Structure Identification of Fractional-Order Dynamical Network with Different Orders
Abstract
:1. Introduction
2. Model Description and Preliminaries
3. Main Results
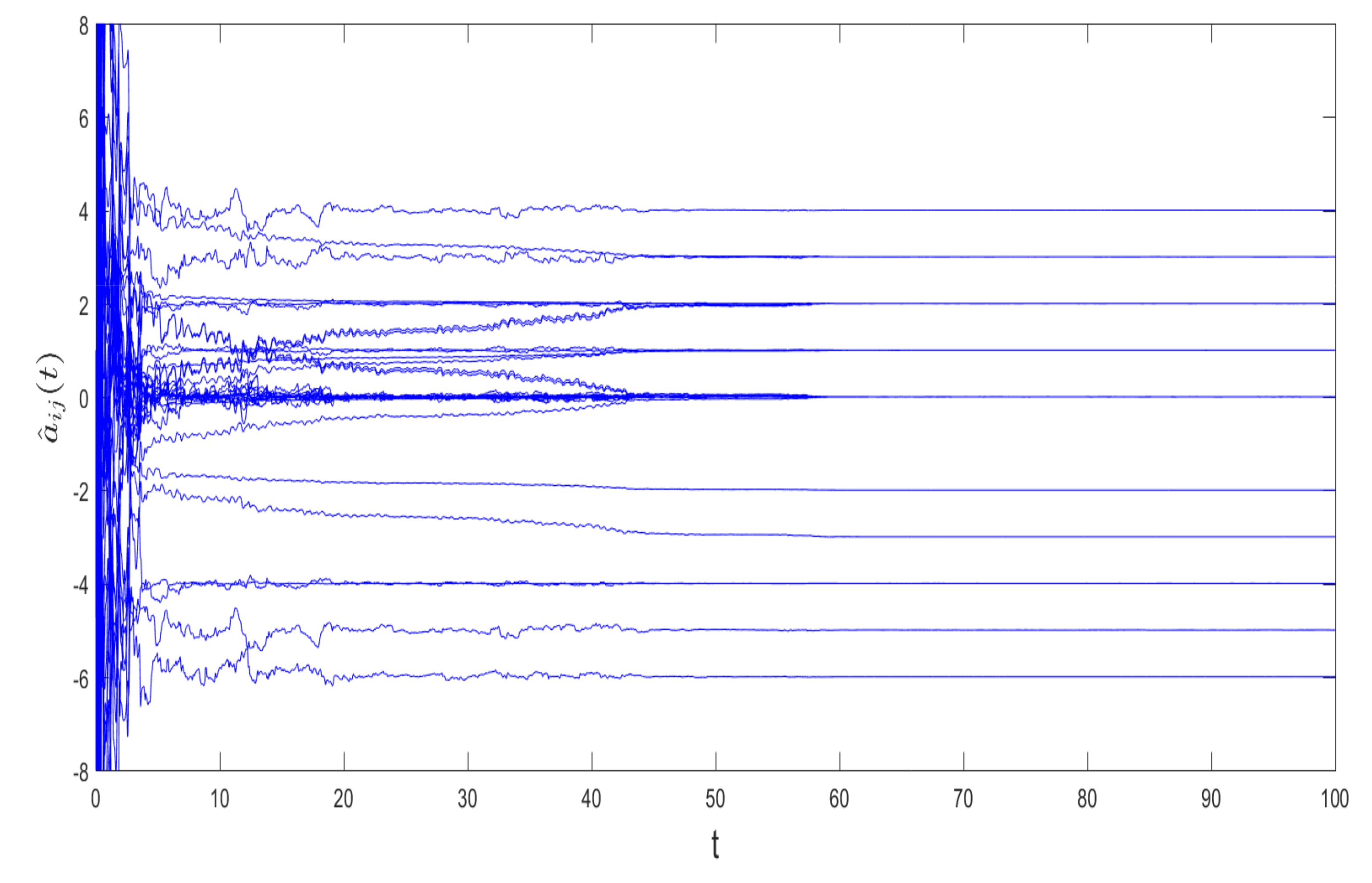
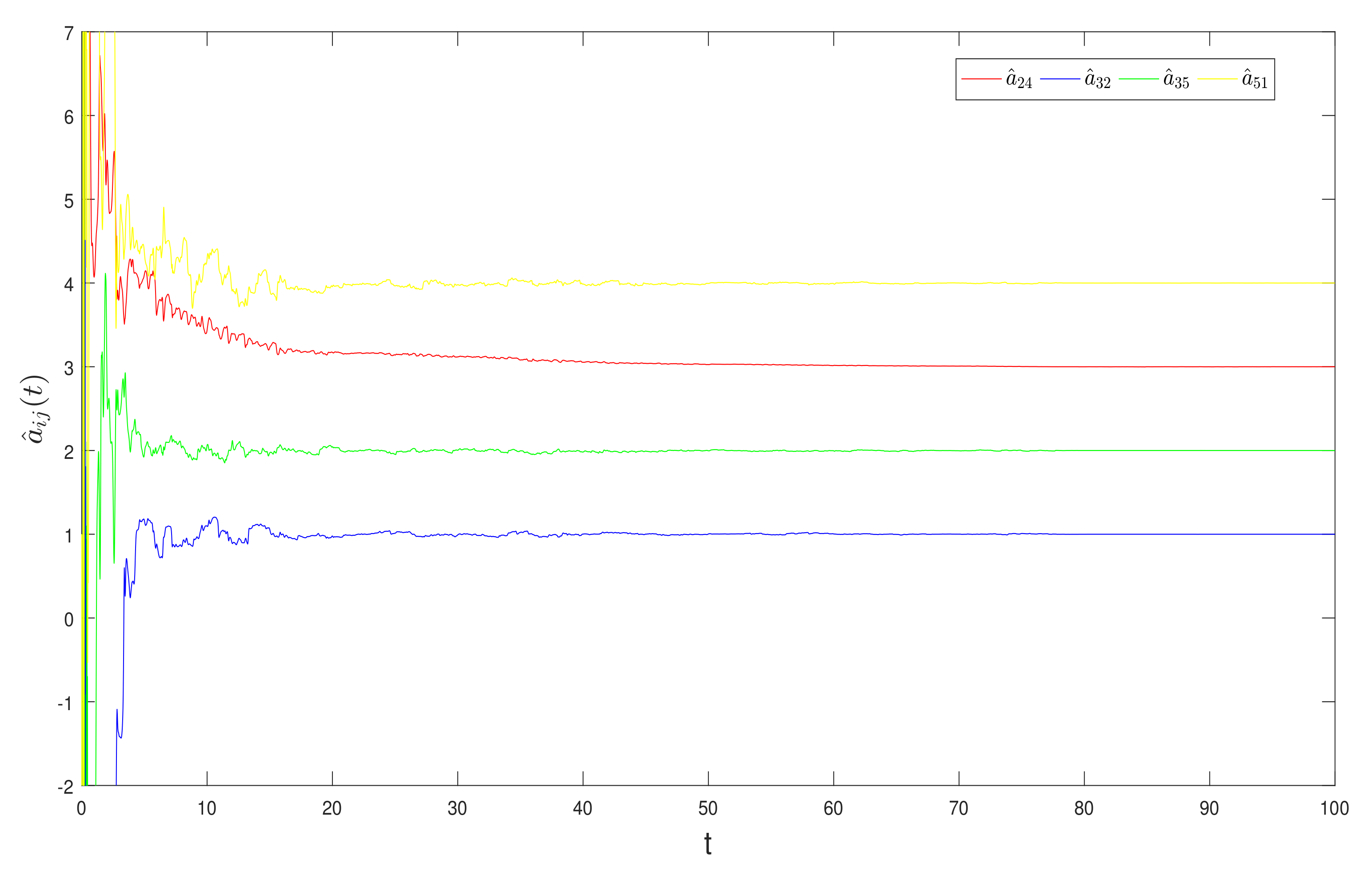
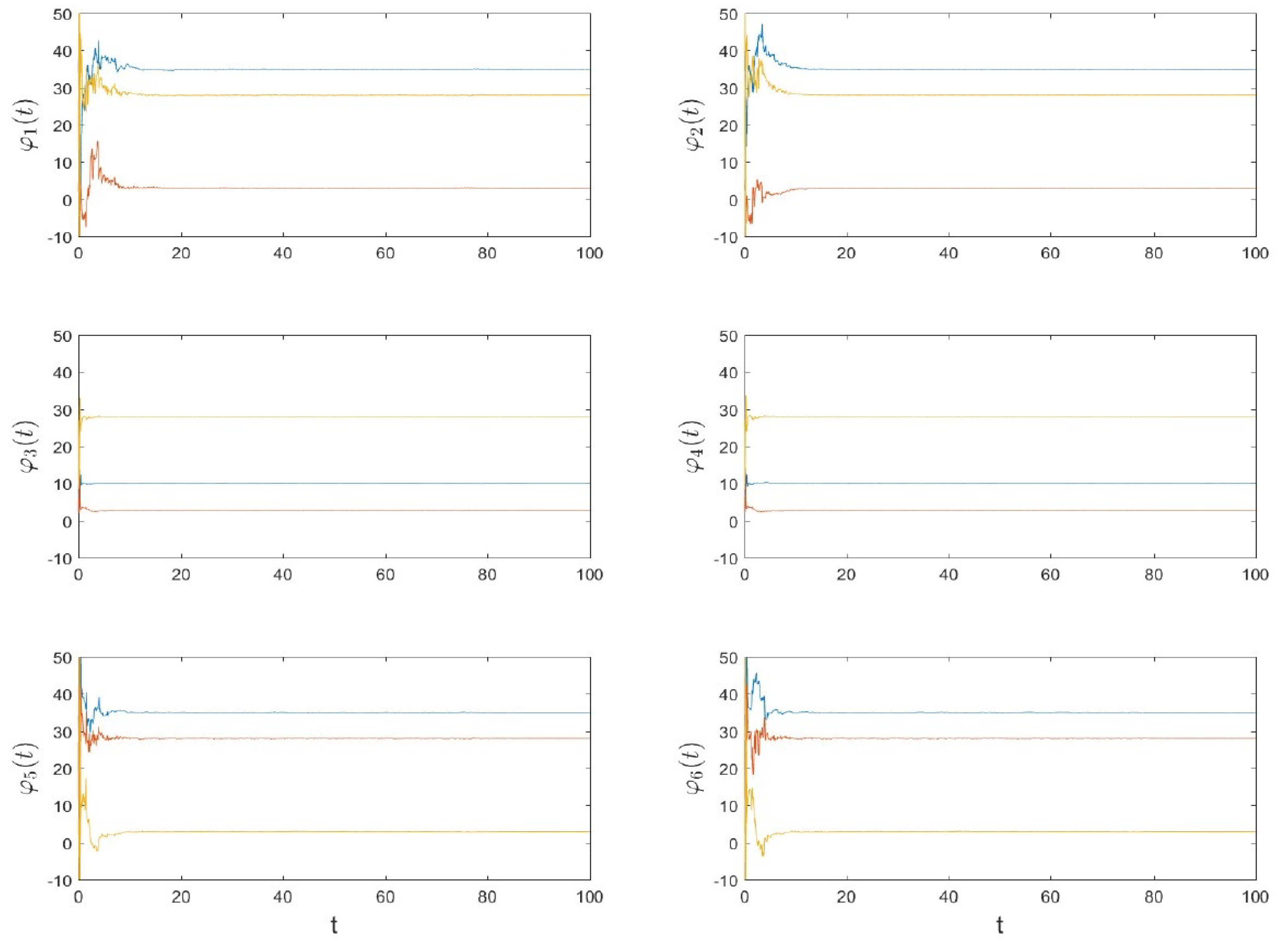
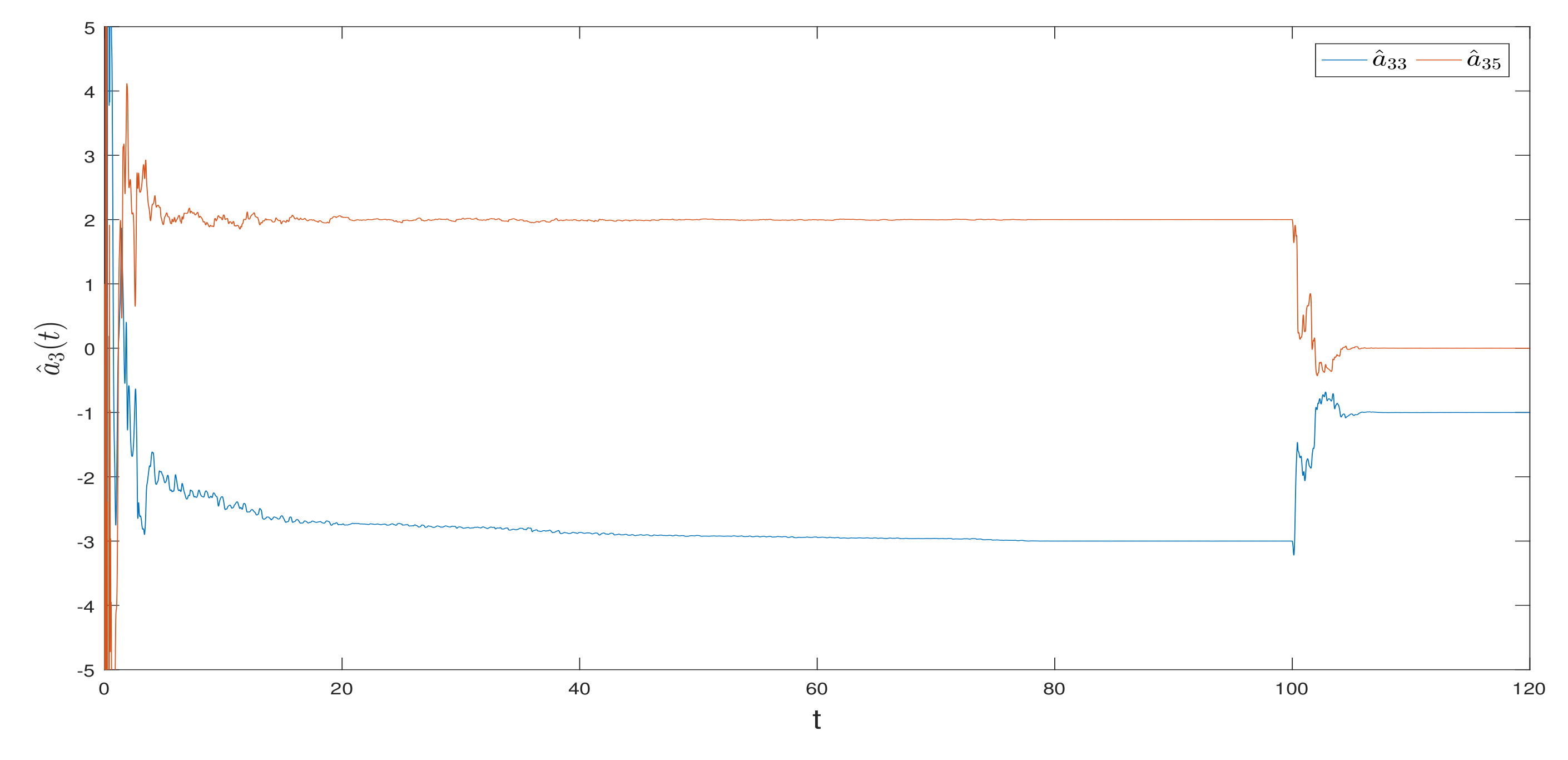
4. Numerical Examples
5. Conclusions and Discussions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Su, H.; Chen, D.; Pan, G.J.; Zeng, Z. Identification of Network Topology Variations Based on Spectral Entropy. IEEE Trans. Cybern. 2021. [Google Scholar] [CrossRef]
- Zhu, S.; Zhou, J.; Lu, J.A. Identifying partial topology of complex dynamical networks via a pinning mechanism. Chaos 2018, 28. [Google Scholar] [CrossRef]
- Li, G.; Li, N.; Liu, S.; Wu, X. Compressive sensing-based topology identification of multilayer networks. Chaos 2019, 29. [Google Scholar] [CrossRef]
- Van Waarde, H.J.; Tesi, P.; Camlibel, M.K. Topology reconstruction of dynamical networks via constrained lyapunov equations. IEEE Trans. Autom. Control 2019, 64, 4300–4306. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Gu, H.; Chen, Y.; Lü, J. Recovering node parameters and topologies of uncertain non-linearly coupled complex networks. IET Control Theory Appl. 2020, 14, 105–115. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, X.; Lu, J.; Lu, J.A.; Dsouza, R.M. Topology Identification in Two-Layer Complex Dynamical Networks. IEEE Trans. Netw. Sci. Eng. 2020, 7, 538–548. [Google Scholar] [CrossRef]
- Zhu, S.; Zhou, J.; Chen, G.; Lu, J.A. A New Method for Topology Identification of Complex Dynamical Networks. IEEE Trans. Cybern. 2021, 51, 2224–2231. [Google Scholar] [CrossRef]
- Yao, X.; Xia, D.; Zhang, C. Topology identification of multi-weighted complex networks based on adaptive synchronization: A graph-theoretic approach. Math. Methods Appl. Sci. 2021, 44, 1570–1584. [Google Scholar] [CrossRef]
- Ding, L.; Li, W.; Nie, S.; Hu, P. Topology Identification for Power Systems via Compressive Sensing Based on Transient Dynamics. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 3202–3206. [Google Scholar] [CrossRef]
- Farajollahi, M.; Shahsavari, A.; Mohsenian-Rad, H. Topology Identification in Distribution Systems Using Line Current Sensors: An MILP Approach. IEEE Trans. Smart Grid 2020, 11, 1159–1170. [Google Scholar] [CrossRef]
- Coutino, M.; Isufi, E.; Maehara, T.; Leus, G. State-Space Network Topology Identification from Partial Observations. IEEE Trans. Signal Inf. Process. Over Netw. 2020, 6, 211–225. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Wang, Y.; Weng, Y.; Zhang, N. Topology Identification and Line Parameter Estimation for Non-PMU Distribution Network: A Numerical Method. IEEE Trans. Smart Grid 2020, 11, 4440–4453. [Google Scholar] [CrossRef]
- Liu, H.; Li, Y.; Li, Z.; Lu, J.; Lu, J.A. Topology Identification of Multilink Complex Dynamical Networks via Adaptive Observers Incorporating Chaotic Exosignals. IEEE Trans. Cybern. 2021. [Google Scholar] [CrossRef]
- He, X.; Qiu, R.C.; Ai, Q.; Zhu, T. A Hybrid Framework for Topology Identification of Distribution Grid with Renewables Integration. IEEE Trans. Power Syst. 2021, 36, 1493–1503. [Google Scholar] [CrossRef]
- van Waarde, H.J.; Tesi, P.; Camlibel, M.K. Topology identification of heterogeneous networks: Identifiability and reconstruction. Automatica 2021, 123, 109331. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution (Mathematics in Science and Engineering); Academic Press: Cambridge, MA, SUA, 1999; Volume 198. [Google Scholar]
- Kilbas, A.; Srivastava, H.; Trujillo, J. Theory and Application of Fractional Differential Equations; Elsevier: New York, NY, USA, 1964; Volume 1, p. 1489. [Google Scholar]
- Si, G.; Sun, Z.; Zhang, H.; Zhang, Y. Parameter estimation and topology identification of uncertain fractional order complex networks. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 5158–5171. [Google Scholar] [CrossRef]
- Du, L.; Yang, Y.; Lei, Y. Synchronization in a fractional-order dynamic network with uncertain parameters using an adaptive control strategy. Appl. Math. Mech. (Engl. Ed.) 2018, 39, 353–364. [Google Scholar] [CrossRef]
- Li, H.L.; Cao, J.; Jiang, H.; Alsaedi, A. Finite-time synchronization and parameter identification of uncertain fractional-order complex networks. Phys. A Stat. Mech. Its Appl. 2019, 533. [Google Scholar] [CrossRef]
- Du, H. Modified function projective synchronization between two fractional-order complex dynamical networks with unknown parameters and unknown bounded external disturbances. Phys. A Stat. Mech. Its Appl. 2019, 526. [Google Scholar] [CrossRef]
- Jia, Y.; Wu, H. Global synchronization in finite time for fractional-order coupling complex dynamical networks with discontinuous dynamic nodes. Neurocomputing 2019, 358, 20–32. [Google Scholar] [CrossRef]
- Xu, Y.; Li, Y.; Li, W.; Feng, J. Synchronization of multi-links impulsive fractional-order complex networks via feedback control based on discrete-time state observations. Neurocomputing 2020, 406, 224–233. [Google Scholar] [CrossRef]
- Yang, Q.; Wu, H.; Cao, J. Pinning exponential cluster synchronization for fractional-order complex dynamical networks with switching topology and mode-dependent impulses. Neurocomputing 2021, 428, 182–194. [Google Scholar] [CrossRef]
- Zheng, Y.; Wu, X.; He, G.; Wang, W. Topology identification of fractional-order complex dynamical networks based on auxiliary-system approach. Chaos 2021, 31. [Google Scholar] [CrossRef] [PubMed]
- Xiao, J.; Cao, J.; Cheng, J.; Zhong, S.; Wen, S. Novel methods to finite-time Mittag-Leffler synchronization problem of fractional-order quaternion-valued neural networks. Inf. Sci. 2020, 526, 221–244. [Google Scholar] [CrossRef]
- Cheng, Y.; Hu, T.; Li, Y.; Zhang, X.; Zhong, S. Delay-dependent consensus criteria for fractional-order Takagi-Sugeno fuzzy multi-agent systems with time delay. Inf. Sci. 2021, 560, 456–475. [Google Scholar] [CrossRef]
- Hu, T.; He, Z.; Zhang, X.; Zhong, S. Event-triggered consensus strategy for uncertain topological fractional-order multiagent systems based on Takagi–Sugeno fuzzy models. Inf. Sci. 2021, 551, 304–323. [Google Scholar] [CrossRef]
- Kaczorek, T. Positive linear systems consisting of n subsystems with different fractional orders. IEEE Trans. Circuits Syst. I Regul. Pap. 2011, 58, 1203–1210. [Google Scholar] [CrossRef]
- Datsko, B.Y.; Gafiychuk, V.V. Mathematical modeling of fractional reaction-diffusion systems with different order time derivatives. J. Math. Sci. 2010, 165, 392–402. [Google Scholar] [CrossRef]
- Li, C.; Deng, W. Remarks on fractional derivatives. Appl. Math. Comput. 2007, 187, 777–784. [Google Scholar] [CrossRef]
- Aguila-Camacho, N.; Duarte-Mermoud, M.A.; Gallegos, J.A. Lyapunov functions for fractional order systems. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 2951–2957. [Google Scholar] [CrossRef]
- Li, C.; Chen, G. Chaos in the fractional order Chen system and its control. Chaos Solitons Fractals 2004, 22, 549–554. [Google Scholar] [CrossRef]
- Grigorenko, I.; Grigorenko, E. Chaotic Dynamics of the Fractional Lorenz System. Phys. Rev. Lett. 2003, 91. [Google Scholar] [CrossRef] [PubMed]
- Lu, J.G. Chaotic dynamics of the fractional-order Lü system and its synchronization. Phys. Lett. Sect. A Gen. At. Solid State Phys. 2006, 354, 305–311. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, M.; Wu, Z. Structure Identification of Fractional-Order Dynamical Network with Different Orders. Mathematics 2021, 9, 2096. https://doi.org/10.3390/math9172096
Zhou M, Wu Z. Structure Identification of Fractional-Order Dynamical Network with Different Orders. Mathematics. 2021; 9(17):2096. https://doi.org/10.3390/math9172096
Chicago/Turabian StyleZhou, Mingcong, and Zhaoyan Wu. 2021. "Structure Identification of Fractional-Order Dynamical Network with Different Orders" Mathematics 9, no. 17: 2096. https://doi.org/10.3390/math9172096
APA StyleZhou, M., & Wu, Z. (2021). Structure Identification of Fractional-Order Dynamical Network with Different Orders. Mathematics, 9(17), 2096. https://doi.org/10.3390/math9172096





