Wind Power Extraction Optimization by Dynamic Gain Scheduling Approximation Based on Non-Linear Functions for a WECS Based on a PMSG

Abstract

Mathematical models and algorithms for maximizing power extraction have become an essential topic in renewable energies in the last years, especially in wind energy conversion systems. This study proposes maximum power point tracking using gain scheduling approximations for an emulated wind system in a direct-drive connection. Power extraction is obtained by controlling the duty cycle of a Multilevel Boost Converter, which directly varies the rotational speed of a permanent magnet synchronous generator directly coupled to a three-phase induction motor that emulates the wind turbine. The system’s complexity is linked to the inherent non-linearities associated with the diverse electrical, mechanical, and power electronic elements. In order to present a synthesized model without losing the system dynamic richness, several physical tests were made to obtain parameters for building several mathematical approaches, resulting in non-linear dynamic equations for the controller gains, which are dependant on wind speed. Thirty real operational wind speeds considering typical variations were used in several tests to demonstrate the mathematical models’ performance. Results among these gain scheduling approaches and a typical controller constant gains mathematical model were compared based on standard deviations, absolute error, and the time for reaching the optimum generator angular speed related to every wind speed.

1. Introduction

In the last decades, renewable energies have become the core of several investigations because of their essential and beneficial features for the environment and nature; their use and management are elements that support a crucial strategy to diminish climate alterations [1,2]. It is a fact that energy represents a substantial element that constitutes a possibility for economic and social development not only for not interconnected territories such as small island states but also for most countries worldwide [3,4,5].

Among the renewable energies, wind power has especially become a significant source of energy in the world. According to the last report of the Global Wind Energy Council (GWEC), the world installed capacity has grown considerably in the last 20 years, reaching several hundreds of GW [6]. The relevance of wind energy is a decisive factor in solving the energetic issues around the world, according to [7]. In the beginning, wind energy was just an emerging technology, but it has evolved to a very competitive energy source through the years. Adding with an increasing global interest in political trends concerning energy supply diversification and environmental care, this fact has ensured wind energy has a crucial role in the future electricity market.

Wind energy technologies have considerably been increased during the last 20 years, so several wind types of research overviews have been published to organize and offer to the specialized and general audience the information related to new and diverse wind energy technologies [8,9,10,11,12].

One of the significant problems related to wind power generation is that the wind is continuously varying its velocity and direction [13]. Because of this, diverse and advanced technologies have been developed in order to obtain the highest wind power efficiency and to ensure the most profitable wind energy technologies [14,15,16,17]. Some studies, for example, are specialized in methods, techniques, and technologies to guarantee a proper connection between wind power generation and the electrical grid [18,19]. Other studies are focused on sophisticated controllers for maximizing wind power extraction [20,21].

When studying wind energy conversion systems (WECS), there is a significant concept to deal with known as the power coefficient ($C_p$), representing the wind power extracted by the turbine divided by the input wind power. Typically, this coefficient is represented by several models such as exponential, sinusoidal, and polynomial, as a function of the tip speed ratio ($\lambda$) and the pitch angle ($\beta$) [22]. $\lambda$ is defined as the quotient of velocities; this is, the tangential velocity at the turbine blade outer edge divided by the wind speed.

When fixed-pitch angle operations are considered, then the $C_p$-$\lambda$ curve presents a point where the maximum power coefficient ($C_{p_{max}}$) corresponds to a specific tip speed ratio value (${\lambda }_{max}$); then, considering the definition of $\lambda$, there exists a particular turbine angular speed that maximizes $C_p$ for every wind speed. This phenomenon has been the core of various studies dealing with power coefficient optimization.

A remarkable method for maximizing $C_p$ is known as Maximum Power Point Tracking (MPPT) [23], and several techniques have been developed such as Perturb and Observe (P&O) [24,25,26,27], Optimal Torque Control (OTC) [28,29], Hill-Climb Searching (HCS) [30,31], Power Signal Feedback (PSF) [32,33], Tip Speed Ratio (TSR) [34,35] and some based on neural-networks algorithms [36,37].

It is common to connect a Multilevel Boost Converter (MBC) to the generator output to modify the turbine rotational speed. A controller based on different algorithms for maximizing power coefficient is typically used to manage the MBC duty cycle. First, the power extracted from the turbine is adjusted, so the optimum turbine angular speed is reached [38,39,40].

The main components of a WECS are usually the turbine, generator, controller, power electronic converters, and a three-phase inverter connected to the load. The system is very complex because of its different components, so a complete model would probably be represented by a set of many non-linear differential equations. In order to represent a less complex mathematical model maintaining the system dynamic richness, some methods have been developed to set a unified system [41,42].

At the end of the last century, some papers presented a new concept known as gain scheduling approximation [43]. The method consists of linearizing a complex dynamic time-varying system around the neighborhood of a set of selected points. Interpolation methods typically obtain the gains of a linear controller. The most standard approach utilizes constant gains for a PI discrete controller, obtained as the average of the diverse mathematical representations built using the recorded system responses before the tests’ applied inputs.

Many applications where gain scheduling approximation can be found in WECS and diverse scientific fields, such as chemical, mechanical, energy, and aerospace engineering; this is because of gain scheduling advantages and its relative facility of implementation [43].

In the field of WECS, several studies have been successfully applied to reach the control purposes. For example, in [44], a gain scheduling pitch and MPPT are used in a vertical axis wind turbine. Linear matrix inequalities are solved to design a gain scheduled controller and utilized for the rotor turbine stability control. As a result, the turbine efficiency was improved, providing excellent response to wind gusts.

Similarly, in [45], a robust gain scheduling baseline controller is implemented for a floating offshore wind turbine. The study proposes a standard PI controller only using the rotor angular speed error as the feedback. Results showed good performance when compared against an advanced controller and the fixed-bottom version of the same turbine.

In other research, dynamic gains for a controller in a hybrid wind-solar system are scheduled to maintain the voltage regulation in a standalone system over a wide range and under unpredictable atmospheric conditions. The proposed dynamic gains controller showed a better performance than the standard fixed gain proportional-integral controller [46].

In [47] a gain-scheduled controller is proposed to provide MPPT operation by achieving an effective pitch angle regulation. The wind turbine is modeled as a linear parameter varying system, while wind speed was set as the scheduling parameter to cope with the varying system dynamics. As a result, reliable controller performance and stability were obtained.

Another important application for gain scheduling was published in [48]. In that paper, the influence of the de-rating on the turbine controller gain-scheduling and its consequences to power output and fatigue damage of the critical turbine components were studied. The results showed that the turbine response was refined by tuning for the different operation points; as a result, the minor fatigue damage of the critical turbine components was obtained.

As it can be seen, several and diverse researches related to gain scheduling in WECS have been developed; still, they are usually established for maximizing wind power extraction by controlling the pitch angle. In these works, dynamic controller gains are typically calculated using linear interpolation as a function of wind speed; nevertheless, in this research, exponential interpolation, second and third-degree mathematical models are proposed to determine the dynamic controller gains. Furthermore, to reach the optimum turbine angular speed and ensure maximum wind power extraction, the poles in the Z plane were appropriately chosen to improve the controller response. In addition, the performance of the three proposed controlling models is compared versus a linear and a fix-gains controller models, which were also proposed.

The rest of this manuscript is organized as follows: Section 2 presents the preliminary theory about the fundamentals related to optimizing wind power extraction. Section 3 introduces a general overview of the physical wind energy conversion system. The Section 4 describes the tests and procedures for obtaining the parameters for building the mathematical models to establish the equations to determine the dynamic controller gains as a function of wind speed. In Section 5, the mathematical model of the controller, including the dynamic gains for every proposed function, is shown. Finally, Section 6 reports the obtained results, while the conclusions are discussed in Section 7.

2. Wind Power Extraction Fundamentals

As it can be found in [43], by definition, the power coefficient $C_p$ in a wind turbine is given by Equation (1) where P represents the wind power extracted by the turbine and $P_1$ is the total wind power, this is, wind power upstream:

$$C_p=\frac{P}{P_1}$$

(1)

There is a very well known relationship that includes tip speed ratio ($\lambda$), turbine angular speed (${\omega }_r$), turbine radius ($R_{wt}$), and wind speed ($v_w$) which is represented in Equation (2).

$$\lambda =\frac{{\omega }_r{R}_{wt}}{v_w}$$

(2)

It is widespread to represent $C_p$ as a function of tip speed ratio $\lambda$ and the blades pitch angle $\beta$; exponential, polynomial, and sinusoidal representations have been widely used by diverse authors [22]. In this work, a sinusoidal representation was used as shown in Equation (3). The values of the coefficients that were selected are indicated in Table 1, while the selected pitch angle was zero. Figure 1 represents the associated curve to Equation (3) considering a typical operational span of tip speed ratio.

$$C_p\left(\lambda ,\beta \right)=\left[a_0+a_1\left(b_0\beta +a_2\right)\right]sin\left(\frac{\pi \left(\lambda +a_3\right)}{a_4+a_5\left(b_1\beta +a_6\right)}\right)+a_7\left(\lambda +a_8\left)\right(b_2\beta +a_9\right)$$

(3)

Table 1. Coefficients values for Equation (3).

Coefficient	${\mathit{a}}_{\mathbf{0}}$	${\mathit{a}}_{\mathbf{1}}$	${\mathit{a}}_{\mathbf{2}}$	${\mathit{a}}_{\mathbf{3}}$	${\mathit{a}}_{\mathbf{4}}$	${\mathit{a}}_{\mathbf{5}}$	${\mathit{a}}_{\mathbf{6}}$	${\mathit{a}}_{\mathbf{7}}$	${\mathit{a}}_{\mathbf{8}}$	${\mathit{a}}_{\mathbf{9}}$	${\mathit{b}}_{\mathbf{0}}$	${\mathit{b}}_{\mathbf{1}}$	${\mathit{b}}_{\mathbf{2}}$
Value	0.5	−0.00167	−2	0.1	18.5	−0.3	−2	0.00184	−3	−2	1	1	1

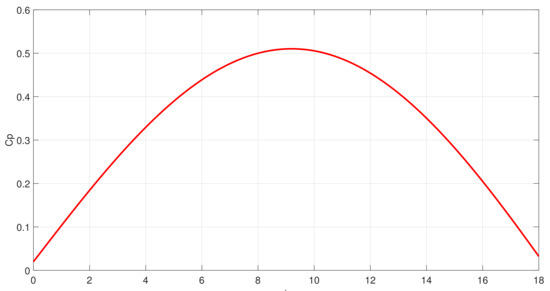
Figure 1. $C_p$ curve used in the project as a function of tip speed ratio.

It is especially important the value of $\lambda$ that maximizes $C_p$; this element (${\lambda }_{crit}$) was obtained by using first and second derivative criteria; its value is approximately 9.1949, as shown in Appendix A.

Suppose ${\omega }_r$ is isolated and evaluated in ${\lambda }_{crit}$. In that case, a meaningful relationship is obtained since it defines the value of ${\omega }_r$ that maximizes wind power extraction for every wind speed as shown in Equation (4). The main idea is to define a set of dynamic gains equations for the controller in order to reach optimum turbine angular speed (${\omega }_{r_{sp}}$).

$${\omega }_{r_{sp}}=\frac{{\lambda }_{crit}{v}_w}{R_{wt}}$$

(4)

3. Experimental Setup

In this research, an emulated wind energy conversion system was used as the physical setup to provide the data for establishing the control law for maximizing wind power extraction as shown in Figure 2.

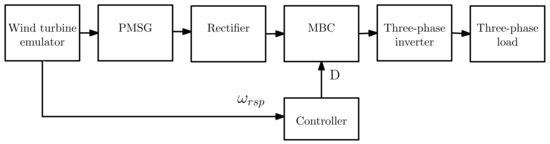
Figure 2. General overview of the WECS used in this research.

The turbine emulator shown in Figure 2 uses a Linux real-time platform where a particular wind speed is set, then $\lambda$ is calculated using Equation (2) (${\omega }_r$ is measured). In the next step, $C_p$ is obtained by Equation (3). The wind turbine aerodynamic torque ($T_m$) depends on the turbine blades rotational speed and on the wind speed [49,50], and it is calculated in the real-time application interface (RTAI) program using the Equation (5), where $\rho$ is the air density.

$$T_m=\frac{C_p}{2\lambda }\rho \pi R_{wt}{v}_w$$

(5)

Then a signal is sent to a variable speed drive; this element is responsible for providing the appropriate torque to an induction motor so that its angular speed ${\omega }_r$ reaches the correspondent value associated with the specified wind speed as it is shown in Figure 3. Additionally, the value of ${\omega }_r$ that maximizes wind power extraction (${\omega }_{rsp}$) is determined for a closed-loop operation.

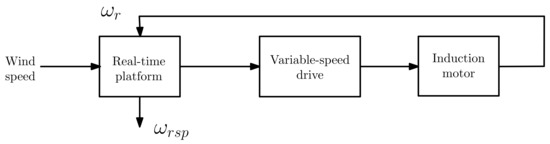
Figure 3. Wind turbine emulator.

The induction motor and the PMSG are in a direct-drive connection; on the other hand, the PMSG is a four-pole three-phase type. One of the advantages of using a generator of low speed type is that the WECS avoid problems related to the use of a gearbox [51,52,53,54], becoming less expensive. In addition, because of the extensive length of its operating speed in the asynchronous mode, PMSG is preferred over other electrical generators [42]. Table 2 shows the parameters associated with the PMSG, while Figure 4 shows a photo of the experimental setup which includes the speed variator as well as the direct drive connection between the three-phase induction motor and the PMSG.

Table 2. Parameters associated to the PMSG.

Symbol	Value	Units	Description
$R_s$	$0.69$	$\mathsf{\Omega }$	Stator resistance
p	4	Poles	Number of poles
${\lambda }_m$	$0.4411$	Vs	Flux linkages amplitude
$R_{Lmin}$	$3.3647$	$\mathsf{\Omega }$	Minimum equivalent electrical load resistance
$R_{Lmax}$	115	$\mathsf{\Omega }$	Maximum equivalent electrical load resistance
$R_L$	3.3647–115	$\mathsf{\Omega }$	Equivalent electrical load resistance
J	$0.1488$	kgm${}^2$	Combined inertia

Figure 4. Experimental setup for speed variator-induction motor-PMSG.

This WECS contains a full-rated full-wave uncontrolled rectifier for converting the variable frequency voltage at the terminals of the PMSG to a variable DC voltage. The rectifier’s output is connected to the input of a custom-made full-rated 2N-MBC [55,56]; the pulse-width modulation frequency is 50 kHz. The controller sends the duty cycle of the 2N-MBC. An IGBT-based full-rated voltage source inverter was employed to convert the DC voltage at the output of the 2N-MBC to 60 Hz three-phase voltages applied to a balanced Y-connected electrical load. A voltage source inverter is operated in a 180-degree switching mode.

4. Tests for Obtaining the Parameters

In order to calculate the system parameters, a set of six steps were sent from the controller to the MBC input in open-loop operation for a certain programmed wind speed; then, the transient responses were stored. The WECS was approximated by using Equation (6), where $x\left(t\right)$ is the state, $y\left(t\right)$ is the output, $u\left(t\right)$ is the input, while A, B, and C are 1 × 1 matrices. For this study, C = 1 while

$$x\left(t\right)$$

is the turbine-generator angular speed and $u\left(t\right)$ = 1 − D. D is the MBC duty cycle. For every transient response, the time constant $\tau$ was obtained, and A is inversely related to $\tau$. B was calculated from Equation (6) for the steady-state. Table 3 shows the relationship among the duty cycle applied to the MBC, A, B, and the steady-state angular speed.

$$\left\{\begin{array}{ccc}\hfill \frac{d}{dt}x\left(t\right)& =& Ax\left(t\right)+Bu\left(t\right)\hfill \\ \hfill y\left(t\right)& =& Cx\left(t\right)\hfill \end{array}\right.$$

(6)

Table 3. Values of the system parameters for the correspondent duty cycle.

D(%)	${\mathbf{\omega }}_{\mathit{r}}$ (rad/s)	A	B
20	$185.85$	$-0.76684$	$1.7815$
30	$174.69$	$-1.0176$	2.5393
40	$146.8$	$-1.3482$	3.2987
50	$123.61$	$-2.2479$	5.5573
60	$103.17$	$-2.4095$	6.2147
70	$74.69$	$-3.0511$	7.5962

A is associated with the state and can be determined by Equation (7), where $\tau$ is the system’s time constant; this is the time that the system needs to reach 63.2% of its steady-state. Once the system is fed by $u\left(t\right)$, the transient behavior of $x\left(t\right)$ is stored and plotted, then $\tau$ is obtained directly from the graphic, and A is calculated. For example, when D = 70, then the input $u\left(t\right)$ = 30, $\tau$ = 0.32775 and A is determined by Equation (7). The correspondent steady state is x = ${\omega }_r$ = 74.69 rad/s, then the first Equation in Equation (6) equals zero since $x\left(t\right)$ is constant and B can be calculated as shown in Equation (8). This process allowed for a simplified model, diminishing the inherent non-linearities associated with the WECS because of its electrical and mechanical components without losing the system’s dynamic richness. The parameter values were used to obtain the mathematical proposed models presented in the next section.

$$\left\{\begin{array}{ccc}\hfill A& =& -\frac{1}{\tau }\hfill \\ \hfill A& =& -3.0511\hfill \end{array}\right.$$

(7)

$$\left\{\begin{array}{ccc}\hfill 0& =& Ax\left(t\right)+Bu\left(t\right)\hfill \\ \hfill B& =& -\frac{Ax\left(t\right)}{u\left(t\right)}\hfill \\ \hfill B& =& -\frac{(-3.0511)74.69}{30}\hfill \\ \hfill B& =& 7.5962\hfill \end{array}\right.$$

(8)

5. Mathematical Model

Let us consider Equation (9) which represents a SISO discrete time-invariant linear dynamic system

$$\left\{\begin{array}{ccc}\hfill x(k+1)& =& Gx\left(k\right)+Hu\left(k\right)\hfill \\ \hfill y\left(k\right)& =& Cx\left(k\right)\hfill \end{array}\right.$$

(9)

where $x\left(k\right)$ is the state, $y\left(k\right)$ is the output, u(k) is the input, while G, H, and C are 1 × 1 matrices. For this study, C = 1 while $x\left(k\right)$ is the turbine-generator angular speed. On the other hand, Equation (10) represents a discrete-time equation for an integral action of a state-space controller.

$$x_I(k+1)=x_I\left(k\right)+Cx\left(k\right)-r\left(k\right)$$

(10)

where $x_I\left(k\right)$ is the state variable of the integrator, and $r\left(k\right)$ is the reference for the output to be controlled. Equation (11) shows the augmented system that is composed by the discrete-time model of the system to be controlled and the expression for the discrete-time integral controller.

$$\begin{array}{cc}\hfill \left[\begin{array}{c}{x}_I(k+1)\\ x(k+1)\end{array}\right]=& \left[\begin{array}{cc}1& C\\ 0& G\end{array}\right]\left[\begin{array}{c}{x}_I\left(k\right)\\ x\left(k\right)\end{array}\right]+\left[\begin{array}{c}0\\ H\end{array}\right]u\left(k\right)-\left[\begin{array}{c}1\\ 0\end{array}\right]r\left(k\right)\hfill \end{array}$$

(11)

where the augmented state vector is defined as ${\left[x_I\left(k\right)x\left(k\right)\right]}^T$. State feedback for the augmented system is represented by Equation (12)

$$u\left(k\right)=-\left[\begin{array}{cc}{k}_1& k_2\end{array}\right]\left[\begin{array}{c}{x}_I\left(k\right)\\ x\left(k\right)\end{array}\right]$$

(12)

where $k_1$ and $k_2$ are the integral and proportional gains of the controller, respectively.

In this work, five mathematical models for the associated gains $k_1,k_2$ were established: the constant gains model and the dynamic gains models dependant on wind speed which include linear, second grade, third grade, and exponential approaches. A Matlab code was programmed to obtain the mathematical models for the dynamical gains and validate the controller performance for each model.

For determining the constant gains, the continuous state equation was built using the average of A and B values resulting in Equation (13). The system was discretized using a time base of 0.05 s, and the associated coefficients from the discrete equation were extracted. In the next step, the augmented system including the integrator was set; then, the state feedback gains were established around the desired poles in the Z plane, which values were found as 0.92 and 0.93; finally, the integrator and the state variable constants were obtained, resulting in $k_1=0.026042$ and $k_2=0.29585$. The pole placement method was used to build the discrete model.

$$\frac{d}{dx}x\left(t\right)=-1.807x\left(t\right)+4.498u\left(t\right)$$

(13)

For calculating the dynamic gains approaches, in the first place, the same procedure described for the constant gains was followed (also considering the same desired poles in the Z plane), but repeating the calculations for every pair (A, B) shown in Table 4.

Table 4. Associated gains for every pair (A, B).

${\mathit{k}}_{\mathbf{1}}$	${\mathit{k}}_{\mathbf{2}}$	${\mathbf{\omega }}_{\mathit{r}}$ (rad/s)	A	B
$0.064083$	$1.2861$	$185.85$	$-0.76684$	$1.7815$
$0.045238$	$0.811$	$174.69$	$-1.0176$	2.5393
$0.03511$	$0.53173$	$146.8$	$-1.3482$	3.2987
$0.021308$	$0.16624$	$123.61$	$-2.2479$	5.5573
$0.019129$	$0.12467$	$103.17$	$-2.4095$	6.2147
$0.015897$	$0.024168$	$74.69$	$-3.0511$	7.5962

In the second place, an exponential and three polynomial approaches were established using interpolation based on ${\omega }_r$, which also depends on wind speed. Dynamic gains are calculated as functions dependant on this speed (${\omega }_{r_{opt}}$). Equation (14) shows the exponential function for $k_1$ while Equation (15) corresponds to the function for calculating $k_2$.

$$k_1=c_1{e}^{a_1{\omega }_{r_{opt}}}=0.014797e^{0.027665{\omega }_{r_{opt}}}$$

(14)

$$k_2=c_2{e}^{a_2{\omega }_{r_{opt}}}=0.046404e^{0.051246{\omega }_{r_{opt}}}$$

(15)

On the other hand, Equation (16) represents the power expansion for calculating $k_1$, while Equation (17) shows the function structure for determining $k_2$. Table 5 contains the different coefficients associated to the polynomial equation for $k_1$ while Table 6 presents the diverse coefficients related to the polynomial function for $k_2$. Figure 5 shows the graphics related to the functions used to calculate the integrator state variable gains. In contrast, Figure 6 represents the plotting associated with the functions utilized to determine the state variable gains.

$$k_1=\sum _{j=0}^n{\psi }_j{\left({\omega }_{r_{opt}}\right)}^j$$

(16)

$$k_2=\sum _{j=0}^n{\zeta }_j{\left({\omega }_{r_{opt}}\right)}^j$$

(17)

Table 5. Polynomial function coefficients for calculating $k_1$.

j	0	1	2	3
Linear	$-0.059728$	$0.0024695$	0	0
Quadratic	$0.13001$	$-0.0044641$	$5.7809\times {10}^{-5}$	0
Cubic	$-0.063472$	$0.0066006$	$-0.00014071$	$1.1262x{10}^{-6}$

Table 6. Polynomial function coefficients for calculating $k_2$.

j	0	1	2	3
Linear	$-2.4293$	$0.065121$	0	0
Quadratic	$2.5188$	$-0.1157$	$0.0015076$	0
Cubic	$-2.6282$	$0.17865$	$-0.0037734$	$2.996\times {10}^{-5}$

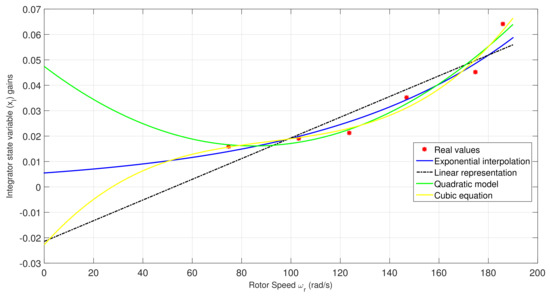
Figure 5. Graphics related to the functions for calculating the integrator state variable gains.

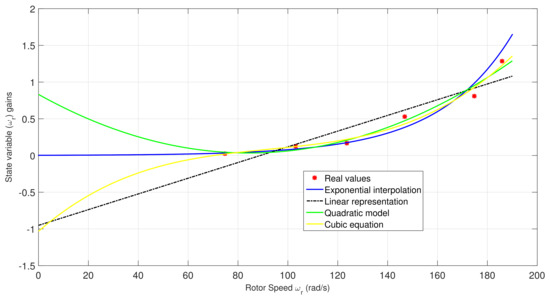
Figure 6. Graphics related to the functions for calculating the state variable gains.

In order to show an example of the complexity and non-linearities associated with the mathematical model for the controller, the state feedback and discrete non-linear system in closed-loop are presented in Equations (18) and (19) for the particular case of the exponential model.

$$\left\{\begin{array}{ccc}\hfill u\left(k\right)& =& -k_1{x}_I\left(k\right)-k_{2}x\left(k\right)=-c_1{e}^{a_1{\omega }_{r_{opt}}}{x}_I\left(k\right)-c_2{e}^{a_2{\omega }_{r_{opt}}}x\left(k\right)\hfill \\ \hfill u\left(k\right)& =& -c_1{e}^{\frac{a_1{\lambda }_{crit}{v}_w}{R}}{x}_I\left(k\right)-c_2{e}^{\frac{a_2{\lambda }_{crit}{v}_w}{R}}\hfill \end{array}\right.$$

(18)

$$\begin{array}{cc}\hfill \left[\begin{array}{c}{x}_I(k+1)\\ x(k+1)\end{array}\right]=& \left[\begin{array}{cc}1& 1\\ 0& 0.58155\end{array}\right]\left[\begin{array}{c}{x}_I\left(k\right)\\ x\left(k\right)\end{array}\right]+\left[\begin{array}{c}0\\ 1.0417\end{array}\right]\left(-c_1{e}^{\frac{a_1{\lambda }_{crit}{v}_w}{R}}{x}_I\left(k\right)-c_2{e}^{\frac{a_2{\lambda }_{crit}{v}_w}{R}}\right)-\left[\begin{array}{c}1\\ 0\end{array}\right]{\omega }_{r_{opt}}\hfill \end{array}$$

(19)

6. Results

In order to test the mathematical model’s performance for the controller, a set of 30 real wind values were used; they were extracted from an IEEE dataset [57]. The wind speed values were selected to include a sudden high variation as shown in Table 7. The time between measurements is ten seconds.

Table 7. Real wind speed values used for testing controller mathematical model performance.

Time (s)	Wind Speed (m/s)	Time (s)	Wind Speed (m/s)	Time (s)	Wind Speed (m/s)
10	6.01	110	6.47	210	5.76
20	6.53	120	7.17	220	4.53
30	5.26	130	8.85	230	4.61
40	6.53	140	10.05	240	9.87
50	8.01	150	7.14	250	8.53
60	7.77	160	6.79	260	9.24
70	8.77	170	6.66	270	7.68
80	8.68	180	6.3	280	6.82
90	10.25	190	5.1	290	6.59
100	6.72	200	4.58	300	7.79

In Figure 7 the behavior of each proposed model is shown from 0 to 300 s, the red line represents ${\omega }_{r_{opt}}$, that is, the value of ${\omega }_r$ which optimizes power extraction for the correspondent wind speed. The blue, green, dashed-dot black, dot cyan, and dashed magenta lines represent the transient evolution of ${\omega }_r$ before wind speed changes based on exponential, average (fixed gains), linear, quadratic, and cubic models respectively.

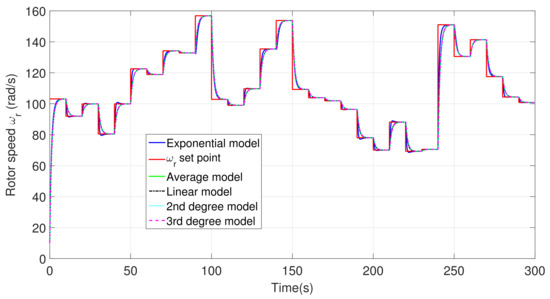
Figure 7. Whole span rotor speed control and tracking.

To show a better perspective of the proposed model’s performance, Figure 8 presents four changes of optimum rotational speed correspondent to wind changes between 190 and 230 s. As it can be seen, the exponential model presents better behavior with respect to the other models not only in the decreasing intervals but also in the increasing ones; in addition, Figure 9 presents the duty cycle related to each proposed model in the whole time span, while Figure 10 shows the duty cycle associated to everyone on the dynamic gains mathematical models from 190 to 230 s as well as the average model just as an example for having a better perspective.

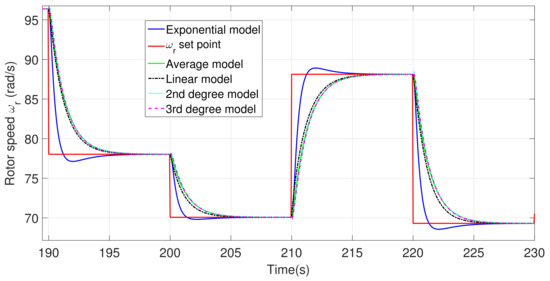
Figure 8. Rotor speed control and tracking from 190 to 230 s.

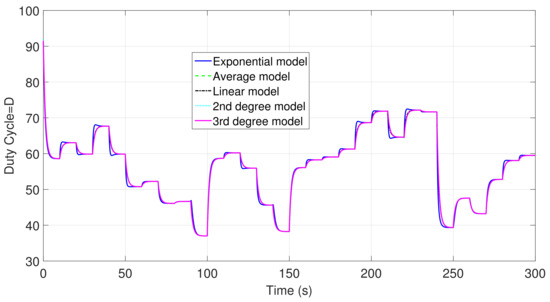
Figure 9. Whole span duty cycle for the proposed models.

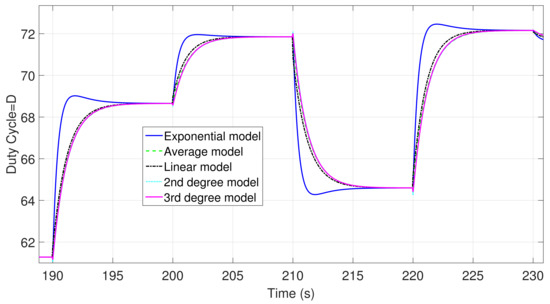
Figure 10. Duty cycle for the proposed models from 190 to 230 s.

Excluding the exponential model, the performance of the other models was very similar. Table 8 shows the standard deviations of every model from two perspectives. In the first, the difference between optimum rotor speed and the instantaneous rotor speed for every gain scheduling model was calculated (absolute error); then, the standard deviations of the whole span were determined. In the second, the absolute error was calculated in the first three seconds after applying every one of the 30 rotor speed steps; this represents approximately the average time for the exponential function to reach the steady-state. This error was used to calculate a more representative standard deviation.

Table 8. Standard deviations for the different proposed models.

Interval	Exponential	Average	Linear	2nd-Degree	3rd-Degree
0–300 s	6.7179	7.6387	7.4255	7.6024	7.5917
First 3 s section of all steps	10.055	11.878	11.349	11.69	11.693

On the other hand, in Table 9, the average absolute error between optimum rotor speed and instantaneous rotor speed for each dynamic gain scheduling approach is shown for the whole span (0–300 s), as well as for the first 3 s section of all steps. Table 10 shows the time that every proposed model needs for reaching the 99.9% of ${\omega }_{r_{opt}}$ in every one of the 30 wind steps applied from 0–300 s; $t_1$, $t_2$, $t_3$, $t_4$, and $t_5$ represent the time in seconds for exponential, average, linear, second and 3rd-degree models respectively. The average time of the 30 intervals for each model is presented in Table 11.

Table 9. Average absolute error for the different proposed models.

Interval	Exponential	Average	Linear	2nd-Degree	3rd-Degree
0–300 s	1.8931	2.6603	2.5459	2.6341	2.6335
First 3s section of all steps	5.0482	7.1726	6.8249	7.0859	7.0848

Table 10. Time to reach 99.9% of ${\omega }_{r_{opt}}$ for the different proposed models.

Interval(s)	${\mathit{t}}_{\mathbf{1}}\left(\mathbf{s}\right)$	${\mathit{t}}_{\mathbf{2}}\left(\mathbf{s}\right)$	${\mathit{t}}_{\mathbf{3}}\left(\mathbf{s}\right)$	${\mathit{t}}_{\mathbf{4}}\left(\mathbf{s}\right)$	${\mathit{t}}_{\mathbf{5}}\left(\mathbf{s}\right)$	Interval(s)	${\mathit{t}}_{\mathbf{1}}\left(\mathbf{s}\right)$	${\mathit{t}}_{\mathbf{2}}\left(\mathbf{s}\right)$	${\mathit{t}}_{\mathbf{3}}\left(\mathbf{s}\right)$	${\mathit{t}}_{\mathbf{4}}\left(\mathbf{s}\right)$	${\mathit{t}}_{\mathbf{5}}\left(\mathbf{s}\right)$
0–10	7.55	8.5	8.45	8.4	8.45	150–160	6.65	7.7	7.65	7.6	7.65
10–20	1.25	6	5.8	5.9	5.95	160–170	1.4	5.1	5	5.05	5.05
20–30	1.2	5.6	5.45	5.55	5.55	170–180	1.15	3.85	3.75	3.8	3.85
30–40	1.25	6.7	6.3	6.55	6.55	180–190	1.2	5.1	5	5.05	5.1
40–50	1.2	6.7	6.5	6.65	6.65	190–200	1.25	6.6	6.15	6.5	6.5
50–60	2.25	6.9	6.85	6.85	6.85	200–210	1.35	5.6	4.8	5.5	5.45
60–70	2.65	4.6	4.6	4.55	4.6	210–220	1.3	6.6	6.25	6.5	6.55
70–80	4.75	6.4	6.4	6.35	6.35	220–230	1.35	6.65	5.75	6.55	6.45
80–90	2.9	3.4	3.4	4.35	3.35	230–240	1.15	3.25	2.65	3.25	3.2
90–100	6.95	6.95	7	6.95	6.95	240–250	6.3	8.45	8.45	8.55	8.5
100–110	7	7.95	7.85	7.8	7.85	250–260	6.1	6.75	6.75	6.7	6.7
110–120	1.2	4.7	4.55	4.6	4.65	260–270	5.2	5.95	6	5.95	5.95
120–130	1.4	5.95	5.85	5.9	5.9	270–280	5.55	6.95	6.9	6.85	6.9
130–140	4.95	7.05	7.05	7	7.05	280–290	1.85	6.2	6.1	6.1	6.15
140–150	6.55	6.6	6.65	6.6	6.6	290–300	1.2	4.55	4.45	4.5	4.55

Table 11. Average time to reach 99.9% of ${\omega }_{r_{opt}}$ for the different dynamic gains models.

Interval(s)	${\mathit{t}}_{\mathbf{1}}\left(\mathbf{s}\right)$	${\mathit{t}}_{\mathbf{2}}\left(\mathbf{s}\right)$	${\mathit{t}}_{\mathbf{3}}\left(\mathbf{s}\right)$	${\mathit{t}}_{\mathbf{4}}\left(\mathbf{s}\right)$	${\mathit{t}}_{\mathbf{5}}\left(\mathbf{s}\right)$
0–300	3.2017	6.11	5.945	6.0483	6.0617

Finally, Figure 11 shows the ideal power as well as the instantaneous power for every proposed model for the entire interval (0–300 s). It can be noticed that the proposed models’ power curves are very similar to the ideal power graphic, so maximum power is rapidly reached. On the other hand, Figure 12 presents the ideal power and instantaneous power curves in the interval 190–230 s to have a better appreciation of the different models’ performance. As it can be seen, the exponential model provides the best results.

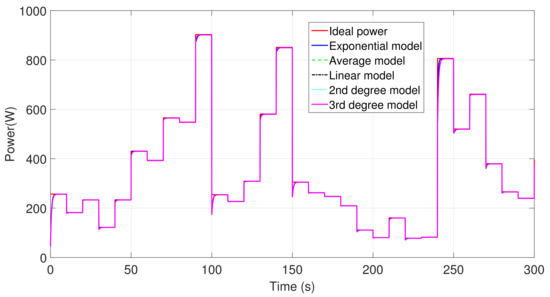
Figure 11. Whole span ideal and instantaneous power for the proposed models.

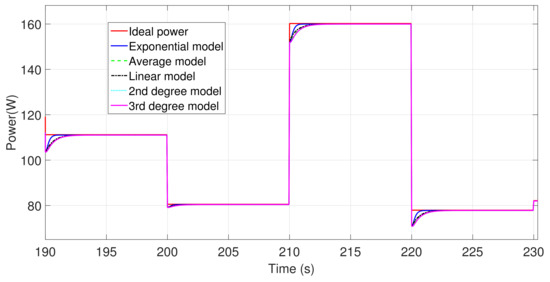
Figure 12. Ideal and instantaneous power for the proposed models from 190 to 230 s.

In order to compare the proposed controllers with the state of the art, the achieved results in the instantaneous power shown in Figure 11, are compared to the power results obtained in a constant PI controller with the feed-forward aerodynamic torque disturbance compensation using an aerodynamic torque observer, like the one proposed in [49]. As it can be noticed, the results are similar; nevertheless, in this work, real and diverse wind steps were used for the system excitation so that the reliability of the different proposed models can be verified.

7. Conclusions

A set of mathematical models for determining the dynamic gains for a discrete PI non-linear controller was proposed. Different tests were established in a particular WECS based on a PMSG to assess the system response and reduce its complexity, obtaining a linearized approach. The mathematical models’ performance was measured according to standard deviation, absolute error, and the time to reach the optimum generator angular speed. Unlike other investigations based on a fixed gains model or a linear model, this work is the first to present a set of mathematical models for calculating dynamic gains based on non-linear functions that depend on wind speed, such as the exponential, 2nd order, and 3rd order approaches.

The dynamic adjustment of the controller gains is a crucial factor for optimization purposes, allowing high performance for reaching the optimum angular rotor speed. It was verified that, in general, the dynamic approaches presented a better performance than the fixed gains model, especially the proposed exponential model.

When comparing the instantaneous power performance between the dynamic proposed models and state of the art; (especially to specialized constant gains PI controllers); the results were similar; nevertheless, a remarkable contribution of this paper is that, unlike other works, a set of different real wind speeds were provided as steps for testing the controller’s performance, even more, significant wind speed changes were also provided, and wind steps were applied just in 10 s, in order to demonstrate the controller’s reliability.

The graphics of angular speed and instantaneous power derived from the proposed methods show that ${\omega }_{r_{opt}}$ and maximum power are reached quickly. The statistical analysis supports the remarkable exponential model performance.