On Some Properties of the Limit Points of (z(n)/n)_n

Abstract

Let ${\left(F_n\right)}_{n\ge 0}$ be the sequence of Fibonacci numbers. The order of appearance of an integer $n\ge 1$ is defined as $z\left(n\right):=min\{k\ge 1:n\mid F_k\}$. Let ${\mathcal{Z}}^{\prime }$ be the set of all limit points of $\left\{z\right(n)/n:n\ge 1\}$. By some theoretical results on the growth of the sequence ${(z\left(n\right)/n)}_{n\ge 1}$, we gain a better understanding of the topological structure of the derived set ${\mathcal{Z}}^{\prime }$. For instance, $\{0,1,\frac{3}{2},2\}\subseteq {\mathcal{Z}}^{\prime }\subseteq [0,2]$ and ${\mathcal{Z}}^{\prime }$ does not have any interior points. A recent result of Trojovská implies the existence of a positive real number $t<2$ such that ${\mathcal{Z}}^{\prime }\cap (t,2)$ is the empty set. In this paper, we improve this result by proving that $(\frac{12}{7},2)$ is the largest subinterval of $[0,2]$ which does not intersect ${\mathcal{Z}}^{\prime }$. In addition, we show a connection between the sequence ${\left(x_n\right)}_n$, for which $z\left(x_n\right)/x_n$ tends to $r>0$ (as $n\to \infty$), and the number of preimages of r under the map $m\mapsto z\left(m\right)/m$.

1. Introduction

Let ${\left(F_n\right)}_n$ be the Fibonacci sequence. For any positive integer n, the order of apparition (or the rank of appearance) of n in the Fibonacci sequence, denoted by $z\left(n\right)$, as the minimum element of the set $\{k\ge 1:n\mid F_k\}$. This function is well-defined by a result of Lucas [1] (p. 300) (in 1878) and, in 1975, Sallé [2] proved the sharpest upper bound $z\left(n\right)\le 2n$, for all $n\ge 1$. Moreover, he also found the explicit form of all integers n for which the equality is attained. Indeed, it holds that

$$z\left(n\right)=2nifandonlyifn=6\times 5^k,fork\ge 0.$$

(1)

In particular, ${lim\; sup}_{n\to \infty }z\left(n\right)/n=2$. Set $\mathcal{Z}:=\{z\left(n\right)/n:n\in {\mathbb{Z}}_{\ge 1}\}$ and denote by ${\mathcal{Z}}^{\prime }$ its derived set (i.e., the set of all limit points of $\mathcal{Z}$). In 2013, Marques [3] proved the ${lim\; inf}_{n\to \infty }z\left(n\right)/n=inf{\mathcal{Z}}^{\prime }=0$. Recently, Trojovský [4] generalized this result by showing that the natural density of ${\mathcal{Z}}^{\prime }\cap (0,ϵ)$ is 1, for all $ϵ>0$. Recall that the natural density of $\mathcal{A}\subseteq {\mathbb{Z}}_{>0}$ is the following limit (if it exists)

$${\displaystyle \delta \left(\mathcal{A}\right):=\underset{x\to \infty }{lim}\frac{\#\mathcal{A}\left(x\right)}{x},}$$

where, $\mathcal{A}\left(x\right):=\mathcal{A}\cap [1,x]$ for $x>0$ (see, e.g., recent paper [5] on natural density of sets related to generalized Fibonacci numbers of order r).

Summarizing, we have some important properties of ${\mathcal{Z}}^{\prime }$, namely:

• ${\mathcal{Z}}^{\prime }\subseteq [0,2]$ and $sup{\mathcal{Z}}^{\prime }=2$ (Sallé [2]);
• $inf{\mathcal{Z}}^{\prime }=0$ (Marques [3]) and $1\in {\mathcal{Z}}^{\prime }$ (Marques [6], see also [7]);
• ${\mathcal{Z}}^{\prime }$ does not contain any (non-degenerated) interval (Trojovský [4]).

In 2020, Trojovská [8] solved completely the Diophantine equation $z\left(n\right)=(2-1/k)n$, with $k\ge 1$. She proved that all solutions are related to the cases $k=1$ or 2 (and there are two infinite families of solutions for each of these cases). In particular, $3/2\in {\mathcal{Z}}^{\prime }$ and since $2-1/k$ tends to 2 as $k\to \infty$, then (by her result) there exists some real number $t<2$ such that $(t,2)$ does not contain any limit point of $\mathcal{Z}$ (i.e., ${\mathcal{Z}}^{\prime }\cap (t,2)=⌀$). This seems to be more apparent by Figure 1 (indeed, seemingly $t>1.8$ should work).

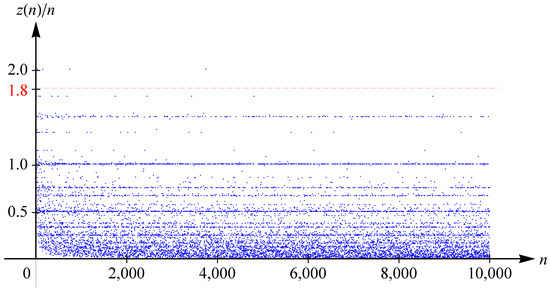
Figure 1. The scatterplot of the function $z\left(n\right)/n$ for values of n from 1 to $10,000$.

Our first goal is to find the largest subinterval of $[0,2]$ which does not intersect ${\mathcal{Z}}^{\prime }$. More precisely, we proved that

Theorem 1.

It holds that $(\frac{12}{7},2)$ is the largest subinterval of $[0,2]$ which does not intersect ${\mathcal{Z}}^{\prime }$.

Now, we turn our attention to the arithmetic properties of the sequences which “realize” the elements of ${\mathcal{Z}}^{\prime }$. For that, let us make some definitions. First, for any $r\in {\mathcal{Z}}^{\prime }$, we denote ${\Sigma }_r$ as

$${\Sigma }_r:=\left\{{\left(x_n\right)}_n\in {\mathbb{Z}}_{\ge 1}^{\infty }:\underset{n\to \infty }{lim}\frac{z\left(x_n\right)}{x_n}=r\right\},$$

i.e., ${\Sigma }_r$ is the set of all sequences $\sigma ={\left(x_n\right)}_n$ (of positive integers) for which $z\left(x_n\right)/x_n$ tends to r as $n\to \infty$. For example, ${\sigma }_1={\left(5^n\right)}_n\in {\Sigma }_1$ (see [3]). Also, it is conjectured that $z\left(q_n\right)=q_n+1$ holds for infinitely many prime numbers $q_n$ (the first few of them are $2,3,7,23,43,67,\dots$, see sequence A000057 in OEIS [9]). If this conjecture is true, then ${\sigma }_2:={\left(q_n\right)}_n$ also belongs to ${\Sigma }_1$. However, if ${\mathcal{F}}_r$ denotes the set of preimages of r under the function $m\mapsto z\left(m\right)/m$ (i.e., ${\mathcal{F}}_r:=\{m\ge 1:z\left(m\right)=rm\}$), then ${\sigma }_1\cap {\mathcal{F}}_1={\sigma }_1$, while ${\sigma }_2\cap {\mathcal{F}}_1=\varnothing$.

The next result provides a characterization for $\sigma \cap {\mathcal{F}}_r$ to be finite (for $\sigma \in {\Sigma }_r$) depending on the prime factors of the terms of $\sigma$. As usual, $P\left(n\right)$ denotes the greatest prime factor of n and, for $\sigma \in {\mathbb{Z}}_{\ge 1}^{\infty }\backslash \left\{{\left\{1\right\}}^{\infty }\right\}$ we define $P\left(\sigma \right):=sup\{P\left(x_n\right):n\ge 1\}$.

Theorem 2.

For any $r\in {\mathcal{Z}}^{\prime }\backslash \left\{0\right\}$ and $\sigma \in {\Sigma }_r$, we have that $\sigma \cap {\mathcal{F}}_r$ is an infinite set if and only if $P\left(\sigma \right)$ is finite.

Remark 1.

Observe that the case $r=0$ is not considered in the previous theorem. The reason is that ${\mathcal{F}}_0$ is the empty set, since $z\left(n\right)\ge 1$, for all $n\ge 1$.

The proof of the theorems combines the growth properties of $z\left(n\right)$ with some Diophantine aspects of its prime factors.

2. Auxiliary Results

In this section, we shall present some results which will be very important tools in the proof. The first ingredients are about the growth of $z\left(n\right)$ related to the number of its distinct primes factors of n (denoted, as usual, by $\omega \left(n\right)$):

Lemma 1.

We have

(i) 

(Theorem 1.1 of [3]) $z\left(2^k\right)=3\times 2^{k-2}$ (for $k\ge 3$), $z\left(3^k\right)=4\times 3^{k-1}$ (for $k\ge 1$), and $z\left(5^k\right)=5^k$ (for $k\ge 0$).

(ii) 

(Theorem 2.4 of [10]) If p is an odd prime, then

$$z\left(p^k\right)=p^{max\{k-e(p),0\}}z\left(p\right),$$

where $e\left(p\right)={\nu }_p\left(F_{z\left(p\right)}\right)\ge 1$. In particular, since $z\left(p\right)\mid p-\left(\frac{5}{p}\right)$, it holds that

$$z\left(p^k\right) divides \left(p-\left({\displaystyle \frac{5}{p}}\right)\right)p^{k-1}, for all k\ge 1,$$

where, as usual, ${\nu }_p\left(m\right)$ denotes the p-adic valuation of m and $\left(\frac{a}{q}\right)$ denotes the Legendre symbol of an integer a with respect to an odd prime q.

Lemma 2

(Theorem 1.2 of [3]). Let n be an odd integer with $\omega \left(n\right)\ge 2$, then

$$z\left(n\right)\le 2\times {\left({\displaystyle \frac{2}{3}}\right)}^{\omega \left(n\right)-{\delta }_n}n,$$

where

$${\delta }_n=\left\{\begin{array}{cc}\hfill 0,& if5\nmid n;\hfill \\ \hfill 1,& if5\mid n.\hfill \end{array}\right.$$

Lemma 3

(Theorem 1.3 of [3]). Let n be an even integer with $\omega \left(n\right)\ge 2$ and let ${\delta }_n$ as in the previous lemma, we have that

(i) 

If ${\nu }_2\left(n\right)\ge 4$, then

$${\displaystyle z\left(n\right)\le \frac{3}{4}\times {\left({\displaystyle \frac{2}{3}}\right)}^{\omega \left(n\right)-{\delta }_n-1}n.}$$

(ii) 

If ${\nu }_2\left(n\right)=1$, then

$$z\left(n\right)\le \left\{\begin{array}{cc}\hfill 3n/2,& if\omega \left(n\right)=2and5\mid n;\hfill \\ \hfill 2n,& if\omega \left(n\right)=2and5\nmid n;\hfill \\ \hfill 3\times {(2/3)}^{\omega \left(n\right)-{\delta }_n-1}n,& if\omega \left(n\right)>2.\hfill \end{array}\right.$$

(iii) 

If ${\nu }_2\left(n\right)\in \{2,3\}$, then

$$z\left(n\right)\le \left\{\begin{array}{cc}\hfill 3n/2,& if\omega \left(n\right)=2and5\mid n;\hfill \\ \hfill n,& if\omega \left(n\right)=2and5\nmid n;\hfill \\ \hfill {(2/3)}^{\omega \left(n\right)-{\delta }_n-2}n,& if\omega \left(n\right)>2.\hfill \end{array}\right.$$

The next tool is a kind of “formula" for $z\left(n\right)$ depending on $z\left(p^a\right)$ for all primes p dividing n. The proof of this fact can be found in [11].

Lemma 4

(Theorem 3.3 of [11]). Let $n>1$ be an integer with prime factorization $n=p_1^{a_1}\dots p_k^{a_k}$. Then

$$z\left(n\right)=lcm(z\left(p_1^{a_1}\right),\dots ,z\left(p_k^{a_k}\right)).$$

In general, it holds that

$$z\left(lcm(m_1,\dots ,m_k)\right)=lcm(z\left(m_1\right),\dots ,z\left(m_k\right)).$$

Our last auxiliary result is the following

Lemma 5.

Let $a\ge 1$ be an integer and let $q>3$ be a prime number. If $P\left(a\right)<q$, then $gcd\left(z\right(a),q)=1$.

Proof .

Set $a=p_1^{a_1}\dots p_k^{a_k}$ be the factorization of a, where $p_1<\dots <p_k$ are prime numbers, with $p_k>2$ and $a_i\ge 1$. By Lemma 1 (ii), we have

$$z\left(a\right)=\mathrm{lcm}(z\left(p_1^{a_1}\right),\dots ,z\left(p_k^{a_k}\right))=\mathrm{lcm}(p_1^{b_1}z\left(p_1\right),\dots ,p_k^{b_k}z\left(p_k\right)),$$

for some $b_i\ge 0$. Striving for a contradiction, suppose that q divides $z\left(a\right)$ (i.e., $gcd\left(z\right(a),q)>1$), then q divides $\mathrm{lcm}(p_1^{b_1}z\left(p_1\right),\dots ,p_k^{b_k}z\left(p_k\right))$ which divides $p_1^{b_1}z\left(p_1\right)\dots p_k^{b_k}z\left(p_k\right)$. Since $p_k<q$, then q divides $z\left(p_i\right)$, for some $i\in [1,k]$. This implies that

$$q\le z\left(p_i\right)\le p_i+1\le p_k+1\le q$$

and so $q=p_k+1$ (where we used that $z\left(p\right)\le p+1$, for all prime numbers p, also by Lemma 1 (ii)). Therefore, $q=3$ and $p_k=2$ (the only consecutive primes) leading to a contradiction (since $q>3$), which completes the proof. □

Now, we are ready to deal with the proof of the theorems.

3. The Proof of Theorem 1

Since $z\left(n\right)/n=2$ if and only if $n=6\times 5^k$, then, in order to prove that $12/7=max({\mathcal{Z}}^{\prime }\backslash \left\{2\right\})$, it suffices to show that $z\left(n\right)/n\le 12/7$ whenever n is not of the form $n=6\times 5^k$ and that $z\left(n\right)=12n/7$ for infinitely many positive integers n. This proof will be divided into four cases according to $\omega \left(n\right)$ and the parity of n.

Case 1.$\omega \left(n\right)=1$. In this case, n is a power of a prime number, say $n=p^k$. By Lemma 1 (ii), we have

$${\displaystyle \frac{z\left(p^k\right)}{p^k}}\le {\displaystyle \frac{p-(5/p)}{p}}\le 1+{\displaystyle \frac{1}{p}}\le \frac{3}{2}<{\displaystyle \frac{12}{7}}.$$

Case 2.n odd and $\omega \left(n\right)\ge 2$. By Lemma 2, we obtain

$${\displaystyle \frac{z\left(n\right)}{n}}\le 2\times {\left({\displaystyle \frac{2}{3}}\right)}^{\omega \left(n\right)-{\delta }_n}\le {\displaystyle \frac{4}{3}}<{\displaystyle \frac{12}{7}},$$

since $2/3<1$ and the minimum of $\omega \left(n\right)-{\delta }_n$ is 1.

Case 3.n even, $\omega \left(n\right)\ge 2$ and ${\nu }_2\left(n\right)>1$. For this case, we must split the proof into 2 sub-cases:

• If ${\nu }_2\left(n\right)\ge 4$, then Lemma 3 (i) yields

  $${\displaystyle \frac{z\left(n\right)}{n}}\le {\displaystyle \frac{3}{4}}\times {\left({\displaystyle \frac{2}{3}}\right)}^{\omega \left(n\right)-{\delta }_n}\le {\displaystyle \frac{3}{4}}<{\displaystyle \frac{12}{7}}.$$
• If ${\nu }_2\left(n\right)\in \{2,3\}$, then Lemma 3 (iii) implies that

  $${\displaystyle \frac{z\left(n\right)}{n}}\le max\left\{{\displaystyle \frac{3}{2}},1,{\left({\displaystyle \frac{2}{3}}\right)}^{1-{\delta }_n}\right\}\le {\displaystyle \frac{3}{2}}<{\displaystyle \frac{12}{7}}.$$

Case 4.n even, $\omega \left(n\right)\ge 2$ and ${\nu }_2\left(n\right)=1$. This is the most delicate case, since it contains the extremal values $n=6\times 5^k$ (for $k\ge 0$). Thus, Lemma 3 (in its item (ii)) only settles the case in which $\omega \left(n\right)=2$ and $n\equiv 0(mod5)$. Indeed, in this situation, one has

$${\displaystyle \frac{z\left(n\right)}{n}}\le {\displaystyle \frac{3}{2}}<{\displaystyle \frac{12}{7}}.$$

In order to deal with the other cases, we need to improve the inequalities in Lemma 3 (ii).

• Suppose that $\omega \left(n\right)=2$ and $n\equiv 0(mod5)$, then $n=2p^k$, for some prime number $p\ne 5$. If $p=3$, we have by Lemmas 1 (i) and 4 that

  $$z(2\times 3^k)=\mathrm{lcm}(z\left(2\right),z\left(3^k\right))=\mathrm{lcm}(3,4\times 3^{k-1})=4\times 3^{k-1}$$

  and so

  $${\displaystyle \frac{z\left(n\right)}{n}}={\displaystyle \frac{z(2\times 3^k)}{2\times 3^k}}={\displaystyle \frac{2}{3}}<{\displaystyle \frac{12}{7}}.$$
  Let us assume that $p\ge 7$. Thus

  $$z(2\times p^k)=\mathrm{lcm}(z\left(2\right),z\left(p^k\right))=\mathrm{lcm}(3,z\left(p^k\right))\le 3z\left(p^k\right)\le 3(p+1)p^{k-1},$$

  where we used that $\mathrm{lcm}(a,b)\le ab$ and that $z\left(p^k\right)\le (p+1)p^{k-1}$, from Lemma 1 (ii). Therefore,

  $${\displaystyle \frac{z\left(n\right)}{n}}={\displaystyle \frac{z\left(2p^k\right)}{2p^k}}\le {\displaystyle \frac{3(p+1)}{2p}}\le {\displaystyle \frac{3}{2}}\times \left(1+{\displaystyle \frac{1}{p}}\right)\le {\displaystyle \frac{3}{2}}\times \left(1+{\displaystyle \frac{1}{7}}\right)={\displaystyle \frac{12}{7}}.$$
  Also, since $z\left(7\right)=8$, Lemma 1 (ii), yields that $z\left(7^k\right)=8\times 7^{k-1}$ (here we used that $e\left(7\right)={\nu }_7\left(F_8\right)={\nu }_7\left(21\right)=1$). We then get

  $${\displaystyle \frac{z(2\times 7^k)}{2\times 7^k}}={\displaystyle \frac{\mathrm{lcm}(z\left(2\right),z\left(7^k\right))}{2\times 7^k}}={\displaystyle \frac{\mathrm{lcm}(3,8\times 7^{k-1})}{2\times 7^k}}={\displaystyle \frac{24\times 7^{k-1}}{2\times 7^k}}={\displaystyle \frac{12}{7}}$$

  for all $k\ge 1$ and so $12/7\in {\mathcal{Z}}^{\prime }$.
• The remaining case is $\omega \left(n\right)\ge 3$. Note that by Lemma 3 (ii), we infer that

  $${\displaystyle \frac{z\left(n\right)}{n}}\le {\displaystyle \frac{9}{2}}\times {\left({\displaystyle \frac{2}{3}}\right)}^{\omega \left(n\right)-{\delta }_n}.$$
  If $\omega \left(n\right)-{\delta }_n\ge 3$, then $z\left(n\right)/n\le (9/2)\times {(2/3)}^3=4/3<12/7$. However, the minimum value of $\omega \left(n\right)-{\delta }_n$ is 2 which is attained only if $\omega \left(n\right)=3$ and n is a multiple of 5, i.e., $n=2\times 5^k{p}^r$, for some prime number p with $gcd(p,10)=1$. When $p\ge 7$, we deduce that

  $$\begin{array}{ccc}\hfill {\displaystyle \frac{z\left(n\right)}{n}}& =& {\displaystyle \frac{z(2\times 5^k{p}^r)}{2\times 5^k{p}^r}}={\displaystyle \frac{\mathrm{lcm}(z\left(2\right),z\left(5^k\right),z\left(p^r\right))}{2\times 5^k{p}^r}}\hfill \\ & \le & {\displaystyle \frac{\mathrm{lcm}(3,5^k,z\left(p^r\right))}{2\times 5^k{p}^r}}\le {\displaystyle \frac{3\times 5^{k}z\left(p^r\right)}{2\times 5^k{p}^r}}\hfill \\ & \le & {\displaystyle \frac{3\times 5^k(p+1)p^{r-1}}{2\times 5^k{p}^r}}={\displaystyle \frac{3}{2}}\times \left(1+{\displaystyle \frac{1}{p}}\right)\hfill \\ & \le & {\displaystyle \frac{3}{2}}\times \left(1+{\displaystyle \frac{1}{7}}\right)={\displaystyle \frac{12}{7}}\hfill \end{array}$$

  for all $p\ge 7$ (as before, one has that $z\left(n\right)=12n/7$, for all $n=2\times 5^k\times 7^r$, with $(k,r)\in {\mathbb{Z}}_{\ge 0}\times {\mathbb{Z}}_{\ge 1}$).
  Now, we must deal with the case that $n=2\times 3^r\times 5^k$. Indeed, one has
  $$\begin{gathered} z(2\times 3^r\times 5^k)=\mathrm{lcm}(z\left(2\right),z\left(3^r\right),z\left(5^k\right))=\mathrm{lcm}(3,4\times 3^{r-1},5^k)=12\times 5^k \mathrm{o}\mathrm{r} \\ 4\times 3^{r-1}\times 5^k \end{gathered}$$

  according to $r=1$ or $r>1$, respectively. In conclusion, we arrive at

  $${\displaystyle \frac{z(2\times 3^r\times 5^k)}{2\times 3^r\times 5^k}}=\left\{\begin{array}{cc}\hfill 2,& ifr=1;\hfill \\ \hfill 2/3,& ifr>1.\hfill \end{array}\right.$$

Summarizing, we proved that $z\left(n\right)/n\in [\frac{12}{7},2]$ if and only if $n=2\times 7^k$ or $n=2\times 5^k\times 7^r$ (for which $z\left(n\right)/n=12/7$) as well as $n=6\times 5^k$ (for which $z\left(n\right)/n=2$). Hence ${\mathcal{Z}}^{\prime }\cap (\frac{12}{7},2)$ is the empty set.

To finish the proof, we must show that $(\frac{12}{7},2)$ is the largest subinterval of $[0,2]$ without limit points of ${(z\left(n\right)/n)}_{n\ge 1}$ (observe that the length of $(\frac{12}{7},2)$ is $2/7\approx 0.285$). For proving this, it is enough to exhibit a partition of the interval $[0,\frac{12}{7}]$ by subintervals of length smaller than $2/7$ and whose endpoints belong to ${\mathcal{Z}}^{\prime }$. Indeed, consider the following partition (and see Figure 2)

$$\left[0,\frac{12}{7}\right]=\left[0,\frac{1}{4}\right)\cup \left[\frac{1}{4},\frac{1}{2}\right)\cup \left[\frac{1}{2},\frac{3}{4}\right)\cup \left[\frac{3}{4},1\right)\cup \left[1,\frac{8}{7}\right)\cup \left[\frac{8}{7},\frac{4}{3}\right)\cup \left[\frac{4}{3},\frac{3}{2}\right)\cup \left[\frac{3}{2},\frac{12}{7}\right].$$

Figure 2. Partition of $[0,\frac{12}{7}]$ into subintervals intersecting ${\mathcal{Z}}^{\prime }$ and with the length smaller than $0.285$.

Graphically, the endpoints are positioned as below:

The largest among the intervals of partition has length $1/4$ (which is smaller than $2/7$). Hence, we only need to prove that all endpoints belong to ${\mathcal{Z}}^{\prime }$ (since $0\in {\mathcal{Z}}^{\prime }$, we may consider only nonzero endpoints). This is a consequence of Lemmas 1 and 4 and a straightforward calculation (we shall leave the details to the reader):

$${\displaystyle \frac{z\left(n\right)}{n}}=\left\{\begin{array}{cc}1/4,\hfill & ifn=3\times 2^k(k\ge 4);\hfill \\ 1/2,\hfill & ifn=24\times 5^k(k\ge 0);\hfill \\ 3/4,\hfill & ifn=2^k(k\ge 3);\hfill \\ 1,\hfill & ifn=5^k(k\ge 0);\hfill \\ 8/7,\hfill & ifn=7^k(k\ge 1);\hfill \\ 4/3,\hfill & ifn=3^k(k\ge 1);\hfill \\ 3/2,\hfill & ifn=2\times 5^k(k\ge 1);\hfill \\ 12/7,\hfill & ifn=2\times 7^k(k\ge 1)\hfill \end{array}\right.$$

The proof is then complete. □

4. The Proof of Theorem 2

4.1. Proof of “If” Part

Let $\sigma :={\left(x_n\right)}_n\in {\Sigma }_r$ with $P\left(\sigma \right)<\infty$. So, $z\left(x_n\right)/x_n$ tends to r ($r>0$) and ${\left(P\left(x_n\right)\right)}_n$ is a bounded sequence. Thus, there exist distinct prime numbers $q_1,\dots ,q_k$ and an infinite set $\mathcal{S}\subseteq {\mathbb{Z}}_{\ge 1}$ such that

$$x_n=q_1^{a_{n,1}}\dots q_k^{a_{n,k}},$$

for all $n\in \mathcal{S}$, where $a_{n,k}\ge 1$. By Lemma 4, we have that

$$z\left(x_n\right)=\mathrm{lcm}(z\left(q_1^{a_{n,1}}\right),\dots ,z\left(q_k^{a_{n,k}}\right)).$$

By Lemma 1 (ii), one has

$$z\left(x_n\right)=\mathrm{lcm}(q_1^{{\delta }_{n,1}}z\left(q_1\right),\dots ,q_k^{{\delta }_{n,k}}z\left(q_k\right)),$$

where ${\delta }_{n,i}:=max\{a_{n,i}-e\left(q_i\right),0\}$. We infer that $z\left(x_n\right)$ divides $q_1^{{\delta }_{n,1}}\dots q_k^{{\delta }_{n,k}}z\left(q\right)$ (where we denote $q=q_1\dots q_k$) and so

$$z\left(x_n\right)=q_1^{c_{n,1}}\dots q_k^{c_{n,k}}t,$$

for all n belonging to an infinite set ${\mathcal{S}}_1\subseteq \mathcal{S}$, where $0\le c_{n,i}\le {\delta }_{n,i}$ and t is a divisor of $z\left(q\right)$. Thus

$${\displaystyle \frac{z\left(x_n\right)}{x_n}}={\displaystyle \frac{q_1^{c_{n,1}}\dots q_k^{c_{n,k}}t}{q_1^{a_{n,1}}\dots q_k^{a_{n,k}}}}={\displaystyle \frac{t}{q_1^{{\theta }_{n,1}}\dots q_k^{{\theta }_{n,k}}}},$$

where ${\theta }_{n,i}:=a_{n,i}-c_{n,i}$ (it is important to notice that ${\theta }_{n,i}>0$, because $c_{n,i}\le {\delta }_{n,i}<a_{n,i}$, since $min\{a_{n,i},e\left(q_n\right)\}\ge 1$).

Since $z\left(x_n\right)/x_n$ does not tend to 0 as $n\to \infty$, then ${max}_{n\in {\mathcal{S}}_1}\{{\theta }_{n,i}:i\in [1,k]\}$ is bounded. Therefore, by the pigeonhole principle, there exists a k-tuple $({\theta }_1,\dots ,{\theta }_k)\in {\mathbb{Z}}_{\ge 1}^k$ such that

$$({\theta }_{n,1},\dots ,{\theta }_{n,k})=({\theta }_1,\dots ,{\theta }_k)$$

for all n belonging to an infinite set ${\mathcal{S}}_2\subseteq {\mathcal{S}}_1$. In conclusion,

$${\displaystyle \frac{z\left(x_n\right)}{x_n}}={\displaystyle \frac{t}{q_1^{{\theta }_1}\dots q_k^{{\theta }_k}}}=r$$

for all $n\in {\mathcal{S}}_2$. Thus $\sigma \cap {\mathcal{F}}_r$ is an infinite set (since it contains ${\left(x_n\right)}_{n\in {\mathcal{S}}_2}$). □

4.2. Proof of the “Only If” Part

Let $\sigma :={\left(x_n\right)}_n\in {\Sigma }_r$ with $P\left(\sigma \right)=\infty$. Then, we can write $x_n=y_n{q}_n^{a_n}$, where $P\left(y_n\right)<q_n$, $a_n\ge 1$ and $q_n$ tends to infinity as $n\to \infty$. Passing through a subsequence, if necessary, we may assume that ${\left(q_n\right)}_n$ is an increasing sequence with $q_n>5$, for all $n\ge 1$. By Lemmas 1 (ii) and 4, we have

$$z\left(x_n\right)=\mathrm{lcm}(z\left(y_n\right),z\left(q_n^{a_n}\right))=\mathrm{lcm}(z\left(y_n\right),q_n^{{\delta }_n}z\left(q_n\right)),$$

where ${\delta }_n=max\{a_n-e\left(q_n\right),0\}$. Since $max\{P\left(y_n\right),3\}<q_n$, we have, by Lemma 5, that $gcd(z\left(y_n\right),q_n)=1$ and then

$$z\left(x_n\right)=q_n^{{\delta }_n}·\mathrm{lcm}(z\left(y_n\right),z\left(q_n\right)),$$

where we used that $\mathrm{lcm}(a,qb)=q·\mathrm{lcm}(a,b)$ if $gcd(a,q)=1$. Thus

$${\displaystyle \frac{z\left(x_n\right)}{x_n}}=\left\{\begin{array}{cc}\hfill {\displaystyle \frac{\mathrm{lcm}(z\left(y_n\right),z\left(q_n\right))}{y_n·q_n^{a_n}}},& if{\delta }_n=0;\hfill \\ \hfill {\displaystyle \frac{\mathrm{lcm}(z\left(y_n\right),z\left(q_n\right))}{y_n·q_n^{e\left(q_n\right)}}},& if{\delta }_n\ne 0.\hfill \end{array}\right.$$

Note that, in any case, if $t_n:=min\{a_n,e\left(q_n\right)\}$, then

$${\displaystyle \frac{z\left(x_n\right)}{x_n}}\le {\displaystyle \frac{\mathrm{lcm}(z\left(y_n\right),z\left(q_n\right))}{y_n·q_n^{t_n}}}\le {\displaystyle \frac{z\left(y_n\right)z\left(q_n\right)}{y_n·q_n^{t_n}}}\le {\displaystyle \frac{2y_n(q_n+1)}{y_n·q_n^{t_n}}}={\displaystyle \frac{2(q_n+1)}{q_n^{t_n}}},$$

where we used Sallé’s bound $z\left(m\right)\le 2m$, for any m. However, $z\left(x_n\right)/x_n$ tends to $r>0$ and $q_n$ tends to infinity (as $n\to \infty$) which forces $t_n$ to be 1, for all n sufficiently large, say $n\ge n_0$. Therefore

$${\displaystyle \frac{z\left(x_n\right)}{x_n}}={\displaystyle \frac{\mathrm{lcm}(z\left(y_n\right),z\left(q_n\right))}{y_n·q_n}},$$

(2)

for all $n\ge n_0$.

Suppose that $z\left(x_n\right)=r{x}_n$, for all n belonging to an infinite set $\mathcal{S}$. Then $r=a/b$, for positive coprime integers a and b and, by (2), we obtain

$$a{y}_n{q}_n=b·\mathrm{lcm}(z\left(y_n\right),z\left(q_n\right)),$$

(3)

for all $n\in S\cap [n_0,+\infty )$. However, $gcd(q_n,z\left(y_n\right))=gcd(q_n,z\left(q_n\right))=1$ (since $q_n>5$) and thus the relation (3) implies that $q_n$ divides b for all $n\in S\cap [n_0,+\infty )$ which is an absurd since ${\left(q_n\right)}_{n\in \mathcal{S}}$ is unbounded and $b>0$. Thus $\sigma \cap {\mathcal{F}}_r$ must be a finite set. This completes the proof. □

5. Conclusions

In this paper, we study some properties of the set of limit points, say ${\mathcal{Z}}^{\prime }$, of the sequence ${(z\left(n\right)/n)}_{n\ge 1}$, where $z\left(n\right):=min\{k\ge 1:n\mid F_k\}$ is the order of appearance in the Fibonacci sequence. For instance, some results in the literature imply that $0,1,3/2$ and 2 belongs to ${\mathcal{Z}}^{\prime }$. Thus, in this work, we improve some growth results of $z\left(n\right)$ in order to prove that $(\frac{12}{7},2)$ is the largest subinterval of $[0,2]$ which does not contain any element of ${\mathcal{Z}}^{\prime }$. Moreover, we show a connection between some arithmetic properties of the sequence ${\left(x_n\right)}_n$, for which $z\left(x_n\right)/x_n$ tends to $r>0$ (as $n\to \infty$), and the number of preimages of r under the map $m\mapsto z\left(m\right)/m$.