Fixed-Time Third-Order Super-Twisting-like Sliding Mode Motion Control for Piezoelectric Nanopositioning Stage

Abstract

This paper presents a novel third-order super-twisting-like integral sliding mode controller (3-ISMC) for trajectory tracking of nanopositioning applications. Different from traditional sliding mode control methods presenting with chattering problems, the proposed approach provides continuous control inputs, which brings much convenience for practical applications. Moreover, the fixed-time convergence of the proposed 3-ISMC is guaranteed independently of initial conditions. The estimation of the fixed convergence time and stability are derived based on the Lyapunov method. Simulation results demonstrate that the proposed controller exhibits chattering free and quick transient response performance for a piezoelectric nanopositioning system under model uncertainties and external disturbances.

1. Introduction

The last decades have witnessed the increasing popularity of piezoelectric actuators among nanopositioning platforms, which provide several advantages including ultra-fine resolution, quick response speed, large energy density, and no backlash. Such piezoelectric-driven nanopositioning devices exhibit a variety of applications, such as atomic force microscope [1,2], biological manipulation [3] and precision machining [4]. Nevertheless, the intrinsic hysteresis of piezo-driven stages, which is amplitude- and rate-dependent, leads to challenges of its precise positioning. These nonlinear characteristics need to be suppressed so that piezoelectric actuators can be utilized in nanopositioning applications.

Various control methods have been proposed to cope with this limitation in the literature; voltage based control methods can be mainly divided into three parts: (1) feedforward control with inverse hysteresis model; (2) closed-loop control with an approximate hysteresis model; and (3) adaptive control by considering hysteresis as disturbances. The first category constructs mathematical models that describe hysteresis behaviors precisely, and using its inverse model cancels the hysteresis characteristic. Several kinds of hysteresis model have been developed, for example, the Bouc–Wen model, the Prandtl–Ishlinskii model, the Duhem model, the polynomial model, and so forth [5,6,7]. More sophisticated methods are also proposed to deal with the rate-dependent characteristic of hysteresis, for example, machine learning-based models [8], neural network-based modesl [9,10], modified PI models [11], and rate-dependent Bouc–Wen models [12], and so forth. However, these hysteresis models often exist in complicated structures, it is time-consuming to identify the parameters accurately, and the system dynamics always change with load variance that deteriorates the accuracy of feedforward controllers.

Sliding mode control (SMC) is an effective nonlinear control approach to cope with various disturbances and system uncertainties [13]. However, the traditional SMC algorithms guarantee the convergence of tracking errors only asymptotically, which means that to drive the tracking errors to zero takes infinite time. To alleviate this shortcoming, a terminal sliding surface is proposed in the literature, which can achieve finite-time convergence using a nonlinear sliding surface. The crucial feature lies in the nonlinear fractional order manifold, which leads the system to achieve finite-time convergence to zero. Although the faster convergence rate can be obtained in the neighborhood of the origin, the convergence rate deteriorates prominently when the system states of the system are far away from the origin. This indicates that convergence time may become unacceptably large for large initial conditions. To improve the performance in terms of convergence rate, the design of SMC with fixed-time convergence, which is independent of initial conditions, has increasingly attracted the attention of researchers [14,15].

Furthermore, the chattering problem, which is caused by discontinuous control inputs, is another disadvantage of the conventional SMC algorithm. This problem may excite undesirable dynamics behavior of the system and is prone to damaging the actuator. Moreover, the actual actuator always has a response time, which means that it cannot change infinitely fast [16]. To tackle control chattering, high-order sliding mode control (HOSMC) is proposed in the literature [17,18]. To enhance control performance further, integral sliding surface is adopted to eliminate the reaching phase of control law [19,20]. Combined with the above two methods, a third-order SMC with an integral type of terminal sliding surface is proposed in [21], and it achieves a finite-time convergence and eliminates the chattering problem. The second-order sliding mode controller with a fixed time convergence time has been also designed in [22], in which the upper bound of its fixed convergence time was estimated. Nevertheless, to achieve better precision positioning and a faster transient response, a third-order sliding mode control with fixed convergence time is needed.

The main contribution of this paper is the development of a fixed-time 3-ISMC algorithm. The proposed approach guarantees that the convergence time is fixed and is independent of initial conditions. The structure of the following parts is as follows. Section 2 formulates the problem. Section 3 presents the controller design of fixed-time third-order SMC. Section 4 illustrates the simulation results, and conclusions are summarized in Section 5.

2. Problem Formulation

2.1. Dynamical Model

Consider a second order piezoelectric nanopositioning stage system [21]:

$$M\ddot{x}\left(t\right)+B\dot{x}\left(t\right)+Kx\left(t\right)=Du\left(t\right)+F_h\left(t\right)+P\left(t\right),$$

(1)

where $x\left(t\right)\in \mathbb{R}$ is the displacement output, and M, B and K are positive constants which represent the mass, damping coefficient and stiffness of the dynamical system, respectively. The constant D is the scaled coefficient of the control input. $u\left(t\right)\in \mathbb{R}$ signifies the excitation voltage. $F_h\left(t\right)$ denotes the nonlinear effects and $P\left(t\right)$ represents the total bounded perturbations and model uncertainties.

The objective of this work is to design a state-feedback control law $u(·)$, such that the displacement $x\left(t\right)$ tracks the desired reference trajectory $x_d\left(t\right)$ precisely. Specifically, the origin of the resulting closed-loop system needs to be globally fixed-time stable, and the convergence time of the trajectories can be estimated.

The dynamical model (1) can be represented as follows:

$$\ddot{x}\left(t\right)+a_1\dot{x}\left(t\right)+a_{0}x\left(t\right)=b_{0}u\left(t\right)+d\left(t\right),$$

(2)

where $a_1=\frac{B}{M}$, $a_0=\frac{K}{M}$, $b_0=\frac{D}{M}$, and $d\left(t\right)=\frac{F_h\left(t\right)+P\left(t\right)}{M}$. Instead of building an accurate nonlinear effect model, the nonlinearity and uncertainties are considered as lumped disturbance $d\left(t\right)$, which can be estimated online in the following subsection.

2.2. Disturbance Estimation

The lumped disturbance $d\left(t\right)$ can be estimated in real time by the perturbation estimation approach proposed in [23]

$$\widehat{d}\left(t\right)=\ddot{x}\left(t\right)+a_1\dot{x}\left(t\right)+a_{0}x\left(t\right)-b_{0}u(t-T),$$

(3)

where T denotes the sampling time. Hence, the nonlinear dynamics (2) can be rewritten into the form of double-integrator dynamics with a matched disturbance:

$$\left\{\begin{array}{cc}\hfill {\dot{x}}_1\left(t\right)& =x_2\left(t\right),\hfill \\ \hfill {\dot{x}}_2\left(t\right)& =-a_1{x}_2\left(t\right)-a_0{x}_1\left(t\right)+b_{0}u\left(t\right)+\widehat{d}\left(t\right)+\tilde{d}\left(t\right),\hfill \end{array}\right.$$

(4)

where $x_1\left(t\right):=x\left(t\right)$ is the displacement of the nanopositioning stage system, $x_2\left(t\right)$ is the linear velocity of the displacement, and $\tilde{d}\left(t\right):=d\left(t\right)-\widehat{d}\left(t\right)$ is the disturbance estimation error.

It is observed that the disturbance estimation error $\tilde{d}\left(t\right)$ is always present due to the sampling time T in practice. However, as the sampling time is usually a small number, it is reasonable to assume that $\tilde{d}\left(t\right)$ is bounded. Thus, the variation rate can be considered to be bounded, that is, $|\dot{\tilde{d}}\left(t\right)|<\delta$, where $\delta$ is a known constant bound.

Definition 1.

A control law is said to globally stabilize the plant (1) in finite-time, if for any initial condition $x_0:=[x_{10},x_{20}]\in {\mathbb{R}}^2$ there exists a time moment $T\left(x_0\right)$ such that one has $x\left(t\right)=0$ for all $t\ge T\left(x_0\right)$, for any admissible disturbance $d\left(t\right)$.

Definition 2.

A control law is said to globally stabilize the plant (1) in fixed-time, if for any initial condition $x_0:=[x_{10},x_{20}]\in {\mathbb{R}}^2$ there exists a time moment T, which is independent of the initial conditions, such that one has $x\left(t\right)=0$ for all $t\ge T$, for any admissible disturbance $d\left(t\right)$.

3. Design of Controller

For the convenience of control design, we denote the tracking error as

$$e\left(t\right):=x\left(t\right)-x_d\left(t\right),$$

(5)

where $x_d\left(t\right)$ is the desired tracking trajectory. The integral type of terminal sliding surface is defined as

$$s\left(t\right):=e\left(t\right)+c_1{\int }_{t_0}^t{e}^{\alpha }\left(\tau \right)\mathrm{d}\tau +c_2{\int }_{t_0}^t{e}^{\beta }\left(\tau \right)\mathrm{d}\tau +\zeta ,$$

(6)

where $c_1,c_2>0$, $\alpha >1$, $\frac{1}{2}<\beta <1$ are constants, and $\zeta$ is a constant control parameter depending on the initial conditions. The time derivative of s is computed as

$$\dot{s}\left(t\right)=\dot{e}\left(t\right)+c_1{e}^{\alpha }\left(t\right)+c_2{e}^{\beta }\left(t\right).$$

(7)

Theorem 1.

Consider the second-order system (2) with the sliding surface given by (6). Then, the sliding surface is a fixed-time stable manifold, and the reaching time of the trajectories is estimated as

$$T\left(e_0\right)<T_{max}:=\frac{1}{c_1}\frac{1}{\alpha -1}+\frac{1}{c_2}\frac{1}{1-\beta }.$$

(8)

Proof. 

Consider the Lyapunov candidate $V\left(e\right)=e^2\ge 0$, where the time derivative along the trajectories is

$$\dot{V}\left(e\right)=2e\dot{e}.$$

(9)

Assume that $s\equiv 0$, which yields the following expression from (7)

$$\dot{e}\left(t\right)=-c_1{e}^{\alpha }\left(t\right)-c_2{e}^{\beta }\left(t\right).$$

(10)

Then, substituting (10) into (9) yields

$$\begin{array}{cc}\hfill \dot{V}\left(e\left(t\right)\right)& =2e\left(t\right)\left(-c_1{e}^{\alpha }\left(t\right)-c_2{e}^{\beta }\left(t\right)\right)\hfill \\ \hfill & =-2c_1{\left(e{\left(t\right)}^2\right)}^{\frac{\alpha +1}{2}}-2c_2{\left(e{\left(t\right)}^2\right)}^{\frac{\beta +1}{2}}\hfill \\ \hfill & =-2\left(c_{1}V{\left(e\left(t\right)\right)}^{\frac{\alpha -\beta }{2}}+c_2\right)V{\left(e\left(t\right)\right)}^{\frac{\beta +1}{2}}.\hfill \end{array}$$

(11)

Since $c_1{V}^{(\alpha -\beta )/2}\ge 0$, the following inequality holds:

$$\dot{V}\left(e\right)+c{\left(V\left(e\right)\right)}^{\eta }\le 0,$$

(12)

where $c=2c_2$, $\eta =(\beta +1)/2$, and $0<\eta <1$. Then, the error dynamics on the sliding manifold are global finite-time stable [24] and the reaching-time function is given by

$$T_f\left(e_0\right)\le {\displaystyle \frac{1}{c(1-\eta )}}{V}^{(1-\eta )}\left(e_0\right).$$

(13)

It is noted that the finite-time reaching time depends on the initial condition $e_0$. To eliminate the dependence of the initial condition, assuming that $V\left(e\right(t\left)\right)\ne 0$, one obtains

$$\frac{1}{V^{\frac{\beta +1}{2}}}\frac{\mathrm{d}V}{\mathrm{d}t}=-2\left(c_1{V}^{\frac{\alpha -\beta }{2}}+c_2\right),$$

which yields

$$\frac{1}{1-\beta }\frac{\mathrm{d}{V}^{\frac{1-\beta }{2}}}{\mathrm{d}t}=-\left(c_1{V}^{\frac{\alpha -\beta }{2}}+c_2\right).$$

Let $z=V^{\frac{1-\beta }{2}}$, we have

$$\frac{1}{c_1{z}^{1+ϵ}+c_2}\mathrm{d}z=-(1-\beta )\mathrm{d}t,$$

where $ϵ:=(\alpha -1)/(1-\beta )$. Let $\phi \left(l\right)={\int }_0^l\frac{1}{c_1{z}^{1+ϵ}+c_2}\mathrm{d}z$, integrating both sides of the above equation yields

$$\phi \left(z\right(t\left)\right)=\phi \left(z\right(0\left)\right)-(1-\beta )t.$$

Note that the function $\phi \left(l\right)$ is monotonically increasing. Since $\phi \left(z\right)=0$ if and only if $z=0$ (implying that $V=0$), one obtains

$$\underset{t\to T\left(e_0\right)}{lim}V\left(e\left(t\right)\right)=0,$$

where $T\left(e_0\right)$ is the settling time given by

$$T\left(e_0\right)=\frac{1}{1-\beta }\phi \left(z\left(0\right)\right)=\frac{1}{1-\beta }\phi \left(e^{1-\beta }\left(0\right)\right).$$

Then, the bounded $T\left(e_0\right)$ can be obtained by

$$\begin{array}{cc}\hfill \underset{e_0\to +\infty }{lim}& T\left(e_0\right)=\underset{z_0\to +\infty }{lim}\frac{1}{1-\beta }\phi \left(z\left(0\right)\right)\hfill \\ \hfill & =\frac{1}{1-\beta }\left({\int }_0^1\frac{1}{c_1{z}^{1+ϵ}+c_2}\mathrm{d}z+{\int }_1^{+\infty }\frac{1}{c_1{z}^{1+ϵ}+c_2}\mathrm{d}z\right)\hfill \\ \hfill & \le \frac{1}{1-\beta }\left({\int }_0^1\frac{1}{c_2}\mathrm{d}z+{\int }_1^{+\infty }\frac{1}{c_1{z}^{1+ϵ}}\mathrm{d}z\right)\hfill \\ \hfill & =\frac{1}{1-\beta }\left(\frac{1}{c_2}+\frac{1}{c_1ϵ}\right)\hfill \\ \hfill & =\frac{1}{c_1}\frac{1}{\alpha -1}+\frac{1}{c_2}\frac{1}{1-\beta }.\hfill \end{array}$$

Note that $V\left(e\right(t\left)\right)=0$ implies that $e\left(t\right)=0$.

It can be observed that the settling time function eliminates the dependence of the initial condition $e_0$. As a result, the convergence time can be prescribed.  □

We summarize our main results in the following theorem.

Theorem 2.

Consider the second-order system (2) with the feedback control law (14). Then, the control law (14) globally stabilizes system (2) in fixed-time with a continuous control input.

$$u=\frac{1}{b_0}(u_{eq}+u_n),$$

(14)

with

$$\begin{array}{cc}\hfill u_{eq}& =a_0{x}_1+a_1{x}_2+{\ddot{x}}_d-c_1\alpha e^{\alpha -1}\dot{e}-c_2\beta e^{\beta -1}\dot{e},\hfill \\ \hfill u_n& =-k_1{\left|\varphi \right|}^{1/2}\mathrm{sign}\left(\varphi \right)-k_2{\left|\varphi \right|}^p\mathrm{sign}\left(\varphi \right)+\psi ,\hfill \\ \hfill \dot{\psi }& =-k_3\mathrm{sign}\left(\varphi \right),\hfill \\ \hfill \varphi & =\dot{s}+k_4{\left|s\right|}^{2/3}\mathrm{sign}\left(s\right),\hfill \end{array}$$

(15)

where $k_1,k_2,k_4>0$ are positive control gains, $k_3>\left|\dot{\widehat{d}}\right|$, and $\alpha >1$, $\frac{1}{2}<\beta <1$.

Proof. 

Taking the time derivative of both sides of (7) yields

$$\ddot{s}=\ddot{e}+c_1\alpha e^{\alpha -1}\dot{e}+c_2\beta e^{\beta -1}\dot{e}.$$

(16)

Then, take the time derivative of (5) twice, and substitute it into (16) resulting in

$$\begin{array}{cc}\hfill \ddot{s}=& (\ddot{x}-{\ddot{x}}_d)+c_1\alpha e^{\alpha -1}\dot{e}+c_2\beta e^{\beta -1}\dot{e}\hfill \\ \hfill =& b_{0}u-a_0{x}_1-a_1{x}_2+d-{\ddot{x}}_d+c_1\alpha e^{\alpha -1}\dot{e}+c_2\beta e^{\beta -1}\dot{e}.\hfill \end{array}$$

(17)

Substituting control law (14) into (17), we have

$$\begin{array}{cc}\hfill \ddot{s}& =-k_1{\left|\varphi \right|}^{1/2}\mathrm{sign}\left(\varphi \right)-k_2{\left|\varphi \right|}^p\mathrm{sign}\left(\varphi \right)+\psi +\widehat{d},\hfill \\ \hfill \dot{\psi }& =-k_3\mathrm{sign}\left(\varphi \right).\hfill \end{array}$$

(18)

Denoting $\xi :=\psi +\widehat{d}$, the above equations become

$$\begin{array}{cc}\hfill \ddot{s}& =-k_1{\left|\varphi \right|}^{1/2}\mathrm{sign}\left(\varphi \right)-k_2{\left|\varphi \right|}^p\mathrm{sign}\left(\varphi \right)+\xi ,\hfill \\ \hfill \dot{\xi }& =-k_3\mathrm{sign}\left(\varphi \right)+\dot{\widehat{d}}.\hfill \end{array}$$

(19)

Let us denote ${\sigma }_1:=s$, and then the above equations can be rewritten into the following form:

$$\begin{array}{cc}\hfill {\dot{\sigma }}_1& ={\sigma }_2,\hfill \\ \hfill {\dot{\sigma }}_2& =-k_1{\left|\varphi \right|}^{1/2}\mathrm{sign}\left(\varphi \right)-k_2{\left|\varphi \right|}^p\mathrm{sign}\left(\varphi \right)+{\sigma }_3,\hfill \\ \hfill \dot{{\sigma }_3}& =-k_3\mathrm{sign}\left(\varphi \right)+\dot{\widehat{d}},\hfill \end{array}$$

(20)

where $\varphi ={\sigma }_2+k_4{\left|{\sigma }_1\right|}^{2/3}\mathrm{sign}\left({\sigma }_1\right)$. Note that Equation (20) has a structure similar to that of the third-order super-twisting algorithm (3-STA) with the assumption that $\dot{\tilde{d}}$ is bounded [17].

Denote ${\lfloor ·\rceil }^q={|·|}^{q}sign(·)$, and consider the following continuous Lyapunov candidate for the stability analysis of (20)

$$\begin{array}{cc}\hfill U\left(\sigma \right)& =q_1{\left|{\sigma }_1\right|}^{\frac{4}{3}}-q_{12}{⌊{\sigma }_1⌉}^{\frac{2}{3}}\left({\sigma }_2+k_4{⌊{\sigma }_1⌉}^{2/3}\right)\hfill \\ \hfill & +q_2{\left|{\sigma }_2+k_4{⌊{\sigma }_1⌉}^{2/3}\right|}^2+q_{13}{⌊{\sigma }_1⌉}^{\frac{2}{3}}{⌊{\sigma }_3⌉}^2\hfill \\ \hfill & -q_{23}\left({\sigma }_2+k_4{⌊{\sigma }_1⌉}^{2/3}\right){⌊{\sigma }_3⌉}^2+q_3{\left|{\sigma }_3\right|}^4.\hfill \end{array}$$

(21)

Note that the Lyapunov function (21) is differentiable everywhere but it is not Lipschitz at the origin. Lyapunov function (21) can also be rewritten into a quadratic form of the vector ${\Xi }^{\mathrm{T}}=\left[{⌊{\sigma }_1⌉}^{2/3}\varphi {⌊{\sigma }_3⌉}^2\right]$, that is,

$$U\left(\Xi \right)={\Xi }^{T}Q\Xi ,\mathrm{where}Q=\left[\begin{array}{ccc}{q}_1& -\frac{1}{2}{q}_{12}& \frac{1}{2}{q}_{13}\\ -\frac{1}{2}{q}_{12}& q_2& -\frac{1}{2}{q}_{23}\\ \frac{1}{2}{q}_{13}& -\frac{1}{2}{q}_{23}& q_3\end{array}\right].$$

(22)

Select parameters in the Lyapunov function (21) such that

$$\begin{array}{cc}\hfill & q_1>0,q_1{q}_2>\frac{1}{4}{q}_{12}^2,\hfill \\ \hfill & q_1\left(q_2{q}_3-q_{23}^2\right)+\frac{q_{12}}{2}\left(-\frac{q_{12}{q}_3}{2}+\frac{q_{13}{q}_{23}}{4}\right)\hfill \\ \hfill & +\frac{q_{13}}{2}\left(\frac{q_{12}{q}_{23}}{4}-\frac{q_2{q}_{13}}{2}\right)>0.\hfill \end{array}$$

(23)

Then, the matrix $Q>0$ and therefore $U\left(\sigma \right)$ are positive definite and radically unbounded. In this case, $\dot{U}\left(\sigma \right)$ satisfies the following inequality,

$$\dot{U}\le -{\kappa }_1{U}^{3/4}-{\kappa }_2{U}^p,$$

(24)

for some positive constants ${\kappa }_1$ and ${\kappa }_2$ for the set of control gains $k_1,k_2,k_3$ and $k_4$. It follows from (24) that the closed-loop system (20) is fixed-time stable. Then, the reaching time of the sliding variable can be further estimated using the inequality (24) [25]. Finally, it follows from Theorem 1 that on the sliding manifold the error trajectories converge to the origin in fixed time (8), which completes the proof. □

4. Simulation Results

This section illustrates the effectiveness of the proposed third-order fixed-time super-twisting-like sliding mode controller by conducting a simulation study. The Hammerstein-based model is adopted to describe the dynamic characteristics of the piezoelectric nanopositioning stage. In particular, the Bounc–Wen model is employed to express static nonlinear, and a transfer function is used for capturing the rate-dependent hysteresis of the stage, where the framework is described in Figure 1.

Figure 1. The framework of the Hammerstein model.

The nonlinear dynamics of the piezoelectric nanopositioning stage in simulations are given as:

$$\left\{\begin{array}{cc}\hfill & w\left(t\right)=du\left(t\right)-h\left(t\right),\hfill \\ \hfill & \dot{h}\left(t\right)=b_1\dot{u}\left(t\right)-b_2|\dot{u}\left(t\right)|h\left(t\right)-b_3\dot{u}\left(t\right)\left|h\left(t\right)\right|,\hfill \end{array}\right.$$

(25)

in which the model parameters are identified by the particle swarm optimization algorithm as $b_1=13.6612$$\mathsf{\mu }$m/V, $b_2=0.6449$V${}^{-1}$, $b_3=0.0118$V${}^{-1}$, and $d=27.1141$N · V${}^{-1}$.

The transfer function is identified as:

$$G\left(s\right)=\frac{3.2066\times {10}^6}{s^2+1502s+3.2066\times {10}^6}(\mu m/V).$$

(26)

The parameters of dynamic model (2) are calculated as $a_0=3.2066\times {10}^6$N$·\mathsf{\mu }$m${}^{-1}·$Kg${}^{-1}$, $a_1=1502$N·s$·\mathsf{\mu }$m${}^{-1}$Kg${}^{-1}$, and $b_0=8.7\times {10}^7$N·V${}^{-1}$·Kg${}^{-1}$, respectively. Hence, it can be seen that the hysteresis loop varies dramatically with input frequency from 1Hz to 100 Hz in Figure 2.

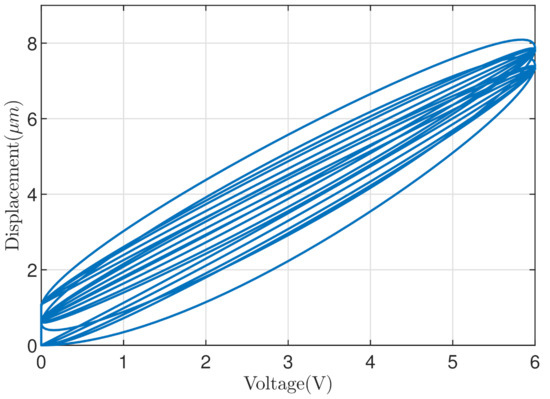
Figure 2. The hysteresis loop of the simulated model from 1Hz to 100 Hz.

The controller parameters of the proposed 3-ISMC in (14) are shown in Table 1; the sampling time is $1\times {10}^{-4}$ s. The position output is available for the nanopositioning stage, and thus the initial position error $\zeta$ can be calculated in advance. Therefore, the value of sliding surface (6) can always be set to zero in the initialization. As a result, the reaching phase of the control law can be eliminated.

Table 1. Control Parameters of the Proposed Controller.

Parameter	$\mathit{\alpha }$	$\mathit{\beta }$	${\mathit{c}}_1$	${\mathit{c}}_2$	${\mathit{k}}_1$	${\mathit{k}}_2$	${\mathit{k}}_3$	${\mathit{k}}_4$
Value	2	0.6	3	10	$6\times {10}^4$	8	$1\times {10}^{10}$	340

Remark 1.

The nonlinear control law $u_n$ in (14) is divided by $b_0$, where the magnitude is at the level of ${10}^7$. The reason for the parameter $b_0$ being so large is that the displacement of the nanopositioning system is at the micron level, which results in a consequence that the magnitudes of control gains $k_1,k_2,k_3,k_4$ vary considerably. For the three terms in the control law $u_n$, they are expected at similar magnitude levels to be effective in the control law, which leads to the following gain tuning rule. Specifically, $k_4$ can be chosen first to make the controller sensitive to the tracking error. Then, $k_2,k_3,k_4$ can be determined by the rule of guaranteeing each term in $u_n$ at similar magnitude levels to be effective in the control law.

(1) Convergence Properties of the Proposed Fixed-time Sliding Surface: A high initial condition $\sigma \left(0\right)$=[10, 100, 0] is used for illustrating the performance of the proposed fixed-time sliding surface, as shown in Figure 3. It can be observed that the states of (20) converge to zero very fast, which indicates that the convergence time is independent of the initial conditions.

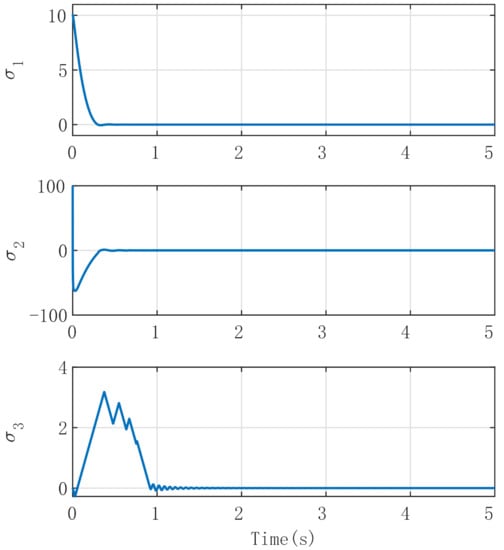
Figure 3. Proposed 3-ISMC control: Time histories of ${\sigma }_0$, ${\sigma }_1$, and ${\sigma }_2$ corresponding to initial condition of $\sigma \left(0\right)$ = [10, 100, 0].

(2) Step Position Tracking: In general, the trade-off between the response speed and overshoot has to be considered during the controller design. The controllers for nanopositioning applications have to be sensitive to minor tracking errors while the overshoot of step response needs to be reduced. Step position tracking is conducted to illustrate the response performance of the proposed 3-ISMC algorithm. It can be observed from Figure 4 that the states exhibit a fast response without the overshoot phenomenon, while the control input keeps continuous. However, the conventional 3-STA algorithm has a weaker performance compared with 3-ISMC.

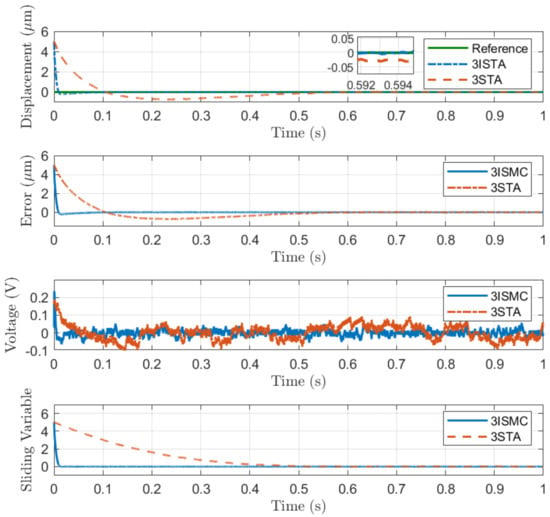
Figure 4. Proposed 3-ISMC control: Time histories of state variables and control inputs corresponding to initial condition of $x_0$ = [5, 100].

(3) Sinusoidal Position Tracking: To demonstrate the performance of the proposed control approach for particular applications, a 20 μm peak-to-peak sinusoidal reference trajectory with frequency of 10Hz is used in simulations for position tracking control, as shown in Figure 5. Even though the nonlinear hysteresis $h\left(t\right)$ of plant (25) is unknown for the proposed control law, the desired trajectory is tracked preciously. The conventional 3-STA controller presents a maximum absolute error (MAXE) of 76.2 nm and a root mean square error (RMSE) of 27.4 nm and the proposed 3-ISMC controller generates a MAXE of 11.9 nm and an RMSE of 3.6 nm, which are reduced to 15.62% and 13.12% by the proposed 3-ISMC method, respectively. Additionally, an initial position error of 10 μm is imposed for sinusoidal reference trajectory tracking simulation to describe the superiority of convergence, as shown in Figure 6.

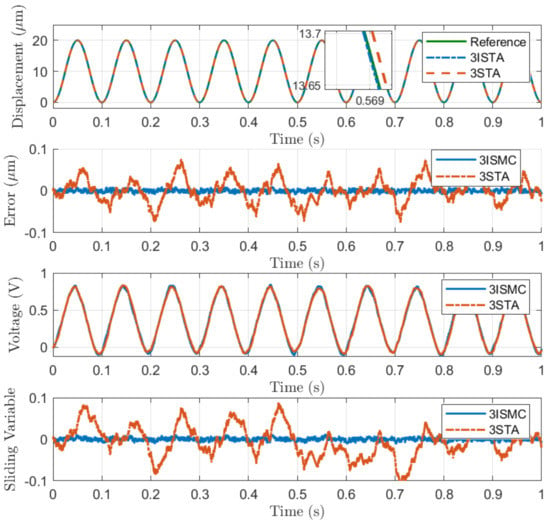
Figure 5. Simulation results of 10Hz sinusoidal trajectory tracking. (a) Position tracking results. (b) Position tracking error. (c) Control inputs. (d) Sliding variable.

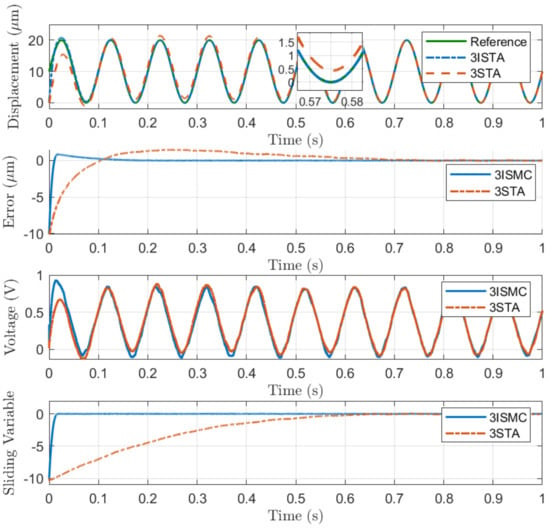
Figure 6. Simulation results of 10Hz sinusoidal trajectory tracking. (a) Position tracking results. (b) Position tracking error. (c) Control inputs. (d) Sliding variable.

(4) Robustness Testing: In order to illustrate the robustness of the proposed controller, system parameters adopted in the proposed controller $a_0$, $a_1$, $b_0$ float up to 1.1 times of the original values, and the following external disturbance signal (27) is injected into 20 μm peak-to-peak sinusoidal trajectories with a frequency of 10Hz for position tracking control, as shown in Figure 7.

$$d\left(t\right)=[0.05sin(100\pi t)+0.25sin(2\pi t)+0.3]\mu m.$$

(27)

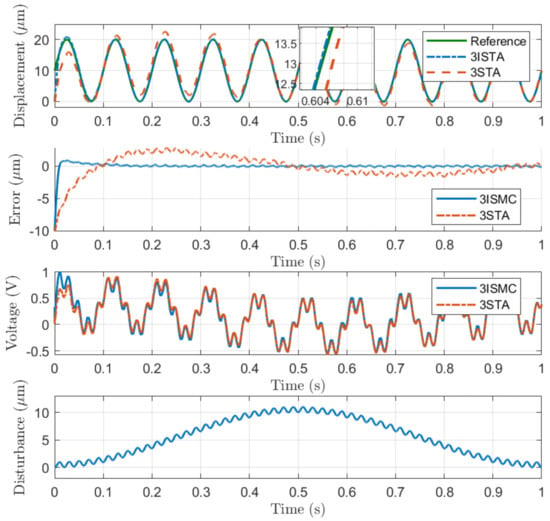
Figure 7. Simulation results of 10Hz sinusoidal trajectory tracking with external disturbance. (a) Position tracking results. (b) Position tracking error. (c) Control inputs. (d) External disturbance signal.

It can be seen that both 3-STA and 3-ISMC offer a continuous sliding surface and smooth control efforts while the hyper external disturbance is alleviated. Particularly, the proposed 3-ISMC achieves an RMSE of 0.5188 μm for 10Hz sinusoidal trajectories with disturbance, which is smaller than the RMSE of 1.7780 μm achieved by 3-STA. The comparison results of trajectory tracking with disturbance under difference frequencies (5–50 Hz) is shown in Table 2; it can be seen that the proposed method maintains a superior performance of RMSE compared with conventional 3-STA, which proves that the developed 3-ISMC method exhibits better robustness under system uncertainties and external disturbances.

Table 2. Comparison Results of Trajectory Tracking with Disturbance.

Controller Type	5 Hz Sinewave	10 Hz Sinewave	20 Hz Sinewave	50 Hz Sinewave
3-STA (μm)	1.7782	1.7780	1.7778	4.3219
3-ISMC (μm)	0.5914	0.5188	0.9703	0.7348

It is noted that, although restrictions on the magnitude of control inputs are not imposed in the simulations, from a practical viewpoint, the applied voltages are still realistic in all shown simulation results. However, as shown in Figure 7, the control voltage gradually decreases as the amplitude of the disturbance increases. In practice, the range of control voltages for the piezoelectric stages is, in general, from −1 V to 10 V. Thus, it may exceed the lower bounds of the control voltage while the disturbance reaches a certain large value, which leads to the actuator being in saturation with the proposed controller.

5. Conclusions

In this paper, the third-order super-twisting-like sliding mode controller (3-ISMC) has been developed for trajectory tracking of the piezoelectric nanopositioning stage. The stability and fixed-time convergence properties of the proposed method have been theoretically demonstrated, and the effectiveness of 3-ISMC has been verified on a series of simulation studies. Particularly, the 3-ISMC shows a quick response independently of initial conditions, a smooth control input without chattering, and excellent performance of disturbance reduction. In future work, the proposed approach will be implemented on a physical piezo-driven nanopositioning stage to verify its performance for practical applications; an adaptive gain method will also be developed to adjust control gains online to improve performance further.