A Modified Rao-2 Algorithm for Optimal Power Flow Incorporating Renewable Energy Sources

Abstract

In this paper, a modified Rao-2 (MRao-2) algorithm is proposed to solve the problem of optimal power flow (OPF) in a power system incorporating renewable energy sources (RES). Quasi-oppositional and Levy flight methods are used to improve the performance of the Rao algorithm. To demonstrate effectiveness of the MRao-2 technique, it is tested on two standard test systems: an IEEE 30-bus system and an IEEE 118-bus system. The objective function of the OPF is the minimization of fuel cost in five scenarios. The IEEE 30-bus system reflects fuel cost minimization in three scenarios (without RES, with RES, and with RES under contingency state), while the IEEE 118-bus system reflects fuel cost minimization in two scenarios (without RES and with RES). The achieved results of various scenarios using the suggested MRao-2 technique are compared with those obtained using five recent techniques: Atom Search Optimization (ASO), Turbulent Flow of Water-based Optimization (TFWO), Marine Predators Algorithm (MPA), Rao-1, Rao-3 algorithms, as well as the conventional Rao-2 algorithm. Those comparisons confirm the superiority of the MRao-2 technique over those other algorithms in solving the OPF problem.

1. Introduction

In recent decades, the optimal power flow (OPF) problem has had an important role in the operation and planning of electrical systems [1]. OPF aims to adjust the independent control variables parameters of power systems to reach the needed objective function, which are normally reducing the fuel cost, emission, and active power loss, to satisfy the needed demand load, concurrently meeting the boundaries of inequality and equality constraints [2].

The critical necessity to address global warming and climate change have placed renewable energy sources (RES) such as solar energy systems, wind energy systems, and hydropower plants in the center of energy conversion as well as the quickly dropping renewable power generation costs, we need to face the challenges, arising from using a high scale of renewable energy sources in the power system [3]. In recent years, RES contributes to decreasing the power losses of the grid, enhancing the quality and reliability of the electrical grid [4]; furthermore, they affect the electricity market. By increasing the added energy from RES inside the electrical power grid, it is required to set the best energy production for the system to satisfy the objective functions such as minimizing the fuel cost, total emission from the conventional power generation stations, and transmission losses and enhancing the voltage profile [5].

The OPF problem is generally non-convex, non-smooth, and non-differentiable objective functions. Consequently, it is very significant to develop new techniques to reach the global best solution for this problem. The conventional approaches such as Gradient’s method [6], nonlinear programming [6], quadratic programming [7], and interior-point methods [8] have been successfully applied in the previous researches to solve the OPF problem. The nonlinear properties may produce the obtained solutions to be confined in local minima, and these methods need a huge quantity of computational effort and time. Therefore, several optimization techniques need to be developed to defeat these weaknesses [9].

Thus, different heuristic techniques are utilized to solve the OPF problem such as a multi-objective hybrid firefly and PSO (MOHFPSO) [10], modified grasshopper optimization algorithm (MGOA) [11], forced initialized differential evolution algorithm [12], an adaptive multiple teams perturbation-guiding Jaya (AMTPG-Jaya) technique [13], modified Sine-Cosine algorithm (MSCA) [14], Developed Grey Wolf Optimizer (DGWO) [15], improved salp swarm algorithm (ISSA) [16], Barnacles Mating Optimizer (BMO) [17], and Lévy Coyote optimization algorithm (LCOA) [18].

Although these three versions of the Rao algorithm have been recently published, many optimization problems have been solved using them and using their modifications such as the photovoltaic cell parameter estimation [19,20,21,22], design optimization of mechanical system components [23], selected thermodynamic [24], Optimal weight design of a spur gear train [25], 2D truss structures [26], multi-objective design optimization of selected heat sinks [27], optimal reactive power dispatch with renewable energy and time-varying demand uncertainty [28], and Classification of Parkinson disease [29].

In this article, the main contribution is summarized as follows.

• The proposed MRao-2 technique is used to achieve the accurate values of control variables of the OPF problem without RES, with RES, and with RES under contingency state.
• The fuel cost is the main objective function in five scenarios for the two IEEE 30 -bus and 118-bus systems to test the validation of the proposed algorithm.
• To check the robustness of this modified algorithm, its results are compared with five recent algorithms—ASO, TFWO, MPA, Rao-1, and Rao-3—as well as the original Rao-2 which are the strong algorithms in solving the modern power system problems and they are used in many published papers in the last two years so far.

The rest of the paper is organized as follows. The problem formulation is presented in Section 2. Section 3 introduces the proposed MRao-2 algorithm applied to solve the OPF problem with various scenarios. Section 4 gives a discussion and analysis of the simulation results. Section 5 presents the conclusion.

2. Problem Formulation

2.1. General Structure of OPF

The OPF solution provides the best value of the control variables by minimizing an objective function with satisfying equality and inequality limitations. Commonly, the mathematical formulation of the optimization problem may be expressed as follows [30]:

$$\mathrm{Minimize}\mathrm{F}\left(\mathrm{x},\mathrm{u}\right)$$

(1)

Subject to

$${\mathrm{g}}_{\mathrm{i}}\left(\mathrm{x},\mathrm{u}\right)=0\mathrm{i}=1,2,3,\dots ,\mathrm{m}$$

(2)

$${\mathrm{h}}_{\mathrm{j}}\left(\mathrm{x},\mathrm{u}\right)\le 0\mathrm{j}=1,2,3,\dots ,\mathrm{n}$$

(3)

where F is the objective function; $\mathrm{x}$,$\mathrm{u}$ are the state variables (dependent variables) and the control variables (independent variables) vectors, respectively; ${\mathrm{g}}_{\mathrm{i}}$ is the equality constraints$;\mathrm{m}$ is the number of equality constraints; ${\mathrm{h}}_{\mathrm{j}}$ is the number of inequality constraints; and $\mathrm{n}$ is the number of inequality constraints.

The state variables are represented in a vector as follows [16]:

$$\mathrm{x}=\left[{\mathrm{P}}_{\mathrm{G}1},{\mathrm{V}}_{\mathrm{L}1}\dots {\mathrm{V}}_{\mathrm{LNPQ}},{\mathrm{Q}}_{\mathrm{G}1}\dots {\mathrm{Q}}_{\mathrm{GNPV}},{\mathrm{S}}_{\mathrm{TL}1}\dots {\mathrm{S}}_{\mathrm{TLNTL}}\right]$$

(4)

where ${\mathrm{P}}_{\mathrm{G}1}$ refers to the active power generation of slack bus, V_L is the voltage magnitude of the load bus, NPQ is the number of load buses, Q_G is the generated reactive power, NPV is the number of generation buses, S_TL is the loading of transmission line, and NTL is Number of transmission lines.

The control variables are represented in a vector as follows [16]:

$$\mathrm{u}=\left[{\mathrm{P}}_{\mathrm{G}2}\dots {\mathrm{P}}_{\mathrm{GNG}},{\mathrm{V}}_{\mathrm{G}1}\dots {\mathrm{V}}_{\mathrm{GNG}},{\mathrm{Q}}_{\mathrm{C}1}\dots {\mathrm{Q}}_{\mathrm{CNC}},{\mathrm{T}}_1\dots {\mathrm{T}}_{\mathrm{NT}}\right]$$

(5)

where P_G is the generated active power, and NG is the number of generators. V_G is the voltage magnitude of the generation bus. Q_C is the injected imaginary power by the shunt compensator. NC is the number of shunt compensators. T is the tapping ratio of the transformer. NT is the number of transformers.

2.2. Objective Functions

2.2.1. Quadratic Total Fuel Cost

The total fuel cost of all thermal generation units is represented based on the polynomial quadratic function as the following equation [2]:

$${\mathrm{F}}_1={\displaystyle \sum }_{\mathrm{i}=1}^{\mathrm{N}}\left({\mathrm{a}}_{\mathrm{i}}{\mathrm{P}}_{\mathrm{gi}}^2+{\mathrm{b}}_{\mathrm{i}}{\mathrm{P}}_{\mathrm{gi}}+{\mathrm{c}}_{\mathrm{i}}\right)\$/\mathrm{h}$$

(6)

where a_i, b, and c_i are the cost coefficients of ith generator.

2.2.2. Total Emission

Various types of noxious emissions are emitted from those plants because of using several types of fossil fuels in thermal power plants. Newly, one of the principal goals of the OPF problem is reducing these emissions without affecting the generated power to satisfy the load demands in the electrical power system. This emission is calculated from the following equation: [31]:

$$\mathrm{E}={\displaystyle \sum }_{\mathrm{i}=1}^{\mathrm{N}}\left[{10}^{-2}({\mathsf{\alpha }}_{\mathrm{i}}+{\mathsf{\beta }}_{\mathrm{i}}{\mathrm{P}}_{\mathrm{i}}+{\mathsf{\gamma }}_{\mathrm{i}}{\mathrm{P}}_{\mathrm{i}}^2)\right]$$

(7)

where ${\mathsf{\alpha }}_{\mathrm{i}}$, ${\mathsf{\beta }}_{\mathrm{i}}$, and ${\mathsf{\gamma }}_{\mathrm{i}}$ represent the emission coefficients for the ith unit.

2.2.3. Power Loss Function

The total active power losses in the system can be expressed as follows [32]:

$${\mathrm{P}}_{\mathrm{loss}}={\displaystyle \sum }_{\mathrm{k}=1}^{\mathrm{nl}}{\mathrm{G}}_{\mathrm{k}}\left[{\mathrm{V}}_{\mathrm{i}}^2+{\mathrm{V}}_{\mathrm{j}}^2-2{\mathrm{V}}_{\mathrm{i}}{\mathrm{V}}_{\mathrm{j}}\cos ({\mathsf{\delta }}_{\mathrm{i}}-{\mathsf{\delta }}_{\mathrm{j}})\right]\mathrm{MW}$$

(8)

where $\mathrm{nl}$ is the number of network nodes; ${\mathrm{V}}_{\mathrm{i}}$ and ${\mathrm{V}}_{\mathrm{j}}$ are the voltage magnitudes for the i-th and j-th nodes, respectively; ${\mathsf{\delta }}_{\mathrm{i}}$ and ${\mathsf{\delta }}_{\mathrm{j}}$ are the node voltage angles of the i-th–j-th branch; and ${\mathrm{G}}_{\mathrm{k}}$ refers to the conductivity between node i and node j.

2.2.4. Voltage Deviation (VD) Function (Voltage Profile Improvement)

One of the effective methods is the voltage magnitude fluctuation from 1.0 per unit at each load bus which is defined as follows [32]:

$$\mathrm{VD}={\displaystyle \sum }_{\mathrm{p}=1}^{\mathrm{NL}}\left|{\mathrm{V}}_{{\mathrm{L}}_{\mathrm{p}}}-1\right|$$

(9)

where ${\mathrm{V}}_{{\mathrm{L}}_{\mathrm{p}}}$ is the ith voltage of load buses.

2.3. Constraints

2.3.1. Equality Constraints

The balanced load flow equations represent the equality constraints. The following equations express the active and reactive power constraints that fulfill the load demands requirements and also the power losses of the transmission line [33]:

$${\mathrm{P}}_{\mathrm{Gi}}-{\mathrm{P}}_{\mathrm{Di}}={\mathrm{V}}_{\mathrm{i}}{\displaystyle \sum }_{\mathrm{j}=1}^{\mathrm{NB}}{\mathrm{V}}_{\mathrm{j}}[{\mathrm{G}}_{\mathrm{ij}}\cos \left({\mathsf{\delta }}_{\mathrm{i}}-{\mathsf{\delta }}_{\mathrm{j}}\right)+{\mathrm{B}}_{\mathrm{ij}}\sin \left({\mathsf{\delta }}_{\mathrm{i}}-{\mathsf{\delta }}_{\mathrm{j}}\right)]$$

(10)

$${\mathrm{Q}}_{\mathrm{Gi}}-{\mathrm{Q}}_{\mathrm{Di}}={\mathrm{V}}_{\mathrm{i}}{\displaystyle \sum }_{\mathrm{j}=1}^{\mathrm{NB}}{\mathrm{V}}_{\mathrm{j}}[{\mathrm{G}}_{\mathrm{ij}}\cos \left({\mathsf{\delta }}_{\mathrm{i}}-{\mathsf{\delta }}_{\mathrm{j}}\right)-{\mathrm{B}}_{\mathrm{ij}}\sin \left({\mathsf{\delta }}_{\mathrm{i}}-{\mathsf{\delta }}_{\mathrm{j}}\right)]$$

(11)

where P_G is the generated real power, Q_G is the reactive power generation, $\mathrm{NB}$ is the number of buses, and P_D and Q_D are the real and imaginary load demands, respectively. ${\mathrm{G}}_{\mathrm{ij}}$ and ${\mathrm{B}}_{\mathrm{ij}}$ are the conductance and substance between buses i and j.${\mathsf{\delta }}_{\mathrm{i}}$ and ${\mathsf{\delta }}_{\mathrm{j}}$ are the voltage angles bus i and j.

2.3.2. Inequality Constraints

The inequality constraints are described as follows [34]:

(a) Generator constraints (thermal or renewable as applicable):

$${\mathrm{P}}_{\mathrm{Gi}}^{\min }\le {\mathrm{P}}_{\mathrm{Gi}}\le {\mathrm{P}}_{\mathrm{Gi}}^{\max }\mathrm{i}=1,2,\dots ,\mathrm{NG}$$

(12)

$${\mathrm{V}}_{\mathrm{Gi}}^{\min }\le {\mathrm{V}}_{\mathrm{Gi}}\le {\mathrm{V}}_{\mathrm{Gi}}^{\max }\mathrm{i}=1,2,\dots ,\mathrm{NPV}$$

(13)

$${\mathrm{Q}}_{\mathrm{Gi}}^{\min }\le {\mathrm{Q}}_{\mathrm{Gi}}\le {\mathrm{Q}}_{\mathrm{Gi}}^{\max }\mathrm{i}=1,2,\dots ,\mathrm{NPV}$$

(14)

(b) Security constraints

$${\mathrm{S}}_{\mathrm{Li}}\le {\mathrm{S}}_{\mathrm{li}}^{\max }\mathrm{i}=1,2,\dots ,\mathrm{NTL}$$

(15)

$${\mathrm{V}}_{\mathrm{i}}^{\min }\le {\mathrm{V}}_{\mathrm{i}}\le {\mathrm{V}}_{\mathrm{i}}^{\max }\mathrm{i}=1,2,\dots ,\mathrm{NPQ}$$

(16)

(c) Shunt VAR compensator constraints:

$${\mathrm{Q}}_{\mathrm{ci}}^{\min }\le {\mathrm{Q}}_{\mathrm{Ci}}\le {\mathrm{Q}}_{\mathrm{ci}}^{\max }\mathrm{i}=1,2,\dots ,\mathrm{NC}$$

(17)

(d) Transformer constraints:

$${\mathrm{T}}_{\mathrm{i}}^{\min }\le {\mathrm{T}}_{\mathrm{i}}\le {\mathrm{T}}_{\mathrm{i}}^{\max }\mathrm{i}=1,2,\dots ,\mathrm{NT}$$

(18)

The mathematical formulation of the fitness function combined with the quadratic penalty is as follows:

$${\mathrm{F}}_{\mathrm{g}}\left(\mathrm{x},\mathrm{u}\right)={\mathrm{F}}_{\mathrm{i}}\left(\mathrm{x},\mathrm{u}\right)+\mathrm{Penalty}$$

(19)

$$\mathrm{Penalty}={\mathsf{\lambda }}_{\mathrm{p}}{\left(\Delta {\mathrm{P}}_{\mathrm{G}1}\right)}^2+{\mathsf{\lambda }}_{\mathrm{v}}{\displaystyle \sum }_{\mathrm{i}=1}^{\mathrm{NPQ}}{\left(\Delta {\mathrm{V}}_{\mathrm{Li}}\right)}^2+{\mathsf{\lambda }}_{\mathrm{Q}}{\displaystyle \sum }_{\mathrm{i}=1}^{\mathrm{NPV}}{\left(\Delta {\mathrm{Q}}_{\mathrm{Gi}}\right)}^2+{\mathsf{\lambda }}_{\mathrm{s}}{\displaystyle \sum }_{\mathrm{i}=1}^{\mathrm{NTL}}{\left(\Delta {\mathrm{S}}_{\mathrm{Li}}\right)}^2$$

(20)

$$\Delta {\mathrm{P}}_{\mathrm{G}1}=\left\{\begin{array}{c}{\mathrm{P}}_{\mathrm{G}1}{}^{\max }-{\mathrm{P}}_{\mathrm{G}1}{\mathrm{P}}_{\mathrm{G}1}>{\mathrm{P}}_{\mathrm{G}1}{}^{\max }\\ {\mathrm{P}}_{\mathrm{G}1}-{\mathrm{P}}_{\mathrm{G}1}{}^{\min }{\mathrm{P}}_{\mathrm{G}1}<{\mathrm{P}}_{\mathrm{G}1}{}^{\min }\end{array}\right.$$

(21)

$$\Delta {\mathrm{V}}_{\mathrm{Li}}=\left\{\begin{array}{c}\Delta {\mathrm{V}}_{\mathrm{Li}}{}^{\max }-\Delta {\mathrm{V}}_{\mathrm{Li}}\Delta {\mathrm{V}}_{\mathrm{Li}}>\Delta {\mathrm{V}}_{\mathrm{Li}}{}^{\max }\\ \Delta {\mathrm{V}}_{\mathrm{Li}}-\Delta {\mathrm{V}}_{\mathrm{Li}}{}^{\min }\Delta {\mathrm{V}}_{\mathrm{Li}}<\Delta {\mathrm{V}}_{\mathrm{Li}}{}^{\min }\end{array}\right.$$

(22)

$$\Delta {\mathrm{Q}}_{\mathrm{Gi}}=\left\{\begin{array}{c}\Delta {\mathrm{Q}}_{\mathrm{Gi}}{}^{\max }-\Delta {\mathrm{Q}}_{\mathrm{Gi}}\Delta {\mathrm{Q}}_{\mathrm{Gi}}>\Delta {\mathrm{Q}}_{\mathrm{Gi}}{}^{\max }\\ \Delta {\mathrm{Q}}_{\mathrm{Gi}}-\Delta {\mathrm{Q}}_{\mathrm{Gi}}{}^{\min }\Delta {\mathrm{Q}}_{\mathrm{Gi}}<\Delta {\mathrm{Q}}_{\mathrm{Gi}}{}^{\min }\end{array}\right.$$

(23)

$$\Delta {\mathrm{S}}_{\mathrm{Li}}=\left\{\begin{array}{c}\Delta {\mathrm{S}}_{\mathrm{Li}}{}^{\max }-\Delta {\mathrm{S}}_{\mathrm{Li}}\Delta {\mathrm{S}}_{\mathrm{Li}}>\Delta {\mathrm{S}}_{\mathrm{Li}}{}^{\max }\\ \Delta {\mathrm{S}}_{\mathrm{Li}}-\Delta {\mathrm{S}}_{\mathrm{Li}}{}^{\min }\Delta {\mathrm{S}}_{\mathrm{Li}}<\Delta {\mathrm{S}}_{\mathrm{Li}}{}^{\min }\end{array}\right.$$

(24)

where ${\mathsf{\lambda }}_{\mathrm{p}}$,${\mathsf{\lambda }}_{\mathrm{v}}$,${\mathsf{\lambda }}_{\mathrm{Q}}$, ${\mathsf{\lambda }}_{\mathrm{s}}$ are the Penalty factors.

2.3.3. Power Balance Considering RES

Adding the RES to the power system has different shapes in the studying of the OPF problem. In this article, the RES is employed as a negative load [35,36]. This implies that all RES (such as solar, wind, hydro, and biomass) that are added to the system will be utilized first to produce the part of the required power to loads then the remainder of the loads and power losses will be covered from the thermal power plants.

3. The Proposed Optimization Technique

3.1. Rao Algorithm

Rao algorithms have recently been implemented in [37]. The key benefit of these algorithms is that they do not need any complex control parameters, only ordinary parameters such as population size and the number of iterations are required. Rao-1, Rao-2, and Rao-3 are three algorithms that have been developed in [37]. The Rao-2 algorithm is used in this study as it has a high convergence rate.

The following equation can be used to describe the mathematical formulation of the Rao-2 algorithm:

$${\mathrm{X}}_{\mathrm{j},\mathrm{k}\mathrm{p},\mathrm{i}}^{\prime }={\mathrm{X}}_{\mathrm{j},\mathrm{k}\mathrm{p},\mathrm{i}}+\mathrm{R}{\mathrm{d}}_{1,\mathrm{j},\mathrm{i}}\left({\mathrm{X}}_{\mathrm{j},\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t},\mathrm{i}}-{\mathrm{X}}_{\mathrm{j},\mathrm{w}\mathrm{o}\mathrm{r}\mathrm{s}\mathrm{t},\mathrm{i}}\right)+\mathrm{R}{\mathrm{d}}_{2,\mathrm{j},\mathrm{i}}\left(\left|{\mathrm{X}}_{\mathrm{j},\mathrm{k}\mathrm{p},\mathrm{i}}\mathrm{o}\mathrm{r}{\mathrm{X}}_{\mathrm{j},\mathrm{l}\mathrm{m},\mathrm{i}}\right|-\left({\mathrm{X}}_{\mathrm{j},\mathrm{l}\mathrm{m},\mathrm{i}}\mathrm{o}\mathrm{r}{\mathrm{X}}_{\mathrm{j},\mathrm{k}\mathrm{p},\mathrm{i}}\right)\right)$$

(25)

where ${\mathrm{X}}_{\mathrm{j},\mathrm{kp},\mathrm{i}}$ denotes the value of jth variable design for kpth candidate solution after the ith iteration, and ${\mathrm{X}}_{\mathrm{j},\mathrm{kp},\mathrm{i}}^{\prime }$denotes the updated value of the next iteration. ${\mathrm{X}}_{\mathrm{j},\mathrm{best},\mathrm{i}}$ and${\mathrm{X}}_{\mathrm{j},\mathrm{worst},\mathrm{i}}$are the values of the j for the best and worst candidate solutions during the ith iteration, respectively.${\mathrm{Rd}}_{1,\mathrm{j},\mathrm{i}}{\mathrm{and}\mathrm{Rd}}_{2,\mathrm{j},\mathrm{i}}$are random numbers in the range [0, 1] for the jth variable during the ith iteration.

The terminology (${\mathrm{X}}_{\mathrm{j},\mathrm{kp},\mathrm{i}}{\mathrm{or}\mathrm{X}}_{\mathrm{j},\mathrm{lm},\mathrm{i}}{\mathrm{and}\mathrm{X}}_{\mathrm{j},\mathrm{lm},\mathrm{i}}{\mathrm{or}\mathrm{X}}_{\mathrm{j},\mathrm{kp},\mathrm{i}}$) are used to compare the fitness values of a candidate solution k and a randomly chosen candidate solution.

The following are the key steps of the Rao-2 algorithm.

• Step 1: Randomly distribute the population within the vector ranges.
• Step 2: Determine the objective value for each variable.
• Step 3: Define the worst and best solutions depending on the objective function’s values.
• Step 4: Upgrade the solutions by (25).
• Step 5: If any of the updated values fall outside of the range, they should be returned.
• Step 6: Evaluate the value of each search agent’s objective function.
• Step 7: Increase the number of iterations of the new one $it=it+1$
• Step 8: If the iteration has reached its end, return the best value so far. If not, go on to Step 3.

Figure 1 illustrates the main flowchart for the Rao-2.

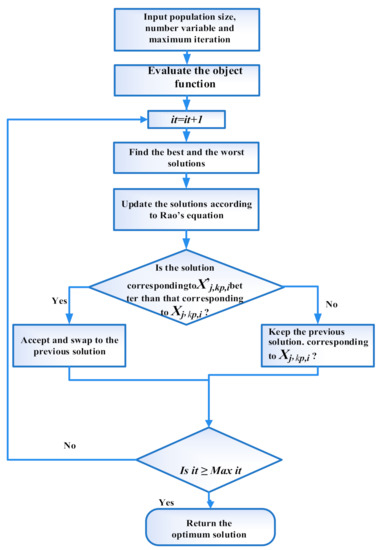
Figure 1. Flowchart of Rao-2 algorithm.

3.2. Modified Rao Algorithm

The quasi-oppositional and Levy flight methods are used to enhance the conventional Rao technique in this paper.

3.2.1. Quasi-Oppositional

Opposition-based learning (OBL) [38] is a commonly used way to enhance several optimization algorithms such as Quasi-oppositional swine influenza model-based optimization with quarantine (QOSIMBO-Q) [39], quasi-oppositional teaching-learning (QOTLBO) [40], quasi oppositional bonobo optimizer (QOBO) [41], and Oppositional Jaya Algorithm [42].

The OBL can be improved by simultaneously using the candidate solution and the opposite. Therefore, this work will express the opposite solution of ${\mathrm{X}}_{\mathrm{B}}^{\mathrm{i}}$ in the Rao algorithm as

$${\mathrm{X}}_{\mathrm{j},\mathrm{kp},\mathrm{i}}^{\prime \mathrm{qi}}=\left\{\begin{array}{c}C+{\mathrm{r}}_1\left(C-{\mathrm{X}}_{\mathrm{j},\mathrm{kp},\mathrm{i}}^{\prime }\right),|{\mathrm{X}}_{\mathrm{j},\mathrm{kp},\mathrm{i}}^{\prime })<C\\ C-{\mathrm{r}}_1\left({\mathrm{X}}_{\mathrm{j},\mathrm{kp},\mathrm{i}}^{\prime }\right)-C),|{\mathrm{X}}_{\mathrm{j},\mathrm{kp},\mathrm{i}}^{\prime })\ge C\end{array}\right.$$

(26)

where ${\mathrm{r}}_1$ is a random number between [0, 1], and $\mathrm{C}$ is a middle point between ${\mathrm{X}}_{\min }^{\mathrm{i}}$ and ${\mathrm{X}}_{\max }^{\mathrm{i}}$, which can be calculated as follows:

$$\mathrm{C}=\frac{{\mathrm{X}}_{\min }^{\mathrm{i}}+{\mathrm{X}}_{\max }^{\mathrm{i}}}{2}$$

(27)

3.2.2. Levy Flight

The delivery of levy flight is used to boost the exploration phase using the following equation:

$${\mathrm{X}}_{\mathrm{j},\mathrm{kp},\mathrm{i}}^{\prime }{}^{\mathrm{levy}}={\mathrm{X}}_{\mathrm{j},\mathrm{kp},\mathrm{i}}^{\prime }+\mathrm{S}\times \mathrm{LF}\left(\mathrm{D}\right)$$

(28)

where D is the problem dimension, and$\mathrm{S}$ is a vector of random values with size $1\times \mathrm{D}$. The LF is the levy flight function, which is calculated by the following equations:

$$\mathrm{LF}\left(\mathrm{x}\right)=0.01\times \frac{\mathsf{\mu }\times \mathsf{\sigma }}{{\left|\mathrm{v}\right|}^{\frac{1}{\mathsf{\beta }}}}$$

(29)

$$\mathsf{\sigma }={\left(\frac{\mathsf{\Gamma }\left(1+\mathsf{\beta }\right)\times \sin \left(\frac{\mathsf{\pi }\mathsf{\beta }}{2}\right)}{\mathsf{\Gamma }\left(\frac{1+\mathsf{\beta }}{2}\right)\times \mathsf{\beta }\times 2^{\left(\frac{\mathsf{\beta }-1}{2}\right)}}\right)}^{\frac{1}{\mathsf{\beta }}}$$

(30)

where $\mathsf{\mu }$ and $\mathrm{v}$ are random values inside (0,1), $\mathsf{\beta }$ is a default constantset to 1.5, and $\mathsf{\Gamma }$ is a gamma function.

The updated Rao positions will then be chosen based on the value of the objective function where if the objective function of the updated Rao position using levy $\mathrm{F}\left({\mathrm{X}}_{\mathrm{j},\mathrm{kp},\mathrm{i}}^{\prime }{}^{\mathrm{levy}}\right)\mathrm{is}\mathrm{lower}\mathrm{than}$the objective function of the conventional Rao position $\mathrm{F}\left({\mathrm{X}}_{\mathrm{j},\mathrm{kp},\mathrm{i}}^{\prime }\right)$ then the new position will be the ${\mathrm{X}}_{\mathrm{j},\mathrm{kp},\mathrm{i}}^{\prime }{}^{\mathrm{levy}}$ otherwise the position will not be updated. Therefore, the following equation can be used to update the modified Rao:

$${\mathrm{X}}_{\mathrm{j},\mathrm{kp},\mathrm{i}}^{\prime }=\left\{\begin{array}{c}{\mathrm{X}}_{\mathrm{j},\mathrm{kp},\mathrm{i}}^{\prime }\mathrm{if}\mathrm{F}\left({\mathrm{X}}_{\mathrm{j},\mathrm{kp},\mathrm{i}}^{\prime }\right)<\mathrm{F}\left({\mathrm{X}}_{\mathrm{j},\mathrm{kp},\mathrm{i}}^{\prime }{}^{\mathrm{levy}}\right)\\ {\mathrm{X}}_{\mathrm{j},\mathrm{kp},\mathrm{i}}^{\prime }{}^{\mathrm{levy}},\mathrm{if}\mathrm{F}\left({\mathrm{X}}_{\mathrm{j},\mathrm{kp},\mathrm{i}}^{\prime }{}^{\mathrm{levy}}\right)<\mathrm{F}\left({\mathrm{X}}_{\mathrm{j},\mathrm{kp},\mathrm{i}}^{\prime }\right)\end{array}\right.$$

(31)

4. Simulation Results

4.1. Test Systems

In this paper, the IEEE 30-bus and IEEE 118-bus systems are used to prove the efficient performance of the proposed MRao-2. The data of lines and buses for the IEEE 30-bus system can be found in [43], while the data of lines and buses for the IEEE 118-bus system can be found in [28,44]. The IEEE 30-bus system has 41 transmission lines and 6 generating units. Bus 1 is selected as the slack bus and the load demand is 283.4 MW. Table 1 displays the upper and lower limits of the control variables in 30- bus system. The IEEE 118-bus system has 54 generation units and 186 transmission lines. Bus 69 is chosen as the slack bus and the total load of the network is 3733.07 MW [45]. The upper and lower limits of the control variables in 118-bus systems are also displayed in Table 1 [4]. The emission coefficients of the generators are taken from [46].

Table 1. Limit setting for control variables of the all-test systems [4].

	IEEE 30-Bus System		IEEE 118-Bus System
Variables	Lower limit	Upper limit	Lower limit	Upper limit
Voltages for all generator bus	0.95 p.u	1.1 p.u	0.94 p.u	1.06 p.u
Voltages for all load bus	0.95 p.u	1.05 p.u	0.95 p.u	1.05 p.u
Tap setting	0.9 p.u	1.1 p.u	0.9 p.u	1.1 p.u
Reactive power of capacitor banks	0	0.05 p.u	0	0.3 p.u

The modification to the IEEE 30-bus system is by adding the RES. The selection of the proper location of these RES in the test system is based on the power loss sensitivity and generation cost to each real and imaginary power as stated in [47]. The results in [47] presented that the optimum location is bus 30 and the value chosen of RES is 20MW. Figure 2 shows a single line diagram of the modified IEEE 30-bus system.

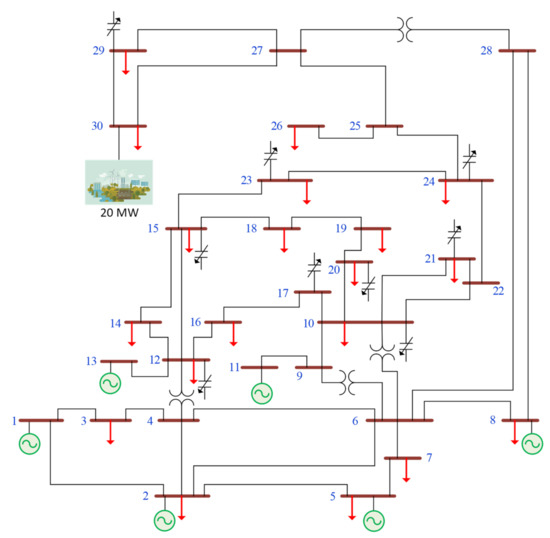
Figure 2. Single-line diagram of the modified IEEE 30-bus test system.

The modification to the standard IEEE 118-bus test system is by adding RES based on that in [48]. The location and values of the RES in the IEEE 118-bus test systems are tabulated in Table 2. A single line diagram of the modified IEEE 118-bus system is presented in Figure 3.

Table 2. The location and values of the RES in the IEEE 118-bus test systems.

Type of RES	No. of Bus	Value (MW)
biomass	12	18.2
wind	31	156
solar	54	264
hydro	76	77
hydro	116	286

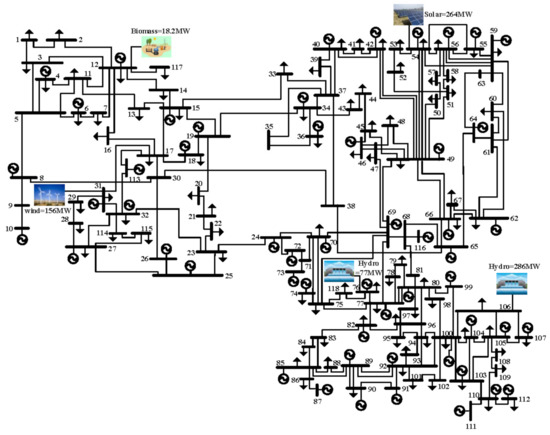
Figure 3. Single-line diagram of IEEE 118-bus test system.

In this article, the numerical simulations studies have been run on an Intel ^®® core TM i5-7200U CPU with 8 GB of RAM using MATLAB 2016a. The proposed MRao-2 technique is employed to find the best solution for the OPF problem in different cases considering the fuel cost, emission, transmission loss, and improvement of the voltage profile. The results of MRao-2 are compared with the ASO Algorithm [49], TFWO [50], MPA [51], and Rao algorithms: Three metaphor-less simple algorithms (Rao-1, Rao-2, and Rao-3) [37]. The parameters settings of the different optimization techniques are shown in Table 3.

Table 3. The parameter settings of different optimization techniques.

Algorithms	Parameters Setting
Common settings	Population size: nPop = 30 Maximum iterations: Max_iter = 200 for IEEE 30-bus test system and Max_iter = 300 for IEEE 118-bus test system. Number of independent runs: 20.
ASO	depth weight a = 50. multiplier weight β = 0.2.
MPA	FADs = 0.2, P = 0.5, C = 0.05, e = 0.25

4.2. Case 1: The OPF without RES for the IEEE 30-Bus System

The proposed MRao-2 is used in this case to achieve the best solution for the OPF problem without RES and considering the fuel cost, power loss, emission, and voltage profile improvement. Table 4 presents the results of the MRao-2 algorithm in comparison with other techniques. These results confirm that the MRao-2 technique outperforms other algorithms. Its objective function (Fuel Cost = 800.4412 $/h) is better than all other algorithms and it performs without any violation of the constraints. The voltage profile of the proposed MRao-2 is displayed in Figure 4. It can be observed from this figure that all voltage magnitudes at all buses of the power system are within the boundaries presented in Table 1. Given the convergence characteristics of all algorithms for the optimal solutions that have been achieved by the ASO, TFWO, MPA, Rao algorithms, and MRao-2 in this case, the proposed MRao-2 has a smooth convergence characteristics curve to the best solution with a rapid convergence rate and without oscillations in comparison with all other techniques as displayed in Figure 5. It is shown in Figure 5 that the supremacy of the MRao-2 over the recent other techniques is proven in the last iterations as it converges to the best solution.

Table 4. Results of the proposed MRao-2 algorithm and other algorithms for case 1.

	ASO	TFWO	MPA	Rao-1	Rao-2	Rao-3	MRao-2
PG1 (MW)	176.9732	177.2422	176.8351	179.8369	177.887	177.5088	176.3625
PG2 (MW)	48.91006	48.64558	48.67575	49.49712	49.36524	48.76959	49.07412
PG5 (MW)	21.30213	21.36803	21.45982	22.21521	21.54786	20.94155	21.24651
PG8 (MW)	20.9253	21.35596	21.88621	18.77388	21.6564	21.53046	21.37135
PG11 (MW)	12.45411	11.86476	11.54409	10.38348	10.00796	11.80911	12.21261
PG13 (MW)	12.00137	12.00148	12.02418	12	12.04775	12.0039	12.10508
V1 (p.u.)	1.080029	1.079984	1.082237	1.078675	1.084304	1.080698	1.083304
V2 (p.u.)	1.080992	1.030047	1.083237	1.027824	1.094344	1.099999	1.092657
V5 (p.u.)	1.028033	1.082677	1.031479	1.085737	1.031264	1.028262	1.029766
V8 (p.u.)	1.034358	1.035451	1.037666	1.033404	1.037539	1.036411	1.037062
V11 (p.u.)	1.006403	1.05873	1.065692	1.078167	1.077243	1.031184	1.059477
V13 (p.u.)	1.036055	1.067677	1.029076	1.057387	1.034243	1.099824	1.046984
T11 (6–9)	0.96365	0.972727	0.963545	1.014786	1.031208	0.916034	1.002334
T12 (6–10)	1.014561	1.012358	1.05331	0.983026	0.9	1.099979	0.953247
T15 (4–12)	1.056913	0.994481	0.989785	1.001	0.964418	1.031275	0.971027
T36 (28–27)	0.99403	0.971573	1.000675	0.975213	0.980459	0.987251	0.971058
QC10 (MVAR)	3.0526	4.9784	3.2035	0.5727	0.1362	0.00562	3.7024
QC12 (MVAR)	3.5939	0.5594	4.639	0.7186	1.3228	0.00426	2.0306
QC15 (MVAR)	2.5611	4.635	3.9502	5	4.9242	4.9567	2.2152
QC17 (MVAR)	1.6444	3.7878	1.5066	3.3725	4.2338	0.0702	4.6995
QC20 (MVAR)	1.9898	4.5001	4.8618	4.4774	3.1484	4.9871	3.859
QC21 (MVAR)	3.4191	4.1061	3.5977	3.9993	0.2586	4.8557	4.8858
QC23 (MVAR)	4.7618	0.00168	4.3476	0.818	3.2847	0.0451	3.9984
QC24 (MVAR)	1.1282	2.1995	4.5618	4.9692	4.9243	4.9741	4.8289
QC29 (MVAR)	1.5646	0.4415	3.5686	2.1977	4.9685	2.3785	1.6698
Fuel cost ($/h)	801.0005	800.6477	800.5804	800.8944	800.6166	800.848	800.4412
Emission (ton/h)	0.295736	0.296049	0.295644	0.297821	0.296313	0.296384	0.295152
Power loss (MW)	9.177889	9.083431	9.036827	9.312149	9.123883	9.163424	8.983817
Voltage deviation (p.u.)	0.334805	0.749458	0.575301	0.707313	0.916652	0.469378	0.868108
Time (s)	95.06342	104.1479	166.5552	101.91743	94.84023	101.83725	169.6059

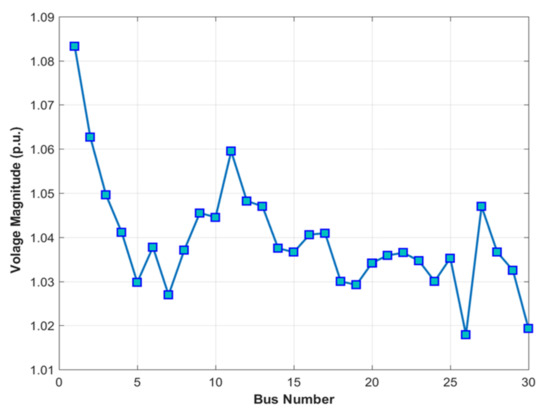
Figure 4. The voltage profile of the MRao-2 for the best solutions of case 1.

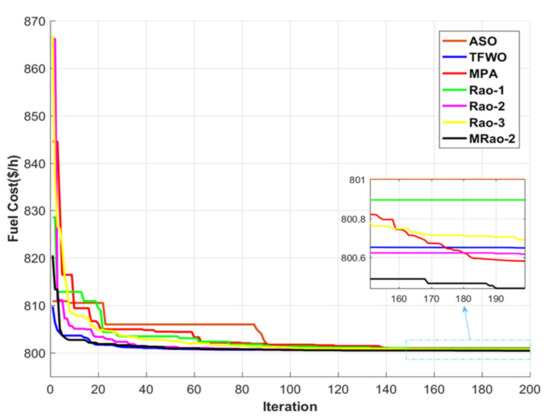
Figure 5. Convergence characteristics of the proposed MRao-2 and other recent algorithms for case 1.

Furthermore, Figure 6 shows graphic comparisons for 20 individual runs (i.e., fuel cost) obtained from the proposed algorithm compared with the other six algorithms in the form of a boxplot graph. These boxplots present the mean performance of techniques that can be compared visually. There are five elements that can be defined from each boxplot as follows: first quartile, minimum, third quartile, maximum, and median. The median value is the line inside the box. These boxplots are drawn after 20 individual runs for each technique, and they display the classification precision. It can be seen that the MRao-2 algorithm has a lower boxplot compared to the other well-known techniques. Furthermore, the median of the proposed MRao-2 has a minimum value compared to the other techniques. It can be observed from this figure that the proposed MRao-2 is competitive and often superior to the other recent algorithms. Furthermore, the proposed MRao-2 technique delivers the optimal results in terms of precision and reliability compared to the other techniques. The optimal fuel cost listed in Table 5 shows that the proposed MRao-2 technique is more effective than other approaches in obtaining the best solutions as its fuel cost is less than those of others.

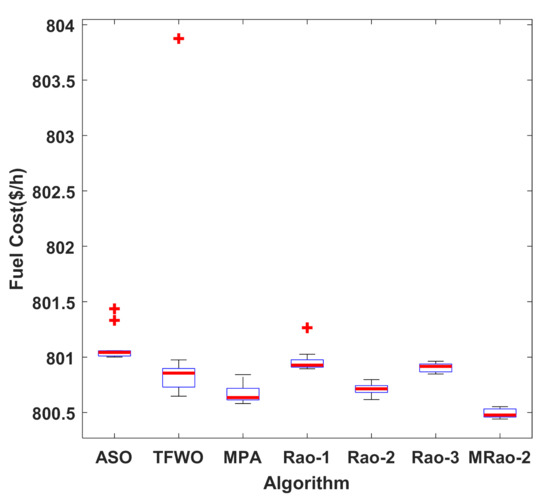
Figure 6. Boxplot graph of best Fuel cost in 20 runs of the proposed MRao-2 and other recent algorithms for case 1.

Table 5. Simulation results of MRao-2 and other algorithms for Case 1.

Algorithm	Min	Max	Average
MRao-2	800.4412	800.553	800.4872
Rao-2	800.6166	800.7965	800.7118
Rao-1	800.8944	801.2647	800.9678
Rao-3	800.848	800.9628	800.9067
MPA	800.5804	800.8416	800.6659
TFWO	800.6477	803.8754	801.1159
ASO	801.0005	801.4358	801.101
MGOA [11]	800.4744	NA	NA
ABC [52]	800.6600	800.8715	801.8674
Jaya [47]	800.4794	800.4928	800.5306
ARCBBO [53]	800.5159	800.6412	800.9262
MSA [54]	800.5099	NA	NA
Hybrid SFLA SA [55]	801.79	NA	NA
HHO [33]	801.4228	NA	NA
HHODE [33]	800.9959	NA	NA
DE [56]	801.23	801.622	801.282

4.3. Case 2: OPF Incorporating RES for the IEEE 30-Bus System

The proposed MRao-2 technique is employed in the second case to reach the optimum solution for the OPF problem incorporating RES, considering the generation cost, transmission loss, emission, and improvement of voltage profile. Next, the obtained results using the proposed MRao-2 algorithm are compared with ASO, TFWO, MPA, Rao-1, Rao-2, and Rao-3 algorithms. The results of all the techniques for this case are listed in Table 6.

Table 6. Results of the proposed MRao-2 algorithm and other algorithms for case 2.

	ASO	TFWO	MPA	Rao-1	Rao-2	Rao-3	MRao-2
PG1 (MW)	166.3103	167.0352	166.5015	167.7043	167.5941	167.2709	167.2508
PG2 (MW)	45.88087	46.29256	46.03059	47.38566	45.71914	47.19775	46.42704
PG5 (MW)	20.9709	20.64382	20.45905	20.90393	20.6118	20.69004	20.64984
PG8 (MW)	15.69756	15.68206	15.17763	13.74229	15.13705	14.47554	15.27324
PG11 (MW)	10.79724	10.00009	11.10394	10	10.53956	10.00813	10
PG13 (MW)	12.00262	12	12.32851	12	12.03885	12.04529	12
V1 (p.u.)	1.077967	1.081966	1.0788	1.077875	1.080078	1.080089	1.07852
V2 (p.u.)	1.072375	1.006269	1.1	1.094477	1.051656	1.063304	1.1
V5 (p.u.)	1.033146	1.057191	1.031388	1.076221	1.077262	1.0572	1.032235
V8 (p.u.)	1.031798	1.036781	1.038591	1.038888	1.039808	1.040699	1.026295
V11 (p.u.)	1.02098	1.099826	1.093579	1.049587	1.04657	1.078359	1.047772
V13 (p.u.)	1.042508	1.022207	1.014105	1.01495	1.009777	1.022799	1.062827
T11(6–9)	0.986874	0.989094	1.027745	0.99534	1.09646	0.991078	0.98482
T12(6–10)	1.005378	1.1	0.957009	0.928192	0.908495	1.073045	0.977984
T15(4–12)	0.975554	0.987607	0.981413	0.981491	0.971842	0.970377	0.981403
T36(28–27)	1.001887	0.99311	0.99195	0.997822	1.017273	1.010252	1.001331
QC10 (MVAR)	4.1156	4.7537	2.7651	4.7977	2.8059	4.9307	4.9494
QC12 (MVAR)	2.8466	4.821	3.8682	3.6157	1.4147	0.0171	0
QC15 (MVAR)	3.4126	4.8818	0.5251	4.3005	1.2958	3.8049	0.0184
QC17 (MVAR)	2.9106	4.2942	4.9994	0.3354	4.6224	3.1239	4.8752
QC20 (MVAR)	2.3832	2.9394	4.6997	4.691	4.394	3.1954	4.8711
QC21 (MVAR)	2.9478	5	0.3764	1.8647	3.3121	0	5
QC23 (MVAR)	1.4159	1.9167	2.9807	1.0238	4.9937	5	5
QC24 (MVAR)	2.6985	5	0.8889	3.9491	4.9191	4.7007	4.9522
QC29 (MVAR)	2.7382	0.3091	2.0465	1.5414	4.2786	2.302	2.282
Fuel cost ($/h)	729.9074	729.6002	729.6347	729.6406	729.5025	729.5657	729.3429
Emission (ton/h)	0.287894	0.288436	0.288163	0.288493	0.289114	0.28828	0.288559
Power loss (MW)	8.271074	8.264871	8.212681	8.341641	8.245904	8.293049	8.21248
Voltage deviation (p.u.)	0.487935	0.587188	0.723005	0.74643	0.599303	0.554658	0.890863
Time (s)	96.3905	101.40315	154.3002	93.26448	92.40164	95.84038	166.5166

It is seen from these results that the MRao-2 technique is also more effective than other techniques in reaching the best solution for the OPF problem with fuel cost and RES. Its fitness function (Fuel cost = 729.3429 $/h) is less than all other algorithms and it does not violate the constraints. Furthermore, the objective function of the MRao-2 technique is reduced from 800.4412 $/h (case 1) to 729.3429 $/h (case 2) by 8.88% after incorporating the RES as expected. By entering the RES as a negative load, the total load of the power system is decreased, which reduces the generation cost of the conventional thermal generators.

Furthermore, as in the previous case, the voltage magnitude of all buses is within their boundaries as shown in Figure 7. After incorporating the RES, the proposed MRao-2 has also smooth and speedy convergence curves in comparison with other algorithms as presented in Figure 8. The Boxplot graph of best Fuel cost in 20 runs of the proposed MRao-2 and other recent algorithms for case 2 is presented in Figure 9.

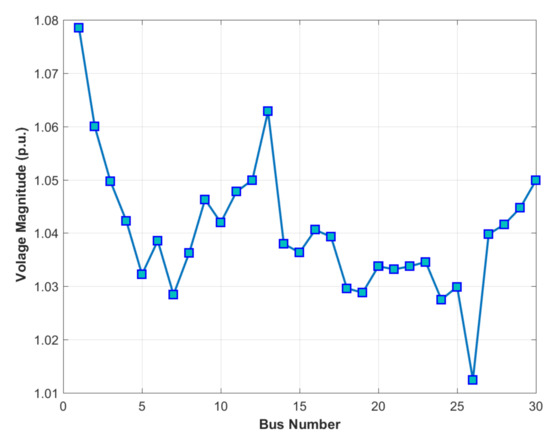
Figure 7. The voltage profile of the MRao-2 for case 2.

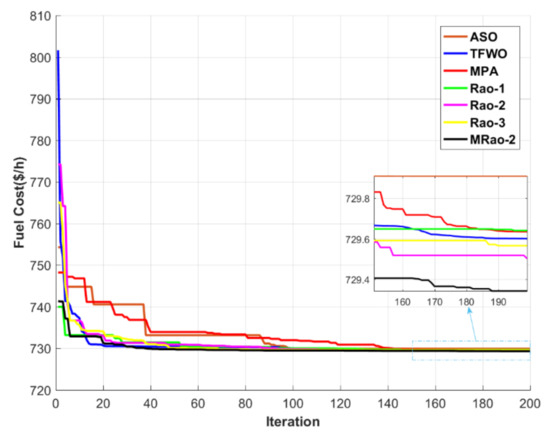
Figure 8. Convergence characteristics curves of all algorithms for case 2.

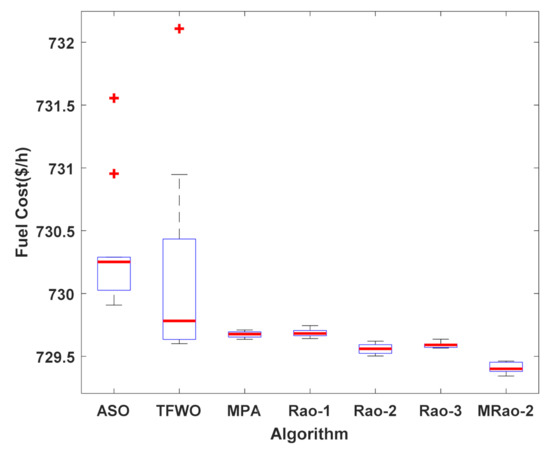
Figure 9. Boxplot graph of best Fuel cost in 20 runs of the proposed MRao-2 and other recent algorithms for case 2.

4.4. Case 3: OPF Incorporating RES under Contingency State for IEEE 30-Bus System

In this case, a contingency state is simulated by the outage of two lines. These lines are line (10–17) and line (10–21). Table 7 tabulates the obtained results using the proposed MRao-2 and other algorithms. According to these results, the proposed MRao-2 technique provides the best solution for the fitness function in comparison with other algorithms including RES during the contingency state and without any violation of the constraints. Figure 10 displays the voltage profile of the MRao-2 technique, while Figure 11 shows the convergence characteristics of all algorithms. From these figures, it is clear that all voltage magnitudes are within the constraints and the proposed MRao-2 has smooth convergence features with speedy convergence in comparison with other techniques. Furthermore, Figure 12 displays the Boxplot graph of best Fuel cost in individual 20 runs of the proposed MRao-2 and other recent algorithms for this case.

Table 7. Results of the proposed method and other methods for case 3.

	ASO	TFWO	MPA	Rao-1	Rao-2	Rao-3	MRao-2
PG1 (MW)	169.1157	167.646	168.4079	166.1685	168.162	168.2884	167.6707
PG2 (MW)	47.10122	46.38156	46.73768	46.29319	46.34349	46.35133	46.43635
PG5 (MW)	20.77245	20.68947	20.8021	20.22988	20.61748	20.70681	20.82097
PG8 (MW)	12.4257	15.29242	13.2599	17.28305	14.80192	14.45443	14.76838
PG11 (MW)	10.9089	10	10.93876	10	10.09605	10.24194	10.22822
PG13 (MW)	12.0136	12	12.00331	12.02535	12.00538	12.00845	12.05377
V1 (p.u.)	1.071178	1.080797	1.082793	1.088881	1.082847	1.081143	1.08205
V2 (p.u.)	1.091177	1.0925	1.033038	1.063013	1.084106	1.082092	1.083835
V5 (p.u.)	1.018346	1.031645	1.086276	1.054294	1.031456	1.026707	1.032011
V8 (p.u.)	1.023794	1.036661	1.037818	1.034209	1.033635	1.033571	1.03592
V11 (p.u.)	1.038897	1.071995	1.083139	1.059527	1.029808	1.074468	1.029754
V13 (p.u.)	1.019225	1.042984	1.047633	1.039893	1.046966	1.045277	1.04714
T11 (6–9)	0.966049	0.965995	1.05369	0.973616	1.040438	1.078513	1.06788
T12 (6–10)	0.970151	1.099986	0.939359	1.016485	0.906038	0.9	0.900135
T15 (4–12)	0.96075	0.984042	0.957996	0.961999	0.984907	0.988115	0.980633
T36 (28–27)	1.014058	1.006899	1.011424	1.01808	1.017749	1.010059	1.010374
QC10 (MVAR)	3.3514	1.8078	1.993	4.6449	0.0643	0.1501	0.0246
QC12 (MVAR)	2.4055	4.5298	2.4846	0.515	0.9183	3.2165	0.0275
QC15 (MVAR)	3.0776	5	4.3023	4.5803	4.4913	4.9203	1.5989
QC17 (MVAR)	3.3283	5	2.7311	4.2387	4.9964	4.7269	4.994
QC20 (MVAR)	3.9248	0	2.5187	0.2183	1.9472	0.0149	4.8959
QC21 (MVAR)	4.4199	5	0.24	3.2204	5	5	4.9499
QC23 (MVAR)	2.5112	0.702	1.7923	4.9999	4.9924	0	3.431
QC24 (MVAR)	4.5875	5	2.9447	1.9501	4.8343	4.9989	5
QC29 (MVAR)	2.7613	0	2.76 × 10−5	0	0.00259	0.0514	0.0739
Fuel cost ($/h)	731.4898	730.6851	731.0095	731.0468	730.6201	730.688	730.583
Emission (ton/h)	0.289802	0.288885	0.289341	0.287874	0.289345	0.289416	0.288841
Power loss (MW)	8.949145	8.620926	8.755022	8.605339	8.63787	8.662901	8.589888
Voltage deviation (p.u.)	0.595555	0.626741	0.73608	0.693286	0.695892	0.665941	0.665648
Time (s)	94.1653	98.40031	153.3302	95.61418	98.2997	97.24576	164.5099

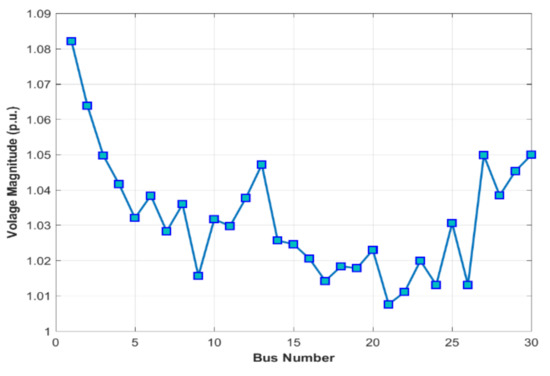
Figure 10. The voltage profile of the MRao-2 for case 3.

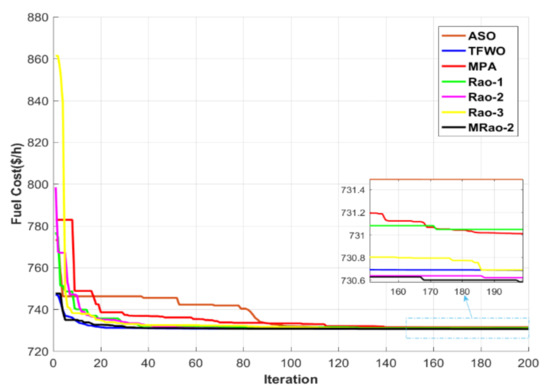
Figure 11. Convergence characteristics of all methods for case 3.

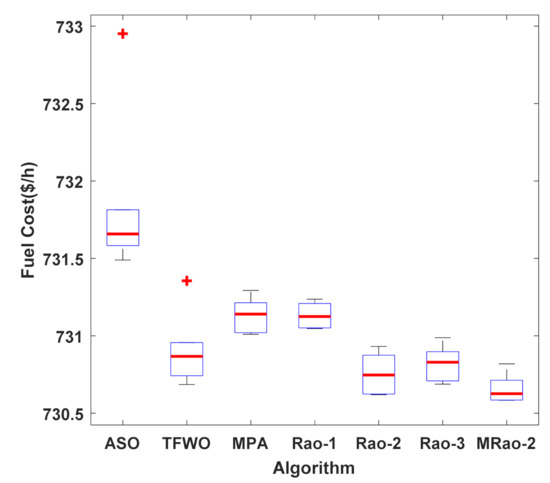
Figure 12. Boxplot graph of best Fuel cost in 20 runs of the proposed MRao-2 and other recent algorithms for case 3.

The statistical results of the proposed MRao-2 and the other recently algorithms for 20 individual runs for each case are presented in Table 8. Most researchers choose the minimum, mean, median, maximum, and standard deviation (STD) values to demonstrate the superiority and effectiveness of a technique. Table 8 shows the minimum, average, median, maximum, and STD values of the fuel cost as the objective function for all cases. These results confirm the supremacy of the proposed algorithm on the other algorithms.

Table 8. Statistical results comparison of investigated cases for IEEE 30-bus system for different recent optimization algorithm.

Case No.	Algorithm	Min	Average	Median	Max	STD
Case 1	MRao-2	800.4412	800.4872	800.4769	800.553	0.038822
	Rao-2	800.6166	800.7118	800.7135	800.7965	0.052478
	Rao-1	800.8944	800.9678	800.9277	801.2647	0.111619
	Rao-3	800.848	800.9067	800.9167	800.9628	0.0403
	MPA	800.5804	800.6659	800.6347	800.8416	0.081797
	TFWO	800.6477	801.1159	800.855	803.8754	0.975128
	ASO	801.0005	801.101	801.0422	801.4358	0.152133
Case 2	MRao-2	729.3429	729.4065	729.4001	729.4615	0.042289
	Rao-2	729.5025	729.5599	729.5596	729.6205	0.040197
	Rao-1	729.6406	729.6845	729.6815	729.7441	0.031135
	Rao-3	729.5657	729.5888	729.5903	729.6361	0.021254
	MPA	729.6347	729.674	729.6771	729.7095	0.024818
	TFWO	729.6002	730.1646	729.782	732.1079	0.813312
	ASO	729.9074	730.3542	730.251	731.555	0.513813
Case 3	MRao-2	730.583	730.6588	730.6266	730.8189	0.09241
	Rao-2	730.6201	730.7573	730.747	730.9311	0.141165
	Rao-1	731.0468	731.132	731.1247	731.2359	0.090685
	Rao-3	730.688	730.8235	730.8296	730.9879	0.113336
	MPA	731.0095	731.136	731.14	731.2927	0.111756
	TFWO	730.6851	730.9124	730.8677	731.3553	0.23962
	ASO	731.4898	731.8588	731.6576	732.9515	0.546641

4.5. Case 4: OPF without RES for the IEEE 118-Bus System

In this case, the MRao-2 is utilized to find the optimum solution for the OPF problem for the IEEE 118-bus system considering the fuel cost, transmission loss, and improvement of the voltage profile and without considering the RES. In this paper, this system is chosen to test the scalability of the MRao-2 technique and demonstrate its robustness to apply it to solve the OPF for large-scale systems. Table 9 presents the obtained results using the proposed MRao-2 algorithm. These results are compared with ASO, TFWO, MPA, Rao-1, Rao-2, and Rao-3, and this comparison is listed in Table 10. These results confirm the supremacy of the MRao-2 algorithm over other techniques in achieving the best solution for the OPF problem with the Fuel cost as an objective function for the large-scale electrical power system without considering the RES.

Table 9. Optimal settings of control variables for case 4 using MRao-2.

Variables	Value	Variables	Value	Variables	Value	Variables	Value	Variables	Value
PG1 (MW)	1.984061	PG62 (MW)	0.04968	PG113 (MW)	86.1052	VG59 (p.u.)	0.94707	VG111 (p.u.)	1.05221
PG4 (MW)	0.351443	PG65 (MW)	343.880	PG116 (MW)	4.20199	VG61 (p.u.)	1.02331	VG112 (p.u.)	1.04184
PG6 (MW)	1.344034	PG66 (MW)	340.152	VG1 (p.u.)	0.94	VG62 (p.u.)	0.95129	VG113 (p.u.)	1.02649
PG8 (MW)	10.24637	PG69 (MW)	415.633	VG4 (p.u.)	1.00609	VG65 (p.u.)	0.94352	VG116 (p.u.)	0.96645
PG10 (MW)	376.1126	PG70 (MW)	4.69474	VG6 (p.u.)	1.00546	VG66 (p.u.)	1.01735	T8 (8–5)	0.91057
PG12 (MW)	76.80127	PG72 (MW)	7.50899	VG8 (p.u.)	0.94545	VG69 (p.u.)	1.03288	T32 (25–26)	1.09451
PG15 (MW)	1.528393	PG73 (MW)	10.3911	VG10 (p.u.)	0.94035	VG70 (p.u.)	0.97696	T36 (17–30)	1.09266
PG18 (MW)	46.72157	PG74 (MW)	5.8267	VG12 (p.u.)	0.99321	VG72 (p.u.)	1.03499	T51 (37–38)	0.9
PG19 (MW)	0.067021	PG76 (MW)	20.4488	VG15 (p.u.)	1.01157	VG73 (p.u.)	0.98931	T93 (59–63)	1.00128
PG24 (MW)	2.611653	PG77 (MW)	5.51401	VG18 (p.u.)	0.96454	VG74 (p.u.)	0.99958	T95 (61–64)	1.03762
PG25 (MW)	196.2022	PG80 (MW)	451.524	VG19 (p.u.)	1.04577	VG76 (p.u.)	0.99539	T102 (65–66)	0.95931
PG26 (MW)	280.9463	PG85 (MW)	0	VG24 (p.u.)	0.99640	VG77 (p.u.)	0.97826	T107 (68–69)	0.95758
PG27 (MW)	98.34095	PG87 (MW)	0.95058	VG25 (p.u.)	0.97686	VG80 (p.u.)	1.01302	T127 (80–81)	1.05250
PG31 (MW)	0.751755	PG89 (MW)	483.822	VG26 (p.u.)	0.94265	VG85 (p.u.)	0.97493	QC34 (MVAR)	3.111
PG32 (MW)	18.9298	PG90 (MW)	2.75380	VG27 (p.u.)	1.01799	VG87 (p.u.)	0.94034	QC44 (MVAR)	29.931
PG34 (MW)	0.070676	PG91 (MW)	0	VG31 (p.u.)	1.03403	VG89 (p.u.)	1.03117	QC45 (MVAR)	29.497
PG36 (MW)	4.986125	PG92 (MW)	1.17943	VG32 (p.u.)	0.99471	VG90 (p.u.)	1.02089	QC46 (MVAR)	28.169
PG40 (MW)	1.913409	PG99 (MW)	16.5592	VG34 (p.u.)	1.00824	VG91 (p.u.)	1.04970	QC48 (MVAR)	0
PG42 (MW)	1.394682	PG100 (MW)	200.116	VG36 (p.u.)	0.99818	VG92 (p.u.)	1.01643	QC74 (MVAR)	24.96
PG46 (MW)	13.76368	PG103 (MW)	23.1161	VG40 (p.u.)	0.99148	VG99 (p.u.)	1.02329	QC79 (MVAR)	28.765
PG49 (MW)	209.701	PG104 (MW)	99.6802	VG42 (p.u.)	1.02358	VG100 (p.u.)	0.99312	QC82 (MVAR)	27.479
PG54 (MW)	48.30631	PG105 (MW)	0.13269	VG46 (p.u.)	0.98153	VG103 (p.u.)	1.05004	QC83 (MVAR)	24.519
PG55 (MW)	26.09714	PG107 (MW)	0.19020	VG49 (p.u.)	1.00041	VG104 (p.u.)	1.05559	QC105 (MVAR)	27.063
PG56 (MW)	80.54259	PG110 (MW)	0.42630	VG54 (p.u.)	0.99326	VG105 (p.u.)	0.96614	QC107 (MVAR)	6.934
PG59 (MW)	128.7814	PG111 (MW)	33.7688	VG55 (p.u.)	1.05871	VG107 (p.u.)	0.94274	QC110 (MVAR)	29.781
PG61 (MW)	146.4049	PG112 (MW)	5.1539	VG56 (p.u.)	1.05977	VG110 (p.u.)	1.00997
					Fuel cost ($/h)			131457.8
					Power loss (MW)			96.68278
					Voltage deviation (p.u.)			0.730363

Table 10. Results of the proposed MRao-2 algorithm and other algorithms for case 4.

Algorithm	ASO	TFWO	MPA	Rao-1	Rao-2	Rao-3	MRao-2
Fuel cost ($/h)	133,610.8	132,132.2	131,942.6	131,817.9	131,490.7	131,793.1	131,457.8
Power loss (MW)	61.83332	65.55476	71.94402	93.85931	95.46617	93.95222	96.68278
Voltage deviation (p.u.)	0.658779	0.961026	1.152593	1.328297	0.998901	1.192274	0.730363
Time (s)	800.709	809.028	1022.262	807.969	804.5724	806.71149	1160.264

The MRao-2’s objective function (Fuel cost = 131,457.8 $/h) is less than the fitness function of other algorithms without any violation of the restraints. Figure 13 displays the magnitudes of the voltages of all buses are within the limits. Moreover, the MRao-2 has smooth and speedy convergence curves in comparison with other algorithms as shown in Figure 14.

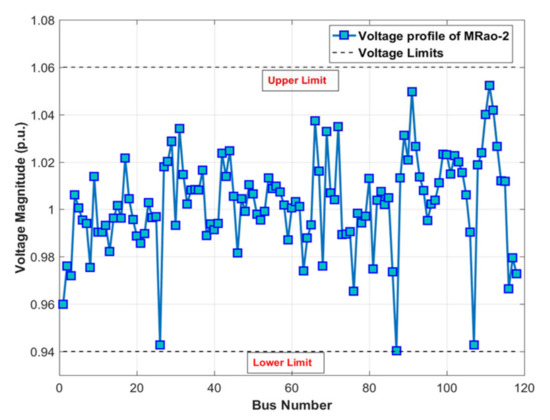
Figure 13. The voltage profile of the MRao-2 for case 4.

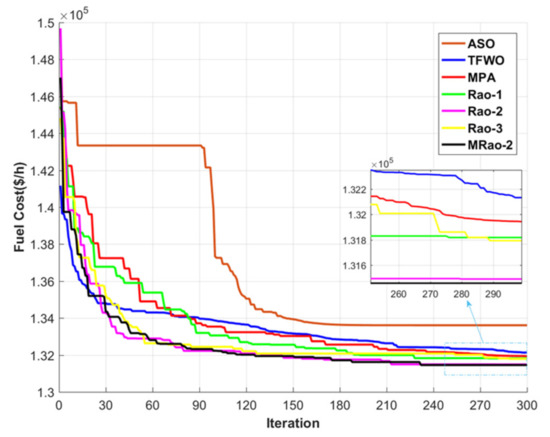
Figure 14. Convergence characteristics of all methods for case 4.

4.6. Case 5: OPF Incorporating RES for the IEEE 118-Bus System

In this case, the proposed MRao-2 technique is applied to the IEEE 118-bus system to check the ability of the proposed algorithm to solve the OPF for the large-scale system considering the RES. Table 11 tabulates the obtained results using the proposed MRao-2 algorithm. Furthermore, the results of the MRao-2 technique and other algorithms for this case are presented in Table 12. These results of the fuel cost for this case by ASO, TFWO, MPA, Rao-1, Rao-2, Rao-3, and MRao-2 algorithms are 103,847.47, 101,747.68, 101,981.69, 101,981.17, 101,078.92, 101,297.12, and 100,738.54 $/h, respectively. These results show that the proposed MRao-2 achieves a better solution than other algorithms in solving the OPF considering RES using the large-scale system and without any violation of the limits. Furthermore, adding RES to the IEEE 118-bus system decreases the fuel cost as an objective function of the MRao-2 by 23.4%. Figure 15 displays the magnitudes of the voltage of all buses of the MRao-2 are within the limits. Figure 16 shows that the proposed MRao-2 has smooth and speedy convergence curves in comparison with other techniques even for large-scale systems.

Table 11. Optimal settings of control variables for case 5 using the proposed MRao-2.

Variables	Value	Variables	Value	Variables	Value	Variables	Value	Variables	Value
PG1 (MW)	3.0911	PG62 (MW)	6.37571	PG113 (MW)	7.09147	VG59 (p.u.)	1.036427	VG111 (p.u.)	1.03604
PG4 (MW)	7.265278	PG65 (MW)	298.824	PG116 (MW)	0	VG61 (p.u.)	0.956257	VG112 (p.u.)	0.97545
PG6 (MW)	79.79656	PG66 (MW)	284.31	VG1 (p.u.)	1.01134	VG62 (p.u.)	1.054308	VG113 (p.u.)	1.04051
PG8 (MW)	0.20039	PG69 (MW)	400.029	VG4 (p.u.)	1.03191	VG65 (p.u.)	0.974536	VG116 (p.u.)	0.97347
PG10 (MW)	332.3392	PG70 (MW)	7.71916	VG6 (p.u.)	1.02025	VG66 (p.u.)	1.00127	T8 (8–5)	1.09856
PG12 (MW)	73.21883	PG72 (MW)	0.27496	VG8 (p.u.)	0.94257	VG69 (p.u.)	1.020322	T32 (25–26)	0.90257
PG15 (MW)	6.500848	PG73 (MW)	6.45688	VG10 (p.u.)	0.94115	VG70 (p.u.)	0.979919	T36 (17–30)	0.9
PG18 (MW)	5.979357	PG74 (MW)	5.52285	VG12 (p.u.)	0.97438	VG72 (p.u.)	1.030921	T51 (37–38)	0.90084
PG19 (MW)	1.346065	PG76 (MW)	2.53255	VG15 (p.u.)	1.05303	VG73 (p.u.)	1.005468	T93 (59–63)	1.09369
PG24 (MW)	1.582226	PG77 (MW)	0.22016	VG18 (p.u.)	1.04361	VG74 (p.u.)	1.020992	T95 (61–64)	0.96853
PG25 (MW)	159.4184	PG80 (MW)	363.967	VG19 (p.u.)	0.98928	VG76 (p.u.)	1.019236	T102 (65–66)	0.93325
PG26 (MW)	215.2208	PG85 (MW)	0.07633	VG24 (p.u.)	0.96523	VG77 (p.u.)	1.034034	T107 (68–69)	0.91076
PG27 (MW)	0.110372	PG87 (MW)	4.60698	VG25 (p.u.)	1.04943	VG80 (p.u.)	1.036756	T127 (80–81)	0.9
PG31 (MW)	1.978596	PG89 (MW)	434.560	VG26 (p.u.)	1.00787	VG85 (p.u.)	1.049239	QC34 (MVAR)	0.20760
PG32 (MW)	2.320654	PG90 (MW)	0.12767	VG27 (p.u.)	0.97993	VG87 (p.u.)	1.059658	QC44 (MVAR)	0.00941
PG34 (MW)	0.120587	PG91 (MW)	17.5246	VG31 (p.u.)	0.98609	VG89 (p.u.)	1.010104	QC45 (MVAR)	0.26098
PG36 (MW)	5.158081	PG92 (MW)	1.45348	VG32 (p.u.)	0.94097	VG90 (p.u.)	0.963199	QC46 (MVAR)	0.07600
PG40 (MW)	32.66632	PG99 (MW)	4.11549	VG34 (p.u.)	0.94553	VG91 (p.u.)	1.042132	QC48 (MVAR)	0.24244
PG42 (MW)	3.238611	PG100 (MW)	206.177	VG36 (p.u.)	1.00105	VG92 (p.u.)	1.040622	QC74 (MVAR)	0.2194
PG46 (MW)	4.574268	PG103 (MW)	35.1167	VG40 (p.u.)	0.97223	VG99 (p.u.)	0.943471	QC79 (MVAR)	5.6 × 10−5
PG49 (MW)	161.9397	PG104 (MW)	1.01542	VG42 (p.u.)	0.97289	VG100 (p.u.)	0.951227	QC82 (MVAR)	0.00622
PG54 (MW)	28.01801	PG105 (MW)	15.1016	VG46 (p.u.)	0.98664	VG103 (p.u.)	1.004165	QC83 (MVAR)	0.27248
PG55 (MW)	0.389909	PG107 (MW)	0	VG49 (p.u.)	1.00712	VG104 (p.u.)	0.987921	QC105 (MVAR)	0.03938
PG56 (MW)	12.21136	PG110 (MW)	18.5235	VG54 (p.u.)	1.04523	VG105 (p.u.)	0.943759	QC107 (MVAR)	0.27336
PG59 (MW)	108.0116	PG111 (MW)	35.5095	VG55 (p.u.)	1.05831	VG107 (p.u.)	0.960449	QC110 (MVAR)	0.23428
PG61 (MW)	122.726	PG112 (MW)	2.19141	VG56 (p.u.)	0.96064	VG110 (p.u.)	1.00083
					Fuel cost ($/h)		100738.5
					Power loss (MW)		88.04623
					Voltage deviation (p.u.)		0.778536

Table 12. Results of the proposed MRao-2 algorithm and other algorithms for case 5.

Algorithm	ASO	TFWO	MPA	Rao-1	Rao-2	Rao-3	MRao-2
Fuel cost ($/h)	103,847.47	101,747.68	101,981.69	101,981.17	101,078.92	101,297.12	100,738.54
Power loss (MW)	58.3333	85.062475	71.168974	89.992651	90.296046	91.006497	88.04623
Voltage deviation (p.u.)	0.6645742	04387701	0.7712916	1.1227076	1.1595186	0.9923019	0.778536
Time (s)	792.735	802.82732	1013.509	800.827	803.4047	798.4426	1136.06

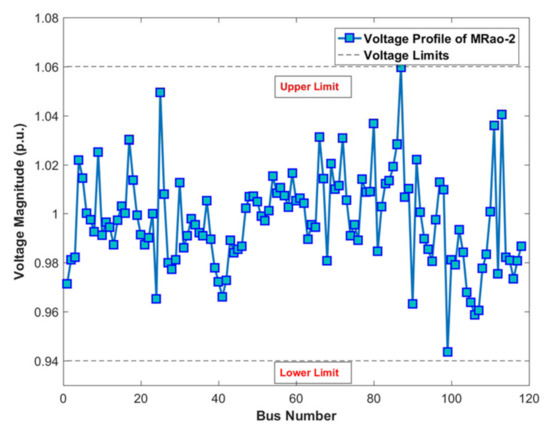
Figure 15. The voltage profile of the MRao-2 for case 5.

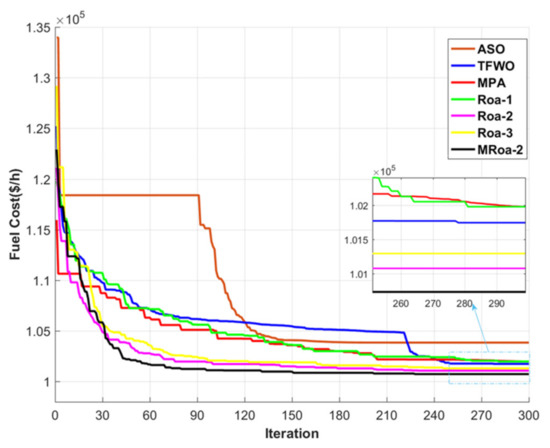
Figure 16. Convergence characteristics of all methods for case 5.

5. Conclusions

In this article, a new technique has been proposed for finding the optimum solution to the OPF problem incorporating renewable energy sources considering the fuel cost, transmission loss, emission, and improvement of the voltage profile. To overcome the shortcomings of the original Rao-2, the MRao-2 algorithm has been proposed using the quasi-oppositional and levy methods. The superiority and effectiveness of MRao-2 have been checked based on two standard test systems (IEEE 30-bus system and IEEE 118-bus system) with or without RES. It is obvious from the results that the MRao-2 provided a better solution of the objective function for all cases over other algorithms employed in the comparison. The obtained results using MRao-2 in comparison with those obtained using other recent techniques show that the proposed MRao-2 is superior to these algorithms for normal, contingency states and with incorporating RES whatsoever the scale of the power system which shows the strength of the MRao-2 to solve the real-life application.