A Modified Rao-2 Algorithm for Optimal Power Flow Incorporating Renewable Energy Sources
Abstract
:1. Introduction
- The proposed MRao-2 technique is used to achieve the accurate values of control variables of the OPF problem without RES, with RES, and with RES under contingency state.
- The fuel cost is the main objective function in five scenarios for the two IEEE 30 -bus and 118-bus systems to test the validation of the proposed algorithm.
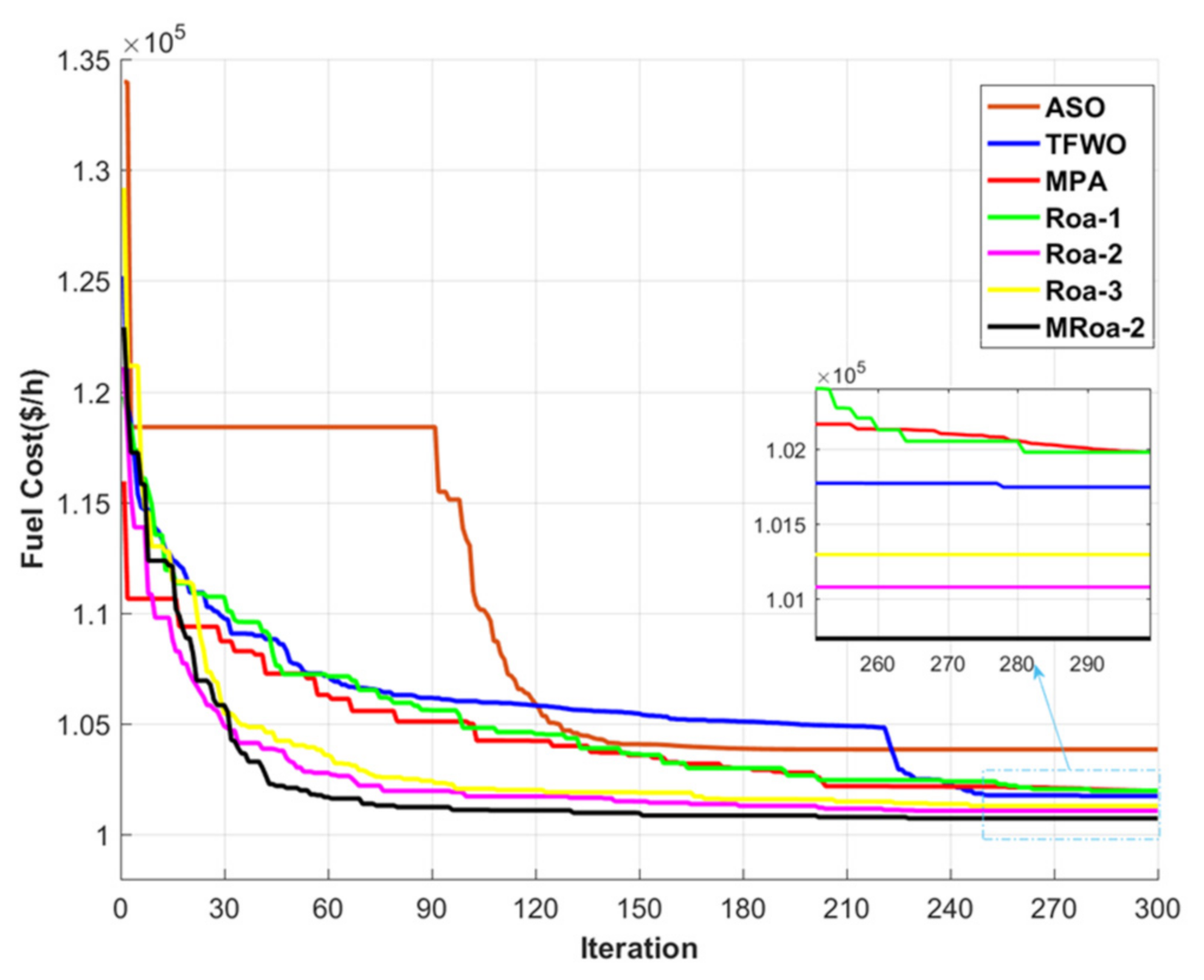
- To check the robustness of this modified algorithm, its results are compared with five recent algorithms—ASO, TFWO, MPA, Rao-1, and Rao-3—as well as the original Rao-2 which are the strong algorithms in solving the modern power system problems and they are used in many published papers in the last two years so far.
2. Problem Formulation
2.1. General Structure of OPF
2.2. Objective Functions
2.2.1. Quadratic Total Fuel Cost
2.2.2. Total Emission
2.2.3. Power Loss Function
2.2.4. Voltage Deviation (VD) Function (Voltage Profile Improvement)
2.3. Constraints
2.3.1. Equality Constraints
2.3.2. Inequality Constraints
2.3.3. Power Balance Considering RES
3. The Proposed Optimization Technique
3.1. Rao Algorithm
- Step 1: Randomly distribute the population within the vector ranges.
- Step 2: Determine the objective value for each variable.
- Step 3: Define the worst and best solutions depending on the objective function’s values.
- Step 4: Upgrade the solutions by (25).
- Step 5: If any of the updated values fall outside of the range, they should be returned.
- Step 6: Evaluate the value of each search agent’s objective function.
- Step 7: Increase the number of iterations of the new one
- Step 8: If the iteration has reached its end, return the best value so far. If not, go on to Step 3.
3.2. Modified Rao Algorithm
3.2.1. Quasi-Oppositional
3.2.2. Levy Flight
4. Simulation Results
4.1. Test Systems
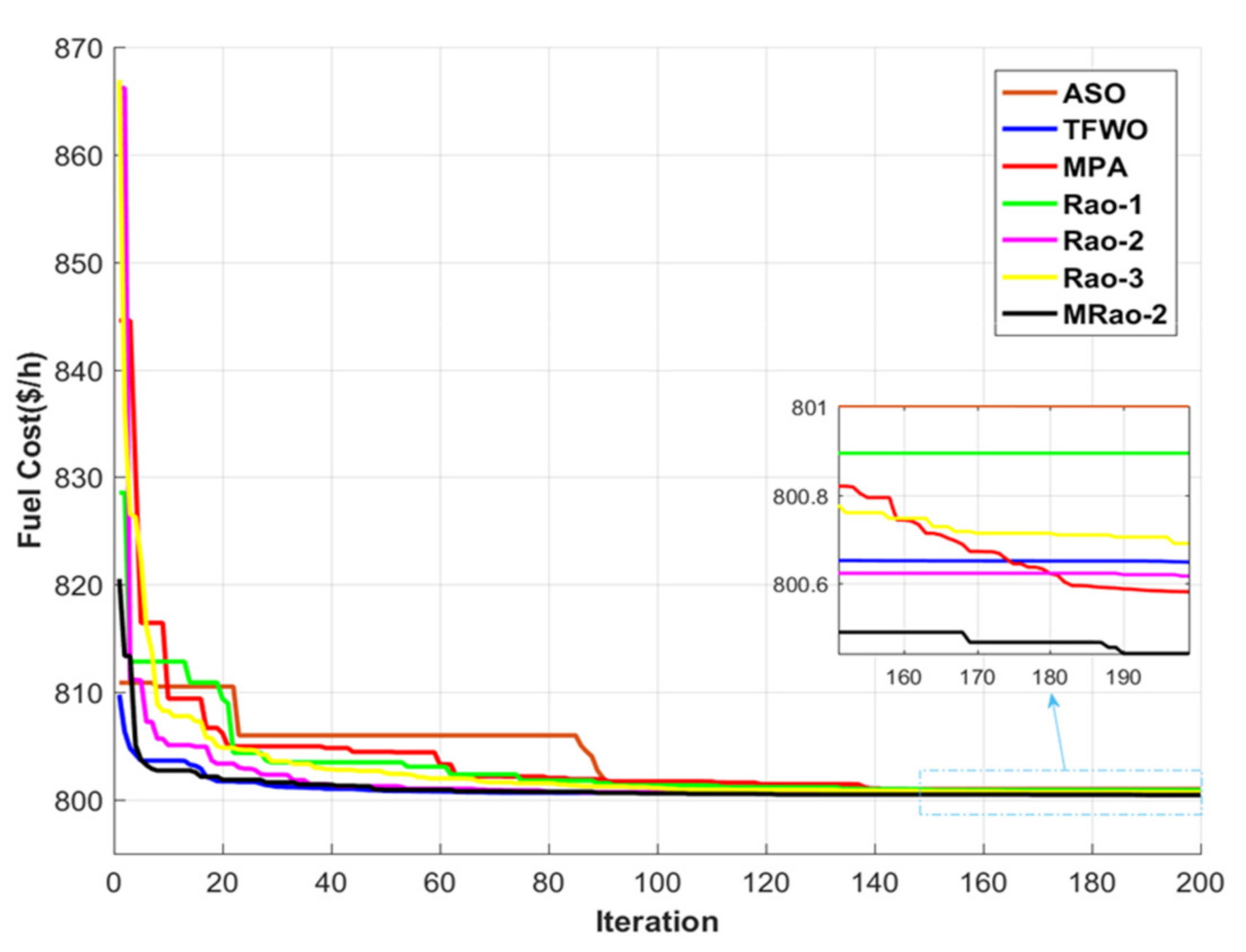
4.2. Case 1: The OPF without RES for the IEEE 30-Bus System
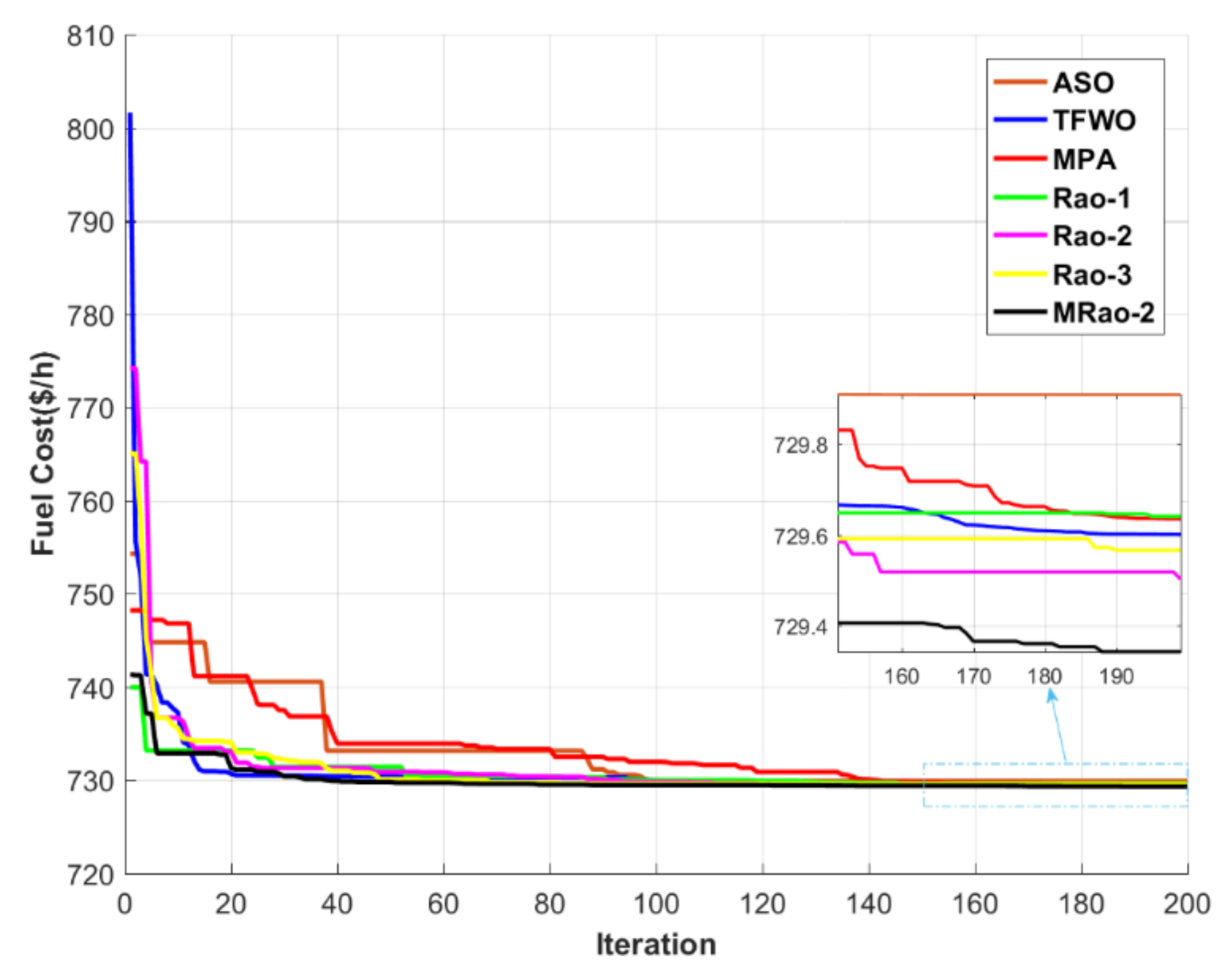
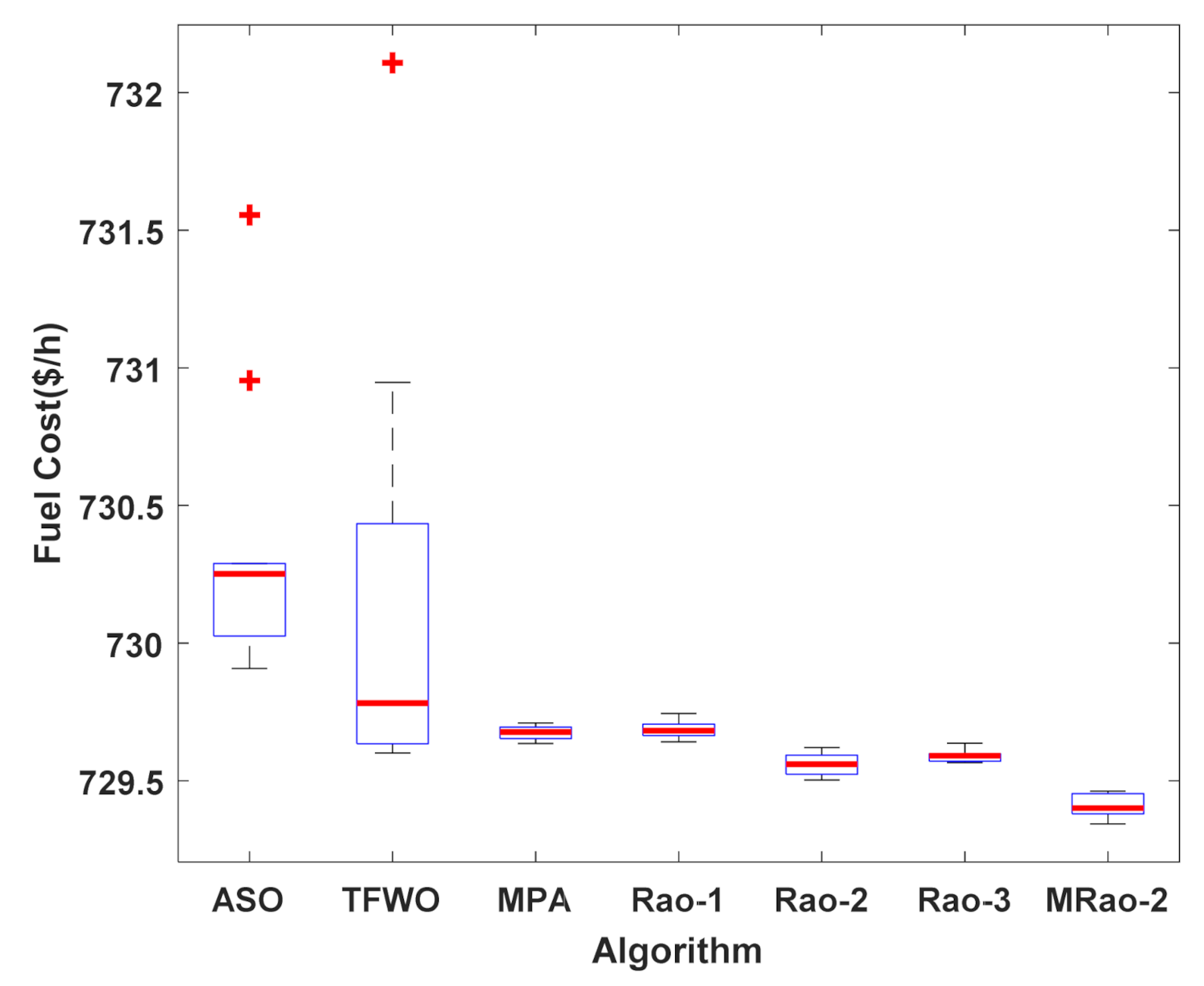
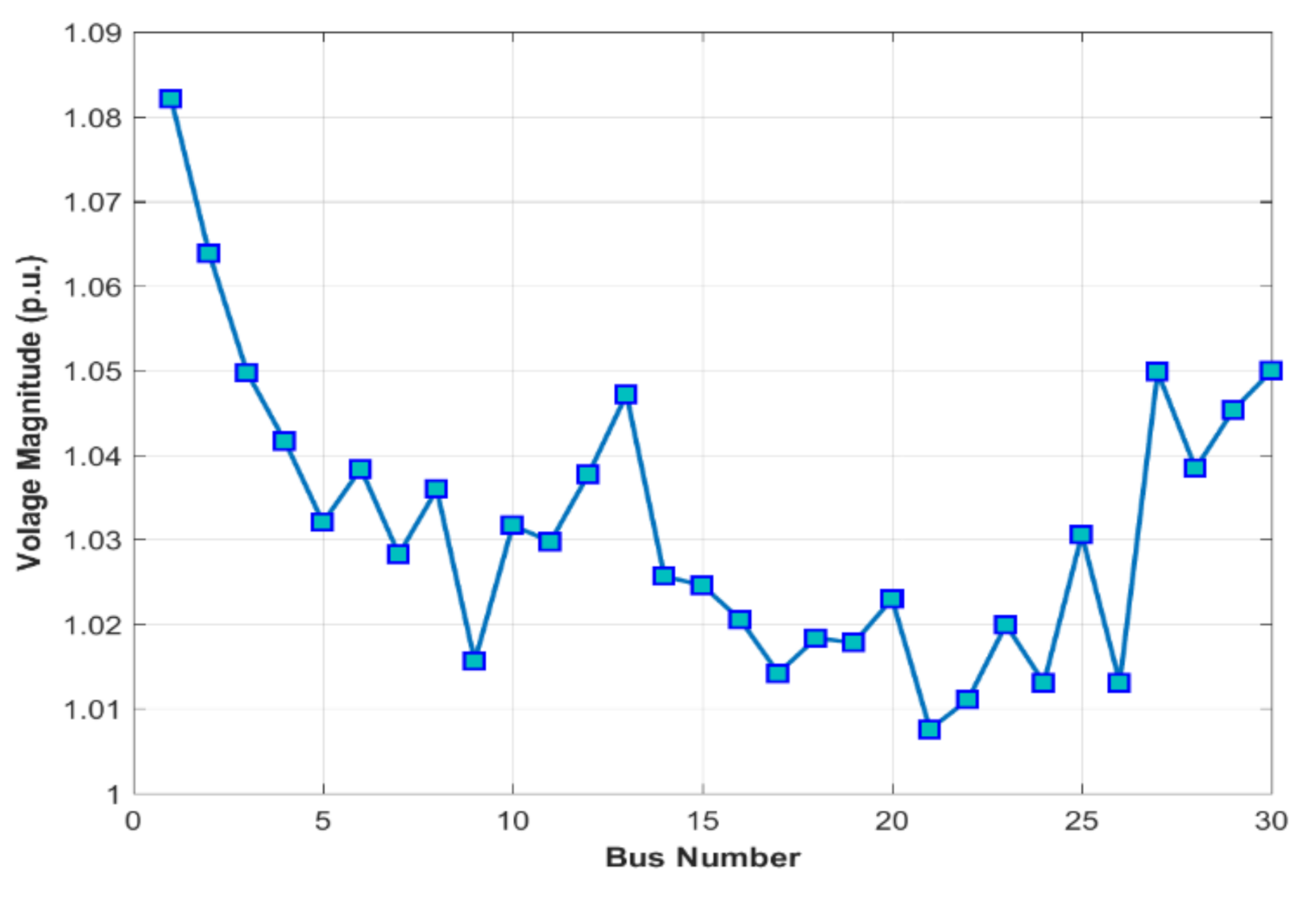
4.3. Case 2: OPF Incorporating RES for the IEEE 30-Bus System
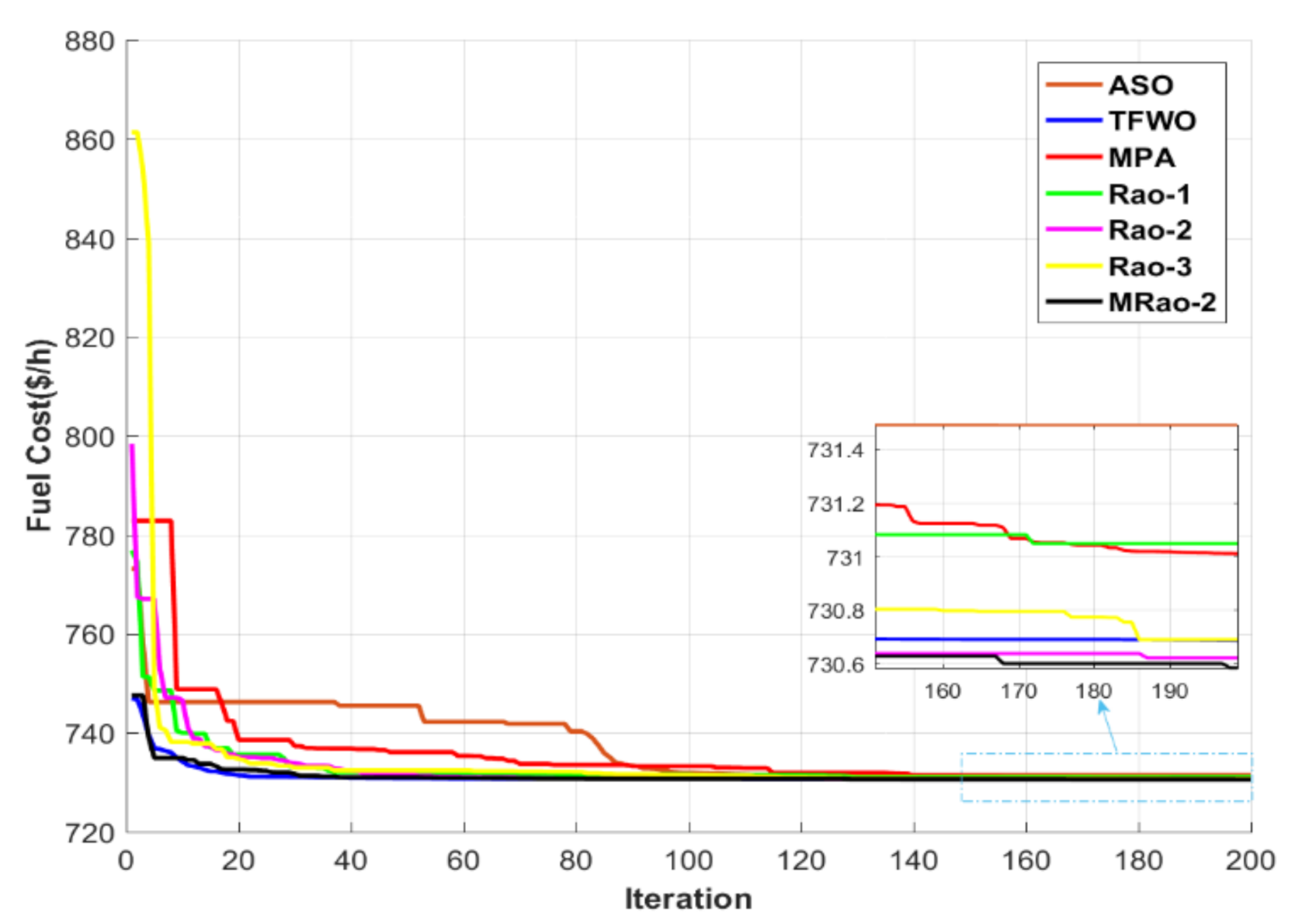
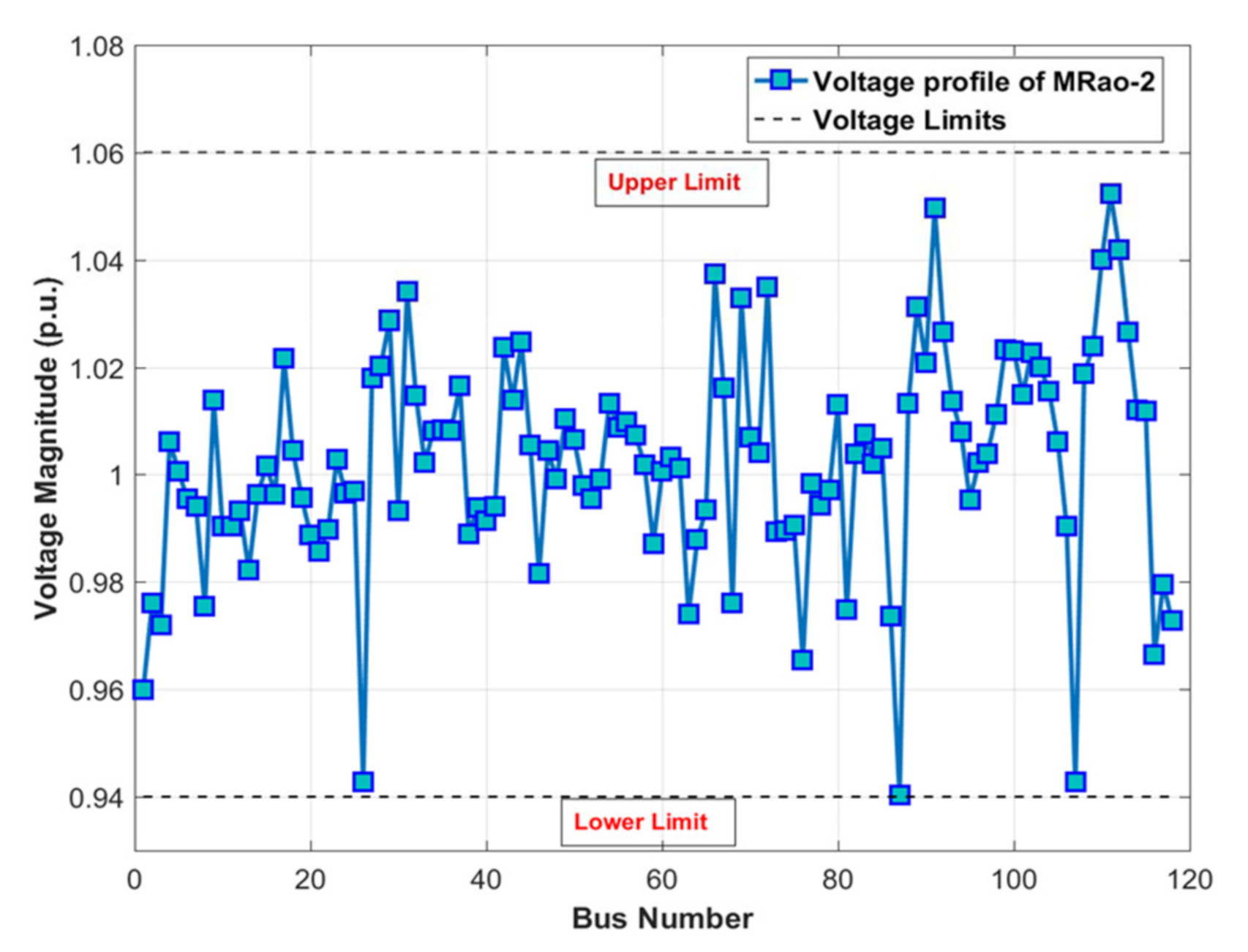
4.4. Case 3: OPF Incorporating RES under Contingency State for IEEE 30-Bus System
4.5. Case 4: OPF without RES for the IEEE 118-Bus System
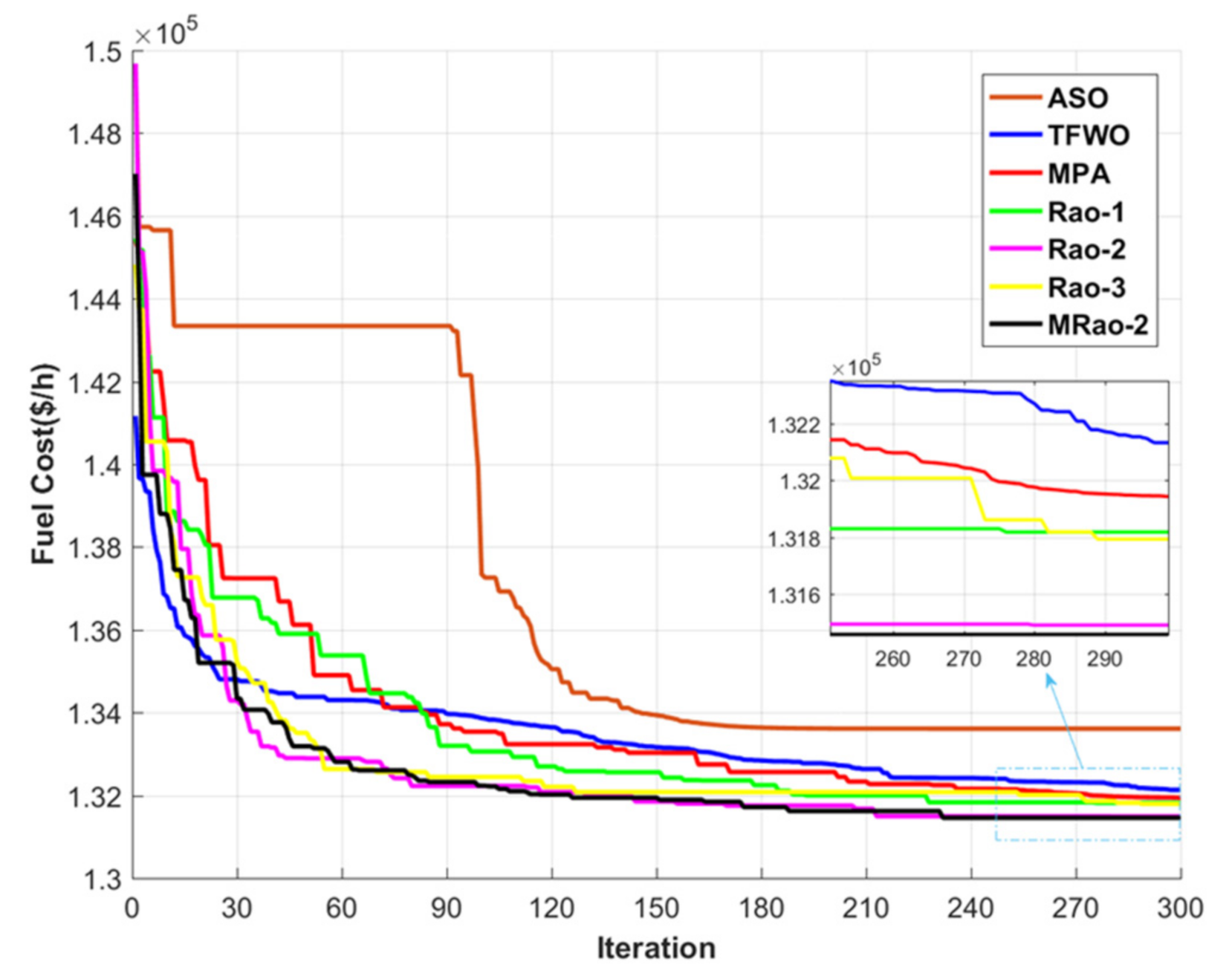
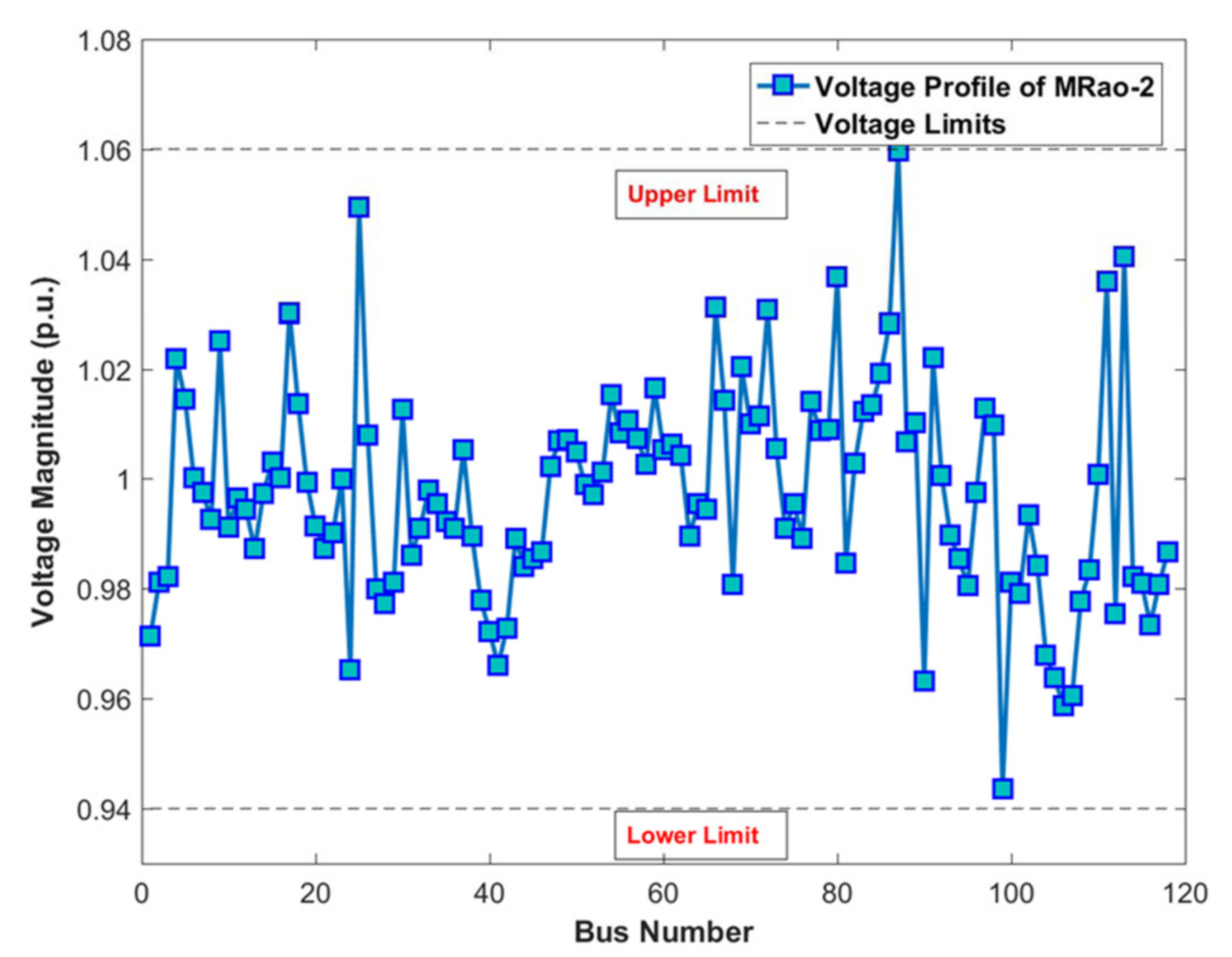
4.6. Case 5: OPF Incorporating RES for the IEEE 118-Bus System
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sulaiman, M.H.; Mustaffa, Z.; Mohamad, A.J.; Saari, M.M.; Mohamed, M.R. Optimal power flow with stochastic solar power using barnacles mating optimizer. Int. Trans. Electr. Energy Syst. 2021, 31, e12858. [Google Scholar] [CrossRef]
- Abaci, K.; Yamacli, V. Differential search algorithm for solving multi-objective optimal power flow problem. Int. J. Electr. Power Energy Syst. 2016, 79, 1–10. [Google Scholar] [CrossRef]
- Ben Hmida, J.; Chambers, T.; Lee, J. Solving constrained optimal power flow with renewables using hybrid modified imperialist competitive algorithm and sequential quadratic programming. Electr. Power Syst. Res. 2019, 177, 105989. [Google Scholar] [CrossRef]
- Elattar, E.E.; ElSayed, S.K. Modified JAYA algorithm for optimal power flow incorporating renewable energy sources considering the cost, emission, power loss and voltage profile improvement. Energy 2019, 178, 598–609. [Google Scholar] [CrossRef]
- Shaheen, M.A.M.; Hasanien, H.M.; Al-Durra, A. Solving of Optimal Power Flow Problem Including Renewable Energy Resources Using HEAP Optimization Algorithm. IEEE Access 2021, 9, 35846–35863. [Google Scholar] [CrossRef]
- Frank, S.; Steponavice, I.; Rebennack, S. Optimal power flow: A bibliographic survey I. Energy Syst. 2012, 3, 221–258. [Google Scholar] [CrossRef]
- Momoh, J.A.; Adapa, R.; El-Hawary, M.E. A review of selected optimal power flow literature to 1993. I. Nonlinear and quadratic programming approaches. IEEE Trans. Power Syst. 1999, 14, 96–104. [Google Scholar] [CrossRef]
- Yan, X.; Quintana, V.H. Improving an interior-point-based OPF by dynamic adjustments of step sizes and tolerances. IEEE Trans. Power Syst. 1999, 14, 709–717. [Google Scholar] [CrossRef]
- Khunkitti, S.; Siritaratiwat, A.; Premrudeepreechacharn, S.; Chatthaworn, R.; Watson, N. A Hybrid DA-PSO Optimization Algorithm for Multiobjective Optimal Power Flow Problems. Energies 2018, 11, 2270. [Google Scholar] [CrossRef] [Green Version]
- Khan, A.; Hizam, H.; Abdul-Wahab, N.I.; Othman, M.L. Solution of Optimal Power Flow Using Non-Dominated Sorting Multi Objective Based Hybrid Firefly and Particle Swarm Optimization Algorithm. Energies 2020, 13, 4265. [Google Scholar] [CrossRef]
- Taher, M.A.; Kamel, S.; Jurado, F.; Ebeed, M. Modified grasshopper optimization framework for optimal power flow solution. Electr. Eng. 2019, 101, 121–148. [Google Scholar] [CrossRef]
- Shaheen, A.M.; El-Sehiemy, R.A.; Farrag, S.M. Solving multi-objective optimal power flow problem via forced initialised differential evolution algorithm. IET Gener. Transm. Distrib. 2016, 10, 1634–1647. [Google Scholar] [CrossRef]
- Warid, W. Optimal power flow using the AMTPG-Jaya algorithm. Appl. Soft Comput. 2020, 91, 106252. [Google Scholar] [CrossRef]
- Attia, A.-F.; El Sehiemy, R.A.; Hasanien, H.M. Optimal power flow solution in power systems using a novel Sine-Cosine algorithm. Int. J. Electr. Power Energy Syst. 2018, 99, 331–343. [Google Scholar] [CrossRef]
- Abdo, M.; Kamel, S.; Ebeed, M.; Yu, J.; Jurado, F. Solving Non-Smooth Optimal Power Flow Problems Using a Developed Grey Wolf Optimizer. Energies 2018, 11, 1692. [Google Scholar] [CrossRef] [Green Version]
- Abd el-sattar, S.; Kamel, S.; Ebeed, M.; Jurado, F. An improved version of salp swarm algorithm for solving optimal power flow problem. Soft Comput. 2021, 25, 4027–4052. [Google Scholar] [CrossRef]
- Sulaiman, M.H.; Mustaffa, Z. Solving optimal power flow problem with stochastic wind–solar–small hydro power using barnacles mating optimizer. Control Eng. Pract. 2021, 106, 104672. [Google Scholar] [CrossRef]
- Kaymaz, E.; Duman, S.; Guvenc, U. Optimal power flow solution with stochastic wind power using the Lévy coyote optimization algorithm. Neural Comput. Appl. 2021, 33, 6775–6804. [Google Scholar] [CrossRef]
- Premkumar, M.; Babu, T.S.; Umashankar, S.; Sowmya, R. A new metaphor-less algorithms for the photovoltaic cell parameter estimation. Optik 2020, 208, 164559. [Google Scholar] [CrossRef]
- Wang, L.; Wang, Z.; Liang, H.; Huang, C. Parameter estimation of photovoltaic cell model with Rao-1 algorithm. Optik (Stuttgart) 2020, 210, 163846. [Google Scholar] [CrossRef]
- Jian, X.; Zhu, Y. Parameters identification of photovoltaic models using modified Rao-1 optimization algorithm. Optik (Stuttgart) 2021, 231, 166439. [Google Scholar] [CrossRef]
- Lekouaghet, B.; Boukabou, A.; Boubakir, C. Estimation of the photovoltaic cells/modules parameters using an improved Rao-based chaotic optimization technique. Energy Convers. Manag. 2021, 229, 113722. [Google Scholar] [CrossRef]
- Rao, R.V.; Pawar, R.B. Constrained design optimization of selected mechanical system components using Rao algorithms. Appl. Soft Comput. 2020, 89, 106141. [Google Scholar] [CrossRef]
- Rao, R.V.; Keesari, H.S. Rao algorithms for multi-objective optimization of selected thermodynamic cycles. Eng. Comput. 2020. [Google Scholar] [CrossRef]
- Venkata Rao, R.; Pawar, R.B. Optimal Weight Design of a Spur Gear Train Using Rao Algorithms. In Proceedings of the International Conference on Sustainable and Innovative Solutions for Current Challenges in Engineering & Technology, Gwalior, India, 2–3 November 2019; pp. 351–362. [Google Scholar]
- Grzywiński, M.; Dede, T. New Optimization Algorithms and their Application for 2d Truss Structures. Zesz. Nauk. Politech. Częstochowskiej. Bud. 2020, 175, 50–54. [Google Scholar] [CrossRef]
- Rao, R.V.; Pawar, R.B. Quasi-oppositional-based Rao algorithms for multi-objective design optimization of selected heat sinks. J. Comput. Des. Eng. 2020, 7, 830–863. [Google Scholar] [CrossRef]
- Hassan, M.H.; Kamel, S.; El-Dabah, M.A.; Khurshaid, T.; Dominguez-Garcia, J.L. Optimal Reactive Power Dispatch With Time-Varying Demand and Renewable Energy Uncertainty Using Rao-3 Algorithm. IEEE Access 2021, 9, 23264–23283. [Google Scholar] [CrossRef]
- Sharma, S.R.; Singh, B.; Kaur, M. Classification of Parkinson disease using binary Rao optimization algorithms. Expert Syst. 2021, 38, e12674. [Google Scholar] [CrossRef]
- Zabaiou, T.; Dessaint, L.; Kamwa, I. Preventive control approach for voltage stability improvement using voltage stability constrained optimal power flow based on static line voltage stability indices. IET Gener. Transm. Distrib. 2014, 8, 924–934. [Google Scholar] [CrossRef] [Green Version]
- Elattar, E.E. Modified harmony search algorithm for combined economic emission dispatch of microgrid incorporating renewable sources. Energy 2018, 159, 496–507. [Google Scholar] [CrossRef]
- Biswas, P.P.; Suganthan, P.N.; Mallipeddi, R.; Amaratunga, G.A.J. Optimal power flow solutions using differential evolution algorithm integrated with effective constraint handling techniques. Eng. Appl. Artif. Intell. 2018, 68, 81–100. [Google Scholar] [CrossRef]
- Birogul, S. Hybrid Harris Hawk Optimization Based on Differential Evolution (HHODE) Algorithm for Optimal Power Flow Problem. IEEE Access 2019, 7, 184468–184488. [Google Scholar] [CrossRef]
- Duong, T.L.; Nguyen, N.A.; Nguyen, T.T. A Newly Hybrid Method Based on Cuckoo Search and Sunflower Optimization for Optimal Power Flow Problem. Sustainability 2020, 12, 5283. [Google Scholar] [CrossRef]
- Farhat, I.A.; El-Hawary, M.E. Dynamic adaptive bacterial foraging algorithm for optimum economic dispatch with valve-point effects and wind power. IET Gener. Transm. Distrib. 2010, 4, 989. [Google Scholar] [CrossRef]
- Nwulu, N.I.; Xia, X. Optimal dispatch for a microgrid incorporating renewables and demand response. Renew. Energy 2017, 101, 16–28. [Google Scholar] [CrossRef]
- Rao, R.V. Rao algorithms: Three metaphor-less simple algorithms for solving optimization problems. Int. J. Ind. Eng. Comput. 2020, 11, 107–130. [Google Scholar] [CrossRef]
- Tizhoosh, H.R. Opposition-Based Learning: A New Scheme for Machine Intelligence. In Proceedings of the International Conference on Computational Intelligence for Modelling, Control and Automation and International Conference on Intelligent Agents, Web Technologies and Internet Commerce (CIMCA-IAWTIC’06), Vienna, Austria, 28–30 November 2005; Volume 1, pp. 695–701. [Google Scholar]
- Sharma, S.; Bhattacharjee, S.; Bhattacharya, A. Quasi-Oppositional Swine Influenza Model Based Optimization with Quarantine for optimal allocation of DG in radial distribution network. Int. J. Electr. Power Energy Syst. 2016, 74, 348–373. [Google Scholar] [CrossRef]
- Sultana, S.; Roy, P.K. Multi-objective quasi-oppositional teaching learning based optimization for optimal location of distributed generator in radial distribution systems. Int. J. Electr. Power Energy Syst. 2014, 63, 534–545. [Google Scholar] [CrossRef]
- Kharrich, M.; Mohammed, O.H.; Kamel, S.; Selim, A.; Sultan, H.M.; Akherraz, M.; Jurado, F. Development and Implementation of a Novel Optimization Algorithm for Reliable and Economic Grid-Independent Hybrid Power System. Appl. Sci. 2020, 10, 6604. [Google Scholar] [CrossRef]
- Yu, J.; Kim, C.-H.; Rhee, S.-B. Oppositional Jaya Algorithm With Distance-Adaptive Coefficient in Solving Directional Over Current Relays Coordination Problem. IEEE Access 2019, 7, 150729–150742. [Google Scholar] [CrossRef]
- Taha, I.B.M.; Elattar, E.E. Optimal reactive power resources sizing for power system operations enhancement based on improved grey wolf optimiser. IET Gener. Transm. Distrib. 2018, 12, 3421–3434. [Google Scholar] [CrossRef]
- Christie, R. Power Systems Test Case Archive, University of Washington. Available online: http://www.ee.washington.edu/research/pstca/ (accessed on 26 May 2021).
- Duman, S.; Rivera, S.; Li, J.; Wu, L. Optimal power flow of power systems with controllable wind-photovoltaic energy systems via differential evolutionary particle swarm optimization. Int. Trans. Electr. Energy Syst. 2020, 30, 1–28. [Google Scholar] [CrossRef]
- Hazra, J.; Sinha, A.K. A multi-objective optimal power flow using particle swarm optimization. Eur. Trans. Electr. Power 2011, 21, 1028–1045. [Google Scholar] [CrossRef]
- Warid, W.; Hizam, H.; Mariun, N.; Abdul-Wahab, N. Optimal Power Flow Using the Jaya Algorithm. Energies 2016, 9, 678. [Google Scholar] [CrossRef]
- Pena, I.; Martinez-Anido, C.B.; Hodge, B.-M. An Extended IEEE 118-Bus Test System With High Renewable Penetration. IEEE Trans. Power Syst. 2018, 33, 281–289. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, L.; Zhang, Z. Atom search optimization and its application to solve a hydrogeologic parameter estimation problem. Knowl.-Based Syst. 2019, 163, 283–304. [Google Scholar] [CrossRef]
- Ghasemi, M.; Davoudkhani, I.F.; Akbari, E.; Rahimnejad, A.; Ghavidel, S.; Li, L. A novel and effective optimization algorithm for global optimization and its engineering applications: Turbulent Flow of Water-based Optimization (TFWO). Eng. Appl. Artif. Intell. 2020, 92, 103666. [Google Scholar] [CrossRef]
- Faramarzi, A.; Heidarinejad, M.; Mirjalili, S.; Gandomi, A.H. Marine Predators Algorithm: A nature-inspired metaheuristic. Expert Syst. Appl. 2020, 152, 113377. [Google Scholar] [CrossRef]
- Rezaei Adaryani, M.; Karami, A. Artificial bee colony algorithm for solving multi-objective optimal power flow problem. Int. J. Electr. Power Energy Syst. 2013, 53, 219–230. [Google Scholar] [CrossRef]
- Ramesh Kumar, A.; Premalatha, L. Optimal power flow for a deregulated power system using adaptive real coded biogeography-based optimization. Int. J. Electr. Power Energy Syst. 2015, 73, 393–399. [Google Scholar] [CrossRef]
- Mohamed, A.-A.A.; Mohamed, Y.S.; El-Gaafary, A.A.M.; Hemeida, A.M. Optimal power flow using moth swarm algorithm. Electr. Power Syst. Res. 2017, 142, 190–206. [Google Scholar] [CrossRef]
- Niknam, T.; Narimani, M.R.; Azizipanah-Abarghooee, R. A new hybrid algorithm for optimal power flow considering prohibited zones and valve point effect. Energy Convers. Manag. 2012, 58, 197–206. [Google Scholar] [CrossRef]
- El-Fergany, A.A.; Hasanien, H.M. Single and Multi-objective Optimal Power Flow Using Grey Wolf Optimizer and Differential Evolution Algorithms. Electr. Power Compon. Syst. 2015, 43, 1548–1559. [Google Scholar] [CrossRef]







| IEEE 30-Bus System | IEEE 118-Bus System | |||
|---|---|---|---|---|
| Variables | Lower limit | Upper limit | Lower limit | Upper limit |
| Voltages for all generator bus | 0.95 p.u | 1.1 p.u | 0.94 p.u | 1.06 p.u |
| Voltages for all load bus | 0.95 p.u | 1.05 p.u | 0.95 p.u | 1.05 p.u |
| Tap setting | 0.9 p.u | 1.1 p.u | 0.9 p.u | 1.1 p.u |
| Reactive power of capacitor banks | 0 | 0.05 p.u | 0 | 0.3 p.u |
| Type of RES | No. of Bus | Value (MW) |
|---|---|---|
| biomass | 12 | 18.2 |
| wind | 31 | 156 |
| solar | 54 | 264 |
| hydro | 76 | 77 |
| hydro | 116 | 286 |
| Algorithms | Parameters Setting |
|---|---|
| Common settings |
|
| ASO |
|
| MPA | FADs = 0.2, P = 0.5, C = 0.05, e = 0.25 |
| ASO | TFWO | MPA | Rao-1 | Rao-2 | Rao-3 | MRao-2 | |
|---|---|---|---|---|---|---|---|
| PG1 (MW) | 176.9732 | 177.2422 | 176.8351 | 179.8369 | 177.887 | 177.5088 | 176.3625 |
| PG2 (MW) | 48.91006 | 48.64558 | 48.67575 | 49.49712 | 49.36524 | 48.76959 | 49.07412 |
| PG5 (MW) | 21.30213 | 21.36803 | 21.45982 | 22.21521 | 21.54786 | 20.94155 | 21.24651 |
| PG8 (MW) | 20.9253 | 21.35596 | 21.88621 | 18.77388 | 21.6564 | 21.53046 | 21.37135 |
| PG11 (MW) | 12.45411 | 11.86476 | 11.54409 | 10.38348 | 10.00796 | 11.80911 | 12.21261 |
| PG13 (MW) | 12.00137 | 12.00148 | 12.02418 | 12 | 12.04775 | 12.0039 | 12.10508 |
| V1 (p.u.) | 1.080029 | 1.079984 | 1.082237 | 1.078675 | 1.084304 | 1.080698 | 1.083304 |
| V2 (p.u.) | 1.080992 | 1.030047 | 1.083237 | 1.027824 | 1.094344 | 1.099999 | 1.092657 |
| V5 (p.u.) | 1.028033 | 1.082677 | 1.031479 | 1.085737 | 1.031264 | 1.028262 | 1.029766 |
| V8 (p.u.) | 1.034358 | 1.035451 | 1.037666 | 1.033404 | 1.037539 | 1.036411 | 1.037062 |
| V11 (p.u.) | 1.006403 | 1.05873 | 1.065692 | 1.078167 | 1.077243 | 1.031184 | 1.059477 |
| V13 (p.u.) | 1.036055 | 1.067677 | 1.029076 | 1.057387 | 1.034243 | 1.099824 | 1.046984 |
| T11 (6–9) | 0.96365 | 0.972727 | 0.963545 | 1.014786 | 1.031208 | 0.916034 | 1.002334 |
| T12 (6–10) | 1.014561 | 1.012358 | 1.05331 | 0.983026 | 0.9 | 1.099979 | 0.953247 |
| T15 (4–12) | 1.056913 | 0.994481 | 0.989785 | 1.001 | 0.964418 | 1.031275 | 0.971027 |
| T36 (28–27) | 0.99403 | 0.971573 | 1.000675 | 0.975213 | 0.980459 | 0.987251 | 0.971058 |
| QC10 (MVAR) | 3.0526 | 4.9784 | 3.2035 | 0.5727 | 0.1362 | 0.00562 | 3.7024 |
| QC12 (MVAR) | 3.5939 | 0.5594 | 4.639 | 0.7186 | 1.3228 | 0.00426 | 2.0306 |
| QC15 (MVAR) | 2.5611 | 4.635 | 3.9502 | 5 | 4.9242 | 4.9567 | 2.2152 |
| QC17 (MVAR) | 1.6444 | 3.7878 | 1.5066 | 3.3725 | 4.2338 | 0.0702 | 4.6995 |
| QC20 (MVAR) | 1.9898 | 4.5001 | 4.8618 | 4.4774 | 3.1484 | 4.9871 | 3.859 |
| QC21 (MVAR) | 3.4191 | 4.1061 | 3.5977 | 3.9993 | 0.2586 | 4.8557 | 4.8858 |
| QC23 (MVAR) | 4.7618 | 0.00168 | 4.3476 | 0.818 | 3.2847 | 0.0451 | 3.9984 |
| QC24 (MVAR) | 1.1282 | 2.1995 | 4.5618 | 4.9692 | 4.9243 | 4.9741 | 4.8289 |
| QC29 (MVAR) | 1.5646 | 0.4415 | 3.5686 | 2.1977 | 4.9685 | 2.3785 | 1.6698 |
| Fuel cost ($/h) | 801.0005 | 800.6477 | 800.5804 | 800.8944 | 800.6166 | 800.848 | 800.4412 |
| Emission (ton/h) | 0.295736 | 0.296049 | 0.295644 | 0.297821 | 0.296313 | 0.296384 | 0.295152 |
| Power loss (MW) | 9.177889 | 9.083431 | 9.036827 | 9.312149 | 9.123883 | 9.163424 | 8.983817 |
| Voltage deviation (p.u.) | 0.334805 | 0.749458 | 0.575301 | 0.707313 | 0.916652 | 0.469378 | 0.868108 |
| Time (s) | 95.06342 | 104.1479 | 166.5552 | 101.91743 | 94.84023 | 101.83725 | 169.6059 |
| Algorithm | Min | Max | Average |
|---|---|---|---|
| MRao-2 | 800.4412 | 800.553 | 800.4872 |
| Rao-2 | 800.6166 | 800.7965 | 800.7118 |
| Rao-1 | 800.8944 | 801.2647 | 800.9678 |
| Rao-3 | 800.848 | 800.9628 | 800.9067 |
| MPA | 800.5804 | 800.8416 | 800.6659 |
| TFWO | 800.6477 | 803.8754 | 801.1159 |
| ASO | 801.0005 | 801.4358 | 801.101 |
| MGOA [11] | 800.4744 | NA | NA |
| ABC [52] | 800.6600 | 800.8715 | 801.8674 |
| Jaya [47] | 800.4794 | 800.4928 | 800.5306 |
| ARCBBO [53] | 800.5159 | 800.6412 | 800.9262 |
| MSA [54] | 800.5099 | NA | NA |
| Hybrid SFLA SA [55] | 801.79 | NA | NA |
| HHO [33] | 801.4228 | NA | NA |
| HHODE [33] | 800.9959 | NA | NA |
| DE [56] | 801.23 | 801.622 | 801.282 |
| ASO | TFWO | MPA | Rao-1 | Rao-2 | Rao-3 | MRao-2 | |
|---|---|---|---|---|---|---|---|
| PG1 (MW) | 166.3103 | 167.0352 | 166.5015 | 167.7043 | 167.5941 | 167.2709 | 167.2508 |
| PG2 (MW) | 45.88087 | 46.29256 | 46.03059 | 47.38566 | 45.71914 | 47.19775 | 46.42704 |
| PG5 (MW) | 20.9709 | 20.64382 | 20.45905 | 20.90393 | 20.6118 | 20.69004 | 20.64984 |
| PG8 (MW) | 15.69756 | 15.68206 | 15.17763 | 13.74229 | 15.13705 | 14.47554 | 15.27324 |
| PG11 (MW) | 10.79724 | 10.00009 | 11.10394 | 10 | 10.53956 | 10.00813 | 10 |
| PG13 (MW) | 12.00262 | 12 | 12.32851 | 12 | 12.03885 | 12.04529 | 12 |
| V1 (p.u.) | 1.077967 | 1.081966 | 1.0788 | 1.077875 | 1.080078 | 1.080089 | 1.07852 |
| V2 (p.u.) | 1.072375 | 1.006269 | 1.1 | 1.094477 | 1.051656 | 1.063304 | 1.1 |
| V5 (p.u.) | 1.033146 | 1.057191 | 1.031388 | 1.076221 | 1.077262 | 1.0572 | 1.032235 |
| V8 (p.u.) | 1.031798 | 1.036781 | 1.038591 | 1.038888 | 1.039808 | 1.040699 | 1.026295 |
| V11 (p.u.) | 1.02098 | 1.099826 | 1.093579 | 1.049587 | 1.04657 | 1.078359 | 1.047772 |
| V13 (p.u.) | 1.042508 | 1.022207 | 1.014105 | 1.01495 | 1.009777 | 1.022799 | 1.062827 |
| T11(6–9) | 0.986874 | 0.989094 | 1.027745 | 0.99534 | 1.09646 | 0.991078 | 0.98482 |
| T12(6–10) | 1.005378 | 1.1 | 0.957009 | 0.928192 | 0.908495 | 1.073045 | 0.977984 |
| T15(4–12) | 0.975554 | 0.987607 | 0.981413 | 0.981491 | 0.971842 | 0.970377 | 0.981403 |
| T36(28–27) | 1.001887 | 0.99311 | 0.99195 | 0.997822 | 1.017273 | 1.010252 | 1.001331 |
| QC10 (MVAR) | 4.1156 | 4.7537 | 2.7651 | 4.7977 | 2.8059 | 4.9307 | 4.9494 |
| QC12 (MVAR) | 2.8466 | 4.821 | 3.8682 | 3.6157 | 1.4147 | 0.0171 | 0 |
| QC15 (MVAR) | 3.4126 | 4.8818 | 0.5251 | 4.3005 | 1.2958 | 3.8049 | 0.0184 |
| QC17 (MVAR) | 2.9106 | 4.2942 | 4.9994 | 0.3354 | 4.6224 | 3.1239 | 4.8752 |
| QC20 (MVAR) | 2.3832 | 2.9394 | 4.6997 | 4.691 | 4.394 | 3.1954 | 4.8711 |
| QC21 (MVAR) | 2.9478 | 5 | 0.3764 | 1.8647 | 3.3121 | 0 | 5 |
| QC23 (MVAR) | 1.4159 | 1.9167 | 2.9807 | 1.0238 | 4.9937 | 5 | 5 |
| QC24 (MVAR) | 2.6985 | 5 | 0.8889 | 3.9491 | 4.9191 | 4.7007 | 4.9522 |
| QC29 (MVAR) | 2.7382 | 0.3091 | 2.0465 | 1.5414 | 4.2786 | 2.302 | 2.282 |
| Fuel cost ($/h) | 729.9074 | 729.6002 | 729.6347 | 729.6406 | 729.5025 | 729.5657 | 729.3429 |
| Emission (ton/h) | 0.287894 | 0.288436 | 0.288163 | 0.288493 | 0.289114 | 0.28828 | 0.288559 |
| Power loss (MW) | 8.271074 | 8.264871 | 8.212681 | 8.341641 | 8.245904 | 8.293049 | 8.21248 |
| Voltage deviation (p.u.) | 0.487935 | 0.587188 | 0.723005 | 0.74643 | 0.599303 | 0.554658 | 0.890863 |
| Time (s) | 96.3905 | 101.40315 | 154.3002 | 93.26448 | 92.40164 | 95.84038 | 166.5166 |
| ASO | TFWO | MPA | Rao-1 | Rao-2 | Rao-3 | MRao-2 | |
|---|---|---|---|---|---|---|---|
| PG1 (MW) | 169.1157 | 167.646 | 168.4079 | 166.1685 | 168.162 | 168.2884 | 167.6707 |
| PG2 (MW) | 47.10122 | 46.38156 | 46.73768 | 46.29319 | 46.34349 | 46.35133 | 46.43635 |
| PG5 (MW) | 20.77245 | 20.68947 | 20.8021 | 20.22988 | 20.61748 | 20.70681 | 20.82097 |
| PG8 (MW) | 12.4257 | 15.29242 | 13.2599 | 17.28305 | 14.80192 | 14.45443 | 14.76838 |
| PG11 (MW) | 10.9089 | 10 | 10.93876 | 10 | 10.09605 | 10.24194 | 10.22822 |
| PG13 (MW) | 12.0136 | 12 | 12.00331 | 12.02535 | 12.00538 | 12.00845 | 12.05377 |
| V1 (p.u.) | 1.071178 | 1.080797 | 1.082793 | 1.088881 | 1.082847 | 1.081143 | 1.08205 |
| V2 (p.u.) | 1.091177 | 1.0925 | 1.033038 | 1.063013 | 1.084106 | 1.082092 | 1.083835 |
| V5 (p.u.) | 1.018346 | 1.031645 | 1.086276 | 1.054294 | 1.031456 | 1.026707 | 1.032011 |
| V8 (p.u.) | 1.023794 | 1.036661 | 1.037818 | 1.034209 | 1.033635 | 1.033571 | 1.03592 |
| V11 (p.u.) | 1.038897 | 1.071995 | 1.083139 | 1.059527 | 1.029808 | 1.074468 | 1.029754 |
| V13 (p.u.) | 1.019225 | 1.042984 | 1.047633 | 1.039893 | 1.046966 | 1.045277 | 1.04714 |
| T11 (6–9) | 0.966049 | 0.965995 | 1.05369 | 0.973616 | 1.040438 | 1.078513 | 1.06788 |
| T12 (6–10) | 0.970151 | 1.099986 | 0.939359 | 1.016485 | 0.906038 | 0.9 | 0.900135 |
| T15 (4–12) | 0.96075 | 0.984042 | 0.957996 | 0.961999 | 0.984907 | 0.988115 | 0.980633 |
| T36 (28–27) | 1.014058 | 1.006899 | 1.011424 | 1.01808 | 1.017749 | 1.010059 | 1.010374 |
| QC10 (MVAR) | 3.3514 | 1.8078 | 1.993 | 4.6449 | 0.0643 | 0.1501 | 0.0246 |
| QC12 (MVAR) | 2.4055 | 4.5298 | 2.4846 | 0.515 | 0.9183 | 3.2165 | 0.0275 |
| QC15 (MVAR) | 3.0776 | 5 | 4.3023 | 4.5803 | 4.4913 | 4.9203 | 1.5989 |
| QC17 (MVAR) | 3.3283 | 5 | 2.7311 | 4.2387 | 4.9964 | 4.7269 | 4.994 |
| QC20 (MVAR) | 3.9248 | 0 | 2.5187 | 0.2183 | 1.9472 | 0.0149 | 4.8959 |
| QC21 (MVAR) | 4.4199 | 5 | 0.24 | 3.2204 | 5 | 5 | 4.9499 |
| QC23 (MVAR) | 2.5112 | 0.702 | 1.7923 | 4.9999 | 4.9924 | 0 | 3.431 |
| QC24 (MVAR) | 4.5875 | 5 | 2.9447 | 1.9501 | 4.8343 | 4.9989 | 5 |
| QC29 (MVAR) | 2.7613 | 0 | 2.76 × 10−5 | 0 | 0.00259 | 0.0514 | 0.0739 |
| Fuel cost ($/h) | 731.4898 | 730.6851 | 731.0095 | 731.0468 | 730.6201 | 730.688 | 730.583 |
| Emission (ton/h) | 0.289802 | 0.288885 | 0.289341 | 0.287874 | 0.289345 | 0.289416 | 0.288841 |
| Power loss (MW) | 8.949145 | 8.620926 | 8.755022 | 8.605339 | 8.63787 | 8.662901 | 8.589888 |
| Voltage deviation (p.u.) | 0.595555 | 0.626741 | 0.73608 | 0.693286 | 0.695892 | 0.665941 | 0.665648 |
| Time (s) | 94.1653 | 98.40031 | 153.3302 | 95.61418 | 98.2997 | 97.24576 | 164.5099 |
| Case No. | Algorithm | Min | Average | Median | Max | STD |
|---|---|---|---|---|---|---|
| Case 1 | MRao-2 | 800.4412 | 800.4872 | 800.4769 | 800.553 | 0.038822 |
| Rao-2 | 800.6166 | 800.7118 | 800.7135 | 800.7965 | 0.052478 | |
| Rao-1 | 800.8944 | 800.9678 | 800.9277 | 801.2647 | 0.111619 | |
| Rao-3 | 800.848 | 800.9067 | 800.9167 | 800.9628 | 0.0403 | |
| MPA | 800.5804 | 800.6659 | 800.6347 | 800.8416 | 0.081797 | |
| TFWO | 800.6477 | 801.1159 | 800.855 | 803.8754 | 0.975128 | |
| ASO | 801.0005 | 801.101 | 801.0422 | 801.4358 | 0.152133 | |
| Case 2 | MRao-2 | 729.3429 | 729.4065 | 729.4001 | 729.4615 | 0.042289 |
| Rao-2 | 729.5025 | 729.5599 | 729.5596 | 729.6205 | 0.040197 | |
| Rao-1 | 729.6406 | 729.6845 | 729.6815 | 729.7441 | 0.031135 | |
| Rao-3 | 729.5657 | 729.5888 | 729.5903 | 729.6361 | 0.021254 | |
| MPA | 729.6347 | 729.674 | 729.6771 | 729.7095 | 0.024818 | |
| TFWO | 729.6002 | 730.1646 | 729.782 | 732.1079 | 0.813312 | |
| ASO | 729.9074 | 730.3542 | 730.251 | 731.555 | 0.513813 | |
| Case 3 | MRao-2 | 730.583 | 730.6588 | 730.6266 | 730.8189 | 0.09241 |
| Rao-2 | 730.6201 | 730.7573 | 730.747 | 730.9311 | 0.141165 | |
| Rao-1 | 731.0468 | 731.132 | 731.1247 | 731.2359 | 0.090685 | |
| Rao-3 | 730.688 | 730.8235 | 730.8296 | 730.9879 | 0.113336 | |
| MPA | 731.0095 | 731.136 | 731.14 | 731.2927 | 0.111756 | |
| TFWO | 730.6851 | 730.9124 | 730.8677 | 731.3553 | 0.23962 | |
| ASO | 731.4898 | 731.8588 | 731.6576 | 732.9515 | 0.546641 |
| Variables | Value | Variables | Value | Variables | Value | Variables | Value | Variables | Value |
|---|---|---|---|---|---|---|---|---|---|
| PG1 (MW) | 1.984061 | PG62 (MW) | 0.04968 | PG113 (MW) | 86.1052 | VG59 (p.u.) | 0.94707 | VG111 (p.u.) | 1.05221 |
| PG4 (MW) | 0.351443 | PG65 (MW) | 343.880 | PG116 (MW) | 4.20199 | VG61 (p.u.) | 1.02331 | VG112 (p.u.) | 1.04184 |
| PG6 (MW) | 1.344034 | PG66 (MW) | 340.152 | VG1 (p.u.) | 0.94 | VG62 (p.u.) | 0.95129 | VG113 (p.u.) | 1.02649 |
| PG8 (MW) | 10.24637 | PG69 (MW) | 415.633 | VG4 (p.u.) | 1.00609 | VG65 (p.u.) | 0.94352 | VG116 (p.u.) | 0.96645 |
| PG10 (MW) | 376.1126 | PG70 (MW) | 4.69474 | VG6 (p.u.) | 1.00546 | VG66 (p.u.) | 1.01735 | T8 (8–5) | 0.91057 |
| PG12 (MW) | 76.80127 | PG72 (MW) | 7.50899 | VG8 (p.u.) | 0.94545 | VG69 (p.u.) | 1.03288 | T32 (25–26) | 1.09451 |
| PG15 (MW) | 1.528393 | PG73 (MW) | 10.3911 | VG10 (p.u.) | 0.94035 | VG70 (p.u.) | 0.97696 | T36 (17–30) | 1.09266 |
| PG18 (MW) | 46.72157 | PG74 (MW) | 5.8267 | VG12 (p.u.) | 0.99321 | VG72 (p.u.) | 1.03499 | T51 (37–38) | 0.9 |
| PG19 (MW) | 0.067021 | PG76 (MW) | 20.4488 | VG15 (p.u.) | 1.01157 | VG73 (p.u.) | 0.98931 | T93 (59–63) | 1.00128 |
| PG24 (MW) | 2.611653 | PG77 (MW) | 5.51401 | VG18 (p.u.) | 0.96454 | VG74 (p.u.) | 0.99958 | T95 (61–64) | 1.03762 |
| PG25 (MW) | 196.2022 | PG80 (MW) | 451.524 | VG19 (p.u.) | 1.04577 | VG76 (p.u.) | 0.99539 | T102 (65–66) | 0.95931 |
| PG26 (MW) | 280.9463 | PG85 (MW) | 0 | VG24 (p.u.) | 0.99640 | VG77 (p.u.) | 0.97826 | T107 (68–69) | 0.95758 |
| PG27 (MW) | 98.34095 | PG87 (MW) | 0.95058 | VG25 (p.u.) | 0.97686 | VG80 (p.u.) | 1.01302 | T127 (80–81) | 1.05250 |
| PG31 (MW) | 0.751755 | PG89 (MW) | 483.822 | VG26 (p.u.) | 0.94265 | VG85 (p.u.) | 0.97493 | QC34 (MVAR) | 3.111 |
| PG32 (MW) | 18.9298 | PG90 (MW) | 2.75380 | VG27 (p.u.) | 1.01799 | VG87 (p.u.) | 0.94034 | QC44 (MVAR) | 29.931 |
| PG34 (MW) | 0.070676 | PG91 (MW) | 0 | VG31 (p.u.) | 1.03403 | VG89 (p.u.) | 1.03117 | QC45 (MVAR) | 29.497 |
| PG36 (MW) | 4.986125 | PG92 (MW) | 1.17943 | VG32 (p.u.) | 0.99471 | VG90 (p.u.) | 1.02089 | QC46 (MVAR) | 28.169 |
| PG40 (MW) | 1.913409 | PG99 (MW) | 16.5592 | VG34 (p.u.) | 1.00824 | VG91 (p.u.) | 1.04970 | QC48 (MVAR) | 0 |
| PG42 (MW) | 1.394682 | PG100 (MW) | 200.116 | VG36 (p.u.) | 0.99818 | VG92 (p.u.) | 1.01643 | QC74 (MVAR) | 24.96 |
| PG46 (MW) | 13.76368 | PG103 (MW) | 23.1161 | VG40 (p.u.) | 0.99148 | VG99 (p.u.) | 1.02329 | QC79 (MVAR) | 28.765 |
| PG49 (MW) | 209.701 | PG104 (MW) | 99.6802 | VG42 (p.u.) | 1.02358 | VG100 (p.u.) | 0.99312 | QC82 (MVAR) | 27.479 |
| PG54 (MW) | 48.30631 | PG105 (MW) | 0.13269 | VG46 (p.u.) | 0.98153 | VG103 (p.u.) | 1.05004 | QC83 (MVAR) | 24.519 |
| PG55 (MW) | 26.09714 | PG107 (MW) | 0.19020 | VG49 (p.u.) | 1.00041 | VG104 (p.u.) | 1.05559 | QC105 (MVAR) | 27.063 |
| PG56 (MW) | 80.54259 | PG110 (MW) | 0.42630 | VG54 (p.u.) | 0.99326 | VG105 (p.u.) | 0.96614 | QC107 (MVAR) | 6.934 |
| PG59 (MW) | 128.7814 | PG111 (MW) | 33.7688 | VG55 (p.u.) | 1.05871 | VG107 (p.u.) | 0.94274 | QC110 (MVAR) | 29.781 |
| PG61 (MW) | 146.4049 | PG112 (MW) | 5.1539 | VG56 (p.u.) | 1.05977 | VG110 (p.u.) | 1.00997 | ||
| Fuel cost ($/h) | 131457.8 | ||||||||
| Power loss (MW) | 96.68278 | ||||||||
| Voltage deviation (p.u.) | 0.730363 | ||||||||
| Algorithm | ASO | TFWO | MPA | Rao-1 | Rao-2 | Rao-3 | MRao-2 |
|---|---|---|---|---|---|---|---|
| Fuel cost ($/h) | 133,610.8 | 132,132.2 | 131,942.6 | 131,817.9 | 131,490.7 | 131,793.1 | 131,457.8 |
| Power loss (MW) | 61.83332 | 65.55476 | 71.94402 | 93.85931 | 95.46617 | 93.95222 | 96.68278 |
| Voltage deviation (p.u.) | 0.658779 | 0.961026 | 1.152593 | 1.328297 | 0.998901 | 1.192274 | 0.730363 |
| Time (s) | 800.709 | 809.028 | 1022.262 | 807.969 | 804.5724 | 806.71149 | 1160.264 |
| Variables | Value | Variables | Value | Variables | Value | Variables | Value | Variables | Value |
|---|---|---|---|---|---|---|---|---|---|
| PG1 (MW) | 3.0911 | PG62 (MW) | 6.37571 | PG113 (MW) | 7.09147 | VG59 (p.u.) | 1.036427 | VG111 (p.u.) | 1.03604 |
| PG4 (MW) | 7.265278 | PG65 (MW) | 298.824 | PG116 (MW) | 0 | VG61 (p.u.) | 0.956257 | VG112 (p.u.) | 0.97545 |
| PG6 (MW) | 79.79656 | PG66 (MW) | 284.31 | VG1 (p.u.) | 1.01134 | VG62 (p.u.) | 1.054308 | VG113 (p.u.) | 1.04051 |
| PG8 (MW) | 0.20039 | PG69 (MW) | 400.029 | VG4 (p.u.) | 1.03191 | VG65 (p.u.) | 0.974536 | VG116 (p.u.) | 0.97347 |
| PG10 (MW) | 332.3392 | PG70 (MW) | 7.71916 | VG6 (p.u.) | 1.02025 | VG66 (p.u.) | 1.00127 | T8 (8–5) | 1.09856 |
| PG12 (MW) | 73.21883 | PG72 (MW) | 0.27496 | VG8 (p.u.) | 0.94257 | VG69 (p.u.) | 1.020322 | T32 (25–26) | 0.90257 |
| PG15 (MW) | 6.500848 | PG73 (MW) | 6.45688 | VG10 (p.u.) | 0.94115 | VG70 (p.u.) | 0.979919 | T36 (17–30) | 0.9 |
| PG18 (MW) | 5.979357 | PG74 (MW) | 5.52285 | VG12 (p.u.) | 0.97438 | VG72 (p.u.) | 1.030921 | T51 (37–38) | 0.90084 |
| PG19 (MW) | 1.346065 | PG76 (MW) | 2.53255 | VG15 (p.u.) | 1.05303 | VG73 (p.u.) | 1.005468 | T93 (59–63) | 1.09369 |
| PG24 (MW) | 1.582226 | PG77 (MW) | 0.22016 | VG18 (p.u.) | 1.04361 | VG74 (p.u.) | 1.020992 | T95 (61–64) | 0.96853 |
| PG25 (MW) | 159.4184 | PG80 (MW) | 363.967 | VG19 (p.u.) | 0.98928 | VG76 (p.u.) | 1.019236 | T102 (65–66) | 0.93325 |
| PG26 (MW) | 215.2208 | PG85 (MW) | 0.07633 | VG24 (p.u.) | 0.96523 | VG77 (p.u.) | 1.034034 | T107 (68–69) | 0.91076 |
| PG27 (MW) | 0.110372 | PG87 (MW) | 4.60698 | VG25 (p.u.) | 1.04943 | VG80 (p.u.) | 1.036756 | T127 (80–81) | 0.9 |
| PG31 (MW) | 1.978596 | PG89 (MW) | 434.560 | VG26 (p.u.) | 1.00787 | VG85 (p.u.) | 1.049239 | QC34 (MVAR) | 0.20760 |
| PG32 (MW) | 2.320654 | PG90 (MW) | 0.12767 | VG27 (p.u.) | 0.97993 | VG87 (p.u.) | 1.059658 | QC44 (MVAR) | 0.00941 |
| PG34 (MW) | 0.120587 | PG91 (MW) | 17.5246 | VG31 (p.u.) | 0.98609 | VG89 (p.u.) | 1.010104 | QC45 (MVAR) | 0.26098 |
| PG36 (MW) | 5.158081 | PG92 (MW) | 1.45348 | VG32 (p.u.) | 0.94097 | VG90 (p.u.) | 0.963199 | QC46 (MVAR) | 0.07600 |
| PG40 (MW) | 32.66632 | PG99 (MW) | 4.11549 | VG34 (p.u.) | 0.94553 | VG91 (p.u.) | 1.042132 | QC48 (MVAR) | 0.24244 |
| PG42 (MW) | 3.238611 | PG100 (MW) | 206.177 | VG36 (p.u.) | 1.00105 | VG92 (p.u.) | 1.040622 | QC74 (MVAR) | 0.2194 |
| PG46 (MW) | 4.574268 | PG103 (MW) | 35.1167 | VG40 (p.u.) | 0.97223 | VG99 (p.u.) | 0.943471 | QC79 (MVAR) | 5.6 × 10−5 |
| PG49 (MW) | 161.9397 | PG104 (MW) | 1.01542 | VG42 (p.u.) | 0.97289 | VG100 (p.u.) | 0.951227 | QC82 (MVAR) | 0.00622 |
| PG54 (MW) | 28.01801 | PG105 (MW) | 15.1016 | VG46 (p.u.) | 0.98664 | VG103 (p.u.) | 1.004165 | QC83 (MVAR) | 0.27248 |
| PG55 (MW) | 0.389909 | PG107 (MW) | 0 | VG49 (p.u.) | 1.00712 | VG104 (p.u.) | 0.987921 | QC105 (MVAR) | 0.03938 |
| PG56 (MW) | 12.21136 | PG110 (MW) | 18.5235 | VG54 (p.u.) | 1.04523 | VG105 (p.u.) | 0.943759 | QC107 (MVAR) | 0.27336 |
| PG59 (MW) | 108.0116 | PG111 (MW) | 35.5095 | VG55 (p.u.) | 1.05831 | VG107 (p.u.) | 0.960449 | QC110 (MVAR) | 0.23428 |
| PG61 (MW) | 122.726 | PG112 (MW) | 2.19141 | VG56 (p.u.) | 0.96064 | VG110 (p.u.) | 1.00083 | ||
| Fuel cost ($/h) | 100738.5 | ||||||||
| Power loss (MW) | 88.04623 | ||||||||
| Voltage deviation (p.u.) | 0.778536 | ||||||||
| Algorithm | ASO | TFWO | MPA | Rao-1 | Rao-2 | Rao-3 | MRao-2 |
|---|---|---|---|---|---|---|---|
| Fuel cost ($/h) | 103,847.47 | 101,747.68 | 101,981.69 | 101,981.17 | 101,078.92 | 101,297.12 | 100,738.54 |
| Power loss (MW) | 58.3333 | 85.062475 | 71.168974 | 89.992651 | 90.296046 | 91.006497 | 88.04623 |
| Voltage deviation (p.u.) | 0.6645742 | 04387701 | 0.7712916 | 1.1227076 | 1.1595186 | 0.9923019 | 0.778536 |
| Time (s) | 792.735 | 802.82732 | 1013.509 | 800.827 | 803.4047 | 798.4426 | 1136.06 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hassan, M.H.; Kamel, S.; Selim, A.; Khurshaid, T.; Domínguez-García, J.L. A Modified Rao-2 Algorithm for Optimal Power Flow Incorporating Renewable Energy Sources. Mathematics 2021, 9, 1532. https://doi.org/10.3390/math9131532
Hassan MH, Kamel S, Selim A, Khurshaid T, Domínguez-García JL. A Modified Rao-2 Algorithm for Optimal Power Flow Incorporating Renewable Energy Sources. Mathematics. 2021; 9(13):1532. https://doi.org/10.3390/math9131532
Chicago/Turabian StyleHassan, Mohamed H., Salah Kamel, Ali Selim, Tahir Khurshaid, and José Luis Domínguez-García. 2021. "A Modified Rao-2 Algorithm for Optimal Power Flow Incorporating Renewable Energy Sources" Mathematics 9, no. 13: 1532. https://doi.org/10.3390/math9131532
APA StyleHassan, M. H., Kamel, S., Selim, A., Khurshaid, T., & Domínguez-García, J. L. (2021). A Modified Rao-2 Algorithm for Optimal Power Flow Incorporating Renewable Energy Sources. Mathematics, 9(13), 1532. https://doi.org/10.3390/math9131532










