Abstract
This paper addresses the problem of predicting time series data using the autoregressive integrated moving average (ARIMA) model in an online manner. Existing algorithms require model selection, which is time consuming and unsuitable for the setting of online learning. Using adaptive online learning techniques, we develop algorithms for fitting ARIMA models without hyperparameters. The regret analysis and experiments on both synthetic and real-world datasets show that the performance of the proposed algorithms can be guaranteed in both theory and practice.
1. Introduction
The autoregressive integrated moving average (ARIMA) model is an important tool for time series analysis [1], and has been successfully applied to a wide range of domains including the forecasting of household electric consumption [2], scheduling in smart grids [3], finance [4], and environment protection [5]. It specifies that the values of a time series depend linearly on their previous values and error terms. In recent years, online learning (OL) methods have been applied to estimate the univariate [6,7] and multivariate [8,9] ARIMA models for their efficiency and scalability. These methods are based on the fact that any ARIMA model can be approximated by a finite dimensional autoregressive (AR) model, which can be fitted incrementally using online convex optimization algorithms. However, to guarantee accurate predictions, these methods require a proper configuration of hyperparameters, such as the diameter of the decision set, the learning rate, the order of differencing, and the lag of the AR model. Theoretically, these hyperparameters need to be set according to prior knowledge about the data generation, which is impossible to obtain. In practice, the hyperparameters are usually tuned to optimize the goodness of fit on the unseen data, which requires numerical simulation (e.g., cross-validation) on a previously collected dataset. The numerical simulation is notoriously expensive, since it requires multiple training runs for each candidate hyperparameter configuration. Furthermore, a previously collected dataset containing ground truth is needed for validation of the fitted model, which is unsuited for the online setting. Unfortunately, the expensive tuning process needs to be regularly repeated if the statistical properties of the time series change over time in an unforeseen way.
Given a new problem of predicting time series values, it appears that tuning the hyperparameters of the online algorithms can negate the benefits of the online setting. This paper addresses this problem in the online learning framework by proposing new parameter-free algorithms for learning ARIMA models, while their performance can still be guaranteed in both theory and practice. A naive attempt for this would be to directly apply parameter-free online convex optimization (PF-OCO) algorithms to the AR approximation. However, the theoretical performance of the AR approximation and the parameter-free algorithms rely on the bounded gradient vectors of the loss function, which is unreasonable for the widely used squared error with an unbounded domain.
The key contribution of this paper is the design of online learning algorithms for ARIMA models, avoiding regular and expensive hyperparameter tuning without damaging the power of the models. Our algorithms update the model incrementally with a computational complexity that is linearly related to the size of the model parameters and the number of candidate models in each iteration. To obtain a solid theoretical foundation, we first show that, for any locally Lipschitz-continuous function, ARIMA models with fixed order of differencing can be approximated using an AR model of the same order for a large enough lag. Based on this, new algorithms are proposed for learning the AR model adaptively without requiring any prior knowledge about the model parameters. For Lipschitz-continuous loss functions, we apply a new algorithm based on the adaptive follow the regularized leader (FTRL) framework [10] and show that our algorithm achieves a sublinear regret bound depending on the data sequence and the Lipschitz constant. A special treatment on the commonly used squared error is required due to its non-Lipschitz continuity. To obtain a data-dependent regret bound, we combine a polynomial regularizer [11] with the adaptive FTRL framework. Finally, to find the proper order and lag of the AR model in an online manner, multiple AR models are simultaneously maintained, and an adaptive hedge algorithm is applied to aggregate their predictions. In the previous attempts [12,13] to solve this online model selection (OMS) problem, the exponentiated gradient (EG) algorithm has been directly applied to aggregate the predictions, which not only requires tuning the learning rate, but also yields a regret bound depending on the loss incurred by the worst model. Our adaptive hedge algorithm is parameter-free and guarantees a regret bound depending on the time series sequence. Table 1 provides a comparison of the online learning algorithms applied to the learning of the ARIMA models. In addition to the theoretical analysis, we also demonstrate the performance of the proposed algorithm using both synthetic and real-world datasets.

Table 1.
Algorithms for online learning of ARIMA.
The rest of the paper is organized as follows. Section 2 reviews the existing work on the subject. The notation, learning model, and formal description of the problem are introduced in Section 3. Next, we present and analyze our algorithms in Section 4. Section 5 demonstrates the empirical performance of the proposed methods. Finally, we conclude our work with some future research directions in Section 6.
| Algorithm 1 ARIMA-AdaFTRL. |
Input: Initialize arbitrarily, , for for to T do for to m do if then else end if end for Play Observe and for to m do end for end for |
| Algorithm 2 ARIMA-AdaFTRL-Poly. |
Input: Initialize arbitrarily, for to T do if then Select satisfying else end if Play Observe and end for |
| Algorithm 3 ARIMA-AO-Hedge. |
Input: predictor , d Initialize , for for to T do Get prediction from for Set Set for if then Set for some else Set for end if Predict Observe , update , and set for end for |
2. Related Work
An ARIMA model can be fitted using statistical methods such as recursive least square and maximum likelihood estimation, which are not only based on strong assumptions such as the Gaussian distributed noise terms [18], linear dependencies [19], and data generated by a stationary process [20], but also require solution of non-convex optimization problems [21]. Although these assumptions can be relaxed by considering non-Gaussian noise [22,23], non-stationary processes [24], or a convex relaxation [21], the pre-trained models still cannot deal with concept drift [7]. Moreover, retraining is time consuming and memory intensive, especially for large-scale datasets. The idea of applying regret minimization techniques to autoregressive moving average (ARMA) prediction was first introduced in [6]. The authors propose online algorithms incrementally producing predictions close to the values generated by the best ARMA model. This idea was extended to models in [7] by learning the model of the higher-order differencing of the time series. Further extensions to multiple time series can be found in [8,9], while the problem of predicting time series with missing data was addressed in [25].
In order to obtain accurate predictions, the lag of the AR model and the order of differencing have to be tuned, which has been well studied in the offline setting. In some textbooks [20,26,27], Akaike’s Information Criterion (AIC) and the Bayesian Information Criterion (BIC) are recommended for this task. Both require prior knowledge and strong assumptions about the variance of the noise [20], and are time and space consuming as they require numerical simulation such as cross-validation on previously collected datasets. Nevertheless, given a properly selected lag m and order d, online convex optimization techniques such as online Newton step (ONS) or online gradient descent (OGD) can be applied to fitting the model in the regret minimization framework [6,7,8,9]. However, both algorithms introduce additional hyperparameters to control the learning rate and numerical stability.
The idea of selecting hyperparameters for online time series prediction was proposed in [12,13]. Regarding the online AR predictor with different lags as experts, the authors aggregate over predictors by applying a multiplicative weights algorithm for prediction with expert advice. The proposed algorithm is not optimal for time series prediction, since the regret bound of the chosen algorithm depends on the largest loss incurred by the experts [28]. Furthermore, each individual expert still requires that the parameters are taken from a compact decision set, the diameter of which needs to be tuned in practice. A series of recent works on parameter-free online learning have provided possibilities of achieving sublinear regret without prior information on the decision set. In [14], the unconstrained online learning problem is modeled as a betting game, based on which a parameter-free algorithm is developed. The algorithm was further extended in [15], so a better regret bound can be achieved for strongly convex loss functions. However, the coin betting algorithm requires that the gradient vectors are normalized, which is unrealistic for unbounded time series and the squared error loss. In [16,17], the authors introduced parameter-free algorithms without requiring normalized gradient vectors. Unfortunately, the regret upper bounds of the proposed algorithms depend on the norm of the gradient vectors, which could be extremely large in our setting.
The main idea of the current work is based on the combination of the adaptive FTRL framework [10] and the idea of handling relative Lipschitz continuous functions [11], which makes it possible to devise an online algorithm with a data-dependent regret upper bound. To aggregate the results, an adaptive optimistic algorithm is proposed, such that the overall regret depends on the data sequence instead of the worst-case loss.
3. Preliminary and Learning Model
Let denote the value observed at time t of a time series. We assume that is taken from a finite dimensional real vector space with norm . We denote by the vector space of bounded linear operators from to and the corresponding operator norm. An model is given by
where is a linear operator and is an error term. The model extends the model by adding a moving average (MA) component as follows:
where is the error term and . We define the d-th order differencing of the time series as for and . The model assumes that the d-th order differencing of the time series follows an model. In this section, this general setting suffices for introducing the learning model. In the following sections, we fix the basis of to obtain implementable algorithms, for which different kinds of norms and inner products for vectors and matrices are needed. We provide a table of required notation in Appendix C.
In this paper, we consider the setting of online learning, which can be described as an iterative game between a player and an adversary. In each round t of the game, the player makes a prediction . Next, the adversary chooses some and reveals it to the player, who then suffers the loss for some convex loss function . The ultimate goal is to design a strategy for the player to minimize the cumulative loss of T rounds. For simplicity, we define
In classical textbooks about time series analysis, the signal is assumed to be generated by a model, based on which the predictions are made. In this paper, we make no assumptions on the data generation. Therefore, minimizing the cumulative loss is generally impossible. An achievable objective is to keep a possibly small regret of not having chosen some model to generate the prediction . Formally, we denote by the prediction using the model parameterized by and , given by (in this paper, we do not directly address the problem of the cointegration, where the third term should be applied to a low-rank linear operator):
The cumulative regret of T rounds is then given by
The goal of this paper is to design a strategy for the player such that the cumulative regret grows sublinearly in T. In the ideal case, in which the data are actually generated by an ARIMA process, the prediction generated by the player yields a small loss. Otherwise, the predictions are always close to those produced by the best ARIMA model, independent of the data generation. Following the adversarial setting in [6], we allow the sequences , and the parameters , to be selected by the adversary. Without any restrictions on the model, this is no different than the impossible task of minimizing the cumulative loss, since can always be selected such that holds for all t. Therefore, we make the following assumptions throughout this paper:
Assumption 1.
, and there is some such that for all .
Assumption 2.
The coefficients satisfy for some .
Since we are interested in competing against predictions generated by ARIMA models, we assume that is selected as if is generated by the ARIMA process. Furthermore, we assume the norm is upper bounded within T iterations. Assumption 2 is a sufficient condition for the MA component to be invertible, which prevents it from going to infinity as [27].
Our work is based on the fact that we can compete against an model by taking predictions from an model of the d-th order differencing for large enough m, which is shown in the following lemma, the proof of which can be found in Appendix A.
Lemma 1.
Let , , α, and β be as assumed in Assumptions 1 and 2. Then there is some with such that
holds for all , where we define .
As can be seen from the lemma, a prediction generated by the process
is close to the prediction generated by the ARIMA process. In the previous works [6,7], the loss function is assumed to be Lipschitz continuous to control the difference of loss incurred by the approximation. In general, this does not hold for squared error. However, from Assumption 1 and Lemma 1, it follows that both and lie in a compact set around with a bounded diameter. Given the convexity of l, which is local Lipschitz continuous in the compact convex domain, we obtain a similar property:
where is some constant depending on . For squared error, it is easy to verify that the Lipschitz constant depends on , the boundedness of which can be reasonably assumed. To avoid extraneous details, we simply add the third assumption:
Assumption 3.
Define set . There is a compact convex set , such that is L-Lipschitz continuous in for .
The next corollary shows that the losses incurred by the ARIMA and its approximation are close, which allows us to take predictions from the approximation.
Corollary 1.
Let , , α, β, and l be as assumed in Assumptions 1–3. Then there is some with , such that
holds for all .
Proof.
It follows from Assumption 1 and Lemma 1 that holds for all . Together with Assumption 3, we obtain
Applying Lemma 1, we obtain the claimed result. □
4. Algorithms and Analysis
From Corollary 1, it follows clearly that an ARIMA(p,q,d) model can be approximated by an integrated AR model with large enough m. However, neither the order of differencing d nor the lag m is known. To circumvent tuning them using a previously collected dataset, we propose a framework with a two-level hierarchical construction, which is described in Algorithm 4.
| Algorithm 4 Two-level framework. |
Input: K instances of the slave algorithm . An instance of master algorithm . for to T do Get from each Get from ▹ is the standard K-simplex Integrate the prediction: Observe Define with Update using for Update using end for |
The idea is to maintain a master algorithm and a set of slave algorithms . At each step t, the master algorithm receives predictions from for . Then it comes up with a convex combination for some in the simplex. Next, it observes and computes the loss for each slave , which is then used to update and . Let be the sequence generated by some slave k. We define the regret of not having chosen the prediction generated by slave k as
and the regret of the slave k
where is the prediction generated by an integrated AR model parameterized by . Let be some slave. Then the regret of this two-level framework can obviously be decomposed as
For , , and satisfying the condition in Corollary 1 (this is not a condition of having a correct algorithm—with more slaves, there are more satisfying the condition; we increase the freedom of the model by increasing the number of slaves), the marked term above is upper bounded by a constant, that is,
If the regret of the master and the slaves grow sublinearly in T, we can achieve an overall sublinear regret upper bound, which is formally described in the following corollary.
Corollary 2.
Let be an online learning algorithm against an model parameterized by for . For any ARIMA model parameterized by α and β, if there is a such that , and satisfy Assumptions 1–3, then running Algorithm 4 with and guarantees
Next, we design and analyze parameter-free algorithms for the slaves and the master.
4.1. Parameter-Free Online Learning Algorithms
4.1.1. Algorithms for Lipschitz Loss
Given fixed m and d, an integrated model can be treated as an ordinary linear regression model. In each iteration t, we select and make prediction
Since is convex, there is some subdifferential such that
for all . Define . The regret can be further upper bounded by
Thus, we can cast the online linear regression problem to an online linear optimization problem. Unlike the previous work, we focus on the unconstrained setting, where is not picked from a compact decision set. In this setting, we can apply an FTRL algorithm with an adaptive regularizer. To obtain an efficient implementation, we fix a basis for both and . Now we can assume and work with the matrix representation of . It is easy to verify that (2) can be rewritten as
where is the Frobenius inner product. It is well known that the Frobenius inner product can be considered as a dot product of vectorized matrices, with which we obtain a simple first-order (the computational complexity per iteration depends linearly on the dimension of the parameter, i.e., ) algorithm described in Algorithm 1.
The cumulative regret of Algorithm 1 can be upper bounded using the following theorem.
Theorem 1.
Let be any sequence of vectors taken from . Algorithm 1 guarantees
For an L-Lipschitz loss function , in which is upper bounded by L, we obtain a sublinear regret upper bound depending on the sequence of d-th order differencing . In case L is known, we can set , otherwise picking arbitrarily from a reasonable range (e.g., ) would not have a devastating impact on the performance of the algorithms.
4.1.2. Algorithms for Squared Errors
For the commonly used squared error given by
it can be verified that can be represented as a vector
for all t. Existing algorithms, which have a regret upper bound depending on , could fail since can be set arbitrarily large due to the adversarially selected data sequence . To design a parameter-free algorithm for the squared error, we equip FTRL with a time-varying polynomial regularizer described in Algorithm 2.
Define
and consider the matrix representation . Then we have , and the upper bound of the regret can be rewritten as
The idea of Algorithm 2 is to run the FTRL algorithm with a polynomial regularizer
for increasing sequences and , which leads to updating rule given by
for c satisfying . Since we have and for , c exists and has a closed-form expression. The computational complexity per iteration has a linear dependency on the dimension of . The following theorem provides a regret upper bound of Algorithm 2.
Theorem 2.
Let be any sequence of vectors taken from and
be the squared error. We define and , the matrix representation of . Then, Algorithm 2 guarantees
for all .
For squared error, Algorithm 2 does not require a compact decision set and ensures a sublinear regret bound depending on the data sequence. Similar to Algorithm 1, one can set according to the prior knowledge about the bounds of the time series. Alternatively, we can simply set to obtain a reasonable performance.
4.2. Online Model Selection Using Master Algorithms
The straightforward choice of the master algorithm would be the exponentiated gradient algorithm for prediction with expert advice. However, this algorithm requires tuning of the learning rate and losses bounded by a small quantity, which can not be assumed for our case. The AdaHedge algorithm [29] solves these problems. However, it yields a worst-case regret bound depending on the largest loss observed, which could be much worse compared to a data-dependent regret bound.
Our idea is based on the adaptive optimistic follow the regularized leader (AO-FTRL) framework [10]. Given a sequence of hints and loss vectors , AO-FTRL guarantees a regret bound related to for some time-varying norm . In our case, where the loss incurred by a slave is given by at iteration t, we simply choose . If l is L-Lipschitz in its first argument, then we have , which leads to a data-dependent regret. The obtained algorithm is described in Algorithm 3. Its regret is upper bounded by the following theorem, the proof of which is provided in Appendix B.
Theorem 3.
Let , , , , and be as generated in Algorithm 3. Assume l is L-Lipschitz in its first argument and convex in its second argument. Then for any sequence and slave algorithm , we have
By Corollary 2, combining Algorithm 3 with Algorithms 1 or 2 guarantees a data-dependent regret upper bound sublinear in T. Note that there is an input parameter d for Algorithm 3, which can be adjusted according to the prior knowledge of the dataset such that can be bounded by a small quantity. In case no prior knowledge can be obtained, we can set d to the maximal order of differencing used in the slave algorithms. Arguably, the Lipschitz continuity is not a reasonable assumption for squared error with unbounded domain. With a bounded , we can assume that the loss function is locally Lipschitz, but with a Lipschitz constant depending on the prediction. In the next section, we show the performance of Algorithm 3 in combination with Algorithms 1 and 2 in different experimental settings.
5. Experiments and Results
In this section, we carry out experiments on both synthetic and real-world data to show that the proposed algorithms can generate promising predictions without tuning hyperparameters.
5.1. Experiment Settings
The synthetic data was generated randomly. We run 20 trials for each synthetic experiment and average the results. For numerical stability, we scale the real-world data down so that the values are between 0 and 10. Note that the range of the data are not assumed or used in the algorithms.
Setting 1: Sanity Check
For a sanity check, we generate a stationary 10-dimensional process using randomly drawn coefficients.
Setting 2: Time-Varying Parameters
Aimed at demonstrating the effectiveness of the proposed algorithm in the non-stationary case, we generate the non-stationary 10-dimensional process using time-varying parameters. We draw , and randomly and independent, and generate data at iteration t with the model parameterized by and .
Setting 3: Time-Varying Models
To get more adversarially selected time series values, we generate the first half of the values using a stationary 10-dimensional model and the second half of the values using a stationary 10-dimensional model. The model parameters are drawn randomly.
Stock Data: Time Series with Trend
Following the experiments in [8], we collect the daily stock prices of seven technology companies from Yahoo Finance together with the S&P 500 index for over twenty years, which has an obvious increasing trend and is believed to exhibit integration.
Google Flu Data: Time Series with Seasonality
We collect estimates of influenza activity of the northern hemisphere countries, which has an obvious seasonal pattern. In the experiment, we examine the performance of the algorithms for handling regular and predictable changes that occur over a fixed period.
Electricity Demand: Trend and Seasonality
In this setting, we collect monthly load, gross electricity production, net electricity consumption, and gross demand in Turkey from 1976 to 2010. The dataset contains both trend and seasonality.
5.2. Experiments for the Slave Algorithms
We first fix and and compare our slave algorithms with ONS and OGD from [9] for squared error and Euclidean distance . ONS and OGD stack and vectorize the parameter matrices, and incrementally update the vectorized parameter respectively using the following rules
and
where is the vectorized gradient at step t, is the decision set satisfying , and the operator projects v into . We select a list of candidate values for each hyperparameter, evaluate their performance on the whole dataset, and select the configuration with the best performance for comparison. Since the synthetic data are generated randomly, we average the results over 20 trials for stability. The corresponding results are shown in Figure 1, Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6 (to amplify the differences of the algorithms, we use plots for the y-axis for all settings; for the synthetic datasets, we also use plot for the x-axis, so that the behavior of the algorithms in the first 1000 steps can be better observed). To show the impact of the hyperparameters on the performance of the baseline algorithm, we also plot their performance using sub-optimal configurations. Note that since the error term cannot be predicted, an ideal predictor would suffer an average error rate of at least and for the two kinds of loss function. This is known for the synthetic datasets and plotted in the figures.
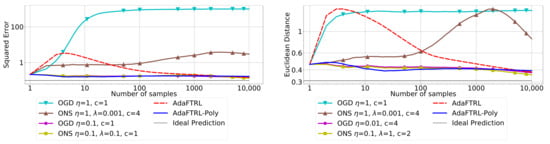
Figure 1.
Results for setting 1 (sanity check), using a stationary ARIMA(5,2,1) model.
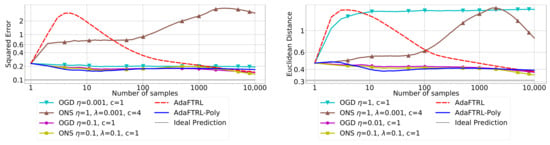
Figure 2.
Results for setting 2 (time-varying parameters), using a non-stationary ARIMA(5,2,1) model.
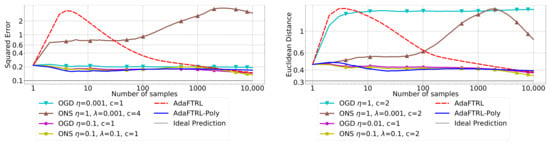
Figure 3.
Results for setting 3 (time-varying models), using a combination of stationary ARIMA(5,2,1) and ARIMA(5,2,0) models.
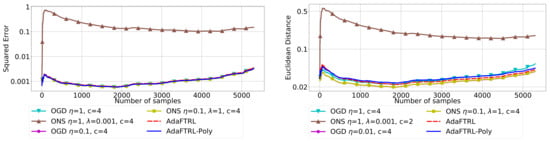
Figure 4.
Results for stock data.
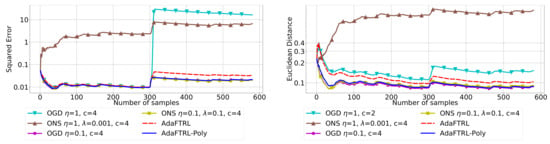
Figure 5.
Results for Google Flu data.
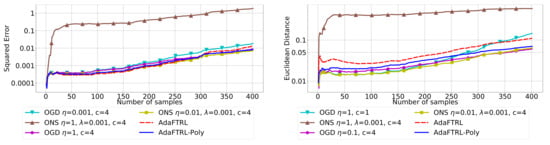
Figure 6.
Results for electricity demand data.
In all settings, both AdaFTRL and AdaFTRL-Poly have a performance on par with well-tuned OGD and ONS, which can have extremely bad performance using sub-optimal hyperparameter configurations. In the experiments using synthetic datasets, AdaFTRL suffers large loss at the beginning while generating accurate predictions after 1000 iterations. The relative performances of the proposed algorithms after the first 1000 iterations compared to the best tuned baseline algorithms are plotted in Appendix D. AdaFTRL-Poly has more stable performance compared to AdaFTRL. In the experiment with Google Flu data, all algorithms suffer huge losses around iteration 300 due to an abrupt change in the dataset. OGD and ONS with sub-optimal hyperparameter configurations, despite good performance for the first half of the data, generate very inaccurate predictions after the abrupt change in the dataset. This could lead to a catastrophic failure in practice, when certain patterns do not appear in the dataset collected for hyperparameter tuning. Our algorithms are more robust against this change and perform similarly to OGD and ONS with optimal hyperparameter configurations.
5.3. Experiments for Online Model Selection
The performance of the two-level framework and Algorithm 3 for online model selection is demonstrated in Figure 7, Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12. We simultaneously maintain 96 models of d-th-order differencing for and , which are updated by Algorithms 1 and 2 for squared error and Euclidean distance, respectively. The predictions generated by the AR models are aggregated using Algorithm 3 and the aggregation algorithm (AA) introduced in [13] with learning rate set to . We compare the average losses incurred by the aggregated predictions with those incurred by the best AR model. To show the impact of m and d, we also plot the average loss of some other sub-optimal AR models.
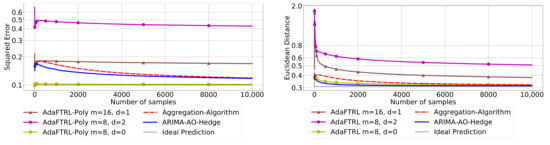
Figure 7.
Model selection in setting 1.
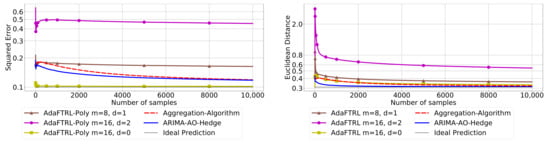
Figure 8.
Model selection in setting 2.
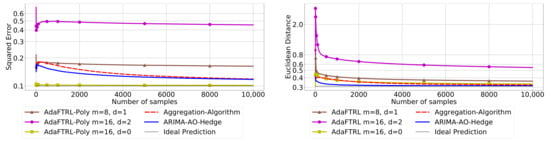
Figure 9.
Model selection in setting 3.
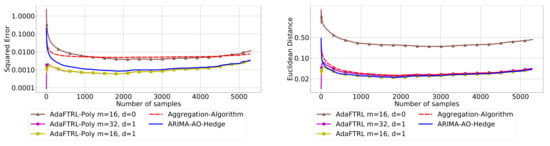
Figure 10.
Model selection for stock data.
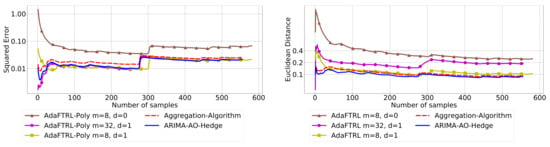
Figure 11.
Model selection for Google Flu.
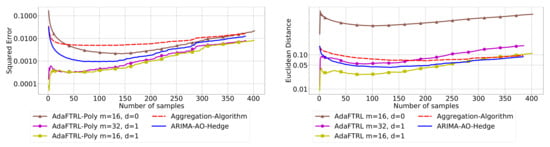
Figure 12.
Model Selection for electricity demand.
In all settings, AO-Hedge outperforms AA, although the differences are very slight in some of the experiments. We would like to stress again that the choice of the hyperparameters has a great impact on the performance of the AR model. In settings 1–3, the AR model with 0-th-order differencing has the best performance, although the data are generated using , which suggests that the prior knowledge about the data generation may not be helpful for the model selection in all cases. The experimental results also show that AO-Hedge has a performance similar to the best AR model.
6. Conclusions
We proposed algorithms for fitting ARIMA models in an online manner without requiring prior knowledge or tuning hyperparameters. We showed that the cumulative regret of our method grows sublinearly with the number of iterations and depends on the values of the time series. The comparison study on both synthetic and real-world datasets suggests that the proposed algorithms have a performance on par with the well-tuned state-of-the-art algorithms.
There are still several remaining issues that we want to address in future research. Firstly, it would be interesting to also develop a parameter-free algorithm for the cointegrated vector ARMA model. Secondly, we believe that the strong assumption on the coefficient can be relaxed for multi-dimensional time series by generalizing Lemma 2 in [7]. Furthermore, we are also interested in applying online learning to other time series models such as the (generalized) ARCH model [30]. Finally, the proposed algorithms need to be empirically analyzed using more real-world datasets and loss functions, and compared with more recent predictive models such as recurrent neural networks and the models combining neural networks and ARIMA models [31].
Author Contributions
Conceptualization, W.S.; methodology, W.S. and L.F.R.; validation, W.S., L.F.R., and F.S.; formal analysis, W.S.; investigation, W.S. and L.F.R.; writing—original draft preparation, W.S. and L.F.R.; writing—review and editing, W.S., L.F.R., F.S., and S.A.; visualization, L.F.R.; supervision, F.S. and S.A. All authors have read and agreed to the published version of the manuscript.
Funding
We acknowledge support by the German Research Foundation and the Open Access Publication Fund of TU Berlin.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The source code for generating the synthetic data set, the implementation of the algorithms, and the detailed information about our experiments are available on GitHub: https://github.com/OnlinePredictorTS/AOLForTimeSeries (accessed on March 2021). The stock data are collected from https://finance.yahoo.com/ (accessed on March 2021). The Google Flu data are available in https://github.com/datalit/googleflutrends/ (accessed on March 2021). The detailed information about the electricity demand can be found in [32].
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
We prove Lemma 1 in this section. Consider the ARIMA model given by
with for . Let
be the t-th value generated by the ARIMA process. To prove Lemma 1, we generalize the proof provided in [6]. To remove the MA component, we first recursively define a growing process of the d-th-order differencing
with for . Let
be the t-th value generated by this process.
The next lemma shows that it approximates an process.
Lemma A1.
For any α, β, and satisfying Assumptions 1 and 2, we have, for ,
Proof.
First of all, we have
for . Define . W.l.o.g. we can assume for . Next, we prove by induction on t that holds for all . For the induction basis, we have
for all . We assume the claim holds for some t, then we have
which concludes the induction. Finally, we have
which is the claimed result. □
Next, we recursively define the following process:
where for . Let be the sequence generated as follows:
We show in the next lemma that it is close to .
Lemma A2.
For any α, β, , and satisfying A1–A2, we have
for .
Proof.
Define . We prove by induction on m that
holds for all and . For , we have for
By the definition of the stochastic process , we have
where is defined as in the proof of Lemma A1. From the assumption, we have , and, as we have proved in Lemma A1, holds. Therefore, we obtain , which is the induction basis. Next, assume the claim holds for all . Then we have
From the induction hypothesis, we have
From the proof of the induction basis, we have
Therefore, can be further bounded using
Choosing , we have
which is the claimed result. □
This process of the d-th-order differencing is actually an integrated process with order d, which is shown in the following lemma.
Lemma A3.
Proof.
Let be the sequence generated by (A1). We prove by induction on m that for all there is a such that
holds for all α and β. The induction basis follows directly from the definition that
Assume that the claim holds for some m. Let be the zero linear functional for and be the zero linear functional for . Then we have
where the second equality follows from the fact that for , the third line uses the induction hypothesis and the last line is obtained by rearranging and setting for . The induction step is obtained by setting
for , and the claimed result follows. □
Finally, we prove Lemma 1 by combining the results.
Proof of Lemma 1.
From Lemmas A1, A2, and A3, there is some with such that
which is the claimed result. □
Appendix B
In this section, we prove the theorems in Section 4. The required notation is summarized in Appendix C. We apply some important properties of convex functions and their convex conjugate defined on a general vector space, which can be found in [17]. The proposed algorithms are instances of the adaptive optimistic follow the regularized leader (AO-FTRL) [10], which is described in Algorithm A1.
| Algorithm A1 AO-FTRL. |
Input: closed convex set Initialize: arbitrary for to T do Get hint Observe end for |
Lemma A4.
We run AO-FTRL with closed convex regularizers defined on satisfying for all and . Then, for all , we have
where is the Bregman divergence associated with .
Proof.
W.l.o.g. we assume , since it is not involved in the algorithm. Then we have
Furthermore, we have
Combining the inequalities above, rearranging and adding to both sides, we obtain
which is the claimed result. □
Proof of Theorem 1.
First of all, since we have
the overall regret can be considered as the sum of the regrets . Next, we analyse the regret of each . Define . It is easy to verify for . Applying Lemma A4 with , we obtain
From the updating rule of , we have for . Let be the smallest index such that . Then we have
For , is -strongly convex with respect to . From the duality of strong convexity and strong smoothness (see Proposition 2 in [17]), we have
From the definition of Frobenius norm, we have
Then, we obtain
where the second inequality uses Lemma 4 in [17] and the last inequality follows from the fact that . Furthermore, we have
and . Adding up from 1 to m, we have
□
Proof of Theorem 2.
Define . First of all, it is easy to verify that . Applying Lemma A4 with , we have
Define . Then we have
where we define and . From the properties of the Frobenius norm, we have
Following the idea of [33], we can upper bound as follows:
Thus, for , we have
where the second inequality uses the fact that . Let be the smallest index such that . Then we have
where the last inequality uses Lemma 4 in [17]. Similarly, let be the smallest index such that . Then we obtain the upper bound
Combining (A3)–(A6), we obtain
For , it is easy to verify that . By putting this in the inequality above, we obtain the claimed result. □
Proof of Theorem 3
Proof.
Define
where . It can be verified that . Applying Lemma A4, we obtain
From the definition of , it follows that and hold. Define . Next, we bound the third term as follows:
where the first inequality uses the fact that is strongly convex w.r.t. . Adding up from 1 to T, we have
Combining the inequalities, we obtain
where the first inequality follows from Jensen’s inequality. Furthermore, if l is L-Lipschitz in its first argument, then we have
Finally, we obtain the regret upper bound
which is the claimed result. □
Appendix C
We summarize the main notations used throughout the article in Table A1.

Table A1.
Nomenclature.
Table A1.
Nomenclature.
| finite dimensional norm space | |
| the dual space with dual norm of | |
| vector space of bounded linear operators | |
| the operator norm of | |
| 2 norm for | |
| 1 norm for | |
| max norm for | |
| Frobenius inner product | |
| Frobenius norm | |
| standard d-simplex | |
| closed convex function | |
| the set of subdifferential of at w | |
| convex conjugate of | |
| , where | the Bregman divergence |
Appendix D
For the synthetic data, the relative performance of the proposed algorithms after the first 1000 iterations are plotted in Figure A1, Figure A2, and Figure A3. For each setting, we calculate the average loss after the first 1000 iterations and plot the difference of the proposed algorithms compared to the average loss incurred by the best baseline algorithm.
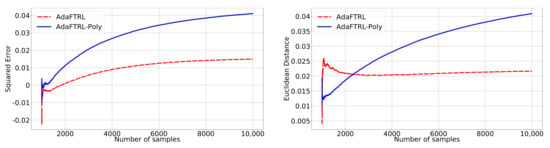
Figure A1.
Relative performance for setting 1.
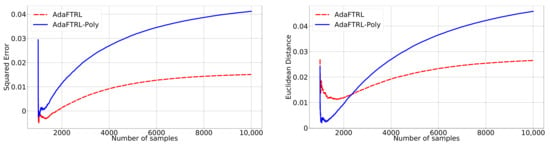
Figure A2.
Relative performance for setting 2.
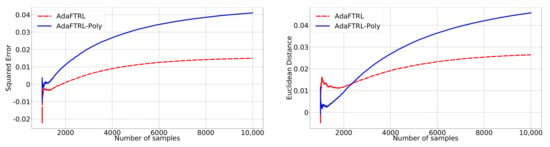
Figure A3.
Relative performance for setting 3.
Similarly, we plot the relative performance for the real-world data over the time horizon in Figure A4, Figure A5 and Figure A6.
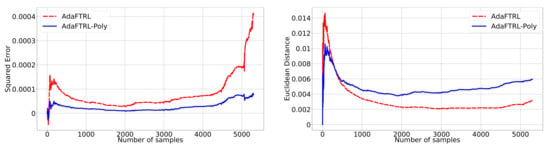
Figure A4.
Relative performance for stock data.
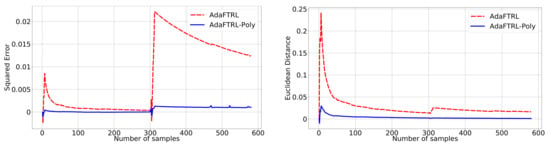
Figure A5.
Relative performance for Google Flu.
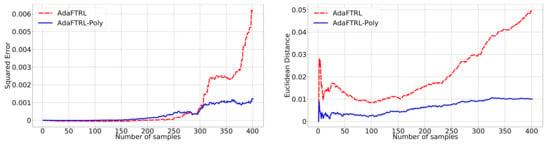
Figure A6.
Relative Performance for electricity demand.
References
- Shumway, R.; Stoffer, D. Time Series Analysis and Its Applications: With R Examples; Springer Texts in Statistics; Springer: New York, NY, USA, 2010. [Google Scholar]
- Chujai, P.; Kerdprasop, N.; Kerdprasop, K. Time series analysis of household electric consumption with ARIMA and ARMA models. In Proceedings of the International MultiConference of Engineers and Computer Scientists, Hong Kong, China, 13–15 March 2013; Volume 1, pp. 295–300. [Google Scholar]
- Ghofrani, M.; Arabali, A.; Etezadi-Amoli, M.; Fadali, M.S. Smart scheduling and cost-benefit analysis of grid-enabled electric vehicles for wind power integration. IEEE Trans. Smart Grid 2014, 5, 2306–2313. [Google Scholar] [CrossRef]
- Rounaghi, M.M.; Zadeh, F.N. Investigation of market efficiency and financial stability between S&P 500 and London stock exchange: Monthly and yearly forecasting of time series stock returns using ARMA model. Phys. A Stat. Mech. Its Appl. 2016, 456, 10–21. [Google Scholar]
- Zhu, B.; Chevallier, J. Carbon price forecasting with a hybrid Arima and least squares support vector machines methodology. In Pricing and Forecasting Carbon Markets; Springer: Berlin/Heidelberg, Germany, 2017; pp. 87–107. [Google Scholar]
- Anava, O.; Hazan, E.; Mannor, S.; Shamir, O. Online learning for time series prediction. In Proceedings of the Conference on Learning Theory, Princeton, NJ, USA, 23–26 June 2013; pp. 172–184. [Google Scholar]
- Liu, C.; Hoi, S.C.; Zhao, P.; Sun, J. Online ARIMA algorithms for time series prediction. In Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016; pp. 1867–1873. [Google Scholar]
- Xie, C.; Bijral, A.; Ferres, J.L. Nonstop: A nonstationary online prediction method for time series. IEEE Signal Process. Lett. 2018, 25, 1545–1549. [Google Scholar] [CrossRef] [Green Version]
- Yang, H.; Pan, Z.; Tao, Q.; Qiu, J. Online learning for vector autoregressive moving-average time series prediction. Neurocomputing 2018, 315, 9–17. [Google Scholar] [CrossRef]
- Joulani, P.; György, A.; Szepesvári, C. A modular analysis of adaptive (non-) convex optimization: Optimism, composite objectives, variance reduction, and variational bounds. Theor. Comput. Sci. 2020, 808, 108–138. [Google Scholar] [CrossRef]
- Zhou, Y.; Sanches Portella, V.; Schmidt, M.; Harvey, N. Regret Bounds without Lipschitz Continuity: Online Learning with Relative-Lipschitz Losses. Adv. Neural Inf. Process. Syst. 2020, 33, 15823–15833. [Google Scholar]
- Jamil, W.; Bouchachia, A. Model selection in online learning for times series forecasting. In UK Workshop on Computational Intelligence; Springer: Berlin/Heidelberg, Germany, 2018; pp. 83–95. [Google Scholar]
- Jamil, W.; Kalnishkan, Y.; Bouchachia, H. Aggregation Algorithm vs. Average For Time Series Prediction. In Proceedings of the ECML PKDD 2016 Workshop on Large-Scale Learning from Data Streams in Evolving Environments, Riva del Garda, Italy, 23 September 2016; pp. 1–14. [Google Scholar]
- Orabona, F.; Pál, D. Coin betting and parameter-free online learning. In Proceedings of the 30th International Conference on Neural Information Processing Systems, Barcelona, Spain, 4–9 December 2016; pp. 577–585. [Google Scholar]
- Cutkosky, A.; Orabona, F. Black-box reductions for parameter-free online learning in banach spaces. In Proceedings of the Conference on Learning Theory, Stockholm, Sweden, 6–9 July 2018; pp. 1493–1529. [Google Scholar]
- Cutkosky, A.; Boahen, K. Online learning without prior information. In Proceedings of the Conference on Learning Theory, Amsterdam, The Netherlands, 7–10 July 2017; pp. 643–677. [Google Scholar]
- Orabona, F.; Pál, D. Scale-free online learning. Theor. Comput. Sci. 2018, 716, 50–69. [Google Scholar] [CrossRef] [Green Version]
- Hamilton, J.D. Time Series Analysis; Princeton University Press: Princeton, NJ, USA, 1994; Volume 2. [Google Scholar]
- Box, G.E.; Jenkins, G.M.; Reinsel, G.C.; Ljung, G.M. Time Series Analysis: Forecasting and Control; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Brockwell, P.J.; Davis, R.A. Time Series: Theory and Methods; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Georgiou, T.T.; Lindquist, A. A convex optimization approach to ARMA modeling. IEEE Trans. Autom. Control 2008, 53, 1108–1119. [Google Scholar] [CrossRef]
- Lii, K.S. Identification and estimation of non-Gaussian ARMA processes. IEEE Trans. Acoust. Speech Signal Process. 1990, 38, 1266–1276. [Google Scholar] [CrossRef]
- Huang, S.J.; Shih, K.R. Short-term load forecasting via ARMA model identification including non-Gaussian process considerations. IEEE Trans. Power Syst. 2003, 18, 673–679. [Google Scholar] [CrossRef] [Green Version]
- Ding, F.; Shi, Y.; Chen, T. Performance analysis of estimation algorithms of nonstationary ARMA processes. IEEE Trans. Signal Process. 2006, 54, 1041–1053. [Google Scholar] [CrossRef]
- Yang, H.; Pan, Z.; Tao, Q. Online Learning for Time Series Prediction of AR Model with Missing Data. Neural Process. Lett. 2019, 50, 2247–2263. [Google Scholar] [CrossRef]
- Ding, J.; Noshad, M.; Tarokh, V. Order selection of autoregressive processes using bridge criterion. In Proceedings of the 2015 IEEE International Conference on Data Mining Workshop (ICDMW), Atlantic City, NJ, USA, 14–17 November 2015; pp. 615–622. [Google Scholar]
- Lütkepohl, H. New Introduction to Multiple Time Series Analysis; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Steinhardt, J.; Liang, P. Adaptivity and optimism: An improved exponentiated gradient algorithm. In Proceedings of the International Conference on Machine Learning, PMLR, Bejing, China, 22–24 June 2014; pp. 1593–1601. [Google Scholar]
- De Rooij, S.; Van Erven, T.; Grünwald, P.D.; Koolen, W.M. Follow the leader if you can, hedge if you must. J. Mach. Learn. Res. 2014, 15, 1281–1316. [Google Scholar]
- Bollerslev, T. Generalized autoregressive conditional heteroskedasticity. J. Econom. 1986, 31, 307–327. [Google Scholar] [CrossRef] [Green Version]
- Deng, Y.; Fan, H.; Wu, S. A hybrid ARIMA-LSTM model optimized by BP in the forecast of outpatient visits. J. Ambient. Intell. Humaniz. Comput. 2020. [Google Scholar] [CrossRef]
- Tutun, S.; Chou, C.A.; Canıyılmaz, E. A new forecasting framework for volatile behavior in net electricity consumption: A case study in Turkey. Energy 2015, 93, 2406–2422. [Google Scholar] [CrossRef]
- Lu, H. “Relative Continuity” for Non-Lipschitz Nonsmooth Convex Optimization Using Stochastic (or Deterministic) Mirror Descent. Informs J. Optim. 2019, 1, 288–303. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).