Weak Dependence Notions and Their Mutual Relationships

Abstract

New weak notions of positive dependence between the components X and Y of a random pair $(X,Y)$ have been considered in recent papers that deal with the effects of dependence on conditional residual lifetimes and conditional inactivity times. The purpose of this paper is to provide a structured framework for the definition and description of these notions, and other new ones, and to describe their mutual relationships. An exhaustive review of some well-know notions of dependence, with a complete description of the equivalent definitions and reciprocal relationships, some of them expressed in terms of the properties of the copula or survival copula of $(X,Y)$, is also provided.

1. Introduction

In the past few decades, a number of different concepts and notions of dependence between the components X and Y of a random pair $(X,Y)$ have been defined and applied in a variety of fields like reliability theory or actuarial sciences. Since the main motivation for these notions is in the understanding of the effects of the dependence between X and Y on the reliability of one of them given the behavior of the other, most of these notions have been described and defined by using classical stochastic comparisons, comparing in some stochastic sense the distribution of one variable under different conditions for the other. For example, a well-known notion is the stochastically increasing property: given $(X,Y)$, the variable X is said to be stochastically increasing in Y if, and only if, $Pr(X>x|Y=y)$ increases in y for all fixed x (respectively in the corresponding supports of Y and X), or equivalently, if, and only if, $\left(X\right|Y=y_1){\le }_{ST}\left(X\right|Y=y_2)$ for all $y_1\le y_2$, where ${\le }_{ST}$ denotes the usual stochastic order (whose definition is recalled next). Similarly, other notions have been defined (and studied in detail) by replacing the usual stochastic order with other common stochastic comparisons and considering other conditional events, such as, for example, $\{Y>y\}$.

The purpose of this paper is twofold: on the one hand, it is our intention to provide a complete review of the main notions introduced so far, clearly describing equivalent definitions and reciprocal relationships; on the other hand, it is to enlarge the set of dependence notions with two properties recently considered in [1,2] and with other new ones, all defined as above, but considering stochastic orders for which the corresponding notions have not been characterized in the previous literature. The first point is motivated by the fact that characterizations of the previously defined notions can be found in many different articles and books, where the equivalent definitions and mutual connections are separately and partially analyzed, so that it is difficult to find them in a few exhaustive statements. For the second point, the aim is also to describe in an systematic manner some notions introduced in recent literature and to define a unified framework for dependence notions and their mutual relationships.

The paper also contains a result of general interest in the context of total positivity theory, for which we have not found the statement in the literature. This result, stated and proven in Section 2, deals with the preservation properties of total positivity and is used to provide sufficient conditions for the new notions of dependence.

The paper is structured as follows. The definitions of the stochastic orders used to describe the old and new dependence properties are recalled in Section 2, together with other useful properties and characterizations. Section 3 contains the survey on the notions introduced so far in the literature; all of them imply the Positively Quadrant Dependent ($PQD$) property, defined later, which is a necessary condition for a property of a vector $(X,Y)$ to be considered a dependence property according to the classical definition described in [3]. The new dependence notions, which are called here “weak dependence notions” since they imply the non-negativity of the linear correlation index, but not the $PQD$ property, are described in Section 4 and Section 5. Finally, Section 6 contains counterexamples showing that equivalences among some of these notions are not satisfied.

Throughout the paper, we will consider bivariate vectors $(X,Y)$ having an absolutely continuous joint distribution, unless otherwise stated, and the supports of X and Y will be denoted as ${\mathcal{S}}_X$ and ${\mathcal{S}}_Y$. For any random variable or random vector X and an event A, the notation $\left(X\right|A)$ describes the random variable whose distribution is the conditional distribution of X given A (tacitly assuming that it exists). The terms “increasing” and “decreasing” are used in place of “nondecreasing” and “nonincreasing”, respectively. Furthermore, for a function $h(x,y):{\mathbb{R}}^2\to \mathbb{R}$, the notations ${\partial }_{1}h(x,y)$ and ${\partial }_{2}h(x,y)$ are used for the partial derivatives with respect to the first or the second component, respectively, while ${\partial }_{12}^{2}h(x,y)$ is used for the mixed second partial derivative.

2. Preliminaries

First, we briefly recall the definitions of the stochastic orders that will be used throughout this paper. Most of them are mainly used to compare random lifetimes or inactivity times. To this aim, let X and Y be two absolutely continuous random variables having supports ${\mathcal{S}}_X$ and ${\mathcal{S}}_Y$, distribution functions $F_X$ and $F_Y$, reliability (survival) functions ${\overline{F}}_X=1-F_X$ and ${\overline{F}}_Y=1-F_Y$, and density functions $f_X$ and $f_Y$, respectively. Furthermore, for $t\in \mathbb{R}$, let $X_t=(X-t|X>t)$ and $Y_t=(Y-t|Y>t)$ be the corresponding residual lifetimes (RL), and let ${}_{t}X=(t-X|X<t)$ and ${}_{t}Y=(t-Y|Y<t)$ denote the corresponding inactivity times (IT). Then, we say that X is smaller than Y:

• in the stochastic order (denoted by $X{\le }_{ST}Y$) if ${\overline{F}}_X\le {\overline{F}}_Y$ in $\mathbb{R}$;
• in the likelihood ratio order (denoted by $X{\le }_{LR}Y$) if the ratio $f_Y/f_X$ is increasing in ${\mathcal{S}}_X\cup {\mathcal{S}}_Y$;
• in the hazard rate order (denoted by $X{\le }_{HR}Y$) if the ratio ${\overline{F}}_Y/{\overline{F}}_X$ is increasing in $\mathbb{R}$;
• in the reversed hazard rate order (denoted by $X{\le }_{RHR}Y$) if the ratio $F_Y/F_X$ is increasing in $\mathbb{R}$;
• in the mean residual life order (denoted by $X{\le }_{MRL}Y$) if $E\left(X_t\right)\le E\left(Y_t\right)$ for all t for which the expectations exist;
• in the mean inactivity time order (denoted by $X{\le }_{MIT}Y$) if $E{(}_{t}X)\ge E{(}_{t}Y)$ for all t for which the expectations exist;
• in the increasing convex order (denoted by $X{\le }_{ICX}Y$) if $E\left(\varphi \right(X\left)\right)\le E\left(\varphi \right(Y\left)\right)$ for all increasing and convex functions $\varphi$ for which the expectations exist;
• in the increasing concave order (denoted by $X{\le }_{ICV}Y$) if $E\left(\varphi \right(X\left)\right)\le E\left(\varphi \right(Y\left)\right)$ for all increasing and concave functions $\varphi$ for which the expectations exist.

We address the reader to [4] for a detailed description of these stochastic orders (except for the MIT order, for which we address the reader to [5]) and to [6] or [7] for a list of examples of applications in reliability theory and in actuarial sciences. Among these stochastic orders, there exist the well-known relationships shown in Table 1. The proof of all these relationships may be found in [4], except for those involving the MIT order, which can be found in [5].

Table 1. Relationships among the main stochastic orders.

$\mathit{X}{\le }_{\mathit{L}\mathit{R}}\mathit{Y}$	⇒	$\mathit{X}{\le }_{\mathit{H}\mathit{R}}\mathit{Y}$	⇒	$\mathit{X}{\le }_{\mathit{M}\mathit{R}\mathit{L}}\mathit{Y}$
⇓		⇓		⇓
$X{\le }_{RHR}Y$	⇒	$X{\le }_{ST}Y$	⇒	$X{\le }_{ICX}Y$
⇓		⇓		⇓
$X{\le }_{MIT}Y$	⇒	$X{\le }_{ICV}Y$	⇒	$E\left(X\right)\le E\left(Y\right)$

We recall here some immediate properties and equivalent conditions of these stochastic orders. The proofs of the following statements, unless stated, can be found in [4] or are straightforward.

Proposition 1.

The following conditions are equivalent:

(i) 

$X{\le }_{LR}Y$;

(ii) 

$X_t{\le }_{LR}{Y}_t$ for all t;

(iii) 

$X_t{\le }_{RHR}{Y}_t$ for all t;

(iv) 

$\left(X\right|s<X<t){\le }_{ST}\left(Y\right|s<Y<t)$ for all $s<t$.

Note that the third and the fourth conditions in the proposition above can be used to define the order also for variables that are not absolutely continuous.

Proposition 2.

The following conditions are equivalent:

(i) 

$X{\le }_{HR}Y$;

(ii) 

$X_t{\le }_{HR}{Y}_t$ for all t;

(iii) 

$X_t{\le }_{ST}{Y}_t$ for all t.

Proposition 3.

The following conditions are equivalent:

(i) 

$X{\le }_{MRL}Y$;

(ii) 

$X_t{\le }_{MRL}{Y}_t$ for all t;

(iii) 

$X_t{\le }_{ICX}{Y}_t$ for all t.

The proofs of the propositions above may be found in [4] or easily follow from statements there. For example, to prove the last one, we note that if $m_X\left(t\right)=E\left(X_t\right)=E(X-t|X>t)$ is the MRL of X, then the MRL of $X_t$ is $m_{X_t}\left(x\right)=m_X(x+t)$. Therefore, we get $\left(i\right)\Rightarrow \left(ii\right)$. Furthermore, $\left(ii\right)\Rightarrow \left(iii\right)$ holds because the MRL order implies the ICX order. Finally, $\left(iii\right)\Rightarrow \left(i\right)$ holds because the ICX order implies the order in expectations.

Similar results can be stated for inactivity times. The proofs of the following results, again, can be found in [4] or are straightforward.

Proposition 4.

The following conditions are equivalent:

(i) 

$X{\le }_{RHR}Y$;

(ii) 

${}_{t}X{\ge }_{HR}{}_{t}Y$ for all t;

(iii) 

${}_{t}X{\ge }_{ST}{}_{t}Y$ for all t.

Proposition 5.

The following conditions are equivalent:

(i) 

$X{\le }_{LR}Y$;

(ii) 

${}_{t}X{\ge }_{LR}{}_{t}Y$ for all t;

(iii) 

${}_{t}X{\ge }_{RHR}{}_{t}Y$ for all t;

Finally, we include the equivalences for the MIT order.

Proposition 6.

The following conditions are equivalent:

(i) 

$X{\le }_{MIT}Y$;

(ii) 

${}_{t}X{\ge }_{MRL}{}_{t}Y$ for all t;

(iii) 

${}_{t}X{\ge }_{ICX}{}_{t}Y$ for all t.

The proof of the equivalence between Conditions (i) and (iii) in the previous proposition may be found in [8], while the equivalence with (ii) can be proven in a similar manner.

For the proof of some of the results stated in the next sections, we will use a few preliminary results whose proofs are given here. These results, for which we have not found the statements in the literature, are of general interest in the context of total positivity theory, regardless of their applications in the following sections.

For them, we recall the notion of total positivity of order two (see, e.g., [9]).

Definition 1.

A bivariate function $l:{\mathbb{R}}^2\mapsto {\mathbb{R}}^{+}$ is said to be totally positive of order two $\left(T{P}_2\right)$ if:

$$l(x_1,y_1)l(x_2,y_2)\ge l(x_1,y_2)l(x_2,y_1),\mathit{for}\mathit{all}{x}_1\le x_2,y_1\le y_2.$$

We also recall the following useful property, the proof of which is given in Lemma 7.1(a) in Chapter 4 of [6] (see also the remark after the lemma).

Lemma 1.

Let W be a Lebesgue–Stieltjes measure, not necessarily positive, defined on the interval $(a,b)$, and let ϕ be a non-negative function defined on $(a,b)$. If ${\int }_t^{b}dW\left(x\right)\ge 0$ for all $t\in (a,b)$ and ϕ is increasing, then ${\int }_t^b\varphi \left(x\right)dW\left(x\right)\ge 0$ for all $t\in (a,b).$

We can now state and prove the first one of the preliminary results.

Theorem 1.

Let $f:{\mathbb{R}}^2\mapsto {\mathbb{R}}^{+}.$ If $h(x,y)={\int }_x^{b}f(s,y)ds$ is $T{P}_2$ in $\left(x,y\right)$, with $x\in (a,b)\subseteq \mathbb{R}$, then:

$$H(x,y)={\int }_x^{b}f(s,y)\varphi \left(s\right)ds$$

is also $T{P}_2$ in $\left(x,y\right)$ for all increasing and non-negative real functions $\varphi .$

Proof. 

We assume that $h(x,y)$ is $T{P}_2$ in $\left(x,y\right)$, which means that:

$$\frac{{\int }_x^{b}f(s,y_1)ds}{{\int }_x^{b}f(s,y_2)ds}\mathrm{decreases}\mathrm{in}x,\mathrm{for}{y}_1\le y_2.$$

(1)

Now observe that (1) holds if, and only if:

$$\frac{f(x,y_1)}{f(x,y_2)}\ge \frac{{\int }_x^{b}f(s,y_1)ds}{{\int }_x^{b}f(s,y_2)ds}\mathrm{for}{y}_1\le y_2.$$

(2)

From (1) and (2), we can rewrite the $T{P}_2$ property of $h(x,y)$ as:

$$\frac{f(x,y_1)}{f(x,y_2)}\ge \frac{{\int }_t^{b}f(s,y_1)ds}{{\int }_t^{b}f(s,y_2)ds},\mathrm{for}a<x\le t<b,y_1\le y_2.$$

Now, given $y_1\le y_2$, this is the same as:

$${\int }_t^{b}d{W}_x\left(s\right)\ge 0,\mathrm{for}\mathrm{all}a<x\le t<b,$$

(3)

where:

$$d{W}_x\left(s\right)=\left[f(s,y_2)f(x,y_1)-f(s,y_1)f(x,y_2)\right]ds.$$

(4)

Now, consider the function:

$$\mathsf{\Phi }\left(u\right)={\int }_u^b{I}_{[t,\infty )}\left(s\right)d{W}_x\left(s\right),u\in (a,b),$$

where:

$$I_{[t,\infty )}\left(s\right)=\left\{\begin{array}{cc}1,& s\ge t\\ 0,& s<t,\end{array}\right.t\in (a,b).$$

Then, by noting that:

$$\mathsf{\Phi }\left(u\right)=\left\{\begin{array}{cc}{\int }_u^{b}d{W}_x\left(s\right),& u>t\\ & \\ {\int }_t^{b}d{W}_x\left(s\right),& u\le t,\end{array}\right.$$

we see that (3) is equivalent to:

$${\int }_u^b{I}_{[t,\infty )}\left(s\right)d{W}_x\left(s\right)\ge 0,\mathrm{for}\mathrm{all}u,\mathrm{for}\mathrm{all}a<x\le t<b.$$

Since $\varphi$ is increasing and non-negative, by using Lemma 1, we have:

$${\int }_u^b{I}_{[t,\infty )}\left(s\right)\varphi \left(s\right)d{W}_x\left(s\right)\ge 0,\mathrm{for}\mathrm{all}u,\mathrm{for}\mathrm{all}a<x\le t<b.$$

By repeating the argument in the opposite direction, we see that the last inequality is the same as:

$${\int }_t^b\varphi \left(s\right)d{W}_x\left(s\right)\ge 0,\mathrm{for}\mathrm{all}a<x\le t<b.$$

Therefore, we have proven that (1) implies:

$${\int }_t^b\left[f(s,y_2)f(x,y_1)-f(s,y_1)f(x,y_2)\right]\varphi \left(s\right)ds\ge 0,y_1\le y_2,a<x\le t<b.$$

Rewriting this inequality as:

$$\frac{f(x,y_1)}{f(x,y_2)}\ge \frac{{\int }_t^{b}f(s,y_1)\varphi \left(s\right)ds}{{\int }_t^{b}f(s,y_2)\varphi \left(s\right)ds},\mathrm{for}x\le t,y_1\le y_2$$

and taking $x=t,$ we see that:

$$\frac{{\int }_x^{b}f(s,y_1)\varphi \left(s\right)ds}{{\int }_x^{b}f(s,y_2)\varphi \left(s\right)ds}\mathrm{decreases}\mathrm{in}x,\mathrm{for}{y}_1\le y_2.$$

This means that ${\int }_x^{\infty }f(s,y)\varphi \left(s\right)ds$ is $T{P}_2$ in $\left(x,y\right).$ □

The following is an immediate consequence of Theorem 1.

Corollary 1.

Let $f:{\mathbb{R}}^2\mapsto {\mathbb{R}}^{+}.$ If $h(x,y)={\int }_x^{b}f(s,y)ds$ is $T{P}_2$ in $\left(x,y\right)$, with $x\in (a,b)$, then:

$$H(x,y)={\int }_x^{{\psi }^{-1}\left(b\right)}f(\psi \left(s\right),y)ds$$

is also $T{P}_2$ in $\left(x,y\right)$, with $x\in ({\psi }^{-1}\left(a\right),{\psi }^{-1}\left(b\right))$, for all strictly increasing and concave real functions $\psi .$

Proof. 

Since $h(x,y)$ is $T{P}_2$ in $\left(x,y\right)$ and $\psi$ is increasing, it follows from Theorem 1.1 of [9], p. 99, that $h(\psi \left(x\right),y)$ is $T{P}_2$ in $\left(x,y\right).$ This is equivalent to stating that:

$$\frac{{\int }_{\psi \left(x\right)}^{b}f(s,y_1)ds}{{\int }_{\psi \left(x\right)}^{b}f(s,y_2)ds}\mathrm{decreases}\mathrm{in}x,\mathrm{for}{y}_1\le y_2,$$

which is the same as:

$$\frac{{\int }_x^{{\psi }^{-1}\left(b\right)}f(\psi \left(s\right),y_1){\psi }^{\prime }\left(s\right)ds}{{\int }_x^{{\psi }^{-1}\left(b\right)}f(\psi \left(s\right),y_2){\psi }^{\prime }\left(s\right)ds}\mathrm{decreases}\mathrm{in}x,\mathrm{for}{y}_1\le y_2.$$

Equivalently, we can say that:

$${\int }_x^{{\psi }^{-1}\left(b\right)}f(\psi \left(s\right),y){\psi }^{\prime }\left(s\right)ds$$

(5)

is $T{P}_2$ in $\left(x,y\right)$. Since $\psi$ is strictly increasing and concave, the result follows from (5) by applying Theorem 1 with $\varphi \left(s\right)=\frac{1}{{\psi }^{\prime }\left(s\right)}.$ □

Using the same procedure as above, but applying Lemma 7.1(b) in Chapter 4 of [6] instead of Lemma 7.1(a), one can also prove the following statements.

Theorem 2.

Let $f:{\mathbb{R}}^2\mapsto {\mathbb{R}}^{+}.$ If $h(x,y)={\int }_a^{x}f(s,y)ds$ is $T{P}_2$ in $\left(x,y\right)$, with $x\in (a,b)\subseteq \mathbb{R}$, then:

$$H(x,y)={\int }_a^{x}f(s,y)\varphi \left(s\right)ds$$

is also $T{P}_2$ in $\left(x,y\right)$ for all non-negative and decreasing real functions $\varphi .$

Corollary 2.

Let $f:{\mathbb{R}}^2\mapsto {\mathbb{R}}^{+}.$ If $h(x,y)={\int }_a^{x}f(s,y)ds$ is $T{P}_2$ in $\left(x,y\right)$, with $x\in (a,b)\subseteq \mathbb{R}$, then:

$$H(x,y)={\int }_{{\psi }^{-1}\left(a\right)}^{x}f(\psi \left(s\right),y)ds$$

is also $T{P}_2$ in $\left(x,y\right)$, with $x\in ({\psi }^{-1}\left(a\right),{\psi }^{-1}\left(b\right))$, for all strictly increasing and convex real functions $\psi .$

3. Strong Dependence Notions

Starting from the seminal paper by Kimeldorf and Sampson [3], where a unified framework to deal with dependence concepts was proposed, many alternative notions of dependence (either positive or negative) have been investigated and applied in the literature with the intent of mathematically describing the different properties and aspects of this intuitive concept. According to [3], a bivariate property can be considered as a positive dependence notion if it satisfies a number of conditions, the first of which is the $PQD$ property, whose definition and relevance in this context is recalled later.

Since all the monotone dependence properties based on the level of concordance between the components of a random vector are entirely described by its copula, whenever it is unique, one can rewrite the conditions described in [3] in terms of families of copulas, without taking care of the marginal distributions. See, e.g., [10] or [11] for the relationships between copulas and positive dependence notions or indexes. For this reason, we briefly recall here the definition of the copula and the survival copula of a random vector $(X,Y)$.

Given a random vector $(X,Y)$ with joint distribution function F and marginal distributions $F_X$ and $F_Y$, the function $C:{[0,1]}^2\to [0,1]$ is called copula of the vector $(X,Y)$ if it is such that, for all $(x,y)\in {\mathbb{R}}^2$,

$$F(x,y)=C(F_X\left(x\right),F_Y\left(y\right)).$$

In this case, it also holds, if $F_X$ and $F_Y$ are continuous, that:

$$C(u,v)=F(F_X^{-1}\left(u\right),F_Y^{-1}\left(v\right)),$$

for all $u,v\in [0,1]$, where $F_X^{-1}$ denotes the quasi-inverse of $F_X$ (and similarly for $F_Y^{-1}$). Actually, the copula of a vector $(X,Y)$, which is unique whenever $F_X$ and $F_Y$ are continuous, is the joint distribution function of a vector having uniformly distributed margins on $[0,1]\subset \mathbb{R}$, which entirely describes the dependence between the components of the vector. Moreover, since in some applicative fields, like reliability theory, the dependence among components of a vector is analyzed through the survival copula instead of through the copula, then we recall its definition as well: given $(X,Y)$, and denoting $\overline{F}$, ${\overline{F}}_X$, and ${\overline{F}}_Y$ as its joint survival function and the two marginal survival functions, the survival copula $\widehat{C}$ is defined as:

$$\widehat{C}(u,v)=\overline{F}({\overline{F}}_X^{-1}\left(u\right),{\overline{F}}_Y^{-1}\left(v\right))=u+v-1+C(1-u,1-v)$$

for all $u,v\in [0,1]$. If $\widehat{C}$ exists, then one also has:

$$\overline{F}(x,y)=\widehat{C}({\overline{F}}_X\left(x\right),{\overline{F}}_Y\left(y\right))$$

for all x and y. For the basic properties of copulas and survival copulas, we refer the reader to [11,12].

The definitions of the dependence properties considered throughout the paper, and previously defined in the literature, are recalled here.

Definition 2.

Given a vector $(X,Y)$, it is said to be:

• $PQD$ (Positively Quadrant Dependent) iff $X{\le }_{ST}\left(X\right|Y>t)$ for all t (see, e.g., [11], p. 187).
• $NQD$ (Negatively Quadrant Dependent) iff $X{\ge }_{ST}\left(X\right|Y>t)$ for all t (see, e.g., [11], p. 187).
• $RTI\left(X\right|Y)$ (Right Tail Increasing) iff $\left(X\right|Y>t)$ is ST-increasing in t (see, e.g., [11], p. 191).
• $RTD\left(X\right|Y)$ (Right Tail Decreasing) iff $\left(X\right|Y>t)$ is ST-decreasing in t (see, e.g., [10], p. 22).
• $LTD\left(X\right|Y)$ (Left Tail Decreasing) iff $\left(X\right|Y\le t)$ is ST-increasing in t (see, e.g., [11], p. 191).
• $LTI\left(X\right|Y)$ (Left Tail Increasing) iff $\left(X\right|Y\le t)$ is ST-decreasing in t (see, e.g., [10], p. 22).
• $SI\left(X\right|Y)$ (Stochastically Increasing) iff $\left(X\right|Y=t)$ is ST-increasing in $t\in {\mathcal{S}}_Y$ (see, e.g., [11], p. 196).
• $SD\left(X\right|Y)$ (Stochastically Decreasing) iff $\left(X\right|Y=t)$ is ST-decreasing in $t\in {\mathcal{S}}_Y$ (see, e.g., [11], p. 196).
• $RCSI$ (Right Corner Set Increasing) iff $Pr(X>x,Y>y|X>s,Y>t)$ is increasing in s and t for all $(x,y)\in {\mathbb{R}}^2$ (see [11], p. 198) or, equivalently, iff $\left(X\right|Y>t)$ is HR-increasing in t (see [13], p. 166).
• $RCSD$ (Right Corner Set Decreasing) iff $Pr(X>x,Y>y|X>s,Y>t)$ is decreasing in s and t for all $(x,y)\in {\mathbb{R}}^2$ (see [11], p. 198) or, equivalently, iff $\left(X\right|Y>t)$ is HR-decreasing in t (see [13], p. 166).
• $LCSD$ (Left Corner Set Decreasing) iff $Pr(X\le x,Y\le y|X\le s,Y\le t)$ is decreasing in s and t for all $(x,y)\in {\mathbb{R}}^2$ (see [11], p. 198) or, equivalently, iff $\left(X\right|Y\le t)$ is RHR-increasing in t.
• $LCSI$ (Left Corner Set Increasing) iff $Pr(X\le x,Y\le y|X\le s,Y\le t)$ is increasing in s and t for all $(x,y)\in {\mathbb{R}}^2$ (see [11], p. 198) or, equivalently, iff $\left(X\right|Y\le t)$ is RHR-decreasing in t.
• $SIRL\left(X\right|Y)$ (Stochastically Increasing in Residual Life), defined in [14], iff $\left(X\right|Y=t)$ is HR-increasing in $t\in {\mathcal{S}}_Y$.
• $SDRL\left(X\right|Y)$ (Stochastically Decreasing in Residual Life), defined in [14], iff $\left(X\right|Y=t)$ is HR-decreasing in $t\in {\mathcal{S}}_Y$.
• $PRLD$ (Positive Likelihood Ratio Dependent) iff its joint density function is $T{P}_2$ (see [11], p. 200, where it is denoted as $PLR(X,Y)$) or, equivalently, iff $\left(X\right|Y=t)$ is LR-increasing in $t\in {\mathcal{S}}_Y$ (see [14]).
• $NRLD$ (Negative Likelihood Ratio Dependent) iff its joint density function is $R{R}_2$ (see [11], p. 200, and [9] for $R{R}_2$ notion) or, equivalently, iff $\left(X\right|Y=t)$ is LR-decreasing in $t\in {\mathcal{S}}_Y$.

Note that some of these notions, like the $PQD$, are “symmetric”, in the sense that they describe both the properties of X given Y and the properties of Y given X, while other notions, like $RTI\left(X\right|Y)$, describe only the properties of X given Y, while the opposite notions (e.g., $RTI\left(Y\right|X)$) describe the properties of Y given X. For these cases, the symmetric notions can be defined similarly and will be denoted as $P\left(Y\right|X)$, where P is the specific property.

As pointed out before, for all the above-mentioned notions, there exist equivalent definitions given in terms of the survival copula $\widehat{C}$ (or connecting copula C) of the vector $(X,Y)$. These alternative definitions, proven in [11,13], or [14], will be pointed out in the following statements, which also describe more interesting equivalences. Here, and throughout the rest of the paper, the notations $X_{t,s}$ and $Y_{t,s}$ are used to describe double conditioning, i.e., $X_{t,s}=(X-t|X>t,Y>s)$ and $Y_{t,s}=(Y-s|X>t,Y>s)$.

Proposition 7.

For continuous ${\overline{F}}_X$ and ${\overline{F}}_Y$, the following conditions are equivalent:

(i) 

$X{\le }_{HR}\left(X\right|Y>s)$ for all $s\in \mathbb{R}$ and all ${\overline{F}}_X,{\overline{F}}_Y$;

(ii) 

$X_t{\le }_{HR}{X}_{t,s}$ for all $(t,s)\in {\mathbb{R}}^2$ and all ${\overline{F}}_X,{\overline{F}}_Y$;

(iii) 

$X_t{\le }_{ST}{X}_{t,s}$ for all $(t,s)\in {\mathbb{R}}^2$ and all ${\overline{F}}_X,{\overline{F}}_Y$;

(iv) 

$\widehat{C}(u,v)/u$ is decreasing in u for all $v\in [0,1]$;

(v) 

$RTI\left(Y\right|X)$.

The equivalences between the first three conditions can be obtained from the equivalences given in the preceding section. The equivalences between $\left(i\right)$ and $\left(iv\right)$ can be obtained both from Proposition 3.1 in [2] or from Proposition 3.3 $\left(iii\right)$ in [13]. The equivalence between $\left(iv\right)$ and $\left(v\right)$ can be found in [11] (Theorem 5.2.5). It is interesting to observe that, even if $RTI\left(Y\right|X)$ refers to a property describing the behavior of the law of Y given X, Conditions $\left(i\right)$, $\left(ii\right)$, and $\left(iii\right)$ refer to the behavior of X given Y. A discussion of and the formal motivation for this fact were clearly provided in [14].

Note that a similar proposition could be stated just for a fixed s. Note that if $\left(i\right)$ holds for a fixed $s>0$ and all ${\overline{F}}_X,{\overline{F}}_Y$, then $\left(iv\right)$ holds for all $u={\overline{F}}_X\left(t\right)>0$ and $v={\overline{F}}_Y\left(s\right)>0$; by changing ${\overline{F}}_Y$, we cover the interval $(0,1)$. However, if we fix ${\overline{F}}_X$ and ${\overline{F}}_Y$, then the equivalence is not true when we also fix s (the $RTI\left(Y\right|X)$ property is no longer satisfied). In this case, $\left(v\right)$ does not hold, but one could write $\left(iv\right)$ for a fixed value $v={\overline{F}}_Y\left(s\right)$.

The following statement deals with the SI notion.

Proposition 8.

The following conditions are equivalent:

(i) 

$X{\le }_{LR}\left(X\right|Y>s)$ for all $s\in \mathbb{R}$ and all ${\overline{F}}_X,{\overline{F}}_Y$;

(ii) 

$X_t{\le }_{LR}{X}_{t,s}$ for all $(t,s)\in {\mathbb{R}}^2$ and all ${\overline{F}}_X,{\overline{F}}_Y$;

(iii) 

$X_t{\le }_{RHR}{X}_{t,s}$ for all $(t,s)\in {\mathbb{R}}^2$ and all ${\overline{F}}_X,{\overline{F}}_Y$;

(iv) 

$\widehat{C}(u,v)$ is concave in u (or ${\partial }_1\widehat{C}(u,v)$ is decreasing in u) for all $v\in [0,1]$;

(v) 

$SI\left(Y\right|X)$.

The equivalences between the first three conditions can be obtained from the equivalences given in the preceding section. The equivalences with $\left(iv\right)$ can be obtained both from Proposition 3.2 in [2] or from Proposition 3.3 (v), in [13]. Again, it is interesting to observe that $SI\left(Y\right|X)$ refers to a property describing the behavior of the law of Y given X, while Conditions $\left(i\right)$, $\left(ii\right)$, and $\left(iii\right)$ refer to the behavior of X given Y (see [14]).

The following statement describes equivalent definitions for the $RCSI$ notion.

Proposition 9.

The following conditions are equivalent:

(i) 

$\left(X\right|Y>s_1){\le }_{HR}\left(X\right|Y>s_2)$ for all $s_1\le s_2$ and all ${\overline{F}}_X,{\overline{F}}_Y$;

(ii) 

$\left(Y\right|X>t_1){\le }_{HR}\left(Y\right|X>t_2)$ for all $t_1\le t_2$ and all ${\overline{F}}_X,{\overline{F}}_Y$;

(iii) 

$X_{t,s_1}{\le }_{HR}{X}_{t,s_2}$ for all t, all $s_1\le s_2$ and all ${\overline{F}}_X,{\overline{F}}_Y$;

(iv) 

$X_{t,s_1}{\le }_{ST}{X}_{t,s_2}$ for all t, all $s_1\le s_2$ and all ${\overline{F}}_X,{\overline{F}}_Y$;

(v) 

$Y_{t_1,s}{\le }_{HR}{Y}_{t_2,s}$ for all s, all $t_1\le t_2$ and all ${\overline{F}}_X,{\overline{F}}_Y$;

(vi) 

$Y_{t_1,s}{\le }_{ST}{Y}_{t_2,s}$ for all s, all $t_1\le t_2$ and all ${\overline{F}}_X,{\overline{F}}_Y$;

(vii) 

$\widehat{C}(u,v)$ is $T{P}_2$ in $(u,v)\in {[0,1]}^2$;

(viii) 

$(X,Y)$ is $RCSI$.

The proofs of the equivalences in the above proposition can be found in [1,14] or [13].

The preceding propositions can be completed with the following result (extracted from Proposition 3.3 in [13]) that does not have an equivalent result based on residual lifetimes. For the equivalence between Conditions $\left(iv\right)$ and $\left(v\right)$, see [15].

Proposition 10.

The following conditions are equivalent:

(i) 

$X{\le }_{ST}\left(X\right|Y>s)$ for all s and all ${\overline{F}}_X,{\overline{F}}_Y$;

(ii) 

$Y{\le }_{ST}\left(Y\right|X>t)$ for all t and all ${\overline{F}}_X,{\overline{F}}_Y$;

(iii) 

$\widehat{C}(u,v)\ge uv$ for all $u,v\in [0,1]$;

(iv) 

$Cov\left(\tau \right(X),\varphi (Y\left)\right)\ge 0$ for all increasing real functions τ and ϕ for which the covariance exists;

(v) 

$(X,Y)$ is $PQD$.

The following two propositions hold as well.

Proposition 11.

The following conditions are equivalent:

(i) 

$\left(X\right|Y>s_1){\le }_{LR}\left(X\right|Y>s_2)$ for all $s_1<s_2$ and all ${\overline{F}}_X,{\overline{F}}_Y$;

(ii) 

$\left(X_t\right|Y>s_1){\le }_{LR}\left(X_t\right|Y>s_2)$ for all t, $s_1<s_2,s_1,s_2$ and all ${\overline{F}}_X,{\overline{F}}_Y$;

(iii) 

$\left(X_t\right|Y>s_1){\le }_{RHR}\left(X_t\right|Y>s_1)$ for all t, $s_1<s_2$ and all ${\overline{F}}_X,{\overline{F}}_Y$;

(iv) 

${\partial }_1\widehat{C}(u,v)$ is $T{P}_2$ in $(u,v)\in {[0,1]}^2$;

(v) 

$SIRL\left(Y\right|X)$.

The proof of equivalence among $\left(i\right)$, $\left(iv\right)$, and $\left(v\right)$ can be found in [13] or [14]. The proof of equivalence among $\left(ii\right)$, $\left(iii\right)$, and $\left(v\right)$ can be found in [1]. Once more, it is interesting to observe that $SIRL\left(Y\right|X)$ refers to a property describing the behavior of the law of Y given X, while Conditions $\left(i\right)$, $\left(ii\right)$, and $\left(iii\right)$ refer to the behavior of X given Y (see [14]).

Proposition 12.

The following conditions are equivalent:

(i) 

$\left(Y\right|X=t_1){\le }_{LR}\left(Y\right|X=t_2)$ for all $t_1<t_2,t_1,t_2\in {\mathcal{S}}_X$ and all ${\overline{F}}_X,{\overline{F}}_Y$;

(ii) 

$\left(X\right|Y=s_1){\le }_{LR}\left(X\right|Y=s_2)$ for all $s_1<s_2,s_1,s_2\in {\mathcal{S}}_Y$ and all ${\overline{F}}_X,{\overline{F}}_Y$;

(iii) 

$\left(X_t\right|Y=s_1){\le }_{LR}\left(X_t\right|Y=s_2)$ for all t, $s_1<s_2,s_1,s_2\in {\mathcal{S}}_Y$ and all ${\overline{F}}_X,{\overline{F}}_Y$;

(iv) 

$\left(X_t\right|Y=s_1){\le }_{RHR}\left(X_t\right|Y=s_2)$ for all t, $s_1<s_2,s_1,s_2\in {\mathcal{S}}_Y$ and all ${\overline{F}}_X,{\overline{F}}_Y$;

(v) 

$\left(Y_s\right|X=t_1){\le }_{LR}\left(Y_s\right|X=t_2)$ for all s, $t_1<t_2,t_1,t_2\in {\mathcal{S}}_X$ and all ${\overline{F}}_X,{\overline{F}}_Y$;

(vi) 

$\left(Y_s\right|X=t_1){\le }_{RHR}\left(Y_s\right|X=t_2)$ for all s, $t_1<t_2,t_1,t_2\in {\mathcal{S}}_X$ and all ${\overline{F}}_X,{\overline{F}}_Y$;

(vii) 

${\partial }_{1,2}^2\widehat{C}(u,v)$ is $T{P}_2$ in $(u,v)\in {[0,1]}^2$;

(viii) 

${\partial }_{1,2}^{2}C(u,v)$ is $T{P}_2$ in $(u,v)\in {[0,1]}^2$;

(ix) 

$(X,Y)$ is $PLRD$.

The proof of equivalence between $\left(vii\right)$ and $\left(viii\right)$ can be found in [11]. The proof of equivalence among $\left(i\right)$, $\left(ii\right)$, and $\left(viii\right)$ can be found in [13] or [14]. The proof of equivalence among $\left(iii\right)$, $\left(iv\right)$, $\left(v\right)$, and $\left(vi\right)$ follows from Proposition 2.1.

In order to synthesize all these properties with a uniform notation and to introduce similarly defined new properties, the definitions that follow were proposed in [13,14]. The first one of them deals with the $SI$ notion.

Definition 3.

We say that $(X,Y)$ is stochastically increasing (decreasing) in the order $ORD$, denoted $S{I}_{ORD}\left(X\right|Y)$ ($S{D}_{ORD}\left(X\right|Y)$), if:

$$\left(X\right|Y=s_1){\le }_{ORD}\left(X\right|Y=s_2)\left({\ge }_{ORD}\right)$$

holds for all $s_1<s_2$, with $s_1,s_2\in {\mathcal{S}}_Y$, for a given stochastic order ORD.

The classes for $\left(Y\right|X)$ are defined in a similar manner. With this definition, the class $SI\left(X\right|Y)$ can also be written as $S{I}_{ST}\left(X\right|Y)$; the class $SIRL\left(X\right|Y)$ can also be written as $S{I}_{HR}\left(X\right|Y)$; and the condition $\left(i\right)$ in Proposition 12 as $S{I}_{LR}\left(Y\right|X)$. Note that in this last case, $S{I}_{LR}\left(Y\right|X)$ is equivalent to $S{I}_{LR}\left(X\right|Y)$, and so, we can just write $S{I}_{LR}$.

One can do the same with the $RTI$ and $LTD$ classes by proposing the following definitions (see [14]).

Definition 4.

We say that $(X,Y)$ is right tail increasing (decreasing) in the order $ORD$, denoted $RT{I}_{ORD}\left(X\right|Y)$ ($RT{D}_{ORD}\left(X\right|Y)$), if:

$$\left(X\right|Y>s_1){\le }_{ORD}\left(X\right|Y>s_2)\left({\ge }_{ORD}\right)$$

holds for all $s_1<s_2$ for a given stochastic order ORD.

Definition 5.

We say that $(X,Y)$ is left tail decreasing (increasing) in the order $ORD$, denoted $LT{D}_{ORD}\left(X\right|Y)$ ($LT{I}_{ORD}\left(X\right|Y)$), if:

$$\left(X\right|Y\le s_1){\le }_{ORD}\left(X\right|Y\le s_2)\left({\ge }_{ORD}\right)$$

holds for all $s_1<s_2$ for a given stochastic order ORD.

The classes for $\left(Y\right|X)$ are defined in a similar manner. With this definition, the class $RTI\left(X\right|Y)$ can also be written as $RT{I}_{ST}\left(X\right|Y)$; the conditions $\left(i\right)$ and $\left(ii\right)$ in Proposition 9 can also be written as $RT{I}_{HR}\left(X\right|Y)$ and $RT{I}_{HR}\left(Y\right|X)$; and the condition $\left(i\right)$ in Proposition 11 as $RT{I}_{LR}\left(X\right|Y)$.

We can add more notions by considering the following definitions.

Definition 6.

We say that $(X,Y)$ is right tail increasing (decreasing) at zero in the order $ORD$, denoted $RT{I}_{ORD}^0\left(X\right|Y)$ ($RT{D}_{ORD}^0\left(X\right|Y)$), if:

$$X{\le }_{ORD}\left(X\right|Y>s)\left({\ge }_{ORD}\right)$$

holds for all s for a given stochastic order ORD.

Definition 7.

We say that $(X,Y)$ is left tail decreasing (increasing) at infinity in the order $ORD$, denoted $LT{D}_{ORD}^{\infty }\left(X\right|Y)$ ($LT{I}_{ORD}^{\infty }\left(X\right|Y)$), if:

$$X{\ge }_{ORD}\left(X\right|Y\le s)\left({\le }_{ORD}\right)$$

holds for all s for a given stochastic order ORD.

With these definitions, $PQD$ can also be written as $RT{I}_{ST}^0\left(Y\right|X)$ or $RT{I}_{ST}^0\left(X\right|Y)$, but also as $LT{D}_{ST}^{\infty }\left(Y\right|X)$ or $LT{D}_{ST}^{\infty }\left(X\right|Y)$. Analogously, $RTI\left(Y\right|X)$ and $LTD\left(Y\right|X)$ can be written as $RT{I}_{HR}^0\left(X\right|Y)$ and $LT{D}_{RHR}^{\infty }\left(X\right|Y)$, respectively. Furthermore, $SI\left(Y\right|X)$ can be written as $RT{I}_{LR}^0\left(X\right|Y)$ or as $LT{D}_{LR}^{\infty }\left(X\right|Y)$. The proofs of these equivalences can be found in [2,13]. Note also that some of these notions are actually equivalent, like, e.g., $RT{I}_{LR}^0\left(Y\right|X)$ and $S{I}_{ST}\left(X\right|Y)$ or $RT{I}_{HR}^0\left(Y\right|X)$ and $RT{I}_{ST}\left(X\right|Y)$ (see [14] for details).

The preceding propositions can be connected by using the relationships among the stochastic orders shown in Table 1. They are summarized in Table 2. For example, to prove $SIRL\left(X\right|Y)\Rightarrow RCSI(X,Y)$, we just note that $RCSI(X,Y)=RT{I}_{HR}\left(X\right|Y)$, that $SIRL\left(X\right|Y)=RT{I}_{LR}\left(X\right|Y)$, and that the LR order implies the HR order. These relationships prove that they are positive dependence properties, since all of them imply the PQD property. Analogously, the corresponding negative dependence properties imply the NQD property. Some of these relationships were given in [13], p. 166, and in [14]. Connections with the ordering properties of coherent systems and extremes values were given in [16,17].

Table 2. Relationships among positive dependence properties.

$\mathit{P}\mathit{Q}\mathit{D}(\mathit{X},\mathit{Y})$	⇐	$\mathit{R}\mathit{T}\mathit{I}\left(\mathit{Y}\right|\mathit{X})$	⇐	$\mathit{S}\mathit{I}\left(\mathit{Y}\right|\mathit{X})$
⇑		⇑		⇑
$RTI\left(X\right|Y)$	⇐	$RCSI(X,Y)$	⇐	$SIRL\left(Y\right|X)$
⇑		⇑		⇑
$SI\left(X\right|Y)$	⇐	$SIRL\left(X\right|Y)$	⇐	$PLRD(X,Y)$

The relationships for the reversed properties (i.e., based on cumulative distributions rather than survival functions) are given in Table 3. For them, observe, e.g., that $S{I}_{RHR}\left(Y\right|X)$ iff ${\partial }_{1}C(u,v)$ is $T{P}_2$ and that $S{I}_{RHR}\left(X\right|Y)$ iff ${\partial }_{2}C(u,v)$ is $T{P}_2$ (see [13], where more equivalences were also provided). More equivalences can be seen in [13]. Note that two of the notions described in this table ($S{I}_{RHR}\left(Y\right|X)$ and $S{I}_{RHR}\left(X\right|Y)$) were previously considered in [13].

Table 3. Relationships among reversed positive dependence properties.

$\mathit{S}\mathit{I}\left(\mathit{Y}\right|\mathit{X})$	⇒	$\mathit{L}\mathit{T}\mathit{D}\left(\mathit{Y}\right|\mathit{X})$	⇒	$\mathit{P}\mathit{Q}\mathit{D}(\mathit{X},\mathit{Y})$
⇑		⇑		⇑
$S{I}_{RHR}\left(Y\right|X)$	⇒	$LCSD(X,Y)$	⇒	$LTD\left(X\right|Y)$
⇑		⇑		⇑
$PLRD(X,Y)$	⇒	$S{I}_{RHR}\left(X\right|Y)$	⇒	$SI\left(X\right|Y)$

Negative dependence properties can be considered as well. For them, one has to consider the $RTD$ and $LTI$ properties, obtaining relationships similar to those described in Table 2 and Table 3.

4. Weak Dependence Notions

In this section, new dependence notions are introduced and discussed. These notions, which are defined as those satisfying $RT{I}_{ORD}\left(X\right|Y)$ and $RT{I}_{ORD}^0\left(X\right|Y)$ where ORD is one of the orders $ICX$, or $MRL$, or simply in Expectation (E), are “weak” in the sense that they do not imply the $PQD$ property, which is a necessary condition for a property to be considered a “dependence notion” according to the classical definition given in [3]. However, they imply the non-negativity of the linear correlation coefficient $r_{X,Y}$, as mentioned after Proposition 15, and this is the reason to consider them as “weak dependence notions”. Note that some of these notions have been already considered and applied in the literature; this is the case, for example, of $RT{I}_{ICX}^0\left(X\right|Y)$, which was named positive stop-loss dependence in [7].

For $RT{I}_{ICX}^0\left(X\right|Y)$, we have the following properties.

Proposition 13.

Let $(X,Y)$ be a random vector with a continuous marginal distribution functions $F_X$ and $F_Y$. Then, the following conditions are equivalent:

(i) 

$X{\le }_{ICX}\left(X\right|Y>y)$ for all $y\in \mathbb{R}$ (i.e., $RT{I}_{ICX}^0\left(X\right|Y)$);

(ii) 

The survival copula $\widehat{C}$ satisfies:

$${\int }_0^z[\widehat{C}(u,v)-uv]d{\overline{F}}_X^{-1}\left(u\right)\le 0,\forall z\in [0,1],\forall v\in [0,1].$$

(6)

Proof. 

It is clear that $X{\le }_{ICX}\left(X\right|Y>y)$ for all y, if, and only if,

$${\int }_t^{\infty }Pr\left(X>x\right)dx\le {\int }_t^{\infty }Pr\left(X>x|Y>y\right)dx,\forall t,y\in \mathbb{R}.$$

This is equivalent to:

$${\int }_t^{\infty }[\widehat{C}({\overline{F}}_X\left(x\right),{\overline{F}}_Y\left(y\right))-{\overline{F}}_X\left(x\right){\overline{F}}_Y\left(y\right)]dx\ge 0,\forall t,y\in \mathbb{R}$$

or

$${\int }_0^{{\overline{F}}_X\left(t\right)}[\widehat{C}(u,v)-uv]d{\overline{F}}_X^{-1}\left(u\right)\le 0,\forall t\in \mathbb{R},v\in [0,1].$$

Since $F_X$ is continuous, this is the same as:

$${\int }_0^z[\widehat{C}(u,v)-uv]d{\overline{F}}_X^{-1}\left(u\right)\le 0,\forall z\in [0,1],v\in [0,1].$$

(7)

□

Corollary 3.

Under the above assumptions, if ${\overline{F}}_X$ is convex and:

$${\int }_0^z[\widehat{C}(u,v)-uv]du\ge 0,\forall z\in [0,1],\forall v\in [0,1],$$

(8)

then $X{\le }_{ICX}\left(X\right|Y>y)$ for all $y\in \mathbb{R}$ and all ${\overline{F}}_Y$.

Proof. 

Since ${\overline{F}}_X$ is decreasing and convex, then ${\overline{F}}_X^{-1}\left(u\right)$ is decreasing and convex and $-{\overline{F}}_X^{-1}\left(u\right)$ is increasing and concave. Then, by applying Lemma 7.1(b), of [6], to Equation (8) above, we obtain:

$${\int }_0^z[\widehat{C}(u,v)-uv]d\left(-{\overline{F}}_X^{-1}\left(u\right)\right)\ge 0,\forall z\in [0,1],\forall v\in [0,1],$$

(9)

which is the same as (7). □

In particular, we have that the PQD property implies both $RT{I}_{ICX}^0\left(X\right|Y)$ for all ${\overline{F}}_Y$ and all convex ${\overline{F}}_X$ and $RT{I}_{ICX}^0\left(Y\right|X)$ for all ${\overline{F}}_X$ and all convex ${\overline{F}}_Y$. Note also that if $RT{I}_{ICX}^0\left(X\right|Y)$ holds for a continuous survival function ${\overline{F}}_Y$, then it holds for all continuous survival functions ${\overline{F}}_Y$ (since (6) holds for any $v={\overline{F}}_Y\left(y\right)$ and all y).

For $RT{I}_{MRL}^0\left(X\right|Y)$, we have the following properties.

Proposition 14.

Let $(X,Y)$ be a random vector with continuous marginal distribution functions $F_X$ and $F_Y$. Then, the following conditions are equivalent:

(i) 

$X{\le }_{MRL}\left(X\right|Y>y)$ for all $y\in \mathbb{R}$ (i.e., $RT{I}_{MRL}^0\left(X\right|Y)$);

(ii) 

$X_t{\le }_{MRL}{X}_{t,s}$ for all $(t,s)\in {\mathbb{R}}^2$;

(iii) 

$X_t{\le }_{ICX}{X}_{t,s}$ for all $(t,s)\in {\mathbb{R}}^2$;

(iv) 

The survival copula $\widehat{C}$ satisfies:

$${\int }_0^z[z\widehat{C}(u,v)-u\widehat{C}(z,v))d{\overline{F}}_X^{-1}\left(u\right)\le 0\forall z,v\in [0,1].$$

(10)

Proof. 

The equivalence between the first three items follows from Proposition 3. For the equivalence with $\left(iv\right)$, observe that $X{\le }_{MRL}\left(X\right|Y>y)$ for all $y\in {\mathcal{S}}_Y$ if, and only if,

$$\frac{{\int }_t^{\infty }\overline{F}(x,0)dx}{{\int }_t^{\infty }\overline{F}(x,y)dx/\overline{F}(0,y)}\mathrm{decreases}\mathrm{in}t\forall y,$$

i.e., if, and only if,

$$\frac{{\int }_t^{\infty }\widehat{C}(\overline{F_X}\left(x\right),1)dx}{{\int }_t^{\infty }\widehat{C}({\overline{F}}_X\left(x\right),v)dx}\mathrm{decreases}\mathrm{in}t\forall v\in [0,1].$$

This is equivalent to:

$$-\widehat{C}({\overline{F}}_X\left(t\right),1){\int }_t^{\infty }\widehat{C}({\overline{F}}_X\left(x\right),v)dx+\widehat{C}({\overline{F}}_X\left(t\right),v){\int }_t^{\infty }\widehat{C}({\overline{F}}_X\left(x\right),1)dx\le 0$$

for all $v\in [0,1]$ and t. The latter can be written as:

$${\int }_t^{\infty }[\widehat{C}({\overline{F}}_X\left(x\right),v){\overline{F}}_X\left(t\right)-\widehat{C}({\overline{F}}_X\left(t\right),v){\overline{F}}_X\left(x\right)]dx\ge 0,\forall v\in [0,1],\forall t,$$

which is the same as:

$${\int }_z^0[z\widehat{C}(u,v)-u\widehat{C}(z,v)]d{\overline{F}}_X^{-1}\left(u\right)\ge 0\forall v,z\in [0,1],$$

i.e., (10). □

Corollary 4.

Under the above assumptions, if ${\overline{F}}_X$ is strictly monotone and convex and:

$$\frac{{\int }_0^z\widehat{C}(u,v)du}{{\int }_0^z\widehat{C}(u,1)du}\mathrm{is}\mathrm{decreasing}\mathrm{in}z\mathrm{for}\mathrm{all}v\in [0,1]$$

(11)

then $X{\le }_{MRL}\left(X\right|Y>y)$ for all $y\in {\mathcal{S}}_Y$ and all ${\overline{F}}_Y$.

Proof. 

Observe that (11) is equivalent to:

$$\frac{{\int }_z^1\widehat{C}(1-u,1)du}{{\int }_z^1\widehat{C}(1-u,1-v)du}\mathrm{is}\mathrm{decreasing}\mathrm{in}z\mathrm{for}\mathrm{all}v\in [0,1].$$

(12)

Defining:

$$K\left(1-u,i\right)=\left\{\begin{array}{cc}\widehat{C}(1-u,1),& i=0\\ & \\ \widehat{C}(1-u,1-v),& i=1,\end{array}\right.$$

then (11) can be restated as $T{P}_2$ in the $(z,i)$ property of ${\int }_z^{1}K(1-u,i)du$. Thus, by applying Corollary 1 one gets that ${\int }_t^{\infty }K(1-F_X\left(u\right),i)du$ is also $T{P}_2$ in $(t,i)$, i.e., that:

$$\frac{{\int }_t^{\infty }\widehat{C}(1-F_X\left(u\right),1-F_Y\left(0\right))du}{{\int }_t^{\infty }\widehat{C}(1-F_X\left(u\right),1-F_Y\left(v\right))du}\mathrm{is}\mathrm{decreasing}\mathrm{in}t\mathrm{for}\mathrm{all}v\in [0,1],$$

which means:

$$\frac{{\int }_t^{\infty }\overline{F}(u,0)du}{{\int }_t^{\infty }\overline{F}(u,s)du}\mathrm{is}\mathrm{decreasing}\mathrm{in}t\mathrm{for}\mathrm{all}s\ge 0,$$

i.e., $X{\le }_{MRL}\left(X\right|Y>y)$ for all y. Note that the strict monotonicity of $F_X$ is required in this proof. □

Note that the sufficient conditions for $RT{I}_{MRL}^0\left(X\right|Y)$ described in Corollary 4 were proven already in [2] with a different and longer proof. However, the strict monotonicity of ${\overline{F}}_X$ is not required in the proof provided there. Moreover, note that (11) is also a necessary condition since equation (3.5) appearing in [2] is what one gets by choosing uniform distributions. However, we think that the convexity of ${\overline{F}}_X$ is not a necessary condition.

Alternative conditions for $RT{I}_{MRL}^0\left(X\right|Y)$ are described also in Proposition 3.3 (vi), of [13] (obtained from [18]), and are:

$$E\left(X\right)\le E\left(X\right|Y>y)\forall y\in \mathbb{R}$$

(13)

and:

$$\frac{1}{u}\widehat{C}(u,v)\mathrm{is}\mathrm{the}\mathrm{bathtub}\mathrm{in}u\mathrm{for}\mathrm{all}v\in [0,1].$$

(14)

Clearly, (13) is a necessary condition (because they are the values of the respective MRL functions at zero).

It is useful to point out that the counterexamples provided in Section 6 show that there exist no relationships between PQD (i.e., $\widehat{C}(u,v)\ge uv$ for all $u,v\in [0,1]$) and both (11) and (14).

The Positive Quadrant Dependence in Expectation property ($PQDE$), defined in [19], is considered in the following statement. According to the definition provided in [19], and the notation used here, we say that the vector $(X,Y)$ satisfies $PQDE\left(X\right|Y)$ if, and only if, $E\left(X\right)\le E\left(X\right|Y>y)$ for all $y\in \mathbb{R}$ (and similarly for $PQDE\left(Y\right|X)$). Note that, actually, a study on a negative dependence notion analog of the property $PQDE\left(Y\right|X)$ goes back to [20].

Proposition 15.

Let $(X,Y)$ be a vector of non-negative variables having continuous marginal distribution functions $F_X$ and $F_Y$, respectively. Assuming that $E\left(X\right|Y>y)$ and $E\left(X\right|Y\le y)$ exist for all y, then the following conditions are equivalent:

(i) 

$E\left(X\right)\le E\left(X\right|Y>y)$ for all $y\in \mathbb{R}$ (i.e., $PQDE\left(X\right|Y)$);

(ii) 

$E\left(X\right)\ge E\left(X\right|Y\le y)$ for all $y\in \mathbb{R}$;

(iii) 

$Cov(X,\varphi (Y\left)\right)\ge 0$ for all increasing real functions ϕ for which the covariance exists;

(iv) 

The survival copula $\widehat{C}$ satisfies:

$${\int }_0^1(\widehat{C}(u,v)-uv)d{\overline{F}}_X^{-1}\left(u\right)\le 0,\forall v\in [0,1].$$

(15)

Proof. 

For the equivalence between $\left(i\right)$ and $\left(ii\right)$, note that, for fixed $y\in \mathbb{R}$, one has:

$$E\left(X\right)=Pr(Y>y)E\left(X\right|Y>y)+Pr(Y\le y\left)E\right(X|Y\le y),$$

which implies:

$$\left[E\right(X)-E(X|Y>y)\left]P\right(Y>y)=P(Y\le y\left)\right[E\left(X\right|Y\le y)-E(X\left)\right].$$

(16)

Thus, $E\left(X\right)-E\left(X\right|Y>y)$ and $E\left(X\right|Y\le y)-E(X)$ must have the same sign, and the equivalence follows. In a similar manner, again by using Inequality (16), one can prove the equivalence between $\left(i\right)$ and $\left(iii\right)$ (see [20], Theorem 3.1, for details). For the relationship between $\left(i\right)$ and $\left(iv\right)$, observe that:

$$E\left(X\right)=-{\int }_{-\infty }^{0}F\left(x\right)dx+{\int }_0^{\infty }\overline{F}\left(x\right)dx,$$

and similarly for $E\left(X\right|Y>y)$. If the marginal expectations are finite, then:

$$E\left(X|Y>y\right)-E\left(X\right)={\int }_{-\infty }^{\infty }\left[Pr(X>x|Y>y)-Pr(X>x)\right]dx.$$

We can thus verify that $E\left(X\right)\le E\left(X\right|Y>y)$ for all y if, and only if,

$${\int }_{-\infty }^{\infty }[\widehat{C}({\overline{F}}_X\left(x\right),{\overline{F}}_Y\left(y\right))-{\overline{F}}_X\left(x\right){\overline{F}}_Y\left(y\right)]dx\ge 0,\forall y$$

or:

$${\int }_0^1(\widehat{C}(u,v)-uv)d{\overline{F}}_X^{-1}\left(u\right)\le 0,\forall t,\forall v\in [0,1].$$

□

Note that, as an immediate consequence of the preceding proposition, we have that the PQD property implies $E\left(X\right)\le E\left(X\right|Y>y)$ for all y and all ${\overline{F}}_X,{\overline{F}}_Y$, if the expectations exist. Moreover, it is easy to verify that $r_{X,Y}\ge 0$ if $E\left(X\right)\le E\left(X\right|Y>y)$ for all y, where:

$$r_{X,Y}=\frac{1}{{\sigma }_X{\sigma }_Y}{\int }_0^1{\int }_0^1(\widehat{C}(u,v)-uv)d{\overline{F}}_X^{-1}\left(u\right)d{\overline{F}}_Y^{-1}\left(v\right)$$

is the Pearson’s correlation coefficient (here, ${\sigma }_X$ and ${\sigma }_Y$ are the standard deviations of X and Y, respectively). For the formula of $r_{X,Y}$, see, e.g., [21].

For $RT{I}_{MRL}\left(X\right|Y)$, we have the following property.

Proposition 16.

Let $(X,Y)$ be a random vector with continuous marginal distribution functions $F_X$ and $F_Y$. Then, the following conditions are equivalent:

(i) 

$\left(X\right|Y>y_1){\le }_{MRL}\left(X\right|Y>y_2)$ for all $y_1\le y_2,y_1,y_2\in \mathbb{R}$ (i.e., $RT{I}_{MRL}\left(X\right|Y)$);

(ii) 

$\left(X_t\right|Y>y_1){\le }_{MRL}\left(X_t\right|Y>y_2)$ for all $y_1\le y_2,y_1,y_2\in \mathbb{R}$, and for all $t\in \mathbb{R}$;

(iii) 

$\left(X_t\right|Y>y_1){\le }_{ICX}\left(X_t\right|Y>y_2)$ for all $y_1\le y_2,y_1,y_2\in \mathbb{R}$, and for all $t\in \mathbb{R}$;

(iv) 

The survival copula $\widehat{C}$ satisfies:

$${\int }_0^z[\widehat{C}(z,v_1)\widehat{C}(u,v_2)-\widehat{C}(z,v_2)\widehat{C}(u,v_1)]d{\overline{F}}_X^{-1}\left(u\right)\le 0$$

(17)

for all $z\in [0,1]$ and $0\le v_1\le v_2\le 1.$

Proof. 

The equivalence between the first three items follows from Proposition 3. For the equivalence with $\left(iv\right)$, observe that $\left(X\right|Y>y_1){\le }_{MRL}\left(X\right|Y>y_2)$ for all $y_1\le y_2$ if, and only if,

$$\frac{{\int }_t^{\infty }\overline{F}(x,y_1)dx}{{\int }_t^{\infty }\overline{F}(x,y_2)dx}\mathrm{decreases}\mathrm{in}t\forall y_1\le y_2,$$

i.e., if, and only if,

$$\frac{{\int }_t^{\infty }\widehat{C}({\overline{F}}_X\left(x\right),v_1)dx}{{\int }_t^{\infty }\widehat{C}({\overline{F}}_X\left(x\right),v_2)dx}\mathrm{decreases}\mathrm{in}t\forall 0\le v_2\le v_1\le 1.$$

This is equivalent to:

$$-\widehat{C}({\overline{F}}_X\left(t\right),v_1){\int }_t^{\infty }\widehat{C}({\overline{F}}_X\left(x\right),v_2)dx+\widehat{C}({\overline{F}}_X\left(t\right),v_2){\int }_t^{\infty }\widehat{C}({\overline{F}}_X\left(x\right),v_1)dx\le 0$$

for all $0\le v_2\le v_1\le 1$ and $t\in {\mathcal{S}}_X$. The latter can be written as:

$${\int }_z^0[\widehat{C}(z,v_1)\widehat{C}(u,v_2)-\widehat{C}(z,v_2)\widehat{C}(u,v_1)]d{\overline{F}}_X^{-1}\left(u\right)\ge 0$$

for all $z\in [0,1]$ and $0\le v_2\le v_1\le 1$, which is equivalent to (17). □

Note that, as an immediate consequence of the preceding proposition, we have that the RCSI property (i.e., $\widehat{C}$ is $T{P}_2$) implies $\left(X\right|Y>y_1){\le }_{MRL}\left(X\right|Y>y_2)$ for all $y_1\le y_2$ and all ${\overline{F}}_X,{\overline{F}}_Y$.

Corollary 5.

Under the above assumptions, if ${\overline{F}}_X$ is strictly monotone and convex and:

$${\int }_0^z\widehat{C}(u,v)du\mathrm{is}T{P}_2\mathrm{in}(z,v)\in {[0,1]}^2$$

(18)

then $\left(X\right|Y>y_1){\le }_{MRL}\left(X\right|Y>y_2)$ for all $y_1\le y_2,y_1,y_2\in \mathbb{R}$ and all ${\overline{F}}_Y$.

Proof. 

From (18) and the convexity of ${\overline{F}}_X$, by applying Corollary 1, one gets that ${\int }_t^1\overline{C}(1-F_X\left(u\right),1-v)du$ is also $T{P}_2$ in $(t,v)$. This implies that:

$$\frac{{\int }_t^{\infty }\overline{C}(1-F_X\left(u\right),1-F_Y\left(v_1\right))du}{{\int }_t^{\infty }\overline{C}(1-F_X\left(u\right),1-F_Y\left(v_2\right))du}\mathrm{is}\mathrm{decreasing}\mathrm{in}t\mathrm{for}\mathrm{all}0\le v_1\le v_2\le 1,$$

which means:

$$\frac{{\int }_t^{\infty }\overline{F}(u,s_1)du}{{\int }_t^{\infty }\overline{F}(u,s_2)du}\mathrm{is}\mathrm{decreasing}\mathrm{in}t\mathrm{for}\mathrm{all}0\le s_1\le s_2,$$

i.e., $\left(X\right|Y>s_1){\le }_{MRL}\left(X\right|Y>s_2)$. □

Note that the sufficient conditions for $RT{I}_{MRL}\left(X\right|Y)$ described in Corollary 5 were proven already in [1] with a different and less immediate proof. However, the strict monotonicity of ${\overline{F}}_X$ is not required in the proof provided there.

The relationships between these new dependence notions and the ones described in the previous section are summarized in the following Table 4. Note that the fact that $PQD(X,Y)$ is not implied by $RT{I}_{MRL}\left(X\right|Y)$, mentioned in the table, is because the MRL order does not imply the ST order.

Table 4. Relationships among weak positive dependence properties.

${\mathit{r}}_{\mathit{X},\mathit{Y}}\ge 0$
⇑
$PQDE\left(X\right|Y)$	⇐	$RT{I}_{ICX}^0\left(X\right|Y)$	⇐	$RT{I}_{MRL}^0\left(X\right|Y)$
⇑		⇑		⇑
$RT{I}_{ICX}^0\left(Y\right|X)$	⇐	$PQD(X,Y)$	$\nLeftarrow$	$RT{I}_{MRL}\left(X\right|Y)$
⇑		$\cancel{\Uparrow }$		⇑
$RT{I}_{MRL}^0\left(Y\right|X)$	⇐	$RT{I}_{MRL}\left(Y\right|X)$	⇐	$RCSI(X,Y)$

To avoid false implications in Table 4, one can try to replace the PQD property with the $RT{I}_{ICX}\left(X\right|Y)$ property, for which we have the following statements.

Proposition 17.

Let $(X,Y)$ be a random vector with continuous distribution functions $F_X$ and $F_Y$. Then, the following conditions are equivalent:

(i) 

$\left(X\right|Y>y_1){\le }_{ICX}\left(X\right|Y>y_2)$ for all $y_1\le y_2,y_1,y_2\in \mathbb{R}$ (i.e., $RT{I}_{ICX}\left(X\right|Y)$);

(ii) 

The survival copula $\widehat{C}$ satisfies:

$${\int }_0^z[v_2\widehat{C}(u,v_1)-v_1\widehat{C}(u,v_2)]d{\overline{F}}_X^{-1}\left(u\right)\le 0,\forall z\in [0,1]\mathrm{and}\forall 0\le v_1\le v_2\le 1.$$

(19)

Proof. 

Observe that $\left(X\right|Y>y_1){\le }_{ICX}\left(X\right|Y>y_2)$ for $y_1\le y_2$, if, and only if,

$${\int }_t^{\infty }\left[\frac{\overline{F}(x,y_1)}{\overline{F}(0,y_1)}-\frac{\overline{F}(x,y_2)}{\overline{F}(0,y_2)}\right]dx\le 0\forall t,$$

i.e., if, and only if,

$${\int }_t^{\infty }\left[\overline{F}(x,y_1)\overline{F}(0,y_2)-\overline{F}(x,y_2)\overline{F}(0,y_1)\right]dx\le 0\forall t.$$

The latter is the same as:

$${\int }_t^{\infty }\left[\widehat{C}(\overline{F}\left(x\right),v_1)v_2-\widehat{C}(\overline{F}\left(x\right),v_2)v_1\right]dx\le 0$$

for $v_1\ge v_2$ and $t\in \mathbb{R}$, which can be also restated as:

$${\int }_0^{\overline{F}\left(t\right)}\left[\widehat{C}(u,v_1)v_2-\widehat{C}(u,v_2)v_1\right]d{\overline{F}}_X^{-1}\left(u\right)\ge 0$$

for $v_1\ge v_2$ and $t\in \mathbb{R}$. This is the same as (19). □

Corollary 6.

Under the above assumptions, if ${\overline{F}}_X$ is convex and:

$${\int }_0^z[v_2\widehat{C}(u,v_1)-v_1\widehat{C}(u,v_2)]du\ge 0,\forall z\in [0,1]\mathrm{and}\forall 0\le v_1\le v_2\le 1,$$

(20)

then $\left(X\right|Y>y_1){\le }_{ICX}\left(X\right|Y>y_2)$ for $y_1\le y_2,y_1,y_2\in \mathbb{R}$ and all $F_Y$.

Proof. 

Since ${\overline{F}}_X$ is decreasing and convex, then ${\overline{F}}_X^{-1}\left(u\right)$ is decreasing and convex and $-{\overline{F}}_X^{-1}\left(u\right)$ is increasing and concave. Then, by applying Lemma 7.1(b) of [6] to Equation (20) above, we obtain:

$${\int }_0^z[v_2\widehat{C}(u,v_1)-v_1\widehat{C}(u,v_2)]d\left(-{\overline{F}}_X^{-1}\left(u\right)\right)\ge 0$$

(21)

for all $z\in [0,1]$ and $0\le v_1\le v_2\le 1$, which is the same as (19). □

Thus, the relationships between the new dependence notions (and some of the strong ones) are summarized in the following Table 5, where only the dependencies of X given Y are considered (due to the fact that the $RT{I}_{ICX}\left(X\right|Y)$ is not symmetric, i.e., that $RT{I}_{ICX}\left(X\right|Y)$ is different than $RT{I}_{ICX}\left(Y\right|X)$). However, a similar table can be obtained for $\left(Y\right|X)$.

Table 5. Relationships among weak positive dependence properties.

${\mathit{r}}_{\mathit{X},\mathit{Y}}\ge 0$
⇑
$PQDE\left(X\right|Y)$	⇐	$RT{I}_{ICX}^0\left(X\right|Y)$	⇐	$RT{I}_{MRL}^0\left(X\right|Y)$
⇑		⇑		⇑
$RT{I}_{ICX}^0\left(X\right|Y)$	⇐	$RT{I}_{ICX}\left(X\right|Y)$	⇐	$RT{I}_{MRL}\left(X\right|Y)$
⇑		⇑		⇑
$PQD(X,Y)$	⇐	$RT{I}_{ST}\left(X\right|Y)$	⇐	$RCSI(X,Y)$

All the properties mentioned above are not independent of the marginal distributions of $(X,Y)$, and the convexity of the marginal survival functions is required. However, interesting properties of the survival copula of the vector are introduced. In the following, these particular properties are studied in detail, and their mutual relationships are pointed out.

To this aim, first observe that considering the property of the copula rather than the property of the vector, one gets a different final result in terms of dependence indexes. In fact, letting P denote the property:

$${\int }_0^z[\widehat{C}(u,v)-uv]du\ge 0,\forall z\in [0,1],\forall v\in [0,1],$$

and letting $\tilde{P}$ denote the property:

$$X{\le }_{ICX}\left(X\right|Y>y)\forall y\in \mathbb{R}\mathrm{and}\mathrm{for}\mathrm{fixed}\mathrm{continuous}\mathrm{survival}\mathrm{functions}{\overline{F}}_X,{\overline{F}}_Y,$$

one immediately observes that both are positive dependence properties weaker than $PQD$, but with different implications. Property P verifies:

$$PQD\Rightarrow P\Rightarrow {\rho }_{X,Y}\ge 0,$$

where:

$${\rho }_{X,Y}=12{\int }_0^1{\int }_0^{1}C(u,v)dudv-3$$

is the Spearman’s rho coefficient for X and Y (for the formula of ${\rho }_{X,Y},$, see equation (5.1.15c) in [11]), and the first implication follows from (6). Property $\tilde{P}$ verifies:

$$PQD\Rightarrow \tilde{P}\Rightarrow r_{X,Y}\ge 0.$$

(22)

Because of this fact, one can define weak dependence properties as has been done for P, by letting the margins be uniformly distributed on $(0,1)$ in the definitions above. Doing this, one gets the weak positive dependence properties described in the statement that follows (easy to prove). Note that property P described above is denoted here as $P_2$.

Proposition 18.

Let $(U,V)$ be a random vector having uniformly $U[0,1]$ distributed margins. Then:

($P_1)$

$E\left(U\right)\le E\left(U\right|V>v)$ for all v (i.e., $PQDE\left(U\right|V)$) if, and only if,

$${\int }_0^1[\widehat{C}(u,v)-uv]du\ge 0\mathrm{for}\mathrm{all}v\in [0,1];$$

(23)

($P_2)$

$U{\le }_{ICX}\left(U\right|V>v)$ for all v (i.e., $RT{I}_{ICX}^0\left(U\right|V)$) if, and only if,

$${\int }_0^z[\widehat{C}(u,v)-uv]du\ge 0\mathrm{for}\mathrm{all}v,z\in [0,1];$$

(24)

($P_3)$

$U{\le }_{MRL}\left(U\right|V>v)$ for all v (i.e., $RT{I}_{MRL}^0\left(U\right|V)$) if, and only if,

$${\int }_0^z[z\widehat{C}(u,v)-u\widehat{C}(z,v)]du\ge 0\mathrm{for}\mathrm{all}v,z\in [0,1];$$

(25)

($P_4)$

$\left(U\right|V>v_1){\le }_{ICX}\left(U\right|V>v_2)$ for all $v_1\le v_2$ (i.e., $RT{I}_{ICX}\left(U\right|V)$) if, and only if,

$${\int }_0^z[v_2\widehat{C}(u,v_1)-v_1\widehat{C}(u,v_2)]du\ge 0\mathrm{for}\mathrm{all}z\in [0,1]\mathrm{and}{v}_1\le v_2;$$

(26)

($P_5)$

$\left(U\right|V>v_1){\le }_{MRL}\left(U\right|V>v_2)$ for all $v_1\le v_2$ (i.e., $RT{I}_{MRL}\left(U\right|V)$) if, and only if,

$${\int }_0^z[\widehat{C}(z,v_2)\widehat{C}(u,v_1)-\widehat{C}(z,v_1)\widehat{C}(u,v_2)]du\ge 0\mathrm{for}\mathrm{all}z\in [0,1]\mathrm{and}{v}_1\le v_2.$$

(27)

Remark 1.

The relationships between these properties can be better understood by considering their equivalent formulations described as follows.

For (23), observe that it is the same as:

$${\int }_0^1[\widehat{C}(u,v)\widehat{C}(1,1)-\widehat{C}(u,1)\widehat{C}(1,v)]du\ge 0\mathrm{for}\mathrm{all}v\in [0,1],$$

i.e.,

$$\frac{{\int }_0^1\widehat{C}(u,v)du}{\widehat{C}(1,v)}\ge \frac{{\int }_0^1\widehat{C}(u,1)du}{\widehat{C}(1,1)}\forall v\in [0,1].$$

(28)

In a similar manner, one has that (24) holds if, and only if,

$$\frac{{\int }_0^z\widehat{C}(u,v)du}{\widehat{C}(1,v)}\ge \frac{{\int }_0^z\widehat{C}(u,1)du}{\widehat{C}(1,1)}\forall v,z\in [0,1].$$

(29)

Clearly, (29) implies (28), i.e., property $P_2$ implies $P_1$.

For (25), observe that it is the same as:

$$\widehat{C}(z,1){\int }_0^z\widehat{C}(u,v)du-\widehat{C}(z,v){\int }_0^z\widehat{C}(u,1)du\ge 0\mathit{for}\mathit{all}v,z\in [0,1],$$

which in turn means that:

$$\frac{{\int }_0^z\widehat{C}(u,v)du}{{\int }_0^z\widehat{C}(u,1)du}\mathit{decreases}\mathit{in}z\in [0,1]\mathit{for}\mathit{every}\mathit{fixed}v\in [0,1].$$

(30)

Note that (30) is the same as:

$$\frac{{\int }_0^z\widehat{C}(u,v)du}{\widehat{C}(z,v)}\ge \frac{{\int }_0^z\widehat{C}(u,1)du}{\widehat{C}(z,1)}\forall z,v\in [0,1].$$

Thus it follows that, if (25) holds, then:

$$\frac{{\int }_0^z\widehat{C}(u,v)du}{{\int }_0^z\widehat{C}(u,1)du}\ge \frac{{\int }_0^1\widehat{C}(u,v)du}{{\int }_0^1\widehat{C}(u,1)du}\ge \frac{\widehat{C}(1,v)}{\widehat{C}(1,1)}\forall v,z\in [0,1],$$

and (24) holds. Thus, property $P_3$ implies $P_2$.

For (26), just observe that we can rewrite it as:

$${\int }_0^z[\widehat{C}(1,v_2)\widehat{C}(u,v_1)-\widehat{C}(1,v_1)\widehat{C}(u,v_2)]du\ge 0\mathit{for}\mathit{all}{v}_1\le v_2,$$

i.e.,

$$\frac{{\int }_0^z\widehat{C}(u,v_1)du}{\widehat{C}(1,v_1)}\ge \frac{{\int }_0^z\widehat{C}(u,v_2)du}{\widehat{C}(1,v_2)}\forall z\in [0,1]\mathit{and}0\le v_1\le v_2\le 1.$$

(31)

Clearly, (31) implies (29), i.e., property $P_4$ implies $P_2$.

Finally, (27) is the same as:

$$\frac{{\int }_0^z\widehat{C}(u,v_1)du}{\widehat{C}(z,v_1)}\ge \frac{{\int }_0^z\widehat{C}(u,v_2)du}{\widehat{C}(z,v_2)}\forall z\in [0,1]\mathit{and}0\le v_1\le v_2\le 1,$$

which means that:

$$\frac{{\int }_0^z\widehat{C}(u,v_1)du}{{\int }_0^z\widehat{C}(u,v_2)du}\mathit{decreases}\mathit{in}z\in [0,1]\mathit{for}\mathit{every}\mathit{fixed}{v}_1\le v_2,$$

(32)

i.e., ${\int }_0^z\widehat{C}(u,v)du$ is $T{P}_2$ in $(z,v)\in {[0,1]}^2$. Clearly, (32) implies (30) (i.e., $P_5$ implies $P_3$). Moreover, it implies (31) (i.e., $P_4$), as it can be proven in a similar manner as we proved that (30) implies (29).

These equivalent formulations of the properties of $\widehat{C}$, and their mutual implications, are described in the following Table 6. Note that all these properties only depend on the copula, thus being actually dependence properties. Some strong dependence properties are included in the chain of relationships, i.e., the $PQD$ ($PQD(U,V)$), the $RTI$ ($RT{I}_{ST}\left(U\right|V)$), and the $RCSI$ ($RCSI(U,V)$) properties.

Table 6. Relationships among weak positive dependence properties.

${\mathit{\rho }}_{\mathit{U},\mathit{V}}\ge 0$
⇑
$PQDE\left(U\right|V)$	⇐	$RT{I}_{ICX}^0\left(U\right|V)$	⇐	$RT{I}_{MRL}^0\left(U\right|V)$
⇑		⇑		⇑
$RT{I}_{ICX}^0\left(U\right|V)$	⇐	$RT{I}_{ICX}\left(U\right|V)$	⇐	$RT{I}_{MRL}\left(U\right|V)$
⇑		⇑		⇑
$PQD(U,V)$	⇐	$RT{I}_{ST}\left(U\right|V)$	⇐	$RCSI(U,V)$

5. Reversed Weak Dependence Notions

By considering relationships between inactivity times rather than residual times, one can define other dependence notions, which we call “reversed weak dependence notions”. In particular, the notions considered here are based on comparisons in the MIT and the ICV orders and on the $LTD$ property. Thus, the notions considered here are $LT{D}_{ICV}^{\infty }\left(X\right|Y)$, $LT{D}_{MIT}^{\infty }\left(X\right|Y)$, $LT{D}_{ICV}\left(X\right|Y)$, $LT{D}_{MIT}\left(X\right|Y)$, and the one based on inequality $E\left(X\right)\ge E\left(X\right|Y\le y)$ for all $y\ge 0$ (which is actually equivalent to $PQDE\left(X\right|Y)$, as seen in Proposition 15).

All the proofs of the statements described in this section follow the same lines of those described in Section 4 and are therefore omitted, except for the first one (given as an example).

Proposition 19.

Let $(X,Y)$ be a random vector with continuous marginal distribution functions $F_X$ and $F_Y$. Then, $X{\ge }_{ICV}\left(X\right|Y\le y)$ for all $y\in \mathbb{R}$ (i.e., $LT{D}_{ICV}^{\infty }\left(X\right|Y)$) if, and only if:

$${\int }_0^z(C(u,v)-uv)d{F}_X^{-1}\left(u\right)\ge 0,\forall z,v\in [0,1].$$

(33)

Proof. 

It is clear that $X{\ge }_{ICV}\left(X\right|Y\le y)$ for all y, if, and only if,

$${\int }_{-\infty }^{t}Pr\left(X\le x\right)dx\le {\int }_{-\infty }^{t}Pr\left(X\le x|Y\le y\right)dx,\forall t,\forall y.$$

This is equivalent to:

$${\int }_{-\infty }^t[C(F_X\left(x\right),F_Y\left(y\right))-F_X\left(x\right)F_Y\left(y\right)]dx\ge 0,\forall t,\forall y$$

or:

$${\int }_0^{F_X\left(t\right)}(C(u,v)-uv)d{F}_X^{-1}\left(u\right)\ge 0,\forall t,\forall v\in [0,1].$$

Since $F_X$ is continuous, this is the same as (33). □

Corollary 7.

Under the above assumptions, if $F_X$ is convex and:

$${\int }_0^t(C(u,v)-uv)du\ge 0,\forall t,v\in [0,1],$$

(34)

then $X{\ge }_{ICV}\left(X\right|Y\le y)$ for all $y\in \mathbb{R}$ (i.e., $LT{D}_{ICV}^{\infty }\left(X\right|Y)$) for all $F_Y$.

Proof. 

The result follows by applying Lemma 7.1(b) of [6] to Equation (34) above. □

From Proposition 6, we obtain the following result.

Proposition 20.

Let $(X,Y)$ be a random vector with continuous marginal distribution functions $F_X$ and $F_Y$. Then, the following conditions are equivalent:

(i) 

$X{\ge }_{MIT}\left(X\right|Y\le y)$ for all $y\in \mathbb{R}$ (i.e., $LT{D}_{MIT}^{\infty }\left(X\right|Y)$);

(ii) 

${}_{t}X{\le }_{MIT}{(}_{t}X|Y\le y)$ for all $y,t\in \mathbb{R}$;

(iii) 

${}_{t}X{\le }_{ICX}{(}_{t}X|Y\le y)$ for all $y,t\in \mathbb{R}$;

(iv) 

${\int }_0^t[tC(u,v)-uC(t,v))d{F}_X^{-1}\left(u\right)\le 0,\forall t,v\in [0,1]$.

Corollary 8.

Under the above assumptions, if $F_X$ is convex and:

$${\int }_0^t[tC(u,v)-uC(t,v))du\ge 0,\forall t,v\in [0,1],$$

(35)

then $X{\ge }_{MIT}\left(X\right|Y\le y)$ for all $y\in \mathbb{R}$ (i.e., $LT{D}_{MIT}^{\infty }\left(X\right|Y)$) for all $F_Y$.

Proposition 21.

Let $(X,Y)$ be a random vector with continuous distribution functions $F_X$ and $F_Y$. Then, $\left(X\right|Y\le y_2){\ge }_{ICV}\left(X\right|Y\le y_1)$ for all $y_1\le y_2,y_1,y_2\in \mathbb{R}$ (i.e., $LT{D}_{ICV}\left(X\right|Y)$) if, and only if:

$${\int }_0^t[v_{2}C(u,v_1)-v_{1}C(u,v_2)]d{F}_X^{-1}\left(u\right)\ge 0,\forall t\in [0,1],\forall 0\le v_1\le v_2\le 1.$$

(36)

Corollary 9.

Under the above assumptions, if $F_X$ is convex and:

$${\int }_0^t[v_{2}C(u,v_1)-v_{1}C(u,v_2)]du\ge 0,\forall t\in [0,1],\forall v_1\le v_2,$$

(37)

then $\left(X\right|Y\le y_2){\ge }_{ICV}\left(X\right|Y\le y_1)$ for all $y_1\le y_2,y_1,y_2\in \mathbb{R}$ (i.e., $LT{D}_{ICV}\left(X\right|Y)$) for all $F_Y$.

The following theorem can also be obtained from Proposition 6.

Proposition 22.

Let $(X,Y)$ be a random vector with continuous marginal distribution functions $F_X$ and $F_Y$. Then, the following conditions are equivalent:

(i) 

$\left(X\right|Y\le y_2){\ge }_{MIT}\left(X\right|Y\le y_1)$ for all $y_1\le y_2,y_1,y_2\in \mathbb{R}$ (i.e., $LT{D}_{MIT}\left(X\right|Y)$);

(ii) 

${(}_{t}X|Y\le y_2){\le }_{MIT}{(}_{t}X|Y\le y_1)$ for all $y_1\le y_2,y_1,y_2\in \mathbb{R}$ and $t\in \mathbb{R}$;

(iii) 

${(}_{t}X|Y\le y_2){\le }_{ICX}{(}_{t}X|Y\le y_1)$ for all $y_1\le y_2,y_1,y_2\in \mathbb{R}$ and $t\in \mathbb{R}$;

(iv) 

${\int }_0^t[C(t,v_2)C(u,v_1)-C(t,v_1)C(u,v_2)]d{F}_X^{-1}\left(u\right)\ge 0,\forall t\in [0,1],\forall 0\le v_1\le v_2\le 1.$

Corollary 10.

Under the above assumptions, if $F_X$ is convex and:

$${\int }_0^t[C(t,v_2)C(u,v_1)-C(t,v_1)C(u,v_2)]du\ge 0,\forall t\in [0,1],\forall 0\le v_1\le v_2\le 1,$$

(38)

then $\left(X\right|Y\le y_2){\ge }_{MIT}\left(X\right|Y\le y_1)$ for all $y_1\le y_2,y_1,y_2\in \mathbb{R}$ (i.e., $LT{D}_{MIT}\left(X\right|Y)$) for all $F_Y$.

Proposition 23.

Let $(X,Y)$ be a random vector with continuous marginal distribution functions $F_X$ and $F_Y$. Then, $E\left(X\right)\ge E\left(X\right|Y\le y)$ for all $y\in \mathbb{R}$, whenever the expectations exist, if, and only if:

$${\int }_0^1(C(u,v)-uv)d{F}_X^{-1}\left(u\right)\ge 0,\forall t,v\in [0,1].$$

(39)

Note that the following chain of implications holds.

$$\mathrm{PQD}⟹X{\ge }_{ICV}\left(X\right|Y\le y)\forall y⟹E\left(X\right)\ge E\left(X\right|Y\le y)\forall y⟹r_{X,Y}\ge 0.$$

Thus, all the notions described above are positive dependence notions, depending on the marginal distributions of $(X,Y)$, whose relationships are described in Table 7.

Table 7. Relationships among reversed weak dependence properties.

				${\mathit{r}}_{\mathit{X},\mathit{Y}}\ge 0$
				⇑
$LT{D}_{MIT}^{\infty }\left(X\right|Y)$	⇒	$LT{D}_{ICV}^{\infty }\left(X\right|Y)$	⇒	$PQDE\left(X\right|Y)$
⇑		⇑		⇑
$LT{D}_{MIT}\left(X\right|Y)$	⇒	$LT{D}_{ICV}\left(X\right|Y)$	⇒	$LT{D}_{ICV}^{\infty }\left(X\right|Y)$
⇑		⇑		⇑
$RCSI(X,Y)$	⇒	$LT{D}_{ST}\left(X\right|Y)$	⇒	$PQD(X,Y)$

As has been done for the positive dependence notions in the previous section, one can again define weak dependence properties that are independent of the margins by considering only the properties of the connecting copula C, thus letting the margins be uniformly distributed on $(0,1)$ in the definitions above. Doing so, one gets the weak positive dependence properties described in the statement that follows.

Proposition 24.

Let $(U,V)$ be a random vector having uniformly $U[0,1]$ distributed margins. Then:

($P_1^R$)

$E\left(U\right)\ge E\left(U\right|V\le v)$ for all v (i.e., $PQDE\left(U\right|V)$) if, and only if,

$${\int }_0^1[C(u,v)-uv]du\ge 0\mathrm{for}\mathrm{all}v\in [0,1];$$

($P_2^R$)

$U{\ge }_{ICV}\left(U\right|V\le v)$ for all v (i.e., $LT{D}_{ICV}^{\infty }\left(U\right|V)$) if, and only if,

$${\int }_0^z[C(u,v)-uv]du\ge 0\mathrm{for}\mathrm{all}v,z\in [0,1];$$

($P_3^R$)

$U{\ge }_{MIT}\left(U\right|V\le v)$ for all v (i.e., $LT{D}_{MIT}^{\infty }\left(U\right|V)$) if, and only if,

$${\int }_0^z[zC(u,v)-uC(z,v)]du\ge 0\mathrm{for}\mathrm{all}v,z\in [0,1];$$

($P_4^R$)

$\left(U\right|V\le v_2){\ge }_{ICV}\left(U\right|V\le v_1)$ for all $0\le v_1\le v_2\le 1$ (i.e., $LT{D}_{ICV}\left(U\right|V)$) if, and only if,

$${\int }_0^z[v_{2}C(u,v_1)-v_{1}C(u,v_2)]du\ge 0\mathrm{for}\mathrm{all}z\in [0,1]\mathrm{and}0\le v_1\le v_2\le 1;$$

($P_5^R$)

$\left(U\right|V\le v_2){\ge }_{MIT}\left(U\right|V\le v_1)$ for all $v_1\le v_2$ (i.e., $LT{D}_{MIT}\left(U\right|V)$) if, and only if,

$${\int }_0^z[C(z,v_2)C(u,v_1)-C(z,v_1)C(u,v_2)]du\ge 0\mathrm{for}\mathrm{all}z\in [0,1]\mathrm{and}0\le v_1\le v_2\le 1.$$

The relationships among these notions can be proven as described for the weak positive dependence properties and are listed in Table 8.

Table 8. Relationships among reversed weak dependence properties.

				${\mathit{\rho }}_{\mathit{U},\mathit{V}}\ge 0$
				⇑
$LT{D}_{MIT}^{\infty }\left(U\right|V)$	⇒	$LT{D}_{ICV}^{\infty }\left(U\right|V)$	⇒	$PQDE\left(U\right|V)$
⇑		⇑
$LT{D}_{MIT}\left(U\right|V)$	⇒	$LT{D}_{ICV}\left(U\right|V)$	⇒	$LT{D}_{ICV}^{\infty }\left(U\right|V)$
⇑		⇑		⇑
$RCSI(U,V)$	⇒	$LT{D}_{ST}\left(U\right|V)$	⇒	$PQD(U,V)$

6. Counterexamples

Comments on the relationships among the above-described properties of copulas are given here, together with other useful counterexamples, like the first one that follows, which shows that the convexity of ${\overline{F}}_X$ is not a necessary condition for $RT{I}_{MRL}^0\left(X\right|Y)$.

Example 1.

Let us consider an FGM survival copula, that is,

$$\widehat{C}(u,v)=uv+\theta uv(1-u)(1-v)$$

for $\theta \in [-1,1]$. Then:

$${\partial }_1\widehat{C}(u,v)=v+\theta v(1-v)-2\theta uv(1-v)$$

is decreasing in u when $\theta \ge 0$. Hence, from Proposition 8, we get $X{\le }_{LR}\left(X\right|Y>s)$ for all s and all ${\overline{F}}_X,{\overline{F}}_Y$ (i.e., $RT{I}_{LR}^0\left(X\right|Y)$). Therefore, $X{\le }_{MRL}\left(X\right|Y>s)$ for all s and all ${\overline{F}}_X,{\overline{F}}_Y$. Therefore, we do not need the condition “${\overline{F}}_X$ is convex” for $RT{I}_{MRL}^0\left(X\right|Y)$ to hold. A straightforward calculation shows that (11) holds for this copula when $\theta \ge 0$.

In the next example, we discuss the relationships between $\widehat{C}(u,v)\ge uv$ ($PQD$ property) and the conditions on $\widehat{C}$ for $RT{I}_{MRL}^0\left(X\right|Y)$ to hold, i.e., (11) (which is the same as $RT{I}_{MRL}^0\left(U\right|V)$) and (14). In particular, it proves that the $PQD$ property does not imply (11) or (14). Moreover, it also proves that $RT{I}_{ICX}^0\left(X\right|Y)$ does not imply $RT{I}_{MRL}^0\left(X\right|Y)$.

Example 2.

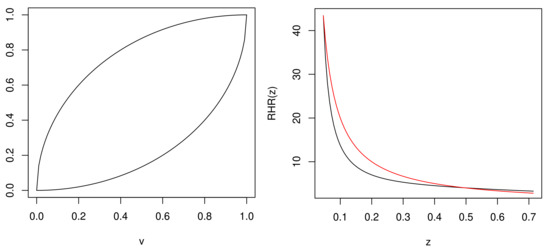
Let us consider a random vector $(X,Y)$ with the following Fredricks–Nelsen survival copula (see, e.g., p. 32 in [12]):

$$\widehat{C}(u,v)=min\left(u,v,\frac{u^2+v^2}{2}\right).$$

Clearly, $\widehat{C}(u,v)\ge uv$ since $u^2+v^2\ge 2uv$ for all $u,v\in [0,1]$. Hence, $(X,Y)$ is $PQD$, and so, $X{\le }_{ST}\left(X\right|Y>s)$ for all s and all $F_X,F_Y$ (i.e., $RT{I}_{ST}^0\left(X\right|Y)$ holds). Therefore, $RT{I}_{ICX}^0\left(X\right|Y)$ and $RT{I}_{ICX}^0\left(U\right|V)$ hold as well. A straightforward calculation shows that $\widehat{C}(u,v)/u$ is not decreasing in u for all $v\in [0,1]$, that is $(X,Y)$ is not $RTI\left(Y\right|X)$. Therefore, $X{\le }_{HR}\left(X\right|Y>s)$ does not hold for all s and all $F_X,F_Y$.

Let us see now that $(X,Y)$ (or $\widehat{C}$) does not satisfy (11). Hence, $X{\le }_{MRL}\left(X\right|Y>s)$ does not hold for all s and all $F_X,F_Y$ (e.g., for uniform distributions). For a fixed $v\in (0,1)$, let us consider an r.v. $Z_v$ having density defined as:

$$g_v\left(u\right)=\frac{\widehat{C}(u,v)}{k_v}=\left\{\begin{array}{cc}u/k_v& \mathrm{for}0\le u\le {\alpha }_1\left(v\right);\hfill \\ \frac{u^2+v^2}{2k_v}& \mathrm{for}{\alpha }_1\left(v\right)<u\le {\alpha }_2\left(v\right);\hfill \\ v/k_v& \mathrm{for}{\alpha }_2\left(v\right)<u\le 1;\hfill \\ 0& \mathrm{for}u\notin [0,1];\hfill \end{array}\right.$$

with $k_v:={\int }_0^1\widehat{C}(u,v)du>0$, $0<{\alpha }_1\left(v\right)<{\alpha }_2\left(v\right)<1$,

$${\alpha }_1\left(v\right):=1-\sqrt{1-v^2}$$

and:

$${\alpha }_2\left(v\right):=\sqrt{2v-v^2}.$$

They are plotted in Figure 1, left. Note that (11) is equivalent to $Z_1{\ge }_{RHR}{Z}_v$ for all $0<v<1$. The associated distribution and reversed hazard rate functions are:

$$G_v\left(z\right)={\int }_0^z{g}_v\left(u\right)du=\frac{1}{k_v}{\int }_0^{z}udu=\frac{z^2}{2k_v}$$

Figure 1. Functions (left) ${\alpha }_1$ (down) and ${\alpha }_2$ (top) for the copula in Example 2. Reversed hazard rate functions (right) for $Z_v$ (black) and $Z_1$ (red) when $v=0.3$ for the copula in Example 2.

and:

$${\overline{h}}_v\left(z\right)=\frac{g_v\left(z\right)}{G_v\left(z\right)}=\frac{2}{z}$$

for $0\le z\le {\alpha }_1\left(v\right)$. Analogously, for ${\alpha }_1\left(v\right)<z\le {\alpha }_2\left(v\right)$, we get:

$$G_v\left(z\right)={\int }_0^z{g}_v\left(u\right)du=\frac{{\alpha }_1^2\left(v\right)}{2k_v}+{\int }_{{\alpha }_1\left(v\right)}^z\frac{u^2+v^2}{2k_v}du=\frac{{\alpha }_1^2\left(v\right)}{2k_v}+\frac{z^3-{\alpha }_1^3\left(v\right)}{6k_v}+\frac{z-{\alpha }_1\left(v\right)}{2k_v}{v}^2$$

and:

$${\overline{h}}_v\left(z\right)=\frac{g_v\left(z\right)}{G_v\left(z\right)}=\frac{z^2+v^2}{{\alpha }_1^2\left(v\right)+(z^3-{\alpha }_1^3\left(v\right))/3+v^2(z-{\alpha }_1\left(v\right))}$$

for ${\alpha }_1\left(v\right)<z\le {\alpha }_2\left(v\right)$. By plotting ${\overline{h}}_v$, we see that ${\overline{h}}_v\left(z\right)$ and $h_1\left(z\right)=2/z$ are not ordered for ${\alpha }_1\left(v\right)<z\le {\alpha }_2\left(v\right)$. For example, if $v=0.3$, then ${\alpha }_1\left(v\right)=0.0460608$ and ${\alpha }_2\left(v\right)=0.7141428$, and we obtain the reversed hazard rate functions ${\overline{h}}_v\left(z\right)$ plotted in Figure 1, right, for $0.0460608<z<0.7141428$. Therefore, $Z_v$ and $Z_1$ are not RHR-ordered, and (11) does not hold.

Finally, we prove that (14) does not hold. For $0<u\le {\alpha }_1\left(v\right)$,

$${\beta }_v\left(u\right):=\frac{1}{u}\widehat{C}(u,v)=1$$

and for ${\alpha }_1\left(v\right)<u<{\alpha }_2\left(v\right)$:

$${\beta }_v\left(u\right):=\frac{1}{u}\widehat{C}(u,v)=\frac{u}{2}+\frac{v^2}{2u}.$$

Then:

$${\beta }_v^{\prime }\left(u\right)=\frac{1}{2}-\frac{v^2}{2u^2}=\frac{u^2-v^2}{2u^2}$$

for ${\alpha }_1\left(v\right)<u<{\alpha }_2\left(v\right)$. Hence, ${\beta }_v\left(u\right)$ is decreasing for ${\alpha }_1\left(v\right)<u<v$ and increasing for $v<u<{\alpha }_2\left(v\right)$. Thus, for ${\alpha }_2\left(v\right)<u<1$, we get:

$${\beta }_v\left(u\right)=\frac{1}{u}\widehat{C}(u,v)=\frac{v}{u}$$

is decreasing in u for ${\alpha }_2\left(v\right)<u<1$. Therefore, (14) does not hold.

The following is a copula that satisfies both (11) (i.e., $RT{I}_{MRL}^0\left(U\right|V)$) and (14), but not the $PQD$ property.

Example 3.

Let us consider a random vector $(X,Y)$ with the following survival copula:

$$\widehat{C}(u,v)=uv+\theta \gamma \left(u\right)g\left(v\right),$$

where $\theta \in [0,1]$, $\gamma \left(u\right)=sin\left(2\pi u\right)/\left(2\pi \right)$, and $g\left(v\right)=v(1-v)$. It can be verified that γ satisfy all the conditions for $\widehat{C}$ to be a copula (see [22], for details). It is easy to see that it is not PQD (the difference $\widehat{C}(u,v)-uv$ is positive for $0<u<1/2$ and negative for $1/2<u<1$). To study (11), we consider the function:

$$\frac{{\int }_0^z\widehat{C}(u,v)du}{{\int }_0^z\widehat{C}(u,1)du}=\frac{1}{z^2}{\int }_0^z\widehat{C}(u,v)du=\frac{v}{2}+\frac{\theta v(1-v)}{{\left(2\pi \right)}^2}\frac{1-cos\left(2\pi z\right)}{z^2}.$$

It is easy to see that $(1-cos\left(2\pi z\right))/z^2$ is decreasing for $z\in (0,1)$, so (11) holds. Moreover, by plotting $\widehat{C}(u,v)/u$, we see that it is a bathtub in u for all $v\in (0,1)$. Hence, (14) also holds.

7. Conclusions

In the paper, we analyzed the dependence properties related to orderings of conditional distributions. The main novelties are new weak dependence notions related to mean residual life, increasing concave, mean inactivity time, and increasing convex orders. All these new classes imply positive or negative correlation coefficients and can be related to the classical dependence properties defined in a similar way as the stochastic, hazard rate, reversed hazard rate, and likelihood ratio orders. The relationships for all the positive dependence notions (summarized in Table 9) are described in Figure 2. The relationships for the negative dependence notions are similar.

Table 9. Positive dependence notions.

N	Name
0	$PQDE$	$E\left(X\right)\le E\left(X\right|Y>s)$	$E\left(X\right)\ge E\left(X\right|Y\le s)$
1	$PQD$	$RT{I}_{ST}^0\left(Y\right|X)$	$RT{I}_{ST}^0\left(X\right|Y)$	$LT{D}_{ST}^{\infty }\left(Y\right|X)$	$LT{D}_{ST}^{\infty }\left(X\right|Y)$
2	$RTI\left(Y\right|X)$	$RT{I}_{ST}\left(Y\right|X)$	$RT{I}_{HR}^0\left(X\right|Y)$
2’	$RTI\left(X\right|Y)$	$RT{I}_{ST}\left(X\right|Y)$	$RT{I}_{HR}^0\left(Y\right|X)$
3	$SI\left(Y\right|X)$	$S{I}_{ST}\left(Y\right|X)$	$RT{I}_{LR}^0\left(X\right|Y)$	$LT{D}_{LR}^{\infty }\left(X\right|Y)$
3’	$SI\left(X\right|Y)$	$S{I}_{ST}\left(X\right|Y)$	$RT{I}_{LR}^0\left(Y\right|X)$	$LT{D}_{LR}^{\infty }\left(Y\right|X)$
4	$LTD\left(Y\right|X)$	$LT{D}_{ST}\left(Y\right|X)$	$LT{D}_{RHR}^{\infty }\left(X\right|Y)$
4’	$LTD\left(X\right|Y)$	$LT{D}_{ST}\left(X\right|Y)$	$LT{D}_{RHR}^{\infty }\left(Y\right|X)$
5	$RCSI$	$RT{I}_{HR}\left(Y\right|X)$	$RT{I}_{HR}\left(X\right|Y)$
6	$LCSD$	$LT{D}_{RHR}\left(Y\right|X)$	$LT{D}_{RHR}\left(X\right|Y)$
7	$SIRL\left(Y\right|X)$	$S{I}_{HR}\left(Y\right|X)$	$RT{I}_{LR}\left(X\right|Y)$
7’	$SIRL\left(X\right|Y)$	$S{I}_{HR}\left(X\right|Y)$	$RT{I}_{LR}\left(Y\right|X)$
8		$S{I}_{RHR}\left(Y\right|X)$	$LT{D}_{LR}\left(X\right|Y)$
8’		$S{I}_{RHR}\left(X\right|Y)$	$LT{D}_{LR}\left(Y\right|X)$
9	$PLRD$	$S{I}_{LR}\left(Y\right|X)$	$S{I}_{LR}\left(X\right|Y)$
10		$RT{I}_{MRL}\left(Y\right|X)$
10’		$RT{I}_{MRL}\left(X\right|Y)$
11		$RT{I}_{MRL}^0\left(Y\right|X)$
11’		$RT{I}_{MRL}^0\left(X\right|Y)$
12		$RT{I}_{ICX}\left(Y\right|X)$
12’		$RT{I}_{ICX}\left(X\right|Y)$
13		$RT{I}_{ICX}^0\left(Y\right|X)$
13’		$RT{I}_{ICX}^0\left(X\right|Y)$
14		$LT{D}_{MIT}\left(Y\right|X)$
14’		$LT{D}_{MIT}\left(X\right|Y)$
15		$LT{D}_{MIT}^{\infty }\left(Y\right|X)$
15’		$LT{D}_{MIT}^{\infty }\left(X\right|Y)$
16		$LT{D}_{ICV}\left(Y\right|X)$
16’		$LT{D}_{ICV}\left(X\right|Y)$
17		$LT{D}_{ICV}^{\infty }\left(Y\right|X)$
17’		$LT{D}_{ICV}^{\infty }\left(X\right|Y)$

Figure 2. Relationships among the positive dependence notions in Table 9.

The main disadvantage of the new dependence notions proposed here is that they depend on the marginal distributions (as the Pearson’s correlation coefficient). This problem can be solved by replacing them with the respective copula properties obtained by assuming uniform marginals. In this case, they imply a positive Spearman’s rho coefficient. Moreover, we must say that there are other weak dependence notions that come through in papers devoted to more specific areas, which are not studied here for the sake of brevity. This is the case, for example, of the Gini correlation introduced in economics in [23] and further studied in [24,25]. Given two random variables X and Y, the Gini correlation is a non-symmetric measure given by:

$${\rho }_{X\circ Y}=\frac{Cov\left(X,F_Y\left(Y\right)\right)}{Cov\left(X,F_X\left(X\right)\right)}$$

whose properties are a mixture of Pearson’s and Spearman’s correlations. It follows from Proposition 15(iii) that $PQDE\left(X\right|Y)$ implies ${\rho }_{X\circ Y}\ge 0.$ Furthermore, for simplicity, we have just studied the bivariate case. The study of other notions and the extensions of these dependence properties to n-dimensional random vectors are not straightforward and will be studied in future research projects.