A Method of Generating Fuzzy Implications from n Increasing Functions and n + 1 Negations

Abstract

In this paper, we introduce a new construction method of a fuzzy implication from n increasing functions ${\mathrm{g}}_{\mathrm{i}}:\left[0,1\right]\to \left[0,\infty \right), \left(\mathrm{g}\left(0\right)=0\right)$ ($\mathrm{i}=1,2,\dots ,\mathrm{n}, \mathrm{n} \in \mathbb{\mathbb{N}}$) and $\mathrm{n}+1$ fuzzy negations ${\mathrm{N}}_{\mathrm{i}}$ ($\mathrm{i}=1,2,\dots ,\mathrm{n}+1, \mathrm{n} \in \mathbb{\mathbb{N}}$). Imagine that there are plenty of combinations between $\mathrm{n}$ increasing functions ${\mathrm{g}}_{\mathrm{i}}$ and $\mathrm{n}+1$ fuzzy negations ${\mathrm{N}}_{\mathrm{i}}$ in order to produce new fuzzy implications. This method allows us to use at least two fuzzy negations ${\mathrm{N}}_{\mathrm{i}}$ and one increasing function $\mathrm{g}$ in order to generate a new fuzzy implication. Choosing the appropriate negations, we can prove that some basic properties such as the exchange principle (EP), the ordering property (OP), and the law of contraposition with respect to $\mathrm{N}$ are satisfied. The worth of generating new implications is valuable in the sciences such as artificial intelligence and robotics. In this paper, we have found a novel method of generating families of implications. Therefore, we would like to believe that we have added to the literature one more source from which we could choose the most appropriate implication concerning a specific application. It should be emphasized that this production is based on a generalization of an important form of Yager’s implications.

1. Introduction

Fuzzy implications are the generalization of the classical (Boolean) implication in the interval of [0,1]. They play an important role in the area of fuzzy logic, decision theory, and fuzzy control. We can generate fuzzy implications from aggregation functions and fuzzy negations [1,2,3,4,5]. Other ways of generating fuzzy implications can be achieved by additive generating functions or by some initials implications [6,7,8,9,10,11]. Fuzzy implications are used for the application of the ‘if-then’ rule in fuzzy systems and inference processes, through Modus Ponens and Modus Tollens [12].

This paper is inspired by Yager’s f-generated implications where $\mathrm{f}:\left[0,1\right]\to \left[0,\infty \right]$ is a strictly decreasing and continuous function and $\mathrm{f}\left(1\right)=0$. In addition, a fuzzy implication $\mathrm{I}:{\left[0,1\right]}^2\to \left[0,1\right]$ is defined by: $\mathrm{I}\left(\mathrm{x},\mathrm{y}\right)={\mathrm{f}}^{-1}\left(\mathrm{xf}\left(\mathrm{y}\right)\right), \mathrm{x},\mathrm{y} \in \left[0,1\right]$ with the understanding 0·∞ = 0 (see [1] Definition 3.1.1). In this paper, we use functions ${\mathrm{g}}_{\mathrm{i}}:\left[0,1\right]\to \left[0,\infty \right)$, which are increasing and continuous, and also ${\mathrm{g}}_{\mathrm{i}}\left(0\right)=0$. We present a new production machine of fuzzy implications. Such a type of generating fuzzy implications can be found in the literature [1,2,5,6,7,8], for example, ${\mathrm{I}}_{\mathrm{RC}}=1-\mathrm{x}+\mathrm{xy}$. The production of new fuzzy implications is accomplished with the help of any fuzzy negations and increasing functions. These generated fuzzy implications fulfill the necessary properties required to be fuzzy implications (see [1] Definition 1.1.1.). Moreover, if the negations are selected with certain properties, then the generated implications may also fulfill additional properties like the neutrality property (NP), exchange principle (EP), identity principle (IP), and some others. The worth of this production of implications could be estimated at artificial intelligence, robotics science, etc. [13,14,15]. This method of producing implications gives us the possibility, in a fuzzy environment, to find a large number of implications, which could help any researcher choose the most appropriate one.

The paper is organized as follows. In Section 2, we recall the basic concepts and definitions used in the paper. In Section 3, we study the new constructed method of fuzzy implications. Firstly, we present a constructed method using one increasing function $\mathrm{g}$ and two negations ${\mathrm{N}}_1,{\mathrm{N}}_2$, then a second method using two increasing functions ${\mathrm{g}}_1,{\mathrm{g}}_2$ and three negations ${\mathrm{N}}_1,{\mathrm{N}}_2,{\mathrm{N}}_3$. Finally, we generalize our constructed method using $\mathrm{n}$ functions ${\mathrm{g}}_1,{\mathrm{g}}_2,\dots ,{\mathrm{g}}_{\mathrm{n}}$ and $\mathrm{n}+1$ negations ${\mathrm{N}}_1,{\mathrm{N}}_2,\dots ,{\mathrm{N}}_{\mathrm{n}},{\mathrm{N}}_{\mathrm{n}+1}.$

2. Preliminaries

In order to help the reader get familiar with the theory, we recall here some of the concepts and results employed in the rest of the paper.

Definition 1.

(see [1] Definition 1.1.1).A function$I:{\left[0, 1\right]}^2\to \left[0, 1\right]$is called a fuzzy implication if it satisfies, for all$x,x_{1, }{x}_2, y, y_1,y_{2 }\in \left[0, 1\right],$the following conditions:

$${\mathrm{x}}_1\le {\mathrm{x}}_2 \mathrm{then} \mathrm{I} ({\mathrm{x}}_{1, } \mathrm{y})\ge \mathrm{I}({\mathrm{x}}_2, \mathrm{y}),\mathrm{i}.\mathrm{e}.,\text{\hspace{1em}I is is decreasing in the first variable}$$

(1)

$${\mathrm{y}}_1\le {\mathrm{y}}_2 \mathrm{then} \mathrm{I} \left(\mathrm{x},{ \mathrm{y}}_1\right)\le \mathrm{I}\left(\mathrm{x},{ \mathrm{y}}_2\right),\mathrm{i}.\mathrm{e}., \text{I is increasing in the second variable}.$$

(2)

$$\mathrm{I}\left(0,0\right)=1$$

(3)

$$\mathrm{I}\left(1,1\right)=1$$

(4)

$$\mathrm{I}\left(1,0\right)=0$$

(5)

The set of all fuzzy implications will be denoted by$FI$.

A fuzzy negation N is a generalization of the classical complement or negation ¬, whose truth table consists of the two conditions: ¬0 = 1 and ¬1 = 0.

Definition 2.

(see [1] Definition 1.4.1).A function$N:\left[0,1\right]\to \left[0,1\right]$is called a fuzzy negation if it satisfies the following conditions:

$$\mathrm{N}\left(0\right)=1, \mathrm{N}\left(1\right)=0$$

(6)

$$\mathrm{N} \text{is decreasing}$$

(7)

Definition 3.

(see [1] Definition 1.4.2 (i)).A fuzzy negation$N$is called strict if, in addition,

$$\mathrm{N} \text{is strictly decreasing}$$

(8)

$$\mathrm{N} \text{is continuous}$$

(9)

Definition 4.

(see [1] Definition 1.4.2 (ii)).A fuzzy negation$N$is called strong if it is an involution, i.e.,

$$\mathrm{N}\left(\mathrm{N}\left(\mathrm{x}\right)\right)=\mathrm{x}, \mathrm{x}\in \left[0,1\right]$$

(10)

Definition 5.

(see [1] Definition 1.4.2 (ii)).A fuzzy negation$N$is said to be non-vanishing if

N(x) = 0 ⟺ x = 1

(11)

Definition 6.

(see [1] Definition 1.4.2 (ii)).A fuzzy negation$N$ is said to be non-filling if

N(x) = 1 ⟺ x = 0

(12)

Definition 7.

(see [1] Definition 1.4.15 (ii)).Let I ∈ FI. The function$N_I:\left[0,1\right]⟶\left[0,1\right]$defined by

$${\mathrm{N}}_{\mathrm{I}}\left(\mathrm{x}\right):=\mathrm{I}\left(\mathrm{x},0\right), \mathrm{x}\in \left[0,1\right]$$

(13)

is called the natural negation of I.

Example 1.

(see [1] example 1.4.4, [2] Section 2.1 Example 1).Important negations that will be used throughout this paper are the standard negation$N_C=1-x,$the least or Godel, and the greatest or dual Godel fuzzy negations given respectively by

$${\mathrm{N}}_{{\mathrm{D}}_1}\left(\mathrm{x}\right)=\{\begin{array}{ll}1& \mathrm{if}\hspace{1em}x=0\\ 0& \mathrm{if}\hspace{1em}x\in \left(0,1\right]\end{array}{\mathrm{N}}_{{\mathrm{D}}_2}\left(x\right)=\{\begin{array}{ll}1& \mathrm{if} x\in \left[0,1\right)\\ 0& \mathrm{if} x=1\end{array}$$

Definition 8.

(see [1] Definitions 1.3.1, 1.5.1).A Fuzzy Implication$I$is said to satisfy

i. 

The left neutrality property if:

$$\mathrm{I}\left(1,\mathrm{y}\right)=\mathrm{y}, \mathrm{y}\in \left[0,1\right]$$

(14)

ii. 

The exchange principle if:

$$\mathrm{I}\left(\mathrm{x},\mathrm{I}\left(\mathrm{y},\mathrm{z}\right)\right)=\mathrm{I}\left(\mathrm{y},\mathrm{I}\left(\mathrm{x},\mathrm{z}\right)\right), \mathrm{x},\mathrm{y},\mathrm{z} \in \left[0,1\right]$$

(15)

iii. 

The identity principle if:

$$\mathrm{I}\left(\mathrm{x},\mathrm{x}\right)=1, \mathrm{x}\in \left[0,1\right]$$

(16)

iv. 

The ordering property if:

$$\mathrm{I}\left(\mathrm{x},\mathrm{y}\right)=1 \iff \mathrm{x}\le \mathrm{y}, \mathrm{x},\mathrm{y}\in \left[0,1\right]$$

(17)

v. 

The law of contraposition with respect to$N$if:

$$\mathrm{I}\left(\mathrm{x},\mathrm{y}\right)=\mathrm{I}\left(\mathrm{N}\left(\mathrm{y}\right),\mathrm{N}\left(\mathrm{x}\right)\right) ,\mathrm{x},\mathrm{y} \in \left[0,1\right]$$

(18)

vi. 

The law of left contraposition with respect to$N$if:

$$\mathrm{I}\left(\mathrm{N}\left(\mathrm{x}\right),\mathrm{y}\right)=\mathrm{I}\left(\mathrm{N}\left(\mathrm{y}\right),\mathrm{x}\right), \mathrm{x},\mathrm{y} \in \left[0,1\right]$$

(19)

vii. 

The law of right contraposition with respect to N if:

$$\mathrm{I}\left(\mathrm{x},\mathrm{N}\left(\mathrm{y}\right)\right)=\mathrm{I}\left(\mathrm{y},\mathrm{N}\left(\mathrm{x}\right)\right), \mathrm{x},\mathrm{y} \in \left[0,1\right]$$

(20)

Definition 9.

(see [1] Notations and Some Preliminaries).We say that functions$f, g :{\left[0,1\right]}^n\to \left[0,1\right]$are Φ-conjugate if there exists a φ ∈ Φ such that $g=f_{\phi }$, where

$${\mathrm{f}}_{\mathsf{\phi }}\left({\mathrm{x}}_1,\mathrm{x},\dots ,{\mathrm{x}}_{\mathrm{n}}\right)={\mathsf{\phi }}^{-1}\left(\mathrm{f}\left(\mathsf{\phi }\left({\mathrm{x}}_1\right),\mathsf{\phi }\left({\mathrm{x}}_2\right),\dots \mathsf{\phi }\left({\mathrm{x}}_{\mathrm{n}}\right)\right)\right),{ \mathrm{x}}_1,{\mathrm{x}}_2,\dots ,{\mathrm{x}}_{\mathrm{n}} \in \left[0,1\right].$$

(21)

Definition 10.

(see [1] Definition 2.2.1).A function$S:{\left[0,1\right]}^2 ⟶\left[0,1\right]$is called a triangular conorm (t-conorm) if it satisfies, for all$x,y,z\in \left[0,1\right],$the following conditions:

$$\mathrm{S}\left(\mathrm{x},\mathrm{y}\right)=\mathrm{S}\left(\mathrm{y},\mathrm{x}\right)$$

(22)

$$\mathrm{S}\left(\mathrm{x},\mathrm{S}\left(\mathrm{y},\mathrm{z}\right)\right)=\mathrm{S}\left(\mathrm{S}\left(\mathrm{x},\mathrm{y}\right),\mathrm{z}\right)$$

(23)

$$\mathrm{If} \mathrm{y}\le \mathrm{z}, \mathrm{then} \mathrm{S}\left(\mathrm{x},\mathrm{y}\right)\le \mathrm{S}\left(\mathrm{x},\mathrm{z}\right), \mathrm{i}.\mathrm{e}., \mathrm{S}\left(\mathrm{x},·\right) \text{is increasing}$$

(24)

$$\mathrm{S}\left(\mathrm{x},0\right)=\mathrm{x}$$

(25)

Definition 11.

(see [1] Definition 2.1.1).A function$S: {\left[0,1\right]}^2 ⟶\left[0,1\right]$is called a triangular norm (t-norm) if it satisfies, for all$x,y,z \in \left[0,1\right],$the following conditions:

$$\mathrm{T}\left(\mathrm{x},\mathrm{y}\right)=\mathrm{T}\left(\mathrm{y},\mathrm{x}\right)$$

(26)

$$\mathrm{T}\left(\mathrm{x},\mathrm{T}\left(\mathrm{y},\mathrm{z}\right)\right)=\mathrm{T}\left(\mathrm{T}\left(\mathrm{x},\mathrm{y}\right),\mathrm{z}\right)$$

(27)

$$\mathrm{If} \mathrm{y}\le \mathrm{z}, \mathrm{then} \mathrm{T}\left(\mathrm{x},\mathrm{y}\right)\le \mathrm{T}\left(\mathrm{x},\mathrm{z}\right) , \mathrm{i}.\mathrm{e}., \mathrm{T}\left(\mathrm{x},·\right) \text{is increasing}$$

(28)

$$\mathrm{T}\left(\mathrm{x},1\right)=\mathrm{x}$$

(29)

Remark 1.

(see [1] Propositions 1.1.8, 1.4.8 and Remarks 2.1.4 (vii), 2.2.5 (vii)).It is proved that, if φ ∈ Φ, T is a continuous t-norm,$S$is a continuous t-conorm,$N$is a fuzzy (strict, strong) negation, and$I$is a fuzzy implication, then$T_{\phi }$is a t-norm,$S_{\phi }$is a t-conorm,$N_{\phi }$is a fuzzy (strict, strong) negation, and$I_{\phi }$is a fuzzy implication.

Definition 12.

(see [1] Definition 2.4.1).The equation p → q ≡ ¬p ∨ q creates a new class of fuzzy implications.

A function$I:{\left[0,1\right]}^2⟶\left[0,1\right]$is called an (S, N)-Implication if there exist a t-conorm S and a fuzzy negation$N$such that:

$$\mathrm{I}\left(\mathrm{x},\mathrm{y}\right)=\mathrm{S}\left(\mathrm{N}\left(\mathrm{x}\right),\mathrm{y}\right) ,\mathrm{x}, \mathrm{y}\in \left[0,1\right]$$

(30)

Definition 13.

(see [1] Subsection 7.3).The equation (p ∧ q) → r ≡ (p → (q → r)) is known as the law of importation and is a tautology in classical logic. The general form of the above equivalence is given by

$$\mathrm{I}\left(\mathrm{T}\left(\mathrm{x},\mathrm{y}\right),\mathrm{z}\right)=\mathrm{I}\left(\mathrm{x},\mathrm{I}\left(\mathrm{y},\mathrm{z}\right)\right),\mathrm{x},\mathrm{y},\mathrm{z} \in \left[0,1\right]$$

(31)

Definition 14.

(see [1] Definition 7.4.1).An implication I and a t-norm T satisfy the T-conditionality property if and only if

$$\mathrm{T}\left(\mathrm{x},\mathrm{I}\left(\mathrm{x},\mathrm{y}\right)\right)\le \mathrm{y},\mathrm{x},\mathrm{y} \in \left[0,1\right]$$

(32)

Proposition 1.

(see [1] Definition 7.4.2).If I ∈ FI is such that there exist x, y ∈ (0, 1) such that x > y and I(x, y) = 1, then I does not satisfy (32) with any t-norm T.

Proposition 2.

(see [1] Definition 7.4.3).Let I ∈ FI, a t-norm T satisfy (32),$N_I$is the natural negation of I and$N_T$is the natural negation of T, then $N_I\le N_T$, the natural negation of T.

Definition 15.

(see [1] Definition 1.6.1).Let N be a fuzzy negation and I be a fuzzy implication. A function$I_N:{\left[0,1\right]}^2\to \left[0,1\right]$defined by

$${\mathrm{I}}_{\mathrm{N}}\left(\mathrm{x},\mathrm{y}\right)=\mathrm{I}\left(\mathrm{N}\left(\mathrm{y}\right),\mathrm{N}\left(\mathrm{x}\right)\right), \mathrm{x},\mathrm{y} \in \left[0,1\right]$$

(33)

is called the N-reciprocal of I.

When N is the classical negation$N_C$, then$I_N$is called the reciprocal of I and is denoted by$I^{\prime }$.

3. The Main Results

In this section, we give definitions of new generated implications and prove some useful properties of them.

3.1. Fuzzy Implications Generated by One Increasing Function $g$ and Two fuzzy negations $N_1,N_2$

Theorem 1.

If$N_1, N_2$are two fuzzy negations and$g:\left[0,1\right]\to \left[0,\infty \right)$is an increasing and continuous function with g(0) = 0, then the function$I :{\left[0,1\right]}^2\to \left[0,1\right]$defined by

$$\mathrm{I}\left(\mathrm{x},\mathrm{y}\right)={\mathrm{N}}_2\left(\frac{\mathrm{g}\left(\mathrm{x}\right)}{\mathrm{g}\left(1\right)}ˑ{\mathrm{N}}_1\left(\mathrm{y}\right)\right),\mathrm{x},\mathrm{y}\in \left[0,1\right]$$

(34)

is a fuzzy implication.

Proof. 

Let $\mathrm{g}:\left[0,1\right]\to \left[0,\infty \right)$ be an increasing and continuous function with g(0) = 0 and ${\mathrm{x}}_1,{\mathrm{x}}_2,\mathrm{y} \in \left[0,1\right].$

• If ${\mathrm{x}}_1\le {\mathrm{x}}_2$ then
• $\mathrm{g}\left({\mathrm{x}}_1\right)\le \mathrm{g}\left({\mathrm{x}}_2\right) \Rightarrow \frac{\mathrm{g}\left({\mathrm{x}}_1\right)}{\mathrm{g}\left(1\right)}ˑ{\mathrm{N}}_1\left(\mathrm{y}\right) \le \frac{\mathrm{g}\left({\mathrm{x}}_2\right)}{\mathrm{g}\left(1\right)}ˑ{\mathrm{N}}_1\left(\mathrm{y}\right) \Rightarrow { \mathrm{N}}_2\left(\frac{\mathrm{g}\left({\mathrm{x}}_1\right)}{\mathrm{g}\left(1\right)}ˑ{\mathrm{N}}_1\left(\mathrm{y}\right)\right) \ge {\mathrm{N}}_2\left(\frac{\mathrm{g}\left({\mathrm{x}}_2\right)}{\mathrm{g}\left(1\right)}ˑ{\mathrm{N}}_1\left(\mathrm{y}\right)\right) \mathrm{I}\left({\mathrm{x}}_1,\mathrm{y}\right)\ge \mathrm{I}\left({\mathrm{x}}_2,\mathrm{y}\right), \mathrm{i}.\mathrm{e}., \mathrm{I}\left(ˑ,\mathrm{y}\right))$ is decreasing, i.e., I satisfies (1)
• Let ${\mathrm{y}}_1,{\mathrm{y}}_2,\mathrm{x} \in \left[0,1\right]$. If ${\mathrm{y}}_1\le {\mathrm{y}}_2$, then ${\mathrm{N}}_1\left({\mathrm{y}}_1\right)\ge {\mathrm{N}}_1\left({\mathrm{y}}_2\right) \Rightarrow \frac{\mathrm{g}\left(\mathrm{x}\right)}{\mathrm{g}\left(1\right)}ˑ{\mathrm{N}}_1\left({\mathrm{y}}_1\right)\ge \frac{\mathrm{g}\left(\mathrm{x}\right)}{\mathrm{g}\left(1\right)}ˑ{\mathrm{N}}_1\left({\mathrm{y}}_2\right) \Rightarrow { \mathrm{N}}_2\left(\frac{\mathrm{g}\left(\mathrm{x}\right)}{\mathrm{g}\left(1\right)}ˑ{\mathrm{N}}_1\left({\mathrm{y}}_1\right)\right)\le {\mathrm{N}}_2\left(\frac{\mathrm{g}\left(\mathrm{x}\right)}{\mathrm{g}\left(1\right)}ˑ{\mathrm{N}}_1\left({\mathrm{y}}_2\right)\right)$
• $\Rightarrow \mathrm{I}\left(\mathrm{x},{\mathrm{y}}_1\right)\le \mathrm{I}\left(\mathrm{x},{\mathrm{y}}_2\right), \mathrm{i}.\mathrm{e}., \mathrm{I}\left(\mathrm{x},ˑ\right)$ is increasing, i.e., I satisfies (2)
• $\mathrm{I}\left(0,0\right)={\mathrm{N}}_2\left(\frac{\mathrm{g}\left(0\right)}{\mathrm{g}\left(1\right)}ˑ{\mathrm{N}}_1\left(0\right)\right)={\mathrm{N}}_2\left(0\right)=1$, i.e., I satisfies (3)
• $\mathrm{I}\left(1,1\right)={\mathrm{N}}_2\left(\frac{\mathrm{g}\left(1\right)}{\mathrm{g}\left(1\right)}ˑ{\mathrm{N}}_1\left(1\right)\right)={\mathrm{N}}_2\left(0\right)=1$, i.e., I satisfies (4)
• $\mathrm{I}\left(1,0\right)={\mathrm{N}}_2\left(\frac{\mathrm{g}\left(1\right)}{\mathrm{g}\left(1\right)}ˑ{\mathrm{N}}_1\left(0\right)\right)={\mathrm{N}}_2\left(1\right)=0$, i.e., I satisfies (5)
• Therefore, I ∈ FI.  □

Proposition 3.

Let I be the fuzzy implication of Theorem 1, then the fuzzy implication N-reciprocal of I is

$${\mathrm{I}}_{\mathrm{N}}\left(\mathrm{x},\mathrm{y}\right)=\mathrm{I}\left(\mathrm{N}\left(\mathrm{y}\right),\mathrm{N}\left(\mathrm{x}\right)\right)={\mathrm{N}}_2\left(\frac{\mathrm{g}\left(\mathrm{N}\left(\mathrm{y}\right)\right) }{\mathrm{g}\left(1\right)}ˑ{\mathrm{N}}_1\left(\mathrm{N}\left(\mathrm{x}\right)\right)\right)$$

(35)

Proposition 4.

If$N_1=N_2=N$are strong negations, then the fuzzy implication of Theorem 1 satisfies additionally the left neutrality property (14) and the exchange principle (15).

Proof. 

$\mathrm{I}\left(1,\mathrm{y}\right)= \mathrm{N}\left(\frac{\mathrm{g}\left(1\right)}{\mathrm{g}\left(1\right)}ˑ\mathrm{N}\left(\mathrm{y}\right)\right)=$$\mathrm{N}\left(\mathrm{N}\left(\mathrm{y}\right)\right)=\mathrm{y}$, y ∈ [0, 1], i.e., I satisfies (14)

$$\begin{array}{l}\mathrm{I}\left(\mathrm{a},\mathrm{I}\left(\mathrm{b},\mathrm{x}\right)\right)=\mathrm{N}\left(\frac{\mathrm{g}\left(\mathrm{a}\right)}{\mathrm{g}\left(1\right)}ˑ\mathrm{N}\left(\mathrm{I}\left(\mathrm{b},\mathrm{x}\right)\right)\right)=\mathrm{N}\left(\frac{\mathrm{g}\left(\mathrm{a}\right)}{\mathrm{g}\left(1\right)}ˑ\mathrm{N}\left(\mathrm{N}\left(\frac{\mathrm{g}\left(\mathrm{b}\right)}{\mathrm{g}\left(1\right)}ˑ\mathrm{N}\left(\mathrm{x}\right)\right)\right)\right)\stackrel{\mathrm{N}: \mathrm{strong} \mathrm{negation}}{=}\mathrm{N}\left(\frac{\mathrm{g}\left(\mathrm{a}\right)\mathrm{g}\left(\mathrm{b}\right)}{\mathrm{g}{\left(1\right)}^2} \mathrm{N}\left(\mathrm{x}\right)\right)\\ \mathrm{I}\left(\mathrm{b},\mathrm{I}\left(\mathrm{a},\mathrm{x}\right)\right)=\mathrm{N}\left(\frac{\mathrm{g}\left(\mathrm{b}\right)}{\mathrm{g}\left(1\right)}ˑ\mathrm{N}\left(\mathrm{I}\left(\mathrm{a},\mathrm{x}\right)\right)\right)=\mathrm{N}\left(\frac{\mathrm{g}\left(\mathrm{b}\right)}{\mathrm{g}\left(1\right)}ˑ\mathrm{N}\left(\mathrm{N}\left(\frac{\mathrm{g}\left(\mathrm{a}\right)}{\mathrm{g}\left(1\right)}ˑ\mathrm{N}\left(\mathrm{x}\right)\right)\right)\right)\stackrel{\mathrm{N}: \mathrm{strong} \mathrm{negation}}{=}\mathrm{N}\left(\frac{\mathrm{g}\left(\mathrm{a}\right)\mathrm{g}\left(\mathrm{b}\right)}{\mathrm{g}{\left(1\right)}^2} \mathrm{N}\left(\mathrm{x}\right)\right)\end{array}$$

Thus, we have $\mathrm{I}\left(\mathrm{a},\mathrm{I}\left(\mathrm{b},\mathrm{x}\right)\right)= \mathrm{I}\left(\mathrm{b},\mathrm{I}\left(\mathrm{a},\mathrm{x}\right)\right),$ i.e., I satisfies (15).  □

Theorem 2.

If φ ∈ Φ and I is the fuzzy implication of Theorem 1, then I_φ is a fuzzy implication.

Proof. 

According to Remark 1, ${\mathrm{I}}_{\mathsf{\phi }}$ is a fuzzy implication.  □

Proposition 5.

If $N_1\left(x\right)=N_{D_1}\left(x\right)$ = $\{\begin{array}{c}1, if x=0\\ 0, if x\in \left(0,1\right]\end{array}$ (the least fuzzy negation), then the fuzzy implication of Theorem 1 satisfies the Identity Principle (16).

Proof. 

$$\begin{gathered} \mathrm{I}\left(\mathrm{x},\mathrm{x}\right)={\mathrm{N}}_2\left(\frac{\mathrm{g}\left(\mathrm{x}\right)}{\mathrm{g}\left(1\right)}ˑ{\mathrm{N}}_1\left(\mathrm{x}\right)\right)\stackrel{ \mathrm{x}=0}{=}{\mathrm{N}}_2\left(\frac{\mathrm{g}\left(0\right)}{\mathrm{g}\left(1\right)}ˑ{\mathrm{N}}_1\left(0\right)\right)={\mathrm{N}}_1\left(0\right)=1 \\ \mathrm{I}\left(\mathrm{x},\mathrm{x}\right)={\mathrm{N}}_2\left(\frac{\mathrm{g}\left(\mathrm{x}\right)}{\mathrm{g}\left(1\right)}ˑ{\mathrm{N}}_1\left(\mathrm{x}\right)\right)\stackrel{ \mathrm{x}\in \left(0,1\right] }{=}{\mathrm{N}}_2\left(\frac{\mathrm{g}\left(0\right)}{\mathrm{g}\left(1\right)}ˑ{\mathrm{N}}_1\left(0\right)\right)={\mathrm{N}}_1\left(0\right)=1 \end{gathered}$$

i.e., I satisfies (16).  □

Proposition 6.

If the fuzzy implication of Theorem 1 satisfies the Identity Principle (16), then it satisfies the Ordering Property (17).

Proof. 

Let x,y ∈ [0,1] and x ≤ y, then I(x,y) ≥ I(y, y) = 1. Thus, I(x, y) = 1.

• If $\mathrm{I}\left(\mathrm{x},\mathrm{y}\right)=1$ ⇔
• $\mathrm{I}\left(\mathrm{x},\mathrm{y}\right)={\mathrm{N}}_2\left(\frac{\mathrm{g}\left(\mathrm{x}\right)}{\mathrm{g}\left(1\right)}ˑ{\mathrm{N}}_1\left(\mathrm{y}\right)\right)=1$ ⇔
• $\frac{\mathrm{g}\left(\mathrm{x}\right)}{\mathrm{g}\left(1\right)}ˑ{\mathrm{N}}_1\left(\mathrm{y}\right)=0$ ⇔
• $\mathrm{g}\left(\mathrm{x}\right)=0{ \mathrm{or} \mathrm{N}}_1\left(\mathrm{y}\right)=0$ ⇔
• x = 0 ≤ y or y = 1≥ x.
• Thus, we have x ≤ y.  □

Proposition 7.

The natural negation$N_I$of the fuzzy implication of Theorem 1 is

$${\mathrm{N}}_{\mathrm{I}}\left(\mathrm{x}\right)={\mathrm{N}}_2\left(\frac{\mathrm{g}\left(\mathrm{x}\right)}{\mathrm{g}\left(1\right)}\right)$$

Proof. 

$$\begin{array}{l}{\mathrm{N}}_{\mathrm{I}}\left(\mathrm{x}\right)=\mathrm{I}\left(\mathrm{x},0\right)={\mathrm{N}}_2\left(\frac{\mathrm{g}\left(\mathrm{x}\right)}{\mathrm{g}\left(1\right)}ˑ{\mathrm{N}}_1\left(0\right)\right)={\mathrm{N}}_2\left(\frac{\mathrm{g}\left(\mathrm{x}\right)}{\mathrm{g}\left(1\right)}\right).\end{array}$$

 □

Proposition 8.

When$N_1\left(x\right)=N_2\left(x\right)=N\left(x\right)$are strong negations, then the fuzzy implication of Theorem 1 is an (S, N)–implication.

Proof. 

When ${\mathrm{N}}_1\left(\mathrm{x}\right)={\mathrm{N}}_2\left(\mathrm{x}\right)=\mathrm{N}\left(\mathrm{x}\right)$ are strong negations, according to Theorem 1 and Proposition 4, the fuzzy implication $\mathrm{I}\left(\mathrm{x},\mathrm{y}\right)={\mathrm{N}}_2\left(\frac{\mathrm{g}\left(\mathrm{x}\right)}{\mathrm{g}\left(1\right)}ˑ{\mathrm{N}}_1\left(\mathrm{y}\right)\right)$ satisfies (I1) and (EP). Moreover, if ${\mathrm{N}}_1\left(\mathrm{x}\right),{\mathrm{N}}_2\left(\mathrm{x}\right)$ are continuous negations, then ${\mathrm{N}}_{\mathrm{I}}$ is also a continuous fuzzy negation. We deduce that I is an (S, N) – implication (see [1] Theorem 2.4.10).  □

Example 2.

Let $g\left(x\right)=x , N_2\left(x\right)=1-x , N_1\left(x\right)=1-x^2$.

• Then,$I\left(x,y\right)=N_2\left(x\left(1-y^2\right)\right)=1-x\left(1-y^2\right)=1-x+x{y}^2$
• The graph of the above surface is plotted in Figure 1.
  

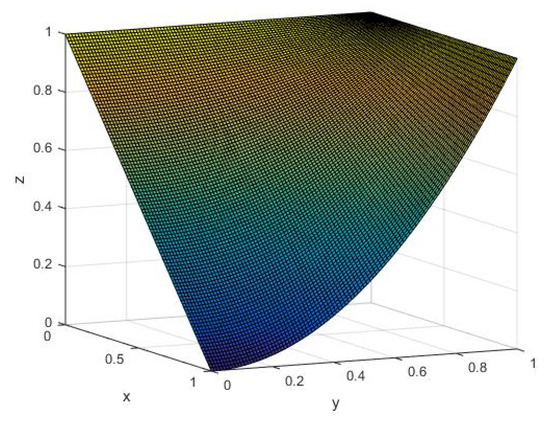  Figure 1. I implication of example 2.

Example 3.

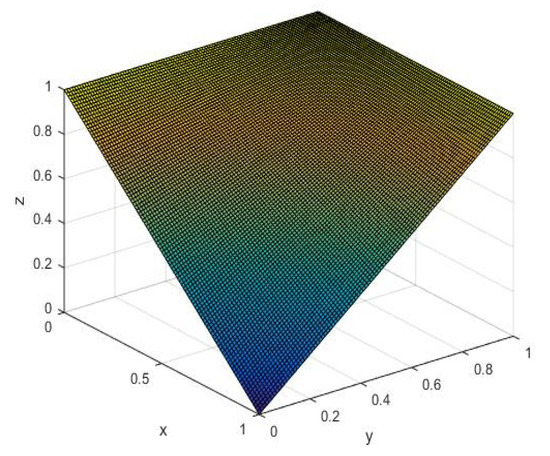
Let$g\left(x\right)=x, N_1\left(x\right)=N_2\left(x\right)=1-x.$Thus,$I\left(x,y\right)=N_2\left(x\left(1-y\right)\right)=1-x\left(1-y\right)=1-x+xy$Then, it is the Reinchenbach Implication.

The graph of the above surface is plotted in Figure 2.

Figure 2. I implication of example 3.

Example 4.

$Let g\left(x\right)=x , N_2\left(x\right)=1-x , N_1\left(x\right)=\frac{1-x}{1+x}$. Then,$I\left(x,y\right)=N_2\left(x·\frac{1-y}{1+y}\right)=$$\frac{1+y-x+xy}{1+y}.$

The graph of the above surface is plotted in Figure 3.

Figure 3. I implication of example 4.

Proposition 9.

Let$N_1,N_2,N_3$be three fuzzy negations. Let us suppose also that$N_3$is a strong fuzzy negation. If g: [0,1] → [0,∞) is an increasing and continuous function with g(0) = 0 and$g\left(x\right)=N_1\left(N_3\left(x\right)\right)$, then the fuzzy implication$I\left(x,y\right)=N_2\left(\frac{g\left(x\right)}{g\left(1\right)}ˑN_1\left(y\right)\right)$defined in Theorem 1 satisfies the law of contraposition (18) with respect to$N_3$.

Proof. 

g: [0,1] → [0,∞) is an increasing and continuous function

$\mathrm{I}\left({\mathrm{N}}_3\left(\mathrm{y}\right),{\mathrm{N}}_3\left(\mathrm{x}\right)\right)={\mathrm{N}}_2\left(\frac{\mathrm{g}\left({\mathrm{N}}_3\left(\mathrm{y}\right)\right)}{\mathrm{g}\left(1\right)}·{\mathrm{N}}_1\left({\mathrm{N}}_3\left(\mathrm{x}\right)\right)\right)={ \mathrm{N}}_2\left(\frac{{\mathrm{N}}_1\left({\mathrm{N}}_3\left({\mathrm{N}}_3\left(\mathrm{y}\right)\right)\right)}{\mathrm{g}\left(1\right)}·{\mathrm{N}}_1\left({\mathrm{N}}_3\left(\mathrm{x}\right)\right)\right)\stackrel{{\mathrm{N}}_3:\mathrm{strong} \mathrm{negation}}{=}$

${\mathrm{N}}_2\left(\frac{{\mathrm{N}}_1\left(\mathrm{y}\right)}{\mathrm{g}\left(1\right)}·{\mathrm{N}}_1\left({\mathrm{N}}_3\left(\mathrm{x}\right)\right)\right)={\mathrm{N}}_2\left(\frac{{\mathrm{N}}_1\left(\mathrm{y}\right)}{\mathrm{g}\left(1\right)}·\mathrm{g}\left(\mathrm{x}\right)\right)={\mathrm{N}}_2\left(\frac{\mathrm{g}\left(\mathrm{x}\right)}{\mathrm{g}\left(1\right)}·{\mathrm{N}}_1\left(\mathrm{y}\right)\right)= \mathrm{I}\left(\mathrm{x},\mathrm{y}\right), \mathrm{i}.\mathrm{e}., \mathrm{I} \mathrm{satisfies} \left(18\right).$  □

Lemma  1.

(see [1] Proposition 1.5.3).Let$N_1,N_2,N_3$be three fuzzy negations with the properties$N_1, N_3$being strict ones and$N_3$additionally being a strong negation. If g: [0,1] → [0,∞) is an increasing and continuous function with g(0) = 0 and$g\left(x\right)=N_1\left(N_3\left(x\right)\right)$, then the fuzzy implication$I\left(x,y\right)=N_2\left(\frac{g\left(x\right)}{g\left(1\right)}ˑN_1\left(y\right)\right), x,y\in \left[0,1\right]$defined by Theorem 1 satisfies the left (L-CP) and the right (R-CP) law of the contraposition.

Proof. 

According to Proposition 1.5.3 [1], I satisfies the left (19) and the right (20) law of the contraposition.  □

Using Definition 14 and Proposition 2 of Section 2, we prove the following:

Proposition 10.

Let I be the fuzzy implication defined by Theorem 1, $I\left(x,y\right)=N_2\left(\frac{g\left(x\right)}{g\left(1\right)}ˑN_1\left(y\right)\right), x,y\in \left[0,1\right]$. Let us suppose that T is a t-norm and T satisfies (32), then:

i. 

$N_2\left(x\right)\le N_1\left(x\right), if N_2 is a strong negation$.

ii. 

$g\left(x\right)\ge g\left(1\right)ˑN_1\left(N_T\left(x,y\right)\right)$, if$N_1$ is a strong negation.

Proof. 

As I and T satisfy (TC), then $\mathrm{T}\left(\mathrm{x},\mathrm{I}\left(\mathrm{x},\mathrm{y}\right)\right)\le \mathrm{y}$ for all $\mathrm{x},\mathrm{y} \in \left[0,1\right]$.

i.

Let $\mathrm{x}=1 , \mathrm{we} \mathrm{have} \mathrm{I}\left(1,\mathrm{y}\right)\le \mathrm{y}, \mathrm{y} \in \left[0,1\right]{ \mathrm{then} \mathrm{N}}_2\left(\frac{\mathrm{g}\left(1\right)}{\mathrm{g}\left(1\right)}ˑ{\mathrm{N}}_1\left(\mathrm{y}\right)\right)\le \mathrm{y}\Rightarrow { \mathrm{N}}_2\left({\mathrm{N}}_1\left(\mathrm{y}\right)\right)\le \mathrm{y}$ ⇒ ${\mathrm{N}}_2\left({\mathrm{N}}_2\left({\mathrm{N}}_1\left(\mathrm{y}\right)\right)\right) \ge { \mathrm{N}}_2\left(\mathrm{y}\right) \stackrel{{\mathrm{N}}_2 : \mathrm{strong} \mathrm{negation}}{\Rightarrow }{ \mathrm{N}}_2\left(\mathrm{y}\right)\le {\mathrm{N}}_1\left(\mathrm{y}\right)$.

ii.

From Proposition 2, we have ${\mathrm{N}}_{\mathrm{I}} \le {\mathrm{N}}_{\mathrm{T}}$ ⇒ ${\mathrm{N}}_2\left(\frac{\mathrm{g}\left(\mathrm{x}\right)}{\mathrm{g}\left(1\right)}\right)\le { \mathrm{N}}_{\mathrm{T}}\left(\mathrm{x},\mathrm{y}\right)$ $\stackrel{{\mathrm{N}}_2 : \mathrm{strong} \mathrm{negation}}{\Rightarrow }{ \mathrm{N}}_2\left({\mathrm{N}}_2\left(\frac{\mathrm{g}\left(\mathrm{x}\right)}{\mathrm{g}\left(1\right)}\right)\right)\ge {\mathrm{N}}_2\left({\mathrm{N}}_{\mathrm{T}}\left(\mathrm{x},\mathrm{y}\right)\right) \Rightarrow \frac{\mathrm{g}\left(\mathrm{x}\right)}{\mathrm{g}\left(1\right)} \ge {\mathrm{N}}_2\left({\mathrm{N}}_{\mathrm{T}}\left(\mathrm{x},\mathrm{y}\right)\right) \Rightarrow \mathrm{g}\left(\mathrm{x}\right)$ $\ge \mathrm{g}\left(1\right)ˑ{\mathrm{N}}_2\left({\mathrm{N}}_{\mathrm{T}}\left(\mathrm{x},\mathrm{y}\right)\right)$

 □

3.2. Fuzzy Implications Generated by Two Increasing Functions $g_1,g_2$ and Three Fuzzy Negations $N_1,N_2,N_3$

Theorem 3.

If $g_1\left(x\right), g_2\left(x\right):\left[0,1\right]\to \left[0,\infty \right)$ are increasing and continuous functions with$g_1\left(0\right)=g_2\left(0\right)=0$and$N_1 ,N_2 N_3$are fuzzy negations, then the function$I :{\left[0,1\right]}^2\to \left[0,1\right]$defined by

$$\mathrm{I}\left(\mathrm{x},\mathrm{y}\right)={ \mathrm{N}}_3\left(\frac{\frac{{\mathrm{g}}_1\left(\mathrm{x}\right)}{{\mathrm{g}}_1\left(1\right)}{\mathrm{N}}_1\left(\mathrm{y}\right)+\frac{{\mathrm{g}}_2\left(\mathrm{x}\right)}{{\mathrm{g}}_2\left(1\right)}{\mathrm{N}}_2\left(\mathrm{y}\right)}{2}\right),\mathrm{x},\mathrm{y}\in \left[0,1\right]$$

(36)

is a fuzzy implication.

Proof. 

• Let ${\mathrm{x}}_1 ,{\mathrm{x}}_2 ,\mathrm{y}$ ∈ [0,1].
  • If

    $$\begin{array}{c}{\mathrm{x}}_1\le {\mathrm{x}}_2\Rightarrow \frac{{\mathrm{g}}_1\left({\mathrm{x}}_1\right)}{{\mathrm{g}}_1\left(1\right)}\le \frac{{\mathrm{g}}_1\left({\mathrm{x}}_2\right)}{{\mathrm{g}}_1\left(1\right)} \mathrm{and} \frac{{\mathrm{g}}_2\left({\mathrm{x}}_1\right)}{{\mathrm{g}}_2\left(1\right)}\le \frac{{\mathrm{g}}_2\left({\mathrm{x}}_2\right)}{{\mathrm{g}}_2\left(1\right)},\hfill \\ \mathrm{then},{ \mathrm{N}}_1\left(\mathrm{y}\right)\frac{{\mathrm{g}}_1\left({\mathrm{x}}_1\right)}{{\mathrm{g}}_1\left(1\right)}\le {\mathrm{N}}_1\left(\mathrm{y}\right)\frac{{\mathrm{g}}_1\left({\mathrm{x}}_2\right)}{{\mathrm{g}}_1\left(1\right)}{ \mathrm{and} \mathrm{N}}_2\left(\mathrm{y}\right)\frac{{\mathrm{g}}_2\left({\mathrm{x}}_1\right)}{{\mathrm{g}}_2\left(1\right)}\le {\mathrm{N}}_2\left(\mathrm{y}\right)\frac{{\mathrm{g}}_2\left({\mathrm{x}}_2\right)}{{\mathrm{g}}_2\left(1\right)}\hfill \\ ⟹ \frac{{\mathrm{N}}_1\left(\mathrm{y}\right){\frac{{\mathrm{g}}_1\left({\mathrm{x}}_1\right)}{{\mathrm{g}}_1\left(1\right)}}_1+{\mathrm{N}}_2\left(\mathrm{y}\right)\frac{{\mathrm{g}}_2\left({\mathrm{x}}_1\right)}{{\mathrm{g}}_2\left(1\right)}}{2} \le \frac{{\mathrm{N}}_1\left(\mathrm{y}\right){\frac{{\mathrm{g}}_1\left({\mathrm{x}}_2\right)}{{\mathrm{g}}_1\left(1\right)}}_1+{\mathrm{N}}_2\left(\mathrm{y}\right)\frac{{\mathrm{g}}_2\left({\mathrm{x}}_2\right)}{{\mathrm{g}}_2\left(1\right)}}{2} ⟹\hfill \\ {\mathrm{N}}_3(\frac{{\mathrm{N}}_1\left(\mathrm{y}\right){\frac{{\mathrm{g}}_1\left({\mathrm{x}}_1\right)}{{\mathrm{g}}_1\left(1\right)}}_1+{\mathrm{N}}_2\left(\mathrm{y}\right)\frac{{\mathrm{g}}_2\left({\mathrm{x}}_1\right)}{{\mathrm{g}}_2\left(1\right)}}{2}\le {\mathrm{N}}_3\left(\frac{{\mathrm{N}}_1\left(\mathrm{y}\right){\frac{{\mathrm{g}}_1\left({\mathrm{x}}_2\right)}{{\mathrm{g}}_1\left(1\right)}}_1+{\mathrm{N}}_2\left(\mathrm{y}\right)\frac{{\mathrm{g}}_2\left({\mathrm{x}}_2\right)}{{\mathrm{g}}_2\left(1\right)}}{2}\right)\hfill \end{array}$$
  • $\mathrm{I}\left({\mathrm{x}}_1,\mathrm{y}\right)\ge \mathrm{I}\left({\mathrm{x}}_2,\mathrm{y}\right)$, i.e., I(∙,y) is decreasing, i.e., I satisfies (1).
• Let ${\mathrm{y}}_1,{ \mathrm{y}}_2,\mathrm{x}$ ∈ [0, 1]
  • If ${\mathrm{y}}_1\le { \mathrm{y}}_2$, then ${\mathrm{N}}_1\left({\mathrm{y}}_1\right)\ge {\mathrm{N}}_2\left({\mathrm{y}}_2\right)$ ⇒ $\frac{{\mathrm{g}}_1\left(\mathrm{x}\right)}{\mathrm{g}\left(1\right)}{\mathrm{N}}_1\left({\mathrm{y}}_1\right)\ge \frac{{\mathrm{g}}_1\left(\mathrm{x}\right)}{\mathrm{g}\left(1\right)}{\mathrm{N}}_1\left({\mathrm{y}}_2\right) \mathrm{and} \frac{{\mathrm{g}}_2\left(\mathrm{x}\right)}{\mathrm{g}\left(1\right)}{\mathrm{N}}_2\left({\mathrm{y}}_1\right)\ge \frac{{\mathrm{g}}_2\left(\mathrm{x}\right)}{\mathrm{g}\left(1\right)}{\mathrm{N}}_2\left({\mathrm{y}}_2\right)$

    $$\Rightarrow \frac{\frac{{\mathrm{g}}_1\left(\mathrm{x}\right)}{\mathrm{g}\left(1\right)}{\mathrm{N}}_1\left({\mathrm{y}}_1\right)+\frac{{\mathrm{g}}_1\left(\mathrm{x}\right)}{\mathrm{g}\left(1\right)}{\mathrm{N}}_2\left({\mathrm{y}}_1\right)}{2}\ge \frac{\frac{{\mathrm{g}}_2\left(\mathrm{x}\right)}{\mathrm{g}\left(1\right)}{\mathrm{N}}_1\left({\mathrm{y}}_2\right)+\frac{{\mathrm{g}}_2\left(\mathrm{x}\right)}{\mathrm{g}\left(1\right)}{\mathrm{N}}_2\left({\mathrm{y}}_2\right)}{2}\text{⇒} {\mathrm{N}}_3\left(\frac{\frac{{\mathrm{g}}_1\left(\mathrm{x}\right)}{\mathrm{g}\left(1\right)}{\mathrm{N}}_1\left({\mathrm{y}}_1\right)+\frac{{\mathrm{g}}_1\left(\mathrm{x}\right)}{\mathrm{g}\left(1\right)}{\mathrm{N}}_2\left({\mathrm{y}}_1\right)}{2}\right) \le {\mathrm{N}}_3\left( \frac{\frac{{\mathrm{g}}_2\left(\mathrm{x}\right)}{\mathrm{g}\left(1\right)}{\mathrm{N}}_1\left({\mathrm{y}}_2\right)+\frac{{\mathrm{g}}_2\left(\mathrm{x}\right)}{\mathrm{g}\left(1\right)}{\mathrm{N}}_2\left({\mathrm{y}}_2\right)}{2}\right)$$
  • $\Rightarrow \mathrm{I}\left(\mathrm{x},{\mathrm{y}}_1\right)\le \mathrm{I}\left(\mathrm{x},{\mathrm{y}}_2\right),$ i.e., $\mathrm{I}\left(\mathrm{x},·\right)$ is increasing, i.e., I satisfies (2).

    $$\begin{array}{l}\mathrm{I}\left(0,0\right)= \mathrm{N}\left(0\right)=1 \mathrm{i}.\mathrm{e}., \mathrm{I} \mathrm{satisfies} \left(3\right)\\ \mathrm{I}\left(1,1\right)= \mathrm{N}\left(0\right)=1 \mathrm{i}.\mathrm{e}., \mathrm{I} \mathrm{satisfies} \left(4\right)\hfill \\ \mathrm{I}\left(1,0\right)= \mathrm{N}\left(1\right)=0 \mathrm{i}.\mathrm{e}., \mathrm{I} \mathrm{satisfies} \left(5\right).\hfill \end{array}$$

     □

Proposition 11.

Let$I$be the fuzzy implication of Theorem 3. If$N_1\left(x\right)=N_2\left(x\right)=N_3\left(x\right)=N\left(x\right)$are strong negations, then the neutrality property (14) and the exchange principle (15) are satisfied.

Proof. 

$\mathrm{I}\left(1,\mathrm{x}\right)=\mathrm{N}\left(\frac{\mathrm{N}\left(\mathrm{x}\right)+\mathrm{N}\left(\mathrm{x}\right)}{2}\right)=\mathrm{N}\left(\frac{2\mathrm{N}\left(\mathrm{x}\right)}{2}\right)=\mathrm{N}\left(\mathrm{N}\left(\mathrm{x}\right)\right)= \mathrm{x}$, i.e., I satisfies (14)

$$\begin{array}{c}\mathrm{I}\left(\mathrm{a},\mathrm{I}\left(\mathrm{b},\mathrm{x}\right)\right)=\mathrm{N}\left(\frac{\frac{{\mathrm{g}}_1\left(\mathrm{a}\right)}{{\mathrm{g}}_1\left(1\right)}\mathrm{N}\left(\mathrm{I}\left(\mathrm{b},\mathrm{x}\right)\right)+\frac{{\mathrm{g}}_2\left(\mathrm{a}\right)}{{\mathrm{g}}_2\left(1\right)}\mathrm{N}\left(\mathrm{I}\left(\mathrm{b},\mathrm{x}\right)\right)}{2}\right)=\hfill \\ \mathrm{N}\left(\frac{\frac{{\mathrm{g}}_1\left(\mathrm{a}\right)}{{\mathrm{g}}_1\left(1\right)}\mathrm{N}\left(\mathrm{N}\left( \frac{\frac{{\mathrm{g}}_1\left(\mathrm{b}\right)}{{\mathrm{g}}_1\left(1\right)}\mathrm{N}\left(\mathrm{x}\right)+\frac{{\mathrm{g}}_2\left(\mathrm{b}\right)}{{\mathrm{g}}_2\left(1\right)}\mathrm{N}\left(\mathrm{x}\right)}{2}\right)\right)+\frac{{\mathrm{g}}_2\left(\mathrm{a}\right)}{{\mathrm{g}}_2\left(1\right)}\mathrm{N}\left(\mathrm{N}\left( \frac{\frac{{\mathrm{g}}_1\left(\mathrm{b}\right)}{{\mathrm{g}}_1\left(1\right)}\mathrm{N}\left(\mathrm{x}\right)+\frac{{\mathrm{g}}_2\left(\mathrm{b}\right)}{{\mathrm{g}}_2\left(1\right)}\mathrm{N}\left(\mathrm{x}\right)}{2} \right)\right)}{2}\right)\stackrel{ \mathrm{N}:\mathrm{strong} \mathrm{negation}}{=}\hfill \\ =\mathrm{N}\left(\frac{\frac{{\mathrm{g}}_1\left(\mathrm{a}\right)}{{\mathrm{g}}_1\left(1\right)}ˑ\frac{\frac{{\mathrm{g}}_1\left(\mathrm{b}\right)}{{\mathrm{g}}_1\left(1\right)}\mathrm{N}\left(\mathrm{x}\right)+\frac{{\mathrm{g}}_2\left(\mathrm{b}\right)}{{\mathrm{g}}_2\left(1\right)}\mathrm{N}\left(\mathrm{x}\right)}{2}+\frac{{\mathrm{g}}_2\left(\mathrm{a}\right)}{{\mathrm{g}}_2\left(1\right)}ˑ \frac{\frac{{\mathrm{g}}_1\left(\mathrm{b}\right)}{{\mathrm{g}}_1\left(1\right)}\mathrm{N}\left(\mathrm{x}\right)+\frac{{\mathrm{g}}_2\left(\mathrm{b}\right)}{{\mathrm{g}}_2\left(1\right)}\mathrm{N}\left(\mathrm{x}\right)}{2}}{2}\right)=\hfill \\ =\mathrm{N}\left(\frac{\frac{{\mathrm{g}}_1\left(\mathrm{a}\right)}{{\mathrm{g}}_1\left(1\right)}ˑ\frac{{\mathrm{g}}_1\left(\mathrm{b}\right)}{{\mathrm{g}}_1\left(1\right)}\mathrm{N}\left(\mathrm{x}\right)+\frac{{\mathrm{g}}_1\left(\mathrm{a}\right)}{{\mathrm{g}}_1\left(1\right)}ˑ\frac{{\mathrm{g}}_2\left(\mathrm{b}\right)}{{\mathrm{g}}_2\left(1\right)}\mathrm{N}\left(\mathrm{x}\right)+\frac{{\mathrm{g}}_2\left(\mathrm{a}\right)}{{\mathrm{g}}_2\left(1\right)}ˑ\frac{{\mathrm{g}}_1\left(\mathrm{b}\right)}{{\mathrm{g}}_1\left(1\right)}\mathrm{N}\left(\mathrm{x}\right)+\frac{{\mathrm{g}}_2\left(\mathrm{a}\right)}{{\mathrm{g}}_2\left(1\right)}ˑ\frac{{\mathrm{g}}_2\left(\mathrm{b}\right)}{{\mathrm{g}}_2\left(1\right)}\mathrm{N}\left(\mathrm{x}\right)}{4}\right). \hfill \end{array}$$

$$\begin{array}{c}\mathrm{I}\left(\mathrm{b},\mathrm{I}\left(\mathrm{a},\mathrm{x}\right)\right)=\mathrm{N}\left(\frac{\frac{{\mathrm{g}}_1\left(\mathrm{b}\right)}{{\mathrm{g}}_1\left(1\right)}\mathrm{N}\left(\mathrm{I}\left(\mathrm{a},\mathrm{x}\right)\right)+\frac{{\mathrm{g}}_2\left(\mathrm{b}\right)}{{\mathrm{g}}_2\left(1\right)}\mathrm{N}\left(\mathrm{I}\left(\mathrm{a},\mathrm{x}\right)\right)}{2}\right)=\hfill \\ \mathrm{N}\left(\frac{\frac{{\mathrm{g}}_1\left(\mathrm{b}\right)}{{\mathrm{g}}_1\left(1\right)}\mathrm{N}\left(\mathrm{N}\left( \frac{\frac{{\mathrm{g}}_1\left(\mathrm{a}\right)}{{\mathrm{g}}_1\left(1\right)}\mathrm{N}\left(\mathrm{x}\right)+\frac{{\mathrm{g}}_2\left(\mathrm{a}\right)}{{\mathrm{g}}_2\left(1\right)}\mathrm{N}\left(\mathrm{x}\right)}{2} \right)\right)+\frac{{\mathrm{g}}_2\left(\mathrm{b}\right)}{{\mathrm{g}}_2\left(1\right)}\mathrm{N}\left(\mathrm{N}\left( \frac{\frac{{\mathrm{g}}_1\left(\mathrm{a}\right)}{{\mathrm{g}}_1\left(1\right)}\mathrm{N}\left(\mathrm{x}\right)+\frac{{\mathrm{g}}_2\left(\mathrm{a}\right)}{{\mathrm{g}}_2\left(1\right)}\mathrm{N}\left(\mathrm{x}\right)}{2} \right)\right)}{2}\right)\stackrel{ \mathrm{N}:\mathrm{strong} \mathrm{negation}}{=}\hfill \\ =\mathrm{N}\left(\frac{\frac{{\mathrm{g}}_1\left(\mathrm{b}\right)}{{\mathrm{g}}_1\left(1\right)}ˑ\frac{\frac{{\mathrm{g}}_1\left(\mathrm{a}\right)}{{\mathrm{g}}_1\left(1\right)}\mathrm{N}\left(\mathrm{x}\right)+\frac{{\mathrm{g}}_2\left(\mathrm{a}\right)}{{\mathrm{g}}_2\left(1\right)}\mathrm{N}\left(\mathrm{x}\right)}{2}+\frac{{\mathrm{g}}_2\left(\mathrm{b}\right)}{{\mathrm{g}}_2\left(1\right)}ˑ \frac{\frac{{\mathrm{g}}_1\left(\mathrm{a}\right)}{{\mathrm{g}}_1\left(1\right)}\mathrm{N}\left(\mathrm{x}\right)+\frac{{\mathrm{g}}_2\left(\mathrm{a}\right)}{{\mathrm{g}}_2\left(1\right)}\mathrm{N}\left(\mathrm{x}\right)}{2}}{2}\right)\hfill \\ =\mathrm{N}\left(\frac{\frac{{\mathrm{g}}_1\left(\mathrm{a}\right)}{{\mathrm{g}}_1\left(1\right)}ˑ\frac{{\mathrm{g}}_1\left(\mathrm{b}\right)}{{\mathrm{g}}_1\left(1\right)}\mathrm{N}\left(\mathrm{x}\right)+\frac{{\mathrm{g}}_1\left(\mathrm{a}\right)}{{\mathrm{g}}_1\left(1\right)}ˑ\frac{{\mathrm{g}}_2\left(\mathrm{b}\right)}{{\mathrm{g}}_2\left(1\right)}\mathrm{N}\left(\mathrm{x}\right)+\frac{{\mathrm{g}}_2\left(\mathrm{a}\right)}{{\mathrm{g}}_2\left(1\right)}ˑ\frac{{\mathrm{g}}_1\left(\mathrm{b}\right)}{{\mathrm{g}}_1\left(1\right)}\mathrm{N}\left(\mathrm{x}\right)+\frac{{\mathrm{g}}_2\left(\mathrm{a}\right)}{{\mathrm{g}}_2\left(1\right)}ˑ\frac{{\mathrm{g}}_2\left(\mathrm{b}\right)}{{\mathrm{g}}_2\left(1\right)}\mathrm{N}\left(\mathrm{x}\right)}{4}\right)\hfill \end{array}$$

We conclude that (15) is satisfied.  □

Proposition 12.

Let$I$be the fuzzy implication of Theorem 3and$N_1,N_2,N_3$be fuzzy negations. If$N_1\left(x\right)=N_2\left(x\right)=N_{D_1}\left(x\right)=$$\{\begin{array}{c}1 , if x=0 \\ 0 , if x\in \left(0,1\right]\end{array}$(the least fuzzy negation), then the identity principle (16) is satisfied.

Proof. 

$$\begin{gathered} \mathrm{I}\left(\mathrm{x},\mathrm{y}\right)={ \mathrm{N}}_3\left( \frac{\frac{{\mathrm{g}}_1\left(\mathrm{x}\right)}{{\mathrm{g}}_1\left(1\right)}{\mathrm{N}}_1\left(\mathrm{y}\right)+\frac{{\mathrm{g}}_2\left(\mathrm{x}\right)}{{\mathrm{g}}_2\left(1\right)}{\mathrm{N}}_2\left(\mathrm{y}\right)}{2}\right)\stackrel{\mathrm{x}=0}{=} {\mathrm{N}}_3\left(0\right)=1 \\ \mathrm{I}\left(\mathrm{x},\mathrm{y}\right)={ \mathrm{N}}_3\left( \frac{\frac{{\mathrm{g}}_1\left(\mathrm{x}\right)}{{\mathrm{g}}_1\left(1\right)}{\mathrm{N}}_1\left(\mathrm{y}\right)+\frac{{\mathrm{g}}_2\left(\mathrm{x}\right)}{{\mathrm{g}}_2\left(1\right)}{\mathrm{N}}_2\left(\mathrm{y}\right)}{2}\right)\stackrel{\mathrm{x}\in \left(0,1\right]}{=} {\mathrm{N}}_3\left(0\right)=1 \end{gathered}$$

Thus, I satisfies (16).  □

Proposition 13.

If the fuzzy implication of Theorem 3 satisfies the identity principle (16), then it satisfies the ordering property (17).

Proof. 

Let x,y ∈ [0,1] and x ≤ y, then I(x,y) ≥ I(y, y) = 1. Thus, I(x, y) = 1.

If $\mathrm{I}\left(\mathrm{x},\mathrm{y}\right)=1$ ⇔

$$\mathrm{I}\left(\mathrm{x},\mathrm{y}\right)={ \mathrm{N}}_3\left( \frac{\frac{{\mathrm{g}}_1\left(\mathrm{x}\right)}{{\mathrm{g}}_1\left(1\right)}{\mathrm{N}}_1\left(\mathrm{y}\right)+\frac{{\mathrm{g}}_2\left(\mathrm{x}\right)}{{\mathrm{g}}_2\left(1\right)}{\mathrm{N}}_2\left(\mathrm{y}\right)}{2} \right)=1 ⟺ \frac{\frac{{\mathrm{g}}_1\left(\mathrm{x}\right)}{{\mathrm{g}}_1\left(1\right)}{\mathrm{N}}_1\left(\mathrm{y}\right)+\frac{{\mathrm{g}}_2\left(\mathrm{x}\right)}{{\mathrm{g}}_2\left(1\right)}{\mathrm{N}}_2\left(\mathrm{y}\right)}{2}=0 ⟺$$

• ${\mathrm{g}}_1\left(\mathrm{x}\right){\mathrm{N}}_1\left(\mathrm{x}\right)=0$ and ${\mathrm{g}}_2\left(\mathrm{x}\right){\mathrm{N}}_2\left(\mathrm{x}\right)=0$ (${\mathrm{g}}_1,{\mathrm{g}}_2,{\mathrm{N}}_1,{\mathrm{N}}_2\ge 0)$
• ${\mathrm{g}}_1\left(\mathrm{x}\right)=0{ \mathrm{or} \mathrm{N}}_1\left(\mathrm{y}\right)=0$ and ${\mathrm{g}}_2\left(\mathrm{x}\right)=0$ or ${\mathrm{N}}_2\left(\mathrm{x}\right)=0$
• x = 0 ≤ y or y = 1 ≥ x.
• Thus, we have x ≤ y. □

Proposition 14.

Let$N_1,N_2,N_3,N_4$be four fuzzy negations. Let us suppose also that$N_4$is a strong fuzzy negation. If$g_1,g_2$: [0,1] → [0,∞) are increasing and continuous functions with$g_1\left(0\right)=g_2\left(0\right)=0$and$g_1\left(x\right)=N_1\left(N_4\left(x\right)\right)$, and$g_2\left(x\right)=N_2\left(N_4\left(x\right)\right)$, then the fuzzy implication defined in Theorem 3 satisfies the law of contraposition (16) with respect to$N_4$.

Proof. 

$$\begin{array}{c}\mathrm{I}\left({\mathrm{N}}_4\left(\mathrm{y}\right),{\mathrm{N}}_4\left(\mathrm{x}\right)\right)={\mathrm{N}}_3\left( \frac{\frac{{\mathrm{g}}_1\left({\mathrm{N}}_4\left(\mathrm{y}\right)\right)}{{\mathrm{g}}_1\left(1\right)}{\mathrm{N}}_1\left({\mathrm{N}}_4\left(\mathrm{x}\right)\right)+\frac{{\mathrm{g}}_2\left({\mathrm{N}}_4\left(\mathrm{y}\right)\right)}{{\mathrm{g}}_2\left(1\right)}{\mathrm{N}}_2\left({\mathrm{N}}_4\left(\mathrm{x}\right)\right)}{2}\right)=\hfill \\ ={\mathrm{N}}_3\left(\frac{\frac{{\mathrm{N}}_1\left({\mathrm{N}}_4\left({\mathrm{N}}_4\left(\mathrm{y}\right)\right)\right)}{{\mathrm{g}}_1\left(1\right)}{\mathrm{N}}_1\left({\mathrm{N}}_4\left(\mathrm{x}\right)\right)+\frac{{\mathrm{N}}_2\left({\mathrm{N}}_4\left({\mathrm{N}}_4\left(\mathrm{y}\right)\right)\right)}{{\mathrm{g}}_2\left(1\right)}{\mathrm{N}}_2\left({\mathrm{N}}_4\left(\mathrm{x}\right)\right)}{2}\right)\hfill \\ \stackrel{N_4:strong negation}{=}{\mathrm{N}}_3\left(\frac{\frac{{\mathrm{N}}_1\left(\mathrm{y}\right)}{{\mathrm{g}}_1\left(1\right)}{\mathrm{N}}_1\left({\mathrm{N}}_4\left(\mathrm{x}\right)\right)+\frac{{\mathrm{N}}_2\left(\mathrm{y}\right)}{{\mathrm{g}}_2\left(1\right)}{\mathrm{N}}_2\left({\mathrm{N}}_4\left(\mathrm{x}\right)\right)}{2}\right)\hfill \\ ={\mathrm{N}}_3\left( \frac{\frac{{\mathrm{g}}_1\left(\mathrm{x}\right)}{{\mathrm{g}}_1\left(1\right)}{\mathrm{N}}_1\left(\mathrm{y}\right)+\frac{{\mathrm{g}}_2\left(\mathrm{x}\right)}{{\mathrm{g}}_2\left(1\right)}{\mathrm{N}}_2\left(\mathrm{y}\right)}{2}\right)=\mathrm{I}(\mathrm{x}, \mathrm{y})\hfill \end{array}$$

Thus, I satisfies (16). □

Proposition 15.

The natural negation$N_I$of the fuzzy implication of Theorem 3 is

$${ \mathrm{N}}_{\mathrm{I}}\left(\mathrm{x}\right)={ \mathrm{N}}_3\left( \frac{\frac{{\mathrm{g}}_1\left(\mathrm{x}\right)}{{\mathrm{g}}_1\left(1\right)}+\frac{{\mathrm{g}}_2\left(\mathrm{x}\right)}{{\mathrm{g}}_2\left(1\right)}}{2}\right)$$

Proof. 

$${\mathrm{N}}_{\mathrm{I}}\left(\mathrm{x}\right)=\mathrm{I}\left(\mathrm{x},0\right)={ \mathrm{N}}_3\left( \frac{\frac{{\mathrm{g}}_1\left(\mathrm{x}\right)}{{\mathrm{g}}_1\left(1\right)}{\mathrm{N}}_1\left(0\right)+\frac{{\mathrm{g}}_2\left(\mathrm{x}\right)}{{\mathrm{g}}_2\left(1\right)}{\mathrm{N}}_2\left(0\right)}{2}\right)={\mathrm{N}}_3\left( \frac{\frac{{\mathrm{g}}_1\left(\mathrm{x}\right)}{{\mathrm{g}}_1\left(1\right)}+\frac{{\mathrm{g}}_2\left(\mathrm{x}\right)}{{\mathrm{g}}_2\left(1\right)}}{2}\right).$$

 □

Example 5.

Let$g_1\left(x\right)=g_2\left(x\right)=x , N_3\left(x\right)=1-x=N_1\left(x\right) , N_2\left(x\right)=1-x^2$

• Then,$I\left(x,y\right)=N_3\left( \frac{x\left(1-y\right)+x\left(1-y^2\right)}{2} \right)==N_3\left( \frac{2x-xy-x{y}^2}{2}\right)=\frac{2-2x+xy+x{y}^2}{2}$
• The graph of the above surface is plotted in Figure 4.
  

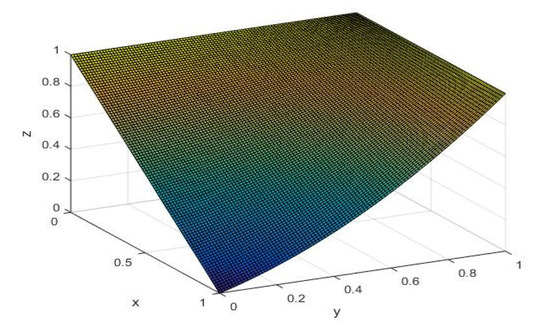  Figure 4. I implication of example 5.

Example 6.

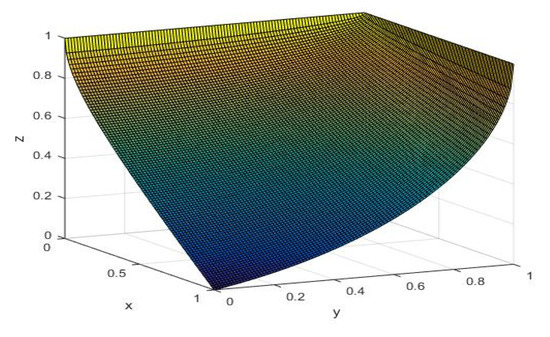
Let $g_1\left(x\right)=x^2 , g_2\left(x\right)=x , N_3\left(x\right)=1-\sqrt{x} , N_1\left(x\right)=1-x , N_2\left(x\right)=1-x^2$.

Then, $I\left(x,y\right)=N_3\left(\frac{x^2\left(1-y\right)+x\left(1-y^2\right)}{2}\right)=1-\sqrt{\frac{x^2-x^{2}y+x-x{y}^2}{2}}$.

The graph of the above surface is plotted in Figure 5.

Figure 5. I implication of example 6.

3.3. Fuzzy Implications Generated by n Increasing Function $g_i\left(i=1,2,\dots n,n\in \mathbb{\mathbb{N}}\right)$ and n + 1 Fuzzy Negations $N_i , \left( i=1,2,\dots n+1 , n \in \mathbb{\mathbb{N}}\right)$

Theorem 4.

If $g_i\left(x\right)$: [0,1] → [0,∞) are increasing and continuous functions, where $g_i\left(0\right)=0$ (i = 1, 2, …n, n ∈ ℕ) and $N_i$ are fuzzy negations (i = 1,2,…n + 1 , n ∈ ℕ), then the function $I :{\left[0,1\right]}^2\to \left[0,1\right]$ defined by

$$\mathrm{I}\left(\mathrm{x},\mathrm{y}\right)={\mathrm{N}}_{\mathrm{n}+1}\left({\sum }_{\mathrm{i}=1}^{\mathrm{n}}\left(\frac{\frac{{\mathrm{g}}_{\mathrm{i}}\left(\mathrm{x}\right)}{{\mathrm{g}}_{\mathrm{i}}\left(1\right)}ˑ{\mathrm{N}}_{\mathrm{i}}\left(\mathrm{y}\right) }{\mathrm{n}} \right)\right) \mathrm{x},\mathrm{y}\in \left[0,1\right],$$

(37)

is a fuzzy implication.

Proof. 

Let ${\mathrm{x}}_1,{\mathrm{x}}_2, \mathrm{y}$ ∈ [0, 1].

If ${\mathrm{x}}_1\le {\mathrm{x}}_2 \Rightarrow {\mathrm{g}}_1\left({\mathrm{x}}_1\right)\le {\mathrm{g}}_1\left({\mathrm{x}}_2\right),{ \mathrm{g}}_2\left({\mathrm{x}}_1\right)\le {\mathrm{g}}_2\left({\mathrm{x}}_2\right),\dots ,{ \mathrm{g}}_{\mathrm{n}}\left({\mathrm{x}}_1\right)\le {\mathrm{g}}_{\mathrm{n}}\left({\mathrm{x}}_2\right)$ ⇒ ${\sum }_{\mathrm{i}=1}^{\mathrm{n}}\frac{{\mathrm{g}}_{\mathrm{i}}\left({\mathrm{x}}_1\right)}{{\mathrm{g}}_{\mathrm{i}}\left(1\right)} \le {\sum }_{\mathrm{i}=1}^{\mathrm{n}}\frac{{\mathrm{g}}_{\mathrm{i}}\left({\mathrm{x}}_2\right)}{{\mathrm{g}}_{\mathrm{i}}\left(1\right)}$, then ${\mathrm{N}}_1\left(\mathrm{y}\right){\mathrm{g}}_1\left({\mathrm{x}}_1\right)\le {\mathrm{N}}_1\left(\mathrm{y}\right){\mathrm{g}}_1\left({\mathrm{x}}_2\right),{ \mathrm{N}}_2\left(\mathrm{y}\right){\mathrm{g}}_2\left({\mathrm{x}}_1\right)\le {\mathrm{N}}_2\left(\mathrm{y}\right){\mathrm{g}}_2\left({\mathrm{x}}_2\right),\dots ,{\mathrm{N}}_{\mathrm{n}}\left(\mathrm{y}\right){ \mathrm{g}}_{\mathrm{n}}\left({\mathrm{x}}_1\right)\le {\mathrm{N}}_{\mathrm{n}}\left(\mathrm{y}\right){\mathrm{g}}_{\mathrm{n}}\left({\mathrm{x}}_2\right)$ ${\sum }_{\mathrm{i}=1}^{\mathrm{n}}\frac{1}{\mathrm{n}}{\mathrm{N}}_{\mathrm{i}}\left(\mathrm{y}\right)\frac{{\mathrm{g}}_{\mathrm{i}}\left({\mathrm{x}}_1\right)}{{\mathrm{g}}_{\mathrm{i}}\left(1\right)} \le {\sum }_{\mathrm{i}=1}^{\mathrm{n}}\frac{1}{\mathrm{n}}{\mathrm{N}}_{\mathrm{i}}\left(\mathrm{y}\right)\frac{{\mathrm{g}}_{\mathrm{i}}\left({\mathrm{x}}_2\right)}{{\mathrm{g}}_{\mathrm{i}}\left(1\right)}\Rightarrow {\mathrm{N}}_{\mathrm{n}+1}\left({\sum }_{\mathrm{i}=1}^{\mathrm{n}}\left(\frac{1}{\mathrm{n}}{\mathrm{N}}_{\mathrm{i}}\left(\mathrm{y}\right)\frac{{\mathrm{g}}_{\mathrm{i}}\left({\mathrm{x}}_1\right)}{{\mathrm{g}}_{\mathrm{i}}\left(1\right)}\right)\right)\ge {\mathrm{N}}_{\mathrm{n}+1}\left({\sum }_{\mathrm{i}=1}^{\mathrm{n}}(\frac{1}{\mathrm{n}}{\mathrm{N}}_{\mathrm{i}}\left(\mathrm{y}\right)\frac{{\mathrm{g}}_{\mathrm{i}}\left({\mathrm{x}}_2\right)}{{\mathrm{g}}_{\mathrm{i}}\left(1\right)})\right)$

• ⇒ $\mathrm{I}\left({\mathrm{x}}_1,\mathrm{y}\right)\ge \mathrm{I}\left({\mathrm{x}}_2,\mathrm{y}\right)$, i.e., I(,y) is decreasing, i.e., I satisfies (1)
• Let ${\mathrm{y}}_1,{ \mathrm{y}}_2,$ x ∈ [0, 1]. If ${\mathrm{y}}_1\le {\mathrm{y}}_2$, then ${\mathrm{N}}_{\mathrm{i}}({\mathrm{y}}_1)\ge {\mathrm{N}}_{\mathrm{i}}\left({\mathrm{y}}_2\right)\Rightarrow \frac{{\mathrm{g}}_{\mathrm{i}}\left(\mathrm{x}\right)}{{\mathrm{g}}_{\mathrm{i}}\left(1\right)}{\mathrm{N}}_{\mathrm{i}}\left({\mathrm{y}}_1\right)\ge \frac{{\mathrm{g}}_{\mathrm{i}}\left(\mathrm{x}\right)}{{\mathrm{g}}_{\mathrm{i}}\left(1\right)}{\mathrm{N}}_{\mathrm{i}}\left({\mathrm{y}}_2\right)\Rightarrow {\sum }_{\mathrm{i}=1}^{\mathrm{n}}\frac{1}{\mathrm{n}}\frac{{\mathrm{g}}_{\mathrm{i}}\left(\mathrm{x}\right)}{{\mathrm{g}}_{\mathrm{i}}\left(1\right)}{\mathrm{N}}_{\mathrm{i}}\left({\mathrm{y}}_1\right) \ge {\sum }_{\mathrm{i}=1}^{\mathrm{n}}\frac{1}{\mathrm{n}}\frac{{\mathrm{g}}_{\mathrm{i}}\left(\mathrm{x}\right)}{{\mathrm{g}}_{\mathrm{i}}\left(1\right)}{\mathrm{N}}_{\mathrm{i}}\left({\mathrm{y}}_2\right) \Rightarrow$
• ${\mathrm{N}}_{\mathrm{n}+1}\left({\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{n}}}\left(\frac{1}{\mathrm{n}}\mathrm{N}\left({\mathrm{y}}_1\right)\frac{{\mathrm{g}}_{\mathrm{i}}\left(\mathrm{x}\right)}{{\mathrm{g}}_{\mathrm{i}}\left(1\right)}\right)\right)\le { \mathrm{N}}_{\mathrm{n}+1}\left({\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{n}}}\left(\frac{1}{\mathrm{n}}\mathrm{N}\left({\mathrm{y}}_2\right)\frac{{\mathrm{g}}_{\mathrm{i}}\left(\mathrm{x}\right)}{{\mathrm{g}}_{\mathrm{i}}\left(1\right)}\right)\right)$
• $\Rightarrow \mathrm{I}\left(\mathrm{x},{\mathrm{y}}_1\right)\le \mathrm{I}\left(\mathrm{x},{\mathrm{y}}_2\right)$, i.e., I(x,ˑ) is increasing, i.e., I satisfies (2)
• $\mathrm{I}\left(0,0\right)=\mathrm{N}\left(0\right)=1$, i.e., I satisfies (3)
  $\mathrm{I}\left(1,1\right)=\mathrm{N}\left(0\right)=1$, i.e., I satisfies (4)
• $\mathrm{I}\left(1,0\right)=\mathrm{N}\left(\frac{1+1+\dots +1}{\mathrm{n}}\right)=\mathrm{N}\left( \frac{\mathrm{n}}{\mathrm{n}} \right)=\mathrm{N}\left(1\right)=0$, i.e., I satisfies (5).  □

Proposition 16.

Let$I$be the fuzzy implication of Theorem 4. If$N_{n+1}\left(x\right)=N_1\left(x\right)=\dots =N_n\left(x\right)=N\left(x\right)$are strong negations, then the left neutrality property (14) and the exchange principle (15) are satisfied.

Proof. 

$\mathrm{I}\left(1,\mathrm{y}\right)=\mathrm{N}\left({\sum }_{\mathrm{i}=1}^{\mathrm{n}}\left(\frac{\frac{{\mathrm{g}}_{\mathrm{i}}\left(1\right)}{{\mathrm{g}}_{\mathrm{i}}\left(1\right)}ˑ\mathrm{N}\left(\mathrm{y}\right) }{\mathrm{n}} \right)\right)=\mathrm{N}\left(\mathrm{N}\left(\mathrm{y}\right)\right)=\mathrm{y},$ y ∈ [0, 1], i.e., I satisfies (14)

$$\begin{gathered} \mathrm{I}\left(\mathrm{a},\mathrm{I}\left(\mathrm{b},\mathrm{x}\right)\right)=\mathrm{N}\left({\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{n}}}\left(\frac{\frac{{\mathrm{g}}_{\mathrm{i}}\left(\mathrm{a}\right)}{{\mathrm{g}}_{\mathrm{i}}\left(1\right)}ˑ\mathrm{N}\left(\mathrm{I}\left(\mathrm{b},\mathrm{x}\right)\right) }{\mathrm{n}} \right)\right) \\ =\mathrm{N}\left({\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{n}}}\left(\frac{\frac{{\mathrm{g}}_{\mathrm{i}}\left(\mathrm{a}\right)}{{\mathrm{g}}_{\mathrm{i}}\left(1\right)}ˑ\mathrm{N}\left(\mathrm{N}\left({\sum }_{\mathrm{i}=1}^{\mathrm{n}}\left(\frac{\frac{{\mathrm{g}}_{\mathrm{i}}\left(\mathrm{b}\right)}{{\mathrm{g}}_{\mathrm{i}}\left(1\right)}ˑ\mathrm{N}\left(\mathrm{x}\right)}{\mathrm{n}} \right)\right)\right) }{\mathrm{n}}\right)\right) \end{gathered}$$

$$\stackrel{\mathrm{N}: \mathrm{strong} \mathrm{negation}}{=}\mathrm{N}\left({\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{n}}}\left(\frac{\frac{{\mathrm{g}}_{\mathrm{i}}\left(\mathrm{a}\right)}{{\mathrm{g}}_{\mathrm{i}}\left(1\right)}ˑ{\sum }_{\mathrm{i}=1}^{\mathrm{n}}\left(\frac{\frac{{\mathrm{g}}_{\mathrm{i}}\left(\mathrm{b}\right)}{{\mathrm{g}}_{\mathrm{i}}\left(1\right)}ˑ\mathrm{N}\left(\mathrm{x}\right)}{\mathrm{n}} \right) }{\mathrm{n}}\right)\right)$$

$$\begin{gathered} \mathrm{I}\left(\mathrm{b},\mathrm{I}\left(\mathrm{a},\mathrm{x}\right)\right)=\mathrm{N}\left({\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{n}}}\left(\frac{\frac{{\mathrm{g}}_{\mathrm{i}}\left(\mathrm{b}\right)}{{\mathrm{g}}_{\mathrm{i}}\left(1\right)}ˑ\mathrm{N}\left(\mathrm{I}\left(\mathrm{a},\mathrm{x}\right)\right) }{\mathrm{n}}\right)\right)= \\ =\mathrm{N}\left({\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{n}}}\left(\frac{\frac{{\mathrm{g}}_{\mathrm{i}}\left(\mathrm{b}\right)}{{\mathrm{g}}_{\mathrm{i}}\left(1\right)}ˑ\mathrm{N}\left(\mathrm{N}\left({\sum }_{\mathrm{i}=1}^{\mathrm{n}}\left(\frac{\frac{{\mathrm{g}}_{\mathrm{i}}\left(\mathrm{a}\right)}{{\mathrm{g}}_{\mathrm{i}}\left(1\right)}ˑ\mathrm{N}\left(\mathrm{x}\right)}{\mathrm{n}} \right)\right)\right) }{\mathrm{n}} \right)\right) \\ \stackrel{\mathrm{N}:\mathrm{strong} \mathrm{negation}}{=}\mathrm{N}\left({\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{n}}}\left(\frac{\frac{{\mathrm{g}}_{\mathrm{i}}\left(\mathrm{b}\right)}{{\mathrm{g}}_{\mathrm{i}}\left(1\right)}ˑ{\sum }_{\mathrm{i}=1}^{\mathrm{n}}\left(\frac{\frac{{\mathrm{g}}_{\mathrm{i}}\left(\mathrm{a}\right)}{{\mathrm{g}}_{\mathrm{i}}\left(1\right)}ˑ\mathrm{N}\left(\mathrm{x}\right) }{\mathrm{n}}\right) }{\mathrm{n}}\right)\right) \end{gathered}$$

We conclude that (15) is satisfied, $\mathrm{I}\left(\mathrm{a},\mathrm{I}\left(\mathrm{b},\mathrm{x}\right)\right)= \mathrm{I}\left(\mathrm{b},\mathrm{I}\left(\mathrm{a},\mathrm{x}\right)\right).$  □

Proposition 17.

Let$I\left(x,y\right)=N_{n+1}\left({\sum }_{i=1}^n\left(\frac{\frac{g_i\left(x\right)}{g_i\left(1\right)}ˑN_i\left(y\right) }{n}\right)\right), x,y\in \left[0,1\right],$the fuzzy implication defined by Theorem 4. Then, if$N_1=N_2=\dots N_n=N_{D_1}=\{\begin{array}{c}1 , if x=0\\ 0 , if x\in \left(0,1\right]\end{array}$(the least fuzzy negation), the identity principle (16) is satisfied.

Proof. 

$$\begin{gathered} \mathrm{I}\left(\mathrm{x},\mathrm{x}\right)={\mathrm{N}}_{\mathrm{n}+1}\left({\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{n}}}\left(\frac{\frac{{\mathrm{g}}_{\mathrm{i}}\left(\mathrm{x}\right)}{{\mathrm{g}}_{\mathrm{i}}\left(1\right)}ˑ{\mathrm{N}}_{\mathrm{i}}\left(\mathrm{x}\right) }{\mathrm{n}}\right)\right)\stackrel{ \mathrm{x}=0}{=}{ \mathrm{N}}_{\mathrm{n}+1}\left(0\right)=1 \\ \mathrm{I}\left(\mathrm{x},\mathrm{x}\right)={\mathrm{N}}_{\mathrm{n}+1}\left({\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{n}}}\left(\frac{\frac{{\mathrm{g}}_{\mathrm{i}}\left(\mathrm{x}\right)}{{\mathrm{g}}_{\mathrm{i}}\left(1\right)}ˑ{\mathrm{N}}_{\mathrm{i}}\left(\mathrm{x}\right) }{\mathrm{n}} \right)\right)\stackrel{ \mathrm{x}\in \left(0,1\right]}{=}{ \mathrm{N}}_{\mathrm{n}+1}\left(0\right)=1 \end{gathered}$$

Thus, I satisfies (16).  □

Proposition 18.

Let$N_1,\dots ,N_{n+1},N_{n+2}$n + 2 be fuzzy negations. Let us suppose also that$N_{n+2}$is a strong fuzzy negation. If$g_i$: [0,1] → [0,∞) (i = 1, …, n , n ∈ ℕ) are increasing and continuous functions with$g_i\left(0\right)=\dots =g_n\left(0\right)=0$and$g_i\left(x\right)=N_i\left(N_{n+2}\left(x\right)\right)$, then the function$I :{\left[0,1\right]}^2\to \left[0,1\right]$defined by Theorem 4,$I\left(x,y\right)=N_{n+1}\left({\sum }_{i=1}^n\left(\frac{\frac{g_i\left(x\right)}{g_i\left(1\right)}ˑN_i\left(y\right) }{n} \right)\right)$$x,y\in \left[0,1\right],$satisfies the law of contraposition (18) with respect to$N_{n+2}$.

Proof. 

$$\begin{gathered} \mathrm{I}\left({\mathrm{N}}_{\mathrm{n}+2}\left(\mathrm{y}\right),{ \mathrm{N}}_{\mathrm{n}+2}\left(\mathrm{x}\right)\right)={\mathrm{N} }_{\mathrm{n}+1}\left({\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{n}}}\left(\frac{\frac{{\mathrm{g}}_{\mathrm{i}}\left({\mathrm{N}}_{\mathrm{n}+2}\left(\mathrm{y}\right)\right) }{{\mathrm{g}}_{\mathrm{i}}\left(1\right)}ˑ{\mathrm{N}}_{\mathrm{i}}\left({\mathrm{N}}_{\mathrm{n}+2}\left(\mathrm{x}\right)\right) }{\mathrm{n}}\right)\right)= \\ ={\mathrm{N} }_{\mathrm{n}+1}\left({\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{n}}}\left(\frac{\frac{{\mathrm{N}}_{\mathrm{i}}\left({\mathrm{N}}_{\mathrm{n}+2}\left({\mathrm{N}}_{\mathrm{n}+2}\left(\mathrm{y}\right)\right)\right)}{{\mathrm{g}}_{\mathrm{i}}\left(1\right)}ˑ{\mathrm{N}}_{\mathrm{i}}\left({\mathrm{N}}_{\mathrm{n}+2}\left(\mathrm{x}\right)\right)}{\mathrm{n}}\right)\right) \end{gathered}$$

$$\begin{gathered} \stackrel{N_{n+2}: strong negation}{=}{\mathrm{N}}_{\mathrm{n}+1}\left({\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{n}}}\left(\frac{\frac{{\mathrm{N}}_{\mathrm{i}}\left(\mathrm{y}\right)}{{\mathrm{g}}_{\mathrm{i}}\left(1\right)}ˑ{\mathrm{N}}_{\mathrm{i}}\left({\mathrm{N}}_{\mathrm{n}+2}\left(\mathrm{x}\right)\right) }{\mathrm{n}} \right)\right) \\ =\mathrm{I}\left(\mathrm{x},\mathrm{y}\right). \end{gathered}$$

Thus, I satisfies (16).  □

Proposition 19.

The natural negation$N_I$of the fuzzy negation of Theorem 4 is

$${\mathrm{N}}_{\mathrm{I}}\left(\mathrm{x}\right)={ \mathrm{N}}_{\mathrm{n}+1}\left({\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{n}}}\left(\frac{\frac{{\mathrm{g}}_{\mathrm{i}}\left(\mathrm{x}\right)}{{\mathrm{g}}_{\mathrm{i}}\left(1\right)} }{\mathrm{n}} \right)\right)$$

Proof. 

$${\mathrm{N}}_{\mathrm{I}}\left(\mathrm{x}\right)=\mathrm{I}\left(\mathrm{x},0\right)={\mathrm{N}}_{\mathrm{n}+1}\left({\sum }_{\mathrm{i}=1}^{\mathrm{n}}\left(\frac{\frac{{\mathrm{g}}_{\mathrm{i}}\left(\mathrm{x}\right)}{{\mathrm{g}}_{\mathrm{i}}\left(1\right)}ˑ{\mathrm{N}}_{\mathrm{i}}\left(0\right) }{\mathrm{n}}\right)\right)={\mathrm{N}}_{\mathrm{n}+1}\left({\sum }_{\mathrm{i}=1}^{\mathrm{n}}\left(\frac{\frac{{\mathrm{g}}_{\mathrm{i}}\left(\mathrm{x}\right)}{{\mathrm{g}}_{\mathrm{i}}\left(1\right)} }{\mathrm{n}} \right)\right).$$

 □

4. Conclusions

In this paper, a new production machine of fuzzy implications from n continuous increasing functions and n + 1 negation are introduced. We studied certain properties of these new fuzzy implications, as the left neutrality property (14), exchange principle (15), identity principle (16), ordering property (17), law of contraposition (18), and T-Conditionality (32), where some results are obtained if the fuzzy negations are strong or the least fuzzy negations. The advance of this method relies on the fact that we can combine a lot of fuzzy negations ${\mathrm{N}}_{\mathrm{i}}$ and increasing functions ${\mathrm{g}}_{\mathrm{i}}$ in order to generate fuzzy implications.

Finally, we believe that this production machine needs to be investigated further. It has been observed that in order to be satisfied, certain desirable properties by the implications generated by this method must use strong fuzzy negations or the least fuzzy negation. A question that arises is the following one:

Are there non-strong fuzzy negations that satisfy the left neutrality property (14) or the exchange principle (15)? In addition, in a future paper, we will study the behavior of non-continuous functions in terms of the validity of certain basic properties.