Abstract
In the paper, we investigate a local boundary value problem with transmitting condition of the integral form for mixed parabolic-hyperbolic equation with non-characteristic line of type changing. Theorem on strong solvability of the considered problem has been proved and integral representation of the solution is obtained in a functional space. Using Lidskii Theorem on coincidences of matrix and spectral traces of nuclear operator and Gaal’s formula for evaluating traces of nuclear operator, which is represented as a product of two Hilbert-Schmidt operators, we prove the existence of eigenvalues of the considered problem.
MSC:
35M10
1. Introduction
Main problems of the spectral theory of boundary value problems (BVPs) for mixed type equations can be divided as follows:
(1) characterization of the spectrum of boundary problems;
(2) construction of root (eigenfunctions and associated functions) functions;
(3) investigation of the completeness and basis property of root functions in various functional spaces.
Investigation of BVPs for mixed type equations becomes one of the main problems of the general theory of partial differential equations due to several applications of it in both in practice and theory. Nevertheless, despite the great attention to this problem by mathematicians, questions of the spectral theory of BVPs, in particular, for equations of mixed parabolic-hyperbolic type equations with integral transmitting conditions, remained hitherto unexplored.
In the work [], an analog problem to the generalized Tricomi problem, with integral gluing conditions for mixed parabolic-hyperbolic equation, was studied. Theorems on strong solvability and on the absence of eigenvalues were proved. In [] one can find historical information and notation on main scientific results on the related field.
Omitting huge amount of work, we just note some of them, which are closely related to the present problem. One of the first investigations of BVPs with non-continuous transmitting conditions for parabolic-hyperbolic equations was work []. In [] authors investigated initial-boundary value problems for mixed type equations in multi-dimensional domains, which appear at studying problems on motion of conducting fluid in an electromagnetic field.
In the work [] the propagation of electrical oscillations in composite lines, when on the interval of the semi-infinite line losses are neglected, and the rest of the line is considered as a cable without leakage was reduced to solving the system of equations
with initial
and boundary conditions
together with requirement of the continuity of the voltage and current
Here are inductance and capacitance (per unit length) of the first part of the line; are resistance and capacitance of the second part.
It is not difficult to verify that if one excludes current from the system, the following parabolic-hyperbolic equation
can be deduced together with boundary conditions
In this case transmitting condition will have form of
where
Another example of an application can be found in the work [].
Investigation of the unique solvability and spectral questions of some BVPs with integral transmitting conditions for parabolic-hyperbolic equations were done in works [,,,,]. Regarding the investigation of semilinear parabolic-equations we refer the readers to the works [,].
We note that in [,,], classical and generalized solvability questions of local and nonlocal problems for mixed parabolic-hyperbolic type equations were discussed. Spectral properties of boundary problems with a shift for wave equation was studied in []. The spectrum and basis properties of the operator eigenfunction systems, comparable to the boundary value problem for some linear systems of PDEs have been studied in []. Properties of the spectrum of an elliptic boundary value problem were the subject of study in [].
In general, spectral theory for elliptic type equations is well-developed, while similar theory for the wave type and mixed type equations is still under development. Strong solvability and the Volterra property (the absence of eigenvalues) for the analog of the Tricomi problem for mixed parabolic-hyperbolic type equation with non-characteristic line of type-changing (in the domain with the deviation from characteristics) was studied in []. The existence of eigenvalues for a class of local boundary problems for the second and third order parabolic-hyperbolic type equations were investigated in [,].
In this regard, there is a question on the possibility of formulation and investigation of boundary problems with special transmitting condition for such equations, whose eigenvalues does exist. Therefore, the main aim of the present work is to answer this question. We formulate the correct problem with integral transmitting condition for a mixed parabolic-hyperbolic type equation and prove the existence of eigenvalues for this problem.
It is well-known that general spectral theory has many applications in different branches of mathematics. Especially, spectral theory of differential operators becomes main tool of many investigations related to real-life problems [,]. We would like also note that spectral properties of BVPs for mixed type equations will be used at studying qualitative properties of higher order mixed type PDEs.
2. Formulation of the Problem
Let be a finite simple-connected domain (See Figure 1), bounded at by segments , and at by characteristics , of the equation
where ,
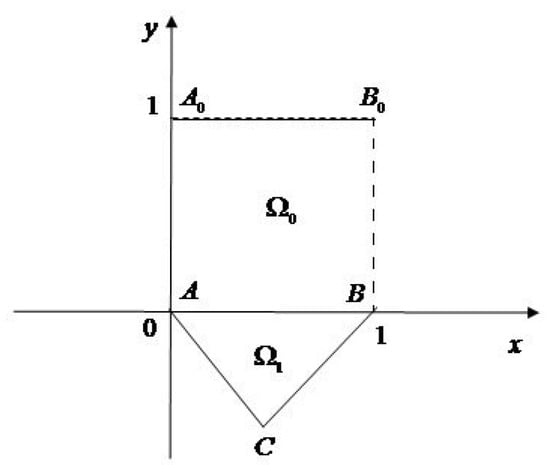
Figure 1.
Domain .
We consider the following variant of the Tricomi problem for a parabolic-hyperbolic equation.
Problem A. Find a solution of the Equation (1), satisfying boundary conditions
and transmitting condition on the type-changing line
where , such that .
Denote . We introduce the following set of functions:
Function we call as strong solution of the problem, if there exists a sequence of functions , , such that , for . Here and further, by we denote norm of the Sobolev space , where .
Remark 1.
We note that, generally speaking, the strong solution (in our understanding) does not satisfy neither equation nor boundary conditions (in classical sense) and it is associated with the closure of differential operator L in of the corresponding problem.
If by we denote the closure of differential operator L in on the set W, then, , the set of definition of operator , consists of the strong solutions to the Problem A in the sense of our definition
3. Main Result
Theorem 1.
For any function there exists a unique strong solution of Problem A. This solution belongs to the class of functions , satisfies the following inequality
and represented as
where .
Remark 2.
It should be noted that the kernel is expressed in the explicit form through the Green’s function and the solutions of the second kind Volterra type integral equation. The kernel K is presented in the Proof of Theorem 1 (see the Formula (20)).
Proof of Theorem 1.
According to the unique solvability of the first boundary problem for the heat equation with conditions (2) and , [], and the Darboux problem for the wave equation with conditions (3), , [], solution of the Equation (1) can be represented as follows
where , , , and is Green’s function of the first boundary problem for heat equation in a rectangle , which has a form []:
Considering (8), calculating derivative , and passing to the limit as y tends to zero in , we obtain first functional relation between functions and given as
where
or, which is the same,
Similarly, we find another integral-differential relation between functions and on , reduced from the domain . It has the form
Let . From (9) and (13) based on transmitting conditions (4), we deduce integral equation with respect to :
Here
Thus, the problem is equivalently reduced to the second kind Volterra integral Equation (14). Since by (10), the kernel can be represented as
where , then from (15) it follows that has a weak singularity. Therefore, Problem (14) has a unique solution and it has a form
where is the resolvent kernel of (14), which is defined as
Considering after some evaluations, from (17) we get
where
Substituting (18) into (7), we deduce the Formula (6), where
Similarly as in [] (see proof of the Lemma 1), one can prove that
Here one can face bulky expressions, which should be carefully considered.
Considering (11) by virtue of direct calculations from (16) we can state that the estimate
is valid. Therefore, from (17) we have
Based on this and properties of solution for the first boundary problem for heat equation [], it follows that solution of the Problem A belongs to the class of functions and satisfies inequality (5).
Now we show that the obtained solution will be strong. Since is dense in , then for any function there exists a sequence of functions such that , . Here is a set of differentiable functions in , which are equal to zero in neighborhood of ( is a boundary of the domain ). Denote that , where is inverse of the operator of Problem A defined as
It is not difficult to verify that for any . Here by we denote representation similar to (16), where should be replaced with . Hence, Equation (14) we can consider as the second kind Volterra integral equation in the space . Consequently, . Based on properties of the first boundary problem for heat equation and the Darboux problem for wave equation [], considering representation (6), we get that for all .
By virtue of the inequality (5) we obtain
Therefore, sequence satisfies all requirements of the definition of the strong solution. Now we can state that the Problem A is strongly solvable for any , and strong solution belongs to the class of functions .
Theorem 1 is proved. □
From Theorem 1 we can conclude that operator of the Problem A is invertible, and inverse operator is Hilbert-Schmidt operator. There is a natural question on the existence of eigenvalues of the operator , consequently, of the Problem A as well.
Before answering this question, we introduce the following result
Lemma 1.
[] If operator T is nuclear in a Hilbert space H, then for any orthonormal basis in H, the equality
holds true. Here are the eigenvalues of the operator T.
Theorem 2.
Let . There exists such that the equation
has a non-trivial solution .
Proof of Theorem 2.
We denote by a closure in of the differential operator given in by equality (1). From Theorem 1 it follows that is invertible and defined by (6) is the Hilbert-Schmidt operator. Then operator is nuclear in . Therefore, we apply the result of the Lidskii [] on the coincidences of the matrix and spectral traces to the operator .
It is very well known that if operator T is nuclear in , it can be represented as the composition of two Hilbert-Schmidt operators
and
Then, by using Gaal’s formula for calculating traces [], we have that
is true.
From (21) and (22) we deduce that
From (20) it follows that
Therefore,
where
Let us show that . In fact
Since, due to (10), (15), (19) and , then
Now consider . We have
Function we represent as
Taking (12) into account, we study the sign of the first term. For this, we use the following transformations:
From here we get
The equality in (27) will be true only when , i.e.,
Then considering , with respect to the second item of (26) we have
Similarly, we can prove that the second item of (25) is as well positive. Hence, from (25) we can state that . From (23)–(25) it follows that .
Then by virtue of (20), we have
where are eigenvalues of . It means that , where are eigenvalues of the problem (1)–(3). From here, the existence of eigenvalues of the Problem A follows.
Theorem 2 is proved. □
4. Conclusions
In this work, we formulate correct boundary problem with integral transmitting condition for parabolic-hyperbolic type equation and proved strong solvability and the existence of eigenvalues for considered problem. Due to integral transmitting conditions, expressions obtained during evaluations have composite forms and we carefully used necessary actions on them in order to get required results. General idea of investigation tool is similar to previous works, cited in the paper, but one needs some modifications due to specific form of transmitting condition. This work shows that a transmitting condition has a specific role on solvability of considered problem. The same problem with different transmitting conditions will have different spectral properties (See []).
Author Contributions
Conceptualization, A.B. and A.C.; methodology, E.K.; validation, A.B., A.C. and E.K.; formal analysis, A.B., A.C. and E.K..; investigation, A.B., A.C. and E.K.; writing—original draft preparation, E.K.; writing—review and editing, A.B., A.C.; supervision, A.C.; project administration, A.B.; funding acquisition, A.B., A.C. All authors have read and agreed to the published version of the manuscript.
Funding
The research of the first author is supported by the grant of the Committee of Sciences, Ministry of Education and Science of the Republic of Kazakhstan to the Institute of Information and Computational Technologies, project AP05131026. Second author is supported by the Agencia Estatal de Investigación (AEI) of Spain under grant MTM2016-75140-P, co-financed by the European Community fund FEDER and by Xunta de Galicia, project ED431C 2019/02 (Spain).
Acknowledgments
The third author would like to thank “FracDiff” research group of the Sultan Qaboos University for hosting in SQU. The authors would like to thank the referees of the paper for their careful reviews.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Berdyshev, A.S.; Cabada, A.; Karimov, E.T.; Akhtaeva, N.S. On the Volterra property of a boundary problem with integral gluing condition for a mixed parabolic-hyperbolic equation. Bound. Value Probl. 2013, 2013, 94. [Google Scholar] [CrossRef]
- Struchina, G.M. A problem of pairing two equations. Injenerno Fiz. J. 1961, 11, 99–104. [Google Scholar]
- Ladizhenskaya, O.A.; Stupyalis, L. On mixed type equations. Vestnik LGU, seriya matematika, mexanika i astronomia 1965, 19, 38–46. [Google Scholar]
- Uflyand, Y.S. On the question of the distribution of fluctuations in composite electrical lines. Injenerno Fiz. J. 1964, 7, 89–92. [Google Scholar]
- Terlyga, O.; Bellout, H.; Bloom, F. A hyperbolic-parabolic system arising in pulse combustion: Existence of solutions for the linearized problem. Electron. J. Differ. Equ. 2013, 46, 1–42. [Google Scholar]
- Moiseev, E.I.; Kapustin, N.Y. On spectral problems with a spectral parameter in the boundary conditions. Differ. Uravn. (Minsk) 1997, 33, 115–119. Translation in Differ. Equ. 1997, 33, 116–120. (In Russian) [Google Scholar]
- Sadybekov, M.A.; Tojzhanova, G.D. Spectral properties of a class of parabolic-hyperbolic equations. Differ. Uravn. (Minsk) 1992, 28, 176–179. [Google Scholar]
- Akhtaeva, N.S.; Karimov, E.T. On a boundary problem with gluing conditions of integral form for mixed parabolic-hyperbolic equation with non-characteristic line of type changing. Vestnik KazNU Seriya Matem. Mexan. Inform 2013, 77, 64–77. [Google Scholar]
- Berdyshev, A.S. On the existence of eigenvalues of a boundary problem for parabolic-hyperbolic equation of the third order. Uzb. Math. J. 1998, 2, 19–25. [Google Scholar]
- Karimov, E.T. Non-local problems with special gluing condition for the parabolic-hyperbolic type equation with complex spectral parameter. Panam. Math. J. 2007, 17, 11–20. [Google Scholar]
- Ferreira, J. On weak solutions of semilinear hyperbolic-parabolic equations. Int. J. Math. Math. Sci. 1996, 19, 751–758. [Google Scholar] [CrossRef]
- Ashyralyev, A.; Yurtsever, A. On a nonlocal boundary value problem for semilinear hyperbolic-parabolic equations. Nonlinear Anal. 2001, 47, 3585–3592. [Google Scholar] [CrossRef]
- Esirkegenov, N.A.; Sadybekov, M.A. Spectral Properties of Boundary-Value Problem With a Shift for Wave Equation. Russ. Math. (Iz. VUZ) 2016, 60, 41–46. [Google Scholar] [CrossRef]
- Kornienko, D. Spectral Properties of the Cauchy Problem for Some Linear Systems of Partial Differential Equations. J. Comput. Theor. Nanosci. 2019, 16, 2780–2789. [Google Scholar] [CrossRef]
- Pavlenko, V.N.; Potapov, D.K. Properties of the spectrum of an elliptic boundary value problem with a parameter and a discontinuous nonlinearity. Sb. Math. 2019, 210, 1043–1066. [Google Scholar] [CrossRef]
- Laugesen, R.S. Spectral theory of partial differential equations. Contemp. Math. 2018, 720, 23–55. [Google Scholar]
- Ruzhansky, M.; Tokmagambetov, N.; Torebek, B. Inverse source problems for positive operators. I: Hypoelliptic diffusion and subdiffusion equations. J. Inverse Ill-Posed Probl. 2019, 27, 891–911. [Google Scholar] [CrossRef]
- Dzhuraev, T.D.; Sopuev, A.; Mamazhanov, M. Boundary Value Problems for Parabolic-Hyperbolic Type Equations; FAN: Tashkent, Uzbekistan, 1986. (In Russian) [Google Scholar]
- Tikhonov, A.N.; Samarskij, A.A. Equations of Mathematical Physics; Nauka: Moscow, Russia, 1966. (In Russian) [Google Scholar]
- Ladyzhenskaya, O.A.; Solonnikov, V.A.; Ural’tseva, N.N. Linear and Quasilinear Equations of Parabolic Type; Nauka: Moscow, Russia, 1967. (In Russian) [Google Scholar]
- Lidskii, V.B. Non-adjoint operators with traces. Doklady AN SSSR 1959, 125, 485–488. [Google Scholar]
- Brislawn, C. Kernels of trace class operators. Proc. Amer. Math. Soc. 1988, 104, 1181–1190. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).