From Grammar Inference to Semantic Inference—An Evolutionary Approach

Abstract

This paper describes a research work on Semantic Inference, which can be regarded as an extension of Grammar Inference. The main task of Grammar Inference is to induce a grammatical structure from a set of positive samples (programs), which can sometimes also be accompanied by a set of negative samples. Successfully applying Grammar Inference can result only in identifying the correct syntax of a language. With the Semantic Inference a further step is realised, namely, towards inducing language semantics. When syntax and semantics can be inferred, a complete compiler/interpreter can be generated solely from samples. In this work Evolutionary Computation was employed to explore and exploit the enormous search space that appears in Semantic Inference. For the purpose of this research work the tool LISA.SI has been developed on the top of the compiler/interpreter generator tool LISA. The first results are encouraging, since we were able to infer the semantics only from samples and their associated meanings for several simple languages, including the Robot language.

1. Introduction

Grammar Inference, also called Grammar Induction or Grammatical Inference, is the process of learning grammar from examples, either positive (i.e., the grammar generates a string) and/or negative (i.e., the grammar does not generate a string) [1,2]. Grammar Inference has been applied successfully to many diverse domains, such as Speech Recognition [3], Computational Biology [4,5], Robotics, and Software Engineering [6]. In our previous research we developed a memetic algorithm [7], called MAGIc (Memetic Algorithm, for Grammar Inference) [8,9,10], which is a population-based Evolutionary Algorithm enhanced with local search and a generalisation process, and used this to infer a wide range of Domain-Specific Language (DSL) grammars from programs in a variety of DSLs, including DSLs embedded in general purpose programming languages (GPLs) and extensions of GPLs. MAGIc can be improved further with enhanced local search with the information from a grammar repository (a collection of GPL and DSL grammars). However, this will only improve the syntax part of inferred DSL specifications. In this work, we concentrated on Semantic Inference, which is currently underdeveloped. Applications of Grammar Inference with semantics will go much beyond DSL grammar design (e.g., covering context sensitive grammars where context is given by static semantics). There are several key challenges and research questions to accomplish the above goals:

• Grammar Inference is able to infer only the syntactic structure, whilst, in many problems, there are additional restrictions on allowed structures [11,12] which can’t be described by Context-Free Grammars (CFGs). Hence, we also need to know the static semantics, or even the meaning of the structure (e.g., in the area of programming languages a program might be syntactically correct, but contains semantic errors such as undeclared identifiers). How can we extend Grammar Inference beyond discovering only the syntactic structure?
• The search space is enormous, even in the case for inferring regular and context-free languages [13], and it becomes substantially bigger for the context-sensitive languages (context-free languages with static semantics). How can we assure sufficient exploration and exploitation of the search space [14] for Semantic Inference? Note that the search space is too large for the exhaustive (brute-force) approach.

With Semantic Inference we will be able to infer DSL formal specifications from given sample programs annotated with a meaning that can be provided even by domain-experts. Hence, creating formal specifications of DSLs will be greatly simplified. Note that, from a formal specification, many other tools (editor, compiler, debugger, test engine) can be generated automatically [15]. With the fundamental work on Semantic Inference further advances on Grammar Inference would be possible, which may also have new applications in other areas of Computer Science (e.g., Spam Modelling, Bioinformatics, Speech Recognition, Protocol Security etc.), not only for easier development of DSLs for domain experts.

This paper is organised as follows—In Section 2, related work on Grammar Inference is reviewed briefly, as well as a few existing research works on Semantic Inference. Section 3 starts with necessary preliminaries about Attribute Grammars, a suitable formalism for describing language semantics, followed by suggested extensions of our previous work on Grammar Inference to support also Semantic Inference. In this Section, a description is also given of a newly developed tool called $LISA.SI$ (LISA with Semantic Inference). The extensive experimental part is given in Section 4, where Semantic inference are investigated on three languages: $a^n{b}^n{c}^n$, simple arithmetic expression, and the Robot language. Finally, the paper concludes in Section 5.

2. Related Work on Grammar Inference and Semantic Inference

2.1. Grammar Inference

The Grammar Inference process [1,2] can be stated as follows—Given a set of positive samples $S^{+}$ and set of negative samples $S^{-}$, which might also be empty, find at least one grammar G, such that $S^{+}\subseteq L\left(G\right)$ and $S^{-}\subseteq \overline{L\left(G\right)}$, where $L\left(G\right)$ and $\overline{L\left(G\right)}$ are the set of strings in and not in, respectively, the language generated by G ($L\left(G\right)$). Grammar Inference has been investigated now for more than 40 years, and has found applications in several research domains, such as Language Acquisition [16], Pattern Recognition [17], Computational Biology [4], and Software Engineering [6,8,10]. In language acquisition a child, being exposed only to positive samples, is able to discover the syntactic representation of the language (grammar). The aim of research on Grammar Inference is to provide different models on how language acquisition takes place [16]. Grammars have also been used as an efficient representation of artifacts that are inherently structural and/or recursive (e.g., neural networks, structured data and patterns) [18]. In pattern recognition, pattern grammars are used for pattern description and recognition [17]. Such a pattern grammar consists of primitives (e.g., circle, square, line), a set of predicates that describe the structural relationships among defined primitives (e.g., left, above, inside), and a set of productions, which describe the composition of the predicates and primitives. Given the set of patterns, the problem is to infer a pattern grammar that fits the given set of patterns. In Computational Biology Grammar Inference has been used for analysis of DNA, RNA, and protein sequences. For example, Grammar Inference has been applied successfully to predict secondary structures and functions of the biological molecules [4]. An early application of Grammar Inference in Software Engineering was programming language design [19], where an inference algorithm was proposed for a very restricted grammar, namely operator precedence grammar.

So far, Grammar Inference has been successful mainly in inferring regular languages. Researchers have developed various algorithms which can learn regular languages from positive and negative samples. A number of algorithms (e.g., RPNI [20]) first construct the finite automaton from positive samples, and generalise the automaton by using a state merging process. By merging states, an automaton is obtained that accepts a bigger set of strings, and generalises according to the increasing number of positive samples presented. CFG Inference is more difficult than regular Grammar Inference. Using structurally complete positive samples along with negative samples did not result in the same level of success as with regular Grammar Inference. Hence, some researchers resorted to using additional knowledge to assist in the inference process. Sakakibara [21] used a set of skeleton parse trees (unlabelled parse trees), where the input to the inference process is a sentence with parentheses inserted to indicate the shape of the parse tree. An enhancement to this algorithm was proposed in Reference [22], where CFG inference was possible from partially structured sentences. However, in many application domains it is impractical to assume that completely or partially structured samples exist.

Our previous research focused on various aspects (e.g., domain analysis, design, implementation) of DSLs [23,24]. In contrast with GPLs, where one can address large classes of problems (e.g., scientific computing, business processing, symbolic processing, etc.), a DSL facilitates the solution of problems in a particular domain (e.g., Aerospace, Automotive, Graphics, etc.). One of the open problems in DSL research stated in the survey paper on DSLs [23] is: “How can DSL design and implementation be made easier for domain experts not versed in GPL development?” Namely, domain experts are not versed in compilers and designing languages, but know how to express problems and their solutions in their domain of expertise. In other words, they know domain notations and abstractions, and can provide DSL programs. Here, Grammar Inference can find the underlying structure of the provided DSL programs. Hence, a DSL grammar can be constructed and a DSL parser generated [25]. On the other hand, the inferred grammar can be examined further by a Software Language Engineer to enhance the design of the language further. DSLs, also called little languages, are usually small and declarative. Therefore, it is more likely that the Grammar Inference process would be successful. In our previous work in inferring DSLs from examples, we developed a memetic algorithm, MAGIc, which improves the Grammar Inference process [10] and facilitates grammar learning. MAGIc may assist domain experts and Software Language Engineers in developing DSLs by producing a grammar which describes a set of sample DSL programs automatically [9]. We also researched the problem of embedding DSLs into GPLs, an approach that is often used to express domain-specific problems using the domain’s natural syntax inside GPL programs. In Reference [8], MAGIc is extended by embedding the inferred DSL into existing GPL grammar. Additionally, negative examples were also incorporated into the inference process. From the results it can be concluded that MAGIc is successful in DSL embedding, and that the inference process is improved with the use of negative examples. To give a glimpse of what kind of grammars is inferred successfully by MAGIc, we provide a small example (more realistic examples are presented in References [9,10]). From the positive samples of DESK language [26] shown on Listing 1, MAGIc inferred CFG grammar for DESK language correctly (shown on Listing 2).

Listing 1. Positive samples S⁺ of DESK language.

1. print a

2. print 23

3. print a + 23

4. print a + b + c

5. print a where a = 23

6. print 23 where b = 11

7. print 23 + c where c = 28

8. print 23 + 11 where c = 28

9. print a where a = 23; a = 28

10. print 28 where a = 23; b = 11

11. print 1 + 2 where b = 23; a = 5

12. print a + b + c where a = 1; b = 2; c = 3

Listing 1. Positive samples S⁺ of DESK language.

1. print a

2. print 23

3. print a + 23

4. print a + b + c

5. print a where a = 23

6. print 23 where b = 11

7. print 23 + c where c = 28

8. print 23 + 11 where c = 28

9. print a where a = 23; a = 28

10. print 28 where a = 23; b = 11

11. print 1 + 2 where b = 23; a = 5

12. print a + b + c where a = 1; b = 2; c = 3

Listing 2. Inferred DESK grammar.

N1 → print N3 N5

N2 → + N3 |  ε

N3 → num N2 | id N2

N4 → ; id = num N4 | ε

N5 → where id = num N4 | ε

Listing 2. Inferred DESK grammar.

N1 → print N3 N5

N2 → + N3 |  ε

N3 → num N2 | id N2

N4 → ; id = num N4 | ε

N5 → where id = num N4 | ε

Although all positive samples are syntactically correct, not all the aforementioned samples are semantically correct (e.g., undefined identifiers in samples 1, 3 and 4; double declaration of identifier in sample 9). Since, in our previous research work, we dealt only with the syntax, those context sensitive violations (e.g., undefined identifier, double declaration) were undetected. To support DSL development to the full extent the static semantics should be inferred as well. This is an objective of the current research work. It is important to notice that, although we did not address semantics in our previous research work, the results were still successful and encouraging. We were able to infer grammars which were much larger in size, and for DSLs in actual use. However, the syntax structure of GPLs is still too complex for current Grammar Inference algorithms to be successful. As mentioned before, MAGIc applies the Memetic Algorithm (MA) [7] to explore and exploit the search space efficiently. Furthermore, References [8,9,10] were also extended to Domain-Specific Modelling Languages (DSMLs) [27], which can be regarded as a special class of DSLs, and to graph grammar induction [28]. Distinguishing features of DSMLs are—Concrete syntax is often graphical, structures of phrases are often defined with metamodels instead of CFGs, and often used in an earlier software development phase (design phase instead of implementation phase). The MetAmodel Recovery System (MARS) [29] was extended to become scalable for larger metamodels, such as the ESML (Embedded Systems Modeling Language). This approach is called Metamodel Inference from Models (MIM) [30].

2.2. Semantic Inference

In the past, some other versions of Evolutionary Algorithms (EAs) [31] have been used to solve different optimisation problems where grammars have been employed as efficient encoding. For example, Grammatical Evolution (GE) [32] can be seen as a language independent Genetic Programming (GP) [33] approach that uses a predefined grammar to minimise the generation of syntactically invalid solutions. GE has been extended to Attribute Grammar Evolution (AGE) in Reference [34] and Christiansen Grammar Evolution (CGE) in Reference [35]. Note that, in all the aforementioned cases (GE, AGE, CGE), CFG, Attribute Grammar and Christiansen Grammar had been provided in advance, and were not the subject of learning, as is the case in this work.

We are aware of only a few research works [36,37,38,39,40] which manifest some application of Semantic Inference. They are explained briefly in the continuation. In Reference [36], communication systems’ workload models have been described with Attribute Grammars. Protocol data units and their interdependencies have been captured by inferred regular grammar, whilst characteristic workload parameters, such as packet length and timeouts, have been described with attributes and predefined semantic rules to compute attributes. The Lyrebird algorithm developed by Reference [37] uses Grammar Inference in combination with a templating technique for programming spoken dialogues. To enhance Speech Recognition Attribute Grammars have been used to attach meaning to phrases. The system starts from a simple description, and then learns from examples to improve the spoken dialogue interface. The Lyrebird algorithm is capable of inferring simple Attribute Grammars with only synthesised attributes with only copy rules. This work was extended in Reference [38] for inferring reversible Attribute Grammars from tagged natural language sentences. Hence, it is not only possible to attach meanings (attributes) to phrases, but also to generate phrases given meanings. Grammar Inference with semantics and its application to compilers of programming languages have been discussed in Reference [39], using the Synapse system for incremental learning of Definite Clause Grammars (DCG) and syntax directed translation schema (Attribute Grammars with synthesised attributes only). As an example, simple arithmetic expressions were translated into an intermediate language based on inverse Polish notation. A syntax-directed translation scheme was inferred from positive and negative samples to which the meanings were attached. The closest work to ours was recently published in Reference [40], where, instead of Attribute Grammars (AGs) [26,41] the Answer Set Grammars (ASGs) were used to express context-sensitive constraints, written as Answer Set Programming (ASP) annotations. The other difference is that, for learning ASGs, the authors of Reference [40] are using Inductive Logic Programming [42], whilst, in our work for learning AGs, we applied Evolutionary Computations [31]. With the proposed framework [40], the ASP part of ASG can be learned, which corresponds to learning semantic constraints. As in our case, the CFG is fixed, assuming that the syntax of the target language is known or can be inferred by Grammar Inference, but the semantic is unknown. The approach has been evaluated on simple languages, such as $a^n{b}^n{c}^n$. The authors concluded that “we are not aware of any work on learning Attribute Grammars, or learning semantic conditions on top of existing CFG.” In this respect, the presented work in this paper is novel.

Semantic Inference is also a hot topic in other fields, such as Natural Language Processing, Semantic Web, Image Processing, Mobile and Pervasive Computing, and Recommendation Systems for inferring semantically meaningful profiles [43], to name a few. In Natural Language Processing the aim of Semantics Inference is to interpret better abstract terms [44], for word sense disambiguation [45], to annotate semantic roles on bilingual or multilingual text, facilitating machine translation and cross-lingual information retrieval [46,47]. Resource Description Framework (RDF) is a standard model for knowledge representation in the Semantic Web, where Semantic inference is used to infer non-existing triples (subject, predicate, object) from existing triples [48,49]. Semantic Inference in Image Processing and Image Understanding is used for relationship detection among visual objects [50]. In Mobile and Pervasive Computing an indoor semantic inference is used to improve indoor location based services, such as indoor positioning and indoor tracking [51].

3. Semantic Inference with LISA

As stated earlier, MAGIc [8,9,10] has proven to be useful for inferring grammars from real DSL samples. However, MAGIc still has some problems inferring grammars, due to its inability to deal with context sensitive information (static semantics). This problem can’t be solved without dealing with the semantics. The first step is to extend the representation of individuals in MAGIc, which are currently only CFGs. Namely, the current population in MAGIc consists of CFGs which are evolved during evolution to such a CFG which parses all positive samples and rejects all negative samples. To include also the semantics, the individuals need to change from CFGs to Attribute Grammars (AGs) [26,41,52,53,54]. AGs are a generalisation of CFGs in which each symbol has an associated set of attributes that carry semantic information. Attribute values are defined by attribute evaluation rules associated with each production of the CFG. These rules specify how to compute the values of certain attribute occurrences as a function of other attribute occurrences. Semantic rules are localised to each CFG production. Formally, an $AG$ consists of three components, a Context-Free Grammar $CFG$, a set of attributes A, and set of semantic rules R: $AG=(CFG,A,R)$. A grammar $CFG=(T,N,S,P)$, where T and N are sets of terminal and non-terminal symbols; $S\in N$ is the start symbol, which appears only on the left-hand side of the first production rule; and P is a set of productions $(P=\{p_0,p_1,\dots ,p_z\},z>0)$ in which elements (also called grammar symbols) of set $V\in N\cup T$ appear in the form of pairs $X\to \alpha$ (the left-hand side of a production is X and the right-hand side is $\alpha$), where $X\in N$ and $\alpha \in V^{*}$. An empty right-hand side of a production is denoted by the symbol $\epsilon$. A set of attributes $A\left(X\right)$ is associated with each symbol $X\in N$. $A\left(X\right)$ is divided into two mutually disjointed subsets $I\left(X\right)$ of inherited attributes and $S\left(X\right)$ of synthesised attributes. Now $A=\cup A\left(X\right)$. A set of semantic rules R is defined within the scope of a single production. A production $p\in P$, $p:X_0\to X_1\dots X_n(n\ge 0)$ has an attribute occurrence $X_i.a$ if $a\in A\left(X_i\right)$, $0\le i\le n$. A finite set of semantic rules $R_p$ contains rules for computing values of attributes that occur in the production p, that is, it contains exactly one rule for each synthesised attribute $X_0.a$, and exactly one rule for each inherited attribute $X_i.a$, $1\le i\le n$. Thus, $R_p$ is a collection of rules of the form $X_i.a=f(y_1,\dots ,y_k)$, $k\ge 0$, where $y_j$, $1\le j\le k$, is an attribute occurrence in p, and f is a semantic function. In the rule $X_i.a=f(y_1,\dots ,y_k)$, the occurrence $X_i.a$ depends on each attribute occurrence $y_j$, $1\le j\le k$. Now set $R=\cup R_p$. For each production $p\in P$, $p:X_0\to X_1\dots X_n(n\ge 0)$ the set of defining attribute occurrences is $DefAttr\left(p\right)=\{X_i.a|X_i.a=f(...)\in Rp\}$. An attribute $X.a$ is called synthesised ($X.a\in S\left(X\right)$) if there exists a production $p:X\to X_1\dots X_n$ and $X.a\in DefAttr\left(p\right)$. It is called inherited ($X.a\in I\left(X\right)$) if there exists a production $q:Y\to X_1\dots X\dots X_n$ and $X.a\in DefAttr\left(q\right)$. The meaning of a program (values of the synthesised attributes of a starting non-terminal symbol) is defined during the attribute evaluation process, where the values of attribute occurrences are calculated for each node of an attributed tree of a particular program. For those who are less proficient in AGs let us present a small example. Listing 3 shows LISA specifications (Language Implementation System based on Attribute grammars) [55,56,57] for a simple language of $a^n{b}^n{c}^n$. Since CFGs are not capable of counting more than two things, the underlying CFG grammar is actually $a^i{b}^j{c}^k$ and the original language is obtained if $i=j=k$. In Listing 3, we can observe how language is defined with the LISA specifications. The lexical part is defined within a $lexicon$ block, whilst syntax and semantics are merged within a $rule$ block. For each CFG production semantics are provided by semantic equations specifying how attributes are computed. For the language $a^n{b}^n{c}^n$ semantic rules are quite simple, and we are actually counting occurrences of a’s, b’s and c’s. If there are the same numbers of a’s, b’s and c’s, the value of attribute $S.ok$ in the production $S::=ABC$ is set to $true$ (see Figure 1 and Figure 2). Note that, in LISA, there is no need to specify the kind of attributes, inherited or synthesised, since the kind of attributes is inferred from the provided equations. On the other hand, the types of attributes (e.g., int, boolean) must be provided. Since MAGIc already used LISA [55,56,57] it was also natural to use LISA in our current work. Previously, MAGIc was using only LISA’s parsing feature, whilst, in the current work, we are using the fully-fledged LISA semantic evaluator, which is able to evaluate absolutely non-circular AGs [26,41,52,53,54].

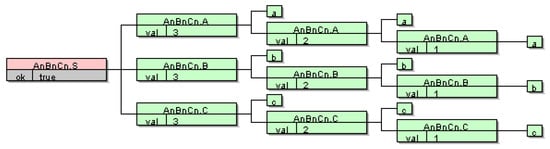
Figure 1. Computation of attributes for sentence “aaabbbccc”.

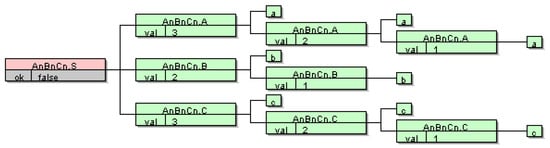
Figure 2. Computation of attributes for sentence “aaabbccc”.

Listing 3. LISA specifications for language aⁿbⁿcⁿ.

language AnBnCn {   lexicon {     TokenA a     TokenB b     TokenC c     ignore [\ \0x0D\0x0A\0x09]+   }   attributes int ∗.val; boolean ∗.ok;   rule S {     S ::= A B C compute {  // production P1       S.ok = (A.val == B.val) && (B.val == C.val);     };   }   rule A {     A ::= a A compute {  // production P2       A[0].val = 1 + A[1].val;     };     A ::= a compute {  // production P3       A.val = 1;     };   }   rule B {     B ::= b B compute {  // production P4       B[0].val = 1 + B[1].val;     };     B ::= b compute {  // production P5       B.val = 1;     };   }   rule C {     C ::= c C compute {  // production P6       C[0].val = 1 + C[1].val;     };     C ::= c compute {  // production P7       C.val = 1;     };   } }

Listing 3. LISA specifications for language aⁿbⁿcⁿ.

language AnBnCn {   lexicon {     TokenA a     TokenB b     TokenC c     ignore [\ \0x0D\0x0A\0x09]+   }   attributes int ∗.val; boolean ∗.ok;   rule S {     S ::= A B C compute {  // production P1       S.ok = (A.val == B.val) && (B.val == C.val);     };   }   rule A {     A ::= a A compute {  // production P2       A[0].val = 1 + A[1].val;     };     A ::= a compute {  // production P3       A.val = 1;     };   }   rule B {     B ::= b B compute {  // production P4       B[0].val = 1 + B[1].val;     };     B ::= b compute {  // production P5       B.val = 1;     };   }   rule C {     C ::= c C compute {  // production P6       C[0].val = 1 + C[1].val;     };     C ::= c compute {  // production P7       C.val = 1;     };   } }

In our previous work [13] we have shown that the search space of regular and context-free Grammar Inference is too large for the exhaustive (brute-force) approach. The same is true for Semantic Inference, where the following equations describe how enormous the search space is in the case of Semantic Inference. The search space can be calculated as the product of the total number of permutations ($SumP\left(\right)$) for each semantic equation. The number of semantic equations K depends on the number of synthesised and inherited attributes, which need to be defined in each CFG production [26,41,52,53,54]. Hence, the size of search space depends heavily on the number of semantic equations. The more semantic equations need to be found the bigger the search space is.

$$SearchSpace=\prod _{semanticEquation=1}^{K}SumP\left(maxDepth\right).$$

The total number of permutations ($SumP\left(\right)$) for a single semantic equation, where an expression represented as a binary tree of max depth ($maxDepth$) is then calculated as:

$$SumP\left(maxDepth\right)=\sum _{treeDepth=0}^{maxDepth}P\left(treeDepth\right)$$

where $P\left(treeDepth\right)$ denotes the number of all possible permutations of binary trees of depth $treeDepth$ with different operands and operators (assuming only binary operators), where internal nodes are operators and leaves are operands. Hence, the size of the search space also depends heavily on the number of different operands and operators. If a binary tree has depth $maxDepth$, then the minimum number of nodes is between $maxDepth+1$ (in the case of a left skewed and right skewed binary tree), and $2^{maxDepth+1}-1$ (in the case of a full binary tree). In the former case, the number of leaves is 1, in the latter case the number of leaves is the number of internal nodes plus 1. First, we calculate the maximum number of permutations at levels [0..$maxDepth$] of the expression tree, where $operands$ represent possible attribute occurrences in a particular production and constants, and $operators$ represent the various operations on attributes. In our experiments we generated simple semantic equations with a $maxDepth$ of no more than 2. In that case, $P\left(0\right)$, $P\left(1\right)$ and $P\left(2\right)$ can be calculated easily by the following equations:

$$P\left(0\right)=operands$$

$$P\left(1\right)=operand{s}^2\ast operators$$

$$P\left(2\right)=operand{s}^4\ast operator{s}^3+2\ast operand{s}^3\ast operator{s}^2.$$

Search space calculation for the $a^n{b}^n{c}^n$ language is demonstrated in Table 1. Even in this simple case there are more than 55 billion possible semantic equations. For example, in the first production $P1$ (Listing 3) three attributes ($A.val$, $B.val$, $C.val$) and constant 1, can act as operands, while three operators +, $\&\&$ and $==$ can be applied on operands. Therefore, there are 8116 (4+48+8064) different semantic equations for production $P1$. Similarly, in the second production $P2$ (Listing 3), only one attribute A[1].val and constant 1 can be used as operands, on which only operator + can be applied. Since operators $\&\&$ and $==$ return boolean value, the assignment statement for the attribute A[0].val in the production $P2$ would cause a type error. Hence, operators $\&\&$ and $==$ cannot be used in the semantic equation for production $P2$, and there are only 38 different semantic equations.

Table 1. Search space calculation for $a^n{b}^n{c}^n$ language when $maxDepth=2$.

Attribute	Operands	Operators	P(0)	P(1)	P(2)	SumP
P1:S.ok	4	3	4	48	8064	8116
P2:A.val	2	1	2	4	32	38
P3:A.val	1	1	1	1	3	5
P4:B.val	2	1	2	4	32	38
P5:B.val	1	1	1	1	3	5
P6:C.val	2	1	2	4	32	38
P7:C.val	1	1	1	1	3	5
SearchSpace						55.667.644.000

It is quite obvious that a need arose for a different and more efficient approach to explore the search space. Evolutionary Computation [31] is particularly suitable for these kinds of problems. Yet another evolutionary approach, Genetic Programming (GP), is proposed to solve the problem of Semantic Inference. Genetic programming [33] is a successful technique for getting computers to solve problems automatically. It has been used successfully in a wide variety of application domains, such as Data Mining, Image Classification and Robotic Control. GP has also been used previously for Grammar Inference [58,59,60]. Semantic rules attached to particular CFG productions in AGs for DSLs are small enough so that we can expect that a successful solution can be found using GP. In GP a program is constructed from the terminal set T and the user-defined function set F [33]. The set T contains variables and constants, and the set F contains functions that are a priori believed to be useful for the problem domain. In our case, set T consists of attributes and constants attached to nonterminal symbols, whilst set F consists of various functions/operators. Both sets, T and F, need to be provided by domain experts. Appropriate semantic rules can be evolved from these two sets. Note that, in addition to attributes which will be attached to nonterminal symbols, also the kind (synthesised or inherited) and type (e.g., int, boolean) of those attributes need to be provided by a domain expert. For example, the sets T and F for the language $a^n{b}^n{c}^n$ are defined as:

$$T=\{S.ok,A[0].val,B[0].val,C[0].val,A[1].val,B[1].val,C[1].val,1\}$$

$$F=\{+(int),\&\&(int),==(int\left)\right\}.$$

From such an input, the number of semantic rules which are attached to CFG production rules can be computed (one semantic rule for each synthesised attribute attached to a nonterminal symbol on the left-hand side, and one semantic rule for each inherited attribute attached to nonterminal symbols on the right-hand side of CFG production [26,41,52,53,54]). Hence, it is necessary to infer only expressions in assignment statements, and, for this task, GP seems to be a feasible approach. A complete Attribute Grammar for a language can be generated in such a manner.

For the purpose of this research, a tool, $LISA.SI$ (LISA with Semantic Inference), was developed, that implements GP and attempts to find appropriate semantic equations for the productions of the given grammar. It was developed using the C++ programming language, C++ Builder 10.3 IDE and VCL (Visual Component Library) framework. As shown in Figure 3, the first step is to load the input data (grammar productions, attributes, operators and functions). Due to its size and complexity, the input data are loaded from a manually prepared XML document. Subsequently, our tool determines the defining attributes ($DefAttr\left(p\right)$) of each production p (attributes for which semantic equations must be generated), and a set of values that can be used to generate a semantic equation for each of the defining attributes. Semantic equations are generated as expressions formed from an expression tree with limited (predefined) depth $maxDepth$.

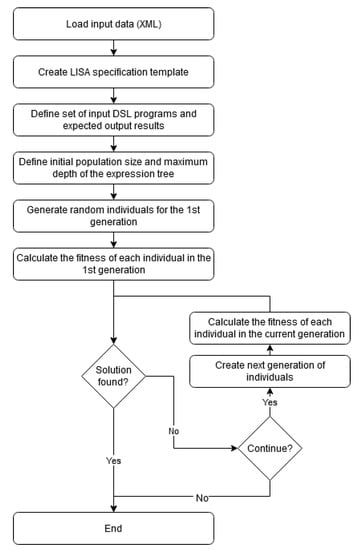
Figure 3. Application flow diagram.

We used the LISA compiler-compiler tool [55,56,57] to calculate the fitness value of individuals in the population. First, we defined an Attribute Grammar-based language specification template. Based on this template, our tool generated LISA specifications containing grammar productions with candidate semantic equations automatically. To calculate the fitness value of an individual, we provided N input DSL programs with N output results. The fitness value is then represented as a ratio between the correct and maximum number of output results (e.g., 4/6). It should be noted that a higher fitness value indicates a better individual. The LISA compiler-compiler tool was used as an external Java application that loaded inputs (LISA specification, input DSL programs and expected results) using command line arguments, and output the results (fitness value) into a text file.

The time required to calculate the fitness value depends largely on the LISA specification, that is, the number of attributes that must be computed. On a Windows 10 desktop machine with a 3.4 GHz AMD Ryzen™ Threadripper 1950X processor (16-core/32-thread), 64 GB RAM and solid-state drive, it takes approximately 5.1 s to calculate the fitness value for one LISA $a^n{b}^n{c}^n$ language specification. Due to the large search space, it was crucial to improve the performance by implementing a multi-threaded fitness calculation and a hash table (Figure 4). On the same desktop machine, but now utilising all 32 threads, we could calculate the fitness values of 112 individuals in 60 s (1.87 LISA specifications per second), which was a 957% performance improvement over a single-threaded approach. In addition, performance was improved by using a hash table. After the fitness value of an individual is calculated, its hash and fitness value are stored, and reused when dealing with the same individual again [61].

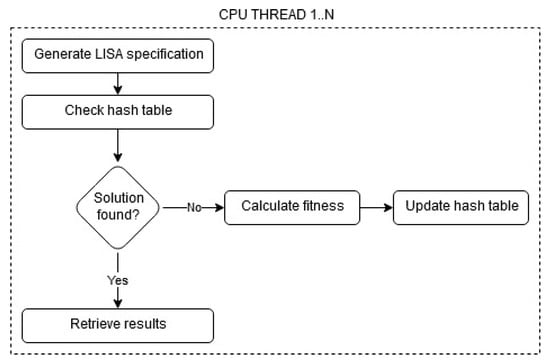
Figure 4. Multi-threaded fitness calculation.

The initial population consists of random individuals. If the solution is not found in the initial population, we define the elitism (percentage of the best individuals that will automatically move on to the next generation), selection pressure (percentage of the best individuals whose genes can be used in crossover) and mutation probability parameters, to generate the next generation [31]. Two random parents are selected when creating a new individual. Based on their fitness values and mutation probability, the crossover operator can decide that a new individual will inherit a gene from one parent or the other, or if a mutation will occur. To calculate the probability of these events the following equations are used.

parentFitnessRatio = (parentFitness + 1) / maxFitness ∗ 100;

If the fitness ratio of both parents is 0 (corner case) the probability to inherit a gene from one of the parents is

parentProbability = 50 - mutationProbability / 2;

otherwise, the probability is calculated as

parent1Probability = (parent1FitnessRatio ∗ (100 - mutationProbability)) /        (parent1FitnessRatio + parent2FitnessRatio);

parent2Probability = (parent2FitnessRatio ∗ (100 - mutationProbability)) /        (parent1FitnessRatio + parent2FitnessRatio);

For example, when having parents P1 (fitness: $1/5$) and P2 (fitness: $2/5$) with mutation probability of $10\%$, there is a $36\%$ chance that the child will inherit a gene from parent P1 and $54\%$ chance to inherit a gene from parent P2.

After setting all the necessary parameters, our tool $LISA.SI$ is capable of seeking for a solution constantly, and stops only at the user’s intervention or when a solution is found. The tool $LISA.SI$ shows the progress of the evolutionary process by displaying maximum fitness per generation (Figure 5), fitness distribution per generation, and by displaying the content of the hash table. These features help a researcher to understand the processes of Evolutionary Computation better, to identify common problems (e.g., local maxima), and to understand the effects of different control parameter setting (e.g., population size, number of generations, elitism, selection pressure, mutation probability) [62,63].

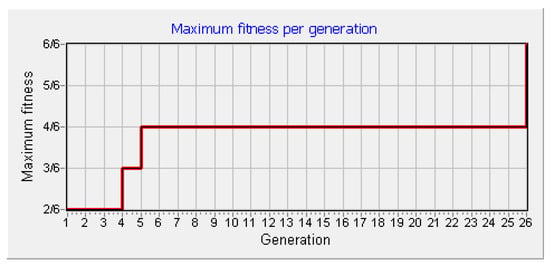
Figure 5. Maximum fitness per generation.

4. Experiments

In the experimental part we tested our approach on three examples—Language $a^n{b}^n{c}^n$, simple arithmetic expression with operator +, and the Robot language [64]. As noted in Reference [40], learning of AGs is non-existent and no common benchmarks exist. For this reason, it is our future intent to provide a suitable benchmark that can be used by other researchers for Semantic Inference.

4.1. Example 1

In References [39,40], the language $a^n{b}^n{c}^n$ was used in the experiments. The input language was a CFG representing $a^i{b}^j{c}^k$ and the task was to learn that $i=j=k$. Therefore, we tested our approach on this example as well. Note that, in this example, only synthesised attributes can be used, and AG is going to be S-attributed AG [26,41], where semantic evaluation can be computed during top-down or bottom-up parsing [65].

Control parameter setting:

T = {S.ok, A[0].val, B[0].val, C[0].val, A[1].val, B[1].val, C[1].val, 1}

F = {+(int), ==(int), &&(int)}

Max tree depth: 2

Population size: 2500

Elitism: 20%

Selection pressure: 50%

Mutation probability: 10%

From the number of CFG productions, sets T and F, and $maxDepth$, the search space can be computed (see Section 3). There are 55,667,644,000 possible AGs. From the following input statements and their meanings (a meaning is stored in the synthesised attributes of the starting nonterminal; in this case, it is attribute $ok$), our tool found in the 9th generation the AG (Listing 4), which assigned meanings correctly to the following input statements:

(abc, ok=true)

(aabbcc, ok=true)

(aaabbbccc, ok=true)

(aaaabbbbcccc, ok=true)

(abbcc, ok=false)

(aabcc, ok=false)

(aabbc, ok=false)

(aabbbccc, ok=false)

(aaabbccc, ok=false)

(aaabbbcc, ok=false)

(abbccc, ok=false)

Listing 4. Inferred AG for language aⁿbⁿcⁿ.

language AnBnCn {   lexicon {     TokenA a     TokenB b     TokenC c     ignore [\ \0x0D\0x0A\0x09]+   }   attributes int *.val; boolean *.ok;   rule S {     S ::= A B C compute {       S.ok = A.val==(B.val+C.val);     };   }   rule A {     A ::= a A compute {      A[0].val = 1+(1+A[1].val);     };     A ::= a compute {       A.val = 1+1;     };   }   rule B {     B ::= b B compute {      B[0].val = B[1].val+1;     };     B ::= b compute {       B.val = 1;     };   }   rule C {     C ::= c C compute {      C[0].val = 1+C[1].val;     };     C ::= c compute {       C.val = 1;     };   } }

Listing 4. Inferred AG for language aⁿbⁿcⁿ.

language AnBnCn {   lexicon {     TokenA a     TokenB b     TokenC c     ignore [\ \0x0D\0x0A\0x09]+   }   attributes int *.val; boolean *.ok;   rule S {     S ::= A B C compute {       S.ok = A.val==(B.val+C.val);     };   }   rule A {     A ::= a A compute {      A[0].val = 1+(1+A[1].val);     };     A ::= a compute {       A.val = 1+1;     };   }   rule B {     B ::= b B compute {      B[0].val = B[1].val+1;     };     B ::= b compute {       B.val = 1;     };   }   rule C {     C ::= c C compute {      C[0].val = 1+C[1].val;     };     C ::= c compute {       C.val = 1;     };   } }

If we compare LISA specifications for the language $a^n{b}^n{c}^n$ from Section 3 and inferred LISA specifications in the 9th generation, we can notice several differences. First, attribute $S.ok$ is evaluated to true when $A.val$ is equal to $B.val+C.val$. Hence, the counting of a’s must be steeper than for b’ and c’s. Indeed, when only one a is recognised, the counter $A.val$ is set to 2. But, in the same basic step, the counters for $B.val$ and $C.val$ are set to 1. In this basic step, indeed $A.val$ is equal to $B.val+C.val$. In the recursive step $A::=aA$, the counter $A\left[0\right].val$ is incremented by 2, whilst, in the recursive steps, the counters $B\left[0\right].val$ and $C\left[0\right].val$ are incremented by 1. Again, in the recursive steps $A.val$ is equal to $B.val+C.val$. This equation is true only if there is the same number of a’s, b’s and c’s. Note that, in the specified input, we just specify when the input statement belongs to the language $a^n{b}^n{c}^n$. When additional semantics (to compute n and store it into attribute $val$) are provided as input:

(abc, ok=true, val=1)

(aabbcc, ok=true, val=2)

(aaabbbccc, ok=true, val=3)

(aaaabbbbcccc, ok=true, val=4)

(abbcc, ok=false, val=1)

(aabcc, ok=false, val=2)

(aabbc, ok=false, val=2)

(aabbbccc, ok=false, val=2)

(aaabbccc, ok=false, val=3)

(aaabbbcc, ok=false, val=3)

(abbccc, ok=false, val=1)

the following AG was found in the 15th generation (Listing 5). While this inferred AG is closer to the AG from Section 3, there are still some important differences. Besides the semantic equation $S.val=A.val$, which is added to the first production and computes the number n in $a^n{b}^n{c}^n$, there are the following differences: Attribute $S.ok$ is computed as $(S.val+B.val)==(1+C.val)$, which is the same as $(A.val+B.val)==(1+C.val)$, since $S.val=A.val$. This equation indicates that the sum of attributes $A.val$ and $B.val$ is equal to $C.val+1$. By incrementing $A.val$ and $B.val$ by 1 on each occurrence of a’s and b’s, it is the same as incrementing by two for $C.val$. This is true for recursive case $C::=cC$. In the base case $A.val$, $B.val$, and $C.val$ are set to 1. Hence, at the end, we need to add 1 to $C.val$ and equation $(A.val+B.val)==(1+C.val)$ holds whenever there is the same amount of a’s, b’s, and c’s.

Listing 5. 2^nd inferred AG for language aⁿbⁿcⁿ.

language AnBnCn {   lexicon {     TokenA a     TokenB b     TokenC c     ignore [\ \0x0D\0x0A\0x09]+   }   attributes int ∗.val; boolean ∗.ok;   rule S {     S ::= A B C compute {       S.ok = (S.val+B.val)==(1+C.val);       S.val = A.val;     };   }   rule A {     A ::= a A compute {      A[0].val = A[1].val+1;     };     A ::= a compute {       A.val = 1;     };   }   rule B {     B ::= b B compute {      B[0].val = B[1].val+1;     };     B ::= b compute {       B.val = 1;     };   }   rule C {     C ::= c C compute {      C[0].val = 1+(C[1].val+1);     };     C ::= c compute {       C.val = 1;     };   } }

Listing 5. 2^nd inferred AG for language aⁿbⁿcⁿ.

language AnBnCn {   lexicon {     TokenA a     TokenB b     TokenC c     ignore [\ \0x0D\0x0A\0x09]+   }   attributes int ∗.val; boolean ∗.ok;   rule S {     S ::= A B C compute {       S.ok = (S.val+B.val)==(1+C.val);       S.val = A.val;     };   }   rule A {     A ::= a A compute {      A[0].val = A[1].val+1;     };     A ::= a compute {       A.val = 1;     };   }   rule B {     B ::= b B compute {      B[0].val = B[1].val+1;     };     B ::= b compute {       B.val = 1;     };   }   rule C {     C ::= c C compute {      C[0].val = 1+(C[1].val+1);     };     C ::= c compute {       C.val = 1;     };   } }

For the language $a^n{b}^n{c}^n$ the used input CFG was also $a^n{b}^n{c}^m$, and the task was to learn that $n=m$ [40]. This is a somehow easier problem, and our approach found the solution presented in Listing 6 in the 3rd generation (note that, again, computing n was not part of semantics, only the same number of a’s, b’s and c’s). In this inferred AG attribute $S.ok$ is computed as $S.ok=(AB.val+AB.val)==(C.val+AB.val)$. After simplification this is the same as $S.ok=(AB.val==C.val)$. GP often generates a code which is redundant, but semantically identical [33]. This was also true for our experiments.

Listing 6. 3rd inferred AG for language aⁿbⁿcⁿ.

language AnBnCn {   lexicon {     TokenA a     TokenB b     TokenC c     ignore [\ \0x0D\0x0A\0x09]+   }   attributes int ∗.val; boolean ∗.ok;   rule S {     S ::= AB C compute {       S.ok = (AB.val+AB.val)==(C.val+AB.val);     };   }   rule AB {     AB ::= a AB b compute {      AB[0].val = AB[1].val+1;     };     AB ::= a b compute {       AB.val = 1;     };   }   rule C {     C ::= c C compute {      C[0].val = C[1].val+1;     };     C ::= c compute {       C.val = 1;     };   } }

Listing 6. 3rd inferred AG for language aⁿbⁿcⁿ.

language AnBnCn {   lexicon {     TokenA a     TokenB b     TokenC c     ignore [\ \0x0D\0x0A\0x09]+   }   attributes int ∗.val; boolean ∗.ok;   rule S {     S ::= AB C compute {       S.ok = (AB.val+AB.val)==(C.val+AB.val);     };   }   rule AB {     AB ::= a AB b compute {      AB[0].val = AB[1].val+1;     };     AB ::= a b compute {       AB.val = 1;     };   }   rule C {     C ::= c C compute {      C[0].val = C[1].val+1;     };     C ::= c compute {       C.val = 1;     };   } }

4.2. Example 2

Our second example is the language of simple arithmetic expression with the operator +, where the underlying grammar is LL(1) [65] and, as such, suitable for top-down parsing. On the other hand, such a grammar requires inherited attributes. In our previous example, only synthesised attributes were used for the language $a^n{b}^n{c}^n$. With this example we demonstrated that our approach is able to learn AGs with inherited attributes. The inferred grammar is L-attributed AG [26,41], where synthesised and inherited attributes can still be evaluated during parsing using left-to-right traversal [65].

Control parameter setting:

T = {E.val, T.val, EE[0].val, EE[0].inVal, EE[1].val, EE[1].inVal, #Int.value()}

F = {+(int), int Integer.valueOf(String).intValue()}

Max tree depth: 1

Population size: 1000

Elitism: 20%

Selection pressure: 50%

Mutation probability: 10%

From the number of CFG productions, sets T and F, and $maxDepth$, the search space can be computed (see Section 3). There are 230,400 possible AGs. Input statements with associated semantics were:

(5, val=5)

(2+5, val=7)

(10+5+8, val=23)

The following correct solution was found in the 3rd generation (Listing 7):

Listing 7. Inferred AG for simple arithmetic expression.

language SimpleArithmeticExpression {   lexicon {     Operator \+     Int [0-9]+     ignore [\ \0x0D\0x0A\0x09]+   }   attributes int ∗.val, ∗.inVal;   rule Expr {     E ::= T EE compute {       E.val = EE.val;       EE.inVal = T.val;     };     EE ::= + T EE compute {       EE[0].val = EE[0].inVal+EE[1].val;       EE[1].inVal = T.val;     };     EE ::= epsilon compute {       EE.val = EE.inVal;     };   }   rule Term {     T ::= #Int compute {       T.val = Integer.valueOf(#Int.value()).intValue();     };   } }

Listing 7. Inferred AG for simple arithmetic expression.

language SimpleArithmeticExpression {   lexicon {     Operator \+     Int [0-9]+     ignore [\ \0x0D\0x0A\0x09]+   }   attributes int ∗.val, ∗.inVal;   rule Expr {     E ::= T EE compute {       E.val = EE.val;       EE.inVal = T.val;     };     EE ::= + T EE compute {       EE[0].val = EE[0].inVal+EE[1].val;       EE[1].inVal = T.val;     };     EE ::= epsilon compute {       EE.val = EE.inVal;     };   }   rule Term {     T ::= #Int compute {       T.val = Integer.valueOf(#Int.value()).intValue();     };   } }

Although this example is simple, the inferred AG contains synthesised, as well as inherited, attributes. The latter attributes were not included in the existing Semantic Inference algorithms [37,38,39]. We are strongly convinced that both kinds of attributes are needed in inferring semantics of DSLs, as well as for checking context sensitiveness in grammar.

4.3. Example 3

Our last example is the Robot language for simple movement of a robot in four directions [64] (Listing 8). The meaning of the Robot program is the final position of robot movements, whilst the starting position of the robot is $(0,0)$. Although this is an L-attributed AG [26], it has the largest search space ($5.22214E+36$ possible AGs).

An example for the Robot language, begin right up up end, is shown in Figure 6. The current position of the robot is adjusted with four commands: left (decrease the x coordinate by 1), right (increase the x coordinate by 1), down (decrease the y coordinate by 1) and up (increase the y coordinate by 1). After executing the first command right, the robot moved to the position (1,0) (inx=0, iny=0, outx=1, outy=0 on Figure 6). Similarly, after executing the next command up, the robot moved to the position (1,1) (inx=1, iny=0, outx=1, outy=1 in Figure 6). Finally, the robot stopped at position (1, 2) (see Figure 6).

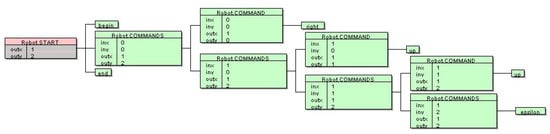
Figure 6. Example of Robot language.

Listing 8. AG for the Robot language.

language Robot {     lexicon {         keywords  begin | end         operation left | right | up | down            ignore [\0x0D\0x0A\ ]     }     attributes int ∗.inx; int ∗.iny;                int ∗.outx; int ∗.outy;     rule start {           START ::= begin COMMANDS end compute {            START.outx = COMMANDS.outx;            START.outy = COMMANDS.outy;            COMMANDS.inx = 0;            COMMANDS.iny = 0;         };     }     rule commands {           COMMANDS ::= COMMAND COMMANDS compute {            COMMANDS.outx = COMMANDS[1].outx;            COMMANDS.outy = COMMANDS[1].outy;            COMMAND.inx = COMMANDS.inx;            COMMAND.iny = COMMANDS.iny;            COMMANDS[1].inx = COMMAND.outx;            COMMANDS[1].iny = COMMAND.outy;         }       | epsilon compute {            COMMANDS.outx = COMMANDS.inx;            COMMANDS.outy = COMMANDS.iny;         };     }     rule command {           COMMAND ::= left compute {            COMMAND.outx = COMMAND.inx - 1;            COMMAND.outy = COMMAND.iny;         };           COMMAND ::= right compute {            COMMAND.outx = COMMAND.inx + 1;            COMMAND.outy = COMMAND.iny;         };           COMMAND ::= up compute {            COMMAND.outx = COMMAND.inx;            COMMAND.outy = COMMAND.iny + 1;         };           COMMAND ::= down compute {            COMMAND.outx = COMMAND.inx;            COMMAND.outy = COMMAND.iny - 1;         };    } }

Listing 8. AG for the Robot language.

language Robot {     lexicon {         keywords  begin | end         operation left | right | up | down            ignore [\0x0D\0x0A\ ]     }     attributes int ∗.inx; int ∗.iny;                int ∗.outx; int ∗.outy;     rule start {           START ::= begin COMMANDS end compute {            START.outx = COMMANDS.outx;            START.outy = COMMANDS.outy;            COMMANDS.inx = 0;            COMMANDS.iny = 0;         };     }     rule commands {           COMMANDS ::= COMMAND COMMANDS compute {            COMMANDS.outx = COMMANDS[1].outx;            COMMANDS.outy = COMMANDS[1].outy;            COMMAND.inx = COMMANDS.inx;            COMMAND.iny = COMMANDS.iny;            COMMANDS[1].inx = COMMAND.outx;            COMMANDS[1].iny = COMMAND.outy;         }       | epsilon compute {            COMMANDS.outx = COMMANDS.inx;            COMMANDS.outy = COMMANDS.iny;         };     }     rule command {           COMMAND ::= left compute {            COMMAND.outx = COMMAND.inx - 1;            COMMAND.outy = COMMAND.iny;         };           COMMAND ::= right compute {            COMMAND.outx = COMMAND.inx + 1;            COMMAND.outy = COMMAND.iny;         };           COMMAND ::= up compute {            COMMAND.outx = COMMAND.inx;            COMMAND.outy = COMMAND.iny + 1;         };           COMMAND ::= down compute {            COMMAND.outx = COMMAND.inx;            COMMAND.outy = COMMAND.iny - 1;         };    } }

Control parameter setting:

T = {START.outx, START.outy, COMMANDS.outx, COMMANDS.outy, COMMANDS.inx,              COMMANDS.iny, COMMAND.outx, COMMAND.outy, COMMAND.inx,              COMMAND.iny,COMMANDS[1].outx, COMMANDS[1].outy, COMMANDS[1].inx,              COMMANDS[1].iny, 0, 1}

F = {+(int), -(int)}

Max tree depth: 1

Population size: 2000

Elitism: 20%

Selection pressure: 50%

Mutation probability: 10%

Input statements with associated semantics were:

(begin end, outx=0, outy=0)

(begin down end, outx=0, outy=-1)

(begin up end, outx=0, outy=1)

(begin left end, outx=-1, outy=0)

(begin right end, outx=1, outy=0)

(begin left left left end, outx=-3, outy=0)

(begin up left up end, outx=-1, outy=2)

(begin left down up right up up end, outx=0, outy=2)

(begin up left up end, outx=-1, outy=2)

(begin right down right up down end, outx=2, outy=-1)

(begin right down down up end, outx=1, outy=-1)

(begin left down left up end, outx=-2, outy=0)

The following interesting and unusual, but correct, solution was found in the 59th generation (Listing 9):

Listing 9. Inferred AG for the Robot language.

language Robot {     lexicon {         Command      left | right | up | down         ReservedWord begin | end         ignore       [\0x0D\0x0A\ ]     }       attributes int ∗.inx; int ∗.iny;                int ∗.outx; int ∗.outy;       rule start {         START ::= begin COMMANDS end compute {           // exchanging x and y coordinates           START.outx = COMMANDS.outy;           // simplified to COMMANDS.outx and exchanging x and y coordinates           START.outy = COMMANDS.iny+COMMANDS.outx;           COMMANDS.inx=0;  // predefined starting position           COMMANDS.iny=0;  // predefined starting position         };       }       rule commands {         COMMANDS ::= COMMAND COMMANDS compute {           // summing x-coordinates           COMMANDS.outx = COMMANDS[1].outx+COMMAND.outx;           // subtracting y-coordinates           COMMANDS.outy = COMMANDS[1].outy-COMMAND.outy;           // position is not propagated and always set to 0           COMMAND.inx = 0;           // position is not propagated and always set to 0           COMMAND.iny = 0;           // simplified to 0           COMMANDS[1].inx = 0+COMMANDS[1].outy;           // simplified to 0           COMMANDS[1].iny = COMMAND.iny;         }         | epsilon compute {             // simplified to 0             COMMANDS.outx = COMMANDS.iny-COMMANDS.outy;             COMMANDS.outy = 0;         };     }       rule command {         // note that COMMAND.iny and COMMAND.inx are 0         COMMAND ::= left compute {           // simplified to 0           COMMAND.outx = COMMAND.iny-0;           // increasing y, which will be moved to x in starting production           COMMAND.outy = 1+0;         };         COMMAND ::= right compute {           // simplified to 0           COMMAND.outx = COMMAND.inx-COMMAND.iny;           // decreasing y, which will be moved to x in starting production           COMMAND.outy = 0-1;         };         COMMAND ::= up compute {           // increasing x, which will be moved to y in starting production           COMMAND.outx = 1;           COMMAND.outy = 0+0;         };         COMMAND ::= down compute {           // decreasing x, which will be moved to y in starting production           COMMAND.outx = 0-1;           // simplified to 0           COMMAND.outy = COMMAND.iny;         };    } }

Listing 9. Inferred AG for the Robot language.

language Robot {     lexicon {         Command      left | right | up | down         ReservedWord begin | end         ignore       [\0x0D\0x0A\ ]     }       attributes int ∗.inx; int ∗.iny;                int ∗.outx; int ∗.outy;       rule start {         START ::= begin COMMANDS end compute {           // exchanging x and y coordinates           START.outx = COMMANDS.outy;           // simplified to COMMANDS.outx and exchanging x and y coordinates           START.outy = COMMANDS.iny+COMMANDS.outx;           COMMANDS.inx=0;  // predefined starting position           COMMANDS.iny=0;  // predefined starting position         };       }       rule commands {         COMMANDS ::= COMMAND COMMANDS compute {           // summing x-coordinates           COMMANDS.outx = COMMANDS[1].outx+COMMAND.outx;           // subtracting y-coordinates           COMMANDS.outy = COMMANDS[1].outy-COMMAND.outy;           // position is not propagated and always set to 0           COMMAND.inx = 0;           // position is not propagated and always set to 0           COMMAND.iny = 0;           // simplified to 0           COMMANDS[1].inx = 0+COMMANDS[1].outy;           // simplified to 0           COMMANDS[1].iny = COMMAND.iny;         }         | epsilon compute {             // simplified to 0             COMMANDS.outx = COMMANDS.iny-COMMANDS.outy;             COMMANDS.outy = 0;         };     }       rule command {         // note that COMMAND.iny and COMMAND.inx are 0         COMMAND ::= left compute {           // simplified to 0           COMMAND.outx = COMMAND.iny-0;           // increasing y, which will be moved to x in starting production           COMMAND.outy = 1+0;         };         COMMAND ::= right compute {           // simplified to 0           COMMAND.outx = COMMAND.inx-COMMAND.iny;           // decreasing y, which will be moved to x in starting production           COMMAND.outy = 0-1;         };         COMMAND ::= up compute {           // increasing x, which will be moved to y in starting production           COMMAND.outx = 1;           COMMAND.outy = 0+0;         };         COMMAND ::= down compute {           // decreasing x, which will be moved to y in starting production           COMMAND.outx = 0-1;           // simplified to 0           COMMAND.outy = COMMAND.iny;         };    } }

Some examples are illustrated with semantic trees (see Figure 7 and Figure 8):

Figure 7. Robot language example 1.

Figure 8. Robot language example 2.

5. Conclusions

In this paper, we described Semantic Inference as an extension of Grammar Inference. To achieve this goal, the representation of a solution needs to be extended from Context-Free Grammars to Attribute Grammars. To solve the problem of Semantic Inference successfully a Genetic Programming approach was employed, which is a population based evolutionary search. The first results were encouraging, and we were able to infer S-attributed and L-attributed Attribute Grammars [26,41,52,53,54]. The main contributions of this work are:

• Few previous approaches were able to learn Attribute Grammars with synthesised attributes only. This limitation has been overcome in this paper, and we were able to learn Attribute Grammars with synthesised and inherited attributes. Consequently, few previous approaches inferred only S-attributed Attribute Grammars, whilst our approach inferred also L-attributed Attribute Grammars.
• The search space of all possible semantic equations is enormous and quantified in Section 3.
• We have shown that Genetic Programming can be used effectively to explore and exploit the search space solving the problem of Semantic Inference successfully.
• The tool $LISA.SI$ has been developed on the top of the compiler/interpreter generator tool LISA [55,56,57], which performed Semantic Inference seamlessly.

The proposed approach can be used for designing and implementing DSLs by giving the syntax and semantics in the form of samples and associated meanings. Furthermore, applications of Grammar Inference with semantics will be greatly extended, and might become useful in numerous other applications (e.g., spam filtering [66], intrusion detection [67,68], to facilitate communicative contexts for beginning communicators [69]). Many applications of Semantics Inference can hardly be anticipated at this moment.

Although we have inferred semantics successfully in the form of Attribute Grammars for several simple languages (e.g., Robot Language), our work will be continued and heading towards different directions. Firstly, we would like to solve more difficult examples, where dependency relations among synthesised and inherited attributes are more complex and required to infer absolutely non-circular Attribute Grammars. To achieve this goal, we anticipated developing sophisticated local searches. Secondly, we would like to build a benchmark of problems suitable for others working in the field of Semantic Inference. Namely, standard benchmarks for Semantic Inference are not currently available. Thirdly, we will investigate the influence of different control parameter settings (e.g., population size, probability of mutation, selection pressure), as well as inputs (e.g., number of input statements) towards the successfulness of evolutionary search. Fourthly, we would like to apply Semantic Inference not only to DSL development, but also for spam filtering and intrusion detection [67,68].