Stochastic Memristive Quaternion-Valued Neural Networks with Time Delays: An Analysis on Mean Square Exponential Input-to-State Stability

Abstract

In this paper, we study the mean-square exponential input-to-state stability (exp-ISS) problem for a new class of neural network (NN) models, i.e., continuous-time stochastic memristive quaternion-valued neural networks (SMQVNNs) with time delays. Firstly, in order to overcome the difficulties posed by non-commutative quaternion multiplication, we decompose the original SMQVNNs into four real-valued models. Secondly, by constructing suitable Lyapunov functional and applying It $\widehat{o}$’s formula, Dynkin’s formula as well as inequity techniques, we prove that the considered system model is mean-square exp-ISS. In comparison with the conventional research on stability, we derive a new mean-square exp-ISS criterion for SMQVNNs. The results obtained in this paper are the general case of previously known results in complex and real fields. Finally, a numerical example has been provided to show the effectiveness of the obtained theoretical results.

1. Introduction

In 1971, Chua proposed the theoretical idea of memristor [1], and its prototype was produced by the HP lab successfully in 2008 [2,3]. A memristor is the fourth fundamental element of an electrical circuit that can be used to construct a new artificial neural network. It has a tremendous potential to be utilized in synapsis for simulation of the human brain by replacing a resistor with a memristor [4,5,6]. In view of these characteristics, a new neural network (NN) model, namely, the memristive neural network (MNN) has been widely studied, and many theoretical papers regarding various dynamics of MNNs have been published in recent years [7,8,9,10,11,12,13]. From the real-world application perspective, time delays inherently arise in many practical systems including NNs. Indeed, time delays appear as the main cause of instability, compromising the system performance in real environments [10,14,15,16,17,18]. Typically, two main types of time delays exist, i.e., either constant delays or time-varying delays. The time-varying delays can be viewed as a general case of constant time delays. Up to now, a number of investigations with respect to the dynamics of NN models along with time-varying delays are available in the literature [10,15,16,17,18,19,20,21].

It has been reported that real-valued neural networks (RVNNs) are useful in various scientific fields, for example, optimization, image and signal processing, as well as associative memory [10,16,17]. However, RVNN models perform poorly in tackling the XOR problem and in 2D affine transformations [18,19]. In view of this, complex properties have been incorporated into RVNNs to formulate complex-valued neural networks (CVNNs), which can effectively solve the XOR problem and $2D$ affine transformations [18,19]. As a result, CVNN-related models have received significant research attention in both mathematical and practical analyses [20,21,22,23,24]. Nevertheless, CVNN models are inefficient in handling higher dimension transformations including color night vision, color image compression, and $3D$ and $4D$ problems [25,26,27]. Meanwhile, several engineering problems involve quaternion-valued signals and quaternion functions, such as 3D wind forecasting, polarized signal classification, color night vision, as well as color night vision [26,27,28]. Undoubtedly, quaternion-based networks present good mathematical models to undertake these applications due to the quaternion features. In view of this, quaternion-valued neural networks (QVNNs) have been developed by implementing quaternion algebra into CVNNs, in order to generalize RVNN and CVNN models with quaternion-valued activation functions, connection weights, as well as signals states [11,29,30,31,32]. Therefore, the investigation of the dynamics of QVNN models is essential and important. Recently, many computational approaches for various QVNN models and their learning algorithms have been proposed. Among the studies include global $\mu$ stability, global asymptotic stability as well as global synchronization [29,30,31]. Other studies of QVNN models are also available, for example, exponential input-to-state stability (exp-ISS) and global Mittag-Leffler stability and synchronization [32,33]. Similarly, some other stability conditions have been defined for QVNN models [12,34,35].

In modeling problems, we have to consider the existence of noise, since it is inherent in nonlinear dynamic systems. In fact, when a system is influenced by external disturbance, the stochastic neural network (SNN) models become very useful for describing a real system, as compared with a deterministic NN. Therefore, it is crucial to examine the dynamic properties pertaining to SNN models. As a result, several research studies have extensively analyzed the dynamics of SNN models [36,37], stochastic Hopfield NN models [38], stochastic memristive NN models [13], and stochastic CVNN models [13]. On the other hand, it is clear that the external inputs can influence the dynamic behaviors of NNs in practical applications. As such, the ISS criterion is important to characterize the effects of external inputs [10,39,40]. Recently, several useful ISS results for stochastic RVNN and CVNN models have been published [13,39,40,41]. It should be noted that most studies on QVNN dynamic behaviors are concerned with global asymptotic stability and synchronization analysis [11,29,30,31,32]. There are only a few studies on the exponential stability of QVNN models. According to our survey, the study on mean-square exp-ISS analysis with respect to SMQVNN models with time-varying delays is new in the literature, and our paper contributes toward this research area.

Inspired by the above-mentioned discussions, our analysis mainly focuses on the mean-square exp-ISS problem for the SMQVNN models. The current SMQVNN model encompasses stochastic memristive CVNN and stochastic memristive RVNN as its special cases. We divide the original QVNN into four RVNN models, in order to avoid the issue of non-commutative of quaternion multiplication. By constructing suitable Lyapunov functional and utilizing Dynkin’s and It $\widehat{o}$’s formulae, as well as other inequality methods, we establish new sufficient conditions for exp-ISS with respect to the considered SMQVNN model. We illustrate the usefulness of the obtained results by a numerical example.

This study has the following contributions: (1) this is the first analysis on the mean-square exp-ISS pertaining to SMQVNN models with time-varying delays; (2) unlike the conventional stability criteria, we establish new mean-square exp-ISS pertaining to the SMQVNN by dividing the original QVNN into four RVNN models; (3) the main results of this paper are new and more general than those in the QVNN literature.

This paper is structured as follows. We formally define the proposed model and analyze the new exp-ISS criteria in Section 2 and Section 3, respectively. We present the numerical example and the associated simulation results in Section 4. In Section 5, we present the key conclusions and some suggestions for future research.

2. Mathematical Fundamentals and Problem Formulation

2.1. Mathematical Notations

The real field, complex field, and skew field of quaternion are denoted as $\mathbb{R},\mathbb{C}$, and $\mathbb{Q}$, respectively. Their n-dimension vector with elements of $\mathbb{R},\mathbb{C}$ and $\mathbb{Q}$ are denoted as ${\mathbb{R}}^n,{\mathbb{C}}^n$ and ${\mathbb{Q}}^n$, while their $n\times n$ matrices with entries from $\mathbb{R},\mathbb{C}$ and $\mathbb{Q}$ are denoted as ${\mathbb{R}}^{n\times n},{\mathbb{C}}^{n\times n}$ and ${\mathbb{Q}}^{n\times n}$, respectively. In addition, the space of a continuous function mapping $\phi$ from $[-\tau ,0]$ into ${\mathbb{Q}}^n$ is denoted as $\mathcal{C}([-\tau ,0];{\mathbb{Q}}^n)$. The closure of the convex hull of ${\mathbb{Q}}^n$, which is formulated from quaternion numbers ∇ and ∆, is denoted as $co\{\nabla ,▵\}$. A class of essentially bounded function u from $[0,\infty )$ to ${\mathbb{Q}}^n$ with ${\parallel u\parallel }_{\infty }=ess{sup}_{-\tau \le s\le 0}|u(s)|<\infty$ is denoted as ${\ell }_{\infty }$, while the family of all ${\mathcal{F}}_0$ measurable is denoted as ${\mathcal{L}}_{{\mathcal{F}}_0}^2([-\tau ,0];{\mathbb{Q}}^n)$. Besides that, $\mathcal{C}([-\tau ,0];{\mathbb{Q}}^n)$-valued stochastic variables $\{\phi (s):-\tau \le s\le 0\}$ is in a way that ${\int }_{-\tau }^0\mathbb{E}{|\phi (s)|}^{2}ds<\infty$, in which the mathematical expectation operation pertaining to a probability measure $\mathcal{P}$ is denoted as $\mathbb{E}\{·\}$. Superscripts * and T represent the complex conjugate transpose and matrix transposition, while $i,j,k$ represent the imaginary units, respectively, and $N=1,2,\dots ,n$.

2.2. Quaternion Algebra

Firstly, we address the quaternion and its operating rules. We can express the quaternion, which consists of a real part along and three imaginary parts, as:

$$\begin{array}{c}\mathbf{m}={\mathbf{m}}^R+i{\mathbf{m}}^I+j{\mathbf{m}}^J+k{\mathbf{m}}^K\in \mathbb{Q},\hfill \end{array}$$

where ${\mathbf{m}}^R,{\mathbf{m}}^I,{\mathbf{m}}^J,{\mathbf{m}}^K\in \mathbb{R}$. The multiplication rules of Hamilton are satisfied by the imaginary roots $i,j,k$:

$$\begin{array}{c}{i}^2=j^2=k^2=ijk=-1,ij=-ji=k,jk=-kj=i,ki=-ik=j.\hfill \end{array}$$

(1)

The quaternion-valued function is denoted by $\mathbf{m}(t)={\mathbf{m}}^R(t)+i{\mathbf{m}}^I(t)+j{\mathbf{m}}^J(t)+k{\mathbf{m}}^K(t)\in \mathbb{Q}$, where ${\mathbf{m}}^R(t)$, ${\mathbf{m}}^I(t)$, ${\mathbf{m}}^J(t)$, ${\mathbf{m}}^K(t)\in \mathbb{R}$. Let $\mathbf{p}={\mathbf{p}}^R+i{\mathbf{p}}^I+j{\mathbf{p}}^J+k{\mathbf{p}}^K$ and $\mathbf{q}={\mathbf{q}}^R+i{\mathbf{q}}^I+j{\mathbf{q}}^J+k{\mathbf{q}}^K$ are two quaternions, the addition and subtraction of $\mathbf{p}\pm \mathbf{q}$ are defined as

$$\begin{array}{c}\mathbf{p}\pm \mathbf{q}=({\mathbf{p}}^R\pm {\mathbf{q}}^R)+i({\mathbf{p}}^I\pm {\mathbf{q}}^I)+j({\mathbf{p}}^J\pm {\mathbf{q}}^J)+k({\mathbf{p}}^K\pm {\mathbf{q}}^K).\hfill \end{array}$$

We can express the product of $\mathbf{p}\mathbf{q}$ with respect to the multiplication rules of Hamilton as:

$$\begin{array}{cc}\mathbf{p}\mathbf{q}=\hfill & \left({\mathbf{p}}^R{\mathbf{q}}^R-{\mathbf{p}}^I{\mathbf{q}}^I-{\mathbf{p}}^J{\mathbf{q}}^J-{\mathbf{p}}^K{\mathbf{q}}^K\right)+i\left({\mathbf{p}}^R{\mathbf{q}}^I+{\mathbf{p}}^I{\mathbf{q}}^R+{\mathbf{p}}^J{\mathbf{q}}^K-{\mathbf{p}}^K{\mathbf{q}}^J\right)\hfill \\ & +j\left({\mathbf{p}}^R{\mathbf{q}}^J+{\mathbf{p}}^J{\mathbf{q}}^R-{\mathbf{p}}^I{\mathbf{q}}^K+{\mathbf{p}}^K{\mathbf{q}}^I\right)+k\left({\mathbf{p}}^R{\mathbf{q}}^K+{\mathbf{p}}^K{\mathbf{q}}^R+{\mathbf{p}}^I{\mathbf{q}}^J-{\mathbf{p}}^J{\mathbf{q}}^I\right).\hfill \end{array}$$

Note that given any $\mathbf{m}(t)\in \mathbb{Q}$, $\parallel \mathbf{m}\parallel =\sqrt{{\displaystyle \sum _{\mathfrak{x}=1}^n}{({\mathbf{m}}^R)}^2+{\displaystyle \sum _{\mathfrak{x}=1}^n}{({\mathbf{m}}^I)}^2+{\displaystyle \sum _{\mathfrak{x}=1}^n}{({\mathbf{m}}^J)}^2+{\displaystyle \sum _{\mathfrak{x}=1}^n}{({\mathbf{m}}^K)}^2}$ represents the norm of $\mathbf{m}$, while $|\mathbf{m}|=\sqrt{\mathbf{m}{\mathbf{m}}^{\ast }}=\sqrt{{({\mathbf{m}}^R)}^2+{({\mathbf{m}}^I)}^2+{({\mathbf{m}}^J)}^2+{({\mathbf{m}}^K)}^2}$ represents the modulus of $\mathbf{m}$, in which the conjugate transpose of $\mathbf{m}$ is denoted as ${\mathbf{m}}^{\ast }={\mathbf{m}}^R(t)-i{\mathbf{m}}^I(t)-j{\mathbf{m}}^J(t)-k{\mathbf{m}}^K(t)$.

2.3. Problem Formation

In this section, we define a SMQVNN model as:

$$\begin{array}{cc}d{\mathbf{m}}_{\mathfrak{x}}(t)=\hfill & [-{\mathbf{c}}_{\mathfrak{x}}{\mathbf{m}}_{\mathfrak{x}}(t)+\sum _{\mathfrak{z}=1}^n{\mathbf{a}}_{\mathfrak{x}\mathfrak{z}}({\mathbf{m}}_{\mathfrak{x}}(t)){\mathbf{f}}_{\mathfrak{z}}({\mathbf{m}}_{\mathfrak{z}}(t))+\sum _{\mathfrak{z}=1}^n{\mathbf{b}}_{\mathfrak{x}\mathfrak{z}}({\mathbf{m}}_{\mathfrak{x}}(t)){\mathbf{g}}_{\mathfrak{z}}({\mathbf{m}}_{\mathfrak{z}}(t-\tau (t)))+{\mathbf{u}}_{\mathfrak{x}}(t)]dt\hfill \\ & +\sum _{\mathfrak{z}=1}^n{\sigma }_{\mathfrak{x}\mathfrak{z}}(t,{\mathbf{m}}_{\mathfrak{z}}(t),{\mathbf{m}}_{\mathfrak{z}}(t-\tau (t)))d{w}_{\mathfrak{z}}(t),t\ge 0,\mathfrak{x}\in N,\hfill \end{array}$$

(2)

Subject to the initial condition of

$$\begin{array}{c}{\mathbf{m}}_{\mathfrak{x}}(t)={\phi }_{\mathfrak{x}}(t),t\in [-\tau ,0],\mathfrak{x}\in N,\hfill \end{array}$$

(3)

where ${\mathbf{c}}_{\mathfrak{x}}>0$ is a constant and the state variable is ${\mathbf{m}}_{\mathfrak{x}}(t)$; the external input vector is ${\mathbf{u}}_{\mathfrak{x}}(t)$. In addition, the time delay is $\tau (t)$, which is differentiable and it is able to satisfy $0\le \tau (t)\le \tau ,\dot{\tau }(t)\le \mu <1$, with positive constants $\mu$ and $\tau$; ${\phi }_{\mathfrak{x}}(t)\in \mathcal{C}([-\tau ,0];{\mathbb{Q}}^n)$ is the initial condition. In addition, ${\mathbf{f}}_{\mathfrak{x}}({\mathbf{m}}_{\mathfrak{x}}(t))$ and ${\mathbf{g}}_{\mathfrak{x}}({\mathbf{m}}_{\mathfrak{x}}(t-\tau (t)))$ are quaternion-valued activation functions. The standard Brownian motion is denoted by $w_{\mathfrak{z}}$. Note that it is defined on a probability space of $(\mathsf{\Omega },\mathcal{F},\mathcal{P})$ subject to a natural filtration ${\left\{{\mathcal{F}}_t\right\}}_{t\ge 0}$. Besides that, ${\sigma }_{\mathfrak{x}\mathfrak{z}}:\mathbb{R}\times {\mathbb{Q}}^n\times {\mathbb{Q}}^n\to {\mathbb{Q}}^{n\times n}$ is a Borel measurable function; while the quaternion-valued connection weights are ${\mathbf{a}}_{\mathfrak{x}\mathfrak{z}}({\mathbf{m}}_{\mathfrak{z}}(t))$ and ${\mathbf{b}}_{\mathfrak{x}\mathfrak{z}}({\mathbf{m}}_{\mathfrak{z}}(t))$, which can be expressed as:

$$\begin{array}{cc}\hfill {\mathbf{a}}_{\mathfrak{x}\mathfrak{z}}({\mathbf{m}}_{\mathfrak{z}}(t))=& \frac{{\mathbf{W}}_{f\mathfrak{x}\mathfrak{z}}}{{\mathbf{C}}_{\mathfrak{x}}}\times sig{n}_{\mathfrak{x}\mathfrak{z}},\hfill \\ \hfill {\mathbf{b}}_{\mathfrak{x}\mathfrak{z}}({\mathbf{m}}_{\mathfrak{z}}(t))=& \frac{{\mathbf{W}}_{g\mathfrak{x}\mathfrak{z}}}{{\mathbf{C}}_{\mathfrak{x}}}\times sig{n}_{\mathfrak{x}\mathfrak{z}},\hfill \\ \hfill sig{n}_{\mathfrak{x}\mathfrak{z}}=& \left\{\begin{array}{c}-1,\mathfrak{x}=\mathfrak{z}\hfill \\ 1,\mathfrak{x}\ne \mathfrak{z}\hfill \end{array}\right.\hfill \end{array}$$

with ${\mathbf{C}}_{\mathfrak{x}}$ is the capacitor, ${\mathbf{W}}_{f\mathfrak{x}\mathfrak{z}}$ and ${\mathbf{W}}_{g\mathfrak{x}\mathfrak{z}}$ are the memductances of memristors ${\mathbf{R}}_{f\mathfrak{x}\mathfrak{z}}$ and ${\mathbf{R}}_{g\mathfrak{x}\mathfrak{z}}$, respectively, that represent a memristor from ${\mathbf{f}}_{\mathfrak{x}}({\mathbf{m}}_{\mathfrak{x}}(t))$ and ${\mathbf{m}}_{\mathfrak{x}}(t)$ and a memristor from ${\mathbf{g}}_{\mathfrak{x}}({\mathbf{m}}_{\mathfrak{x}}(t-\tau (t)))$ and ${\mathbf{m}}_{\mathfrak{x}}(t)$. Based on the memristor current-voltage properties, the memristive connection weights are chosen to be state-dependent switching as follows:

$$\begin{array}{cc}{\mathbf{a}}_{\mathfrak{x}\mathfrak{z}}({\mathbf{m}}_{\mathfrak{z}}(t))=\hfill & \left\{\begin{array}{c}{\widehat{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}},|{\mathbf{m}}_{\mathfrak{z}}(t)|<{\psi }_{\mathfrak{z}}\hfill \\ {\check{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}},|{\mathbf{m}}_{\mathfrak{z}}(t)|>{\psi }_{\mathfrak{z}},\hfill \end{array}\right.{\mathbf{b}}_{\mathfrak{x}\mathfrak{z}}({\mathbf{m}}_{\mathfrak{z}}(t))=\left\{\begin{array}{c}{\widehat{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}},|{\mathbf{m}}_{\mathfrak{z}}(t)|<{\psi }_{\mathfrak{z}}\hfill \\ {\check{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}},|{\mathbf{m}}_{\mathfrak{z}}(t)|>{\psi }_{\mathfrak{z}},\hfill \end{array}\right.\hfill \\ {\mathbf{a}}_{\mathfrak{x}\mathfrak{z}}^R({\mathbf{m}}_{\mathfrak{z}}^R(t))=\hfill & \left\{\begin{array}{c}{\widehat{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^R,|{\mathbf{m}}_{\mathfrak{z}}^R(t)|<{\psi }_{\mathfrak{z}}\hfill \\ {\check{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^R,|{\mathbf{m}}_{\mathfrak{z}}^R(t)|>{\psi }_{\mathfrak{z}},\hfill \end{array}\right.{\mathbf{a}}_{\mathfrak{x}\mathfrak{z}}^I({\mathbf{m}}_{\mathfrak{z}}^I(t))=\left\{\begin{array}{c}{\widehat{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^I,|{\mathbf{m}}_{\mathfrak{z}}^I(t)|<{\psi }_{\mathfrak{z}}\hfill \\ {\check{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^I,|{\mathbf{m}}_{\mathfrak{z}}^I(t)|>{\psi }_{\mathfrak{z}},\hfill \end{array}\right.\hfill \\ {\mathbf{a}}_{\mathfrak{x}\mathfrak{z}}^J({\mathbf{m}}_{\mathfrak{z}}^J(t))=\hfill & \left\{\begin{array}{c}{\widehat{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^J,|{\mathbf{m}}_{\mathfrak{z}}^J(t)|<{\psi }_{\mathfrak{z}}\hfill \\ {\check{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^J,|{\mathbf{m}}_{\mathfrak{z}}^J(t)|>{\psi }_{\mathfrak{z}},\hfill \end{array}\right.{\mathbf{a}}_{\mathfrak{x}\mathfrak{z}}^K({\mathbf{m}}_{\mathfrak{z}}^K(t))=\left\{\begin{array}{c}{\widehat{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^K,|{\mathbf{m}}_{\mathfrak{z}}^K(t)|<{\psi }_{\mathfrak{z}}\hfill \\ {\check{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^K,|{\mathbf{m}}_{\mathfrak{z}}^K(t)|>{\psi }_{\mathfrak{z}},\hfill \end{array}\right.\hfill \\ {\mathbf{b}}_{\mathfrak{x}\mathfrak{z}}^R({\mathbf{m}}_{\mathfrak{z}}^R(t))=\hfill & \left\{\begin{array}{c}{\widehat{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^R,|{\mathbf{m}}_{\mathfrak{z}}^R(t)|<{\psi }_{\mathfrak{z}}\hfill \\ {\check{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^R,|{\mathbf{m}}_{\mathfrak{z}}^R(t)|>{\psi }_{\mathfrak{z}},\hfill \end{array}\right.{\mathbf{b}}_{\mathfrak{x}\mathfrak{z}}^I({\mathbf{m}}_{\mathfrak{z}}^I(t))=\left\{\begin{array}{c}{\widehat{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^I,|{\mathbf{m}}_{\mathfrak{z}}^I(t)|<{\psi }_{\mathfrak{z}}\hfill \\ {\check{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^I,|{\mathbf{m}}_{\mathfrak{z}}^I(t)|>{\psi }_{\mathfrak{z}},\hfill \end{array}\right.\hfill \\ {\mathbf{b}}_{\mathfrak{x}\mathfrak{z}}^J({\mathbf{m}}_{\mathfrak{z}}^J(t))=\hfill & \left\{\begin{array}{c}{\widehat{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^J,|{\mathbf{m}}_{\mathfrak{z}}^J(t)|<{\psi }_{\mathfrak{z}}\hfill \\ {\check{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^J,|{\mathbf{m}}_{\mathfrak{z}}^J(t)|>{\psi }_{\mathfrak{z}},\hfill \end{array}\right.{\mathbf{b}}_{\mathfrak{x}\mathfrak{z}}^K({\mathbf{m}}_{\mathfrak{z}}^K(t))=\left\{\begin{array}{c}{\widehat{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^K,|{\mathbf{m}}_{\mathfrak{z}}^K(t)|<{\psi }_{\mathfrak{z}}\hfill \\ {\check{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^K,|{\mathbf{m}}_{\mathfrak{z}}^K(t)|>{\psi }_{\mathfrak{z}},\hfill \end{array}\right.\hfill \end{array}$$

for $\mathfrak{x},\mathfrak{z}\in N$, the switching jumps ${\psi }_{\mathfrak{z}}>0$, and, where ${\mathbf{a}}_{\mathfrak{x}\mathfrak{z}}^R({\mathbf{m}}_{\mathfrak{z}}^R(t))=Re({\mathbf{a}}_{\mathfrak{x}\mathfrak{z}}({\mathbf{m}}_{\mathfrak{z}}(t)))$, ${\mathbf{a}}_{\mathfrak{x}\mathfrak{z}}^I({\mathbf{m}}_{\mathfrak{z}}^I(t))=Im({\mathbf{a}}_{\mathfrak{x}\mathfrak{z}}({\mathbf{m}}_{\mathfrak{z}}(t)))$, ${\mathbf{a}}_{\mathfrak{x}\mathfrak{z}}^J({\mathbf{m}}_{\mathfrak{z}}^J(t))=Im({\mathbf{a}}_{\mathfrak{x}\mathfrak{z}}({\mathbf{m}}_{\mathfrak{z}}(t)))$, ${\mathbf{a}}_{\mathfrak{x}\mathfrak{z}}^K({\mathbf{m}}_{\mathfrak{z}}^K(t))=Im({\mathbf{a}}_{\mathfrak{x}\mathfrak{z}}({\mathbf{m}}_{\mathfrak{z}}(t)))$, ${\mathbf{b}}_{\mathfrak{x}\mathfrak{z}}^R({\mathbf{m}}_{\mathfrak{z}}^R(t))=Re({\mathbf{b}}_{\mathfrak{x}\mathfrak{z}}({\mathbf{m}}_{\mathfrak{z}}(t)))$, ${\mathbf{b}}_{\mathfrak{x}\mathfrak{z}}^I({\mathbf{m}}_{\mathfrak{z}}^I(t))=Im({\mathbf{b}}_{\mathfrak{x}\mathfrak{z}}({\mathbf{m}}_{\mathfrak{z}}(t)))$, ${\mathbf{b}}_{\mathfrak{x}\mathfrak{z}}^J({\mathbf{m}}_{\mathfrak{z}}^J(t))=Im({\mathbf{b}}_{\mathfrak{x}\mathfrak{z}}({\mathbf{m}}_{\mathfrak{z}}(t)))$, ${\mathbf{b}}_{\mathfrak{x}\mathfrak{z}}^K({\mathbf{m}}_{\mathfrak{z}}^K(t))=Im({\mathbf{b}}_{\mathfrak{x}\mathfrak{z}}({\mathbf{m}}_{\mathfrak{z}}(t)))$ and ${\widehat{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}},{\check{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}$, ${\widehat{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^R,{\check{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^R$, ${\widehat{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^I,{\check{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^I$, ${\widehat{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^J,{\check{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^J$, ${\widehat{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^K,{\check{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^K$, ${\widehat{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}},{\check{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}$, ${\widehat{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^R,{\check{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^R$, ${\widehat{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^I,{\check{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^I$, ${\widehat{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^J,{\check{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^J$, ${\widehat{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^K,{\check{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^K$ are constants.

A1: [32] For any $\mathfrak{z}\in N$, ${\mathbf{f}}_{\mathfrak{z}}({\mathbf{m}}_{\mathfrak{z}}(·))$ and ${\mathbf{g}}_{\mathfrak{z}}({\mathbf{m}}_{\mathfrak{z}}(·))$ are bounded and continuous along with positive constants ${\mathbf{G}}_{\mathfrak{z}}$, ${\mathbf{H}}_{\mathfrak{z}}$ such that

$$\begin{array}{c}\left\{\begin{array}{c}|{\mathbf{f}}_{\mathfrak{z}}({\mathbf{m}}_1)-{\mathbf{f}}_{\mathfrak{z}}({\mathbf{m}}_2)|\le {\mathbf{G}}_{\mathfrak{z}}|{\mathbf{m}}_1-{\mathbf{m}}_2|,\hfill \\ |{\mathbf{g}}_{\mathfrak{z}}({\mathbf{m}}_1)-{\mathbf{g}}_{\mathfrak{z}}({\mathbf{m}}_2)|\le {\mathbf{H}}_{\mathfrak{z}}|{\mathbf{m}}_1-{\mathbf{m}}_2|,\hfill \end{array}\right.\hfill \end{array}$$

(4)

for all ${\mathbf{m}}_1,{\mathbf{m}}_2\in \mathbb{Q}$ and ${\mathbf{f}}_{\mathfrak{z}}(0)=0$, ${\mathbf{g}}_{\mathfrak{z}}(0)=0$.

Remark 1.

The activation functions are the fundamental factors in the structure of the NN model. The choice of appropriate quaternion-valued activation functions remains an open question in the QVNNs study. Recently, several activation functions have recently been used to study QVNNs. For example, nonmonotonic piecewise nonlinear activation functions, linear threshold activation functions, and real-imaginary separate type activation functions. The main results of this paper will be derived based on the assumption A1 that the activation functions can be divided into real and imaginary parts.

As similar in [13,41], by using the set valued map as well as the differential inclusion theory, from Equation (2), we obtain

$$\begin{array}{cc}d{\mathbf{m}}_{\mathfrak{x}}(t)\in \hfill & [-{\mathbf{c}}_{\mathfrak{x}}{\mathbf{m}}_{\mathfrak{x}}(t)+\sum _{\mathfrak{z}=1}^{n}co[{\overline{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}},{\underline{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}]{\mathbf{f}}_{\mathfrak{z}}({\mathbf{m}}_{\mathfrak{z}}(t))+\sum _{\mathfrak{z}=1}^{n}co[{\overline{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}},{\underline{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}]{\mathbf{g}}_{\mathfrak{z}}({\mathbf{m}}_{\mathfrak{z}}(t-\tau (t)))+{\mathbf{u}}_{\mathfrak{x}}(t)]dt\hfill \\ & +\sum _{\mathfrak{z}=1}^n{\sigma }_{\mathfrak{x}\mathfrak{z}}(t,{\mathbf{m}}_{\mathfrak{z}}(t),{\mathbf{m}}_{\mathfrak{z}}(t-\tau (t)))d{w}_{\mathfrak{z}}(t),\hfill \end{array}$$

(5)

or equivalently, for all $\mathfrak{x},\mathfrak{z}\in N$, where ${\overline{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}=max\{{\widehat{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}},{\check{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}\}$, ${\underline{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}=min\{{\widehat{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}},{\check{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}\}$, ${\overline{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}=max\{{\widehat{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}},{\check{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}\}$, ${\underline{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}=min\{{\widehat{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}},{\check{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}\}$. There exist measurable functions ${\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}\in co[{\overline{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}},{\underline{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}]$, ${\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}\in co[{\overline{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}},{\underline{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}]$, such that

$$\begin{array}{cc}d{\mathbf{m}}_{\mathfrak{x}}(t)=\hfill & [-{\mathbf{c}}_{\mathfrak{x}}{\mathbf{m}}_{\mathfrak{x}}(t)+\sum _{\mathfrak{z}=1}^n{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}{\mathbf{f}}_{\mathfrak{z}}({\mathbf{m}}_{\mathfrak{z}}(t))+\sum _{\mathfrak{z}=1}^n{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}{\mathbf{g}}_{\mathfrak{z}}({\mathbf{m}}_{\mathfrak{z}}(t-\tau (t)))+{\mathbf{u}}_{\mathfrak{x}}(t)]dt\hfill \\ & +\sum _{\mathfrak{z}=1}^n{\sigma }_{\mathfrak{x}\mathfrak{z}}(t,{\mathbf{m}}_{\mathfrak{z}}(t),{\mathbf{m}}_{\mathfrak{z}}(t-\tau (t)))d{w}_{\mathfrak{z}}(t),\hfill \end{array}$$

(6)

Now, let ${\overline{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^R=max\{{\widehat{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^R,{\check{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^R\}$, ${\underline{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^R=min\{{\widehat{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^R,{\check{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^R\}$, ${\overline{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^I=max\{{\widehat{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^I,{\check{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^I\}$, ${\underline{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^I=min\{{\widehat{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^I,{\check{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^I\}$, ${\overline{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^J=max\{{\widehat{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^J,{\check{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^J\}$, ${\underline{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^J=min\{{\widehat{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^J,{\check{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^J\}$, ${\overline{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^K=max\{{\widehat{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^K,{\check{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^K\}$, ${\underline{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^K=min\{{\widehat{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^K,{\check{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^K\}$, ${\overline{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^R=max\{{\widehat{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^R,{\check{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^R\}$, ${\underline{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^R=min\{{\widehat{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^R,{\check{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^R\}$, ${\overline{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^I=max\{{\widehat{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^I,{\check{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^I\}$, ${\underline{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^I=min\{{\widehat{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^I,{\check{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^I\}$, ${\overline{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^J=max\{{\widehat{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^J,{\check{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^J\}$, ${\underline{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^J=min\{{\widehat{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^J,{\check{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^J\}$, ${\overline{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^K=max\{{\widehat{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^K,{\check{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^K\}$, ${\underline{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^K=min\{{\widehat{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^K,{\check{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^K\}$. We assume that the NN model (6) can be separated into real and imaginary parts. Therefore, there exist measurable functions ${\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^R\in co[{\overline{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^R,{\underline{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^R]$, ${\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^I\in co[{\overline{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^I,{\underline{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^I]$, ${\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^J\in co[{\overline{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^J,{\underline{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^J]$, ${\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^K\in co[{\overline{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^K,{\underline{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^K]$, ${\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^R\in co[{\overline{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^R,{\underline{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^R]$, ${\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^I\in co[{\overline{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^I,{\underline{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^I]$, ${\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^J\in co[{\overline{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^J,{\underline{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^J]$, ${\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^K\in co[{\overline{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^K,{\underline{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^K]$, such that the NN model (6) can be express as follows:

$$\begin{array}{c}\left\{\begin{array}{cc}d{\mathbf{m}}_{\mathfrak{x}}^R(t)=\hfill & [-{\mathbf{c}}_{\mathfrak{x}}{\mathbf{m}}_{\mathfrak{x}}^R(t)+{\displaystyle \sum _{\mathfrak{z}=1}^n}\left[{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^R{\mathbf{f}}_{\mathfrak{z}}^R({\mathbf{m}}_{\mathfrak{z}}^R(t))-{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^I{\mathbf{f}}_{\mathfrak{z}}^I({\mathbf{m}}_{\mathfrak{z}}^I(t))-{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^J{\mathbf{f}}_{\mathfrak{z}}^J({\mathbf{m}}_{\mathfrak{z}}^J(t))-{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^K{\mathbf{f}}_{\mathfrak{z}}^K({\mathbf{m}}_{\mathfrak{z}}^K(t))\right]\hfill \\ & +{\displaystyle \sum _{\mathfrak{z}=1}^n}[{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^R{\mathbf{g}}_{\mathfrak{z}}^R({\mathbf{m}}_{\mathfrak{z}}^R(t-\tau (t)))-{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^I{\mathbf{g}}_{\mathfrak{z}}^I({\mathbf{m}}_{\mathfrak{z}}^I(t-\tau (t)))-{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^J{\mathbf{g}}_{\mathfrak{z}}^J({\mathbf{m}}_{\mathfrak{z}}^J(t-\tau (t)))\hfill \\ & -{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^K{\mathbf{g}}_{\mathfrak{z}}^K({\mathbf{m}}_{\mathfrak{z}}^K(t-\tau (t)))]+{\mathbf{u}}_{\mathfrak{x}}^R(t)]dt+{\displaystyle \sum _{\mathfrak{z}=1}^n}{\sigma }_{\mathfrak{x}\mathfrak{z}}^R(t,{\mathbf{m}}_{\mathfrak{z}}^R(t),{\mathbf{m}}_{\mathfrak{z}}^R(t-\tau (t)))d{w}_{\mathfrak{z}}(t),\hfill \\ d{\mathbf{m}}_{\mathfrak{x}}^I(t)=\hfill & [-{\mathbf{c}}_{\mathfrak{x}}{\mathbf{m}}_{\mathfrak{x}}^I(t)+{\displaystyle \sum _{\mathfrak{z}=1}^n}\left[{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^R{\mathbf{f}}_{\mathfrak{z}}^I({\mathbf{m}}_{\mathfrak{z}}^I(t))+{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^I{\mathbf{f}}_{\mathfrak{z}}^R({\mathbf{m}}_{\mathfrak{z}}^R(t))+{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^J{\mathbf{f}}_{\mathfrak{z}}^K({\mathbf{m}}_{\mathfrak{z}}^K(t))-{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^K{\mathbf{f}}_{\mathfrak{z}}^J({\mathbf{m}}_{\mathfrak{z}}^J(t))\right]\hfill \\ & +{\displaystyle \sum _{\mathfrak{z}=1}^n}[{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^R{\mathbf{g}}_{\mathfrak{z}}^I({\mathbf{m}}_{\mathfrak{z}}^I(t-\tau (t)))+{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^I{\mathbf{g}}_{\mathfrak{z}}^R({\mathbf{m}}_{\mathfrak{z}}^R(t-\tau (t)))+{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^J{\mathbf{g}}_{\mathfrak{z}}^K({\mathbf{m}}_{\mathfrak{z}}^K(t-\tau (t)))\hfill \\ & -{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^K{\mathbf{g}}_{\mathfrak{z}}^J({\mathbf{m}}_{\mathfrak{z}}^J(t-\tau (t)))]+{\mathbf{u}}_{\mathfrak{x}}^I(t)]dt+{\displaystyle \sum _{\mathfrak{z}=1}^n}{\sigma }_{\mathfrak{x}\mathfrak{z}}^I(t,{\mathbf{m}}_{\mathfrak{z}}^I(t),{\mathbf{m}}_{\mathfrak{z}}^I(t-\tau (t)))d{w}_{\mathfrak{z}}(t),\hfill \\ d{\mathbf{m}}_{\mathfrak{x}}^J(t)=\hfill & [-{\mathbf{c}}_{\mathfrak{x}}{\mathbf{m}}_{\mathfrak{x}}^J(t)+{\displaystyle \sum _{\mathfrak{z}=1}^n}\left[{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^R{\mathbf{f}}_{\mathfrak{z}}^J({\mathbf{m}}_{\mathfrak{z}}^J(t))+{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^J{\mathbf{f}}_{\mathfrak{z}}^R({\mathbf{m}}_{\mathfrak{z}}^R(t))+{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^K{\mathbf{f}}_{\mathfrak{z}}^I({\mathbf{m}}_{\mathfrak{z}}^I(t))-{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^I{\mathbf{f}}_{\mathfrak{z}}^K({\mathbf{m}}_{\mathfrak{z}}^K(t))\right]\hfill \\ & +{\displaystyle \sum _{\mathfrak{z}=1}^n}[{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^R{\mathbf{g}}_{\mathfrak{z}}^J({\mathbf{m}}_{\mathfrak{z}}^J(t-\tau (t)))+{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^J{\mathbf{g}}_{\mathfrak{z}}^R({\mathbf{m}}_{\mathfrak{z}}^R(t-\tau (t)))+{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^K{\mathbf{g}}_{\mathfrak{z}}^I({\mathbf{m}}_{\mathfrak{z}}^I(t-\tau (t)))\hfill \\ & -{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^I{\mathbf{g}}_{\mathfrak{z}}^K({\mathbf{m}}_{\mathfrak{z}}^K(t-\tau (t)))]+{\mathbf{u}}_{\mathfrak{x}}^J(t)]dt+{\displaystyle \sum _{\mathfrak{z}=1}^n}{\sigma }_{\mathfrak{x}\mathfrak{z}}^J(t,{\mathbf{m}}_{\mathfrak{z}}^J(t),{\mathbf{m}}_{\mathfrak{z}}^J(t-\tau (t)))d{w}_{\mathfrak{z}}(t),\hfill \\ d{\mathbf{m}}_{\mathfrak{x}}^K(t)=\hfill & [-{\mathbf{c}}_{\mathfrak{x}}{\mathbf{m}}_{\mathfrak{x}}^K(t)+{\displaystyle \sum _{\mathfrak{z}=1}^n}\left[{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^R{\mathbf{f}}_{\mathfrak{z}}^K({\mathbf{m}}_{\mathfrak{z}}^K(t))+{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^I{\mathbf{f}}_{\mathfrak{z}}^J({\mathbf{m}}_{\mathfrak{z}}^J(t))+{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^K{\mathbf{f}}_{\mathfrak{z}}^R({\mathbf{m}}_{\mathfrak{z}}^R(t))-{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^J{\mathbf{f}}_{\mathfrak{z}}^I({\mathbf{m}}_{\mathfrak{z}}^I(t))\right]\hfill \\ & +{\displaystyle \sum _{\mathfrak{z}=1}^n}[{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^R{\mathbf{g}}_{\mathfrak{z}}^K({\mathbf{m}}_{\mathfrak{z}}^K(t-\tau (t)))+{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^I{\mathbf{g}}_{\mathfrak{z}}^J({\mathbf{m}}_{\mathfrak{z}}^J(t-\tau (t)))+{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^K{\mathbf{g}}_{\mathfrak{z}}^R({\mathbf{m}}_{\mathfrak{z}}^R(t-\tau (t)))\hfill \\ & -{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^J{\mathbf{g}}_{\mathfrak{z}}^I({\mathbf{m}}_{\mathfrak{z}}^I(t-\tau (t)))]+{\mathbf{u}}_{\mathfrak{x}}^K(t)]dt+{\displaystyle \sum _{\mathfrak{z}=1}^n}{\sigma }_{\mathfrak{x}\mathfrak{z}}^K(t,{\mathbf{m}}_{\mathfrak{z}}^K(t),{\mathbf{m}}_{\mathfrak{z}}^K(t-\tau (t)))d{w}_{\mathfrak{z}}(t),\hfill \end{array}\right.\hfill \end{array}$$

(7)

for $t\in [0,+\infty )$, where $\mathfrak{x},\mathfrak{z}\in N$, ${\mathbf{u}}_{\mathfrak{x}}^R(t)=Re({\mathbf{u}}_{\mathfrak{x}}(t))$, ${\mathbf{u}}_{\mathfrak{x}}^I(t)=Im({\mathbf{u}}_{\mathfrak{x}}(t))$, ${\mathbf{u}}_{\mathfrak{x}}^J(t)=Im({\mathbf{u}}_{\mathfrak{x}}(t))$, ${\mathbf{u}}_{\mathfrak{x}}^K(t)=Im({\mathbf{u}}_{\mathfrak{x}}(t))$, and

$$\begin{array}{cc}{\sigma }_{\mathfrak{x}\mathfrak{z}}^R(t,{\mathbf{m}}_{\mathfrak{z}}^R(t),{\mathbf{m}}_{\mathfrak{z}}^R(t-\tau (t)))=\hfill & Re({\sigma }_{\mathfrak{x}\mathfrak{z}}(t,{\mathbf{m}}_{\mathfrak{z}}(t),{\mathbf{m}}_{\mathfrak{z}}(t-\tau (t)))),\hfill \\ {\sigma }_{\mathfrak{x}\mathfrak{z}}^I(t,{\mathbf{m}}_{\mathfrak{z}}^I(t),{\mathbf{m}}_{\mathfrak{z}}^I(t-\tau (t)))=\hfill & Im({\sigma }_{\mathfrak{x}\mathfrak{z}}(t,{\mathbf{m}}_{\mathfrak{z}}(t),{\mathbf{m}}_{\mathfrak{z}}(t-\tau (t)))),\hfill \\ {\sigma }_{\mathfrak{x}\mathfrak{z}}^J(t,{\mathbf{m}}_{\mathfrak{z}}^J(t),{\mathbf{m}}_{\mathfrak{z}}^J(t-\tau (t)))=\hfill & Im({\sigma }_{\mathfrak{x}\mathfrak{z}}(t,{\mathbf{m}}_{\mathfrak{z}}(t),{\mathbf{m}}_{\mathfrak{z}}(t-\tau (t)))),\hfill \\ {\sigma }_{\mathfrak{x}\mathfrak{z}}^K(t,{\mathbf{m}}_{\mathfrak{z}}^K(t),{\mathbf{m}}_{\mathfrak{z}}^K(t-\tau (t)))=\hfill & Im({\sigma }_{\mathfrak{x}\mathfrak{z}}(t,{\mathbf{m}}_{\mathfrak{z}}(t),{\mathbf{m}}_{\mathfrak{z}}(t-\tau (t)))).\hfill \end{array}$$

Consider Model (7), its initial condition is

$$\begin{array}{c}{\mathbf{m}}_{\mathfrak{x}}^R(t)={\phi }_{\mathfrak{x}}^R(t),{\mathbf{m}}_{\mathfrak{x}}^I(t)={\phi }_{\mathfrak{x}}^I(t),{\mathbf{m}}_{\mathfrak{x}}^J(t)={\phi }_{\mathfrak{x}}^J(t),{\mathbf{m}}_{\mathfrak{x}}^K(t)={\phi }_{\mathfrak{x}}^K(t),\hfill \end{array}$$

(8)

for $t\in [-\tau ,0],$ where ${\phi }_{\mathfrak{x}}^R(t)=Re({\phi }_{\mathfrak{x}}(t))$, ${\phi }_{\mathfrak{x}}^I(t)=Im({\phi }_{\mathfrak{x}}(t))$, ${\phi }_{\mathfrak{x}}^J(t)=Im({\phi }_{\mathfrak{x}}(t))$, ${\phi }_{\mathfrak{x}}^K(t)=Im({\phi }_{\mathfrak{x}}(t))$.

A2: [32] For any $\mathfrak{z}\in N$, ${\mathbf{f}}_{\mathfrak{z}}^s({\mathbf{m}}_{\mathfrak{z}}(·))$ and ${\mathbf{g}}_{\mathfrak{z}}^s({\mathbf{m}}_{\mathfrak{z}}(·)),s=R,I,J,K$ are bounded and continuous, along with ${\mathbf{G}}_{\mathfrak{z}}^s$, ${\mathbf{H}}_{\mathfrak{z}}^s$ as the positive constants, in which

$$\begin{array}{c}\left\{\begin{array}{c}|{\mathbf{f}}_{\mathfrak{z}}^s({\mathbf{m}}_1)-{\mathbf{f}}_{\mathfrak{z}}^s({\mathbf{m}}_2)|\le {\mathbf{G}}_{\mathfrak{z}}^s|{\mathbf{m}}_1-{\mathbf{m}}_2|,\hfill \\ |{\mathbf{g}}_{\mathfrak{z}}^s({\mathbf{m}}_1)-{\mathbf{g}}_{\mathfrak{z}}^s({\mathbf{m}}_2)|\le {\mathbf{H}}_{\mathfrak{z}}^s|{\mathbf{m}}_1-{\mathbf{m}}_2|,\hfill \end{array}\right.\hfill \end{array}$$

(9)

for all ${\mathbf{m}}_1,{\mathbf{m}}_2\in \mathbb{R}$ and ${\mathbf{f}}_{\mathfrak{z}}^s(0)=0$, ${\mathbf{g}}_{\mathfrak{z}}^s(0)=0,s=R,I,J,K$.

Let $\mathbf{C}=diag\{{\mathbf{c}}_1,\dots ,{\mathbf{c}}_n\}\in {\mathbb{R}}^n$, ${\mathbf{A}}^R={({\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^R)}_{n\times n}\in {\mathbb{R}}^{n\times n}$, ${\mathbf{A}}^I={({\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^I)}_{n\times n}\in {\mathbb{R}}^{n\times n}$, ${\mathbf{A}}^J={({\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^J)}_{n\times n}\in {\mathbb{R}}^{n\times n}$, ${\mathbf{A}}^K={({\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^K)}_{n\times n}\in {\mathbb{R}}^{n\times n}$, ${\mathbf{B}}^R={({\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^R)}_{n\times n}\in {\mathbb{R}}^{n\times n}$, ${\mathbf{B}}^I={({\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^I)}_{n\times n}\in {\mathbb{R}}^{n\times n}$, ${\mathbf{B}}^J={({\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^J)}_{n\times n}\in {\mathbb{R}}^{n\times n}$, ${\mathbf{B}}^K={({\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^K)}_{n\times n}\in {\mathbb{R}}^{n\times n}$, ${\mathbf{f}}^R({\mathbf{m}}^R(t))={[{\mathbf{f}}_1^R({\mathbf{m}}_1^R(t)),\dots ,{\mathbf{f}}_n^R({\mathbf{m}}_n^R(t))]}^T\in {\mathbb{R}}^n$, ${\mathbf{f}}^I({\mathbf{m}}^I(t))={[{\mathbf{f}}_1^I({\mathbf{m}}_1^I(t)),\dots ,{\mathbf{f}}_n^I({\mathbf{m}}_n^I(t))]}^T\in {\mathbb{R}}^n$, ${\mathbf{f}}^J({\mathbf{m}}^J(t))={[{\mathbf{f}}_1^J({\mathbf{m}}_1^J(t)),\dots ,{\mathbf{f}}_n^J({\mathbf{m}}_n^J(t))]}^T\in {\mathbb{R}}^n$, ${\mathbf{f}}^K({\mathbf{m}}^K(t))={[{\mathbf{f}}_1^K({\mathbf{m}}_1^K(t)),\dots ,{\mathbf{f}}_n^K({\mathbf{m}}_n^K(t))]}^T\in {\mathbb{R}}^n$, ${\mathbf{g}}^R({\mathbf{m}}^R(t-\tau (t)))={[{\mathbf{g}}_1^R({\mathbf{m}}_1^R(t-\tau (t))),\dots ,{\mathbf{g}}_n^R({\mathbf{m}}_n^R(t-\tau (t)))]}^T\in {\mathbb{R}}^n$, ${\mathbf{g}}^I({\mathbf{m}}^I(t-\tau (t)))={[{\mathbf{g}}_1^I({\mathbf{m}}_1^I(t-\tau (t))),\dots ,{\mathbf{g}}_n^I({\mathbf{m}}_n^I(t-\tau (t)))]}^T\in {\mathbb{R}}^n$, ${\mathbf{g}}^J({\mathbf{m}}^J(t-\tau (t)))={[{\mathbf{g}}_1^J({\mathbf{m}}_1^J(t-\tau (t))),\dots ,{\mathbf{g}}_n^J({\mathbf{m}}_n^J(t-\tau (t)))]}^T\in {\mathbb{R}}^n$, ${\mathbf{g}}^K({\mathbf{m}}^K(t-\tau (t)))={[{\mathbf{g}}_1^K({\mathbf{m}}_1^K(t-\tau (t))),\dots ,{\mathbf{g}}_n^K({\mathbf{m}}_n^K(t-\tau (t)))]}^T\in {\mathbb{R}}^n$, ${\mathbf{u}}^R(t)={[{\mathbf{u}}_1^R(t),\dots ,{\mathbf{u}}_n^R(t)]}^T\in {\mathbb{R}}^n$, ${\mathbf{u}}^I(t)={[{\mathbf{u}}_1^I(t),\dots ,{\mathbf{u}}_n^I(t)]}^T\in {\mathbb{R}}^n$, ${\mathbf{u}}^J(t)={[{\mathbf{u}}_1^J(t),\dots ,{\mathbf{u}}_n^J(t)]}^T\in {\mathbb{R}}^n$, ${\mathbf{u}}^K(t)={[{\mathbf{u}}_1^K(t),\dots ,{\mathbf{u}}_n^K(t)]}^T\in {\mathbb{R}}^n$, ${\sigma }^R(t)={({\sigma }_{\mathfrak{x}\mathfrak{z}}^R(t))}_{n\times n}:\mathbb{R}\times {\mathbb{R}}^n\times {\mathbb{R}}^n\to {\mathbb{R}}^{n\times n}$, ${\sigma }^I(t)={({\sigma }_{\mathfrak{x}\mathfrak{z}}^I(t))}_{n\times n}:\mathbb{R}\times {\mathbb{R}}^n\times {\mathbb{R}}^n\to {\mathbb{R}}^{n\times n}$, ${\sigma }^J(t)={({\sigma }_{\mathfrak{x}\mathfrak{z}}^J(t))}_{n\times n}:\mathbb{R}\times {\mathbb{R}}^n\times {\mathbb{R}}^n\to {\mathbb{R}}^{n\times n}$, ${\sigma }^K(t)={({\sigma }_{\mathfrak{x}\mathfrak{z}}^K(t))}_{n\times n}:\mathbb{R}\times {\mathbb{R}}^n\times {\mathbb{R}}^n\to {\mathbb{R}}^{n\times n}$, ${\sigma }_{\mathfrak{x}\mathfrak{z}}^R(t)={\sigma }_{\mathfrak{x}\mathfrak{z}}^R(t,{\mathbf{m}}_{\mathfrak{z}}^R(t),{\mathbf{m}}_{\mathfrak{z}}^R(t-\tau (t)))$, ${\sigma }_{\mathfrak{x}\mathfrak{z}}^I(t)={\sigma }_{\mathfrak{x}\mathfrak{z}}^I(t,{\mathbf{m}}_{\mathfrak{z}}^I(t),{\mathbf{m}}_{\mathfrak{z}}^I(t-\tau (t)))$, ${\sigma }_{\mathfrak{x}\mathfrak{z}}^J(t)={\sigma }_{\mathfrak{x}\mathfrak{z}}^J(t,{\mathbf{m}}_{\mathfrak{z}}^J(t),{\mathbf{m}}_{\mathfrak{z}}^J(t-\tau (t)))$, ${\sigma }_{\mathfrak{x}\mathfrak{z}}^K(t)={\sigma }_{\mathfrak{x}\mathfrak{z}}^K(t,{\mathbf{m}}_{\mathfrak{z}}^K(t),{\mathbf{m}}_{\mathfrak{z}}^K(t-\tau (t)))$.

Now, we can express Model (7) as

$$\begin{array}{c}\left\{\begin{array}{cc}d{\mathbf{m}}^R(t)=\hfill & [-\mathbf{C}{\mathbf{m}}^R(t)+{\mathbf{A}}^R{\mathbf{f}}^R({\mathbf{m}}^R(t))-{\mathbf{A}}^I{\mathbf{f}}^I({\mathbf{m}}^I(t))-{\mathbf{A}}^J{\mathbf{f}}^J({\mathbf{m}}^J(t))-{\mathbf{A}}^K{\mathbf{f}}^K({\mathbf{m}}^K(t))\hfill \\ & +{\mathbf{B}}^R{\mathbf{g}}^R({\mathbf{m}}^R(t-\tau (t)))-{\mathbf{B}}^I{\mathbf{g}}^I({\mathbf{m}}^I(t-\tau (t)))-{\mathbf{B}}^J{\mathbf{g}}^J({\mathbf{m}}^J(t-\tau (t)))\hfill \\ & -{\mathbf{B}}^K{\mathbf{g}}^K({\mathbf{m}}^K(t-\tau (t)))+{\mathbf{u}}^R(t)]dt+{\sigma }^R(t)dw(t),\hfill \\ d{\mathbf{m}}^I(t)=\hfill & [-\mathbf{C}{\mathbf{m}}^I(t)+{\mathbf{A}}^R{\mathbf{f}}^I({\mathbf{m}}^I(t))+{\mathbf{A}}^I{\mathbf{f}}^R({\mathbf{m}}^R(t))+{\mathbf{A}}^J{\mathbf{f}}^K({\mathbf{m}}^K(t))-{\mathbf{A}}^K{\mathbf{f}}^J({\mathbf{m}}^J(t))\hfill \\ & +{\mathbf{B}}^R{\mathbf{g}}^I({\mathbf{m}}^I(t-\tau (t)))+{\mathbf{B}}^I{\mathbf{g}}^R({\mathbf{m}}^R(t-\tau (t)))+{\mathbf{B}}^J{\mathbf{g}}^K({\mathbf{m}}^K(t-\tau (t)))\hfill \\ & -{\mathbf{B}}^K{\mathbf{g}}^J({\mathbf{m}}^J(t-\tau (t)))+{\mathbf{u}}^I(t)]dt+{\sigma }^I(t)dw(t),\hfill \\ d{\mathbf{m}}^J(t)=\hfill & [-\mathbf{C}{\mathbf{m}}^J(t)+{\mathbf{A}}^R{\mathbf{f}}^J({\mathbf{m}}^J(t))+{\mathbf{A}}^J{\mathbf{f}}^R({\mathbf{m}}^R(t))+{\mathbf{A}}^K{\mathbf{f}}^I({\mathbf{m}}^I(t))-{\mathbf{A}}^I{\mathbf{f}}^K({\mathbf{m}}^K(t))\hfill \\ & +{\mathbf{B}}^R{\mathbf{g}}^J({\mathbf{m}}^J(t-\tau (t)))+{\mathbf{B}}^J{\mathbf{g}}^R({\mathbf{m}}^R(t-\tau (t)))+{\mathbf{B}}^K{\mathbf{g}}^I({\mathbf{m}}^I(t-\tau (t)))\hfill \\ & -{\mathbf{B}}^I{\mathbf{g}}^K({\mathbf{m}}^K(t-\tau (t)))+{\mathbf{u}}^J(t)]dt+{\sigma }^J(t)dw(t),\hfill \\ d{\mathbf{m}}^K(t)=\hfill & [-\mathbf{C}{\mathbf{m}}^K(t)+{\mathbf{A}}^R{\mathbf{f}}^K({\mathbf{m}}^K(t))+{\mathbf{A}}^I{\mathbf{f}}^J({\mathbf{m}}^J(t))+{\mathbf{A}}^K{\mathbf{f}}^R({\mathbf{m}}^R(t))-{\mathbf{A}}^J{\mathbf{f}}^I({\mathbf{m}}^I(t))\hfill \\ & +{\mathbf{B}}^R{\mathbf{g}}^K({\mathbf{m}}^K(t-\tau (t)))+{\mathbf{B}}^I{\mathbf{g}}^J({\mathbf{m}}^J(t-\tau (t)))+{\mathbf{B}}^K{\mathbf{g}}^R({\mathbf{m}}^R(t-\tau (t)))\hfill \\ & -{\mathbf{B}}^J{\mathbf{g}}^I({\mathbf{m}}^I(t-\tau (t)))+{\mathbf{u}}^K(t)]dt+{\sigma }^K(t)dw(t),\hfill \end{array}\right.\hfill \end{array}$$

(10)

Denote

$$\begin{array}{cc}\hfill \overline{\mathbf{m}}(t)=& {[{({\mathbf{m}}^R(t))}^T,{({\mathbf{m}}^I(t))}^T,{({\mathbf{m}}^J(t))}^T,{({\mathbf{m}}^K(t))}^T]}^T,\hfill \\ \hfill \overline{\mathbf{f}}(\overline{\mathbf{m}}(t))=& [({\mathbf{f}}^R{({\mathbf{m}}^R(t))}^T,({\mathbf{f}}^I{({\mathbf{m}}^I(t))}^T,({\mathbf{f}}^J{({\mathbf{m}}^J(t))}^T,{({\mathbf{f}}^K{({\mathbf{m}}^K(t))}^T]}^T,\hfill \\ \hfill \overline{\mathbf{g}}(\overline{\mathbf{m}}(t-\tau (t)))=& [({\mathbf{g}}^R{({\mathbf{m}}^R(t-\tau (t)))}^T,({\mathbf{g}}^I{({\mathbf{m}}^I(t-\tau (t)))}^T,({\mathbf{g}}^J{({\mathbf{m}}^J(t-\tau (t)))}^T,{({\mathbf{g}}^K{({\mathbf{m}}^K(t-\tau (t)))}^T]}^T,\hfill \\ \hfill \overline{\sigma }(t)=& {[{({\sigma }^R(t))}^T,{({\sigma }^I(t))}^T,{({\sigma }^J(t))}^T,{({\sigma }^K(t))}^T]}^T,\hfill \\ \hfill \overline{\mathbf{U}}=& {[{({\mathbf{u}}^R(t))}^T,{({\mathbf{u}}^I(t))}^T,{({\mathbf{u}}^J(t))}^T,{({\mathbf{u}}^K(t))}^T]}^T,\overline{\mathbf{C}}=diag\{\mathbf{C},\mathbf{C},\mathbf{C},\mathbf{C}\},\hfill \\ \hfill \overline{\mathbf{A}}=& \left[\begin{array}{cccc}{\mathbf{A}}^R& -{\mathbf{A}}^I& -{\mathbf{A}}^J& -{\mathbf{A}}^K\\ {\mathbf{A}}^I& {\mathbf{A}}^R& -{\mathbf{A}}^K& {\mathbf{A}}^J\\ {\mathbf{A}}^J& {\mathbf{A}}^K& {\mathbf{A}}^R& -{\mathbf{A}}^I\\ {\mathbf{A}}^K& -{\mathbf{A}}^J& {\mathbf{A}}^I& {\mathbf{A}}^R\end{array}\right],\overline{\mathbf{B}}=\left[\begin{array}{cccc}{\mathbf{B}}^R& -{\mathbf{B}}^I& -{\mathbf{B}}^J& -{\mathbf{B}}^K\\ {\mathbf{B}}^I& {\mathbf{B}}^R& -{\mathbf{B}}^K& {\mathbf{B}}^J\\ {\mathbf{B}}^J& {\mathbf{B}}^K& {\mathbf{B}}^R& -{\mathbf{B}}^I\\ {\mathbf{B}}^K& -{\mathbf{B}}^J& {\mathbf{B}}^I& {\mathbf{B}}^R\end{array}\right].\hfill \end{array}$$

Therefore, the model in Equation (10) can be rewritten as

$$\begin{array}{cc}d\overline{\mathbf{m}}(t)=\hfill & [-\overline{\mathbf{C}}\overline{\mathbf{m}}(t)+\overline{\mathbf{A}}\overline{\mathbf{f}}(\overline{\mathbf{m}}(t))+\overline{\mathbf{B}}\overline{\mathbf{g}}(\overline{\mathbf{m}}(t-\tau (t)))+\overline{\mathbf{U}}]dt+\overline{\sigma }(t)dw(t).\hfill \end{array}$$

(11)

Note that the model in Equation (11) has the following initial condition

$$\begin{array}{c}\overline{\mathbf{m}}(t)=\varphi (t),t\in [-\tau ,0],\hfill \end{array}$$

(12)

where $\varphi (t)={[{\phi }^R(t),{\phi }^I(t),{\phi }^J(t),{\phi }^K(t)]}^T$, with $\parallel {\phi }^R(t)\parallel =\underset{-\tau \le t\le 0}{sup}|{\phi }^R(t)|$, $\parallel {\phi }^I(t)\parallel =\underset{-\tau \le t\le 0}{sup}|{\phi }^I(t)|,$ $\parallel {\phi }^J(t)\parallel =\underset{-\tau \le t\le 0}{sup}|{\phi }^J(t)|,$ $\parallel {\phi }^K(t)\parallel =\underset{-\tau \le t\le 0}{sup}|{\phi }^K(t)|$.

A3: [13] There exist nonnegative constants ${\widehat{\alpha }}_{\mathfrak{x}\mathfrak{z}},{\check{\alpha }}_{\mathfrak{x}\mathfrak{z}},{\overline{\alpha }}_{\mathfrak{x}\mathfrak{z}},{\tilde{\alpha }}_{\mathfrak{x}\mathfrak{z}}$, ${\widehat{\beta }}_{\mathfrak{x}\mathfrak{z}},{\check{\beta }}_{\mathfrak{x}\mathfrak{z}},{\overline{\beta }}_{\mathfrak{x}\mathfrak{z}},{\tilde{\beta }}_{\mathfrak{x}\mathfrak{z}}$ such that

$$\begin{array}{cc}{[{\sigma }_{\mathfrak{x}\mathfrak{z}}^R(t,{\acute{\mathbf{m}}}^R,{\stackrel{`}{\mathbf{m}}}^R)-{\sigma }_{\mathfrak{x}\mathfrak{z}}^R(t,{\acute{\overline{\mathbf{m}}}}^R,{\stackrel{`}{\overline{\mathbf{m}}}}^R)]}^2\le \hfill & {\widehat{\alpha }}_{\mathfrak{x}\mathfrak{z}}{({\acute{\mathbf{m}}}^R-{\acute{\overline{\mathbf{m}}}}^R)}^2+{\widehat{\beta }}_{\mathfrak{x}\mathfrak{z}}{({\stackrel{`}{\mathbf{m}}}^R-{\stackrel{`}{\overline{\mathbf{m}}}}^R)}^2,\hfill \\ {\sigma }_{\mathfrak{x}\mathfrak{z}}^I(t,{\acute{\mathbf{m}}}^I,{\stackrel{`}{\mathbf{m}}}^I)-{\sigma }_{\mathfrak{x}\mathfrak{z}}^I(t,{\acute{\overline{\mathbf{m}}}}^I,{\stackrel{`}{\overline{\mathbf{m}}}}^I){]}^2\le \hfill & {\check{\alpha }}_{\mathfrak{x}\mathfrak{z}}{({\acute{\mathbf{m}}}^I-{\acute{\overline{\mathbf{m}}}}^I)}^2+{\check{\beta }}_{\mathfrak{x}\mathfrak{z}}{({\stackrel{`}{\mathbf{m}}}^I-{\stackrel{`}{\overline{\mathbf{m}}}}^I)}^2,\hfill \\ {\sigma }_{\mathfrak{x}\mathfrak{z}}^J(t,{\acute{\mathbf{m}}}^J,{\stackrel{`}{\mathbf{m}}}^J)-{\sigma }_{\mathfrak{x}\mathfrak{z}}^J(t,{\acute{\overline{\mathbf{m}}}}^J,{\stackrel{`}{\overline{\mathbf{m}}}}^J){]}^2\le \hfill & {\overline{\alpha }}_{\mathfrak{x}\mathfrak{z}}{({\acute{\mathbf{m}}}^J-{\acute{\overline{\mathbf{m}}}}^J)}^2+{\overline{\beta }}_{\mathfrak{x}\mathfrak{z}}{({\stackrel{`}{\mathbf{m}}}^J-{\stackrel{`}{\overline{\mathbf{m}}}}^J)}^2,\hfill \\ {\sigma }_{\mathfrak{x}\mathfrak{z}}^K(t,{\acute{\mathbf{m}}}^K,{\stackrel{`}{\mathbf{m}}}^K)-{\sigma }_{\mathfrak{x}\mathfrak{z}}^K(t,{\acute{\overline{\mathbf{m}}}}^K,{\stackrel{`}{\overline{\mathbf{m}}}}^K){]}^2\le \hfill & {\tilde{\alpha }}_{\mathfrak{x}\mathfrak{z}}{({\acute{\mathbf{m}}}^K-{\acute{\overline{\mathbf{m}}}}^K)}^2+{\tilde{\beta }}_{\mathfrak{x}\mathfrak{z}}{({\stackrel{`}{\mathbf{m}}}^K-{\stackrel{`}{\overline{\mathbf{m}}}}^K)}^2,\hfill \end{array}$$

for all ${\acute{\mathbf{m}}}^R,{\stackrel{`}{\mathbf{m}}}^R,{\acute{\overline{\mathbf{m}}}}^R,{\stackrel{`}{\overline{\mathbf{m}}}}^R$, ${\acute{\mathbf{m}}}^I,{\stackrel{`}{\mathbf{m}}}^I,{\acute{\overline{\mathbf{m}}}}^I,{\stackrel{`}{\overline{\mathbf{m}}}}^I$, ${\acute{\mathbf{m}}}^J,{\stackrel{`}{\mathbf{m}}}^J,{\acute{\overline{\mathbf{m}}}}^J,{\stackrel{`}{\overline{\mathbf{m}}}}^J$, ${\acute{\mathbf{m}}}^K,{\stackrel{`}{\mathbf{m}}}^K,{\acute{\overline{\mathbf{m}}}}^K,{\stackrel{`}{\overline{\mathbf{m}}}}^K\in \mathbb{R},\mathfrak{x},\mathfrak{z}\in N$.

A4: [13] ${\sigma }_{\mathfrak{x}\mathfrak{z}}^R(t,0,0)=0$, ${\sigma }_{\mathfrak{x}\mathfrak{z}}^I(t,0,0)=0$, ${\sigma }_{\mathfrak{x}\mathfrak{z}}^J(t,0,0)=0$, ${\sigma }_{\mathfrak{x}\mathfrak{z}}^K(t,0,0)=0$, for all $\mathfrak{x},\mathfrak{z}\in N$.

Definition 1.

[13] There existence of positive scalars $\alpha >0,\beta >0,\gamma >0$, the SMQVNN model in Equation (2) has a trivial solution that is mean-square exp-ISS, in which

$$\begin{array}{c}{\mathbb{E}[|\mathbf{m}(t;\phi )|}^2]\le \alpha e^{-\beta t}{\mathbb{E}[\parallel \phi \parallel }^2{]+\gamma \parallel \mathbf{u}\parallel }_{\infty }^2,\hfill \end{array}$$

(13)

for any $\phi \in {\mathcal{L}}_{{\mathcal{F}}_0}^2([-\tau ,0];{\mathbb{Q}}^n),\mathbf{u}(t)\in {\ell }_{\infty }$.

Now, consider the initial data $\overline{\mathbf{m}}(t)=\varphi (t)$ on $-\tau \le t\le 0$ in ${\mathcal{L}}_{{\mathcal{F}}_0}^2([-\tau ,0];{\mathbb{R}}^{4n})$ has the solution of $\overline{\mathbf{m}}(t;\varphi )$. Obviously, under assumptions A2 and A4, subject to the input $\overline{\mathbf{U}}=0$, the model in Equation (11) has a trivial solution, or a zero solution $\overline{\mathbf{m}}(t;0)=0$.

3. Main Results

We derive the sufficient conditions that assure the mean-square exp-ISS with respect to the trivial solution of the SMQVNN model in Equation (2).

Theorem 1.

Suppose that A1–A4 hold, subject to the existence of positive scalars $\lambda ,{\mathbf{p}}_{\mathfrak{x}},{\mathbf{q}}_{\mathfrak{x}},{\mathbf{r}}_{\mathfrak{x}},{\mathbf{s}}_{\mathfrak{x}}$, ${\mathbf{d}}_{\mathfrak{x}},{\mathbf{h}}_{\mathfrak{x}},{\mathbf{u}}_{\mathfrak{x}},{\mathbf{v}}_{\mathfrak{x}},\mathfrak{x}\in N$, the SMQVNN model in Equation (2) has a trivial solution, which is mean-square exp-ISS, in which

$$\begin{array}{cc}2{\mathbf{p}}_{\mathfrak{x}}{\mathbf{c}}_{\mathfrak{x}}\ge \hfill & \lambda {\mathbf{p}}_{\mathfrak{x}}+\sum _{\mathfrak{z}=1}^n{\mathbf{p}}_{\mathfrak{z}}{\widehat{\alpha }}_{\mathfrak{z}\mathfrak{x}}+{\mathbf{d}}_{\mathfrak{x}}+{\mathbf{p}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{G}}_{\mathfrak{z}}^R+{\mathbf{p}}_{\mathfrak{z}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{z}\mathfrak{x}}^R|{\mathbf{G}}_{\mathfrak{x}}^R+{\mathbf{p}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{G}}_{\mathfrak{z}}^I\hfill \\ & +{\mathbf{p}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^J|{\mathbf{G}}_{\mathfrak{z}}^J+{\mathbf{p}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^K|{\mathbf{G}}_{\mathfrak{z}}^K+{\mathbf{p}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{H}}_{\mathfrak{z}}^R+{\mathbf{p}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{H}}_{\mathfrak{z}}^I\hfill \\ & +{\mathbf{p}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^J|{\mathbf{H}}_{\mathfrak{z}}^J+{\mathbf{p}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^K|{\mathbf{H}}_{\mathfrak{z}}^K+{\mathbf{p}}_{\mathfrak{x}}+{\mathbf{q}}_{\mathfrak{z}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{z}\mathfrak{x}}^I|{\mathbf{G}}_{\mathfrak{x}}^R+{\mathbf{r}}_{\mathfrak{z}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{z}\mathfrak{x}}^J|{\mathbf{G}}_{\mathfrak{x}}^I+{\mathbf{s}}_{\mathfrak{z}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{z}\mathfrak{x}}^K|{\mathbf{G}}_{\mathfrak{x}}^K,\hfill \end{array}$$

(14)

$$\begin{array}{cc}(1-\mu ){\mathbf{d}}_{\mathfrak{x}}\ge \hfill & e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{p}}_{\mathfrak{z}}{\widehat{\beta }}_{\mathfrak{z}\mathfrak{x}}+e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{p}}_{\mathfrak{z}}|{\tilde{\mathbf{b}}}_{\mathfrak{z}\mathfrak{x}}^R|{\mathbf{H}}_{\mathfrak{x}}^R+e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{q}}_{\mathfrak{z}}|{\tilde{\mathbf{b}}}_{\mathfrak{z}\mathfrak{x}}^I|{\mathbf{H}}_{\mathfrak{x}}^R+e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{r}}_{\mathfrak{z}}|{\tilde{\mathbf{b}}}_{\mathfrak{z}\mathfrak{x}}^J|{\mathbf{H}}_{\mathfrak{x}}^R+e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{s}}_{\mathfrak{z}}|{\tilde{\mathbf{b}}}_{\mathfrak{z}\mathfrak{x}}^K|{\mathbf{H}}_{\mathfrak{x}}^R,\hfill \end{array}$$

(15)

$$\begin{array}{cc}2{\mathbf{q}}_{\mathfrak{x}}{\mathbf{c}}_{\mathfrak{x}}\ge \hfill & \lambda {\mathbf{q}}_{\mathfrak{x}}+\sum _{\mathfrak{z}=1}^n{\mathbf{q}}_{\mathfrak{z}}{\check{\alpha }}_{\mathfrak{z}\mathfrak{x}}+{\mathbf{h}}_{\mathfrak{x}}+{\mathbf{q}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{G}}_{\mathfrak{z}}^I+{\mathbf{q}}_{\mathfrak{z}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{z}\mathfrak{x}}^R|{\mathbf{G}}_{\mathfrak{x}}^I+{\mathbf{p}}_{\mathfrak{z}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{z}\mathfrak{x}}^I|{\mathbf{G}}_{\mathfrak{x}}^I\hfill \\ & +{\mathbf{q}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{G}}_{\mathfrak{z}}^R+{\mathbf{q}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^J|{\mathbf{G}}_{\mathfrak{z}}^K+{\mathbf{q}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^K|{\mathbf{G}}_{\mathfrak{z}}^J+{\mathbf{q}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{H}}_{\mathfrak{z}}^I\hfill \\ & +{\mathbf{q}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{H}}_{\mathfrak{z}}^R+{\mathbf{q}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^J|{\mathbf{H}}_{\mathfrak{z}}^K+{\mathbf{q}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^K|{\mathbf{H}}_{\mathfrak{z}}^J+{\mathbf{q}}_{\mathfrak{x}}+{\mathbf{r}}_{\mathfrak{z}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{z}\mathfrak{x}}^K|{\mathbf{G}}_{\mathfrak{x}}^I+{\mathbf{s}}_{\mathfrak{z}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{z}\mathfrak{x}}^J|{\mathbf{G}}_{\mathfrak{x}}^I,\hfill \end{array}$$

(16)

$$\begin{array}{cc}(1-\mu ){\mathbf{h}}_{\mathfrak{x}}\ge \hfill & e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{q}}_{\mathfrak{z}}{\check{\beta }}_{\mathfrak{z}\mathfrak{x}}+e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{p}}_{\mathfrak{z}}|{\tilde{\mathbf{b}}}_{\mathfrak{z}\mathfrak{x}}^I|{\mathbf{H}}_{\mathfrak{x}}^I+e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{q}}_{\mathfrak{z}}|{\tilde{\mathbf{b}}}_{\mathfrak{z}\mathfrak{x}}^R|{\mathbf{H}}_{\mathfrak{x}}^I+e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{r}}_{\mathfrak{z}}|{\tilde{\mathbf{b}}}_{\mathfrak{z}\mathfrak{x}}^K|{\mathbf{H}}_{\mathfrak{x}}^I+e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{s}}_{\mathfrak{z}}|{\tilde{\mathbf{b}}}_{\mathfrak{z}\mathfrak{x}}^J|{\mathbf{H}}_{\mathfrak{x}}^I,\hfill \end{array}$$

(17)

$$\begin{array}{cc}2{\mathbf{r}}_{\mathfrak{x}}{\mathbf{c}}_{\mathfrak{x}}\ge \hfill & \lambda {\mathbf{r}}_{\mathfrak{x}}+\sum _{\mathfrak{z}=1}^n{\mathbf{r}}_{\mathfrak{z}}{\overline{\alpha }}_{\mathfrak{z}\mathfrak{x}}+{\mathbf{u}}_{\mathfrak{x}}+{\mathbf{r}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{G}}_{\mathfrak{z}}^J+{\mathbf{r}}_{\mathfrak{z}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{z}\mathfrak{x}}^R|{\mathbf{G}}_{\mathfrak{x}}^J+{\mathbf{p}}_{\mathfrak{z}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{z}\mathfrak{x}}^J|{\mathbf{G}}_{\mathfrak{x}}^J\hfill \\ & +{\mathbf{q}}_{\mathfrak{z}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{z}\mathfrak{x}}^K|{\mathbf{G}}_{\mathfrak{x}}^J+{\mathbf{r}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^J|{\mathbf{G}}_{\mathfrak{z}}^R+{\mathbf{r}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^K|{\mathbf{G}}_{\mathfrak{z}}^I+{\mathbf{r}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{G}}_{\mathfrak{z}}^K\hfill \\ & +{\mathbf{r}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{H}}_{\mathfrak{z}}^J+{\mathbf{r}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^J|{\mathbf{H}}_{\mathfrak{z}}^R+{\mathbf{r}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^K|{\mathbf{H}}_{\mathfrak{z}}^I+{\mathbf{r}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{H}}_{\mathfrak{z}}^K+{\mathbf{r}}_{\mathfrak{x}}+{\mathbf{s}}_{\mathfrak{z}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{z}\mathfrak{x}}^I|{\mathbf{G}}_{\mathfrak{x}}^J,\hfill \end{array}$$

(18)

$$\begin{array}{cc}(1-\mu ){\mathbf{u}}_{\mathfrak{x}}\ge \hfill & e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{r}}_{\mathfrak{z}}{\overline{\beta }}_{\mathfrak{z}\mathfrak{x}}+e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{p}}_{\mathfrak{z}}|{\tilde{\mathbf{b}}}_{\mathfrak{z}\mathfrak{x}}^J|{\mathbf{H}}_{\mathfrak{x}}^J+e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{q}}_{\mathfrak{z}}|{\tilde{\mathbf{b}}}_{\mathfrak{z}\mathfrak{x}}^K|{\mathbf{H}}_{\mathfrak{x}}^J+e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{r}}_{\mathfrak{z}}|{\tilde{\mathbf{b}}}_{\mathfrak{z}\mathfrak{x}}^R|{\mathbf{H}}_{\mathfrak{x}}^J+e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{s}}_{\mathfrak{z}}|{\tilde{\mathbf{b}}}_{\mathfrak{z}\mathfrak{x}}^I|{\mathbf{H}}_{\mathfrak{x}}^J,\hfill \end{array}$$

(19)

$$\begin{array}{cc}2{\mathbf{s}}_{\mathfrak{x}}{\mathbf{c}}_{\mathfrak{x}}\ge \hfill & \lambda {\mathbf{s}}_{\mathfrak{x}}+\sum _{\mathfrak{z}=1}^n{\mathbf{s}}_{\mathfrak{z}}{\tilde{\alpha }}_{\mathfrak{z}\mathfrak{x}}+{\mathbf{v}}_{\mathfrak{x}}+{\mathbf{s}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{G}}_{\mathfrak{z}}^K+{\mathbf{s}}_{\mathfrak{z}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{z}\mathfrak{x}}^R|{\mathbf{G}}_{\mathfrak{x}}^K+{\mathbf{p}}_{\mathfrak{z}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{z}\mathfrak{x}}^K|{\mathbf{G}}_{\mathfrak{x}}^K\hfill \\ & +{\mathbf{q}}_{\mathfrak{z}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{z}\mathfrak{x}}^J|{\mathbf{G}}_{\mathfrak{x}}^K+{\mathbf{r}}_{\mathfrak{z}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{G}}_{\mathfrak{x}}^K+{\mathbf{s}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{G}}_{\mathfrak{z}}^I+{\mathbf{s}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^K|{\mathbf{G}}_{\mathfrak{z}}^R\hfill \\ & +{\mathbf{s}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^J|{\mathbf{G}}_{\mathfrak{z}}^I+{\mathbf{s}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{H}}_{\mathfrak{z}}^K+{\mathbf{s}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{H}}_{\mathfrak{z}}^J+{\mathbf{s}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^K|{\mathbf{H}}_{\mathfrak{z}}^R+{\mathbf{s}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^J|{\mathbf{H}}_{\mathfrak{z}}^I+{\mathbf{s}}_{\mathfrak{x}},\hfill \end{array}$$

(20)

$$\begin{array}{cc}(1-\mu ){\mathbf{v}}_{\mathfrak{x}}\ge \hfill & e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{s}}_{\mathfrak{z}}{\tilde{\beta }}_{\mathfrak{z}\mathfrak{x}}+e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{p}}_{\mathfrak{z}}|{\tilde{\mathbf{b}}}_{\mathfrak{z}\mathfrak{x}}^K|{\mathbf{H}}_{\mathfrak{x}}^K+e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{q}}_{\mathfrak{z}}|{\tilde{\mathbf{b}}}_{\mathfrak{z}\mathfrak{x}}^J|{\mathbf{H}}_{\mathfrak{x}}^K+e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{r}}_{\mathfrak{z}}|{\tilde{\mathbf{b}}}_{\mathfrak{z}\mathfrak{x}}^I|{\mathbf{H}}_{\mathfrak{x}}^K+e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{s}}_{\mathfrak{z}}|{\tilde{\mathbf{b}}}_{\mathfrak{z}\mathfrak{x}}^R|{\mathbf{H}}_{\mathfrak{x}}^K.\hfill \end{array}$$

(21)

Proof. 

A Lyapunov functional is formulated as

$$\begin{array}{c}\mathcal{V}(t,\overline{\mathbf{m}}(t))=e^{\lambda t}\sum _{\mathfrak{x}=1}^{4n}{\xi }_{\mathfrak{x}}{\overline{\mathbf{m}}}_{\mathfrak{x}}^2(t)+{\int }_{t-\tau (t)}^t{e}^{\lambda s}\sum _{\mathfrak{x}=1}^{4n}{\zeta }_{\mathfrak{x}}{\overline{\mathbf{m}}}_{\mathfrak{x}}^2(s)ds,\hfill \end{array}$$

(22)

where

$$\begin{array}{cc}{\xi }_{\mathfrak{x}}=\hfill & \left\{\begin{array}{c}{\mathbf{p}}_{\mathfrak{x}},\mathfrak{x}=1,2,\dots ,n,\hfill \\ {\mathbf{q}}_{\mathfrak{x}},\mathfrak{x}=n+1,n+2,\dots ,2n,\hfill \\ {\mathbf{r}}_{\mathfrak{x}},\mathfrak{x}=2n+1,2n+2,\dots ,3n,\hfill \\ {\mathbf{s}}_{\mathfrak{x}},\mathfrak{x}=3n+1,3n+2,\dots ,4n,\hfill \end{array}\right.,\hfill \\ {\zeta }_{\mathfrak{x}}=\hfill & \left\{\begin{array}{c}{\mathbf{d}}_{\mathfrak{x}},\mathfrak{x}=1,2,\dots ,n,\hfill \\ {\mathbf{h}}_{\mathfrak{x}},\mathfrak{x}=n+1,n+2,\dots ,2n,\hfill \\ {\mathbf{u}}_{\mathfrak{x}},\mathfrak{x}=2n+1,2n+2,\dots ,3n,\hfill \\ {\mathbf{v}}_{\mathfrak{x}},\mathfrak{x}=3n+1,3n+2,\dots ,4n.\hfill \end{array}\right.\hfill \end{array}$$

Then,

$$\begin{array}{c}\mathcal{V}(t,\overline{\mathbf{m}}(t))={\mathcal{V}}_1(t,{\mathbf{m}}^R(t))+{\mathcal{V}}_1(t,{\mathbf{m}}^I(t))+{\mathcal{V}}_1(t,{\mathbf{m}}^J(t))+{\mathcal{V}}_1(t,{\mathbf{m}}^K(t)),\hfill \end{array}$$

(23)

where

$$\begin{array}{cc}{\mathcal{V}}_1(t,{\mathbf{m}}^R(t))=\hfill & e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{p}}_{\mathfrak{x}}{{\mathbf{m}}^R}_{\mathfrak{x}}^2(t)+{\int }_{t-\tau (t)}^t{e}^{\lambda s}\sum _{\mathfrak{x}=1}^n{\mathbf{d}}_{\mathfrak{x}}{{\mathbf{m}}^R}_{\mathfrak{x}}^2(s)ds,\hfill \\ {\mathcal{V}}_2(t,{\mathbf{m}}^I(t))=\hfill & e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{q}}_{\mathfrak{x}}{{\mathbf{m}}^I}_{\mathfrak{x}}^2(t)+{\int }_{t-\tau (t)}^t{e}^{\lambda s}\sum _{\mathfrak{x}=1}^n{\mathbf{h}}_{\mathfrak{x}}{{\mathbf{m}}^I}_{\mathfrak{x}}^2(s)ds,\hfill \\ {\mathcal{V}}_3(t,{\mathbf{m}}^J(t))=\hfill & e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{r}}_{\mathfrak{x}}{{\mathbf{m}}^J}_{\mathfrak{x}}^2(t)+{\int }_{t-\tau (t)}^t{e}^{\lambda s}\sum _{\mathfrak{x}=1}^n{\mathbf{u}}_{\mathfrak{x}}{{\mathbf{m}}^J}_{\mathfrak{x}}^2(s)ds,\hfill \\ {\mathcal{V}}_4(t,{\mathbf{m}}^K(t))=\hfill & e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{s}}_{\mathfrak{x}}{{\mathbf{m}}^K}_{\mathfrak{x}}^2(t)+{\int }_{t-\tau (t)}^t{e}^{\lambda s}\sum _{\mathfrak{x}=1}^n{\mathbf{v}}_{\mathfrak{x}}{{\mathbf{m}}^K}_{\mathfrak{x}}^2(s)ds.\hfill \end{array}$$

Based on the It $\widehat{o}$’s formula, we have

$$\begin{array}{c}d\mathcal{V}(t,\overline{\mathbf{m}}(t))=\mathcal{L}\mathcal{V}(t,\overline{\mathbf{m}}(t))dt+{\mathcal{V}}_{\overline{\mathbf{m}}}(t,\overline{\mathbf{m}}(t))\overline{\sigma }(t)dw(t),\hfill \end{array}$$

(24)

where

$$\begin{array}{c}{\mathcal{V}}_{\overline{\mathbf{m}}}(t,\overline{\mathbf{m}}(t))=\left(\frac{\partial \mathcal{V}(t,\overline{\mathbf{m}}(t))}{\partial {\overline{\mathbf{m}}}_1},\dots ,\frac{\partial \mathcal{V}(t,\overline{\mathbf{m}}(t))}{\partial {\overline{\mathbf{m}}}_{4n}}\right).\hfill \end{array}$$

where the It $\widehat{o}$’s operator is $\mathcal{L}$, such that

$$\begin{array}{cc}\mathcal{L}{\mathcal{V}}_1(t,{\mathbf{m}}^R(t))=\hfill & \lambda e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{p}}_{\mathfrak{x}}{{\mathbf{m}}^R}_{\mathfrak{x}}^2(t)+2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{p}}_{\mathfrak{x}}{{\mathbf{m}}^R}_{\mathfrak{x}}(t)[-{\mathbf{c}}_{\mathfrak{x}}{{\mathbf{m}}^R}_{\mathfrak{x}}(t)+\sum _{\mathfrak{z}=1}^n{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^R{\mathbf{f}}_{\mathfrak{z}}^R({\mathbf{m}}_{\mathfrak{z}}^R(t))\hfill \\ & -\sum _{\mathfrak{z}=1}^n{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^I{\mathbf{f}}_{\mathfrak{z}}^I({\mathbf{m}}_{\mathfrak{z}}^I(t))-\sum _{\mathfrak{z}=1}^n{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^J{\mathbf{f}}_{\mathfrak{z}}^J({\mathbf{m}}_{\mathfrak{z}}^J(t))-\sum _{\mathfrak{z}=1}^n{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^K{\mathbf{f}}_{\mathfrak{z}}^K({\mathbf{m}}_{\mathfrak{z}}^K(t))\hfill \\ & +\sum _{\mathfrak{z}=1}^n{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^R{\mathbf{g}}_{\mathfrak{z}}^R({\mathbf{m}}_{\mathfrak{z}}^R(t-\tau (t)))-\sum _{\mathfrak{z}=1}^n{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^I{\mathbf{g}}_{\mathfrak{z}}^I({\mathbf{m}}_{\mathfrak{z}}^I(t-\tau (t)))-\sum _{\mathfrak{z}=1}^n{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^J{\mathbf{g}}_{\mathfrak{z}}^J({\mathbf{m}}_{\mathfrak{z}}^J(t-\tau (t)))\hfill \\ & -\sum _{\mathfrak{z}=1}^n{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^K{\mathbf{g}}_{\mathfrak{z}}^K({\mathbf{m}}_{\mathfrak{z}}^K(t-\tau (t)))+{\mathbf{u}}_{\mathfrak{x}}^R(t)]+e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{p}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n[{{\sigma }^R}_{\mathfrak{x}\mathfrak{z}}^2{(t,{\mathbf{m}}_{\mathfrak{z}}^R(t),{\mathbf{m}}_{\mathfrak{z}}^R(t-\tau (t))]}^2\hfill \\ & +e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{d}}_{\mathfrak{x}}{{\mathbf{m}}^R}_{\mathfrak{x}}^2(t)-(1-\dot{\tau }(t))e^{\lambda (t-\tau (t))}\sum _{\mathfrak{x}=1}^n{\mathbf{d}}_{\mathfrak{x}}{{\mathbf{m}}^R}_{\mathfrak{x}}^2(t-\tau (t)).\hfill \end{array}$$

(25)

According to A2 and A3, we have

$$\begin{array}{cc}\mathcal{L}{\mathcal{V}}_1(t,{\mathbf{m}}^R(t))=\hfill & e^{\lambda t}\sum _{\mathfrak{x}=1}^n(\lambda {\mathbf{p}}_{\mathfrak{x}}-2{\mathbf{p}}_{\mathfrak{x}}{\mathbf{c}}_{\mathfrak{x}}+\sum _{\mathfrak{z}=1}^n{\mathbf{p}}_{\mathfrak{z}}{\widehat{\alpha }}_{\mathfrak{z}\mathfrak{x}}+{\mathbf{d}}_{\mathfrak{x}}){{\mathbf{m}}^R}_{\mathfrak{x}}^2(t)+2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{p}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^R(t)|\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{G}}_{\mathfrak{z}}^R|{\mathbf{m}}_{\mathfrak{z}}^R(t)|\hfill \\ & +2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{p}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^R(t)|\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{G}}_{\mathfrak{z}}^I|{\mathbf{m}}_{\mathfrak{z}}^I(t)|+2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{p}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^R(t)|\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^J|{\mathbf{G}}_{\mathfrak{z}}^J|{\mathbf{m}}_{\mathfrak{z}}^J(t)|\hfill \\ & +2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{p}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^R(t)|\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^K|{\mathbf{G}}_{\mathfrak{z}}^K|{\mathbf{m}}_{\mathfrak{z}}^K(t)|+2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{p}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^R(t)|\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{H}}_{\mathfrak{z}}^R|{\mathbf{m}}_{\mathfrak{z}}^R(t-\tau (t))|\hfill \\ & +2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{p}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^R(t)|\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{H}}_{\mathfrak{z}}^I|{\mathbf{m}}_{\mathfrak{z}}^I(t-\tau (t))|+2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{p}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^R(t)|\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^J|{\mathbf{H}}_{\mathfrak{z}}^J|{\mathbf{m}}_{\mathfrak{z}}^J(t-\tau (t))|\hfill \\ & +2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{p}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^R(t)|\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^K|{\mathbf{H}}_{\mathfrak{z}}^K|{\mathbf{m}}_{\mathfrak{z}}^K(t-\tau (t))|+2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{p}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^R(t)||{\mathbf{u}}_{\mathfrak{x}}^R(t)|\hfill \\ & +e^{\lambda t}\sum _{\mathfrak{x}=1}^n[-(1-\mu )e^{-\lambda \tau }{\mathbf{d}}_{\mathfrak{x}}+\sum _{\mathfrak{z}=1}^n{\mathbf{p}}_{\mathfrak{z}}{\widehat{\beta }}_{\mathfrak{z}\mathfrak{x}}]{{\mathbf{m}}^R}_{\mathfrak{x}}^2(t-\tau (t)).\hfill \end{array}$$

(26)

By using similar techniques, we can estimate the derivatives of $\mathcal{L}{\mathcal{V}}_2(t,{\mathbf{m}}^I(t)),\mathcal{L}{\mathcal{V}}_3(t,{\mathbf{m}}^J(t))$ and $\mathcal{L}{\mathcal{V}}_4(t,{\mathbf{m}}^K(t))$ along the solution with respect to the model in Equation (7) as

$$\begin{array}{cc}\mathcal{L}{\mathcal{V}}_2(t,{\mathbf{m}}^I(t))=\hfill & \lambda e^{\lambda t}\sum _{\mathfrak{x}=1}^n(\lambda {\mathbf{q}}_{\mathfrak{x}}-2{\mathbf{q}}_{\mathfrak{x}}{\mathbf{c}}_{\mathfrak{x}}+\sum _{\mathfrak{z}=1}^n{\mathbf{q}}_{\mathfrak{z}}{\check{\alpha }}_{\mathfrak{z}\mathfrak{x}}+{\mathbf{h}}_{\mathfrak{x}}){{\mathbf{m}}^I}_{\mathfrak{x}}^2(t)+2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{q}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^I(t)|\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{G}}_{\mathfrak{z}}^I|{\mathbf{m}}_{\mathfrak{z}}^I(t)|\hfill \\ & +2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{q}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^I(t)|\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{G}}_{\mathfrak{z}}^R|{\mathbf{m}}_{\mathfrak{z}}^R(t)|+2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{q}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^I(t)|\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^J|{\mathbf{G}}_{\mathfrak{z}}^K|{\mathbf{m}}_{\mathfrak{z}}^K(t)|\hfill \\ & +2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{q}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^I(t)|\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^K|{\mathbf{G}}_{\mathfrak{z}}^J|{\mathbf{m}}_{\mathfrak{z}}^J(t)|+2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{q}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^I(t)|\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{H}}_{\mathfrak{z}}^I|{\mathbf{m}}_{\mathfrak{z}}^I(t-\tau (t))|\hfill \\ & +2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{q}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^I(t)|\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{H}}_{\mathfrak{z}}^R|{\mathbf{m}}_{\mathfrak{z}}^R(t-\tau (t))|+2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{q}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^I(t)|\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^J|{\mathbf{H}}_{\mathfrak{z}}^K|{\mathbf{m}}_{\mathfrak{z}}^K(t-\tau (t))|\hfill \\ & +2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{q}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^I(t)|\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^K|{\mathbf{H}}_{\mathfrak{z}}^J|{\mathbf{m}}_{\mathfrak{z}}^J(t-\tau (t))|+2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{q}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^I(t)||{\mathbf{u}}_{\mathfrak{x}}^I(t)|\hfill \\ & +e^{\lambda t}\sum _{\mathfrak{x}=1}^n[-(1-\mu )e^{-\lambda \tau }{\mathbf{h}}_{\mathfrak{x}}+\sum _{\mathfrak{z}=1}^n{\mathbf{q}}_{\mathfrak{z}}{\check{\beta }}_{\mathfrak{z}\mathfrak{x}}]{{\mathbf{m}}^I}_{\mathfrak{x}}^2(t-\tau (t)).\hfill \end{array}$$

(27)

$$\begin{array}{cc}\mathcal{L}{\mathcal{V}}_3(t,{\mathbf{m}}^J(t))=\hfill & \lambda e^{\lambda t}\sum _{\mathfrak{x}=1}^n(\lambda {\mathbf{r}}_{\mathfrak{x}}-2{\mathbf{r}}_{\mathfrak{x}}{\mathbf{c}}_{\mathfrak{x}}+\sum _{\mathfrak{z}=1}^n{\mathbf{r}}_{\mathfrak{z}}{\overline{\alpha }}_{\mathfrak{z}\mathfrak{x}}+{\mathbf{u}}_{\mathfrak{x}}){{\mathbf{m}}^J}_{\mathfrak{x}}^2(t)+2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{r}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^J(t)|\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{G}}_{\mathfrak{z}}^J|{\mathbf{m}}_{\mathfrak{z}}^J(t)|\hfill \\ & +2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{r}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^J(t)|\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^J|{\mathbf{G}}_{\mathfrak{z}}^R|{\mathbf{m}}_{\mathfrak{z}}^R(t)|+2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{r}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^J(t)|\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^K|{\mathbf{G}}_{\mathfrak{z}}^I|{\mathbf{m}}_{\mathfrak{z}}^I(t)|\hfill \\ & +2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{r}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^J(t)|\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{G}}_{\mathfrak{z}}^K|{\mathbf{m}}_{\mathfrak{z}}^K(t)|+2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{r}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^J(t)|\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{H}}_{\mathfrak{z}}^J|{\mathbf{m}}_{\mathfrak{z}}^J(t-\tau (t))|\hfill \\ & +2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{r}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^J(t)|\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^J|{\mathbf{H}}_{\mathfrak{z}}^R|{\mathbf{m}}_{\mathfrak{z}}^R(t-\tau (t))|+2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{r}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^J(t)|\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^K|{\mathbf{H}}_{\mathfrak{z}}^I|{\mathbf{m}}_{\mathfrak{z}}^I(t-\tau (t))|\hfill \\ & +2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{r}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^J(t)|\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{H}}_{\mathfrak{z}}^K|{\mathbf{m}}_{\mathfrak{z}}^K(t-\tau (t))|+2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{r}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^J(t)||{\mathbf{u}}_{\mathfrak{x}}^J(t)|\hfill \\ & +e^{\lambda t}\sum _{\mathfrak{x}=1}^n[-(1-\mu )e^{-\lambda \tau }{\mathbf{u}}_{\mathfrak{x}}+\sum _{\mathfrak{z}=1}^n{\mathbf{r}}_{\mathfrak{z}}{\overline{\beta }}_{\mathfrak{z}\mathfrak{x}}]{{\mathbf{m}}^J}_{\mathfrak{x}}^2(t-\tau (t)).\hfill \end{array}$$

(28)

$$\begin{array}{cc}\mathcal{L}{\mathcal{V}}_4(t,{\mathbf{m}}^K(t))=\hfill & \lambda e^{\lambda t}\sum _{\mathfrak{x}=1}^n(\lambda {\mathbf{s}}_{\mathfrak{x}}-2{\mathbf{s}}_{\mathfrak{x}}{\mathbf{c}}_{\mathfrak{x}}+\sum _{\mathfrak{z}=1}^n{\mathbf{s}}_{\mathfrak{z}}{\tilde{\alpha }}_{\mathfrak{z}\mathfrak{x}}+{\mathbf{v}}_{\mathfrak{x}}){{\mathbf{m}}^K}_{\mathfrak{x}}^2(t)+2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{s}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^K(t)|\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{G}}_{\mathfrak{z}}^K|{\mathbf{m}}_{\mathfrak{z}}^K(t)|\hfill \\ & +2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{s}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^K(t)|\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{G}}_{\mathfrak{z}}^J|{\mathbf{m}}_{\mathfrak{z}}^J(t)|+2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{s}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^K(t)|\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^K|{\mathbf{G}}_{\mathfrak{z}}^R|{\mathbf{m}}_{\mathfrak{z}}^R(t)|\hfill \\ & +2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{s}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^K(t)|\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^J|{\mathbf{G}}_{\mathfrak{z}}^I|{\mathbf{m}}_{\mathfrak{z}}^I(t)|+2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{s}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^K(t)|\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{H}}_{\mathfrak{z}}^K|{\mathbf{m}}_{\mathfrak{z}}^K(t-\tau (t))|\hfill \\ & +2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{s}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^K(t)|\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{H}}_{\mathfrak{z}}^J|{\mathbf{m}}_{\mathfrak{z}}^J(t-\tau (t))|+2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{s}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^K(t)|\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^K|{\mathbf{H}}_{\mathfrak{z}}^R|{\mathbf{m}}_{\mathfrak{z}}^R(t-\tau (t))|\hfill \\ & +2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{s}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^K(t)|\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}^J{I}_{\mathfrak{x}\mathfrak{z}}|{\mathbf{H}}_{\mathfrak{z}}^I|{\mathbf{m}}_{\mathfrak{z}}^I(t-\tau (t))|+2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{s}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^K(t)||{\mathbf{u}}_{\mathfrak{x}}^K(t)|\hfill \\ & +e^{\lambda t}\sum _{\mathfrak{x}=1}^n[-(1-\mu )e^{-\lambda \tau }{\mathbf{v}}_{\mathfrak{x}}+\sum _{\mathfrak{z}=1}^n{\mathbf{s}}_{\mathfrak{z}}{\tilde{\beta }}_{\mathfrak{z}\mathfrak{x}}]{{\mathbf{m}}^K}_{\mathfrak{x}}^2(t-\tau (t)).\hfill \end{array}$$

(29)

Using the well-known Young inequality, it follows that

$$\begin{array}{cc}\hfill 2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{p}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^R(t)|\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{G}}_{\mathfrak{z}}^R|{\mathbf{m}}_{\mathfrak{z}}^R(t)|\le & e^{\lambda t}\sum _{\mathfrak{x}=1}^n\sum _{\mathfrak{z}=1}^n{\mathbf{p}}_{\mathfrak{x}}|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{G}}_{\mathfrak{z}}^R(|{\mathbf{m}}_{\mathfrak{x}}^R{(t)|}^2+{\mathbf{m}}_{\mathfrak{z}}^R(t){|}^2),\hfill \\ \hfill 2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{p}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^R(t)|\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{G}}_{\mathfrak{z}}^I|{\mathbf{m}}_{\mathfrak{z}}^I(t)|\le & e^{\lambda t}\sum _{\mathfrak{x}=1}^n\sum _{\mathfrak{z}=1}^n{\mathbf{p}}_{\mathfrak{x}}|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{G}}_{\mathfrak{z}}^I(|{\mathbf{m}}_{\mathfrak{x}}^R{(t)|}^2+{\mathbf{m}}_{\mathfrak{z}}^I(t){|}^2),\hfill \\ \hfill 2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{p}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^R(t)|\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^J|{\mathbf{G}}_{\mathfrak{z}}^J|{\mathbf{m}}_{\mathfrak{z}}^J(t)|\le & e^{\lambda t}\sum _{\mathfrak{x}=1}^n\sum _{\mathfrak{z}=1}^n{\mathbf{p}}_{\mathfrak{x}}|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^J|{\mathbf{G}}_{\mathfrak{z}}^J(|{\mathbf{m}}_{\mathfrak{x}}^R{(t)|}^2+{\mathbf{m}}_{\mathfrak{z}}^J(t){|}^2),\hfill \\ \hfill 2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{p}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^R(t)|\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^K|{\mathbf{G}}_{\mathfrak{z}}^K|{\mathbf{m}}_{\mathfrak{z}}^K(t)|\le & e^{\lambda t}\sum _{\mathfrak{x}=1}^n\sum _{\mathfrak{z}=1}^n{\mathbf{p}}_{\mathfrak{x}}|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^K|{\mathbf{G}}_{\mathfrak{z}}^K(|{\mathbf{m}}_{\mathfrak{x}}^R{(t)|}^2+{\mathbf{m}}_{\mathfrak{z}}^K(t){|}^2),\hfill \\ \hfill 2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{p}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^R(t)|\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{H}}_{\mathfrak{z}}^R|{\mathbf{m}}_{\mathfrak{z}}^R(t-\tau (t))|\le & e^{\lambda t}\sum _{\mathfrak{x}=1}^n\sum _{\mathfrak{z}=1}^n{\mathbf{p}}_{\mathfrak{x}}|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{H}}_{\mathfrak{z}}^R(|{\mathbf{m}}_{\mathfrak{x}}^R{(t)|}^2+{\mathbf{m}}_{\mathfrak{z}}^R(t-\tau (t)){|}^2),\hfill \\ \hfill 2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{p}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^R(t)|\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{H}}_{\mathfrak{z}}^I|{\mathbf{m}}_{\mathfrak{z}}^I(t-\tau (t))|\le & e^{\lambda t}\sum _{\mathfrak{x}=1}^n\sum _{\mathfrak{z}=1}^n{\mathbf{p}}_{\mathfrak{x}}|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{H}}_{\mathfrak{z}}^I(|{\mathbf{m}}_{\mathfrak{x}}^R{(t)|}^2+{\mathbf{m}}_{\mathfrak{z}}^I(t-\tau (t)){|}^2),\hfill \\ \hfill 2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{p}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^R(t)|\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^J|{\mathbf{H}}_{\mathfrak{z}}^J|{\mathbf{m}}_{\mathfrak{z}}^J(t-\tau (t))|\le & e^{\lambda t}\sum _{\mathfrak{x}=1}^n\sum _{\mathfrak{z}=1}^n{\mathbf{p}}_{\mathfrak{x}}|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^J|{\mathbf{H}}_{\mathfrak{z}}^J(|{\mathbf{m}}_{\mathfrak{x}}^R{(t)|}^2+{\mathbf{m}}_{\mathfrak{z}}^J(t-\tau (t)){|}^2),\hfill \\ \hfill 2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{p}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^R(t)|\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^K|{\mathbf{H}}_{\mathfrak{z}}^K|{\mathbf{m}}_{\mathfrak{z}}^K(t-\tau (t))|\le & e^{\lambda t}\sum _{\mathfrak{x}=1}^n\sum _{\mathfrak{z}=1}^n{\mathbf{p}}_{\mathfrak{x}}|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^K|{\mathbf{H}}_{\mathfrak{z}}^K(|{\mathbf{m}}_{\mathfrak{x}}^R{(t)|}^2+{\mathbf{m}}_{\mathfrak{z}}^K(t-\tau (t)){|}^2),\hfill \\ \hfill 2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{p}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^R(t)|{\mathbf{u}}_{\mathfrak{x}}^R(t)|\le & e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{p}}_{\mathfrak{x}}(|{\mathbf{m}}_{\mathfrak{x}}^R{(t)|}^2+|{\mathbf{u}}_{\mathfrak{x}}^R(t){|}^2),\hfill \\ \hfill 2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{q}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^I(t)|\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{G}}_{\mathfrak{z}}^I|{\mathbf{m}}_{\mathfrak{z}}^I(t)|\le & e^{\lambda t}\sum _{\mathfrak{x}=1}^n\sum _{\mathfrak{z}=1}^n{\mathbf{q}}_{\mathfrak{x}}|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{G}}_{\mathfrak{z}}^I(|{\mathbf{m}}_{\mathfrak{x}}^I{(t)|}^2+{\mathbf{m}}_{\mathfrak{z}}^I(t){|}^2),\hfill \\ \hfill 2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{q}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^I(t)|\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{G}}_{\mathfrak{z}}^R|{\mathbf{m}}_{\mathfrak{z}}^R(t)|\le & e^{\lambda t}\sum _{\mathfrak{x}=1}^n\sum _{\mathfrak{z}=1}^n{\mathbf{q}}_{\mathfrak{x}}|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{G}}_{\mathfrak{z}}^R(|{\mathbf{m}}_{\mathfrak{x}}^I{(t)|}^2+{\mathbf{m}}_{\mathfrak{z}}^R(t){|}^2),\hfill \\ \hfill 2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{q}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^I(t)|\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^J|{\mathbf{G}}_{\mathfrak{z}}^K|{\mathbf{m}}_{\mathfrak{z}}^K(t)|\le & e^{\lambda t}\sum _{\mathfrak{x}=1}^n\sum _{\mathfrak{z}=1}^n{\mathbf{q}}_{\mathfrak{x}}|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^J|{\mathbf{G}}_{\mathfrak{z}}^K(|{\mathbf{m}}_{\mathfrak{x}}^I{(t)|}^2+{\mathbf{m}}_{\mathfrak{z}}^K(t){|}^2),\hfill \\ \hfill 2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{q}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^I(t)|\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^K|{\mathbf{G}}_{\mathfrak{z}}^J|{\mathbf{m}}_{\mathfrak{z}}^J(t)|\le & e^{\lambda t}\sum _{\mathfrak{x}=1}^n\sum _{\mathfrak{z}=1}^n{\mathbf{q}}_{\mathfrak{x}}|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^K|{\mathbf{G}}_{\mathfrak{z}}^J(|{\mathbf{m}}_{\mathfrak{x}}^I{(t)|}^2+{\mathbf{m}}_{\mathfrak{z}}^J(t){|}^2),\hfill \\ \hfill 2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{q}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^I(t)|\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{H}}_{\mathfrak{z}}^I|{\mathbf{m}}_{\mathfrak{z}}^I(t-\tau (t))|\le & e^{\lambda t}\sum _{\mathfrak{x}=1}^n\sum _{\mathfrak{z}=1}^n{\mathbf{q}}_{\mathfrak{x}}|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{H}}_{\mathfrak{z}}^I(|{\mathbf{m}}_{\mathfrak{x}}^I{(t)|}^2+{\mathbf{m}}_{\mathfrak{z}}^I(t-\tau (t)){|}^2),\hfill \\ \hfill 2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{q}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^I(t)|\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{H}}_{\mathfrak{z}}^R|{\mathbf{m}}_{\mathfrak{z}}^R(t-\tau (t))|\le & e^{\lambda t}\sum _{\mathfrak{x}=1}^n\sum _{\mathfrak{z}=1}^n{\mathbf{q}}_{\mathfrak{x}}|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{H}}_{\mathfrak{z}}^R(|{\mathbf{m}}_{\mathfrak{x}}^I{(t)|}^2+{\mathbf{m}}_{\mathfrak{z}}^R(t-\tau (t)){|}^2),\hfill \\ \hfill 2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{q}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^I(t)|\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^J|{\mathbf{H}}_{\mathfrak{z}}^K|{\mathbf{m}}_{\mathfrak{z}}^K(t-\tau (t))|\le & e^{\lambda t}\sum _{\mathfrak{x}=1}^n\sum _{\mathfrak{z}=1}^n{\mathbf{q}}_{\mathfrak{x}}|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^J|{\mathbf{H}}_{\mathfrak{z}}^K(|{\mathbf{m}}_{\mathfrak{x}}^I{(t)|}^2+{\mathbf{m}}_{\mathfrak{z}}^K(t-\tau (t)){|}^2),\hfill \\ \hfill 2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{q}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^I(t)|\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^K|{\mathbf{H}}_{\mathfrak{z}}^J|{\mathbf{m}}_{\mathfrak{z}}^J(t-\tau (t))|\le & e^{\lambda t}\sum _{\mathfrak{x}=1}^n\sum _{\mathfrak{z}=1}^n{\mathbf{q}}_{\mathfrak{x}}|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^K|{\mathbf{H}}_{\mathfrak{z}}^J(|{\mathbf{m}}_{\mathfrak{x}}^I{(t)|}^2+{\mathbf{m}}_{\mathfrak{z}}^J(t-\tau (t)){|}^2),\hfill \\ \hfill 2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{q}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^I(t)|{\mathbf{u}}_{\mathfrak{x}}^I(t)|\le & e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{q}}_{\mathfrak{x}}(|{\mathbf{m}}_{\mathfrak{x}}^I{(t)|}^2+|{\mathbf{u}}_{\mathfrak{x}}^I(t){|}^2),\hfill \end{array}$$

$$\begin{array}{cc}\hfill 2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{r}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^J(t)|\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{G}}_{\mathfrak{z}}^J|{\mathbf{m}}_{\mathfrak{z}}^J(t)|\le & e^{\lambda t}\sum _{\mathfrak{x}=1}^n\sum _{\mathfrak{z}=1}^n{\mathbf{r}}_{\mathfrak{x}}|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{G}}_{\mathfrak{z}}^J(|{\mathbf{m}}_{\mathfrak{x}}^J{(t)|}^2+{\mathbf{m}}_{\mathfrak{z}}^J(t){|}^2),\hfill \\ \hfill 2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{r}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^J(t)|\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^J|{\mathbf{G}}_{\mathfrak{z}}^R|{\mathbf{m}}_{\mathfrak{z}}^R(t)|\le & e^{\lambda t}\sum _{\mathfrak{x}=1}^n\sum _{\mathfrak{z}=1}^n{\mathbf{r}}_{\mathfrak{x}}|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^J|{\mathbf{G}}_{\mathfrak{z}}^R(|{\mathbf{m}}_{\mathfrak{x}}^J{(t)|}^2+{\mathbf{m}}_{\mathfrak{z}}^R(t){|}^2),\hfill \\ \hfill 2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{r}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^J(t)|\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^K|{\mathbf{G}}_{\mathfrak{z}}^I|{\mathbf{m}}_{\mathfrak{z}}^I(t)|\le & e^{\lambda t}\sum _{\mathfrak{x}=1}^n\sum _{\mathfrak{z}=1}^n{\mathbf{r}}_{\mathfrak{x}}|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^K|{\mathbf{G}}_{\mathfrak{z}}^I(|{\mathbf{m}}_{\mathfrak{x}}^J{(t)|}^2+{\mathbf{m}}_{\mathfrak{z}}^I(t){|}^2),\hfill \\ \hfill 2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{r}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^J(t)|\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{G}}_{\mathfrak{z}}^K|{\mathbf{m}}_{\mathfrak{z}}^K(t)|\le & e^{\lambda t}\sum _{\mathfrak{x}=1}^n\sum _{\mathfrak{z}=1}^n{\mathbf{r}}_{\mathfrak{x}}|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{G}}_{\mathfrak{z}}^K(|{\mathbf{m}}_{\mathfrak{x}}^J{(t)|}^2+{\mathbf{m}}_{\mathfrak{z}}^K(t){|}^2),\hfill \\ \hfill 2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{r}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^J(t)|\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{H}}_{\mathfrak{z}}^J|{\mathbf{m}}_{\mathfrak{z}}^J(t-\tau (t))|\le & e^{\lambda t}\sum _{\mathfrak{x}=1}^n\sum _{\mathfrak{z}=1}^n{\mathbf{r}}_{\mathfrak{x}}|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{H}}_{\mathfrak{z}}^J(|{\mathbf{m}}_{\mathfrak{x}}^J{(t)|}^2+{\mathbf{m}}_{\mathfrak{z}}^J(t-\tau (t)){|}^2),\hfill \\ \hfill 2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{r}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^J(t)|\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^J|{\mathbf{H}}_{\mathfrak{z}}^R|{\mathbf{m}}_{\mathfrak{z}}^R(t-\tau (t))|\le & e^{\lambda t}\sum _{\mathfrak{x}=1}^n\sum _{\mathfrak{z}=1}^n{\mathbf{r}}_{\mathfrak{x}}|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^J|{\mathbf{H}}_{\mathfrak{z}}^R(|{\mathbf{m}}_{\mathfrak{x}}^J{(t)|}^2+{\mathbf{m}}_{\mathfrak{z}}^R(t-\tau (t)){|}^2),\hfill \\ \hfill 2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{r}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^J(t)|\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^K|{\mathbf{H}}_{\mathfrak{z}}^I|{\mathbf{m}}_{\mathfrak{z}}^I(t-\tau (t))|\le & e^{\lambda t}\sum _{\mathfrak{x}=1}^n\sum _{\mathfrak{z}=1}^n{\mathbf{r}}_{\mathfrak{x}}|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^K|{\mathbf{H}}_{\mathfrak{z}}^I(|{\mathbf{m}}_{\mathfrak{x}}^J{(t)|}^2+{\mathbf{m}}_{\mathfrak{z}}^I(t-\tau (t)){|}^2),\hfill \\ \hfill 2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{r}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^J(t)|\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{H}}_{\mathfrak{z}}^K|{\mathbf{m}}_{\mathfrak{z}}^K(t-\tau (t))|\le & e^{\lambda t}\sum _{\mathfrak{x}=1}^n\sum _{\mathfrak{z}=1}^n{\mathbf{r}}_{\mathfrak{x}}|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{H}}_{\mathfrak{z}}^K(|{\mathbf{m}}_{\mathfrak{x}}^J{(t)|}^2+{\mathbf{m}}_{\mathfrak{z}}^K(t-\tau (t)){|}^2),\hfill \\ \hfill 2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{r}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^J(t)|{\mathbf{u}}_{\mathfrak{x}}^J(t)|\le & e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{r}}_{\mathfrak{x}}(|{\mathbf{m}}_{\mathfrak{x}}^J{(t)|}^2+|{\mathbf{u}}_{\mathfrak{x}}^J(t){|}^2),\hfill \\ \hfill 2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{s}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^K(t)|\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{G}}_{\mathfrak{z}}^K|{\mathbf{m}}_{\mathfrak{z}}^K(t)|\le & e^{\lambda t}\sum _{\mathfrak{x}=1}^n\sum _{\mathfrak{z}=1}^n{\mathbf{s}}_{\mathfrak{x}}|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{G}}_{\mathfrak{z}}^K(|{\mathbf{m}}_{\mathfrak{x}}^K{(t)|}^2+{\mathbf{m}}_{\mathfrak{z}}^K(t){|}^2),\hfill \\ \hfill 2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{s}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^K(t)|\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{G}}_{\mathfrak{z}}^J|{\mathbf{m}}_{\mathfrak{z}}^J(t)|\le & e^{\lambda t}\sum _{\mathfrak{x}=1}^n\sum _{\mathfrak{z}=1}^n{\mathbf{s}}_{\mathfrak{x}}|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{G}}_{\mathfrak{z}}^J(|{\mathbf{m}}_{\mathfrak{x}}^K{(t)|}^2+{\mathbf{m}}_{\mathfrak{z}}^J(t){|}^2),\hfill \\ \hfill 2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{s}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^K(t)|\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^K|{\mathbf{G}}_{\mathfrak{z}}^R|{\mathbf{m}}_{\mathfrak{z}}^R(t)|\le & e^{\lambda t}\sum _{\mathfrak{x}=1}^n\sum _{\mathfrak{z}=1}^n{\mathbf{s}}_{\mathfrak{x}}|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^K|{\mathbf{G}}_{\mathfrak{z}}^R(|{\mathbf{m}}_{\mathfrak{x}}^K{(t)|}^2+{\mathbf{m}}_{\mathfrak{z}}^R(t){|}^2),\hfill \\ \hfill 2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{s}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^K(t)|\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^J|{\mathbf{G}}_{\mathfrak{z}}^I|{\mathbf{m}}_{\mathfrak{z}}^I(t)|\le & e^{\lambda t}\sum _{\mathfrak{x}=1}^n\sum _{\mathfrak{z}=1}^n{\mathbf{s}}_{\mathfrak{x}}|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^J|{\mathbf{G}}_{\mathfrak{z}}^I(|{\mathbf{m}}_{\mathfrak{x}}^K{(t)|}^2+{\mathbf{m}}_{\mathfrak{z}}^I(t){|}^2),\hfill \\ \hfill 2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{s}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^K(t)|\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{H}}_{\mathfrak{z}}^K|{\mathbf{m}}_{\mathfrak{z}}^K(t-\tau (t))|\le & e^{\lambda t}\sum _{\mathfrak{x}=1}^n\sum _{\mathfrak{z}=1}^n{\mathbf{s}}_{\mathfrak{x}}|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{H}}_{\mathfrak{z}}^K(|{\mathbf{m}}_{\mathfrak{x}}^K{(t)|}^2+{\mathbf{m}}_{\mathfrak{z}}^K(t-\tau (t)){|}^2),\hfill \\ \hfill 2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{s}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^K(t)|\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{H}}_{\mathfrak{z}}^J|{\mathbf{m}}_{\mathfrak{z}}^J(t-\tau (t))|\le & e^{\lambda t}\sum _{\mathfrak{x}=1}^n\sum _{\mathfrak{z}=1}^n{\mathbf{s}}_{\mathfrak{x}}|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{H}}_{\mathfrak{z}}^J(|{\mathbf{m}}_{\mathfrak{x}}^K{(t)|}^2+{\mathbf{m}}_{\mathfrak{z}}^J(t-\tau (t)){|}^2),\hfill \\ \hfill 2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{s}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^K(t)|\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^K|{\mathbf{H}}_{\mathfrak{z}}^R|{\mathbf{m}}_{\mathfrak{z}}^R(t-\tau (t))|\le & e^{\lambda t}\sum _{\mathfrak{x}=1}^n\sum _{\mathfrak{z}=1}^n{\mathbf{s}}_{\mathfrak{x}}|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^K|{\mathbf{H}}_{\mathfrak{z}}^R(|{\mathbf{m}}_{\mathfrak{x}}^K{(t)|}^2+{\mathbf{m}}_{\mathfrak{z}}^R(t-\tau (t)){|}^2),\hfill \\ \hfill 2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{s}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^K(t)|\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^J|{\mathbf{H}}_{\mathfrak{z}}^I|{\mathbf{m}}_{\mathfrak{z}}^I(t-\tau (t))|\le & e^{\lambda t}\sum _{\mathfrak{x}=1}^n\sum _{\mathfrak{z}=1}^n{\mathbf{s}}_{\mathfrak{x}}|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^J|{\mathbf{H}}_{\mathfrak{z}}^I(|{\mathbf{m}}_{\mathfrak{x}}^K{(t)|}^2+{\mathbf{m}}_{\mathfrak{z}}^I(t-\tau (t)){|}^2),\hfill \\ \hfill 2e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{s}}_{\mathfrak{x}}|{\mathbf{m}}_{\mathfrak{x}}^K(t)|{\mathbf{u}}_{\mathfrak{x}}^K(t)|\le & e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{s}}_{\mathfrak{x}}(|{\mathbf{m}}_{\mathfrak{x}}^K{(t)|}^2+|{\mathbf{u}}_{\mathfrak{x}}^K(t){|}^2),\hfill \end{array}$$

Substituting the above inequalities into Equations (26)–(29), we have

$$\begin{array}{c}\mathcal{L}{\mathcal{V}}_1(t,{\mathbf{m}}^R(t))=e^{\lambda t}\sum _{\mathfrak{x}=1}^n(\lambda {\mathbf{p}}_{\mathfrak{x}}-2{\mathbf{p}}_{\mathfrak{x}}{\mathbf{c}}_{\mathfrak{x}}+\sum _{\mathfrak{z}=1}^n{\mathbf{p}}_{\mathfrak{z}}{\widehat{\alpha }}_{\mathfrak{z}\mathfrak{x}}+{\mathbf{d}}_{\mathfrak{x}}){{\mathbf{m}}^R}_{\mathfrak{x}}^2(t)+e^{\lambda t}\sum _{\mathfrak{x}=1}^n\sum _{\mathfrak{z}=1}^n{\mathbf{p}}_{\mathfrak{x}}|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{G}}_{\mathfrak{z}}^R(|{\mathbf{m}}_{\mathfrak{x}}^R{(t)|}^2+{\mathbf{m}}_{\mathfrak{z}}^R(t){|}^2)\hfill \\ +e^{\lambda t}\sum _{\mathfrak{x}=1}^n\sum _{\mathfrak{z}=1}^n{\mathbf{p}}_{\mathfrak{x}}|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{G}}_{\mathfrak{z}}^I(|{\mathbf{m}}_{\mathfrak{x}}^R{(t)|}^2+{\mathbf{m}}_{\mathfrak{z}}^I{(t)|}^2)+e^{\lambda t}\sum _{\mathfrak{x}=1}^n\sum _{\mathfrak{z}=1}^n{\mathbf{p}}_{\mathfrak{x}}|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^J|{\mathbf{G}}_{\mathfrak{z}}^J(|{\mathbf{m}}_{\mathfrak{x}}^R{(t)|}^2+{\mathbf{m}}_{\mathfrak{z}}^J(t){|}^2)\hfill \\ +e^{\lambda t}\sum _{\mathfrak{x}=1}^n\sum _{\mathfrak{z}=1}^n{\mathbf{p}}_{\mathfrak{x}}|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^K|{\mathbf{G}}_{\mathfrak{z}}^K(|{\mathbf{m}}_{\mathfrak{x}}^R{(t)|}^2+{\mathbf{m}}_{\mathfrak{z}}^K{(t)|}^2)+e^{\lambda t}\sum _{\mathfrak{x}=1}^n\sum _{\mathfrak{z}=1}^n{\mathbf{p}}_{\mathfrak{x}}|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{H}}_{\mathfrak{z}}^R(|{\mathbf{m}}_{\mathfrak{x}}^R{(t)|}^2+{\mathbf{m}}_{\mathfrak{z}}^R(t-\tau (t)){|}^2)\hfill \\ +e^{\lambda t}\sum _{\mathfrak{x}=1}^n\sum _{\mathfrak{z}=1}^n{\mathbf{p}}_{\mathfrak{x}}|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{H}}_{\mathfrak{z}}^I(|{\mathbf{m}}_{\mathfrak{x}}^R{(t)|}^2+{\mathbf{m}}_{\mathfrak{z}}^I{(t-\tau (t))|}^2)+e^{\lambda t}\sum _{\mathfrak{x}=1}^n\sum _{\mathfrak{z}=1}^n{\mathbf{p}}_{\mathfrak{x}}|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^J|{\mathbf{H}}_{\mathfrak{z}}^J(|{\mathbf{m}}_{\mathfrak{x}}^R{(t)|}^2+{\mathbf{m}}_{\mathfrak{z}}^J(t-\tau (t)){|}^2)\hfill \\ +e^{\lambda t}\sum _{\mathfrak{x}=1}^n\sum _{\mathfrak{z}=1}^n{\mathbf{p}}_{\mathfrak{x}}|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^K|{\mathbf{H}}_{\mathfrak{z}}^K(|{\mathbf{m}}_{\mathfrak{x}}^R{(t)|}^2+{\mathbf{m}}_{\mathfrak{z}}^K{(t-\tau (t))|}^2)+e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{p}}_{\mathfrak{x}}(|{\mathbf{m}}_{\mathfrak{x}}^R{(t)|}^2+|{\mathbf{u}}_{\mathfrak{x}}^R(t){|}^2)\hfill \\ +e^{\lambda t}\sum _{\mathfrak{x}=1}^n[-(1-\mu )e^{-\lambda \tau }{\mathbf{d}}_{\mathfrak{x}}+\sum _{\mathfrak{z}=1}^n{\mathbf{p}}_{\mathfrak{z}}{\widehat{\beta }}_{\mathfrak{z}\mathfrak{x}}]{{\mathbf{m}}^R}_{\mathfrak{x}}^2(t-\tau (t)),\hfill \end{array}$$

(30)

$$\begin{array}{cc}\hfill \mathcal{L}& {\mathcal{V}}_2(t,{\mathbf{m}}^I(t))=\lambda e^{\lambda t}\sum _{\mathfrak{x}=1}^n(\lambda {\mathbf{q}}_{\mathfrak{x}}-2{\mathbf{q}}_{\mathfrak{x}}{\mathbf{c}}_{\mathfrak{x}}+\sum _{\mathfrak{z}=1}^n{\mathbf{q}}_{\mathfrak{z}}{\check{\alpha }}_{\mathfrak{z}\mathfrak{x}}+{\mathbf{h}}_{\mathfrak{x}}){{\mathbf{m}}^I}_{\mathfrak{x}}^2(t)+e^{\lambda t}\sum _{\mathfrak{x}=1}^n\sum _{\mathfrak{z}=1}^n{\mathbf{q}}_{\mathfrak{x}}|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{G}}_{\mathfrak{z}}^I(|{\mathbf{m}}_{\mathfrak{x}}^I{(t)|}^2+{\mathbf{m}}_{\mathfrak{z}}^I(t){|}^2)\hfill \\ & +e^{\lambda t}\sum _{\mathfrak{x}=1}^n\sum _{\mathfrak{z}=1}^n{\mathbf{q}}_{\mathfrak{x}}|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{G}}_{\mathfrak{z}}^R(|{\mathbf{m}}_{\mathfrak{x}}^I{(t)|}^2+{\mathbf{m}}_{\mathfrak{z}}^R{(t)|}^2)+e^{\lambda t}\sum _{\mathfrak{x}=1}^n\sum _{\mathfrak{z}=1}^n{\mathbf{q}}_{\mathfrak{x}}|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^J|{\mathbf{G}}_{\mathfrak{z}}^K(|{\mathbf{m}}_{\mathfrak{x}}^I{(t)|}^2+{\mathbf{m}}_{\mathfrak{z}}^K(t){|}^2)\hfill \\ & +e^{\lambda t}\sum _{\mathfrak{x}=1}^n\sum _{\mathfrak{z}=1}^n{\mathbf{q}}_{\mathfrak{x}}|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^K|{\mathbf{G}}_{\mathfrak{z}}^J(|{\mathbf{m}}_{\mathfrak{x}}^I{(t)|}^2+{\mathbf{m}}_{\mathfrak{z}}^J{(t)|}^2)+e^{\lambda t}\sum _{\mathfrak{x}=1}^n\sum _{\mathfrak{z}=1}^n{\mathbf{q}}_{\mathfrak{x}}|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{H}}_{\mathfrak{z}}^I(|{\mathbf{m}}_{\mathfrak{x}}^I{(t)|}^2+{\mathbf{m}}_{\mathfrak{z}}^I(t-\tau (t)){|}^2)\hfill \\ & +e^{\lambda t}\sum _{\mathfrak{x}=1}^n\sum _{\mathfrak{z}=1}^n{\mathbf{q}}_{\mathfrak{x}}|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{H}}_{\mathfrak{z}}^R(|{\mathbf{m}}_{\mathfrak{x}}^I{(t)|}^2+{\mathbf{m}}_{\mathfrak{z}}^R{(t-\tau (t))|}^2)+e^{\lambda t}\sum _{\mathfrak{x}=1}^n\sum _{\mathfrak{z}=1}^n{\mathbf{q}}_{\mathfrak{x}}|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^J|{\mathbf{H}}_{\mathfrak{z}}^K(|{\mathbf{m}}_{\mathfrak{x}}^I{(t)|}^2+{\mathbf{m}}_{\mathfrak{z}}^K(t-\tau (t)){|}^2)\hfill \\ & +e^{\lambda t}\sum _{\mathfrak{x}=1}^n\sum _{\mathfrak{z}=1}^n{\mathbf{q}}_{\mathfrak{x}}|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^K|{\mathbf{H}}_{\mathfrak{z}}^J(|{\mathbf{m}}_{\mathfrak{x}}^I{(t)|}^2+{\mathbf{m}}_{\mathfrak{z}}^J{(t-\tau (t))|}^2)+e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{q}}_{\mathfrak{x}}(|{\mathbf{m}}_{\mathfrak{x}}^I{(t)|}^2+|{\mathbf{u}}_{\mathfrak{x}}^I(t){|}^2)\hfill \\ & +e^{\lambda t}\sum _{\mathfrak{x}=1}^n[-(1-\mu )e^{-\lambda \tau }{\mathbf{h}}_{\mathfrak{x}}+\sum _{\mathfrak{z}=1}^n{\mathbf{q}}_{\mathfrak{z}}{\check{\beta }}_{\mathfrak{z}\mathfrak{x}}]{{\mathbf{m}}^I}_{\mathfrak{x}}^2(t-\tau (t)),\hfill \end{array}$$

(31)

$$\begin{array}{cc}\mathcal{L}\hfill & {\mathcal{V}}_3(t,{\mathbf{m}}^J(t))=\lambda e^{\lambda t}\sum _{\mathfrak{x}=1}^n(\lambda {\mathbf{r}}_{\mathfrak{x}}-2{\mathbf{r}}_{\mathfrak{x}}{\mathbf{c}}_{\mathfrak{x}}+\sum _{\mathfrak{z}=1}^n{\mathbf{r}}_{\mathfrak{z}}{\overline{\alpha }}_{\mathfrak{z}\mathfrak{x}}+{\mathbf{u}}_{\mathfrak{x}}){{\mathbf{m}}^J}_{\mathfrak{x}}^2(t)+e^{\lambda t}\sum _{\mathfrak{x}=1}^n\sum _{\mathfrak{z}=1}^n{\mathbf{r}}_{\mathfrak{x}}|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{G}}_{\mathfrak{z}}^J(|{\mathbf{m}}_{\mathfrak{x}}^J{(t)|}^2+{\mathbf{m}}_{\mathfrak{z}}^J(t){|}^2)\hfill \\ & +e^{\lambda t}\sum _{\mathfrak{x}=1}^n\sum _{\mathfrak{z}=1}^n{\mathbf{r}}_{\mathfrak{x}}|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^J|{\mathbf{G}}_{\mathfrak{z}}^R(|{\mathbf{m}}_{\mathfrak{x}}^J{(t)|}^2+{\mathbf{m}}_{\mathfrak{z}}^R{(t)|}^2)+e^{\lambda t}\sum _{\mathfrak{x}=1}^n\sum _{\mathfrak{z}=1}^n{\mathbf{r}}_{\mathfrak{x}}|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^K|{\mathbf{G}}_{\mathfrak{z}}^I(|{\mathbf{m}}_{\mathfrak{x}}^J{(t)|}^2+{\mathbf{m}}_{\mathfrak{z}}^I(t){|}^2)\hfill \\ & +e^{\lambda t}\sum _{\mathfrak{x}=1}^n\sum _{\mathfrak{z}=1}^n{\mathbf{r}}_{\mathfrak{x}}|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{G}}_{\mathfrak{z}}^K(|{\mathbf{m}}_{\mathfrak{x}}^J{(t)|}^2+{\mathbf{m}}_{\mathfrak{z}}^K{(t)|}^2)+e^{\lambda t}\sum _{\mathfrak{x}=1}^n\sum _{\mathfrak{z}=1}^n{\mathbf{r}}_{\mathfrak{x}}|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{H}}_{\mathfrak{z}}^J(|{\mathbf{m}}_{\mathfrak{x}}^J{(t)|}^2+{\mathbf{m}}_{\mathfrak{z}}^J(t-\tau (t)){|}^2)\hfill \\ & +e^{\lambda t}\sum _{\mathfrak{x}=1}^n\sum _{\mathfrak{z}=1}^n{\mathbf{r}}_{\mathfrak{x}}|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^J|{\mathbf{H}}_{\mathfrak{z}}^R(|{\mathbf{m}}_{\mathfrak{x}}^J{(t)|}^2+{\mathbf{m}}_{\mathfrak{z}}^R{(t-\tau (t))|}^2)+e^{\lambda t}\sum _{\mathfrak{x}=1}^n\sum _{\mathfrak{z}=1}^n{\mathbf{r}}_{\mathfrak{x}}|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^K|{\mathbf{H}}_{\mathfrak{z}}^I(|{\mathbf{m}}_{\mathfrak{x}}^J{(t)|}^2+{\mathbf{m}}_{\mathfrak{z}}^I(t-\tau (t)){|}^2)\hfill \\ & +e^{\lambda t}\sum _{\mathfrak{x}=1}^n\sum _{\mathfrak{z}=1}^n{\mathbf{r}}_{\mathfrak{x}}|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{H}}_{\mathfrak{z}}^K(|{\mathbf{m}}_{\mathfrak{x}}^J{(t)|}^2+{\mathbf{m}}_{\mathfrak{z}}^K{(t-\tau (t))|}^2)+e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{r}}_{\mathfrak{x}}(|{\mathbf{m}}_{\mathfrak{x}}^J{(t)|}^2+|{\mathbf{u}}_{\mathfrak{x}}^J(t){|}^2)\hfill \\ & +e^{\lambda t}\sum _{\mathfrak{x}=1}^n[-(1-\mu )e^{-\lambda \tau }{\mathbf{u}}_{\mathfrak{x}}+\sum _{\mathfrak{z}=1}^n{\mathbf{r}}_{\mathfrak{z}}{\overline{\beta }}_{\mathfrak{z}\mathfrak{x}}]{{\mathbf{m}}^J}_{\mathfrak{x}}^2(t-\tau (t)),\hfill \end{array}$$

(32)

$$\begin{array}{cc}\mathcal{L}\hfill & {\mathcal{V}}_4(t,{\mathbf{m}}^K(t))=\lambda e^{\lambda t}\sum _{\mathfrak{x}=1}^n(\lambda {\mathbf{s}}_{\mathfrak{x}}-2{\mathbf{s}}_{\mathfrak{x}}{\mathbf{c}}_{\mathfrak{x}}+\sum _{\mathfrak{z}=1}^n{\mathbf{s}}_{\mathfrak{z}}{\tilde{\alpha }}_{\mathfrak{z}\mathfrak{x}}+{\mathbf{v}}_{\mathfrak{x}}){{\mathbf{m}}^K}_{\mathfrak{x}}^2(t)+e^{\lambda t}\sum _{\mathfrak{x}=1}^n\sum _{\mathfrak{z}=1}^n{\mathbf{s}}_{\mathfrak{x}}|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{G}}_{\mathfrak{z}}^K(|{\mathbf{m}}_{\mathfrak{x}}^K{(t)|}^2+{\mathbf{m}}_{\mathfrak{z}}^K(t){|}^2)\hfill \\ & +e^{\lambda t}\sum _{\mathfrak{x}=1}^n\sum _{\mathfrak{z}=1}^n{\mathbf{s}}_{\mathfrak{x}}|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{G}}_{\mathfrak{z}}^J(|{\mathbf{m}}_{\mathfrak{x}}^K{(t)|}^2+{\mathbf{m}}_{\mathfrak{z}}^J{(t)|}^2)+e^{\lambda t}\sum _{\mathfrak{x}=1}^n\sum _{\mathfrak{z}=1}^n{\mathbf{s}}_{\mathfrak{x}}|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^K|{\mathbf{G}}_{\mathfrak{z}}^R(|{\mathbf{m}}_{\mathfrak{x}}^K{(t)|}^2+{\mathbf{m}}_{\mathfrak{z}}^R(t){|}^2)\hfill \\ & +e^{\lambda t}\sum _{\mathfrak{x}=1}^n\sum _{\mathfrak{z}=1}^n{\mathbf{s}}_{\mathfrak{x}}|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^J|{\mathbf{G}}_{\mathfrak{z}}^I(|{\mathbf{m}}_{\mathfrak{x}}^K{(t)|}^2+{\mathbf{m}}_{\mathfrak{z}}^I{(t)|}^2)+e^{\lambda t}\sum _{\mathfrak{x}=1}^n\sum _{\mathfrak{z}=1}^n{\mathbf{s}}_{\mathfrak{x}}|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{H}}_{\mathfrak{z}}^K(|{\mathbf{m}}_{\mathfrak{x}}^K{(t)|}^2+{\mathbf{m}}_{\mathfrak{z}}^K(t-\tau (t)){|}^2)\hfill \\ & +e^{\lambda t}\sum _{\mathfrak{x}=1}^n\sum _{\mathfrak{z}=1}^n{\mathbf{s}}_{\mathfrak{x}}|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{H}}_{\mathfrak{z}}^J(|{\mathbf{m}}_{\mathfrak{x}}^K{(t)|}^2+{\mathbf{m}}_{\mathfrak{z}}^J{(t-\tau (t))|}^2)+e^{\lambda t}\sum _{\mathfrak{x}=1}^n\sum _{\mathfrak{z}=1}^n{\mathbf{s}}_{\mathfrak{x}}|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^K|{\mathbf{H}}_{\mathfrak{z}}^R(|{\mathbf{m}}_{\mathfrak{x}}^K{(t)|}^2+{\mathbf{m}}_{\mathfrak{z}}^R(t-\tau (t)){|}^2)\hfill \\ & +e^{\lambda t}\sum _{\mathfrak{x}=1}^n\sum _{\mathfrak{z}=1}^n{\mathbf{s}}_{\mathfrak{x}}|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^J|{\mathbf{H}}_{\mathfrak{z}}^I(|{\mathbf{m}}_{\mathfrak{x}}^K{(t)|}^2+{\mathbf{m}}_{\mathfrak{z}}^I{(t-\tau (t))|}^2)+e^{\lambda t}\sum _{\mathfrak{x}=1}^n{\mathbf{s}}_{\mathfrak{x}}(|{\mathbf{m}}_{\mathfrak{x}}^K{(t)|}^2+|{\mathbf{u}}_{\mathfrak{x}}^K(t){|}^2)\hfill \\ & +e^{\lambda t}\sum _{\mathfrak{x}=1}^n[-(1-\mu )e^{-\lambda \tau }{\mathbf{v}}_{\mathfrak{x}}+\sum _{\mathfrak{z}=1}^n{\mathbf{s}}_{\mathfrak{z}}{\tilde{\beta }}_{\mathfrak{z}\mathfrak{x}}]{{\mathbf{m}}^K}_{\mathfrak{x}}^2(t-\tau (t)).\hfill \end{array}$$

(33)

With further simplification, we have

$$\begin{array}{cc}\mathcal{L}\mathcal{V}(t,\overline{\mathbf{m}}(t))=\hfill & -e^{\lambda t}\underset{1\le \mathfrak{x}\le n}{min}[2{\mathbf{p}}_{\mathfrak{x}}{\mathbf{c}}_{\mathfrak{x}}-\lambda {\mathbf{p}}_{\mathfrak{x}}-\sum _{\mathfrak{z}=1}^n{\mathbf{p}}_{\mathfrak{z}}{\widehat{\alpha }}_{\mathfrak{z}\mathfrak{x}}-{\mathbf{d}}_{\mathfrak{x}}-{\mathbf{p}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{G}}_{\mathfrak{z}}^R-{\mathbf{p}}_{\mathfrak{z}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{z}\mathfrak{x}}^R|{\mathbf{G}}_{\mathfrak{x}}^R\hfill \\ & -{\mathbf{p}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{G}}_{\mathfrak{z}}^I-{\mathbf{p}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^J|{\mathbf{G}}_{\mathfrak{z}}^J-{\mathbf{p}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^K|{\mathbf{G}}_{\mathfrak{z}}^K-{\mathbf{p}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{H}}_{\mathfrak{z}}^R-{\mathbf{p}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{H}}_{\mathfrak{z}}^I\hfill \\ & -{\mathbf{p}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^J|{\mathbf{H}}_{\mathfrak{z}}^J-{\mathbf{p}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^K|{\mathbf{H}}_{\mathfrak{z}}^K-{\mathbf{p}}_{\mathfrak{x}}-{\mathbf{q}}_{\mathfrak{z}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{z}\mathfrak{x}}^I|{\mathbf{G}}_{\mathfrak{x}}^R-{\mathbf{r}}_{\mathfrak{z}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{z}\mathfrak{x}}^J|{\mathbf{G}}_{\mathfrak{x}}^J\hfill \\ & -{\mathbf{s}}_{\mathfrak{z}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{z}\mathfrak{x}}^K|{\mathbf{G}}_{\mathfrak{x}}^K]\sum _{\mathfrak{x}=1}^n{{\mathbf{m}}^R}_{\mathfrak{x}}^2(t)-e^{\lambda t}\underset{1\le \mathfrak{x}\le n}{min}[(1-\mu ){\mathbf{d}}_{\mathfrak{x}}-e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{p}}_{\mathfrak{z}}{\widehat{\beta }}_{\mathfrak{z}\mathfrak{x}}-e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{p}}_{\mathfrak{z}}|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{H}}_{\mathfrak{x}}^R\hfill \\ & -e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{q}}_{\mathfrak{z}}|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{H}}_{\mathfrak{x}}^R-e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{r}}_{\mathfrak{z}}|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^J|{\mathbf{H}}_{\mathfrak{x}}^R-e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{s}}_{\mathfrak{z}}|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^K|{\mathbf{H}}_{\mathfrak{x}}^R]\sum _{\mathfrak{x}=1}^n{{\mathbf{m}}^R}_{\mathfrak{x}}^2(t-\tau (t))\hfill \\ & -e^{\lambda t}\underset{1\le \mathfrak{x}\le n}{min}[2{\mathbf{q}}_{\mathfrak{x}}{\mathbf{c}}_{\mathfrak{x}}-\lambda {\mathbf{q}}_{\mathfrak{x}}-\sum _{\mathfrak{z}=1}^n{\mathbf{q}}_{\mathfrak{z}}{\check{\alpha }}_{\mathfrak{z}\mathfrak{x}}-{\mathbf{h}}_{\mathfrak{x}}-{\mathbf{q}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{G}}_{\mathfrak{z}}^I-{\mathbf{q}}_{\mathfrak{z}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{z}\mathfrak{x}}^R|{\mathbf{G}}_{\mathfrak{x}}^I\hfill \\ & -{\mathbf{p}}_{\mathfrak{z}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{z}\mathfrak{x}}^I|{\mathbf{G}}_{\mathfrak{x}}^I-{\mathbf{q}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{G}}_{\mathfrak{z}}^R-{\mathbf{q}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^J|{\mathbf{G}}_{\mathfrak{z}}^K-{\mathbf{q}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^K|{\mathbf{G}}_{\mathfrak{z}}^J-{\mathbf{q}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{H}}_{\mathfrak{z}}^I\hfill \\ & -{\mathbf{q}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{H}}_{\mathfrak{z}}^R-{\mathbf{q}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^J|{\mathbf{H}}_{\mathfrak{z}}^K-{\mathbf{q}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^K|{\mathbf{H}}_{\mathfrak{z}}^J-{\mathbf{q}}_{\mathfrak{x}}-{\mathbf{r}}_{\mathfrak{z}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{z}\mathfrak{x}}^K|{\mathbf{G}}_{\mathfrak{x}}^I\hfill \\ & -{\mathbf{s}}_{\mathfrak{z}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{z}\mathfrak{x}}^J|{\mathbf{G}}_{\mathfrak{x}}^I]\sum _{\mathfrak{x}=1}^n{{\mathbf{m}}^I}_{\mathfrak{x}}^2(t)-e^{\lambda t}\underset{1\le \mathfrak{x}\le n}{min}[(1-\mu ){\mathbf{h}}_{\mathfrak{x}}-e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{q}}_{\mathfrak{z}}{\check{\beta }}_{\mathfrak{z}\mathfrak{x}}-e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{p}}_{\mathfrak{z}}|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{H}}_{\mathfrak{x}}^I\hfill \\ & -e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{q}}_{\mathfrak{z}}|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{H}}_{\mathfrak{x}}^I-e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{r}}_{\mathfrak{z}}|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^K|{\mathbf{H}}_{\mathfrak{x}}^I-e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{s}}_{\mathfrak{z}}|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^J|{\mathbf{H}}_{\mathfrak{x}}^I]\sum _{\mathfrak{x}=1}^n{{\mathbf{m}}^I}_{\mathfrak{x}}^2(t-\tau (t))\hfill \\ & -e^{\lambda t}\underset{1\le \mathfrak{x}\le n}{min}[2{\mathbf{r}}_{\mathfrak{x}}{\mathbf{c}}_{\mathfrak{x}}-\lambda {\mathbf{r}}_{\mathfrak{x}}-\sum _{\mathfrak{z}=1}^n{\mathbf{r}}_{\mathfrak{z}}{\overline{\alpha }}_{\mathfrak{z}\mathfrak{x}}-{\mathbf{u}}_{\mathfrak{x}}-{\mathbf{r}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{G}}_{\mathfrak{z}}^J-{\mathbf{r}}_{\mathfrak{z}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{z}\mathfrak{x}}^R|{\mathbf{G}}_{\mathfrak{x}}^J\hfill \\ & -{\mathbf{p}}_{\mathfrak{z}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{z}\mathfrak{x}}^J|{\mathbf{G}}_{\mathfrak{x}}^J-{\mathbf{q}}_{\mathfrak{z}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{z}\mathfrak{x}}^K|{\mathbf{G}}_{\mathfrak{x}}^J-{\mathbf{r}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^J|{\mathbf{G}}_{\mathfrak{z}}^R-{\mathbf{r}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^K|{\mathbf{G}}_{\mathfrak{z}}^I-{\mathbf{r}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{G}}_{\mathfrak{z}}^K\hfill \\ & -{\mathbf{r}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{H}}_{\mathfrak{z}}^J-{\mathbf{r}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^J|{\mathbf{H}}_{\mathfrak{z}}^R-{\mathbf{r}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^K|{\mathbf{H}}_{\mathfrak{z}}^I-{\mathbf{r}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{H}}_{\mathfrak{z}}^K-{\mathbf{r}}_{\mathfrak{x}}\hfill \\ & -{\mathbf{s}}_{\mathfrak{z}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{z}\mathfrak{x}}^I|{\mathbf{G}}_{\mathfrak{x}}^J]\sum _{\mathfrak{x}=1}^n{{\mathbf{m}}^J}_{\mathfrak{x}}^2(t)-e^{\lambda t}\underset{1\le \mathfrak{x}\le n}{min}[(1-\mu ){\mathbf{u}}_{\mathfrak{x}}-e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{r}}_{\mathfrak{z}}{\overline{\beta }}_{\mathfrak{z}\mathfrak{x}}-e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{p}}_{\mathfrak{z}}|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^J|{\mathbf{H}}_{\mathfrak{x}}^J\hfill \\ & -e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{q}}_{\mathfrak{z}}|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^K|{\mathbf{H}}_{\mathfrak{x}}^J-e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{r}}_{\mathfrak{z}}|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{H}}_{\mathfrak{x}}^J-e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{s}}_{\mathfrak{z}}|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{H}}_{\mathfrak{x}}^J]\sum _{\mathfrak{x}=1}^n{{\mathbf{m}}^J}_{\mathfrak{x}}^2(t-\tau (t))\hfill \\ & -e^{\lambda t}\underset{1\le \mathfrak{x}\le n}{min}[2{\mathbf{s}}_{\mathfrak{x}}{\mathbf{c}}_{\mathfrak{x}}-\lambda {\mathbf{s}}_{\mathfrak{x}}-\sum _{\mathfrak{z}=1}^n{\mathbf{s}}_{\mathfrak{z}}{\tilde{\alpha }}_{\mathfrak{z}\mathfrak{x}}-{\mathbf{v}}_{\mathfrak{x}}-{\mathbf{s}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{G}}_{\mathfrak{z}}^K-{\mathbf{s}}_{\mathfrak{z}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{z}\mathfrak{x}}^R|{\mathbf{G}}_{\mathfrak{x}}^K\hfill \\ & -{\mathbf{p}}_{\mathfrak{z}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{z}\mathfrak{x}}^K|{\mathbf{G}}_{\mathfrak{x}}^K-{\mathbf{q}}_{\mathfrak{z}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{z}\mathfrak{x}}^J|{\mathbf{G}}_{\mathfrak{x}}^K-{\mathbf{r}}_{\mathfrak{z}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{G}}_{\mathfrak{x}}^K-{\mathbf{s}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{G}}_{\mathfrak{z}}^I-{\mathbf{s}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^K|{\mathbf{G}}_{\mathfrak{z}}^R\hfill \\ & -{\mathbf{s}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^J|{\mathbf{G}}_{\mathfrak{z}}^I-{\mathbf{s}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{H}}_{\mathfrak{z}}^K-{\mathbf{s}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{H}}_{\mathfrak{z}}^J-{\mathbf{s}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^K|{\mathbf{H}}_{\mathfrak{z}}^R\hfill \\ & -{\mathbf{s}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^J|{\mathbf{H}}_{\mathfrak{z}}^I-{\mathbf{s}}_{\mathfrak{x}}]\sum _{\mathfrak{x}=1}^n{{\mathbf{m}}^K}_{\mathfrak{x}}^2(t)-e^{\lambda t}\underset{1\le \mathfrak{x}\le n}{min}[(1-\mu ){\mathbf{v}}_{\mathfrak{x}}-e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{s}}_{\mathfrak{z}}{\tilde{\beta }}_{\mathfrak{z}\mathfrak{x}}-e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{p}}_{\mathfrak{z}}|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^K|{\mathbf{H}}_{\mathfrak{x}}^K\hfill \\ & -e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{q}}_{\mathfrak{z}}|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^J|{\mathbf{H}}_{\mathfrak{x}}^K-e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{r}}_{\mathfrak{z}}|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{H}}_{\mathfrak{x}}^K-e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{s}}_{\mathfrak{z}}|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{H}}_{\mathfrak{x}}^K]\sum _{\mathfrak{x}=1}^n{{\mathbf{m}}^K}_{\mathfrak{x}}^2(t-\tau (t))+e^{\lambda \tau }\sum _{\mathfrak{x}=1}^{4n}{\xi }_{\mathfrak{x}}{|\overline{\mathbf{U}}(t)|}^2,\hfill \end{array}$$

(34)

where

$$\begin{array}{c}\overline{\mathbf{U}}(t)=\left\{\begin{array}{c}{\mathbf{u}}_{\mathfrak{x}}^R(t),\mathfrak{x}=1,2,\dots ,n,\hfill \\ {\mathbf{u}}_{\mathfrak{x}}^I(t),\mathfrak{x}=n+1,n+2,\dots ,2n,\hfill \\ {\mathbf{u}}_{\mathfrak{x}}^J(t),\mathfrak{x}=2n+1,2n+2,\dots ,3n,\hfill \\ {\mathbf{u}}_{\mathfrak{x}}^K(t),\mathfrak{x}=3n+1,3n+2,\dots ,4n.\hfill \end{array}\right.\hfill \end{array}$$

According to Equations (14)–(21), we can easily obtain

$$\begin{array}{c}\mathcal{L}\mathcal{V}(t,\overline{\mathbf{m}}(t))\le e^{\lambda t}\sum _{\mathfrak{x}=1}^{4n}{\xi }_{\mathfrak{x}}|\overline{\mathbf{U}}{(t)|}^2\le e^{\lambda t}\underset{1\le \mathfrak{x}\le 4n}{max}{\xi }_{\mathfrak{x}}{\parallel \overline{\mathbf{U}}\parallel }_{\infty }^2.\hfill \end{array}$$

(35)

Now, similar to the study in [13], the Markov time or stopping time is defined as ${\varrho }_{ħ}:=inf\{s\ge 0:|\overline{\mathbf{m}}(s)|\ge ħ\}$. The Dynkin formula is then used to yield

$$\begin{array}{c}\mathbb{E}[\mathcal{V}(t\wedge {\varrho }_{ħ},\overline{\mathbf{m}}(t\wedge {\varrho }_{ħ}))]=\mathbb{E}[\mathcal{V}(0,\overline{\mathbf{m}}(0))]+\mathbb{E}\left[{\int }_0^{t\wedge {\varrho }_{ħ}}\mathcal{L}\mathcal{V}(s,\overline{\mathbf{m}}(s))ds\right].\hfill \end{array}$$

(36)

With respect to the monotone convergence theorem, we have the following when ℏ goes to ∞

$$\begin{array}{c}\mathbb{E}[\mathcal{V}(t,\overline{\mathbf{m}}(t))]\le \sum _{\mathfrak{x}=1}^{4n}{\xi }_{\mathfrak{x}}\mathbb{E}[{\overline{\mathbf{m}}}_{\mathfrak{x}}^2(0)]+{\int }_{-\tau (0)}^0{e}^{\lambda s}\mathbb{E}\left[\sum _{\mathfrak{x}=1}^{4n}{\zeta }_{\mathfrak{x}}{\overline{\mathbf{m}}}_{\mathfrak{x}}^2(s)]ds\right]+\frac{1}{\lambda }{\parallel \overline{\mathbf{U}}\parallel }_{\infty }^2\underset{1\le \mathfrak{x}\le 4n}{min}{\xi }_{\mathfrak{x}}(e^{\lambda t}-1).\hfill \end{array}$$

(37)

Based on Equation (22), we have

$$\begin{array}{cc}\mathbb{E}[\mathcal{V}(t,\overline{\mathbf{m}}(t))]\ge \hfill & \mathbb{E}\left[e^{\lambda t}\sum _{\mathfrak{x}=1}^{4n}{\xi }_{\mathfrak{x}}\mathbb{E}|{\overline{\mathbf{m}}}_{\mathfrak{x}}^2(t)|\right]\hfill \\ & \ge e^{\lambda t}\underset{1\le \mathfrak{x}\le 4n}{min}{\xi }_{\mathfrak{x}}\mathbb{E}[|\overline{\mathbf{m}}(t){|}^2].\hfill \end{array}$$

(38)

Combining Equations (37) and (38), we have

$$\begin{array}{c}{e}^{\lambda t}\underset{1\le \mathfrak{x}\le 4n}{min}{\xi }_{\mathfrak{x}}\mathbb{E}[|\overline{\mathbf{m}}{(t)|}^2]\le \underset{1\le \mathfrak{x}\le 4n}{max}{\xi }_{\mathfrak{x}}\sum _{\mathfrak{x}=1}^{4n}\mathbb{E}[{\overline{\mathbf{m}}}_{\mathfrak{x}}^2(0)]+\underset{1\le \mathfrak{x}\le 4n}{max}{\zeta }_{\mathfrak{x}}{\int }_{-\tau }^0{e}^{\lambda s}\sum _{\mathfrak{x}=1}^{4n}\mathbb{E}[{\overline{\mathbf{m}}}_{\mathfrak{x}}^2(s)]ds+\frac{1}{\lambda }{e}^{\lambda t}{\parallel \overline{\mathbf{U}}\parallel }_{\infty }^2\underset{1\le \mathfrak{x}\le 4n}{max}{\xi }_{\mathfrak{x}}.\hfill \end{array}$$

(39)

Consequently, we can derive

$$\begin{array}{c}\mathbb{E}[|\overline{\mathbf{m}}{(t)|}^2]\le \alpha e^{-\lambda t}{\mathbb{E}[\parallel \varphi \parallel }^2]+\gamma \parallel \overline{\mathbf{U}}{\parallel }_{\infty }^2,\hfill \end{array}$$

(40)

where

$$\begin{array}{c}\alpha =\frac{\underset{1\le \mathfrak{x}\le 4n}{max}{\xi }_{\mathfrak{x}}+\tau \underset{1\le \mathfrak{x}\le 4n}{max}{\zeta }_{\mathfrak{x}}}{\underset{1\le \mathfrak{x}\le 4n}{min}{\xi }_{\mathfrak{x}}},\gamma =\frac{\underset{1\le \mathfrak{x}\le 4n}{max}{\xi }_{\mathfrak{x}}}{\lambda \underset{1\le \mathfrak{x}\le 4n}{min}{\xi }_{\mathfrak{x}}},\hfill \end{array}$$

which implies that the SMQVNN model in Equation (2) has a trivial solution, which is mean-square exp ISS. The proof is completed. □

Remark 2.

Suppose that the time-varying delay $\tau (t)$ is assumed to satisfy $0\le \tau (t)\le \tau$, where τ is a positive real constant. As we mentioned in the introduction, constant delays can be seen as a special case of time-varying delays when the delays vary in a fixed point. Therefore, the mean-square exp-ISS criterion of the NN Model (2) can be derived based on the same approaches as in Theorem (1) with constant delays in the following Corollary (1).

Corollary 1.

Suppose that A1-A4 hold, and subject to the existence of positive scalars $\lambda ,{\mathbf{p}}_{\mathfrak{x}},{\mathbf{q}}_{\mathfrak{x}},{\mathbf{r}}_{\mathfrak{x}},{\mathbf{s}}_{\mathfrak{x}}$, ${\mathbf{d}}_{\mathfrak{x}},{\mathbf{h}}_{\mathfrak{x}},{\mathbf{u}}_{\mathfrak{x}},{\mathbf{v}}_{\mathfrak{x}},\mathfrak{x}\in N$, the SMQVNN model in Equation (2) with a constant delay has a trival solution, which is mean-square exp-ISS, in which

$$\begin{array}{cc}2{\mathbf{p}}_{\mathfrak{x}}{\mathbf{c}}_{\mathfrak{x}}\ge \hfill & \lambda {\mathbf{p}}_{\mathfrak{x}}+\sum _{\mathfrak{z}=1}^n{\mathbf{p}}_{\mathfrak{z}}{\widehat{\alpha }}_{\mathfrak{z}\mathfrak{x}}+{\mathbf{d}}_{\mathfrak{x}}+{\mathbf{p}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{G}}_{\mathfrak{z}}^R+{\mathbf{p}}_{\mathfrak{z}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{z}\mathfrak{x}}^R|{\mathbf{G}}_{\mathfrak{x}}^R+{\mathbf{p}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{G}}_{\mathfrak{z}}^I\hfill \\ & +{\mathbf{p}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^J|{\mathbf{G}}_{\mathfrak{z}}^J+{\mathbf{p}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^K|{\mathbf{G}}_{\mathfrak{z}}^K+{\mathbf{p}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{H}}_{\mathfrak{z}}^R+{\mathbf{p}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{H}}_{\mathfrak{z}}^I\hfill \\ & +{\mathbf{p}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^J|{\mathbf{H}}_{\mathfrak{z}}^J+{\mathbf{p}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^K|{\mathbf{H}}_{\mathfrak{z}}^K+{\mathbf{p}}_{\mathfrak{x}}+{\mathbf{q}}_{\mathfrak{z}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{z}\mathfrak{x}}^I|{\mathbf{G}}_{\mathfrak{x}}^R+{\mathbf{r}}_{\mathfrak{z}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{z}\mathfrak{x}}^J|{\mathbf{G}}_{\mathfrak{x}}^J+{\mathbf{s}}_{\mathfrak{z}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{z}\mathfrak{x}}^K|{\mathbf{G}}_{\mathfrak{x}}^K,\hfill \end{array}$$

(41)

$$\begin{array}{cc}{\mathbf{d}}_{\mathfrak{x}}\ge \hfill & e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{p}}_{\mathfrak{z}}{\widehat{\beta }}_{\mathfrak{z}\mathfrak{x}}+e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{p}}_{\mathfrak{z}}|{\tilde{\mathbf{b}}}_{\mathfrak{z}\mathfrak{x}}^R|{\mathbf{H}}_{\mathfrak{x}}^R+e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{q}}_{\mathfrak{z}}|{\tilde{\mathbf{b}}}_{\mathfrak{z}\mathfrak{x}}^I|{\mathbf{H}}_{\mathfrak{x}}^R+e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{r}}_{\mathfrak{z}}|{\tilde{\mathbf{b}}}_{\mathfrak{z}\mathfrak{x}}^J|{\mathbf{H}}_{\mathfrak{x}}^R+e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{s}}_{\mathfrak{z}}|{\tilde{\mathbf{b}}}_{\mathfrak{z}\mathfrak{x}}^K|{\mathbf{H}}_{\mathfrak{x}}^R,\hfill \end{array}$$

(42)

$$\begin{array}{cc}2{\mathbf{q}}_{\mathfrak{x}}{\mathbf{c}}_{\mathfrak{x}}\ge \hfill & \lambda {\mathbf{q}}_{\mathfrak{x}}+\sum _{\mathfrak{z}=1}^n{\mathbf{q}}_{\mathfrak{z}}{\check{\alpha }}_{\mathfrak{z}\mathfrak{x}}+{\mathbf{h}}_{\mathfrak{x}}+{\mathbf{q}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{G}}_{\mathfrak{z}}^I+{\mathbf{q}}_{\mathfrak{z}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{z}\mathfrak{x}}^R|{\mathbf{G}}_{\mathfrak{x}}^I+{\mathbf{p}}_{\mathfrak{z}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{z}\mathfrak{x}}^I|{\mathbf{G}}_{\mathfrak{x}}^I\hfill \\ & +{\mathbf{q}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{G}}_{\mathfrak{z}}^R+{\mathbf{q}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^J|{\mathbf{G}}_{\mathfrak{z}}^K+{\mathbf{q}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^K|{\mathbf{G}}_{\mathfrak{z}}^J+{\mathbf{q}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{H}}_{\mathfrak{z}}^I\hfill \\ & +{\mathbf{q}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{H}}_{\mathfrak{z}}^R+{\mathbf{q}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^J|{\mathbf{H}}_{\mathfrak{z}}^K+{\mathbf{q}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^K|{\mathbf{H}}_{\mathfrak{z}}^J+{\mathbf{q}}_{\mathfrak{x}}+{\mathbf{r}}_{\mathfrak{z}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{z}\mathfrak{x}}^K|{\mathbf{G}}_{\mathfrak{x}}^I+{\mathbf{s}}_{\mathfrak{z}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{z}\mathfrak{x}}^J|{\mathbf{G}}_{\mathfrak{x}}^I,\hfill \end{array}$$

(43)

$$\begin{array}{cc}{\mathbf{h}}_{\mathfrak{x}}\ge \hfill & e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{q}}_{\mathfrak{z}}{\check{\beta }}_{\mathfrak{z}\mathfrak{x}}+e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{p}}_{\mathfrak{z}}|{\tilde{\mathbf{b}}}_{\mathfrak{z}\mathfrak{x}}^I|{\mathbf{H}}_{\mathfrak{x}}^I+e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{q}}_{\mathfrak{z}}|{\tilde{\mathbf{b}}}_{\mathfrak{z}\mathfrak{x}}^R|{\mathbf{H}}_{\mathfrak{x}}^I+e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{r}}_{\mathfrak{z}}|{\tilde{\mathbf{b}}}_{\mathfrak{z}\mathfrak{x}}^K|{\mathbf{H}}_{\mathfrak{x}}^I+e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{s}}_{\mathfrak{z}}|{\tilde{\mathbf{b}}}_{\mathfrak{z}\mathfrak{x}}^J|{\mathbf{H}}_{\mathfrak{x}}^I,\hfill \end{array}$$

(44)

$$\begin{array}{cc}2{\mathbf{r}}_{\mathfrak{x}}{\mathbf{c}}_{\mathfrak{x}}\ge \hfill & \lambda {\mathbf{r}}_{\mathfrak{x}}+\sum _{\mathfrak{z}=1}^n{\mathbf{r}}_{\mathfrak{z}}{\overline{\alpha }}_{\mathfrak{z}\mathfrak{x}}+{\mathbf{u}}_{\mathfrak{x}}+{\mathbf{r}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{G}}_{\mathfrak{z}}^J+{\mathbf{r}}_{\mathfrak{z}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{z}\mathfrak{x}}^R|{\mathbf{G}}_{\mathfrak{x}}^J+{\mathbf{p}}_{\mathfrak{z}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{z}\mathfrak{x}}^J|{\mathbf{G}}_{\mathfrak{x}}^J\hfill \\ & +{\mathbf{q}}_{\mathfrak{z}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{z}\mathfrak{x}}^K|{\mathbf{G}}_{\mathfrak{x}}^J+{\mathbf{r}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^J|{\mathbf{G}}_{\mathfrak{z}}^R+{\mathbf{r}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^K|{\mathbf{G}}_{\mathfrak{z}}^I+{\mathbf{r}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{G}}_{\mathfrak{z}}^K\hfill \\ & +{\mathbf{r}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{H}}_{\mathfrak{z}}^J+{\mathbf{r}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^J|{\mathbf{H}}_{\mathfrak{z}}^R+{\mathbf{r}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^K|{\mathbf{H}}_{\mathfrak{z}}^I+{\mathbf{r}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{H}}_{\mathfrak{z}}^K+{\mathbf{r}}_{\mathfrak{x}}+{\mathbf{s}}_{\mathfrak{z}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{z}\mathfrak{x}}^I|{\mathbf{G}}_{\mathfrak{x}}^J,\hfill \end{array}$$

(45)

$$\begin{array}{cc}{\mathbf{u}}_{\mathfrak{x}}\ge \hfill & e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{r}}_{\mathfrak{z}}{\overline{\beta }}_{\mathfrak{z}\mathfrak{x}}+e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{p}}_{\mathfrak{z}}|{\tilde{\mathbf{b}}}_{\mathfrak{z}\mathfrak{x}}^J|{\mathbf{H}}_{\mathfrak{x}}^J+e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{q}}_{\mathfrak{z}}|{\tilde{\mathbf{b}}}_{\mathfrak{z}\mathfrak{x}}^K|{\mathbf{H}}_{\mathfrak{x}}^J+e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{r}}_{\mathfrak{z}}|{\tilde{\mathbf{b}}}_{\mathfrak{z}\mathfrak{x}}^R|{\mathbf{H}}_{\mathfrak{x}}^J+e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{s}}_{\mathfrak{z}}|{\tilde{\mathbf{b}}}_{\mathfrak{z}\mathfrak{x}}^I|{\mathbf{H}}_{\mathfrak{x}}^J,\hfill \end{array}$$

(46)

$$\begin{array}{cc}2{\mathbf{s}}_{\mathfrak{x}}{\mathbf{c}}_{\mathfrak{x}}\ge \hfill & \lambda {\mathbf{s}}_{\mathfrak{x}}+\sum _{\mathfrak{z}=1}^n{\mathbf{s}}_{\mathfrak{z}}{\tilde{\alpha }}_{\mathfrak{z}\mathfrak{x}}+{\mathbf{v}}_{\mathfrak{x}}+{\mathbf{s}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{G}}_{\mathfrak{z}}^K+{\mathbf{s}}_{\mathfrak{z}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{z}\mathfrak{x}}^R|{\mathbf{G}}_{\mathfrak{x}}^K+{\mathbf{p}}_{\mathfrak{z}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{z}\mathfrak{x}}^K|{\mathbf{G}}_{\mathfrak{x}}^K\hfill \\ & +{\mathbf{q}}_{\mathfrak{z}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{z}\mathfrak{x}}^J|{\mathbf{G}}_{\mathfrak{x}}^K+{\mathbf{r}}_{\mathfrak{z}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{G}}_{\mathfrak{x}}^K+{\mathbf{s}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{G}}_{\mathfrak{z}}^I+{\mathbf{s}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^K|{\mathbf{G}}_{\mathfrak{z}}^R\hfill \\ & +{\mathbf{s}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^J|{\mathbf{G}}_{\mathfrak{z}}^I+{\mathbf{s}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{H}}_{\mathfrak{z}}^K+{\mathbf{s}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{H}}_{\mathfrak{z}}^J+{\mathbf{s}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^K|{\mathbf{H}}_{\mathfrak{z}}^R+{\mathbf{s}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^J|{\mathbf{H}}_{\mathfrak{z}}^I+{\mathbf{s}}_{\mathfrak{x}},\hfill \end{array}$$

(47)

$$\begin{array}{cc}{\mathbf{v}}_{\mathfrak{x}}\ge \hfill & e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{s}}_{\mathfrak{z}}{\tilde{\beta }}_{\mathfrak{z}\mathfrak{x}}+e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{p}}_{\mathfrak{z}}|{\tilde{\mathbf{b}}}_{\mathfrak{z}\mathfrak{x}}^K|{\mathbf{H}}_{\mathfrak{x}}^K+e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{q}}_{\mathfrak{z}}|{\tilde{\mathbf{b}}}_{\mathfrak{z}\mathfrak{x}}^J|{\mathbf{H}}_{\mathfrak{x}}^K+e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{r}}_{\mathfrak{z}}|{\tilde{\mathbf{b}}}_{\mathfrak{z}\mathfrak{x}}^I|{\mathbf{H}}_{\mathfrak{x}}^K+e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{s}}_{\mathfrak{z}}|{\tilde{\mathbf{b}}}_{\mathfrak{z}\mathfrak{x}}^R|{\mathbf{H}}_{\mathfrak{x}}^K,\hfill \end{array}$$

(48)

Remark 3.

The exp-ISS criteria pertaining to the SMQVNN model is yet to be reported in the study of QVNNs dynamics. In order to fill this gap, Theorem (1) and Corollary (1) reveal several new sufficient conditions for the SMQVNN model.

Based on the complex number definition, the model in Equation (10) becomes:

$$\begin{array}{c}\left\{\begin{array}{cc}d{\mathbf{m}}_{\mathfrak{x}}^R(t)=\hfill & [-{\mathbf{c}}_{\mathfrak{x}}{\mathbf{m}}_{\mathfrak{x}}^R(t)+\sum _{\mathfrak{z}=1}^n\left[{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^R{\mathbf{f}}_{\mathfrak{z}}^R({\mathbf{m}}_{\mathfrak{z}}^R(t))-{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^I{\mathbf{f}}_{\mathfrak{z}}^I({\mathbf{m}}_{\mathfrak{z}}^I(t))\right]+\sum _{\mathfrak{z}=1}^n[{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^R{\mathbf{g}}_{\mathfrak{z}}^R({\mathbf{m}}_{\mathfrak{z}}^R(t-\tau (t)))\hfill \\ & -{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^I{\mathbf{g}}_{\mathfrak{z}}^I({\mathbf{m}}_{\mathfrak{z}}^I(t-\tau (t)))]+{\mathbf{u}}_{\mathfrak{x}}^R(t)]dt+\sum _{\mathfrak{z}=1}^n{\sigma }_{\mathfrak{x}\mathfrak{z}}^R(t,{\mathbf{m}}_{\mathfrak{z}}^R(t),{\mathbf{m}}_{\mathfrak{z}}^R(t-\tau (t)))d{w}_{\mathfrak{z}}(t),\hfill \\ d{\mathbf{m}}_{\mathfrak{x}}^I(t)=\hfill & [-{\mathbf{c}}_{\mathfrak{x}}{\mathbf{m}}_{\mathfrak{x}}^I(t)+\sum _{\mathfrak{z}=1}^n\left[{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^R{\mathbf{f}}_{\mathfrak{z}}^I({\mathbf{m}}_{\mathfrak{z}}^I(t))+{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^I{\mathbf{f}}_{\mathfrak{z}}^R({\mathbf{m}}_{\mathfrak{z}}^R(t))\right]+\sum _{\mathfrak{z}=1}^n[{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^R{\mathbf{g}}_{\mathfrak{z}}^I({\mathbf{m}}_{\mathfrak{z}}^I(t-\tau (t)))\hfill \\ & +{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^I{\mathbf{g}}_{\mathfrak{z}}^R({\mathbf{m}}_{\mathfrak{z}}^R(t-\tau (t)))]+{\mathbf{u}}_{\mathfrak{x}}^I(t)]dt+\sum _{\mathfrak{z}=1}^n{\sigma }_{\mathfrak{x}\mathfrak{z}}^I(t,{\mathbf{m}}_{\mathfrak{z}}^I(t),{\mathbf{m}}_{\mathfrak{z}}^I(t-\tau (t)))d{w}_{\mathfrak{z}}(t).\hfill \end{array}\right.\hfill \end{array}$$

(49)

Corollary 2.

Suppose that A1-A4 hold, and subject to the existence of positive scalars $\lambda ,{\mathbf{p}}_{\mathfrak{x}},{\mathbf{q}}_{\mathfrak{x}}$, ${\mathbf{d}}_{\mathfrak{x}},{\mathbf{h}}_{\mathfrak{x}},\mathfrak{x}\in N$, the SMCVNN model in Equation (49) has a trivial solution that is the mean-square exp ISS, such that

$$\begin{array}{cc}2{\mathbf{p}}_{\mathfrak{x}}{\mathbf{c}}_{\mathfrak{x}}\ge \hfill & \lambda {\mathbf{p}}_{\mathfrak{x}}+\sum _{\mathfrak{z}=1}^n{\mathbf{p}}_{\mathfrak{z}}{\widehat{\alpha }}_{\mathfrak{z}\mathfrak{x}}+{\mathbf{d}}_{\mathfrak{x}}+{\mathbf{p}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{G}}_{\mathfrak{z}}^R+{\mathbf{p}}_{\mathfrak{z}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{z}\mathfrak{x}}^R|{\mathbf{G}}_{\mathfrak{x}}^R+{\mathbf{p}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{G}}_{\mathfrak{z}}^I\hfill \\ & +{\mathbf{p}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{H}}_{\mathfrak{z}}^R+{\mathbf{p}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{H}}_{\mathfrak{z}}^I+{\mathbf{p}}_{\mathfrak{x}}+{\mathbf{q}}_{\mathfrak{z}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{z}\mathfrak{x}}^I|{\mathbf{G}}_{\mathfrak{x}}^R,\hfill \end{array}$$

(50)

$$\begin{array}{c}(1-\mu ){\mathbf{d}}_{\mathfrak{x}}\ge e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{p}}_{\mathfrak{z}}{\widehat{\beta }}_{\mathfrak{z}\mathfrak{x}}+e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{p}}_{\mathfrak{z}}|{\tilde{\mathbf{b}}}_{\mathfrak{z}\mathfrak{x}}^R|{\mathbf{H}}_{\mathfrak{x}}^R+e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{q}}_{\mathfrak{z}}|{\tilde{\mathbf{b}}}_{\mathfrak{z}\mathfrak{x}}^I|{\mathbf{H}}_{\mathfrak{x}}^R,\hfill \end{array}$$

(51)

$$\begin{array}{cc}2{\mathbf{q}}_{\mathfrak{x}}{\mathbf{c}}_{\mathfrak{x}}\ge \hfill & \lambda {\mathbf{q}}_{\mathfrak{x}}+\sum _{\mathfrak{z}=1}^n{\mathbf{q}}_{\mathfrak{z}}{\check{\alpha }}_{\mathfrak{z}\mathfrak{x}}+{\mathbf{h}}_{\mathfrak{x}}+{\mathbf{q}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{G}}_{\mathfrak{z}}^I+{\mathbf{q}}_{\mathfrak{z}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{z}\mathfrak{x}}^R|{\mathbf{G}}_{\mathfrak{x}}^I+{\mathbf{p}}_{\mathfrak{z}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{z}\mathfrak{x}}^I|{\mathbf{G}}_{\mathfrak{x}}^I\hfill \\ & +{\mathbf{q}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{G}}_{\mathfrak{z}}^R+{\mathbf{q}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{H}}_{\mathfrak{z}}^I+{\mathbf{q}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{H}}_{\mathfrak{z}}^R+{\mathbf{q}}_{\mathfrak{x}},\hfill \end{array}$$

(52)

$$\begin{array}{c}(1-\mu ){\mathbf{h}}_{\mathfrak{x}}\ge e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{q}}_{\mathfrak{z}}{\check{\beta }}_{\mathfrak{z}\mathfrak{x}}+e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{p}}_{\mathfrak{z}}|{\tilde{\mathbf{b}}}_{\mathfrak{z}\mathfrak{x}}^I|{\mathbf{H}}_{\mathfrak{x}}^I+e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{q}}_{\mathfrak{z}}|{\tilde{\mathbf{b}}}_{\mathfrak{z}\mathfrak{x}}^R|{\mathbf{H}}_{\mathfrak{x}}^I.\hfill \end{array}$$

(53)

Remark 4.

When the external inputs ${\mathbf{u}}^R(t)$, ${\mathbf{u}}^J(t)$, ${\mathbf{u}}^I(t)$ and ${\mathbf{u}}^K(t)$ in Equation (10) are bounded, then $\overline{\mathbf{U}}=[{({\mathbf{u}}^R(t))}^T,{({\mathbf{u}}^I(t))}^T,$${({\mathbf{u}}^J(t))}^T,{({\mathbf{u}}^K(t))}^T{]}^T$ is bounded in Equation (12). From Equation (40), we can acquire that $\mathbb{E}|\overline{\mathbf{m}}{(t)|}^2$ is bounded. Therefore, the model in Equation (2) is stable with respect to a bounded input bounded output (BIBO) condition subject to validity of the conditions of Equations (14)–(21).

Remark 5.

In [39,40], the authors have studied the exp-ISS stability criteria for a class of stochastic RVNNs. Recently, in [13,41], the authors have extended the results proposed in [39,40], to the complex domain. The exp-ISS stability criteria for stochastic CVNNs has also been analyzed. Compared to the previous results, in this paper, we have generalized the results proposed in [13,39,40,41] to the quaternion domain. Furthermore, the results obtained in previous studies [13,39,40,41] can be seen as special cases of this paper.

4. Illustrative Examples

A simulation example is presented to ascertain the efficiency of the results.

Example 1.

A 2D SMQVNN model with a time-varying delay is considered as follows:

$$\begin{array}{cc}d\mathbf{m}(t)=\hfill & [-\mathbf{C}\mathbf{m}(t)+\mathbf{A}(\mathbf{m}(t))\mathbf{f}(\mathbf{m}(t))+\mathbf{B}(\mathbf{m}(t))\mathbf{g}(\mathbf{m}(t-\tau (t)))+\mathbf{U}]dt+\sigma (t,\mathbf{m}(t),\mathbf{m}(t-\tau (t)))dw(t),\hfill \end{array}$$

(54)

where

$$\begin{array}{cc}{\mathbf{a}}_{11}({\mathbf{m}}_1(t))=\hfill & \left\{\begin{array}{c}0.5-0.5i+0.3j-0.4k,|{\mathbf{m}}_1(t)|<0.5\hfill \\ 0.4-0.5i+0.3j-0.4k,|{\mathbf{m}}_1(t)|>0.5,\hfill \end{array}\right.\hfill \\ {\mathbf{a}}_{12}({\mathbf{m}}_2(t))=\hfill & \left\{\begin{array}{c}0.5+0.4i-0.4j+0.3k,|{\mathbf{m}}_2(t)|<0.5\hfill \\ 0.4+0.3i-0.4j+0.3k,|{\mathbf{m}}_2(t)|>0.5,\hfill \end{array}\right.\hfill \\ {\mathbf{a}}_{21}({\mathbf{m}}_1(t))=\hfill & \left\{\begin{array}{c}0.4+0.5i-0.4j-0.5k,|{\mathbf{m}}_1(t)|<0.5\hfill \\ 0.2+0.4i-0.4j-0.4k,|{\mathbf{m}}_1(t)|>0.5,\hfill \end{array}\right.\hfill \\ {\mathbf{a}}_{22}({\mathbf{m}}_2(t))=\hfill & \left\{\begin{array}{c}0.5-0.5i+0.4j+0.4k,|{\mathbf{m}}_2(t)|<0.5\hfill \\ 0.3-0.3i+0.2j+0.2k,|{\mathbf{m}}_2(t)|>0.5,\hfill \end{array}\right.\hfill \\ {\mathbf{b}}_{11}({\mathbf{m}}_1(t))=\hfill & \left\{\begin{array}{c}0.5-0.4i+0.4j+0.3k,|{\mathbf{m}}_1(t)|<0.5\hfill \\ 0.4-0.3i+0.3j+0.3k,|{\mathbf{m}}_1(t)|>0.5,\hfill \end{array}\right.\hfill \\ {\mathbf{b}}_{12}({\mathbf{m}}_2(t))=\hfill & \left\{\begin{array}{c}0.4+0.4i-0.4j-0.5k,|{\mathbf{m}}_2(t)|<0.5\hfill \\ 0.3+0.4i-0.3j-0.5k,|{\mathbf{m}}_2(t)|>0.5,\hfill \end{array}\right.\hfill \end{array}$$

$$\begin{array}{cc}{\mathbf{b}}_{21}({\mathbf{m}}_1(t))=\hfill & \left\{\begin{array}{c}0.4+0.3i-0.4j-0.5k,|{\mathbf{m}}_1(t)|<0.5\hfill \\ -0.3+0.3i-0.3j-0.4k,|{\mathbf{m}}_1(t)|>0.5,\hfill \end{array}\right.\hfill \\ {\mathbf{b}}_{22}({\mathbf{m}}_2(t))=\hfill & \left\{\begin{array}{c}0.5-0.5i+0.4j+0.5k,|{\mathbf{m}}_2(t)|<0.5\hfill \\ 0.4-0.4i+0.3j+0.4k,|{\mathbf{m}}_2(t)|>0.5,\hfill \end{array}\right.\hfill \end{array}$$

and ${\mathbf{c}}_1=6$, ${\mathbf{c}}_2=6$. The the activation functions and external input are as follows $\mathbf{f}(\mathbf{m}(·))=\mathbf{g}(\mathbf{m}(·))=tanh{\mathbf{m}}^R(·)+itanh{\mathbf{m}}^I(·)+jtanh{\mathbf{m}}^J(·)+ktanh{\mathbf{m}}^K(·)$ and $\mathbf{U}={[0.1sin(t)+isin(0.1t)+jsin(0.1t)+ksin(0.1t),0.1cos(t)+icos(0.1t)+jcos(0.1t)+kcos(0.1t)]}^T.$

According to the above analysis, we have $\sigma (t,\mathbf{m}(t),\mathbf{m}(t-\tau (t)))={\sigma }^R(t,{\mathbf{m}}^R(t),{\mathbf{m}}^R(t-\tau (t)))+i{\sigma }^I(t,{\mathbf{m}}^I(t),{\mathbf{m}}^I(t-\tau (t)))$$+j{\sigma }^J(t,{\mathbf{m}}^J(t),{\mathbf{m}}^J(t-\tau (t)))+k{\sigma }^K(t,{\mathbf{m}}^K(t),{\mathbf{m}}^K(t-\tau (t)))$, where

$$\begin{array}{cc}\hfill {\sigma }^R(t,{\mathbf{m}}^R(t),{\mathbf{m}}^R(t-\tau (t)))=& \left[\begin{array}{cc}0.5{\mathbf{m}}_1^R(t)& 0.7{\mathbf{m}}_1^R(t-\tau (t))\\ 0.4{\mathbf{m}}_2^R(t)+0.5{\mathbf{m}}_2^R(t-\tau (t))& 0.3{\mathbf{m}}_2^R(t-\tau (t))\end{array}\right],\hfill \\ \hfill {\sigma }^I(t,{\mathbf{m}}^I(t),{\mathbf{m}}^I(t-\tau (t)))=& \left[\begin{array}{cc}0.4{\mathbf{m}}_1^I(t)& 0.3{\mathbf{m}}_1^I(t-\tau (t))\\ 0.2{\mathbf{m}}_2^I(t)+0.3{\mathbf{m}}_2^I(t-\tau (t))& 0.1{\mathbf{m}}_2^I(t-\tau (t))\end{array}\right],\hfill \\ \hfill {\sigma }^J(t,{\mathbf{m}}^J(t),{\mathbf{m}}^J(t-\tau (t)))=& \left[\begin{array}{cc}0.5{\mathbf{m}}_1^J(t)& 0.3{\mathbf{m}}_1^J(t-\tau (t))\\ 0.4{\mathbf{m}}_2^J(t)+0.1{\mathbf{m}}_2^J(t-\tau (t))& 0.5{\mathbf{m}}_2^J(t-\tau (t))\end{array}\right],\hfill \\ \hfill {\sigma }^K(t,{\mathbf{m}}^K(t),{\mathbf{m}}^K(t-\tau (t)))=& \left[\begin{array}{cc}0.2{\mathbf{m}}_1^K(t)& 0.4{\mathbf{m}}_1^K(t-\tau (t))\\ 0.4{\mathbf{m}}_2^K(t)+0.4{\mathbf{m}}_2^K(t-\tau (t))& 0.2{\mathbf{m}}_2^K(t-\tau (t))\end{array}\right].\hfill \end{array}$$

Take, $\tau =0.3,\tau (t)=0.2cos(t)+0.1,\lambda =0.1,{\mathbf{p}}_1=0.4,{\mathbf{p}}_2=0.5,{\mathbf{q}}_1=0.3,{\mathbf{q}}_2=0.4,{\mathbf{r}}_1=0.6,{\mathbf{r}}_2=0.5,{\mathbf{s}}_1=0.4$, ${\mathbf{s}}_2=0.5,{\mathbf{d}}_1=1.5,{\mathbf{d}}_2=1.6,{\mathbf{h}}_1=1.5,{\mathbf{h}}_2=1.3,{\mathbf{u}}_1=1.4,{\mathbf{u}}_2=1.6,{\mathbf{v}}_1=1.2,{\mathbf{v}}_2=1.4,\mu =0.1$, ${\mathbf{G}}_1^s={\mathbf{G}}_2^s=0.2$, ${\mathbf{H}}_1^s={\mathbf{H}}_2^s=0.2,(s=R,I,J,K)$. By simple computation, the following conditions as given in Equations (55)–(62) are true for all $\mathfrak{x},\mathfrak{z}=1,2$.

$$\begin{array}{cc}2{\mathbf{p}}_{\mathfrak{x}}{\mathbf{c}}_{\mathfrak{x}}>\hfill & \lambda {\mathbf{p}}_{\mathfrak{x}}+\sum _{\mathfrak{z}=1}^n{\mathbf{p}}_{\mathfrak{z}}{\widehat{\alpha }}_{\mathfrak{z}\mathfrak{x}}+{\mathbf{d}}_{\mathfrak{x}}+{\mathbf{p}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{G}}_{\mathfrak{z}}^R+{\mathbf{p}}_{\mathfrak{z}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{z}\mathfrak{x}}^R|{\mathbf{G}}_{\mathfrak{x}}^R+{\mathbf{p}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{G}}_{\mathfrak{z}}^I\hfill \\ & +{\mathbf{p}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^J|{\mathbf{G}}_{\mathfrak{z}}^J+{\mathbf{p}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^K|{\mathbf{G}}_{\mathfrak{z}}^K+{\mathbf{p}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{H}}_{\mathfrak{z}}^R+{\mathbf{p}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{H}}_{\mathfrak{z}}^I\hfill \\ & +{\mathbf{p}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^J|{\mathbf{H}}_{\mathfrak{z}}^J+{\mathbf{p}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^K|{\mathbf{H}}_{\mathfrak{z}}^K+{\mathbf{p}}_{\mathfrak{x}}+{\mathbf{q}}_{\mathfrak{z}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{z}\mathfrak{x}}^I|{\mathbf{G}}_{\mathfrak{x}}^R+{\mathbf{r}}_{\mathfrak{z}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{z}\mathfrak{x}}^J|{\mathbf{G}}_{\mathfrak{x}}^J+{\mathbf{s}}_{\mathfrak{z}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{z}\mathfrak{x}}^K|{\mathbf{G}}_{\mathfrak{x}}^K,\hfill \end{array}$$

(55)

$$\begin{array}{cc}(1-\mu ){\mathbf{d}}_{\mathfrak{x}}>\hfill & e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{p}}_{\mathfrak{z}}{\widehat{\beta }}_{\mathfrak{z}\mathfrak{x}}+e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{p}}_{\mathfrak{z}}|{\tilde{\mathbf{b}}}_{\mathfrak{z}\mathfrak{x}}^R|{\mathbf{H}}_{\mathfrak{x}}^R+e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{q}}_{\mathfrak{z}}|{\tilde{\mathbf{b}}}_{\mathfrak{z}\mathfrak{x}}^I|{\mathbf{H}}_{\mathfrak{x}}^R+e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{r}}_{\mathfrak{z}}|{\tilde{\mathbf{b}}}_{\mathfrak{z}\mathfrak{x}}^J|{\mathbf{H}}_{\mathfrak{x}}^R+e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{s}}_{\mathfrak{z}}|{\tilde{\mathbf{b}}}_{\mathfrak{z}\mathfrak{x}}^K|{\mathbf{H}}_{\mathfrak{x}}^R,\hfill \end{array}$$

(56)

$$\begin{array}{cc}2{\mathbf{q}}_{\mathfrak{x}}{\mathbf{c}}_{\mathfrak{x}}>\hfill & \lambda {\mathbf{q}}_{\mathfrak{x}}+\sum _{\mathfrak{z}=1}^n{\mathbf{q}}_{\mathfrak{z}}{\check{\alpha }}_{\mathfrak{z}\mathfrak{x}}+{\mathbf{h}}_{\mathfrak{x}}+{\mathbf{q}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{G}}_{\mathfrak{z}}^I+{\mathbf{q}}_{\mathfrak{z}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{z}\mathfrak{x}}^R|{\mathbf{G}}_{\mathfrak{x}}^I+{\mathbf{p}}_{\mathfrak{z}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{z}\mathfrak{x}}^I|{\mathbf{G}}_{\mathfrak{x}}^I\hfill \\ & +{\mathbf{q}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{G}}_{\mathfrak{z}}^R+{\mathbf{q}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^J|{\mathbf{G}}_{\mathfrak{z}}^K+{\mathbf{q}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^K|{\mathbf{G}}_{\mathfrak{z}}^J+{\mathbf{q}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{H}}_{\mathfrak{z}}^I\hfill \\ & +{\mathbf{q}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{H}}_{\mathfrak{z}}^R+{\mathbf{q}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^J|{\mathbf{H}}_{\mathfrak{z}}^K+{\mathbf{q}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^K|{\mathbf{H}}_{\mathfrak{z}}^J+{\mathbf{q}}_{\mathfrak{x}}+{\mathbf{r}}_{\mathfrak{z}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{z}\mathfrak{x}}^K|{\mathbf{G}}_{\mathfrak{x}}^I+{\mathbf{s}}_{\mathfrak{z}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{z}\mathfrak{x}}^J|{\mathbf{G}}_{\mathfrak{x}}^I,\hfill \end{array}$$

(57)

$$\begin{array}{cc}(1-\mu ){\mathbf{h}}_{\mathfrak{x}}>\hfill & e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{q}}_{\mathfrak{z}}{\check{\beta }}_{\mathfrak{z}\mathfrak{x}}+e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{p}}_{\mathfrak{z}}|{\tilde{\mathbf{b}}}_{\mathfrak{z}\mathfrak{x}}^I|{\mathbf{H}}_{\mathfrak{x}}^I+e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{q}}_{\mathfrak{z}}|{\tilde{\mathbf{b}}}_{\mathfrak{z}\mathfrak{x}}^R|{\mathbf{H}}_{\mathfrak{x}}^I+e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{r}}_{\mathfrak{z}}|{\tilde{\mathbf{b}}}_{\mathfrak{z}\mathfrak{x}}^K|{\mathbf{H}}_{\mathfrak{x}}^I+e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{s}}_{\mathfrak{z}}|{\tilde{\mathbf{b}}}_{\mathfrak{z}\mathfrak{x}}^J|{\mathbf{H}}_{\mathfrak{x}}^I,\hfill \end{array}$$

(58)

$$\begin{array}{cc}2{\mathbf{r}}_{\mathfrak{x}}{\mathbf{c}}_{\mathfrak{x}}>\hfill & \lambda {\mathbf{r}}_{\mathfrak{x}}+\sum _{\mathfrak{z}=1}^n{\mathbf{r}}_{\mathfrak{z}}{\overline{\alpha }}_{\mathfrak{z}\mathfrak{x}}+{\mathbf{u}}_{\mathfrak{x}}+{\mathbf{r}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{G}}_{\mathfrak{z}}^J+{\mathbf{r}}_{\mathfrak{z}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{z}\mathfrak{x}}^R|{\mathbf{G}}_{\mathfrak{x}}^J+{\mathbf{p}}_{\mathfrak{z}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{z}\mathfrak{x}}^J|{\mathbf{G}}_{\mathfrak{x}}^J\hfill \\ & +{\mathbf{q}}_{\mathfrak{z}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{z}\mathfrak{x}}^K|{\mathbf{G}}_{\mathfrak{x}}^J+{\mathbf{r}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^J|{\mathbf{G}}_{\mathfrak{z}}^R+{\mathbf{r}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^K|{\mathbf{G}}_{\mathfrak{z}}^I+{\mathbf{r}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{G}}_{\mathfrak{z}}^K\hfill \\ & +{\mathbf{r}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{H}}_{\mathfrak{z}}^J+{\mathbf{r}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^J|{\mathbf{H}}_{\mathfrak{z}}^R+{\mathbf{r}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^K|{\mathbf{H}}_{\mathfrak{z}}^I+{\mathbf{r}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{H}}_{\mathfrak{z}}^K+{\mathbf{r}}_{\mathfrak{x}}+{\mathbf{s}}_{\mathfrak{z}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{z}\mathfrak{x}}^I|{\mathbf{G}}_{\mathfrak{x}}^J,\hfill \end{array}$$

(59)

$$\begin{array}{cc}(1-\mu ){\mathbf{u}}_{\mathfrak{x}}>\hfill & e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{r}}_{\mathfrak{z}}{\overline{\beta }}_{\mathfrak{z}\mathfrak{x}}+e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{p}}_{\mathfrak{z}}|{\tilde{\mathbf{b}}}_{\mathfrak{z}\mathfrak{x}}^J|{\mathbf{H}}_{\mathfrak{x}}^J+e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{q}}_{\mathfrak{z}}|{\tilde{\mathbf{b}}}_{\mathfrak{z}\mathfrak{x}}^K|{\mathbf{H}}_{\mathfrak{x}}^J+e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{r}}_{\mathfrak{z}}|{\tilde{\mathbf{b}}}_{\mathfrak{z}\mathfrak{x}}^R|{\mathbf{H}}_{\mathfrak{x}}^J+e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{s}}_{\mathfrak{z}}|{\tilde{\mathbf{b}}}_{\mathfrak{z}\mathfrak{x}}^I|{\mathbf{H}}_{\mathfrak{x}}^J,\hfill \end{array}$$

(60)

$$\begin{array}{cc}2{\mathbf{s}}_{\mathfrak{x}}{\mathbf{c}}_{\mathfrak{x}}>\hfill & \lambda {\mathbf{s}}_{\mathfrak{x}}+\sum _{\mathfrak{z}=1}^n{\mathbf{s}}_{\mathfrak{z}}{\tilde{\alpha }}_{\mathfrak{z}\mathfrak{x}}+{\mathbf{v}}_{\mathfrak{x}}+{\mathbf{s}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{G}}_{\mathfrak{z}}^K+{\mathbf{s}}_{\mathfrak{z}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{z}\mathfrak{x}}^R|{\mathbf{G}}_{\mathfrak{x}}^K+{\mathbf{p}}_{\mathfrak{z}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{z}\mathfrak{x}}^K|{\mathbf{G}}_{\mathfrak{x}}^K\hfill \\ & +{\mathbf{q}}_{\mathfrak{z}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{z}\mathfrak{x}}^J|{\mathbf{G}}_{\mathfrak{x}}^K+{\mathbf{r}}_{\mathfrak{z}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{G}}_{\mathfrak{x}}^K+{\mathbf{s}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{G}}_{\mathfrak{z}}^I+{\mathbf{s}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^K|{\mathbf{G}}_{\mathfrak{z}}^R\hfill \\ & +{\mathbf{s}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{a}}}_{\mathfrak{x}\mathfrak{z}}^J|{\mathbf{G}}_{\mathfrak{z}}^I+{\mathbf{s}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^R|{\mathbf{H}}_{\mathfrak{z}}^K+{\mathbf{s}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^I|{\mathbf{H}}_{\mathfrak{z}}^J+{\mathbf{s}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^K|{\mathbf{H}}_{\mathfrak{z}}^R+{\mathbf{s}}_{\mathfrak{x}}\sum _{\mathfrak{z}=1}^n|{\tilde{\mathbf{b}}}_{\mathfrak{x}\mathfrak{z}}^J|{\mathbf{H}}_{\mathfrak{z}}^I+{\mathbf{s}}_{\mathfrak{x}},\hfill \end{array}$$

(61)

$$\begin{array}{cc}(1-\mu ){\mathbf{v}}_{\mathfrak{x}}>\hfill & e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{s}}_{\mathfrak{z}}{\tilde{\beta }}_{\mathfrak{z}\mathfrak{x}}+e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{p}}_{\mathfrak{z}}|{\tilde{\mathbf{b}}}_{\mathfrak{z}\mathfrak{x}}^K|{\mathbf{H}}_{\mathfrak{x}}^K+e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{q}}_{\mathfrak{z}}|{\tilde{\mathbf{b}}}_{\mathfrak{z}\mathfrak{x}}^J|{\mathbf{H}}_{\mathfrak{x}}^K+e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{r}}_{\mathfrak{z}}|{\tilde{\mathbf{b}}}_{\mathfrak{z}\mathfrak{x}}^I|{\mathbf{H}}_{\mathfrak{x}}^K+e^{\lambda \tau }\sum _{\mathfrak{z}=1}^n{\mathbf{s}}_{\mathfrak{z}}|{\tilde{\mathbf{b}}}_{\mathfrak{z}\mathfrak{x}}^R|{\mathbf{H}}_{\mathfrak{x}}^K.\hfill \end{array}$$

(62)

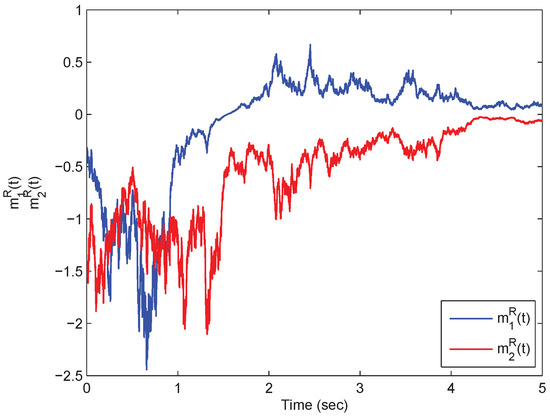
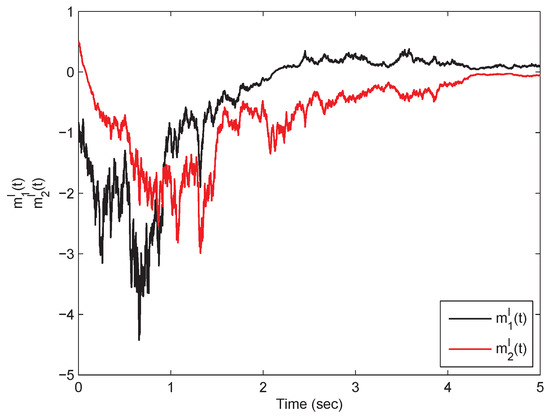
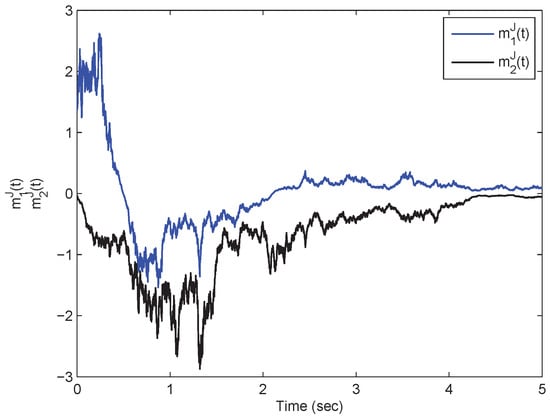
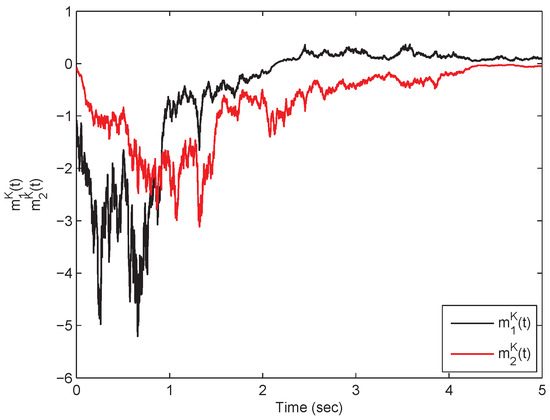
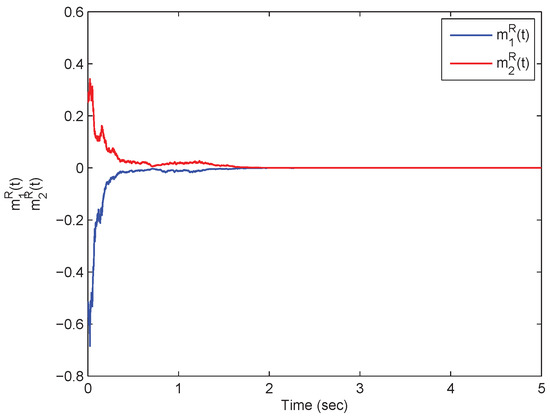
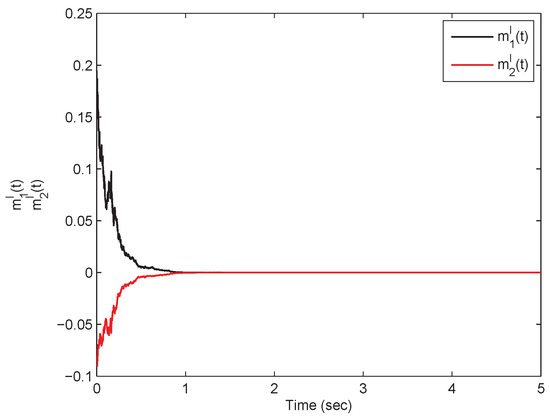
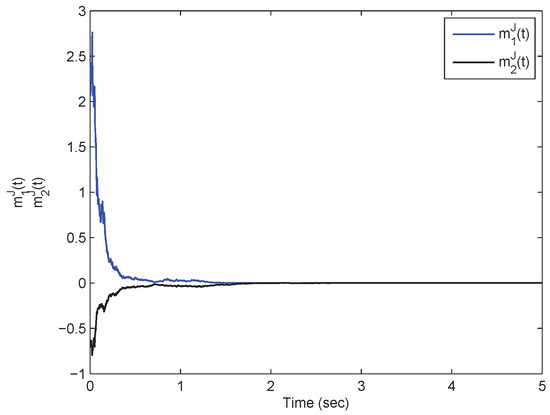
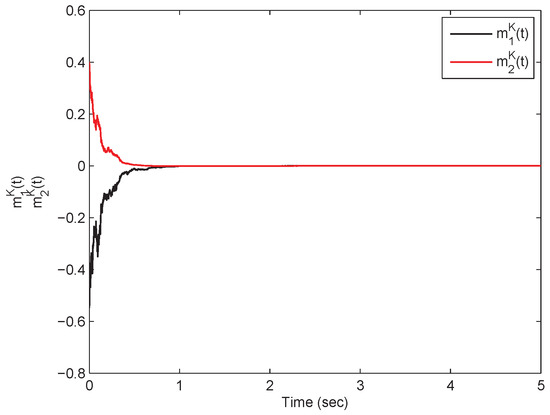
From Theorem (1), it is clear that the model in Equation (54) is mean-square exp-ISS. Referring to the model in Equation (54) in the presence of inputs, its state responses with respect to the real and imaginary parts are plotted in Figure 1, Figure 2, Figure 3 and Figure 4. On the other hand, the model in Equation (54) in the absence of the inputs has the state responses with respect to the real and imaginary parts shown in Figure 5, Figure 6, Figure 7 and Figure 8. Therefore, it is clear that the model in Equation (54) is mean-square exponentially stable.

5. Summary

In this paper, we have studied the mean-square exponential input-to-state stability problem for a new class of SMQVNNs with time-varying delays. Firstly, we decomposed the original SMQVNNs into four real-valued models, in order to avoid the difficulties posed by non-commutative quaternion multiplication. Secondly, by constructing suitable Lyapunov functional and applying It $\widehat{o}$’s formula, Dynkin’s formula as well as inequity techniques, several new sufficient conditions have been obtained to guarantee that the considered system model is mean-square exp-ISS. The results obtained in this paper are the general case of previously known results in complex and real fields. Finally, a numerical example shows the effectiveness of the obtained theoretical results.

Based on the proposed method in this paper, it is possible to analyze different QVNN models. The proposed approach can be applied to the analysis of stochastic QVNN models for the discrete-time case. In future studies, the stability and synchronization analysis for discrete-time stochastic QVNN models will also be investigated. The results will be useful for the dynamical analysis of discrete-time stochastic QVNN models.