A Class of Quantum Briot–Bouquet Differential Equations with Complex Coefficients

Abstract

Quantum inequalities (QI) are local restraints on the magnitude and range of formulas. Quantum inequalities have been established to have a different range of applications. In this paper, we aim to introduce a study of QI in a complex domain. The idea basically, comes from employing the notion of subordination. We shall formulate a new q-differential operator (generalized of Dunkl operator of the first type) and employ it to define the classes of QI. Moreover, we employ the q-Dunkl operator to extend the class of Briot–Bouquet differential equations. We investigate the upper solution and exam the oscillation solution under some analytic functions.

1. Introduction

Quantum calculus exchanges the traditional derivative by a difference operator, which permits dealing with sets of non-differentiable curves and admits several formulas. The most common formula of quantum calculus is constructed by the q-operator (q-indicates for the quantum), which is created by the Jackson q-difference operator [1] as follows: let ${\delta }_q$ be the q-calculus which is formulated by

$${\delta }_q(⋎\left(\xi \right))=⋎\left(q\xi \right)-⋎\left(\xi \right),$$

then the derivatives of functions are presented as fractions by the q-derivative

$${\displaystyle D_q(⋎\left(\xi \right))=\frac{{\delta }_q(⋎\left(\xi \right))}{{\delta }_q\left(\xi \right)}=\frac{⋎\left(q\xi \right)-⋎\left(\xi \right)}{(q-1)\xi }},\xi \ne 0.$$

For example, the q-derivative of the function ${\xi }^n$ (for some positive integer n) is

$$D_q\left({\xi }^n\right)=\frac{q^n-1}{q-1}{\xi }^{n-1}={\left[n\right]}_q{\xi }^{n-1},{\left[n\right]}_q=\frac{q^n-1}{q-1}.$$

Recently, quantum inequalities (differential and integral) have extensive applications not only in mathematical physics but also in other sciences. In variation problems, Cruz et al. [2] presented a new variational calculus created by the general quantum difference operator of $D_q$. Rouze and Datta used the quantum functional inequalities to describe the transportation cost functional inequality [3]. Giacomo and Trevisan proved the conditional Entropy Power Inequality for Gaussian quantum systems [4]. Bharti et al. provided a novel algorithm to self-test local quantum systems employing non-contextuality quantum inequalities [5]. The class of quantum energy inequalities is studied by Fewster and Kontou [6]. In the control system, Ibrahim et al. established different classes of quantum differential inequalities [7]. In quantum information processing, Mao et al formulated a new quantum key distribution based on quantum inequalities [8].

In this investigation, we formulate a novel q-differential operator of complex coefficients and discuss its behavior in view of the theory of geometric functions. The suggested q-differential operator indicates a generalization of well-known differential operators in the open unit disk, such as the Dunkl operator and the Sàlàgean operator. It will be considered in some subclasses of starlike functions. Quantum inequalities involve the q-differential operator and some special functions are studied. Sharpness of QI is studied in the sequel. As an application, we employ the q-differential operator to define the q-Briot–Bouquet differential equations (q-BBE). Special cases are discussed and compared with recent works. Moreover, we illustrate a set of examples of q-BBE (for q = 1/2) and exam its oscillated solutions.

2. Related Works

The quantum calculus receives the attention of many investigators. This calculus, for the first time appeared in complex analysis by Ismail et al. [9]. They defined a class of complex analytic functions dealing with the inequality condition $|⋎(q\xi \left)\right|<|⋎(\xi \left)\right|$ on the open unit disk. Grinshpan [10] presented some interesting outcomes filled with geometric observations are of very significant in the univalent function theory. Newly, q-calculus becomes very attractive in the field of special functions. Srivastava and Bansal [11] presented a generalization of the well-known Mittag–Leffler functions and they studied the sufficient conditions under which it is close-to-convex in the open unit disk. Srivastava et al. [12] established a new subclass of normalized smooth and starlike functions in $\cup$. Mahmood et al. [13] introduced a family of q-starlike functions which are based on the Ruscheweyh-type q-derivative operator. Shi et al. [14] examined some recent problems concerning the concept of q-starlike functions. Ibrahim and Darus [15] employed the notion of quantum calculus and the Hadamard product to amend an extended Sàlàgean q-differential operator. Srivastava [16] developed many functions and classes of smooth functions based on the q-calculus. The q-Subordination inequality presented by Ul-Haq et al. [17]. Govindaraj and Sivasubramanian [18] as well as Ibrahim et al. [7] used the quantum calculus and the Hadamard product to deliver some subclasses of analytic functions involving the modified Sàlàgean q-differential operator and the generalized symmetric Sàlàgean q-differential operator respectively.

3. q-Differential Operator

Assume that ⋀ is the set of the smooth functions formulating by the followed power series

$$⋎\left(\xi \right)=\xi +\sum _{n=2}^{\infty }{⋎}_n{\xi }^n,\xi \in \cup =\{\xi :|\xi |<1\}.$$

For a function $⋎\in \bigwedge ,$ the Sàlàgean operator expansion is formulated by the expansion

$${\varsigma }^m⋎\left(\xi \right)=\xi +\sum _{n=2}^{\infty }{n}^m{⋎}_n{\xi }^n.$$

For $⋎\in \bigwedge ,$ we get

$$D_q⋎\left(\xi \right)=\sum _{n=1}^{\infty }{⋎}_n{\left[n\right]}_q{\xi }^{n-1},\xi \in \cup ,{⋎}_1=1.$$

Now, let $⋎\in \bigwedge$, the Sàlàgean q-differential operator [18] is formulated by

$${\varsigma }_q^0⋎\left(\xi \right)=⋎\left(\xi \right),{\varsigma }_q^1⋎\left(\xi \right)=\xi D_q⋎\left(\xi \right),\dots ,{\varsigma }_q^m⋎\left(\xi \right)=\xi D_q\left({\varsigma }_q^{m-1}⋎\left(\xi \right)\right),$$

where m is a positive integer. A calculation associated by the formula of $D_q$, yields ${\varsigma }_q^m⋎\left(\xi \right)=⋎\left(\xi \right)\ast {\mathsf{\Theta }}_q^m\left(\xi \right)$, where ∗ is the convolution product,

$${\mathsf{\Theta }}_q^m\left(\xi \right)=\xi +\sum _{n=2}^{\infty }{\left[n\right]}_q^m{\xi }^n$$

and

$${\varsigma }_q^m⋎\left(\xi \right)=\xi +\sum _{n=2}^{\infty }{\left[n\right]}_q^m{⋎}_n{\xi }^n.$$

Next, we present the q-differential operator as follows:

$$\begin{array}{cc}\hfill & {}_q{\mathsf{\Lambda }}_{\lambda }^0⋎\left(\xi \right)=⋎\left(\xi \right)\hfill \\ \hfill & {}_q{\mathsf{\Lambda }}_{\lambda }^1⋎\left(\xi \right)=\xi D_q⋎\left(\xi \right)+\left(\left(\lambda ⋎\left(\xi \right)-\xi \right)-\lambda \left(⋎(-\xi )+\xi \right)\right),\hfill \\ \hfill & ⋮\hfill \\ \hfill & {}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right){=}_q{\mathsf{\Lambda }}_{\lambda }{(}_q{\mathsf{\Lambda }}_{\lambda }^{m-1}⋎\left(\xi \right))\hfill \\ \hfill & =\xi +\sum _{n=2}^{\infty }{\left({\left[n\right]}_q+({(-1)}^{n+1}+1)\lambda \right)}^m{⋎}_n{\xi }^n,\hfill \end{array}$$

(1)

where $\lambda \in \mathbb{C}.$ For $\lambda =0,q\to 1^{-},$ the operator subjects to the Sàlàgean operator [19]. In addition, the operator ${}_q{\mathsf{\Lambda }}_{\lambda }^m$ represents to the q-Dunkl operator of first rank [20], such that the value of $\lambda$ is the Dunkl parameter. The term ${({\left[n\right]}_q+\lambda (1+{(-1)}^{n+1}))}^m$ indicates a major law in oscillation study (see [21]). Furthermore, the term $e^{2i\pi }$ is denoting the quantum number q when $\hslash =1$. That is there is a connection between the definition of the ${}_q{\mathsf{\Lambda }}_{\lambda }^m$ and its coefficients.

Two functions ⋎ and ⋏ in ⋀ are subordinated ( $⋎\prec ⋏$), if there occurs a Schwarz function $\zeta \in \cup$ with $\zeta \left(0\right)=0$ and $\left|\zeta \right(\xi \left)\right|<1,$ whenever $⋎\left(\xi \right)=⋏\left(\zeta \right(\xi \left)\right)$ for all $\xi \in \cup$ (see [22]). Literally, the subordination inequality is indicated the equality at the origin and inclusion regarding $\cup .$

Definition 1.

Assume that $\lambda \in \mathbb{C},$$m\in \mathbb{N}$ and $⋎\in \bigwedge .$ Then it is in the set ${}_q{\mathfrak{S}}_m^{\ast }(\lambda ,\varsigma )$ if and only if

$${\displaystyle \frac{\xi {{(}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right))}^{\prime }}{{}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right)}}\prec \varsigma \left(\xi \right),\xi \in \cup ,$$

where ς is univalent function of a positive real part in ∪ realizing $\varsigma \left(0\right)=1,\Re \left({\varsigma }^{\prime }\left(\xi \right)\right)>0$.

The set of functions ${}_q{\mathfrak{S}}_m^{\ast }(\alpha ,\lambda ,\varsigma )$ is an extension of types related to the Ma and Minda classes (see [23,24,25,26,27]). Next result indicates the upper and lower bound of a convex formula involving special functions, which will be useful in the next section.

Theorem 1.

Assume that $0\le \beta \le 1$. Then for $\varsigma \in \cup$ as follows:

1. 

$\varsigma \left(\xi \right)=(1-\beta )\sqrt{1+\xi }+\beta ,$

2. 

$\varsigma \left(\xi \right)=(1-\beta )e^{\xi }+\beta ,$

3. 

$\varsigma \left(\xi \right)=(1-\beta )(1+sin(\xi \left)\right)+\beta ,$

4. 

$\varsigma \left(\xi \right)=(1-\beta )e^{e^{\xi }-1}+\beta ,$

satisfying

$$\underset{\left|\xi \right|=r}{min}\Re \left(\varsigma \left(\xi \right)\right)=\varsigma (-r)=\underset{\left|\xi \right|=r}{min}\left|\varsigma \left(\xi \right)\right|,r<1$$

and

$$\underset{\left|\xi \right|=r}{max}\Re \left(\varsigma \left(\xi \right)\right)=\varsigma \left(r\right)=\underset{\left|\xi \right|=r}{max}\left|\varsigma \left(\xi \right)\right|,r<1.$$

Proof. 

For $\vartheta \in (0,2\pi ),$$\Re \left(\varsigma \left(r{e}^{i\vartheta }\right)\right)=(1-\beta )e^{rcos\left(\vartheta \right)}cos(rsin\left(\vartheta \right))+\beta$, the first and second formula can be found in [25]. In the same manner, we show the third formal. When $\beta =0$ this implies that $\varsigma \left(\xi \right)=1+sin\left(\xi \right)$ (see [24]). Obviously,

$$sin\left(r{e}^{i\vartheta }\right)=sin(rcos\left(\vartheta \right))cosh(rsin\left(\vartheta \right))+icos(rcos\left(\vartheta \right))sinh(rsin\left(\vartheta \right))$$

thus, this yields

$$\Re \left(\varsigma \right(\xi \left)\right)=sin(rcos(\vartheta \left)\right)cosh(rsin(\vartheta \left)\right)+1.$$

Now, let $r\to 0,$ this leads to

$$\underset{\left|\xi \right|=r}{min}\Re \left(\varsigma \left(\xi \right)\right)=1-sin\left(r\right)=\underset{\left|\xi \right|=r}{min}\left|\varsigma \left(\xi \right)\right|=1.$$

Consequently, we indicate that

$$|sin\left(r{e}^{i\vartheta }\right){|}^2={cos}^2(rcos\vartheta )sinh2(rsin\vartheta )+{sin}^{2}2(rcos\vartheta )cosh2(rsinr)\le {sinh}^2\left(r\right);$$

thus, this yields

$$\underset{\left|\xi \right|=r}{max}\Re \left(\varsigma \left(\xi \right)\right)=1+sin\left(r\right)=\underset{\left|\xi \right|=r}{max}\left|\varsigma \left(\xi \right)\right|\le 1+{sinh}^2\left(r\right).$$

Extend the above outcome, for $\beta >0,$ we obtain

$$\underset{\left|\xi \right|=r}{min}\Re \left(\varsigma \left(\xi \right)\right)=\beta +(1-\beta )(1-sin\left(r\right))=\underset{\left|\xi \right|=r}{min}\left|\varsigma \left(\xi \right)\right|=1,$$

and

$$\underset{\left|\xi \right|=r}{max}\Re \left(\varsigma \left(\xi \right)\right)=\beta +(1-\beta )(1+sin\left(r\right))=\underset{\left|\xi \right|=r}{max}\left|\varsigma \left(\xi \right)\right|\le \beta +(1-\beta )(1+{sinh}^2\left(r\right)).$$

Similarly, for the last assertion, where for $\beta =0,$ we have a result in [27]. □

The next result can be found in [22].

Lemma 1.

Suppose that $\tau >0$ and $\varsigma \in \mathfrak{H}[1,n]$. Then for two constants $\wp >0$ and $\nu >0$ with $\nu =\nu (\wp ,\tau ,n)$ are achieving

$$\varsigma \left(\xi \right)+\tau \xi {\varsigma }^{\prime }\left(\xi \right)\prec {\left[{\displaystyle \frac{1+\xi }{1-\xi }}\right]}^{\nu }\Rightarrow \varsigma \left(\xi \right)\prec {\left[{\displaystyle \frac{1+\xi }{1-\xi }}\right]}^{\wp }.$$

Lemma 2.

Consider $\phi \left(\xi \right)$ is a convex function in ∪ and $h\left(\xi \right)=\phi \left(\xi \right)+n\nu \left(\xi {\phi }^{\prime }\left(\xi \right)\right)$ for $\nu >0$ and n is a positive integer. If $\varrho \in \mathfrak{H}\left[\phi \right(0),n],$ and

$$\varrho \left(\xi \right)+\nu \xi {\varrho }^{\prime }\left(\xi \right)\prec h\left(\xi \right),\xi \in \cup ,$$

then $\varrho \left(\xi \right)\prec \phi \left(\xi \right),$ and this outcome is sharp.

4. q-Subordination Relations

In this section, we deal with the set ${}_q{\mathfrak{S}}_m^{\ast }(\lambda ,\varsigma )$ for some $\varsigma .$

Theorem 2.

Assume that ${}_q{\mathfrak{S}}_m^{\ast }(\lambda ,\varsigma )$ fulfills the next relation:

$${}_q{\mathfrak{S}}_m^{\ast }(\lambda ,\varsigma )\subset {}_q{\mathfrak{S}}_m^{\ast }(\lambda ,\gamma )\subset {}_q{\mathfrak{S}}_m^{\ast }\left(\lambda \right),$$

where γ is non-negative real number (depending on β) and ς is one of the form in Theorem 1 and

$${}_q{\mathfrak{S}}_m^{\ast }(\lambda ,\gamma ):=\{⋎\in \bigwedge :\Re ({\displaystyle \frac{\xi {{(}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right))}^{\prime }}{{}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right)}})>\gamma ,\gamma \ge 0\};$$

$${}_q{\mathfrak{S}}_m^{\ast }\left(\lambda \right):=\{⋎\in \bigwedge :\Re ({\displaystyle \frac{\xi {{(}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right))}^{\prime }}{{}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right)}})>0\}.$$

Proof. 

Suppose that $⋎{\in }_q{\mathfrak{S}}_m^{\ast }(\lambda ,\varsigma )$ and $\varsigma \left(\xi \right)=(1-\beta )\sqrt{1+\xi }+\beta .$ This implies the inequality

$${\displaystyle \frac{\xi {{(}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right))}^{\prime }}{{}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right)}}\prec (1-\beta )\sqrt{1+\xi }+\beta ,\xi \in \cup .$$

According to Theorem 1, one can find

$$\underset{\left|\xi \right|=1^{-}}{min}\Re ((1-\beta ){(\xi +1)}^{0.5}+\beta )<\Re ({\displaystyle \frac{\xi {{(}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right))}^{\prime }}{{}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right)}})<\underset{\left|\xi \right|=1^{+}}{max}{\Re ((1-\beta )(\xi +1)}^{0.5}+\beta ,$$

which indicates

$$\beta <\Re ({\displaystyle \frac{\xi {{(}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right))}^{\prime }}{{}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right)}})<(1-\beta )\sqrt{2}+\beta .$$

Hence, we have

$$\Re ({\displaystyle \frac{\xi {{(}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right))}^{\prime }}{{}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right)}})>\beta :=\gamma \ge 0,$$

which leads to the requested result. Assume that $\varsigma \left(\xi \right)=(1-\beta )e^{\xi }+\beta ,$ then we conclude the next minimization and maximization inequality

$$\underset{\left|\xi \right|=1}{min}\Re ((1-\beta )e^{\xi }+\beta )<\Re ({\displaystyle \frac{\xi {{(}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right))}^{\prime }}{{}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right)}})<\underset{\left|\xi \right|=1}{max}\Re ((1-\beta )e^{\xi }+\beta ),$$

which implies

$$((1-\beta ){\displaystyle \frac{1}{e}}+\beta )<\Re ({\displaystyle \frac{\xi {{(}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right))}^{\prime }}{{}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right)}})<((1-\beta )e+\beta ),$$

that is

$$\Re ({\displaystyle \frac{\xi {{(}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right))}^{\prime }}{{}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right)}})>((1-\beta ){\displaystyle \frac{1}{e}}+\beta ):=\gamma \ge 0.$$

Now, suppose that $\varsigma \left(\xi \right)=(1-\beta )(1+sin(\xi )+\beta ),$ which implies that

$$\underset{\left|\xi \right|=1}{min}\Re ((1-\beta )(1+sin\left(\xi \right))+\beta )<\Re ({\displaystyle \frac{\xi {{(}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right))}^{\prime }}{{}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right)}})<\underset{\left|\xi \right|=1}{max}\Re ((1-\beta )(1+sin\left(\xi \right))+\beta ).$$

A calculation yields

$$(0.158(1-\beta )+\beta )<\Re ({\displaystyle \frac{\xi {{(}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right))}^{\prime }}{{}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right)}})<(1.841(1-\beta )+\beta ),$$

this yields

$$\Re ({\displaystyle \frac{\xi {{(}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right))}^{\prime }}{{}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right)}})>(0.158(1-\beta )+\beta ):=\gamma \ge 0.$$

□

Remark 1.

In Theorem 2,

• When $m=0,\beta =0,\varsigma \left(\xi \right)=1+sin\xi ⟹{}_q{\mathfrak{S}}_0^{\ast }(\lambda ,1+sin\xi )\subset {}_q{\mathfrak{S}}_0^{\ast }(\lambda ,\gamma )\subset {}_q{\mathfrak{S}}_0^{\ast }\left(\lambda \right)$ for non-negative γ (see [24]);
• When $m=0⟹{}_q{\mathfrak{S}}_0^{\ast }(\lambda ,\varsigma )\subset {}_q{\mathfrak{S}}_0^{\ast }(\lambda ,\gamma )\subset {}_q{\mathfrak{S}}_0^{\ast }\left(\lambda \right)$ for all ς in Theorem 2 and non-negative real number γ (see [25]);
• When $m=0,\beta =0,\varsigma \left(\xi \right)=e^{\xi }⟹{}_q{\mathfrak{S}}_0^{\ast }(\lambda ,e^{\xi })\subset {}_q{\mathfrak{S}}_0^{\ast }(\lambda ,\gamma )\subset {}_q{\mathfrak{S}}_0^{\ast }\left(\lambda \right)$ for all non-negative γ (see [28]);
• When $m=0,\beta =0,\varsigma \left(\xi \right)={(\xi +1)}^{0.5}⟹{}_q{\mathfrak{S}}_0^{\ast }(\lambda ,{(\xi +1)}^{0.5})\subset {}_q{\mathfrak{S}}_0^{\ast }(\lambda ,\gamma )\subset {}_q{\mathfrak{S}}_0^{\ast }\left(\lambda \right)$ for all non-negative γ (see [28]).

Next outcome shows the inclusion relation between the class ${}_q{\mathfrak{S}}_m^{\ast }(\lambda ,\sigma )$ and other geometric class.

Theorem 3.

The set ${}_q{\mathfrak{S}}_m^{\ast }(\lambda ,\varsigma )$ satisfies the inclusion:

$${}_q{\mathfrak{S}}_m^{\ast }(\lambda ,\varsigma )\subset {}_q{\mathfrak{M}}_m(\lambda ,\alpha ):=\{⋎\in \bigwedge :\Re ({\displaystyle \frac{\xi {{(}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right))}^{\prime }}{{}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right)}})<\alpha ,\alpha >1\},$$

where ς is given in Theorem 1.

The class ${}_q{\mathfrak{M}}_m(\lambda ,\alpha )$ is an extension of the Uralegaddi set (see [29])

$$\mathfrak{M}\left(\alpha \right):=\{⋎\in \bigwedge :\Re ({\displaystyle \frac{\xi {(⋎\left(\xi \right))}^{\prime }}{⋎\left(\xi \right)}})<\alpha ,\alpha >1\}.$$

Proof. 

Suppose that $⋎\in {}_q{\mathfrak{S}}_m^{\ast }(\lambda ,\varsigma ),$ where $\varsigma$ is termed in Theorem 1. Then we obtain

$$\Re ({\displaystyle \frac{\xi {{(}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right))}^{\prime }}{{}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right)}})<(1-\beta )\sqrt{2}+\beta :=\alpha ,$$

$$\Re ({\displaystyle \frac{\xi {{(}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right))}^{\prime }}{{}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right)}})<(1-\beta )e+\beta :=\alpha$$

and

$$\Re ({\displaystyle \frac{\xi {{(}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right))}^{\prime }}{{}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right)}})<1.841(1-\beta )+\beta :=\alpha ,$$

Thus, $⋎\in {}_q{\mathfrak{M}}_m(⋎\left(\xi \right),\alpha ).$ □

Remark 2.

We have the following special cases from Theorem 3,

• $m=0,\beta =0,\varsigma \left(\xi \right)=1+sin\xi {⟹}_q{\mathfrak{S}}_0^{\ast }(\lambda ,1+sin\xi )\subset {}_q{\mathfrak{M}}_0(\lambda ,\alpha )$ for $\alpha >1$ (see [24]);
• $m=0,\varsigma \left(\xi \right)=\beta +(1-\beta )e^{\xi }{⟹}_q{\mathfrak{S}}_0^{\ast }(\lambda ,(1-\beta )e^{\xi })+\beta \subset {}_q{\mathfrak{M}}_0(\lambda ,\alpha )$ for $\alpha >1$ (see [25], Theorem 2.5);
• $m=0,\varsigma \left(\xi \right)=(1-\beta )({(\xi +1)}^{0.5})+\beta {⟹}_q{\mathfrak{S}}_0^{\ast }(\lambda ,\beta +(1-\beta ){(\xi +1)}^{0.5})+\beta )\subset {}_q{\mathfrak{M}}_0(\lambda ,\alpha )$ for $\alpha >1$ (see [25], Theorem 2.6).
• $m=0,\beta =0,\varsigma \left(\xi \right)=({(\xi +1)}^{0.5}){⟹}_q{\mathfrak{S}}_0^{\ast }(\lambda ,{(\xi +1)}^{0.5})\subset {}_q{\mathfrak{M}}_0(\lambda ,\alpha )$ where $\alpha >1$ (see [25], Corollary 2.7).

The following theorem confirms the belonging of a normalized function in the class ${}_q{\mathfrak{S}}_m^{\ast }(\lambda ,\varsigma ),$ where $\varsigma$ indicates the Janowski formula of order $\wp >0$.

Theorem 4.

If $⋎\in \bigwedge$ satisfies the subordination

$$\left({\displaystyle \frac{\xi {{(}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right))}^{\prime }}{{}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right)}}\right)\left(2+{\displaystyle \frac{\xi {{(}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right))}^{″}}{{{(}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right))}^{\prime }}}-{\displaystyle \frac{\xi {{(}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right))}^{\prime }}{{}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right)}}\right)\prec {\left({\displaystyle \frac{\xi +1}{1-\xi }}\right)}^{\tau }$$

then $⋎{\in }_q{\mathfrak{S}}_m^{\ast }(\lambda ,\varsigma ),$ where $\varsigma \left(\xi \right)={\left({\displaystyle \frac{\xi +1}{1-\xi }}\right)}^{\wp }$ for $\wp >0,\tau >0.$

Proof. 

In virtue of Lemma 1, a computation yields

$$\begin{array}{cc}\hfill & \left({\displaystyle \frac{\xi {{(}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right))}^{\prime }}{{}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right)}}\right)+\xi {\left({\displaystyle \frac{\xi {{(}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right))}^{\prime }}{{}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right)}}\right)}^{\prime }\hfill \\ \hfill & =\left({\displaystyle \frac{\xi {{(}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right))}^{\prime }}{{}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right)}}\right)\left({\displaystyle \frac{\xi {{(}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right))}^{″}}{{{(}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right))}^{\prime }}}-{\displaystyle \frac{\xi {{(}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right))}^{\prime }}{{}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right)}}+2\right)\hfill \\ \hfill & \prec {\left({\displaystyle \frac{\xi +1}{1-\xi }}\right)}^{\tau }.\hfill \end{array}$$

Now, according to Lemma 1, we attain

$$\left({\displaystyle \frac{\xi {{(}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right))}^{\prime }}{{}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right)}}\right)\prec {\left({\displaystyle \frac{\xi +1}{1-\xi }}\right)}^{\wp }:=\varsigma \left(\xi \right),$$

which indicates that $⋎{\in }_q{\mathfrak{S}}_m^{\ast }(\lambda ,\varsigma )$. □

The next result shows the iteration inequality including the q-differential operator ${}_q{\mathsf{\Lambda }}_{\lambda }^m$ and ${}_q{\mathsf{\Lambda }}_{\lambda }^{m+1}$.

Theorem 5.

Suppose that φ is convex with $\phi \left(0\right)=0$ and g is defined as follows:

$$g\left(\xi \right)=\phi \left(\xi \right)+({\displaystyle \frac{1}{1-\ell }})\left(\xi {\phi }^{\prime }\left(\xi \right)\right),\ell \in (0,1),\xi \in \cup .$$

If $⋎\in \bigwedge$ fulfills the inequality

$${({\displaystyle \frac{\xi }{{}_q{\mathsf{\Lambda }}_{\lambda }^{m+1}⋎\left(\xi \right)}})}^{\ell }{\displaystyle \frac{{}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right)}{1-\ell }}({\displaystyle \frac{{\left({}_q{\mathsf{\Lambda }}_{\lambda }^{m+1}⋎\left(\xi \right)\right)}^{\prime }}{{}_q{\mathsf{\Lambda }}_{\lambda }^{m+1}⋎\left(\xi \right)}}-\ell {\displaystyle \frac{{\left({}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right)\right)}^{\prime }}{{}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right)}})\prec g\left(\xi \right)$$

then

$$({\displaystyle \frac{{}_q{\mathsf{\Lambda }}_{\lambda }^{m+1}⋎\left(\xi \right)}{\xi }}){({\displaystyle \frac{\xi }{{}_q{\mathsf{\Lambda }}_{\lambda }^{m+1}⋎\left(\xi \right)}})}^{\ell }\prec \phi \left(\xi \right).$$

Proof. 

For all $\xi \in \cup ,$ we define

$$\varrho \left(\xi \right)=({\displaystyle \frac{{}_q{\mathsf{\Lambda }}_{\lambda }^{m+1}⋎\left(\xi \right)}{\xi }}){({\displaystyle \frac{\xi }{{}_q{\mathsf{\Lambda }}_{\lambda }^{m+1}⋎\left(\xi \right)}})}^{\ell }.$$

Please note that the term

$${\left({\displaystyle \frac{\xi }{{}_q{\mathsf{\Lambda }}_{\lambda }^{m+1}⋎\left(\xi \right)}}\right)}^{\ell }={\left({\displaystyle \frac{\xi }{\xi +{\sum }_{n=2}^{\infty }{\left({\left[n\right]}_q+(1+{(-1)}^{n+1})\lambda \right)}^{m+1}}}\right)}^{\ell }=1+\dots ;$$

therefore, ${({\displaystyle \frac{\xi }{{}_q{\mathsf{\Lambda }}_{\lambda }^{m+1}⋎\left(\xi \right)}})}^{\ell }{|}_{\xi =0}=1.$ A differentiation implies that

$$\begin{array}{cc}\hfill & {\left({\displaystyle \frac{\xi }{{}_q{\mathsf{\Lambda }}_{\lambda }^{m+1}⋎\left(\xi \right)}}\right)}^{\ell }\left({\displaystyle \frac{{}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right)}{1-\ell }}\right)\left({\displaystyle \frac{{\left({}_q{\mathsf{\Lambda }}_{\lambda }^{m+1}⋎\left(\xi \right)\right)}^{\prime }}{{}_q{\mathsf{\Lambda }}_{\lambda }^{m+1}⋎\left(\xi \right)}}-\ell {\displaystyle \frac{{\left({}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right)\right)}^{\prime }}{{}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right)}}\right)\hfill \\ \hfill & =\left({\displaystyle \frac{1}{1-\ell }}\right)\left(\xi {\varrho }^{\prime }\left(\xi \right)\right)+\varrho \left(\xi \right)\hfill \end{array}$$

Consequently, we indicate that

$$\left({\displaystyle \frac{1}{1-\ell }}\right)\left(\xi {\varrho }^{\prime }\left(\xi \right)\right)+\varrho \left(\xi \right)\prec g\left(\xi \right)=\left({\displaystyle \frac{1}{1-\ell }}\right)\left(\xi {\phi }^{\prime }\left(\xi \right)\right)+\phi \left(\xi \right).$$

In virtue of Lemma 2, we conclude that $\varrho \left(\xi \right)\prec g\left(\xi \right),$ which leads to

$$\left({\displaystyle \frac{{}_q{\mathsf{\Lambda }}_{\lambda }^{m+1}⋎\left(\xi \right)}{\xi }}\right){\left({\displaystyle \frac{\xi }{{}_q{\mathsf{\Lambda }}_{\lambda }^{m+1}⋎\left(\xi \right)}}\right)}^{\ell }\prec \phi \left(\xi \right).$$

□

5. Q-Differential Equations

This section deals with a class of differential equations type complex Briot–Bouquet (see [30,31] for recent works) and its analytic solutions. The main formula of BBE is $\frac{\xi {(⋎\left(\xi \right))}^{\prime }}{⋎\left(\xi \right)}=\mathsf{{\rm Y}}\left(\xi \right).$ The operator (1) can be used to extend q-BBE as follows:

$${\displaystyle \frac{\xi {{(}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right))}^{\prime }}{{}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right)}}=\mathsf{{\rm Y}}\left(\xi \right),\xi \in \cup ,⋎\in \bigwedge ,$$

(2)

where $\mathsf{{\rm Y}}\left(\xi \right)\in \mathcal{C}$ (the set of univalent and convex in ∪). The aim is to discuss the maximum outcome of (2) by using $q$-inequalities.

Theorem 6.

Suppose that $⋎\in \bigwedge$ and $\mathsf{{\rm Y}}\left(\xi \right)\in \mathcal{C}$ satisfy

$${\displaystyle \frac{\xi {({}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right))}^{\prime }}{{}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right)}}\prec \mathsf{{\rm Y}}\left(\xi \right).$$

(3)

Then the maximum solution of (3) is

$${}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right)\prec \left(exp\left({\int }_0^{\xi }{\displaystyle \frac{\mathsf{{\rm Y}}\left(\mathsf{\Phi }\right(\iota \left)\right)-1}{\iota }}d\iota \right)\right)\xi ,$$

where $\mathsf{\Phi }\left(\xi \right)$ is smooth in $\cup ,$ such that $\mathsf{\Phi }\left(0\right)=0,$$\left|\mathsf{\Phi }\right(\xi \left)\right|<1$ and it is the upper limit in the above integral. Also, for $\left|\xi \right|=\iota$, ${}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right)$ achieves the inequality

$$exp\left({\int }_0^1{\displaystyle \frac{\mathsf{{\rm Y}}\left(\mathsf{\Phi }\right(-\iota \left)\right)-1}{\iota }}d\iota \right)\le \left|{\displaystyle \frac{{}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right)}{\xi }}\right|\le exp\left({\int }_0^1{\displaystyle \frac{\mathsf{{\rm Y}}\left(\mathsf{\Phi }\right(\iota \left)\right)-1}{\iota }}d\iota \right).$$

Proof. 

By the definition of the subordination, inequality (3) achieves that there exists a Schwarz function $\mathsf{\Phi }$ satisfying $\left|\mathsf{\Phi }\right(\xi \left)\right|<1,$$\mathsf{\Phi }\left(0\right)=0$ and

$${\displaystyle \frac{\xi {{(}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right))}^{\prime }}{{}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right)}}=\mathsf{{\rm Y}}\left(\mathsf{\Phi }\left(\xi \right)\right),\xi \in \cup .$$

This implies

$${\displaystyle \frac{{{(}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right))}^{\prime }}{{}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right)}}-{\displaystyle \frac{1}{\xi }}={\displaystyle \frac{\mathsf{{\rm Y}}\left(\mathsf{\Phi }\right(\xi \left)\right)-1}{\xi }}.$$

Integrating both sides yields

$${log}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right)-log\xi ={\int }_0^{\xi }{\displaystyle \frac{\mathsf{{\rm Y}}\left(\mathsf{\Phi }\right(\iota \left)\right)-1}{\iota }}d\iota .$$

A calculation indicates

$$log({\displaystyle \frac{{}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right)}{\xi }})={\int }_0^{\xi }{\displaystyle \frac{\mathsf{{\rm Y}}\left(\mathsf{\Phi }\right(\iota \left)\right)-1}{\iota }}d\iota .$$

(4)

Then, we have

$${}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right)\prec \xi exp\left({\int }_0^{\xi }{\displaystyle \frac{\mathsf{{\rm Y}}\left(\mathsf{\Phi }\right(\iota \left)\right)-1}{\iota }}d\iota \right)$$

for some Schwarz function. In addition, by the behavior of the function $\mathsf{{\rm Y}}$ on the disk $0<\left|\xi \right|<\iota <1$ we have

$$\mathsf{{\rm Y}}(-\iota |\xi \left|\right)\le \Re \left(\mathsf{{\rm Y}}\right(\mathsf{\Phi }\left(\iota \xi \right)\left)\right)\le \mathsf{{\rm Y}}\left(\iota \right|\xi \left|\right),\iota \in (0,1),$$

and

$$\mathsf{{\rm Y}}(-\iota )\le \mathsf{{\rm Y}}(-\iota |\xi \left|\right),\mathsf{{\rm Y}}\left(\iota \right|\xi \left|\right)\le \mathsf{{\rm Y}}\left(\iota \right).$$

Thus, we conclude that

$${\int }_0^1{\displaystyle \frac{\mathsf{{\rm Y}}\left(\mathsf{\Phi }\right(-\iota \left|\xi \right|\left)\right)-1}{\iota }}d\iota \le \Re \left({\int }_0^1{\displaystyle \frac{\mathsf{{\rm Y}}\left(\mathsf{\Phi }\right(\iota \left)\right)-1}{\iota }}d\iota \right)\le {\int }_0^1{\displaystyle \frac{\mathsf{{\rm Y}}\left(\mathsf{\Phi }\right(\iota \left|\xi \right|\left)\right)-1}{\iota }}d\iota ,$$

which implies

$${\int }_0^1{\displaystyle \frac{\mathsf{{\rm Y}}\left(\mathsf{\Phi }\right(-\iota \left|\xi \right|\left)\right)-1}{\iota }}d\iota \le log\left|{\displaystyle \frac{{}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right)}{\xi }}\right|\le {\int }_0^1{\displaystyle \frac{\mathsf{{\rm Y}}\left(\mathsf{\Phi }\right(\iota \left|\xi \right|\left)\right)-1}{\iota }}d\iota ,$$

and

$$exp\left({\int }_0^1{\displaystyle \frac{\mathsf{{\rm Y}}\left(\mathsf{\Phi }\right(-\iota \left|\xi \right|\left)\right)-1}{\iota }}d\iota \right)\le \left|{\displaystyle \frac{{}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right)}{\xi }}\right|\le exp\left({\int }_0^1{\displaystyle \frac{\mathsf{{\rm Y}}\left(\mathsf{\Phi }\right(\iota \left|\xi \right|\left)\right)-1}{\iota }}d\iota \right).$$

We conclude that

$$exp\left({\int }_0^1{\displaystyle \frac{\mathsf{{\rm Y}}\left(\mathsf{\Phi }\right(-\iota \left)\right)-1}{\iota }}d\iota \right)\le \left|{\displaystyle \frac{{}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right)}{\xi }}\right|\le exp\left({\int }_0^1{\displaystyle \frac{\mathsf{{\rm Y}}\left(\mathsf{\Phi }\right(\iota \left)\right)-1}{\iota }}d\iota \right).$$

□

Next result presents the condition on the coefficients of the normalized function ⋎ to satisfy the upper bound in Theorem 6.

Theorem 7.

Suppose that $⋎\in \bigwedge$ has non-negative coefficients. If $\mathsf{{\rm Y}}\in \mathcal{C}$ in Equation (2) and $\Re \left(\lambda \right)>0$ then there is a solution satisfying the maximum bound inequality

$${}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right)\prec \xi exp\left({\int }_0^{\xi }{\displaystyle \frac{\mathsf{{\rm Y}}\left(\mathsf{\Phi }\right(\iota \left)\right)-1}{\iota }}d\iota \right),$$

(5)

where $\mathsf{\Phi }\left(\xi \right)$ is smooth with $\left|\mathsf{\Phi }\right(\xi \left)\right|<1$ and $\mathsf{\Phi }\left(0\right)=0$.

Proof. 

By the condition of the theorem, we get the following assertions:

$$\begin{array}{cc}\hfill & \Re ({\displaystyle \frac{\xi {{(}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right))}^{\prime }}{{}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right)}})>0\hfill \\ \hfill & \iff \Re \left(\frac{\xi +{\sum }_{n=2}^{\infty }n{[{\left[n\right]}_q+\lambda (1+{(-1)}^{n+1})]}^m{⋎}_n{\xi }^n}{\xi +{\sum }_{n=2}^{\infty }{[{\left[n\right]}_q+\lambda (1+{(-1)}^{n+1})]}^m{⋎}_n{\xi }^n}\right)>0\hfill \\ \hfill & \iff \Re \left(\frac{1+{\sum }_{n=2}^{\infty }n{[{\left[n\right]}_q+\lambda (1+{(-1)}^{n+1})]}^m{⋎}_n{\xi }^{n-1}}{1+{\sum }_{n=2}^{\infty }{[{\left[n\right]}_q+\lambda (1+{(-1)}^{n+1})]}^m{⋎}_n{\xi }^{n-1}}\right)>0\hfill \\ \hfill & \iff \left(\frac{1+{\sum }_{n=2}^{\infty }n{[{\left[n\right]}_q+\lambda (1+{(-1)}^{n+1})]}^m{⋎}_n}{1+{\sum }_{n=2}^{\infty }{[{\left[n\right]}_q+\lambda (1+{(-1)}^{n+1})]}^m{⋎}_n}\right)>0\hfill \\ \hfill & \iff \left(1+\sum _{n=2}^{\infty }n{[{\left[n\right]}_q+(1+{(-1)}^{n+1})\lambda ]}^m{⋎}_n\right)>0.\hfill \end{array}$$

Moreover, we have ${(}_q{\mathsf{\Lambda }}_{\lambda }^m⋎)\left(0\right)=0$, which leads to

$${\displaystyle \frac{\xi {{(}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right))}^{\prime }}{{}_q{\mathsf{\Lambda }}_{\lambda }^m⋎\left(\xi \right)}}\in \mathcal{P}.$$

Hence the proof. □

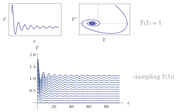
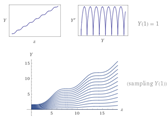
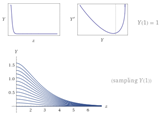
We illustrate an example to find the upper and oscillation solution of q-BBE when $q=1/2$, see Table 1 and Table 2.

Table 1. The upper bound solution of q-BBE for different $\mathsf{{\rm Y}}\left(\xi \right).$

$\mathsf{{\rm Y}}\left(\mathit{\xi }\right)$	Upper Solution	Graph	Polynomial
$cos\left(\xi \right)$	$(\xi \ast exp(sin\left(\xi \right)-\xi \left)\right)$		$\xi -{\xi }^4/6+O\left({\xi }^6\right)$
$1-sin\left(\xi \right)$	$(\xi \ast exp(cos\left(\xi \right)+\xi -1\left)\right)$		$\xi +{\xi }^2-\frac{{\xi }^4}{3}-\frac{{\xi }^5}{24}+O\left({\xi }^6\right)$
$1/(1-\xi )$	$(\xi \ast exp(-\xi -log(1-\xi )\left)\right)$		$\xi +\frac{{\xi }^3}{2}+\frac{{\xi }^4}{3}+\frac{3{\xi }^5}{8}+O\left({\xi }^6\right)$
$1/{(1-\xi )}^2$	$(\xi \ast exp\left(\frac{{\xi }^2}{1-\xi }\right))$		$\xi +{\xi }^3+{\xi }^4+\frac{3{\xi }^5}{2}+O\left({\xi }^6\right)$
$1-\xi$	$(\xi \ast exp(-{\xi }^2/2))$		$\xi -\frac{{\xi }^3}{2}+\frac{{\xi }^5}{8}-\frac{{\xi }^7}{48}+O\left({\xi }^9\right)$

Table 2. The oscillation solution for different $\mathsf{{\rm Y}}\left(\xi \right)$.

$\frac{1}{2}$-BBE (2)	Oscillation Solution	Graph
$cos\left(\xi \right)$	$c_1{e}^{Ci\left(\xi \right)}$
$1-sin\left(\xi \right)$	$c_1\xi e^{(-Si(\xi \left)\right)}$
$1/(1-\xi )$	$c_1{e}^{(1/(1-\xi \left)\right)}\xi$
$1-\xi$	$c_1{e}^{(-\xi )}\xi$

Where $Ci$ is the cos integral function and $Si$ is the sin integral function. The first example of $\frac{1}{2}$-BBE of (2) is $Y\left(\xi \right)=cos\left(\xi \right)$ which has an oscillation solution with one branch point at the origin and has a local maximum at $\xi =\frac{\pi }{2}+2n\pi$ and local minimum at $\xi =\frac{\pi }{2}-2n\pi .$ While, for $Y\left(\xi \right)=1-sin\left(\xi \right),$ the oscillation solution has no branch point in the disk. Moreover, for $Y\left(\xi \right)=1/(1-\xi )$ the oscillation solution has no branch point. Finally, when $Y\left(\xi \right)=1-\xi ,$ the oscillation solution has a global maximum equal to $1/e$ at $\xi =1.$

6. Conclusions

From above, we conclude that in view of the quantum calculus, some generalized differential operators in the open unit disk can have connections (coefficients) convergence of quantum numbers. These numbers might change the behavior of the operator and its classes of analytic functions. We investigated the oscillation solution and asymptotic solutions of different differential equations of the Briot–Bouquet type. For future work, one can employ the q-operator (1) in different classes of analytic functions such as the meromorphic and multivalent functions (see [32,33,34]).