Applications of the Periodogram Method for Perturbed Block Toeplitz Matrices in Statistical Signal Processing

Abstract

In this paper, we combine the periodogram method for perturbed block Toeplitz matrices with the Cholesky decomposition to give a parameter estimation method for any perturbed vector autoregressive (VAR) or vector moving average (VMA) process, when we only know a perturbed version of the sequence of correlation matrices of the process. In order to combine the periodogram method for perturbed block Toeplitz matrices with the Cholesky decomposition, we first need to generalize a known result on the Cholesky decomposition of Toeplitz matrices to perturbed block Toeplitz matrices.

1. Introduction

The Cholesky decomposition has been widely used in statistical signal processing. For instance, it has been used for parameter estimation of vector autoregressive (VAR) processes and for parameter estimation of vector moving average (VMA) processes. Specifically, the parameters of a VAR process can be directly obtained from the Cholesky decomposition of the inverses of its correlation matrices, and the parameters of a VMA process can be directly obtained from the Cholesky decomposition of its correlation matrices. However, when real-world problems are considered, what we usually know is a perturbed version of the sequence of correlation matrices of the process involved.

In this paper, we use the Cholesky decomposition to give a parameter estimation method for any perturbed VAR or VMA process, whenever the sequence of correlation matrices of the perturbed process is asymptotically equivalent to the sequence of correlation matrices of the original process in the Gray sense [1]. Specifically, our parameter estimation method combines the Cholesky decomposition with the periodogram method for perturbed block Toeplitz matrices presented in [2]. In order to combine them, we first need to generalize a result given in [3] on the Cholesky decomposition of Toeplitz matrices to perturbed block Toeplitz matrices.

The paper is organized as follows. In Section 2, we set up notation and we review the periodogram method for perturbed block Toeplitz matrices presented in [2]. In Section 3, we generalize a result given in [3] on the Cholesky decomposition of Toeplitz matrices to perturbed block Toeplitz matrices. In Section 4, we give a parameter estimation method for perturbed VAR and VMA processes. Our parameter estimation method for perturbed VMA processes is there also applied in another statistical signal processing problem, namely, in multiple-input multiple-output (MIMO) channel identification.

2. Preliminaries

In this section, we set up notation and we review the periodogram method for perturbed block Toeplitz matrices presented in [2].

2.1. Notation

In this paper, $\mathbb{N}$, $\mathbb{Z}$, $\mathbb{R}$, and $\mathbb{C}$ denote the set of natural numbers (that is, the set of positive integers), the set of integer numbers, the set of real numbers, and the set of complex numbers, respectively. ${\mathbb{C}}^{M\times N}$ is the set of all $M\times N$ complex matrices, $I_N$ stands for the $N\times N$ identity matrix, $0_{M\times N}$ denotes the $M\times N$ zero matrix, and $V_n$ is the $n\times n$ Fourier unitary matrix, i.e.,

$${\left[V_n\right]}_{j,k}:=\frac{1}{\sqrt{n}}{\mathrm{e}}^{-\frac{2\pi (j-1)(k-1)}{n}\mathrm{i}},j,k\in \{1,\dots ,n\},$$

with $\mathrm{i}$ being the imaginary unit. We denote by ${\lambda }_1\left(A\right),\dots ,{\lambda }_n\left(A\right)$ the eigenvalues of an $n\times n$ Hermitian matrix A arranged in decreasing order, * denotes conjugate transpose, ⊗ is the Kronecker product, E stands for expectation, and ${\chi }_S$ denotes the characteristic (or indicator) function of $S\subseteq \mathbb{R}$, that is,

$${\chi }_S\left(\omega \right):=\left\{\begin{array}{cc}1\hfill & \mathrm{if}\omega \in \mathrm{S},\hfill \\ 0\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

If $x_k\in {\mathbb{C}}^{N\times 1}$ for all $k\in \{1,\dots ,n\}$, then $x_{n:1}$ is the $nN$-dimensional vector given by

$$x_{n:1}=\left(\begin{array}{c}{x}_n\\ x_{n-1}\\ ⋮\\ x_1\end{array}\right).$$

If $x_n$ is a (complex) random N-dimensional vector for all $n\in \mathbb{N}$, $\left\{x_n\right\}$ denotes the corresponding (complex) random N-dimensional vector process.

Let $A_n$ and $B_n$ be $nM\times nN$ matrices for all $n\in \mathbb{N}$. We write $\left\{A_n\right\}\sim \left\{B_n\right\}$ if the sequences $\left\{A_n\right\}$ and $\left\{B_n\right\}$ are asymptotically equivalent (i.e., $\{\parallel A_n{\parallel }_2\}$ and $\{\parallel B_n{\parallel }_2\}$ are bounded and ${lim}_{n\to \infty }\frac{\parallel A_n-B_n{\parallel }_F}{\sqrt{n}}=0$ with ${\parallel ·\parallel }_2$ and ${\parallel ·\parallel }_F$ being the spectral norm and the Frobenius norm, respectively). We recall that the concept of asymptotically equivalent sequences of matrices was introduced by Gray in [1] for the case in which $M=N=1$.

If $F:\mathbb{R}\to {\mathbb{C}}^{M\times N}$ is a continuous $2\pi$-periodic function, we denote by $T_n\left(F\right)$ the block Toeplitz matrix generated by F whose blocks are given by

$${\left[T_n\left(F\right)\right]}_{j,k}:={\mathsf{F}}_{j-k},n\in \mathbb{N},j,k\in \{1,\dots ,n\},$$

where ${\left\{{\mathsf{F}}_k\right\}}_{k\in \mathbb{Z}}$ is the sequence of Fourier coefficients of F, that is,

$${\mathsf{F}}_k:=\frac{1}{2\pi }{\int }_0^{2\pi }{\mathrm{e}}^{-k\omega \mathrm{i}}F\left(\omega \right)d\omega \forall k\in \mathbb{Z}.$$

2.2. The Periodogram Method for Perturbed Block Toeplitz Matrices

The following theorem, which was given in ([2], Theorem 4), provides a method to estimate the generating function F when we only know a perturbed version of the sequence of block Toeplitz matrices $\left\{T_n\left(F\right)\right\}$, namely, we only know a sequence of matrices $\left\{A_n\right\}$ which is asymptotically equivalent to $\left\{T_n\left(F\right)\right\}$.

Theorem 1.

Let$A_n$be an$nM\times nN$matrix for all$n\in \mathbb{N}$. Suppose that there exists a continuous$2\pi$-periodic function$F:\mathbb{R}\to {\mathbb{C}}^{M\times N}$such that${\lim }_{n\to \infty }\frac{\parallel A_n-T_n{\left(F\right)\parallel }_F}{\sqrt{n}}=0$. Then

$${\displaystyle \underset{n\to \infty }{\lim }}\frac{1}{2\pi }{\int }_0^{2\pi }{\parallel {\widehat{P}}_{A_n}\left(\omega \right)-F\left(\omega \right)\parallel }_F^{2}d\omega =0,$$

(1)

where${\widehat{P}}_{A_n}:\mathbb{R}\to {\mathbb{C}}^{M\times N}$is the$2\pi$-periodic step function given by

$${\widehat{P}}_{A_n}\left(\omega \right):={\displaystyle \sum _{k=1}^n}{\chi }_{\left.\left[\frac{2\pi (k-1)}{n},\frac{2\pi k}{n}\right.\right)}\left(\omega \right){\left[{(V_n\otimes I_M)}^{*}{A}_n(V_n\otimes I_N)\right]}_{k,k}\forall \omega \in [0,2\pi ).$$

Moreover, if F is a trigonometric polynomial there exists$K\in [0,\infty )$such that

$$\sqrt{\frac{1}{2\pi }{\int }_0^{2\pi }{\parallel {\widehat{P}}_{A_n}\left(\omega \right)-F\left(\omega \right)\parallel }_F^{2}d\omega }\le \frac{\parallel A_n-T_n{\left(F\right)\parallel }_F}{\sqrt{n}}+\frac{K}{\sqrt{n}}\forall n\in \mathbb{N}.$$

The estimation method of the generating function F provided in Theorem 1 consists of the sequence of functions $\left\{{\widehat{P}}_{A_n}\right\}$. Observe that from Equation (1) the squared error made, when F is estimated (approximated) by ${\widehat{P}}_{A_n}$, tends to zero as n grows.

The correlation matrix of a random vector is a positive semidefinite matrix. Furthermore, if A is a positive semidefinite matrix, then there exists a zero-mean random vector whose correlation matrix is A. Therefore, $\left\{T_n\left(F\right)\right\}$ is a sequence of positive semidefinite matrices if and only if $\left\{T_n\left(F\right)\right\}$ is the sequence of correlation matrices of certain wide sense stationary (WSS) N-dimensional vector process (we recall that a random vector process $\left\{x_n\right\}$ is said to be WSS if its correlation matrices $E\left(x_{n:1}{x}_{n:1}^{*}\right)$ are block Toeplitz and its random vectors $x_n$ have the same mean). If $\left\{T_n\left(F\right)\right\}$ is the sequence of correlation matrices of a WSS vector process, the generating function F is called the power spectral density (PSD) of the process. Therefore, Theorem 1 provides a method to estimate the PSD (a spectral estimation method) of any WSS vector process, when we only know a perturbed version of its sequence of correlation matrices. This spectral estimation method is a modified version of the (averaged) periodogram method, because if $N=1$ then

$$\begin{array}{c}{\widehat{P}}_{T_n}\left(\frac{2\pi (h-1)}{n}\right)={\left[V_n^{*}{T}_n{V}_n\right]}_{h,h}={\sum }_{k=1}^n{\left[V_n^{*}{T}_n\right]}_{h,k}{\left[V_n\right]}_{k,h}={\sum }_{k=1}^n{\left[V_n\right]}_{k,h}{\sum }_{j=1}^n{\left[V_n^{*}\right]}_{h,j}{\left[T_n\right]}_{j,k}\hfill \\ ={\sum }_{j,k=1}^n{\left[V_n\right]}_{k,h}{\displaystyle \overline{{\left[V_n\right]}_{j,h}}}{\left[T_n\right]}_{j,k}=\frac{1}{n}{\sum }_{j,k=1}^n{\mathrm{e}}^{\frac{2\pi (j-k)(h-1)}{n}\mathrm{i}}{\left[T_n\right]}_{j,k}=P_{T_n}\left(\frac{2\pi (h-1)}{n}\right),n\in \mathbb{N},h\in \{1,\dots ,n\},\hfill \end{array}$$

where $\left\{P_{T_n}\right\}$ is the conventional spectral estimator, which is also known as the method of (averaged) periodogram or as the Bartlett method (see, e.g., [4]), defined as

$$P_{T_n}\left(\omega \right):=\frac{1}{n}{\displaystyle \sum _{j,k=1}^n}{\mathrm{e}}^{(j-k)\omega \mathrm{i}}{\left[T_n\right]}_{j,k},n\in \mathbb{N},\omega \in \mathbb{R}.$$

3. A Note on the Cholesky Decomposition of Perturbed Block Toeplitz Matrices

We recall that if A is an $n\times n$ positive definite matrix, then there exists a unique $n\times n$ lower triangular matrix L with ${\left[L\right]}_{j,j}>0$ for all $j\in \{1,\dots ,n\}$ satisfying that $A=L{L}^{*}$. This decomposition of A ($A=L{L}^{*}$) is called the Cholesky decomposition of A. In ([3], Section 6.3) Gray gave a result on the Cholesky decomposition of Toeplitz matrices. The following theorem generalizes this result to perturbed block Toeplitz matrices. Furthermore, unlike in ([3], Section 6.3) we also give the convergence speed of our result.

Theorem 2.

Consider a continuous$2\pi$-periodic function$F:\mathbb{R}\to {\mathbb{C}}^{N\times N}$whose sequence of Fourier coefficients${\left\{{\mathsf{F}}_k\right\}}_{k\in \mathbb{Z}}$satisfies that${\mathsf{F}}_0$is lower triangular with${\left[{\mathsf{F}}_0\right]}_{j,j}>0$for all$j\in \{1,\dots ,N\}$and${\mathsf{F}}_{-k}=0_{N\times N}$for all$k\in \mathbb{N}$. Suppose that$A_n$is an$nN\times nN$positive definite matrix for all$n\in \mathbb{N}$with$\left\{A_n\right\}\sim \left\{T_n\left(F\right){\left(T_n\left(F\right)\right)}^{*}\right\}$(or equivalently,$\left\{A_n\right\}\sim \left\{T_n\left(F{F}^{*}\right)\right\}$, where$F{F}^{*}\left(\omega \right)=F\left(\omega \right){\left(F\left(\omega \right)\right)}^{*}$,$\omega \in \mathbb{R}$). Let$A_n=L_n{L}_n^{*}$be the Cholesky decomposition of$A_n$for all$n\in \mathbb{N}$. If$\left\{L_n\right\}$and$\left\{T_n\left(F\right)\right\}$are stable (that is,$\{\parallel L_n^{-1}{\parallel }_2\}$and$\{\parallel {\left(T_n\left(F\right)\right)}^{-1}{\parallel }_2\}$are bounded) then

$$\left\{L_n\right\}\sim \left\{T_n\left(F\right)\right\}.$$

(2)

Moreover, there exists$K\in [0,\infty )$such that

$$\frac{\parallel L_n-T_n{\left(F\right)\parallel }_F}{\sqrt{n}}\le K\frac{\parallel A_n-T_n\left(F\right){\left(T_n\left(F\right)\right)}^{*}{\parallel }_F}{\sqrt{n}}\forall n\in \mathbb{N}.$$

(3)

Proof. 

Applying ([5], Lemma 4.2) and ([5], Theorem 6.2) yields $\left\{T_n\left(F\right){\left(T_n\left(F\right)\right)}^{*}\right\}=\left\{T_n\left(F\right)T_n\left(F^{*}\right)\right\}\sim \left\{T_n\left(F{F}^{*}\right)\right\}$ (we recall that ([5], Theorem 6.2) was previously given for Hermitian generating functions (see, e.g., [6,7], or ([8], Theorem 2))). Hence, since the relation ∼ is symmetric and transitive (see ([5], Lemma 3.1)), $\left\{A_n\right\}\sim \left\{T_n\left(F\right){\left(T_n\left(F\right)\right)}^{*}\right\}$ if and only if $\left\{A_n\right\}\sim \left\{T_n\left(F{F}^{*}\right)\right\}$.

The sequence $\{\parallel T_n\left(F\right){\parallel }_2\}$ is bounded (see, e.g., ([5], Theorem 4.3) or ([9], Corollary 4.2)). As $\{\parallel A_n{\parallel }_2\}$ is bounded and

$$\{\parallel L_n{\parallel }_2\}=\{\parallel L_n^{*}{\parallel }_2\}=\left\{\sqrt{{\lambda }_1\left(L_n{L}_n^{*}\right)}\right\}=\left\{\sqrt{\parallel L_n{L}_n^{*}{\parallel }_2}\right\}=\left\{\sqrt{\parallel A_n{\parallel }_2}\right\},$$

$\{\parallel L_n{\parallel }_2\}$ is also bounded. Consequently, to finish the proof we only need to show Equation (3), or equivalently, we only need to show that there exists $K\in [0,\infty )$ such that

$$\parallel L_n-T_n{\left(F\right)\parallel }_F\le K{\parallel A_n-T_n\left(F\right){\left(T_n\left(F\right)\right)}^{*}\parallel }_F\forall n\in \mathbb{N}.$$

(4)

We have

$$\begin{array}{cc}\hfill \parallel L_n-T_n{\left(F\right)\parallel }_F& =\parallel T_n\left(F\right){\left(T_n\left(F\right)\right)}^{-1}{L}_n-T_n{\left(F\right)\parallel }_F\hfill \\ & \le \parallel T_n{\left(F\right)\parallel }_2\parallel {\left(T_n\left(F\right)\right)}^{-1}{L}_n-I_{nN}{\parallel }_F\le \parallel T_n{\left(F\right)\parallel }_2(\parallel {\left(T_n\left(F\right)\right)}^{-1}{L}_n-D_n{\parallel }_F+\parallel D_n-I_{nN}{\parallel }_F),\hfill \end{array}$$

(5)

where $D_n$ denotes the $nN\times nN$ diagonal matrix satisfying that ${\left[D_n\right]}_{j,j}={\left[{\left(T_n\left(F\right)\right)}^{-1}{L}_n\right]}_{j,j}$ for all $j\in \{1,\dots ,nN\}$ and $n\in \mathbb{N}$. Since $T_n\left(F\right)$ is lower triangular for all $n\in \mathbb{N}$, ${\left(T_n\left(F\right)\right)}^{-1}$ is lower triangular for all $n\in \mathbb{N}$ (see, e.g., ([10], p. 44)), and therefore,

$$1={\left[I_{nN}\right]}_{j,j}={\left[T_n\left(F\right){\left(T_n\left(F\right)\right)}^{-1}\right]}_{j,j}={\displaystyle \sum _{k=1}^{nN}}{\left[T_n\left(F\right)\right]}_{j,k}{\left[{\left(T_n\left(F\right)\right)}^{-1}\right]}_{k,j}={\left[T_n\left(F\right)\right]}_{j,j}{\left[{\left(T_n\left(F\right)\right)}^{-1}\right]}_{j,j}$$

for all $j\in \{1,\dots ,nN\}$ and $n\in \mathbb{N}$. Thus,

$${\left[D_n\right]}_{j,j}={\left[{\left(T_n\left(F\right)\right)}^{-1}{L}_n\right]}_{j,j}={\displaystyle \sum _{k=1}^{nN}}{\left[{\left(T_n\left(F\right)\right)}^{-1}\right]}_{j,k}{\left[L_n\right]}_{k,j}={\left[{\left(T_n\left(F\right)\right)}^{-1}\right]}_{j,j}{\left[L_n\right]}_{j,j}=\frac{{\left[L_n\right]}_{j,j}}{{\left[T_n\left(F\right)\right]}_{j,j}}>0$$

for all $j\in \{1,\dots ,nN\}$ and $n\in \mathbb{N}$, and hence,

$$\begin{array}{c}\parallel D_n-I_{nN}{\parallel }_F\hfill \\ =\sqrt{{\sum }_{j=1}^{nN}{\left|{[D_n-I_{nN}]}_{j,j}\right|}^2}=\sqrt{{\sum }_{j=1}^{nN}{|{\left[D_n\right]}_{j,j}-1|}^2}=\sqrt{{\sum }_{j=1}^{nN}{\left|\frac{{\left({\left[D_n\right]}_{j,j}\right)}^2-1}{{\left[D_n\right]}_{j,j}+1}\right|}^2}=\sqrt{{\sum }_{j=1}^{nN}\frac{|{\left[D_n{D}_n\right]}_{j,j}{-1|}^2}{{({\left[D_n\right]}_{j,j}+1)}^2}}\hfill \\ \le \sqrt{{\sum }_{j=1}^{nN}{|{\left[D_n{D}_n\right]}_{j,j}-1|}^2}=\parallel D_n{D}_n-I_{nN}{\parallel }_F=\parallel D_n{D}_n^{*}-I_{nN}{\parallel }_F={\parallel D_n{D}_n^{*}-{\left(T_n\left(F\right)\right)}^{-1}{L}_n{\left(L_n\right)}^{-1}{T}_n\left(F\right)\parallel }_F\hfill \\ \le \parallel D_n{D}_n^{*}-{\left(T_n\left(F\right)\right)}^{-1}{L}_n{D}_n^{*}{\parallel }_F+{\parallel {\left(T_n\left(F\right)\right)}^{-1}{L}_n{D}_n^{*}-{\left(T_n\left(F\right)\right)}^{-1}{L}_n{\left(L_n\right)}^{-1}{T}_n\left(F\right)\parallel }_F\hfill \\ \le \parallel D_n-{\left(T_n\left(F\right)\right)}^{-1}{L}_n{\parallel }_F\parallel D_n^{*}{\parallel }_2+\parallel {\left(T_n\left(F\right)\right)}^{-1}{L}_n{\parallel }_2{\parallel D_n^{*}-{\left(L_n\right)}^{-1}{T}_n\left(F\right)\parallel }_F\hfill \\ =\parallel D_n-{\left(T_n\left(F\right)\right)}^{-1}{L}_n{\parallel }_F\parallel D_n{\parallel }_2+\parallel {\left(T_n\left(F\right)\right)}^{-1}{L}_n{\parallel }_2{\parallel D_n-{\left(T_n\left(F\right)\right)}^{*}{\left(L_n^{*}\right)}^{-1}\parallel }_F\hfill \\ \le \parallel D_n-{\left(T_n\left(F\right)\right)}^{-1}{L}_n{\parallel }_F{\parallel D_n\parallel }_2\hfill \\ +\parallel {\left(T_n\left(F\right)\right)}^{-1}{\parallel }_2\parallel L_n{\parallel }_2(\parallel D_n-{\left(T_n\left(F\right)\right)}^{-1}{L}_n{\parallel }_F+\parallel {\left(T_n\left(F\right)\right)}^{-1}{L}_n-{\left(T_n\left(F\right)\right)}^{*}{\left(L_n^{*}\right)}^{-1}{\parallel }_F)\forall n\in \mathbb{N}.\hfill \end{array}$$

(6)

As $T_n\left(F\right)$ and $L_n$ are lower triangular for all $n\in \mathbb{N}$, ${\left(T_n\left(F\right)\right)}^{-1}{L}_n$ and $L_n^{-1}{T}_n\left(F\right)$ are lower triangular for all $n\in \mathbb{N}$ (see, e.g., ([11], p. 240)). Consequently, ${\left(T_n\left(F\right)\right)}^{*}{\left(L_n^{*}\right)}^{-1}$ is upper triangular for all $n\in \mathbb{N}$, and therefore,

$$\begin{array}{c}\parallel {\left(T_n\left(F\right)\right)}^{-1}{L}_n-D_n{\parallel }_F=\sqrt{\parallel {\left(T_n\left(F\right)\right)}^{-1}{L}_n-D_n{\parallel }_F^2}\le \sqrt{\parallel {\left(T_n\left(F\right)\right)}^{-1}{L}_n-D_n{\parallel }_F^2+{\parallel D_n-{\left(T_n\left(F\right)\right)}^{*}{\left(L_n^{*}\right)}^{-1}\parallel }_F^2}\hfill \\ =\sqrt{\parallel {\left(T_n\left(F\right)\right)}^{-1}{L}_n-{\left(T_n\left(F\right)\right)}^{*}{\left(L_n^{*}\right)}^{-1}{\parallel }_F^2}={\parallel {\left(T_n\left(F\right)\right)}^{-1}{L}_n-{\left(T_n\left(F\right)\right)}^{*}{\left(L_n^{*}\right)}^{-1}\parallel }_F\forall n\in \mathbb{N}.\hfill \end{array}$$

(7)

Combining Equations (6), (7), and (8) yields

$$\begin{array}{c}\parallel L_n-T_n{\left(F\right)\parallel }_F\hfill \\ \le \parallel T_n{\left(F\right)\parallel }_2(1+\parallel D_n{\parallel }_2+2\parallel {\left(T_n\left(F\right)\right)}^{-1}{\parallel }_2\parallel L_n{\parallel }_2)\parallel {\left(T_n\left(F\right)\right)}^{-1}{L}_n-{\left(T_n\left(F\right)\right)}^{*}{\left(L_n^{*}\right)}^{-1}{\parallel }_F\hfill \\ \le \parallel T_n{\left(F\right)\parallel }_2(1+\parallel D_n{\parallel }_2+2\parallel {\left(T_n\left(F\right)\right)}^{-1}{\parallel }_2\parallel L_n{\parallel }_2)\parallel {\left(T_n\left(F\right)\right)}^{-1}{\parallel }_2{\parallel L_n-T_n\left(F\right){\left(T_n\left(F\right)\right)}^{*}{\left(L_n^{*}\right)}^{-1}\parallel }_F\hfill \\ \le \parallel T_n{\left(F\right)\parallel }_2(1+\parallel D_n{\parallel }_2+2\parallel {\left(T_n\left(F\right)\right)}^{-1}{\parallel }_2\parallel L_n{\parallel }_2)\parallel {\left(T_n\left(F\right)\right)}^{-1}{\parallel }_2\parallel L_n{L}_n^{*}-T_n\left(F\right){\left(T_n\left(F\right)\right)}^{*}{\parallel }_F{\parallel {\left(L_n^{*}\right)}^{-1}\parallel }_2\hfill \\ =K_n{\parallel A_n-T_n\left(F\right){\left(T_n\left(F\right)\right)}^{*}\parallel }_F\hfill \end{array}$$

with $K_n=\parallel T_n{\left(F\right)\parallel }_2(1+\parallel D_n{\parallel }_2+2\parallel {\left(T_n\left(F\right)\right)}^{-1}{\parallel }_2\parallel L_n{\parallel }_2)\parallel {\left(T_n\left(F\right)\right)}^{-1}{\parallel }_2{\parallel L_n^{-1}\parallel }_2$ for all $n\in \mathbb{N}$. To prove Equation (4) we only need to show that $\left\{K_n\right\}$ is bounded, or equivalently, we only need to show that $\{\parallel D_n{\parallel }_2\}$ is bounded. For every $n\in \mathbb{N}$ there exists $j_0\in \{1,\dots ,nN\}$ such that

$$\parallel D_n{\parallel }_2={\lambda }_1\left(D_n\right)={\left[D_n\right]}_{j_0,j_0}=\frac{\parallel D_n{e}_{j_0}{\parallel }_F}{\parallel e_{j_0}{\parallel }_F}\le \frac{\parallel {\left(T_n\left(F\right)\right)}^{-1}{L}_n{e}_{j_0}{\parallel }_F}{\parallel e_{j_0}{\parallel }_F}\le \parallel {\left(T_n\left(F\right)\right)}^{-1}{L}_n{\parallel }_2\le \parallel {\left(T_n\left(F\right)\right)}^{-1}{\parallel }_2{\parallel L_n\parallel }_2,$$

where $e_{j_0}$ is the $nN$-dimensional (column) vector whose entries are given by ${\left[e_{j_0}\right]}_{j,1}={\delta }_{j,j_0}$, $j\in \{1,\dots ,nN\}$, with $\delta$ being the Kronecker delta. Thus, $\{\parallel D_n{\parallel }_2\}$ is bounded. □

Observe that Equation (3) shows that the sequence $\left\{\frac{\parallel L_n-T_n{\left(F\right)\parallel }_F}{\sqrt{n}}\right\}$ converges to zero at least as fast as the sequence $\left\{\frac{\parallel A_n-T_n\left(F\right){\left(T_n\left(F\right)\right)}^{*}{\parallel }_F}{\sqrt{n}}\right\}$ does.

Equation (2) generalizes ([3], Section 6.3). Specifically, in ([3], Section 6.3) Gray proved Equation (2), but only for the special case in which $N=1$, F is in the Wiener class, and $\left\{A_n\right\}=\left\{T_n\left(F{F}^{*}\right)\right\}$ (or equivalently, $\left\{A_n\right\}=\{T_n{\left(\right|F|}^2\left)\right\}$). It should be mentioned that unlike here, the convergence speed of $\left\{\frac{\parallel L_n-T_n{\left(F\right)\parallel }_F}{\sqrt{n}}\right\}$ was not given in ([3], Section 6.3) for the special case there studied.

4. Applications of the Periodogram Method in Parameter Estimation

Using Theorems 1 and 2 we give in this section a parameter estimation method for perturbed VAR processes and another for perturbed VMA processes. These methods can be applied in any real-world problem where the random process involved is modeled as a VAR process or as a VMA process, e.g., in damage detection for aeronautical structures or in MIMO channel identification.

4.1. Parameter Estimation Method for Perturbed VAR Processes

We begin by reviewing the concept of VAR process.

Definition 1.

A zero-mean random N-dimensional vector process$\left\{x_n\right\}$is said to be a VAR process if

$$x_n=w_n-{\displaystyle \sum _{k=1}^{n-1}}{\mathsf{F}}_{-k}{x}_{n-k}\forall n\in \mathbb{N},$$

(8)

where${\mathsf{F}}_{-k}\in {\mathbb{C}}^{N\times N}$for all$k\in \mathbb{N}$, and$\left\{w_n\right\}$is a zero-mean random N-dimensional vector process whose sequence of correlation matrices is given by$\left\{E\left(w_{n:1}{w}_{n:1}^{*}\right)\right\}=\left\{T_n\left(\mathsf{\Lambda }\right)\right\}$with Λ being an $N\times N$ positive definite matrix. If there exists $p\in \mathbb{N}$ such that ${\mathsf{F}}_{-k}=0_{N\times N}$ for all $k>p$, then $\left\{x_n\right\}$ is called a VAR process of (finite) order p or a VAR$\left(p\right)$ process.

Let $\left\{x_n\right\}$ be as in Definition 1. Assume that ${\left\{{\mathsf{F}}_k\right\}}_{k\in \mathbb{Z}}$, with ${\mathsf{F}}_0=I_N$ and ${\mathsf{F}}_k=0_{N\times N}$ for all $k\in \mathbb{N}$, is the sequence of Fourier coefficients of a continuous $2\pi$-periodic function $F:\mathbb{R}\to {\mathbb{C}}^{N\times N}$. From Equation (8) we can obtain (see, e.g., ([12], Equation (20)))

$${\left(E\left(x_{n:1}{x}_{n:1}^{*}\right)\right)}^{-1}=T_n\left(F^{*}\right)T_n\left({\Lambda }^{-1}\right)T_n\left(F\right)\forall n\in \mathbb{N}.$$

If ${\mathsf{\Lambda }}^{-1}=L_{{\mathsf{\Lambda }}^{-1}}{L}_{{\mathsf{\Lambda }}^{-1}}^{*}$ is the Cholesky decomposition of the positive definite matrix ${\mathsf{\Lambda }}^{-1}$, then

$${\left(E\left(x_{n:1}{x}_{n:1}^{*}\right)\right)}^{-1}=T_n\left(F^{*}{L}_{{\mathsf{\Lambda }}^{-1}}\right){\left(T_n\left(F^{*}{L}_{{\mathsf{\Lambda }}^{-1}}\right)\right)}^{*}$$

(9)

is the Cholesky decomposition of the positive definite matrix ${\left(E\left(x_{n:1}{x}_{n:1}^{*}\right)\right)}^{-1}$ for all $n\in \mathbb{N}$, since

$$\begin{array}{cc}\hfill {\left(E\left(x_{n:1}{x}_{n:1}^{*}\right)\right)}^{-1}& =T_n\left(F^{*}\right)T_n\left(L_{{\mathsf{\Lambda }}^{-1}}{L}_{{\mathsf{\Lambda }}^{-1}}^{*}\right)T_n\left(F\right)=T_n\left(F^{*}\right)T_n\left(L_{{\mathsf{\Lambda }}^{-1}}\left)T_n\right(L_{{\mathsf{\Lambda }}^{-1}}^{*}\right)T_n\left(F\right)\hfill \\ & =T_n\left(F^{*}{L}_{{\mathsf{\Lambda }}^{-1}}\right)T_n\left(L_{{\mathsf{\Lambda }}^{-1}}^{*}F\right)=T_n\left(F^{*}{L}_{{\mathsf{\Lambda }}^{-1}}\right)T_n\left({\left(F^{*}{L}_{{\mathsf{\Lambda }}^{-1}}\right)}^{*}\right)\forall n\in \mathbb{N}.\hfill \end{array}$$

Observe that if we know the correlation matrix $E\left(x_{n:1}{x}_{n:1}^{*}\right)$ for certain $n\in \mathbb{N}$, then the Cholesky decomposition of ${\left(E\left(x_{n:1}{x}_{n:1}^{*}\right)\right)}^{-1}$ provides $\mathsf{\Lambda }$ and the parameters ${\mathsf{F}}_{-1},\dots ,{\mathsf{F}}_{1-n}$ of the VAR process, because

$$T_n\left(F^{*}{L}_{{\mathsf{\Lambda }}^{-1}}\right)=\left(\begin{array}{ccccc}{L}_{{\mathsf{\Lambda }}^{-1}}& 0_{N\times N}& 0_{N\times N}& \cdots & 0_{N\times N}\\ {\mathsf{F}}_{-1}^{*}{L}_{{\mathsf{\Lambda }}^{-1}}& L_{{\mathsf{\Lambda }}^{-1}}& 0_{N\times N}& \cdots & 0_{N\times N}\\ {\mathsf{F}}_{-2}^{*}{L}_{{\mathsf{\Lambda }}^{-1}}& {\mathsf{F}}_{-1}^{*}{L}_{{\mathsf{\Lambda }}^{-1}}& L_{{\mathsf{\Lambda }}^{-1}}& \cdots & 0_{N\times N}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ {\mathsf{F}}_{1-n}^{*}{L}_{{\mathsf{\Lambda }}^{-1}}& {\mathsf{F}}_{2-n}^{*}{L}_{{\mathsf{\Lambda }}^{-1}}& {\mathsf{F}}_{3-n}^{*}{L}_{{\mathsf{\Lambda }}^{-1}}& \cdots & L_{{\mathsf{\Lambda }}^{-1}}\end{array}\right).$$

(10)

However, in practice what we usually know is a perturbed version $\left\{A_n\right\}$ of the sequence of correlation matrices $\left\{E\left(x_{n:1}{x}_{n:1}^{*}\right)\right\}$ of the process. The following theorem allows us to estimate $\mathsf{\Lambda }$ and the parameters ${\left\{{\mathsf{F}}_{-k}\right\}}_{k\in \mathbb{N}}$ of the VAR process from the Cholesky decomposition of the matrices of the sequence $\left\{A_n^{-1}\right\}$, when $\left\{A_n\right\}\sim \left\{E\left(x_{n:1}{x}_{n:1}^{*}\right)\right\}$.

Theorem 3.

Let$\left\{x_n\right\}$be as in Definition 1. Assume that${\left\{{\mathsf{F}}_k\right\}}_{k\in \mathbb{Z}}$, with${\mathsf{F}}_0=I_N$and${\mathsf{F}}_k=0_{N\times N}$for all$k\in \mathbb{N}$, is the sequence of Fourier coefficients of a continuous$2\pi$-periodic function$F:\mathbb{R}\to {\mathbb{C}}^{N\times N}$. Suppose that$A_n$is an$nN\times nN$positive definite matrix for all$n\in \mathbb{N}$satisfying that$\left\{A_n\right\}$is stable and$\left\{A_n\right\}\sim \left\{E\left(x_{n:1}{x}_{n:1}^{*}\right)\right\}$. Let$A_n^{-1}=L_n{L}_n^{*}$be the Cholesky decomposition of$A_n^{-1}$for all$n\in \mathbb{N}$. Then

$${\displaystyle \underset{n\to \infty }{\lim }}\frac{1}{2\pi }{\int }_0^{2\pi }{\parallel {\widehat{P}}_{L_n}\left(\omega \right)-{\left(F\left(\omega \right)\right)}^{*}{L}_{{\mathsf{\Lambda }}^{-1}}\parallel }_F^{2}d\omega =0$$

(11)

and

$${∥\frac{1}{2\pi }{\int }_0^{2\pi }{\mathrm{e}}^{-k\omega \mathrm{i}}{\widehat{P}}_{L_n}\left(\omega \right)d\omega -{\mathsf{F}}_{-k}^{*}{L}_{{\mathsf{\Lambda }}^{-1}}∥}_F^2\le \frac{1}{2\pi }{\int }_0^{2\pi }{∥{\widehat{P}}_{L_n}\left(\omega \right)-{\left(F\left(\omega \right)\right)}^{*}{L}_{{\mathsf{\Lambda }}^{-1}}∥}_F^{2}d\omega$$

for all$n\in \mathbb{N}$and$k\in \{0,1,\dots ,n-1\}$, where${\mathsf{\Lambda }}^{-1}=L_{{\mathsf{\Lambda }}^{-1}}{L}_{{\mathsf{\Lambda }}^{-1}}^{*}$is the Cholesky decomposition of${\mathsf{\Lambda }}^{-1}$. Moreover, if$\left\{x_n\right\}$is of finite order there exist$K_1,K_2\in [0,\infty )$such that

$$\sqrt{\frac{1}{2\pi }{\int }_0^{2\pi }{\parallel {\widehat{P}}_{L_n}\left(\omega \right)-{\left(F\left(\omega \right)\right)}^{*}{L}_{{\mathsf{\Lambda }}^{-1}}\parallel }_F^{2}d\omega }\le K_1\frac{\parallel A_n-E\left(x_{n:1}{x}_{n:1}^{*}\right){\parallel }_F}{\sqrt{n}}+\frac{K_2}{\sqrt{n}}\forall n\in \mathbb{N}.$$

Proof. 

Since $A_n$ is positive definite matrix for all $n\in \mathbb{N}$, $A_n^{-1}$ is positive definite matrix for all $n\in \mathbb{N}$. From ([12], Equation (20)) and ([5], Lemma 4.2) we have

$$\begin{array}{cc}\hfill {∥{\left(E\left(x_{n:1}{x}_{n:1}^{*}\right)\right)}^{-1}∥}_2& =\parallel T_n\left(F^{*}\right)T_n\left({\mathsf{\Lambda }}^{-1}\right)T_n\left(F\right){\parallel }_2\le \parallel T_n\left(F^{*}\right){\parallel }_2\parallel T_n\left({\mathsf{\Lambda }}^{-1}\right){\parallel }_2{\parallel T_n\left(F\right)\parallel }_2\hfill \\ & =\parallel {\left(T_n\left(F\right)\right)}^{*}{\parallel }_2\parallel {\mathsf{\Lambda }}^{-1}{\parallel }_2\parallel T_n{\left(F\right)\parallel }_2=\parallel {\mathsf{\Lambda }}^{-1}{\parallel }_2{\parallel T_n\left(F\right)\parallel }_2^2\forall n\in \mathbb{N}.\hfill \end{array}$$

Hence, as $\{\parallel T_n\left(F\right){\parallel }_2\}$ is bounded (see, e.g., ([5], Theorem 4.3) or ([9], Corollary 4.2)), $\left\{{∥{\left(E\left(x_{n:1}{x}_{n:1}^{*}\right)\right)}^{-1}∥}_2\right\}$ is also bounded. Consequently, applying ([13], Lemma A1) and Equation (9) yields

$$\left\{A_n^{-1}\right\}\sim \left\{{\left(E\left(x_{n:1}{x}_{n:1}^{*}\right)\right)}^{-1}\right\}=\left\{T_n\left(F^{*}{L}_{{\mathsf{\Lambda }}^{-1}}\right){\left(T_n\left(F^{*}{L}_{{\mathsf{\Lambda }}^{-1}}\right)\right)}^{*}\right\}.$$

As $\{\parallel A_n{\parallel }_2\}$ and $\{\parallel E\left(x_{n:1}{x}_{n:1}^{*}\right){\parallel }_2\}$ are bounded, the sequences

$$\{\parallel L_n^{-1}{\parallel }_2\}=\left\{\sqrt{{\lambda }_1\left({\left(L_n^{-1}\right)}^{*}{L}_n^{-1}\right)}\right\}=\left\{\sqrt{{∥{\left(L_n^{-1}\right)}^{*}{L}_n^{-1}∥}_2}\right\}=\left\{\sqrt{{∥{\left(L_n{L}_n^{*}\right)}^{-1}∥}_2}\right\}=\left\{\sqrt{{∥A_n∥}_2}\right\}$$

and

$$\{\parallel {\left(T_n\left(F^{*}{L}_{{\mathsf{\Lambda }}^{-1}}\right)\right)}^{-1}{\parallel }_2\}=\left\{\sqrt{{∥{\left(T_n\left(F^{*}{L}_{{\mathsf{\Lambda }}^{-1}}\right){\left(T_n\left(F^{*}{L}_{{\mathsf{\Lambda }}^{-1}}\right)\right)}^{*}\right)}^{-1}∥}_2}\right\}=\left\{\sqrt{{∥E\left(x_{n:1}{x}_{n:1}^{*}\right)∥}_2}\right\}$$

are also bounded. Thus, from Theorem 2 we have that $\left\{L_n\right\}\sim \left\{T_n\left(F^{*}{L}_{{\mathsf{\Lambda }}^{-1}}\right)\right\}$ and that there exists $K\in [0,\infty )$ such that

$$\frac{\parallel L_n-T_n\left(F^{*}{L}_{{\mathsf{\Lambda }}^{-1}}\right){\parallel }_F}{\sqrt{n}}\le K\frac{\parallel A_n^{-1}-T_n\left(F^{*}{L}_{{\mathsf{\Lambda }}^{-1}}\right){\left(T_n\left(F^{*}{L}_{{\mathsf{\Lambda }}^{-1}}\right)\right)}^{*}{\parallel }_F}{\sqrt{n}}=K\frac{\parallel A_n^{-1}-{\left(E\left(x_{n:1}{x}_{n:1}^{*}\right)\right)}^{-1}{\parallel }_F}{\sqrt{n}}$$

for all $n\in \mathbb{N}$. Hence, applying Theorem 1 we conclude that Equation (11) holds.

Applying the Schwarz inequality (see, e.g., ([14], p. 139) yields

$$\begin{array}{cc}\hfill {∥\frac{1}{2\pi }{\int }_0^{2\pi }{\mathrm{e}}^{-k\omega \mathrm{i}}{\widehat{P}}_{L_n}\left(\omega \right)d\omega -{\mathsf{F}}_{-k}^{*}{L}_{{\mathsf{\Lambda }}^{-1}}∥}_F& ={∥\frac{1}{2\pi }{\int }_0^{2\pi }{\mathrm{e}}^{-k\omega \mathrm{i}}{\widehat{P}}_{L_n}\left(\omega \right)d\omega -\frac{1}{2\pi }{\int }_0^{2\pi }{\mathrm{e}}^{-k\omega \mathrm{i}}{\left(F\left(\omega \right)\right)}^{*}d\omega L_{{\mathsf{\Lambda }}^{-1}}∥}_F\hfill \\ & =\frac{1}{2\pi }{∥{\int }_0^{2\pi }{\mathrm{e}}^{-k\omega \mathrm{i}}\left({\widehat{P}}_{L_n}\left(\omega \right)-{\left(F\left(\omega \right)\right)}^{*}{L}_{{\mathsf{\Lambda }}^{-1}}\right)d\omega ∥}_F\hfill \\ & =\frac{1}{2\pi }\sqrt{{\displaystyle \sum _{r,s=1}^N}{\left|{\left[{\int }_0^{2\pi }{\mathrm{e}}^{-k\omega \mathrm{i}}\left({\widehat{P}}_{L_n}\left(\omega \right)-{\left(F\left(\omega \right)\right)}^{*}{L}_{{\mathsf{\Lambda }}^{-1}}\right)d\omega \right]}_{r,s}\right|}^2}\hfill \\ & =\frac{1}{2\pi }\sqrt{{\displaystyle \sum _{r,s=1}^N}{\left|{\int }_0^{2\pi }{\mathrm{e}}^{-k\omega \mathrm{i}}{\left[{\widehat{P}}_{L_n}\left(\omega \right)-{\left(F\left(\omega \right)\right)}^{*}{L}_{{\mathsf{\Lambda }}^{-1}}\right]}_{r,s}d\omega \right|}^2}\hfill \\ & \le \frac{1}{2\pi }\sqrt{{\displaystyle \sum _{r,s=1}^N}2\pi {\int }_0^{2\pi }{\left|{\mathrm{e}}^{-k\omega \mathrm{i}}{\left[{\widehat{P}}_{L_n}\left(\omega \right)-{\left(F\left(\omega \right)\right)}^{*}{L}_{{\mathsf{\Lambda }}^{-1}}\right]}_{r,s}\right|}^{2}d\omega }\hfill \\ & =\sqrt{\frac{1}{2\pi }{\int }_0^{2\pi }{\displaystyle \sum _{r,s=1}^N}{\left|{\mathrm{e}}^{-k\omega \mathrm{i}}\right|}^2{\left|{\left[{\widehat{P}}_{L_n}\left(\omega \right)-{\left(F\left(\omega \right)\right)}^{*}{L}_{{\mathsf{\Lambda }}^{-1}}\right]}_{r,s}\right|}^{2}d\omega }\hfill \\ & =\sqrt{\frac{1}{2\pi }{\int }_0^{2\pi }{\displaystyle \sum _{r,s=1}^N}{\left|{\left[{\widehat{P}}_{L_n}\left(\omega \right)-{\left(F\left(\omega \right)\right)}^{*}{L}_{{\mathsf{\Lambda }}^{-1}}\right]}_{r,s}\right|}^{2}d\omega }\hfill \\ & =\sqrt{\frac{1}{2\pi }{\int }_0^{2\pi }{∥{\widehat{P}}_{L_n}\left(\omega \right)-{\left(F\left(\omega \right)\right)}^{*}{L}_{{\mathsf{\Lambda }}^{-1}}∥}_F^{2}d\omega }\hfill \end{array}$$

for all $n\in \mathbb{N}$ and $k\in \mathbb{Z}$.

Moreover, if $\left\{x_n\right\}$ is of finite order from Theorem 1 there exists $K_2\in [0,\infty )$ such that

$$\begin{array}{c}\sqrt{\frac{1}{2\pi }{\int }_0^{2\pi }{\parallel {\widehat{P}}_{L_n}\left(\omega \right)-{\left(F\left(\omega \right)\right)}^{*}{L}_{{\mathsf{\Lambda }}^{-1}}\parallel }_F^{2}d\omega }\hfill \\ \le \frac{\parallel L_n-T_n\left(F^{*}{L}_{{\mathsf{\Lambda }}^{-1}}\right){\parallel }_F}{\sqrt{n}}+\frac{K_2}{\sqrt{n}}\hfill \\ \le K\frac{\parallel A_n^{-1}-{\left(E\left(x_{n:1}{x}_{n:1}^{*}\right)\right)}^{-1}{\parallel }_F}{\sqrt{n}}+\frac{K_2}{\sqrt{n}}\hfill \\ =K\frac{\parallel {\left(E\left(x_{n:1}{x}_{n:1}^{*}\right)\right)}^{-1}-A_n^{-1}{\parallel }_F}{\sqrt{n}}+\frac{K_2}{\sqrt{n}}\hfill \\ =K\frac{\parallel {\left(E\left(x_{n:1}{x}_{n:1}^{*}\right)\right)}^{-1}\left(A_n-E\left(x_{n:1}{x}_{n:1}^{*}\right)\right)A_n^{-1}{\parallel }_F}{\sqrt{n}}+\frac{K_2}{\sqrt{n}}\hfill \\ \le K\parallel {\left(E\left(x_{n:1}{x}_{n:1}^{*}\right)\right)}^{-1}{\parallel }_2\frac{\parallel \left(A_n-E\left(x_{n:1}{x}_{n:1}^{*}\right)\right)A_n^{-1}{\parallel }_F}{\sqrt{n}}+\frac{K_2}{\sqrt{n}}\hfill \\ \le K\parallel {\left(E\left(x_{n:1}{x}_{n:1}^{*}\right)\right)}^{-1}{\parallel }_2{\parallel A_n^{-1}\parallel }_2\frac{\parallel A_n-E\left(x_{n:1}{x}_{n:1}^{*}\right){\parallel }_F}{\sqrt{n}}+\frac{K_2}{\sqrt{n}}\forall n\in \mathbb{N}.\hfill \end{array}$$

 □

If we know $A_n$ for certain $n\in \mathbb{N}$, Theorem 3 provides an estimation of the block entry ${\mathsf{F}}_{-k}^{*}{L}_{{\mathsf{\Lambda }}^{-1}}$ of the matrix $T_n\left(F^{*}{L}_{{\mathsf{\Lambda }}^{-1}}\right)$ in Equation (10) given by

$$\begin{array}{c}\frac{1}{2\pi }{\int }_0^{2\pi }{\mathrm{e}}^{-k\omega \mathrm{i}}{\widehat{P}}_{L_n}\left(\omega \right)d\omega \hfill \\ =\frac{1}{2\pi }{\int }_0^{2\pi }{\mathrm{e}}^{-k\omega \mathrm{i}}{\displaystyle \sum _{h=1}^n}{\chi }_{\left.\left[\frac{2\pi (h-1)}{n},\frac{2\pi h}{n}\right.\right)}\left(\omega \right){\left[{(V_n\otimes I_N)}^{*}{L}_n(V_n\otimes I_N)\right]}_{h,h}d\omega \hfill \\ =\frac{1}{2\pi }{\displaystyle \sum _{h=1}^n}{\int }_0^{2\pi }{\chi }_{\left.\left[\frac{2\pi (h-1)}{n},\frac{2\pi h}{n}\right.\right)}\left(\omega \right){\mathrm{e}}^{-k\omega \mathrm{i}}d\omega {\left[{(V_n\otimes I_N)}^{*}{L}_n(V_n\otimes I_N)\right]}_{h,h}\hfill \\ =\frac{1}{2\pi }{\displaystyle \sum _{h=1}^n}{\int }_{\frac{2\pi (h-1)}{n}}^{\frac{2\pi h}{n}}{\mathrm{e}}^{-k\omega \mathrm{i}}d\omega {\left[{(V_n\otimes I_N)}^{*}{L}_n(V_n\otimes I_N)\right]}_{h,h}\hfill \\ =\left\{\begin{array}{cc}\frac{1}{n}{\displaystyle {\sum }_{h=1}^n}{\left[{(V_n\otimes I_N)}^{*}{L}_n(V_n\otimes I_N)\right]}_{h,h}\hfill & \mathrm{if}k=0,\hfill \\ \frac{\mathrm{i}}{2\pi k}{\displaystyle {\sum }_{h=1}^n}\left({\mathrm{e}}^{-k\frac{2\pi h}{n}\mathrm{i}}-{\mathrm{e}}^{-k\frac{2\pi (h-1)}{n}\mathrm{i}}\right){\left[{(V_n\otimes I_N)}^{*}{L}_n(V_n\otimes I_N)\right]}_{h,h}\hfill & \mathrm{if}k\in \{1,\dots ,n-1\}.\hfill \end{array}\right.\hfill \end{array}$$

Therefore, if we know $A_n$ for certain $n\in \mathbb{N}$, Theorem 3 allows us to estimate $\mathsf{\Lambda }$ and the parameters ${\mathsf{F}}_{-1},\dots ,{\mathsf{F}}_{1-n}$ of the VAR process as follows

$$\widehat{\mathsf{\Lambda }}\left(n\right)={\left(\left(\frac{1}{2\pi }{\int }_0^{2\pi }{\widehat{P}}_{L_n}\left(\omega \right)d\omega \right){\left(\frac{1}{2\pi }{\int }_0^{2\pi }{\widehat{P}}_{L_n}\left(\omega \right)d\omega \right)}^{*}\right)}^{-1}$$

and

$${\widehat{\mathsf{F}}}_{-k}\left(n\right)={\left(\left(\frac{1}{2\pi }{\int }_0^{2\pi }{\mathrm{e}}^{-k\omega \mathrm{i}}{\widehat{P}}_{L_n}\left(\omega \right)d\omega \right){\left(\frac{1}{2\pi }{\int }_0^{2\pi }{\widehat{P}}_{L_n}\left(\omega \right)d\omega \right)}^{-1}\right)}^{*}\forall k\in \{1,\dots ,n-1\}.$$

Example 1.

We consider the zero-mean 2-dimensional VAR$\left(1\right)$process$\left\{x_n\right\}$in ([15], Example 2.3), where

$$\mathsf{\Lambda }=\left(\begin{array}{cc}4& 1\\ 1& 2\end{array}\right)$$

and

$$F_{-1}=\left(\begin{array}{cc}-0.8& -0.7\\ 0.4& -0.6\end{array}\right).$$

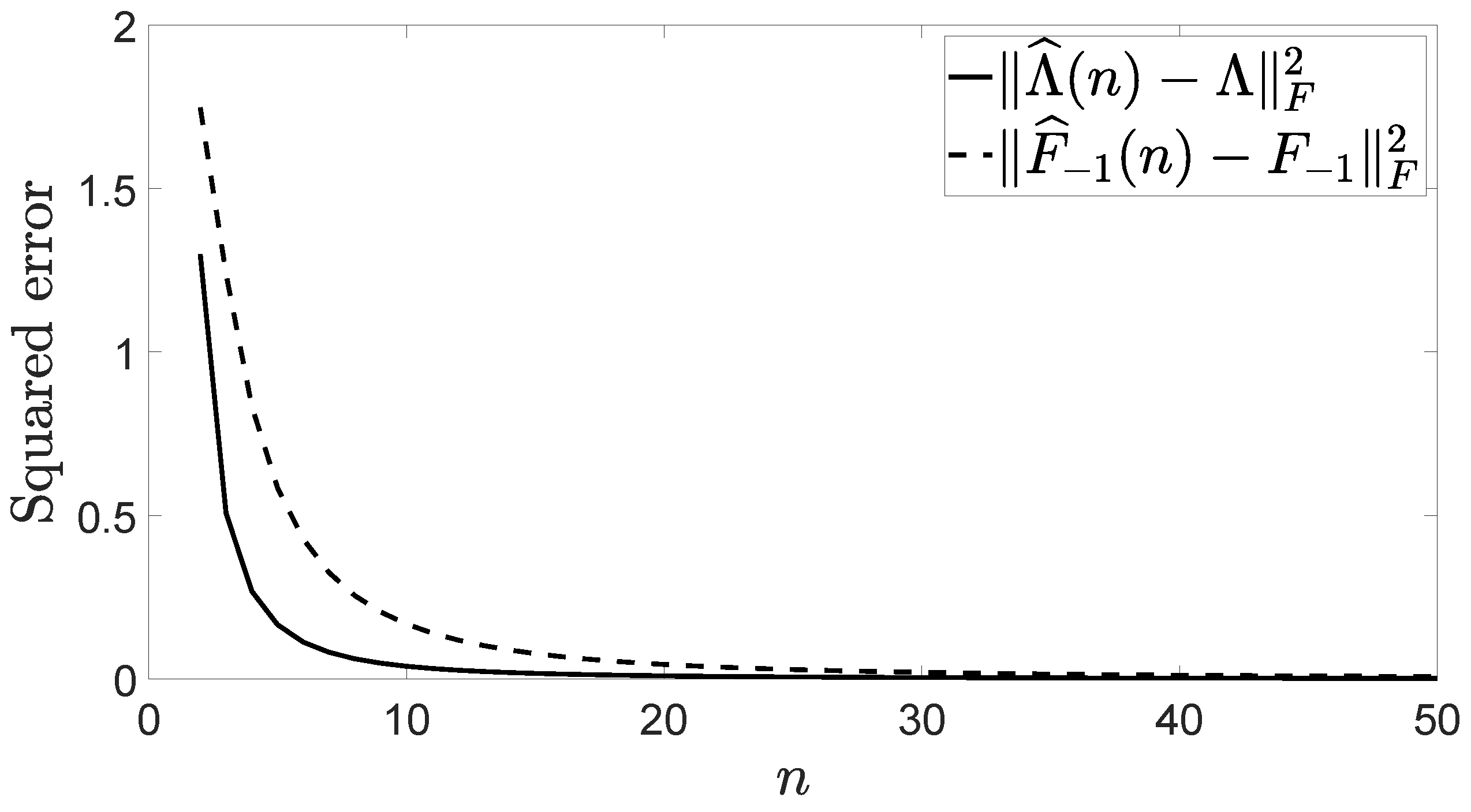
Figure 1 shows the squared error made when Λ and $F_{-1}$ are estimated from the perturbed VAR$\left(1\right)$ process whose sequence of correlation matrices is

$$\left\{A_n\right\}=\left\{E\left(x_{n:1}{x}_{n:1}^{*}\right)+\left(\begin{array}{cc}{0}_{2n-2\times 2n-2}& 0_{2n-2\times 2}\\ 0_{2\times 2n-2}& I_2\end{array}\right)\right\}.$$

Observe that this perturbed process has been generated by corrupting the VAR$\left(1\right)$ process in ([15], Example 2.3) by an impulse at $n=1$.

Figure 1. Squared error made when $\mathsf{\Lambda }$ and $F_{-1}$ are estimated by $\widehat{\mathsf{\Lambda }}\left(n\right)$ and ${\widehat{F}}_{-1}\left(n\right)$, respectively.

4.2. Parameter Estimation Method for Perturbed VMA Processes

We begin by reviewing the concept of VMA process.

Definition 2.

A zero-mean random N-dimensional vector process$\left\{x_n\right\}$is said to be a VMA process if

$$x_n=w_n+{\displaystyle \sum _{k=1}^{n-1}}{\mathsf{G}}_k{w}_{n-k}\forall n\in \mathbb{N},$$

(12)

where${\mathsf{G}}_k\in {\mathbb{C}}^{N\times N}$for all$k\in \mathbb{N}$, and$\left\{w_n\right\}$is a zero-mean random N-dimensional vector process whose sequence of correlation matrices is given by$\left\{E\left(w_{1:n}{w}_{1:n}^{*}\right)\right\}=\left\{T_n\left(\mathsf{\Lambda }\right)\right\}$with Λ being an $N\times N$ positive definite matrix and

$$w_{1:n}=\left(\begin{array}{c}{w}_1\\ ⋮\\ w_n\end{array}\right)\forall n\in \mathbb{N}.$$

If there exists $q\in \mathbb{N}$ such that ${\mathsf{G}}_k=0_{N\times N}$ for all $k>q$, then $\left\{x_n\right\}$ is called a VMA process of (finite) order q or a VMA$\left(q\right)$ process.

Let $\left\{x_n\right\}$ be as in Definition 2. Assume that ${\left\{{\mathsf{G}}_k\right\}}_{k\in \mathbb{Z}}$, with ${\mathsf{G}}_0=I_N$ and ${\mathsf{G}}_{-k}=0_{N\times N}$ for all $k\in \mathbb{N}$, is the sequence of Fourier coefficients of a continuous $2\pi$-periodic function $G:\mathbb{R}\to {\mathbb{C}}^{N\times N}$. Since Equation (12) can be rewritten as

$$x_n=\left(\begin{array}{cccc}{\mathsf{G}}_{n-1}& \cdots & {\mathsf{G}}_1& I_N\end{array}\right)w_{1:n}\forall n\in \mathbb{N},$$

we have

$$x_{1:n}=\left(\begin{array}{ccccc}{I}_N& 0_{N\times N}& 0_{N\times N}& \cdots & 0_{N\times N}\\ {\mathsf{G}}_1& I_N& 0_{N\times N}& \cdots & 0_{N\times N}\\ {\mathsf{G}}_2& {\mathsf{G}}_1& I_N& \cdots & 0_{N\times N}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ {\mathsf{G}}_{n-1}& {\mathsf{G}}_{n-2}& {\mathsf{G}}_{n-3}& \cdots & I_N\end{array}\right)w_{1:n}=T_n\left(G\right)w_{1:n}\forall n\in \mathbb{N},$$

and consequently,

$$\begin{array}{cc}\hfill \left\{E\left(x_{1:n}{x}_{1:n}^{*}\right)\right\}& =\left\{E\left(T_n\left(G\right)w_{1:n}{w}_{1:n}^{*}{\left(T_n\left(G\right)\right)}^{*}\right)\right\}\hfill \\ & =\left\{T_n\left(G\right)E\left(w_{1:n}{w}_{1:n}^{*}\right){\left(T_n\left(G\right)\right)}^{*}\right\}=\left\{T_n\left(G\right)T_n\left(\mathsf{\Lambda }\right){\left(T_n\left(G\right)\right)}^{*}\right\}.\hfill \end{array}$$

(13)

If $\mathsf{\Lambda }=L_{\mathsf{\Lambda }}{L}_{\mathsf{\Lambda }}^{*}$ is the Cholesky decomposition of $\mathsf{\Lambda }$, then

$$E\left(x_{1:n}{x}_{1:n}^{*}\right)=T_n\left(G{L}_{\mathsf{\Lambda }}\right){\left(T_n\left(G{L}_{\mathsf{\Lambda }}\right)\right)}^{*}$$

(14)

is the Cholesky decomposition of the positive definite matrix $E\left(x_{1:n}{x}_{1:n}^{*}\right)$ for all $n\in \mathbb{N}$, because

$$\begin{array}{cc}\hfill E\left(x_{1:n}{x}_{1:n}^{*}\right)& =T_n\left(G\right)T_n\left(L_{\mathsf{\Lambda }}{L}_{\mathsf{\Lambda }}^{*}\right){\left(T_n\left(G\right)\right)}^{*}=T_n\left(G\right)T_n\left(L_{\mathsf{\Lambda }}\right)T_n\left(L_{\mathsf{\Lambda }}^{*}\right){\left(T_n\left(G\right)\right)}^{*}\hfill \\ & =T_n\left(G{L}_{\mathsf{\Lambda }}\right){\left(T_n\left(L_{\mathsf{\Lambda }}\right)\right)}^{*}{\left(T_n\left(G\right)\right)}^{*}=T_n\left(G{L}_{\mathsf{\Lambda }}\right){\left(T_n\left(G\right)T_n\left(L_{\mathsf{\Lambda }}\right)\right)}^{*}\forall n\in \mathbb{N}.\hfill \end{array}$$

Observe that if we know the correlation matrix $E\left(x_{1:n}{x}_{1:n}^{*}\right)$ for certain $n\in \mathbb{N}$, then its Cholesky decomposition provides $\mathsf{\Lambda }$ and the parameters ${\mathsf{G}}_1,\dots ,{\mathsf{G}}_{n-1}$ of the VMA process, since

$$T_n\left(G{L}_{\mathsf{\Lambda }}\right)=\left(\begin{array}{ccccc}{L}_{\mathsf{\Lambda }}& 0_{N\times N}& 0_{N\times N}& \cdots & 0_{N\times N}\\ {\mathsf{G}}_1{L}_{\mathsf{\Lambda }}& L_{\mathsf{\Lambda }}& 0_{N\times N}& \cdots & 0_{N\times N}\\ {\mathsf{G}}_2{L}_{\mathsf{\Lambda }}& {\mathsf{G}}_1{L}_{\mathsf{\Lambda }}& L_{\mathsf{\Lambda }}& \cdots & 0_{N\times N}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ {\mathsf{G}}_{n-1}{L}_{\mathsf{\Lambda }}& {\mathsf{G}}_{n-2}{L}_{\mathsf{\Lambda }}& {\mathsf{G}}_{n-3}{L}_{\mathsf{\Lambda }}& \cdots & L_{\mathsf{\Lambda }}\end{array}\right).$$

(15)

However, in practice what we usually know is a perturbed version $\left\{A_n\right\}$ of the sequence of correlation matrices $\left\{E\left(x_{1:n}{x}_{1:n}^{*}\right)\right\}$ of the process. The following theorem allows us to estimate $\mathsf{\Lambda }$ and the parameters ${\left\{{\mathsf{G}}_k\right\}}_{k\in \mathbb{N}}$ of the VMA process from the Cholesky decomposition of the matrices of the sequence $\left\{A_n\right\}$, when $\left\{A_n\right\}\sim \left\{E\left(x_{1:n}{x}_{1:n}^{*}\right)\right\}$.

Theorem 4.

Let$\left\{x_n\right\}$be as in Definition 2. Assume that${\left\{{\mathsf{G}}_k\right\}}_{k\in \mathbb{Z}}$, with${\mathsf{G}}_0=I_N$and${\mathsf{G}}_{-k}=0_{N\times N}$for all$k\in \mathbb{N}$, is the sequence of Fourier coefficients of a continuous$2\pi$-periodic function$G:\mathbb{R}\to {\mathbb{C}}^{N\times N}$. Suppose that$A_n$is an$nN\times nN$positive definite matrix for all$n\in \mathbb{N}$satisfying that$\left\{A_n\right\}$is stable and$\left\{A_n\right\}\sim \left\{E\left(x_{1:n}{x}_{1:n}^{*}\right)\right\}$. Let$A_n=L_n{L}_n^{*}$be the Cholesky decomposition of$A_n$for all$n\in \mathbb{N}$. If$\left\{E\left(x_{1:n}{x}_{1:n}^{*}\right)\right\}$is stable then

$${\displaystyle \underset{n\to \infty }{\lim }}\frac{1}{2\pi }{\int }_0^{2\pi }{\parallel {\widehat{P}}_{L_n}\left(\omega \right)-G\left(\omega \right)L_{\mathsf{\Lambda }}\parallel }_F^{2}d\omega =0,$$

(16)

and

$${∥\frac{1}{2\pi }{\int }_0^{2\pi }{\mathrm{e}}^{-k\omega \mathrm{i}}{\widehat{P}}_{L_n}\left(\omega \right)d\omega -{\mathsf{G}}_k{L}_{\mathsf{\Lambda }}∥}_F^2\le \frac{1}{2\pi }{\int }_0^{2\pi }{∥{\widehat{P}}_{L_n}\left(\omega \right)-G\left(\omega \right)L_{\mathsf{\Lambda }}∥}_F^{2}d\omega$$

for all$n\in \mathbb{N}$and$k\in \{0,1,\dots ,n-1\}$, where$\mathsf{\Lambda }=L_{\mathsf{\Lambda }}{L}_{\mathsf{\Lambda }}^{*}$is the Cholesky decomposition of Λ. Moreover, if$\left\{x_n\right\}$is of finite order there exist$K_1,K_2\in [0,\infty )$such that

$$\sqrt{\frac{1}{2\pi }{\int }_0^{2\pi }{\parallel {\widehat{P}}_{L_n}\left(\omega \right)-G\left(\omega \right)L_{\mathsf{\Lambda }}\parallel }_F^{2}d\omega }\le K_1\frac{\parallel A_n-E\left(x_{1:n}{x}_{1:n}^{*}\right){\parallel }_F}{\sqrt{n}}+\frac{K_2}{\sqrt{n}}\forall n\in \mathbb{N}.$$

Proof. 

From Equation (14) we have $\left\{A_n\right\}\sim \left\{E\left(x_{1:n}{x}_{1:n}^{*}\right)\right\}=\left\{T_n\left(G{L}_{\mathsf{\Lambda }}\right){\left(T_n\left(G{L}_{\mathsf{\Lambda }}\right)\right)}^{*}\right\}$. As $\{\parallel A_n^{-1}{\parallel }_2\}$ and $\{\parallel {\left(E\left(x_{1:n}{x}_{1:n}^{*}\right)\right)}^{-1}{\parallel }_2\}$ are bounded, the sequences

$$\{\parallel L_n^{-1}{\parallel }_2\}=\left\{\sqrt{{\lambda }_1\left({\left(L_n^{-1}\right)}^{*}{L}_n^{-1}\right)}\right\}=\left\{\sqrt{{∥{\left(L_n^{-1}\right)}^{*}{L}_n^{-1}∥}_2}\right\}=\left\{\sqrt{{∥{\left(L_n{L}_n^{*}\right)}^{-1}∥}_2}\right\}=\left\{\sqrt{{∥A_n^{-1}∥}_2}\right\}$$

and

$$\{\parallel {\left(T_n\left(G{L}_{\mathsf{\Lambda }}\right)\right)}^{-1}{\parallel }_2\}=\left\{\sqrt{{∥{\left(T_n\left(G{L}_{\mathsf{\Lambda }}\right){\left(T_n\left(G{L}_{\mathsf{\Lambda }}\right)\right)}^{*}\right)}^{-1}∥}_2}\right\}=\left\{\sqrt{{∥{\left(E\left(x_{1:n}{x}_{1:n}^{*}\right)\right)}^{-1}∥}_2}\right\}$$

are also bounded. Consequently, from Theorem 2 we have that $\left\{L_n\right\}\sim \left\{T_n\left(G{L}_{\mathsf{\Lambda }}\right)\right\}$ and that there exists $K_1\in [0,\infty )$ such that

$$\frac{\parallel L_n-T_n\left(G{L}_{\mathsf{\Lambda }}\right){\parallel }_F}{\sqrt{n}}\le K_1\frac{{∥A_n-T_n\left(G{L}_{\mathsf{\Lambda }}\right){\left(T_n\left(G{L}_{\mathsf{\Lambda }}\right)\right)}^{*}∥}_F}{\sqrt{n}}=K_1\frac{{∥A_n-E\left(x_{1:n}{x}_{1:n}^{*}\right)∥}_F}{\sqrt{n}}\forall n\in \mathbb{N}.$$

Therefore, applying Theorem 1 we conclude that Equation (16) holds.

Applying the Schwarz inequality (see, e.g., ([14], p. 139)) yields

$$\begin{array}{cc}\hfill {∥\frac{1}{2\pi }{\int }_0^{2\pi }{\mathrm{e}}^{-k\omega \mathrm{i}}{\widehat{P}}_{L_n}\left(\omega \right)d\omega -{\mathsf{G}}_k{L}_{\mathsf{\Lambda }}∥}_F& ={∥\frac{1}{2\pi }{\int }_0^{2\pi }{\mathrm{e}}^{-k\omega \mathrm{i}}{\widehat{P}}_{L_n}\left(\omega \right)d\omega -\frac{1}{2\pi }{\int }_0^{2\pi }{\mathrm{e}}^{-k\omega \mathrm{i}}G\left(\omega \right)d\omega L_{\mathsf{\Lambda }}∥}_F\hfill \\ & =\frac{1}{2\pi }{∥{\int }_0^{2\pi }{\mathrm{e}}^{-k\omega \mathrm{i}}\left({\widehat{P}}_{L_n}\left(\omega \right)-G\left(\omega \right)L_{\mathsf{\Lambda }}\right)d\omega ∥}_F\hfill \\ & =\frac{1}{2\pi }\sqrt{{\sum }_{r,s=1}^N{\left|{\left[{\int }_0^{2\pi }{\mathrm{e}}^{-k\omega \mathrm{i}}\left({\widehat{P}}_{L_n}\left(\omega \right)-G\left(\omega \right)L_{\mathsf{\Lambda }}\right)d\omega \right]}_{r,s}\right|}^2}\hfill \\ & =\frac{1}{2\pi }\sqrt{{\displaystyle \sum _{r,s=1}^N}{\left|{\int }_0^{2\pi }{\mathrm{e}}^{-k\omega \mathrm{i}}{\left[{\widehat{P}}_{L_n}\left(\omega \right)-G\left(\omega \right)L_{\mathsf{\Lambda }}\right]}_{r,s}d\omega \right|}^2}\hfill \\ & \le \frac{1}{2\pi }\sqrt{{\displaystyle \sum _{r,s=1}^N}2\pi {\int }_0^{2\pi }{\left|{\mathrm{e}}^{-k\omega \mathrm{i}}{\left[{\widehat{P}}_{L_n}\left(\omega \right)-G\left(\omega \right)L_{\mathsf{\Lambda }}\right]}_{r,s}\right|}^{2}d\omega }\hfill \\ & =\sqrt{\frac{1}{2\pi }{\int }_0^{2\pi }{\displaystyle \sum _{r,s=1}^N}{\left|{\mathrm{e}}^{-k\omega \mathrm{i}}\right|}^2{\left|{\left[{\widehat{P}}_{L_n}\left(\omega \right)-G\left(\omega \right)L_{\mathsf{\Lambda }}\right]}_{r,s}\right|}^{2}d\omega }\hfill \\ & =\sqrt{\frac{1}{2\pi }{\int }_0^{2\pi }{\displaystyle \sum _{r,s=1}^N}{\left|{\left[{\widehat{P}}_{L_n}\left(\omega \right)-G\left(\omega \right)L_{\mathsf{\Lambda }}\right]}_{r,s}\right|}^{2}d\omega }\hfill \\ & =\sqrt{\frac{1}{2\pi }{\int }_0^{2\pi }{∥{\widehat{P}}_{L_n}\left(\omega \right)-G\left(\omega \right)L_{\mathsf{\Lambda }}∥}_F^{2}d\omega }\hfill \end{array}$$

for all $n\in \mathbb{N}$ and $k\in \mathbb{Z}$.

Moreover, if $\left\{x_n\right\}$ is of finite order from Theorem 1 there exists $K_2\in [0,\infty )$ such that

$$\begin{array}{c}\sqrt{\frac{1}{2\pi }{\int }_0^{2\pi }{\parallel {\widehat{P}}_{L_n}\left(\omega \right)-G\left(\omega \right)L_{\mathsf{\Lambda }}\parallel }_F^{2}d\omega }\hfill \\ \le \frac{\parallel L_n-T_n\left(G{L}_{\mathsf{\Lambda }}\right){\parallel }_F}{\sqrt{n}}+\frac{K_2}{\sqrt{n}}\le K_1\frac{{∥A_n-E\left(x_{1:n}{x}_{1:n}^{*}\right)∥}_F}{\sqrt{n}}+\frac{K_2}{\sqrt{n}}\forall n\in \mathbb{N}.\hfill \end{array}$$

 □

If we know $A_n$ for certain $n\in \mathbb{N}$, Theorem 4 provides an estimation of the block entry ${\mathsf{G}}_k{L}_{\mathsf{\Lambda }}$ of the matrix $T_n\left(G{L}_{\mathsf{\Lambda }}\right)$ in Equation (15) given by

$$\begin{array}{c}\frac{1}{2\pi }{\int }_0^{2\pi }{\mathrm{e}}^{-k\omega \mathrm{i}}{\widehat{P}}_{L_n}\left(\omega \right)d\omega \hfill \\ =\left\{\begin{array}{cc}\frac{1}{n}{\sum }_{h=1}^n{\left[{(V_n\otimes I_N)}^{*}{L}_n(V_n\otimes I_N)\right]}_{h,h}\hfill & \mathrm{if}k=0,\hfill \\ \frac{\mathrm{i}}{2\pi k}{\sum }_{h=1}^n\left({\mathrm{e}}^{-k\frac{2\pi h}{n}\mathrm{i}}-{\mathrm{e}}^{-k\frac{2\pi (h-1)}{n}\mathrm{i}}\right){\left[{(V_n\otimes I_N)}^{*}{L}_n(V_n\otimes I_N)\right]}_{h,h}\hfill & \mathrm{if}k\in \{1,\dots ,n-1\}.\hfill \end{array}\right.\hfill \end{array}$$

Therefore, if we know $A_n$ for certain $n\in \mathbb{N}$, Theorem 4 allows us to estimate $\mathsf{\Lambda }$ and the parameters ${\mathsf{G}}_1,\dots ,{\mathsf{G}}_{n-1}$ of the VMA process as follows

$$\widehat{\mathsf{\Lambda }}\left(n\right)=\left(\frac{1}{2\pi }{\int }_0^{2\pi }{\widehat{P}}_{L_n}\left(\omega \right)d\omega \right){\left(\frac{1}{2\pi }{\int }_0^{2\pi }{\widehat{P}}_{L_n}\left(\omega \right)d\omega \right)}^{*}$$

and

$${\widehat{\mathsf{G}}}_k\left(n\right)=\left(\frac{1}{2\pi }{\int }_0^{2\pi }{\mathrm{e}}^{-k\omega \mathrm{i}}{\widehat{P}}_{L_n}\left(\omega \right)d\omega \right){\left(\frac{1}{2\pi }{\int }_0^{2\pi }{\widehat{P}}_{L_n}\left(\omega \right)d\omega \right)}^{-1}\forall k\in \{1,\dots ,n-1\}.$$

Example 2.

We consider the zero-mean 2-dimensional VMA$\left(1\right)$process$\left\{x_n\right\}$in ([15], Example 2.1), where

$$\mathsf{\Lambda }=\left(\begin{array}{cc}4& 1\\ 1& 2\end{array}\right)$$

and

$$G_1=\left(\begin{array}{cc}-0.8& -0.7\\ 0.4& -0.6\end{array}\right).$$

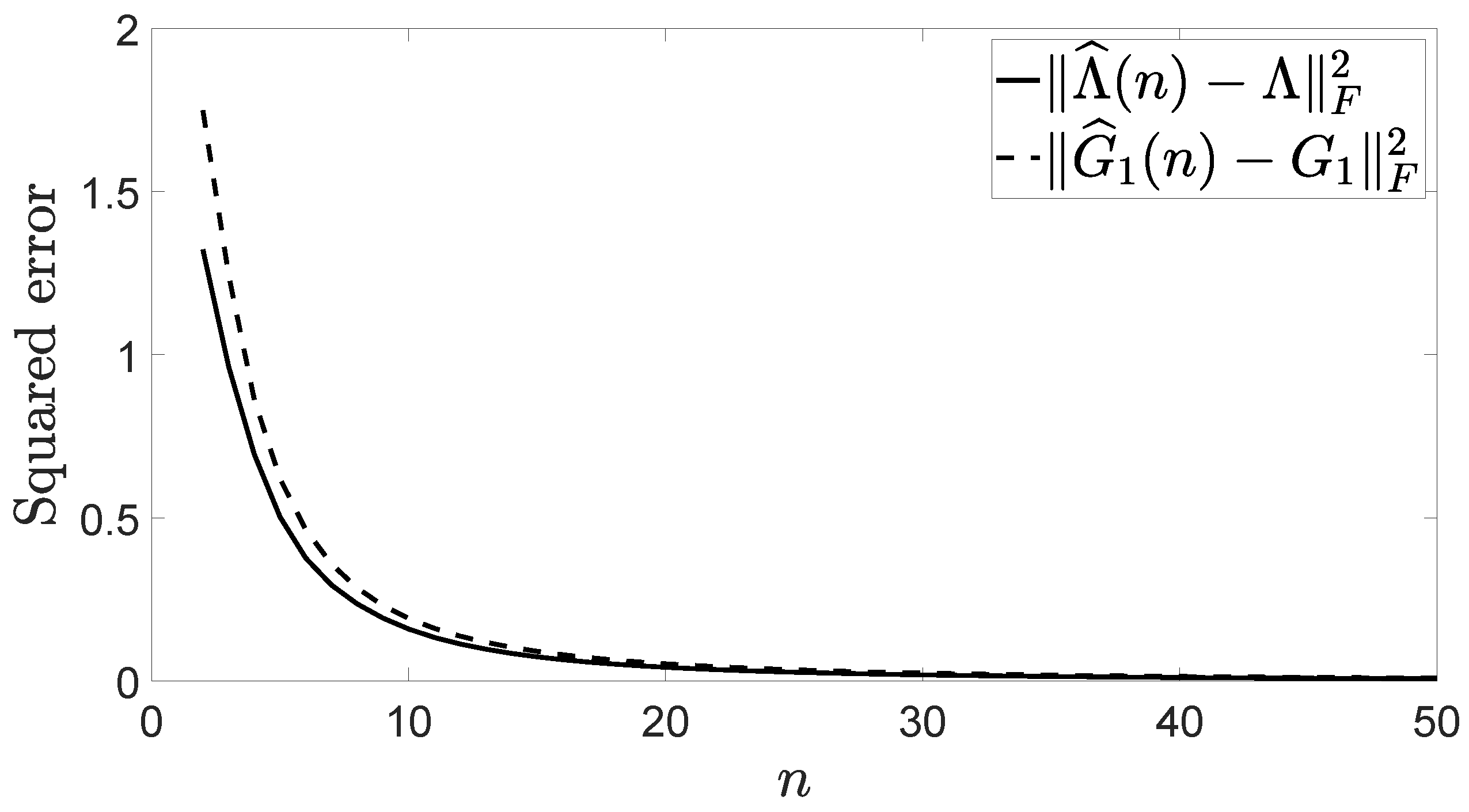
Figure 2 shows the squared error made when Λ and $G_1$ are estimated from the perturbed VMA$\left(1\right)$ process whose sequence of correlation matrices is

$$\left\{A_n\right\}=\left\{E\left(x_{1:n}{x}_{1:n}^{*}\right)+\left(\begin{array}{cc}{I}_2& 0_{2\times 2n-2}\\ 0_{2n-2\times 2}& 0_{2n-2\times 2n-2}\end{array}\right)\right\}.$$

Observe that this perturbed process has been generated by corrupting the VMA$\left(1\right)$ process in ([15], Example 2.1) by an impulse at $n=1$.

Figure 2. Squared error made when $\mathsf{\Lambda }$ and $G_1$ are estimated by $\widehat{\mathsf{\Lambda }}\left(n\right)$ and ${\widehat{G}}_1\left(n\right)$, respectively.

In [2], the periodogram method for perturbed block Toeplitz matrices was applied in spectral estimation. In Theorems 3 and 4, it has been also applied in parameter estimation for perturbed VAR processes and in parameter estimation for perturbed VMA processes, respectively. We finish the paper by showing that the periodogram method for perturbed block Toeplitz matrices can be applied in a fourth statistical signal processing problem, namely, in MIMO channel identification with perturbed additive WSS noise.

In [16], an asymptotic result on block Toeplitz matrices was applied in single-input multiple-output (SIMO) channel identification. We finish the paper by showing that Theorem 4 can be applied in MIMO channel identification when the number of channel inputs and the number of channel outputs are equal.

We consider a MIMO channel with a discrete-time causal infinite impulse response (IIR) filter and additive noise. Thus, the channel output process $\left\{y_n\right\}$ is of the form

$$y_n=x_n+{ϵ}_n={\displaystyle \sum _{k=0}^{n-1}}{\mathsf{G}}_k{w}_{n-k}+{ϵ}_n\forall n\in \mathbb{N}.$$

We assume that the filter tap ${\mathsf{G}}_k\in {\mathbb{C}}^{N\times N}$ for all $k\in \mathbb{N}$ and ${\mathsf{G}}_0=I_N$. We also assume that ${\left\{{\mathsf{G}}_k\right\}}_{k\in \mathbb{Z}}$, with ${\mathsf{G}}_{-k}=0_{N\times N}$ for all $k\in \mathbb{N}$, is the sequence of Fourier coefficients of a continuous $2\pi$-periodic function $G:\mathbb{R}\to {\mathbb{C}}^{N\times N}$. We consider that the input process $\left\{w_n\right\}$ is a zero-mean WSS N-dimensional vector process with $\left\{E\left(w_{1:n}{w}_{1:n}^{*}\right)\right\}=\left\{T_n\left(\mathsf{\Lambda }\right)\right\}$, where $\mathsf{\Lambda }$ is an $N\times N$ positive definite matrix. We assume that the noise process $\left\{{ϵ}_n\right\}$ is a zero-mean random N-dimensional vector process satisfying that there exists a continuous $2\pi$-periodic function $\mathsf{{\rm Y}}:\mathbb{R}\to {\mathbb{C}}^{N\times N}$ such that $\left\{E\left({ϵ}_{1:n}{ϵ}_{1:n}^{*}\right)\right\}\sim \left\{T_n\left(\mathsf{{\rm Y}}\right)\right\}$. We also assume that the noise process is uncorrelated with the input process.

Suppose that $\left\{E\left(x_{1:n}{x}_{1:n}^{*}\right)\right\}$ is stable and $\left\{A_n\right\}=\{E\left(y_{1:n}{y}_{1:n}^{*}\right)-T_n\left(\mathsf{{\rm Y}}\right)\}$ is a stable sequence of positive definite matrices. To show that Theorem 4 can be here applied, we only need to prove that $\left\{A_n\right\}\sim \left\{E\left(x_{1:n}{x}_{1:n}^{*}\right)\right\}$.

From Equation (13) we obtain

$${∥E\left(x_{1:n}{x}_{1:n}^{*}\right)∥}_2=\parallel T_n\left(G\right)T_n\left(\mathsf{\Lambda }\right){\left(T_n\left(G\right)\right)}^{*}{\parallel }_2\le \parallel T_n{\left(G\right)\parallel }_2\parallel T_n{\left(\mathsf{\Lambda }\right)\parallel }_2\parallel {\left(T_n\left(G\right)\right)}^{*}{\parallel }_2={\parallel \mathsf{\Lambda }\parallel }_2{\parallel T_n\left(G\right)\parallel }_2^2$$

for all $n\in \mathbb{N}$. Hence, as $\{\parallel T_n\left(G\right){\parallel }_2\}$ is bounded (see, e.g., ([5], Theorem 4.3) or ([9], Corollary 4.2)), $\{\parallel E\left(x_{1:n}{x}_{1:n}^{*}\right){\parallel }_2\}$ is also bounded and $\left\{E\left(x_{1:n}{x}_{1:n}^{*}\right)\right\}\sim \left\{E\left(x_{1:n}{x}_{1:n}^{*}\right)\right\}$. Since $\{\parallel -T_n{\left(\mathsf{{\rm Y}}\right)\parallel }_2\}=\{\parallel T_n\left(\mathsf{{\rm Y}}\right){\parallel }_2\}$ is bounded, $\{-T_n\left(\mathsf{{\rm Y}}\right)\}\sim \{-T_n\left(\mathsf{{\rm Y}}\right)\}$, and consequently, applying ([5], Lemma 3.1) yields $\{E\left({ϵ}_{1:n}{ϵ}_{1:n}^{*}\right)-T_n\left(\mathsf{{\rm Y}}\right)\}\sim \left\{0_{nN\times nN}\right\}$. Therefore, from ([5], Lemma 3.1) we conclude that

$$\begin{array}{cc}\hfill \left\{A_n\right\}& =\{E\left(\left(x_{1:n}+{ϵ}_{1:n}\right){\left(x_{1:n}+{ϵ}_{1:n}\right)}^{*}\right)-T_n\left(\mathsf{{\rm Y}}\right)\}\hfill \\ & =\{E\left(x_{1:n}{x}_{1:n}^{*}\right)+E\left(x_{1:n}{ϵ}_{1:n}^{*}\right)+E\left({ϵ}_{1:n}{x}_{1:n}^{*}\right)+E\left({ϵ}_{1:n}{ϵ}_{1:n}^{*}\right)-T_n\left(\mathsf{{\rm Y}}\right)\}\hfill \\ & =\{E\left(x_{1:n}{x}_{1:n}^{*}\right)+E\left(x_{1:n}\right)E{\left({ϵ}_{1:n}\right)}^{*}+E\left({ϵ}_{1:n}\right)E{\left(x_{1:n}\right)}^{*}+E\left({ϵ}_{1:n}{ϵ}_{1:n}^{*}\right)-T_n\left(\mathsf{{\rm Y}}\right)\}\hfill \\ & =\{E\left(x_{1:n}{x}_{1:n}^{*}\right)+E\left({ϵ}_{1:n}{ϵ}_{1:n}^{*}\right)-T_n\left(\mathsf{{\rm Y}}\right)\}\sim \left\{E\left(x_{1:n}{x}_{1:n}^{*}\right)\right\}.\hfill \end{array}$$

Thus, Theorem 4 can be applied in the considered MIMO channel identification problem, that is, it can be used to identify $\mathsf{\Lambda }$ and the filter taps ${\left\{{\mathsf{G}}_k\right\}}_{k\in \mathbb{N}}$.

5. Conclusions

In ([2], Theorem 4) the (averaged) periodogram method for positive semidefinite Toeplitz matrices was generalized to perturbed block Toeplitz matrices. Moreover, ([2], Theorem 4) was there applied to perturbed positive semidefinite block Toeplitz matrices to solve a statistical signal processing problem: spectral estimation for perturbed WSS vector processes.

In the present paper, ([2], Theorem 4) (Theorem 1) has been applied to perturbed lower triangular block Toeplitz matrices to solve three statistical signal processing problems: parameter estimation for perturbed VAR processes, parameter estimation for perturbed VMA processes, and MIMO channel identification with perturbed additive WSS noise. To solve those problems we have first generalized a result given in [3] on the Cholesky decomposition of Toeplitz matrices to perturbed block Toeplitz matrices.