Derived Hyperstructures from Hyperconics

Abstract

In this paper, we introduce generalized quadratic forms and hyperconics over quotient hyperfields as a generalization of the notion of conics on fields. Conic curves utilized in cryptosystems; in fact the public key cryptosystem is based on the digital signature schemes (DLP) in conic curve groups. We associate some hyperoperations to hyperconics and investigate their properties. At the end, a collection of canonical hypergroups connected to hyperconics is proposed.

1. Introduction

In 1934, Marty initiated the notion of hypergroups as a generalization of groups and referred to its utility in solving some problems of groups, algebraic functions and rational fractions [1]. To review this theory one can study the books of Corsini [2], Davvaz and Leoreanu-Fotea [3], Corsini and Leoreanu [4], Vougiouklis [5] and in papers of Hoskova and Chvalina [6] and Hoskova-Mayerova and Antampoufis [7]. In recent years, the connection of hyperstructures theory with various fields has been entered into a new phase. For this we advise the researchers to see the following papers. (i) For connecting it to number theory, incidence geometry, and geometry in characteristic one [8,9,10]. (ii) For connecting it to tropical geometry, quadratic forms [11,12] and real algebraic geometry [13,14]. (iii) For relating it to some other objects see [15,16,17,18,19]. M. Krasner introduced the concept of the hyperfield and hyperring in Algebra [20,21]. The theory which was developed for the hyperrings is generalizing and extending the ring theory [22,23,24,25]. There are different types of hyperrings [22,25,26]. In the most general case a triplet $(R,+,·)$ is a hyperring if $(R,+)$ is a hypergroup, $(R,·)$ is a semihypergroup and the multiplication is bilaterally distributive with regards to the addition [3]. If $(R,·)$ is a semigroup instead of semihypergroup, then the hyperring is called additive. A special type of additive hyperring is the Krasner’s hyperring and hyperfield [20,21,24,27,28]. The construction of different classes of hyperrings can be found in [29,30,31,32,33]. There are different kinds of curves that basically are used in cryptography [34,35]. An elliptical curve is a curve of the form $y^2=p(x)$, where $p(x)$ is a cubic polynomial with no-repeat roots over the field F. This kind of curves are considered and extended over Krasner’s hyperfields in [13]. Now let $g(x,y)=a{x}^2+bxy+c{y}^2+dx+ey+f\in F[x,y]$ and $g(x,y)=0$ be the quadratic equation of two variables in field of F, if $a=c=0$ and $b\ne 0$ then the equation $g(x,y)=0$ is called homographic transformation. In [14] Vahedi et. al extended this particular quadratic equation on Krasner’s quotient hyperfield $\frac{F}{G}.$ The motivation of this paper goes in the same direction of [14]. If in the general form of the equation of quadratic form one suppose that $ae\ne 0$ and $b=0$ then initiate an important quadratic equation which is called a conic. Notice that the conditions which are considered for the coefficients of the equations of a conic curve and a homographic curve are completely different. Until now the study of conic curves has been on fields. At the recent works the authors have investigated some main classes of curves; elliptic curves and homographics over Krasner’s hyperfields (see [13,14]). In the present work, we study the conic curves over some quotients of Krasner’s hyperfields.

2. Preliminaries

In the following, we recall some basic notions of Pell conics and hyperstructures theory that these topics can be found in the books [2,36,37]. Moreover, we fix here the notations that are used in this paper.

2.1. Conics

According to [36] a conic is a plane affine curve of degree 2. Irreducible conics C come in three types: we say that C is a hyperbola, a parabola, or an ellipse according as the number of points at infinity on (the projective closure of) C equals $2,1$, or 0. Over an algebraically closed field, every irreducible conic is a hyperbola. Let d be a square free integer nonequal to 1 and put

$$\Delta =\left\{\begin{array}{cc}d\hfill & \mathrm{if}d\equiv 1(mod4),\hfill \\ 4d\hfill & \mathrm{if}d\equiv 2,3(mod4).\hfill \end{array}\right.$$

The conic $C:Q_0(x,y)=1$ associated to the principal quadratic form of discriminant $\Delta$,

$$Q_0(x,y)=\left\{\begin{array}{cc}{x}^2+xy+\frac{1-d}{4}{y}^2\hfill & \mathrm{if}d\equiv 1(mod4),\hfill \\ x^2-d{y}^2\hfill & \mathrm{if}d\equiv 2,3(mod4),\hfill \end{array}\right.$$

is called the Pell conic of discriminant. Pell conics are irreducible nonsingular affine curves with a distinguished integral point N = (1, 0). The problem corresponding to the determination of E(Q) is finding the integral points on a Pell conic. The idea that certain sets of points on curves can be given a group structure is relatively modern. For elliptic curves, the group structure became well known only in the 1920s; implicitly it can be found in the work of Clebsch, and Juel, in a rarely cited article, wrote down the group law for elliptic curves defined over $\mathbb{R}$ and $\mathbb{C}$ at the end of the 19th century. The group law on Pell conics defined over a field F. For two rational points $p,q\in Q(F)$, draw the line through $\mathcal{O}$ parallel to line $p,q$, and denote its second point of intersection with $p\ast q$ which is the sum of two $p,q,$ where $\mathcal{O}$ is an arbitrary point in pell conic perchance in infinity, is identity element of group. In the Figure 1 the operation is picturised on the conic section $Q_{\mathbb{R}}(f_{1,1})$.

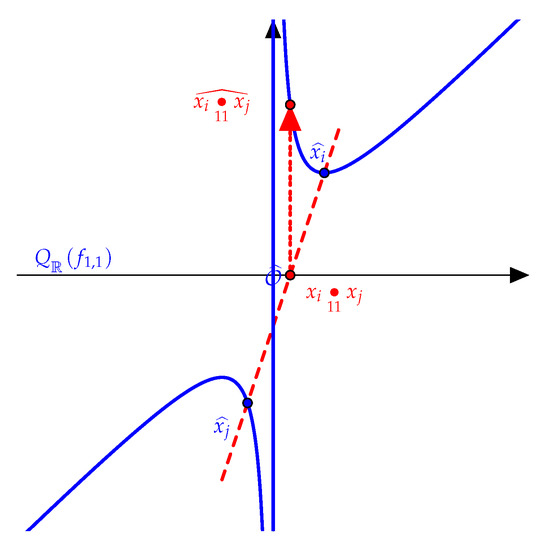
Figure 1. Conic section $Q_{\mathbb{R}}(f_{1,1})$.

Example 1.

Consider $f_{1,1}(x)=x^{-1}+x$ over finite field $F={\mathbb{Z}}_7$. Then we have a Caley table of points (Table 1):

Table 1. Conic group $\left(Q_{{\mathbb{Z}}_7}(f_{1,1}),{•}_{a,b}\right)$.

•11	(0, ∞)	(1, 2)	(2, −1)	(3, 1)	(−3, −1)	(−2, 1)	(−1, −2)	(∞, ∞)
$(0,\infty )$	$(0,\infty )$	$(1,2)$	$(2,-1)$	$(3,1)$	$(-3,-1)$	$(-2,1)$	$(-1,-2)$	$(\infty ,\infty )$
$(1,2)$	$(1,2)$	$(-1,-2)$	$(-3,-1)$	$(-2,1)$	$(3,1)$	$(2,-1)$	$(0,\infty )$	$(\infty ,\infty )$
$(2,-1)$	$(2,-1)$	$(-3,-1)$	$(1,2)$	$(-1,-2)$	$(\infty ,\infty )$	$(0,\infty )$	$(-2,1)$	$(3,1)$
$(3,1)$	$(3,1)$	$(-2,1)$	$(-1,-2)$	$(1,2)$	$(0,\infty )$	$(\infty ,\infty )$	$(-3,-1)$	$(2,-1)$
$(-3,-1)$	$(-3,-1)$	$(3,1)$	$(\infty ,\infty )$	$(0,\infty )$	$(-1,-2)$	$(1,2)$	$(2,-1)$	$(-2,1)$
$(-2,1)$	$(-2,1)$	$(2,-1)$	$(0,\infty )$	$(\infty ,\infty )$	$(1,2)$	$(-1,-2)$	$(3,1)$	$(-3,-1)$
$(-1,-2)$	$(-1,-2)$	$(0,\infty )$	$(-2,1)$	$(-3,-1)$	$(2,-1)$	$(3,+1)$	$(\infty ,\infty )$	$(1,2)$
$(\infty ,\infty )$	$(\infty ,\infty )$	$(-1,-2)$	$(3,1)$	$(2,-1)$	$(-2,+1)$	$(-3,-1)$	$(1,2)$	$(0,\infty )$

The associativity of the group law is induced from a special case of Pascal’s Theorem. In the following, we recall Pascal’s Theorem which is a very special case of Bezout’s Theorem.

Theorem 1

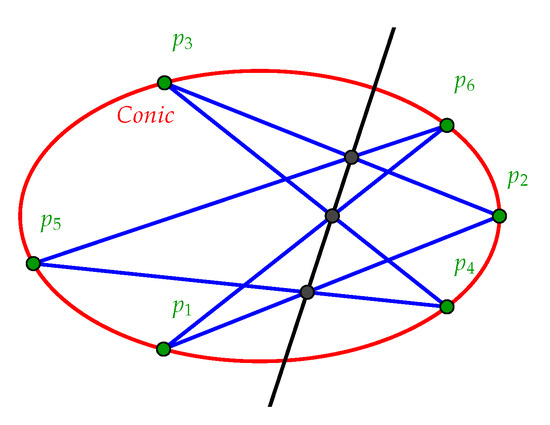
([38] Pascal’s Theorem). For any conic and any six points $p_1,p_2,\dots ,p_6$ on it, the opposite sides of the resulting hexagram, extended if necessary, intersect at points lying on some straight line. More specifically, let $L(p,q)$ denote the line through the points p and q. Then the points $L(p_1,p_2)\cap L(p_4,p_5),L(p_2,p_3)\cap L(p_5,p_6)$, and $L(p_3,p_4)\cap L(p_6,p_1)$ lie on a straight line, called the Pascal line of the hexagon Figure 2.

Figure 2. Pascal line of the hexagon.

2.2. Krasner’s Hyperrings and Hyperfields

Let H be a non-empty set and ${\mathcal{P}}^{\ast }(H)$ denotes the set of all non-empty subsets of H. Any function · from the cartesian product $H\times H$ into ${\mathcal{P}}^{\ast }(H)$ is called a hyperoperation on H. The image of the pair $(a,b)\in H\times H$ under the hyperoperation · in ${\mathcal{P}}^{\ast }(H)$ is denoted by $a·b$. The hyperoperation can be extended in a natural way to subsets of H as follows: for non-empty subsets $A,B$ of H, define $A·B={\displaystyle \bigcup _{a\in A,b\in B}}a·b$. The notation $a·A$ is applied for $\left\{a\right\}·A$ and also $A·a$ for $A·\left\{a\right\}$. Generally, we mean $H^k=H\times H\dots \times H$ (k times), for all $k\in \mathbb{N}$ and also the singleton $\left\{a\right\}$ is identified with its element a. The hyperstructure $(H,·)$ is called a semihypergroup if $x·(y·z)=(x·y)·z$ for all $x,y,z\in H$, which means that

$${\displaystyle \bigcup _{u\in x·y}}u·z={\displaystyle \bigcup _{v\in y·z}}x·v.$$

A semihypergroup $(H,·)$ is called a hypergroup if the reproduction law holds: $x·H=H·x=H$, for all $x\in H$.

Definition 1

([2]).Let $(H,·)$ be a hypergroup and K be a non-empty subset of H. We say that $(K,·)$ is a subhypergroup of H and it denotes $K⩽H,$ if for all $x\in K$ we have $K·x=K=x·K$.

Let $(H,·)$ be a hypergroup, an element $e_r$ (resp. $e_l$) of H is called a right identity (resp. left identity $e_l$) if for all $a\in H$, $x\in a·e_r$ (resp. $a\in e_l·a$). An element e is called an identity if, for all $a\in H$, $a\in a·e\cap e·a.$ A right identity $e_r$ (resp. left identity $e_l$) of H is called a scalar right identity (resp. scalar left identity) if for all $a\in H$, $a=a·e_r$ ($a=e_l·x$). An element e is called a scalar identity if for all $a\in H$, $a=a·e=e·x.$ An element $a^{\prime }\in H$ is called a right inverse (resp. left inverse) of a in H if $e_r\in a·a^{\prime }$, for some right identities $e_r$ in H ($e_l\in a^{\prime }·a$). An element $a^{\prime }\in H$ is called an inverse of $a\in H$ if $e\in a^{\prime }·a\cap a·a^{\prime },$ for some identities in $H.$ We denote the set of all right inverses, left inverses and inverses of $a\in H$ by $i_r(a),$$i_l(a),$ and $i(a),$ respectively.

Definition 2

([2]).A hypergroup $(H,·)$ is called reversible, if the following conditions hold:

(i) 

At least H has one identity e;

(ii) 

every element x of H has one inverse, that is $i(x)\ne \varnothing$;

(iii) 

$x\in y·z$ implies that $y\in x·z^{\prime }$ and $z\in y^{\prime }·x$, where $z^{\prime }\in i(z)$ and $y^{\prime }\in i(y)$.

Definition 3

([2,23]).A hypergroup $(H,+)$ is called canonical, if the following conditions hold:

(i) 

for every $x,y,z\in H,x+(y+z)=(x+y)+z,$

(ii) 

for every $x,y\in H,x+y=y+x,$

(iii) 

there exists $0\in H$ such that $0+x=\left\{x\right\}$ for every $x\in H$,

(iv) 

for every $x\in H$ there exists a unique element $x^{\prime }\in H$ such that $0\in x+x^{\prime }$; (we shall write $-x$ for $x^{\prime }$ and we call it the opposite of x.)

(v) 

$z\in x+y$ implies $y\in z-x$ and $x\in z-y$;

Definition 4

([2]).Suppose that $(H,·)$ and $(K,\circ )$ are two hypergroups. A function $f:H\to K$ is called a homomorphism if $f(x·y)\subseteq f(x)\circ f(y),$ for all x and y in H. We say that f is a good homomorphism if for all x and y in H, $f(x·y)=f(x)\circ f(y)$.

The more general hyperstructure that satisfies the ring-like conditions is the hyperring. The notion of the hyperring and hyperfield was introduced in Algebra by M. Krasner in 1956 [21]. According to the current terminology, these initial hypercompositional structures are additive hyperrings and hyperfields whose additive part is a canonical hypergroup. Nowadays such hypercompositional structures are called Krasner’s hyperrings and hyperfields.

Definition 5

([20]).A Krasner’s hyperring is an algebraic structure $(R,+,·)$ which satisfies the following axioms:

(1) 

$(R,+)$ is a canonical hypergroup,

(2) 

$(R,·)$ is a semigroup having zero as a bilaterally absorbing element, i.e., $x·0=0·x=0$.

(3) 

The multiplication is distributive with respect to the hyperoperation +.

A Krasner’s hyperring is called commutative if the multiplicative semigroup is a commutative monoid. A Krasner’s hyperring is called a Krasner’s hyperfield, if $(R-\{0\},·)$ is a commutative group. In [20] Krasner presented a class of hyperrings which is constructed from rings. He proved that if R is a ring and G is a normal subgroup of $R^{\prime }$s multiplicative semigroup, then the multiplicative classes $\overline{x}=xG,x\in R$, form a partition of R. He also proved that the product of two such classes, as subsets of R, is a class $mod$G as well, while their sum is a union of such classes. Next, he proved that the set $\overline{R}=\frac{R}{G}$ of these classes becomes a hyperring, when:

(i)

$xG\oplus yG=\left\{zG\right|z\in xG+yG\},$ and

(ii)

$xG\odot yG=xyG,$

Moreover, he observed that if R is a field, then $\frac{R}{G}$ is a hyperfield. Krasner named these hypercompositional structures quotient hyperring and quotient hyperfield, respectively. At the same time, he raised the question if there exist non-quotient hyperrings and hyperfields [20]. Massouros in [27] generalized Krasner’s construction using not normal multiplicative subgroups, and proved the existence of non-quotient hyperrings and hyperfields. Since the paper deals only with Krasner’s hyperfields we will write simply quotient hyperfields instead of Krasner’s quotient hyperfields.

3. Hyperconic

The notion of hyperconics on a quotient hyperfield will be studied in this section. By the use of hyperconic $Q_{\overline{F}}(f_{{}_{\overline{A},\overline{B}}}),$ we present some hyperoperations as a generalization group operations on fields. We investigate some attributes of the associated hypergroups from the hyperconics and the associated $H_v$-groups on the hyperconics.

Let $g(x,y)=a{x}^2+bxy+c{y}^2+dx+ey+f\in F[x,y]$ and $g(x,y)=0$ be the quadratic equation of two variables in field of F. If $c=0$ and equation $g(x,y)=0$ still stay in quadratic and two variables or the other word $c=0$ and $(a,b)\ne 0\ne (e,b)$, then it can be calculated as an explicit function y in terms of x, also with a change of variables, can be expressed in the form of $Y=A{X}^2+BX$ or $A{X}^{-1}+BX,$ where $A,B\in F.$

For this purpose if $a,e\ne 0=b$ set $x=X$ and $y=Y-f{e}^{-1}$ then $Y=A{X}^2+BX,$ where $A=-a{e}^{-1},B=-d{e}^{-1}.$ If $b\ne 0=a$ set $x=X-e{b}^{-1}$ and $y=Y-d{b}^{-1}$ then $Y=A{X}^{-1},$ where $A=ed{b}^{-2}-f{b}^{-1}.$ If $b\ne 0\ne a$ set $x=X-e{b}^{-1}$ and $y=Y+2ae{b}^{-2}{\alpha }_{{}_F}-d{b}^{-1}$ that

$${\alpha }_{{}_F}=\left\{\begin{array}{cc}0,\hfill & \mathrm{if}char(F)=2\hfill \\ 1,\hfill & \mathrm{if}char(F)\ne 2,\hfill \end{array}\right.$$

then $Y=A{X}^{-1}+BX,$ where $A=-a{e}^2{b}^{-3}+ed{b}^{-2}-f{b}^{-1}$ and $B=-a{b}^{-1}$. Reduced quadratic equation of two variables $a{x}^2+bxy+dx+ey+f=0$ in field of F can be generalized in quotient hyperfield $\overline{F}$.

Definition 6.

Let $\overline{F}$ be the quotient hyperfield and $(\overline{A},\overline{B})\in {\overline{F}}^2$ and $f_{\overline{A},\overline{B}}(\overline{x})$ be equal to $\overline{A}{\overline{x}}^{-1}\oplus \overline{B}\overline{x}$ or $\overline{A}{\overline{x}}^2\oplus \overline{B}\overline{x}$. Then the relation $\overline{y}\in f_{\overline{A},\overline{B}}(\overline{x})$, is called generalized reduced two variable quadratic equation in ${\overline{F}}^2.$ Moreover the set $Q(f_{\overline{A},\overline{B}},\overline{F})=\{(\overline{x},\overline{y})\in {\overline{F}}^2|\overline{y}\in f_{\overline{A},\overline{B}}(\overline{x})\}$ is called conic hypersection, and if $\overline{A}\ne 0$, $Q(f_{\overline{A},\overline{B}},\overline{F})$ is named non-degenerate conic hypersection. For all $a\in \overline{A}$ and $b\in \overline{B}$, $Q(f_{a,b},F)=\{(x,y)\in F^2|y=f_{a,b}(x)\}$ is conic section and for $a\ne 0$ is non-degenerate conic section, in which $f_{a,b}(z)=a{z}^2+bz$ or $a{z}^{-1}+bz$ corresponding to $f_{\overline{A},\overline{B}}$. It is also said to $Q(f_{\overline{A},\overline{B}},F)={\displaystyle \bigcup _{(\overline{x},\overline{y})\in Q(f_{\overline{A},\overline{B}},\overline{F})}}\overline{x}\times \overline{y},$ conic hypersection, as a subset of $F^2,$ and $Q(f_{a,b},\overline{F})=\overline{Q(f_{a,b},F)}=\left\{\overline{(x,y)}|(x,y)\in Q(f_{{}_{a,b}},F)\right\},$ where $\overline{(x,y)}=(\overline{x},\overline{y})$ for all $(x,y)\in Q(f_{\overline{A},\overline{B}},F).$

Theorem 2.

Using the above notions we have $Q(f_{\overline{A},\overline{B}},F)={\displaystyle \bigcup _{a\in \overline{A},b\in \overline{B}}}Q(f_{a,b},F).$

Proof. 

Let $(x,y)\in Q(f_{\overline{A},\overline{B}},F)$ and without losing of generality $f(x)=A{x}^2+Bx$. Then

$$\begin{array}{cc}(\overline{x},\overline{y})\in Q(f_{\overline{A},\overline{B}},\overline{F})\hfill & ⟺\overline{y}\in \overline{A}{\overline{x}}^2\oplus \overline{B}\overline{x}\hfill \\ & ⟺\overline{y}\in \overline{\overline{A}{x}^2+\overline{B}x}\hfill \\ & ⟺\overline{y}=\overline{a{x}^2+bx},forsome(a,b)\in \overline{A}\times \overline{B}\hfill \\ & ⟺y=ag{x}^2+bgxforsomeg\in G\hfill \\ & ⟺y=a^{\prime }{x}^2+b^{\prime }x,where{a}^{\prime }=ag,b^{\prime }=bg\hfill \\ & ⟺(x,y)\in Q(f_{a^{\prime },b^{\prime }},F),forsome(a^{\prime },b^{\prime })\in \overline{A}\times \overline{B}\hfill \\ & ⟺(x,y)\in \bigcup _{a\in \overline{A},b\in \overline{B}}Q(f_{a,b},F).\hfill \end{array}$$

Consequently, $Q(f_{\overline{A},\overline{B}},F)={\displaystyle \bigcup _{a\in \overline{A},b\in \overline{B}}}Q(f_{a,b},F).$ □

Example 2.

Let $F={\mathbb{Z}}_5$ be the field of order 5, $G=\{\pm 1\}⩽F^{\ast }$ and $f_{{}_{\overline{1},\overline{0}}}(\overline{x})={\overline{x}}^2$. Then we have $\overline{F}=\left\{\overline{0},\overline{1},\overline{2}\right\},$$Q(f_{{}_{\overline{1},\overline{0}}},\overline{F})=\overline{Q(f_{{}_{1,0}},F)}\cup \overline{Q(f_{{}_{(-1),0}},F)},$ where

$$Q(f_{{}_{1,0}},F)=\{(0,0),(1,1),(-1,1),(2,-1),(-2,-1)\},$$

$$Q(f_{{}_{(-1),0}},F)=\{(0,0),(1,-1),(-1,-1),(2,1),(-2,1)\},$$

and $Q(f_{{}_{1,0}},\overline{F})=\overline{Q(f_{{}_{1,0}},F)}=\{(\overline{0},\overline{0}),(\overline{1},\overline{1}),(\overline{2},\overline{1})\}=\overline{Q(f_{{}_{(-1),0}},F)}=Q(f_{{}_{(-1),0}},\overline{F}).$ In this case $Q(f_{{}_{\overline{1},\overline{0}}},\overline{F})$ is a non-degenerate conic hypersection because $\overline{A}=\overline{1}\ne \overline{0}$.

Definition 7.

Let F be a field, $x\in F$ and G be a subgroup in $F^{\ast }.$ We take

$$\mathcal{O}=\left\{\begin{array}{cc}{0}^{-1},& if{f}_{a,b}(z)=a{z}^2+bz\hfill \\ 0,& if{f}_{a,b}(z)=a{z}^{-1}+bz\hfill \end{array}\right.$$

$${\mathcal{G}}_x(f_{a,b})=\left\{\begin{array}{cc}\left\{x\right\},& ifG=\left\{1\right\}\hfill \\ \{z\in F|f_{a,b}(z)=f_{a,b}(x)\},& ifG\ne \left\{1\right\},f_{a,b}(z)=a{z}^2+bz\hfill \\ \{-x,x\},& ifG\ne \left\{1\right\},f_{a,b}(z)=a{z}^{-1}+bz.\hfill \end{array}\right.$$

Obviously, $0^{-1}$ is an element outside of F. We denote $0^{-1}=\frac{1}{0}$ by $\infty ,$ where $\infty \notin F$, and $\overline{\infty }=\infty$. Suppose that ${\mathcal{G}}_{\infty }(f_{a,b})=\{\infty \}$, $f_{a,b}(\infty )=\infty$, $f_{a,b}(\mathcal{O})=\infty$, for all $a\in \overline{A},b\in \overline{B}$, also $\widehat{X}=\left\{\widehat{x}\right|x\in X\}$ where $\widehat{x}=(x,f_{a,b}(x))$ and $X\subseteq F\cup \left\{\mathcal{O}\right\}$. Moreover, $\mathcal{O}·\mathcal{O}=\mathcal{O}=\mathcal{O}+\mathcal{O}$, $x·\mathcal{O}=\left\{\begin{array}{cc}\mathcal{O},\hfill & ifx\ne 0\hfill \\ 0,\hfill & ifx=0\hfill \end{array}\right.$ and $x+\mathcal{O}=\left\{\begin{array}{cc}\mathcal{O},\hfill & if\mathcal{O}=0^{-1}\hfill \\ x,\hfill & if\mathcal{O}=0\hfill \end{array}\right.$, for all x in field of $(F,+,·)$.

Remark 1.

It should be noted that associativity by adding $\mathcal{O}$ to field of $(F,+,·)$ for two operations of "+" and "·" remains preserved.

Definition 8.

Let $Q(f_{\overline{A},\overline{B}},\overline{F})$ be a non-degenerate conic hypersection, $F_{{}_{\infty }}=F\cup \{\infty \}$ and

$$Q_F(f_{a,b})=\{\widehat{x}:x\in F_{{}_{\infty }},\widehat{x}\notin L_0\},$$

$$Q_F(f_{\overline{A},\overline{B}})=\bigcup _{a\in \overline{A},b\in \overline{B}}{Q}_F(f_{a,b}),$$

where $L_0=\left\{(x,0)\right|x\in F_{{}_{\mathcal{O}}}\}.$ For all $\widehat{x_i},\widehat{x_i}\in Q_F(f_{a,b})$

$$\widehat{x_i{•}_{{}_{ab}}{x}_j}=(x_i{•}_{{}_{ab}}{x}_j,f_{a,b}(x_i{•}_{{}_{ab}}{x}_j))inwhich\left\{(x_i{•}_{{}_{ab}}{x}_j,0)\right\}=L_0\cap L_{a,b}(\widehat{x_i},\widehat{x_j}),$$

and

$$L_{a,b}({\widehat{x}}_i,{\widehat{x}}_j)=\left\{\begin{array}{cc}\{(x,y)\in F^2|y-f_{a,b}(x_i)=\frac{f_{a,b}(x_j)-f_{a,b}(x_i)}{(x_j-x_i)}(x-x_i)\},\hfill & x_i\ne x_j,\mathcal{O}\notin \{x_i,x_j\}\hfill \\ \{(x,y)\in F^2|y-f_{a,b}(x_i)=f_{a,b}^{\prime }(x_i)(x-x_i)\},\hfill & x_i=x_j\notin \left\{\mathcal{O}\right\}\hfill \\ \{(x,y)\in F^2|\mathcal{O}\ne x\in \{x_i,x_j\}\}\cup \left\{\widehat{\mathcal{O}}\right\},\hfill & x_i\ne x_j,\mathcal{O}\in \{x_i,x_j\}\hfill \\ \left\{(\mathcal{O},y)\right|y\in F_{{}_{\infty }}=F\cup \{\infty \}\},\hfill & (x_i,x_j)=(\mathcal{O},\mathcal{O}),\hfill \end{array}\right.$$

and $f_{a,b}^{{}^{\prime }}$ is meant by formal derivative $f_{a,b}$.

We denote $\overline{Q_F(f_{a,b})}$ by $Q_{\overline{F}}(f_{a,b})$ and $\overline{Q_F(f_{\overline{A},\overline{B}})}$ by $Q_{\overline{F}}(f_{\overline{A},\overline{B}})$ also take $\overline{\mathcal{O}}=\left\{\mathcal{O}\right\}=\mathcal{O},$$\overline{f(\mathcal{O})}=\left\{f(\mathcal{O})\right\}=f(\mathcal{O})$ and, $\overline{(\mathcal{O},f(\mathcal{O}))}=(\overline{\mathcal{O}},\overline{f(\mathcal{O})})=(\mathcal{O},f(\mathcal{O}))$. Moreover, $\mathcal{O}\odot \mathcal{O}=\mathcal{O}$ and $\mathcal{O}\oplus \mathcal{O}=\mathcal{O}$ also, for all $\overline{x}$ in hyperfield of $(\overline{F},\oplus ,\odot )$, $\overline{x}\odot \mathcal{O}=\left\{\begin{array}{cc}\mathcal{O},\hfill & ifx\ne 0\hfill \\ \overline{0},\hfill & ifx=0\hfill \end{array}\right.$$\overline{x}\oplus \mathcal{O}=\left\{\begin{array}{cc}\mathcal{O},\hfill & if\mathcal{O}=0^{-1}\hfill \\ \overline{x},\hfill & if\mathcal{O}=0\hfill \end{array}\right.$ and agree to $L_o\cap L(\widehat{x_i},\widehat{x_j})=\left\{(\infty ,0)\right\}$ if $f_{a,b}(x_i)=f_{a,b}(x_j).$ In addition say to $L_{a,b}({\widehat{x}}_i,{\widehat{x}}_j)$ the line passing from ${\widehat{x}}_i,{\widehat{x}}_j,$ Intuitively each line passing from $(\mathcal{O},\infty )$ is called vertical line, and every vertical line pass through $(\mathcal{O},\infty )$. $\widehat{\mathcal{O}}$ is playing an asymptotic extension role for function $f_{a,b}$

Remark 2.

By adding $\mathcal{O}$ to hyperfield of $(F,\oplus ,\odot )$ associativity for two hyperoperations of "⊕" and "⊙" remains preserved.

Suppose that $\widehat{x}\in Q(f_{a,b},F)$ and $\tilde{x}=\left\{\begin{array}{cc}\left\{x\right\},& f_{a,b}(x)=a{x}^2+bx\hfill \\ \{x,-x\},& f_{a,b}(x)=a{x}^{-1}+bx\hfill \end{array}\right.$ Hence, we the following proposition

Proposition 1.

if $|Q_F({\tilde{f}}_{{}_{a_1,b_1}})\cap Q_F({\tilde{f}}_{{}_{a_2,b_2}})|\ge 2$ then $Q(f_{{}_{a_1,b_1}},F)=Q(f_{{}_{a_2,b_2}},F)$.

Proof. 

Let $\{{\tilde{x}}_1,{\tilde{x}}_2\}\subseteq Q_F({\tilde{f}}_{{}_{a_1,b_1}})\cap Q_F({\tilde{f}}_{{}_{a_2,b_2}})$, ${\tilde{x}}_1\ne {\tilde{x}}_2$ and $i,j=1,2$. Then

$$y_i=a_j{x}_i^2+b_j{x}_i⟹x_1\ne x_2⟹\left\{\begin{array}{c}{a}_1=a_2={\displaystyle \frac{x_2{y}_1-x_1{y}_2}{x_1^2{x}_2-x_2^2{x}_1}},\hfill \\ b_1=b_2={\displaystyle \frac{-x_2^2{y}_1+x_1^2{y}_2}{x_1^2{x}_2-x_2^2{x}_1}},\hfill \end{array}\right.$$

$$y_i=a_j{x}_i^{-1}+b_j{x}_i⟹x_1\ne \pm x_2⟹\left\{\begin{array}{c}{a}_1=a_2={\displaystyle \frac{x_2{y}_1-x_1{y}_2}{x_2{x}_1^{-1}-x_1{x}_2^{-1}}},\hfill \\ b_1=b_2={\displaystyle \frac{-x_2^{-1}{y}_1+x_1^{-1}{y}_2}{x_2{x}_1^{-1}-x_1{x}_2^{-1}}}.\hfill \end{array}\right.$$

Hence $Q(f_{{}_{a_1,b_1}},F)=Q(f_{{}_{a_2,b_2}},F)$, as we expected. □

Definition 9.

Let $Q(f_{\overline{A},\overline{B}},\overline{F})$ be a non-degenerate conic hypersection then it is named hyperconic and denoted to $Q_{\overline{F}}(f_{\overline{A},\overline{B}}),$ if the following implication for all $a,c\in \overline{A}$ and $b,d\in \overline{B}$ holds:

$$Q_F(f_{a,b})\cap Q_F(f_{c,d})\ne \left\{\begin{array}{cc}\left\{\widehat{\mathcal{O}}\right\},& f_{a,b}(x)=a{x}^2+bx\hfill \\ \{\widehat{\mathcal{O}},\widehat{\infty }\},& f_{a,b}(z)=a{x}^{-1}+bx\hfill \end{array}\right.⟹Q_F(f_{a,b})=Q_F(f_{c,d}).$$

Proposition 2.

Let $\widehat{x_i}=(x_i,f(x_i))$ and $\widehat{x_j}=(x_j,f(x_j))$ belong to $Q_F(f_{a,b})$, then

$$x_i{•}_{{}_{ab}}{x}_j=\left\{\begin{array}{cc}{\displaystyle \frac{x_i{f}_{{}_{a,b}}(x_j)-x_j{f}_{{}_{a,b}}(x_i)}{f_{{}_{a,b}}(x_j)-f_{{}_{a,b}}(x_i)}}\hfill & x_i\ne x_j,\mathcal{O}\notin \{x_i,x_j\},\hfill \\ x_i-{\displaystyle \frac{f_{{}_{a,b}}(x_i)}{f_{{}_{a,b}}^{{}^{\prime }}(x_i)}}\hfill & x_i=x_j\notin \left\{\mathcal{O}\right\},\hfill \\ x_i\hfill & x_i\ne \mathcal{O}=x_j,\hfill \\ x_j\hfill & x_j\ne \mathcal{O}=x_i,\hfill \\ \mathcal{O}\hfill & (x_i,x_j)=(\mathcal{O},\mathcal{O}).\hfill \end{array}\right.$$

Proof. 

The proof is straightforward for the first two cases. If $f_{a,b}(x_i)=f_{a,b}(x_j)$ then

$$x_i{•}_{{}_{ab}}{x}_j={\displaystyle \frac{x_i{f}_{{}_{a,b}}(x_j)-x_j{f}_{{}_{a,b}}(x_i)}{f_{{}_{a,b}}(x_j)-f_{{}_{a,b}}(x_i)}}={\displaystyle \frac{x_i{f}_{{}_{a,b}}(x_j)-x_j{f}_{{}_{a,b}}(x_i)}{0}}=\infty ,$$

$$\left\{(x_i{•}_{{}_{ab}}{x}_j,0)\right\}=L_o\cap L(\widehat{x_i},\widehat{x_j})=\left\{(\infty ,0)\right\}⟹x_i{•}_{{}_{ab}}{x}_j=\infty .$$

Suppose that $(x_i,x_j)\in Q_F^2(f_{a,b})$ by regarding Definition 8 if $x_i\ne \mathcal{O}=x_j$ then

$$\left\{(x_i{•}_{{}_{ab}}\mathcal{O},0)\right\}=L_0\cap L_{a,b}(\widehat{x_i},\widehat{\mathcal{O}})=\left\{(x_i,0)\right\}⟹x_i{•}_{{}_{ab}}\mathcal{O}=x_i,$$

if $x_j\ne \mathcal{O}=x_i$ then proof is similar to previous manner, ultimately if $x_i=x_j=\mathcal{O}$ then

$$\left\{(\mathcal{O}{•}_{{}_{a,b}}\mathcal{O},0)\right\}=L_0\cap L(\widehat{\mathcal{O}},\widehat{\mathcal{O}})=\left\{(\mathcal{O},0)\right\}⟹\mathcal{O}{•}_{{}_{a,b}}\mathcal{O}=\mathcal{O}.$$

□

Remark 3.

$\left(Q_F(f_{a,b}),{•}_{{}_{ab}}\right)$ is a conic group, for all $(a,b)\in \overline{A}\times \overline{B}$. Notice that ${•}_{{}_{ab}}$ is the group operation on the conic $Q_F(f_{a,b}).$

Example 3.

Let $F={\mathbb{Z}}_5$ the field of order 5, $G=\{\pm 1\}⩽F^{\ast }$ and $f_{{}_{\overline{1},\overline{0}}}(\overline{x})={\overline{x}}^2$. Then we have $\overline{F}=\{\overline{0},\overline{1},\overline{2}\},$$Q_{\overline{F}}(f_{{}_{\overline{1},\overline{0}}})=\overline{Q_F(f_{{}_{1,0}}})\cup \overline{Q_F(f_{{}_{(-1),0}}})$, where $Q_F(f_{{}_{1,0}})=\{\widehat{\mathcal{O}},(1,1),(-1,1),(2,-1),(-2,-1)\}$ and $\overline{Q_F(f_{{}_{1,0}})}=\{\widehat{\mathcal{O}},(\overline{1},\overline{1}),(\overline{2},\overline{1})\},Q_F(f_{{}_{(-1),0}})=\{\widehat{\mathcal{O}},(1,-1),(-1,-1),(2,1),(-2,1)\}$, and $\overline{Q_F(f_{{}_{(-1),0})}}=\{\widehat{\mathcal{O}},(\overline{1},\overline{1}),(\overline{2},\overline{1})\}$, in this case $Q_{\overline{F}}(f_{{}_{\overline{1},\overline{0}}})$ is a hyperconic because $Q_F(f_{{}_{1,0}})\cap Q_F(f_{{}_{(-1),0}})=\widehat{\mathcal{O}}$.

Definition 10.

We introduce hyperoperation “∘” on $Q_F(f_{\overline{A},\overline{B}})$ as follows:

Let $(x,y),(x^{\prime },y^{\prime })\in Q_F(f_{\overline{A},\overline{B}})$. If $(x,y)\in Q_F(f_{a,b})$ and $(x^{\prime },y^{\prime })\in Q_F(f_{a^{\prime },b^{\prime }})$ for some $a,a^{\prime }\in \overline{A}$ and $b,b^{\prime }\in \overline{B}$.

$$(x,y)\circ (x^{\prime },y^{\prime })=\left\{\begin{array}{cc}\left\{\widehat{x_i{•}_{{}_{ab}}{x}_j}\right|(x_i,x_j)\in {\mathcal{G}}_x(f_{a,b})\times {\mathcal{G}}_{x^{\prime }}(f_{a^{\prime },b^{\prime }})\},& if{Q}_F(f_{a,b})=Q_F(f_{a^{\prime },b^{\prime }})\hfill \\ Q_F(f_{a,b})\cup Q_F(f_{a^{\prime },b^{\prime }}),& otherwise.\hfill \end{array}\right.$$

Theorem 3.

$\left(Q_F(f_{\overline{A},\overline{B}}),\circ \right)$ is a hypergroup.

Proof. 

Suppose that $\{X,Y,Z\}\subseteq Q_F(f_{\overline{A},\overline{B}})$, by Bezout’s Theorem $(x,y)\circ (x^{\prime },y^{\prime })\subseteq P^{\ast }(Q_F(f_{a,b})).$ Now let $X=(x,y)\in Q_F(f_{a,b}),Y=(x^{\prime },y^{\prime })\in Q_F(f_{a^{\prime },b^{\prime }}),Z=(x^{″},y^{″})\in Q_F(f_{a^{″},b^{″}})$, where $J=\{(a,b),(a^{\prime },b^{\prime }),(a^{″},b^{″})\}\subseteq \overline{A}\times \overline{B}$. If $(x,y)=(x_1,y_1)$ and $(x^{\prime },y^{\prime })=(x_1^{\prime },y_1^{\prime })$ then $x=x_1$ and $x^{\prime }=x_1^{\prime }.$ Because ${\mathcal{G}}_x(f_{a,b})={\mathcal{G}}_{x_1}(f_{a,b})$ and ${\mathcal{G}}_{x^{\prime }}(f_{a,b})={\mathcal{G}}_{x_1^{\prime }}(f_{a,b})$ we have ${\mathcal{G}}_x(f_{a,b})\times {\mathcal{G}}_{x^{\prime }}(f_{a,b})={\mathcal{G}}_{x_1}(f_{a,b})\times {\mathcal{G}}_{x_1^{\prime }}(f_{a,b})$ thus

$$\left\{\widehat{z{•}_{{}_{ab}}w}\right|(z,w)\in {\mathcal{G}}_x(f_{a,b})\times {\mathcal{G}}_{x^{\prime }}(f_{a,b})\}=\left\{\widehat{z{•}_{{}_{ab}}w}\right|(z,w)\in {\mathcal{G}}_{x_1}(f_{a,b})\times {\mathcal{G}}_{x_1^{\prime }}(f_{a,b})\}$$

and that is $(x,y)\circ (x^{\prime },y^{\prime })=(x_1,y_1)\circ (x_1^{\prime },y_1^{\prime })$, consequently "∘" is well defined. If $X=(\mathcal{O},\infty )$ or $Y=(\mathcal{O},\infty )$ or $Z=(\mathcal{O},\infty ),$ associativity is evident. If this property is not met, the following cases may occur:

Case 1. If $\left|J\right|=1$. In this case we have $Q_F(f_{a,b})=Q_F(f_{a^{\prime },b^{\prime }})=Q_F(f_{a^{″},b^{″}})$.

$$\begin{array}{cc}[(x,y)\circ (x^{\prime },y^{\prime })]\circ (x^{″},y^{″})\hfill & =\left\{\widehat{(x_i{•}_{{}_{ab}}{x}_j^{\prime })}|(x_i,x_j^{\prime })\in {\mathcal{G}}_x(f_{a,b})\times {\mathcal{G}}_{x^{\prime }}(f_{a,b})\right\}\circ (x^{″},y^{″})\hfill \\ \hfill & =\left\{\widehat{(x_i{•}_{{}_{ab}}{x}_j^{\prime }){•}_{{}_{ab}}{x}_k^{″}}|(x_i,x_j^{\prime },x_k^{″})\in {\mathcal{G}}_x(f_{a,b})\times {\mathcal{G}}_{x^{\prime }}(f_{a,b})\times {\mathcal{G}}_{x^{″}}(f_{a,b})\right\}.\hfill \end{array}$$

Similarly

$$(x,y)\circ [(x^{\prime },y^{\prime })\circ (x^{″},y^{″})]=\left\{\widehat{x_i{•}_{{}_{ab}}(x_j^{\prime }{•}_{{}_{ab}}{x}_k^{″})}|(x_i,x_j^{\prime },x_k^{″})\in {\mathcal{G}}_x(f_{a,b})\times {\mathcal{G}}_{x^{\prime }}(f_{a,b})\times {\mathcal{G}}_{x^{″}}(f_{a,b})\right\}.$$

On the other hand we have

$$\begin{array}{c}L(\widehat{x_i},\widehat{x_j^{\prime }})\cap L(\widehat{x_i{•}_{{}_{ab}}{x}_j^{\prime }},\widehat{\mathcal{O}})=\left\{(x_i{•}_{{}_{ab}}{x}_j,0)\right\}\subseteq L_0,\hfill \\ L(\widehat{x_j^{\prime }},\widehat{x_k^{″}})\cap L(\widehat{\mathcal{O}},\widehat{x_j^{\prime }{•}_{{}_{ab}}{x}_k^{″}})=\left\{(x_j{•}_{{}_{ab}}{x}_k,0)\right\}\subseteq L_0.\hfill \end{array}$$

Therefore by Pascal’s Theorem we have

$$L(\widehat{x_k^{″}},\widehat{x_i{•}_{{}_{ab}}{x}_j^{\prime }})\cap L(\widehat{x_j^{\prime }}{•}_{{}_{ab}}\widehat{x_k^{″}},\widehat{x_i})\subseteq L_0,$$

and in addition

$$\left\{((x_i{•}_{{}_{ab}}{x}_j^{\prime }){•}_{{}_{ab}}{x}_k^{″},0)\right\}=L_0\cap L(\widehat{x_i{•}_{{}_{ab}}{x}_j^{\prime }},\widehat{x_k^{″}}),$$

$$\left\{(x_i{•}_{{}_{ab}}(x_j^{\prime }{•}_{{}_{ab}}{x}_k^{″}),0)\right\}=L_0\cap L(\widehat{x_i},\widehat{x_j^{\prime }{•}_{{}_{ab}}{x}_k^{″}}),$$

$$L_0\cap L(\widehat{x_i{•}_{{}_{ab}}{x}_j^{\prime }},\widehat{x_k^{″}})=L(\widehat{x_k^{″}},\widehat{x_i{•}_{{}_{ab}}{x}_j^{\prime }})\cap L(\widehat{x_j^{\prime }{•}_{{}_{ab}}{x}_k^{″}},\widehat{x_i})=L_0\cap L(\widehat{x_i},\widehat{x_j^{\prime }{•}_{{}_{ab}}{x}_k^{″}}).$$

On the other word

$$(x_i{•}_{{}_{ab}}{x}_j^{\prime }){•}_{{}_{ab}}{x}_k^{″}=x_i{•}_{{}_{ab}}(x_j^{\prime }{•}_{{}_{ab}}{x}_k^{″}).$$

So

$$\widehat{\left((x_i{•}_{{}_{ab}}{x}_j^{\prime }){•}_{{}_{ab}}{x}_k^{″}\right)}=\widehat{\left(x_i{•}_{{}_{ab}}(x_j^{\prime }{•}_{{}_{ab}}{x}_k^{″})\right)}\mathrm{for}\mathrm{all}(x_i,x_j^{\prime },x_k^{″})\in {\mathcal{G}}_x(f_{a,b})\times {\mathcal{G}}_{x^{\prime }}(f_{a,b})\times {\mathcal{G}}_{x^{″}}(f_{a,b})$$

Case 2. If $\left|J\right|=2$. (i) If $Q_F(f_{a,b})=Q_F(f_{a^{\prime },b^{\prime }})\ne Q_F(f_{a^{″},b^{″}})$. We have

$$\begin{array}{cc}[(x,y)\circ (x^{\prime },y^{\prime })]\circ (x^{″},y^{″})\hfill & =\left[\left\{\widehat{z{•}_{{}_{ab}}w}\right|(z,w)\in {\mathcal{G}}_x(f_{a,b})\times {\mathcal{G}}_{x^{\prime }}(f_{a,b})\}\right]\circ (x^{″},y^{″})\hfill \\ & =\bigcup _{(u,v)\in (x,y)\circ (x^{\prime },y^{\prime })}(u,v)\circ (x^{″},y^{″})\hfill \\ & =Q_F(f_{a,b})\cup Q_F(f_{a^{″},b^{″}}).\hfill \end{array}$$

Otherwise

$$\begin{array}{cc}(x,y)\circ [(x^{\prime },y^{\prime })\circ (x^{″},y^{″})]\hfill & =(x,y)\circ \left(Q_F(f_{a^{\prime },b^{\prime }})\cup Q_F(f_{a^{″},b^{″}})\right)\hfill \\ & =Q_F(f_{a^{\prime },b^{\prime }})\cap Q_F(f_{a,b})\cup Q_F(f_{a^{″},b^{″}})\hfill \\ & =Q_F(f_{a,b})\cup Q_F(f_{a^{″},b^{″}}).\hfill \end{array}$$

(ii) If $Q_F(f_{a,b})\ne Q_F(f_{a^{\prime },b^{\prime }})=Q_F(f_{a^{″},b^{″}})$. This case similar to (i).

(iii) If $Q_F(f_{a,b})=Q_F(f_{a^{″},b^{″}})\ne Q_F(f_{a^{\prime },b^{\prime }})$. We have

$$\begin{array}{cc}[(x,y)\circ (x^{\prime },y^{\prime })]\circ (x^{″},y^{″})\hfill & =\left(Q_F(f_{a,b})\cup Q_F(f_{a^{\prime },b^{\prime }})\right)\circ (x^{″},y^{″})\hfill \\ \hfill & =Q_F(f_{a,b})\cup Q_F(f_{a^{\prime },b^{\prime }})\cup Q_F(f_{a^{″},b^{″}})\hfill \\ \hfill & =Q_F(f_{a,b})\cup Q_F(f_{a^{\prime },b^{\prime }}).\hfill \end{array}$$

On the other hand

$$\begin{array}{cc}(x,y)\circ [(x^{\prime },y^{\prime })\circ (x^{″},y^{″})]\hfill & =(x,y)\circ (Q_F(f_{a^{\prime },b^{\prime }})\cup Q_F(f_{a^{″},b^{″}}))\hfill \\ & =Q_F(f_{a,b})\cup Q_F(f_{a^{\prime },b^{\prime }})\cup Q_F(f_{a^{″},b^{″}})\hfill \\ & =Q_F(f_{a,b})\cup Q_F(f_{a^{\prime },b^{\prime }}).\hfill \end{array}$$

Case 3. If $\left|J\right|=3$. In this case we have

$$\begin{array}{cc}[(x,y)\circ (x^{\prime },y^{\prime })]\circ (x^{″},y^{″})\hfill & =\left(Q_F(f_{a,b})\cup Q_F(f_{a^{\prime },b^{\prime }})\right)\circ (x^{″},y^{″})\hfill \\ & =Q_F(f_{a,b})\cup Q_F(f_{a^{\prime },b^{\prime }})\cup Q_F(f_{a^{″},b^{″}}).\hfill \end{array}$$

On the other hand

$$\begin{array}{cc}(x,y)\circ [(x^{\prime },y^{\prime })\circ (x^{″},y^{″})]\hfill & =(x,y)\circ \left(Q_F(f_{a^{\prime },b^{\prime }})\cup Q_F(f_{a^{″},b^{″}})\right)\hfill \\ & =Q_F(f_{a,b})\cup Q_F(f_{a^{\prime },b^{\prime }})\cup Q_F(f_{a^{″},b^{″}}).\hfill \end{array}$$

To prove the validity of reproduction axiom for ”∘” let us consider two cases:

Case 1. If $|\overline{A}\times \overline{B}|=1$ then $\overline{F}=F$ and $Q_F(f_{\overline{A},\overline{B}})=Q_F(f_{a,b}),$ where $a\in \overline{A},b\in \overline{B}$ also $(Q_F(f_{a,b}),\circ )$ is a conic group, hence there is nothing to prove.

Case 2. If $|\overline{A}\times \overline{B}|>1,$ consider arbitrary element $\widehat{x}\in Q_F(f_{a,b})\subseteq Q_F(f_{\overline{A},\overline{B}}),$ then

$$\begin{array}{cc}\widehat{x}\circ Q_F(f_{\overline{A},\overline{B}})\hfill & =\left(\widehat{x}\circ {\displaystyle \bigcup _{a\ne i\in \overline{A},b\ne j\in \overline{B}}}{Q}_F(f_{i,j}))\cup (\widehat{x}\circ Q_F(f_{a,b})\right),\hfill \\ & =\left({\displaystyle \bigcup _{a\ne i\in \overline{A},b\ne j\in \overline{B}}}\widehat{x}\circ Q_F(f_{i,j})\right)\cup Q_F(f_{a,b}),\hfill \\ & =\left({\displaystyle \bigcup _{i\in \overline{A},j\in \overline{B}}}{Q}_F(f_{i,j})\right)\cup Q_F(f_{a,b}),\hfill \\ & =Q_F(f_{\overline{A},\overline{B}}).\hfill \end{array}$$

Similarly, $Q_F(f_{\overline{A},\overline{B}})\circ \widehat{x}=Q_F(f_{\overline{A},\overline{B}})$ and reproduction axiom is established. Thus, $\left(Q_F(f_{\overline{A},\overline{B}}),\circ \right)$ is a hypergroup. □

Remark 4.

The hyperconic and the associated hypergroup are conic and conic group, respectively, if $G=\left\{1\right\}$.

Example 4.

Let $F={\mathbb{Z}}_5$ be the field of order 5 and $G=\{\pm 1\}⩽F^{\ast }$. We have $\overline{F}=\{\overline{0},\overline{1},\overline{2}\}.$ In addition, if we go back to Example 3 then $Q_{\overline{F}}(f_{{}_{\overline{1},\overline{0}}})=\overline{Q_F(f_{{}_{1,0}}})\cup \overline{Q_F(f_{{}_{(-1),0}}})$ is hyperconic, where $Q_F(f_{{}_{1,0}})=\{\widehat{\mathcal{O}},(1,1),(-1,1),(2,-1),(-2,-1)\}$

$Q_F(f_{{}_{(-1),0}})=\{\widehat{\mathcal{O}},(1,-1),(-1,-1),(2,1),(-2,1)\}$, $Q_{\overline{F}}(f_{{}_{\overline{1},\overline{0}}})=\{\widehat{\mathcal{O}},(\overline{1},\overline{1}),(\overline{2},\overline{1})\}.$ Now let $H=Q_F(f_{{}_{1,0}})$ and $K=Q_F(f_{{}_{(-1),0}}).$ Then H and K are reversible subhypergroups of $Q_F(f_{{}_{\overline{1},\overline{0}}})$, which are defined by the Caley Table 2 and Table 3, respectively.

Table 2. Cayle table $\left(Q_{{\mathbb{Z}}_5}(f_{1,0}),\circ \right)$.

∘	$\widehat{\mathcal{O}}$	$(\mathbf{1}\mathbf{,}\mathbf{1})$	$(\mathbf{-}\mathbf{1}\mathbf{,}\mathbf{1})$	$(\mathbf{2}\mathbf{,}\mathbf{-}\mathbf{1})$	$(\mathbf{-}\mathbf{2}\mathbf{,}\mathbf{-}\mathbf{1})$
$\widehat{\mathcal{O}}$	$\widehat{\mathcal{O}}$	$(\pm 1,1)$	$(\pm 1,1)$	$(\pm 2,-1)$	$,(\pm 2,-1)$
$(1,1)$	$(\pm 1,1)$	$\widehat{\mathcal{O}},(\pm 2,-1)$	$\widehat{\mathcal{O}},(\pm 2,-1)$	$(\pm 1,1),(\pm 2,-1)$	$(\pm 1,1),(\pm 2,-1)$
$(-1,1)$	$(\pm 1,1)$	$\widehat{\mathcal{O}},(\pm 2,-1)$	$\widehat{\mathcal{O}},(\pm 2,-1)$	$(\pm 1,1),(\pm 2,-1)$	$(\pm 1,1),(\pm 2,-1)$
$(2,-1)$	$(\pm 2,-1)$	$(\pm 1,1),(\pm 2,-1)$	$(\pm 1,1),(\pm 2,-1)$	$(\pm 1,1),\widehat{\mathcal{O}}$	$(\pm 1,1),\widehat{\mathcal{O}}$
$(-2,-1)$	$(\pm 2,-1)$	$(\pm 1,1),(\pm 2,-1)$	$(\pm 1,1),(\pm 2,-1)$	$(\pm 1,1),\widehat{\mathcal{O}}$	$(\pm 1,1),\widehat{\mathcal{O}}$

Table 3. Caley table $\left(Q_{{\mathbb{Z}}_5}(f_{(-1),0}),\circ \right)$.

∘	$\widehat{\mathcal{O}}$	$(1,-1)$	$(-1,-1)$	$(2,1)$	$(-2,1)$
$\widehat{\mathcal{O}}$	$\widehat{\mathcal{O}}$	$(\pm 1,-1)$	$(\pm 1,-1)$	$(\pm 2,1)$	$,(\pm 2,1)$
$(1,-1)$	$(\pm 1,-1)$	$\widehat{\mathcal{O}},(\pm 2,1)$	$\widehat{\mathcal{O}},(\pm 2,1)$	$(\pm 1,-1),(\pm 2,1)$	$(\pm 1,-1),(\pm 2,1)$
$(-1,-1)$	$(\pm 1,-1)$	$\widehat{\mathcal{O}},(\pm 2,1)$	$\widehat{\mathcal{O}},(\pm 2,1)$	$(\pm 1,-1),(\pm 2,1)$	$(\pm 1,-1),(\pm 2,1)$
$(2,1)$	$(\pm 2,1)$	$(\pm 1,-1),(\pm 2,1)$	$(\pm 1,-1),(\pm 2,1)$	$(\pm 1,-1),\widehat{\mathcal{O}}$	$(\pm 1,-1),\widehat{\mathcal{O}}$
$(-2,1)$	$(\pm 2,1)$	$(\pm 1,-1),(\pm 2,1)$	$(\pm 1,-1),(\pm 2,1)$	$(\pm 1,-1),\widehat{\mathcal{O}}$	$(\pm 1,-1),\widehat{\mathcal{O}}$

Proposition 3.

H is subhypergroup of $Q_F(f_{\overline{A},\overline{B}})$ if and only if $H={\displaystyle \bigcup _{(i,j)\in I\subseteq \overline{A}\times \overline{B}}}{Q}_F(f_{i,j})$ or $H⩽Q_{i,j}(F)$, for some $(i,j)\in \overline{A}\times \overline{B}$.

Proof. 

$(\Rightarrow )$. Let us assume that $H\nleqq Q_F(f_{i,j})$ for every $(i,j)$ in $\overline{A}\times \overline{B}$. Then in $\overline{A}\times \overline{B}$ exist $(i,j)\ne (s,t)$ such that $H\cap Q_F(f_{i,j})\ne \varnothing \ne H\cap Q_F(f_{s,t})$. Now let $I=\{(i,j)\in \overline{A}\times \overline{B}|H\cap Q_F(f_{i,j})\ne \varnothing \}$, thus we have $H\subseteq {\displaystyle \bigcup _{(i,j)\in I}}{Q}_F(f_{i,j})\subseteq {\displaystyle \bigcup _{(s,t),(i,j)\in I}}(Q_F(f_{i,j})\cap H)\circ (Q_F(f_{s,t})\cap H)\subseteq H$. Accordingly, $H={\displaystyle \bigcup _{(i,j)\in I}}{Q}_F(f_{i,j})$.

$(\Leftarrow )$. It is obvious. □

Proposition 4.

Let H be a subhypergroup of $Q_F(f_{\overline{A},\overline{B}})$. Then H is reversible hypergroup if and only if $H⩽Q_F(f_{i,j})$, for some $(i,j)\in \overline{A}\times \overline{B}$.

Proof. 

$(\Leftarrow )$. First we prove that $H⩽Q_F(f_{i,j})$ is a regular reversible hypergroup for all $(i,j)\in \overline{A}\times \overline{B}$. Let $(x,y)$ and $(x^{\prime },y^{\prime })$ are elements in $Q_F(f_{i,j})$.

Case 1. If $x^{\prime }\notin {\mathcal{G}}_x(f_{a,b})$, then

$$\begin{array}{cc}(x^{″},y^{″})\in (x,y)\circ (x^{\prime },y^{\prime })\hfill & ⟹(x^{″},y^{″})=\widehat{z{•}_{ij}w},forsome(z,w)\in {\mathcal{G}}_x(f_{a,b})\times {\mathcal{G}}_{x^{\prime }}(f_{a,b})\hfill \\ & ⟹x^{″}=z{•}_{ij}w,\hfill \\ & ⟹z=x^{″}{•}_{ij}h\mathrm{where},w{•}_{ij}h=\mathcal{O},\hfill \\ & ⟹(z,f_{a,b}(z))=\widehat{x^{″}{•}_{ij}h}\mathrm{and}h\in {\mathcal{G}}_w(f_{a,b})={\mathcal{G}}_{x^{\prime }}(f_{a,b})\hfill \\ & ⟹(z,f_{a,b}(z))\in (x^{″},f_{a,b}(x^{″}))\circ (x^{\prime },f_{a,b}(x^{\prime })).\hfill \end{array}$$

Case 2. If $x^{\prime }\in {\mathcal{G}}_x(f_{a,b})$, then $z,w\in {\mathcal{G}}_x(f_{{}_{a,b}})$ and $\widehat{m}\in \widehat{z}\circ \widehat{w}=\{\widehat{x{•}_{ab}x},\widehat{n{•}_{ab}n},\widehat{\mathcal{O}}\}$, where $x{•}_{ab}n=\mathcal{O}$ then $\widehat{z}\in \widehat{m}\circ \widehat{w}$ and $\widehat{w}\in \widehat{z}\circ \widehat{m}$.

Case 3. If $Y\in \infty \circ X=X\circ \infty$, then $\infty \in Y\circ X$ and $X\in \infty \circ Y$. Notice that $\infty \in X\circ X$, for all $X\in Q_F(f_{i,j})$ (i.e., every element is one of its inverses).

$(\Rightarrow )$. Assume that $(x,y)\in H\cap Q_F(f_{i,j})$ and $(x^{\prime },y^{\prime })\in H\cap Q_F(f_{s,t})$, in which $(i,j)\ne (s,t)$, $(x,y)\ne \widehat{\mathcal{O}}\ne (x^{\prime },y^{\prime })$ and $(x^{″},y^{″})\in (x,y)\circ (x^{\prime },y^{\prime })\cap Q_F(f_{i,j})$. Then $(x^{\prime },y^{\prime })\in (z,w)\circ (x^{″},y^{″})\subseteq Q_F(f_{i,j})$, where $z\in {\mathcal{G}}_x(f_{a,b})$. Hence $Q_F(f_{i,j})=Q_F(f_{s,t})$ and this means reversibility conditions do not hold. □

The class of $H_v$- groups is more general than the class of hypergroups which is introduced by Th. Vougiouklis [39]. The hyperstructure $(H,\circ )$ is called an $H_v—$group if $x\circ H=H=H\circ x,$ and also the weak associativity condition holds, that is $x\circ (y\circ z)\cap (x\circ y)\circ z\ne \varnothing$ for all $x,y,z\in H$. In [13,14] the authors have investigated some hyperoperations denoted by $\overline{\circ }$ and ⋄ on some main classes of curves; elliptic curves and homographics over Krasner’s hyperfields. In the following, we study them on hyperconic. Consider the following hyperoperation on the hyperconic; $(Q_{\overline{F}}(f_{\overline{A},\overline{B}})$:

$$(\overline{x},\overline{y})\overline{\circ }(\overline{x^{\prime }},\overline{y^{\prime }})=\left\{(\overline{v},\overline{w})\right|(v,w)\in (\overline{x}\times \overline{y})\circ (\overline{x^{\prime }}\times \overline{y^{\prime }})\},$$

for all $(\overline{x},\overline{y})$, $(\overline{x^{\prime }},\overline{y^{\prime }})$ in $Q_{\overline{F}}(f_{\overline{A},\overline{B}}).$

Proposition 5.

$(Q_{\overline{F}}(f_{\overline{A},\overline{B}}),\overline{\circ })$ is an $H_v$-group.

Proof. 

The proof is straightforward. □

Proposition 6.

If ${\psi }_{{}_{\overline{A},\overline{B}}}:Q_F(f_{\overline{A},\overline{B}})⟶Q_{\overline{F}}(f_{\overline{A},\overline{B}})$, ${\psi }_{{}_{\overline{A},\overline{B}}}(x,y)=(\overline{x},\overline{y})$, then ${\psi }_{{}_{\overline{A},\overline{B}}}$ is an epimorphism of $H_v$-groups.

Proof. 

The base of the proof is similar to the proof of Proposition 3 in [14]. □

Example 5.

Let $G=\{\pm 1\}$ be a subgroup of $F^{\ast }$, where $F={\mathbb{Z}}_5.$ Consider $f_{{}_{\overline{1},\overline{1}}}(\overline{x})={\overline{x}}^2\oplus \overline{x}$ on $\overline{F}=\{\overline{0},\overline{1},\overline{2}\}$. Consequently $Q_{\overline{F}}(f_{\overline{1},\overline{1}})=\{\widehat{\mathcal{O}},(\overline{1},\overline{2}),(\overline{2},\overline{1}),(\overline{2},\overline{2})\}$ is a hyperconic, a calculation gives us the Table 4 of $H_v$-group.

Table 4. Conic $H_v$-group, $\left(Q_{\overline{{\mathbb{Z}}_5}}(f_{\overline{1},\overline{1}}),\overline{\circ }\right)$.

$\overline{\circ }$	$\widehat{\mathcal{O}}$	$(\overline{1},\overline{2})$	$(\overline{2},\overline{1})$	$(\overline{2},\overline{2})$
$\widehat{\mathcal{O}}$	$\widehat{\mathcal{O}}$	$(\overline{1},\overline{2}),(\overline{2},\overline{2})$	$(\overline{2},\overline{1})$	$(\overline{2},\overline{2}),(\overline{1},\overline{2})$
$(\overline{1},\overline{2})$	$(\overline{1},\overline{2}),(\overline{2},\overline{2})$	$(\overline{1},\overline{2}),(\overline{2},\overline{1}),(\overline{2},\overline{2})$	$(\overline{1},\overline{2}),(\overline{2},\overline{1}),(\overline{2},\overline{2})$	$(\overline{1},\overline{2}),(\overline{2},\overline{1}),(\overline{2},\overline{2})$
$(\overline{2},\overline{1})$	$(\overline{2},\overline{1})$	$(\overline{1},\overline{2}),(\overline{2},\overline{1}),(\overline{2},\overline{2})$	$Q_{\overline{F}}(f_{\overline{1},\overline{1}})$	$(\overline{1},\overline{2}),(\overline{2},\overline{1}),(\overline{2},\overline{2})$
$(\overline{2},\overline{2})$	$(\overline{1},\overline{2}),(\overline{2},\overline{2})$	$(\overline{1},\overline{2}),(\overline{2},\overline{1}),(\overline{2},\overline{2})$	$(\overline{1},\overline{2}),(\overline{2},\overline{1}),(\overline{2},\overline{2})$	$(\overline{1},\overline{2}),(\overline{2},\overline{1}),(\overline{2},\overline{2})$

Let A be a finite set called alphabet and let K be a non-empty subset of $A,$ called key-set and also let “·” be a hyperoperation on $A.$ In [40] Berardi et.al. utilized the hyperoperations with the following condition $k·x=k·y\Rightarrow x=y,$ for all $(x,y)\in A^2$ and $k\in K.$ Let the subhypergroup $\left(Q_F(f_{m,n}),\circ \right)$ of $\left(Q_F(f_{\overline{m},\overline{n}}),\circ \right)$ and $A=\left\{a_x\right|\widehat{x}\in Q_F(f_{m,n})\},$ where $a_x=i(x).$ Notice that $i(x)=\widehat{{\mathcal{G}}_x(f_{a,b})},$ is the set of all inverses of $\widehat{x},$ for all $\widehat{x}\in Q_F(f_{m,n})$. We define the hyperoperation ⋄ on A as bellow:

$$a_u\diamond a_v=\left\{a_w\right|w\in u\circ v\}.$$

Theorem 4.

$(A,\diamond )$ is a canonical hypergroup which satisfies Berardi’s condition.

Proof. 

The proof is similar to the one of Theorem 4.1 in [13]. □

4. Conclusions

Conic curve cryptography (CCC) is rendering efficient digital signature schemes (CCDLP). They have a high level of security with small keys size. Let $g(x,y)=a{x}^2+bxy+c{y}^2+dx+ey+f\in F[x,y]$ and $g(x,y)=0$ be the quadratic equation of two variables in field of F, if $a=c=0$ and $b\ne 0$ then the equation $g(x,y)=0$ is called homographic transformation. In [14] Vahedi et. al extended this particular quadratic equation on the quotient hyperfield $\frac{F}{G}.$ Now suppose that $ae\ne 0$ and $b=0$ in $g(x,y)$. Then the curve is called a conic. The motivation of this paper goes in the same direction of [14]. In fact, by a similar way the notion of conic on a field extended to hyperconic over a quotient hyperfield hyperfield, as picturized in Figure 3. Notice that as one can see the group structures of these two classes of curves have different applications, the associated hyperstructures can be different in applications. In the last part of the paper a canonical hypergroup which is assigned by $\left(Q_F(f_{{}_{n,m}}),\diamond \right)$ is investigated.

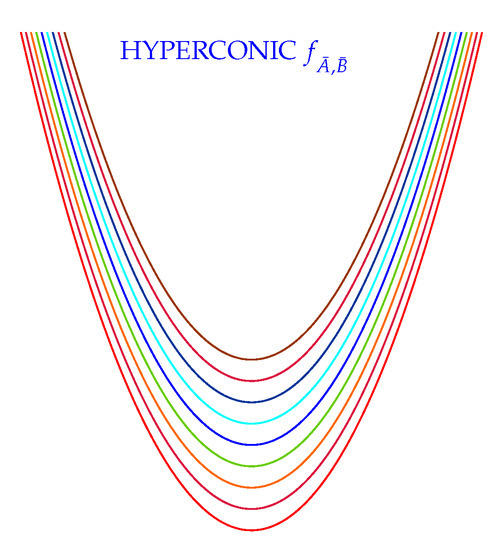
Figure 3. Hyperconic, $Q_{\mathbb{R}}(f_{\overline{A},\overline{B}})$.