On the (29, 5)-Arcs in PG(2, 7) and Some Generalized Arcs in PG(2, q)

Abstract

Using an exhaustive computer search, we prove that the number of inequivalent $(29,5)$-arcs in PG$(2,7)$ is exactly 22. This generalizes a result of Barlotti (see Barlotti, A. Some Topics in Finite Geometrical Structures, 1965), who constructed the first such arc from a conic. Our classification result is based on the fact that arcs and linear codes are related, which enables us to apply an algorithm for classifying the associated linear codes instead. Related to this result, several infinite families of arcs and multiple blocking sets are constructed. Lastly, the relationship between these arcs and the Barlotti arc is explored using a construction that we call transitioning.

1. Introduction

Let ${\mathbb{F}}_q$ be the finite field with q elements, q a prime power. We denote by $\mathrm{PG}(2,q)$ the projective plane over ${\mathbb{F}}_q$. Two subsets $K_1$ and $K_2$ in $\mathrm{PG}(2,q)$ are projectively equivalent (denoted by $K_1\sim K_2$) if there exists a projectivity $\tau$ such that $\tau \left(K_1\right)=K_2$. An $(n,r)$-arcK in $\mathrm{PG}(2,q)$ is an n-set in $\mathrm{PG}(2,q)$ such that each line contains at most r points of K and some lines contain exactly r points of K. An $(n,2)$-arc in $\mathrm{PG}(2,q)$ is simply called an n-arc. A fundamental problem of $(n,r)$-arcs in $\mathrm{PG}(2,q)$ is the following.

Problem. 

Let r be an integer with $2\le r\le q-1$.

(1)

Find $m_r(2,q)$, the maximum value of n for which an $(n,r)$-arc exists in $\mathrm{PG}(2,q)$.

(2)

Classify $(n,r)$-arcs in $\mathrm{PG}(2,q)$ for $n=m_r(2,q)$ up to projective equivalence.

In the cases $3\le q\le 16$, the values of $m_r(2,q)$ are known as given in Table 1, see [1,2]. It is also known that every $(q+1)$-arc is projectively equivalent to a conic $V(x_1^2-x_0{x}_2)$ when q is odd, and that every $(q+2)$-arc is projectively equivalent to a conic plus a point (called the nucleus) when $q=4$ or 8 [3]. Marcugini et al. [4,5] proved with the aid of a computer that $(15,3)$-arcs in $\mathrm{PG}(2,7)$ are unique, and Hill and Love [6] showed that there are three $(22,4)$-arcs in $\mathrm{PG}(2,7)$ up to projective equivalence, see Table 2 (see also [7,8] for $q=8,9$). In unpublished work, the authors of [7] have classified the $(33,5)$-arcs in $\mathrm{PG}(2,8)$.

Table 1. The known values and bounds on $m_r(2,q)$, $3\le q\le 16$.

$\mathit{r}\backslash \mathit{q}$	3	4	5	7	8	9	11	13	16
2	4	6	6	8	10	10	12	14	18
3		9	11	15	15	17	21	23	28
4			16	22	28	28	32	38–40	52
5				29	33	37	43–45	49–53	65
6				36	42	48	56	64–66	78–82
7					49	55	67	79	93–97
8						65	78	92	120
9							89–90	105	129–130
10							100–102	118–119	142–148
11								132–133	159–164
12								145–147	180–181
13									195–199
14									210–214
15									231

Table 2. The number of inequivalent $(m_r(2,q),r)$-arcs.

$\mathit{r}\backslash \mathit{q}$	3	4	5	7	8	9
2	1	1	1	1	1	1
3		3	2	1	19	4
4			6	3	1	?
5				22	6	?
6				194	5	1
7					?	?
8						?

For 5-arcs in $\mathrm{PG}(2,7)$, it has been known that the maximal size is $n=29$ [9,10], but it was not known how many inequivalent arcs of maximal size exist. In [11], the second author presented 13 inequivalent $(29,5)$-arcs in $\mathrm{PG}(2,7)$. Subsequently, Professor M. Grassl, attending the same conference, found in total 22 inequivalent linear codes corresponding to $(29,5)$-arcs with the help of the computer algebra system Magma [12]. Those results have been presented in [13]. Finally, using the package Q-Extension developed by the first author [14] (see Section 2), the following extended result has been confirmed.

Theorem 1.

There are exactly 22 inequivalent $(29,5)$-arcs in $\mathrm{PG}(2,7)$ as listed in Table 3.

Table 3. The $(29,5)$-arcs in $\mathrm{PG}(2,7)$.

Arc	${\mathit{a}}_0$	${\mathit{a}}_1$	${\mathit{a}}_2$	${\mathit{a}}_3$	${\mathit{a}}_4$	${\mathit{a}}_5$	$\left|\mathbf{Aut}\right|$	Construction
$K_1$	0	5	3	9	6	24	6
$K_2$	0	8	0	0	21	28	336	Barlotti [10]
$K_3$	1	3	4	8	8	33	2
$K_4$	1	4	3	5	13	31	2
$K_5$	2	1	5	7	10	32	2
$K_6$	2	1	6	4	13	31	1
$K_7$	2	2	2	10	9	32	2
$K_8$	2	2	4	4	15	30	2
$K_9$	2	2	4	4	15	30	2
$K_{10}$	2	3	2	4	17	29	2
$K_{11}$	3	0	3	9	11	31	1	Theorem 4 (3)
$K_{12}$	3	0	3	9	11	31	6
$K_{13}$	3	0	4	6	14	30	2	Theorem 3
$K_{14}$	3	1	1	9	13	30	1	Theorem 4 (2)
$K_{15}$	3	1	2	6	16	29	1
$K_{16}$	3	1	2	6	16	29	1
$K_{17}$	3	1	2	6	16	29	2
$K_{18}$	3	1	3	3	19	28	3
$K_{19}$	3	2	0	6	18	28	2
$K_{20}$	3	2	0	6	18	28	6	Theorem 5
$K_{21}$	4	0	0	8	17	28	8	Example 2.3 in [15]
$K_{22}$	4	0	1	5	20	27	2	Theorem 7

In Section 2, we explain the algorithms in the package Q-Extension, which is used for classification of linear codes with many different parameters over different fields including codes with given restrictions (self-orthogonal, self-complementary, etc.). Many published results are based on calculations with Q-Extension and most of them are verified with other software, programs and theoretical proofs (for example [16]).

An ${[n,k]}_q$ code $\mathcal{C}$ is a linear code over ${\mathbb{F}}_q$ of length n and dimension k. $\mathcal{C}$ is called an ${[n,k,d]}_q$ code if it has minimum weight d. A $k\times n$ matrix over ${\mathbb{F}}_q$ whose rows form a basis of $\mathcal{C}$ is called a generator matrix of $\mathcal{C}$. A code $\mathcal{C}$ is projective if any two columns of G are linearly independent. Consequently, G has no all-zero column if $\mathcal{C}$ is projective. Two q-ary codes are equivalent if one can be obtained from the other by a sequence of the following transformations: (1) a permutation of the coordinate positions of all codewords; (2) a multiplication of a coordinate of all codewords with a nonzero element of ${\mathbb{F}}_q$; (3) a field automorphism. The set of all automorphisms of $\mathcal{C}$ forms the automorphism group of $\mathcal{C}$, denoted by $\mathrm{Aut}\left(\mathcal{C}\right)$. Two codes are monomially equivalent if one can be obtained from the other by a sequence of the transformations (1) and (2). The equivalent codes over a prime field are monomially equivalent. For $i=1,2$, let $G_i$ be a generator matrix of a projective ${[n,k,d]}_q$ code ${\mathcal{C}}_i$ and let $K_i$ be the n-set in $\mathrm{PG}(k-1,q)$ corresponding to the n columns of $G_i$. Then ${\mathcal{C}}_1$ and ${\mathcal{C}}_2$ are monomially equivalent if and only if $K_1\sim K_2$.

For a projective ${[n,3,d]}_q$ code $\mathcal{C}$ with a generator matrix G, the n columns of G can be considered as an $(n,n-d)$-arc in $\mathrm{PG}(2,q)$ and vice versa. For more details about the equivalence between sets in projective spaces over a finite field and linear codes, see Chapter 16 in [17].

An $(f,m)$-blocking set B in $\mathrm{PG}(2,q)$ is an f-set such that each line contains at least m points of B and some lines contain exactly m points of B. If $n+f=q^2+q+1$ and $r+m=q+1$, then the complement $K^c$ of an $(n,r)$-arc K in PG$(2,q)$ is an $(f,m)$-blocking set. Thus, $(n,r)$-arcs and $(f,m)$-blocking sets are equivalent objects.

Lemma 1

([17,18]). Let $\mathcal{C}$ be a projective ${[n,3]}_q$ code with a generator matrix G and let K be the n-set in PG$(2,q)$ given by the n columns of G. Then, $\mathcal{C}$ has minimum weight d if and only if K is an $(n,n-d)$-arc (equivalently, $K^c$ is a $(q^2+q+1-n,q+1-(n-d))$-blocking set) in $\mathrm{PG}(2,q)$.

For an ${[n,k,d]}_q$ code, we have $n\ge d+\lceil \frac{d}{q}\rceil +\cdots +\lceil \frac{d}{q^{k-1}}\rceil$, which is called the Griesmer bound. A linear code attaining the Griesmer bound is called a Griesmer code. Since Griesmer ${[n,k,d]}_q$ codes with $d\le q^{k-1}$ are projective [18], the $(29,5)$-arcs in PG$(2,7)$ and the ${[29,3,24]}_7$ codes are equivalent objects. For a set K in $\mathrm{PG}(2,q)$, a line is called an i-line if it meets K in exactly i points. We denote $a_i\left(K\right)$ (or simply $a_i$ when no confusion arises) the number of i-lines of K. The list $\left\{a_i\right\}$ is called the spectrum of K. Let $\mathrm{Aut}\left(K\right)$ be the automorphism group of K, that is, the set of projectivities $\tau$ in $PGL(3,q)$ with $\tau \left(K\right)=K$. The spectra, together with the order of the automorphism group for the 22 projectively inequivalent $(29,5)$-arcs in $\mathrm{PG}(2,7)$ are given in Table 3.

In Section 3, we construct the arcs $K_1,\dots ,K_{22}$ in Table 3 without computer. We show how to construct these arcs from the well-known arc found by Barlotti [10] by exchanging some points, an operation called transition. From the geometrical point of view, we show how to distinguish $K_8$ and $K_9$ (also $K_{15}$ and $K_{16}$), which can not be distinguished from their spectra and automorphism group orders.

In Section 4, we generalize some of the $(29,5)$-arcs given in Section 3 to $(q^2-3q+1,q-2)$-arcs (equivalently, $(4q,3)$-blocking sets) in $\mathrm{PG}(2,q)$.

Remark 1.

We have also confirmed that there are exactly 194 inequivalent $(36,6)$-arcs in $\mathrm{PG}(2,7)$ by exhaustive search using the package Q-Extension as in Table 2. For the 194 inequivalent $(36,6)$-arcs in $\mathrm{PG}(2,7)$, see http://mars39.lomo.jp/opu/36_3_30.txt.

Remark 2.

A similar interesting problem in the real projective plane is so called the real configuration problem. A configuration of lines and points is called an $\left(n_k\right)$ configuration if it consists of n lines and n points, each of which is incident to exactly k of the other type. It is called geometric if these are points and lines in the real projective plane. Especially, the problem concerning the existence of geometric $\left(n_4\right)$ configurations remains open only for the case $n=23$, see [19].

Remark 3.

The $(29,5)$-arc $K_2$ in Table 3 is given as $K_2=C\cup \mathcal{I}\left(C\right)$, in Section 3, where C is a conic and $\mathcal{I}\left(C\right)$ is the interior of C. In [20], they gave a realization of the configuration (${21}_4$) and Coxeter’s coordinates of them in the plane PG$(2,7)$, which is equals to $\mathcal{I}\left(C\right)$ where C is the conic defined by the equation $x^2+y^2+z^2=0$.

2. Algorithms in the Package Q-Extension

We have proved that there are exactly 22 inequivalent $(29,5)$-arcs (and also 194 inequivalent $(36,6)$-arcs) in PG$(2,7)$ by exhaustive computer search using the package Q-Extension [14]. It is available on the web page http://www.moi.math.bas.bg/~iliya/Q_ext.htm of the first author for fields with $q\le 5$ elements (for larger fields write to Iliya Bouyukliev). In this section we briefly describe the algorithms in the package. We present the explanation in terms of linear codes because Q-Extension is a software for construction and investigations of linear codes. We discuss the background and give the main ideas.

Each linear code is completely determined by its generator matrix. The main problem we solve is how to construct generator matrices of all inequivalent linear codes with length n, dimension k, and minimum distance d over the field ${\mathbb{F}}_p$, where p is a prime. If we know a part of the generator matrix, the problem will be much easier. This previously given part (submatrix) can be a generator matrix of a residual code or the identity matrix of size k, since any code has a generator matrix in systematic form.

Let G be a generator matrix of an ${[n,k,d]}_p$ code $\mathcal{C}$. Then the residual code $Res(\mathcal{C},c)$ of $\mathcal{C}$ with respect to a codeword c is the code generated by the restriction of G to the columns where c has zero entries.

Lemma 2

([21]). Let $\mathcal{C}$ be an $[n,k,d]$ code over ${\mathbb{F}}_p$ and let $c\in \mathcal{C}$ be a codeword of weight $w<(p/(p-1\left)\right)d$. Then $Res(\mathcal{C},c)$ is an $[n-w,k-1,d^{\prime }]$ code with $d^{\prime }\ge d-w+\lceil w/p\rceil$.

Let $\mathcal{C}$ be an ${[n,k,d]}_p$ code with generator matrix G and let $G_0$ be a $k\times (n-m)$ matrix with rows $g_1,\cdots ,g_k$ such that $G=\left(G_{0}X\right)$. The main idea of our approach is to construct all inequivalent codes with given parameters on the current step and to use these codes (their generator matrices) in the next step of the extension.

Let ${\Omega }_1$ be the set consisting of the codes generated by a matrix in the form

$$G_1=\left(\begin{array}{cc}{g}_1& a_{11}\cdots a_{1m}\\ g_2\\ ⋮& O\\ g_k\end{array}\right),$$

where O is the zero matrix, and $a=(a_{11},\cdots ,a_{1m})$ is such a vector that the first row of G has weight $\ge d$. We can assume that $a_{11}=\dots =a_{1j}=0$ and $a_{1,j+1}=\dots ,a_{1m}=1$. The codes from ${\Omega }_1$ form the root of our search tree. We define ${\Omega }_s$ to be the set of all codes which have a generator matrix of the form

$$G_s=\left(\begin{array}{cccc}{g}_1& a_{11}& \cdots & a_{1m}\\ ⋮& ⋮& \ddots & ⋮\\ g_s& a_{s1}& \cdots & a_{sm}\\ g_{s+1}\\ ⋮& & O& \\ g_k\end{array}\right),$$

such that the first s rows of $G_s$ generate an ${[n,s]}_p$ code whose minimum weight is at least d.

We use the equivalence of codes in terms of group action on a proper set. We consider the action of the group $M_n$ of all monomial matrices of size n on the set $\Omega$ of linear codes with length n over the field ${\mathbb{F}}_p$. This action induces an equivalence relation in $\Omega$ as two codes ${\mathcal{C}}_1,{\mathcal{C}}_2\in \Omega$ are equivalent if and only if they belong to the same orbit. Hence the equivalence classes for the defined relation are the orbits with respect to this action. The set of matrices $\sigma \in M_n$ such that $\mathcal{C}\sigma =\mathcal{C}$ form the automorphism group $\mathrm{Aut}\left(\mathcal{C}\right)$ of the linear code $\mathcal{C}$.

The nodes in our search tree are objects from the search space $\Omega ={\Omega }_1\cup {\Omega }_2\cup \cdots \cup {\Omega }_k$. From a linear code $A\in {\Omega }_{s-1}$ corresponding to the node $\overline{A}$, we obtain linear codes from ${\Omega }_s$ which are children of the code A. We denote the set of inequivalent children by $\mathit{Child}\left(A\right)$. The elements of $\mathit{Child}\left(A\right)$ correspond to the nodes of the next level which are connected to $\overline{A}$ by edges. To find only the inequivalent children in ${\Omega }_s$, $s<k$, we use a special type of equivalence which we call equivalence up to extension. This type of equivalence is defined considering the action of the subgroup of $M_n$ consisting of the monomial matrices of block-diagonal form with two blocks of sizes $n-m$ and m, respectively. Obviously, such a matrix acts on the first $n-m$ coordinates and the last m coordinates of the given linear code $\mathcal{C}$ separately.

It is easy to see that two equivalent codes up to extension have equivalent children. Practically, the rule $A\to \mathit{Child}\left(A\right)$, which connects all children to a code, defines our search tree. The execution of the algorithm can be considered as traversing the search tree and visiting all nodes through the edges. This can be done by a depth first search.

We use the algorithm only in the case when the search tree is not so big. That is why our isomorph rejection approach is very natural, and it is known as isomorph rejection with recorded objects [22]. The basic idea of this technique is to keep a global record R of the objects seen so far during traversal of a search tree. Whenever an object $\mathcal{C}$ is constructed, it is checked for equivalence against the recorded objects in R. If $\mathcal{C}$ is equivalent to an object in R, then the subtree rooted at $\mathcal{C}$ is pruned. This approach is fast enough for us because of concepts of canonical form. The use of canonical form reduces the problem of equivalence test of codes to comparison of codes (for more details see [22]).

We obtain the automorphism group and a canonical form of a given code $\mathcal{C}$ using a modification of the algorithm presented in [23]. This algorithm gives the order of the group, a set of generating elements, and a canonical permutation. One of the advantages of the algorithm is the effective construction of child codes. We give an example.

Example 1.

Let us try to construct all ${[13,3,9]}_3$ codes taking their generator matrices in a systematic form:

$$G=\left(\begin{array}{c}100\\ 010& X\\ 001\end{array}\right).$$

Any row in the unknown matrix X must have at least eight nonzero coordinates. For a row a in X, consider the triple $(x_0,x_1,x_2)$, where $x_i$ is the number of coordinates in a equal to i, $i=0,1,2$. We are looking for all triples with $x_0+x_1+x_2=10$ and $x_1+x_2\ge 8$. The number of nonnegative triples which satisfy these constrains is 30. They form the set $S_1$ of possible solutions.

Without loss of generality we can take the first row of X to be $\left(0011111111\right)$, $\left(0111111111\right)$ or $\left(1111111111\right)$. This means that the root ${\Omega }_1$ consists of three codes with generator matrices

$$\left(\begin{array}{cc}100& 0011111111\\ 010& 0000000000\\ 001& 0000000000\end{array}\right),\left(\begin{array}{cc}100& 0111111111\\ 010& 0000000000\\ 001& 0000000000\end{array}\right),\left(\begin{array}{cc}100& 1111111111\\ 010& 0000000000\\ 001& 0000000000\end{array}\right).$$

Consider in detail the first node. We can divide the matrix X into two parts, $X=\left(X_1{X}_2\right)$ where $X_1$ and $X_2$ have 2 and 8 columns respectively. Using the possible solutions from $S_1$, the algorithm finds by exhaustive search all possible solutions for the next rows as tuples of triples $\{(x_{00},x_{01},x_{02}),(x_{10},x_{11},x_{12})\}$ such that $x_{0i}=\left|\{b_j=i,1\le j\le 2\}\right|$, $x_{1i}=\left|\{b_j=i,3\le j\le 10\}\right|$, where $b=(b_1,b_2,\cdots ,b_{10})$ is the second or third row of X. The constrains for $x_{ij}$ are

$$x_{00}+x_{01}+x_{02}=2,x_{10}+x_{11}+x_{12}=8,x_{0i}+x_{1i}=x_i,i=0,1,2.$$

We denote by $S_2$ the set of all possible solutions in this step. Furthermore, the code generated by the vectors $\left(100011111111\right)$ and $\left(010\right|b)$ must have minimum distance at least 9 which reduces the possibilities and the algorithm obtains

$$S_2=\{\{(0,2,0),(2,3,3)\},\{(0,1,1),(2,3,3)\},\{(0,0,2),(2,3,3)\}\}.$$

This gives us the information that the first two coordinates of b are not zeros, but two of the other 8 coordinates are zeros, three of them are 1 and three are equal to 2. It turns out that, up to a permutation, the second row of X must be $\left(1100111222\right)$, $\left(1200111222\right)$ or $\left(2200111222\right)$. The codes which correspond to these solutions have generator matrices

$$\left(\begin{array}{cc}100& 0011111111\\ 010& 1100111222\\ 001& 0000000000\end{array}\right),\left(\begin{array}{cc}100& 0011111111\\ 010& 1200111222\\ 001& 0000000000\end{array}\right),\left(\begin{array}{cc}100& 0011111111\\ 010& 2200111222\\ 001& 0000000000\end{array}\right).$$

Obviously, these three codes are equivalent, therefore there is only one node in the second level of the tree connected with the considered root node.

Now we divide the matrix X into four parts (cells), $X=\left(X_1{X}_{20}{X}_{21}{X}_{22}\right)$ where $X_{20}$, $X_{21}$ and $X_{22}$ have 2, 3 and 3 columns respectively. One possible solution for the matrix G is

$$\left(\begin{array}{cc}100& 0011111111\\ 010& 1100111222\\ 001& 1212012012\end{array}\right).$$

This solution turns out to be unique up to equivalence. The solution for the third row comes from $\{(0,1,1),(2,3,3)\}\in S_2$. The algorithm also provides that the code $\mathcal{C}$ must be projective. It is easy to prove that the matrix G in systematic form cannot have rows with weights 9 and 10 (the algorithm proves this by exhaustive search).

The same code can be constructed using as a prescribed part its residual code with respect to a codeword of weight 9. The residual code has parameters ${[4,2,3]}_3$. There is a unique ternary code with these parameters, so we are looking for a generator matrix of $\mathcal{C}$ in the form

$$\left(\begin{array}{cc}0000& 111111111\\ 1011& \cdots \\ 0112& \cdots \end{array}\right).$$

The algorithm in this case works in a similar way and it is even more effective, but it is a little bit more complicated to explain.

Consider now the construction of the ${[29,3,24]}_7$ codes. If $\mathcal{C}$ is a code with these parameters, then its residual code with respect to a codeword of weight 24 is a ${[5,2,4]}_7$ code. It is easy to prove (even by hand) that the code with a generator matrix $\left(\begin{array}{c}10111\\ 01123\end{array}\right)$ is, up to equivalence, the only ${[5,2,4]}_7$ code. Therefore we are looking for a generator matrix of $\mathcal{C}$ of the form

$$G=\left(\begin{array}{cc}00000& 111111111111111111111111\\ 10111& \cdots \\ 01123& \cdots \end{array}\right).$$

The program finds all inequivalent solutions in about 23 hours on a computer with Intel Xeon E5-2640 processor. The constructed tree consists of 8 nodes on the second level and 22 nodes on the third level. In this case the tree is not big, but finding solutions for the last level is computationally expensive. Since this search is exhaustive, we can conclude that there are exactly 22 ${[29,3,24]}_7$ codes up to equivalence, which proves Theorem 1.

Remark 4.

Many problems for classification of combinatorial objects are solved using computer programs. But there are only a few more general software packages for such classification, for example “Split” by David Jaffe [24] and “Orbiter” by Anton Betten [25]. Q-Extension is convenient for our purposes, we have experience with it and therefore we use exactly this package in our classification.

3. Construction of $(\mathbf{29},\mathbf{5})$-Arcs in $\mathrm{PG}(\mathbf{2},\mathbf{7})$

We start with the conic

$$C=\left\{\mathbf{P}(1,a,a^2)\right|a\in {\mathbb{F}}_q\}\cup \left\{\mathbf{P}(0,0,1)\right\}.$$

A line ℓ in $\mathrm{PG}(2,q)$ is called external, tangent or secant to C if $|C\cap \ell |=0$, 1 or 2, respectively. For odd q, a point $P\notin C$ in $\mathrm{PG}(2,q)$ is called internal or external if the number of tangent lines on P is 0 or 2, respectively. Let $\mathcal{I}\left(C\right)$ (resp. $\mathcal{E}\left(C\right)$) be the set of all internal (resp. external) points of C. Then, $\left|\mathcal{I}\right(C\left)\right|=q(q-1)/2$, $\left|\mathcal{E}\right(C\left)\right|=q(q+1)/2$, see ([3] Chapter 8). The following construction of a $(\frac{q^2+q+2}{2},\frac{q+3}{2})$-arc in $\mathrm{PG}(2,q)$ is due to [10].

Theorem 2.

For q odd, let $K=\mathcal{I}\left(C\right)\cup C$. Then

(1)

K forms a $(\frac{q^2+q+2}{2},\frac{q+3}{2})$-arc in $\mathrm{PG}(2,q)$ with spectrum

$$(a_1,a_{(q+1)/2},a_{(q+3)/2})=(q+1,q(q-1)/2,q(q+1)/2).$$

(2)

$\mathrm{Aut}\left(K\right)\cong PGL(2,q)$ and $\left|\mathrm{Aut}\left(K\right)\right|=q(q^2-1)$.

Proof. 

The tangents, the secants and the external lines of C are 1-lines, $(q+3)/2$-lines and $(q+1)/2$-lines for the arc K, respectively. Recall that $\mathrm{Aut}\left(C\right)\cong PGL(2,q)$ [3]. Since any automorphism $\sigma$ of K satisfies $\sigma \left(\mathcal{E}\right(C\left)\right)=\mathcal{E}\left(C\right)$, $\sigma$ maps any tangent line of C to a tangent line. Then, $\sigma \left(C\right)=C$ and $\sigma \left(\mathcal{I}\right(C\left)\right)=\mathcal{I}\left(C\right)$. Hence, we get the assertion. □

Let $K_2$ be the above arc K for $q=7$. We denote the line $\left\{\mathbf{P}\right(x,y,z)\in \mathrm{PG}(2,q)\mid ax+by+cz=0\}$ by $[a,b,c]$ or $\left[abc\right]$. There is another simple construction of a $(29,5)$-arc in $\mathrm{PG}(2,7)$.

Lemma 3

(Example 2.3 in [15]). Let $B_0$ be the set of points on the lines $\left[100\right]$, $\left[010\right]$, $\left[001\right]$, $\left[111\right]$ together with the points $\mathbf{P}(-1,1,1)$, $\mathbf{P}(1,-1,1)$. Then, the complement of $B_0$ forms a $(q^2-3q+2,q-2)$-arc if q is even and a $(q^2-3q+1,q-2)$-arc if q is odd.

The arc $K_{21}$ given below is such an arc obtained by the above lemma for $q=7$. We give another construction for $K_{21}$ later. See Section 4 for the spectra of the arcs in Lemma 3.

In the following, we show how to construct the arcs in Table 3 from $K_2=C\cup \mathcal{I}\left(C\right)$. For two $(29,5)$-arcs $K_i$ and $K_j$, we define the distance between them as

$$d(K_i,K_j)=\underset{K^{\prime }\sim K_j}{min}(29-|K_i\cap K^{\prime }\left|\right).$$

We also define the transition number of $K_i$ as

$$t\left(K_i\right)=\underset{K_j\nsim K_i}{min}d(K_i,K_j).$$

Then, one can obtain some arc $K_j(\nsim K_i)$ from $K_i$ by exchanging $t\left(K_i\right)$ or $t\left(K_j\right)$ points, denoted by $K_i\to K_j$, that is, $K_j=(K_i\backslash D)\cup A$ for some disjoint t-sets $D\subset K_i$ and $A\subset \mathrm{PG}(2,7)\backslash K_i$ with $t=t\left(K_i\right)$ or $t\left(K_j\right)$, see Table 4. In what follows, we discuss how to find the set D to be deleted from the arc $K_i$ and the set A to be added to get $K_j$ in Table 4. Here by $xyz$ we denote the point $\mathbf{P}(x,y,z)$ in $\mathrm{PG}(2,7)$. For two points P and Q, $⟨P,Q⟩$ denotes the line through P and Q. Table 4 follows from the following lemmas.

Table 4. Transition $K_i\to K_j=(K_i\backslash D)\cup A$, together with the values $t_i=t\left(K_i\right)$ and $t_j=t\left(K_j\right)$.

${\mathit{K}}_{\mathit{i}}$	${\mathit{t}}_{\mathit{i}}$	D	A	${\mathit{K}}_{\mathit{j}}$	${\mathit{t}}_{\mathit{j}}$	${\mathit{K}}_{\mathit{i}}$	${\mathit{t}}_{\mathit{i}}$	D	A	${\mathit{K}}_{\mathit{j}}$
$K_2$	3	001, 100, 111	131, 145, 153	$K_{20}$	2	$K_{22}$	1	146	120	$K_{14}$
$K_2$	3	136, 146, 151	131, 145, 153	$K_1$	3	$K_{22}$	1	133	120	$K_{15}$
$K_{20}$	2	115, 163, 165	015, 103, 106	$K_3$	3	$K_{22}$	1	165	120	$K_{16}$
$K_{20}$	2	101, 131	015, 130	$K_4$	2	$K_{22}$	1	101	120	$K_{17}$
$K_{20}$	2	124, 131	015, 114	$K_{10}$	2	$K_{22}$	1	152	120	$K_{19}$
$K_{20}$	2	131, 132	015, 122	$K_{18}$	2	$K_{22}$	1	131	111	$K_{21}$
$K_{20}$	2	132, 154	152, 164	$K_{22}$	1	$K_{17}$	1	134	014	$K_7$
$K_{10}$	2	102, 144	016, 141	$K_6$	2	$K_{17}$	1	113	014	$K_8$
$K_{22}$	1	113, 155	103, 105	$K_9$	2	$K_{14}$	1	126	130	$K_{11}$
$K_9$	2	145, 153	123, 135	$K_5$	2	$K_{14}$	1	104	130	$K_{13}$
$K_{21}$	1	102, 146	120, 140	$K_{12}$	2

Lemma 4.

$K_{20}=(K_2\backslash \{001,100,111\})\cup \{131,145,153\}$ and $t\left(K_2\right)=3$.

Proof. 

Since every external point Q of the conic C is on the three 5-lines (the secants through Q), we have $t\left(K_2\right)\ge 3$. We construct $K_{20}$ from $K_2$ by three point exchanges, which implies $t\left(K_2\right)=3$. Note that the tangents of C are the 1-lines for $K_2$. Take three points $P_1,P_2,P_3$ on the conic C. Since $\mathrm{Aut}\left(C\right)$ is 3-transitive, we may assume that $P_1=161$, $P_2=142$, $P_3=124$. Let ${\ell }_i$ be the tangent of C at $P_i$ for $i=1,2,3$, i.e., ${\ell }_1=\left[121\right]$, ${\ell }_2=\left[134\right]$, ${\ell }_3=\left[162\right]$, and let $Q_k={\ell }_i\cap {\ell }_j$ for $\{i,j,k\}=\{1,2,3\}$. For $i=1,2,3$, the line ${\ell }_i^{\prime }=⟨P_i,Q_i⟩$ is a secant meeting C in $P_i$ and $P_{i+3}$ say. Then, $Q_1=131$, $Q_2=145$, $Q_3=153$, ${\ell }_1^{\prime }=\left[106\right]$, ${\ell }_2^{\prime }=\left[150\right]$, ${\ell }_3^{\prime }=\left[013\right]$, $P_4=111$, $P_5=001$, $P_6=100$. Taking $D=\{P_4,P_5,P_6\}$ and $A=\{Q_1,Q_2,Q_3\}$, one obtains the transition $K_2\to K_{20}$. Actually, the tangents at $P_4,P_5,P_6$ are the 0-lines and the tangents at $P_7=132$ and $P_8=154$ are the 1-lines for $K_{20}$, where $C=\{P_1,P_2,\dots ,P_8\}$. □

We confirmed that $\left|\mathrm{Aut}\right(K_{20}\left)\right|=6$ (and similar for the other values of $\left|\mathrm{Aut}\right|$ in Table 3 by computer. In what follows, let $C=\{P_1,P_2,\dots ,P_8\}$, ${\ell }_1^{\prime }$, ${\ell }_2^{\prime }$, ${\ell }_3^{\prime }$, $Q_1$, $Q_2$, $Q_3$, be as in the proof of Lemma 4 and let ${\ell }_i$ be the tangent at $P_i$ to C for $1\le i\le 8$ and ${\ell }_{ij}=⟨P_i,P_j⟩$ for $1\le i<j\le 8$. Then, ${\ell }_4=\left[151\right]$, ${\ell }_5=\left[100\right]$, ${\ell }_6=\left[001\right]$, ${\ell }_7=\left[144\right]$, ${\ell }_8=\left[112\right]$, ${\ell }_{12}=\left[165\right]$, ${\ell }_{13}=\left[143\right]$, ${\ell }_{14}=l_1^{\prime }=\left[106\right]$, ${\ell }_{18}=\left[154\right]$, ${\ell }_{28}=\left[126\right]$, ${\ell }_{23}=\left[111\right]$, ${\ell }_{24}=\left[142\right]$, ${\ell }_{25}=l_2^{\prime }=\left[150\right]$, ${\ell }_{36}=l_3^{\prime }=\left[013\right]$, ${\ell }_{37}=\left[156\right]$, ${\ell }_{38}=\left[105\right]$, ${\ell }_{45}=\left[160\right]$, ${\ell }_{46}=\left[016\right]$, ${\ell }_{56}=\left[010\right]$, ${\ell }_{57}=\left[120\right]$, ${\ell }_{68}=\left[014\right]$, ${\ell }_{78}=\left[161\right]$. Note that ${\ell }_{14},{\ell }_{57},{\ell }_{68}$ are the secants through $Q_1$. Let $Q_{ij}={\ell }_i\cap {\ell }_j$ apart from $Q_1=Q_{23}$, $Q_2=Q_{13}$, $Q_3=Q_{12}$. For any point R and for a given arc $K_i$, we state that R is of type $i_1^{j_1}{i}_2^{j_2}\cdots$ if there exist $j_1$$i_1$-lines and $j_2$$i_2$-lines and so on through R for $K_i$.

Lemma 5.

$K_1=(K_2\backslash \{136,146,151\})\cup \{131,145,153\}$ and $t\left(K_1\right)=3$.

Proof. 

Let $R_i={\ell }_i^{\prime }\cap {\ell }_{jk}$ for $\{i,j,k\}=\{1,2,3\}$. Then, $R_1=151$, $R_2=146$, $R_3=136$. Taking $D=\{R_1,R_2,R_3\}$ and $A=\{Q_1,Q_2,Q_3\}$, one can get the transition $K_2\to K_1$. The tangents at $P_1,P_2,P_3$ are 3-lines for $K_1$, while the other five tangents remain 1-lines. The three external lines $⟨R_i,R_j⟩$ ($1\le i<j\le 3$) to C form the 2-lines for $K_1$. Now, take $R\notin K_1$. Then the possible types of R are: $1^1{2}^1{3}^2{5}^4$, $1^1{3}^3{4}^1{5}^3$, $1^1{2}^1{3}^1{4}^2{5}^3$, $1^2{2}^1{5}^5$, $1^2{3}^1{4}^1{5}^4$, $2^2{3}^2{4}^1{5}^3$, $1^2{4}^3{5}^3$. So, $t\left(K_1\right)\ge 3$. Now, by the transition $K_2\to K_1$, we get $K_1$ by exchanging three points. Hence, we determine $t\left(K_1\right)=3$. □

For a point $R\notin K_{20}$, the possible types of R are: $1^1{3}^2{4}^3{5}^2$, $0^1{3}^1{4}^4{5}^2$, $0^1{3}^2{4}^2{5}^3$, $0^2{4}^1{5}^5$, $0^1{1}^1{4}^2{5}^4$, $0^1{3}^2{4}^2{5}^3$, $1^2{4}^3{5}^3$. Since every point out of $K_{20}$ is on at least two 5-lines, we get $t\left(K_{20}\right)\ge 2$. By exhaustive computer search, we get the following.

Lemma 6.

$t\left(K_i\right)\ge 2$ for $i=4,5,6,9,10,12,18,20$.

Lemma 7.

$K_4=(K_{20}\backslash \{101,131\})\cup \{015,130\}$ and $t\left(K_4\right)=t\left(K_{20}\right)=2$.

Proof. 

Let $S_1={\ell }_{57}\cap {\ell }_1$, $S_2={\ell }_{68}\cap {\ell }_1$ and $R_4={\ell }_{56}\cap {\ell }_1^{\prime }$. Then, $S_1=130$, $S_2=015$, $R_4=101$. Taking $D=\{Q_1,R_4\}$ and $A=\{S_1,S_2\}$, one can get the transition $K_{20}\to K_4$. Since the two tangents ${\ell }_5$ and ${\ell }_6$ contain the points $S_2$ and $S_1$, respectively, the two tangents at ${\ell }_5$, ${\ell }_6$ are 1-lines for $K_4$, while the tangent at ${\ell }_4$ remains a 0-line. The two 1-lines for $K_{20}$ remain 1-lines for $K_4$. Now, the transition $K_{20}\to K_4$ yields $t\left(K_4\right)=t\left(K_{20}\right)=2$ by Lemma 6. □

Lemma 8.

$K_{18}=(K_{20}\backslash \{131,132\})\cup \{015,122\}$ and $t\left(K_{18}\right)=2$.

Proof. 

Take $Q_{18}={\ell }_1\cap {\ell }_8=122$. Setting $D=\{Q_1,P_7\}$ and $A=\{S_2,Q_{18}\}$, we get the transition $K_{20}\to K_{18}$. As for the 0-lines ${\ell }_4$, ${\ell }_5$, ${\ell }_6$ for $K_{20}$, two lines ${\ell }_4$ and ${\ell }_6$ are also 0-lines for $K_{18}$, but ${\ell }_5$ is a 1-line for $K_{18}$. Two 1-lines ${\ell }_7$ and ${\ell }_8$ for $K_{20}$ are a 0-line and a 2-line for $K_{18}$, respectively. The other 2-lines for $K_{18}$ are ${\ell }_2$ and ${\ell }_3$. The transition $K_{20}\to K_{18}$ yields $t\left(K_{18}\right)=2$ by Lemma 6. □

Lemma 9.

$K_{10}=(K_{20}\backslash \{124,131\})\cup \{015,114\}$ and $t\left(K_{10}\right)=2$.

Proof. 

Let $T_1={\ell }_{37}\cap {\ell }_1$, $T_2={\ell }_{38}\cap {\ell }_1$. Then, $T_1=S_2=015$, $T_2=114$. Taking $D=\{Q_1,P_3\}$ and $A=\{T_1,T_2\}$, one can get the transition $K_{20}\to K_{10}$. Since the tangent ${\ell }_5$ contains $T_1$, it is a 1-line for $K_{10}$, while the tangents ${\ell }_4$ and ${\ell }_6$ remain 0-lines. The other 1-lines for $K_{10}$ are the tangents ${\ell }_3$ and ${\ell }_8$. The transition $K_{20}\to K_{10}$ yields $t\left(K_{10}\right)=2$ by Lemma 6. □

Lemma 10.

$K_{22}=(K_{20}\backslash \{132,154\})\cup \{052,164\}$.

Proof. 

Take $Q_{24}={\ell }_2\cap {\ell }_4=164$ and $Q_{34}={\ell }_3\cap {\ell }_4=152$. Setting $D=\{P_7,P_8\}$ and $A=\{Q_{24},Q_{34}\}$, we get the transition $K_{20}\to K_{22}$. The tangent ${\ell }_4$ is a 0-line for $K_{20}$, but a 2-line for $K_{22}$, while the tangents ${\ell }_5$ and ${\ell }_6$ remain 0-lines. The tangents ${\ell }_7$ and ${\ell }_8$ are 1-lines for $K_{20}$, but 0-lines for $K_{22}$. □

Lemma 11.

$K_6=(K_{10}\backslash \{102,144\})\cup \{016,141\}$ and $t\left(K_6\right)=2$.

Proof. 

Let $V_1=⟨Q_2,P_4⟩\cap {\ell }_{23}$, $V_2=⟨Q_2,P_4⟩\cap {\ell }_{13}$, $V_3=⟨Q_2,P_5⟩\cap {\ell }_{46}$, $V_4=⟨Q_2,P_5⟩\cap {\ell }_{14}$. Then, $V_1=016$, $V_2=102$, $V_3=144$, $V_4=141$. Taking $D=\{V_2,V_3\}$ and $A=\{V_1,V_4\}$, one can get the transition $K_{10}\to K_6$. The 0-lines for $K_{10}$ are also 0-lines for $K_6$. The tangent ${\ell }_3$ remains a 1-line, but the other 1-lines for $K_{10}$ are 2-lines for $K_6$. The transition $K_{10}\to K_6$ yields $t\left(K_6\right)=2$ by Lemma 6. □

Lemma 12.

$K_9=(K_{22}\backslash \{113,155\})\cup \{103,105\}$ and $t\left(K_9\right)=2$.

Proof. 

Take $W_1={\ell }_{56}\cap {\ell }_2=103$, $W_2={\ell }_{56}\cap {\ell }_3=105$, $W_3={\ell }_{13}\cap {\ell }_{45}=113$, $W_4={\ell }_{12}\cap {\ell }_{46}=155$. Setting $D=\{W_3,W_4\}$ and $A=\{W_1,W_2\}$, we get the transition $K_{22}\to K_9$. The tangents ${\ell }_5$, ${\ell }_6$ are 0-lines for $K_9$ and the tangents ${\ell }_7$, ${\ell }_8$ are 1-lines for $K_9$. We note that three of the four 2-lines ${\ell }_4$, ${\ell }_{45}$, ${\ell }_{46}$ and $\left[131\right]$ are concurrent at the point $P_4$. The transition $K_{22}\to K_9$ yields $t\left(K_9\right)=2$ by Lemma 6. □

Lemma 13.

$K_5=(K_9\backslash \{145,153\})\cup \{123,135\}$ and $t\left(K_5\right)=2$.

Proof. 

Take the two points ${\ell }_{13}\cap {\ell }_4=135$ and ${\ell }_{12}\cap {\ell }_4=123$ for the set A to be deleted from $K_9$. Setting $D=\{Q_2,Q_3\}$, we get the transition $K_9\to K_5$. The 0-lines for $K_9$ are also 0-lines for $K_5$. The tangents ${\ell }_7$ and ${\ell }_8$ are 2-lines for $K_5$ and the unique 1-line for $K_5$ is ${\ell }_1$. The transition $K_9\to K_5$ yields $t\left(K_5\right)=2$ by Lemma 6. □

Lemma 14.

$K_{14}=(K_{22}\backslash \left\{146\right\})\cup \left\{120\right\}$, $K_{15}=(K_{22}\backslash \left\{133\right\})\cup \left\{120\right\}$, $K_{16}=(K_{22}\backslash \left\{165\right\})\cup \left\{120\right\}$, $K_{17}=(K_{22}\backslash \left\{101\right\})\cup \left\{120\right\}$, $K_{19}=(K_{22}\backslash \left\{152\right\})\cup \left\{120\right\}$.

Proof. 

Take the point $Q_{34}={\ell }_3\cap {\ell }_4=152$ and let $L=⟨Q_{34},R_4⟩=\left[136\right]$, $U=L\cap {\ell }_2=120$ and $K^{\prime }=K\cup \left\{U\right\}$. Then, $K^{\prime }$ has spectrum $(a_0,a_1,a_2,a_3,a_4,a_5,a_6)=(3,1,1,5,14,32,1)$ and L is the unique 6-line for $K^{\prime }$. The 1-points of L other than U are $U_1(=R_2)=146$, $U_2=133$, $U_3=165$, $U_4(=R_4)=101$, $U_5(=Q_{34})=152$. Then, $K_{13+j}=K^{\prime }\backslash \left\{U_j\right\}$ for $1\le j\le 4$ and $K_{19}=K^{\prime }\backslash \left\{U_5\right\}$. As can be seen in Table 3, $K_{15}$, $K_{16}$ and $K_{17}$ have the same spectrum. Nevertheless, one can distinguish them as follows. The 3-lines for $K_{15}$ are ${\ell }_1$, ${\ell }_{18}$, ${\ell }_{45}$, ${\ell }_{56}$, ${\ell }_{57}$, ${\ell }_{78}$. And there are two points on three 3-lines; the point 106 on ${\ell }_1$, ${\ell }_{56}$, ${\ell }_{78}$ and the point $P_5$ on ${\ell }_{45}$, ${\ell }_{56}$, ${\ell }_{57}$. As for $K_{16}$, the 3-lines are ${\ell }_{24}$, ${\ell }_{45}$, ${\ell }_{46}$, ${\ell }_{56}$, $\left[123\right]$, ${\ell }_1$ and there is only one point on three 3-lines; the point $P_4$ on the three lines ${\ell }_{24}$, ${\ell }_{45}$, ${\ell }_{46}$. Meanwhile, the 3-lines for $K_{17}$: ${\ell }_1$, ${\ell }_{28}$, ${\ell }_{37}$, ${\ell }_{45}$, ${\ell }_{46}$, ${\ell }_{78}$ form a 6-arc of lines (no three of which are concurrent). Thus, $K_{15}$, $K_{16}$ and $K_{17}$ are projectively inequivalent. $K_{19}$ and $K_{20}$ can be also distinguished similarly as follows. Let $\mathcal{L}$ and ${\mathcal{L}}^{\prime }$ be the sets of 3-lines for $K_{19}$ and $K_{20}$, respectively. Then, ${\mathcal{L}}^{\prime }=\{{\ell }_1,{\ell }_2,{\ell }_3,{\ell }_{45},{\ell }_{46},{\ell }_{56}\}$ is a 6-arc of lines, but $\mathcal{L}=\{{\ell }_1,{\ell }_3,{\ell }_{45},{\ell }_{46},{\ell }_{56},{\ell }_{78}\}$ is not, for $106=l_1\cap {\ell }_{56}\cap {\ell }_{78}$ and $110=l_3\cap {\ell }_{45}\cap {\ell }_{78}$. Hence, $K_{19}$ and $K_{20}$ are projectively inequivalent. □

Lemma 15.

$K_{21}=(K_{22}\backslash \left\{131\right\})\cup \left\{111\right\}$.

Proof. 

Taking $D=\left\{Q_1\right\}$ and $A=\left\{P_4\right\}$, we get the transition $K_{22}\to K_{21}$. The tangents ${\ell }_5$, ${\ell }_6$, ${\ell }_7$, ${\ell }_8$, no three of which are concurrent, remain 0-lines. The two 0-points out of the 0-lines are ${\ell }_{23}\cap {\ell }_1=106$ and $Q_1$. It turns out that $K_{21}$ is projectively equivalent to the arc constructed in Lemma 3. The tangent ${\ell }_4$ is the 2-line for $K_{22}$, but a 3-line for $K_{21}$. □

Lemma 16.

$K_7=(K_{17}\backslash \left\{134\right\})\cup \left\{014\right\}$, $K_8=(K_{17}\backslash \left\{113\right\})\cup \left\{014\right\}$.

Proof. 

Take the points $Q_{24}={\ell }_2\cap {\ell }_4=164$ and $X=⟨Q_{24},R_4⟩\cap {\ell }_3=014$, where $R_4={\ell }_{56}\cap {\ell }_1^{\prime }$, and let $K_{17}^{\prime }=K_{17}\cup \left\{X\right\}$. Then, the arc $K_{17}^{\prime }$ has spectrum $(a_0,a_1,a_2,a_3,a_4,a_5,a_6)=(2,2,2,6,10,34,1)$ and the unique 6-line for $K^{\prime }$ is $L_1=⟨X,U⟩=\left[131\right]$. The 1-points of $L_1$ other than X are $X_1=134$, $X_2=113$, $X_3=162$, $X_4=155$, $X_5=120$. Then, $K_7=K_{17}^{\prime }\backslash \left\{X_1\right\}$ and $K_8=K_{17}^{\prime }\backslash \left\{X_2\right\}$. $K_{17}^{\prime }\backslash \left\{X_3\right\}$, $K_{17}^{\prime }\backslash \left\{X_4\right\}$, $K_{17}^{\prime }\backslash \left\{X_5\right\}$ are projectively equivalent to $K_7$, $K_8$, $K_{17}$, respectively. We can distinguish $K_8$ and $K_9$ as follows. The 2-lines for $K_8$ are ${\ell }_4$, ${\ell }_{28}$, ${\ell }_{45}$, ${\ell }_{56}$, which form a 4-arc of lines. On the other hand, the 2-lines for $K_9$ are ${\ell }_4$, ${\ell }_{45}$, ${\ell }_{46}$, $L_1$, the first three of which are concurrent at the point $P_4$. □

Lemma 17.

$K_{11}=(K_{14}\backslash \left\{126\right\})\cup \left\{130\right\}$, $K_{13}=(K_{14}\backslash \left\{104\right\})\cup \left\{130\right\}$.

Proof. 

Let $E=l_1^{\prime }\cap {\ell }_2^{\prime }\cap {\ell }_3^{\prime }=141$, $L_2=⟨Q_{34},E⟩$ and $Y=L_2\cap {\ell }_1=130$, where $Q_{34}=152$. Then, $K_{14}^{\prime }=K_{14}\cup \left\{Y\right\}$ has spectrum $(a_0,a_1,a_2,a_3,a_4,a_5,a_6)=(3,0,2,8,9,34,1)$ and the unique 6-line for $K_{14}^{\prime }$ is $L_2=\left[125\right]$. The 1-points of $L_2$ other than Y are $Y_1=126$, $Y_2=104$, $Y_3=163$, $Y_4=115$, $Y_5=130$. Then, $K_{11}=K_{14}^{\prime }\backslash \left\{Y_1\right\}$ and $K_{13}=K_{14}^{\prime }\backslash \left\{Y_2\right\}$. $K_{14}^{\prime }\backslash \left\{Y_3\right\}$, $K_{14}^{\prime }\backslash \left\{Y_4\right\}$, $K_{14}^{\prime }\backslash \left\{Y_5\right\}$ are projectively equivalent to $K_{11}$, $K_{13}$, $K_{14}$, respectively. □

Lemma 18.

$K_{12}=(K_{21}\backslash \{102,146\})\cup \{120,140\}$ and $t\left(K_{12}\right)=2$.

Proof. 

Take the two points ${\ell }_{13}\cap {\ell }_2^{\prime }(=R_2)=146$ and ${\ell }_{13}\cap {\ell }_{56}(=V_2)=102$ for the 2-set D to be deleted and take $A=\{Q_{26}=120,Q_{46}=140\}$. Then, we get the transition $K_{21}\to K_{12}$. The 0-line ${\ell }_6$ for $K_{21}$ becomes a 2-line for $K_{12}$, while the tangents ${\ell }_5$, ${\ell }_7$, ${\ell }_8$ remain 0-lines. The arcs $K_{11}$ and $K_{12}$ are projectively inequivalent since their automorphism group orders are different. In addition, we can distinguish $K_{11}$ and $K_{12}$ as follows. The 2-lines for $K_{11}$ are $\left[101\right]$, ${\ell }_4$, ${\ell }_6$, having no common point. On the other hand, the 2-lines for $K_{12}$ are $\left[101\right]$, ${\ell }_5$, ${\ell }_6$, which are concurrent at the point 010. The transition $K_{21}\to K_{12}$ yields $t\left(K_{12}\right)=2$ by Lemma 6. □

Lemma 19.

$K_3=(K_{20}\backslash \{115,163,165\})\cup \{015,103,106\}$ and $t\left(K_3\right)=3$.

Proof. 

Take the points $Z_1={\ell }_{68}\cap {\ell }_1(=S_2)=015$, $Z_2={\ell }_{68}\cap {\ell }_{23}=115$, $Z_3={\ell }_{23}\cap {\ell }_1=106$, $Z_4={\ell }_{24}\cap {\ell }_3(=W_1)=103$, $Z_5={\ell }_{24}\cap {\ell }_{78}=165$, $Z_6={\ell }_{37}\cap ⟨Z_3,Q_1⟩=163$. Setting $D=\{Z_2,Z_5,Z_6\}$ and $A=\{Z_1,Z_3,Z_4\}$, we get the transition $K_{20}\to K_3$. The 0-lines ${\ell }_4$, ${\ell }_5$ for $K_{20}$ are 1-lines for $K_3$, while the ${\ell }_6$ remains a 0-line. The 1-lines ${\ell }_7$ and ${\ell }_8$ for $K_{20}$ are a 1-line and a 2-line for $K_3$, respectively. Now, there are only two points out of $K_3$, namely 122 and 165, which are on at most two 5-lines. The types of 122 and 165 are $2^1{3}^3{4}^2{5}^2$ and $2^1{3}^3{4}^2{5}^2$, respectively. Hence $t\left(K_3\right)\ge 2$. Suppose $t\left(K_3\right)=2$. Then, we have a transition $K_3\to (K_3\backslash \{Z,Z^{\prime }\})\cup \{122,165\}$ for some points $Z,Z^{\prime }\in K_3$. Since the five lines $⟨122,143⟩=\left[103\right]$, $⟨122,106⟩=\left[121\right]$, $⟨165,142⟩=\left[142\right]$, $⟨165,106⟩=\left[161\right]$, $⟨122,165⟩=\left[155\right]$ are 6-lines for $K_3\cup \{122,165\}$, the points Z and $Z^{\prime }$ must be on the five lines, which is impossible. Thus, $t\left(K_3\right)\ge 3$. Now, by the transition $K_{20}\to K_3$, we determine $t\left(K_3\right)=3$.

In summary, we have determined the transition numbers of each $K_i$ as in Table 4. Considering the graph with vertex set $\{K_i:t\left(K_i\right)=1\}$, where two vertices $K_i,K_j$ are joined if $d(K_i,K_j)=1$, we get Figure 1.

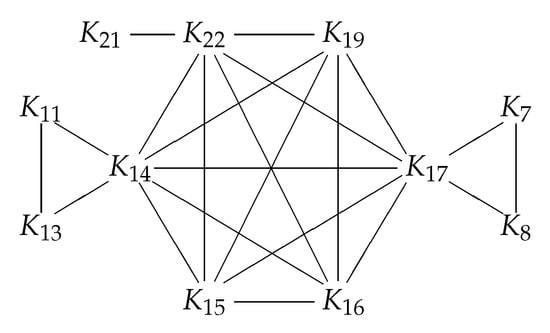
Figure 1. Graph of $(29,5)$-arcs with distance 1.

4. Construction of Some Generalized Arcs in $\mathrm{PG}(\mathbf{2},\mathbf{q})$

Recall from Lemma 1 that the complement of a $(b,3)$-blocking set B is a $(q^2+q+1-b,q-2)$ -arc in $\mathrm{PG}(2,q)$. When q is odd, for a $(b,3)$-blocking set B is known that $b=\left|B\right|\ge 4q$ if B contains a line [26]. The set $B_0$ for odd q in Lemma 3 is such a $(4q,3)$-blocking set.

In this section, we generalize some construction results in Section 3 by constructing some $(4q,3)$-blocking sets in $\mathrm{PG}(2,q)$ for odd q. Obviously, we have $a_i\left(K\right)=a_{q+1-i}\left(K^c\right)$, where $K^c$ is the complement of K in $\mathrm{PG}(2,q)$.

Theorem 3.

For odd $q\ge 5$, let C be a conic in $\mathrm{PG}(2,q)$. For any three points $P_1$, $P_2$, $P_3$ in C, let ${\ell }_i$ be the tangent of C through $P_i$ and ${\ell }_{ij}$ be the secant of C through $P_i$ and $P_j$, and let $P_{ij}={\ell }_i\cap {\ell }_j$ for $1\le i\le j\le 3$. Take any two points P and Q from the three points $P_{12}$, $P_{23}$, $P_{13}$, and let $B=C\cup {\ell }_{12}\cup {\ell }_{23}\cup {\ell }_{13}\cup \{P,Q\}$. Then $K=B^c$ is a $(q^2-3q+1,q-2)$-arc with spectrum

$(a_0,a_1,a_2,a_3)=(5,1,10,15)$ for $q=5$ and

$(a_0,a_{q-5},a_{q-4},a_{q-3},a_{q-2})=(3,q-3,\frac{(q-3)(q-4)}{2},2q,\frac{(q+5)(q-2)}{2})$ for $q\ge 7$.

Proof. 

Let $C=\{P_1,P_2,\cdots ,P_{q+1}\}$ be a conic in $\mathrm{PG}(2,q)$ and let ℓ be a line. If ℓ contains none of $P_1,P_2,P_3$, then ℓ meets ${\ell }_{12}\cup {\ell }_{23}\cup {\ell }_{13}$ at three points. Thus, $|\ell \cap B|\ge 3$. If ℓ contains exactly one of $P_1$, $P_2$, $P_3$, say $P^{\prime }$, ℓ meets ${\ell }_{12}\cup {\ell }_{23}\cup {\ell }_{13}$ at two points. Then, ℓ is a secant or a tangent of C. If ℓ is a secant of C, ℓ meets C at $P^{\prime }$ and another point. So, $|\ell \cap B|\ge 3$. If ℓ is a tangent of C, ℓ is ${\ell }_1$, ${\ell }_2$ or ${\ell }_3$, and ℓ contains at least one of the points P and Q. So, $|\ell \cap B|\ge 3$. If ℓ contains two of $P_1$, $P_2$ and $P_3$, then ℓ is ${\ell }_{12}$, ${\ell }_{23}$ or ${\ell }_{13}$. Thus, B is a $(4q,3)$-blocking set. Without loss of generality, we may take $P=P_{13}$ and $Q=P_{12}$. Assume $q\ge 7$. The $(q+1)$-lines for B are ${\ell }_{12}$, ${\ell }_{23}$, ${\ell }_{13}$. So, $a_{q+1}\left(B\right)=3$. The 6-lines are the secants through P or Q except $⟨P,P_2⟩$ and $⟨Q,P_3⟩$. Hence $a_6\left(B\right)=2\left(\frac{q-1}{2}-1\right)=q-3$. For $q=5$, the above $(q+1)$-lines are also 6-lines for B, and $a_6\left(B\right)=5$. Now, assume $q\ge 5$. The 5-lines are the secants of C passing through none of $P_1$, $P_2$, $P_3$ except the 6-lines. So, $a_5\left(B\right)=\left(\genfrac{}{}{0pt}{}{q+1-3}{2}\right)-a_6\left(B\right)=(q-3)(q-4)/2$. The 4-lines are the external lines of C through P or Q, the secants $⟨P,P_2⟩$, $⟨Q,P_3⟩$, the tangents at $P_4,P_5,\dots ,P_{q+1}$ and $⟨P,Q⟩$. Hence, $a_4\left(B\right)=q-1+2+(q+1-3)+1=2q$. Finally, $a_3\left(B\right)=q^2+q+1-a_4\left(B\right)-a_5\left(B\right)-a_6\left(B\right)-a_{q+1}\left(B\right)=(q+5)(q-2)/2$. □

By some transitions from B in Theorem 3, we get the following.

Theorem 4.

Under the conditions of Theorem 3 with $q\ge 7$, take $P=P_{13}$, $Q=P_{12}$ and a point $Q^{\prime }$ in ${\ell }_2$ with $Q^{\prime }\notin \{Q,P_2,l_{13}\cap {\ell }_2\}$. Let $B^{\prime }=(B\backslash \left\{Q\right\})\cup \left\{Q^{\prime }\right\}$ and $\ell =⟨P,Q^{\prime }⟩$. Then $K={\left(B^{\prime }\right)}^c$ forms a $(q^2-3q+1,q-2)$-arc with spectrum

(1)

$(a_0,a_{q-5},a_{q-4},a_{q-3},a_{q-2})=(3,q-3,\frac{(q-3)(q-4)}{2},2q,\frac{(q+5)(q-2)}{2})$ if ℓ is a tangent,

(2)

$(a_0,a_{q-6},a_{q-5},a_{q-4},a_{q-3},a_{q-2})=(3,1,q-6,\frac{q^2-7q+18}{2},2q-1,\frac{(q+5)(q-2)}{2})$ if ℓ is a secant,

(3)

$(a_0,a_{q-5},a_{q-4},a_{q-3},a_{q-2})=(3,q-4,\frac{q^2-7q+18}{2},2q-3,\frac{q^2+3q-8}{2})$ if ℓ is an external line.

Proof. 

Since ℓ is a tangent of C if and only if $Q^{\prime }=P_{23}$, we get the spectrum (1) from Theorem 3 if ℓ is a tangent. As we have already seen in the proof of Theorem 3, the tangent $⟨Q,P⟩$ and the secant $⟨Q,P_3⟩$ are 4-lines, the other $(q-3)/2$ secants through Q are 6-lines and the $(q-1)/2$ external lines through Q are 4-lines for B. Note that $a_{q+1}\left(B^{\prime }\right)=a_{q+1}\left(B\right)$, for $Q^{\prime }\in {\ell }_2\backslash \{P_2,{\ell }_{13}\cap {\ell }_2\}$.

If ℓ is a secant, then for B, the tangent ($\ne {\ell }_2$) through $Q^{\prime }$ is a 4-line, the secant ℓ is a 6-line, the secants $⟨Q^{\prime },P_1⟩$, $⟨Q^{\prime },P_3⟩$ are 3-lines, other $(q-7)/2$ secants on $Q^{\prime }$ are 5-lines and the $(q-1)/2$ external lines on $Q^{\prime }$ are 3-lines. Hence, $a_3\left(B^{\prime }\right)=a_3\left(B\right)+2+(q-1)/2-2-(q-1)/2=a_3\left(B\right)$, $a_4\left(B^{\prime }\right)=a_4\left(B\right)-2-(q-1)/2-1+2+(q-1)/2=a_4\left(B\right)-1$, $a_5\left(B^{\prime }\right)=a_5\left(B\right)+(q-3)/2+1-(q-7)/2=a_5\left(B\right)+3$, $a_6\left(B^{\prime }\right)=a_6\left(B\right)-(q-3)/2-1+(q-7)/2=a_6\left(B\right)-3$, $b_7^{\prime }=1$.

If ℓ is an external line, then for B, the tangent ($\ne {\ell }_2$) through $Q^{\prime }$ is a 4-line, the secants $⟨Q^{\prime },P_1⟩$, $⟨Q^{\prime },P_3⟩$ are 3-lines, other $(q-5)/2$ secants on $Q^{\prime }$ are 5-lines, the external line ℓ is a 4-line and the $(q-3)/2$ external lines on $Q^{\prime }$ are 3-lines. Hence, $a_3\left(B^{\prime }\right)=a_3\left(B\right)+2+(q-1)/2-2-(q-3)/2=a_3\left(B\right)+1$, $a_4\left(B^{\prime }\right)=a_4\left(B\right)-2-(q-1)/2-1+2-1+(q-3)/2=a_4\left(B\right)-3$, $a_5\left(B^{\prime }\right)=a_5\left(B\right)+(q-3)/2+1-(q-5)/2+1=a_5\left(B\right)+3$, $a_6\left(B^{\prime }\right)=a_6\left(B\right)-(q-3)/2+(q-5)/2=a_6\left(B\right)-1$. □

We note that the construction of a $(4q,3)$-blocking set with spectrum (1) or (3) in Theorem 4 is also valid for $q=5$, but not for the spectrum (2) since ℓ is a secant if and only if $Q^{\prime }={\ell }_{13}\cap {\ell }_2$ when $q=5$.

For $q=7$, the $(q^2-3q+1,q-2)$-arcs of Theorem 4 (1), (2) and (3) are equivalent to $K_{13}$, $K_{14}$ and $K_{11}$, respectively. The next lemma is given in [3, Corollary 7.5].

Lemma 20

([3]). In $\mathrm{PG}(2,q)$ with $q\ge 4$, there is a unique conic through a 5-arc.

We can get one more $(4q,3)$-blocking set in $\mathrm{PG}(2,q)$ from the set B in Theorem 3 by exchanging two points.

Theorem 5.

Let $q=p^h\ge 7$ for an odd prime $p\ne 3$. Under the conditions of Theorem 3, let C be the conic $\{\mathbf{P}(1,a,a^2):a\in {\mathbb{F}}_q\}\cup \left\{\mathbf{P}(0,0,1)\right\}$ and take $P_1=\mathbf{P}(1,1,1)$, $P_2=\mathbf{P}(0,0,1)$, $P_3=\mathbf{P}(1,0,0)$, $P_4=\mathbf{P}(1,2^{-1},2^{-2})$, $P_5=\mathbf{P}(1,2,2^2)$, $S=⟨P_1,P_4⟩\cap ⟨P_2,P_5⟩$ and $T=⟨P_1,P_5⟩\cap ⟨P_3,P_4⟩$. Let $B_1=(B\backslash \{P_4,P_5\})\cup \{S,T\}$. Then $K^{\prime }={\left(B_1\right)}^c$ is a $(q^2-3q+1,q-2)$-arc, which is not projectively equivalent to any arc in Theorems 3 and 4.

Proof. 

Note that $P_4\ne P_5$ if $p\ne 3$ and that $S=\mathbf{P}(1,2,2+2^{-1})$, $T=\mathbf{P}(2+2^{-1},2,1)$. Since $P={\ell }_1\cap {\ell }_3=\mathbf{P}(1,2^{-1},0)$ and $Q={\ell }_1\cap {\ell }_2=\mathbf{P}(0,1,2)$, the lines $⟨P,P_2⟩$ and $⟨Q,P_3⟩$ are passing through $P_4$ and $P_5$, respectively. Let $B_1^{-}=B\backslash \{P_4,P_5\}$. Then, the 2-lines for $B_1^{-}$ are $⟨P_1,P_4⟩$, $⟨P_1,P_5⟩$, $⟨P_2,P_5⟩$ and $⟨P_3,P_4⟩$. Hence, adding $S=⟨P_1,P_4⟩\cap ⟨P_2,P_5⟩$ and $T=⟨P_1,P_5⟩\cap ⟨P_3,P_4⟩$ to $B_1^{-}$, $B_1=B_1^{-}\cup \{S,T\}$ forms a $(4q,3)$-blocking set. It can be checked using computer that $B_1$ has spectrum $(a_3\left(B_1\right),a_4\left(B_1\right),a_5\left(B_1\right),a_7\left(B_1\right),a_8\left(B_1\right))=(28,18,6,2,3)$ for $q=7$, $(a_3\left(B_1\right),a_4\left(B_1\right),a_5\left(B_1\right),a_6\left(B_1\right),a_7\left(B_1\right),a_{12}\left(B_1\right))=(66,38,16,8,2,3)$ for $q=11$ and $(a_3\left(B_1\right),a_4\left(B_1\right),a_5\left(B_1\right),a_6\left(B_1\right),a_{14}\left(B_1\right))=(93,44,27,16,3)$ for $q=13$. Hence, $B_1$ is not projectively equivalent to any blocking set in Theorems 3 and 4. Assume $q\ge 17$ and suppose $B_1$ contains a conic $C^{\prime }$. Since $C\ne C^{\prime }$, it follows from Lemma 20 that $C^{\prime }$ could contain at most 4 points from C, 6 points from ${\ell }_{12}\cup {\ell }_{13}\cup {\ell }_{23}$ and the other 4 points, in total at most 14 points from $B_1$, a contradiction. Thus, $B_1$ contains no conic for $q\ge 17$. On the other hand, the blocking sets in Theorem 3 and 4 contain a conic. Hence, the arc ${\left(B_1\right)}^c$ is not projectively equivalent to any of the arcs in the previous theorems. □

For $q=7$, the $(q^2-3q+1,q-2)$-arc of Theorem 5 is equivalent to $K_{20}$.

Remark 5.

(1) Assume $q=5$ in Theorem 5. From Table 2 in Section 1, there exist two inequivalent $(11,3)$-arcs (equivalently, $(20,3)$-blocking sets) in $\mathrm{PG}(2,5)$, see also ([3], Table 12.5). The $(11,3)$-arcs have spectrum

(a)

$(a_0,a_1,a_2,a_3)=(5,1,10,15)$ or

(b)

$(a_0,a_1,a_2,a_3)=(4,4,7,16)$.

There are four 6-lines ${\ell }_{12}$, ${\ell }_{13}$, ${\ell }_{23}$ and $⟨S,T⟩$ for the arc ${\left(B_1\right)}^c$ in Theorem 5 when $q=5$. So, ${\left(B_1\right)}^c$ has spectrum (b) and hence ${\left(B_1\right)}^c$ is projectively equivalent to the arc in Theorem 4 (3).

(2) When $q=7$, the line $⟨P,S⟩$ in the proof of Theorem 5 is a secant of C. On the other hand, when $q=13$, $⟨P,S⟩$ is an external line of C. Thus, depending on the value of q, the line $⟨P,S⟩$ can form a tangent, a secant or an external line of C. That is why we could not determine the spectrum of the $(q^2-3q+1,q-2)$-arc in Theorem 5.

Next, we determine the spectrum of the arc $B_0$ in Lemma 3 for odd q to find one more inequivalent arc.

Theorem 6.

For odd $q\ge 5$, let $B={\ell }_1\cup {\ell }_2\cup {\ell }_3\cup {\ell }_4\cup \{P_1,P_2\}$, consisting of the lines ${\ell }_1=\left[100\right]$, ${\ell }_2=\left[010\right]$, ${\ell }_3=\left[001\right]$, ${\ell }_4=\left[111\right]$ and the points $P_1=\mathbf{P}(-1,1,1)$, $P_2=\mathbf{P}(1,-1,1)$. Then, $B^c$ forms a $(q^2-3q+1,q-2)$-arc with spectrum $(a_0,a_{q-4},a_{q-3},a_{q-2})=(4,2q-6,q^2-7q+17,6q-14)$.

Proof. 

Note that no three of the lines ${\ell }_1,{\ell }_2,{\ell }_3,{\ell }_4$ are concurrent. Let $\mathcal{Q}=\{Q_{ij}=l_i\cap {\ell }_j:1\le i<j\le 4\}$, $r_1=⟨Q_{14},Q_{23}⟩$, $r_2=⟨Q_{13},Q_{24}⟩$ and $r_3=⟨Q_{12},Q_{34}⟩$. Then, $P_1$ and $P_2$ are equal to $r_2\cap r_3$ and $r_1\cap r_3$, respectively. Hence, $r_3=⟨P_1,P_2⟩$ is a 4-line. Let ℓ be a line. Then ℓ meets ${\bigcup }_{i=1}^4{\ell }_i$ at two, three or four points. When $|\ell \cap ({\bigcup }_{i=1}^4{\ell }_i)|=2$, ℓ is $r_1$, $r_2$ or $r_3$. So, ℓ contains $P_1$ or $P_2$. Thus, $B^c$ is a $(q^2-3q+1,q-2)$-arc. Now, the $(q+1)$-lines for B are ${\ell }_1,\dots ,{\ell }_4$, and $a_{q+1}\left(B\right)=4$. The 5-lines for B are the lines containing one of $P_1$, $P_2$ but none of $\mathcal{Q}$. Hence, $a_5\left(B\right)=2(q+1-4)$. The 3-lines for B are the lines through one of two points $Q_{12}$, $Q_{34}$ containing no other point of $\mathcal{Q}$, the lines through one point $(\ne Q_{12},Q_{34})$ of $\mathcal{Q}$ containing none of $\{P_1,P_2\}$, and two more lines $r_1,r_2$. Thus, $a_3\left(B\right)=2(q+1-3)+4(q+1-4)+2=6q-14$. Finally, $a_4\left(B\right)=q^2+q+1-a_{q+1}\left(B\right)-a_5\left(B\right)-a_3\left(B\right)=q^2-7q+17$. □

Theorem 7.

Under the conditions of Theorem 6, let $P_3=r_1\cap r_2$. Take $P_2^{\prime }\in r_1\backslash \{P_2,P_3,Q_{14},Q_{23}\}$ and let $B^{\prime }=(B\backslash \left\{P_2\right\})\cup \left\{P_2^{\prime }\right\}$. Then, $K={\left(B^{\prime }\right)}^c$ is a $(q^2-3q+1,q-2)$-arc with spectrum $(a_0,a_1,a_2,a_3)=(5,1,10,15)$ for $q=5$ and $(a_0,a_{q-5},a_{q-4},a_{q-3},a_{q-2})=(4,1,2q-9,q^2-7q+20,6q-15)$ for $q\ge 7$.

Proof. 

Since the 3-line for B through $P_2$ is $r_1$ only, $B^{\prime }$ forms a $(4q,3)$-blocking set. The lines through $P_2$ for K except $r_1=⟨P_2,P_2^{\prime }⟩$ are three 4-lines $⟨P_2,Q_{13}⟩$, $⟨P_2,Q_{24}⟩$, $⟨P_1,P_2⟩$ and $(q-3)$ 5-lines. On the other hand, the lines through $P_2^{\prime }$ for K other than $r_1$ are four 3-lines $⟨P_2^{\prime },Q_{ij}⟩$ with $Q_{ij}\in \mathcal{Q}\backslash r_1$, one 5-line $⟨P_2^{\prime },P_1⟩$ and $(q-5)$ 4-lines. Hence, $a_3\left(B^{\prime }\right)=a_3\left(B\right)+3-4$, $a_4\left(B^{\prime }\right)=a_4\left(B\right)-3+(q-3)+4-(q-5)$, $a_5\left(B^{\prime }\right)=a_5\left(B\right)-(q-3)-1+(q-5)$, $a_6\left(B^{\prime }\right)=1$ (or $a_6\left(B^{\prime }\right)=1+4=5$ for $q=5$). Now, our assertion follows from Theorem 6. □

From the above theorems we get the following.

Corollary 1.

There exist at least six projectively inequivalent $(q^2-3q+1,q-2)$-arcs in $\mathrm{PG}(2,q)$ for $q=p^h\ge 7$ with odd prime $p\ne 3$.

Finally, we consider the case q is even. Assume $q\ge 4$. Then, it is known that a $(b,3)$-blocking set B containing a line satisfies $b\ge 4q-1$ [27]. The set $B_0$ for even q in Lemma 3 is such a $(4q-1,3)$-blocking set with spectrum

$$(a_3\left(B_0\right),a_4\left(B_0\right),a_5\left(B_0\right),a_{q+1}\left(B_0\right))=(6q-9,q^2-6q+8,q-2,4).$$

When $q=4$, the complement of a $(4q-1,3)$-blocking set is a 6-arc (a hyperoval). So, assume $q\ge 8$. We can construct two more $(4q-1,3)$-blocking sets as follows.

Theorem 8.

For even $q\ge 8$, let C be a conic in $\mathrm{PG}(2,q)$ with nucleus N. For any three points $P_1$, $P_2$, $P_3$ in $C\cup \left\{N\right\}$ with $P_1,P_2\in C$, let ${\ell }_{ij}=⟨P_i,P_j⟩$ for $1\le i<j\le 3$. Then,

(1)

$B=C\cup {\ell }_{12}\cup {\ell }_{23}\cup {\ell }_{13}$ is a $(4q-1,3)$-blocking set with spectrum

$$(a_3\left(B\right),a_5\left(B\right),a_{q+1}\left(B\right))=\left(\frac{(q+6)(q-1)}{2},\frac{(q-1)(q-2)}{2},3\right)$$

with $\left|\mathrm{Aut}\right(B\left)\right|=2(q-1)$ if $P_3=N$,

(2)

$B=C\cup {\ell }_{12}\cup {\ell }_{23}\cup {\ell }_{13}\cup \left\{N\right\}$ is a $(4q-1,3)$-blocking set with spectrum

$$(a_3\left(B\right),a_5\left(B\right),a_{q+1}\left(B\right))=\left(\frac{(q+6)(q-1)}{2},\frac{(q-1)(q-2)}{2},3\right)$$

with $\left|\mathrm{Aut}\right(B\left)\right|=6$ if $P_3\ne N$.

The $(4q-1,3)$-blocking sets in Theorem 8 were first found for $q=8$, see [7].

Corollary 2.

There exist at least three projectively inequivalent $(q^2-3q+2,q-2)$-arcs (equivalently, $(4q-1,3)$-blocking sets) in $\mathrm{PG}(2,q)$ for every even $q\ge 8$.

Remark 6.

From Table 1, $(q^2-3q+2,q-2)$-arcs are optimal for $q=4,8$ and give the known lower bound on $m_{14}(2,16)$ for $q=16$.