Two-Tailed Fuzzy Hypothesis Testing for Unilateral Specification Process Quality Index

Abstract

The quality characteristics with unilateral specifications include the smaller-the-better (STB) and larger-the-better (LTB) quality characteristics. Roundness, verticality, and concentricity are categorized into the STB quality characteristics, while the wire pull and the ball shear of gold wire bonding are categorized into the LTB quality characteristics. In terms of the tolerance, zero and infinity ($\infty$) can be viewed as the target values in line with the STB and LTB quality characteristics, respectively. However, cost and timeliness considerations, or the restrictions of practical technical capabilities in the industry, mean that the process mean is generally far more than 1.5 standard deviations away from the target value. Researchers have accordingly proposed a process quality index conforming to the STB quality characteristics. In this study, we come up with a process quality index conforming to the LTB quality characteristics. We refer to these two types of indices as the unilateral specification process quality indices. These indices and the process yield have a one-to-one mathematical relationship. Besides, the process quality levels can be completely reflected as well. These indices possess unknown parameters. Therefore, sample data are required for calculation. Nevertheless, interval estimates can lower the misjudgment risk resulting from sampling errors more than point estimates can. In addition, considering cost and timeliness in the industry, samples are generally small, which lowers estimation accuracy. In an attempt to increase the accuracy of estimation as well as overcome the uncertainty of measured data, we first derive the confidence interval for unilateral specification process quality indices, and then propose a fuzzy membership function on the basis of the confidence interval to establish the two-tailed fuzzy testing rules for a single indicator. Lastly, we determine whether the process quality has improved.

1. Introduction

According to a number of studies, process capability indices (PCIs) are convenient tools for process quality assessment, such that they are widely employed in the manufacturing industry [1,2,3,4,5,6,7,8]. Six Sigma is also a widely-used approach which can enhance process quality levels in manufacturing [9,10,11,12]. Many researchers examined the relations of various PCIs with Six Sigma quality levels [13,14,15]. According to the definitions of Six Sigma quality levels, Chen et al. [13] and Huang et al. [16] proposed a Six Sigma quality index—when the process mean shifts 1.5 standard deviations from the target value and the standard deviation of the process is one-sixth of the tolerance, the quality level of the process is exactly 6 standard deviations, which means the Six Sigma quality index is exactly 6.

Chen et al. [13] noted that the PCIs for unilateral specifications do not have specific target values. Although zero and infinity ( $\infty$ ) can respectively be considered the target values of STB and LTB quality characteristics, considerations of cost and timeliness and the restrictions of practical technical capabilities in the industry mean that the process mean is generally far more than 1.5 standard deviations away from the target value. The STB quality characteristics include roundness, verticality, and concentricity, while the LTB quality characteristics include the wire pull and ball shear of gold wire bonding. Chang et al. [17] accordingly presented a process quality index in line with STB. In this study, a process quality index is proposed to conform with LTB. Under the assumption of normality, we let the random variable $X$ follow the normal distribution with the process mean $\mu$ and process standard deviation σ. Therefore, the process quality index of the unilateral specification can be expressed as follows:

$$P_{QI}=\{\begin{array}{l}\frac{USL-\mu }{\sigma },smaller-the-better\\ \frac{\mu -LSL}{\sigma },larger-the-better\end{array}$$

(1)

where $USL$ and $LSL$ respectively represent the upper as well as lower specification limits. On the basis of the concept put forward by Chang et al. [17], when $\mu +k\sigma =USL$, then the process quality level reaches $k-sigma$ for STB quality characteristics. Therefore,

$$P_{QI}=\frac{USL-\mu }{\sigma }=\frac{\left(\mu +k\sigma \right)-\mu }{\sigma }=\frac{k\sigma }{\sigma }=k$$

(2)

Similarly, when $\mu -k\sigma =LSL$, then the process quality level reaches k sigma for LTB quality characteristics. Therefore,

$$P_{QI}=\frac{\mu -LSL}{\sigma }=\frac{\mu -\left(\mu -k\sigma \right)}{\sigma }=\frac{k\sigma }{\sigma }=k$$

(3)

Based on the above description, if the process quality level attains to k sigma, then the unilateral specification process quality index value will be equal to k. The process yield for the STB quality characteristic can be calculated as follows:

$$yield\%=p\left(X\le USL\right)={\displaystyle {\int }_{-\infty }^{\left(USL-\mu \right)/\sigma }\frac{1}{\sqrt{2\pi }}exp\left\{\frac{t^2}{2}\right\}{d}_t}=\Phi \left(P_{QI}\right)$$

(4)

Similarly, for LTB quality characteristics, the process yield can be displayed in the following:

$$yield\%=p\left(X\ge LSL\right)={\displaystyle {\int }_{\left(\mu -LSL\right)/\sigma }^{\infty }\frac{1}{\sqrt{2\pi }}exp\left\{\frac{t^2}{2}\right\}{d}_t}=\Phi \left(P_{QI}\right)$$

(5)

where $Z$$=$$\left(X-\mu \right)/\sigma$ complies with the standard normal distribution. $\Phi \left(z\right)$, a cumulative function of the standard normal distribution, is expressed as follows:

$$\Phi \left(z\right)=p\left(Z\le z\right)={\displaystyle {\int }_{-\infty }^z\frac{1}{\sqrt{2\pi }}exp\left\{\frac{t^2}{2}\right\}{d}_t}$$

(6)

Based on the above description, the process yield and unilateral specification process quality indices have a one-to-one mathematical relationship. Obviously, the process quality indices of the unilateral specification show the process yield as well as the quality level, so they are good quality assessment tools for processes with unilateral specifications. These indices include unknown parameters, so sample data are required for calculation [18,19]. However, interval estimates can decrease the misjudgment risk resulting from sampling errors more than point estimates can [20,21]. In addition, due to cost and timeliness considerations, samples are generally small, which lowers estimation accuracy. To increase the accuracy of estimation and decrease the uncertainty of measurement data, many researchers use the confidence interval of indices to construct confidence interval-based fuzzy evaluation models [22,23,24,25,26]. In this study, we first derive the confidence interval for the unilateral specification process’ quality indices, and then propose a confidence interval-based fuzzy membership function to establish the two-tailed fuzzy testing rules for a single index. Lastly, we determine whether process quality has improved. Obviously, the fuzzy evaluation model proposed by this study can make a more accurate judgment in a short period of time on whether the process has improved through a smaller sample size and the integration of accumulated past expert experience [20,22,23,24,25]. Besides, grasping the opportunity for improvement can not only reduce the testing cost but also make the quality level quickly meet the requirements of the specifications. At the same time, it has the advantage of reducing the ratio of rework and scrap as well as further reducing social losses, such as carbon emissions [26,27]. Central Taiwan holds a strategic position in the global machine-tool and machinery industries, and is home to a complete industry chain, including upstream, midstream and downstream manufacturers [28,29]. We therefore demonstrated the application of the proposed approach using the roundness of a gear-grinding process at a factory in Central Taiwan.

As to the rest of this paper, it will be arranged as follows: Section 2 indicates the confidence interval of a unilateral specification process quality index; Section 3 presents the two-tailed statistical hypothesis testing of a unilateral specification process quality index; Section 4 develops the two-tailed fuzzy testing model on the basis of the above rules with critical values; Section 5 employs an application to demonstrate the efficacy of the proposed approach. Last but not least, conclusions are given in Section 6.

2. Confidence Intervals

It is assumed that ( $X_1$,…, $X_i$,…, $X_n$ ) is a random sample derived from $N\left(\mu ,{\sigma }^2\right)$ using sample size n. Then, the estimator of $\mu$ and $\sigma$ is

$$\overline{X}=\frac{1}{n}{\displaystyle \sum _{i=1}^n{X}_i}=S\sqrt{\frac{1}{n-1}{\displaystyle \sum _{i=1}^n{\left(X_i-\overline{X}\right)}^2}}$$

As a result, the estimator of these two process quality indices can be expressed as follows:

$$P_{QI}^{\ast }=\{\begin{array}{l}\frac{USL-\overline{X}}{S},smaller-the-better\\ \frac{\overline{X}-LSL}{S},larger-the-better\end{array}$$

(7)

Let the random variable $K$$=$$\left(n-1\right)S^2/{\sigma }^2$. The characteristic function of $K$ is ${\varphi }_K\left(t\right)={\left(1-2it\right)}^{-\left(n-1\right)/2}$; therefore, $K$ proceeds with the chi-square distribution using $n-1$ degrees of freedom, expressed as ${\chi }_{n-1}^2$. If we let ${\alpha }^{\prime }$$=$1$-$$\sqrt{1-\alpha }$, then

$$\mathrm{p}\left\{{\chi }_{{\alpha }^{\prime }/2;n-1}^2\le K\le {\chi }_{1-{\alpha }^{\prime }/2;n-1}^2\right\}=\sqrt{1-\alpha }$$

(8)

where ${\chi }_{{\alpha }^{\prime }/2;n-1}^2$ refers to the lower ${\alpha }^{\prime }/2$ quantile of the chi-square distribution using $n-1$ degrees of freedom. Therefore,

$$\mathrm{p}\left\{\sqrt{\frac{{\chi }_{{\alpha }^{\prime }/2;n-1}^2}{n-1}}\le \frac{S}{\sigma }\le \sqrt{\frac{{\chi }_{1-{\alpha }^{\prime }/2;n-1}^2}{n-1}}\right\}=\sqrt{1-\alpha }$$

(9)

If we let the random variable

$$Z=\{\begin{array}{l}\frac{\sqrt{n}\left[\left(USL-\mu \right)-\left(USL-\overline{X}\right)\right]}{\sigma },smaller-the-better\\ \frac{\sqrt{n}\left[\left(\overline{X}-LSL\right)-\left(\mu -LSL\right)\right]}{\sigma },larger-the-better\end{array}$$

(10)

then $Z$ follows the standard normal distribution, denoted as $N\left(0,1\right)$. We also let ${\alpha }^{\prime }$$=$ 1 $-$$\sqrt{1-\alpha }$. Then

$$\mathrm{p}\left\{-Z_{{\alpha }^{\prime }/2}\le Z\le Z_{{\alpha }^{\prime }/2}\right\}=\sqrt{1-\alpha }$$

(11)

where $Z_{{\alpha }^{\prime }/2}$ means the upper ${\alpha }^{\prime }/2$ quantile of the standard normal distribution. Therefore,

$$p\left\{P_{QI}^{\ast }\left(\frac{S}{\sigma }\right)-\frac{Z_{{\alpha }^{\prime }/2}}{\sqrt{n}}\le P_{QI}\le P_{QI}^{\ast }\left(\frac{S}{\sigma }\right)+\frac{Z_{{\alpha }^{\prime }/2}}{\sqrt{n}}\right\}=\sqrt{1-\alpha }$$

(12)

We set event $A$ and event $B$ as:

$$A=\left\{P_{QI}^{\ast }\left(\frac{S}{\sigma }\right)-\frac{Z_{{\alpha }^{\prime }/2}}{\sqrt{n}}\le P_{QI}\le P_{QI}^{\ast }\left(\frac{S}{\sigma }\right)+\frac{Z_{{\alpha }^{\prime }/2}}{\sqrt{n}}\right\}$$

(13)

$$B=\left\{\sqrt{\frac{{\chi }_{{\alpha }^{\prime }/2;n-1}^2}{n-1}}\le \frac{S}{\sigma }\le \sqrt{\frac{{\chi }_{1-{\alpha }^{\prime }/2;n-1}^2}{n-1}}\right\}$$

(14)

$\overline{X}$ and $S^2$ are independent, and so are $Z$ and $K$. Therefore, event $A$ and event $B$ are independent.

$$p\left\{A\cap B\right\}=p\left\{A\right\}\times p\left\{B\right\}=1-\alpha$$

(15)

Thus,

$$p\left\{\begin{array}{l}{P}_{QI}^{\ast }\left(\frac{S}{\sigma }\right)-\frac{Z_{{\alpha }^{\prime }/2}}{\sqrt{n}}\le P_{QI}\le P_{QI}^{\ast }\left(\frac{S}{\sigma }\right)+\frac{Z_{{\alpha }^{\prime }/2}}{\sqrt{n}},\\ \sqrt{\frac{{\chi }_{{\alpha }^{\prime }/2;n-1}^2}{n-1}}\le \frac{S}{\sigma }\le \sqrt{\frac{{\chi }_{1-{\alpha }^{\prime }/2;n-1}^2}{n-1}}\end{array}\right\}=1-\alpha$$

(16)

and we have

$$p\left\{\begin{array}{l}{P}_{QI}^{\ast }\times \sqrt{\frac{{\chi }_{{\alpha }^{\prime }/2;n-1}^2}{n-1}}-\frac{Z_{{\alpha }^{\prime }/2}}{\sqrt{n}}\le P_{QI}\\ \le P_{QI}^{\ast }\times \sqrt{\frac{{\chi }_{1-{\alpha }^{\prime }/2;n-1}^2}{n-1}}+\frac{Z_{{\alpha }^{\prime }/2}}{\sqrt{n}}\end{array}\right\}\ge 1-\alpha$$

(17)

Based on the above description, $\left[L-P_{QI},U-P_{QI}\right]$ is the 100(1 $-$$\alpha$)% confidence interval of the index $P_{QI}$ where

$$L-P_{QI}=P_{QI}^{\ast }\sqrt{\frac{{\chi }_{{\alpha }^{\prime }/2;n-1}^2}{n-1}}-\frac{Z_{{\alpha }^{\prime }/2}}{\sqrt{n}}$$

(18)

$$U-P_{QI}=P_{QI}^{\ast }\sqrt{\frac{{\chi }_{1-{\alpha }^{\prime }/2;n-1}^2}{n-1}}+\frac{Z_{{\alpha }^{\prime }/2}}{\sqrt{n}}$$

(19)

3. Two-Tailed Statistical Hypothesis Testing

Statistical hypothesis testing is an effective approach determining whether the process quality index of the unilateral specification value is equal to k, which demonstrates that the process quality has attained to the $k\sigma$ level. Therefore, the hypotheses for testing at significance level α can be described as below:

$$\mathrm{null}\mathrm{hypothesis}{H}_0:P_{QI}=k$$

(20)

$$\mathrm{alternative}\mathrm{hypothesis}{H}_a:P_{QI}\ne k$$

(21)

If we let $Z$$=$${\left(X_1,\cdots ,X_i,\cdots ,X_n\right)}^{\prime }$, then the statistical test function for the null hypothesis $H_0$ is given by

$$\varphi (Z)=\{\begin{array}{l}1,if{P}_{QI}^{\ast }<C_{0L}\mathrm{or}{P}_{QI}^{\ast }<C_{0R}\\ 0,otherwise,\end{array}$$

(22)

Furthermore, suppose the random variable $T^{\prime }$$=$$\sqrt{n}$$\times$$P_{QI}^{\ast }$, then

$$T^{\prime }=\frac{Z^{\prime }}{\sqrt{S^2/{\sigma }^2}}=\frac{N\left(\delta ,1\right)}{\sqrt{{\chi }_{n-1}^2/n-1}}$$

(23)

proceeds with the non-central t-distribution at $n-1$ degrees of freedom using the non-centrality parameter $\delta$$=$$\sqrt{n}$$\times$$P_{QI}$, denoted as ${t^{\prime }}_{n-1}\left(\delta \right)$ and

$$Z^{\prime }=\{\begin{array}{l}\sqrt{n}\left(USL-\overline{X}\right)/\sigma ,smaller-the-better\\ \sqrt{n}\left(\overline{X}-LSL\right)/\sigma ,larger-the-better\end{array}$$

(24)

is denoted as $N(\delta ,1)$. Then the critical value $C_0^{-}$, is controlled by

$$\begin{array}{l}p\left\{P_{QI}^{\ast }<C_0^{-}|P_{QI}=k\right\}=\frac{\alpha }{2}\\ \Rightarrow p\left\{{t^{\prime }}_{n-1}\left(\delta =\sqrt{n}k\right)<\sqrt{n}\times C_0^{-}\right\}=\frac{\alpha }{2}\\ \Rightarrow C_0^{-}=\frac{{t^{\prime }}_{\alpha /2,n-1}\left(\delta =\sqrt{n}k\right)}{\sqrt{n}}\end{array}$$

(25)

where ${t^{\prime }}_{\alpha /2,n-1}\left(\delta =\sqrt{n}k\right)$ is the lower $\alpha /2$ quantile of ${t^{\prime }}_{n-1}\left(\delta =\sqrt{n}k\right)$. Similarly, the critical value $C_0^{+}$, is determined by

$$\begin{array}{l}p\left\{P_{QI}^{\ast }>C_0^{+}|P_{QI}=k\right\}=\frac{\alpha }{2}\\ \Rightarrow p\left\{{t^{\prime }}_{n-1}\left(\delta =\sqrt{n}k\right)<\sqrt{n}\times C_0^{+}\right\}=1-\frac{\alpha }{2}\\ \Rightarrow C_0^{+}=\frac{{t^{\prime }}_{1-\alpha /2,n-1}\left(\delta =\sqrt{n}k\right)}{\sqrt{n}}\end{array}$$

(26)

where ${t^{\prime }}_{1-\alpha /2,n-1}\left(\delta =\sqrt{n}k\right)$ is the lower 1 $-$$\alpha /2$ quantile of ${t^{\prime }}_{n-1}\left(\delta =\sqrt{n}k\right)$. If we let ($x_1$,…, $x_i$,…, $x_n$) be the observed value of ($X_1$,…, $X_i$,…, $X_n$ ), then the observed values of $\overline{X}$ and $S$ are

$$\overline{x}=\frac{1}{n}{\displaystyle \sum _{i=1}^n{x}_i}$$

(27)

and

$$s=\sqrt{\frac{1}{n-1}{\displaystyle \sum _{i=1}^n{\left(x_i-\overline{x}\right)}^2}}$$

(28)

Therefore, the observed value of $P_{QI}^{\ast }$ can be displayed as follows:

$$p_{qi}^{\ast }=\{\begin{array}{l}\frac{USL-\overline{x}}{s},smaller-the-better\\ \frac{\overline{x}-LSL}{s},larger-the-better\end{array}$$

(29)

The statistical testing rules are listed below:

(1)

If $C_0^{-}$$\le$$p_{qi}^{\ast }$$\le$$C_0^{+}$, then $H_0$ is not rejected, and it is concluded that $H_0$$=$$k$;

(2)

If $p_{qi}^{\ast }$$<$$C_{0L}$, then $H_0$ is rejected, and it is concluded that $P_{QI}$$<$$k$;

(3)

If $C_0^{+}$$<$$p_{qi}^{\ast }$, then $H_0$ is rejected, and it is concluded that $k$$<$$P_{QI}$.

4. Two-Tailed Fuzzy Testing

As noted by Chen [30], sample size n can affect the statistical inference results. Thus, this paper develops a two-tailed fuzzy testing model on the basis of the above rules with critical values $C_0^{-}$ and $C_0^{+}$. Furthermore, the observed values of $L-P_{QI}$ and $U-P_{QI}$, respectively, are

$$l-p_{qi}=p_{qi}^{\ast }\times \sqrt{\frac{{\chi }_{0.5-\sqrt{1-\alpha }/2,n-1}^2}{n-1}}-\frac{Z_{0.5-\sqrt{1-\alpha }/2}}{\sqrt{n}}$$

(30)

$$u-p_{qi}=p_{qi}^{\ast }\times \sqrt{\frac{{\chi }_{0.5+\sqrt{1-\alpha }/2,n-1}^2}{n}}+\frac{Z_{0.5-\sqrt{1-\alpha }/2}}{\sqrt{n}}$$

(31)

According to the observed values of the confidence interval $\left[l-p_{qi},u-p_{qi}\right]$ and the proposal made by Chen [22], the $\alpha -\mathrm{cuts}$ of the triangular fuzzy number ${\tilde{p}}_{qi}^{\ast }$ is ${\tilde{p}}_{qi}^{\ast }$$\left[\alpha \right]$$=$ $\left[p_{qi1}^{\ast }(\alpha ),p_{qi2}^{\ast }(\alpha )\right]$ for $0.01\le \alpha \le 1$, where

$$p_{qi1}^{\ast }\left(\alpha \right)=p_{qi}^{\ast }\times \sqrt{\frac{{\chi }_{0.5-\sqrt{1-\alpha }/2,n-1}^2}{n-1}}-\frac{Z_{0.5-\sqrt{1-\alpha }/2}}{\sqrt{n}}$$

(32)

$$p_{qi2}^{\ast }\left(\alpha \right)=p_{qi}^{\ast }\times \sqrt{\frac{{\chi }_{0.5+\sqrt{1-\alpha }/2,n-1}^2}{n}}+\frac{Z_{0.5-\sqrt{1-\alpha }/2}}{\sqrt{n}}$$

(33)

It is recalled that the $\alpha -\mathrm{cuts}$ of triangular fuzzy number ${\tilde{p}}_{qi}^{\ast }$$\left[\alpha \right]$ for $0\le \alpha <0.01$ is equal to ${\tilde{p}}_{qi}^{\ast }$$\left[0.01\right]$. In the case of $\alpha =1$, $p_{qi1}^{\ast }$$(1)$$=$$p_{qi2}^{\ast }$$(1)$$=$$p_{qi}^{\ast }$$\times$$\sqrt{\frac{{\chi }_{0.5,n-1}^2}{n-1}}$$\ne$$p_{qi}^{\ast }$. According to Chen [22], considering the convenience in practice, we let

$$x^{\prime }=\sqrt{\frac{n-1}{{\chi }_{0.5,n-1}^2}}x$$

(34)

Thus:

(1)

When $x$$=$$p_{qi1}^{\ast }$$(\alpha )$, then

$$x^{\prime }={\widetilde{p^{\prime }}}_{qi1}(\alpha )=p_{qi}^{\ast }\sqrt{\frac{{\chi }_{0.5-\sqrt{1-\alpha }/2,n-1}^2}{{\chi }_{0.5,n-1}^2}}-\frac{Z_{0.5-\sqrt{1-\alpha }/2}}{\sqrt{{\chi }_{0.5,n-1}^2}}$$

(35)

(2)

When $x$$=$$p_{qi2}^{\ast }$$(\alpha )$, then

$$x^{\prime }={\widetilde{p^{\prime }}}_{qi2}(\alpha )=p_{qi}^{\ast }\sqrt{\frac{{\chi }_{0.5+\sqrt{1-\alpha }/2,n-1}^2}{{\chi }_{0.5,n-1}^2}}+\frac{Z_{0.5-\sqrt{1-\alpha }/2}}{\sqrt{{\chi }_{0.5,n-1}^2}}$$

(36)

Therefore, the α-cuts of the new triangular fuzzy number of $p_{qi}^{\ast }$ is ${\tilde{p}}_{qi}^{\prime }$$\left[\alpha \right]$$=$$\left[{p^{\prime }}_{qi1}(\alpha ),{p^{\prime }}_{qi2}(\alpha )\right]$ for $0.01\le \alpha \le 1$, where

$${p^{\prime }}_{qi1}(\alpha )=p_{qi}^{\ast }\times \sqrt{\frac{{\chi }_{0.5-\sqrt{1-\alpha }/2,n-1}^2}{{\chi }_{0.5,n-1}^2}}-\frac{Z_{0.5-\sqrt{1-\alpha }/2}}{\sqrt{{\chi }_{0.5,n-1}^2}}$$

(37)

$${p^{\prime }}_{qi2}(\alpha )=p_{qi}^{\ast }\times \sqrt{\frac{{\chi }_{0.5+\sqrt{1-\alpha }/2,n-1}^2}{{\chi }_{0.5,n-1}^2}}+\frac{Z_{0.5-\sqrt{1-\alpha }/2}}{\sqrt{{\chi }_{0.5,n-1}^2}}$$

(38)

It is suggested that all of the α-cuts of ${\widetilde{p^{\prime }}}_{qi}$$\left[\alpha \right]$ for $0\le \alpha <0.01$ be equal to ${{\tilde{p}}^{\prime }}_{qi}$$\left[0.01\right]$. Obviously, if $\alpha =1$, then ${p^{\prime }}_{qi1}$$(1)$$=$${p^{\prime }}_{qi2}$$(1)$$=$$p_{qi}^{\ast }$. The new triangular fuzzy number of $p_{qi}^{\ast }$ is ${\widetilde{p^{\prime }}}_{qi}$$=$$\mathsf{\Delta }\left(p_L,p_M,p_R\right)$, where

$$p_L=p_{qi}^{\ast }\times \sqrt{\frac{{\chi }_{0.0025,n-1}^2}{{\chi }_{0.5,n-1}^2}}-\frac{Z_{0.0025}}{\sqrt{{\chi }_{0.5,n-1}^2}}$$

(39)

$$p_M=p_{qi}^{\ast }$$

(40)

$$p_R=p_{qi}^{\ast }\times \sqrt{\frac{{\chi }_{0.9975,n-1}^2}{{\chi }_{0.5,n-1}^2}}+\frac{Z_{0.0025}}{\sqrt{{\chi }_{0.5,n-1}^2}}$$

(41)

Then, the membership function of the triangular fuzzy number ${\widetilde{p^{\prime }}}_{qi}$ is

$$\eta (x)=\{\begin{array}{l}0 if x<p_L\\ {\alpha }_{1}if{p}_L\le x<p_{qi}^{\ast }\\ 1 if x=p_M\\ {\alpha }_2 if{p}_{qi}^{\ast }<x\le p_R\\ 0 if{p}_R<x\end{array}$$

(42)

where ${\alpha }_1$ and ${\alpha }_2$ are determined by ${p^{\prime }}_{qi1}({\alpha }_1)$$=$$x$ and ${p^{\prime }}_{qi2}({\alpha }_2)$$=$$x$. The membership function $\eta (x)$ is presented in Figure 1.

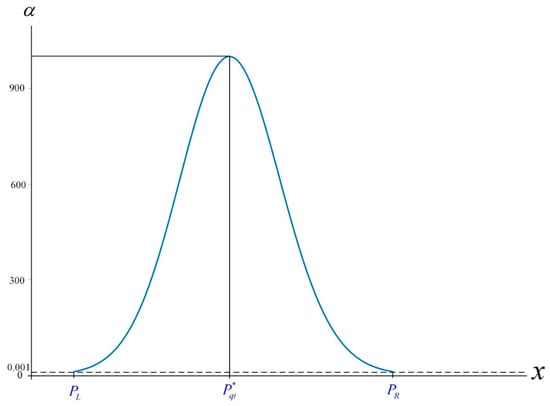
Figure 1. Membership function η(x).

Suppose $A_T$ is the area in the graph of η(x), and then

$$A_T=\left\{\left(x,\alpha \right)|{p^{\prime }}_{qi1}(\alpha )\le x\le {p^{\prime }}_{qi2}(\alpha ),0\le \alpha \le 1\right\}$$

(43)

As noted by Chen [31] and Buckley [32], the area of set $A_T$ can be computed as follows:

$$a_T={\displaystyle \underset{p_L}{\overset{p_R}{\int }}\eta (x)}{d}_x$$

(44)

Based on Chen [31], it is difficult to calculate $a_T$ directly via integration, so we let $l$$=$$\lfloor 1000\alpha \rfloor$, $l$$=$ 0,1,…,1000 for 0$\le$$\alpha$ 1, where $\lfloor 1000\alpha \rfloor$ refers to the largest integer less than or equal to 1000$\alpha$. We let $\alpha$$=$ 0.001 $\times$$l$ and $l$$=$ 0,1,…,1000, showing that $A_T$ is divided into 1000 trapezoid-shaped blocks by 1001 horizontal lines. Therefore, the $l$ th block for $l$$=$ 0, 1, 2, …, 999 can be stated in the following equation:

$$A_{Tl}=\left\{\begin{array}{l}\left(x,\alpha \right)|{p^{\prime }}_{qi1}(0.001\times l)\le x\le {p^{\prime }}_{qi2}(0.001\times l),\\ 0.001\times l\le \alpha \le 0.001\times (l+1)\end{array}\right\}$$

(45)

We also let the coordinates of the two intersection points of horizontal line $\alpha$$=$ 0.001 $\times$$l$ and set $A_T$ be $\left(x_{l1}^T,0.001\times l\right)$ and $\left(x_{l2}^L,0.001\times l\right)$. Thus, the distance between these two points is $d_l^T$$=$$x_{l2}^T$$-$$x_{l1}^T$ as shown below:

$$d_l^T=p_{qi}^{\ast }\times \left(\sqrt{\frac{{\chi }_{0.5+\sqrt{1-0.001\times l}/2,n-1}^2}{{\chi }_{0.5,n-1}^2}}-\sqrt{\frac{{\chi }_{0.5-\sqrt{1-0.001\times l}/2,n-1}^2}{{\chi }_{0.5,n-1}^2}}\right)+2\frac{Z_{0.5-\sqrt{1-0.001\times l}/2}}{\sqrt{{\chi }_{0.5,n-1}^2}}$$

(46)

Obviously, $d_0^T$$=$$d_1^T$$=$…$=$$d_{10}^T$, $d_{1000}^T$$=$ 0 and $A_{Tl}$ is a trapezoid-shaped block containing lower base $d_{l-1}^T$, upper base $d_l^T$, and height 0.001. As a result, the approximate value of its area $a_{Tl}$ for $l$ = 1, 2, …, 1000 can be written as

$$a_{Tl}=(0.001)\times \left(\frac{d_{l-1}^T+d_l^T}{2}\right)$$

(47)

Therefore,

$$\begin{array}{ll}{a}_T& ={\displaystyle \sum _{l=1}^{1000}{a}_{Tl}}\\ & =\left(0.001\right)\times {\displaystyle \sum _{l=1}^{1000}\left(\frac{d_{l-1}^T+d_l^T}{2}\right)}\\ & =0.001\times \left\{\left(\frac{d_0^T}{2}+\frac{d_1^T}{2}\right)+\left(\frac{d_1^T}{2}+\frac{d_2^T}{2}\right)+\dots +\left(\frac{d_9^T}{2}+\frac{d_{10}^T}{2}\right)+\left(\frac{d_{10}^T}{2}+\frac{d_{11}^T}{2}\right)\right\}\\ & +0.001\times \left\{\left(\frac{d_{11}^T}{2}+\frac{d_{12}^T}{2}\right)+\dots +\left(\frac{d_{999}^T}{2}+\frac{d_{1000}^T}{2}\right)\right\}\\ & =\left(0.001\right)\times \left\{\left(\frac{d_0^T}{2}+d_1^T+\dots +d_{10}^T\right)+\left(d_{11}^T+d_{12}^T+\dots +d_{999}^T+\frac{d_{1000}^T}{2}\right)\right\}\\ & =\left(0.001\right)\times \left(10.5\times d_{10}^T+{\displaystyle \sum _{l=11}^{999}{d}_l^T}\right)\end{array}$$

(48)

As noted by Chen [22], since the test is two-tailed, the following two cases must be taken into account:

Case 1: $p_{qi}^{\ast }$$<$$k$

Similar to ${\widetilde{p^{\prime }}}_{qi}$$\left[\alpha \right]$, when $p_{qi}^{\ast }$$<$$k$, the $\alpha -\mathrm{cuts}$ of triangular fuzzy critical value number ${\tilde{C}}_0^{-}$ is ${\tilde{C}}_0^{-}$$\left[\alpha \right]$$=$$\left[C_{01}^{-}(\alpha ),C_{02}^{-}(\alpha )\right]$ for $0.01\le \alpha \le 1$, where

$$C_{01}^{-}(\alpha )=C_0^{-}\times \sqrt{\frac{{\chi }_{0.5-\sqrt{1-\alpha }/2,n-1}^2}{{\chi }_{0.5,n-1}^2}}-\frac{Z_{0.5-\sqrt{1-\alpha }/2}}{\sqrt{{\chi }_{0.5,n-1}^2}}$$

(49)

$$C_{02}^{-}(\alpha )=C_0^{-}\times \sqrt{\frac{{\chi }_{0.5+\sqrt{1-\alpha }/2,n-1}^2}{{\chi }_{0.5,n-1}^2}}+\frac{Z_{0.5-\sqrt{1-\alpha }/2}}{\sqrt{{\chi }_{0.5,n-1}^2}}$$

(50)

It is suggested that all of the $\alpha -\mathrm{cuts}$ of ${\tilde{C}}_0^{-}$$\left[\alpha \right]$ for $0\le \alpha <0.01$ are equal to ${\tilde{C}}_0^{-}$$\left[0.01\right]$. Obviously, if $\alpha =1$, then $C_{01}^{-}$$(1)$$=$$C_{02}^{-}$$(1)$$=$$C_0^{-}$ and the triangular fuzzy number of $C_0^{-}$ is ${\tilde{C}}_0^{-}$$=$ $\mathsf{\Delta }\left(C_L^{-},C_0^{-},C_R^{-}\right)$, where $C_L^{-}=C_{01}^{-}(0.01)$ and $C_R^{-}=C_{02}^{-}(0.01)$. Then, the membership function of the triangular-shaped fuzzy number ${\tilde{C}}_0^{-}$ is

$${\eta }^{-}(x)=\{\begin{array}{l}0ifx<C_L^{-}\\ {\alpha }_1^{-}if{C}_L^{-}\le x<C_0^{-}\\ 1ifx=C_0^{-}\\ {\alpha }_2^{-}if{C}_0^{-}<x\le C_R^{-}\\ 0if{C}_R^{-}<x\end{array}$$

(51)

where ${\alpha }_1^{-}$ and ${\alpha }_2^{-}$ are determined by $C_{01}^{-}$$({\alpha }_1^{-})$$=$$x$ and $C_{02}^{-}$$({\alpha }_2^{-})$$=$$x$. Therefore, the membership functions $\eta (x)$ and ${\eta }^{-}(x)$ are presented in Figure 2.

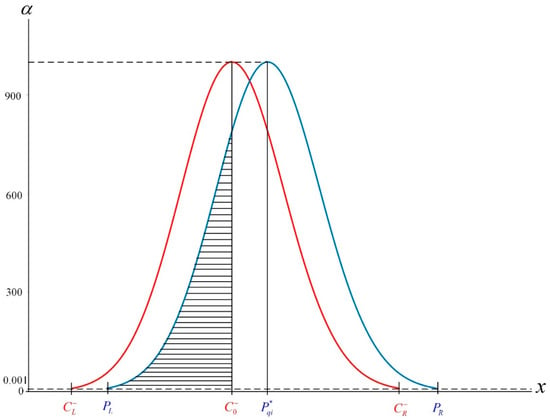
Figure 2. Membership functions η(x) and ${\eta }^{-}(x)$.

Suppose $A_L$ is the area attaining to the left of the vertical line x $=$$C_0^{-}$ in the graph of ${\eta }^{-}(x)$, and then

$$A_L=\left\{\left(x,\alpha \right)|{p^{\prime }}_{qi1}(\alpha )\le x\le C_0^{-},0\le \alpha \le 0.001\times b\right\}$$

(52)

where $C_0^{-}$$=$${p^{\prime }}_{qi1}$$(0.001\times b)$. We also let $\alpha$$=$ 0.001 $\times$$l$ and $l$$=$ 1,…, $b$, which indicate that $b+1$ horizontal lines divide $A_L$ into $b$ trapezoid-shaped blocks. Then, the $l\mathrm{th}$ block can be displayed as follows:

$$A_{Ll}=\left\{\begin{array}{l}\left(x,\alpha \right)|{p^{\prime }}_{qi1}(0.001\times l)\le x\le {p^{\prime }}_{qi1}(0.001\times b),\\ 0.001\times (l-1)\le \alpha \le 0.001\times l\end{array}\right\}$$

(53)

We also let the coordinates of the two intersection points of horizontal line $\alpha$$=$ 0.001 $\times$$l$ and set $A_L$ be $\left(x_{l1}^L,0.001\times l\right)$ and $\left(x_{l2}^L,0.001\times l\right)$. Thus, the distance between these two points is $d_l^L$$=$$x_{l2}^L$$-$$x_{l1}^L$, as shown below:

$$d_l^L=p_{qi}^{\ast }\times \frac{\sqrt{{\chi }_{0.5-\sqrt{1-0.001\times b}/2,n-1}^2}-\sqrt{{\chi }_{0.5-\sqrt{1-0.001\times l}/2,n-1}^2}}{\sqrt{{\chi }_{0.5,n-1}^2}}-\frac{Z_{0.5-\sqrt{1-0.001\times b}/2}-Z_{0.5-\sqrt{1-0.001\times l}/2}}{\sqrt{{\chi }_{0.5,n-1}^2}}$$

(54)

Obviously, $d_0^L$$=$$d_1^L$$=$ … $=$$d_{10}^L$, $d_b^L$$=$ 0 and $A_{Ll}$ is a trapezoid-shaped block, including lower base $d_{l-1}^L$, upper base $d_l^L$, and height 0.001. Consequently, the approximate value of its area $a_{Ll}$ for $l$ 1,…, $b$ can be expressed below:

$$a_{Ll}=(0.001)\times \left(\frac{d_{l-1}^L+d_l^L}{2}\right)$$

(55)

Therefore,

$$\begin{array}{ll}{a}_L& ={\displaystyle \sum _{l=1}^b{a}_{Ll}}\\ & =(0.001)\times {\displaystyle \sum _{l=1}^b\left(\frac{d_{l-1}^L+d_l^L}{2}\right)}\\ & =0.001\times \left\{\left(\frac{d_0^L}{2}+\frac{d_1^L}{2}\right)+\left(\frac{d_1^L}{2}+\frac{d_2^L}{2}\right)+\dots +\left(\frac{d_9^L}{2}+\frac{d_{10}^L}{2}\right)+\left(\frac{d_{10}^L}{2}+\frac{d_{11}^L}{2}\right)\right\}\\ & +0.001\times \left\{\left(\frac{d_{11}^L}{2}+\frac{d_{12}^L}{2}\right)+\dots +\left(\frac{d_{b-1}^L}{2}+\frac{d_b^L}{2}\right)\right\}\\ & =\left(0.001\right)\times \left\{\left(\frac{d_0^L}{2}+d_1^L+\dots +d_{10}^L\right)+\left(d_{11}^L+d_{12}^L+\dots +d_{b-1}^L+\frac{d_b^L}{2}\right)\right\}\\ & =\left(0.001\right)\times \left(10.5\times d_{10}^L+{\displaystyle \sum _{l=11}^{b-1}{d}_l^L}\right)\end{array}$$

(56)

Case 2: $k$$\le$$p_{qi}^{\ast }$

Similar to ${\tilde{C}}_0^{-}$$\left[\alpha \right]$, when $k$$\le$$p_{qi}^{\ast }$, the $\alpha -\mathrm{cuts}$ of triangular fuzzy critical value number ${\tilde{C}}_0^{+}$ will be ${\tilde{C}}_0^{+}$$\left[\alpha \right]$$=$$\left[C_{01}^{+}(\alpha ),C_{02}^{+}(\alpha )\right]$ for $0.01\le \alpha \le 1$, where

$$C_{01}^{+}(\alpha )=C_0^{+}\times \sqrt{\frac{{\chi }_{0.5-\sqrt{1-\alpha }/2,n-1}^2}{{\chi }_{0.5,n-1}^2}}-\frac{Z_{0.5-\sqrt{1-\alpha }/2}}{\sqrt{{\chi }_{0.5,n-1}^2}}$$

(57)

$$C_{02}^{+}(\alpha )=C_0^{+}\times \sqrt{\frac{{\chi }_{0.5+\sqrt{1-\alpha }/2,n-1}^2}{{\chi }_{0.5,n-1}^2}}+\frac{Z_{0.5-\sqrt{1-\alpha }/2}}{\sqrt{{\chi }_{0.5,n-1}^2}}$$

(58)

Suppose the $\alpha -\mathrm{cuts}$ of ${\tilde{C}}_0^{+}$$\left[\alpha \right]$ for $0\le \alpha <0.01$ equals ${\tilde{C}}_0^{+}$$\left[0.01\right]$. Obviously, if $\alpha =1$, then $C_{01}^{+}$$(1)$$=$$C_{02}^{+}$$(1)$$=$$C_0^{+}$ and the triangular fuzzy number of $C_0^{+}$ is ${\tilde{C}}_0^{+}$$=$ $\mathsf{\Delta }\left(C_L^{+},C_0^{+},C_R^{+}\right)$ where $C_L^{+}=C_{01}^{+}(0.01)$ and $C_R^{+}=C_{02}^{+}(0.01)$. Then, the membership function of triangular fuzzy number ${\tilde{C}}_0^{+}$ is

$${\eta }^{+}(x)=\{\begin{array}{l}0ifx<C_L^{+}\\ {\alpha }_1^{+}if{C}_L^{+}\le x<C_0^{+}\\ 1ifx=C_0^{+}\\ {\alpha }_2^{+}if{C}_0^{+}<x\le C_R^{+}\\ 0if{C}_R^{+}<x\end{array}$$

(59)

where ${\alpha }_1^{+}$ and ${\alpha }_2^{+}$ are determined by $C_{01}^{+}$$({\alpha }_1^{+})$$=$$x$ and $C_{02}^{+}$$({\alpha }_2^{+})$$=$$x$. Therefore, the membership functions η(x) and ${\eta }^{+}(x)$ are as presented in Figure 3:

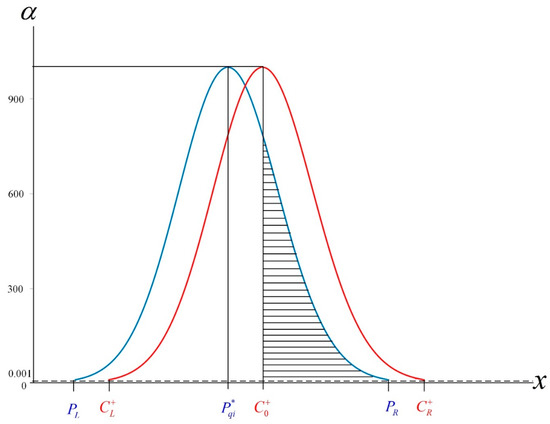
Figure 3. Membership functions η(x) and ${\eta }^{+}(x)$.

It is assumed that $A_R$ is the area extending to the right of the vertical line x = $C_0^{+}$ in the graph of η(x), and then

$$A_R=\left\{\left(x,\alpha \right)|C_0^{+}\le x\le {p^{\prime }}_{qi2}(\alpha ),0\le \alpha \le 0.001\times a\right\}$$

(60)

where $C_0^{+}$$=$${p^{\prime }}_{qi2}$$(0.001\times a)$. We let $\alpha$$=$ 0.001 $\times$$l$ and $l$$=$ 1,…, $a$, which indicate that $a+1$ horizontal lines divide $A_R$ into $a$ trapezoid-shaped blocks. Therefore, the $l\mathrm{th}$ block can be expressed in the following equation:

$$A_{Rl}=\left\{\begin{array}{l}\left(x,\alpha \right)|{p^{\prime }}_{qi2}(0.001\times a)\le x\le {p^{\prime }}_{qi2}(0.001\times l),\\ 0.001\times (l-1)\le \alpha \le 0.001\times l\end{array}\right\}$$

(61)

We also set the coordinates of the two intersection points of horizontal line $\alpha$ = 0.001 × $l$ and set $A_R$ as $\left(x_{l1}^R,0.001\times l\right)$ and $\left(x_{l2}^R,0.001\times l\right)$. Thus, the distance between these two points is $d_l^R$$=$$x_{l2}^R$$-$$x_{l1}^R$ as shown below:

$$d_l^R=p_{qi}^{\ast }\times \frac{\sqrt{{\chi }_{0.5+\sqrt{1-0.001\times l}/2,n-1}^2}-\sqrt{{\chi }_{0.5+\sqrt{1-0.001\times a}/2,n-1}^2}}{\sqrt{{\chi }_{0.5,n-1}^2}}+\frac{Z_{0.5-\sqrt{1-0.001\times l}/2}-Z_{0.5-\sqrt{1-0.001\times a}/2}}{\sqrt{{\chi }_{0.5,n-1}^2}}$$

(62)

Obviously, $d_0^R$$=$$d_1^R$$=$ … $=$$d_{10}^R$, $d_a^R$$=$ 0 and $A_{Rl}$ is a trapezoid-shaped block with a lower base $d_{l-1}^R$, upper base $d_l^R$, and height 0.001. As a result, the approximate value of its area $a_{Rl}$ for $l$$=$ 1,..., $a$ can be written as follows:

$$a_{Rl}=(0.001)\times \left(\frac{d_{l-1}^R+d_l^R}{2}\right)$$

(63)

Therefore,

$$\begin{array}{ll}{a}_R& ={\displaystyle \sum _{l=1}^a{a}_{Rl}}\\ & =(0.001)\times {\displaystyle \sum _{l=1}^a\left(\frac{d_{l-1}^R+d_l^R}{2}\right)}\\ & =0.001\times \left\{\left(\frac{d_0^R}{2}+\frac{d_1^R}{2}\right)+\left(\frac{d_1^R}{2}+\frac{d_2^R}{2}\right)+\dots +\left(\frac{d_9^R}{2}+\frac{d_{10}^R}{2}\right)+\left(\frac{d_{10}^R}{2}+\frac{d_{11}^R}{2}\right)\right\}\\ & +0.001\times \left\{\left(\frac{d_{11}^R}{2}+\frac{d_{12}^R}{2}\right)+\dots +\left(\frac{d_{a-1}^R}{2}+\frac{d_a^R}{2}\right)\right\}\\ & =\left(0.001\right)\times \left\{\left(\frac{d_0^R}{2}+d_1^R+\dots +d_{10}^R\right)+\left(d_{11}^R+d_{12}^R+\dots +d_{a-1}^R+\frac{d_a^R}{2}\right)\right\}\\ & =(0.001)\times \left(10.5\times d^R{\displaystyle \sum _{l=11}^{a-1}{d}_l^R}\right)\end{array}$$

(64)

According to the above-mentioned inferences, the fuzzy testing rules can be based on case 1 ($p_{qi}^{\ast }$$<$$k$) and case 2 ($k$$\le$$p_{qi}^{\ast }$ ). Letting 0$<$${\varphi }_1$$<$${\varphi }_2$$<$ 0.5, the fuzzy hypothesis testing rules can be listed as follows:

Case 1: $p_{qi}^{\ast }$$<$$k$.

(1)

If $a_L/a_T$$<$${\varphi }_1$, then $H_0$ is not rejected, and it is concluded that $P_{QI}$$=$$k$;

(2)

If ${\varphi }_1$$\le$$a_L/a_T$$\le$${\varphi }_2$, then no decision is made;

(3)

If ${\varphi }_2$$<$$a_L/a_T$, then $H_0$ is rejected, and it is concluded that $P_{QI}$$<$$k$.

Case 2: $p_{qi}^{\ast }$$\ge$$k$.

(1)

If $a_R/a_T$$<$${\varphi }_1$, then $H_0$ is not rejected, and it is concluded that $P_{QI}$$=$$k$;

(2)

If ${\varphi }_1$$\le$$a_R/a_T$$\le$${\varphi }_2$, then no decision is made;

(3)

If ${\varphi }_2$$<$$a_R/a_T$, then $H_0$ is rejected, and it is concluded that $P_{QI}$$>$$k$.

5. A Practical Application

As noted by Wu et al. [28] and Chen et al. [29], Central Taiwan boasts a large machinery industry including various upstream, midstream, and downstream manufacturers. We therefore used the roundness of a gear-grinding process at a factory in Central Taiwan to illustrate the two-tailed fuzzy hypothesis testing method with process quality indices of the unilateral specification. The roundness of the inner hole in a gear is an STB quality characteristic, and the upper specification limit USL $=$ 0.01 µm. Based on Equations (27) and (28), we can compute the values of $\overline{x}$ and s with sample size n = 100 as follows:

$$\overline{x}=\frac{1}{n}{\displaystyle \sum _{i=1}^n{x}_i}=\frac{1}{100}{\displaystyle \sum _{i=1}^{100}{x}_i}=0.0067$$

$$s=\sqrt{\frac{1}{n-1}{\displaystyle \sum _{i=1}^n{\left(x_i-\overline{x}\right)}^2}}=\sqrt{\frac{1}{99}{\displaystyle \sum _{i=1}^{100}{\left(x_i-0.0067\right)}^2}}=0.0008.$$

Therefore,

$$p_{qi}^{\ast }=\frac{USL-\overline{x}}{s}=4.125$$

According to Equations (39)–(41), we have ${\widetilde{p^{\prime }}}_{qi}$$=$$\mathsf{\Delta }\left(p_L,p_M,p_R\right)$$=$$\mathsf{\Delta }\left(3.047,4.125,5.259\right)$, and the membership function $\eta (x)$ with $p_{qi}^{\ast }$$=$ 4.125 is

$$\eta (x)=\{\begin{array}{l}0 if x<3.047\\ {\alpha }_{1}if 3.047\le x<4.125\\ 1 if x=4.125\\ {\alpha }_{2}if4.125<x\le 5.259\\ 0 if 5.259<x\end{array}$$

where ${\alpha }_1$ and ${\alpha }_2$ are determined by ${p^{\prime }}_{qi1}({\alpha }_1)$$=$$x$ and ${p^{\prime }}_{qi2}({\alpha }_2)$$=$$x$. Since $d_0^T=d_1^T=\dots =d_{10}^T$ and $d_{1000}^T=0$, then, based on Equation (48), we have

$$\begin{array}{ll}{a}_T& =\left(0.001\right)\times \left\{\left(\frac{d_0^T}{2}+d_1^T+\dots +d_{10}^T\right)+\left(d_{11}^T+d_{12}^T+\dots +d_{999}^T\right)\right\}\\ & =(0.001)\times \left(10.5\times d_{10}^T+{\displaystyle \sum _{l=11}^{999}{d}_l^T}\right)\\ & =(0.001)\times \left(10.5\times 2.2122+864.9726\right)\\ & =0.8882\end{array}$$

Our goal is to test whether the unilateral specification process quality index value is equal to k $=$ 5 with sample size n$=$ 100 and α = 0.01. The null hypothesis is $H_0$: $P_{QI}$ $=$ 5, and the alternative hypothesis is $H_1$: $P_{QI}$ $\ne$ 5. Obviously, $p_{qi}^{\ast }$ $=$ 4.125 $<$ 5 belongs to case 1. Thus, based on Equation (25), we can compute the values of $C_0^{-}$ as follows:

$$C_0^{-}=\frac{{t^{\prime }}_{\alpha /2,n-1}\left(\delta =\sqrt{n}k\right)}{\sqrt{n}}=\frac{{t^{\prime }}_{0.005,99}\left(\delta =\sqrt{100}\times 5\right)}{\sqrt{100}}=4.060$$

According to Equations (49) and (50), we have ${\tilde{C}}_0^{-}$$=$$\mathsf{\Delta }\left(C_L^{-},C_0^{-},C_R^{-}\right)$$=$$\mathsf{\Delta }\left(2.994,4.060,5.180\right)$, and the membership function ${\eta }^{-}(x)$ with $C_0^{-}$$=$ 4.060 is

$${\eta }^{-}(x)=\{\begin{array}{l}0if x<2.994\\ {\alpha }_{1}if 2.994\le x<4.060\\ 1if x=4.060\\ {\alpha }_{2}if 4.060<x\le 5.180\\ 0if 5.180<x\end{array}$$

(65)

where ${\alpha }_1^{-}$ and ${\alpha }_2^{-}$ are determined by $C_{01}^{-}$$({\alpha }_1^{-})$$=$$x$ and $C_{02}^{-}$$({\alpha }_2^{-})$ $=$$x$. Therefore, the membership functions $\eta (x)$ and ${\eta }^{-}(x)$ are as presented in Figure 4.

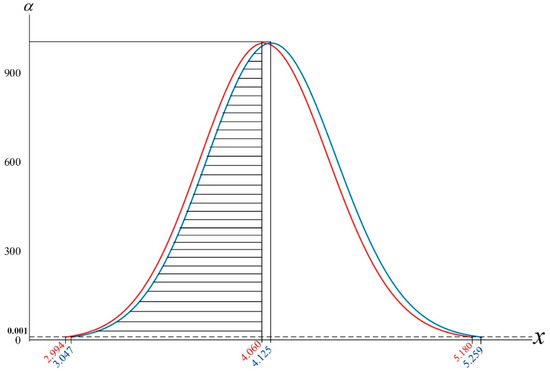
Figure 4. Membership functions η(x) with $p_{qi}^{\ast }$$=$ 4.125 and ${\eta }^{-}(x)$ with $C_0^{-}$ $=$ 4.060.

Since $d_0^L=d_1^L=\dots =d_{10}^L$ and $d_b^L=0$ (b = 983), then based on Equation (56), we have

$$\begin{array}{ll}{a}_L& =\left(0.001\right)\times \left\{\left(\frac{d_0^L}{2}+d_1^L+\dots +d_{10}^L\right)+\left(d_{11}^L+d_{12}^L+\dots +d_{b-1}^L\right)\right\}\\ & =(0.001)\times \left(10.5\times d_{10}^L+{\displaystyle \sum _{l=11}^{b-1}{d}_l^L}\right)\\ & =(0.001)\times \left(10.5\times 1.0135+{\displaystyle \sum _{l=11}^{983-1}{d}_l^L}\right)\\ & =(0.001)\times \left(10.5\times 1.0135+363.1641\right)\\ & =0.3738\end{array}$$

Based on Chen [30] and setting ${\varphi }_2$ = 0.40,

$$a_L/a_T=\frac{0.3738}{0.8882}=0.421>{\varphi }_2$$

Based on the fuzzy testing rule (3) of case 1, we can conclude that $P_{QI}$$<$ 5. According to the statistical testing rules, since $p_{qi}^{\ast }$ $=$ 4.125 $>$ 4.060 $=$$C_0^{-}$, the null hypothesis cannot be rejected ($P_{QI}$ = 5). However, $p_{qi}^{\ast }$ = 4.125 is much smaller than 5, so the conclusion that $Q_{pk}$ = 5 is obviously unreasonable. The conclusion that $P_{QI}$ < 5, received via the fuzzy testing method suggested in this study, is obviously more reasonable than the conclusion of the statistical testing method [20,22,24,25,26,31].

In order to facilitate the use of the industry, this study summarizes the above and provides an application process as follows:

Step 1: Calculate the sample mean $\overline{x}$, and sample standard deviation s;

Step 2: Calculate the estimated value of the indicator, $p_{qi}^{\ast }$, and the critical value, $C_0$;

Step 3: Apply the Statistical software (e.g., SAS programming), first, enter the required value $K$ of the quality level, and then enter the estimated value of the index, $p_{qi}^{\ast }$, as well as the critical value, $C_0$;

Step 4: Execute the completed Statistical software and then simply calculate to get the value $a_L/a_T$.

Step 5: Then, judgments can be made based on the fuzzy evaluation criteria.

6. Conclusions

The unilateral specification process quality index reflects process yield and quality level. In addition, it serves as a good bridge between the industry and customers as well as a tool for internal engineers. This study proposes a two-tailed fuzzy test method built on the basis of the process quality indices of the unilateral specification for performance evaluation conducted by the industry. First, we derived the confidence interval of the unilateral specification process quality index based on the results of statistical inferences. Next, we used the confidence interval to develop the two-tailed fuzzy testing model based on the above rules with critical values. This two-tailed test provides an effective method for process quality assessment as well as improvement. We also present a case study evaluating the roundness of a gear-grinding process at a factory in Central Taiwan. The results of the case study illustrate the application of the two-tailed fuzzy hypothesis testing method for the unilateral specification process quality index, and further prove that the proposed method provides more reasonable results than statistical testing [20,22,24,25,26,31]. Our proposed method can decrease the testing cost and make the quality level reach the standard rapidly. Besides, it diminishes the ratio of rework and scrap, as well as further reducing social losses such as carbon emissions [26,27]. Obviously, this method is an innovation for sustainable concept and application. In view of global warming, sustainable development is the premise for all companies to maintain the advantages of high quality and production efficiency. The sustainability concept is different from the traditional one, which focuses on the profits only. Increasingly more and more companies apply our proposed method and concept, not only to improve production efficiency, but also to reduce waste for the goal of sustainability.

After the enterprise has completed the process improvement, it should carry out the improvement verification [33] in order to practice the spirit of total quality management. Therefore, this study suggests that the fuzzy improvement verification model be developed in the future. In addition, considering that many process distributions are abnormal, the future research can focus on exploring how to imitate a normal process as well as create a fuzzy evaluation model of the abnormal process distribution when the process distribution is abnormal, the median replaces the average, and ($1-\alpha /2$ upper quantile—$\alpha /2$ upper quantile)/6 replaces the standard deviation [34,35].