Abstract
Computational thinking is a highly appreciated skill by mathematicians. It was forecasted that, in the next few years, half of the jobs in science, mathematics, technology and engineering (abbreviated as STEM, including arts as STEAM) will use some kind of computation. It is therefore necessary to enhance the learning of mathematics by collaborative problem-solving activities focused on both learning mathematics and developing computational thinking. The problems in science offer a reasonable context in which to investigate the common overarching concepts (e.g., measuring the length). An interdisciplinary STEAM collaborative problem-solving activity was designed and piloted with 27 lower secondary students aged 13.07 ± 1.21 years. Different levels of willingness to use the technology were observed and the factors influencing it were identified. We found that strong background knowledge implies high demands when controlling the used device. On the other hand, when a nice and user-friendly application was used, students did not need to perceive any control over it. After the intervention, the students’ views on the tablet changed and they reported more STEAM-related functions of the device.
1. Introduction
To learn mathematics in the 21st century not only means obtaining mathematical proficiency, but also critical thinking, creativity and technology literacy [1]. Collaborative problem solving is one of the recommended pedagogies to promote the active learning of mathematics. Furthermore, collaborative problem solving led to better performance in standardized tests in mathematics than a traditional transmissive approach [2,3,4,5], particularly when the problems were related to the real life of the students [6] and used technology [7]. It was also reported that students educated using collaborative problem solving appreciate their knowledge of mathematics and science even in their future workplace. This influenced their academic performance and career choice [8].
Furthermore, it is predicted that, in the next few years, half of STEAM-related jobs will be in computing [9,10]. Children and young people use smartphones and tablets on a daily basis, but their use is mainly for entertainment, not for learning purposes. On the contrary, mathematicians consider the effective use of technological tools as a “valuable component of the practice of doing mathematics” [11] (p. 9). A similar perception can be given of the scientists [10,12]. This has led to the large-scale development and piloting of materials aimed at fostering computational thinking [13], but not all of them are suitable for problem-based learning. Cápay and Magdin [14] used black boxes as the main concept for tasks developing computational thinking and they provoked very intensive reaction. Burbaite et al. [15] designed an activity where the students could learn about the physical principles of functioning an ultrasonic sensor, connecting knowledge of physics with knowledge from computer science. Students were able to gain conceptual knowledge in physics and design the algorithm at the same time. Another example of an interdisciplinary approach can be found in the work of Lytle et al. [16], aimed at an agent-based simulation with a special focus on student-perceived ownership of developed programs. Students using the use–modify–create approach felt more confident and perceived the code developed in the guided part, with their slight changes, as more familiar compared to the transmissive approach in the control group. Several studies [17,18] have shown that the design-based approach can improve the computational thinking of participating students and enhance the students’ awareness of the different tasks that can be performed using the computer and their self-efficacy in using computers.
1.1. Interdisciplinary Teaching
A lot of current scientific problems can be addressed only if experts from several scientific fields collaborate together. New scientific fields (e.g., physical chemistry, biostatistics, and theoretical physics) have even been established. However, the school curriculum is divided into separate subjects. In Slovakia, even science subjects are separated to physics, chemistry and biology in secondary education [19]. Both mathematics and science education aim to enable students to understand the wonder of the world around us. They share strategies for solving problems and for scientific inquiry. These approaches include logical thinking, hypothesizing, observations, analysis and experimentation. Even university students are not used to solving practical problems and, therefore, they are not able to interpret the obtained results [20].
St. Clair and Hough [21] grouped arguments supporting an interdisciplinary approach to education into six groups. An interdisciplinary approach (i) is in agreement with the current body of knowledge about the needs of the secondary students; (ii) offers a substantial learning environment and, therefore, has a positive impact on the learning process as well as on achievement; (iii) provides students with a more holistic approach to problems; (iv) is global in content and better prepares participating students for critical citizenship; (v) improves the skills necessary for problem-solving by demonstrating different views and perspectives; (vi) encourages collaboration among teachers.
1.2. Computational Thinking
Weintrop et al. [9] stress the ability of mathematics and science to develop key skills in computation. Departing from the poor-technological view, we can focus on four main categories: “data practices, modelling and simulation practices, modelling and simulation practices, computational problem-solving practices and systems thinking practices” (p. 127). It is important to realize that computational thinking is more than using technology: it is a way of thinking while solving complex problems [22]. Computational thinking was defined by Aho as “the thought processes involved in formulating problems so their solutions can be represented as computational steps and algorithms” [23] (p. 832).
Similar to proficiency in mathematics [24], computational thinking may be also developed via problem-solving activities [25]. Gretter and Yadav [26] see “collecting, analysing and representing data, decomposing problems, using algorithms and procedures, making simulation” as the key component of computational thinking (p. 511). Bocconi et al. [27], based on studies [28,29], define six components constituting computational thinking: (1) abstraction, (2) algorithmic thinking, (3) automation, (4) decomposition, (5) debugging, and (6) generalization. Abstraction is understood as reducing the details in order to make the artefact more understandable. The essence of abstraction is competence in choosing the proper feature to hide and proper representation, so that the hiding results in easier problems with a suitable solution. Algorithmic thinking is a systematic way of thinking applied to splitting a complex problem into a series of (not necessarily ordered) steps utilising the different tools available in the moment. Automation can be defined as a procedure aimed at saving the labour which the computer is uses to perform a (ordered) set of repetitive tasks instead of the slow and inefficient work of humans. Decomposition is a way of breaking down the artefacts into smaller parts that can be “understood, solved, developed and evaluated separately” [28] (p. 8), which makes complex systems simpler to design. Debugging is a looking-back ability when the outcomes are analysed and evaluated. Generalization, as a part of computer thinking, is connected to “identifying patterns, similarities and connections, and exploiting those features” [28] (p. 8), relating to previous experience with similar problems and adopting developed algorithms to solve the comprehensive class of similar problems. Although the positive effect of the use of technology on students’ performance in mathematics and science was confirmed, very few studies investigated the use of these applications for mathematics. The results of Kosko et al. [30] suggest that integration of the applications over a three-week period significantly increased the mathematics achievements of participating students.
The ability to use the technology is not self-developing. The fact that students are able to use tablets or smartphones or any other technology for communication or browsing the internet does not imply an ability to use it for more sophisticated purposes, such as measuring the distance, temperature or size of an angle, calculating repetitive tasks or processing the measured data. It is necessary to provide students with the opportunity to experience this kind of use of the technology. The invention of mobile technologies allowed students to unplug the computers, leave the classroom and move outdoors [31].
The instrumental approach [32] seems to be a reliable framework to understand what is going on during the activities, supporting both mathematical learning and computational thinking. The technology introduced in the classroom can be considered as an artefact. Only when students learn to use it, when they develop the utilization scheme, does the artefact become a tool, an instrument [33]. The development of the utilization scheme can be described as having three levels: (1) usage schemes, (2) instrumental action schemes including gestures and operative invariants, and (3) instrumented collective activity schemes [34]. Usage schemes are directly related to the artefacts themselves. They are developed through manipulations and examinations by the artefact. Instrumented action schemes or instrument-mediated action schemes are higher-order, coherent and meaningful mental schemes, acquired from existing elementary usage schemes when a student manipulates an instrument with the aim of solving the problem. The developed schemes are specific to each activity. When an application is introduced in the classroom, students first have to become familiar with its basic features, developing the usage scheme. Only then they can use it for solving the problem and fostering the instrumental action schemes. Instrumented collective activity schemes or collective instrument-mediated activity schemes are the schemes developed in the context of collective, particularly collaborative, activity. The students are both influenced by artefacts’ potentialities and constraints (instrumentation) and influencing the artefact via their preconceptions, knowledge, beliefs and usual ways of work (instrumentalisation) [34]. The two described dual processes are united in the instrumental genesis when the instrument arises as the result of the interactions between the student (subject of the activity) and the artefact [35,36,37,38].
The main aim of this study is to demonstrate the potential of interdisciplinary problem-solving activities, including several STEAM disciplines, to develop both the mathematical proficiency and computational thinking of involved students. Various activities were designed to develop computational thinking [13,14], but only a few of them were focused on the students’ tendency to use technology to solve problems. In this article, we looked for the answer to the research question formulated as follows: What components of computational thinking may be developed by involving students in interdisciplinary STEAM activities using technology? How is this development manifested?
2. Methodology
The presented research was conducted with a more than 15-year longitudinal study about summer camps for lower-secondary students focused on STEAM, particularly physics and mathematics (mainly as the language of physics). The study based on the design research principles involved the following phases: (i) the preparation and design of instructional materials, (ii) implementation of the materials, and (iii) retrospective analyses, cyclically repeating from 2006 to 2020, described in more detail in the work of Cobb [39,40]. The outputs from each year informed preparation and design in the following year. Development of the design and the overarching topic of each year are summarised in Supplementary Materials (Table S1). The camp leader had an input and primary responsibility for implementing the activity with the group of 3–4 students. In this article, we focus on one particular activity implemented in the year 2019. As the activity was held in the 14th year of the study, the design was informed by each activity implemented in previous years of the camp.
2.1. Participants
The camp in 2019 was attended by 27 students of grade 6–10 (age 13.07 ± 1.21 years), nine of whom were girls. The leaders in the group were a graduate student of Physics Education and a bachelor student of physics. The 27 participating students were divided into three big groups, and each group was further divided into three sub-groups to enable students to try the hands-on activities on their own. For some of the activities, the groups were divided into two smaller subgroups, one with younger students (YS) aged 11–12 and the second with older students (OS) aged 13–14. Written informed consent was collected from the parents of all participating students.
2.2. Preparation Phase: Design of the Activity
During all years, the camp was organized to last from Monday till Friday. Usually, there is an overarching topic for all the activities in the camp. On top of this, the overall design of the 2019 camp was focused on the development of students’ skills in the area of project management including the development of related soft skills, e.g., leadership, organization and communication. The main topic of the camp was the construction of a rocket. Students were supposed to design a rocket in an environment simulating a real funding programme. They had to write a project proposal to get funding, prepare the budget and milestones, and defend their project at the ending of the camp-week. One of the required tasks in the final project was to assess their developed rocket based on various indicators, including the maximum height their rocket could achieve.
The design of the activity was led by the categorization of the strategies of interdisciplinary teaching into three groups, as proposed by Nikitina [27]: (1) contextualizing, providing a reasonable context for the interdisciplinary activity (preparation of estimating the height of the rocket), (2) conceptualizing, meaning that the activity is based on an overarching concept that is central for two or more disciplines (i.e., measuring and length) and (3) problem-centring, particularly using real-life or realistic problems in which concepts, processes and ideas of different disciplines have to be used in the solution. The main aim of the activities rooted in this strategy was to create a tangible outcome or product, in our case, a procedure to estimate the height.
In order to prepare students to solve the problem, e.g., to estimate the rocket range height, a series of three smaller activities was designed. The primary designers were two of the authors of this article, who were involved in the longitudinal study since its very beginning and therefore were informed in detail about the outcomes of the previously implemented activities. The camp leaders adjusted the ideas and prepared the worksheets for the students.
2.3. Implementation and Reflection
The designed activity was performed three times during camp-week. After each implementation, the leaders reflected on their experience with the guidance of the designers of the activity. After the first piloting, the activity was slightly changed. The second pilot did not lead to any significant change in the worksheet.
2.4. Data Analysis
The implementation of the activity was audio-recorded and transcribed. The students’ actions connected to the use of technology (i.e., tablets) were analysed using the components of computational thinking, as described by Bocconi et al. [27], and the episodes where computational thinking was observable were chosen.
In order to compare the responses of the participating students in the items related to computational thinking in the beginning and at the end of camp-week, a McNemar test of symmetry [41] with Yates correction [42] was performed using the calculations, carried out in the programme STATISTICA 13.3 (StatSoft Inc., TIBCO Software, Palo Alto, CA, USA).
3. Results and Discussion
The activity was designed to teach children the procedure for measuring or estimating the height of the object. The overarching concept involved was measuring the distance. Length was seen as both the physical quantity and also the geometrical characteristics. On the other hand, the main aim of the activity was to estimate the height of the statue, so problem-centring was used as a strategy to create interdisciplinary teaching. The whole activity took approximately 90 min for each group. It was divided into the three phases: motivation and introduction, problem-solving, and concluding. Each of the three strategies took approximately 20 min.
3.1. Strategy 1: Shadow
The first strategy offered to students in order to solve the problem used measuring tape and a pole (140 cm). First, pupils measured the length of the pole when the pole was laid down on the flat surface. After that, the pole was placed to be orthogonal with the floor, and the length of the shadow of the pole was measured. The next step was to measure the shadow of the statue.
The first phase of the strategy was the introduction into similarity. Teacher explained the concept of similarity, and when she found that some of the pupils knew and understood, she left him/her to explain it to the other members of the group. The teacher facilitated the discussion and posed questions to lead the students to come up with the expression , where means height of the statue, height of its shadow, means height of the pole and height of the pole’s shadow. Students later expressed the height of the statue as . The intention was to use the spreadsheet to calculate the height of the statue (). After expressing , the teacher asked the students how to calculate the height of the statue using the measured data.
| T | Have you seen this kind of expression? How would you use it? |
| YS1 | This [points finger on ] reminds me a fraction, so we might substitute our numbers and we will get something. |
| T | So, you can start to calculate. Add a column to the table and write down the results. |
| YS2 | Isn’t it possible to write the numbers to the table in the tablet, so the tablet can calculate instead of us? (1) |
| T | Try to find an app which can calculate. What kind of software would you look for? |
| YS3 | I am going to ask some of the older students of the group. |
| T | Check the installed apps in the tablets. Maybe you can find an appropriate app on your own. |
The two students remaining at the stage with the Statue problem started to run the different applications in the tablet. The students had two minutes, so the remaining students did not get a chance to check more than three apps.
| OS1 | Just find excel or something resembling excel [takes the tablet, starts MS Excel, creates a table] and do not delete it, is will remain for the next group [then he leaves the subgroup of younger members and joins his subgroup] |
| YS1 | I do not know how and based on what that excel calculates (2). |
| YS2 | Neither do I. |
| YS3 | It’s kind of a black box (3). It gives the data but we do not know where the formula is hidden. |
The students resisted using the spreadsheet prepared by their groupmate without understanding it. The teacher made them insert the data into the table and then showed them the formula written in the last column. Even though the students could see it, they were not familiar with the syntax and they were not able to see the formula they came up with before (see Figure 1). Their previous experience and usual ways of work were not satisfactory to understand the potentialities of the application.
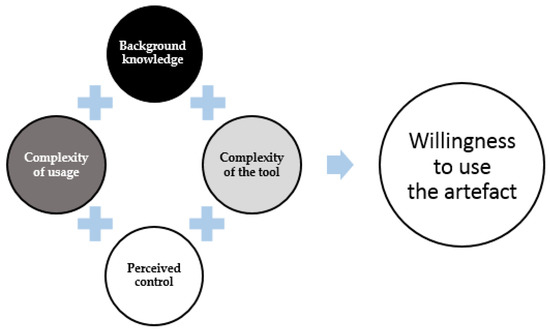
Figure 1.
Low student willingness to use the artefact as influenced by the low perceived control.
One of the older students gained this ability and did not expect that the younger members of his group would not understand his product. Therefore, the teacher asked the younger students to create a new file and introduced them to the basics of typing formulae in a spreadsheet. Then, the students were able to see their formula in the prepared spreadsheet and they were willing to use it for calculations (see Figure 2). The knowledge of basic syntax allowed them to use the spreadsheet while fully understanding how it works. As the students were fully aware of the method used to estimate the height of the state, they felt the need to influence the artefact in the process of instrumentalisation. In this case, students understood the formula and how it was developed, they had full background knowledge and resisted using the spreadsheet without controlling the process of computing.
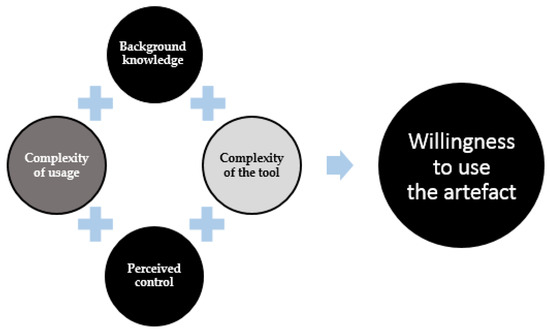
Figure 2.
High student willingness to use the artefact as influenced by the high perceived control.
This episode gives us two interesting moments. In contrast with the rest of the group, the young student YS2 did not perceive the tablet as an artefact; she intended to use it as a tool, but did not have the appropriate knowledge. She showed an unexpected level of computational thinking in the area of automation (1), understood as a labour-saving process when the computer executes repetitive tasks instead of humans [29], but she was able to come up with either a concrete application or the kind of software needed. Conversely, the older student OS1 had the utilization scheme at their disposal and was able to develop a needed spreadsheet, so he acted using the tablet as with an instrument.
We consider it a very positive sign that the younger students complained that they did not understand what the spreadsheet developed by their group-mate computed [2], and pushed the teacher to show them how to create it. The process of instrumental genesis was present in both ways: students’ knowledge of mathematics led to their own development of the artefact and the unknown calculations provoked the students’ perception that they need to understand how the artefact works. This need may indicate some level of evaluation [43], or at least a tendency toward the evaluation of results provided by the software. After a detailed explanation by the teacher, they could understand the process of how the formula was transformed into the spreadsheet. Even though we did not test whether they could create the spreadsheet on their own, they were able to use it, and developed an instrumented action scheme capable of solving the problem.
3.2. Strategy 2: Protractor
The second implemented strategy followed the successful solution by strategy 1, described above. The main objective of the activity was to give the students the opportunity of learning how to estimate the height of the object based on the angle between the horizon and the line connecting the observer’s eyes and the object. The intention of this activity was to prepare students to use the application for measuring angles by giving them experience measuring them with a homemade tool.
This strategy did not depend on the weather, as it did not use the length of the shadow. It also needed less information compared to the shadow strategy. Instead, it used other manipulatives: a homemade protractor from cardboard and a rope. With the first of the six groups, we tried to create the protractor, but it took too long, as the students did not have satisfactory skills. As they used corrugated cardboard, the nib of the pen pierced the upper layer of the paper. Therefore, the other groups got the pre-prepared cardboard and had to finish the protractor. The students first fastened the rope to the paper. Then, they had to decide what kind of plummet they would use.
| T | I should point out that to ensure the correct measurement the rope should be tight. |
| YS2 | How to ensure that the rope will be tight? |
| YS3 | We can hold it stretched. |
| OS1 | And how would you measure it, if it should be tight all the time? What should we put there? |
The teacher provided students with the box of different things, including the 20 g weight. All the groups intended to find an object that was easy to fasten and heavy enough to tighten the rope. One of the three groups wanted to find some object with a spike to point to the exact line. All the groups used the weight, but one of them tried to use the pen first (the nip should serve as the pointer).
After finishing the cardboard protractor, the students could finally measure the angle under which they see the top of the statue. The students were already familiar with the similarity of triangles. All the groups came up with the idea that if they knew the ratio and distance from the statue, they could calculate the height of it. All the groups started to calculate, and they came up with results different than those obtained using strategy 1. The students were confused, but the teacher asked them where they held the protractor. Then, they realized that they should subtract the height of the person doing the measuring. The results were quite different again. In each group, the teacher tried to question the students to lead them to realise that they should subtract the height of the eyes (see Figure 3), not the top of the head of the measuring person. With this correction, all the groups obtained results not very different to the ones estimated by strategy 1.

Figure 3.
The sketch used to calculate the height of the statue based on the view angle.
In the final discussion after this strategy, the teacher provided the students with the definition of a tangent as the ratio of the length of the opposite side to the length of the adjacent side of the right triangle. The teacher put the formula into the tablet and developed a spreadsheet calculating the height of the statue based on the distance between the statue and observer and the viewing angle. Contrasting with the previous strategy, the children did not ask for an explanation of the formula. This may indicate that they did not understand the idea of the tangent in depth, but accepted the existence of it and believed that the teacher could teach it to them through a worksheet. Their background knowledge was lower and they did not perceive the need to fully control the method (see Figure 4). Furthermore, the worksheet gave the same result as the one they understood. Their knowledge was not deep enough to shape the instrument. The students were able to deal with the spreadsheet, as with the black box providing the same result. We assume that the same instrumented action scheme is needed to use the spreadsheet as in the previous case. However, none of the students tested whether the results would be the same when measuring the height of the known object. This fact may indicate that the students did not have advanced computational thinking in the area of debugging, defined by Csizmadia et al. [28] as the evaluation of developed application by testing, tracing or critical thinking.
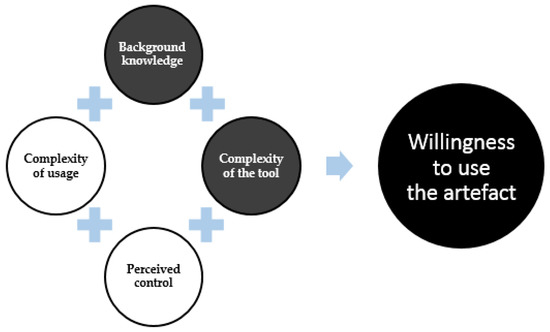
Figure 4.
High student willingness to use the artefact as influenced by a similar level of background knowledge and perceived control.
3.3. Strategy 3: Application
The third strategy used to solve the statue problem involved directly measuring the height of the statue with the SmartMeasure application on a tablet. The input for the application is the height of the eyes of the observer. Then, two other measurements are carried out: measuring the distance between the observer and the bottom of the statue and measuring the viewing angle of the observer. The application then gives the height of the statue as the output. We expected that with direct use of the application, the students may be confused by the reason for inputting this particular information. The students were already familiar with the application, as they used it for measuring the length of the corridor. The students were pleased when they found out that they would use the tablets. The teacher instructed them to use the application.
| YS1 | What should we look for in the app menu? |
| T | Try to look and guess what we can use. |
| YS2 | There is a picture like the protractor we used, so may be that one (1). |
After the confirmation of the teacher, the students launched the application and tried to use it without any previous instruction, but with the guidance of the teacher.
| YS3 | We need to set here something. |
| OS2 | We need to know the height of the tablet. What height we should use? |
| YS3 | My height. |
| YS1 | Do you have the tablet on your head? |
| YS3 | No, I hold it in my hands. But I think I should put it close to my eyes, same as we measured by paper protractor. (2) |
| T | So, what height should you set? |
| YS3 | The height of my eyes. |
The students very smoothly used the application to measure the distance between the ground and the observer’s eyes and use it as the input for the estimation of the height. We assume that the students were able to use the table so naturally because the utilization scheme for the cardboard protractor was very similar to the utilization scheme for the tablets. The relation with the previous experience was signalled by the icon of the software (1). The student YS3 said this explicitly.
The students had the same background knowledge in mathematics as in strategy 2, and the application uses the same principle to estimate the height of the object. On the other hand, their constructed protractor was fully controlled by them but, when using the tablet, they did not know how the technology measures the angle or the source calculating the height. Their background knowledge was even lower than in the previous case (Figure 5). The work was automated by the table, and the tool used was more complex.
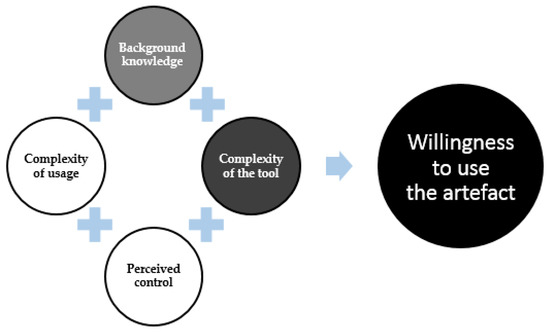
Figure 5.
High student willingness to use the artefact as influenced by higher complexity of the tool.
The students demonstrated a certain amount of abstraction when they were able to abstract from the concrete artefact and transfer the utilization scheme from a paper tool to an electronic one. We believe that the previous experience with the cardboard protractor enabled students to adopt the instrumented action scheme with a satisfactory depth for specific transfer. Furthermore, the simplicity of the homemade tool provided students with the opportunity to learn the process behind the estimation, and to concentrate on the mathematical basis used by the application without the disturbance caused by the more sophisticated affordances of the tablet.
The above analysis shows that there are more factors affecting the proper use of technology than the elements of computational thinking. Although students were not able to do this, they wanted to use the tablets for calculations. On the other hand, they refused to use the technology they did not understand. The need to understand the technology was influenced by both (1) the characteristics of subject (students), namely the background knowledge and perceived control over the artefact, and (2) the constraints and potentialities of the tool, its complexity and the complexity of its utilisation schemes. We believe that this is an important factor to be considered when assessing the computational thinking of students, particularly in the area of automation.
3.4. Remarks about the Impacts of the Activity
Besides the identification of the process of instrumental genesis, we would like to show how participation in the activity further influenced students’ work and perception of the technologies.
Just after solving the statue problem, the students had to answer the question of which methods they would use to estimate the height of an object. All of them chose using tablets and the SmartMeasure app as the most appropriate approach, so we might assume that the artefact became an instrument. The students’ reasoning varied. Students stressed the different potentialities of the application: (1) its simplicity of usage “we did not need to do anything, the tablet did the measure instead of us”, “tablet needed just one number”, “we can stand at one place”, “we did not need any other equipment”; (2) independence of the weather “we can measure using the tablet if there is a shadow or not” or (3) the universal usage “I can install the same app to my smartphone that I always have on disposal”. In the feedback for the activity, the students complained that they had to estimate the height of the statue using the shadow or protractor when the tablet offered a very convenient way to measure it. Even though they were not happy with the demanding process, we believe that the procedure gave students the opportunity to learn some new geometry, as well as stimulating their critical thinking in the further use of the technology. They were actors in the situation when they misused the technology by inputting the height of the person instead of the height of his/her eyes. When they inputted the wrong information in the application, the result was wrong.
Their experience with measuring the height of the statue was also observable in other activities performed during the week, mainly during estimating the height of their constructed rockets. When measuring the rocket range height, all the groups chose the tablet. This fact might be considered as partial evidence that the automation and abstraction components of computational thinking were developed. It is worth mentioning that younger students (age 10–11 years) referred to the measuring of the height as “statue”, while older students (age 12–13 years) referred to it as “estimating the height by a protractor”. The different terminology used may reflect the different levels of cognitive development of the students. While the younger students named the action according to the surface characteristic, the particular object measured in the problem, the older students focused more on the structure of the solution when the angle was used to calculate the height, so, surprisingly for them, the height was estimated by a protractor.
Besides this qualitative evidence, we may support our findings about the changed perception of the tablets from the participating students by the change that occurred in their responses to specific items in the questionnaires administered at the very beginning and at the end of the camp week. The responses are summarized in Table 1. In the first question, students were asked to list different means of measuring distance. In the pre-test, none of the participating students mentioned any electronic device, while in the post-test 17 of the 27 participating students mentioned the tablet or the SmartMeasure application (). When students listed what tablets can be useful for, they mainly listed calling and messaging in the pre-test, while in the post-test they listed different features useful for solving STEAM problems, e.g., calculator, measuring, GPS or compass The measurement of different characteristics was listed by 14 of 27 participating students () in the post-test. The change in students’ responses supports the hypothesis that involving students in problem-solving activities when technology (i.e., tablet) is used as a tool to simplify their work can enhance their computational thinking, mainly in the automation component.

Table 1.
Students’ responses to the chosen items in pre- and post-questionnaire.
The episodes reported in the qualitative analysis indicate that the abstraction can be enhanced too. The process of the instrumental genesis of the students was not studied in great detail, but we assume that using the physical aid before the virtual one enhanced students’ understanding of the process of how height is obtained based on the viewing angle. Similar results are reported by Vagova et al. [44], who used 3D-printed manipulatives before the virtual manipulation with cubes in the computer environment. The findings also support Lieban’s [45] conjecture that the results obtained using a virtual environment should be confronted by results using physical aids. The implementation of both physical manipulatives and computers enhances the mathematical modelling skills of secondary students [46].
3.5. Limitations of the Study
We are aware of the limitations of the study, mainly the fact that the participants of the study were not regular students, but students choosing a summer camp focused on physics, so their enthusiasm and willingness to solve the problem is much higher than in the common population. Their interest in STEAM subjects allowed us to analyse the processes appearing when introducing technology without the need of demanding classroom management. When generalising the results, one should keep in mind that the sample comprised only 27 students. The arrangement of the activities in the summer camp, where a small group of students work under the supervision of one or two camp leaders, allowed us to see what is going on during the process of instrumentation genesis in detail. On the other hand, neither the teachers’ (camp-leaders) work nor the teachers’ influence on the process were analysed. Furthermore, the activity in which they were involved provided a plausible context to solve problems in mathematics and/or physics, and we therefore assume that similar processes would happen in usual classrooms.
4. Conclusions
The main aim of the presented study was to demonstrate the effect of incorporating ICT in solving STEM interdisciplinary problems on the computational thinking of the students. The concept of measuring connects mathematics and physics, and the problem-based orientation of the analysed activity supported the interdisciplinary learning of participating students. The mathematical apparatus was used in the procedural way or as a toolbox, but enhanced the mathematical repertoire of models of right-angled triangles by a nontrivial separated model. On the other hand, the students could develop skills in measuring the distance and length by concrete tools, as is usual in physics. The progressive involvement of technology in the problem-solving process allowed students to understand the way the application works and enhanced their computational thinking in a very meaningful way. They were able to progressively develop their utilisation schemes.
The detailed process of instrumental genesis during a problem-solving activity involving mathematics and physics should be studied further. The influence of different orchestrations should be researched in order to maximize the students’ gain from the educational activity.
Supplementary Materials
The following are available online at https://www.mdpi.com/2227-7390/8/12/2128/s1, Table S1: Development of the design of the camp in years 2006–2020.
Author Contributions
Conceptualization, Ľ.V. and J.M.; methodology, Ľ.V. and J.O.; software, J.O.; validation, Ľ.Z.; formal analysis, J.M. and V.C.; investigation, Ľ.V.; resources, Ľ.V.; data curation, V.C.; writing—original draft preparation, J.M.; writing—review and editing, J.M.; supervision, Ľ.Z.; project administration, Ľ.V. and J.M.; funding acquisition, Ľ.V. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Slovak Research and Development Agency under the contract No. APVV-15-0368, by the Scientific Grant Agency of the Ministry of Education, Science, Research and Sport of the Slovak Republic and the Slovak Academy of Sciences under the contract No. VEGA 1/0815/18, and by European Commission within the ERASMUS+ programme under the project no 2020-1-DE03-KA201-077363.
Acknowledgments
The tablets used in the study were loaned by the civic association VAU (More than Learning), Slovakia.
Conflicts of Interest
The authors declare no conflict of interest.
References
- National Research Council. Assessing 21st Century Skills; National Academies Press: Washington, DC, USA, 2011. [Google Scholar]
- Bottge, B.A. Effects of Contextualized Math Instruction on Problem Solving of Average and Below-Average Achieving Students. J. Spec. Educ. 1999, 33, 81–92. [Google Scholar] [CrossRef]
- Boaler, J. Open and Closed Mathematics: Student Experiences and Understandings. J. Res. Math. Educ. 1998, 29, 41–62. [Google Scholar] [CrossRef]
- Boaler, J. Experiencing School Mathematics: Traditional and Reform Approaches to Teaching and Their Impact on Student Learning; Routledge: Abingdon, UK, 2002. [Google Scholar]
- Boaler, J. Mathematical Mindsets: Unleashing Students’ Potential Through Creative Math, Inspiring Messages and Innovative Teaching; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Plothová, L.; Páleníková, K.; Naštická, Z.; Florková, M.; Šubová, L. An Analysis of Students’ Use of Mathematical Models in Solving Tasks with Real-life Context. In Proceedings of the 16th Conference on Applied Mathematics (APLIMAT 2017), Bratislava, Slovakia, 31 January–2 February 2017; pp. 1207–1223. [Google Scholar]
- Hill, A.M. Problem Solving in Real-Life Contexts: An Alternative for Design in Technology Education. Int. J. Technol. Des. Educ. 1998, 8, 203–220. [Google Scholar] [CrossRef]
- Boaler, J.; Selling, S.K. Psychological Imprisonment or Intellectual Freedom? A Longitudinal Study of Contrasting School Mathematics Approaches and Their Impact on Adults’ Lives. J. Res. Math. Educ. 2017, 48, 78–105. [Google Scholar] [CrossRef]
- Weintrop, D.; Beheshti, E.; Horn, M.S.; Orton, K.; Jona, K.; Trouille, L.; Wilensky, U. Defining computational thinking for mathematics and science classrooms. J. Sci. Educ. Technol. 2016, 25, 127–147. [Google Scholar] [CrossRef]
- Foster, I. A two-way street to science’s future. Nat. Cell Biol. 2006, 440, 419. [Google Scholar] [CrossRef] [PubMed]
- Lockwood, E. Algorithmic thinking: An initial characterization of computational thinking in mathematics. In Proceedings of the 38th Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education, Tucson, AZ, USA, 3–6 November 2016. [Google Scholar]
- Jona, K.; Wilensky, U.; Trouille, L.; Horn, M.; Orton, K.; Weintrop, D.; Beheshti, E. Embedding computational thinking in science, technology, engineering, and math (CT-STEM). In Proceedings of the Future Directions in Computer Science Education Summit Meeting, Orlando, FL, USA, 8–9 January 2014. [Google Scholar]
- Milicic, G.; Wetzel, S.; Ludwig, M. Generic Tasks for Algorithms. Future Internet 2020, 12, 152. [Google Scholar] [CrossRef]
- Cápay, M.; Magdin, M. Tasks for teaching scientific approach using the black box method. In Proceedings of the ECEL2013—The 12th European Conference on eLearning, Sophia Antipolis, France, 30–31 October 2013. [Google Scholar]
- Burbaitė, R.; Drąsutė, V.; Štuikys, V. Integration of computational thinking skills in STEM-driven computer science education. In Proceedings of the 2018 IEEE Global Engineering Education Conference (EDUCON), Tenerife, Spain, 17–20 April 2018. [Google Scholar]
- Lytle, N.; Cateté, V.; Boulden, D.; Dong, Y.; Houchins, J.; Milliken, A.; Isvik, A.; Bounajim, D.; Wiebem, E.; Barnes, T. Use, Modify, Create: Comparing Computational Thinking Lesson Progressions for STEM Classes. In Proceedings of the 2019 ACM Conference on Innovation and Technology in Computer Science Education, Aberdeen, UK, 12–17 July 2019; pp. 395–401. [Google Scholar]
- Ball, L.J.; Christensen, B.T. Advancing an understanding of design cognition and design metacognition: Progress and prospects. Des. Stud. 2019, 65, 35–59. [Google Scholar] [CrossRef]
- Jun, S.; Han, S.; Kim, S. Effect of design-based learning on improving computational thinking. Behav. Infor. Technol. 2017, 36, 43–53. [Google Scholar] [CrossRef]
- Maass, K. Enhancing Mathematics and Science Learning through Interdisciplinary Enquiry; Pädagogische Hochschule: Freiburg, Germany, 2011. [Google Scholar]
- Boboňová, I.; Čeretková, S.; Tirpáková, A.; Markechová, D. Inclusion of Interdisciplinary Approach in the Mathematics Education of Biology Trainee Teachers in Slovakia, in Interdisciplinary Mathematics Education; Springer: Cham, Switzerland, 2019; pp. 263–280. [Google Scholar]
- St Clair, B.; Hough, D.L. Interdisciplinary Teaching: A Review of the Literature; ERIC: Kingswood, UK, 1992.
- McClelland, K.; Grata, L. A Review of the Importance of Computational Thinking in K-12. In Proceedings of the eLmL 2018—The Tenth International Conference on Mobile, Hybrid, and On-line Learning, Rome, Italy, 25–29 March 2018. [Google Scholar]
- Aho, A.V. Computation and computational thinking. Comput. J. 2012, 55, 832–835. [Google Scholar] [CrossRef]
- Schoenfeld, A.H. Learning to think mathematically: Problem solving, metacognition, and sense making in mathematics. In Handbook of Research on Mathematics Teaching and Learning; Grouws, D., Ed.; Macmillan: New York, NY, USA, 1992. [Google Scholar]
- Charlton, P.; Luckin, R. Time to Reload? Computational Thinking and Computer Science in Schools. What Researches Says? Knowledge Lab-Institute of Education, University of London: London, UK, 2012. [Google Scholar]
- Gretter, S.; Yadav, A. Computational Thinking and Media & Information Literacy: An Integrated Approach to Teaching Twenty-First Century Skills. TechTrends 2016, 60, 510–516. [Google Scholar]
- Bocconi, S.; Chioccariello, A.; Dettori, G.; Ferrari, A.; Engelhardt, K.; Kampylis, P.; Punie, Y. Developing Computational Thinking in Compulsory Education; Kampylis, P., Punie, Y., Eds.; European Commission, Joint Research Centre: Luxembourg, 2016. [Google Scholar]
- Csizmadia, A.; Curzon, P.; Dorling, M.; Humphreys, S.; Ng, T.; Selby, C. Computational Thinking-A Guide for Teachers; Computing At School: Swindon, UK, 2015. [Google Scholar]
- Lee, I.; Martin, F.; Denner, J.; Coulter, B.; Allan, W.; Erickson, J.; Malyn-Smith, J.; Werner, L. Computational thinking for youth in practice. ACM Inroads 2011, 2, 32–37. [Google Scholar] [CrossRef]
- Kosko, K.; Ferdig, R. Effects of a Tablet-Based Mathematics Application for Pre-School Children. J. Comput. Math. Sci. Teach. 2016, 35, 61–79. [Google Scholar]
- Crompton, H. Contextualizing STEM Learning: Frameworks & Strategies. In Research on Outdoor STEM Education in the Digital Age, Proceedings of the ROSETA Online Conference, 16–19 June 2020; WTM: Munster, Germany, 2020; pp. 13–22. [Google Scholar]
- Rabardel, P. Instrument mediated activity in situations. In People and Computers XV—Interaction without Frontiers; Springer: Berlin, Germnay, 2001; pp. 17–30. [Google Scholar]
- Trouche, L. Managing the Complexity of Human/Machine Interactions in Computerized Learning Environments: Guiding Students’ Command Process through Instrumental Orchestrations. Int. J. Comput. Math. Learn. 2004, 9, 281. [Google Scholar] [CrossRef]
- Vágová, R. Designing Combinations of Physical and Digital Manipulatives to Develop Students’ Visualisation. Open Educ. Stud. 2020, 2, 1–27. [Google Scholar]
- Rabardel, P. People and Technology: A Cognitive Approach to Contemporary Instruments; Université Paris 8: Paris, France, 2002; Available online: https://hal.archives-ouvertes.fr/hal-01020705 (accessed on 20 September 2020).
- Drijvers, P.; Trouche, L. From artifacts to instruments: A theoretical framework behind the orchestra metaphor. In Research on Technology and the Teaching and Learning of Mathematics; IAP: Charlotte, NC, USA, 2008; Volume 2, pp. 363–392. [Google Scholar]
- Gueudet, G.; Buteau, C.; Mesa, V.; Misfeldt, M. Instrumental and documentational approaches: From technology use to documentation systems in university mathematics education. Res. Math. Educ. 2014, 16, 139–155. [Google Scholar] [CrossRef]
- Laisney, P.; Chatoney, M. Instrumented Activity and Theory of Instrument of Pierre Rabardel. In Philosophy of Technology for Technology Education; Sense/Brill: Boston, MA, USA, 2018. [Google Scholar]
- Cobb, P.; Confrey, J.; Disessa, A.; Lehrer, R.; Schauble, L. Design Experiments in Educational Research. Educ. Res. 2003, 32, 9–13. [Google Scholar] [CrossRef]
- Cobb, P.; Jackson, K.; Munoz, C. Design research: A critical analysis. In Handbook of International Research in Mathematics Education; Routledge: Abingdon, UK, 2016; pp. 481–503. [Google Scholar]
- McNemar, Q. Note on the sampling error of the difference between correlated proportions or percentages. Psychometrika 1947, 12, 153–157. [Google Scholar] [CrossRef] [PubMed]
- Yates, F. Contingency Tables Involving Small Numbers and the χ2 Test. Suppl. J. R. Statist. Soc. 1934, 1, 217–235. [Google Scholar] [CrossRef]
- Selby, C.; Woollard, J. Computational Thinking: The Developing Definition; University of Southampton: Southampton, UK, 2013. [Google Scholar]
- Vagova, R.; Kmetova, M.; Lieban, D. The Interplay of Physical and Digital Resources to Explore Cube Cross-Sections. In Proceedings of the APLIMAT 2020 19th Conference on Applied Mathematics, Bratislava, Slovakia, 4–6 February 2020; pp. 1067–1081. [Google Scholar]
- Donevska-Todorova, A.; Lieban, D. Fostering heuristic strategies in mathematical problem solving with virtual and tangible manipulatives. In Proceedings of the Tenth ERME Topic Conference (ETC 10) on Mathematics Education in the Digital Age (MEDA), Linz, Austria, 16–18 September 2020; pp. 175–182. [Google Scholar]
- Haas, B.; Kreis, Y.; Lavicza, Z. Connecting the real world to mathematical models in elementary schools in Luxemburg. Proc. Br. Soc. Res. Learn. Math. 2020, 40, 1–6. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).