Abstract
In this paper, the problem of robust stability for a class of linear switched positive time-varying delay systems with all unstable subsystems and interval uncertainties is investigated. By establishing suitable time-scheduled multiple copositive Lyapunov-Krasovskii functionals (MCLKF) and adopting a mode-dependent dwell time (MDDT) switching strategy, new delay-dependent sufficient conditions guaranteeing global uniform asymptotic stability of the considered systems are formulated. Apart from past studies that studied switched systems with at least one stable subsystem, in the present study, the MDDT switching technique has been applied to ensure robust stability of the considered systems with all unstable subsystems. Compared with the existing results, our results are more general and less conservative than some of the previous studies. Two numerical examples are provided to illustrate the effectiveness of the proposed methods.
1. Introduction
Positive systems are systems whose state variables take only non-negative values [1,2,3,4]. Examples of positive systems are discovered in real-world systems such as biological systems, pharmacological models, and physiological processes. Switched systems, which are composed of a family of subsystems and a switching rule orchestrating the switching among subsystems, are an important class of hybrid systems [5,6,7]. For specific switched systems with all individual positive subsystems, these systems are called switched positive systems and widely arise in various applications such as wireless power control [8], congestion control [9], compartmental model [2], water-quality model [6,10], and so on. Stabilities of switched positive systems have been extensively investigated under an appropriate switching rule; for example, the stability analysis of switched positive systems [11,12,13,14,15,16,17], robust stability analysis of switched positive systems [18,19], and -gain analysis of switched positive systems [19,20].
The evolution of the state variables relies not only on their present values but also on their past values. Such dynamical systems are called time-delay systems, which are appeared in practical systems [21,22,23,24]. It is well-known that the existence of a time-delay in the system can usually degrade the system performance or even cause instability. Results from the study related to time-delay can be divided into two kinds: delay-independent and delay-dependent results. The delay-independent results apply to the arbitrary size of the time-delay, while the delay-dependent results contain the information on the size of the time-delay. Generally speaking, the delay-dependent results are less conservative than the delay-independent ones when the size of the time-delay is small [7]. For these reasons, the topics of stability analysis for dynamical systems with time-delay have been studied by several researchers; especially switched positive systems with constant time-delay [25,26] and time-varying delay [27,28,29,30,31]. Most dynamical systems often contain uncertainties owing to some unpredictable factors such as the existence of modeling error or parameter fluctuation during hardware implementation. These systems can be modeled in the form of interval uncertainties [32,33]. Consequently, there are many results on the interval uncertainties systems; for example, switched systems [34,35], switched positive systems [18,19,32,33,36], and switched positive time-delay systems [37].
During recent decades, the existing research articles about switched systems mainly concentrate on the (robust) stability and (robust) stabilization problems. In accordance with the dynamic behavior of the subsystems, switched systems can be classified into three types; (i) all subsystems are stable, (ii) there is at least one stable subsystem, (iii) all subsystems are unstable. The main idea of analyzing the stability for the second type is that the stable subsystems are activated for a sufficiently long time to compensate for the state divergence made by unstable subsystems. Nevertheless, the above idea fails when all subsystems are unstable. Therefore, the stabilization problems of switched systems without delay [34,38], stability problems of switched sytems with time-delay [39,40], and without delay [41,42,43,44] have drawn much attention in the control community. By employing the discretized Lyapunov function method, a set of sufficient conditions ensuring the asymptotic stability of switched continuously-time systems with all unstable subsystems was derived in [38]. In 2016, Wang et al. [40] constructed multiple discretized Lyapunov-Krasovskii functionals to study the stability of switched delay systems with all unstable subsystems. Both results were mainly focused on the dwell time (DT) switching law. Recently, the problems of exponential stability for switched systems with all unstable subsystems under the bounded maximum average dwell time switching law were discussed for continuous-time case [43] and for discrete-time case [44]. The methods of the discretized Lyapunov function and the multiple discretized Lyapunov-Krasovskii functionals can also be extended to the discretized copositive Lyapunov function and the multiple discretized copositive Lyapunov-Krasovskii functionals, which have been used in formulating stability conditions of (some) switched positive (delay) systems with all unstable subsystems [18,28]. DT and MDDT are common switching laws that are designed to investigate the stability and stabilization problems for the switched positive (delay) systems. The main advantage of the MDDT switching law is that each mode in the underlying system not only has its own DT but also has its own control strategy. Therefore, the MDDT switching law is more suitable in practice than the DT switching law. Past studies on switched positive systems with all unstable subsystems were investigated in [18,28,31]. In 2018, Liu et al. [28] investigated the stabilization problem of linear switched positive delay systems with all unstable subsystems by employing the multiple discretized copositive Lyapunov-Krasovskii functionals and the DT switching law. In 2019, Feng et al. [18] studied the stability and robust stability for linear switched positive systems with all unstable subsystems by utilizing the discretized copositive Lyapunov function and the MDDT switching rule, but the existence of the time-delay was not taken into account. More recently, Yang et al. [31] proposed a time-scheduled MCLKF technique combining with fast average dwell time switching law to derive a sufficient stability criterion for continuous-time switched positive delay systems with all unstable subsystems. Note that the interval uncertainties were not considered in [28,31]. To the best of our knowledge, there is no work in the literature on the robust stability analysis for linear uncertain switched positive time-varying delay systems with all unstable subsystems.
The above discussions motivate us to study the robust stability for a class of continuous-time linear switched positive time-varying delay systems with all unstable subsystems and interval uncertainties under the MDDT switching strategy. The main contributions of this paper are summarized as follows.
(1) A time-scheduled MCLKF method combined with the MDDT switching law is utilized to derive new delay-dependent sufficient conditions for global uniform asymptotic stability of the underlying systems.
(2) The stability criteria for continuous-time switched positive time-varying delay systems without the interval uncertainties are also obtained.
(3) Apart from the studies in [12,15,25,36] that proposed stability conditions for switched positive systems with at least one stable subsystem, our research mainly concentrates on the (robust) stability of switched positive time-varying delay systems with all unstable subsystems. Note that conditions in [18] also guarantee globally asymptotically stable of switched positive systems under all unstable subsystems, but the existence of the time-delay was not taken into account.
(4) Unlike the existing results in [28,31,36,38,40], the MDDT switching law, which is less conservative and more applicable in practice than the DT switching law, is utilized for the robust stability analysis of the continuous-time linear switched positive time-varying delay systems with all unstable subsystems and interval uncertainties in the present study.
The rest of this work is organized as follows. In Section 2, necessary preliminaries are presented. The main results are shown in Section 3. Two numerical simulations are provided to justify the efficiency of our theoretical results in Section 4. The conclusions are given in Section 5.
Notations: Throughout this paper, the sets of non-negative and positive integers are represented by and , respectively. For any . and are the vectors of n-tuples of real and positive real numbers, respectively. stands for the set of all real matrices. is the dimensional identity matrix. symbolizes the transpose of matrix A. For , is non-negative (positive) vector meaning that . Matrix A is called non-negative if all entries are non-negative and denoted by . The notation means that . For , define as the 1-norm, as the Euclidean norm, and , respectively. Moreover, , stand for the maximal and minimal elements of , respectively.
2. Preliminaries
In this paper, we consider the following class of continuous-time linear switched positive time-varying delay systems, with and being in the form of interval uncertainties, satisfying
where is the state vector. The switching signal is a piecewise constant function depending on time t. is the number of subsystems or modes of the overall switched system. The switching instants are expressed by a sequence , where and . When , we suppose that and the ith subsystem is activated which implies that the trajectory of system (1) is the trajectory of this subsystem. Note that the switching signal is continuous from the right at . Under the control of the switching signal at the switching instant , system (1) switches from the jth subsystem to the ith subsystem, where . The time-varying delay satisfies and for known constants and d. Moreover, is a continuous and differentiable initial function.
As mentioned in [18,19], the system matrices and are constant matrices with appropriate dimensions and i denotes the ith subsystem with . These system matrices are supposed to be interval uncertain, namely, ,
and
which can be denoted by and where are constant matrices with appropriate dimensions.
The main goal in this paper is to derive robust stability criteria for a class of continuous-time linear switched positive time-varying delay systems with all unstable subsystems and interval uncertainties by designing switching signals based on the MDDT switching law.
First, we introduce some definitions and the lemma used in this research.
Definition 1.
[28] System (1) is said to be positive if for any initial condition and any switching signal , the corresponding trajectory satisfies for any .
Definition 2.
[18] A matrix A is said to be a Metzler matrix if its offdiagonal entries are non-negative.
Lemma 1.
[28] System (1) is positive if and only if are Metzler matrices and .
Then, we provide required assumptions and definitions which are useful for deriving the main results in this research.
Assumption 1.
[18,32,37] For each and in system (1), there are the known Metzler matrices and such that and , .
Remark 1.
It is well known that most existing control engineerings contain some uncertainties [18,32,37]. The uncertain systems can be represented in the form of interval uncertain systems. Consequently, Assumption 1 is reasonable.
Assumption 2.
[18,40] The state of switched systems does not jump at each switching instant, namely, the state trajectory is continuous everywhere.
Assumption 3.
[18,28] All subsystems of system (1) are unstable.
Definition 3.
[38] System (1) with switching signal is said to be uniformly stable (US) with respect to if such that whenever . When we have then system (1) is globally uniformly stable (GUS) with respect to . Moreover, if system (1) is GUS and satisfies , system (1) is globally uniformly asymptotically stable (GUAS) with respect to .
Remark 2.
Generally, the robust stability analysis of switched systems can be achieved whenever either all subsystems are stable or there is at least one stable subsystem for compensating another unstable one. However, the above existing idea is invalid for the case that all subsystems are unstable. How to design appropriate switching laws to stabilize the switched positive time-varying delay systems with all unstable subsystems and interval uncertainties? This question not only considers finding the appropriate switching laws for the system but also regards the positivity and the existence of the time-delay of the system. Therefore, it is challenging to cope with this problem.
A switching signal plays an important role in the research of robust stability analysis for switched systems. In this paper, the switching signal used to study robust stability for a class of linear switched positive time-varying delay systems with all unstable subsystems and interval uncertainties is a time-dependent switching signal. There are well-known types of time-dependent switching signals, namely, DT and MDDT switching laws. To describe a sufficiently long active interval, the notion of a DT switching law is stated as follows.
Definition 4.
[5,7] For given two successive switching times and , if there exists a constant such that holds for any , then the constant τ is called DT.
Recently, the concept of the DT switching law is extended to the concept of the MDDT switching law. It has been recognized that the MDDT switching law is more general and less conservative than the DT switching law. The definition of MDDT is given as follows.
Definition 5.
[19,41] For the length between successive switching instants during which the ith subsystem is activated, if there exists a constant such that holds for any , then the constant is called MDDT.
Remark 3.
It is well-known that too small or too large DT switching would make system (1) unstable with respect to [18]. Thus, the MDDT switching strategy is confined by a pair of upper and lower bounds to ensure the asymptotic stability, namely, where . Moreover, we call the set of all switching policies with MDDT , .
Assumption 4.
[18] Every subsystem has its own DT. Namely, the DT of the ith subsystem is denoted by .
3. Main Results
In this present section, we utilize the time-scheduled MCLKF technique to formulate the robust stability conditions for a class of linear switched positive time-varying delay systems with all unstable subsystems and interval uncertainties (1) under the MDDT switching strategy. Moreover, we propose new delay-dependent sufficient conditions to guarantee global uniform asymptotic stability of system (1) without the interval uncertainties.
For convenience, the essential symbols are firstly introduced as follows:
where represents the kth row and lth column entry of system matrices . We are now ready to derive new delay-dependent sufficient conditions to ensure the global uniform asymptotic stability of system (1) satisfying Assumptions 1–4 as in the following theorem.
Theorem 1.
Proof.
By Assumption 1, we obtain that are also Metzler matrices and , respectively. By Lemma 1, we can conclude that system (1) is positive.
For a given , suppose that , and the interval is divided into L segments with equal length . Furthermore, we define , then .
Based on the concept of discretized Lyapunov function used in [28,38], we establish the following vector function
where with , and are positive vectors for . For we obtain
For each subsystem, we construct the time-scheduled MCLKF in the form of
It follows that
Together with and , one has
When , we obtain
and
This yields
For , we observe that
and
Using condition (9), we get
Integrating both sides of (16) over for , we have
It follows from condition (10) that which implies
According to condition (11), it is immediate that
Hence, we get
Moreover, let and , then
From (13), we have the following estimation:
and
where . From (20)–(22), we obtain
where . Then, for , we choose
Therefore,
This implies that system (1) is uniformly stable.
Next, we will show that . From (18), we get
Hence, we get . Since and by assumption that there exists a set of positive vectors , we obtain
Furthermore, from the positivity of system (1), we get
For the proof in the final part that , it is similar to that of Theorem 1 in [18]. Thus, it is omitted here. Consequently, system (1) is GUAS with respect to switching signal . □
Remark 4.
As in [18,28,38], the time-scheduled MCLKF in Theorem 5 was applied to study the stability of their considered systems with all unstable subsystems. The use of time-scheduled MCLKF allows one to enlarge the bounded rate of convergence, , described by , when unstable subsystems work. However, the increment of the time-scheduled MCLKF can be compensated by switching behavior expressed by and the advantage of the MDDT approach applied in this paper. In other words, are nonincreasing at the switching instants. Therefore, stabilization can be achieved and demonstrated in numerical examples.
Remark 5.
As in [18,38], the number of discretized positive vectors is which has to be given in advance. It is commonly known that different choices of L can lead to different analysis results. Namely, if larger L is chosen, then the denser the division of interval must be.
From Theorem 5, we can acquire new delay-dependent sufficient conditions to guarantee global uniform asymptotic stability of system (1) without interval uncertainties (2) and (3). To obtain the result, we first define important symbols used in Corollary 5 as follows:
where represents the kth row and lth column entry of system matrices . Next, the new delay-dependent sufficient conditions guaranteeing global uniform asymptotic stability of system (1) without interval uncertainties (2) and (3) satisfying Assumptions 2–4 will be stated in the following corollary.
Corollary 1.
Consider system (1) without interval uncertainties (2) and (3) satisfying Assumptions 2–4. Let be the Metzler matrices and . Given constants , and . If there exist a set of positive vectors and constants , such that for any , and for any the following inequalities hold
where
and D is defined as in (24). Then, system (1) without interval uncertainties (2) and (3) is GUAS under any switching signal .
Proof.
Since is the Metzler matrices and , system (1) without interval uncertainties (2) and (3) is positive by employing Lemma 1. Under the same notations and vector function (12) in Theorem 5, we can prove this corollary by using the time-scheduled MCLKF:
The rest of the proof is similar to that of Theorem 5. Therefore, it is omitted. □
Remark 6.
Different from the discretized quadratic Lyapunov function used in [38] and the discretized copositive Lyapunov function used in [18], in this research, the time-scheduled MCLKFs in (13) and (25) are specifically constructed for the switched positive system with time-varying delay. Moreover, unlike the discretized copositive Lyapunov-Krasovskii functional used in [28] and the time-scheduled MCLKF used in [31], our time-scheduled MCLKFs are specially established to derive a set of delay-dependent sufficient conditions under the MDDT approach for being the global uniform asymptotic stability of the considered system.
4. Numerical Examples
In this section, we present two numerical examples to demonstrate the effectiveness and applicability of our theoretical results. For the first example, we investigate global uniform asymptotic stability of linear interval uncertain switched positive system with time-varying delay by modifying linear interval uncertain switched positive system studied in [18]. In the second example, we study global uniform asymptotic stability of linear switched positive system with time-varying delay which is used to control water-quality [6,7,10].
Example 1.
Consider the following continuous-time linear switched interval system with time-varying delay (1) consisting of two subsystems. The bounds of the system matrices are provided as
and
From the considered time-varying delay above, we chooseand. By Definition 2, it can be seen thatandare Metzler matrices. Moreover,andThus, the system in this example is positive.
For the numerical simulations, we set the initial condition as, and the system matrices
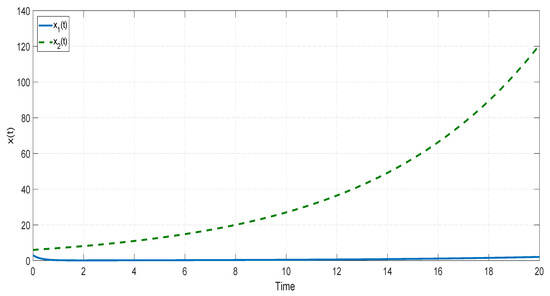
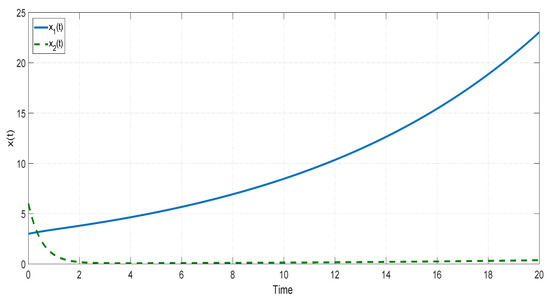
The state trajectories of two subsystems are presented in Figure 1 and Figure 2, respectively. From these two subsystems, it is easy to see that both subsystems are unstable. Let. From the bounds of the system matrices above, it is obviously that

Figure 1.
The state trajectory of the first subsystem in Example 1.

Figure 2.
The state trajectory of the second subsystem in Example 1.
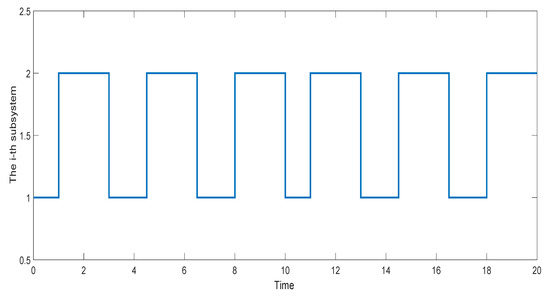
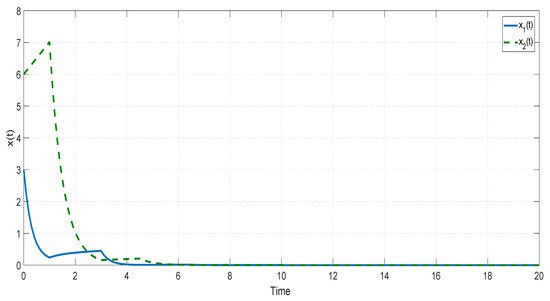
According to Theorem 5, the system in this example is GUAS under the switching signal. The designed switching signaland the state responses of the system are depicted in Figure 3 and Figure 4, respectively. It is clear that the considered system can be stabilized by the above switching signal.

Figure 3.
The switching signal for the switched positive delay system in Example 1.

Figure 4.
The state trajectory of the switched positive delay system in Example 1.
Remark 7.
For the comparison results between the previous studies and our results, one can see that the results of Theorem 2 and Example 1 in [18] are a special case of our results. This shows that our results are more general than that of Theorem 2 and Example 1 in [18]. In addition, the results of Theorem 3.1 in [28] and Theorem 1 in [31] used dwell time switching and fast average dwell time switching techniques, respectively. Their considered switched systems do not include the interval uncertainties. Meanwhile, our main results apply the MDDT switching, in which each subsystem has its own dwell time switching, and the considered switched system includes the interval uncertainties. Hence, our results are less conservative and more applicable than those of Theorem 3.1 in [28] and Theorem 1 in [31].
For the next example, we consider the switched system used in a water-quality model adopted from [6,7,10]. This model is used to preserve the water-quality in multireach fresh water streams of the River Nile. The state vector in this model stands for water-quality constituents such as algae, ammonia nitrogen, dissolved oxygen, and biochemical oxygen demand. The time-varying delay in this model reflects the mixing effect of biochemical constituents in the reach at time t. However, in this study, we do not have information about the complexity or noise affecting the water-quality constituents. Therefore, the model can be described as a switched positive time-varying delay system, which is consistent with the system (1) without interval uncertainties (2) and (3). The main purpose of studying in this model is to restore water-quality constituents to standard levels by designing the MDDT switching law based on Corollary 5.
Example 2.
To simulate this model, we set the initial condition as . The state trajectories of the two subsystems under this initial condition are plotted in Figure 5 and Figure 6, respectively. Obviously, these subsystems are unstable. Thus, our theoretical results can apply to investigate the stability of this model.
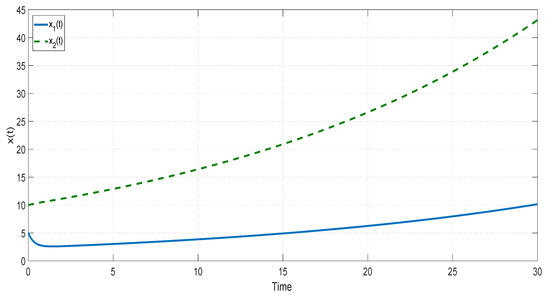
Figure 5.
The state trajectory of the first subsystem in Example 2.
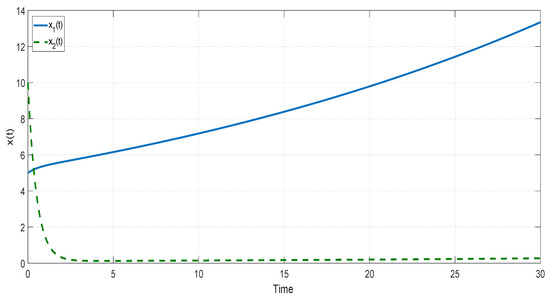
Figure 6.
The state trajectory of the second subsystem in Example 2.
Let . From the system matrices above, it is obviously that
Solving all conditions in Corollary 5, we obtain the following feasible solution , ,
According to Corollary 5, the considered system in this example is GUAS under the switching signal . The designed switching signal and the state responses of the system are depicted in Figure 7 and Figure 8, respectively. It can be seen from Figure 8 that the switched positive time-varying delay system containing two unstable subsystems can be stabilized under the above switching signal. This shows that our theoretical results can be applied to the simple water-quality model without uncertainty.
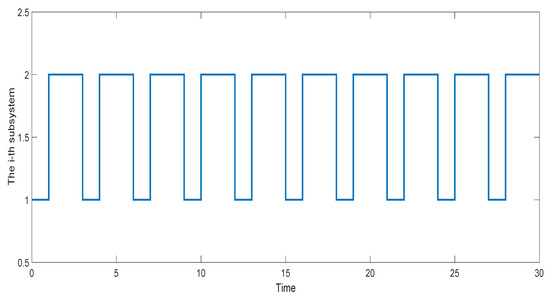
Figure 7.
The switching signal for the switched positive delay system in Example 2.
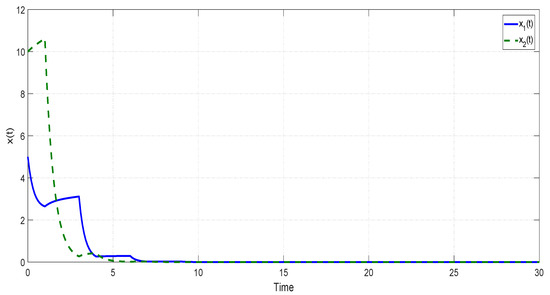
Figure 8.
The state trajectory of the switched positive delay system in Example 2.
5. Conclusions
The concept of the stabilization for a class of linear switched positive time-varying delay systems with all unstable subsystems and interval uncertainties has been studied in this research. Under the assumptions, the time-scheduled MCLKF method combined with the MDDT switching law has been utilized to derive sufficient conditions for guaranteeing the global uniform asymptotic stability of continuous-time linear switched positive time-varying delay systems with all unstable subsystems and interval uncertainties. Based on the above approach, the stability conditions of the considered systems without the interval uncertainties have also been obtained. All conditions are given in terms of the solvability to a set of linear vector inequalities. Two numerical examples have been presented to validate the theoretical results. The comparison between our results and the existing results has shown that our results are more general and less conservative than that of previous studies. Finally, it is worth noting that no research applies the MDDT technique to formulate stability conditions to guarantee GUAS of some switched neutral or discrete-time systems with time-varying delay and all unstable subsystems. Thus, in future research, it will be interesting to develop some stability conditions of these systems using a similar approach discussed in the current research.
Author Contributions
Conceptualization, P.N.; Formal analysis, T.R., S.Y.; Investigation, all authors; Methodology, all authors; Software, S.Y.; Validation, T.R., P.N.; Visualization, S.Y.; Writing—original draft, S.Y.; Writing—review and editing by all authors. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially supported by Chiang Mai University and the Centre of Excellence in Mathematics, The Commission on Higher Education, Thailand.
Acknowledgments
We would like to thank the reviewers for their valuable comments to improve the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Farina, L.; Rinaldi, S. Positive Linear Systems: Theory and Applications; Wiley: New York, NY, USA, 2000. [Google Scholar]
- Haddad, W.M.; Chellaboina, V.; Hui, Q. Nonnegative and Compartmental Dynamical Systems; Princeton University Press: Princeton, NJ, USA, 2010. [Google Scholar]
- Kaczorek, T. Positive 1D and 2D Systems; Springer: London, UK, 2002. [Google Scholar]
- Sau, N.H.; Niamsup, P.; Phat, V.N. Positivity and stability analysis for linear implicit difference delay equations. Linear Algebra Appl. 2016, 510, 25–41. [Google Scholar] [CrossRef]
- Liberzon, D. Switching in Systems and Control; Birkhauser: Boston, MA, USA, 2003. [Google Scholar]
- Mahmoud, M.S. Switched Time-Delay Systems: Stability and Control; Springer: New York, NY, USA, 2010. [Google Scholar]
- Wang, D.; Shi, P.; Wang, W. Robust Filtering and Fault Detection of Switched Delay Systems; Springer: Berlin, Germany, 2013. [Google Scholar]
- Mason, O.; Shorten, R. On linear copositive Lyapunov functions and the stability of switched positive linear systems. IEEE Trans. Autom. Control 2007, 52, 1346–1349. [Google Scholar] [CrossRef]
- Bolajraf, M.; Tadeo, F.; Alvarez, T.; Rami, M.A. State-feedback with memory for controlled positivity with application to congestion control. IET Control Theory Appl. 2010, 4, 2041–2048. [Google Scholar] [CrossRef]
- Mahmoud, M.S. Switched delay-dependent control policy for water-quality systems. IET Control Theory Appl. 2009, 3, 1599–1610. [Google Scholar] [CrossRef]
- Blanchini, F.; Colaneri, P.; Valcher, M.E. Co-positive Lypunov functions for the stabilization of positive switched systems. IEEE Trans. Autom. Control 2012, 57, 3038–3050. [Google Scholar] [CrossRef]
- Lian, J.; Liu, J. New results on stability of switched positive systems: An average dwell-time approach. IET Control Theory Appl. 2013, 7, 1651–1658. [Google Scholar] [CrossRef]
- Tian, Y.; Sun, Y. Stability analysis of switched positive nonlinear systems by mode-dependent average dwell time method. IEEE Access 2019, 7, 15584–15589. [Google Scholar] [CrossRef]
- Wang, G.; Liu, Y.; Lu, J.; Wang, Z. Stability analysis of totally positive switched linear systems with average dwell time switching. Nonlinear Anal. Hybrid Syst. 2020, 36, 100877. [Google Scholar] [CrossRef]
- Zhang, J.S.; Wang, Y.W.; Xiao, J.W.; Shen, Y.J. Stability analysis of switched positive linear systems with stable and unstable subsystems. Int. J. Syst. Sci. 2014, 45, 2458–2465. [Google Scholar] [CrossRef]
- Zhao, H.; Li, Y. Exponential stability of switched positive linear systems without stable subsystems. In Proceedings of the IEEE 2017 4th International Conference on Information Science and Control Engineering (ICISCE), Changsha, China, 21–23 July 2017; pp. 984–988. [Google Scholar]
- Zhou, Z.-Y.; Wang, Y.-W.; Yang, W.; Hu, M.-J. Exponential stability of switched positive systems with all modes being unstable. Int. J. Robust Nonlinear Control 2020. [Google Scholar] [CrossRef]
- Feng, S.; Wang, J.; Zhao, J. Stability and robust stability of switched positive linear systems with all modes unstable. IEEE/CAA J. Autom. Sin. 2019, 6, 167–176. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, H.B.; Zheng, Q.X. Robust stability and L1-gain analysis of interval positive switched T-S fuzzy systems with mode-dependent dwell time. Neurocomputing 2017, 235, 90–97. [Google Scholar] [CrossRef]
- Xiang, W.; Lam, J.; Shen, J. Stability analysis and L1-gain characterization for switched positive systems under dwell-time constraint. Automatica 2017, 58, 1–8. [Google Scholar] [CrossRef]
- Fridman, E. Introduction to Time-Delay Systems: Analysis and Control; Springer: Basel, Switzerland, 2014. [Google Scholar]
- Kharitonov, V. Time-Delay Systems: Lyapunov Functionals and Matrices; Springer: New York, NY, USA, 2012. [Google Scholar]
- Wu, M.; He, Y.; She, J.-H. Stability Analysis and Robust Control of Time-Delay Systems; Springer: Berlin, Germany, 2010. [Google Scholar]
- Elmadssia, S.; Saadaoui, K. New stability conditions for a class of nonlinear discrete-time systems with time-varying delay. Mathematics 2020, 8, 1531. [Google Scholar] [CrossRef]
- Liu, L.-J.; Zhao, X.; Wu, D. Stability of switched positive linear time-delay systems. IET Control Theory Appl. 2019, 13, 912–919. [Google Scholar] [CrossRef]
- Zhao, X.; Zhang, L.; Shi, P. Stability of a class of switched positive linear time-delay systems. Int. J. Robust Nonlinear Control 2013, 23, 578–589. [Google Scholar] [CrossRef]
- Liu, X.; Dang, C. Stability analysis of positive switched linear systems with delays. IEEE Trans. Autom. Control 2011, 56, 1684–1690. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, X.; Lu, X.; Liu, Q. Stabilization of positive switched delay systems with all modes unstable. Nonlinear Anal. Hybrid Syst. 2018, 29, 110–120. [Google Scholar] [CrossRef]
- Shi, R.; Tian, X.; Zhao, X.; Zheng, X. Stability and L1-gain analysis for switched delay positive systems with stable and unstable subsystems. Circuits Syst. Signal Process. 2015, 34, 1683–1696. [Google Scholar] [CrossRef]
- Xiang, M.; Xiang, Z.; Lu, X.; Liu, Q. Stability, L1-gain and control synthesis for positive switched systems with time-varying delay. Nonlinear Anal. Hybrid Syst. 2013, 9, 9–17. [Google Scholar] [CrossRef]
- Yang, G.; Hao, F.; Zhang, L.; Li, B. Exponential stability for continue-time switched positive delay systems with all unstable subsystems. IEEE Access 2019, 7, 165428–165436. [Google Scholar] [CrossRef]
- Ma, R.; Wang, X.; Liu, Y. Robust stability of switched positive linear systems with interval uncertainties via multiple time-varying linear copositive Lyapunov functions. Nonlinear Anal. Hybrid Syst. 2018, 30, 285–292. [Google Scholar] [CrossRef]
- Zhang, J.; Han, Z. Robust stabilization of switched positive linear systems with uncertainties. Int. J. Control Autom. Syst. 2013, 11, 41–47. [Google Scholar] [CrossRef]
- Allerhand, L.; Shaked, U. Robust stability and stabilization of linear switched systems with dwell time. IEEE Trans. Autom. Control 2011, 56, 381–386. [Google Scholar] [CrossRef]
- Rodriguse-Licea, M.-A.; Perez-Pinal, F.-J.; Olivares, J.P. Robust stabilization of linear switched systems with unstable subsystems. Appl. Sci. 2018, 8, 2620. [Google Scholar] [CrossRef]
- Liu, J.J.; Zhang, K.J.; Wei, H.K. Robust stability of positive switched systems with dwell time. Int. J. Syst. Sci. 2016, 47, 2553–2562. [Google Scholar] [CrossRef]
- Liu, J.; Zhu, C.; Li, Z. Robust stabilization for constrained switched positive linear systems with uncertainties and delays. In Proceedings of the IEEE Proceedings 2017 29th Chinese Control and Decision Conference (CCDC), Chongqing, China, 28–30 May 2017; pp. 2459–2464. [Google Scholar]
- Xiang, W.; Xiao, J. Stabilization of switched continuous-time systems with all modes unstable via dwell time switching. Automatica 2014, 50, 940–945. [Google Scholar] [CrossRef]
- Tian, Y.; Cai, Y.; Sun, Y. Stability of switched nonlinear time-delay systems with stable and unstable subsystems. Nonlinear Anal. Hybrid Syst. 2017, 24, 58–68. [Google Scholar] [CrossRef]
- Wang, Q.; Sun, H.; Zong, G. Stability analysis of switched delay systems with all subsystems unstable. Int. J. Control Autom. Syst. 2016, 14, 1262–1269. [Google Scholar] [CrossRef]
- Dehghan, M.; Ong, C.-J. Computations of mode-dependent dwell times for discrete-time switching system. Automatica 2013, 49, 1804–1808. [Google Scholar] [CrossRef]
- Lee, T.C.; Jiang, Z.P. Uniform asymptotic stability of nonlinear switched systems with an application to mobile robots. IEEE Trans. Autom. Control 2008, 53, 1235–1252. [Google Scholar] [CrossRef]
- Mao, X.; Zhu, H.; Chen, W.; Zhang, H. New results on stability of switched continuous-time systems with all subsystems unstable. ISA Trans. 2019, 87, 28–33. [Google Scholar] [CrossRef] [PubMed]
- Mao, X.; Zhu, H.; Chen, W.; Zhang, H. Results on stability of switched discrete-time systems with all subsystems unstable. IET Control Theory Appl. 2019, 13, 152–158. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).