Serial and Parallel Iterative Splitting Methods: Algorithms and Applications to Fractional Convection-Diffusion Equations

Abstract

The benefits and properties of iterative splitting methods, which are based on serial versions, have been studied in recent years, this work, we extend the iterative splitting methods to novel classes of parallel versions to solve nonlinear fractional convection-diffusion equations. For such interesting partial differential examples with higher dimensional, fractional, and nonlinear terms, we could apply the parallel iterative splitting methods, which allow for accelerating the solver methods and reduce the computational time. Here, we could apply the benefits of the higher accuracy of the iterative splitting methods. We present a novel parallel iterative splitting method, which is based on the multi-splitting methods, The flexibilisation with multisplitting methods allows for decomposing large scale operator equations. In combination with iterative splitting methods, which use characteristics of waveform-relaxation (WR) methods, we could embed the relaxation behavior and deal better with the nonlinearities of the operators. We consider the convergence results of the parallel iterative splitting methods, reformulating the underlying methods with a summation of the individual convergence results of the WR methods. We discuss the numerical convergence of the serial and parallel iterative splitting methods with respect to the synchronous and asynchronous treatments. Furthermore, we present different numerical applications of fluid and phase field problems in order to validate the benefit of the parallel versions.

1. Introduction

Nowadays, iterative splitting methods are important solver methods to solve large systems of ordinary, partial, or stochastic differential equations, see [1,2,3,4,5,6]. Iterative splitting methods are based on two solver ideas: In the first part, we separate the full operators into different sub-operators and reduce the computational time for such sub-computation. An additional benefit is the iterative technique, which allows for solving a relaxation problem, as in the waveform-relaxation method or Picard’s iterative method, see [7,8,9,10]. Both parts reduce the computational time and the complexity as if we solved all parts (full operator and direct method) together, see [11]. Such iterative splitting methods can be used to compute, with less computational burden, an approximate solution of the ordinary differential equations (ODEs) or semi-discretized partial differential equations (PDEs), see [10,11]. Moreover, we consider parallel splitting methods, which are nowadays important to solve large problems, see [3]. Such parallel splitting methods are applied to the splitted subproblems and computed independently by the different processors. Therefore, in a second part we consider the parallelization-techniques, which are given with the multi-splitting approach, see [5]. Such approaches allow for embedding the splitting techniques of the first part into a parallelized version, see [12]. Based on the parallel versions of our methods, we can consider large computational problems.

For the computational problems, we consider the interesting part of higher dimensional and nonlinear PDEs as nonlinear and fractional convection-diffusion equations, see [13,14]. The nonlinear PDEs are applied in nonlinear flow problems, for example, to simulate traffic-flow problems, see [15] and flow problems that are related to Navier–Stokes equations, see [16], which can be modeled with the Burgers’ equation.

Furthermore, we take into account the fractional PDEs, e.g., fractional convection-diffusion equations. Nowadays, the fractional calculus is applied to several fields of science and engineering, for example, in visco-elastic and thermal diffusion in fractal domains, see [17,18], or in phase-field models with mixtures of fluids [19,20], or in biological models to deal with fractional multi-models [21]. It is also interesting on a theoretical aspect, e.g., physical and geometrical interpretation [22], fractional Dirac operators [23].

The treatment of such delicate fractional and nonlinear partial differential equations (PDEs) needs additional spatial and nonlinear approximations of higher order, see [24]. We apply flexible iterative splitting methods, see [13,25], which can be extended to parallel algorithms.

The underlying modeling equations are given as nonlinear fractional convection-diffusion equations:

$${\partial }_{t}u=-\nu u\nabla u+\mu ({\mathcal{L}}_x^{\alpha }u+{\mathcal{L}}_y^{\beta }u)+f(x,y,t), (x,y,t)\in \Omega \times [0,T],$$

(1)

$$u(x,y,0)=u_0(x,y,0), (x,y)\in \Omega ,$$

(2)

$$u(x,y,t)=0, (x,y,t)\in \partial \Omega \times [0,T],$$

(3)

where $\Omega \in {IR}^d$ is the spatial domain with d as the dimension and $T\in {IR}^{+}$. We denote by $\nu \in {IR}^{+}$ a scalar parameter of the convection part and by $\mu \in {IR}^{+}$ the viscosity of the diffusion part, while f is a right hand side function.

We have different cases:

• $\alpha =\beta =2$: viscous Burgers’ equation, see [2,26],
• $\alpha =\beta =2$ and $\nu =0$: Diffusion equation, see [2,26], and
• $\alpha ,\beta \in (1,2)$: fractional diffusion equation, see [14,27].

Further interesting examples that are related to fractional and nonlinear PDE can be found in [24,28].

Equations (1)–(3) can be derived in a more general setting with the idea of the least action principle, see [29,30]. Here, we are not restricted by the specific Lagrangian or Hamiltonian principle, such that we can account for a much larger number of fractional differential equations.

Here, the fractional Laplace operator replaces the standard Laplacian operator, see [14], and it is denoted as a sum of one-dimensional spatial operators, ${\mathcal{L}}_{\alpha ,\beta }={\mathcal{L}}_x^{\alpha }+{\mathcal{L}}_y^{\beta }$:

$$\begin{array}{c}{\mathcal{L}}_x^{\alpha }u:=\frac{{\partial }^{\alpha }u}{\partial x^{\alpha }},\hfill \end{array}$$

(4)

where we have defined the Riemann fractional derivative of order $\alpha$, as:

$$\begin{array}{c}\frac{{\partial }^{\alpha }u}{\partial x^{\alpha }}=\frac{1}{\mathrm{\Gamma }(2-\alpha )}\frac{{\partial }^2}{\partial x^2}{\int }_L^x\frac{u(\xi )}{{(x-\xi )}^{\alpha -1}}d\xi \hfill \end{array}$$

(5)

In the next step, we apply a semi-discretisation with higher order finite-difference methods for $\alpha =\beta =2$, see [31] or with higher order Grünwald formula for the fractional operators with $\alpha ,\beta \in (1,2)$, see [27,32]. Thus, we could reduce the computational cost of the time-splitting approaches, which are given as an iterative splitting approach, see [33]. With such an approximation and the consideration of the semi-discretization with higher order schemes, we obtain the nonlinear differential equation system in a Cauchy-form, which is given as:

$${\partial }_{t}c=\tilde{A}(c) c+\tilde{B} c+F(t), t\in [0,T],$$

(6)

$$c(0)=c_0,$$

(7)

where $c\in \mathcal{X}\subset {IR}^M$, while $M=m^d$, where d is the dimension and m is the number of grid-points in each spatial direction. Furthermore, $\tilde{A}(c):\mathcal{X}\to \mathcal{X}\times \mathcal{X}$ is a nonlinear matrix, which includes the spatial discretization of the nonlinear convection in Equation (1) with the boundary conditions and with higher order spatial finite difference schemes, see [31]. The operator $\tilde{B}\in \mathcal{X}\times \mathcal{X}$ is a linear matrix, which includes the spatial discretization of the fractional diffusion term with the boundary conditions and with the underlying fractional discretization methods, see [24,32]. The function $F(t)$: ${IR}^{+}\to \mathcal{X}$ is the discretized right-hand side. We assume $\mathcal{X}$ to be an appropriate Banach space with a vector and induced matrix norm $\left|\right|·\left|\right|$, see [10,34,35].

For the nonlinear term, we apply the linearisation that is based on the Picard’s iteration, which is also a special iterative splitting approach, see [7,36]. We have:

$${\partial }_t{v}_j=\tilde{A}(v_{j-1}) v_j+\tilde{B} v_j+F(t), t\in [0,T],$$

(8)

$$v(0)=c_0,$$

(9)

where $j=1,2,\dots ,J$ with some $J\in IN$ (number of the iterations for the nonlinear part) and starting condition $v_0(t)=c_0$. Furthermore, we assume to have a sufficiently large J, such that $\left|\right|v_J-v_{J-1}\left|\right|\le err$, where $err$ is an error-bound. For simplification, we assume $F(t)=0$, while $F(t)$ is a right hand side, which can be approached by an integral equation, see [35].

Therefore, we obtain a linearised differential equation system, which is solved by the outer-iterations with $j=1,\dots ,J$. In the following, we concentrate on solving such linearised evolution equations by decomposing them with respect to their underlying matrix-operator in submatrix-operators, so that we obtain the following differential equation,

$$\begin{array}{c}{\partial }_t c=Ac=\sum _{l=1}^L{A}_l c, c(0)=c_0,\hfill \end{array}$$

(10)

where $A=\tilde{A}(v_J)+\tilde{B}\in {IR}^M\times {IR}^M$ is the full operator, and $A_l$ are the sub-operators. Further, $c \in C^1([0,T];{IR}^M)$ is the solution and $c_0\in {IR}^M$ is the initial condition.

The bottleneck of the iterative methods is due to the large sizes of the iteration matrices, see [4,5]; therefore, we consider parallel versions of the iterative splitting method, see [3,12]. Based on the decomposition of the large scale differential equation with operator A into different smaller sub-differential equations with operators $A_l$, where $l=1,\dots ,L$, and L is the number of processors, we distribute the computational time to many processors and reduce the overall computational time, see [5]. Furthermore, we modify the synchronous parallel splitting method with chaotic (asynchronous) ideas, such that the computation and communication of the various processors can be done independently, see [37].

In addition, we have considered different examples of the literature that also discuss optimized computational cost and error bounds, see [28]. Here, we deal with models of viscous Burgers’ equation, which are applied in flow-problems, and fractional convection-diffusion equations, which are applied in diffusion interface phase field problems, see [20].

The outline of this paper is as follows. Section 2 explains the serial iterative splitting method. Section 3 introduces the parallel iterative splitting method. We discuss the theoretical results in Section 4. The numerical examples are presented in Section 5. In Section 6, we discuss the theoretical and practical results.

2. Serial Iterative Splitting Method

We consider a two-level iterative splitting method, which is discussed for two operators in [2] and for L operators in [38].

In this work, we also apply the recent theoretical results of our work in [26]. While in that work we took the adaptivity of the splitting results into account, here we consider the application of multi-operator splitting approaches and multi-splitting methods.

Based on the differential Equation (10), we have the following decomposition of the operator A:

• $A={\sum }_{l=1}^L{A}_l$, while $A_l$ are the sub-operators for the iterative part (solver part), and
• and $B_l=A-A_l$ are the sub-operators for the relaxation part (right hand side part).

where we have $l=1,\dots ,L$.

The serial iterative splitting method is given in the following algorithm. Here, we consider discretization step-size $\tau =t^{n+1}-t^n$, which can also be set adaptively, see [26]. We assume to have time-interval $[t^n,t^{n+1}]$ with $n=0,1,\dots ,N$, where $t_0$ is the initial time and $t_N=T$ is the end time. We consecutively solve the following sub-problems for $i=0,L,\dots ,(m-1)L$:

$$\frac{\partial c_{i+1}(t)}{\partial t}=A_1{c}_{i+1}(t) + B_1{c}_i(t), with c_{i+1}(t^n)=c^n,$$

(11)

$$\frac{\partial c_{i+2}(t)}{\partial t}=A_2{c}_{i+2}(t) + B_2{c}_{i+1}(t), with c_{i+2}(t^n)=c^n,$$

(12)

$$\dots$$

(13)

$$\frac{\partial c_{i+L}(t)}{\partial t}=A_L{c}_{i+L}(t) + B_L{c}_{i+L-1}(t), with c_{i+L}(t^n)=c^n ,$$

(14)

where we can assume for the first initialisation $c_0(t)=0$, or a different initial-function, see [2]. $c^n=c(t^n)$ is the known split approximation, which is computed in the previous iterative procedure. The current split approximation at time $t=t^{n+1}$ is defined as $c^{n+1}=c_{(m-1)L}(t^{n+1})$, where $(m-1)L$ is the maximal number of iterative steps. The stopping criterion is $\left|\right|c_{(m-1)L}-c_{(m-2)L}\left|\right|\le err$ and, then we have the solution $c(t^{n+1})=c_{(m-1)L}(t^{n+1})$.

The solutions are given as:

$$c_{i+1}(t)=exp(A_1 (t-t^n))c^n+{\int }_{t^n}^{t}exp(A_1 (t-s)) B_1 c_i(s) ds,$$

(15)

$$c_{i+2}(t)=exp(A_2 (t-t^n))c^n+{\int }_{t^n}^{t}exp(A_2 (t-s)) B_2 c_{i+1}(s) ds,$$

(16)

$$\dots ,$$

(17)

$$c_{i+L}(t)=exp(A_L (t-t^n))c^n+{\int }_{t^n}^{t}exp(A_L (t-s)) B_L c_{i+L-1}(s) ds,$$

(18)

where $t\in [t^n,t^{n+1}]$.

Remark 1.

We approximate the integral operator with a higher order integration scheme, e.g., exp-matrix computations, see [39,40], exp-Runge–Kutta methods, see [41], Pade- or Magnus-expansions, see [42,43] or with higher order numerical integration methods, as Trapezoidal- or Simpsons-rule, see [44].

We define the error-function as $e_i(t)=c(t)-c_i(t)$ with $e_0(t)=c(t)-c_0$, the maximum-norm $\left|\right|e_i\left|\right|={max}_{t\in [0,T]}\left|\right|e_i(t){\left|\right|}_{\infty }$, and the maximum operator norm $\left|\right|A_l\left|\right|=\left|\right|A_l{\left|\right|}_{\infty }$.

Theorem 1.

Consider the bounded operators $A_l\in {IR}^m\times {IR}^m$ for $l=1,\dots ,L$, where L is the number of operators. The iterations (11)–(14) for the Cauchy-problem (10), which are applied with $i=0,L,\dots ,(m-1)L$, are of order $\mathcal{O}({\tau }^{mL})$.

Proof. 

The result for the 2-level method is given in [38]. We apply a recursive argument to the iterative scheme with L operators and obtain:

$$\begin{array}{c}\left|\right|e_{mL}\left|\right|\le {\left({\mathrm{\Pi }}_{l=1}^L{C}_l\left|\right|B_l\left|\right|\right)}^m\left|\right|e_0\left|\right|,\hfill \end{array}$$

(19)

where $C_l$ is given with $C_l=\mathcal{O}(\tau )$, see also [38].  □

Remark 2.

The operators are based on the spatial discretization with higher order methods, e.g., [27,31]. Further, we assume that all of the operators, including the fractional discretized operators, are bounded, see [24]. Based on such assumption, we could generalize the results with respect to fractional operators.

3. Parallel Iterative Splitting Method

In the following, we parallelise the serial iterative splitting approach.

We present the following approaches:

• multi-splitting iterative approach, and
• two operator iterative splitting approach.

3.1. Multi-Splitting Iterative Approach

The problem is given as $\frac{\partial c}{\partial t}=Ac(t)={\sum }_{l=1}^L{A}_{l}c(t), c=c_0$.

The idea is a multiple decomposition of

$$A=A_l+B_l, l=1,\dots ,L,$$

(20)

$$B_l=A-A_l,$$

(21)

where $A_l$ is a non-singular and $B_l$ is the rest matrix.

Further, we have the decomposition of the parallel computable vectors:

$$\begin{array}{c}{c}_i=\sum _{l=1}^L{E}_l{c}_{i,l}, and E=\sum _{l=1}^L{E}_l,\hfill \end{array}$$

(22)

where $c_i$ is the i-th iterative solution and $c_{i,l}$ are the parallel computable solutions in the i-th iterative step. E is the identity matrix and $E_l$ are diagonal matrices with positive entries.

The multisplitting iterative approach is given as:

$$\begin{array}{c}\frac{\partial c_{i,l}(t)}{\partial t}=A_l{c}_{i,l}(t) + B_l{c}_{i-1}(t), for t\in [t^n,t^{n+1}]\hfill \\ with c_{i,l}(t^n)=c(t^n),l=1,\dots L,\hfill \end{array}$$

(23)

where the initialisation is $c_0(t)=c(t^n)$, and $i=1,\dots ,I$ are the iterative steps. The stopping criterion is $\left|\right|c_i-c_{i-1}\left|\right|\le err$ and then we have the solution $c(t^{n+1})=c_i(t^{n+1})$.

The splitting error of the iterative splitting is of $k+1$ order, i.e. $O({\tau }^{k+1})$, with

$$\begin{array}{c}\left|\right|er{r}_{i+1}\left|\right|=K_i{\tau }_n^i\left|\right|er{r}_0\left|\right|+O({\tau }_n^{i+1}) ,\hfill \end{array}$$

(24)

where $K_i={\sum }_{l=1}^L\frac{1}{{\omega }_l} \left|\right|B_l\left|\right|$ and ${\sum }_{l=1}^L\frac{1}{{\omega }_l}=1$ are the weights (${\omega }_l>1$) and $\left|\right|er{r}_0\left|\right|=\left|\right|c_0(t)\left|\right|$, while $c_{-1}(t)=0$.

Benefit:

• Parallel implementation (the method is designed for parallel contributions), and
• Good error balance between the different operators

Drawback:

• Balances in the decomposition of $E_l$ important to damp large errors

3.2. Parallel Splitting: Classical Version (Synchronous Version)

Here, we consider the classical version of the parallel splitting algorithm that is applied with synchronisation, see also [45]. We assume to deal with L processors and $i=1,\dots ,I$ are the iterative steps, while I is the maximum number of iterative steps.

We deal with the parallel splitting in the synchronous version as:

$$\frac{\partial c_{i,1}(t)}{\partial t}=A_1{c}_{i,1}(t) + B_1{c}_{i-1}(t), with c_{i,1}(t^n)=c^n,$$

(25)

$$\frac{\partial c_{i,2}(t)}{\partial t}=A_2{c}_{i,2}(t) + B_2{c}_{i-1}(t), with c_{i,2}(t^n)=c^n,$$

(26)

$$\dots$$

(27)

$$\frac{\partial c_{i,L}(t)}{\partial t}=A_l{c}_{i,L}(t) + B_l{c}_{i-1}(t), with c_{i,L}(t^n)=c^n,$$

(28)

$$c_i(t)=\sum _{l=1}^L{E}_l{c}_{i,l}(t),and E=\sum _{l=1}^L{E}_l,$$

(29)

where we assume for the initialisation of the first step $c_0(t)=0$. E is the identity matrix and $E_l$ are diagonal matrices with positive entries. $A_l$ and $B_l$ are given in the Equations (20) and (21). Furthermore, $c^n=c(t^n)$ is the known split approximation at the time-level $t=t^n$, which is computed in the previous iterative process. The split approximation at the time-level $t=t^{n+1}$ is defined as $c^{n+1}=c_i(t^{n+1})$, which is computed in the current iterative process.

The solutions are given as:

$$c_{i,1}(t)=exp(A_1 (t-t^n))c^n+{\int }_{t^n}^{t}exp(A_1 (t-s)) B_1 c_{i-1}(s) ds,$$

(30)

$$c_{i,2}(t)=exp(A_2 (t-t^n))c^n+{\int }_{t^n}^{t}exp(A_2 (t-s)) B_2 c_{i-1}(s) ds,$$

(31)

$$\dots ,$$

(32)

$$c_{i,L}(t)=exp(A_L (t-t^n))c^n+{\int }_{t^n}^{t}exp(A_L (t-s)) B_L c_{i-1}(s) ds,$$

(33)

$$c_i(t)=\sum _{l=1}^L{E}_l{c}_{i,l}(t),and E=\sum _{l=1}^L{E}_l,$$

(34)

where $t\in [t^n,t^{n+1}]$.

The stopping criterion is given as:

$$\begin{array}{c}\left|\right|c_i-c_{i-1}\left|\right|\le err.\hfill \end{array}$$

(35)

The integrals can be solved by higher order integration-rules, see Remark 1.

In the classical algorithm, we have a synchronisation point, so that the next iterative step can only start if all processors have submitted the results, see Equation (34). Such a hard point allows for applying a simpler stopping criterion, which is given in Equation (35).

The bottleneck of the synchronous algorithm is that the finished processors could not go on with the next iterative step and the computational time is wasted. Therefore, we explain the ideas of the asynchronous algorithms, which are used to apply the parallel splitting method in an asynchronous version.

3.3. Asynchronous Algorithm

The idea of an asynchronous algorithm is that each processor works independently and has access to a common memory. If one processor needs an update of a solution of another processor, then he can read the solution in the common memory. The processors are independent and the convergence is given with the weighted norm, see [3].

An asynchronous algorithm is defined, as follows:

Definition 1.

For $i\in IN$, let ${\{I(i)\}}_{i\in IN}$ be the subset indicating which components are computed at the i-th iteration. Additionally, we have an iteration count $s_l(i)\in {IN}_0$ (prior to i), which indicates the iteration when the l-th component was computed in processor l.

For $i\in IN$, we have $I(i)\in \{1,\dots ,L\}$, where L is the number of processors and $(s_1(i),\dots ,s_L(i))\in {IN}_0^L$, such that:

$$s_l(i)\le i-1, for l\in \{1,\dots ,L\}, i\in IN,$$

(36)

$$\underset{i\to \infty }{lim}{s}_l(i)=\infty , forl\in \{1,\dots ,L\},$$

(37)

$$|\{i\in IN:l\in I(i)\}|=\infty , forl\in \{1,\dots ,L\}.$$

(38)

Subsequently, we define the asynchronous algorithm:

$$\begin{array}{c}\hfill x_l^i=\left\{\begin{array}{cc}{x}_l^{i-1},& for l\notin I(i),\\ H_l(x_1^{s_1(i)},\dots ,x_L^{s_L(i)}),& for l\in I(i),\end{array}\right.\end{array}$$

(39)

where ${\mathbf{x}}^0={(x_1^0,\dots ,x_L^0)}^t$ are the initialisations and $H_l$ is the solver function of the l-th component, see [3].

In the following, the convergence of the asynchronous algorithm is presented with respect to the weighted norm, see [3].

Definition 2.

We assume that each component space ${\epsilon }_i$ has a normed linear space $({\epsilon }_i,||·|{|}_i)$. We can define an appropriate norm for the parallel methods, which can be given as the weighted maximum norm:

$$\begin{array}{c}\hfill {\left|\right|x\left|\right|}_w=\underset{i=1}{\overset{m}{max}}\frac{\left|\right|x_i{\left|\right|}_i}{w_i}\end{array}$$

(40)

where the vector $w={(w_1,\dots ,w_m)}^t$ is positive in each component $w_i>0$ for all $i=1,\dots ,m$.

Theorem 2.

We assume that we have a fixed point ${\mathbf{x}}^{*}\in \epsilon ={\epsilon }_1\times \dots \times {\epsilon }_L$ with ${\mathbf{H}}^i({\mathbf{x}}^{*})={\mathbf{x}}^{*}$ for all i. Further, we assume that there exists $\gamma \in [0,1)$ and a positive vector $w\in {IR}^m$, such that:

$$\begin{array}{c}\left|\right|{\mathbf{H}}^i(\mathbf{x})-{\mathbf{x}}^{*}{\left|\right|}_w\le \gamma \left|\right|\mathbf{x}-{\mathbf{x}}^{*}{\left|\right|}_w.\hfill \end{array}$$

(41)

Based on the assumptions, we conclude that the asynchronous iterates $x^k$ converge to $x^{*}$, which is the unique fixed point of ${\mathbf{H}}^i={(H_1^i,\dots ,H_l^i)}^t$.

Proof. 

The proof is given in [3].  □

3.4. Parallel Splitting: Modern Version (Asynchronous Version)

We have to apply the following asynchronous algorithm, which is given in Definitions 1 and 2 and with the convergence results in Theorem 2. We assume to deal with L processors and $i=1,\dots ,I$ are the iterative steps, while I is the maximum number of iterative steps.

We deal with the parallel splitting in the synchronous version as:

$$\frac{\partial c_{s_1(i+1)}(t)}{\partial t}=A_1{c}_{s_1(i+1)}(t) + B_1{c}_i(t), with c_{s_1(i+1)}(t^n)=c^n,$$

(42)

$$\frac{\partial c_{s_2(i+1)}(t)}{\partial t}=A_2{c}_{s_2(i+1)}(t) + B_2{c}_i(t), with c_{s_L(i+1)}(t^n)=c^n,$$

(43)

$$\dots$$

(44)

$$\frac{\partial c_{s_L(i+1)}(t)}{\partial t}=A_L{c}_{s_L(i+1)}(t) + B_l{c}_i(t), with c_{s_l(i+1)}(t^n)=c^n,$$

(45)

$$c_{i+1,l}(t)=\left\{\begin{array}{cc}{x}_l^i,& \mathrm{for} l\notin I(i+1),\hfill \\ x_l^{s_l(i+1)},& \mathrm{for} l\in I(i+1),\hfill \end{array}\right.$$

(46)

$$c_{i+1}(t)=\sum _{l=1}^L{E}_l{c}_{i+1,l}(t), \mathrm{and} E=\sum _{l=1}^L{E}_l,$$

(47)

where we assume for the initialisation of the first step $c_0(t)=0$. E is the identity matrix and $E_l$ are diagonal matrices with positive entries. $A_l$ and $B_l$ are given in Equations (20) and (21). Further, $c^n$ is the known split approximation at time $t=t^n$, which is computed in the previous iterative process. The split approximation at time $t=t^{n+1}$ is given as $c^{n+1}=c_i(t^{n+1})$, which is computed in the current iterative process.

The solutions are given as:

$$c_{s_1(i+1)}=exp(A_1 (t-t^n))c^n+{\int }_{t^n}^{t}exp(A_1 (t-s)) B_1 c_i(s) ds,$$

(48)

$$c_{s_2(i+1)}=exp(A_2 (t-t^n))c^n+{\int }_{t^n}^{t}exp(A_2 (t-s)) B_2 c_i(s) ds,$$

(49)

$$\dots ,$$

(50)

$$c_{s_L(i+1)}(t)=exp(A_L (t-t^n))c^n+{\int }_{t^n}^{t}exp(A_L (t-s)) B_L c_i(s) ds,$$

(51)

$$c_{i+1,l}(t)=\left\{\begin{array}{cc}{x}_l^i,& \mathrm{for} l\notin I(i+1),\hfill \\ x_l^{s_l(i+1)},& \mathrm{for} l\in I(i+1),\hfill \end{array}\right.$$

(52)

$$c_{i+1}(t)=\sum _{l=1}^L{E}_l{c}_{i+1,l}(t), \mathrm{and} E=\sum _{l=1}^L{E}_l,$$

(53)

where $t\in [t^n,t^{n+1}]$.

The stopping criterion is given as:

$$\begin{array}{c}\hfill \left|\right|c_{i+1}-c_i{\left|\right|}_w\le \underset{l=1}{\overset{L}{max}}\frac{\left|\right|c_{i+1,l}-c_{i,l}\left|\right|}{w_l}\le err,\end{array}$$

(54)

where $w={(w_1,\dots ,w_L)}^t$ and we have the maximum-norm with $w_l=1$ for all $l=1,\dots ,L$.

The integrals can be solved by higher order integration-rules, see Remark 1.

In the modern algorithm, we do not have a synchronisation point, so that each processor can work independently. For the stopping criterion, we apply a weighted norm, which means that all of the single results of the processors have to be lower than the given error-bound, see the stopping criterion in Equation (54).

4. Theoretical Results

In the following, we deal with the m-dimensional initial value problem in the non-homogeneous form, also see the homogeneous form in Equation (10):

$$\begin{array}{c}\hfill c^{\prime }(t)=Ac(t)+f(t), c(0)=c_0,\end{array}$$

(55)

where A is conveniently decomposed in two operators $A=M+N$, and f is the right hand side.

Further, we deal in the following with the proof-ideas that are related to Waveform-relaxation methods, see [37,45].

The initial value problem (55) is solved with the multisplitting Waveform-relaxation method, which is given as:

$$\begin{array}{c}\hfill c_{i+1}^{\prime }(t)=M{c}_{i+1}(t)+N{c}_i(t)+f(t), c(0)=c_0,\end{array}$$

(56)

where A is given in Equation (10). Further, $c_0(t)=c_0$ is the starting condition.

For the multisplitting approach, we have the following Definition:

Definition 3.

Let $L\ge 1$ be the number of splittings, and $A,A_l,B_l,E_l$ real-valued $m\times m$ matrices. We say that $(A_l,B_l,E_l)$ for $l=1,\dots ,L$ is a multisplitting triple if:

• $A=A_l+B_l$ and $B_l={\sum }_{k=1,k\ne l}^L{A}_k$ with $l=1,\dots ,L$,
• The matrices $E_l$ are non-negative diagonal matrices and satisfy: ${\sum }_{l=1}^L{E}_l=I$,
  where I is the identity matrix, and
• $s_l(i+1)\le i+1$ indicates the iteration, where the l-th component is computed prior to $i+1$.

• The multisplitting approach that is based on the Waveform-relaxation in the classical version is given by:

  $$c_{l,i+1}^{\prime }(t)=A_l{c}_{l,i+1}(t)+B_l{c}_i+f(t), c_{l,i+1}(0)=c_0,$$

  (57)

  $$c_{i+1}(t)=\sum _{l=1}^L{E}_l{c}_{l,i+1}(t).$$

  (58)
• The multisplitting approach based on the Waveform-relaxation in the modern version is given by:

  $$c_{s_l(i+1)}^{\prime }(t)=A_l{c}_{s_l(i+1)}(t)+B_l{c}_i+f(t), c_{s_l(i+1)}(0)=c_0,$$

  (59)

  $$c_{i+1}(t)=\sum _{l=1}^L{E}_l{c}_{s_l(i+1)}(t).$$

  (60)

4.1. Stability Analysis

We deal with the following system:

$$\begin{array}{c}\hfill c_{l,i+1}(t)=K_l{c}_i(t)+{\varphi }_l(t),\end{array}$$

(61)

where we have

$$K_{l}c(t)={\int }_0^t{k}_l(t-s) c(s)ds, for l=1,\dots ,L,$$

(62)

$${\varphi }_l(t)=exp(t{A}_l)c_0+{\int }_0^{t}exp((t-s)A_l)f(s) ds, for l=1,\dots ,L.$$

(63)

where $k_l(t)=exp(t{A}_l) B_l$ for $l=1,\dots ,L$, and we apply the multisplitting notation (58), with:

$$Kc(t)=\sum _{l=1}^L{E}_l{K}_{l}c(t),$$

(64)

$$\varphi (t)=\sum _{l=1}^L{E}_l{\varphi }_l(t),$$

(65)

where $k(t)={\sum }_{l=1}^L{E}_l{k}_l(t)$ and we obtain the standard Waveform-relaxation method as:

$$\begin{array}{c}{c}_{i+1}(t)=K{c}_i(t)+\varphi (t).\hfill \end{array}$$

(66)

We can rewrite into an recursive notation and without loss of generality, we assume $f(t)=0$, then we obtain:

$$\begin{array}{c}\hfill c_{i+1}(t)=\sum _{l=1}^L{E}_l{\int }_0^{t}exp((t-s)A_l)B_l{c}_i(s)ds+\sum _{l=1}^L{E}_{l}exp(t{A}_l)c_0.\end{array}$$

(67)

Given a well-conditioned system of eigenvectors, we can consider the eigenvalues ${\lambda }_{1,l}$ of $A_l$ and ${\lambda }_{2,l}$ of $B_l$ instead of the operators $A_l,B_l$ themselves, for $l=1,\dots ,L$. For the matrices $E_l$ we have the eigenvalues ${\lambda }_{E_l}$ with $0\le {\lambda }_{E_l}\le 1$ and ${\sum }_{l=1}^L{\lambda }_{E_l}=1$.

We can rewrite into the eigenvalue-notation and obtain:

$$\begin{array}{c}\hfill c_{i+1}(t)=\sum _{l=1}^L{\lambda }_{E_l}{\int }_0^{t}exp((t-s){\lambda }_{A_l}){\lambda }_{B_l}{c}_i(s)ds+\sum _{l=1}^L{\lambda }_{E_l}exp(t{\lambda }_{A_l})c_0.\end{array}$$

(68)

We assume that all of the initial values $c_i(t^n)=c_{approx}(t^n)$ with $i=0,1,2,\dots ,$ are as $\left|\right|c_{approx}(t_n)-c_n\left|\right|\le O({\tau }^I)$ where I is the order, following the ideas in the iterative splitting approach [46].

Further, we also assume that the pairs ${\lambda }_{1,l}\ne {\lambda }_{2,l}$ for $l=1,\dots ,L$, otherwise we do not consider the iterative splitting approach, while the time-scales are equal, see [34].

In the following, we apply the $A(\alpha )$-stability.

$A(\alpha )$-Stability

We define $z_{1,l}=\tau {\lambda }_{1,l}$ and $z_{2,l}=\tau {\lambda }_{2,l}$ with $\tau =t^{n+1}-t^n$, $l=1,\dots ,L$.

We have the following proposition 1:

Proposition 1.

Starting with $c(t^n)=c_n$ and a time-step $\tau =t^{n+1}-t^n$, we obtain:

$$\begin{array}{ccc}\hfill c_i(t^{n+1})& =& \sum _{i=0}^i{S}_j(z_{1,l},z_{2,l},\tau ) c_n,\hfill \end{array}$$

(69)

where $S_i$ is the stability function of the scheme. The $S_i$ are given as:

$$\begin{array}{c}\hfill S_0(z_{1,l},z_{2,l},t)=\sum _{l=1}^L{\lambda }_{E_l}exp(t{\lambda }_{1,l})c_n.\end{array}$$

(70)

$$\begin{array}{c}\hfill S_1(z_{1,l},z_{2,l},t)=\sum _{l=1}^L{\lambda }_{E_l}{\int }_0^{t}exp((t-s){\lambda }_{1,l}){\lambda }_{2,l}\sum _{l_1=1}^L{\lambda }_{E_{l_1}}exp(s{\lambda }_{1,l_1})c_n ds,\\ \hfill S_1(z_{1,l},z_{2,l},t)=\sum _{l=1}^L{\lambda }_{E_l}{\int }_0^{t}exp((t-s){\lambda }_{1,l}){\lambda }_{2,l}{S}_0(z_{1,l},z_{2,l},s)c_n ds.\end{array}$$

(71)

and

$$\begin{array}{c}{S}_i(z_{1,l},z_{2,l},t)=\hfill \\ =\sum _{l=1}^L{\lambda }_{E_l}{\int }_0^{t}exp((t-s){\lambda }_{1,l}){\lambda }_{2,l}\left(\sum _{l_1=1}^L{\lambda }_{E_{l_1}}{\int }_0^{s}exp((s-s_1){\lambda }_{1,l_1}){\lambda }_{1,l_1}·\right.\hfill \\ ·\left.\left(\dots (\sum _{l_i=1}^L{\lambda }_{E_{l_1}}{\int }_0^{s_{i-1}}exp((s_{i-1}-s_i){\lambda }_{1,l_i}){\lambda }_{2,l_i}{c}_n d{s}_i)\dots d{s}_1\right)ds\right),\hfill \end{array}$$

(72)

$$\begin{array}{c}{S}_i(z_{1,l},z_{2,l},t)=\sum _{l=1}^L{\lambda }_{E_l}{\int }_0^{t}exp((t-s){\lambda }_{1,l}){\lambda }_{2,l}{S}_{i-1}(z_{1,l},z_{2,l},s)c_n ds.\hfill \end{array}$$

(73)

with i-iterations.

Proof. 

We apply the complete induction.

We start with $i=0$ and obtain:

$$c_0(t^{n+1})=\sum _{i=0}^0{S}_j(z_{1,l},z_{2,l},\tau ) c_n,$$

(74)

$$c_0(t^{n+1})=\sum _{l=1}^L{\lambda }_{E_l}exp((t{\lambda }_{A_l})c_n.$$

(75)

We apply the induction step $i\to i+1$, while we apply Equation (68):

$$c_{i+1}(t^{n+1})=S_0(z_1,z_2,\tau )c_n+ {\int }_0^t\sum _{l=1}^L{\lambda }_{E_l}exp((t-s){\lambda }_{1,l}) {\lambda }_{2,l}{c}_i(s)ds,$$

(76)

$$c_{i+1}(t^{n+1})=S_0(z_1,z_2,\tau )c_n+ {\int }_0^t\sum _{l=1}^L{\lambda }_{E_l}exp((t-s){\lambda }_{1,l}) {\lambda }_{2,l}\sum _{j=0}^i{S}_j(z_1,z_2,s)c_{n}ds,$$

(77)

we apply the Equation (71) and obtain:

$$c_{i+1}(t^{n+1})=S_0(z_1,z_2,\tau )c_n+\sum _{j=1}^{i+1}{S}_j(z_1,z_2,s)c_{n}ds,$$

(78)

$$c_{i+1}(t^{n+1})=\sum _{j=0}^{i+1}{S}_j(z_1,z_2,s)c_{n}ds,$$

(79)

and we obtain the results.  □

Let us consider the $A(\alpha )$-stability that is given by the following eigenvalues in a wedge:

$$\mathcal{W}=\{\zeta \in \mathbb{C}:|arg(\zeta )\le \alpha \}.$$

For the A-stability we have $|S_m(z_1,z_2)|\le 1$ whenever $z_1\in {\mathcal{W}}_{\pi /2}$. This means that we have the stiff operator, where we assume that $z_2$ is the non-stiff operator.

The stability of the two iterations is given in the following theorem with respect to A and $A(\alpha )$-stability.

Theorem 3.

We have the following stability for the iterative operator splitting scheme (71):

For the stability function $S_i$, where i is the iterative step, we have the following A-stability

$$\begin{array}{c}\hfill \underset{z_1\in W_{\alpha },z_2\le 0}{max}\left|S_i(z_1,z_2)\right|\le 1 , \forall \alpha \in [0,\pi /2],\end{array}$$

(80)

with $\omega \in [0,1]$, the initialization is given as $c_{-1}=0$ and the initial conditions are $c_i(t^n)=c_n$.

Proof. 

We consider the $z_1\to -\infty$, while $z_2\le 0$ is bounded as a nonstiff operator.

We apply the complete induction.

We start with $i=0$:

$$\begin{array}{c}|S_0(-\infty ,z_2,t)|=|\sum _{l=1}^L{\lambda }_{E_l}exp(t{\lambda }_{1,l})|\le 1,\hfill \end{array}$$

(81)

with the assumption of the nonstiff operators ${\lambda }_{2,l}\le 0$ with $l=1,\dots ,L$.

Further we also have $i=1$:

$$|S_1(-\infty ,z_1,t)|=|\sum _{l=1}^L{\lambda }_{E_l}{\int }_0^{t}exp((t-s){\lambda }_{1,l}){\lambda }_{2,l}{S}_0(z_{1,l},z_{2,l},s) ds|$$

(82)

$$\le |\sum _{l=1}^L{\lambda }_{E_l} t exp(t{\lambda }_{1,l}){\lambda }_{2,l}\left|S_0(z_{1,l},z_{2,l},t)\right|=0\le 1.$$

(83)

Subsequently, we apply the induction step for $i\to i+1$:

$$\begin{array}{ccc}\hfill |S_{i+1}(z_1,z_2,t)|& =& \left|\right|S_0(z_1,z_2,\tau )+ {\int }_0^t\sum _{l=1}^L{\lambda }_{E_l}exp((t-s){\lambda }_{1,l}) {\lambda }_{2,l}\sum _{j=0}^i{S}_j(z_1,z_2,s)ds\left|\right|\hfill \end{array}$$

(84)

$$\begin{array}{ccc}& \le & \left|\right|S_0(z_1,z_2,\tau )\left|\right|+\left|\right|\sum _{l=1}^L{\lambda }_{E_l} t exp(t{\lambda }_{1,l}) {\lambda }_{2,l}\sum _{j=0}^i{S}_j(z_1,z_2,t)\left|\right|=0\le 1,\hfill \end{array}$$

(85)

where we applied $\left|\right|{\sum }_{j=0}^i{S}_j(z_1,z_2,t)\left|\right|=0$.

Afterwards, we obtain our results, also see the ideas of the stability proofs in [47].  □

4.2. Convergence Analysis

In order to apply the multisplitting Waveform-relaxation method (57) and (58), we write the solutions of the individual Equation (57) as:

$$\begin{array}{c}\hfill c_{l,i+1}(t)=K_l{c}_i(t)+{\varphi }_l(t),\end{array}$$

(86)

where we have

$$K_{l}c(t)={\int }_0^t{k}_l(t-s) c(s)ds, for l=1,\dots ,L,$$

(87)

$${\varphi }_l(t)=exp(t{A}_l)c_0+{\int }_0^{t}exp((t-s)A_l)f(s) ds, for l=1,\dots ,L.$$

(88)

where $k_l(t)=exp(t{A}_l)B_l$ for $l=1,\dots ,L$.

Further, we apply the multisplitting notation (58) and obtain the summations:

$$Kc(t)=\sum _{l=1}^L{E}_l{K}_{l}c(t),$$

(89)

$$\varphi (t)=\sum _{l=1}^L{E}_l{\varphi }_l(t),$$

(90)

where $k(t)={\sum }_{l=1}^L{E}_l{k}_l(t)$ and we obtain the standard Waveform-relaxation method as:

$$\begin{array}{c}{c}_{i+1}(t)=K{c}_i(t)+\varphi (t).\hfill \end{array}$$

(91)

We assume that Lemma 1 is fulfilled, see also [45].

Lemma 1.

The following items are equivalent:

• $c(t)$ is a solution of the initial value problem (55).
• $c(t)$ is a solution of each multisplitted equation $c(t)=K_{l}c(t)+{\varphi }_l(t), c(0)=c_0, l=1,\dots ,L$.
• $c(t)$ is the solution of the fixed point equation $c(t)=Kc(t)+{\varphi }_l(t)$.

We define ${\left|\right|c\left|\right|}_T={max}_{t\in [0,T]}\left|c(t)\right|$ as maximum norm and we also denote by $\left|\right|·\left|\right|$ the matrix norm induced by the vector norm $|·|$.

Based on these assumptions, in the following we derive the errors and convergence results.

In Theorem 4, we derive the error of the i-th approximation, see also [45].

Theorem 4.

There exists a constant $C:={\sum }_{l=1}^L{C}_l$, which is given to estimate the kernel k of the multisplitting waveform-relaxation operator, such that we obtain ${\left|\right|k\left|\right|}_T=C$. Subsequently, the error of the i-th approximation of the classical multisplitting WR method (57) and (58) is given by

$$\begin{array}{c}\hfill \left|\right|c^i-{c\left|\right|}_T\le \frac{{(CT)}^i}{i!}{(exp(CT)|\left|\varphi \right||}_T+\left|\right|c_0{\left|\right|}_T).\end{array}$$

(92)

Proof. 

We have given

$$\begin{array}{c}\hfill c_i(t)=K{c}_{i-1}(t)+\varphi (t),\end{array}$$

(93)

We apply the Lemma 1 and follow with the iterative approach:

$$\begin{array}{c}\hfill c_i(t)=K^i{c}_0(t)+\sum _{j=0}^{i-1}{K}^i\varphi (t),\end{array}$$

(94)

where is $K^{i}u(t)$ is the i-times convolution

$K^{i}u(t)={\int }_0^{t}k(t-s_i)({\int }_0^{s_i}k(t-s_i-s_{i-1})(\dots {\int }_0^{t-{\sum }_{j=0}^i{s}_{i-j}}k(t-{\sum }_{j=0}^i{s}_{i-j})u(s_1)d_{s_1}\dots )d{s}_{i-1})d{s}_i$.

Further, we have ${\left|\right|u\left|\right|}_T={max}_{t\in [0,t]}\left|u(t)\right|$, where $|·|$ is an appropriate Banach-Norm.

There exists:

$$\begin{array}{c}\hfill \left|\right|k_l{\left|\right|}_T\le C_l, for l=1,\dots ,L,\end{array}$$

(95)

and we have

$$\begin{array}{c}\left|k(t)\right|\le {\left|\right|k\left|\right|}_T=\left|\right|\sum _{l=1}^L{E}_l{k}_l\left|\right|\le \sum _{l=1}^L{C}_l=C.\hfill \end{array}$$

(96)

We apply the estimation of the Waveform-relaxation, see [8], and obtain:

$$\begin{array}{c}\hfill \left|\right|K^i{\left|\right|}_T\le \frac{{(CT)}^i}{i!},\end{array}$$

(97)

where we have ${lim}_{i\to \infty }\left|\right|K^i{\left|\right|}_T\to 0$.

The error estimate is then given as

$$\begin{array}{c}\left|\right|c-c^i{\left|\right|}_T=\left|\right|(\underset{j\to \infty }{lim}{K}^j{c}_0-\sum _{j=0}^{\infty }{K}^j\varphi (t))-(K^i{c}_0-\sum _{j=0}^{i-1}{K}^j\varphi (t))\left|\right|\hfill \\ \le \left|\right|\sum _{j=i}^{\infty }{K}^j\varphi (t)+K^i{c}_0\left|\right|\le \left|\right|K^i{\left|\right|}_T(||\sum _{j=0}^{\infty }\left|\right|K^j{\left|\right|}_T{ \left|\right|\varphi (t)\left|\right|}_T+\left|\right|c_0{\left|\right|}_T).\hfill \end{array}$$

(98)

We apply

$$\begin{array}{c}\sum _{j=0}^{\infty }\left|\right|K^j{\left|\right|}_T=\left|\right|K^0{\left|\right|}_T+\left|\right|K^1{\left|\right|}_T+\dots +\left|\right|K^{\infty }{\left|\right|}_T\le exp(CT).\hfill \end{array}$$

(99)

Subsequently, we obtain the estimation

$$\begin{array}{c}\left|\right|c-c^i{\left|\right|}_T=\le \frac{{(CT)}^i}{i!}{(exp(CT)|\left|\varphi \right||}_T+\left|\right|c_0{\left|\right|}_T).\hfill \end{array}$$

(100)

 □

We have the following new convergence Theorem 5 based on the extension of the classical convergence Theorem version 4.

Theorem 5.

There exists a constant $C:={\sum }_{l=1}^L{C}_l$, which is given to estimate the kernel k of the multisplitting waveform-relaxation operator, such that we obtain ${\left|\right|k\left|\right|}_T=C$. Subsequently, the convergence of the modern multisplittting WR method (59) and (60) is given by

$$\begin{array}{c}\hfill \left|\right|c^{i_{min}}-{c\left|\right|}_T\le \frac{{(C T)}^{i_{min}}}{i_{min}!}\left|\right|c^0-c{\left|\right|}_T,\end{array}$$

(101)

where $i_{min}={min}_{l=1}^L{s}_l(i)$, where $s_l(i)\le i$ are the retarded iterations of the l-th processor.

Proof. 

We start with the estimation of the i-th iteration:

$$\left|\right|c^{i_{min}}-{c\left|\right|}_T\le \left|\right|\sum _{l=1}{E}_l{K}_l(c^{s_l(i)}-c){\left|\right|}_T\le$$

(102)

$$\le \left|\right|\sum _{l=1}{E}_l{K}_l(c^{i_{min}-1}-c){\left|\right|}_T\le {\left|\right|K\left|\right|}_T \left|\right|(c^{i_{min}-1}-c){\left|\right|}_T.$$

(103)

Afterwards, we have the recursion:

$$\begin{array}{c}\hfill \left|\right|c^{i_{min}}-{c\left|\right|}_T\le \left|\right|K^{i_{min}}{\left|\right|}_T\left|\right|(c^0-c){\left|\right|}_T.\end{array}$$

(104)

where we apply $\left|\right|K^{i_{min}}{\left|\right|}_T\le \frac{{(C T)}^{i_{min}}}{i_{min}!}$, based on the idea in [8], and we obtain:

$$\begin{array}{c}\hfill \left|\right|c^{i_{min}}-{c\left|\right|}_T\le \frac{{(C T)}^{i_{min}}}{i_{min}!} \left|\right|(c^0-c){\left|\right|}_T,\end{array}$$

(105)

where $i_{min}={min}_{l=1}^L{s}_l(i)$.  □

Remark 3.

For the parallel error, we obtain order $\mathcal{O}({\tau }^m)$ if we assume that all processors have at least m iterative cycles, while, for the serial error, we have order $\mathcal{O}({\tau }^{mL})$. Thus, in the serial version, we have to apply $mL$ iterative steps in sum to obtain the result, while in the parallel version, we only apply m iterative steps, while L processors share the computation to solve the L sub-equations. Furthermore, we can assume that the sub-equations are faster to solve, because the sub-operators are much smaller and simpler to handle. Subsequently, we have $t_{sub}\le \frac{t_{full}}{L}$, where $t_{sub}$ is the time to solve a sub-problem and $t_{full}$ the time to solve the full problem. Therefore, we have a benefit in the parallel distribution and obtain faster the higher order $\mathcal{O}({\tau }^{mL})$ than with the serial version.

Remark 4.

While the classical version of the parallel splitting method has order $\mathcal{O}({\tau }^m)$, see the Theorem 4, the modern version of the parallel splitting method can improve the order partially to higher order. We obtain $\mathcal{O}({\tau }^{m_{partial}})$ with $m\le m_{partial}\le m{L}_{fast}$, when we split into slow and fast convergent processors and assume that the faster results of the fast convergent processors are sufficient for the update. We can define a new $c_i={\sum }_{l\in \mathrm{Fast}}{\tilde{E}}_l{c}_{i,l}$ with $E={\sum }_{l\in \mathrm{Fast}}{\tilde{E}}_l$ and the set $\mathrm{Fast}$ is given with the fast convergent processors, see also the ideas of [37,48]. Therefore, we circumvent the slow processors and, later, we redistribute the decomposition of the matrices to gain a more balanced load of the processors.

5. Numerical Examples

In what follows, we deal with different numerical examples, which are motivated by real-life applications in fluid-flow and phase-field problems. We verify and test our theoretical results of the novel parallel iterative splitting approaches.

We deal with:

• Only time-dependent linear problem: we apply ordinary differential equation to verify the theoretical results.
• Time and space dependent linear problem: we apply a diffusion equation with different spatial dependent operators and test the application to partial differential equations.
• Time and space dependent nonlinear problem: we apply a mixed diffusion-convection with Burgers’ equation to test and verify the application to nonlinear problems.
• Time and space dependent fractional problem: we apply a fractional diffusion equation with different spatial dependent operators and, furthermore, we test the application to fractional differential equations.

5.1. First Example: Matrix Problem

In the first test example, we consider the following matrix equation,

$$\begin{array}{ccc}\hfill u^{\prime }(t)& =& \left[\begin{array}{cc}1& 2\\ 0& 1\end{array}\right]u,\hspace{1em}u(0)=u_0=\left(\begin{array}{c}1\\ 1\end{array}\right),\hfill \end{array}$$

(106)

whose exact solution is

$$\begin{array}{c}\hfill exp(\left[\begin{array}{cc}1& 2\\ 0& 1\end{array}\right] t)=\left(\begin{array}{cc}exp(t)& 2t exp(t)\\ 0& exp(t)\end{array}\right).\end{array}$$

(107)

We split the matrix as:

• Two operator approach

  $$\begin{array}{ccc}\hfill A+B=\left[\begin{array}{cc}1& 2\\ 0& 1\end{array}\right]& =& \left[\begin{array}{cc}0.3& 1\\ 0& 0.3\end{array}\right]+\left[\begin{array}{cc}0.7& 1\\ 0& 0.7\end{array}\right]\hfill \end{array}$$

  (108)
• Multiple operator approach

  $$\begin{array}{ccc}\hfill A_1+B_1=\left[\begin{array}{cc}1& 2\\ 0& 1\end{array}\right]& =& \left[\begin{array}{cc}0.1& 1.0\\ 0& 0.1\end{array}\right]+\left[\begin{array}{cc}0.9& 1.0\\ 0& 0.9\end{array}\right]\hfill \end{array}$$

  (109)

  $$\begin{array}{ccc}\hfill A_2+B_2=\left[\begin{array}{cc}1& 2\\ 0& 1\end{array}\right]& =& \left[\begin{array}{cc}0.5& 0.1\\ 0& 0.5\end{array}\right]+\left[\begin{array}{cc}0.5& 1.9\\ 0& 0.5\end{array}\right]\hfill \end{array}$$

  (110)

  where the $E_1$ and $E_2$ are given as:

  $$\begin{array}{c}\hfill E_1=\left[\begin{array}{cc}0.9& 0\\ 0& 0.1\end{array}\right], E_2=\left[\begin{array}{cc}0.1& 0\\ 0& 0.9\end{array}\right].\end{array}$$

  (111)

We include Table 1 and Table 2 that correspond to multi-splitting iterative approach classical and modern version with the above partitions and using different discretizations in $[0,1]$ of step h allowing for a maximum of 10 iterations and a tolerance of ${10}^{-3}.$ We can see in the results the relative and absolute errors for each component of the solution and the average iterations performed in order to reach the tolerance.

Table 1. Multisplitting classic version.

h	max ${\mathit{e}}_1$	max ${\mathit{e}}_2$	rel ${\mathit{e}}_1$	rel ${\mathit{e}}_2$	it 1	it 2
0.1	0.008308	0.00040332	0.0010188	0.00014837	4	4
0.05	0.00043184	$2.906\times {10}^{-5}$	$5.2955\times {10}^{-5}$	$1.069\times {10}^{-5}$	3	3
0.025	0.00010623	$7.2291\times {10}^{-6}$	$1.3027\times {10}^{-5}$	$2.6595\times {10}^{-6}$	3	3
0.0125	$2.6335\times {10}^{-5}$	$1.8026\times {10}^{-6}$	$3.2294\times {10}^{-6}$	$6.6316\times {10}^{-7}$	3	3
0.00625	$6.5553\times {10}^{-6}$	$4.5007\times {10}^{-7}$	$8.0385\times {10}^{-7}$	$1.6557\times {10}^{-7}$	3	3

Table 2. Multisplitting Modern version.

h	max ${\mathit{e}}_1$	max ${\mathit{e}}_2$	rel ${\mathit{e}}_1$	rel ${\mathit{e}}_2$	it 1	it 2
0.1	0.0081586	0.0003996	0.0010005	0.000147	4	4
0.05	0.00030027	$3.1292\times {10}^{-5}$	0.00012447	$1.1512\times {10}^{-5}$	3.35	3
0.025	0.00027348	$1.3123\times {10}^{-5}$	$3.3536\times {10}^{-5}$	$4.8277\times {10}^{-6}$	3	3
0.0125	$6.8274\times {10}^{-5}$	$3.281\times {10}^{-6}$	$8.3723\times {10}^{-6}$	$1.207\times {10}^{-6}$	3	3
0.00625	$1.7056\times {10}^{-5}$	$8.2026\times {10}^{-7}$	$2.0915\times {10}^{-6}$	$3.0176\times {10}^{-7}$	3	3

Figure 1 shows the influence of the tolerance value in the error of the modern version of the algorithm. Each group of bars represents the error for the different step sizes indicated in the legend. It can be seen that the error decreases with the step h if the tolerance is small enough. This is the case, except for $tol={10}^{-2}$, where higher errors appear for smaller steps. Looking at the bars that correspond to the same step and different tolerances, it can be observed that the error for a given temporal step h reaches a minimum as the tolerance decreases and, beyond this point, the errors stabilize or even increase slightly for smaller tolerances.

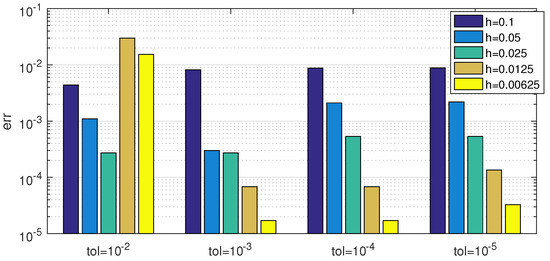
Figure 1. Matrix problem. Precision of the modern version of the multi-splitting iterative approach in terms of the time step h and the tolerance.

Remark 5.

We applied the multisplitting method with the classical (synchronous) and modern (chaotic) approach. We receive the same accuracy of the numerical results, which means that the methods are equally accurate. We obtain some more benefits of the modern method if we apply large time-steps, such that the solution of one sub-problem can be achieved faster and benefit the solution of the second sub-problem. For such small computational unbalances, the modern approach is more efficient.

5.2. Second Example: Diffusion Problem

We deal with the following diffusion problem:

$$u^{\prime }(\mathbf{x},t)=\Delta u(\mathbf{x},t), (\mathbf{x},t)\in \partial \Omega \times [0,T],$$

(112)

$$u(\mathbf{x},0)=sinx siny sinz, \mathbf{x}\in \Omega ,$$

(113)

$$u(\mathbf{x},t)=0, (\mathbf{x},t)\in \partial \Omega \times [0,T],$$

(114)

where we have the analytical solution $u_{an}(\mathbf{x},t)=exp(-3t) sinx siny sinz$, with $\mathbf{x}={(x,y,z)}^t$ and $\Omega =[-\pi ,\pi ]\times [-\pi ,\pi ]\times [-\pi ,\pi ]$.

In operator notation, we write:

$$\begin{array}{c}\hfill A=A_1+A_2+A_3,\end{array}$$

(115)

where $A_1=\frac{{\partial }^2}{\partial x^2}, A_2=\frac{{\partial }^2}{\partial y^2}, A_3=\frac{{\partial }^2}{\partial z^2}$ and we assume that the zero-boundary conditions (Dirichlet boundary conditions) are fulfilled.

The problem is discretized by using a four-dimensional (4-D) mesh in $\Omega \times [0,T]$. Denote by $u_{i,j,k,t}$ the approximated value of the solution at node $(x_i,y_j,z_k,t)$ for a given t. For the time-integration, we apply the integral formulation, see Equations (15)–(18).

For the spatial discretization, we test a second order scheme:

$$\begin{array}{c}\hfill \frac{{\partial }^2}{\partial x^2}{u}_{i,j,k,t}=\frac{u_{i+1,j,k,t}-2u_{i,j,k,t}+u_{i-1,j,k,t}}{\Delta x^2},\end{array}$$

(116)

and a fourth order scheme:

$$\begin{array}{c}\hfill \frac{{\partial }^2}{\partial x^2}{u}_{i,j,k,t}=\frac{-u_{i+2,j,k,t}+16u_{i+1,j,k,t}-30u_{i,j,k,t}+16u_{i-1,j,k,t}-u_{i-2,j,k,t}}{12\Delta x^2},\end{array}$$

(117)

where we have the analogous operators for the y and z derivatives.

We compute the solution $u(\Delta x,h)$ obtained using spatial and temporal steps $\Delta x=\Delta y=\Delta z$ and $h,$ respectively, in order to establish the convergence of the algorithms. We use different measures to estimate the convergence. On one hand, we can compare the outcome of the method $u(\Delta x,h)$ with the exact solution $u_{ana}$ for every point of the mesh, which shows the convergence of the method. On the other hand, we can compare $u(\Delta x,h)$ with the result that was obtained halving the time steps, $h/2$, at the points shared by the corresponding meshes. This allows for analyzing how the results depend on these steps.

Denote by $e_{i,j,k}(\Delta x,h)$ the difference between the results at a mesh point in the final time T, $(x_i,y_j,z_k,T)$, obtained using time steps h and $h/2$, and by ${\delta }_{i,j,k}(\Delta x,h)$ the difference with the analytical solution at the same point. In the tables, we will denote the maximum errors by

$$\begin{array}{c}\hfill e_{\max }=\underset{i,j,k}{\max } \left|e_{i,j,k}(\Delta x,h)\right|,\end{array}$$

(118)

and

$$\begin{array}{c}\hfill {\delta }_{\max }=\underset{i,j,k}{\max } \left|{\delta }_{i,j,k}(\Delta x,h)\right|,\end{array}$$

(119)

and the mean errors by

$$\begin{array}{c}\hfill e_{\mathrm{mean}}=\frac{1}{N}\sum _{i,j,k}\left|e_{i,j,k}(\Delta x,h)\right|,\end{array}$$

(120)

and

$$\begin{array}{c}\hfill {\delta }_{\mathrm{mean}}=\frac{1}{N}\sum _{i,j,k}\left|{\delta }_{i,j,k}(\Delta x,h)\right|,\end{array}$$

(121)

where N is the number of spatial nodes at time T.

In the following, we discuss different decompositions of the multi-operator splitting approach:

• Directional decomposition: We decompose into the different directions:

  $$\begin{array}{c}{A}_1=\frac{{\partial }^2}{\partial x^2}, A_2=\frac{{\partial }^2}{\partial y^2}, A_3=\frac{{\partial }^2}{\partial z^2}.\hfill \end{array}$$

  (122)

  Here, we have the benefit of decomposing the different directions.
  The drawback is related to the unbalanced decomposition, where the matrices have different sparse entries. Therefore, the exponential matrices of the operators are different in their sparse behaviour and the error can not be optimally reduced.
  We can reduce the unbalanced problem, if we deal with the idea to use $\Delta t\approx \Delta x$, see [38]. Subsequently, we obtain at least a second order scheme (related to the spatial discretization).
  We compare our sequential and parallel iterative splitting methods with standard ones such as the sequential operator splitting [49] and the Strang–Marchuk splitting [50]. We apply the splitting algorithms with directional decomposition in $[0,1]$. The splitting is iterated until a tolerance of ${10}^{-8}$ or a maximum of 10 iterations is reached. The values that are shown in the tables correspond to maximum or mean values at $T=1$. Table 3 and Table 4 present the results obtained using different number of temporal steps and the second and fourth order schemes for the spatial discretization, respectively.
  Table 3. Diffusion problem. Results of the directional decomposition using the second order scheme for the spatial discretization, with 10 spatial subintervals and different number of temporal steps.

  Splitting Algorithm	Time Steps	${\mathit{e}}_{\mathbf{max}}$	${\mathit{e}}_{\mathbf{mean}}$	${\mathit{\delta }}_{\mathbf{max}}$	${\mathit{\delta }}_{\mathbf{mean}}$	Average Iterations
  Sequential Operator	20	$6.3838\times {10}^{-16}$	$8.4685\times {10}^{-17}$	$3.2022\times {10}^{-2}$	$4.0127\times {10}^{-3}$	1.0000
  	40	$2.1580\times {10}^{-15}$	$2.1350\times {10}^{-16}$	$3.2022\times {10}^{-2}$	$4.0127\times {10}^{-3}$	1.0000
  	80	$1.6133\times {10}^{-15}$	$2.3525\times {10}^{-16}$	$3.2022\times {10}^{-2}$	$4.0127\times {10}^{-3}$	1.0000
  	160	$3.6013\times {10}^{-15}$	$3.2583\times {10}^{-16}$	$3.2022\times {10}^{-2}$	$4.0127\times {10}^{-3}$	1.0000
  Strang-Marchuk	20	$9.7838\times {10}^{-16}$	$6.7970\times {10}^{-17}$	$3.2022\times {10}^{-2}$	$4.0127\times {10}^{-3}$	1.6667
  	40	$2.4702\times {10}^{-15}$	$1.5928\times {10}^{-16}$	$3.2022\times {10}^{-2}$	$4.0127\times {10}^{-3}$	1.6667
  	80	$6.6128\times {10}^{-15}$	$5.9749\times {10}^{-16}$	$3.2022\times {10}^{-2}$	$4.0127\times {10}^{-3}$	1.6667
  	160	$1.4572\times {10}^{-14}$	$9.5031\times {10}^{-16}$	$3.2022\times {10}^{-2}$	$4.0127\times {10}^{-3}$	1.6667
  Serial Iterative	20	$4.7546\times {10}^{-3}$	$1.6356\times {10}^{-4}$	$2.0304\times {10}^{-2}$	$2.1113\times {10}^{-3}$	3.0000
  	40	$2.2831\times {10}^{-3}$	$7.5764\times {10}^{-5}$	$2.0135\times {10}^{-2}$	$2.0213\times {10}^{-3}$	3.0000
  	80	$1.1013\times {10}^{-3}$	$3.6053\times {10}^{-5}$	$2.0059\times {10}^{-2}$	$1.9958\times {10}^{-3}$	2.0688
  	160	$5.3905\times {10}^{-4}$	$1.7569\times {10}^{-5}$	$2.0024\times {10}^{-2}$	$1.9835\times {10}^{-3}$	2.0031
  Classical Parallel	20	$6.1563\times {10}^{-4}$	$7.1759\times {10}^{-5}$	$2.0942\times {10}^{-2}$	$2.2622\times {10}^{-3}$	7.0000
  	40	$3.1759\times {10}^{-4}$	$3.7914\times {10}^{-5}$	$2.1295\times {10}^{-2}$	$2.3328\times {10}^{-3}$	5.0750
  	80	$1.6070\times {10}^{-4}$	$1.9398\times {10}^{-5}$	$2.1479\times {10}^{-2}$	$2.3701\times {10}^{-3}$	4.8688
  	160	$8.0751\times {10}^{-5}$	$9.7999\times {10}^{-6}$	$2.1574\times {10}^{-2}$	$2.3891\times {10}^{-3}$	4.0031
  Modern Parallel	20	$5.4241\times {10}^{-4}$	$8.2138\times {10}^{-5}$	$2.0487\times {10}^{-2}$	$2.2348\times {10}^{-3}$	7.9750
  	40	$3.0696\times {10}^{-4}$	$4.5356\times {10}^{-5}$	$2.1029\times {10}^{-2}$	$2.3158\times {10}^{-3}$	6.0000
  	80	$1.6316\times {10}^{-4}$	$2.3798\times {10}^{-5}$	$2.1336\times {10}^{-2}$	$2.3605\times {10}^{-3}$	4.9938
  	160	$8.4106\times {10}^{-5}$	$1.2186\times {10}^{-5}$	$2.1499\times {10}^{-2}$	$2.3841\times {10}^{-3}$	4.0031

  Table 4. Diffusion problem. Results of the directional decomposition using the fourth order scheme for the spatial discretization, with 10 subintervals in each dimension and different number of temporal steps.

  Splitting Algorithm	Time Steps	${\mathit{e}}_{\mathbf{max}}$	${\mathit{e}}_{\mathbf{mean}}$	${\mathit{\delta }}_{\mathbf{max}}$	${\mathit{\delta }}_{\mathbf{mean}}$	Average Iterations
  Sequential Operator	20	$2.8449\times {10}^{-16}$	$2.3056\times {10}^{-17}$	$2.6024\times {10}^{-4}$	$4.7017\times {10}^{-5}$	1.0000
  	40	$2.9143\times {10}^{-16}$	$2.6939\times {10}^{-17}$	$2.6024\times {10}^{-4}$	$4.7017\times {10}^{-5}$	1.0000
  	80	$1.2490\times {10}^{-16}$	$1.5822\times {10}^{-17}$	$2.6024\times {10}^{-4}$	$4.7017\times {10}^{-5}$	1.0000
  	160	$7.9103\times {10}^{-16}$	$1.2310\times {10}^{-16}$	$2.6024\times {10}^{-4}$	$4.7017\times {10}^{-5}$	1.0000
  Strang-Marchuk	20	$1.6653\times {10}^{-16}$	$1.4661\times {10}^{-17}$	$2.6024\times {10}^{-4}$	$4.7017\times {10}^{-5}$	1.6667
  	40	$3.2613\times {10}^{-16}$	$3.9698\times {10}^{-17}$	$2.6024\times {10}^{-4}$	$4.7017\times {10}^{-5}$	1.6667
  	80	$3.1919\times {10}^{-16}$	$2.0470\times {10}^{-17}$	$2.6024\times {10}^{-4}$	$4.7017\times {10}^{-5}$	1.6667
  	160	$1.5127\times {10}^{-15}$	$2.1817\times {10}^{-16}$	$2.6024\times {10}^{-4}$	$4.7017\times {10}^{-5}$	1.6667
  Serial Iterative	20	$5.3739\times {10}^{-5}$	$1.0912\times {10}^{-5}$	$3.1645\times {10}^{-4}$	$6.1276\times {10}^{-5}$	3.0000
  	40	$1.3425\times {10}^{-5}$	$2.7263\times {10}^{-6}$	$2.7126\times {10}^{-4}$	$5.0429\times {10}^{-5}$	3.0000
  	80	$3.3557\times {10}^{-6}$	$6.8147\times {10}^{-7}$	$2.6299\times {10}^{-4}$	$4.7851\times {10}^{-5}$	2.0063
  	160	$8.3886\times {10}^{-7}$	$1.7036\times {10}^{-7}$	$2.6093\times {10}^{-4}$	$4.7225\times {10}^{-5}$	2.0031
  Classical Parallel	20	$5.3681\times {10}^{-5}$	$1.0912\times {10}^{-5}$	$3.1644\times {10}^{-4}$	$6.1276\times {10}^{-5}$	6.0250
  	40	$1.3412\times {10}^{-5}$	$2.7263\times {10}^{-6}$	$2.7125\times {10}^{-4}$	$5.0429\times {10}^{-5}$	5.0125
  	80	$3.3528\times {10}^{-6}$	$6.8152\times {10}^{-7}$	$2.6299\times {10}^{-4}$	$4.7851\times {10}^{-5}$	4.0062
  	160	$8.3793\times {10}^{-7}$	$1.7032\times {10}^{-7}$	$2.6093\times {10}^{-4}$	$4.7225\times {10}^{-5}$	4.0031
  Modern Parallel	20	$5.3684\times {10}^{-5}$	$1.0912\times {10}^{-5}$	$3.1644\times {10}^{-4}$	$6.1276\times {10}^{-5}$	6.0250
  	40	$1.3412\times {10}^{-5}$	$2.7263\times {10}^{-6}$	$2.7125\times {10}^{-4}$	$5.0429\times {10}^{-5}$	5.0125
  	80	$3.3528\times {10}^{-6}$	$6.8152\times {10}^{-7}$	$2.6299\times {10}^{-4}$	$4.7851\times {10}^{-5}$	4.0062
  	160	$8.3794\times {10}^{-7}$	$1.7032\times {10}^{-7}$	$2.6093\times {10}^{-4}$	$4.7225\times {10}^{-5}$	4.0031

  The standard methods, sequential operator, and Strang–Marchuk splitting give almost the same results independently of the number of time steps, because of the linearity of the equation. The e error estimates are negligible, whereas the $\delta$ error estimates are independent of the time step, reflecting the spatial discretization error.
  Table 3 and Table 4 show that the estimated errors $e_{\max }$ and $e_{\mathrm{mean}}$ of the iterative splitting methods are proportional to h for the second order scheme of discretization of the directional derivatives, whereas they are proportional to $h^2$ for the fourth order scheme. The mean differences with the analytical solution, ${\delta }_{\mathrm{mean}}$, of the iterative splitting methods tend to those of the non iterative ones as h decreases. The $\delta$ error estimates are more than one order of magnitude better for the fourth order scheme than for the second order scheme. Figure 2 and Figure 3 depict these results.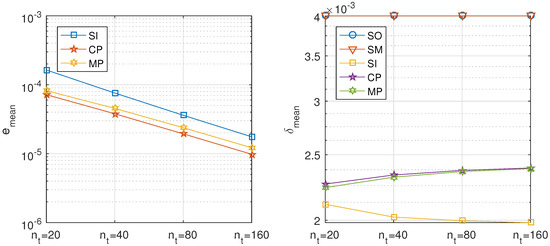
  

  Figure 2. Diffusion problem, directional decomposition. Precision of the proposed methods: sequential iterative SI, classical parallel CP, and modern parallel MP, as compared with the classical ones: sequential operator SO and Strang–Marchuk SM, with second order approximations for the spatial derivatives for different number of time steps.
  

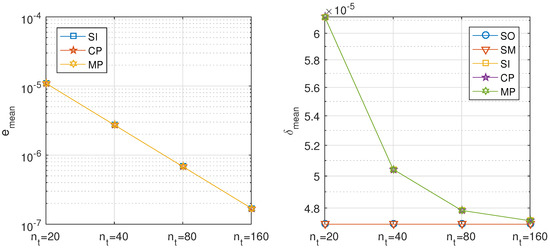  Figure 3. Diffusion problem, directional decomposition. Precision of the proposed methods: sequential iterative SI, classical parallel CP, and modern parallel MP, compared with the classical ones: sequential operator SO and Strang–Marchuk SM, with fourth order approximations for the spatial derivatives for different number of time steps.
  Now, we analyze the influence of the number of spatial intervals on the convergence properties of the iterative splitting algorithms. The spatial step is reduced simultaneously in the three dimensions, in order to keep the increments equal, because the performance of the method is better in this case. The time step is small enough to ensure the convergence in the case of the smaller spatial subinterval and is the same in all of the cases to allow the comparison depending only on the spatial step.
  For the second order scheme (see Table 5), the e error estimates are proportional to the number of spatial subintervals in each dimension, whereas the $\delta$ error estimates decrease, indicating a better approximation to the analytical solution as the spatial step decreases.The parallel methods obtain slightly less approximation to the analytical result and they require more iterations than the serial iterative method. The modern parallel method needs more iterations per step to converge than the classical parallel method.
  Table 5. Diffusion problem. Results of the directional decomposition using the second order scheme for the spatial discretization, with 320 temporal steps and different number of spatial subintervals.

  Splitting Algorithm	Space Intervals	${\mathit{e}}_{\mathbf{max}}$	${\mathit{e}}_{\mathbf{mean}}$	${\mathit{\delta }}_{\mathbf{max}}$	${\mathit{\delta }}_{\mathbf{mean}}$	Average Iterations
  Sequential Operator	10	$1.8437\times {10}^{-14}$	$2.3626\times {10}^{-15}$	$3.2022\times {10}^{-2}$	$4.0127\times {10}^{-3}$	1.0000
  	20	$2.2100\times {10}^{-14}$	$4.3596\times {10}^{-15}$	$1.8587\times {10}^{-2}$	$2.7497\times {10}^{-3}$	1.0000
  	40	$3.7588\times {10}^{-14}$	$6.9991\times {10}^{-15}$	$9.7462\times {10}^{-3}$	$1.5908\times {10}^{-3}$	1.0000
  Strang-Marchuk	10	$2.8838\times {10}^{-14}$	$2.2970\times {10}^{-15}$	$3.2022\times {10}^{-2}$	$4.0127\times {10}^{-3}$	1.6667
  	20	$3.7408\times {10}^{-14}$	$3.9795\times {10}^{-15}$	$1.8587\times {10}^{-2}$	$2.7497\times {10}^{-3}$	1.6667
  	40	$6.2721\times {10}^{-14}$	$8.1078\times {10}^{-15}$	$9.7462\times {10}^{-3}$	$1.5908\times {10}^{-3}$	1.6667
  Serial Iterative	10	$2.6647\times {10}^{-4}$	$8.6700\times {10}^{-6}$	$2.0006\times {10}^{-2}$	$1.9774\times {10}^{-3}$	2.0000
  	20	$4.4399\times {10}^{-4}$	$9.5320\times {10}^{-6}$	$1.1625\times {10}^{-2}$	$1.1212\times {10}^{-3}$	2.0000
  	40	$7.4728\times {10}^{-4}$	$9.9603\times {10}^{-6}$	$5.8701\times {10}^{-3}$	$6.0205\times {10}^{-4}$	2.0078
  Classical Parallel	10	$4.0467\times {10}^{-5}$	$4.9240\times {10}^{-6}$	$2.1621\times {10}^{-2}$	$2.3988\times {10}^{-3}$	4.0000
  	20	$8.2970\times {10}^{-5}$	$1.1843\times {10}^{-5}$	$1.2119\times {10}^{-2}$	$1.7252\times {10}^{-3}$	4.0016
  	40	$1.5751\times {10}^{-4}$	$2.4059\times {10}^{-5}$	$6.1534\times {10}^{-3}$	$9.8751\times {10}^{-4}$	4.4063
  Modern Parallel	10	$4.2699\times {10}^{-5}$	$6.1656\times {10}^{-6}$	$2.1583\times {10}^{-2}$	$2.3962\times {10}^{-3}$	4.0000
  	20	$9.7992\times {10}^{-5}$	$1.5103\times {10}^{-5}$	$1.2050\times {10}^{-2}$	$1.7183\times {10}^{-3}$	4.9828
  	40	$1.7725\times {10}^{-4}$	$2.9509\times {10}^{-5}$	$6.0466\times {10}^{-3}$	$9.7394\times {10}^{-4}$	6.9922

  For the fourth order scheme (see Table 6), the e error estimates are unaffected by the number of spatial subintervals, so that the convergence is maintained. The $\delta$ error estimates are proportional to a power of the spatial step of degree between 3 and 5, greatly improving the approximation of the second order scheme.
  Table 6. Diffusion problem, directional decomposition. Results using the fourth order scheme for the spatial discretization, with 320 temporal steps and different number of subintervals in each dimension.

  Splitting Algorithm	Space Intervals	${\mathit{e}}_{\mathbf{max}}$	${\mathit{e}}_{\mathbf{mean}}$	${\mathit{\delta }}_{\mathbf{max}}$	${\mathit{\delta }}_{\mathbf{mean}}$	Average Iterations
  Sequential Operator	10	$9.6451\times {10}^{-16}$	$1.5113\times {10}^{-16}$	$2.6024\times {10}^{-4}$	$4.7017\times {10}^{-5}$	1.0000
  	20	$1.0686\times {10}^{-15}$	$1.0900\times {10}^{-16}$	$1.2606\times {10}^{-5}$	$3.0953\times {10}^{-6}$	1.0000
  	40	$3.9899\times {10}^{-15}$	$8.3332\times {10}^{-16}$	$4.1987\times {10}^{-7}$	$1.1088\times {10}^{-7}$	1.0000
  Strang-Marchuk	10	$1.7972\times {10}^{-15}$	$2.6813\times {10}^{-16}$	$2.6024\times {10}^{-4}$	$4.7017\times {10}^{-5}$	1.6667
  	20	$1.5821\times {10}^{-15}$	$1.8215\times {10}^{-16}$	$1.2606\times {10}^{-5}$	$3.0953\times {10}^{-6}$	1.6667
  	40	$1.3531\times {10}^{-15}$	$2.0462\times {10}^{-16}$	$4.1987\times {10}^{-7}$	$1.1088\times {10}^{-7}$	1.6667
  Serial Iterative	10	$2.0971\times {10}^{-7}$	$4.2590\times {10}^{-8}$	$2.6041\times {10}^{-4}$	$4.7069\times {10}^{-5}$	2.0000
  	20	$2.4313\times {10}^{-7}$	$5.2851\times {10}^{-8}$	$1.2777\times {10}^{-5}$	$3.1437\times {10}^{-6}$	2.0000
  	40	$2.4310\times {10}^{-7}$	$5.7886\times {10}^{-8}$	$4.1609\times {10}^{-7}$	$1.1596\times {10}^{-7}$	2.0000
  Classical Parallel	10	$2.0952\times {10}^{-7}$	$4.2587\times {10}^{-8}$	$2.6041\times {10}^{-4}$	$4.7069\times {10}^{-5}$	4.0000
  	20	$2.4312\times {10}^{-7}$	$5.2848\times {10}^{-8}$	$1.2777\times {10}^{-5}$	$3.1437\times {10}^{-6}$	4.0000
  	40	$2.4309\times {10}^{-7}$	$5.7883\times {10}^{-8}$	$4.1609\times {10}^{-7}$	$1.1596\times {10}^{-7}$	4.0000
  Modern Parallel	10	$2.0952\times {10}^{-7}$	$4.2587\times {10}^{-8}$	$2.6041\times {10}^{-4}$	$4.7069\times {10}^{-5}$	4.0000
  	20	$2.4312\times {10}^{-7}$	$5.2848\times {10}^{-8}$	$1.2777\times {10}^{-5}$	$3.1437\times {10}^{-6}$	4.0000
  	40	$2.4309\times {10}^{-7}$	$5.7883\times {10}^{-8}$	$4.1609\times {10}^{-7}$	$1.1596\times {10}^{-7}$	4.0000

  Figure 4 and Figure 5 present the results that were obtained by the analyzed splitting methods with different number of spatial steps, using the second and the fourth order schemes for the spatial discretization, respectively.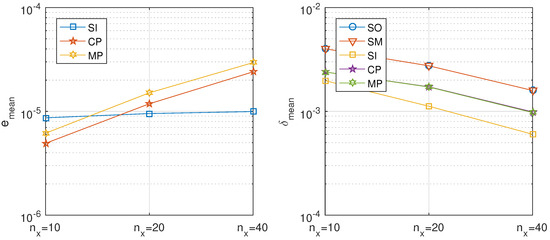
  

  Figure 4. Diffusion problem, directional decomposition. Precision of the proposed methods: sequential iterative SI, classical parallel CP, and modern parallel MP, compared with the classical ones: sequential operator SO and Strang–Marchuk SM, with second order approximations for the spatial derivatives with 320 time steps and different number of spatial steps.
  

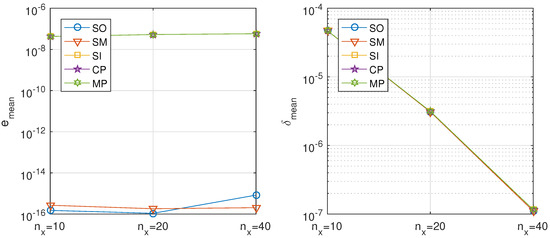  Figure 5. Diffusion problem, directional decomposition. Precision of the proposed methods: sequential iterative SI, classical parallel CP, and modern parallel MP, compared with the classical ones: sequential operator SO and Strang–Marchuk SM, with fourth order approximations for the spatial derivatives for different number of spatial steps.
• Balanced decomposition: We decompose into:

  $$\begin{array}{c}{A}_1=\frac{1}{3}A, A_2=\frac{1}{3}A, A_3=\frac{1}{3}A.\hfill \end{array}$$

  (123)

  Here, we have the benefit of equal load balances of the matrices, such that the exp-matrices have the same sparse structure. The results of the splitting algorithms with balanced decomposition are shown in Table 7 and Table 8 for the second and fourth order schemes for the spatial discretization, and in Figure 6 and Figure 7, respectively. The numerical behaviour is similar to that of the directional decomposition.
  Table 7. Diffusion problem. Results of the balanced decomposition using the second order scheme for the spatial discretization, with 10 spatial subintervals and different number of temporal steps.

  Splitting Algorithm	Time Steps	${\mathit{e}}_{\mathbf{max}}$	${\mathit{e}}_{\mathbf{mean}}$	${\mathit{\delta }}_{\mathbf{max}}$	${\mathit{\delta }}_{\mathbf{mean}}$	Average Iterations
  Sequential Operator	20	$4.2674\times {10}^{-15}$	$4.9711\times {10}^{-16}$	$4.3817\times {10}^{-3}$	$8.9251\times {10}^{-4}$	1.0000
  	40	$7.5459\times {10}^{-15}$	$9.4849\times {10}^{-16}$	$4.3817\times {10}^{-3}$	$8.9251\times {10}^{-4}$	1.0000
  	80	$7.9486\times {10}^{-15}$	$1.0959\times {10}^{-15}$	$4.3817\times {10}^{-3}$	$8.9251\times {10}^{-4}$	1.0000
  	160	$3.1839\times {10}^{-14}$	$4.4734\times {10}^{-15}$	$4.3817\times {10}^{-3}$	$8.9251\times {10}^{-4}$	1.0000
  Strang-Marchuk	20	$3.9690\times {10}^{-15}$	$3.6874\times {10}^{-16}$	$4.3817\times {10}^{-3}$	$8.9251\times {10}^{-4}$	1.6667
  	40	$7.9000\times {10}^{-15}$	$1.2019\times {10}^{-15}$	$4.3817\times {10}^{-3}$	$8.9251\times {10}^{-4}$	1.6667
  	80	$2.3551\times {10}^{-14}$	$3.5211\times {10}^{-15}$	$4.3817\times {10}^{-3}$	$8.9251\times {10}^{-4}$	1.6667
  	160	$8.0304\times {10}^{-14}$	$1.1365\times {10}^{-14}$	$4.3817\times {10}^{-3}$	$8.9251\times {10}^{-4}$	1.6667
  Serial Iterative	20	$5.3493\times {10}^{-5}$	$1.0896\times {10}^{-5}$	$4.3104\times {10}^{-3}$	$8.7798\times {10}^{-4}$	3.0000
  	40	$1.3365\times {10}^{-5}$	$2.7223\times {10}^{-6}$	$4.3639\times {10}^{-3}$	$8.8888\times {10}^{-4}$	3.0000
  	80	$3.3408\times {10}^{-6}$	$6.8047\times {10}^{-7}$	$4.3773\times {10}^{-3}$	$8.9160\times {10}^{-4}$	2.0063
  	160	$8.3516\times {10}^{-7}$	$1.7011\times {10}^{-7}$	$4.3806\times {10}^{-3}$	$8.9228\times {10}^{-4}$	2.0031
  Classical Parallel	20	$5.3493\times {10}^{-5}$	$1.0896\times {10}^{-5}$	$4.3104\times {10}^{-3}$	$8.7798\times {10}^{-4}$	6.0000
  	40	$1.3365\times {10}^{-5}$	$2.7223\times {10}^{-6}$	$4.3639\times {10}^{-3}$	$8.8888\times {10}^{-4}$	5.0125
  	80	$3.3410\times {10}^{-6}$	$6.8052\times {10}^{-7}$	$4.3773\times {10}^{-3}$	$8.9160\times {10}^{-4}$	4.0062
  	160	$8.3499\times {10}^{-7}$	$1.7008\times {10}^{-7}$	$4.3806\times {10}^{-3}$	$8.9228\times {10}^{-4}$	4.0031
  Modern Parallel	20	$5.3493\times {10}^{-5}$	$1.0896\times {10}^{-5}$	$4.3104\times {10}^{-3}$	$8.7798\times {10}^{-4}$	6.0000
  	40	$1.3365\times {10}^{-5}$	$2.7223\times {10}^{-6}$	$4.3639\times {10}^{-3}$	$8.8888\times {10}^{-4}$	5.0125
  	80	$3.3410\times {10}^{-6}$	$6.8052\times {10}^{-7}$	$4.3773\times {10}^{-3}$	$8.9160\times {10}^{-4}$	4.0062
  	160	$8.3499\times {10}^{-7}$	$1.7008\times {10}^{-7}$	$4.3806\times {10}^{-3}$	$8.9228\times {10}^{-4}$	4.0031

  Table 8. Diffusion problem. Results of the balanced decomposition using the fourth order scheme for the spatial discretization, with 10 spatial subintervals and different number of temporal steps.

  Splitting Algorithm	Time Steps	${\mathit{e}}_{\mathbf{max}}$	${\mathit{e}}_{\mathbf{mean}}$	${\mathit{\delta }}_{\mathbf{max}}$	${\mathit{\delta }}_{\mathbf{mean}}$	Average Iterations
  Sequential Operator	20	$1.1796\times {10}^{-15}$	$1.0685\times {10}^{-16}$	$2.6024\times {10}^{-4}$	$4.7017\times {10}^{-5}$	1.0000
  	40	$2.9143\times {10}^{-15}$	$3.5778\times {10}^{-16}$	$2.6024\times {10}^{-4}$	$4.7017\times {10}^{-5}$	1.0000
  	80	$4.3715\times {10}^{-15}$	$5.4513\times {10}^{-16}$	$2.6024\times {10}^{-4}$	$4.7017\times {10}^{-5}$	1.0000
  	160	$1.3073\times {10}^{-14}$	$1.7961\times {10}^{-15}$	$2.6024\times {10}^{-4}$	$4.7017\times {10}^{-5}$	1.0000
  Strang-Marchuk	20	$8.4655\times {10}^{-16}$	$6.8614\times {10}^{-17}$	$2.6024\times {10}^{-4}$	$4.7017\times {10}^{-5}$	1.6667
  	40	$1.9776\times {10}^{-15}$	$2.8005\times {10}^{-16}$	$2.6024\times {10}^{-4}$	$4.7017\times {10}^{-5}$	1.6667
  	80	$3.6429\times {10}^{-15}$	$2.9301\times {10}^{-16}$	$2.6024\times {10}^{-4}$	$4.7017\times {10}^{-5}$	1.6667
  	160	$4.2882\times {10}^{-15}$	$5.7185\times {10}^{-16}$	$2.6024\times {10}^{-4}$	$4.7017\times {10}^{-5}$	1.6667
  Serial Iterative	20	$5.3718\times {10}^{-5}$	$1.0912\times {10}^{-5}$	$3.1641\times {10}^{-4}$	$6.1276\times {10}^{-5}$	3.0000
  	40	$1.3421\times {10}^{-5}$	$2.7263\times {10}^{-6}$	$2.7124\times {10}^{-4}$	$5.0429\times {10}^{-5}$	3.0000
  	80	$3.3547\times {10}^{-6}$	$6.8147\times {10}^{-7}$	$2.6299\times {10}^{-4}$	$4.7851\times {10}^{-5}$	2.0063
  	160	$8.3865\times {10}^{-7}$	$1.7036\times {10}^{-7}$	$2.6093\times {10}^{-4}$	$4.7225\times {10}^{-5}$	2.0031
  Classical Parallel	20	$5.3718\times {10}^{-5}$	$1.0912\times {10}^{-5}$	$3.1641\times {10}^{-4}$	$6.1276\times {10}^{-5}$	6.0250
  	40	$1.3421\times {10}^{-5}$	$2.7263\times {10}^{-6}$	$2.7124\times {10}^{-4}$	$5.0429\times {10}^{-5}$	5.0125
  	80	$3.3550\times {10}^{-6}$	$6.8152\times {10}^{-7}$	$2.6299\times {10}^{-4}$	$4.7851\times {10}^{-5}$	4.0062
  	160	$8.3847\times {10}^{-7}$	$1.7032\times {10}^{-7}$	$2.6093\times {10}^{-4}$	$4.7225\times {10}^{-5}$	4.0031
  Modern Parallel	20	$5.3718\times {10}^{-5}$	$1.0912\times {10}^{-5}$	$3.1641\times {10}^{-4}$	$6.1276\times {10}^{-5}$	6.0250
  	40	$1.3421\times {10}^{-5}$	$2.7263\times {10}^{-6}$	$2.7124\times {10}^{-4}$	$5.0429\times {10}^{-5}$	5.0125
  	80	$3.3550\times {10}^{-6}$	$6.8152\times {10}^{-7}$	$2.6299\times {10}^{-4}$	$4.7851\times {10}^{-5}$	4.0062
  	160	$8.3847\times {10}^{-7}$	$1.7032\times {10}^{-7}$	$2.6093\times {10}^{-4}$	$4.7225\times {10}^{-5}$	4.0031

  

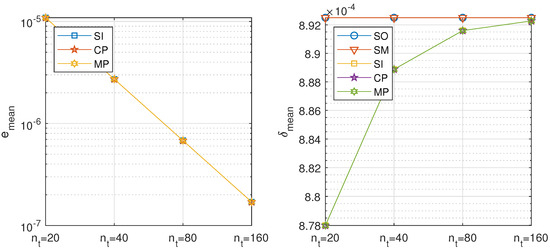  Figure 6. Diffusion problem, balanced decomposition. Precision of the proposed methods: sequential iterative SI, classical parallel CP, and modern parallel MP, compared with the classical ones: sequential operator SO and Strang–Marchuk SM, with second order approximations for the spatial derivatives for different number of time steps.
  

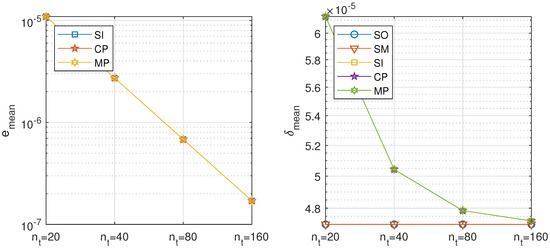  Figure 7. Diffusion problem, balanced decomposition. Precision of the proposed methods: sequential iterative SI, classical parallel CP, and modern parallel MP, compared with the classical ones: sequential operator SO and Strang–Marchuk SM, with fourth order approximations for the spatial derivatives for different number of time steps.
• Mixed decomposition: We decompose into:

  $$A_1=(1-ϵ)\frac{{\partial }^2}{\partial x^2}+\frac{ϵ}{2}(\frac{{\partial }^2}{\partial y^2}+\frac{{\partial }^2}{\partial z^2}), A_2=(1-ϵ)\frac{{\partial }^2}{\partial y^2}+\frac{ϵ}{2}(\frac{{\partial }^2}{\partial x^2}+\frac{{\partial }^2}{\partial z^2}),$$

  (124)

  $$A_3=(1-ϵ)\frac{{\partial }^2}{\partial z^2}+\frac{ϵ}{2}(\frac{{\partial }^2}{\partial x^2}+\frac{{\partial }^2}{\partial y^2}),$$

  (125)

  where $ϵ=[0,2/3]$. For $ϵ=0$, we have the directional decomposition, while, for $ϵ=2/3$, we have the balanced decomposition.

Remark 6.

Based on the balanced decomposition with $ϵ=2/3$, we do not have problems with the splitting approaches and obtain optimal results. For the pure unbalanced decomposition, which means $ϵ=0$, we decompose into different directions. Here, we have to restrict us to the exact second order approach, which is $\Delta t\approx \Delta x$.

Remark 7.

We obtain the benefit of the classical and modern parallel iterative splitting method that is based on larger time-steps and more iterative steps. In such an optimal version, we are much faster than the serial version and also the result is more accurate. For very fine time-steps, we do not see an improvement in the accuracy, but we see a benefit in the computational time; the parallel versions are faster.

5.3. Third Example: Mixed Convection-Diffusion and Burgers’ Equation

We consider a partial differential equation, which is a two-dimesnional (2D) example of a mixed convection-diffusion and Burgers’ equation. Such mixed PDEs are used to model fluid flow problems in traffic or population dynamics, see [15,16,51]. For testing the numerical methods, we consider a Burgers’ equation, where we can find an analytical solution. The model problem is:

$$\begin{array}{cc}\hfill {\partial }_{t}u=& -1/2u{\partial }_{x}u-1/2u{\partial }_{y}u-1/2{\partial }_{x}u-1/2{\partial }_{y}u\hfill \\ & +\mu ({\partial }_{xx}u+{\partial }_{yy}u)+f(x,y,t), (x,y,t)\in \Omega \times [0,T],\hfill \end{array}$$

(126)

$$\begin{array}{cc}\hfill u(x,y,0)=& u_{\mathrm{ana}}(x,y,0), (x,y)\in \Omega ,\hfill \end{array}$$

(127)

$$\begin{array}{cc}\hfill u(x,y,t)=& u_{\mathrm{ana}}(x,y,t) on \partial \Omega \times [0,T],\hfill \end{array}$$

(128)

where $\Omega =[0,1]\times [0,1]$, $T=1.25$, and $\mu$ is the viscosity.

The analytical solution is given by

$$\begin{array}{c}{u}_{\mathrm{ana}}(x,y,t)={(1+exp(\frac{x+y-t}{2\mu }))}^{-1}+exp(\frac{x+y-t}{2\mu }),\hfill \end{array}$$

(129)

where we compute $f(x,y,t)$ accordingly.

As in the previous example, denote, by $u(\Delta ,h)$, the numerical solution obtained using spatial subintervals of amplitude $\Delta =\Delta x=\Delta y$, time steps h and a tolerance of $tol={10}^{-6}$, allowing a maximum of 40 iterations. On one hand, we will compare the numerical solution with the exact one $u_{ana}$ for every point of the mesh, which shows the convergence of the method. On the other hand, we will compare $u(\Delta ,h)$ with the result obtained halving the time steps, $h/2$, at the points that are shared by the corresponding meshes. Denote by $e_{i,j,k}(\Delta ,h)$ the difference between the results obtained using two different time steps, h and $h/2$, at a common mesh point $(x_i,y_j,t_k)$, and by ${\delta }_{i,j,k}(\Delta ,h)$ the difference with the analytical solution at the same point. In the tables, we will use the error estimates given by

$$\begin{array}{c}\hfill e_{\max }=\underset{i,j,k}{\max } \left|e_{i,j,k}(\Delta ,h)\right|,\end{array}$$

(130)

and

$$\begin{array}{c}\hfill {\delta }_{\max }=\underset{i,j,k}{\max } \left|{\delta }_{i,j,k}(\Delta ,h)\right|,\end{array}$$

(131)

and the mean errors by

$$\begin{array}{c}\hfill e_{\mathrm{mean}}=\frac{1}{N}\sum _{i,j,k}\left|e_{i,j,k}(\Delta ,h)\right|,\end{array}$$

(132)

and

$$\begin{array}{c}\hfill {\delta }_{\mathrm{mean}}=\frac{1}{N}\sum _{i,j,k}\left|{\delta }_{i,j,k}(\Delta ,h)\right|,\end{array}$$

(133)

where N is the total number of nodes $(x_i,y_j,t_k)$.

We measure the time consumed by processor l in each iteration m, in $[t_k,t_{k+1}]$, $t{p}_{k,l,m}$ in order to obtain the temporal cost of the parallel schemes. In the classical parallel scheme, the processors synchronize at each iteration, so the cost for this time interval is $t{p}_k={\sum }_m\underset{l=1,2}{\max } t{p}_{k,l,m}$, whereas, in the modern parallel scheme, the processors iterate independently in $[t_k,t_{k+1}]$ performing $m_l, l=1,2$ iterations until convergence, thus the cost is $t{p}_k=\underset{l=1,2}{\max }{\sum }_m t{p}_{k,l,m}$. The final cost is obtained adding the results of all time subintervals.

In the following, we discuss different decompositions of the multi-operator splitting approach:

• Directional decomposition

We decompose into the different directions (x and y direction):

$$A(u)u=-1/2u{\partial }_{x}u-1/2{\partial }_{x}u+\mu {\partial }_{xx}u,$$

(134)

$$B(u)u=-1/2u{\partial }_{y}u-1/2{\partial }_{y}u+\mu {\partial }_{yy}u+f(x,y,t).$$

(135)

Let us first analyze the influence of parameter $\mu$ on the convergence of the algorithms.

Table 9 and Table 10 show the error estimations of the considered algorithms for different values of $\mu$ using the second and the fourth order discretization scheme, respectively, taking 10 subintervals in each spatial dimension and 640 time steps. The results for the different algorithms are similar. As it could be expected, higher viscosity values give lower error estimates.

Table 9. Mixed convection-diffusion and Burgers’ equation. Results of the directional decomposition using the second order scheme for the spatial discretization, with 10 spatial subintervals, 640 temporal intervals and different values of $\mu$.

Splitting Algorithm	$\mathit{\mu }$	${\mathit{e}}_{\mathbf{max}}$	${\mathit{e}}_{\mathbf{mean}}$	${\mathit{\delta }}_{\mathbf{max}}$	${\mathit{\delta }}_{\mathbf{mean}}$	Average Iterations	Time
Sequential Operator	0.25	$5.8112\times {10}^{-1}$	$8.0638\times {10}^{-3}$	$9.3476\times {10}^{-1}$	$1.1794\times {10}^{-2}$	1.0000	10.9421
	0.5	$4.5508\times {10}^{-3}$	$2.1796\times {10}^{-4}$	$7.9207\times {10}^{-3}$	$5.7747\times {10}^{-4}$	1.0000	11.8920
	1	$2.8491\times {10}^{-4}$	$1.0611\times {10}^{-4}$	$6.0982\times {10}^{-4}$	$2.3120\times {10}^{-4}$	1.0000	11.2869
	2	$1.3365\times {10}^{-4}$	$5.5167\times {10}^{-5}$	$2.7611\times {10}^{-4}$	$1.1307\times {10}^{-4}$	1.0000	11.8224
Strang-Marchuk	0.25	$1.1244\times {10}^{-1}$	$8.2317\times {10}^{-4}$	$6.5305\times {10}^{-2}$	$7.8549\times {10}^{-3}$	1.5000	16.2900
	0.5	$1.8260\times {10}^{-3}$	$3.3699\times {10}^{-4}$	$4.8191\times {10}^{-3}$	$1.0202\times {10}^{-3}$	1.5000	16.4826
	1	$4.5546\times {10}^{-4}$	$1.4794\times {10}^{-4}$	$9.5796\times {10}^{-4}$	$3.1493\times {10}^{-4}$	1.5000	17.5409
	2	$1.4546\times {10}^{-4}$	$6.5449\times {10}^{-5}$	$2.9273\times {10}^{-4}$	$1.3371\times {10}^{-4}$	1.5000	16.8117
Serial Iterative	0.25	$1.3150\times {10}^{-2}$	$1.2382\times {10}^{-3}$	$2.2903\times {10}^{-1}$	$1.0361\times {10}^{-2}$	2.1500	22.3302
	0.5	$2.0471\times {10}^{-3}$	$3.7850\times {10}^{-4}$	$5.3038\times {10}^{-3}$	$1.1031\times {10}^{-3}$	2.0031	21.5187
	1	$4.6720\times {10}^{-4}$	$1.5130\times {10}^{-4}$	$9.7092\times {10}^{-4}$	$3.2097\times {10}^{-4}$	2.5313	27.0622
	2	$1.5460\times {10}^{-4}$	$6.6664\times {10}^{-5}$	$3.0698\times {10}^{-4}$	$1.3545\times {10}^{-4}$	3.0141	34.6163
Classical Parallel	0.25	$1.2263\times {10}^{-2}$	$1.2385\times {10}^{-3}$	$2.2913\times {10}^{-1}$	$1.0361\times {10}^{-2}$	3.2531	17.8904
	0.5	$2.0418\times {10}^{-3}$	$3.7840\times {10}^{-4}$	$5.2987\times {10}^{-3}$	$1.1030\times {10}^{-3}$	3.9859	22.5435
	1	$4.5870\times {10}^{-4}$	$1.5117\times {10}^{-4}$	$9.6710\times {10}^{-4}$	$3.2087\times {10}^{-4}$	4.0078	24.1887
	2	$1.4252\times {10}^{-4}$	$6.6562\times {10}^{-5}$	$2.9093\times {10}^{-4}$	$1.3539\times {10}^{-4}$	5.0328	32.4515
Modern Parallel	0.25	$1.2348\times {10}^{-2}$	$1.2388\times {10}^{-3}$	$2.2923\times {10}^{-1}$	$1.0361\times {10}^{-2}$	3.7172	25.2081
	0.5	$2.0354\times {10}^{-3}$	$3.7825\times {10}^{-4}$	$5.2929\times {10}^{-3}$	$1.1029\times {10}^{-3}$	4.0062	24.5462
	1	$4.5939\times {10}^{-4}$	$1.5113\times {10}^{-4}$	$9.6862\times {10}^{-4}$	$3.2087\times {10}^{-4}$	5.0109	30.8930
	2	$1.4410\times {10}^{-4}$	$6.6516\times {10}^{-5}$	$2.9168\times {10}^{-4}$	$1.3524\times {10}^{-4}$	10.0828	63.1537

Table 10. Mixed convection-diffusion and Burgers’ equation. Results of the directional decomposition using the fourth order scheme for the spatial discretization, with 10 spatial subintervals, 640 temporal intervals and different values of $\mu$.

Splitting Algorithm	$\mathit{\mu }$	${\mathit{e}}_{\mathbf{max}}$	${\mathit{e}}_{\mathbf{mean}}$	${\mathit{\delta }}_{\mathbf{max}}$	${\mathit{\delta }}_{\mathbf{mean}}$	Average Iterations	Time(s)
Sequential Operator	0.25	$5.8896\times {10}^{-1}$	$7.9743\times {10}^{-3}$	1.1575	$1.5807\times {10}^{-2}$	1.0000	9.7930
	0.5	$4.5804\times {10}^{-3}$	$2.1804\times {10}^{-4}$	$8.9458\times {10}^{-3}$	$4.3546\times {10}^{-4}$	1.0000	9.7708
	1	$2.8621\times {10}^{-4}$	$1.0646\times {10}^{-4}$	$5.8378\times {10}^{-4}$	$2.1488\times {10}^{-4}$	1.0000	10.0130
	2	$1.3465\times {10}^{-4}$	$5.5478\times {10}^{-5}$	$2.7645\times {10}^{-4}$	$1.1254\times {10}^{-4}$	1.0000	10.7038
Strang-Marchuk	0.25	$1.7993\times {10}^{-2}$	$6.0015\times {10}^{-4}$	$5.4593\times {10}^{-2}$	$1.2833\times {10}^{-3}$	1.5000	14.9624
	0.5	$1.8507\times {10}^{-3}$	$3.3834\times {10}^{-4}$	$3.7379\times {10}^{-3}$	$6.7850\times {10}^{-4}$	1.5000	14.9328
	1	$4.5736\times {10}^{-4}$	$1.4837\times {10}^{-4}$	$9.4192\times {10}^{-4}$	$2.9859\times {10}^{-4}$	1.5000	15.6433
	2	$1.4761\times {10}^{-4}$	$6.5866\times {10}^{-5}$	$2.9398\times {10}^{-4}$	$1.3333\times {10}^{-4}$	1.5000	15.4479
Serial Iterative	0.25	$1.5854\times {10}^{-2}$	$1.2976\times {10}^{-3}$	$3.1234\times {10}^{-2}$	$2.5814\times {10}^{-3}$	2.1922	18.4870
	0.5	$2.0512\times {10}^{-3}$	$3.7922\times {10}^{-4}$	$4.1861\times {10}^{-3}$	$7.6029\times {10}^{-4}$	2.0031	17.0251
	1	$4.6948\times {10}^{-4}$	$1.5139\times {10}^{-4}$	$9.5395\times {10}^{-4}$	$3.0419\times {10}^{-4}$	2.1734	18.9489
	2	$3.5872\times {10}^{-4}$	$6.7393\times {10}^{-5}$	$3.5875\times {10}^{-4}$	$1.3508\times {10}^{-4}$	3.0781	28.1390
Classical Parallel	0.25	$1.6499\times {10}^{-2}$	$1.2986\times {10}^{-3}$	$3.1931\times {10}^{-2}$	$2.5824\times {10}^{-3}$	3.2641	15.7949
	0.5	$2.0442\times {10}^{-3}$	$3.7916\times {10}^{-4}$	$4.1796\times {10}^{-3}$	$7.6023\times {10}^{-4}$	4.0000	18.9540
	1	$4.6044\times {10}^{-4}$	$1.5136\times {10}^{-4}$	$9.5063\times {10}^{-4}$	$3.0417\times {10}^{-4}$	4.0094	20.2018
	2	$4.9841\times {10}^{-4}$	$6.7084\times {10}^{-5}$	$4.9845\times {10}^{-4}$	$1.3493\times {10}^{-4}$	5.8922	30.5905
Modern Parallel	0.25	$1.7037\times {10}^{-2}$	$1.2990\times {10}^{-3}$	$3.2501\times {10}^{-2}$	$2.5830\times {10}^{-3}$	4.0906	20.3866
	0.5	$2.0357\times {10}^{-3}$	$3.7908\times {10}^{-4}$	$4.1717\times {10}^{-3}$	$7.6017\times {10}^{-4}$	4.0062	20.6630
	1	$4.6092\times {10}^{-4}$	$1.5129\times {10}^{-4}$	$9.5182\times {10}^{-4}$	$3.0411\times {10}^{-4}$	5.0813	26.9929
	2	$2.4848\times {10}^{-2}$	$8.3803\times {10}^{-5}$	$2.4848\times {10}^{-2}$	$1.5144\times {10}^{-4}$	40.0000	221.3149

Figure 8 shows the dependence on $\mu$ of the values of $e_{\mathrm{mean}}$ for the different algorithms, using second and fourth order approximations for the spatial derivatives. In contrast with the former example, the use of higher order approximations for the spatial derivatives produces only a slight improvement in the error estimations, in both cases being of the same order with respect to the time step.

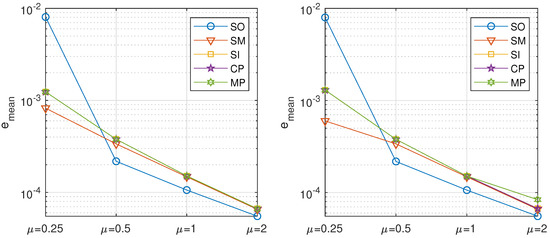
Figure 8. Mixed convection-diffusion and Burgers’ equation, directional decomposition. Precision of the proposed methods: sequential iterative SI, classical parallel CP, and modern parallel MP, compared with the classical ones: sequential operator SO and Strang–Marchuk SM, for different viscosities $\mu$. Left: order 2 approximation and right: order 4 approximation for the discretization of the spatial derivatives.

As we can observe, the mean error is approximately proportional to the inverse of the viscosity, $\mu$, and it is not much affected by the order of approximation of the spatial derivatives. The number of iterations and the execution time are not affected by the viscosity changes, except for the case of $\mu =2$ in the modern parallel algorithm, where the maximum number of iterations is reached in each step, also consuming more execution time. In what follows, we will take the viscosity parameter $\mu =0.5$ and use second order approximations for the spatial derivatives.

We will now analyze the influence of the number of time steps on the convergence of the algorithms.

Table 11 shows that the estimated error is roughly proportional to the time step, although, in the end, the differences $\delta$ with the analytical solution decrease more slowly, due to the discretization error. All of the considered methods have errors of the same order. The sequential operator splitting method presents higher estimates than the iterative schemes for the maximum error, but lower estimates of the mean error, as seen in Figure 9.

Table 11. Mixed convection-diffusion and Burgers’ equation. Results of the directional decomposition with 10 spatial subintervals and different number of temporal steps.

Splitting Algorithm	Time Steps	${\mathit{e}}_{\mathbf{max}}$	${\mathit{e}}_{\mathbf{mean}}$	${\mathit{\delta }}_{\mathbf{max}}$	${\mathit{\delta }}_{\mathbf{mean}}$	Average Iterations	Time
Sequential Operator	160	$2.1627\times {10}^{-2}$	$8.8698\times {10}^{-4}$	$3.9223\times {10}^{-2}$	$1.8270\times {10}^{-3}$	1.0000	1.8802
	320	$9.6835\times {10}^{-3}$	$4.3790\times {10}^{-4}$	$1.7596\times {10}^{-2}$	$9.7195\times {10}^{-4}$	1.0000	3.7410
	640	$4.5508\times {10}^{-3}$	$2.1796\times {10}^{-4}$	$7.9207\times {10}^{-3}$	$5.7747\times {10}^{-4}$	1.0000	7.5102
	1280	$2.2024\times {10}^{-3}$	$1.0880\times {10}^{-4}$	$3.3878\times {10}^{-3}$	$4.1692\times {10}^{-4}$	1.0000	14.3002
Strang-Marchuk	160	$6.7325\times {10}^{-3}$	$1.2989\times {10}^{-3}$	$1.5103\times {10}^{-2}$	$2.9795\times {10}^{-3}$	1.5000	2.7755
	320	$3.5515\times {10}^{-3}$	$6.6569\times {10}^{-4}$	$8.3706\times {10}^{-3}$	$1.6847\times {10}^{-3}$	1.5000	5.5802
	640	$1.8260\times {10}^{-3}$	$3.3699\times {10}^{-4}$	$4.8191\times {10}^{-3}$	$1.0202\times {10}^{-3}$	1.5000	11.0716
	1280	$9.2592\times {10}^{-4}$	$1.6954\times {10}^{-4}$	$2.9931\times {10}^{-3}$	$6.8365\times {10}^{-4}$	1.5000	22.0197
Serial Iterative	160	$8.0785\times {10}^{-3}$	$1.4732\times {10}^{-3}$	$1.6809\times {10}^{-2}$	$3.3199\times {10}^{-3}$	5.0375	9.8504
	320	$3.8934\times {10}^{-3}$	$7.4966\times {10}^{-4}$	$9.1969\times {10}^{-3}$	$1.8514\times {10}^{-3}$	3.0062	11.2158
	640	$2.0471\times {10}^{-3}$	$3.7850\times {10}^{-4}$	$5.3038\times {10}^{-3}$	$1.1031\times {10}^{-3}$	2.0031	14.7620
	1280	$1.0522\times {10}^{-3}$	$1.9023\times {10}^{-4}$	$3.2567\times {10}^{-3}$	$7.2500\times {10}^{-4}$	2.0008	28.9387
Classical Parallel	160	$6.9233\times {10}^{-3}$	$1.4687\times {10}^{-3}$	$1.6080\times {10}^{-2}$	$3.3149\times {10}^{-3}$	10.0938	10.1398
	320	$3.8634\times {10}^{-3}$	$7.4911\times {10}^{-4}$	$9.1617\times {10}^{-3}$	$1.8507\times {10}^{-3}$	5.0125	9.7186
	640	$2.0418\times {10}^{-3}$	$3.7840\times {10}^{-4}$	$5.2987\times {10}^{-3}$	$1.1030\times {10}^{-3}$	3.9859	15.7576
	1280	$1.0525\times {10}^{-3}$	$1.9024\times {10}^{-4}$	$3.2570\times {10}^{-3}$	$7.2501\times {10}^{-4}$	3.0016	22.4570
Modern Parallel	160	$6.7471\times {10}^{-3}$	$1.4653\times {10}^{-3}$	$1.5863\times {10}^{-2}$	$3.3107\times {10}^{-3}$	20.0562	21.0610
	320	$3.8313\times {10}^{-3}$	$7.4855\times {10}^{-4}$	$9.1238\times {10}^{-3}$	$1.8501\times {10}^{-3}$	6.0188	12.0327
	640	$2.0354\times {10}^{-3}$	$3.7825\times {10}^{-4}$	$5.2929\times {10}^{-3}$	$1.1029\times {10}^{-3}$	4.0062	16.4724
	1280	$1.0530\times {10}^{-3}$	$1.9026\times {10}^{-4}$	$3.2575\times {10}^{-3}$	$7.2504\times {10}^{-4}$	3.0023	23.0908

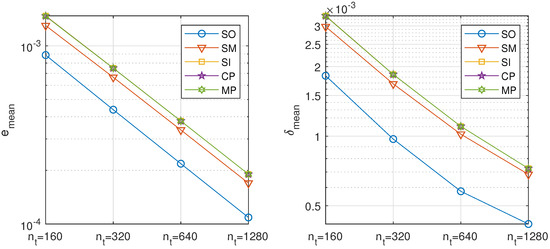
Figure 9. Mixed convection-diffusion and Burgers’ equation, directional decomposition. Precision of the proposed methods: sequential iterative SI, classical parallel CP, and modern parallel MP, compared with the classical ones: sequential operator SO and Strang–Marchuk SM, for different number of time steps.

Now, we analyze the dependence on the number of spatial subintervals. Table 12 displays the errors obtained varying the number of space subintervals, considering 1280 time steps, $\mu =0.5$, tolerance ${10}^{-6}$ and maximum number of iterations 40.

Table 12. Mixed convection-diffusion and Burgers’ equation. Results of the directional decomposition using the second order scheme for the spatial discretization, with 1280 time subintervals and different number of spatial steps.

Splitting Algorithm	Space Steps	${\mathit{e}}_{\mathbf{max}}$	${\mathit{e}}_{\mathbf{mean}}$	${\mathit{\delta }}_{\mathbf{max}}$	${\mathit{\delta }}_{\mathbf{mean}}$	Average Iterations	Time(s)
Sequential operator	5	$1.9600\times {10}^{-2}$	$1.0751\times {10}^{-4}$	$3.8363\times {10}^{-2}$	$1.1866\times {10}^{-3}$	1.0000	2.5386
	10	$5.4143\times {10}^{-2}$	$2.7859\times {10}^{-4}$	$1.0181\times {10}^{-1}$	$6.0435\times {10}^{-4}$	1.0000	7.0674
	20	$1.5522\times {10}^{-1}$	$2.4284\times {10}^{-3}$	$2.4936\times {10}^{-1}$	$3.3760\times {10}^{-3}$	1.0000	19.1647
Strang-Marchuk	5	$1.9504\times {10}^{-2}$	$1.1148\times {10}^{-4}$	$3.8228\times {10}^{-2}$	$1.2082\times {10}^{-3}$	1.5000	3.7953
	10	$5.3092\times {10}^{-2}$	$2.2084\times {10}^{-4}$	$1.0038\times {10}^{-1}$	$5.9598\times {10}^{-4}$	1.5000	9.3821
	20	$1.4010\times {10}^{-1}$	$1.5951\times {10}^{-3}$	$2.2965\times {10}^{-1}$	$2.2729\times {10}^{-3}$	1.5000	24.3018
Serial Iterative	5	$1.5415\times {10}^{-4}$	$1.5346\times {10}^{-5}$	$6.7133\times {10}^{-3}$	$1.0434\times {10}^{-3}$	2.0008	6.7669
	10	$1.2967\times {10}^{-3}$	$1.3550\times {10}^{-4}$	$2.2505\times {10}^{-3}$	$4.2699\times {10}^{-4}$	2.0008	8.3770
	20	$3.0299\times {10}^{-2}$	$1.6372\times {10}^{-3}$	$3.9211\times {10}^{-2}$	$2.1837\times {10}^{-3}$	2.4992	27.8058
Classical Parallel	5	$1.5192\times {10}^{-4}$	$9.4243\times {10}^{-6}$	$6.7124\times {10}^{-3}$	$1.0434\times {10}^{-3}$	3.0008	4.2199
	10	$1.0957\times {10}^{-3}$	$1.0800\times {10}^{-4}$	$2.2581\times {10}^{-3}$	$3.5285\times {10}^{-4}$	3.0016	10.2357
	20	$1.8765\times {10}^{-2}$	$1.0091\times {10}^{-3}$	$2.5443\times {10}^{-2}$	$1.4653\times {10}^{-3}$	4.0047	34.6686
Modern Parallel	5	$1.5292\times {10}^{-4}$	$9.4575\times {10}^{-6}$	$6.7112\times {10}^{-3}$	$1.0434\times {10}^{-3}$	3.0008	4.8821
	10	$1.1220\times {10}^{-3}$	$1.1151\times {10}^{-4}$	$2.2857\times {10}^{-3}$	$3.5492\times {10}^{-4}$	3.0023	8.1929
	20	$2.0590\times {10}^{-2}$	$1.1583\times {10}^{-3}$	$2.7563\times {10}^{-2}$	$1.6374\times {10}^{-3}$	7.0039	51.4063

Figure 10 shows, on the left, that the convergence properties degrade with the number of spatial steps for a fixed time step and, on the right, that the best approximations are obtained for 10 subintervals in each spatial dimension. The error increment for more space intervals can be due to the fact that the condition number of the exponential matrix utilized in order to solve the differential system increases fast with the number of spatial intervals, making the solution less reliable.

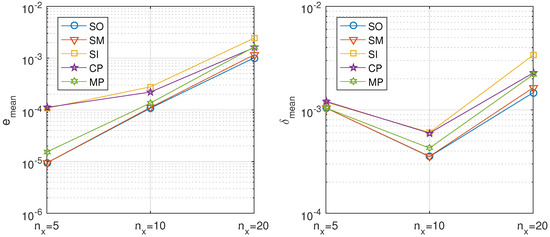
Figure 10. Mixed convection-diffusion and Burgers’ equation, directional decomposition. Precision of the proposed methods: sequential iterative SI, classical parallel CP, and modern parallel MP, compared with the classical ones: sequential operator SO and Strang–Marchuk SM, for different number of spatial steps in the directional decomposition.

• Convection and diffusion decomposition

Here, we decompose to an explicit part, which is the convection, and into an implicit part, which is the diffusion.

$$\begin{array}{cc}\hfill A(u)u& =-1/2u({\partial }_{x}u+{\partial }_{y}u)-1/2({\partial }_{x}u+{\partial }_{y}u),\hfill \end{array}$$

(136)

$$\begin{array}{cc}\hfill Bu& =\frac{1}{2}\mu ({\partial }_{xx}u+{\partial }_{yy}u)+f(x,y,t).\hfill \end{array}$$

(137)

Table 13 analyzes the convergence of the different splitting methods for the convection and diffusion decomposition varying the time step. The errors are proportional to the time step, as shown in the log-log diagrams in Figure 11. The iterative methods have slightly better accuracy than the reference methods, particularly better than the sequential operator splitting method. The modern parallel version does not converge for 160 time steps.

Table 13. Mixed convection-diffusion and Burgers’ equation. Results for the convection diffusion decomposition using the second order scheme for the spatial discretization with 10 spatial subintervals and different number of temporal steps.

Splitting Algorithm	Time Steps	${\mathit{e}}_{\mathbf{max}}$	${\mathit{e}}_{\mathbf{mean}}$	${\mathit{\delta }}_{\mathbf{max}}$	${\mathit{\delta }}_{\mathbf{mean}}$	Average Iterations	Time(s)
Sequential Operator	160	$5.5916\times {10}^{-2}$	$3.9170\times {10}^{-3}$	$1.1155\times {10}^{-1}$	$7.5286\times {10}^{-3}$	1.0000	2.2217
	320	$2.8229\times {10}^{-2}$	$1.9781\times {10}^{-3}$	$5.5638\times {10}^{-2}$	$3.6224\times {10}^{-3}$	1.0000	4.1601
	640	$1.4194\times {10}^{-2}$	$9.9398\times {10}^{-4}$	$2.7412\times {10}^{-2}$	$1.6466\times {10}^{-3}$	1.0000	8.1867
	1280	$7.1179\times {10}^{-3}$	$4.9822\times {10}^{-4}$	$1.3220\times {10}^{-2}$	$6.5429\times {10}^{-4}$	1.0000	16.1663
Strang-Marchuk	160	$1.0750\times {10}^{-2}$	$1.8276\times {10}^{-3}$	$2.2543\times {10}^{-2}$	$3.9088\times {10}^{-3}$	1.5000	3.2557
	320	$5.3570\times {10}^{-3}$	$8.8281\times {10}^{-4}$	$1.1836\times {10}^{-2}$	$2.0865\times {10}^{-3}$	1.5000	6.1221
	640	$2.6780\times {10}^{-3}$	$4.3354\times {10}^{-4}$	$6.4794\times {10}^{-3}$	$1.2052\times {10}^{-3}$	1.5000	12.2784
	1280	$1.3392\times {10}^{-3}$	$2.1479\times {10}^{-4}$	$3.8023\times {10}^{-3}$	$7.7212\times {10}^{-4}$	1.5000	23.9329
Serial Iterative	160	$1.1984\times {10}^{-2}$	$1.3870\times {10}^{-3}$	$2.2076\times {10}^{-2}$	$3.0691\times {10}^{-3}$	3.7250	7.0300
	320	$4.8721\times {10}^{-3}$	$6.7652\times {10}^{-4}$	$1.0137\times {10}^{-2}$	$1.6865\times {10}^{-3}$	3.0062	10.7644
	640	$2.1637\times {10}^{-3}$	$3.3484\times {10}^{-4}$	$5.2782\times {10}^{-3}$	$1.0112\times {10}^{-3}$	2.0031	14.1231
	1280	$1.0151\times {10}^{-3}$	$1.6667\times {10}^{-4}$	$3.1179\times {10}^{-3}$	$6.7675\times {10}^{-4}$	2.0008	29.3916
Classical Parallel	160	$9.7517\times {10}^{-3}$	$1.4278\times {10}^{-3}$	$1.9648\times {10}^{-2}$	$3.1946\times {10}^{-3}$	10.1000	11.5662
	320	$4.5454\times {10}^{-3}$	$7.1452\times {10}^{-4}$	$9.9089\times {10}^{-3}$	$1.7712\times {10}^{-3}$	5.0125	10.6269
	640	$2.1597\times {10}^{-3}$	$3.5723\times {10}^{-4}$	$5.3681\times {10}^{-3}$	$1.0580\times {10}^{-3}$	4.0031	17.3560
	1280	$1.0506\times {10}^{-3}$	$1.7865\times {10}^{-4}$	$3.2100\times {10}^{-3}$	$7.0114\times {10}^{-4}$	3.0016	25.8503
Modern Parallel	320	$4.5794\times {10}^{-3}$	$7.1442\times {10}^{-4}$	$9.9479\times {10}^{-3}$	$1.7711\times {10}^{-3}$	9.6687	20.3683
	640	$2.1612\times {10}^{-3}$	$3.5716\times {10}^{-4}$	$5.3734\times {10}^{-3}$	$1.0579\times {10}^{-3}$	4.8344	20.8872
	1280	$1.0537\times {10}^{-3}$	$1.7866\times {10}^{-4}$	$3.2137\times {10}^{-3}$	$7.0116\times {10}^{-4}$	3.0047	26.5525

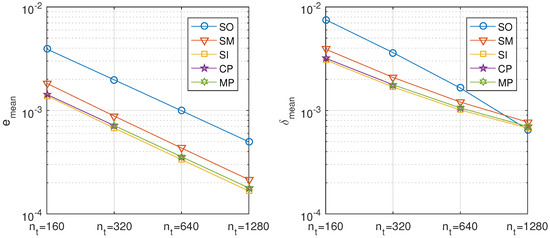
Figure 11. Mixed convection-diffusion and Burgers’ equation, convection-diffusion decomposition. Precision of the proposed methods: sequential iterative SI, classical parallel CP, and modern parallel MP, compared with the classical ones: sequential operator SO and Strang–Marchuk SM, for different number of time steps.

Table 14 analyzes the dependence on the spatial step. The behavior is similar to the case of the directional decomposition, presenting an increment of the estimated error with the number of spatial subintervals for a fixed time step. In the second order scheme, the $\delta$-errors decrease with the space step. The temporal cost is relatively high in the case of 20 subintervals, due to the computational overhead for dealing with big matrices.

Table 14. Mixed convection-diffusion and Burgers’ equation. Results for the convection diffusion decomposition using the second order scheme for the spatial discretization with 10 temporal steps and different number of spatial subintervals.

Splitting Algorithm	Spatial Intervals	${\mathit{e}}_{\mathbf{max}}$	${\mathit{e}}_{\mathbf{mean}}$	${\mathit{\delta }}_{\mathbf{max}}$	${\mathit{\delta }}_{\mathbf{mean}}$	Average Iterations	Time(s)
Sequential operator	5	$4.1014\times {10}^{-3}$	$3.1046\times {10}^{-4}$	$3.0286\times {10}^{-3}$	$4.4136\times {10}^{-4}$	1.0000	4.9225
	10	$7.1179\times {10}^{-3}$	$4.9822\times {10}^{-4}$	$1.3220\times {10}^{-2}$	$6.5429\times {10}^{-4}$	1.0000	13.9807
	20	$9.5637\times {10}^{-3}$	$6.3048\times {10}^{-4}$	$1.9117\times {10}^{-2}$	$1.1655\times {10}^{-3}$	1.0000	246.2290
Strang-Marchuk	5	$1.0128\times {10}^{-3}$	$1.3655\times {10}^{-4}$	$8.9821\times {10}^{-3}$	$1.3134\times {10}^{-3}$	1.5000	8.8805
	10	$1.3392\times {10}^{-3}$	$2.1479\times {10}^{-4}$	$3.8023\times {10}^{-3}$	$7.7212\times {10}^{-4}$	1.5000	25.2552
	20	$1.5215\times {10}^{-3}$	$2.6922\times {10}^{-4}$	$3.1757\times {10}^{-3}$	$6.3273\times {10}^{-4}$	1.5000	379.1765
Serial Iterative	5	$5.6621\times {10}^{-4}$	$1.0099\times {10}^{-4}$	$8.0418\times {10}^{-3}$	$1.2428\times {10}^{-3}$	2.0008	21.1443
	10	$1.0151\times {10}^{-3}$	$1.6667\times {10}^{-4}$	$3.1179\times {10}^{-3}$	$6.7675\times {10}^{-4}$	2.0008	49.0657
	20	$1.5741\times {10}^{-3}$	$2.1460\times {10}^{-4}$	$3.1037\times {10}^{-3}$	$5.2448\times {10}^{-4}$	2.0016	707.5677
Classical Parallel	5	$6.4980\times {10}^{-4}$	$1.1055\times {10}^{-4}$	$8.2248\times {10}^{-3}$	$1.2617\times {10}^{-3}$	3.0008	18.2641
	10	$1.0506\times {10}^{-3}$	$1.7865\times {10}^{-4}$	$3.2100\times {10}^{-3}$	$7.0114\times {10}^{-4}$	3.0016	43.1654
	20	$1.4562\times {10}^{-3}$	$2.2646\times {10}^{-4}$	$2.9778\times {10}^{-3}$	$5.4990\times {10}^{-4}$	4.0039	792.4449
Modern Parallel	5	$6.4782\times {10}^{-4}$	$1.1048\times {10}^{-4}$	$8.2242\times {10}^{-3}$	$1.2617\times {10}^{-3}$	3.0016	8.3758
	10	$1.0537\times {10}^{-3}$	$1.7866\times {10}^{-4}$	$3.2137\times {10}^{-3}$	$7.0116\times {10}^{-4}$	3.0047	21.2526
	20	$1.4709\times {10}^{-3}$	$2.2651\times {10}^{-4}$	$2.9890\times {10}^{-3}$	$5.4993\times {10}^{-4}$	6.0141	687.0917

Figure 12 compares the estimated mean errors $e_{\mathrm{mean}}$ and ${\delta }_{\mathrm{mean}}$ of the different methods with the convection-diffusion decomposition and second order approximation of the spatial derivatives for different number of spatial steps. The sequential operator splitting has poorer convergence properties than the other methods, and its result differs more from the analytical solution as the number of spatial nodes increases.

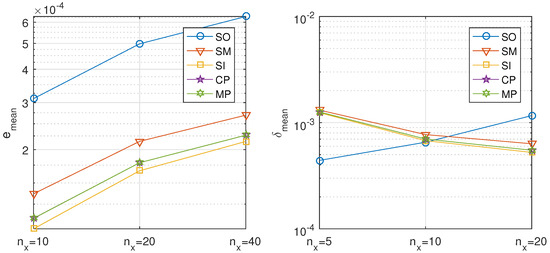
Figure 12. Mixed convection-diffusion and Burgers’ equation, convection-diffusion decomposition. Precision of the proposed methods: sequential iterative SI, classical parallel CP, and modern parallel MP, compared with the classical ones: sequential operator SO and Strang–Marchuk SM, for different number of spatial steps.

• Balanced decomposition

We decompose into:

$$\begin{array}{c}A(u)u=(1-ϵ)\left(-1/2u{\partial }_{x}u-1/2{\partial }_{x}u+\mu {\partial }_{xx}u\right)+ϵ\left(-1/2u{\partial }_{y}u-1/2{\partial }_{y}u+\mu {\partial }_{yy}u\right)+ϵf(x,y,t),\hfill \\ B(u)u=ϵ\left(-1/2u{\partial }_{x}u-1/2{\partial }_{x}u+\mu {\partial }_{xx}u\right)+(1-ϵ)\left(-1/2u{\partial }_{y}u-1/2{\partial }_{y}u+\mu {\partial }_{yy}u\right)+(1-ϵ)f(x,y,t).\hfill \end{array}$$

(138)

where $ϵ$ is an arbitrary parameter that can be tuned in order to achieve the maximum efficiency.

We first examine the influence of parameter $ϵ$ on the convergence of the different splitting schemes, see Table 15, The method has the same behavior for parameter values symmetric with respect to 0.5. The results are quite uniform for $ϵ$ in the range $[-0.1,1.1]$, whereas, for other parameter values, the method may diverge. The classical parallel algorithm yields results for $ϵ=2$, whereas the serial and the modern parallel iterative methods fail for $ϵ=2$.

Table 15. Mixed convection-diffusion and Burgers’ equation, balanced decomposition. Results for the balanced decomposition using the second order scheme for the spatial discretization with 640 temporal subintervals and different values of parameter $ϵ$.

Splitting Algorithm	$\mathit{ϵ}$	${\mathit{e}}_{\mathbf{max}}$	${\mathit{e}}_{\mathbf{mean}}$	${\mathit{\delta }}_{\mathbf{max}}$	${\mathit{\delta }}_{\mathbf{mean}}$	Average Iterations	Time(s)
Sequential operator	0.5	$4.5184\times {10}^{-3}$	$2.1168\times {10}^{-4}$	$7.8771\times {10}^{-3}$	$5.6809\times {10}^{-4}$	1.0000	6.6720
	1	$4.5508\times {10}^{-3}$	$2.1796\times {10}^{-4}$	$7.9207\times {10}^{-3}$	$5.7747\times {10}^{-4}$	1.0000	7.5672
	2	$4.8177\times {10}^{-3}$	$2.7309\times {10}^{-4}$	$8.2784\times {10}^{-3}$	$6.6081\times {10}^{-4}$	1.0000	7.8492
Strang-Marchuk	0.5	$1.8701\times {10}^{-3}$	$3.3767\times {10}^{-4}$	$4.8778\times {10}^{-3}$	$1.0211\times {10}^{-3}$	1.0000	9.7979
	1	$1.8260\times {10}^{-3}$	$3.3699\times {10}^{-4}$	$4.8191\times {10}^{-3}$	$1.0202\times {10}^{-3}$	1.0000	12.8640
	2	$1.4965\times {10}^{-3}$	$3.3155\times {10}^{-4}$	$4.3586\times {10}^{-3}$	$1.0130\times {10}^{-3}$	1.0000	13.6113
Serial Iterative	0.5	$2.0353\times {10}^{-3}$	$3.7750\times {10}^{-4}$	$5.2893\times {10}^{-3}$	$1.1017\times {10}^{-3}$	2.8812	20.1360
	1	$1.8680\times {10}^{-3}$	$3.7128\times {10}^{-4}$	$5.4439\times {10}^{-3}$	$1.1173\times {10}^{-3}$	2.0031	20.5409
	2	$8.3539\times {10}^{29}$	NaN	Inf	NaN	1.3125	10.5239
Classical Parallel	0.5	$2.0337\times {10}^{-3}$	$3.7747\times {10}^{-4}$	$5.2887\times {10}^{-3}$	$1.1017\times {10}^{-3}$	3.9859	15.0469
	1	$1.9713\times {10}^{-3}$	$3.7521\times {10}^{-4}$	$5.2081\times {10}^{-3}$	$1.0988\times {10}^{-3}$	3.9859	21.0260
	2	$1.9719\times {10}^{-3}$	$3.4606\times {10}^{-4}$	$5.2186\times {10}^{-3}$	$1.0635\times {10}^{-3}$	3.9875	19.8748
Modern Parallel	0.5	$2.0337\times {10}^{-3}$	$3.7747\times {10}^{-4}$	$5.2887\times {10}^{-3}$	$1.1017\times {10}^{-3}$	3.9859	15.9368
	1	$1.9721\times {10}^{-3}$	$3.7521\times {10}^{-4}$	$5.2139\times {10}^{-3}$	$1.0990\times {10}^{-3}$	4.0062	19.0337
	2	$2.0550\times {10}^{11}$	NaN	$2.0550\times {10}^{11}$	NaN	2.7375	12.0642

The dependence on the time and space steps of the algorithms with the convection-diffusion decomposition is similar to that of the previously analyzed decompositions. Table 16 compares the behavior of the considered methods with different decompositions.

Table 16. Mixed convection-diffusion and Burgers’ equation with 10 spatial intervals and 640 temporal steps. Results of the different splitting methods with directional decomposition, D, convection-diffusion decomposition, CD, and $ϵ$-balanced decomposition, $ϵ$ B.

Splitting Algorithm	Decomposition	${\mathit{e}}_{\mathbf{max}}$	${\mathit{e}}_{\mathbf{mean}}$	${\mathit{\delta }}_{\mathbf{max}}$	${\mathit{\delta }}_{\mathbf{mean}}$	Average Iterations	Time
Sequential operator	D	$1.1412\times {10}^{-1}$	$9.7183\times {10}^{-4}$	$1.0181\times {10}^{-1}$	$6.0435\times {10}^{-4}$	1.0000	3.4686
	CD	$1.4194\times {10}^{-2}$	$9.9398\times {10}^{-4}$	$1.3220\times {10}^{-2}$	$6.5429\times {10}^{-4}$	1.0000	12.5035
	$ϵD$	$4.5184\times {10}^{-3}$	$2.1168\times {10}^{-4}$	$3.3769\times {10}^{-3}$	$4.1340\times {10}^{-4}$	1.0000	12.5689
Strang-Marchuk	D	$1.0966\times {10}^{-1}$	$6.9728\times {10}^{-4}$	$1.0038\times {10}^{-1}$	$5.9598\times {10}^{-4}$	1.0000	5.1649
	CD	$2.6780\times {10}^{-3}$	$4.3354\times {10}^{-4}$	$3.8023\times {10}^{-3}$	$7.7212\times {10}^{-4}$	1.0000	19.4012
	$ϵ$ B	$1.8701\times {10}^{-3}$	$3.3767\times {10}^{-4}$	$3.0078\times {10}^{-3}$	$6.8387\times {10}^{-4}$	1.0000	20.3991
Serial Iterative	D	$5.1944\times {10}^{-3}$	$5.5729\times {10}^{-4}$	$2.2505\times {10}^{-3}$	$4.2699\times {10}^{-4}$	2.0008	8.1039
	CD	$2.1637\times {10}^{-3}$	$3.3484\times {10}^{-4}$	$3.1179\times {10}^{-3}$	$6.7675\times {10}^{-4}$	2.0008	29.1385
	$ϵ$ B	$2.0353\times {10}^{-3}$	$3.7750\times {10}^{-4}$	$3.2541\times {10}^{-3}$	$7.2469\times {10}^{-4}$	2.0008	30.3495
Classical Parallel	D	$4.0117\times {10}^{-3}$	$4.0302\times {10}^{-4}$	$2.2581\times {10}^{-3}$	$3.5285\times {10}^{-4}$	3.0016	6.8251
	CD	$2.1597\times {10}^{-3}$	$3.5723\times {10}^{-4}$	$3.2100\times {10}^{-3}$	$7.0114\times {10}^{-4}$	3.0016	24.2979
	$ϵ$ B	$2.0337\times {10}^{-3}$	$3.7747\times {10}^{-4}$	$3.2550\times {10}^{-3}$	$7.2471\times {10}^{-4}$	3.0016	24.4019
Modern Parallel	D	$4.2148\times {10}^{-3}$	$4.3094\times {10}^{-4}$	$2.2857\times {10}^{-3}$	$3.5492\times {10}^{-4}$	3.0023	6.3850
	CD	$2.1612\times {10}^{-3}$	$3.5716\times {10}^{-4}$	$3.2137\times {10}^{-3}$	$7.0116\times {10}^{-4}$	3.0047	24.3399
	$ϵ$ B	$2.0337\times {10}^{-3}$	$3.7747\times {10}^{-4}$	$3.2550\times {10}^{-3}$	$7.2471\times {10}^{-4}$	3.0016	24.6888

Figure 13 shows that the non-iterative splitting methods give better results with the $ϵ$-balanced decomposition, whereas the iterative methods give similar results with all of the decompositions, being slightly better for the directional decomposition.

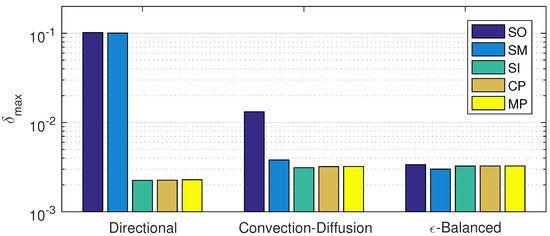
Figure 13. Mixed convection-diffusion and Burgers’ equation with 10 spatial intervals and 1280 temporal steps. Precision of the proposed methods: sequential iterative SI, classical parallel CP, and modern parallel MP, compared with the classical ones: sequential operator SO and Strang–Marchuk SM, for different decomposition methods.

Figure 14 compares the temporal costs that are shown in Table 16. The results indicate that the directional decomposition is better than the convection-diffusion decomposition and the $ϵ$-balanced decomposition for all the considered splitting algorithms.

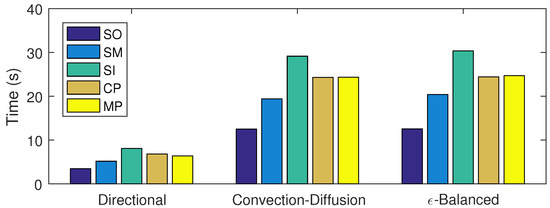
Figure 14. Mixed convection-diffusion and Burgers’ equation with 10 spatial intervals and 640 time steps. Temporal cost in seconds of the proposed methods: sequential iterative SI, classical parallel CP, and modern parallel MP, compared with the classical ones: sequential operator SO and Strang–Marchuk SM, for different decomposition methods.

5.4. Fourth Example: Fractional Diffusion Problem

We deal with the following fractional diffusion problem, see also [27]:

$$u^{\prime }(\mathbf{x},t)=d(\mathbf{x})\frac{{\partial }^{1.8}u(\mathbf{x},t)}{\partial x^{1.8}}+e(\mathbf{x})\frac{{\partial }^{1.6}u(\mathbf{x},t)}{\partial y^{1.6}}+q(\mathbf{x},t), (\mathbf{x},t)\in \Omega \times [0,T],$$

(139)

$$u(\mathbf{x},0)=x^3 y^{3.6}, \mathbf{x}\in \Omega ,$$

(140)

$$u(\mathbf{x},t)=exp(-t) x^3 y^{3,6}, (\mathbf{x},t)\in \partial \Omega \times [0,T],$$

(141)

where we have the analytical solution $u_{an}(\mathbf{x},t)=exp(-t) x^3 y^{3.6}$, with $\mathbf{x}={(x,y)}^t$ and $\Omega =[0,1]\times [0,1]$ and $t\in [0,T]$ with $T=1.0$. $q(\mathbf{x},t)=-(1+2xy)exp(-t) x^3 y^{3.6}$ and $d(\mathbf{x})=\mathrm{\Gamma }(2.2)x^{2.8}y/6$, $e(\mathbf{x})=2x{y}^{2.6}/\mathrm{\Gamma }(4.6)$.

In operator notation, we write:

$$\begin{array}{c}\hfill A=A_1+A_2,\end{array}$$

(142)

where $A_1=d(\mathbf{x})\frac{{\partial }^{\alpha }}{\partial x^{\alpha }}, A_2=e(\mathbf{x})\frac{{\partial }^{\beta }}{\partial y^{\beta }}+q(\mathbf{x},t)$ and we assume that the Dirichlet boundary conditions are embedded into the operators.

We apply the normalized Grünwald weights by:

$$\begin{array}{c}\hfill g_{\alpha ,k}=\frac{\mathrm{\Gamma }(k-\alpha )}{\mathrm{\Gamma }(-\alpha ) \mathrm{\Gamma }(k+1)}={(-1)}^k\left(\genfrac{}{}{0pt}{}{\alpha }{k}\right),\end{array}$$

(143)

for the right-shifted Grünwald formula, see [32].

We apply:

$$\begin{array}{c}d(x_i,y_j)\frac{{\partial }^{\alpha }u(x_i,y_j,t)}{\partial x^{\alpha }}\simeq \frac{d_{i,j}}{{(\Delta x)}^{\alpha }}\sum _{k=0}^{i+1}{g}_{\alpha ,k} u_{i-k+1,j},\hfill \end{array}$$

(144)

$$\begin{array}{c}e(x_i,y_j)\frac{{\partial }^{\beta }u(x_i,y_j,t)}{\partial y^{\beta }}\simeq \frac{e_{i,j}}{{(\Delta y)}^{\beta }}\sum _{k=0}^{j+1}{g}_{\beta ,k} u_{i,j-k+1}.\hfill \end{array}$$

(145)

In order to establish the convergence of the algorithms, we compute the solution $u(\Delta ,h)$ obtained while using spatial and temporal steps $\Delta =\Delta x=\Delta y$ and $h$, respectively. We use different measures to estimate the convergence. On one hand, we compare the outcome of the method $u(\Delta ,h)$ with the exact solution $u_{an}$ for every point of the mesh, which shows the convergence of the method. On the other hand, we can compare $u(\Delta ,h)$ with the result obtained halving the time or space steps, $h/2$, at the final time $T=1$. Denote, by $e_{i,j}(\Delta ,h)$, the difference between the results at a mesh point $(x_i,y_j,1)$, obtained using two different time steps, h and $h/2$, and by ${\delta }_{i,j}(\Delta ,h)$ the difference with the analytical solution at the same point. In the tables, we will denote the maximum errors by

$$e_{\max }=\underset{i,j}{\max } \left|e_{i,j}(\Delta x,h)\right|,$$

(146)

and

$${\delta }_{\max }=\underset{i,j}{\max } \left|{\delta }_{i,j}(\Delta x,h)\right|,$$

(147)

and the mean errors by

$$e_{\mathrm{mean}}=\frac{1}{N}\sum _{i,j}\left|e_{i,j}(\Delta x,h)\right|,$$

(148)

and

$${\delta }_{\mathrm{mean}}=\frac{1}{N}\sum _{i,j}\left|{\delta }_{i,j}(\Delta x,h)\right|,$$

(149)

where N is the number of spatial nodes at time T.

In the following, we discuss different decompositions of the multi-operator splitting approach:

• Directional decomposition:

We decompose into the different directions:

$$A_1=d(\mathbf{x})\frac{{\partial }^{\alpha }}{\partial x^{\alpha }},$$

(150)

$$A_2=e(\mathbf{x})\frac{{\partial }^{\beta }}{\partial y^{\beta }}+q(\mathbf{x},t).$$

(151)

The directional decomposition allows obtaining the solution solving linear systems of size $n_x-1$, where $n_x$ is the number of spatial subintervals. Table 17 shows the results of the considered splitting algorithms for 20 spatial subintervals and different time steps, allowing for a maximum of three iterations and using tolerance ${10}^{-4}$. Figure 15 shows, on the left, that the parallel iterative methods perform slightly better than the serial iterative method and, on the right, the approximation to the analytical solution for different number of time steps.

Table 17. Fractional diffusion equation. Results for the directional decomposition with 20 spatial subintervals and different number of temporal steps.

Splitting Algorithm	Time Steps	${\mathit{e}}_{\mathbf{max}}$	${\mathit{e}}_{\mathbf{mean}}$	${\mathit{\delta }}_{\mathbf{max}}$	${\mathit{\delta }}_{\mathbf{mean}}$	Average Iterations	Time(s)
Sequential Operator	40	$3.6909\times {10}^{-3}$	$2.1918\times {10}^{-4}$	$7.4079\times {10}^{-3}$	$4.3302\times {10}^{-4}$	1.0000	0.0595
	80	$1.9763\times {10}^{-3}$	$1.1228\times {10}^{-4}$	$3.7171\times {10}^{-3}$	$2.4365\times {10}^{-4}$	1.0000	0.1169
	160	$1.0222\times {10}^{-3}$	$5.6858\times {10}^{-5}$	$1.7407\times {10}^{-3}$	$1.7337\times {10}^{-4}$	1.0000	0.2488
	320	$5.1954\times {10}^{-4}$	$2.8614\times {10}^{-5}$	$8.8420\times {10}^{-4}$	$1.5956\times {10}^{-4}$	1.0000	0.4207
Strang-Marchuk	40	$6.1536\times {10}^{-4}$	$7.5827\times {10}^{-5}$	$1.0176\times {10}^{-3}$	$1.8768\times {10}^{-4}$	1.5000	1.1779
	80	$3.4782\times {10}^{-4}$	$4.2854\times {10}^{-5}$	$1.3636\times {10}^{-3}$	$2.3792\times {10}^{-4}$	1.5000	0.1476
	160	$1.7770\times {10}^{-4}$	$2.1897\times {10}^{-5}$	$1.1561\times {10}^{-3}$	$2.0663\times {10}^{-4}$	1.5000	0.3029
	320	$8.9844\times {10}^{-5}$	$1.1077\times {10}^{-5}$	$1.0605\times {10}^{-3}$	$1.9393\times {10}^{-4}$	1.5000	0.6012
Serial Iterative	40	$4.3494\times {10}^{-2}$	$3.7787\times {10}^{-3}$	$3.9615\times {10}^{-2}$	$4.8916\times {10}^{-3}$	1.1625	1.1494
	80	$2.6689\times {10}^{-2}$	$2.2996\times {10}^{-3}$	$7.8003\times {10}^{-2}$	$8.5729\times {10}^{-3}$	3.0000	0.3391
	160	$1.1493\times {10}^{-2}$	$1.0086\times {10}^{-3}$	$5.2376\times {10}^{-2}$	$6.3074\times {10}^{-3}$	2.9625	0.6819
	320	$5.3112\times {10}^{-3}$	$4.7046\times {10}^{-4}$	$4.3672\times {10}^{-2}$	$5.3400\times {10}^{-3}$	1.9625	0.9298
Classical Parallel	40	$5.3373\times {10}^{-3}$	$4.4982\times {10}^{-4}$	$3.9545\times {10}^{-2}$	$4.8664\times {10}^{-3}$	1.7414	1.6636
	80	$8.1666\times {10}^{-3}$	$2.3243\times {10}^{-4}$	$3.4634\times {10}^{-2}$	$4.4640\times {10}^{-3}$	3.0000	0.3520
	160	$1.2229\times {10}^{-2}$	$6.1940\times {10}^{-4}$	$3.5694\times {10}^{-2}$	$4.4046\times {10}^{-3}$	2.9750	0.6967
	320	$4.3711\times {10}^{-3}$	$1.9453\times {10}^{-4}$	$4.2061\times {10}^{-2}$	$4.9619\times {10}^{-3}$	2.5344	1.2122
Modern Parallel	40	$2.5500\times {10}^{-3}$	$1.1787\times {10}^{-4}$	$3.7503\times {10}^{-2}$	$7.5934\times {10}^{-3}$	1.5680	1.5756
	80	$2.7226\times {10}^{-3}$	$7.5531\times {10}^{-5}$	$3.8166\times {10}^{-2}$	$7.6333\times {10}^{-3}$	3.0000	0.3567
	160	$5.7234\times {10}^{-4}$	$2.0251\times {10}^{-5}$	$3.8201\times {10}^{-2}$	$7.7009\times {10}^{-3}$	2.9937	0.7005
	320	$1.4722\times {10}^{-3}$	$1.2626\times {10}^{-4}$	$3.8233\times {10}^{-2}$	$7.7196\times {10}^{-3}$	2.5500	1.2045

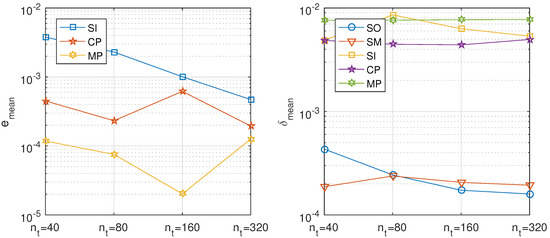
Figure 15. Fractional diffusion equation, directional decomposition. Precision of the proposed methods: sequential iterative SI, classical parallel CP, and modern parallel MP, compared with the classical ones: sequential operator SO and Strang–Marchuk SM, for different number of time steps.

Table 18 shows the results of the considered splitting algorithms for 320 time steps and different number of spatial subintervals, allowing for a maximum of three iterations and using tolerance ${10}^{-4}$. Figure 16 presents graphically the results.

Table 18. Fractional diffusion equation. Results for the directional decomposition with 320 time steps and different number of spatial subintervals.

Splitting Algorithm	Spatial Intervals	${\mathit{e}}_{\mathbf{max}}$	${\mathit{e}}_{\mathbf{mean}}$	${\mathit{\delta }}_{\mathbf{max}}$	${\mathit{\delta }}_{\mathbf{mean}}$	Average Iterations	Time(s)
Sequential Operator	10	$3.1792\times {10}^{-4}$	$2.4488\times {10}^{-5}$	$1.7691\times {10}^{-3}$	$3.5031\times {10}^{-4}$	1.0000	0.2665
	20	$5.1954\times {10}^{-4}$	$2.8614\times {10}^{-5}$	$8.8420\times {10}^{-4}$	$1.5956\times {10}^{-4}$	1.0000	0.4556
	40	$6.7834\times {10}^{-4}$	$3.0654\times {10}^{-5}$	$1.2946\times {10}^{-3}$	$8.9356\times {10}^{-5}$	1.0000	2.0992
Strang-Marchuk	10	$6.7693\times {10}^{-5}$	$9.4661\times {10}^{-6}$	$1.9450\times {10}^{-3}$	$3.9668\times {10}^{-4}$	1.5000	0.1661
	20	$8.9844\times {10}^{-5}$	$1.1077\times {10}^{-5}$	$1.0605\times {10}^{-3}$	$1.9393\times {10}^{-4}$	1.5000	0.5920
	40	$1.2152\times {10}^{-4}$	$1.1864\times {10}^{-5}$	$5.9024\times {10}^{-4}$	$1.0142\times {10}^{-4}$	1.5000	3.1666
Serial Iterative	10	$9.7111\times {10}^{-4}$	$1.0946\times {10}^{-4}$	$2.1149\times {10}^{-2}$	$2.6542\times {10}^{-3}$	1.7750	0.2555
	20	$5.3112\times {10}^{-3}$	$4.7046\times {10}^{-4}$	$4.3672\times {10}^{-2}$	$5.3400\times {10}^{-3}$	1.9625	0.9364
	40	$2.7080\times {10}^{-2}$	$2.2282\times {10}^{-3}$	$8.9409\times {10}^{-2}$	$1.0208\times {10}^{-2}$	1.9937	4.5270
Classical Parallel	10	$7.3233\times {10}^{-4}$	$5.9725\times {10}^{-5}$	$2.0834\times {10}^{-2}$	$2.6001\times {10}^{-3}$	1.8281	0.2669
	20	$4.3711\times {10}^{-3}$	$1.9453\times {10}^{-4}$	$4.2061\times {10}^{-2}$	$4.9619\times {10}^{-3}$	2.5344	1.1800
	40	$4.3727\times {10}^{-2}$	$1.6621\times {10}^{-3}$	$4.8885\times {10}^{-2}$	$5.8880\times {10}^{-3}$	2.9406	6.5080
Modern Parallel	10	$4.3702\times {10}^{-4}$	$5.3345\times {10}^{-5}$	$4.1936\times {10}^{-2}$	$9.1615\times {10}^{-3}$	2.0875	0.2990
	20	$1.4722\times {10}^{-3}$	$1.2626\times {10}^{-4}$	$3.8233\times {10}^{-2}$	$7.7196\times {10}^{-3}$	2.5500	1.2041
	40	$4.5579\times {10}^{-3}$	$1.1580\times {10}^{-4}$	$3.5053\times {10}^{-2}$	$6.3818\times {10}^{-3}$	2.9000	6.6945

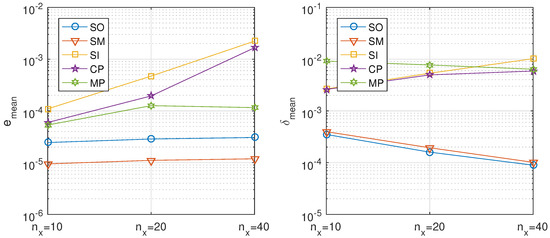
Figure 16. Fractional diffusion equation, directional decomposition. Precision of the proposed methods: sequential iterative SI, classical parallel CP, and modern parallel MP, compared with the classical ones: sequential operator SO and Strang–Marchuk SM, for 320 temporal steps and different number of spatial subintervals.

• Balanced decomposition:

We decompose into:

$$\begin{array}{c}{A}_1=\frac{1}{2}A, A_2=\frac{1}{2}A.\hfill \end{array}$$

(152)

Here, we have the benefit of equal load balances of the matrices, such that the exp-matrices have the same sparse structure.

Table 19 shows the results of the considered splitting algorithms for 20 spatial subintervals and different time steps, allowing a maximum of three iterations and using tolerance ${10}^{-4}$. Figure 17 shows, on the left, that the parallel iterative methods perform slightly better than the serial iterative method and, on the right, the approximation to the analytical solution for different number of time steps.

Table 19. Fractional diffusion equation. Results for the balanced decomposition with 20 spatial subintervals and different number of temporal steps.

Splitting Algorithm	Time Steps	${\mathit{e}}_{\mathbf{max}}$	${\mathit{e}}_{\mathbf{mean}}$	${\mathit{\delta }}_{\mathbf{max}}$	${\mathit{\delta }}_{\mathbf{mean}}$	Average Iterations	Time(s)
Sequential Operator	40	$5.3158\times {10}^{-4}$	$4.9157\times {10}^{-5}$	$1.1895\times {10}^{-3}$	$2.1594\times {10}^{-4}$	1.0000	0.9777
	80	$3.1002\times {10}^{-4}$	$2.5518\times {10}^{-5}$	$1.0759\times {10}^{-3}$	$1.8993\times {10}^{-4}$	1.0000	1.8580
	160	$1.7340\times {10}^{-4}$	$1.3021\times {10}^{-5}$	$1.0190\times {10}^{-3}$	$1.8313\times {10}^{-4}$	1.0000	3.6733
	320	$9.2152\times {10}^{-5}$	$6.5802\times {10}^{-6}$	$9.9049\times {10}^{-4}$	$1.8186\times {10}^{-4}$	1.0000	7.4484
Strang Marchuk	40	$7.5805\times {10}^{-4}$	$5.9623\times {10}^{-5}$	$1.3763\times {10}^{-3}$	$1.6935\times {10}^{-4}$	1.5000	1.4172
	80	$4.2151\times {10}^{-4}$	$3.0984\times {10}^{-5}$	$8.6828\times {10}^{-4}$	$1.5511\times {10}^{-4}$	1.5000	2.8931
	160	$2.3309\times {10}^{-4}$	$1.5810\times {10}^{-5}$	$9.1488\times {10}^{-4}$	$1.6222\times {10}^{-4}$	1.5000	5.6685
	320	$1.2289\times {10}^{-4}$	$7.9883\times {10}^{-6}$	$9.3832\times {10}^{-4}$	$1.7070\times {10}^{-4}$	1.5000	11.1808
Serial Iterative	40	$4.9767\times {10}^{-4}$	$6.4003\times {10}^{-5}$	$1.3036\times {10}^{-1}$	$7.6993\times {10}^{-3}$	3.0000	0.9013
	80	$2.4927\times {10}^{-4}$	$3.1592\times {10}^{-5}$	$1.3045\times {10}^{-1}$	$7.7224\times {10}^{-3}$	3.0000	1.5581
	160	$1.2439\times {10}^{-4}$	$1.6482\times {10}^{-5}$	$1.3041\times {10}^{-1}$	$7.7335\times {10}^{-3}$	2.5875	2.6810
	320	$6.2430\times {10}^{-5}$	$8.1657\times {10}^{-6}$	$1.3047\times {10}^{-1}$	$7.7399\times {10}^{-3}$	1.6688	3.5020
Classical Parallel	40	$9.3505\times {10}^{-4}$	$7.4913\times {10}^{-5}$	$1.2923\times {10}^{-1}$	$7.6842\times {10}^{-3}$	2.0000	1.8878
	80	$7.2531\times {10}^{-4}$	$5.4398\times {10}^{-5}$	$1.3017\times {10}^{-1}$	$7.7186\times {10}^{-3}$	2.0000	2.1625
	160	$1.9158\times {10}^{-4}$	$2.1530\times {10}^{-5}$	$1.3089\times {10}^{-1}$	$7.7522\times {10}^{-3}$	1.8062	3.8818
	320	$1.0043\times {10}^{-4}$	$6.3991\times {10}^{-6}$	$1.3071\times {10}^{-1}$	$7.7557\times {10}^{-3}$	1.3406	6.4414
Modern Parallel	40	$4.9675\times {10}^{-4}$	$6.3589\times {10}^{-5}$	$1.3077\times {10}^{-1}$	$7.7019\times {10}^{-3}$	3.0000	0.8175
	80	$3.8832\times {10}^{-4}$	$5.0606\times {10}^{-5}$	$1.3053\times {10}^{-1}$	$7.7228\times {10}^{-3}$	3.0000	1.7332
	160	$1.9024\times {10}^{-4}$	$2.1449\times {10}^{-5}$	$1.3089\times {10}^{-1}$	$7.7524\times {10}^{-3}$	2.6000	2.6822
	320	$1.0046\times {10}^{-4}$	$6.3750\times {10}^{-6}$	$1.3071\times {10}^{-1}$	$7.7557\times {10}^{-3}$	1.6719	3.4380

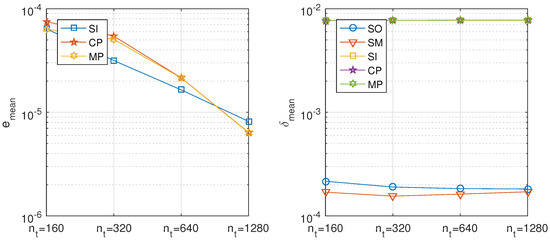
Figure 17. Fractional diffusion equation, balanced decomposition. Precision of the proposed methods: sequential iterative SI, classical parallel CP, and modern parallel MP, compared with the classical ones: sequential operator SO and Strang–Marchuk SM, for different number of time steps.

Table 20 shows the results of the considered splitting algorithms for 320 time steps and different number of spatial subintervals, allowing a maximum of three iterations and using tolerance ${10}^{-4}$. Figure 18 graphically presents the results.

Table 20. Fractional diffusion equation. Results for the balanced decomposition with 320 time steps and different number of spatial subintervals.

Splitting Algorithm	Spatial Intervals	${\mathit{e}}_{\mathbf{max}}$	${\mathit{e}}_{\mathbf{mean}}$	${\mathit{\delta }}_{\mathbf{max}}$	${\mathit{\delta }}_{\mathbf{mean}}$	Average Iterations	Time(s)
Sequential Operator	5	$1.4662\times {10}^{-5}$	$4.4384\times {10}^{-6}$	$3.3195\times {10}^{-3}$	$8.1165\times {10}^{-4}$	1.0000	0.1604
	10	$6.0500\times {10}^{-5}$	$5.6659\times {10}^{-6}$	$1.8656\times {10}^{-3}$	$3.8575\times {10}^{-4}$	1.0000	0.6763
	20	$9.2152\times {10}^{-5}$	$6.5802\times {10}^{-6}$	$9.9049\times {10}^{-4}$	$1.8186\times {10}^{-4}$	1.0000	14.9386
Strang Marchuk	5	$3.9269\times {10}^{-5}$	$4.6669\times {10}^{-6}$	$3.2665\times {10}^{-3}$	$8.0162\times {10}^{-4}$	1.5000	0.1949
	10	$9.0735\times {10}^{-5}$	$6.8613\times {10}^{-6}$	$1.8124\times {10}^{-3}$	$3.7471\times {10}^{-4}$	1.5000	0.8352
	20	$1.2289\times {10}^{-4}$	$7.9883\times {10}^{-6}$	$9.3832\times {10}^{-4}$	$1.7070\times {10}^{-4}$	1.5000	21.1158
Serial Iterative	5	$4.4368\times {10}^{-5}$	$7.8056\times {10}^{-6}$	$3.0745\times {10}^{-2}$	$3.9191\times {10}^{-3}$	1.2875	0.1144
	10	$5.7553\times {10}^{-5}$	$8.1817\times {10}^{-6}$	$8.9020\times {10}^{-2}$	$6.4615\times {10}^{-3}$	1.6063	0.4583
	20	$6.2430\times {10}^{-5}$	$8.1657\times {10}^{-6}$	$1.3047\times {10}^{-1}$	$7.7399\times {10}^{-3}$	1.6688	7.4995
Classical Parallel	5	$1.4093\times {10}^{-5}$	$3.0061\times {10}^{-6}$	$3.0875\times {10}^{-2}$	$3.9338\times {10}^{-3}$	1.1469	0.1123
	10	$6.3414\times {10}^{-5}$	$5.1056\times {10}^{-6}$	$8.9191\times {10}^{-2}$	$6.4759\times {10}^{-3}$	1.3062	0.4936
	20	$1.0043\times {10}^{-4}$	$6.3991\times {10}^{-6}$	$1.3071\times {10}^{-1}$	$7.7557\times {10}^{-3}$	1.3406	5.5945
Modern Parallel	5	$1.4149\times {10}^{-5}$	$3.0076\times {10}^{-6}$	$3.0875\times {10}^{-2}$	$3.9338\times {10}^{-3}$	1.2906	0.1332
	10	$6.3456\times {10}^{-5}$	$5.1059\times {10}^{-6}$	$8.9192\times {10}^{-2}$	$6.4759\times {10}^{-3}$	1.6094	0.4803
	20	$1.0046\times {10}^{-4}$	$6.3750\times {10}^{-6}$	$1.3071\times {10}^{-1}$	$7.7557\times {10}^{-3}$	1.6719	6.4903

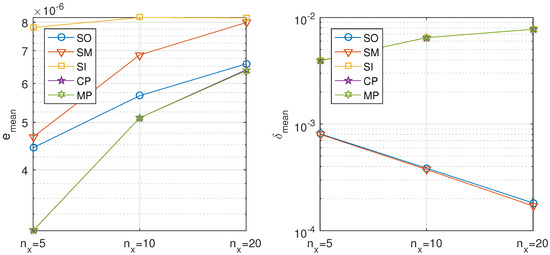
Figure 18. Fractional diffusion equation, balanced decomposition. Precision of the proposed methods: sequential iterative SI, classical parallel CP, and modern parallel MP, compared with the classical ones: sequential operator SO and Strang–Marchuk SM, for 320 temporal steps and different number of spatial subintervals.

• Mixed decomposition

We decompose into the different directions:

$$A_1=(1-ϵ)d(\mathbf{x})\frac{{\partial }^{\alpha }}{\partial x^{\alpha }}+ϵ(e(\mathbf{x})\frac{{\partial }^{\beta }}{\partial y^{\beta }}+q(\mathbf{x},t)),$$

(153)

$$A_2=ϵ d(\mathbf{x})\frac{{\partial }^{\alpha }}{\partial x^{\alpha }}+(1-ϵ)(e(\mathbf{x})\frac{{\partial }^{\beta }}{\partial y^{\beta }}+q(\mathbf{x},t)),$$

(154)

where $ϵ=[0,1/2]$. For $ϵ=0$, we have the directional decomposition, while, for $ϵ=1/2$, we have the balanced decomposition.

Table 21 shows the influence of $ϵ$ on the convergence of the different splitting methods with mixed decomposition for the fractional diffusion problem using 20 subintervals in each spatial direction and 320 time steps. The same information can be seen in Figure 19.

Table 21. Fractional diffusion equation. Results for the mixed decomposition with 20 subintervals in each spatial direction, 320 time steps, and different values of $ϵ$.

Splitting Algorithm	$\mathit{ϵ}$	${\mathit{e}}_{\mathbf{max}}$	${\mathit{e}}_{\mathbf{mean}}$	${\mathit{\delta }}_{\mathbf{max}}$	${\mathit{\delta }}_{\mathbf{mean}}$	Average Iterations	Time(s)
Sequential Operator	0.1	$4.0169\times {10}^{-4}$	$2.2303\times {10}^{-5}$	$8.9352\times {10}^{-4}$	$1.6047\times {10}^{-4}$	1.0000	11.7929
	0.2	$2.9957\times {10}^{-4}$	$1.7062\times {10}^{-5}$	$9.1842\times {10}^{-4}$	$1.6368\times {10}^{-4}$	1.0000	11.6719
	0.3	$2.2243\times {10}^{-4}$	$1.2715\times {10}^{-5}$	$9.4435\times {10}^{-4}$	$1.6863\times {10}^{-4}$	1.0000	11.4894
	0.4	$1.5449\times {10}^{-4}$	$9.1917\times {10}^{-6}$	$9.6838\times {10}^{-4}$	$1.7504\times {10}^{-4}$	1.0000	12.7896
Strang Marchuk	0.1	$1.2924\times {10}^{-4}$	$9.3575\times {10}^{-6}$	$9.9183\times {10}^{-4}$	$1.8011\times {10}^{-4}$	1.5000	22.0758
	0.2	$1.0913\times {10}^{-4}$	$7.1597\times {10}^{-6}$	$9.7285\times {10}^{-4}$	$1.7825\times {10}^{-4}$	1.5000	18.4355
	0.3	$9.9531\times {10}^{-5}$	$6.6577\times {10}^{-6}$	$9.6026\times {10}^{-4}$	$1.7604\times {10}^{-4}$	1.5000	18.5075
	0.4	$1.0929\times {10}^{-4}$	$7.1156\times {10}^{-6}$	$9.5002\times {10}^{-4}$	$1.7349\times {10}^{-4}$	1.5000	21.7024
Serial Iterative	0.1	$8.5542\times {10}^{-3}$	$1.5771\times {10}^{-4}$	$1.9578\times {10}^{-1}$	$1.3803\times {10}^{-2}$	1.8375	6.1359
	0.2	$5.8233\times {10}^{-3}$	$1.0769\times {10}^{-4}$	$1.7232\times {10}^{-1}$	$1.1791\times {10}^{-2}$	1.8062	6.9199
	0.3	$3.4843\times {10}^{-3}$	$6.5522\times {10}^{-5}$	$1.5323\times {10}^{-1}$	$1.0007\times {10}^{-2}$	1.7688	6.2609
	0.4	$1.5374\times {10}^{-3}$	$3.1802\times {10}^{-5}$	$1.4154\times {10}^{-1}$	$8.5870\times {10}^{-3}$	1.7188	5.8413
Classical Parallel	0.1	$1.4317\times {10}^{-3}$	$4.2833\times {10}^{-5}$	$1.3293\times {10}^{-1}$	$7.8025\times {10}^{-3}$	1.3375	4.7969
	0.2	$8.3872\times {10}^{-4}$	$2.5891\times {10}^{-5}$	$1.3196\times {10}^{-1}$	$7.7821\times {10}^{-3}$	1.3375	5.5666
	0.3	$4.1720\times {10}^{-4}$	$1.4159\times {10}^{-5}$	$1.3126\times {10}^{-1}$	$7.7674\times {10}^{-3}$	1.3375	5.7738
	0.4	$1.6622\times {10}^{-4}$	$8.0251\times {10}^{-6}$	$1.3085\times {10}^{-1}$	$7.7586\times {10}^{-3}$	1.3406	4.7526
Modern Parallel	0.1	$6.0380\times {10}^{-4}$	$2.1615\times {10}^{-5}$	$1.3061\times {10}^{-1}$	$7.7407\times {10}^{-3}$	3.0000	10.3976
	0.2	$8.3108\times {10}^{-4}$	$2.5046\times {10}^{-5}$	$1.3055\times {10}^{-1}$	$7.7404\times {10}^{-3}$	3.0000	10.1307
	0.3	$1.1571\times {10}^{-3}$	$2.8534\times {10}^{-5}$	$1.3007\times {10}^{-1}$	$7.7378\times {10}^{-3}$	2.9297	11.0316
	0.4	$1.6138\times {10}^{-4}$	$1.1869\times {10}^{-5}$	$1.3084\times {10}^{-1}$	$7.7536\times {10}^{-3}$	2.3078	7.8798

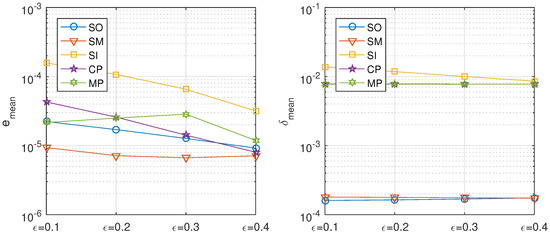
Figure 19. Fractional diffusion equation, mixed decomposition. Precision of the proposed methods: sequential iterative SI, classical parallel CP, and modern parallel MP, compared with the classical ones: sequential operator SO and Strang–Marchuk SM, for 20 temporal steps, 320 temporal steps, and different values of $ϵ$.

Remark 8.

For the fractional diffusion model, we could also obtain the same results as in the previous diffusion and Burgers’ equation. We could stabilize the schemes with respect to $ϵ\ne 0$ and obtain a good load balance of the matrices. Here, we could apply real-life problems with respect to the fractional differential equations, while we developped a stable novel parallel solver scheme.

6. Conclusions

In the paper, we have discussed the extensions of the iterative splitting approaches to parallel solver methods. Such novel methods allow for reducing the computational time. We can achieve the same accuracy as in the serial version. The improvements are obtained with larger time-steps and additional iterative steps, where we could reduce the computational time with the parallel methods. The benefit is, of course, the balance to multiple processors with additional memories. Further, we could apply the resources to improve with additional steps the accuracy of the approximations. We circumvent the problem of the memory of the algorithm, see [38], which we have if we only apply a serial method. Based on the parallel distribution, we have additional iterative steps for each processor and we distribute such a memory to all processors. For large scale numerical experiments, we could present the benefit of the parallel resources.

In our proposed iterative methods, we gain accuracy if we apply more iterative cycles, so that we have to devote additional computational time. We could reduce the computational cost more than with serial iterative methods due to the application of parallel ideas. On the other hand, it is important to optimize the parallel amount of work with additional adaptive and distributed ideas that improve the efficiency of the proposed parallel methods.

In summary, we optimize the reduction of computational time and the results accuracy with the help of parallel iterative splitting methods. In the future, we will consider more real-life problems and stochastic processes. Furthermore, we will extend the parallel iterative methods to more efficient adaptive schemes.