Expanded Fréchet Model: Mathematical Properties, Copula, Different Estimation Methods, Applications and Validation Testing

Abstract

The extreme value theory is expanded by proposing and studying a new version of the Fréchet model. Some new bivariate type extensions using Farlie–Gumbel–Morgenstern copula, modified Farlie–Gumbel–Morgenstern copula, Clayton copula, and Renyi’s entropy copula are derived. After a quick study for its properties, different non-Bayesian estimation methods under uncensored schemes are considered, such as the maximum likelihood estimation method, Anderson–Darling estimation method, ordinary least square estimation method, Cramér–von-Mises estimation method, weighted least square estimation method, left-tail Anderson–Darling estimation method, and right-tail Anderson–Darling estimation method. Numerical simulations were performed for comparing the estimation methods using different sample sizes for three different combinations of parameters. The Barzilai–Borwein algorithm was employed via a simulation study. Three applications were presented for measuring the flexibility and the importance of the new model for comparing the competitive distributions under the uncensored scheme. Using the approach of the Bagdonavicius–Nikulin goodness-of-fit test for validation under the right censored data, we propose a modified chi-square goodness-of-fit test for the new model. The modified goodness-of-fit statistic test was applied for the right censored real data set, called leukemia free-survival times for autologous transplants. Based on the maximum likelihood estimators on initial data, the modified goodness-of-fit test recovered the loss in information while the grouping data and followed chi-square distributions. All elements of the modified goodness-of-fit criteria tests are explicitly derived and given.

1. Introduction

The extreme value theory (EVT) was firstly introduced by [1] then followed by [2] and completed by [3,4]. The EVT is devoted to stochastic series of independent and identical distributed (iid) random variables (RVs). The EVT was originally devoted toward studying the behavior of extreme values (EVs), even though these extremes have a very low chance to appear, these EVs can turn out to have a very high effect to the observed experiment. Insurance and finance are the best fields of research to observe the importance of extreme events in EVT. The EVT started in the last century as an equivalent theory to the central limit theory (CLT), which was devoted toward studying the asymptotic distribution of the average of a sequence of RVs. Assume that $Z_1$, $Z_2$, $\dots$, $Z_n$ is a sequence of iid-RVs with common cumulative distribution function (CDF) $F(\cdot )$. One of the most interesting statistics is the sample maximum $S_{1:n}=max\left\{Z_1,Z_2,\dots ,Z_n\right\}.$ One is interested in the behavior of $M_{1:n}$ as the sample size $n$ increases to infinity.

$$Pr\left\{M_{1:n}\le z\right\}=Pr\left\{Z_1\le z,Z_2\le z,\dots ,Z_n\le z,\right\},$$

(1)

then,

$$Pr\left\{M_{1:n}\le z\right\}=Pr\left\{Z_1\le z\right\}Pr\left\{Z_2\le z\right\}\dots Pr\left\{Z_n\le z\right\}=F{\left(z\right)}^n.$$

(2)

Suppose there are sequences of constants $\left\{A_{1:n}|A_{1:n}⟩0\right\}$ and $\left\{B_{1:n}\right\}$, such that

$$Pr\left\{\frac{S_{1:n}-B_{1:n}}{A_{1:n}}\le z\right\}\to G\left(z\right)\mathrm{as}n\to \infty .$$

(3)

Then, for any non-degenerate CDF, it will belong to one of the three main types of classic extreme value families, which include the Gumbel, Fréchet, and Weibull distributions. The Fréchet (F) model is one of the most important distributions in modeling extreme values. The F model was originally proposed by [1]. It has many applications, in ranging, accelerated life testing, earthquakes, floods, wind speed, horse racing, rainfall, queues in supermarkets, and sea waves. One can find more details about the F model in the literature, for example [5] investigated the exponentiated F distribution. Moreover, [6] discussed the odd Chen F random variables (RVs), [7] defined and applied a new version of the F distribution for relief times and survival times data. Eliwa et al. [8] proposed the exponentiated odd Chen F distribution, [9] proposed some applications of the Marshall–Olkin F (MO-F) distribution, [10] investigated the odd flexible Weibull F distribution, among others. Many other useful F model extensions are defined and studied by [11,12,13,14,15,16].

In this article, we expanded the EVT with proposing and studying a new version the F model, called the odd-Burr generalized Fréchet (OB-F) model. The new model is derived based on compiling the standard F model with the odd-Burr generalized (OB-G) family (see [17]). Many new bivariate type extensions using the Farlie–Gumbel–Morgenstern (FGM) copula, modified FGM copula, Clayton copula, and Renyi’s entropy copula, are derived. The bivariate type extensions may e useful in modeling the bivariate real data sets.

After a quick studying for its properties, different classical estimation methods under uncensored schemes are considered, such as the maximum likelihood estimation (MLE) method, Anderson–Darling estimation (ADE) method, ordinary least square estimation (OLSE) method, Cramér-von Mises estimation (CVME) method, weighted least square estimation (WLSE) method, left-tail Anderson–Darling estimation ($L{T}_{\left(ADE\right)}$) method, and right-tail Anderson–Darling estimation ($R{T}_{\left(ADE\right)}$) method. Numerical simulations are performed for comparing the estimation methods using different sample sizes for the three different combinations of parameters. The Barzilai–Borwein (BB) algorithm is employed via a simulation study for assessing the performance of the estimators with different sample sizes, as sample size tends to $\infty .$ Three applications for measuring the flexibility and the importance of the OB-F model are presented and are also used for comparing the competitive distributions under the uncensored scheme. Using the approach of the Bagdonavicius–Nikulin goodness-of-fit (BN-GOF) test for validation under the right censored data, we propose a modified chi-square GOF tests for the OB-F model. The modified GOF statistic test is applied for the right censored real data set, called leukemia free-survival times (in months) for autologous transplants. Based on the maximum likelihood estimators (MLEs) on initial data, the modified BN-GOF test recovers the loss in information, while the grouping data follow chi-square distributions. All elements of the modified BN-GOF criteria tests are explicitly derived and given.

A RV $Z$ is said to have the F distribution if its probability density function (PDF) and CDF are given by

$$g_{\theta }\left(z\right)=\theta z^{-\left(\theta +1\right)}exp\left(-z^{-\theta }\right){|}_{z\ge 0},$$

(4)

and

$$G_{\theta }\left(z\right)=exp\left(-z^{-\theta }\right){|}_{z\ge 0},$$

(5)

where $\theta >0$ is a shape parameter. For $\theta =2$ we get the Inverse Rayleigh (IR) model. Due to [17], the CDF of the OB-G family is given by

$$F_{a,b,\underset{\_}{\Phi }}\left(z\right)=1-\frac{{\overline{G}}_{\underset{\_}{\Phi }}{\left(z\right)}^{ab}}{{\left[G_{\underset{\_}{\Phi }}{\left(z\right)}^a+{\overline{G}}_{\underset{\_}{\Phi }}{\left(z\right)}^a\right]}^b},$$

(6)

where ${\overline{G}}_{\underset{\_}{\Phi }}\left(z\right)=1-G_{\underset{\_}{\Phi }}\left(z\right).$ The PDF corresponding to (6) is given by

$$f_{a,b,\underset{\_}{\Phi }}\left(z\right)=\frac{ab{g}_{\underset{\_}{\Phi }}\left(z\right)G_{\underset{\_}{\Phi }}{\left(z\right)}^{a-1}{\overline{G}}_{\underset{\_}{\Phi }}{\left(z\right)}^{ab-1}}{{\left[G_{\underset{\_}{\Phi }}{\left(z\right)}^a+{\overline{G}}_{\underset{\_}{\Phi }}{\left(z\right)}^a\right]}^{1+b}}.$$

(7)

For $b=1$, the OB-G family reduces to the Odd G (O-G) family (see [18]). For $a=1$, the OB-G family reduces to the proportional reversed hazard rate (PRHR) family (see [19]). In this work, we define and study a new Fréchet model based on OB-G family, called generalized odd log-logistic F (OB-F) model. The OB-F survival function (SF) is given by

$$S_{\underset{\_}{P}}\left(z\right)=\frac{{\left[1-exp\left(-z^{-\theta }\right)\right]}^{ab}}{{\left\{exp\left(-a{z}^{-\theta }\right)+{\left[1-exp\left(-z^{-\theta }\right)\right]}^a\right\}}^b},$$

(8)

where $S_{\underset{\_}{P}}\left(z\right)=1-F_{\underset{\_}{P}}\left(z\right){|}_{\left(\underset{\_}{P}=a,b,\theta \right)}.$ For $b=1$, the OB-F reduces to the O-F. For $a=1$, the OB-F reduces to the PRHR-F. The PDF corresponding to (8) is given by

$$f_{\underset{\_}{P}}\left(z\right)=\frac{ab\theta z^{-\left(\theta +1\right)}exp\left(-a{z}^{-\theta }\right){\left[1-exp\left(-z^{-\theta }\right)\right]}^{ab-1}}{{\left\{exp\left(-a{z}^{-\theta }\right)+{\left[1-exp\left(-z^{-\theta }\right)\right]}^a\right\}}^{1+b}}.$$

(9)

The hazard rate function (HRF) for the new model can be given from $f_{\underset{\_}{P}}\left(z\right)/S_{\underset{\_}{P}}\left(z\right)$. Let $c=\inf \left\{z{|}_{G\left(z;\underset{\_}{\Phi }\right)>0}\right\}$, the asymptotics of the CDF, PDF, and HRF as $z\to c$ are given by

$$F_{\underset{\_}{P}}\left(z\right)\sim bexp\left(-a{z}^{-\theta }\right){|}_{z\to c},$$

(10)

$$f_{\underset{\_}{P}}\left(z\right)\sim ab\theta z^{-\left(\theta +1\right)}exp\left(-a{z}^{-\theta }\right){|}_{z\to c}$$

(11)

and

$$h_{\underset{\_}{P}}\left(z\right)\sim ab\theta z^{-\left(\theta +1\right)}exp\left(-a{z}^{-\theta }\right){|}_{z\to c}.$$

(12)

The asymptotes of CDF, PDF, and HRF as $z\to \infty$ are given by

$$1-F_{\underset{\_}{P}}\left(z\right)\sim a^b{\left[1-exp\left(-z^{-\theta }\right)\right]}^b{|}_{z\to \infty },$$

(13)

$$f_{\underset{\_}{P}}\left(z\right)\sim b{a}^b\theta \frac{z^{-\left(\theta +1\right)exp\left(-z^{-\theta }\right)}}{{\left[1-exp\left(-z^{-\theta }\right)\right]}^{1-b}}{|}_{z\to \infty }$$

(14)

and

$$h_{\underset{\_}{P}}\left(z\right)\sim \frac{b\theta z^{-\left(\theta +1\right)}exp\left(-z^{-\theta }\right)}{1-exp\left(-z^{-\theta }\right)}{|}_{z\to \infty }.$$

(15)

For simulation of this new model, we obtain the quantile function (QF) of $Z$ (by inverting $F_{\underset{\_}{P}}\left(z\right)$ based on (8)), say $z_u=h\left(u\right)=F^{-1}\left(u\right)$, as

$$z_u={\left(-\ln \left\{\frac{{\left[1-{\left(u^{*}\right)}^{\frac{1}{b}}\right]}^{\frac{1}{a}}}{{\left(1-u\right)}^{\frac{1}{ab}}+{\left[1-{\left(u^{*}\right)}^{\frac{1}{b}}\right]}^{\frac{1}{a}}}\right\}\right)}^{-\frac{1}{\theta }}{|}_{u^{*}=1-u}.$$

(16)

Equation (16) is used for simulating the new model (see Section 5). The now OB-F model can be used in modeling extreme data, such as extreme floods, maximum sizes of ecological populations, the size of freak waves, the amount of large insurance losses, equity risks, day-to-day market risk, side effects of drugs (e.g., ximelagatran), survival times, large wildfires, repair data, and estimate fastest time of running (e.g., 100 m sprint) (see [11,12,13,14,15,16]).

2. Copula

For modeling the bivariate real data sets, we can consider the bivariate OB-F type generated via the FGM copula, modified FGM copula, Clayton copula, and Renyi’s entropy copula. Many other types of copula could be considered in separate works. In this section, we derive a new bivariate type OB-F (BOB-F) model using the theorems of FGM Copula, modified FGM Copula, Clayton Copula and Renyi’s entropy. The Multivariate OB-F (MvOB-F) type is also presented. However, future works may be allocated to study these new models. First, we consider the joint CDF of the FGM family, where $C_{\rho }\left(m,w\right)=mw\left(1+\rho m^{*}{w}^{*}\right){|}_{m^{*}=1-m},$ where the marginal function $m=F_1$, $w=F_2$, $\rho \in \left(-1,1\right)$ is a dependence parameter and for every $m,w\in \left(0,1\right)$, $C(m,0)=C(0,m)=0$ which is “grounded minimum” and $C\left(m,1\right)=m$ and $C\left(1,w\right)=w$ which is “grounded maximum”, $C\left(m_1,w_1\right)+C\left(m_2,w_2\right)-C\left(m_1,w_2\right)-C\left(m_2,w_1\right)\ge 0$.

2.1. Via FGM Copula

Due to [20,21,22,23], a Copula is continuous in $m$ and $w$ where

$$\left|C\left(m_2,w_2\right)-C\left(m_1,w_1\right)|\le |m_2-m_1|+|w_2-w_1\right|,$$

(17)

is the stronger Lipschitz condition. For $0\le m_1\le m_2\le 1$ and $0\le w_1\le w_2\le 1,$ we have

$$\stackrel{}{Pr}\left(m_1\le M\le m_2,w_1\le W\le w_2\right)=C\left(m_1,w_1\right)+C\left(m_2,w_2\right)-C\left(m_1,w_2\right)-C\left(m_2,w_1\right)\ge 0.$$

(18)

Then, setting $m^{*}=1-F_{{\underset{\_}{P}}_1}\left(x_1\right){|}_{\left[m^{*}=\left(1-m\right)\in \left(0,1\right)\right]}$ and $w^{*}=1-F_{{\underset{\_}{P}}_2}\left(x_2\right){|}_{\left[w^{*}=\left(1-w\right)\in \left(0,1\right)\right]}.$ We can easily obtain the joint CDF of the FGM family from

$$C_{\rho }\left(m,w\right)=mw\left(1+\rho m^{*}{w}^{*}\right){|}_{m^{*}=1-m}.$$

(19)

The joint PDF can then be derived from

$$c_{\rho }\left(m,w\right)=1+\rho m^{\cdot }{w}^{\cdot }{|}_{\left(m^{\cdot }=1-2m\mathrm{and}{w}^{\cdot }=1-2w\right)}$$

(20)

or from

$$f\left(x_1,x_2\right)=C\left(F_1,F_2\right)f_1{f}_2.$$

(21)

2.2. Via Modified FGM Copula

According to [24], the modified FGM copula is defined as

$$C_{\rho }\left(m,w\right)=mw\left[1+\rho \vee \left(m\right)\wedge \left(w\right)\right]{|}_{\rho \in \left(-1,1\right)}$$

(22)

or

$$C_{\rho }\left(m,w\right)=mw+\rho \dot{\vee }\left(m\right)\dot{\wedge }\left(w\right){|}_{\rho \in \left(-1,1\right)},$$

(23)

where $\dot{\vee }\left(m\right)=m\vee \left(m\right)$, and $\dot{\wedge }\left(w\right)=w\wedge \left(w\right)$, where $\vee \left(m\right)$ and $\wedge \left(w\right)$ are being two continuous functions on $\left(0,1\right)$ where $\vee \left(0\right)=\vee \left(1\right)=\wedge \left(0\right)=\wedge \left(1\right)=0.$ Let

$$c_1=inf\left\{\frac{\partial }{\partial m}\dot{\vee }\left(m\right)|t_1\left(m\right)\right\}<0,c_2=sup\left\{\frac{\partial }{\partial m}\dot{\vee }\left(m\right)|t_1\left(m\right)\right\}<0,$$

(24)

$$d_2=inf\left\{\frac{\partial }{\partial w}\dot{\wedge }\left(w\right)|t_2\left(w\right)\right\}>0and{d}_2=sup\left\{\frac{\partial }{\partial w}\dot{\wedge }\left(w\right)|t_2\left(w\right)\right\}>0.$$

(25)

Then, $1\le min\left({\mathrm{c}}_1{\mathrm{c}}_1,{\mathrm{d}}_2{\mathrm{d}}_2\right)\le \infty ,$ where

$$\frac{\partial }{\partial m}\vee \left(m\right)=\vee \left(m\right)+m\frac{\partial }{\partial m}\vee \left(m\right),$$

(26)

$$t_1\left(u\right)=\left\{m:m\in \left(0,1\right)|\frac{\partial \dot{\vee }\left(m\right)}{\partial m}\mathrm{exists}\right\}$$

(27)

and

$$t_2\left(w\right)=\left\{w:w\in \left(0,1\right)|\frac{\partial \dot{\wedge }\left(w\right)}{\partial w}\mathrm{exists}\right\}.$$

(28)

• Type-I

Recalling the following functional form for both $\vee \left(m\right)$ and $\wedge \left(w\right)$. Then, the BOB-F–FGM (Type-I) can be derived from

$$C_{\rho }\left(m,w\right)=mw+\rho \dot{\vee }\left(m\right)\dot{\wedge }\left(w\right){|}_{\rho \in \left(-1,1\right)}$$

(29)

where

$$\dot{\vee }\left(m\right)=m{S}_{{\underset{\_}{P}}_1}\left(m\right)\mathrm{and}\dot{\wedge }\left(w\right)=w{S}_{{\underset{\_}{P}}_2}\left(w\right).$$

(30)

• Type-II

Let $\vee {\left(m\right)}^{*}$ and $\wedge {\left(w\right)}^{*}$ be two functional forms satisfying all the conditions stated earlier where $\vee {\left(m\right)}^{*}{|}_{\left({\rho }_1>0\right)}={\left(1-m\right)}^{1-{\rho }_1}{m}^{{\rho }_1}$ and

$$\wedge {\left(w\right)}^{*}{|}_{\left({\rho }_2>0\right)}={\left(1-w\right)}^{1-{\rho }_2}{w}^{{\rho }_2}.$$

(31)

Then, the corresponding BOB-F–FGM (Type-II) can be derived from

$$C_{\rho ,{\rho }_1,{\rho }_2}\left(m,w\right)=mw\left[1+\rho \vee {\left(m\right)}^{*}\wedge {\left(w\right)}^{*}\right].$$

(32)

• Type-III

Let $\ddot{\vee }\left(m\right){|}_{m\in \left(0,1\right)}$ and $\ddot{\wedge }\left(w\right){|}_{w\in \left(0,1\right)}$ be two functional form for satisfy all the conditions stated earlier where

$$m^{-1}\ddot{\vee }\left(m\right)=\log \left(1+\dot{m}\right){|}_{\dot{m}+m=1}$$

(33)

and

$$w^{-1}\ddot{\wedge }\left(w\right)=\log \left(1+\dot{w}\right){|}_{\dot{w}+w=1}.$$

(34)

In this case, one can also derive a closed form expression for the associated CDF of the BOB-F–FGM (Type-III) from

$$C_{\rho }\left(m,w\right)=mw\left[1+\rho \ddot{\vee }\left(m\right)\ddot{\wedge }\left(m\right)\right].$$

(35)

• Type-IV

The CDF of the BOB-F–FGM (Type-IV) model can be derived from

$$C\left(m,w\right)=m{F}_{{\underset{\_}{P}}_2}^{-1}\left(w\right)+w{F}_{{\underset{\_}{P}}_1}^{-1}\left(m\right)-F_{{\underset{\_}{P}}_1}^{-1}\left(m\right)F_{{\underset{\_}{P}}_2}^{-1}\left(w\right)$$

(36)

where $F_{{\underset{\_}{P}}_1}^{-1}\left(m\right)$ and $\hspace{0.17em}{F}_{{\underset{\_}{P}}_2}^{-1}\left(w\right)$ can be derived using (16).

2.3. Via Clayton Copula

The Clayton Copula can be considered as

$$C\left(w_1,w_2\right)={\left[{\left(1/w_1\right)}^{\rho }+{\left(1/w_2\right)}^{\rho }-1\right]}^{-{\rho }^{-1}}{|}_{\rho \in \left(0,\infty \right)}.$$

(37)

Setting $w_1\in \left(0,1\right)=F_{{\underset{\_}{P}}_1}\left(t\right)$ and $w_2\in \left(0,1\right)=F_{{\underset{\_}{P}}_2}\left(x\right).$ Then, the BOB-F type can be derived from $C\left(w_1,w_2\right)=C\left(F_{{\underset{\_}{P}}_1}\left(t\right),F_{{\underset{\_}{P}}_2}\left(x\right)\right).$ Similarly, the MvOB-F ($m$-dimensional extension) from the above can be derived from

$$C\left(w_h\right)={\left({\displaystyle \sum }_{h=1}^m{w}_h^{-\rho }+1-m\right)}^{-{\rho }^{-1}}.$$

(38)

2.4. Via Renyi’s Entropy

Let $m\in \left(0,1\right)=F_{{\underset{\_}{P}}_1}\left(x_1\right)$ and $w\in \left(0,1\right)=F_{{\underset{\_}{P}}_2}\left(x_2\right).$ Then, using the theorem of [25], the Renyi’s entropy Copula can be expressed as

$$C\left(m,w\right)=x_{2}m+x_{1}w-x_1{x}_2.$$

(39)

Then, the associated BOB-F can be directly derived from $C\left(m,w\right)=C\left(F_{{\underset{\_}{P}}_1}\left(x_1\right),F_{{\underset{\_}{P}}_2}\left(x_2\right)\right)$.

3. Mathematical Properties

3.1. Useful Representations

Due to [17], the PDF in (9) can be expressed as

$$f\left(z\right)={\displaystyle \sum }_{\kappa =0}^{\infty }{\Delta }_{\kappa }{\pi }_{\left(1+\kappa \right)}\left(z;\theta \right),$$

(40)

where

$${\Delta }_{\kappa }=\frac{ab}{1+\kappa }{\displaystyle \sum }_{i_1,i_2=0}^{\infty }{\displaystyle \sum }_{i_3=\kappa }^{\infty }{\left(-1\right)}^{i_2+k+\kappa }\left(\begin{array}{c}-\left(1+b\right)\\ i_1\end{array}\right)\left(\begin{array}{c}-a\left(1+i_1\right)-1\\ i_2\end{array}\right)\left(\begin{array}{c}a\left(1+i_1\right)+i_2+1\\ i_3\end{array}\right)\left(\begin{array}{c}{i}_3\\ \kappa \end{array}\right),$$

(41)

and ${\pi }_{\left(1+\kappa \right)}\left(z;\theta \right)$ is the PDF of the F model with scale parameter ${\left(1+\kappa \right)}^{\frac{1}{\theta }}$ and shape parameter $\theta$. By integrating Equation (40), the CDF of $Z$ becomes

$$F\left(z\right)={\displaystyle \sum }_{\kappa =0}^{\infty }{\Delta }_{\kappa }{\Pi }_{\left(1+\kappa \right)}\left(z;\theta \right),$$

(42)

where ${\Pi }_{\left(1+\kappa \right)}\left(z;\theta \right)$ is the CDF of the F distribution with scale parameter ${\left(1+\kappa \right)}^{\frac{1}{\theta }}$ and shape parameter $\theta$.

3.2. Moments and Incomplete Moments

The ${\rho }^{th}$ ordinary moment of $Z$ is given by

$${\mu }_{\rho }^{\prime }=E\left(Z^{\rho }\right)=\hspace{0.17em}\underset{-\infty }{\overset{\infty }{{\displaystyle \int }}}{z}^{\rho }f\left(z\right)dz,$$

(43)

then we obtain

$${\mu }_{\rho }^{\prime }{|}_{\left(\theta >\rho \right)}={\displaystyle \sum }_{\kappa =0}^{\infty }{\Delta }_{\kappa }^{\left(\rho ,\theta \right)}\Gamma \left(1-\frac{\rho }{\theta }\right),$$

(44)

where ${\mathsf{\Delta }}_{\kappa }^{\left(\rho ,\theta \right)}={\mathsf{\Delta }}_{\kappa }{\left(1+\kappa \right)}^{\frac{\rho }{\theta }}$ and $\Gamma \left(1+\delta \right){|}_{\left(\delta \in R^{+}\right)}=\delta !={\displaystyle \prod }_{h=0}^{\delta -1}\left(\delta -h\right).$ Setting $\rho =1,2,3$ and $4$ in (44), we have

$$\begin{array}{c}E\left(Z\right){|}_{\left(\theta >1\right)}={\displaystyle {\displaystyle \sum }_{\kappa =0}^{\infty }}{\mathsf{\Delta }}_{\kappa }^{\left(1,\theta \right)}\Gamma \left(1-\frac{1}{\theta }\right),E\left(Z^2\right){|}_{\left(\theta >2\right)}={\displaystyle {\displaystyle \sum }_{\kappa =0}^{\infty }}{\mathsf{\Delta }}_{\kappa }^{\left(2,\theta \right)}\Gamma \left(1-\frac{2}{\theta }\right),\\ E\left(Z^3\right){|}_{\left(\theta >3\right)}={\displaystyle {{\displaystyle \sum }}_{\kappa =0}^{\infty }}{\mathsf{\Delta }}_{\kappa }^{\left(3,\theta \right)}\Gamma \left(1-\frac{3}{\theta }\right)\mathrm{and}E\left(Z^4\right){|}_{\left(\theta >4\right)}={\displaystyle {{\displaystyle \sum }}_{\kappa =0}^{\infty }}{\Delta }_{\kappa }^{\left(4,\theta \right)}\Gamma \left(1-\frac{4}{\theta }\right),\end{array}$$

(45)

where $E\left(Z\right)={\mu }_1^{\prime }$ is the mean of $Z$. The ${\rho }^{th}$ incomplete moment, say ${\varphi }_{\rho }\left(\tau \right)$, of $Z$ can be expressed, from (42), as

$${\varphi }_{\rho }\left(\tau \right)=\underset{-\infty }{\overset{\tau }{{\displaystyle \int }}}{z}^{\rho }f\left(z\right)dz={\displaystyle \sum }_{\kappa =0}^{\infty }{\Delta }_{\kappa }\underset{-\infty }{\overset{\tau }{{\displaystyle \int }}}{z}^{\rho }{\pi }_{\left(1+\kappa \right)}\left(z;\theta \right)dz$$

(46)

then

$${\varphi }_{\rho }\left(\tau \right){|}_{\left(\theta >\rho \right)}={\displaystyle \sum }_{\kappa =0}^{\infty }{\Delta }_{\kappa }^{\left(\rho ,\theta \right)}\gamma \left(1-\frac{\rho }{\theta },\left(1+\kappa \right){\left(a/\tau \right)}^{\theta }\right),$$

(47)

where $\gamma \left(\delta ,\rho \right)$ is the incomplete gamma function.

$$\gamma \left(\delta ,\rho \right){|}_{\left(\delta \ne 0,-1,-2,\dots \right)}=\underset{0}{\overset{\rho }{{\displaystyle \int }}}{z}^{\delta -1}exp\left(-z\right)dz={\displaystyle \sum }_{\kappa =0}^{\infty }{\rho }^{\delta +\kappa }\frac{{\left(-1\right)}^{\kappa }}{\kappa !\left(\delta +\kappa \right)},$$

(48)

The first incomplete moment given by (11) with $\rho =1$ as

$${\varphi }_1\left(\tau \right){|}_{\left(\theta >1\right)}={\displaystyle \sum }_{\kappa =0}^{\infty }{\Delta }_{\kappa }^{\left(1,\theta \right)}\Gamma \left(1-\frac{1}{\theta },\left(1+\kappa \right){\left(a/\tau \right)}^{\theta }\right).$$

(49)

3.3. Moment Generating Function (MGF)

The MGF $M_Z\left(\tau \right)=E\left(exp\left(\tau Z\right)\right)$ of $Z$ can be derived from equation (40) as

$$M_Z\left(\tau \right)={\displaystyle \sum }_{\kappa =0}^{\infty }{\Delta }_{\kappa }{M}_{\left(1+\kappa \right)}\left(\tau ;\theta \right),$$

(50)

where $M_{\left(1+\kappa \right)}\left(\tau ;\theta \right)$ is the MGF of the F model with scale parameter ${\left(1+\kappa \right)}^{\frac{1}{\theta }}$ and shape parameter $\theta$, then

$$M_Z\left(\tau \right){|}_{\left(\theta >\rho \right)}={\displaystyle \sum }_{\kappa =0}^{\infty }{\displaystyle \sum }_{\rho =0}^{\infty }{\Delta }_{\kappa }^{\left(\rho ,\theta \right)}\frac{{\tau }^{\rho }}{\rho !}\Gamma \left(1-\frac{\rho }{\theta }\right).$$

(51)

3.4. Residual Life and Reversed Residual Life Functions

The $h^{th}$ moment of the residual life can be derived using

$$w_h\left(\tau \right)=E\left[{(Z-\tau )}^h\hspace{0.17em}{|}_{Z>\tau ,h=1,2,\dots }\right].$$

(52)

Then, the $h^{th}$ moment of the residual life of $Z$ is given also by

$$w_h\left(\tau \right)=\frac{1}{1-F\left(\tau \right)}\underset{\tau }{\overset{\infty }{{\displaystyle \int }}}{(Z-\tau )}^{h}dF\left(Z\right).$$

(53)

Therefore, using (40), we have

$$w_h\left(\tau \right)=\frac{1}{1-F\left(\tau \right)}{\displaystyle \sum }_{\kappa =0}^{\infty }{\Delta }_{\kappa }^{\left(h,\theta \right)*}\Gamma \left(1-\frac{h}{\theta },\left(1+\kappa \right){\left(a/\tau \right)}^{\theta }\right){|}_{\theta >h},$$

(54)

where ${\Delta }_{\kappa }^{\left(h,\theta \right)*}={\Delta }_{\kappa }{\displaystyle \sum }_{\rho =0}^h\left(\begin{array}{c}h\\ \rho \end{array}\right){\left(-\tau \right)}^h,$ $\Gamma \left(\delta ,\rho \right){|}_{\rho >0}=\underset{\rho }{\overset{\infty }{{\displaystyle \int }}}{z}^{\delta -1}exp\left(-z\right)dz$ and $\Gamma \left(\delta ,\rho \right)=\Gamma \left(\delta \right)-\gamma \left(\delta ,\rho \right)$.

Analogously, the $h^{th}$ moment of the reversed residual life is

$$W_h\left(\tau \right)=E\left[{(\tau -Z)}^h\hspace{0.17em}{|}_{Z\le \tau ,\tau >0\mathrm{and}h=1,2,\dots }\right]\hspace{0.17em}$$

(55)

uniquely determines $F\left(z\right)$. We obtain $W_h\left(\tau \right)=\frac{1}{F\left(\tau \right)}\underset{0}{\overset{\tau }{{\displaystyle \int }}}{(\tau -Z)}^{h}dF\left(z\right).$ Then, the $h^{th}$ moment of the reversed residual life of $Z$ becomes

$$W_h\left(\tau \right)=\frac{1}{F\left(\tau \right)}{\displaystyle \sum }_{\kappa =0}^{\infty }{\Delta }_{\kappa }^{\left(h,\theta \right)**}\gamma \left(1-\frac{h}{\theta },\left(1+\kappa \right){\left(a/\tau \right)}^{\theta }\right){|}_{\theta >h},$$

(56)

where ${\Delta }_{\kappa }^{\left(h,\theta \right)**}={\Delta }_{\kappa }\stackrel{h}{\underset{\rho =0}{{{\displaystyle \sum }}^{}}}{\left(-1\right)}^{\rho }\left(\begin{array}{c}h\\ \rho \end{array}\right){\tau }^{h-\rho }.$

3.5. Numerical Calculations and Relevant Analysis

Numerical analysis for the mean $\left[E\left(Z\right)\right]$, variance $\left[\mathrm{Var}\left(Z\right)\right]$, skewness $\left[Skew\left(Z\right)\right]$, kurtosis $\left[Kur\left(Z\right)\right],{\varphi }_1\left(1000\right)$ and ${\varphi }_2\left(1000\right)$ are calculated in Table 1 (for the OB-F model) and Table 2 (for the F model) for some carefully selected parameters value. Based on Table 1 and Table 2 we note that, the ${\mathrm{Skew}}_{\mathrm{OB}-\mathrm{F}}\left(Z\right)\in$($5.78075$, $\infty$), whereas the ${\mathrm{Skew}}_{\mathrm{F}}\left(Z\right)\in$(1.199258, 5.601109). Further, the spread for the ${\mathrm{Kur}}_{\mathrm{OB}-\mathrm{F}}\left(Z\right)$ is ranging from nearly 39.75302 to nearly $\infty$, whereas the spread for the ${\mathrm{Kur}}_{\mathrm{F}}\left(Z\right)$ only varies from 5.69888 to 54524.95. Based on Table 1, the 1st and the 2nd incomplete moments ${\varphi }_1\left(1000\right)$ and ${\varphi }_2\left(1000\right)$ decreases as $a,b$ and $\theta$ increases. Based on Table 2, the 1st and the 2nd incomplete moments ${\varphi }_1\left(1000\right)$ and ${\varphi }_2\left(1000\right)$ decreases as $\theta$ increases.

Table 1. E(Z), Var(Z), Skew(Z) and Kur(Z) of the GOLLRW model.

$\mathit{a}$	$\mathit{b}$	$\mathit{\theta }$	E(Z)	Var(Z)	Skew(Z)	Kur(Z)	${\mathit{\varphi }}_1\left(1000\right)$	${\mathit{\varphi }}_2\left(1000\right)$
1	0.5	0.25	24575.64	10930984115	5.873463	40.9488	24575.64	11534945965
5			336.9234	86392744	61.89353	4675.322	336.9234	86506262
10			11.25069	60850.12	1681.481	4309801	11.25069	60976.70
50			1.9$\times {10}^{-14}$	2.1$\times {10}^{-11}$	$\cong \infty$	$\cong \infty$	1.92903$\times {10}^{-14}$	2.09453$\times {10}^{-11}$
2	0.05	1.25	25403.99	11209836646	5.78075	39.75302	25403.99	11855199133
	0.15		3374.045	1286326804.0	17.1300	345.0779	3374.045	1297710986
	0.25		296.3798	80743061	64.40085	5042.712	296.3798	80830902
	0.35		39.3637	4372214.0	253.2212	82348.29	39.3637	4373764
5	0.5	0.01	5266.967	2675972773	12.82974	186.0085	5266.967	2703713717
		0.25	336.9234	86392744.0	61.89353	4675.322	336.9234	86506262
		0.35	37.53839	4461785	249.7617	80324.18	37.53839	4463194
		0.45	9.305143	230220.7	970.2972	1318254	9.305143	230307.3
		0.5	6.235529	52934.94	1859.104	5140488	6.235529	52973.83
		0.55	4.731619	12405.41	3448.200	19161060	4.731619	12427.8
0.5	0.5	0.5	23851.02	10675812761	5.960493	42.09073	23851.02	11244684106
1	1	1	13.2383	999816.3000	500.0971	333428.8	13.2383	999991.6000
0.15	0.15	1	14391.58	6992893577	7.685724	68.12830	14391.6	7200011193
0.25	0.05	0.25	2073.379	1038694167	20.62117	479.5531	2073.379	1042993067
0.01	0.01	0.01	0.7453203	371968.3000	1092.416	1342959	0.745320	371968.9000

Table 2. E(Z), Var(Z), Skew(Z) and Kur(Z) of the RW model.

$\mathit{\theta }$	E(Z)	Var(Y)	Skew(Z)	Kur(Z)	${\mathit{\varphi }}_1\left(1000\right)$	${\mathit{\varphi }}_2\left(1000\right)$
4.001	1.22533	0.270577	5.60111	54524.95	1.225334	1.772017
4.010	1.22459	0.268511	5.56508	5436.60	1.224588	1.768125
4.100	1.21739	0.249111	5.23632	529.592	1.217387	1.731142
4.250	1.20633	0.221216	4.79036	204.831	1.206332	1.676453
4.500	1.19015	0.184256	4.23884	98.8015	1.190151	1.600716
5	1.16423	0.133761	3.53507	48.0915	1.16423	1.489192
7	1.10577	0.053272	2.42510	17.5340	1.105767	1.275993
10	1.06863	0.022262	1.91034	10.9786	1.068629	1.164230
12	1.05555	0.014609	1.74981	9.46172	3.368633$\times {10}^{-5}$	1.128787
15	1.04317	0.008858	1.60525	8.28249	1.213482$\times {10}^{-6}$	3.957999$\times {10}^{-6}$
20	1.03145	0.0047328	1.47388	7.33349	4.382908$\times {10}^{-9}$	1.429566$\times {10}^{-8}$
25	1.02473	0.0029403	1.40049	6.85240	1.4841$0\times {10}^{-11}$	4.840664$\times {10}^{-11}$
30	1.02037	0.0020027	1.35357	6.56231	4.824307$\times {10}^{-14}$	1.573536$\times {10}^{-13}$
35	1.01732	0.0014515	1.32097	6.36853	1.524658$\times {10}^{-16}$	4.972951 $\times {10}^{-16}$
45	1.01333	0.0008625	1.27863	6.12607	1.438461$\times {10}^{-21}$	4.691805$\times {10}^{-21}$
55	1.010827	0.000571	1.252304	5.98124	1.290118$\times {10}^{-26}$	4.207958$\times {10}^{-26}$
65	1.009118	0.000406	1.234393	5.88325	1.118823$\times {10}^{-31}$	3.649247$\times {10}^{-31}$
75	1.007874	0.000303	1.221374	5.81438	9.473066$\times {10}^{-37}$	3.089815$\times {10}^{-36}$
85	1.006929	0.0002349	1.211503	5.76240	7.878245$\times {10}^{-42}$	2.569635$\times {10}^{-41}$
95	1.006187	0.0001874	1.203757	5.72214	6.461233$\times {10}^{-47}$	2.10745$\times {10}^{-46}$
100	1.00587	0.000169	1.20048	5.70518	1.842394$\times {10}^{-49}$	6.009306$\times {10}^{-49}$
102	1.00576	0.0001623	1.19926	5.69890	1.76644$0\times {10}^{-50}$	5.761569$\times {10}^{-50}$

4. Classical Estimation under Uncensored Scheme

4.1. The MLE Method

Let $z_1,z_2,\dots ,z_h$ be a random sample from size $h$ from the OB-F distribution with parameters $a,b\hspace{0.17em}$ and $\theta$. Let ${\underset{\_}{P}}^{\mathrm{T}}$ be the $3\times 1$ parameter vector. For determining the MLE of $\underset{\_}{P}$, we have the log-likelihood function

$$\begin{array}{c}\ell =\ell \left(\underset{\_}{P}\right)=h\log \left(ab\theta \right)-\left(\theta +1\right){\displaystyle {\displaystyle \sum }_{i=1}^h}\log \left(z_{\left[i,h\right]}\right)-ab{\displaystyle {\displaystyle \sum }_{i=1}^h}{z}_{\left[i,h\right]}^{-\theta }\\ +2{\displaystyle {\displaystyle \sum }_{i=1}^h}\log \left(\begin{array}{c}exp\left[-ab{z}_{\left[i,h\right]}^{-\theta }\right]\\ +{\left\{1-exp\left[-b{z}_{\left[i,h\right]}^{-\theta }\right]\right\}}^a\end{array}\right)+\left(a-1\right){\displaystyle {\displaystyle \sum }_{i=1}^h}\log \left\{1-exp\left[-b{z}_{\left[i,h\right]}^{-\theta }\right]\right\}.\end{array}$$

(57)

The components of the score vector is available if needed. Setting $L_a=L_b=L_{\theta }=0$ and solving them simultaneously yields the MLE, where $L_s=\partial \ell /\partial s$. To solve these equations, it is usually more convenient to use nonlinear optimization methods, such as the quasi-Newton algorithm to numerically maximize $\ell$. For interval estimation of the parameters, we obtain the $3\times 3$ observed information matrix

$$J\left(\underset{\_}{P}\right)=\left\{{\partial }^2\ell /\partial r\partial s\right\}{|}_{\left(r,s=a,b,\theta \right)},$$

(58)

whose elements can be computed numerically.

4.2. The CVME Method

The CVME of the parameters $\underset{\_}{P}$ are obtained via minimizing the following expression with respect to (WRT) to the parameters $\underset{\_}{P}$ respectively, where

$$CV{M}_{\left(\underset{\_}{P}\right)}=\frac{1}{12}{h}^{-1}+{\displaystyle \sum }_{i=1}^h{\left[F_{\underset{\_}{P}}\left(z_{\left[i,h\right]}\right)-c_{\left(h,i\right)}^{\left[1\right]}\right]}^2,$$

(59)

where $c_{\left(h,i\right)}^{\left[1\right]}=\frac{2i-1}{2h}$ and

$$CV{M}_{\left(\underset{\_}{P}\right)}={\displaystyle \sum }_{i=1}^h{\left\{1-\frac{{\left[1-exp\left(-z_{\left[i,h\right]}^{-\theta }\right)\right]}^{ab}}{{\left\{exp\left(-a{z}_{\left[i,h\right]}^{-\theta }\right)+{\left[1-exp\left(-z_{\left[i,h\right]}^{-\theta }\right)\right]}^a\right\}}^b}-c_{\left(h,i\right)}^{\left[1\right]}\right\}}^2.$$

(60)

Then, the CVME of the parameters $\underset{\_}{P}$ are obtained by solving the two following non-linear equations

$$0={\displaystyle \sum }_{i=1}^h{\delta }_{\left(a\right)}\left(z_{\left[i,h\right]},\underset{\_}{P}\right)\left\{1-\frac{{\left[1-exp\left(-z_{\left[i,h\right]}^{-\theta }\right)\right]}^{ab}}{{\left\{exp\left(-a{z}_{\left[i,h\right]}^{-\theta }\right)+{\left[1-exp\left(-z_{\left[i,h\right]}^{-\theta }\right)\right]}^a\right\}}^b}-c_{\left(h,i\right)}^{\left[1\right]}\right\},$$

(61)

$$0={\displaystyle \sum }_{i=1}^h{\delta }_{\left(b\right)}\left(z_{\left[i,h\right]},\underset{\_}{P}\right)\left\{1-\frac{{\left[1-exp\left(-z_{\left[i,h\right]}^{-\theta }\right)\right]}^{ab}}{{\left\{exp\left(-a{z}_{\left[i,h\right]}^{-\theta }\right)+{\left[1-exp\left(-z_{\left[i,h\right]}^{-\theta }\right)\right]}^a\right\}}^b}-c_{\left(h,i\right)}^{\left[1\right]}\right\},$$

(62)

and

$$0={\displaystyle \sum }_{i=1}^h{\delta }_{\left(\theta \right)}\left(z_{\left[i,h\right]},\underset{\_}{P}\right)\left\{1-\frac{{\left[1-exp\left(-z_{\left[i,h\right]}^{-\theta }\right)\right]}^{ab}}{{\left\{exp\left(-a{z}_{\left[i,h\right]}^{-\theta }\right)+{\left[1-exp\left(-z_{\left[i,h\right]}^{-\theta }\right)\right]}^a\right\}}^b}-c_{\left(h,i\right)}^{\left[1\right]}\right\},$$

(63)

where ${\delta }_{\left(a\right)}\left(z_{\left[i,h\right]},\underset{\_}{P}\right)=\partial F_{\underset{\_}{P}}\left(z_{\left[i,h\right]}\right)/\partial a,$ ${\delta }_{\left(b\right)}\left(z_{\left[i,h\right]},\underset{\_}{P}\right)=\partial F_{\underset{\_}{P}}\left(z_{\left[i,h\right]}\right)/\partial b$ and ${\delta }_{\left(\theta \right)}\left(z_{\left[i,h\right]},\underset{\_}{P}\right)=\partial F_{\underset{\_}{P}}\left(z_{\left[i,h\right]}\right)/\partial \theta$.

4.3. OLS Method

Let $F_{\underset{\_}{P}}\left(z_{\left[i,h\right]}\right)$ denotes the CDF of OB-F model and let $z_1<z_2<\cdots <z_h$ be the $h$ ordered RS. The OLSEs are obtained upon minimizing

$$OLSE\left(\underset{\_}{P}\right)={\displaystyle \sum }_{i=1}^h{\left[F_{\underset{\_}{P}}\left(z_{\left[i,h\right]}\right)-c_{\left(h,i\right)}^{\left[2\right]}\right]}^2,$$

(64)

then, we have

$$OLSE\left(\underset{\_}{P}\right)={\displaystyle \sum }_{i=1}^h{\left\{1-\frac{{\left[1-exp\left(-z_{\left[i,h\right]}^{-\theta }\right)\right]}^{ab}}{{\left\{exp\left(-a{z}_{\left[i,h\right]}^{-\theta }\right)+{\left[1-exp\left(-z_{\left[i,h\right]}^{-\theta }\right)\right]}^a\right\}}^b}-c_{\left(h,i\right)}^{\left[2\right]}\right\}}^2,$$

(65)

where $c_{\left(h,i\right)}^{\left[2\right]}=\frac{i}{h+1}$.The LSEs are obtained via solving the following non-linear equations

$$0={\displaystyle \sum }_{i=1}^h{\delta }_{\left(a\right)}\left(z_{\left[i,h\right]},\underset{\_}{P}\right)\left\{1-\frac{{\left[1-exp\left(-z_{\left[i,h\right]}^{-\theta }\right)\right]}^{ab}}{{\left\{exp\left(-a{z}_{\left[i,h\right]}^{-\theta }\right)+{\left[1-exp\left(-z_{\left[i,h\right]}^{-\theta }\right)\right]}^a\right\}}^b}-c_{\left(h,i\right)}^{\left[2\right]}\right\},$$

(66)

$$0={\displaystyle \sum }_{i=1}^h{\delta }_{\left(b\right)}\left(z_{\left[i,h\right]},\underset{\_}{P}\right)\left\{1-\frac{{\left[1-exp\left(-z_{\left[i,h\right]}^{-\theta }\right)\right]}^{ab}}{{\left\{exp\left(-a{z}_{\left[i,h\right]}^{-\theta }\right)+{\left[1-exp\left(-z_{\left[i,h\right]}^{-\theta }\right)\right]}^a\right\}}^b}-c_{\left(h,i\right)}^{\left[2\right]}\right\}$$

(67)

and

$$0={\displaystyle \sum }_{i=1}^h{\delta }_{\left(\theta \right)}\left(z_{\left[i,h\right]},\underset{\_}{P}\right)\left\{1-\frac{{\left[1-exp\left(-z_{\left[i,h\right]}^{-\theta }\right)\right]}^{ab}}{{\left\{exp\left(-a{z}_{\left[i,h\right]}^{-\theta }\right)+{\left[1-exp\left(-z_{\left[i,h\right]}^{-\theta }\right)\right]}^a\right\}}^b}-c_{\left(h,i\right)}^{\left[2\right]}\right\},$$

(68)

where ${\delta }_{\left(a\right)}\left(z_{\left[i,h\right]},\underset{\_}{P}\right),$ ${\delta }_{\left(b\right)}\left(z_{\left[i,h\right]},\underset{\_}{P}\right)$ and ${\delta }_{\left(\theta \right)}\left(z_{\left[i,h\right]},\underset{\_}{P}\right)$ defined above.

4.4. WLSE Method

The WLSE is obtained by minimizing the function $WLSE\left(\underset{\_}{P}\right)$ WRT $\underset{\_}{P}$

$$WLSE\left(\gamma ,b,a\right)={\displaystyle \sum }_{i=1}^h{c}_{\left(h,i\right)}^{\left[3\right]}{\left[F_{\underset{\_}{P}}\left(z_{\left[i,h\right]}\right)-c_{\left(h,i\right)}^{\left[2\right]}\right]}^2,$$

(69)

where

$$c_{\left(h,i\right)}^{\left[3\right]}=\left[{(1+h)}^2\left(2+h\right)\right]/\left[i\left(1+h-i\right)\right].$$

(70)

The WLSEs are obtained by solving

$$0={\displaystyle \sum }_{i=1}^h{\delta }_{\left(a\right)}\left(z_{\left[i,h\right]},\underset{\_}{P}\right)c_{\left(h,i\right)}^{\left[3\right]}\left\{1-\frac{{\left[1-exp\left(-z_{\left[i,h\right]}^{-\theta }\right)\right]}^{ab}}{{\left\{exp\left(-a{z}_{\left[i,h\right]}^{-\theta }\right)+{\left[1-exp\left(-z_{\left[i,h\right]}^{-\theta }\right)\right]}^a\right\}}^b}-c_{\left(h,i\right)}^{\left[2\right]}\right\},$$

(71)

$$0={\displaystyle \sum }_{i=1}^h{\delta }_{\left(b\right)}\left(z_{\left[i,h\right]},\underset{\_}{P}\right)c_{\left(h,i\right)}^{\left[3\right]}\left\{1-\frac{{\left[1-exp\left(-z_{\left[i,h\right]}^{-\theta }\right)\right]}^{ab}}{{\left\{exp\left(-a{z}_{\left[i,h\right]}^{-\theta }\right)+{\left[1-exp\left(-z_{\left[i,h\right]}^{-\theta }\right)\right]}^a\right\}}^b}-c_{\left(h,i\right)}^{\left[2\right]}\right\}$$

(72)

and

$$0={\displaystyle \sum }_{i=1}^h{\delta }_{\left(\theta \right)}\left(z_{\left[i,h\right]},\underset{\_}{P}\right)c_{\left(h,i\right)}^{\left[3\right]}\left\{1-\frac{{\left[1-exp\left(-z_{\left[i,h\right]}^{-\theta }\right)\right]}^{ab}}{{\left\{exp\left(-a{z}_{\left[i,h\right]}^{-\theta }\right)+{\left[1-exp\left(-z_{\left[i,h\right]}^{-\theta }\right)\right]}^a\right\}}^b}-c_{\left(h,i\right)}^{\left[2\right]}\right\},$$

(73)

where ${\delta }_{\left(a\right)}\left(z_{\left[i,h\right]},\underset{\_}{P}\right),$ ${\delta }_{\left(b\right)}\left(z_{\left[i,h\right]},\underset{\_}{P}\right)$ and ${\delta }_{\left(\theta \right)}\left(z_{\left[i,h\right]},\underset{\_}{P}\right)$ defined above.

4.5. The ADE Method

The ADE are obtained by minimizing the function

$$ADE\left(\underset{\_}{P}\right)=-h-h^{-1}{\displaystyle \sum }_{i=1}^h\left(2i-1\right)\left\{\log F_{\underset{\_}{P}}\left(z_{\left[i,h\right]}\right)+\log {\overline{F}}_{\underset{\_}{P}}\left(z_{\left[-i+1+h\hspace{0.17em}\hspace{0.17em}:\hspace{0.17em}\hspace{0.17em}h\right]}\right)\right\}.$$

(74)

where

$${\overline{F}}_{\underset{\_}{P}}\left(z_{\left[-i+1+h\hspace{0.17em}\hspace{0.17em}:\hspace{0.17em}\hspace{0.17em}h\right]}\right)=\left[1-F_{\underset{\_}{P}}\left(z_{\left[-i+1+h\hspace{0.17em}\hspace{0.17em}:\hspace{0.17em}\hspace{0.17em}h\right]}\right)\right].$$

(75)

The parameter estimates follow by solving the nonlinear equations

$$0=\frac{\partial }{\partial a}\left[ADE\left(\underset{\_}{P}\right)\right]=\frac{\partial }{\partial b}\left[ADE\left(\underset{\_}{P}\right)\right]=\frac{\partial }{\partial \theta }\left[ADE\left(\underset{\_}{P}\right)\right].$$

(76)

4.6. The $R{T}_{\left(ADE\right)}$ Method

The $R{T}_{\left(ADE\right)}$ are obtained by minimizing

$$R{T}_{\left(ADE\right)}\left(a,b,\theta \right)=\frac{1}{2}h-2{\displaystyle \sum }_{i=1}^h{F}_{\underset{\_}{P}}\left(z_{\left[i,h\right]}\right)-\frac{1}{h}{\displaystyle \sum }_{i=1}^h\left(2i-1\right)\left\{\log {\overline{F}}_{\underset{\_}{P}}\left(z_{\left[-i+1+h\hspace{0.17em}\hspace{0.17em}:\hspace{0.17em}\hspace{0.17em}h\right]}\right)\right\}.$$

(77)

The parameter estimates follow by solving the nonlinear equations

$$0=\frac{\partial }{\partial a}\left[R{T}_{\left(ADE\right)}\left(\underset{\_}{P}\right)\right]=\frac{\partial }{\partial b}\left[R{T}_{\left(ADE\right)}\left(\underset{\_}{P}\right)\right]=\frac{\partial }{\partial \theta }\left[R{T}_{\left(ADE\right)}\left(\underset{\_}{P}\right)\right].$$

(78)

4.7. The $L{T}_{\left(ADE\right)}$ Method

The $L{T}_{\left(ADE\right)}$ are obtained by minimizing

$$L{T}_{\left(ADE\right)}\left(\underset{\_}{P}\right)=-\frac{3}{2}h+2{\displaystyle \sum }_{i=1}^h{F}_{\underset{\_}{P}}\left(z_{\left[i,h\right]}\right)-\frac{1}{h}{\displaystyle \sum }_{i=1}^h\left(2i-1\right)\log F_{\underset{\_}{P}}\left(z_{\left[i,h\right]}\right).$$

(79)

The parameter estimates follow by solving the nonlinear equations

$$0=\frac{\partial }{\partial a}\left[L{T}_{\left(ADE\right)}\left(\underset{\_}{P}\right)\right]=\frac{\partial }{\partial b}\left[L{T}_{\left(ADE\right)}\left(\underset{\_}{P}\right)\right]=\frac{\partial }{\partial \theta }\left[L{T}_{\left(ADE\right)}\left(\underset{\_}{P}\right)\right].$$

(80)

5. Simulation Studies for Comparing Estimation Methods under Uncensored Scheme

A numerical simulation is performed in to compare the classical estimation methods. The simulation study is based on N = $1000$ generated data sets from the OB-F version where $n=50,100,300,$ and $500$, and under the following three scenarios: $\mathrm{Scenario}1:\left(a=0.80,b=0.80,\theta =0.80\right)$, $\mathrm{Scenario}2:\left(a=1.25,b=0.80,\theta =0.50\right)$ and $\mathrm{Scenario}3:\left(a=0.50,b=0.75,\theta =0.50\right)$. Figure 1a, Figure 1b and Figure 1c gives the density functions for three scenarios. The estimates are compared in terms of

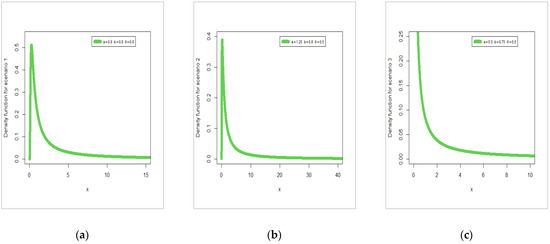
Figure 1. Density functions for the three scenarios.

• Bias $\left({BIAS}_{\left(\underset{\_}{P}\right)}\right);$
• Root mean-standard error $\left({RMSE}_{\left(\underset{\_}{P}\right)}\right);$
• The mean of the absolute difference between the theoretical and the estimates $\left(D_{\left(abs\right)}\right)$; and
• The maximum absolute difference between the true parameters and estimates $\left(D_{\left(max\right)}\right)$.

From Table 3, Table 4 and Table 5 we note that:

Table 3. Simulation results for parameters a = b = θ = 0.8.

	n	BIAS(a)	BIAS(b)	BIAS(θ)	RMSE(a)	RMSE(b)	RMSE(θ)	${\mathit{D}}_{\left(\mathbf{abs}\right)}$	${\mathit{D}}_{\left(\mathbf{max}\right)}$
MLE	50	0.00807	0.00975	0.011514	0.100754	0.117999	0.09090	0.005825	0.01072
CVM		−0.01243	0.00856	−0.00391	0.12232	0.13539	0.13791	0.00262	0.0053
OLS		−0.02486	−0.01852	−0.02408	0.12368	0.13114	0.13735	0.01337	0.02473
WLS		0.06774	−0.02485	0.06358	0.14211	0.11892	0.12843	0.02101	0.03235
ADE		−0.02272	0.00426	−0.02246	0.10632	0.12608	0.10436	0.00827	0.0147
RT		−0.00077	0.0006	0.00077	0.14007	0.12008	0.14141	0.00023	0.00177
LT		−0.01324	0.01587	−0.02012	0.12197	0.15242	0.10291	0.00505	0.01126
MLE	100	0.00839	0.007981	0.008815	0.06959	0.08209	0.06066	0.00492	0.00914
CVM		−0.0012	0.0059	0.00315	0.0854	0.09367	0.09853	0.00213	0.00339
OLS		−0.00761	−0.00762	−0.00717	0.08559	0.09196	0.0978	0.00445	0.00827
WLS		0.05163	−0.00878	0.04946	0.09626	0.08525	0.08648	0.01766	0.02943
ADE		−0.00517	0.0056	−0.0059	0.07434	0.08772	0.07298	0.00168	0.00446
RT		0.00405	0.00318	0.00468	0.09677	0.08363	0.09794	0.00232	0.00547
LT		−0.00214	0.00773	−0.00676	0.08418	0.1034	0.06898	0.0016	0.00434
MLE	300	0.001745	0.002581	0.00208	0.039482	0.046039	0.03379	0.00130	0.00240
CVM		0.00091	0.00315	0.00242	0.04947	0.05326	0.05582	0.0014	0.00251
OLS		−0.00261	−0.00131	−0.00204	0.04906	0.05374	0.0552	0.00114	0.00211
WLS		0.02453	−0.00271	0.02406	0.05089	0.0477	0.04483	0.00886	0.01500
ADE		−0.00258	−0.00145	−0.00351	0.04331	0.04882	0.04256	0.00147	0.00362
RT		0.00115	0.00159	0.0016	0.05452	0.04804	0.05515	0.00087	0.00261
LT		−0.00112	0.00422	−0.00228	0.05039	0.0603	0.0396	0.00101	0.00251
MLE	500	0.000087	0.00033	0.002176	0.03039	0.03483	0.02604	0.00088	0.00157
CVM		−0.00162	−0.00112	−0.00159	0.03845	0.03965	0.04254	0.00084	0.00156
OLS		−0.00191	−0.0033	−0.00261	0.03842	0.03999	0.04284	0.00162	0.00297
WLS		0.01934	−0.00232	0.01896	0.03948	0.03627	0.03472	0.00699	0.01178
ADE		−0.00153	0.00096	−0.00156	0.03339	0.0379	0.03251	0.00049	0.00176
RT		−0.00003	−0.00068	−0.00017	0.04258	0.03645	0.04276	0.00023	0.00134
LT		0.00097	−0.00057	−0.00055	0.03775	0.0438	0.03037	0.00018	0.0012

Table 4. Simulation results for parameters a = 1.25, b = 0.8, and θ = 0.5.

	n	BIAS(a)	BIAS(b)	BIAS(θ)	RMSE(a)	RMSE(b)	RMSE(θ)	${\mathit{D}}_{\left(\mathbf{abs}\right)}$	${\mathit{D}}_{\left(\mathbf{max}\right)}$
MLE	50	0.023764	0.015476	0.009473	0.158557	0.118178	0.060194	0.009302	0.017345
CVM		0.00057	0.01991	0.01226	0.19723	0.14069	0.09586	0.00954	0.01659
OLS		−0.02333	−0.01548	−0.00822	0.19277	0.13196	0.0894	0.00906	0.01685
WLS		0.11877	−0.02027	0.03617	0.22408	0.12112	0.07859	0.02202	0.03713
ADE		−0.02229	0.00738	−0.00574	0.1661	0.1261	0.06905	0.00366	0.00672
RT		0.01091	0.00561	0.00498	0.21508	0.11939	0.08265	0.00416	0.00863
LT		−0.00621	0.0156	−0.01253	0.19069	0.15363	0.06628	0.00311	0.0072
MLE	100	0.012492	0.007061	0.004961	0.108888	0.084967	0.041468	0.004651	0.008701
CVM		0.00045	0.00364	0.00351	0.13773	0.09388	0.06539	0.00221	0.00394
OLS		−0.01263	−0.0079	−0.00407	0.13407	0.09501	0.06444	0.00462	0.00863
WLS		0.07746	−0.01107	0.02659	0.14821	0.0864	0.05507	0.01589	0.02729
ADE		−0.01174	0.00377	−0.00259	0.11517	0.09125	0.05095	0.00181	0.0037
RT		0.0064	0.00315	0.00289	0.15524	0.08717	0.06034	0.0024	0.00523
LT		−0.00251	0.00733	−0.00609	0.13087	0.10775	0.04765	0.00145	0.00367
MLE	300	0.00250	0.004189	0.001343	0.060440	0.044982	0.022886	0.001799	0.003203
CVM		−0.00046	0.0032	0.00139	0.04903	0.05418	0.05534	0.00113	0.00179
OLS		−0.00374	−0.00047	−0.00042	0.07542	0.05235	0.0353	0.00066	0.00124
WLS		0.03905	−0.00102	0.01497	0.08009	0.04668	0.02983	0.00937	0.01681
ADE		−0.00413	0.00350	−0.00031	0.06396	0.04941	0.02798	0.00086	0.00206
RT		0.00414	0.00281	0.00191	0.08320	0.04685	0.03209	0.00175	0.00386
LT		−0.0028	0.00251	−0.00294	0.07627	0.0586	0.02573	0.00095	0.00214
MLE	500	0.000621	−0.000011	0.000328	0.045951	0.035669	0.017223	0.00018	0.00033
CVM		−0.00061	−0.00061	−0.00055	0.03839	0.04001	0.04284	0.00035	0.00065
OLS		−0.00415	−0.00237	−0.00151	0.05778	0.05778	0.02771	0.00151	0.00284
WLS		0.02756	−0.00279	0.01058	0.05966	0.03746	0.02229	0.0063	0.01105
ADE		−0.00405	−0.00012	−0.00127	0.04947	0.03904	0.02188	0.00093	0.00225
RT		−0.0011	−0.00045	−0.00028	0.0653	0.03703	0.02523	0.00031	0.00118
LT		−0.00237	0.00264	−0.00148	0.05933	0.04566	0.02094	0.00054	0.00172

Table 5. Simulation results for parameters a = 0.5, b = 0.75, and θ = 1.5.

	n	BIAS(a)	BIAS(b)	BIAS(θ)	RMSE(a)	RMSE(b)	RMSE(θ)	${\mathit{D}}_{\left(\mathbf{abs}\right)}$	${\mathit{D}}_{\left(\mathbf{max}\right)}$
MLE	50	0.004824	0.008576	0.017762	0.062856	0.11083	0.146539	0.005268	0.009642
CVM		−0.00328	0.00745	−0.00994	0.08249	0.13242	0.24642	0.00185	0.00391
OLS		−0.01345	−0.01617	−0.03945	0.0814	0.12269	0.24364	0.01201	0.02205
WLS		0.03881	−0.02391	0.11541	0.09030	0.11182	0.22718	0.01998	0.03209
ADE		−0.01273	0.0046	−0.04379	0.06803	0.11777	0.17922	0.00808	0.01505
RT		0.00023	0.00116	0.00112	0.08905	0.11295	0.26643	0.00049	0.00385
LT		−0.00843	0.01549	−0.02432	0.07607	0.14224	0.17088	0.00431	0.01136
MLE	100	0.00216	0.006975	0.010667	0.04356	0.074849	0.102224	0.003484	0.00628
CVM		0.00175	0.01084	0.00553	0.05642	0.08787	0.16508	0.00411	0.00699
OLS		−0.00700	−0.00502	−0.02016	0.05542	0.08567	0.16202	0.00539	0.00975
WLS		0.02786	−0.01039	0.07939	0.05873	0.07681	0.14387	0.01518	0.02409
ADE		−0.0048	0.00555	−0.01785	0.0465	0.0809	0.11966	0.00278	0.00707
RT		0.00164	0.00337	0.00474	0.05934	0.07746	0.17643	0.00179	0.00534
LT		−0.00574	0.01244	−0.01276	0.05401	0.1003	0.12148	0.00305	0.00815
MLE	300	−0.000001	0.002677	0.002529	0.02484	0.043363	0.058097	0.001031	0.001723
CVM		−0.00042	0.0017	−0.00124	0.03171	0.05039	0.09336	0.00046	0.00069
OLS		−0.00309	−0.00188	−0.00834	0.0316	0.05064	0.09313	0.00223	0.00403
WLS		0.01449	−0.00199	0.04067	0.03221	0.04515	0.07681	0.00845	0.01409
ADE		−0.00302	0.00031	−0.00981	0.02675	0.04743	0.06873	0.00195	0.00501
RT		−0.00051	0.00077	−0.00105	0.03376	0.04436	0.10063	0.00022	0.00235
LT		−0.00309	0.00518	−0.00618	0.03032	0.05385	0.06829	0.00138	0.0047
MLE	500	0.00018	0.000744	0.00097	0.019156	0.033038	0.044046	0.000348	0.000621
CVM		−0.00061	0.00048	−0.00183	0.02386	0.03801	0.0702	0.00032	0.00056
OLS		−0.00150	−0.00102	−0.00410	0.02475	0.0377	0.07232	0.00111	0.00201
WLS		0.01072	−0.00200	0.02987	0.02404	0.03453	0.0568	0.00616	0.01019
ADE		−0.00205	0.00152	−0.00621	0.02039	0.03665	0.05255	0.00111	0.00351
RT		−0.00042	−0.00025	−0.00121	0.02642	0.03386	0.07828	0.00031	0.00243
LT		−0.00071	0.00149	−0.00204	0.02330	0.04110	0.05204	0.00038	0.00245

Overall, MLE is providing better estimation compared to other methods for all sample sizes and for all initials “a = b = θ = 0.8”, “a = 1.25, b = 0.8 and θ = 0.5”, and “a = 0.5, b = 0.75 and θ = 1.5”.

• The BIAS $\left(\underset{\_}{P}\right)$ (BIAS(a), BIAS(b) and BIAS(θ)) tends to $0$ when n increases and tends to $\infty ,$ which means that all estimators are non-biased.
• The RMSE $\left(\underset{\_}{P}\right)$ (RMSE(a), RMSE (b) and RMSE (θ)) tends to $0$ when n increases, and tends to $\infty$, which means incidence of consistency property.

• For “a = b = θ = 0.8” (see Table 3), the MLE has the lowest RMSE as illustrated below:
  • RMSE (a)${|}_{n=50,100,300,500}$= (0.100754, 0.06959, 0.039482, and 0.03039).
  • RMSE (b)${|}_{n=50,100,300,500}$= (0.117999, 0.082085, 0.046039, and 0.03483).
  • RMSE (θ)${|}_{n=50,100,300,500}$= (0.09090, 0.060655, 0.03379, and 0.02604).
• For “a = 1.25, b = 0.8 and θ = 0.5” (Table 4), the MLE has the lowest RMSE as illustrated below:
  • RMSE(a)${|}_{n=50,100,300,500}$= (0.158557, 0.108888, 0.060440, and 0.045951).
  • RMSE(b)${|}_{n=50,100,300,500}$= (0.118178, 0.084967, 0.044982, and 0.035669).
  • RMSE(θ)${|}_{n=50,100,300,500}$= (0.060194, 0.041468, 0.022886, and 0.017223).
• For “a = 0.5, b = 0.75 and θ = 1.5” (Table 5), the MLE has the lowest RMSE as illustrated below:
  • RMSE(a)${|}_{n=50,100,300,500}$= (0.062856, 0.04356, 0.043363, and 0.019156).
  • RMSE(b)${|}_{n=50,100,300,500}$= (0.11083, 0.074849, 0.058097, and 0.033038).
  • RMSE(θ)${|}_{n=50,100,300,500}$= (0.146539, 0.102224, 0.001031, and 0.044046).
• The worst estimation method cannot be determined obviously since all other estimation methods perform well, especially when n increases and tends to $\infty$, where in Table 3, Table 4 and Table 5 we have

  $$\mathrm{RT}=R{T}_{\left(ADE\right)}\mathrm{and}\mathrm{LT}=L{T}_{\left(ADE\right)}$$

  (81)

6. Modeling Uncensored Real Data for Comparing the Competitive Models

For illustrating the wide applicability of the new OB-F model, we consider the Cramér–von Mises (C$1$) statistic, the Anderson–Darling (C$2$) statistic, the Kolmogorov–Smirnov (K-S) statistic, and its corresponding p-value $\left(\mathrm{P}-\mathrm{V}\right)$. Table 6 below gives the competitive models.

Table 6. The competitive models.

Competitive Models (Abbreviation)	Author(s)
Kumaraswamy Fréchet (Kum-F)	[26]
Transmuted Fréchet (T-F)	[27,28]
Exponentiated Fréchet (EF)	[5,28]
Beta Fréchet (B-F)	[29]
Marshal–Olkin-Fréchet (MO-F)	[9]
McDonald Fréchet (Mc-F)	[30]
odd log-logistic inverse Rayleigh (OLL-IR)	[13]
Fréchet (F)	[1]
odd log-logistic exponentiated Fréchet (OLL-EF)	New
odd log-logistic exponentiated inverse Rayleigh (OLL-EIR)	New
Generalized odd log-logistic inverse Rayleigh (GOLL-IR)	New

6.1. Stress Data

The first data set is an uncensored data set consisting of 100 observations on breaking stress of carbon fibers (in Gba) given by [31] and these data are used by [32,33,34,35]. For exploring the empirical HRF of data set I, the total time test (TTT) (see [36]) plot is plotted in Figure 2a. Due to Figure 2a, the empirical HRF of data sets I is “monotonically increasing”. For exploring the initial shape of real data set I, the nonparametric Kernel density estimation (KDE) is provided in Figure 2b. In Figure 2b, it is noted that the nonparametric density of data I is “asymmetric right skewed with heavy tail”. For exploring the extreme value, the box plot is plotted in Figure 2c. Based on Figure 2c, we note that some extreme values were found and the quantile–quantile (Q–Q) plot (Figure 2d) confirms this fact.

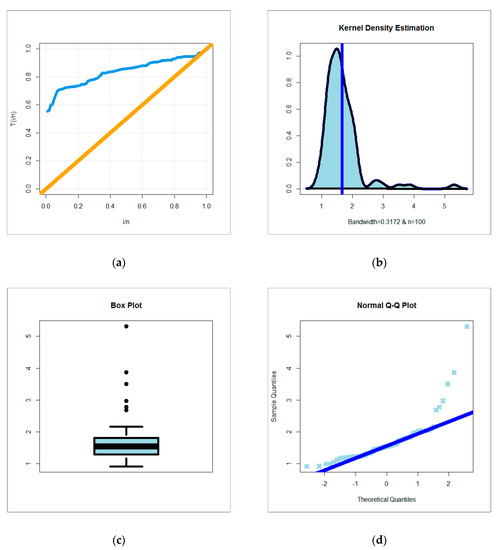
Figure 2. (a) Total time test (TTT) plot; (b) Kernel density estimation (KDE) plot; (c) box plot; (d) quantile–quantile (Q–Q) plot for data set I.

The statistics C$1$, C$2$, K-S, and P-V for all fitted models are presented in Table 7. The MLEs and corresponding standard errors (SEs) are given in Table 8. From Table 7, the OB-F model gives the lowest values the C$1$, C$2$, K-S and the biggest P-V statistics (bold values) as compared to further F models, therefore, the OB-F can be chosen as the best model. Figure 3a, Figure 3b, Figure 3c and Figure 3d give the estimated (E-PDF), estimated CDF (E-CDF), probability-probability (P-P) plot and estimated HRF (E-HRF), respectively, for data set I. Based on Table 8 and for a = 5.8786, b = 0.5825 and θ = 1.1017 we have, mean = 1.653321, variance = 0.3408465, skewness = 6.36955$>0$ and kurtosis = 906.9166$>3$.

Table 7. C$1$, C$2$, K-S and P-V for data set I.

Model	Goodness of Fit Criteria
	$\mathbf{C}1$	$\mathbf{C}2$	K-S	P-V
OB-F	0.0669	0.473	0.06317	0.8198
OLL-EF	0.1203	0.9639	0.5561	2.2 × 10⁻¹⁶
OLL-EIR	0.1553	1.21197	0.65497	2.2 × 10⁻¹⁶
OLL-IR	0.15532	1.21201	0.6550	2.2 × 10⁻¹⁶
F	0.1090	0.7657	0.0874	0.4282
Kum-F	0.0812	0.6217	0.0759	0.6118
EF	0.1091	0.7658	0.0874	0.4287
Beta-F	0.0809	0.6207	0.0757	0.6147
T-F	0.0871	0.6209	0.0782	0.5734
MO-F	0.0886	0.6142	0.0763	0.5168
Mc-F	0.1333	1.0608	0.0807	0.5332

Table 8. MLEs and their standard errors (in parentheses) for data set I.

Model	Estimates
	a	b	c	β	θ
OB-F	5.8786	0.5825			1.1017
	(0.6645)	(0.1711)			(0.1801)
OLL-EF	0.1351		3.7216	0.9296	21.319
	(0.011)		(0.0034)	(0.0033)	(0.0034)
OLL-EIR	0.4946		0.067	1.74262
	(0.04135)		(0.7195)	(9.3007)
OLL-IR	0.49459			0.45242
	0.04135			0.03869
F				1.3968	4.3724
				(0.0336)	(0.3278)
Kum-F		0.8489	1.6239	1.6341	3.4208
		(16.083)	(0.6979)	(9.049)	(0.7635)
EF		0.9395		1.4169	0.9395
		(3.543)		(2.568)	(0.3278)
Beta-F		0.7346	1.5830	1.6684	3.5112
		(1.5290)	(0.7132)	(0.7662)	(0.9683)
T-F	−0.7166			1.2656	4.7121
	(0.2616)			(0.0579)	(0.3657)
MO-F		0.0033		6.2296	1.2419
		(0.0009)		(1.0134)	(0.1181)
Mc-F	0.8503	44.423	19.859	0.0203	46.974
	(0.1353)	(25.100)	(6.706)	(0.0060)	(21.871)

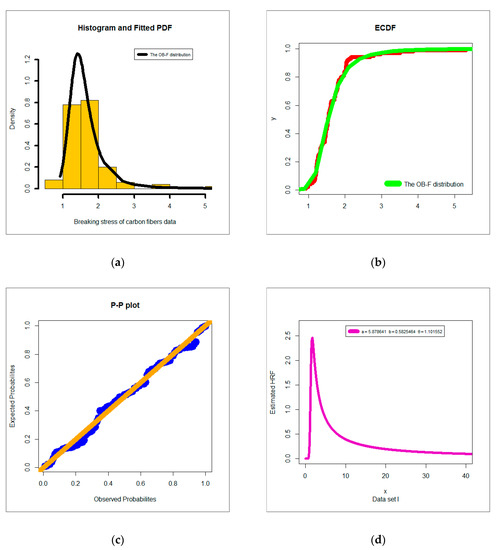
Figure 3. (a) Estimated density; (b) estimated cumulative distribution function (CDF); (c) P-P plot; (d) estimated hazard rate function (HRF) for data set I.

6.2. Glass Fibers Data

The second data set is generated data to simulate the strengths of glass fibers, given by [37]. For exploring the empirical HRF of data set II, the TTT plot is plotted in Figure 4a. Due to Figure 4a, the empirical HRF of data sets II is “monotonically increasing”. For exploring the initial shape of real data II non-parametrically, the KDE is provided in Figure 4b. In Figure 4b, it is noted that the nonparametric density of data II is “asymmetric right skewed with heavy tail”. For exploring the extreme value, the box plot is plotted in Figure 4c. Based on Figure 4c, we note that some extreme values were found and the Q–Q plot (Figure 4d) confirms this fact. The C$1$, C$2,$ K-S, and P-V are listed in Table 9. The MLEs and SEs are given in Table 10. From Table 9, the OB-F model gives the lowest values the C$1$, C$2,$ K-S, and the biggest value of the P-V, therefore, the OB-F can be chosen as the best model. Figure 5a, Figure 5b, Figure 5c and Figure 5d gives the E-PDF, E-CDF, P-P plot, and E-HRF for data set II. Based on Table 10 and for a = 7.5535, b = 0.4841 and θ = 1.1588 we have, mean = 1.611337, variance = 0.2134206, skewness = 4.838406 $>0$ and kurtosis = 232.3354$>3$.

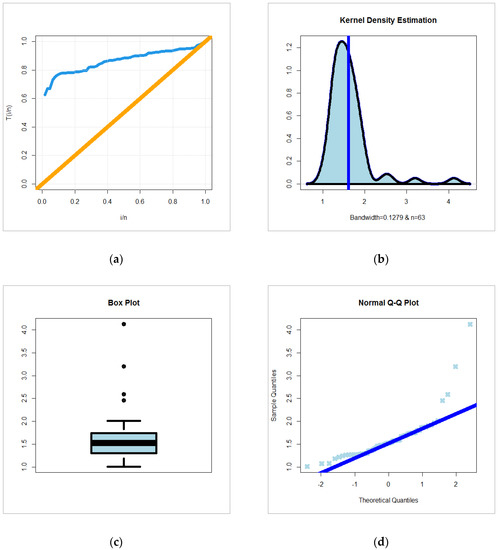
Figure 4. (a) TTT plot; (b) KDE plot; (c) box plot; (d) Q–Q plot for data set II.

Table 9. C$1$, C$2$, K-S, and P-V for data set II.

Model	Goodness of Fit Criteria
	$\mathbf{C}1$	$\mathbf{C}2$	K-S	P-V
OB-F	0.0548	0.38734	0.0705	0.8914
OLL-EF	0.10487	0.8325	0.55196	6.7 × 10⁻¹⁶
OLL-EIR	0.1502	1.14697	0.67949	6.7 × 10⁻¹⁶
OLL-IR	0.15021	1.14697	0.67951	6.7 × 10⁻¹⁶
F	0.0707	0.5332	0.0772	0.8185
Kum-F	0.0634	0.4981	0.0715	0.8810
EF	0.0707	0.5332	0.0772	0.8187
Beta-F	0.0640	0.5008	0.0716	0.8804
T-F	0.0655	0.4939	0.0735	0.8470
MO-F	0.0629	0.4902	0.0813	0.7685
Mc-F	0.1161	0.9193	0.0831	0.7455

Table 10. MLEs and their standard errors (in parentheses) for data set II.

Model	Estimates
	a	b	c	β	θ
OB-F	7.5535	0.4841			1.1588
	(1.13)	(0.184)			(0.192)
OLL-EF	0.1449		0.0088	1.2997	24.878
	(0.013)		(0.000)	(0.000)	(0.000)
OLL-EIR	0.5025		0.0716	1.7048
	(0.053)		(1.1306)	(13.47)
OLL-IR	0.50251			0.45599
	0.05295			0.04865
F				1.4108	5.4377
				(0.0344)	(0.5192)
Kum-F		0.2855	1.2824	1.9142	4.7731
		(9.1338)	(0.6388)	(12.836)	(1.3134)
EF		0.9059		1.4367	5.4379
		(2.764)		(4.324)	(0.5193)
B-F		1.2996	1.2649	1.3945	4.7927
		(4.4378)	(0.6640)	(0.9304)	(1.4641)
T-F	0.7778			1.5491	4.3139
	(0.2477)			(0.0655)	(0.5849)
MO-F		0.0023		5.2383	1.4537
		(0.0004)		(0.8209)	(0.1650)
Mc-F		56.227	14.953	0.0073	29.104
		(30.539)	(4.733)	(0.0013)	(11.304)

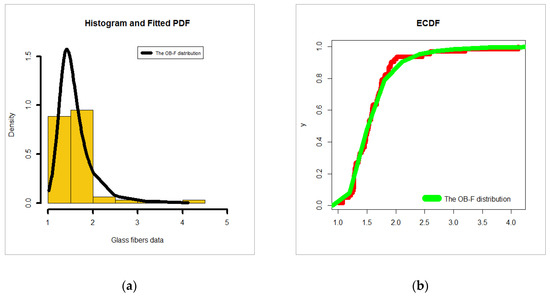
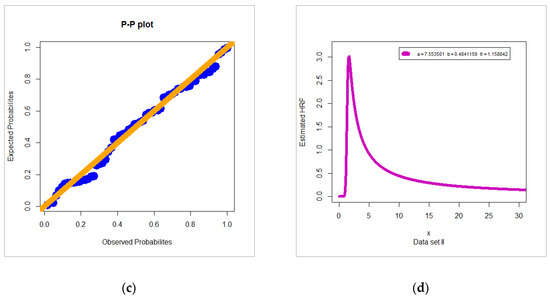
Figure 5. (a) Estimated density; (b) estimated CDF; (c) P-P plot; (d) estimated HRF for data set II.

6.3. Relief Time Data

The 3rd data set (Wingo data) represents a complete sample from a clinical trial describe a relief time (in hours) for 50 arthritic patients [38]. For exploring the empirical HRF of data set III, the TTT plot is plotted in Figure 6 a. Due to Figure 6a the empirical HRF of data sets III is “monotonically increasing”. For exploring the initial shape of real data III, the nonparametric KDE is provided in Figure 6b. Figure 6b it is noted that the nonparametric density of data III is “nearly symmetric”. The box plot is presented in Figure 6c. Based on Figure 6c, we note no extreme values were found and the Q–Q plot (Figure 6d) confirms this fact. The C$1$, C$2,$ K-S, and P-V are listed in Table 11. The MLEs and SEs are given in Table 12. From Table 11, the OB-F model gives the lowest values the C$1$, C$2,$ K-S and the biggest value of the P-V, therefore the OB-F can be chosen as the best model. Figure 7a, Figure 7b, Figure 7c and Figure 7d gives the E-PDF, E-CDF, P-P plot and E-HRF for data set III. Based on Table 12 and for a = 29.50356, b = 0.64127 and θ = 0.14316 we have, mean = 16.20257, variance = 67.31756, skewness = 9.75092$>0$ and kurtosis = 1520.895$>3$.

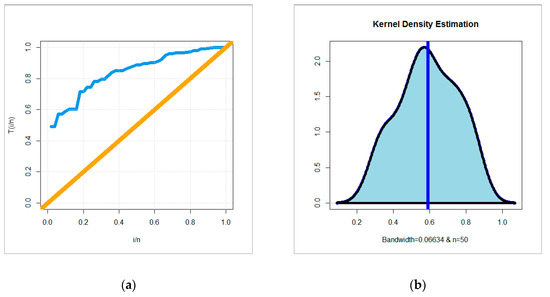
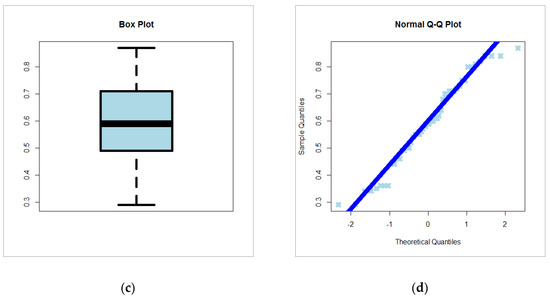
Figure 6. (a) TTT plot; (b) KDE plot; (c) box plot; (d) Q–Q plot for data set III.

Table 11. C$1$, C$2$, K-S, and P-V for data set III.

Model	Goodness of Fit Criteria
	$\mathbf{C}1$	$\mathbf{C}2$	K-S	P-V
OB-F	0.1038	0.8163	0.1043	0.6482
GOLL-IR	0.1955	1.3498	0.11008	0.5797
OLL-EF	0.1577	1.09876	0.53498	7.4 × 10⁻¹³
F	0.3233	2.0301	0.1506	0.2066
EF	0.3233	2.0301	0.1506	0.2064
Beta-F	0.3611	2.5131	0.1433	0.3601
T-F	0.2823	1.8152	0.1370	0.3045

Table 12. MLEs and their standard errors (in parentheses) for data set III.

Model	Estimates
	a	b	c	β	θ
OB-F	29.50356	0.64127			0.14316
	(49.14)	(0.083)			(0.238)
GOLL-IR	1.961	0.111		1.4123
	(0.234)	(0.000)		(0.000)
OLL-EF	0.0669		0.0046	0.3558	32.561
	(0.0076)		(0.003)	(0.0047)	(0.006)
F				0.4859	3.2078
				(0.023)	(0.326)
EF			0.9047	0.5013	3.2077
			(18.784)	(3.244)	(0.326)
Beta-F		4.015	1.3349	2.0022	0.87017
		(0.111)	(0.147)	(0.321)	(0.0033)
T-F	−0.5816			0.4400	3.4974
	(0.2787)			(0.0290)	(0.3527)

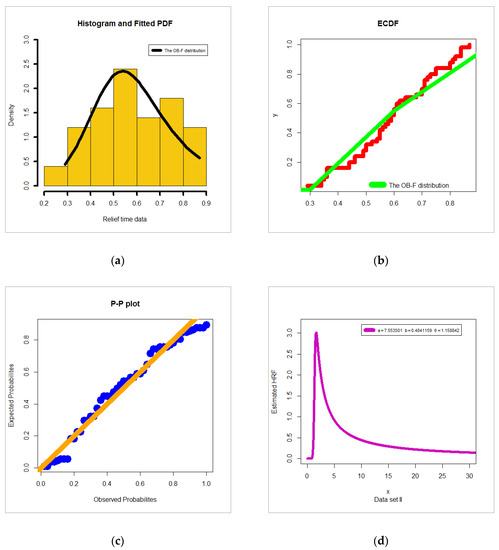
Figure 7. (a) Estimated density; (b) estimated CDF; (c) P-P plot; (d) estimated HRF for data set III.

7. Validation under Censored Scheme

7.1. Maximum Likelihood Estimation for Censored Data

In reliability studies and survival analysis, data are often censored. If $Z_1,Z_2,.....,Z_h$ is a censored sample from the OB-F distribution, each observation can be written as

$$z_{\left[i,h\right]}=\left(Z_i,C_i\right)=\{\begin{array}{c}{Z}_{i}if{Z}_i<C_i\\ C_{i}if{Z}_i>C_i\end{array},$$

(82)

where $Z_i$ are failure times and $C_i$ censoring times. The likelihood function is

$$l_i\left(\underset{\_}{P}\right)={\displaystyle \prod }_{i=1}^h{\left[f_{\underset{\_}{P}}\left(z_{\left[i,h\right]}\right)\right]}^{O_i}{\left[S_{\underset{\_}{P}}\left(z_{\left[i,h\right]}\right)\right]}^{1-O_i}{|}_{\left(O_i=1_{z_{\left[i,h\right]}<C_i}\right)}.$$

(83)

The right censoring is assumed to be non-informative, so the log-likelihood function can be written as:

$${ℒ}_{\left[i,h\right]}\left(\underset{\_}{P}\right)={\displaystyle \sum }_{i=1}^h{O}_i\log f_{\underset{\_}{P}}\left(z_{\left[i,h\right]}\right)+{\displaystyle \sum }_{i=1}^h\overline{O_i}\log S_{\underset{\_}{P}}\left(z_{\left[i,h\right]}\right){|}_{\left(\overline{O_i}=1-O_i\right)}$$

(84)

we pose

$${\upsilon }_i=exp\left(-z_{\left[i,h\right]}^{-\theta }\right)\hspace{0.17em}\mathrm{and}{\psi }_i=1-exp\left(-z_{\left[i,h\right]}^{-\theta }\right)$$

(85)

$${ℒ}_{\left[i,h\right]}\left(\underset{\_}{P}\right)={\displaystyle \sum }_{i=1}^h{O}_i\left[\begin{array}{c}\ln (ab\theta )-\left(\theta -1\right)\ln z_{\left[i,h\right]}-a{z}_{\left[i,h\right]}^{-\theta }\\ +\left(ab-1\right)\ln {\psi }_i-\left(b-1\right)\ln ({\upsilon }_i+{\psi }_i^a)\end{array}\right]+{\displaystyle \sum }_{i=1}^h\overline{O_i}\left[ab\ln {\psi }_i-b\ln ({\upsilon }_i+{\psi }_i^a)\right].$$

(86)

The MLEs of the unknown parameters $a,b$ and $\theta$ are derived from the nonlinear following score equations:

$$\frac{\partial {ℒ}_{\left[i,h\right]}\left(\underset{\_}{P}\right)}{\partial a}={\displaystyle \sum }_{i=1}^h{O}_i\left(\frac{1}{a}-z_{\left[i,h\right]}^{-\theta }+b\ln {\psi }_i-\left(b-1\right)\frac{{\psi }_i^a\ln {\psi }_i}{{\upsilon }_i+{\psi }_i^{\alpha }}\right)+{\displaystyle \sum }_{i=1}^h\overline{O_i}\left(b\ln s_i-\frac{b{\psi }_i^{a_1}\ln {\psi }_i}{{\upsilon }_i+{\psi }_i^a}\right)$$

(87)

$$\frac{\partial {ℒ}_{\left[i,h\right]}\left(\underset{\_}{P}\right)}{\partial b}={\displaystyle \sum }_{i=1}^h{O}_i\left[\frac{1}{b}+a\ln s_i-\ln ({\tau }_i+s_i^a)\right]+{\displaystyle \sum }_{i=1}^h\overline{O_i}\left[a\ln s_i-\ln ({\tau }_i+s_i^a)\right]$$

(88)

$$\begin{array}{c}\frac{\partial {ℒ}_{\left[i,h\right]}\left(\underset{\_}{P}\right)}{\partial \theta }{\displaystyle {\displaystyle \sum }_{i=1}^h}{O}_i{}_{}\left[\begin{array}{c}\frac{1}{\theta }+\left(a{z}_{\left[i,h\right]}^{-\theta }-1\right)\ln z_{\left[i,h\right]}\\ -\frac{\left(ab-1\right)z_{\left[i,h\right]}^{-\theta }\ln z_{\left[i,h\right]}{\tau }_i}{s_i}-\frac{\left(b-1\right)z_{\left[i,h\right]}^{-\theta }\ln z_{\left[i,h\right]}{\tau }_i\left(1-a{s}_i^{a-1}\right)}{{\tau }_i+s_i^a}\end{array}\right]\\ -{\displaystyle {\displaystyle \sum }_{i=1}^h}\overline{O_i}\left[\frac{ab{z}_{\left[i,h\right]}^{-\theta }\ln z_{\left[i,h\right]}{\tau }_i}{s_i}+\frac{b{z}_{\left[i,h\right]}^{-\theta }\ln z_{\left[i,h\right]}{\tau }_i\left(1-a{s}_i^{a-1}\right)}{{\tau }_i+s_i^a}\right].\end{array}$$

(89)

The explicit form of cannot be obtained, so we use numerical methods.

7.2. Test Statistic for Right Censored Data

Let $Z_1,Z_2,.....,Z_h$ be $h$ i.i.d. random variables grouped into $r$ classes $I_j$. To assess the adequacy of a parametric model

$$H_0:\stackrel{}{Pr}\left(Z_i\le z\hspace{0.17em}|\hspace{0.17em}{H}_0\right)=F_0\left(z;\underset{\_}{P}\right),z\ge 0{|}_{\left(\underset{\_}{P}={({\underset{\_}{P}}_1,{\underset{\_}{P}}_1,\dots ,{\underset{\_}{P}}_s)}^T\in \underset{\_}{P}\subset R^s\right)},\hspace{0.17em}$$

(90)

when data are right censored and the parameter vector $\underset{\_}{P}$ is unknown, [39] proposed a statistic test $T^2$ based on the vector

$$Y_j=\frac{1}{\sqrt{h}}\left(V_j-e_j\right){|}_{\left(\hspace{0.17em}j=1,2,\dots ,r\mathrm{and}r\succ s\right)}.$$

(91)

This one represents the differences between observed and expected numbers of failures ($V_j$ and $e_j)$ to fall into these grouping intervals

$$I_j=\left({\rho }_{j-1},{\rho }_j\right]{|}_{\left({\rho }_0=0,{\rho }_r=\tau \right)},$$

(92)

where $\tau$ is a finite time. The authors considered ${\rho }_j$ as random data functions such as the $r$ intervals chosen to have equal expected numbers of failures $e_j$. The statistic test $T^2$ is defined by

$${\mathrm{T}}_n^2={\displaystyle \sum }_{j=1}^n\frac{1}{V_j}{\left(V_j-e_j\right)}^2+Q$$

(93)

where $e_j$ and $V_j$ are the expected and the observed numbers of failure in grouping intervals, other elements were defined in [38,39,40,41,42,43,44], where

$$Q=W^T{\widehat{G}}^{-}W,\widehat{G}={\left[{\widehat{g}}_{l{l}^{\prime }}\right]}_{s\times s},$$

(94)

$$\widehat{W}=\widehat{C}{\widehat{A}}^{-1}Z={\left({\widehat{W}}_1,\dots ,{\widehat{W}}_s\right)}^T,$$

(95)

$$Z_j=\frac{1}{\sqrt{n}}\left(V_j-e_j\right),W_l={{\displaystyle \sum }}_{j=1}^r{\widehat{C}}_{lj}{\widehat{A}}_j^{-1}{Z}_j,$$

(96)

$${\widehat{g}}_{l{l}^{\prime }}={\widehat{ı}}_{l{l}^{\prime }}-{\displaystyle \sum }_{j=1}^r{\widehat{C}}_{lj}{\widehat{C}}_{l^{\prime }j}{\widehat{A}}_j^{-1},i=1,\dots ,n,j=1,\dots ,r,l,l\prime =1,\dots ,s$$

(97)

The limits $a_j$ of $r$ random gouging intervals $I_j=\left[a_{j-1},a_j\right]$ were chosen, such as the expected failure times to fall into these intervals, which were the same for each; $j=1,\dots ,r-1,$ ${\widehat{a}}_r=\max \left(x_{\left(l\right)},\tau \right).$ The estimated ${\widehat{\rho }}_j$ is defined by

$${\widehat{\rho }}_j=H^{-1}\left(\frac{E_j-{{\displaystyle \sum }}_{l=1}^{i-1}{H}_{\widehat{\underset{\_}{P}}}\left(x_l\right)}{n-i+1},\widehat{\underset{\_}{P}}\right),{\widehat{a}}_r=\stackrel{\underset{}{}}{max}\left(x_{\left(n\right),}\tau \right)$$

(98)

where $H_{\widehat{\underset{\_}{P}}}\left(x_l\right)$ is the cumulative HRF (CHRF) of the new distribution. This statistic test $Y_n^2$ follows a chi-squared distribution. To calculate the quadratic form $Q$ of the statistic $Y_n^2$, and, as its distribution doesn’t depend on the parameters, we can use the estimated matrices $\widehat{W}$ and $\widehat{C}$ and the estimated information matrix $\widehat{I}.$ The elements of $\widehat{C}$ defined by

$${\widehat{C}}_{lj}=\frac{1}{n}{\displaystyle \sum }_{i:x_i\in I_j}^n{O}_i\frac{\partial }{\partial {\widehat{\underset{\_}{P}}}_l}\ln h_{\widehat{\underset{\_}{P}}}\left(x_i\right)$$

(99)

7.3. Criteria Test for OB-F

For testing the null hypothesis $H_0$ that data belong to the OB-F model, we construct a modified chi-squared type goodness-of-fit test based on the statistic $T^2$. Suppose that $\tau$ is a finite time, and observed data are grouped into $r>s$ sub-intervals $I_j=\left({\rho }_{j-1},{\rho }_j\right]$ of $\left[0,\tau \right].$ The limit intervals ${\rho }_j$ are considered as random variables, such that the expected number of failures in each interval $I_j$ are the same, so the expected number of failures $e_j$ are obtained as

$$E_j{|}_{\left(j=1,..r-1\right)}=\frac{-j}{r-1}{\displaystyle \sum }_{i=1}^f\log \left[ab\ln {\psi }_i-b\ln ({\upsilon }_i+{\psi }_i^a)\right],$$

(100)

Therefore, the quadratic form of the test statistic can be obtained easily:

$$T_n^2\left(\underset{\_}{P}\right)\hspace{0.17em}\hspace{0.17em}={{\displaystyle \sum }}_{j=1}^r\frac{1}{V_j}{\left(V_j-e_j\right)}^2+{\widehat{W}}^T{\left[{\widehat{ı}}_{l{l}^{\prime }}-{{\displaystyle \sum }}_{j=1}^r{\widehat{C}}_{lj}{\widehat{C}}_{l^{\prime }j}{\widehat{A}}_j^{-1}\right]}^{-1}\widehat{W},$$

(101)

where matrices $\widehat{W}$, $\widehat{C}$ and the estimated information matrix $\widehat{I}$ are derived as given in [40,41,42,43,44,45]. The matrix $\widehat{C}$ is defined in (99) and its elements are ${\widehat{C}}_{1j},{\widehat{C}}_{2j}$ and ${\widehat{C}}_{2j}$ are numerically evaluated in Section 8.

7.4. Simulations

An important simulation study is carried out to show the performance of the techniques used and the feasibility of the goodness-of-fit test developed in this work. At this end, we generated $N=10,000$ right censored samples with different sizes $\left(h=15,25,50,130,350,500\right)$ from the OB-F model with parameter values $\left(a=2,b=0.5,\theta =1.5\right).$ Firstly, we compute the MLEs of the unknown parameters, and then the criteria $T^2$ of the corresponding samples are provided. Using $R$ statistical software and the BB algorithm (see [46]), we calculate the MLEs of the unknown parameters, the corresponding bias and mean square errors (MSE). The BB algorithm is recently applied by [47,48,49,50]. The results are given in Table 13.

Table 13. MLEs of a, b, θ, and MSE.

N = 10,000	h₁ = 15	h₂ = 25	h₃ = 50	h₄ = 130	h₅ = 350	h₆ = 500
a	1.9568	1.9612	1.9734	1.9786	1.9856	1.9923
MSE	0.0137	0.0109	0.0090	0.0073	0.0048	0.00029
b	0.5436	0.5326	0.5289	0.5203	0.5176	0.5066
MSE	0.0186	0.0152	0.0123	0.0095	0.0078	0.0059
θ	1.5286	1.5243	1.5182	1.5126	1.5064	1.5022
MSE	0.0158	0.0128	0.0092	0.0079	0.0062	0.0046

7.5. Test Statistic $T^2$

For testing the null hypothesis $H_0$ that right censored data become from OB-F model, we compute the criteria statistic $T_h^2\left(\underset{\_}{P}\right)$ as defined above for $10,000$ simulated samples from the hypothezised distribution with different sizes $\left(h=50,130,350,500\right)$.Then, we calculate empirical levels of significance, when $T²>{\chi }_{\epsilon }^2\left(r\right)$, correponding to theoretical levels of significance $\left(\epsilon =0.10,0.05,0.01\right)$, We choose $r=5$. The results are reported in Table 14.

Table 14. Simulated levels of significance for $T_h^2\left(\underset{\_}{P}\right)$ test for OB-F model against their theoretical values (ε 0.01, 0.05, 0.10).

N = 10,000	h = 50	h = 130	h = 350	h = 500
ε = 1%	0.0079	0.0092	0.0098	0.0107
ε = 5%	0.0461	0.0478	0.0492	0.0503
ε = 10%	0.0971	0.0985	0.0990	0.1002

The null hypothesis $H_0$ for which simulated samples are fitted by OB-F distribution, is widely validated for the different levels of significance. Therefore, the test proposed in this work, can be used to fit data from this new distribution.

8. Application to Leukemia Free-Survival Times

We consider sample data of 51 patients with advanced acute myelogenous leukemia reported to the International Bone Marrow Transplant Registry. These patients had received an autologous (auto) bone marrow transplant in which, after high doses of chemotherapy, their own marrow was reinfused to replace their destroyed immune system. Leukemia free-survival times (in months) for Autologous Transplants: 0.658, 0.822, 1.414, 2.5, 3.322, 3.816, 4.737, 4.836 *, 4.934, 5.033, 5.757, 5.855, 5.987, 6.151, 6.217, 6.447 *, 8.651, 8.717, 9.441 *, 10.329, 11.48, 12.007, 12.007 *, 12.237, 12.401 *, 13.059 *, 14.474 *, 15 *, 15.461, 15.757, 16.48, 16.711, 17.204*, 17.237, 17.303 *, 17.664 *, 18.092, 18.092 *, 18.75 *, 20.625 *, 23.158, 27.73 *, 31.184 *, 32.434 *, 35.921 *, 42.237 *,44.638 *, 46.48 *, 47.467 *, 48.322 *, 56.086. (* indicates the censorship). We use the statistic test provided above to verify if these data are modeled by the transmuted generalized linear exponential distribution OB-F, and at that end, we first calculate the MLEs of the unknown parameters

$$\widehat{P}={\left({\widehat{a}}_{},{\widehat{b}}_{},\widehat{\theta }\right)}^T={\left(1.5364,2.6397,1.2639\right)}^T.$$

(102)

Data are grouped into $r=5$ intervals $I_j$. We give the necessary calculus in the following Table 15.

Table 15. Values of the limits (${\widehat{\rho }}_j)$, observed numbers of failures ($V_j$), and expected numbers of failures ($e_j$).

${\widehat{\rho }}_j$	4.425	8.702	14.253	22.968	56.086
$V_j$	6	11	9	14	11
${\widehat{C}}_{2j}$	−1.635	−1.236	−0.986	−2.635	−7.956
${\widehat{C}}_{2j}$	2.272	3.030	1.894	2.272	0.757
${\widehat{C}}_{3j}$	−0.723	1.136	−0.986	0.9763	−2.953
$e_j$	5.5246	5.5246	5.5246	5.5246	5.5246

Then we obtain the value of the statistic test $Y_h^2$:

$$Y_h^2=X^2+Q=4.5263+3.4968=8.0231$$

(103)

For significance level $\epsilon =0.05$, the critical value ${\chi }_5^2=11.0705$ is superior than the value of $Y_h^2=8.0231,$ so we can say that the proposed OB-F model fit these data.

9. Concluding Remarks

In this article, we expanded the extreme value theory by proposing and studying a new version of the Fréchet model called the odd-Burr generalized Fréchet model. The new model is based on compiling the standard Fréchet model with the odd-Burr generalized family. Many new bivariate type extensions using Farlie–Gumbel–Morgenstern Copula, modified Farlie–Gumbel–Morgenstern, Clayton Copula, and Renyi’s entropy Copula are derived. After a quick study for its properties, different classical estimation methods under an uncensored scheme are considered, such as the maximum likelihood estimation method, Anderson–Darling estimation method, ordinary least square estimation method, Cramér–von Mises estimation method, weighted least square estimation method, left-tail Anderson–Darling estimation method, and right-tail Anderson–Darling estimation method. Simulations were performed by comparing the estimation methods using different sample sizes for three different combinations of parameters. The Barzilai–Borwein algorithm is employed via simulation studies, assessing the performance of the estimators with different sample sizes as sample size tends to $\infty .$ Three applications for measuring the flexibility and the importance of the new model are presented and used for comparing the competitive distributions under the uncensored scheme. Using the approach of the Bagdonavicius–Nikulin goodness-of-fit test for validation under the right censored data, we propose a modified chi-square goodness-of-fit test for the new model. The modified goodness-of-fit statistic test is applied for right censored real data set called leukemia free-survival times (in months) for autologous transplants. Based on the maximum likelihood estimators on initial data, the modified goodness-of-fit test recovers the loss of information. All elements of the modified GOF criteria tests are explicitly derived and given.