New Approach for a Weibull Distribution under the Progressive Type-II Censoring Scheme

Abstract

This paper proposes a new approach based on the regression framework employing a pivotal quantity to estimate unknown parameters of a Weibull distribution under the progressive Type-II censoring scheme, which provides a closed form solution for the shape parameter, unlike its maximum likelihood estimator counterpart. To resolve serious rounding errors for the exact mean and variance of the pivotal quantity, two different types of Taylor series expansion are applied, and the resulting performance is enhanced in terms of the mean square error and bias obtained through the Monte Carlo simulation. Finally, an actual application example, including a simple goodness-of-fit analysis of the actual test data based on the pivotal quantity, proves the feasibility and applicability of the proposed approach.

1. Introduction

The progressive Type-II censoring scheme is one of the useful censoring schemes capable of saving experimental cost and time. Under the progressive Type-II censoring scheme, $m\in (1,\dots ,n)$ is the pre-fixed failure number and $R_i$ denotes the number of removed units when the ith failure arises. When the 1st failure arises, $R_1$ units are randomly removed from $n-1$ surviving units. After some time, $R_2$ units are randomly removed from $n-2-R_1$ surviving units when the 2nd failure arises and so on. The experiment is terminated when the mth failure arises, removing all remaining $R_m=n-m-R_1-\dots -R_{m-1}$ units. Many studies in various fields have discussed the progressive Type-II censoring scheme and used a Weibull distribution as the lifetime distribution because of the flexibility afforded by its wide variety of shapes. This paper proposes a new estimation method based on the regression framework employing a pivotal quantity when a progressive Type-II censored sample is available from a Weibull distribution with the cumulative distribution function and the probability density function (pdf), as given by

$$\begin{array}{cc}\hfill & F(x;\theta ,\lambda )=1-e^{-\theta x^{\lambda }}\hfill \end{array}$$

and

$$\begin{array}{c}f(x;\theta ,\lambda )=\lambda \theta x^{\lambda -1}{e}^{-\theta x^{\lambda }},x>0,\theta >0,\lambda >0,\hfill \end{array}$$

(1)

respectively, where $\theta$ is the scale parameter and $\lambda$ is the shape parameter. As mentioned earlier, the versatility of the Weibull distribution enables it model the characteristics of other types of distribution, due to the shape parameter. For this reason, this distribution has been studied by many researchers under various censoring schemes, especially the progressive Type-II censoring scheme. Pareek etal. [1] provided the maximum likelihood estimators (MLEs), approximate MLEs (AMLEs) and the Fisher information matrix based on the competing risks data from a Weibull distribution under the progressive Type-II censoring scheme. Wang etal. [2] proposed an inverse estimation and exact confidence intervals based on a pivotal quantity for the proportional hazard distributions such as the Weibull, Gompertz, and Lomax distributions under the progressive Type-II censoring scheme. Abdel-Hamid and Al-Hussaini [3] provided a progressive stress-accelerated life test model based on a progressive Type-II sample from a Weibull distribution through graphical and maximum likelihood methods of estimations. Valiollahi etal. [4] studied the estimation of the stress strength reliability that represents the system stress less than its strength when the system stress and its strength are independent Weibull random variables under the progressive Type-II censoring scheme.

However, these approaches suffer a disadvantage in that the shape parameter must be numerically estimated, despite its importance. Instead of these approaches, the present article develops a closed form for the parameter of interest, i.e., the shape parameter, by proposing a weighted linear regression framework based on a pivotal quantity under the progressive Type-II censoring scheme. In our approach, the concept proposed by Lu and Tao [5] is extended to the progressive Type-II censoring scheme and the rounding error which was revealed by Balakrishnan and Aggarwala [6] in the exact determination of the single and product moments for large samples is resolved by utilizing two different Taylor series expansions. The superiority of the approach relative to the maximum likelihood estimation is proved in terms of the mean square error (MSE) and bias through the Monte Carlo simulation.

The rest of this paper is organized. Section 2 proposes a new estimation method using the weighted least squares method based on the linear regression framework, which provides a closed form for the shape parameter that may be of interest and also enhances the performance in terms of the MSE and bias, compared to the MLEs. Section 3 proves the superiority of the proposed method through the Monte Carlo simulations and the real data analysis. Section 4 concludes the paper.

2. Weighted Least Squares Estimation

Let $X_{1:m:n},\dots ,X_{m:m:n}$ be a progressive Type-II censored sample from the Weibull distribution with the pdf (1). Then the corresponding likelihood function is given by

$$\begin{array}{c}\hfill L(\theta ,\lambda )\propto {\theta }^m{\lambda }^m\exp \left(-\theta \sum _{i=1}^m{x}_{i:m:n}^{\lambda }\left(1+R_i\right)\right)\prod _{i=1}^m{x}_{i:m:n}^{\lambda -1},\end{array}$$

and the MLEs $\widehat{\lambda }$ and $\widehat{\theta }$ can be found by maximizing its logarithm. Although estimation based on the likelihood function is most commonly used, it does not provide a closed form for the shape parameter $\lambda$ that can be of interest. To resolve this shortcoming, estimation methods based on a linear regression-type framework are proposed in this section. First, a pivotal quantity is provided.

Let

$$\begin{array}{cc}\hfill Y_{i:m:n}=& -log[1-F(x_{i:m:n};\theta ,\lambda )]\hfill \\ \hfill =& \theta x_{i:m:n}^{\lambda },i=1,\dots ,m.\hfill \end{array}$$

(2)

Then, $Y_{1:m:n}\le \cdots \le Y_{m:m:n}$ are progressive Type-II censored order statistics that have a standard exponential distribution with a mean $E\left(Y_{i:m:n}\right)={\sum }_{j=1}^{i}1/{\gamma }_j$, where ${\gamma }_j={\sum }_{k=j}^m\left(1+R_k\right)$. To obtain a simple linear model, $log{Y}_{i:m:n}$ is considered, which is a progressive Type-II censored sample from a standard extreme value distribution with

$$\begin{array}{cc}\hfill E(log{Y}_{i:m:n})& =-\mathcal{C}-\prod _{j=1}^i{\gamma }_j\sum _{j=1}^i\frac{a_{j,i}}{{\gamma }_j}log{\gamma }_j\hfill \end{array}$$

(3)

and

$$\begin{array}{cc}\hfill Var(log{Y}_{i:m:n})& =\frac{{\pi }^2}{6}+\prod _{j=1}^i{\gamma }_j\sum _{j=1}^i\frac{a_{j,i}}{{\gamma }_j}{\left(\mathcal{C}+log{\gamma }_j\right)}^2-{\left[E(log{Y}_{i:m:n})\right]}^2,i=1,\dots ,m,\hfill \end{array}$$

(4)

respectively, where $a_{j,i}$=${\prod }_{k=1,k\ne j}^i{\left({\gamma }_k-{\gamma }_j\right)}^{-1}$ and $\mathcal{C}$ is the Euler’s constant.

From the quantity $log{Y}_{i:m:n}$ and its mean (3), a simple linear regression model can be obtained as

$$\begin{array}{c}\hfill E(log{Y}_{i:m:n})=log\theta +\lambda log{X}_{i:m:n}+{\epsilon }_i,i=1,\dots ,m,\end{array}$$

(5)

where ${\epsilon }_i$ is the error term with $E\left({\epsilon }_i\right)=0$. Now, an approach based on the weighted least squares method is proposed since the weight of each data point is not identical constant, as mentioned in Lu and Tao [5].

Theorem 1.

The weighted least squares estimators (WLSEs) of θ and λ are

$$\begin{array}{cc}\hfill \tilde{\theta }& =exp\left(\frac{Q_2{Q}_4-Q_3{Q}_5}{Q_1{Q}_4-Q_3^2}\right)\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill \tilde{\lambda }& =\frac{Q_5-Q_{3}log\tilde{\theta }}{Q_4},\hfill \end{array}$$

respectively, where

$$\begin{array}{cc}\hfill Q_1& =\sum _{i=1}^m{w}_{i:m:n},\hfill \\ \hfill Q_2& =\sum _{i=1}^m{w}_{i:m:n}E(log{Y}_{i:m:n}),\hfill \\ \hfill Q_3& =\sum _{i=1}^m{w}_{i:m:n}log{X}_{i:m:n},\hfill \\ \hfill Q_4& =\sum _{i=1}^m{w}_{i:m:n}{\left(log{X}_{i:m:n}\right)}^2,\hfill \\ \hfill Q_5& =\sum _{i=1}^m{w}_{i:m:n}E(log{Y}_{i:m:n})log{X}_{i:m:n}.\hfill \end{array}$$

Proof. 

The weighted least squares equation corresponding to the progressive Type-II censoring scheme is

$$\begin{array}{c}\hfill \sum _{i=1}^m{w}_{i:m:n}{\left[E(log{Y}_{i:m:n})-log\theta -\lambda log{X}_{i:m:n}\right]}^2.\end{array}$$

(6)

Then, by letting $w_{i:m:n}=1/Var(log{Y}_{i:m:n})$ and minimizing the quantity (6) for each parameter, it completes the proof. ☐

Note that Balakrishnan and Aggarwala [6] pointed out the serious rounding errors arising in the exact determination of the single and product moments for a large sample size n. To resolve that, two types of Taylor series expansion for $log{Y}_{i:m:n}$ are provided.

First, $log{Y}_{i:m:n}$ can be approximated in a Taylor series around $E\left(U_{i:m:n}\right)=1-{\prod }_{j=1}^i{\gamma }_j{\left(1+{\gamma }_j\right)}^{-1}$ due to $F(x_{i:m:n};\theta ,\lambda )\stackrel{d}{=}{U}_{i:m:n}$, where $U_{i:m:n}$ is the ith order statistic from a standard uniform distribution under the progressive Type-II censoring scheme. For notation simplicity, $E\left(U_{i:m:n}\right)$ is denoted as $p_{i:m:n}$. Then, we have

$$\begin{array}{c}\hfill log{Y}_{i:m:n}\approx log\left[-log\left(1-p_{i:m:n}\right)\right]-\frac{F(x_{i:m:n};\theta ,\lambda )-p_{i:m:n}}{\left(1-p_{i:m:n}\right)log\left(1-p_{i:m:n}\right)}.\end{array}$$

(7)

By (7), the mean (3) and variance (4) are approximated as

$$\begin{array}{cc}\hfill E(log{Y}_{i:m:n})& \approx log\left[-log\left(1-p_{i:m:n}\right)\right]\hfill \end{array}$$

(8)

and

$$\begin{array}{cc}\hfill Var(log{Y}_{i:m:n})& \approx \frac{Var\left(F(x_{i:m:n};\theta ,\lambda )\right)}{{\left[\left(1-p_{i:m:n}\right)log\left(1-p_{i:m:n}\right)\right]}^2},\hfill \end{array}$$

(9)

respectively, where $Var\left(F(x_{i:m:n};\theta ,\lambda )\right)={\prod }_{j=1}^i{\gamma }_j{\left(2+{\gamma }_j\right)}^{-1}-{\prod }_{j=1}^i{\gamma }_j^2{\left(1+{\gamma }_j\right)}^{-2}$. The approximate WLSEs are provided by substituting the mean (3) and variance (4) in Theorem 1 with their approximations (8) and (9), which are denoted as ${\tilde{\theta }}_{approx1.}$ and ${\tilde{\lambda }}_{approx1.}$, respectively.

Second, by approximating $log{Y}_{i:m:n}$ in a Taylor series around $E\left(Y_{i:m:n}\right)={\sum }_{j=1}^{i}1/{\gamma }_j$ because $Y_{i:m:n}$ be a progressive Type-II sample from a standard exponential distribution, we have

$$\begin{array}{c}\hfill log{Y}_{i:m:n}\approx logE\left(Y_{i:m:n}\right)+\frac{1}{E\left(Y_{i:m:n}\right)}\left(Y_{i:m:n}-E\left(Y_{i:m:n}\right)\right),i=1,\dots ,m.\end{array}$$

(10)

Then, the mean (3) and variance (4) are approximated as

$$\begin{array}{cc}\hfill E(log{Y}_{i:m:n})& \approx logE\left(Y_{i:m:n}\right)\hfill \end{array}$$

(11)

and

$$\begin{array}{cc}\hfill Var(log{Y}_{i:m:n})& \approx \frac{Var\left(Y_{i:m:n}\right)}{{\left[E\left(Y_{i:m:n}\right)\right]}^2},\hfill \end{array}$$

(12)

respectively, where $Var\left(Y_{i:m:n}\right)={\sum }_{j=1}^{i}1/{\gamma }_j^2$. Then, another approximate WLSEs can be obtained as in the case of ${\tilde{\theta }}_{approx1.}$ and ${\tilde{\lambda }}_{approx1.}$, and they are denoted as ${\tilde{\theta }}_{approx2.}$ and ${\tilde{\lambda }}_{approx2.}$, respectively.

3. Application

This section assesses the proposed estimators in terms of the MSE and bias through the Monte Carlo simulations, and analyzes a real dataset to illustrate the validity and application of the proposed approach.

3.1. Simulation Result

To assess the proposed estimators, the progressive censored samples are generated from the Weibull distribution with $\lambda$ = 0.5(1.0)2.5 and $\theta$ = 1.0 under the following progressive Type-II censoring schemes (Lee etal. [7])

$$\begin{array}{cc}\hfill \mathrm{Scheme}& \mathrm{I}:R_m=n-m\mathrm{and}{R}_i=0\mathrm{for}i\ne m\hfill \\ \hfill & \mathrm{II}:R_1=n-m\mathrm{and}{R}_i=0\mathrm{for}i\ne 1\hfill \\ \hfill & \mathrm{III}:R_1=R_m=\frac{n-m}{2}\mathrm{and}{R}_i=0\mathrm{for}i\ne 1\mathrm{and}m\hfill \\ \hfill & \mathrm{IV}:R_{m/2}=n-m\mathrm{and}{R}_i=0\mathrm{for}i\ne \frac{m}{2}\hfill \end{array}$$

by using the algorithm in Balakrishnan and Sandhu [8]. The sample size n and the pre-fixed failure number m are considered as follows.

$$\begin{array}{cc}\hfill & n=20,m=14,18,20,\hfill \\ \hfill & n=30,m=18,26,30.\hfill \end{array}$$

Then, for each scheme, the MSEs and biases are obtained over 10,000 replications after computing all the estimators considered in Section 2. The results are reported in Figure 1 and Figure 2.

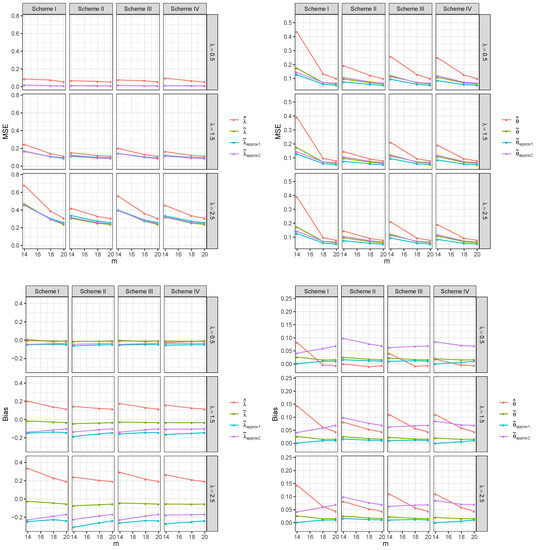
Figure 1. The MSEs and biases of the estimators for the sample size n = 20.

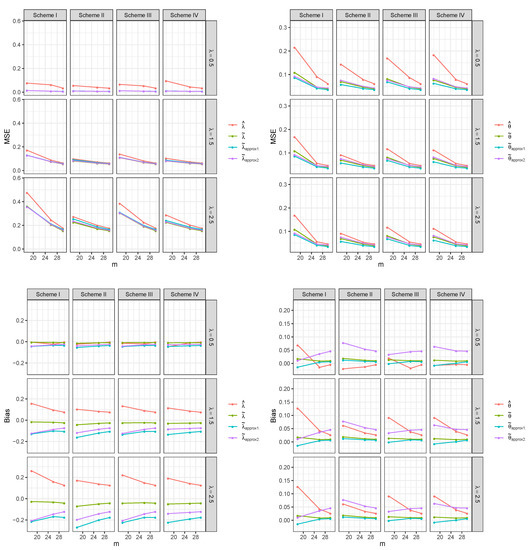
Figure 2. The MSEs and biases of the estimators for the sample size n = 30.

Figure 1 and Figure 2 show that the proposed WLSEs are more efficient than the MLEs in terms of the MSE. Among the WLSEs, for $\lambda$, ${\tilde{\lambda }}_{approx1.}$ has larger values than other WLSEs in some cases but the differences are small. In addition, $\tilde{\lambda }$ shows the best result in that the bias values are close to zero. In the case of $\theta$, ${\tilde{\theta }}_{approx1.}$ generally has better performance than that of other WLSEs in terms of the MSE. As expected, the MSEs decrease as the sample size n increases. In addition, for the fixed sample size n, the same pattern is observed as the pre-fixed failure number m increases. One interesting thing is that the MSEs generally decrease as $\lambda$ decreases for the estimators of $\lambda$.

3.2. Real Data

Wind is increasingly used worldwide as an alternative clean energy source. The most important parameter of wind energy is the wind speed, which is a random parameter that can be estimated by using the proposed approach. This subsection considers 30 monthly average wind speed values (Table 1) presented in Abd-Elfattah [9], which was computed from the daily wind speed values of the index Swedish Meteorological and Hydrological Institute records for 2006 to 2008. In addition, the progressive Type-II censored sample (Table 2) generated by Zhang and Gui [10] from Table 1 is analyzed and Table 3 reports the results.

Table 1. 30 monthly observed average wind speed data from 2006 to 2008.

2	2	2.5	2.5	2.6	2.6	2.7	2.8	2.8	2.9	3.2	3.3	3.3	3.4	3.5
3.7	3.8	3.8	3.9	4	4	4.1	4.1	4.7	5.3	5.4	5.5	5.7	6.7	6.9

Table 2. Progressive Type-II censored sample generated by Zhang and Gui [10] from the real data.

i	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18
$x_{i:18:30}$	2	2.7	2.8	2.9	3.2	3.3	3.3	3.4	3.5	3.9	4	4.7	5.3	5.4	5.5	5.7	6.7	6.9
$R_i$	1	0	1	1	0	1	1	0	1	1	0	1	1	0	1	1	0	1

Table 3. Estimates of $\lambda$ and $\theta$ for the observed progressive Type-II censored sample.

$\widehat{\mathit{\lambda }}$	$\tilde{\mathit{\lambda }}$	${\tilde{\mathit{\lambda }}}_{\mathit{approx}1.}$	${\tilde{\mathit{\lambda }}}_{\mathit{approx}2.}$	$\widehat{\mathit{\theta }}$	$\tilde{\mathit{\theta }}$	${\tilde{\mathit{\theta }}}_{\mathit{approx}1.}$	${\tilde{\mathit{\theta }}}_{\mathit{approx}2.}$
3.2694	2.7791	2.6553	2.7205	0.0039	0.0084	0.0103	0.0097

To examine the goodness-of-fit of a Weibull distribution to the observed progressive Type-II censored sample, two approaches are considered: One is to use the replicated data $X_{i:m:n}^{rep}$ that are generated from the following steps

(a)

Compute the estimates of $\theta$ and $\lambda$.

(b)

Generate $x_{i:m:n}^{rep}$ from the marginal density function $f_{X_{i:m:n}}(x;\theta ,\lambda )$ with the estimates obtained in (a), where

$$\begin{array}{c}\hfill f_{X_{i:m:n}}(x;\theta ,\lambda )=\lambda \theta x^{\lambda -1}exp\left(-\theta x^{\lambda }\right)\prod _{j=1}^i{\gamma }_j\sum _{j=1}^i{a}_{j,i}exp\left[-\theta x^{\lambda }({\gamma }_j-1)\right].\end{array}$$

(c)

Repeat $N(\ge$10,000), (b).

Other is to compare $Y_{i:m:n}$ with its mean $E\left(Y_{i:m:n}\right)$ as follows:

(a)

Compute the estimates of $\theta$ and $\lambda$.

(b)

Compute $Y_{i:m:n}$=$\theta x_{i:m:n}^{\lambda }$ with the estimates obtained in (a).

Figure 3 plots the $95\%$ predictive regions for $X_{i:m:n}^{rep}$ and the scatter plot between the observed progressive Type-II censored sample and $E\left(X_{i:m:n}^{rep}\right)$. The result shows that the Weibull distribution fits the observed progressive Type-II censored sample very well for all estimates, while the MLE has better performance than the WLSEs in terms of the uncertainty because of its smaller predictive regions. Figure 4 illustrates the relationship and the sample correlation coefficient r between $Y_{i:m:n}$ and $E\left(Y_{i:m:n}\right)$. The strong correlation coefficients in Figure 4 indicate that the Weibull distribution fits the observed progressive Type-II censored sample very well for all estimates, as in the case of Figure 3.

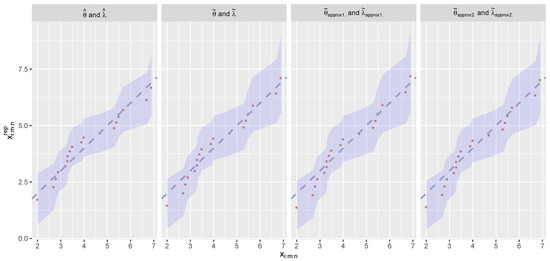
Figure 3. 95% predictive regions for $X_{i:m:n}^{rep}$ and the scatter plot between the observed progressive Type-II censored sample and $E\left(X_{i:m:n}^{rep}\right)$.

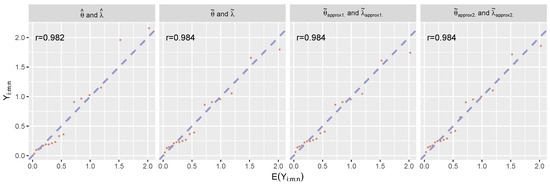
Figure 4. The scatter plots between $Y_{i:m:n}$ and $E\left(Y_{i:m:n}\right)$.

4. Conclusions

This study proposes a new estimation method based on the weighted least squares method under the progressive Type-II censoring scheme, which provides a closed form solution of the shape parameter that can be of interest, unlike the MLE. Whereas many studies have generally used a pivotal quantity $Y_{i:m:n}$, this article employed $log{Y}_{i:m:n}$, which leads to a simple linear regression model. To obtain the WLSEs based on the regression model, the exact mean and variance of $log{Y}_{i:m:n}$ are employed, but they suffer serious rounding errors for large samples. For this reason, two different types of Taylor series expansion are provided to approximate the mean and variance of $log{Y}_{i:m:n}$. To prove the superiority of the proposed estimation method, the Monte Carlo simulation is conducted, and the results demonstrate the superiority of all the proposed WLSEs to the MLE in terms of the MSE. Our approach offers three benefits: it can be expressed in a closed form of a shape parameter that can be a parameter of interest, the resulting performance is enhanced in terms of MSE, and it can be applied to other censoring schemes.