Abstract
For a controlled system of coupled Markov chains, which share common control parameters, a tensor description is proposed. A control optimality condition in the form of a dynamic programming equation is derived in tensor form. This condition can be reduced to a system of coupled ordinary differential equations and admits an effective numerical solution. As an application example, the problem of the optimal control for a system of water reservoirs with phase and balance constraints is considered.
1. Introduction
The analysis and optimization of systems of coupled Markov Chains (MC) appear in various applied areas such as environmental management [1,2], control of dams [3,4,5], control of data transmission systems for the avoidance of congestion [6,7,8], and many others. In general, the optimal control of MC with constraints and various criteria leads to the solution of a system of ordinary differential equations. However, the coupled MC produces serious difficulties due to a dramatic increase in the number of states, which renders impossible the numerical solution of the optimization problem with the aid of standard computers in a reasonable time [9]. Moreover, the presence of constraints very often leads to rather complicated and cumbersome mathematical problems.
The evolution of single controlled MC may be effectively represented via a vector-valued function satisfying stochastic differential equations with a control dependent generator [10]. If a set of MCs shares common control parameters, they no longer can be analyzed separately, since the system becomes coupled. Approaching the coupled system as a whole leads to the necessity of the consideration of a global system state, which incorporates the states of all individual MCs involved. Joining together the states of all MCs as a set of vectors (perhaps of different dimensions) leads to the description of their evolution in tensor form. The next step of the control synthesis for this coupled system is the derivation of the optimality conditions in the form of a special dynamic programming equation (DPE). The demand for accuracy leads, however, to the extension of MCs’ state space, and by that, to the increase of the dimensionality of the DPE. At the same time, the numerical solution of DPE allows the parallelization of the most time-consuming operations, and this is one of the advantages of the tensor representation. Here we give an algorithm for DPE derivation, which is the principal step for its numerical solution. It should be noted that this paper follows the previously published works [6,9,11] and provides a proper mathematical justification for the results presented there.
As an example, we consider the management of coupled dams under non-stationary seasonally changing random inflows/outflows. The presentation of a dam’s state as a continuous-time MC permits one to take into account the random character of the incoming and outgoing water flow due to rain, evaporation, and, of course, customer demands. However, sometimes it is necessary to organize the interflow between the different parts of a system, such as controlled flow from one dam to another or controlled release, to avoid overflow. In all these cases, it is necessary to consider the system as a whole, that is, the global state of the dam system. The current water level of each dam is described by the state of a continuous-time MC, hence the state of the whole system of the coupled dams is represented in tensor form. The connection of MCs is a result of the controlled flow between the dams. The control aims to maintain the required water levels in given weather conditions, and at the same time, to satisfy the customer demands. The general approach is based on the solution of DPE in tensor form. This equation may be reduced to a system of ordinary differential equations. We suggest here the procedure for the generation of this system and also the approach to the minimization in its right-hand side (RHS), which may be realized for each state of the coupled MC independently.
The structure of the paper is as follows: in Section 2 we describe the model of the controlled MC system. The martingale representation and stochastic evolution of the global state of coupled MC is given in Section 3. The optimal control and Kolmogorov equation for the distribution of states of the controlled coupled system of MC is in Section 4. A numerical example motivated by the Goulburn River water cascade is presented in Section 5.
2. Model of Controlled Markov Chains System
In this section we give the definition of the model of the controlled coupled MCs. Let us consider a set of M MCs. The m-th MC has possible states and a time- and control-dependent generator , :
- , for ;
- .
The controlparameter , where U is a compact set in some complete metric space, and the matrix valued functions , are assumed to be continuous in both parameters , where . The control parameter u is shared by all the MCs, and hence defines their interconnection.
2.1. Global State
Let the local state space of the m-th MC be given by a set of standard basis vectors , then its dynamics can be described by the following stochastic differential equation [10]:
where is the initial state of the m-th MC and the process is a square integrable martingale with bounded quadratic variation. We assume that the martingales and are independent for , and hence the MCs do not experience simultaneous transitions.
The first approach to the controlled coupled MCs was presented in References [6,9,11], where the global system state was described as a tensor product of the individual MCs’ states:
, , where × denotes the Cartesian product (the definition of tensor product can be found in Appendix A). For the combination of local states , the global state can be represented as a multidimensional array of shape with single non-zero element . This representation allows us to significantly simplify the expressions involved in the DPE and makes the implementation of the control optimization algorithms rather straightforward, especially with programming tools that allow multidimensional array objects (e.g., Matlab, Python NumPy or Julia).
Let the set of admissible controls be defined as a set of -predictable controls taking values in U (here stands for a natural filtration associated with the stochastic process ). This assumption ensures the measurability of the admissible controls. In other words, if the number of global state transitions of the coupled MC system up to the current time is and is the time of the k-th jump and
is the history of the m-th MC on the time interval (set of state and jump time pairs), then for the controls are measurable with respect to t and the global history [9].
2.2. Performance Criterion
Let be a running cost function defined for the global state and time , and be a terminal condition. Then a general performance criterion to be minimized is given by
Here is, in fact, a multidimensional array-valued function defined for any possible global state of the coupled MC system . For example, the running cost function can be represented as
where denotes the inner product and is the indicator function. Thus, for given t and , the state selects a single value from the multidimensional array . The same is valid for the terminal condition , which is defined by a multidimensional array .
Assumption A1.
The elements of are bounded from below and are continuous functions on .
3. Martingale Representation of the Global State
In this section we derive the martingale representation for the global state of the controlled coupled MC system analogous to (1). To that end, we need to introduce some additional notations. Let denote an identity matrix of the same shape as the matrix , , and denote the tensor product of matrices A and B (see Appendix A). Then
is called the tensor sum [12] of the square matrices , .
Theorem 1.
Let be the global state of the coupled MC system, where each MC satisfies the representation (1). Then satisfies the representation
where is a square integrable martingale.
Note that from Theorem 1 it follows, that piece-wise constant right-continuous process and square integrable martingale give the solution of the martingale problem (see Reference [13], [Chapter III] for details) for SDE (6).
Proof.
The theory of stochastic differential equations with values from finite-dimensional Hilbert spaces can be found in Reference [14], and the present proof is based on the corollary from the Ito formula for a finite-dimensional Hilbert space [14], [Section 4.1]. This result, applied for the case of , that is, for tensor product , brings the following:
where stands for the tensor mutual variation of the processes , , which is a zero tensor due to the independence of the martingales , .
Substituting the martingale representation of the individual MCs (1) for we obtain
where , so is a square integrable martingale.
Proceeding further for , we finally have
Now using the definition of tensor product of matrices (see Appendix A), we can factorize the summands in the last expression as
which, along with the definition of the tensor sum (5), yields the theorem statement. □
Note that Formula (7) provides an efficient way to calculate the tensor contraction :
4. Optimal Control
4.1. Value Function Representation
The value function of the coupled MC system is a function, which is equal to the minimum total cost for the system given the starting time and state :
where
As in Formula (4) for the running cost function, we now represent the value function as
where is a multidimensional array-valued function defined for any possible global state of the coupled MC system .
4.2. Dynamic Programming Equation
Further, we generalize the approach to the control optimization of ordinary MC [7] to the controlled MC systems. Define the dynamic programming equation with respect to :
with terminal condition [7,10,15]. Our aim is to show that (10) has a unique solution , and that from the value function representation (9). This will allow us to present an optimal Markov control, which minimizes the performance criterion (3).
If Assumption 1 holds, then is continuous in , and hence for any there exists
which minimizes this continuous function on a compact set U. Moreover, is affine in for any , so is Lipschitz in , and hence Equation (10) has a unique solution on .
The existence of an -predictable (i.e., -measurable) optimal control, provided that Assumption 1 is true, follows from a general result [16], [Theorem 4.2]. The following theorem states that the optimal control can be chosen among the Markov controls, which depend not on the whole process history , but on the left limit only. It should be noted that this result is a generalization of Theorem 2.8 [7] for controlled MCs to the case of controlled MC systems.
Theorem 2.
If Assumption 1 holds, then the Markov control and the value function is defined by the solution of the DPE (10), that is, and
is the optimal control.
Proof.
Since is a predictable control, then for any initial condition there exists a unique solution of the martingale problem (6). That is, there exists a process , where is a class of -valued right continuous functions with left limits, which satisfies Equation (6), that is,
where is a square integrable martingale.
Let us take some admissible control and corresponding solution of the martingale problem (6). Applying Ito’s formula to the process we get
Since the first integrand in the RHS is the minimum in (10), and in the second integrand obeys the martingale representation (6), we can transform the last equation into the following inequality:
Taking the expectation of both parts of the inequality, we get
since is a continuous deterministic function and the expectation of the integral over the martingale is equal to zero. Substitution of the control yields the equality, which means that the solution to the DPE (10) defines the value function and is the optimal control. □
4.3. Optimal Control Calculation
In the previous section it was shown that the solution to the DPE (10) is unique and from Theorem 2 it follows that the Markov control, which minimizes the RHS of this equation, is optimal. Now if we let , then we get a system of ordinary differential equations (ODEs):
The inner product in the right-hand side of the ODEs (11) can be simplified as follows:
where we used the definition of tensor sum (5), the representation of the inner product as a component-wise sum, and denoted
Finally, we get the following tensor form for the system of ODEs (11):
The system (12) provides a method of simultaneous calculation of the optimal Markov control and the DPE solution. This system is solved backwards in time, starting from the terminal condition . The minimizations of the RHSs of the equations of this system are independent of each other and, in the case of the numerical solution, these time-consuming operations can be performed in parallel. The result of the minimization yields a set of control functions , which define the Markov optimal control:
4.4. Kolmogorov Equation
Once the optimal control is obtained, there arises the problem of the state probabilities calculation. The main difficulty is that the optimal Markov control depends on the state , so one cannot directly compute the generator using the tensor sum Formula (5). To overcome this issue for a single controlled MC with the generator , it suffices to substitute in the j-th column with control , which corresponds to the state . For the controlled MC system, the generator can be constructed in a similar block-wise manner. Indeed, for any global state , the corresponding Markov control is equal to and
where is defined by Formula (5) for .
Finally, Equation (14) defines the transition rate tensor , which is nonrandom, and the state probabilities for the process satisfy the Kolmogorov equation
5. Numerical Study: Goulburn River Cascade
To illustrate our approach to the modeling of real-world systems as coupled MCs and optimal control synthesis, in this section we present a numerical study based on real-world data. The usual area of applications for MCs and numerous generalizations is service systems, which can be described in terms of Poisson arrival flows, queues, and servers. For example, in References [6,17], one can find an application of coupled MCs for congestion control in networks. Specifically, an optimal control strategy was proposed for a multi-homing network connection, where the packets (portions of incoming traffic) could be sent through one of two lines of different speed and price or discarded. However, in the present paper, we stick to another application area, namely, the control of water reservoirs. The reason is that the proposed approach allows successful modeling of these systems, accounting for the stochastic nature of the incoming and outgoing flows, being dependent on the weather condition and users’ behavior. Moreover, the proposed form of the performance criterion (3) permits a variety of optimization goals, for example, minimization of the difference between the actual and desired demand intensities, maintenance of the balance between the incoming and outgoing flows, minimization of the probability that either dam falls below some critical level on average or at the terminal time [9]. Besides, this criterion allows penalizing control in certain states, so that natural restrictions (such as the impossibility to transfer water from an empty or to an overflowing reservoir) can also be taken into account. The terminal condition can reflect the desire to bring the system to a certain state by the end of the control interval.
The object of our study is a system of interconnected dams of the Goulburn River cascade. The model is deliberately simplified to avoid cumbersome details, which are unnecessary for a journal on mathematical subjects, nevertheless, it demonstrates all the necessary techniques, such as MCs states’ choice, relations between the discharges and state transition intensities, accounting for the natural inflows and outflows, consumer demands, and environmental constraints.
The Goulburn River Basin is located in the south-western part of State Victoria, Australia. The description of the region and a review of the literature devoted to water resource modeling and planning can be found, for instance, in References [18,19,20]. The review of papers on allocation modeling in this region and water trading can be found in References [21,22,23]. The Goulburn Basin, together with the Upper Murray, Ovens, Kiewa, Broken, Loddon, and Campaspe Basins constitute an area called the Goulburn-Murray Irrigation District (common abbreviation is GMW from Goulburn-Murray Water—an organization governing water resources in this area). Since the Goulburn River is a major waterway and a major contributor of water supply in the district, it is an object of very intensive research and modeling. The GMW uses the Goulburn simulation model (GSM) for the optimization and planning of water supply in the region. The GSM represents the Goulburn system as a set of nodes of different types: storages, demands, and streamflow inputs. These nodes are connected by a network of carriers characterized by their capacities and delivery penalties (penalty functions). The GSM was calibrated using a trial-and-error procedure, which optimizes the model parameters related to the water supply infrastructure [24]. The model presented here reflects a part of the GSM and involves Lake Eildon—a major storage of water, which can be required by farmers during the irrigation season, and Lake Nagambie with the Goulbourn Weir, which is connected by three major channels to the end-users. The Goulburn River connects the two water storages and continues to run after Nagambie, serving as its fourth outflow. Based on the request of irrigators, the water is released from Lake Eildon to Lake Nagambie, and then by one of three channels or the river delivered to the farmers (water right holders). The important point is that apart from irrigation requests, the system must satisfy environmental demand, which means the levels in rivers and channels should exceed some minimal threshold that will allow the support of healthy ecosystems and provide some required minimal inflows to satisfy downstream demands.
The scheme of the Goulburn River cascade is presented in Figure 1. We assume that the water level of Lake Eildon is affected by two major flows. One is the incoming flow, which reflects the sum of all the natural water arrivals and losses, including precipitation, upstream tributaries, evaporation, and other causes. The single outcoming flow is the controlled discharge of the Goulburn River, which also serves as the single incoming flow of Lake Nagambie (other natural inflows and outflows into this lake are ignored here due to a significant difference in the size of the two lakes). From Lake Nagambie, there are four controlled discharges, namely the Stuart Murray Canal, Cattanach Canal, East Goulburn Main Channel, and the Goulburn River.
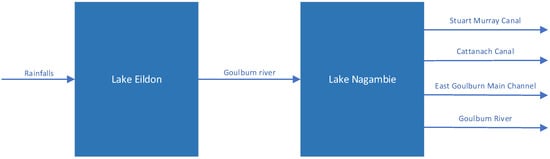
Figure 1.
Goulburn River cascade scheme.
5.1. Mcs and Generators
The states of the water reservoirs indicate their water levels, expressed in equal portions of their volume. So for Lake Eildon with a total volume equal to = 3,390,000 ML, the bounds of the states are , where and is the desired number of states, which is chosen according to accuracy demands. The same state division is considered for Lake Nagambie with volume = 25,500 ML: the bounds are , , — desired number of states for this reservoir. Association of the states with water volumes instead of the water surface levels leads to the same dependency of the transitions on the incoming and outcoming flows and hence simplifies the resulting model.
We model the reservoirs as MCs, so the evolution of the reservoirs’ states in time is described by the stochastic differential Equation (1), where and and stand for Lakes Eildon and Nagambie respectively. Due to natural reasons, the transitions are only possible between adjacent states, so the generators reflect a birth-and-death processes:
where is the intensity of the incoming flow of natural water arrivals and losses, and is the controlled intensity, which reflects the flow from Lake Eildon to Lake Nagambie. The variables and have a purely probabilistic sense, which has to be translated into the common units of water discharge measurement, say . Here the basic assumption is the equality of the average transition times, which for the constant rate and constant discharge u are equal to from the one side, and to from the other. Here v is the volume of water, which corresponds to the difference between the levels, for example, for Lake Eildon, . Thus, in terms of the discharges, the generator can be represented as follows:
where is the discharge from Lake Eildon, and is the sum of all the natural inflows expressed in common units .
Denote the controlled discharges from Lake Nagambie by , , , , which stand respectively for the discharges of the Stuart Murray, Cattanach, East Goulburn Main Channels, and the Goulburn River, and the sum of these discharges as . Since the outflow of Lake Eildon is at the same time the incoming flow of Lake Nagambie, we have the following representation of the generator :
It should be noted that the capacity of Lake Eildon is more than 100 times larger than the capacity of Lake Nagambie. This causes certain problems for the numerical simulation since the same discharge values affect the transition rates in different scales. To overcome this issue, one can normalize the transition rates by adjusting the number of states, providing . Another way is to scale down the time discretization step, ensuring adequate probabilities of state transitions for the MC, which corresponds to Lake Nagambie.
5.2. Performance Criterion and Constraints
The performance criterion should take into account the customer demands and ensure the balance of the water reservoirs inflows and outflows. We assume that there are some reference values for the demands in the channels and the Goulburn River: , , , , which an optimal control aims to satisfy. Let
where i and j stand for the state number of Lakes Eildon and Nagambie respectively, C is some large number, and is an indicator function.
The running cost function (4) with the state-related cost given by (18) reflects the mentioned aim along with the intention to balance the arriving and outgoing flows of Lake Nagambie. Plus, this running cost penalizes the nonzero discharges from both lakes, when they are in the states , , which corresponds to the lowest possible level, or drought.
The terminal condition in (3) is defined by matrix with elements , which correspond to the combination of states and . Let be the desired terminal state of the system, then define the terminal condition as follows:
where is the norm (sum of absolute values). This condition penalizes any deviation of the system’s state at the end of the control interval T from the desired and, moreover, it assigns a larger penalty for greater deviations.
For all the control variables we also define phase constraints in the form of upper and lower bounds:
These constraints bound the maximal possible discharges for the channels and the Goulburn River and guarantee the environmental demand, mentioned earlier.
5.3. Parameters Definition
In previous subsections, the Goulburn River cascade model was defined in general. Nevertheless, there still are some undefined parameters, which will be specified using real-world data. To define the reference demand values , , , , we use the data on the discharges of the corresponding channels and river available from the Water Measurement Information System of the Department of Environment, Land, Water & Planning of Victoria State Government [25]. The data on the daily discharges was grouped by the day of year, and for each group, the mean value was calculated. The resulting time series were approximated by functions
where days and coefficients , are chosen using the Least-Squares method. The resulting functions are smooth and have a period equal to one year, which makes them suitable for the reference values of the irrigation demands in the proposed model. The time series of the average daily discharges and the approximating functions are presented in Figure 2.
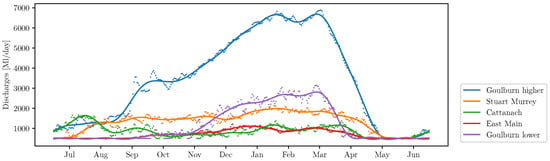
Figure 2.
Average daily discharges (dotted lines) and the approximating smooth periodic functions (solid lines).
The data for the Lake Eildon incoming flow is obtained from the Climate Data Online service of the Bureau of Meteorology of the Australian Government [26]. The rainfall data is collected at the weather station situated there. This data is averaged on a daily basis and approximated by a smooth periodic function in the same way as the daily discharges. The resulting function serves as an incoming flow pattern . For this model, we assume that the irrigation demands agree with the total available natural resources, so the incoming flow pattern is normalized to make the incoming flow satisfy the following condition:
The resulting flow approximation along with normalized rainfall averages is presented in Figure 3.
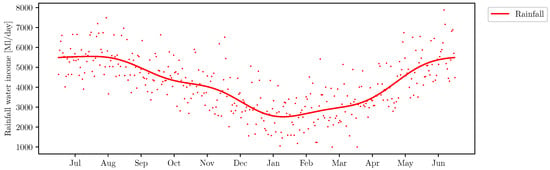
Figure 3.
Normalized rainfall daily averages (dotted line) and the approximation (solid line).
Specifying of the upper and lower bounds for the control parameters and by maximum and minimum registered values of the corresponding discharges time series obtained from Reference [25] finalizes the definition of our Goulburn River cascade model.
5.4. Simulation Results
The complete definition of the control optimization problem is given by
- phase constraints (20);
- incoming flow , reference values of the irrigation demands , , , and upper and lower bounds for the control parameters defined in Section 5.3.
Now the optimal Markov control (13) can be calculated as a solution to the system of ODEs (12). Remember that the minimization in the RHS of the ODEs can be done independently and hence can be effectively parallelized. The system (12) was solved numerically using the Euler method with the discretization step , while the time scale and all the necessary functions were normalized so that . The number of MCs’ states for both lakes was chosen as , and the desired terminal state .
In Figure 4 and Figure 5, the optimal control values are presented for the states and . One can see the nontrivial behavior of the optimal discharges, which differs from the reference values even for the desired terminal state. The evolution of the value function components exhibits the influence both from the integral part of the criterion and the terminal condition. Indeed, for it monotonically decreases since the demands here are mostly satisfied and the system is already in the desired state. For the state , on the contrary, there are intervals of monotonic growth: the first is because of insufficient supplies in late summer and autumn months, and the second starts in spring and shows the necessity to transit to the desired terminal state .
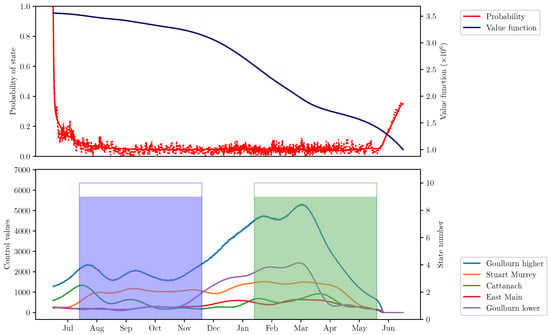
Figure 4.
Probability of the state , , corresponding value function component and optimal Markov control .
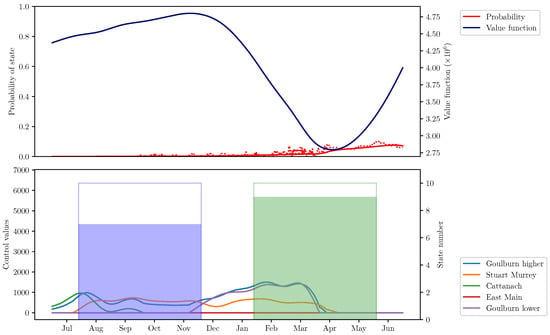
Figure 5.
Probability of the state , , corresponding value function component and optimal Markov control .
The Kolmogorov Equation (15) allows us to calculate the probabilities of the global system states given the initial state or distribution. The probabilities for states and are presented in Figure 4 and Figure 5 on the upper subplots. The initial state here was chosen to be equal to the terminal . The solid red lines present the solution of (15), and the dotted lines are the result of Monte-Carlo sampling: the state rate was estimated using a set of 100 sample paths governed by the optimal control strategy. The state probabilities allow us to also calculate the average states of MCs, which can be converted into the average levels of Lakes Eildon and Nagambie. In Figure 6, the average levels calculated by means of the Kolmogorov Equation (15) are presented by solid lines. The corresponding averages calculated using the Monte-Carlo sampling are depicted with dotted lines.
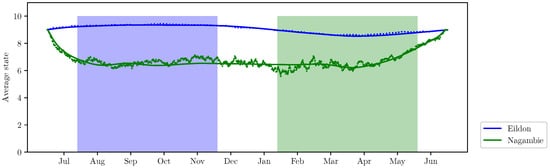
Figure 6.
Average levels of Lakes Eildon and Nagambie for optimal control.
As an alternative to the optimal control we present here a program control which aims to fully satisfy the customer demands:
The indicator functions make sure that the natural constraints are satisfied, that is, the water cannot be taken from an empty dam. In Figure 7, the average levels calculated by means of the Kolmogorov equation and Monte-Carlo sampling are presented. One can observe that this program control leads to overuse of the resources in contrast with the optimal one, which is able to refill the dams after the winter demand growth and rainfall shortage.
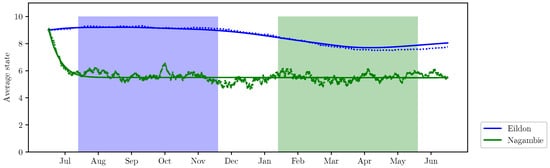
Figure 7.
Average levels of Lakes Eildon and Nagambie for program control.
6. Conclusions
The paper presents a framework of controlled coupled MC optimization. The specific character of the problem requires the usage of tensor representation of the set of MCs, which permits us to derive the joint set of DPEs and organize the calculation in a parallel manner. This is important, especially for the most time-consuming minimization of the right-hand side in each discretization step of the numerical solution of the DPE. For a demonstration of the method, we chose a model of the Goulburn River cascade. The model was deliberately simplified to provide a clear demonstration of the approach; however, it is just a first step in a possible detailed analysis of this dam system, which would rely on more detailed data on natural and agricultural processes in the district.
Author Contributions
Conceptualization, B.M., G.M.and S.S.; Data curation, G.M.; Formal analysis, D.M., B.M., G.M.and S.S.; Investigation, D.M., B.M., G.M.and S.S.; Methodology, B.M. and S.S.; Software, G.M.; Supervision, B.M. and S.S.; Validation, B.M.; Visualization, G.M.; Writing–original draft, D.M., B.M., G.M.and S.S.; Writing–review–editing, D.M., G.M.and S.S. All authors have read and agreed to the published version of the manuscript.
Funding
The work of G. Miller was partially supported by the Russian Foundation of Basic Research (RFBR Grant No. 19-07-00187-A).
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| DPE | Dynamic programming equation |
| GMW | Goulburn-Murray water |
| GSM | Goulburn simulation model |
| MC | Markov chain |
| ODE | Ordinary differential equation |
| RHS | Right-hand side |
Appendix A. Tensor Product Properties
In this Section we provide the tensor related definitions used throughout the paper. For more details we refer the reader to Reference [27].
For the present paper it is sufficient to define a tensor by its entries like an M-dimensional array of elements , where is multi-index (tuple) given by indices . The set of such objects we denote as .
Definition A1.
Let , then is called tensor product of vectors
if its entries are equal to .
From Definition A1 it follows that the tensor space can be defined as a set of all finite linear combinations of tensor products of vectors from vector spaces :
Definition A2.
Let be a set of matrices, then the tensor product of these matrices is the linear mapping
defined for any by
References
- Filar, J.; Vrieze, K. Competitive Markov Decision Processes; Springer: New York, NY, USA, 1997. [Google Scholar] [CrossRef]
- Williams, B.K. Markov decision processes in natural resources management: Observability and uncertainty. Ecol. Model. 2015, 220, 830–840. [Google Scholar] [CrossRef]
- Delebecque, F.; Quadrat, J.P. Optimal control of markov chains admitting strong and weak interactions. Automatica 1981, 17, 281–296. [Google Scholar] [CrossRef]
- Miller, B.M.; McInnes, D.J. Management of dam systems via optimal price control. Procedia Comput. Sci. 2011, 4, 1373–1382. [Google Scholar] [CrossRef][Green Version]
- McInnes, D.; Miller, B. Optimal control of time-inhomogeneous Markov chains with application to dam management. In Proceedings of the 2013 Australian Control Conference, Perth, Australia, 4–5 November 2013; pp. 230–237. [Google Scholar] [CrossRef]
- Miller, A.; Miller, B. Control of connected Markov chains. Application to congestion avoidance in the Internet. In Proceedings of the 2011 50th IEEE Conference on Decision and Control and European Control Conference, Orlando, FL, USA, 12–15 December 2011; pp. 7242–7248. [Google Scholar] [CrossRef]
- Miller, B.M. Optimization of queuing system via stochastic control. Automatica 2009, 45, 1423–1430. [Google Scholar] [CrossRef]
- Miller, A. Using methods of stochastic control to prevent overloads in data transmission networks. Autom. Remote. Control 2010, 71, 1804–1815. [Google Scholar] [CrossRef]
- Miller, B.; McInnes, D. Optimal management of a two dam system via stochastic control: Parallel computing approach. In Proceedings of the 2011 50th IEEE Conference on Decision and Control and European Control Conference, Orlando, FL, USA, 12–15 December 2011; pp. 1417–1423. [Google Scholar] [CrossRef]
- Elliott, R.J.; Aggoun, L.; Moore, J.B. Hidden Markov Models. Estimation and Control; Stochastic Modelling and Applied Probability; Springer: New York, NY, USA, 1995. [Google Scholar] [CrossRef]
- Miller, A.; Miller, B.; Popov, A.; Stepanyan, K. Towards the development of numerical procedure for control of connected Markov chains. In Proceedings of the 2015 5th Australian Control Conference (AUCC), Gold Coast, Australia, 5–6 November 2015; pp. 336–341. [Google Scholar]
- Fourneau, J.; Plateau, B.; Stewart, W. Product form for Stochastic Automata Networks. In Proceedings of the 2nd International ICST Conference on Performance Evaluation Methodologies and Tools (Valuetools), Nantes, France, 23–25 October 2007. [Google Scholar] [CrossRef]
- Jacod, J.; Shiryaev, A. Limit Theorems for Stochastic Processes. In Grundlehren Der Mathematischen Wissenschaften; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar] [CrossRef]
- Metivier, M.; Pellaumail, J. Stochastic Integration. In Probability and Mathematical Statistics; Academic Press: New York, NY, USA, 1980. [Google Scholar] [CrossRef]
- Miller, B.; Miller, G.; Siemenikhin, K. Towards the optimal control of Markov chains with constraints. Automatica 2010, 46, 1495–1502. [Google Scholar] [CrossRef]
- Wan, C.B.; Davis, M.H.A. Existence of Optimal Controls for Stochastic Jump Processes. SIAM J. Control Optim. 1978, 17, 511–524. [Google Scholar] [CrossRef]
- Miller, A.; Miller, B. Application of stochastic control to analysis and optimization of TCP. In Proceedings of the 2013 Australian Control Conference, Victoria, Australia, 4–5 November 2013; pp. 238–243. [Google Scholar] [CrossRef]
- Schreider, S.; Whetton, P.; Jakeman, A.; Pittock, A. Runoff modelling for snow-affected catchments in the Australian alpine region, eastern Victoria. J. Hydrol. 1997, 200, 1–23. [Google Scholar] [CrossRef]
- Schreider, S.; Jakeman, A.; Letcher, R.; Nathan, R.; Neal, B.; Beavis, S. Detecting changes in streamflow response to changes in non-climatic catchment conditions: Tarm dam development in the Murray–Darling basin, Australia. J. Hydrol. 2002, 262, 84–98. [Google Scholar] [CrossRef]
- Griffith, M.; Codner, G.; Weinmann, E.; Schreider, S. Modelling hydroclimatic uncertainty and short-run irrigator decision making: The Goulburn system. Aust. J. Agric. Resour. Econ. 2009, 53, 565–584. [Google Scholar] [CrossRef]
- Cui, J.; Schreider, S. Modelling of pricing and market impacts for water options. J. Hydrol. 2009, 371, 31–41. [Google Scholar] [CrossRef]
- Dixon, P.; Schreider, S.; Wittwer, G. Combining engineering-based water models with a CGE model. In Quantitative Tools in Microeconomic Policy Analysis; Pincus, J., Ed.; Australian Productivity Commission: Canberra, Australia, 2005; Chapter 2; pp. 17–30. [Google Scholar]
- Schreider, S.; Weinmann, P.E.; Codner, G.; Malano, H.M. Integrated Modelling System for Sustainable Water Allocation Planning. In Proceedings of the International Congress on Modelling and Simulation MODSIM01, Canberra, Australia, 1 January 2001; Ghassemi, F., McAleer, M., Oxley, L., Scoccimarro, M., Eds.; 2001; Volume 3, pp. 1207–1212. [Google Scholar]
- Perera, B.; James, B.; Kularathna, M. Computer software tool REALM for sustainable water allocation and management. J. Environ. Manag. 2005, 77, 291–300. [Google Scholar] [CrossRef] [PubMed]
- Water Measurement Information System of the Department of Environment, Land, Water & Planning of Victoria State Government. Available online: https://data.water.vic.gov.au/ (accessed on 25 July 2020).
- Climate Data Online Service of the Bureau of Meteorology of the Australian Government. Available online: http://www.bom.gov.au// (accessed on 25 July 2020).
- Hackbusch, W. Tensor Spaces and Numerical Tensor Calculus; Springer Series in Computational Mathematics; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).