New Refinements of the Erdös–Mordell Inequality and Barrow’s Inequality

Abstract

In this paper, two new refinements of the Erdös–Mordell inequality and three new refinements of Barrow’s inequality are established. Some related interesting conjectures are put forward.

1. Introduction

In 1935, Erdös [1] proposed the following geometric inequality:

For any interior point P of the triangle $ABC$, let $R_1,R_2,R_3$ be the distances from P to the vertices $A,B,C$, respectively, and let $r_1,r_2,r_3$ be the distances from P to the sides $BC,CA,AB$, respectively. Then

$$\sum R_1\ge 2\sum r_1,$$

(1)

where ∑ denotes the cyclic sums (we shall use this symbol in the sequel). Equality in (1) holds if and only if the triangle $ABC$ is equilateral and P is its center.

Two years later, Mordell and Barrow [2] first proved the inequality (1), and the latter actually obtained the following sharpness:

$$\sum R_1\ge 2\sum w_1,$$

(2)

where $w_1,w_2,w_3$ are the lengths of the bisectors of $\angle BPC,\angle CPA,\angle APB$, respectively.

The above two inequalities have long been famous results in the field of geometric inequalities. The former is called the Erdös–Mordell inequality, which has attracted the interest of many authors and motivated a large number of research papers (see [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28] and the references cited therein).

In 1957, Ozeki [22] first obtained the following generalization of Barrow’s inequality (2) for convex polygons: For any interior point P of the convex polygon $A_1{A}_2\cdots A_n$, it holds that

$$\sum _{i=1}^n{R}_i\ge \sec \frac{\pi }{n}\sum _{i=1}^n{w}_i,$$

(3)

where $R_i=P{A}_i$ and $w_i$ denote the lengths of the bisectors of $\angle A_{i}P{A}_{i+1}(i=1,2,\cdots ,n$ and $A_{n+1}=A_1)$.

Some other discussions about Barrow’s inequality and (3) can be found in [4,14,19,21,23,27].

In 2012, when the author considered Oppenheim’s inequality (see [24])

$$\sum R_2{R}_3\ge 2\sum (r_3+r_1)(r_1+r_2),$$

(4)

the following sharpened version of the Erdös–Mordell inequality was found:

$$R_2+R_3\ge 2r_1+\frac{{(r_2+r_3)}^2}{R_1},$$

(5)

with equality if and only if $▵ABC$ is an isosceles right triangle and P is its circumcenter. Furthermore, by using inequalities (4), (5), and other results, the author obtained a series of refinements for the Erdös–Mordell inequality in [14,16].

In this paper, we shall give two new refinements of the Erdös–Mordell inequality and three new refinements of Barrow’s inequality. In addition, we shall present several interesting related conjectures in the last section.

2. Refinements of the Erdös–Mordell Inequality

In [11], the author proved the following refinement of the Erdös–Mordell inequality:

$$\sum R_1\ge 2\sqrt{\sum h_a{r}_1}\ge 2\sum r_1$$

(6)

where $h_a,h_b,h_c$ are the corresponding altitudes of the sides $BC,CA,AB$ of the triangle $ABC$.

Here, we further give the following result:

Theorem 1.

For any interior point P of the triangle $ABC$, it holds that

$$\sum R_1\ge 2\sqrt{\sum h_a{w}_1}\ge 2\sqrt{\sum h_a{r}_1}\ge 2\sum r_1.$$

(7)

Equalities in (7) all hold if and only if $▵ABC$ is equilateral and P is its center.

To prove Theorem 1, we first give several lemmas.

Lemma 1.

For any triangle $ABC$ with sides $a,b,c$ and real numbers $x,y,z$, it holds that

$${\left(\sum xa\right)}^2\ge \left(2\sum bc-\sum a^2\right)\sum yz,$$

(8)

with equality if and only if $x:y:z=(b+c-a):(c+a-b):(a+b-c)$.

For any triangle $ABC$ with sides $a,b,c$, we have $\sqrt{b}+\sqrt{c}>\sqrt{b+c}>\sqrt{a}$. Thus, $\sqrt{a},\sqrt{b},\sqrt{c}$ can be viewed sides of a triangle, and we see that inequality (8) can be obtained by using the following weighted Oppenheim inequality (see [19], p. 681):

$${\left(\sum x{a}^2\right)}^2\ge 16S^2\sum yz$$

(9)

(where S is the area of $▵ABC$) and the following equivalent form of the Heron formula:

$$16S^2=2\sum b^2{c}^2-\sum a^4.$$

(10)

Remark 1.

In the sixth chapter of the monograph [17], the author proved that inequality (8) is equivalent with (9) and the Wolstenholme inequality (52) below.

In the Appendix A of my monograph [17], Theorem A3 gives an equivalent theorem for the geometric transformations, which includes the following conclusion: An inequality involving any interior point P of the triangle $ABC$,

$$f(a,b,c,R_1,R_2,R_3,r_1,r_2,r_3)\ge 0,$$

(11)

is equivalent to

$$f\left(\frac{a{R}_1}{2R},\frac{b{R}_2}{2R},\frac{c{R}_3}{2R},r_1,r_2,r_3,\frac{r_2{r}_3}{R_1},\frac{r_3{r}_1}{R_2},\frac{r_1{r}_2}{R_3}\right)\ge 0.$$

(12)

In fact, this conclusion can be extended to the following:

Lemma 2.

With above notations, the inequality

$$f(a,b,c,R_1,R_2,R_3,r_1,r_2,r_3,w_1,w_2,w_3)\ge 0$$

(13)

is equivalent to

$$\begin{array}{l}f\left(\frac{a{R}_1}{2R},\frac{b{R}_2}{2R},\frac{c{R}_3}{2R},r_1,r_2,r_3,\frac{r_2{r}_3}{R_1},\frac{r_3{r}_1}{R_2},\frac{r_1{r}_2}{R_3},\right.\hfill \\ \left.\frac{2r_2{r}_3}{r_2+r_3}\sin \frac{A}{2},\frac{2r_3{r}_1}{r_3+r_1}\sin \frac{B}{2},\frac{2r_1{r}_2}{r_1+r_2}\sin \frac{C}{2}\right)\ge 0.\hfill \end{array}$$

(14)

Proof. 

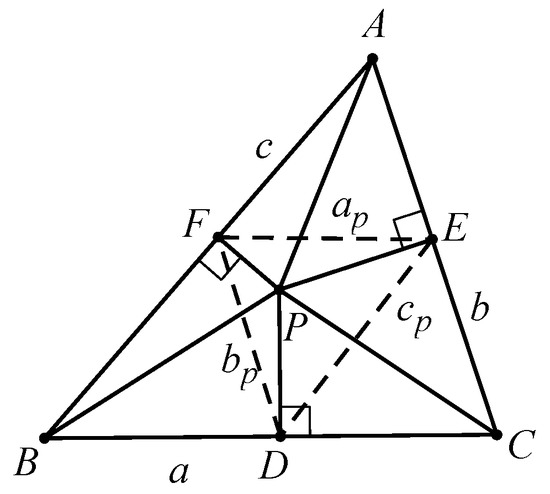
Let $DEF$ be the pedal triangle of P with respect to the triangle $ABC$ (see Figure 1), and let $EF=a_p,FD=b_p,DE=c_p$, then it is easy to get

$$a_p=\frac{a{R}_1}{2R},b_p=\frac{b{R}_2}{2R},c_p=\frac{c{R}_3}{2R}.$$

(15)

Figure 1. An inequality involving any point P inside triangle $ABC$ is equivalent to the one involving the point P and its pedal triangle $DEF$ with respect to $ABC$.

Let $h_1,h_2,h_3$ be the distances from P to the side lines $EF,FD,DE$, respectively, we also easily obtain

$$h_1=\frac{r_2{r}_3}{R_1},h_2=\frac{r_3{r}_1}{R_2},h_3=\frac{r_1{r}_2}{R_3}.$$

(16)

In addition, by means of the known formula in the triangle $ABC$

$$w_a=\frac{2bc}{b+c}\cos \frac{A}{2}$$

(17)

(where $w_a$ is the bisector of $\angle BAC$) and the fact that $\angle EPF=\pi -A$, we get

$$w_1^{\prime }=\frac{2r_2{r}_3}{r_2+r_3}\sin \frac{A}{2},$$

(18)

where $w_1^{\prime }$ is the bisector of $\angle EPF$. Two similar relations hold for the bisectors $w_2^{\prime },w_3^{\prime }$ of $\angle FPD,\angle DPE$, respectively.

If we apply inequality (13) to triangle $DEF$ and point P, then

$$f(a_p,b_p,c_p,r_1,r_2,r_3,h_1,h_2,h_3,w_1^{\prime },w_2^{\prime },w_3^{\prime })\ge 0.$$

Substituting (15), (16), and (18) into this inequality, (14) follows immediately. Conversely, we can obtain (13) from (14) by using the method of proving Theorem A3 in Appendix A of the monograph [17]. Thus, inequality (13) is equivalent with (14). The proof of Lemma 2 is completed. □

Lemma 3.

For any interior point P of the triangle $ABC$, it holds that

$$r_2+r_3\le 2R_1\sin \frac{A}{2},$$

(19)

with equality if and only if $r_2=r_3$.

Inequality (19) is well-known and is easily proved (see [29], p. 111).

Next, we prove Theorem 1.

Proof. 

Since $w_1\ge r_1$ etc., the second inequality in (7) is evidently valid. In addition, the third inequality of (7) is easily obtained (see [11]).

We now prove the first inequality in (7), i.e.,

$${\left(\sum R_1\right)}^2\ge 4\sum h_a{w}_1.$$

(20)

By the area formula $h_a=2S/a$ and the identity

$$\sum a{r}_1=2S,$$

(21)

we see that (20) is equivalent to

$${\left(\sum R_1\right)}^2\ge 4\sum a{r}_1\sum \frac{w_1}{a}.$$

(22)

According to Lemma 2 and the relations (15) and (16), we further know that inequality (22) is equivalent to

$${\left(\sum r_1\right)}^2\ge 4\sum \frac{a{R}_1}{2R}·\frac{r_2{r}_3}{R_1}\sum \frac{2R}{a{R}_1}·\frac{2r_2{r}_3}{r_2+r_3}\sin \frac{A}{2},$$

i.e.,

$${\left(\sum r_1\right)}^2\ge 8\sum a{r}_2{r}_3\sum \frac{r_2{r}_3}{a(r_2+r_3)R_1}\sin \frac{A}{2}.$$

(23)

But using $r_2{r}_3\le {(r_2+r_3)}^2/4$, Lemma 3, and the known formula

$$\sin \frac{A}{2}=\sqrt{\frac{(s-b)(s-c)}{bc}}$$

(24)

(where $s=(a+b+c)/2$), we have

$$\begin{array}{c}\sum \frac{r_2{r}_3}{a(r_2+r_3)R_1}\sin \frac{A}{2}\hfill \\ \le \frac{1}{4}\sum \frac{r_2+r_3}{a{R}_1}\sin \frac{A}{2}\hfill \\ \le \frac{1}{2}\sum \frac{1}{a}{\sin }^2\frac{A}{2}\hfill \\ =\frac{1}{2abc}\sum (s-b)(s-c).\hfill \end{array}$$

Thus, in order to prove inequality (23), we only need to prove that

$${\left(\sum r_1\right)}^2\ge 4\sum \frac{r_2{r}_3}{bc}\sum (s-b)(s-c).$$

(25)

Putting $x=r_1/a,y=r_2/b,z=r_3/c$ in inequality (8) of Lemma 1 and noting the fact that

$$2\sum bc-\sum a^2=4\sum (s-b)(s-c),$$

(26)

we get inequality (25) immediately. Thus, inequality (20) is proved. It is easily known that the equality in (20) holds if and only if $▵ABC$ is equilateral and P is its center. This completes the proof of Theorem 1. □

Now we state and prove the second refinement of the Erdös–Mordell inequality.

Theorem 2.

For any interior point P of the triangle $ABC$, it holds that

$$\begin{array}{c}\sum R_1\ge \sqrt{\frac{1}{2}\sum a^2+\sum R_2{R}_3+2\sum r_1^2}\hfill \\ \ge \sqrt{\frac{1}{2}\sum a^2+\frac{3}{2}\sum {(r_2+r_3)}^2}\ge 2\sum r_1.\hfill \end{array}$$

(27)

The first equality in (27) holds if and only if P is the circumcenter of the triangle $ABC$. The second and third equalities in (27) hold if and only if the triangle $ABC$ is equilateral and P is its center.

Proof. 

In triangle $ABC$, we have the following known angle bisector formula:

$$w_a=\frac{2}{b+c}\sqrt{sbc(s-a)}.$$

(28)

Noting that $\sqrt{bc}\le (b+c)/2$ and $s=(a+b+c)/2$, we have

$$w_a\le \frac{1}{2}\sqrt{\left[{(b+c)}^2-a^2\right]},$$

(29)

with equality if and only if $b=c$. Applying this inequality to $▵BPC$, we get

$$\sqrt{{(R_2+R_3)}^2-a^2}\ge 2w_1.$$

(30)

Hence, we have

$$\sum {(R_2+R_3)}^2\ge \sum a^2+4\sum w_1^2,$$

(31)

that is,

$$\sum R_1^2+\sum R_2{R}_3\ge \frac{1}{2}\sum a^2+2\sum w_1^2.$$

Adding $\sum R_2{R}_3$ to both sides of the above inequality and then squaring root, we obtain

$$\sum R_1\ge \sqrt{\frac{1}{2}\sum a^2+\sum R_2{R}_3+2\sum w_1^2}.$$

(32)

Sine $w_1\ge r_1$ etc., the first inequality in (27) obviously holds. Note that the equality in (30) holds if and only if $R_2=R_3$, thus the equality in (31) holds if and only if $R_1=R_2=R_3$, which means that P is the circumcenter of the triangle $ABC$. Furthermore, we can conclude that the first equality in (27) holds if and only if P is the circumcenter of the triangle $ABC$.

Clearly, the second inequality in (27) is equivalent to

$$\sum R_2{R}_3+2\sum r_1^2\ge \frac{3}{2}\sum {(r_2+r_3)}^2.$$

Removing $2\sum r_1^2$ to the right and arranging gives the previous Oppenheim inequality (4), which has been proved by the author in different ways (see [12,14]).

For the third inequality in (27), by squaring both sides and arranging, we know that it is equivalent to

$$2\sum r_1^2+10\sum r_2{r}_3\le \sum a^2,$$

(33)

which was first established by Chu in [30] and proved by the author in another way in [15]. In addition, we have known that both equalities in (4) and (33) hold if and only if $▵ABC$ is equilateral and P is its center. This completes the proof of Theorem 2. □

From Theorem 2, we have

Corollary 1.

For any interior point P of the triangle $ABC$, it holds that

$$2{\left(\sum R_1\right)}^2-3\sum {(r_2+r_3)}^2\ge \sum a^2.$$

(34)

Furthermore, we can easily obtain the following inequality:

Corollary 2.

For any interior point P of the triangle $ABC$, it holds that

$${\left(\sum R_1\right)}^2-2{\left(\sum r_1\right)}^2\ge \frac{1}{2}\sum a^2.$$

(35)

3. Refinements of Barrow’s Inequality

In [14], Theorem 4.3 gives the following refinement of the Erdös–Mordell inequality:

$$\sum R_1\ge \sqrt{\sum \left[R_1^2+2r_1{R}_1+{(r_2+r_3)}^2\right]}\ge 2\sum r_1,$$

(36)

which is actually equivalent to

$$\sum R_1\ge \sqrt{\sum {(R_1+r_1)}^2+{\left(\sum r_1\right)}^2}\ge 2\sum r_1.$$

(37)

Now, we point out that for Barrow’s inequality (2), the following similar result holds:

Theorem 3.

For any interior point P of the triangle $ABC$, it holds that

$$\sum R_1\ge \sqrt{\sum {(R_1+w_1)}^2+{\left(\sum w_1\right)}^2}\ge 2\sum w_1.$$

(38)

Equalities in (38) hold if and only if $▵ABC$ is equilateral and P is its center.

Clearly, the first inequality in (38) is also equivalent to the following interesting form:

$${\left(\sum R_1\right)}^2-{\left(\sum w_1\right)}^2\ge \sum {(R_1+w_1)}^2.$$

(39)

To prove this inequality, we first prove a strengthening of the previous inequality (5), which is posed by the author in [12] as a conjecture.

Lemma 4.

For any interior point P of the triangle $ABC$, it holds that

$$R_2+R_3\ge 2w_1+\frac{{(w_2+w_3)}^2}{R_1},$$

(40)

with equality if and only if $CA=AB$ and P is the circumcenter of the triangle $ABC$.

Proof. 

We let $\angle BPC=2{\delta }_1,\angle CPA=2{\delta }_2,\angle APB=2{\delta }_3$. By the previous Formula (17), we know that inequality (40) is equivalent to

$$R_2+R_3\ge \frac{4R_2{R}_3}{R_2+R_3}\cos {\delta }_1+\frac{1}{R_1}{\left(\frac{2R_3{R}_1}{R_3+R_1}\cos {\delta }_2+\frac{2R_1{R}_2}{R_1+R_2}\cos {\delta }_3\right)}^2.$$

Since $R_3+R_1\ge 2\sqrt{R_3{R}_1}$ and $R_1+R_2\ge 2\sqrt{R_1{R}_2}$, to prove the above inequality we only need to prove that

$$R_2+R_3\ge \frac{4R_2{R}_3}{R_2+R_3}\cos {\delta }_1+{\left(\sqrt{R_3}\cos {\delta }_2+\sqrt{R_2}\cos {\delta }_3\right)}^2.$$

(41)

Letting $\sqrt{R_2}=y$ and $\sqrt{R_3}=z,$ (41) then becomes

$$y^2+z^2\ge \frac{4y^2{z}^2}{y^2+z^2}\cos {\delta }_1+{\left(z\cos {\delta }_2+y\cos {\delta }_3\right)}^2.$$

(42)

Note that ${\delta }_1,{\delta }_2,{\delta }_3$ can be viewed angles of a non-obtuse triangle. To prove inequality (42), we only need to prove that the following inequality holds for non-obtuse triangles $ABC$ and real numbers $y,z$:

$$y^2+z^2\ge \frac{4y^2{z}^2}{y^2+z^2}\cos A+{\left(z\cos B+y\cos C\right)}^2,$$

(43)

that is,

$${(y^2+z^2)}^2-4y^2{z}^2\cos A-(y^2+z^2){\left(z\cos B+y\cos C\right)}^2\ge 0.$$

(44)

Multiplying both sides by $4{\left(abc\right)}^2$ and using the law of cosines, we can transform the proof to the following weighted inequality:

$$\begin{array}{c}4{\left(abc\right)}^2{(y^2+z^2)}^2-8bc{a}^2{y}^2{z}^2(b^2+c^2-a^2)\hfill \\ -(y^2+z^2){\left[zb(c^2+a^2-b^2)+yc(a^2+b^2-c^2)\right]}^2\ge 0.\hfill \end{array}$$

(45)

If we denote by $Q_0$ the value of the left-hand side of (45), then it is easy to check the following identity:

$$\begin{array}{cc}{Q}_0\hfill & =(y^2+z^2){(yc-zb)}^2(c^2+a^2-b^2)(a^2+b^2-c^2)\hfill \\ & +2a^2(b^2+c^2-a^2)[{(y^{2}c-z^{2}b)}^2+y^2{z}^2{(b-c)}^2],\hfill \end{array}$$

(46)

which shows that inequality $Q_0\ge 0$ holds clearly. Moreover, from (46) we can obtain the following conclusions: (i) if $A=\pi /2$, then the equality in (43) holds if and only if $yc=zb$; (ii) if $A<\pi /2$, then the equality in (43) holds if and only if $y=z$ and $b=c$. According to this conclusion, we can further determine the equality condition of (40), just as mentioned in Lemma 4. This completes the proof of Lemma 4. □

Remark 2.

Adding $R_1$ to both sides of (40) and noting that

$$R_1+\frac{{(w_2+w_3)}^2}{R_1}\ge 2(w_2+w_3),$$

we obtain Barrow’s inequality (2). Therefore, inequality (43) is actually stronger than Barrow’s inequality (2).

We now prove Theorem 3.

Proof. 

As the proof of the first inequality (36) given in [14], we can easily prove the first inequality of (38) by using Lemma 4 (we omit the details here). By the power means inequality and Barrow’s inequality (2), we have

$$\begin{array}{c}\sum {(R_1+w_1)}^2\ge \frac{1}{3}{\left[\sum (R_1+w_1)\right]}^2=\frac{1}{3}{\left(\sum R_1+\sum w_1\right)}^2\hfill \\ \ge 3{\left(\sum w_1\right)}^2.\hfill \end{array}$$

Hence, the second inequality of (38) follows immediately. Moreover, it is easily known that both equalities in (38) hold if and only if $▵ABC$ is equilateral and P is its center. The proof of Theorem 3 is completed. □

Next, we state and prove the second new refinement of Barrow’s inequality (2).

Theorem 4.

For any interior point P of the triangle $ABC$, it holds that

$$\sum R_1\ge \sum \sqrt{{(R_2+R_3)}^2-a^2}\ge 2\sum w_1.$$

(47)

The second equality in (47) holds if and only if P is the circumcenter of the triangle $ABC$.

Proof. 

Firstly, we prove the first of (47):

$$\sum R_1\ge \sum \sqrt{{(R_2+R_3)}^2-a^2}.$$

(48)

According to Lemma 2, we only need to prove that

$$\sum r_1\ge \sum \sqrt{{(r_2+r_3)}^2-a_p^2}.$$

(49)

Using the law of cosines in triangle $EPF$ and the fact that $\angle EPF=\pi -A$ (see Figure 1), we have

$$a_p^2=r_2^2+r_3^2-2r_2{r}_3\cos \angle EPF=r_2^2+r_3^2+2r_2{r}_3\cos A,$$

and then

$${(r_2+r_3)}^2-a_p^2=4r_2{r}_3{\sin }^2\frac{A}{2}.$$

(50)

Thus, we see that inequality (49) is equivalent to

$$\sum r_1\ge 2\sum \sqrt{r_2{r}_3}\sin \frac{A}{2}.$$

(51)

But, for any real numbers $x,y,z$ and $▵ABC$, we have the following Wolstenholme inequality (see [19]):

$$\sum x^2\ge 2\sum yz\cos A,$$

(52)

with equality if and only if $x:y:z=\sin A:\sin B:\sin C$. Putting $x=\sqrt{r_1},y=\sqrt{r_2},z=\sqrt{r_3}$ in (52) and substituting $A\to (\pi -A)/2$ etc., we get inequality (51) at once. Thus, inequality (48) is proved.

The second inequality in (47) follows immediately by adding the previous inequality (30) and its two analogues. Note that the equality in (30) holds if and only if $R_2=R_3$. We conclude that the second equality in (47) holds if and only if $R_1=R_2=R_3$, which means that the point P is the circumcenter of $▵ABC$. The proof of Theorem 4 is completed. □

Remark 3.

The author knows that the triangle $ABC$ need not be equilateral when the first equality in (47) holds but does not know what are the barycentric coordinates of P with respect to the triangle $ABC$.

Now we give an application of Theorem 4.

Squaring both sides of the first inequality of (47), we have

$$\begin{array}{c}{\left(\sum R_1\right)}^2\hfill \\ \ge \sum \left[{(R_2+R_3)}^2-a^2\right]+2\sum \sqrt{{(R_3+R_1)}^2-b^2}·\sqrt{{(R_1+R_2)}^2-c^2}.\hfill \end{array}$$

Then, applying inequality (30), we further get

$${\left(\sum R_1\right)}^2\ge \sum {(R_2+R_3)}^2-\sum a^2+8\sum w_2{w}_3.$$

Expanding gives the following:

Corollary 3.

For any interior point P of the triangle $ABC$, it holds that

$$\sum R_1^2+8\sum w_2{w}_3\le \sum a^2.$$

(53)

In fact, by using the previous inequality (30), we have the following extension:

$$\sum R_1^2+8\sum w_2{w}_3\le \sum a^2\le \sum {(R_2+R_3)}^2-4\sum w_1^2,$$

(54)

which implies Barrow’s inequality (2).

Finally, we give the third new refinement of Barrow’s inequality:

Theorem 5.

For any interior point P of the triangle $ABC$, it holds that

$$\sum R_1\ge \sqrt{\frac{1}{2}\sum a^2+\sum R_2{R}_3+2\sum w_1^2}\ge 2\sum w_1$$

(55)

The first equality in (55) holds if and only if P is the circumcenter of $▵ABC$. The second equality in (55) holds if and only if $▵ABC$ is equilateral and P is its center.

Proof. 

In the proof of Theorem 2, we have proved the first inequality in (55). The second inequality in (55) is easily obtained as follows: By (53), we have

$$\begin{array}{c}\frac{1}{2}\sum a^2+\sum R_2{R}_3+2\sum w_1^2\hfill \\ \ge \frac{1}{2}\sum R_1^2+4\sum w_2{w}_3+\sum R_2{R}_3+2\sum w_1^2\hfill \\ =\frac{1}{2}{\left(\sum R_1\right)}^2+2{\left(\sum w_1\right)}^2\hfill \\ \ge {\left(\sum w_1\right)}^2,\hfill \end{array}$$

where the last step used Barrow’s inequality (2). It is not difficult to know the equality conditions of inequality chain (55). The proof of Theorem 5 is completed. □

4. Some Open Problems

In this section, we present some interesting conjectures as open problems.

For the second inequality in (27), the author guesses that the following refinement is valid.

Conjecture 1.

For any interior point P of the triangle $ABC$, it holds that

$$\begin{array}{c}\sqrt{\frac{1}{2}\sum a^2+\sum R_2{R}_3+2\sum r_1^2}\ge \frac{1}{2}\sum \sqrt{a^2+4r_1^2}\hfill \\ \ge \sqrt{\frac{1}{2}\sum a^2+\frac{3}{2}\sum {(r_2+r_3)}^2}.\hfill \end{array}$$

(56)

A similar conjecture is as follows.

Conjecture 2.

For any interior point P of the triangle $ABC$, it holds that

$$\begin{array}{c}\sqrt{\frac{1}{2}\sum a^2+\sum R_2{R}_3+2\sum w_1^2}\ge \frac{1}{2}\sum \sqrt{a^2+4w_1^2}\hfill \\ \ge \sqrt{\frac{1}{2}\sum a^2+\frac{3}{2}\sum {(w_2+w_3)}^2}\ge 2\sum w_1.\hfill \end{array}$$

(57)

Remark 4.

The last inequality of (57) is actually equivalent to

$$2\sum w_1^2+10\sum w_2{w}_3\le \sum a^2,$$

(58)

which is Conjecture 2 posed by the author in [15].

Next, we give a reversed inequality similar to the previous inequality (34).

Conjecture 3.

For any interior point P of the triangle $ABC$, it holds that

$${\left(\sum R_1\right)}^2+12\sum r_2{r}_3\le 2\sum a^2.$$

(59)

Considering generalizations of the first inequality of (47), the author presents the following conjecture:

Conjecture 4.

Let P be an interior point of a convex polygon $A_1{A}_2\cdots A_n$($n>3$) and $P{A}_i=R_i(i=1,2,\cdots ,n)$, $R_{n+1}=R_1$, $A_i{A}_{i+1}=a_i(i=1,2,\cdots ,n,$ and $A_{n+1}=A_1$). Then

$$2\cos \frac{\pi }{n}\sum _{i=1}^n{R}_i\ge \sum _{i=1}^n\sqrt{{(R_i+R_{i+1})}^2-a_i^2}.$$

(60)

Remark 5.

By the previous inequality, (30) we know that the above inequality is stronger than inequality (3).

We have the following refinement of the Erdös–Mordell inequality (see [10]):

$$\sum R_1\ge \frac{1}{2}\sum \sqrt{a^2+4r_1^2}\ge 2\sum r_1,$$

(61)

in which the first inequality can easily be generalized to polygons by applying inequality (30) and $w_1\ge r_1$. The author believes that the second inequality can also be generalized to polygons as follows:

Conjecture 5.

Let P be an interior point of convex polygon $A_1{A}_2\cdots A_n$($n>3$), and let $r_i$ denote the distances from P to the side lines $A_i{A}_{i+1}(i=1,2,\cdots ,n$ and $A_{n+1}=A_1$). Then

$$\sum _{i=1}^n\sqrt{a_i^2+4r_i^2}\ge 2\sec \frac{\pi }{n}\sum _{i=1}^n{r}_i.$$

(62)

Similarly, we put forward the following conjecture:

Conjecture 6.

Let P be an interior point of convex polygon $A_1{A}_2\cdots A_n$($n>3$), and let $w_i$ denote the angle bisectors of $\angle A_{i}P{A}_{i+1}$($i=1,2,\cdots ,n$ and $A_{n+1}=A_1$). Then

$$\sum _{i=1}^n\sqrt{a_i^2+4w_i^2}\ge 2\sec \frac{\pi }{n}\sum _{i=1}^n{w}_i.$$

(63)

If the above inequality holds, then we can obtain the following refinement of inequality (3):

$$\sum _{i=1}^n{R}_i\ge \frac{1}{2}\sum _{i=1}^n\sqrt{a_i^2+4w_i^2}\ge \sec \frac{\pi }{n}\sum _{i=1}^n{w}_i,$$

(64)

where $R_i=P{A}_i(i=1,2,\cdots ,n)$.