Construction and Application of Nine-Tic B-Spline Tensor Product SS

Abstract

In this paper, we propose and analyze a tensor product of nine-tic B-spline subdivision scheme (SS) to reduce the execution time needed to compute the subdivision process of quad meshes. We discuss some essential features of the proposed SS such as continuity, polynomial generation, joint spectral radius, holder regularity and limit stencil. Some results of the SS using surface modeling with the help of computer programming are shown.

1. Introduction

Computer Aided Geometric Design (CAGD) considers the mathematical description of curves and surfaces utilized in computer graphics, data structure and computational algebra. CAGD has many fields of research interests. However, surface modeling is one of the important studies and an interesting area in the field of CAGD and computer graphics. Subdivision schemes (SSs) are iterative algorithms of surface modeling in CAGD. They are a type of models from discrete to discrete data having methods of generating curves/surfaces more effectively.

Nowadays, CAGD is the most common tool in the presentation of curves/surfaces. In CAGD, geometric shapes are related to the mathematical representations that satisfy approximation and interpolation properties of curves and surfaces. One of the common tools in CAGD are SSs, which provide an elegant way to describe curves and surfaces. Rham [1] was the first scholar who started work on SSs. He constructed a SS which generated a function with the first derivative. Chaikin [2] also used subdivision to design a curve. SSs gained importance when people generalized the tensor product in an arbitrary topology. This idea was presented by Doo and Sabin [3]. Catmull and Clark [4] used SSs to surface design and to control meshes in an arbitrary topology. Dyn et al. [5] generalized the SS of Dubuc and Deslauriers, known as butterfly SS, and concluded that the SS has $C^1$ smoothness in a certain range of shape parameter. In 1995, Dyn and Levin [6] introduced a technique for analyzing the Hermite-Type SSs for surface designs. In 1998, Stam [7] showed that surfaces and their derivatives can be described in terms of eigen basis functions. In 2002, Hassan et al. [8,9] worked on arity and number of control points. In 2005, Mustafa and Liu [10] worked on the SS of Bajaj with a new parameter that controlled the shape of models and gave them more flexibility to design a model over the soft and rough mesh network. Beccari et al. [11] produced an interpolating SS, which produced conic curve shapes. Mustafa et al. [12] unified the m-point approximating SS and showed that his SS has higher smoothness as compared to other SSs. Aslam et al. [13] introduced a formula that gives the mask of $(2n-1)$-point ternary interpolating as well as approximating SSs.

Zheng et al. [14] used B-spline to construct a $2n$-ary SS. In 2013, Mustafa et al. [15] worked on odd point ternary families of approximating SSs, in which they showed that their SSs have high smoothness. They also worked on subdivision regularization, in which they proposed that unified framework can work well for both over-fitting and noise removal in subdivision as well as regularization. In 2013, Ghaffar et al. [16] designed a three-point tensor product SS and showed some of its applications. Mustafa et al. [17] described a family of $(2n-1)$-point binary approximating SSs with tension parameters for generating curves. Again, Mustafa et al. [18] presented a general algorithm to generate a new class of binary approximating SSs and also have the derivation of some family members. In 2016, Hameed and Mustafa [19] constructed and analyzed binary SSs using Lane-Riesenfeld algorithm for curves and surfaces with Chaikin SS. In 2016, Ghaffar and Mustafa [20] proposed three different algorithms for approximating SS with application in curve modeling. In 2017, Cheng and Zhou [21] explained the necessary conditions of SSs with finite masks. During 2017, Akram et al. [22] discussed the properties of the binary four-point interpolating non-stationary SS [11]. In 2018, Manan et al. [23] focused on an algorithm to solve the third-order boundary value problem using eight-point approximating SS. In 2019, Kanwal et al. [24] formulated a numerical approximating collocation algorithm that is based on binary six-point approximating SS to generate the curves. Ghaffar et al. [25] introduced odd and even point non-stationary binary SSs for curve designing.

A simple smoothing tool for polygonal meshes is introduced which provide the motivation of our proposed work. The refine versions of the models are achieved by applying smoothing operation. The significance of the research problem to the success of such a model is that the transitions between the different resolutions of the meshes are almost imperceptible. This paper aims to construct a tensor product of nine-tic B-spline subdivision scheme to reduce the execution time needed to compute the subdivision process of quad meshes. The scheme, when computing the tetrahedron (four faces), as the number of faces increases, shows that the suggested technique performs better in model computation. The numerical results illustrate that the proposed SS reconstruct refined version of the models by using smoothing operation on regular meshes, but it doesn’t reproduced parametric curves/surfaces that have logarithmic functions and division terms i.e non-exponential polynomials, which actually needs non-uniform masks of SS for the exact reproduction of such models.

The remainder of this work is organized as follows. Section 2 describe properties of the SS. Section 3 is devoted to the construction and analysis of nine-tic B-spline tensor product SS. Section 4 gives numerical examples. Section 5 is concerned with the conclusion.

2. Properties of the SS

Here, firstly we introduce the nine-tic B-spline SS. We analyze the SS by examining the important features: continuity, hölder exponent, polynomial generation and reproduction, joint spectral radius, local analysis with invariant neighborhood and limiting curve produced by the nine-tic B-spline SS. It is defined as:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mu }_{2i}^{k+1}=\frac{10}{512}{\mu }_{i-2}^k+\frac{120}{512}{\mu }_{i-1}^k+\frac{252}{512}{\mu }_i^k+\frac{120}{512}{\mu }_{i+1}^k+\frac{10}{512}{\mu }_{i+2}^k,\hfill \\ {\mu }_{2i+1}^{k+1}=\frac{1}{512}{\mu }_{i-2}^k+\frac{45}{512}{\mu }_{i-1}^k+\frac{210}{512}{\mu }_i^k+\frac{210}{512}{\mu }_{i+1}^k+\frac{45}{512}{\mu }_{i+2}^k+\frac{1}{512}{\mu }_{i+3}^k.\hfill \end{array}\right.\end{array}$$

(1)

2.1. Smoothness of the SS

Theorem 1

([26]). The SS is convergent if and only if the SS $S_d$ is contractive, then for contractiveness $\parallel d_n\parallel <1$ for some $n>0$ with $\parallel d_n\parallel =\mathit{max}{\mathsf{\Sigma }}_u\left|d_{v-2_u^l}^n\right|:0\le v<2^n$, where $d_u^n$ are the coefficients of the SS $S_d^n$ with symbol $d^n\left(x\right)=d\left(x\right)d\left(x^2\right)...d\left(x^{2^n-1}\right)$.

Theorem 2.

If $S_{\eta }$ converges, then the limit curves can be denoted by $\eta \left(x\right)={\left(\frac{1+x}{2}\right)}^{q}d\left(x\right)$. $S_d$ is the SS for the qth divided differences.

Proof. 

Laurent polynomial of proposed SS (Equation (1)) can be elaborated as:

$$\begin{array}{ccc}\hfill \eta \left(x\right)& =& \frac{{(1+x)}^{10}}{512},\hfill \end{array}$$

where

$$\begin{array}{ccc}\hfill \eta \left(x\right)& =& \left\{x^{10}+10x^9+45x^8+120x^7+210x^6+252x^5+210x^4+120x^3\right.\hfill \\ & & \left.+45x^2+10x+1\right\}/512.\hfill \end{array}$$

To prove $C^0$ continuity of the SS $S_{\eta }$ related to $\eta \left(x\right)$, we have to show the convergence of $d_1\left(x\right)$. To see this we generate another SS $S_{{\mu }_1}$ related to ${\mu }_1\left(x\right)$ collected from $d_1\left(x\right)$ as:

$$\begin{array}{c}\hfill \eta \left(x\right)=\left(\frac{1+x}{2}\right)d_1\left(x\right)\end{array}$$

where

$$\begin{array}{ccc}\hfill d_1\left(x\right)& =& \left\{1+9x+36x^2+84x^3+126x^4+126x^5+84x^6+36x^7\right.\hfill \\ & & \left.+9x^8+x^9\right\}/256.\hfill \end{array}$$

The SS $S_{{\mu }_1}$ is contractive. For this, we have,

$$\begin{array}{ccc}\hfill \le {∥S_{{\mu }_1}∥}_{\infty }& =& \frac{1}{2}\max \left\{\left|\frac{1+36+126+84+9}{256}\right|,\left|\frac{9+84+126+36+1}{256}\right|\right\},\hfill \\ \hfill \le {∥S_{{\mu }_1}∥}_{\infty }& =& \frac{1}{2}\max \left\{\left|\frac{1}{256}\right|+\left|\frac{36}{256}\right|+\left|\frac{126}{256}\right|+\left|\frac{84}{256}\right|+\left|\frac{9}{256}\right|,\right.\hfill \\ & & \left.\left|\frac{1}{256}\right|+\left|\frac{36}{256}\right|+\left|\frac{126}{256}\right|+\left|\frac{84}{256}\right|+\left|\frac{9}{256}\right|\right\},\hfill \end{array}$$

$$\begin{array}{ccc}\hfill {∥S_{{\mu }_1}∥}_{\infty }& =& \frac{1}{2}\max \left\{\left|\frac{1}{256}\right|+\left|\frac{36}{256}\right|+\left|\frac{126}{256}\right|+\left|\frac{84}{256}\right|+\left|\frac{9}{256}\right|,\right.\hfill \\ & & \left.\left|\frac{1}{256}\right|+\left|\frac{36}{256}\right|+\left|\frac{126}{256}\right|+\left|\frac{84}{256}\right|+\left|\frac{9}{256}\right|\right\}<1.\hfill \end{array}$$

Thus, SS $S_{{\mu }_1}$ is contractive, $S_{d_1}$ is convergent and $S_{\eta }$ is $C^0$ continuous.

For $C^1$ continuity of the SS, we can rewrite as:

$$\begin{array}{c}\hfill \eta \left(x\right)={\left(\frac{1+x}{2}\right)}^2{d}_2\left(x\right),\end{array}$$

where

$$\begin{array}{ccc}\hfill d_2\left(x\right)& =& \left\{1+8x+28x^2+56x^3+70x^4+56x^5+28x^6+8x^7+x^8\right\}/128.\hfill \end{array}$$

To prove $C^1$ continuity of the SS $S_{\eta }$ related to $\eta \left(x\right)$, we have to show the convergence of $d_2\left(x\right)$. To see this, we generate another SS $S_{{\mu }_2}$ related to ${\mu }_2\left(x\right)$ collected from $d_2\left(x\right)$ as:

$$\begin{array}{ccc}\hfill {\mu }_2\left(x\right)& =& \left\{x^{-5}+8x^{-4}+28x^{-3}+56x^{-2}+70x^{-1}+56x^0+28x^1+8x^2+x^3\right\}/128.\hfill \end{array}$$

For the contractivity of the SS $S_{{\mu }_2}$, we have

$$\begin{array}{ccc}\hfill {∥S_{{\mu }_2}∥}_{\infty }& =& \frac{1}{2}\max \left\{\left|\frac{1}{128}\right|+\left|\frac{28}{128}\right|+\left|\frac{70}{128}\right|+\left|\frac{28}{128}\right|+\left|\frac{1}{128}\right|,\right.\hfill \\ & & \left.\left|\frac{8}{128}\right|+\left|\frac{56}{128}\right|+\left|\frac{56}{128}\right|+\left|\frac{8}{128}\right|\right\}<1.\hfill \end{array}$$

Thus, SS $S_{{\mu }_2}$ is contractive, $S_{d_2}$ is convergent and $S_{\eta }$ is $C^1$ continuous.

For $C^8$ continuity of the SS, we can rewrite as

$$\begin{array}{c}\hfill \eta \left(x\right)={\left(\frac{1+x}{2}\right)}^9{d}_9\left(x\right),\end{array}$$

where

$$\begin{array}{c}\hfill d_9\left(x\right)=1+x.\end{array}$$

To prove $C^8$ continuity of the SS $S_{\eta }$ related to $\eta \left(x\right)$, we have to show the convergence of $d_9\left(x\right)$. To see this, we generate another SS $S_{{\mu }_9}$ related to ${\mu }_9\left(x\right)$ collected from $d_9\left(x\right)$ as:

$$\begin{array}{c}\hfill {\mu }_9\left(x\right)=\left\{x^{-5}+x^{-4}\right\}.\end{array}$$

For the contractivity of the SS $S_{{\mu }_9}$, we have

$$\begin{array}{ccc}\hfill {∥S_{{\mu }_9}∥}_{\infty }& =& \frac{1}{2}\max \left\{\left|\frac{1}{2}\right|,\left|\frac{1}{2}\right|\right\}<1.\hfill \end{array}$$

Hence, the SS $S_{{\mu }_9}$ is contractive. This implies the $S_{\eta }$ has $C^8$ smoothness. □

2.2. Holder Exponent

Here, we find holder continuity of the nine-tic B-spline.

Theorem 3.

Consider that the SS (Equation (1)) $S_{\eta }$ with symbol $\eta \left(x\right)={\left(\frac{1+x}{2}\right)}^{l}d\left(x\right)$ produces limit curves with Holder continuity $r\ge l-{log}_2\frac{\parallel d^m\parallel }{m}$ for some m.

Proof. 

The symbol of the SS (Equation (1)) is:

$$\begin{array}{ccc}\hfill \eta \left(x\right)& =& \frac{x^{-5}}{512}\left\{1+10x+45x^2+120x^3+210x^4+252x^5+210x^6+120x^7\right.\hfill \\ & & \left.+45x^8+10x^9+x^{10}\right\}\hfill \\ & =& {\left(\frac{1+x}{2}\right)}^{10}d\left(x\right),\hfill \end{array}$$

where

$$\begin{array}{ccc}\hfill d\left(x\right)& =& \frac{2}{x^5}.\hfill \end{array}$$

Here, $l=10$ and $d=\left[2\right]$, which implies that $r\ge 10-{log}_2\left(2\right)=9.$ □

2.3. Polynomial Generation and Reproduction

In this section, we discuss the degree of polynomial generation and polynomial reproduction of nine-tic B-spline SS.

Theorem 4.

The degree of polynomial generation of SS (Equation (1)) is 9.

Proof. 

Since the Laurent polynomial $\eta \left(x\right)$ of the SS (Equation (1)) is

$$\begin{array}{c}\hfill \eta \left(x\right)={(1+x)}^{(9+1)}d\left(x\right),\end{array}$$

where

$$\begin{array}{ccc}\hfill d\left(x\right)& =& \frac{1}{512x^5}\left\{1+x\right\},\hfill \end{array}$$

then 9 is the degree of polynomial generation.

$$\begin{array}{c}\hfill \eta \left(x\right)={(1+x)}^{9+1}\left(\frac{1}{512x^5}\right),\end{array}$$

which shows that degree of polynomial generation is 9. □

Theorem 5.

The polynomial reproduction of SS (Equation (1)) is primal parameterization.

Proof. 

For any SS that generates linear functions with symbol

$$\begin{array}{c}\eta \left(x\right)={(1+x)}^{10}d\left(x\right),\hfill \end{array}$$

let $\tau =\frac{a^{\prime }\left(x\right)}{2}$ attach the data ${\mu }_u^v$ to parameter

$$\begin{array}{c}{t}_u^v=-\tau +\frac{u+\tau }{2^v}\hfill \end{array}$$

(2)

then the SS also reproduces linear functions. The Laurent polynomial of the SS (Equation (1)) is:

$$\begin{array}{ccc}\hfill \eta \left(x\right)& =& \frac{x^{-5}}{512}\left\{1+10x+45x^2+120x^3+210x^4+252x^5+210x^6+120x^7\right.\hfill \\ & & \left.+45x^8+10x^9+x^{10}\right\},\hfill \\ & =& {\left(\frac{1+x}{2}\right)}^{10}d\left(x\right).\hfill \end{array}$$

$$\begin{array}{ccc}\hfill {\eta }^{\prime }\left(x\right)& =& \{-5x^{-6}-40x^{-5}-135x^{-4}-240x^{-3}-210x^{-2}+210+240x+135x^2+40x^3\hfill \\ & & +5x^4\}/512.\hfill \end{array}$$

After putting $x=1$, we get

$$\begin{array}{c}{\eta }^{\prime }\left(1\right)=\{-5-40-135-240-210+210+240+135+40+5\}/512=0.\hfill \end{array}$$

Thus, the value of $\tau =\frac{{\eta }^{\prime }\left(1\right)}{2}=\frac{0}{2}=0$, putting the value of τ in above Equation (2):

$$\begin{array}{c}{t}_u^v=-\tau +\frac{u+\tau }{2^v},\hfill \end{array}$$

$$\begin{array}{c}{t}_u^v=0+\frac{u+0}{2^v}=\frac{u}{2^v}.\hfill \end{array}$$

Thus, the nine-tic B-spline SS generates linear reproduction with respect to primal parameterization. This SS is primal parameterization. □

2.4. Local Analysis with Invariant Neighborhood

In this section, we calculate the limit stencil of Nine-tic B-Spline SS by using local analysis. Using limit stencil, we locate the confine position of control point of initial control polygon on the point of confinement curve. For this, by considering the SS (Equation (1)), we can write it in matrix form as:

$$\left[\begin{array}{c}\hfill {\mu }_{-4}^u\\ \hfill {\mu }_{-3}^u\\ \hfill {\mu }_{-2}^u\\ \hfill {\mu }_{-1}^u\\ \hfill {\mu }_0^u\\ \hfill {\mu }_1^u\\ \hfill {\mu }_2^u\\ \hfill {\mu }_3^u\\ \hfill {\mu }_4^u\end{array}\right]=\left[\begin{array}{ccccccccc}\frac{10}{512}& \frac{120}{512}& \frac{252}{512}& \frac{120}{512}& \frac{10}{512}& 0& 0& 0& 0\\ \frac{1}{512}& \frac{45}{512}& \frac{210}{512}& \frac{210}{512}& \frac{45}{512}& \frac{1}{512}& 0& 0& 0\\ 0& \frac{10}{512}& \frac{120}{512}& \frac{252}{512}& \frac{120}{512}& \frac{10}{512}& 0& 0& 0\\ 0& \frac{1}{512}& \frac{45}{512}& \frac{210}{512}& \frac{210}{512}& \frac{45}{512}& \frac{1}{512}& 0& 0\\ 0& 0& \frac{10}{512}& \frac{120}{512}& \frac{252}{512}& \frac{120}{512}& \frac{10}{512}& 0& 0\\ 0& 0& \frac{1}{512}& \frac{45}{512}& \frac{210}{512}& \frac{210}{512}& \frac{45}{512}& \frac{1}{512}& 0\\ 0& 0& 0& \frac{10}{512}& \frac{120}{512}& \frac{252}{512}& \frac{120}{512}& \frac{10}{512}& 0\\ 0& 0& 0& \frac{1}{512}& \frac{45}{512}& \frac{210}{512}& \frac{210}{512}& \frac{45}{512}& \frac{1}{512}\\ 0& 0& 0& 0& \frac{10}{512}& \frac{120}{512}& \frac{252}{512}& \frac{120}{512}& \frac{10}{512}\end{array}\right]\left[\begin{array}{c}\hfill {\mu }_{-4}^{u-1}\\ \hfill {\mu }_{-3}^{u-1}\\ \hfill {\mu }_{-2}^{u-1}\\ \hfill {\mu }_{-1}^{u-1}\\ \hfill {\mu }_0^{u-1}\\ \hfill {\mu }_1^{u-1}\\ \hfill {\mu }_2^{u-1}\\ \hfill {\mu }_3^{u-1}\\ \hfill {\mu }_4^{u-1}\end{array}\right]$$

(3)

The local subdivision matrix of the presented SS is:

$$\begin{array}{c}\hfill \mathbf{S}=\left[\begin{array}{ccccccccc}\frac{10}{512}& \frac{120}{512}& \frac{252}{512}& \frac{120}{512}& \frac{10}{512}& 0& 0& 0& 0\\ \frac{1}{512}& \frac{45}{512}& \frac{210}{512}& \frac{210}{512}& \frac{45}{512}& \frac{1}{512}& 0& 0& 0\\ 0& \frac{10}{512}& \frac{120}{512}& \frac{252}{512}& \frac{120}{512}& \frac{10}{512}& 0& 0& 0\\ 0& \frac{1}{512}& \frac{45}{512}& \frac{210}{512}& \frac{210}{512}& \frac{45}{512}& \frac{1}{512}& 0& 0\\ 0& 0& \frac{10}{512}& \frac{120}{512}& \frac{252}{512}& \frac{120}{512}& \frac{10}{512}& 0& 0\\ 0& 0& \frac{1}{512}& \frac{45}{512}& \frac{210}{512}& \frac{210}{512}& \frac{45}{512}& \frac{1}{512}& 0\\ 0& 0& 0& \frac{10}{512}& \frac{120}{512}& \frac{252}{512}& \frac{120}{512}& \frac{10}{512}& 0\\ 0& 0& 0& \frac{1}{512}& \frac{45}{512}& \frac{210}{512}& \frac{210}{512}& \frac{45}{512}& \frac{1}{512}\\ 0& 0& 0& 0& \frac{10}{512}& \frac{120}{512}& \frac{252}{512}& \frac{120}{512}& \frac{10}{512}\end{array}\right]\end{array}$$

The proposed SS has invariant neighborhood size 9 and the corresponding eigenvalues of the subdivision matrix $\mathbf{S}$ are $\lambda =\{1,\frac{1}{2},\frac{1}{4},\frac{1}{8},\frac{1}{16},\frac{1}{32},\frac{1}{64},\frac{1}{128},\frac{1}{256}\}$. For eigenvectors related to eigenvalues, we obtain:

$$\begin{array}{c}\hfill \left[\begin{array}{c}1\\ \frac{1}{2}\\ \frac{1}{4}\\ \frac{1}{8}\\ \frac{1}{16}\\ \frac{1}{32}\\ \frac{1}{64}\\ \frac{1}{128}\\ \frac{1}{256}\end{array}\right]\left[\begin{array}{ccccccccc}1& -1& 1& 1& 1& -1& 1& -1& -1\\ -\frac{1}{8}& -\frac{13}{36}& 1& \frac{7}{13}& -\frac{16}{29531}& \frac{223}{3044}& \frac{229}{1069}& -\frac{3}{4}& -\frac{101}{1068}\\ \frac{1}{28}& -\frac{1}{18}& 1& \frac{19}{91}& -\frac{331}{29531}& -\frac{19}{1522}& -\frac{11}{1069}& -\frac{1}{2}& \frac{13}{534}\\ -\frac{1}{56}& \frac{1}{36}& 1& \frac{1}{91}& \frac{236}{29531}& \frac{9}{3044}& -\frac{11}{1069}& -\frac{1}{4}& -\frac{7}{1068}\\ \frac{1}{70}& 0& 1& -\frac{5}{91}& -\frac{205}{29531}& 0& \frac{13}{1069}& 0& 0\\ -\frac{1}{56}& -\frac{1}{36}& 1& \frac{1}{91}& \frac{236}{29531}& -\frac{9}{3044}& -\frac{11}{1069}& \frac{1}{4}& \frac{7}{1068}\\ \frac{11}{28}& \frac{1}{18}& 1& \frac{19}{91}& -\frac{331}{29531}& \frac{19}{1522}& -\frac{11}{1069}& \frac{1}{2}& -\frac{13}{534}\\ -\frac{1}{8}& \frac{13}{36}& 1& \frac{7}{13}& -\frac{16}{29531}& -\frac{223}{3044}& \frac{229}{1069}& \frac{3}{4}& \frac{101}{1068}\\ 1& 1& 1& 1& 1& 1& 1& 1& 1\end{array}\right]\end{array}$$

Thus,

$$\begin{array}{c}\hfill Q=\left[\begin{array}{ccccccccc}1& -\frac{1}{8}& \frac{1}{28}& -\frac{1}{56}& \frac{1}{70}& -\frac{1}{56}& \frac{1}{28}& -\frac{1}{8}& 1\\ -1& -\frac{13}{36}& -\frac{1}{18}& \frac{1}{36}& 0& -\frac{1}{36}& \frac{1}{18}& \frac{13}{36}& 1\\ 1& 1& 1& 1& 1& 1& 1& 1& 1\\ 1& \frac{7}{13}& \frac{19}{91}& \frac{1}{91}& -\frac{5}{91}& \frac{1}{91}& \frac{19}{91}& \frac{7}{13}& 1\\ 1& -\frac{16}{29531}& -\frac{331}{29531}& \frac{236}{29531}& -\frac{205}{29531}& \frac{236}{29531}& -\frac{331}{29531}& -\frac{16}{29531}& 1\\ -1& \frac{223}{3044}& -\frac{19}{1522}& \frac{9}{3044}& 0& -\frac{9}{3044}& \frac{19}{1522}& -\frac{223}{3044}& 1\\ 1& \frac{229}{1069}& -\frac{11}{1069}& -\frac{11}{1069}& \frac{13}{1069}& -\frac{11}{1069}& -\frac{11}{1069}& \frac{229}{1069}& 1\\ -1& -\frac{3}{4}& -\frac{1}{2}& -\frac{1}{4}& 0& \frac{1}{4}& \frac{1}{2}& \frac{3}{4}& 1\\ -1& -\frac{101}{1068}& \frac{13}{534}& -\frac{7}{1068}& 0& \frac{7}{1068}& -\frac{13}{534}& \frac{101}{1068}& 1\end{array}\right]\end{array}$$

and

$$\begin{array}{c}\hfill Q^{-1}=\left[\begin{array}{ccccccccc}\frac{1}{9}& -\frac{1}{80}& \frac{1}{362880}& \frac{13}{8640}& \frac{29531}{90720}& -\frac{761}{2520}& \frac{1069}{17280}& -\frac{1}{10080}& -\frac{89}{480}\\ -\frac{8}{9}& -\frac{27}{40}& \frac{251}{181440}& \frac{767}{4320}& -\frac{29531}{45360}& \frac{761}{420}& \frac{11759}{8640}& -\frac{41}{1680}& -\frac{89}{80}\\ \frac{28}{9}& -\frac{67}{40}& \frac{913}{22680}& \frac{1547}{1080}& -\frac{29531}{11340}& -\frac{761}{180}& -\frac{1069}{540}& -\frac{289}{720}& \frac{1513}{240}\\ -\frac{56}{9}& \frac{217}{40}& \frac{44117}{181440}& \frac{1001}{4320}& \frac{502027}{45360}& \frac{761}{180}& -\frac{45967}{8640}& -\frac{809}{720}& -\frac{2047}{240}\\ \frac{70}{9}& 0& \frac{15619}{36288}& -\frac{3185}{864}& -\frac{147655}{9072}& 0& \frac{20311}{1728}& 0& 0\\ -\frac{56}{9}& -\frac{217}{40}& \frac{44117}{181440}& \frac{1001}{4320}& \frac{502027}{45360}& -\frac{761}{180}& -\frac{45967}{8640}& \frac{809}{720}& \frac{2047}{240}\\ \frac{28}{9}& \frac{67}{40}& \frac{913}{22680}& \frac{1547}{1080}& -\frac{29531}{11340}& \frac{761}{180}& -\frac{1069}{540}& \frac{289}{720}& -\frac{1513}{240}\\ -\frac{8}{9}& \frac{27}{40}& \frac{251}{181440}& \frac{767}{4320}& -\frac{29531}{45360}& -\frac{761}{420}& \frac{11759}{8640}& \frac{41}{1680}& \frac{89}{80}\\ \frac{1}{9}& \frac{1}{80}& \frac{1}{362880}& \frac{13}{8640}& \frac{29531}{90720}& \frac{761}{2520}& \frac{1069}{17280}& \frac{1}{10080}& \frac{89}{480}\end{array}\right]\end{array}$$

and the eigen decomposition of $\mathbf{S}$ is

$$\mathbf{S}=Q\wedge Q^{-1},$$

where

$$\begin{array}{c}\hfill \wedge =\left[\begin{array}{ccccccccc}1& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& \frac{1}{2}& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& \frac{1}{4}& 0& 0& 0& 0& 0\\ 0& 0& 0& \frac{1}{8}& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& \frac{1}{16}& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& \frac{1}{32}& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& \frac{1}{64}& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& \frac{1}{128}& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& \frac{1}{256}\end{array}\right]\end{array}$$

Using diagonalization process of a matrix $\wedge ={\mathbf{S}}^{-1}A\mathbf{S}$, whereas ∧ = diagonal matrix, $\mathbf{S}=Q\wedge Q^{-1}$ indicates that ${\mathbf{S}}^u=Q{\wedge }^u{Q}^{-1}$, where $\wedge ={\mathbf{S}}^{-1}A\mathbf{S}$, and $A=\mathbf{S}\wedge {\mathbf{S}}^{-1}$ shows that $A^u=\mathbf{S}{\wedge }^u{\mathbf{S}}^{-1}.$ Since ∧ is a diagonal matrix, for some diagonal matrix, ${\wedge }^2$ means square of entries diagonally and so on. Thus,

$$\begin{array}{c}\hfill {\wedge }^u=\left[\begin{array}{ccccccccc}1& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& {\left(\frac{1}{2}\right)}^u& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& {\left(\frac{1}{4}\right)}^u& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& {\left(\frac{1}{8}\right)}^u& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& {\left(\frac{1}{16}\right)}^u& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& {\left(\frac{1}{32}\right)}^u& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& {\left(\frac{1}{64}\right)}^u& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& {\left(\frac{1}{128}\right)}^u& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& {\left(\frac{1}{256}\right)}^u\end{array}\right]\end{array}$$

In addition, then ${\mathbf{S}}^u=Q{\wedge }^u{Q}^{-1}$. Thus, using eigen decomposition of $\mathbf{S}$, we have, $X^u=\mathbf{S}{X}^{u-1}=\mathbf{S}\left(\mathbf{S}{X}^{u-2}\right)={\mathbf{S}}^2{X}^{u-2}$ and so on. $X^u={\mathbf{S}}^u{X}^0$ shows that $X^u=\left(Q{\wedge }^u{Q}^{-1}\right)X^0.$ Now, by applying limit $u\to \infty$, $X^{\infty }={lim}_{u\to \infty }{\mathbf{S}}^u{X}^0={\mathbf{S}}^{\infty }{X}^0$ implies that $X^{\infty }=Q{\bigwedge }^{\infty }{Q}^{-1}{X}^0$.

$$\left[\begin{array}{c}\hfill {\mu }_{-4}^u\\ \hfill {\mu }_{-3}^u\\ \hfill {\mu }_{-2}^u\\ \hfill {\mu }_{-1}^u\\ \hfill {\mu }_0^u\\ \hfill {\mu }_1^u\\ \hfill {\mu }_2^u\\ \hfill {\mu }_3^u\\ \hfill {\mu }_4^u\end{array}\right]=\left[\begin{array}{ccccccccc}\frac{1}{9}& -\frac{1}{80}& \frac{1}{362880}& \frac{13}{8640}& \frac{29531}{90720}& -\frac{761}{2520}& \frac{1069}{17280}& -\frac{1}{10080}& -\frac{89}{480}\\ -\frac{1}{9}& \frac{1}{80}& -\frac{1}{362880}& -\frac{13}{8640}& -\frac{29531}{90720}& \frac{761}{2520}& -\frac{1069}{17280}& \frac{1}{10080}& \frac{89}{480}\\ \frac{1}{9}& -\frac{1}{80}& \frac{1}{362880}& \frac{13}{8640}& \frac{29531}{90720}& -\frac{761}{2520}& \frac{1069}{17280}& -\frac{1}{10080}& -\frac{89}{480}\\ \frac{1}{9}& -\frac{1}{80}& \frac{1}{362880}& \frac{13}{8640}& \frac{29531}{90720}& -\frac{761}{2520}& \frac{1069}{17280}& -\frac{1}{10080}& -\frac{89}{480}\\ \frac{1}{9}& -\frac{1}{80}& \frac{1}{362880}& \frac{13}{8640}& \frac{29531}{90720}& -\frac{761}{2520}& \frac{1069}{17280}& -\frac{1}{10080}& -\frac{89}{480}\\ -\frac{1}{9}& \frac{1}{80}& -\frac{1}{362880}& -\frac{13}{8640}& -\frac{29531}{90720}& \frac{761}{2520}& -\frac{1069}{17280}& \frac{1}{10080}& \frac{89}{480}\\ \frac{1}{9}& -\frac{1}{80}& \frac{1}{362880}& \frac{13}{8640}& \frac{29531}{90720}& -\frac{761}{2520}& \frac{1069}{17280}& -\frac{1}{10080}& -\frac{89}{480}\\ -\frac{1}{9}& \frac{1}{80}& -\frac{1}{362880}& -\frac{13}{8640}& -\frac{29531}{90720}& \frac{761}{2520}& -\frac{1069}{17280}& \frac{1}{10080}& \frac{89}{480}\\ -\frac{1}{9}& \frac{1}{80}& -\frac{1}{362880}& -\frac{13}{8640}& -\frac{29531}{90720}& \frac{761}{2520}& -\frac{1069}{17280}& \frac{1}{10080}& \frac{89}{480}\end{array}\right]\left[\begin{array}{c}\hfill {\mu }_{-4}^{u-1}\\ \hfill {\mu }_{-3}^{u-1}\\ \hfill {\mu }_{-2}^{u-1}\\ \hfill {\mu }_{-1}^{u-1}\\ \hfill {\mu }_0^{u-1}\\ \hfill {\mu }_1^{u-1}\\ \hfill {\mu }_2^{u-1}\\ \hfill {\mu }_3^{u-1}\\ \hfill {\mu }_4^{u-1}\end{array}\right].$$

Hence, the limit stencils are: $[\frac{1}{9},\frac{-1}{80},\frac{1}{362880},\frac{13}{8640},\frac{29531}{90720},\frac{-761}{2520},\frac{1069}{17280},\frac{-1}{10080},\frac{-89}{480}].$

3. Construction and Analysis of Nine-tic B-Spline Tensor Product SS

3.1. Preliminaries

In this section, we construct nine-tic B-Spline tensor product SS. We analyze the SS by reviewing the continuity of the SS and limiting behavior of the curve generated by nine-tic B-spline tensor product SS. The Laurent polynomial of tensor product SS can be acquired by the accompanying principle:

$$\begin{array}{c}\hfill \eta \left(x\right)=\eta (x_1,x_2)=\eta \left(x_1\right)\eta \left(x_2\right),\end{array}$$

(4)

where $\eta \left(x_1\right)$ and $\eta \left(x_2\right)$ are the Laurent polynomials of univariate SSs.

A general compact form of binary SS $\mathbf{S}$ which maps a polygon ${\mu }^k={\left\{{\mu }_{u,v}^k\right\}}_{u,v\in \mathbb{Z}}$ to a refined polygon ${\mu }^{k+1}={\left\{{\mu }_{u,v}^{k+1}\right\}}_{u,v\in \mathbb{Z}}$ is defined by

$$\begin{array}{c}\hfill {\mu }_{\delta }^{k+1}=\sum _{\gamma \in {\mathbb{Z}}^s}{\eta }_{\delta -2\gamma }{\mu }_{\gamma }^k,\delta \in {\mathbb{Z}}^s.\end{array}$$

(5)

where $\mathbf{S}=1$ for curve and $\mathbf{S}=2$ for surface. In the case of univariate SSs, the two rules ( for u is even and odd) are given below as:

Let $u=2m$, then

$$\begin{array}{c}\hfill {\mu }_{2m}^{k+1}=\sum _{v\in \mathbb{Z}}{\eta }_{2m-2v}{\mu }_u^k.\end{array}$$

To get second rule, we assume $u=2m+1$, then

$$\begin{array}{c}\hfill {\mu }_{2l+1}^{k+1}=\sum _{v\in \mathbb{Z}}{\eta }_{(2m+1)-2v}{\mu }_u^k.\end{array}$$

In the case of tensor product (bivariate) SS, we have four rules subject to the uniformity of each component in the multi-index $u=(u_1,u_2)$.

$${\mu }_{2u_1,2u_2}^{k+1}=\sum _{l_1,l_2\in \mathbb{Z}}{\eta }_{2l_1,2l_2}{\mu }_{u_1-l_1,u_2-l_2}^k,{\mu }_{2u_1+1,2u_2}^{k+1}=\sum _{l_1,l_2\in \mathbb{Z}}{\eta }_{2l_1+1,2l_2}{\mu }_{u_1-l_1,u_2-l_2}^k,$$

$${\mu }_{2u_1,2u_2+1}^{k+1}=\sum _{l_1,l_2\in \mathbb{Z}}{\eta }_{2l_1,2l_2+1}{\mu }_{u_1-l_1,u_2-l_2}^k,{\mu }_{2u_1+1,2u_2+1}^{k+1}=\sum _{l_1,l_2\in \mathbb{Z}}{\eta }_{2l_1+1,2l_2+1}{\mu }_{u_1-l_1,u_2-l_2}^k.$$

A necessary condition for uniform convergence of SS (Equation (5)) is given in the following theorem.

Theorem 6 

([26]). Let $\eta \left(x\right)=\eta (x_1,x_2)={\sum }_{u,v}{\eta }_{u,v}{x}_1^u{x}_2^v$ be the symbol or Laurent polynomial of bivariate SS $\mathbf{S}$, which is defined on quad-meshes. Then, a necessary condition for the convergence of $\mathbf{S}$ is:

$$\begin{array}{c}\hfill \sum _{\gamma \in {\mathbb{Z}}^2}{\eta }_{\delta -2\gamma }=1,\delta \in \{(0,0),(0,1),(1,0),(1,1)\}.\end{array}$$

(6)

This implies that:

$$\begin{array}{c}\hfill \eta (1,1)=4,\eta (-1,1)=\eta (1,-1)=\eta (-1,-1)=0.\end{array}$$

(7)

Theorem 7 

([26]). Suppose the SSs with symbols ${\eta }^{\left[1\right]}\left(x\right)=\frac{\eta \left(x\right)}{1+x_1}=(1+x_2)b\left(x\right)$ and ${\eta }^{\left[2\right]}\left(x\right)=\frac{\eta \left(x\right)}{1+x_2}=(1+x_1)b\left(x\right)$, are both contractive, namely

$$\begin{array}{c}\hfill \underset{k\to \infty }{lim}{\left(S_{{\eta }^{\left[1\right]}}\right)}^k{\mu }^0=0,\underset{k\to \infty }{lim}{\left(S_{{\eta }^{\left[2\right]}}\right)}^k{\mu }^0=0,\end{array}$$

for any initial data ${\mu }^0$ then the SS $S_{\eta }$ with the symbol: $\eta \left(x\right)=(1+x_1)(1+x_2)b\left(x\right),x=(x_1,x_2),$ is convergent. Conversely, if $S_{\eta }$ is convergent, then $S_{{\eta }^{\left[1\right]}}$ and $S_{{\eta }^{\left[2\right]}}$ are contractive.

Remark 1 

([26]). Thus, convergence is checked in this case by checking the contractivity of two SSs $S_{{\eta }_1},S_{{\eta }_2}.$ If $b(x_1,x_2)=b(x_2,x_1)$, which is typical for SSs having the symmetry of the square grid, then $\eta (x_1,x_2)=\eta (x_2,x_1)$, and the contractivity of only one SS has to be checked.

Theorem 8 

([26]). Let

$$\begin{array}{c}\hfill \eta (x_1,x_2)={(1+x_1)}^n{(1+x_2)}^{n}b\left(x\right).\end{array}$$

(8)

If the SSs with the masks

$$\begin{array}{c}\hfill {\eta }_{u,v}(x_1,x_2)=\frac{2^{u+v}\eta (x_1,x_2)}{{(1+x_1)}^u{(1+x_2)}^v},u,v=0,...,n\end{array}$$

(9)

are convergent, then $S_{\eta }$ generate $C^n$ function.

Remark 2 

([26]). For $C^n$ continuity of $S_{\eta }$, we have to show that the SSs $S_{u,v}$, corresponding to masks ${\eta }_{u,v}(x_1,x_2)$ for $u,v=0,1,...,n$ are convergent and it is equivalent to checking whether SSs $\left\{S_{u,v}^{\left[1\right]}\right\}$ and $\left\{S_{u,v}^{\left[2\right]}\right\}$ corresponding to the masks ${\eta }_{u,v}^{\left[1\right]}(x_1,x_2)=\frac{{\eta }_{u,v}(x_1,x_2)}{1+x_1}$ and ${\eta }_{u,v}^{\left[2\right]}(x_1,x_2)=\frac{{\eta }_{u,v}(x_1,x_2)}{1+x_2}$ are contractive, which is equivalent to checking whether ${∥{\left(\frac{1}{2}{S}_{u,v}^{\left[1\right]}\right)}^L∥}_{\infty }<1$ and ${∥{\left(\frac{1}{2}{S}_{u,v}^{\left[2\right]}\right)}^L∥}_{\infty }<1$, for some integer $L>0$. Since there are four rules for computing the values at next refinement level, we define the norm as:

$$\begin{array}{ccc}\hfill {∥\frac{1}{2}{S}_{u,v}^{\left[k\right]}∥}_{\infty }& =& \frac{1}{2}max\left\{\sum _{s,t\in \mathbb{Z}}|{\eta }_{2s,2t}^{\left[k\right]}|,\sum _{s,t\in \mathbb{Z}}|{\eta }_{2s+1,2t}^{\left[k\right]}|,\sum _{s,t\in \mathbb{Z}}|{\eta }_{2s,2t+1}^{\left[k\right]}|,\sum _{s,t\in \mathbb{Z}}|{\eta }_{2s+1,2t+1}^{\left[k\right]}|\right\},\hfill \end{array}$$

(10)

where $k=1,2.$

3.2. Construction of Nine-tic B-Spline Tensor Product SS

Consider the proposed nine-tic B-spline SS (Equation (1)), and its mask is:

$$\begin{array}{c}\hfill \eta =\left[...,0,0,\frac{1}{512},\frac{10}{512},\frac{45}{512},\frac{120}{512},\frac{210}{512},\frac{252}{512},\frac{210}{512},\frac{120}{512},\frac{45}{512},\frac{10}{512},\frac{1}{512},0,0,...\right],\end{array}$$

and its Laurent polynomial is given as:

$$\begin{array}{ccc}\hfill \eta \left(x\right)& =& \frac{x^{-5}}{512}\left\{1+10x+45x^2+120x^3+210x^4+252x^5+210x^6+120x^7\right.\hfill \\ & & \left.+45x^8+10x^9+x^{10}\right\}.\hfill \end{array}$$

This implies that

$$\begin{array}{ccc}\hfill \eta \left(x_1\right)& =& \frac{x_1^{-5}}{512}\left\{1+10x_1+45{x_1}^2+120{x_1}^3+210{x_1}^4+252{x_1}^5+210{x_1}^6+120{x_1}^7\right.\hfill \\ & & \left.+45{x_1}^8+10{x_1}^9+{x_1}^{10}\right\},\hfill \\ \hfill \eta \left(x_2\right)& =& \frac{x_2^{-5}}{512}\left\{1+10x_2+45{x_2}^2+120{x_2}^3+210{x_2}^4+252{x_2}^5+210{x_2}^6+120{x_2}^7\right.\hfill \\ & & \left.+45{x_2}^8+10{x_2}^9+{x_2}^{10}\right\}.\hfill \end{array}$$

Since $\eta (x_1,x_2)=\eta \left(x_1\right)\eta \left(x_2\right)$, then we have the following Laurent polynomial of nine-tic B-spline SS $S_{\eta }$:-

$$\begin{array}{ccc}\hfill \eta (x_1,x_2)& =& \frac{x_1^{-5}{x}_2^{-5}}{262144}(1+45{x_1}^2+25200{x_1}^4{x_2}^7+9450{x_1}^4{x_2}^8+2100{x_1}^4{x_2}^9+45{x_2}^2\hfill \\ & & +45{x_2}^8+1200{x_1}^3{x_2}^9+5400{x_1}^3{x_2}^8+210{x_1}^4{x_2}^{10}+2520{x_1}^5{x}_2\hfill \\ & & +11340{x_1}^5{x_2}^2+30240{x_1}^5{x_2}^3+52920{x_1}^5{x_2}^4+63504{x_1}^5{x_2}^5+52920{x_1}^5{x_2}^6\hfill \\ & & +30240{x_1}^5{x_2}^7+11340{x_1}^5{x_2}^8+2520{x_1}^5{x_2}^9+252{x_1}^5{x_2}^{10}+2100{x_1}^6{x}_2\hfill \\ & & +9450{x_1}^6{x_2}^2+25200{x_1}^6{x_2}^3+44100{x_1}^6{x_2}^4+52920{x_1}^6{x_2}^5+44100{x_1}^6{x_2}^6\hfill \\ & & +25200{x_1}^6{x_2}^7+9450{x_1}^6{x_2}^8+2100{x_1}^6{x_2}^9+210{x_1}^6{x_2}^{10}+1200{x_1}^7{x}_2\hfill \\ & & +5400{x_1}^7{x_2}^2+14400{x_1}^7{x_2}^3+25200{x_1}^7{x_2}^4+30240{x_1}^7{x_2}^5\hfill \\ & & +25200{x_1}^7{x_2}^6+14400{x_1}^7{x_2}^7+5400{x_1}^7{x_2}^8+1200{x_1}^7{x_2}^9+120{x_1}^7{x_2}^{10}\hfill \\ & & +450{x_1}^8{x}_2+2025{x_1}^8{x_2}^2+5400{x_1}^8{x_2}^3+9450{x_1}^8{x_2}^4+11340{x_1}^8{x_2}^5\hfill \\ & & +9450{x_1}^8{x_2}^6+5400{x_1}^8{x_2}^7+2025{x_1}^8{x_2}^8+450{x_1}^8{x_2}^9+45{x_1}^8{x_2}^{10}\hfill \\ & & +100{x_1}^9{x}_2+450{x_1}^9{x_2}^2+1200{x_1}^9{x_2}^3+2100{x_1}^9{x_2}^4+2520{x_1}^9{x_2}^5\hfill \\ & & +2100{x_1}^9{x_2}^6+1200{x_1}^9{x_2}^7+450{x_1}^9{x_2}^8+100{x_1}^9{x_2}^9+10{x_1}^9{x_2}^{10}\hfill \\ & & +10{x_1}^{10}{x}_2+45{x_1}^{10}{x_2}^2+120{x_1}^{10}{x_2}^3+210{x_1}^{10}{x_2}^4+252{x_1}^{10}{x_2}^5\hfill \\ & & +210{x_1}^{10}{x_2}^6+120{x_1}^{10}{x_2}^7+45{x_1}^{10}{x_2}^8+10{x_1}^{10}{x_2}^9+{x_1}^{10}{x_2}^{10}+210{x_2}^4\hfill \\ & & +44100{x_1}^4{x_2}^4+52920{x_1}^4{x_2}^5+44100{x_1}^4{x_2}^6+252{x_2}^5+210{x_2}^6+120{x_2}^7\hfill \\ & & +{x_2}^{10}+120{x_2}^3+10{x_2}^9+252{x_1}^5+210{x_1}^4+120{x_1}^3+120{x_1}^7+210{x_1}^6\hfill \\ & & +45{x_1}^8+{x_1}^{10}+10{x_1}^9+100x_1{x}_2+450x_1{x_2}^2+1200x_1{x_2}^3+2100x_1{x_2}^4\hfill \\ & & +2520x_1{x_2}^5+2100x_1{x_2}^6+1200x_1{x_2}^7+450x_1{x_2}^8+100x_1{x_2}^9+10x_1{x_2}^{10}\hfill \\ & & +450{x_1}^2{x}_2+2025{x_1}^2{x_2}^2+5400{x_1}^2{x_2}^3+9450{x_1}^2{x_2}^4+11340{x_1}^2{x_2}^5\hfill \\ & & +9450{x_1}^2{x_2}^6+5400{x_1}^2{x_2}^7+2025{x_1}^2{x_2}^8+450{x_1}^2{x_2}^9+45{x_1}^2{x_2}^{10}\hfill \\ & & +1200{x_1}^3{x}_2+5400{x_1}^3{x_2}^2+14400{x_1}^3{x_2}^3+25200{x_1}^3{x_2}^4+30240{x_1}^3{x_2}^5\hfill \\ & & +25200{x_1}^3{x_2}^6+14400{x_1}^3{x_2}^7+2100{x_1}^4{x}_2+9450{x_1}^4{x_2}^2+120{x_1}^3{x_2}^{10}\hfill \\ & & +10x_1+10x_2+25200{x_1}^4{x_2}^3).\hfill \\ & =& \frac{x_1^{-5}{x}_2^{-5}}{262144}{\left(1+x_1\right)}^{10}{\left(1+x_2\right)}^{10}.\hfill \end{array}$$

(11)

From Equation (1), we suggest the following nine-tic B-spline tensor product SS:

$$\begin{array}{ccc}\hfill {\mu }_{2u,2v}^{k+1}& =& \frac{100}{262144}{\mu }_{u-2,v-2}^k+\frac{1200}{262144}{\mu }_{u-1,v-2}^k+\frac{2520}{262144}{\mu }_{u,v-2}^k+\frac{1200}{262144}{\mu }_{u+1,v-2}^k+\frac{100}{262144}{\mu }_{u+2,v-2}^k\hfill \\ & & +\frac{1200}{262144}{\mu }_{u-2,v-1}^k+\frac{14400}{262144}{\mu }_{u-1,v-1}^k+\frac{30240}{262144}{\mu }_{u,v-1}^k+\frac{14400}{262144}{\mu }_{u+1,v-1}^k+\frac{1200}{262144}{\mu }_{u+2,v-1}^k\hfill \\ & & +\frac{2520}{262144}{\mu }_{u-2,v}^k+\frac{30240}{262144}{\mu }_{u-1,v}^k+\frac{63504}{262144}{\mu }_{u,v}^k+\frac{30240}{262144}{\mu }_{u+1,v}^k+\frac{2520}{262144}{\mu }_{u+2,v}^k\hfill \\ & & +\frac{1200}{262144}{\mu }_{u-2,v+1}^k+\frac{14400}{262144}{\mu }_{u-1,v+1}^k+\frac{30240}{262144}{\mu }_{u,v+1}^k+\frac{14400}{262144}{\mu }_{u+1,v+1}^k+\frac{1200}{262144}{\mu }_{u+2,v+1}^k\hfill \\ & & +\frac{100}{262144}{\mu }_{u-2,v+2}^k+\frac{1200}{262144}{\mu }_{u-1,v+2}^k+\frac{2520}{262144}{\mu }_{u,v+2}^k+\frac{1200}{262144}{\mu }_{u+1,v+2}^k+\frac{100}{262144}{\mu }_{u+2,v+2}^k,\hfill \\ \hfill {\mu }_{2u+1,2v}^{k+1}& =& \frac{10}{262144}{\mu }_{u-2,v-2}^k+\frac{450}{262144}{\mu }_{u-1,v-2}^k+\frac{2100}{262144}{\mu }_{u,v-2}^k+\frac{2100}{262144}{\mu }_{u+1,v-2}^k+\frac{450}{262144}{\mu }_{u+2,v-2}^k\hfill \\ & & +\frac{10}{262144}{\mu }_{u+3,v-2}^k+\frac{120}{262144}{\mu }_{u-2,v-1}^k+\frac{5400}{262144}{\mu }_{u-1,v-1}^k+\frac{25200}{262144}{\mu }_{u,v-1}^k+\frac{25200}{262144}{\mu }_{u+1,v-1}^k\hfill \\ & & +\frac{5400}{262144}{\mu }_{u+2,v-1}^k+\frac{120}{262144}{\mu }_{u+3,v-1}^k+\frac{252}{262144}{\mu }_{u-2,v}^k+\frac{11340}{262144}{\mu }_{u-1,v}^k+\frac{52920}{262144}{\mu }_{u,v}^k\hfill \\ & & +\frac{52920}{262144}{\mu }_{u+1,v}^k+\frac{11340}{262144}{\mu }_{u+2,v}^k+\frac{252}{262144}{\mu }_{u+3,v}^k+\frac{120}{262144}{\mu }_{u-2,v+1}^k+\frac{5400}{262144}{\mu }_{u-1,v+1}^k\hfill \\ & & +\frac{25200}{262144}{\mu }_{u,v+1}^k+\frac{25200}{262144}{\mu }_{u+1,v+1}^k+\frac{5400}{262144}{\mu }_{u+2,v+1}^k+\frac{120}{262144}{\mu }_{u+3,v+1}^k+\frac{10}{262144}{\mu }_{u-2,v+2}^k\hfill \\ & & +\frac{450}{262144}{\mu }_{u-1,v+2}^k+\frac{2100}{262144}{\mu }_{u,v+2}^k+\frac{2100}{262144}{\mu }_{u+1,v+2}^k+\frac{450}{262144}{\mu }_{u+2,v+2}^k+\frac{10}{262144}{\mu }_{u+3,v+2}^k,\hfill \\ \hfill {\mu }_{2u,2v+1}^{k+1}& =& \frac{10}{262144}{\mu }_{u-2,v-2}^k+\frac{120}{262144}{\mu }_{u-1,v-2}^k+\frac{252}{262144}{\mu }_{u,v-2}^k+\frac{120}{262144}{\mu }_{u+1,v-2}^k+\frac{10}{262144}{\mu }_{u+2,v-2}^k\hfill \\ & & +\frac{450}{262144}{\mu }_{u-2,v-1}^k+\frac{5400}{262144}{\mu }_{u-1,v-1}^k+\frac{11340}{262144}{\mu }_{u,v-1}^k+\frac{5400}{262144}{\mu }_{u+1,v-1}^k+\frac{450}{262144}{\mu }_{u+2,v-1}^k\hfill \\ & & +\frac{2100}{262144}{\mu }_{u-2,v}^k+\frac{25200}{262144}{\mu }_{u-1,v}^k+\frac{52920}{262144}{\mu }_{u,v}^k+\frac{25200}{262144}{\mu }_{u+1,v}^k+\frac{2100}{262144}{\mu }_{u+2,v}^k\hfill \\ & & +\frac{2100}{262144}{\mu }_{u-2,v+1}^k+\frac{25200}{262144}{\mu }_{u-1,v+1}^k+\frac{52920}{262144}{\mu }_{u,v+1}^k+\frac{25200}{262144}{\mu }_{u+1,v+1}^k+\frac{2100}{262144}{\mu }_{u+2,v+1}^k\hfill \\ & & +\frac{450}{262144}{\mu }_{u-2,v+2}^k+\frac{5400}{262144}{\mu }_{u-1,v+2}^k+\frac{11340}{262144}{\mu }_{u,v+2}^k+\frac{5400}{262144}{\mu }_{u+1,v+2}^k+\frac{450}{262144}{\mu }_{u+2,v+2}^k\hfill \\ & & +\frac{10}{262144}{\mu }_{u-2,v+3}^k+\frac{120}{262144}{\mu }_{u-1,v+3}^k+\frac{252}{262144}{\mu }_{u,v+3}^k+\frac{120}{262144}{\mu }_{u+1,v+3}^k+\frac{10}{262144}{\mu }_{u+2,v+3}^k,\hfill \\ \hfill {\mu }_{2u+1,2v+1}^{k+1}& =& \frac{1}{262144}{\mu }_{u-2,v-2}^k+\frac{45}{262144}{\mu }_{u-1,v-2}^k+\frac{210}{262144}{\mu }_{u,v-2}^k+\frac{210}{262144}{\mu }_{u+1,v-2}^k+\frac{45}{262144}{\mu }_{u+2,v-2}^k\hfill \\ & & +\frac{1}{262144}{\mu }_{u+3,v-2}^k+\frac{45}{262144}{\mu }_{u-2,v-1}^k+\frac{2025}{262144}{\mu }_{u-1,v-1}^k+\frac{9450}{262144}{\mu }_{u,v-1}^k+\frac{9450}{262144}{\mu }_{u+1,v-1}^k\hfill \\ & & +\frac{2025}{262144}{\mu }_{u+2,v-1}^k+\frac{45}{262144}{\mu }_{u+3,v-1}^k+\frac{210}{262144}{\mu }_{u-2,v}^k+\frac{9450}{262144}{\mu }_{u-1,v}^k+\frac{44100}{262144}{\mu }_{u,v}^k\hfill \\ & & +\frac{44100}{262144}{\mu }_{u+1,v}^k+\frac{9450}{262144}{\mu }_{u+2,v}^k+\frac{210}{262144}{\mu }_{u+3,v}^k+\frac{210}{262144}{\mu }_{u-2,v+1}^k+\frac{9450}{262144}{\mu }_{u-1,v+1}^k\hfill \\ & & +\frac{44100}{262144}{\mu }_{u,v+1}^k+\frac{44100}{262144}{\mu }_{u+1,v+1}^k+\frac{9450}{262144}{\mu }_{u+2,v+1}^k+\frac{210}{262144}{\mu }_{u+3,v+1}^k+\frac{45}{262144}{\mu }_{u-2,v+2}^k\hfill \\ & & +\frac{2025}{262144}{\mu }_{u-1,v+2}^k+\frac{9450}{262144}{\mu }_{u,v+2}^k+\frac{9450}{262144}{\mu }_{u+1,v+2}^k+\frac{2025}{262144}{\mu }_{u+2,v+2}^k+\frac{45}{262144}{\mu }_{u+3,v+2}^k\hfill \\ & & +\frac{1}{262144}{\mu }_{u-2,v+3}^k+\frac{45}{262144}{\mu }_{u-1,v+3}^k+\frac{210}{262144}{\mu }_{u,v+3}^k+\frac{210}{262144}{\mu }_{u+1,v+3}^k+\frac{45}{262144}{\mu }_{u+2,v+3}^k\hfill \\ & & +\frac{1}{262144}{\mu }_{u+3,v+3}^k.\hfill \end{array}$$

(12)

3.3. Analysis of Nine-tic B-Spline Tensor Product SS

In this section, we present $C^9$ continuous nine-tic B-Spline tensor product SS. To check the continuity of the nine-tic B-Spline tensor product SS (Equation (11)), we apply similar analysis tools to those in the case. From Equation (8) for $u=0,v=0$ and then from Equation (9), we get

$$\begin{array}{c}\hfill {\eta }_{0,0}(x_1,x_2)=\eta (x_1,x_2)=\frac{x_1^{-5}{x}_2^{-5}}{262144}{\left(1+x_1\right)}^{10}{\left(1+x_2\right)}^{10}.\end{array}$$

This implies

$$\begin{array}{ccc}\hfill {\eta }_{0,0}(x_1,x_2)& =& \frac{x_1^{-5}{x}_2^{-5}}{262144}(1+45{x_1}^2+25200{x_1}^4{x_2}^7+9450{x_1}^4{x_2}^8+2100{x_1}^4{x_2}^9\hfill \\ & & +45{x_2}^2+45{x_2}^8+1200{x_1}^3{x_2}^9+5400{x_1}^3{x_2}^8+210{x_1}^4{x_2}^{10}\hfill \\ & & +2520{x_1}^5{x}_2+11340{x_1}^5{x_2}^2+30240{x_1}^5{x_2}^3+52920{x_1}^5{x_2}^4\hfill \\ & & +63504{x_1}^5{x_2}^5+52920{x_1}^5{x_2}^6+30240{x_1}^5{x_2}^7+11340{x_1}^5{x_2}^8\hfill \\ & & +2520{x_1}^5{x_2}^9+252{x_1}^5{x_2}^{10}+2100{x_1}^6{x}_2+9450{x_1}^6{x_2}^2\hfill \\ & & +25200{x_1}^6{x_2}^3+44100{x_1}^6{x_2}^4+52920{x_1}^6{x_2}^5+44100{x_1}^6{x_2}^6\hfill \\ & & +25200{x_1}^6{x_2}^7+9450{x_1}^6{x_2}^8+2100{x_1}^6{x_2}^9+210{x_1}^6{x_2}^{10}\hfill \\ & & +1200{x_1}^7{x}_2+5400{x_1}^7{x_2}^2+14400{x_1}^7{x_2}^3+25200{x_1}^7{x_2}^4\hfill \\ & & +30240{x_1}^7{x_2}^5+25200{x_1}^7{x_2}^6+14400{x_1}^7{x_2}^7+5400{x_1}^7{x_2}^8\hfill \\ & & +1200{x_1}^7{x_2}^9+120{x_1}^7{x_2}^{10}+450{x_1}^8{x}_2+2025{x_1}^8{x_2}^2+5400{x_1}^8{x_2}^3\hfill \\ & & +9450{x_1}^8{x_2}^4+11340{x_1}^8{x_2}^5+9450{x_1}^8{x_2}^6+5400{x_1}^8{x_2}^7+2025{x_1}^8{x_2}^8\hfill \\ & & +450{x_1}^8{x_2}^9+45{x_1}^8{x_2}^{10}+100{x_1}^9{x}_2+450{x_1}^9{x_2}^2+1200{x_1}^9{x_2}^3\hfill \\ & & +2100{x_1}^9{x_2}^4+2520{x_1}^9{x_2}^5+2100{x_1}^9{x_2}^6+1200{x_1}^9{x_2}^7+450{x_1}^9{x_2}^8\hfill \\ & & +100{x_1}^9{x_2}^9+10{x_1}^9{x_2}^{10}+10{x_1}^{10}{x}_2+45{x_1}^{10}{x_2}^2+120{x_1}^{10}{x_2}^3\hfill \\ & & +210{x_1}^{10}{x_2}^4+252{x_1}^{10}{x_2}^5+210{x_1}^{10}{x_2}^6+120{x_1}^{10}{x_2}^7+45{x_1}^{10}{x_2}^8\hfill \\ & & +10{x_1}^{10}{x_2}^9+{x_1}^{10}{x_2}^{10}+210{x_2}^4+44100{x_1}^4{x_2}^4+52920{x_1}^4{x_2}^5\hfill \\ & & +44100{x_1}^4{x_2}^6+252{x_2}^5+210{x_2}^6+120{x_2}^7+{x_2}^{10}+120{x_2}^3+10{x_2}^9\hfill \\ & & +252{x_1}^5+210{x_1}^4+120{x_1}^3+120{x_1}^7+210{x_1}^6+45{x_1}^8+{x_1}^{10}\hfill \\ & & +10{x_1}^9+100x_1{x}_2+450x_1{x_2}^2+1200x_1{x_2}^3+2100x_1{x_2}^4+2520x_1{x_2}^5\hfill \\ & & +2100x_1{x_2}^6+1200x_1{x_2}^7+450x_1{x_2}^8+100x_1{x_2}^9+10x_1{x_2}^{10}\hfill \\ & & +450{x_1}^2{x}_2+2025{x_1}^2{x_2}^2+5400{x_1}^2{x_2}^3+9450{x_1}^2{x_2}^4+11340{x_1}^2{x_2}^5\hfill \\ & & +9450{x_1}^2{x_2}^6+5400{x_1}^2{x_2}^7+2025{x_1}^2{x_2}^8+450{x_1}^2{x_2}^9+45{x_1}^2{x_2}^{10}\hfill \\ & & +1200{x_1}^3{x}_2+5400{x_1}^3{x_2}^2+14400{x_1}^3{x_2}^3+25200{x_1}^3{x_2}^4+30240{x_1}^3{x_2}^5\hfill \\ & & +25200{x_1}^3{x_2}^6+14400{x_1}^3{x_2}^7+2100{x_1}^4{x}_2+9450{x_1}^4{x_2}^2+120{x_1}^3{x_2}^{10}\hfill \\ & & +10x_1+10x_2+25200{x_1}^4{x_2}^3).\hfill \end{array}$$

If $S_{0,0}^{\left[1\right]}$ and $S_{0,0}^{\left[2\right]}$ are SSs corresponding to the masks ${\eta }_{0,0}^{\left[1\right]}(x_1,x_2)$ and ${\eta }_{0,0}^{\left[2\right]}(x_1,x_2)$, respectively, then

$$\begin{array}{c}\hfill {\eta }_{0,0}^{\left[1\right]}(x_1,x_2)=\frac{{\eta }_{0,0}(x_1,x_2)}{1+x_1}=\frac{x_1^{-5}{x}_2^{-5}}{262144}{\left(1+x_1\right)}^9{\left(1+x_2\right)}^{10}\end{array}$$

and

$$\begin{array}{c}\hfill {\eta }_{0,0}^{\left[2\right]}(x_1,x_2)=\frac{{\eta }_{0,0}(x_1,x_2)}{1+x_2}=\frac{x_1^{-5}{x}_2^{-5}}{262144}{\left(1+x_1\right)}^{10}{\left(1+x_2\right)}^9.\end{array}$$

This implies

$$\begin{array}{ccc}\hfill {\eta }_{0,0}^{\left[1\right]}(x_1,x_2)& =& \frac{x_1^{-5}{x}_2^{-5}}{262144}\{1+1260{x_1}^5{x_2}^9+5670{x_1}^4{x_2}^8+3780{x_1}^6{x_2}^2+5670{x_1}^5{x_2}^8\hfill \\ & & +15120{x_1}^5{x_2}^7+3780{x_1}^3{x_2}^2+26460{x_1}^5{x_2}^6+31752{x_1}^5{x_2}^5+9x_1\hfill \\ & & +26460{x_1}^5{x_2}^4+15120{x_1}^5{x_2}^3+5670{x_1}^5{x_2}^2+84{x_1}^3+126{x_1}^4{x_2}^{10}\hfill \\ & & +1260{x_1}^5{x}_2+15120{x_1}^4{x_2}^7+126{x_1}^4+1260{x_1}^4{x_2}^9+26460{x_1}^4{x_2}^6\hfill \\ & & +126{x_1}^5+840{x_1}^6{x}_2+84{x_1}^6+36{x_1}^2+45{x_2}^2+10x_2+360{x_1}^2{x}_2\hfill \\ & & +9x_1{x_2}^{10}+90x_1{x_2}^9+405x_1{x_2}^8+1080x_1{x_2}^7+1890x_1{x_2}^6\hfill \\ & & +2268x_1{x_2}^5+1890x_1{x_2}^4+1080x_1{x_2}^3+405x_1{x_2}^2+90x_1{x}_2\hfill \\ & & +7560{x_1}^2{x_2}^4+4320{x_1}^2{x_2}^3+1620{x_1}^2{x_2}^2+9072{x_1}^2{x_2}^5+36{x_1}^7\hfill \\ & & +31752{x_1}^4{x_2}^5+36{x_1}^2{x_2}^{10}+360{x_1}^2{x_2}^9+1620{x_1}^2{x_2}^8+4320{x_1}^2{x_2}^7\hfill \\ & & +7560{x_1}^2{x_2}^6+4320{x_1}^7{x_2}^3+1620{x_1}^7{x_2}^2+360{x_1}^7{x}_2+84{x_1}^6{x_2}^{10}\hfill \\ & & +840{x_1}^6{x_2}^9+3780{x_1}^6{x_2}^8+10080{x_1}^6{x_2}^7+17640{x_1}^6{x_2}^6\hfill \\ & & +21168{x_1}^6{x_2}^5+17640{x_1}^6{x_2}^4+10080{x_1}^6{x_2}^3+840{x_1}^3{x}_2+360{x_1}^7{x_2}^9\hfill \\ & & +1620{x_1}^7{x_2}^8+4320{x_1}^7{x_2}^7+7560{x_1}^7{x_2}^6+9072{x_1}^7{x_2}^5+7560{x_1}^7{x_2}^4\hfill \\ & & +26460{x_1}^4{x_2}^4+9{x_1}^8+405{x_1}^8{x_2}^2+90{x_1}^8{x}_2+36{x_1}^7{x_2}^{10}\hfill \\ & & +1890{x_1}^8{x_2}^4+1080{x_1}^8{x_2}^3+90{x_1}^8{x_2}^9+405{x_1}^8{x_2}^8+1080{x_1}^8{x_2}^7\hfill \\ & & +1890{x_1}^8{x_2}^6+120{x_2}^3+2268{x_1}^8{x_2}^5+120{x_1}^9{x_2}^3+45{x_1}^9{x_2}^2\hfill \\ & & +10{x_1}^9{x}_2+9{x_1}^8{x_2}^{10}+{x_1}^9+15120{x_1}^4{x_2}^3+10{x_1}^9{x_2}^9+45{x_1}^9{x_2}^8\hfill \\ & & +120{x_1}^9{x_2}^7+210{x_1}^9{x_2}^6+252{x_1}^9{x_2}^5+210{x_1}^9{x_2}^4+210{x_2}^4\hfill \\ & & +252{x_2}^5+1260{x_1}^4{x}_2+84{x_1}^3{x_2}^{10}+5670{x_1}^4{x_2}^2+{x_1}^9{x_2}^{10}\hfill \\ & & +840{x_1}^3{x_2}^9+120{x_2}^7+10080{x_1}^3{x_2}^7+45{x_2}^8+210{x_2}^6+3780{x_1}^3{x_2}^8\hfill \\ & & +126{x_1}^5{x_2}^{10}+17640{x_1}^3{x_2}^6+{x_2}^{10}+17640{x_1}^3{x_2}^4+10080{x_1}^3{x_2}^3\hfill \\ & & +10{x_2}^9+21168{x_1}^3{x_2}^5\},\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill {\eta }_{0,0}^{\left[2\right]}(x_1,x_2)& =& \frac{x_1^{-5}{x}_2^{-5}}{262144}\{1+252{x_1}^5{x_2}^9+1890{x_1}^4{x_2}^8+7560{x_1}^6{x_2}^2+2268{x_1}^5{x_2}^8\hfill \\ & & +9072{x_1}^5{x_2}^7+4320{x_1}^3{x_2}^2+21168{x_1}^5{x_2}^6+31752{x_1}^5{x_2}^5+10x_1\hfill \\ & & +31752{x_1}^5{x_2}^4+21168{x_1}^5{x_2}^3+9072{x_1}^5{x_2}^2+120{x_1}^3+2268{x_1}^5{x}_2\hfill \\ & & +7560{x_1}^4{x_2}^7+210{x_1}^4+210{x_1}^4{x_2}^9+17640{x_1}^4{x_2}^6+252{x_1}^5\hfill \\ & & +1890{x_1}^6{x}_2+210{x_1}^6+45{x_1}^2+36{x_2}^2+9x_2+405{x_1}^2{x}_2\hfill \\ & & +10x_1{x_2}^9+90x_1{x_2}^8+360x_1{x_2}^7+840x_1{x_2}^6+1260x_1{x_2}^5\hfill \\ & & +1260x_1{x_2}^4+840x_1{x_2}^3+360x_1{x_2}^2+90x_1{x}_2+5670{x_1}^2{x_2}^4\hfill \\ & & +3780{x_1}^2{x_2}^3+1620{x_1}^2{x_2}^2+5670{x_1}^2{x_2}^5+120{x_1}^7+26460{x_1}^4{x_2}^5\hfill \\ & & +45{x_1}^2{x_2}^9+405{x_1}^2{x_2}^8+1620{x_1}^2{x_2}^7+3780{x_1}^2{x_2}^6+10080{x_1}^7{x_2}^3\hfill \\ & & +4320{x_1}^7{x_2}^2+1080{x_1}^7{x}_2+210{x_1}^6{x_2}^9+1890{x_1}^6{x_2}^8+7560{x_1}^6{x_2}^7\hfill \\ & & +17640{x_1}^6{x_2}^6+26460{x_1}^6{x_2}^5+26460{x_1}^6{x_2}^4+17640{x_1}^6{x_2}^3\hfill \\ & & +1080{x_1}^3{x}_2+120{x_1}^7{x_2}^9+1080{x_1}^7{x_2}^8+4320{x_1}^7{x_2}^7+10080{x_1}^7{x_2}^6\hfill \\ & & +15120{x_1}^7{x_2}^5+15120{x_1}^7{x_2}^4+26460{x_1}^4{x_2}^4+45{x_1}^8+1620{x_1}^8{x_2}^2\hfill \\ & & +405{x_1}^8{x}_2+5670{x_1}^8{x_2}^4+3780{x_1}^8{x_2}^3+45{x_1}^8{x_2}^9+405{x_1}^8{x_2}^8\hfill \\ & & +1620{x_1}^8{x_2}^7+3780{x_1}^8{x_2}^6+84{x_2}^3+5670{x_1}^8{x_2}^5+840{x_1}^9{x_2}^3\hfill \\ & & +360{x_1}^9{x_2}^2+90{x_1}^9{x}_2+10{x_1}^9+17640{x_1}^4{x_2}^3+10{x_1}^9{x_2}^9\hfill \\ & & +90{x_1}^9{x_2}^8+360{x_1}^9{x_2}^7+840{x_1}^9{x_2}^6+1260{x_1}^9{x_2}^5+1260{x_1}^9{x_2}^4\hfill \\ & & +126{x_2}^4+126{x_2}^5+1890{x_1}^4{x}_2+7560{x_1}^4{x_2}^2+120{x_1}^3{x_2}^9\hfill \\ & & +36{x_2}^7+4320{x_1}^3{x_2}^7+9{x_2}^8+84{x_2}^6+1080{x_1}^3{x_2}^8+10080{x_1}^3{x_2}^6\hfill \\ & & +15120{x_1}^3{x_2}^4+10080{x_1}^3{x_2}^3+{x_2}^9+15120{x_1}^3{x_2}^5+{x_1}^{10}+9{x_1}^{10}{x}_2\hfill \\ & & +36{x_1}^{10}{x_2}^2+84{x_1}^{10}{x_2}^3+126{x_1}^{10}{x_2}^4+126{x_1}^{10}{x_2}^5+84{x_1}^{10}{x_2}^6\hfill \\ & & +36{x_1}^{10}{x_2}^7+9{x_1}^{10}{x_2}^8+{x_1}^{10}{x_2}^9\}.\hfill \end{array}$$

By utilizing Equation (10), we get

$$\begin{array}{ccc}\hfill {∥\frac{1}{2}{S}_{0,0}^{\left[1\right]}∥}_{\infty }& =& \frac{1}{2}max\left\{\left|\frac{1}{262144}\left(1+5670+3780+126+126+26460+84\right.\right.\right.\hfill \\ & & +36+45+7560+1620+36+1620+7560+84+3780\hfill \\ & & +17640+17640+26460+9+405+1890+405+1890\hfill \\ & & +9+210+5670+45+210+1\left)\right|,\hfill \\ & & \left|\frac{1}{262144}\left(10+10+120+252+120+90+1080+2268\right.\right.\hfill \\ & & +1080+90+840+10080+21168+10080+840+1260\hfill \\ & & +15120+31752+15120+1260+360+4320+9072\hfill \\ & & \left.\left.+4320+360\right)\right|,\hfill \\ & & \left|\frac{1}{262144}\left(9+45+1+210+84+126+36+1+45+405\right.\right.\hfill \\ & & +1890+1890+405+9+3780+17640+17640+3780+84\hfill \\ & & +5670+26460+26460+5670+126+1620+7560+7560\hfill \\ & & \left.\left.+1620+36+210\right)\right|,\hfill \\ & & \left|\frac{1}{262144}\left(10+1080+360+4320+9072+4320+360\right.\right.\hfill \\ & & +1260+15120+31752+15120+1260+840+10080\hfill \\ & & +21168+10080+840+90+1080+2268+120+252\hfill \\ & & \left.\left.+120+10+90\right)\right|\}\hfill \\ & =& \frac{1}{2}max\left\{\frac{1}{2},\frac{1}{2},\frac{1}{2},\frac{1}{2}\right\}<1,\hfill \end{array}$$

(13)

$$\begin{array}{ccc}\hfill {∥\frac{1}{2}{S}_{0,0}^{\left[2\right]}∥}_{\infty }& =& \frac{1}{2}max\left\{\left|\frac{1}{262144}\left(1+45+210+210+126+1+45+36+84\right.\right.\right.\hfill \\ & & +9+3780+405+1620+5670+7560+26460+17640+1890\hfill \\ & & +7560+26460+17640+1890+1620+5670+3780+405\hfill \\ & & \left.\left.+84+9+36+126\right)\right|,\hfill \\ & & \left|\frac{1}{262144}\left(90+840+1080+10080+1260+360+10+15120\right.\right.\hfill \\ & & +4320+120+2268+21168+31752+9072+252+90\hfill \\ & & \left.\left.+10080+15120+4320+120+1080+1260+840+360+10\right)\right|,\hfill \\ & & \left|\frac{1}{262144}\left(120+252+120+10+1260+10+360+4320\right.\right.\hfill \\ & & +15120+840+90+10080+1080+9072+31752+21168\hfill \\ & & \left.\left.+2268+4320+15120+10080+1080+360+1260+840+90\right)\right|,\hfill \\ & & \left|\frac{1}{262144}\left(84+126+36+1+5670+1620+45+405+3780\right.\right.\hfill \\ & & +1890+17640+26460+7560+210+1890+17640+26460\hfill \\ & & +7560+210+3780+5670+1620+45+405+126+36\hfill \\ & & \left.\left.\left.+9+1+9+84\right)\right|\right\}\hfill \\ & =& \frac{1}{2}max\left\{\frac{1}{2},\frac{1}{2},\frac{1}{2},\frac{1}{2}\right\}<1.\hfill \end{array}$$

(14)

Let $S_{0,0}$ be the SS corresponding to the Laurent polynomial, ${\eta }_{0,0}(x_1,x_2),$ then, by using Equation (10), from Equations (13) and (14), we have that $\left\{S_{u,v}^{\left[k\right]};k=1,2,\&u,v=0\right\}$ are contractive, thus by Theorem 7, the SSs $S_{u,v}$, corresponding to masks ${\eta }_{u,v}(x_1,x_2)$ for $u,v=0$ are convergent. Hence, by Theorem 8, the proposed SS $S_{\eta }$ is $C^0$ continuous.

By applying the above procedure repeatedly, we found that the proposed SS has $C^9$ continuity (the proof is given in Appendix A).

4. Numerical Examples

In this section, performance of our nine-tic B spline tensor product SS is discussed. The refinement algorithm of nine-tic B spline tensor product SS creates a new vertex position corresponding to both vertex and face of the original mesh. It is observed that the new vertices are weighted averages of the vertex points belonging to each pair (face, vertex) of the original mesh. For the nine-tic B spline tensor product case, these weights (going around a face) are:

$$\begin{array}{c}\{\frac{100}{262144},\frac{1200}{262144},\frac{2520}{262144},\frac{1200}{262144},\frac{100}{262144},\frac{1200}{262144},\frac{14400}{262144},\frac{30240}{262144},\frac{14400}{262144},\frac{1200}{262144},\frac{2520}{262144},\frac{30240}{262144},\hfill \\ \frac{63504}{262144},\frac{30240}{262144},\frac{2520}{262144},\frac{1200}{262144},\frac{14400}{262144},\frac{30240}{262144},\frac{14400}{262144},\frac{1200}{262144},\frac{100}{262144},\frac{1200}{262144},\frac{2520}{262144},\frac{1200}{262144},\frac{100}{262144}\}.\hfill \end{array}$$

The newly created vertices are then connected to form the faces of the refined control mesh.

The refined model is generated from the control polygon in the following way. Each vertex point is obtained in the proportion of [10: 120: 252: 120: 10:]/512 and each edge point is obtained in the proportion of [1: 45: 210: 210: 45: 1:]/512. A face point is achieved as the centroid of every mesh of the given control polygon, and vertex point is achieved as the normal of a vertex mesh in the control polygon. The new points are then associated with each other. There are two edges along each side of each vertex of the previous mesh. These pairs are related and form quadrilaterals over the old edges. Inside every control polygon, there are the same number of new vertices. These are related to each other inside the control polygon. Lastly, around every old vertex there is another vertex in the adjoining corner of each old polygon. These are associated to form another polygon with the same number of edges. The new mesh generates quadrilaterals for each edge in the old vertex, and makes a little n-sided polygon. Each n-sided polygon produces a n-sided polygon for each n-valence (valence being the number of edges that touch the vertex). After the first iteration of our SS, all vertices have a valence of four, thus resulting applications generate quadrilaterals for the vertices. To make a smooth model, the SS is applied repeatedly. In Figure 1, Figure 2 and Figure 3, show the visual performance of our proposed SS. We used MATLAB software for the implementation of our proposed SS as a plug in inanimation and modeling industry and achieved required refine model after applying the 5th level of the proposed SS.

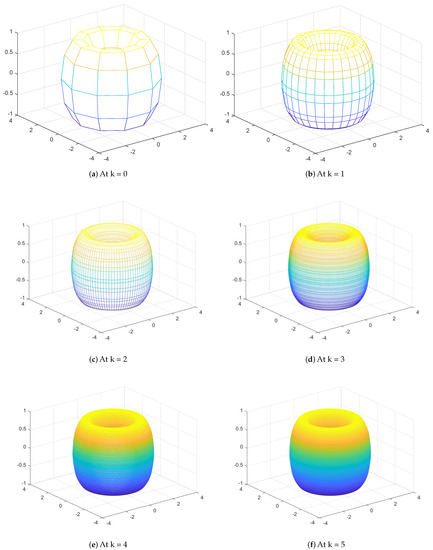
Figure 1. (a) The initial polygon; and (b–f) the results up to fifth subdivision levels.

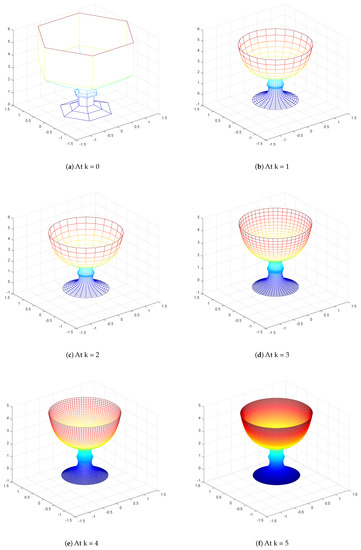
Figure 2. (a) The initial polygon; and (b–f) the results up to fifth subdivision levels.

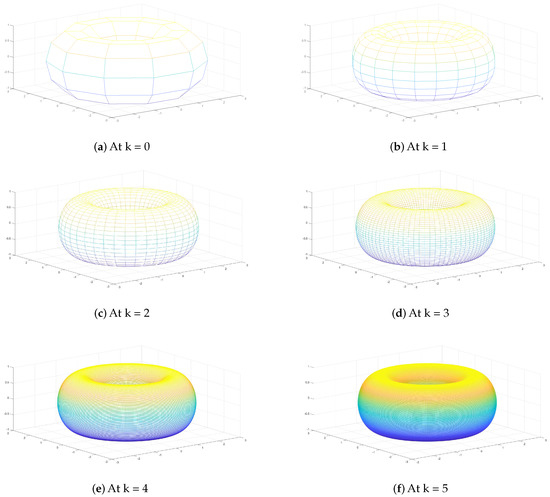
Figure 3. (a) The initial polygon; and (b–f) the results up to fifth subdivision levels.

Comparison of NURBS & Proposed SS

This section defines the comparison of the proposed scheme with NURBS. The NURBS is either a torus, disk or a tube and many NURBS patches are applied to form a surface models as shown in Figure 4. After the deformation of the NURBS surfaces, the cracks appears at the joints. In Figure 1, Figure 2 and Figure 3 shows that continues surfaces are generated as the limit of a sequence of successive refinements. All theother properties such as efficiency, compact support, local definition, affine invariance, simplicity and smoothness are the same properties as the NURBS have, but it will work for any topology. Subdivision is a data structure used to store mesh data in a convenient way so that the mesh information can be easily accessed. It is clearly seen that proposed SS shows smoothness in generating different curves.

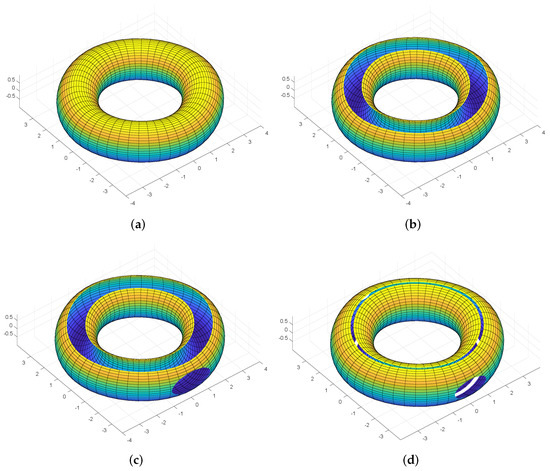
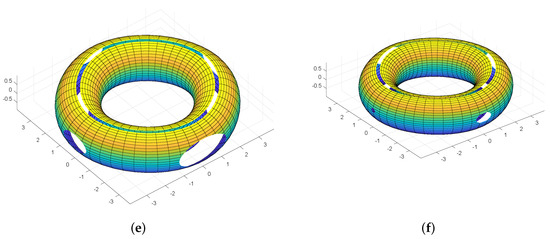
Figure 4. (a) The results of the NURBS; and (b–f) the deformation of a surface made of NURBS patches.

5. Conclusions and Future Work

This paper contributes the nine-tic B-spline approximating bivariate SS to reduce the execution time needed to compute the subdivision process of quad meshes. We have discussed some interesting features such as polynomial generation, smoothness, joint spectral radius, holder continuity, limit stencils of the proposed SS. We used Laurent polynomial (symbol) method to find the smoothness of our proposed SS and it is observed that our proposed SS gives good results for modeling of curves and surfaces as shown in figures. There are many directions of future work. Firstly, spreading of tensor product SS to a mesh with arbitrary topology. We are also interested to work on reproducing exact surface models by SS. If we could generate exact surface models having singular points, we will be able to solve some additional issues regarding SS.