Abstract
The Fisher information metric provides a smooth family of probability measures with a Riemannian manifold structure, which is an object in information geometry. The information geometry of the gamma manifold associated with the family of gamma distributions has been well studied. However, only a few results are known for the generalized gamma family that adds an extra shape parameter. The present article gives some new results about the generalized gamma manifold. This paper also introduces an application in medical imaging that is the classification of Alzheimer’s disease population. In the medical field, over the past two decades, a growing number of quantitative image analysis techniques have been developed, including histogram analysis, which is widely used to quantify the diffuse pathological changes of some neurological diseases. This method presents several drawbacks. Indeed, all the information included in the histogram is not used and the histogram is an overly simplistic estimate of a probability distribution. Thus, in this study, we present how using information geometry and the generalized gamma manifold improved the performance of the classification of Alzheimer’s disease population.
1. Introduction
In the medical field, the use of medical imaging techniques, such as Magnetic Resonance Imaging (MRI), is particularly important for measuring brain activity in different parts of the anatomy of the central nervous system. This technique is of major interest in the context of neurodegenerative diseases such as Alzheimer’s disease [1,2,3]. By measuring the cortical thickness of the brain, it is possible to estimate the brain atrophy that is considered as a crucial marker of neurodegeneration in Alzheimer’s disease [4,5]. Previous works have already studied measures of central tendency of biomarkers of the brain activity. These are next implemented in a statistical data analysis, such as classification algorithms for detecting changes in the pathological disease. The commonly used summaries are the mean, the median or the mode, but these are not informative enough on the distribution of the data.
In most recent studies [6,7], histograms have been used as an approximation of the probability density functions, but only a few of their characteristics, such as mean, percentiles, peak location, peak height, skweeness and kurtosis, were used in a statistical data analysis. In the context of multiple sclerosis, the entire histogram information was implemented in a k-nearest neighbors classifier, with higher classification performances than in previous studies [8]. However, the quality of the histogram estimation depends on the choice of the bin size. The histogram may then be a too rough estimate of the probability density function, and provide poor estimates of the characteristics cited above. For overcoming this drawback and using the entire information included in the data, the underlying probability density functions themselves should be used as a biomarker of the whole brain. The general framework of the information geometry, in which the probability distributions are considered as points on a manifold, is particularly relevant to reach this goal.
The generalized gamma distribution was introduced in [9], and can be viewed as a special case of the Amoroso distribution [10] in which the location parameter is dropped [11]. Apart from the gamma distribution, it generalizes also the Weibull distribution and is of common use in survival models. Moreover, the generalized gamma distribution is particularly relevant in the medical field previously described.
The purpose of the present work is to investigate some information geometric properties of the generalized gamma family, especially when restricted to the gamma submanifold. First, in Section 2, the Fisher information as a Riemannian metric and results in the case of the gamma manifold will be briefly introduced. Next, in Section 3, the case of the generalized gamma manifold will be detailed, using an approach based on diffeomorphism groups. In Section 4, the extrinsic curvature of the gamma submanifold will be computed. Finally, an example of application in the medical imaging domain will be given in the last section. A clustering technique has been successfully extended by using a geodesic distance of which an approximation is computed in two steps for numerical considerations.
2. Information Geometry and the Gamma Manifold
Information geometry deals with parameterized families of distributions whose parameters are understood as coordinates and provided with a Riemannian structure by the Fisher metric [12]. Let be a smooth manifold and a family of probability distributions defined on a common event space, parameterized by , and absolutely continuous with respect to a fixed measure . It is further assumed that the corresponding density functions are smooth with respect to the parameter. In the sequel, will denote the density function for a given . Thorough the paper, the Einstein summation convention on repeated indices will be used.
Definition 1.
The Fisher information metric on Θ is defined at point by the symmetric order 2 tensor:
where:
When the support of the density functions does not depend on , the information metric can be rewritten as:
It gives rise to a Riemannian metric on .
The Fisher information metric is invariant under change of variables by sufficient statistics [13,14]. When the parameterized family is of natural exponential type, the Fisher information metric can be expressed as
where is the log-partition function.
A manifold with such a Riemannian metric is referred to as a Hessian structure [15]. Many important tools from Riemannian geometry, like the Levi–Civita connection, are greatly simplified within this frame. In the sequel, all partial derivatives will be abbreviated by .
Proposition 1.
For a parameterized density family pertaining to the natural exponential class with log-partition function ϕ, the Christoffel symbols of the first kind for the Levi–Civita connection of the associated Hessian structure are given by [16]:
The gamma distribution can be written as a natural exponential family on two parameters , defined on the parameter space by:
Definition 2.
The gamma distribution is the probability law on with density relative to the Lebesgue measure given by:
with parameters .
The next proposition comes directly from the definition:
Proposition 2.
The gamma distribution defines a natural exponential family with natural parameters λ and and potential function .
Using (2), the Fisher metric is obtained by a straightforward computation:
where is the digamma function.
It is sometimes convenient to perform a change of parameterization in order to have a diagonal form for the metric. The next proposition is of common use and allows the computation of a pullback metric in local coordinates:
Proposition 3.
Let be a smooth manifold and be a smooth Riemannian manifold. For a smooth diffeomorphism , the pullback metric has matrix expressed in local coordinates at the point by:
with the Jacobian matrix of f at m and the matrix of the metric g at .
Performing the change of parameterization yields:
Using Proposition 3 then gives for the pullback metric matrix:
The information geometry of the gamma distribution is studied in detail in [17], with explicit calculations of the Christoffel symbols and the geodesic equation.
3. The Geometry of the Generalized Gamma Manifold
While the gamma distribution is well suited to study departure to full randomness, as pointed out in [17], it is not general enough in many applications. In particular, the Weibull distribution that also generalizes the exponential distribution is not a gamma distribution. A more general family was thus introduced, by adding a power term.
Definition 3.
The generalized gamma distribution is the probability measure on with density respective to the Lesbesgue measure given by:
where .
Due to the exponent , the generalized gamma distribution does not define a natural exponential family. However, keeping fixed, the mapping is a diffeomorphism of to itself, and the image density of under is a gamma density with parameters . For any , the submanifold of the generalized gamma manifold is diffeomorphic to the gamma manifold. Using the invariance of the Fisher metric under diffeomorphisms, the induced metric on the above submanifold can be obtained.
Proposition 4.
Let be a fixed real number. The induced Fisher metric matrix on the submanifold of the generalized gamma manifold is given in local coordinates by:
Proof.
In local coordinates , the Fisher metric matrix of a gamma distribution manifold is
The Jacobian matrix of the transformation is the matrix and the change of parameterization yields:
The Fisher metric matrix on the submanifold is directly obtained from the invariance by using the diffeomorphism . □
Proposition 5.
In local coordinates, the Fisher information metric matrix of the generalized gamma manifold is given by:
Proof.
The submatrix corresponding to the local coordinates has already been obtained in Proposition 4. The remaining terms can be computed by differentiating the log-likelihood function twice, but an alternative will be given below in a more general setting. □
The usual definition of the generalized gamma distribution Definition 3 does stem from the gamma one by a simple change of variable, thus making some computation less natural. Starting with the above diffeomorphism and applying it to a gamma distribution yields an equivalent, but more intuitive form. Furthermore, it is advisable to express the gamma density as a natural exponential family distribution:
where , are the natural parameters of the distribution.
Definition 4.
The generalized gamma distribution on is the probability measure with density:
with , and .
Due to the invariance by diffeomorphism property of the Fisher information metric, the induced metric on the submanifolds is independent of , and is exactly the one of the gamma manifold, here given by the matrix:
An important fact about the family of diffeomorphisms is the group property . It turns out that all the computation can be conducted in a general Lie group setting, as detailed below. Let be a parameterized family of probability densities defined on an open subset U of and let W be a Lie group acting on U by diffeomorphisms preserving orientation. For any w in W and in , the image density under the diffeomorphism is given by:
Note that we consider diffeomorphisms preserving orientation. For simplicity of calculus, the absolute value may be removed in the above expression. Denoting the log-likelihood of and the one of , it comes, by obvious computation:
In this section, the symbol stands for the partial derivative with respect to the i-th variable. Higher order derivatives are written similarly as by repeating the variable k times to indicate a partial derivative of order k.
Proposition 6.
For any , :
where e is the identity of W and is the right translation mapping .
Proof.
Since comes from a group action:
Then, taking the derivative with respect to h at identity:
Since by the chain rule, the claimed result is proved. □
This property allows for computing the Fisher information metric in a convenient way.
Proposition 7.
The element of the Fisher metric matrix of is given by:
Proof.
Since:
it comes:
and thus:
Now, using Proposition 6:
Taking the expectation with respect to yields:
and the result follows by the change of variable . □
The case of the elements is a little bit more complex, due to the non-vanishing extra term in the log-likelihood . Taking the first derivative with respect to w yields:
where tr denotes the trace of the linear application with respect to the x components. The second term on the right-hand side can be further simplified using the next proposition that is a direct consequence of Proposition 6.
Proposition 8.
For any :
Applying it to the log-likelihood derivative and using again Proposition 6 yields:
Proposition 9.
The element of the Fisher metric matrix of is given in matrix form by:
with:
Proof.
Starting with the definition:
the result follows after the change of variable in the expectation. □
An important corollary of Propositions 7 and 9 is that the Fisher metric can be expressed as a right invariant metric on the Lie group .
Propositions 7 and 9 allow for computing the coefficients in the Fisher metric matrix, thus yielding the next proposition.
Proposition 10.
The Fisher information matrix in natural coordinates has coefficients:
Recalling that the Christoffel symbols of the first kind for the Levi–Civita connection are obtained using the formula:
one can obtain them as:
4. The Gamma Submanifold
The submanifolds of the generalized gamma manifold are all isometric to the gamma manifold. This section is dedicated to the study of their properties using the Gauss–Codazzi equations. In the sequel, the generalized gamma manifold will be denoted by M while will stand for the embedded submanifold .
Proposition 11.
The normal bundle to is generated at on the gamma submanifold by the vector:
Proof.
The matrix of the Fisher metric at can be written in block form as:
with:
and
Any multiple of the vector:
is normal to the tangent space to the submanifold . The result follows by simple computation. □
Let ∇ be the Levi–Civita connection of the gamma manifold and that of the generalized gamma. It is well known [18] (pp. 60–63) that these two connections are related by the Gauss formula:
where is a symmetric bilinear form with values in the normal bundle. Letting with , it comes, with :
Since takes its values in the normal bundle, it exists a smooth real value mapping such that . Equation (12) yields:
From [18] (p. 63), the sectional curvature of M can be obtained from the one of as:
or:
Using the expressions of the Christoffel symbols and the metric, the coefficients can be computed as:
with:
Finally:
with:
and:
Proposition 12.
The term is strictly positive.
Proof.
Using the expressions of the coefficients:
with:
The function satisfies the next inequality [19]:
from which it comes:
and it turns:
To obtain the sign of , a different bound is needed for the polygamma function. Again from [19]:
Using again (20) with yields finally:
Since both and are strictly negative, is strictly positive as claimed. □
Proposition 13.
The sectional curvature of the generalized gamma manifold in the satisfies:
Proof.
The sectional curvature of the gamma manifold satisfies [17]:
It is thus only needed to estimate the limit of (19) when . The asymptotics of the polygamma functions at 0 are given by:
The term:
can thus be approximated by:
and the term:
is approximated by:
Finally, the quotient is equal at to
and the result follows by summation with . □
It is conjectured that the sectional curvature of the generalized gamma manifold in the directions is strictly positive, bounded from above by 1/2 as it appears to be the case numerically.
5. Medical Imaging Application
Magnetic Resonance Imaging (MRI) seeks to identify, localize and measure different parts of the anatomy of the central nervous system. It is of common use for the diagnosis of neurodegenerative diseases such as Alzheimer’s disease [1,2,3]. The brain atrophy can be estimated from the measure of the cortical thickness [4,5].
Many of these studies limited their work by using aggregated measures such as the mean or the median while the most recent ones used histogram-analysis [20,21]. In the present work, a generalized gamma density function will be used in place of the histogram to model the distribution of the cortical thickness.
5.1. Study Set-Up and Design
Data used in this paper were obtained from the Alzheimer’s disease Neuroimaging Initiative (ADNI) database http://adni.loni.usc.edu/about/ which aims at providing researchers with an expertized database of several biomarkers. Access is granted upon an online approval process. The details of the experimental setup can be found on the ADNI website under the “MRI Acquisition” tab.
Our study is based on a selected subset of the ADNI population, comprising 143 subjects; 71 healthy controls (HC) subjects and 72 Alzheimer’s disease (AD) patients whose characteristics are summarized in Table 1.

Table 1.
Demographic and clinical characteristics of the study population.
Raw images were preprocessed by gradwarping, intensity correction and scaling. Only high quality images were kept in the final dataset.
5.2. Cortical Thickness Measurement and Distribution
Cortical thickness was chosen as the MRI biomarker because of its ability to quantify morphological alterations of the cortical mantle in early stage of AD. Cortical Thickness (CTh) was measured using the Matlab Toolbox CorThiZon [22] and delivered as a vector of thickness values sampled evenly along the medial axis of the cortex.
On each vector of cortical thicknesses, a generalized gamma density in the form (6) is fitted using the method of moments described in [23], yielding the estimates of three generalized gamma parameters () which are then converted to natural parameters. At the end of the data processing phase, a dataset of 143 estimated generalized gamma densities is released.
5.3. Clustering
Clustering, also called unsupervised classification, has been extensively studied for years in many fields, such as data mining, pattern recognition, image segmentation and bioinformatics. This technique aims at grouping samples in subsets of the original dataset, such that all elements in a given subset are as similar as possible, while they differ as much as possible from the ones belonging to other subsets. Depending on the exact quality criterion, several formulations can be made. Three principal categories of clustering exist in literature, partitioning clustering, hierarchical clustering and density-based clustering. In the first category, the popular k-means problem applies to vector samples in and finds a partition of the original dataset D into k subsets that minimize the total intra-class variance:
where denotes the number of elements in . It can be formulated as a vector quantization problem that is to find an optimal sequence of vectors from that minimizes:
where is the subset of points from the dataset located in the Voronoï cell of center . It was proved to be NP-hard [24], even with only two classes. Existing algorithms will thus only seek locally optimal solutions. A popular choice is Llyod’s algorithm [25], which is a gradient based local minimization procedure. It can be extended to the Riemannian case [26], but requires at each iteration the computation of the geodesics between a sample and the cell centers. In our study, the experiments were conducted using a slightly different partitioning algorithm, the k-medoids [27]. Compared to Llyod’s algorithm, it is generally considered to be slower, but requires only a dissimilarity measure between pairs of points of the dataset instead of a true distance. It is more suited to small samples, since iterations are made without having to recompute distances. In the context of clustering on Riemannian manifolds, this is a distinguished advantage as geodesic computations are expensive. It is also robust to outliers [28]. The different steps of our k-medoids algorithm are summarized in Algorithm 1.
| Algorithm 1k-medoids algorithm. |
| Initialization: Select randomly k samples as the initial medoids. repeat Calculate dissimilarity between each medoid m and the remaining data objects. Assign the non-medoid object to the closest medoid m. Compute the total cost variation of swapping the medoid m with . if then swap m with to form the new set of medoids. end if until No improvement on total cost. |
The dissimilarity matrix used in the k-medoids algorithm was computed using the following similarity measures:
- Geodesic distance on the generalized gamma manifold (DGG1),
- Approximate geodesic distance on the generalized gamma manifold (DGG2),
- Geodesic distance on the gamma manifold (DG),
- Absolute value distance between empirical means (DM),
- Kullback–Leibler divergence for generalized gamma distributions (KL).
The (DGG1) and (DG) distances are computed between two points on the respective manifold by solving the geodesic equation:
A shooting method was selected for this boundary value problem. It converges in any cases for (DG) but failed to converge on ten pairs for (DG1). The approximate geodesic distance (DGG2) was defined to circumvent this issue. It is based on the observation that the gamma manifold is isometrically embedded in the generalized gamma manifold when is constant. There is thus a Riemannian submersion defined in coordinates by . An approximate distance can then be obtained by considering separately the vertical and the horizontal part. Let be two generalized gamma densities. The energy of the vertical path is computed using the formula:
Then, the energy of the geodesic joining and is computed on the gamma submanifold as the infimum of the integrals:
where is a smooth path joining the two previous points with constant equal to . The overall approximate distance is then taken to be . Please note that it is only a similarity measure, like the Kullback–Leibler divergence, as it fails to be symmetric.
5.4. Results
The overall process is summarized in Figure 1 below.
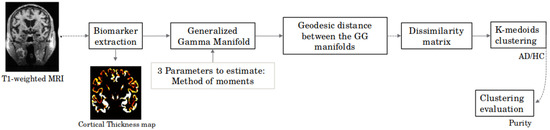
Figure 1.
General scheme of the proposed approach.
The quality of the clustering results was assessed using purity that is the proportion of well classified samples. Since the k-medoids algorithm has a random initialization, the values given in Table 2 were computed as the mean of the purity on 100 runs.

Table 2.
Performance of clustering with different similarity measures.
The best results were obtained using (DGG1) and (DGG2), but, in the first case, one must keep in mind that some distances were impossible to compute: the corresponding samples were thus removed from the dataset. The reference method in the medical imaging community is (DM), which performs slightly better than (DG) and (KL). Due to the small size of the dataset, more testing is needed. A new study with different biomarkers is ongoing.
Author Contributions
F.N. and S.P. have contributed equally to the geometry of the generalized gamma manifold. S.R. has written the part on medical applications.
Funding
This research was funded by by the Fondation pour la Recherche Medicale (FRM Grant No. ECO20160736068 to S.R) and by the ANR grant ANR-14-CE27-0006.
Acknowledgments
Data used in the preparation of this article were obtained from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) database (adni.loni.ucla.edu). As such, the investigators within the ADNI contributed to the design and implementation of ADNI and/or provided data but did not participate in analysis or writing of this report. A complete listing of ADNI investigators can be found at: http://adni.loni.ucla.edu/wp-content/uploads/how_to_apply/ADNI_Acknowledgement_List.pdf.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Vemuri, P.; Jack, C.R. Role of structural MRI in Alzheimer’s disease. Alzheimers Res. Ther. 2010, 2, 23. [Google Scholar] [CrossRef] [PubMed]
- Cuingnet, R.; Gerardin, E.; Tessieras, J.; Auzias, G.; Lehéricy, S.; Habert, M.O.; Chupin, M.; Benali, H.; Colliot, O.; Alzheimer’s Disease Neuroimaging Initiative. Automatic classification of patients with Alzheimer’s disease from structural MRI: a comparison of ten methods using the ADNI database. NeuroImage 2011, 56, 766–781. [Google Scholar] [CrossRef] [PubMed]
- Lama, R.K.; Gwak, J.; Park, J.S.; Lee, S.W. Diagnosis of Alzheimer’s Disease Based on Structural MRI Images Using a Regularized Extreme Learning Machine and PCA Features. J. Healthc. Eng. 2017, 2017, 5485080. [Google Scholar] [CrossRef] [PubMed]
- Pini, L.; Pievani, M.; Bocchetta, M.; Altomare, D.; Bosco, P.; Cavedo, E.; Galluzzi, S.; Marizzoni, M.; Frisoni, G.B. Brain atrophy in Alzheimer’s Disease and aging. Ageing Res. Rev. 2016, 30, 25–48. [Google Scholar] [CrossRef] [PubMed]
- Busovaca, E.; Zimmerman, M.E.; Meier, I.B.; Griffith, E.Y.; Grieve, S.M.; Korgaonkar, M.S.; Williams, L.M.; Brickman, A.M. Is the Alzheimer’s disease cortical thickness signature a biological marker for memory? Brain Imaging Behav. 2016, 10, 517–523. [Google Scholar] [CrossRef] [PubMed]
- Cercignani, M.; Inglese, M.; Pagani, E.; Comi, G.; Filippi, M. Mean Diffusivity and Fractional Anisotropy Histograms of Patients with Multiple Sclerosis. Am. J. Neuroradiol. 2001, 22, 952–958. [Google Scholar] [PubMed]
- Dehmeshki, J.; Silver, N.; Leary, S.; Tofts, P.; Thompson, A.; Miller, D. Magnetisation transfer ratio histogram analysis of primary progressive and other multiple sclerosis subgroups. J. Neurol. Sci. 2001, 185, 11–17. [Google Scholar] [CrossRef]
- Rebbah, S.; Delahaye, D.; Puechmorel, S.; Maréchal, P.; Nicol, F.; Berry, I. Classification of Multiple Sclerosis patients using a histogram-based K-Nearest Neighbors algorithm. In Proceedings of the OHBM 2019, 25th Annual Meeting of Organization for Human Brain Mapping, Rome, Italy, 14 June 2019. [Google Scholar]
- Stacy, E.W. A Generalization of the Gamma Distribution. Ann. Math. Stat. 1962, 33, 1187–1192. [Google Scholar] [CrossRef]
- Amoroso, L. Ricerche intorno alla curva dei redditi. Annali di Matematica Pura ed Applicata 1925, 2, 123–159. [Google Scholar] [CrossRef]
- Crooks, G.E. The Amoroso Distribution. arXiv 2010, arXiv:1005.3274. [Google Scholar]
- Amari, S. Information Geometry and Its Applications; Applied Mathematical Sciences; Springer: Tokyo, Japan, 2016. [Google Scholar]
- Calin, O.; Udrişte, C. Geometric Modeling in Probability and Statistics; Mathematics and Statistics; Springer International Publishing: Cham, Switzerland, 2014. [Google Scholar]
- Amari, S.; Nagaoka, H. Methods of Information Geometry; Translations of Mathematical Monographs; American Mathematical Society: Providence, RI, USA, 2007. [Google Scholar]
- Shima, H. Geometry of Hessian Structures. In Geometric Science of Information; Nielsen, F., Barbaresco, F., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 37–55. [Google Scholar]
- Duistermaat, J. On Hessian Riemannian structures. Asian J. Math. 2001, 5, 79–91. [Google Scholar] [CrossRef]
- Arwini, K.; Dodson, C.; Doig, A.; Sampson, W.; Scharcanski, J.; Felipussi, S. Information Geometry: Near Randomness and Near Independence; Information Geometry: Near Randomness and Near Independence; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Chavel, I. Riemannian Geometry: A Modern Introduction; Cambridge Studies in Advanced Mathematics; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Guo, B.-N.; Qi, F.; Zhao, J.-L.; Luo, Q.-M. Sharp Inequalities for Polygamma Functions. Math. Clovaca 2015, 65, 103–120. [Google Scholar]
- Ruiz, E.; Ramírez, J.; Górriz, J.M.; Casillas, J.; Alzheimer’s Disease Neuroimaging Initiative. Alzheimer’s Disease Computer-Aided Diagnosis: Histogram-Based Analysis of Regional MRI Volumes for Feature Selection and Classification. J. Alzheimers Dis. 2018, 65, 819–842. [Google Scholar] [CrossRef] [PubMed]
- Giulietti, G.; Torso, M.; Serra, L.; Spanò, B.; Marra, C.; Caltagirone, C.; Cercignani, M.; Bozzali, M.; Alzheimer’s Disease Neuroimaging Initiative (ADNI). Whole brain white matter histogram analysis of diffusion tensor imaging data detects microstructural damage in mild cognitive impairment and alzheimer’s disease patients. J. Magn. Reson. Imaging 2018. [Google Scholar] [CrossRef] [PubMed]
- Querbes, O.; Aubry, F.; Pariente, J.; Lotterie, J.A.; Démonet, J.F.; Duret, V.; Puel, M.; Berry, I.; Fort, J.C.; Celsis, P.; et al. Early diagnosis of Alzheimer’s disease using cortical thickness: impact of cognitive reserve. Brain J. Neurol. 2009, 132, 2036–2047. [Google Scholar] [CrossRef] [PubMed]
- Stacy, E.W.; Mihram, G.A. Parameter Estimation for a Generalized Gamma Distribution. Technometrics 1965, 7, 349–358. [Google Scholar] [CrossRef]
- Garey, M.; Johnson, D.; Witsenhausen, H. The complexity of the generalized Lloyd - Max problem (Corresp.). IEEE Trans. Inf. Theory 1982, 28, 255–256. [Google Scholar] [CrossRef]
- Lloyd, S. Least squares quantization in PCM. IEEE Trans. Inf. Theory 1982, 28, 129–137. [Google Scholar] [CrossRef]
- Brigant, A.L.; Puechmorel, S. Quantization and clustering on Riemannian manifolds with an application to air traffic analysis. J. Multivar. Anal. 2019, 173, 685–703. [Google Scholar] [CrossRef]
- Kaufman, L.; Rousseeuw, P. Clustering by means of Medoids. In Statistical Data Analysis Based on the L1—Norm and Related Methods; Dodge, Y., Ed.; Springer: North-Holland, The Netherlands, 1987; pp. 405–416. [Google Scholar]
- Soni, K.G.; Patel, D.A. Comparative Analysis of K-means and K-medoids Algorithm on IRIS Data. Int. J. Comput. Intell. Res. 2017, 13, 899–906. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).