Construction and Application of Nine-Tic B-Spline Tensor Product SS
Abstract
1. Introduction
2. Properties of the SS
2.1. Smoothness of the SS
2.2. Holder Exponent
2.3. Polynomial Generation and Reproduction
2.4. Local Analysis with Invariant Neighborhood
3. Construction and Analysis of Nine-tic B-Spline Tensor Product SS
3.1. Preliminaries
3.2. Construction of Nine-tic B-Spline Tensor Product SS
3.3. Analysis of Nine-tic B-Spline Tensor Product SS
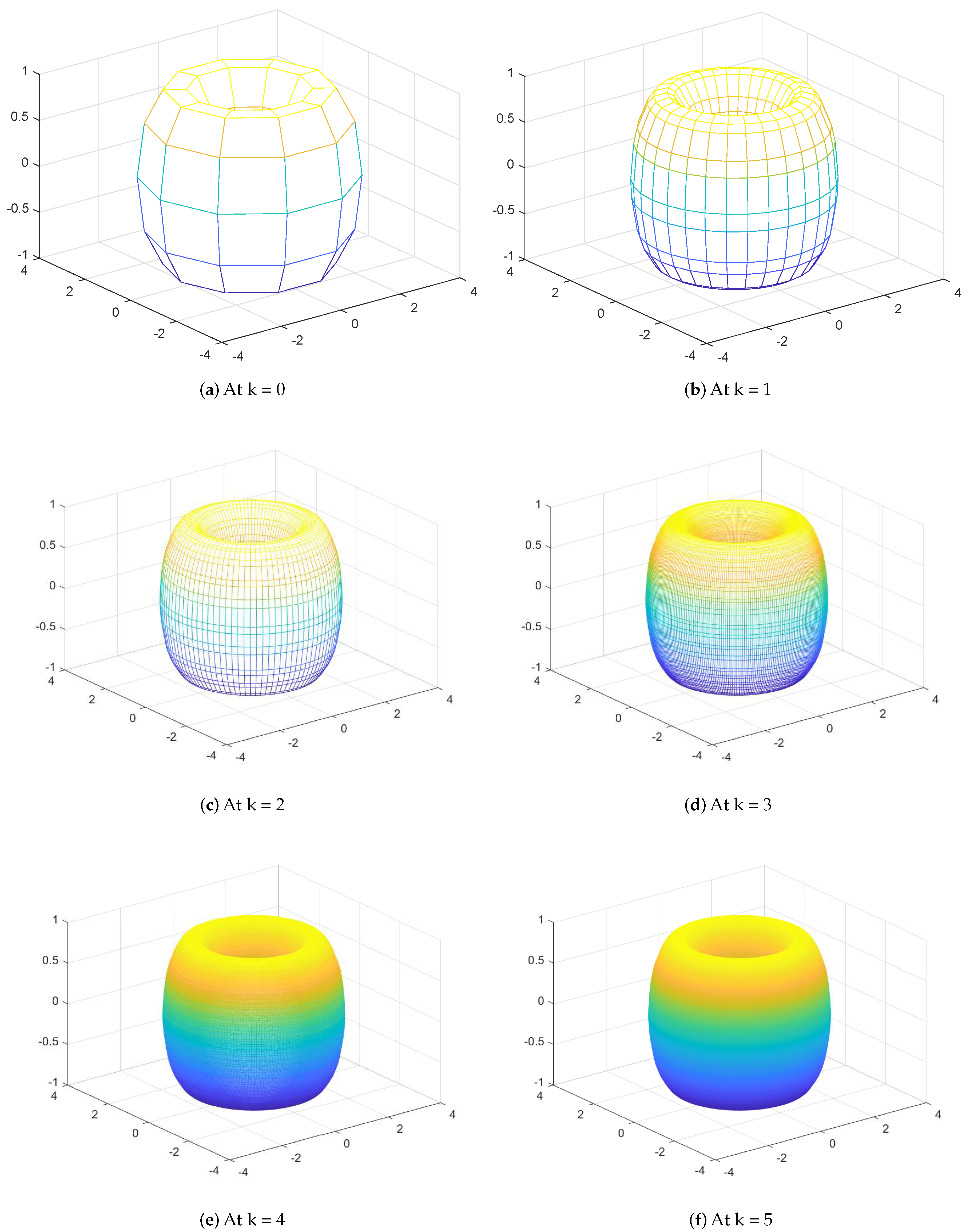
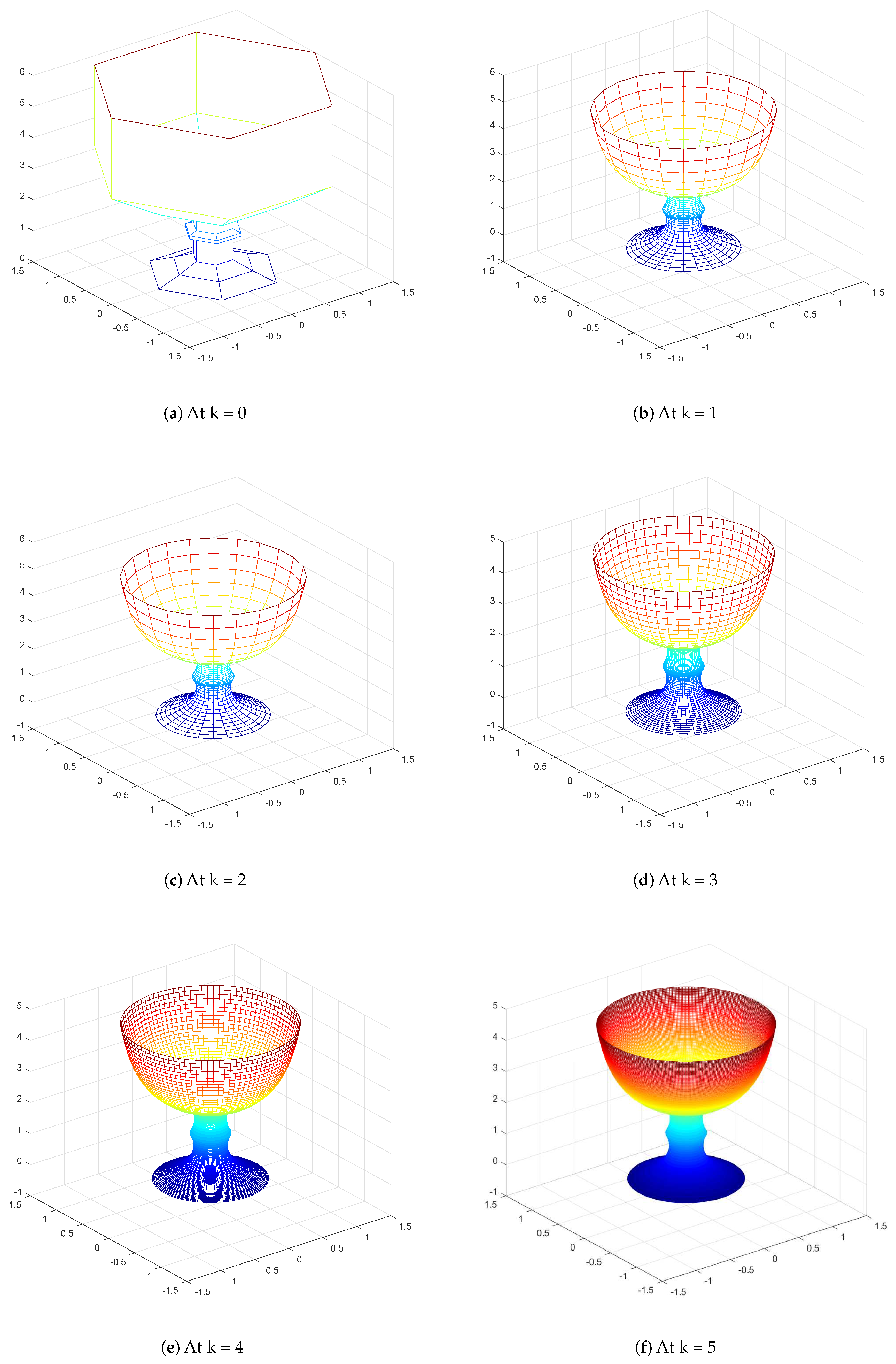
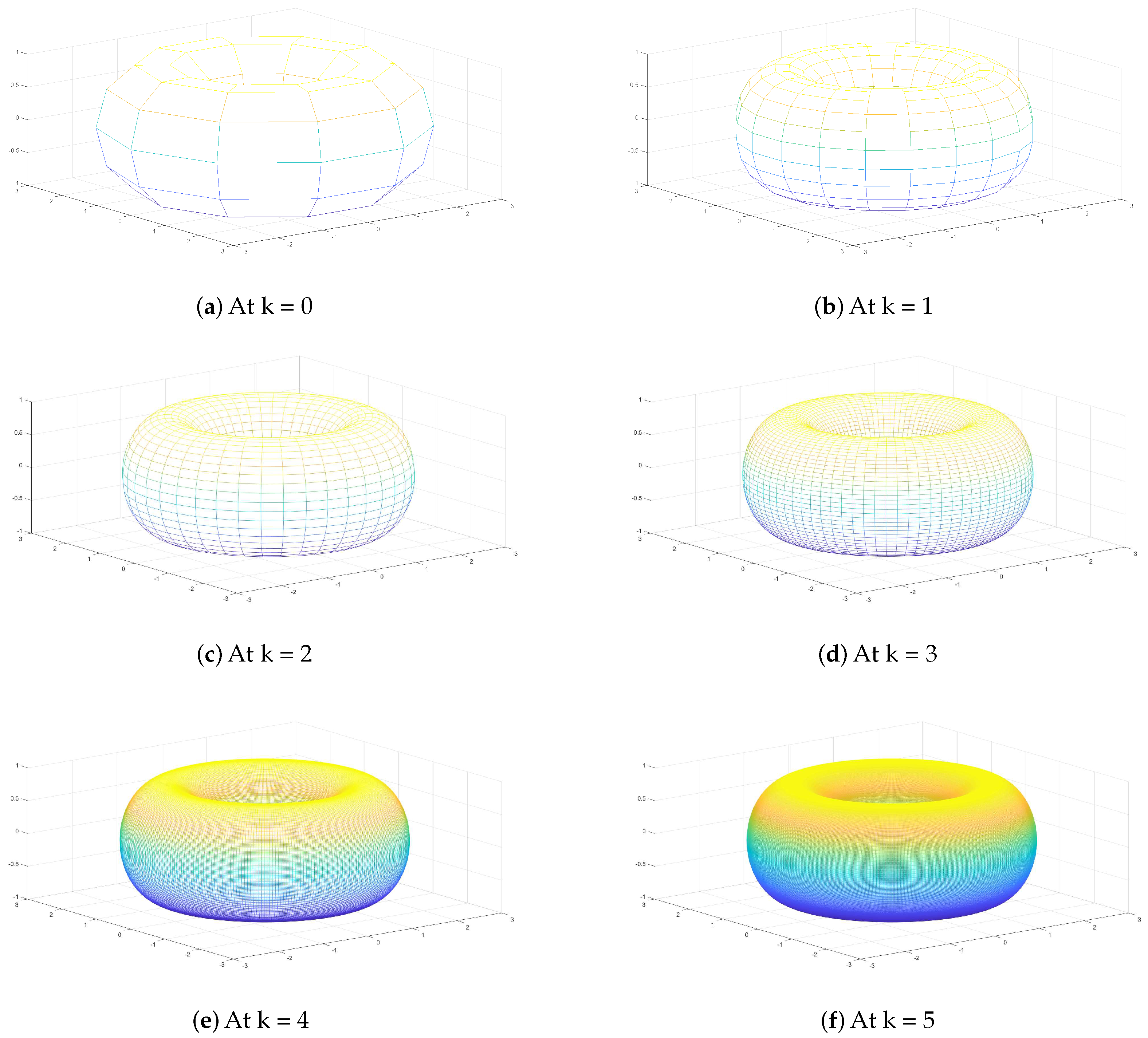
4. Numerical Examples
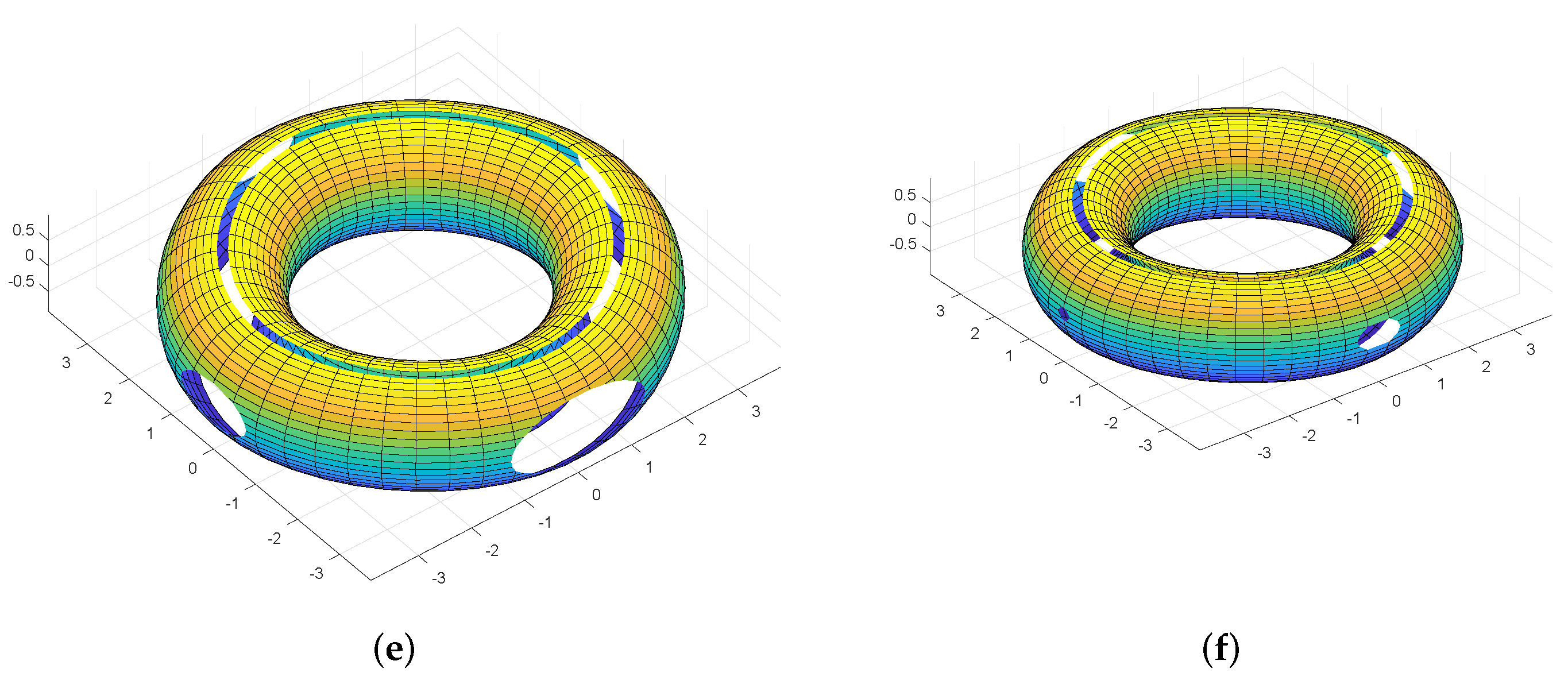
Comparison of NURBS & Proposed SS
5. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- De Rham, G. Un peu de mathématiques à propos d’une courbe plane. Elem. Der Math. 1947, 2, 73–76. [Google Scholar]
- Chaikin, G.M. An algorithm for high-speed curve generation. Comput. Graph. Image Process. 1974, 3, 346–349. [Google Scholar] [CrossRef]
- Doo, D.; Sabin, M. Behaviour of recursive division surfaces near extraordinary points. Comput. Aided Des. 1978, 10, 356–360. [Google Scholar] [CrossRef]
- Catmull, E.; Clark, J. Recursively generated B-spline surfaces on arbitrary topological meshes. Comput. Aided Des. 1978, 10, 350–355. [Google Scholar] [CrossRef]
- Dyn, N.; Levine, D.; Gregory, J.A. A butterfly subdivision scheme for surface interpolation with tension control. ACM Trans. Graph. 1990, 9, 160–169. [Google Scholar] [CrossRef]
- Dyn, N.; Levin, D. Analysis of Hermite-type subdivision schemes. Ser. Approx. Decompos. 1995, 6, 117–124. [Google Scholar]
- Stam, J. Exact evaluation of Catmull-Clark subdivision surfaces at arbitrary parameter values. In Proceedings of the 25th Annual Conference on Computer Graphics and Interactive Techniques, Orlando, FL, USA, 19–24 July 1998; pp. 395–404. [Google Scholar]
- Hassan, M.; Dodgson, N.A. Ternary and Three-Point Univariate Subdivision Schemes; No. UCAM-CL-TR-520; University of Cambridge, Computer Laboratory: Cambridge, UK, 2001; pp. 1–15. [Google Scholar]
- Hassan, M.F.; Ivrissimitzis, I.P.; Dodgson, N.A.; Sabin, M.A. An interpolating 4-point C2 ternary stationary subdivision scheme. Comput. Aided Geom. Des. 2002, 19, 1–18. [Google Scholar] [CrossRef]
- Mustafa, G.; Liu, X. A subdivision scheme for volumetric models. Appl. Math. J. Chin. Univ. 2005, 20, 213–224. [Google Scholar] [CrossRef]
- Beccari, C.; Casciola, G.; Romani, L. An interpolating 4-point C2 ternary non-stationary subdivision scheme with tension control. Comput. Aided Geom. Des. 2007, 24, 210–219. [Google Scholar] [CrossRef]
- Mustafa, G.; Khan, F.; Ghaffar, A. The m-point approximating subdivision scheme. Lobachevskii J. Math. 2009, 30, 138–145. [Google Scholar] [CrossRef]
- Aslam, M.; Mustafa, G.; Ghaffar, A. The (2n-1)-Point Ternary Approximating and Interpolating subdivision schemes. J. Appl. Math. 2011, 2011. [Google Scholar] [CrossRef]
- Zheng, H.; Hu, M.; Peng, G. Ternary even symmetric 2n-point subdivision. In Proceedings of the Computational Intelligence and Software Engineering, CiSE, Wuhan, China, 11–13 December 2009; pp. 1–4. [Google Scholar]
- Mustafa, G.; Ghaffar, A.; Aslam, M. A subdivision-regularization framework for preventing over fitting of data by a model. Appl. Appl. Math. Int. J. 2013, 8, 178–190. [Google Scholar]
- Ghaffar, A.; Mustafa, G.; Qin, K. Construction and application of 3-point tensor product subdivision scheme. Appl. Math. 2013, 4, 477–485. [Google Scholar] [CrossRef][Green Version]
- Mustafa, G.; Ghaffar, A.; Bari, M. The (2n-1)-point binary approximating subdivision scheme. In Proceedings of the Eighth International Conference on Digital Information Management (ICDIM 2013), Islamabad, Pakistan, 10–12 September 2013; pp. 363–368. [Google Scholar]
- Mustafa, G.; Ashraf, P.; Saba, N. A new class of binary approximating subdivision schemes. J. Teknol. 2016, 78, 65–72. [Google Scholar] [CrossRef]
- Hameed, R.; Mustafa, G. Construction and analysis of binary subdivision schemes for curves and surfaces originated from Chaikin points. Int. J. Anal. 2016, 2016. [Google Scholar] [CrossRef]
- Ghaffar, A.; Mustafa, G. An Alternative Method for Constructing Subdivision Algorithm. Sci. Int. 2016, 28, 5011–5015. [Google Scholar]
- Cheng, L.; Zhou, X. Necessary conditions for the convergence of subdivision schemes with finite masks. Appl. Math. Comput. 2017, 303, 34–41. [Google Scholar] [CrossRef]
- Akram, G.; Bibi, K.; Rehan, K.; Siddiqi, S.S. Shape preservation of 4-point interpolating non-stationary subdivision scheme. J. Comput. Appl. Math. 2017, 319, 480–492. [Google Scholar] [CrossRef]
- Manan, S.A.; Ghaffar, A.; Rizwan, M.; Rahman, G.; Kanwal, G. A subdivision approach to the approximate solution of 3rd order boundary value problem. Commun. Math. Appl. 2018, 9, 499–512. [Google Scholar]
- Kanwal, G.; Ghaffar, A.; Hafeezullah, M.M.; Manan, S.A.; Rizwan, M.; Rahman, G. Numerical solution of 2-point boundary value problem by subdivision scheme. Commun. Math. Appl. 2019, 10, 1–11. [Google Scholar]
- Ghaffar, A.; Ullah, Z.; Bari, M.; Nisar, K.S.; Baleanu, D. Family of odd point non-stationary subdivision schemes and their applications. Adv. Differ. Equ. 2019, 2019, 171. [Google Scholar] [CrossRef]
- Dyn, N. Analysis of convergence and smoothness by the formalism of Laurent polynomials. In Tutorials on Multiresolution in Geometric Modelling; Springer: Berlin/Heidelberg, Germany, 2002; pp. 51–68. [Google Scholar]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghaffar, A.; Iqbal, M.; Bari, M.; Muhammad Hussain, S.; Manzoor, R.; Sooppy Nisar, K.; Baleanu, D. Construction and Application of Nine-Tic B-Spline Tensor Product SS. Mathematics 2019, 7, 675. https://doi.org/10.3390/math7080675
Ghaffar A, Iqbal M, Bari M, Muhammad Hussain S, Manzoor R, Sooppy Nisar K, Baleanu D. Construction and Application of Nine-Tic B-Spline Tensor Product SS. Mathematics. 2019; 7(8):675. https://doi.org/10.3390/math7080675
Chicago/Turabian StyleGhaffar, Abdul, Mudassar Iqbal, Mehwish Bari, Sardar Muhammad Hussain, Raheela Manzoor, Kottakkaran Sooppy Nisar, and Dumitru Baleanu. 2019. "Construction and Application of Nine-Tic B-Spline Tensor Product SS" Mathematics 7, no. 8: 675. https://doi.org/10.3390/math7080675
APA StyleGhaffar, A., Iqbal, M., Bari, M., Muhammad Hussain, S., Manzoor, R., Sooppy Nisar, K., & Baleanu, D. (2019). Construction and Application of Nine-Tic B-Spline Tensor Product SS. Mathematics, 7(8), 675. https://doi.org/10.3390/math7080675







