Abstract
This paper examines unsteady magnetohydrodynamic (MHD) convective fluid flow described by the Oldroyd-B model using ramped wall temperature and velocity simultaneously. The fluid flow is closed to an infinite vertical flat plate immersed through a porous medium. Laplace transformation is used to find solutions of momentum and energy equations. Afterwards, the Nusselt number and skin friction coefficient are obtained. A parametric study is performed to investigate the effects of ramped velocity and temperature (at wall) on the considered fluid flow model.
MSC:
76D03; 76S05; 76W05; 76M25
1. Introduction
Non-Newtonian fluids gained a wide deal of attention due to their practical utility in modern technologies. Examples of non-Newtonian fluids are blood, paints, oils, greases and polymer solutions and so forth [1,2,3]. Mixed convective flows of non-Newtonian fluids under the action of magnetohydrodynamic (MHD) force, are of great importance in MHD pumps and power generators, accelerators, energy generators, aerodynamic heating, polymer fabrication and purification of mineral oil and so forth. Convective flows through a porous medium play an imperative role in locating gas and oil reservoirs in the earth [4]. In agriculture, convective flows are used to locate the sub-ground water reservoirs [5]. In metallurgy, the flow of liquid metal under the strong magnetic field in a porous medium takes place during a solidification process [6].
The above mentioned practical applications are the main motivations behind this work. Many complex fluids exhibit a combination of elastic and viscous behavior for example, polymer solutions and melts, oil, toothpaste and clay. The Oldroyd-B model is one of the simplest models that includes the history of the flow and capable of describing viscoelastic fluids. In this study, we investigated the MHD convective fluid flow of the Oldroyd-B model subject to ramped velocity and ramped temperature (at wall), through a porous medium. The literature reveals that the simultaneous implementation of above mentioned conditions, ramped velocity and ramped temperature (at wall), have attracted a little attention of the researchers examining such flows. The simultaneous use of ramped wall temperature and velocity conditions are physically important, but mathematically difficult to handle. Ergometers or treadmill testing (TT) is an application of ramped velocity which is currently applied to diagnose cardiovascular diseases. Furthermore, there are many applications of Ramped velocity in making diagnoses, determining prognosis, establishing treatments and examining the functioning of heart and blood vessels system [7]. Bruce [8], Astrand and Rodahl [9] and Myers and Bellin [10] are contributed on TT.
Hayday [11], Schetz [12] and Malhotra et al. [13] presented their work on ramped wall temperature conditions. An efficient and effective way to estimate the increase in temperature due to adiabatic conditions can be controlled with the help of ramped heating. Another important application of controlled temperature boundary conditions (BCs) is reported by Kundu [14]. Kundu [14] affirmed that the thermal therapy is helpful in treating cancerous cells as the therapy has insignificant side effects. Kundu [14] further suggested five types of temperature BCs for better treatment of cancerous cells depending upon Fourier and non-Fourier heating. Seth et al. presented their work on the heat and mass transfer considering ramped temperature (at wall) with the impulsive and moving vertical plate [15,16,17,18,19]. Recently, Chandran et al. [20] used the ramped wall temperature condition with convective viscous fluid flow. Some researches taking into account the ramped temperature conditions can be found in the recent literature [21,22,23,24,25,26].
The conditions of ramped velocity and temperature at wall have significant importance in human health and in many daily life related procedures. The Oldroyd-B fluid model considers the memory effects and elasticity and memory effects. The model also retains rheological effects even for unidirectional flows. The Oldroyd B model gives good approximations of viscoelastic fluids in shear flow and has an unphysical singularity in extensional flow. The model contains Maxwell and viscous fluid as its special cases. If the solvent viscosity is zero, the Oldroyd-B becomes the Upper Convected Maxwell model. Therefore Oldroyd-B model can be regarded as an extension of the Upper Convected Maxwell model which is named after its creator James G. Oldroyd. The focus of the present work is to use the velocity and temperature conditions on ramped wall simultaneously for the convective flow of Oldroyd-B fluid model. Laplace transformation is implemented to solve the Oldroyd-B fluid model subject to ramped velocity and temperature at wall.
2. Model Formulation
The unsteady, incompressible and MHD flow of Oldroyd-B fluid over an infinite vertical plate under the Boussinesq’s approximations can be described by the subsequent equations [27,28]. The Boussinesq’s approximations is used to find the buoyancy force [29].
where
and satisfies the following relation:
where accounts for the unidirectional and unidimensional velocity profile as given below:
is defined as follows:
refers to the indeterminate stress tensor, denotes the Cauchy stress tensor of Oldroyd-B fluid, is the extra stress tensor, represents the fluid density, is defined as the fluid viscosity, is the material time derivative. Moreover, , and represent the relaxation and retardation times and Darcy’s resistance, respectively. The Rivlin-Ericksen tensor is as follows:
The modified version of Darcy’s law for the Oldroyd-B fluid flow is given below:
The Maxwell’s equations are defined as below:
and
where , , and represent electric field, total magnetic field, current density and magnetic permeability, respectively.
The aggregate magnetic field is . Here, and represent the induced magnetic field and the applied magnetic field, respectively. In the light of Equations (3)–(8), Equation (2) takes the following form:
Multiplying Equation (11) by () and using Equations (8)–(10) we get the form as given below:
Geometry of the considered flow model is presented in Figure 1.
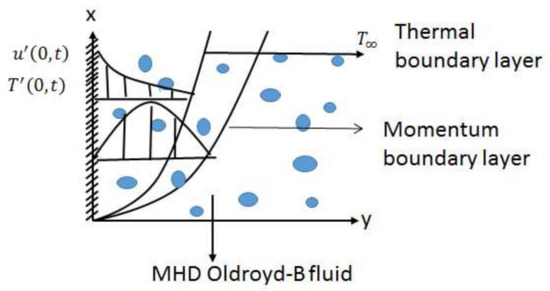
Figure 1.
Geometry of the considered flow model.
Using small magnetic Reynolds number and Boussinesq’s approximation, the equation of motion and the energy equation for Oldroyd-B fluid are as under:
with initial conditions (ICs) as given below:
and corresponding (BCs) as follows:
and
Dimensionless quantities are defined as:
After applying Equation (20) in Equations (14)–(19), the obtained coupled PDEs system is presented as follows:
where
and the energy equation:
where Pr and Gr are the Prandtl’s and Grashof’s numbers respectively. The corresponding ICs and BCs can be rewritten as:
and
3. Analytical Solution of the Problem
Laplace and Inverse Laplace Transforms
We use the Laplace transform tool [30] to tackle the problem because the other analytical method like Homotopy analysis method, perturbation techniques, Adomian decomposition, and method of separation of variables and so forth, do not work because of non-uniform boundary conditions. In order to solve the problem specified through Equations (21)–(26), we define the Laplace transform pair of an almost piecewise continuous function (of exponential order), as an integral of the form:
which is convergent for , where , and is some real number. The inverse Laplace transform of can be evaluated as:
where denotes the Bromwich type contour integral over the contour to , while R approaches ∞ and also the Gaver-Stehfest method is required when there are multivalued functions involved (as in the velocity ) as:
where and are the constants to be determined [31,32,33]. Now using definitions given in Equations (27)–(29), we define Laplace and inverse Laplace transforms of and as:
The solution of model Equation (23) in the transformed domain s after implementing ICs and BCs, we get the following result:
Afterwards, implementing inverse Laplace transform with the help of Equation (28), results in the form of subsequent equation:
with
where Heaviside function is denoted by F.
Now, putting the value of (c.f. Equation (32)) into Equation (36) leads us to the subsequent equation:
where
As the velocity field contains the multivalued functions in terms of constants and , therefore we apply the Gaver-Stehfest method described in [31,32,33] to evaluate the inverse Laplace transform of which results in a series solution of the form:
The shear stress on the wall and local Nusselt number is derived and presented as follows:
where
and is given below:
In this study, one dimensional unsteady flow problem was taken into account for which the advection term becomes zero. The advection term can be considered in the two dimensional problem, which makes the problem nonlinear and the Laplace method cannot be applied.
4. Limiting Models
This section contains two limiting cases:
4.1. Case 1
The velocity and temperature profiles of Oldroyd-B fluid for constant wall velocity and constant wall temperature (isothermal) are as follows:
where
4.2. Case 2
The results of Maxwell model can be deduced when and the viscous fluid flow with ramped wall temperature can be obtained when [34,35].
5. Results and Discussion
The present section comprises of solution profiles considering different parameter values, such as, Prandtl number (Pr), Grashof number (Gr), magnetic parameter (M), porosity (K), relaxation time , and dimensionless time (t). The numerical results are divided into two main categories: (1) Oldroyd-B fluid model with ramped wall temperature and ramped wall velocity and (2) Oldroyd-B fluid model with constant temperature at wall and ramped wall velocity. In the numerical results, the solid line is used for Oldroyd-B model considering ramped temperature profiles and velocity conditions, while the dashed lines are used for Oldroyd-B model with constant temperature and ramped velocity conditions. Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10 are produced by using the software “Wolfram Mathematica 9.0” (Wolfram Research, Champaign, IL, USA).
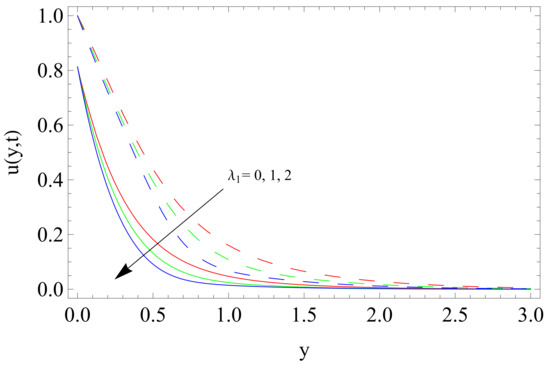
Figure 2.
Influence of relaxation time on velocity profile u.
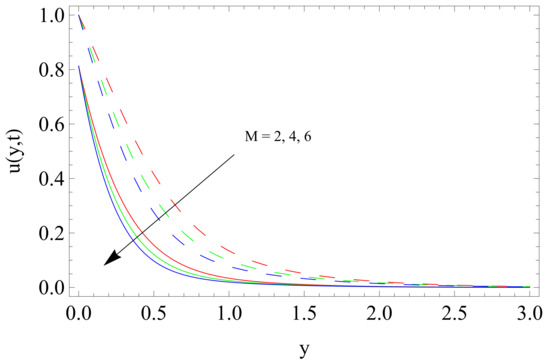
Figure 3.
Influence of magnetic parameter M on velocity profile u.
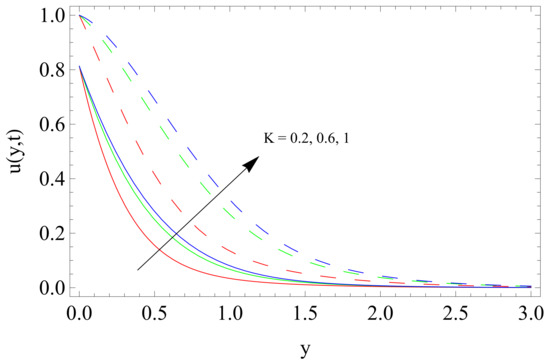
Figure 4.
Influence of porosity K on velocity u.
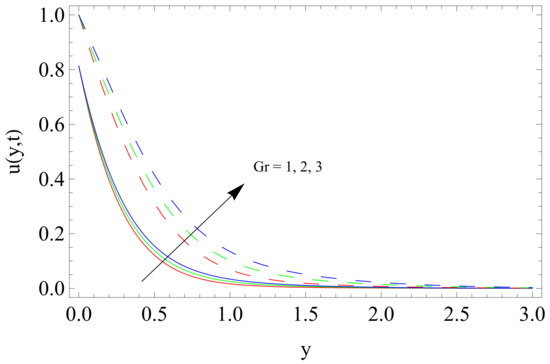
Figure 5.
Influence of Grashof number Gr on velocity u.
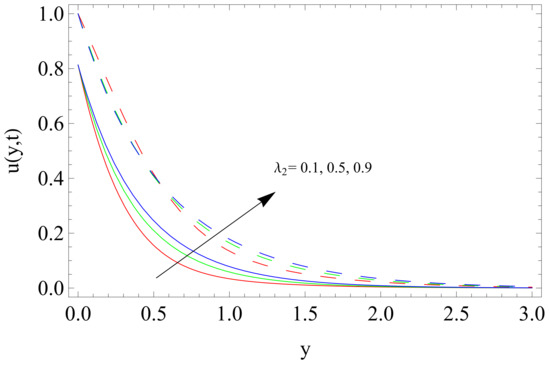
Figure 6.
Influence of retardation time on velocity u.
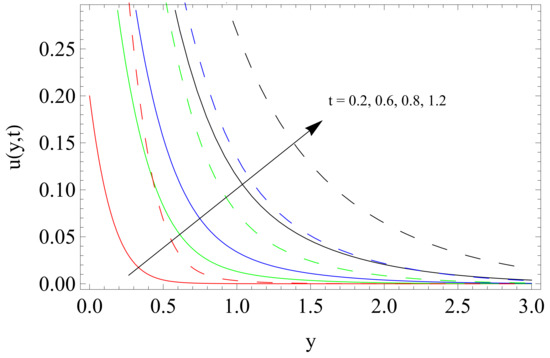
Figure 7.
Influence of time t on velocity u.
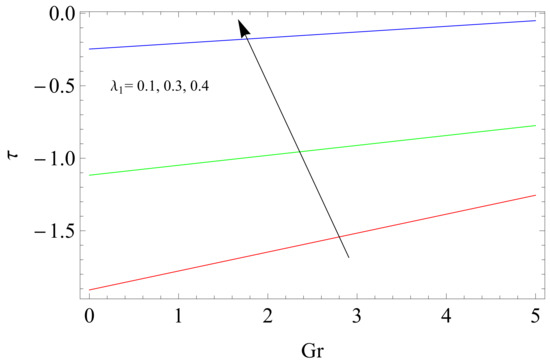
Figure 8.
The graphs of shear stress on the wall Gr for different values of the .
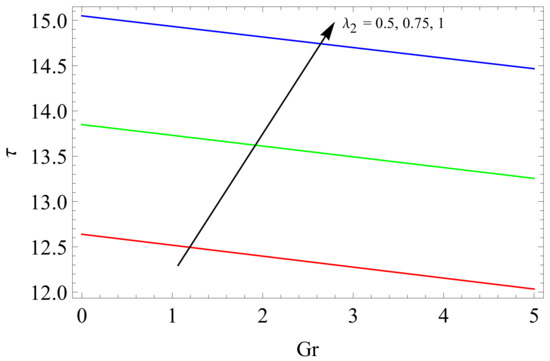
Figure 9.
The graphs of shear stress on the wall Gr for various values of the .
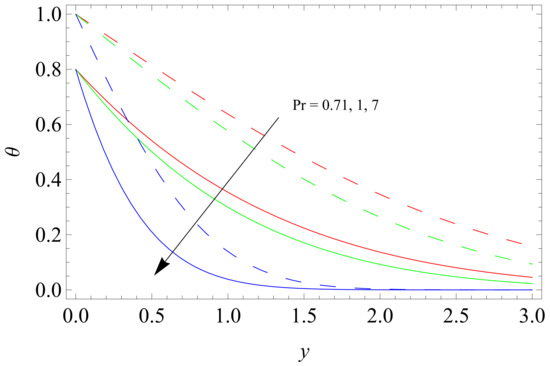
Figure 10.
Influence of Pr on temperature profile.
The impact of time on velocity distribution is shown in Figure 2. It is found that by increasing relaxation time , velocity profile decreases as relaxation time causes the thickness of momentum boundary layer. Moreover, the velocity becomes slower for non-isothermal plate than the isothermal one.
The effect of M on the velocity for isothermal plate and ramped temperature is illustrated in Figure 3. Figure 3 depicts that the velocity reduces as the value of M increases because of the Lorentz force which occurs due to imposed magnetic field on an electrically conducting fluid. Consequently, a drag force is produced and fluid motion is retarded and Lorentz force along with other forces becomes weaker therefore the fluid gradually calmed.
The variation in K is shown in Figure 4. The change in parameter K brings acceleration in the velocity field for both the conditions, ramped temperature and isothermal one. It is found that the drag force reduces when permeability of mushy (porous) medium increases, thus, velocity is accelerated in both cases. Moreover, the velocity is higher for the isothermal case as compared to ramped temperature condition.
The effects of Gr for both thermal and isothermal conditions are illustrated in Figure 5. Physically, Gr accounts for the weight of thermal buoyancy force to viscous force. The buoyancy forces increase near the plate and decrease far from the plate with an increase in Gr. Thus, the buoyancy forces with allied forces get weaker and fluid, far from the plate, on free stream surface achieves zero velocity.
Figure 6 shows the results of retardation time on the velocity for both thermal and isothermal conditions. It is found that the flow is accelerated due to the retardation time for both cases. Figure 6 illustrate that the velocity is increased when time is increased for both the cases.
Figure 7 presents the effects of time t (dimensionless) considering both isothermal conditions and ramped temperature on the solution .
Figure 8 shows the relationship between shear stress on the wall and Gr under the influence of relaxation time . The increase in brings decrease in magnitude of the . Internal friction is significantly decreased owing to small viscosity. Figure 9 illustrates that retardation time causes the shear stress on the wall to increase. Figure 10 shows the effects of Prandtl numbers Pr on the temperature profile. It is observed that the temperature profile decreases as Pr increases because the moving fluid gets less heat transfer from the solid plate as Pr increases from 0.7 to 7.
6. Conclusions
The MHD convective fluid flow of Oldroyd-B model is solved analytically subject to ramped velocity and temperature (at wall) simultaneously. The results of the considered model subject to ramped temperature are compared with the isothermal model in a porous medium. It is worthwhile mentioning that the simultaneous use of both the conditions (ramped velocity and ramped temperature), which was the main focus of this study, is limited in the literature though both the conditions are physically important. The solution of the Oldroyd-B fluid model, considering ramped velocity and ramped temperature at the same time, is mathematically difficult. We used Laplace transformation and the Gaver-Stehfest method to solve the model problem. The parametric study is performed and presented graphically and discussed.
Important findings are as follows:
- An increase in the magnetic parameter (M) on velocity causes decrease in the thickness of the momentum boundary layer.Momentum boundary layer increases as parameters values such as, , K, Gr and increase.
- An increase in relaxation time results in a decrease in velocity (related to skin friction) on the plate.
- Rate of heat transfer (related to Nusselt numbers Nu) increases when thermal diffusivity related to Pr number increases. For lower Prandtl numbers Pr, the fluid has higher thermal conductivity whereas higher Pr numbers cause resistance in the transfer of heat into the fluid (see [36,37,38]).
Author Contributions
Conceptualization, M.H.T., A.B.M. and K.M.; methodology, M.H.T., A.B.M., K.M. and S.J.; software, K.M. and S.J; validation, M.R., K.M.; formal analysis, A.B.M. and K.M.; resources, M.R., S.R. and M.S.K.; writing—original draft preparation, K.M., S.J.; writing—review and editing, M.R., S.J., S.R. and M.S.K.; project administration, S.J.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| B | Total magnetic field |
| J | Current density |
| E | Electric field |
| T | Cauchy Stress Tensor |
| r | Darcy resistance vector |
| S | Extra Stress tensor |
| A1 | Rivlin-Erickson tensor |
| Velocity components | |
| Space variables | |
| T | Temperature |
| p | Pressure |
| g | Acceleration due to gravity |
| Fluid density | |
| Magnetic permeability | |
| Electrical conductivity of the fluid | |
| Porosity parameter | |
| Viscosity of the fluid | |
| Relaxation, retardation times | |
| Non-dimensional velocity | |
| Non-dimensional time | |
| Non-dimensional temperature | |
| M | Hartmann Number |
| K | Non-dimensional porosity parameter |
| Non-dimensional relaxation & retardation times | |
| Gr | Grashof’s number |
| Pr | Prandtl’s Number |
| Laplace transform operator | |
| s | Laplace transform parameter |
References
- Khan, M. Partial slip effects on the oscillatory flows of a fractional Jeffery fluid in a porous medium. J. Porous Media 2007, 10, 473–487. [Google Scholar] [CrossRef]
- Ghosh, A.K.; Sana, P. On hydromagnetic flow of an Oldroyd-B fluid near a pulsating plate. Acta Astronaut. 2009, 64, 272–280. [Google Scholar] [CrossRef]
- Nadeem, S.; Mehmood, R.; Akbar, N.S. Non-orthogonal stagnation point flow of a nano non-Newtonian fluid towards a stretching surface with heat transfer. Int. J. Heat Mass Transf. 2013, 57, 679–689. [Google Scholar] [CrossRef]
- Nadeem, S.; Saleem, S. Analytical study of third grade fluid over a rotating vertical cone in the presence of nanoparticles. Int. J. Heat Mass Transf. 2015, 85, 1041–1048. [Google Scholar] [CrossRef]
- Sharmilaa, K.; Kaleeswari, S. Dufour effects on unsteady free convection and mass transfer through a porous medium in a slip regime with heat source/sink. Int. J. Sci. Eng. Appl. Sci. (IJSEAS) 2015, 1, 307–320. [Google Scholar]
- Geindreau, C.; Auriault, J.-L. Magnetohydrodynamic flows in porous media. J. Fluid Mech. 2002, 466, 343–363. [Google Scholar] [CrossRef]
- Sobral Filho, D.C. A new proposal to guide velocity and inclination in the ramp protocol for the Treadmill Ergometer. Arq. Bras. Cardiol. 2003, 81, 48–53. [Google Scholar]
- Bruce, R.A. Evaluation of functional capacity and exercise tolerance of cardiac patients. Mod. Concepts Cardiovasc. Dis. 1956, 25, 321–326. [Google Scholar]
- Ästrand, P.O.; Rodahl, K. Avaliação da capacidade de trabalho físico na base dos testes. In Tratado de Fisiologia do Exercício, 2nd ed.; Interamericana: Rio de Janeiro, Brazil, 1977; pp. 304–336. [Google Scholar]
- Myers, J.; Bellin, D. Ramp exercise protocol for clinical and cardiopulmonary exercise testing. Sports Med. 2000, 30, 23–29. [Google Scholar] [CrossRef] [PubMed]
- Hayday, A.A.; Bowlus, D.A.; McGraw, R.A. Free convection from a vertical flat plate with step discontinuities in surface temperature. J. Heat Transf. 1967, 89, 244–249. [Google Scholar] [CrossRef]
- Schetz, J.A. On the approximate solution of viscous flow problems. ASME J. Appl. Mech. 1963, 30, 263–268. [Google Scholar] [CrossRef]
- Malhotra, C.P.; Mahajan, R.L.; Sampath, W.S.; Barth, K.L.; Enzenroth, R.A. Control of temperature uniformity during the manufacture of stable thin-film photovoltaic devices. Int. J. Heat Mass Transf. 2006, 49, 2840–2850. [Google Scholar] [CrossRef]
- Kundu, B. Exact analysis for propagation of heat in a biological tissue subject to different surface conditions for therapeutic applications. Appl. Math. Comput. 2016, 285, 204–216. [Google Scholar] [CrossRef]
- Seth, G.S.; Hussain, S.M.; Sarkar, S. Hydromagnetic natural convection flow with heat and mass transfer of a chemically reacting and heat absorbing fluid past an accelerated moving vertical plate with ramped temperature and ramped surface concentration through a porous medium. J. Egypt. Math. Soc. 2015, 23, 197–207. [Google Scholar] [CrossRef]
- Seth, G.S.; Sharma, R.; Sarkar, S. Natural convection heat and mass transfer flow with Hall current, rotation, radiation and heat absorption past an accelerated moving vertical plate with ramped temperature. J. Appl. Fluid Mech. 2015, 8, 7–20. [Google Scholar]
- Seth, G.S.; Sarkar, S.; Hussain, S.M.; Mahato, G.K. Effects of hall current and rotation on hydromagnetic natural convection flow with heat and mass transfer of a heat absorbing fluid past an impulsively moving vertical plate with ramped temperature. J. Appl. Fluid Mech. 2015, 8, 159–171. [Google Scholar]
- Seth, G.S.; Sarkar, S. MHD natural convection heat and mass transfer flow past a time dependent moving vertical plate with ramped temperature in a rotating medium with hall effects, radiation and chemical reaction. J. Mech. 2015, 31, 91–104. [Google Scholar] [CrossRef]
- Seth, G.S.; Sarkar, S. Hydromagnetic natural convection flow with induced magnetic field and nth order chemical reaction of a heat absorbing fluid past an impulsively moving vertical plate with ramped temperature. Bulg. Chem. Commun. 2015, 47, 66–79. [Google Scholar]
- Chandran, P.; Sacheti, N.C.; Singh, A.K. Natural convection near a vertical plate with ramped wall temperature. Heat Mass Transf. 2005, 41, 459–464. [Google Scholar] [CrossRef]
- Seth, G.S.; Ansari, M.S. MHD natural convection flow past an impulsively moving vertical plate with ramped wall temperature in the presence of thermal diffusion with heat absorption. Int. J. Appl. Mech. Eng. 2010, 15, 199–215. [Google Scholar]
- Das, S.; Jana, M.; Jana, R.N. Radiation effect on natural convection near a vertical plate embedded in a porous medium with ramped wall temperature. Open J. Fl. Dyn. 2011, 1, 1. [Google Scholar] [CrossRef][Green Version]
- Nandkeolyar, R.; Das, M.; Sibanda, P. Exact solutions of unsteady MHD free convection in a heat absorbing fluid flow past a flat plate with ramped wall temperature. Bound. Value Probl. 2013, 2013, 247. [Google Scholar] [CrossRef]
- Zin, N.A.B.M.; Khan, I.; Shafie, S. Influence of thermal radiation on unsteady MHD free convection flow of Jeffrey fluid over a vertical plate with ramped wall temperature. Math. Probl. Eng. 2016. [Google Scholar] [CrossRef]
- Ahmed, N.; Dutta, M. Transient mass transfer flow past an impulsively started infinite vertical plate with ramped plate velocity and ramped temperature. Int. J. Phys. Sci. 2013, 8, 254–263. [Google Scholar]
- Maqbool, K.; Mann, A.B.; Tiwana, M.H. Unsteady MHD convective flow of a Jeffery fluid embedded in a porous medium with ramped wall velocity and temperature. Alex. Eng. J. 2018, 57, 1071–1078. [Google Scholar] [CrossRef]
- Hayat, T.; Siddiqui, A.M.; Asghar, S. Some simple flows of an Oldroyd-B fluid. Int. J. Eng. Sci. 2001, 39, 135–147. [Google Scholar] [CrossRef]
- Asghar, S.; Parveen, S.; Hanif, S.; Siddiqui, A.M.; Hayat, T. Hall effects on the unsteady hydromagnetic flows of an Oldroyd-B fluid. Int. J. Eng. Sci. 2003, 41, 609–619. [Google Scholar] [CrossRef]
- Rajagopal, K.R.; Ruzicka, M.; Srinivasa, A.R. On the Oberbeck-Boussinesq approximation. Math. Mod. Methods Appl. Sci. 1996, 6, 1157–1167. [Google Scholar] [CrossRef]
- Wilbur, R. Lepage. In Complex Variables and the Laplace Transform for Engineers; McGraw Hill Book Company: New York, NY, USA, 1961. [Google Scholar]
- Knight, J.H.; Raiche, A.P. Transient electromagnetic calculations using the Gaver-Stehfest inverse Laplace transform method. Geophysics 1982, 47, 47–50. [Google Scholar] [CrossRef]
- Zakian, V. Numerical inversion of Laplace transform. Electr. Lett. 1969, 5, 120–121. [Google Scholar] [CrossRef]
- Kenny, S. Crump, Numerical inversion of Laplace transforms using a Fourier series approximation. J. Assoc. Comput. Mach. 1976, 23, 89–96. [Google Scholar]
- Khan, A.; Khan, I.; Ali, F. Sami ulhaq and S. Shafie, Effects of wall shear stress on unsteady MHD conjugate flow in a porous medium with ramped wall temperature. PLoS ONE 2014, 9, e90280. [Google Scholar]
- Seth, G.S.; Nandkeolyar, R.; Ansari, M.S. Effect of rotation on unsteady hydromagnetic natural convection flow past an impulsively moving vertical plate with ramped temperature in a porous medium with thermal diffusion and heat absorption. Int. J. Appl. Math. Mech. 2011, 7, 52–69. [Google Scholar]
- Gargano, F.; Ponetti, G.; Sammartino, M.; Sciacca, V. Route to chaos in the weakly stratified Kolmogorov flow. Phys. Fluids 2019, 31, 024106. [Google Scholar] [CrossRef]
- Balmforth, N.J.; Young, Y.N. Stratified Kolmogorov flow. J. Fluid Mech. 2002, 450, 131–167. [Google Scholar] [CrossRef]
- Vadasz, P.; Olek, S. Route to Chaos for Moderate Prandtl Number Convection in a Porous Layer Heated from Below. Transp. Porous Med. 2000, 41, 211–239. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).