Child Development Influence Environmental Factors Determined Using Spherical Fuzzy Distance Measures

Abstract

This paper aims to resolve the issue of the ranking of the fuzzy numbers in decision analysis, artificial intelligence, and optimization. In the literature, many ideas have been established for the ranking of the fuzzy numbers, and those ideas have some restrictions and limitations. We propose a method based on spherical fuzzy numbers (SFNs) for ranking to overcome the existing restrictions. Further, we investigate the basic properties of SFNs, compare the idea of spherical fuzzy set with the picture fuzzy set, and establish some distance operators, namely spherical fuzzy distance-weighted averaging (SFDWA), spherical fuzzy distance order-weighted averaging (SFDOWA), and spherical fuzzy distance order-weighted average weighted averaging (SFDOWA WA) operators with the attribute weights’ information incompletely described. Further, we design an algorithm to solve decision analysis problems. Finally, to validate the usage and applicability of the established procedure, we assume the child development influence environmental factors problem as a practical application.

1. Introduction

In the actual decision-making environment, it is of great importance to derive exact assessment information. However, due to the indeterminacy of the practical environment, we can not always achieve this goal. Then, to overcome this limitation, the concept of the fuzzy set (FS) [1] was defined. The FS is mainly characterized by the degree of membership and can provide more reasonable decision-making information. After their prosperous and successful applications, Atanassov [2] generalized this concept and improved the notion of FS as the intuitionistic fuzzy set (IFS), in which each element can be written in the form of an ordered pair. Under this situation, many scholars have paid more attention to IFSs to aggregate the different options using different methods and operators. Yager [3] proposed the order-weighted averaging (OWA) operator to aggregate the IFNs. In [4], Xu and Yager explored the idea of geometric and order geometric operators of IFNs and also developed their application for selecting the best options in daily life problems. In [5], Xu explored the idea of the weighed averaging operator based on IFNs. In [6,7], Wang and Liu explored the notion of many operators such as the intuitionistic fuzzy Einstein weighted geometric operator, order weighted geometric operator, weighted averaging operator, and order weighted averaging operator based on the Einstein operations and applied these operators to decision-making problems.

After many applications of IFSs, Yager observed that there are many shortcomings in this theory and introduced the notion of the Pythagorean fuzzy set (PyFS) [8] to generalize the concept of the Atanassov IFS. Many researchers contributed to PyFS by proposing different techniques for decision-making problems to deal with uncertainties. Khan et al. [9] proposed the Pythagorean fuzzy Dombi aggregation operators and discussed their applications. Zhang and Xu [10] proposed the TOPSIS method for PyFS information to deal with uncertainty in the form of the Pythagorean fuzzy set. Yager and Abbasov [11] established Pythagorean fuzzy aggregation operators and proposed their application in multi-attribute decision-making problems. For more study of decision-making techniques, we refer to [12,13,14].

The picture fuzzy set (PFS), as an extension of the intuitionistic fuzzy set, was firstly proposed by Cuong [15]. After that, in order to solve multi-criteria group decision-making (MCGDM) problems, it was proposed to use the picture fuzzy information. With regard to measurement, Singh et al. developed the approach with picture fuzzy correlation coefficients [16], Wei et al. [17] introduced a novel method to solve MCGDM voting problems using cross-entropy of the picture fuzzy set. As for the aggregation operators, Wei et al. [18] used the picture two-tuple linguistic-based operators, including the Bonferroni mean operator, the weighted averaging operator, and the ordered weighted averaging operator. In [19], a series of aggregation operators was proposed to aggregate the picture fuzzy information and to solve the MCGDM issues well. Ashraf et al. [20] developed the picture linguistic fuzzy set and discussed its application in decision-making problems. For more study of the decision-making techniques using picture fuzzy information, we refer to [21,22,23,24,25].

Cuong’s PFS possessed the same problem as IFS had, i.e., it bounds the sum of positive membership, neutral membership, and negative membership grades between zero and one. This restriction does not allow decision makers to select the values of the three characteristic functions. Realizing this issue, Ashraf and Abdullah [26] developed a new model of the spherical fuzzy set (SFS). It basically bounds the square sum of positive, neutral, and negative membership grades between zero and one. Ashraf et al. [27] developed the aggregation operators to aggregate the uncertainty in the form of spherical fuzzy information and proposed the GRAmethod [28] to deal the decision-making problems. Ashraf et al. [29] developed the spherical fuzzy measure on the basis of the cosine and tangent function and a proposed related application in decision making. Rafiq et al. [30] proposed the spherical fuzz set representation on the basis of the t-norm and the t-conorm. Zeng et al. [31] proposed the spherical fuzzy rough set model and discussed its application using the TOPSIS approach. Ashraf et al. [32] introduced the spherical fuzzy Dombi aggregation operators and their applications. Jin et al. [33] proposed the spherical fuzzy logarithmic aggregation operators based on entropy and gave some applications related to decision support systems. In [34], Jin et al. proposed the linguistic spherical fuzzy set and discussed its applications in decision making.

From the previous studies, we see that the use of spherical fuzzy set is growing well and that it is effective in decision-making problems. In this paper, we propose the spherical distance measure on the basis of distance operators. The main contributions of this paper are as follows:

Firstly, based on the concept of the spherical fuzzy set, a spherical fuzzy measure is defined.

Secondly, utilizing the concept of the proposed spherical distance measure, the spherical fuzzy distance aggregation operators are introduced to deal the uncertainty and inaccurate information in decision making problems in the form of a spherical fuzzy set.

Thirdly, we propose an algorithm using spherical distance measures to deal with decision-making problems.

Fourthly, to show the effectiveness and reliability of the proposed technique, a real-life problem of the child development influence environmental factors is demonstrated.

The rest of this study is organized as follows. Section 2 briefly introduces the basic knowledge about the extension of fuzzy sets. In Section 3, the distance measure of SFSs is proposed. Four phases, like calculating the overall criteria weights and establishing difference techniques, are included. In Section 4, the detailed evaluation procedures of the proposed method are exemplified by a case study after the evaluation criteria system is built. Section 5 gives some discussions on the application of the proposed method, and essential conclusions are drawn in Section 6. The paper structure is shown in Figure 1.

Figure 1. Paper structure.

2. Preliminaries

We assume that the reader is familiar with the classical results of fuzzy algebras, but to make this work more self-contained, we introduce the basic notations used in the text and briefly mention some of the concepts and results employed in the rest of the work.

Definition 1

([35]). A mapping $OWA:{\mathbb{R}}^n\to \mathbb{R}$ with weighted vectors $\tau ={\left({\tau }_1,{\tau }_2,\dots ,{\tau }_n\right)}^T$ such that:

$$OWA\left(E_1,E_2,\dots E_n\right)=\sum _{p=1}^n{\tau }_p{E}_p$$

where $E_p$ is the $p^{\mathrm{th}}$ largest distance of $E_n$ with ${\tau }_p\in \left[0,1\right],{\displaystyle \sum _{p=1}^n}{\tau }_p=1.$ The OWA operator satisfies the commutation, monotonicity, boundedness, and idempotency properties.

Definition 2

([35]). An order-weighted averaging distance mapping $OWAD:{\mathbb{R}}^n\times {\mathbb{R}}^n\to \mathbb{R}$ with weighted vectors $\tau ={\left({\tau }_1,{\tau }_2,\dots ,{\tau }_n\right)}^T$ such that:

$$OWAD\left(⟨P_1,Q_1⟩,⟨P_2,Q_2⟩,\dots ,⟨P_n,Q_n⟩\right)=\sum _{p=1}^n{\tau }_p{E}_p$$

where $E_p$ is the $p^{\mathrm{th}}$ largest distance of $⟨P_n,Q_n⟩$ with ${\tau }_p\in \left[0,1\right],{\displaystyle \sum _{p=1}^n}{\tau }_p=1.$ The OWAD operator satisfies the commutation, monotonicity, boundedness, and idempotency properties.

Definition 3

([35]). An order weighted distance measure mapping $OWDM:{\mathbb{R}}^n\times {\mathbb{R}}^n\to \mathbb{R}$ with weighted vectors $\tau ={\left({\tau }_1,{\tau }_2,\dots ,{\tau }_n\right)}^T$ such that:

$$OWDM\left(⟨P_1,Q_1⟩,⟨P_2,Q_2⟩,\dots ,⟨P_n,Q_n⟩\right)={\left(\sum _{p=1}^n{\tau }_p{\left(E\left(P_{\delta \left(p\right)},Q_{\delta \left(p\right)}\right)\right)}^{\lambda }\right)}^{\frac{1}{\lambda }},\lambda >0$$

where $E\left(P_n,Q_n\right)$ is the distance of $⟨P_n,Q_n⟩$ with ${\tau }_p\in \left[0,1\right],{\displaystyle \sum _{p=1}^n}{\tau }_p=1$ and $(\delta \left(1\right),\delta \left(2\right),\dots ,\delta \left(n\right))$ is any permutation of $\left(1,2,\dots ,n\right)$, such that $E\left(P_{\delta \left(p-1\right)},Q_{\delta \left(p-1\right)}\right)\ge E\left(P_{\delta \left(p\right)},Q_{\delta \left(p\right)}\right),$ $p=2,3,\dots ,n.$

Definition 4

([1]). A fuzzy set (FS) ${\breve{E}}_j$ on the universe of discourse $\mathbb{R}\ne \varphi$ is defined as:

$${\breve{E}}_j=\left\{⟨r,P_{{\breve{E}}_j}\left(r\right)|r\in \mathbb{R}⟩\right\}.$$

An FS in a set $\mathbb{R}$ is indicated by $P_{{\breve{E}}_j}:\mathbb{R}\to \left[0,1\right].$ The function $P_{{\breve{E}}_j}\left(r\right)$ indicates the positive membership degree of each $r\in$ $\mathbb{R}.$

Definition 5

([2]). An intuitionistic fuzzy set (IFS) ${\breve{E}}_j$ on the universe of discourse $\mathbb{R}\ne \varphi$ is defined as:

$${\breve{E}}_j=\left\{⟨r,P_{{\breve{E}}_j}\left(r\right),N_{{\breve{E}}_j}\left(r\right)|r\in \mathbb{R}⟩\right\}.$$

An IFS in a set $\mathbb{R}$ is indicated by $P_{{\breve{E}}_j}:\mathbb{R}\to \left[0,1\right]$ and $N_{{\breve{E}}_j}:\mathbb{R}\to \left[0,1\right].$ The functions $P_{{\breve{E}}_j}\left(r\right)$ and $N_{{\breve{E}}_j}\left(r\right)$ indicate the positive and the negative membership degrees of each $r\in$ $\mathbb{R},$ respectively. Furthermore, $P_{{\breve{E}}_j}$ and $N_{{\breve{E}}_j}$ satisfy $0\le P_{{\breve{E}}_j}\left(r\right)+N_{{\breve{E}}_j}\left(r\right)\le 1,$ for all $r\in \mathbb{R}.$

Definition 6

([3]). A Pythagorean fuzzy set (PyFS) ${\breve{E}}_j$ on the universe of discourse $\mathbb{R}\ne \varphi$ is defined as:

$${\breve{E}}_j=\left\{⟨r,P_{{\breve{E}}_j}\left(r\right),N_{{\breve{E}}_j}\left(r\right)|r\in \mathbb{R}⟩\right\}.$$

A PyFS in a set $\mathbb{R}$ is indicated by $P_{{\breve{E}}_j}:\mathbb{R}\to [0,1]$ and $N_{{\breve{E}}_j}:\mathbb{R}\to [0,1]$ are the positive and negative membership degrees of each $r\in \mathbb{R}$, respectively. Furthermore, $P_{{\breve{E}}_j}$ and $N_{{\breve{E}}_j}$ satisfy $0\le P_{{\breve{E}}_j}^2\left(r\right)+N_{{\breve{E}}_j}^2\left(r\right)\le 1$ for all $r\in \mathbb{R}.$

Definition 7

([15]). A PFS ${\breve{E}}_j$ on the universe of discourse $\mathbb{R}\ne \varphi$ is defined as:

$${\breve{E}}_j=\left\{⟨r,P_{{\breve{E}}_j}\left(r\right),I_{{\breve{E}}_j}\left(r\right),N_{{\breve{E}}_j}\left(r\right)|r\in \mathbb{R}⟩\right\}.$$

A PFS in a set $\mathbb{R}$ is indicated by $P_{{\breve{E}}_j}:\mathbb{R}\to [0,1]$, $I_{{\breve{E}}_j}:\mathbb{R}\to [0,1]$, and $N_{{\breve{E}}_j}:\mathbb{R}\to [0,1]$ are the positive, neutral, and negative membership degrees of each $r\in \mathbb{R}$, respectively. Furthermore, $P_{{\breve{E}}_j}$, $I_{{\breve{E}}_j}$ and $N_{{\breve{E}}_j}$ satisfy $0\le P_{{\breve{E}}_j}\left(r\right)+I_{{\breve{E}}_j}\left(r\right)+N_{{\breve{E}}_j}\left(r\right)\le 1$ for all $r\in \mathbb{R}.$

Cuong in 2014 [15] introduced the distance of two picture fuzzy numbers (PFNs), which are discussed here:

Definition 8

([15]). For a set F and any two PFNs ${\breve{E}}_{{\breve{u}}_j},{\breve{E}}_{{\breve{u}}_l}$ in F. The normalized Hamming distance $d_{NHD}({\breve{E}}_{{\breve{u}}_j},{\breve{E}}_{{\breve{u}}_l})$ is given as, for all $r_{⋎}\in F$,

$$d_{NHD}({\breve{E}}_{{\breve{u}}_j},{\breve{E}}_{{\breve{u}}_l})=\frac{1}{n}\sum _{p=1}^n\left(\begin{array}{c}\left|P_{{}_{{\check{e}}_{{\breve{u}}_j}}}\left(r_p\right)-P_{{\check{e}}_{{\breve{u}}_l}}\left(r_p\right)\right|+\left|I_{{\check{e}}_{{\breve{u}}_j}}\left(r_p\right)-I_{{\check{e}}_{{\breve{u}}_l}}\left(r_p\right)\right|+\\ \left|N_{{\check{e}}_{{\breve{u}}_j}}\left(r_p\right)-N_{{\check{e}}_{{\breve{u}}_l}}\left(r_p\right)\right|\end{array}\right).$$

Definition 9

([15]). For a set F and any two PFNs ${\breve{E}}_{{\breve{u}}_j},{\breve{E}}_{{\breve{u}}_l}$ in F. The normalized Euclidean distance $d_{NED}({\breve{E}}_{{\breve{u}}_j},{\breve{E}}_{{\breve{u}}_l})$ is given as, for all $r_{⋎}\in F$,

$$\begin{array}{ccc}\hfill d_{NED}({\breve{E}}_{{\breve{u}}_j},{\breve{E}}_{{\breve{u}}_l})& =& \sqrt{\frac{1}{n}\sum _{p=1}^n\left(\begin{array}{c}{\left(P_{{}_{{\check{e}}_{{\breve{u}}_j}}}\left(r_p\right)-P_{{\check{e}}_{{\breve{u}}_l}}\left(r_p\right)\right)}^2+{\left(I_{{\check{e}}_{{\breve{u}}_j}}\left(r_p\right)-I_{{\check{e}}_{{\breve{u}}_{\mathrm{l}}}}\left(r_p\right)\right)}^2+\\ {\left(N_{{\check{e}}_{{\breve{u}}_j}}\left(r_p\right)-N_{{\check{e}}_{{\breve{u}}_l}}\left(r_p\right)\right)}^2\end{array}\right)}.\hfill \end{array}$$

Definition 10

([26]). A SFS ${\breve{E}}_j$ on the universe of discourse $\mathbb{R}\ne \varphi$ is defined as:

$${\breve{E}}_j=\left\{⟨r,P_{{\breve{E}}_j}\left(r\right),I_{{\breve{E}}_j}\left(r\right),N_{{\breve{E}}_j}\left(r\right)|r\in \mathbb{R}⟩\right\}.$$

An SFS in a set $\mathbb{R}$ is indicated by $P_{{\breve{E}}_j}:\mathbb{R}\to [0,1]$, $I_{{\breve{E}}_j}:\mathbb{R}\to [0,1]$, and $N_{{\breve{E}}_j}:\mathbb{R}\to [0,1]$ are the positive, neutral, and negative membership degrees of each $r\in \mathbb{R}$, respectively. Furthermore, $P_{{\breve{E}}_j}$, $I_{{\breve{E}}_j}$ and $N_{{\breve{E}}_j}$ satisfy $0\le P_{{\breve{E}}_j}^2\left(r\right)+I_{{\breve{E}}_j}^2\left(r\right)+N_{{\breve{E}}_j}^2\left(r\right)\le 1$ for all $r\in \mathbb{R}.$

${\chi }_A\left(r\right)=\sqrt{1-\left(P_{{\breve{E}}_j}^2\left(r\right)+I_{{\breve{E}}_j}^2\left(r\right)+N_{{\breve{E}}_j}^2\left(r\right)\right)}$ is said to be the refusal degree of r in $\mathbb{R}$, for SFS $\left\{⟨r,P_{{\breve{E}}_j},I_{{\breve{E}}_j},N_{{\breve{E}}_j}|r\in \mathbb{R}⟩\right\}$, for which triple components $⟨P_{{\breve{E}}_j},I_{{\breve{E}}_j},N_{{\breve{E}}_j}⟩$ are said to be SFN, and each SFN can be denoted by $E=⟨P_e,I_e,N_e⟩$, where $P_e,I_e$ and $N_e\in [0,1]$, with the condition that $0\le P_e^2+I_e^2+N_e^2\le 1.$

Definition 11.

Let ${\breve{E}}_j=⟨P_{{\breve{E}}_j},I_{{\breve{E}}_j},N_{{\breve{E}}_j}⟩$ and ${\breve{E}}_k=⟨P_{{\breve{E}}_k},I_{{\breve{E}}_k},N_{{\breve{E}}_k}⟩$ be two SFNs defined on the universe of discourse $\mathbb{R}\ne \varphi$; some operations on SFNs are defined as follows:

(1) 

${\breve{E}}_j\subseteq {\breve{E}}_k$$iff$$\forall r\in R,$

$$P_{{\breve{E}}_j}\le P_{{\breve{E}}_k},I_{{\breve{E}}_j}\le I_{{\breve{E}}_k}and{N}_{{\breve{E}}_j}\ge N_{{\breve{E}}_k};$$

(2) 

${\breve{E}}_j={\breve{E}}_k$$iff$:

$${\breve{E}}_j\subseteq {\breve{E}}_{k}and{E}_k\subseteq {\breve{E}}_j;$$

(2) 

Union:

$${\breve{E}}_j\cup {\breve{E}}_k=⟨max\left(P_{{\breve{E}}_j},P_{{\breve{E}}_k}\right),min\left(I_{{\breve{E}}_j},I_{{\breve{E}}_k}\right),min\left(N_{{\breve{E}}_j},N_{{\breve{E}}_k}\right)⟩;$$

(4) 

Intersection:

$${\breve{E}}_j\cap {\breve{E}}_k=⟨min\left(P_{{\breve{E}}_j},P_{{\breve{E}}_k}\right),min\left(I_{{\breve{E}}_j},I_{{\breve{E}}_k}\right),max\left(N_{{\breve{E}}_j},N_{{\breve{E}}_k}\right)⟩;$$

(5) 

Compliment:

$${\breve{E}}_j^c=⟨N_{{\breve{E}}_j},I_{{\breve{E}}_j},P_{{\breve{E}}_j}⟩.$$

Proposition 1.

Assume that ${\breve{E}}_j,{\breve{E}}_k$, and ${\breve{E}}_l$ are any three SFNs on the universe of discourse $\mathbb{R}\ne \varphi$. Then, the following properties are satisfied:

(1) 

Associativity:

$$\begin{array}{ccc}\hfill {\breve{E}}_j\cap ({\breve{E}}_k\cap {\breve{E}}_k)& =& ({\breve{E}}_j\cap {\breve{E}}_k)\cap {\breve{E}}_k,\hfill \\ \hfill {\breve{E}}_j\cup ({\breve{E}}_k\cup {\breve{E}}_k)& =& ({\breve{E}}_j\cup {\breve{E}}_k)\cup {\breve{E}}_k\hfill \end{array}$$

(2) 

Commutativity:

$$\begin{array}{ccc}\hfill ({\breve{E}}_j\cap {\breve{E}}_k)& =& ({\breve{E}}_k\cap {\breve{E}}_j),\hfill \\ \hfill ({\breve{E}}_j\cup {\breve{E}}_k)& =& ({\breve{E}}_k\cup {\breve{E}}_j)\hfill \end{array}$$

(3) 

Distributivity:

$$\begin{array}{ccc}\hfill {\breve{E}}_j\cap ({\breve{E}}_k\cup {\breve{E}}_k)& =& ({\breve{E}}_j\cap {\breve{E}}_k)\cup ({\breve{E}}_j\cap {\breve{E}}_k),\hfill \\ \hfill {\breve{E}}_j\cup ({\breve{E}}_k\cap {\breve{E}}_k)& =& ({\breve{E}}_j\cup {\breve{E}}_k)\cap ({\breve{E}}_j\cup {\breve{E}}_k)\hfill \end{array}$$

(4) 

De Morgan laws:

$$\begin{array}{ccc}\hfill {({\breve{E}}_j\cap {\breve{E}}_k)}^{/}& =& {\breve{E}}_j\cup {\breve{E}}_k,\hfill \\ \hfill {({\breve{E}}_j\cup {\breve{E}}_k)}^{/}& =& {\breve{E}}_j\cap {\breve{E}}_k.\hfill \end{array}$$

Definition 12.

Let ${\breve{E}}_j=⟨P_{{\breve{E}}_j},I_{{\breve{E}}_j},N_{{\breve{E}}_j}⟩$ and ${\breve{E}}_k=⟨P_{{\breve{E}}_k},I_{{\breve{E}}_k},N_{{\breve{E}}_k}⟩$ be two SFNs defined on the universe of discourse $\mathbb{R}\ne \varphi$; some operations on SFNs are defined as follows with $\tau \ge 0.$

(1) 

${\breve{E}}_j\oplus {\breve{E}}_k=\left\{\sqrt{P_{{\breve{E}}_j}^2+P_{{\breve{E}}_k}^2-P_{{\breve{E}}_j}^2·P_{{\breve{E}}_k}^2},I_{{\breve{E}}_j}·I_{{\breve{E}}_k},N_{{\breve{E}}_j}·N_{{\breve{E}}_k}\right\}.$

(2) 

$\tau ·{\breve{E}}_j=\left\{\sqrt{1-{(1-P_{{\breve{E}}_j}^2)}^{\tau }},{(I_{{\breve{E}}_j})}^{\tau },{(N_{{\breve{E}}_j})}^{\tau }\right\}.$

Definition 13.

Let ${\breve{E}}_k=⟨P_{{\breve{E}}_k},I_{{\breve{E}}_k},N_{{\breve{E}}_k}⟩$ be any SFNs. Then:

(1) 

$sco({\breve{E}}_k)=\frac{\left(P_{{\breve{E}}_k}+1-I_{{\breve{E}}_k}+1-N_{{\breve{E}}_k}\right)}{3}=\frac{1}{3}(2+P_{{\breve{E}}_k}-I_{{\breve{E}}_k}-N_{{\breve{E}}_k})$, which is denoted as the score function.

(2) 

$acu({\breve{E}}_k)=P_{{\breve{E}}_k}-N_{{\breve{E}}_k}$, which is denoted as the accuracy function.

(3) 

$cr({\breve{E}}_k)=P_{{\breve{E}}_k}$, which is denoted as the certainty function.

The idea taken from Definition 13 is the technique used for equating the SFNs and can be described as:

Definition 14.

Assume that ${\breve{E}}_j=⟨P_{{\breve{E}}_j},I_{{\breve{E}}_j},N_{{\breve{E}}_j}⟩$ and ${\breve{E}}_k=⟨P_{{\breve{E}}_k},I_{{\breve{E}}_k},N_{{\breve{E}}_k}⟩$ are any two SFNs on the universe of discourse $\mathbb{R}\ne \varphi$. Then, by using the Definition 13, the equating technique can be described as,

(1) 

If $sco({\breve{E}}_j)\succ sco({\breve{E}}_j)$, then ${\breve{E}}_j\succ {\breve{E}}_j.$

(2) 

If $sco({\breve{E}}_j)\approx sco({\breve{E}}_j)$ and $acu({\breve{E}}_j)\succ acu({\breve{E}}_j)$, then ${\breve{E}}_j\succ {\breve{E}}_j.$

(3) 

If $sco({\breve{E}}_j)\approx sco({\breve{E}}_j),$ $acu({\breve{E}}_j)\approx acu({\breve{E}}_j)$ and $cr({\breve{E}}_j)\succ cr({\breve{E}}_j),$ then ${\breve{E}}_j\succ {\breve{E}}_j.$

(4) 

If $sco({\breve{E}}_j)\approx sco({\breve{E}}_j),$ $acu({\breve{E}}_j)\approx acu({\breve{E}}_j)$ and $cr({\breve{E}}_j)\approx cr({\breve{E}}_j),$ then ${\breve{E}}_j\approx {\breve{E}}_j.$

Definition 15.

Let any collections ${\breve{E}}_p=⟨P_{{\breve{E}}_p},I_{{\breve{E}}_p},N_{{\breve{E}}_p}⟩,$ $p\in N$ be the SFNs and $SFWA:SF{N}^n\to SFN.$ The $SFWA$ operator is described as,

$$SFWA({\breve{E}}_1,{\breve{E}}_2,\dots ,{\breve{E}}_n)=\sum _{p=1}^n{\tau }_p{\breve{E}}_p,$$

in which $\tau =\left\{{\tau }_1,{\tau }_2,\dots ,{\tau }_n\right\}$ is the weight vector of ${\breve{E}}_p=⟨P_{{\breve{E}}_p},I_{{\breve{E}}_p},N_{{\breve{E}}_p}⟩,$ $p\in N$, with ${\tau }_p\ge 0$ and ${\sum }_{p=1}^n{\tau }_p=1.$

Theorem 1.

Let any collections ${\breve{E}}_p=⟨P_{{\breve{E}}_p},I_{{\breve{E}}_p},N_{{\breve{E}}_p}⟩,$ $p\in N$ be the SFNs. Then, by utilizing Definition 15 and the operational properties of SFNs, we can obtain the following outcome.

$$SFWA({\breve{E}}_1,{\breve{E}}_2,\dots ,{\breve{E}}_n)=\left\{\begin{array}{c}\sqrt{1-{\mathsf{\Pi }}_{p=1}^n{(1-P_{{\breve{E}}_p}^2)}^{{\tau }_p}},\\ {\mathsf{\Pi }}_{p=1}^n{(I_{{\breve{E}}_p})}^{{\tau }_p},\\ {\mathsf{\Pi }}_{p=1}^n{(N_{{\breve{E}}_p})}^{{\tau }_p}\end{array}\right\}.$$

3. Spherical Fuzzy Distance Measure

Due to the motivation and inspiration of the concept discussed in Definitions 8 and 9, we introduce the distance between any SFNs.

Definition 16.

(1) For a set $\mathbb{R}\ne \varphi$ and any two SFNs ${\breve{E}}_{{\breve{u}}_j},{\breve{E}}_{{\breve{u}}_l}$ in $\mathbb{R}$, then the maximum distance $d_{Max}({\breve{E}}_{{\breve{u}}_j},{\breve{E}}_{{\breve{u}}_l})$ is given as for all $r_{⋎}\in \mathbb{R}$,

$$d_{Max}({\breve{E}}_{{\breve{u}}_j},{\breve{E}}_{{\breve{u}}_l})=\frac{1}{n}\sum _{p=1}^{n}max\left(\left\{\begin{array}{c}\left|P_{{}_{{\breve{u}}_j}}\left(r_p\right)-P_{{\breve{u}}_l}\left(r_p\right)\right|+\left|I_{{\breve{u}}_j}\left(r_p\right)-I_{{\breve{u}}_l}\left(r_p\right)\right|+\\ \left|N_{{\breve{u}}_j}\left(r_p\right)-N_{{\breve{u}}_l}\left(r_p\right)\right|\end{array}\right\}\right).$$

(2) For a set $\mathbb{R}\ne \varphi$ and any two SFNs ${\breve{E}}_{{\breve{u}}_j},{\breve{E}}_{{\breve{u}}_l}$ in $\mathbb{R}$, then the minimum distance $d_{Min}({\breve{E}}_{{\breve{u}}_j},{\breve{E}}_{{\breve{u}}_l})$ is given as for all $r_{⋎}\in \mathbb{R}$,

$$d_{Min}({\breve{E}}_{{\breve{u}}_j},{\breve{E}}_{{\breve{u}}_l})=\frac{1}{n}\sum _{p=1}^{n}min\left(\left\{\begin{array}{c}\left|P_{{}_{{\breve{u}}_j}}\left(r_p\right)-P_{{\breve{u}}_l}\left(r_p\right)\right|+\left|I_{{\breve{u}}_j}\left(r_p\right)-I_{{\breve{u}}_l}\left(r_p\right)\right|+\\ \left|N_{{\breve{u}}_j}\left(r_p\right)-N_{{\breve{u}}_l}\left(r_p\right)\right|\end{array}\right\}\right).$$

(3) For a set $\mathbb{R}\ne \varphi$ and any two SFNs ${\breve{E}}_{{\breve{u}}_j},{\breve{E}}_{{\breve{u}}_l}$ in $\mathbb{R}$, then the normalized Hamming distance $d_{NHD}({\breve{E}}_{{\breve{u}}_j},{\breve{E}}_{{\breve{u}}_l})$ is given for all $r_{⋎}\in \mathbb{R}$ as,

$$d_{NHD}({\breve{E}}_{{\breve{u}}_j},{\breve{E}}_{{\breve{u}}_l})=\frac{1}{n}\sum _{p=1}^n\left(\left\{\begin{array}{c}\left|P_{{}_{{\breve{u}}_j}}\left(r_p\right)-P_{{\breve{u}}_l}\left(r_p\right)\right|+\left|I_{{\breve{u}}_j}\left(r_p\right)-I_{{\breve{u}}_l}\left(r_p\right)\right|+\\ \left|N_{{\breve{u}}_j}\left(r_p\right)-N_{{\breve{u}}_l}\left(r_p\right)\right|\end{array}\right\}\right).$$

Definition 17.

(1) For a set $\mathbb{R}\ne \varphi$ and any two SFNs ${\breve{E}}_{{\breve{u}}_j},{\breve{E}}_{{\breve{u}}_l}$ in $\mathbb{R}$, then the normalized Euclidean distance $d_{NED}({\breve{E}}_{{\breve{u}}_j},{\breve{E}}_{{\breve{u}}_l})$ is given for all $r_{⋎}\in \mathbb{R}$ as,

$$d_{NED}({\breve{E}}_{{\breve{u}}_j},{\breve{E}}_{{\breve{u}}_l})=\sqrt{\frac{1}{n}\sum _{p=1}^n\left(\begin{array}{c}{(P_{{}_{{\breve{u}}_j}}\left(r_p\right)-P_{{\breve{u}}_l}\left(r_p\right))}^2+{(I_{{\breve{u}}_j}\left(r_p\right)-I_{{\breve{u}}_l}\left(r_p\right))}^2+\\ {(N_{{\breve{u}}_j}\left(r_p\right)-N_{{\breve{u}}_l}\left(r_p\right))}^2\end{array}\right)}.$$

(2) For a set $\mathbb{R}\ne \varphi$ and any two SFNs ${\breve{E}}_{{\breve{u}}_j},{\breve{E}}_{{\breve{u}}_l}$ in $\mathbb{R}$, then the generalized normalized Euclidean distance $d_{GNHD}({\breve{E}}_{{\breve{u}}_j},{\breve{E}}_{{\breve{u}}_l})$ is given for all $r_{⋎}\in \mathbb{R}$ as,

$$d_{NGED}({\breve{E}}_{{\breve{u}}_j},{\breve{E}}_{{\breve{u}}_l})={\left[\frac{1}{n}\sum _{p=1}^n\left(\begin{array}{c}{(P_{{}_{{\breve{u}}_j}}(r_p)-P_{{\breve{u}}_l}(r_p))}^{\lambda }+{(I_{{\breve{u}}_j}(r_p)-I_{{\breve{u}}_l}(r_p))}^{\lambda }+\\ {(N_{{\breve{u}}_j}(r_p)-N_{{\breve{u}}_l}(r_p))}^{\lambda }\end{array}\right)\right]}^{\frac{1}{\lambda }}.$$

Definition 18.

The distance measure of any SFNs ${\breve{E}}_j$ and ${\breve{E}}_l$ is a mapping $d:SF{N}^n\times SF{N}^n\to \left[0,1\right]$ subject to the following conditions:

(1) 

$0\le d({\breve{E}}_j,{\breve{E}}_l)\le 1$;

(2) 

$d({\breve{E}}_j,{\breve{E}}_l)=d({\breve{E}}_l,{\breve{E}}_j)$.

In order to measure the deviation between any two SFNs ${\breve{E}}_j=⟨P_{{\breve{E}}_j},I_{{\breve{E}}_j},N_{{\breve{E}}_j}⟩$ and ${\breve{E}}_l=⟨P_{{\breve{E}}_l},I_{{\breve{E}}_l},N_{{\breve{E}}_l}⟩$, we define the distance measure of ${\breve{E}}_j$ and ${\breve{E}}_l$ as follows:

$$d_{SFD}({\breve{E}}_j,{\breve{E}}_l)=\frac{1}{2}\left(\left|P_{{\breve{E}}_j}-P_{{\breve{E}}_l}\right|+\left|I_{{\breve{E}}_j}-I_{{\breve{E}}_l}\right|+\left|N_{{\breve{E}}_j}-N_{{\breve{E}}_l}\right|\right),$$

so $d_{SFD}({\breve{E}}_j,{\breve{E}}_l)$ is called the spherical fuzzy distance (SFD) measure between ${\breve{E}}_j$ and ${\breve{E}}_l$.

Theorem 2.

Assuming that ${\breve{E}}_j=⟨P_{{\breve{E}}_j},I_{{\breve{E}}_j},N_{{\breve{E}}_j}⟩$, ${\breve{E}}_l=⟨P_{{\breve{E}}_l},I_{{\breve{E}}_l},N_{{\breve{E}}_l}⟩$, and ${\breve{E}}_k=⟨P_{{\breve{E}}_k},I_{{\breve{E}}_k},N_{{\breve{E}}_k}⟩$ are any three SFNs on the universe of discourse $\mathbb{R}\ne \varphi$, we have:

(1) 

Non-negativity: $d_{SFD}\left({\breve{E}}_j,{\breve{E}}_l\right)\ge 0$;

(2) 

Commutativity: $d_{SFD}\left({\breve{E}}_j,{\breve{E}}_l\right)=d_{PFD}\left({\breve{E}}_l,{\breve{E}}_j\right)$;

(3) 

Reflexivity: $d_{SFD}\left({\breve{E}}_l,{\breve{E}}_l\right)=0$;

(4) 

Triangle inequality: $d_{SFD}\left({\breve{E}}_j,{\breve{E}}_l\right)+d_{PFD}({\breve{E}}_l,{\breve{E}}_k)\ge d_{PFD}\left({\breve{E}}_j,{\breve{E}}_k\right)$.

Proof. 

(1) Non-negativity: $d_{SFD}\left({\breve{E}}_j,{\breve{E}}_l\right)\ge 0$. Since the distance measure of two spherical fuzzy sets is denoted by,

$$d_{SFD}\left({\breve{E}}_j,{\breve{E}}_l\right)=\frac{1}{2}\left(\left|P_{{\breve{E}}_j}-P_{{\breve{E}}_l}\right|+\left|I_{{\breve{E}}_j}-I_{{\breve{E}}_l}\right|+\left|N_{{\breve{E}}_j}-N_{{\breve{E}}_l}\right|\right),$$

thus we have $\left|P_{{\breve{E}}_j}-P_{{\breve{E}}_l}\right|\ge 0$, $\left|I_{{\breve{E}}_j}-I_{{\breve{E}}_l}\right|\ge 0$ and $\left|N_{{\breve{E}}_j}-N_{{\breve{E}}_l}\right|\ge 0$, and this implies $\left|P_{{\breve{E}}_j}-P_{{\breve{E}}_l}\right|+\left|I_{{\breve{E}}_j}-I_{{\breve{E}}_l}\right|+\left|N_{{\breve{E}}_j}-N_{{\breve{E}}_l}\right|\ge 0$. Therefore,

$$\frac{1}{2}\left(\left|P_{{\breve{E}}_j}-P_{{\breve{E}}_l}\right|+\left|I_{{\breve{E}}_j}-I_{{\breve{E}}_l}\right|+\left|N_{{\breve{E}}_j}-N_{{\breve{E}}_l}\right|\right)\ge 0$$

$$d_{SFD}\left({\breve{E}}_j,{\breve{E}}_l\right)\ge 0.$$

(2) Commutativity: $d_{SFD}\left({\breve{E}}_j,{\breve{E}}_l\right)=d_{PFD}\left({\breve{E}}_l,{\breve{E}}_j\right)$. Since the distance measure of two spherical fuzzy sets is denoted by,

$$d_{SFD}\left({\breve{E}}_j,{\breve{E}}_l\right)=\frac{1}{2}\left(\left|P_{{\breve{E}}_j}-P_{{\breve{E}}_l}\right|+\left|I_{{\breve{E}}_j}-I_{{\breve{E}}_l}\right|+\left|N_{{\breve{E}}_j}-N_{{\breve{E}}_l}\right|\right),$$

if we have, $\left|P_{{\breve{E}}_j}-P_{{\breve{E}}_l}\right|=\left|P_{{\breve{E}}_l}-P_{{\breve{E}}_j}\right|,\left|I_{{\breve{E}}_j}-I_{{\breve{E}}_l}\right|=\left|I_{{\breve{E}}_l}-I_{{\breve{E}}_j}\right|$ and $\left|N_{{\breve{E}}_j}-N_{{\breve{E}}_l}\right|=\left|N_{{\breve{E}}_l}-N_{{\breve{E}}_j}\right|$, therefore,

$$\frac{1}{2}\left(\begin{array}{c}\left|P_{{\breve{E}}_j}-P_{{\breve{E}}_l}\right|+\\ \left|I_{{\breve{E}}_j}-I_{{\breve{E}}_l}\right|+\\ \left|N_{{\breve{E}}_j}-N_{{\breve{E}}_l}\right|\end{array}\right)=\frac{1}{2}\left(\begin{array}{c}\left|P_{{\breve{E}}_l}-P_{{\breve{E}}_j}\right|+\\ \left|I_{{\breve{E}}_l}-I_{{\breve{E}}_j}\right|+\\ \left|N_{{\breve{E}}_l}-N_{{\breve{E}}_j}\right|\end{array}\right)$$

$$d_{SFD}\left({\breve{E}}_j,{\breve{E}}_l\right)=d_{SFD}\left({\breve{E}}_l,{\breve{E}}_j\right)$$

(3) Reflexivity: $d_{SFD}\left({\breve{E}}_l,{\breve{E}}_l\right)=0$. Since,

$$\frac{1}{2}\left(\begin{array}{c}\left|P_{{\breve{E}}_l}-P_{{\breve{E}}_l}\right|+\\ \left|I_{{\breve{E}}_l}-I_{{\breve{E}}_l}\right|+\\ \left|N_{{\breve{E}}_l}-N_{{\breve{E}}_l}\right|\end{array}\right)=0+0+0=0$$

⇒$d_{SFD}\left({\breve{E}}_l,{\breve{E}}_l\right)=0$.

(4) Triangular inequality: $d_{SFD}\left({\breve{E}}_j,{\breve{E}}_l\right)+d_{PFD}({\breve{E}}_l,{\breve{E}}_k)\ge d_{PFD}\left({\breve{E}}_j,{\breve{E}}_k\right)$. Thus, we have,

$$\begin{array}{lll}\left|P_{{\breve{E}}_j}-P_{{\breve{E}}_k}\right|& =& \left|P_{{\breve{E}}_j}-P_{{\breve{E}}_l}+P_{{\breve{E}}_l}-P_{{\breve{E}}_k}\right|\\ & \le & \left|P_{{\breve{E}}_j}-P_{{\breve{E}}_l}\right|+\left|P_{{\breve{E}}_l}-P_{{\breve{E}}_k}\right|,\\ \left|I_{{\breve{E}}_j}-I_{{\breve{E}}_k}\right|& =& \left|I_{{\breve{E}}_j}-I_{{\breve{E}}_l}+I_{{\breve{E}}_l}-I_{{\breve{E}}_k}\right|\\ & \le & \left|I_{{\breve{E}}_j}-I_{{\breve{E}}_l}\right|+\left|I_{{\breve{E}}_l}-I_{{\breve{E}}_k}\right|\mathrm{and}\\ \left|N_{{\breve{E}}_j}-N_{{\breve{E}}_k}\right|& =& \left|N_{{\breve{E}}_j}-N_{{\breve{E}}_l}+N_{{\breve{E}}_l}-N_{{\breve{E}}_k}\right|\\ & \le & \left|N_{{\breve{E}}_j}-N_{{\breve{E}}_l}\right|+\left|N_{{\breve{E}}_l}-N_{{\breve{E}}_k}\right|.\end{array}$$

Therefore,

$$\begin{array}{ll}& \frac{1}{2}\left(\left|P_{{\breve{E}}_j}-P_{{\breve{E}}_k}\right|+\left|I_{{\breve{E}}_j}-I_{{\breve{E}}_k}\right|+\left|N_{{\breve{E}}_j}-N_{{\breve{E}}_k}\right|\right)\\ \le & \frac{1}{2}\left(\begin{array}{c}\left|P_{{\breve{E}}_j}-P_{{\breve{E}}_l}\right|+\\ \left|I_{{\breve{E}}_j}-I_{{\breve{E}}_l}\right|+\\ \left|N_{{\breve{E}}_j}-N_{{\breve{E}}_l}\right|\end{array}\right)+\frac{1}{2}\left(\begin{array}{c}\left|P_{{\breve{E}}_l}-P_{{\breve{E}}_k}\right|+\\ \left|I_{{\breve{E}}_l}-I_{{\breve{E}}_k}\right|+\\ \left|N_{{\breve{E}}_l}-N_{{\breve{E}}_k}\right|\end{array}\right)\end{array}$$

which implies that $d_{SFD}\left({\breve{E}}_j,{\breve{E}}_l\right)+d_{PFD}({\breve{E}}_l,{\breve{E}}_k)\ge d_{PFD}\left({\breve{E}}_j,{\breve{E}}_k\right)$.  □

Spherical Fuzzy Distance Aggregation Operators

Definition 19.

Let any collections ${\breve{E}}_p=⟨P_{{\breve{E}}_p},I_{{\breve{E}}_p},N_{{\breve{E}}_p}⟩,$ $p\in N$ of SFNs, $SFDWA:SF{N}^n\times SF{N}^n\to SFN.$ The $SFDWA$ operator is describe as,

$$SFDWA\left(⟨Q_1,L_1⟩,⟨Q_2,L_2⟩,\dots ,⟨Q_n,L_n⟩\right)={\left(\sum _{p=1}^n{\tau }_p{\left(d\left(Q_p,L_p\right)\right)}^{\lambda }\right)}^{\frac{1}{\lambda }},\lambda >0.$$

In which the weight vector $\tau =\left\{{\tau }_1,{\tau }_2,\dots ,{\tau }_n\right\}$ of ${\breve{E}}_p=⟨P_{{\breve{E}}_p},I_{{\breve{E}}_p},N_{{\breve{E}}_p}⟩,$ $p\in N$, with ${\tau }_p\ge 0$ and ${\sum }_{p=1}^n{\tau }_p=1$ and $d\left(Q_p,L_p\right)\left(p\in N\right)$ represents the distances of $⟨Q_p,L_p⟩$ $p\in N.$

Example 1.

Let $Q_1=⟨0.5,0.6,0.4⟩,$ $Q_2=⟨0.5,0.8,0.3⟩,Q_3=⟨0.3,0.4,0.8⟩$, $Q_4=⟨0.7,0.5,0.4⟩,$ $L_1=⟨0.7,0.6,0.2⟩,$ $L_2=⟨0.1,0.9,0.3⟩, L_3=⟨0.4,0.8,0.4⟩$, and $L_4=⟨0.5,0.8,0.2⟩$ be spherical fuzzy values on the universe of discourse $\mathbb{R}\ne \varphi$. The weighted weight vectors are ${(0.2,0.3,0.1,0.4)}^T$. Then,

$$\begin{array}{ccc}\hfill d_{SFN}\left(Q_1,L_1\right)& =& \frac{1}{2}\left(\left|0.5-0.7\right|+\left|0.6-0.6\right|+\left|0.4-0.2\right|\right)=0.20\hfill \\ \hfill d_{SFN}\left(Q_2,L_2\right)& =& \frac{1}{2}\left(\left|0.5-0.1\right|+\left|0.8-0.9\right|+\left|0.3-0.3\right|\right)=0.25\hfill \\ \hfill d_{SFN}\left(Q_3,L_3\right)& =& \frac{1}{2}\left(\left|0.3-0.4\right|+\left|0.4-0.8\right|+\left|0.8-0.4\right|\right)=0.45\hfill \\ \hfill d_{SFN}\left(Q_4,L_4\right)& =& \frac{1}{2}\left(\left|0.7-0.5\right|+\left|0.5-0.8\right|+\left|0.4-0.2\right|\right)=0.35\hfill \end{array}$$

Now, use the $SFDWA$ operator to aggregate the information as:

$$\begin{array}{ll}& SFDWA\left(⟨Q_1,L_1⟩,⟨Q_2,L_2⟩,⟨Q_3,L_3⟩,⟨Q_4,L_4⟩\right)\\ =& {\left({\displaystyle \sum _{p=1}^4}{\tau }_p{\left(d\left(Q_p,L_p\right)\right)}^2\right)}^{\frac{1}{2}},\lambda =2>0\\ =& {\left(0.2{\left(0.20\right)}^2+0.3{\left(0.25\right)}^2+0.1{\left(0.45\right)}^2+0.4{\left(0.35\right)}^2\right)}^{\frac{1}{2}}\\ =& 0.3098\end{array}$$

The $SFDWA$ operator is commutative, monotonic, bounded, idempotent, non-negative, and reflexive, but it cannot always achieve the triangle inequality. These properties can be proven with the following lemma:

Lemma 1 (Commutativity).

Assume that the $SFDWA$ operator satisfies the commutativity, i.e.,

$$SFDWA\left(\begin{array}{c}⟨Q_1,L_1⟩,\\ ⟨Q_2,L_2⟩,\\ \dots ,\\ ⟨Q_n,L_n⟩\end{array}\right)=SFDWA\left(\begin{array}{c}⟨L_1,Q_1⟩,\\ ⟨L_2,Q_2⟩,\\ \dots ,\\ ⟨L_n,Q_n⟩\end{array}\right),$$

where $Q_l$ $\left(l\in N\right)$ and $L_l\left(l\in N\right)$ are the collections of SFNs.

Proof. 

$$\begin{array}{ccc}\hfill SFDWA\left(⟨Q_1,L_1⟩,⟨Q_2,L_2⟩,\dots ,⟨Q_n,L_n⟩\right)& =& {\left(\sum _{p=1}^n{\tau }_p{\left(d\left(Q_p,L_p\right)\right)}^{\lambda }\right)}^{\frac{1}{\lambda }},\lambda >0,\hfill \\ \hfill SFDWA\left(⟨L_1,Q_1⟩,⟨L_2,Q_2⟩,\dots ,⟨L_n,Q_n⟩\right)& =& {\left(\sum _{p=1}^n{\tau }_p{\left(d\left(L_p,Q_p\right)\right)}^{\lambda }\right)}^{\frac{1}{\lambda }},\lambda >0.\hfill \end{array}$$

Since the distance satisfies the commutativity, we have $d_{SFD}\left(Q_{\mathrm{p}},L_{\mathrm{p}}\right)=d_{SFD}\left(L_{\mathrm{p}},Q_{\mathrm{p}}\right)$ for all p. Thus,

$$SFDWA\left(\begin{array}{c}⟨Q_1,L_1⟩,\\ ⟨Q_2,L_2⟩,\\ \dots ,\\ ⟨Q_n,L_n⟩\end{array}\right)=SFDWA\left(\begin{array}{c}⟨L_1,Q_1⟩,\\ ⟨L_2,Q_2⟩,\\ \dots ,\\ ⟨L_n,Q_n⟩\end{array}\right).$$

  □

Lemma 2 (Monotonicity).

Assume that the $SFDWA$ operator satisfies the monotonicity, i.e.,

$$SFDWA\left(\begin{array}{c}⟨Q_1,L_1⟩,\\ ⟨Q_2,L_2⟩,\\ \dots ,\\ ⟨Q_n,L_n⟩\end{array}\right)\ge SFDWA\left(\begin{array}{c}⟨L_1,K_1⟩,\\ ⟨L_2,K_2⟩,\\ \dots ,\\ ⟨L_n,K_n⟩\end{array}\right)$$

where $Q_{\mathrm{p}}$ $\left(\mathrm{p}\in N\right)$, $L_{\mathrm{p}}\left(\mathrm{p}\in N\right)$, and $K_{\mathrm{p}}$ $\left(\mathrm{p}\in N\right)$ are the collections of SFNs.

Proof. 

$$\begin{array}{ccc}\hfill SFDWA\left(⟨Q_1,L_1⟩,⟨Q_2,L_2⟩,\dots ,⟨Q_n,L_n⟩\right)& =& {\left(\sum _{p=1}^n{\tau }_p{\left(d\left(Q_p,L_p\right)\right)}^{\lambda }\right)}^{\frac{1}{\lambda }},\lambda >0,\hfill \\ \hfill SFDWA\left(⟨L_1,K_1⟩,⟨L_2,K_2⟩,\dots ,⟨L_n,K_n⟩\right)& =& {\left(\sum _{p=1}^n{\tau }_p{\left(d\left(L_p,K_p\right)\right)}^{\lambda }\right)}^{\frac{1}{\lambda }},\lambda >0.\hfill \end{array}$$

Since the distance satisfies the monotonicity, so we have $d_{SFD}\left(Q_{\mathrm{p}},L_{\mathrm{p}}\right)\ge d_{SFD}\left(L_{\mathrm{p}},K_{\mathrm{p}}\right)$ for all p. Thus,

$$SFDWA\left(\begin{array}{c}⟨Q_1,L_1⟩,\\ ⟨Q_2,L_2⟩,\\ \dots ,\\ ⟨Q_n,L_n⟩\end{array}\right)\ge SFDWA\left(\begin{array}{c}⟨L_1,K_1⟩,\\ ⟨L_2,K_2⟩,\\ \dots ,\\ ⟨L_n,K_n⟩\end{array}\right)$$

  □

Lemma 3 (Boundary).

Assume that the $SFDWA$ operator satisfies the following:

$$\underset{p}{min}\left|Q_p,L_p\right|\le SFDWA\left(⟨Q_1,L_1⟩,⟨Q_2,L_2⟩,\dots ,⟨Q_n,L_n⟩\right)\le \underset{p}{max}\left|Q_p,L_p\right|.$$

Proof. 

Assuming that ${max}_{\mathrm{p}}\left|Q_{\mathrm{p}},L_{\mathrm{p}}\right|=\check{d}$ and ${min}_{\mathrm{p}}\left|Q_{\mathrm{p}},L_{\mathrm{p}}\right|=\breve{g}$ with weight vector $\tau =\left\{{\tau }_1,{\tau }_2,\dots ,{\tau }_n\right\}$, ${\tau }_{\mathrm{p}}\ge 0$, and ${\sum }_{\mathrm{p}=1}^n{\tau }_{\mathrm{p}}=1$, then,

$$SFDWA\left(⟨Q_1,L_1⟩,⟨Q_2,L_2⟩,\dots ,⟨Q_n,L_n⟩\right)={\left(\sum _{p=1}^n{\tau }_p{\left(d\left(Q_p,L_p\right)\right)}^{\lambda }\right)}^{\frac{1}{\lambda }},\lambda >0,$$

$$\le {\left(\sum _{p=1}^n{\tau }_p{\check{d}}^{\lambda }\right)}^{{}^{\frac{1}{{}^{\lambda }}}}={\left({\check{d}}^{\lambda }\sum _{p=1}^n{\tau }_p\right)}^{{}^{\frac{1}{{}^{\lambda }}}}=\check{d}$$

$$SFDWA\left(⟨Q_1,L_1⟩,⟨Q_2,L_2⟩,\dots ,⟨Q_n,L_n⟩\right)={\left(\sum _{p=1}^n{\tau }_p{\left(d\left(Q_p,L_p\right)\right)}^{\lambda }\right)}^{\frac{1}{\lambda }},\lambda >0,$$

$$\ge {\left(\sum _{p=1}^n{\tau }_p{\breve{g}}^{\lambda }\right)}^{{}^{\frac{1}{{}^{\lambda }}}}={\left({\breve{g}}^{\lambda }\sum _{p=1}^n{\tau }_p\right)}^{{}^{\frac{1}{{}^{\lambda }}}}=\breve{g}.$$

Hence,

$$\underset{p}{min}\left|Q_p,L_p\right|\le SFDWA\left(⟨Q_1,L_1⟩,⟨Q_2,L_2⟩,\dots ,⟨Q_n,L_n⟩\right)\le \underset{p}{max}\left|Q_p,L_p\right|.$$

  □

Lemma 4 (Idempotency).

Assume that the $SFDWA$ operator satisfies that $\left|Q_{\mathrm{p}},L_{\mathrm{p}}\right|=I$ for all p. Then:

$$SFDWA\left(⟨Q_1,L_1⟩,⟨Q_2,L_2⟩,\dots ,⟨Q_n,L_n⟩\right)=I.$$

Proof. 

Since,

$$SFDWA\left(⟨Q_1,L_1⟩,⟨Q_2,L_2⟩,\dots ,⟨Q_n,L_n⟩\right)={\left(\sum _{p=1}^n{\tau }_p{\left(d\left(Q_p,L_p\right)\right)}^{\lambda }\right)}^{\frac{1}{\lambda }},\lambda >0,$$

because $d_{SFD}\left(Q_{\mathrm{p}},L_{\mathrm{p}}\right)=\left|Q_{\mathrm{p}},L_{\mathrm{p}}\right|=I$ for all p, then also:

$$SFDWA\left(⟨Q_1,L_1⟩,⟨Q_2,L_2⟩,\dots ,⟨Q_n,L_n⟩\right)={\left(\sum _{p=1}^n{\tau }_p{\left(d\left(Q_p,L_p\right)\right)}^{\lambda }\right)}^{\frac{1}{\lambda }}=I$$

Hence, we get the required results.  □

Lemma 5 (Non-negativity).

Assume that the $SFDWA$ operator satisfies the following:

$$SFDWA\left(⟨Q_1,L_1⟩,⟨Q_2,L_2⟩,\dots ,⟨Q_n,L_n⟩\right)\ge 0.$$

Proof. 

Since, as $d_{SFD}\left(Q_1,L_1\right)=\left|Q_1,L_1\right|\ge 0$, similarly, we have:

$$d_{SFD}\left(Q_p,L_p\right)=\left|Q_p,L_p\right|\ge 0\mathrm{for}\mathrm{all}p\in N$$

Therefore, we use the above information and gain:

$$SFDWA\left(⟨Q_1,L_1⟩,⟨Q_2,L_2⟩,\dots ,⟨Q_n,L_n⟩\right)\ge 0$$

  □

Lemma 6 (Reflexivity).

Assume that the $SFDWA$ operator satisfies the following:

$$SFDWA\left(⟨L_1,L_1⟩,⟨L_2,L_2⟩,\dots ,⟨L_n,L_n⟩\right)=0.$$

Proof. 

Since, as $d_{SFD}\left(L_1,L_1\right)=\left|L_1,L_1\right|=0$, similarly, we have:

$$d_{SFD}\left(L_p,L_p\right)=\left|L_p,L_p\right|=0\mathrm{for}\mathrm{all}p\in N$$

Therefore, we use the above information and gain:

$$SFDWA\left(⟨L_1,L_1⟩,⟨L_2,L_2⟩,\dots ,⟨L_n,L_n⟩\right)=0.$$

  □

Definition 20.

Let any collections ${\breve{E}}_{\mathrm{p}}=⟨P_{{\breve{E}}_{\mathrm{p}}},I_{{\breve{E}}_{\mathrm{p}}},N_{{\breve{E}}_{\mathrm{p}}}⟩,$ $p\in N$ of SFNs, $SFODWA:SF{N}^n\times SF{N}^n\to SFN.$ The $SFODWA$ operator is described as,

$$SFODWA\left(⟨Q_1,L_1⟩,⟨Q_2,L_2⟩,\dots ,⟨Q_n,L_n⟩\right)={\left(\sum _{p=1}^n{\tau }_p{\left(d\left(Q_{\eta \left(p\right)},L_{\eta \left(p\right)}\right)\right)}^{\lambda }\right)}^{\frac{1}{\lambda }},\lambda >0.$$

In which the weight vector $\tau =\left\{{\tau }_1,{\tau }_2,\dots ,{\tau }_n\right\}$, ${\tau }_p\ge 0$, and ${\sum }_{p=1}^n{\tau }_p=1$. Where $d\left(Q_{\eta \left(p\right)},L_{\eta \left(p\right)}\right)$ is the p^th largest distance of $⟨Q_p,L_p⟩$, consequently by total order, $d\left(Q_{\eta \left(1\right)},L_{\eta \left(1\right)}\right)\ge d\left(Q_{\eta \left(2\right)},L_{{\eta }_{\left(2\right)}}\right)\ge \dots \ge d\left(Q_{\eta \left(n\right)},L_{\eta \left(n\right)}\right)$.

Example 2.

Let $Q_1=⟨0.5,0.6,0.4⟩,$ $Q_2=⟨0.5,0.8,0.3⟩,Q_3=⟨0.3,0.4,0.8⟩$, $Q_4=⟨0.7,0.5,0.4⟩,$ $L_1=⟨0.7,0.6,0.2⟩,$ $L_2=⟨0.1,0.9,0.3⟩, L_3=⟨0.4,0.8,0.4⟩$, and $L_4=⟨0.5,0.8,0.2⟩$ be spherical fuzzy values on the universe of discourse $\mathbb{R}\ne \varphi$. The weighted weight vectors are ${(0.2,0.3,0.1,0.4)}^T$. Use Definition 13 to calculate the score functions as:

$$\begin{array}{cc}\hfill Sco\left(Q_1\right)=\frac{1}{3}(2+0.5-0.6-0.4)=0.50& Sco\left(L_1\right)=\frac{1}{3}(2+0.7-0.6-0.2)=0.63\\ \hfill Sco\left(Q_2\right)=\frac{1}{3}(2+0.5-0.8-0.3)=0.46& Sco\left(L_2\right)=\frac{1}{3}(2+0.1-0.9-0.3)=0.30\\ \hfill Sco\left(Q_3\right)=\frac{1}{3}(2+0.3-0.4-0.8)=0.36& Sco\left(L_3\right)=\frac{1}{3}(2+0.4-0.8-0.4)=0.40\\ \hfill Sco\left(Q_4\right)=\frac{1}{3}(2+0.7-0.5-0.4)=0.60& Sco\left(L_4\right)=\frac{1}{3}(2+0.5-0.8-0.2)=0.50\end{array}$$

Now, use the comparison technique in Definition 14 to rank the spherical fuzzy numbers as:

$$Sco\left(Q_4\right)>Sco\left(Q_1\right)>Sco\left(Q_2\right)>Sco\left(Q_3\right)$$

and:

$$Sco\left(L_1\right)>Sco\left(L_4\right)>Sco\left(L_3\right)>Sco\left(L_2\right)$$

Then, we obtain,

$$\begin{array}{ccc}\hfill Q_4& >& Q_1>Q_2>Q_3\hfill \\ \hfill L_1& >& L_4>L_3>L_2\hfill \end{array}$$

and hence, $Q_{\eta \left(1\right)}=Q_4=⟨0.7,0.5,0.4⟩,Q_{\eta \left(2\right)}=Q_1=⟨0.5,0.6,0.4⟩,Q_{\eta \left(3\right)}=Q_2=⟨0.5,0.8,0.3⟩$, and $Q_{\eta \left(4\right)}=Q_3=⟨0.3,0.4,0.8⟩.$ Similarly, $L_{\eta \left(1\right)}=L_1=⟨0.7,0.6,0.2⟩,L_{\eta \left(2\right)}=L_4=⟨0.5,0.8,0.2⟩,L_{\eta \left(3\right)}=L_3=⟨0.4,0.8,0.4⟩$, and $L_{\eta \left(4\right)}=L_2=⟨0.1,0.9,0.3⟩.$ Then:

$$\begin{array}{ccc}\hfill d_{SFN}\left(Q_{\eta \left(1\right)},L_{\eta \left(1\right)}\right)& =& \frac{1}{2}\left(\left|0.7-0.7\right|+\left|0.5-0.6\right|+\left|0.4-0.2\right|\right)=0.15\hfill \\ \hfill d_{SFN}\left(Q_{\eta \left(2\right)},L_{\eta \left(2\right)}\right)& =& \frac{1}{2}\left(\left|0.5-0.5\right|+\left|0.6-0.8\right|+\left|0.4-0.2\right|\right)=0.20\hfill \\ \hfill d_{SFN}\left(Q_{\eta \left(3\right)},L_{\eta \left(3\right)}\right)& =& \frac{1}{2}\left(\left|0.5-0.4\right|+\left|0.8-0.8\right|+\left|0.3-0.4\right|\right)=0.10\hfill \\ \hfill d_{SFN}\left(Q_{\eta \left(4\right)},L_{\eta \left(4\right)}\right)& =& \frac{1}{2}\left(\left|0.3-0.1\right|+\left|0.4-0.9\right|+\left|0.8-0.3\right|\right)=0.60\hfill \end{array}$$

Now, use the $SFODWA$ operator to aggregate the information as:

$$\begin{array}{ll}& SFDWA\left(⟨Q_{\eta \left(1\right)},L_{\eta \left(1\right)}⟩,⟨Q_{\eta \left(2\right)},L_{\eta \left(2\right)}⟩,⟨Q_{\eta \left(3\right)},L_{\eta \left(3\right)}⟩,⟨Q_{\eta \left(4\right)},L_{\eta \left(4\right)}⟩\right)\\ =& {\left({\displaystyle \sum _{p=1}^n}{\tau }_p{\left(d\left(Q_{\eta \left(p\right)},L_{\eta \left(p\right)}\right)\right)}^2\right)}^{\frac{1}{2}},\lambda =2>0\\ =& {\left(0.2{\left(0.15\right)}^2+0.3{\left(0.20\right)}^2+0.1{\left(0.10\right)}^2+0.4{\left(0.60\right)}^2\right)}^{\frac{1}{2}}\\ =& 0.4018\end{array}$$

The $SFODWA$ operator is commutative, monotonic, bounded, idempotent, non-negative, and reflexive, but it cannot always achieve the triangle inequality. These properties can be proven similarly as defined above, so we omit them here.

Definition 21.

Let any collections ${\breve{E}}_p=⟨P_{{\breve{E}}_p},I_{{\breve{E}}_p},N_{{\breve{E}}_p}⟩,$ $p\in N$ of SFNs, $SFDOWAWA:SF{N}^n\times SF{N}^n\to SFN.$ The $SFDOWAWA$ operator is described with the associated weights $\tau =\left\{{\tau }_1,{\tau }_2,\dots ,{\tau }_n\right\}$, ${\tau }_p\ge 0$ and ${\sum }_{p=1}^n{\tau }_p=1.$

$$SFDOWAWA\left(⟨Q_1,L_1⟩,⟨Q_2,L_2⟩,\dots ,⟨Q_n,L_n⟩\right)={\left(\sum _{p=1}^n\widehat{{\tau }_p}{\left(d\left(Q_{\eta \left(p\right)},L_{\eta \left(p\right)}\right)\right)}^{\lambda }\right)}^{\frac{1}{\lambda }},\lambda >0$$

where $d\left(Q_{\eta \left(p\right)},L_{\eta \left(p\right)}\right)$ is p the largest distance of $⟨Q_p,L_p⟩$, consequently by total order, $d\left(Q_{\eta \left(1\right)},L_{\eta \left(1\right)}\right)\ge d\left(Q_{\eta \left(2\right)},L_{\eta \left(2\right)}\right)\ge \dots \ge d\left(Q_{\eta \left(n\right)},L_{\eta \left(n\right)}\right)$, in which the weighted weight vector $v=\left\{v_1,v_2,\dots ,v_n\right\}$, $v_p\ge 0$ and ${\sum }_{p=1}^n{v}_p=1,$ $\widehat{{\tau }_p}=\xi {\tau }_p+\left(1-\xi \right)v_p$ with $\xi \in \left[0,1\right].$

As we can see, if $\xi =1$, we get the SFDOWA operator and if $\xi =0$ the SFDWA. The SFDOWAWA operator accomplishes similar properties as the usual distance aggregation operators. Note that we can distinguish between descending and ascending orders, extend it by using mixture operators, and so on.

Example 3.

Let $Q_1=⟨0.5,0.6,0.4⟩,$ $Q_2=⟨0.5,0.8,0.3⟩,Q_3=⟨0.3,0.4,0.8⟩$, $Q_4=⟨0.7,0.5,0.4⟩,$ $L_1=⟨0.7,0.6,0.2⟩,$ $L_2=⟨0.1,0.9,0.3⟩, L_3=⟨0.4,0.8,0.4⟩$, and $L_4=⟨0.5,0.8,0.2⟩$ be spherical fuzzy values on the universe of discourse $\mathbb{R}\ne \varphi$. The associated weight vectors are ${(0.2,0.3,0.1,0.4)}^T$, and assume that the weighted weight vectors are ${\left(0.2,0.3,0.2,0.3\right)}^T$. Use Definition 13 to calculate the score functions as:

$$\begin{array}{cc}\hfill Sco\left(Q_1\right)=\frac{1}{3}(2+0.5-0.6-0.4)=0.50& Sco\left(L_1\right)=\frac{1}{3}(2+0.7-0.6-0.2)=0.63\\ \hfill Sco\left(Q_2\right)=\frac{1}{3}(2+0.5-0.8-0.3)=0.46& Sco\left(L_2\right)=\frac{1}{3}(2+0.1-0.9-0.3)=0.30\\ \hfill Sco\left(Q_3\right)=\frac{1}{3}(2+0.3-0.4-0.8)=0.36& Sco\left(L_3\right)=\frac{1}{3}(2+0.4-0.8-0.4)=0.40\\ \hfill Sco\left(Q_4\right)=\frac{1}{3}(2+0.7-0.5-0.4)=0.60& Sco\left(L_4\right)=\frac{1}{3}(2+0.5-0.8-0.2)=0.50\end{array}$$

Now, use the comparison technique in Definition 14 to rank the spherical fuzzy numbers as:

$$Sco\left(Q_4\right)>Sco\left(Q_1\right)>Sco\left(Q_2\right)>Sco\left(Q_3\right)$$

and:

$$Sco\left(L_1\right)>Sco\left(L_4\right)>Sco\left(L_3\right)>Sco\left(L_2\right)$$

Then, we obtain,

$$\begin{array}{ccc}\hfill Q_4& >& Q_1>Q_2>Q_3\hfill \\ \hfill L_1& >& L_4>L_3>L_2\hfill \end{array}$$

and hence, $Q_{\eta \left(1\right)}=Q_4=⟨0.7,0.5,0.4⟩,Q_{\eta \left(2\right)}=Q_1=⟨0.5,0.6,0.4⟩,Q_{\eta \left(3\right)}=Q_2=⟨0.5,0.8,0.3⟩$, and $Q_{\eta \left(4\right)}=Q_3=⟨0.3,0.4,0.8⟩.$ Similarly, $L_{\eta \left(1\right)}=L_1=⟨0.7,0.6,0.2⟩,L_{\eta \left(2\right)}=L_4=⟨0.5,0.8,0.2⟩,L_{\eta \left(3\right)}=L_3=⟨0.4,0.8,0.4⟩$, and $L_{\eta \left(4\right)}=L_2=⟨0.1,0.9,0.3⟩.$ Then:

$$\begin{array}{ccc}\hfill d_{SFN}\left(Q_{\eta \left(1\right)},L_{\eta \left(1\right)}\right)& =& \frac{1}{2}\left(\left|0.7-0.7\right|+\left|0.5-0.6\right|+\left|0.4-0.2\right|\right)=0.15\hfill \\ \hfill d_{SFN}\left(Q_{\eta \left(2\right)},L_{\eta \left(2\right)}\right)& =& \frac{1}{2}\left(\left|0.5-0.5\right|+\left|0.6-0.8\right|+\left|0.4-0.2\right|\right)=0.20\hfill \\ \hfill d_{SFN}\left(Q_{\eta \left(3\right)},L_{\eta \left(3\right)}\right)& =& \frac{1}{2}\left(\left|0.5-0.4\right|+\left|0.8-0.8\right|+\left|0.3-0.4\right|\right)=0.10\hfill \\ \hfill d_{SFN}\left(Q_{\eta \left(4\right)},L_{\eta \left(4\right)}\right)& =& \frac{1}{2}\left(\left|0.3-0.1\right|+\left|0.4-0.9\right|+\left|0.8-0.3\right|\right)=0.60\hfill \end{array}$$

Now, we calculate the weights as:

$$\begin{array}{ccc}\hfill \widehat{{\tau }_1}& =& 0.4\times 0.2+\left(1-0.4\right)0.2=0.20\hfill \\ \hfill \widehat{{\tau }_2}& =& 0.4\times 0.3+\left(1-0.4\right)0.3=0.30\hfill \\ \hfill \widehat{{\tau }_3}& =& 0.4\times 0.1+\left(1-0.4\right)0.2=0.16\hfill \\ \hfill \widehat{{\tau }_4}& =& 0.4\times 0.4+\left(1-0.4\right)0.3=0.34\hfill \end{array}$$

Now, use the $SFDOWAWA$ operator to aggregate the information as:

$$\begin{array}{ll}& SFDOWAWA\left(⟨Q_1,L_1⟩,⟨Q_2,L_2⟩,⟨Q_3,L_3⟩,⟨Q_4,L_4⟩\right)\\ =& {\left({\displaystyle \sum _{p=1}^4}\widehat{{\tau }_p}·{\left(d\left(Q_{\eta \left(p\right)},L_{\eta \left(p\right)}\right)\right)}^2\right)}^{\frac{1}{2}},\lambda =2>0.\\ =& {\left(0.20{\left(0.15\right)}^2+0.30{\left(0.20\right)}^2+0.16{\left(0.10\right)}^2+0.34{\left(0.60\right)}^2\right)}^{\frac{1}{2}}\\ =& 0.3748\end{array}$$

The $SFDOWAWA$ operator is commutative, monotonic, bounded, idempotent, non-negative, and reflexive, but it cannot always achieve the triangle inequality. These properties can be proven similarly as defined above, so we omit them here.

Without weights, we cannot aggregate the spherical fuzzy information. If the weights are given, then we use the given weights to aggregate our spherical fuzzy information straightforwardly. If the weights are unknown, then firstly, we find the weights. Here, we introduce the mean-squared deviation models to determine the weights, which are as follows:

• Assume that:

  $${\tau }_p=\frac{d_{SFD}\left(Q_{\eta \left(p\right)},L_{\eta \left(p\right)}\right)}{{\displaystyle \sum _{p=1}^n}{d}_{SFD}\left(Q_{\eta \left(p\right)},L_{\eta \left(p\right)}\right)},p=1,2,\dots n.$$

  (1)

  such that ${\tau }_{p+1}\ge {\tau }_p\ge 0$, $p=1,2,\dots n-1$, and ${\displaystyle \sum _{p=1}^n}{\tau }_p=1$.
• Assume that:

  $${\tau }_p=\frac{e^{-d_{SFD}\left(Q_{\eta \left(p\right)},L_{\eta \left(p\right)}\right)}}{{\displaystyle \sum _{p=1}^n}{e}^{-d_{SFD}\left(Q_{\eta \left(p\right)},L_{\eta \left(p\right)}\right)}},p=1,2,\dots ,n.$$

  (2)

  where $0\le {\tau }_{p+1}\le {\tau }_p$, $p=1,2,\dots n-1$ and ${\displaystyle \sum _{p=1}^n}{\tau }_p=1$.
• Assume that:

  $$d_{SFD}^{/}\left(Q_{\eta \left(p\right)},L_{\eta \left(p\right)}\right)=\frac{1}{n}\sum _{p=1}^n{d}_{SFD}\left(Q_{\eta \left(p\right)},L_{\eta \left(p\right)}\right)$$

  and $d^{//}\left(d_{SFD}\left(Q_{\eta \left(p\right)},L_{\eta \left(p\right)}\right),d_{SFD}^{/}\left(Q_{\eta \left(p\right)},L_{\eta \left(p\right)}\right)\right)=\left|d_{SFD}\left(Q_{\eta \left(p\right)},L_{\eta \left(p\right)}\right)-d_{SFD}^{/}\left(Q_{\eta \left(p\right)},L_{\eta \left(p\right)}\right)\right|,$ then we can find,

  $$\begin{array}{ccc}\hfill {\tau }_p& =& \frac{1-d^{//}\left(d_{SFD}\left(Q_{\eta \left(p\right)},L_{\eta \left(p\right)}\right),d_{SFD}^{/}\left(Q_{\eta \left(p\right)},L_{\eta \left(p\right)}\right)\right)}{{\displaystyle \sum _{p=1}^n}\left(1-d^{//}\left(d_{SFD}\left(Q_{\eta \left(p\right)},L_{\eta \left(p\right)}\right),d_{SFD}^{/}\left(Q_{\eta \left(p\right)},L_{\eta \left(p\right)}\right)\right)\right)}\hfill \end{array}$$

  (3)

  $$\begin{array}{cc}=& \frac{1-\left|d_{SFD}\left(Q_{\eta \left(p\right)},L_{\eta \left(p\right)}\right)-\frac{1}{n}{\displaystyle \sum _{p=1}^n}{d}_{SFD}\left(Q_{\eta \left(p\right)},L_{\eta \left(p\right)}\right)\right|}{{\displaystyle \sum _{p=1}^n}\left(1-\left|d_{SFD}\left(Q_{\eta \left(p\right)},L_{\eta \left(p\right)}\right)-\frac{1}{n}{\displaystyle \sum _{p=1}^n}{d}_{SFD}\left(Q_{\eta \left(p\right)},L_{\eta \left(p\right)}\right)\right|\right)}\hfill \end{array}$$

  (4)

  in which $\tau =\left\{{\tau }_1,{\tau }_2,\dots ,{\tau }_n\right\}$, ${\tau }_p\ge 0$, and ${\sum }_{p=1}^n{\tau }_p=1$.

Example 4.

Let $Q_1=⟨0.5,0.6,0.4⟩,$ $Q_2=⟨0.5,0.8,0.3⟩,Q_3=⟨0.3,0.4,0.8⟩$, $Q_4=⟨0.7,0.5,0.4⟩,$ $L_1=⟨0.7,0.6,0.2⟩,$ $L_2=⟨0.1,0.9,0.3⟩, L_3=⟨0.4,0.8,0.4⟩$, and $L_4=⟨0.5,0.8,0.2⟩$ be spherical fuzzy values on the universe of discourse $\mathbb{R}\ne \varphi$. The weighted weight vectors are unknown. Then, firstly, we find the weights by using any one of their technique. Therefore,

$$\begin{array}{ccc}\hfill d_{SFN}\left(Q_1,L_1\right)& =& \frac{1}{2}\left(\left|0.5-0.7\right|+\left|0.6-0.6\right|+\left|0.4-0.2\right|\right)=0.20\hfill \\ \hfill d_{SFN}\left(Q_2,L_2\right)& =& \frac{1}{2}\left(\left|0.5-0.1\right|+\left|0.8-0.9\right|+\left|0.3-0.3\right|\right)=0.25\hfill \\ \hfill d_{SFN}\left(Q_3,L_3\right)& =& \frac{1}{2}\left(\left|0.3-0.4\right|+\left|0.4-0.8\right|+\left|0.8-0.4\right|\right)=0.45\hfill \\ \hfill d_{SFN}\left(Q_4,L_4\right)& =& \frac{1}{2}\left(\left|0.7-0.5\right|+\left|0.5-0.8\right|+\left|0.4-0.2\right|\right)=0.35\hfill \end{array}$$

Now, use the technique (1) to determine that the weight are ${\left(0.16,0.20,0.36,0.28\right)}^T$. Now, use the $SFDWA$ operator to aggregate the information as:

$$\begin{array}{ll}& SFDWA\left(⟨Q_1,L_1⟩,⟨Q_2,L_2⟩,⟨Q_3,L_3⟩,⟨Q_4,L_4⟩\right)\\ =& {\left({\displaystyle \sum _{p=1}^4}{\tau }_p{\left(d\left(Q_p,L_p\right)\right)}^2\right)}^{\frac{1}{2}},\lambda =2>0\\ =& {\left(0.16{\left(0.20\right)}^2+0.20{\left(0.25\right)}^2+0.36{\left(0.45\right)}^2+0.28{\left(0.35\right)}^2\right)}^{\frac{1}{2}}\\ =& 0.3551\end{array}$$

Similarly, us the other techniques (2) and (3) to determine the unknown weights, and after that, use the aggregation operator to aggregate the spherical fuzzy information.

4. Algorithm

In this section, we develop an application of spherical fuzzy distance-weighted aggregation operators for multiple criteria decision-making problems. Let $G=\left\{G_1,G_2,\dots ,G_m\right\}$ be the finite set of m alternatives, $A=\left\{A_1,A_2,\dots ,A_n\right\}$ be the set of n attributes, and $D=\left\{D_1,D_2,\dots ,D_k\right\}$ be the set of k decision makers. Let $\tau ={\left({\tau }_1,{\tau }_2,\dots {\tau }_n\right)}^T$ be the weighted vector of the attributes $A_p\left(p=1,2,\dots ,n\right)$ such that $w_p\in \left[0,1\right]$ and ${\displaystyle \sum _{p=1}^n}{w}_p=1,$ and let $\omega ={\left({\omega }_1,{\omega }_2,\dots ,{\omega }_k\right)}^T$ be the weighted vector of the decision makers $D^s\left(s=1,2,3,\dots ,k\right),$ such that ${\omega }_s\in \left[0,1\right]$ and ${\displaystyle \sum _{s=1}^k}{\omega }_s=1.$ This method has the following steps.

Step 1: In this step, we construct the spherical fuzzy decision making matrices, $D^s={\left[E_{ip}^{\left(s\right)}\right]}_{m\times n}\left(s=1,2,\dots ,k\right)$, for the decision. It is noted that the criteria are of two types, benefit criteria and cost criteria. If the spherical fuzzy decision matrices, $D^s={\left[E_{ip}^s\right]}_{{}_{m\times n}}$, have cost criteria, then they will be converted into the normalized spherical fuzzy decision matrices, $R^s={\left[r_{ip}^{\left(s\right)}\right]}_{{}_{m\times n}}$, where $r_{ip}^s=\left\{\begin{array}{c}{E}_{ip}^s,\mathrm{for}\mathrm{benefit}\mathrm{criteria}{A}_p\\ {\overline{E}}_{ip}^s,\mathrm{for}\cos \mathrm{t}\mathrm{criteria}{A}_p,\end{array}\right.j=1,2,\dots ,n,$ and ${\overline{E}}_{ip}^s$ is the complement of $E_{ip}^s.$ If all the criteria have the same type, then there is no need for normalization.

Step 2: Use the details of the ideal levels of each criterion to construct the ideal strategy.

Step 3: Use the family of the $SFDWA$ operator to aggregate the spherical fuzzy decision matrix with the constructed ideal strategy.

Step 4: Arrange the values of the all alternatives in ascending order, and select that alternative that has the highest value. The alternative that has the highest value will be our best result or a suitable alternative according to decision makers.

5. An Application to the Child Development Influence Environmental Factors

In this section, the proposed ranking method is applied to deal with the child development influence environmental factors. Consider a committee of decision makers performing an evaluation and selecting the environmental factor that influences the child development process, among three countries $G_1($Pakistan), $G_2($China), and $G_3($Japan), with DM weights $\left(0.4,0.2,0.4\right)$. The decision maker evaluates this according to five criteria, which are given as follows:

(1)

Housing$\left(C_1\right):$ Does the child have space to play and explore? Is the child safe from injury or contaminants such as lead?

(2)

Income$\left(C_2\right):$ Does the child receive adequate nutrition, fresh fruits, and vegetables? Does the child have adequate clothing, e.g., snow coat and boots in winter weather?

(3)

Employment$\left(C_3\right)$: Does the child have quality child care, when the parents are working?

(4)

Education$\left(C_4\right):$ Does someone read and play with the child? Does the child have access to books and toys that stimulate literacy development?

(5)

Environment$\left(C_5\right):$ The environment plays a critical role in the development of children, and it represents the sum total of the physical and psychological stimulation that the child receives.

Step 1: We construct the decision matrices as shown in Table 1, Table 2 and Table 3.

Table 1. Child development influence of environmental factors’ information $D^1$.

	Housing	Income	Employment	Education	Environment
$G_1$	$⟨0.3,0.8,0.5⟩$	$⟨0.8,0.4,0.3⟩$	$⟨0.4,0.5,0.7⟩$	$⟨0.3,0.3,0.4⟩$	$⟨0.8,0.3,0.5⟩$
$G_2$	$⟨0.2,0.6,0.7⟩$	$⟨0.3,0.9,0.1⟩$	$⟨0.5,0.3,0.7⟩$	$⟨0.5,0.4,0.2⟩$	$⟨0.5,0.4,0.2⟩$
$G_3$	$⟨0.4,0.8,0.4⟩$	$⟨0.5,0.8,0.2⟩$	$⟨0.2,0.3,0.7⟩$	$⟨0.6,0.6,0.1⟩$	$⟨0.4,0.2,0.3⟩$

Table 2. Child development influence of environmental factors’ information $D^2$.

	Housing	Income	Employment	Education	Environment
$G_1$	$⟨0.1,0.5,0.7⟩$	$⟨0.6,0.3,0.4⟩$	$⟨0.3,0.8,0.6⟩$	$⟨0.6,0.3,0.2⟩$	$⟨0.8,0.4,0.3⟩$
$G_2$	$⟨0.4,0.4,0.8⟩$	$⟨0.5,0.7,0.1⟩$	$⟨0.4,0.2,0.7⟩$	$⟨0.6,0.1,0.6⟩$	$⟨0.5,0.6,0.4⟩$
$G_3$	$⟨0.2,0.9,0.3⟩$	$⟨0.7,0.1,0.4⟩$	$⟨0.3,0.6,0.4⟩$	$⟨0.6,0.2,0.4⟩$	$⟨0.8,0.1,0.4⟩$

Table 3. Child development influence of environmental factors’ information $D^3$.

	Housing	Income	Employment	Education	Environment
$G_1$	$⟨0.4,0.2,0.8⟩$	$⟨0.4,0.4,0.3⟩$	$⟨0.5,0.4,0.6⟩$	$⟨0.5,0.1,0.4⟩$	$⟨0.7,0.3,0.5⟩$
$G_2$	$⟨0.2,0.5,0.7⟩$	$⟨0.6,0.5,0.4⟩$	$⟨0.2,0.5,0.8⟩$	$⟨0.7,0.2,0.4⟩$	$⟨0.8,0.5,0.2⟩$
$G_3$	$⟨0.6,0.4,0.5⟩$	$⟨0.9,0.3,0.1⟩$	$⟨0.3,0.1,0.9⟩$	$⟨0.6,0.2,0.6⟩$	$⟨0.4,0.4,0.4⟩$

Since $C_1$ and $C_3$ are cost-type criteria and $C_2$, $C_4$, and $C_5$ are benefit-type criteria, we need to normalized the decision matrices. The normalized decision matrices are shown in Table 4, Table 5 and Table 6.

Table 4. Child development influence of environmental factors’ information $R^1$.

	Housing	Income	Employment	Education	Environment
$G_1$	$⟨0.5,0.8,0.3⟩$	$⟨0.8,0.4,0.3⟩$	$⟨0.7,0.5,0.4⟩$	$⟨0.3,0.3,0.4⟩$	$⟨0.8,0.3,0.5⟩$
$G_2$	$⟨0.7,0.6,0.2⟩$	$⟨0.3,0.9,0.1⟩$	$⟨0.7,0.3,0.5⟩$	$⟨0.5,0.4,0.2⟩$	$⟨0.5,0.4,0.2⟩$
$G_3$	$⟨0.4,0.8,0.4⟩$	$⟨0.5,0.8,0.2⟩$	$⟨0.7,0.3,0.2⟩$	$⟨0.6,0.6,0.1⟩$	$⟨0.4,0.2,0.3⟩$

Table 5. Child development influence of environmental factors’ information $R^2$.

	Housing	Income	Employment	Education	Environment
$G_1$	$⟨0.7,0.5,0.1⟩$	$⟨0.6,0.3,0.4⟩$	$⟨0.6,0.8,0.3⟩$	$⟨0.6,0.3,0.2⟩$	$⟨0.8,0.4,0.3⟩$
$G_2$	$⟨0.8,0.4,0.4⟩$	$⟨0.5,0.7,0.1⟩$	$⟨0.7,0.2,0.4⟩$	$⟨0.6,0.1,0.6⟩$	$⟨0.5,0.6,0.4⟩$
$G_3$	$⟨0.3,0.9,0.2⟩$	$⟨0.7,0.1,0.4⟩$	$⟨0.4,0.6,0.3⟩$	$⟨0.6,0.2,0.4⟩$	$⟨0.8,0.1,0.4⟩$

Table 6. Child development influence of environmental factors’ information $R^3$.

	Housing	Income	Employment	Education	Environment
$G_1$	$⟨0.8,0.2,0.4⟩$	$⟨0.4,0.4,0.3⟩$	$⟨0.6,0.4,0.5⟩$	$⟨0.5,0.1,0.4⟩$	$⟨0.7,0.3,0.5⟩$
$G_2$	$⟨0.7,0.5,0.2⟩$	$⟨0.6,0.5,0.4⟩$	$⟨0.8,0.5,0.2⟩$	$⟨0.7,0.2,0.4⟩$	$⟨0.8,0.5,0.2⟩$
$G_3$	$⟨0.5,0.4,0.6⟩$	$⟨0.9,0.3,0.1⟩$	$⟨0.9,0.1,0.3⟩$	$⟨0.6,0.2,0.6⟩$	$⟨0.4,0.4,0.4⟩$

Step 2: The ideal strategy for choosing the best results is given in Table 7 and graphical representation is shown in Figure 2.

Table 7. Ideal strategy.

	Housing	Income	Employment	Education	Environment
ideal levels	$⟨0.9,0.3,0.1⟩$	$⟨0.9,0.2,0.1⟩$	$⟨0.9,0.1,0.2⟩$	$⟨0.9,0.1,0.1⟩$	$⟨0.9,0.1,0.2⟩$

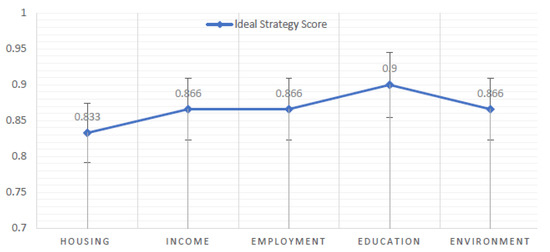
Figure 2. Ideal strategy.

Step 3: Use the $SFWA$ aggregation operator defined in Theorem 1 to aggregate all the individual normalized spherical fuzzy decision matrices. The aggregated spherical fuzzy decision matrix is shown in Table 8:

Table 8. Collective spherical fuzzy decision information matrix R.

	Housing	Income	Employment	Education	Environment
$G_1$	$⟨0.69,0.42,0.22⟩$	$⟨0.64,0.36,0.33⟩$	$⟨0.63,0.54,0.38⟩$	$⟨0.49,0.20,0.31⟩$	$⟨0.77,0.33,0.41⟩$
$G_2$	$⟨0.74,0.48,0.25⟩$	$⟨0.49,0.67,0.15⟩$	$⟨0.73,0.30,0.34⟩$	$⟨0.61,0.19,0.37⟩$	$⟨0.66,0.56,0.29⟩$
$G_3$	$⟨0.40,0.66,0.35⟩$	$⟨0.76,0.27,0.20⟩$	$⟨0.74,0.26,0.26⟩$	$⟨0.60,0.28,0.29⟩$	$⟨0.61,0.19,0.36⟩$

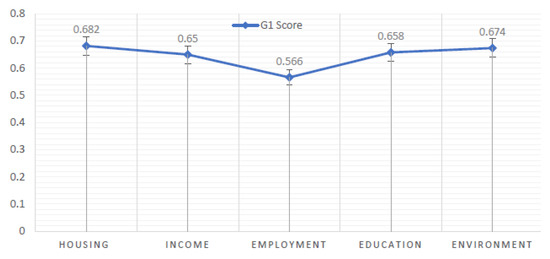
The graphical representation for each alternatives is shown in Figure 3, Figure 4 and Figure 5.

Figure 3. $G_1$ representation.

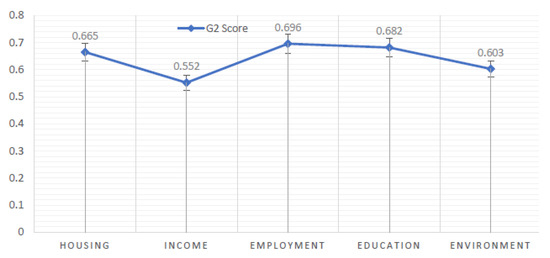
Figure 4. $G_2$ representation.

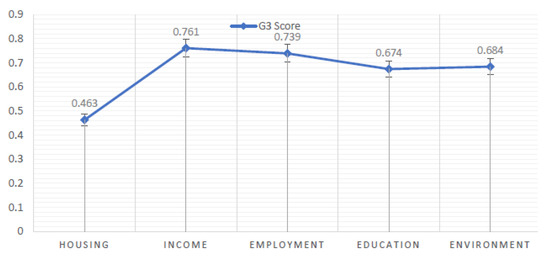
Figure 5. $G_3$ representation.

Step 4: Use the family of the $SFDWA$ operator to aggregate the spherical individual fuzzy decision matrix with the constructed ideal strategy. Here, the weight information is unknown. Therefore, firstly, we utilize the above defined techniques (1)–(3) to calculate the associated weights. The weights using the technique (1) are calculated as $\tau ={(0.124,0.216,0.274,0.154,0.232)}^T.$ Furthermore, the given weighted weights are ${\left(0.2,0.3,0.2,0.1,0.2\right)}^T.$ Use the associated and weighted weights to find the weighted averaging weights as:

$$\begin{array}{cc}\hfill \widehat{{\tau }_1}& 0.3\times 0.124+\left(1-0.3\right)0.2=0.1772\\ \hfill \widehat{{\tau }_2}& 0.3\times 0.216+\left(1-0.3\right)0.3=0.2748\\ \hfill \widehat{{\tau }_3}& 0.3\times 0.274+\left(1-0.3\right)0.2=0.2222\\ \hfill \widehat{{\tau }_4}& 0.3\times 0.154+\left(1-0.3\right)0.1=0.1162\\ \hfill \widehat{{\tau }_5}& 0.3\times 0.232+\left(1-0.3\right)0.2=0.2096\end{array}$$

Now, use the SFDWA operator to find the distances form the ideal Strategy shown in Table 9 and Table 10.

Table 9. Aggregated distance information matrix.

Normalized Hamming Distance
	Max Distance	Min. Distance	SFDWA	SFDOWA	SFDOWAWA
$G_1$	0.4505	0.2265	0.3524	0.2354	0.2281
$G_2$	0.4710	0.2515	0.3552	0.2922	0.2922
$G_3$	0.5555	0.1575	0.2977	0.4452	0.4568

Table 10. Aggregated distance information matrix.

Normalized Euclidean Distance
	Max Distance	Min. Distance	SFDWA	SFDOWA	SFDOWAWA
$G_1$	0.3913	0.1903	0.3044	0.2053	0.1981
$G_2$	0.4452	0.2061	0.3246	0.2433	0.2430
$G_3$	0.4684	0.1320	0.2542	0.4016	0.4116

The graphical representation of the distance from each alternative using the normalized Hamming distance is shown in Figure 6.

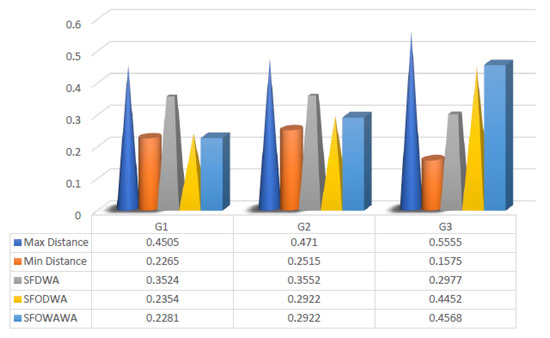
Figure 6. Distance of alternative using the normalized Hamming distance.

The graphical representation of the distance from each alternative using the normalized Euclidean distance is shown in Figure 7.

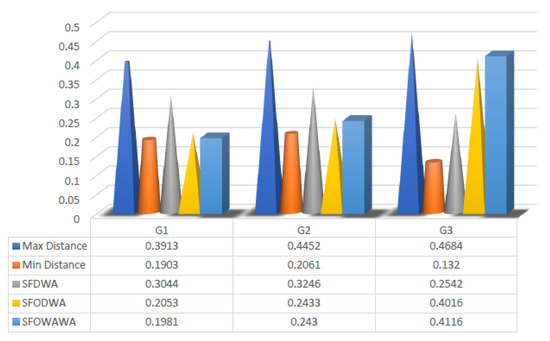
Figure 7. Distance of alternative using Normalized Euclidean Distance.

Step 5: The ranking is shown in Table 11 and Table 12.

Table 11. Final ranking.

		Ranking
Normalized Hamming Distance	Max Distance	$G_3>G_2>G_1$
	Min. Distance	$G_2>G_1>G_3$
	SFDWA	$G_2>G_1>G_3$
	SFDOWA	$G_3>G_2>G_1$
	SFDOWAWA	$G_3>G_2>G_1$

Table 12. Final ranking.

		Ranking
Normalized Euclidean Distance	Max Distance	$G_3>G_2>G_1$
	Min. Distance	$G_2>G_1>G_3$
	SFDWA	$G_2>G_1>G_3$
	SFDOWA	$G_3>G_2>G_1$
	SFDOWAWA	$G_3>G_2>G_1$

The graphical representation of the final ranking for each alternative using the normalized Hamming distance is shown in Figure 8.

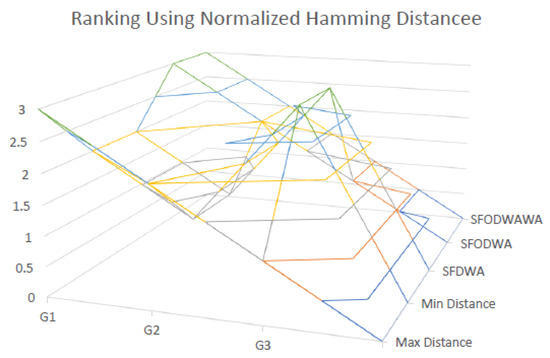
Figure 8. Final ranking for each alternative using the normalized Hamming distance.

The graphical representation of the final ranking for each alternative using the normalized Euclidean distance is shown in Figure 9.

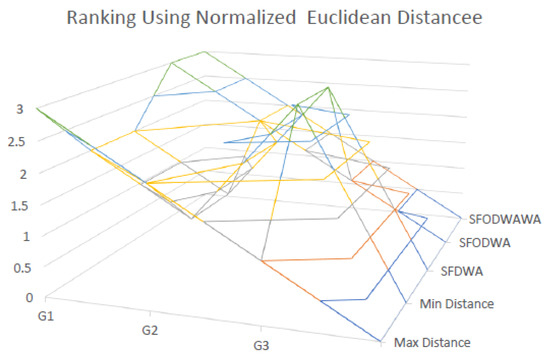
Figure 9. Final Ranking for each alternative using the normalized Euclidean distance.

Then, the ranking order of the alternative is $G_3>G_2>G_1,$ and the best outcome is $G_3.$

6. Conclusions

The distance-weighted averaging operators are generally suitable for dealing with the MCGDM problems in which the information takes the form of numerical values, yet they will fail when dealing with MCGDM problems in which the information takes the form of spherical fuzzy information. In this paper, we establish the multiple objective optimization models based on the distance-weighted averaging operators. Since in decision making, distance aggregation operators play a vital role, therefore, in this paper, we developed distance aggregation operators, namely spherical fuzzy distance-weighted averaging (SFDWA), spherical fuzzy distance order-weighted averaging (SFDOWA), and spherical fuzzy weighted averaging order-weighted averaging (SFDOWAWA) operators with information about attribute weights incompletely known. We also saw that how the SFDWA operator provided a parametric family of aggregation operator and distance measures. To determine the attribute, we proposed the optimization models based on these distance aggregated operators. Finally, we designed an algorithm to solve MCGDM problems based on these distance-weighted averaging operators under spherical fuzzy information with unknown information about the weights. The child development influence environmental factors problem was given as a practical application to demonstrate the usage and applicability of the proposed ranking approach. We saw graphically how aggregated information of an attribute is similar to the ideal strategy, the calculated distance of each attribute to the ideal strategy, and the ranking of the attributes.