The Existence and Global Exponential Stability of Almost Periodic Solutions for Neutral-Type CNNs on Time Scales

Abstract

In this paper, neutral-type competitive neural networks with mixed time-varying delays and leakage delays on time scales are proposed. Based on the contraction fixed-point theorem, some sufficient conditions that are independent of the backwards graininess function of the time scale are obtained for the existence and global exponential stability of almost periodic solutions of neural networks under consideration. The results obtained are brand new, indicating that the continuous time and discrete-time conditions of the network share the same dynamic behavior. Finally, two examples are given to illustrate the validity of the results obtained.

1. Introduction

Competitive neural networks (CNNs), which are used to characterize the dynamics of cortical maps, have two types of state variables—the short-term memory variables (STM) that characterize the fast neural activity and the long-term memory (LTM) variables that characterize the slow unsupervised synaptic modifications. Consequently, there are two time scales in CNNs, one corresponding to a rapid change in the state of the neural networks and the other corresponding to a slow change in the external stimulus to the synapse. As they are widely used in image processing, pattern recognition, signal processing and so on [1,2,3,4], many achievements have been made in the research of dynamics of CNNs in recent years [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19]. For example, the exponential stability of CNNs with multi-proportional delays was studied in [13]; the multiplicity of CNNs were studied in [14,15]; the multiperiodicity of higher-order CNNs was investigated in [16]; the anti-periodic dynamics of CNNs was discussed in [17]; the adaptive synchronization of stochastic CNNs was investigated in [18]; the finite-time synchronization of delayed CNNs with non-identical perturbations was dealt with in [19]. It is well known that the phenomenon of approximate periodicity in nature is very common, such as the motion of the sun, the moon, and stars, including repetitions in large alphabets [20]. However, the real periodicity is really rare. What is ubiquitous is the almost periodic phenomenon. However, to the best of our knowledge, so far, there have been few papers on the existence of almost periodic solutions for CNNs, especially for discrete-time CNNs. Nonetheless, because time scale theory can unify continuous and discrete systems [21], we do not have to study discrete-time neural networks alone.

On the one hand, since Bohr [22,23] introduced almost periodic functions into the field of mathematics, the concept of almost periodic functions has attracted the attention of mathematicians, and proposed various extensions of this concept, such as pseudo almost periodic functions, weighted pseudo almost periodic functions and almost automorphic functions and so on. However, to the best of our knowledge, there has been no paper published on the existence and global exponential stability of almost periodic solutions of neutral-type CNNs with mixed time-varying delays and leakage delays on time scales. Therefore, it is a challenging and important issue in theory and application.

On the other hand, to study almost periodic functions on time scales, it is necessary that time scales have some translation invariance. In [24], a concept of time scales with some global translation invariance is proposed, which is called almost periodic time scales. On such almost periodic time scales, the definitions of almost periodicity [24], pseudo almost periodicity [25], almost automorphicity [26], weighted pseudo almost automorphicity [27], set-valued functions’ almost periodicity [28], almost periodicity in the sense of Stepanov [29] and so forth are given one after another. At the same time, some research results have been obtained on this type of almost periodic time scales (see [30,31,32,33,34,35,36,37,38,39]). Since the almost periodic time scale proposed in [24] has some global translation invariance, it can effectively unify the continuous and discrete cases, while eliminating many interesting time scales. Therefore, it is a challenging and significant problem in theory and application to study almost periodic problems on time scales without such a global invariance.

Besides, it is well known that time lag is inevitable in real systems. For neural network systems, there are usually three types of time delays to consider, namely, delays in transmission, delays in leakage terms, and neutral-type delays.

Motivated by the above, in this paper, we propose the following CNNs with mixed time-varying delays and leakage delays on time scales:

$$\begin{array}{c}\hfill \left\{\begin{array}{lll}STM:x_i^{\nabla }\left(t\right)& =& -{\alpha }_i\left(t\right)x_i(t-{\eta }_i\left(t\right))+{\displaystyle \sum _{j=1}^n}{D}_{ij}\left(t\right)f_j\left(x_j\left(t\right)\right)+{\displaystyle \sum _{j=1}^n}{D}_{ij}^{\tau }\left(t\right)f_j\left(x_j(t-{\tau }_{ij}\left(t\right))\right)\\ & & +{\displaystyle \sum _{j=1}^n}{\overline{D}}_{ij}\left(t\right){\int }_{t-{\sigma }_{ij}\left(t\right)}^t{f}_j\left(x_j\left(s\right)\right)\nabla s+{\displaystyle \sum _{j=1}^n}{\tilde{D}}_{ij}\left(t\right){\int }_{t-{\zeta }_{ij}\left(t\right)}^t{f}_j(x_j^{\nabla }\left(s\right))\nabla s\\ & & +B_i\left(t\right)S_i\left(t\right)y_j+I_i\left(t\right),\\ LTM:m_{ij}^{\nabla }\left(t\right)& =& -c_i\left(t\right)m_{ij}(t-{\varsigma }_i\left(t\right))+y_j{E}_i\left(t\right)f_i\left(x_i\left(t\right)\right)+J_i\left(t\right),\end{array}\right.\end{array}$$

where $i=1,2,\dots ,n$, $\mathbb{T}$ is an almost periodic time scale, $x_i^{\nabla }\left(t\right)$ and $m_{ij}^{\nabla }\left(t\right)$ denote the nabla derivatives of $x_i\left(t\right)$ and $m_{ij}\left(t\right)$ at time t, respectively, $x_i\left(t\right)$ is the neuron current activity level, ${\alpha }_i\left(t\right),c_i\left(t\right)$ are the time variable of the neuron, $f_j\left(x_j\left(t\right)\right)$ is the output of neurons, $m_{ij}\left(t\right)$ is the synaptic efficiency, $y_i$ is the constant external stimulus, $D_{ij}\left(t\right)$ and $D_{ij}^{\tau }\left(t\right)$, ${\overline{D}}_{ij}\left(t\right)$ and ${\tilde{D}}_{ij}\left(t\right)$ are the connection weights and the synaptic weights of delayed feedback between the ith neuron and the jth neuron, respectively, $B_i\left(t\right)$ corresponds to the strength of the external stimulus, $E_i\left(t\right)$ represents disposable scale, $I_i\left(t\right)$, $J_i\left(t\right)$ are the external inputs on the ith neuron at time t, ${\eta }_i\left(t\right)$ and ${\varsigma }_i\left(t\right)$ correspond to leakage delays and satisfy $t-{\eta }_i\left(t\right)\in \mathbb{T}$, $t-{\varsigma }_i\left(t\right)\in \mathbb{T}$ for $t\in \mathbb{T}$, ${\tau }_{ij}\left(t\right)$, ${\sigma }_{ij}\left(t\right)$ and ${\zeta }_{ij}\left(t\right)$ are transmission delays and satisfy $t-{\tau }_{ij}\left(t\right)\in \mathbb{T}$, $t-{\sigma }_{ij}\left(t\right)\in \mathbb{T}$, $t-{\zeta }_{ij}\left(t\right)\in \mathbb{T}$ for $t\in \mathbb{T}$.

Setting $S_i={\displaystyle {\displaystyle \sum }_{j=1}^n}{m}_{ij}\left(t\right)y_i={\mathbf{y}}^T{\mathbf{m}}_i\left(t\right)$, where $\mathbf{y}={(y_1,y_2,\dots ,y_n)}^T,{\mathbf{m}}_i={(m_{i1},m_{i2},\dots ,m_{in})}^T$ and, without loss of generality, the input stimulus $\mathbf{y}$ is assumed to be normalized with unit magnitude ${\left|\mathbf{y}\right|}^2=1$, summing up the LTM over j, then the above networks are simplified as the networks:

$$\begin{array}{c}\hfill \left\{\begin{array}{lll}STM:x_i^{\nabla }\left(t\right)& =& -{\alpha }_i\left(t\right)x_i(t-{\eta }_i\left(t\right))+{\displaystyle \sum _{j=1}^n}{D}_{ij}\left(t\right)f_j\left(x_j\left(t\right)\right)+{\displaystyle \sum _{j=1}^n}{D}_{ij}^{\tau }\left(t\right)f_j\left(x_j(t-{\tau }_{ij}\left(t\right))\right)\\ & & +{\displaystyle \sum _{j=1}^n}{\overline{D}}_{ij}\left(t\right){\int }_{t-{\sigma }_{ij}\left(t\right)}^t{f}_j\left(x_j\left(s\right)\right)\nabla s+{\displaystyle \sum _{j=1}^n}{\tilde{D}}_{ij}\left(t\right){\int }_{t-{\zeta }_{ij}\left(t\right)}^t{f}_j(x_j^{\nabla }\left(s\right))\nabla s\\ & & +B_i\left(t\right)S_i\left(t\right)+I_i\left(t\right),\\ LTM:S_i^{\nabla }\left(t\right)& =& -c_i\left(t\right)S_i(t-{\varsigma }_i\left(t\right))+E_i\left(t\right)f_i\left(x_i\left(t\right)\right)+J_i\left(t\right).\end{array}\right.\end{array}$$

(1)

For convenience, for almost periodic functions on time scales, we introduce the following notations:

$${\alpha }_i^{+}={\displaystyle \underset{t\in \mathbb{T}}{sup}}|{\alpha }_i\left(t\right)|,{\alpha }_i^{-}={\displaystyle \underset{t\in \mathbb{T}}{inf}}|{\alpha }_i\left(t\right)|,c_i^{+}={\displaystyle \underset{t\in \mathbb{T}}{sup}}|c_i\left(t\right)|,c_i^{-}={\displaystyle \underset{t\in \mathbb{T}}{inf}}|c_i\left(t\right)|,$$

$${\eta }_i^{+}={\displaystyle \underset{t\in \mathbb{T}}{sup}}|{\eta }_i\left(t\right)|,{\varsigma }_i^{+}={\displaystyle \underset{t\in \mathbb{T}}{sup}}|{\varsigma }_i\left(t\right)|,D_{ij}^{+}={\displaystyle \underset{t\in \mathbb{T}}{sup}}|D_{ij}\left(t\right)|,{(D_{ij}^{\tau })}^{+}={\displaystyle \underset{t\in \mathbb{T}}{sup}}|D_{ij}^{\tau }\left(t\right)|,$$

$${\overline{D}}_{ij}^{+}={\displaystyle \underset{t\in \mathbb{T}}{sup}}|{\overline{D}}_{ij}\left(t\right)|,{\tilde{D}}_{ij}^{+}={\displaystyle \underset{t\in \mathbb{T}}{sup}}|{\tilde{D}}_{ij}\left(t\right)|,B_i^{+}={\displaystyle \underset{t\in \mathbb{T}}{sup}}|B_i\left(t\right)|,E_i^{+}={\displaystyle \underset{t\in \mathbb{T}}{sup}}|E_i\left(t\right)|,$$

$${\tau }_{ij}^{+}={\displaystyle \underset{t\in \mathbb{T}}{sup}}|{\tau }_{ij}\left(t\right)|,{\sigma }_{ij}^{+}={\displaystyle \underset{t\in \mathbb{T}}{sup}}|{\sigma }_{ij}\left(t\right)|,{\zeta }_{ij}^{+}={\displaystyle \underset{t\in \mathbb{T}}{sup}}|{\zeta }_{ij}\left(t\right)|,i,j=1,2,\cdots ,n.$$

We denote ${[a,b]}_{\mathbb{T}}=\left\{t\right|t\in [a,b]\cap \mathbb{T}\}$. The initial condition associated with system (1) is

$$\begin{array}{c}{x}_i\left(s\right)={\varphi }_i\left(s\right),s\in {[-\theta ,0]}_{\mathbb{T}},\hfill \end{array}$$

(2)

$$\begin{array}{c}{S}_i\left(s\right)={\psi }_i\left(s\right),s\in {[-\theta ,0]}_{\mathbb{T}},\hfill \end{array}$$

(3)

where $i=1,2,\cdots ,n$, $\theta =max\{\delta ,\tau ,\sigma ,\zeta ,\varsigma \}$, $\delta ={\displaystyle \underset{1\le i\le n}{max}}\{{\delta }_i^{+}\}$, $\tau ={\displaystyle \underset{1\le i,j\le n}{max}}\{{\tau }_{ij}^{+}\}$, $\sigma ={\displaystyle \underset{1\le i,j\le n}{max}}\{{\sigma }_{ij}^{+}\}$, $\zeta ={\displaystyle \underset{1\le i,j,\le n}{max}}\{{\zeta }_{ij}^{+}\}$, $\varsigma ={\displaystyle \underset{1\le i\le n}{max}}\{{\varsigma }_i^{+}\}$, $i,j=1,2,\dots ,n$, ${\varphi }_i(·)$, ${\psi }_i(·)$ are real-valued bounded ∇-differentiable functions defined on ${[-\theta ,0]}_{\mathbb{T}}$.

Our main purpose of this paper is to study the existence and stability of almost periodic solutions of $\left(1\right)$ on a new almost periodic time scale $\mathbb{T}$ which will be defined in the next section.

This paper is organized as follows. In Section 2, we make some preparations for later sections. In Section 3, we study the existence of almost periodic solutions of $\left(1\right)$. In Section 4, we investigate the stability of the almost periodic solution of $\left(1\right)$. In Section 5, we present an example to illustrate the feasibility of the obtained results. Finally, we give a brief discussion in Section 6.

2. Preliminaries

A time scale $\mathbb{T}$ is a nonempty closed subset of the real set $\mathbb{R}$ with the topology from $\mathbb{R}$. The forward jump and the backwards jump operators $\sigma ,\rho \left(t\right):\mathbb{T}\to \mathbb{T}$ are defined by $\sigma \left(t\right)=inf\left\{s\in \mathbb{T},s>t\right\}$ and $\rho \left(t\right)=sup\left\{s\in \mathbb{T},s<t\right\}$, respectively, and the backwards graininess function $\nu :{\mathbb{T}}_k\to [0,\infty )$ is defined by $\nu \left(t\right)=t-\rho \left(t\right)$. For more terminology and symbols of time scale theory, see [21].

Definition 1.

Let $f:\mathbb{T}\to \mathbb{R}$ be a function and $t\in {\mathbb{T}}_k$ [21]. Then we define $f^{\nabla }\left(t\right)$ to be the number (provided it exists) with the property that given any $\epsilon >0$, there is a neighborhood U of t (i.e., $U=(t-\delta ,t+\delta )\cap \mathbb{T}$ for some $\delta >0$) such that

$$|f\left(\rho \left(t\right)\right)-f\left(s\right)-f^{\nabla }\left(t\right)(\rho \left(t\right)-s)|\le \epsilon |\rho \left(t\right)-s|$$

for all $s\in U$, we call $f^{\nabla }\left(t\right)$ the nabla derivative of f at t.

For every ld-continuous function $f:\mathbb{T}\to \mathbb{R}$, if $F^{\nabla }\left(t\right)=f\left(t\right)$, then we define ${\int }_a^{b}f\left(t\right)\nabla t=F\left(b\right)-F\left(a\right)$.

A function $p:\mathbb{T}\to \mathbb{R}$ is said to be $\nu$-regressive if $1-\nu \left(t\right)p\left(t\right)\ne 0$ for $t\in {\mathbb{T}}_k$. We denote by ${\mathcal{R}}_{\nu }={\mathcal{R}}_{\nu }(\mathbb{T},\mathbb{R})$, the set of all $\nu$-regressive and ld-continuous functions, and define ${\mathcal{R}}_{\nu }^{+}=\{p\in {\mathcal{R}}_{\nu }:1-\nu \left(t\right)p\left(t\right)>0,\forall t\in \mathbb{T}\}$.

For $p\in {\mathcal{R}}_{\nu }$, we define the nabla exponential function as follow:

$${\widehat{e}}_p(t,s)=exp\left({\int }_s^t{\widehat{\xi }}_{\nu \left(\tau \right)}\left(p\left(\tau \right)\right)\nabla \tau \right),\mathrm{for}t,s\in \mathbb{T},$$

where

$${\widehat{\xi }}_h\left(z\right)=\{\begin{array}{ll}-\frac{\log (1-hz)}{h}& \mathrm{if}h\ne 0,\\ z& \mathrm{if}h=0.\end{array}$$

For $p,q\in {\mathcal{R}}_{\nu }$, we define a circle plus addition by $\left(p{\oplus }_{\nu }q\right)\left(t\right)=p\left(t\right)+q\left(t\right)-\nu \left(t\right)p\left(t\right)q\left(t\right)$, for all $t\in {\mathbb{T}}_k$. For $p\in {\mathcal{R}}_{\nu }$, define a circle minus p by ${\ominus }_{\nu }p=-\frac{p}{1-\nu p}$.

Lemma 1.

Let $p,q\in {\mathcal{R}}_{\nu }$, and $s,t,r\in \mathbb{T}$ [21]. Then

(i)

${\widehat{e}}_p(\rho \left(t\right),s)=(1-\nu \left(t\right)p\left(t\right)){\widehat{e}}_p(t,s)$;

(ii)

${\widehat{e}}_p(t,s)=\frac{1}{{\widehat{e}}_p(s,t)}={\widehat{e}}_{{\ominus }_{\nu }p}(s,t)$;

(iii)

${\widehat{e}}_p(t,s){\widehat{e}}_p(s,r)={\widehat{e}}_p(t,r)$;

(iv)

${\left({\widehat{e}}_p(t,s)\right)}^{\nabla }=p\left(t\right){\widehat{e}}_p(t,s)$.

Lemma 2.

Assume $p\in {\mathcal{R}}_{\nu }$ and $t_0\in \mathbb{T}$. If $1-\nu \left(t\right)p\left(t\right)>0$ for $t\in \mathbb{T}$, then ${\widehat{e}}_p(t,t_0)>0$ for all $t\in \mathbb{T}$ [21].

Definition 2.

A time scale $\mathbb{T}$ is called an almost periodic time scale [24] if

$$\mathsf{\Pi }=\left\{\tau \in \mathbb{R}:t\pm \tau \in \mathbb{T},\forall t\in \mathbb{T}\right\}\ne \left\{0\right\}.$$

Definition 3.

A time scale $\mathbb{T}$ is called an almost periodic time scale [40] if the set

$${\mathsf{\Lambda }}_0:=\left\{\tau \in \mathbb{R}:{\mathbb{T}}_{\pm \tau }\ne \varnothing \right\}\ne \left\{0\right\},$$

where ${\mathbb{T}}_{\pm \tau }=\mathbb{T}\cap \{\mathbb{T}\mp \tau \}=\mathbb{T}\cap \{t\mp \tau :t\in \mathbb{T}\}$, and there exists a set Λ satisfying

(a)

$0\in \mathsf{\Lambda }\subseteq {\mathsf{\Lambda }}_0$,

(b)

$\mathsf{\Pi }\left(\mathsf{\Lambda }\right)\backslash \left\{0\right\}\ne \varnothing$,

(c)

$\tilde{\mathbb{T}}:=\mathbb{T}\left(\mathsf{\Pi }\right)={\displaystyle {\displaystyle \bigcap }_{\tau \in \mathsf{\Pi }}}{\mathbb{T}}_{\tau }\ne \varnothing$,

where $\mathsf{\Pi }:=\mathsf{\Pi }\left(\mathsf{\Lambda }\right)=\{\tau \in \mathsf{\Lambda }\subseteq {\mathsf{\Lambda }}_0:\sigma \pm \tau \in \mathsf{\Lambda },\forall \sigma \in \mathsf{\Lambda }\}$.

Obviously, if $t\in {\mathbb{T}}_{\tau }$, then $t+\tau \in \mathbb{T}.$ If $t\in \tilde{\mathbb{T}}$, then $t\pm \tau \in \mathbb{T}$ for $\tau \in \mathsf{\Pi }$.

Lemma 3.

Let $\mathbb{T}$ be almost periodic in the sense of Definition 3 [40]. Then $\tilde{\mathbb{T}}$ is also almost periodic in the sense of Definition 2.

In the following, we restrict our discussion on an almost periodic time scale $\mathbb{T}$ that is defined by Definition 3.

Lemma 4.

Let t be a right-dense point in time scale $\tilde{\mathbb{T}}$ [40]. Then it is also a right-dense point in time scale $\mathbb{T}$.

Lemma 5.

Let t be a left-dense point in time scale $\tilde{\mathbb{T}}$ [40]. Then t is a left-dense point in time scale $\mathbb{T}$.

Let $f\in C(\mathbb{T},\mathbb{R})$, we denote by $\tilde{f}$ the restriction of f on $\tilde{\mathbb{T}}$. It follows from Lemmas 4 and 5 that $\tilde{f}\in C(\tilde{\mathbb{T}},\mathbb{R})$. Hence,

$$F\left(t\right)={\int }_{t_0}^t\tilde{f}\left(\tau \right)\tilde{\nabla }\tau ,t_0,t\in \tilde{\mathbb{T}}$$

is an antiderivative of f on $\tilde{\mathbb{T}}$, where $\tilde{\nabla }$ denotes the ∇-derivative on $\tilde{\mathbb{T}}$.

For each $f\in C(\mathbb{T},\mathbb{R})$, we define $\tilde{f}:\tilde{\mathbb{T}}\to \mathbb{R}$ by $\tilde{f}\left(t\right)=f\left(t\right)$ for $t\in \tilde{\mathbb{T}}$. From Lemmas 4 and 5, we can get that $\tilde{f}\in C(\tilde{\mathbb{T}},\mathbb{R})$. Therefore, F defined by

$$F\left(t\right):={\int }_{t_0}^t\tilde{f}\left(\tau \right)\tilde{\nabla }\tau ,t_0,t\in \tilde{\mathbb{T}}$$

is an antiderivative of f on $\tilde{\mathbb{T}}$, where $\tilde{\nabla }$ denotes the ∇-derivative on $\tilde{\mathbb{T}}$.

Let $BUC(\mathbb{T}\times D,{\mathbb{R}}^n)$ denote the collection of all bounded uniformly continuous functions from $\mathbb{T}\times S$ to ${\mathbb{R}}^n$, where $S\subset D$ is any compact set. We introduce the following definition of almost periodic functions on time scales as follows.

Definition 4.

In the sense of Definition 3, let $\mathbb{T}$ be almost periodic [40]. Function $f\in BUC(\mathbb{T}\times D,{\mathbb{E}}^n)$ is said to be almost periodic in $t\in \mathbb{T}$ uniformly for $x\in D$ if for every $\epsilon >0$ and each compact subset S of D, there exists a constant $l(\epsilon ,S)>0$ such that in each interval of length $l(\epsilon ,S)$ in $\mathbb{T}$, one can find a $\tau (\epsilon ,S)$ such that

$$|f(t+\tau ,x)-f(t,x)|<\epsilon ,\forall (t,x)\in \tilde{\mathbb{T}}\times S.$$

The set of all such functions will be denoted by $AP(\mathbb{T}\times D,{\mathbb{E}}^n)$.

Definition 5.

Let $A\left(t\right)$ be an $n\times n$ matrix-valued function on $\mathbb{T}$ [41]. Then the linear system

$$x^{\nabla }\left(t\right)=A\left(t\right)x\left(t\right),t\in \mathbb{T}$$

(4)

is said to admit an exponential dichotomy on $\mathbb{T}$ if there exist positive constants $K,\alpha$, projection P, and the fundamental solution matrix $X\left(t\right)$ of (4), satisfying

$$\begin{array}{r}\parallel X\left(t\right)P{X}^{-1}{\left(s\right)\parallel }_0\le K{\widehat{e}}_{{\ominus }_{\nu }\alpha }(t,s),s,t\in \mathbb{T},t\ge s,\\ \parallel X\left(t\right)(I-P)X^{-1}{\left(s\right)\parallel }_0\le K{\widehat{e}}_{{\ominus }_{\nu }\alpha }(s,t),s,t\in \mathbb{T},t\le s,\end{array}$$

where ${\parallel ·\parallel }_0$ is a matrix norm on $\mathbb{T}$.

Consider the linear non-homogeneous system

$$x^{\nabla }\left(t\right)=A\left(t\right)x\left(t\right)+f\left(t\right),t\in \mathbb{T},$$

(5)

where $A\left(t\right)$ is a matrix function, $f\left(t\right)$ is a vector function.

Lemma 6.

If system (4) admits exponential dichotomy [41], then system (5) has a bounded solution

$$x\left(t\right)={\int }_{-\infty }^{t}X\left(t\right)P{X}^{-1}\left(\rho \left(s\right)\right)f\left(s\right)\nabla s-{\int }_t^{+\infty }X\left(t\right)(I-P)X^{-1}\left(\rho \left(s\right)\right)f\left(s\right)\nabla s,$$

where $X\left(t\right)$ is the fundamental solution matrix of (4).

Lemma 7.

Let $c_i\in AP(\mathbb{T},\mathbb{R})$ [41], where $c_i\in {\mathcal{R}}_{\nu }^{+}$ and ${\displaystyle \underset{1\le i\le n}{min}}\{{\displaystyle \underset{t\in \mathbb{T}}{inf}}{c}_i\left(t\right)\}>0$, then the linear system

$$x^{\nabla }\left(t\right)=\mathrm{diag}(-c_1\left(t\right),-c_2\left(t\right),\cdots ,-c_n\left(t\right))x\left(t\right)$$

(6)

admits an exponential dichotomy on $\mathbb{T}$.

By Lemma 2.7 in [41], we have

Lemma 8.

In system (5), assume that $A\left(t\right)$ and $f\left(t\right)$ are almost periodic. Then, if system (4) admits an exponential dichotomy, then system (5) has one and only one almost periodic solution:

$$x\left(t\right)={\int }_{-\infty }^t\tilde{X}\left(t\right)P{\tilde{X}}^{-1}\left(\tilde{\sigma }\left(s\right)\right)\tilde{f}\left(s\right)\tilde{\nabla }s-{\int }_t^{+\infty }\tilde{X}\left(t\right)(I-P){\tilde{X}}^{-1}\left(\tilde{\sigma }\left(s\right)\right)\tilde{f}\left(s\right)\tilde{\nabla }s,t\in \tilde{\mathbb{T}},$$

where $\tilde{X}\left(t\right)$ is the restriction of the fundamental solution matrix of (4) on $\tilde{\mathbb{T}}$.

From Definition 4 and Lemmas 6 and 8, one can easily get the following lemma.

Lemma 9.

If linear system (4) admits an exponential dichotomy, then system (5) has an almost periodic solution $x\left(t\right)$ can be expressed as:

$$x\left(t\right)={\int }_{-\infty }^{t}X\left(t\right)P{X}^{-1}\left(\sigma \left(s\right)\right)f\left(s\right)\nabla s-{\int }_t^{+\infty }X\left(t\right)(I-P)X^{-1}\left(\sigma \left(s\right)\right)f\left(s\right)\nabla s,t\in \mathbb{T},$$

where $X\left(t\right)$ is the fundamental solution matrix of (4).

3. The Existence of Almost Periodic Solution

In this section, we will state and prove the sufficient conditions for the existence of almost periodic solutions of (1).

Let $\mathbb{X}=\left\{z={({\varphi }_1,{\varphi }_2,\dots ,{\varphi }_n,{\psi }_1,{\psi }_2,\dots ,{\psi }_n)}^T:{\varphi }_i,{\psi }_i\in C^1(\mathbb{T},\mathbb{R})\cap AP(\mathbb{T},\mathbb{R}),i=1,2,\dots ,n\right\}$ with the norm ${\parallel z\parallel }_{\mathbb{X}}={\displaystyle \underset{t\in \mathbb{T}}{sup}}\parallel z\left(t\right)\parallel$, where $\parallel z\left(t\right)\parallel ={\displaystyle \underset{1\le i\le n}{max}}\left\{\right|{\varphi }_i\left(t\right)|,|{\psi }_i\left(t\right)|,|{\varphi }_i^{\nabla }\left(t\right)|,|{\psi }_i^{\nabla }\left(t\right)\left|\right\}$, then $\mathbb{X}$ is a Banach space.

In the sequel, we make the following assumptions:

$\left(A_1\right)$ 

For $i,j=1,2,\cdots ,n$, ${\alpha }_i,c_i\in {\mathcal{R}}_{\nu }^{+}\cap AP(\mathbb{T},\mathbb{R})$ with ${\alpha }_i^{-}>0$ and $c_i^{-}>0,$ $D_{ij},D_{ij}^{\tau },{\overline{D}}_{ij},{\tilde{D}}_{ij},B_i,E_i,{\eta }_i,{\varsigma }_i,{\tau }_{ij},{\sigma }_{ij},{\zeta }_{ij},I_i,J_i\in AP(\mathbb{T},\mathbb{R})$.

$\left(A_2\right)$ 

The function $f_j\in C(\mathbb{R},\mathbb{R})$ and there exists positive constant $L_j$ such that

$$|f_j\left(x\right)-f_j\left(y\right)|\le L_j|x-y|,x,y\in \mathbb{R},j=1,2,\cdots ,n.$$

Theorem 1.

Assume that Let $\left(A_1\right)$, $\left(A_2\right)$ and the following condition hold:

$\left(A_3\right)$

there exists a constant K such that

$$\begin{array}{l}{\displaystyle \underset{1\le i\le n}{max}}\left\{\frac{P_i}{{\alpha }_i^{-}},\left(1+\frac{{\alpha }_i^{+}}{{\alpha }_i^{-}}\right)P_i,\frac{Q_i}{c_i^{-}},\left(1+\frac{c_i^{+}}{c_i^{-}}\right)Q_i\right\}\le K,\\ {\displaystyle \underset{1\le i\le n}{max}}\left\{\frac{\overline{P_i}}{{\alpha }_i^{-}},\left(1+\frac{{\alpha }_i^{+}}{{\alpha }_i^{-}}\right)\overline{P_i},\frac{\overline{Q_i}}{c_i^{-}},\left(1+\frac{c_i^{+}}{c_i^{-}}\right)\overline{Q_i}\right\}:=\kappa <1,\end{array}$$

where

$$\begin{array}{ccc}\hfill P_i& =& {\alpha }_i^{+}{\eta }_i^{+}K+{\displaystyle \sum _{j=1}^n}{D}_{ij}^{+}(L_{j}K+|f_j\left(0\right)\left|\right)+{\displaystyle \sum _{j=1}^n}{\left(D_{ij}^{\tau }\right)}^{+}(L_{j}K+|f_j\left(0\right)\left|\right)\hfill \\ & & +{\displaystyle \sum _{j=1}^n}{\overline{D}}_{ij}^{+}{\sigma }_{ij}^{+}(L_{j}K+|f_j\left(0\right)\left|\right)+{\displaystyle \sum _{j=1}^n}{\tilde{D}}_{ij}^{+}{\zeta }_{ij}^{+}(L_{j}K+|f_j\left(0\right)\left|\right)+B_i^{+}K+I_i^{+},\hfill \\ \hfill Q_i& =& c_i^{+}{\varsigma }_i^{+}K+E_i^{+}(L_{i}K+|f_i\left(0\right)\left|\right)+J_i^{+},\hfill \\ \hfill \overline{P_i}& =& a_i^{+}{\eta }_i^{+}+{\displaystyle \sum _{j=1}^n}{D}_{ij}^{+}{L}_j+{\displaystyle \sum _{j=1}^n}{\left(D_{ij}^{\tau }\right)}^{+}{L}_j+{\displaystyle \sum _{j=1}^n}{\overline{D}}_{ij}^{+}{\sigma }_{ij}^{+}{L}_j+{\displaystyle \sum _{j=1}^n}{\tilde{D}}_{ij}^{+}{\zeta }_{ij}^{+}{L}_j+B_i^{+},\hfill \\ \hfill \overline{Q_i}& =& c_i^{+}{\varsigma }_i^{+}+E_i^{+}{L}_i,i=1,2,\dots ,n.\hfill \end{array}$$

Then (1) has a unique almost periodic solution in ${\mathbb{X}}^{*}={\{z\in \mathbb{X}:\parallel z\parallel }_{\mathbb{X}}\le K\}$.

Proof. 

System (1) can be written as

$$\begin{array}{ccc}\hfill x_i^{\nabla }\left(t\right)& =& -{\alpha }_i\left(t\right)x_i\left(t\right)+{\alpha }_i\left(t\right){\int }_{t-{\eta }_i\left(t\right)}^t{x}_i^{\nabla }\left(s\right)\nabla s+{\displaystyle \sum _{j=1}^n}{D}_{ij}\left(t\right)f_j\left(x_j\left(t\right)\right)\hfill \\ & & +{\displaystyle \sum _{j=1}^n}{D}_{ij}^{\tau }\left(t\right)f_j\left(x_j(t-{\tau }_{ij}\left(t\right))\right)+{\displaystyle \sum _{j=1}^n}{\overline{D}}_{ij}\left(t\right){\int }_{t-{\sigma }_{ij}\left(t\right)}^t{f}_j\left(x_j\left(s\right)\right)\nabla s\hfill \\ & & +{\displaystyle \sum _{j=1}^n}{\tilde{D}}_{ij}\left(t\right){\int }_{t-{\zeta }_{ij}\left(t\right)}^t{f}_j\left(x_j^{\nabla }\left(s\right)\right)\nabla s+B_i\left(t\right)S_i\left(t\right)+I_i\left(t\right),i=1,2,\cdots ,n,\hfill \\ \hfill S_i^{\nabla }\left(t\right)& =& -c_i\left(t\right)S_i\left(t\right)+c_i\left(t\right){\int }_{t-{\varsigma }_i\left(t\right)}^t{S}_i^{\nabla }\left(s\right)\nabla s+E_i\left(t\right)f_i\left(x_i\left(t\right)\right)+J_i\left(t\right),i=1,2,\cdots ,n.\hfill \end{array}$$

For every $z=({\varphi }_1,{\varphi }_2,\dots ,{\varphi }_n,{\psi }_1,{\psi }_2,\dots ,{\psi }_n)\in \mathbb{X}$, consider the following auxiliary system

$$\begin{array}{c}\hfill \left\{\begin{array}{ccc}{x}_i^{\nabla }\left(t\right)\hfill & =\hfill & -{\alpha }_i\left(t\right)x_i\left(t\right)+{\mathsf{\Gamma }}_i(t,\varphi ),t\in \mathbb{T},i=1,2,\dots ,n,\hfill \\ S_i^{\nabla }\left(t\right)\hfill & =\hfill & -c_i\left(t\right)S_i\left(t\right)+{\Theta }_i(t,\psi ),t\in \mathbb{T},i=1,2,\dots ,n,\hfill \end{array}\right.\end{array}$$

(7)

in which

$$\begin{array}{ccc}\hfill {\mathsf{\Gamma }}_i(t,\varphi )& =& {\alpha }_i\left(t\right){\int }_{t-{\eta }_i\left(t\right)}^t{\varphi }_i^{\nabla }\left(s\right)\nabla s+{\displaystyle \sum _{j=1}^n}{D}_{ij}\left(t\right)f_j\left({\varphi }_j\left(t\right)\right)\hfill \\ & & +{\displaystyle \sum _{j=1}^n}{D}_{ij}^{\tau }\left(t\right)f_j\left({\varphi }_j(t-{\tau }_{ij}\left(t\right))\right)+{\displaystyle \sum _{j=1}^n}{\overline{D}}_{ij}\left(t\right){\int }_{t-{\sigma }_{ij}\left(t\right)}^t{f}_j\left({\varphi }_j\left(s\right)\right)\nabla s\hfill \\ & & +{\displaystyle \sum _{j=1}^n}{\tilde{D}}_{ij}\left(t\right){\int }_{t-{\zeta }_{ij}\left(t\right)}^t{f}_j\left({\varphi }_j^{\nabla }\left(s\right)\right)\nabla s+B_i\left(t\right){\psi }_i\left(t\right)+I_i\left(t\right),i=1,2,\dots ,n,\hfill \\ \hfill {\Theta }_i(t,\psi )& =& c_i\left(t\right){\int }_{t-{\varsigma }_i\left(t\right)}^t{\psi }_i^{\nabla }\left(s\right)\nabla s+E_i\left(t\right)f_i\left({\varphi }_i\left(t\right)\right)+J_i\left(t\right),i=1,2,\dots ,n.\hfill \end{array}$$

According to $\left(A_1\right)$ and Lemma 7, we see that the corresponding homogeneous linear system of (7) admits an exponential dichotomy on $\mathbb{T}$. Therefore, in view of Lemma 9, we obtain that system (7) has a unique almost periodic solution

$$y_z\left(t\right)={(x_{{\varphi }_1}\left(t\right),x_{{\varphi }_2}\left(t\right),\dots ,x_{{\varphi }_n}\left(t\right),S_{{\psi }_1}\left(t\right),S_{{\psi }_2}\left(t\right),\dots ,S_{{\psi }_n}\left(t\right))}^T,$$

where

$$\left\{\begin{array}{c}{x}_{{\varphi }_i}\left(t\right)={\int }_{-\infty }^t{\widehat{e}}_{-{\alpha }_i}(t,\rho \left(s\right)){\mathsf{\Gamma }}_i(s,\varphi )\nabla s,i=1,2,\dots ,n,\hfill \\ S_{{\psi }_i}\left(t\right)={\int }_{-\infty }^t{\widehat{e}}_{-c_i}(t,\rho \left(s\right)){\Theta }_i(s,\psi )\nabla s,i=1,2,\dots ,n.\hfill \end{array}\right.$$

(8)

Define a mapping $\mathcal{F}:{\mathbb{X}}^{*}\to \mathbb{X}$ by setting

$$\mathcal{F}\left(z\left(t\right)\right)=y_z\left(t\right),z\in {\mathbb{X}}^{*}.$$

We will prove that $\mathcal{F}$ is a self-mapping and a contraction mapping.

First, we shall prove that $\mathcal{F}z\in {\mathbb{X}}^{*}$ for all $z\in {\mathbb{X}}^{*}$. In fact, for $i=1,2,\dots ,n$,

$$\begin{array}{cc}& |{\mathsf{\Gamma }}_i(s,\varphi )|\hfill \\ =& |{\alpha }_i(s){\int }_{s-{\eta }_i(s)}^s{\varphi }_i^{\nabla }(u)\nabla u+{\displaystyle \sum _{j=1}^n}{D}_{ij}(s)f_j({\varphi }_j(s))\hfill \\ & +{\displaystyle \sum _{j=1}^n}{D}_{ij}^{\tau }(s)f_j({\varphi }_j(s-{\tau }_{ij}(s)))+{\displaystyle \sum _{j=1}^n}{\overline{D}}_{ij}(s){\int }_{s-{\sigma }_{ij}(s)}^s{f}_j({\varphi }_j(u))\nabla u\hfill \\ & +{\displaystyle \sum _{j=1}^n}{\tilde{D}}_{ij}(s){\int }_{s-{\zeta }_{ij}(s)}^s{f}_j({\varphi }_j^{\nabla }(u))\nabla u+B_i(s){\psi }_i(s)+I_i(s)|\hfill \\ \le & {\alpha }_i^{+}{\int }_{s-{\eta }_i(s)}^s|{\varphi }_i^{\nabla }(u)|\nabla u+{\displaystyle \sum _{j=1}^n}{D}_{ij}^{+}\left|f_j({\varphi }_j(s))\right|\hfill \\ & +{\displaystyle \sum _{j=1}^n}{(D_{ij}^{\tau })}^{+}|f_j({\varphi }_j(s-{\tau }_{ij}(s)))|+{\displaystyle \sum _{j=1}^n}{\overline{D}}_{ij}^{+}{\int }_{s-{\sigma }_{ij}(s)}^s\left|f_j({\varphi }_j(u))\right|\nabla u\hfill \\ & +{\displaystyle \sum _{j=1}^n}{\tilde{D}}_{ij}^{+}{\int }_{s-{\zeta }_{ij}(s)}^s|f_j({\varphi }_j^{\nabla }(u))|\nabla u+B_i^{+}\left|{\psi }_i(s)\right|+I_i^{+}\hfill \\ \le & {\alpha }_i^{+}{\eta }_i^{+}K+{\displaystyle \sum _{j=1}^n}{D}_{ij}^{+}(L_j|{\varphi }_j(s)|+|f_j(0)|)+{\displaystyle \sum _{j=1}^n}{(D_{ij}^{\tau })}^{+}(L_j|{\varphi }_j(s-{\tau }_{ij}(s))|+|f_j(0)|)\hfill \\ & +{\displaystyle \sum _{j=1}^n}{\overline{D}}_{ij}^{+}{\sigma }_{ij}^{+}(L_{j}K+|f_j(0)|)+{\displaystyle \sum _{j=1}^n}{\tilde{D}}_{ij}^{+}{\zeta }_{ij}^{+}(L_{j}K+|f_j(0)|)+B_i^{+}\left|{\psi }_i(s)\right|+I_i^{+}\hfill \\ \le & {\alpha }_i^{+}{\eta }_i^{+}K+{\displaystyle \sum _{j=1}^n}{D}_{ij}^{+}(L_{j}K+|f_j(0)|)+{\displaystyle \sum _{j=1}^n}{(D_{ij}^{\tau })}^{+}(L_{j}K+|f_j(0)|)\hfill \\ & +{\displaystyle \sum _{j=1}^n}{\overline{D}}_{ij}^{+}{\sigma }_{ij}^{+}(L_{j}K+|f_j(0)|)+{\displaystyle \sum _{j=1}^n}{\tilde{D}}_{ij}^{+}{\zeta }_{ij}^{+}(L_{j}K+|f_j(0)|)+B_i^{+}K+I_i^{+}=P_i\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill |{\Theta }_i(s,\psi )|& =& |c_i(s){\int }_{s-{\varsigma }_i(s)}^s{\psi }_i^{\nabla }(u)\nabla s+E_i(s)f_i({\varphi }_i(s))+J_i(s)|\hfill \\ & \le & c_i^{+}{\int }_{s-{\varsigma }_i(s)}^s|{\psi }_i^{\nabla }(u)|\nabla u+E_i^{+}\left|f_i({\varphi }_i(s))\right|+J_i^{+}\hfill \\ & \le & c_i^{+}{\varsigma }_i^{+}|{\psi }_i^{\nabla }(s)|+E_i^{+}(L_i|{\varphi }_i(s)|+|f_i(0)|)+J_i^{+}\hfill \\ & \le & c_i^{+}{\varsigma }_i^{+}K+E_i^{+}(L_{i}K+|f_i(0)|)+J_i^{+}=Q_i.\hfill \end{array}$$

Hence, based on the above inequalities and (8), for $i=1,2,\dots ,n$, we find

$$\begin{array}{cc}& {\displaystyle \underset{t\in \mathbb{T}}{sup}}\left|x_{{\varphi }_i}\left(t\right)\right|\hfill \\ =& {\displaystyle \underset{t\in \mathbb{T}}{sup}}|{\int }_{-\infty }^t{\widehat{e}}_{-{\alpha }_i}(t,\rho \left(s\right)){\mathsf{\Gamma }}_i(s,\varphi )\nabla s|\hfill \\ \le & {\displaystyle \underset{t\in \mathbb{T}}{sup}}{\int }_{-\infty }^t{\widehat{e}}_{-{\alpha }_i^{-}}(t,\rho \left(s\right))|{\mathsf{\Gamma }}_i(s,\varphi )|\nabla s\hfill \\ \le & \frac{1}{{\alpha }_i^{-}}\left[\right({\alpha }_i^{+}{\eta }_i^{+}+{\displaystyle \sum _{j=1}^n}{D}_{ij}^{+}(L_j+|f_j\left(0\right)\left|\right)+{\displaystyle \sum _{j=1}^n}{(D_{ij}^{\tau })}^{+}(L_j+|f_j\left(0\right)\left|\right)\hfill \\ & +{\displaystyle \sum _{j=1}^n}{\overline{D}}_{ij}^{+}{\sigma }_{ij}^{+}(L_j+|f_j\left(0\right)\left|\right)+{\displaystyle \sum _{j=1}^n}{\tilde{D}}_{ij}^{+}{\zeta }_{ij}^{+}(L_j+|f_j\left(0\right)\left|\right)+B_i^{+})K+I_i^{+}]=\frac{P_i}{{\alpha }_i^{-}}\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill {\displaystyle \underset{t\in \mathbb{T}}{sup}}\left|S_{{\psi }_i}\left(t\right)\right|& =& {\displaystyle \underset{t\in \mathbb{T}}{sup}}|{\int }_{-\infty }^t{\widehat{e}}_{-c_i}(t,\rho \left(s\right)){\Theta }_i(s,\psi )\nabla s|\hfill \\ & \le & {\displaystyle \underset{t\in \mathbb{T}}{sup}}{\int }_{-\infty }^t{\widehat{e}}_{-c_i^{-}}(t,\rho \left(s\right))|{\Theta }_i(s,\psi )|\nabla s\hfill \\ & \le & \frac{1}{c_i^{-}}\left(c_i^{+}{\varsigma }_i^{+}K+E_i^{+}(L_{i}K+|f_i\left(0\right)\left|\right)+J_i^{+}\right)=\frac{Q_i}{c_i^{-}}.\hfill \end{array}$$

In addition, for $i=1,2,\dots ,n$, we have

$$\begin{array}{cc}& {\displaystyle \underset{t\in \mathbb{T}}{sup}}\left|x_{{\varphi }_i}^{\nabla }\left(t\right)\right|\hfill \\ =& {\displaystyle \underset{t\in \mathbb{T}}{sup}}\left|{\left({\int }_{-\infty }^t{\widehat{e}}_{-{\alpha }_i}(t,\rho \left(s\right)){\mathsf{\Gamma }}_i(s,\varphi )\nabla s\right)}^{\nabla }\right|\hfill \\ =& {\displaystyle \underset{t\in \mathbb{T}}{sup}}|{\mathsf{\Gamma }}_i(t,\varphi )-{\alpha }_i\left(t\right){\int }_{-\infty }^t{\widehat{e}}_{-{\alpha }_i}(t,\rho \left(s\right)){\mathsf{\Gamma }}_i(s,\varphi )\nabla s|\hfill \\ \le & {\alpha }_i^{+}{\eta }_i^{+}K+{\displaystyle \sum _{j=1}^n}{D}_{ij}^{+}(L_{j}K+|f_j(0)|)+{\displaystyle \sum _{j=1}^n}{(D_{ij}^{\tau })}^{+}(L_{j}K+|f_j(0)|)\hfill \\ & +{\displaystyle \sum _{j=1}^n}{\overline{D}}_{ij}^{+}{\sigma }_{ij}^{+}(L_{j}K+|f_j(0)\left|\right)+{\displaystyle \sum _{j=1}^n}{\tilde{D}}_{ij}^{+}{\zeta }_{ij}^{+}(L_{j}K+|f_j(0)\left|\right)+B_i^{+}K\hfill \\ & +I_i^{+}+\frac{{\alpha }_i^{+}}{{\alpha }_i^{-}}({\alpha }_i^{+}{\eta }_i^{+}+{\displaystyle \sum _{j=1}^n}{D}_{ij}^{+}(L_{j}K+|f_j\left(0\right)\left|\right)+{\displaystyle \sum _{j=1}^n}{\left(D_{ij}^{\tau }\right)}^{+}(L_{j}K+|f_j\left(0\right)\left|\right)\hfill \\ & +{\displaystyle \sum _{j=1}^n}{\overline{D}}_{ij}^{+}{\sigma }_{ij}^{+}(L_{j}K+|f_j\left(0\right)\left|\right)+{\displaystyle \sum _{j=1}^n}{\tilde{D}}_{ij}^{+}{\zeta }_{ij}^{+}(L_{j}K+|f_j\left(0\right)\left|\right)+B_i^{+}K)+\frac{{\alpha }_i^{+}{I}_i^{+}}{{\alpha }_i^{-}}\hfill \\ =& \left(1+\frac{{\alpha }_i^{+}}{{\alpha }_i^{-}}\right)({\alpha }_i^{+}{\eta }_i^{+}K+{\displaystyle \sum _{j=1}^n}{D}_{ij}^{+}(L_{j}K+|f_j\left(0\right)\left|\right)+{\displaystyle \sum _{j=1}^n}{\left(D_{ij}^{\tau }\right)}^{+}(L_{j}K+|f_j\left(0\right)\left|\right)\hfill \\ & +{\displaystyle \sum _{j=1}^n}{\overline{D}}_{ij}^{+}{\sigma }_{ij}^{+}(L_{j}K+|f_j\left(0\right)\left|\right)+{\displaystyle \sum _{j=1}^n}{\tilde{D}}_{ij}^{+}{\zeta }_{ij}^{+}(L_{j}K+|f_j\left(0\right)\left|\right)+B_i^{+}K+I_i^{+})\hfill \\ =& \left(1+\frac{{\alpha }_i^{+}}{{\alpha }_i^{-}}\right)P_i\hfill \end{array}$$

and

$$\begin{array}{cc}& {\displaystyle \underset{t\in \mathbb{T}}{sup}}\left|S_{{\psi }_i}^{\nabla }\left(t\right)\right|\hfill \\ =& {\left({\int }_{-\infty }^t{\widehat{e}}_{-c_i}(t,\rho \left(s\right)){\Theta }_i(s,\psi )\nabla s\right)}^{\nabla }\hfill \\ =& {\displaystyle \underset{t\in \mathbb{T}}{sup}}|{\Theta }_i(s,\psi )-c_i\left(t\right){\int }_{-\infty }^t{\widehat{e}}_{-c_i}(t,\rho \left(s\right)){\Theta }_i(s,\psi )\nabla s|\hfill \\ \le & c_i^{+}{\varsigma }_i^{+}K+E_i^{+}(L_{i}K+|f_i\left(0\right)\left|\right)+J_i^{+}+\frac{c_i^{+}}{c_i^{-}}\left(c_i^{+}{\varsigma }_i^{+}K+E_i^{+}(L_{i}K+|f_i\left(0\right)\left|\right)\right)+\frac{c_i^{+}{J}_i^{+}}{c_i^{-}}\hfill \\ =& \left(1+\frac{c_i^{+}}{c_i^{-}}\right)\left(c_i^{+}{\varsigma }_i^{+}K+E_i^{+}(L_{i}K+|f_i\left(0\right)\left|\right)+J_i^{+}\right)\hfill \\ =& \left(1+\frac{c_i^{+}}{c_i^{-}}\right)Q_i.\hfill \end{array}$$

In view of $\left(A_3\right)$, we have

$${\parallel \mathcal{F}\left(z\right)\parallel }_{\mathbb{X}}\le K,$$

which means that $\mathcal{F}z\in {\mathbb{X}}^{*}$, so the mapping $\mathcal{F}$ is a self-mapping.

Next, we shall show that $\mathcal{F}$ is a contraction mapping. To this end, for any $z={({\varphi }_1,{\varphi }_2,\dots ,{\varphi }_n,{\psi }_1,{\psi }_2,\dots ,{\psi }_n)}^T,\omega ={(u_1,u_2,\dots ,u_n,v_1,v_2,\dots ,v_n)}^T\in {\mathbb{X}}^{*}$, we make the following estimations:

$$\begin{array}{ccc}\hfill {\displaystyle \underset{t\in \mathbb{T}}{sup}}|x_{{\varphi }_i}\left(t\right)-x_{u_i}\left(t\right)|& \le & \frac{1}{{\alpha }_i^{-}}(a_i^{+}{\eta }_i^{+}|{\varphi }_i^{\nabla }\left(s\right)-u_i^{\nabla }\left(s\right)|+{\displaystyle \sum _{j=1}^n}{D}_{ij}^{+}{L}_j|{\varphi }_j\left(s\right)-u_j\left(s\right)|\hfill \\ & & +{\displaystyle \sum _{j=1}^n}{\left(D_{ij}^{\tau }\right)}^{+}{L}_j|{\varphi }_j(s-{\tau }_{ij}\left(s\right))-u_j(s-{\tau }_{ij}\left(s\right))|\hfill \\ & & +{\displaystyle \sum _{j=1}^n}{\overline{D}}_{ij}^{+}{\sigma }_{ij}^{+}{L}_j|{\varphi }_j\left(s\right)-u_j\left(s\right)|+{\displaystyle \sum _{j=1}^n}{\tilde{D}}_{ij}^{+}{\zeta }_{ij}^{+}{L}_j|{\varphi }_j^{\nabla }\left(s\right)-u_j^{\nabla }\left(s\right)|\hfill \\ & & +B_i^{+}|{\psi }_i\left(s\right)-u_i\left(s\right)|)\hfill \\ & \le & \frac{1}{{\alpha }_i^{-}}(a_i^{+}{\eta }_i^{+}+{\displaystyle \sum _{j=1}^n}{D}_{ij}^{+}{L}_j+{\displaystyle \sum _{j=1}^n}{\left(D_{ij}^{\tau }\right)}^{+}{L}_j\hfill \\ & & +{\displaystyle \sum _{j=1}^n}{\overline{D}}_{ij}^{+}{\sigma }_{ij}^{+}{L}_j+{\displaystyle \sum _{j=1}^n}{\tilde{D}}_{ij}^{+}{\zeta }_{ij}^{+}{L}_j+B_i^{+}\left)\right||z-{\omega \left|\right|}_{\mathbb{X}}\hfill \\ & =& \frac{\overline{P_i}}{{\alpha }_i^{-}}\left|\right|z-{\omega \left|\right|}_{\mathbb{X}},i=1,2,\dots ,n\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill {\displaystyle \underset{t\in \mathbb{T}}{sup}}|{(x_{{\varphi }_i}\left(t\right)-x_{u_i}\left(t\right))}^{\nabla }|& \le & {\displaystyle \underset{s\in \mathbb{T}}{sup}}[a_i^{+}{\eta }_i^{+}|{\varphi }_i^{\nabla }\left(s\right)-u_i^{\nabla }\left(s\right)|+{\displaystyle \sum _{j=1}^n}{D}_{ij}^{+}{L}_j|{\varphi }_j\left(s\right)-u_j\left(s\right)|\hfill \\ & & +{\displaystyle \sum _{j=1}^n}{\left(D_{ij}^{\tau }\right)}^{+}{L}_j|{\varphi }_j(s-{\tau }_{ij}\left(s\right))-u_j(s-{\tau }_{ij}\left(s\right))|\hfill \\ & & +{\displaystyle \sum _{j=1}^n}{\overline{D}}_{ij}^{+}{\sigma }_{ij}^{+}{L}_j|{\varphi }_j\left(s\right)-u_j\left(s\right)|+{\displaystyle \sum _{j=1}^n}{\tilde{D}}_{ij}^{+}{\zeta }_{ij}^{+}{L}_j|{\varphi }_j^{\nabla }\left(s\right)-u_j^{\nabla }\left(s\right)|\hfill \\ & & +B_i^{+}|{\psi }_i\left(s\right)-u_i\left(s\right)|\hfill \\ & & +\frac{{\alpha }_i^{+}}{{\alpha }_i^{-}}(a_i^{+}{\eta }_i^{+}|{\varphi }_i^{\nabla }\left(s\right)-u_i^{\nabla }\left(s\right)|+{\displaystyle \sum _{j=1}^n}{D}_{ij}^{+}{L}_j|{\varphi }_j\left(s\right)-u_j\left(s\right)|\hfill \\ & & +{\displaystyle \sum _{j=1}^n}{\left(D_{ij}^{\tau }\right)}^{+}{L}_j|{\varphi }_j(s-{\tau }_{ij}\left(s\right))-u_j(s-{\tau }_{ij}\left(s\right))|\hfill \\ & & +{\displaystyle \sum _{j=1}^n}{\overline{D}}_{ij}^{+}{\sigma }_{ij}^{+}{L}_j|{\varphi }_j\left(s\right)-u_j\left(s\right)|+{\displaystyle \sum _{j=1}^n}{\tilde{D}}_{ij}^{+}{\zeta }_{ij}^{+}{L}_j|{\varphi }_j^{\nabla }\left(s\right)-u_j^{\nabla }\left(s\right)|\hfill \\ & & +B_i^{+}|{\psi }_i\left(s\right)-u_i\left(s\right)|\left)\right]\hfill \\ & \le & (a_i^{+}{\eta }_i^{+}+{\displaystyle \sum _{j=1}^n}{D}_{ij}^{+}{L}_j+{\displaystyle \sum _{j=1}^n}{\left(D_{ij}^{\tau }\right)}^{+}{L}_j\hfill \\ & & +{\displaystyle \sum _{j=1}^n}{\overline{D}}_{ij}^{+}{\sigma }_{ij}^{+}{L}_j+{\displaystyle \sum _{j=1}^n}{\tilde{D}}_{ij}^{+}{\zeta }_{ij}^{+}{L}_j+B_i^{+}\hfill \\ & & +\frac{{\alpha }_i^{+}}{{\alpha }_i^{-}}(a_i^{+}{\eta }_i^{+}+{\displaystyle \sum _{j=1}^n}{D}_{ij}^{+}{L}_j+{\displaystyle \sum _{j=1}^n}{\left(D_{ij}^{\tau }\right)}^{+}{L}_j\hfill \\ & & +{\displaystyle \sum _{j=1}^n}{\overline{D}}_{ij}^{+}{\sigma }_{ij}^{+}{L}_j+{\displaystyle \sum _{j=1}^n}{\tilde{D}}_{ij}^{+}{\zeta }_{ij}^{+}{L}_j+B_i^{+}\left)\right)\left|\right|z-{\omega \left|\right|}_{\mathbb{X}}\hfill \\ & =& \left(1+\frac{{\alpha }_i^{+}}{{\alpha }_i^{-}}\right)(a_i^{+}{\eta }_i^{+}+{\displaystyle \sum _{j=1}^n}{D}_{ij}^{+}{L}_j+{\displaystyle \sum _{j=1}^n}{\left(D_{ij}^{\tau }\right)}^{+}{L}_j\hfill \\ & & +{\displaystyle \sum _{j=1}^n}{\overline{D}}_{ij}^{+}{\sigma }_{ij}^{+}{L}_j+{\displaystyle \sum _{j=1}^n}{\tilde{D}}_{ij}^{+}{\zeta }_{ij}^{+}{L}_j+B_i^{+}\left)\right||z-{\omega \left|\right|}_{\mathbb{X}}\hfill \\ & =& \left(1+\frac{{\alpha }_i^{+}}{{\alpha }_i^{-}}\right)\overline{P_i}\left|\right|z-{\omega \left|\right|}_{\mathbb{X}},i=1,2,\dots ,n.\hfill \end{array}$$

In a similar way, we have

$$\begin{array}{ccc}\hfill {\displaystyle \underset{t\in \mathbb{T}}{sup}}|S_{{\psi }_i}\left(t\right)-S_{v_i}\left(t\right)|& \le & \frac{1}{c_i^{-}}\left(c_i^{+}{\varsigma }_i^{+}+E_i^{+}{L}_i\right)\left|\right|z-{\omega \left|\right|}_{\mathbb{X}}\hfill \\ & =& \frac{1}{c_i^{-}}\overline{Q_i}\left|\right|z-{\omega \left|\right|}_{\mathbb{X}},i=1,2,\dots ,n\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill {\displaystyle \underset{t\in \mathbb{T}}{sup}}|{(S_{{\psi }_i}\left(t\right)-S_{v_i}\left(t\right))}^{\nabla }|& \le & \left(1+\frac{c_i^{+}}{c_i^{-}}\right)\left(c_i^{+}{\varsigma }_i^{+}+E_i^{+}{L}_i\right)\left|\right|z-{\omega \left|\right|}_{\mathbb{X}}\hfill \\ & =& \left(1+\frac{c_i^{+}}{c_i^{-}}\right)\overline{Q_i}\left|\right|z-{\omega \left|\right|}_{\mathbb{X}},i=1,2,\dots ,n.\hfill \end{array}$$

From $\left(A_3\right)$, we obtain

$${\parallel \mathcal{F}\left(z\right)-\mathcal{F}\left(\omega \right)\parallel }_{\mathbb{X}}\le \kappa {\parallel z-\omega \parallel }_{\mathbb{X}}.$$

Since $\kappa <1$, $\mathcal{F}$ is a contraction mapping. Therefore, (1) has a unique almost periodic solution in ${\mathbb{X}}^{*}={\{z\in \mathbb{X}:\parallel z\parallel }_{\mathbb{X}}\le K\}$. The proof is completed.

4. Global Exponential Stability of Almost Periodic Solutions

This section addresses the exponential stability of the almost periodic solution of (1).

Definition 6.

Let $Z^{*}={(x_1^{*},x_2^{*},\dots ,x_n^{*},S_1^{*},S_2^{*},\dots ,S_n^{*})}^T$ be an almost periodic solution of (1) with initial value $z^{*}={({\varphi }_1^{*},{\varphi }_2^{*},\dots ,{\varphi }_n^{*},{\psi }_1^{*},{\psi }_2^{*},\dots ,{\psi }_n^{*})}^T$ and $Z={(x_1,x_2,\dots ,x_n,S_1,S_2,\dots ,S_n)}^T$ be an arbitrary solution of (1) with initial value $z={({\varphi }_1,{\varphi }_2,\dots ,{\varphi }_n,{\psi }_1,{\psi }_2,\dots ,{\psi }_n)}^T$. If there exist positive constants λ with $\ominus \lambda \in {\mathcal{R}}^{+}$ and $M>1$ such that

$$\parallel Z\left(t\right)-Z^{*}\left(t\right)\parallel \le M{e}_{\ominus \lambda }(t,t_0){\parallel z-z^{*}\parallel }_0,\forall t\in {(0,+\infty )}_{\mathbb{T}},t\ge t_0,$$

where $\parallel Z\left(t\right)-Z^{*}\left(t\right)\parallel ={\displaystyle \underset{1\le i\le n}{max}}\left\{|x_i\left(t\right)-x_i^{*}\left(t\right)|,S_i\left(t\right)-S_i^{*}\left(t\right)|,|{(x_i\left(t\right)-x_i^{*}\left(t\right))}^{\nabla }|,|{(S_i\left(t\right)-S_i^{*}\left(t\right)|)}^{\nabla }\right\}$, $\parallel z-z^{*}{\parallel }_0={\displaystyle \underset{s\in {[-\theta ,0]}_{\mathbb{T}}}{sup}}{\displaystyle \underset{1\le i\le n}{max}}\left\{|{\varphi }_i\left(s\right)-{\varphi }_i^{*}\left(s\right)|,|{\psi }_i\left(s\right)-{\psi }_i^{*}\left(s\right)|,|{({\varphi }_i\left(s\right)-{\varphi }_i^{*}\left(s\right))}^{\nabla }|,|{({\psi }_i\left(s\right)-{\psi }_i^{*}\left(s\right))}^{\nabla }|\right\}.$ Then $Z^{*}\left(t\right)$ is said to be globally exponentially stable.

Theorem 2.

Assume that ${\displaystyle \underset{t\in \mathbb{T}}{sup}}\nu \left(t\right)<+\infty$ and $\left(H_1\right)$–$\left(H_3\right)$ hold, then (1) has a unique almost periodic solution which is globally exponentially stable.

Proof. 

By Theorem 1 it follows that system (1) has an almost periodic solution $Z^{*}={(x_1^{*},x_2^{*},\dots ,x_n^{*},S_1^{*},S_2^{*},\dots ,S_n^{*})}^T$. Assume that its initial value is $z^{*}={({\varphi }_1^{*},{\varphi }_2^{*},\dots ,{\varphi }_n^{*},{\psi }_1^{*},{\psi }_2^{*},\dots ,{\psi }_n^{*})}^T$. Suppose that $Z={(x_1,x_2,\dots ,x_n,S_1,S_2,\dots ,S_n)}^T$ is an arbitrary solution of (1) with the initial value $z={({\varphi }_1,{\varphi }_2,\dots ,{\varphi }_n,{\psi }_1,{\psi }_2,\dots ,{\psi }_n)}^T$. By system (1), we obtain

$$\begin{array}{c}\hfill \left\{\begin{array}{ccc}{u}_i^{\nabla }\left(t\right)\hfill & =\hfill & -{\alpha }_i\left(t\right)u_i\left(t\right)+{\alpha }_i\left(t\right){\int }_{t-{\eta }_i\left(t\right)}^t{u}_i^{\nabla }\left(s\right)\nabla s+{\displaystyle \sum _{j=1}^n}{D}_{ij}\left(t\right)p_j\left(u_j\left(t\right)\right)\hfill \\ & & +{\displaystyle \sum _{j=1}^n}{D}_{ij}^{\tau }\left(t\right)p_j\left(u_j(t-{\tau }_{ij}\left(t\right))\right)+{\displaystyle \sum _{j=1}^n}{\overline{D}}_{ij}\left(t\right){\int }_{t-{\sigma }_{ij}\left(t\right)}^t{p}_j\left(u_j\left(s\right)\right)\nabla s\hfill \\ & & +{\displaystyle \sum _{j=1}^n}{\tilde{D}}_{ij}\left(t\right){\int }_{t-{\zeta }_{ij}\left(t\right)}^t{h}_j\left(u_j^{\nabla }\left(s\right)\right)\nabla s+B_i\left(t\right)v_i\left(t\right),i=1,2,\cdots ,n,\hfill \\ v_i^{\nabla }\left(t\right)\hfill & =\hfill & -c_i\left(t\right)v_i\left(t\right)+c_i\left(t\right){\int }_{t-{\varsigma }_i\left(t\right)}^t{u}_i^{\nabla }\left(s\right)\nabla s+E_i\left(t\right)p_i\left(u_i\left(t\right)\right),i=1,2,\cdots ,n,\hfill \end{array}\right.\end{array}$$

(9)

where $u_i\left(t\right)=x_i\left(t\right)-x_i^{*}\left(t\right)$, $v_i\left(t\right)=S_i\left(t\right)-S_i^{*}\left(t\right)$, $p_j\left(u_j\left(t\right)\right))=f_j\left(x_j\left(t\right)\right)-f_j\left(x_j^{*}\left(t\right)\right),h_j\left(x_j^{\nabla }\left(s\right)\right)=f_j\left(x_j^{\nabla }\left(s\right)\right)-f_j\left({x_j^{*}}^{\nabla }\left(s\right)\right)$ and $i,j=1,2,\dots ,n$.

The initial value of (9) is

$$\begin{array}{l}{u}_i\left(s\right)={\varphi }_i\left(s\right)-{\varphi }_i^{*}\left(s\right),s\in {[-\theta ,0]}_{\mathbb{T}},i=1,2,\cdots ,n,\\ v_i\left(s\right)={\psi }_i\left(s\right)-{\psi }_i^{*}\left(s\right),s\in {[-\theta ,0]}_{\mathbb{T}},i=1,2,\cdots ,n.\end{array}$$

Multiplying both sides of the first and the second equations of (9) by ${\widehat{e}}_{-{\alpha }_i}(t_0,\rho \left(s\right))$ and ${\widehat{e}}_{-c_i}(t_0,\rho \left(s\right))$, respectively, and integrating over the interval ${[t_0,t]}_{\mathbb{T}}$, we have

$$\begin{array}{c}\hfill \left\{\begin{array}{ccc}{u}_i\left(t\right)\hfill & =\hfill & u_i\left(t_0\right){\widehat{e}}_{-{\alpha }_i}(t,t_0)+{\int }_{t_0}^t{\widehat{e}}_{-{\alpha }_i}(t,\rho \left(s\right))({\alpha }_i\left(s\right){\int }_{s-{\eta }_i\left(s\right)}^s{u}_i^{\nabla }\left(u\right)\nabla u+{\displaystyle \sum _{j=1}^n}{D}_{ij}\left(s\right)p_j\left(u_j\left(s\right)\right)\hfill \\ & & +{\displaystyle \sum _{j=1}^n}{D}_{ij}^{\tau }\left(s\right)p_j\left(u_j(s-{\tau }_{ij}\left(s\right))\right)+{\displaystyle \sum _{j=1}^n}{\overline{D}}_{ij}\left(s\right){\int }_{s-{\sigma }_{ij}\left(s\right)}^s{p}_j\left(u_j\left(u\right)\right)\nabla u\hfill \\ & & +{\displaystyle \sum _{j=1}^n}{\tilde{D}}_{ij}\left(s\right){\int }_{s-{\zeta }_{ij}\left(s\right)}^s{h}_j\left(u_j^{\nabla }\left(u\right)\right)\nabla u+B_i\left(s\right)v_i\left(s\right))\nabla s,\hfill \\ v_i\left(t\right)\hfill & =\hfill & v_i\left(t_0\right){\widehat{e}}_{-c_i}(t,t_0)+{\int }_{t_0}^t{\widehat{e}}_{-c_i}(t,\rho \left(s\right))\left(c_i\left(s\right){\int }_{s-{\varsigma }_i\left(s\right)}^s{v}_i^{\nabla }\left(u\right)\nabla u+E_i\left(s\right)p_i\left(u_i\left(s\right)\right)\right)\nabla s,\hfill \end{array}\right.\end{array}$$

(10)

where $t_0\in {[-\theta ,0]}_{\mathbb{T}},i=1,2,\cdots ,n$.

For $i=1,2,\cdots ,n$, we introduce the following notation:

$$\begin{array}{ccc}\hfill H_i\left(\beta \right)& =& {\alpha }_i^{-}-\beta -(exp\left(\beta {\displaystyle \underset{s\in \mathbb{T}}{sup}}\nu \left(s\right)\right)({\alpha }_i^{+}{\eta }_i^{+}exp\left(\beta {\eta }_i^{+}\right)\hfill \\ & & +{\displaystyle \sum _{j=1}^n}{D}_{ij}^{+}{L}_j+{\displaystyle \sum _{j=1}^n}{\left(D_{ij}^{\tau }\right)}^{+}{L}_{j}exp\left(\beta {\tau }_{ij}^{+}\right)+{\displaystyle \sum _{j=1}^n}{\overline{D}}_{ij}^{+}{L}_j{\sigma }_{ij}^{+}exp\left(\beta {\sigma }_{ij}^{+}\right)\hfill \\ & & +{\displaystyle \sum _{j=1}^n}{\tilde{D}}_{ij}^{+}{L}_j{\zeta }_{ij}^{+}exp\left(\beta {\zeta }_{ij}^{+}\right))+B_i^{+}),\hfill \\ \hfill \overline{H_i}\left(\beta \right)& =& c_i^{-}-\beta -\left(exp\left(\beta {\displaystyle \underset{s\in \mathbb{T}}{sup}}\nu \left(s\right)\right)c_i^{+}{\varsigma }_i^{+}exp\left(\beta {\varsigma }_i^{+}\right)+E_i^{+}{L}_i\right),\hfill \\ \hfill H_i^{*}\left(\beta \right)& =& {\alpha }_i^{-}-\beta -\left({\alpha }_i^{+}exp\left(\beta {\displaystyle \underset{s\in \mathbb{T}}{sup}}\nu \left(s\right)\right)+{\alpha }_i^{-}-\beta \right)({\alpha }_i^{+}{\eta }_i^{+}exp\left(\beta {\eta }_i^{+}\right)\hfill \\ & & +{\displaystyle \sum _{j=1}^n}{D}_{ij}^{+}{L}_j+{\displaystyle \sum _{j=1}^n}{\left(D_{ij}^{\tau }\right)}^{+}{L}_{j}exp\left(\beta {\tau }_{ij}^{+}\right)+{\displaystyle \sum _{j=1}^n}{\overline{D}}_{ij}^{+}{L}_j{\sigma }_{ij}^{+}exp\left(\beta {\sigma }_{ij}^{+}\right)\hfill \\ & & +{\displaystyle \sum _{j=1}^n}{\tilde{D}}_{ij}^{+}{L}_j{\zeta }_{ij}^{+}exp\left(\beta {\zeta }_{ij}^{+}\right)+B_i^{+})\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill \overline{H_i^{*}}(\beta )& =& c_i^{-}-\beta -\left(c_i^{+}exp\left(\beta {\displaystyle \underset{s\in \mathbb{T}}{sup}}\nu (s)\right)+c_i^{-}-\beta \right)\left(c_i^{+}{\varsigma }_i^{+}exp(\beta {\varsigma }_i^{+})+E_i^{+}{L}_i\right).\hfill \end{array}$$

From $\left(A_3\right)$, for $i=1,2,\cdots ,n$, we obtain

$$\begin{array}{ccc}\hfill H_i\left(0\right)& =& {\alpha }_i^{-}-({\alpha }_i^{+}{\eta }_i^{+}+{\displaystyle \sum _{j=1}^n}{D}_{ij}^{+}{L}_j+{\displaystyle \sum _{j=1}^n}{\left(D_{ij}^{\tau }\right)}^{+}{L}_j\hfill \\ & & +{\displaystyle \sum _{j=1}^n}{\overline{D}}_{ij}^{+}{L}_j{\sigma }_{ij}^{+}+{\displaystyle \sum _{j=1}^n}{\tilde{D}}_{ij}^{+}{L}_j{\zeta }_{ij}^{+}+B_i^{+})>0,\hfill \\ \hfill \overline{H_i}\left(0\right)& =& c_i^{-}-\left(c_i^{+}{\varsigma }_i^{+}+E_i^{+}{L}_i\right)>0,\hfill \\ \hfill H_i^{*}\left(0\right)& =& {\alpha }_i^{-}-({\alpha }_i^{+}+{\alpha }_i^{-})({\alpha }_i^{+}{\eta }_i^{+}+{\displaystyle \sum _{j=1}^n}{D}_{ij}^{+}{L}_j+{\displaystyle \sum _{j=1}^n}{\left(D_{ij}^{\tau }\right)}^{+}{L}_j\hfill \\ & & +{\displaystyle \sum _{j=1}^n}{\overline{D}}_{ij}^{+}{L}_j{\sigma }_{ij}^{+}+{\displaystyle \sum _{j=1}^n}{\tilde{D}}_{ij}^{+}{L}_j{\zeta }_{ij}^{+}+B_i^{+})>0\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill \overline{H_i^{*}}\left(0\right)& =& c_i^{-}-(c_i^{+}+c_i^{-})\left(c_i^{+}+E_i^{+}{L}_i\right)>0.\hfill \end{array}$$

From the continuity of functions $H_i,\overline{H_i},H_i^{*}$ and $\overline{H_i^{*}}$, and the fact that $H_i\left(\beta \right),\overline{H_i}\left(\beta \right),H_i^{*}\left(\beta \right)$ and $\overline{H_i^{*}}\left(\beta \right)\to -\infty$, as $\beta \to +\infty$ it follows that there exist ${\xi }_i,\overline{{\xi }_i},{\gamma }_i,\overline{{\gamma }_i}>0$ such that $H_i\left({\xi }_i\right)=\overline{H_i}\left(\overline{{\xi }_i}\right)=H_i^{*}\left({\gamma }_i\right)=\overline{H_i^{*}}\left(\overline{{\gamma }_i}\right)=0$ and $H_i\left(\beta \right)>0$ for $\beta \in (0,{\xi }_i)$, $\overline{H_i}\left(\beta \right)>0$ for $\beta \in (0,\overline{{\xi }_i})$, $H_i^{*}\left(\beta \right)>0$ for $\beta \in (0,{\gamma }_i)$, $\overline{H_i^{*}}\left(\beta \right)>0$ for $\beta \in (0,\overline{{\gamma }_i})$. Take $a={\displaystyle \underset{1\le i\le n}{min}}\left\{{\xi }_i,\overline{{\xi }_i},{\gamma }_i,\overline{{\gamma }_i}\right\}$, then $H_i\left(a\right)\ge 0,\overline{H_i}\left(a\right)\ge 0,H_i^{*}\left(a\right)\ge 0,\overline{H_i^{*}}\left(a\right)\ge 0$. Therefore, we can select a positive number $0<\lambda <min\left\{a,{\displaystyle \underset{1\le i\le n}{min}}\{{\alpha }_i^{-},c_i^{-}\}\right\}$ such that

$$H_i\left(\lambda \right)>0,\overline{H_i}\left(\lambda \right)>0,H_i^{*}\left(\lambda \right)>0,\overline{H_i^{*}}\left(\lambda \right)>0,i=1,2,\dots ,n,$$

(11)

which imply that for $i=1,2,\dots ,n,$

$$\begin{array}{c}\frac{1}{{\alpha }_i^{-}-\lambda }(exp\left(\lambda {\displaystyle \underset{s\in \mathbb{T}}{sup}}\nu \left(s\right)\right)({\alpha }_i^{+}{\eta }_i^{+}+{\displaystyle \sum _{j=1}^n}{D}_{ij}^{+}{L}_j+{\displaystyle \sum _{j=1}^n}{\left(D_{ij}^{\tau }\right)}^{+}{L}_j+{\displaystyle \sum _{j=1}^n}{\overline{D}}_{ij}^{+}{L}_j{\sigma }_{ij}^{+}\hfill \\ +{\displaystyle \sum _{j=1}^n}{\tilde{D}}_{ij}^{+}{L}_j{\zeta }_{ij}^{+})+B_i^{+})<1,\hfill \end{array}$$

$$\frac{1}{c_i^{-}-\lambda }\left(exp\left(\lambda {\displaystyle \underset{s\in \mathbb{T}}{sup}}\nu \left(s\right)\right)c_i^{+}{\varsigma }_i^{+}+E_i^{+}{L}_i\right)<1,$$

$$\begin{array}{c}\left(1+\frac{{\alpha }_i^{+}exp\left(\lambda {\displaystyle \underset{s\in \mathbb{T}}{sup}}\nu \left(s\right)\right)}{{\alpha }_i^{-}-\lambda }\right)({\alpha }_i^{+}{\eta }_i^{+}+{\displaystyle \sum _{j=1}^n}{D}_{ij}^{+}{L}_j+{\displaystyle \sum _{j=1}^n}{\left(D_{ij}^{\tau }\right)}^{+}{L}_j+{\displaystyle \sum _{j=1}^n}{\overline{D}}_{ij}^{+}{L}_j{\sigma }_{ij}^{+}\hfill \\ +{\displaystyle \sum _{j=1}^n}{\tilde{D}}_{ij}^{+}{L}_j{\zeta }_{ij}^{+}+B_i^{+})<1\hfill \end{array}$$

and

$$\begin{array}{c}\hfill \left(1+\frac{c_i^{+}exp\left(\lambda {\displaystyle \underset{s\in \mathbb{T}}{sup}}\nu \left(s\right)\right)}{c_i^{-}-\lambda }\right)\left(c_i^{+}{\varsigma }_i^{+}+E_i^{+}{L}_i\right)<1.\end{array}$$

Denote

$$\begin{array}{ccc}\hfill M& =& {\displaystyle \underset{1\le i\le n}{max}}\{\frac{{\alpha }_i^{-}}{{\alpha }_i^{+}{\eta }_i^{+}+{\displaystyle \sum _{j=1}^n}{D}_{ij}^{+}{L}_j+{\displaystyle \sum _{j=1}^n}{\left(D_{ij}^{\tau }\right)}^{+}{L}_j+{\displaystyle \sum _{j=1}^n}{\overline{D}}_{ij}^{+}{L}_j{\sigma }_{ij}^{+}+{\displaystyle \sum _{j=1}^n}{\tilde{D}}_{ij}^{+}{L}_j{\zeta }_{ij}^{+}+B_i^{+}},\hfill \\ & & \frac{c_i^{-}}{c_i^{+}{\varsigma }_i^{+}+E_i^{+}{L}_i}\}.\hfill \end{array}$$

From $\left(A_3\right)$, $M>1$.

Obviously,

$$\parallel Z\left(t\right)-Z^{*}\left(t\right)\parallel \le M{\widehat{e}}_{{\ominus }_{\nu }\lambda }(t,t_0){\parallel \varphi \parallel }_0,\forall t\in {[t_0,0]}_{\mathbb{T}},i=1,2,\dots ,n,$$

where ${\ominus }_{\nu }\lambda \in {\mathcal{R}}_{\nu }^{+}$ and $\lambda$ satisfies (11). Below we will prove that the following inequality is established.

$$\parallel Z\left(t\right)-Z^{*}\left(t\right)\parallel \le M{\widehat{e}}_{{\ominus }_{\nu }\lambda }(t,t_0){\parallel z\parallel }_0,\forall t\in {[t_0,+\infty )}_{\mathbb{T}}.$$

(12)

To this end, for every $P>1$, we prove

$$\parallel Z\left(t\right)-Z^{*}\left(t\right)\parallel <PM{\widehat{e}}_{{\ominus }_{\nu }\lambda }(t,t_0){\parallel z\parallel }_0,\forall t\in {[t_0,+\infty )}_{\mathbb{T}}.$$

(13)

If (13) is not true, then there exist some $t_1\in {(0,+\infty )}_{\mathbb{T}}$ and $c\ge 1$ such that

$$\parallel Z\left(t_1\right)-Z^{*}\left(t_1\right)\parallel =cPM{\widehat{e}}_{{\ominus }_{\nu }\lambda }(t_1,t_0){\parallel z\parallel }_0$$

(14)

and

$$\parallel Z\left(t\right)-Z^{*}\left(t\right)\parallel \le cPM{\widehat{e}}_{{\ominus }_{\nu }\lambda }(t,t_0){\parallel z\parallel }_0,t\in {[t_0,t_1]}_{\mathbb{T}}.$$

(15)

By (10), (14), (15) and $\left(A_1\right)$–$\left(A_3\right)$, we obtain for $i=1,2,\dots ,n$,

$$\begin{array}{cc}\hfill & |u_i\left(t_1\right)|\hfill \\ \le & {\widehat{e}}_{-{\alpha }_i}(t_1,t_0){\parallel z\parallel }_0+cPM{\widehat{e}}_{{\ominus }_{\nu }\lambda }(t_1,t_0){\parallel z\parallel }_0{\int }_{t_0}^{t_1}{\widehat{e}}_{-{\alpha }_i}(t_1,\rho \left(s\right)){\widehat{e}}_{\lambda }(t_1,\rho \left(s\right))\hfill \\ & \times ({\alpha }_i^{+}{\int }_{s-{\eta }_i\left(s\right)}^s{\widehat{e}}_{\lambda }(\rho \left(u\right),u)\nabla u+{\displaystyle \sum _{j=1}^n}{D}_{ij}^{+}{L}_j{\widehat{e}}_{\lambda }(\rho \left(s\right),s)\hfill \\ & +{\displaystyle \sum _{j=1}^n}{\left(D_{ij}^{\tau }\right)}^{+}{L}_j{\widehat{e}}_{\lambda }(\rho \left(s\right),s-{\tau }_{ij}\left(s\right))+{\displaystyle \sum _{j=1}^n}{\overline{D}}_{ij}^{+}{L}_j{\int }_{s-{\sigma }_{ij}\left(s\right)}^s{\widehat{e}}_{\lambda }(\rho \left(u\right),u)\nabla u\hfill \\ & +{\displaystyle \sum _{j=1}^n}{\tilde{D}}_{ij}^{+}{L}_j{\int }_{s-{\zeta }_{ij}\left(s\right)}^s{\widehat{e}}_{\lambda }(\rho \left(u\right),u)\nabla u+B_i^{+})\nabla s\hfill \\ \le & {\widehat{e}}_{-{\alpha }_i}(t_1,t_0){\parallel z\parallel }_0+cPM{\widehat{e}}_{{\ominus }_{\nu }\lambda }(t_1,t_0){\parallel z\parallel }_0{\int }_{t_0}^{t_1}{\widehat{e}}_{-{\alpha }_i{\oplus }_{\nu }\lambda }(t_1,\rho \left(s\right))\hfill \\ & \times ({\alpha }_i^{+}{\eta }_i^{+}{\widehat{e}}_{\lambda }(\rho \left(s\right),s-{\eta }_i\left(s\right))+{\displaystyle \sum _{j=1}^n}{D}_{ij}^{+}{L}_j{\widehat{e}}_{\lambda }(\rho \left(s\right),s)\hfill \\ & +{\displaystyle \sum _{j=1}^n}{\left(D_{ij}^{\tau }\right)}^{+}{L}_j{\widehat{e}}_{\lambda }(\rho \left(s\right),s-{\tau }_{ij}\left(s\right))+{\displaystyle \sum _{j=1}^n}{\overline{D}}_{ij}^{+}{L}_j{\sigma }_{ij}^{+}{\widehat{e}}_{\lambda }(\rho \left(s\right),s-{\sigma }_{ij}\left(s\right))\hfill \\ & +{\displaystyle \sum _{j=1}^n}{\tilde{D}}_{ij}^{+}{L}_j{\zeta }_{ij}^{+}{\widehat{e}}_{\lambda }(\rho \left(s\right),s-{\zeta }_{ij}\left(s\right))+B_i^{+})\nabla s\hfill \\ \le & {\widehat{e}}_{-{\alpha }_i}(t_1,t_0){\parallel z\parallel }_0+cPM{\widehat{e}}_{{\ominus }_{\nu }\lambda }(t_1,t_0){\parallel z\parallel }_0{\int }_{t_0}^{t_1}{\widehat{e}}_{-{\alpha }_i{\oplus }_{\nu }\lambda }(t_1,\rho \left(s\right))\hfill \\ & \times ({\alpha }_i^{+}{\eta }_i^{+}exp\left[\lambda ({\eta }_i^{+}+{\displaystyle \underset{s\in \mathbb{T}}{sup}}\nu \left(s\right))\right]+{\displaystyle \sum _{j=1}^n}{D}_{ij}^{+}{L}_{j}exp\left(\lambda {\displaystyle \underset{s\in \mathbb{T}}{sup}}\nu \left(s\right)\right)\hfill \\ & +{\displaystyle \sum _{j=1}^n}{\left(D_{ij}^{\tau }\right)}^{+}{L}_{j}exp\left[\lambda ({\tau }_{ij}^{+}+{\displaystyle \underset{s\in \mathbb{T}}{sup}}\nu \left(s\right))\right]+{\displaystyle \sum _{j=1}^n}{\overline{D}}_{ij}^{+}{L}_j{\sigma }_{ij}^{+}exp\left[\lambda ({\sigma }_{ij}^{+}+{\displaystyle \underset{s\in \mathbb{T}}{sup}}\nu \left(s\right))\right]\hfill \\ & +{\displaystyle \sum _{j=1}^n}{\tilde{D}}_{ij}^{+}{L}_j{\zeta }_{ij}^{+}exp\left[\lambda ({\zeta }_{ij}^{+}+{\displaystyle \underset{s\in \mathbb{T}}{sup}}\nu \left(s\right))\right]+B_i^{+})\nabla s\hfill \\ <& cPM{\widehat{e}}_{{\ominus }_{\nu }\lambda }(t_1,t_0){\parallel z\parallel }_0\{\frac{1}{M}{\widehat{e}}_{-{\alpha }_i{\oplus }_{\nu }\lambda }(t_1,t_0)+[exp\left(\lambda {\displaystyle \underset{s\in \mathbb{T}}{sup}}\nu \left(s\right)\right)\hfill \\ & \times ({\alpha }_i^{+}{\eta }_i^{+}exp\left(\lambda {\eta }_i^{+}\right)+{\displaystyle \sum _{j=1}^n}{D}_{ij}^{+}{L}_j+{\displaystyle \sum _{j=1}^n}{\left(D_{ij}^{\tau }\right)}^{+}{L}_{j}exp\left(\lambda {\tau }_{ij}^{+}\right)\hfill \\ & +{\displaystyle \sum _{j=1}^n}{\overline{D}}_{ij}^{+}{L}_j{\sigma }_{ij}^{+}exp\left(\lambda {\sigma }_{ij}^{+}\right)+{\displaystyle \sum _{j=1}^n}{\tilde{D}}_{ij}^{+}{L}_j{\zeta }_{ij}^{+}exp\left(\lambda {\zeta }_{ij}^{+}\right))\hfill \\ & +B_i^{+}\left]\frac{1-{\widehat{e}}_{-{\alpha }_i{\oplus }_{\nu }\lambda }(t_1,t_0)}{{\alpha }_i^{-}-\lambda }\right\}\hfill \\ \le & cPM{\widehat{e}}_{{\ominus }_{\nu }\lambda }(t_1,t_0){\parallel z\parallel }_0\left\{\right[\frac{1}{M}-\frac{1}{{\alpha }_i^{-}-\lambda }(exp\left(\lambda {\displaystyle \underset{s\in \mathbb{T}}{sup}}\nu \left(s\right)\right)({\alpha }_i^{+}{\eta }_i^{+}exp\left(\lambda {\eta }_i^{+}\right)\hfill \\ & +{\displaystyle \sum _{j=1}^n}{D}_{ij}^{+}{L}_j+{\displaystyle \sum _{j=1}^n}{\left(D_{ij}^{\tau }\right)}^{+}{L}_{j}exp\left(\lambda {\tau }_{ij}^{+}\right)+{\displaystyle \sum _{j=1}^n}{\overline{D}}_{ij}^{+}{L}_j{\sigma }_{ij}^{+}exp\left(\lambda {\sigma }_{ij}^{+}\right)\hfill \\ & +{\displaystyle \sum _{j=1}^n}{\tilde{D}}_{ij}^{+}{L}_j{\zeta }_{ij}^{+}exp\left(\lambda {\zeta }_{ij}^{+}\right))+B_i^{+})]{\widehat{e}}_{-{\alpha }_i{\oplus }_{\nu }\lambda }(t_1,t_0)\hfill \\ & +\frac{1}{{\alpha }_i^{-}-\lambda }(exp\left(\lambda {\displaystyle \underset{s\in \mathbb{T}}{sup}}\nu \left(s\right)\right)({\alpha }_i^{+}{\eta }_i^{+}exp\left(\lambda {\eta }_i^{+}\right)+{\displaystyle \sum _{j=1}^n}{D}_{ij}^{+}{L}_j\hfill \\ & +{\displaystyle \sum _{j=1}^n}{\left(D_{ij}^{\tau }\right)}^{+}{L}_{j}exp\left(\lambda {\tau }_{ij}^{+}\right)+{\displaystyle \sum _{j=1}^n}{\overline{D}}_{ij}^{+}{L}_j{\sigma }_{ij}^{+}exp\left(\lambda {\sigma }_{ij}^{+}\right)\hfill \\ & +{\displaystyle \sum _{j=1}^n}{\tilde{D}}_{ij}^{+}{L}_j{\zeta }_{ij}^{+}exp\left(\lambda {\zeta }_{ij}^{+}\right))+B_i^{+})\}\hfill \\ \le & cPM{\widehat{e}}_{{\ominus }_{\nu }\lambda }(t_1,t_0){\parallel z\parallel }_0\hfill \end{array}$$

(16)

and

$$\begin{array}{cc}\hfill & |v_i\left(t_1\right)|\hfill \\ \le & {\widehat{e}}_{-c_i}(t_1,t_0){\parallel z\parallel }_0+cPM{\widehat{e}}_{{\ominus }_{\nu }\lambda }(t_1,t_0){\parallel z\parallel }_0{\int }_{t_0}^{t_1}{\widehat{e}}_{-c_i}(t_1,\rho \left(s\right)){\widehat{e}}_{\lambda }(t_1,\rho \left(s\right))\hfill \\ & \times \left(c_i^{+}{\int }_{s-{\varsigma }_i\left(s\right)}^s{\widehat{e}}_{\lambda }(\rho \left(u\right),u)\nabla u+E_i^{+}{L}_i\right)\nabla s\hfill \\ \le & {\widehat{e}}_{-c_i}(t_1,t_0){\parallel z\parallel }_0+cPM{\widehat{e}}_{{\ominus }_{\nu }\lambda }(t_1,t_0){\parallel z\parallel }_0{\int }_{t_0}^{t_1}{\widehat{e}}_{-c_i{\oplus }_{\nu }\lambda }(t_1,\rho \left(s\right))\hfill \\ & \times \left(c_i^{+}{\varsigma }_i^{+}{\widehat{e}}_{\lambda }(\rho \left(s\right),s-{\varsigma }_i\left(s\right))+E_i^{+}{L}_i\right)\nabla s\hfill \\ \le & {\widehat{e}}_{-c_i}(t_1,t_0){\parallel z\parallel }_0+cPM{\widehat{e}}_{{\ominus }_{\nu }\lambda }(t_1,t_0){\parallel z\parallel }_0{\int }_{t_0}^{t_1}{\widehat{e}}_{-c_i{\oplus }_{\nu }\lambda }(t_1,\rho \left(s\right))\hfill \\ & \times \left(c_i^{+}{\varsigma }_i^{+}exp\left[\lambda ({\varsigma }_i^{+}+{\displaystyle \underset{s\in \mathbb{T}}{sup}}\nu \left(s\right))\right]+E_i^{+}{L}_i\right)\nabla s\hfill \\ <& cPM{\widehat{e}}_{{\ominus }_{\nu }\lambda }(t_1,t_0){\parallel z\parallel }_0\{\frac{1}{M}{\widehat{e}}_{-c_i{\oplus }_{\nu }\lambda }(t_1,t_0)\hfill \\ & +\left[exp\left(\lambda {\displaystyle \underset{s\in \mathbb{T}}{sup}}\nu \left(s\right)\right)c_i^{+}{\varsigma }_i^{+}exp\left(\lambda {\varsigma }_i^{+}\right)+E_i^{+}{L}_i\right]\frac{1-{\widehat{e}}_{-c_i{\oplus }_{\nu }\lambda }(t_1,t_0)}{c_i^{-}-\lambda }\}\hfill \\ \le & cPM{\widehat{e}}_{{\ominus }_{\nu }\lambda }(t_1,t_0){\parallel z\parallel }_0\left\{\right[\frac{1}{M}-\frac{1}{c_i^{-}-\lambda }(exp\left(\lambda {\displaystyle \underset{s\in \mathbb{T}}{sup}}\nu \left(s\right)\right)c_i^{+}{\varsigma }_i^{+}exp\left(\lambda {\varsigma }_i^{+}\right)\hfill \\ & +E_i^{+}{L}_i\left)\right]{\widehat{e}}_{-c_i{\oplus }_{\nu }\lambda }(t_1,t_0)+\frac{1}{c_i^{-}-\lambda }\left(exp\left(\lambda {\displaystyle \underset{s\in \mathbb{T}}{sup}}\nu \left(s\right)\right)c_i^{+}{\varsigma }_i^{+}exp\left(\lambda {\varsigma }_i^{+}\right)+E_i^{+}{L}_i\right)\}\hfill \\ \le & cPM{\widehat{e}}_{{\ominus }_{\nu }\lambda }(t_1,t_0){\parallel z\parallel }_0.\hfill \end{array}$$

(17)

Similarly, in view of (10), we have for $i=1,2,\dots ,n$,

$$\begin{array}{cc}\hfill & |u_i^{\nabla }\left(t_1\right)|\hfill \\ \le & {\alpha }_i^{+}{\widehat{e}}_{-{\alpha }_i}(t_1,t_0){\parallel z\parallel }_0+cPM{\widehat{e}}_{{\ominus }_{\nu }\lambda }(t_1,t_0){\parallel z\parallel }_0({\alpha }_i^{+}{\int }_{t_1-{\eta }_i\left(t_1\right)}^{t_1}{\widehat{e}}_{\lambda }(t_1,u)\nabla u\hfill \\ & +{\displaystyle \sum _{j=1}^n}{D}_{ij}^{+}{L}_j{\widehat{e}}_{\lambda }(t_1,t_1)+{\displaystyle \sum _{j=1}^n}{\left(D_{ij}^{\tau }\right)}^{+}{L}_j{\widehat{e}}_{\lambda }(t_1,t_1-{\tau }_{ij}\left(t_1\right))\hfill \\ & +{\displaystyle \sum _{j=1}^n}{\overline{D}}_{ij}^{+}{L}_j{\int }_{t_1-{\sigma }_{ij}\left(t_1\right)}^{t_1}{\widehat{e}}_{\lambda }(\rho \left(u\right),u)\nabla u\hfill \\ & +{\displaystyle \sum _{j=1}^n}{\tilde{D}}_{ij}^{+}{L}_j{\int }_{t_1-{\zeta }_{ij}\left(t_1\right)}^{t_1}{\widehat{e}}_{\lambda }(\rho \left(u\right),u)\nabla u+B_i^{+})\hfill \\ & +{\alpha }_i^{+}cPM{\widehat{e}}_{{\ominus }_{\nu }\lambda }(t_1,t_0){\parallel z\parallel }_0{\int }_{t_0}^{t_1}{\widehat{e}}_{-{\alpha }_i}(t_1,\rho \left(s\right)){\widehat{e}}_{\lambda }(t_1,\rho \left(s\right))\hfill \\ & \times \{{\alpha }_i^{+}{\int }_{s-{\eta }_i\left(s\right)}^s{\widehat{e}}_{\lambda }(\rho \left(u\right),u)\nabla u+{\displaystyle \sum _{j=1}^n}{D}_{ij}^{+}{L}_j{\widehat{e}}_{\lambda }(\rho \left(s\right),s)\hfill \\ & +{\displaystyle \sum _{j=1}^n}{\left(D_{ij}^{\tau }\right)}^{+}{L}_j{\widehat{e}}_{\lambda }(\rho \left(s\right),s-{\tau }_{ij}\left(t\right))+{\displaystyle \sum _{j=1}^n}{\overline{D}}_{ij}^{+}{L}_j{\int }_{s-{\sigma }_{ij}\left(s\right)}^s{\widehat{e}}_{\lambda }(\rho \left(u\right),u)\nabla u\hfill \\ & +{\displaystyle \sum _{j=1}^n}{\tilde{D}}_{ij}^{+}{L}_j{\int }_{s-{\zeta }_{ij}\left(s\right)}^s{\widehat{e}}_{\lambda }(\rho \left(u\right),u)\nabla u+B_i^{+}\}\nabla s\hfill \\ \le & {\alpha }_i^{+}{e}_{-{\alpha }_i}(t_1,t_0){\parallel z\parallel }_0+cPM{\widehat{e}}_{{\ominus }_{\nu }\lambda }(t_1,t_0){\parallel z\parallel }_0({\alpha }_i^{+}{\eta }_i^{+}exp\left(\lambda {\eta }_i^{+}\right)+{\displaystyle \sum _{j=1}^n}{D}_{ij}^{+}{L}_j\hfill \\ & +{\displaystyle \sum _{j=1}^n}{\left(D_{ij}^{\tau }\right)}^{+}{L}_{j}exp\left(\lambda {\tau }_{ij}^{+}\right)+{\displaystyle \sum _{j=1}^n}{\overline{D}}_{ij}^{+}{L}_j{\sigma }_{ij}^{+}exp\left(\lambda {\sigma }_{ij}^{+}\right)\hfill \\ & +{\displaystyle \sum _{j=1}^n}{\tilde{D}}_{ij}^{+}{L}_j{\zeta }_{ij}^{+}exp\left(\lambda {\zeta }_{ij}^{+}\right)+B_i^{+})\hfill \\ & \times \left(1+{\alpha }_i^{+}exp\left(\lambda {\displaystyle \underset{s\in \mathbb{T}}{sup}}\nu \left(s\right)\right){\int }_{t_0}^{t_1}{\widehat{e}}_{-{\alpha }_i\oplus \lambda }(t_1,\rho \left(s\right))\nabla s\right)\hfill \\ \le & cPM{\widehat{e}}_{{\ominus }_{\nu }\lambda }(t_1,t_0){\parallel z\parallel }_0\left\{\right[\frac{1}{M}-\frac{exp\left(\lambda {\displaystyle \underset{s\in \mathbb{T}}{sup}}\nu \left(s\right)\right)}{{\alpha }_i^{-}-\lambda }({\alpha }_i^{+}{\eta }_i^{+}exp\left(\lambda {\eta }_i^{+}\right)\hfill \\ & +{\displaystyle \sum _{j=1}^n}{D}_{ij}^{+}{L}_j+{\displaystyle \sum _{j=1}^n}{\left(D_{ij}^{\tau }\right)}^{+}{L}_{j}exp\left(\lambda {\tau }_{ij}^{+}\right)+{\displaystyle \sum _{j=1}^n}{\overline{D}}_{ij}^{+}{L}_j{\sigma }_{ij}^{+}exp\left(\lambda {\sigma }_{ij}^{+}\right)\hfill \\ & +{\displaystyle \sum _{j=1}^n}{\tilde{D}}_{ij}^{+}{L}_j{\zeta }_{ij}^{+}exp\left(\lambda {\zeta }_{ij}^{+}\right)+B_i^{+}\left)\right]{\alpha }_i^{+}{\widehat{e}}_{-{\alpha }_i{\oplus }_{\nu }\lambda }(t_1,t_0)\hfill \\ & +\left(1+\frac{{\alpha }_i^{+}exp\left(\lambda {\displaystyle \underset{s\in \mathbb{T}}{sup}}\nu \left(s\right)\right)}{{\alpha }_i^{-}-\lambda }\right)({\alpha }_i^{+}{\eta }_i^{+}exp\left(\lambda {\eta }_i^{+}\right)+{\displaystyle \sum _{j=1}^n}{D}_{ij}^{+}{L}_j\hfill \\ & +{\displaystyle \sum _{j=1}^n}{\left(D_{ij}^{\tau }\right)}^{+}{L}_{j}exp\left(\lambda {\tau }_{ij}^{+}\right)+{\displaystyle \sum _{j=1}^n}{\overline{D}}_{ij}^{+}{L}_j{\sigma }_{ij}^{+}exp\left(\lambda {\sigma }_{ij}^{+}\right)\hfill \\ & +{\displaystyle \sum _{j=1}^n}{\tilde{D}}_{ij}^{+}{L}_j{\zeta }_{ij}^{+}exp\left(\lambda {\zeta }_{ij}^{+}\right)+B_i^{+}\left)\right\}\hfill \\ <& cPM{\widehat{e}}_{{\ominus }_{\nu }\lambda }(t_1,t_0){\parallel z\parallel }_0\hfill \end{array}$$

(18)

and

$$\begin{array}{cc}\hfill & |v_i^{\nabla }\left(t_1\right)|\hfill \\ \le & c_i^{+}{\widehat{e}}_{-c_i}(t_1,t_0){\parallel z\parallel }_0+cPM{\widehat{e}}_{{\ominus }_{\nu }\lambda }(t_1,t_0){\parallel z\parallel }_0(c_i^{+}{\int }_{t_1-{\varsigma }_i\left(t_1\right)}^{t_1}{\widehat{e}}_{\lambda }(t_1,u)\nabla u\hfill \\ & +E_i^{+}{L}_i)+c_i^{+}cPM{\widehat{e}}_{{\ominus }_{\nu }\lambda }(t_1,t_0){\parallel z\parallel }_0{\int }_{t_0}^{t_1}{\widehat{e}}_{-c_i}(t_1,\rho \left(s\right)){\widehat{e}}_{\lambda }(t_1,\rho \left(s\right))\hfill \\ & \times \left\{c_i^{+}{\int }_{s-{\varsigma }_i\left(s\right)}^s{\widehat{e}}_{\lambda }(\rho \left(u\right),u)\nabla u+E_i^{+}{L}_i\right\}\nabla s\hfill \\ \le & c_i^{+}{e}_{-c_i}(t_1,t_0){\parallel z\parallel }_0+cPM{\widehat{e}}_{{\ominus }_{\nu }\lambda }(t_1,t_0){\parallel z\parallel }_0\left(c_i^{+}{\varsigma }_i^{+}exp\left(\lambda {\varsigma }_i^{+}\right)+E_i^{+}{L}_i\right)\hfill \\ & \times \left(1+c_i^{+}exp\left(\lambda {\displaystyle \underset{s\in \mathbb{T}}{sup}}\nu \left(s\right)\right){\int }_{t_0}^{t_1}{\widehat{e}}_{-c_i\oplus \lambda }(t_1,\rho \left(s\right))\nabla s\right)\hfill \\ \le & cPM{\widehat{e}}_{{\ominus }_{\nu }\lambda }(t_1,t_0){\parallel z\parallel }_0\left\{\right[\frac{1}{M}-\frac{exp\left(\lambda {\displaystyle \underset{s\in \mathbb{T}}{sup}}\nu \left(s\right)\right)}{c_i^{-}-\lambda }(c_i^{+}{\varsigma }_i^{+}exp\left(\lambda {\varsigma }_i^{+}\right)\hfill \\ & +E_i^{+}{L}_i\left)\right]c_i^{+}{\widehat{e}}_{-c_i{\oplus }_{\nu }\lambda }(t_1,t_0)+\left(1+\frac{c_i^{+}exp\left(\lambda {\displaystyle \underset{s\in \mathbb{T}}{sup}}\nu \left(s\right)\right)}{c_i^{-}-\lambda }\right)\left(c_i^{+}{\varsigma }_i^{+}exp\left(\lambda {\varsigma }_i^{+}\right)+E_i^{+}{L}_i\right)\}\hfill \\ <& cPM{\widehat{e}}_{{\ominus }_{\nu }\lambda }(t_1,t_0){\parallel z\parallel }_0.\hfill \end{array}$$

(19)

In view of (16)–(19), we have

$$\parallel Z\left(t_1\right)-Z^{*}\left(t_1\right)\parallel <cPM{\widehat{e}}_{{\ominus }_{\nu }\lambda }(t_1,t_0){\parallel z\parallel }_0,$$

which contradicts (14), and so (13) holds. Let $p\to 1$, then, (12) is established. Therefore, the almost periodic solution of (1) is globally exponentially stable. This completes the proof.

Remark 1.

Since conditions $\left(A_1\right)$–$\left(A_3\right)$ are independent of the backwards graininess function of the time scale, according to Theorems 1 and 2, both the continuous time and the discrete-time cases of system (1) share the same dynamical behavior.

5. Numerical Examples

In this section, we present an example to show the feasibility of our results of this paper.

Example 1.

In system (1), suppose ${\displaystyle \underset{t\in \mathbb{T}}{sup}}\nu \left(t\right)<+\infty$, let $i,j=3$ and take coefficients as follows:

$$f_1\left(t\right)=0.1\left(\right|x+1|+|x|-1),f_2\left(t\right)=0.2sinx,f_3\left(t\right)=0.2|cosx-1|,$$

$${\alpha }_1\left(t\right)=0.2+0.1|sin\sqrt{3}t|,{\alpha }_2\left(t\right)=0.5-0.1|cost|,{\alpha }_1\left(t\right)=0.6-0.1|sin\sqrt{5}t|,$$

$$B_1\left(t\right)=0.05cos\sqrt{2}t,B_2\left(t\right)=0.15sin2t,B_3\left(t\right)=0.2+0.05sin\sqrt{5}t,$$

$$c_1\left(t\right)=0.05+0.01|cos2t|,c_2\left(t\right)=0.06+0.02|sint|,c_3\left(t\right)=0.09-0.01|sin\sqrt{3}t|,$$

$$E_1\left(t\right)=0.03cos2t,E_2\left(t\right)=0.045+0.005sin\sqrt{2}t,E_3\left(t\right)=0.03+0.01|cost|,$$

$$I_1\left(t\right)=0.02sin\sqrt{5}t,I_2\left(t\right)=0.04cost,I_3\left(t\right)=0.05sin2t,$$

$$J_1\left(t\right)=0.01sint,J_2\left(t\right)=0.012cos2t,J_3\left(t\right)=0.009sint,$$

$${\eta }_1\left(t\right)=0.02|sin\pi t|,{\eta }_2\left(t\right)=0.04|cos\left(\pi t+\frac{3\pi }{2}\right)|,{\eta }_3\left(t\right)=0.05|sin2\pi t|,$$

$${\varsigma }_1\left(t\right)=0.5|sin3\pi t|,{\varsigma }_2\left(t\right)=0.4|sin2\pi t|,{\varsigma }_3\left(t\right)=0.6|cos\left(\pi t+\frac{\pi }{2}\right)|,$$

$$D_{ij}\left(t\right)=0.08sint,D_{ij}^{\tau }\left(t\right)=0.04cost,{\overline{D}}_{ij}\left(t\right)=0.06sin2t,{\tilde{D}}_{ij}\left(t\right)=0.05sint,$$

$${\tau }_{ij}\left(t\right)=0.8|sin\pi t|,{\sigma }_{ij}\left(t\right)=0.5|sin2\pi t|,{\zeta }_{ij}\left(t\right)=0.6|sin\pi t|,i,j=1,2,3.$$

By a calculation, we obtain

$${\alpha }_1^{+}=0.3,{\alpha }_1^{-}=0.2,{\alpha }_2^{+}=0.5,{\alpha }_2^{-}=0.4,{\alpha }_3^{+}=0.6,{\alpha }_3^{-}=0.5,$$

$$c_1^{+}=0.06,c_1^{-}=0.05,c_2^{+}=0.08,c_2^{-}=0.06,c_3^{+}=0.09,c_3^{-}=0.08,$$

$$B_1^{+}=0.05,B_2^{+}=0.15,B_3^{+}=0.25,E_1^{+}=0.03,E_2^{+}=0.05,E_3^{+}=0.04,$$

$$I_1^{+}=0.02,I_2^{+}=0.04,I_3^{+}=0.05,J_1^{+}=0.01,J_2^{+}=0.012,J_3^{+}=0.009,$$

$${\eta }_1^{+}=0.02,{\eta }_2^{+}=0.04,{\eta }_3^{+}=0.05,{\varsigma }_1^{+}=0.5,{\varsigma }_2^{+}=0.4,{\varsigma }_3^{+}=0.6,$$

$$D_{ij}^{+}=0.08,{\left(D_{ij}^{\tau }\right)}^{+}=0.04,{\overline{D}}_{ij}^{+}=0.06,{\tilde{D}}_{ij}^{+}=0.05,$$

$${\sigma }_{ij}^{+}=0.5,{\zeta }_{ij}^{+}=0.6,i,j=1,2,3.$$

Take $L_1=L_2=L_3=0.2$, $|f_1\left(0\right)|=|f_2\left(0\right)|=|f_3\left(0\right)|=0$ and $K=0.8$, we have

$$\begin{array}{ccc}\hfill P_1& =& {\alpha }_1^{+}{\eta }_1^{+}K+{\displaystyle \sum _{j=1}^3}{D}_{1j}^{+}(L_{j}K+|f_j\left(0\right)\left|\right)+{\displaystyle \sum _{j=1}^3}{\left(D_{1j}^{\tau }\right)}^{+}(L_{j}K+|f_j\left(0\right)\left|\right)\hfill \\ & & +{\displaystyle \sum _{j=1}^3}{\overline{D}}_{1j}^{+}{\sigma }_{1j}^{+}(L_{j}K+|f_j\left(0\right)\left|\right)+{\displaystyle \sum _{j=1}^3}{\tilde{D}}_{1j}^{+}{\zeta }_{1j}^{+}(L_{j}K+|f_j\left(0\right)\left|\right)+B_1^{+}K+I_1^{+}\hfill \\ & =& 0.3\times 0.02\times 0.8+\left(0.08+0.04+0.06\times 0.5+0.05\times 0.6\right)\hfill \\ & & \times 0.2\times 0.8\times 3+0.05\times 0.8+0.02=0.1512,\hfill \\ \hfill P_2& =& {\alpha }_2^{+}{\eta }_2^{+}K+{\displaystyle \sum _{j=1}^3}{D}_{2j}^{+}(L_{j}K+|f_j\left(0\right)\left|\right)+{\displaystyle \sum _{j=1}^3}{\left(D_{2j}^{\tau }\right)}^{+}(L_{j}K+|f_j\left(0\right)\left|\right)\hfill \\ & & +{\displaystyle \sum _{j=1}^3}{\overline{D}}_{2j}^{+}{\sigma }_{2j}^{+}(L_{j}K+|f_j\left(0\right)\left|\right)+{\displaystyle \sum _{j=1}^3}{\tilde{D}}_{2j}^{+}{\zeta }_{2j}^{+}(L_{j}K+|f_j\left(0\right)\left|\right)+B_2^{+}K+I_2^{+}\hfill \\ & =& 0.5\times 0.04\times 0.8+\left(0.08+0.04+0.06\times 0.5+0.05\times 0.6\right)\hfill \\ & & \times 0.2\times 0.8\times 3+0.15\times 0.8+0.04=0.2624,\hfill \\ \hfill P_3& =& {\alpha }_3^{+}{\eta }_3^{+}K+{\displaystyle \sum _{j=1}^3}{D}_{3j}^{+}(L_{j}K+|f_j\left(0\right)\left|\right)+{\displaystyle \sum _{j=1}^3}{\left(D_{3j}^{\tau }\right)}^{+}(L_{j}K+|f_j\left(0\right)\left|\right)\hfill \\ & & +{\displaystyle \sum _{j=1}^3}{\overline{D}}_{3j}^{+}{\sigma }_{3j}^{+}(L_{j}K+|f_j\left(0\right)\left|\right)+{\displaystyle \sum _{j=1}^3}{\tilde{D}}_{3j}^{+}{\zeta }_{3j}^{+}(L_{j}K+|f_j\left(0\right)\left|\right)+B_3^{+}K+I_3^{+}\hfill \\ & =& 0.6\times 0.05\times 0.8+\left(0.08+0.04+0.06\times 0.5+0.05\times 0.6\right)\hfill \\ & & \times 0.2\times 0.8\times 3+0.25\times 0.8+0.05=0.3604,\hfill \\ \hfill Q_1& =& c_1^{+}{\varsigma }_1^{+}K+E_1^{+}(L_{1}K+|f_1\left(0\right)\left|\right)+J_1^{+}=0.06\times 0.5\times 0.8+0.03\times 0.2\times 0.8\hfill \\ & & +0.01=0.0388,\hfill \\ \hfill Q_2& =& c_2^{+}{\varsigma }_2^{+}K+E_2^{+}(L_{2}K+|f_2\left(0\right)\left|\right)+J_2^{+}=0.08\times 0.4\times 0.8+0.05\times 0.2\times 0.8\hfill \\ & & +0.012=0.0456,\hfill \\ \hfill Q_3& =& c_3^{+}{\varsigma }_3^{+}K+E_3^{+}(L_{3}K+|f_3\left(0\right)\left|\right)+J_3^{+}=0.09\times 0.6\times 0.8+0.04\times 0.2\times 0.8\hfill \\ & & +0.009=0.0586,\hfill \\ \hfill \overline{P_1}& =& {\alpha }_1^{+}{\eta }_1^{+}+{\displaystyle \sum _{j=1}^3}{D}_{1j}^{+}{L}_j+{\displaystyle \sum _{j=1}^3}{\left(D_{1j}^{\tau }\right)}^{+}{L}_j+{\displaystyle \sum _{j=1}^3}{\overline{D}}_{1j}^{+}{\sigma }_{1j}^{+}{L}_j+{\displaystyle \sum _{j=1}^3}{\tilde{D}}_{1j}^{+}{\zeta }_{1j}^{+}{L}_j+B_1^{+}\hfill \\ & =& 0.3\times 0.02+\left(0.08+0.04+0.06\times 0.5+0.05\times 0.6\right)\times 0.2\times 3+0.05=0.164,\hfill \\ \hfill \overline{P_2}& =& {\alpha }_2^{+}{\eta }_2^{+}+{\displaystyle \sum _{j=1}^3}{D}_{2j}^{+}{L}_j+{\displaystyle \sum _{j=1}^3}{\left(D_{2j}^{\tau }\right)}^{+}{L}_j+{\displaystyle \sum _{j=1}^3}{\overline{D}}_{2j}^{+}{\sigma }_{2j}^{+}{L}_j+{\displaystyle \sum _{j=1}^3}{\tilde{D}}_{2j}^{+}{\zeta }_{2j}^{+}{L}_j+B_2^{+}\hfill \\ & =& 0.5\times 0.04+\left(0.08+0.04+0.06\times 0.5+0.05\times 0.6\right)\times 0.2\times 3+0.15=0.278,\hfill \\ \hfill \overline{P_3}& =& {\alpha }_3^{+}{\eta }_3^{+}+{\displaystyle \sum _{j=1}^3}{D}_{3j}^{+}{L}_j+{\displaystyle \sum _{j=1}^3}{\left(D_{3j}^{\tau }\right)}^{+}{L}_j+{\displaystyle \sum _{j=1}^3}{\overline{D}}_{3j}^{+}{\sigma }_{3j}^{+}{L}_j+{\displaystyle \sum _{j=1}^3}{\tilde{D}}_{3j}^{+}{\zeta }_{3j}^{+}{L}_j+B_3^{+}\hfill \\ & =& 0.6\times 0.05+\left(0.08+0.04+0.06\times 0.5+0.05\times 0.6\right)\times 0.2\times 3+0.25=0.398,\hfill \\ \hfill \overline{Q_1}& =& c_1^{+}{\varsigma }_1^{+}+E_1^{+}{L}_1=0.06\times 0.5+0.03\times 0.2=0.036,\hfill \\ \hfill \overline{Q_2}& =& c_2^{+}{\varsigma }_2^{+}+E_2^{+}{L}_2=0.08\times 0.4+0.05\times 0.2=0.042,\hfill \\ \hfill \overline{Q_3}& =& c_3^{+}{\varsigma }_3^{+}+E_3^{+}{L}_3=0.09\times 0.6+0.04\times 0.2=0.062.\hfill \end{array}$$

Obviously, conditions $\left(A_1\right)$ and $\left(A_2\right)$ hold. Since

$$\begin{array}{c}{\displaystyle \underset{1\le i\le 3}{max}}\left\{\frac{P_i}{{\alpha }_i^{-}},\left(1+\frac{{\alpha }_i^{+}}{{\alpha }_i^{-}}\right)P_i,\frac{Q_i}{c_i^{-}},\left(1+\frac{c_i^{+}}{c_i^{-}}\right)Q_i\right\}\le K,\hfill \\ {\displaystyle \underset{1\le i\le 3}{max}}\left\{\frac{\overline{P_i}}{{\alpha }_i^{-}},\left(1+\frac{{\alpha }_i^{+}}{{\alpha }_i^{-}}\right)\overline{P_i},\frac{\overline{Q_i}}{c_i^{-}},\left(1+\frac{c_i^{+}}{c_i^{-}}\right)\overline{Q_i}\right\}<1,\hfill \end{array}$$

that is,

$$\begin{array}{l}{\displaystyle \underset{1\le i\le 3}{max}}\{0.756,0.378,0.656,0.5904,0.7208,0.7929,0.776,0.0854,0.76,0.1664,\\ 0.7325,0.1245\}=0.7929\le r=0.8,\\ {\displaystyle \underset{1\le i\le 3}{max}}\{0.82,0.41,0.695,0.6255,0.796,0.8756,0.72,0.0792,0.7,0.0980,\\ 0.775,0.1318\}=0.8756<1,\end{array}$$

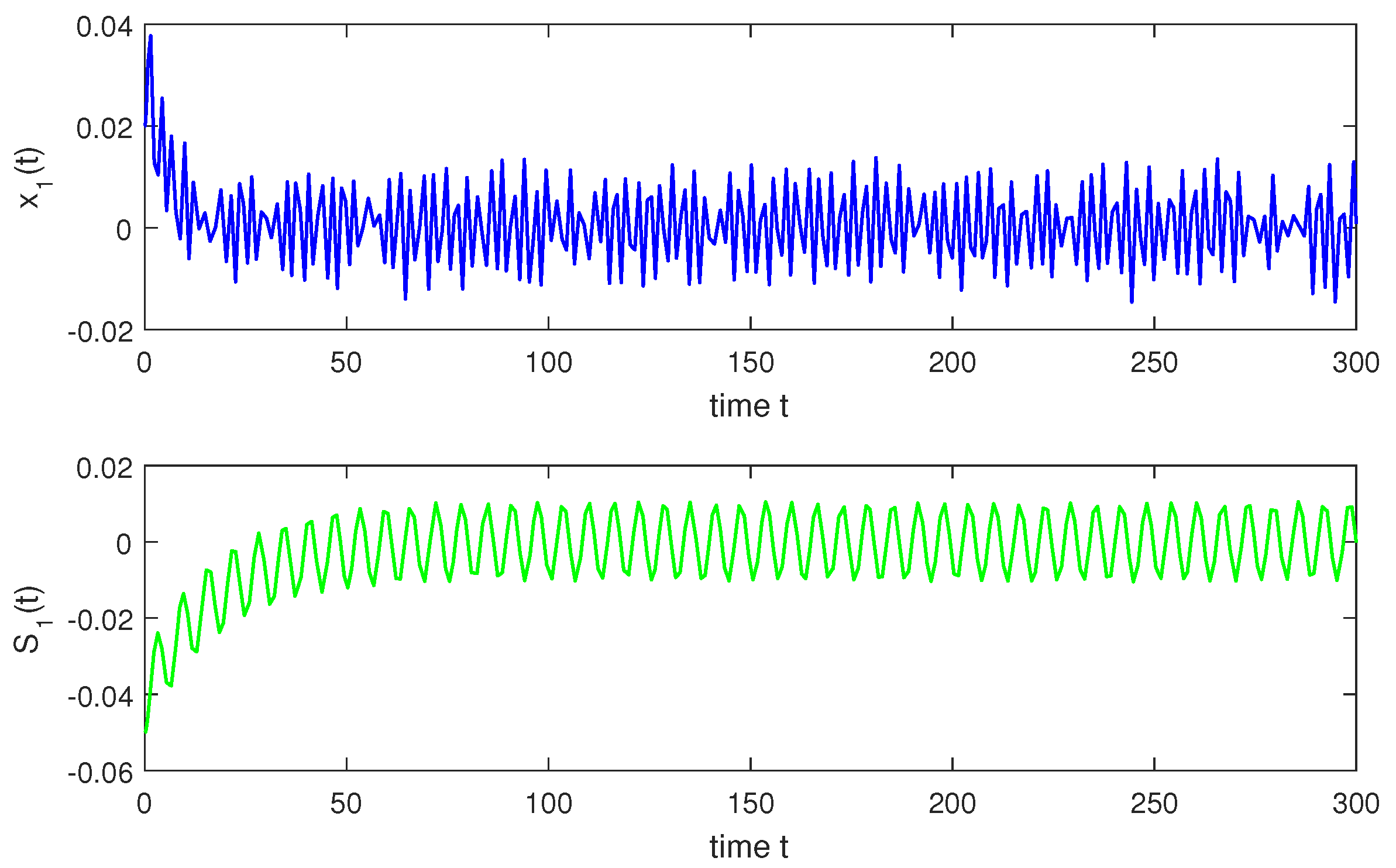
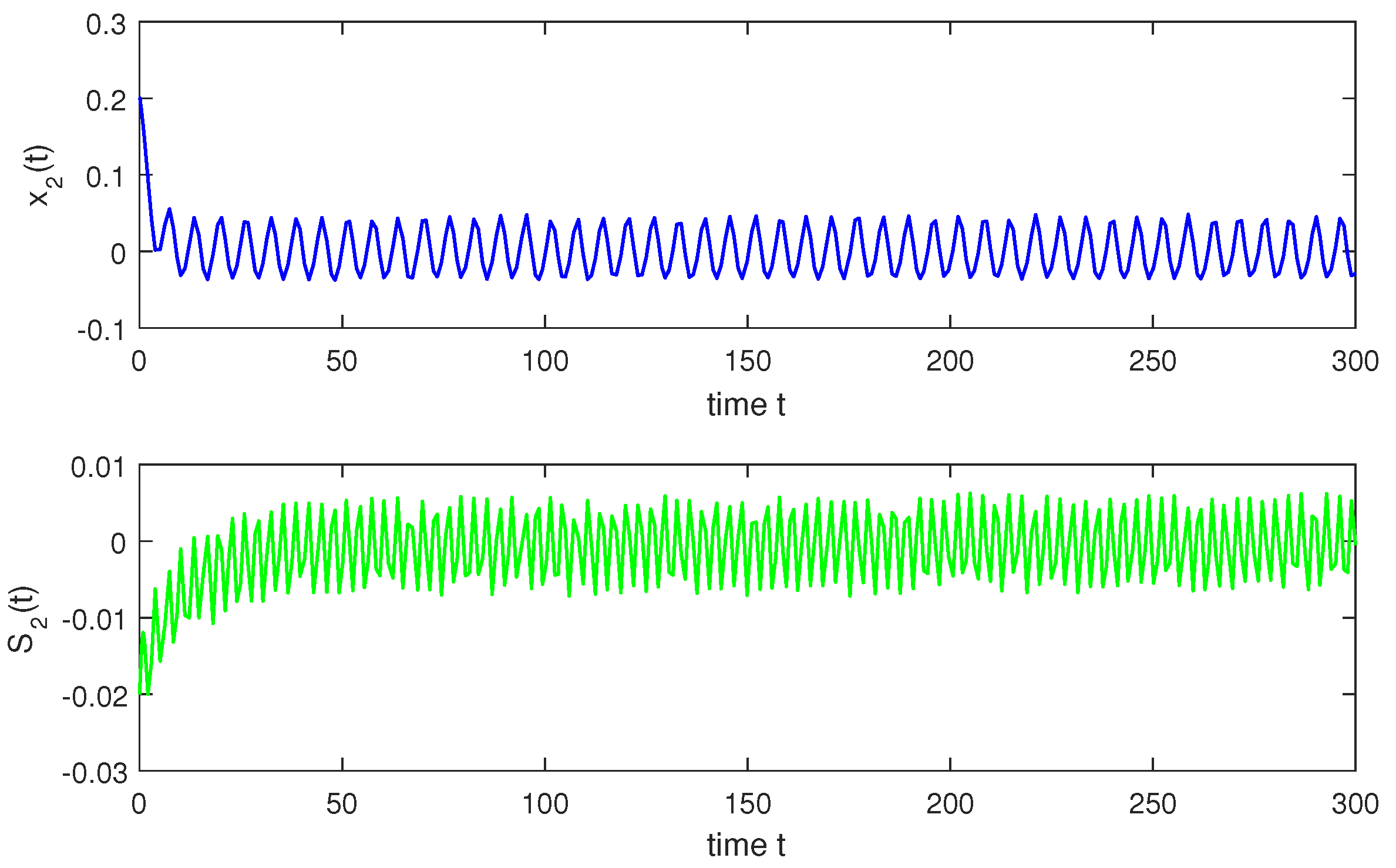
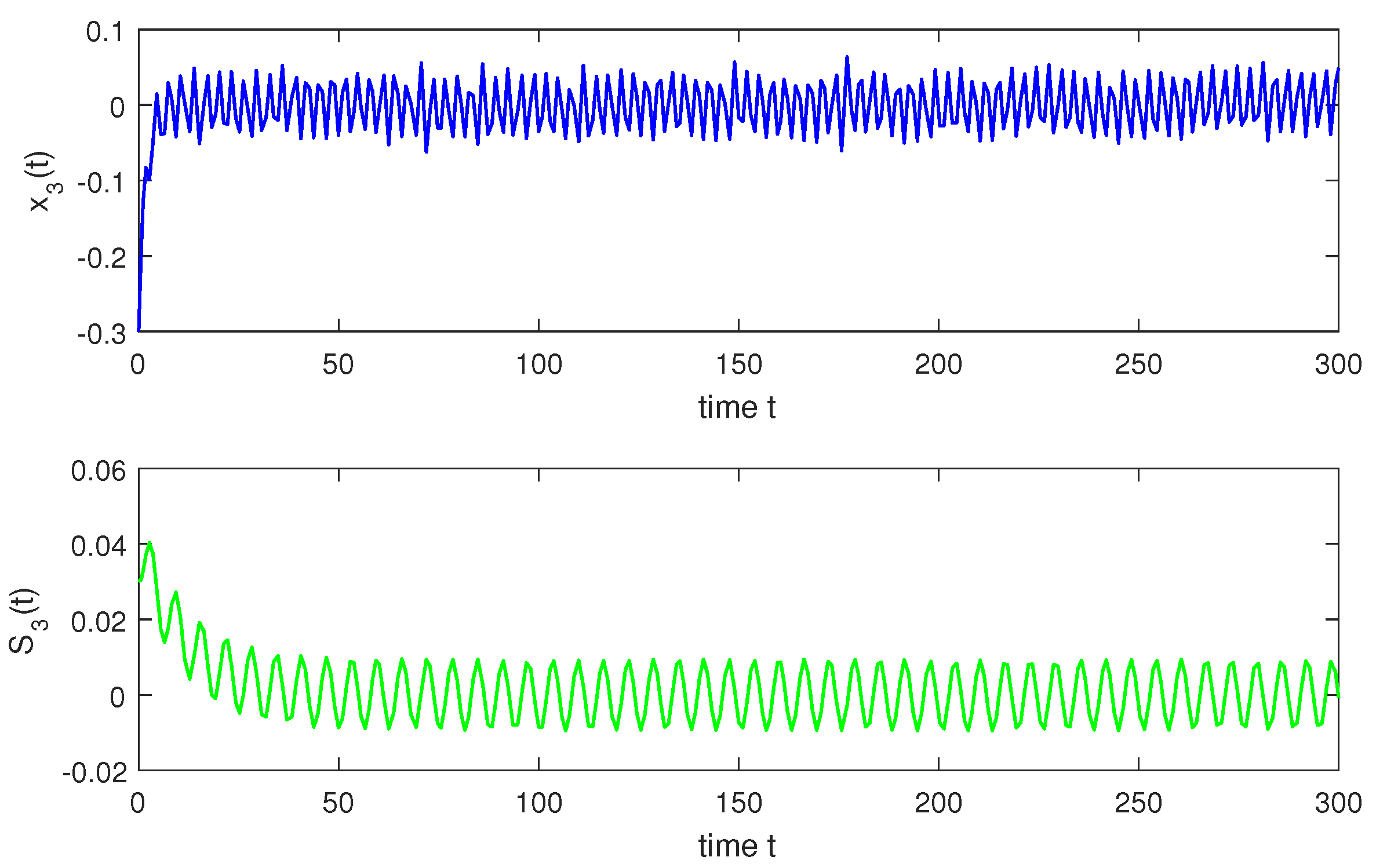
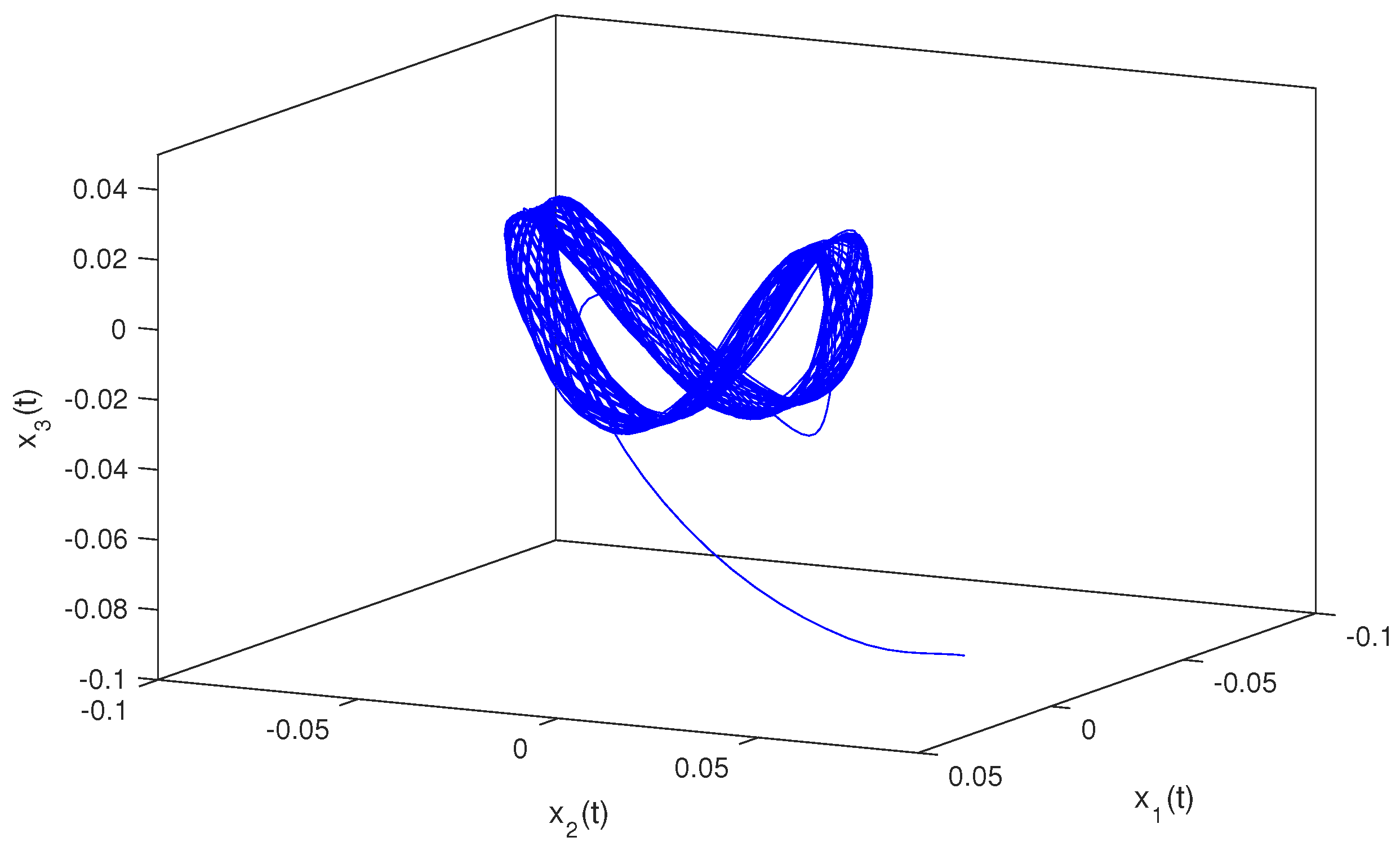
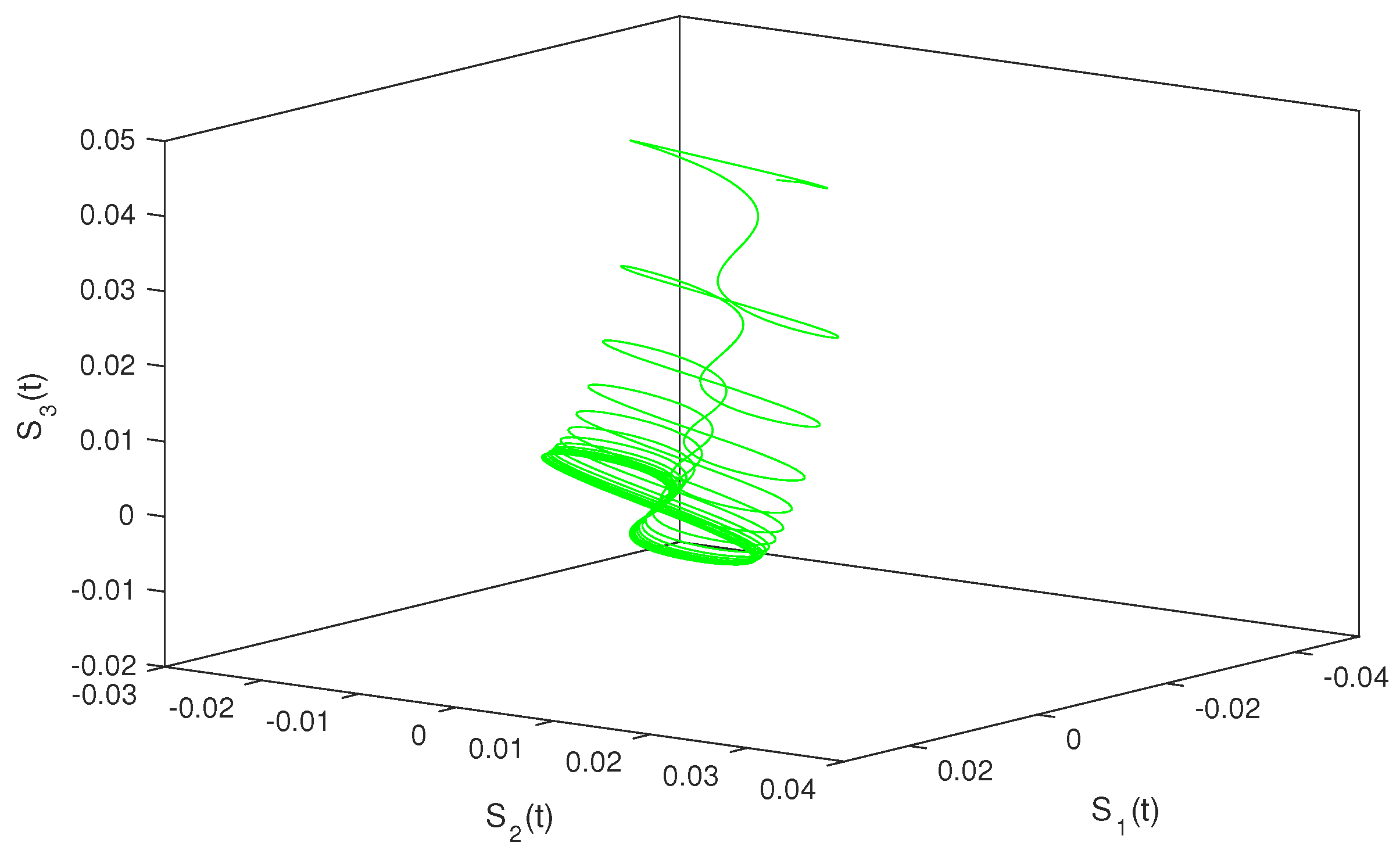
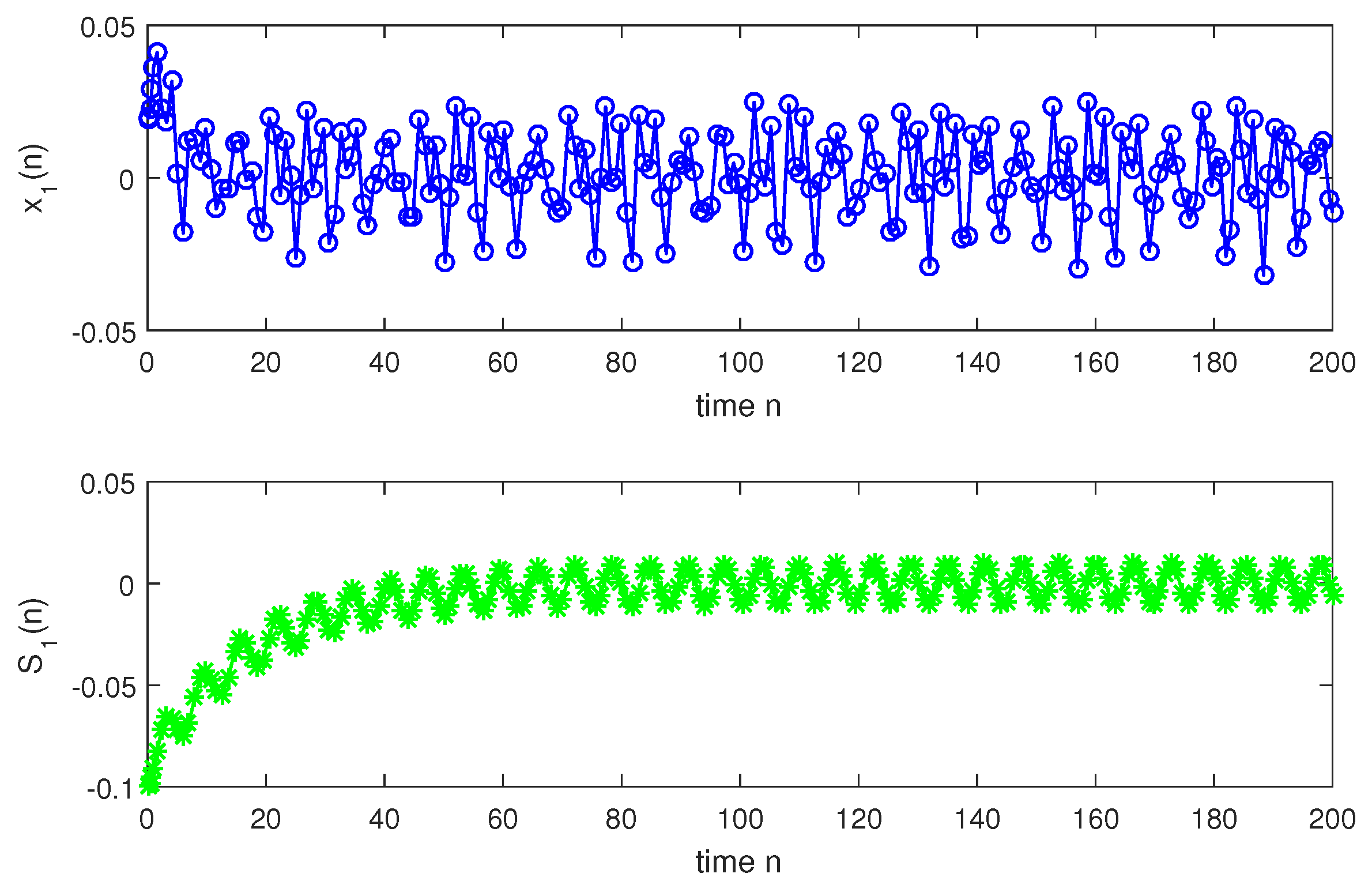
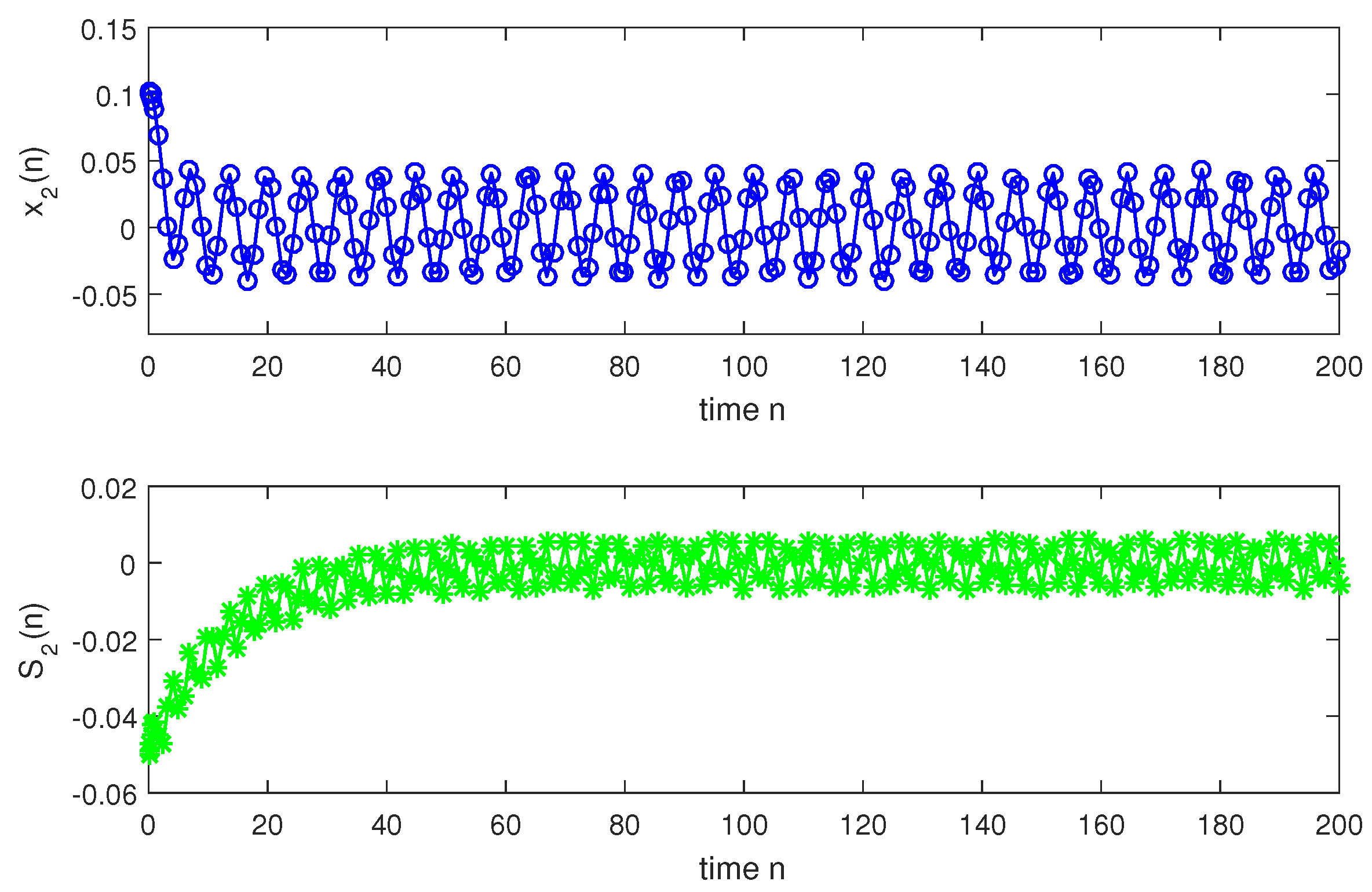
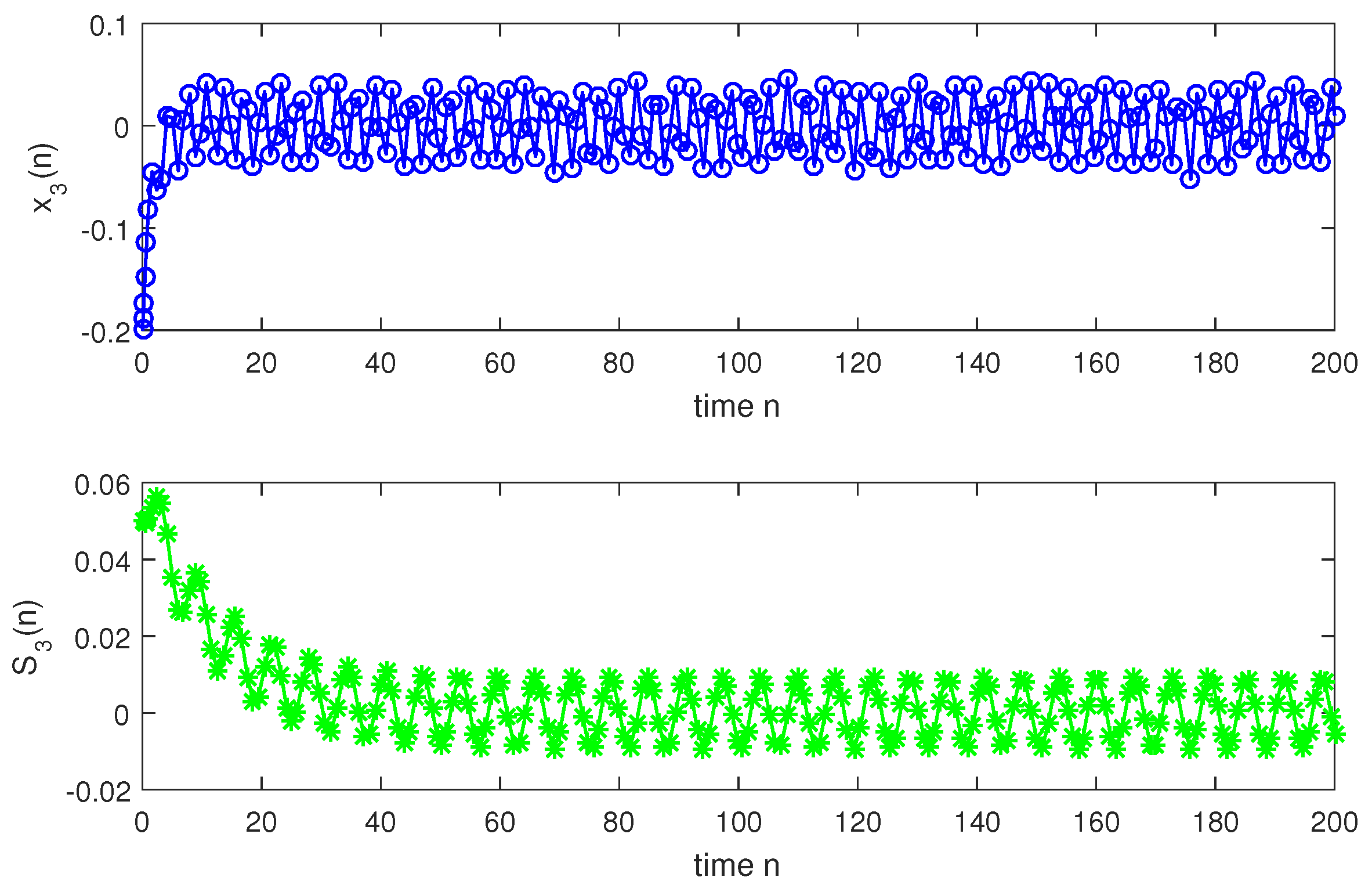
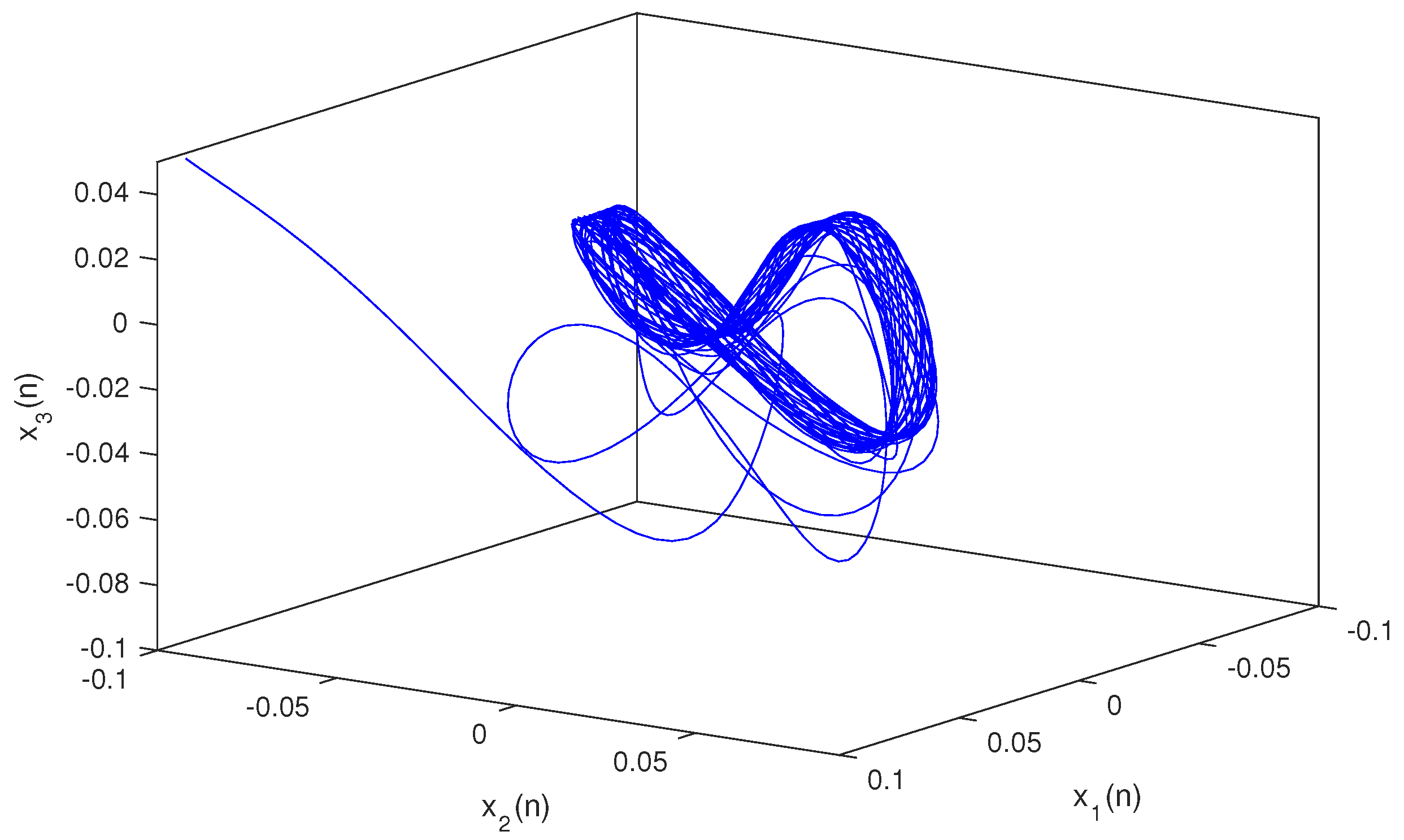
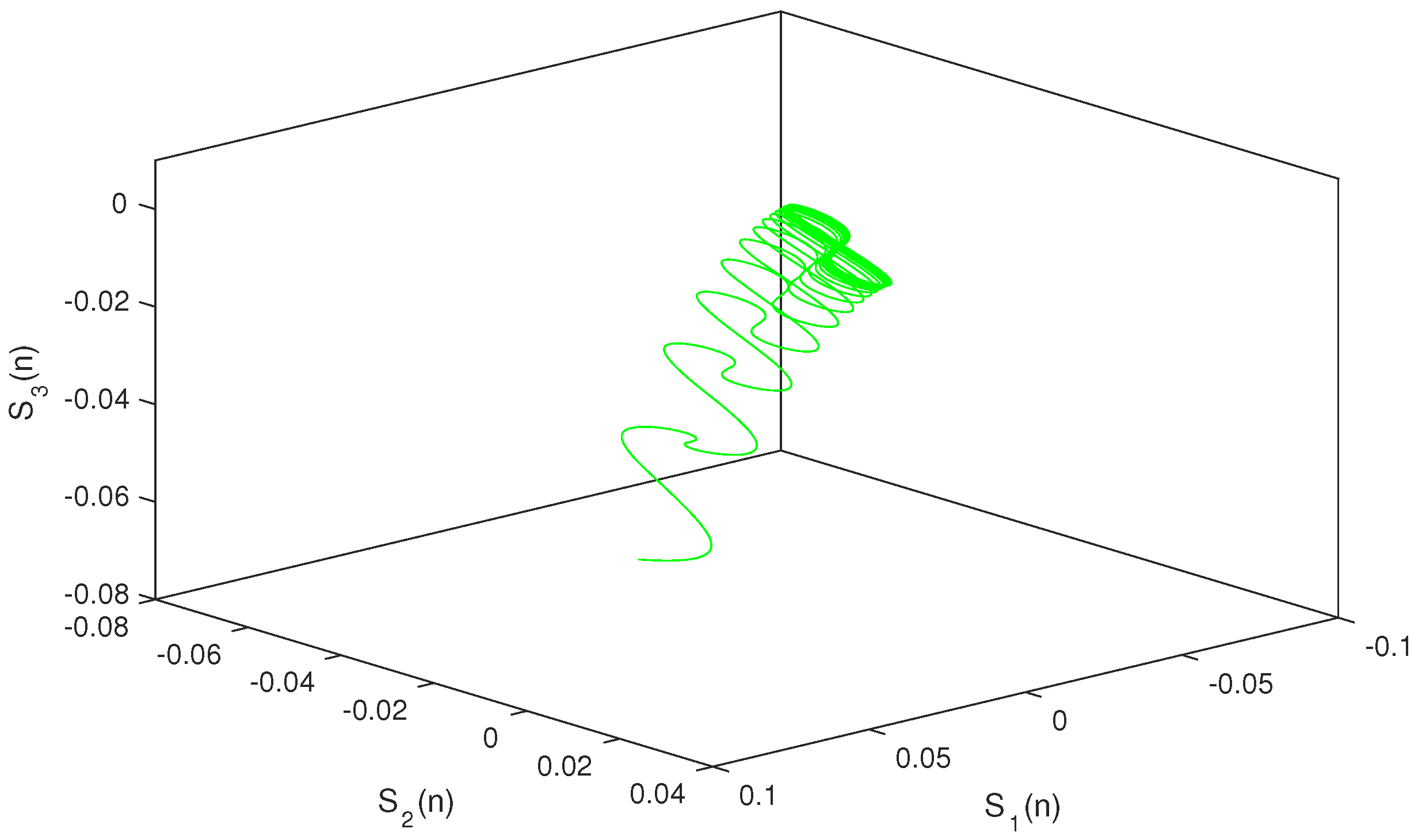
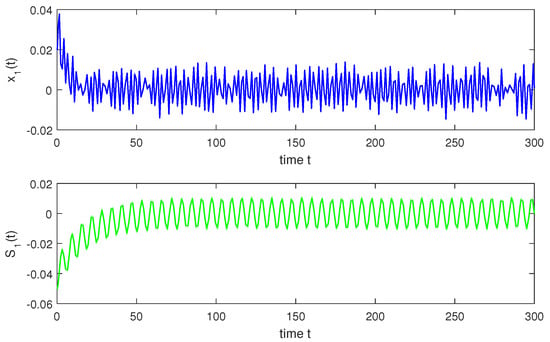
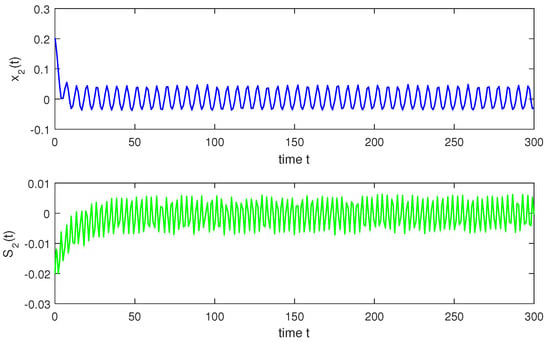
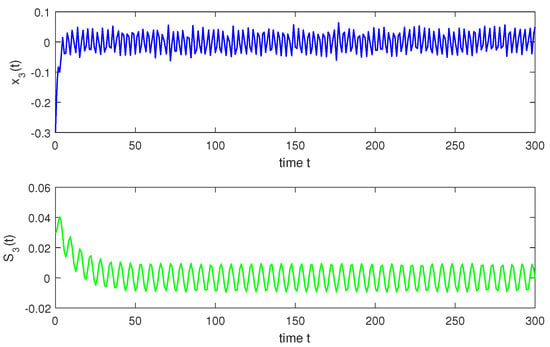
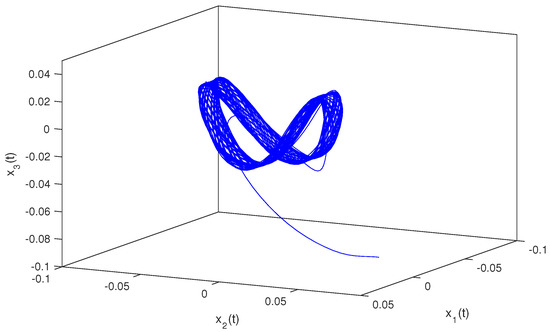
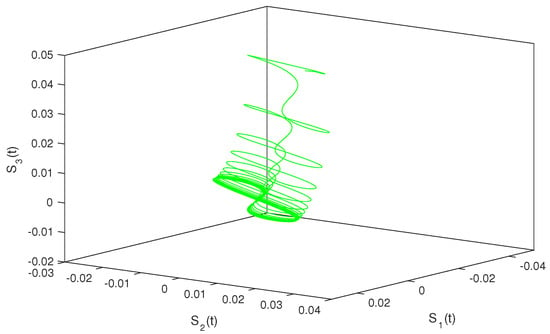
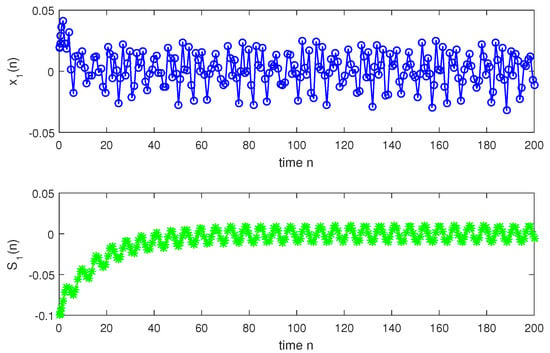
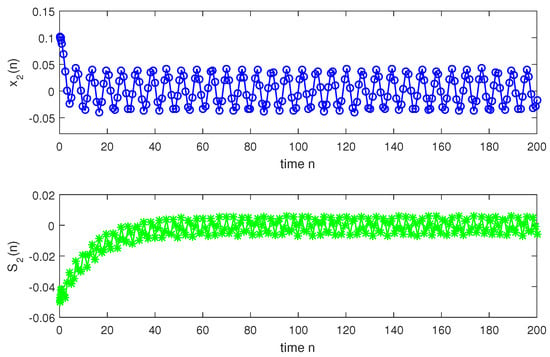
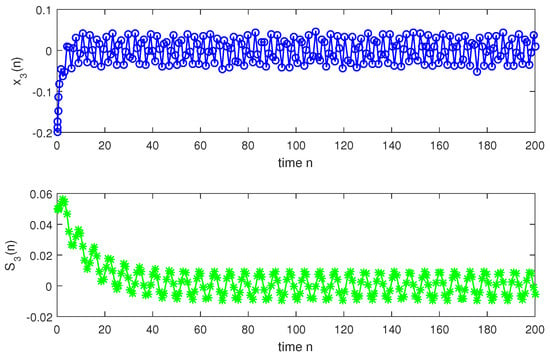
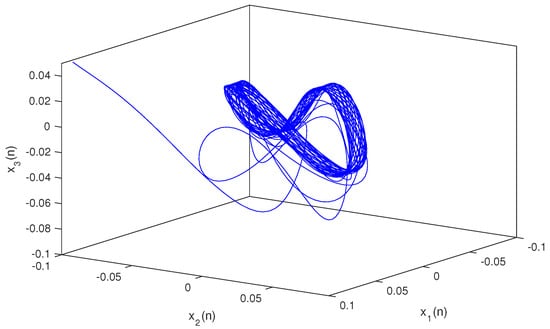
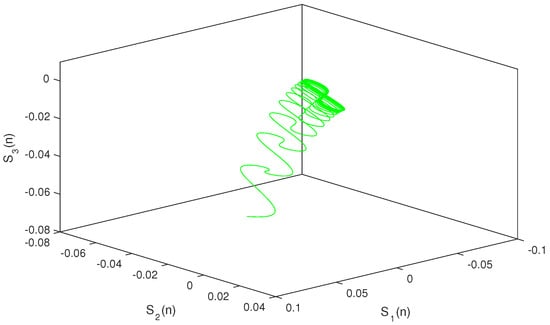
so, condition $\left(A_3\right)$ holds. Hence, conditions $\left(A_1\right)$–$\left(A_3\right)$ are verified. Therefore, according to Theorem 2, system (1) has a unique almost periodic solution which is globally exponentially stable. In particular, for both the discrete-time and continuous-time cases, system (1) has a unique almost periodic solution which is globally exponentially stable (see Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10).

Figure 1. Continuous situation $\mathbb{T}=\mathbb{R}:x_1,S_1$ with t.

Figure 2. Continuous situation $\mathbb{T}=\mathbb{R}:x_2,S_2$ with t.

Figure 3. Continuous situation $\mathbb{T}=\mathbb{R}:x_3,S_3$ with t.

Figure 4. Continuous situation $\mathbb{T}=\mathbb{R}:x_1\left(t\right),x_2\left(t\right),x_3\left(t\right)$.

Figure 5. Continuous situation $\mathbb{T}=\mathbb{R}:S_1\left(t\right),S_2\left(t\right),S_3\left(t\right)$.

Figure 6. Discrete situation $\mathbb{T}=\mathbb{Z}:x_1,S_1$ with n.

Figure 7. Discrete situation $\mathbb{T}=\mathbb{Z}:x_2,S_2$ with n.

Figure 8. Discrete situation $\mathbb{T}=\mathbb{Z}:x_3,S_3$ with n.

Figure 9. Discrete situation $\mathbb{T}=\mathbb{Z}:x_1\left(n\right),x_2\left(n\right),x_3\left(n\right)$.

Figure 10. Discrete situation $\mathbb{T}=\mathbb{Z}:S_1\left(n\right),S_2\left(n\right),S_3\left(n\right)$.

6. Conclusions

In this paper, we proposed a class of neutral-type CNNs on a new type of almost periodic time scales. We established the existence and uniqueness of almost periodic solutions for this class of neural networks without assuming the boundedness of the activation functions by the contraction fixed-point theorem. Besides, under the same assumptions, we also obtained the global exponential stability of the almost periodic solutions. Our approaches of this paper maybe further be used for other dynamical systems. However, if we modify Definition 3 to be the following form:

Definition 7.

Let $\mathbb{T}$ be time scale, it is said to be almost periodic if

$${\mathsf{\Lambda }}_0:=\left\{\tau \in \mathbb{R}:{\mathbb{T}}_{\tau }\ne \varnothing \right\}\ne \left\{0\right\},$$

where ${\mathbb{T}}_{\tau }=\mathbb{T}\cap \{\mathbb{T}-\tau \}=\mathbb{T}\cap \{t-\tau :t\in \mathbb{T}\}$, and there exists a set Λ satisfying

$\left(a\right)$

$0\in \mathsf{\Lambda }\subseteq {\mathsf{\Lambda }}_0$,

$\left(b\right)$

$\mathsf{\Pi }\left(\mathsf{\Lambda }\right)\backslash \left\{0\right\}\ne \varnothing$,

$\left(c\right)$

$\tilde{\mathbb{T}}:=\mathbb{T}\left(\mathsf{\Pi }\right)={\displaystyle {\displaystyle \bigcap }_{\tau \in \mathsf{\Pi }}}{\mathbb{T}}_{\tau }\ne \varnothing$,

where $\mathsf{\Pi }:=\mathsf{\Pi }\left(\mathsf{\Lambda }\right)=\{\tau \in \mathsf{\Lambda }\subseteq {\mathsf{\Lambda }}_0:\sigma +\tau \in \mathsf{\Lambda },\forall \sigma \in \mathsf{\Lambda }\}$.

Then, how to study the problem of almost periodic and almost automorphic solutions for dynamic equations on the almost periodic time scale defined by Definition 7 with or without condition $\left(c\right)$ is a more challenge task. This is our future goals.