1. Introduction
One of the most frequent problems in engineering, scientific computing and applied mathematics, in general, is the problem of solving a nonlinear equation . In most of the cases, whenever real problems are faced, such as weather forecasting, accurate positioning of satellite systems in the desired orbit, measurement of earthquake magnitudes and other high-level engineering problems, only approximate solutions may get resolved. However, only in rare cases, it is possible to solve the governing equations exactly. The most familiar method of solving non linear equation is Newton’s iteration method. The local order of convergence of Newton’s method is two and it is an optimal method with two function evaluations per iterative step.
In the past decade, several higher order iterative methods have been developed and analyzed for solving nonlinear equations that improve classical methods such as Newton’s method, Chebyshev method, Halley’s iteration method, etc. As the order of convergence increases, so does the number of function evaluations per step. Hence, a new index to determine the efficiency called the efficiency index is introduced in [
1] to measure the balance between these quantities. Kung-Traub [
2] conjectured that the order of convergence of any multi-point without memory method with
d function evaluations cannot exceed the bound
, the optimal order. Thus the optimal order for three evaluations per iteration would be four, four evaluations per iteration would be eight, and so on. Recently, some fourth and eighth order optimal iterative methods have been developed (see [
3,
4,
5,
6,
7,
8,
9,
10,
11,
12,
13,
14] and references therein). A more extensive list of references as well as a survey on the progress made in the class of multi-point methods is found in the recent book by Petkovic et al. [
11].
This paper is organized as follows. An optimal fourth, eighth and sixteenth order methods are developed by using divided difference techniques in
Section 2. In
Section 3, convergence order is analyzed. In
Section 4, tested numerical examples to compare the proposed methods with other known optimal methods. The problem of Projectile motion is discussed in
Section 5 where the presented methods are applied on this problem with some existing ones. In
Section 6, we obtain the conjugacy maps of these methods to make a comparison from dynamical point of view. In
Section 7, the proposed methods are studied in the complex plane using basins of attraction.
Section 8 gives concluding remarks.
2. Design of an Optimal Fourth, Eighth and Sixteenth Order Methods
Definition 1 ([
15])
. If the sequence tends to a limit in such a way that for , then the order of convergence of the sequence is said to be p, and C is known as the asymptotic error constant. If , or , the convergence is said to be linear, quadratic or cubic, respectively.Let , then the relationis called the error equation. The value of p is called the order of convergence of the method. Definition 2 ([
1])
. The Efficiency Index is given bywhere d is the total number of new function evaluations (the values of f and its derivatives) per iteration. Let
define an Iterative Function (IF). Let
be determined by new information at
. No old information is reused. Thus,
Then is called a multipoint IF without memory.
The Newton (also called Newton-Raphson) IF (2
ndNR) is given by
The 2ndNR IF is one-point IF with two function evaluations and it satisfies the Kung-Traub conjecture with . Further, .
2.1. An Optimal Fourth Order Method
We attempt to get a new optimal fourth order IF as follows, let us consider two step Newton’s method
The above one is having fourth order convergence with four function evaluations. But, this is not an optimal method. To get an optimal, need to reduce a function and preserve the same convergence order, and so we estimate
by the following polynomial
which satisfies
On implementing the above conditions on Equation (
6), we obtain three unknowns
,
and
. Let us define the divided differences
From conditions, we get
,
and
, respectively, by using divided difference techniques. Now, we have the estimation
Finally, we propose a new optimal fourth order method as
The efficiency of the method (
7) is
.
2.2. An Optimal Eighth Order Method
Next, we attempt to get a new optimal eighth order IF as following way
The above one is having eighth order convergence with five function evaluations. But, this is not an optimal method. To get an optimal, need to reduce a function and preserve the same convergence order, and so we estimate
by the following polynomial
which satisfies
On implementing the above conditions on (
8), we obtain four linear equations with four unknowns
,
,
and
. From conditions, we get
and
. To find
and
, we solve the following equations:
Thus by applying divided differences, the above equations simplifies to
Solving Equations (
9) and (
14), we have
Further, using Equation (
11), we have the estimation
Finally, we propose a new optimal eighth order method as
The efficiency of the method (
12) is
. Remark that the method is seems a particular case of the method of Khan et al. [
16], they used weight function to develop their methods. Whereas we used finite difference scheme to develop proposed methods. We can say the methods
and
are reconstructed of Khan et al. [
16] methods.
2.3. An Optimal Sixteenth Order Method
Next, we attempt to get a new optimal sixteenth order IF as following way
The above one is having eighth order convergence with five function evaluations. However, this is not an optimal method. To get an optimal, need to reduce a function and preserve the same convergence order, and so we estimate
by the following polynomial
which satisfies
On implementing the above conditions on (
13), we obtain four linear equations with four unknowns
,
,
and
. From conditions, we get
and
. To find
,
and
, we solve the following equations:
Thus by applying divided differences, the above equations simplifies to
Solving Equation (
14), we have
Further, using Equation (
15), we have the estimation
Finally, we propose a new optimal sixteenth order method as
The efficiency of the method (
16) is
.
3. Convergence Analysis
In this section, we prove the convergence analysis of proposed with help of Mathematica software.
Theorem 1. Let be a sufficiently smooth function having continuous derivatives. If has a simple root in the open interval D and chosen in sufficiently small neighborhood of , then the methodIFs (7) is of local fourth order convergence, and theIFs (12) is of local eighth order convergence. Proof. Let
and
. Expanding
and
about
by Taylor’s method, we have
and
Expanding
about
by Taylor’s method, we have
Using Equations (
17)–(
20) in divided difference techniques. We have
Substituting Equations (
18)–(
21) into Equation (
7), we obtain, after simplifications,
Expanding
about
by Taylor’s method, we have
Substituting Equations (
19)–(
21), (
23) and (
24) into Equation (
12), we obtain, after simplifications,
Hence from Equations (
22) and (
25), we concluded that the convergence order of the 4
thYM and 8
thYM are four and eight respectively. □
The following theorem is given without proof, which can be worked out with the help of Mathematica.
Theorem 2. Let be a sufficiently smooth function having continuous derivatives. If has a simple root in the open interval D and chosen in sufficiently small neighborhood of , then the method (16) is of local sixteenth order convergence and and it satisfies the error equation = ((c[2]4)((c[2]2 − c[3])2)(c[2]3 − c[2]c[3] + c[4])(c[2]4 − c[2]2c[3] + c[2]c[4] − c[5]))e16 + O(e17).
4. Numerical Examples
In this section, numerical results on some test functions are compared for the new methods 4
thYM, 8
thYM and 16
thYM with some existing eighth order methods and Newton’s method. Numerical computations have been carried out in the
Matlab software with 500 significant digits. We have used the stopping criteria for the iterative process satisfying
, where
and
N is the number of iterations required for convergence. The computational order of convergence is given by ([
17])
We consider the following iterative methods for solving nonlinear equations for the purpose of comparison:
, a method proposed by Sharma et al. [
18]:
, a method proposed by Chun et al. [
19]:
, a method proposed by Singh et al. [
20]:
, a method proposed by Kung-Traub [
2]:
, a method proposed by Liu et al. [
8]
, a method proposed by Petkovic et al. [
11]
where, a method proposed by Sharma et al. [
12]
, a method proposed by Sharma et al. [
13]
, a method proposed by Cordero et al. [
6]
, a method proposed by Cordero et al. [
7]
Table 1 shows the efficiency indices of the new methods with some known methods.
The following test functions and their simple zeros for our study are given below [
10]:
Table 2, shows that corresponding results for
. We observe that proposed method
is converge in a lesser or equal number of iterations and with least error when compare to compared methods. Note that
and
methods are getting diverge in
function. Hence, the proposed method
can be considered competent enough to existing other compared equivalent methods.
Also, from
Table 3,
Table 4 and
Table 5 are shows the corresponding results for
. The computational order of convergence agrees with the theoretical order of convergence in all the functions. Note that
method is getting diverge in
function and all other compared methods are converges with least error. Also, function
having least error in
, function
having least error in
, functions
and
having least error in
, function
having least error in
, function
having least error in
. The proposed
method converges less number of iteration with least error in all the tested functions. Hence, the
can be considered competent enough to existing other compared equivalent methods.
5. Applications to Some Real World Problems
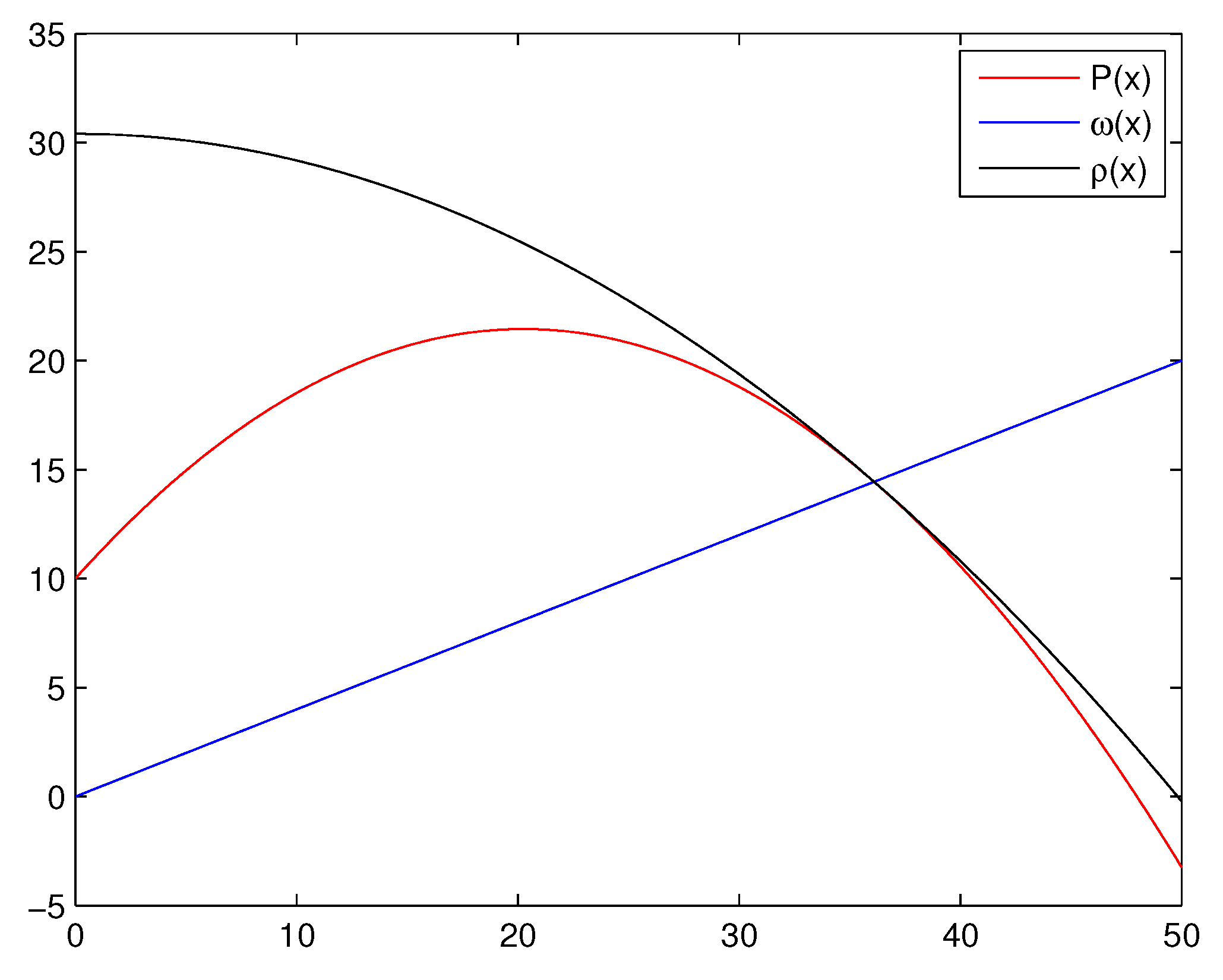
5.1. Projectile Motion Problem
We consider the classical projectile problem [
21,
22] in which a projectile is launched from a tower of height
, with initial speed
v and at an angle
θ with respect to the horizontal onto a hill, which is defined by the function
ω, called the impact function which is dependent on the horizontal distance,
x. We wish to find the optimal launch angle
which maximizes the horizontal distance. In our calculations, we neglect air resistances.
The path function
that describes the motion of the projectile is given by
When the projectile hits the hill, there is a value of
x for which
for each value of
x. We wish to find the value of
θ that maximize
x.
Differentiating Equation (
37) implicitly w.r.t.
θ, we have
Setting
in Equation (
38), we have
or
An enveloping parabola is a path that encloses and intersects all possible paths. Henelsmith [
23] derived an enveloping parabola by maximizing the height of the projectile fora given horizontal distance
x, which will give the path that encloses all possible paths. Let
, then Equation (
36) becomes
Differentiating Equation (
41) w.r.t.
w and setting
, Henelsmith obtained
so that the enveloping parabola defined by
The solution to the projectile problem requires first finding
which satisfies
and solving for
in Equation (
40) because we want to find the point at which the enveloping parabola
ρ intersects the impact function
ω, and then find
θ that corresponds to this point on the enveloping parabola. We choose a linear impact function
with
and
. We let
. Then we apply our IFs starting from
to solve the non-linear equation
whose root is given by
and
Figure 1 shows the intersection of the path function, the enveloping parabola and the linear impact function for this application. The approximate solutions are calculated correct to 500 significant figures. The stopping criterion
, where
is used.
Table 6 shows that proposed method 16
thYM is converging better than other compared methods. Also, we observe that the computational order of convergence agrees with the theoretical order of convergence.
5.2. Planck’s Radiation Law Problem
We consider the following Planck’s radiation law problem found in [
24]:
which calculates the energy density within an isothermal blackbody. Here,
λ is the wavelength of the radiation,
T is the absolute temperature of the blackbody,
k is Boltzmann’s constant,
h is the Planck’s constant and
c is the speed of light. Suppose, we would like to determine wavelength
λ which corresponds to maximum energy density
. From (
44), we get
It can be checked that a maxima for
φ occurs when
, that is, when
Here putting
, the above equation becomes
The aim is to find a root of the equation
. Obviously, one of the root
is not taken for discussion. As argued in [
24], the left-hand side of (
45) is zero for
and
. Hence, it is expected that another root of the equation
might occur near
. The approximate root of the Equation (
46) is given by
with
. Consequently, the wavelength of radiation (
λ) corresponding to which the energy density is maximum is approximated as
Table 7 shows that proposed method 16
thYM is converging better than other compared methods. Also, we observe that the computational order of convergence agrees with the theoretical order of convergence.
Hereafter, we will study the optimal fourth and eighth order methods along with Newton’s method.
6. Corresponding Conjugacy Maps for Quadratic Polynomials
In this section, we discuss the rational map arising from , proposed methods and applied to a generic polynomial with simple roots.
Theorem 3. () [18] For a rational map arising from Newton’s method (4) applied to , , is conjugate via the a Möbius transformation given by to Theorem 4. () For a rational map arising from Proposed Method (7) applied to , , is conjugate via the a Möbius transformation given by to Proof. Let
,
, and let
M be Möbius transformation given by
with its inverse
, which may be considered as map from
. We then have
□
Theorem 5. () For a rational map arising from Proposed Method (12) applied to , , is conjugate via the a Möbius transformation given by to Proof. Let
,
, and let
M be Möbius transformation given by
with its inverse
, which may be considered as map from
. We then have
□
Remark 1. The methods (29)–(35) are given without proof, which can be worked out with the help of Mathematica. Remark 2. All the maps obtained above are of the form , where is either unity or a rational function and p is the order of the method.
7. Basins of Attraction
The study of dynamical behavior of the rational function associated to an iterative method gives important information about convergence and stability of the method. The basic definitions and dynamical concepts of rational function which can found in [
4,
25].
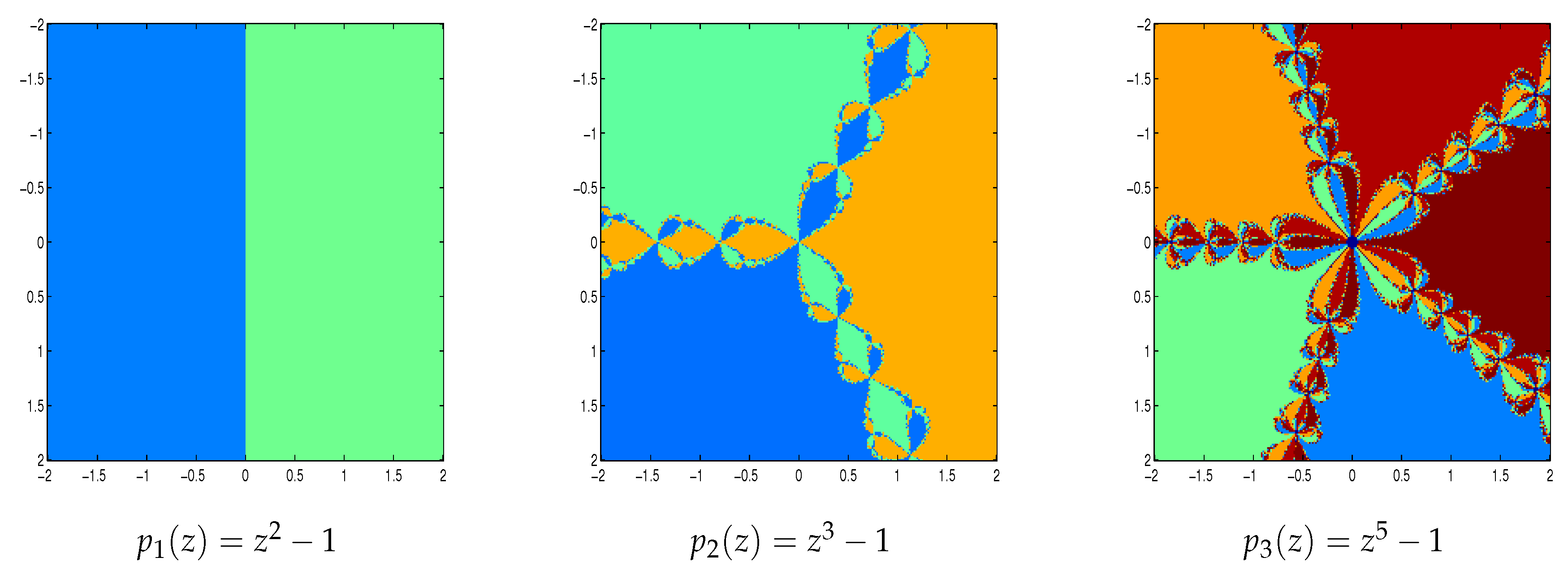
We take a square of points and we apply our iterative methods starting in every in the square. If the sequence generated by the iterative method attempts a zero of the polynomial with a tolerance and a maximum of 100 iterations, we decide that is in the basin of attraction of this zero. If the iterative method starting in reaches a zero in N iterations (), then we mark this point with colors if . If , we conclude that the starting point has diverged and we assign a dark blue color. Let be a number of diverging points and we count the number of starting points which converge in 1, 2, 3, 4, 5 or above 5 iterations. In the following, we describe the basins of attraction for Newton’s method and some higher order Newton type methods for finding complex roots of polynomials , and .
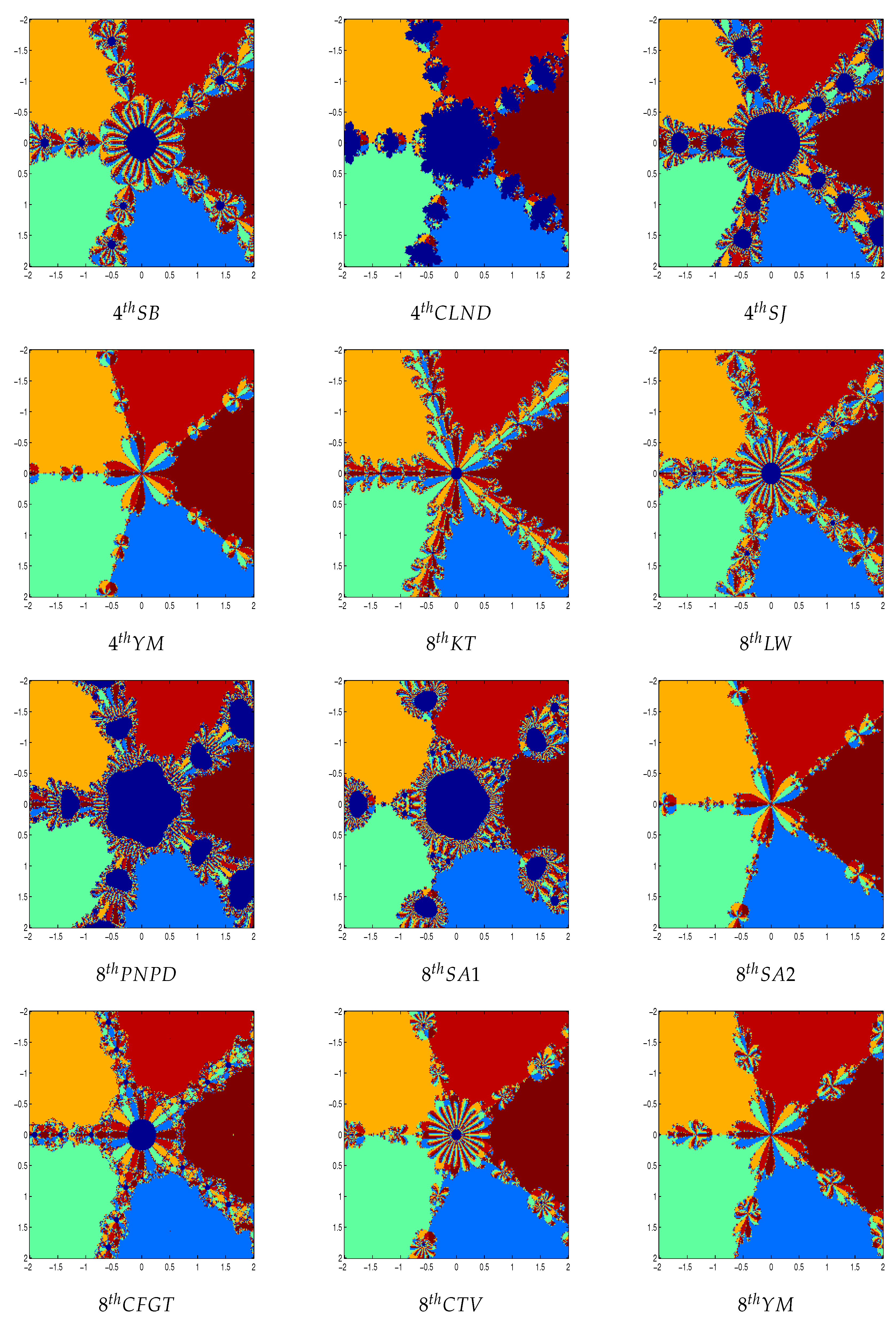
Figure 2 and
Figure 3 shows the polynomiographs of the methods for the polynomial
. We can see that the methods 2
ndNR, 4
thYM, 8
thSA2 and 8
thYM performed very nicely. The methods 4
thSB, 4
thSJ, 8
thKT, 8
thLW, 8
thPNPD, 8
thSA1, 8
thCFGT and 8
thCTV are shows some chaotic behavior near the boundary points. The method 4
thCLND have sensitive to the choice of initial guess in this case.
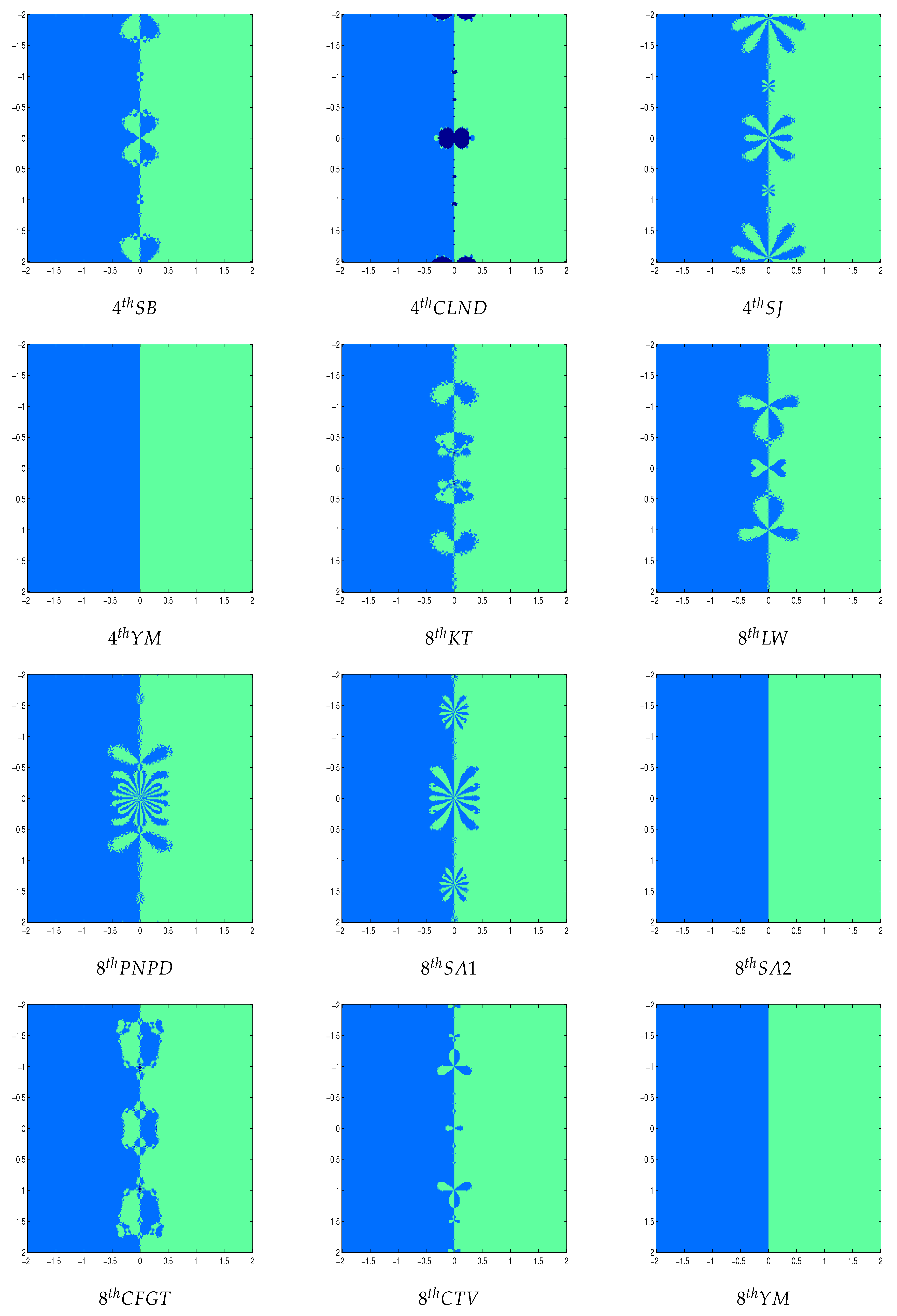
Figure 2 and
Figure 4 shows the polynomiographs of the methods for the polynomial
. We can see that the methods 2
ndNR, 4
thYM, 8
thSA2 and 8
thYM performed very nicely. The methods 4
thSB, 8
thKT, 8
thLW and 8
thCTV are shows some chaotic behavior near the boundary points. The methods 4
thCLND, 4
thSJ, 8
thPNPD, 8
thSA1, and 8
thCFGT have sensitive to the choice of initial guess in this case.
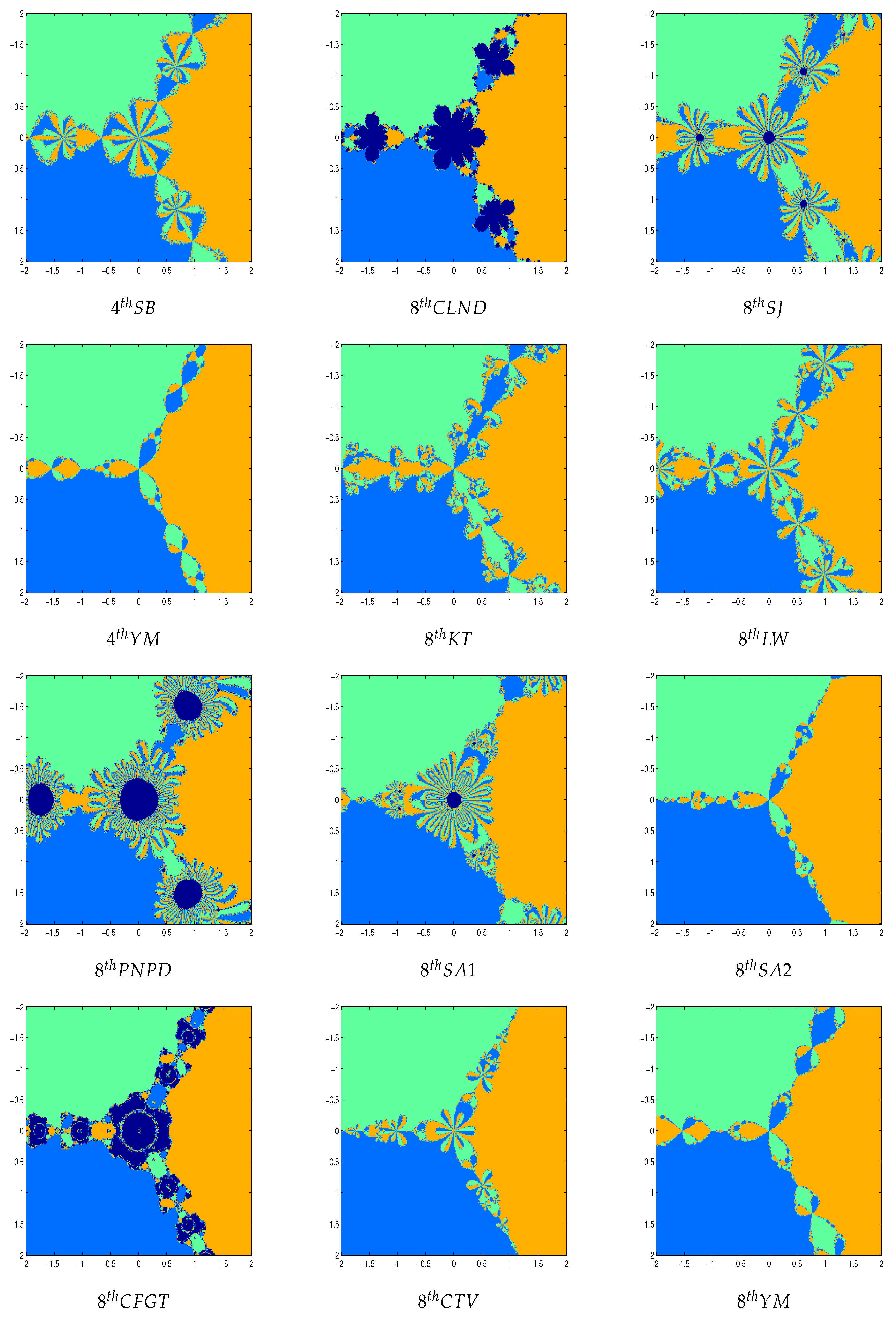
Figure 2 and
Figure 5 shows the polynomiographs of the methods for the polynomial
. We can see that the methods 4
thYM, 8
thSA2 and 8
thYM are shows some chaotic behavior near the boundary points. The methods 2
ndNR, 4
thSB, 4
thCLND, 4
thSJ, 8
thKT, 8
thLW, 8
thPNPD, 8
thSA1, 8
thCFGT and 8
thCTV have sensitive to the choice of initial guess in this case. In
Table 8,
Table 9 and
Table 10, we classify the number of converging and diverging grid points for each iterative method.
We note that a point belongs to the Julia set if and only if the dynamics in a neighborhood of displays sensitive dependence on the initial conditions, so that nearby initial conditions lead to wildly different behavior after a number of iterations. For this reason, some of the methods are getting divergent points. The common boundaries of these basins of attraction constitute the Julia set of the iteration function. It is clear that one has to use quantitative measures to distinguish between the methods, since we have a different conclusion when just viewing the basins of attraction.
In order to summarize the results, we have compared mean number of iteration and total number of functional evaluations (TNFE) for each polynomials and each methods in
Table 11. The best method based on the comparison in
Table 11 is 8
thSA2. The method with the fewest number of functional evaluations per point is 8
thSA2 followed closely by 4
thYM. The fastest method is 8
thSA2 followed closely by 8
thYM. The method with highest number of functional evaluation and slowest method is 8
thPNPD.
8. Concluding Remarks and Future Work
In this work, we have developed optimal fourth, eighth and sixteenth order iterative methods for solving nonlinear equations using the divided difference approximation. The methods require the computations of three functions evaluations reaching order of convergence is four, four functions evaluations reaching order of convergence is eight and five functions evaluations reaching order of convergence is sixteen. In the sense of convergence analysis and numerical examples, the Kung-Traub’s conjecture is satisfied. We have tested some examples using the proposed schemes and some known schemes, which illustrate the superiority of the proposed method 16thYM. Also, proposed methods and some existing methods have been applied on the Projectile motion problem and Planck’s radiation law problem. The results obtained are interesting and encouraging for the new method 16thYM. The numerical experiments suggests that the new methods would be valuable alternative for solving nonlinear equations. Finally, we have also compared the basins of attraction of various fourth and eighth order methods in the complex plane.
Future work includes:
Now we are investigating the proposed scheme to develop optimal methods of arbitrarily high order with Newton’s method, as in [
26].
Also, we are investigating to develop derivative free methods to study dynamical behavior and local convergence, as in [
27,
28].