Matrix Method for the Optimal Scale Selection of Multi-Scale Information Decision Systems

Abstract

In multi-scale information systems, the information is often characterized at multi scales and multi levels. To facilitate the computational process of multi-scale information systems, we employ the matrix method to represent the multi-scale information systems and to select the optimal scale combination of multi-scale decision information systems in this study. To this end, we first describe some important concepts and properties of information systems using some relational matrices. The relational matrix is then introduced into multi-scale information systems, and used to describe some main concepts in systems, including the lower and upper approximate sets and the consistence of systems. Furthermore, from the view of the relation matrix, the scale significance is defined to describe the global optimal scale and the local optimal scale of multi-scale information systems. Finally, the relational matrix is used to compute the scale significance and to construct the optimal scale selection algorithms. The efficiency of these algorithms is examined by several practical examples and experiments.

1. Introduction

Granular computing [1,2] originated from fuzzy information granulation is a mathematical method for knowledge representation and data mining. The purpose is to solve complex problems by dividing the massive information into relatively simple blocks according to its respective characteristics and performance. Since the concept of granular computing was put forward, it has become a hot research topic and has been widely used in many practical applications [3,4,5,6,7,8,9,10,11,12,13].

The theory of rough set plays an important role in the promotion and development of granular computing [14,15,16,17,18,19,20]. Pawlak [14] used an information system to study granular computing. If a decision is required, it is usually an information system with decision attributes.

People can process a lot of information at different levels and scales. Based on this view point, multi-scale information systems have been developed and widely studied [21,22,23,24,25,26,27]. Ferone et al. used feature granulation to study feature selection [12,13]. In papers [21,22], Wu and Leung et al. proposed a multi-scale decision information system model. In their model, the objects are granulated with granularity methods from fine to coarse. The optimal scale selection of multi-scale decision tables was also investigated. Gu and Wu [23] presented a formal method of knowledge acquisition measured at different granularity. Wu and Qian [24] measured the uncertainty in incomplete multi-scale information tables with the Dempster-Shafer evidence theory [28]. Shen et al. [25] employed a local method to induce decision rules in multi-scale decision tables. Li and Hu [26] introduced a step-wise method for the optimal scale selection of multi-scale decision tables.

Due to the massive information provided in multi-scale information systems, which leads to much time consuming in the computation of the concepts in the systems, this article aims to employ the Boolean matrix and matrix computation in order to facilitate the knowledge description and the optimal scale selection in multi-scale decision tables. Indeed, the matrix method has had a computation advantage in many backgrounds [29,30,31,32,33,34,35,36,37], such as in classical rough set and Information systems [29,30,31], static and dynamic information systems [32,35,36], covering information systems [33,34], and so on. For multi-scale information systems, it is worthy to use the relational matrix to obtain the optimal scale selection and develop some matrix methods to facilitate the computational process.

The paper is structured as follows. We first introduce a relational matrix to represent the relative concepts in information systems. We then examine some properties of information systems based on the Boolean matrix. In Section 3, we introduce multi-scale information systems and the Boolean matrix representation. In Section 4, we use the relational matrix to define the scale significance, and to investigate the optimal scale selection of multi-scale information systems. In Section 5, we seek the optimal scale of multi-scale information systems by using the scale significance based on the relation matrix. The paper is finally concluded with a summary. In Section 7, the effectiveness of the matrix method is illustrated by experiments.

2. Preliminary Background

2.1. Rough Set and Information Systems

In this section we introduce some basic concepts of rough set and information systems.

Definition 1

([1]). The Pawlak approximate space is defined as $(U,R)$, where $U=\{x_1,x_2,\cdots ,x_n\}$ is a non-empty finite set called the universe, and R is the equivalent relation on U, the lower and the upper approximation sets of $X\subseteq U$ are defined as $\underline{R}\left(X\right)$, $\overline{R}\left(X\right)$, respectively:

$$\underline{R}\left(X\right)=\{x\in U|{\left[x\right]}_R\subseteq X\},\overline{R}\left(X\right)=\{x\in U|{\left[x\right]}_R\cap X\ne \varnothing \}.$$

where ${\left[x\right]}_R=\{y\in U|(x,y)\in R\}$ is the equivalent class containing x.

Definition 2

([14]). Let $S=(U,A)$ be an information system, where $U=\{x_1,x_2,\cdots ,x_n\}$ is a non-empty finite set called the universe, $A=\{a_1,a_2,\cdots ,a_m\}$ is a non-empty finite set of attributes. For any $a\in A$, there is a surjective map $a:U\to V_a$ ie. $a\left(x\right)\in V_a,x\in U$, where $V_a=\left\{a\right(x\left)\right|x\in U\}$ is called the domain of attribute a. For any $B\subseteq A$, the equivalent relation $R_B$ On U is determined as

$$R_B=\{(x,y)\in U\times U|a\left(x\right)=a\left(y\right),\forall x\in B\}$$

The equivalence class of $x\in U$ in terms of $R_B$ is denoted as ${\left[x\right]}_B=\{y\in U|(x,y)\in R_B\}.$

The lower approximation set and the upper approximate set of $X\subseteq U$ corresponding to the attribute subset B are represented as ${\underline{R}}_B\left(X\right)$ and ${\overline{R}}_B\left(X\right)$, respectively,

$${\underline{R}}_B\left(X\right)=\{x\in U|{\left[x\right]}_B\subseteq X\},{\overline{R}}_B\left(X\right)=\{x\in U|{\left[x\right]}_B\cap X\ne \varnothing \}.$$

Definition 3

([14]). Let $S=(U,A\bigcup d)$ be a decision information system, where $S=(U,A)$ is an information system, $d\notin A$ is called the decision attribute, and $d:U⟶V_d$ is a surjective map, where $V_d=\left\{d\left(x\right)\right|x\in U\}$ is called the domain of d.

Similarly, the equivalent relation on U induced by $R_d$ is given by

$$R_d=\{(x,y)\in U\times U|d\left(x\right)=d\left(y\right)\}.$$

The equivalence class of $x\in U$ is denoted as ${\left[x\right]}_d=\{y\in U|(x,y)\in R_d\}.$

Let $S=(U,A\bigcup d)$ be a decision information system, we summarize the following two kinds of consistent:

(1) If $R_A\subseteq R_d$, then S is globally consistent;

(2) For $x\in U$, if ${\left[x\right]}_A\subseteq {\left[x\right]}_d$, then S is locally consistent for x.

2.2. Boolean Matrix Characterization of Decision Information Systems

Definition 4.

A non-negative matrix $M_B={\left(r_{ij}\right)}_{n\times n}$ is called a Boolean matrix, where $r_{ij}\in \{0,1\}$. Let $A={\left(a_{ij}\right)}_{n\times m},$ $B={\left(b_{ij}\right)}_{n\times m},$ $C={\left(c_{ij}\right)}_{m\times l}$ are Boolean matrices, define the following operations:

(1) Order relation $A⩽B\iff a_{ij}⩽b_{ij}$;

(2) Meet $A\wedge B={(a_{ij}\wedge b_{ij})}_{n\times m};$

(3) Boolean product $AC={\left(d_{ij}\right)}_{n\times l}$, where $d_{ij}={\sum }_{k=1}^m{a}_{ik}\vee c_{kj}$;

(4) Complement $\sim A={(1-a_{ij})}_{n\times m}$.

where $a_{ik}\vee c_{kj}=max\{a_{ik},c_{kj}\}$, $a_{ij}\wedge b_{ij}=min\{a_{ij},b_{ij}\}.$

It can be seen that $a_{ij}\wedge b_{ij}=a_{ij}\times b_{ij}$ and $A⩽B\iff A\wedge (\sim B)=0.$

Definition 5

([33]). Let $U=\{x_1,x_2,\cdots ,x_n\}$ and $X\subseteq U$, The characteristic function of X is defined as $f\left(X\right)=(f\left(x_1\right),f\left(x_2\right),\cdots ,f\left(x_n\right))$, where

$$f\left(x_i\right)=\left\{\begin{array}{cc}1,& x_i\in X,\\ 0,& x_i\notin X.\end{array}\right.$$

It can be seen that $X\subseteq Y\iff f\left(X\right)⩽f\left(Y\right)\iff f\left(X\right)\wedge (\sim f(Y\left)\right)=0.$

Definition 6

([33]). Let $(U,R)$ be an approximate space, $U=\{x_1,x_2,\cdots ,x_n\}$, The relation matrix of R is defined as $M_R={\left(r_{ij}\right)}_{n\times n}$, where

$$m_{ij}=\left\{\begin{array}{cc}1,& (x_i,x_j)\in R,\\ 0,& (x_i,x_j)\notin R.\end{array}\right.$$

Obviously, by Definitions 5 and 6, we have

$$M_R=\left[\begin{array}{c}f\left({\left[x_1\right]}_R\right)\\ f\left({\left[x_2\right]}_R\right)\\ ⋮\\ f\left({\left[x_n\right]}_R\right)\end{array}\right]$$

Theorem 1

([30]). Let $(U,R)$ be an approximate space, $U=\{x_1,x_2,\cdots ,x_n\}$, and $X\subseteq U$, then

$$f\left(\underline{R}\left(X\right)\right)=\sim f(\sim X)M_R,f\left(\overline{R}\left(X\right)\right)=f\left(X\right)M_R.$$

Proof. 

Let $f\left(\underline{R}\left(X\right)\right)=(f_1,f_2,\cdots ,f_n)$, $f(\sim X)M_R=(g_1,g_2,\cdots ,g_n)$, $\sim f(\sim X)M_R=(h_1,h_2,\cdots ,h_n)$.

According to the symmetry of matrix $M_R$ and Definition 6, we have $M_R=M_R^T=(f{\left({\left[x_1\right]}_R\right)}^T,f{\left({\left[x_2\right]}_R\right)}^T,\cdots ,f{\left({\left[x_n\right]}_R\right)}^T)$ and $g_i=f(\sim X)f{\left({\left[x_i\right]}_R\right)}^T$. Therefore $f_i=1\iff x_i\in \underline{R}\left(X\right)\iff {\left[x_i\right]}_R\subseteq X\iff {\left[x_i\right]}_R\cap (\sim X)=⌀\iff f(\sim X)f{\left({\left[x_i\right]}_R\right)}^T)=0\iff g_i=0\iff h_i=1$. Similarly, $f_i=0\iff h_i=0$. Therefore $f\left(\underline{R}\left(X\right)\right)=\sim f(\sim X)M_R.$

By $\overline{R}\left(X\right)=\sim \underline{R}(\sim X)$, we have $f\left(\overline{R}\left(X\right)\right)=f(\sim \underline{R}(\sim X))=\sim f\left(\underline{R}(\sim X)\right)=\sim f(\sim X))M_R=f\left(X\right)M_R.$  □

Example 1.

Let $U=\{x_1,x_2,x_3,x_4,x_5\}, U/R=\{\left\{x_1\right\},\left\{x_2\right\},\{x_3,x_4\},\left\{x_5\right\}\}, X=\{x_1,x_2,x_3\}$

$$f\left(\underline{R}\left(X\right)\right)=\sim f(\sim X)M_R=\sim \left[\begin{array}{ccccc}0& 0& 0& 1& 1\end{array}\right]\left[\begin{array}{ccccc}1& 0& 0& 0& 0\\ 0& 1& 0& 0& 0\\ 0& 0& 1& 1& 0\\ 0& 0& 1& 1& 0\\ 0& 0& 0& 0& 1\end{array}\right]=\left[\begin{array}{ccccc}1& 1& 0& 0& 0\end{array}\right],$$

$$f\left(\overline{R}\left(X\right)\right)=f\left(X\right)M_R=\left[\begin{array}{ccccc}1& 1& 1& 0& 0\end{array}\right]\left[\begin{array}{ccccc}1& 0& 0& 0& 0\\ 0& 1& 0& 0& 0\\ 0& 0& 1& 1& 0\\ 0& 0& 1& 1& 0\\ 0& 0& 0& 0& 1\end{array}\right]=\left[\begin{array}{ccccc}1& 1& 1& 1& 0\end{array}\right].$$

Therefore, $\underline{R}\left(X\right)=\{x_1,x_2\},\overline{R}\left(X\right))=\{x_1,x_2,x_3,x_4\}$.

Theorem 2

([29]). Let U be an universe, $R_1,R_2$ are equivalent relations on U, then the following conclusions hold:

(1) $M_{R_1\cap R_2}=M_{R_1}\wedge M_{R_2}$;

(2) If $R_1\subseteq R_2$, then $M_{R_1}⩽M_{R_2}.$

Let $S=(U,A\bigcup d)$ be an decision information system, $B\subseteq A$, the relation matrix of the equivalent relation $R_B$ is denote as $M_B$, the relation matrix corresponding to $R_d$ is denoted as $M_d$,

Theorem 3.

Let $S=(U,A\bigcup d)$ be an decision information system, $B\subseteq A$, then $M_B={\left(m_{ij}\right)}_{n\times n}$, where

$$m_{ij}=\left\{\begin{array}{cc}1,& a\left(x_i\right)=a\left(x_j\right),\forall a\in B,\\ 0,& else.\end{array}\right.$$

and $M_d={\left(r_{ij}\right)}_{n\times n}$, where

$$r_{ij}=\left\{\begin{array}{cc}1,& d\left(x_i\right)=d\left(x_j\right),\\ 0,& else.\end{array}\right.$$

Proof. 

By Definition 2, $(x_i,x_j)\in R_B\iff a\left(x_i\right)=a\left(x_j\right),\forall a\in B$, by Definition 6, we have $m_{ij}=1\iff a\left(x_i\right)=a\left(x_j\right),\forall a\in B$. Similarly $r_{ij}=1\iff d\left(x_i\right)=d\left(x_j\right).$  □

Theorem 4.

Let $S=(U,A\bigcup d)$ be a decision information system, then the following conclusions are obtained:

(1) S is locally consistent for $x\in U$ if and only $f\left({\left[x\right]}_A\right)⩽f\left({\left[x\right]}_d\right)$ hold;

(2) S is globally consistent if and only if $M_A⩽M_d$ is hold.

Proof. 

By Definition 5, S is locally consistent for $x\in U\iff {\left[X\right]}_A\subseteq {\left[x\right]}_d\iff f\left({\left[x\right]}_A\right)⩽f\left({\left[x\right]}_d\right)$;

By Theorem 2, we have S is globally consistent $\iff R_A\subseteq R_d$ $\iff M_A⩽M_d$.  □

Example 2.

Determining the globally consistent of the following system Table 1.

Table 1. A decision syetem.

U	${\mathit{a}}_1$	${\mathit{a}}_2$	${\mathit{a}}_3$	${\mathit{a}}_4$	d
$x_1$	2	1	1	1	1
$x_2$	3	2	2	2	2
$x_3$	2	1	1	1	1
$x_4$	2	2	1	1	3
$x_5$	1	1	4	2	5
$x_6$	1	1	3	2	1
$x_7$	3	2	2	2	2

$M_A$ is the relational matrix corresponding to A, $M_d$ is the relational matrix corresponding to d. According to Theorem 3, by calculation

$$M_A=\left[\begin{array}{ccccccc}1& 0& 1& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& 0& 1\\ 1& 0& 1& 0& 0& 0& 0\\ 0& 0& 0& 1& 0& 0& 0\\ 0& 0& 0& 0& 1& 0& 0\\ 0& 0& 0& 0& 0& 1& 0\\ 0& 1& 0& 0& 0& 0& 1\end{array}\right],\hspace{1em}{M}_d=\left[\begin{array}{ccccccc}1& 0& 1& 0& 0& 1& 0\\ 0& 1& 0& 0& 0& 0& 1\\ 1& 0& 1& 0& 0& 1& 0\\ 0& 0& 0& 1& 0& 0& 0\\ 0& 0& 0& 0& 1& 0& 0\\ 1& 0& 1& 0& 0& 1& 0\\ 0& 1& 0& 0& 0& 0& 1\end{array}\right]$$

Obviously $M_A\le M_d$, by Theorem 4, the $(U,A\cup \{d\left\}\right)$ is globally consistent.

3. Relational Matrix in Generalized Multi-Scale Information Systems

The theoretical model of multi-scale decision information systems was first proposed by Wu and Leung [21]. Some scholars have participated in this study [21,22,23,24,25,26,27,38,39,40,41], Li and Hu generalized this model in paper [27]. Among many studies, optimal scale selection is an important subject. Wu, Li et al. [29,38,40] studied the optimal scale selection of multi-scale decision information systems. Gu et al. [39] studied the optimal scale selection of incomplete multi-scale decision information systems. Li and Hu [27] studied the optimal scale selection for generalized multi-scale decision information systems. Li et al. [26] gave an attribute significance of generalized multi-scale decision information systems to search for optimal scale selection. Decision information system models involve a large number of set operations. The matrix itself is a powerful tool. The use of matrices to study multi-scale information systems helps to improve algorithm efficiency and further develop multi-scale information table theory. In this part, we introduce relation matrix into multi-scale information systems to prepare for optimal scale selection.

Definition 7

([21,27]). A multi-scale information system is a tuple $S=(U,A)$, where $U=\{x_1,x_2,\cdots ,x_n\}$ is a nonempty and finite set of objects called the universe, $A=\{a_1,a_2,\cdots ,a_m\}$ is a nonempty and finite set of attributes, and each $a_j$ has $I_j(j=1,2,\cdots ,n)$ scales. Then a multi-scale information system $S=(U,A)$ can be represented as

$$S=(U,\left\{a_j^k\right|k=1,2,\cdots ,I_j,j=1,2,\cdots ,m\}).$$

where $a_j^k:U⟶V_j^k$ is a surjective function and $V_j^k$ is the domain of $a_j$ corresponding to the kth scale, and furthermore, for any $j=1,2,\cdots ,m,1⩽k⩽I_j-1$, there exists a surjective $g_j^{k,k+1}:V_j^k⟶V_j^{k+1}$ such that $a_j^{k+1}=g_j^{k,k+1}.a_j^{k+1}$, i.e., $a_j^{k+1}\left(x\right)=g_j^{k,k+1}.a_j^{k+1}\left(x\right),x\in U$, $g_j^{k,k+1}$ is called the information granularity transformation function.

When $I_1=I_2=\cdots =I_j=I$, the information system defined above is the multi-scale information system proposed by Wu-Leung in paper [21].

The equivalent relation determined by attribute $a_j^{l_j}(1⩽l_j⩽I_j)$ is

$$R_{a_j^{l_j}}=\{(x,y)\in U\times U|a_j^{l_j}\left(x\right)=a_j^{l_j}\left(y\right)\}.$$

By the existence of the surjective $g_j^{k,k+1}:V_j^k⟶V_j^{k+1}$, for any $a_j\in U$, we have

$$R_{a_j^1}\subseteq R_{a_j^2}\subseteq \cdots \subseteq R_{a_j^{I_j}}.$$

For a multi-scale information system $S=(U,A)$, if the attribute $a_j\in U$ is restricted on their $l_j$ scale, we call $K=(l_1,l_1,\cdots ,l_m)$ to be a scale combination of the system $S=(U,A)$, and all the scale combinations of the system $S=(U,A)$ are denoted as ∑ and ∑ forms a partial ordered lattice [27].

The information system corresponding to the $K=(l_1,l_1,\cdots ,l_m)$ scale combination is denoted as

$$S^K=(U,A^K)=(U,\{a_1^{l_1},a_2^{l_2},\cdots ,a_m^{l_m}\}).$$

The equivalent relation induced by $A^K$ is denoted as $R_{A^K}$, while the relation matrix of $R_{A^K}$ is denoted as $M_{A^K}$.

Definition 8

([27]). Let $S=(U,A)$ be a multi-scale information system, $K,L\in \sum ,$ $K=(l_1,l_2,\cdots ,l_m),$ $L=(h_1,h_2,\cdots ,h_m)$, if $l_i⩽h_i(i=1,2,\cdots ,m)$, we called the scale combination to be K is finer than L, denoted as $K⩽L$, and further if $K⩽L$ and there is at least one of $i\in \{1,2,\cdots ,m\}$ such that $l_i<h_i$, we called K is strictly finer than L, denoted as $K<L$.

Example 3.

The following example gives a comprehensive evaluation of three courses for eight students, and scores are divided into four criteria, as shown in Table 2.

Table 2. Evaluation criteria.

$\mathit{Score}$	$\mathit{Evaluation}\mathit{Criteria}1$	$\mathit{Evaluation}\mathit{Criteria}2$	$\mathit{Evaluation}\mathit{Criteria}3$	$\mathit{Evaluation}\mathit{Criteria}4$
$(90,100]$	1	$excellent$	$super$	Y
$[80,89)$	2	$good$	$super$	Y
$[70,79)$	3	$fair$	$middle$	Y
$[60,69)$	4	$pass$	$middle$	Y
$[50,59)$	5	$bad$	$low$	N
$[0,49)$	6	$bad$	$low$	N

We use attribute $a_1$ to evaluate the results of the first course, which divided into four levels, attribute $a_2$ for the second course, which divided into three levels, and attribute $a_3$ for the third course, which divided into two levels. Attribute d is called decision attribute, 1 is qualified and 0 is unqualified. According to the scores of each student, the following multi-scale decision-making information system is obtained, as shown in Table 3. In order to facilitate the expression below, we denote excellent by "E", and similarly "G" denotes good, "F" denotes fair, "P" denotes pass, "B" denotes bad, "S" denotes super, "M" denotes middle, "L" denotes low, "Y" denotes yes, "N" denotes no.

Table 3. A generalized multi-scale information system.

U	$\mathit{Subject}1$${\mathit{a}}_1^1$	${\mathit{a}}_1^2$	${\mathit{a}}_1^3$	${\mathit{a}}_1^4$	$\mathit{Subject}2$	${\mathit{a}}_2^1$	${\mathit{a}}_2^2$	${\mathit{a}}_2^3$	$\mathit{Subject}3$	${\mathit{a}}_3^1$	${\mathit{a}}_3^2$	d
$x_1$	78	3	F	M	Y	94	1	E	Y	75	3	Y	1
$x_2$	61	4	P	M	Y	62	4	P	Y	60	4	Y	0
$x_3$	69	4	P	M	Y	78	3	F	Y	68	4	Y	1
$x_4$	98	1	E	S	Y	58	5	B	N	97	1	Y	1
$x_5$	36	6	B	L	N	72	3	F	Y	92	1	Y	0
$x_6$	63	4	P	M	Y	76	3	F	Y	47	5	N	0
$x_7$	58	5	B	L	N	95	1	E	Y	92	1	Y	1
$x_8$	35	6	B	L	N	90	1	E	Y	73	3	Y	0

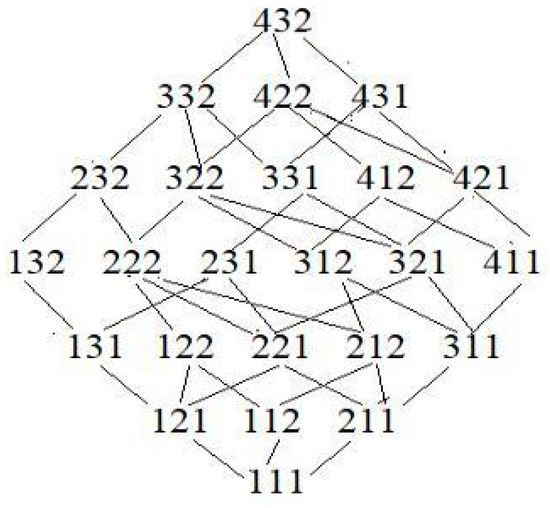
There are 24 different scale combinations in multi-scale information system in Table 3. According to the scale relation in Definition 8, we can obtain a partial ordered lattices [27], as shown in Figure 1.

Figure 1. Partial ordered lattices of scale combinations.

We now discuss some properties of multi-scale information systems using the relation matrix.

Let $S=(U,A)$ be a multi-scale information system and ∑ is the set of all scale combinations for the system, $K=(l_1,l_2,\cdots ,l_m)\in \sum ,$ the decision information system corresponding to the scale combination K is $S^K=(U,A^K\bigcup d)$, the relation matrix of $R_{A^K}$ is denote as $M_{A^K}$.

Theorem 5.

Let $S=(U,A)$ be a multi-scale information system, $K=(l_1,l_2,\cdots ,l_m)\in \sum ,$ then $M_{A^K}={\left(m_{ij}\right)}_{n\times n}$, where

$$m_{ij}=\left\{\begin{array}{cc}1,& a_k^{l_k}\left(x_i\right)=a_k^{l_k}\left(x_j\right),k=1,2,\cdots ,m\\ 0,& else.\end{array}\right.$$

Proof. 

This conclusion can be obtained from Theorem 3.  □

Theorem 6.

Let $S=(U,A)$ be a multi-scale information system and ∑ is the set of all scale combinations for the system, $K,L\in \sum ,$ $K<L,$ $X\subseteq U$. Then the following conclusions hold:

(1) For any attribute $a_j\in A(j=1,2,\cdots ,m),$ $M_{a_j}^1⩽M_{a_j}^2⩽\cdots ⩽M_{a_j}^{I_j}$;

(2) $M_{A^K}⩽M_{A^L}$;

(3) $M_{A^K}={\wedge }_{l\in K}{M}_{a^l}$;

(4) $f\left(\underline{R_{A^K}}\left(X\right)\right)=\sim \left(f(\sim X)\right)M_{A^K}$;

(5) $f\left(\overline{R_{A^K}}\left(X\right)\right)=\left(f\left(X\right)\right)M_{A^K}$;

(6) $f\left(\underline{R_{A^L}}\left(X\right)\right)⩽f\left(\underline{R_{A^K}}\left(X\right)\right)$;

(7) $f\left(\overline{R_{A^K}}\left(X\right)\right)⩽f\left(\overline{R_{A^L}}\left(X\right)\right)$.

Proof. 

(1) By Definition 7, as a result of $R_{a_j^1}\subseteq R_{a_j^2}\subseteq \cdots \subseteq R_{a_j^{I_j}}$, according to Theorem 2, we have $M_{a_j^1}⩽M_{a_j^2}⩽\cdots ⩽M_{a_j^{I_j}}$;

(2) $K⩽L\Rightarrow R_{A^K}\subseteq R_{A^L}\Rightarrow M_{A^K}⩽M_{A^L}$;

(3) Suppose $K=(l_1,l_2,\cdots ,l_m)$, then $A^K=(a^{l_1},a^{l_2},\cdots ,a^{l_m})$, $R_{A^K}=R_{A^{l_1}}\cap R_{A^{l_2}}\cap \cdots \cap R_{A^{l_m}}$, by Theorem 2, we have $M_{A^K}=M_{A_1^l}\wedge M_{A_2^l}\wedge \cdots \wedge M_{A_m^l}={\wedge }_{l\in K}{M}_{a^l}$;

(4) (4) and (5) can be directly obtained by Theorem 1;

(6) $K<L\Rightarrow R_{A^K}\subseteq R_{A^L}\Rightarrow \underline{R_{A^L}}\left(X\right)\subseteq \underline{R_{A^K}}\left(X\right)\Rightarrow f\left(\underline{R_{A^L}}\left(X\right)\right)⩽f\left(\underline{R_{A^K}}\left(X\right)\right)$;

(7) $K<L\Rightarrow R_{A^K}\subseteq R_{A^L}\Rightarrow \overline{R_{A^K}}\left(X\right)\subseteq \overline{R_{A^L}}\left(X\right)\Rightarrow f\left(\overline{R_{A^K}}\left(X\right)\right)⩽f\left(\overline{R_{A^K}}\left(X\right)\right)$.  □

4. Optimal Scale Selection for Consistent Multi-Scale Decision Information Systems

Definition 9

([21,27]). Let $S=(U,A\cup d)$ be a multi-scale decision information system, where $S=(U,A)$ is a multi-scale information system, ∑ is the collection of all scale combinations, $d\notin A$ is a decision attribute and $d:V\to V_d$ is a surjective map, where $V_d=\left\{d\left(x\right)\right|x\in U\}$ is called the domain of d.

4.1. Global Optimal Scale

The decision information system corresponding to the $K=(l_1,l_1,\cdots ,l_m)$ scale combination is denoted as

$$S^K=(U,A^K\cup d)=(U,\{a_1^{l_1},a_2^{l_2},\cdots ,a_m^{l_m}\}\cup d).$$

Obviously, $S^K=(U,A^K\cup d)$ is globally consistent if and only if $R_{A^K}\subseteq R_d$

The relation matrix corresponding to the equivalent relation $R_{A^k}$ is $M_{A^K}$, the relation matrix corresponding to the equivalent relation $R_d$ is $M_d$.

By Theorem 2, $S^K=(U,A^K\cup d)$ is globally consistent if and only if $M_{A^K}⩽M_d$.

Definition 10

([21]). Let $S=(U,A\cup d)$ be a multi-scale decision information system, and ∑ is the collection of all scale combinations, For the finer scale $K_0=(1,1,\cdots ,1)$, if $R_{A^{K_0}}\subseteq R_d$, then we call S to be consistent. If there is a $K\in \sum$ such that $R_{A^K}\subseteq R_d$, but for any $H\in \sum$, $K<H$, $R_{A^H}\subseteq R_d$ does not hold, we call K is a global optimal scale combination.

Theorem 7.

Let $S=(U,A\cup d)$ be a multi-scale decision information system, and ∑ the collection of all scale combinations. Then the following conclusions hold:

(1) S is globally consistent if and only if $M_{A^{K_0}}⩽M_d$;

(2) S is globally consistent if and only if $M_{A^{K_0}}\wedge (\sim M_d)=0$;

(3) A scale combination $K\in \sum$ is the global optimal scale combination if and only if $M_{A^K}⩽M_d$ holds, and for any $H\in \sum$ with $K<H$, $M_{A^H}⩽M_d$ does not hold;

(4) Suppose $K=(l_1,l_2,\cdots ,l_m)\in \sum ,$ let $K_j=(l_1,\cdots ,l_j,\cdots ,l_m)$, then $M_{A^{K_j}}=M_{A^K}\wedge M_{a^{l_j-1}}$.

Proof. 

(1)S is global consistent $\iff R_{A^{K_0}}\subseteq R_{A^d}\iff M_{A^{K_0}}⩽M_d$;

(2) The result is obvious;

(3) By the definition of the global optimal scale combination, it is easy to be obtained;

(4) As a result of $M_{a^{l_j-1}}⩽M_{a^{l_j}}$, we have $M_{a^{l_j-1}}\wedge M_{a^{l_j}}=M_{a^{l_j-1}}$, Therefore, $M_{A^{K_j}}=M_{a^{l_1}\cdots a^{l_j-1}\cdots a^{l_m}}=M_{a^{l_1}}\wedge \cdots M_a^{l_j-1}\wedge \cdots M_a^{l_m}=M_{A^K}\wedge M_{a^{l_j-1}}.$  □

Definition 11.

Let $S=(U,A\cup d)$ be a multi-scale decision information system and ∑ is the collection of all scale combinations, $K=(l_1,l_2,\cdots ,l_m)\in \sum$. Define the significance of scale combination K as

$$sig\left(K\right)=\parallel M_{A^K}\wedge (\sim M_d)\parallel$$

where $\parallel A\parallel$ represents the numbers of 1 in the matrix A.

Let $S=(U,A\cup d)$ be a multi-scale decision information system, and ∑ is the collection of all scale combinations. By Definition 7, the decision information system corresponding to scale combination K is represented as $S^K=(U,A^K\cup d)$. Obviously, $S^K=(U,A^K\cup d)$ is globally consistent if $sig\left(K\right)=0$.

For the scale combination $K=(l_1,l_2,\cdots ,l_m)$, if the decision information system $S^K=(U,A^K\cup d)$ is globally inconsistent, then $M_{A^K}⩽M_d$ is not true, i.e., $sig\left(K\right)\ne 0$. The direct subsequent scale of scale combination K is denoted as $K_j=(l_1,\cdots ,l_j-1,\cdots ,l_m)(j=1,2,\cdots ,m)$, The global consistence of the decision information system $S^{K_j}$ is compared, i.e., the following significance is calculated as

$$sig\left(K_j\right)=\parallel M_{A^{K_j}}\wedge (\sim M_d)\parallel =\parallel M_{A^K}\wedge M_{a_j^{l_j-1}}\wedge (\sim M_d)\parallel$$

It can be seen that if $sig\left(K_j\right)$ is more smaller, the scale $K_j=(l_1,\cdots ,l_j-1,\cdots ,l_m)$ becomes more significant. This means that this metric combination is selected first, in other words, the information system corresponding to this scale combination is closer to consistent. Based on this idea, a global optimal scale combination selection algorithm of a multi-scale decision system can be described as Algorithm 1.

As Algorithm 1 shows, the algorithm sets up the scale combination variable $optK$ and significant variable $optSig$ with the coarsest scale and maximun value initially, and then the scale combination K is put into a queue and starts a iteration. In the iteration, the current scale combination K is take out from the queue and $sig\left(K\right)$ is calculated. If the current $sig\left(K\right)$ is smaller than $optSig$, then $optSig$ and $optK$ are replaced by the current scale combination K and $sig\left(K\right)$. During the iterating, if the value of $optSig$ become zero then iteration is terminal and optimal scale combination is come out. When the queue is empty and $optSig\ne 0$, consequence finer scale combinations are constructed from $optK$ and are put into the queue, and starts another iteration.

Algorithm 1: Selecting the global optimal scale combination of a multi-scale decision system

Input: A multi-scale decision system $S=(U,A\cup d)$;  Output: The global optimal scale combination.  calculates $M_d$;  Let Queue=NULL  Let $optK=(I_1,I_2,\cdots ,I_m)$               //set the coarsest scale combination initially  Let $optSig$= Integer. MAX $\underline{}$VALUE               //set maximum value to $optSig$ initially  Queue. put($optK$)  While (true)       While (not Queue. empty)           Let $K=$ Queue. get()              //pick a scale combination K from Queue           Let $sig\left(K\right)=\parallel M_{A^K}\wedge (\sim M_d)\parallel$        //calculate $sig\left(K\right)$           If ($sig\left(K\right)⩽$ $optSig$)              //choose the minimum $sig\left(K\right)$ and its K                Let $optSig$=$sig\left(K\right)$                Let $optK$=K           EndIf           If ($optSig$==0)       //if the optimal scale combination is found, return.                return $optK$           EndIf      EndWhile              //loop until Queue. empty      Queue.clear()       //empty the Queue, and construct next finer scale combination      Let $(l_1,l_2,\cdots ,l_m)=optK$      For each $j\in (1,2,\cdots ,m)$              //set finer scale to each attribute, respectively           If $(l_j>1)$                Let $K=(l_1,l_2,\cdots ,l_{j-1},l_j-1,l_{j+1},\cdots ,l_m)$                Queue. put(K)           EndIf      EndFor               //next to search finer scale combination  EndWhile

Example 4.

In Example 2, we seek the global optimal scale combination of the system corresponding to Table 3.

By Definition 11, the sufficient condition for the decision information system $S^K=(U,A^K\bigcup d)$ being global consistent is $sig\left(K\right)=\parallel M_{A^K}\wedge (\sim M_d)\parallel =0$, where $K=(l_1,l_2,\cdots ,l_j,\cdots ,l_m)\in \sum$.

We apply scale combination relation diagram 1 to illustrate the calculation steps of optimal scale selection in Table 3. We first judge whether the system is consistent or not, and then, according to the definition of scale significant, we look for the optimal scale combination from the scale relation diagram 1 from top to bottom.

(1) For the smallest scale combination $K_0=(1,1,1)$, according to Theorems 3 and 5, by calculation

$$M_{A^{K_0}}=\left(\begin{array}{cccccccc}1& 0& 0& 0& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& 0& 0& 0\\ 0& 0& 1& 0& 0& 0& 0& 0\\ 0& 0& 0& 1& 0& 0& 0& 0\\ 0& 0& 0& 0& 1& 0& 0& 0\\ 0& 0& 0& 0& 0& 1& 0& 0\\ 0& 0& 0& 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 0& 0& 0& 1\end{array}\right),\hspace{1em}\sim M_d=\left(\begin{array}{cccccccc}0& 1& 0& 0& 1& 1& 0& 1\\ 1& 0& 1& 1& 0& 0& 1& 0\\ 0& 1& 0& 0& 1& 1& 0& 1\\ 0& 1& 0& 0& 1& 1& 0& 1\\ 1& 0& 1& 1& 0& 0& 1& 0\\ 1& 0& 1& 1& 0& 0& 1& 0\\ 0& 1& 0& 0& 1& 1& 0& 1\\ 1& 0& 1& 1& 0& 0& 1& 0\end{array}\right)$$

By Definition 11, $sig\left(K_0\right)=\parallel M_{A_0^K}\wedge (\sim M_d)\parallel =0$, So, the decision information system $S^{K_0}=(U,A^{K_0}\cup d)$ is global consistent, by Definition 10, we see that $S=(U,A\cup d)$ is global consistent;

(2) For the coarsest scale combination $K=(4,3,2)$, similarly, by calculation, $sig(4,3,2)=8$;

(3) For each scale combination that belongs to (4,3,2) for the second layer, similarly, by calculation, $sig(3,3,2)=8;$ $sig(4,2,2)=2;$ $sig(4,3,1)=4$, therefore, the scale combination $K=(4,2,2)$ is the most important. We continue to search for the optimal scale according to this branch;

(4) For each scale combination that belongs to (4,2,2) for the third layer, by calculation, $sig(3,2,2)=2;$ $sig(4,1,2)=2$, $sig(4,2,1)=0$ therefore the decision information system $S^{(4,2,2)}$ is global consistent and the scale combination $(4,2,1)$ is the global optimal scale combination.

This means that the evaluation of the eight students in Table 3 can be fully decision-making and (4, 2, 2) is an optimal scale combination for maintaining decision-making.

4.2. Local Optimal Scale

Definition 12.

Let $S=(U,A\cup d)$ be a consistent multi-scale decision system. and ∑ is the collection of all scale combinations, For $x\in U$ and the scale combination $K\in \sum$, if ${\left[x\right]}_{A^K}\subseteq {\left[x\right]}_d$, but for any $H\in \sum ,K<H,{\left[x\right]}_{A^H}\subseteq {\left[x\right]}_d$ does not hold, we call K is a local optimal scale combination of S for x.

Theorem 8.

Let $S=(U,A\cup d)$ be a consistent multi-scale decision system, and ∑ the collection of all scale combinations. Given a scale combination $K\in \sum$, the following conclusion holds:

$${\left[x\right]}_{A^K}\subseteq {\left[x\right]}_d\iff f\left({\left[x\right]}_{A^K}\right)⩽f\left({\left[x\right]}_d\right).$$

Definition 13.

Let $S=(U,A\cup d)$ be a multi-scale decision information system, and ∑ is the collection of all scale combinations, $K\in \sum$. then the significance of scale combination K for $x_i$ is defined as

$$sig(x_i,K)=\parallel f\left({\left[x_i\right]}_{A^K}\right)\wedge (\sim f\left({\left[x_i\right]}_d\right))\parallel$$

where $\parallel f\left({\left[x_i\right]}_{A^K}\right)\wedge (\sim f\left({\left[x_i\right]}_d\right))\parallel$ represents the the numbers of 1 in the boolean vector $f\left({\left[x_i\right]}_{A^K}\right)\wedge (\sim f\left({\left[x_i\right]}_d\right))$.

If $sig(x_i,K)=0$, then $f\left({\left[x\right]}_{A^K}\right)\subseteq f\left({\left[x\right]}_d\right)$, then the decision information system $S^K=(U,A^K\cup d)$ is locally consistent for $x_i$. Based on this idea, a local optimal scale combination selection algorithm of a multi-scale decision system can be described as Algorithm 2.

The computation process of Algorithm 2 is similar to Algorithm 1, except the value of $sig\left(K\right)$ is the value of $sig(x,K)$ relevant to the given object x.

Example 5.

Look for the local optimal scale combination for $x_1$ in Table 3.

We apply scale combination relation diagram 1 to illustrate the calculation steps of optimal local scale selection for $x_1$, by Definition 13, $sig(x_i,K)=\parallel f\left({\left[x_i\right]}_{A^K}\right)\wedge (\sim f\left({\left[x_i\right]}_d\right))\parallel .$

(1) For the smallest scale combination, $K_0=(1,1,1),$ by calculation, $sig(x_1,K)=0$, the system $S^{K_0}$ is local consistent for $x_1$;

(2) For the coarsest scale combination $K=(4,3,2),$ by calculation, $sig(x_1,K)=1$, Hence, $S^K=(U,A^K\cup d)$ is local inconsistent for $x_1$;

(3) For each scale combination that belongs to (4,3,2) for the second layer, by calculation, $sig(x_1,3,3,2)=1;$ $sig(x_1,4,2,2)=0;$ $sig(x_1,4,3,1)=1$, Hence the scale combination $(4,2,2)$ is the local optimal scale combination for $x_1$.

Algorithm 2: Selecting the local optimal scale combination of a multi-scale decision system

Input: A consistent multi-scale decision systems $S=(U,A\cup d)$ and an object $x\in U$.  Output: A local optimal scale combination for x.  Calculates $f\left({\left[x\right]}_d\right)$;  Let Queue=NULL  Let $optK=(I_1,I_2,\cdots ,I_m)$               //set the coarsest scale combination initially  Let $optSig$= Integer. MAX $\underline{}$VALUE               //set maximum value to $optSig$ initially  Queue. put($optK$)  While (true)       While (not Queue.empty)           Let $K=$ Queue.get()                     //pick a scale combination K from Queue           Let $sig\left(K\right)=\parallel f\left({\left[x\right]}_{A^K}\right)\wedge (\sim f\left({\left[x\right]}_d\right)\parallel$        //calculate $sig(x,K)$           If ($sig\left(K\right)⩽$ $optSig$)              //choose the minimum $sig(x,K)$ and its K                Let $optSig$=$sig\left(K\right)$                Let $optK=K$           EndIf           If ($optSig$==0)       //if the optimal scale combination is found, return.                return $optK$           EndIf      EndWhile              //loop until Queue. empty      Queue.clear()       //empty the Queue, and construct next finer scale combination      Let $(l_1,l_2,\cdots ,l_m)=optK$      For each $j\in (1,2,\cdots ,m)$              //set finer scale to each attribute, respectively           If $(l_j>1)$                Let $K=(l_1,l_2,\cdots ,l_{j-1},l_j-1,l_{j+1},\cdots ,l_m)$                Queue. put(K)           EndIf      EndFor                                    //next to search finer scale combinations  EndWhile

5. Local Optimal Scale Selection for Inconsistent Generalized Decision Information Systems

Let $S=(U,A\bigcup d)$ be a decision information system which defined by Definition 3, where $U=\{x_1,x_2,\cdots ,x_n\}$ is the universe, $A=\{a_1,a_2,\cdots ,a_m\}$ is the set of conditional attributes, $d\notin A$ is the decision attribute. If the decision information system S is locally consistent for $x\in U$, then $d\left({\left[x\right]}_A\right)$ is unique. If the decision information system is globally consistent, $d\left({\left[x\right]}_A\right)$ is unique for any $x\in U$. For an inconsistent decision information system, $\exists x\in U$, such that $d\left({\left[x\right]}_A\right)$ is not unique. For this reason, Wu and Leung put forward a definition of generalized decision in their paper [21].

Definition 14

([21]). Let $S=(U,A\bigcup d)$ be a decision information system. For $B\subseteq A$, the generalized decisions of object $x\in U$ is defined as

$${\partial }_B\left(x\right)=d\left({\left[x\right]}_B\right)=\left\{d\left(y\right)\right|y\in {\left[x\right]}_B\}.$$

Definition 15.

let $A={\left(a_{ij}\right)}_{m\times n}$, $B={\left(b_{ij}\right)}_{m\times n}$ are $m\times n$ matrices. Define $A•B={(a_{ij}\times b_{ij})}_{m\times n}.$

The following theorem is easily obtained from Definitions 14 and 15.

Theorem 9.

Let $S=(U,A\bigcup d)$ be a decision information system, Let $d_j=d\left(x_j\right),x_j\in U$, $K_A\left(i\right)=f\left({\left[x_i\right]}_A\right)•(d_1,d_2,\cdots ,d_n)$, $H_A\left(i\right)$ represents the set of all component elements in vector $K_A\left(i\right)$, for convenience, we denote $H_A\left(i\right)=\left\{d\right|d\in K_A\left(i\right)\}$. If $d_j\ne 0,(j=1,2,\cdots ,n)$, then

$${\partial }_A\left(x_i\right)=H_A\left(i\right).$$

It should be pointed out that if there exist a $x\in U$ and $d\left(x\right)=0$, the above theorem is not suitable. For this case, we may assign another value to the attribute d for x, which does not affect the classification and decision making.

Example 6.

Find the generalized decision of each object in the following inconsistent decision information system Table 4.

Table 4. An inconsistent decision system.

U	${\mathit{a}}_1$	${\mathit{a}}_2$	${\mathit{a}}_3$	d
$x_1$	0	E	S	4
$x_2$	0	E	S	2
$x_3$	1	F	L	1
$x_4$	2	B	M	3
$x_5$	0	F	S	2
$x_6$	1	F	L	2

By calculation $d=(d\left(x_1\right),d\left(x_2\right),\cdots ,d\left(x_n\right))=(4,2,1,3,2,2)$, $f\left({\left[x_1\right]}_A\right)=(1,1,0,0,0,0)$. According to Theorem 9, we have $K_A\left(1\right)=f\left({\left[x_1\right]}_A\right)•d=(4,2,0,0,0,0)$, therefore ${\partial }_A\left(x_1\right)=H_A\left(1\right)=\{2,4\}$. ${\partial }_A\left(x_1\right)=\{2,4\},{\partial }_A\left(x_2\right)=\{2,4\},{\partial }_A\left(x_3\right)=\{1,2\},{\partial }_A\left(x_4\right)=\left\{3\right\},{\partial }_A\left(x_5\right)=\left\{2\right\},{\partial }_A\left(x_6\right)=\{1,2\}$ can be obtained by the same method.

Definition 16.

Let $S=(U,A\cup d)$ be a multi-scale inconsistent decision information system, and ∑ is the collection of all scale combinations, the decision information systems corresponding to the scale combination K is $S^K=(U,A^K\cup d)$. If ${\partial }_{A^K}\left(x\right)={\partial }_{A^{K_0}}\left(x\right)$ holds, we call $S^K$ to be local generalized consistent for x. If $S^K$ is local generalized consistent for x, but for any $L=(l_1,l_2,\cdots ,l_m)$ with $K<L$, $S^L=(U,A^L\cup d)$ is local generalized inconsistent for x, we call K the optimal local generalized consistence for x.

Theorem 10.

$S^K$ is a local generalized consistence for $x_i$ if and only if $H_{A^K}\left(i\right)=H_{A^{K_0}}\left(i\right)$ holds.

Proof. 

By Theorem 9, $S^K$ is local consistent for $x_i\iff {\partial }_{A^K}\left(x_i\right)={\partial }_{A_0^K}\left(x_i\right)\iff H_{A^K}\left(i\right)=H_{A^{K_0}}\left(i\right).$

Theorem 11.

Let $S=(U,A\cup d)$ be an inconsistent multi-scale decision system, and ∑ is the collection of all scale combinations, $K\in \sum$. Then K is the optimal scale combination for $x_i$ if and only if $H_{A^K}\left(i\right)=H_{A^{K_0}}\left(i\right)$ holds. Additionally, for any $K<L,H_{A^L}\left(i\right)\ne H_{A^{K_0}}\left(i\right).$

Definition 17.

Let $S=(U,A\cup d)$ be an inconsistent multi-scale decision system, and ∑ is the collection of all scale combinations, $K=(l_1,\cdots ,l_j,\cdots ,l_m)\in \sum$. Then the significance of scale combination K for $x_i$ is defined as

$$SIG(x_i,K)=\parallel H_{A^K}\left(i\right)-H_{A^{K_0}}\left(i\right)\parallel$$

where $\parallel H_{A^K}\left(i\right)-H_{A^{K_0}}\left(i\right)\parallel$ represents the cardinality of the set $H_{A^K}\left(i\right)-H_{A^{K_0}}\left(i\right)$.

If $SIG(x_i,K)=0$, then $H_{A^K}\left(i\right)-H_{A^{K_0}}\left(i\right)$. Therefore, the decision information system $S=(U,A\cup d)$ is locally generalized consistent for $x_i$. The computation process of Algorithm 3 is similar to Algorithm 2.

Algorithm 3: Selecting the global optimal scale combination of a multi-scale decision system

Input: A inconsistent multi-scale decision system $S=(U,A\cup d)$ and an object $x\in U$.  Output: A local generalized optimal scale combination for x.  Let $K_0=(1,1,\cdots ,1)$;                                     //set the finest scale combination  Calculates $H_{A^{K_0}}\left(x\right)$;       //$H_{A^{K_0}}\left(x\right)$ correspondents to $H_A\left(i\right)$ with $K_0$ and $x_i$ in Theorem 9  Let Queue=NULL  Let $optK=(I_1,I_2,\cdots ,I_m)$               //set the coarsest scale combination initially  Let $optSig$= Integer. MAX $\underline{}$VALUE               //set maximum value to $optSig$ initially  Queue. put($optK$)  While (true)       While (not Queue.empty)           Let $K=$ Queue. get()              //pick a scale combination K from Queue           Calculates $H_{A^K}\left(x\right)$;    //$H_{A^K}\left(x\right)$ correspondents to $H_A\left(i\right)$ with K and $x_i$ in Theorem 9           Let $sig(x,K)=\parallel H_{A^K}\left(x\right)-H_{A^{K_0}}\left(x\right)\parallel$              //calculate $sig(x,K)$           If ($sig(x,K)⩽$ $optSig$)              //choose the minimum $sig(x,K)$ and its K                Let $optSig$=$sig(x,K)$                Let $optK=K$           EndIf           If ($optSig$==0)       //if the optimal scale combination is found, return.                return $optK$           EndIf          EndWhile              //loop until Queue. empty      Queue.clear()       //empty the Queue, and construct next finer scale combination      Let $(l_1,l_2,\cdots ,l_m)=optK$      For each $j\in 1,2,\cdots ,m$       //set finer scale to each attribute, respectively           If $(l_j>1)$                Let $K=(l_1,l_2,\cdots ,l_{j-1},l_j-1,l_{j+1},\cdots ,l_m)$                Queue. put(K)           EndIf      EndFor              //next to search finer scale combination  EndWhile

Example 7.

Search for the generalized local optimal scale combination of the following system Table 5 for $x_i.$

Table 5. A generalized inconsistent multi-scale information system.

U	${\mathit{a}}_1^1$	${\mathit{a}}_1^2$	${\mathit{a}}_1^3$	${\mathit{a}}_2^1$	${\mathit{a}}_2^2$	${\mathit{a}}_2^3$	${\mathit{a}}_3^1$	${\mathit{a}}_3^2$	d
$x_1$	G	S	Y	2	S	Y	1	S	1
$x_2$	G	S	Y	2	S	Y	1	S	2
$x_3$	F	M	Y	4	M	Y	2	S	4
$x_4$	B	L	N	5	M	Y	8	L	4
$x_5$	B	L	N	7	L	N	6	M	4
$x_6$	E	S	Y	3	S	Y	2	S	3

(1) $d=(d\left(x_1\right),d\left(x_2\right),d\left(x_3\right),d\left(x_4\right),d\left(x_5\right),d\left(x_6\right))=(1,2,4,4,4,3)$, for scale combination $K_0=(1,1,1),f\left({\left[x_1\right]}_{A^{K_0}}\right)\wedge d=(1,2,0,0,0,0),$ $H_{A^{K_0}}\left(1\right)=(1,2)$,

(2) For the coarsest scale $K=(3,3,2),$ $f\left({\left[x_1\right]}_{A^K}\right)•d=(1,2,4,0,0,3),$ $H_{A^K}\left(1\right)=(1,2,3,4)$ and $SIG(x_1,K)=2$ therefore, $K=(3,3,2)$ is not the generalized local optimal scale for $x_1;$

(3) For each scale combination that belongs to (3,3,2) for the second layer, by calculation, $SIG(x_1,2,3,2)=1;$ $SIG(x_1,3,2,2)=1;$ $SIG(x_1,3,3,1)=0,$ and hence the $(3,3,1)$ is the generalized local optimal scale combination for $x_1$.

6. Conclusions

This paper introduces relational matrices and matrix calculations into multi-scale decision information systems. Some properties of multi-scale decision information systems are discussed based on matrix methods. Using the relation matrix to introduce the significance of scale combination, the method of optimal scale combination selection is studied, and the related algorithm is designed. The effectiveness of the method is illustrated by experiments. In the future, we will use the matrix method to study the classification and decision-making methods of multi-scale information systems.

7. Experiments and Analysis

In order to verify whether the Algorithms 1 and 2 are able to practically apply to choose the optimal combined-scale in multi-scale decision information system, some University of California Irvine (UCI) datasets are applied in the experiments. Table 6 shows the description of these datasets.

Table 6. The UCI dataset description.

Datasets	Instances	Attributes	Classes
Auto_MPG	392	7	3
CarEvaluation	1728	6	3
Wine	178	13	3
German	1000	20	2
WDBC	569	30	2
Ionosphere	351	34	2

These data sets in Table 6 are single-scale decision datasets, and to extend these datasets from single-scale to multi-scale, some methods in [27] are adopted, which are described below.

Firstly, the finest level of scale of each attribute, that is, $a^1\left(x\right)$ is the value of $x\in U$ at attribute a in the original dataset.

Secondly, for each attribute a, the standard deviation and minimum are denoted as $std\left(a\right)$ and $min\left(a\right)$, then the second level of scale of $x\in U$ at the attribute a in multi-scale dataset is denoted:

$$a^2\left(x\right)=⌊\frac{a\left(x\right)-min\left(a\right)}{std\left(a\right)}⌋,$$

where $⌊y⌋$ means the largest integer v satisfied $v\le y$.

Thirdly, based on the previous level of scale, the next scale of attribute a can be made by merging some equivalence classes in previous level of scale. For example, suppose the equivalence classes of previous level of scale denoted $S^k=\left\{a^k\left(x\right)\right|x\in U\}=\{\left\{5\right\},\left\{6\right\},\left\{8\right\},\left\{12\right\},\left\{20\right\}\}$, then in the next level of scale, the class $\left\{5\right\}$ and class $\left\{6\right\}$ are merged into $\{5,6\}$, which denoted by $\left\{6\right\}$. That is, if $a^k\left(x\right)$ is belong to $\left\{5\right\}$ or $\left\{6\right\}$, then $a^{k+1}\left(x\right)$ is $\left\{6\right\}$, and the consequence equivalence classes is $S^{k+1}=\{\left\{6\right\},\left\{8\right\},\left\{12\right\},\left\{20\right\}\}$.

Table 7 shows the result of experiments using multi-scale optimal combined dataset according to the Algorithm 1. In Table 7 it presents the Support Vector Machine (SVM) classification accuracy both under the raw datasets and the refined datasets of optimal combined multi-scale, and it demonstrates the Algorithm 1 works well.

Table 7. Experiments results of Algorithm 1.

Datasets	Orignal-Dataset (SVM)	Optimal MSC-Dataset (SVM)	Rates of Optimal	Average of LoS
Auto_MPG	0.6611	0.6949	42.9%	2.43
CarEvaluation	0.9267	0.9499	50.0%	1.50
Wine	0.3518	0.8703	92.3%	5.15
German	0.7271	0.7233	80.0%	2.65
WDBC	0.6141	0.9592	93.3%	4.43
Ionosphere	0.9152	0.9339	91.2%	3.76

The Table 7 also presents the rates of optimal, that is the percent of the attributes with level of scale ≥2 in the given refined dataset. For example, there are seven attributes in Auto_MPG raw dataset, the optimal combined scale of the refined dataset outcomes in the experiment is $[1,1,1,5,5,3,1]$, which indicates three of seven attributes are optimal, and the rate of optimal is $\frac{3}{7}=42.9\%$. Similarly, the average of level of scale (LoS) in the refined Auto_MPG dataset is $\frac{17}{7}=2.43$, and relatively the LoS of raw Auto_MPG dataset is 1.

To compare the local multi-scale optimal method of Algorithm 2 with the global multi-scale optimal method of Algorithm 1, each datasets randomly select ≤5% instances of all and the final optimal combined-scale is the intersection of every optimal combined-scales obtained by the every single instance. For example, two instances are randomly selected in Auto_MPG, and their optimal combined-scales are [1,3,4,5,5,7,4] and [3,2,4,5,5,6,1] respectively, thus their final intersected combined-scale is [1,3,4,5,5,7,4]∧[3,2,4,5,5,6,1]=[1,2,4,5,5,6,1].

Table 8 shows the SVM accuracy, Rate of optimal, Average of LoS and time cost in Algorithm 2 relatively compare to Algorithm 2. It demonstrates that, the same as optimal performances of global multi-scale optimal algorithm can be achieved by choosing a small amount of instances in local multi-scale optimal algorithm.

Table 8. The experiments results of Algorithm 2 compares to Algorithm 1.

Datasets	Percent of	Relative Accuracy	Relative Rate	Relative Average	Relative Time
	Instances	(SVM)	of Optimal	of LoS	Cost
Auto_MPG	0.5%	108.5%	200.0%	158.8%	40.2%
CarEvaluation	0.8%	98.2%	133.3%	111.1%	203.1%
Wine	2.2%	104.3%	108.3%	100.0%	78.3%
German	1.0%	95.4%	125.0%	128.3%	14.8%
WDBC	0.4%	87.8%	103.6%	151.1%	70.6%
Ionosphere	4.8%	99.0%	100.0%	97.7%	60.9%