Matrix Method for the Optimal Scale Selection of Multi-Scale Information Decision Systems
Abstract
:1. Introduction
2. Preliminary Background
2.1. Rough Set and Information Systems
2.2. Boolean Matrix Characterization of Decision Information Systems
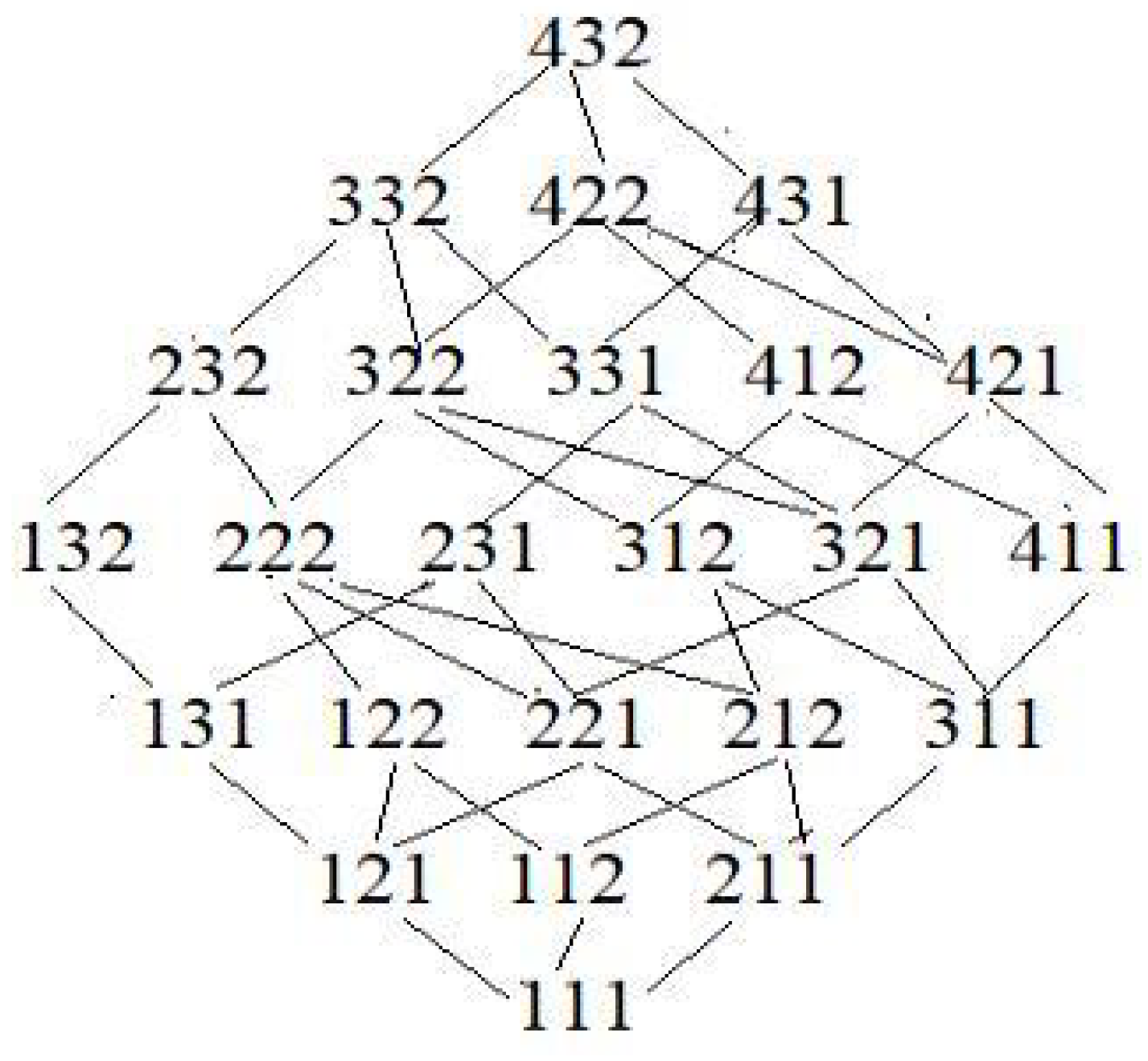
3. Relational Matrix in Generalized Multi-Scale Information Systems
4. Optimal Scale Selection for Consistent Multi-Scale Decision Information Systems
4.1. Global Optimal Scale
| Algorithm 1: Selecting the global optimal scale combination of a multi-scale decision system |
| Input: A multi-scale decision system ; Output: The global optimal scale combination. calculates ; Let Queue=NULL Let //set the coarsest scale combination initially Let = Integer. MAX VALUE //set maximum value to initially Queue. put() While (true) While (not Queue. empty) Let Queue. get() //pick a scale combination K from Queue Let //calculate If ( ) //choose the minimum and its K Let = Let =K EndIf If (==0) //if the optimal scale combination is found, return. return EndIf EndWhile //loop until Queue. empty Queue.clear() //empty the Queue, and construct next finer scale combination Let For each //set finer scale to each attribute, respectively If Let Queue. put(K) EndIf EndFor //next to search finer scale combination EndWhile |
4.2. Local Optimal Scale
| Algorithm 2: Selecting the local optimal scale combination of a multi-scale decision system |
| Input: A consistent multi-scale decision systems and an object . Output: A local optimal scale combination for x. Calculates ; Let Queue=NULL Let //set the coarsest scale combination initially Let = Integer. MAX VALUE //set maximum value to initially Queue. put() While (true) While (not Queue.empty) Let Queue.get() //pick a scale combination K from Queue Let //calculate If ( ) //choose the minimum and its K Let = Let EndIf If (==0) //if the optimal scale combination is found, return. return EndIf EndWhile //loop until Queue. empty Queue.clear() //empty the Queue, and construct next finer scale combination Let For each //set finer scale to each attribute, respectively If Let Queue. put(K) EndIf EndFor //next to search finer scale combinations EndWhile |
5. Local Optimal Scale Selection for Inconsistent Generalized Decision Information Systems
| Algorithm 3: Selecting the global optimal scale combination of a multi-scale decision system |
| Input: A inconsistent multi-scale decision system and an object . Output: A local generalized optimal scale combination for x. Let ; //set the finest scale combination Calculates ; // correspondents to with and in Theorem 9 Let Queue=NULL Let //set the coarsest scale combination initially Let = Integer. MAX VALUE //set maximum value to initially Queue. put() While (true) While (not Queue.empty) Let Queue. get() //pick a scale combination K from Queue Calculates ; // correspondents to with K and in Theorem 9 Let //calculate If ( ) //choose the minimum and its K Let = Let EndIf If (==0) //if the optimal scale combination is found, return. return EndIf EndWhile //loop until Queue. empty Queue.clear() //empty the Queue, and construct next finer scale combination Let For each //set finer scale to each attribute, respectively If Let Queue. put(K) EndIf EndFor //next to search finer scale combination EndWhile |
6. Conclusions
7. Experiments and Analysis
Author Contributions
Funding
Conflicts of Interest
References
- Zadeh, L.A. Fuzzy sets and information granularity. Adv. Fuzzy Set Theory Appl. 1979, 11, 3–18. [Google Scholar]
- Pedrycz, W. Granular Computing: An Introduction; Physica-Verlag: Heidelberg, Germany, 2000; pp. 309–328. [Google Scholar] [CrossRef]
- Yao, Y.Y.; Miao, D.Q.; Xu, F.F. Granular Structures and Approximations in Rough Sets and Knowledge Spaces. In Rough Set Theory: A True Landmark in Data Analysis; Springer: Berlin/Heidelberg, Germany, 2009; pp. 71–84. [Google Scholar] [CrossRef]
- Li, J.; Ren, Y.; Mei, C.; Qian, Y.; Yang, X. A comparative study of multigranulation rough sets and concept lattices via rule acquisition. Knowl.-Based Syst. 2016, 91, 152–164. [Google Scholar] [CrossRef]
- Pal, S.K.; Ray, S.S.; Ganivada, A. Introduction to Granular Computing, Pattern Recognition and Data Mining. In Granular Neural Networks, Pattern Recognition and Bioinformatics; Springer International Publishing: Cham, Switzerland, 2017; pp. 1–37. [Google Scholar] [CrossRef]
- Han, S.E. Roughness measures of locally finite covering rough sets. Int. J. Approx. Reason. 2019, 105, 368–385. [Google Scholar] [CrossRef]
- Liu, H.; Cocea, M. Granular computing-based approach for classification towards reduction of bias in ensemble learning. Granul. Comput. 2017, 2, 131–139. [Google Scholar] [CrossRef]
- Wang, G.; Yang, J.; Xu, J. Granular computing: From granularity optimization to multi-granularity joint problem solving. Granul. Comput. 2017, 2, 105–120. [Google Scholar] [CrossRef]
- Sun, B.Z.; Ma, W.M.; Qian, Y.H. Multigranulation fuzzy rough set over two universes and its application to decision making. Knowl.-Based Syst. 2017, 123, 61–74. [Google Scholar] [CrossRef]
- Yao, Y. Three-way decision and granular computing. Int. J. Approx. Reason. 2018, 103, 107–123. [Google Scholar] [CrossRef]
- Mo, J.; Huang, H.L. (T, S)-Based Single-Valued Neutrosophic Number Equivalence Matrix and Clustering Method. Mathematics 2019, 7, 36. [Google Scholar] [CrossRef]
- Petrosino, A.; Ferone, A. Feature Discovery through Hierarchies of Rough Fuzzy Sets. In Granular Computing and Intelligent Systems: Design with Information Granules of Higher Order and Higher Type; Pedrycz, W., Chen, S.M., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 57–73. [Google Scholar] [CrossRef]
- Ferone, A. Feature selection based on composition of rough sets induced by feature granulation. Int. J. Approx. Reason. 2018, 101, 276–292. [Google Scholar] [CrossRef]
- Pawlak, Z. Imprecise Categories, Approximations and Rough Sets. In Rough Sets: Theoretical Aspects of Reasoning about Data; Springer: Dordrecht, The Netherlands, 1991; pp. 9–32. [Google Scholar] [CrossRef]
- Zhu, P.F.; Hu, Q.H.; Zuo, W.M.; Yang, M. Multi-granularity distance metric learning via neighborhood granule margin maximization. Inf. Sci. 2014, 282, 321–331. [Google Scholar] [CrossRef]
- Zhu, P.F.; Hu, Q.H. Adaptive neighborhood granularity selection and combination based on margin distribution optimization. Inf. Sci. 2013, 249, 1–12. [Google Scholar] [CrossRef]
- Tan, A.H.; Wu, W.Z.; Li, J.J.; Lin, G.P. Evidence-theory-based numerical characterization of multigranulation rough sets in incomplete information systems. Fuzzy Sets Syst. 2016, 294, 18–35. [Google Scholar] [CrossRef]
- Yao, Y.; She, Y. Rough set models in multigranulation spaces. Inf. Sci. 2016, 327, 40–56. [Google Scholar] [CrossRef]
- Lin, G.P.; Liang, J.Y.; Qian, Y.H. An information fusion approach by combining multigranulation rough sets and evidence theory. Inf. Sci. 2015, 314, 184–199. [Google Scholar] [CrossRef]
- Yang, X.B.; Song, X.N.; Chen, Z.H.; Yang, J.Y. On multigranulation rough sets in incomplete information system. Int. J. Mach. Learn. Cybern. 2012, 3, 223–232. [Google Scholar] [CrossRef]
- Wu, W.Z.; Leung, Y. Theory and applications of granular labelled partitions in multi-scale decision tables. Inf. Sci. 2011, 181, 3878–3897. [Google Scholar] [CrossRef]
- Wu, W.Z.; Leung, Y. Optimal scale selection for multi-scale decision tables. Int. J. Approx. Reason. 2013, 54, 1107–1129. [Google Scholar] [CrossRef]
- Gu, S.M.; Wu, W.Z. On knowledge acquisition in multi-scale decision systems. Int. J. Mach. Learn. Cybern. 2013, 4, 477–486. [Google Scholar] [CrossRef]
- Wu, W.Z.; Qian, Y.; Li, T.J.; Gu, S.M. On rule acquisition in incomplete multi-scale decision tables. Inf. Sci. 2017, 378, 282–302. [Google Scholar] [CrossRef]
- She, Y.H.; Li, J.H.; Yang, H.L. A local approach to rule induction in multi-scale decision tables. Knowl.-Based Syst. 2015, 89, 398–410. [Google Scholar] [CrossRef]
- Li, F.; Hu, B.Q.; Wang, J. Stepwise optimal scale selection for multi-scale decision tables via attribute significance. Knowl.-Based Syst. 2017, 129, 4–16. [Google Scholar] [CrossRef]
- Li, F.; Hu, B.Q. A new approach of optimal scale selection to multi-scale decision tables. Inf. Sci. 2017, 381, 193–208. [Google Scholar] [CrossRef]
- Shafer, G. A Mathematical Theory of Evidence; Princeton University Press: Princeton, NJ, USA, 1976. [Google Scholar]
- Guan, J.W.; Bell, D.A.; Guan, Z. Matrix computation for information systems. Inf. Sci. 2001, 131, 129–156. [Google Scholar] [CrossRef]
- Liu, G.L. Rough Sets over the Boolean Algebras. In Rough Sets, Fuzzy Sets, Data Mining, and Granular Computing; Ślęzak, D., Wang, G., Szczuka, M., Düntsch, I., Yao, Y., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 124–131. [Google Scholar]
- Wang, L.; Li, T.R. Matrix-Based Computational Method for Upper and Lower Approximations of Rough Sets. Pattern Recognit. Artif. Intell. 2011, 24, 756–762. [Google Scholar] [CrossRef]
- Huang, Y.Y.; Li, T.R.; Luo, C.; Horng, S.J. Matrix-Based Rough Set Approach for Dynamic Probabilistic Set-Valued Information Systems. In Rough Sets; Springer International Publishing: Cham, Switzerland, 2016; pp. 197–206. [Google Scholar]
- Tan, A.H.; Li, J.J.; Lin, Y.J.; Lin, G.P. Matrix-based set approximations and reductions in covering decision information systems. Int. J. Approx. Reason. 2015, 59, 68–80. [Google Scholar] [CrossRef]
- Tan, A.H.; Li, J.J.; Lin, G.P.; Lin, Y.J. Fast approach to knowledge acquisition in covering information systems using matrix operations. Knowl.-Based Syst. 2015, 79, 90–98. [Google Scholar] [CrossRef]
- Luo, C.; Li, T.R.; Yi, Z.; Fujita, H. Matrix approach to decision-theoretic rough sets for evolving data. Knowl.-Based Syst. 2016, 99, 123–134. [Google Scholar] [CrossRef]
- Hu, C.X.; Liu, S.X.; Liu, G.X. Matrix-based approaches for dynamic updating approximations in multigranulation rough sets. Knowl.-Based Syst. 2017, 122, 51–63. [Google Scholar] [CrossRef]
- Karczmarek, P.; Kiersztyn, A.; Pedrycz, W. An Application of Graphic Tools and Analytic Hierarchy Process to the Description of Biometric Features. In Artificial Intelligence and Soft Computing; Rutkowski, L., Scherer, R., Korytkowski, M., Pedrycz, W., Tadeusiewicz, R., Zurada, J.M., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 137–147. [Google Scholar]
- Xu, Y.H.; Wu, W.Z.; Tan, A.H. Optimal Scale Selections in Consistent Generalized Multi-scale Decision Tables. Rough Sets 2017, 10313, 185–198. [Google Scholar] [CrossRef]
- Gu, S.; Gu, J.; Wu, W.; Li, T.; Chen, C. Local optimal granularity selections in incomplete multi-granular decision systems. J. Comput. Res. Dev. 2017, 54, 1500–1509. [Google Scholar] [CrossRef]
- Wu, W.Z.; Chen, C.J.; Li, T.J.; Xu, Y.H. Comparative Study on Optimal Granularities in Inconsistent Multi-granular Labeled Decision Systems. Pattern Recognit. Artif. Intell. 2016, 29, 1095–1103. [Google Scholar] [CrossRef]
- Wu, W.Z.; Yang, L.; Tan, A.H.; Xu, Y.H. Granularity Selections in Generalized Incomplete Multi-Granular Labeled Decision Systems. J. Comput. Res. Dev. 2018, 55, 1263–1272. [Google Scholar] [CrossRef]
| U | d | ||||
|---|---|---|---|---|---|
| 2 | 1 | 1 | 1 | 1 | |
| 3 | 2 | 2 | 2 | 2 | |
| 2 | 1 | 1 | 1 | 1 | |
| 2 | 2 | 1 | 1 | 3 | |
| 1 | 1 | 4 | 2 | 5 | |
| 1 | 1 | 3 | 2 | 1 | |
| 3 | 2 | 2 | 2 | 2 |
| 1 | Y | |||
| 2 | Y | |||
| 3 | Y | |||
| 4 | Y | |||
| 5 | N | |||
| 6 | N |
| U | d | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 78 | 3 | F | M | Y | 94 | 1 | E | Y | 75 | 3 | Y | 1 | |
| 61 | 4 | P | M | Y | 62 | 4 | P | Y | 60 | 4 | Y | 0 | |
| 69 | 4 | P | M | Y | 78 | 3 | F | Y | 68 | 4 | Y | 1 | |
| 98 | 1 | E | S | Y | 58 | 5 | B | N | 97 | 1 | Y | 1 | |
| 36 | 6 | B | L | N | 72 | 3 | F | Y | 92 | 1 | Y | 0 | |
| 63 | 4 | P | M | Y | 76 | 3 | F | Y | 47 | 5 | N | 0 | |
| 58 | 5 | B | L | N | 95 | 1 | E | Y | 92 | 1 | Y | 1 | |
| 35 | 6 | B | L | N | 90 | 1 | E | Y | 73 | 3 | Y | 0 |
| U | d | |||
|---|---|---|---|---|
| 0 | E | S | 4 | |
| 0 | E | S | 2 | |
| 1 | F | L | 1 | |
| 2 | B | M | 3 | |
| 0 | F | S | 2 | |
| 1 | F | L | 2 |
| U | d | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| G | S | Y | 2 | S | Y | 1 | S | 1 | |
| G | S | Y | 2 | S | Y | 1 | S | 2 | |
| F | M | Y | 4 | M | Y | 2 | S | 4 | |
| B | L | N | 5 | M | Y | 8 | L | 4 | |
| B | L | N | 7 | L | N | 6 | M | 4 | |
| E | S | Y | 3 | S | Y | 2 | S | 3 |
| Datasets | Instances | Attributes | Classes |
|---|---|---|---|
| Auto_MPG | 392 | 7 | 3 |
| CarEvaluation | 1728 | 6 | 3 |
| Wine | 178 | 13 | 3 |
| German | 1000 | 20 | 2 |
| WDBC | 569 | 30 | 2 |
| Ionosphere | 351 | 34 | 2 |
| Datasets | Orignal-Dataset (SVM) | Optimal MSC-Dataset (SVM) | Rates of Optimal | Average of LoS |
|---|---|---|---|---|
| Auto_MPG | 0.6611 | 0.6949 | 42.9% | 2.43 |
| CarEvaluation | 0.9267 | 0.9499 | 50.0% | 1.50 |
| Wine | 0.3518 | 0.8703 | 92.3% | 5.15 |
| German | 0.7271 | 0.7233 | 80.0% | 2.65 |
| WDBC | 0.6141 | 0.9592 | 93.3% | 4.43 |
| Ionosphere | 0.9152 | 0.9339 | 91.2% | 3.76 |
| Datasets | Percent of | Relative Accuracy | Relative Rate | Relative Average | Relative Time |
|---|---|---|---|---|---|
| Instances | (SVM) | of Optimal | of LoS | Cost | |
| Auto_MPG | 0.5% | 108.5% | 200.0% | 158.8% | 40.2% |
| CarEvaluation | 0.8% | 98.2% | 133.3% | 111.1% | 203.1% |
| Wine | 2.2% | 104.3% | 108.3% | 100.0% | 78.3% |
| German | 1.0% | 95.4% | 125.0% | 128.3% | 14.8% |
| WDBC | 0.4% | 87.8% | 103.6% | 151.1% | 70.6% |
| Ionosphere | 4.8% | 99.0% | 100.0% | 97.7% | 60.9% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.S.; Li, J.J.; Huang, J.X. Matrix Method for the Optimal Scale Selection of Multi-Scale Information Decision Systems. Mathematics 2019, 7, 290. https://doi.org/10.3390/math7030290
Chen YS, Li JJ, Huang JX. Matrix Method for the Optimal Scale Selection of Multi-Scale Information Decision Systems. Mathematics. 2019; 7(3):290. https://doi.org/10.3390/math7030290
Chicago/Turabian StyleChen, Ying Sheng, Jin Jin Li, and Jian Xin Huang. 2019. "Matrix Method for the Optimal Scale Selection of Multi-Scale Information Decision Systems" Mathematics 7, no. 3: 290. https://doi.org/10.3390/math7030290
APA StyleChen, Y. S., Li, J. J., & Huang, J. X. (2019). Matrix Method for the Optimal Scale Selection of Multi-Scale Information Decision Systems. Mathematics, 7(3), 290. https://doi.org/10.3390/math7030290




