A Dilation Invariance Method and the Stability of Inhomogeneous Wave Equations

Abstract

We apply the method of a kind of dilation invariance to prove the generalized Hyers-Ulam stability of the (inhomogeneous) wave equation with a source, $u_{tt}(x,t)-c^2▵u(x,t)=f(x,t)$, for a class of real-valued functions with continuous second partial derivatives in each of spatial and the time variables.

1. Introduction

The stability problems for the functional equations and (ordinary or partial) differential equations originate from the question of Ulam [1]: Under what conditions does there exist an additive function near an approximately additive function? In 1941, Hyers [2] answered the question of Ulam in the affirmative for the Banach space cases. Indeed, Hyers’ theorem states that the following statement is true for all $\epsilon \ge 0$: if a function f satisfies the inequality $\parallel f(x+y)-f\left(x\right)-f\left(y\right)\parallel \le \epsilon$ for all x, then there exists an exact additive function F such that $\parallel f\left(x\right)-F\left(x\right)\parallel \le \epsilon$ for all x. In that case, the Cauchy additive functional equation, $f(x+y)=f\left(x\right)+f\left(y\right)$, is said to have (satisfy) the Hyers-Ulam stability.

Assume that V is a normed space and I is an open interval of $\mathbb{R}$. The nth order linear differential equation

$$\begin{array}{c}\hfill a_n\left(x\right)y^{\left(n\right)}\left(x\right)+a_{n-1}\left(x\right)y^{(n-1)}\left(x\right)+\cdots +a_1\left(x\right)y^{\prime }\left(x\right)+a_0\left(x\right)y\left(x\right)+h\left(x\right)=0\end{array}$$

(1)

is said to have (satisfy) the Hyers-Ulam stability provided the following statement is true for all $\epsilon \ge 0$: If a function $u:I\to V$ satisfies the differential inequality

$$\begin{array}{c}\hfill \parallel a_n\left(x\right)u^{\left(n\right)}\left(x\right)+a_{n-1}\left(x\right)u^{(n-1)}\left(x\right)+\cdots +a_1\left(x\right)u^{\prime }\left(x\right)+a_0\left(x\right)u\left(x\right)+h\left(x\right)\parallel \le \epsilon \end{array}$$

for all $x\in I$, then there exists a solution $u_0:I\to V$ to the differential Equation (1) and a continuous function K such that $\parallel u\left(x\right)-u_0\left(x\right)\parallel \le K\left(\epsilon \right)$ for any $x\in I$ and $\underset{\epsilon \to 0}{lim}K\left(\epsilon \right)=0$.

When the above statement is true even if we replace $\epsilon$ and $K\left(\epsilon \right)$ by $\phi \left(x\right)$ and $\Phi \left(x\right)$, where $\phi ,\Phi :I\to [0,\infty )$ are functions not depending on u and $u_0$ explicitly, the corresponding differential Equation (1) is said to have (satisfy) the generalized Hyers-Ulam stability. (This type of stability is sometimes called the Hyers-Ulam-Rassias stability.)

These terminologies will also be applied for other differential equations and partial differential equations. For more detailed definitions, we refer the reader to [1,2,3,4,5,6,7,8,9].

To the best of our knowledge, Obłoza was the first author who investigated the Hyers-Ulam stability of differential equations (see [10,11]): Assume that $g,r:(a,b)\to \mathbb{R}$ are continuous functions with ${\int }_a^b\left|g\left(x\right)\right|dx<\infty$ and $\epsilon$ is an arbitrary positive real number. Obłoza’s theorem states that there exists a constant $\delta >0$ such that $|y\left(x\right)-y_0\left(x\right)|\le \delta$ for all $x\in (a,b)$ whenever a differentiable function $y:(a,b)\to \mathbb{R}$ satisfies the inequality $|y^{\prime }\left(x\right)+g\left(x\right)y\left(x\right)-r\left(x\right)|\le \epsilon$ for all $x\in (a,b)$ and a function $y_0:(a,b)\to \mathbb{R}$ satisfies $y_0^{\prime }\left(x\right)+g\left(x\right)y_0\left(x\right)=r\left(x\right)$ for all $x\in (a,b)$ and $y\left(\tau \right)=y_0\left(\tau \right)$ for some $\tau \in (a,b)$. Since then, a number of mathematicians have dealt with this subject (see [3,12,13,14,15]).

Prástaro and Rassias are the first authors who investigated the Hyers-Ulam stability of partial differential equations (see [16]). Thereafter, the first author [17], together with Lee, proved the Hyers-Ulam stability of the first-order linear partial differential equation of the form, $a{u}_x(x,y)+b{u}_y(x,y)+cu(x,y)+d=0$, where $a,b\in \mathbb{R}$ and $c,d\in \mathbb{C}$ are constants with $\Re \left(c\right)\ne 0$. As a further step, the first author proved the generalized Hyers-Ulam stability of the wave equation without source (see [18,19]).

One of the typical examples of hyperbolic partial differential equations is the wave equation with spatial variables $x_1,\dots ,x_n$ and the time variable t

$$\begin{array}{c}\hfill u_{tt}(x,t)-c^2▵u(x,t)=f(x,t),\end{array}$$

(2)

where $c>0$ is a constant, n is a fixed positive integer, $▵={\displaystyle \sum _{i=1}^n}\frac{{\partial }^2}{\partial x_i^2}$ is the Laplace operator and $x=(x_1,\dots ,x_n)\in {\mathbb{R}}^n$. The solution of the wave Equation (2) is a scalar function $u=u(x,t)$ describing the propagation of a wave at a speed c in all spatial directions.

In this paper, applying the method of dilation invariance (see [18,20]), we investigate the generalized Hyers-Ulam stability of the (inhomogeneous) wave Equation (2) with a source. The main advantages of this present paper over the previous works [18,19,21] are that this paper deals with the inhomogeneous wave equation and its time variable runs through the whole half line $(0,\infty )$ while the previous one [18] deals with the homogeneous wave equation and its time variable is not allowed to run through the whole half line (roughly speaking, the relevant domain seems somewhat artificial) and the other previous ones [19,21] deal with the one-dimensional homogeneous case only. In addition, the present work gives a partial answer to the open problem raised in ([18], Remark 3) concerning the domains of relevant functions.

2. Regular Solutions

If $u(x,t)$ is a solution to the inhomogeneous wave Equation (2) for $n=1$ and a is a positive constant, then the dilated function $w(x,t):=u(ax,at)$ satisfies the equality, $w_{tt}(x,t)-c^2{w}_{xx}(x,t)=a^{2}f(ax,at)$, for all $x\in \mathbb{R}$ and $t>0$. When the source term $f(x,t)$ satisfies the additional condition

$$\begin{array}{c}\hfill a^{2}f(ax,at)=f(x,t),\end{array}$$

(3)

i.e., when $f(x,t)$ is a homogeneous function of degree $-2$, $w(x,t)$ is also a solution to the inhomogeneous wave Equation (2) for $n=1$. This property is called the invariance under dilation.

In this section, we will search for regular solutions to (2) for $n=1$ which have the special form $u(x,t)=tv\left(\right|x|/t)$, where v is a twice continuously differentiable function. Such a method will be called the method of dilation invariance. We will restrict the solutions of (2) within the special class of functions, each of whose functions depends on the value of $\left|x\right|/t$ only. Indeed, this special class is a proper subclass of the class of functions with (independent) two variables x and t. The reason for selecting the dilation invariance of the form $u(x,t)=tv\left(\right|x|/t)$ rather than $u(x,t)=w(x/a,t/a)$ is due to a technical complexity.

Based on this argument, we define

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\overline{D}}_1& :=\left\{(x,t)\in \mathbb{R}\setminus \left\{0\right\}\times (0,\infty )\left|\right|x|<ct\right\},\hfill \\ \hfill {\overline{U}}_1& :=\{u:{\overline{D}}_1\to \mathbb{R}|\mathrm{there} \mathrm{exists} \mathrm{a} \mathrm{twice} \mathrm{continuously} \mathrm{differentiable}\hfill \\ & \mathrm{function} v: (0,c)\to \mathbb{R} \mathrm{such} \mathrm{that} u(x,t)=tv\left(\frac{\left|x\right|}{t}\right) \mathrm{for} \mathrm{all}\hfill \\ & (x,t)\in {\overline{D}}_1, \underset{r\to 0^{+}}{lim}v\left(r\right)=0 \mathrm{and} \underset{r\to 0^{+}}{lim}{v}^{\prime }\left(r\right) \mathrm{exists}\}.\hfill \end{array}\end{array}$$

We note that $(x,t)\in {\overline{D}}_1$ if and only if $0<\left|x\right|/t<c$ (see Figure 1).

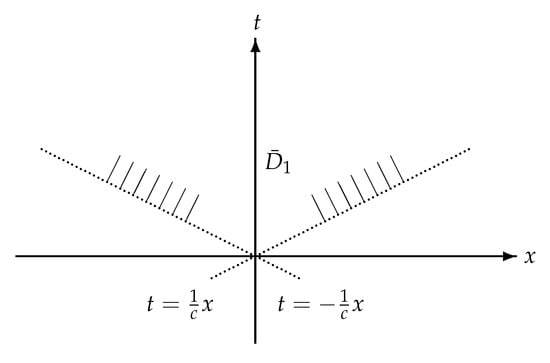
Figure 1. |x| < ct.

Theorem 1.

Assume that $f:{\overline{D}}_1\to \mathbb{R}$ is a function for which there exists a continuous function $g:(0,c)\to \mathbb{R}$ such that

$$\begin{array}{c}\hfill f(x,t)=\frac{1}{t}g\left(\frac{\left|x\right|}{t}\right)\end{array}$$

(4)

and

$$\begin{array}{c}\hfill {\int }_0^r{\int }_0^s\frac{g\left(w\right)}{c^2-w^2}dwds<\infty \end{array}$$

(5)

for all $r\in (0,c)$. A function $u\in {\overline{U}}_1$ is a solution to the inhomogeneous wave Equation $\left(2\right)$ for $n=1$ if and only if there exists a real constant $c_1$ with

$$\begin{array}{c}\hfill u(x,t)=c_1\left|x\right|-t{\int }_0^{\left|x\right|/t}{\int }_0^s\frac{g\left(w\right)}{c^2-w^2}dwds\end{array}$$

(6)

for all $(x,t)\in {\overline{D}}_1$.

Proof. 

Our assumption $u\in {\overline{U}}_1$ implies that there exist a twice continuously differentiable function $v:(0,c)\to \mathbb{R}$ and a real number $c_1$ such that

$$\begin{array}{c}\hfill u(x,t)=tv\left(r\right),\underset{r\to 0^{+}}{lim}v\left(r\right)=0,\underset{r\to 0^{+}}{lim}{v}^{\prime }\left(r\right)=c_1\end{array}$$

(7)

for any $(x,t)\in {\overline{D}}_1$, where we set $r=\left|x\right|/t$. Using this notation and chain rule as well as the partial derivatives

$$\begin{array}{c}\hfill \frac{\partial r}{\partial t}=-\frac{r}{t},\frac{\partial r}{\partial x}=\frac{1}{t}\frac{x}{\left|x\right|},\frac{\partial \left|x\right|}{\partial x}=\frac{x}{\left|x\right|}\end{array}$$

with $\left|x\right|=\sqrt{x^2}$, we calculate the following partial derivatives:

$$\begin{array}{c}\hfill \begin{array}{cc}{\displaystyle u_t(x,t)=v\left(r\right)-r{v}^{\prime }\left(r\right)},\hfill & {\displaystyle u_{tt}(x,t)=\frac{r^2}{t}{v}^{″}\left(r\right)},\hfill \\ {\displaystyle u_x(x,t)=\frac{x}{\left|x\right|}{v}^{\prime }\left(r\right)},\hfill & {\displaystyle u_{xx}(x,t)=\frac{1}{t}{v}^{″}\left(r\right)}\hfill \end{array}\end{array}$$

(8)

Since $u(x,t)$ is assumed to be a solution to the wave Equation (2) with $n=1$, by (4), we have

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill u_{tt}(x,t)-c^2{u}_{xx}(x,t)-f(x,t)& =\frac{r^2}{t}{v}^{″}\left(r\right)-\frac{c^2}{t}{v}^{″}\left(r\right)-\frac{1}{t}g\left(r\right)\hfill \\ & =-\frac{1}{t}\left(\left(c^2-r^2\right)v^{″}\left(r\right)+g\left(r\right)\right)\hfill \\ & =0\hfill \end{array}\end{array}$$

for any $(x,t)\in {\overline{D}}_1$, and hence for all $r\in (0,c)$. Thus, it holds that

$$\begin{array}{c}\hfill \left(c^2-r^2\right)v^{″}\left(r\right)+g\left(r\right)=0\mathrm{or}{v}^{″}\left(r\right)+\frac{g\left(r\right)}{c^2-r^2}=0\end{array}$$

for any $r\in (0,c)$. Therefore, we get

$$\begin{array}{c}\hfill \begin{array}{c}\hfill v^{\prime }\left(r\right)=c_1-{\int }_0^r\frac{g\left(w\right)}{c^2-w^2}dw\end{array}\end{array}$$

for $r\in (0,c)$.

Taking account of the first limit condition in the definition of ${\overline{U}}_1$ and (5), it follows from the last equation that

$$\begin{array}{c}\hfill v\left(r\right)=v\left(r\right)-\underset{s\to 0^{+}}{lim}v\left(s\right)={\int }_0^r{v}^{\prime }\left(s\right)ds=c_{1}r-{\int }_0^r{\int }_0^s\frac{g\left(w\right)}{c^2-w^2}dwds\end{array}$$

for all $r\in (0,c)$. Moreover, we get

$$\begin{array}{c}\hfill u(x,t)=tv\left(\frac{\left|x\right|}{t}\right)=c_1\left|x\right|-t{\int }_0^{\left|x\right|/t}{\int }_0^s\frac{g\left(w\right)}{c^2-w^2}dwds\end{array}$$

for each $(x,t)\in {\overline{D}}_1$.

Conversely, if a function $u:{\overline{D}}_1\to \mathbb{R}$ has the form given in (6), then we can easily compute the following partial derivatives:

$$\begin{array}{c}\hfill u_{tt}(x,t)=-\frac{r^2}{t}\frac{g\left(r\right)}{c^2-r^2}\mathrm{and}{u}_{xx}(x,t)=-\frac{1}{t}\frac{g\left(r\right)}{c^2-r^2}\end{array}$$

Hence, we obtain

$$\begin{array}{c}\hfill u_{tt}(x,t)-c^2{u}_{xx}(x,t)=-\frac{r^2}{t}\frac{g\left(r\right)}{c^2-r^2}+\frac{c^2}{t}\frac{g\left(r\right)}{c^2-r^2}=\frac{1}{t}g\left(r\right)=f(x,t)\end{array}$$

for each $(x,t)\in {\overline{D}}_1$, i.e., $u(x,t)$ is a solution to the wave Equation (2) for $n=1$.

Moreover, if we define a function $v:(0,c)\to \mathbb{R}$ by

$$\begin{array}{c}\hfill v\left(r\right):=c_{1}r-{\int }_0^r{\int }_0^s\frac{g\left(w\right)}{c^2-w^2}dwds,\end{array}$$

then $u(x,t)=tv\left(r\right)$, v is twice continuously differentiable, $\underset{r\to 0^{+}}{lim}v\left(r\right)=0$ and $\underset{r\to 0^{+}}{lim}{v}^{\prime }\left(r\right)=c_1$.

These facts imply that u belongs to ${\overline{U}}_1$. ☐

We now define

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\overline{D}}_2& :=\left\{(x,t)\in \mathbb{R}\setminus \left\{0\right\}\times (0,\infty )\left|\right|x|>ct\right\},\hfill \\ \hfill {\overline{U}}_2& :=\{u:{\overline{D}}_2\to \mathbb{R}|\mathrm{there} \mathrm{exists} \mathrm{a} \mathrm{twice} \mathrm{continuously} \mathrm{differentiable}\hfill \\ & \mathrm{function} v: (c,\infty )\to \mathbb{R} \mathrm{such} \mathrm{that} u(x,t)=tv\left(\frac{\left|x\right|}{t}\right) \mathrm{for} \mathrm{all}\hfill \\ & (x,t)\in {\overline{D}}_2, \underset{r\to c^{+}}{lim}v\left(r\right)=0 \mathrm{and} \underset{r\to c^{+}}{lim}{v}^{\prime }\left(r\right) \mathrm{exists}\}.\hfill \end{array}\end{array}$$

We note that $(x,t)\in {\overline{D}}_2$ if and only if $\left|x\right|/t>c$ (see Figure 2).

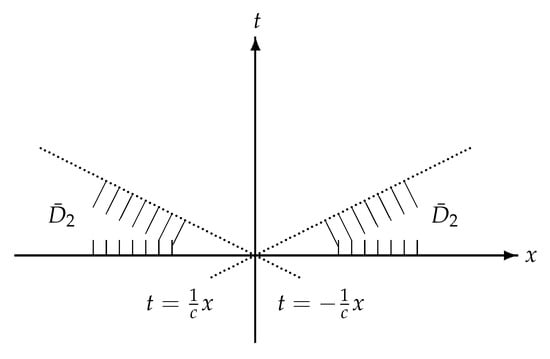
Figure 2. |x| > ct.

Theorem 2.

Assume that $f:{\overline{D}}_2\to \mathbb{R}$ is a function for which there exists a continuous function $g:(c,\infty )\to \mathbb{R}$ with the expression in $\left(4\right)$ and satisfying the condition

$$\begin{array}{c}\hfill {\int }_c^r{\int }_c^s\frac{g\left(w\right)}{c^2-w^2}dwds<\infty \end{array}$$

(9)

for all $r\in (c,\infty )$. A function $u\in {\overline{U}}_2$ is a solution to the inhomogeneous wave Equation $\left(2\right)$ for $n=1$ if and only if there exists a real constant $c_2$ with

$$\begin{array}{c}\hfill u(x,t)=c_2\left(\left|x\right|-ct\right)-t{\int }_c^{\left|x\right|/t}{\int }_c^s\frac{g\left(w\right)}{c^2-w^2}dwds\end{array}$$

(10)

for all $(x,t)\in {\overline{D}}_2$.

Proof. 

Our assumption $u\in {\overline{U}}_2$ implies that there exists a twice continuously differentiable function $v:(c,\infty )\to \mathbb{R}$ and a real number $c_2$ such that

$$\begin{array}{c}\hfill u(x,t)=tv\left(r\right),\underset{r\to c^{+}}{lim}v\left(r\right)=0,\underset{r\to c^{+}}{lim}{v}^{\prime }\left(r\right)=c_2\end{array}$$

(11)

for any $(x,t)\in {\overline{D}}_2$, where we set $r=\left|x\right|/t$. By using this notation and chain rule, we calculate the partial derivatives in (8).

Since $u(x,t)$ is a solution to the wave Equation (2) for $n=1$, it follows from (4) and the partial derivatives in (8) that

$$\begin{array}{c}\hfill u_{tt}(x,t)-c^2{u}_{xx}(x,t)-f(x,t)=-\frac{1}{t}\left(\left(c^2-r^2\right)v^{″}\left(r\right)+g\left(r\right)\right)=0\end{array}$$

for any $(x,t)\in {\overline{D}}_2$, and hence for all $r\in (c,\infty )$. Hence, it is true that

$$\begin{array}{c}\hfill v^{″}\left(r\right)+\frac{g\left(r\right)}{c^2-r^2}=0\end{array}$$

for all $r\in (c,\infty )$. Thus, we obtain

$$\begin{array}{c}\hfill v^{\prime }\left(r\right)=c_2-{\int }_c^r\frac{g\left(w\right)}{c^2-w^2}dw\end{array}$$

for $r\in (c,\infty )$.

On account of the first limit condition in the definition of ${\overline{U}}_2$ and (9), it follows from the last equation that

$$\begin{array}{c}\hfill v\left(r\right)=v\left(r\right)-\underset{s\to c^{+}}{lim}v\left(s\right)={\int }_c^r{v}^{\prime }\left(s\right)ds=c_2(r-c)-{\int }_c^r{\int }_c^s\frac{g\left(w\right)}{c^2-w^2}dwds\end{array}$$

for each $r\in (c,\infty )$. Further, we get

$$\begin{array}{c}\hfill u(x,t)=tv\left(\frac{\left|x\right|}{t}\right)=c_2\left|x\right|-c_{2}ct-t{\int }_c^{\left|x\right|/t}{\int }_c^s\frac{g\left(w\right)}{c^2-w^2}dwds\end{array}$$

for each $(x,t)\in {\overline{D}}_2$.

Conversely, if a function $u:{\overline{D}}_2\to \mathbb{R}$ is expressed as (10), then we have the following partial derivatives:

$$\begin{array}{c}\hfill u_{tt}(x,t)=-\frac{r^2}{t}\frac{g\left(r\right)}{c^2-r^2}\mathrm{and}{u}_{xx}(x,t)=-\frac{1}{t}\frac{g\left(r\right)}{c^2-r^2}\end{array}$$

Hence, we obtain

$$\begin{array}{c}\hfill u_{tt}(x,t)-c^2{u}_{xx}(x,t)=-\frac{r^2}{t}\frac{g\left(r\right)}{c^2-r^2}+\frac{c^2}{t}\frac{g\left(r\right)}{c^2-r^2}=\frac{1}{t}g\left(r\right)=f(x,t)\end{array}$$

for every $(x,t)\in {\overline{D}}_2$, i.e., $u(x,t)$ is a solution to the wave Equation (2) for $n=1$.

Moreover, if we define a function $v:(c,\infty )\to \mathbb{R}$ by

$$\begin{array}{c}\hfill v\left(r\right):=c_{2}r-c_{2}c-{\int }_c^r{\int }_c^s\frac{g\left(w\right)}{c^2-w^2}dwds,\end{array}$$

then $u(x,t)=tv\left(r\right)$, v is twice continuously differentiable, $\underset{r\to c^{+}}{lim}v\left(r\right)=0$ and $\underset{r\to c^{+}}{lim}{v}^{\prime }\left(r\right)=c_2$.

These facts imply that $u\in {\overline{U}}_2$. ☐

3. Main Results

In this section, n is a fixed positive integer and each point x in ${\mathbb{R}}^n$ is expressed as $x=(x_1,\dots ,x_i,\dots ,x_n)$, where $x_i$ denotes the ith coordinate of x. Moreover, $\left|x\right|$ denotes the Euclidean distance of x from the origin:

$$\begin{array}{c}\hfill \left|x\right|=\sqrt{x_1^2+\cdots +x_i^2+\cdots +x_n^2}\end{array}$$

We will now search for approximate solutions to (2), which belong to a special class of scalar functions of the form $u(x,t)=tv\left(\right|x|/t)$, where v is a twice continuously differentiable function. That is, $u(x,t)$ depends on x and t mainly through the term $\left|x\right|/t$. Based on this argument, we define

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill D_1^n& :=\left\{(x,t)\in {\mathbb{R}}^n\setminus \left\{(0,\dots ,0)\right\}\times (0,\infty )\left|\right|x|<ct\right\},\hfill \\ \hfill U_1^n& :=\{u:D_1^n\to \mathbb{R}|\mathrm{there} \mathrm{exists} \mathrm{a} \mathrm{twice} \mathrm{continuously} \mathrm{differentiable}\hfill \\ & \mathrm{function} v: (0,c)\to \mathbb{R} \mathrm{with} u(x,t)=tv\left(\frac{\left|x\right|}{t}\right) \mathrm{for} \mathrm{all} (x,t)\in D_1^n\hfill \\ & \mathrm{and} \underset{r\to 0^{+}}{lim}v\left(r\right)=0\}.\hfill \end{array}\end{array}$$

Then it is obvious that $(x,t)\in D_1^n$ if and only if $0<\left|x\right|/t<c$.

If we define

$$\begin{array}{c}\hfill (u_1+u_2)(x,t)=u_1(x,t)+u_2(x,t)\mathrm{and}\left(\lambda u_1\right)(x,t)=\lambda u_1(x,t)\end{array}$$

for all $u_1,u_2\in U_1^n$ and $\lambda \in \mathbb{R}$, then $U_1^n$ is a vector space over real numbers. That is, $U_1^n$ is a large class of scalar functions in a sense that it is a vector space.

The conditions (12) and (15) below might seem to be too strict at first look. However, we shall see in Corollaries 1 and 2 in the next section that those conditions are not as strict as they look.

Theorem 3.

Let functions $\phi :(0,c)\to [0,\infty )$ and $\psi :(0,\infty )\to [0,\infty )$ be given such that

$$\begin{array}{c}\hfill {\int }_0^{\left|x\right|/t}{\int }_0^y\frac{\phi \left(s\right)}{c^2-s^2}{\left(\frac{s^2}{y^2}·\frac{c^2-y^2}{c^2-s^2}\right)}^{(n-1)/2}dsdy<\infty \end{array}$$

(12)

for all $(x,t)\in D_1^n$ and there exists a positive real number k with

$$\begin{array}{c}\hfill k:=\underset{t>0}{inf}t\psi \left(t\right)>0.\end{array}$$

(13)

Assume that $f:D_1^n\to \mathbb{R}$ is a function for which there exists a continuous function $g:(0,c)\to \mathbb{R}$ such that

$$\begin{array}{c}\hfill f(x,t)=\frac{1}{t}g\left(\frac{\left|x\right|}{t}\right)\end{array}$$

(14)

and

$$\begin{array}{c}\hfill {\int }_0^{\left|x\right|/t}\frac{\left|g\right(s\left)\right|}{c^2-s^2}{\left(\frac{s^2}{c^2-s^2}\right)}^{(n-1)/2}ds<\infty \end{array}$$

(15)

for all $(x,t)\in D_1^n$. If a $u\in U_1^n$ satisfies the inequality

$$\begin{array}{c}\hfill |u_{tt}(x,t)-c^2▵u(x,t)-f(x,t)|\le \phi \left(\frac{\left|x\right|}{t}\right)\psi \left(t\right)\end{array}$$

(16)

for all $(x,t)\in D_1^n$, then there exists a solution $u_0\in U_1^n$ of the wave Equation $\left(2\right)$ such that

$$\begin{array}{c}\hfill |u(x,t)-u_0(x,t)|\le kt{\int }_0^{\left|x\right|/t}{\int }_0^y\frac{\phi \left(s\right)}{c^2-s^2}{\left(\frac{s^2}{y^2}·\frac{c^2-y^2}{c^2-s^2}\right)}^{(n-1)/2}dsdy\end{array}$$

for all $(x,t)\in D_1^n$.

Proof. 

Our assumption $u\in U_1^n$ implies that there exists a twice continuously differentiable function $v:(0,c)\to \mathbb{R}$ such that

$$\begin{array}{c}\hfill u(x,t)=tv\left(r\right)\end{array}$$

(17)

for all $(x,t)\in D_1^n$, where we set $r=\left|x\right|/t$. Then we have

$$\begin{array}{c}\hfill \frac{\partial r}{\partial t}=-\frac{r}{t},\frac{\partial \left|x\right|}{\partial x_i}=\frac{x_i}{\left|x\right|},\frac{\partial r}{\partial x_i}=\frac{1}{t}\frac{x_i}{\left|x\right|},\frac{\partial }{\partial x_i}\frac{x_i}{\left|x\right|}=\frac{{\left|x\right|}^2-x_i^2}{{\left|x\right|}^3}\end{array}$$

for $i\in \{1,\dots ,n\}$. Using these partial derivatives, we obtain

$$\begin{array}{c}\hfill \begin{array}{cc}{u}_t(x,t)=v\left(r\right)-r{v}^{\prime }\left(r\right),\hfill & {\displaystyle u_{tt}(x,t)=\frac{r^2}{t}{v}^{″}\left(r\right)},\hfill \\ {\displaystyle u_{x_i}(x,t)=\frac{x_i}{\left|x\right|}{v}^{\prime }\left(r\right)},\hfill & {\displaystyle u_{x_i{x}_i}(x,t)=\frac{{\left|x\right|}^2-x_i^2}{{\left|x\right|}^3}{v}^{\prime }\left(r\right)+\frac{1}{t}\frac{x_i^2}{{\left|x\right|}^2}{v}^{″}\left(r\right)}\hfill \end{array}\end{array}$$

(18)

for $i\in \{1,\dots ,n\}$.

Therefore, in view of (14) and (18), we have

$$\begin{array}{c}\hfill \begin{array}{c}{u}_{tt}(x,t)-c^2▵u(x,t)-f(x,t)\hfill \\ =\frac{r^2}{t}{v}^{″}\left(r\right)-c^2\sum _{i=1}^n\left(\frac{{\left|x\right|}^2-x_i^2}{{\left|x\right|}^3}{v}^{\prime }\left(r\right)+\frac{1}{t}\frac{x_i^2}{{\left|x\right|}^2}{v}^{″}\left(r\right)\right)-\frac{1}{t}g\left(r\right)\hfill \\ =-\frac{1}{t}\left(\left(c^2-r^2\right)v^{″}\left(r\right)+c^2\frac{n-1}{r}{v}^{\prime }\left(r\right)+g\left(r\right)\right)\hfill \end{array}\end{array}$$

and hence, by (16), we get

$$\begin{array}{c}\hfill \begin{array}{c}|u_{tt}(x,t)-c^2▵u(x,t)-f(x,t)|\hfill \\ =\frac{1}{t}|\left(c^2-r^2\right)v^{″}\left(r\right)+c^2\frac{n-1}{r}{v}^{\prime }\left(r\right)+g\left(r\right)|\hfill \\ \le \phi \left(r\right)\psi \left(t\right)\hfill \end{array}\end{array}$$

or

$$\begin{array}{c}\hfill |\left(c^2-r^2\right)v^{″}\left(r\right)+c^2\frac{n-1}{r}{v}^{\prime }\left(r\right)+g\left(r\right)|\le \phi \left(r\right)\left\{t\psi \left(t\right)\right\}\end{array}$$

for all $r\in (0,c)$ and $t>0$ (for each fixed $r\in (0,c)$ and for any $t>0$, we can select an $x_t\in {\mathbb{R}}^n\setminus \left\{(0,\dots ,0)\right\}$ such that $(x_t,t)\in D_1^n$ and $r=|x_t|/t$). In addition, due to (13), it holds that

$$\begin{array}{c}\hfill |v^{″}\left(r\right)+\frac{n-1}{r}\frac{c^2}{c^2-r^2}{v}^{\prime }\left(r\right)+\frac{1}{c^2-r^2}g\left(r\right)|\le \frac{k}{|c^2-r^2|}\phi \left(r\right)\end{array}$$

for all $r\in (0,c)$.

If we define $w\left(r\right):=v^{\prime }\left(r\right)$ in the previous inequality, then we obtain

$$\begin{array}{c}\hfill |w^{\prime }\left(r\right)+\frac{n-1}{r}\frac{c^2}{c^2-r^2}w\left(r\right)+\frac{1}{c^2-r^2}g\left(r\right)|\le \frac{k}{c^2-r^2}\phi \left(r\right)\end{array}$$

(19)

for any $r\in (0,c)$. Moreover, we set

$$\begin{array}{c}\hfill h\left(r\right):=-\left(c^2-r^2\right)w^{\prime }\left(r\right)-\frac{(n-1)c^2}{r}w\left(r\right)\end{array}$$

or equivalently

$$\begin{array}{c}\hfill w^{\prime }\left(r\right)+\frac{n-1}{r}\frac{c^2}{c^2-r^2}w\left(r\right)+\frac{1}{c^2-r^2}h\left(r\right)=0\end{array}$$

(20)

for all $r\in (0,c)$. Then it follows from (19) and (20) that

$$\begin{array}{c}\hfill \left|h\right(r)-g(r\left)\right|\le k\phi \left(r\right)\end{array}$$

(21)

for any $r\in (0,c)$.

According to ([22], Section 1.8), as a solution to (20), $w\left(r\right)$ has the following form

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill w\left(r\right)=& exp\left\{-{\int }_{r_0}^r\frac{n-1}{z}\frac{c^2}{c^2-z^2}dz\right\}·\hfill \\ & ·\left(c_1-{\int }_{r_0}^r\frac{h\left(s\right)}{c^2-s^2}exp\left\{{\int }_{r_0}^s\frac{n-1}{z}\frac{c^2}{c^2-z^2}dz\right\}ds\right),\hfill \end{array}\end{array}$$

(22)

where $r_0\in (0,c)$ is a constant, and we apply the following integral formula

$$\begin{array}{c}\hfill {\int }_{r_0}^r\frac{n-1}{z}\frac{c^2}{c^2-z^2}dz=ln{\left(\frac{r^2}{r_0^2}·\frac{|c^2-r_0^2|}{|c^2-r^2|}\right)}^{(n-1)/2}\end{array}$$

(23)

to get

$$\begin{array}{c}\hfill w\left(r\right)=c_1{\left(\frac{r_0^2}{r^2}·\frac{c^2-r^2}{c^2-r_0^2}\right)}^{(n-1)/2}-{\int }_{r_0}^r\frac{h\left(s\right)}{c^2-s^2}{\left(\frac{s^2}{r^2}·\frac{c^2-r^2}{c^2-s^2}\right)}^{(n-1)/2}ds\end{array}$$

(24)

for $r\in (0,c)$, where $c_1$ is an arbitrary real constant and the last integral exists due to (12), (15) and (21).

Now, let us define a function $w_0:(0,c)\to \mathbb{R}$ by

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill w_0\left(r\right):=& exp\left\{-{\int }_{r_0}^r\frac{n-1}{z}\frac{c^2}{c^2-z^2}dz\right\}·\hfill \\ & ·\left(c_1-{\int }_{r_0}^r\frac{g\left(s\right)}{c^2-s^2}exp\left\{{\int }_{r_0}^s\frac{n-1}{z}\frac{c^2}{c^2-z^2}dz\right\}ds\right)\hfill \end{array}\end{array}$$

(25)

or

$$\begin{array}{c}\hfill w_0\left(r\right)=c_1{\left(\frac{r_0^2}{r^2}·\frac{c^2-r^2}{c^2-r_0^2}\right)}^{(n-1)/2}-{\int }_{r_0}^r\frac{g\left(s\right)}{c^2-s^2}{\left(\frac{s^2}{r^2}·\frac{c^2-r^2}{c^2-s^2}\right)}^{(n-1)/2}ds.\end{array}$$

(26)

Then, in view of ([22], Section 1.8) or by comparing (25) with (22), we can simply replace $h\left(r\right)$ in (20) by $g\left(r\right)$ to verify that $w_0\left(r\right)$ satisfies

$$\begin{array}{c}\hfill w_0^{\prime }\left(r\right)+\frac{n-1}{r}\frac{c^2}{c^2-r^2}{w}_0\left(r\right)+\frac{1}{c^2-r^2}g\left(r\right)=0\end{array}$$

(27)

for all $r\in (0,c)$. Moreover, it follows from (21), (24) and (26) that

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill |w\left(r\right)-w_0\left(r\right)|=& \left|{\int }_{r_0}^r\frac{g\left(s\right)-h\left(s\right)}{c^2-s^2}{\left(\frac{s^2}{r^2}·\frac{c^2-r^2}{c^2-s^2}\right)}^{(n-1)/2}ds\right|\hfill \\ \hfill \le & {\int }_0^r\frac{\left|g\right(s)-h(s\left)\right|}{c^2-s^2}{\left(\frac{s^2}{r^2}·\frac{c^2-r^2}{c^2-s^2}\right)}^{(n-1)/2}ds\hfill \\ \hfill \le & k{\int }_0^r\frac{\phi \left(s\right)}{c^2-s^2}{\left(\frac{s^2}{r^2}·\frac{c^2-r^2}{c^2-s^2}\right)}^{(n-1)/2}ds\hfill \end{array}\end{array}$$

(28)

for each $r\in (0,c)$.

Noticing $v^{\prime }\left(r\right)=w\left(r\right)$ and regarding (25) or (26), we define functions $u_0:D_1^n\to \mathbb{R}$ and $v_0:(0,c)\to \mathbb{R}$ by

$$\begin{array}{c}\hfill v_0^{\prime }\left(r\right):=w_0\left(r\right)\mathrm{and}{u}_0(x,t):=t{v}_0\left(r\right)\end{array}$$

for all $(x,t)\in D_1^n$ and $r\in (0,c)$, where $v_0\left(r\right)$ is a twice continuously differentiable and satisfies $\underset{r\to 0^{+}}{lim}{v}_0\left(r\right)=0$ by (15).

Then, in view of (18) replacing u and v with $u_0$ and $v_0$, respectively, and by following the lines just below the formula (18) and then considering (14) and (27), we get

$$\begin{array}{c}\hfill \begin{array}{c}\frac{{\partial }^2}{\partial t^2}{u}_0(x,t)-c^2▵u_0(x,t)-f(x,t)\hfill \\ =\frac{r^2}{t}{v}_0^{″}\left(r\right)-c^2\sum _{i=1}^n\left(\frac{{\left|x\right|}^2-x_i^2}{{\left|x\right|}^3}{v}_0^{\prime }\left(r\right)+\frac{1}{t}\frac{x_i^2}{{\left|x\right|}^2}{v}_0^{″}\left(r\right)\right)-\frac{1}{t}g\left(r\right)\hfill \\ =-\frac{c^2-r^2}{t}\left(v_0^{″}\left(r\right)+\frac{n-1}{r}\frac{c^2}{c^2-r^2}{v}_0^{\prime }\left(r\right)+\frac{1}{c^2-r^2}g\left(r\right)\right)\hfill \\ =-\frac{c^2-r^2}{t}\left(w_0^{\prime }\left(r\right)+\frac{n-1}{r}\frac{c^2}{c^2-r^2}{w}_0\left(r\right)+\frac{1}{c^2-r^2}g\left(r\right)\right)\hfill \\ =0\hfill \end{array}\end{array}$$

for any $(x,t)\in D_1^n$, i.e., $u_0(x,t)$ is a solution to the inhomogeneous wave Equation (2).

Finally, since $\underset{r\to 0^{+}}{lim}v\left(r\right)=\underset{r\to 0^{+}}{lim}{v}_0\left(r\right)=0$, $v\left(r\right)={\int }_0^{r}w\left(y\right)dy$ and $v_0\left(r\right)={\int }_0^r{w}_0\left(y\right)dy$, it follows from (17) and (28) that

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill |u(x,t)-u_0(x,t)|& =|tv\left(r\right)-t{v}_0\left(r\right)|=|t{\int }_0^{r}w\left(y\right)dy-t{\int }_0^r{w}_0\left(y\right)dy|\hfill \\ & \le t{\int }_0^r|w\left(y\right)-w_0\left(y\right)|dy\hfill \\ & \le kt{\int }_0^r{\int }_0^y\frac{\phi \left(s\right)}{c^2-s^2}{\left(\frac{s^2}{y^2}·\frac{c^2-y^2}{c^2-s^2}\right)}^{(n-1)/2}dsdy\hfill \\ & =kt{\int }_0^{\left|x\right|/t}{\int }_0^y\frac{\phi \left(s\right)}{c^2-s^2}{\left(\frac{s^2}{y^2}·\frac{c^2-y^2}{c^2-s^2}\right)}^{(n-1)/2}dsdy\hfill \end{array}\end{array}$$

for any $(x,t)\in D_1^n$. ☐

Let us define

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill D_2^n& :=\left\{(x,t)\in {\mathbb{R}}^n\times (0,\infty )\left|\right|x|>ct\right\},\hfill \\ \hfill U_2^n& :=\{u:D_2^n\to \mathbb{R}|\mathrm{there} \mathrm{exists} \mathrm{a} \mathrm{twice} \mathrm{continuously} \mathrm{differentiable}\hfill \\ & \mathrm{function} v: (c,\infty )\to \mathbb{R} \mathrm{with} u(x,t)=tv\left(\frac{\left|x\right|}{t}\right) \mathrm{for} \mathrm{all} (x,t)\in D_2^n\hfill \\ & \mathrm{and} \underset{r\to c^{+}}{lim}v\left(r\right)=0\}.\hfill \end{array}\end{array}$$

Since the propagation speed of each solution $u(x,t)$ to the wave Equation (2) is c, the ‘shape’ of the wave travels at the speed of c. Roughly speaking, $u(x,t)$ seems to have a similar shape at each $(x,t)$ provided $\left|x\right|/t=c$. Furthermore, v strongly depends on $\left|x\right|/t$ rather than x and t separately. Therefore, the limit condition in the definition of $U_2^n$ has a natural affinity in connection with that of $U_1^n$.

Moreover, we see that $(x,t)\in D_2^n$ if and only if $c<\left|x\right|/t<\infty$. As we mentioned in the first part of this section, $U_2^n$ is also a large class of scalar functions in the sense that it is a vector space over real numbers. Even if the conditions (29) and (31) below seem somewhat strict at first look, they are actually not so strict, as we shall see in Corollary 3.

Theorem 4.

Let functions $\phi :(c,\infty )\to [0,\infty )$ and $\psi :(0,\infty )\to [0,\infty )$ be given such that

$$\begin{array}{c}\hfill {\int }_c^{\left|x\right|/t}{\int }_c^y\frac{\phi \left(s\right)}{s^2-c^2}{\left(\frac{s^2}{y^2}·\frac{y^2-c^2}{s^2-c^2}\right)}^{(n-1)/2}dsdy<\infty \end{array}$$

(29)

for all $(x,t)\in D_2^n$ and there exists a positive real number k with

$$\begin{array}{c}\hfill k:=\underset{t>c}{inf}t\psi \left(t\right)>0.\end{array}$$

(30)

Assume that $f:D_2^n\to \mathbb{R}$ is a function for which there exists a continuous function $g:(c,\infty )\to \mathbb{R}$ satisfying the relation $\left(14\right)$ and

$$\begin{array}{c}\hfill {\int }_c^{\left|x\right|/t}\frac{\left|g\right(s\left)\right|}{s^2-c^2}{\left(\frac{s^2}{s^2-c^2}\right)}^{(n-1)/2}ds<\infty \end{array}$$

(31)

for all $(x,t)\in D_2^n$. If a $u\in U_2^n$ satisfies the inequality $\left(16\right)$ for all $(x,t)\in D_2^n$, then there exists a solution $u_0\in U_2^n$ of the wave Equation $\left(2\right)$ such that

$$\begin{array}{c}\hfill |u(x,t)-u_0(x,t)|\le kt{\int }_c^{\left|x\right|/t}{\int }_c^y\frac{\phi \left(s\right)}{s^2-c^2}{\left(\frac{s^2}{y^2}·\frac{y^2-c^2}{s^2-c^2}\right)}^{(n-1)/2}dsdy\end{array}$$

for all $(x,t)\in D_2^n$.

Proof. 

Due to our assumption $u\in U_2^n$, there exists a twice continuously differentiable function $v:(c,\infty )\to \mathbb{R}$ with the relation (17) for all $(x,t)\in D_2^n$, where we set $r=\left|x\right|/t$. In the same way as in the first part of the proof of Theorem 3, we obtain the same derivatives in (18). Moreover, by (14) and (18), we have

$$\begin{array}{c}\hfill u_{tt}(x,t)-c^2▵u(x,t)-f(x,t)=-\frac{1}{t}\left(\left(c^2-r^2\right)v^{″}\left(r\right)+c^2\frac{n-1}{r}{v}^{\prime }\left(r\right)+g\left(r\right)\right)\end{array}$$

and thus, by following the lines of the first part of the proof of Theorem 3 and by (16) and (30) and then defining $w\left(r\right):=v^{\prime }\left(r\right)$, we get

$$\begin{array}{c}\hfill |w^{\prime }\left(r\right)+\frac{n-1}{r}\frac{c^2}{c^2-r^2}w\left(r\right)+\frac{1}{c^2-r^2}g\left(r\right)|\le \frac{k}{r^2-c^2}\phi \left(r\right)\end{array}$$

for any $r\in (c,\infty )$. Moreover, in a similar way as in the proof of the previous theorem, we set

$$\begin{array}{c}\hfill h\left(r\right):=-\left(c^2-r^2\right)w^{\prime }\left(r\right)-\frac{(n-1)c^2}{r}w\left(r\right)\end{array}$$

or we let the equality (20) hold true for all $r\in (c,\infty )$ and then we see that the inequality (21) holds for any $r\in (c,\infty )$.

Since $w\left(r\right)$ is a solution to (20), by considering ([22], Section 1.8), we may use the integral formula (23) to show that $w\left(r\right)$ has the following form

$$\begin{array}{c}\hfill w\left(r\right)=c_2{\left(\frac{r_0^2}{r^2}·\frac{r^2-c^2}{r_0^2-c^2}\right)}^{(n-1)/2}-{\int }_{r_0}^r\frac{h\left(s\right)}{c^2-s^2}{\left(\frac{s^2}{r^2}·\frac{r^2-c^2}{s^2-c^2}\right)}^{(n-1)/2}ds\end{array}$$

(32)

for all $r\in (c,\infty )$, where $r_0\in (c,\infty )$ is a constant and $c_2$ is an arbitrary real constant.

Now, let us define a function $w_0:(c,\infty )\to \mathbb{R}$ by the formula (25) or

$$\begin{array}{c}\hfill w_0\left(r\right)=c_2{\left(\frac{r_0^2}{r^2}·\frac{r^2-c^2}{r_0^2-c^2}\right)}^{(n-1)/2}-{\int }_{r_0}^r\frac{g\left(s\right)}{c^2-s^2}{\left(\frac{s^2}{r^2}·\frac{r^2-c^2}{s^2-c^2}\right)}^{(n-1)/2}ds\end{array}$$

(33)

for each $r\in (c,\infty )$. Then, by ([22], Section 1.8) or a direct calculation with (25), $w_0\left(r\right)$ satisfies the equality (27) for all $r\in (c,\infty )$. Moreover, it follows from (21), (32) and (33) that

$$\begin{array}{c}\hfill |w\left(r\right)-w_0\left(r\right)|\le k{\int }_c^r\frac{\phi \left(s\right)}{s^2-c^2}{\left(\frac{s^2}{r^2}·\frac{r^2-c^2}{s^2-c^2}\right)}^{(n-1)/2}ds\end{array}$$

(34)

for each $r\in (c,\infty )$.

We now define functions $u_0:D_2^n\to \mathbb{R}$ and $v_0:(c,\infty )\to \mathbb{R}$ by $v_0^{\prime }\left(r\right):=w_0\left(r\right)$ and $u_0(x,t):=t{v}_0\left(r\right)$ for all $(x,t)\in D_2^n$ and $r\in (c,\infty )$, where $v_0\left(r\right)$ is a twice continuously differentiable and satisfies $\underset{r\to c^{+}}{lim}{v}_0\left(r\right)=0$. Then, by using the same argument as in the proof of Theorem 3, we can verify that $u_0(x,t)$ is a solution to the inhomogeneous wave Equation (2).

Finally, since $\underset{r\to c^{+}}{lim}v\left(r\right)=\underset{r\to c^{+}}{lim}{v}_0\left(r\right)=0$, $v\left(r\right)={\int }_c^{r}w\left(y\right)dy$ and $v_0\left(r\right)={\int }_c^r{w}_0\left(y\right)dy$, it follows from (17) and (34) that

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill |u(x,t)-u_0(x,t)|& =|tv\left(r\right)-t{v}_0\left(r\right)|=|t{\int }_c^{r}w\left(y\right)dy-t{\int }_c^r{w}_0\left(y\right)dy|\hfill \\ & \le kt{\int }_c^{\left|x\right|/t}{\int }_c^y\frac{\phi \left(s\right)}{s^2-c^2}{\left(\frac{s^2}{y^2}·\frac{y^2-c^2}{s^2-c^2}\right)}^{(n-1)/2}dsdy\hfill \end{array}\end{array}$$

for any $(x,t)\in D_2^n$. ☐

4. Corollaries

In this section, we start with an example for Theorem 3 in the case of $n=1$. Let us denote by $D_1$ and $U_1$ the $D_1^n$ and $U_1^n$ for $n=1$, respectively, whose definitions were introduced in the first part of Section 3. Then we note that $(x,t)\in D_1$ if and only if $0<\left|x\right|/t<c$.

Corollary 1.

Given real constants $\epsilon >0$, $\alpha \in \mathbb{R}$ and $\beta >0$, let $f:D_1\to \mathbb{R}$ be a function of the form

$$\begin{array}{c}\hfill f(x,t)=\alpha \frac{{\left|x\right|}^{\beta }}{t^{\beta +1}}.\end{array}$$

If a $u\in U_1$ satisfies the inequality

$$\begin{array}{c}\hfill |u_{tt}(x,t)-c^2{u}_{xx}(x,t)-f(x,t)|\le \frac{\epsilon }{t}\end{array}$$

for all $(x,t)\in D_1$, then there exists a solution $u_0\in U_1$ of the wave Equation $\left(2\right)$ with $n=1$ such that

$$\begin{array}{c}\hfill |u(x,t)-u_0(x,t)|\le \frac{\epsilon t}{2c}\left(\left(c+\frac{\left|x\right|}{t}\right)ln\left(c+\frac{\left|x\right|}{t}\right)+\left(c-\frac{\left|x\right|}{t}\right)ln\left(c-\frac{\left|x\right|}{t}\right)\right)-\epsilon tlnc\end{array}$$

(35)

for any $(x,t)\in D_1$.

Proof. 

First, we define functions $\phi :(0,c)\to [0,\infty )$ and $\psi :(0,\infty )\to [0,\infty )$ by

$$\begin{array}{c}\hfill \phi \left(r\right):={\epsilon }_1\mathrm{and}\psi \left(t\right):=\frac{{\epsilon }_2}{t},\end{array}$$

where ${\epsilon }_1>0$ and ${\epsilon }_2>0$ are arbitrarily chosen constants with $\epsilon ={\epsilon }_1{\epsilon }_2$. Then, considering the integral formula

$$\begin{array}{c}\hfill {\int }_0^r\frac{ds}{c^2-s^2}=\frac{1}{2c}\left(ln(c+r)-ln(c-r)\right)\end{array}$$

(36)

for any $r\in (0,c)$, we get

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\int }_0^r{\int }_0^y\frac{\phi \left(s\right)}{c^2-s^2}dsdy& =\frac{{\epsilon }_1}{2c}{\int }_0^r\left(ln(c+y)-ln(c-y)\right)dy\hfill \\ & =\frac{{\epsilon }_1}{2c}rln\frac{c+r}{c-r}-{\epsilon }_1\left(lnc-\frac{1}{2}ln\left(c^2-r^2\right)\right)\hfill \\ & <\infty \hfill \end{array}\end{array}$$

for all $r\in (0,c)$, i.e., the control function $\phi$ satisfies the condition (12) for $n=1$.

On the other hand, if we define a function $g:(0,c)\to \mathbb{R}$ by $g\left(r\right):=\alpha r^{\beta }$, then we use (36) to show

$$\begin{array}{c}\hfill {\int }_0^r\frac{\left|g\right(s\left)\right|}{c^2-s^2}ds={\int }_0^r\frac{\left|\alpha \right|s^{\beta }}{c^2-s^2}ds<\frac{\left|\alpha \right|c^{\beta }}{2c}ln\frac{c+r}{c-r}<\infty \end{array}$$

for all $r\in (0,c)$, i.e., the source function g satisfies the condition (15) for $n=1$.

According to Theorem 3, there exists a solution $u_0\in U_1$ to the wave Equation $\left(2\right)$ with $n=1$ such that the inequality (35) holds true for any $(x,t)\in D_1$. ☐

When n is an integer larger than 1, we will evaluate the integral

$$\begin{array}{c}\hfill {\int }_0^r\frac{\phi \left(s\right)}{c^2-s^2}{\left(\frac{s^2}{c^2-s^2}\right)}^{(n-1)/2}ds={\int }_0^r\frac{s^{n-1}\phi \left(s\right)}{{(c^2-s^2)}^{(n+1)/2}}ds\end{array}$$

for any $r\in (0,c)$. We now substitute $s=csin\theta$ $(0<\theta <\pi /2)$ to get

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\int }_0^r\frac{\phi \left(s\right)}{c^2-s^2}{\left(\frac{s^2}{c^2-s^2}\right)}^{(n-1)/2}ds={\int }_0^{{sin}^{-1}(r/c)}\frac{1}{c}sin\theta \phi (csin\theta ){tan}^{n-2}\theta {sec}^2\theta d\theta \end{array}\end{array}$$

(37)

for all $r\in (0,c)$.

Corollary 2.

Given a real constant α and an integer $n\ge 2$, let $f:D_1^n\to \mathbb{R}$ be a function of the form $f(x,t)=\alpha /\left|x\right|$. Let $\epsilon >0$ be an arbitrary real constant. If a $u\in U_1^n$ satisfies the inequality

$$\begin{array}{c}\hfill |u_{tt}(x,t)-c^2▵u(x,t)-f(x,t)|\le \frac{\epsilon }{\left|x\right|}\end{array}$$

for all $(x,t)\in D_1^n$, then there exists a solution $u_0\in U_1^n$ of the wave Equation $\left(2\right)$ such that

$$\begin{array}{c}\hfill |u(x,t)-u_0(x,t)|\le \frac{\epsilon }{(n-1)c^2}\left|x\right|\end{array}$$

for all $(x,t)\in D_1^n$.

Proof. 

We first define the functions $\phi :(0,c)\to [0,\infty )$ and $\psi :(0,\infty )\to [0,\infty )$ by

$$\begin{array}{c}\hfill \phi \left(r\right):=\frac{{\epsilon }_1}{r}\mathrm{and}\psi \left(t\right):=\frac{{\epsilon }_2}{t},\end{array}$$

where ${\epsilon }_1>0$ and ${\epsilon }_2>0$ are arbitrarily chosen constants with $\epsilon ={\epsilon }_1{\epsilon }_2$ and we set $r=\left|x\right|/t$. Then we see that $\phi \left(\right|x|/t)\psi \left(t\right)=\epsilon /\left|x\right|$.

We now consider the integral formula (37) to get

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\int }_0^r& {\int }_0^y\frac{\phi \left(s\right)}{c^2-s^2}{\left(\frac{s^2}{y^2}·\frac{c^2-y^2}{c^2-s^2}\right)}^{(n-1)/2}dsdy\hfill \\ & =\frac{{\epsilon }_1}{c^2}{\int }_0^r{\left(\frac{c^2-y^2}{y^2}\right)}^{(n-1)/2}{\int }_0^{{sin}^{-1}(y/c)}{tan}^{n-2}\theta {sec}^2\theta d\theta dy\hfill \\ & =\frac{{\epsilon }_1}{(n-1)c^2}{\int }_0^r{\left(\frac{c^2-y^2}{y^2}\right)}^{(n-1)/2}{\left(\frac{y}{\sqrt{c^2-y^2}}\right)}^{n-1}dy\hfill \\ & =\frac{{\epsilon }_1}{(n-1)c^2}{\int }_0^{r}dy\hfill \\ & <\infty \hfill \end{array}\end{array}$$

(38)

for all $r\in (0,c)$, i.e., the control function $\phi$ satisfies the condition (12).

On the other hand, if we define a continuous function $g:(0,c)\to \mathbb{R}$ by $g\left(r\right):=\alpha /r$, then we see

$$\begin{array}{c}\hfill f(x,t)=\frac{1}{t}g\left(\frac{\left|x\right|}{t}\right)\end{array}$$

and we use (37) to see

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\int }_0^r\frac{\left|g\right(s\left)\right|}{c^2-s^2}{\left(\frac{s^2}{c^2-s^2}\right)}^{(n-1)/2}ds& ={\int }_0^{{sin}^{-1}(r/c)}\frac{\left|\alpha \right|}{c^2}{tan}^{n-2}\theta {sec}^2\theta d\theta \hfill \\ & =\frac{\left|\alpha \right|}{(n-1)c^2}{\left(\frac{r^2}{c^2-r^2}\right)}^{(n-1)/2}\hfill \\ & <\infty \hfill \end{array}\end{array}$$

for all $r\in (0,c)$, i.e., the source function g satisfies the condition (15).

According to Theorem 3 and in view of (38), there exists a solution $u_0\in U_1^n$ to the wave Equation $\left(2\right)$ such that

$$\begin{array}{c}\hfill |u(x,t)-u_0(x,t)|\le \frac{\epsilon }{(n-1)c^2}\left|x\right|\end{array}$$

for any $(x,t)\in D_1^n$. ☐

In case of $D_2^n$ for $n\ge 1$, we prove the following corollary.

Corollary 3.

Given a real constant α and an integer $n\ge 1$, let $f:D_2^n\to \mathbb{R}$ be a function of the form

$$\begin{array}{c}\hfill f(x,t)=\frac{\alpha }{\left|x\right|}{\left(1-\frac{c^2{t}^2}{{\left|x\right|}^2}\right)}^{(n+1)/2}.\end{array}$$

Let $\epsilon >0$ be an arbitrary real constant. If a $u\in U_2^n$ satisfies the inequality

$$\begin{array}{c}\hfill |u_{tt}(x,t)-c^2▵u(x,t)-f(x,t)|\le \frac{\epsilon }{\left|x\right|}{\left(1-\frac{c^2{t}^2}{{\left|x\right|}^2}\right)}^{(n+1)/2}\end{array}$$

for all $(x,t)\in D_2^n$, then there exists a solution $u_0\in U_2^n$ of the wave Equation $\left(2\right)$ such that

$$\begin{array}{c}\hfill |u(x,t)-u_0(x,t)|\le \frac{\epsilon t}{2c^2}{\int }_c^{\left|x\right|/t}{\left(1-\frac{c^2}{s^2}\right)}^{(n+1)/2}ds\end{array}$$

for all $(x,t)\in D_2^n$.

Proof. 

Let us define the functions $\phi :(c,\infty )\to [0,\infty )$ and $\psi :(0,\infty )\to [0,\infty )$ by

$$\begin{array}{c}\hfill \phi \left(r\right):=\frac{{\epsilon }_1}{r}{\left(1-\frac{c^2}{r^2}\right)}^{(n+1)/2}\mathrm{and}\psi \left(t\right):=\frac{{\epsilon }_2}{t},\end{array}$$

where ${\epsilon }_1>0$ and ${\epsilon }_2>0$ are arbitrarily chosen constants with $\epsilon ={\epsilon }_1{\epsilon }_2$ and we set $r=\left|x\right|/t$. Then we get

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\int }_c^r& {\int }_c^y\frac{\phi \left(s\right)}{s^2-c^2}{\left(\frac{s^2}{y^2}·\frac{y^2-c^2}{s^2-c^2}\right)}^{(n-1)/2}dsdy\hfill \\ & ={\int }_c^r{\left(\frac{y^2-c^2}{y^2}\right)}^{(n-1)/2}{\int }_c^y\frac{{\epsilon }_1}{s^3}dsdy\hfill \\ & =\frac{{\epsilon }_1}{2c^2}{\int }_c^r{\left(\frac{y^2-c^2}{y^2}\right)}^{(n+1)/2}dy\hfill \\ & <\infty \hfill \end{array}\end{array}$$

(39)

for all $r\in (c,\infty )$, i.e., the control function $\phi$ satisfies the condition (29).

Furthermore, if we define a continuous function $g:(c,\infty )\to \mathbb{R}$ by

$$\begin{array}{c}\hfill g\left(r\right):=\frac{\alpha }{r}{\left(1-\frac{c^2}{r^2}\right)}^{(n+1)/2},\end{array}$$

then we see

$$\begin{array}{c}\hfill f(x,t)=\frac{1}{t}g\left(\frac{\left|x\right|}{t}\right)\end{array}$$

and we obtain

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\int }_c^r\frac{\left|g\right(s\left)\right|}{s^2-c^2}{\left(\frac{s^2}{s^2-c^2}\right)}^{(n-1)/2}ds& ={\int }_c^r\frac{s^{n-1}\left|g\left(s\right)\right|}{{(s^2-c^2)}^{(n+1)/2}}ds\hfill \\ & ={\int }_c^r\frac{\left|\alpha \right|}{s^3}ds\hfill \\ & =\frac{\left|\alpha \right|}{2c^2}·\frac{r^2-c^2}{r^2}\hfill \\ & <\infty \hfill \end{array}\end{array}$$

for all $r\in (c,\infty )$, i.e., the source function g satisfies the condition (31).

Due to Theorem 4 and in view of (39), there exists a solution $u_0\in U_2^n$ to the wave Equation $\left(2\right)$ such that

$$\begin{array}{c}\hfill |u(x,t)-u_0(x,t)|\le \frac{\epsilon t}{2c^2}{\int }_c^{\left|x\right|/t}{\left(1-\frac{c^2}{y^2}\right)}^{(n+1)/2}dy\end{array}$$

for any $(x,t)\in D_2^n$. ☐