Sustainable Supplier Selection Process in Edible Oil Production by a Hybrid Fuzzy Analytical Hierarchy Process and Green Data Envelopment Analysis for the SMEs Food Processing Industry

Abstract

Today, business organizations are facing increasing pressure from a variety of sources to operate using sustainable processes. Thus, most companies need to focus on their supply chains to enhance sustainability to meet customer demands and comply with environmental legislation. To achieve these goals, companies must focus on criteria that include CO₂ (carbon footprint) and toxic emissions, energy use and efficiency, wastage generations, and worker health and safety. As in other industries, the food processing industry requires large inputs of resources, which results in several negative environmental effects; thus, decision-makers have to evaluate qualitative and quantitative factors. This work identifies the best supplier for edible oil production in the small and medium enterprise (SME) food processing industry in Vietnam. This study also processes a hybrid multicriteria decision-making (MCDM) model using a fuzzy analytical hierarchy process (FAHP) and green data envelopment analysis (GDEA) model to identify the weight of all criteria of a supplier’s selection process based on opinions from company procurement experts. Subsequently, GDEA is applied to rank all potential supplier lists. The primary objective of this work is to present a novel approach which integrates FAHP and DEA for supplier selection and also consider the green issue in edible oil production in uncertain environments. The aim of this research is also to provide a useful guideline for supplier selection based on qualitative and quantitative factors to improve the efficiency of supplier selection in the food industry and other industries. The results reveal that Decision-Making Unit 1 (DMU 1), DMU 3, DMU 7, and DMU 9 are identified as extremely efficient for five DEA models, which are the optimal suppliers for edible oil production. The contributions of this research include a proposed MCDM model using a hybrid FAHP and GDEA model for supplier selection in the SME food processing industry under a fuzzy environment conditions in Vietnam. This research also is part of an evolution of a new hybrid model that is flexible and practical for decision-makers. In addition, the research also provides a useful guideline in supplier selection in the food processing industry and a guideline for supplier selection in other industries.

1. Introduction

The global edible oil market is expected to witness significant growth due to the increasing prevalence of unrefined, unprocessed, healthy, and organic oil. In the years to come, vegetable oil that is low in cholesterol, fat, and calories is likely to receive great attention due to increased health awareness. In addition, major improvements in retail networks, increased crop yields, oil production, and developing economies are among the key factors supporting the growth of the global edible oil market. Furthermore, the growing popularity of canola oil, trans fat-free soybean oil, and emerging olive oil will fuel the global edible oil market [1].

However, under pressure from the global oil market, the importance of edible supply chain management has to develop at the industrial and scientific levels. Challenges faced in the food supply chain are not only a concern with minimizing costs and delivering on time but also achieving sustainable levels of production. According to the Lowell Center for Sustainable Manufacturing, “Sustainability can be viewed as having three parts: environmental, economic and social (including political) with no pollution; social reward and creativity for everyone working; economic viability; conserve energy and natural resources; and safe and healthy for employees, communities and consumers” [2], and global warming, due to the excessive use of fossil fuels, has driven researchers to focus on sustainable energy sources for the future. For clean production systems, biofuel is expanding the domain of renewable and sustainable energy supplies. An efficient and sustainable supply chain plays a pivotal role in ensuring this supply [3]. Thus, to achieve these goals, companies have to pay attention to a lot of criteria that include CO₂ (carbon footprint) and toxic emissions, energy use and efficiency, wastage generations, and worker health and safety. The sustainable manufacturing concept is shown in Figure 1.

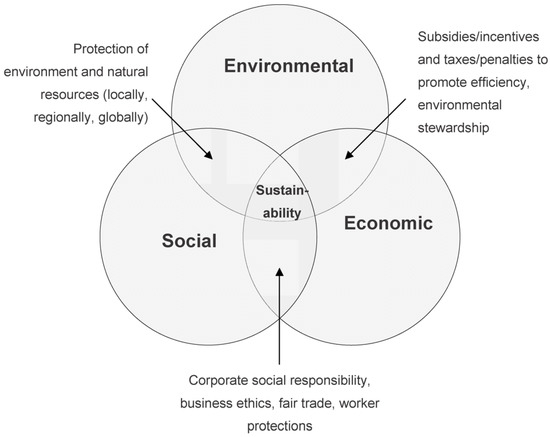
Figure 1. Sustainable manufacturing concept [4].

In order to achieve sustainability in production operations, sustainability needs to be incorporated in all stages of an organization’s supply chain. Supplier selection plays an important role in supply chain management, contributing to the success of production-business organizations. Selecting a green supplier and appropriate management, which helps organizations to reduce input costs, improves the quality of goods and services provided to customers and improves market competitiveness.

Many research studies have applied the multicriteria decision-making (MCDM) model to various fields of science and engineering, and this trend has been increasing for many years. One of the fields that the MCDM model has been applied to is for supplier selection, yet few studies, to the best of our knowledge, consider this problem under uncertainly environmental conditions in the food processing industry. For the selection process of sustainable edible oil suppliers, many environmental and economic criteria need to be considered in the assessment process. Particularly in the food processing industry, companies have to deal with higher uncertainties both upstream and downstream of the supply chain. Consequently, the sustainable supplier selection process can be considered as an MCDM. However, most criteria of sustainable supplier selection are evaluated by decision-makers. Thus, to solve this problem, the author proposes a hybrid model using a fuzzy analytical hierarchy process (FAHP) and green data envelopment analysis (GDEA), which is an effective tool for quantifying ambiguous and incomplete information. Initially, the FAHP model identifies the weight of all criteria of the supplier’s selection process based on opinions of company procurement experts. Subsequently, GDEA is applied for ranking all potential suppliers’ lists.

The remainder of the paper introduces background materials to assist the authors in developing the MCDM model. Then, a hybrid model using the FAHP and GDEA approaches is presented to select the best supplier for edible oil production in the food industry. The results and contributions are discussed at the end of this article.

2. Literature Review

Supplier evaluation and selection problems have attracted serious research attention in the last decade. The role of the supplier selection function of supply chain management in these newer supply chain practices has only been partly explored in the literature. A number of conceptual papers have been published in the last decades that have solved selection problems with mathematical models; for example, Lin et al. [5] applied six main criteria for selecting suppliers.

Jia et al. [6] developed the framework based on the number of factors in the supplier selection process. Mendoza-Fong et al. [7] proposed some criteria for selecting and evaluating suppliers through traditional standards, such as cost, quality, delivery time, and time (JIT), and seeking continuous improvement in processes and products to face competition.

Pearson and Ellram [8] proposed supplier selection and evaluation criteria in small and large electronic firms. Wang et al. [9] applied the multicriteria group decision-making (MCGDM) model for supplier selection in a rice supply chain. In this research, all potential suppliers were to be selected based on financial, delivery and services, qualitative, and environmental management system factors. Zaimes et al. [10] discussed key research opportunities and challenges in the design of supply chains. Deng et at. [11] developed multiple attribute decision making (MADM) with some 2-tuple linguistic Pythagorean fuzzy Hamy mean operators. Wang et al. [12] developed an MADM model with interval-valued 2-tuple linguistic Pythagorean fuzzy information.

Habib and Sarkar [13] proposed an integrated location–allocation model for temporary disaster debris management under an uncertain environment. Stanković [14] used the FAHP model to select criteria and for the assessment of the impact of traffic accessibility on the development of suburbs. Hadi-Vencheh [15] proposed a hybrid model using FAHP–DEA for multiple criteria ABC inventory classification. Ulutas et al. [16] developed an integrated model including FAHP, Fuzzy Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS), and AHP, axiomatic design (AD), and DEA for evaluating and selecting optimal suppliers. Gan et al. [17] used the triangular fuzzy number (TFN), AHP, and DEA approaches for analyzed economic feasibility. Rouyendegh et al. [18] combined a hybrid DEA–Analytic Network Process (ANP) for selecting the process within Iran Amirkabir University.

Based on the literature review and experts’ opinion, there are some factors must be considered in edible oil supplier selection process, such as financial, delivery and devices, qualitative, and environmental management systems, and there are many researchers who have applied the MCDM model to various fields of science and engineering, a trend that has been increasing for many years. One of the fields that the MCDM model has been applied to is for supplier selection, yet very few studies consider this problem under uncertainly environmental conditions in the food processing industry. This is the reason the author has proposed a MCDM model in this research.

3. Methodology

In order to build an effective supplier selection model, the implementation process is carried out in three stages, as shown in Figure 2.

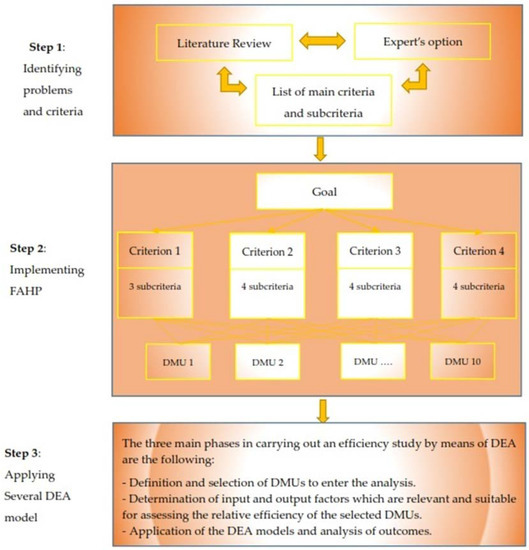
Figure 2. Research process. DMU: Decision-making unit. DEA: Data envelopment analysis.

Stage 1: Identify Problems

Identify problems to analyze and evaluate the current status of a company’s selection process; the first step is to understand the procurement process and the supplier selection criteria. Collect sufficient data as criteria for selecting suppliers from experts, articles, and scientific research works related to the problem being studied (e.g., potential suppliers; data on criteria that suppliers meet).

Stage 2: Fuzzy Hybrid Analytical Hierarchy Process (FAHP)

An advantage of AHP is its stability and flexibility regarding changes within and additions to the hierarchy. Moreover, the method is able to rank criteria according to buyer needs, which also leads to more precise decisions concerning supplier selection. After receiving the overall information of each supplier in the first stage, to overcome the disadvantages of the AHP method, we used the FAHP model to determine the weight of all potential edible oil suppliers.

Stage 3: Green Data Envelopment Analysis (GDEA)

The increase in popularity of bibliographies and the large number of investigators who deal with the DEA method indicate the advantages of using the DEA method (opportunities in the estimation of return, evolution and contrast evaluation, capability of referring/marking nonprofit ability for every entry and exit in every unit, which is ideal for examining a large number of units, the requirement of low calculating power, input and outputs (units do not have to be equal)), as the leader of nonparametric methods and the FAHP may not provide a correct solution [19,20]. Thus, the author applied the GDEA model in this step. All potential suppliers were ranked by several DEA models, and optimal suppliers were determined efficient in all proposed DEA models [9].

3.1. Fuzzy Analytic Hierarchy Process (FAHP)

3.1.1. Fuzzy Sets and Fuzzy Number

In 1965, Zadeh developed a new solution to solve existing problems in an uncertain environment. It was called a Fuzzy set, which is a function that shows the dependence degree of one fuzzy number on a set number. The value of the membership function is between [0; 1] [21,22]. The triangular fuzzy number (TFN) can be defined as (o, g, p); o, g, and p (o ≤ g ≤ p) are parameters, indicating the smallest, the most promising, and the largest value in TFN, respectively. The TFNs are shown in Figure 3.

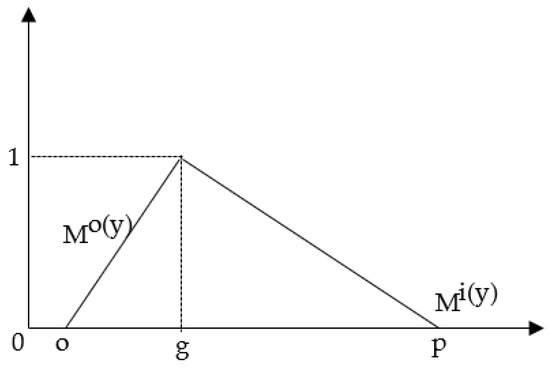
Figure 3. Traingular fuzzy number.

TFN also can be defined as follows:

$$\mu \left(\frac{x}{\tilde{M}}\right)=\{\begin{array}{c}0,\\ \frac{x-o}{g-o}\\ \frac{p-x}{p-g}\\ 0,\end{array} \begin{array}{c}x<l,\\ o\le x\le g,\\ g\le x\le p,\\ x>p,\end{array}$$

(1)

The representatives of each level of membership given a fuzzy number are as follows:

$$\tilde{M}=(M^{o\left(y\right)},M^{i\left(y\right)})=\left[o+\left(g-o\right)y,p+\left(g-p\right)y\right],y\in \left[0,1\right],$$

(2)

where o(y), i(y) indicates both the left side and the right side of a fuzzy number as:

$$\begin{gathered} \left(o_1,g_1,p_1\right)+\left(l_2,g_2,p_2\right)=\left(o_1+o_2,g_1+g_2,p_1+p_2\right) \\ \left(o_1,g_1,p_1\right)-\left(l_2,g_2,p_2\right)=\left(o_1-o_2,g_1-g_2,p_1-p_2\right) \\ \left(o_1,g_1,p_1\right)\times \left(l_2,m_2,u_2\right)=\left(o_1\times o_2,g_1\times g_2,p_1\times p_2\right) \\ \frac{\left(o_1,g_1,p_1\right)}{\left(l_2,g_2,p_2\right)}=\left(o_1/p_2,g_1/g_2,p_1/p_2\right). \end{gathered}$$

(3)

A pairwise comparisons matrix is used to determine the priorities on each level of the hierarchy that are quantified using a 1 ÷ 9 scale, which is used by the FAHP method.

3.1.2. Fuzzy AHP

In this paper, AHP using fuzzy logic was applied to define the weight of each potential edible oil supplier. We had eight steps in the FAHP process:

Step 1: Calculation of Triangular Fuzzy Number

All criteria were considered by a pairwise comparison matrix. In place of a numeral value, the FAHP is a range of values that are combined to evaluate the weight of criteria [23]. The fuzzy prioritization method uses this scale in Parkash’s study [24]. The fuzzy conversion scale is presented in Table 1.

Table 1. Triangular fuzzy scale (TFS).

Importance Intensity	TFS	Importance Intensity	TFS
1	(1, 1, 1)	1/1	(1, 1, 1)
2	(1, 2, 3)	1/2	(1/3, 1/2, 1/1)
3	(2, 3, 4)	1/3	(1/4, 1/3, 1/2)
4	(3, 4, 5)	1/4	(1/5, 1/4, 1/3)
5	(4, 5, 6)	1/5	(1/6, 1/5, 1/4)
6	(5, 6, 7)	1/6	(1/7, 1/6, 1/5)
7	(6, 7, 8)	1/7	(1/8, 1/7, 1/6)
8	(7, 8, 9)	1/8	(1/9, 1/8, 1/7)
9	(9, 9, 9)	1/9	(1/9, 1/9, 1/9)

Step 2: Calculation of ${\tilde{P}}_d$

$$\widetilde{P_d}=\left(o_d,g_d,p_d\right)$$

(4)

$$o_d={\left(o_{d1}\otimes o_{d2}\otimes \dots \otimes o_{da}\right)}^{\frac{1}{a}}, d=1,2,\dots a$$

(5)

$$g_d={\left(g_{d1}\otimes g_{d2}\otimes \dots \otimes g_{da}\right)}^{\frac{1}{a}}, d=1,2,\dots a$$

(6)

$$p_d={\left(p_{d1}\otimes p_{d2}\otimes \dots \otimes p_{da}\right)}^{\frac{1}{a}}, a=1,2,\dots a$$

(7)

Step 3: Calculation of ${\tilde{P}}_Y$

$${\tilde{P}}_Y=\left({\displaystyle \sum }_{d=1}^a{o}_d,{\displaystyle \sum }_{d=1}^a{g}_d,{\displaystyle \sum }_{d=1}^a{p}_d\right)$$

(8)

Step 4: Calculation of $\tilde{R}$

$$\tilde{R}=\frac{{\tilde{P}}_d}{{\tilde{P}}_Y}=\frac{\left(o_d,g_d,p_d\right)}{{{\displaystyle \sum }}_{d=1}^a{l}_d,{{\displaystyle \sum }}_{d=1}^a{g}_d,{{\displaystyle \sum }}_{d=1}^a{p}_a}=\left[\frac{o_d}{{{\displaystyle \sum }}_{d=1}^a{p}_d},\frac{g_d}{{{\displaystyle \sum }}_{d=1}^a{p}_d},\frac{p_d}{{{\displaystyle \sum }}_{d=1}^a{o}_d}\right]$$

(9)

Step 5: Calculation of $t{d}_{\beta o}$

The criteria depend on β cut values, which are defined for the calculated β. The fuzzy priorities shall apply for lower and upper bounds for each β value:

$$T{d}_{\beta o}=(Td{o}_{\beta o},Td{p}_{\beta o});d=1,2,\dots a;o=1,2,\dots O$$

(10)

Step 6: Calculation of T_do, T_dp

$$T_{do}=\frac{{{\displaystyle \sum }}_{d=1}^a\beta {\left(T_{do}\right)}_o}{{{\displaystyle \sum }}_{o=1}^O{\beta }_o};d=1,2,\dots a;o=1,2,\dots O$$

(11)

$$T_{dp}=\frac{{{\displaystyle \sum }}_{d=1}^a\beta {\left(t_{dp}\right)}_o}{{{\displaystyle \sum }}_{o=1}^O{\beta }_o};d=1,2,\dots a;o=1,2,\dots O$$

(12)

Step 7: Calculation of T_wd

The optimism index (γ) to order to defuzzy was used by combining the upper and the lower bounds values.

$$T_{wd}=\gamma ·W_{dp}+\left(1-\gamma \right)·W_{do};\gamma \in \left[0,1\right]da=1,2,\dots a$$

(13)

Step 8: Calculation of T_dz

The defuzzification values priorities are normalized by:

$$T_{dz}=\frac{T_{wd}}{{{\displaystyle \sum }}_{d=1}^a{T}_{wd}};d=1,2,\dots a$$

(14)

3.2. Data Envelopment Analysis Model

3.2.1. Charnes–Cooper–Rhodes Model (CCR Model)

The Charnes–Cooper–Rhodes model (CCR) is a basic DEA model [25]. The definition of the CCR model is as follows:

$$\begin{array}{cc}\hfill & \hfill \underset{e.d}{\max }\mathrm{F}=\frac{d^F{y}_0}{w^F{x}_0},\hfill \\ \mathrm{subject}\mathrm{to}:\hfill & \hfill \hfill \\ \hfill & \hfill d^F{y}_e-w^F{x}_e\le 0,n=1,2,\dots ,l\hfill \\ \hfill & \hfill d\ge 0\hfill \\ \hfill & \hfill w\ge 0\hfill \end{array}$$

(15)

In addition, the fractional program as a linear program (LP) is as follows [26] if:

$$\begin{array}{cc}\hfill & \hfill \underset{d.w}{\max }\xi =d^F{y}_0\hfill \\ \mathrm{subject}\mathrm{to}:\hfill & \hfill \hfill \\ \hfill & \hfill w^F{x}_0-1=0\hfill \\ \hfill & \hfill d^F{y}_n-w^F{x}_n\le 0, n=1,2,\mathrm{\dots },l\hfill \\ \hfill & \hfill w\ge 0\hfill \\ \hfill & \hfill \hspace{1em}d\ge 0\hfill \end{array}$$

(16)

The linear program (Equation (1)) is equal to the fractional program (Equation (2)) [27].

The Farrell model of the linear program (Equation (1)) with variable ξ and a nonnegative vector α $={\alpha }_1,{\alpha }_2,{\alpha }_3,\dots ,{\alpha }_f$ as [26]:

$$\begin{array}{cc}\hfill & \hfill \max {\displaystyle {\displaystyle \sum }_{h=1}^g}{s}_i^{-}+{\displaystyle {\displaystyle \sum }_{i=1}^k}{s}_r^{+},\hfill \\ \mathrm{subject}\mathrm{to}:\hfill & \hfill \hfill \\ \hfill & \hfill {\displaystyle {\displaystyle \sum }_{e=1}^n}{x}_{hn}{\alpha }_h+s_h^{-}=\xi x_{h0},h=1,2,\dots ,j\hfill \\ \hfill & \hfill {\displaystyle {\displaystyle \sum }_{e=1}^n}{y}_{in}{\alpha }_n-s_i^{+}=y_{i0},i=1,2,\dots ,k\hfill \\ \hfill & \hfill {\alpha }_n\ge 0,e=1,2,\dots ,l\hfill \\ \hfill & \hfill s_h^{-}\ge 0,b=1,2,\dots ,j\hfill \\ \hfill & \hfill \hspace{1em}{s}_i^{+}\ge 0,r=1,2,\dots ,k\hfill \end{array}$$

(17)

Avoid the inefficiency border point by invoking a linear program as follows [26]:

$$\begin{array}{cc}\hfill & \hfill \max {\displaystyle {\displaystyle \sum }_{h=1}^g}{s}_b^{-}+{\displaystyle {\displaystyle \sum }_{i=1}^m}{s}_r^{+},\hfill \\ \mathrm{subject}\mathrm{to}:\hfill & \hfill \hfill \\ \hfill & \hfill {\displaystyle {\displaystyle \sum }_{n=1}^l}{x}_{hn}{\alpha }_e+s_h^{-}=\xi x_{h0},h=1,2,\dots ,j\hfill \\ \hfill & \hfill {\displaystyle {\displaystyle \sum }_{n=1}^l}{y}_{in}{\alpha }_n-s_i^{+}=y_{i0},i=1,2,\dots ,k\hfill \\ \hfill & \hfill {\alpha }_n\ge 0,n=1,2,\dots ,l\hfill \\ \hfill & \hfill s_h^{-}\ge 0,h=1,2,\dots ,j\hfill \\ \hfill & \hfill s_i^{+}\ge 0,i=1,2,\dots ,k\hfill \end{array}$$

(18)

In this case, however, note that the choices the $s_h^{-}$ and $s_i^{+}$ do not affect the optimal ${\xi }^{*}$. DMU₀ achieves 100% efficiency if and only if both (15) ξ $=1$ and (2) $s_h^{-*}$ = $s_i^{+}=0$. Only if both (15) ${\xi }^{*}=1$ and (16) $s_h^{-*}\ne 0$ and $s_i^{+}\ne 0$ for a or i in optimal options, so the performance of DMU₀ is inefficient. Therefore, the preceding development amounts to solving the problem as follows [26]:

$$\begin{array}{cc}\hfill & \hfill \min \theta -\mu \left({\displaystyle {\displaystyle \sum }_{h=1}^g}{s}_b^{-}+{\displaystyle {\displaystyle \sum }_{i=1}^m}{s}_r^{+}\right),\hfill \\ \mathrm{subject}\mathrm{to}:\hfill & \hfill \hfill \\ \hfill & \hfill {\displaystyle {\displaystyle \sum }_{h=1}^l}{x}_{hn}{\alpha }_n+s_h^{-}=\xi x_{h0},h=1,2,\dots ,j\hfill \\ \hfill & \hfill {\displaystyle {\displaystyle \sum }_{n=1}^n}{y}_{in}{\alpha }_n-s_i^{+}=y_{i0},i=1,2,\dots ,k\hfill \\ \hfill & \hfill {\alpha }_n\ge 0,n=1,2,\dots ,l\hfill \\ \hfill & \hfill s_h^{-}\ge 0,h=1,2,\dots ,j\hfill \\ \hfill & \hfill \hspace{1em}{s}_i^{+}\ge 0,i=1,2,\dots ,j\hfill \end{array}$$

(19)

In this case, the $s_h^{-}$ and $s_i^{+}$ variables are used to convert the inequalities into tantamount equations. Reducing min ξ at the first phase will resolve the resolution, and then fixing ξ $={\xi }^{*}$, where the slacks variables achieve a maximum value, but do not affect the previously determined value of $\xi ={\xi }^{*}$. The objective will be converted from max to min, to obtain [26]:

$$\begin{array}{cc}\hfill & \hfill \underset{d.w}{\max }\xi =\frac{d^F{x}_0}{w^F{y}_n},\hfill \\ \mathrm{subject}\mathrm{to}:\hfill & \hfill \hfill \\ \hfill & \hfill d^F{x}_0\le w^F{y}_n,n=1,2,\dots ,l\hfill \\ \hfill & \hfill w\ge \epsilon >0\hfill \\ \hfill & \hfill d\ge \epsilon >0\hfill \end{array}$$

(20)

If the non-Archimedean element is defined and the ε > 0, the input models are as follows [26]:

$$\begin{array}{cc}\hfill & \hfill \underset{d.w}{\max }\xi =w^F{x}_0\hfill \\ \mathrm{subject}\mathrm{to}:\hfill & \hfill \hfill \\ \hfill & \hfill d^F{y}_0=1\hfill \\ \hfill & \hfill w^F{x}_o-d^F{y}_n\ge 0, n=1,2,\dots ,l\hfill \\ \hfill & \hfill w\ge \epsilon >0\hfill \\ \hfill & \hfill d\ge \epsilon >0\hfill \end{array}$$

(21)

And:

$$\begin{array}{cc}\hfill & \hfill \max \varphi -\epsilon \left({\displaystyle {\displaystyle \sum }_{h=1}^g}{s}_i^{-}+{\displaystyle {\displaystyle \sum }_{i=1}^m}{s}_r^{+}\right),\hfill \\ \mathrm{subject}\mathrm{to}:\hfill & \hfill \hfill \\ \hfill & \hfill {\displaystyle {\displaystyle \sum }_{n=1}^l}{x}_{hn}{\alpha }_n+s_h^{-}=x_{h0},h=1,2,\dots ,j\hfill \\ \hfill & \hfill {{\displaystyle \sum }}_{n=1}^l{y}_{in}{\alpha }_n-s_i^{+}=\varnothing y_{r0},i=1,2,\dots ,k\hfill \\ \hfill & \hfill {\alpha }_n\ge 0,n=1,2,\dots ,l\hfill \\ \hfill & \hfill s_h^{-}\ge 0,h=1,2,\dots ,j\hfill \\ \hfill & \hfill \hspace{1em}{s}_i^{+}\ge 0,i=1,2,\dots ,k\hfill \end{array}$$

(22)

The CCR input-oriented (CCR–I) has the dual multiplier model expressed as [26]:

$$\begin{array}{cc}\hfill & \hfill \max z={\displaystyle {\displaystyle \sum }_{i=1}^k}{\partial }_i{y}_{i0}\hfill \\ \mathrm{subject}\mathrm{to}:\hfill & \hfill \hfill \\ \hfill & \hfill {\displaystyle {\displaystyle \sum }_{i=1}^k}{\partial }_i{y}_{in}-{\displaystyle {\displaystyle \sum }_{i=1}^k}{a}_i{y}_{in}\le 0\hfill \\ \hfill & \hfill {\displaystyle {\displaystyle \sum }_{h=1}^j}{a}_h{x}_{h0}=1\hfill \\ \hfill & \hfill \hspace{1em}{c}_i,a_h\ge \epsilon >0\hfill \end{array}$$

(23)

The CCR output-oriented (CCR–O) has the dual multiplier model expressed as [26]:

$$\begin{array}{cc}\hfill & \hfill \min k={\displaystyle {\displaystyle \sum }_{h=1}^j}{a}_h{x}_{h0,}\hfill \\ \mathrm{subject}\mathrm{to}:\hfill & \hfill \hfill \\ \hfill & \hfill {\displaystyle {\displaystyle \sum }_{h=1}^j}{a}_h{x}_{hn}-{\displaystyle {\displaystyle \sum }_{i=1}^q}{\partial }_i{y}_{in}\le 0\hfill \\ \hfill & \hfill {\displaystyle {\displaystyle \sum }_{i=1}^k}{\partial }_i{y}_{i0}=1\hfill \\ \hfill & \hfill \hspace{1em}{w}_i,d_h\ge \epsilon >0\hfill \end{array}$$

(24)

3.2.2. Banker Charnes Cooper Model (BCC Model)

Banker et al. introduced an input-oriented BCC model (BCC–I), which is able to assess the efficiency of DMU₀ by solving the following linear program:

$$\begin{array}{cc}\hfill & \hfill {\xi }_H=min\xi ,\hfill \\ \mathrm{subject}\mathrm{to}:\hfill & \hfill \hfill \\ \hfill & \hfill {\displaystyle {\displaystyle \sum }_{n=1}^l}{x}_{hn}{\alpha }_n+s_h^{-}=\xi x_{h0},h=1,2,\dots ,j\hfill \\ \hfill & \hfill {\displaystyle {\displaystyle \sum }_{n=1}^l}{y}_{in}{\alpha }_n-s_i^{+}=y_{i0},i=1,2,\dots ,k\hfill \\ \hfill & \hfill {\displaystyle {\displaystyle \sum }_{c=1}^l}{\alpha }_c=1\hfill \\ \hfill & \hfill {\alpha }_c\ge 0,c=1,2,\dots ,l\hfill \end{array}$$

(25)

Avoid the inefficiency border point by invoking the linear program as follows [26]:

$$\begin{array}{cc}\hfill & \hfill \max {\displaystyle {\displaystyle \sum }_{h=1}^g}{s}_b^{-}+{\displaystyle {\displaystyle \sum }_{i=1}^m}{s}_r^{+},\hfill \\ \mathrm{subject}\mathrm{to}:\hfill & \hfill \hfill \\ \hfill & \hfill {\displaystyle {\displaystyle \sum }_{n=1}^l}{x}_{hn}{\alpha }_n+s_h^{-}=\xi x_{h0},h=1,2,\dots ,j\hfill \\ \hfill & \hfill {\displaystyle {\displaystyle \sum }_{n=1}^l}{y}_{in}{\alpha }_n-s_i^{+}=y_{i0},i=1,2,\dots ,k\hfill \\ \hfill & \hfill {\displaystyle {\displaystyle \sum }_{c=1}^l}{\alpha }_c=1\hfill \\ \hfill & \hfill {\alpha }_c\ge 0,c=1,2,\dots ,l\hfill \\ \hfill & \hfill s_h^{-}\ge 0,h=1,2,\dots ,j\hfill \\ \hfill & \hfill s_i^{+}\ge 0,i=1,2,\dots ,k\hfill \end{array}$$

(26)

Therefore, this is the first multiplier form to the solve problem as follows [26]:

$$\begin{array}{cc}\hfill & \hfill \min \xi -\epsilon \left({\displaystyle {\displaystyle \sum }_{h=1}^g}{s}_b^{-}+{\displaystyle {\displaystyle \sum }_{i=1}^m}{s}_r^{+}\right),\hfill \\ \mathrm{subject}\mathrm{to}:\hfill & \hfill \hfill \\ \hfill & \hfill {\displaystyle {\displaystyle \sum }_{n=1}^l}{x}_{hn}{\alpha }_n+s_h^{-}=\xi x_{a0},h=1,2,\dots ,j\hfill \\ \hfill & \hfill {\displaystyle {\displaystyle \sum }_{n=1}^l}{y}_{in}{\alpha }_n-s_i^{+}=y_{i0},i=1,2,\dots ,k\hfill \\ \hfill & \hfill {\displaystyle {\displaystyle \sum }_{k=1}^n}{\alpha }_k=1\hfill \\ \hfill & \hfill {\alpha }_c\ge 0,c=1,2,\dots ,l\hfill \\ \hfill & \hfill d_h^{-}\ge 0,h=1,2,\dots ,j\hfill \\ \hfill & \hfill d_i^{+}\ge 0,i=1,2,\dots ,k\hfill \end{array}$$

(27)

The second multiplier form given by the linear program is expressed as [26]:

$$\begin{array}{cc}\hfill & \hfill \underset{d.w,d_0}{\max }{\xi }_H=d^F{y}_0-d_0,\hfill \\ \mathrm{subject}\mathrm{to}:\hfill & \hfill \hfill \\ \hfill & \hfill w^F{x}_0=1\hfill \\ \hfill & \hfill d^F{y}_n-w^F{x}_n-d_0\le 0, n=1,2,\dots ,l\hfill \\ \hfill & \hfill w\ge 0\hfill \\ \hfill & \hfill d\ge 0\hfill \end{array}$$

(28)

The cases f and u are vectors, and the scalar $v_0$ may be positive or disclaim or zero. Therefore, the dual program [26] has the equivalent BCC fractional program:

$$\begin{array}{cc}\hfill & \hfill \underset{d.w}{\max }\xi =\frac{d^F{y}_0-d_0}{w^F{x}_0},\hfill \\ \mathrm{subject}\mathrm{to}:\hfill & \hfill \hfill \\ \hfill & \hfill \frac{d^F{y}_e-d_0}{w^F{x}_e}\le 1,n=1,2,\dots ,l\hfill \\ \hfill & \hfill w\ge 0\hfill \\ \hfill & \hfill d\ge 0\hfill \end{array}$$

(29)

BCC is effectively the DMU₀ if an optimal solution $({\xi }_B^{*},s^{-*},s^{+*})$ is required in this two-phase process for satisfying ${\xi }_B^{*}=1$, and has no slack s $s^{-*}=s^{+*}$ = 0. Alternatively, the BCC is non-efficient. The BCC effective illustration [26] is the improved activity $\left({\xi }^{*}x-s^{-*},y+s^{+*}\right)$. In addition, a DMU has a minimum input value for any input item, or a maximum output value for any output item.

3.2.3. Slacks-Based Measure Model (SBM Model):

The stacks-based measure model SBM input effective Input-Oriented SBM (SBM–I–C) is Input-oriented SBM under a constant-returns-to-scale assumption [26]:

$$\begin{array}{cc}\hfill & \hfill {\rho }_I^{*}=\underset{\alpha ,s^{-},s^{+}}{\min }1-\frac{1}{g}{\displaystyle {\displaystyle \sum }_{h=1}^g}\frac{s_h^{-}}{x_{he}},\hfill \\ \mathrm{subject}\mathrm{to}:\hfill & \hfill \hfill \\ \hfill & \hfill x_{hw}={\displaystyle {\displaystyle \sum }_{n=1}^g}{x}_{hw}{\alpha }_h+s_h^{-},h=1,2,\dots j\hfill \\ \hfill & \hfill y_{wi}={\displaystyle {\displaystyle \sum }_{n=1}^g}{y}_{wi}{\alpha }_n-s_i^{+},i=1,2,\dots k\hfill \\ \hfill & \hfill {\alpha }_n\ge 0,c\left(\forall j\right),s_h^{-}\ge 0\left(\forall n\right),s_i^{+}\ge 0\left(\forall n\right)\hfill \end{array}$$

(30)

The output-oriented SBM effective ${\rho }_O^{*}$ of DMU_z = (x_z, y_z) is outlined by SBM–O–C [27]:

$$\begin{array}{cc}\hfill & \hfill \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{${\rho }_O^{*}$}\right.=\underset{\alpha ,s^{-},s^{+}}{\max }1+\frac{1}{s}{{\displaystyle \sum }}_{i=1}^k\frac{s_r^{+}}{y_{iz}},\hfill \\ \mathrm{subject}\mathrm{to}:\hfill & \hfill \hfill \\ \hfill & \hfill x_{rh}={\displaystyle {\displaystyle \sum }_{n=1}^l}{x}_{hn}{\alpha }_n+s_n^{-}\left(h=1,\dots j\right)\hfill \\ \hfill & \hfill y_{hr}={{\displaystyle \sum }}_{n=1}^l{y}_{hn}{\alpha }_n+s_h^{+}\left(h=1,\dots j\right)\hfill \\ \hfill & \hfill {\alpha }_n\ge 0\left(\forall n\right), s_n^{-}\ge 0\left(\forall h\right), s_n^{+}\ge 0 \left(\forall i\right)\hfill \end{array}$$

(31)

4. Case Study

Edible oil suppliers are important in business operations for the small and medium enterprise (SME) food processing industry. The supplier ensures that raw materials are of sufficient quantity, quality, and stability and accuracy to meet the requirements of production and business with a low cost and delivery time. Therefore, selecting good suppliers and managing them are prerequisites for organizing the production of quality products as desired, according to schedules, with reasonable prices and competitiveness in the market and also to obtain supplier support to continue to achieve a higher goal. Thus, with MCDM used in edible oil supplier selection, the decision-maker must consider both qualitative and quantitative factors.

Thus, the main aim of this work is the proposed suppliers’ selection processes, using FAHP and DEA with green factors for edible oil suppliers based on financial, delivery, environmental management system, and qualitative factors.

The proposed model was used to rank potential soybean suppliers of a well-known food processing industry in Vietnam. After preliminary evaluation, 10 potential suppliers (decision-making units (DMU)) were selected by interviewing experts and heads of purchasing departments based on product capacity, time of delivery, supplier’s location, and unit price. A supplier’s list and their symbol in the proposed model are shown in Table 2.

Table 2. The symbol of ten edible Oil suppliers.

No	Name	Symbol
1	Wilmar argo Vietnam Company Limited	DMU1
2	Truong Thinh Joint Stock Company	DMU2
3	Long Gia Company Limited	DMU3
4	Binh Minh Joint Stock Incorporated Company	DMU4
5	Kim Hai Rice Private Business	DMU5
6	Van Nam Export-Production Joint Stock Company	DMU6
7	Thi Hien Joint Stock Company	DMU7
8	Binh Dien Export-Production Joint Stock Company	DMU8
9	Nuy Uyn Joint Stock Company	DMU9
10	Sa Dec Joint Stock Company	DMU10

The list of main criteria and subcriteria for selecting edible oil suppliers from experts, articles, and scientific research works are shown in Table 3.

Table 3. List of main criteria and subcriteria for selecting the best suppliers.

Main Criteria	Subcriteria
C1: Financial	C11: Capital and finance status
	C12: Prices
	C13: Transportation cost to the geographical location
C2: Delivery and services	C21: Delivery
	C22: Customer service
	C23: Communication system
	C24: Production capacity
C3: Qualitative	C31: Quality of Products
	C32: Operational Control
	C33: Expert labor, technical capabilities, and facilities
	C34: Business experience and position among competitors
C4: Environmental management system	C41: Environmental emissions (carbon footprint)
	C42: Environmental planning
	C43: Environmentally friendly material
	C44: Environmentally friendly technology

The weight of potential suppliers, defined by the AHP model using fuzzy logic, is shown in Table 4.

Table 4. The weight of each supplier.

No	DMU	Weight
1	DMU1	0.252
2	DMU2	0.087
3	DMU3	0.093
4	DMU4	0.053
5	DMU5	0.089
6	DMU6	0.103
7	DMU7	0.081
8	DMU8	0.085
9	DMU9	0.070
10	DMU10	0.085

Based on literature reviews and experts, five factors were considered in the DEA model, including unit price, carbon footprint, delivery time, quality of edible oil, and qualitative benefits factor. In summary, a graphic of the green DEA model for the analysis of potential suppliers along with two inputs and three outputs is shown in Figure 4.

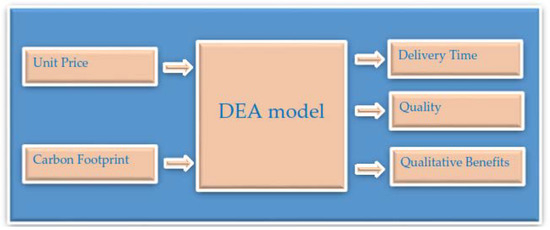
Figure 4. A Graphic of the green data envelopment analysis (GDEA) model.

The data used in the DEA model are shown in Table 5. The unit price and carbon footprint provided by suppliers are inputs. The delivery, and quality of edible oil are outputs of the DEA model; the quality of edible oil was ranked by the team of experts (on a Likert scale 1–9) [28]. Additionally, the results of the FANP model for the ranking of various suppliers on qualitative factors were utilized in the output qualitative benefits of the DEA model [29].

Table 5. Data used in the DEA model.

DMU	(I) Unit Price	(I) Carbon Footprint	(O) Delivery	(O) Quality	(O) Qualitative Benefits
DMU1	0.989	0.953	7	8	0.252
DMU2	0.997	0.978	7	8	0.087
DMU3	0.982	1.310	9	7	0.093
DMU4	1.000	0.978	5	8	0.053
DMU5	0.991	0.998	7	8	0.089
DMU6	1.006	1.010	5	8	0.103
DMU7	0.910	0.999	8	8	0.081
DMU8	1.003	1.013	6	8	0.085
DMU9	0.969	0.665	8	6	0.070
DMU10	0.787	1.001	4	5	0.085

The variables of inputs and outputs for the correlation coefficient matrix should comply with the Isotonicity premise. The results of the Pearson correlation test are in Table 6; all correlation coefficients are positive, so they meet the basic requirements of the DEA model.

Table 6. Pearson correlation coefficient.

	Unit Price	Carbon Footprint	Delivery	Quality	Qualitative Benefits
Unit price	1	0.020	0.332	0.759	0.127
Carbon footprint	0.020	1	0.117	0.203	0.021
Delivery	0.332	0.117	1	0.170	0.105
Quality	0.759	0.203	0.170	1	0.207
Qualitative benefits	0.127	0.021	0.105	0.207	1

5. Results and Discussion

In order to promote the selection of suppliers in the food industry, the selection of suppliers in the edible oil sector is important in achieving supply chain goals. However, the edible oil selection process tends to be incomplete, inaccurate, and vague.

The MCDM model has been applied in various fields of science and engineering; moreover, this trend has been increasing for many years. One of the fields that the MCDM model has been applied to is for supplier selection in edible oil production, yet very few studies consider this problem with green issues and under fuzzy environmental conditions. Thus, we have developed a supplier selection process for the SME food processing industry. In this research, to define the weight of each potential supplier, the AHP model with the combination of fuzzy logic was presented in the first stage of this study; further, the FAHP model focuses on the suppliers’ ratings with four main and 15 subcriteria derived from research-relevant documents and experts. As per the literature review, FAHP was proven to be an appropriate method for evaluating and making multicriteria decisions. Then, several DEA models were proposed for ranking edible oil suppliers. The results showed that DMU 1, DMU 3, DMU 7, and DMU 9 were identified as extremely efficient for five DEA models, as shown in Table 7 [30], which have a condition response to the enterprises’ supply requirement.

Table 7. Results of the DEA model.

DMU	CCR–I	CCR–O	BCC–I	SBM–I–C	SBM–O–C
DMU 1	1	1	1	1	1
DMU 2	0.981	0.981	0.981	0.975	0.608
DMU 3	1	1	1	1	1
DMU 4	0.980	0.980	0.980	0.973	0.415
DMU 5	0.971	0.970	0.971	0.961	0.621
DMU 6	0.958	0.958	0.958	0.949	0.610
DMU 7	1	1	1	1	1
DMU 8	0.957	0.957	0.957	0.947	0.577
DMU 9	1	1	1	1	1
DMU 10	0.743	0.743	1	0.679	0.598

6. Conclusions

Supplier selection plays an important role in supply chain management and contributes to the success of production-business organizations. Selecting a green supplier and appropriate management, which helps organizations reduce input costs, improves the quality of goods and services provided to customers, and improves competitiveness in the market.

Many studies have applied the MCDM model to various fields of science and engineering, and this trend has been increasing for many years. One of the fields that the MCDM model has been applied to is for supplier selection in supply chain management, such as in Diouf and Kwak [31], Kim and Changhee [32], Wang and Tsai [33], etc. Nevertheless, few studies consider this problem under uncertain environmental conditions, and the edible oil supplier selection process can be considered as an MCDM. Thus, the author proposed a hybrid model using FAHP and GDEA, which is an effective tool for quantifying ambiguous and incomplete information. Initially, the FAHP model identified the weight of all criteria of the supplier’s selection process based on the opinion of company procurement experts. Subsequently, GDEA was applied to rank all potential suppliers. The results revealed that DMU 1, DMU 3, DMU 7, and DMU 9 were identified as extremely efficient for five DEA models. Further, the study results suggest that the proposed model is feasible. This study gives businesses more choices in decision-making.

The contribution of this research is proposing new and feasible approaches for supplier evaluation and selection in the food processing industry under a fuzzy environment. This is a useful model in the academic and practical fronts. In addition, this research can be broadened, thus creating a premise for applying supplier selection in other industries and, in particular, extending the model in evaluating and selecting green suppliers.

For future research, it is suggested that applications be increased through the development of new criteria and approached, such as Preference Ranking Organizational Method for Enrichment Evaluation (PROMETHEE) and FANP. A lexicographic optimization algorithm will also be considered for other fields within the food processing industry.