New Refinements and Improvements of Jordan’s Inequality

Abstract

The polynomial bounds of Jordan’s inequality, especially the cubic and quartic polynomial bounds, have been studied and improved in a lot of the literature; however, the linear and quadratic polynomial bounds can not be improved very much. In this paper, new refinements and improvements of Jordan’s inequality are given. We present new lower bounds and upper bounds for strengthened Jordan’s inequality using polynomials of degrees 1 and 2. Our bounds are tighter than the previous results of polynomials of degrees 1 and 2. More importantly, we give new improvements of Jordan’s inequality using polynomials of degree 5, which can achieve much tighter bounds than those previous methods.

1. Introduction

The following inequality

$$\frac{2}{\pi }\le sinc\left(x\right)=\frac{sinx}{x}<1,x\in (0,2/\pi ],$$

(1)

with equality holds if and only if $x=\pi /2$, is the famous Jordan’s inequality [1]. $sinc\left(x\right)$ is also called the “sampling function” that arises frequently in signal processing and the theory of Fourier transforms. The Jordan’s inequality plays an important role in many areas of pure and applied mathematics. Many improvements and refinements of Jordan’s inequality were presented in the recent period [2,3,4,5,6,7]. There are some sharp lower and upper bounds for the $sinc\left(x\right)$ function by using polynomial degrees from 1 to 4.

Zhang et al. [8] gave that

$$\frac{2}{\pi }+\frac{\pi -2}{{\pi }^2}(\pi -2x)\le \frac{sinx}{x}\le \frac{2}{\pi }+\frac{2}{{\pi }^2}(\pi -2x),x\in (0,2/\pi ].$$

(2)

Qi et al. [9] proved that

$$\frac{2}{\pi }+\frac{1}{{\pi }^3}({\pi }^2-4x^2)\le \frac{sinx}{x}\le \frac{2}{\pi }+\frac{\pi -2}{{\pi }^3}({\pi }^2-4x^2),x\in (0,2/\pi ].$$

(3)

Deng [10] presented

$$\frac{2}{\pi }+\frac{2}{3{\pi }^4}({\pi }^3-8x^3)\le \frac{sinx}{x}\le \frac{2}{\pi }+\frac{\pi -2}{{\pi }^4}({\pi }^3-8x^3),x\in (0,2/\pi ],$$

(4)

and Jiang et al. [11], similarly, gave the result

$$\frac{2}{\pi }+\frac{1}{2{\pi }^5}({\pi }^4-16x^4)\le \frac{sinx}{x}\le \frac{2}{\pi }+\frac{\pi -2}{{\pi }^5}({\pi }^4-16x^4),x\in (0,2/\pi ].$$

(5)

Equalities in Labels (2)–(5) are valid if and only if $x=\pi /2$. As $x\to 0^{+}$, the equalities on the right-hand sides of (3)–(5) are valid, but strict inequalities on the left-hand sides of (3)–(5) and two sides of (2) persist. Debnath et al. [12] gave the improvements of (3) and (5)

$$\begin{array}{c}\hfill g_{4,D1}^l\left(x\right)\le \frac{sinx}{x}\le g_{4,D1}^u\left(x\right),x\in (0,2/\pi ]\end{array}$$

(6)

and

$$\begin{array}{c}\hfill g_{4,D2}^l\left(x\right)\le \frac{sinx}{x}\le g_{4,D2}^u\left(x\right),x\in (0,2/\pi ],\end{array}$$

(7)

where $$\begin{gathered} g_{4,D1}^l\left(x\right)=\frac{2}{\pi }+\frac{1}{{\pi }^3}({\pi }^2-4x^2)+(1-\frac{3}{\pi })-(\frac{1}{6}-\frac{4}{{\pi }^3})x^2, g_{4,D1}^u\left(x\right)=\frac{2}{\pi }+\frac{1}{{\pi }^3}({\pi }^2-4x^2)+(1- \\ \frac{3}{\pi })-(\frac{1}{6}-\frac{4}{{\pi }^3})x^2+\frac{1}{120}{x}^4, g_{4,D2}^l\left(x\right)=\frac{2}{\pi }+\frac{1}{2{\pi }^5}({\pi }^4-16x^4)+(1-\frac{5}{2\pi })-\frac{1}{6}{x}^2, g_{4,D2}^u\left(x\right)=\frac{2}{\pi }+\frac{\pi -2}{2{\pi }^5}({\pi }^4- \\ 16x^4)+(1-\frac{5}{2\pi })-\frac{1}{6}{x}^2+(\frac{8}{{\pi }^5}+\frac{1}{120})x^4. \end{gathered}$$

As $x\to 0^{-}$, equalities on two sides of (6) and (7) are valid; however, as $x\to {\frac{\pi }{2}}^{-}$, the lower and upper limits of (6) and (7) are different from that of $sinc\left(x\right)$. The problem of strict inequalities of (6) and (7) still exists.

In order to ensure that the equality of Jorand’s inequality is valid near zero and $\pi /2$, Agarwal et al. [13] and Chen et al. [14] gave new lower and upper bounds by using polynomials of degree of 3 and 4,

$$\begin{array}{c}\hfill g_{3,A}^l\left(x\right)\le \frac{sinx}{x}\le g_{3,A}^u\left(x\right),x\in (0,2/\pi ],\end{array}$$

(8)

$$\begin{array}{c}\hfill g_{3,C}^l\left(x\right)\le \frac{sinx}{x}\le g_{3,C}^u\left(x\right),x\in (0,2/\pi ],\end{array}$$

(9)

$$\begin{array}{c}\hfill g_{4,C}^l\left(x\right)\le \frac{sinx}{x}\le g_{4,C}^u\left(x\right),x\in (0,2/\pi ),\end{array}$$

(10)

where $$\begin{gathered} g_{3,A}^l\left(x\right)=1+\frac{4(66-43\pi +7{\pi }^2)}{{\pi }^2}x-\frac{4(124-83\pi +14{\pi }^2)}{{\pi }^3}{x}^2-\frac{4(12-4\pi )}{{\pi }^4}{x}^3, g_{3,A}^u\left(x\right)=1+\frac{4(75-49\pi +8{\pi }^2)}{{\pi }^2}x-\frac{4(142-95\pi +16{\pi }^2)}{{\pi }^3}{x}^2-\frac{4(12-4\pi )}{{\pi }^4}{x}^3, g_{3,C}^l\left(x\right)=1-\frac{4(3\pi -8)}{{\pi }^3}{x}^2+\frac{16(\pi -3)}{{\pi }^4}{x}^3, g_{3,C}^u\left(x\right)= \\ 1-\frac{2(5\pi -2-16\sqrt{2}+2\sqrt{2}\pi )}{{\pi }^2}x+\frac{8(4\pi -4-16\sqrt{2}+3\sqrt{2}\pi )}{{\pi }^3}{x}^2-\frac{32(\pi -2-4\sqrt{2}+\sqrt{2}\pi )}{{\pi }^4}{x}^3, g_{4,C}^l\left(x\right)=1- \\ \frac{4(-48\sqrt{2}-2+17\pi +4\sqrt{2}\pi )}{{\pi }^3}{x}^2+\frac{32(-28\sqrt{2}-2+9\pi +3\sqrt{2}\pi )}{{\pi }^4}{x}^3-\frac{64(-16\sqrt{2}-2+5\pi +2\sqrt{2}\pi )}{{\pi }^5}{x}^4, g_{4,C}^u\left(x\right)=1- \\ \frac{4(-8\sqrt{2}-7+3\pi +2\sqrt{2}\pi )}{{\pi }^2}x+\frac{4(-32\sqrt{2}-68+13\pi +16\sqrt{2}\pi )}{{\pi }^3}{x}^2-\frac{32(-4\sqrt{2}-26+3\pi +5\sqrt{2}\pi )}{{\pi }^4}{x}^3+\frac{64(-12+\pi +2\sqrt{2}\pi )}{{\pi }^5}{x}^4. \end{gathered}$$

Zeng and Wu [15] gave the polynomial bounds of degree $m(m\ge 2)$ for sinc(x)

$$\frac{2}{\pi }+\frac{2}{m{\pi }^{m+1}}({\pi }^m-2^m{x}^m)\le \frac{sinx}{x}\le \frac{2}{\pi }+\frac{\pi -2}{{\pi }^{m+1}}({\pi }^m-2^m{x}^m),x\in (0,2/\pi ].$$

(11)

Putting $m=2,3,4$ in (11) results in (3), (4) and (5), respectively.

The cubic and quartic polynomial lower and upper bounds of $sinc\left(x\right)$ have been improved in a lot of literature; however, the linear and quadratic polynomial lower and upper bounds can not be improved very well. To give new tighter linear and quadratic polynomial bounds is the first aim of the paper. The second aim is to further refine and generalize the Jordan’s inequality.

The paper gives improvements of the polynomial bounds of degrees 1 and 2. More importantly, we present new improvements of Jordan’s inequality using polynomials of degree 5, which can achieve much tighter bounds than those previous methods.

2. Results

In this section, we will give some results about the n-th-order derivative and two-sides bounds of $sinc\left(x\right)$. Firstly, we present a Lemma that is very useful for our proof [16].

Lemma 1.

Let $w_0,w_1,\cdots ,w_r$ be $r+1$ distinct points in $[a,b]$, and $n_0,n_1,\cdots n_r$ be $r+1$ integers ≥ 0. Let $N=n_0+\cdots +n_r+r.$ Suppose that $g\left(t\right)$ is a polynomial of degree N such that

$$g^{\left(i\right)}\left(w_j\right)=f^{\left(i\right)}\left(w_j\right),i=0,\cdots ,n_j,j=0,\cdots ,r.$$

Then, there exists $\xi \left(t\right)\in [a,b]$ such that

$$f\left(t\right)-g\left(t\right)=\frac{f^{(N+1)}\left(\xi \left(x\right)\right)}{(N+1)!}\prod _{i=0}^r{(t-w_i)}^{n_i+1}.$$

Next, we give Theorems of n-th-order derivative and two sides bounds of $sinc\left(x\right)$ using polynomials of degrees 1 and 2.

Theorem 1.

For $x\in (0,\pi /2]$, we have

$$sin{c}^{\left(n\right)}\left(x\right)=\frac{f_n\left(x\right)}{x^{n+1}},$$

where $f_n\left(x\right)=x{f}_{n-1}^{\prime }\left(x\right)-n{f}_{n-1}\left(x\right)$, $f_n^{\prime }\left(x\right)=-x^{n}sin(x+\frac{n\pi }{2})$, $f_1\left(x\right)=-sin\left(x\right)+xcos\left(x\right)$, and $sin{c}^{(n}\left(x\right)$ denotes the n-th-order derivative of $sinc\left(x\right)$.

Proof. 

For the definition of $sinc\left(x\right)$, we have

$$sin{c}^{\prime }\left(x\right)=\frac{-sin\left(x\right)+xcos\left(x\right)}{x^2};$$

then, $f_1\left(x\right)=-sin\left(x\right)+xcos\left(x\right)$, $f_1^{\prime }\left(x\right)=-xsin\left(x\right)$.

Let $sin{c}^{\left(m\right)}\left(x\right)=\frac{f_m\left(x\right)}{x^{m+1}}=\frac{x{f}_{m-1}^{\prime }\left(x\right)-m{f}_{m-1}\left(x\right)}{x^{m+1}}$, $f_m^{\prime }\left(x\right)=-x^{m}sin(x+\frac{m\pi }{2})$; then, as $n=m+1$,

$$sin{c}^{(m+1)}\left(x\right)=\frac{d}{dx}sin{c}^{\left(m\right)}\left(x\right)=\frac{d}{dx}\frac{f_m\left(x\right)}{x^{m+1}}=\frac{x{f}_m^{\prime }\left(x\right)-(m+1)f_m\left(x\right)}{x^{m+2}}=\frac{f_{m+1}\left(x\right)}{x^{m+2}},$$

$$f_{m+1}^{\prime }\left(x\right)=x{f}_m^{″}\left(x\right)-m{f}_m^{\prime }\left(x\right)=-x^{(m+1)}sin(x+\frac{(m+1)\pi }{2}).$$

The proof of Theorem 1 is completed. □

Theorem 2.

For $x\in (0,\pi /2]$,

$$\begin{array}{c}\hfill 1+\frac{4-2\pi }{{\pi }^2}x\le \frac{sinx}{x}\le \frac{8\sqrt{2}-\sqrt{2}\pi }{2\pi }+\frac{2\sqrt{2}-8\sqrt{2}}{{\pi }^2}x.\end{array}$$

(12)

Proof. 

Let $b=\pi /2,c=\pi /4,e_{1,l}\left(x\right)=sinc\left(x\right)-1-\frac{4-2\pi }{{\pi }^2}x,$ and $e_{1,u}\left(x\right)=sinc\left(x\right)-\frac{8\sqrt{2}-\sqrt{2}\pi }{2\pi }+\frac{2\sqrt{2}-8\sqrt{2}}{{\pi }^2}x,$ for $x\in (0,\pi /2]$, we have

$$e_{1,l}\left(0\right)=e_{l,1}\left(b\right)=0,e_{1,u}\left(c\right)=e_{1,u}^{\prime }\left(c\right)=0.$$

By Lemma 1 and Theorem 1, $e_{1,l}^{″}\left(x\right)=e_{u,1}^{″}\left(x\right)=sin{c}^{″}\left(x\right)\le 0,$ and there exists ${\xi }_j\left(x\right)\in [0,\pi /2],$ $j=1,2,$ such that

$$e_{1,l}\left(x\right)=e_{l,1}^{″}\left({\xi }_1\left(x\right)\right)x(x-b)\ge 0,e_{1,u}\left(x\right)=e_{1,u}^{″}\left({\xi }_2\left(x\right)\right){(x-c)}^2\le 0.$$

The proof is finished. □

Theorem 3.

For $x\in (0,\pi /2]$,

$$\begin{array}{c}\hfill g_2^l\left(x\right)\le \frac{sinx}{x}\le g_2^u\left(x\right),\end{array}$$

(13)

where $g_2^l\left(x\right)=1+\frac{12-4\pi }{{\pi }^2}x+\frac{4\pi -16}{{\pi }^3}{x}^2, g_2^u=1+\frac{8-4\pi }{{\pi }^3}{x}^2.$

Proof. 

Let $b=\pi /2, e_{2,l}\left(x\right)=sinc\left(x\right)-g_2^l\left(x\right)$,

$$e_{2,l}\left(0\right)=e_{2,l}\left(b\right)=e_{2,l}^{\prime }\left(b\right)=0,e_{2,u}\left(0\right)=e_{2,u}\left(b\right)=e_{2,u}^{\prime }\left(0\right)=0.$$

By Lemma 1 and Theorem 1, $e_{1,l}^{\left(3\right)}\left(x\right)=e_{u,1}^{\left(3\right)}\left(x\right)=sin{c}^{\left(3\right)}\left(x\right)\ge 0,$ and there exists ${\xi }_j\left(x\right)\in [0,\pi /2], j=3,4,$ such that

$$e_{2,l}\left(x\right)=e_{2,l}^{\left(3\right)}\left(\xi \left(x\right)\right)x{(x-b)}^2\ge 0,e_{2,u}\left(x\right)=e_{2,u}^{\left(3\right)}\left(\xi \left(x\right)\right)x^2(x-b)\le 0.$$

The proof is finished. □

Theorems 2 and 3 give new bounds of $sinc\left(x\right)$ using polynomials of degrees 1 and 2. Figure 1 and Figure 2 give the error between sinc(x) and the polynomial bounds from degree 1 to 2. Both figures show that our bounds are tighter than the previous results. The same conclusion can also be shown in Table 1. $Erro{r}_{low}$ and $Erro{r}_{upp}$ denote the maximum errors between $sinc\left(x\right)$ and the lower and upper bounds, respectively. It is obvious that the maximum errors are less than or equal to those of previous methods using polynomials of degrees 1 and 2.

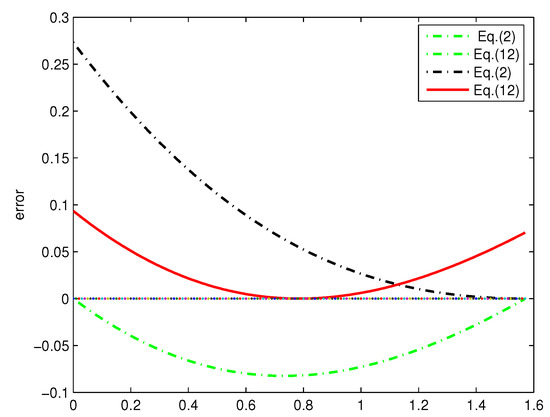
Figure 1. Error plots between sinc(x) and the bounds of Equations (2) and (12).

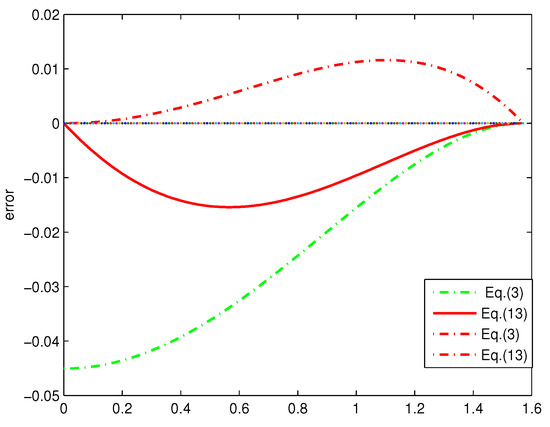
Figure 2. Error plots between sinc(x) and the bounds of Equations (3) and (13).

Table 1. Maximum errors from different methods.

Method	Error
	Errorlow	Errorupp
Linear polynomial (Equation (2))	0.08239552616791	0.27319901792837
Linear polynomial (Equation (12))	0.08239552616791	0.09343987891909
Quadratic polynomial (Equation (3))	0.04507034107202	0.01161202091677
Quadratic polynomial (Equation (13))	0.01541234761755	0.01161202091677
Cubic polynomial (Equation (4))	0.15117363517661	0.06535850279048
Cubic polynomial (Equation (8))	0.00263153345090	0.00098638493116
Cubic polynomial (Equation (9))	0.18004172509621	0.00065651979512
Quartic polynomial (Equation (5))	0.20422528287386	0.10245473620764
Quartic polynomial (Equation (6))	0.04777095540497	0.00287304555420
Quartic polynomial (Equation (7))	0.20664387547518	0.20422528454052
Quartic polynomial (Equation (10))	0.00010491761462	0.00011278132149
Quintic Polynomial (Equation (11) m = 5)	0.236056271492236	0.129868221438454
Quintic Polynomial (Equation (14))	0.00001059989622	0.00000545628343
Octic Polynomial (Equation (11) m = 8)	0.283802754419804	0.182471527648186
Decic Polynomial (Equation (11) m = 10)	0.299718248728994	0.204647143136328

Theorem 4.

For $x\in (0,\pi /2]$,

$$\begin{array}{c}\hfill g_5^l\left(x\right)\le \frac{sinx}{x}\le g_5^u\left(x\right),\end{array}$$

(14)

where $$\begin{gathered} g_5^l\left(x\right)=1+\frac{32-2048\sqrt{2}+2187\sqrt{3}-(113+128\sqrt{2})\pi }{2{\pi }^2}x+\frac{-448+26624\sqrt{2}-27702\sqrt{3}+(1255+1536\sqrt{2})\pi }{2{\pi }^3}{x}^2 \\ +\frac{1168-62464\sqrt{2}+64152\sqrt{3}-(2825+3392\sqrt{2})\pi }{{\pi }^4}{x}^3+\frac{-2688+125952\sqrt{2}-128304\sqrt{3}+(5664+6528\sqrt{2})\pi }{{\pi }^5}{x}^4 \\ +\frac{2304-92160\sqrt{2}+93312\sqrt{3}-(4176+4608\sqrt{2})\pi }{{\pi }^6}{x}^5 \end{gathered}$$, $$\begin{gathered} g_5^u\left(x\right)=1+\frac{64+256\sqrt{2}-(92+32\sqrt{2})\pi }{{\pi }^3}{x}^2+ \\ \frac{-624-1536\sqrt{2}+(528+256\sqrt{2})\pi }{{\pi }^4}{x}^3 \\ +\frac{1920+3072\sqrt{2}-(1088+640\sqrt{2})\pi }{{\pi }^5}{x}^4+\frac{-1792-2048\sqrt{2}+(768+512\sqrt{2})\pi }{{\pi }^6}{x}^5. \end{gathered}$$

Proof. 

Let $b=\frac{\pi }{2}, c=\frac{\pi }{4}, d=\frac{\pi }{3}$, $e_{5,l}\left(x\right)=sinc\left(x\right)-g_5^l\left(x\right), e_{5,u}\left(x\right)=sinc\left(x\right)-g_5^u\left(x\right).$ It is obvious that for $x\in (0,\pi /2]$, $e_{5,l}^{\left(6\right)}\left(x\right)=e_{5,u}^{\left(6\right)}\left(x\right)=sin{c}^{\left(6\right)}\left(x\right)$. □

By Theorem 1 and Lemma 1, we have $sin{c}^{\left(6\right)}\left(x\right)\le 0$ and there exists $\epsilon \in (0,\pi /2]$ such that

$$e_{5,l}\left(0\right)=e_{5,l}\left(b\right)=e_{5,l}\left(c\right)=e_{5,l}\left(d\right)=e_{5,l}^{\prime }\left(c\right)=e_{5,l}^{\prime }\left(d\right)=0,$$

$$e_{5,l}\left(x\right)=e_{5,l}^{\left(6\right)}\left(\epsilon \right)x(x-b){(x-c)}^2{(x-d)}^2\ge 0,$$

$$e_{5,u}\left(0\right)=e_{5,u}\left(b\right)=e_{5,u}\left(c\right)=e_{5,l}^{\prime }\left(0\right)=e_{5,l}^{\prime }\left(b\right)=e_{5,l}^{\prime }\left(c\right)=0,$$

$$e_{5,u}\left(x\right)=e_{5,u}^{\left(6\right)}\left(\eta \right)x^2{(x-b)}^2{(x-c)}^2\le 0,$$

which means that $g_5^l\left(x\right)\le \frac{sinx}{x}\le g_5^u\left(x\right)$. The theorem is proved.

Theorem 4 gives new two-sided bounds of $sinc\left(x\right)$ using polynomials of degree 5. The conclusion that Equation (14) achieves much tighter bounds than those of previous methods is easy to be verified. Figure 3 gives the errors between $sinc\left(x\right)$ and polynomial bounds of degree 3 and 5. However, the results of Equations (8), (9) and (14) are close in Figure 3; in particular, we give the errors between sinc(x) and the polynomial bounds of Equations (8), (9) and (14) in Figure 4. Figure 4 shows that Equations (8) and (9) have similar errors and the error of Equation (14) is obviously smaller than that of Equations (8) and (9).

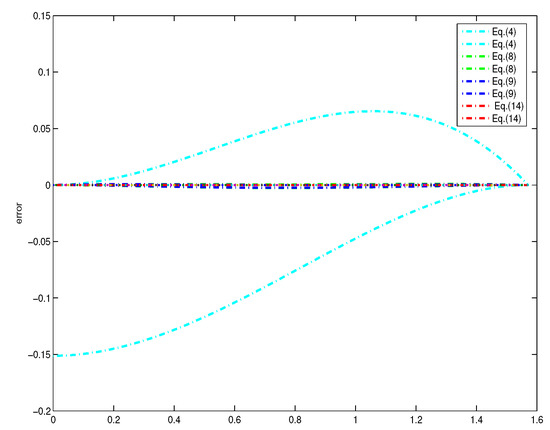
Figure 3. Error plots between sinc(x) and the polynomial bounds of degrees 3 and 5.

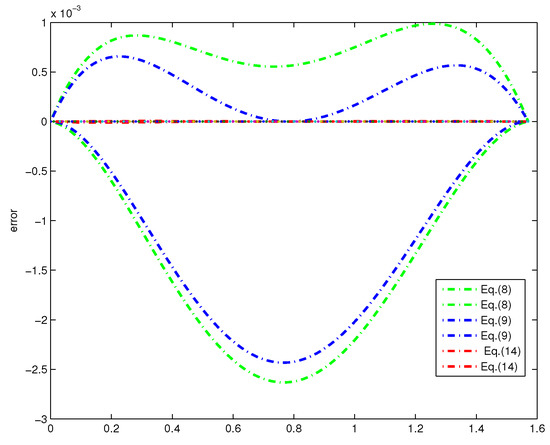
Figure 4. Error plots between sinc(x) and the polynomial bounds of Equations (8), (9) and (14).

Figure 5 gives the errors between $sinc\left(x\right)$ and the polynomial bounds of degrees 4 and 5. For the same reason, we also give the errors between sinc(x) and the polynomial bounds of Equations (10) and (14) in Figure 6.

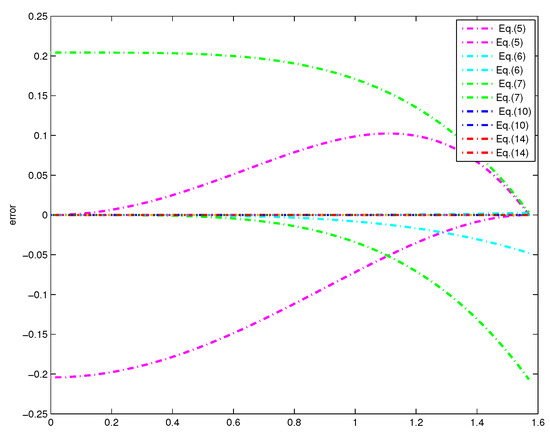
Figure 5. Error plots between sinc(x) and the polynomial bounds of degrees 4 and 5.

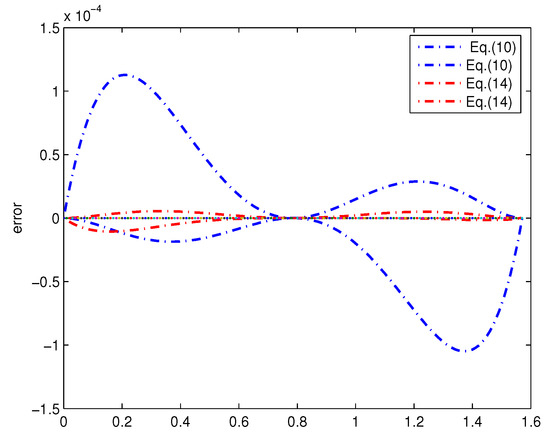
Figure 6. Error plots between sinc(x) and the polynomial bounds of Equations (10) and (14).

Figure 7 gives a comparison between Equations (14) and (11); here, we set $m=5,8,10$ in Equation (11), where m is the degree of the polynomial. Our results are obviously better than that of Zeng [15]; meanwhile, we find that the error is even greater with the increase of m’s value of Equation (11). Maximum errors of different methods are presented in Table 1. Although Equation (11) gives the polynomial bounds of degree m for sinc(x), the error of Equation (11) is relatively large. The maximum errors of Equation (10) is close to the results of Equation (14); however, it is still very obvious that the maximum error of Equation (14) is the smallest.

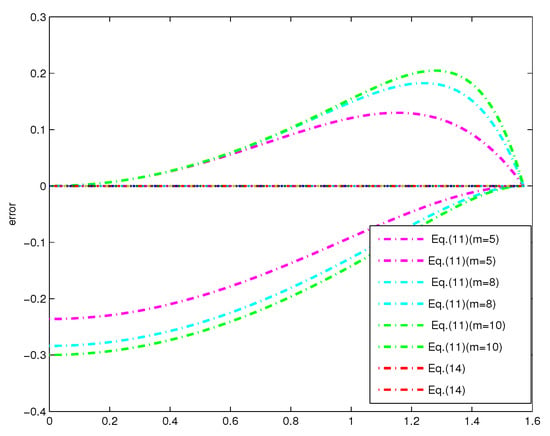
Figure 7. Error plots between sinc(x) and the polynomial bounds of Equations (11) and (14).

3. Conclusions

In this paper, we gave new refinements and improvements of Jordan’s inequality. Firstly, the new polynomial bounds of degrees 1 and 2 were given. The results show that our bounds are tighter than the previous results of polynomials of degrees 1 and 2. Meanwhile, we presented new improvements of Jordan’s inequality using polynomials of degree 5, which can achieve much tighter bounds than those previous methods.

Much work still remains. The polynomial bounds of degree 5 were given in this paper, and the polynomial bounds of higher degree are needed for tighter bounds. However, it will require more complicated calculations. Furthermore, it is still an important problem to find tighter polynomial bounds of lower degrees.