Resistance Distance in H-Join of Graphs G₁,G₂,…,G_k

Abstract

In view of the wide application of resistance distance, the computation of resistance distance in various graphs becomes one of the main topics. In this paper, we aim to compute resistance distance in H-join of graphs $G_1,G_2,\dots ,G_k$. Recall that H is an arbitrary graph with $V\left(H\right)=\{1,2,\dots ,k\}$, and $G_1,G_2,\dots ,G_k$ are disjoint graphs. Then, the H-join of graphs $G_1,G_2,\dots ,G_k$, denoted by ${\bigvee }_H\{G_1,G_2,\dots ,G_k\}$, is a graph formed by taking $G_1,G_2,\dots ,G_k$ and joining every vertex of $G_i$ to every vertex of $G_j$ whenever i is adjacent to j in H. Here, we first give the Laplacian matrix of ${\bigvee }_H\{G_1,G_2,\dots ,G_k\}$, and then give a $\left\{1\right\}$-inverse $L{\left({\bigvee }_H\{G_1,G_2,\dots ,G_k\}\right)}^{\left\{1\right\}}$ or group inverse $L{\left({\bigvee }_H\{G_1,G_2,\dots ,G_k\}\right)}^{\#}$ of $L\left({\bigvee }_H\{G_1,G_2,\dots ,G_k\}\right)$. It is well know that, there exists a relationship between resistance distance and entries of $\left\{1\right\}$-inverse or group inverse. Therefore, we can easily obtain resistance distance in ${\bigvee }_H\{G_1,G_2,\dots ,G_k\}$. In addition, some applications are presented in this paper.

1. Introduction

Throughout this paper, “G is a graph” always means that “G is a simple and undirected graph”. Moreover, we denote a graph G by $G=\left(V\right(G),E(G\left)\right)$, where $V\left(G\right)=\{v_1,v_2,\dots ,v_n\}$ is the vertex set and $E\left(G\right)=\{e_1,e_2,\dots ,e_m\}$ is the edge set of G. Associated with a graph G, some matrices characterize the structure of G, such as the adjacency matrix $A\left(G\right)$, which is an $n\times n$ matrix with entry $a_{ij}=1$ if $v_i$ and $v_j$ are adjacent in G, and $a_{ij}=0$ otherwise, the diagonal matrix $D\left(G\right)$ with diagonal entries $d_G\left(v_1\right),d_G\left(v_2\right),\dots ,d_G\left(v_n\right)$ and the Laplacian matrix $L\left(G\right)$, which is $D\left(G\right)-A\left(G\right)$. Let $I_n$ denote the unit matrix of order n, 1_n be the all-one column vector of dimension n and $J_{n\times m}$ be the all-one $n\times m$-matrix. For more detail, one can refer to [1,2] for the definitions and notions in the paper.

It is rather clear that, from some given graphs, a big graph arises by the help of graph operations, such as the Cartesian product, the Kronecker product, the corona graph, the neighborhood corona graph and subdivision-vertex join and subdivision-edge join of graphs (see [3,4,5,6,7]). Furthermore, following [8], from an arbitrary graph H of order k and graphs $G_1,G_2,\dots ,G_k$, we obtain a new graph called H-join of graphs $G_1,G_2,\dots ,G_k$, which is denoted by ${\bigvee }_H\{G_1,G_2,\dots ,G_k\}$, for detail:

Definition 1.

Let H be an arbitrary graph with $V\left(H\right)=\{1,2,\dots ,k\}$, and $G_1,G_2,\dots ,G_k$ be disjoint graphs of orders $n_1,n_2,\dots ,n_k$. The H-join of graphs $G_1,G_2,\dots ,G_k$, which is denoted by ${\bigvee }_H\{G_1,G_2,\dots ,G_k\}$, is a graph formed by taking $G_1,G_2,\dots ,G_k$ and joining every vertex of $G_i$ to every vertex of $G_j$ whenever i is adjacent to j in H. Particularly, ${\bigvee }_H\{G_1,G_1,\dots ,G_1\}$ is denoted by $H⨀G_1$.

Example 1.

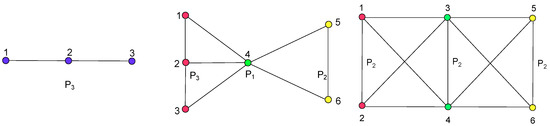
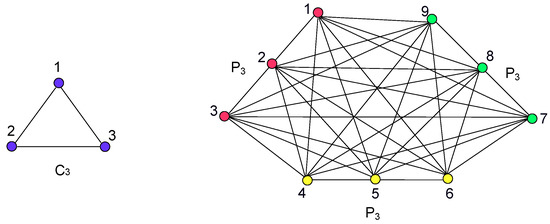
Let $P_n$ and $C_n$ be a path and a cycle with n vertices. Then, ${\bigvee }_{P_3}\{P_3,P_1,P_2\}$, $P_3⨀P_2$ and $C_3⨀P_3$ are as follows (Figure 1 and Figure 2).

As we know, the length of a shortest path between vertices $v_i$ and $v_j$, which is denoted by $d_{ij}$, is the conventional distance. However, it does not apply to some practical situations, such as electrical network. Thus, based on electrical network theory, Klein and Randić introduced a new distance called resistance distance ([9]). The resistance distance between vertices $v_i$ and $v_j$ is denoted by $r_{ij}$, and, in fact, $r_{ij}$ is the effective electrical resistance between $v_i$ and $v_j$ if every edge of G is replaced by a unit resistor. In view of its practical application, resistance distance was widely explored by many authors. One of the main topics in the study of resistance distance is to determine it in various graphs. For example, from [10], one would know that how $r_{ij}$ can be computed from the Laplacian matrix of the graph; in [11], authors gave the resistance distance between any two vertices of a wheel and a fan; in [3], authors obtained formulae for resistance distance in subdivision-vertex join and subdivision-edge join of graphs; recently, in [12], authors gave the resistance distance in corona and the neighborhood corona graphs of two disjoint graphs. Except for the above, one can refer to [13,14,15,16,17,18,19,20] for more information.

Motivated by the study of resistance distance and graph operations, a natural question arises: what is the resistance distance in ${\bigvee }_H\{G_1,G_2,\dots ,G_k\}$? In fact, this paper focuses on this question, gives resistance distance in H-join of graphs $G_1,G_2,\dots ,G_k$ and finally presents some applications.

2. Preliminaries

Recall that, for a matrix M, a $\left\{1\right\}$-inverse of M, which is always denoted by $M^{\left\{1\right\}}$, is a matrix X such that $MXM=M$. For a square matrix M, the group inverse of M, which is denoted by $M^{\#}$, is the unique matrix X such that the following hold: $\left(1\right)MXM=M;\left(2\right)XMX=X;\left(3\right)MX=XM$. It is well-known that $M^{\#}$ exists if and only if rank(M)=rank($M^2$). Therefore, $A^{\#}$ exists and it is a $\left\{1\right\}$-inverse of A, whenever A is a real symmetric. In fact, assume that A is a real symmetric matrix and U is an orthogonal matrix (i.e., $U{U}^T=U^{T}U=I$), such that $A=U^{T}diag\{{\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_n\}U$, where ${\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_n$ are eigenvalues of A. Then, $A^{\#}=U^{T}diag\{f\left({\lambda }_1\right),f\left({\lambda }_2\right),\cdots ,f\left({\lambda }_n\right)\}U$, where

$$f\left({\lambda }_i\right)=\left\{\begin{array}{cc}1/{\lambda }_i,& \mathrm{if}{\lambda }_i\ne 0,\hfill \\ 0,& \mathrm{if}{\lambda }_i=0.\hfill \end{array}\right.$$

Note that the Laplacian matrix $L\left(G\right)$ of a graph G is real symmetric. Thus, $L{\left(G\right)}^{\#}$ exists. For more detail about the group inverse of the Laplacian matrix of a graph, see [21].

Lemma 1

([3,22]). Let $L=\left(\begin{array}{cc}{L}_1& L_2\\ L_2^T& L_3\end{array}\right)$ be the Laplacian matrix of a connected graph. Assume that $L_1$ is nonsingular. Denote $S=L_3-L_2^T{L}_1^{-1}{L}_2$. Then,

(1)

$\left(\begin{array}{cc}{L}_1^{-1}+L_1^{-1}{L}_2{S}^{\#}{L}_2^T{L}_1^{-1}& -L_1^{-1}{L}_2{S}^{\#}\\ -S^{\#}{L}_2^T{L}_1^{-1}& S^{\#}\end{array}\right)$ is a symmetric $\left\{1\right\}$-inverse of L.

(2)

If each column vector of $L_2$ is $\mathbf{1}$ or a zero vector, then $\left(\begin{array}{cc}{L}_1^{-1}& 0\\ 0& S^{\#}\end{array}\right)$ is a symmetric $\left\{1\right\}$-inverse of L.

In order to compute the inverse of a matrix, the next lemma is useful.

Lemma 2

([3]). Let $M=\left(\begin{array}{cc}A& B\\ C& D\end{array}\right)$ be a nonsingular matrix. If A and D are nonsingular, then

$$M^{-1}=\left(\begin{array}{cc}{A}^{-1}+A^{-1}B{S}^{-1}C{A}^{-1}& -A^{-1}B{S}^{-1}\\ -S^{-1}C{A}^{-1}& S^{-1}\end{array}\right),$$

where $S=D-C{A}^{-1}B$ is the Schur complement of A in M.

One of the important applications of group inverse $L{\left(G\right)}^{\#}$ or $\left\{1\right\}$-inverse $L{\left(G\right)}^{\left\{1\right\}}$ is based on the following fact, which gives the formulae for resistance distance.

Lemma 3

([3]). Let G be a connected graph and ${\left(L\left(G\right)\right)}_{ij}$ be the $(i,j)$-entry of the Laplacian matrix $L\left(G\right)$. Then,

$$\begin{array}{cc}\hfill r_{ij}\left(G\right)& ={\left(L{\left(G\right)}^{\left\{1\right\}}\right)}_{ii}+{\left(L{\left(G\right)}^{\left\{1\right\}}\right)}_{jj}-{\left(L{\left(G\right)}^{\left\{1\right\}}\right)}_{ij}-{\left(L{\left(G\right)}^{\left\{1\right\}}\right)}_{ji}\hfill \\ & ={\left(L{\left(G\right)}^{\#}\right)}_{ii}+{\left(L{\left(G\right)}^{\#}\right)}_{jj}-2{\left(L{\left(G\right)}^{\#}\right)}_{ij}.\hfill \end{array}$$

3. Main Results

Now, we turn to compute resistance distance in H-join of graphs $G_1,G_2,\dots ,G_k$. Denote $G={\bigvee }_H\{G_1,G_2,\dots ,G_k\}$. Keeping Lemma 3 in mind, we only need to compute the group inverse $L{\left(G\right)}^{\#}$ or a $\left\{1\right\}$-inverse $L{\left(G\right)}^{\left\{1\right\}}$.

First, we give the Laplacian matrix $L\left(G\right)$ of G.

Theorem 1.

Let H be an arbitrary graph with $V\left(H\right)=\{1,2,\dots ,k\}$, and $G_i$ be the disjoint graph of order $n_i(i=1,2,\dots ,k)$. Assume that the adjacency matrix of H is $A\left(H\right)={\left(a_{ij}\right)}_k$ and

$$A\left(H\right){(n_1,n_2,\dots ,n_k)}^T={(m_1,m_2,\dots ,m_k)}^T.$$

Denote $G={\bigvee }_H\{G_1,G_2,\dots ,G_k\}$, and label the $n_i$ vertices of $G_i$ with

$$V\left(G_i\right)=\{v_i^{n_1+\cdots +n_{i-1}+1},v_i^{n_1+\cdots +n_{i-1}+2},\dots ,v_i^{n_1+\cdots +n_{i-1}+n_i}\}.$$

Then, $V\left(G\right)=\{v_1^1,\dots ,v_1^{n_1},\dots ,v_i^{n_1+\cdots +n_{i-1}+1},\dots ,v_i^{n_1+\cdots +n_{i-1}+n_i},\dots ,v_k^{n_1+\cdots +n_{k-1}+1},\dots ,v_k^{n_1+\cdots +n_{k-1}+n_k}\}$, and the Laplacian matrix $L\left(G\right)$ of G is

$$\left(\begin{array}{cccc}L\left(G_1\right)+m_1{I}_{n_1}& 0& \cdots & 0\\ 0& L\left(G_2\right)+m_2{I}_{n_2}& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & L\left(G_k\right)+m_k{I}_{n_k}\end{array}\right)-\left(\begin{array}{cccc}{a}_{11}{J}_{n_1\times n_1}& a_{12}{J}_{n_1\times n_2}& \cdots & a_{1k}{J}_{n_1\times n_k}\\ a_{21}{J}_{n_2\times n_1}& a_{22}{J}_{n_2\times n_2}& \cdots & a_{2k}{J}_{n_2\times n_k}\\ ⋮& ⋮& ⋮\\ a_{k1}{J}_{n_k\times n_1}& a_{k2}{J}_{n_k\times n_2}& \cdots & a_{kk}{J}_{n_k\times n_k}\end{array}\right).$$

Proof. 

Clearly, all of the diagonal matrix $D\left(G\right)$, the adjacency matrix $A\left(G\right)$ and the Laplacian matrix $L\left(G\right)$ are partitioned $k\times k$-matrixes, whose $\left(ij\right)$-entry is a $n_i\times n_j$-matrix. We proceed via the following steps:

(1) The diagonal matrix $D\left(G\right)$ of G.

Obviously, the degree increment of $V\left(G_i\right)$ depends on the i-th line $(a_{i1}{a}_{i2}\cdots a_{ik})$ of $A\left(H\right)$. For detail, if $a_{ij}=1,j=1,2,\cdots ,k$, then every vertex of $G_j$ is joined to every vertex of $G_i$, that is, the increment of each vertex in $V\left(G_i\right)$ is $a_{ij}{n}_j$. Otherwise, that is $a_{ij}=0$, the increment is zero, which can also be written by $a_{ij}{n}_j$. In general, the degree increment of each vertex of $V\left(G_i\right)$ is

$$a_{i1}{n}_1+a_{i2}{n}_2+\cdots +a_{ik}{n}_k=m_i$$

.

Consequently, the diagonal matrix of G is

$$D\left(G\right)=\left(\begin{array}{cccc}D\left(G_1\right)+m_1{I}_{n_1}& 0& \cdots & 0\\ 0& D\left(G_2\right)+m_2{I}_{n_2}& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & D\left(G_k\right)+m_k{I}_{n_k}\end{array}\right).$$

(2) The adjacency matrix $A\left(G\right)$ of G.

Similarly, the i-th line of the partitioned matrixes $A\left(G\right)$ also relies on $(a_{i1}{a}_{i2}\cdots a_{ik})$. Assume that $a_{ij}=1$. Then, every vertex of $G_j$ is joined to every vertex of $G_i$. Thus, the $\left(ij\right)$-entry of $A\left(G\right)$ is $J_{n_i\times n_j}$, which is $a_{ij}{J}_{n_i\times n_j}$. If $a_{ij}=0$, then there is no edge between $V\left(G_i\right)$ and $V\left(G_j\right)$, that is, the $\left(ij\right)$-entry of $A\left(G\right)$ is zero. However, in this case, we can also denote it by $a_{ij}{J}_{n_i\times n_j}$. Note that the above holds for $i=j$. Therefore, the adjacency matrix of G is

$$A\left(G\right)=\left(\begin{array}{cccc}A\left(G_1\right)& 0& \cdots & 0\\ 0& A\left(G_2\right)& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & A\left(G_k\right)\end{array}\right)+\left(\begin{array}{cccc}{a}_{11}{J}_{n_1\times n_1}& a_{12}{J}_{n_1\times n_2}& \cdots & a_{ik}{J}_{n_1\times n_k}\\ a_{21}{J}_{n_2\times n_1}& a_{22}{J}_{n_1\times n_2}& \cdots & a_{2k}{J}_{n_2\times n_k}\\ ⋮& ⋮& ⋮\\ a_{k1}{J}_{n_k\times n_1}& a_{k2}{J}_{n_k\times n_2}& \cdots & a_{2k}{J}_{n_k\times n_k}\end{array}\right).$$

(3) The Laplacian matrix $L\left(G\right)$ of G.

With respect to the above results, the Laplacian matrix $L\left(G\right)$ of G is the Theorem 1.  ☐

According to Theorem 1 and Lemma 1, we finally obtain a symmetric $\left\{1\right\}$-inverse of $L\left(G\right)$.

Theorem 2.

Let H be an arbitrary connected graph with $V\left(H\right)=\{1,2,\dots ,k\}$, and $G_i$ be disjoint connected graph of order $n_i$$(i=1,2,\dots ,k)$. Assume that $A\left(H\right)={\left(a_{ij}\right)}_k$ and $A\left(H\right){(n_1,n_2,\dots ,n_k)}^T={(m_1,m_2,\dots ,m_k)}^T$. Denote $G={\bigvee }_H\{G_1,G_2,\dots ,G_k\}$. Then, the following matrix

$$\left(\begin{array}{cc}{L}_1^{-1}+L_1^{-1}{L}_2{S}^{\#}{L}_2^T{L}_1^{-1}& -L_1^{-1}{L}_2{S}^{\#}\\ -S^{\#}{L}_2^T{L}_1^{-1}& S^{\#}\end{array}\right)$$

is a symmetric $\left\{1\right\}$-inverse of $L\left(G\right)$, where

$$\begin{array}{cc}\hfill L_1& =L\left(G_1\right)+m_1{I}_{n_1};\hfill \\ \hfill L_2& =-(a_{12}{J}_{n_1\times n_2}{a}_{13}{J}_{n_1\times n_3}\cdots a_{1k}{J}_{n_1\times n_k});\hfill \\ \hfill L_3& =diag\{L\left(G_2\right)+m_2{I}_{n_2},\dots ,L\left(G_k\right)+m_k{I}_{n_k}\}-{\left(a_{ij}{J}_{n_i\times n_j}\right)}_{i,j=2,3,\dots ,k};\hfill \\ \hfill S& =L_3-L_2^T{L}_1^{-1}{L}_2\hfill \\ & =diag\{L\left(G_2\right)+m_2{I}_{n_2},\dots ,L\left(G_k\right)+m_k{I}_{n_k}\}-{\left((a_{ij}+a_{i1}{a}_{1j}s)J_{n_i\times n_j}\right)}_{i,j=2,3,\dots ,k}\hfill \\ & =L_3-{\left(\left(a_{i1}{a}_{1j}s\right)J_{n_i\times n_j}\right)}_{i,j=2,3,\dots ,k}\hfill \\ & =L_3-sB{B}^T.\hfill \end{array}$$

Here, $s={\mathbf{1}}_{n_1}^T{L}_1^{-1}{\mathbf{1}}_{n_1}$ and $B^T=\left(a_{12}{\mathbf{1}}_{n_2}^T{a}_{13}{\mathbf{1}}_{n_3}^T\cdots a_{1k}{\mathbf{1}}_{n_k}^T\right)$.

Proof. 

Note that all of H and $G_1,G_2,\dots ,G_k$ are connected. Thus, it is easy to show that G is connected. By Theorem 1, we have the Laplacian matrix $L\left(G\right)$ of G. In order to give a $\left\{1\right\}$-inverse of $L\left(G\right)$ with the help of Lemma 1, we further divide $L\left(G\right)$ into blocks $L\left(G\right)=\left(\begin{array}{cc}{L}_1& L_2\\ L_2^T& L_3\end{array}\right)$, where

$$\begin{array}{cc}\hfill L_1=& L\left(G_1\right)+m_1{I}_{n_1}-a_{11}{J}_{n_1\times n_1}=L\left(G_1\right)+m_1{I}_{n_1};\hfill \\ \hfill L_2=& -(a_{12}{J}_{n_1\times n_2}{a}_{13}{J}_{n_1\times n_3}\cdots a_{1k}{J}_{n_1\times n_k});\hfill \\ \hfill L_3=& \left(\begin{array}{ccc}L\left(G_2\right)+m_2{I}_{n_2}& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & L\left(G_k\right)+m_k{I}_{n_k}\end{array}\right)-\left(\begin{array}{ccc}{a}_{22}{J}_{n_2\times n_2}& \cdots & a_{2k}{J}_{n_2\times n_k}\\ ⋮& ⋮\\ a_{k2}{J}_{n_k\times n_2}& \cdots & a_{kk}{J}_{n_k\times n_k}\end{array}\right).\hfill \end{array}$$

Note that $L_2^T=\left(\begin{array}{c}-a_{12}{J}_{n_2\times n_1}\\ -a_{13}{J}_{n_3\times n_1}\\ ⋮\\ -a_{1k}{J}_{n_k\times n_1}\end{array}\right)$. Thus, we have

$$\begin{array}{cc}\hfill L_2^T{L}_1^{-1}{L}_2=& \left(\begin{array}{c}{a}_{12}{J}_{n_2\times n_1}\\ a_{13}{J}_{n_3\times n_1}\\ \ddots \\ a_{1k}{J}_{n_k\times n_1}\end{array}\right)L_1^{-1}(a_{12}{J}_{n_1\times n_2}{a}_{13}{J}_{n_1\times n_3}\cdots a_{1k}{J}_{n_1\times n_k})\hfill \\ \hfill =& \left(\begin{array}{ccc}{a}_{12}{a}_{12}{J}_{n_2\times n_1}{L}_1^{-1}{J}_{n_1\times n_2}& \cdots & a_{12}{a}_{1k}{J}_{n_2\times n_1}{L}_1^{-1}{J}_{n_1\times n_k}\\ a_{13}{a}_{12}{J}_{n_3\times n_1}{L}_1^{-1}{J}_{n_1\times n_2}& \cdots & a_{13}{a}_{1k}{J}_{n_3\times n_1}{L}_1^{-1}{J}_{n_1\times n_k}\\ ⋮& ⋮\\ a_{1k}{a}_{12}{J}_{n_k\times n_1}{L}_1^{-1}{J}_{n_1\times n_2}& \cdots & a_{1k}{a}_{1k}{J}_{n_k\times n_1}{L}_1^{-1}{J}_{n_1\times n_k}\end{array}\right).\hfill \end{array}$$

Since $J_{n_i\times n_1}{L}_1^{-1}{J}_{n_1\times n_j}=s{J}_{n_i\times n_j}$, where $s={\mathbf{1}}_{n_1}^T{L}_1^{-1}{\mathbf{1}}_{n_1}\in \mathbb{R}$, we have

$$\begin{array}{cc}\hfill L_2^T{L}_1^{-1}{L}_2& =s\left(\begin{array}{ccc}{a}_{12}{a}_{12}{J}_{n_2\times n_2}& \cdots & a_{12}{a}_{1k}{J}_{n_2\times n_k}\\ a_{13}{a}_{12}{J}_{n_3\times n_2}& \cdots & a_{13}{a}_{1k}{J}_{n_3\times n_k}\\ ⋮& ⋮\\ a_{1k}{a}_{12}{J}_{n_k\times n_2}& \cdots & a_{1k}{a}_{1k}{J}_{n_k\times n_k}\end{array}\right)\hfill \\ & =s\left(\begin{array}{c}{a}_{12}{\mathbf{1}}_{n_2}\\ a_{13}{\mathbf{1}}_{n_3}\\ ⋮\\ a_{1k}{\mathbf{1}}_{n_k}\end{array}\right)(a_{12}{\mathbf{1}}_{n_2}^T{a}_{13}{\mathbf{1}}_{n_3}^T\dots a_{1k}{\mathbf{1}}_{n_k}^T).\hfill \end{array}$$

Assume that B is a column vector of dimension $n_2+n_3+\cdots +n_k$ satisfying

$$B^T=\left(a_{12}{\mathbf{1}}_{n_2}^T{a}_{13}{\mathbf{1}}_{n_3}^T\dots a_{1k}{\mathbf{1}}_{n_k}^T\right).$$

Therefore, $S=L_3-L_2^T{L}_1^{-1}{L}_2$ has three forms:

$$\begin{array}{cc}\hfill S& =diag\{L\left(G_2\right)+m_2{I}_{n_2},\dots ,L\left(G_k\right)+m_k{I}_{n_k}\}-{\left((a_{ij}+a_{i1}{a}_{1j}s)J_{n_i\times n_j}\right)}_{i,j=2,3,\dots ,k}\hfill \\ & =L_3-s{\left(a_{i1}{a}_{1j}{J}_{n_i\times n_j}\right)}_{i,j=2,3,\dots ,k}\hfill \\ & =L_3-sB{B}^T.\hfill \end{array}$$

By Lemma 1, we know that Theorem 2 holds.  ☐

Recall that the Kronecker product $A\otimes B$ ([23]) of two matrices $A={\left(a_{ij}\right)}_{m\times n}$ and $B={\left(b_{ij}\right)}_{p\times q}$ is an $mp\times nq$-matrix obtained from A by replacing every element $a_{ij}$ by $a_{ij}B$. As an application of Theorem 2, we easily obtain a symmetric $\left\{1\right\}$-inverse of $L(H⨀G)$.

Corollary 1.

Let H be an arbitrary connected graph with k vertices and G be a connected graph with n vertices. Assume that $A\left(H\right)=\left(\begin{array}{cc}{0}_{1\times 1}& H_2\\ H_2^T& H_3\end{array}\right)$ and $nA\left(H\right){\mathbf{1}}_n=nD\left(H\right){\mathbf{1}}_n={(m_1,m_2,\dots ,m_k)}^T$. Then, the following matrix

$$\left(\begin{array}{cc}{L}_1^{-1}+L_1^{-1}{L}_2{S}^{\#}{L}_2^T{L}_1^{-1}& -L_1^{-1}{L}_2{S}^{\#}\\ -S^{\#}{L}_2^T{L}_1^{-1}& S^{\#}\end{array}\right)$$

is a symmetric $\left\{1\right\}$-inverse of $L(H⨀G)$, where

$$\begin{array}{cc}\hfill L_1& =L\left(G\right)+m_1{I}_n;\hfill \\ \hfill L_2& =-H_2\otimes J_{n\times n};\hfill \\ \hfill L_3& =I_{k-1}\otimes L\left(G\right)+diag\{m_2,\dots ,m_k\}\otimes I_n-H_3\otimes J_{n\times n};\hfill \\ \hfill S& =L_3-L_2^T{L}_1^{-1}{L}_2\hfill \\ & =L_3-s(H_2^T\otimes {\mathbf{1}}_n)(H_2\otimes {\mathbf{1}}_n^T)\hfill \\ & =L_3-s\left(H_2^T{H}_2\right)\otimes J_{n\times n}.\hfill \end{array}$$

Here, $s={\mathbf{1}}_n^T{L}_1^{-1}{\mathbf{1}}_n$.

4. Some Applications

Now, we give a specific application of formation mentioned in the Section 2. Let A be a real symmetric such that ${\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_{n-1},0$ are eigenvalues of A and 0 is a simple eigenvalue. Assume that A is a real symmetric and U is an orthogonal matrix such that $A=U^{T}diag\{{\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_{n-1},0\}U$. Then, $A^{\#}=U^{T}diag\{\frac{1}{{\lambda }_1},\frac{1}{{\lambda }_2},\cdots ,\frac{1}{{\lambda }_{n-1}},0\}U$.

Example 2.

Compute resistance distance in $G={\bigvee }_{P_3}\{P_3,P_1,P_2\}$ (see Figure 1).

Step 1. We label the vertices $P_3=\{v_1^1,v_1^2,v_1^3\},P_1=\left\{v_2^4\right\},P_2=\{v_3^5,v_3^6\}$. Then,

$$V\left(G\right)=\{v_1^1,v_1^2,v_1^3,v_2^4,v_3^5,v_3^6\}.$$

Note that $A\left(P_3\right)\left(\begin{array}{c}3\\ 1\\ 2\end{array}\right)=\left(\begin{array}{ccc}0& 1& 0\\ 1& 0& 1\\ 0& 1& 0\end{array}\right)\left(\begin{array}{c}3\\ 1\\ 2\end{array}\right)=\left(\begin{array}{c}1\\ 5\\ 1\end{array}\right).$ Thus, the Laplacian matrix of G is

$$L\left(G\right)=\left(\begin{array}{ccc}L\left(P_3\right)+I_3& 0& 0\\ 0& L\left(P_1\right)+5I_1& 0\\ 0& 0& L\left(P_2\right)+I_2\end{array}\right)-\left(\begin{array}{ccc}{0}_{3\times 3}& J_{3\times 1}& 0_{3\times 2}\\ J_{1\times 3}& 0_{1\times 1}& J_{1\times 2}\\ 0_{2\times 3}& J_{2\times 1}& 0_{2\times 2}\end{array}\right)=\left(\begin{array}{cc}{L}_1& L_2\\ L_2^T& L_3\end{array}\right),$$

where $L_1=L\left(P_3\right)+I_3=\left(\begin{array}{ccc}2& -1& 0\\ -1& 3& -1\\ 0& -1& 2\end{array}\right)$, $L_2=-\left(J_{3\times 1}{0}_{3\times 2}\right)=\left(\begin{array}{ccc}-1& 0& 0\\ -1& 0& 0\\ -1& 0& 0\end{array}\right)$ and

$$L_3=\left(\begin{array}{cc}L\left(P_1\right)+5I_1& -J_{1\times 2}\\ -J_{2\times 1}& L\left(P_2\right)+I_2\end{array}\right)=\left(\begin{array}{ccc}5& -1& -1\\ -1& 2& -1\\ -1& -1& 2\end{array}\right).$$

Step 2.$L_1^{-1}={\displaystyle \frac{1}{8}}\left(\begin{array}{ccc}5& 2& 1\\ 2& 4& 2\\ 1& 2& 5\end{array}\right)$ and so $s={\mathbf{1}}_3^T{L}_1^{-1}{\mathbf{1}}_3=3$. By Theorem 2, $B=\left(\begin{array}{c}1\\ 0\\ 0\end{array}\right)$ and $S=\left(\begin{array}{ccc}2& -1& -1\\ -1& 2& -1\\ -1& -1& 2\end{array}\right).$ By the formula at the beginning of this section, $S^{\#}={\displaystyle \frac{1}{9}}\left(\begin{array}{ccc}2& -1& -1\\ -1& 2& -1\\ -1& -1& 2\end{array}\right).$ Furthermore, $-L_1^{-1}{L}_2{S}^{\#}={\displaystyle \frac{1}{9}}\left(\begin{array}{ccc}2& -1& -1\\ 2& -1& -1\\ 2& -1& -1\end{array}\right)$ and $L_1^{-1}{L}_2{S}^{\#}{L}_2^T{L}_1^{-1}={\displaystyle \frac{2}{9}}{J}_{3\times 3}$.

Step 3. By Lemma 1 or Theorem 2, $\left(\begin{array}{cc}{\displaystyle \frac{1}{8}}\left(\begin{array}{ccc}5& 2& 1\\ 2& 4& 2\\ 1& 2& 5\end{array}\right)+{\displaystyle \frac{2}{9}}{J}_{3\times 3}& {\displaystyle \frac{1}{9}}\left(\begin{array}{ccc}2& -1& -1\\ 2& -1& -1\\ 2& -1& -1\end{array}\right)\\ {\displaystyle \frac{1}{9}}\left(\begin{array}{ccc}2& 2& 2\\ -1& -1& -1\\ -1& -1& -1\end{array}\right)& {\displaystyle \frac{1}{9}}\left(\begin{array}{ccc}2& -1& -1\\ -1& 2& -1\\ -1& -1& 2\end{array}\right)\end{array}\right)$ is a $\left\{1\right\}$-inverse of $L\left(G\right)$.

Step 4. In view of Lemma 3, the matrix whose $(i,j)$-entry is the resistance distance $r_{ij}$ between vertices $v^i$ and $v^j$ is

$$\left(\begin{array}{cccccc}0& {\displaystyle \frac{5}{8}}& 1& {\displaystyle \frac{5}{8}}& {\displaystyle \frac{31}{24}}& {\displaystyle \frac{31}{24}}\\ {\displaystyle \frac{5}{8}}& 0& {\displaystyle \frac{5}{8}}& {\displaystyle \frac{1}{2}}& {\displaystyle \frac{7}{6}}& {\displaystyle \frac{7}{6}}\\ 1& {\displaystyle \frac{5}{8}}& 0& {\displaystyle \frac{5}{8}}& {\displaystyle \frac{31}{24}}& {\displaystyle \frac{31}{24}}\\ {\displaystyle \frac{5}{8}}& {\displaystyle \frac{1}{2}}& {\displaystyle \frac{5}{8}}& 0& {\displaystyle \frac{2}{3}}& {\displaystyle \frac{2}{3}}\\ {\displaystyle \frac{31}{24}}& {\displaystyle \frac{7}{6}}& {\displaystyle \frac{31}{24}}& {\displaystyle \frac{2}{3}}& 0& {\displaystyle \frac{2}{3}}\\ {\displaystyle \frac{31}{24}}& {\displaystyle \frac{7}{6}}& {\displaystyle \frac{31}{24}}& {\displaystyle \frac{2}{3}}& {\displaystyle \frac{2}{3}}& 0\end{array}\right).$$

Example 3.

Assume that $G=P_3⨀P_2$ (see Figure 1). Then, the Laplacian matrix of G is

$$L\left(G\right)=\left(\begin{array}{ccc}L\left(P_2\right)+2I_2& 0& 0\\ 0& L\left(P_2\right)+4I_2& 0\\ 0& 0& L\left(P_2\right)+2I_2\end{array}\right)-\left(\begin{array}{ccc}{0}_{2\times 2}& J_{2\times 2}& 0_{2\times 2}\\ J_{2\times 2}& 0_{2\times 2}& J_{2\times 2}\\ 0_{2\times 2}& J_{2\times 2}& 0_{2\times 2}\end{array}\right).$$

From Theorem 2, we have that the matrix $\left(\begin{array}{cc}{\displaystyle \frac{1}{16}}\left(\begin{array}{cc}7& 3\\ 3& 7\end{array}\right)& {\displaystyle \frac{1}{16}}\left(\begin{array}{cccc}1& 1& -1& -1\\ 1& 1& -1& -1\end{array}\right)\\ {\displaystyle \frac{1}{16}}\left(\begin{array}{cc}1& 1\\ 1& 1\\ -1& -1\\ -1& -1\end{array}\right)& {\displaystyle \frac{1}{48}}\left(\begin{array}{cccc}7& -1& -3& -3\\ -1& 7& -3& -3\\ -3& -3& 9& -3\\ -3& -3& -3& 9\end{array}\right)\end{array}\right)$ is a $\left\{1\right\}$-inverse of $L\left(G\right)$.

Thus, the matrix whose $(i,j)$-entry is $r_{ij}$ is

$$\left(\begin{array}{cccccc}0& {\displaystyle \frac{1}{2}}& {\displaystyle \frac{11}{24}}& {\displaystyle \frac{11}{24}}& {\displaystyle \frac{3}{4}}& {\displaystyle \frac{3}{4}}\\ {\displaystyle \frac{1}{2}}& 0& {\displaystyle \frac{11}{24}}& {\displaystyle \frac{11}{24}}& {\displaystyle \frac{3}{4}}& {\displaystyle \frac{3}{4}}\\ {\displaystyle \frac{11}{24}}& {\displaystyle \frac{11}{24}}& 0& {\displaystyle \frac{1}{3}}& {\displaystyle \frac{11}{24}}& {\displaystyle \frac{11}{24}}\\ {\displaystyle \frac{11}{24}}& {\displaystyle \frac{11}{24}}& {\displaystyle \frac{1}{3}}& 0& {\displaystyle \frac{11}{24}}& {\displaystyle \frac{11}{24}}\\ {\displaystyle \frac{3}{4}}& {\displaystyle \frac{3}{4}}& {\displaystyle \frac{11}{24}}& {\displaystyle \frac{11}{24}}& 0& {\displaystyle \frac{1}{2}}\\ {\displaystyle \frac{3}{4}}& {\displaystyle \frac{3}{4}}& {\displaystyle \frac{11}{24}}& {\displaystyle \frac{11}{24}}& {\displaystyle \frac{1}{2}}& 0\end{array}\right).$$

Example 4.

Assume that $G=C_3⨀P_3$ (see Figure 2). Then, the Laplacian matrix of G is

$$L\left(G\right)=\left(\begin{array}{ccc}L\left(P_3\right)+6I_3& 0& 0\\ 0& L\left(P_3\right)+6I_3& 0\\ 0& 0& L\left(P_3\right)+6I_3\end{array}\right)-\left(\begin{array}{ccc}{0}_{3\times 3}& J_{3\times 3}& J_{3\times 3}\\ J_{3\times 3}& 0_{3\times 3}& J_{3\times 3}\\ J_{3\times 3}& J_{3\times 3}& 0_{3\times 3}\end{array}\right).$$

Based on Theorem 2, the matrix $\left(\begin{array}{ccc}A& {\displaystyle \frac{1}{27}}{J}_{3\times 3}& 0_{3\times 3}\\ {\displaystyle \frac{1}{27}}{J}_{3\times 3}& B& 0_{3\times 3}\\ 0_{3\times 3}& 0_{3\times 3}& S^{\#}\end{array}\right)$ is a $\left\{1\right\}$-inverse of $L\left(G\right)$, where

$$A=B=\left(\begin{array}{ccc}{\displaystyle \frac{31}{189}}& {\displaystyle \frac{1}{27}}& {\displaystyle \frac{4}{189}}\\ {\displaystyle \frac{1}{27}}& {\displaystyle \frac{4}{27}}& {\displaystyle \frac{1}{27}}\\ {\displaystyle \frac{4}{189}}& {\displaystyle \frac{1}{27}}& {\displaystyle \frac{31}{189}}\end{array}\right),S^{\#}=\left(\begin{array}{ccc}{\displaystyle \frac{17}{189}}& {\displaystyle \frac{-1}{27}}& {\displaystyle \frac{-10}{189}}\\ {\displaystyle \frac{-1}{27}}& {\displaystyle \frac{2}{27}}& {\displaystyle \frac{-1}{27}}\\ {\displaystyle \frac{-10}{189}}& {\displaystyle \frac{-1}{27}}& {\displaystyle \frac{17}{189}}\end{array}\right).$$

Thus, the matrix whose $(i,j)$-entry is $r_{ij}$ is

$$\left(\begin{array}{ccccccccc}0& {\displaystyle \frac{5}{21}}& {\displaystyle \frac{2}{7}}& {\displaystyle \frac{16}{63}}& {\displaystyle \frac{5}{21}}& {\displaystyle \frac{16}{63}}& {\displaystyle \frac{16}{63}}& {\displaystyle \frac{5}{21}}& {\displaystyle \frac{16}{63}}\\ {\displaystyle \frac{5}{21}}& 0& {\displaystyle \frac{5}{21}}& {\displaystyle \frac{5}{21}}& {\displaystyle \frac{2}{9}}& {\displaystyle \frac{5}{21}}& {\displaystyle \frac{5}{21}}& {\displaystyle \frac{2}{9}}& {\displaystyle \frac{5}{21}}\\ {\displaystyle \frac{2}{7}}& {\displaystyle \frac{5}{21}}& 0& {\displaystyle \frac{16}{63}}& {\displaystyle \frac{5}{21}}& {\displaystyle \frac{16}{63}}& {\displaystyle \frac{16}{63}}& {\displaystyle \frac{5}{21}}& {\displaystyle \frac{16}{63}}\\ {\displaystyle \frac{16}{63}}& {\displaystyle \frac{5}{21}}& {\displaystyle \frac{16}{63}}& 0& {\displaystyle \frac{5}{21}}& {\displaystyle \frac{2}{7}}& {\displaystyle \frac{16}{63}}& {\displaystyle \frac{5}{21}}& {\displaystyle \frac{16}{63}}\\ {\displaystyle \frac{5}{21}}& {\displaystyle \frac{2}{9}}& {\displaystyle \frac{5}{21}}& {\displaystyle \frac{5}{21}}& 0& {\displaystyle \frac{5}{21}}& {\displaystyle \frac{5}{21}}& {\displaystyle \frac{2}{9}}& {\displaystyle \frac{5}{21}}\\ {\displaystyle \frac{16}{63}}& {\displaystyle \frac{5}{21}}& {\displaystyle \frac{16}{63}}& {\displaystyle \frac{2}{7}}& {\displaystyle \frac{5}{21}}& 0& {\displaystyle \frac{16}{63}}& {\displaystyle \frac{5}{21}}& {\displaystyle \frac{16}{63}}\\ {\displaystyle \frac{16}{63}}& {\displaystyle \frac{5}{21}}& {\displaystyle \frac{16}{63}}& {\displaystyle \frac{16}{63}}& {\displaystyle \frac{5}{21}}& {\displaystyle \frac{16}{63}}& 0& {\displaystyle \frac{5}{21}}& {\displaystyle \frac{2}{7}}\\ {\displaystyle \frac{5}{21}}& {\displaystyle \frac{2}{9}}& {\displaystyle \frac{5}{21}}& {\displaystyle \frac{5}{21}}& {\displaystyle \frac{2}{9}}& {\displaystyle \frac{5}{21}}& {\displaystyle \frac{5}{21}}& 0& {\displaystyle \frac{5}{21}}\\ {\displaystyle \frac{16}{63}}& {\displaystyle \frac{5}{21}}& {\displaystyle \frac{16}{63}}& {\displaystyle \frac{16}{63}}& {\displaystyle \frac{5}{21}}& {\displaystyle \frac{16}{63}}& {\displaystyle \frac{2}{7}}& {\displaystyle \frac{5}{21}}& 0\end{array}\right).$$

5. Conclusions

This paper focuses on resistance distance in H-join of graphs $G_1,G_2,\dots ,G_k$. Let G be H-join of graphs $G_1,G_2,\dots ,G_k$. Here we first give the Laplacian matrix $L\left(G\right)$ of G. Then we compute a symmetric $\left\{1\right\}$-inverse of $L\left(G\right)$. Note that there exists a relationship between resistance distance and entries of $\left\{1\right\}$-inverse. So we can easily obtain resistance distance in G.