Hybrid-Frequency-Aware Mixture-of-Experts Method for CT Metal Artifact Reduction

Abstract

In clinical CT imaging, high-density metallic implants often induce severe metal artifacts that obscure critical anatomical structures and degrade image quality, thereby hindering accurate diagnosis. Although deep learning has advanced CT metal artifact reduction (CT-MAR), many methods do not effectively use frequency information, which can limit the recovery of both fine details and overall image structure. To address this limitation, we propose a Hybrid-Frequency-Aware Mixture-of-Experts (HFMoE) network for CT-MAR. The proposed method synergizes the spatial-frequency localization of the wavelet transform with the global spectral representation of the Fourier transform to achieve precise multi-scale modeling of artifact characteristics. Specifically, we design a hybrid-frequency interaction encoder with three specialized branches, incorporating wavelet-domain, Fourier-domain, and cascaded wavelet–Fourier modulation, to distinctively refine local details, global structures, and complex cross-domain features. Then, they are fused via channel attention to yield a comprehensive representation. Furthermore, a Frequency-Aware Mixture-of-Experts (MoE) mechanism is introduced to dynamically route features to specific frequency experts based on the degradation severity, thereby adaptively assigning appropriate receptive fields to handle varying metal artifacts. Evaluations on synthetic (DeepLesion) and clinical (SpineWeb, CLINIC-metal) datasets show that HFMoE outperforms existing methods in both quantitative metrics and visual quality. Our method demonstrates the value of explicit frequency-domain adaptation for CT-MAR and could inform the design of other image restoration tasks.

1. Introduction

Computed tomography (CT) is a fundamental tool in modern diagnostic radiology. However, high-density metallic implants, e.g., dental fillings, hip prostheses, and surgical clips, can corrupt projection data, leading to severe metal artifacts in reconstructed images [1]. These artifacts manifest as dark bands and bright streaks, which not only degrade perceived image quality but also obscure critical anatomical details of surrounding tissues. Moreover, metal artifacts can compromise downstream clinical tasks, such as target delineation in radiotherapy and computer-aided diagnosis. Therefore, developing effective CT metal artifact reduction (MAR) techniques is crucial for restoring diagnostic information.

Early solutions primarily relied on projection inpainting methods, such as linear interpolation (LI) [2] and normalized MAR (NMAR) [3]. Although these methods can reduce strong streaks, they often introduce secondary artifacts and blur fine details because they do not account for the nonlinear effects of beam hardening and scattering. In recent years, deep learning (DL) [4] has significantly advanced this field owing to its powerful nonlinear representation capacity and hierarchical architecture. Existing DL-based MAR methods are generally categorized into image domain [5,6], sinogram domain [7,8], and dual-domain collaboration approaches [9,10,11,12,13]. Among these, dual-domain methods have shown strong performance by combining information from both projection and image domains.

Despite progress, current deep learning methods remain limited in adapting to the varying frequency characteristics of artifacts. From the perspective of imaging physics, metal artifacts exhibit distinct spectral characteristics. Beam hardening typically induces low-frequency global shading (cupping effects), whereas photon starvation and scattering manifest as high-frequency radiating streaks and edge discontinuities. The distribution of these frequency components varies with the implant’s geometry, material, and location. However, conventional spatial-domain CNNs encounter a key limitation in balancing global context modeling and local detail preservation. Although increasing network depth can enlarge the theoretical receptive field, the effective receptive field (ERF) remains substantially constrained in practice [14], limiting the ability of the network to model long-range artifact streaks. As a result, many approaches adopt coarse-scale representations through spatial downsampling to aggregate global context, which unavoidably compromises high-frequency anatomical details. This design choice leads to a notable trade-off between artifact suppression and fine-structure preservation. Transformer-based architectures offer an alternative for modeling long-range dependencies [15]; however, their quadratic computational complexity with respect to image resolution hinders practical deployment in high-resolution medical imaging. Such limitations are clinically nontrivial, as the loss or blurring of subtle textures may introduce diagnostic ambiguity by obscuring or mimicking pathological structures. Consequently, it is necessary to propose a reconstruction framework that explicitly decouples artifact elimination from structural fidelity restoration.

To resolve this diagnostic trade-off and address these issues, we propose that an effective MAR model should adapt to frequency content and employ dynamic computation. We propose a Hybrid-Frequency-Aware Mixture-of-Experts (HFMoE) framework, which separates artifact processing into frequency bands and dynamically routes features to specialized modules. The core strategy is two-fold: First, to overcome the spectral bias, we introduce a hybrid frequency analysis strategy. We combine the wavelet transform, which provides joint spatial-frequency localization to preserve local textures, and the Fourier transform, which offers a global receptive field to effectively model and suppress long-range artifact signatures without destructive downsampling. Furthermore, a cascaded wavelet-Fourier branch is introduced to capture non-stationary spectral dependencies across different resolution scales. Second, to address the limitation of static networks, we integrate the mixture-of-experts (MoE) philosophy into the decoder. Unlike static layers, our frequency-aware experts specialize in different artifact types. A dynamic gating mechanism learns to assign higher weights to the most relevant experts based on the local frequency content of the input, realizing a “divide-and-conquer” strategy for artifact removal. The encoder includes a hybrid-frequency module with parallel wavelet, Fourier, and cascaded branches, fused via channel attention. In the decoder, the MoE architecture takes both spatial and wavelet high-frequency features as input, dynamically allocating computational resources to suppress artifacts while preserving tissue details. Experiments on Synthesized DeepLesion, Clinical SpineWeb, and CLINIC-metal datasets show that HFMoE improves upon current methods in artifact reduction and detail preservation.

In summary, our main contributions are as follows:

• We propose HFMoE, a unified network that integrates wavelet and Fourier transforms to effectively exploit the complementary benefits of spatial-frequency and global spectral information for robust CT-MAR.
• A hybrid-frequency interaction encoder is developed to capture multi-scale features, which incorporates concurrent wavelet, Fourier, and cascaded wavelet-Fourier modulation branches to facilitate multi-resolution spectral refinement, ensuring the restoration of local textures, global structures, and the complex cross-domain dependencies between them.
• A Frequency-Aware MoE strategy is implemented in the decoder to dynamically allocate frequency-specific experts according to the degradation severity of the input, enabling adaptive artifact correction.
• Extensive evaluations on multiple benchmarks, including synthesized and clinical datasets, validate that our method outperforms existing state-of-the-art methods in terms of both quantitative metrics and visual quality.

2. Related Works

2.1. CT Metal Artifact Reduction

Early MAR methods, such as linear interpolation [2] and normalized MAR [3], relied on heuristic inpainting or filtering, often introducing secondary artifacts or blurring. While foundational, they lack the adaptability for complex, patient-specific artifact patterns.

Deep learning [16,17] has significantly advanced MAR, leading to single-domain, dual-domain, and multi-domain paradigms. Single-domain approaches operate either in the sinogram space (e.g., CNN-MAR [7] and Deep-MAR [8]) or the image space (e.g., OSCNet+ [6]). Although effective, sinogram-domain methods can be prone to error propagation, while image-domain methods lack explicit physical data consistency [5]. Dual-domain methods, such as DuDoNet [9] and its successors [10,11,18], integrate both domains to enforce physical constraints, improving robustness. More recently, multi-domain frameworks like Quad-Net [19] and TFT-MAR [20] have begun exploring complementary representations beyond the spatial and sinogram domains, demonstrating the potential of frequency-aware processing.

However, a critical gap persists—existing methods predominantly operate on spatially-localized features, either from convolutional operations or local window-based attention. They lack a dedicated mechanism to explicitly model, decompose, and adaptively process the distinct frequency components that characterize metal artifacts, which span both global low-frequency shadows and local high-frequency streaking. This oversight limits their ability to achieve optimal fidelity and structural preservation across diverse clinical scenarios.

2.2. Frequency-Domain Modeling for Image Restoration

Leveraging frequency-domain transformations (e.g., Fourier, wavelet) is a well-established strategy for separating and processing different image components in general vision tasks [14]. Classical methods used thresholding in transform domains [21], while modern architectures integrate these transforms into networks [22]. For instance, some works decompose features into high- and low-frequency subbands for targeted enhancement [23,24,25], or use Fourier convolutions to capture global context [26,27], which is similar to Transformer [28]. In medical imaging, wavelet transforms have been used for super-resolution to preserve detail [29,30], and hybrid spatial–Fourier models aim to balance local and global processing [31,32].

Despite these advances, most current methods are limited in two ways: (1) They often rely on a single type of frequency transform (e.g., only Fourier or only wavelet), failing to capture the hybrid frequency characteristics (global spectral shifts and multi-scale local discontinuities) that define CT metal artifacts. (2) Their processing is typically static; the same network path handles all frequency content, without the adaptability to specialize for the varied spectral signatures of different artifacts and anatomies.

2.3. Mixture-of-Experts in Low-Level Vision

The mixture-of-experts (MoE) paradigm provides an effective framework for adaptive computation by employing multiple specialized sub-networks (experts) and a dynamic routing mechanism [33,34,35]. In low-level vision, MoE has been successfully applied to weather restoration [36], multi-task learning [37], and MRI denoising/super-resolution [38,39]. The principal advantage lies in its ability to conditionally activate different experts based on input features, allowing for task-aware or region-aware specialization. Recent innovations include gating mechanisms guided by semantic prompts [40] or designed for complexity-aware routing [41].

While promising, the application of MoE in CT-MAR is still in early stages. Existing MoE designs in medical imaging seldom route information based on frequency-domain characteristics. An MoE architecture where experts are specialized for distinct frequency bands or spectral patterns, and where routing is informed by a hybrid-frequency analysis of the input artifact, remains unexplored. This presents a potential direction to move beyond spatial-only adaptive processing.

3. Materials and Methods

3.1. Frequency-Domain Foundations: DWT and FFT

Our method is based on the complementary analysis provided by the discrete wavelet transform (DWT) and the fast Fourier transform (FFT). Metal artifacts in CT scans exhibit a complex, hybrid-frequency nature, comprising both localized high-frequency streaking and globally distributed low-frequency shading. Notably, these components are often spatially entangled and non-stationary rather than cleanly separable in clinical CT images, due to scattering effects that depend on implant geometry and material properties. Individually, DWT and FFT offer distinct advantages for modeling different aspects of this problem, yet neither alone is sufficient to fully characterize such entangled artifacts. Their combination, therefore, forms the basis of our hybrid-frequency approach.

3.1.1. Discrete Wavelet Transform for Localized Analysis

The 2D DWT performs a multi-resolution decomposition of an image, enabling joint analysis in space and frequency. For an input image or feature map $\mathbf{X}\in {\mathbb{R}}^{H\times W}$, a single decomposition level applies quadrature mirror filter banks, producing four subbands:

$$\{{\mathbf{X}}_{LL},{\mathbf{X}}_{LH},{\mathbf{X}}_{HL},{\mathbf{X}}_{HH}\}=\mathrm{DWT}\left(\mathbf{X}\right),$$

(1)

where ${\mathbf{X}}_{LL}$ represents the low-frequency approximation component, capturing coarse-grained structural information. The subbands ${\mathbf{X}}_{LH}$, ${\mathbf{X}}_{HL}$, and ${\mathbf{X}}_{HH}$ correspond to high-frequency details along the horizontal, vertical, and diagonal directions, respectively. The original signal can be exactly reconstructed via the Inverse DWT (IWT): $\mathbf{X}=\mathrm{IWT}({\mathbf{X}}_{LL},{\mathbf{X}}_{LH},{\mathbf{X}}_{HL},{\mathbf{X}}_{HH})$.

Specifically, DWT provides fine-grained space-frequency localization, which enables effective modeling of localized discontinuities and edge distortions induced by metal artifacts, i.e., sharp intensity transitions near metal–tissue interfaces and fine structural perturbations in surrounding anatomy. However, due to its limited receptive field within each subband, DWT alone is insufficient for capturing long-range, globally coherent streak artifacts that span large spatial extents. Thus, DWT is suitable for preserving local structural details but cannot fully represent the global organization of metal-induced corruption.

3.1.2. Fast Fourier Transform for Global Context

In contrast, the FFT provides a global representation of an image’s frequency content. For the 2D feature map $\mathbf{X}$, its 2D FFT is defined as follows:

$$\mathcal{F}\left(\mathbf{X}\right)[u,v]=\sum _{h=0}^{H-1}\sum _{w=0}^{W-1}\mathbf{X}[h,w]·e^{-j2\pi (uh/H+vw/W)},$$

(2)

with the inverse transform (IFFT) denoted by ${\mathcal{F}}^{-1}(·)$. The magnitude spectrum $\left|\mathcal{F}\right(\mathbf{X}\left)\right|$ reveals the global energy distribution across all frequencies, while the phase spectrum encodes essential structural information. The key attribute of the FFT is its inherent global receptive field; each point in the frequency domain depends on every pixel in the spatial domain.

This property makes the FFT effective for modeling globally correlated and directionally coherent components of metal artifacts, such as long-range streak backbones and low-frequency shading caused by beam hardening. The FFT and IFFT operations are efficient, with a computational complexity of $O(HWlog(HW\left)\right)$. However, due to the lack of spatial localization in the FFT basis functions, purely Fourier-domain processing risks suppressing anatomical structures whose frequency orientations resemble those of metal streaks.

3.1.3. Motivation for a Hybrid Frequency-Aware Design

DWT and FFT have complementary characteristics [42]. While DWT offers precise spatial localization that is well-suited for high-frequency and localized artifact features, its ability to capture long-range dependencies is inherently limited. Conversely, the FFT provides a global spectral view that captures global artifact structure but sacrifices spatial selectivity.

Importantly, CT metal artifacts often depart from the implicit assumption that local and global components can be cleanly separated. They frequently exhibit globally coherent spectral patterns whose local appearance varies across spatial locations and resolution scales. Therefore, we propose to construct a unified wavelet–Fourier hybrid frequency-aware representation that is designed to model this entanglement rather than assume a simple decomposition. By jointly leveraging wavelet-based spatial-scale representations and Fourier-based global spectral analysis, the network can capture scale-dependent spectral characteristics of metal artifacts. Integrating both domains thus provides a richer and more robust feature space for artifact reduction compared to single-domain methods.

3.2. Overview

Our proposed HFMoE follows an encoder–decoder architecture with skip connections. Given a metal-corrupted CT image $\mathbf{Y}\in {\mathbb{R}}^{H\times W}$, the network first extracts shallow features via a convolutional stem: ${\mathbf{F}}_0={\mathrm{Conv}}_{3\times 3}\left(\mathbf{Y}\right)$.

The encoder comprises four stages, each performing feature downsampling via DWT. Each stage contains a Hybrid-Frequency Interaction Module (HFIM) (Section 3.3) that processes features in the spatial and frequency domains. The bottleneck layer employs multiple HFIMs for deep feature refinement.

The decoder symmetrically upsamples features via IWT. Crucially, each decoder stage incorporates the proposed Frequency-Aware Mixture-of-Experts Module (FAME) (Section 3.4), which dynamically routes features to experts specialized for different frequency patterns and receptive fields. Skip connections aggregate multi-scale features from the encoder to the decoder.

The final restored image $\widehat{\mathbf{X}}$ is obtained through a reconstruction layer and a residual connection:

$$\widehat{\mathbf{X}}={\mathrm{Conv}}_{3\times 3}\left({\mathit{F}}_d\right)+\mathbf{Y},$$

(3)

where ${\mathit{F}}_d$ denotes the output of the decoder. This residual design enables the network learn the artifact component.

3.3. Hybrid-Frequency Interaction Module (HFIM)

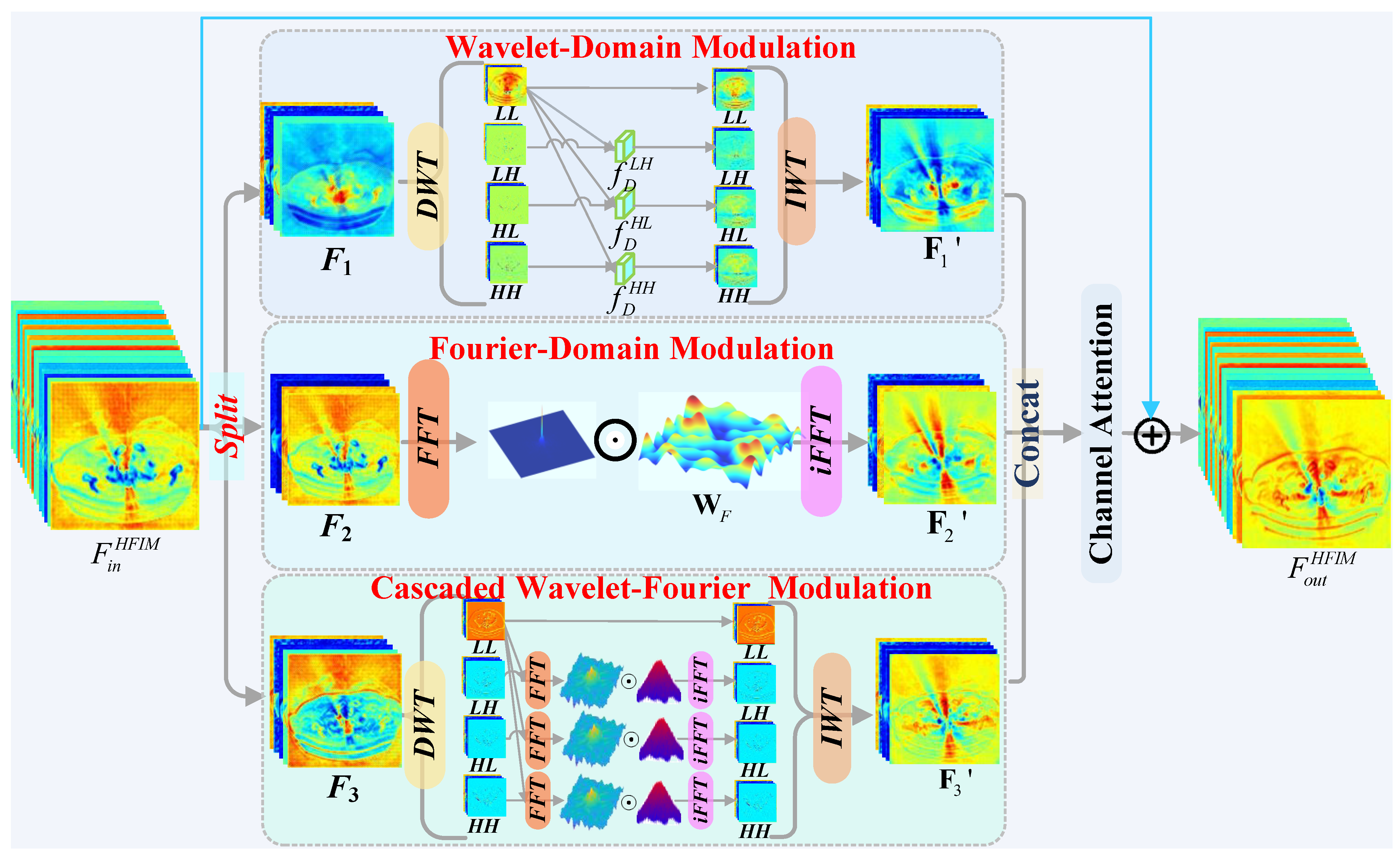
The proposed HFIM is designed to jointly leverage the complementary strengths of wavelet and Fourier transforms for local detail preservation and global artifact suppression. As shown in Figure 1, given an input feature ${\mathit{F}}_{in}^{HFIM}\in {\mathbb{R}}^{H\times W\times C}$, it is first projected to $\mathit{F}={\mathrm{Conv}}_{1\times 1}\left({\mathit{F}}_{in}\right)$. $\mathit{F}$ is then split into three parallel branches.

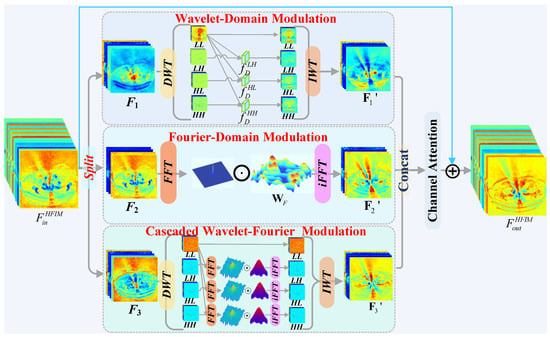
Figure 1. The architecture of the Hybrid-Frequency Interaction Module (HFIM).

• Branch 1: Wavelet-Domain Modulation. This branch focuses on localized details. ${\mathit{F}}_1$ is decomposed via DWT into four subbands: $\{{\mathit{F}}_1^{LL},{\mathit{F}}_1^{LH},{\mathit{F}}_1^{HL},{\mathit{F}}_1^{HH}\}$. The high-frequency (HF) subbands are concatenated with the low-frequency (LF) component and processed by depthwise-separable convolution blocks $f_D^{(·)}$:

$${\mathit{F}}_{1,H}^{\prime }=\mathrm{Concat}\left(f_D^{LH}\left([{\mathit{F}}_1^{LL},{\mathit{F}}_1^{LH}]\right),f_D^{HL}\left([{\mathit{F}}_1^{LL},{\mathit{F}}_1^{HL}]\right),f_D^{HH}\left([{\mathit{F}}_1^{LL},{\mathit{F}}_1^{HH}]\right)\right).$$

(4)

The processed features are then reconstructed via IWT: ${\mathit{F}}_1^{\prime }=\mathrm{IWT}({\mathit{F}}_1^{LL},{\mathit{F}}_{1,H}^{\prime })$.

• Branch 2: Fourier-Domain Modulation. This branch targets globally distributed artifacts. The feature is transformed via 2D FFT: $\mathcal{F}\left({\mathit{F}}_2\right)\in {\mathbb{C}}^{H\times W\times C/3}$. A learnable frequency filter ${\mathbf{W}}_F\in {\mathbb{C}}^{H\times W\times C/3}$ performs element-wise modulation, followed by the inverse FFT (iFFT):

  $${\mathit{F}}_2^{\prime }={\mathcal{F}}^{-1}\left({\mathbf{W}}_F\odot \mathcal{F}\left({\mathit{F}}_2\right)\right).$$

  (5)

• Branch 3: Cascaded Wavelet–Fourier Modulation. This branch models interactions across scales and frequencies. The HF subbands from an initial DWT of ${\mathit{F}}_3$ are first transformed to the Fourier domain, filtered, and then transformed back:

  $${\mathit{F}}_{3,i}^{\prime }={\mathcal{F}}^{-1}\left({\mathbf{W}}_{F,i}\odot \mathcal{F}\left(f_F^i\left([{\mathit{F}}_3^{LL},{\mathit{F}}_3^i]\right)\right)\right),i\in \{LH,HL,HH\}.$$

  (6)

• The final output is obtained via IWT, i.e., ${\mathit{F}}_3^{\prime }=\mathrm{IWT}({\mathit{F}}_3^{LL},{\mathit{F}}_{3,LH}^{\prime },{\mathit{F}}_{3,HL}^{\prime },{\mathit{F}}_{3,HH}^{\prime })$.

The outputs of the three branches are aggregated via channel attention and passed through a feedforward network (FFN), resulting in the final output ${\mathit{F}}_{out}^{HFIM}$ of the HFIM.

3.4. Frequency-Aware Mixture-of-Experts Module (FAME)

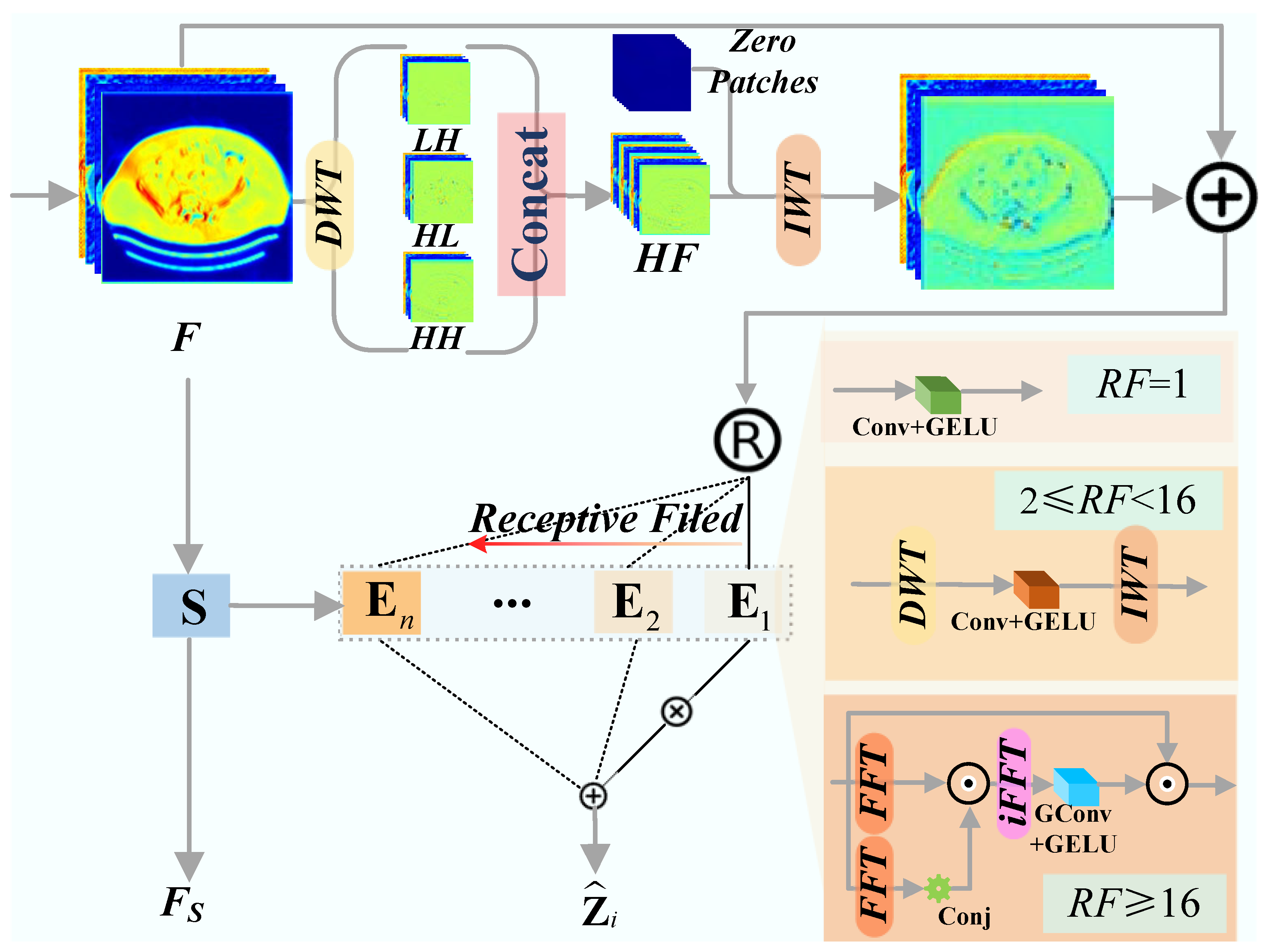
Building upon the MoE paradigm, the FAME module dynamically selects specialized experts based on the frequency characteristics of input features. This architecture enables the network to adapt its ERF to varying artifact scales, a critical requirement for handling non-stationary metal degradations. As illustrated in Figure 2, the input feature ${\mathit{F}}_{in}^{FAME}\in {\mathbb{R}}^{H\times W\times C}$ is first enriched with high-frequency cues extracted via DWT. This hybrid feature serves as input to the gating network and the expert pool.

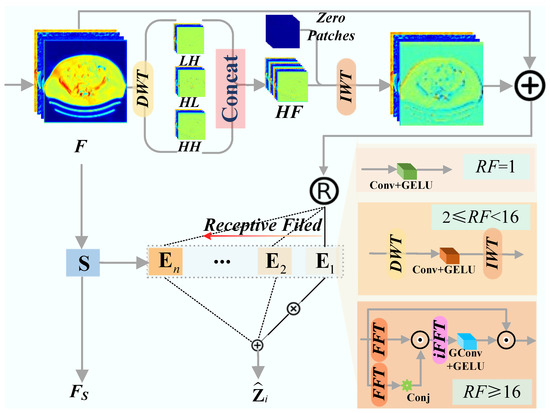
Figure 2. The architecture of Frequency-Aware Mixture-of-Experts (FAME).

• Expert Design. Our expert pool ${\left\{{\mathbf{E}}_i\right\}}_{i=1}^N$ consists of three types of experts with heterogeneous receptive fields designed to handle different degradation patterns via multi-scale feature arbitration:

  $${\widehat{\mathit{Z}}}_E^i=\left\{\begin{array}{c}{\mathrm{Conv}}_{1\times 1}\left({\mathit{Z}}_E^1\right), RF=1\hfill \\ \mathrm{IWT}\left({\mathrm{Conv}}_{k\times k}\left(\mathrm{DWT}\left({\mathit{Z}}_E^i\right)\right)\right),2\le RF<16\hfill \\ {\mathit{Z}}_E^i\odot {\mathcal{F}}^{-1}\left(\mathcal{F}\left({\mathbf{w}}_Q\left({\mathit{Z}}_E^i\right)\right)\odot {\left(\mathcal{F}\left({\mathbf{w}}_K\left({\mathit{Z}}_E^i\right)\right)\right)}^H\right), RF\ge 16\hfill \end{array}\right.$$

  (7)

• Local Expert ($RF=1$): Employs pointwise convolution ($1\times 1$ Conv) for pixel-wise adjustment, minimizing the risk of blurring fine textures during artifact-free region restoration.
• Wavelet Expert ($2\le RF<16$): Applies a DWT-IWT sandwich with a $k\times k$ depthwise convolution in the wavelet domain, providing mid-range context to suppress localized streaks while preserving sub-band edges.
• Fourier Expert ($RF\ge 16$): Approximates global self-attention via Fourier autocorrelation, offering a holistic RF to neutralize large-scale, cross-image streaks.

• The i-th expert processes a routed feature ${\mathit{Z}}_i$ and produces an output ${\widehat{\mathit{Z}}}_i$.
• Frequency-Aware Routing. The gating network $\mathcal{G}$ facilitates input-conditional execution by mapping frequency signatures to the most appropriate expert. A lightweight router, implemented as a linear layer followed by softmax, generates a routing weight vector $\mathit{g}=\mathcal{G}\left(\mathit{F}\right)\in {\mathbb{R}}^N$. For each spatial position (or token), only the expert with the highest weight is activated (Top-1 routing). By dynamically selecting the optimal RF for each token, the model circumvents the limitations of static architectures, thereby ensuring robust MAR performance across varying levels of artifact severity. To encourage balanced utilization and align expert choice with frequency content, we employ an auxiliary load-balancing loss ${\mathcal{L}}_{aux}$ [41].

The final output of the FAME module is the aggregated expert outputs, modulated by a shared feature projection $\mathbf{S}\left(\mathit{F}\right)$, and processed by an FFN:

$${\mathit{F}}_{out}^{FAME}=\mathrm{FFN}\left(\sum _{i=1}^N{g}_i·({\widehat{\mathit{Z}}}_i\odot \mathbf{S}\left(\mathit{F}\right))\right).$$

(8)

3.5. Loss Functions

Our training objective combines three complementary losses, as follows:

• 1. Reconstruction Loss (${\mathcal{L}}_{rec}$): An ${\mathcal{l}}_1$ loss [43] ensures pixel-level fidelity, weighted inside ($\mathcal{M}$) and outside the metal trace region:

  $${\mathcal{L}}_{rec}=\parallel (\widehat{\mathbf{X}}-{\mathbf{X}}^{gt}){\odot \mathcal{M}\parallel }_1+{\lambda }_{bg}{\parallel (\widehat{\mathbf{X}}-{\mathbf{X}}^{gt})\odot (1-\mathcal{M})\parallel }_1.$$

  (9)
• 2. Hybrid Frequency Loss (${\mathcal{L}}_{freq}$): This loss enforces consistency in both wavelet and Fourier domains. Let ${\mathcal{D}}_W(·)$ and ${\mathcal{D}}_F(·)$ denote operations extracting high-frequency wavelet subbands and Fourier magnitude spectra, respectively.

  $${\mathcal{L}}_{freq}=\sum _{s\in \{LH,HL,HH\}}{\alpha }_s\parallel {\mathcal{D}}_W^s(\widehat{\mathbf{X}})-{\mathcal{D}}_W^s({\mathbf{X}}^{gt}){\parallel }_1+\beta {\parallel {\mathcal{D}}_F(\widehat{\mathbf{X}})-{\mathcal{D}}_F({\mathbf{X}}^{gt})\parallel }_1.$$

  (10)
• 3. Routing Auxiliary Loss (${\mathcal{L}}_{aux}$): Adopted from [41], this loss balances expert utilization and encourages alignment between routing decisions and task complexity.

The total loss is a weighted sum: ${\mathcal{L}}_{total}={\mathcal{L}}_{rec}+{\lambda }_f{\mathcal{L}}_{freq}+{\lambda }_a{\mathcal{L}}_{aux}$. The hyperparameters ${\lambda }_{bg},{\lambda }_f,{\lambda }_a,{\alpha }_s,\beta$ are selected based on empirical observations.

4. Experiments

4.1. Physically-Informed Artifact Simulation and Clinical Dataset

To comprehensively evaluate the proposed method, we utilize one synthesized dataset for training and quantitative benchmarking, and two clinical datasets for assessing cross-domain generalizability.

• Synthesized DeepLesion Dataset. Following the protocol established in [6,44], we constructed a synthesized dataset based on the DeepLesion collection. The training set consisted of 1000 paired clean and metal-corrupted volumes, generated by simulating metal artifacts on 1200 randomly sampled metal-free abdominal/thoracic CT images using 90 distinct implant types [7]. To faithfully replicate complex clinical scenarios, the pipeline integrated a polychromatic X-ray model (with $2\times {10}^7$ incident photons) to couple beam-hardening and partial-volume effects with realistic Poisson noise, while extensively randomizing metal mask size, orientation, and position within diverse anatomical regions to reflect clinical variations in patient habitus and implant trajectories. For evaluation, 200 pairs featuring 10 unseen implant types were reserved, focusing on physical attenuation characteristics and geometric morphology rather than specific chemical compositions. These test implants covered a wide range of spatial scales, from 35 pixels (tiny fragments) to 2061 pixels (large prostheses). Consistent with prior works [6,44], all volumes were resampled into 640 projection views under a standard fan-beam geometry and reconstructed at a resolution of $416\times 416$.
• Clinical SpineWeb Dataset (available at https://csi-workshop.weebly.com/ or https://zenodo.org/records/7049844, accessed on 1 June 2014). To validate clinical generalization ability, we employed the SpineWeb dataset as an external testbed. This dataset consists of post-operative spinal CT scans with thoracolumbar instrumentation. We selected a set of spine volumes with implants that were not used in training. Metal implants were segmented using a standard threshold of 2500 HU. This dataset served to evaluate the model’s performance on real-world metallic hardware distinct from the training distribution.
• Clinical CLINIC-metal Dataset. We also utilized the CLINIC-metal pelvic CT dataset [45] to test generalization to different anatomies. This multi-center dataset contained pelvic CT scans with severe artifacts, which challenged the model across different anatomies and acquisition protocols.

4.2. Implementation Details

Table 1 outlines the architectural specifications of HFMoE. We employed progressive multi-resolution training, increasing input size from $256\times 256$ to $384\times 384$, then to $416\times 416$. The model was optimized using the AdamW optimizer with a cosine annealing schedule, where the learning rate decayed from an initial $1\times {10}^{-3}$ to $1\times {10}^{-6}$ following [46]. Data augmentation techniques, including random flipping, rotation, cropping, and MixUp, were applied to prevent overfitting. The framework was implemented in PyTorch 2.9.1. All experiments were conducted on a single NVIDIA RTX 4080S GPU. The model was trained for 2000 epochs, requiring approximately 72 h.

Table 1. HFMoE network configurations.

Task	Features	${\mathit{L}}_{\mathit{E}1}$	${\mathit{L}}_{\mathit{E}2}$	${\mathit{L}}_{\mathit{E}3}$	${\mathit{L}}_{\mathit{E}4}$	${\mathit{L}}_{\mathit{D}4}$	${\mathit{L}}_{\mathit{D}3}$	${\mathit{L}}_{\mathit{D}2}$	${\mathit{L}}_{\mathit{D}1}$
CT-MAR	16	1	2	4	6	6	4	2	1

4.3. Experimental Results and Discussion

4.3.1. Evaluation Metrics

In this paper, we employ Peak Signal-to-Noise Ratio (PSNR) and the Structural Similarity Index (SSIM) as quantitative evaluation metrics to comprehensively and objectively assess the performance of the proposed model on the synthetic dataset. PSNR quantifies pixel-level fidelity based on the Mean Squared Error (MSE), while SSIM assesses structural preservation, which correlates more closely with diagnostic perception.

For two images, $\mathbf{I}$ and $\mathbf{K}$ (from $[-1000,3071]$ HU normalized to range $[0,255]$), PSNR is defined as follows:

$$PSNR=10·{log}_{10}\left({\displaystyle \frac{MA{X}_I^2}{MSE}}\right),\mathrm{where}MSE={\displaystyle \frac{1}{HW}}\sum _{i,j}{[\mathbf{I}(i,j)-\mathbf{K}(i,j)]}^2$$

(11)

The SSIM index is calculated as follows:

$$SSIM(x,y)={\displaystyle \frac{(2{\mu }_x{\mu }_y+C_1)(2{\sigma }_{xy}+C_2)}{({\mu }_x^2+{\mu }_y^2+C_1)({\sigma }_x^2+{\sigma }_y^2+C_2)}}$$

(12)

where $\mu$ and ${\sigma }^2$ represent the local mean and variance, ${\sigma }_{xy}$ is the covariance, and $C_1,C_2$ are stability constants. These definitions ensure the evaluation criteria are transparent.

4.3.2. Quantitative Evaluation

Table 2 compares our proposed HFMoE with 16 existing MAR methods. For fair comparison, models with open-source code (e.g., OSCNet+, InDuDoNet) were evaluated using official pre-trained weights, while others were retrained following their original protocols. HFMoE achieves superior performance across all metrics. As detailed in Table 2, our method obtains the highest PSNR across all implant sizes. Specifically, HFMoE surpasses the best-performing MoE-based competitor, MoCE-IR, by 0.57 dB in PSNR, and outperforms the leading dual-domain method, InDuDoNet+, by a considerable margin of ∼3 dB. The improved SSIM scores also indicate enhanced structural preservation.

Table 2. Performance evaluation in terms of PSNR/SSIM on the Synthesized DeepLesion benchmark. Five distinct implant pairs with varying pixel counts ($[2061,890]$, $[81,451]$, $[254,124]$, $[118,112]$, $[53,35]$, from large to small) were evaluated to validate the robustness of our HFMoE against different implant sizes. Bold numbers denote the highest scores.

Methods	Large Metal	⟶	Medium Metal	⟶	Small Metal	Average
Input	24.12/0.6761	26.13/0.7471	27.75/0.7659	28.53/0.7964	28.78/0.8076	27.06/0.7586
LI (1987) [2]	27.21/0.8920	28.31/0.9185	29.86/0.9464	30.40/0.9555	30.57/0.9608	29.27/0.9347
NMAR (2010) [3]	27.66/0.9114	28.81/0.9373	29.69/0.9465	30.44/0.9591	30.79/0.9669	29.48/0.9442
CNNMAR (2018) [7]	28.92/0.9433	29.89/0.9588	30.84/0.9706	31.11/0.9743	31.14/0.9752	30.38/0.9644
DuDoNet (2019) [9]	29.87/0.9723	30.60/0.9786	31.46/0.9839	31.85/0.9858	31.91/0.9862	31.14/0.9814
DuDoNet++ (2020) [18]	36.17/0.9784	38.34/0.9891	40.32/0.9913	41.56/0.9919	42.08/0.9921	39.69/0.9886
DSCMAR (2020) [44]	34.04/0.9343	33.10/0.9362	33.37/0.9384	32.75/0.9393	32.77/0.9395	33.21/0.9375
DAN-Net (2021) [47]	30.82/0.9750	31.30/0.9796	33.39/0.9852	35.02/0.9883	43.61/0.9950	34.83/0.9846
InDuDoNet (2021) [1]	36.74/0.9742	39.32/0.9893	41.86/0.9944	44.47/0.9948	45.01/0.9958	41.48/0.9897
DICDNet (2021) [48]	37.19/0.9853	39.53/0.9908	42.25/0.9941	44.91/0.9953	45.27/0.9958	41.83/0.9923
ACDNet (2022) [5]	37.91/0.9872	39.30/0.9920	41.14/0.9949	42.43/0.9961	42.64/0.9965	40.68/0.9933
OSCNet (2022) [49]	37.70/0.9883	39.88/0.9902	42.92/0.9950	45.04/0.9958	45.45/0.9962	42.19/0.9931
InDuDoNet+ (2023) [50]	36.28/0.9736	39.23/0.9872	41.81/0.9937	45.03/0.9952	45.15/0.9959	41.50/0.9891
OSCNet+ (2023) [6]	38.98/0.9897	40.72/0.9930	43.46/0.9956	45.51/0.9965	45.99/0.9968	42.93/0.9943
DuDoDp (2024) [51]	29.11/0.9580	29.30/0.9631	29.07/0.9668	28.33/0.9673	28.33/0.9673	28.83/0.9645
MARFormer (2024) [52]	40.56/0.9903	42.32/0.9933	43.90/0.9947	45.78/0.9956	45.70/0.9957	43.65/0.9939
MoCE-IR (2025) [41]	41.23/0.9889	42.44/0.9912	44.02/0.9923	45.48/0.9932	45.98/0.9931	43.86/0.9917
HFMoE (Ours)	41.70/0.9916	43.09/0.9940	44.43/0.9951	46.20/0.9961	46.71/0.9963	44.43/0.9946

To validate these improvements, a paired-sample t-test was conducted between HFMoE and the second-best method, i.e., MoCE-IR, yielding $p<0.001$ ($p=8.75\times {10}^{-15}$). This confirms that the performance gains are statistically significant. Moreover, HFMoE achieved a lower standard deviation in PSNR ($1.74$ vs. $1.98$ in Table 3), demonstrating superior stability across diverse anatomical structures and implant geometries. These quantitative advantages align with our radiologist study, where HFMoE was preferred in $81\%$ of clinical cases for its higher diagnostic fidelity.

Table 3. Standard deviation analysis of PSNR performance. Comparison of stability across varying metal artifact severities on the Synthesized DeepLesion benchmark. Lower standard deviation indicates higher consistency. Bold indicates the best stability.

Methods	Large Metal	⟶	Medium Metal	⟶	Small Metal	All
MARFormer (2024) [52]	3.4027	2.9308	2.8868	3.0317	1.8288	1.7979
MoCE-IR (2025) [41]	3.2286	2.7271	2.6668	3.0740	2.0365	1.9791
HFMoE (Ours)	3.1001	2.5992	2.5328	3.2013	2.0181	1.7377

Note: Group 1 represents the largest implants (>890 pixels), while Group 5 represents the smallest (<53 pixels).

4.3.3. Qualitative Evaluation

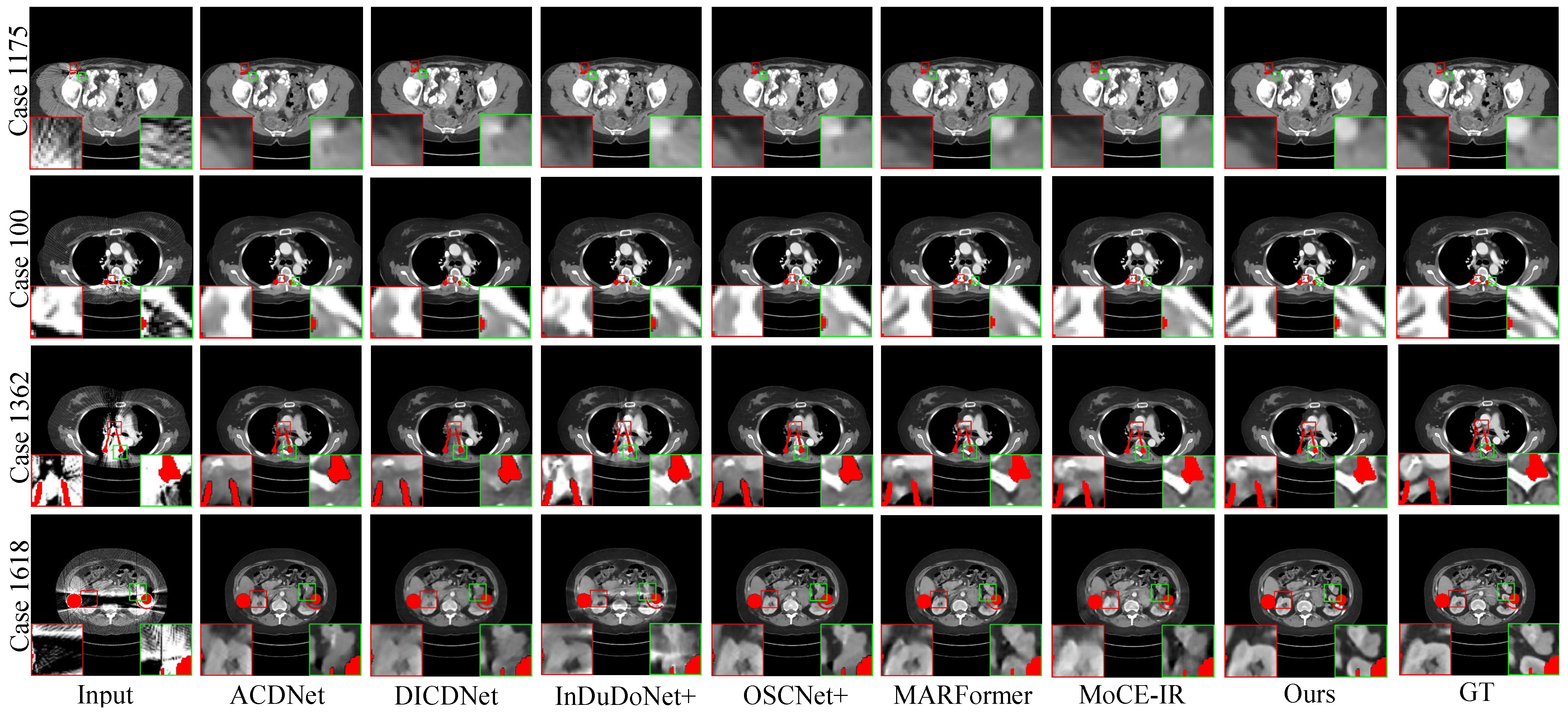
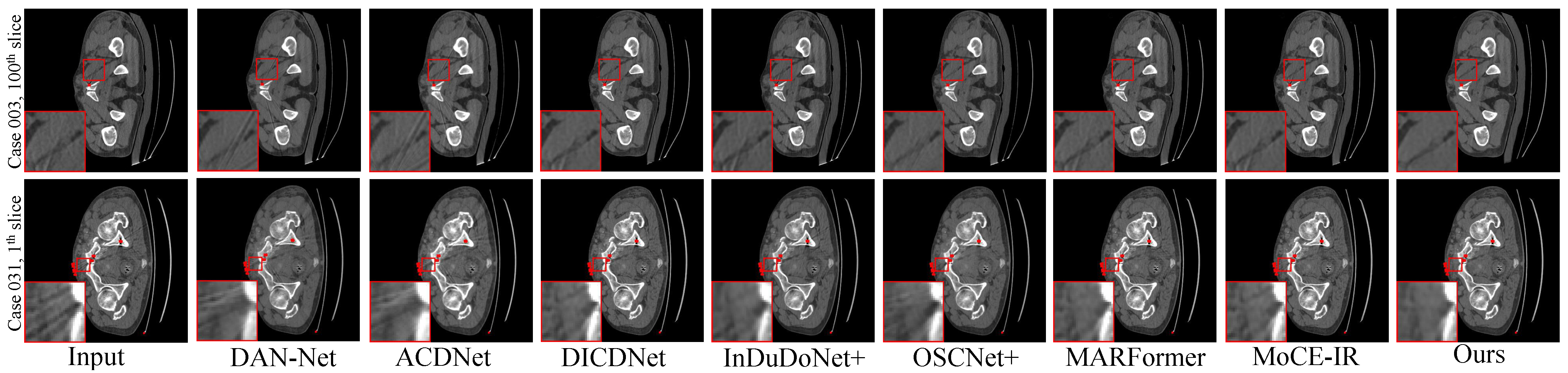
• Synthesized DeepLesion. Figure 3 presents the reconstruction results for cases with varying implant sizes. HFMoE demonstrates robust artifact suppression, particularly in regions surrounding large implants. While competing methods often leave noticeable residual streaks (indicated by circles), our approach effectively mitigates these artifacts and better preserves anatomical boundaries. For small implants, HFMoE also achieves higher texture fidelity compared to existing methods.
  

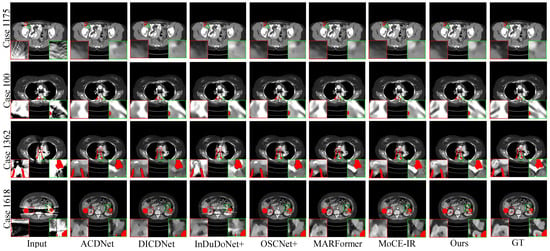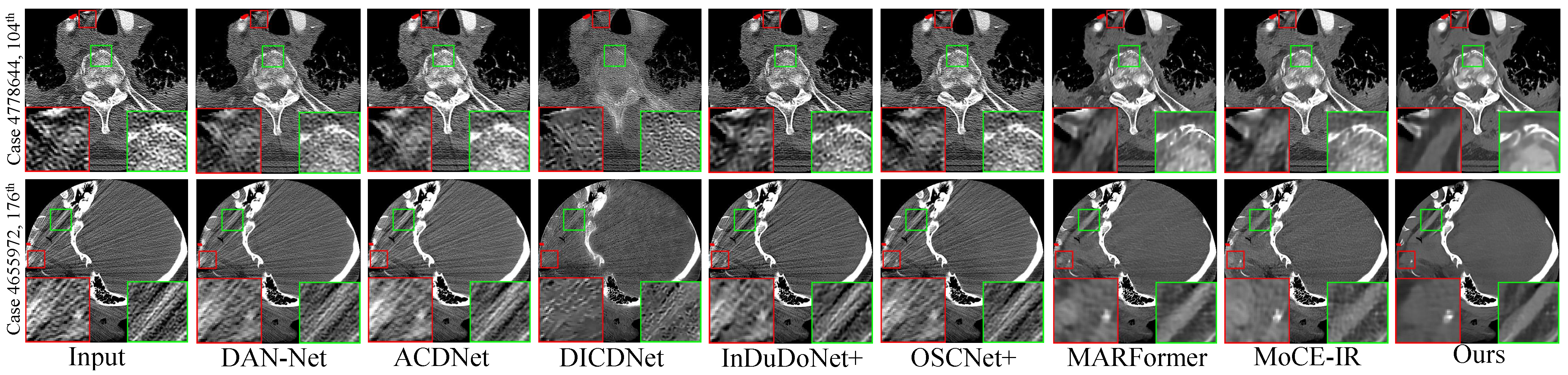
  Figure 3. Visual comparisons of the MAR results on four representative test cases with varying implant sizes and geometries. (Row 1) Case 1175: 112 px staple-like implant; (Row 2) Case 100: 124 px columnar implant; (Row 3) Case 1362: 892 px parallel implants; (Row 4) Case 1618: 2061 px large pelvic scaffold. Red and green boxes highlight critical regions where our method effectively suppresses streaking and shading artifacts, successfully restoring fine anatomical textures and maintaining morphological fidelity (e.g., the circular structure in Case 1175 and sharp boundaries in Case 1618) that are lost or distorted in other methods. Display: [−175, 275] HU; metal (red). ROIs are enlarged. Zoom in for a better view.
• Clinical Datasets. Qualitative results on the clinical SpineWeb and CLINIC-metal datasets are presented in Figure 4 and Figure 5, respectively. Unlike synthetic benchmarks, these clinical datasets involve real-world metal implants and noise patterns that are complex and difficult to model, presenting substantial challenges for robust artifact reduction. On SpineWeb, HFMoE effectively reduces beam-hardening streaks induced by spinal fixation hardware. It suppresses long-range artifacts while maintaining the continuity and visibility of vertebral structures, in contrast to baseline methods that either leave residual streaks or over-smooth anatomical details. On the CLINIC-metal dataset, which contains complex pelvic anatomy and diverse implant configurations, our method demonstrates robustness to various degradation patterns and generalizes well across different tissue textures, indicating its capacity to handle heterogeneous clinical scenarios. Moreover, HFMoE consistently achieves an effective trade-off between noise suppression and detail preservation. It preserves tissue boundaries and structural sharpness more effectively than other methods, which often introduce blurring, texture loss, or local distortions when confronted with severe noise and unknown implants.
  

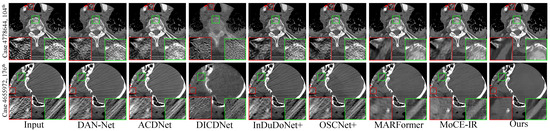  Figure 4. Qualitative comparison of clinical spine CT scans. (Row 1) An elliptical implant: the red box showcases our method’s superior noise reduction performance, providing a cleaner restoration of the underlying tissues, while the green box highlights its ability to preserve fine-grained anatomical textures during the denoising process. (Row 2) A small implant with prominent streak artifacts: the red box demonstrates effective artifact suppression, and the green box underscores our method’s ability to not only remove interfering streaks but also restore sharper anatomical boundaries and improve overall structural fidelity.Display window: [50, 500] HU. ROIs are enlarged. Zoom in for a better view.
  

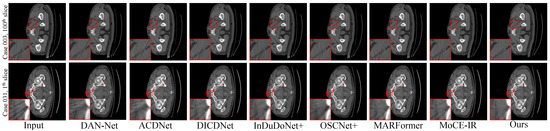  Figure 5. Qualitative comparison on the CLINIC-Metal dataset. (Top row): For the near-circular implant, the zoomed-in ROIs highlight that our method is the only one to achieve complete artifact elimination while maintaining sharp and clear structural boundaries. (Bottom row): In the presence of multiple metal implants, our approach exhibits the highest efficacy in suppressing streak artifacts and restoring latent tissue information, outperforming existing state-of-the-art techniques. Display window: [50, 500] HU. ROIs are enlarged. Zoom in for a better view.

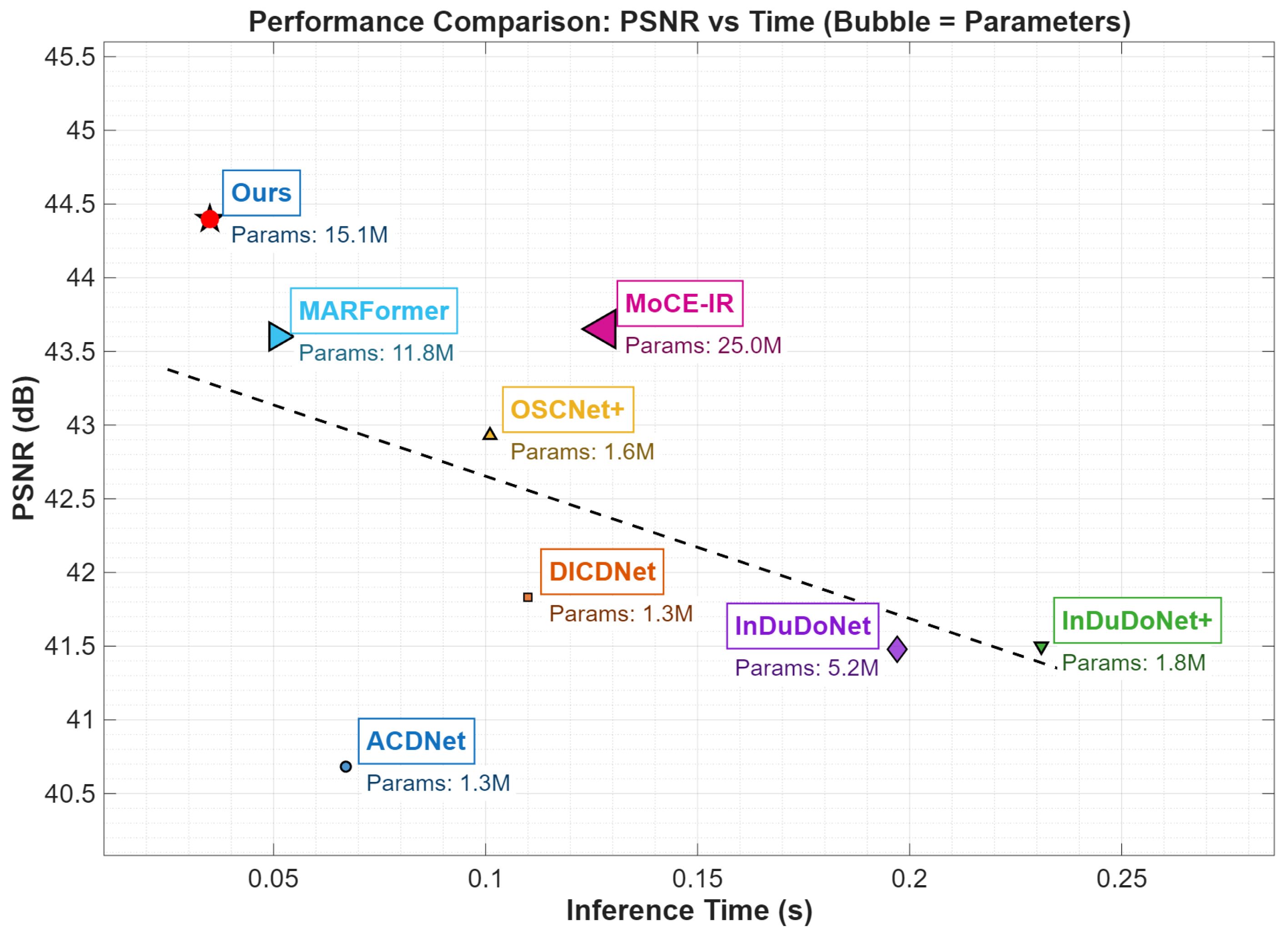
4.4. Computational Efficiency

Figure 6 contrasts the inference efficiency of leading MAR methods. HFMoE has an inference time of 38 ms per slice ($416\times 416$), tested on a standard NVIDIA RTX 4080S GPU. This represents a 40% speed improvement over ACDNet (65 ms), while simultaneously achieving a ∼0.8 dB higher PSNR than MARFormer and MoCE-IR. The model has a small memory footprint: training uses ∼32 GB VRAM (batch size 4), and inference requires ∼180 MB per slice. Our algorithm relies on FFT and DWT operations that are natively supported by the vast majority of modern hardware, including high-end NVIDIA RTX GPUs or mobile-grade processors like the Mali-G31. Such computational efficiency and broad hardware compatibility ensure that HFMoE can be integrated into existing clinical CT reconstruction workflows without introducing significant latency.

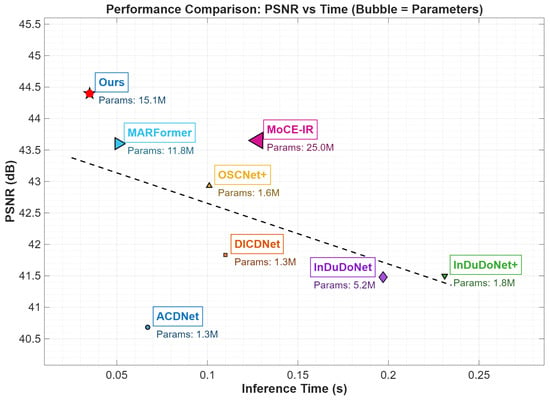
Figure 6. Runtime vs. PSNR with model complexity. Horizontal axis: running time (s); vertical axis: PSNR (dB); parameter count is noted below each method.

4.5. Ablation Study

We conducted a comprehensive ablation study on the Synthesized DeepLesion dataset to validate the contributions of three core components: the Hybrid-Frequency Interaction Module (HFIM), the Frequency-Aware Mixture-of-Experts (FAME), and the multi-scale loss function.

4.5.1. Efficacy of HFIM

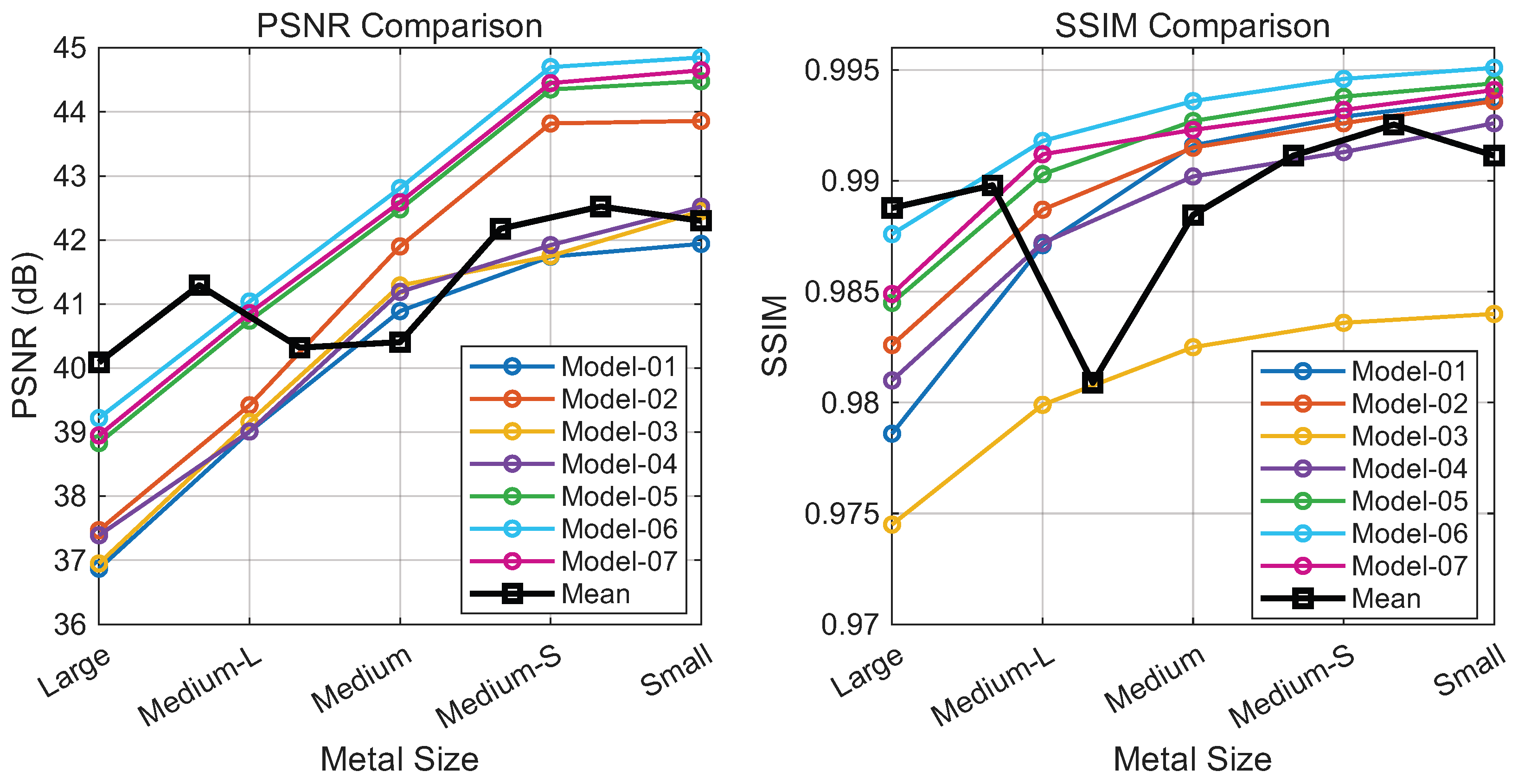
The HFIM leverages complementary information from the wavelet and Fourier domains. To analyze its impact, we constructed a baseline model (Model-01) based on the Transformer architecture, where the self-attention mechanism was replaced by channel attention as the primary interaction mechanism, and we progressively integrated frequency modulation blocks.

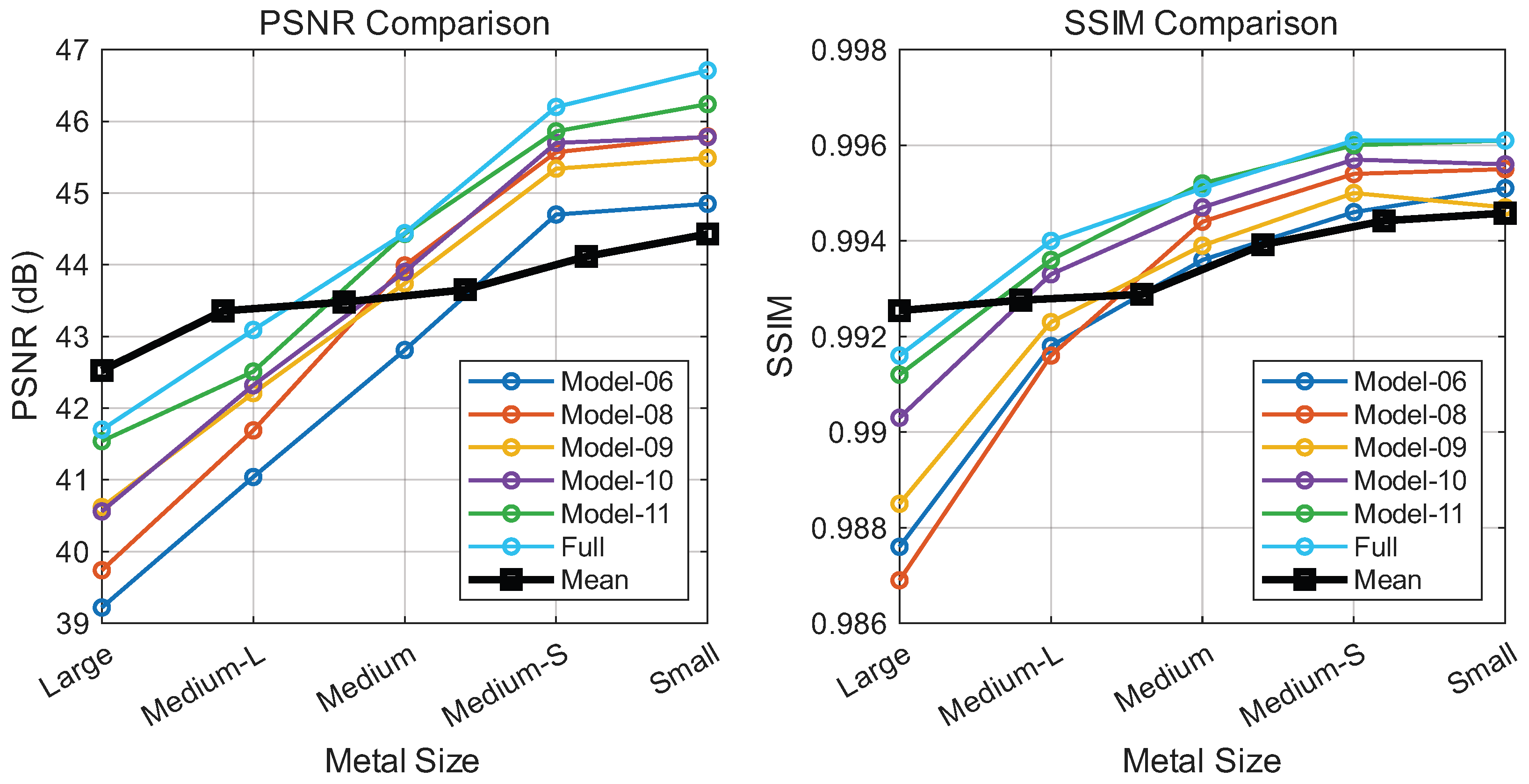
As shown in Figure 7, introducing wavelet-domain modulation (Model-02) yields performance gains by capturing local high-frequency details. While Fourier-domain modulation alone (Model-03) and cascaded wavelet-Fourier modulation (Model-04) prove less stable due to spectral sensitivity, their parallel combination with wavelet modulation (Model-05) produces a notable improvement, suggesting that the two domains offer complementary representations.

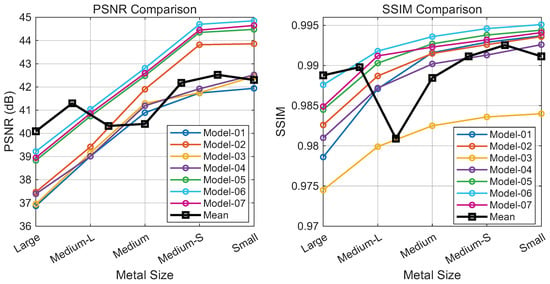
Figure 7. Contribution analysis of HFIM variants: PSNR (left) and SSIM (right) versus implant size (large to small). Curves represent different model configurations. Note: The black curve sequences Model-1 to Model-7 (left to right), not implant size.

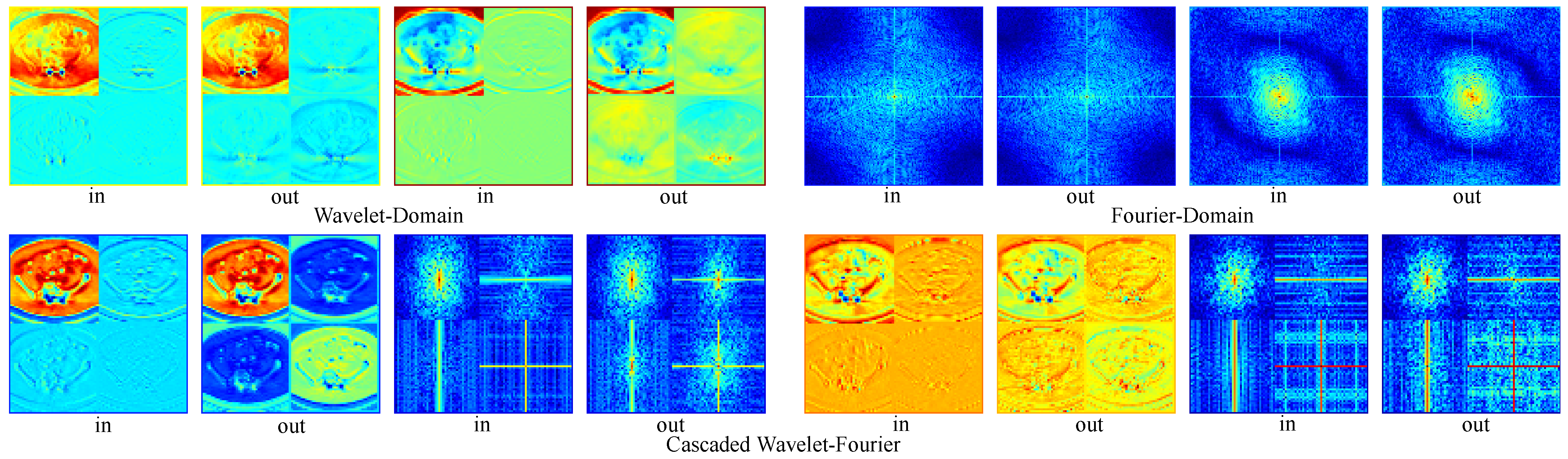
Moreover, we provide visualizations of feature maps across different branches in Figure 8. These visualizations demonstrate that wavelet-domain modulation selectively processes local details, while Fourier-domain modulation captures global structural information. The cascaded wavelet–Fourier modulation effectively integrates both capabilities, handling cases where high- and low-frequency components are not distinctly separated. The final configuration (Model-06), which incorporates a cascaded wavelet-Fourier strategy, achieves the optimal performance, confirming the synergy of the proposed triple-branch mechanism. Ablating the channel attention module (Model-07) leads to a performance drop, indicating that such a mechanism plays a crucial role in regulating the fusion of diverse frequency components.

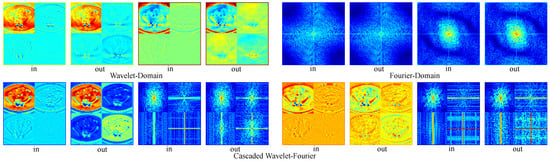
Figure 8. Visualization of feature inputs and outputs across frequency-aware modeling branches. Red denotes higher values, whereas blue signifies lower values. The left half of the first row compares wavelet-domain subband inputs and outputs, while the right half presents FFT magnitude spectra of Fourier-domain features. The second row illustrates the inputs and outputs of the cascaded wavelet–Fourier branch, showing wavelet subbands alongside their corresponding spectral energy distributions.

4.5.2. Role of FAME

The FAME module utilizes a gating mechanism to dynamically route features based on local frequency content. We compared our frequency-aware design against standard MoE and single-domain variants (Figure 9). While replacing standard MoE experts (Model-08) or multi-scale convolutions (Model-09) with a standard feedforward network (Model-06) offers baseline results, employing domain-specific experts, either wavelet-based (Model-10) or Fourier-based (Model-11), leads to noticeable improvements. The full FAME module, which adaptively selects between local wavelet experts for stationary regions and global Fourier experts for complex textures, achieves optimal performance.

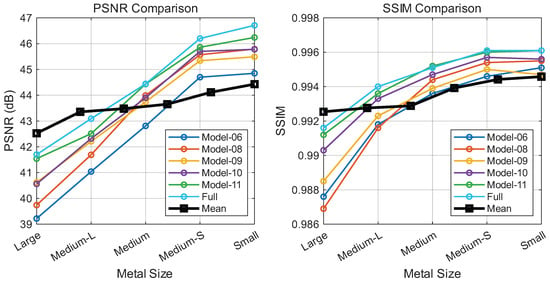
Figure 9. Performance of FAME variants across implant sizes (large to small). (Left): PSNR; (Right): SSIM. Each curve denotes a model configuration. Note: The black curve sequences Model-6 to Model-11 (left to right), not implant size.

This architecture enables an adaptive routing strategy, where the gating logic analyzes the input’s artifact intensity and spectral distribution to achieve input-dependent feature processing. Specifically, by prioritizing Fourier experts for globally coherent streaks and wavelet experts for localized anatomical recovery, FAME effectively disentangles artifacts from underlying anatomical structures. This indicates that the proposed FAME module can adaptively assign appropriate receptive fields and domain-specific priors to handle varying metal artifacts, ranging from subtle localized distortions to severe global artifacts.

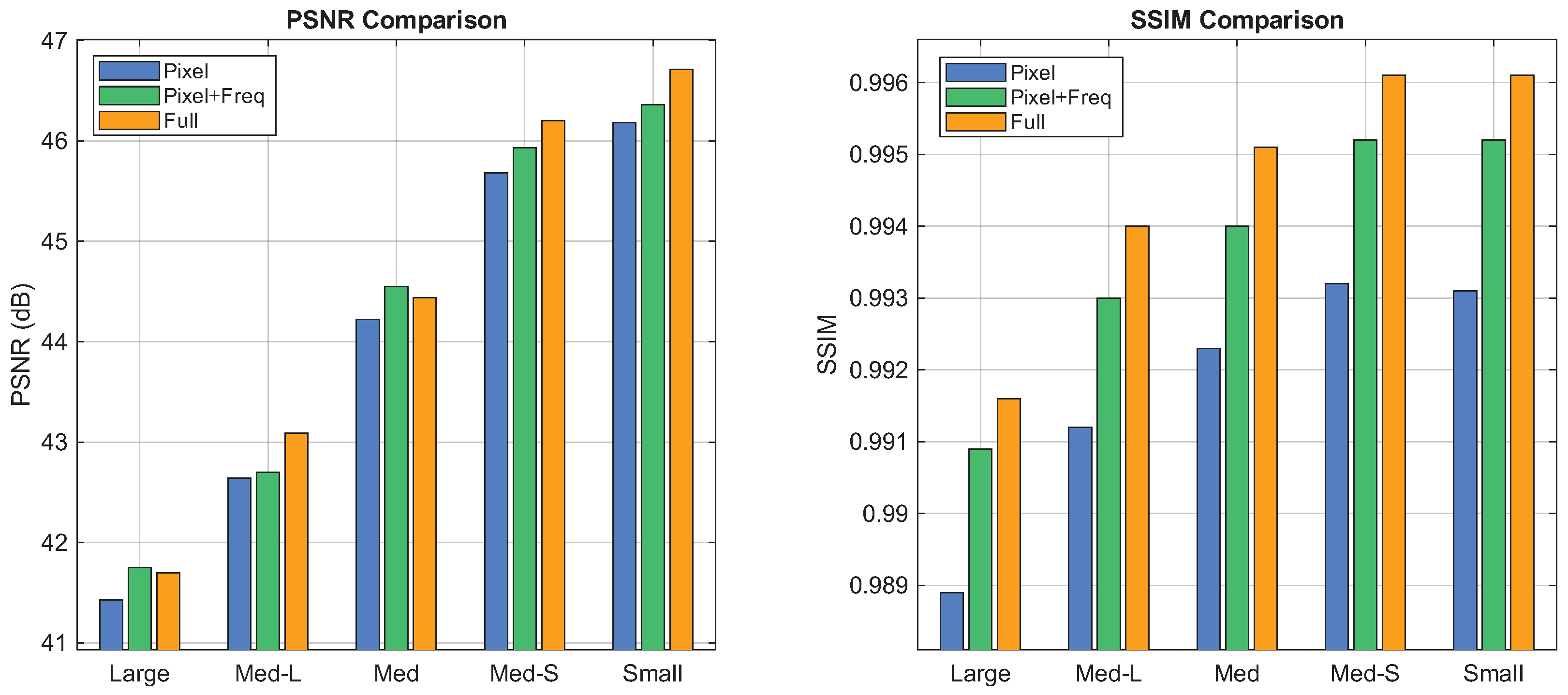
4.5.3. Impact of Loss Function

We finally evaluate the composite loss function, which incorporates reconstruction, frequency-aware, and routing-assisted terms. Ablation results in Figure 10 indicate that reliance solely on the reconstruction loss is limited in restoring subtle structural details. The inclusion of the frequency-aware loss enhances performance by explicitly constraining artifact removal within the spectral domain. Furthermore, the routing-assisted loss refines the model by promoting balanced expert utilization, leading to superior visual fidelity.

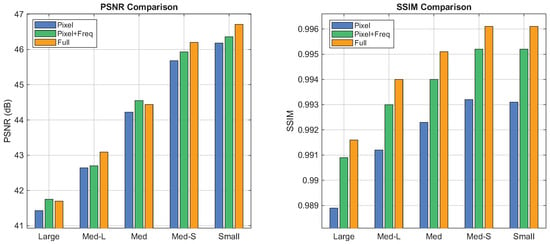
Figure 10. Performance of loss function variants evaluated by PSNR (left) and SSIM (right). Implant size decreases along the horizontal axis; colored bars denote the metric values of each variant.

5. Discussion

In medical image processing, wavelet and Fourier transforms offer complementary frequency-domain representations: wavelets capture localized spatial-frequency features and edges, while Fourier analysis characterizes global periodic structures and spectral distributions. While each transform has been utilized independently in CNNs or Transformers for tasks such as denoising, few methods combine them to leverage their inherent complementary strengths. We propose a Hybrid-Frequency-Aware Mixture-of-Experts (HFMoE) model for CT metal artifact reduction (MAR). This model employs a gating mechanism to dynamically combine wavelet and Fourier features, adapting the artifact suppression process to varying frequency content.

Our work has several limitations that suggest directions for future research. First, the model is trained exclusively on synthetic data, which may not fully capture the diverse artifact patterns in real clinical scans, potentially affecting its generalization. This reliance on simulation poses a risk where high quantitative scores on synthetic benchmarks might obscure performance gaps in handling complex, real-world physical effects. Second, our method processes 2D slices independently, without fully exploiting 3D spatial context. Third, imaging parameters (e.g., scanner settings, X-ray energy) that influence artifact formation are not yet incorporated. Future work could (i) use more realistic training data or domain adaptation techniques to improve clinical generalization; (ii) extend HFMoE to 3D to utilize volumetric context; and (iii) incorporate acquisition parameters to enhance robustness across diverse clinical protocols.

6. Conclusions

This paper presents a Hybrid-Frequency-Aware Mixture-of-Experts (HFMoE) model for metal artifact reduction in CT imaging. The core of this work lies in the systematic integration of wavelet and Fourier transforms to exploit their complementary properties: wavelet transforms capture localized spatial-frequency details, while Fourier transforms characterize global spectral structures. The proposed method consists of two key components. First, a hybrid module processes features in parallel through wavelet, Fourier, and combined branches, followed by adaptive fusion. Second, a routing mechanism dynamically selects specialized experts tailored to handle different artifact patterns based on local frequency content. Experiments on synthetic and clinical datasets demonstrate that HFMoE improves artifact reduction and preserves anatomical details more effectively than existing methods, as validated by quantitative metrics and visual inspection. Future work will extend this framework to 3D reconstruction. Furthermore, the multi-frequency approach of HFMoE offers a generalizable framework for other modalities, such as MRI denoising and PET motion correction; this would involve adapting the input encoding for k-space data or re-specializing experts to model modality-specific statistical noise.