Structure Fault Tolerance of Fully Connected Cubic Networks

Abstract

An interconnection network is usually modeled by a graph, and fault tolerance of the interconnection network is often measured by connectivity of the graph. Given a connected subgraph L of a graph G and non-negative integer t, the t-extra connectivity ${\kappa }_t\left(G\right)$, the L-structure connectivity $\kappa (G;L)$ and the t-extra L-structure connectivity ${\kappa }_g(G;L)$ of G can provide new metrics to measure the fault tolerance of a network represented by G. Fully connected cubic networks ${\mathcal{FC}}_n$ are a class of hierarchical networks which enjoy the strengths of a constant vertex degree and good expansibility. In this paper, we determine ${\kappa }_t\left({\mathcal{FC}}_n\right)$, $\kappa ({\mathcal{FC}}_n;L)$ and ${\kappa }_t({\mathcal{FC}}_n;L)$ for $t=1$ and $L\in \{K_{1,1},K_{1,2},K_{1,3}\}$. We also establish the edge versions ${\lambda }_t\left({\mathcal{FC}}_n\right)$, $\lambda ({\mathcal{FC}}_n;L)$ and ${\lambda }_t({\mathcal{FC}}_n;L)$ for $t=1$ and $L\in \{K_{1,1},K_{1,2}\}$.

1. Introduction

To improve the flexibility and effectiveness of interconnection networks, a major measure is to mend its fault-tolerant performance. Fault tolerance refers to the ability of an interconnection network to run normally when some components fail. The fault-tolerance ability of interconnection networks increases the overall consistency of the parallel systems and improves its functionality. Therefore, the fault tolerance of an interconnection network is an important issue and has been studied extensively [1]. It is well known that when the underlying topology of an interconnection network is modeled by a graph G, the classical connectivity and edge connectivity of G are used as deterministic measures of fault tolerance of the interconnection network. The connectivity (resp., edge connectivity) of a graph G, denoted $\kappa \left(G\right)$ (resp., $\lambda \left(G\right)$), is the cardinality of a minimal set S of vertices (resp., edges) whose removal disconnects G or makes $G-S$ an isolated vertex. In general, the interconnection network becomes more reliable as the connectivity and edge connectivity rise.

However, these two measures are bounded by the minimum degree of the graph. Thus, they cannot accurately reflect the real fault-tolerant ability of networks under some particular cases. In order to overcome this shortcoming and reflect the reliability of interconnection networks more accurately, some generalizations of these two measures have been proposed. Esfahanian and Hakimi introduced the concept of restricted connectivity, which requires that each vertex has at least one good neighbor [2,3]. Over the past few years, the restricted connectivity has found applications in several interconnection networks; see, for example, the works in [4,5] and the references therein. Fábrega et al. introduced the t-extra connectivity by adding extra conditions on every component of a faulty network [6]. As an important measure, extra connectivity has been widely studied. Yang et al. determined the t-extra connectivity of the n-dimensional hypercube $Q_n$ for $0\le t\le n$ and $n\ge 4$. More generally, Chang et al. studied the t-extra connectivity of hypercube-like networks for $t=2,3$. Recently, An et al. investigated the t-extra connectivity of the data center network RRect for $t=1,2,3$ [7]. For further reviewing of t-extra connectivity, the readers can refer to [8,9,10,11,12].

It is worth noting that the above-mentioned research only deals with the faults of a single vertex and fails to take into account the possible impact that these faulty vertices may have on their neighboring vertices. In fact, in a real-world network environment, adjacent vertices usually have an influence on one another. Specifically, when a vertex is faulty, the vertices adjacent to the faulty one are often more prone to being affected, with an increased likelihood of suffering subsequent faults. By taking into account this case, Lin et al. introduced the L-structure connectivity $\kappa (G;L)$ and L-substructure connectivity ${\kappa }^s(G;L)$ of a graph G and determined $\kappa (Q_n;L)$ and ${\kappa }^s(Q_n;L)$ for a hypercube $Q_n$ and $L\in \{K_{1,1},K_{1,2},K_{1,3},C_4\}$ [13]. Following this trend, the two measurements have been studied extensively for other interconnection networks like two-dimensional torus networks [14], alternating group networks [15], split-star networks [16] and divide-and-swap cube [17]. In addition, the further promotion of these concepts and studies also demonstrates the strong vitality of this topic. Recently, combining t-extra connectivity and L-structure connectivity, Zhu et al. proposed t-extra L-structure connectivity and investigated this property of hypercubes [18]. In 2021, Sabir et al., inspired by the impacts brought about by structure edge faults, proposed structure edge connectivity and used the measurement to evaluate the fault tolerance of some recursive interconnection networks [19]. Later, Wang et al. studied the structure edge connectivity and substructure edge connectivity of regular networks [20]. In this paper, combining t-extra connectivity and L-structure edge connectivity, we introduce t-extra L-structure edge connectivity.

This paper focuses on fully connected cubic networks, represented as $FCC{N}_n$. They are recursively defined using the three-dimensional hypercube as the base graph. As a result, $FCC{N}_n$ networks possess the advantages of a constant vertex degree and excellent expandability [21]. For simplicity, we represent $FCC{N}_n$ as ${\mathcal{FC}}_n$ hereafter. Some basic properties including the connectivity, diameter and maximally fault-tolerant capability of ${\mathcal{FC}}_n$ were also discussed in [21]. Later, Yang et al. provided the shortest-path routing algorithm in ${\mathcal{FC}}_n$ [22]. Ho et al. studied the fault-tolerant Hamiltonian property of ${\mathcal{FC}}_n$ [23]. Chin et al. proved that ${\mathcal{FC}}_n$ was super-spanning-connected [24]. Anitha investigated the total domination problem in fully connected cubic networks [25]. Rao et al. explored some forcing parameters in fully connected cubic networks [26]. In this paper, we discuss the t-extra connectivity (resp., t-extra edge connectivity), L-structure connectivity (resp., L-structure edge connectivity) and t-extra L-structure connectivity (resp., t-extra L-structure edge connectivity) of the fully connected cubic networks ${\mathcal{FC}}_n$ for $t=1$ and $L\in \{K_{1,1},K_{1,2},K_{1,3}\}$.

The rest of this article is organized as follows: In Section 2, we introduce the definitions and notations of graphs applied in this paper. The principal contributions of this paper are presented in Section 3 and Section 4. The results of the paper are summarized in Section 5.

We list some symbols in Table 1.

Table 1. Notations and descriptions.

Notation	Description
$G=(V,E)$	A graph with vertex set V and edge set E
$S\subset V\left(G\right)$	A vertex subset of G
$N_G\left(S\right)$	Neighbor set of a vertex subset of G
$N_G^{\prime }\left(S\right)$	Edge neighbor set of a vertex subset of G
$K_n$	A complete graph
$K_{1,r}$	Star graph
$Q_n$	Hypercube
${\mathcal{FC}}_n$	n-Dimensional fully connected cubic networks
$\kappa \left(G\right)$	Connectivity of the graph G
$\lambda \left(G\right)$	Edge connectivity of the graph G
${\kappa }_g\left(G\right)$	g-Extra connectivity of the graph G
${\lambda }_g\left(G\right)$	g-Extra edge connectivity of the graph G
$\kappa (G;L)$	L-structure connectivity of the graph G
$\lambda (G;L)$	L-structure edge connectivity of the graph G
${\kappa }_g(G;L)$	g-Extra L-structure connectivity of the graph G
${\lambda }_g(G;L)$	g-Extra L-structure edge connectivity of the graph G
$\mathbb{N}$	Set of natural numbers

2. Preliminaries

2.1. Graph Definitions and Notations

For a graph $G=(V,E)$, denote by $V\left(G\right)$ and $E\left(G\right)$ the vertex set and edge set. The order of G is the cardinality of $V\left(G\right)$, and the size of G is the cardinality of $E\left(G\right)$. Let $u,v\in V\left(G\right)$, and $(u,v)$ denotes the edge if u is adjacent to v. For a vertex subset $S\subset V\left(G\right)$, we denote $N_G\left(S\right)$ as the set $\{y\in V(G-S)\mid (x,y)\in E(G)$ for some $x\in S\}$. This set includes all vertices outside S that are adjacent to at least one vertex in S. In particular, $G-u$ is a subgraph of graph G, which is obtained by removing vertex u and its adjacent edges from graph G. The degree of a vertex u is $deg\left(u\right)=|N_G\left(u\right)|$. If $deg\left(u\right)=0$, we call it an isolated vertex. We denote by $\delta \left(G\right)$ and $\mathrm{\Delta }\left(G\right)$ the minimum degree and maximum degree of graph G. We use $K_n$ to denote a complete graph with n vertices, where every pair of vertices is connected by an edge. Additionally, we use $K_{1,n}$ to denote a star which consists of a central vertex connected to n leaf vertices.

Definition 1

([6]). Let $t\in \mathbb{N}$ and $S\subset V\left(G\right)$. Then, we call S a t-extra vertex cut if $G-S$ becomes disconnected and every component of $G-S$ contains at least $t+1$ vertices. Moreover, ${\kappa }_t\left(G\right)$, the t-extra connectivity, is defined as the minimum size of all t-extra vertex cuts.

By the definition above, we infer ${\kappa }_0\left(G\right)=\kappa \left(G\right)$.

In the following five lemmas, let L be a connected subgraph of a graph G.

Definition 2

([13]). Assume that a set of vertex-disjoint connected subgraphs in G is denoted by $\mathcal{FC}$. When $\mathcal{FC}$’s every element is isomorphic to L and $G-\mathcal{FC}$ is not connected, we call $\mathcal{FC}$ an L-structure cut. The cardinality of a minimum L-structure cut of G is said to be the L-structure connectivity of G, written as $\kappa (G;L)$. If $G-\mathcal{FC}$ is disconnected and every element of $\mathcal{FC}$ is isomorphic to a connected subgraph of L, then we call $\mathcal{FC}$ an L-substructure cut. A minimum L-substructure cut’s cardinality is said to be the L-substructure connectivity, denoted by ${\kappa }^s(G;L)$, of G.

By definition, it is not difficult to see that ${\kappa }^s(G;L)\le \kappa (G;L)$. Moreover, $\kappa (G;K_1)$ and ${\kappa }^s(G;K_1)$ reduce to the classical connectivity $\kappa \left(G\right)$, i.e., $\kappa (G;K_1)={\kappa }^s(G;K_1)=\kappa \left(G\right)$.

Definition 3

([18]). Let $t\in \mathbb{N}$. For L and a set of vertex-disjoint subgraphs $\mathcal{V}$ of G, we call $\mathcal{V}$ a t-extra L-structure cut if $\mathcal{V}$’s every element is isomorphic to L, $G-\mathcal{V}$ is not connected, and $G-\mathcal{V}$’s every remaining component contains more than t vertices. The cardinality of a minimum t-extra L-structure cut of G is said to be the t-extra L-structure connectivity of G, written as ${\kappa }_t(G;L)$. Moreover, we call $\mathcal{V}$ a t-extra L-substructure cut if $\mathcal{V}$’s every element is isomorphic to a connected subgraph of L, $G-\mathcal{V}$ is not connected, and $G-\mathcal{V}$’s every component contains more than t vertices. The cardinality of a minimum t-extra L-substructure cut of G is said to be the t-extra L-substructure connectivity of G, written as ${\kappa }_t^s(G;L)$.

By definition, we have that ${\kappa }_t^s(G;L)\le {\kappa }_t(G;L)$ and ${\kappa }_0^s(G;K_1)={\kappa }_0(G;K_1)=\kappa \left(G\right)$.

Definition 4

([6]). For a non-negative integer t, we call an edge subset F of a graph G, a t-extra edge cut if $G-F$ is disconnected and every component of $G-F$ has at least $t+1$ vertices. Moreover, the minimum cardinality over all t-extra edge cuts of G is said to be the t-extra edge connectivity, denoted by ${\lambda }_t\left(G\right)$.

By the definition above, we infer ${\lambda }_0\left(G\right)=\lambda \left(G\right)$.

Definition 5

([19]). Let $\mathcal{E}$ denote a set of edge-disjoint subgraphs of G. Then, we call $E\left(\mathcal{E}\right)$ an L-structure edge cut if $G-E\left(\mathcal{E}\right)$ is not connected and $\mathcal{E}$’s every element is isomorphic to L. If $E\left(\mathcal{E}\right)$ is an L-structure edge cut of G, then the minimum cardinality of $\mathcal{E}$ is said to be the L-structure edge connectivity of G, written as $\lambda (G;L)$. Moreover, if $G-E\left(\mathcal{E}\right)$ is not connected and $\mathcal{E}$’s every element is isomorphic to a connected subgraph of L, then $E\left(\mathcal{E}\right)$ is said to be an L-substructure edge cut. If $E\left(\mathcal{E}\right)$ is a substructure edge cut of G, then the L-substructure edge connectivity of G, denoted by ${\lambda }^s(G;L)$ is the minimum cardinality of $\mathcal{E}$.

By definition, ${\lambda }^s(G;L)\le \lambda (G;L)$. In addition, the $K_{1,1}$-structure edge connectivity and $K_{1,1}$-substructure edge connectivity reduce to the classic edge connectivity. Therefore, structure edge connectivity and substructure edge connectivity can both be regarded as general forms of the classic edge connectivity.

Definition 6.

Let $t\in \mathbb{N}$ and a set of edge-disjoint subgraphs of G be denoted by $\mathcal{E}$. Then, we call $E\left(\mathcal{E}\right)$ a t-extra L-structure edge cut if $\mathcal{E}$’s every element is isomorphic to L, $G-E\left(\mathcal{E}\right)$ is not connected, and every remaining component of $G-E\left(\mathcal{E}\right)$ contains more than t vertices. The t-extra L-structure edge connectivity of G, denoted by ${\lambda }_g(G;L)$ is the minimum cardinality of $\mathcal{E}$ such that $E\left(\mathcal{E}\right)$ is a t-extra L-structure edge cut of G. Moreover, $E\left(\mathcal{E}\right)$ is a t-extra L-substructure edge cut if every element in $\mathcal{E}$ is isomorphic with a connected subgraph of L, $G-E\left(\mathcal{E}\right)$ is not connected, and $G-E\left(\mathcal{E}\right)$’s every component has more than t vertices. The t-extra L-substructure edge connectivity ${\lambda }_t^s(G;L)$ of G is the minimum cardinality of $\mathcal{E}$ such that $E\left(\mathcal{E}\right)$ is a t-extra L-substructure edge cut of G.

By definition, we have ${\lambda }_t^s(G;L)\le {\lambda }_t(G;L)$. Moreover, ${\lambda }_0^s(G;K_{1,1})={\lambda }_0(G;K_{1,1})=\lambda \left(G\right)$.

2.2. Fully Connected Cubic Networks

The Hamming distance between two strings of the same length is the number of positions at which the corresponding characters differ. We set ${\mathbb{Z}}_n$ to be the set $\{0,1,\dots ,n-1\}$.

Definition 7.

The n-dimensional hypercube $Q_n$ consists of the vertex set $\{u_{n-1}{u}_{n-2}\dots u_0\mid u_i\in {\mathbb{Z}}_2$ for each $i\in {\mathbb{Z}}_n\}$. Two vertices x and y are adjacent in $Q_n$ if and only if they differ in exactly one position, meaning the Hamming distance $h(u,v)$ between them is one.

Lemma 1

([27]). For $n\ge 3$, ${\kappa }_1\left(Q_n\right)={\lambda }_1\left(Q_n\right)=2n-2$.

Lemma 2

([13]). When $n\ge 3$, $\kappa (Q_n;K_2)={\kappa }^s(Q_n;K_2)=n-1$, and $\kappa (Q_n;L)={\kappa }^s(Q_n;L)=\lceil {\displaystyle \frac{n}{2}}\rceil$, where $L\in \{K_{1,2},K_{1,3}\}$.

Lemma 3

([18]). ${\kappa }_1(Q_n;K_2)={\kappa }_1^s(Q_n;K_2)=n-1$ for $n\ge 3$.

Lemma 4

([28]). For $n\ge 3$, let $F\subset V\left(Q_n\right)$ with $n\le |F|\le 2n-3$. If $Q_n-F$ is not connected, then it contains exactly two components, and one of them contains $2^n-|F|-1$ vertices.

For any positive integer $\mathbf{r}\ge 1$ and for any $a\in {\mathbb{Z}}_8$, we set $a^{\mathbf{r}}=\underset{\mathbf{r}}{\underbrace{aa\cdots a}}$. For any positive integer $x\le 2^n-1$, let $b_n\left(x\right)$ denote the function that returns the binary representation of x with a fixed length n. For example, $b_3\left(7\right)=111$, and $b_3\left(3\right)=011$.

Definition 8

([21]). For $n\ge 1$, the n-level fully connected cubic networks, ${\mathcal{FC}}_n$, is defined as follows:

1. 

${\mathcal{FC}}_1$ has vertex set $\{0,1,\dots ,7\}$ and edge set $\{(x,y)\mid h(b_3\left(x\right),b_3\left(y\right))=1$ for $x,y\in \{0,1,\dots ,7\}\}$.

2. 

For $n\ge 2$, the graph ${\mathcal{FC}}_n$ is constructed from eight vertex-disjoint copies of ${\mathcal{FC}}_{n-1}$ by adding 28 edges. For $m\in {\mathbb{Z}}_8$, let ${\mathcal{FC}}_{n-1}^m$ represent a copy of ${\mathcal{FC}}_{n-1}$ with each vertex being prefixed by m. Specifically, the vertex set of ${\mathcal{FC}}_{n-1}^m$ is $\{x_{n-1}{x}_{n-2}\cdots x_0\mid x_{n-1}=m$ and $x_i\in {\mathbb{Z}}_8$ for each $i\in {\mathbb{Z}}_{n-1}$. Then, the graph ${\mathcal{FC}}_n$ is defined as $V\left({\mathcal{FC}}_n\right)={\bigcup }_{m=0}^{7}V\left({\mathcal{FC}}_{n-1}^m\right)$ and $E\left({\mathcal{FC}}_n\right)=\left({\bigcup }_{m=0}^{7}E\left({\mathcal{FC}}_{n-1}^m\right)\right)\cup \{(s{t}^{\mathbf{n}-\mathbf{1}},t{s}^{\mathbf{n}-\mathbf{1}})\mid s,t\in {\mathbb{Z}}_8$ with $s\ne t\}$.

Figure 1 shows ${\mathcal{FC}}_1$ and ${\mathcal{FC}}_2$. It is worth mentioning that ${\mathcal{FC}}_1\cong Q_3$. Let $n\ge 2$. If a vertex in ${\mathcal{FC}}_n$ is of the form $s^{\mathbf{n}}$, then it is said to be a boundary vertex, and if it has the form $s{t}^{\mathbf{n}-\mathbf{1}}$ with $s\ne t$, then it is said to be an intercubic vertex. If an edge joins two intercubic vertices, then we call it an intercubic edge. Obviously, every ${\mathcal{FC}}_{n-1}^m$ has seven intercubic vertices and one boundary vertex for $n\ge 2$ and $0\le m\le 7$. Let S be any subset of ${\mathbb{Z}}_8$. For convenience, we set ${\mathcal{FC}}_n^S$ to be the subgraph induced by ${\bigcup }_{i\in S}V({\mathcal{FC}}_{n-1}^i$).

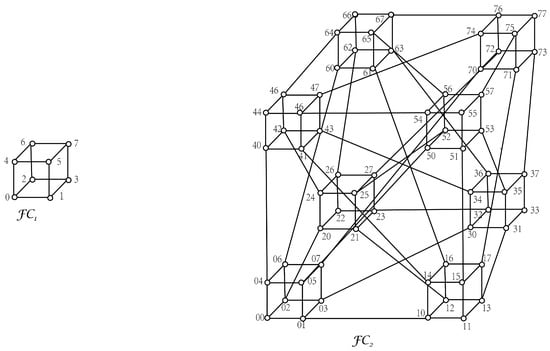
Figure 1. Illustrations of ${\mathcal{FC}}_1$ and ${\mathcal{FC}}_2$.

Lemma 5

([29]). For $n\ge 1$, $\kappa \left({\mathcal{FC}}_n\right)=3$ and $\lambda \left({\mathcal{FC}}_n\right)=3$.

Lemma 6

([24]). For $n\ge 2$ and for any two elements $m,l\in \{0,1,\dots ,7\}$ with $m\ne l$, there is exactly one intercubic edge between ${\mathcal{FC}}_{n-1}^m$ and ${\mathcal{FC}}_{n-1}^l$, denoted by $(m{l}^{\mathbf{n}-\mathbf{1}},l{m}^{\mathbf{n}-\mathbf{1}})$.

3. Extra Connectivity, Structure Connectivity and t-Extra L-Structure Connectivity

For any vertex subset F of ${\mathcal{FC}}_n$, we set $F_i=F\cap V\left({\mathcal{FC}}_{n-1}^i\right)$. Note that $F={\bigcup }_{i\in {\mathbb{Z}}_8}{F}_i$ and $F_j\cap F_k=\varnothing$ if $j\ne k$.

Lemma 7.

Let F be any vertex subset of ${\mathcal{FC}}_n$ with $|F|\le 4$. Define m as $max\{|F_i|\mid i\in {\mathbb{Z}}_8\}$, and let t be an element in ${\mathbb{Z}}_8$ such that $|F_t|=max\{|F_i|\mid i\in {\mathbb{Z}}_8\}$. For $n\ge 2$, ${\mathcal{FC}}_n-F$ is connected if $m\le 2$, and ${\mathcal{FC}}_{n-1}^{{\mathbb{Z}}_8-\left\{t\right\}}-F$ is connected if $m\le 4$.

Proof. 

We set $\{a_0,a_1,\dots ,a_7\}={\mathbb{Z}}_8$ such that $a_0=t$ and $|F_{a_0}|\ge |F_{a_1}|\ge \cdots \ge |F_{a_7}|$. Since $|F|\le 4$ and $|F|={\sum }_{k=0}^7|F_{a_k}|$, $max\{|F_{a_1}|,|F_{a_2}|,|F_{a_3}|\}\le 2$ and $|F_{a_j}|=0$ for $j\in \{4,5,6,7\}$. By Lemma 5, ${\mathcal{FC}}_{n-1}^i-F_i$ is connected for each $i\in \{a_1,a_2,\dots ,a_7\}$. By Lemma 6, there is an edge between ${\mathcal{FC}}_{n-1}^i$ and ${\mathcal{FC}}_{n-1}^j$ for any two elements $i,j\in \{a_4,a_5,a_6,a_7\}$ with $i\ne j$. Thus, the subgraph ${\mathcal{FC}}_{n-1}^{\{a_4,a_5,a_6,a_7\}}$ is connected. We set $S=\{a_1,a_2,\dots ,a_7\}$ and $F_S={\bigcup }_{i\in S}{F}_i$.

• Case 1: $m\le 4$. We set $A_i=\{(a_i{a}_4^{\mathbf{n}-\mathbf{1}},a_4{a}_i^{\mathbf{n}-\mathbf{1}}),(a_i{a}_5^{\mathbf{n}-\mathbf{1}},a_5{a}_i^{\mathbf{n}-\mathbf{1}}),(a_i{a}_6^{\mathbf{n}-\mathbf{1}},a_6{a}_i^{\mathbf{n}-\mathbf{1}}),(a_i{a}_7^{\mathbf{n}-\mathbf{1}},a_7{a}_i^{\mathbf{n}-\mathbf{1}})\}$ for each $i\in \{1,2,3\}$. By Lemma 6, $A_1\subset E\left({\mathcal{FC}}_n\right)$. Since $|F_{a_1}|\le 2$ and $|F_{a_j}|=0$ for each $j\in \{4,5,6,7\}$, there is an edge, say $(x,y)$, in $A_1$ with $\{x,y\}\cap F_{a_1}=\varnothing$. Since ${\mathcal{FC}}_{n-1}^{a_1}-F_{a_1}$ and ${\mathcal{FC}}_{n-1}^{\{a_4,a_5,a_6,a_7\}}$ are both connected, ${\mathcal{FC}}_{n-1}^{\{a_1,a_4,a_5,a_6,a_7\}}-F_{a_1}$ is connected. Similarly, one can deduce that ${\mathcal{FC}}_{n-1}^{a_i}-F_{a_i}$ is connected for each $i\in \{2,3\}$. Thus, we have ${\mathcal{FC}}_{n-1}^S-F_S$ if $m\le 4$.
• Case 2: $m\le 2$. By Case 1, we have that ${\mathcal{FC}}_{n-1}^S-F_S$ is connected. Since $\kappa \left({\mathcal{FC}}_{n-1}\right)=3$, we have that ${\mathcal{FC}}_{n-1}^{\left\{a_0\right\}}$ is connected. We set $A_0=\{(a_0{a}_j^{\mathbf{n}-\mathbf{1}},a_j{a}_0^{\mathbf{n}-\mathbf{1}})\mid j\in \{1,2,\dots ,7\}\}$. By Lemma 6, $A_0\subset E\left({\mathcal{FC}}_n\right)$. Since $|F|\le 4$ and $|A_0|=7$, there exists an edge, say $\{p,q\}$, in $A_0$ with $\{p,q\}\cap F=\varnothing$. From the fact that ${\mathcal{FC}}_{n-1}^{a_0}-F_{a_0}$ and ${\mathcal{FC}}_{n-1}^S-F_S$ are both connected, one can infer that ${\mathcal{FC}}_n-F$ is also connected for $m\le 2$. □

3.1. Extra Connectivity

Lemma 8.

Let $F\subset V\left({\mathcal{FC}}_n\right)$ with $|F|\le 4$. If $n\ge 2$, then ${\mathcal{FC}}_n-F$ contains a component with at least $8^n-|F|-1$ vertices.

Proof. 

We set $\{a_0,a_1,\dots ,a_7\}={\mathbb{Z}}_8$ such that $|F_{a_0}|\ge |F_{a_1}|\ge \cdots \ge |F_{a_7}|$. Suppose that $F_{a_0}\le 2$. We prove this lemma by mathematical induction on n. By Lemma 7, ${\mathcal{FC}}_2-F$ is connected and it contains $8^2-|F|$ vertices. Thus, we consider that $F_{a_0}\ge 3$. Since $|F|\le 4$, we have $|F_{a_1}|\le 1$ and $|F_{a_i}|=0$ for each $i\in \{2,3,\dots ,7\}$. Let $S=\{a_1,a_2,\dots ,a_7\}$. By Lemma 7, the subgraph ${\mathcal{FC}}_1^S-F_{a_1}$ is connected. We have the following cases:

• Case 1: $|F_{a_0}|=3$. Let R be the largest connected component of ${\mathcal{FC}}_1^{a_0}-F_{a_0}$. If ${\mathcal{FC}}_1^{a_0}-F_{a_0}$ is connected, then R contains $8-|F|=5$ vertices. Otherwise, by Lemma 4, it contains four vertices. Consequently, R contains at least three intercubic vertices, and one of these intercubic vertices has a neighbor in ${\mathcal{FC}}_1^S-F_{a_1}$. Hence, the subgraph induced by $V\left(R\right)$ and $V({\mathcal{FC}}_1^S)-F_{a_1}$ is connected and contains at least $4+(7\times 8-|F_{a_1}|)=8^2-|F|-1$ vertices.
• Case 2: $|F_{a_0}|=4$. Since $|F_{a_0}|=4$, there are at least three vertices, say $x_1,x_2$ and $x_3$, in $V({\mathcal{FC}}_1^{a_0})-F_{a_0}$ such that those vertices are not boundary vertex of ${\mathcal{FC}}_1$. By Lemma 6, each vertex of them has a neighbor in ${\mathcal{FC}}_1^S$. Thus, the subgraph induced by $V({\mathcal{FC}}_1^S)\cup \{x_1,x_2,x_3\}$ contains $|V({\mathcal{FC}}_1^S)\cup \{x_1,x_2,x_3\}|=7\times 8+3=59$ vertices. However, $59=8^2-|F|-1$. Therefore, this lemma is valid when $n=2$.

Suppose that it is true for $n\ge 2$. Next, we consider the case for ${\mathcal{FC}}_{n+1}-F$. By Lemma 7, ${\mathcal{FC}}_{n+1}-F$ is connected and it contains $8^{n+1}-|F|$ vertices. Thus, we focus on the case where $F_{a_0}\ge 3$.

Since $|F|\le 4$, we have $|F_{a_1}|\le 1$ and $|F_{a_i}|=0$ for each $i\in \{2,3,\dots ,7\}$. Let $S=\{a_1,a_2,\dots ,a_7\}$. By induction hypothesis, ${\mathcal{FC}}_n^{a_0}-F_{a_0}$ contains a component R which contains a least $8^n-|F_{a_0}|-1$ vertices. Since ${\mathcal{FC}}_n^{a_0}$ has seven intercubic vertices, R has at least two intercubic vertices. Since $|F|-|F_{a_0}|\le 1$, there is at least one intercubic vertex in R such that its neighbor is in ${\mathcal{FC}}_n^S-F_{a_1}$. Hence, the induced subgraph induced by $V\left(R\right)$ and $V\left({\mathcal{FC}}_1^S\right)-F_{a_1}$ is connected and contains at least $(8^n-|F_{a_0}|-1)+(7\times 8^n-|F_{a_1}|)=8^{n+1}-|F|-1$ vertices. □

Theorem 1.

$${\kappa }_1\left({\mathcal{FC}}_n\right)=\left\{\begin{array}{cc}4& \mathit{if}n=1,\hfill \\ 5& \mathit{if}n\ge 2.\hfill \end{array}\right.$$

Proof. 

Since ${\mathcal{FC}}_1$ is isomorphic to $Q_3$, by Lemma 1, we have ${\kappa }_1\left({\mathcal{FC}}_1\right)=4$. Next, we consider the case for $n\ge 2$.

Let F be any subset of vertices of ${\mathcal{FC}}_n$ with $|F|\le 4$. By Lemma 8, ${\mathcal{FC}}_n-F$ is either connected or it contains exactly two components: one trivial component and one nontrivial component. This implies that F is not a one-extra vertex cut of ${\mathcal{FC}}_n$. Hence, ${\kappa }_1\left({\mathcal{FC}}_n\right)\ge 5$.

We set $u=0^{\mathbf{n}}$, $v=0^{\mathbf{n}-\mathbf{1}}1$, $x_1=0^{\mathbf{n}-\mathbf{1}}2$, $x_2=0^{\mathbf{n}-\mathbf{1}}4$, $x_3=1^{\mathbf{n}-\mathbf{1}}3$, $x_4=1^{\mathbf{n}-\mathbf{1}}5$ and $x_5=0^{\mathbf{n}-\mathbf{2}}10$. It is straightforward to see that $\left(1\right)$$(u,v)\in E\left({\mathcal{FC}}_n\right)$, and $\left(2\right)$$N_{{\mathcal{FC}}_n}\left(\{u,v\}\right)=\{x_i\mid 1\le i\le 5\}$. We set R as $N_{{\mathcal{FC}}_n}\left(\right\{u,v\left\}\right)$. Since $|V\left({\mathcal{FC}}_n\right)|=8^n>7=|\{u,v\}\cup R|$, R forms a vertex cut of ${\mathcal{FC}}_n$. Let w be any vertex in ${\mathcal{FC}}_n-(R\cup \{u,v\})$. According to Definition 8, $|N_{{\mathcal{FC}}_n}\left(w\right)\cap N_{{\mathcal{FC}}_n}\left(\{u,v\}\right)|\le 2$. Hence, w has a neighbor in ${\mathcal{FC}}_n-R$. Consequently, R is a one-extra vertex cut of ${\mathcal{FC}}_n$. Thus, ${\kappa }_1\left({\mathcal{FC}}_n\right)\le 5$.

In conclusion, ${\kappa }_1\left({\mathcal{FC}}_n\right)=5$. □

3.2. Structure Connectivity

Theorem 2.

For $n\ge 2$, $\kappa ({\mathcal{FC}}_n;K_{1,1})={\kappa }^s({\mathcal{FC}}_n;K_{1,1})=3$.

Proof. 

We set $u=0^{\mathbf{n}}$, $x_1=0^{\mathbf{n}-\mathbf{1}}1$, $y_1=0^{\mathbf{n}-\mathbf{2}}10$, $x_2=0^{\mathbf{n}-\mathbf{1}}2$, $y_2=0^{\mathbf{n}-\mathbf{2}}20$, $x_3=0^{\mathbf{n}-\mathbf{1}}4$ and $y_3=0^{\mathbf{n}-\mathbf{2}}40$. Then, we set F as $\{\{x_1,y_1\},\{x_2,y_2\},\{x_3,y_3\}\}$. Obviously, every element in F is an edge in ${\mathcal{FC}}_n$. Combining the fact that ${\mathcal{FC}}_n-F$ is not a connected graph with the fact that F is a $K_{1,1}$-structure cut of ${\mathcal{FC}}_n$, $\kappa ({\mathcal{FC}}_n;K_{1,1})\le 3$ and ${\kappa }^s({\mathcal{FC}}_n;K_{1,1})\le 3$.

Let S be a $K_{1,1}$-substructure cut of ${\mathcal{FC}}_n$ with $|S|\le 2$. Since S is a vertex cut and $|V(S)|\le 4$, by Lemma 8, ${\mathcal{FC}}_n-S$ contains one trivial component $C_1=\left\{u\right\}$ and one nontrivial component $C_2$. Moreover, $|V(C_1)|=1$ and $|V\left(C_2\right)|=8^n-|F|-1$. Since each element in S represents either a single vertex or two adjacent vertices, and ${\mathcal{FC}}_n$ is $K_3$-free, u can have at most one neighbor in each element of S. Since ${deg}_{{\mathcal{FC}}_n}\left(u\right)\ge 3$, we must have $|N_{{\mathcal{FC}}_n-V\left(S\right)}\left(u\right)|\ge 1$, which contradicts the fact that $|V(C_1)|=1$. Therefore, S cannot be a $K_{1,1}$-substructure cut. Consequently, ${\kappa }^s({\mathcal{FC}}_n;K_{1,1})\ge 3$ and $\kappa ({\mathcal{FC}}_n;K_{1,1})\ge 3$ for $n\ge 2$. □

Lemma 9.

For $n\ge 2$, $max\{\kappa ({\mathcal{FC}}_n;K_{1,h}),{\kappa }^s({\mathcal{FC}}_n;K_{1,h})\mid h\in \{2,3\}\}\le 2$.

Proof. 

We set $u=0^{\mathbf{n}}$, $x_1=0^{\mathbf{n}-\mathbf{1}}3$, $x_2=0^{\mathbf{n}-\mathbf{1}}1$, $x_3=0^{\mathbf{n}-\mathbf{1}}2$, $x_4=0^{\mathbf{n}-\mathbf{2}}30$, $y_1=0^{\mathbf{n}-\mathbf{1}}6$, $y_2=0^{\mathbf{n}-\mathbf{1}}4$, $y_3=0^{\mathbf{n}-\mathbf{1}}5$ and $y_4=0^{\mathbf{n}-\mathbf{2}}40$. It follows that $(x_1,x_i)\in E\left({\mathcal{FC}}_n\right)$ for every $i\in \{2,3,4\}$ and $(y_1,y_j)\in E\left({\mathcal{FC}}_n\right)$ for every $j\in \{2,3,4\}$.

Let $F_1=\{\{x_1,x_2,x_3\},\{y_1,y_2,y_3\}\}$. Each element in $F_1$ is isomorphic to $K_{1,2}$ and $|F_1|=2$. Since ${\mathcal{FC}}_n-F_1$ is disconnected where $\left\{u\right\}$ is one component of ${\mathcal{FC}}_n-F_1$, we have that $F_1$ is a $K_{1,2}$-structure cut of ${\mathcal{FC}}_n$. Hence, $max\{\kappa ({\mathcal{FC}}_n;K_{1,2}),{\kappa }^s({\mathcal{FC}}_n;K_{1,2})\}\le 2$.

Similarly, define $F_2=\{\{x_1,x_2,\dots ,x_4\},\{y_1,y_2,\dots ,y_4\}\}$. Each element in $F_2$ is isomorphic to $K_{1,3}$ and $|F_2|=2$. From the fact that ${\mathcal{FC}}_n-F_2$ is not connected, we have that $F_2$ is a $K_{1,3}$-structure cut of ${\mathcal{FC}}_n$. Therefore, $max\{\kappa ({\mathcal{FC}}_n;K_{1,2}),{\kappa }^s({\mathcal{FC}}_n;K_{1,2})\}\le 2$.

In conclusion, we have $max\{\kappa ({\mathcal{FC}}_n;K_{1,h}),{\kappa }^s({\mathcal{FC}}_n;K_{1,h})\mid h\in \{2,3\}\}\le 2$. □

Theorem 3.

For $n\ge 2$, $\kappa ({\mathcal{FC}}_n;K_{1,2})={\kappa }^s({\mathcal{FC}}_n;K_{1,2})=2$.

Proof. 

By Lemma 9, we have $max\{\kappa ({\mathcal{FC}}_n;K_{1,2}),{\kappa }^s({\mathcal{FC}}_n;K_{1,2})\}\le 2$. Thus, we only need to show that $min\{{\kappa }^s({\mathcal{FC}}_n;K_{1,2}),\kappa ({\mathcal{FC}}_n;K_{1,2})\}\ge 2$.

We prove it by contradiction. Let S be a $K_{1,2}$-substructure set of ${\mathcal{FC}}_n$ with $|S|\le 1$. Suppose that ${\mathcal{FC}}_n-S$ is not connected. We assume that C is the smallest component of ${\mathcal{FC}}_n-S$. Since $\delta \left({\mathcal{FC}}_n\right)=3$ and ${\mathcal{FC}}_n$ is triangle free, $|V(C)|\ge 2$. However, by Theorem 1, ${\kappa }_1\left({\mathcal{FC}}_n\right)=5$ for $n\ge 2$. This means that under the condition $|V(C)|\ge 2$, if we want to disconnect ${\mathcal{FC}}_n$, we have to delete at least five vertices. However, $|V(S)|\le 3<5$, which is a contradiction. Thus, ${\kappa }^s({\mathcal{FC}}_n;K_{1,2})\ge 2$ and so $\kappa ({\mathcal{FC}}_n;K_{1,2})\ge 2$ for $n\ge 2$. □

Lemma 10.

For $u,v\in V\left({\mathcal{FC}}_n\right)$, we have $|N_{{\mathcal{FC}}_n}\left(u\right)\cap N_{{\mathcal{FC}}_n}\left(v\right)|\le 2$.

Proof. 

Since ${\mathcal{FC}}_1\cong Q_3$, the lemma is valid for $n=1$. Thus, suppose that it is also valid for $n\ge 2$. Next, we consider the case for ${\mathcal{FC}}_{n+1}$. We assume that $u\in {\mathcal{FC}}_n^p$ and $v\in {\mathcal{FC}}_n^q$.

Suppose that $p\ne q$. According to Definition 8, u has at most one neighbor in ${\mathcal{FC}}_n^q$, and v has at most one neighbor in ${\mathcal{FC}}_n^p$. Thus, $|N_{{\mathcal{FC}}_n}\left(u\right)\cap N_{{\mathcal{FC}}_n}\left(v\right)|\le 2$.

Suppose that $p=q$. By induction hypothesis, $|N_{{\mathcal{FC}}_n^p}\left(u\right)\cap N_{{\mathcal{FC}}_n^p}\left(v\right)|\le 2$. Let $S={\mathbb{Z}}_8-\left\{p\right\}$. By Definition 8, the neighbor vertex of u in ${\mathcal{FC}}_n^S$ is not the same as the neighbor vertex of v in ${\mathcal{FC}}_n^S$ if both u and v are intercubic vertices. Thus, $|N_{{\mathcal{FC}}_{n+1}}\left(u\right)\cap N_{{\mathcal{FC}}_{n+1}}\left(v\right)|\le 2$. □

Theorem 4.

For $n\ge 2$$\kappa ({\mathcal{FC}}_n;K_{1,3})={\kappa }^s({\mathcal{FC}}_n;K_{1,3})=2$.

Proof. 

By Lemma 9, we have $max\{\kappa ({\mathcal{FC}}_n;K_{1,3}),{\kappa }^s({\mathcal{FC}}_n;K_{1,3})\}\le 2$. Thus, we only need to show that ${\kappa }^s({\mathcal{FC}}_n;K_{1,3})\ge 2$ and $\kappa ({\mathcal{FC}}_n;K_{1,3})\ge 2$. We prove this by contradiction. Consider a set F which is a subset of the collection of all $K_{1,3}$-substructures of ${\mathcal{FC}}_n$ that satisfies $|F|\le 1$. Assume that ${\mathcal{FC}}_n-F$ is not connected. We suppose that C is the smallest component of ${\mathcal{FC}}_n-F$. Combining the fact that $\delta \left({\mathcal{FC}}_n\right)=3$ and ${\mathcal{FC}}_n$ is triangle free with Lemma 10, $|V(C)|\ge 2$. However, by Theorem 1, ${\kappa }_1\left({\mathcal{FC}}_n\right)=5$ for $n\ge 2$. This means that under the condition $|V(C)|\ge 2$, if we want to disconnect ${\mathcal{FC}}_n$, we have to delete at least five vertices. However, $|V(F)|\le 4<5$, which is a contradiction. Thus, ${\kappa }^s({\mathcal{FC}}_n;K_{1,3})\ge 2$, and so $\kappa ({\mathcal{FC}}_n;K_{1,3})\ge 2$ for $n\ge 2$. □

By Lemma 2, we have $\kappa ({\mathcal{FC}}_1;K_{1,h})={\kappa }^s({\mathcal{FC}}_1;K_{1,h})=2$ for every $h\in \{1,2,3\}$. The following theorem is derived from Theorems 2, 3 and 4.

Theorem 5.

$$\kappa ({\mathcal{FC}}_n;K_{1,h})={\kappa }^s({\mathcal{FC}}_n;K_{1,h})=\left\{\begin{array}{cc}2& \mathrm{if}n=1\mathrm{and}h=1,\mathrm{or}n\ge 1\mathrm{and}h\in \{2,3\},\hfill \\ 3& \mathrm{if}n\ge 2\mathrm{and}h=1.\hfill \end{array}\right.$$

3.3. t-Extra L-Structure Connectivity

Theorem 6.

$${\kappa }_1({\mathcal{FC}}_n;K_{1,1})={\kappa }_1^s({\mathcal{FC}}_n;K_{1,1})=\left\{\begin{array}{cc}2& \mathrm{if}n=1,\hfill \\ 3& \mathrm{if}n\ge 2.\hfill \end{array}\right.$$

Proof. 

According to Lemma 3, one can deduce ${\kappa }_1({\mathcal{FC}}_1;K_{1,1})={\kappa }_1^s({\mathcal{FC}}_1;K_{1,1})=2$. Next, we consider $n\ge 2$.

First, we show that ${\kappa }_1({\mathcal{FC}}_n;K_{1,1})\le 3$ and ${\kappa }_1^s({\mathcal{FC}}_n;K_{1,1})\le 3$ as follows: Let $u=0^{\mathbf{n}}$, $v=0^{\mathbf{n}-\mathbf{1}}1$. Take $u_1=0^{\mathbf{n}-\mathbf{1}}2,u_2=0^{\mathbf{n}-\mathbf{1}}4,v_1=0^{\mathbf{n}-\mathbf{1}}3,v_2=0^{\mathbf{n}-\mathbf{1}}5,v_3=0^{\mathbf{n}-\mathbf{2}}10,v_3^1=0^{\mathbf{n}-\mathbf{2}}11$. Set $F=\{\{u_1,v_1\},\{u_2,v_2\},\{v_3,v_3^1\}\}$. Obviously, every element in F is isomorphic to $K_{1,1}$ and $|F|=3$. Because ${\mathcal{FC}}_n-F$ is not connected and its every component has more than one vertex, we have that F is a one-extra $K_{1,1}$-structure cut of ${\mathcal{FC}}_n$. This means that ${\kappa }_1({\mathcal{FC}}_n;K_{1,1})\le 3$ and ${\kappa }_1^s({\mathcal{FC}}_n;K_{1,1})\le 3$.

Below, we prove that ${\kappa }_1^s({\mathcal{FC}}_n;K_{1,1})\ge 3$ and ${\kappa }_1({\mathcal{FC}}_n;K_{1,1})\ge 3$ for $n\ge 2$. We prove this by contradiction. Let F be a one-extra $K_{1,1}$-substructure cut of ${\mathcal{FC}}_n$ with $|F|\le 2$. Then, ${\mathcal{FC}}_n-F$ is disconnected. We assume that C is the smallest component of ${\mathcal{FC}}_n-F$. Clearly, $|V(C)|\ge 2$. However, by Theorem 1, ${\kappa }_1\left({\mathcal{FC}}_n\right)=5$ for $n\ge 2$. This means that under the condition $|V(C)|\ge 2$, if we want to disconnect ${\mathcal{FC}}_n$, we have to delete at least five vertices. However, $|V(F)|\le 2\times 2=4<5$, which is a contradiction. Thus, ${\kappa }_1^s({\mathcal{FC}}_n;K_{1,1})\ge 3$, and so ${\kappa }_1({\mathcal{FC}}_n;K_{1,1})\ge 3$ for $n\ge 2$. □

4. Extra Edge Connectivity, Structure Edge Connectivity and g-Extra H-Structure Edge Connectivity

Let $\mathcal{E}$ be any subset of edges of ${\mathcal{FC}}_n$. We set ${\mathcal{E}}_i=\mathcal{E}\cap E\left({\mathcal{FC}}_{n-1}^i\right)$ for each $i\in {\mathbb{Z}}_8$, and ${\mathcal{E}}_c=\mathcal{E}-\left({\bigcup }_{i\in {\mathbb{Z}}_8}E\left({\mathcal{FC}}_{n-1}^i\right)\right)$. Note that ${\mathcal{E}}_c$ is the set of faulty intercubic edges. Moreover, $|\mathcal{E}|=|{\mathcal{E}}_c|+{\sum }_{i\in {\mathbb{Z}}_8}|{\mathcal{E}}_i|$.

Lemma 11.

Let $\mathcal{E}$ be a subset of edges of ${\mathcal{FC}}_n$ with $|\mathcal{E}|\le 4$. Define m as $max\{|{\mathcal{E}}_i|\mid i\in {\mathbb{Z}}_8\}$, and let t be an element in ${\mathbb{Z}}_8$ such that $|{\mathcal{E}}_t|=max\{|{\mathcal{E}}_i|\mid i\in {\mathbb{Z}}_8\}$. For $n\ge 2$, ${\mathcal{FC}}_n-\mathcal{E}$ is connected if $m\le 2$, and ${\mathcal{FC}}_{n-1}^{{\mathbb{Z}}_8-\left\{t\right\}}-\mathcal{E}$ is connected if $m\le 4$.

Proof. 

We set $\{a_0,a_1,\dots ,a_7\}={\mathbb{Z}}_8$ such that $a_0=t$ and $|{\mathcal{E}}_{a_0}|\ge |{\mathcal{E}}_{a_1}|\ge \cdots \ge |{\mathcal{E}}_{a_7}|$. Since $|\mathcal{E}|\le 4$ and $|\mathcal{E}|=|{\mathcal{E}}_c|+{\sum }_{k=0}^7|{\mathcal{E}}_{a_k}|$, $max\{|{\mathcal{E}}_{a_j}|\mid j\in \{1,2,\dots ,7\}\}\le 2$. We set $S=\{a_1,a_2,\dots ,a_7\}$, and ${\mathcal{E}}_S=\mathcal{E}-{\mathcal{E}}_{a_0}$. By Lemma 5, ${\mathcal{FC}}_{n-1}^i-{\mathcal{E}}_i$ is connected for each $i\in S$.

• Case 1: $m\le 4$. Let $p,q\in S$, and let R be the set $S-\{p,q\}$. Since $|{\mathcal{E}}_c|\le 4$ and $|R|=5$, by Lemma 6, there is an index z in R such that the edge between ${\mathcal{FC}}_{n-1}^p-{\mathcal{E}}_p$ and ${\mathcal{FC}}_{n-1}^z-{\mathcal{E}}_z$ and the edge between ${\mathcal{FC}}_{n-1}^q-{\mathcal{E}}_q$ and ${\mathcal{FC}}_{n-1}^z-{\mathcal{E}}_z$ are not in ${\mathcal{E}}_c$. Since ${\mathcal{FC}}_{n-1}^z-{\mathcal{E}}_z$ is connected, ${\mathcal{FC}}_{n-1}^p-{\mathcal{E}}_p$ can connect to ${\mathcal{FC}}_{n-1}^q-{\mathcal{E}}_q$ via ${\mathcal{FC}}_{n-1}^z-{\mathcal{E}}_z$. Consequently, for any two distinct indices $\alpha$ and $\beta$ in S, there exists an index $r\in S-\{\alpha ,\beta \}$ such that ${\mathcal{FC}}_{n-1}^{\alpha }-{\mathcal{E}}_{\alpha }$ can connect to ${\mathcal{FC}}_{n-1}^{\beta }-{\mathcal{E}}_{\beta }$ via ${\mathcal{FC}}_{n-1}^r-{\mathcal{E}}_r$. Thus, ${\mathcal{FC}}_{n-1}^S-{\mathcal{E}}_S$ is connected if $m\le 4$.
• Case 2: $m\le 2$. By Case 1, we have that ${\mathcal{FC}}_{n-1}^S-{\mathcal{E}}_S$ is connected. By Lemma 5, ${\mathcal{FC}}_{n-1}^{a_0}-{\mathcal{E}}_{a_0}$ is connected. By Lemma 6, there are seven edges between ${\mathcal{FC}}_{n-1}^{a_0}$ and ${\mathcal{FC}}_{n-1}^S$. Since $|{\mathcal{E}}_c|\le 4$, there is an edge between ${\mathcal{FC}}_{n-1}^{a_0}$ and ${\mathcal{FC}}_n^S$ such that it is not in ${\mathcal{E}}_c$. Thus, ${\mathcal{FC}}_n-\mathcal{E}$ is connected if $m\le 2$. □

4.1. Extra Edge Connectivity

Lemma 12.

If $\mathcal{E}$ is a subset of edges of ${\mathcal{FC}}_2$ with $|\mathcal{E}|\le 4$, then ${\mathcal{FC}}_2-\mathcal{E}$ contains a component with at least $8^2-1$ vertices.

Proof. 

Without loss of generality, we may assume that $|{\mathcal{E}}_0|\ge |{\mathcal{E}}_k|$ for each $k\ge 1$. According to Lemma 11, this lemma is valid for $|{\mathcal{E}}_0|\le 2$. Hence, we consider the case $|{\mathcal{E}}_0|\ge 3$. We have $|{\mathcal{E}}_c|\le 1$. Let $R=\{x_1,x_2,\dots ,x_7\}$ be the set of all intercubic vertices in ${\mathcal{FC}}_1^0$, and let $x_0=00$ be the boundary vertex in ${\mathcal{FC}}_1^0$. Since $|{\mathcal{E}}_c|\le 1$, there is at least six intercubic vertices in ${\mathcal{FC}}_1^0$ such that their corresponding intercubic edges are not in ${\mathcal{E}}_c$. We may suppose that $x_i$’s corresponding intercubic edge is not in ${\mathcal{E}}_c$ for each $i\in \{1,2,\dots ,6\}$. Thus, $x_i$ can connect to ${\mathcal{FC}}_1^S$ via its corresponding intercubic edge. Let e be the $x_7$’s corresponding intercubic edge.

• Case 1: $e\notin {\mathcal{E}}_c$. We have that $x_7$ can connect to ${\mathcal{FC}}_1^S$ via its corresponding intercubic edge. Hence, the subgraph H induced by R and $V({\mathcal{FC}}_1^S)$ is connected and it contains $7+7\times 8=8^2-1$ vertices.
• Case 2: $e\in {\mathcal{E}}_c$. We have $|{\mathcal{E}}_0|=3$.
• Case 2.1: $|N_{{\mathcal{FC}}_1^0}\left(x_0\right)\cap \{x_1,x_2,\dots ,x_6\}|\ge 1$. Let $y\in N_{{\mathcal{FC}}_1^0}\left(x_0\right)\cap \{x_1,x_2,\dots ,x_6\}$. Since $(x_0,y)\notin {\mathcal{E}}_0$ and y can connect to ${\mathcal{FC}}_1^S$ via its corresponding intercubic edge, $x_0$ can connect to ${\mathcal{FC}}_1^S$ via y. Hence, the subgraph H induced by $\left\{x_0\right\}$, $R-\left\{x_7\right\}$ and $V({\mathcal{FC}}_1^S)$ is connected and it contains $7+7\times 8=8^2-1$ vertices.
• Case 2.2: $|N_{{\mathcal{FC}}_1^0}\left(x_0\right)\cap \{x_1,x_2,\dots ,x_6\}|=0$. Since ${deg}_{{\mathcal{FC}}_{n-1}^0}\left(x_0\right)=3$, we have that there are at least two edges corresponding to $x_0$ that are in ${\mathcal{E}}_0$. Since ${deg}_{{\mathcal{FC}}_1^0}\left(x_7\right)=3$, $|N_{{\mathcal{FC}}_1^0}\left(x_7\right)\cap \{x_1,x_2,\dots ,x_6\}|\ge 1$. Similarly to Case 2.1, the subgraph H induced by R and $V({\mathcal{FC}}_1^S)$ is connected and contains $7+7\times 8=8^2-1$ vertices. □

Lemma 13.

Let $F\subset E\left({\mathcal{FC}}_n\right)$ with $|F|\le 4$. If $n\ge 2$, then ${\mathcal{FC}}_n-F$ contains a component with at least $8^n-1$ vertices.

Proof. 

According to Lemma 12, the lemma is valid for $n=2$. Below, we assume that the result is also valid for $n-1$. Without loss of generality, we may assume that $|{\mathcal{E}}_0|\ge |{\mathcal{E}}_k|$ for each $k\ge 1$. According to Lemma 11, this lemma is valid for $|{\mathcal{E}}_0|\le 2$. Hence, we consider the case $|{\mathcal{E}}_0|\ge 3$.

By Lemma 11, ${\mathcal{FC}}_{n-1}^S$ is connected for $S=\{1,2,...,7\}$. By the induction hypothesis, there is a connected component R in ${\mathcal{FC}}_{n-1}^0-{\mathcal{E}}_0$ that contains at least $8^{n-1}-1$ vertices. Consequently, R contains at least six intercubic vertices. Since $|{\mathcal{E}}_c|\le 4$, some of the intercubic vertices in R can connect to ${\mathcal{FC}}_{n-1}^S$ via its intercubic edge. Thus, the subgraph induced by $V\left(R\right)$ and $V\left({\mathcal{FC}}_{n-1}^S\right)$ is connected and it contains at least $(8^{n-1}-1)+7\times 8^{n-1}=8^n-1$ vertices. □

From Lemma 13, we obtain the corollary below.

Corollary 1.

Let $F\subset E\left({\mathcal{FC}}_n\right)$ with $|F|\le 4$. Then, one of the following is true:

1. ${\mathcal{FC}}_n-F$ is connected;

2. ${\mathcal{FC}}_n-F$ contains exactly two components, and one of them contains $8^n-1$ vertices.

Theorem 7.

$${\lambda }_1\left({\mathcal{FC}}_n\right)=\left\{\begin{array}{cc}4& \mathrm{if}n=1,\hfill \\ 5& \mathrm{if}n\ge 2.\hfill \end{array}\right.$$

Proof. 

Combining the fact that ${\mathcal{FC}}_1\cong Q_3$ with Lemma 1, we obtain ${\lambda }_1\left(Q_3\right)=4$. Hence, ${\lambda }_1\left({\mathcal{FC}}_1\right)=4$. Thus, we consider the case $n\ge 2$ below. On one hand, we prove ${\lambda }_1\left({\mathcal{FC}}_n\right)\le 5$. Let $u=0^{\mathbf{n}}$, $v=0^{\mathbf{n}-\mathbf{1}}1$, $F=N_{{\mathcal{FC}}_n}^{\prime }\left(\{u,v\}\right)$. Clearly, $(u,v)\in E\left({\mathcal{FC}}_n\right)$. Because $de{g}_{{\mathcal{FC}}_n}\left(u\right)=3$, $de{g}_{{\mathcal{FC}}_n}\left(v\right)=4$ and u,v have no common vertices, $|F|=5$. Since $\lambda \left({\mathcal{FC}}_n\right)=3$, ${\mathcal{FC}}_n-F-\{u,v\}$ is connected. Thus, every component of ${\mathcal{FC}}_n-F$ has at least two vertices. This means that F is a one-extra edge cut of ${\mathcal{FC}}_n$. Thus, ${\lambda }_1\left({\mathcal{FC}}_n\right)\le 5$. On the other hand, we prove ${\lambda }_1\left({\mathcal{FC}}_n\right)\ge 5$. Suppose, to the contrary, that ${\lambda }_1\left({\mathcal{FC}}_n\right)<5$. Suppose that S is an arbitrary minimum one-extra edge cut of ${\mathcal{FC}}_n$. This means $|F|={\lambda }_1\left({\mathcal{FC}}_n\right)\le 4$. By Corollary 1, ${\mathcal{FC}}_n-F$ contains a component, say C, that satisfies $|V(C)|=1$. Clearly, this is a contradiction. Hence, ${\lambda }_1\left({\mathcal{FC}}_n\right)\ge 5$. In summary, ${\lambda }_1\left({\mathcal{FC}}_n\right)=5$. □

4.2. Structure Edge Connectivity

Theorem 8.

When $1\le h\le 3$, $\lambda ({\mathcal{FC}}_n;K_{1,h})={\lambda }^s({\mathcal{FC}}_n;K_{1,h})=\lceil {\displaystyle \frac{3}{h}}\rceil$.

Proof. 

The result clearly holds for $h=1$ since $\lambda \left({\mathcal{FC}}_n\right)=3$. In the following we consider the case $h\in \{2,3\}$.

First, we show that $min\{{\lambda }^s({\mathcal{FC}}_n;K_{1,h}),\lambda ({\mathcal{FC}}_n;K_{1,h})\}\ge \lceil {\displaystyle \frac{3}{h}}\rceil$ for $h\in \{2,3\}$. Assume that S is a $K_{1,h}$-substructure set of ${\mathcal{FC}}_n$ with $|S|\le \lceil {\displaystyle \frac{3}{h}}\rceil -1$. Since $|E\left(S\right)|\le 2<3=\lambda \left({\mathcal{FC}}_n\right)$, ${\mathcal{FC}}_n-E\left(S\right)$ is connected. Thus, $min\{\lambda ({\mathcal{FC}}_n;K_{1,h}),{\lambda }^s({\mathcal{FC}}_n;K_{1,h})\}\ge \lceil {\displaystyle \frac{3}{h}}\rceil$.

Next, we prove that $max\{{\lambda }^s({\mathcal{FC}}_n;K_{1,h}),\lambda ({\mathcal{FC}}_n;K_{1,h})\}\le \lceil {\displaystyle \frac{3}{h}}\rceil$ for $h\in \{2,3\}$. We set $u=0^{\mathbf{n}}$, $u_1=0^{\mathbf{n}-\mathbf{1}}1$, $u_2=0^{\mathbf{n}-\mathbf{1}}2$, $u_3=0^{\mathbf{n}-\mathbf{1}}4$ and $u_3^1=0^{\mathbf{n}-\mathbf{1}}5$.

• Case 1: $h=2$. Set $S=\{\{u,u_1,u_2\},\{u,u_3,u_3^1\}\}$. Obviously, S’s every element is isomorphic to $K_{1,2}$ and $|S|=2$. Since ${\mathcal{FC}}_n-E\left(F\right)$ is disconnected, we have that $E\left(S\right)$ is clearly a $K_{1,2}$-structure edge cut of ${\mathcal{FC}}_n$. This means that $\lambda ({\mathcal{FC}}_n;K_{1,2})\le 2$ and ${\lambda }^s({\mathcal{FC}}_n;K_{1,2})\le 2$.
• Case 2: $h=3$. Set $S=\left\{\{u,u_1,u_2,u_3\}\right\}$. Obviously, F’S every element isomorphic to $K_{1,3}$ and $|S|=1$. Since ${\mathcal{FC}}_n-E\left(F\right)$ is disconnected, we have that $E\left(F\right)$ is clearly a $K_{1,3}$-structure edge cut of ${\mathcal{FC}}_n$. This implies that $\lambda ({\mathcal{FC}}_n;K_{1,3})\le 1$ and ${\lambda }^s({\mathcal{FC}}_n;K_{1,3})\le 1$.

In conclusion, for $1\le h\le 3$, we have $\lambda ({\mathcal{FC}}_n;K_{1,h})={\lambda }^s({\mathcal{FC}}_n;K_{1,h})=\lceil {\displaystyle \frac{3}{h}}\rceil$. □

4.3. g-Extra H-Structure Edge Connectivity

Theorem 9.

$${\lambda }_1({\mathcal{FC}}_n;K_{1,2})={\lambda }_1^s({\mathcal{FC}}_n;K_{1,2})=\left\{\begin{array}{cc}2& \mathrm{if}n=1,\hfill \\ 3& \mathrm{if}n\ge 2.\hfill \end{array}\right.$$

Proof. 

By definition, we obtain ${\lambda }_1({\mathcal{FC}}_1;K_{1,2})={\lambda }_1^s({\mathcal{FC}}_n;K_{1,2})=2$. In the following, we prove first that ${\lambda }_1({\mathcal{FC}}_n;K_{1,2})\le 3$ and ${\lambda }_1^s({\mathcal{FC}}_n;K_{1,2})\le 3$ for $n\ge 2$. Let $u=0^{\mathbf{n}}$, $v=0^{\mathbf{n}-\mathbf{1}}1$. Take $u_1=0^{\mathbf{n}-\mathbf{1}}2,u_2=0^{\mathbf{n}-\mathbf{1}}4,v_1=0^{\mathbf{n}-\mathbf{1}}3,v_2=0^{\mathbf{n}-\mathbf{1}}5,v_3=0^{\mathbf{n}-\mathbf{2}}10,v_3^1=0^{\mathbf{n}-\mathbf{2}}11$. Set $S=\{\{u,u_1,u_2\},\{v,v_1,v_2\},\{v_3,v,v_3^1\}\}$. Obviously, S’s every element is isomorphic to $K_{1,2}$ and $|S|=3$. Because ${\mathcal{FC}}_n-E\left(S\right)$ is not connected and ${\mathcal{FC}}_n-E\left(S\right)$’s every component has more than one vertices, we infer that $E\left(S\right)$ is a one-extra $K_{1,2}$-structure edge cut of ${\mathcal{FC}}_n$ and so ${\lambda }_1({\mathcal{FC}}_n;K_{1,2})\le 3$ and ${\lambda }_1^s({\mathcal{FC}}_n;K_{1,2})\le 3$. Now, we prove that ${\lambda }_1^s({\mathcal{FC}}_n;K_{1,2})\ge 3$ and ${\lambda }_1({\mathcal{FC}}_n;K_{1,2})\ge 3$ when $n\ge 2$. Assume that S is an arbitrary set of edge disjoint $K_{1,2}$-substructures of ${\mathcal{FC}}_n$ with $|S|\le 2$. Then, $|E\left(S\right)|\le 4<{\lambda }_1\left({\mathcal{FC}}_n\right)=5$. Thus, ${\lambda }_1^s({\mathcal{FC}}_n;K_{1,2})\ge 3$ and so ${\lambda }_1({\mathcal{FC}}_n;K_{1,2})\ge 3$. □

5. Conclusions

Fault tolerance is significant to the reliability analysis of interconnection networks. Extra connectivity, structure connectivity and t-extra L-structure connectivity are important parameters to measure network fault tolerance. In this paper, we explored the t-extra connectivity, L-structure connectivity and t-extra L-structure connectivity of fully connected cubic networks ${\mathcal{FC}}_n$. In detail, we determined that

$$\begin{array}{l}1.{\kappa }_1\left({\mathcal{FC}}_n\right)=\left\{\begin{array}{cc}4& \mathrm{if}n=1,\hfill \\ 5& \mathrm{if}n\ge 2.\hfill \end{array}\right.\\ 2.\kappa ({\mathcal{FC}}_n;K_{1,1})={\kappa }^s({\mathcal{FC}}_n;K_{1,1})=\left\{\begin{array}{cc}2& \mathrm{if}n=1,\hfill \\ 3& \mathrm{if}n\ge 2.\hfill \end{array}\right.\\ 3.\kappa ({\mathcal{FC}}_n;K_{1,h})={\kappa }^s({\mathcal{FC}}_n;K_{1,h})=2\mathrm{for}n\ge 1\mathrm{and}h=2,3.\\ 4.{\kappa }_1({\mathcal{FC}}_n;K_{1,1})={\kappa }_1^s({\mathcal{FC}}_n;K_{1,1})=\left\{\begin{array}{cc}2& \mathrm{if}n=1,\hfill \\ 3& \mathrm{if}n\ge 2.\hfill \end{array}\right.\end{array}$$

We also established the corresponding edge versions of the results $1\sim 4$. On the basis of this research, one can continue to study the t-extra connectivity, L-structure connectivity and t-extra L-structure connectivity of ${\mathcal{FC}}_n$ for more general t and L.