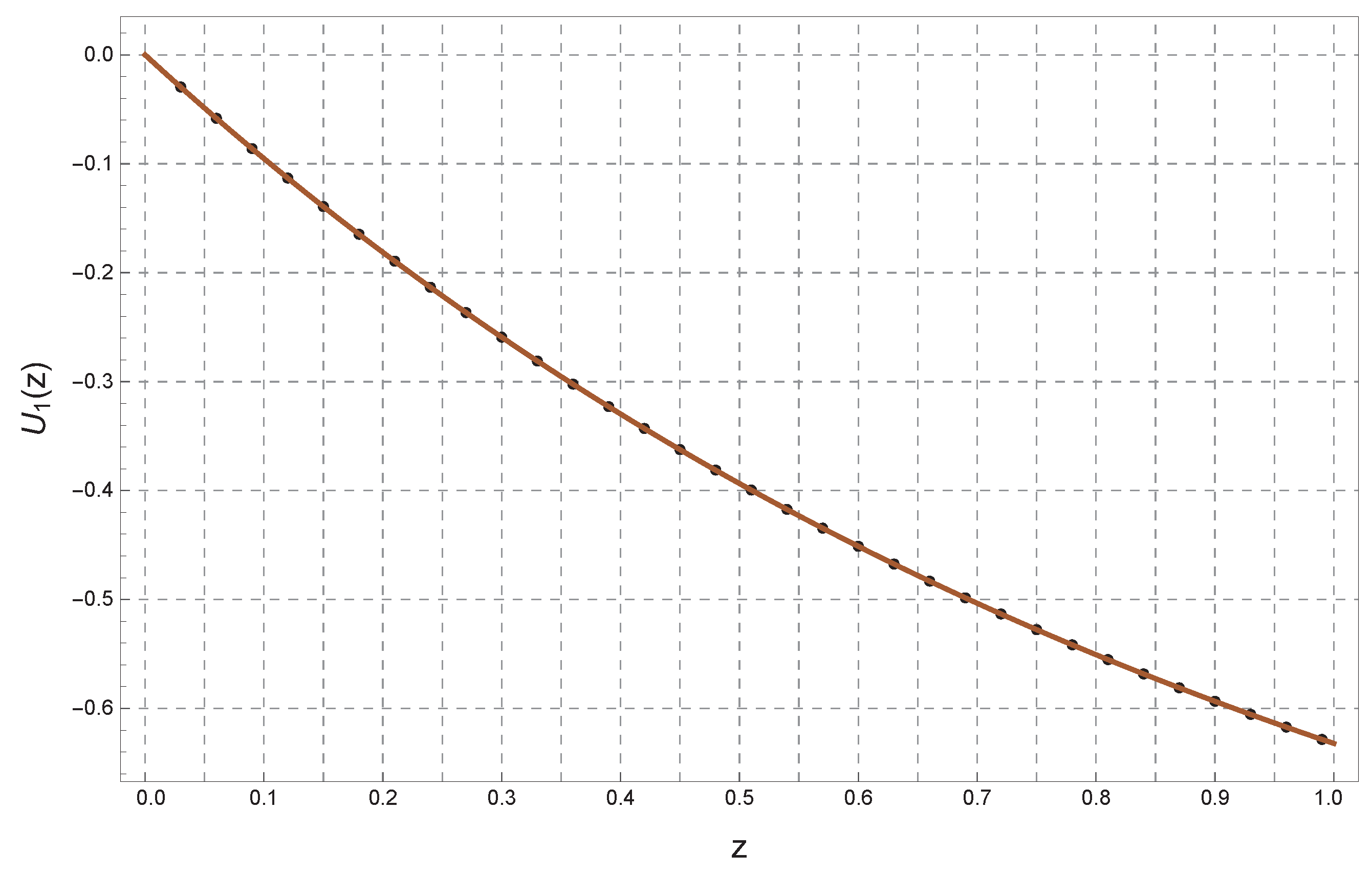Efficient Spectral Galerkin and Collocation Approaches Using Telephone Polynomials for Solving Some Models of Differential Equations with Convergence Analysis

Abstract

This study presents Galerkin and collocation algorithms based on Telephone polynomials (TelPs) for effectively solving high-order linear and non-linear ordinary differential equations (ODEs) and ODE systems, including those with homogeneous and nonhomogeneous initial conditions (ICs). The suggested approach also handles partial differential equations (PDEs), emphasizing hyperbolic PDEs. The primary contribution is to use suitable combinations of the TelPs, which significantly streamlines the numerical implementation. A comprehensive study has been conducted on the convergence of the utilized telephone expansions. Compared to the current spectral approaches, the proposed algorithms exhibit greater accuracy and convergence, as demonstrated by several illustrative examples that prove their applicability and efficiency.

1. Introduction

Polynomials and special functions are crucial in various fields because of their several uses in applied sciences; see, for instance, ref. [1,2,3]. Many theoretical publications have been devoted to the different polynomial sequences. The authors of [4] explored several polynomial sequences and offered a few practical uses for their findings. In ref. [5], the authors investigated different polynomial sequences. In ref. [6], degenerated polynomials of the Apostol type were introduced. The authors of [7] examined Sheffer polynomial sequences. Several articles also examined certain generalized polynomials. For example, the authors of [8] developed several other generalized polynomials. A significant subject in numerical analysis and the solution of various differential equations (DEs) is the utilization of distinct sequences. A great deal of effort has been focused on this area. For example, the authors of [9,10] used specific polynomials to solve some DEs, which are generalizations of the first and second kinds of Chebyshev polynomials. The generalized Bessel polynomials and the generalized Jacobi polynomials were used to address multi-order fractional DEs in [11,12]. The authors of ref. [13] employed a set of generalized Chebyshev polynomials to solve the telegraph DEs.

High-order DEs are central to numerous applications in science and engineering, including structural mechanics, fluid dynamics, and electromagnetic theory. Over the past few decades, significant advancements have been made in developing efficient numerical methods to address these complex problems. Among the most notable techniques are spectral methods, which have demonstrated superior convergence properties compared to traditional finite difference and finite element methods, especially for problems with smooth solutions [14,15,16].

Recent advancements in machine learning have shown promising applications in solving ODEs and PDEs. Various studies have successfully implemented machine learning techniques, providing innovative solutions and insights into complex dynamics. For instance, the work by Qiu et al. [17] explored novel machine learning frameworks for ODEs, while Zhang et al. [18] demonstrated effective methodologies for PDEs. Additionally, the study by Cuomo et al. [19] highlighted the evolving role of machine learning in enhancing computational efficiency and accuracy in this domain. These contributions collectively illustrate the dynamic development of machine learning approaches in addressing differential equations and underscore the potential for further exploration in our research.

In addition to the emerging techniques in machine learning and operational calculus, it is crucial to recognize traditional numerical methods that have been extensively employed in the approximation of differential equations. For instance, Runge–Kutta methods provide a robust framework for solving ordinary differential equations, offering varying degrees of accuracy depending on the specific formulation used. Similarly, differential transformation methods have gained attention for their efficiency and ease of implementation in obtaining numerical solutions. These classical approaches have been explored in literature, as highlighted in recent studies (e.g., [19,20]), and will be discussed further to provide a comprehensive overview of the landscape of numerical techniques applicable to differential equations.

Heat transfer, wave propagation, fluid dynamics, and many more areas of physics and engineering extensively use PDEs. In addition, biology uses them to model population dynamics and disease transmission, while economics uses them to compute price alternatives. Photodynamic enzymes are vital in medical imaging. The geosciences utilize them for weather prediction and groundwater movement simulation, while the material sciences employ them for chemical reaction and diffusion studies. For some applications of different PDEs, see [21,22]. Several numerical techniques exist for solving different PDEs. For example, the authors of [23] followed a variational quantum algorithm for handling PDEs. In [24], some studies of an inverse source problem for the linear parabolic equation were performed.

Spectral methods use global basis functions, such as orthogonal polynomials or trigonometric functions, to approximate the solution to DEs. These methods can be classified into various types (see, for example, [25,26,27,28]). The main spectral methods are collocation, tau, and Galerkin. The collocation method relies on choosing suitable nodes in the domain and, after that, satisfying the equations at these points. Many authors use the collocation method because it is easy to implement and can handle various DEs. For example, the authors of [29] applied a wavelet collocation approach to treat the Benjamin–Bona–Mahony equation. Another collocation approach using third-kind Chebyshev polynomials was followed in [30] to treat the nonlinear fractional Duffing equation. In [31], the authors applied a collocation procedure to specific high-order DEs. The collocation method treated inverse heat equations in [32]. Some other contributions regarding collocation methods can be found in [33,34,35]. The Galerkin method and its variants are also among the essential spectral methods. The main principle of applying this method is to choose basis functions that meet the underlying conditions. For example, the authors of [36] applied a Jacobi Galerkin algorithm for two-dimensional time-dependent PDEs. Some other contributions regarding the Galerkin method can be found in [37,38,39,40]. The tau method can be applied without restrictions on the choice of basis functions. In [41], the authors followed a tau approach for certain Maxwell’s equations. Another tau approach was followed in [42] to solve the two-dimensional ocean acoustic propagation in an undulating seabed environment. A tau–Gegenbauer spectral approach was followed for treating certain systems of fractional integro DEs in [43]. Some other contributions can be found in [44,45,46].

Table 1. Summary of Key Literature on Galerkin’s Approaches to Solving Differential Equations.

Reference	Methodology	Key Findings
Galerkin [47]	Original formulation of the Galerkin method	Introduced the concept of weighted residuals for approximating solutions to differential equations.
Strang and Fix [48]	Variational methods	Discussed the application of Galerkin methods in finite element analysis, providing a comprehensive framework for numerical solutions.
Ciarlet [49]	Finite Element Methods	Established foundational principles for Galerkin methods in Sobolev spaces and their applications in PDEs.
Reddy [50]	Finite Element Methods	Explored advanced Galerkin approaches for nonlinear problems, emphasizing the versatility of the method in engineering applications.
Hughes [51]	Galerkin methods in fluid dynamics	Investigated the application of Galerkin methods in computational fluid dynamics, highlighting stability and convergence.
Quarteroni and Valli [52]	Numerical Approximation of PDEs	Provided a detailed analysis of Galerkin methods for various types of PDEs, with a focus on error estimation.

summarizes the key publications related to Galerkin’s methods for solving DEs, including the types of equations addressed, the specific Galerkin approach used, and notable findings.

In 1800, Heinrich Rothe proposed the Telephone numbers (TelNs) method while computing the involutions in a set of n elements. In a telephone system, where each subscriber may only be linked to a maximum of two other subscribers, the sequence of TelNs can alternatively be seen as the number of feasible methods to make connections between the n subscribers. In graph theory, the quantity of matchings in a whole graph with n vertices is another use of the TelNs. In this paper, we will develop a generalization for the TelNs to build a sequence of polynomials, namely TelPs. We will employ these polynomials to solve some ODEs and PDEs.

In this study, we propose a spectral Galerkin approach for solving some models of DEs. We utilize the TelPs as basis functions. We will propose suitable basis functions for handling some models of DEs. The convergence analysis for the used expansions will be discussed.

The structure of this paper is organized as follows: Section 2 gives an overview of the mathematical properties of TelPs and develops an inversion formula, which is essential for analyzing the error analysis of the used expansion. Section 3 describes the Galerkin formulation for the high-order linear IVPs, while Section 4 proposes a collocation algorithm for treating the non-linear IVPs. Section 5 extends the method to systems of DEs, while Section 6 discusses the application to hyperbolic PDEs. In Section 7, a comprehensive investigation of the convergence and error analysis is performed. Numerical results presented in Section 8 validate the efficiency and accuracy of the presented methods, with concluding remarks and future research directions in Section 9.

2. An Overview of TelNs and Their Corresponding Polynomials

In mathematics, the involution numbers, sometimes called TelNs, are a series of integers that count the possible connections between n individuals through direct telephone calls. These numbers can be generated using the following recursive formula [53]:

$${\mathcal{T}}_n={\mathcal{T}}_{n-1}+(n-1){\mathcal{T}}_{n-2},{\mathcal{T}}_0={\mathcal{T}}_1=1.$$

(1)

These numbers can be represented explicitly as

$${\mathcal{T}}_n=\sum _{\ell =0}^{⌊{\displaystyle \frac{n}{2}}⌋}{\displaystyle \frac{n!}{2^{\ell }\ell !(n-2\ell )!}}.$$

Now, we define a sequence of polynomials ${\mathcal{T}}_n\left(z\right)$ that generalize the numbers ${\mathcal{T}}_n$. We define ${\mathcal{T}}_n\left(z\right)$ of degree n as follows:

$${\mathcal{T}}_n\left(z\right)=\sum _{\ell =0}^{⌊{\displaystyle \frac{n}{2}}⌋}{\displaystyle \frac{n!}{2^{\ell }\ell !(n-2\ell )!}}{z}^{n-2\ell }.$$

(2)

From Formula (2), it can be verified that the recurrence relation given by

$${\mathcal{T}}_n\left(z\right)=z{\mathcal{T}}_{n-1}\left(z\right)+(n-1){\mathcal{T}}_{n-2}\left(z\right),{\mathcal{T}}_0\left(z\right)=1,{\mathcal{T}}_1\left(z\right)=z,$$

(3)

is satisfied by the TelPs that are expressed in (2). Now, we will give the inversion formula to Formula (2) in the following theorem.

Theorem 1.

For every non-negative integer m, the following formula holds:

$$z^i=\sum _{r=0}^{⌊{\displaystyle \frac{i}{2}}⌋}{\displaystyle \frac{{\left(-\frac{1}{2}\right)}^r{(1+i-2r)}_{2r}}{r!}}{\mathcal{T}}_{i-2r}\left(z\right),$$

(4)

where ${\left(A\right)}_r$ is the Pochhammer function defined as ${\displaystyle {\left(A\right)}_r=\frac{\Gamma (A+r)}{\Gamma \left(A\right)}}$.

Proof. 

We will proceed by induction. The formula holds for $i=0$. Assume that Formula (4) is valid, and we have to prove the validity of the following identity:

$$z^{i+1}=\sum _{r=0}^{⌊{\displaystyle \frac{i+1}{2}}⌋}{\displaystyle \frac{{\left(-\frac{1}{2}\right)}^r{(2+i-2r)}_{2r}}{r!}}{\mathcal{T}}_{i-2r+1}\left(z\right).$$

(5)

Now, making use of the inductive hypothesis, we can write

$$z^{i+1}=\sum _{r=0}^{⌊{\displaystyle \frac{i}{2}}⌋}{\displaystyle \frac{{\left(-\frac{1}{2}\right)}^r{(1+i-2r)}_{2r}}{r!}}z{\mathcal{T}}_{i-2r}\left(z\right).$$

(6)

Making use of the recurrence relation (3) in the following form:

$$z{\mathcal{T}}_n\left(z\right)={\mathcal{T}}_{n+1}\left(z\right)-n{\mathcal{T}}_{n-1}\left(z\right),$$

(7)

the following formula can be obtained:

$$z^{i+1}=\sum _{r=0}^{⌊{\displaystyle \frac{i}{2}}⌋}{\displaystyle \frac{{\left(-\frac{1}{2}\right)}^r{(1+i-2r)}_{2r}}{r!}}({\mathcal{T}}_{i-2r+1}\left(z\right)-(i-2r){\mathcal{T}}_{i-2r-1}\left(z\right)).$$

(8)

Some algebraic computations lead to Formula (5). □

Remark 1.

The inversion Formula (4) can be written in the following alternative formula:

$$z^i=\sum _{k=0}^i{d}_{i,k}{\mathcal{T}}_k\left(z\right),$$

(9)

where

$$d_{i,k}=\left\{\begin{array}{cc}{\displaystyle \frac{i!{\left(-\frac{1}{2}\right)}^{\left(\frac{i-k}{2}\right)}}{k!\left(\frac{i-k}{2}\right)!}},\hfill & (i-k)even,\hfill \\ 0,\hfill & otherwise.\hfill \end{array}\right.$$

(10)

3. Treatment of High-Order Initial Value Problems

In this section, we focus on applying the Telephone Galerkin method (TGM) to solve linear higher-order ODEs, both with homogeneous and non-homogeneous ICs.

3.1. Homogeneous ICs

We are interested in handling the following linear higher-order ODEs:

$${\mathcal{U}}^{\left(m\right)}\left(z\right)+\sum _{i=0}^{m-1}{\lambda }_i{\mathcal{U}}^{\left(i\right)}\left(z\right)=\mathit{f}\left(z\right),z\in [0,1],$$

(11)

controlled by the following homogeneous ICs:

$${\mathcal{U}}^{\left(i\right)}\left(0\right)=0,i=0,1,\cdots ,m-1,$$

(12)

where ${\lambda }_0,{\lambda }_1,\cdots ,{\lambda }_{m-1}$ are constants. If we define the following spaces:

$$\begin{array}{cc}\hfill & S_N=\{{\mathcal{T}}_0\left(z\right),{\mathcal{T}}_1\left(z\right),{\mathcal{T}}_2\left(z\right),\cdots ,{\mathcal{T}}_N\left(z\right)\},\hfill \\ & {\Phi }_N=\{\varphi \left(z\right)\in S_N:{\varphi }^{\left(i\right)}\left(0\right)=0,i=0,1,\cdots ,m-1\},\hfill \end{array}$$

(13)

then, the TGM approximation to Equations (11) and (12) is to find ${\mathcal{U}}_N\left(z\right)\in {\Phi }_N$ such that

$$\left({\mathcal{U}}_N^{\left(m\right)}\left(z\right),{\varphi }_j\left(z\right)\right)+\sum _{i=0}^{m-1}{\mu }_i\left({\mathcal{U}}_N^{\left(i\right)}\left(z\right),{\varphi }_j\left(z\right)\right)=\left(\mathit{f}\left(z\right),{\varphi }_j\left(z\right)\right),\forall 0\le j\le N,$$

(14)

where the scalar inner product in the space $L^2(0,1)$ is ${\displaystyle (\mathcal{U}\left(z\right),\mathcal{V}\left(z\right))={\int }_0^1\mathcal{U}\left(z\right)\mathcal{V}\left(z\right)dx}$. To meet the homogenous ICs, we choose suitable basis functions in the form

$${\varphi }_i\left(z\right)=z^m{\mathcal{T}}_i\left(z\right),z\in [0,1].$$

(15)

Now, if we consider the following approximate solution ${\mathcal{U}}_N\left(z\right)$ for (11) and (12):

$${\mathcal{U}}_N\left(z\right)\simeq \sum _{i=0}^N{c}_i{\varphi }_i\left(z\right),z\in [0,1].$$

(16)

then, the Galerkin formulation for (11) and (12) is given by

$$\sum _{i=0}^N{c}_i\left[\left({\varphi }_i^{\left(m\right)}\left(z\right),{\varphi }_j\left(z\right)\right)+\sum _{l=0}^{m-1}{\lambda }_l\left({\varphi }_i^{\left(l\right)}\left(z\right),{\varphi }_j\left(z\right)\right)\right]=\left(\mathit{f}\left(z\right),{\varphi }_j\left(z\right)\right).$$

(17)

Let us denote

$$\begin{array}{cc}\hfill & \mathbf{A}={\left(a_{ij}\right)}_{0\le i,j\le N},a_{ij}=\left({\varphi }_i^{\left(m\right)}\left(z\right),{\varphi }_j\left(z\right)\right),\hfill \\ \hfill & {\mathbf{B}}_l={\left(b_{ij}^l\right)}_{0\le i,j\le N},b_{ij}^l=\left({\varphi }_i^{\left(l\right)}\left(z\right),{\varphi }_j\left(z\right)\right),0\le l\le m-1,\hfill \\ \hfill & \mathbf{F}={(f_0,f_1,\cdots ,f_N)}^T,{\mathit{f}}_j=\left(\mathit{f}\left(z\right),{\varphi }_j\left(z\right)\right).\hfill \end{array}$$

(18)

Then, (17) can be written equivalently in the following form:

$$\left(\mathbf{A}+\sum _{l=0}^{m-1}{\lambda }_l{\mathbf{B}}_l\right)\mathbf{C}=\mathbf{F},$$

(19)

in which the vector of unknowns is $\mathbf{C}={(c_0,c_1,\cdots ,c_N)}^T$. The following theorem presents the nonzero elements of the matrices, $\mathbf{A}$ and ${\mathbf{B}}_l(0\le l\le m-1)$.

Theorem 2.

Consider the basis functions ${\varphi }_i\left(z\right)$ in (15). Setting $a_{ij}=\left({\varphi }_i^{\left(m\right)}\left(z\right),{\varphi }_j\left(z\right)\right)$ and $b_{ij}^l=\left({\varphi }_i^{\left(l\right)}\left(z\right),{\varphi }_j\left(z\right)\right),0\le l\le m-1$. The nonzero elements of the two matrices $\mathit{A}$ and ${\mathit{B}}_l(0\le l\le m-1)$ can be written, respectively, in the following explicit forms:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & a_{ij}=\sum _{k=0}^{\lceil {\displaystyle \frac{i}{2}}\rceil }\sum _{s=0}^{\lceil {\displaystyle \frac{j}{2}}\rceil }{\displaystyle \frac{i!j!(i-2k+m)!}{2^{k+s}k!s!{((i-2k)!)}^2(j-2s)!(i+j-2k-2s+m+1)}},\hfill \end{array}\end{array}$$

(20)

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & b_{ij}^l=\sum _{k=0}^{\lceil {\displaystyle \frac{i}{2}}\rceil }\sum _{s=0}^{\lceil {\displaystyle \frac{j}{2}}\rceil }{\displaystyle \frac{i!j!(i-2k+m)!}{2^{k+s}k!s!(i-2k)!(j-2s)!(i-2k+m-l)!(i+j-2k-2s+2m-l+1)}}.\hfill \end{array}\end{array}$$

(21)

Proof. 

The basis functions ${\varphi }_i\left(z\right)$ are chosen such that the ICs (12) are satisfied. Now, we prove (21). Using (15), we have

$${\varphi }_i\left(z\right)=z^m\sum _{k=0}^{\lceil {\displaystyle \frac{i}{2}}\rceil }{\displaystyle \frac{i!}{2^{k}k!(i-2k)!}}{z}^{i-2k}=\sum _{k=0}^{\lceil {\displaystyle \frac{i}{2}}\rceil }{\displaystyle \frac{i!}{2^{k}k!(i-2k)!}}{z}^{i-2k+m}.$$

(22)

By differentiating both sides of (22) l times with respect to z, we obtain

$${\varphi }_i^{\left(l\right)}\left(z\right)=\sum _{k=0}^{\lceil {\displaystyle \frac{i}{2}}\rceil }{\displaystyle \frac{i!(i-2k+m)!}{2^{k}k!(i-2k)!(i-2k+m-l)!}}{z}^{i-2k+m-l},$$

(23)

and making use of the scalar inner product enables one to obtain

$$b_{ij}^l=\sum _{k=0}^{\lceil {\displaystyle \frac{i}{2}}\rceil }\sum _{s=0}^{\lceil {\displaystyle \frac{j}{2}}\rceil }{\displaystyle \frac{i!j!(i-2k+m)!}{2^{k+s}k!s!(i-2k)!(j-2s)!(i-2k+m-l)!}}{\int }_0^1{z}^{i+j-2k-2s+2m-l}dx,$$

(24)

which leads to the following formula:

$$b_{ij}^l=\sum _{k=0}^{\lceil {\displaystyle \frac{i}{2}}\rceil }\sum _{s=0}^{\lceil {\displaystyle \frac{j}{2}}\rceil }{\displaystyle \frac{i!j!(i-2k+m)!}{2^{k+s}k!s!(i-2k)!(i-2k+m-l)!(j-2s)!(i+j-2k-2s+2m-l+1)}},$$

(25)

which proves (21).

If we replace l in (21) with m, then we obtain (20). □

3.2. Treatment of Nonhomogeneous ICs

In this section, we show how to deal with Equation (11) governed by the following non-homogeneous ICs:

$${\mathcal{U}}^{\left(i\right)}\left(0\right)={\kappa }_i,i=0,1,\cdots ,m-1,$$

(26)

where ${\kappa }_i(i=0,1,\cdots ,m-1)$ are real constants. In such a case, we make use of the transformation

$$V\left(z\right)=\mathcal{U}\left(z\right)-\sum _{r=0}^{m-1}{\displaystyle \frac{{\kappa }_r}{r!}}{z}^r.$$

(27)

It follows that Equation (11) governed by the non-homogeneous conditions (12) turns into the following equation:

$$V^{\left(m\right)}\left(z\right)+\sum _{i=0}^{m-1}{\lambda }_i{V}^{\left(i\right)}\left(z\right)={\mathit{f}}^{*}\left(z\right),z\in [0,1],$$

(28)

governed by the following homogeneous conditions:

$$V^{\left(i\right)}\left(0\right)=0,i=0,1,\cdots ,m-1,$$

(29)

where

$${\mathit{f}}^{*}\left(z\right)=\mathit{f}\left(z\right)-\sum _{i=0}^{m-1}\sum _{r=i}^{m-1}{\displaystyle \frac{{\lambda }_i{\kappa }_r}{(r-i)!}}{z}^{r-i}.$$

4. Treatment of the High-Order Non-Linear IVPs

This section is confined to the numerical treatment of the high-order non-linear IVPs. The typical collocation method, together with the operational matrix of derivatives, will be utilized.

4.1. The Operational Matrix of Derivatives of the TelPs

Here, we establish the operational matrix of derivatives of the TelPs that will be used to solve the non-linear IVPs. The following theorem will be the key to developing the operational matrix.

Theorem 3.

The first derivative of ${\mathcal{T}}_j\left(z\right)$ is given by

$$D{\mathcal{T}}_j\left(z\right)=j{\mathcal{T}}_{j-1}\left(z\right),j\ge 1.$$

(30)

Proof. 

Based on the power form representation in (2), we can write

$$D{\mathcal{T}}_j\left(z\right)=j!\sum _{r=0}^{⌊{\displaystyle \frac{j-1}{2}}⌋}{\displaystyle \frac{2^{-r}(j-2r)}{(j-2r)!r!}}{z}^{j-2r-1}.$$

(31)

If we insert the inversion Formula (4) into (31), then the following formula can be obtained:

$$D{\mathcal{T}}_j\left(z\right)=j!\sum _{r=0}^{⌊{\displaystyle \frac{j-1}{2}}⌋}{\displaystyle \frac{2^{-r}(j-2r)}{(j-2r)!r!}}\sum _{s=0}^{⌊{\displaystyle \frac{j-1}{2}}⌋-r}{\displaystyle \frac{{\left(-\frac{1}{2}\right)}^s{(j-2(r+s))}_{2s}}{s!}}{\mathcal{T}}_{j-2r-2s-1}\left(z\right),$$

(32)

which can be written alternatively as

$$D{\mathcal{T}}_j\left(z\right)=j!\sum _{p=0}^{⌊{\displaystyle \frac{j-1}{2}}⌋}{\displaystyle \frac{2^{-p}}{(j-2p-1)!}}\sum _{r=0}^p{\displaystyle \frac{{(-1)}^{p-r}}{(p-r)!r!}}{\mathcal{T}}_{j-2p-1}\left(z\right).$$

(33)

Using the following identity:

$$\sum _{r=0}^p{\displaystyle \frac{{(-1)}^{p-r}}{(p-r)!r!}}=\left\{\begin{array}{cc}1,\hfill & p=0,\hfill \\ 0,\hfill & p>0.\hfill \end{array}\right.$$

Formula (33) reduces to the following simplified formula:

$$D{\mathcal{T}}_j\left(z\right)=j{\mathcal{T}}_{j-1}\left(z\right),j\ge 1.$$

This ends the proof. □

If we consider the following vector:

$$\mathsf{\Psi }\left(z\right)={[{\mathcal{T}}_0\left(z\right),{\mathcal{T}}_1\left(z\right),\dots ,{\mathcal{T}}_N\left(z\right)]}^T,$$

(34)

then it is easy to see that

$${\displaystyle \frac{d\mathsf{\Psi }}{dx}}=S\mathsf{\Psi },$$

(35)

where S is the operational matrix of derivatives with the following entries:

$$s_{ij}=\left\{\begin{array}{cc}j+1,\hfill & j=i-1,\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

For example, the matrix S for $N=5$ is

$$\left(\begin{array}{cccccc}0& 0& 0& 0& 0& 0\\ 1& 0& 0& 0& 0& 0\\ 0& 2& 0& 0& 0& 0\\ 0& 0& 3& 0& 0& 0\\ 0& 0& 0& 4& 0& 0\\ 0& 0& 0& 0& 5& 0\end{array}\right).$$

4.2. Treatment of the High-Order Non-Linear IVPs

We aim to solve the following nonlinear IVPs numerically:

$$u^{\left(m\right)}\left(z\right)=F\left(z,u\left(z\right),u^{\prime }\left(z\right),\cdots ,u^{(m-1)}\left(z\right)\right),z\in (0,1),n\ge 1,$$

(36)

governed by the following ICs:

$$u^{(\ell )}\left(0\right)=0,0\le \ell \le m-1.$$

(37)

Now, assume a polynomial approximation in terms of the TelPs as

$${\displaystyle u\left(z\right)\simeq u_N\left(z\right)=\sum _{i=0}^N{c}_i{\mathcal{T}}_i\left(z\right),}$$

(38)

which can be expressed as

$${\displaystyle u_N\left(z\right)=\sum _{k=0}^N{c}_k{\mathcal{T}}_k\left(z\right)={\mathit{C}}^T\mathsf{\Psi }\left(z\right),}$$

(39)

where

$${\mathit{C}}^T=[a_0,a_1,\cdots ,a_N],$$

(40)

and $\mathsf{\Psi }\left(z\right)$ is defined in (34).

Now, using the operational matrix S, the ℓth derivative of $u_N\left(z\right)$ can be expressed in the following form:

$$D^{\ell }{u}_N\left(z\right)={\mathit{C}}^T{S}^{\ell }\mathsf{\Psi }\left(z\right),$$

(41)

and accordingly, the residual of Equation (36) has the following form:

$$R\left(z\right)={\mathit{C}}^T{S}^{2n}\mathsf{\Psi }\left(z\right)-F\left(z,{\mathit{C}}^T\mathsf{\Psi }\left(z\right),{\mathit{C}}^{T}S\mathsf{\Psi }\left(z\right),\cdots ,{\mathit{C}}^T{S}^{2n-1}\mathsf{\Psi }\left(z\right)\right).$$

(42)

Now, to apply the collocation method to solve Equation (36), we enforce the residual to be zero at selected suitable points $z_i$. We choose them to be the distinct $(N+1)$ zeros of the shifted Legendre polynomial $P_{N+1}^{*}\left(z\right)$ on $[0,1]$. In such case, we have

$$\begin{array}{cc}\hfill {\mathit{C}}^T{S}^{2n}\mathsf{\Psi }\left(z_i\right)=& F\left(z,{\mathit{C}}^T\mathsf{\Psi }\left(z_i\right),{\mathit{C}}^{T}S\mathsf{\Psi }\left(z_i\right),\cdots ,{\mathit{C}}^T{S}^{2n-1}\mathsf{\Psi }\left(z_i\right)\right),\hfill \\ \hfill & i=0,1,\dots ,N-n.\hfill \end{array}$$

(43)

In addition, the ICs in (37) lead to the following n equations:

$${\mathit{C}}^T{S}^{\ell }\mathsf{\Psi }\left(0\right)=0.$$

(44)

Merging the $(N+1)$ equations in (43) and (44) yields a non-linear algebraic system that can be treated using any suitable numerical algorithm such as Newton’s iterative method, and hence solution $u_N\left(z\right)$ can be obtained.

5. Numerical Treatment of a System of Initial Value Problems

In this section, we present another application of the TGM to solve a system of higher-order DEs with homogeneous ICs. Consider the following system of higher-order DEs.

$$\sum _{i=0}^m\sum _{l=1}^s{\lambda }_{r,l}^i{\mathcal{U}}_l^{\left(i\right)}\left(z\right)={\mathit{f}}_r\left(z\right),r=1,2,\cdots ,k,z\in [0,1],$$

(45)

controlled by following homogeneous ICs:

$${\mathcal{U}}_l^{\left(i\right)}\left(0\right)=0,i=0,1,\cdots ,m-1,l=1,2,\cdots ,s.$$

(46)

Similarly, as in Section 3.1, we have to find ${\mathcal{U}}_{lN}\left(z\right)\in {\Phi }_N,l=1,2,\cdots ,s$, such that

$$\sum _{i=0}^m\sum _{l=1}^s{\lambda }_{r,l}^i\left({\mathcal{U}}_{lN}^{\left(i\right)}\left(z\right),{\varphi }_j\left(z\right)\right)=\left(f_r\left(z\right),{\varphi }_j\left(z\right)\right),\forall 0\le j\le N.$$

(47)

Now, if we approximate ${\mathcal{U}}_{lN}\left(z\right)\in {\Phi }_N,l=1,2,\cdots ,s$, as

$${\mathcal{U}}_{lN}\left(z\right)\simeq \sum _{h=0}^N{c}_{l,h}{\varphi }_h\left(z\right),z\in [0,1],l=1,2,\cdots ,s.$$

(48)

where ${\varphi }_h\left(z\right)\in {\Phi }_N$ is defined as in (15). Now the application of the Galerkin method leads to

$$\sum _{i=0}^m\sum _{l=1}^s\sum _{h=0}^N{\lambda }_{r,l}^i{c}_{l,h}\left({\varphi }_h^{\left(i\right)}\left(z\right),{\varphi }_j\left(z\right)\right)=\left(f_r\left(z\right),{\varphi }_j\left(z\right)\right),r=1,2,\cdots ,k.$$

(49)

Then, (49) is equivalent to the system

$$\sum _{i=0}^m\sum _{l=1}^s{\lambda }_{r,l}^i\mathbf{A}{\mathbf{C}}_l={\mathbf{F}}_r,r=1,2,\cdots ,k,$$

(50)

where

$${\mathbf{C}}_l={(c_{l,0},c_{1,1},\cdots ,c_{l,N})}^T,$$

and

$${\mathbf{F}}_r={({{\mathit{f}}_0}^r,{{\mathit{f}}_1}^r,\cdots ,{{\mathit{f}}_N}^r)}^T,{{\mathit{f}}_j}^r=\left({\mathit{f}}_r\left(z\right),{\varphi }_j\left(z\right)\right).$$

One can use any appropriate numerical solver to solve the $(sN+s)$ algebraic system in the variables $c_{l,h}$, where $1\le l\le s,0\le h\le N$.

6. Numerical Treatment of Hyperbolic PDEs of First-Order

In this section, we focus on applying the TGM to solve one-dimensional first-order hyperbolic PDEs governed by homogeneous and non-homogeneous ICs.

6.1. The Problem Governed by Homogeneous ICs

Consider the following one-dimensional hyperbolic PDE [54]:

$$\begin{array}{c}\hfill {\partial }_t\mathcal{U}(z,t)-{\tau }_1{\partial }_z\mathcal{U}(z,t)-{\tau }_2\mathcal{U}(z,t)=S(z,t),(z,t)\in (0,1)\times (0,1),\end{array}$$

(51)

subject to the following conditions:

$$\begin{array}{cc}\hfill \mathcal{U}(z,0)=& 0,z\in (0,1),\hfill \end{array}$$

(52)

$$\begin{array}{cc}\hfill \mathcal{U}(0,t)=& 0,t\in (0,1),\hfill \end{array}$$

(53)

where ${\tau }_1$ and ${\tau }_2$ are constants, and $S(z,t)$ is the source function. We choose appropriate basis functions to apply the Galerkin method to (51)–(53). The TGM for (51) is to find ${\mathcal{U}}_N\in {\mathcal{W}}_N$ such that

$$\begin{array}{c}\hfill ({\partial }_t{\mathcal{U}}_N,v)-{\tau }_1({\partial }_z{\mathcal{U}}_N,v)-{\tau }_2({\mathcal{U}}_N,v)=(S,v),\forall v\in W_N,\end{array}$$

(54)

where

$$\mathcal{U}(z,t)\backsimeq {\mathcal{U}}_N(z,t)=\sum _{i=0}^{N-1}\sum _{j=0}^{N-1}{c}_{ij}{\xi }_i\left(z\right){\xi }_j\left(t\right),$$

(55)

$${\mathcal{W}}_N=\mathrm{Span}\{{\xi }_i\left(z\right){\xi }_j\left(t\right):i,j=0,1,\cdots ,N\}.$$

(56)

Now, we choose combinations of TelPs to act as basis functions. More precisely, we choose the two following sets of basis functions:

$$\begin{array}{cc}\hfill {\xi }_i\left(z\right)& =z{\mathcal{T}}_i\left(z\right),\hfill \end{array}$$

(57)

$$\begin{array}{cc}\hfill {\xi }_j\left(t\right)& =t{\mathcal{T}}_j\left(t\right).\hfill \end{array}$$

(58)

These choices allow us to convert (54) into

$$\begin{array}{cc}\hfill ({\partial }_t{\mathcal{U}}_N,{\xi }_i\left(z\right){\xi }_j\left(t\right))& -{\tau }_1({\partial }_z{\mathcal{U}}_N,{\xi }_i\left(z\right){\xi }_j\left(t\right))-{\tau }_2({\mathcal{U}}_N,{\xi }_i\left(z\right){\xi }_j\left(t\right))\hfill \\ & =(S(z,t),{\xi }_i\left(z\right){\xi }_j\left(t\right)),i,j=0,1,\dots ,N-1.\hfill \end{array}$$

(59)

Let us denote

$$s_{ij}=(S(z,t),{\xi }_i\left(z\right){\xi }_j\left(t\right))={\int }_0^1{\int }_0^{1}S(z,t){\xi }_i\left(z\right){\xi }_j\left(t\right)dtdx,$$

and

$$\mathcal{S}=\left(s_{ij}\right),i,j=0,1,\dots ,N-1.$$

The proposed approximation ${\mathcal{U}}_N(z,t)$ can be written in the form

$${\mathcal{U}}_N(z,t)=\sum _{i=0}^{N-1}\sum _{j=0}^{N-1}{c}_{ij}{\xi }_i\left(z\right){\xi }_j\left(t\right)={\Omega }_{N-1}^T\left(t\right)\mathit{C}{\Omega }_{N-1}\left(z\right),$$

(60)

and $\mathbf{C}$ is represented as

$$\mathbf{C}=\left(\begin{array}{cccc}{c}_{00}& c_{01}& \cdots & c_{0,N-1}\\ c_{10}& c_{11}& \cdots & c_{1,N-1}\\ ⋮& ⋮& \ddots & ⋮\\ c_{N-1,0}& c_{N-1,1}& \cdots & c_{N-1,N-1}\end{array}\right),$$

where

$${\Omega }_{N-1}\left(z\right)={[{\xi }_0\left(z\right),{\xi }_1\left(z\right),\cdots ,{\xi }_{N-1}\left(z\right)]}^T.$$

In the tensor product notion, Equation (59) can be represented as

$$(\widehat{\mathbf{B}}\otimes \widehat{\mathbf{A}}-{\tau }_1\widehat{\mathbf{A}}\otimes \widehat{\mathbf{B}}-{\tau }_2\widehat{\mathbf{B}}\otimes \widehat{\mathbf{B}})\mathbf{C}=\mathcal{S},$$

(61)

where $\mathcal{S}$ can be represented in the form

$$\mathcal{S}={[s_{00},s_{10},\dots ,s_{N-1,0},s_{01},s_{11},\dots ,s_{N-1,1},s_{0,N-1},s_{1,N-1},\dots ,s_{N-1,N-1}]}^T,$$

and $\widehat{\mathbf{A}}$ and $\widehat{\mathbf{B}}$ are $N\times N$ matrices,

$$\widehat{\mathbf{A}}={\left({\widehat{a}}_{ij}\right)}_{0\le i,j\le N-1},\widehat{\mathbf{B}}={\left({\widehat{b}}_{ij}\right)}_{0\le i,j\le N-1},$$

their elements ${\widehat{a}}_{ij}$ and ${\widehat{b}}_{ij}$ are obtained, respectively, from

$${\widehat{a}}_{ij}=({\partial }_z{\xi }_j\left(z\right),{\xi }_i\left(z\right)),{\widehat{b}}_{ij}=({\xi }_j\left(z\right),{\xi }_i\left(z\right)),$$

where the nonzero elements of the matrices $\widehat{\mathbf{A}}$ and $\widehat{\mathbf{B}}$ are given explicitly by

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & {\widehat{a}}_{ij}=\sum _{k=0}^{\lceil {\displaystyle \frac{i}{2}}\rceil }\sum _{s=0}^{\lceil {\displaystyle \frac{j}{2}}\rceil }{\displaystyle \frac{i!j!(i-2k+1)!}{2^{k+s}k!s!(i-2k)!(j-2s)!(i-2k)!(i+j-2k-2s+2)}},\hfill \end{array}\end{array}$$

(62)

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & {\widehat{b}}_{ij}=\sum _{k=0}^{\lceil {\displaystyle \frac{i}{2}}\rceil }\sum _{s=0}^{\lceil {\displaystyle \frac{j}{2}}\rceil }{\displaystyle \frac{i!j!(i-2k+1)!}{2^{k+s}k!s!(i-2k)!(j-2s)!(i-2k+1)!(i+j-2k-2s+3)}}.\hfill \end{array}\end{array}$$

(63)

Remark 2.

The Kronecker product $\widehat{\mathbf{A}}\otimes \widehat{\mathbf{B}}$ of the $n\times m$ matrix $\widehat{\mathbf{A}}$ and the $p\times q$ matrix $\widehat{\mathbf{B}}$

$$\widehat{\mathbf{A}}=\left(\begin{array}{cccc}{\widehat{a}}_{11}& {\widehat{a}}_{12}& \cdots & {\widehat{a}}_{1m}\\ {\widehat{a}}_{21}& {\widehat{a}}_{22}& \cdots & {\widehat{a}}_{2m}\\ ⋮& ⋮& \ddots & ⋮\\ {\widehat{a}}_{n1}& {\widehat{a}}_{n2}& \cdots & {\widehat{a}}_{nm}\end{array}\right),\widehat{\mathbf{B}}=\left(\begin{array}{cccc}{\widehat{b}}_{11}& {\widehat{b}}_{12}& \cdots & {\widehat{b}}_{1q}\\ {\widehat{b}}_{21}& {\widehat{b}}_{22}& \cdots & {\widehat{b}}_{2q}\\ ⋮& ⋮& \ddots & ⋮\\ {\widehat{b}}_{p1}& {\widehat{b}}_{p2}& \cdots & {\widehat{b}}_{pq}\end{array}\right),$$

is the $np\times mq$ matrix having the following block form:

$$\widehat{\mathbf{A}}\otimes \widehat{\mathbf{B}}=\left(\begin{array}{cccc}{\widehat{a}}_{11}\widehat{\mathbf{B}}& {\widehat{a}}_{12}\widehat{\mathbf{B}}& \cdots & {\widehat{a}}_{1m}\widehat{\mathbf{B}}\\ {\widehat{a}}_{21}\widehat{\mathbf{B}}& {\widehat{a}}_{22}\widehat{\mathbf{B}}& \cdots & {\widehat{a}}_{2m}\widehat{\mathbf{B}}\\ ⋮& ⋮& \ddots & ⋮\\ {\widehat{a}}_{n1}\widehat{\mathbf{B}}& {\widehat{a}}_{n2}\widehat{\mathbf{B}}& \cdots & {\widehat{a}}_{nm}\widehat{\mathbf{B}}\end{array}\right).$$

At last, the differential equation governed by its underlying conditions is converted into a linear system of algebraic equations concerning the unknown expansion coefficients, which can be efficiently solved utilizing the Gaussian elimination method.

6.2. The Problem Governed by the Nonhomogeneous Conditions

In this subsection, we examine the first-order one-dimensional hyperbolic PDEs (51) with non-homogeneous initial and boundary conditions:

$$\begin{array}{c}\hfill \mathcal{U}(z,0)={\mathcal{H}}_1\left(z\right),z\in (0,1),\end{array}$$

(64)

$$\begin{array}{c}\hfill \mathcal{U}(0,t)={\mathcal{H}}_2\left(t\right),t\in (0,1),\end{array}$$

(65)

where ${\mathcal{H}}_1\left(z\right)$ and ${\mathcal{H}}_2\left(t\right)$ are given functions.

We make use of the following transformation:

$$\begin{array}{cc}\hfill \mathcal{V}(z,t)& =\mathcal{U}(z,t)-\left[\right(1-zt\left)\mathcal{U}\right(z,t\left)\right]\hfill \\ & =\mathcal{U}(z,t)-{\mathcal{U}}_{\epsilon }(z,t),\hfill \end{array}$$

where $\mathcal{V}$ is a function that is chosen to satisfy the following homogeneous conditions:

$$\begin{array}{cc}\hfill \mathcal{V}(z,0)& =0,z\in (0,1),\hfill \end{array}$$

(66)

$$\begin{array}{cc}\hfill \mathcal{V}(0,t)& =0,t\in (0,1).\hfill \end{array}$$

(67)

This means that (51) governed by (64), and (65) is equivalent to the following modified equation:

$$\begin{array}{c}\hfill {\partial }_t\mathcal{V}(z,t)-{\tau }_1{\partial }_z\mathcal{V}(z,t)-{\tau }_2\mathcal{V}(z,t)=\Re (z,t),(z,t)\in (0,1)\times (0,1),\end{array}$$

(68)

with

$$\Re (z,t)=S(z,t)-{\partial }_t{\mathcal{U}}_{\epsilon }(z,t)+{\tau }_1{\partial }_z{\mathcal{U}}_{\epsilon }(z,t)+{\tau }_2{\mathcal{U}}_{\epsilon }(z,t),$$

under the homogeneous conditions (66), and (67).

While ${\mathcal{U}}_{\epsilon }(z,t)$ is an arbitrary function that satisfies the original non-homogeneous initial and boundary conditions.

7. Investigation of the Convergence and Error Analysis

This section focuses on specific models discussed in Section 3, Section 4, Section 5 and Section 6. We will analyze the convergence of the proposed expansions employed for the numerical treatment of these models. This ensures that the numerical solutions converge to the exact solution as the discretization parameters approach their limits. Additionally, we will investigate convergence and error analysis. Through rigorous analysis, we aim to establish error bounds and conditions for convergence that affirm the efficiency of our methods in solving the models under consideration. The following lemma is required to continue with our analysis.

Lemma 1.

The polynomials ${\mathcal{T}}_n\left(z\right)$ satisfy the following inequality:

$$|{\mathcal{T}}_n\left(z\right)|\le {\displaystyle \frac{6(n!){\left(\frac{5}{8}\right)}^{⌊\frac{n}{2}⌋}}{⌊\frac{n}{2}⌋!}},z\in [0,1].$$

(69)

Proof. 

In view of (2), we have

$$|{\mathcal{T}}_n\left(z\right)|\le \sum _{k=0}^{⌊{\displaystyle \frac{n}{2}}⌋}{\displaystyle \frac{n!}{2^{k}k!(n-2k)!}}.$$

(70)

For $n=2p$, Formula (70) takes the form:

$$|{\mathcal{T}}_{2p}\left(z\right)|\le \left(2p\right)!\sum _{k=0}^p{\displaystyle \frac{1}{2^{k}k!(2p-2k)!}}=\left(2p\right)!\sum _{k=0}^p{\displaystyle \frac{1}{2^{p-k}(p-k)!\left(2k\right)!}}.$$

(71)

Using the simple identity: $\left(2k\right)!=2^{2k}k!{(1/2)}_k$, we can write

$$|{\mathcal{T}}_{2p}\left(z\right)|\le \left(2p\right)!\sum _{k=0}^p{\displaystyle \frac{1}{2^{p+k}(p-k)!{(1/2)}_{k}k!}}.$$

(72)

In addition, it is not difficult to show that ${(1/2)}_k\ge {\displaystyle \frac{1}{6}}{2}^k$, and accordingly, (72) takes the form

$$|{\mathcal{T}}_{2p}\left(z\right)|\le 6\left(2p\right)!S_p,$$

(73)

where

$$S_p=\sum _{k=0}^p{\displaystyle \frac{1}{2^{p+2k}(p-k)!k!}}.$$

By using computer algebra, especially Zeilberger’s algorithm (see [55]), $S_p$ are able to meet the first-order recurrence relation shown below:

$$8(p+1)S_{p+1}-5S_p=0,S_0=1.$$

(74)

The exact solution to this recurrence relation has the form

$$S_p={\displaystyle \frac{{\left(\frac{5}{8}\right)}^p}{p!}}.$$

(75)

Then, we obtain

$$|{\mathcal{T}}_{2p}\left(z\right)|\le 6\left(2p\right)!{\displaystyle \frac{{\left(\frac{5}{8}\right)}^p}{p!}}.$$

(76)

Similarly, for $n=2p+1$, we can prove that

$$|{\mathcal{T}}_{2p+1}\left(z\right)|\le 6(2p+1)!{\displaystyle \frac{{\left(\frac{5}{8}\right)}^p}{p!}}.$$

(77)

Formulas (76) and (77) lead to (69) and the proof of Lemma 1 is complete. □

The following corollary is a direct consequence of Lemma 1.

Corollary 1.

The polynomials ${\varphi }_n\left(z\right)$ satisfy the following inequality

$$|{\varphi }_n\left(z\right)|\le {\displaystyle \frac{6(n!){\left(\frac{5}{8}\right)}^{⌊\frac{n}{2}⌋}}{⌊\frac{n}{2}⌋!}},z\in [0,1].$$

(78)

7.1. The Model of Initial Value Problem

If the error obtained by solving (11), and (12) numerically is defined by

$$e_N\left(z\right)=\left|\mathcal{U}\left(z\right)-{\mathcal{U}}_N\left(z\right)\right|,$$

(79)

subsequently, the maximum absolute error (MAE) of the proposed technique is estimated as

$$\parallel e_N{\parallel }_{\infty }=\underset{0\le z\le 1}{max}{e}_N\left(z\right),$$

(80)

while the differences between the function ${\mathcal{U}}_j\left(z\right)$ and its estimated value ${\mathcal{U}}_{j,N}\left(z\right)$ for the system (45) and (46) are defined by

$$e_{j,N}\left(z\right)=\left|{\mathcal{U}}_j\left(z\right)-{\mathcal{U}}_{j,N}\left(z\right)\right|,j=1,2,\cdots ,k,$$

(81)

and consequently, the MAEs of the suggested method are estimated by the following:

$$\parallel e_{j,N}{\parallel }_{\infty }=\underset{0\le z\le 1}{max}{e}_{j,N}\left(z\right).$$

(82)

In order to evaluate the precision of the suggested method, we define the following error:

$${\mathcal{E}}_N=max\{\parallel e_{1,N}{\parallel }_{\infty },\cdots ,\parallel e_{k,N}{\parallel }_{\infty }\}.$$

(83)

Theorem 4.

Assume that $\mathcal{U}\left(z\right)=z^{m}u\left(z\right)$, where $u\left(z\right)$ is an infinitely differentiable function at the origin with $|{\displaystyle \frac{d^{i}u\left(0\right)}{d{z}^i}}|<M$. Then, it has the following expansion:

$${\displaystyle \mathcal{U}\left(z\right)=\sum _{i=0}^{\infty }{U}_i{\varphi }_i\left(z\right),}$$

(84)

where

$${\displaystyle U_i=\sum _{p=0}^{\infty }\frac{d^{i+2p}u\left(0\right)}{d{z}^{i+2p}}\frac{{(-1/2)}^p}{i!p!}.}$$

(85)

These expansion coefficients satisfy the following inequality

$$|U_i|<M{e}^{-1/2}{\displaystyle \frac{1}{i!}},i\ge 0,$$

(86)

and the series in (84) converges absolutely.

Proof. 

First, we expand $\mathcal{U}\left(z\right)$ as

$$\mathcal{U}\left(z\right)=z^m\sum _{i=0}^{\infty }{u}_i{z}^i,u_i={\displaystyle \frac{1}{i!}}{\displaystyle \frac{d^{i}u\left(0\right)}{d{z}^i}}.$$

(87)

Inserting the inversion Formula (9) into (87) enables one to write

$$\mathcal{U}\left(z\right)=z^m\sum _{i=0}^{\infty }{u}_i\sum _{k=0}^i{d}_{i,k}{\mathcal{T}}_k\left(z\right).$$

(88)

Expanding the right-hand side of (88) and rearranging similar terms, the following expansion is obtained:

$$\mathcal{U}\left(z\right)=\sum _{i=0}^{\infty }{U}_i{\varphi }_i\left(z\right),$$

(89)

where

$$U_i=\sum _{p=0}^{\infty }{u}_{p+i}{d}_{p+i,i}.$$

(90)

In view of (9), we can obtain (85). The inequality (86) is a direct consequence of (85). Now, direct use of (86) together with the application of Lemma 1 yields

$$\sum _{i=0}^{\infty }|U_i||{\varphi }_i\left(z\right)|\le 6M{e}^{-1/2}\sum _{i=0}^{\infty }{\displaystyle \frac{{(5/8)}^{⌊\frac{i}{2}⌋}}{⌊\frac{i}{2}⌋!}},$$

(91)

we have

$$\sum _{i=0}^{\infty }{\displaystyle \frac{{(5/8)}^{⌊\frac{i}{2}⌋}}{⌊\frac{i}{2}⌋!}}=\underset{ieven}{{\sum }_{i=0}^{\infty }}{\displaystyle \frac{{(5/8)}^i}{i!}}+\underset{iodd}{{\sum }_{i=0}^{\infty }}{\displaystyle \frac{{(5/8)}^i}{i!}}\le \sum _{i=0}^{\infty }{\displaystyle \frac{{(5/8)}^i}{i!}}=e^{5/8},$$

(92)

then

$$\sum _{i=0}^{\infty }|U_i\left|\right|{\varphi }_i\left(z\right)|\le 6M{e}^{-1/2}\sum _{i=0}^{\infty }{\displaystyle \frac{{(5/8)}^i}{i!}}=6M{e}^{1/8},$$

(93)

so, the series converges absolutely. □

Theorem 5.

If $\mathcal{U}\left(z\right)$ satisfies the hypothesis of Theorem 4, and if

$${\displaystyle U_N\left(z\right)=\sum _{i=0}^N{U}_i{\varphi }_i\left(z\right),}$$

(94)

then, the following estimate is satisfied

$$\parallel \mathcal{U}-U_N{\parallel }_{\infty }\le 6M{e}^{9/2}{(1/2)}^{3N+3},N\ge 1.$$

(95)

So

$$\parallel \mathcal{U}-U_N{\parallel }_{\infty }\lesssim {\displaystyle \frac{1}{2^{3N+3}}},$$

(96)

where ≲ means that a generic constant d exists such that $\parallel \mathcal{U}-U_N{\parallel }_{\infty }\le d{(1/2)}^{3N+3}$.

Proof. 

The truncation error may be written as follows:

$$\begin{array}{cc}\hfill \left|\mathcal{U}-U_N\right|=& {\displaystyle \left|{\displaystyle \sum _{i=N+1}^{\infty }{U}_i{\varphi }_i\left(z\right)}\right|\le \sum _{i=N+1}^{\infty }|U_i||{\varphi }_i\left(z\right)|\le 6M{e}^{-1/2}\sum _{i=N+1}^{\infty }\frac{{(5/8)}^{⌊\frac{i}{2}⌋}}{⌊\frac{i}{2}⌋!},}\hfill \end{array}$$

(97)

however, we have

$$\sum _{i=N+1}^{\infty }{\displaystyle \frac{{(5/8)}^{⌊\frac{i}{2}⌋}}{⌊\frac{i}{2}⌋!}}\le \sum _{i=N+1}^{\infty }{\displaystyle \frac{{(5/8)}^i}{i!}}\le {(1/8)}^{N+1}\sum _{i=N+1}^{\infty }{\displaystyle \frac{5^i}{i!}}\le {(1/8)}^{N+1}{e}^5,$$

(98)

then,

$$\left|\mathcal{U}-U_N\right|\le 6M{e}^{9/2}{(1/8)}^{N+1}\lesssim {(1/2)}^{3N+3},$$

(99)

which completes the proof of the theorem. □

Corollary 2.

Suppose that ${\mathcal{U}}_N\left(z\right)$ has the form (16) and represents the best possible approximation for $\mathcal{U}\left(z\right)$ out of Ω. Then, the following estimates for the error $E_N$ are valid:

$$e_N\le 6M{e}^{9/2}{(1/2)}^{3N+3},N\ge 1.$$

(100)

Proof. 

Since ${\mathcal{U}}_N\left(z\right)\in \Omega$ represents the best possible approximation for $\mathcal{U}\left(z\right)$, we have the following:

$$\parallel \mathcal{U}\left(z\right)-{\mathcal{U}}_N{\left(z\right)\parallel }_{\infty }\le {\parallel \mathcal{U}\left(z\right)-h\left(z\right)\parallel }_{\infty },\forall h\in \Omega .$$

(101)

In view of (95) and (101),

$$e_N=\parallel \mathcal{U}\left(z\right)-{\mathcal{U}}_N{\left(z\right)\parallel }_{\infty }\le {\parallel \mathcal{U}\left(z\right)-U_N\left(z\right)\parallel }_{\infty },$$

(102)

and this leads to (100), which completes the proof of the theorem. □

Remark 3.

Theorems 4 and 5 can be extended when the error analysis is considered for the proposed technique for solving the model defined by the system (45) and (46). The most important steps would be as follows:

 (i)

In order to derive the bound expression of the coefficients $c_{i,j}$, it is necessary to establish the matching assumptions in Theorem 4.

 (ii)

In Theorem 5, the error bound formulas for $\parallel e_{j,N}{\parallel }_{\infty },j=1,2,\cdots ,k$ are derived. These expressions are identical to the ones for $\parallel e_N{\parallel }_{\infty }$.

 (iii)

Obtaining the bound expression of the expression ${\mathcal{E}}_N$ that is specified in Equation (100) as

$${\mathcal{E}}_N\lesssim 6M{e}^{9/2}{(1/2)}^{3N+3}.$$

(103)

7.2. Treatment of First-Order Hyperbolic PDEs

The error estimation to assess the numerical scheme’s error is

$$\parallel E_N{\parallel }_{\infty }=\parallel \mathcal{U}-{\mathcal{U}}_N{\parallel }_{\infty }=\underset{(z,t)\in I}{max}|\mathcal{U}(z,t)-{\mathcal{U}}_N(z,t)|.$$

(104)

To proceed in our analysis, the following two theorems are needed in this subsection:

Theorem 6.

Let $\mathcal{U}(z,t)=ztu(z,t)$ be an infinitely differentiable function at the origin with $|{\displaystyle \frac{{\partial }^{i+j}u(0,0)}{\partial z^i\partial t^j}}|<M$. Then, it has the following expansion

$${\displaystyle \mathcal{U}(z,t)=\sum _{i=0}^{\infty }\sum _{j=0}^{\infty }{U}_{i,j}{\xi }_i\left(z\right){\xi }_j\left(t\right),}$$

(105)

where

$${\displaystyle U_{i,j}=\sum _{p=0}^{\infty }\sum _{q=0}^{\infty }\frac{{\partial }^{i+j+2(p+q)}u(0,0)}{\partial z^{i+2p}\partial t^{j+2q}}\frac{{(-1/2)}^{p+q}}{i!j!p!q!}.}$$

(106)

These expansion coefficients satisfy the following inequality

$$|U_{i,j}|<M{e}^{-1}{\displaystyle \frac{1}{i!j!}},i,j\ge 0,$$

(107)

and the series in (105) converges absolutely.

Proof. 

First, we expand $\mathcal{U}(z,t)$ as

$$\mathcal{U}(z,t)=zt\sum _{i=0}^{\infty }\sum _{j=0}^{\infty }{u}_{i,j}{z}^i{t}^j,u_{i,j}={\displaystyle \frac{1}{i!j!}}{\displaystyle \frac{{\partial }^{i+j}u(0,0)}{\partial z^i\partial t^j}}.$$

(108)

This expansion can be written in the form:

$$\mathcal{U}(z,t)=zt\sum _{i=0}^{\infty }{b}_i\left(t\right)z^i,$$

(109)

where

$$b_i\left(t\right)=\sum _{j=0}^{\infty }{u}_{i,j}{t}^j.$$

(110)

Inserting the inversion Formula (9) into (109) enables one to write

$$\mathcal{U}(z,t)=t\sum _{i=0}^{\infty }{b}_i\left(t\right)\sum _{k=0}^i{d}_{i,k}{\xi }_k\left(z\right).$$

(111)

Expanding the right-hand side of (88), and rearranging the similar terms, the following expansion is obtained

$$\mathcal{U}(z,t)=t\sum _{i=0}^{\infty }\left(\sum _{p=0}^{\infty }{b}_{p+i}\left(t\right)d_{p+i,i}\right){\xi }_i\left(z\right).$$

(112)

Now,

$$\sum _{p=0}^{\infty }{b}_{p+i}\left(t\right)d_{p+i,i}=\sum _{p=0}^{\infty }\left(\sum _{j=0}^{\infty }{u}_{p+i,j}{t}^j\right)d_{p+i,i}=\sum _{j=0}^{\infty }\left(\sum _{p=0}^{\infty }{u}_{p+i,j}{d}_{p+i,i}\right)t^j.$$

(113)

Inserting the inversion Formula (9) into (113) and following the same procedures enables one to write

$$\sum _{p=0}^{\infty }{b}_{p+i}\left(t\right)d_{p+i,i}=\sum _{j=0}^{\infty }\left(\sum _{p=0}^{\infty }\sum _{q=0}^{\infty }{u}_{p+i,j+q}{d}_{p+i,i}{d}_{q+j,j}\right){\mathcal{T}}_j\left(t\right).$$

(114)

Substituting (114) for (112) immediately gives

$$\mathcal{U}(z,t)=\sum _{i=0}^{\infty }\sum _{j=0}^{\infty }{U}_{i,j}{\xi }_i\left(z\right){\xi }_j\left(t\right),$$

(115)

where

$$U_{i,j}=\sum _{p=0}^{\infty }\sum _{q=0}^{\infty }{u}_{p+i,j+q}{d}_{p+i,i}{d}_{q+j,j}.$$

(116)

In view of (10), we can obtain (106). The inequality (107) is a direct consequence of (106). Now, direct use of (107) together with the application of Lemma 1 yields

$$\sum _{i,j=0}^{\infty }|U_{i,j}||{\varphi }_i\left(z\right)||{\varphi }_j\left(t\right)|\le 36M{e}^{-1}\sum _{i,j=0}^{\infty }{\displaystyle \frac{{(5/8)}^{⌊\frac{i}{2}⌋}{(5/8)}^{⌊\frac{j}{2}⌋}}{⌊\frac{i}{2}⌋!⌊\frac{j}{2}⌋!}},$$

(117)

we have

$$\sum _{i=0}^{\infty }{\displaystyle \frac{{(5/8)}^{⌊\frac{i}{2}⌋}}{⌊\frac{i}{2}⌋!}}=\underset{ieven}{{\sum }_{i=0}^{\infty }}{\displaystyle \frac{{(5/8)}^i}{i!}}+\underset{iodd}{{\sum }_{i=0}^{\infty }}{\displaystyle \frac{{(5/8)}^i}{i!}}\le \sum _{i=0}^{\infty }{\displaystyle \frac{{(5/8)}^i}{i!}}=e^{5/8},$$

(118)

then

$$\sum _{i,j=0}^{\infty }|U_{i,j}||{\varphi }_i\left(z\right)||{\varphi }_j\left(t\right)|\le 36M{e}^{-1}\sum _{i,j=0}^{\infty }{\displaystyle \frac{{(5/8)}^{i+j}}{i!j!}}=36M{e}^{-1}{e}^{(5/4)},$$

(119)

so the series converges absolutely. □

Theorem 7.

If $\mathcal{U}(z,t)$ satisfies the hypothesis of Theorem 6, and if

$${\displaystyle U_N(z,t)=\sum _{i=0}^N\sum _{j=0}^N{U}_{i,j}{\xi }_i\left(z\right){\xi }_j\left(t\right),}$$

(120)

then the following estimate is satisfied

$$\parallel \mathcal{U}-U_N{\parallel }_{\infty }\lesssim {\displaystyle \frac{1}{2^{3N+3}}}.$$

(121)

Proof. 

The truncation error may be written as follows:

$$\begin{array}{cc}\hfill \left|\mathcal{U}-U_N\right|=& \left|{\displaystyle \sum _{i=0}^{\infty }\sum _{j=0}^{\infty }{U}_{i,j}{\xi }_i\left(z\right){\xi }_j\left(t\right)-\sum _{i=0}^N\sum _{j=0}^N{U}_{i,j}{\xi }_i\left(z\right){\xi }_j\left(t\right)}\right|\hfill \\ & {\displaystyle \le \sum _{i=0}^N\sum _{j=N+1}^{\infty }|U_{i,j}\left|\right|{\xi }_i\left(z\right)\left|\right|{\xi }_j\left(t\right)|+\sum _{i=N+1}^{\infty }\sum _{j=0}^{\infty }|U_{i,j}\left|\right|{\xi }_i\left(z\right)\left|\right|{\xi }_i\left(t\right)|}\hfill \\ & {\displaystyle \le 36M{e}^{-1}\sum _{i=0}^N\sum _{j=N+1}^{\infty }\frac{{(5/8)}^{⌊\frac{i}{2}⌋}{(5/8)}^{⌊\frac{j}{2}⌋}}{⌊\frac{i}{2}⌋!⌊\frac{j}{2}⌋!}}\hfill \\ & {\displaystyle +36M{e}^{-1}\sum _{i=N+1}^{\infty }\sum _{j=0}^{\infty }\frac{{(5/8)}^{⌊\frac{i}{2}⌋}{(5/8)}^{⌊\frac{j}{2}⌋}}{⌊\frac{i}{2}⌋!⌊\frac{j}{2}⌋!},}\hfill \end{array}$$

(122)

we have

$$\sum _{i=0}^N{\displaystyle \frac{{(5/8)}^{⌊\frac{i}{2}⌋}}{⌊\frac{i}{2}⌋!}}=\underset{ieven}{{\sum }_{i=0}^N}{\displaystyle \frac{{(5/8)}^i}{i!}}+\underset{iodd}{{\sum }_{i=0}^N}{\displaystyle \frac{{(5/8)}^i}{i!}}\le \sum _{i=0}^N{\displaystyle \frac{{(5/8)}^i}{i!}}\le e^{5/8},$$

(123)

also,

$$\sum _{j=N+1}^{\infty }{\displaystyle \frac{{(5/8)}^{⌊\frac{j}{2}⌋}}{⌊\frac{j}{2}⌋!}}\le \sum _{j=N+1}^{\infty }{\displaystyle \frac{{(5/8)}^j}{j!}}\le {(1/8)}^{N+1}\sum _{j=N+1}^{\infty }{\displaystyle \frac{5^j}{j!}}\le {(1/8)}^{N+1}{e}^5,$$

(124)

then

$$\left|\mathcal{U}-U_N\right|\le 36M{e}^{-1}{(1/8)}^{N+1}{e}^5{e}^{(5/8)}+36M{e}^{-1}{(1/8)}^{N+1}{e}^5{e}^{5/8}\lesssim {(1/8)}^{N+1},$$

(125)

which completes the proof of the theorem. □

Corollary 3.

Suppose that ${\mathcal{U}}_N(z,t)$ has the form (60) and represents the best possible approximation for $\mathcal{U}(z,t)$ out of $\mathcal{W}$. Then, the following estimates for the error $E_N$ are valid:

$$\parallel E_N{\parallel }_{\infty }\lesssim {(1/2)}^{3N+3},N\ge 1.$$

(126)

Proof. 

Since ${\mathcal{U}}_N(z,t)\in \mathcal{W}$ represents the best possible approximation for $U(z,t)$, we have the following:

$$\parallel E_N{\parallel }_{\infty }=\parallel U-{\mathcal{U}}_N{\parallel }_{\infty }\le {\parallel U-h\parallel }_{\infty },\forall h\in \mathcal{W}.$$

(127)

In view of (121) and (127),

$$\parallel E_N{\parallel }_{\infty }\le {\parallel U-U_N\parallel }_{\infty }\lesssim {(1/2)}^{3N+3},$$

(128)

which completes the proof of the theorem. □

The stability of error, or the process of estimating the propagation of error, is the focus of the subsequent theorem.

Theorem 8.

For any two successive approximations of $\mathcal{U}(z,t)$, we obtain the following:

$$|{\mathcal{U}}_{N+1}-{\mathcal{U}}_N{|\lesssim (1/2)}^{3N+3}.$$

(129)

Proof. 

We have

$$|{\mathcal{U}}_{N+1}-{\mathcal{U}}_N|=|{\mathcal{U}}_{N+1}-\mathcal{U}+\mathcal{U}-{\mathcal{U}}_N|\le |\mathcal{U}-{\mathcal{U}}_{N+1}|+|\mathcal{U}-{\mathcal{U}}_N|\le \parallel E_{N+1}{\parallel }_{\infty }+{\parallel E_N\parallel }_{\infty }.$$

By considering (126), we can obtain (129). □

8. Numerical Results

Several test examples are presented in this section to demonstrate the effectiveness of the proposed algorithms. Comparisons between the results obtained using the proposed method and those from other methods show that the proposed methods are highly effective and convenient. The following examples are considered.

Example 1.

Consider the linear eighth-order problem [56]

$$\begin{array}{c}\hfill {\mathcal{U}}^{\left(8\right)}\left(z\right)-\mathcal{U}\left(z\right)=f\left(z\right),f\left(z\right)=-8e^z,z\in [0,1],\end{array}$$

(130)

subject to the conditions

$$\begin{array}{cc}& \mathcal{U}\left(0\right)=1,{\mathcal{U}}^{\left(1\right)}\left(0\right)=0,{\mathcal{U}}^{\left(2\right)}\left(0\right)=-1,{\mathcal{U}}^{\left(3\right)}\left(0\right)=-2,{\mathcal{U}}^{\left(4\right)}\left(0\right)=-3,\hfill \\ & {\mathcal{U}}^{\left(5\right)}\left(0\right)=-4,{\mathcal{U}}^{\left(6\right)}\left(0\right)=-5,{\mathcal{U}}^{\left(7\right)}\left(0\right)=-6,\hfill \end{array}$$

and the analytical solution is $\mathcal{U}\left(z\right)=(1-z)e^z$.

Table 2. The absolute errors for Example 1 at different values of z and N.

	TGM
$\mathit{z}$	$\mathit{N}=\mathbf{16}$	$\mathit{N}=\mathbf{20}$	$\mathit{N}=\mathbf{24}$
$0.1$	$1.1452\times {10}^{-10}$	$1.7763\times {10}^{-15}$	$1.1102\times {10}^{-16}$
$0.2$	$2.4774\times {10}^{-8}$	$3.3195\times {10}^{-13}$	$0.0000\times {10}^{-00}$
$0.3$	$5.4599\times {10}^{-7}$	$6.8604\times {10}^{-12}$	$1.1102\times {10}^{-16}$
$0.4$	$4.7633\times {10}^{-6}$	$5.7179\times {10}^{-11}$	$7.7715\times {10}^{-16}$
$0.5$	$2.5134\times {10}^{-5}$	$2.9184\times {10}^{-10}$	$5.6621\times {10}^{-15}$
$0.6$	$9.6789\times {10}^{-5}$	$1.0961\times {10}^{-9}$	$2.8754\times {10}^{-14}$
$0.7$	$3.0048\times {10}^{-4}$	$3.3377\times {10}^{-9}$	$1.1390\times {10}^{-13}$
$0.8$	$7.9773\times {10}^{-4}$	$8.7262\times {10}^{-9}$	$3.7525\times {10}^{-13}$
$0.9$	$1.8807\times {10}^{-3}$	$2.0319\times {10}^{-8}$	$1.0758\times {10}^{-12}$

in Example 1 displays three sets of absolute error values using the proposed methods, with different numbers of points N (16, 20, and 24). The absolute errors decrease significantly as N increases, indicating that the method becomes more accurate with a higher number of points. This suggests the method is effective in reducing error and improving numerical precision.

• At smaller values of z (e.g., $z=0.1$), the errors are generally lower.
• At larger values of z (e.g., $z=0.9$), the errors increase, indicating potential challenges in achieving high accuracy in these regions.

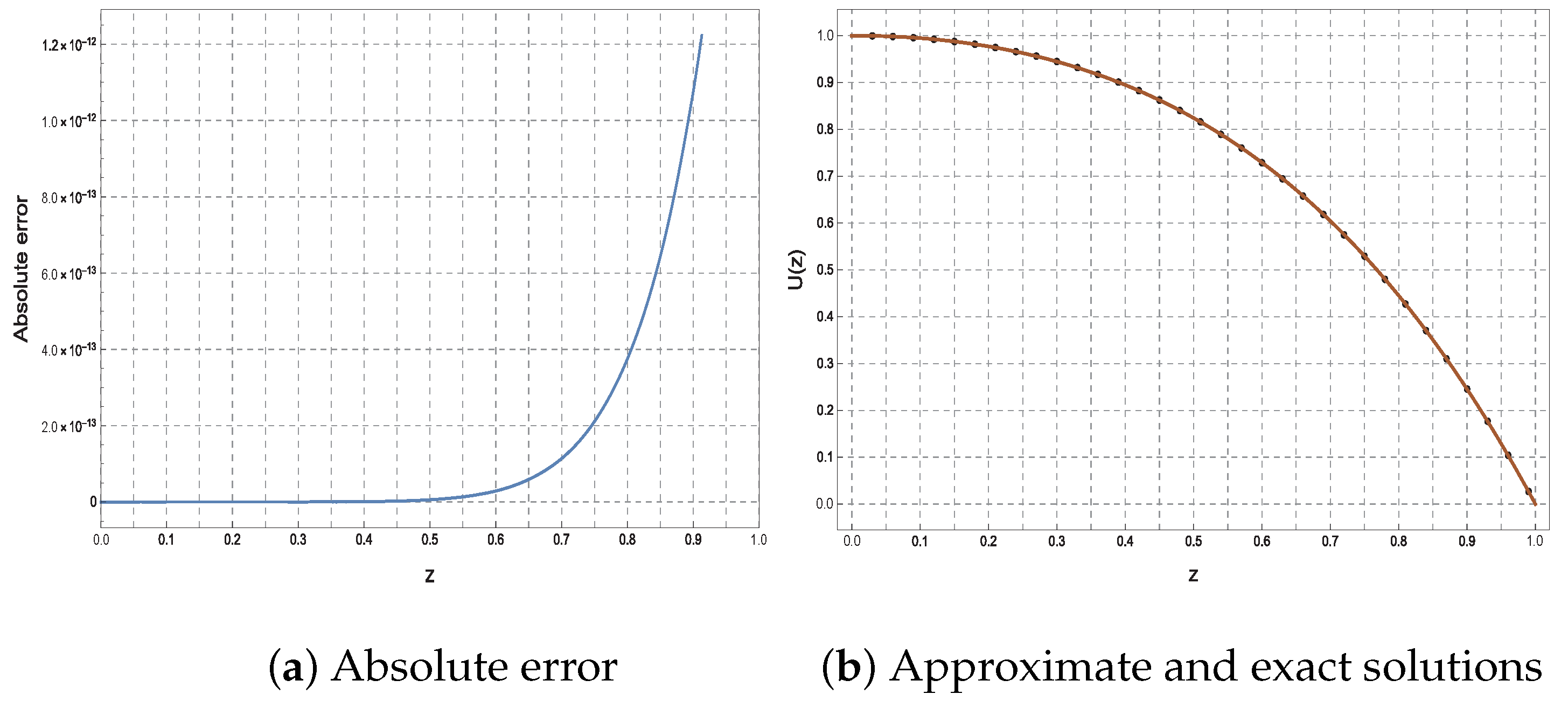
Figure 1 illustrates the corresponding absolute error function (left) and the comparison between the approximate and exact solutions (right) for Example 1 at $N=24$. The plot on the left demonstrates that the absolute error remains very small and increases gradually at $N=24$, confirming the method’s reliability and precision in solving the given problem. The plot on the right shows an excellent agreement between the approximate and exact solutions, indicating the high accuracy of the method.

Example 2.

Consider the linear second-order problem (see [57])

$$\begin{array}{cc}\hfill {\mathcal{U}}^{\left(2\right)}\left(z\right)& -2{\mathcal{U}}^{\left(1\right)}\left(z\right)+2\mathcal{U}\left(z\right)=f\left(z\right),z\in [0,1],\hfill \end{array}$$

with two different sets of initial conditions and corresponding exact solutions:

• First case:
  Initial conditions:

  $$\mathcal{U}\left(0\right)=0,{\mathcal{U}}^{\left(1\right)}\left(0\right)=1.$$
  Exact solution:

  $$\mathcal{U}\left(z\right)=z{e}^z.$$
• Second case:
  Initial conditions:

  $$\mathcal{U}\left(0\right)=0,{\mathcal{U}}^{\left(1\right)}\left(0\right)=0.$$
  Exact solution:

  $$\mathcal{U}\left(z\right)=z^{13/2}sin\left(\pi z^{4/3}\right).$$

In each case, $f\left(z\right)$ is selected accordingly to satisfy the differential equation.

Table 3. The absolute errors and CPU time (s) for Example 2 at different values of N.

N	R-JTM	CPU	N	TGM	CPU
	[57]	Time (s)			Time (s)
8	$5.11\times {10}^{-3}$	$11.845$	7	$1.25\times {10}^{-4}$	$1.062$
12	$3.15\times {10}^{-8}$	$12.016$	10	$8.11\times {10}^{-9}$	$2.078$
16	$1.19\times {10}^{-11}$	$12.375$	13	$1.70\times {10}^{-13}$	$3.125$
20	$2.96\times {10}^{-13}$	$12.907$	15	$8.03\times {10}^{-17}$	$4.499$

presents a comparative analysis of two computational methods, Romanovski–Jacobi tau method (R-JTM) [57] and the proposed TGM, for solving numerical Example 2. The table details each method’s absolute errors and CPU time (s) at varying numbers of discretization points N. The results demonstrate the superior accuracy of the TGM method, achieving significantly smaller absolute errors compared to R-JTM [57]. For instance, at $N=15$, TGM exhibits an absolute error of 8.03 × 10⁻¹⁷, while R-JTM at $N=20$ shows 2.96 × 10⁻¹³. Furthermore, TGM is more computationally efficient, requiring only $4.499$ seconds at $N=15$, in contrast to R-JT’s $12.907$ seconds at $N=20$. The table highlights that TGM offers a better balance between accuracy and efficiency, establishing it as a more favorable choice for solving similar problems with solutions of the form $\mathcal{U}\left(z\right)=z{e}^z$. Notably, while CPU time increases with N in both methods, the rate of increase is substantially lower for TGM. Figure 2 compares the exact solutions of a second-order differential equation in Example 2. In the left plot, the solution $\mathcal{U}\left(z\right)=z{e}^z$ is shown for $N=24$, exhibiting a smooth increasing behavior before decreasing, with a good match between the numerical and analytical solutions. In the right plot, the solution $\mathcal{U}\left(z\right)=z^{13/2}sin\left(\pi z^{4/3}\right)$ is presented for $N=10$, displaying a more oscillatory pattern. The first solution demonstrates exponential behavior, while the second shows strong oscillatory effects. This figure highlights the possibility of obtaining different solutions for the same equation depending on the initial conditions.

Remark 4.

In both accuracy and computational efficiency, the TGM approach beats the R-JTM method [57]. TGM is the better method for this problem as it requires considerably less CPU time and yields much less absolute errors.

Example 3.

The isothermal gas spheres equation [57] is given by the following equation:

$$\begin{array}{c}\hfill {\mathcal{U}}^{\left(2\right)}\left(z\right)+{\displaystyle \frac{2}{z}}{\mathcal{U}}^{\left(1\right)}\left(z\right)+e^{\mathcal{U}\left(z\right)}=0,z\in [0,1],\end{array}$$

(131)

with the following initial conditions:

$$\begin{array}{cc}& \mathcal{U}\left(0\right)=0,{\mathcal{U}}^{\left(1\right)}\left(0\right)=0.\hfill \end{array}$$

An approximate solution to this equation, as obtained by Wazwaz [58], Liao [59], and Singh et al. [60], is given by the following formula:

$$\mathcal{U}\left(z\right)=-{\displaystyle \frac{1}{6}}{z}^2+{\displaystyle \frac{1}{5.4!}}{z}^4-{\displaystyle \frac{8}{21.6!}}{z}^6+{\displaystyle \frac{122}{81.8!}}{z}^8-{\displaystyle \frac{61.67}{495.10!}}{z}^{10}+\cdots .$$

Table 4. Approximate solutions for Lane–Emden Equation (131) for Example 3.

z	TGM	JRPM	VWFML	ADM
	(Our Method)	[61]	Method [62]	Solution [58]
0.1	−0.0016658	−0.0016677	−0.0014253	−0.0016658
0.2	−0.0066534	−0.0066443	−0.0062547	−0.0066534
0.3	−0.014933	−0.0149455	−0.014411	−0.014933
0.4	−0.026456	−0.0264421	−0.025868	−0.026456
0.5	−0.041154	−0.0411573	−0.04051	−0.041154
0.6	−0.058944	−0.058964	−0.058256	−0.058945
0.7	−0.079726	−0.0797169	−0.079011	−0.079728
0.8	−0.10339	−0.103359	0.10264	−0.10339
0.9	−0.12979	−0.129795	0.12904	−0.12981
1.0	−0.15883	−0.158859	−0.15806	−0.15886

presents the approximate values of $u\left(z\right)$ for the standard Lane–Emden equation with $N=8$, obtained using TGM. These results are compared with those derived from the Jacobi Rational Pseudospectral Method (JRPM) [61], the variable weight fuzzy marginal linearization (VWFML) method [62], and the Adomian Decomposition Method (ADM) solution [58].

Example 4.

We consider the following linear ODE system [63],

$$\begin{array}{cc}& \left\{\begin{array}{c}{\mathcal{U}}_1^{\left(1\right)}\left(z\right)+{\mathcal{U}}_2^{\left(1\right)}\left(z\right)+{\mathcal{U}}_1\left(z\right)+{\mathcal{U}}_2\left(z\right)=1,\hfill \\ {\mathcal{U}}_2^{\left(1\right)}\left(z\right)-2{\mathcal{U}}_1\left(z\right)-{\mathcal{U}}_2\left(z\right)=0,\hfill & 0\le z\le 1,\hfill \end{array}\right.\hfill \end{array}$$

(132)

with the ICs

$${\mathcal{U}}_1\left(0\right)=0and{\mathcal{U}}_2\left(0\right)=1.$$

The exact solution of this problem are ${\mathcal{U}}_1\left(z\right)=e^{-z}-1$ and ${\mathcal{U}}_2\left(z\right)=2-e^{-z}$.

Table 5. Comparison of the absolute errors $e_{1,N}$ for ${\mathcal{U}}_1\left(z\right)$ of Equation (132).

${\mathit{x}}_{\mathit{i}}$	DTM [64]	BCM [63]	TGM
	${\mathit{e}}_{\mathbf{1},\mathbf{6}}$	${\mathit{e}}_{\mathbf{1},\mathbf{6}}$	${\mathit{e}}_{\mathbf{1},\mathbf{6}}$	${\mathit{e}}_{\mathbf{1},\mathbf{10}}$
0.0	0	0	0	0
0.2	$1.5575\times {10}^{-2}$	$2.8460\times {10}^{-8}$	$3.8359\times {10}^{-8}$	$1.2216\times {10}^{-10}$
0.4	$5.1209\times {10}^{-2}$	$1.7820\times {10}^{-8}$	$5.9136\times {10}^{-8}$	$5.3899\times {10}^{-11}$
0.6	$1.0150\times {10}^{-1}$	$1.2668\times {10}^{-8}$	$2.9357\times {10}^{-8}$	$8.0393\times {10}^{-10}$
0.8	$1.6630\times {10}^{-1}$	$3.3538\times {10}^{-8}$	$3.6346\times {10}^{-8}$	$1.1373\times {10}^{-9}$
1.0	$2.3351\times {10}^{-1}$	$6.8657\times {10}^{-7}$	$2.5086\times {10}^{-8}$	$1.8155\times {10}^{-9}$

and

Table 6. Comparison of the absolute errors $e_{2,N}$ for ${\mathcal{U}}_2\left(z\right)$ of Equation (132).

${\mathit{x}}_{\mathit{i}}$	DTM [64]	BCM [63]	TGM
	${\mathit{e}}_{\mathbf{2},\mathbf{6}}$	${\mathit{e}}_{\mathbf{2},\mathbf{6}}$	${\mathit{e}}_{\mathbf{2},\mathbf{6}}$	${\mathit{e}}_{\mathbf{2},\mathbf{10}}$
0.0	0	0	0	0
0.2	$2.3262\times {10}^{-3}$	$2.8460\times {10}^{-8}$	$3.8360\times {10}^{-8}$	$2.9631\times {10}^{-10}$
0.4	$1.6867\times {10}^{-2}$	$1.7820\times {10}^{-8}$	$5.9137\times {10}^{-8}$	$4.4937\times {10}^{-10}$
0.6	$5.4499\times {10}^{-2}$	$1.2668\times {10}^{-8}$	$2.9358\times {10}^{-8}$	$6.2494\times {10}^{-10}$
0.8	$1.3194\times {10}^{-1}$	$3.3538\times {10}^{-8}$	$3.6346\times {10}^{-8}$	$6.4809\times {10}^{-10}$
1.0	$2.8038\times {10}^{-1}$	$6.8657\times {10}^{-7}$	$2.5086\times {10}^{-8}$	$6.8342\times {10}^{-10}$

provide a comparison of the absolute errors $e_{1,N}$ and $e_{2,N}$ for the functions ${\mathcal{U}}_1\left(z\right)$ and ${\mathcal{U}}_2\left(z\right)$, solved using different methods. Here are some observations on the tables:

• They show a clear difference in solution accuracy between the three methods used (Differential transformation method (DTM) in [64], Bessel collocation method (BCM) in [63], and the present method). The present method achieves significantly higher accuracy, with much smaller error values at the same points $x_i$.
• In Table 5, it is evident that the errors produced by the present method are much smaller compared to those of the DTM and BCM methods, especially as N increases from 6 to 10.
• In Table 6, the present method again demonstrates notably higher precision than the DTM and BCM methods across all $x_i$ points.

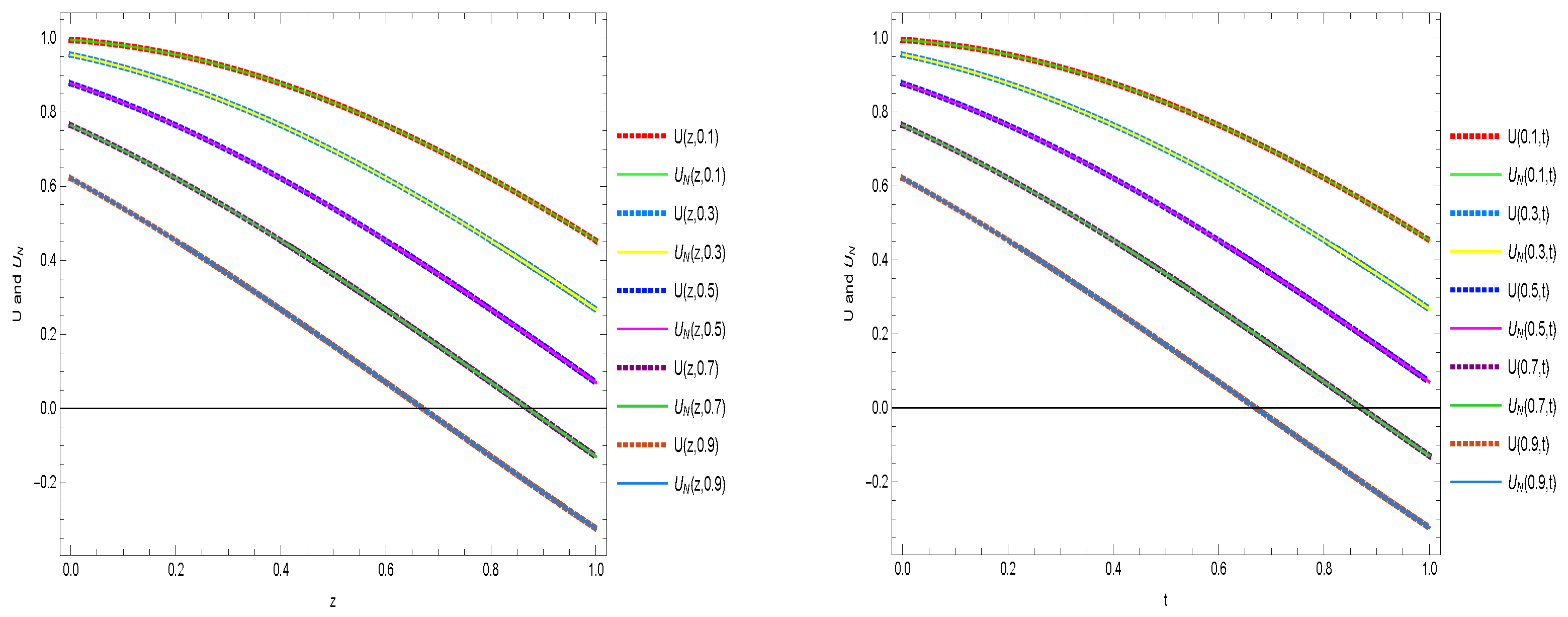
Also, Figure 3 and Figure 4 are plotted to compare the analytic solution with the approximate solution at $N=12$ for Example 4.

Example 5.

We consider the following hyperbolic equation of first-order of the form [33]

$$\begin{array}{c}\hfill {\partial }_t\mathcal{U}(z,t)=-{\partial }_z\mathcal{U}(z,t)-\mathcal{U}(z,t)+S(z,t),z\in (0,1),t\in (0,1),\end{array}$$

(133)

subject to initial and boundary conditions,

$$\begin{array}{cc}& \mathcal{U}(z,0)=cos\left(z\right),z\in (0,1),\mathcal{U}(0,t)=cos\left(t\right),t\in (0,1),\hfill \end{array}$$

where

$$S(z,t)=-2sin(z+t)+cos(z+t).$$

The exact solution is given by

$$\mathcal{U}(z,t)=cos(z+t).$$

Table 7. Comparison of the absolute errors for Example 5 at $N=6$.

	[33]		TGM
$(\mathit{z},\mathit{t})$	LW	CW
$(0.1,0.1)$	$9.12\times {10}^{-5}$	$4.53\times {10}^{-4}$	$2.95\times {10}^{-8}$
$(0.2,0.2)$	$3.36\times {10}^{-5}$	$2.07\times {10}^{-4}$	$4.32\times {10}^{-8}$
$(0.3,0.3)$	$1.86\times {10}^{-5}$	$6.92\times {10}^{-5}$	$1.63\times {10}^{-8}$
$(0.4,0.4)$	$2.42\times {10}^{-5}$	$1.39\times {10}^{-4}$	$8.50\times {10}^{-8}$
$(0.5,0.5)$	$8.30\times {10}^{-5}$	$2.64\times {10}^{-5}$	$6.31\times {10}^{-8}$
$(0.6,0.6)$	$1.38\times {10}^{-4}$	$7.62\times {10}^{-5}$	$3.05\times {10}^{-8}$
$(0.7,0.7)$	$9.90\times {10}^{-5}$	$2.10\times {10}^{-5}$	$3.15\times {10}^{-8}$
$(0.8,0.8)$	$1.20\times {10}^{-6}$	$2.01\times {10}^{-5}$	$1.95\times {10}^{-8}$
$(0.9,0.9)$	$9.00\times {10}^{-5}$	$3.00\times {10}^{-4}$	$8.00\times {10}^{-9}$

compares the absolute errors at various points in the $(z,t)$ domain for Example 5, with $N=6$. The errors are shown for two previous methods (Legendre wavelets (LW) and Chebyshev wavelets (CW) from Singh et al. [33]) and the present method.

• It is notable that the errors in the present method are significantly lower compared to the LW and CW methods. For instance, at point $(z,t)=(0.1,0.1)$, the error in the present method is $2.95\times {10}^{-8}$, while the errors in the other methods are $9.12\times {10}^{-5}$ and $4.53\times {10}^{-4}$, respectively.
• This result highlights the efficiency of the present method in substantially reducing the error compared to the other methods, reflecting higher accuracy.

Table 8. Comparison of the $L^{\infty }$ errors for Example 5 at different values of N.

	[33]		TGM
$\mathit{N}$	LW	CW
2	$4.86\times {10}^{-2}$	$5.94\times {10}^{-2}$	$8.02\times {10}^{-3}$
4	$2.78\times {10}^{-4}$	$6.00\times {10}^{-4}$	$6.49\times {10}^{-5}$
6	$9.90\times {10}^{-5}$	$4.53\times {10}^{-4}$	$1.58\times {10}^{-7}$
7	−	−	$1.74\times {10}^{-8}$
8	−	−	$2.39\times {10}^{-10}$
9	−	−	$2.30\times {10}^{-11}$

compares the $L^{\infty }$ errors for Example 5 at different values of N.

• It is clear that the present method shows reduced errors as the values of N increase, with the error decreasing significantly with larger N. For instance, at $N=6$, the error in the present method is $1.58\times {10}^{-7}$, while the errors in the other methods are $9.90\times {10}^{-5}$ and $4.53\times {10}^{-4}$ for the LW and CW methods, respectively.
• The present method demonstrates excellent performance as N increases, achieving very high accuracy, such as $2.30\times {10}^{-11}$ at $N=9$, indicating the method’s strength in convergence and accuracy.

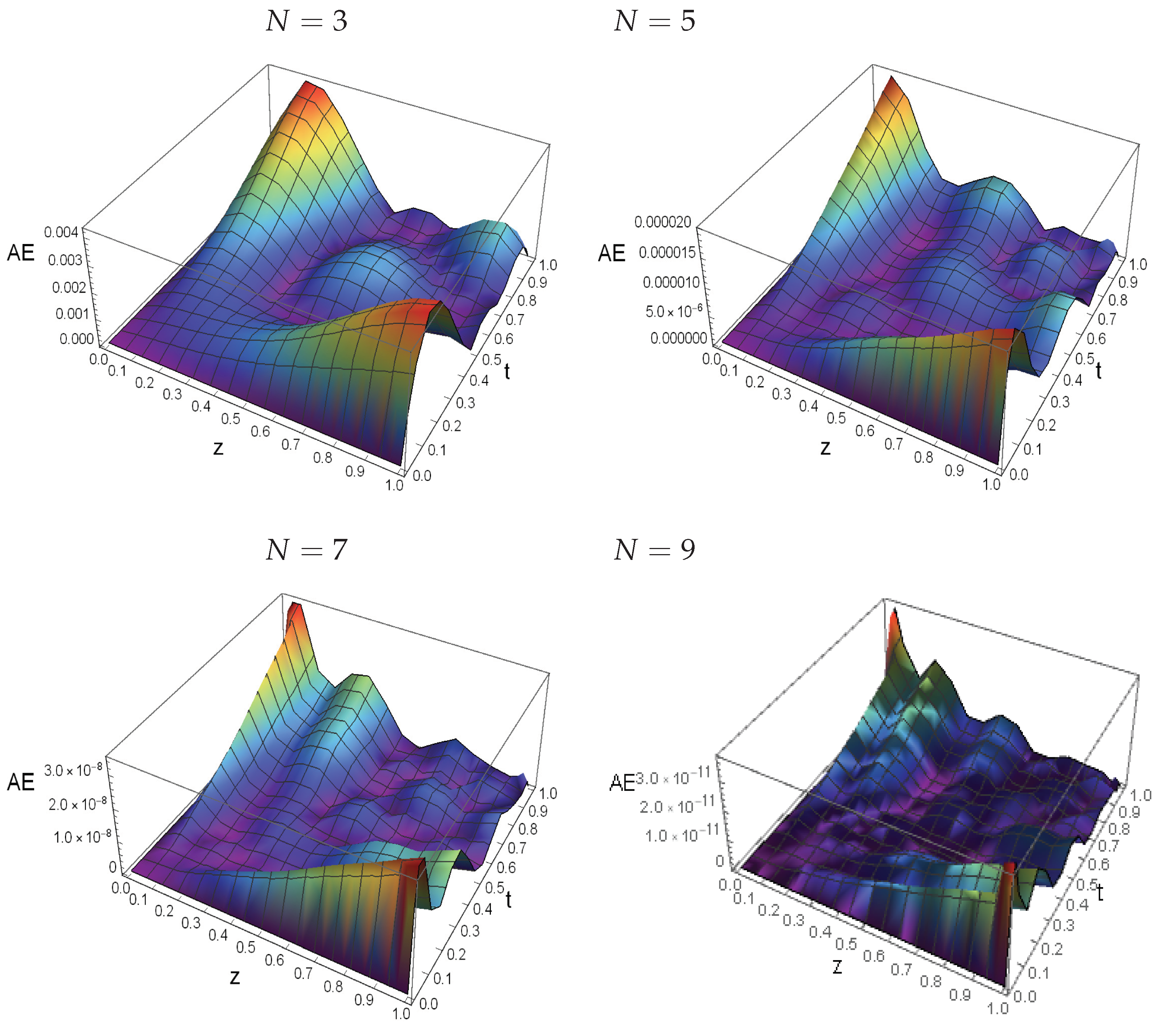
Also, Figure 5 compares the curves of analytical and approximation solutions for Example 5, where $N=9$, at $t=0.1,0.3,0.5,0.7,0.9$ and $z=0.1,0.3,0.5,0.7,0.9$. Finally, Figure 6 illustrates the space-time graphs of the absolute error functions for Example 5 at various choices of N, specifically $N=3$, $N=5$, $N=7$, and $N=9$. The graphs depict the distribution of errors over time and space, reflecting the accuracy of the proposed method in solving the problem. It is evident that increasing the values of N results in a significant reduction in errors, confirming the method’s effectiveness in terms of accuracy and convergence.

9. Conclusions

This paper introduces and utilizes a new set of polynomials known as TelPs, which are considered generalizations of TelNs. We showed that the application of spectral methods, and in particular the Galerkin and collocation methods, is efficient for solving different DEs. We treated numerically some types of DEs using TelPs as basis functions. We conducted a thorough investigation into the convergence analysis of the used expansion. To the best of our knowledge, these kinds of polynomials have not been used to solve DEs before. We plan to employ these polynomials in other types of DEs shortly. In conclusion, our research has significant implications for various real-world applications. For instance, the methodologies developed can be effectively applied to heat transfer problems, enabling more efficient thermal management in engineering systems. Additionally, our findings contribute to the growing field of machine learning-based PDE solvers, which have the potential to revolutionize how complex DEs are approached in disciplines such as fluid dynamics, materials science, and environmental modeling. By bridging the gap between theoretical advancements and practical implementations, we hope to inspire further exploration and application of these techniques in diverse fields.