Abstract
In this paper, the generalized quadratic assignment problem (GQAP) is extended to consider multiple time periods and is called the dynamic GQAP (DGQAP). This problem considers assigning a set of facilities to a set of locations for multiple periods in the planning horizon such that the sum of the transportation, assignment, and reassignment costs is minimized. The facilities may have different space requirements (i.e., unequal areas), and the capacities of the locations may vary during a multi-period planning horizon. Also, multiple facilities may be assigned to each location during each period without violating the capacities of the locations. This research was motivated by the problem of assigning multiple facilities (e.g., equipment) to locations during outages at electric power plants. This paper presents mathematical models, construction algorithms, and two simulated annealing (SA) heuristics for solving the DGQAP problem. The first SA heuristic (SAI) is a direct adaptation of SA to the DGQAP, and the second SA heuristic (SAII) is the same as SAI with a look-ahead/look-back search strategy. In computational experiments, the proposed heuristics are first compared to an exact method on a generated data set of smaller instances (data set 1). Then the proposed heuristics are compared on a generated data set of larger instances (data set 2). For data set 1, the proposed heuristics outperformed a commercial solver (CPLEX) in terms of solution quality and computational time. SAI obtained the best solutions for all the instances, while SAII obtained the best solution for all but one instance. However, for data set 2, SAII obtained the best solution for nineteen of the twenty-four instances, while SAI obtained five of the best solutions. The results highlight the effectiveness and efficiency of the proposed heuristics, particularly SAII, for solving the DGQAP.
Keywords:
dynamic generalized quadratic assignment problem; generalized quadratic assignment problem; mathematical models; simulated annealing; heuristic MSC:
90B06; 90B80; 90C27; 90C59; 49M99; 37N40
1. Introduction
Assignment problems are common combinatorial optimization problems (COPs) that carry much importance in different fields spanning logistics, manufacturing, business, telecommunication, healthcare, etc. There are mainly two types of assignment problems: one-to-one and many-to-one. For example, consider the quadratic assignment problem (QAP), a one-to-one assignment-type problem, which assigns equal-area facilities to locations while minimizing the sum of the costs of transporting materials between facilities and the costs of assigning (or installing) facilities to locations. In the QAP, each facility is assigned to a location, and each location is assigned to a facility (i.e., one-to-one assignment). The QAP was introduced by Koopmans and Beckmann [1] and was proven to be NP Hard by Sahni and Gonzales [2]. See Burkard et al. [3] and Loiola et al. [4] for an extensive review of the solution techniques for the QAP.
There are many variants of the QAP. For some examples of different variants of the QAP see Silva et al. [5]. One of them is the generalized QAP (GQAP) which is a many-to-one assignment-type problem. That is, more than one facility may be assigned to each location without violating location capacities, but each facility is assigned to exactly one location. More specifically, the GQAP is stated as the problem of assigning a set of M facilities to a set of N locations (M > N) without exceeding the capacities of the locations, such that the sum of the assignment and transportation costs is minimized. The formulation of the GQAP is given below and is an adaptation of the model presented by Lee and Ma [6].
where M is the number of facilities, N is the number of locations, aik is the cost of assigning (installing) facility i to (at) location k, fij is the amount of materials flowing from facility i to facility j, dkl is the distance from location k to location l, cijkl is the unit cost per distance unit of transporting materials from facility i (at location k) to facility j (at location l), ri is the resource (or space) requirement of facility i, and Ck is the amount of resource (or space) capacity available at location k. The decision variable xik = 1 indicate that facility i is assigned to location k. When xik = 0, facility i is not assigned to location k. Objective function (1) minimizes the sum of the assignment (or installation) and transportation costs. Constraint (2) ensures that each facility is assigned to only one location. Constraint (3) ensures that the capacity of each location is not exceeded, and the restrictions on the decision variables are given in (4).
The term in objective function (1) used to obtain transportation cost has a quadratic term. As a result, the mathematical formulation (1)–(4) is a binary integer nonlinear programming model. The model is linearized by using a simple standard linear programming transformation (i.e., by substituting wijkl for xikxjl). Then, replace objective function (1) with the following.
In addition, add the following constraints.
As a result, the linearized model, categorized as a mixed integer linear programming (MILP) model, for the GQAP consists of objective function (5) subject to constraints (2)–(4), (6) and (7). For other linearizations of the GQAP see Lee and Ma [6] and Cordeau et al. [7].
The GQAP literature is very limited compared to the QAP literature. Lee and Ma [6] presented the first formulation for the GQAP. Also, the authors presented three methods for the linearization of the formulation, and a branch-and-bound algorithm to optimally solve the GQAP. Hahn et al. [8] proposed a new algorithm based on a reformulation linearization technique (RLT) dual ascent procedure to optimally solve the GQAP. Similarly, Pessoa et al. [9] proposed two exact algorithms for the GQAP which combine a previously proposed branch-and-bound scheme with a new Lagrangean relaxation procedure over a known RLT formulation. Guignard [10] presented RLT models for the GQAP and special cases of the problem (i.e., crossdock door assignment problem and 0-1 quadratic knapsack problem). It is important to note that the exact algorithms presented above are unable to solve large-size problems within a reasonable timeframe. However, the following heuristics (or approximation algorithms) are able to obtain “good” solutions for large-size problems within a reasonable timeframe. Cordeau et al. [7] presented a linearization of the GQAP formulation as well as a memetic heuristic for the GQAP, which combines genetic algorithms (Holland [11]) and tabu search (Glover [12]). Mateus et al. [13] proposed several greedy randomized adaptive search procedures (GRASPs) with path-relinking heuristics for the GQAP using different construction, local search, and path-relinking procedures. McKendall and Li [14] presented three construction algorithms and a tabu search heuristic for the GQAP. Silva et al. [5] proposed a parallel memetic iterated tabu search heuristic for the QAP and four of its variants, which includes the GQAP as one of its variants. More recently, Greistorfer et al. [15] presented a tabu search matheuristic for the GQAP. Also, Fathollahi-Fard et al. [16] proposed a Benders reformulation based on RLT inequalities as well as a construction and a metaheuristic algorithm based on adaptive large neighborhood search (ALNS) for the GQAP. Within the ALNS heuristic, the authors incorporate removal–insertion heuristics, a local search algorithm which uses a tabu list, and a decision rule inspired by simulated annealing. In McKendall and Dhungel [17], the authors presented a simulated annealing heuristic for the GQAP. Sohrabi et al. [18] proposed a modified genetic algorithm (GA) called genetic engineering algorithm.
The GQAP has numerous applications related to facility design, scheduling, and network design. Lee and Ma [6] first introduced the GQAP to solve the problem of assigning a set of production equipment (or facilities) to manufacturing sites (or locations). Cordeau et al. [7] considered the application of GQAP on container yard management where the yard is partitioned into storage areas (or locations) and containers (or facilities) are assigned to these storage areas. McKendall and Li [14] considered the application of assigning a set of machines (or facilities) to a set of locations on the floor of a manufacturing plant. Also, Zou et al. [19] considered a GQAP with an additional capacity constraint to assign tasks to processors. Unal & Uysal [20] implemented GQAP to design the curriculum at a university. As stated above, the crossdock door assignment problem and the 0-1 quadratic knapsack problem are special cases of the GQAP (Guignard [10]). As stated in Greistorfer et al. [15], the GQAP has been used to model several applications such as order picking, storage layout in warehouse management, relational database design, and scheduling activities in semiconductor wafer processing.
In this paper, the dynamic GQAP (DGQAP) is considered. It is defined as the task of assigning a set of facilities to a set of locations for multiple periods in the planning horizon such that the sum of the transportation, assignment, and reassignment costs is minimized. The facilities may have different space requirements, and the capacities of the locations may vary during a multi-period planning horizon. Also, multiple facilities may be assigned to each location during each period without violating the capacities of the locations. To the best of the authors’ knowledge, this extension has not been studied before. Nevertheless, this research was motivated by the problem of assigning multiple facilities (equipment) to locations at electric power plants during planned outages. Since the equipment are of different sizes, the facilities may have different space requirements. More importantly, during planned outages some location capacities and distances between locations may change due to the performance of maintenance activities as well as the storage of the materials required for these activities. A similar application of the DGQAP is the management of construction facilities during construction projects, where construction facilities (e.g., cranes, equipment, materials) are assigned to locations at a construction site for a multiple period planning horizon (Elbeltagi et al. [21]). As the layout changes at the construction site, location capacities and distances between locations may change. In contrast, there are other applications where this may not be the case. Consider the applications presented above for the GQAP in Cordeau et al. [7] where the facilities (containers) are assigned to locations (storage areas) in the container yard during a multi-period planning horizon. This is an application of the DGQAP where the capacities of the locations and the distances between the locations may not change. Nevertheless, the DGQAP can be considered in the other applications presented above for the GQAP where there are multiple periods in the planning horizon such as in Zou et al. [19] (i.e., assigning tasks to processors), Unal & Uysal [20] (i.e., designing the curriculum at a university), and McKendall and Li [14] (i.e., assigning machines to locations in a manufacturing plant). In general, when there are changes in the problem (input) data during the planning horizon—more specifically, if one or more of the following input data changes during the planning horizon—it would be better to solve the resulting problem as a DGQAP as opposed to solving multiple GQAPs, as will be discussed later.
- There are changes in either the amount of materials transported between facilities or the costs of transporting materials between facilities.
- There are changes in the location and location capacities, which may change the distances between the locations.
- There are changes in the facilities’ requirements.
As stated previously, to the best of our knowledge, the GQAP has not been extended to the dynamic GQAP. However, there are many dynamic (or multi-period) COPs in the literature, besides the one mentioned earlier (i.e., assigning facilities to locations at a construction site as in Elbeltagi et al. [21]). In 1986, Rosenblatt [22] extended the QAP to consider multiple discrete time periods and presented a dynamic programming algorithm to solve the problem referred to as the dynamic facility layout problem (DFLP) (i.e., the problem of assigning facilities to locations during a multi-period planning horizon such that sum of the transportation and rearrangement costs is minimized). This problem differs from the DGQAP, since each location is assigned to only one facility during each period as opposed to assigning multiple facilities to a location without exceeding its capacity, as in the DGQAP. For examples of SA algorithms used to solve the DFLP, see McKendall et al. [23] and Khajemahalle et al. [24]. In 1997, Kogan et al. [25] extended the GAP to the dynamic GAP (DGAP), which considers continuous-time. In 2012, Mazzola and Neebe [26] considered an extension of the GAP to multiple discrete time periods. This problem is called MultiGAP, which considers assigning multiple tasks to agents, without exceeding the capacities of the agents, for each period in the planning horizon such that the sum of the assignment and reassignment costs is minimized. The authors presented two mathematical models, a branch-and-bound algorithm, and a Lagrangian heuristic for the problem. It is important to note that MultiGAP is a special case of the DGQAP where the facilities are the tasks and the locations are the agents. In other words, the main difference between MultiGAP and DGQAP is that the latter problem also considers the sum of the transportation costs in the objective function, which adds a quadratic term to the formulation, making the mathematical model nonlinear and more difficult to solve. Moccia et al. [27] present a different DGAP which extends the GAP by considering discrete periods and by associating a start and finish time to each task. Also, they consider additional constraints related to warehouse and yard management applications. In 2005, McKendall et al. [28] presented a mathematical model and SA algorithms for assigning activities to workspaces and resources to either work or storage locations during a multi-period planning horizon while minimizing total distance resources travel during planned outages at electric power plants. The problem is defined as the dynamic space allocation problem and is a generalization of the DGQAP. Notice, there are two types of locations: workspaces and storage spaces where activities (groups of resources required to perform activities) are assigned to workspaces and individual resources are assigned to storage locations. Although there are many other dynamic COPs such as the dynamic vehicle routing problem (Wang et al., [29]) and dynamic facility location problem (Zhang and Li [30]), here are just a few. This shows the importance and relevance for considering the dynamic extensions of several of the well-known COPs.
As mentioned above, SA is used to solve dynamic COPs such as DFLP (e.g., McKendall et al. [23] and Khajemahalle et al. [24]) and the dynamic space allocation problem (McKendall et al. [28]). However, Kirkpatrick et al. [31] was the first to use SA to solve a COP called the Ising spin glass problem. More recently, Huo et al. [32] presented an SA heuristic for a task assignment and path planning problem which is viewed as a three-dimensional vehicle routing problem. This problem is a generalization of the generalized assignment problem combined with multiple traveling salesperson problems. Dai et al. [33] developed an SA heuristic for a home healthcare location-routing problem with a mixed fleet of electric and conventional vehicles that consider battery swapping stations. Also, Leelertkij et al. [34] presented an SA algorithm for a multi-objective vehicle routing problem with time windows. Tole et al. [35] used an SA heuristic to solve a new variant of the bin packing problem called the circular bin packing problem with rectangular items. Lin et al. [36] presented an SA algorithm for the set orienteering problem with mandatory visits. This shows the diversity of problems that are solved using SA. Recently, researchers have used multi-neighborhood SA algorithms to solve COPs. Rosati and Schaerf [37] used a multi-neighborhood SA algorithm to solve the capacitated dispersion problem. The authors stated that their algorithm improved the state-of-the-art methods on almost all instances from public benchmarks. The multi-neighborhood SA algorithm developed for a capacitated facility location problem with incompatibilities presented in Ceschia and Schaerf [38] was able to outperform all previous methods on the publicly available data set. Da Ros et al. [39] proposed a multi-neighborhood SA algorithm for an oven scheduling problem. The authors stated that their algorithm was able to find new best solutions for many instances. Van Bulck et al. [40] presented a multi-neighborhood SA algorithm for a capacitated examination time-tabling problem. The authors stated that the proposed algorithm was able to produce new best solutions for a variety of well-known instances. As stated previously, McKendall and Dhungel [17] presented an SA heuristic for the GQAP, which considers multiple neighborhoods. Compared to the state-of-the-art methods, the proposed SA algorithm was able to produce the best-known solutions using very little computational time on a publicly available data set. Since multi-neighborhood SA was successfully applied to several related COPs (i.e., obtain very good solutions for many complex problems) and is easy to implement, it is used to solve the proposed DGQAP.
In this paper, mathematical models, construction algorithms, and simulated annealing (SA) heuristics are presented for the DGQAP problem. In Section 2, the mathematical models are presented for the DGQAP, and an illustrative example is solved using one of the proposed models. The construction algorithms and the SA heuristics for the DGQAP are presented in Section 3. In Section 4, some computational results of the proposed techniques on a set of randomly generated test problems are given. Finally, Section 5 provides conclusions.
2. Mathematical Models for the DGQAP
2.1. Mathematical Programming Models
The DGQAP is the problem of assigning a set of M facilities to a set of N locations (M > N) for T periods in the planning horizon such that the sum of the transportation, assignment, and reassignment costs is minimized. The assumptions of the DGQAP are as follows.
- (1)
- The planning horizon is divided into multiple periods. Periods may be defined as weeks, months, quarters, or years.
- (2)
- The input data is deterministic and known. That is, for each period t, the number of units of materials transported between facilities i and j (ftij), the distances between locations k and l (dtkl), the space requirement of each facility i (rti), the capacity of each location k (Ctk), the costs of assigning and reassigning each facility i to each location k (atik), and the unit cost per distance unit of transporting materials between each pair of facility i at location k and facility j at location l (ctijkl) are deterministic and known.
- (3)
- One or more facilities may be assigned to each location during each period such that the capacity of the location is not exceeded.
- (4)
- The objective is to minimize the sum of the transportation, assignment, and reassignment costs. The assignment costs are the costs of initially assigning (or installing) facilities to locations during the first period. Reassignment costs are the costs of reassigning facilities to different locations (uninstalling and reinstalling facilities) after the first period. More specifically, reassignment cost of a facility i assigned to location l in period t (atil) consists of the costs of uninstalling facility i assigned to location k at end of period t − 1 plus the cost of reinstalling facility i at a new location l at the beginning of the next period t.
Next, a mathematical formulation is presented for the DGQAP, which is an extension of the GQAP model, but first the decision variables are defined as follows. The decision variable xtik = 1 indicate that facility i is assigned to location k at period t. When xtik = 0, facility i is not assigned to location k at period t.
Objective function (8) minimizes the sum of the assignment, reassignment, and transportation costs. Constraint (9) ensures that each facility is assigned to only one location in each period. Constraint (10) ensures that the capacity of each location is not exceeded in each period. The restrictions on the decision variables are given in (11).
The mathematical formulation presented above for the DGQAP is nonlinear due to the nonlinear terms in Objective function (8) and is categorized as a BINLP model. In order to obtain the global optimal for the DGQAP, the nonlinear model above is linearized by using the simple standard transformation by substituting ytikl for the term x(t−1)ikxtil and wtijkl for the term xtikxtjl. This yields the following linearized objective function.
and the following constraints.
As a result, the linearized mathematical model for the DGQAP, which is categorized as a MILP model, consists of Objective function (12) subject to Constraints (9)–(11) and (13)–(16). Next, a DGQAP instance is presented and solved optimally using the MILP model presented above and the commercial solver CPLEX.
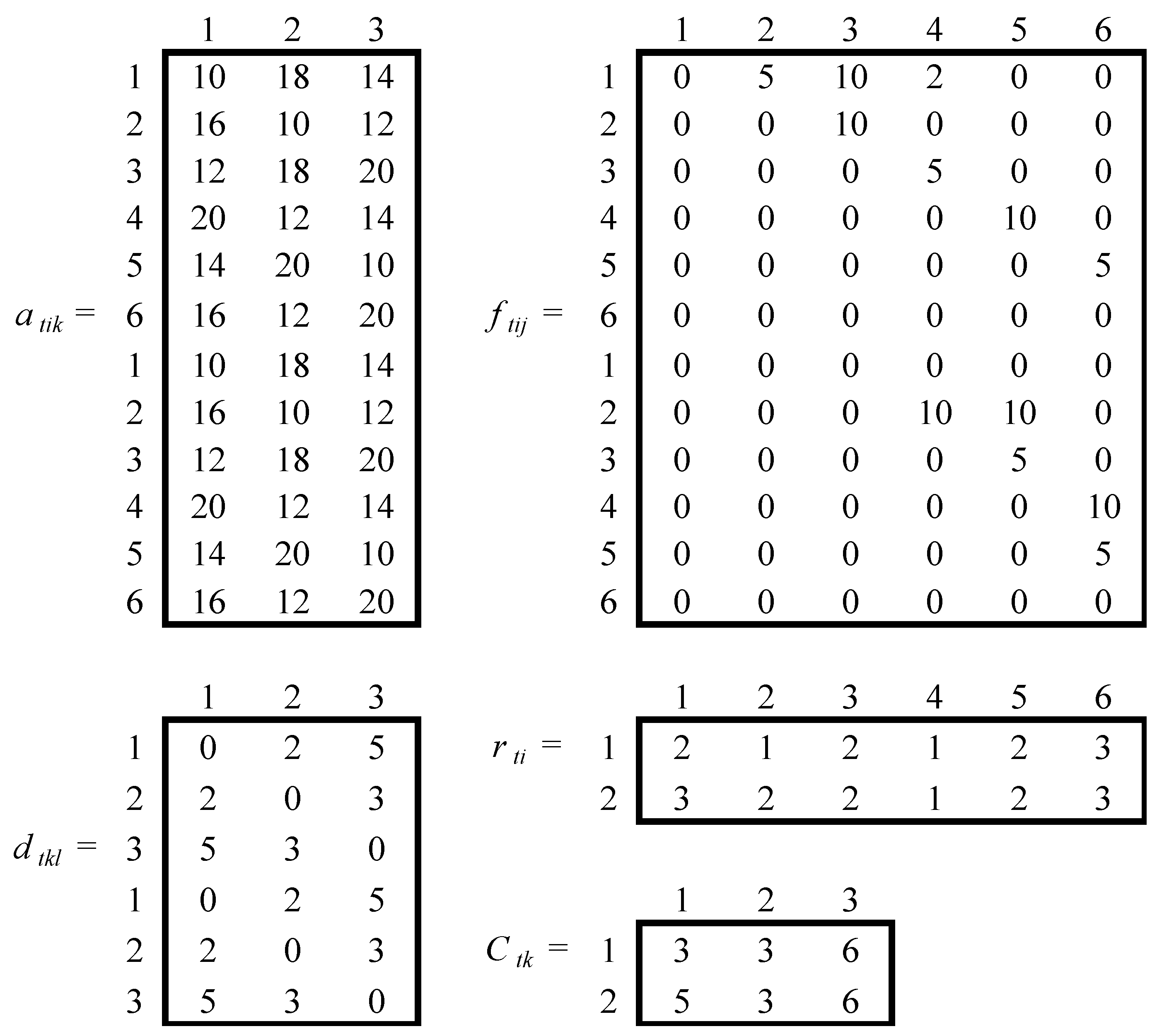
Consider a DGQAP instance in which six facilities are assigned to three locations in a 2-period planning horizon (i.e., M = 6, N = 3, T = 2). The unit cost per distance unit of transporting materials between each pair of the facilities during each period is 2 (i.e., ctijkl = 2). Note, all costs are in USD 1000s. See Figure 1 below for the input data for a small DGQAP instance. For example, the cost of assigning facility 2 to location 3 in period 1 is 12 (i.e., a123 = USD 12,000), and the cost of reassigning facility 2 (located at either location 1 or 2 in period 1) to location 3 in period 2 is also 12 (i.e., a223 = USD 12,000). Furthermore, the distance from location 3 to location 2 for both periods 1 and 2 are same, which is 3 distance units (i.e., d132 = d232 = 3). However, the space requirements of a facility during different periods may change due to either an increase or decrease in production capacity, for example. In the data below, the space requirement for facility 1 increases for period 2 from period 1 (i.e., r11 = 2, r21 = 3), but for facility 3 for each period, the facility requirement is the same (i.e., r13 = r23 = 2). Furthermore, there is a possibility that the space capacity of a location may change during different planning periods, as discussed above for the application of assigning facilities to locations during planned outages at electric power plants. For example, additional space may become available at a location when a maintenance activity is completed. Notice the space capacity of location 1 during period 1 is 3 units (i.e., C11 = 3), but in period 2 it increased to 5 units (i.e., C21 = 5).
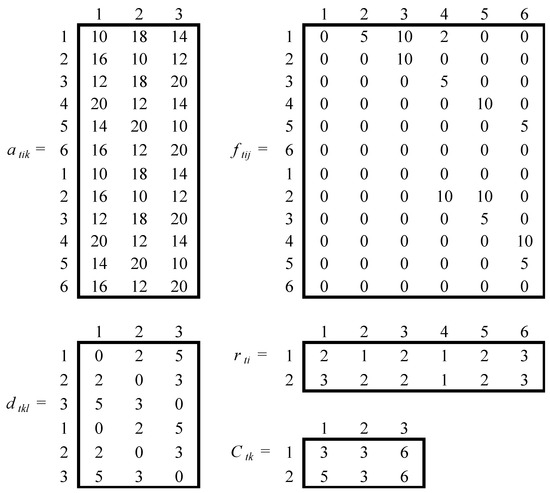
Figure 1.
Input data for a small DGQAP instance.
Using the data given in Figure 1, the MILP model presented for the DGQAP (i.e., objective function (12) subject to constraints (9)–(11) and (13)–(16)) and the commercial solver CPLEX (version 12.4), the following optimal solution is obtained. The nonzero values of the decision variable xtik are as follows.
x113 = x123 = x133 = x141 = x151 = x162 = x213 = x221 = x233 = x241 = x251 = x262 = 1
In other words, in period 1 assign facilities 4 and 5 to location 1, facility 6 to location 2, and facilities 1, 2, and 3 to location 3. In period 2, assign facilities 2, 4, and 5 to location 1, facility 6 to location 2, and facilities 1 and 3 to location 3. See Figure 2 for a display of the solution. Notice at the beginning of period 2, facility 2 (assigned to location 3 in period 1) is reassigned to location 1. Total assignment cost (AC) and transportation cost (TC) for period 1 is USD 92,000 and USD 90,000, respectively, and total reassignment cost (RC) and transportation cost (TC) for period 2 is USD 16,000 and USD 110,000. Thus, the total cost of the optimal solution is USD 308,000.

Figure 2.
Optimal solution for DGQAP model for small DGQAP instance with total cost of USD 308,000.
Since this is the first paper known to the authors, which consider the DGQAP, the DGQAP may be solved (or is oftentimes solved) sequentially as multiple GQAPs. That is, for period 1 the GQAP may be solved, then the GQAP may be solved for period 2, and so on. As stated earlier, it would be better to solve the resulting problem as a DGQAP as opposed to solving multiple GQAPs, since finding the optimal (or good) solution for each subproblem (or period) oftentimes does not yield the optimal (or good) solution for the problem as a whole. Consider the data given in Figure 1, the MILP model presented for the GQAP, objective function (5) subject to constraints (2)–(4), (6), (7) and the commercial solver CPLEX. The GQAP is optimally solved for periods 1 and 2 separately, and the following optimal solution is obtained for both problems where the nonzero values of the decision variables xik are as follows.
x13 = x23 = x33 = x42 = x52 = x61 = 1 for T = 1 and x11 = x23 = x31 = x43 = x52 = x63 = 1 for T = 2
In other words, assign facility 6 to location 1, facilities 4 and 5 to location 2, and facilities 1, 2, and 3 to location 3 in period 1. In period 2, assign facilities 1 and 3 to location 1, facility 5 to location 2, and facilities 2, 4, and 6 to location 3. For a graphical display of the solution, see Figure 3 below. Notice facilities 1, 3, 4, and 6 are reassigned to different locations in period 2. Total AC and TC for period 1 is USD 94,000 and USD 62,000, respectively, and total RC and TC for period 2 is USD 56,000 and USD 110,000, respectively. Thus, the total cost of the solution is USD 322,000, which gives a higher total cost solution (i.e., USD 14,000 higher) than solving the problem as a DGQAP.

Figure 3.
Solution for DGQAP instance where each period is solved as an individual GQAP model with total cost of USD 322,000.
In contrast, if the DGQAP instance is solved for period 1 using the GQAP model, the above solution is obtained for period 1 (i.e., x13 = x23 = x33 = x42 = x52 = x61 = 1). If this solution for period 1 is put into the DGQAP model, then the solution for period 2 is x13 = x22 = x33 = x42 = x51 = x61 = 1. In other words, rearrangement costs are considered, unlike the previous scenario. Nevertheless, see Figure 4 below for a graphical display of the solution. Notice facilities 2 and 5 are reassigned to different locations in period 2, and the total cost of the solution is USD 310,000. Therefore, the savings for solving the complete problem as a DGQAP is USD 2000. Although this may not seem like a lot, it adds up as the number of facilities and planning periods increases.

Figure 4.
Solution for DGQAP instance where period 1 is solved as a GQAP model, and assignment for period 1 is put into the DGQAP model to obtain the assignment for period 2. Here the total cost of the assignments is USD 310,000.
It is important to note that the DGQAP instance has given above in Figure 1 is a tightly constrained problem, which means that it is more difficult to find feasible solutions for this type of problem compared to loosely constrained problems. Consider the total amount of space required for the facilities in periods 1 and 2 are 11 (i.e., r11 + r12 + … + r16 = 2 + 1 + 2 + 1 + 2 + 3 = 11) and 13, respectively, and the total capacity of the locations for periods 1 and 2 are 12 (i.e., C11 + C12 + C13 = 3 + 3 + 6 = 12) and 14, respectively. Thus, the amount of space utilized in periods 1 and 2 are 91.7% and 92.9%, respectively, which averages to 92.3%. Therefore, this is a tightly constrained problem and obtaining feasible solutions are oftentimes difficult, which will be discussed in the next section. However, since this DGQAP instance has 2 periods (T = 2), 6 facilities (M = 6), 3 locations (N = 3), and average space utilization is 92.3%, the instance code for this problem is 2-6-3-92. Note in Cordeau et al. [7] a similar notation is used to identify the complexity (i.e., size of an instance and whether the instance is loosely or tightly constrained) of GQAP instances. This notation will be used later when describing the set of test problems generated to test the performances of the proposed solution techniques. Nevertheless, since only small-size problems can be solved within a reasonable timeframe using the MILP model presented for the proposed problem, which will be shown below in Section 4.3, another formulation is given for the proposed problem.
2.2. Combinatorial Optimization Problem (COP) Model
To overcome the limitation of the mathematical model (i.e., unable to solve large-size problems in reasonable time), heuristics are developed for the DGQAP. As a result, additional notation is used to give another formulation of the DGQAP. Using a combinatorial optimization problem (COP) formulation, the solution for the DGQAP is represented as S = {S1, S2, …, ST} where St is used to represent the assignment of facilities to locations in period t where t = 1, …, T, St = (st(1), st(2), …, st(M)) and st(i) = k indicates that facility i is assigned to location k in period t. Therefore, the solution S is represented as follows.
S = {(s1(1), s1(2), …, s1(M)), (s2(1), s2(2), …, s2(M)), …, (sT(1), sT(2), …, sT(M))}
Considering the small DGQAP instance 2-6-3-92 given earlier in Figure 1, the optimal solution given in Figure 2 is represented as S = {S1, S2} = {(3, 3, 3, 1, 1, 2), (3, 1, 3, 1, 1, 2)}. For example, s1(2) = 3 and s2(2) = 1, which means in period 1 facility 2 is assigned to location 3 and is reassigned to location 1 in period 2. Using the notation defined earlier for the mathematical models, the index representing location k (l) of facilities i (j) in period t is replaced with st(i) (st(j)), and the COP model for the DGQAP is given as follows.
Notice an additional variable rati is introduced into the second term of (18) to determine the reassignment cost of each facility i in period t > 1. That is, if facility i assigned to location k in period t − 1 (i.e., st−1(i) = k) and is reassigned to location l (l ≠ k) in period t (i.e., st(i) = l), then reassignment cost is incurred, and the variable rati = 1. Otherwise, rati = 0, if facility i is not reassigned to a different location l in period t (i.e., st−1(i) = st(i) = k). Regardless, given the solution (17), Equation (18) gives the sum of the assignment, reassignment, and transportation costs (i.e., total cost of solution S). Constraint (19) ensures that the capacity of each location is not exceeded during each period. Next, construction algorithms are presented for the DGQAP.
3. Heuristic Algorithms for the DGQAP
3.1. Construction Algorithms
Two construction algorithms are presented for the proposed DGQAP. The sole purpose of the construction algorithms is to generate solutions for the improvement algorithms (i.e., the proposed SA heuristics) presented later. The first construction algorithm (CAI) begins by assigning facilities to locations for the first time period (t = 1) and then moves to the next time period until all time periods have been considered. Facilities requiring more space are assigned to locations first (i.e., facilities are sorted and assigned based on space requirements). However, if there is not enough capacity at a location for a facility, the next facility in the sorted list is considered. The purpose of this algorithm is to ensure that feasible solutions are obtained for the tightly constrained problems without regards to transportation and assignment/reassignment costs. On the other hand, the second construction algorithm (CAII), attempts to assign facilities to the same location in multiple periods in order to construct solutions with lower reassignment costs. This algorithm performs best on loosely constrained problems.
3.1.1. Construction Algorithm I (CAI)
Algorithm 1 shows the steps of the pseudo-code for the first construction algorithm (CAI) used to generate a solution for the DGQAP. It is similar to the first of three construction algorithms presented in McKendall and Li [14] for the static GQAP. However, it has been extended to include a multi-period planning horizon. This algorithm works well for obtaining feasible solutions for tightly constrained DGQAPs by attempting to assign as many facilities (priority is given to facilities which require the most space) as possible to the first location, then the second location, and so on such that location capacities are not exceeded. This method ensures that feasible solutions are obtained regardless of the total costs of the solutions, since feasible solutions may be very difficult to obtain for tightly constrained problems.
To illustrate the construction algorithm CAI in Algorithm 1 for the small DGQAP instance 2-6-3-92 given in Figure 1, for period 1 (t = 1) the input arguments (capacities of the locations for period 1, C1, and the facility requirements for period 1, r1) are initialized (step 2), where C1 = {3, 3, 6} and r1 = {2, 1, 2, 1, 2, 3}. Next, the set EFS1 = {6, 1, 3, 5, 2, 4} is generated (step 3). Notice facility 6 has the largest facility requirement (i.e., r1(6) = 3) and is listed first in EFS1. However, since r1(1) = r1(3) = r1(5) = 2 and 1 < 3 < 5, facilities 1, 3, and 5 are placed in set EFS1 in that order (break ties by putting lower facility number first). Once set EFS1 is obtained, facilities are assigned to locations based on their order in this set (steps 4–18). More specifically, first the assignment of the first location (k = 1) to facility i in the first position (p = 1) in the vector EFS1 is considered, where i = EFS1(1) = 6 (steps 4–8). Since facility 6 does not exceed the capacity of location 1 (i.e., r1(6) = 3 ≤ C1(1) = 3 holds), assign facility 6 to location 1 (i.e., set s1(6) = 1 = k) and update the capacity of location 1 (i.e., C1(1) = C1(1) − r1(6) = 0) as well as remove facility 6 and update EFS1 which is now {1, 3, 5, 2, 4} (steps 9–12). Since the remaining capacity is zero for location 1 (i.e., C1(1) = 0) which is less than the facility requirement of the last facility in EFS1 (i.e., C1(1) = 0 < r1(4) = 1), exit loop (in steps 7–16) and set k = 2 (step 17) and continue second iteration (steps 5–18). Next, assign facility i (i.e., i = EFS1(1) = 1) to location 2 and update the capacity of location 2 (i.e., set s1(1) = 2 = k and C1(2) = C1(2) − r1(1) = 3 − 2 = 1), since facility 1 does not exceed the capacity of location 2 (steps 6–11). Also, remove facility 1 and update EFS1 which is now {3, 5, 2, 4} (step 12). Since C1(2) = 1 = r1(4), there is still enough capacity in location 2 to assign facility 4 (step 16). However, facility 4 cannot be assigned to location 2, since higher priority is given to other facilities in the set EFS1. So next facility 3 is considered. In the third iteration, facility 3 cannot be assigned to location 2 since there is not enough capacity, i.e., r1(3) = 2 > 1 = C1(2) (steps 9). Therefore, update p such that p = p + 1 = 2 (step 14) and continue the fourth iteration (steps 7–16). Since there is not enough capacity, in iteration 5 (p = 3), facility i = 2 is assigned to location 2 (i.e., set s1(2) = 2 = k and C1(2) = C1(2) − r1(2) = 1 − 1 = 0). Furthermore, update EFS1 which is now {3, 5, 4} (step 12). Since there is no capacity remaining at location 2 (step 16), set k = 3 (step 17) and continue iteration 6 (steps 6–18). In iteration 6, 7, and 8, facilities 3, 5, and 4, respectively, are assigned to location 3. As a result, EFS1 is empty (i.e., EFS1 = {}) and the solution for period 1 is obtained (i.e., S1 = (2, 2, 3, 3, 3, 1)). In other words, all the facilities are assigned to locations in period 1. Therefore, set t = t + 1 = 2 and continue for loop (steps 1–19) to obtain solution S (step 20).
| Algorithm 1: CAI(Ctk, rti) | ||||
| 1: for t ← 1 to T do | ||||
| 2: | Initialize Ct and rt | |||
| 3: | Construct EFSt by sorting i in descending order based on rt(i) (break ties by lower i) | |||
| 4: | k ← 1 % k is the location index in array Ct | |||
| 5: | while k ≤ N and EFSt ≠ {} do % {} is the empty set | |||
| 6: | p ← 1 % p is the position index in array EFSt | |||
| 7: | repeat | |||
| 8: | i ← EFSt(p) % i is the facility number | |||
| 9: | if rt(i) ≤ Ct(k) then | |||
| 10: | st(i) ← k | |||
| 11: | Ct(k) ← Ct(k) − rt(i) | |||
| 12: | Remove(EFSt(p)) % Remove element EFSt(p) from set EFSt | |||
| 13: | else | |||
| 14: | p ← p + 1 | |||
| 15: | end if | |||
| 16: | until Ct(k) < rt(EFSt(Last)) do % EFSt(Last) is the last facility in array EFSt | |||
| 17: | k ← k + 1 | |||
| 18: | end while | |||
| 19: end for | ||||
| 20: return S | ||||
The construction algorithm CAI generates the solution S = {(2, 2, 3, 3, 3, 1), (1, 1, 3, 3, 3, 2)} which gives a total cost of 598 (i.e., TC(S) = 598). As stated earlier, the objective of CAI is to ensure that feasible solutions are generated especially for tightly constrained problems regardless of the total cost of the solutions. Next, the second construction algorithm (CAII) is presented for the DGQAP which attempts to produce feasible solutions with lower reassignment costs.
3.1.2. Construction Algorithm II (CAII)
Algorithm 2 shows the steps of the pseudo-code for the second construction algorithm (CAII) used to construct a solution for the DGQAP. After initializing the parameters (step 1), first assign the facilities to locations in time period 1 using CAI (step 2). Next, construct the set EFSt for each time period t for 2 ≤ t ≤ T (step 3). Then facilities in the current period t (t > 1) are assigned to the same locations as in the previous period t − 1 (e.g., st(i) = st−1(i)), based on their order in the set ESFt, if there is enough capacity at the locations in period t (e.g., rt(i) ≤ Ct(st−1(i)) = Ct(k) if st−1(i) = k) (steps 4–15). More specifically, if there is enough capacity at period t to assign the facility in the first position (p = 1) in the set ESFt to the same location it is assigned to in period t − 1, assign facility to location, update the location capacity and remove facility from set ESFt (steps 7–11). Now, if the facility in the first position in the set ESFt cannot be assigned to the location it was assigned to in the previous period, move to the facility in the next position (p = p + 1) in the set ESFt (step 13) and continue steps 7–14 until all facilities in set ESFt has been considered. The facilities remaining in the set ESFt at step 15 (i.e., the facilities that cannot be assigned to their same locations as in the previous period) are assigned to the first available locations with enough capacity, starting with location 1 then 2 and so on (step 17). For instance, if facility i in period 1 was assigned to location 3 (s1(i) = k = 3), but there is not enough capacity in period 2 to assign facility i to location 3 (r2(i) > C2(s1(i)) = C2(3)), then facility i is assigned to the location k with enough capacity in period 2, starting with location 1. In our problem instance location k = 1 would be considered first, then location k = 2. Note that if it is not possible to assign all the facilities to locations in a period, use the CAI to assign all the facilities to locations for that period (steps 18–20). Repeat this process (continue for loop) for all time periods (steps 4–22) and obtain solution S (step 23). Again, CAII attempts to assign facilities to the same location in multiple periods to construct solutions with lower reassignment costs. This algorithm performs best on loosely constrained problems and on problems with relatively high reassignment cost compared to transportation cost.
| Algorithm 2: CAII(Ctk, rti) | |||
| 1: Initialize Ct and rt for 1 ≤ t ≤ T | |||
| 2: S1 ← CAI(C1, r1) | |||
| 3: Construct EFS2, …, EFST as discussed in CAI | |||
| 4: for t ← 2 to T do | |||
| 5: | p ← 1 % p is the position index in array EFSt | ||
| 6: | while p ≤ Last do % Last is the position of the last facility in array EFSt | ||
| 7: | i ← EFSt(p) % i is the facility number | ||
| 8: | if rt(i) ≤ Ct(st−1(i)) then | ||
| 9: | st(i) ← st−1(i) | ||
| 10: | Ct(st(i)) ← Ct(st(i)) − rt(i) | ||
| 11: | Remove(EFSt(p)) % Remove element EFSt(p) from set EFSt | ||
| 12: | else | ||
| 13: | p ← p + 1 | ||
| 14: | end if | ||
| 15: | end while | ||
| 16: | if EFSt ≠ {} then | ||
| 17: | Assign facilities in EFSt to location with enough capacity | ||
| 18: | if insufficient capacity then | ||
| 19: | St ← CAI(Ct, rt) | ||
| 20: | end if | ||
| 21: | end if | ||
| 22: end for | |||
| 23: return S | |||
CAI will be used to construct starting solutions for the proposed SA heuristic (called SAI) which is a direct adaptation of SA to the DGQAP. However, the CAII will be used to produce starting solutions for the proposed SA heuristic (called SAII) which uses SAI with a look-ahead/look-back search strategy. This strategy works well for DGQAP instances where reassignment cost is relatively high. Therefore, starting with a solution with low rearrangement cost as with the CAII algorithm would aid in converging to a near optimal solution more quickly. On the other hand, the SAI heuristic may work better for DGQAP instances where reassignment cost is relatively low. As a result, the starting solutions produced by the CAI is sufficient. In summary, once a solution is generated using one of the proposed construction algorithms, either CAI or CAII, improvement algorithms which are discussed below are used to obtain “good” local optimums. The proposed improvement algorithms consist of an SA heuristic and a steepest descent heuristic. Next, the SA heuristics are presented for the DGQAP.
3.2. Simulated Annealing (SA) Heuristic
Simulated annealing (SA) is a metaheuristic used to solve many different types of COPs. As mentioned earlier, McKendall et al. [28] presented two SA heuristics to solve the dynamic space allocation problem, and McKendall et al. [23] presented two SA heuristics to solve a dynamic QAP (i.e., DFLP). The SA heuristics presented in the latter paper were modified and extended to solve the proposed problem. The first SA heuristic (SAI) is a direct adaptation of SA to the DGQAP, and the second SA heuristic (SAII) is the same as SAI with a look-ahead/look-back search strategy. Algorithm 3 shows the pseudo-code for the SAI and SAII heuristics. Next, the two SA heuristics are presented and discussed for the proposed problem.
3.2.1. Simulated Annealing I (SAI)
As stated previously, the proposed SAI heuristic is a direct adaptation of SA to the DGQAP. Algorithm 3 shows the steps of the pseudo-code for the SAI heuristic. It starts with an initial solution S0 (also called the current solution) obtained by the proposed construction algorithm CAI (step 2), and Equation (18) is used to obtain the total cost of the solution (step 3). This solution and its cost are defined as the best solution and best cost (step 4). After initializing the current temperature and the iteration counter n, which keeps track of the number of iterations performed at each temperature (step 5), a neighboring solution S is generated randomly using either a drop/add or pairwise exchange operation on the solution S0 (step 7). The details of these operations are given below. Next, constraints (19) of the COP model is used to check the feasibility of the neighboring solution S (step 8). If the neighboring solution S is infeasible, the solution S0 remains as the current solution (return to step 7). Otherwise, the cost of the neighboring solution, TC(S), is obtained, and it is compared with the cost of the current solution, TC(S0), by calculating ∆TC, where ∆TC = TC(S0) – TC(S) (steps 9–10). If the cost of neighboring solution S is better than the cost of the initial solution S0 (i.e., ∆TC > 0), the neighboring solution S becomes the current solution, i.e., set S0 = S (step 11). In addition, if the cost of the neighboring solution S is worse than the cost of the current solution S0 (i.e., ∆TC < 0), then the neighboring solution S is selected as the current solution S0 (i.e., set S0 = S) with respect to an acceptance probability p (steps 10–11). In either of the last two cases mentioned above, the current solution S0 is updated, and if this solution gives the best cost, the best solution and its cost are updated (steps 12). Since we are describing the SAI heuristic, the look-ahead/look-back strategy is not considered (bypass step 13). Next, the iteration counter at the current temperature, n, is updated (step 15). After Ntemp iterations at each temperature Temp, the temperature is reduced, and n is updated (step 17). This process continues until a stopping criterion is met (i.e., Temp ≤ min_Temp). It is important to note that sometimes SA heuristics may not converge to a local optimum. In other words, there may be a neighboring solution S, in the neighborhood of best_sol, that gives a lower total cost (i.e., TC(S) < TC(best_sol) = best_cost). As a result, a steepest descent (local search) heuristic is implemented to ensure that the best solution obtained from the SAI heuristic (S*) is a local optimum (steps 21–22). The details of the local search heuristic and the parameter setting are given below, but first the operations for obtaining a neighboring solution is defined.
| Algorithm 3: SA(Temp0, min_Temp, NTemp, α, p) | |||||||||
| 1: Initialize Temp0, min_Temp, NTemp, α, and p | |||||||||
| 2: S0 ← CAI(Ctk, rti) in SAI and S0 ← CAII(Ctk, rti) in SAII | |||||||||
| 3: Compute TC(S0) using Equation (18) | |||||||||
| 4: best_sol ← S0, best_cost ← TC(S0) | |||||||||
| 5: n ← 0, Temp ← Temp0 % n is the iteration counter at current temperature Temp | |||||||||
| 6: while Temp > min_Temp do | |||||||||
| 7: | Randomly generate period t, move, and obtain neighboring solution S | ||||||||
| 8: | if S is feasible then % Use Equation (19) to check if S is feasible | ||||||||
| 9: | ∆TC ← TC(S0) − TC(S) | ||||||||
| 10: | if ∆TC > 0 or p = exp(-∆TC/Temp) > rand(0, 1) then | ||||||||
| 11: | S0 ← S | ||||||||
| 12: | Update(best_sol, best_cost) | ||||||||
| 13: | S0 ← Look-Ahead/Look-Back Strategy(S0, t, move) //use in SAII only | ||||||||
| 14: | end if | ||||||||
| 15: | n ← n + 1 | ||||||||
| 16: | if n = Ntemp then | ||||||||
| 17: | n ← 0, Temp ← α*Temp | ||||||||
| 18: | end if | ||||||||
| 19: | end if | ||||||||
| 20: end while | |||||||||
| 21: S* ← LocalSearch(best_sol, best_cost) | |||||||||
| 22: return S* | |||||||||
In step 7 of the proposed SAI heuristic, there are two types of operations used to obtain a neighboring solution S from the current solution S0: drop/add and pairwise exchange. The drop/add operation removes one location assigned to a facility and reassigns a different location to it in one of the periods. However, the pairwise exchange operation interchanges the locations of two facilities (assigned to different locations) in one of the periods. For example, consider the solution S0 = {(2, 2, 3, 3, 3, 1), (1, 1, 3, 3, 3, 2)} obtained from the proposed construction algorithm CAI discussed earlier. The proposed SAI heuristic randomly selects an operation, say pairwise exchange. Next, a period is randomly selected, say period 2, and two facilities assigned to different locations are selected, say facilities 2 and 6. As a result, a neighboring solution S is obtained as follows by interchanging the locations of facilities 2 and 6 in period 2, and constraint (19) of the COP model is used to check the feasibility of the new solution S (step 8).
S0 = {(2, 2, 3, 3, 3, 1), (1, 1, 3, 3, 3, 2)} → S = {(2, 2, 3, 3, 3, 1), (1, 2, 3, 3, 3, 1)}
As mentioned earlier, if the solution S is infeasible, the solution S0 remains the current solution. Otherwise, the total cost of the solution S (i.e., TC(S)) is obtained (step 9), and either S0 remains the current solution or S is selected as the current solution (i.e., set S0 = S) if either ∆TC > 0 or ∆TC < 0 and the acceptance probability p = exp(−∆TC/Temp) is more than a randomly generated number between zero and one (i.e., rand(0, 1)) (step 10–11). In contrast, if the drop/add operation is selected randomly as well as a period, say period 1, then a facility is randomly selected, say facility 4 (assigned to location 3) and a different location is randomly selected between location 1 or 2, say 1. Therefore, a neighboring solution S is obtained as follows by replacing location 3 with location 1 for facility 4 in period 1, and constraint (19) of the COP model is used to check the feasibility of the new solution S, as discussed earlier.
S0 = {(2, 2, 3, 3, 3, 1), (1, 1, 3, 3, 3, 2)} → S = {(2, 2, 3, 1, 3, 1), (1, 1, 3, 3, 3, 2)}
Since there are M facilities and T periods where M = 6 and T = 2 for the above example, there are T*M(M − 1)/2 = 30 possible pairwise exchanges. In contrast, since there are N locations where N = 3 in the example above, there are T*M(N − 1) = 24 possible drop/add operations. It is important to note that for tightly constrained DGQAP instances, many of the neighboring solutions generated using either the pairwise exchange or drop/add operation may be infeasible. However, for loosely constrained DGQAP instances, many of the neighboring solutions generated from one of the operations may be feasible.
As mentioned earlier, SA heuristics may not converge to local optimums. In other words, the best_sol obtained after step 20 of Algorithm 3 may not be a local optimum. That is, there may be a neighboring solution S, in the neighborhood of best_sol, that gives a lower total cost (i.e., TC(S) < TC(best_sol) = best_cost). Therefore, a steepest descent (local search) heuristic is implemented (step 21) to ensure the proposed SAI heuristic converges to a local optimum. The steps for the local search heuristic are as follows.
- Given best_sol and best_cost.
- Find all feasible neighboring solutions by considering all possible drop/add and pairwise exchange operations on best_sol.
- Pick the best feasible neighboring solution, S, with respect to total cost, TC(S). If TC(S) < best_cost, set best_sol = S, best_cost = TC(S), and go to step 2. Otherwise, terminate heuristic and return local optimum S* = best_sol.
At the initial temperature, Temp = Temp0, the probability of accepting non-improving solutions is high. This allows the heuristic to search the solution space without quickly converging to a poor local optimum. After a number of iterations, NTemp, at the current temperature Temp, the temperature is reduced (i.e., set Temp = α*Temp) where 0 < α < 1. As the temperature Temp reduces, the probability of accepting non-improving solutions is lower, allowing the heuristic to possibly converge to a good local optimum. The initial temperature (Temp0) is determined using the acceptance probability equation p = exp(−∆TC/Temp0) where ∆TC = TC(S0) − TC(S), and p is the probability of accepting a non-improving neighboring solution S as the current solution. If the probability of accepting a neighboring solution with a cost of 10% above the cost of the initial solution S0 is p, then ∆TC = 0.10TC(S0). When solving the probability equation for Temp0, the following equation is obtained.
Temp0 = −∆TC/ln(p) = −0.10TC(S0)/ln(p)
Before using Equation (20) to obtain the value for the parameter Temp0, S0 is obtained using CAI, and the parameter p is obtained experimentally as with the parameters α, NTemp, and min_Temp which will be discussed in the computational results section of this paper.
It is believed that the SAI heuristic should work well for DGQAP instances with relatively low reassignment costs for each period, allowing for more reassignment of facilities in each period (t = 2, …, T) while attempting to reduce total transportation cost. As a result, the starting solutions produced by the CAI is sufficient. In contrast, the starting solution produced by the CAII oftentimes reduce reassignment cost for each period by attempting to assign facilities to the same location for each period based on location capacities and facility requirements. Therefore, the proposed SAII heuristic, which will be discussed next and uses the CAII to produce a starting solution, works well for DGQAP instances with a relatively high reassignment cost during each period. The heuristic attempts to keep reassignment cost low by keeping facilities assigned to the same locations for each period.
3.2.2. Simulated Annealing II (SAII)
The SAII heuristic is the adaptation of the SAI heuristic with a look-ahead/look-back strategy. The only changes in the SAI heuristic (in Algorithm 3) are in steps 2 and 13. In step 2, the CAII heuristic is used to obtain an initial solution S0, as opposed to CAI, as mentioned above. The only other change is the addition of the look-ahead/look-back strategy (step 13). Algorithm 4 shows the steps of the pseudo-code for the look-ahead/look-back strategy. Recall that step 7 in SAI (Algorithm 3) considers finding a neighboring solution using either the drop/add operation or the pairwise exchange operation. Instead of performing only one operation (i.e., move) at one randomly selected period t to produce a neighboring solution as in the SAI heuristic, in SAII, the same operation, move, is considered in previous and succeeding periods which may result in the same operation being performed in multiple periods. More specifically, if a period t (t = 1, 2, …, T) is randomly selected, and an operation, move, is randomly selected to produce a neighboring solution S (step 7), then if the neighboring solution S is feasible and either better than the current solution S0 (i.e., ∆TC > 0) or worse than the current solution S0 (i.e., ∆TC < 0) and p = exp(−∆TC/Temp) > rand(0, 1), set current solution S0 = S (steps 8–11), as in SAI. Update best_sol and best_cost, if necessary (step 12). However, in SAII the look-ahead/look-back strategy is implemented (step 13). That is, the operation, move, (in step 7 of Algorithm 3) is considered in the preceding period tp = t − 1 and succeeding period ts = t + 1 in Algorithm 4. As above, the operation, move, is accepted in periods tp = t − 1 and/or ts = t + 1 if it improves the total cost of the current solution or does not improve the total cost of the current solution but p > rand(0, 1) (steps 1–7). If necessary, consider tp = tp − 1 where tp ≥ 1 and ts = ts + 1 where ts ≤ T (step 9). Continue process until either tp < 1 and ts > T (steps 2–16). In summary, the operation, move, is considered first in period tp (step 3) until either
- (i)
- S is infeasible (steps 13–14),
- (ii)
- S is feasible, but ∆TC < 0 and p < rand(0, 1) (steps 10–11), or
- (iii)
- tp < 1 (step 16).
| Algorithm 4: Look-Ahead/Look-Back Strategy(S0, t, move) | ||||||||||
| 1: | tp ← t − 1, ts ← t + 1 | |||||||||
| 2: | repeat | |||||||||
| 3: | Perform move in period tp (or ts) and obtain solution S | |||||||||
| 4: | if S is feasible then % Use Equation (19) to check if S is feasible | |||||||||
| 5: | ∆TC ← TC(S0) − TC(S) | |||||||||
| 6: | if ∆TC > 0 or p = exp(−∆TC/Temp) > rand(0, 1) then | |||||||||
| 7: | S0 ← S | |||||||||
| 8: | Update(best_sol, best_cost) | |||||||||
| 9: | tp ← tp − 1 (ts ← ts + 1) | |||||||||
| 10: | else | |||||||||
| 11: | break | |||||||||
| 12: | end if | |||||||||
| 13: | else | |||||||||
| 14: | break | |||||||||
| 15: | end if | |||||||||
| 16: | until tp < 1 (ts > T) do | |||||||||
| 17: | return S0 | |||||||||
Similarly, the operation, move, is considered in period ts (steps 2–16) in a similar fashion, except condition iii above is ts > T (Step 16). This strategy attempts to keep reassignment cost low by reassigning facilities to the same locations in multiple periods. Consider the case where a neighboring solution is obtained by randomly exchanging the locations of two facilities in a period t, and the optimal solution can be obtained by randomly exchanging the same locations of the facilities in the preceding and/or succeeding periods (i.e., periods t − 1 and t + 1). The probability of randomly selecting these facilities to exchange locations in periods t − 1 and/or t + 1 in consecutive iterations in the SAI heuristic is extremely small because of the randomness of the heuristic. However, the SAII heuristic has the capability of performing these operations in only one iteration. As a result, the additional operations implemented by the look-ahead/look-back search strategy are compensated for by possibly being able to perform more exchanges during an iteration, resulting in better solutions. In other words, since the SAII heuristic may perform more than one move during a single iteration, requiring more computational time per iteration, compared to the SAI heuristic, it is capable of producing higher quality solutions. Therefore, the number of runs for SAI is either two or three times more than for the SAII heuristic, which will be illustrated below.
4. Computational Results
This section provides the results obtained from computational experiments performed to test the performances of the proposed SA heuristics. First, the proposed SA heuristics results are compared against the results obtained from solving the MILP model using CPLEX 12.4 for seven test problems (data set 1). This experiment was only performed to show that only very small-size problems can be solved optimally within a reasonable timeframe using the MILP model with CPLEX, and our proposed SA heuristics can perform well for solving small-size problems. In addition, the computational results of the proposed SA heuristics applied to 24 test problems (data set 2) are presented. Data set 1 consists of small-size DGQAP instances (where T = 2, 3, 4) whereas data set 2 consists of larger-size instances (where T = 5, 10). In all experiments, a PC (equipped with Microsoft Windows 10, an Intel Core processor i7 with a CPU speed of 2.90 GHz and 16 GB of RAM) was used to solve the test problems, and the proposed SA heuristics were coded using Matlab R2024a.
4.1. Set of Test Problems
Two data sets (31 test problems total) were developed for the DGQAP to test the performances of the SA heuristics. The test problems are generated following the procedure available in Cordeau et al. [7] for the GQAP and modified for the DGQAP. The authors labeled the test problems using the notation M-N-U where M = number of facilities, N = number of locations, and U = total percent of location space utilized by the facilities (a value between 1 and 100 used to control the tightness of the capacity constraints). Since the DGQAP has more than one period in the planning horizon, in this paper, U = average percent of location space utilized considering all periods. As a result, in this paper the test problems are labeled using the notation T-M-N-U where T = number of periods in the planning horizon. For instance, the small DGQAP instance given in Figure 1 is labeled as 2-6-3-92. Furthermore, the input data are generated for given values for T, M, N, and U as follows.
atik is generated according to a discrete uniform distribution in [1, …, 104 N].
ftij and dtkl are generated according to discrete uniform distribution in [1, …, 100].
rti is generated according to a discrete uniform distribution in [1, …, 100], as discussed below for the different cases (e.g., the rti remains the same for each instance for all periods).
Ctk is generated according to a discrete uniform distribution in [1, …, ].
The seven test problems in data set 1 are generated as mentioned above where the space utilization (U) and the distance matrices are the same for each period (i.e., d1kl = d2kl = … = dTkl). Also, the amount of space required for each facility i is the same for each period (i.e., r1i = r2i = …= rTi). Note that the small DGQAP instance given in Figure 1, labeled as 2-6-3-92, does not consider the last restriction. That is, the amount of space required for a facility may change from one period to another (e.g., r11 = 2 but r21 = 3).
The 24 test problems in data set 2 are generated as mentioned above and are categorized into three different cases considering the different applications in managing facilities in container yards/warehouses, at construction sites and electric power plants during planned outages. Each case consists of eight test problems having either 5 or 10 periods. The first case considers the test problems in which the distances (dtkl) between locations during each period are the same. Also, the facility requirements (rti) and space utilization (U) remain the same for each period. However, capacities of the locations (Ctk), the number of units of materials transported between facilities (ftij), and the costs of assigning and reassigning facilities to locations changes for each period. The second case is like the first case except that the distances (dtkl) between locations changes in each period. In contrast, the third case considers the most general test problems where all the input data changes from one period to the next. Recall that these cases were discussed at the end of Section 1. See Table 1 below for the 24 test problems generated for the different types of cases for data set 2.

Table 1.
Instances of the 24 test problems for data set 2.
4.2. Heuristic Parameter Settings
As discussed earlier, the values of the proposed SA heuristic parameters for SAI and SAII are obtained either theoretically or experimentally. More specifically, based on preliminary experiments, set cooling ratio, α = 0.99, and minimum allowable temperature before terminating heuristic, min_Temp = 0.0001 for data set 1 for SAI and 0.001 for SAII. However, set min_Temp = 0.001 for data set 2 for both the SAI and SAII heuristics. The initial temperature, Temp0, is obtained as discussed earlier using Equation (20). The number of iterations to be performed at each temperature (i.e., epoch length), NTemp, is based on the number of possible neighboring solutions obtained using both drop/add and pairwise exchange operations, which is TM(N − 1) and TM(M − 1)/2, respectively. After careful experimentation, it was decided to set NTemp = . That is, NTemp is q% of the maximum size of the neighborhood of S0, rounded above to the nearest integer. During the experimentation process, q = 40%, 50%, 60%, 70%, 80%, and 90% (and in between) was considered. It was decided for data set 1 to use q = 40% for SAI and q = 70% for SAII. However, the parameter used to determine the probability of accepting a non-improving solution S at the initial temperature Temp0, p, was considered to take on the values p = 0.6, 0.7, 0.8, or 0.9. For data set 1, p = 0.7 (0.9) was used for SAI (II) heuristic. Recall that data set 1 considers only the simplest type of the DGQAP (i.e., case 1), but data set 2 considers all three cases. Therefore, there are nine different parameter settings used for both SAI and SAII for data set 2. For SAI, it was decided to use p = 0.6, 0.7, 0.8 where q = 40%, 50% and p = 0.9 where q = 40%, 50%, 60%. For SAII, it was decided to use p = 0.6, 0.7 where q = 50%, p = 0.8 where q = 60%, and p = 0.9 where q = 40%, 50%, 55%, 60%, 70%, 80%.
4.3. Computational Results for Data Set 1
The results for the proposed SA heuristics for data set 1 are compared against the results obtained from solving the proposed MILP model using the commercial solver CPLEX 12.4. The results of the computational experiments are given in Table 2 below. Notice the small DGQAP instance given in Figure 1 (i.e., 2-6-3-92) is listed first followed by the six test problems randomly generated as discussed above. Since SAII is able to produce higher quality solutions than SAI in a single run but requires more computational time, the number of runs for SAI is twice as long for SAII, which gives a fairer comparison and is discussed below. Each test problem was solved 20 (10) times, since the SAI (II) heuristics are stochastic, and the outcomes may be different for different runs. Thus, the minimum (Min) and average (Avg) best total cost of the best solutions, as well as average computation time (Avg Time) in seconds are given for each problem. Furthermore, the optimal solutions (Opt TC) with run times were obtained for some of the problems using CPLEX (using the default settings), which are bolded, without asterisks. Notice the optimal solutions were obtained for four of the seven problems. However, CPLEX was unable to verify optimality for the other three problems, since CPLEX stopped due to insufficient memory (see Opt TC column with asterisks). In other words, the branch-and-bound search tree became very large and used up most of the RAM and terminated before obtaining or verifying optimality. Notice these problems ran for at least 10,916 s (or 3.03 h). Last, the percent deviation (% Dev) the best total cost obtained from the proposed SA heuristics is from the best total cost obtained from CPLEX is given in the last column for each problem. For instance, considering problem 3-15-4-85, CPLEX obtained its best solution where its total cost is 1,872,699, and the proposed SA heuristics obtained a solution with its Min total cost of 1,652,317, which is 11.8% below the Min total cost obtained from CPLEX. However, the SAII heuristic obtained a Min total cost which was 5.5% above the Min total cost obtained from CPLEX (and SAI) for problem 4-10-5-75. This is the only problem where CPLEX obtained a better solution than the SAII heuristic but notice the run time is a lot longer for CPLEX on average (i.e., 5.47 h = 19,674 s > 130.6 s = 13.06 (10 runs)). Hence, the proposed SA heuristics clearly outperformed CPLEX with respect to solution quality and computation time. However, the Friedman test reveals that there is no significant difference between the three methods when comparing Min values (p = 0.3679).

Table 2.
Computational results for data set 1.
When comparing the performances of SAI against SAII on data set 1, notice that the heuristics obtained the same minimum total cost (Min) for six of the seven problems. However, for problem 4-10-5-75 SAII did not obtain the Min of 822,861 but a total cost which is 5.5% higher. Although SAI average run time (Avg Time) is shorter, the average total run time was longer by approximately 30 s (i.e., 8.01 (20 runs) = 160.2 > 130.6 = 13.06 (10 runs)). As mentioned earlier, the look-ahead/look-back strategy of SAII performs multiple moves and requires more computation time per iteration. Therefore, the number of runs for SAI is doubled in order to fairly compete with SAII. Although it seems to make a difference for this problem, it does not for the other problem or for the problems of data set 2. More specifically, for data set 1, which is the simplest case (i.e., case 1 where the space utilization and the distance matrices are the same in each period) of the three cases mentioned in Section 4.1, SAI performed very well. However, for data set 2, which considers all three cases with larger-size problems, SAI heuristic does not perform as well on the more difficult problems (i.e., cases 2 and 3) which will be discussed below. Next, notice that the average total cost (Avg) for SAII is lower for all the problems (lowest Avgs are bolded). Therefore, one can argue that SAII outperformed SAI. This was confirmed by the Wilcoxon signed-rank test, when comparing Avg for SAI and SAII (p = 0.018, r = 0.89). In other words, there is a significant difference between the Avg values for SAI and SAII with a large effect size.
4.4. Computational Results for Data Set 2
The proposed heuristics SAI and SAII was used to solve data set 2 using the parameter settings previously discussed in Section 4.1. Each test problem was solved 30 times and 10 times using the SAI and SAII heuristics, respectively. This will be discussed in detail below. Nevertheless, considering all the possible combinations of setting the parameters (for parameters p and q) given in Section 4.1 and solving the problems using the proposed SA heuristics, the best total costs and computational times obtained by each were recorded. See the results of the computational experiments in Table 3 where the first eight problems represent case 1-type problems, the second eight problems represent case 2-type problems, and the third eight problems represent case 3-type problems. When comparing the minimum best total cost (Min) obtained for SAI and SAII, SAI and SAII obtained best Min 6 and 19 times (best Mins are bolded), respectively. As the problems become more difficult (e.g., Case 3 problems 17-24), SAI obtained only one solution which gives the best Min. See problem 17. When comparing the average total cost (Avg) for SAI and SAII, SAII obtained lowest Avg (lowest Avgs are bolded) for all problems except for four problems (i.e., problems 8, 11, 12, and 16). As in data set 1, SAI average run time (Time) is shorter, but average total run time is longer, approximately twice as long as SAII. Notice times are given in seconds. For example, the largest discrepancy between average total run times is with problem 10 where SAI ran 2.146 times as long as SAII (i.e., 3573.3 s = 119.11 (30 runs) > 1664.7 s = 166.47 (10 runs)). Nevertheless, SAII outperformed SAI for data set 2. This was confirmed by the Wilcoxon signed-rank test. When comparing Min for SAI and SAII (p = 0.0285, r = 0.45) and Avg for SAI and SAII (p = 0.0397, r = 0.42), both cases represent a medium effect. Last, the percent deviation (% Dev), i.e., the best minimum total cost obtained from SAII is from the best minimum total cost obtained from SAI, is given in the last column. Notice the largest differences (i.e., negative and positive) in % Dev are for problems 13 and 16 of case 2. That is, for problem 13 the best Min obtained from SAII is 1.44% below best Min obtained from SAI, but 1.08% higher for problem 16. In summary, although SAII outperformed SAI with respect to solution quality and computation time, SAII solutions were only better by at most 1.44% Dev.

Table 3.
Computational results for data set 2.
5. Conclusions
In this paper, the GQAP is extended to include multiple time periods and is called the DGQAP. Mathematical models as well as construction algorithms (i.e., CAI and CAII) and improvement algorithms were developed and presented for the proposed problem. The improvement algorithms consist of an SA and a steepest descent heuristic called SAI and SAII. The SAI heuristic is a direct adaptation of SA to the DGQAP, and SAII is like SAI except that it includes a look-ahead/look-back strategy. Computational experiments were conducted on a small data set (i.e., data set 1) and a large data set (i.e., data set 2), generated randomly, and it showed promising results for the proposed SA heuristics. However, SAII clearly outperformed SAI for data set 2. It is believed that the SAI heuristic did not perform well because of its randomness, and its inability to change locations of either one or two facilities in multiple periods simultaneously, especially for tightly constrained problems (U > 70). More specifically, for tightly constrained problems where rearrangement cost is relatively high, changing the location of either one or two facilities in a period (i.e., performing either a drop/add or pairwise exchange operation during one iteration) may require changing the location of one or two of those facilities in either preceding or succeeding periods (i.e., at the next several consecutive iterations) to keep total cost low. However, due to the randomness of the SAI heuristic, the chances of changing the locations of one or both of those facilities in the necessary preceding or succeeding periods in the next several consecutive iterations are very low. In contrast, since the SAII heuristic considers changing the locations of one or both facilities in preceding and succeeding periods during the same iteration (i.e., look-ahead/look-back strategy), it outperformed the SAI heuristic.
The following recommendations are given for future research. Consider extending DGQAP by considering the stochastic nature of the problem (e.g., units of materials flowing between facilities are stochastic) and develop solution techniques for the problems of the proposed algorithms. Adapt other metaheuristics (e.g., tabu search, variable neighborhood search, or genetic algorithm) for solving the DGQAP for a more robust performance comparison. Develop hybrid heuristics for the DGQAP which considers the combination of two metaheuristics to overcome the drawbacks of purely stochastic and deterministic heuristics.
Author Contributions
Conceptualization, A.M.; methodology, A.M. and Y.D.; software, Y.D.; validation, Y.D. and A.M.; formal analysis, A.M.; investigation, A.M. and Y.D.; resources, A.M.; data curation, A.M.; writing—original draft preparation, Y.D. and A.M.; writing—review and editing, Y.D. and A.M.; visualization, Y.D. and A.M.; supervision, A.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Koopmans, T.C.; Beckmann, M.J. Assignment problems and the location of economic activities. Econometrica 1957, 25, 53–76. [Google Scholar] [CrossRef]
- Sahni, S.; Gonzales, T. P-complete Approximation Problems. J. ACM 1976, 23, 555–565. [Google Scholar] [CrossRef]
- Burkard, R.E.; Cela, E.; Pardalos, P.M.; Pitsoulis, L.S. The Quadratic Assignment Problem. In Handbook of Combinatorial Optimization; Du, D.-Z., Pardalos, P.M., Eds.; Kluwer: Boston, MA, USA, 1998; pp. 1713–1809. [Google Scholar] [CrossRef]
- Loiola, E.M.; de Abreu, N.M.M.; Boaventura-Netto, P.O.; Hahn, P.; Querido, T. A survey for the quadratic assignment problem. Eur. J. Oper. Res. 2007, 176, 657–690. [Google Scholar] [CrossRef]
- Silva, A.; Coelho, L.C.; Darvish, M. Quadratic assignment problem variants: A survey and an effective parallel memetic iterated tabu search. Eur. J. Oper. Res. 2021, 292, 1066–1084. [Google Scholar] [CrossRef]
- Lee, C.-G.; Ma, Z. The Generalized Quadratic Assignment Problem; Research Report; Department of Mechanical and Industrial Engineering, University of Toronto: Toronto, ON, Canada, 2004. [Google Scholar]
- Cordeau, J.-F.; Gaudioso, M.; Laporte, G.; Moccia, L. A memetic heuristic for the generalized quadratic assignment problem. INFORMS J. Comput. 2006, 18, 433–443. [Google Scholar] [CrossRef]
- Hahn, P.M.; Kim, B.-J.; Guignard, M.; MacGregor Smith, J.; Zhu, Y.-R. An algorithm for the generalized quadratic assignment problem. Comput. Optim. Appl. 2008, 40, 351–372. [Google Scholar] [CrossRef][Green Version]
- Pessoa, A.A.; Hahn, P.M.; Guignard, M.; Zhu, Y.-R. Algorithms for the generalized quadratic assignment problem combining lagrangean decomposition and the reformulation-linearization technique. Eur. J. Oper. Res. 2010, 206, 54–63. [Google Scholar] [CrossRef]
- Guignard, M. Strong RLT1 bounds from decomposable Lagrangean relaxation for some quadratic 0–1 optimization problems with linear constraints. Ann. Oper. Res. 2020, 286, 173–200. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems; University of Michigan Press: Ann Arbor, MI, USA, 1975. [Google Scholar]
- Glover, F. Future paths for integer programming and links to artificial intelligence. Comput. Oper. Res. 1986, 13, 533–549. [Google Scholar] [CrossRef]
- Mateus, G.R.; Resende, M.G.C.; Silva, R.M.A. GRASP with Path-relinking for the generalized quadratic assignment problem. J. Heuristics 2011, 17, 527–565. [Google Scholar] [CrossRef]
- McKendall, A.; Li, C. A tabu search heuristic for a generalized quadratic assignment problem. J. Ind. Prod. Eng. 2017, 34, 221–231. [Google Scholar] [CrossRef]
- Greistorfer, P.; Staněk, R.; Maniezzo, V. A tabu search matheuristic for the generalized quadratic assignment problem. In Metaheuristics; MIC 2022; Lecture Notes in Computer Science; Di Gaspero, L., Festa, P., Nakib, A., Pavone, M., Eds.; Springer: Cham, Switzerland, 2023; Volume 13838, pp. 544–553. [Google Scholar] [CrossRef]
- Fathollahi-Fard, A.M.; Wong, K.Y.; Aljuaid, M. An efficient adaptive large neighborhood search algorithm based on heuristics and reformulations for the generalized quadratic assignment problem. Eng. Appl. Artif. Intell. 2023, 126, 106802. [Google Scholar] [CrossRef]
- McKendall, A.; Dhungel, Y. A simulated annealing algorithm for the generalized quadratic assignment problem. Algorithms 2024, 17, 540. [Google Scholar] [CrossRef]
- Sohrabi, M.; Fathollahi-Fard, A.M.; Gromov, V.A.; Dulebenets, M.A. A genetic engineering algorithm for the generalized quadratic assignment problem. Neur. Comput. Appl. 2025, 37, 12253–12279. [Google Scholar] [CrossRef]
- Zou, D.; Gao, L.; Li, S.; Wu, J.; Wang, X. A novel global harmony search algorithm for task assignment problem. J. Syst. Soft. 2010, 83, 1678–1688. [Google Scholar] [CrossRef]
- Unal, Y.Z.; Uysal, O. A new mixed integer programming model for curriculum balancing: Application to a Turkish university. Eur. J. Oper. Res. 2014, 238, 339–347. [Google Scholar] [CrossRef]
- Elbeltagi, E.; Hegazy, T.; Eldosouky, A. Dynamic layout of construction temporary facilities considering safety. J. Constr. Eng. Manag. 2004, 130, 534–541. [Google Scholar] [CrossRef]
- Rosenblatt, M.J. The dynamics of plant layout. Manag. Sci. 1986, 32, 76–86. [Google Scholar] [CrossRef]
- McKendall, A.R.; Shang, J.; Kuppusamy, S. Simulated annealing heuristics for the dynamic facility layout problem. Comput. Oper. Res. 2006, 33, 2431–2444. [Google Scholar] [CrossRef]
- Khajemahalle, L.; Emami, S.; Keshteli, R.N. A hybrid nested partitions and simulated annealing algorithm for dynamic facility layout problem: A robust optimization approach. INFOR 2021, 59, 74–101. [Google Scholar] [CrossRef]
- Kogan, K.; Shtub, A.; Levit, V. DGAP-The dynamic generalized assignment problem. Ann. Oper. Res. 1997, 69, 227–239. [Google Scholar] [CrossRef]
- Mazzola, J.B.; Neebe, A.W. A generalized assignment model for dynamic supply chain capacity planning. Nav. Res. Logist. 2012, 59, 470–485. [Google Scholar] [CrossRef]
- Moccia, L.; Cordeau, J.-F.; Monaco, M.F.; Sammarra, M. A column generation heuristic for a dynamic generalized assignment problem. Comput. Oper. Res. 2009, 36, 2670–2681. [Google Scholar] [CrossRef]
- McKendall, A.R.; Noble, J.S.; Klein, C.M. Simulated annealing heuristics for managing resources during planned outages at electric power plants. Comput. Oper. Res. 2005, 32, 107–125. [Google Scholar] [CrossRef]
- Wang, S.; Sun, W.; Huang, M. An adaptive large neighborhood search for the multi-depot dynamic vehicle routing problem with time windows. Comput. Ind. Eng. 2024, 191, 110122. [Google Scholar] [CrossRef]
- Zhang, L.; Li, Q. Approximation algorithm for dynamic facility location problem. J. Comb. Optim. 2025, 49, 48. [Google Scholar] [CrossRef]
- Kirpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Huo, L.; Zhu, J.; Wu, G.; Li, Z. A novel simulated annealing based strategy for balanced UAV task assignment and path planning. Sensors 2020, 20, 4769. [Google Scholar] [CrossRef]
- Dai, Z.; Zhang, Z.; Chen, M. The home health care location-routing problem with a mixed fleet and battery swapping stations using a competitive simulated annealing algorithm. Expert Syst. Appl. 2023, 228, 120374. [Google Scholar] [CrossRef]
- Leelertkij, T.; Buddhakulsomsiri, J.; Huynh, V.-N. A multi-thread simulated annealing for multi-objective vehicle routing problem with time windows and demand priority. Comput. Ind. Eng. 2025, 207, 111253. [Google Scholar] [CrossRef]
- Tole, K.; Moqa, R.; Zheng, J.; He, K. A simulated annealing approach for the circle bin packing problem with rectangular items. Comput. Ind. Eng. 2023, 176, 109004. [Google Scholar] [CrossRef]
- Lin, S.-W.; Guo, S.; Wu, W.-J. Applying the simulated annealing algorithm to the set orienteering problem with mandatory visits. Mathematics 2024, 12, 3089. [Google Scholar] [CrossRef]
- Rosati, R.M.; Schaerf, A. Multi-neighborhood simulated annealing for the capacitated dispersion problem. Expert Syst. Appl. 2024, 255, 124484. [Google Scholar] [CrossRef]
- Ceschia, S.; Schaerf, A. Multi-neighborhood simulated annealing for the capacitated facility location problem with customer incompatibilities. Comput. Ind. Eng. 2024, 188, 109858. [Google Scholar] [CrossRef]
- Da Ros, F.; Di Gaspero, L.; Lackner, M.-L.; Musliu, N.; Winter, F. Multi-neighborhood simulated annealing for the oven scheduling problem. Comput. Oper. Res. 2025, 177, 106999. [Google Scholar] [CrossRef]
- Van Bulck, D.; Goossens, D.; Schaerf, A. Multi-neighbourhood simulated annealing for the ITC-2007 capacitated examination timetabling problem. J. Sched. 2025, 28, 217–232. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).