A Novel Imperialist Competitive Algorithm for Energy-Efficient Permutation Flow Shop Scheduling Problem Considering the Deterioration Effect of Machines

Abstract

This study addresses a critical gap in Energy-Efficient Permutation Flow Shop Scheduling (EPFSP) by integrating the often-overlooked time-accumulative equipment degradation inherent in practical manufacturing. This research formalizes and solves the EPFSP with machine deterioration (EPFSP-DEM), aiming to simultaneously minimize the makespan and total energy consumption. To achieve this objective, this study proposes a Diversity-Constrained Imperialist Competitive Algorithm (DCICA) featuring several novel mechanisms. In DCICA, a differentiated assimilation is developed to improve diversity of the population; a knowledge-guided revolution is designed to allocate computing resources efficiently; the convergence and diversity metrics are defined to evaluate the search quality on assimilation and revolution; a novel imperialist competition is also given to enhance information exchanges among empires and strengthen the search for some worse solutions. Finally, extensive experiments are conducted, and the results demonstrate that DCICA outperforms the existing algorithms in solving the investigated problem.

1. Introduction

Computational intelligence (CI) has revolutionized the solution paradigms for complex combinatorial optimization problems, particularly in cyber-physical production systems where classical operations research methods reach their limits. The permutation flow shop scheduling problem (PFSP) is a prototypical NP-hard challenge [1,2]. At present, meta-heuristics have become a major method in solving PFSP [3,4]. Energy-efficient shop scheduling is an important part of green manufacturing, which is more difficult to solve than traditional scheduling problems and has greater academic research significance and engineering application value. Energy-efficient shop scheduling achieves efficiency, energy conservation, emission reduction, and consumption reduction through rational optimization of resource allocation, operation sorting, and operation modes [5,6].

In recent years, the Energy-Efficient PFSP (EPFSP) has been studied extensively. Due to the NP-hard nature of the problem, meta-heuristics have become the dominant solution approach, which can generally be categorized into local search-based and population-based algorithms. Regarding local search-based methods, Iterated Greedy (IG) algorithms are widely adopted due to their simple structure and strong exploitation ability. For example, a multi-objective IG was developed in [7] to solve EPFSP with sequence-dependent setup times (SDST). Similarly, Ding et al. [8] designed a modified multi-objective IG (MMOIG) for carbon-efficient scheduling. Variable Neighborhood Search (VNS) is another effective approach; for instance, Wu et al. [9] applied VNS to the no-wait EPFSP. In terms of population-based methods, evolutionary algorithms are frequently employed to maintain population diversity. Jiang et al. [10] designed an improved MOEA/D, which decomposes the multi-objective problem into scalar sub-problems. Other swarm intelligence algorithms, such as the Discrete Whale Swarm Optimization (IDWSO) [11] and Hybrid Multi-Objective Backtracking Search Algorithm (HMOBSA) [12], have proven effective in handling complex constraints.

With respect to relevant research on PFSP with a deterioration effect, in [13,14,15], a multi-objective discrete fireworks algorithm (MO-DFWA) was proposed, an artificial-molecule-based chemical reaction algorithm was presented, and an h-MOEA/D was introduced to solve PFSP with deterioration of jobs. In [16], a multi-verse optimizer was employed for the PFSP with the deterioration of jobs. A pseudo-polynomial time algorithm was utilized by Shabtay et al. [17] for proportionate PFSP with step-deteriorating processing times. In [18], a branch-and-bound algorithm was designed to address the problem that is also about deteriorating jobs. A discrete ABC was proposed to solve flexible FSP with assembly and deterioration effects of machines in [19]. In [20], a memetic algorithm was developed by Liu for a distributed hybrid FSP to minimize $C_{max}$. A hybrid genetic algorithm was designed for the PFSP with a deterioration effect to minimize $C_{max}$ in [21].

The relevant works on EPFSP and deterioration are summarized in Table 1. As shown in the table, the vast majority of existing research focuses solely on the deterioration of jobs [13,14,15,16,17,18]. In these studies, the processing time of a job is defined as a function of its starting time (e.g., an ingot cooling down requires more time to roll as it waits longer). This perspective assumes that the machine’s capability remains constant.

Table 1. Summary of the most relevant literature on EFJSP.

Reference	Methodology	Objective	Constraint	Deterioration
ref. [7]	iterated greedy	($C_{max}$, $TEC$)	SDST, learning effect	−
ref. [8]	MMOIG	($C_{max}$, $TEC$)	−	−
ref. [9]	variable neighborhood search	($C_{max}$, $TEC$)	no-wait	−
ref. [10]	MOEA/D	($C_{max}$, $TEC$)	SDST	−
ref. [11]	IDWSO	($C_{max}$, $TEC$)	−	−
ref. [12]	HMOBSA	($C_{max}$, $TEC$)	SDST, transportation	−
ref. [13]	MO-DFWA	($TEC$, total tardiness)	−	jobs
ref. [14]	chemical reaction algorithm	$C_{max}$	−	jobs
ref. [15]	h-MOEA	($TEC$, total tardiness)	stochastic	jobs
ref. [16]	multi-verse optimizer	total tardiness	−	jobs
ref. [17]	pseudo-polynomial time algorithm	($C_{max}$, total load)	−	jobs
ref. [18]	branch-and-bound algorithm	$C_{max}$	−	jobs
ref. [22]	decomposition-based heuristic	$TEC$	SDST, group	−
ref. [23]	simulated annealing	($C_{max}$, $TEC$)	SDST, worker learning, transportation	−
ref. [24]	fix-and-optimize	total electricity costs	−	−
ref. [25]	MODBH	($C_{max}$, total tardiness)	−	−
ref. [26]	memetic algorithm	$TEC$	uncertainty	−
ref. [27]	differential evolution algorithm	($TEC$, mean tardiness)	time-of-use tariff	−
ref. [28]	logic-based benders decomposition	total electricity costs	time-of-use tariff	−
ref. [29]	ant colony algorithm	($C_{max}$, $TEC$)	time-of-use tariff	−
this study	DCICA	($C_{max}$, $TEC$)	−	machines

In contrast, this study addresses the deterioration effect of machines (EPFSP-DEM), a critical yet rarely investigated area. The distinction lies in the source of degradation: machine deterioration implies that the equipment’s processing efficiency declines due to cumulative wear, fatigue, or chemical corrosion during operation [19]. Consequently, the processing time of a job depends on the machine’s historical workload rather than the job’s starting time. This aspect has been largely neglected in the literature primarily due to the modeling complexity. Incorporating machine state-dependency introduces non-linear constraints that make the NP-hard scheduling problem significantly more difficult to solve. However, ignoring machine deterioration in energy-efficient scheduling can lead to substantial errors, as worn machines not only work more slowly but often consume more energy per unit of output.

The imperialist competitive algorithm (ICA) has some advantages, such as fast convergence speed, strong global search capability, and high accuracy, etc. At present, it has been applied to solve many multi-objective production scheduling problems [30] and has obtained better results. Therefore, ICA is a potential algorithm to handle EPFSP-DEM.

The primary objective of this research is to formalize and solve the EPFSP with machine deterioration (EPFSP-DEM), aiming to simultaneously minimize the makespan and total energy consumption. The contributions of this paper are described as follows. (1) EPFSP-DEM with the objectives of minimizing makespan and total energy consumption is investigated. (2) A differentiated assimilation is developed to improve the diversity of the population. (3) A knowledge-guided revolution is designed to reasonably allocate computing resources. (4) The convergence and diversity metrics are defined to evaluate the search quality of assimilation and revolution.

The remainder of the paper is organized below. EPFSP-DEM is described in Section 2, followed by the introduction to ICA in Section 3. An imperialist competitive algorithm considering diversity and convergence (DCICA) for EPFSP-DEM is reported in Section 4. Experiments are shown in Section 5, and conclusions are summarized in the final section.

2. Problem Description

EPFSP-DEM is described below. There are n jobs $J=\left\{J_1 ,J_2, ···, J_n\right\}$ and m machines $M=\left\{M_1, M_2, \right.$$\left.···, M_m\right\}$. Each job $J_i$ is processed in terms of the same production flow: $M_1, M_2,···, M_m$. There is a set V with d different processing speeds for all machines, $V=\left\{v_1,v_2,···v_d\right\}$. When job $J_i$ is processed on $M_k$ at speed $v_l$, the processing time is $p_{ik}/\phantom{p_{ik}{v}_l}{v}_l$. The deterioration rate of $M_k$ is defined as $b_k$. Not all machines turn off completely before the processing of all jobs is finished.

Some assumptions are listed below.

(1)

Job preemption is not allowed.

(2)

Each job can only be processed on one machine at a time.

(3)

All jobs and machines are available at time zero.

(4)

Each machine cannot process more than one job at a time.

(5)

Transportation and setup times are negligible, etc.

This study adopts the step-deterioration effect model, as shown in Equation (1).

$$p_{ik}^{\prime }=p_{ik}+b_k\times \left[max\left\{t-t_k^{min},0\right\}-max\left\{t-t_k^{max},0\right\}\right]$$

(1)

where $t_k^{min}\left(t_k^{max}\right)$ is the lower (upper) bound of the threshold; ${p^{\prime }}_{ik}$ represents the actual processing time of $J_i$ on $M_k$. To accurately describe the scheduling process, let $\pi =[{\pi }_1,{\pi }_2,\dots ,{\pi }_n]$ denote the permutation of jobs to be processed. The completion time $C_{{\pi }_i,k}$ of the i-th job ${\pi }_i$ on machine $M_k$ is calculated recursively using Equation (2). This recursion embodies the two fundamental constraints of flow shop scheduling: (1) Operation Precedence Constraint, meaning a job cannot start on machine $M_k$ until it finishes on $M_{k-1}$; and (2) Machine Availability Constraint, meaning machine $M_k$ cannot process job ${\pi }_i$ until it finishes the previous job ${\pi }_{i-1}$.

$$\left\{\begin{array}{c}{C}_{{\pi }_1,1}=p_{{\pi }_1,1}^{\prime }\hfill \\ C_{{\pi }_i,1}=C_{{\pi }_{i-1},1}+p_{{\pi }_i,1}^{\prime },\hfill & i=2,\dots ,n\hfill \\ C_{{\pi }_1,k}=C_{{\pi }_1,k-1}+p_{{\pi }_1,k}^{\prime },\hfill & k=2,\dots ,m\hfill \\ C_{{\pi }_i,k}=max\{C_{{\pi }_{i-1},k},C_{{\pi }_i,k-1}\}+p_{{\pi }_i,k}^{\prime },\hfill & i=2,\dots ,n;k=2,\dots ,m\hfill \end{array}\right.$$

(2)

Based on the recursive calculation, the two objectives, Makespan ($C_{max}$) and Total Energy Consumption ($TEC$), are formulated as follows:

$$f_1=C_{max}=C_{{\pi }_n,m}\left(min\right)$$

(3)

$$f_2=TEC=E{C}_1+E{C}_2\left(kJ\right)$$

(4)

$$E{C}_1=\sum _{k=1}^m\sum _{i=1}^n\sum _{l=1}^d{E}_{kl}\times p_{ik}^{\prime }\times y_{ikl}$$

(5)

$$E{C}_2=\sum _{k=1}^{m}S{E}_k\times \left(C_{max}-\sum _{i=1}^n{p}_{ik}^{\prime }\right)$$

(6)

where $y_{ikl}$ is a binary variable equal to 1 if job $J_i$ is processed on machine $M_k$ at speed $v_l$, and 0 otherwise. Equation (3) defines the makespan as the completion time of the last job on the last machine. Equation (5) calculates the total processing energy consumption $E{C}_1$ based on the selected speed. Equation (6) calculates the total idle energy consumption $E{C}_2$, where the total idle time is derived by subtracting the total processing time from the makespan. $E_{kl}$ and $S{E}_k$ represent the processing power and stand-by power in kW, respectively.

To verify the model and illustrate the impact of the deterioration effect, a numerical example of EPFSP-DEM is presented. This instance consists of ten jobs ($J_1,\dots ,J_{10}$) and four machines ($M_1,\dots ,M_4$). Table 2 details the standard processing times ($p_{ik}$) for each job on each machine under the base speed ($v=1$), along with the specific deterioration rate ($b_k$) for each machine. For example, machine $M_1$ has a deterioration rate of $b_1=0.13$, implying that its processing efficiency declines faster than $M_3$ ($b_3=0.09$) as the cumulative processing time increases. And Table 3 lists the energy consumption per unit time ($E_{kl}$) corresponding to five distinct speed levels. It reflects the trade-off considered in this study: higher processing speeds ($v_5=2$) significantly reduce operation time but result in higher power intensity ($E_{kl}$) compared to lower speeds ($v_1=1$).

Table 2. An example of EPFSP-DEM.

Job	${\mathit{J}}_1$	${\mathit{J}}_2$	${\mathit{J}}_3$	${\mathit{J}}_4$	${\mathit{J}}_5$	${\mathit{J}}_6$	${\mathit{J}}_7$	${\mathit{J}}_8$	${\mathit{J}}_9$	${\mathit{J}}_{10}$	${\mathit{b}}_{\mathit{k}}$
$M_1$	6	7	9	10	6	5	10	6	7	7	0.13
$M_2$	5	5	8	10	5	5	7	8	7	6	0.12
$M_3$	9	10	7	9	6	6	8	6	7	7	0.09
$M_4$	7	5	9	10	9	7	5	6	10	7	0.10

Table 3. Energy consumption per unit time $E_{kl}$ (kW).

Speed	${\mathit{v}}_1=1$	${\mathit{v}}_2=1.33$	${\mathit{v}}_3=1.5$	${\mathit{v}}_4=1.8$	${\mathit{v}}_5=2$
$M_1$	3.03	5.12	7.28	9.82	12.12
$M_2$	2.47	4.17	5.92	7.99	9.86
$M_3$	2.60	4.39	6.24	8.42	10.39
$M_4$	2.73	4.61	6.55	8.83	10.90

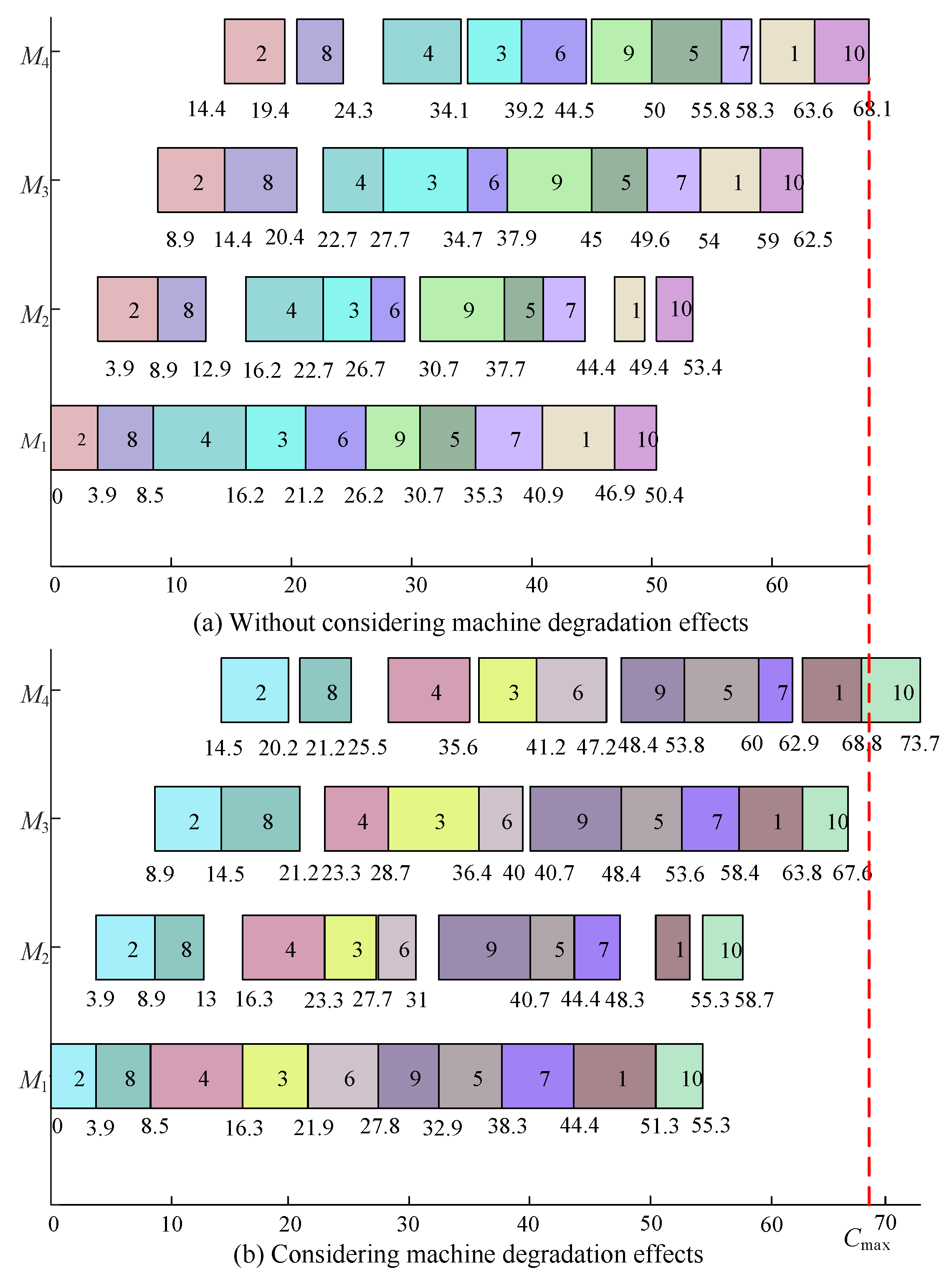
Figure 1 visualizes the scheduling results of this instance using Gantt charts to compare two scenarios: Figure 1a depicts the schedule without considering the deterioration effect (i.e., treating machines as ideal with constant efficiency). Figure 1b shows the schedule for the same job sequence and speed selection but with the deterioration effect derived from Equation (1). By comparing Figure 1b with Figure 1a, the influence of machine aging is evident. As machines operate continuously, the actual processing time $p_{ik}^{\prime }$ for later jobs becomes longer than the standard processing time $p_{ik}$. For instance, consider the last few jobs on Machine 1 ($M_1$). In Figure 1a, the operations are compact. However, in Figure 1b, due to the deterioration rate of $b_1=0.13$, the processing times for the subsequent jobs are prolonged. Consequently, the entire schedule is stretched, pushing the completion time of the final job from 68.1 to 73.7. This comparison visually confirms that neglecting the deterioration effect in practical manufacturing can lead to significant underestimations of both completion time and energy costs.

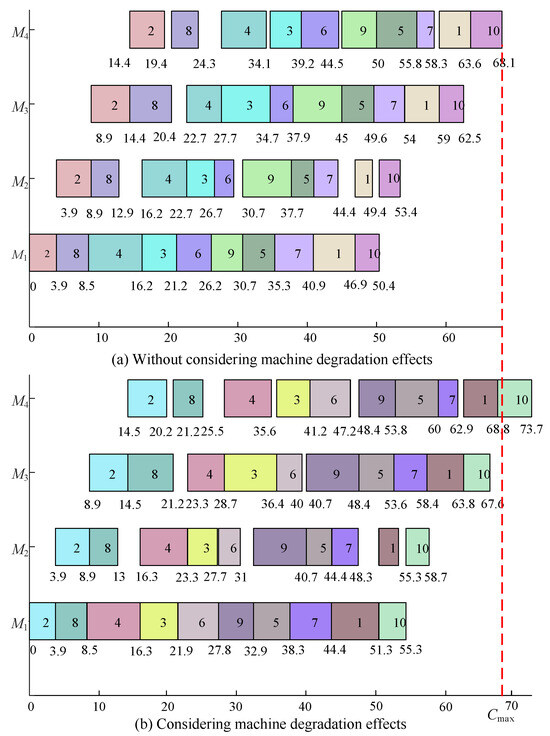
Figure 1. The Gantt charts of the instance.

3. Introduction to ICA

ICA was first proposed by Atashpaz-Gagari and Lucas [31], which consists of initial empires, assimilation, revolution, and imperialist competition. In ICA, one country represents a feasible solution, whose quality is determined by a cost value. Generally, the better the quality of a solution is, the smaller the cost value is. The procedures of ICA are shown in Algorithm 1, where ${\overline{c}}_q$ and $po{w}_q$ represent normalized cost values and the power of the imperialist $I{M}_q$, respectively. $N{C}_q$ indicates the number of colonies possessed by the imperialist $I{M}_q$, $N_{im}$ is the number of imperialists, and $N_{col}$ denotes the total number of colonies.

Algorithm 1 ICA

1: Initialization. Stochastically produce an initial population, $Pop$, and calculate the cost values of all solutions.   2: Initial empires. Choose solutions $N_{im}$ with the smallest cost values as imperialists, calculate ${\overline{c}}_q$ and $N{C}_q$, and stochastically allocate $N{C}_q$ colonies for each imperialist $I{M}_q$.   3: while the termination condition is not met, do   4:      for q=1 to $N_{im}$ do   5:          perform assimilation in the empire q   6:          implement revolution in the empire q   7:          exchange them if the colony is superior to the imperialist $I{M}_q$   8:      end for   9:      execute imperialist competition among all empires 10: end while

$${\overline{c}}_q=\underset{v\in H}{max}\left\{c_v\right\}-c_q$$

(7)

$$po{w}_q=\left|{\overline{c}}_q/\sum _{v\in H}{\overline{c}}_v\right|$$

(8)

$$N{C}_q=round\left(po{w}_q\times N_{col}\right)$$

(9)

$$N_{col}=N-N_{im}$$

(10)

where H denotes the set of all imperialists and $c_q$ is the cost value of the imperialist $I{M}_q$.

In assimilation, each colony in the empire q moves $\overline{\delta }\sim U\left[0,t\times e\right]$ along the e direction toward the imperialist $I{M}_q$, where $t\in \left(1,2\right)$ and e is the distance between the colony and the imperialist $I{M}_q$. To expand the search scope, a deviation $\theta \sim U\left[-\phi ,\phi \right]$ is added on above movement, where $\phi$ is a parameter.

When there is a sudden change in the social and political characteristics of a colony, including culture, language, and religion, a revolution will be carried out in which colonies are first chosen by revolution probability, and then the related search operators are executed on the chosen colony. It is similar to the mutation operator of the genetic algorithm, which can improve the search ability of ICA and prevent premature convergence. After assimilation and revolution, the cost value of each colony is compared with that of the imperialist, one by one. If the cost value of the colony is better than that of the imperialist, they are exchanged.

In imperialist competition, stronger empires continually plunder the colonies of weaker ones to elevate their political standing, whereas weaker empires progressively decline or even perish. Imperialist competition is performed in the following way. Calculate total cost $T{C}_q$, the normalized total cost ${\overline{TC}}_q$ and the power $E{P}_q$ for each empire q, construct a vector Q, decide an empire g with the greatest $E{P}_g-{\epsilon }_g$ and allocate the weakest colony of the weakest empire into empire g.

$$T{C}_q=c_q+\varsigma \times mean\left\{\mathrm{Cost}\left(\mathrm{colonies}\mathrm{of}\mathrm{empire}q\right)\right\}$$

(11)

$${\overline{TC}}_q=\underset{h\in H}{max}\left\{T{C}_h\right\}-T{C}_q$$

(12)

$$E{P}_q=\left|{\overline{TC}}_q/\sum _{v\in H}{\overline{TC}}_v\right|$$

(13)

$$Q=\left[E{P}_1-{\epsilon }_1,E{P}_2-{\epsilon }_2,···,E{P}_{N_{im}}-{\epsilon }_{N_{im}}\right]$$

(14)

where $\varsigma$ is a positive number, ${\epsilon }_i\in U\left[0,1\right]$.

4. DCICA for EPFSP-DEM

In previous ICAs [30], there is only one learning object, which is the imperialist for all colonies. Under these circumstances, the diversity of the population will rapidly decrease. In revolution, the allocation of computing resources is rarely investigated. In addition, only one colony is transferred into the winning empire in imperialist competition. Information communication among empires should be strengthened to improve the search performance of the algorithm. In this paper, a DCICA is proposed to tackle EPFSP-DEM.

4.1. Encoding and Decoding

In EPFSP-DEM, two sub-problems must be solved: scheduling and speed selection. Therefore, this study adopts a two-string encoding method. $\left[{\pi }_1,{\pi }_2,···,{\pi }_n\right]$ and a speed selection string $\left[{w_1}_1,{w_1}_2,···,w_{1m},···,w_{nm}\right]$, where ${\pi }_i\in \left\{1,2,···,n\right\}$, $w_{ik}\in V$ indicates a speed utilized to process jobs.

The procedure of decoding is described as follows: determine the speeds for all machines according to the speed-assignment string; start from the first job ${\pi }_1$ in the scheduling string $\left[{\pi }_1,{\pi }_2,···,{\pi }_n\right]$; and process the jobs on machines $M_1,M_2,···,M_m$ as early as possible until all jobs are completed.

The procedure of decoding determines the speeds for all machines according to the speed assignment string and processes jobs on machines as early as possible. To avoid disrupting the flow of the text, a detailed numerical example illustrating the decoding procedure and specific objective calculations (based on the instance in Table 2) is provided in Appendix A.

4.2. Initialization and Initial Empires

To ensure the diversity of the population, the initial $Pop$ with N colonies is randomly produced. Initial empires are constructed after $Pop$ is obtained. For a colony $x_i$, its normalized cost ${\overline{c}}_i$ is calculated. Then, the $N_{im}$ colonies with the greatest ${\overline{c}}_i$ values are selected as imperialists, and the remaining ones are assigned as colonies. Next, $po{w}_k$ and $N{C}_q$ are calculated for imperialist $I{M}_q$, and $N{C}_q$ colonies are randomly allocated to imperialist $I{M}_q$. ${\overline{c}}_i$ is determined as in Equation (14).

$${\overline{c}}_i=\underset{l=1,2,···,N}{max}\left\{ran{k}_l\right\}-ran{k}_i+{\displaystyle \frac{crow{d}_i}{{\sum }_{j\in {\Theta }_{ran{k}_i}}crow{d}_j}}$$

(15)

where $ran{k}_i$ indicates the rank value of $x_i$ by non-dominated sorting on $Pop$ [32], ${\Theta }_{ran{k}_i}$ is the set of solutions with rank value of $ran{k}_i$, and $crow{d}_i$ is defined by Lei et al [30]. $Round\left(x\right)$ is a function that gives the nearest integer of x.

After $N_{im}$ empires are constructed, each empire q is composed of the imperialist $I{M}_q$ and $N{C}_q$ colonies. For empire q, its normalized total cost ${\overline{TC}}_q$ is defined by Equation (15).

$${\overline{TC}}_q={\overline{c}}_q+\xi {\sum }_{\lambda \in Q_q}{\overline{c}}_{\lambda }/\phantom{{\overline{c}}_{\lambda }N{C}_q}N{C}_q$$

(16)

where $Q_q$ is a set of colonies possessed by the imperialist $I{M}_q$ and $\xi =0.1$.

All empires are sorted in descending order of ${\overline{TC}}_q$. Suppose that ${\overline{TC}}_1\ge {\overline{TC}}_2\ge ···\ge {\overline{TC}}_{N_{im}}$, empire 1($N_{im}$) is the strongest (weakest) one.

4.3. Differentiated Assimilation

Generally, the crossover is utilized to perform assimilation between imperialists and colonies, and imperialists remain invariant [30]. When colonies only move toward their imperialist—that is, there is only one learning object—this leads to more similarities among them. The diversity of $Pop$ will decrease quickly. Therefore, many learning objects should be retained. On the other hand, it is necessary to distinguish some of the best solutions and others, since these best solutions are closer to the Pareto front and make it easier to produce better ones. Based on the above analyses, a differentiated assimilation is designed. Its specific procedure is described in Algorithm 2 and visually illustrated in Figure 2, where $\beta$ is an integer.

Algorithm 2 Differentiated assimilation

1: for u=1 to q do   2:      if $N{C}_u>\beta$ then   3:          perform non-dominated sorting for all colonies in empire u   4:          select $\beta$ best ones and add them into set ${\Lambda }_u$   5:          if $x_i\in {\Lambda }_u$ then   6:               choose one solution y randomly from $\Omega$   7:               execute crossover between $x_i$ and y   8:          else   9:               choose one solution y randomly from ${\Lambda }_u$ 10:               if a random number $rand<0.5$ then 11:                   execute crossover between $x_i$ and y 12:               else 13:                   perform crossover between $x_i$ and $I{M}_u$ 14:               end if 15:          end if 16:      else 17:          perform crossover between $x_i$ and $I{M}_u$ 18:      end if 19:      if the obtained new solution z is not dominated by $x_i$ then 20:          x is replaced with z, and z is used to update $\Omega$ 21:      else 22:          update $\Omega$ using z 23:      end if 24: end for

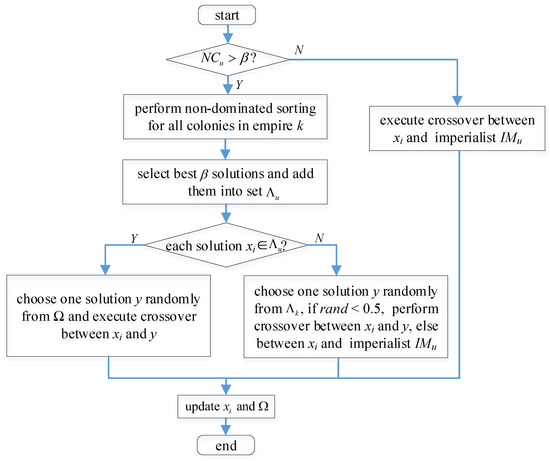
Figure 2. Flowchart of the differentiated assimilation process.

Initial ${\Lambda }_u$ is empty. After assimilation finishes, all solutions in ${\Lambda }_u$ are deleted. Initial $\Omega$ is composed of non-dominated solutions of the initial $Pop$. When a new solution is added to $\Omega$, all dominated ones are deleted. Crossover is described below. Scheduling string and speed string of solutions $x_i$ and $I{M}_u\left(y\right)$ are executed sequentially. In this study, order-based crossover (OBX) and two-point crossover are adopted because of their effectiveness for solving scheduling problems, which are described as follows.

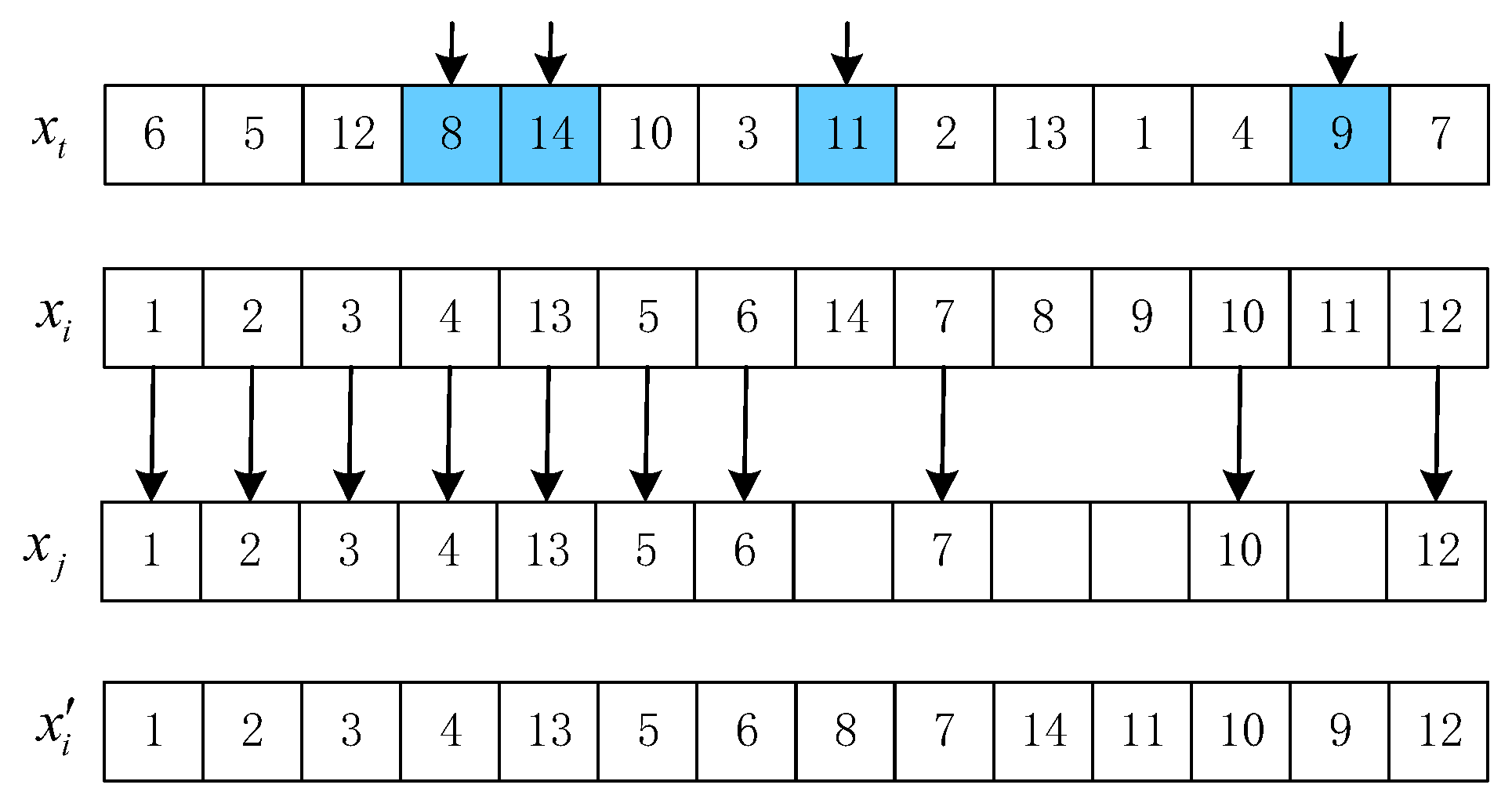
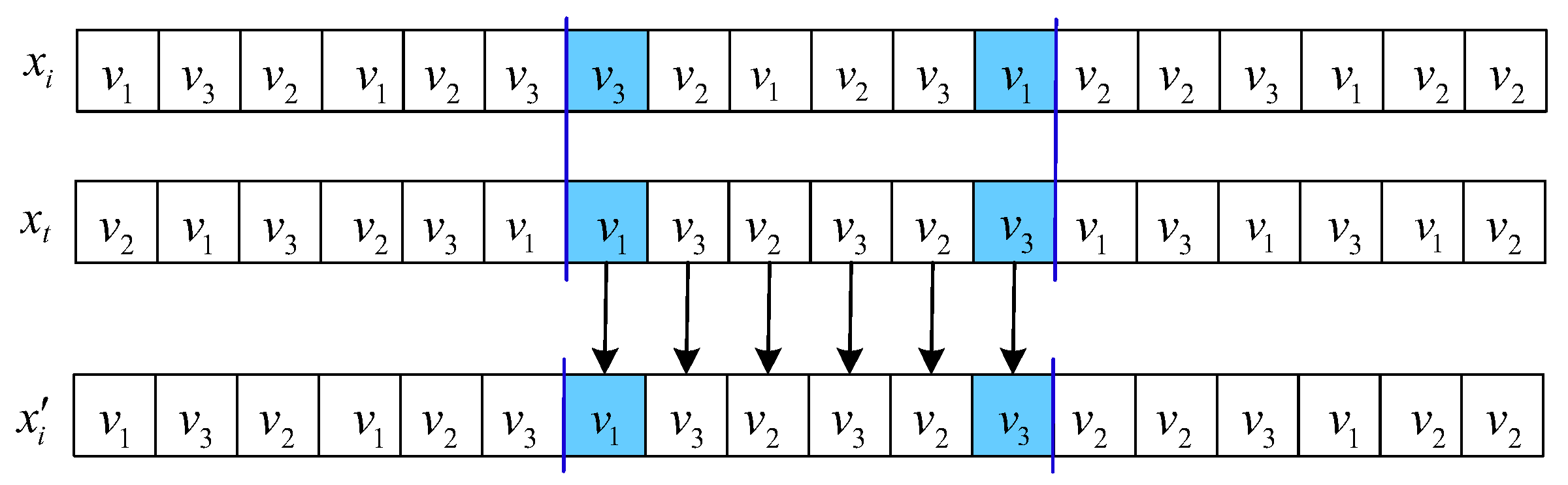
OBX acts on the scheduling string. For solutions $x_i$ and $x_t$, randomly select G genes from $x_t$, delete them from $x_i$, and produce a partial solution $x_j$. Finally, $x_i^{\prime }$ is generated by adding the chosen genes into $x_i$ as a sequence in $x_t$, where G is set to $0.3\times n$ by experiments. Figure 3 describes the process of OBX. Two-point crossover is applied to the speed string. For $x_i$, stochastically select two positions l and h, $1\le l<h\le n\times m$. The speeds between l and h are replaced by the same positions of $x_t$, as shown in Figure 4.

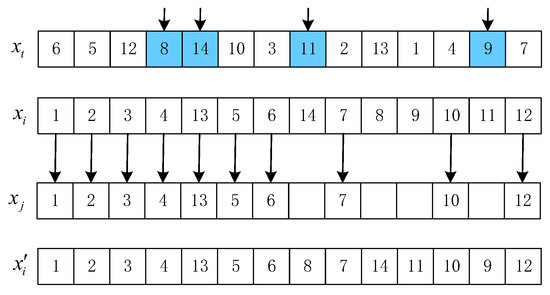
Figure 3. An example of OBX. The colors represent randomly selected jobs, and the arrows indicate that the positions of the jobs remain unchanged.

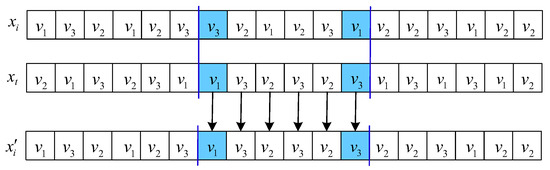
Figure 4. An example of a two-point crossover. The colors represent randomly selected processing speeds, and the arrows illustrate the crossover operation performed at corresponding positions of $x_i$ and $x_t$ to generate $x_i^{\prime }$.

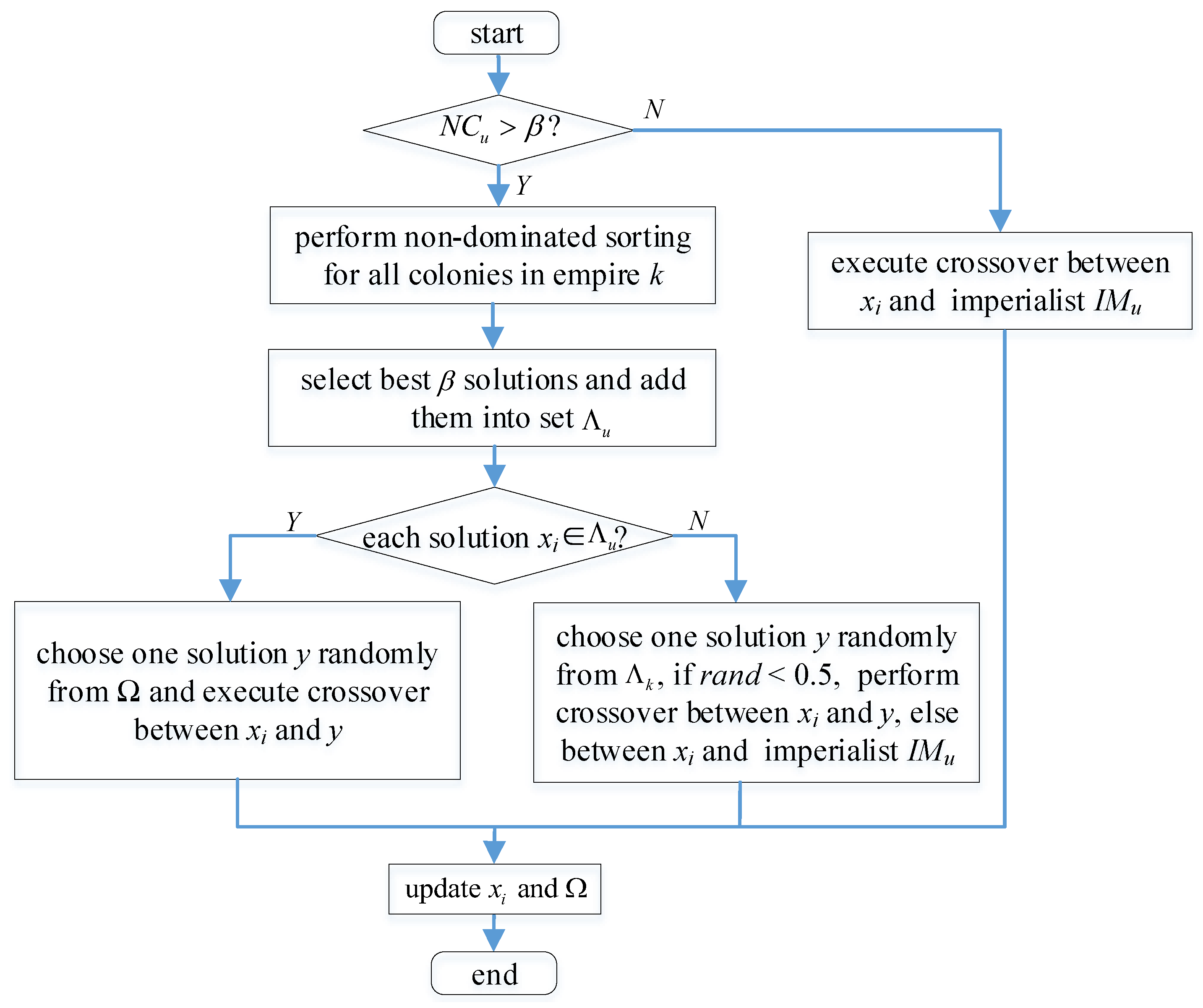
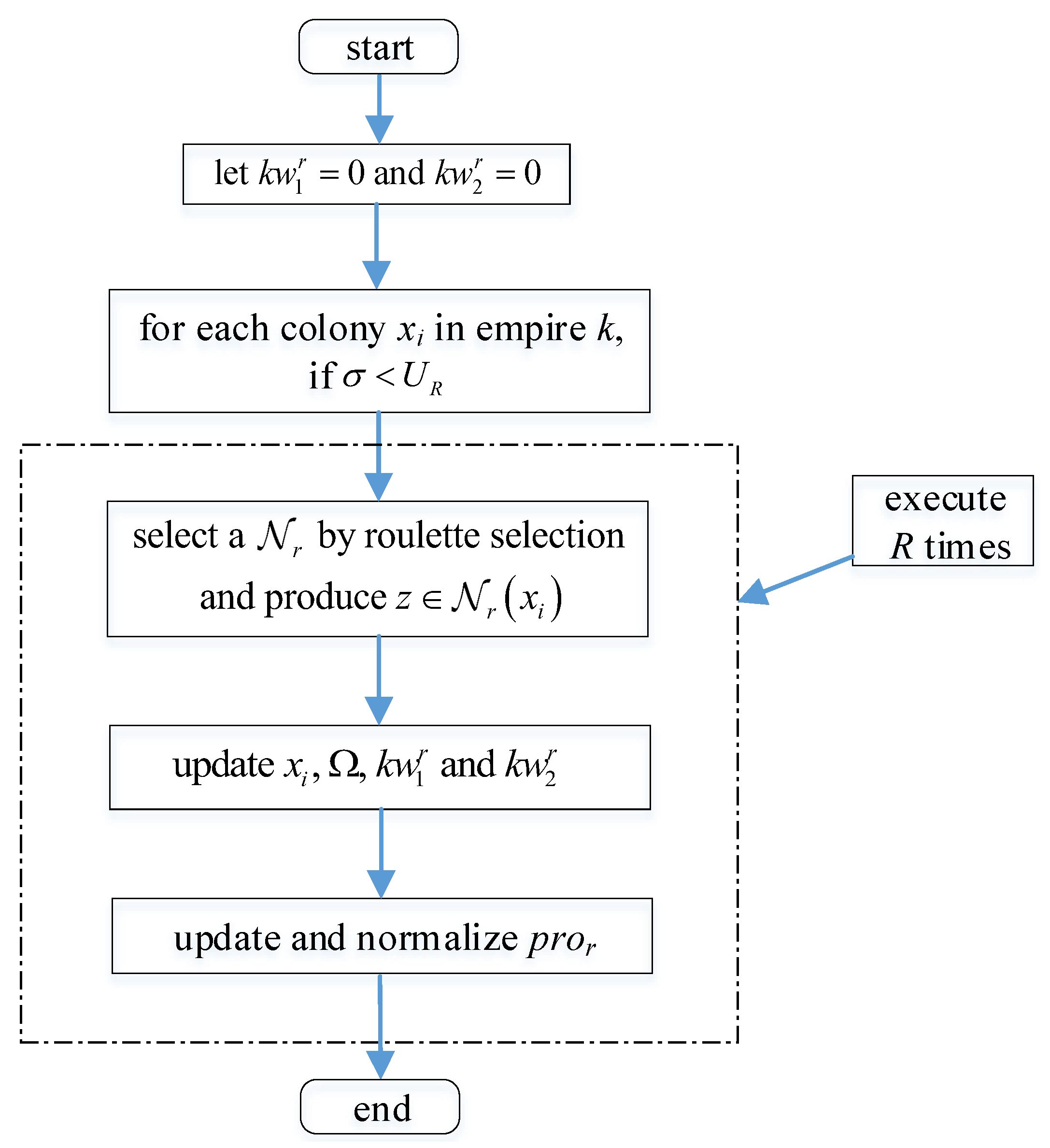
4.4. Knowledge-Guided Revolution

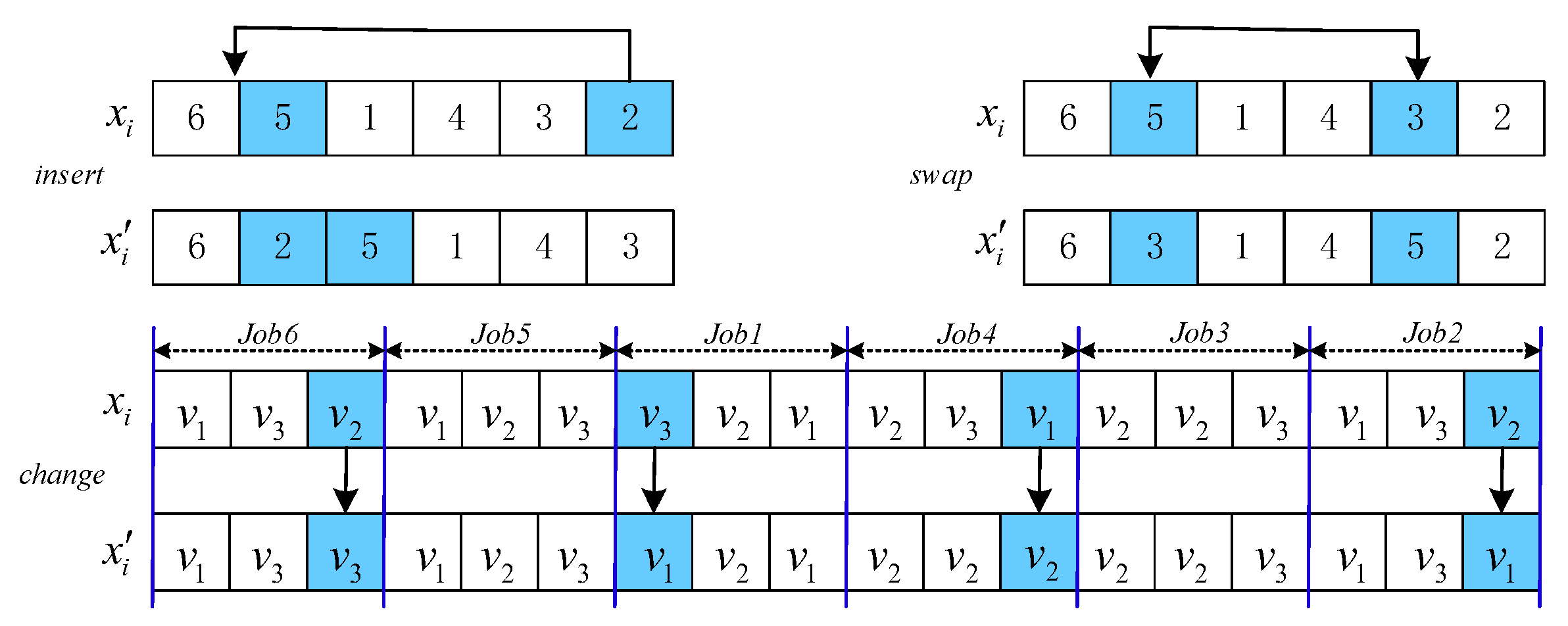
Revolution is another way to produce new solutions. In general, there is a probability $U_R$ that is employed to select colonies as revolutionaries. It is beneficial to exploit current information and enhance search efficiency. In this paper, three neighborhood structures—$insert$, $change$, and $swap$—are adopted to perform revolution, which are represented as ${\mathcal{N}}_1,{\mathcal{N}}_2,{\mathcal{N}}_3$. Figure 5 shows the changes in them.

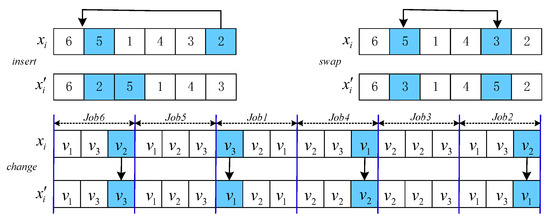
Figure 5. Neighborhood structures ${\mathcal{N}}_1,{\mathcal{N}}_2,{\mathcal{N}}_3$. The colors represent randomly selected jobs or processing speeds. The arrows in the insert, swap, and change operators indicate job insertion, position swapping, and replacement operations, respectively.

To employ ${\mathcal{N}}_1,{\mathcal{N}}_2,{\mathcal{N}}_3$ effectively, a knowledge-guided revolution is developed, where two kinds of knowledge are defined below.

Knowledge 1: The number of updating colonies by ${\mathcal{N}}_r$, denoted $k{w}_1^r$.

Knowledge 2: The number of updating $\Omega$ by ${\mathcal{N}}_r$, denoted $k{w}_2^r$. The probability $pr{o}_r$ of selecting ${\mathcal{N}}_r$ is calculated by

$$pr{o}_r={\displaystyle \frac{1}{3}}+{\displaystyle \frac{\lambda \times k{w}_1^r+\left(1-\lambda \right)\times k{w}_2^r}{{\sum }_{i=1}^3\left(\lambda \times k{w}_1^i+\left(1-\lambda \right)\times k{w}_2^i\right)}}$$

(17)

where $\lambda$ is a weight coefficient.

The proposed knowledge-guided revolution is thoroughly described in Algorithm 3, and its flowchart is presented in Figure 6.

Algorithm 3 Knowledge-guided revolution

1: let $k{w}_1^r=0$ and $k{w}_2^r=0$   2: for each colony $x_i$ in empire q do   3:      if a random number $\sigma <U_R$ then   4:          for l=1 to R do   5:               select a ${\mathcal{N}}_r$ by roulette selection based on $pr{o}_r$ and produce a new solution $z\in {\mathcal{N}}_r\left(x_i\right)$   6:               if z is not dominated by $x_i$ then   7:                   $x_i$ is replaced with z, $k{w}_1^r=k{w}_1^r+1$ and update $\Omega$ using z   8:                   if $\Omega$ is updated then   9:                        $k{w}_1^r=k{w}_1^r+1$ 10:                   end if 11:               else 12:                   update $\Omega$ using z 13:                   if $\Omega$ is updated then 14:                        $k{w}_1^r=k{w}_1^r+1$ 15:                   end if 16:               end if 17:               normalize $pr{o}_r$, $pr{o}_r=pr{o}_r/\phantom{pr{o}_r{\sum }_{i=1}^{3}pr{o}_i}{\sum }_{i=1}^{3}pr{o}_i$ 18:          end for 19:      end if 20: end for

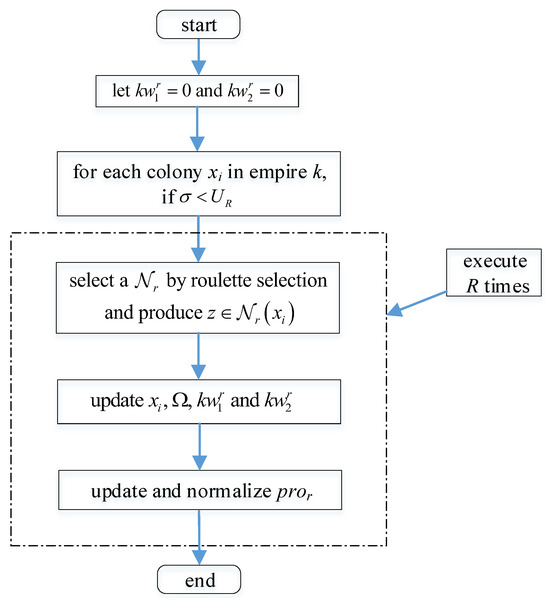
Figure 6. Flowchart of the knowledge-guided revolution strategy.

After assimilation and revolution are finished, each colony $x_i$ is compared with its imperialist in the empire q. If the colony is not dominated by its imperialist $I{M}_q$, the colony becomes the new imperialist, and the old one turns into the colony.

4.5. Definitions on Diversity and Convergence

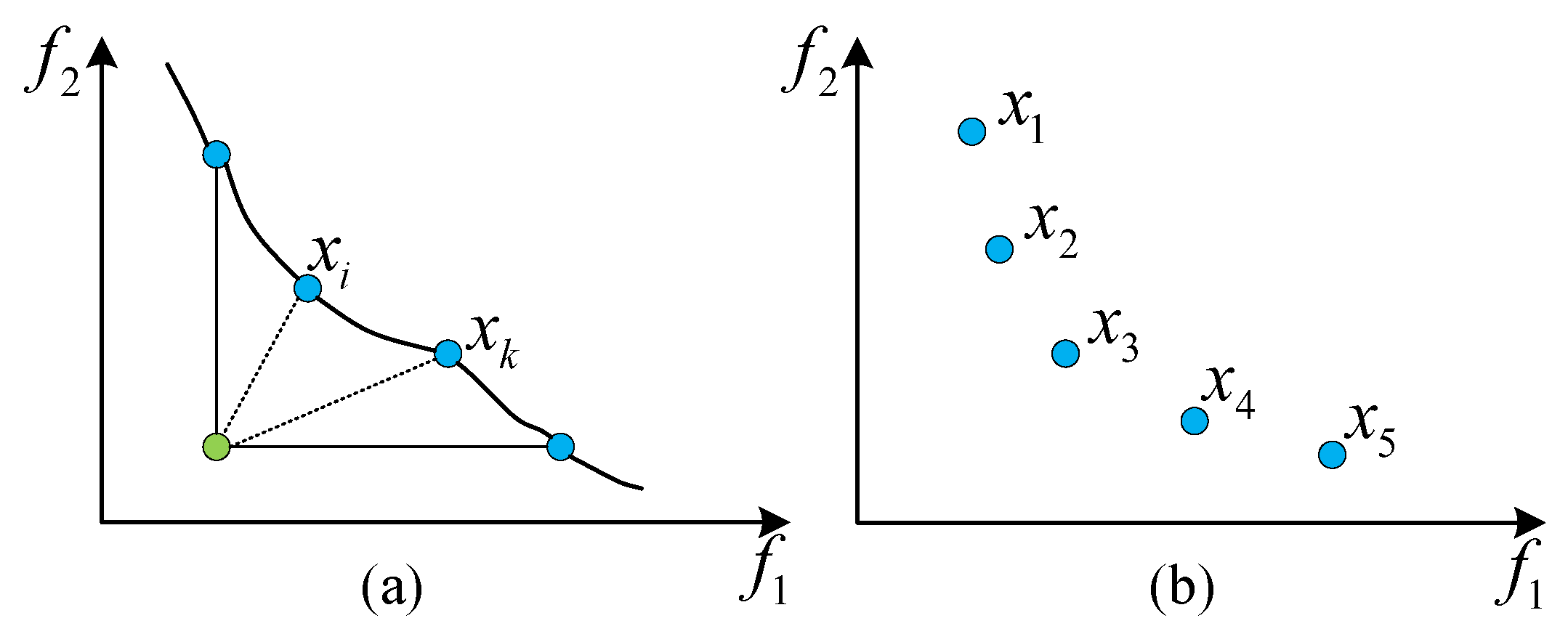
The non-dominated solutions obtained by DCICA should be distributed uniformly in the search space and provide a better convergence performance. For solutions $x_i$ and $x_t$ in $\Omega$, the convergence is diverse although they are non-dominated with respect to each other, as shown in Figure 7a, where $d\left(x_i,f_{1,min}\right)+d\left(x_i,f_{2,min}\right)$ is less than $d\left(x_t,f_{1,min}\right)+d\left(x_t,f_{2,min}\right)$. Here, $d\left(x_{i\left(t\right)},f_{1\left(2\right),min}\right)=x_{i\left(t\right)}-f_{1\left(2\right),min}$. Obviously, $x_i$ is easier to reach the ideal point, marked by the green circle in Figure 7a, than $x_t$ in terms of the moving distance. Moreover, solutions in $\Omega$ should maintain a uniform distribution, which means that they have better diversity, as shown in Figure 7b.

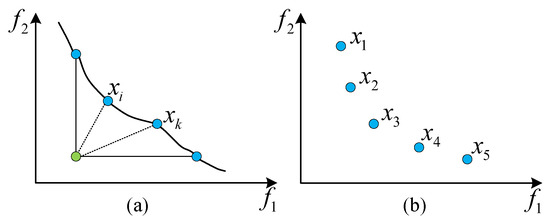
Figure 7. The convergence and diversity of solutions. (a) Schematic of the convergence metric, where the green dot represents the ideal point, blue dots denote the non-dominated solutions, and the dashed and solid lines indicate the distances to the ideal point. (b) Schematic of the diversity metric, illustrating the distribution of solutions.

Based on the above analyses, this study designs two indicators, $Co{n}_{\Omega ,gen}$ and $Di{v}_{\Omega ,gen}$, to evaluate the convergence and diversity of solutions at generation $gen$. The convergence of solutions in $\Omega$ at generation $gen$ is defined by

$$Co{n}_{\Omega ,gen}={\displaystyle \frac{1}{\left|\Omega \right|}}\sum _{j=1}^2\sum _{i=1}^{\left|\Omega \right|}{\displaystyle \frac{f_{i,j}-f_{j,min}}{f_{j,max}-f_{j,min}+\epsilon }}$$

(18)

where $f_{i,j}$ is the j-th objective value of solution $x_i$, and $f_{j,min}\left(f_{j,max}\right)$ indicates the minimum (maximum) value of the j-th objective. After $f_1$ and $f_2$ are sorted in ascending order, the diversity of solutions in $\Omega$ at generation $gen$ is calculated by

$$\begin{array}{c}Di{v}_{\Omega ,gen}={\displaystyle \frac{1}{\left|\Omega \right|-1}}\times {\displaystyle \sum _{j=1}^2}{\displaystyle \sum _{i=2}^{\left|\Omega \right|-1}}{\displaystyle \frac{f_{i+1,j}-f_{i-1,j}}{f_{j,max}-f_{j,min}+\epsilon }}\hfill \\ +{\displaystyle \frac{1}{2}}\times \left({\displaystyle \sum _{j=1}^2}{\displaystyle \frac{f_{2,j}-f_{1,j}+f_{i,j}-f_{i-1,j}}{f_{j,max}-f_{j,min}+\epsilon }}\right)\hfill \end{array}$$

(19)

According to the above evaluation, this study adopts four strategies to perform assimilation and revolution for improving search efficiency, where $Co{n}_{\Omega ,gen}^a\left(Co{n}_{\Omega ,gen}^r\right)$ and $Di{v}_{\Omega ,gen}^a\left(Di{v}_{\Omega ,gen}^r\right)$ represent convergence and diversity of solutions in $\Omega$ at generation $gen$ after performing assimilation and revolution.

(1)

$Co{n}_{\Omega ,gen}^a-Co{n}_{\Omega ,gen-1}^a\ge 0$ and $Di{v}_{\Omega ,gen}^a-Di{v}_{\Omega ,gen-1}^a\le 0$.

When this case occurs, it indicates that the search in assimilation does not change the quality of $\Omega$. More computing resources should be allocated to other areas.

(2)

$Co{n}_{\Omega ,gen}^r-Co{n}_{\Omega ,gen-1}^r\ge 0$ and $Di{v}_{\Omega ,gen}^r-Di{v}_{\Omega ,gen-1}^r\le 0$.

This case is similar to case 1. It means that revolution does not obtain promising results in the current search process; thus, a penalty is imposed, preventing the execution of the revolution.

(3)

$Co{n}_{\Omega ,gen}^{a\left(r\right)}-Co{n}_{\Omega ,gen-1}^{a\left(r\right)}\ge 0$ and $Di{v}_{\Omega ,gen}^{a\left(r\right)}-Di{v}_{\Omega ,gen-1}^{a\left(r\right)}\le 0$.

The non-dominated solutions in $Pop$ are selected to perform local search as in Section 4.4, since they are closer to Pareto-optimal solutions and easier to generate better solutions, which can guide the search further.

(4)

For other cases, DCICA performs a search as the original steps in the next iteration.

For the above case, it indicates that assimilation and revolution improve at least one of the diversity and convergence of the solutions in $\Omega$.

4.6. Imperialist Competition

In the original imperialist competition, when the power of an empire greatly exceeds that of other empires, there are enough opportunities to win and quickly occupy more colonies, which can lead to falling into local optima. In addition, competition only changes the structures of the winning empire and the weakest one. In fact, more colonies should be exchanged among empires, which is beneficial for changing the structures of empires and improving search efficiency. In this study, a novel imperialist competition is proposed and described in Algorithm 4, where W is set to 2.

Algorithm 4 Novel imperialist competition

1: compute $E{P}_q$ for empire q according to ${\overline{TC}}_q$   2: if $N_{im}\ge Z$ then   3:      sort all empires in descending order of $E{P}_q$, suppose that $E{P}_1>E{P}_2>···>E{P}_{N_{im}}$   4:      if $E{P}_1/\phantom{E{P}_{1}E{P}_2\le W}E{P}_2\le W$ then   5:          determine the winning empire u by binary tournament selection based on $E{P}_q$   6:          randomly select a colony from the weakest empire v and transfer it into empire u   7:          rank all empires in $H\setminus \left\{u,v\right\}$ in descending order of $E{P}_q$, suppose the sorted ones are $1,2,···,N_{im}-2$   8:          randomly choose a colony of empire $q+1$ and transfer it into empire $q\left(q=1,2,···,N_{im}-3\right)$   9:      else 10:          randomly choose a colony of empire $q+1$ and transfer it into empire $q\left(q=1,2,···,N_{im}-1\right)$ 11:      end if 12: end if 13: if $N_{im}>2$ and $N_{im}<Z$ then 14:      stochastically pick a colony from empire $q\left(q>1\right)$ and transfer it into empire 1 15: end if 16: select $0.1\times N$ worst colonies from $Pop$ and construct a set $\chi$ 17: for each colony $x_i$ in empire q do 18:      randomly pick a one $y\in \Omega$, execute search as knowledge-guided revolution and produce a new solution z 19:      if z is not dominated by x then 20:          x is replaced with z, and update using z 21:      end if 22: end for

Unlike the original ICA [30], when $E{P}_1/\phantom{E{P}_{1}E{P}_2>W}E{P}_2>W$, the strongest empire does not participate in imperialist competition, which can prevent premature convergence of algorithms. Strengthening the search for the worst solutions in $Pop$ is beneficial for avoiding the wastage of computing resources. Meanwhile, it enhances information exchange among empires and improves the search efficiency of DCICA.

5. Computational Experiments

All experiments are coded by using MATLAB 2018b and run on an Intel Core i7-1260 16.0 G RAM 2.10 GHz win11 640S CPU PC.

5.1. Instances, Metrics, and Comparative Algorithms

To verify the performance of DCICA, 32 test instances are generated. The problem scales (defined by the number of jobs n and machines m) and the standard processing times ($p_{ik}$) are constructed based on the structure of the classical Taillard benchmark set, which is also utilized in the literature [2]. Since the original benchmark does not consider energy consumption and machine deterioration, the specific parameters for EPFSP-DEM are extended as follows. Specifically, the instances cover combinations of $n\in \{10,20,50,100,200,300,400,500\}$ and $m\in \{5,10,15,20\}$. The standard processing time ($p_{ik}$) is generated from a uniform distribution $U[1,99]$. Regarding the energy parameters, the set of discrete speeds is $V=\{1,1.3,1.55,1.8,2\}$, while the power consumption ($E_{kl}$) is calculated by $E_{kl}=\xi \times v_l^2$, where $\xi$ is randomly generated from $U[2,4]$, and the standby power is set to $S{E}_k=1$. Finally, to analyze the impact of machine aging, three levels of deterioration rates ($b_k$) are generated: Low ($U[0.05,0.15]$), Medium ($U[0.15,0.25]$), and High ($U[0.25,0.40]$). The $t_k^{min}$ and $t_k^{max}$ are determined by

$$\left[t_k^{min},t_k^{max}\right]=\left[0.1,0.2\right]\times {\sum }_{i=1}^n{p}_{ik}.$$

(20)

The hypervolume ($HV$) [33] and inverted generational distance ($IGD$) [33] are two widely used performance evaluation metrics to evaluate the performance of the DCICA.

Suppose that $r^{*}={\left(r_1^{*},r_2^{*},···,r_m^{*}\right)}^T$ is a reference point in the objective space that is dominated by any Pareto optimal objective vector in a Pareto front approximation S. The $HV$ value of S (with regard to $r^{*}$) measures the volume of the region in the objective space dominated by S and bounded by $r^{*}$ [33].

$$HV\left(S\right)=Leb\left(\underset{x\in S}{\cup }\left[f_1\left(x\right),r_1^{*}\right]\times ···\left[f_m\left(x\right),r_m^{*}\right]\right)$$

(21)

where $Leb\left(·\right)$ indicates the Lebesgue measure. $HV$ can measure the approximation in terms of both convergence and diversity. Obviously, the higher the $HV$ value, the better the approximation is. In this paper, the $HV$ value of S is calculated based on Equation (20) with reference point ${\left(1.1,1.1,···\right)}^T$ after normalizing S.

Let $P^{*}$ be a set of points uniformly sampled over the true Pareto front, and S be the set of solutions obtained by DCICA. The $IGD$ value of S is computed as:

$$IGD\left(S,P^{*}\right)={\displaystyle \frac{{\sum }_{x\in P^{*}}dist\left(x,S\right)}{\left|P^{*}\right|}}$$

(22)

$$dist\left(x,S\right)=\underset{j=1}{\overset{\left|S\right|}{min}}∥x_i,p_j∥$$

(23)

where $dist\left(x,S\right)$ is the Euclidean distance between a point $x\in P^{*}$ and its nearest neighbor $p_j\in S$, and $\left|P^{*}\right|$ is the cardinality of $P^{*}$. $IGD$ calculates an average minimum distance from each point in $P^{*}$ to those in S, which measures both convergence and diversity of a solution set S. The lower the $IGD$ value is, the better the quality of S is.

In this study, six algorithms are selected for comparison to comprehensively evaluate the performance of DCICA. These algorithms were chosen based on three criteria: providing a baseline, relevance to energy-efficient scheduling, and handling of deterioration constraints. Specifically, the standard ICA is selected to verify whether the proposed strategies effectively improve upon the original algorithm. Regarding the state-of-the-art methods, MODBH [25], IDWSO [11], HMOBSA [12], and MMOIG [8] are chosen because they are representative metaheuristics specifically designed for EPFSP. They optimize the same objectives (Makespan and TEC) or can be directly adapted to the problem structure of this study. For instance, MMOIG reported superior performance in solving carbon-efficient flow shop problems. Furthermore, since this study considers the deterioration effect, MO-DFWA [13] is selected. Although it originally addressed job deterioration, it serves as a robust benchmark for evaluating algorithm performance under deterioration constraints. For fairness, all comparative algorithms were adapted to the EPFSP-DEM model by incorporating the machine deterioration constraints defined in Equation (1) while retaining their original search mechanisms.

5.2. Parameter Settings

The key parameters of DCICA are listed below: N, $N_{im}$, R, $\beta$, $U_R$, $\lambda$, Z. The Taguchi method is utilized to set parameters. The levels of parameters are shown in Table 4. Table 5 provides the orthogonal array $L_{27}\left(3^7\right)$, where $IGD$ represents the average value obtained by DCICA under three cases of $b_k$, and each combination runs 10 times independently; for instance, $500\times 5$.

Table 4. Parameters of DCICA and their levels.

Parameter	Factor Level
	1	2	3
N	60	80	100
$N_{im}$	6	7	8
R	8	12	16
$\beta$	3	4	5
$U_R$	0.05	0.1	0.15
$\lambda$	0.2	0.4	0.6
Z	4	5	6

Table 5. The orthogonal array $L_{27}\left(3^7\right)$.

No.	Factor							IGD
	N	Nim	R	$\beta$	UR	$\lambda$	Z
1	1	1	1	1	1	1	1	0.031
2	1	1	1	1	2	2	2	0.061
3	1	1	1	1	3	3	3	0.011
4	1	2	2	2	1	1	1	0.003
5	1	2	2	2	2	2	2	0.004
6	1	2	2	2	3	3	3	0.053
7	1	3	3	3	1	1	1	0.062
8	1	3	3	3	2	2	2	0.027
9	1	3	3	3	3	3	3	0.037
10	2	1	2	3	1	2	3	0.033
11	2	1	2	3	2	3	1	0.035
12	2	1	2	3	3	1	2	0.009
13	2	2	3	1	1	2	3	0.019
14	2	2	3	1	2	3	1	0.023
15	2	2	3	1	3	1	2	0.037
16	2	3	1	2	1	2	3	0.033
17	2	3	1	2	2	3	1	0.019
18	2	3	1	2	3	1	2	0.005
19	3	1	3	2	1	3	2	0.057
20	3	1	3	2	2	1	3	0.045
21	3	1	3	2	3	2	1	0.035
22	3	2	1	3	1	3	2	0.019
23	3	2	1	3	2	1	3	0.060
24	3	2	1	3	3	2	1	0.008
25	3	3	2	1	1	3	2	0.044
26	3	3	2	1	2	1	3	0.015
27	3	3	2	1	3	2	1	0.031

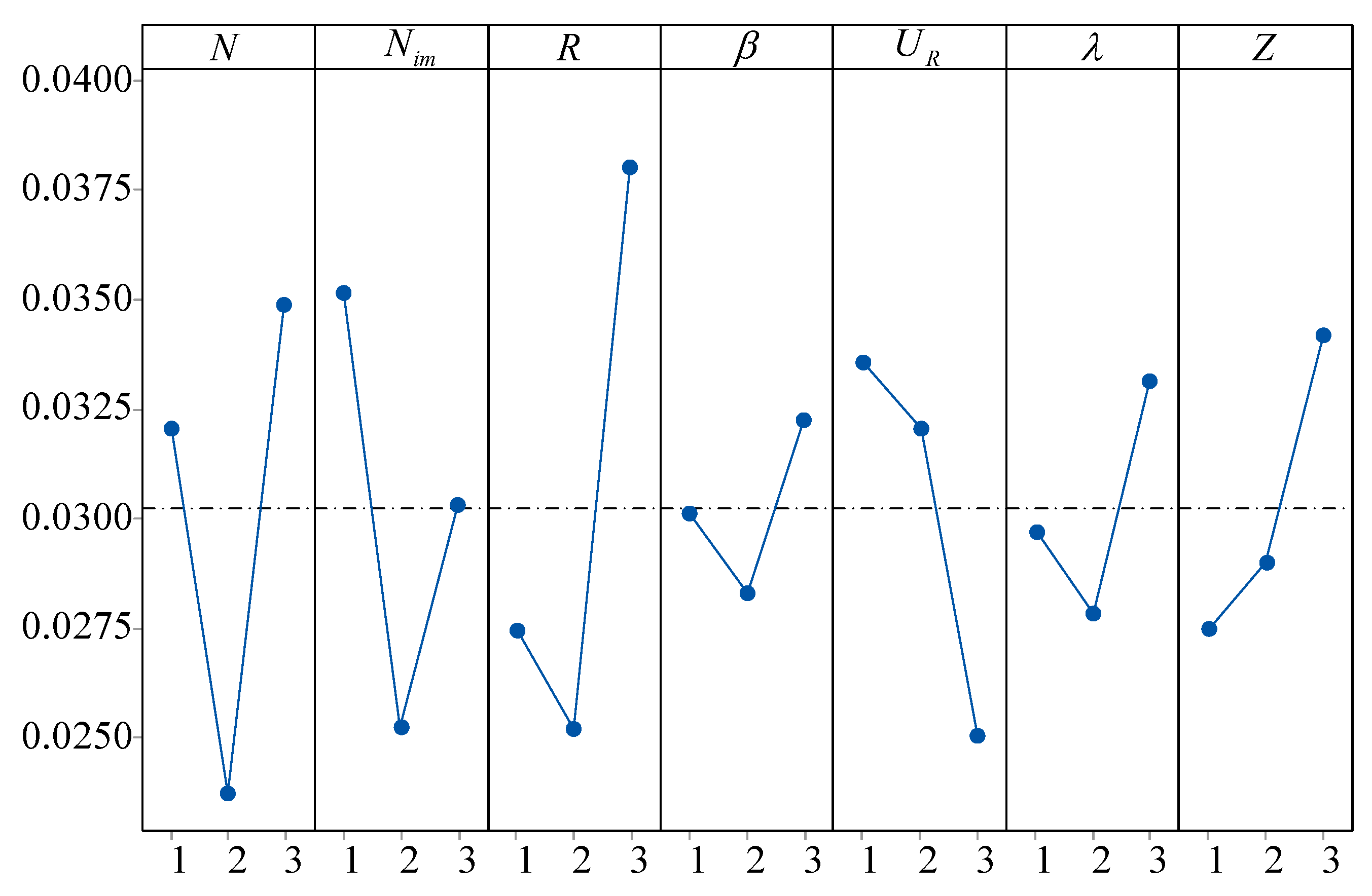
The main effect plot of $IGD$ is presented in Figure 8. As presented in Figure 8, the parameter R has the greatest impact on the performance of DCICA because R determines the depth of local exploration of the algorithm. For population size N, under the premise of fixed total computation time, if N is too large, the total number of evolutionary generations of DCICA will decrease, resulting in insufficient evolution. Otherwise, it will weaken the evolutionary ability of the population at each generation. When a large $U_R$ is determined, DCICA will overly focus on local search, leading to premature convergence. For a small parameter $\beta$, the diversity of DCICA will rapidly decrease. Conversely, it leads to insufficient global search capability. For $N_{im}$, if the value of $N_{im}$ is relatively large, DCICA will fall into a blind search. A large parameter Z is detrimental to information exchange among empires, which will lead to premature convergence of DCICA.

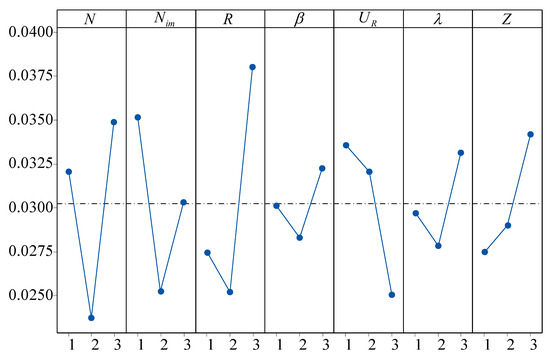
Figure 8. Main effects plot of all parameters on $IGD$. The dashed line represents the total mean value of the IGD metric across all experiments.

Based on the above analysis, the best parameter settings of DCICA are $N=80$, $N_{im}=7$, $R=12$, $\beta =4$, $U_R=0.15$, $\lambda =0.4$, and $Z=4$.

In addition, when $0.2\times n\times m$ seconds of research, DCICA, ICA, MODBH, IDWSO, HMOBSA, MMOIG, and MO-DFWA can converge fully; thus, the stopping condition is set to $0.2\times n\times m$ seconds. To ensure a fair comparison and optimal performance, the parameters for all comparative algorithms were also calibrated using the Taguchi method, identical to the procedure used for DCICA. Extensive preliminary experiments were conducted based on orthogonal arrays to identify the best configuration for each algorithm on the current test instances. Consequently, the resulting optimal parameter settings are listed below: MODBH: $po{p}_{max}=25$, $\tilde{\lambda }=3$. IDWSO: $po{p}_{max}=50$, $F=1$, $T_{max}=2$, $sd=4$. HMOBSA: $po{p}_{max}=50$, $b=0.2$, $p_c=0.9$, $p_m=0.1$. MMOIG: $po{p}_{max}=25$, $\tilde{d}=3$, $\rho =0.4$. MO-DFWA: $po{p}_{max}=30$, $iter\_time=5n$, $lb\_tem=0.3$, $ub\_tem=0.75$, $exp\_r=0.5$.

5.3. Results and Analyses

To reduce the impact of randomness, DCICA, ICA, MODBH, IDWSO, HMOBSA, MMOIG, and MO-DFWA run 10 times independently for all test instances. Since the true Pareto front $P^{*}$ of the investigated problem is unknown, this study adopts the non-dominated solutions of $P_1\cup P_2\cup P_3\cup P_4\cup P_5\cup P_6\cup P_7$ as $P^{*}$ of EPFSP-DEM, where $P_1$, $P_2$, $P_3$, $P_4$, $P_5$, $P_6$ and $P_7$ are the set of non-dominated solutions obtained by DCICA, ICA, MODBH, IDWSO, HMOBSA, MMOIG, and MO-DFWA. Table 6, Table 7, Table 8, Table 9, Table 10 and Table 11 report the results obtained by all algorithms on metrics $IGD$ and $HV$ under three cases of $b_k$.

Table 6. Performance comparison of all algorithms via $IGD$ metric under $b_k\in U\left[0.05,0.15\right]$.

Instance	DCICA	ICA	MODBH	IDWSO	HMOBSA	MMOIG	MO-DFWA
$10\times 5$	0.002	0.327	0.094	0.127	0.110	0.084	0.215
$10\times 10$	0.017	0.209	0.103	0.106	0.115	0.138	0.328
$10\times 15$	0.027	0.215	0.146	0.098	0.160	0.198	0.235
$10\times 20$	0.014	0.203	0.085	0.077	0.109	0.130	0.286
$20\times 5$	0.013	0.265	0.057	0.095	0.097	0.088	0.601
$20\times 10$	0.034	0.209	0.085	0.068	0.138	0.176	0.415
$20\times 15$	0.037	0.162	0.106	0.085	0.101	0.218	0.414
$20\times 20$	0.053	0.226	0.110	0.071	0.131	0.173	0.599
$50\times 5$	0.026	0.285	0.085	0.149	0.137	0.170	0.318
$50\times 10$	0.081	0.198	0.117	0.061	0.152	0.188	0.227
$50\times 15$	0.040	0.218	0.083	0.093	0.136	0.120	0.207
$50\times 20$	0.081	0.206	0.157	0.071	0.207	0.143	0.264
$100\times 5$	0.060	0.171	0.086	0.103	0.119	0.155	0.426
$100\times 10$	0.205	0.639	0.208	0.000	0.373	0.234	0.928
$100\times 15$	0.243	0.339	0.259	0.275	0.228	0.342	0.433
$100\times 20$	0.121	0.174	0.149	0.134	0.146	0.197	0.505
$200\times 5$	0.147	0.274	0.156	0.107	0.206	0.201	0.351
$200\times 10$	0.266	0.291	0.308	0.309	0.305	0.329	0.445
$200\times 15$	0.094	0.183	0.122	0.164	0.180	0.141	0.295
$200\times 20$	0.186	0.255	0.234	0.278	0.278	0.254	0.422
$300\times 5$	0.102	0.221	0.237	0.219	0.205	0.236	0.359
$300\times 10$	0.264	0.288	0.286	0.281	0.285	0.243	0.479
$300\times 15$	0.120	0.250	0.176	0.134	0.192	0.109	0.411
$300\times 20$	0.140	0.633	0.206	0.270	0.362	0.170	0.599
$400\times 5$	0.370	0.454	0.303	0.284	0.345	0.329	0.714
$400\times 10$	0.293	0.389	0.364	0.323	0.355	0.366	0.643
$400\times 15$	0.707	0.920	0.071	0.753	0.345	0.891	0.966
$400\times 20$	0.137	0.352	0.163	0.157	0.136	0.096	0.528
$500\times 5$	0.339	0.364	0.364	0.349	0.363	0.357	0.594
$500\times 10$	0.168	0.237	0.197	0.217	0.205	0.234	0.411
$500\times 15$	0.285	0.333	0.293	0.272	0.319	0.400	0.607
$500\times 20$	0.168	0.165	0.162	0.153	0.157	0.156	0.506

Table 7. Performance comparison of all algorithms via $HV$-metric under $b_k\in U\left[0.05,0.15\right]$.

Instance	DCICA	ICA	MODBH	IDWSO	HMOBSA	MMOIG	MO-DFWA
$10\times 5$	0.731	0.503	0.618	0.611	0.603	0.633	0.451
$10\times 10$	0.788	0.553	0.699	0.669	0.651	0.640	0.499
$10\times 15$	0.714	0.483	0.578	0.674	0.577	0.533	0.440
$10\times 20$	0.762	0.528	0.715	0.722	0.648	0.620	0.428
$20\times 5$	0.828	0.581	0.796	0.753	0.719	0.735	0.328
$20\times 10$	0.813	0.595	0.756	0.768	0.658	0.664	0.412
$20\times 15$	0.752	0.630	0.750	0.732	0.680	0.606	0.512
$20\times 20$	0.769	0.580	0.753	0.712	0.745	0.702	0.414
$50\times 5$	0.789	0.523	0.734	0.711	0.661	0.609	0.486
$50\times 10$	0.679	0.561	0.692	0.764	0.611	0.559	0.451
$50\times 15$	0.769	0.584	0.730	0.770	0.639	0.643	0.495
$50\times 20$	0.823	0.703	0.753	0.868	0.704	0.809	0.536
$100\times 5$	0.721	0.555	0.665	0.632	0.658	0.561	0.425
$100\times 10$	0.767	0.524	0.799	0.923	0.635	0.713	0.543
$100\times 15$	0.725	0.588	0.795	0.657	0.776	0.591	0.301
$100\times 20$	0.875	0.784	0.780	0.853	0.770	0.784	0.365
$200\times 5$	0.716	0.562	0.715	0.736	0.628	0.623	0.441
$200\times 10$	0.701	0.703	0.627	0.654	0.651	0.607	0.283
$200\times 15$	0.754	0.633	0.719	0.734	0.647	0.732	0.467
$200\times 20$	0.608	0.462	0.602	0.536	0.636	0.590	0.360
$300\times 5$	0.726	0.578	0.585	0.527	0.559	0.562	0.306
$300\times 10$	0.555	0.575	0.541	0.545	0.534	0.598	0.293
$300\times 15$	0.744	0.641	0.825	0.787	0.735	0.745	0.447
$300\times 20$	0.740	0.594	0.779	0.708	0.610	0.835	0.568
$400\times 5$	0.716	0.662	0.859	0.809	0.739	0.771	0.115
$400\times 10$	0.627	0.435	0.510	0.573	0.476	0.506	0.142
$400\times 15$	0.546	0.481	0.860	0.529	0.762	0.517	0.447
$400\times 20$	0.685	0.451	0.673	0.756	0.651	0.688	0.386
$500\times 5$	0.538	0.430	0.469	0.500	0.470	0.491	0.182
$500\times 10$	0.760	0.762	0.773	0.721	0.736	0.660	0.369
$500\times 15$	0.648	0.563	0.633	0.674	0.567	0.454	0.164

Table 8. Performance comparison of all algorithms via $IGD$-metric under $b_k\in U\left[0.15,0.25\right]$.

Instance	DCICA	ICA	MODBH	IDWSO	HMOBSA	MMOIG	MO-DFWA
$500\times 20$	0.366	0.387	0.347	0.379	0.399	0.350	0.293
$10\times 5$	0.006	0.286	0.107	0.138	0.124	0.112	0.317
$10\times 10$	0.012	0.239	0.069	0.094	0.107	0.103	0.329
$10\times 15$	0.052	0.154	0.092	0.052	0.085	0.107	0.225
$10\times 20$	0.021	0.171	0.100	0.126	0.128	0.178	0.383
$20\times 5$	0.051	0.214	0.077	0.086	0.093	0.118	0.245
$20\times 10$	0.072	0.184	0.134	0.087	0.133	0.160	0.323
$20\times 15$	0.060	0.137	0.068	0.040	0.125	0.123	0.599
$20\times 20$	0.106	0.226	0.120	0.116	0.136	0.142	0.307
$50\times 5$	0.032	0.193	0.071	0.075	0.090	0.133	0.331
$50\times 10$	0.094	0.253	0.095	0.135	0.170	0.187	0.424
$50\times 15$	0.064	0.196	0.088	0.109	0.200	0.180	0.318
$50\times 20$	0.064	0.257	0.158	0.137	0.141	0.152	0.480
$100\times 5$	0.214	0.376	0.160	0.107	0.258	0.168	0.588
$100\times 10$	0.131	0.255	0.136	0.165	0.198	0.202	0.507
$100\times 15$	0.190	0.273	0.254	0.270	0.331	0.258	0.463
$100\times 20$	0.173	0.297	0.221	0.180	0.226	0.199	0.401
$200\times 5$	0.087	0.240	0.150	0.172	0.194	0.249	0.651
$200\times 10$	0.205	0.291	0.222	0.236	0.238	0.253	0.588
$200\times 15$	0.111	0.411	0.116	0.337	0.181	0.235	0.633
$200\times 20$	0.189	0.224	0.267	0.200	0.185	0.218	0.404
$300\times 5$	0.099	0.232	0.187	0.116	0.112	0.180	0.417
$300\times 10$	0.209	0.379	0.282	0.311	0.256	0.335	0.678
$300\times 15$	0.087	0.315	0.165	0.149	0.308	0.184	0.598
$300\times 20$	0.262	0.269	0.286	0.304	0.264	0.243	0.475
$400\times 5$	0.301	0.327	0.262	0.302	0.308	0.304	0.517
$400\times 10$	0.169	0.256	0.223	0.212	0.231	0.244	0.647
$400\times 15$	0.060	0.307	0.083	0.159	0.188	0.100	0.480
$400\times 20$	0.074	0.217	0.115	0.155	0.177	0.209	0.780
$500\times 5$	0.282	0.363	0.285	0.272	0.315	0.298	0.687
$500\times 10$	0.132	0.276	0.188	0.222	0.321	0.294	0.462
$500\times 15$	0.192	0.242	0.248	0.162	0.293	0.246	0.593
$500\times 20$	0.112	0.177	0.182	0.294	0.152	0.213	0.433

Table 9. Performance comparison of all algorithms via $HV$-metric under $b_k\in U\left[0.15,0.25\right]$.

Instance	DCICA	ICA	MODBH	IDWSO	HMOBSA	MMOIG	MO-DFWA
$10\times 5$	0.732	0.406	0.604	0.558	0.569	0.584	0.426
$10\times 10$	0.783	0.455	0.658	0.629	0.631	0.611	0.375
$10\times 15$	0.623	0.480	0.570	0.639	0.580	0.554	0.454
$10\times 20$	0.679	0.501	0.656	0.595	0.541	0.508	0.294
$20\times 5$	0.615	0.423	0.593	0.573	0.561	0.487	0.383
$20\times 10$	0.759	0.572	0.744	0.709	0.659	0.669	0.416
$20\times 15$	0.761	0.638	0.741	0.764	0.679	0.691	0.353
$20\times 20$	0.796	0.589	0.801	0.776	0.744	0.741	0.471
$50\times 5$	0.757	0.495	0.680	0.689	0.659	0.636	0.412
$50\times 10$	0.841	0.653	0.846	0.823	0.747	0.741	0.396
$50\times 15$	0.640	0.478	0.599	0.610	0.500	0.506	0.380
$50\times 20$	0.809	0.641	0.760	0.718	0.714	0.726	0.453
$100\times 5$	0.728	0.603	0.775	0.860	0.686	0.788	0.285
$100\times 10$	0.805	0.668	0.930	0.851	0.721	0.781	0.405
$100\times 15$	0.903	0.750	0.811	0.806	0.731	0.886	0.370
$100\times 20$	0.693	0.527	0.614	0.562	0.747	0.647	0.309
$200\times 5$	0.751	0.482	0.778	0.699	0.615	0.530	0.210
$200\times 10$	0.893	0.704	0.800	0.774	0.771	0.818	0.271
$200\times 15$	0.728	0.410	0.693	0.493	0.627	0.554	0.274
$200\times 20$	0.398	0.351	0.426	0.392	0.452	0.339	0.397
$300\times 5$	0.722	0.493	0.630	0.694	0.718	0.571	0.343
$300\times 10$	0.930	0.685	0.803	0.744	0.820	0.706	0.181
$300\times 15$	0.795	0.474	0.637	0.704	0.523	0.658	0.204
$300\times 20$	0.787	0.766	0.680	0.697	0.766	0.798	0.328
$400\times 5$	0.617	0.620	0.730	0.639	0.637	0.648	0.222
$400\times 10$	0.800	0.727	0.738	0.788	0.759	0.718	0.225
$400\times 15$	0.765	0.547	0.799	0.619	0.633	0.726	0.319
$400\times 20$	0.795	0.593	0.701	0.694	0.750	0.657	0.341
$500\times 5$	0.474	0.346	0.493	0.534	0.395	0.444	0.140
$500\times 10$	0.817	0.617	0.861	0.823	0.635	0.799	0.400
$500\times 15$	0.756	0.652	0.829	0.758	0.600	0.682	0.247
$500\times 20$	0.894	0.733	0.776	0.550	0.766	0.673	0.411

Table 10. Performance comparison of all algorithms via $IGD$-metric under $b_k\in U\left[0.25,0.40\right]$.

Instance	DCICA	ICA	MODBH	IDWSO	HMOBSA	MMOIG	MO-DFWA
$10\times 5$	0.012	0.305	0.068	0.177	0.109	0.100	0.292
$10\times 10$	0.032	0.239	0.116	0.080	0.131	0.149	0.593
$10\times 15$	0.097	0.206	0.055	0.127	0.124	0.135	0.283
$10\times 20$	0.030	0.201	0.103	0.094	0.143	0.111	0.391
$20\times 5$	0.015	0.169	0.139	0.087	0.124	0.135	0.445
$20\times 10$	0.051	0.232	0.078	0.067	0.177	0.133	0.633
$20\times 15$	0.088	0.189	0.092	0.064	0.173	0.163	0.401
$20\times 20$	0.049	0.188	0.061	0.086	0.106	0.109	0.350
$50\times 5$	0.030	0.269	0.060	0.141	0.134	0.260	0.589
$50\times 10$	0.143	0.398	0.137	0.175	0.355	0.217	0.530
$50\times 15$	0.037	0.283	0.085	0.050	0.128	0.139	0.491
$50\times 20$	0.126	0.362	0.187	0.250	0.279	0.307	0.479
$100\times 5$	0.088	0.194	0.098	0.135	0.148	0.142	0.548
$100\times 10$	0.070	0.486	0.299	0.324	0.313	0.303	0.357
$100\times 15$	0.130	0.250	0.142	0.150	0.229	0.199	0.473
$100\times 20$	0.392	0.475	0.049	0.217	0.432	0.246	0.441
$200\times 5$	0.123	0.297	0.222	0.186	0.258	0.224	0.495
$200\times 10$	0.199	0.419	0.457	0.167	0.662	0.410	0.644
$200\times 15$	0.131	0.336	0.261	0.261	0.374	0.350	0.451
$200\times 20$	0.177	0.879	0.443	0.665	0.825	0.717	0.711
$300\times 5$	0.205	0.282	0.211	0.202	0.184	0.185	0.542
$300\times 10$	0.453	0.426	0.336	0.393	0.373	0.381	0.446
$300\times 15$	0.181	0.344	0.222	0.218	0.220	0.187	0.553
$300\times 20$	0.271	0.479	0.366	0.181	0.317	0.280	0.474
$400\times 5$	0.296	0.373	0.293	0.340	0.328	0.317	0.543
$400\times 10$	0.370	0.403	0.318	0.279	0.352	0.385	0.530
$400\times 15$	0.101	0.292	0.461	0.118	0.291	0.212	0.702
$400\times 20$	0.251	0.237	0.196	0.320	0.208	0.318	0.631
$500\times 5$	0.205	0.227	0.215	0.215	0.219	0.229	0.68
$500\times 10$	0.097	0.243	0.125	0.130	0.138	0.145	0.423
$500\times 15$	0.103	0.164	0.193	0.161	0.148	0.206	0.314
$500\times 20$	0.169	0.213	0.209	0.232	0.267	0.273	0.398

Table 11. Performance comparison of all algorithms via $HV$-metric under $b_k\in U\left[0.25,0.40\right]$.

Instance	DCICA	ICA	MODBH	IDWSO	HMOBSA	MMOIG	MO-DFWA
$10\times 5$	0.762	0.549	0.693	0.659	0.653	0.695	0.434
$10\times 10$	0.870	0.609	0.761	0.837	0.758	0.725	0.370
$10\times 15$	0.615	0.478	0.635	0.579	0.572	0.563	0.409
$10\times 20$	0.698	0.539	0.614	0.663	0.579	0.581	0.316
$20\times 5$	0.696	0.471	0.609	0.601	0.574	0.568	0.356
$20\times 10$	0.748	0.498	0.752	0.744	0.634	0.696	0.337
$20\times 15$	0.715	0.516	0.663	0.686	0.555	0.601	0.516
$20\times 20$	0.725	0.518	0.724	0.690	0.626	0.660	0.356
$50\times 5$	0.743	0.541	0.725	0.586	0.648	0.549	0.354
$50\times 10$	0.715	0.353	0.543	0.561	0.402	0.593	0.389
$50\times 15$	0.774	0.559	0.808	0.833	0.653	0.714	0.299
$50\times 20$	0.787	0.566	0.866	0.684	0.577	0.557	0.346
$100\times 5$	0.614	0.536	0.604	0.566	0.525	0.579	0.214
$100\times 10$	0.949	0.560	0.704	0.700	0.667	0.699	0.551
$100\times 15$	0.705	0.597	0.712	0.735	0.649	0.721	0.359
$100\times 20$	0.501	0.447	0.842	0.700	0.498	0.568	0.538
$200\times 5$	0.657	0.437	0.492	0.564	0.447	0.483	0.246
$200\times 10$	0.902	0.587	0.566	0.890	0.537	0.774	0.567
$200\times 15$	0.744	0.777	0.711	0.741	0.781	0.646	0.399
$200\times 20$	0.831	0.578	0.829	0.693	0.588	0.679	0.649
$300\times 5$	0.653	0.540	0.618	0.637	0.651	0.601	0.210
$300\times 10$	0.569	0.430	0.660	0.543	0.540	0.545	0.287
$300\times 15$	0.805	0.563	0.653	0.657	0.633	0.729	0.521
$300\times 20$	0.746	0.620	0.709	0.816	0.766	0.735	0.243
$400\times 5$	0.468	0.392	0.478	0.413	0.436	0.431	0.296
$400\times 10$	0.454	0.396	0.533	0.614	0.491	0.431	0.230
$400\times 15$	0.753	0.561	0.449	0.628	0.520	0.554	0.367
$400\times 20$	0.793	0.822	0.833	0.754	0.830	0.777	0.268
$500\times 5$	0.650	0.549	0.557	0.622	0.593	0.572	0.156
$500\times 10$	0.783	0.578	0.767	0.737	0.734	0.680	0.421
$500\times 15$	0.576	0.722	0.595	0.565	0.625	0.527	0.404
$500\times 20$	0.718	0.586	0.554	0.622	0.504	0.516	0.357

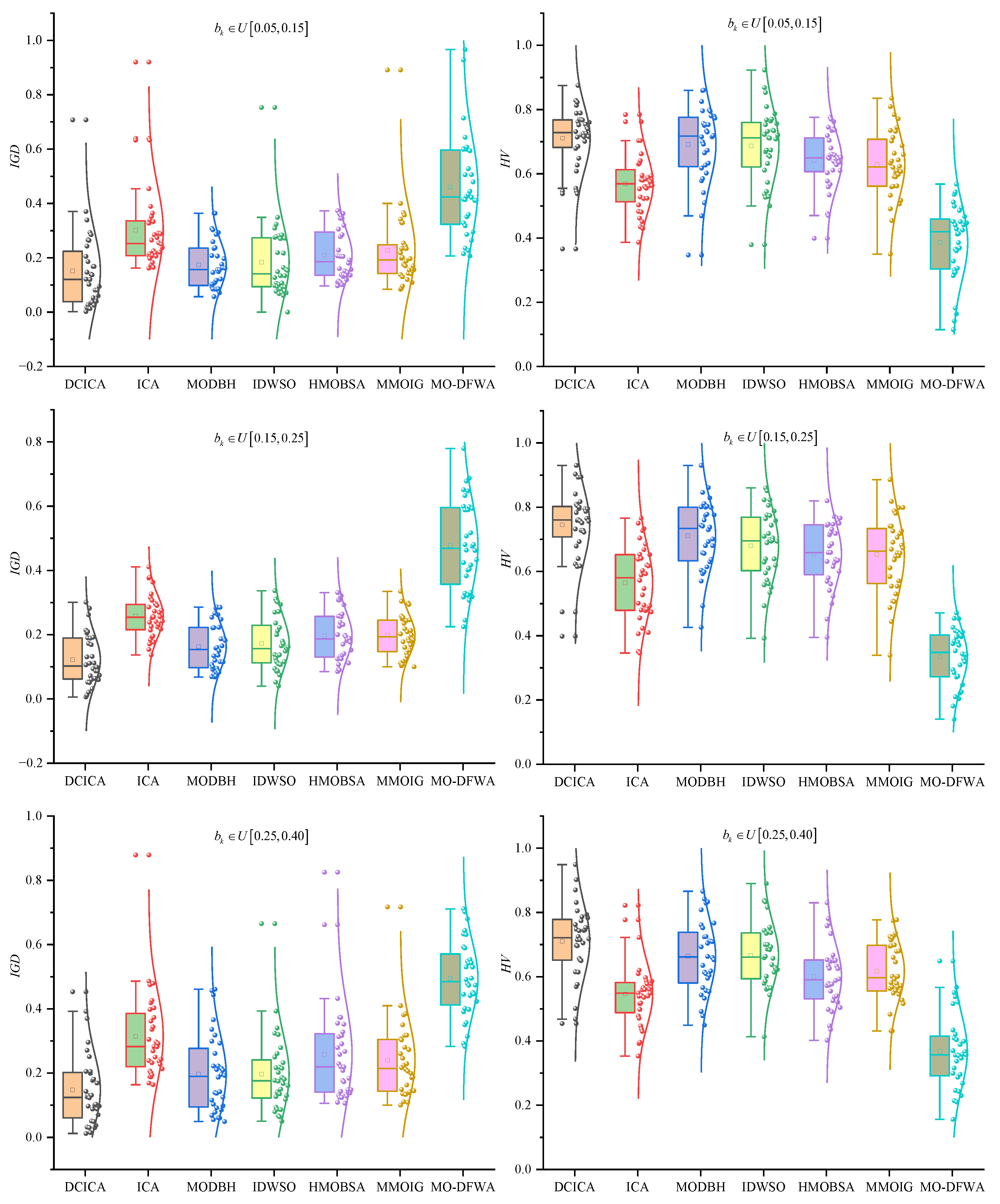
As presented in Table 6, Table 7, Table 8, Table 9, Table 10 and Table 11, the values of the metrics $IGD$ and $HV$ achieved by DCICA are better than those of ICA, MODBH, IDWSO, HMOBSA, MMOIG, and MO-DFWA on most test instances under the three cases of $b_k$, distributed in $U\left[0.05,0.15\right]$, $U\left[0.15,0.25\right]$, $U\left[0.25,0.40\right]$, which is analyzed systematically as follows.

Under the first case $b_k\in U\left[0.05,0.15\right]$, the metric $IGD$ of DCICA performs better than those of ICA, MODBH, IDWSO, HMOBSA, MMOIG, and MO-DFWA on 31, 29, 25, 27, 27, and 32 test instances. The metric $HV$ of DCICA is superior to ICA, MODBH, IDWSO, HMOBSA, MMOIG, and MO-DFWA on 28, 24, 22, 27, 27, and 32 test instances. Therefore, DCICA is superior to ICA, MODBH, IDWSO, HMOBSA, MMOIG, and MO-DFWA on metrics $IGD$ and $HV$ under $b_k\in \left[0.05,0.15\right]$.

Under the second case $b_k\in U\left[0.15,0.25\right]$, the metric $IGD$ of DCICA is less than that of ICA, MODBH, IDWSO, HMOBSA, MMOIG, and MO-DFWA on 32, 30, 27, 31, 30, and 32 test instances. In other words, DCICA obtains better results than comparative algorithms over $87\%$ test instances. For metric $HV$, DCICA outperforms ICA, MODBH, IDWSO, HMOBSA, MMOIG, and MO-DFWA on 31, 21, 24, 29, 29, and 32 instances.

Under the third case $b_k\in U\left[0.25,0.40\right]$, metric $IGD$ produced by DCICA is better than ICA, MODBH, IDWSO, HMOBSA, MMOIG, and MO-DFWA on 29, 27, 26, 29, 30, 32 test instances. For metrics $HV$, DCICA performs better than the compared algorithms on most instances. Moreover, the metric $IGD$ of DCICA performs better than those of ICA over $87\%$ test instances under $b_k\in U\left[0.25,0.40\right]$, which also implies that the new strategies of DCICA are effective in solving EPFSP-DEM.

Table 12 shows the success rates of DCICA on metrics $IGD$ and $HV$ under three cases of $b_k$, namely $b_k\in U\left[0.05,0.15\right]$, $b_k\in U\left[0.15,0.25\right]$, and $b_k\in U\left[0.25,0.40\right]$.

Table 12. The success rates of DCICA on metrics $IGD$ and $HV$ under three cases of $b_k$.

Comparison	Metric	First Case of ${\mathit{b}}_{\mathit{k}}$	First Second of ${\mathit{b}}_{\mathit{k}}$	Third Case of ${\mathit{b}}_{\mathit{k}}$
DCICA vs. ICA	$IGD$	$96.9\%$	$100\%$	$90.9\%$
	$HV$	$84.8\%$	$96.9\%$	$87.9\%$
DCICA vs. MODBH	$IGD$	$87.9\%$	$90.9\%$	$75.8\%$
	$HV$	$72.7\%$	$63.6\%$	$63.6\%$
DCICA vs. IDWSO	$IGD$	$75.8\%$	$81.8\%$	$75.8\%$
	$HV$	$66.7\%$	$72.7\%$	$81.8\%$
DCICA vs. HMOBSA	$IGD$	$81.8\%$	$96.9\%$	$84.8\%$
	$HV$	$81.8\%$	$87.9\%$	$81.8\%$
DCICA vs. MMOIG	$IGD$	$81.8\%$	$90.9\%$	$87.9\%$
	$HV$	$81.8\%$	$87.9\%$	$90.9\%$
DCICA vs. MODFWA	$IGD$	$100\%$	$100\%$	$96.9\%$
	$HV$	$100\%$	$100\%$	$96.9\%$

Figure 9 and Figure 10 are the box plots of metrics and non-dominated solutions produced by all algorithms. As shown in Figure 9, for the metric $IGD\left(HV\right)$, the average values of DCICA are lower (higher) than those of ICA, MODBH, IDWSO, HMOBSA, MMOIG, and MO-DFWA. Hence, it indicates that DCICA is superior to ICA, MODBH, IDWSO, HMOBSA, MMOIG, and MO-DFWA. In Figure 10, it can be observed that the convergence of DCICA is better than that of other methods, and the solutions obtained by DCICA are also uniformly distributed in the search space. Therefore, the non-dominated solution distributions also illustrate that DCICA is superior to ICA, MODBH, IDWSO, HMOBSA, MMOIG, and MO-DFWA in solving EPFSP-DEM.

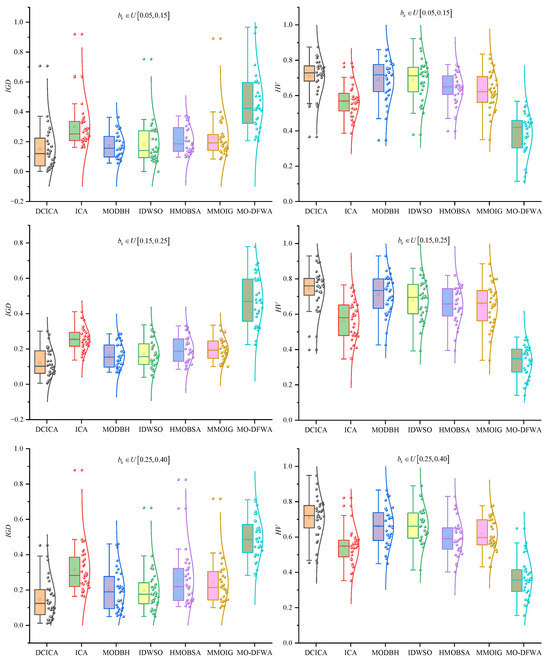
Figure 9. Boxplot of all algorithms on metrics $IGD$ and $HV$.

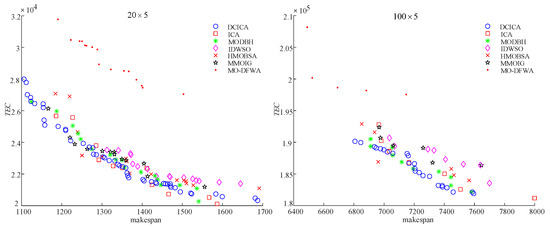
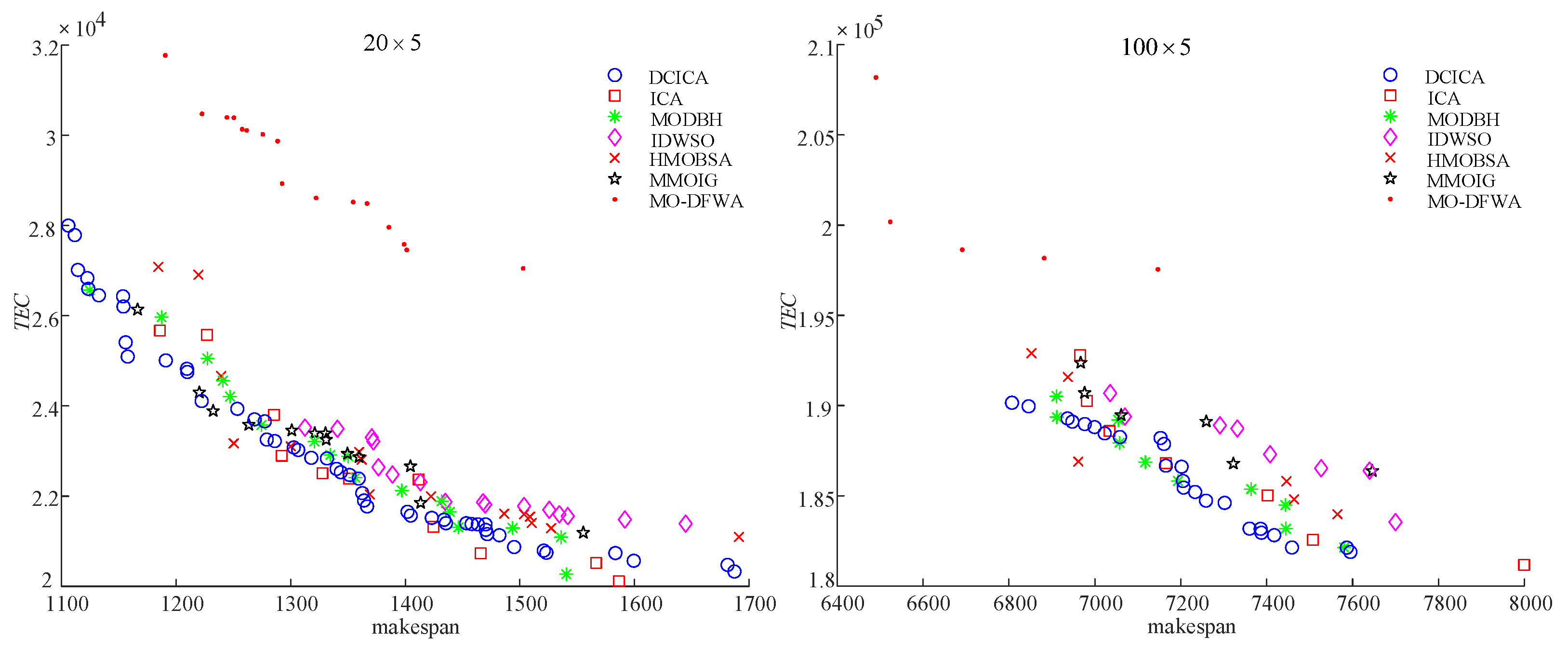
Figure 10. Non-dominated solutions for instances $20\times 5$ and $100\times 5$ under $b_k\in U\left[0.15,0.25\right]$.

Statistics play a vital role in experiment result analyses, which can void influences from random factors. In this section, the Wilcoxon test, as a widely used test method, is adopted to determine the validity between DCICA and other compared algorithms. In principle, the Wilcoxon test utilizes the signed test of paired observation data to deduce the probability when the difference appears. $R^{+}$ represents that the results are outstanding compared with the other algorithms, and $R^{-}$ is the opposite. For each pair, the sum of $R^{+}$ and $R^{-}$ is equal to the total case numbers.

The statistical results through the Wilcoxon test at $95\%$ confidence interval are presented in Table 13, Table 14 and Table 15, where “Yes” represents that a significant difference exists between DCICA and the comparative algorithm. In this study, the confidence level $\alpha$ is set to 0.05. If the p-value is less than $\alpha$ through the Wilcoxon test, it indicates that there are significant differences between the pairwise algorithms. In Table 13, Table 14 and Table 15, it can be found that all p-values are less than $\alpha$ on pairwise algorithms. That is, there are significant differences between DCICA and pairwise algorithms (ICA, MODBH, IDWSO, HMOBSA, MMOIG, and MO-DFWA) in solving EPFSP-DEM.

Table 13. Results achieved by the Wilcoxon test under $b_k\in U\left[0.05,0.15\right]$.

Comparison	Metric	${\mathit{R}}^{+}$	${\mathit{R}}^{-}$	p-Value	$\mathit{\alpha }=0.05$
DCICA vs. ICA	$IGD$	31	1	$8.7321\times {10}^{-7}$	Yes
	$HV$	28	4	$2.0\times {10}^{-6}$	Yes
DCICA vs. MODBH	$IGD$	29	3	$1.08\times {10}^{-4}$	Yes
	$HV$	24	8	$2.669\times {10}^{-2}$	Yes
DCICA vs. IDWSO	$IGD$	25	7	$1.256\times {10}^{-3}$	Yes
	$HV$	22	10	$4.6404\times {10}^{-2}$	Yes
DCICA vs. HMOBSA	$IGD$	27	5	$4.1\times {10}^{-5}$	Yes
	$HV$	27	5	$1.17\times {10}^{-4}$	Yes
DCICA vs. MMOIG	$IGD$	27	5	$6.0\times {10}^{-4}$	Yes
	$HV$	27	5	$2.6\times {10}^{-6}$	Yes
DCICA vs. MODFWA	$IGD$	32	0	$7.9259\times {10}^{-7}$	Yes
	$HV$	32	0	$9.441\times {10}^{-7}$	Yes

Table 14. Results achieved by the Wilcoxon test under $b_k\in U\left[0.15,0.25\right]$.

Comparison	Metric	${\mathit{R}}^{+}$	${\mathit{R}}^{-}$	p-Value	$\mathit{\alpha }=0.05$
DCICA vs. ICA	$IGD$	32	0	$7.9485\times {10}^{-7}$	Yes
	$HV$	31	1	$8.7513\times {10}^{-7}$	Yes
DCICA vs. MODBH	$IGD$	30	2	$1.2\times {10}^{-5}$	Yes
	$HV$	21	11	$1.4672\times {10}^{-2}$	Yes
DCICA vs. IDWSO	$IGD$	27	4	$9.2\times {10}^{-5}$	Yes
	$HV$	24	8	$4.55\times {10}^{-4}$	Yes
DCICA vs. HMOBSA	$IGD$	31	1	$9.6004\times {10}^{-7}$	Yes
	$HV$	29	3	$6.0\times {10}^{-6}$	Yes
DCICA vs. MMOIG	$IGD$	30	2	$2.0\times {10}^{-6}$	Yes
	$HV$	29	3	$4.0\times {10}^{-6}$	Yes
DCICA vs. MODFWA	$IGD$	32	0	$7.9485\times {10}^{-7}$	Yes
	$HV$	32	0	$7.9441\times {10}^{-7}$	Yes

Table 15. Results achieved by the Wilcoxon test under $b_k\in U\left[0.25,0.40\right]$.

Comparison	Metric	${\mathit{R}}^{+}$	${\mathit{R}}^{-}$	p-Value	$\mathit{\alpha }=0.05$
DCICA vs. ICA	$IGD$	30	2	$1.0\times {10}^{-6}$	Yes
	$HV$	29	3	$4.0\times {10}^{-6}$	Yes
DCICA vs. MODBH	$IGD$	25	7	$3.427\times {10}^{-3}$	Yes
	$HV$	21	11	$3.2264\times {10}^{-2}$	Yes
DCICA vs. IDWSO	$IGD$	25	7	$5.179\times {10}^{-3}$	Yes
	$HV$	27	5	$3.2264\times {10}^{-2}$	Yes
DCICA vs. HMOBSA	$IGD$	28	4	$1.0\times {10}^{-5}$	Yes
	$HV$	27	5	$1.8\times {10}^{-5}$	Yes
DCICA vs. MMOIG	$IGD$	29	3	$3.6\times {10}^{-5}$	Yes
	$HV$	30	2	$4.0\times {10}^{-6}$	Yes
DCICA vs. MODFWA	$IGD$	31	1	$8.7465\times {10}^{-7}$	Yes
	$HV$	31	1	$8.7417\times {10}^{-7}$	Yes

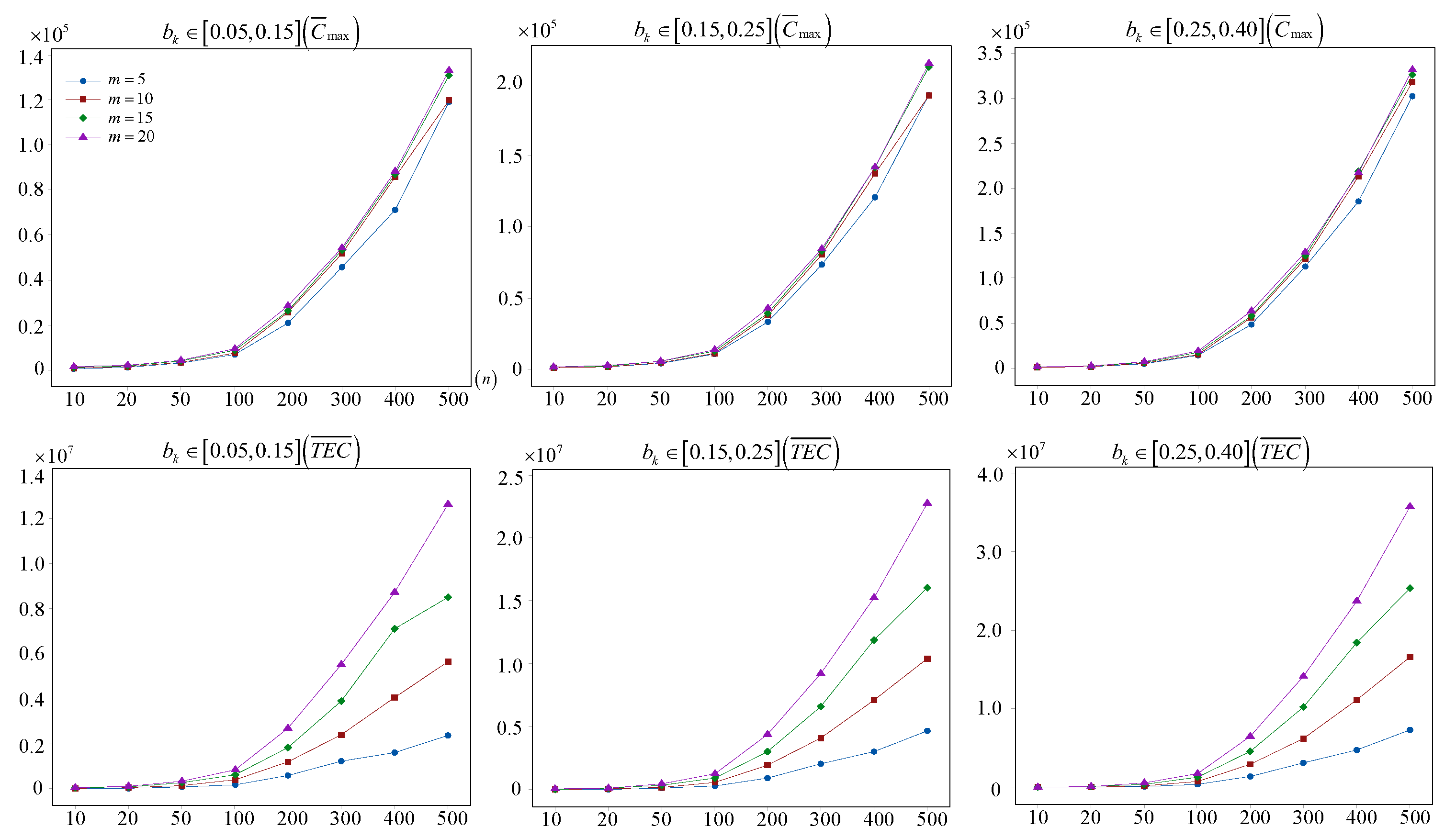
5.4. Analysis of the Deterioration Effect

To observe the results more intuitively and analyze the influence of the deterioration effect for EPFSP-DEM, the results obtained by DCICA are listed in Table 16, Table 17 and Table 18 and presented in Figure 11, where ${\overline{C}}_{max}$ and $\overline{TEC}$ are the average value of $C_{max}$ and $TEC$ of non-dominated solutions produced by DCICA for each instance. Since EPFSP-DEM is a multi-objective optimization problem and many non-dominated solutions are commonly obtained, adopting ${\overline{C}}_{max}$ and $\overline{TEC}$ can better measure variations in $C_{max}$ and $TEC$ that are caused by the deterioration effect of machines.

Table 16. The values of ${\overline{C}}_{max}$ and $\overline{TEC}$ obtained by DCICA under $b_k\in U\left[0.05,0.15\right]$.

n	${\overline{\mathit{C}}}_{max}$				$\overline{\mathit{TEC}}$
	$\mathit{m}$ = 5	$\mathit{m}$ = 10	$\mathit{m}$ = 15	$\mathit{m}$ = 20	$\mathit{m}$ = 5	$\mathit{m}$ = 10	$\mathit{m}$ = 15	$\mathit{m}$ = 20
10	744.8	1022.9	1300.9	1594.7	11,084.7	22,413.1	35,086.6	48,671.4
20	1341.4	1670.2	2002.7	2264.6	23,082.1	51,786.6	81,647.5	106,298.4
50	3297.4	3743.8	4256.9	4458.4	75,562.6	157,673.7	261,638.6	337,398.9
100	7194.6	7699.3	8908.6	9774.5	186,100.6	390,540.9	623,940.8	85,8321.7
200	21,159.0	25,774.7	26,520.3	28,818.9	587,859.2	1,192,689.1	1,826,445.9	2,707,292.7
300	45,943.6	51,905.7	53,300.3	54,482.5	1,230,018.1	2,401,650.7	3,907,046.8	5,513,531.4
400	71,255.2	85,790.1	86,937.6	88,372.9	1,595,467.3	4,068,905.8	7,108,554.4	8,731,750.9
500	119,021.2	119,637.3	130,847.3	133,095.7	2,373,959.9	5,639,544.4	8,534,803.4	12,656,250.6

Table 17. The values of ${\overline{C}}_{max}$ and $\overline{TEC}$ obtained by DCICA under $b_k\in U\left[0.15,0.25\right]$.

n	${\overline{\mathit{C}}}_{max}$				$\overline{\mathit{TEC}}$
	$\mathit{m}$ = 5	$\mathit{m}$ = 10	$\mathit{m}$ = 15	$\mathit{m}$ = 20	$\mathit{m}$ = 5	$\mathit{m}$ = 10	$\mathit{m}$ = 15	$\mathit{m}$ = 20
10	821.1	1081.3	1358.6	1670.9	11,364.9	24,175.2	39,000.6	53,504.9
20	1462.9	1738.8	2166.2	2458.9	27,460.6	63,877.3	97,888.4	126,240.1
50	4166.4	4628.0	5357.3	5617.0	96,621.1	208,098.6	338,520.9	445,132.3
100	10,424.2	11,184.0	12,686.3	13,523.8	275,391.7	584,091.1	926,657.4	1,282,881.9
200	33,251.2	37,595.8	39,050.8	42,939.3	941,765.7	1,953,512.3	3,039,934.7	4,400,782.5
300	73,593.7	80,510.5	82,771.6	84,401.8	2,032,540.3	4,103,816.5	6,633,375.5	9,231,971.7
400	120,621.5	137,227.4	141,618.3	141,637.5	3,045,587.9	7,109,819.7	1,192,7653.4	15,258,051.6
500	192,313.5	192,123.1	212,207.1	214,342.6	4,694,431.3	10,407,974.5	16,050,939.5	22,776,233.6

Table 18. The values of ${\overline{C}}_{max}$ and $\overline{TEC}$ obtained by DCICA under $b_k\in U\left[0.25,0.40\right]$.

n	${\overline{\mathit{C}}}_{max}$				$\overline{\mathit{TEC}}$
	$\mathit{m}$ = 5	$\mathit{m}$ = 10	$\mathit{m}$ = 15	$\mathit{m}$ = 20	$\mathit{m}$ = 5	$\mathit{m}$ = 10	$\mathit{m}$ = 15	$\mathit{m}$ = 20
10	879.1	1207.7	1529.7	1796.5	12,930.1	26,520.6	41,692.1	59,360.6
20	1719.3	2030.3	2498.3	2839.7	29,680.5	71,900.2	112,759.5	147,470.3
50	5245.4	6025.3	6697.2	7284.7	126,074.6	265,801.6	444,319.2	572,209.7
100	14,454.9	15,225.7	17,709.8	18,826.9	376,423.1	806,429.0	1,305,623.8	1,809,725.2
200	49,005.3	56,297.4	58,274.7	63,409.6	1420,049.9	2,937,850.2	4,563,153.9	6,525,644.6
300	113,258.5	121,823.6	124,744.8	129,122.3	3,128,478.3	6,262,951.4	10,204,053.9	14,169,815.8
400	185,333.2	213,760.4	218,618.1	217,330.7	4,744,003.7	11,153,238.0	18,435,567.0	23,661,265.1
500	302,673.9	318,812.1	326,365.1	331,950.2	7,350,983.0	16,608,890.3	25,341,889.6	35,710,311.0

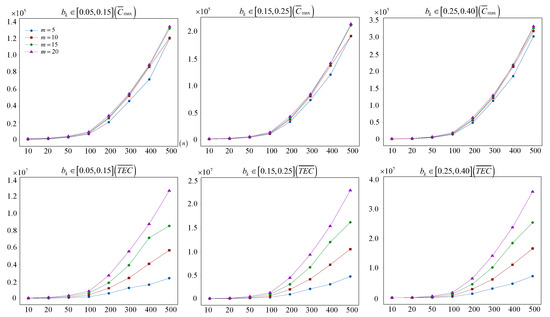
Figure 11. The influence on ${\overline{C}}_{max}$ and $\overline{TEC}$.

As shown in Figure 11, the horizontal comparisons indicate that as the number of jobs increases, the influence of the deterioration effect for variations of ${\overline{C}}_{max}$ and $\overline{TEC}$ generally shows an increasingly serious trend. Especially, the deterioration effect brings notable influences for large-scale test instances under the same number of machines. However, as the number of machines increases, the influence of the deterioration effect on ${\overline{C}}_{max}$ is slightly less than that on $\overline{TEC}$ under the same deterioration rate, as presented in Figure 11.

The search performances of DCICA mainly contribute to the following four aspects: (1) the proposed differentiated assimilation can improve the diversity of the population since many learning objects are kept, which can enlarge the search area and continuously update their status; (2) the knowledge-guided revolution is beneficial to efficiently allocate computing resources, and the blindness of randomly selecting neighborhood structures is avoided; (3) the newly defined convergence and diversity can effectively evaluate the search quality of differentiated assimilation and knowledge-guided revolution, which can guide the search of DCICA further and balance exploration and exploitation; (4) the novel imperialist competition can prevent premature convergence of algorithms, enhance information exchange among empires, and strengthen the search for worse solutions.

6. Conclusions

This paper investigated the Energy-Efficient Permutation Flow Shop Scheduling Problem with Machine Deterioration Effects (EPFSP-DEM) through the lens of computational intelligence theory, providing novel insights into the interplay between scheduling dynamics, energy consumption, and system degradation. Since the investigated problem is NP-hard, this study proposes a DCICA to optimize $C_{max}$ and $TEC$ simultaneously. Extensive experiments were conducted, and the results demonstrated that DCICA outperforms the existing algorithms in solving EPFSP-DEM. In addition, it was also observed that as the number of jobs increases, the impact of the deterioration effect on both makespan and total energy consumption generally exhibits an increasingly serious trend. Especially, the deterioration effect brings notable influences for large-scale test instances under the same number of machines. However, as the number of machines increases, the influence of the deterioration effect on makespan is slightly less than the total energy consumption under the same deterioration rate. However, potential limitations exist. The introduced mechanisms increase computational complexity compared to standard ICA, and the algorithm remains sensitive to parameter settings (e.g., $\beta ,\lambda$), necessitating careful calibration. In the future, this study will investigate Energy-Efficient Permutation Flow Shop Scheduling Problems with other constraints, such as machine preventive maintenance and transportation. Uncertainty dynamic factors, such as job delay and machine breakdowns, are also to be considered in our future work. Moreover, this study will explore other optimization algorithms, such as the particle swarm algorithm and the ant colony algorithm, to solve EPFSP-DEM.