Gaussian Learning-Based Pareto Evolutionary Algorithm for Parallel Machine Planning in Industrial Silicon Production

Abstract

This study focuses on a multi-objective heterogeneous parallel machine planning problem for industrial silicon smelting. Specifically, under the conflicting objectives of minimizing carbon emissions, rollover penalty costs, and load imbalance, the total production demand of industrial silicon is allocated monthly across multiple machines. We first establish the mathematical model of the problem accounting for real-life management requirements. To solve the model, a Gaussian learning-based Pareto evolutionary algorithm (GLPEA) is proposed. The algorithm is developed based on a nondominated sorting framework and incorporates two key innovations: (1) a generation-wise dynamic Gaussian mixture component selection strategy that adaptively fits the multimodal distribution of elite solutions, and (2) a hybrid offspring generation mechanism that integrates traditional evolutionary operators with a Gaussian sampling strategy trained on perturbed solution sets, thereby enhancing exploration capability while maintaining convergence. The effectiveness of GLPEA is validated on 40 problem instances of varying scales. Compared with NSGA-II and MOEA/D, GLPEA achieves average improvements of 5.78% and 89.23% in IGD, and 1.03% and 264.43% in HV, respectively. We make the source codes of GLPEA publicly available to facilitate future research on practical applications.

1. Introduction

Industrial silicon plays an irreplaceable role in strategic emerging industries, such as photovoltaics, semiconductors, and aluminum [1]. Over the past two years, the authors conducted a practical project for a cooperative industrial silicon factory in Yunnan, China. Our task was to make production planning for heterogeneous parallel furnaces. As illustrated in Figure 1, the smelting process involves raw materials including silica, cleaned coal, charcoal, semi-coke, and petroleum coke, yielding molten industrial silicon while substantial ${\mathrm{CO}}_2$. Figure 2 provides an overview of the production planning framework in the factory. The factory has a fixed monthly delivery demand, and the planning task consists of allocating the output of each furnace to meet this demand. Each furnace follows a maintenance planning, and its monthly output must not exceed its rated capacity minus downtime. Furnace load is quantified as the total assigned production during the planning period, and the combined output of all furnaces must equal the total demand. Unfinished tasks are rolled over to subsequent months, incurring a penalty cost, while excess production is treated as early output for the following month. The carbon emission factor, which varies by furnace and month, reflects the ${\mathrm{CO}}_2$ emissions per ton of silicon produced. The rollover penalty factor is the cost per ton of delayed delivery. Reducing rollover penalties requires assigning more tasks to higher-capacity furnaces. This may worsen load imbalance and increase emissions. Conversely, minimizing emissions or balancing loads could raise penalties. Therefore, the three objective functions in nature conflict with each other.

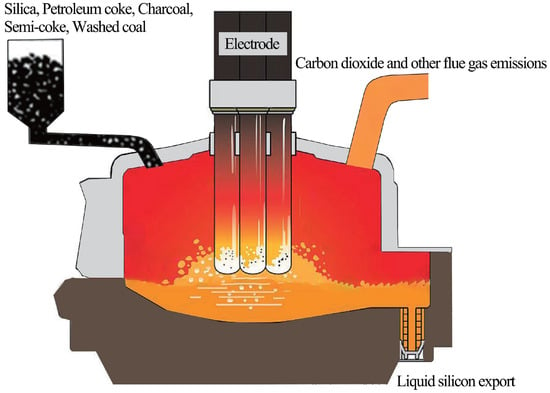
Figure 1. Illustration of industrial silicon smelting process.

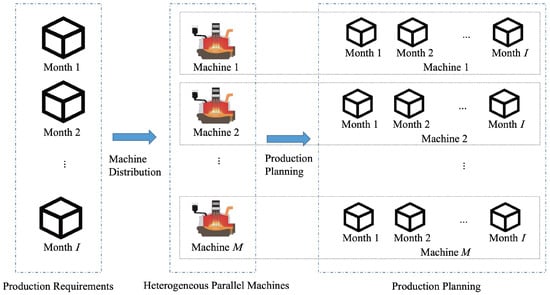
Figure 2. Overview of planning for industrial silicon production.

Given the above real-life applications, we propose introducing a specific heterogeneous parallel machine planning problem (HPMPP). However, no single algorithm can optimize the three conflicting objective functions simultaneously. Therefore, multi-objective evolutionary algorithm (MOEA) can be a suitable solution method. MOEAs use a parallel search framework to find approximate Pareto front (APF) within an acceptable CPU time frame [2].

However, as will be analyzed in detail in Section 2, classical multi-objective evolutionary algorithms (MOEAs) such as NSGA-II, although widely applied, rely heavily on “blind” stochastic search operators. Often, the nondominated sorting model is short for finding promising solutions in certain search regions when there are more than two objective functions. It may also suffer from reduced convergence precision [3,4,5]. To overcome these limitations, machine learning has shown potential to improve MOEAs. Gaussian learning has attracted increasing attention due to its strong capability in distribution fitting. A single-component GMM only offers a unimodal approximation of the primary elite cluster, whereas a multi-component GMM can better represent multimodal distributions of multiple high-quality solution clusters [6]. Therefore, employing different GMM components at different search stages of MOEAs can help yield improved results. In addition, the performance of GMM highly depends on the quality of its training data. If the GMM is trained solely on the current Pareto elite solutions, it tends to perform “local exploitation” around the discovered elites. This leads to a rapid loss of global exploration ability, causing the population to prematurely converge to a local Pareto front. This paper proposes GLPEA for solving HPMPP in industrial silicon smelting. GLPEA employs a Gaussian distribution to discover high-quality offspring solutions and a dedicated GMM training strategy to enhance global exploration. We additionally design a problem-specific repair operator to handle infeasible solutions encountered during the search process. The contributions of this work are summarized as follows.

First, from the modeling perspective, HPMPP aims to optimize rollover penalty costs, carbon emissions, and load imbalance. To our knowledge, this is the first work to model the industrial silicon production planning problem within such a framework. This work provides valuable guidance for managers who desire to balance these objectives. We use 40 problem instances of varying sizes and make the source code of the algorithm publicly available. These resources would be useful to facilitate future research on algorithm benchmarking and applications.

Second, from the algorithm perspective, we introduce a generational dynamic GMM component selection strategy into the nondominated sorting framework. This differs from most studies that use fixed-component GMMs. Our strategy adapts the number of components at each generation, leading to improved model flexibility and sampling effectiveness across different search stages. The perturbed solution set GMM training strategy further enhances exploration during the search. The proposed GLPEA provides useful insights for researchers and practitioners working on complex heterogeneous parallel machine planning problems.

Third, our GMM strategy is of general interest. It can guide the design of new operators within any nondominated sorting framework. Integrating this strategy into other MOEAs could improve their convergence and exploration. Therefore, our findings offer a valuable reference for advancing MOEAs.

The rest of this paper is organized as follows. Section 2 provides a review of the related works. Section 3 presents the mathematical model of HPMPP. Section 4 details the proposed GLPEA. Section 5 reports experimental results and comparisons. In Section 6, we draw concluding comments.

2. Related Work

2.1. Classical MOEAs

With the growing consensus on sustainable manufacturing, scheduling objectives have substantially evolved. Optimization now extends beyond the traditional two-dimensional “efficiency–cost” trade-off to higher-dimensional objectives encompassing “efficiency–cost–environment.” MOEAs have become mainstream tools for addressing such complexity. Generally, MOEAs can be categorized into: (a) dominance-based MOEAs, such as NSGA-II [7] and SPEA-II [8], which rank and select solutions based on Pareto dominance levels and crowding distance (or similar diversity indicators); (b) decomposition-based MOEAs, such as MOEA/D [9] and MOGLS [10], which decompose a multi-objective problem into a set of single-objective subproblems and exploit neighborhood relationships among subproblems for cooperative optimization, and (c) indicator-based MOEAs, such as SMS-EMO [11,12], which directly employ performance indicators (e.g., hypervolume) as selection criteria to drive the population toward a better Pareto front. In particular, the NSGA-II model has shown powerful search performance for solving the parallel machine planning problem [13,14]. Its search process relies on nondominated sorting and crowding distance mechanisms to discover promising search regions. Motivated by these studies, we adopt the nondominated sorting search model of NSGA-II in this work.

Despite their remarkable success, classical MOEAs still face inherent limitations. Their evolutionary operators are often inherently “blind,” relying purely on stochastic perturbations and heuristic selection. This traditional approach lacks the capability to perceive the topological structure of the search space or discern the distribution characteristics of high-quality solutions [15,16]. Such “blind” exploration often leads to limited search efficiency and consequently slow convergence. To overcome these limitations, researchers have introduced machine learning techniques to enhance the performance of MOEAs.

2.2. Surrogate-Assisted MOEAs

The core idea of Surrogate-Assisted MOEAs (SA-MOEAs) is to employ a computationally inexpensive machine learning model (surrogate) to approximate the true objective function, primarily targeting scenarios where evaluations are computationally expensive. Studies by Balekelayi N [17], Rossmann J [18], and Hebbal A [19] have successfully demonstrated that optimization based on Gaussian processes (GP) can achieve faster convergence to the optimal Pareto front than NSGA-II. Wu H [20] and Ravi K [21] further explored sparse and multi-fidelity GPs to improve efficiency on medium-scale problems. Gaussian processes are particularly valuable as they not only provide predictive means but also quantify predictive uncertainty, making them ideal models for Bayesian Optimization (BO) [22], which intelligently balances exploration and exploitation through acquisition functions. Other Surrogate-Assisted MOEAs have also been widely used. For instance, research by Zhang H [23] demonstrated that the Inverse Gaussian Process (IGP)-based MOEA significantly improves performance in dynamic optimization. Research by Yang Z [24] and Niu Y [25] introduced surrogate models based on Radial Basis Functions (RBF), effectively enhancing prediction accuracy. Studies by Sonoda T [26] and Xu D [27] developed surrogate-assisted MOEAs using Support Vector Machines (SVMs), achieving high computational efficiency. Moreover, works by Zhu E [28] and De Moraes M. B [29] demonstrated that surrogate-assisted MOEAs using Random Forests (RF) exhibit outstanding optimization performance.

However, the primary challenge for the HPMPP considered in this study differs significantly from the expensive-evaluation scenario. In this industrial context, production plans are typically established at the beginning of each planning cycle and executed strictly thereafter. The objective function evaluation frequency is thus relatively low. Consequently, the main challenge lies not in computationally expensive evaluations but in the inherently low search efficiency, reflected by slow convergence and limited solution quality improvement. Under such circumstances, the advantages of SA-MOEAs become less pronounced, as their designs are tailored for expensive-evaluation problems and may introduce additional computational overhead, making them less suitable for improving search efficiency in our HPMPP context.

2.3. Estimation of Distribution Algorithms (EDAs)

A distinct paradigm for enhancing MOEAs is the Estimation of Distribution Algorithms (EDAs), which replace traditional genetic operators (crossover and mutation) with a statistical learning or probabilistic generative model. The core principle involves learning the probability distribution of high-quality solutions in the decision space and subsequently sampling new offspring based on this learned model to generate potentially superior solutions [30].

Empirical studies by Wang F [31], Li G [32], and Zou J [33] have demonstrated that GMM-based MOEAs exhibit excellent performance across a wide range of benchmark and real-world problems. Lu C [34] and Aggarwal S [35] proposed MOEAs based on the Covariance Matrix Adaptation Evolution Strategy (CMA-ES), which feature lightweight design and faster execution. Zhang W [36] improved the Regularity Model-based Estimation of Distribution Algorithms (RM-MEDA), enhancing convergence performance. Kalita K [37] introduced the Multi-objective exponential distribution optimizer (MOEDO), which achieves robust performance in balancing diversity and convergence efficiency.

2.4. Analysis and Proposed Approach

For the HPMPP addressed in this study, we aim to solve planning problems that are computationally challenging yet required to be completed within an acceptable CPU time frame. Among existing methods, GMM-based MOEAs are well suited for this purpose. Compared with other probabilistic models, the GMM has been widely validated as effective—particularly in industrial applications—by researchers such as Alghamdi A. S [38], Guerrero-Peña E [39] and Yazdi F [40]. Moreover, GMMs are data-efficient, capable of robustly fitting multimodal distributions even with small to medium sample sizes. Considering practical industrial applicability and algorithmic stability, we adopt the GMM as the probabilistic generative model in this work. In recent years, many studies have sought to enhance the performance of GMM-based sampling strategies. Zhang J [41] decomposed the overall problem into several subproblems and employed multi-component GMMs to capture diverse solution patterns, thereby improving population diversity. Abdulghani A. M [42] proposed the NA-GMM, which integrates adaptive weighting of features and node importance weighting to further enhance diversity.

Most existing studies employ a fixed number of Gaussian components throughout the evolutionary process, which is theoretically suboptimal. During the early evolution stage, the population distribution is broad and dispersed; a simple GMM can adequately capture the global trend, while using an excessive number of components may lead to overfitting. In later stages, when the population converges to a refined and complex Pareto front with multiple distinct elite clusters, a low-component GMM fails to distinguish these clusters, resulting in underfitting. Therefore, we introduce a generation-wise dynamic Gaussian mixture component selection strategy. Furthermore, the training dataset of the GMM has a significant impact on its sampling performance. A training set with greater diversity enables more diverse sampling results. To this end, we propose a GMM training strategy based on perturbed solution sets to enhance the diversity of the solution space and improve global exploration capability.

3. Mathematical Model of HPMPP

HPMPP involves allocating predetermined monthly production targets to a set of heterogeneous parallel machines (furnaces). Given the monthly rollover penalty factors, machine maintenance schedules, capacity limits, and deep learning-predicted carbon emission factors, the objective is to determine the monthly capacity allocation across machines that optimizes the three objective functions detailed below.

3.1. Assumptions

The proposed HPMPP model is based on the following assumptions.

(a) The maximum monthly production capacity of each machine is fixed and time-invariant.

(b) No unexpected interruptions occur during the production process, allowing the analysis to focus on the inherent trade-offs among the optimization objectives.

3.2. Parameters

To clearly construct the model and algorithm, this section classifies all relevant parameters into two categories: Table 1 defines the model parameters of the industrial silicon scheduling problem, while Table 2 defines the algorithm parameters of the proposed GLPEA.

Table 1. The model parameters of the industrial silicon scheduling problem.

Symbol	Recommended Range of Values	Description
M	$\{1,2,\dots ,20\}$	Set of machines and it also denotes the cardinality of the set.
I	$\{1,2,\dots ,12\}$	Set of months and it also denotes the cardinality of the set.
$H_i$	$\{28,29,30,31\}$	Number of days in month $i\in I$. Defines the number of days within the production planning period for each month.
$P_i$	$(0,\infty )$	Production demand for month i. Used to constrain the total production of all machines to be equal to the overall demand.
$C_{ij}$	$(0,\infty )$	Carbon emission factor of machine $j\in M$ in month $i\in I$. The result value is obtained through Section 3.5.5.
$D_i$	$(0,\infty )$	Rollover penalty coefficient for month i. Used to calculate the monthly rollover penalty, defined as the unfinished production of each month multiplied by the monthly rollover penalty coefficient.
$R_{ij}$	$\{1,2,\dots ,31\}$	Scheduled maintenance days for machine j in month i. Used to calculate the remaining monthly rated capacity of machines after subtracting maintenance days from the number of days in the production planning period of each month.
$Ca{p}_j$	$(0,\infty )$	Maximum monthly production capacity of machine j. Used to impose machine load constraints.

Note: Parameter values must also comply with the constraints specified in Section 3.4.

Table 2. The algorithm parameters of the proposed GLPEA.

Symbol	Recommended Range of Values	Description
$PS$	$\{50,100,150,200\}$	Population size. Determines the total number of solutions (individuals) maintained by the algorithm in each generation.
$P_c$	$\{0.6,0.7,0.8,0.9\}$	Crossover probability. Controls the probability of generating new offspring through the crossover process in traditional genetic operations.
$P_m$	$\{0.1,0.2,0.3,0.4\}$	Mutation probability. Controls the probability of random mutation occurring in offspring individuals during traditional genetic operations.
$GSR$	$\{0.3,0.5,0.7,0.9\}$	Gaussian sampling rate. Determines the proportion of individuals in the new generation that are generated through GMM sampling rather than traditional genetic operations.
$BETA$	$\{0.2,0.4,0.6,0.8\}$	Disturbance scaling factor. Controls the scaling factor used when generating perturbed solutions.
$DR$	$\{0.1,0.3,0.5,0.7\}$	Disturbed ratio of the Pareto solutions. Determines the proportion of Pareto solutions used to generate “perturbed solutions” in the perturbed solution set training strategy.

3.3. Decision Variables

$X_{ij}$	Production volume of month $i\in I$ on machine $j\in M$;
$V_i$	Cumulative amount of unfulfilled demand in month i;
$U_i$	Unfulfilled demand in month i;
$L_j$	Load of machine j.

3.4. Objective Functions

The objective of HPMPP is to minimize carbon emissions (f₁), minimize rollover penalty costs (f₂), and minimize load imbalance (f₃). The carbon emissions (f₁) are obtained by multiplying the production of each machine in each month by the corresponding unit carbon emission coefficient and summing over all machines and months. The monthly rollover penalty (f₂) is calculated based on unfinished demand: for each month i, the actual total production is compared with the demand for that month, including any rollover from the previous month. If production is insufficient, an unfinished amount $U_i$ is generated; if production exceeds demand, the surplus offsets the following month’s demand. The unfinished amount for each month is multiplied by the monthly rollover penalty coefficient $D_i$, and the sum over all months gives the total penalty. Load imbalance (f₃) is calculated by first computing the total production load $L_j$ of each machine over the entire scheduling period. The squared deviations of each machine’s total load from the average load are then summed to represent the load imbalance.

$$\mathit{Min}{f}_1=\sum _{i\in I}\sum _{j\in M}{C}_{ij}{X}_{ij}$$

(1)

$$\mathit{Min}{f}_2=\sum _{i\in I}{D}_i{U}_i$$

(2)

$$\mathit{Min}{f}_3=\sum _{j\in M}{\left(L_j-{\displaystyle \frac{1}{M}}\sum _{j\in M}{L}_j\right)}^2$$

(3)

Subject to:

$$X_{ij}\le {\mathit{Cap}}_j\left(1-{\displaystyle \frac{R_{ij}}{H_i}}\right),\forall i\in I,j\in M$$

(4)

$$\sum _{i\in I}\sum _{j\in M}{X}_{ij}=\sum _{i\in I}{P}_i$$

(5)

$$L_j=\sum _{i\in I}{X}_{ij},\forall j\in M$$

(6)

$$V_i=P_i+V_{i-1}-\sum _{j\in M}{X}_{ij},\forall i\in I,V_0=0$$

(7)

$$U_i=max\left\{0,V_i\right\},\forall i\in I,V_0=0$$

(8)

3.5. Carbon Emission Factor Prediction

In the proposed mathematical model, the carbon emission factor denotes the carbon emissions per ton of silicon product. Although emissions generally scale with output, the factor is also influenced by operational efficiency, energy consumption, and climatic conditions (e.g., temperature, humidity, rainfall), leading to monthly variations. Therefore, it can vary from month to month. Accurate prediction of this factor is important for emission management. Hochreiter et al. [43] showed that long short-term memory (LSTM) networks perform well on nonlinear time-series prediction.

3.5.1. Datasets and Preprocessing

We collected five years (2020–2024) of production data from an industrial silicon smelting plant (The data set is available at https://gitee.com/zhangjinsi_p/glpea/blob/master/dataset.xlsx, accessed on 30 September 2024). It covers seven furnaces (#1 to #7), with monthly records for each furnace. In total, there are 60 months, comprising 420 entries of monthly production, carbon dioxide emissions, and carbon emission factors. The monthly production is measured in tons and represents the output of each furnace for the corresponding month. The carbon dioxide emissions are also measured in tons, indicating the ${\mathrm{CO}}_2$ output of each furnace per month. The carbon emission factor represents the ratio of ${\mathrm{CO}}_2$ emissions to production for each furnace in the corresponding month, i.e., the amount of ${\mathrm{CO}}_2$ emitted per ton of industrial silicon produced.

As the dataset is relatively small but of high quality, we performed a thorough inspection and found no missing values or obvious outliers. For data preprocessing, we applied the RobustScaler method for standardization. Bachechi et al. [44] showed that this method reduces the impact of outliers and noise.

The dataset was split into training and test sets at an 80:20 ratio. It is worth noting that when the dataset is limited in size, setting aside a separate validation set can significantly reduce the valuable data available for model training. Therefore, we adopted cross validation for time series [45]. Specifically, we set a validation window corresponding to a complete seasonal cycle (window size = 12) and rolled it forward within the training set, ensuring that each validation set only contains data that the model has not seen during training and occurs later in chronological order.

3.5.2. Feature Engineering

Inspired by Box [46], Ma [47], and Dong [48], we construct multidimensional features to capture periodicity, lag effects, and local statistical properties in time series.

(a) Periodic features. We map the month index to a periodic variable. We encode the 12-month cycle using sine and cosine functions as follows:

$$sinmonth=sin\left({\displaystyle \frac{2\pi {\Phi }_t}{P}}\right),cosmonth=cos\left({\displaystyle \frac{2\pi {\Phi }_t}{P}}\right)$$

(9)

where ${\Phi }_t=(tmod12)+1$ represents the month index in the cycle. The cycle length $P=12$ months. This encoding captures seasonal variation and the periodic effects of temperature, humidity, and rainfall.

(b) Lag features and padding. To reflect the influence of past values, we use the observations from the three most recent time steps as lag features. We denote them ${\mathrm{x}}_{t-1}$, ${\mathrm{x}}_{t-2}$, and ${\mathrm{x}}_{t-3}$.

(c) Sliding-window statistical features. To capture local trends and volatility, we compute statistics over a fixed window of size w = 12 (including the current time t). We have

$${\mu }_t={\displaystyle \frac{1}{w}}\sum _{i=t-w+1}^t{x}_i,{\sigma }_t=\sqrt{{\displaystyle \frac{1}{w}}\sum _{i=t-w+1}^t{(x_i-{\mu }_t)}^2}$$

(10)

We additionally calculate the ratio of the standard deviation to the mean to capture local volatility as follows:

$${\gamma }_t={\displaystyle \frac{{\sigma }_t}{{\mu }_t+ϵ}}$$

(11)

Toward that end, at each time step t, we construct a feature vector $X_t$ as follows:

$$X_t=\left[x_t,sin\left({\displaystyle \frac{2\pi {\Phi }_t}{P}}\right),cos\left({\displaystyle \frac{2\pi {\Phi }_t}{P}}\right),x_{t-1},x_{t-2},x_{t-3},{\mu }_t,{\sigma }_t,{\gamma }_t\right]$$

(12)

3.5.3. Model Structure and Loss Function

We employed a single-layer LSTM encoder, followed by a fully connected (FC) layer, to predict the estimated carbon emission factor for the next time step, ${\widehat{Y}}_{t+1}$, which approximates the true value $Y_{t+1}$. The Mean Squared Error (MSE) [49] was utilized as the loss function:

$$MSE={\displaystyle \frac{1}{N}}\sum _{i=1}^N{(Y_i-{\widehat{Y}}_i)}^2$$

(13)

where N represents the number of samples, $Y_i$ denotes the true (or actual) value, and ${\widehat{Y}}_i$ is the predicted value from the model.

3.5.4. Model Parameters

The number of LSTM hidden units (lstm_unit) and the Dropout rate (dropout_rate) significantly influence the model’s generalization ability and fitting performance. We conducted an experimental grid search involving nine different combinations of these parameters. The results are presented in Table 3. As shown in the table, the combination of lstm_unit = 48 and dropout_rate = 0.3 yielded the lowest MSE score. Consequently, this optimal hyperparameter set was selected for the training of the final model.

Table 3. Experimental results of model parameters.

lstm_unit	dropout_rate	MSE
32	0.1	0.0087
32	0.3	0.0078
32	0.5	0.0091
48	0.1	0.0074
48	0.3	0.0067
48	0.5	0.0080
64	0.1	0.0088
64	0.3	0.0079
64	0.5	0.0081

3.5.5. Evaluation and Prediction Results

The model’s performance was evaluated using the Mean Squared Error (MSE), Root Mean Squared Error (RMSE) [50], and Mean Absolute Error (MAE) [51]. The resulting metrics were $MSE=0.0067$, $RMSE=0.0794$, and $MAE=0.0643$. Overall, the model achieved low prediction errors, demonstrating its excellent predictive performance.

The trained model is used to forecast monthly carbon emission factors for each furnace over a 12-month horizon. The results are reported in Table 4.

Table 4. Predicted carbon emission factors for furnaces #1–#7 over the next 12 months.

Month	#1	#2	#3	#4	#5	#6	#7
1	13.249	12.797	12.305	12.058	11.827	13.084	13.247
2	11.959	11.924	12.484	11.801	11.571	12.353	12.636
3	11.356	11.617	12.146	11.445	11.729	11.750	11.708
4	12.823	12.480	12.511	12.184	12.179	12.765	12.600
5	12.435	12.289	12.025	11.850	12.276	12.484	12.299
6	13.382	12.824	12.107	12.167	12.749	13.124	12.960
7	11.270	11.538	11.047	11.033	12.044	11.663	11.322
8	11.827	11.866	11.176	11.203	12.344	12.034	11.843
9	12.206	12.187	11.195	11.393	13.019	12.504	11.744
10	10.304	10.679	10.131	11.078	11.277	10.844	10.626
11	10.714	11.065	11.210	10.686	11.793	11.210	11.028
12	12.203	12.125	11.640	11.552	13.492	12.564	12.662

4. Proposed GLPEA for HPMPP

In GLPEA, we encode a solution with a two-dimensional matrix X. The matrix has I rows and M columns. Each element $X_{ij}\in {\mathrm{Cap}}_j\left(1-{\displaystyle \frac{R_{ij}}{H_i}}\right), \forall i\in I, j\in M$. represents the production assigned to machine j in month i. Based on this solution representation method, we detail the search components of GLPEA below.

4.1. Proposed Problem-Specific Repair Operator

To ensure all solutions satisfy the problem constraints during the search process of GLPEA, a dedicated repair operator is proposed in Algorithm 1. The repair operator first constructs a capacity upper-bound matrix to represent the available capacity of machine j in month i accounting for maintenance (lines 3–8). Next, the infeasible solution matrix and the capacity matrix are vectorized (lines 9–10). Thereafter, a bisection search determines the shift parameter $\theta$ such that the projection $x_k=min\{max(z_k-\theta ,0),u_k\}$ results a solution satisfying the total production demand with a tolerance $1\times {10}^{-8}$ (lines 13–23), thereby enforcing both bound constraints and demand satisfaction. The repaired vector is then reshaped into the final feasible matrix (Line 24). Note that in determining $\theta$, we set $Nbis=1000$. Based on our preliminary observations, such an $Nbis$ is sufficient to find a suitable $\theta$ value.

Algorithm 1 Proposed problem-specific repair operator

1: Input: X   2: Output: $X_{repaired}$   3: cap_matrix$\leftarrow \mathrm{Matrix}(\mathrm{zeros},I,M);$   4: for i = 1 to I do   5:      for $j=1$ to M do   6:           cap_matrix[i,j]$\leftarrow \mathrm{Cap}\ast (1-R[i]/H[i]);$   7:      end for   8: end for   9: $z\leftarrow \mathrm{flatten}\left(X\right);$ 10: $u\leftarrow \mathrm{flatten}$(cap_matrix); 11: ${\theta }_{lo}\leftarrow min(z-u);$ 12: ${\theta }_{hi}\leftarrow max(z-u);$ 13: for $i=1$ to $Nbis$ do 14:      $\theta \leftarrow ({\theta }_{lo}+{\theta }_{hi})/2;$ 15:      if $\left|\sum (min(max(z-\theta ,0),u))-{\sum }_{i\in I}{P}_i\right|\le 1e-8$ then 16:           $break;$ 17:      end if 18:      if $\sum (min(max(z-\theta ,0),u))>{\sum }_{i\in I}{P}_i$ then 19:           ${\theta }_{lo}\leftarrow \theta ;$ 20:      else 21:           ${\theta }_{hi}\leftarrow \theta ;$ 22:      end if 23: end for 24: $X_{repaired}\leftarrow \mathrm{reshape}(min(max(z-\theta ,0),u),I,M);$ 25: return $X_{repaired}$

4.2. Gaussian Mixture Model

4.2.1. Univariate Gaussian Distribution

The univariate Gaussian distribution (normal distribution) is one of the most common continuous probability distributions. Its probability density function is defined as:

$$p\left(x\right|\mu ,{\sigma }^2)={\displaystyle \frac{1}{\sqrt{2\pi {\sigma }^2}}}exp\left(-{\displaystyle \frac{{(x-\mu )}^2}{2{\sigma }^2}}\right)$$

(14)

where $x\in \mathbb{R}$ is the random variable, $\mu$ is the mean, and ${\sigma }^2$ is the variance. Given a set of independent and identically distributed samples $\{x_1,x_2,\dots ,x_N\}$, the parameters $\mu$ and ${\sigma }^2$ are calculated as follows:

$$\mu ={\displaystyle \frac{1}{N}}\sum _{i=1}^N{x}_i,{\sigma }^2={\displaystyle \frac{1}{N}}\sum _{i=1}^N{(x_i-\mu )}^2$$

(15)

4.2.2. Multivariate Gaussian Distribution

The multivariate Gaussian distribution generalizes the univariate case. It describes the joint distribution of a D-dimensional continuous random vector x. Its probability density function is:

$$p\left(x\right|\mu ,\Sigma )={\displaystyle \frac{1}{{\left(2\pi \right)}^{D/2}{|\Sigma |}^{1/2}}}exp\left(-{\displaystyle \frac{1}{2}}{(x-\mu )}^T{\Sigma }^{-1}(x-\mu )\right)$$

(16)

where $\mu \in \mathbb{R}$ is the mean vector. $\Sigma \in {\mathbb{R}}^{D\times D}$ is the covariance matrix, which describes the correlations among the dimensions. $|\Sigma |$ denotes the determinant of the covariance matrix.

4.2.3. Adopted Gaussian Mixture Model

GMM assumes that each data point x is generated from a weighted combination of K Gaussian distributions [52]. Its probability density function is expressed as follows:

$$p\left(x\right)=\sum _{k=1}^K{\pi }_k\mathcal{N}\left(x\right|{\mu }_k,{\Sigma }_k)$$

(17)

where ${\pi }_k$ denotes the mixing weight of the k-th Gaussian component, satisfying ${\sum }_{k=1}^K{\pi }_k=1$. ${\mu }_k$ and ${\Sigma }_k$ represent the mean vector and covariance matrix of the k-th Gaussian distribution, respectively. The parameters of GMM are usually estimated using the Expectation-Maximization (EM) algorithm [53]. The EM algorithm consists of two steps:

Expectation step (E-step): In this step, the posterior probability that each data point belongs to each Gaussian component, namely the responsibility, is calculated. ${\gamma }_{ik}$ represents the probability that the i-th data point is generated by the k-th Gaussian component, and t denotes the current iteration. The formula is given as follows:

$${\gamma }_{ik}^{\left(t\right)}={\displaystyle \frac{{\pi }_k^{\left(t\right)}N\left(x_i|{\mu }_k^{\left(t\right)},{\Sigma }_k^{\left(t\right)}\right)}{{\sum }_{j=1}^K{\pi }_j^{\left(t\right)}N\left(x_i|{\mu }_j^{\left(t\right)},{\Sigma }_j^{\left(t\right)}\right)}}$$

(18)

Maximization step (M-step): In this step, the parameters are updated using the posterior probabilities obtained from the E-step. The new parameters are estimated by maximizing the log-likelihood function. The mixing weights are updated as follows:

$${\pi }_k^{(\mathrm{t}+1)}={\displaystyle \frac{1}{N}}\sum _{i=1}^N{\gamma }_{ik}^{\left(\mathrm{t}\right)}$$

(19)

where ${\sum }_{i=1}^N{\gamma }_{ik}^{\left(t\right)}$ represents the total responsibility of all data points for the k-th Gaussian component. Note that N is the total number of data points.

Thereby, the mean vector and covariance matrix are updated as follows:

$${\mu }_k^{(\mathrm{t}+1)}={\displaystyle \frac{{\sum }_{i=1}^N{\gamma }_{ik}^{\left(\mathrm{t}\right)}{x}_i}{{\sum }_{i=1}^N{\gamma }_{ik}^{\left(\mathrm{t}\right)}}}$$

(20)

$${\Sigma }_k^{(\mathrm{t}+1)}={\displaystyle \frac{{\sum }_{i=1}^N{\gamma }_{ik}^{\left(\mathrm{t}\right)}(x_i-{\mu }_k^{(\mathrm{t}+1)}){(x_i-{\mu }_k^{(\mathrm{t}+1)})}^T}{{\sum }_{i=1}^N{\gamma }_{ik}^{\left(\mathrm{t}\right)}}}$$

(21)

Toward that end, the EM algorithm can alternates between the E-step and the M-step. It increases the log-likelihood at each iteration until it converges to a local optimum.

4.3. Main Framework of GLPEA

As mentioned earlier, GLPEA employs a Gaussian mixture model-based non-dominated sorting framework. The general framework of the algorithm is given in Algorithm 2. Initially, a population of size $PS$ is randomly generated. The objective function calculation module evaluates three objective values $F=\{f_1,f_2,f_3\}$ for each individual. At each generation, the population first undergoes non-dominated sorting. Subsequently, a perturbed solution set is constructed for Gaussian model training (Section 4.4). Offspring are then generated using a Gaussian mixture model-based evolutionary method (Section 4.5). The parent and offspring populations are merged to form a temporary population, which then undergoes non-dominated sorting and crowding distance calculation. Finally, an elitism preservation strategy selects the top $PS$ optimal individuals to form the new-generation population. This process continues until the maximum generation number $GENS$ is reached, ultimately outputting an approximate Pareto-optimal solution set.

Algorithm 2 Main framework of GLPEA

1: Input: initial_population, GENS, and the other parameters of the algorithm   2: Output: final_population   3: evaluate objectives $F=\{f_1,f_2,f_3\}$ for all individuals;   4: for $gen=1$ to $GENS$ do   5:      perform non-dominated sorting;   6:      hybrid data augmented gaussian model training strategy; /∗ Section 4.4 ∗/   7:      generate offspring by gaussian mixture model combined evolution method; /∗ Section 4.5 ∗/   8:      merge parent and child populations;   9:      perform non-dominated sorting; 10:      selecting the next generation population based on crowding distance; 11: end for 12: return fianl_population

4.4. Proposed Gaussian Model Training Strategy Based on Perturbed Solutions

The proposed training strategy is implemented by constructing a specific GMM training dataset, denoted as training_data. The procedure is presented in Algorithm 3. First, the indices of perturbed points are randomly selected from the current Pareto front solutions, denoted as pareto_solutions. The number of perturbed solutions is determined by the product of the number of current Pareto solutions (n) and the disturbance ratio of Pareto solutions ($DR$) (Lines 1–3). Then, inspired by the mutation operator in differential evolution (DE), multiple diversity-enhanced new solutions are generated for each selected Pareto solution (Lines 4–7). After repairing infeasible solutions, the feasible ones are added to the new solution set (Lines 8–9). Finally, the GMM training dataset is constructed by merging the current Pareto front set with the new solution set (Line 11). The core mutation formula of DE [54] is given as follows:

$$X^{\prime }=X+BETA(X_a-X_b)$$

(22)

In Equation (22), relevant parameters are defined as follows: X is the original Pareto solution; $X_a, X_b$ represent a randomly selected pair of Pareto solutions; and $BETA\in [0,1]$ serves as the perturbation intensity factor.

Algorithm 3 Gaussian model training strategy based on perturbed solutions

1: Input: pareto_solutions, DR, BETA   2: Output: training_data   3: $perturbed\_points\leftarrow \varnothing ;$   4: $n\leftarrow |pareto\_solutions|;/$*$Calculate the number of Pareto frontier solutions$*/   5: $selected\_indices\leftarrow RandomSample\left(\right\{0,1,\dots ,n-1\},\lfloor n·DR\rfloor );$   6: for $each$$idx$ in $selected\_indices$ do   7:      $X\leftarrow pareto\_solutions\left[idx\right];$   8:      $(i1,i2)\leftarrow RandomSample\left(\right\{0,1,\dots ,|pareto\_solutions|-1\},2);$   9:      $X^{\prime }\leftarrow X+BETA·(pareto\_solutions\left[i1\right]-pareto\_solutions\left[i2\right]);$ 10:      $X^{\prime }\leftarrow repair\_solution\left(X^{\prime }\right);$ /∗ Section 4.1 ∗/ 11:      $perturbed\_points\leftarrow perturbed\_points\cup \left\{X^{\prime }\right\};$ 12: end for 13: $training\_data\leftarrow pareto\_solutions\cup perturbed\_points;$ 14: return $training\_data$

4.5. Gaussian Mixture Model Combined Evolutionary Method

In GLPEA, a GMM strategy with dynamically selected component numbers per generation is employed to choose the optimal number of components for each generation. The procedure is presented in Algorithm 4. The hybrid reproduction strategy generates offspring using both GMM sampling and traditional genetic operations. Let $PS$ denote the number of offspring generated per generation and $GSR$ the GMM sampling rate. $training\_data$ denotes the GMM training dataset constructed in Section 4.4, and $population$ represents the population. If the sampling rate criterion is satisfied, GMM sampling is performed; otherwise, traditional genetic operations are applied. During GMM sampling, all candidate points are flattened and normalized to a standard normal distribution (Lines 3–4). The number of components is traversed from 1 to the maximum component number ($componentsMax$), and the Bayesian Information Criterion (BIC) [55] is used to evaluate the models. The model with the smallest BIC corresponds to the optimal number of components, and this GMM is then used for sampling (Lines 5–17). After repairing infeasible solutions, the sampled offspring are added to the offspring solution set (Lines 18–20). Note that $componentsMax$ = 5 is set when determining the optimal number of components. Based on our preliminary observations, this value is sufficient to find an appropriate component number. For the traditional genetic operation, parents are selected by binary tournament selection (Lines 23–24; see Section 4.6), followed by crossover and mutation to generate two offspring, which are then added to the offspring solution set (Lines 25–31).

4.6. Binary Tournament Parent Selection

In the traditional genetic algorithm, binary tournament selection is used to choose the parent individuals for crossover and mutation. We give the binary tournament selection is described in Algorithm 5. Let $fronts$ be the positions of individuals in each non-dominated front within the $population$, and $rank$ the front level to which each individual belongs.

As Algorithm 5 shows, a zero vector $distances$ with a length equal to the population size is first initialized to store the crowding distance of each individual (Line 1). Then, each non-dominated front is traversed (Line 2), and the crowding distance of all individuals in the current front is calculated (Line 3). The calculated distances are assigned to the corresponding positions in the $distances$ vector (Lines 4–5). Next, two distinct indices are randomly sampled from the set of population indices (Line 8). The selected candidate solutions are compared according to their non-dominated sorting ranks, and the solution with a lower rank (i.e., higher quality) is selected (Lines 9–12). If the two candidates have the same rank, the crowding distance is used as the criterion, and the one with a larger crowding distance is selected to maintain population diversity (Lines 14–19).

Algorithm 4 Proposed GMM combined evolutionary method

1: Input: training_data, population, GSR   2: Output: offspring, offspring_obj   3: $offspring\leftarrow \varnothing ;$   4: $offspring\_obj\leftarrow \varnothing ;$   5: $data\leftarrow \left\{flatten\right(point)\mid point\in training\_data\};$   6: $data\_scaled\leftarrow StandardScaler\left(\right).fit\_transform\left(data\right);$   7: $bic\_values\leftarrow \left[\right];$   8: for $n=1$ to $componentsMax$ do   9:    $gmm\_n\leftarrow GaussianMixture(n\_components=n);/$∗ Section 4.2 ∗/ 10:    $gmm\_n.fit(data\_scaled);$ 11:    $bic\_values.append(gmm\_n.BIC(data\_scaled\left)\right);$ 12: end for 13: $gmm\_components\leftarrow argmin(bic\_values)+1;$ 14: $gm\_model\leftarrow GaussianMixture(n\_components=gmm\_components);/$∗ Section 4.2 ∗/ 15: $gm\_model.fit(data\_scaled);$ 16: while $\left|population\right|<PS$do 17:    if $UniformRandom(0,1)<GSR$ then 18:      $/$*$Generating offspring using Gaussian learning$*/ 19:      $child\leftarrow StandardScaler\left(\right).inverse\_transform(gm\_model.Sample(\left)\right).reshape(I,M);$ 20:      $child\leftarrow repair\_solution\left(child\right);/$∗ Section 4.1 ∗/ 21:      $offspring\leftarrow offspring\cup \left\{child\right\};$ 22:      $offspring\_obj\leftarrow offspring\_obj\cup \{calculate\_objectives(child\left)\right\};$ 23:    else 24:      $/$*$Generate offspring using traditional crossover and mutation$*/ 25:      $parent1\leftarrow BinaryTournament\left(population\right);/$∗ Section 4.6 ∗/ 26:      $parent2\leftarrow BinaryTournament\left(population\right);/$∗ Section 4.6 ∗/ 27:      $(child1,child2)\leftarrow Crossover\left(Clone\right(parent1),Clone(parent2\left)\right);$ 28:      $child1\leftarrow mutation\left(child1\right);$ 29:      $child2\leftarrow mutation\left(child2\right);$ 30:      $offspring\leftarrow offspring\cup \left\{child1\right\};$ 31:      $offspring\_obj\leftarrow offspring\_obj\cup \{calculate\_objectives(child1\left)\right\};$ 32:      $offspring\leftarrow offspring\cup \left\{child2\right\};$ 33:      $offspring\_obj\leftarrow offspring\_obj\cup \{calculate\_objectives(child2\left)\right\};$ 34:    end if 35: end while 36: return$(offspring,offspring\_obj)$

Algorithm 5 Adopted binary tournament selection operator

1: Input: population   2: Output: parent   3: $distances\leftarrow ZeroVector(length=|population\left|\right);$   4: for $each$$front$ in $fronts$ do   5:    $front\_dist\leftarrow crowding\_distance\left(front\right);$   6:    for $each$$(idx,d)$ in $zip(front,front\_dist)$ do   7:      $distances\left[idx\right]\leftarrow d;$   8:    end for   9: end for 10: $(i_1,i_2)\leftarrow RandomSample\left(\right\{0,1,\dots ,\left|population\right|-1\},2);$ 11: if  $rank\left[i1\right]<rank\left[i2\right]$  then 12:    $s\leftarrow population\left[i1\right];$ 13: else if $rank\left[i2\right]<rank\left[i1\right]$ then 14:    $s\leftarrow population\left[i2\right];$ 15: else 16:    if $distance\left[i1\right]>distance\left[i2\right]$ then 17:      $s\leftarrow population\left[i1\right];$ 18:    else 19:      $s\leftarrow population\left[i2\right];$ 20:    end if 21: end if 22: return  $parent$

5. Experiment Results and Comparisons

5.1. Test Instances and Experimental Design

We consider the combinations $M\times I=\{3,5,7,9,11,13,15,17\}\times \{4,6,8,10,12\},$ yielding 40 instances. For each instance, GLPEA and the comparison algorithms are each run independently 20 times. Experimental results are reported as Best, Worst, and Mean, representing the best, worst, and average values of the performance metrics. All algorithms are implemented in Python 3.8 and executed on a PC running macOS with an Intel Core i7 2.7 GHz quad-core processor and 16 GB of RAM (The source code, test instances, and results are available at https://gitee.com/zhangjinsi_p/glpea.git, accessed on 30 September 2024).

5.2. Performance Metrics

To evaluate the solution quality achieved by GLPEA and compared algorithms, two well-known MOEA performance metrics are used in this work [56].

IGD quantifies the proximity between the solution sets generated by an algorithm and the reference Pareto front (or true Pareto front). It calculates the average Euclidean distance from each point in the reference Pareto front to its nearest neighbor in the algorithm’s solution set. The metric is formulated as follows:

$$IGD(P^{*},A)={\displaystyle \frac{1}{|P^{*}|}}\sum _{v\in P^{*}}\underset{u\in A}{min}\parallel v-u\parallel$$

(23)

where $P^{*}$ denotes the reference Pareto front (or true Pareto front), and A represents the solution set obtained by a given compared algorithm. Note that we combine the solutions obtained by all compared algorithm and then identify $P^{*}$ from these solutions. A smaller IGD value indicates closer proximity to the true Pareto front, reflecting superior convergence performance.

HV measures the multidimensional space between a reference point r and the solution set, reflecting the breadth and diversity of the distribution. HV is defined as follows:

$$HV\left(A\right)=Volume\left(\bigcup _{x\in A}[x_1,r_1]\times [x_2,r_2]\times \cdots \times [x_m,r_m]\right)$$

(24)

where $r=(r_1,r_2,\dots ,r_m)$ represents a predefined reference point in the objective space. A larger HV value signifies stronger exploration capability, with solutions exhibiting a more comprehensive and balanced distribution in the objective space.

5.3. Parameter Settings

GLPEA has six parameters: population size ($PS$), crossover probability ($P_c$), mutation probability ($P_m$), Gaussian sampling rate ($GSR$), disturbance scaling factor ($BETA$), and disturbed ratio of the Pareto solutions ($DR$). To find a suitable parameter combination of these parameters, the Taguchi method is employed using the instance “m7i12”. In this approach, the search performance of GLPEA under different parameter settings is evaluated using the two performance metrics. A design-of-experiments (DOE) procedure is adopted to generate candidate parameter combinations. As shown in Table 5, four levels are assigned to each parameter, and an $L_4^6$ orthogonal array with 25 experimental runs is used. For each parameter combination, GLPEA is executed independently 20 times with $GENS=1000$. The corresponding performance metrics are given (see Table 6). A proper parameter combination should minimize IGD while maximizing HV. To facilitate comparison, both IGD and HV values are normalized, and the signal-to-noise ratio ($S/N$) is used as the response variable. Our goal is to identify the parameter combination that yields the highest $S/N$ ratio, which is calculated as follows:

$$S/N=-10log\left({\displaystyle \frac{1}{m}}\sum _{k=1}^m{\displaystyle \frac{1}{{\mathrm{sum}}_k^2}}\right)$$

(25)

where m is the number of GLPEA executions, and $su{m}_k^2$ represents the composite performance score obtained from the normalized IGD and HV values in the k-th run.

Table 5. Parameter levels.

Parameter	Level 1	Level 2	Level 3	Level 4
$PS$	50	100	150	200
$P_c$	0.6	0.7	0.8	0.9
$P_m$	0.1	0.2	0.3	0.4
$GSR$	0.3	0.5	0.7	0.9
$BETA$	0.2	0.4	0.6	0.8
$DR$	0.1	0.3	0.5	0.7

Table 6. Orthogonal array and response values.

No.	Combination						$\mathit{S}/\mathit{N}$
	$\mathit{PS}$	$\mathit{Pc}$	$\mathit{Pm}$	$\mathit{GSR}$	$\mathit{BETA}$	$\mathit{DR}$
1	3	3	3	4	1	1	3.075
2	4	2	3	1	4	1	4.106
3	1	1	1	1	1	1	−3.595
4	1	1	3	3	3	4	−8.018
5	4	4	4	3	2	1	4.511
6	4	1	1	1	1	2	4.061
7	3	4	1	1	4	4	3.433
8	1	1	1	2	4	1	−3.975
9	2	2	2	1	3	1	1.692
10	1	2	1	4	2	2	−5.032
11	2	1	4	4	4	3	1.597
12	2	1	1	3	1	1	1.502
13	1	4	2	1	1	3	−1.217
14	3	1	2	2	2	1	2.902
15	1	1	3	1	2	3	−5.308
16	4	1	2	4	1	4	3.643
17	2	4	3	2	1	2	2.415
18	3	2	1	3	1	3	3.059
19	1	3	4	1	1	1	−5.297
20	1	4	1	4	3	1	−5.052
21	1	2	4	2	1	4	−5.454
22	4	3	1	2	3	3	4.153
23	3	1	4	1	3	2	3.031
24	2	3	1	1	2	4	1.142
25	1	3	2	3	4	2	−0.608

Based on the results in Table 6, the level trends of the parameters are illustrated in Figure 3. The six parameters are set as follows: $PS=200$, $P_c=0.9$, $P_m=0.2$, $GSR=0.3$, $\beta =0.2$, and $DR=0.3$. To validate these settings, additional parameter tuning experiments are conducted on the instances “m7i4" and “m11i4", which confirms the above parameter settings.

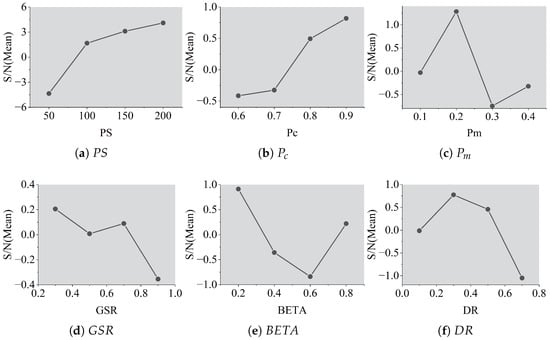
Figure 3. Level trends of parameters ($S/N$).

5.4. Effectiveness of GLPEA’s Search Components

We evaluate the effectiveness of the search components of GLPEA by comparing it with two variant algorithms: GLPEA_V1 and GLPEA_V2. GLPEA_V1 is a variant in which the generational dynamic component-selection strategy of GMM is replaced with a single-component Gaussian model. In GLPEA_V2, the Gaussian model training based on disturbed solutions is removed, and only the GMM sampling mechanism is retained for offspring generation. For fair comparisons, all algorithms are run with $GENS=1000$. The comparative results are given in Table 7 and Table 8.

Table 7. Comparisons of GLPEA, GLPEA_V1, and GLPEA_V2 (IGD).

Instance	GLPEA		GLPEA_V1		GLPEA_V2
	Best	Mean	Best	Mean	Best	Mean
m3i4	0.031	0.035	0.033	0.037	0.406	0.494
m3i6	0.035	0.038	0.036	0.040	0.347	0.415
m3i8	0.046	0.049	0.045	0.050	0.352	0.387
m3i10	0.045	0.050	0.046	0.052	0.342	0.373
m3i12	0.042	0.050	0.045	0.053	0.385	0.429
m5i4	0.032	0.036	0.036	0.042	0.482	0.589
m5i6	0.036	0.056	0.043	0.064	0.395	0.438
m5i8	0.044	0.049	0.045	0.052	0.340	0.407
m5i10	0.044	0.049	0.040	0.052	0.351	0.386
m5i12	0.043	0.053	0.051	0.058	0.388	0.434
m7i4	0.040	0.049	0.045	0.053	0.449	0.500
m7i6	0.036	0.045	0.048	0.054	0.440	0.526
m7i8	0.048	0.056	0.046	0.055	0.351	0.407
m7i10	0.051	0.058	0.046	0.058	0.373	0.416
m7i12	0.049	0.061	0.053	0.064	0.458	0.505
m9i4	0.044	0.050	0.046	0.053	0.385	0.525
m9i6	0.043	0.055	0.047	0.060	0.378	0.520
m9i8	0.046	0.055	0.048	0.057	0.421	0.467
m9i10	0.052	0.064	0.053	0.064	0.400	0.439
m9i12	0.051	0.066	0.056	0.069	0.529	0.560
m11i4	0.043	0.056	0.051	0.072	0.591	0.660
m11i6	0.045	0.055	0.047	0.063	0.477	0.506
m11i8	0.044	0.055	0.046	0.056	0.367	0.388
m11i10	0.055	0.063	0.060	0.069	0.373	0.404
m11i12	0.052	0.064	0.055	0.066	0.458	0.484
m13i4	0.056	0.063	0.057	0.074	0.530	0.574
m13i6	0.039	0.055	0.045	0.060	0.473	0.509
m13i8	0.049	0.060	0.057	0.066	0.414	0.441
m13i10	0.055	0.067	0.054	0.067	0.360	0.391
m13i12	0.050	0.070	0.060	0.076	0.483	0.509
m15i4	0.041	0.048	0.047	0.053	0.540	0.598
m15i6	0.048	0.062	0.058	0.075	0.541	0.570
m15i8	0.052	0.059	0.054	0.065	0.399	0.426
m15i10	0.046	0.059	0.055	0.065	0.390	0.421
m15i12	0.048	0.058	0.049	0.064	0.472	0.497
m17i4	0.047	0.058	0.047	0.064	0.583	0.621
m17i6	0.049	0.063	0.050	0.071	0.538	0.562
m17i8	0.046	0.057	0.054	0.065	0.405	0.430
m17i10	0.053	0.063	0.054	0.067	0.371	0.400
m17i12	0.056	0.068	0.056	0.077	0.451	0.468
p-value	—	—	0.000	0.032	0.000	0.000

Table 8. Comparisons of GLPEA, GLPEA_V1, and GLPEA_V2 (HV).

Instance	GLPEA		GLPEA_V1		GLPEA_V2
	Best	Mean	Best	Mean	Best	Mean
m3i4	0.730	0.724	0.723	0.719	0.418	0.239
m3i6	0.822	0.815	0.814	0.810	0.393	0.329
m3i8	0.848	0.832	0.842	0.831	0.429	0.402
m3i10	0.831	0.817	0.828	0.812	0.435	0.394
m3i12	0.864	0.838	0.845	0.831	0.398	0.358
m5i4	0.776	0.767	0.769	0.762	0.310	0.162
m5i6	0.833	0.823	0.826	0.810	0.351	0.292
m5i8	0.838	0.816	0.832	0.811	0.381	0.314
m5i10	0.864	0.848	0.868	0.839	0.430	0.390
m5i12	0.859	0.845	0.844	0.832	0.381	0.332
m7i4	0.800	0.791	0.789	0.779	0.325	0.242
m7i6	0.781	0.766	0.751	0.740	0.243	0.151
m7i8	0.831	0.805	0.819	0.802	0.376	0.325
m7i10	0.830	0.816	0.832	0.815	0.399	0.362
m7i12	0.839	0.802	0.812	0.794	0.266	0.216
m9i4	0.780	0.767	0.771	0.762	0.346	0.235
m9i6	0.747	0.723	0.729	0.714	0.353	0.236
m9i8	0.820	0.803	0.819	0.793	0.308	0.268
m9i10	0.796	0.776	0.804	0.780	0.305	0.281
m9i12	0.834	0.804	0.827	0.802	0.222	0.194
m11i4	0.710	0.700	0.696	0.685	0.130	0.062
m11i6	0.795	0.778	0.774	0.746	0.192	0.161
m11i8	0.815	0.797	0.814	0.788	0.347	0.322
m11i10	0.786	0.749	0.771	0.741	0.342	0.309
m11i12	0.815	0.786	0.815	0.784	0.274	0.252
m13i4	0.747	0.735	0.736	0.725	0.219	0.160
m13i6	0.819	0.793	0.793	0.767	0.221	0.181
m13i8	0.790	0.769	0.781	0.755	0.265	0.232
m13i10	0.811	0.774	0.796	0.771	0.343	0.313
m13i12	0.828	0.788	0.813	0.783	0.228	0.203
m15i4	0.770	0.753	0.757	0.742	0.167	0.126
m15i6	0.790	0.761	0.750	0.731	0.133	0.102
m15i8	0.825	0.800	0.811	0.780	0.292	0.263
m15i10	0.798	0.772	0.789	0.759	0.283	0.262
m15i12	0.837	0.814	0.841	0.800	0.256	0.233
m17i4	0.748	0.726	0.737	0.718	0.146	0.110
m17i6	0.799	0.774	0.779	0.759	0.213	0.171
m17i8	0.788	0.757	0.756	0.735	0.259	0.237
m17i10	0.786	0.762	0.774	0.750	0.327	0.299
m17i12	0.831	0.803	0.843	0.783	0.279	0.263
p-value	—	—	0.000	0.010	0.000	0.000

As Table 7 and Table 8 show, GLPEA outperforms the two variant algorithms in both IGD and HV, indicating its superior solution quality. To verify the statistical significance of these improvements, we performed the Wilcoxon signed-rank test [57]. Statistical analysis shows that the p-values (presented at the bottom of the table) for all two algorithm pairs are all less than 0.05, confirming the significant improvement in convergence and exploration capabilities achieved by GLPEA. These results validate the effectiveness of the generation-wise dynamic component-selection strategy and the disturbed-solution-based GMM training method, combined with conventional genetic operations for offspring generation, within the nondominated sorting framework. The proposed approach demonstrates considerable potential for applications in other multi-objective evolutionary algorithms.

5.5. Comparisons with State-of-the-Art MOEAs

We evaluate the performance of GLPEA by comparing it with two state-of-the-art MOEAs: NSGA-II and MOEA/D. Both reference algorithms are configured using the parameter settings reported in their original studies, and the same stopping condition described in Section 5.4 is applied. To facilitate a quantitative comparison, we introduce the metric $NB$, which denotes the number of instances in which an algorithm achieves the best value for a given quality indicator. The comparative results are reoprted in Table 9 and Table 10, and the distributions of $NB$ values are shown in Figure 4 and Figure 5.

Table 9. Comparisons of NSGA-II, MOEA/D, and GLPEA (IGD).

Instance	NSGA-II			MOEA/D			GLPEA
	Worst	Best	Mean	Worst	Best	Mean	Worst	Best	Mean
m3i4	0.037	0.024	0.028	0.397	0.286	0.316	0.028	0.022	0.026
m3i6	0.063	0.037	0.043	0.505	0.359	0.440	0.047	0.036	0.040
m3i8	0.053	0.041	0.046	0.420	0.331	0.388	0.051	0.041	0.045
m3i10	0.051	0.041	0.047	0.450	0.328	0.395	0.050	0.040	0.046
m3i12	0.074	0.042	0.050	0.570	0.416	0.508	0.055	0.040	0.049
m5i4	0.049	0.033	0.040	0.678	0.472	0.600	0.044	0.032	0.036
m5i6	0.083	0.045	0.056	0.585	0.427	0.522	0.089	0.035	0.054
m5i8	0.053	0.038	0.044	0.497	0.400	0.438	0.049	0.038	0.043
m5i10	0.055	0.039	0.045	0.496	0.377	0.430	0.051	0.037	0.043
m5i12	0.058	0.042	0.048	0.576	0.455	0.503	0.054	0.037	0.047
m7i4	0.065	0.043	0.053	0.646	0.464	0.571	0.059	0.042	0.048
m7i6	0.055	0.035	0.043	0.633	0.496	0.553	0.050	0.034	0.040
m7i8	0.059	0.041	0.049	0.531	0.406	0.466	0.057	0.041	0.049
m7i10	0.063	0.042	0.049	0.473	0.369	0.413	0.059	0.040	0.048
m7i12	0.074	0.046	0.057	0.616	0.470	0.552	0.069	0.043	0.055
m9i4	0.059	0.044	0.051	0.664	0.502	0.597	0.055	0.042	0.047
m9i6	0.076	0.041	0.056	0.570	0.417	0.519	0.074	0.039	0.054
m9i8	0.062	0.045	0.051	0.627	0.501	0.545	0.057	0.043	0.050
m9i10	0.062	0.044	0.055	0.569	0.385	0.448	0.062	0.042	0.052
m9i12	0.076	0.048	0.060	0.595	0.463	0.512	0.074	0.043	0.059
m11i4	0.106	0.052	0.074	0.678	0.523	0.605	0.088	0.042	0.055
m11i6	0.084	0.045	0.062	0.535	0.413	0.481	0.081	0.042	0.056
m11i8	0.059	0.041	0.049	0.431	0.338	0.391	0.055	0.039	0.045
m11i10	0.069	0.048	0.055	0.474	0.360	0.412	0.066	0.045	0.054
m11i12	0.066	0.049	0.056	0.507	0.396	0.451	0.071	0.043	0.055
m13i4	0.089	0.060	0.073	0.708	0.511	0.600	0.083	0.052	0.065
m13i6	0.098	0.039	0.058	0.464	0.385	0.433	0.065	0.037	0.054
m13i8	0.062	0.044	0.053	0.477	0.409	0.438	0.062	0.041	0.052
m13i10	0.070	0.045	0.058	0.443	0.349	0.393	0.072	0.043	0.055
m13i12	0.088	0.045	0.061	0.516	0.396	0.430	0.086	0.047	0.059
m15i4	0.053	0.041	0.047	0.655	0.497	0.586	0.053	0.035	0.043
m15i6	0.094	0.046	0.065	0.545	0.414	0.482	0.096	0.039	0.063
m15i8	0.062	0.044	0.052	0.490	0.406	0.447	0.059	0.044	0.050
m15i10	0.070	0.042	0.057	0.416	0.326	0.377	0.067	0.042	0.050
m15i12	0.074	0.045	0.057	0.547	0.409	0.480	0.070	0.042	0.052
m17i4	0.087	0.045	0.059	0.710	0.539	0.641	0.083	0.045	0.058
m17i6	0.093	0.061	0.072	0.590	0.488	0.521	0.089	0.047	0.064
m17i8	0.067	0.048	0.055	0.486	0.381	0.425	0.065	0.040	0.051
m17i10	0.077	0.051	0.062	0.456	0.369	0.413	0.079	0.047	0.057
m17i12	0.091	0.050	0.066	0.506	0.432	0.468	0.080	0.049	0.062
$NB$	8	7	1	0	0	0	35	39	40
p-value	0.000	0.000	0.000	0.000	0.000	0.000	—	—	—

Note: For each instance, the superior value among the NSGA-II, MOEA/D, and GLPEA algorithms for the worst, best, and mean metrics is shown in bold. For example, for instance m3i4. Under the Worst case, the values for NSGA-II, MOEA/D, and GLPEA are 0.037, 0.397, and 0.028, respectively; 0.028 is superior. Under the Best case, the values are 0.024, 0.286, and 0.022, respectively; 0.022 is superior. Under the Mean case, the values are 0.028, 0.316, and 0.026, respectively; 0.026 is superior.

Table 10. Comparisons of NSGA-II, MOEA/D, and GLPEA (HV).

Instance	NSGA-II			MOEA/D			GLPEA
	Worst	Best	Mean	Worst	Best	Mean	Worst	Best	Mean
m3i4	0.734	0.748	0.743	0.293	0.520	0.440	0.742	0.753	0.747
m3i6	0.777	0.795	0.787	0.193	0.367	0.270	0.783	0.801	0.793
m3i8	0.820	0.845	0.831	0.307	0.412	0.354	0.824	0.848	0.832
m3i10	0.810	0.846	0.833	0.356	0.454	0.401	0.819	0.848	0.836
m3i12	0.803	0.841	0.818	0.178	0.317	0.254	0.792	0.849	0.820
m5i4	0.779	0.792	0.787	0.164	0.401	0.255	0.782	0.798	0.789
m5i6	0.762	0.804	0.792	0.098	0.302	0.194	0.786	0.817	0.805
m5i8	0.807	0.845	0.827	0.228	0.348	0.298	0.808	0.853	0.834
m5i10	0.818	0.855	0.838	0.227	0.338	0.281	0.811	0.860	0.844
m5i12	0.821	0.858	0.843	0.235	0.341	0.284	0.838	0.866	0.852
m7i4	0.793	0.814	0.804	0.213	0.294	0.248	0.800	0.823	0.815
m7i6	0.768	0.798	0.782	0.135	0.224	0.179	0.779	0.809	0.796
m7i8	0.798	0.841	0.817	0.230	0.356	0.278	0.803	0.833	0.819
m7i10	0.797	0.849	0.818	0.275	0.357	0.316	0.800	0.834	0.820
m7i12	0.795	0.840	0.820	0.186	0.280	0.242	0.795	0.857	0.825
m9i4	0.766	0.789	0.778	0.159	0.320	0.230	0.771	0.797	0.786
m9i6	0.775	0.811	0.793	0.117	0.266	0.190	0.777	0.819	0.802
m9i8	0.773	0.812	0.793	0.144	0.228	0.183	0.773	0.818	0.800
m9i10	0.770	0.815	0.796	0.216	0.318	0.274	0.769	0.831	0.801
m9i12	0.816	0.862	0.838	0.252	0.307	0.281	0.820	0.871	0.839
m11i4	0.750	0.769	0.761	0.111	0.263	0.182	0.760	0.779	0.772
m11i6	0.729	0.784	0.765	0.079	0.233	0.127	0.771	0.807	0.791
m11i8	0.770	0.812	0.794	0.194	0.319	0.238	0.773	0.838	0.800
m11i10	0.732	0.766	0.752	0.206	0.281	0.247	0.713	0.790	0.754
m11i12	0.782	0.831	0.805	0.218	0.325	0.269	0.792	0.830	0.812
m13i4	0.743	0.762	0.755	0.114	0.204	0.168	0.740	0.772	0.761
m13i6	0.775	0.812	0.798	0.168	0.244	0.207	0.796	0.839	0.815
m13i8	0.750	0.815	0.781	0.152	0.241	0.200	0.757	0.802	0.782
m13i10	0.738	0.811	0.775	0.218	0.294	0.252	0.743	0.820	0.786
m13i12	0.767	0.849	0.814	0.210	0.268	0.244	0.799	0.842	0.822
m15i4	0.771	0.807	0.790	0.130	0.226	0.189	0.789	0.814	0.800
m15i6	0.738	0.784	0.761	0.055	0.165	0.109	0.750	0.807	0.780
m15i8	0.775	0.820	0.797	0.164	0.232	0.197	0.790	0.837	0.811
m15i10	0.740	0.810	0.772	0.221	0.319	0.251	0.749	0.812	0.788
m15i12	0.765	0.859	0.810	0.164	0.279	0.211	0.774	0.845	0.823
m17i4	0.725	0.760	0.738	0.067	0.228	0.116	0.735	0.767	0.747
m17i6	0.747	0.794	0.775	0.101	0.194	0.145	0.758	0.809	0.785
m17i8	0.731	0.796	0.763	0.177	0.283	0.228	0.734	0.801	0.772
m17i10	0.730	0.779	0.756	0.226	0.305	0.267	0.743	0.784	0.760
m17i12	0.770	0.848	0.808	0.194	0.288	0.238	0.775	0.845	0.816
$NB$	7	7	0	0	0	0	35	33	40
p-value	0.000	0.000	0.000	0.000	0.000	0.000	—	—	—

Note: For each instance, the superior value among the NSGA-II, MOEA/D, and GLPEA algorithms for the worst, best, and mean metrics is shown in bold. For example, for instance m3i4. Under the Worst case, the values for NSGA-II, MOEA/D, and GLPEA are 0.734, 0.293, and 0.742, respectively; 0.742 is superior. Under the Best case, the values are 0.748, 0.520, and 0.753, respectively; 0.753 is superior. Under the Mean case, the values are 0.743, 0.440, and 0.747, respectively; 0.747 is superior.

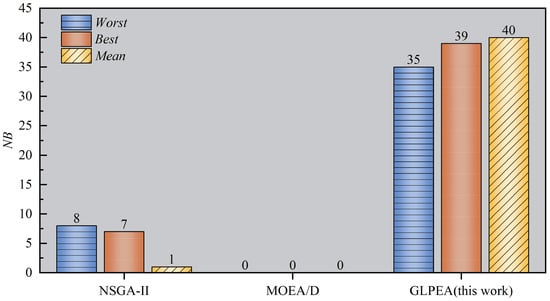
Figure 4. Distributions of NB values obtianed by NSGA-II, MOEA/D, and GLPEA (IGD).

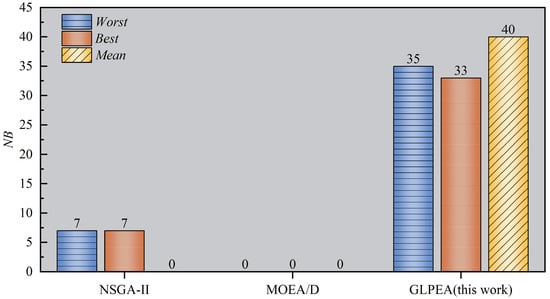
Figure 5. Distributions of NB values obtianed by NSGA-II, MOEA/D, and GLPEA (HV).

From Table 9 and Table 10, one observes that GLPEA outperforms the two reference algorithms in terms of worst, best, and average for almost all these problem instances. The p-values obtained from the Wilcoxon signed-rank test (presented at the bottom of the table) were all substantially less than $0.05$. This indicates that the observed improvements of GLPEA in both convergence and diversity are statistically significant. Furthermore, as shown in Figure 4 and Figure 5, GLPEA achieves higher $NB$ values than those of the reference algorithms, indicating its superior consistency in obtaining the best search performance. The statistical distributions of the results are further analyzed through the box plots for selected instances (“m11i4”, “m13i4”, and “m15i4”) in Figure 6, and violin plots summarizing the IGD and HV results are provided in Figure 7. These distributions collectively confirm the competitive search capability of GLPEA. Based on the comprehensive experimental analysis, GLPEA can be regarded as an effective solution approach for HPMPP. Given the practical relevance of HPMPP, the proposed algorithm holds promise for extension to other production planning problems in industrial silicon manufacturing.

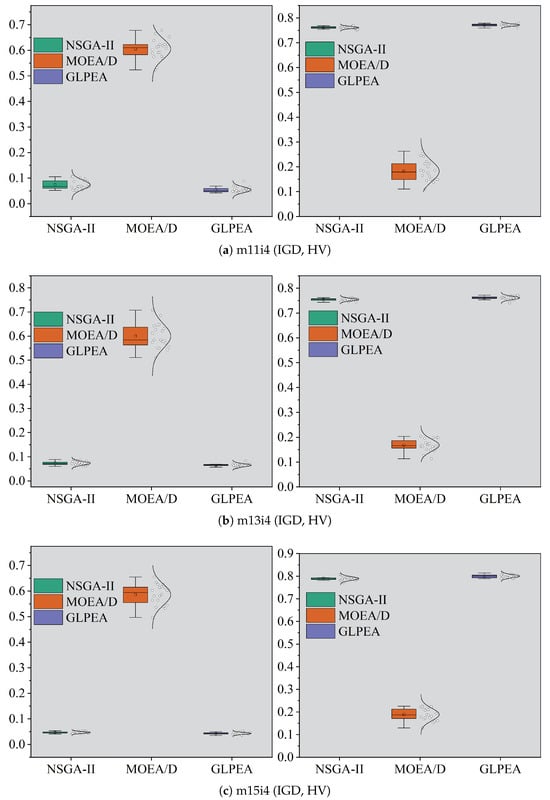
Figure 6. Box plots for NSGA-II, MOEA/D, and GLPEA.

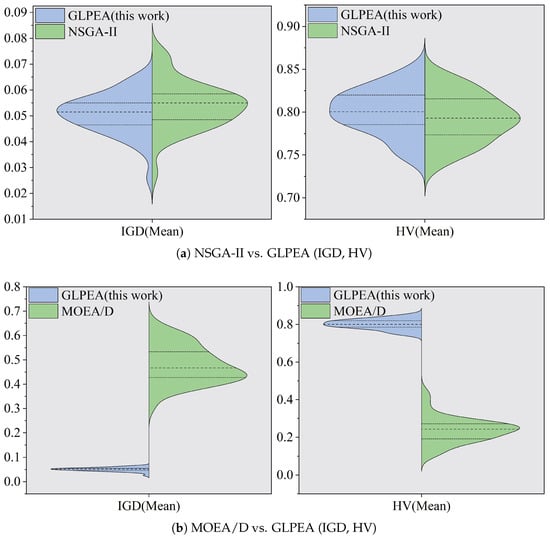
Figure 7. Violin plots for MOEA/D, NSGA-II, and GLPEA (Mean).

5.6. Computational Overhead and Limitations Analysis

5.6.1. Analysis of Computational Time

This section analyzes the computational time of the GLPEA. All experiments were executed on the hardware described in Section 5.1. Notably, the GLPEA does not require specialized hardware resources, such as GPUs, for execution. For each instance, GLPEA and the compared algorithms are executed independently 20 times with $GENS=1000$. To quantitatively compare the execution time, Table 11 presents the average execution time (in seconds) of the three algorithms across 40 instances.

Table 11. The average execution time (in seconds) of the three algorithms.

Instance	NSGA-II	MOEA/D	GLPEA
m3i4	779.726	2000.148	1283.671
m3i6	794.307	4657.909	1330.478
m3i8	828.950	9622.002	1377.809
m3i10	792.819	11,121.178	1377.129
m3i12	808.040	7133.246	1679.763
m5i4	814.061	2907.541	1334.321
m5i6	799.367	2415.997	1341.155
m5i8	791.859	8448.023	1749.291
m5i10	776.201	8627.950	1927.886
m5i12	795.755	6869.132	1065.323
m7i4	804.528	4796.024	1030.131
m7i6	817.014	4019.891	1077.614
m7i8	812.654	6771.598	1096.161
m7i10	803.460	6438.196	1585.894
m7i12	816.046	8097.105	2110.503
m9i4	801.167	5500.998	1646.787
m9i6	807.605	3516.891	2005.195
m9i8	794.848	7504.607	2040.184
m9i10	827.751	9542.724	2134.090
m9i12	829.950	7998.894	2240.898
m11i4	814.927	5035.524	2095.210
m11i6	790.528	3404.547	2029.272
m11i8	824.761	10,279.548	2074.627
m11i10	820.250	8103.275	1128.435
m11i12	836.556	10,684.374	2177.091
m13i4	792.300	4672.910	1996.058
m13i6	831.316	4324.266	2287.419
m13i8	764.265	7660.314	2050.911
m13i10	875.118	11,367.958	2316.989
m13i12	840.692	10,505.099	2359.349
m15i4	766.218	5112.326	1992.162
m15i6	763.724	4651.158	2042.017
m15i8	784.077	7785.538	2024.366
m15i10	806.579	9968.631	2206.082
m15i12	729.105	8401.749	2323.825
m17i4	831.656	2554.879	1744.554
m17i6	842.603	1958.153	2911.123
m17i8	826.641	9448.504	2146.167
m17i10	832.813	10,989.428	2377.331
m17i12	849.449	9877.921	2873.884

As detailed in Table 9, we observed that the computational time generally increases with the size of the problem instance for most cases. The execution time of GLPEA is significantly higher than NSGA-II but lower than MOEA/D. This finding aligns with the higher computational complexity inherent in the Gaussian Mixture Model (GMM) training integrated into GLPEA. This increase in computational overhead is anticipated; unlike the lightweight stochastic operators of NSGA-II, the primary computational burden of GLPEA stems from the GMM training.

5.6.2. Analysis of Computational Complexity

To theoretically analyze the computational overhead of GLPEA, we base our analysis on the HPMPP problem studied in this research, where $PS$ is the population size and $I\times M$ is the dimension of the problem’s decision variables. We analyze the main computational complexity per generation of the algorithm. (1) GLPEA adopts the non-dominated sorting framework of NSGA-II. Since the number of objective functions is a constant (three), the computational complexity of non-dominated sorting can be simplified to $O\left({\left(PS\right)}^2\right)$; the complexity of calculating the crowding distance is $O\left(\right(PS)log(PS\left)\right)$. Thus, the complexity of the traditional evolutionary mechanism is $O\left({\left(PS\right)}^2\right)$. (2) Based on the analysis presented in Section 4.2.3, the computational complexity of the GMM training is primarily determined by the calculation of the covariance matrix, which is approximately $O(t·k·\left(PS\right)·{(I\times M)}^2)$, where t is the number of EM iterations and k is the number of components. Since t and k are constants, the complexity of GMM training is simplified to $O(\left(PS\right)·{(I\times M)}^2)$. In summary, the total computational complexity of GLPEA per generation is $O({\left(PS\right)}^2+\left(PS\right)·{(I\times M)}^2)$.

5.6.3. Method Limitations and Industrial Applicability

As discussed above, the complexity scales with $O(\left(PS\right)·{(I\times M)}^2)$ due to the GMM training as the problem size $I\times M$ increases, leading to a rapid increase in the algorithm’s computational time. This observation is consistent with the computational time trend of GLPEA shown in Table 11. Regarding parameter sensitivity, GLPEA introduces new parameters such as $GSR$, $BETA$, and $DR$. Although this study determined a suitable combination of parameters in Section 5.3, the algorithm’s performance might be sensitive to these parameters. Re-tuning the parameters may be required when applying the algorithm to new problems, which can be time-consuming.

Despite these limitations, in the context of HPMPP, planning is typically executed periodically and offline. Therefore, obtaining a superior Pareto front, as shown in Table 9 and Table 10, within the computational time demonstrated in Table 11 on modern computing hardware, is fully acceptable. Thus, GLPEA retains strong industrial applicability.

5.7. Discussions

We further evaluate the solution quality of GLPEA concerning the following issues: (a) the trends of IGD and HV values for GLPEA, NSGA-II, and MOEA/D; and (b) a comparison of APFs obtained by the three algorithms. These analyses help verify the search behavior of GLPEA and the distribution of its final solutions.

5.7.1. Trends of IGD and HV Achieved by GLPEA, NSGA-II, and MOEA/D

Using the instance “m7i4”, we execute GLPEA, NSGA-II, and MOEA/D with a stopping condition of $GENS=1000$. At each generation, the IGD and HV values are calculated and recorded based on the nondominated solutions identified from the populations of the three algorithms. The resulting trends of IGD and HV of GLPEA and the two reference approaches are given in Figure 8 and Figure 9.

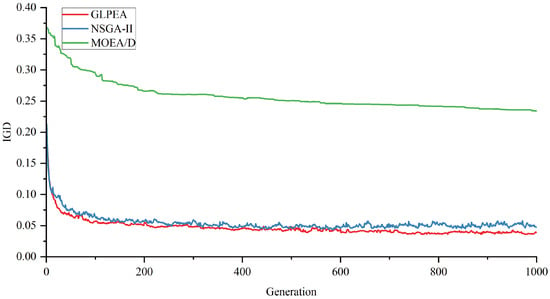
Figure 8. Trends of IGD obtained by GLPEA, NSGA-II, and MOEA/D.

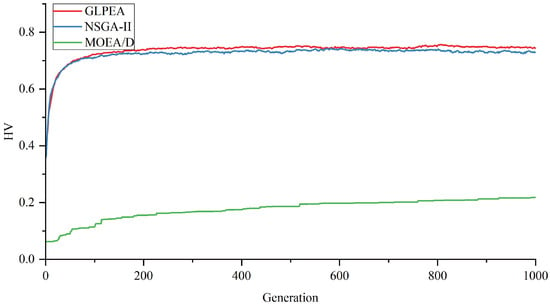
Figure 9. Trends of HV obtained by GLPEA, NSGA-II, and MOEA/D.

As shown in Figure 8 and Figure 9, GLPEA consistently achieves lower IGD values and higher HV values than NSGA-II and MOEA/D throughout the whole iterative process. This indicates a smaller distance to the reference Pareto front and a broader coverage of the objective space, collectively confirming GLPEA’s superior capability in exploring diverse regions of the Pareto front.

5.7.2. APFs Solved by GLPEA, NSGA-II, and MOEA/D

To analyze the distributions of APFs obtained by GLPEA and the two state-of-the-art solution methods, we draw the APFs of the three methods in Figure 10. We note that this analysis is again based on the instance “m7i4” and under the stopping condition of $GENS=1000$.

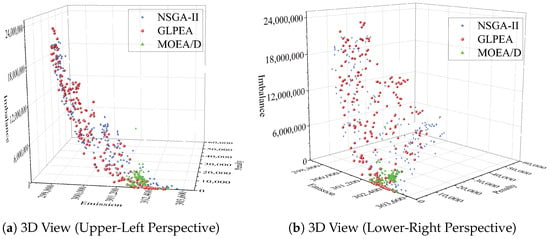
Figure 10. APFs obtained by GLPEA, NSGA-II, MOEA/D.

Based on the distributions of obtained APFs shown in Figure 10, GLPEA achieves superior uniformity and coverage across all three objectives in the Pareto front, outperforming NSGA-II (which ranks second) and MOEA/D (which shows the weakest performance in both coverage and distribution uniformity). Moreover, these results reflect inherent conflicts among the three optimization objectives: emission control, rollover penalty costs, and load balancing. As a result, a significant improvement in one objective generally leads to deterioration in the others, resulting in a dispersed Pareto front rather than a single optimal solution.

6. Conclusions

We investigate a multi-objective heterogeneous parallel machine scheduling problem arising from industrial silicon smelting, with the aim of simultaneously minimizing carbon emissions, rollover penalty costs, and load imbalance. The model incorporates practical constraints including machine maintenance schedules and monthly production demands, while carbon emission factors are predicted using a machine learning approach for a 12-month horizon. From the algorithmic perspective, the proposed GLPEA introduces a generation-wise dynamic component-selection strategy within a GMM framework, enhanced by a disturbed-solution-set-based training scheme, and integrated with conventional genetic operators for offspring generation. Extensive computational experiments demonstrate that GLPEA achieves superior performance compared to state-of-the-art MOEAs in terms of both IGD and HV metrics.

For future research, carbon emission forecasting could be improved through advanced techniques such as multimodal fusion prediction. Further enhancement of the algorithm may also be achieved by developing more adaptive mechanisms for determining the number of Gaussian mixture components during evolution.