Content Value Dynamics in Digital Platforms: Strategic Monetization and Operational Design

Abstract

Digital content platforms rely on value co-creation among users, creators, and the platform. Content value, including historical accumulation, influences platforms’ pricing strategies, quality decisions, and monetization potential. This study explores the impact of content value on pricing and quality strategies under centralized and decentralized content configurations. We capture the relationship between historical content quality and user engagement. The interplay of historical quality and content type is characterized as content value dynamics, which influence platforms in managing content supply, user engagement, and revenue generation under different modes. Results show that operational modes offer distinct advantages depending on subsidy levels, advertising revenue-sharing mechanisms, and the platform development stage. The centralized mode performs better under limited subsidies, particularly by offering content with higher continuity. The decentralized mode benefits from diverse creation and flexible incentives to achieve rapid market scaling when subsidies are sufficient. Notably, higher advertising revenue-sharing is not always optimal, especially in low-advertising environments. Additionally, the platform development stage affects optimal mode selection. The decentralized mode with low subsidies may achieve early profitability, whereas the centralized mode offers greater potential for sustainable long-term growth. This work contributes to platform-based supply chain theory by incorporating dynamic content value into operational decision-making. It provides operational insights for platforms regarding mode design and the optimization of value-based monetization strategies.

1. Introduction

Content platforms operate as digital supply chains, coordinating users, creators, and platform resources to deliver and monetize content. A critical operational decision is the selection between centralized and decentralized content configurations, each offering distinct trade-offs [1,2]. Centralized modes, exemplified by professionally generated content (PGC), rely on substantial investment in content production and support subscription-based monetization, such as Netflix (What can I watch on Netflix? https://www.netflix.com/). Decentralized modes, i.e., user-generated content (UGC), provide diversity through positive user creation and focus on advertising revenue, as exemplified by YouTube (How to earn money on YouTube). In practice, many content platforms adopt a “dual-engine growth” strategy, combining subscription and advertising to diversify revenue streams [3,4]. This strategy can satisfy both paid and freemium users, generating more profit potential.

To determine the optimal operational mode, platforms must weigh content adaptability, market characteristics, user preferences, and revenue potential. Netflix benefits from consistent content quality and subscription-based monetization, demonstrating the success of centralized configurations. Quibi’s failure illustrates the risk of misaligned high subscription pricing and underwhelming content in the centralized PGC mode. For decentralized configurations, YouTube’s success through UGC demonstrates the potential of user engagement, whereas Friendster struggled to sustain a user base due to insufficient network effects. Its recent interest in PGC illustrates the evolution of model configuration. These cases demonstrate that content platforms must integrate resource allocation and market feedback to optimize mode selection and monetization strategy.

A crucial driver of platform performance is the dynamic accumulation of perceived content quality. Given the intangible and abundant nature of content, users often rely on historical quality signals—such as views, likes, and subscriber counts—to support engagement and consumption decisions [5]. This indicates that historical content quality affects subsequent user engagement and characterizes the users’ overall perception of the platform. High historical quality enhances user perceptions and fosters engagement, while poor quality diminishes them. Thus, the perceived value of content accumulates dynamically, influencing consumption behavior and revenue generation.

Content quality also directly influences pricing strategies [6]. Platforms use flexible pricing strategies to align with consumer preferences and optimize revenue structures [7]. For example, YouTube monetizes through advertising and premium subscription models (All YouTube. No interruptions. https://www.youtube.com/premium (accessed on 21 March 2025)) Spotify and Netflix provide tiered payment plans to accommodate varying consumer willingness to pay (NETFLIX: Choose the plan that’s right for you. https://www.netflix.com/signup/planform (accessed on 17 March 2025)). These pricing strategies increasingly rely on dynamic information to enhance operational efficiency within digital platform operations [8].

Diverse operational modes and flexible monetization strategies drive research on the joint effects of pricing and quality strategies [9,10]. To capture the strategy dynamics, they investigate two-stage decision-making through signaling [11], online reviews [12,13], and social learning [14,15,16]. However, few studies have explored the interactions between cumulative content quality and decision dynamics.

Our work develops a dynamic framework for modeling value accumulation within digital content platforms. We synthesize historical quality and content type to characterize value dynamics. Content with higher continuity exerts a greater influence on current decisions. Our work optimizes price and quality decisions based on value dynamics and explores monetization strategies and profitability under centralized and decentralized content configurations, represented by PGC and UGC modes, respectively. We aim to address the following questions:

1.

What factors influence content platforms’ selection between PGC and UGC modes?

2.

How do value dynamics affect quality and pricing strategies?

3.

What dynamic patterns emerge between operational decisions and user behavior?

4.

How can platforms determine optimal operational strategies based on subsidy, content type, and development stage?

Our work highlights significant contributions of value dynamics to digital platform supply chains and information management. First, we develop a dynamic framework to model the temporal accumulation of historical content quality. Second, we formulate a dynamic supply chain system to balance the requirements of the platform, consumers, and creators. We analyze the trade-offs among quality, pricing, and user value dynamics. Then, we model the effects of different user groups and consumption preferences, and discuss the advantageous operational conditions under different modes. Finally, we derive equilibrium strategies under varying subsidy schemes and advertising intensities, offering practical guidance for platform monetization and operational design.

We obtained several insights. First, the PGC mode is more suitable for platforms emphasizing content continuity and subscription-based monetization. The UGC mode relies on supportive incentive programs. However, a higher advertising revenue-sharing ratio does not necessarily improve platform performance. This finding challenges the conventional assumption that more generous creator incentives always stimulate greater engagement [17]. Instead, platforms must balance the effectiveness of incentives against costs to ensure sustainable monetization. Second, PGC and UGC modes perform differently under various subsidy and advertising conditions. The PGC mode can stay competitive even with limited subsidies because of stable content. The UGC mode rapidly enhances profitability with high subsidies. Surprisingly, the UGC mode presents superior performance even with low subsidies or reduced advertising revenue sharing, especially when advertising opportunities are limited. This finding contrasts with Subramanian et al. [9], who suggested that UGC platforms incur higher performance costs. Moreover, advertising intensity further amplifies the performance gap between the two modes. Finally, content platforms should adopt flexible operation modes based on the content’s operational period. The UGC mode is better suited for quick, short-term monetization due to lower costs, especially when subsidies are limited. In contrast, the PGC mode is more effective for long-term growth and sustained value.

In the remainder of this paper, Section 2 reviews relevant literature. Section 3 introduces the value dynamics framework and decision models. Section 4 analyzes equilibrium price and quality strategies under PGC and UGC modes. Section 5 presents numerical results. Section 6 summarizes managerial insights.

2. Literature Review

Our work closely relates to three literature streams: content operation mode, online decision optimization, and user consumption experience.

2.1. Content Operation Mode

The selection of content operation mode significantly influences user behavior and platform competitiveness [18]. Currently, content platforms typically adopt two dominant modes: PGC and UGC. The PGC mode signals more specialized content and higher quality [19]. The UGC mode provides diverse content resources and greater user engagement [20]. Although each mode has distinct advantages, they also present specific operational challenges. The PGC mode has higher content distribution costs and limited resource richness [18], whereas the UGC mode introduces greater uncertainty in value creation [9]. Considering the dependence of the online environment on users, content platforms investigate effective operational methods through factors such as creator influence [17,21,22], consumer preference [23], marketing strategy [9], market characteristics [24], and content type [25]. The study by Sen et al. [26] shows output and value complementary effects between UGC and PGC modes. Caro and Martínez-de-Albéniz [23] demonstrated that optimal content strategies exhibit dynamics, and past information has significant implications. Previous studies have mainly focused on the conceptual framework of content platforms and the analysis of influencing factors. However, content platform operational strategies involve funding, type, market, and the complex interplay of user engagement, quality management, and value perception dynamics. This work investigates the interaction between user consumption perceptions and decision optimization. We examine the impact of historical consumption on users’ purchase intentions and explore differences across operational modes.

2.2. Online Decision Optimization

Quality and price decisions are the primary interest of scholars in online decision optimization. Platforms enhance decisions based on consumer behaviors [27], online reviews [28], and service segmentation [29] to boost marketing competitiveness. Jiang and Yang [28] leveraged user online reviews to investigate two-stage quality and pricing decisions for new experience products. They found that more cost-efficient companies provide higher quality than less efficient ones. However, as the online environment evolves and competition intensifies, content platforms innovate in operational modes [30], expand content development channels [31], leverage user network effects [32], and share information [33]. For instance, Geng and Chen [34] examined the influence of value differences between freemium and premium versions on platform profitability. Du et al. [35] considered consumer uncertainty about valuations and studied the platform revenue optimization through disclosure strategies. They determined optimal subscription prices and advertising allocations based on reference price effects. Wu and Chiu [31] found that developing exclusive content is a dominant strategy benefiting platforms, consumers, and society in multi-homing scenarios. Existing literature gradually recognizes the importance of users in decision optimization and integrates marketing strategies to improve platform profitability [36]. However, due to the intangible nature of online content, users fail to understand content quality and value accurately. Since content quality impacts are historically accumulative, our work emphasizes the historical accumulation of online content quality. It explores the interaction between dynamic quality and user preferences in platform operational decisions.

2.3. User Consumption Experience

As users’ consumption expectations increase, optimizing the consumption experience enhances platform effectiveness and expands the quantity and variety of users. Considering the intangible characteristics of online content, platforms attempt to better portray the consumption value through data analysis [37], user feedback [13,38], and content quality grading [5]. Content quality is a crucial factor in perceived value and directly influences user consumption behavior [39]. Due to the uncertain content quality, users often evaluate the value based on historical information. Specifically, historical content quality exerts an accumulative effect on current consumption behavior [40]. Caro and Martínez-de-Albéniz [23] noted that past successes motivate content providers to enhance their efforts. Zhao et al. [41] also identified that the loading time and prior reading behavior continuously affect user engagement and content consumption. This work captures the accumulative impact of historical information from the perspective of consumption value. We formulate value dynamics based on historical quality to support users’ consumption decisions, creators’ quality improvements, and platforms’ pricing strategies.

3. Model

In content supply chains consisting of creators, platforms, and consumers, two operational modes exist: PGC and UGC. In the PGC mode, platforms distribute content and also actively produce content. Conversely, in the UGC mode, platforms stimulate external content creation by offering financial incentives, such as advertising revenue sharing and subscriber-based rewards. As shown in Figure 1, content creators determine their quality effort $s\left(t\right)$ based on revenue incentives and production costs. Over time, the cumulative quality effort contributes to dynamic content value. This directly influences user engagement and subscription decisions. Content platforms strategically set subscription price $p\left(t\right)$ based on anticipated consumer responses. Users are classified into two engagement types: freemium and subscription. Freemium users obtain content access primarily through advertising exposure. Subscription users pay a fee to experience advertisement-reduced or advertisement-free content. Additionally, they have unlimited access to historical and current content throughout the subscription period. We emphasize operational decisions within given content ecosystems and incentive structures. Therefore, network externalities on the user side are treated as exogenous and stable environmental parameters. Within this operational framework, we propose optimal strategies for platform management and content monetization, aiming to maximize the profitability of the involved entities. The notations used are summarized in Table 1.

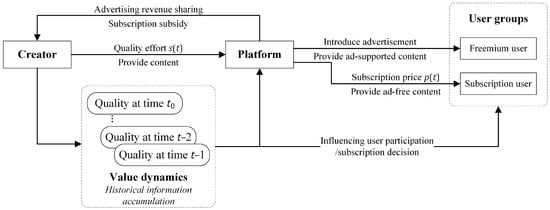
Figure 1. Dynamic decision relationships between content platform involved entities.

Table 1. Main variables and parameters.

	Notation	Description
variable	$p\left(t\right)$	online content subscription price at time $t$
	$s\left(t\right)$	quality effort of online content at time $t$
	$L\left(t\right)$	content value dynamics at time $t$, dynamically accumulated from historical quality
	$D^F\left(t\right)$	demand for freemium users at time $t$
	$D^S\left(t\right)$	demand for subscription users at time $t$
parameter	$g$	advertising revenue-sharing ratio for content creators, $g\in [0,1]$
	$r$	revenue generated by unit advertising intensity
	$a$	advertising intensity
	$c$	user engagement costs, such as time spent searching and cognitive effort
	$f$	unit subsidy provided by the platform to creators for subscription users
	$\delta$	marginal effect of historical quality on value dynamics, also used to portray the dispersion of content type (that is, a more significant $\delta$ results in a lower influence of historical quality and a higher content dispersion)
	$\theta$	advertising revenue-sharing ratio for content creators

3.1. User Utility and Demand Dynamics

In freemium business models, users typically choose between free and paid content access. Freemium users are not charged directly but experience advertisement interruptions [42]. Engagement costs for users include the time spent searching for content, decision-making, and advertisement viewing. We set the baseline engagement cost $c$, which applies directly to subscription users. Freemium users incur an additional cost from advertising, denoted as $a$, making their total engagement cost $c+a$. An empirical study on Pandora Internet Radio found that advertising interruptions significantly reduce user engagement time and prompt more users to choose paid ad-free services [43]. This supports our model that freemium users generate additional advertising engagement costs. In practice, user responses vary according to cost sensitivity, denoted as $\theta$, uniformly distributed within the interval $\left[0,\overline{\theta }\right]$. Using heterogeneous cost sensitivity $\theta$ to simulate user engagement is a common approach in demand modeling for digital platforms, such as in the work of Liu et al. [36], Moorthy and Shahrokhi Tehrani [44]. This approach captures differences in user behavior while simplifying computational complexity.

Users highly sensitive to costs tend to choose paid subscriptions to minimize total expenses. However, users with extremely high-cost sensitivity (approaching $\overline{\theta }$) may opt out. Subscription users pay a fee $p$ to obtain full utility, including historical content value $L$ and the current content quality $s$. Therefore, the utilities of subscription $u_S$ and freemium $u_F$ are defined as follows:

$$\left\{\begin{array}{l}{u}_S=L+s-p-\theta c\\ u_F=s-\theta \left(c+a\right)\end{array}\right.$$

(1)

Notably, the utility of freemium users does not explicitly include historical content. In practice, freemium users can derive value from historical content. However, our model introduces this effect into the engagement cost of advertising disruption, that is, the negative effect of advertisement exposure is greater than the positive utility of accessing historical content. This simplification enhances model tractability and highlights the trade-off between advertising disturbances and subscription charges.

First, when freemium users attempt to access historical content, most platforms impose restrictions or heavy advertising. For example, digital publications such as “The New York Times” and “Financial Times” typically charge for access to historical articles; online education platforms like “Coursera” and “edX” often restrict freemium users from revisiting completed courses. In these cases, the practical utility of historical content for freemium users is significantly reduced.

Second, excluding historical content from freemium utility can be regarded as a lower-bound benchmark. If freemium users derive substantial positive utility from historical content with advertising exposure, the attractiveness of subscription services would be further diminished.

We categorize users based on cost sensitivity $\theta$. By solving for user indifference ($u_S=u_F$), we determine the threshold cost sensitivity ${\theta }_1=\left(p-L\right)/a$, distinguishing subscription and freemium preferences. Users with a cost sensitivity $\theta \in \left[0,{\theta }_1\right]$ prefer the freemium model. Hence, the freemium user demand is $D^F=\left(p-L\right)/a$. Users with a cost sensitivity greater than ${\theta }_1$ will prefer a paid subscription. We further analyze the maximum cost sensitivity threshold for subscription engagement ($u_S=0$), denoted as ${\theta }_2=\left(L-p+s\right)/c$. Users with $\theta >{\theta }_2$ would leave the content platform. Thus, subscription demand depends on ${\theta }_2-{\theta }_1$. Considering that the base cost $c$ uniformly affects all users, it linearly shifts the threshold ${\theta }_2$ without affecting relative comparisons. This threshold-based characterization of subscription and freemium demand aligns with empirical evidence from digital content platforms. Previous research indicates that users’ cost sensitivity and advertising aversion are strong predictors of subscription conversion, consistent with models used for Spotify [45], YouTube Premium [46], and digital news paywalls [47]. We verify that the changes in $c$ linearly shift certain expressions and conditions. Normalize $c=1$ for simplicity without losing generality, allowing a focused analysis on freemium-specific costs. Therefore, the subscription user demand is $D^S=L-p+s-\left(p-L\right)/a$.

3.2. Content Value Dynamics

In content supply chains, the principle that “content is king” significantly drives platform competitiveness is well-established [25]. Continuous content updates and quality accumulation form the basis for user engagement. Platforms and creators formulate user value perceptions and evaluations based on historical content quality [48]. This value depends on content quality and is also influenced by the cumulative effect over time, which is related to the continuity of the content type. For instance, content types with high continuity (such as courses or series) have a longer-lasting impact from historical quality, while content types with low continuity (such as entertainment videos) are more easily forgotten. Therefore, we define the cumulative change in historical information in terms of content quality and type as content value dynamics, denoted as $L\left(t\right)$, represented by the weighted average of historical content quality:

$$L\left(t\right)=\omega \left(t-t_0\right)L\left(t_0\right)+{\int }_{t_0}^t\omega \left(t-\tau \right)s\left(\tau \right)\mathrm{d}\tau$$

(2)

Here, $\omega \left(·\right)$ is a weighting scheme capturing the diminishing impact of past content quality over time. Specifically, $\omega \left(·\right)$ is a non-increasing function, indicating that more recent content has a greater influence on current value than older content. This memory decay effect aligns with the consumption characteristics of online platforms, where historical information gradually declines in influence. We specify the weighting function as $\omega \left(t\right)=\delta e^{-\delta t}$ for computational simplicity, where $\delta$ is the influence intensity of historical content quality on value dynamics. This parameter $\delta$ also indicates the continuity or independence of content type. This model is widely used and standardized in the literature [27,49]. Differentiating Equation (2), we obtain:

$$\dot{L}\left(t\right)=\delta \left(s\left(t\right)-L\left(t\right)\right)$$

(3)

Notably, when $\delta =0$, the content value is constant, that is, it is independent of the current quality. When $\delta > 0$, the value is adjusted based on the quality of newly generated content. As $\delta \to \infty$, $\omega \left(t-\tau \right)$ converges to zero. In this case, the content value adjustment is instantaneous [27]. This indicates that content types are entirely independent, and the historical content has almost no influence.

3.3. Operation Profit Model

In freemium business models, operational revenue mainly derives from two streams: subscription fees $p\left(t\right)D^S\left(t\right)$ and advertising revenue $ra{D}^F\left(t\right)$. Operational costs mainly involve quality-related costs, modeled as ${\displaystyle \frac{k}{2}}{s}^2\left(t\right)$, consistent with the law of increasing marginal costs. In practice, improving content quality requires greater investment of resources and effort to optimize content effectiveness. As creators pursue higher-quality content, they need to coordinate multiple resources including time, expertise, equipment, and financial investment [50]. For example, producing higher-quality video content requires more sophisticated equipment, advanced editing techniques, larger teams, and stricter quality control, resulting in a convex cost structure. Therefore, we assume that content production costs are convex and increase with the intensity of quality investments. This assumption reflects the challenge of balancing content investment costs with operational profitability. Thus, in the PGC scenario (Scenario $P$), platforms determine quality effort and subscription pricing to optimize profits. The profit function under Scenario $P$ is given by

$$\pi =p\left(t\right)D^S\left(t\right)+ra{D}^F\left(t\right)-{\displaystyle \frac{1}{2}}{s}^2\left(t\right)$$

(4)

In the UGC mode (Scenario $U$), the platform operates as a Stackelberg leader by first determining the subscription price $p\left(t\right)$, and creators subsequently decide their quality effort $s\left(t\right)$. The platform incentivizes creators through financial subsidies based on subscription user numbers and advertising revenue-sharing schemes. This dual-subsidy mechanism is widely used by online content platforms. Our model considers the subsidy and advertising revenue-sharing ratio as exogenous parameters. In practice, platforms usually adopt fixed incentive mechanisms based on budget constraints, strategic positioning, and content type. Compared to the flexible time scales for pricing and quality decisions, incentive programs remain stable within a given operational cycle. For example, in YouTube’s Partner Program, creators receive about 55% of advertising revenue generated from freemium users. For subscribers (such as YouTube Premium users), who are not exposed to advertisements, the platform allocates part of subscription revenue to creators based on subscriber viewing time. In our model, the parameter $f$ represents the unit subsidy per subscriber, $g\in \left[0,1\right]$ represents the share of advertising revenue given to creators. The advertising revenue follows the Cost Per Mille model and depends on the number of freemium users. Therefore, operational profit for the platform (${\pi }_P$) and the creator (${\pi }_C$) under Scenario $U$ are given by

$$\left\{\begin{array}{l}{\pi }_P=\left(p\left(t\right)-f\right)D^S\left(t\right)+\left(1-g\right)ra{D}^F\left(t\right)\\ {\pi }_C=gra{D}^F\left(t\right)+f{D}^S\left(t\right)-{\displaystyle \frac{1}{2}}{s}^2\left(t\right)\end{array}\right.$$

(5)

Notably, the differences between the PGC and UGC models are inherent in the model structure. First, the two models differ in decision configurations and incentive mechanisms. In the PGC mode, the platform determines price and quality and fully internalizes the trade-offs between costs and benefits. In contrast, in the UGC mode, the platform sets the price while creators choose quality based on subsidies and revenue-sharing incentives, generating a different dynamic structure. Second, the accumulation efficiency of content value depends on the type continuity parameter δ. Under different decision structures, content value affects stakeholders’ payoffs differently, leading each mode to prefer different content types. For example, the PGC mode benefits more from high-continuity content, whereas the UGC mode accommodates more content types. Third, advertising is introduced into models through dynamic demands. Although the revenue-sharing rate remains fixed, advertising revenue adjusts endogenously with changes in demand and content value.

4. Equilibrium Feedback Strategy

This section discusses the equilibrium strategies for digital content platforms under the PGC mode (Scenario $P$) and UGC mode (Scenario $U$). Let $\varphi$ denote a continuous discount rate. We derive the feedback equilibrium strategies through Hamilton–Jacobi–Bellman (HJB) equations. To ensure the continuity and validity of the model, we assume non-negative control variables and stationarity. On one hand, quality effort $s\left(t\right)$ is crucial for content production. If $s\left(t\right)\le 0$, the platform cannot sustainably provide content. Therefore, we assume that quality investments are strictly positive and focus on this feasible parameter range. On the other hand, stationarity is a critical assumption in the infinite horizon problem [51]. Online content platforms pursue stable operational strategies to ensure sustainability and economic viability. Therefore, we focus on investigating the equilibrium of stationary systems in the infinite horizon problem. Detailed proofs of propositions and corollaries are provided in the Appendix A.

4.1. Equilibrium Feedback Strategies in the PGC Mode

In Scenario $P$, the optimal control model to maximize platform revenue is formulated as follows:

$$\left\{\begin{array}{l}\underset{p\left(t\right),s\left(t\right)}{\max }{\int }_0^{\mathrm{\infty }}{e}^{-\varphi t}\pi \left(t\right)\mathrm{d}t\\ s.t.\dot{L}\left(t\right)=\delta \left(s\left(t\right)-L\left(t\right)\right),L\left(0\right)=L_0\end{array}\right.$$

(6)

The corresponding HJB equation for the value function of Equation (6) is:

$$\varphi V^{PP}=\underset{p,s}{\max }\left(\begin{array}{c}p\left(L-p+s-{\displaystyle \frac{p-L}{a}}\right)+ra\left({\displaystyle \frac{p-L}{a}}\right)-{\displaystyle \frac{1}{2}}{s}^2\\ +V_L^P\delta \left(s-L\right)\end{array}\right)$$

(7)

where $V_L^{PP}={\displaystyle \frac{\partial \left(V^P\right)}{\partial \left(L\right)}}$ and satisfies the value function boundary condition $\underset{t\to \mathrm{\infty }}{\lim } e^{-\varphi t}{V}_L^{PP}\left(L\left(t\right)\right)=0$. The equilibrium feedback strategies under Scenario $P$ are presented below.

Proposition 1.

Equilibrium feedback strategies in the PGC mode

(i) 

In Scenario $P$, the equilibrium feedback strategies for quality and price with respect to value dynamics are

$$p^{P*}\left(t\right)=\left({\displaystyle \frac{1+a}{2+a}}+{\displaystyle \frac{a{N}_1}{4(1+a)\delta \left(2+a\right)}}\right)L^P\left(t\right)+{\displaystyle \frac{ar\left(4\right(1+a)\varphi -N_1)}{2(1+a)\left(2\right(\delta +(2+a)\varphi )-N_1)}}\mathit{,}$$

$$s^{P*}\left(t\right)=\left({\displaystyle \frac{1+a}{2+a}}+{\displaystyle \frac{N_1}{2\delta \left(2+a\right)}}\right)L^P\left(t\right)-{\displaystyle \frac{2r(\delta -a\varphi )}{2(\delta +(2+a\left)\varphi \right)-N_1}}\mathit{,}$$

where $N_1=2\delta +\varphi \left(2+a\right)-\sqrt{{\left(2\delta +\varphi \left(2+a\right)\right)}^2-{\displaystyle \frac{8{(1+a)}^3{\delta }^2}{a}}}$.

(ii) 

In Scenario $P$, the equilibrium trajectory of value dynamics is

$$L^P\left(t\right)=\left({\displaystyle \frac{ar(a\varphi -\delta )}{\delta +2a(1+a)\delta -a\varphi }}+L_0\right)e^{{\displaystyle \frac{N_1-2\delta }{2(2+a)}}t}-{\displaystyle \frac{ar(a\varphi -\delta )}{\delta +2a(1+a)\delta -a\varphi }}.$$

(iii) 

In Scenario $P$, the demand dynamics for freemium and subscription users are

$$D_P^F\left(t\right)={\displaystyle \frac{a{N}_1-4(1+a)\delta }{4a(1+a)(2+a)\delta }}{L}^P\left(t\right)+{\displaystyle \frac{r\left(4\right(1+a)\varphi -N_1)}{2(1+a)\left(2\right(\delta +(2+a)\varphi )-N_1)}},{\displaystyle \frac{\partial D_P^F}{\partial L^P}}<0;$$

$$D_P^S\left(t\right)=\left({\displaystyle \frac{{\left(1+a\right)}^2}{a\left(2+a\right)}}+{\displaystyle \frac{N_1}{8\delta +4a\delta }}\right)L^P\left(t\right)+{\displaystyle \frac{r(-4(\delta +\varphi )+N_1)}{4(\delta +(2+a\left)\varphi \right)-2N_1}},{\displaystyle \frac{\partial D_P^S}{\partial L^P}}>0.$$

Proposition 1 highlights that price and quality strategies are positively and linearly correlated with content value $L^P$ (since $N_1\ge 0$). The value dynamics function is continuously differentiable. This presents various impact mechanisms on different user groups. As content value increases, subscription user quantity increases, whereas freemium user quantity decreases. Thus, enhancing content value through high-quality content is an effective strategy for PGC platforms to improve subscriptions. Conversely, platforms should depend on advertising revenue to sustain profitability when content value is low. Further, we analyze Proposition 1 to draw some corollaries and explore managerial insights.

Corollary 1.

Strategy dynamics and relationships

In Scenario $P$, the price and quality strategies evolve dynamically, and the relationships are as follows

(i) 

$s^{P*}\left(t\right)>0$, $p^{P*}\left(t\right)>0$, $L^P\left(t\right)\ge 0$;

(ii) 

${\displaystyle \frac{\partial L^P\left(t\right)}{\partial t}}>0$, ${\displaystyle \frac{\partial s^{P*}\left(t\right)}{\partial t}}>0$, ${\displaystyle \frac{\partial p^{P*}\left(t\right)}{\partial t}}>0$;

(iii) 

$s^{P*}\left(t\right)-p^{P*}\left(t\right)={\displaystyle \frac{1}{4(1+a)\delta }}\left(N_1{L}^P\left(t\right)+{\displaystyle \frac{2r\delta (a{N}_1-4(1+a\left)\delta \right)}{2(\delta +(2+a\left)\varphi \right)-N_1}}\right)$.

Corollary 1 suggests that quality and price strategies remain effective throughout the operational lifecycle of PGC platforms. Content value, quality, and pricing strategies increase over time. In the early stages of platform development, extensive investment in quality may not be necessary, as platforms primarily aim to recover production costs. Adopting a “low-price, low-quality” strategy can attract initial users while controlling operational costs during this period. As content value accumulates, the gap between quality and price increases monotonically. This implies that the increase in content price is significantly smaller than that in quality. This observation reveals that PGC platforms prioritize enhancing quality rather than aggressively adjusting prices. This strategy allows platforms to leverage improved perceived value to stimulate subscriptions while maintaining competitive pricing.

Proposition 2.

Steady-state conditions and solutions

In Scenario $P$, price, quality and value converge to steady-state solutions if $\delta +2a\left(1+a\right)\delta -a\varphi <0$, where ${\overline{L}}^P={\displaystyle \frac{ar(\delta -a\varphi )}{\delta +2a(1+a)\delta -a\varphi }}$, ${\overline{p}}^P={\displaystyle \frac{ar(\delta +a\delta -a\varphi )}{\delta +2a(1+a)\delta -a\varphi }}$, ${\overline{s}}^P={\displaystyle \frac{ar(\delta -a\varphi )}{\delta +2a(1+a)\delta -a\varphi }}$.

The PGC mode is particularly suitable for platforms characterized by high content continuity, as identified by the condition $\delta <{\displaystyle \frac{a\varphi }{1+2a\left(1+a\right)}}$. In practice, high continuity is often associated with specialized content domains such as online courses, academic research, or serialized media. These domains typically favor the centralized decision configuration pattern, with content produced and reviewed by professional managers to provide high-quality content. Additionally, there is an upper bound constraint on viable advertising intensity under this regime, expressed as $2a^2\delta +a\left(2\delta -\varphi \right)+\delta <0$. This constraint arises because users of specialized content platforms have a greater emphasis on content quality and are less tolerant of advertising interruptions. Excessive advertising in such contexts will affect the user experience negatively and diminish the platform’s credibility. Consequently, PGC platforms prioritize subscription-based monetization while limiting advertising exposure to maintain user engagement and satisfaction. For example, Netflix imposes strict content acquisition and production standards, with centralized managerial control to ensure quality and thematic continuity. In contrast, platforms like YouTube encompass broader and less curated content, depending more heavily on advertising for monetization. Finally, under the steady-state solution, the equilibrium price level is notably lower than the quality effort level. This implies that PGC platforms should focus on enhancing content value and quality rather than engaging in aggressive price competition. Emphasizing quality supports long-term user retention and strengthens the platform’s market differentiation and value proposition.

Corollary 2.

Advertising decisions for platforms

(i) 

When $0<a<{\displaystyle \frac{1}{\sqrt{2}}}$, in the smaller $\delta$ case, ${\overline{p}}^P$, ${\overline{s}}^P$, ${\overline{L}}^P$, ${\overline{D}}^S$ and ${\overline{D}}^F$ increase as $a$ increases; in the larger $\delta$ case, ${\overline{p}}^P$, ${\overline{s}}^P$, ${\overline{L}}^P$ and ${\overline{D}}^S$ decrease, and ${\overline{D}}^F$ increases as $a$ increases; there is a difference in $\delta$ thresholds: ${\tilde{\delta }}_L={\tilde{\delta }}_s\ge {\tilde{\delta }}_p$.

(ii) 

When $a\ge {\displaystyle \frac{1}{\sqrt{2}}}$, ${\overline{p}}^P$, ${\overline{s}}^P$, ${\overline{L}}^P$, ${\overline{D}}^S$ increase, and ${\overline{D}}^F$ decreases as $a$ increases.

In the PGC mode, platforms must design advertising strategies in response to user behavior and content characteristics. Corollary 2 demonstrates that advertising intensity significantly influences strategic decisions and user segmentation outcomes.

When advertising intensity is low ($0<a<{\displaystyle \frac{1}{\sqrt{2}}}$), platform behavior becomes sensitive to content continuity, denoted by $\delta$. For content types with high continuity (i.e., small $\delta$), increases in advertising intensity lead to higher platform prices, greater content quality, enhanced value perception, and expanded freemium and subscription user bases. Under such conditions, platforms can efficiently accumulate content value through sustained quality improvements, making users more tolerant of moderate advertising exposure. PGC platforms with premium content can achieve a balance between advertising and subscription revenue by appropriately adjusting advertising intensity. However, as $\delta$ increases—indicating lower content continuity—the effectiveness of advertising diminishes. Higher advertising intensity results in declining content quality and pricing. Although the freemium user base grows, the quantity of subscription users tends to decline. This occurs because a higher $\delta$ presents more challenges in quality improvement and value accumulation. Users are less willing to pay for content perceived as only moderately valuable. This reveals the critical effect of content continuity in advertising decisions. Notably, platform responses to $\delta$ differ across strategy dimensions: the thresholds ${\tilde{\delta }}_L$ and ${\tilde{\delta }}_s$ for value and quality exceed the threshold ${\tilde{\delta }}_p$ for pricing strategy. Platforms must evaluate different content types’ value formation efficiency in operational practice to develop strategies carefully.

For high advertising intensity ($a\ge {\displaystyle \frac{1}{\sqrt{2}}}$), the influence of content continuity on platform behavior diminishes. In this context, excessive advertising risks exceeding users’ tolerance, negatively affecting the content experience. PGC platforms increasingly rely on subscription-based monetization. Increasing advertising exposure may also be a practical mechanism to convert freemium users into subscribers by increasing the relative disutility of ad interruptions. This guides PGC platforms in balancing advertising intensity with content type to effectively attract and retain various user groups. These findings highlight the importance of an integrated advertising strategy with content type and user expectations to manage platform monetization and consumer retention effectively.

4.2. Equilibrium Feedback Strategies in the UGC Mode

In operational practice, many digital platforms decentralize content-related decisions to creators to generate UGC. Platforms such as YouTube and TikTok support individual users in contributing content independently while offering a monetization opportunity through revenue-sharing programs. These mechanisms aim to incentivize the engagement of high-quality contributors and increase the quantity of premium content. This subsection discusses the monetization strategies in a decentralized UGC framework. We model the interaction between the platform and content creators as a Stackelberg game, where the platform acts as the leader and the creators as followers. In Scenario $U$ (UGC mode), the dynamic optimization problem is formalized as a differential game. The objective functions for the platform and creators are as follows:

$$\left\{\begin{array}{l}\underset{p\left(t\right)}{\max }{\int }_0^{\mathrm{\infty }}{e}^{-\varphi t}\left\{\left(p\left(t\right)-f\right)D^S\left(t\right)+\left(1-g\right)ra{D}^F\left(t\right)\right\}\mathrm{d}t\\ \underset{s\left(t\right)}{\max }{\int }_0^{\mathrm{\infty }}{e}^{-\varphi t}\left\{gra{D}^F\left(t\right)+f{D}^S\left(t\right)-{\displaystyle \frac{1}{2}}{s}^2\left(t\right)\right\}\mathrm{d}t\\ s.t.\dot{L}\left(t\right)=\delta \left(s\left(t\right)-L\left(t\right)\right),L\left(0\right)=L_0\end{array}\right.$$

(8)

The HJB equations capturing the dynamic value functions for the platform and creators are expressed as:

$$\varphi V^{UP}=\underset{p}{\max }\left(\begin{array}{c}\left(p-f\right)\left(L-p+s-{\displaystyle \frac{p-L}{a}}\right)+\left(1-g\right)ra\left({\displaystyle \frac{p-L}{a}}\right)\\ +V_L^{UP}\delta \left(s-L\right)\end{array}\right)$$

(9)

$$\varphi V^{UC}=\underset{s}{\max }\left(\begin{array}{c}gra\left({\displaystyle \frac{p-L}{a}}\right)+f\left(L-p+s-{\displaystyle \frac{p-L}{a}}\right)-{\displaystyle \frac{1}{2}}{s}^2\left(t\right)\\ +V_L^{UC}\delta \left(s-L\right)\end{array}\right)$$

(10)

where $V_L^{Ui}={\displaystyle \frac{\partial \left(V^{Ui}\right)}{\partial \left(L\right)}},i\in \left\{P,C\right\}$, and both value functions satisfy the value function boundary condition $\underset{t\to \mathrm{\infty }}{\lim } e^{-\varphi t}{V}_L^{Ui}\left(L\left(t\right)\right)=0$. We derive the equilibrium feedback strategies in Scenario $U$.

Proposition 3.

Equilibrium feedback strategy in the UGC mode

(i) 

In Scenario $U$, the equilibrium feedback strategies for quality and price with respect to value dynamics are

$$s^{U*}\left(t\right)=f+{\displaystyle \frac{(f+af-agr)\delta }{2a(\delta +\varphi )}}, p^{U*}\left(t\right)={\displaystyle \frac{L^U\left(t\right)}{2}}+{\displaystyle \frac{f+2af+ar-agr+\frac{(f+af-agr)\delta }{2(\delta +\varphi )}}{2(1+a)}}.$$

(ii) 

In Scenario $U$, the equilibrium trajectory of value dynamics is

$$L^U\left(t\right)=\left(-f-{\displaystyle \frac{(f+af-agr)\delta }{2a(\delta +\varphi )}}+L_0\right)e^{-\delta t}+f+{\displaystyle \frac{(f+af-agr)\delta }{2a(\delta +\varphi )}}.$$

(iii) 

In Scenario $U$, the demand dynamics for freemium and subscription users are

$$D_F^U\left(t\right)=-{\displaystyle \frac{L^U\left(t\right)}{2a}}+{\displaystyle \frac{f+2af+ar-agr+\frac{(f+af-agr)\delta }{2(\delta +\varphi )}}{2(1+a)a}},{\displaystyle \frac{\partial D^F}{\partial L^U}}<0;$$

$$D^S={\displaystyle \frac{(1+a)}{2a}}{L}^U\left(t\right)+{\displaystyle \frac{(a-1)f\delta -2f\varphi +ar\left(\right(-2+g)\delta +2(-1+g\left)\varphi \right)}{4a(\delta +\varphi )}},{\displaystyle \frac{\partial D^F}{\partial L^U}}>0.$$

In Scenario $U$, price strategy exhibits a positive correlation with the value $L^U$, while the quality effort determined by creators is independent of $L^U$. This independence stems from the decentralized nature of content creation in the UGC framework, where creators’ incentives to invest in quality are primarily driven by the revenue-sharing mechanisms established by the platform. Specifically, when both the advertising revenue-sharing ratio $g$ and the subscription-based subsidy $f$ are held constant, creators tend to maintain a stable level of effort in content production, regardless of fluctuations in user base value. Furthermore, as $L^U$ increases, freemium users gradually switch to subscription users, similar to the market dynamics observed in Scenario $P$. The following corollaries are derived by analyzing Proposition 3.

Corollary 3.

In Scenario $U$, the price and value strategies evolve dynamically, and the relationships are as

(i) 

$p^{U*}\left(t\right)>0$; $s^{U*}\left(t\right)>0$ and $L^U\left(t\right)>0$ only when $f>{\displaystyle \frac{agr\delta }{\delta +3a\delta +2a\varphi }}$.

(ii) 

${\displaystyle \frac{\partial L^U\left(t\right)}{\partial t}}>0$, ${\displaystyle \frac{\partial p^{U*}\left(t\right)}{\partial t}}>0$.

While the pricing strategy remains strictly positive in the UGC mode, its effectiveness is subject to a critical constraint on content quality and user value generation. Specifically, the condition $f>{\displaystyle \frac{agr\delta }{\delta +3a\delta +2a\varphi }}$ must be satisfied. This indicates that platforms must offer sufficient economic incentives—such as subscription subsidies—to incentivize creators to produce high-quality content consistently. It is conducive to the long-term stability and sustainable development of UGC platforms. Moreover, although creators’ quality efforts remain static over time due to fixed incentive structures, platform pricing and user-perceived value exhibit a dynamic upward trend. This suggests that UGC platforms can gradually enhance pricing strategies by accumulating value through creators’ historical content. Therefore, providing appropriate incentive mechanisms in the early operational stages is essential.

Corollary 4.

In Scenario $U$, the content pricing $p^{U*}\left(t\right)$ and platform subsidy $f$ relationships are closely associated with the advertising intensity and advertising revenue-sharing ratio.

(i) 

In the case of  $a>{\displaystyle \frac{\delta +2\varphi }{\delta }}$ and $f>{\tilde{f}}_L$,

if $0<g\le {\tilde{g}}_1$, $p^{U*}\left(t\right)\ge f$;

if ${\tilde{g}}_1<g\le 1$, (a) $p^{U*}\left(t\right)<f$ when ${\tilde{f}}_L<f<{\tilde{f}}_1$; (b) $p^{U*}\left(t\right)$ is smaller than $f$ in the early stage and larger than $f$ in the later stage when ${\tilde{f}}_1\le f<{\tilde{f}}_2$; (c) $p^{U*}\left(t\right)\ge f$ when $f\ge {\tilde{f}}_2$.

(ii) 

In the case of $a<{\displaystyle \frac{\delta +2\varphi }{\delta }}$ and $f>{\tilde{f}}_L$,

if $0<g\le {\tilde{g}}_1$, (a) $p^{U*}\left(t\right)\ge f$ when ${\tilde{f}}_L<f<{\tilde{f}}_2$; (b) $p^{U*}\left(t\right)$ is smaller than $f$ in the early stage and larger than $f$ in the later stage when $f\ge {\tilde{f}}_2$;

if ${\tilde{g}}_1<g\le 1$, (a) $p^{U*}\left(t\right)<f$ when ${\tilde{f}}_L<f\le {\tilde{f}}_1$; (b) $p^{U*}\left(t\right)$ is smaller than $f$ in the early stage and larger than $f$ in the later stage when $f>{\tilde{f}}_1$;

where ${\tilde{g}}_1={\displaystyle \frac{\delta +3a\delta +2a\varphi }{2(\delta +2a\delta +a\varphi )}}$, ${\tilde{f}}_L={\displaystyle \frac{agr\delta }{\delta +3a\delta +2a\varphi }}$, ${\tilde{f}}_1={\displaystyle \frac{ar(\left(\delta +4a\delta +2a\varphi \right)g-2a\left(\varphi +\delta \right))}{\delta +a(3+4a)\delta +2a^2\varphi }}$, ${\tilde{f}}_2={\displaystyle \frac{ar(\left(3g-2\right)\delta -2(1-g\left)\varphi \right)}{(a-1)\delta -2\varphi }}$.

Corollary 4 discusses that UGC platforms may involve loss-leading subsidies to attract and retain creators. Under conditions of high advertising intensity, the platform’s optimal subsidy level is closely tied to the advertising revenue-sharing ratio $g$. When $g$ is low, the price charged for content consistently exceeds the subsidy offered to creators. The subsidy could be regarded as a portion of the content charge. This pattern is similar to YouTube’s operational strategy, where subscription fees from premium ad-free memberships are distributed to creators proportionally. As $g$ increases, the platform retains a larger portion of advertising revenue. Platforms are inclined to enhance content quality to maximize monetization potential. Hence, a sufficient subsidy becomes a crucial incentive for motivating creators. Insufficient subsidies may lead to disengagement from content producers and long-term losses for the platform. Conversely, a more generous subsidy benefits the platform’s pricing strategy. On one hand, such platforms greatly depend on premium content to attract users and advertisers. It is inevitable to provide generous financial incentives to creators. On the other hand, platforms prefer to attract users by low prices during the early development stage, which could generate rapid value accumulation.

Under relatively low advertising intensity, a small $g$ means that advertising revenue is ineffective in incentivizing creators. In such cases, a lower subsidy scheme allows the platform to balance cost control with subscription revenue, resulting in modest operational growth. However, adopting a higher subsidy scheme in the early stage incurs more costs, while platforms can acquire greater pricing superiority later and realize better monetization due to improved content quality and value accumulation. Note that a low advertising intensity in this case makes the platform implement appropriate subsidies.

Notably, a higher advertising revenue-sharing ratio g is not always optimal. Platforms must balance incentive costs and advertising effectiveness to appropriately determine development positioning and creator incentive programs. The platform can effectively incentivize creators at high advertising intensity by offering a moderate revenue-sharing ratio $g$. This approach allows the platform to develop advertising and subscription revenue channels jointly without incurring excessive incentive costs. Conversely, it may be more effective to prioritize subscription-based monetization over advertising at low advertising intensity. In such cases, reducing advertising revenue-sharing and subsidies can help the platform achieve early profitability while maintaining financial flexibility.

Proposition 4.

In Scenario $U$, the price, quality, and value converge to steady-state solutions, ${\overline{L}}^U=f+{\displaystyle \frac{(f+af-agr)\delta }{2a(\delta +\varphi )}}$, ${\overline{p}}^U={\displaystyle \frac{f(\delta +a(7+8a)\delta +2a(2+3a\left)\varphi \right)-ar\left(\right(g+a(-2+4g))\delta +2a(-1+g\left)\varphi \right)}{4a(1+a)(\delta +\varphi )}}$, ${\overline{s}}^U=f+{\displaystyle \frac{(f+af-agr)\delta }{2a\delta +2a\varphi }}$.

Scenario $U$ offers greater operational flexibility than Scenario $P$, which is often constrained by content types and advertising structures. This flexibility explains why more platforms adopt the UGC mode. It is observed that value, quality, and price are positively correlated with subsidy $f$ and negatively correlated with the advertising revenue-sharing ratio $g$. As platforms evolve into more stable stages, a significant shift occurs wherein freemium users transition into paying subscribers. In this context, subscription revenue becomes the dominant source of monetization. The reduction in $g$ reflects this strategic shift in the platform’s profit patterns. Lower reliance on advertising also reduces commercial interference in content creation, allowing creators to focus more on enhancing content quality and building long-term value. This supports the development of creator reputations based on consistent quality output. For example, despite offering a modest advertising revenue share, TikTok leverages financial subsidies to incentivize creators. These strategies enable the platform to sustain high-quality content production and support long-term platform development.

Corollary 5.

Impact of platform incentive programs on demand

(i) 

As $f$ increases, ${\overline{D}}^S$ always increases, ${\overline{D}}^F$ decreases when $a\le {\displaystyle \frac{\delta +\sqrt{\delta (9\delta +8\varphi )}}{4(\delta +\varphi )}}$ and increases when $a>{\displaystyle \frac{\delta +\sqrt{\delta (9\delta +8\varphi )}}{4(\delta +\varphi )}}$;

(ii) 

As $g$ increases, ${\overline{D}}^F$ increases when $a\le {\displaystyle \frac{\delta }{2(\delta +\varphi )}}$ and decreases when $a>{\displaystyle \frac{\delta }{2(\delta +\varphi )}}$, ${\overline{D}}^S$ decreases when $a\le {\displaystyle \frac{\delta }{2\varphi }}$ and increases when $a>{\displaystyle \frac{\delta }{2\varphi }}$.

An increasing subsidy $f$ provides more economic incentives for premium content generation. This attracts more users to subscribe, leading to the platform’s shift toward subscription-based revenue. Meanwhile, the number of freemium users is correlated with advertising intensity. Limited advertising fails to generate substantial revenue for the platform. This leads the platform to shift its focus towards subscription channels and convert freemium users into subscribers. As a result, platforms prioritize subscription revenue and implement strategies that convert freemium users into paying subscribers. In contrast, when advertising intensity is high, monetization through advertisements becomes an important revenue stream. In such cases, platforms must improve content quality and pricing strategies to attract freemium and subscription users. Moreover, there are differences in the impact of advertising revenue-sharing ratio $g$ on demand under different advertising intensities. At low advertising intensity, a high $g$ results in a market dominated by freemium users, as creators are less motivated by the limited advertising returns. Conversely, at high advertising intensity, a high $g$ contributes to a subscription user-dominated market.

Corollary 6.

Impact of content type on strategy

(i) 

In the case of ${\tilde{f}}_L<f\le {\displaystyle \frac{agr}{1+a}}$, as $\delta$ increases, ${\overline{p}}^U$, ${\overline{s}}^U$ and ${\overline{L}}^U$ decrease, ${\overline{D}}^F$ increases and ${\overline{D}}^S$ decreases.

(ii) 

In the case of $f>{\displaystyle \frac{agr}{1+a}}$, as $\delta$ increases, ${\overline{p}}^U$, ${\overline{s}}^U$ and ${\overline{L}}^U$ increase, ${\overline{D}}^F$ decreases and ${\overline{D}}^S$ increases.

The effect of content continuity on optimal strategies varies depending on the subsidy scheme. With lower subsidies, price, quality, and value tend to decline as content continuity decreases (reflected by an increase in $\delta$). This suggests less specialized or entertainment-oriented content types are more compatible with low-subsidy schemes. In such cases, the number of freemium users increases while the number of paying subscribers declines. The reason is that the limited subsidies generate moderate-quality content, prompting platforms to reduce prices and depend more on advertising revenue from freemium users. For example, TikTok’s business model emphasizes short-form entertainment content and does not rely on subscription revenue. Conversely, higher subsidy schemes demonstrate the opposite effect. The platform’s monetization strategies improve as content continuity decreases (i.e., as $\delta$ increases). In these situations, subscription users will eventually become the primary revenue source. These findings highlight the strategic importance of integrating content type with subsidy funding levels and platform development positioning. Specifically, when subsidies are limited, promoting high-continuity content types allows platforms to accumulate value more rapidly, making it profitable to target a freemium-driven model. When subsidies are high, platforms benefit more from supporting content with lower continuity. This enables stronger differentiation and supports a subscription-based revenue model.

4.3. Comparative Analysis of Modes

This subsection compares monetization strategies, user demand patterns, and platform profits. It summarizes the mode selection and operational strategies within different decision configuration frameworks for content supply chains.

Proposition 5.

Scenario comparison of steady-state strategies

(i) 

For quality strategy and value dynamics, there exists a threshold ${\tilde{f}}_s$, ${\overline{L}}^P\ge {\overline{L}}^U$ and ${\overline{s}}^P\ge {\overline{s}}^U$ when ${\tilde{f}}_L<f\le {\tilde{f}}_s$, ${\overline{L}}^P<{\overline{L}}^U$ and ${\overline{s}}^P<{\overline{s}}^U$ when $f>{\tilde{f}}_s$;

(ii) 

For price strategy, there exists a threshold ${\tilde{f}}_p$, ${\overline{p}}^P\ge {\overline{p}}^U$ when ${\tilde{f}}_L<f\le {\tilde{f}}_p$, ${\overline{p}}^P<{\overline{p}}^U$ when $f>{\tilde{f}}_p$; where ${\tilde{f}}_p<{\tilde{f}}_s$.

Subsidy $f$ is crucial in determining the optimal operational mode for content platforms. When subsidies are high, the UGC mode generates superior content quality and value. Platforms can also enhance their pricing strategies more effectively. Compared to the PGC mode, the UGC mode delegates content creation to individual users and motivates them through financial incentives. This finding suggests that incentivizing creators is more cost-effective than using a platform to produce content. By contrast, the PGC mode is more appropriate when subsidy funding is limited. The PGC mode allows the platform to enter the market quickly with manageable content quality and to attract users with content continuity requirements. Notably, the subsidy thresholds affecting decision superiority vary across different scenarios. Specifically, the subsidy threshold for pricing is lower than that for content quality. The reason is that a high subsidy is critical for motivating creators, whereas pricing depends more on market conditions and operational costs. Consequently, UGC platforms may sometimes offer slightly lower content quality than PGC platforms but achieve higher profitability due to more dynamic pricing and broader monetization channels. For example, premium content produced by social media influencers may lack the professionalism of PGC offerings. However, it still generates substantial revenue through advertising, sponsorships, and strong user engagement driven by creator loyalty and social influence.

Proposition 6.

Scenario comparison of steady-state user demands

(i) 

For freemium user demand, ${\overline{D}}_P^F\le {\overline{D}}_U^F$;

(ii) 

For subscription user demand, there exists a threshold ${\tilde{f}}_{DS}$, ${\overline{D}}_P^S\ge {\overline{D}}_U^S$ when ${\tilde{f}}_L<f\le {\tilde{f}}_{DS}$, ${\overline{D}}_P^S<{\overline{D}}_U^S$ when $f>{\tilde{f}}_{DS}$.

(iii) 

For total user demand, there exists a threshold ${\tilde{f}}_D$, ${\overline{D}}_P\ge {\overline{D}}_U$ when ${\tilde{f}}_L<f\le {\tilde{f}}_D$, ${\overline{D}}_P<{\overline{D}}_U$ when $f>{\tilde{f}}_D$.

As demonstrated by Proposition 6, there are differences in user scales and primary revenue streams across various platform modes. With the low subsidy, the PGC mode attracts more subscribers and achieves higher total user demand than the UGC mode. This preference is primarily attributed to the PGC mode’s controlled quality and high content continuity, which lead users to prefer paying for professional content. Consequently, PGC platforms prioritize subscription users and stabilize subscription revenue through reliable content quality. For instance, Netflix adopts the PGC mode to engage subscriptions by offering serialized, high-quality episodes as its primary monetization stream.

As subsidy levels increase, the UGC mode demonstrates superior performance. Adequate financial subsidies can incentivize creators to provide extensive and premium content. It contributes to the rapid expansion of the platform’s user base. In this scenario, the number of freemium and subscription users in the UGC mode surpasses that in the PGC mode. Platforms such as YouTube, TikTok, Facebook, and Instagram have widely adopted the UGC mode and have attracted a massive number of creators and viewers. In particular, with the introduction of stronger network externalities (e.g., accelerated demand growth driven by increased creator numbers, or the retention-enhancing effects of social interactions among users), this mechanism typically further amplifies the advantages of the UGC model under high-subsidy scenarios.

In summary, the PGC mode is more conducive to attracting subscription users and maintaining high-quality content production under low subsidy conditions. Conversely, under high subsidy conditions, the UGC mode is more efficient for expanding the user base and generating revenue through advertising and subscriptions. These findings suggest that content platforms should strategically decide operational modes based on subsidy level, market characteristics, and content type.

Proposition 7.

Scenario comparison of platform steady-state profits

(i) 

In the case of $0\le a<{\displaystyle \frac{\delta +\sqrt{9{\delta }^2+8\delta \varphi }}{4(\delta +\varphi )}}$, ${\overline{\pi }}_P^P<{\overline{\pi }}_P^U$ when the subsidy is low, ${\overline{\pi }}_P^P>{\overline{\pi }}_P^U$ when the subsidy is moderate, ${\overline{\pi }}_P^P<{\overline{\pi }}_P^U$ when the subsidy is high;

(ii) 

In the case of ${\displaystyle \frac{\delta +\sqrt{9{\delta }^2+8\delta \varphi }}{4(\delta +\varphi )}}\le a<{\displaystyle \frac{1}{2}}(\sqrt{3}-1)$, if $0\le g\le {\tilde{g}}_D$, ${\overline{\pi }}_P^P<{\overline{\pi }}_P^U$; if ${\tilde{g}}_D\le g\le 1$, ${\overline{\pi }}_P^P<{\overline{\pi }}_P^U$ when the subsidy is low, ${\overline{\pi }}_P^P>{\overline{\pi }}_P^U$ when the subsidy is moderate, ${\overline{\pi }}_P^P<{\overline{\pi }}_P^U$ when the subsidy is high;

(iii) 

In the case of $a>{\displaystyle \frac{1}{2}}(\sqrt{3}-1)$, ${\overline{\pi }}_P^P\ge {\overline{\pi }}_P^U$ when the subsidy is low, ${\overline{\pi }}_P^P<{\overline{\pi }}_P^U$ when the subsidy is high.

The platform’s steady-state profitability is closely related to advertising intensity, subsidy levels, and revenue-sharing ratio.

When advertising intensity is low, the incremental advertising revenue generated by freemium users is limited. In this context, platforms prioritize subscription revenue and strict cost control. UGC platforms operating under low-subsidy schemes offer a cost-effective alternative to the PGC mode, although content quality may be lower. On one hand, the platform does not incur production costs under the UGC model, possessing the structural low-cost advantage [52]. On the other hand, in a low-advertising environment, the marginal revenues of high-quality content under the PGC model decline, while production costs remain relatively high. It allows the UGC model to sustain content supply even without high advertising revenue or subsidies, offering the platform greater potential for profitability. This aligns with the findings from the work of Rieder et al. [53] that YouTube content can achieve scalable dissemination even during low-profitability stages. When subsidies are moderate, UGC platforms incur higher incentive expenses but are inferior to the quality and value in the PGC mode. This results in the UGC mode performing worse in monetization than the PGC mode. However, the UGC mode with sufficient subsidies becomes more advantageous.

When advertising intensity is medium, optimal operational mode depends on the advertising revenue-sharing ratio $g$. In the case of a small $g$, the UGC mode generates more profit than the PGC mode. This is due to the platform retaining a larger share of advertising revenue, and the low-cost structure of UGC creation facilitates faster value accumulation. In contrast, in the case of a high $g$, the platform must balance creator incentives with rising production costs and declining retained revenue. This scenario exhibits conditions observed under low advertising intensity, where tight cost control becomes essential.

When advertising intensity is high, the platform focuses on enhancing content quality and value. Due to superior quality control, the PGC mode with low subsidies demonstrates better profit potential. Meanwhile, with generous subsidies, the UGC mode can also achieve high profitability by leveraging the creators’ ability to produce high-quality content.

These insights highlight that content platforms must integrate advertising revenue, subsidy strategies, and content value to determine operational modes strategically. Balancing revenue streams and expenses is essential for optimizing economic performance and user experience.

5. Numerical Analysis

Due to the complexity of the equilibrium strategy expression and scenario comparison, numerical analysis is performed to highlight more dynamic characteristics. We set $g=0.55$, consistent with the YouTube Partner Program’s advertising revenue share. Following experimental results from Pandora Internet Radio, increasing advertising intensity significantly reduces user engagement [43]. This negative effect impacts approximately 20–40% of users. Therefore, we set the additional engagement cost introduced by advertising as $a=0.3$. Previous empirical studies [54] calibrated memory decay parameters between 0.05 and 0.15, and we set the decay rate for historical content value as $\delta =0.1$, representing a moderate baseline. Based on the annual discount rate of 5–10% commonly used in economic research, we set $\varphi =0.06$. For subsidy scenarios, we set the low-subsidy scenario $f=0.1$ as Case I and the high-subsidy scenario $f=0.5$ as Case II. This can be applied to the typical creator reward intensity adopted by platforms like TikTok or Bilibili at different development stages. To ensure the effectiveness and reliability of the model, we set the remaining parameters as follows: $r=0.5$ and $L_0=0$. These calibrations simulate real user response patterns and creator engagement behaviors in market environments. We compare the dynamics of strategies and platform profits across different scenarios to derive managerial insights.

Figure 2 analyzes the dynamic evolution of quality, price strategies, and value in PGC and UGC modes. In the low-subsidy scenario (Case I), the UGC mode initially exhibits higher price, quality, and value during the early stages of platform development. This early-stage advantage stems from the platform’s lower production costs and the consistent content quality provided by creators, enabling rapid user acquisition and a short-term competitive edge. However, limited subsidies constrain sustained investment in quality improvement, diminishing the long-term competitiveness of the UGC mode. In contrast, the PGC mode demonstrates superior value upgrade and user attraction through content quality enhancement. Despite higher quality investment costs, the PGC mode shows greater monetization efficiency and acquires more markets in the long-term competition.

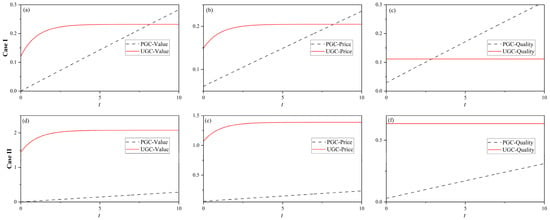
Figure 2. Decision dynamics of the content platform: (a) value in Case I, (b) price in Case I, (c) quality in Case I, (d) value in Case II, (e) price in Case II, (f) quality in Case II.

In the high-subsidy scenario (Case II), the UGC mode benefits from increased creator engagement, resulting in increased content quality and operational flexibility. Enhanced subsidies incentivize diverse and high-quality content creation, improving the platform’s ability to respond to competition. For example, TikTok has successfully attracted numerous creators with a high-reward strategy. The creators produce premium and diverse UGC, rapidly expanding the consumption market globally.

These findings suggest that subsidy levels significantly influence the relative advantages of UGC and PGC modes at different stages of platform development. Content platforms should develop strategies and allocate resources based on the development period to optimize operational performance and long-term development.

Figure 3 compares the platform’s profit trajectories under PGC and UGC modes across different subsidies. In the low-subsidy scenario (Figure 3a), the PGC mode presents an initial decline in profitability due to high content production costs. However, as content quality improves over time, platform profits gradually increase. In contrast, the UGC mode demonstrates a steady increase in profit throughout the development process. Interestingly, the platform’s profitability pattern is characterized by a three-stage process. In the early development stage, the UGC mode is less profitable due to the creator incentive cost and limited advertising revenue, while the PGC mode offers higher profitability. During the mid-stage, the PGC mode invests in content quality, increasing production costs. Meanwhile, the UGC mode benefits from consistent content quality settings and lower operational expenses, resulting in higher profits. In the later stage, the low-subsidy environment weakens creator incentives in the UGC mode, limiting further quality improvement. The PGC mode accumulates more premium content, enhancing user engagement and monetization potential. As a result, although the UGC mode generates moderate profit growth, it fails to reach the potential of the PGC mode in content value and price enhancement.

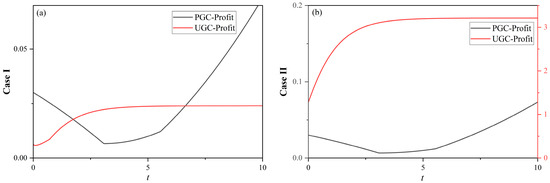
Figure 3. Profit dynamics of the content platform: (a) profit in Case I, (b) profit in Case II.

In the high-subsidy scenario (Figure 3b), the profits under the UGC mode are always higher than those under the PGC mode. Increased subsidies continuously accumulate premium content and leverage the scale effect to enhance platform profitability. This observation supports the proposition that “content is king” in the platform economy.

The PGC mode provides a sustainable advantage through continuous, high-quality content production. Meanwhile, the UGC mode enables rapid monetization under low-subsidy conditions and demonstrates strong profitability and market expansion capabilities when supported by higher subsidies. These insights suggest that platforms should adapt strategies and subsidy mechanisms based on development stages and strategic priorities.

Figure 4 illustrates the variation of decisions with advertising intensity $a$ under system steady-state conditions. In the low-subsidy scenario (Figure 4a–c), the PGC mode performs more robustly with moderate advertising, while the UGC mode declines in value as advertising increases. For instance, Netflix creates differentiation by investing consistently in high-quality content despite minimal advertising. Platforms depending on UGC mode often struggle to maintain consistent quality in such case, making long-term value accumulation more difficult. Therefore, for low-subsidy conditions, platforms should reduce advertising density, strengthen subscription schemes, and focus on content types with high continuity. In the high-subsidy scenario (Figure 4d–f), the value and quality of the UGC mode increase as subsidy increases, and the steady-state superiority is more significant. This aligns with the expansion mechanisms of platforms like YouTube or TikTok. That is, when the platform has sufficient incentive resources, a large-scale creator ecosystem rapidly forms to share the quality fluctuation risk and enhance overall content supply. In this case, reducing advertising interference and adopting differentiated revenue-sharing mechanisms can further motivate creators.

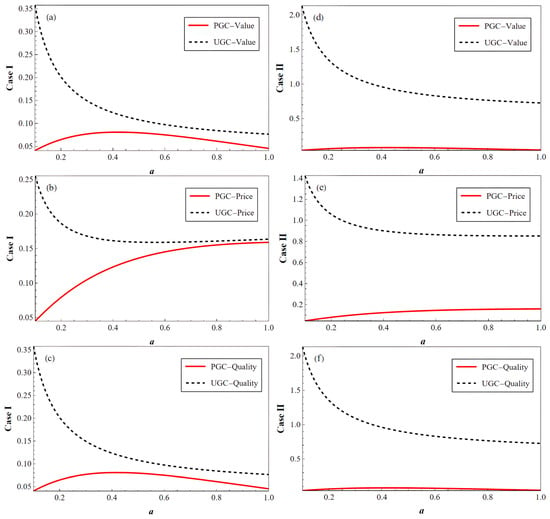
Figure 4. Influence of $a$ on the steady-state value of decisions: (a) value in Case I, (b) price in Case I, (c) quality in Case I, (d) value in Case II, (e) price in Case II, (f) quality in Case II.

We further analyze the impact of advertising intensity $a$ on steady-state profits. As shown in Figure 5, the subsidy level determines the profitability dominance of two modes, while advertising intensity amplifies the difference between them.

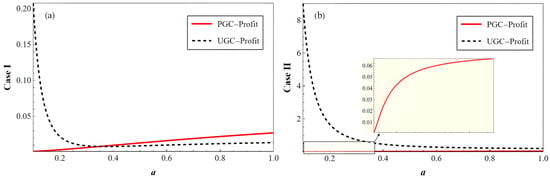
Figure 5. Influence of $a$ on the steady-state value of platform profits: (a) profit in Case I, (b) profit in Case II.

In Case I (low subsidies), the UGC mode presents a profit advantage in low-advertising scenarios, but this advantage rapidly shrinks as $a$ increases. The PGC mode gradually dominates as $a$ increases. This implies that the UGC mode is more sensitive to advertising. A high advertising intensity will reduce user experience and creator revenue, thus compressing platform profits. For instance, short-video platforms generally avoided high advertising exposure in the early stage to maintain creator engagement and user retention. In contrast, the PGC mode benefits from continuity, where advertising may instead supplement the revenue structure. For example, platforms like Hulu and Youku moderately introduce advertisements within professional content to increase revenue. Therefore, these two modes present inverse profit sensitivity on advertising intensity.

In Case II (high subsidies), the UGC mode demonstrates increased profitability and always exceeds PGC mode. Despite increased advertising will reduce revenue, the UGC mode maintains dominance due to the large creator ecosystem and scale effects driven by subsidies. Similar to mechanisms on platforms such as Douyin and TikTok, subsidies amplify content supply and reduce creators’ reliance on advertising. This can help platforms maintain high profitability even when advertising revenue is relatively low.

Figure 6 illustrates the impact of content continuity parameter $\mathsf{\delta }$ on the value and profit.

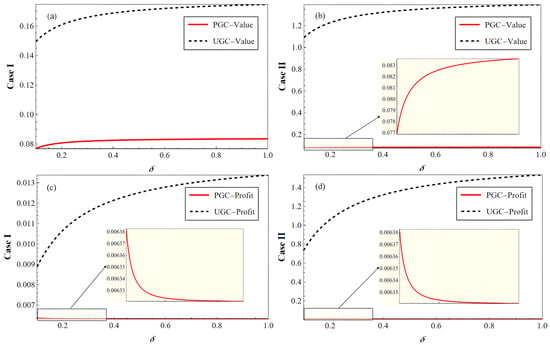
Figure 6. Influence of $\delta$ on the steady-state values and profits: (a) value in Case I, (b) value in Case II, (c) profit in Case I, (d) profit in Case II.

As $\delta$ increases, reducing the influence of historical content on current decisions, content value rises for both modes, with the UGC mode showing greater relative advantage. However, from a profitability perspective, the UGC mode can generate profits as $\delta$ increases, while the PGC mode declines in profitability as historical value effect diminishes. This is because the core competitiveness of the PGC mode derives from the content continuity and serialization. For instance, Netflix’s series rely on accumulated historical quality to generate premium value. An increased $\delta$ indicates that users are less sensitive to historical content, and the long-term content value of PGC mode is reduced, leading to less profit.

The UGC model has diverse content resources. As δ increases, the UGC model can attract continuous user engagement, thereby driving higher monetization. This aligns with the strong monetization performance of TikTok and YouTube in fragmented content environments.

Overall, when platforms operate in scenarios with fragmented content and low continuity (high $\delta$), they should prioritize UGC creator ecosystems and introduce more flexible incentive systems. In contrast, scenarios emphasizing serialization (low $\delta$) are suitable for developing PGC modes, where quality investments enhance historical value effect.

6. Conclusions

This study investigates operational strategies for digital content platforms in the centralized PGC and decentralized UGC modes. Value dynamics are introduced into monetization decisions to optimize pricing and content quality. First, we characterize the value dynamics through the differential accumulation of historical content quality. The interaction between value, content pricing, and quality is explored. Then, we derive and discuss the feedback equilibrium strategies of pricing and quality efforts with the influence of value dynamics. Finally, we compare equilibrium solutions and numerical experiments across PGC and UGC operational scenarios. The results provide managerial insights and extend the existing literature by revealing trade-offs between operational modes under varying subsidy and advertising conditions.

The content platform mode selection depends on the subsidy and advertising monetization strategy. Platforms with limited subsidies prefer the PGC mode, leveraging its long-term quality control and subscription revenue advantage. The consistent investment in high-quality content allows these platforms to establish content value and retain loyal users. Conversely, platforms with sufficient subsidies often adopt the UGC mode to achieve rapid market expansion and scale benefits. Due to the lower content creation costs and flexible incentive mechanisms, the UGC mode can expand the market rapidly and maintain significant profit potential when advertising revenues are sufficient. Interestingly, when advertisements are scarce, the UGC mode demonstrates superior performance even with limited subsidies or low advertising revenue-sharing. This contrasts with previous studies, such as the work of Subramanian et al. [9], who argue that UGC platforms have more value uncertainty and require higher switching costs to capture value from network effects. Our results indicate that in low-advertising environments, freemium users generate marginal revenue. The UGC mode provides greater monetization potential for platforms by minimizing incentive costs and shifting production efforts to creators.

Enhancing content quality is crucial for the PGC mode to attract subscriptions. Strategic pricing adjustments help balance user acquisition with content production investments. Additionally, the advertising strategy is pivotal to attracting various user groups. The PGC mode is particularly well-suited for content types with greater continuity. Limiting advertising interruptions can expand subscription and freemium user bases in such cases. Conversely, increasing advertising exposure can convert freemium users to subscription users.

The UGC mode, in contrast, depends on platform incentives to support content quality. Under low-subsidy conditions, platforms prioritize higher continuity content types and freemium users to accumulate value at a lower cost. Platforms can adopt more flexible strategies with lower content continuity when subsidies are sufficient. In such cases, it is more profitable to focus on subscription users. Significantly, a higher advertising revenue-sharing ratio is not always preferable. While Wang et al. [17] highlight the contribution of higher sharing rates in attracting streamers, our findings suggest that platforms should optimize the balance between subsidy levels and advertising revenue-sharing ratios to generate long-term profitability. In high-advertising scenarios, moderate sharing ratios incentivize creators effectively while controlling platform costs. In low advertising conditions, a reduced sharing ratio helps form a subscription-dominated user base, accelerating the transition to profitability.

Furthermore, the optimal operational mode varies with the platform’s development stage. The UGC mode performs better during the early stages due to low content costs and sufficient quality. However, as platforms mature, their limited capacity for sustained quality investment diminishes competitiveness. Conversely, the PGC mode generates more profit potential in long-term development through continuous quality enhancement. With high subsidies, the UGC mode effectively improves content quality and user expansion, achieving higher monetization than the PGC mode. Generally, the PGC mode has long-term competitive strengths. The UGC mode can accumulate more profit by reducing cost expenses in a shorter period and also generate more profits with high subsidies. This aligns with the operational trajectory of platforms like YouTube, which initially scaled through UGC and later institutionalized content production through PGC to enhance revenue stability.

Our work extends the application of optimal control theory to digital platform operations. Previous studies applied system dynamics models to capture long-term feedback structures, but these typically depended on numerical simulations and rarely provided closed-form behavioral insights [55]. While agent-based models can represent heterogeneous interactions between creators and users, the results often lack analytical transparency and are difficult to recognize mechanisms [56]. In our work, the continuous time optimization and dynamic value framework explicitly provides equilibrium strategies for pricing and quality decisions. This emphasizes the structural effects of incentives, value accumulation, and monetization channels, providing useful insights and policies. Therefore, the implementable conclusions and strategies derived from our work enhance contributions to the platform’s dynamic operations and supply chain coordination.

This work has several limitations. First, we focus on PGC and UGC as separate modes, but some platforms use both together. Second, we set advertising as exogenous, though it affects platform choices. Third, the influences of network externalities are ignored, and we will focus on network uncertainty and user social interactions. Future research will expand the influences of value dynamics and decision interactions with practical scenarios.