An Analytically Derived Gauss–Legendre Quadrature for Axis-Aligned Ellipse–Ellipse Intersection

Abstract

Accurate and efficient evaluation of the intersection area between two axis-aligned ellipses is essential in applications where the coordinate system or underlying geometry naturally imposes alignment. However, most existing numerical integration techniques are designed for arbitrarily oriented ellipses, and their generality typically requires adaptive refinement or solving higher-degree algebraic intersection formulations, leading to greater computational cost than necessary in the axis-aligned case. This study introduces two analytically derived, fixed-cost Gauss–Legendre quadrature formulations for computing the intersection area in the axis-aligned configuration. The first is a sine-mapped Gauss–Legendre quadrature, which applies a trigonometric transformation to improve conditioning near endpoint singularities while retaining constant-time evaluation. The second is an enhanced two-panel affine-normalized formulation, which splits the intersection domain into two sub-intervals to increase local accuracy while maintaining a fixed computational cost. Both methods are benchmarked against adaptive Simpson integration, polygonal discretization, and Monte Carlo sampling over 10,000 randomly generated ellipse pairs. The two-panel formulation achieves a mean relative error of 0.003% with runtimes more than twenty times faster than the adaptive reference and remains consistently more efficient than the polygonal and Monte Carlo approaches while exhibiting comparable or superior numerical behavior across all tested regimes.

1. Introduction

Elliptical geometries play a central role in scientific and engineering domains in which spatial uncertainty, dispersion, or structural footprints must be quantified precisely. Accurate evaluation of the intersection area between two ellipses is essential in various applications, including orbital conjunction analysis, geographic information systems (GIS), medical imaging, industrial inspection, and statistical modeling [1,2,3,4,5]. Despite its widespread occurrence, analytically determining the intersection area between two ellipses remains algebraically intractable in the general case. The intersection boundary is defined by two quadratic curves whose simultaneous solution yields a quartic equation, resulting in up to four real intersection points depending on the configuration [6,7].

Over the past few decades, numerous approaches have been developed to estimate the intersection area between two ellipses, reflecting both the geometric and numerical complexity of the problem. Analytical and semi-analytical methods integrate parametric arcs and polygonal segments using the Gauss–Green theorem to obtain analytical expressions that preserve the true geometric definition of the ellipse boundaries, but they require explicit intersection coordinates and case classification, making them numerically unstable near tangency due to finite-precision arithmetic [8,9]. Polygonal and polyarc approximations discretize each ellipse into a finite number of vertices or arcs, determine the intersection through standard clipping algorithms such as those of Sutherland–Hodgman [10], Weiler–Atherton [11], Vatti [12], and Greiner–Hormann [13], and compute the resulting area using the shoelace formula [14]; however, their accuracy typically improves on the order of N⁻² with the number of segments for smooth boundaries [15]. Numerical quadrature formulations recast the problem as a one-dimensional integral over the horizontal overlap domain and employ adaptive Simpson or other Newton–Cotes schemes, as well as Gaussian quadrature, to integrate the overlap-height function. These achieve deterministic precision for smooth boundaries but require increased computational effort and exhibit reduced stability for highly eccentric or grazing configurations [8,16,17,18,19]. Algebraic–geometric approaches instead operate on the implicit equations of the ellipses, eliminate one variable to yield a quartic polynomial, and compute the area from algebraic segments or level-set integrals; while rigorous, these methods are computationally expensive and numerically fragile near degeneracy [20,21,22,23]. Stochastic methods such as Monte Carlo sampling [24,25,26,27] provide conceptually simple and parallelizable solutions but converge slowly and exhibit high variance, making them unsuitable for precision-demanding applications. Raster-based discretization represents each ellipse as a binary mask and estimates the overlap by counting intersecting pixels or applying sub-pixel interpolation; however, its accuracy deteriorates rapidly with coarse resolution [28,29,30]. Morphological or convolution-based representations treat shapes, for example, using elliptical structuring elements, in a binary indicator-function manner, and recent work links morphological dilation/erosion to discrete convolution, hence enabling Fast Fourier Transform (FFT) acceleration. However, when applied to ellipses, such methods implicitly rely on discretization and thus sacrifice analytical interpretability [30,31,32]. Parametric transformation and reduction techniques apply affine or modular normalization to map elliptic forms into canonical domains—such as transforming one ellipse to a unit circle—simplifying integration and improving numerical conditioning, though these transformations are often limited to specific parameter ranges or symmetry conditions [33,34].

Despite extensive study of the general ellipse–ellipse intersection problem, most existing formulations have been developed for arbitrarily oriented configurations and treat the axis-aligned case merely as a simplified subset. In such general approaches, axis alignment is recognized only as a limiting form of the analytical equations. However, in this configuration, the absence of rotational coupling between coordinate axes allows the intersection area to be expressed, for example, as a single definite integral of the vertical overlap height across the shared horizontal domain.

This study examines the lack of a dedicated fixed-cost quadrature method for the axis-aligned ellipse–ellipse intersection problem, for which general numerical approaches often introduce unnecessary algebraic complexity and adaptive refinement. To address this gap, two complementary Gauss–Legendre quadrature formulations are introduced. First, a sine-mapped Gauss–Legendre quadrature is derived to improve numerical conditioning near tangential boundaries. Second, an affine-normalized two-panel formulation is introduced to balance curvature across sub-intervals and increase accuracy for ellipses with disparate aspect ratios. In addition, a comprehensive stratified benchmark study is conducted across the principal intersection regimes, comparing the proposed formulations with adaptive Simpson integration, polygonal approximation, and Monte Carlo estimation.

The remainder of this paper is organized as follows: Section 2 presents the mathematical derivation of the proposed quadrature formulations and describes the implementation and benchmarking methodology; Section 3 reports quantitative results and comparative analysis; Section 4 discusses the numerical behavior, performance characteristics, and potential extensions; and Section 5 summarizes and concludes the study.

2. Materials and Methods

The proposed computational framework estimates the intersection area between two axis-aligned ellipses using alternative numerical formulations for evaluating the overlap integral. The process begins with the geometric definition of two ellipses, $E_1(x_1, y_1, a_1, b_1)$ and $E_2(x_2, y_2, a_2, b_2)$, from which the horizontal interval of potential overlap $\left[L, R\right]$ is determined. Within this interval, the intersection height function $h\left(x\right)$ defines the vertical extent of overlap between the two boundaries. The integral of $h\left(x\right)$ over $\left[L, R\right]$ yields the total intersection area, forming the analytical foundation for the proposed methods. The mathematical formulation of the overlap integral and the definition of $h\left(x\right)$ are presented in Section 2.1, establishing the deterministic relationship between the input ellipse parameters and the resulting intersection area. Section 2.2 introduces the first formulation—Sine-Mapped Gauss–Legendre Quadrature—which applies a smooth variable substitution to redistribute quadrature nodes toward the interval boundaries and improve conditioning near tangential contact. Section 2.3 describes the second formulation—Enhanced Two-Panel Affine-Normalized Gauss–Legendre Quadrature—which rescales the coordinate system to balance unequal semi-axes and divides the integration domain to handle curvature transitions within the overlap region. Section 2.4 presents the theoretical extensions that distinguish both formulations from standard Gauss–Legendre quadrature, while Section 2.5 discusses the smoothness and boundary behavior of the overlap-height function. Section 2.6 summarizes the theoretical error characteristics of fixed-order quadrature. For comparative evaluation, Section 2.7 outlines two conventional approaches: the polygonal approximation and the Monte Carlo estimator. Section 2.8 details the Adaptive Simpson Integration, used as a deterministic reference to obtain near-machine-precision benchmark solutions. Finally, Section 2.9 defines the evaluation metrics and benchmark scenarios employed to assess the numerical accuracy and computational performance of all methods.

2.1. Mathematical Formulation

The analytical formulation of the axis-aligned ellipse–ellipse intersection problem is expressed as a specific case of the general intersection between two ellipses, where both principal axes are parallel to the Cartesian axes. Let the two ellipses $E_1$ and $E_2$ be defined by their centers $(x_i,y_i)$ and semi-axes $(a_i,b_i)$, with $i=1, 2$. Each ellipse satisfies the implicit quadratic equation:

$${\displaystyle \frac{{(x-x_i)}^2}{a_i^2}}+{\displaystyle \frac{{(y-y_i)}^2}{b_i^2}}=1$$

(1)

Because the ellipses are axis-aligned, the limits of potential horizontal overlap are obtained from the intersection of their projections on the $x$-axis, denoted as:

$$\left[L, R\right]=\left[\max \left(x_1-a_1, x_2-a_2\right),\min (x_1+a_1, x_2+a_2)\right]$$

(2)

If $L\ge R$, the ellipses do not overlap in the horizontal direction, and the intersection area is zero. For any abscissa $x\in [L,R]$, the upper and lower boundaries of each ellipse are derived from Equation (1) as:

$$y_{i, max}\left(x\right)=y_i+b_i\sqrt{1-{\left({\displaystyle \frac{x-x_i}{a_i}}\right)}^2}$$

(3)

$$y_{i, min}\left(x\right)=y_i-b_i\sqrt{1-{\left({\displaystyle \frac{x-x_i}{a_i}}\right)}^2}$$

(4)

The instantaneous vertical extent of the intersection at position $x$ is then:

$$h\left(x\right)=\max \left(0,\min \left(y_{1, max}\left(x\right), y_{2, max}\left(x\right)\right)-\max \left(y_{1, min}\left(x\right), y_{2, min}\left(x\right)\right)\right)$$

(5)

Here, the horizontal integration variable $x$ ranges over the intersection interval $[L,R]$, defined by the leftmost and rightmost abscissas at which the two ellipses overlap. Within this interval, $\min \left(y_{1, max}\left(x\right), y_{2, max}\left(x\right)\right)$ gives the upper boundary of the region common to both ellipses, while $\max \left(y_{1, min}\left(x\right), y_{2, min}\left(x\right)\right)$ gives the corresponding lower boundary. Their difference yields the vertical overlap height at each abscissa, and the outer non-negativity condition ensures that $h\left(x\right)=0$ whenever the vertical profiles do not intersect, so the integrand contributes only in the portion of the domain where the overlap is non-empty. Accordingly, integrating this height function across the horizontal overlap yields the total intersection area:

$$A={\int }_L^{R}h\left(x\right) dx$$

(6)

Equation (6) constitutes the core analytical representation used throughout this study. It reformulates the two-dimensional geometric intersection as a one-dimensional definite integral of the overlap height, allowing the proposed methods to evaluate the intersection without solving quartic systems or performing geometric decomposition.

Boundary conditions are handled explicitly. When $L\ge R$, the ellipses are horizontally disjointed, and $A=0$. If one ellipse lies entirely within the other—verified when all points of the smaller ellipse satisfy Equation (1) for the larger one—the intersection area equals the full area of the contained ellipse, $A=\pi a_{min}{b}_{min}$, where $a_{min}$ and $b_{min}$ denote the semi-axes of the smaller ellipse. Finally, if $h\left(x\right)=0$ for all $x\in [L,R]$, the ellipses are vertically separated, and $A=0$.

2.2. Proposed Method 1: Sine-Mapped Gauss–Legendre Quadrature

Classical Gauss–Legendre quadrature assumes that the integrand $h\left(x\right)$ varies smoothly across the integration interval $\left[L, R\right]$. In the case of axis-aligned ellipses, however, $h\left(x\right)$ often changes sharply near the overlap boundaries because the square root terms in $y_{i, max}\left(x\right)$ and $y_{i, min}\left(x\right)$ approach zero as $\left|x-x_i\right|$ tends to $a_i$. These steep gradients lead to uneven numerical conditioning near $L$ and $R$, causing fixed, non-adaptive quadrature nodes to under-sample the boundary regions. To mitigate this effect, a sine-based coordinate transformation is introduced that redistributes the quadrature abscissas non-uniformly, concentrating them near the endpoints, where $h\left(x\right)$ exhibits the strongest variation. Hence, the transformation is defined as:

$$x={\displaystyle \frac{L+R}{2}}+{\displaystyle \frac{R-L}{2}}\sin \left({\displaystyle \frac{\pi t}{2}}\right), t\in [-1, 1]$$

(7)

which maps the canonical Gauss–Legendre interval $[-1, 1]$ to the physical domain $\left[L, R\right]$, while smoothly compressing both ends of the range. The Jacobian of this mapping is:

$${\displaystyle \frac{dx}{dt}}={\displaystyle \frac{\pi (R-L)}{4}}\cos \left({\displaystyle \frac{\pi t}{2}}\right), t\in [-1, 1]$$

(8)

Therefore, substituting these expressions into Equation (6) gives the integral in the transformed domain, defined as:

$$A={\int }_{-1}^{1}h\left({\displaystyle \frac{L+R}{2}}+{\displaystyle \frac{R-L}{2}}\sin \left({\displaystyle \frac{\pi t}{2}}\right)\right){\displaystyle \frac{\pi \left(R-L\right)}{4}}\cos \left({\displaystyle \frac{\pi t}{2}}\right) dt$$

(9)

This integral is evaluated using an $N$-point Gauss–Legendre rule, where $(t_i, w_i)$ denote the abscissas and weights associated with the Legendre polynomial $P_N\left(t\right)$ on $[-1, 1]$, respectively. The resulting discrete form therefore becomes:

$$A_{GL}={\displaystyle \frac{\pi \left(R-L\right)}{4}}{\sum }_{i=1}^N{w}_i\cos \left({\displaystyle \frac{\pi t_i}{2}}\right)h\left({\displaystyle \frac{L+R}{2}}+{\displaystyle \frac{R-L}{2}}\sin \left({\displaystyle \frac{\pi t_i}{2}}\right)\right)$$

(10)

The sine term determines the mapping of each reference node $t_i$ from the canonical domain to the physical domain, while the cosine term arises from the Jacobian and compensates for local stretching or compression introduced by the transformation. Together they aim to preserve weight normalization and maintain the deterministic character of the quadrature, modifying only the node placement and corresponding weights for a given order $N$. This formulation maintains a fixed computational complexity of $O\left(N\right)$ per ellipse pair and enhances numerical stability in cases where $h\left(x\right)$ exhibits steep boundary gradients or near-tangency behavior. Similar transformation-based quadrature ideas have also been used in recent high-order numerical integration schemes to improve the conditioning of integral evaluations [35].

2.3. Proposed Method 2: Enhanced Two-Panel Affine-Normalized Gauss–Legendre Quadrature

While the sine-mapped quadrature described in Section 2.2 mitigates boundary-related instabilities, additional numerical imbalance can arise when the two ellipses possess highly unequal aspect ratios, such as $a/b>5$ or $b/a>5$. In these configurations, the disparity between horizontal and vertical scales introduces anisotropic curvature in $h\left(x\right)$, where small horizontal variations lead to disproportionately large vertical changes near the ellipse boundaries. To maintain numerical consistency between the horizontal and vertical scales, an affine normalization is introduced prior to integration.

2.3.1. Affine Normalization

Let $s_x=\max (a_1, a_2)$ and $s_y=\max (b_1, b_2)$. Each ellipse is rescaled into a normalized coordinate system in which the larger semi-axes are unity:

$$x_i^{\prime }={\displaystyle \frac{x_i}{s_x}}, y_i^{\prime }={\displaystyle \frac{y_i}{s_y}}, a_i^{\prime }={\displaystyle \frac{a_i}{s_x}}, b_i^{\prime }={\displaystyle \frac{b_i}{s_y}}, i=1, 2$$

(11)

This affine transformation regularizes the curvature and improves integrand conditioning by reducing anisotropy in the domain. After numerical integration, the physical intersection area is recovered through the Jacobian determinant of the scaling:

$$A=s_x{s}_y{A}^{\prime }$$

(12)

where $A^{\prime }$ denotes the intersection area computed in the normalized coordinate space.

2.3.2. Two-Panel Subdivision

Even after normalization, the normalized height function $h^{\prime }\left(x\right)$ may exhibit a change in curvature dominance, meaning that the upper boundary of the overlap region transitions from being governed by one ellipse to the other at an internal abscissa $M$. Evaluating the full normalized domain $[L^{\prime }, R^{\prime }]$ using a single quadrature panel can therefore introduce truncation error, since Gauss–Legendre nodes are symmetrically distributed around the midpoint and cannot adapt to asymmetric curvature behavior. To address this, the interval is divided into two sub-panels, $[L^{\prime }, M]$ and $[M, R^{\prime }]$, where each sub-interval is evaluated independently.

The crossover point $M$ is determined by a dynamic one-step secant approximation strategy. Let the normalized upper and lower boundaries be defined as:

$$y_{i, max}^{\prime }\left(x\right)=y_i^{\prime }+b_i^{\prime }\sqrt{1-{\left({\displaystyle \frac{x-x_i^{\prime }}{a_i^{\prime }}}\right)}^2}$$

(13)

$$y_{i, min}^{\prime }\left(x\right)=y_i^{\prime }-b_i^{\prime }\sqrt{1-{\left({\displaystyle \frac{x-x_i^{\prime }}{a_i^{\prime }}}\right)}^2}$$

(14)

The envelope difference functions are denoted as $g_{max}\left(x\right)=y_{1, max}^{\prime }\left(x\right)-y_{2, max}^{\prime }\left(x\right)$ and $g_{min}\left(x\right)=y_{1, min}^{\prime }\left(x\right)-y_{2, min}^{\prime }\left(x\right)$. Hence, the crossover abscissa point $M$ is determined as:

$$M=\left\{\begin{array}{c}{L}^{\prime }-g_{max}\left(L^{\prime }\right){\displaystyle \frac{R^{\prime }-L^{\prime }}{g_{max}\left(R^{\prime }\right)-g_{max}\left(L^{\prime }\right)}} , g_{max}\left(L^{\prime }\right) g_{max}\left(R^{\prime }\right)<0\\ L^{\prime }-g_{min}\left(L^{\prime }\right){\displaystyle \frac{R^{\prime }-L^{\prime }}{g_{min}\left(R^{\prime }\right)-g_{min}\left(L^{\prime }\right)}} , g_{min}\left(L^{\prime }\right) g_{min}\left(R^{\prime }\right)<0\\ {\displaystyle \frac{L^{\prime }+R^{\prime }}{2}} , otherwise \end{array}\right.$$

(15)

If both envelope differences exhibit sign changes, indicating curvature transitions along both boundaries, the crossover corresponding to the function with the larger magnitude of $\left|g\left(L^{\prime }\right)-g\left(R^{\prime }\right)\right|$ is preferred. This dynamic subdivision aims to ensure that each sub-interval contains a single dominant curvature regime, allowing the quadrature rule to approximate $h^{\prime }\left(x\right)$ within each sub-interval with improved local accuracy.

The corresponding computational procedure (pseudo-code) for selecting the split point $M$ is provided in Algorithm 1.

Algorithm 1: Two-Panel Split Point (M) Selection

Input: Normalized interval $[{\mathrm{L}}^{\prime },{\mathrm{R}}^{\prime }]$ Envelope functions ${\mathrm{g}}_{\mathrm{m}\mathrm{a}\mathrm{x}}\left(\mathrm{x}\right)$ and ${\mathrm{g}}_{\mathrm{m}\mathrm{i}\mathrm{n}}\left(\mathrm{x}\right)$ $\mathrm{Compute} \mathrm{s}1 = {\mathrm{g}}_{\mathrm{m}\mathrm{a}\mathrm{x}}\left({\mathrm{L}}^{\prime }\right)$$\times {\mathrm{g}}_{\mathrm{m}\mathrm{a}\mathrm{x}}\left({\mathrm{R}}^{\prime }\right)$ $\mathrm{Compute} \mathrm{s}2 = {\mathrm{g}}_{\mathrm{m}\mathrm{i}\mathrm{n}}\left({\mathrm{L}}^{\prime }\right)$$\times {\mathrm{g}}_{\mathrm{m}\mathrm{i}\mathrm{n}}\left({\mathrm{R}}^{\prime }\right)$ If s1 < 0: M1 = ${\mathrm{L}}^{\prime }$ $- {\mathrm{g}}_{\mathrm{m}\mathrm{a}\mathrm{x}}\left({\mathrm{L}}^{\prime }\right)$$\times ({\mathrm{R}}^{\prime }$ $- {\mathrm{L}}^{\prime }$$)/({\mathrm{g}}_{\mathrm{m}\mathrm{a}\mathrm{x}}\left({\mathrm{R}}^{\prime }\right)$$- {\mathrm{g}}_{\mathrm{m}\mathrm{a}\mathrm{x}}\left({\mathrm{L}}^{\prime }\right)$) If s2 < 0: M2 = ${\mathrm{L}}^{\prime }$ $- {\mathrm{g}}_{\mathrm{m}\mathrm{i}\mathrm{n}}\left({\mathrm{L}}^{\prime }\right)$$\times ({\mathrm{R}}^{\prime }$ $- {\mathrm{L}}^{\prime }$$)/({\mathrm{g}}_{\mathrm{m}\mathrm{i}\mathrm{n}}\left({\mathrm{R}}^{\prime }\right)$$- {\mathrm{g}}_{\mathrm{m}\mathrm{i}\mathrm{n}}\left({\mathrm{L}}^{\prime }\right)$) If both s1 < 0 and s2 < 0: Choose M as the value (M1 or M2) corresponding to the larger $\left|\mathrm{g}\left({\mathrm{L}}^{\prime }\right)-\mathrm{g}\left({\mathrm{R}}^{\prime }\right)\right|$ Else if s1 < 0: M = M1 Else if s2 < 0: M = M2 Else: $\mathrm{M} = ({\mathrm{L}}^{\prime }$ $+ {\mathrm{R}}^{\prime }$)/2 Output: Split point M

2.3.3. Final Formulation

The total intersection area in the normalized space is expressed as the sum of two sine-mapped Gauss–Legendre quadratures evaluated over the two sub-intervals:

$$A^{\prime }={\int }_{L^{\prime }}^M{h}^{\prime }\left(x\right) dx+{\int }_M^{R^{\prime }}{h}^{\prime }\left(x\right) dx\approx {\sum }_{p=\{1, 2\}}{\displaystyle \frac{\pi \left(R_p^{\prime }-L_p^{\prime }\right)}{4}}{\sum }_{i=1}^N{w}_i\cos \left({\displaystyle \frac{\pi t_i}{2}}\right)h^{\prime }\left(x_p\left(t_i\right)\right)$$

(16)

where $p=\{1, 2\}$ indexes the first and second sub-intervals, and $x_p\left(t_i\right)$ denotes the corresponding sine-mapped abscissas.

The two-panel affine-normalized formulation retains a fixed computational cost of the single-panel quadrature and reduces truncation error in asymmetric intersections or configurations with extreme aspect ratios.

2.4. Theoretical Extensions Beyond Standard Gauss–Legendre Quadrature

The proposed quadrature formulations extend classical Gauss–Legendre (GL) integration through a set of analytic transformations that address geometric features unique to the axis-aligned ellipse–ellipse intersection problem. Standard GL quadrature applies fixed nodes and weights on a symmetric interval and assumes a smoothly varying integrand with well-conditioned derivatives. In contrast, the overlap-height function $h\left(x\right)$ may exhibit steep endpoint gradients, curvature asymmetry, or internal changes in the dominant boundary, all of which degrade the performance of conventional GL rules.

The first extension is the sine-mapped transformation, which applies the variable substitution $x=\varphi \left(t\right)$ with $\varphi$ chosen to cluster quadrature nodes near the interval endpoints. This improves numerical conditioning in cases where the square-root terms inside $h\left(x\right)$ introduce high curvature or near-singular behavior. Such endpoint-focused node redistribution is not part of standard GL formulations and is essential for stabilizing the integral in grazing or near-tangency regimes. The second extension is affine normalization, in which each ellipse is rescaled into a common normalized coordinate system before integration. This transformation equalizes curvature across axes and mitigates anisotropy in the height function, allowing the quadrature rule to operate on a geometrically balanced integrand. Classical GL quadrature does not incorporate curvature conditioning or geometric normalization and therefore cannot compensate for the effect of disparate aspect ratios. The third extension is the two-panel decomposition, which partitions the overlap interval at a curvature crossover point determined from the envelope functions of the upper and lower boundaries. Each sub-interval is integrated independently, isolating regions where $h\left(x\right)$ is governed by a different dominant boundary. Standard GL integration operates on a single symmetric panel and cannot adapt to such curvature transitions, which explains its reduced accuracy in asymmetric configurations.

Together, these modifications preserve the fixed cost and theoretical convergence properties of Gauss–Legendre quadrature while extending its applicability to integrands exhibiting non-uniform curvature and steep endpoint behavior arising from axis-aligned ellipse–ellipse intersections. Similar fixed-order Gaussian quadrature ideas are widely used in finite-element analysis for integrating smooth fields over curved elements [36], and the formulations developed here follow the same numerical paradigm in the specific setting of axis-aligned ellipse–ellipse intersections.

2.5. Smoothness and Boundary Behavior of the Overlap-Height Function

Let each ellipse be defined as in Equation (1), where ($x_c$, $y_c$) denote its center coordinates. For an axis-aligned configuration, the upper and lower boundaries of each ellipse are analytic in $x$:

$$y_{max}\left(x\right)=y_c+b\sqrt{1-{\displaystyle \frac{{\left(x-x_c\right)}^2}{a^2}}}, y_{min}\left(x\right)=y_c-b\sqrt{1-{\displaystyle \frac{{\left(x-x_c\right)}^2}{a^2}}}$$

(17)

Within any non-degenerate intersection interval $(L, R)$, the overlap-height function $h\left(x\right)$ defined in Equation (5) is piecewise analytic on the open region where both square-root terms are defined, i.e., for $x\in (x_c-a, x_c+a)$, since it is the difference of two analytic functions. Consequently, $h\left(x\right)$ is $C^{\infty }$ on each analytic sub-interval, and the only non-analytic points arise at isolated envelope-switching abscissas or at the endpoints $x=L, R$, which are excluded from the integration domain of the quadrature. This property guarantees that the assumptions underlying the Gauss–Legendre error estimate are satisfied.

In near-tangent configurations, numerical instability arises from the derivative of the ellipse boundary:

$$y^{\prime }\left(x\right)=\mp {\displaystyle \frac{b\left(x-x_c\right)}{a^2\sqrt{1-\left(\right(x-x_c)/a{)}^2}}}$$

(18)

whose magnitude diverges as $\left|x-x_c\right|\to a$. Because the overlap-height function satisfies $h^{\prime }\left(x\right)=y_{2,max}^{\prime }\left(x\right)-y_{1,min}^{\prime }\left(x\right)$, the same blow-up appears in $h^{\prime }\left(x\right)$, causing steep endpoint gradients and local loss of floating-point precision. In addition, when the ellipses have high aspect ratios (e.g., $a/b\gg 1$), the denominator $\sqrt{1-\left(\right(x-x_c)/a{)}^2}$ becomes small over a wider portion of the domain, amplifying $h^{\prime }\left(x\right)$ even away from the endpoints and making the integrand more ill-conditioned under uniform sampling. The sine mapping and affine normalization counteract these behaviors by clustering nodes near the endpoints and bounding curvature in the normalized space.

From a conditioning standpoint, the local quadrature error depends on the curvature of the ellipse boundaries and the minimal separation distance between them. In near-tangent configurations where the vertical gap between boundaries behaves like $\delta \left(x\right)\approx \sqrt{2a∆x}$, the derivative magnitude satisfies $\left|h^{\prime }\left(x\right)\right|=O\left({\delta }^{-1}\right)$, increasing the Gauss–Legendre error constant and reducing stability under uniform node placement. High-aspect-ratio cases behave similarly, since curvature grows as $O(a/b)$ along the major axis. The sine mapping reduces this effect by compressing nodes in regions where $\delta \left(x\right)$ is small, while affine normalization bounds curvature by rescaling the ellipse axes. These transformations therefore control the error constant conditionally on boundary curvature and separation, providing qualitative stability guarantees in the regimes that challenge standard Gauss–Legendre quadrature.

2.6. Numerical Accuracy of Fixed-Order Quadrature

Both proposed formulations employ fixed-order Gauss–Legendre quadrature to integrate the overlap-height function $h\left(x\right)$ across the intersection domain $[L, R]$. For such smooth integrands, GL quadrature exhibits exponential convergence with respect to the number of nodes $N$. The classical error estimate for a smooth function whose $2N$-th derivative is bounded in magnitude by a constant $C$, i.e., $\left|h^{\left(2N\right)}(x)\right|\le C$ is [18,37]:

$$\left|E_N\right|\le {\displaystyle \frac{C\left(2N\right)!}{\left(2N+1\right)\left({\left(N!\right)}^4\right)}}$$

(19)

Because the curvature of the ellipse boundaries is finite and bounded after affine normalization, the constant $C$ remains moderate, ensuring that relatively small orders ($N=8-16$) achieve near-machine-precision accuracy in all non-degenerate configurations. This theoretical property underpins the deterministic accuracy and fixed computational cost of both formulations.

2.7. Comparative Methods: Polygonal Approximation and Monte Carlo Estimation

In addition to the proposed quadrature formulations, two established numerical techniques are implemented for comparative evaluation: the polygonal approximation and the Monte Carlo estimation. Both approaches operate independently of the integral representation in Equation (6) and instead rely on geometric discretization or stochastic sampling to estimate the overlap area between the two axis-aligned ellipses.

2.7.1. Polygonal Approximation

The polygonal method replaces each ellipse with a polygon composed of $n$ evenly spaced vertices along its perimeter. Each vertex $(x_k, y_k)$, where $k=0,\dots ,n-1$, is defined parametrically as:

$$\left(x_k, y_k\right)=\left(x_c+a\cos {\theta }_k, y_c+b\sin {\theta }_k\right), {\theta }_k={\displaystyle \frac{2\pi k}{n}}$$

(20)

The intersection between the two polygons is computed using clipping algorithms such as those of Vatti or Greiner–Hormann [12,13]. The area of the resulting intersection polygon, with $m$ vertices $\left(x_j, y_j\right)$, is then obtained using the shoelace formula [14]:

$$A_{Polygon}={\displaystyle \frac{1}{2}}\left|{\sum }_{j=1}^m(x_j{y}_{j+1}-x_{j+1}{y}_j)\right|$$

(21)

where the indices are cyclic, i.e., $x_{m+1}=x_1$ and $y_{m+1}=y_1$.

The accuracy of this method scales approximately with $O(1/n^2)$ for smooth curves, since increasing the vertex count improves the fidelity of the circular arc approximation. In practice, $n=256$ provides moderate accuracy, whereas $n=1024$ yields near-convergent results at a computational cost approximately 5–10 times higher than that of fixed-order quadrature.

2.7.2. Monte Carlo Estimation

The Monte Carlo method estimates the intersection area statistically through random sampling of uniformly distributed points within the joint bounding box of the two ellipses [24,25,26]. Let the bounding rectangle be defined by the smallest and largest coordinate limits of both ellipses. A total of $N_s$ random samples $\left(x_j, y_j\right)$ are drawn from the rectangle, and each point is tested for inclusion according to the implicit condition:

$${\displaystyle \frac{{(x_j-x_i)}^2}{a_i^2}}+{\displaystyle \frac{{(y_j-y_i)}^2}{b_i^2}}\le 1, i=1, 2$$

(22)

The ratio of points lying within both ellipses to the total number of samples provides an estimate of the fractional overlap, which, when multiplied by the bounding-box area $A_{box}$, yields the intersection estimate:

$$A_{MC}=A_{box}{\displaystyle \frac{N_{in}}{N_s}}$$

(23)

where $N_{in}$ denotes the number of points simultaneously contained in both ellipses.

This stochastic formulation is straightforward to implement and easily parallelized, but its accuracy depends on the number of random samples. The statistical error decreases proportionally to $1/\sqrt{N_s}$, implying that higher precision requires substantial increases in sample count.

2.8. Baseline Reference: Adaptive Simpson Integration

To establish a deterministic reference for accuracy evaluation, adaptive Simpson integration [16,17] is employed as the baseline numerical method. This approach provides a high-precision numerical evaluation of the integral in Equation (6) and serves exclusively as the ground truth for assessing the performance of the proposed and comparative models. The method recursively subdivides the interval $\left[L, R\right]$ until successive Simpson estimates converge within a predefined tolerance $\epsilon$. For a given sub-interval $\left[a, b\right]$, the Simpson estimate is defined as:

$$S\left(a, b\right)={\displaystyle \frac{b-a}{6}}\left(h\left(a\right)+4h\left({\displaystyle \frac{a+b}{2}}\right)+h\left(b\right)\right)$$

(24)

The interval is bisected at $u=(a+b)/2$, and two half-intervals $\left[a, u\right]$ and $\left[u, b\right]$ are recursively evaluated, where refinement proceeds until the local convergence criterion $\left|S\left(a, b\right)-(S\left(a, u\right)+S\left(u, b\right))\right|\le 15\epsilon$ is satisfied. When this condition holds, the two sub-intervals are accepted, and Richardson extrapolation [16,17,18] is applied to locally refine the accumulated estimate. The final intersection area is obtained by summing the contributions of all accepted sub-intervals.

The adaptive Simpson method attains near machine-precision accuracy for smooth integrands but exhibits variable computational cost, as the number of recursive subdivisions depends on local curvature and ellipse eccentricity.

2.9. Evaluation Metrics and Benchmark Scenarios

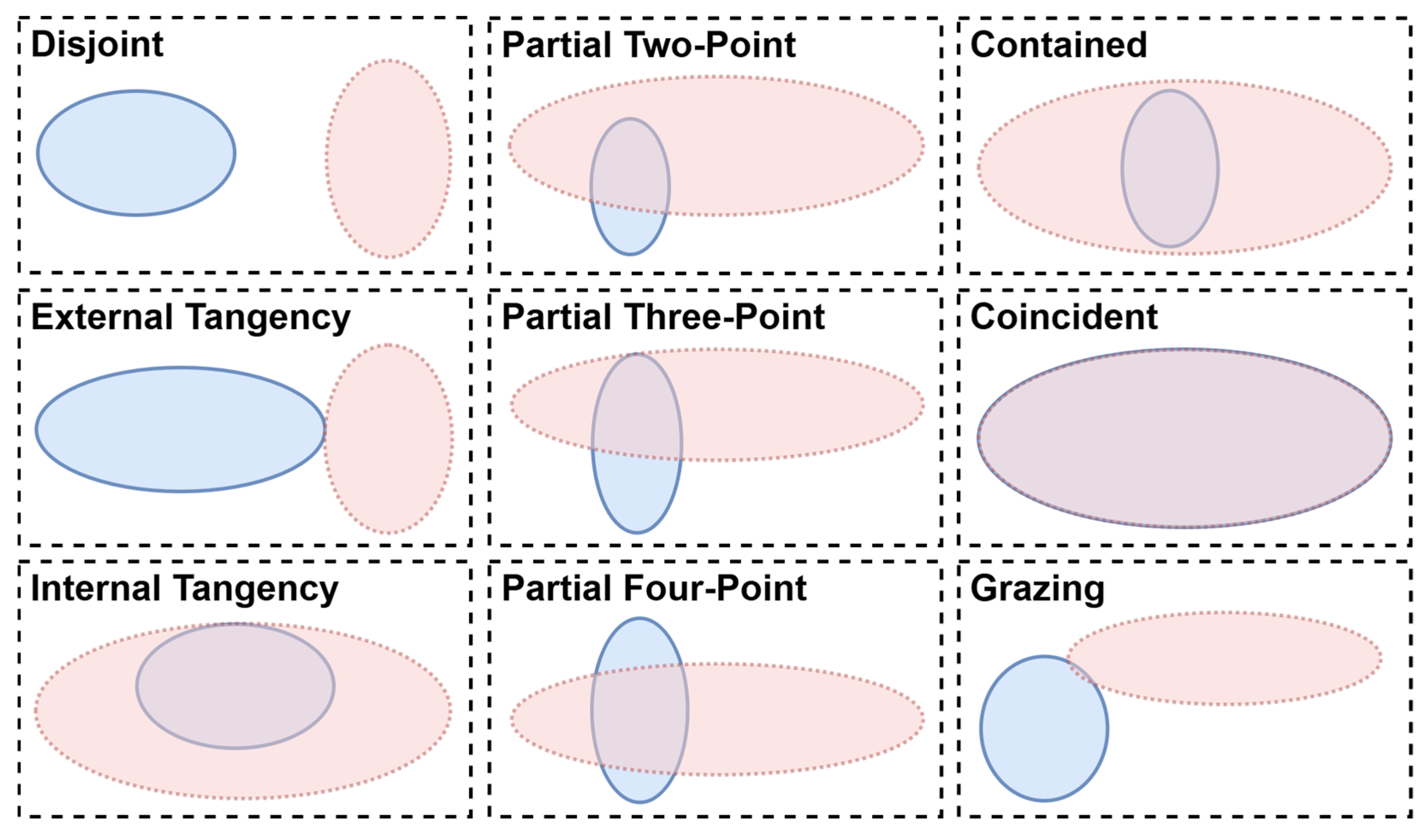
The numerical performance of all methods is evaluated using a stratified benchmark that encompasses the principal geometric configurations of axis-aligned ellipse–ellipse interaction. Each sample pair $(E_1, E_2)$ is generated with randomized centers and semi-axes, constrained to satisfy one of nine positional regimes representing the complete set of intersection topologies illustrated schematically in Figure 1. These include disjoint, external tangency, internal tangency, partial two-point overlap, partial three-point overlap, partial four-point overlap, contained, coincident, and grazing.

Figure 1. Schematic illustration of intersection regimes highlighting disjoint, external tangency, internal tangency, partial two-point overlap, partial three-point overlap, partial four-point overlap, contained, coincident, and grazing configurations.

• Disjoint regime corresponds to ellipses with no spatial intersection.
• External tangency describes ellipses that touch at exactly one boundary point from the outside.
• Internal tangency refers to an internal contact where one ellipse is tangent to the other from within.
• Partial two-point, partial three-point, and partial four-point regimes represent cases of partial overlap where the intersection boundary consists of two, three or four real crossing points, respectively.
• Contained configuration describes the containment of one ellipse entirely within the other, producing a complete but nested intersection.
• Coincident cases correspond to identical ellipses sharing the same geometric parameters, where the intersection equals the full area of either ellipse.
• Grazing cases denote near-tangency conditions where the intersection area approaches zero while the boundaries are nearly coincident.

For each configuration, the reference intersection area $A_{ref}$ is computed using adaptive Simpson integration, as detailed in Section 2.8. All other methods are evaluated relative to this reference based on the mean, median, and standard deviation of the relative error ${ϵ}_{rel}$:

$${ϵ}_{rel}={\displaystyle \frac{\left|A_{method}-A_{ref}\right|}{A_{ref}}}$$

(25)

where $A_{method}$ denotes the intersection area estimated by the evaluated method.

The relative error metrics quantify the deviation of each numerical approximation from the reference area. The runtime $T_{ref}$ of the reference method and $T_{method}$ of each evaluated method are measured as an average of 50 identical runs. The speed-up ratio, $r_S=T_{ref}/T_{method}$, expresses the relative computational efficiency normalized by the baseline reference.

The evaluation is performed both globally over all generated samples to assess overall performance and per-regime to analyze how numerical behavior varies with geometric configuration. Global metrics summarize the mean, median, and variability of relative error and runtime across all cases, while per-regime statistics isolate each method’s response to specific intersection regimes.

In addition to the synthetic benchmarks, a real-world case study is considered to evaluate the behavior of the proposed quadrature formulations in an applied engineering context. Corrosion defects detected during in-line inspections of transmission pipelines are described in the feature tally by their axial position, circumferential position, measured length, width, and depth [38,39,40]. These attributes define an axis-aligned two-dimensional footprint for each defect. Conventional overlap-based matching models [41,42,43] typically approximate each defect using rectangular boxes, as the tally provides no orientation information. However, corrosion metal-loss regions generally exhibit smooth tapered profiles and their footprint is more faithfully represented by axis-aligned ellipses [44,45,46,47,48].

In long-distance pipelines, an inspection may contain tens to hundreds of thousands of metal-loss features, and matching two inspections may require evaluating millions of footprint intersections. Efficient and deterministic computation of axis-aligned overlap areas is therefore operationally relevant for large-scale corrosion analysis workflows. To illustrate computational performance in such a scenario, a 12 m pipeline section containing multiple corrosion defects is modeled using axis-aligned elliptical footprints, and the total overlap area between two successive inspections is computed using adaptive Simpson integration and the two proposed Gauss–Legendre formulations.

3. Experiment and Analysis

The performance of the proposed quadrature formulations is examined through two complementary experiments. The first evaluates accuracy and computational behavior using a large synthetic benchmark spanning the principal intersection regimes, as detailed in Section 3.1. The second applies the methods to a real 12 m pipeline section to illustrate their behavior in a practical inspection setting, as detailed in Section 3.2.

3.1. Synthetic Benchmark Evaluation

The numerical experiments were conducted on a stratified dataset comprising 10,000 randomly generated pairs of axis-aligned ellipses, equally spanning the geometric spectrum of possible mutual configurations illustrated in Figure 1. Each ellipse pair was defined within the unbounded coordinate domain, with semi-axes uniformly distributed in the range [1.0, 15.0], producing a broad range of size ratios, eccentricities, and relative positional offsets that collectively aimed to span all principal intersection configurations.

All computations were performed in IEEE 64-bit floating-point precision under identical runtime conditions. The adaptive Simpson recursive integrator was configured with a recursion depth limit of 20 and a convergence tolerance of ${10}^{-10}$, to yield reference solutions at near-machine-precision accuracy. The proposed two methods were evaluated at node orders $N=16, 32, 64$, denoted, respectively, as 16-GL, 32-GL, and 64-GL (GL denotes Gauss–Legendre quadrature). Polygonal approximations were computed using uniform angular sampling with vertex counts of 64, 256, and 1024, and intersection areas were obtained using a vectorized polygon-clipping implementation provided by Python 3’s ‘shapely 2.1.2’ package. The Monte Carlo estimator employed ${10}^5$ random samples per pair within the bounding box of the ellipses. All methods were implemented in vectorized form and executed in a single CPU thread. Runtimes $T_{ref}$ and $T_{method}$ and speed-up ratios $r_S$ represent full per-run wall-clock times for the 10,000 pairs, including the computation of the height function $h\left(x\right)$ and all auxiliary operations. All experiments were executed on an Intel Core i7-14650HX CPU (Intel Corporation, Santa Clara, CA, USA) with 16 GB RAM, and no GPU acceleration was used.

Overall accuracy statistics and runtime details across the 10,000 benchmark samples are presented in Table 1. Both quadrature formulations exhibit monotonic convergence with increasing node order. The two-panel variant consistently attains lower mean and standard deviation of the error than the sine-mapped formulation, with proportionally higher but still sub-0.7 s runtime attributable to its dual sub-interval evaluation. At 64-GL, it reaches a mean relative error of 0.003% within 0.623 s total runtime, representing a 23.9× speed-up over the adaptive Simpson reference. The sine-mapped quadrature (method 1) follows a similar convergence pattern, with mean errors decreasing from 0.214% at 16-GL to 0.023% at 64-GL and speed-up ratios exceeding 50× at higher orders. Polygonal discretization shows error reduction with increased vertex count, but runtimes remain one to two orders of magnitude higher than those of the quadrature methods. The 1024-vertex configuration, for example, attains a mean error of 0.014% at 6.669 s (≈2.2× speed-up). The Monte Carlo estimator is the least efficient; despite using ${10}^5$ samples per case, it yields a mean error of 2.629% and a standard deviation of 9.356%, with runtimes exceeding 18 s (≈0.8× speed-up). Overall, the two-panel quadrature demonstrates the most favorable trade-off between accuracy and computational efficiency, with sub-0.1% standard deviation at both 32-GL and 64-GL.

Table 1. Global performance of all evaluated methods across 10,000 benchmark samples, showing mean, median, and standard deviation of the relative error, total runtime, and speed-up ratio with respect to the adaptive Simpson reference.

Method	Mean Error (%)	Median Error (%)	Std Dev (%)	${\mathbf{T}}_{\mathbf{m}\mathbf{e}\mathbf{t}\mathbf{h}\mathbf{o}\mathbf{d}}$ (s)	Speed-Up (${\mathbf{r}}_{\mathbf{S}}$)
Sine-Mapped Quadrature (16-GL)	0.214	0.000	3.256	0.074	201.6
Sine-Mapped Quadrature (32-GL)	0.063	0.000	1.527	0.135	110.3
Sine-Mapped Quadrature (64-GL)	0.023	0.000	1.025	0.260	57.1
Two-Panel Quadrature (16-GL)	0.046	0.000	0.302	0.173	85.9
Two-Panel Quadrature (32-GL)	0.011	0.000	0.062	0.321	46.3
Two-Panel Quadrature (64-GL)	0.003	0.000	0.025	0.623	23.9
Polygonal (64 Vertices)	1.997	0.161	6.216	0.906	16.4
Polygonal (256 Vertices)	0.145	0.010	1.061	1.994	7.5
Polygonal (1024 Vertices)	0.014	0.001	0.558	6.669	2.2
Monte Carlo (105 Samples)	2.629	0.241	9.356	18.229	0.8

Table 2 summarizes the per-regime relative-error statistics for all tested configurations. Disjoint and external-tangency regimes yield zero intersection and therefore zero error for all methods. In the contained, coincident, and internal-tangency regimes, both quadrature formulations reproduce the reference area to numerical precision, with mean deviations below 0.01%, while polygonal discretization introduces minor residuals that decrease from 0.167% (64 vertices) to 0.001% (1024 vertices) and Monte Carlo retains small sampling deviations around 0.3%. Across all partial-overlap configurations, both quadrature schemes show consistent monotonic convergence as node order increases, with the two-panel formulation yielding uniformly lower mean and standard deviation of the error. At 64-GL, the two-panel quadrature records mean errors of 0.018%, 0.003%, and 0.003% for the two-, three-, and four-point overlap cases, respectively, while the sine-mapped quadrature yields 0.180%, 0.006%, and 0.006%. Polygonal discretization exhibits the same monotonic reduction in error as the vertex count increases: the mean error decreases from 1.410% to 0.058% in the two-point regime, from 0.227% to 0.001% in the three-point regime, and from 0.184% to 0.001% in the four-point regime. Whereas Monte Carlo remains between 0.561% and 2.325% with high variance. The grazing configuration produces the largest spread in performance: the two-panel quadrature achieves a mean error of 0.004% at 64-GL, surpassing both the sine-mapped quadrature (0.011%) and the polygonal method at 1024 vertices (0.066%), while Monte Carlo remains above 19%. Overall, the two-panel quadrature maintains the highest overall accuracy and stability across all non-trivial intersection regimes, whereas zero-overlap configurations are resolved exactly by all methods.

Table 2. Per-regime relative-error statistics for all evaluated methods across 10,000 benchmark samples, covering the full set of geometric intersection regimes illustrated in Figure 1.

Method	Error Metric (%)	Disjoint	External Tangency	Internal Tangency	Partial Two-Point	Partial Three-Point	Partial Four-Point	Contained	Coincident	Grazing
Sine-Mapped Quadrature (16-GL)	Mean	0.000	0.000	0.003	1.564	0.093	0.104	0.000	0.000	0.165
	Median	0.000	0.000	0.000	0.106	0.041	0.064	0.000	0.000	0.148
	Std Dev	0.000	0.000	0.011	9.657	0.227	0.171	0.000	0.000	0.114
Sine-Mapped Quadrature (32-GL)	Mean	0.000	0.000	0.001	0.474	0.021	0.026	0.000	0.000	0.042
	Median	0.000	0.000	0.000	0.024	0.011	0.016	0.000	0.000	0.038
	Std Dev	0.000	0.000	0.002	4.560	0.044	0.046	0.000	0.000	0.029
Sine-Mapped Quadrature (64-GL)	Mean	0.000	0.000	0.000	0.180	0.006	0.006	0.000	0.000	0.011
	Median	0.000	0.000	0.000	0.006	0.003	0.004	0.000	0.000	0.010
	Std Dev	0.000	0.000	0.001	3.069	0.013	0.010	0.000	0.000	0.007
Two-Panel Quadrature (16-GL)	Mean	0.000	0.000	0.001	0.259	0.050	0.046	0.000	0.000	0.056
	Median	0.000	0.000	0.000	0.045	0.024	0.029	0.000	0.000	0.050
	Std Dev	0.000	0.000	0.002	0.863	0.097	0.075	0.000	0.000	0.043
Two-Panel Quadrature (32-GL)	Mean	0.000	0.000	0.000	0.061	0.012	0.012	0.000	0.000	0.014
	Median	0.000	0.000	0.000	0.012	0.006	0.007	0.000	0.000	0.013
	Std Dev	0.000	0.000	0.000	0.174	0.021	0.019	0.000	0.000	0.011
Two-Panel Quadrature (64-GL)	Mean	0.000	0.000	0.000	0.018	0.003	0.003	0.000	0.000	0.004
	Median	0.000	0.000	0.000	0.003	0.002	0.002	0.000	0.000	0.003
	Std Dev	0.000	0.000	0.000	0.073	0.006	0.005	0.000	0.000	0.003
Polygonal (64 Vertices)	Mean	0.000	0.000	0.167	1.410	0.227	0.184	0.161	0.161	15.668
	Median	0.000	0.000	0.161	0.400	0.194	0.175	0.161	0.161	12.253
	Std Dev	0.000	0.000	0.013	5.524	0.089	0.028	0.000	0.000	10.275
Polygonal (256 Vertices)	Mean	0.000	0.000	0.010	0.198	0.014	0.012	0.010	0.010	1.047
	Median	0.000	0.000	0.010	0.025	0.012	0.011	0.010	0.010	0.797
	Std Dev	0.000	0.000	0.001	2.933	0.006	0.002	0.000	0.000	0.762
Polygonal (1024 Vertices)	Mean	0.000	0.000	0.001	0.058	0.001	0.001	0.001	0.001	0.066
	Median	0.000	0.000	0.001	0.002	0.001	0.001	0.001	0.001	0.050
	Std Dev	0.000	0.000	0.000	1.672	0.000	0.000	0.000	0.000	0.048
Monte Carlo (105 Samples)	Mean	0.000	0.000	0.324	2.325	0.614	0.561	0.563	0.131	19.141
	Median	0.000	0.000	0.259	0.873	0.412	0.370	0.417	0.107	12.842
	Std Dev	0.000	0.000	0.262	6.460	0.714	0.585	0.543	0.100	20.838

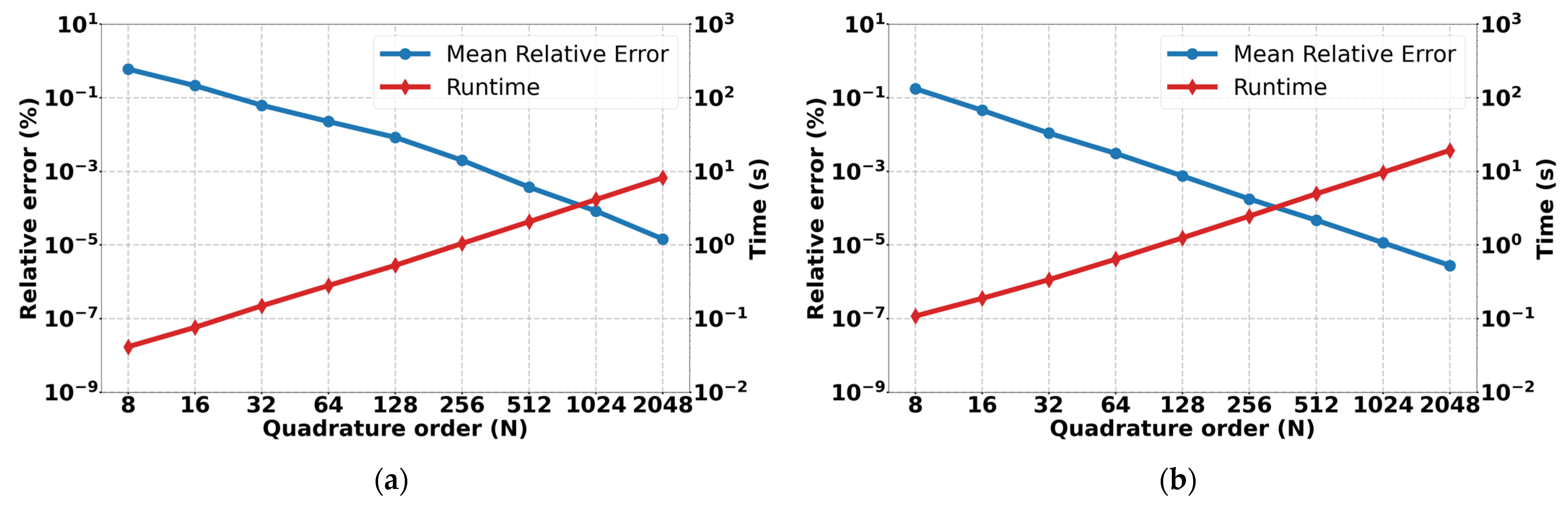
Additionally, convergence analysis is performed for the proposed quadrature formulations. As shown in Figure 2, the sine-mapped single-panel and enhanced two-panel affine-normalized variants exhibit distinct asymptotic behavior as quadrature order $N$ increases. Both demonstrate continuous and monotonic decay of the mean relative error across the entire tested range, with no sign of oscillation or stagnation, while runtime scales linearly with the number of quadrature nodes. The two-panel variant preserves a uniformly lower error envelope at all orders, reflecting reduced sensitivity to curvature-induced parameterization distortions and improved numerical balance across sub-intervals. The convergence trajectories of both schemes remain stable and well-conditioned throughout the examined resolution spectrum, confirming that the underlying integration strategy remains consistent under progressive refinement and that residual errors remain bounded in high-order regimes.

Figure 2. Convergence and runtime characteristics of the proposed Gauss–Legendre quadrature formulations. (a) Sine-mapped single-panel quadrature; (b) Enhanced two-panel affine-normalized quadrature. Both plots show the decay of the mean relative error with respect to the quadrature order N. Log–log scaling reveals near-monotonic convergence, with the enhanced formulation maintaining faster asymptotic error reduction across higher orders, while runtime increases linearly with N for both methods.

3.2. Real-World Case Study: 12 m Section of a Pipeline

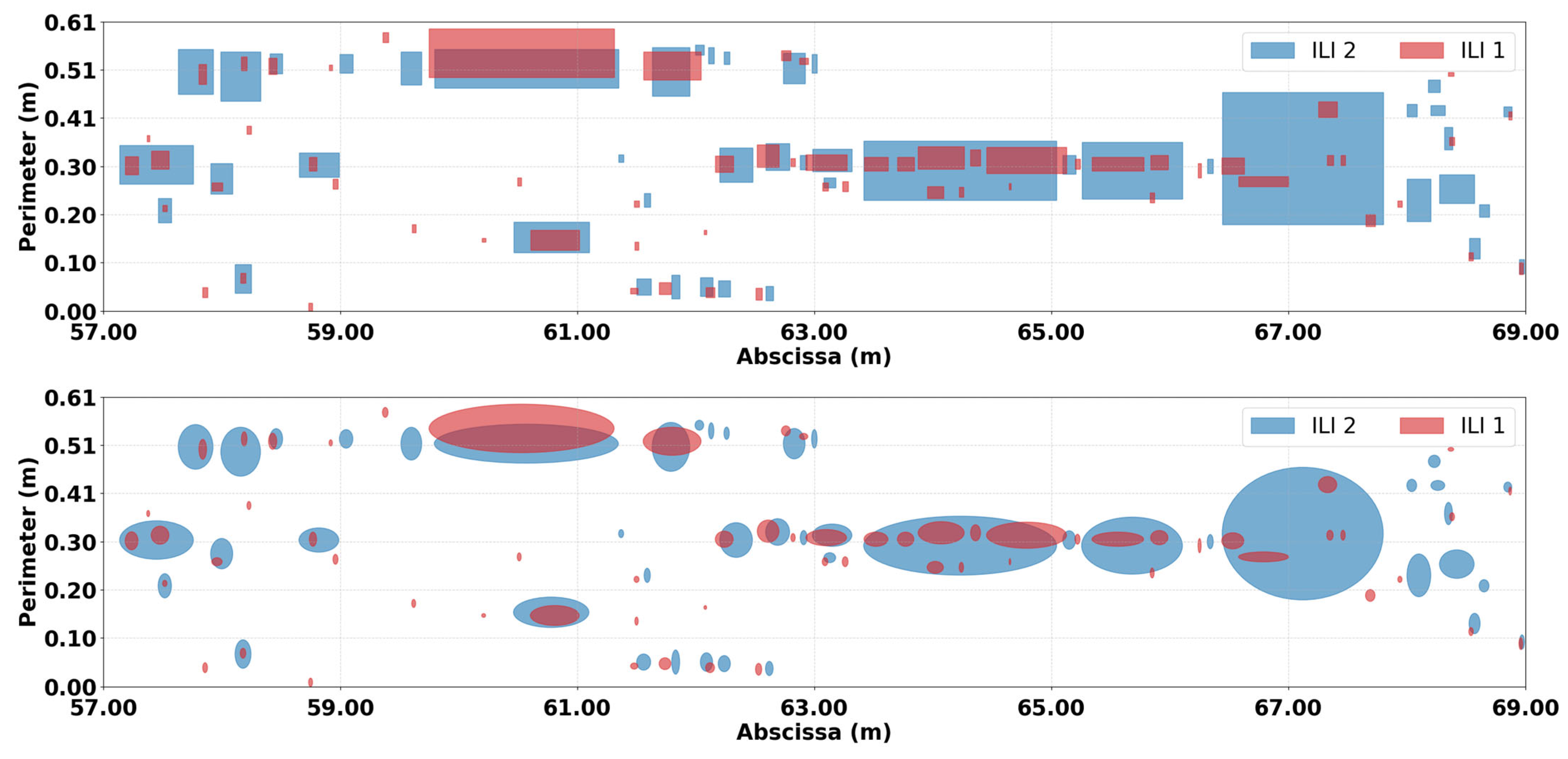
A 12 m water-injection pipeline section with an outer diameter of 219 mm and a wall thickness of 12.7 mm is used as the real-world dataset for evaluating the proposed quadrature formulations. The corrosion features from two successive ILIs are represented using both axis-aligned rectangular boxes and axis-aligned ellipses derived from the reported dimensions, as illustrated in Figure 3.

Figure 3. Visualization of corrosion features from two successive in-line inspections (ILI 2 shown in blue and ILI 1 shown in red) along a 12 m pipeline segment. The top panel represents each defect using its reported axial length and circumferential width as axis-aligned rectangular boxes, consistent with conventional ILI feature tallies. The bottom panel models the same defects as axis-aligned ellipses derived from the same dimensional measurements, providing a smoother geometric representation of metal-loss footprints. Both panels reveal the spatial distribution, relative sizing, and mutual overlap of corresponding features across the two inspections.

For this case study, the total overlap area between the two inspection datasets is computed using the adaptive Simpson reference, the sine-mapped 64-GL formulation, and the two-panel 64-GL variant. The resulting intersection areas are:

• Adaptive Simpson (reference): 1,450,743.75 mm².
• Sine-Mapped Quadrature (64-GL): 1,450,727.79 mm².
• Two-Panel Quadrature (64-GL): 1,450,743.23 mm².

Both quadrature formulations produce area estimates closely aligned with the adaptive reference, with deviations of approximately 0.001% for the sine-mapped variant and 0.00004% for the two-panel variant. These results show that the formulations reproduce the reference overlap area with very small discrepancies when applied to field-recorded corrosion data, indicating consistent numerical behavior in this practical feature matching setting.

4. Discussion

This section discusses the numerical and analytical findings presented in Section 3, with emphasis on computational behavior, numerical conditioning, and stability of the proposed quadrature formulations. Section 4.1 evaluates runtime scaling and computational efficiency, while Section 4.2 consolidates accuracy trends across all intersection regimes. Section 4.3, Section 4.4, Section 4.5, Section 4.6 examine formulation-specific characteristics, sensitivity to geometric conditioning, the stabilizing role of affine normalization, and the runtime behavior and determinism. Section 4.7 identifies sources of numerical instability, and Section 4.8 relates the proposed methods to existing semi-analytical approaches. Section 4.9 outlines methodological limitations and directions for future development.

4.1. Computational Performance

The runtime behavior observed in Table 1 confirms that the computational cost of both quadrature formulations scales linearly with the number of nodes. The sine-mapped GL quadrature (method 1) completed 10,000 integrations in 0.074 s at order 16 and 0.260 s at order 64, while the two-panel variant (method 2) increased proportionally to 0.623 s at order 64 owing to its dual sub-interval processing. Despite this doubling, the two-panel quadrature remained below 0.7 s total across all tested orders, corresponding to an average of roughly 63 µs per ellipse pair.

Compared with polygonal and Monte Carlo approaches, the quadrature formulations achieved between one and two orders of magnitude higher efficiency for equivalent or superior accuracy. The polygonal approximation with 1024 vertices required 6.669 s, approximately ten times slower than the two-panel 64-GL configuration, and the Monte Carlo estimator required 18.229 s, making it impractical for dense evaluation tasks or embedded implementations. Furthermore, because both quadrature methods use a fixed, predetermined sampling grid, their runtimes are deterministic and independent of geometry, unlike adaptive Simpson recursion whose cost varies with curvature and eccentricity.

4.2. Summary of Observations

Across all benchmarks, deterministic methods reproduced exact results for disjoint and external tangency configurations, while only the quadrature-based methods achieved full numerical accuracy for contained and coincident cases. The enhanced two-panel affine-normalized quadrature exhibited the lowest deviations across all intersection regimes, reducing mean errors to below 0.018% at 64-GL compared with 0.18% for the sine-mapped formulation. Polygonal discretization reached comparable precision only at very high vertex counts (≈0.066% at 1024 vertices) but required significantly higher runtime, whereas Monte Carlo integration remained the least stable with percent-level dispersion even at ${10}^5$ samples. Overall, both quadrature formulations demonstrate monotonic convergence and deterministic performance, with the two-panel variant maintaining the most consistent balance between accuracy and computational cost across overlapping configurations.

The convergence trends in Table 1 and Table 2 are consistent with the Gauss–Legendre error expression in Equation (19), whose magnitude depends on the higher-order derivatives of $h\left(x\right)$. Grazing and near-tangency regimes introduce steep endpoint gradients in the overlap-height function, which increase these derivatives and therefore slow the decay of the quadrature error with increasing order. In contrast, smooth overlap configurations exhibit rapid error reduction, consistent with classical expectations for analytic integrands. The two-panel formulation reduces this variation by isolating high-curvature regions within smaller sub-intervals, which explains the steeper convergence slope observed in Figure 2.

4.3. Formulation Independence of the Proposed Methods

Although both quadrature formulations achieve deterministic precision, their numerical behavior remains distinct across geometric regimes. The two-panel variant provides consistently higher accuracy at a modest increase in computational cost, while the sine-mapped formulation executes faster but exhibits higher residual errors. The two approaches are therefore complementary rather than hierarchical, representing an accuracy–performance trade-off whose selection depends on computational constraints and application requirements.

4.4. Sensitivity of Numerical Integration to Geometric Conditioning

The variation in error across intersection regimes originates primarily from the conditioning of the height function $h\left(x\right)$. In disjoint or fully contained cases, $h\left(x\right)$ is either zero or continuous with constant sign, resulting in exact cancelation or stable evaluation in any deterministic method. In contrast, partial overlaps, external tangency, and grazing contacts introduce regions where $h\left(x\right)$ transitions sharply due to near-zero terms under the square roots in $y_{i,max}(x)$. These transitions amplify round-off and truncation errors because $h^{\prime }(x)$ approaches infinity as $\left|x-x_i\right|\to a_i$. The sine-mapped quadrature distributes sampling nodes according to a fixed symmetric pattern, leaving boundary singularities under-resolved. The two-panel scheme mitigates this by segmenting the integration domain at curvature crossover points, confining high-gradient regions to smaller subintervals. This reduces the numerical condition number of the integral operator itself, explaining the order-of-magnitude improvement observed for those cases.

In comparison, polygonal and Monte Carlo methods are both more sensitive to this behavior. Polygonal clipping converts a smooth boundary into a piecewise linear chain, where the discretization error grows as $O(1/n^2)$ but remains spatially uniform. When curvature changes rapidly, uniform vertex spacing overrepresents flat segments and under-samples sharp lobes, leading to localized underestimation of the area. Monte Carlo sampling instead introduces statistical variance that scales as $O(1/\sqrt{N}$); the stochastic noise dominates the small intersection zones characteristic of tangency, explaining the larger standard deviations in those regimes.

4.5. Conditioning and Affine Normalization

Affine normalization stabilizes the integrand by equalizing the scaling between the $x$- and $y$-axes. Without normalization, the partial derivative of $h\left(x\right)$ with respect to $x$ inherits the square-root denominator in Equation (18), so its magnitude increases sharply as $\left|x-x_i\right|\to a_i$, producing steep endpoint gradients. As the aspect ratio $a_i/b_i$ increases, curvature anisotropy causes the vertical range to vary disproportionately to the horizontal sampling density. The transformation $x^{\prime }=x/s_x, y^{\prime }=y/s_y$ normalizes the semi-axes to unity, restoring isotropy and ensuring that the quadrature nodes are evenly distributed with respect to curvature, not Euclidean distance. The resulting Jacobian scaling $s_x{s}_y$ only affects the magnitude of the integrated value and does not alter the relative precision. This normalization is particularly effective for cases where one ellipse is much flatter or more elongated than the other. By conditioning both ellipses in the same normalized space, the intersection boundaries become smoother, reducing the oscillatory component of $h\left(x\right)$ that would otherwise cause alternating over- and underestimation in standard quadrature.

4.6. Runtime Behavior and Determinism

The deterministic complexity $O\left(N\right)$ of Gauss–Legendre rules contrasts sharply with the variable runtime of adaptive or sampling-based methods. Each node–weight pair is precomputed, and function evaluations occur at fixed positions, enabling full vectorization. The two-panel approach doubles the number of evaluations but preserves this linearity. In contrast, adaptive Simpson integration performs recursive subdivision until local convergence, leading to a non-deterministic runtime proportional to the number of generated subintervals, which depends on local curvature. Polygonal discretization also exhibits deterministic scaling but with a substantially higher constant cost due to geometric clipping and vertex-wise intersection checks, and its computational complexity grows quadratically with the number of vertices $n$, i.e., $O\left(n^2\right)$. Monte Carlo integration scales with sample count rather than geometry. This difference in algorithmic structure explains the observed stability in runtime across all geometric configurations for the quadrature methods and the large runtime variance of stochastic sampling, particularly when the overlap region is small. The predictable computational cost of the two-panel quadrature makes it suitable for batch or embedded contexts where bounded runtime is critical.

4.7. Sources of Numerical Instability

Residual numerical instability appears primarily in two forms. First, for extreme eccentricities $(a/b)>10$, the square-root expression inside $h\left(x\right)$ loses precision due to catastrophic cancelation near the ellipse edge, where ${(x-x_i)}^2\approx a_i^2$. This limits the attainable accuracy regardless of integration order. Second, near-tangency cases introduce condition numbers that depend on the reciprocal of the minimal separation distance between ellipses, causing small perturbations in center coordinates to change the intersection classification itself. These instabilities are geometric rather than algorithmic and remain inherent to any method based on direct numerical integration.

4.8. Relation to Semi-Analytical Intersection Methods

Semi-analytical algorithms such as the method of Hughes and Chraibi [9] address the general ellipse–ellipse intersection problem through explicit boundary decomposition, quartic root solving, and case-dependent branching that enumerates all possible geometric configurations. The present work focuses on the axis-aligned configuration, where the absence of rotational coupling reduces the intersection area to a single one-dimensional integral of the overlap-height function. This avoids quartic root solving, geometric decomposition, and multi-case branching entirely. Because semi-analytical methods operate on a fundamentally different computational pipeline designed for arbitrary orientations, they are not directly comparable to the numerical quadrature formulations evaluated in this study. Moreover, while semi-analytical formulations aim for near–machine-precision accuracy, they do not work directly with the height function; therefore, this study prioritizes comparison with adaptive Simpson, which integrates the same one-dimensional representation as the proposed quadratures.

Conceptually, the proposed quadrature formulation may be viewed as an additional branch of the Hughes–Chraibi framework that applies specifically when both ellipses are axis-aligned. In this configuration, the intersection reduces to a smooth one-dimensional integral, and the quadrature methods developed here offer an efficient numerical alternative within that restricted branch.

4.9. Limitations and Directions for Future Work

Although rotated ellipses represent the general case, they fall outside the scope of the present study. When either ellipse is rotated, the boundary is no longer single-valued in $x$, and the intersection area cannot be expressed as the one-dimensional integral $\int h\left(x\right) dx$. Instead, the intersection curve must be computed by solving a quartic equation followed by geometric case branching, such as in Hughes–Chraibi [9]. In contrast, the axis-aligned configuration admits a smooth overlap-height function and a single integral representation. For these reasons, the study is restricted to axis-aligned ellipses.

Future research may address both geometric generality and numerical conditioning. Handling rotated ellipses requires incorporating an angular parameter into the implicit form and performing integration over a transformed coordinate system, since the one-dimensional height-function representation used in the present work is no longer valid. This could be achieved using an orthogonal diagonalization of the quadratic form or via a local coordinate rotation prior to normalization. Second, an adaptive multi-panel variant could dynamically identify curvature breakpoints through zero-crossings in $h^{″}\left(x\right)$, applying higher-order quadrature locally while maintaining a bounded global node count. Third, mixed analytic–geometric approaches may provide further robustness: polygonal clipping could serve to localize the integration region, followed by precise quadrature on subdomains where the implicit boundaries are smooth. Finally, extending the same framework to three-dimensional conic or ellipsoidal intersections could bridge the gap between planar and volumetric overlap estimation, relevant to shape analysis and probabilistic collision modeling.

5. Conclusions

This study analyzed the numerical performance of several ellipse–ellipse intersection strategies derived from a unified analytical framework. Two deterministic quadrature formulations—a sine-mapped and an affine-normalized two-panel scheme—were proposed and benchmarked against polygonal and Monte Carlo approximations using adaptive Simpson integration as the reference. The enhanced two-panel quadrature exhibited the most stable and precise overall performance, particularly under grazing and high-eccentricity conditions, while maintaining linear computational cost and deterministic runtime. These results confirm that integration accuracy is primarily governed by geometric conditioning near boundary singularities and that affine normalization effectively mitigates curvature imbalance.