Prediction of Manufactured-Sand Concrete Compressive Strength Using Hybrid ML Models and Dream Optimization Algorithm

Abstract

This study proposes a predictive framework for the compressive strength (CS) of manufactured-sand concrete (MSC), integrating six machine learning (ML) models—artificial neural network (ANN), random forest (RF), extreme learning machine (ELM), kernel-ELM (KELM), support vector regression (SVR), and extreme gradient boosting (XGBoost) with the newly developed Dream optimization algorithm (DOA) for hyperparameter tuning. A database of 306 samples with eight features is used to train and test models. Results demonstrate that all models achieved satisfactory predictive accuracy, with the DOA-RF model exhibiting the best performance on the testing dataset (R² = 0.9755, RMSE = 2.7836, MAE = 2.1716, WI = 0.9933). The DOA-XGBoost model also yielded competitive results, whereas DOA-ELM showed relatively weaker performance. Compared with existing optimization-based approaches, the proposed DOA-RF model significantly reduced RMSE and MAE, validating the effectiveness of the DOA. SHAP analysis further revealed that the water-to-binder ratio (W/B) and curing age (CA) are the most influential factors in predicting MSC strength. Overall, this work not only establishes an accurate and interpretable predictive tool but also underscores the potential of novel optimization algorithms to advance data-driven concrete design and sustainable construction practices.

1. Introduction

In recent years, concrete composed with manufactured sand has attracted increasing attention as a sustainable alternative to natural river sand, driven by the depletion of natural sand resources and growing ecological constraints [1]. Concrete using manufactured sand (MSC) has been explored in a variety of structural and non-structural applications, including building slabs, precast members, pavements, and marine structures, owing to its controllable gradation, angular particle shape, and availability in many production regions. However, a central metric determining the viability of MSC in load-bearing applications is its compressive strength (CS), which not only governs structural design limits but also correlates with durability, crack resistance, and long-term service performance [2,3,4]. Therefore, accurate assessment of the CS of MSC is essential both for mix design optimization and for ensuring compliance with safety standards.

Over the past decade, researchers have approached the study of MSC’s strength from multiple avenues, notably experimental investigations and numerical modeling. In the experimental domain, many authors have varied mixture proportions (M_p), sand gradation (S_g), stone powder content (SPC), curing ages (CAs), and admixture dosages (A_d) to explore their influence on CS of MSC materials. For instance, Sun et al. [5] tested 12 groups of high-performance MSC mixes with varying SPC. The results observed that the best balance in workability and CS was obtained when the SPC was set near 9 %, and the 28-day compressive strength reached 60 MPa. Ma et al. [6] replaced a portion of fine aggregate with marble powder and used response surface methodology to optimize the contents of superplasticizer (SP), fly ash (FA), and silica fume (SF) in an MSC material. The test results showed that the MSC material achieved a high 28-day strength of 54.5 MPa with 20 % marble powder replacement. Other experimental studies on the strength of MSC materials can be referred to in the literature [7,8,9,10,11]. Although experimental studies are essential for validating the mechanical behavior of MSC materials, they are often costly, time-consuming, and limited in exploring complex parameter interactions [12]. These limitations motivate the use of numerical simulations, which enable controlled, repeatable, and scalable analysis across a broader design space. Numerical modeling of MSC is relatively less common but offers a path to link microstructure and macroscopic strength. Some studies embed manufactured-sand particle geometry, interfacial transition zone (ITZ) behavior, and damage models in finite element (FE) or meso-scale simulations [13,14]. However, such mechanistic models are not without limitations. First, their computational cost can be prohibitive, especially for large-scale or meso-scale simulations requiring fine meshes to resolve complex microstructures [15]. Second, model calibration is laborious and data-intensive, often relying on inverse fitting to experimental data, which may not generalize well across different mix designs or curing conditions [16]. Third, simplifying assumptions (e.g., isotropy, linear elasticity in aggregates, uniform ITZ thickness) may compromise accuracy, especially when applied to real-world MSC with diverse particle shapes and packing densities [17].

Given these constraints, data-driven approaches such as machine learning (ML) have emerged as promising alternatives or complements. Various ML-based prediction models have been used to predict the concrete’s CS, such as artificial neural network (ANN), extreme gradient boosting (XGBoost), support vector regression (SVR), and random forest (RF) [18,19,20,21,22,23]. Among these models, the input features typically include cement content (C_c), water-to-cement (W/B) ratio, fine aggregate proportion (FA), sand ratio (SR), filler or admixture content (e.g., stone powder, fly ash, silica fume), CA, etc. For instance, Dao et al. [24] developed two ML models called ANN and adaptive neuro fuzzy inference (ANFIS) to predict CS of geopolymer concrete materials. The results indicated that the prediction accuracy of ANFIS was higher than that of the ANN model, with a coefficient of determination (R²) of 0.879. Chou and Pham [25] established several ensemble models to predict the CS of high-performance concrete (HPC) materials. Five datasets, including FA, water, coarse and fine aggregate, CA, sand, and cement, were used to train these models. The results illustrated that the ANN model exhibited superior performance across the majority of datasets. Gregori et al. [26] used SVR and Gaussian process regression (GPR) models to predict the CS of rubberized concrete materials. Compared to the SVR model, the GPR model obtained a higher prediction accuracy in the CS prediction. And they also found that the W/B has the main influence on the CS prediction. For the MSC materials, Ly et al. [27] developed an ANFIS model to predict the CS of MSC materials using 289 data samples with features such as compressive strength of cement (CSC), tensile strength of cement (TSC), CA, stone powder content (SPC), W/B, and SR. The results showed that the proposed model obtained a satisfactory predictive performance, with a root mean squared error (RMSE) of 4.93. In addition, they found that the CA was the most important feature in the CS prediction for MSC materials. Liu et al. [28] introduced a paradigm application for predicting the CS of MSC materials using interpretable ML models. All models were trained and tested on 3382 data samples, among which the XGBoost model achieved the highest prediction accuracy (R² = 0.934). In addition, the combination of Shapley additive explanations (SHAPs) and the XGBoost model provided insights into the contributions of 12 input features to the CS prediction. However, the performance of basic ML models depends on the proper selection of hyperparameters. Some optimization methods, such as metaheuristic algorithms, provide effective solutions for hyperparameter optimization [29,30,31]. For example, Zhao et al. [32] applied two nature-inspired metaheuristic algorithms to optimize ANN models for predicting the CS of MSC materials. The results indicated that the optimized ANN model achieved a higher prediction accuracy than the original ANN model, with a decrease in RMSE of 8.84%. However, the application of newly developed optimization algorithms to MSC’s CS prediction is still limited, and no study has systematically explored the development of diverse ML algorithms (e.g., extreme learning machine (ELM) and kernel-ELM (KELM)) for this task.

Thus, this paper aims to use six classical and high-performance ML models (ANN, RF, ELM, KELM, SVR, and XGBoost) to predict the CS of MSC materials, while employing a novel algorithm called Dream optimization algorithm (DOA) proposed by Lang and Gao [33] to optimize the models’ hyperparameters in order to enhance prediction accuracy. The best model for CS prediction is determined through a systematic comparison of the performance among all models, thereby further strengthening the foundation of AI research in this field. The content of the other sections is organized as follows: Section 2 introduces ML models and optimization algorithm used for predicting CS; Section 3 describes the data used and the feature selection process; Section 4 outlines the development procedure of the prediction models, including data processing, model optimization, and model evaluation; Section 5 presents the main prediction results and analyzes the performance differences among all models, as well as feature sensitivity; and Section 6 summarizes the main findings of this work.

2. Methods

2.1. ML Models

2.1.1. ANN Model

ANN models have emerged as a versatile tool for modeling complex, nonlinear relationships in materials science. A typical ANN consists of an input layer, multiple hidden layers, and an output layer, where each hidden layer is composed of neurons interconnected through weighted links. The principal hyperparameters include the number of hidden layers (N_h) and the number of neurons per layer (N_n), which strongly influence the model’s capacity to capture intricate correlations between input variables and target properties. Excessive neurons may lead to overfitting, while insufficient complexity reduces predictive accuracy [34]. Thus, careful tuning is essential for robust regression performance. For regression tasks in concrete materials research, ANNs offer distinct advantages over traditional statistical approaches by flexibly handling high-dimensional and noisy data [35]. Their ability to approximate nonlinear constitutive relationships enables accurate prediction of properties such as CS, durability indices, or thermal performance. The general prediction function of an ANN with one hidden layer is as follows:

$$y=f({\displaystyle \sum _{h=1}^{N_n}{w}_{ho}\sigma \left({\displaystyle \sum _{i=1}^{N_x}{w}_{ih}{x}_i+b_h}\right)}+b_o)$$

(1)

where y and x present output and input features, respectively. N_n and N_x represent the number of features and the number of neurons in a hidden layer, respectively. w_ho is the weight between the hidden layer and output layer, and w_ih is the weight between the input layer and hidden layer. $\sigma$ is the hidden-layer activation function. b_h and b_o are the bias terms of the hidden layer and the output layer, respectively.

2.1.2. RF Model

RF is a robust ensemble learning method widely applied in regression and classification tasks due to its ability to manage nonlinear relationships and high-dimensional datasets [36]. The model constructs multiple decision trees (DTs), each trained on a bootstrap sample of the data, and aggregates their predictions to reduce variance and improve generalization. This prediction mechanism can be described mathematically by Equation (2). Its main hyperparameters include the number of trees (N_t) and maximum tree depth (M_d), all of which determine the balance between accuracy and computational efficiency. In regression problems, increasing the N_t typically enhances stability, while controlling depth prevents overfitting to noise. For applications in concrete materials prediction, RF provides superior interpretability compared with many black-box models, as variable importance measures can highlight influential microstructural or compositional features [37]. Moreover, its tolerance to multicollinearity and capacity to capture nonlinear feature–property linkages make RF a valuable predictive tool for estimating strength, durability, and service-life parameters in civil engineering materials.

$$y={\displaystyle \frac{1}{N}}{\displaystyle \sum _{n=1}^N{p}_n(x)}$$

(2)

where N represents the number of DTs. $p_n(x)$ denotes the prediction made by the n-th DT for sample x.

2.1.3. ELM Model

ELM is a single-hidden-layer feedforward neural network distinguished by its unique training strategy. Unlike conventional backpropagation-based networks, the input weights and hidden biases in ELM are randomly assigned and remain fixed, while the output weights are analytically determined through a least-squares solution. This design eliminates iterative optimization and substantially reduces computational cost, allowing the model to achieve rapid convergence even with large datasets [38]. Key hyperparameters primarily include the N_n, which governs the balance between approximation capability and generalization. In regression-oriented applications, ELM demonstrates a strong capability in approximating nonlinear mappings with minimal training time, making it attractive for engineering domains requiring real-time prediction. Within concrete material research, ELM provides advantages by efficiently capturing multivariate interactions among composition, curing conditions, and mechanical performance, thereby enabling accurate forecasting of strength development and service-related properties in a computationally efficient manner [39,40]. The general prediction function of the ELM model with a single hidden layer is:

$$y=H\beta ,\hspace{1em}\hspace{1em}{H}_{kj}=\sigma \left(w_j{x}_k+b_j\right)$$

(3)

where H is the output matrix of the hidden layer. $\beta$ is the weight matrix of the output layer. $H_{kj}$ denotes the mapped value of the k-th sample at the j-th hidden node. w_j and b_j represent the randomly initialized input weights and randomly initialized biases, respectively.

2.1.4. KELM Model

KELM is a refined variant of the ELM model, designed to combine the efficiency of random hidden-layer mapping with the flexibility of kernel-based learning [41]. In KELM, the hidden layer does not require explicit tuning of neuron weights, while nonlinear transformations are realized through a kernel matrix. The general prediction function of the KELM model is expressed by Equation (4). The first primary hyperparameter is the regularization factor (R_f), which balances model complexity against overfitting. The second hyperparameter is the kernel parameter (k_p), which governs the mapping ability of the chosen kernel function. Compared with conventional neural networks, KELM avoids laborious iterative optimization, allowing rapid model construction even with high-dimensional or noisy datasets [42].

$$y=\Omega (x,X)\cdot {({\displaystyle \frac{1}{C}}I+\Omega )}^{-1}{y}_a$$

(4)

where y_a represents the actual of the samples. $\Omega$ and I are kernel and identity matrices. X and C represent the training sample matrix and the regularization coefficient, respectively.

2.1.5. SVR Model

SVR represents a kernel-based learning framework capable of addressing nonlinear regression problems with high generalization ability. The model seeks to construct an optimal regression function within an allowable error margin while simultaneously maximizing prediction robustness. Its performance is also largely governed by two critical hyperparameters: R_f and k_p. For instance, an excessively high R_f may induce overfitting, whereas a poorly tuned k_p can limit the ability to capture nonlinear interactions [43]. Within the domain of concrete materials, SVR offers notable advantages, particularly in predicting strength development and durability indicators when experimental data are limited or highly variable [44,45]. The general prediction function of the SVR model is expressed by Equation (5).

$$y={\displaystyle \sum _{k=1}^K\left({\alpha }_k-{\alpha }_k^{*}\right)f\left(x_k,x\right)}+b$$

(5)

where K represents the total samples in the training set. ${\alpha }_k$ and ${\alpha }_k^{*}$ are Lagrange multipliers. $x_k$ and b are the k-th samples in training and bias, respectively.

2.1.6. XGBoost Model

XGBoost is a tree-based ensemble algorithm designed to achieve high predictive accuracy and computational efficiency. It constructs an additive sequence of DTs, where each new tree corrects the residual errors of the previous ensemble. The major hyperparameters determining the model’s performance include the number of weak learners (N_w), M_d, and learning rate (L_r). Increasing N_w typically improves model expressiveness but may cause overfitting if not regularized. A larger M_d enables the capture of complex feature interactions, yet excessive depth risks reduced generalization. The L_r parameter governs the step size of updates: smaller values stabilize training and improve accuracy but require more iterations, while larger values accelerate convergence at the expense of precision. For regression tasks in concrete materials research, XGBoost offers remarkable advantages, such as robustness against noisy inputs, ability to manage heterogeneous features, and interpretability through feature importance ranking [46,47]. These characteristics make it a reliable predictive framework for property evaluation and optimization in advanced concrete systems. The general prediction function of the SVR model is expressed by Equations (6) and (7).

$$y=\widehat{y}+f{\left(x\right)}_k$$

(6)

$$\mathrm{minimize}: {\rm Y}={\displaystyle \sum _{k=1}^K\left[G_{k}f{\left(x\right)}_k+0.5S_{k}f{\left(x\right)}_k^2\right]+\Omega f(x)}$$

(7)

where $\widehat{y}$ represents the prediction obtained in the iteration prior to the final update. $f{\left(x\right)}_k$ is the output of the k-th tree in the model. ${\rm Y}$ is the optimization target. G_k and S_k are the first- and second-order derivatives of the loss function, respectively. $\Omega f(x)$ represents the regularization term of the XGBoost model.

2.2. Dream Optimization Algorithm (DOA)

DOA has its theoretical basis in cognitive neuroscience, particularly in the neural processes related to human dreaming during rapid eye movement (REM) sleep. Dream states exhibit features such as incomplete memory preservation, intentional omission of information, and spontaneous reorganization, which together serve as an apt analogy for the balance between exploration and exploitation in metaheuristic search [33]. Building on this perspective, DOA portrays a population of agents undergoing iterative ‘dreaming’ cycles, where members are categorized according to different memory capacities. During each cycle, individuals recall previously discovered optimal solutions (resembling remembered experiences), discard certain dimensions (mimicking memory fading), and regenerate these missing elements either through internal reorganization or information exchange with peers (similar to dream-sharing). In regression modeling contexts, DOA explores complex parameter spaces through structured variation at the initial stages, while later iterations emphasize focused exploitation by narrowing the search scope. As for optimization problems (see Figure 1), the operational structure of DOA can be organized into the following components:

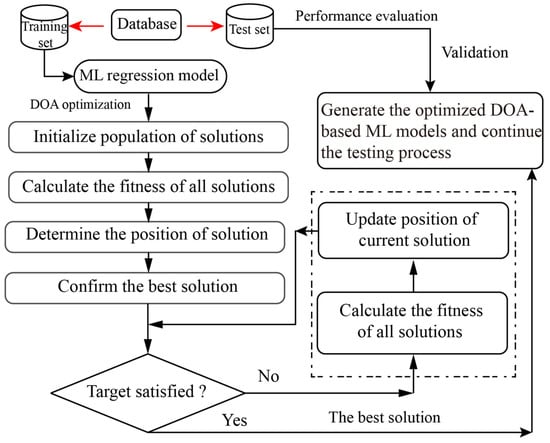
Figure 1. The framework for using DOA to solve the optimization problem.

(1)

Initialization phase

The algorithm commences by dispersing candidate solutions randomly throughout the domain, as described by the following equation:

$$D_i=D_{low}+rand\cdot (D_{up}-D_{low})$$

(8)

where $D_i$ represents the initial position of the i-th candidate solution. $D_{low}$ and $D_{up}$ represent the lower and upper boundaries of the searching space, respectively. $rand$ is a random number within the range of [0, 1].

(2)

Exploration phase

At the onset of the dreaming stage, individuals experience partial forgetting of earlier solutions and explore fresh combinations under guided random perturbations. Grouped by memory ability, they adjust merely a subset of variables:

$$D_i^{t+1}=D_{best}^t+\left(D_{low}+rand\cdot (D_{up}-D_{low})\right)\cdot {\displaystyle \frac{1}{2}}\cdot \left(\cos \left(\pi \cdot {\displaystyle \frac{t+T_{\max }-T_d}{T_{\max }}}\right)+1\right)$$

(9)

where $D_i^{t+1}$ represents the position of the i-th candidate solution at the t + 1 iteration. $D_{best}^t$ represents the best position of the candidate solution at the t iteration. t, T_max, and T_d are the current iteration time, the maximum number of iterations, and the maximum number of iterations in the current phase, respectively.

(3)

Exploitation phase

During later iterations, every agent emphasizes refinement near the globally retained optimum. This transition curtails random exploration and enhances the stability of the process:

$$D_i^{t+1}=D_{best}^t+\left(D_{low}+rand\cdot (D_{up}-D_{low})\right)\cdot {\displaystyle \frac{1}{2}}\cdot \left(\cos \left(\pi \cdot {\displaystyle \frac{t}{T_{\max }}}\right)+1\right)$$

(10)

3. Materials

In this paper, a database containing 306 samples was utilized to train and test six ML models for predicting the CS of manufactured-sand concrete materials. The database was generated by Zhao et al. [32] from published studies. This database included eight features, including CSC, TSC, CA, maximum size of the crushed stone (Smax), SPC, fine modulus (FM), W/B, and SR. The detailed information on the features in the database is illustrated in Table 1. Several statistical metrics, including minimum, maximum, mean, and standard indices, were used to describe the distribution of data. However, not all features should be used to train models for predicting targets limited in computational efficiency. Therefore, a feature selection approach conducted using the Boruta algorithm was adopted to determine the feature importance in the prediction of CS. As shown in Figure 2, the selection process can be organized using steps as follows:

Table 1. The statistical information of features related to the UCS prediction.

Features	Statistical Indices
	Minimum	Maximum	Mean	Standard Deviation
CSC (MPa)	35.50	63.40	48.10	4.32
TSC (MPa)	6.90	10.20	8.26	0.60
CA (day)	1.00	388.00	77.55	100.35
Smax (mm)	16.00	40.00	28.33	4.13
SPC (%)	0.00	20.00	7.88	4.78
FM (GPa)	2.20	3.50	3.05	0.27
W/B	0.25	0.69	0.43	0.09
SR (%)	28.00	45.00	37.50	4.18
CS (MPa)	4.23	96.30	54.80	17.11

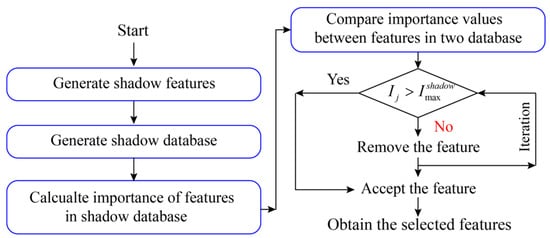
Figure 2. The flowchart of using the Boruta algorithm to select the optimal input features.

(1)

Shadow feature construction

The shadow database ($F^{shadow}$) was generated using original samples to enhance the complexity of the database. The new database can be described using Equation (11).

$$F^{shadow}=\left[perm(f_1),perm(f_1),\dots ,perm(f_F)\right]$$

(11)

where $perm()$ is the randomly shuffled feature. F is the total number of features in the database.

(2)

Feature importance computation

Then, the database was used to build an RF model for predicting CS and calculate the importance scores of all features. The importance value for each feature can be expressed as follows:

$$I_j=\mathrm{RFImportance}(F_j),\hspace{1em}{I}_j^{shadow}=\mathrm{RFImportance}(perm(F_j))$$

(12)

where $I_j$ and $I_j^{shadow}$ are the importance values of the j-th feature in the original and shadow databases, respectively.

(3)

Feature selection rule

In this step, the maximum importance score of features in the shadow database ($I_{\max }^{shadow}$) was considered as a threshold to further select the useful features. Then, the importance scores of all features in the original database were recalculated to compare with the threshold. As expressed in Equation (13), the features with values of importance scores lower than the threshold should be removed from the database. The calculation results of importance scores for each feature are summarized in Table 2. It can be observed that the minimum values of the importance score for all features are greater than the threshold based on the same database. In other words, all features can be considered as input features to generate ML models for forecasting the CS of manufactured-sand concrete materials in this work.

$$\left\{\begin{array}{ll}\mathrm{Accepted},& I_j>I_{\max }^{shadow}\\ \mathrm{Rejected},& I_j>I_{\max }^{shadow}\\ \mathrm{Tentative},& \mathrm{otherwise}\end{array}\right.$$

(13)

Table 2. The results of importance scores for all features using the Boruta algorithm.

Features	Importance Scores
	Mean	Median	Minimum	Maximum
CSC (MPa)	28.01	27.91	27.45	28.77
TSC (MPa)	29.43	29.28	28.41	30.78
CA (day)	70.65	70.38	69.53	72.46
Smax (mm)	17.55	17.47	16.54	18.38
SPC (%)	20.05	19.84	19.40	21.09
FM (GPa)	20.60	20.75	18.18	21.71
W/B	59.07	58.67	57.65	61.51
SR (%)	31.97	32.15	30.78	33.34

4. Prediction Models

In this paper, six common ML models were developed to predict the CS of manufactured-sand concrete materials. DOA was utilized to select the optimal combinations of hyperparameters for each model to improve predictive performance. After that, several evaluation tools were adopted to evaluate the model performance and then to determine the best model for exploring the influence of all features on the CS prediction. As shown in Figure 3, the framework can be divided into the following steps:

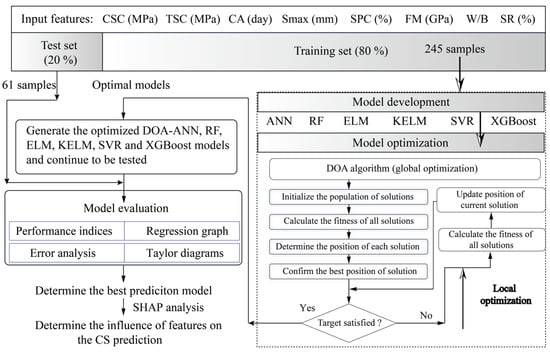
Figure 3. The framework of using DOA and ML models to predict CS of manufactured-sand concrete materials.

(1) Data processing: A total of 306 samples were used to predict CS values. To improve prediction accuracy, more data samples need to be utilized to train models [48]. In this work, 80% of the data samples were assigned to the training set to enable the model to learn the internal relationships between input features and prediction targets. The remaining data samples were allocated to the test set to evaluate the performance of the trained model. In addition, all features were normalized to the range of −1 to 1 to prevent a decline in model predictive performance caused by differences in their scales.

(2) Model optimization: Before employing the DOA algorithm to optimize the best hyperparameter combinations for the models, it is necessary to determine the variation range of each model’s hyperparameters. For example, the candidate values of the parameter N_h in the ANN model were set to 1 and 2 in this study, while the parameter N_n varied within the range of 1 to 10. In the RF model, the range of N_t was set from 1 to 100, and the upper and lower limits of M_d were set to 1 and 10, respectively. The hyperparameter ranges for the other models are presented in Table 3. Furthermore, two parameters called the population size and the number of iterations control the optimization performance of DOA. To that end, four values of population sizes (25, 50, 100, and 200) were selected to search for the optimal candidates during 300 iterations. Moreover, a fitness function organized by RMSE and five-fold cross-validation was established to avoid potential overfitting during DOA-based hyperparameter optimization. This function was defined as follows:

$$\mathrm{Fitness}={\displaystyle \frac{1}{\mathrm{K}}}{\displaystyle \sum _{\mathrm{k}=1}^{\mathrm{K}}{\mathrm{RMSE}}_k}\hspace{1em}(k=1,2,3,\dots ,5)$$

(14)

Table 3. The setting of hyperparameters for all ML models.

ML Models	Hyperparameters	Range
ANN	Nh and Nn	[1, 2] and [1–10]
RF	Nt and Md	[1, 100] and [1, 10]
ELM	Nn	[1–100]
KELM	Rf and kp	[0.25, 256] and [0.125, 8]
SVR	Rf and kp	[0.25, 256] and [0.125, 8]
XGBoost	Nw, Md, and Lr	[50, 500], [1, 20], and [0.001, 0.5]

(3) Model evaluation: To determine the optimal prediction model, the statistical indices were commonly used to evaluate the prediction accuracy of models [49,50,51,52]. The R², RMSE, Willmott’s index (WI), and mean absolute error (MAE) were adopted to compare model performance in this paper. In regression tasks, the value of R² for an ideal model is 1.0, indicating a perfect match between predicted and measured strengths. In contrast, the ideal values for RMSE and MAE are 0, since lower error magnitudes reflect better predictive performance. For WI, the ideal value is 1.0, representing a perfect agreement between model predictions and experimental results. Therefore, better-performing models are characterized by higher R² and WI, together with lower RMSE and MAE. The definitions of these indices are expressed in Equations (5)–(8). In addition, the regression diagrams and prediction curves were also utilized to determine the optimal models for predicting CS values.

$${\mathrm{R}}^2=1-{\displaystyle \frac{{\left[{\displaystyle \sum _{i=1}^n(a_i-p_i)}\right]}^2}{{\left[{\displaystyle \sum _{i=1}^n(a_i-\overline{a})}\right]}^2}}$$

(15)

$$\mathrm{RMSE}=\sqrt{{\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n{\left(a_i-p_i\right)}^2}}$$

(16)

$$\mathrm{MAE}={\displaystyle \frac{1}{N}}{\displaystyle \sum _{n=1}^N\left|a_n-p_n\right|}$$

(17)

$$\mathrm{WI}=1-\left[{\displaystyle \frac{{\displaystyle {\sum }_{i=1}^n{\left(a_i-p_i\right)}^2}}{{\displaystyle {\sum }_{i=1}^n{\left(\left|p_i-\overline{a}\right|+\left|a_i-\overline{a}\right|\right)}^2}}}\right]$$

(18)

where a_i and p_i are the actual and predicted CS values of the i-th sample, respectively. $\overline{a}$ represents the average values of actual values for all samples. N represents the maximum number of samples used in model evaluation.

5. Results and Discussions

In this paper, six ML models were developed using a training set and were optimized using the DOA algorithm, combining various population sizes. Figure 4 shows the iteration curves of all hybrid models during the optimization process. It can be observed that the optimal solutions with the lowest fitness values were obtained before reaching the maximum number of iterations. For example, the optimized ANN model obtained the lowest fitness value when the population size was equal to 50. The optimal hybrid RF model was obtained using a population size of 100. The ELM, KELM, and SVR models also achieved higher performance optimized by DOA with 50 solutions. Especially, the fitness values of the DOA-XGBoost models with population sizes of 50 and 100 are close, indicating a similar predictive performance after iterations. The fitness values of all hybrid models were calculated and recorded in Table 4. In addition, based on the minimum fitness value principle, the selected optimal hyperparameter combinations are also presented in Table 4. In addition, it should be noted that the fitness curves of all hybrid models rapidly decrease in the early stages and approach a plateau after approximately 100–150 iterations, with only minor fluctuations afterwards. This behavior suggests that the near-optimal hyperparameter combinations have already been found, and additional iterations would yield only marginal reductions in RMSE while considerably increasing the computational cost. Therefore, 300 iterations were adopted as a practical upper limit in the optimization process.

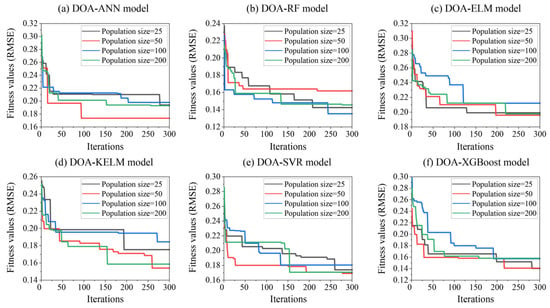
Figure 4. Iteration curves of all hybrid ML models optimized using DOA.

Table 4. The fitness and hyperparameters for all models in the training and testing phases.

Models	Population Size				Hyperparameters
	25	50	100	200
DOA-ANN	0.1940	0.1735	0.1980	0.1929	Nh: 2 and Nn: 4, 2
DOA-RF	0.1425	0.1618	0.1353	0.1456	Nt: 48 and Md: 1
DOA-ELM	0.1992	0.1960	0.2122	0.1977	Nn: 100
DOA-KELM	0.1754	0.1540	0.1844	0.1586	Rf: 128 and kp: 4
DOA-SVR	0.1740	0.1691	0.1804	0.1707	Rf: 75 and kp: 0.15
DOA-XGBoost	0.1404	0.1409	0.1573	0.1581	Nw: 175, Md: 3, and Lr: 0.017

After determining the optimal hyperparameters of all ML models, several tools and methods were utilized to evaluate the model performance. To comprehensively assess the performance differences before and after optimization, all six models were first configured using their default hyperparameter settings (ANN model: N_h = 1 and N_n = 10; RF model: N_t = 100 and M_d = Non; ELM model: N_n = 80; KELM model: R_f = 1 and k_p = 1; SVR model: R_f = 1 and k_p = 0.1; XGBoost model: N_w = 100, M_d = 6, and L_r: 0.3). The same training and testing datasets were then used to develop and evaluate the baseline models for a comparison. Table 5 shows the values of statistical indices for all models calculated using training and test sets. In the training phase, the DOA-RF and DOA-XGBoost models obtained higher prediction accuracy than other models, especially the DOA-ELM model with unideal values of evaluation indices (R² of 0.9141, RMSE of 4.9448, WI of 0.9771, and MAE of 3.7408). On the other hand, the trained models need to be further validated using a test set to avoid overfitting. As illustrated in this table, the DOA-RF also obtained the most satisfactory predictive performance, resulting in the highest values of R² and WI (0.9755 and 0.9933), and the lowest values of RMSE and MAE (2.7836 and 2.1716). After this model, the ranking of other models ordered by performance is as follows: the DOA-XGBoost, DOA-ANN, DOA-SVR, DOA-KELM, and DOA-ELM models. Moreover, it can be seen that all non-optimized models exhibited noticeably lower prediction accuracy. For instance, the original RF model achieved values of indices R² = 0.9536, RMSE = 2.7450, WI = 0.9807, and MAE = 1.9182 compared with the R² = 0.9836, RMSE = 2.1606, WI = 0.9957, and MAE = 1.5104 after DOA optimization during the training phase. These results clearly indicate that the DOA algorithm substantially enhances model accuracy and generalization performance. In addition, although the R² values of the proposed models are close to 1, the RMSE values are not close to 0 because RMSE is sensitive to the scale of the target variable. Given that the compressive strength values in the dataset range from 4.23 to 96.30 MPa, even a small percentage prediction error results in RMSE values greater than 2–4 MPa. Furthermore, R² quantifies the proportion of explained variance and is independent of scale, while RMSE expresses absolute error. Therefore, high R² and non-zero RMSE are consistent and expected. The obtained RMSE values represent small relative errors, confirming that the ML models achieved satisfactory predictive performance.

Table 5. The results of statistical indices for all models in the training and testing phases.

Models	Phases	Statistical Indices
		R2	RMSE	WI	MAE
DOA-ANN	Training	0.9496	3.7880	0.9862	2.8618
DOA-RF	Training	0.9836	2.1606	0.9957	1.5104
DOA-ELM	Training	0.9141	4.9448	0.9771	3.7408
DOA-KELM	Training	0.9635	3.2233	0.9905	2.1812
DOA-SVR	Training	0.9614	3.3128	0.9899	2.1226
DOA-XGBoost	Training	0.9811	2.3197	0.9950	1.5992
ANN	Training	0.9196	4.8108	0.9712	3.6335
RF	Training	0.9536	2.7450	0.9807	1.9182
ELM	Training	0.8841	6.2819	0.9621	4.7498
KELM	Training	0.9335	4.0916	0.9755	2.7681
SVR	Training	0.9314	4.2053	0.9749	2.6967
XGBoost	Training	0.9511	2.9470	0.9800	2.0309
DOA-ANN	Testing	0.9630	3.4173	0.9903	2.3722
DOA-RF	Testing	0.9755	2.7836	0.9933	2.1716
DOA-ELM	Testing	0.8566	6.7287	0.9618	5.4168
DOA-KELM	Testing	0.9358	4.5025	0.9844	3.1712
DOA-SVR	Testing	0.9456	4.1453	0.9867	2.9304
DOA-XGBoost	Testing	0.9732	2.9073	0.9927	2.2176
ANN	Testing	0.9330	4.3410	0.9761	3.0147
RF	Testing	0.9485	3.5372	0.9784	2.7579
ELM	Testing	0.8266	8.5455	0.9466	6.8683
KELM	Testing	0.9108	5.7182	0.9698	4.0256
SVR	Testing	0.9156	5.2687	0.9685	3.7237
XGBoost	Testing	0.9432	3.6923	0.9777	2.8144

Furthermore, a method-based regression graph was adopted to compare the predictive performance between models developed in this paper. In a graph, the position of the data sample was determined using measured and predicted values. If the predicted value equals the measured value, the corresponding data sample lies on the diagonal line. In other words, the greater the deviation between the predicted and measured values, the farther the data points are from the diagonal. As demonstrated in Figure 5, it can be clearly observed that many data points in the DOA-ELM model are located far from the diagonal line. To allow for a certain level of prediction error, a 10% error tolerance line was introduced to further evaluate model performance, i.e., the greater the number of data points outside the tolerance line, the poorer the model performance. Overall, only the DOA-RF and DOA-XGBoost models have data points that are mostly within the tolerance line and even close to the diagonal. This indicates that the predictive performance of these two models is superior to the others, which is consistent with the performance ranking inferred from the evaluation indices.

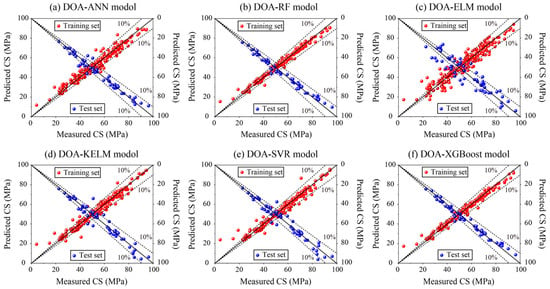
Figure 5. Regression graphs of all hybrid ML models optimized using DOA.

In addition, prediction curves were generated to further evaluate the predictive performance of the models. If the prediction curve coincides with the measured curve, it indicates that the model achieves 100% prediction accuracy. Therefore, this study proposes a curve similarity index based on the R² and RMSE values to assess the degree of overlap between the predicted and measured curves. The R² value directly reflects the goodness of fit between the predicted and actual curves, while the RMSE value describes their variation trend. To integrate these two metrics, RMSE was normalized to the range of 0–1 and then combined with R² to form a new similarity index (SI). The SI values can be calculated using Equation (19). The purpose of introducing SI is to provide an integrated measure that captures both prediction accuracy and curve-shape consistency. While R² evaluates the overall goodness-of-fit, RMSE reflects the magnitude of prediction errors. By combining these two metrics after normalizing RMSE, SI enables a more balanced assessment of how closely the predicted curve follows the measured trend. A higher SI value, therefore, indicates that the model not only fits the data well but also reproduces the variation pattern of the experimental curve more faithfully. As shown in Figure 6, during both the training and testing phases, the ANN model achieved the highest SI values (0.7733 and 0.7808) for the prediction and measured curves, representing the greatest degree of overlap and demonstrating that the ANN model provides the best predictive performance.

$$\mathrm{SI}={\displaystyle \frac{{\mathrm{R}}^2+(1-{\mathrm{RMSE}}_{\mathrm{norm}})}{2}}$$

(19)

where ${\mathrm{RMSE}}_{\mathrm{norm}}$ represents the normalized RMSE values for each prediction model.

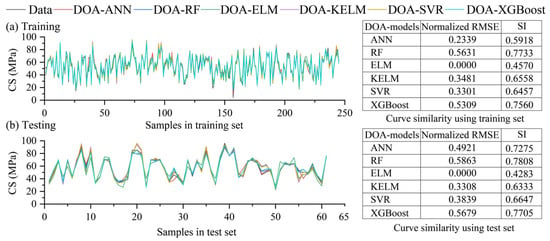
Figure 6. Prediction curves and similarity calculation results of all hybrid ML models.

Although the DOA-RF model was regarded as the best-performing among the proposed models, its relative advantages or disadvantages compared with other published models remain unknown. Therefore, this paper further compares the prediction accuracy of the developed models under the same dataset. As shown in Table 6, the proposed model outperforms the models (ANN models optimized by biogeography-based optimization (BBO) and multi-tracker optimization algorithm (MTOA), i.e., BBONN and MTOANN) provided by Zhao et al. [32] on both the training and testing sets, with lower values of RMSE and MAE (training: 2.1606 and 1.5104; testing: 2.7836 and 2.1716). This result further demonstrates that changes in the optimization algorithm exert a significant influence on improving the predictive performance of the model.

Table 6. Comparison of predictive performance between the proposed model and existing models.

Reference	Models	Training Phase		Testing Phase
		RMSE	MAE	RMSE	MAE
Zhao et al. [32]	BBONN-I	5.4164	3.8850	4.9856	3.9702
	BBONN-II	5.3219	3.8536	5.0105	3.9900
	MTOANN-I	5.3177	3.8529	5.2146	3.8759
	MTOANN-II	5.4785	4.0179	5.0763	3.9284
This paper	DOA-RF	2.1606	1.5104	2.7836	2.1716

In addition, the influence of each feature on the CS prediction needs to be assessed using the optimal model (i.e., DOA-RF model). In this paper, the SHAP analysis was conducted to complete a sensitivity analysis for features in predicting the CS of MSC materials. SHAP is a model-agnostic interpretability method derived from cooperative game theory, where each feature is treated as a ‘player’ that contributes to the final prediction. The SHAP value assigned to each feature reflects its marginal contribution, averaged across all possible feature combinations [53,54,55]. For a trained prediction model, the SHAP value of the j-th feature for the i-th sample is defined as the marginal contribution of that feature to the model output. Mathematically, the SHAP value is expressed as follows:

$${\varphi }_j^i={\displaystyle \sum _{S\subseteq \left\{j\right\}}\frac{\left|S\right|!(\left|F\right|-\left|S\right|-1)!}{\left|F\right|!}\cdot \left[f_S\cup \left\{j\right\}(x^i)-f_S(x^i)\right]}$$

(20)

where ${\varphi }_j^i$ represents the Shapley value (marginal contribution) of feature j for sample i. S and F are two subsets of features. $x^i$ is the input feature vector of the i-th sample. $f_S(x^i)$ is model prediction using only feature subset S. $\left|S\right|$ and $\left|F\right|$ are cardinalities (number of elements) of sets S and F, respectively. SHAP provides two key outputs: (1) feature importance, ranking the variables according to their overall impact on the prediction, and (2) feature effects, showing whether a feature increases or decreases the predicted strength and how this effect varies with its magnitude. To derive the global importance of all features, the absolute SHAP values were averaged across all samples:

$$I_j={\displaystyle \frac{1}{N_s}}{\displaystyle \sum _{i=1}^{N_s}\left|{\varphi }_j^i\right|}$$

(21)

where $N_s$ represents the total number of samples used in the SHAP evaluation. $I_j$ is the global importance score of feature j.

Figure 7a shows the calculation results of importance scores for all features in predicting the CS of manufactured-sand concrete. It can be observed that the W/B and CA features had higher importance scores than other features, especially the W/B (importance score equals 8.73). On the other hand, the contribution of features to CS prediction is also analyzed by calculating the SHAP values. The color map represents the original feature values, where red indicates higher feature values and blue indicates lower values. The SHAP value on the vertical axis shows whether the feature increases or decreases the predicted compressive strength. Thus, the combination of color (feature magnitude) and SHAP value (impact direction) indicates how different levels of each feature influence the model prediction. It can be seen from Figure 7b that W/B and concrete’s CS exhibited a negative correlation, whereby higher W/B values correspond to lower CS values. In the case of CA, it shows a negative correlation with CS at lower values, while higher CA values exert a positive contribution to CS of concrete materials. This finding aligns with the fundamental material mechanisms. For instance, W/B governs the balance between hydration and porosity: lower W/B ratios lead to a denser cement matrix with fewer capillary pores, while higher W/B ratios produce more voids as excess water evaporates, significantly reducing strength. CA represents the progression of hydration and microstructural refinement over time. Longer curing promotes the continued formation of gel and densification of the ITZ, resulting in measurable increases in strength. In MSC materials, the angular geometry of manufactured sand makes the ITZ more sensitive to hydration progress, reinforcing the importance of CA. In short, the SHAP analysis indicates that the W/B and CA are the two most influential variables in predicting MSC material’s compressive strength.

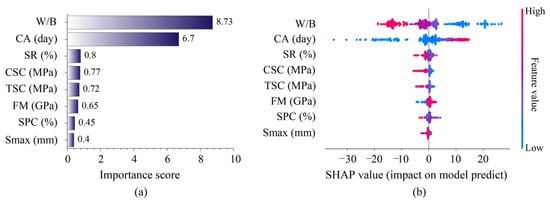
Figure 7. SHAP analysis of CS prediction based on the optimal DOA-RF model: (a) global feature importance ranking; (b) SHAP value distribution and feature impact analysis.

6. Conclusions

This study systematically developed and compared six DOA-optimized machine learning models for predicting the CS of manufactured-sand concrete. By integrating a newly proposed metaheuristic optimization algorithm with multiple ML models, the research provides a comprehensive benchmark for model performance and identifies the governing parameters affecting concrete strength. The major conclusions can be summarized as follows:

(1)

Model performance: Among all the models, DOA-RF achieved the highest predictive accuracy, with testing R² = 0.9755, RMSE = 2.7836, and MAE = 2.1716.

(2)

The introduction of DOA significantly improved predictive performance compared with previously reported optimization techniques such as BBO and MTOA. This demonstrated that algorithmic selection is critical for enhancing the accuracy of ML-based predictions in materials engineering.

(3)

SHAP analysis confirmed that the W/B and CA are the dominant predictors of compressive strength. W/B showed a negative correlation with strength, whereas CA contributed positively to long-term strength development.

Despite the encouraging outcomes, this study is subject to certain limitations. The database consists of only 306 samples, which constrains the generalization of the models across broader ranges of mix designs and environmental conditions. The reliance on a single optimization algorithm (i.e., DOA) also raises questions regarding its robustness under different datasets, suggesting that future work should explore hybrid or comparative optimization strategies. Furthermore, the current validation is limited to laboratory data, and large-scale field applications are required to confirm the reliability and practicality of the proposed models in real engineering environments.