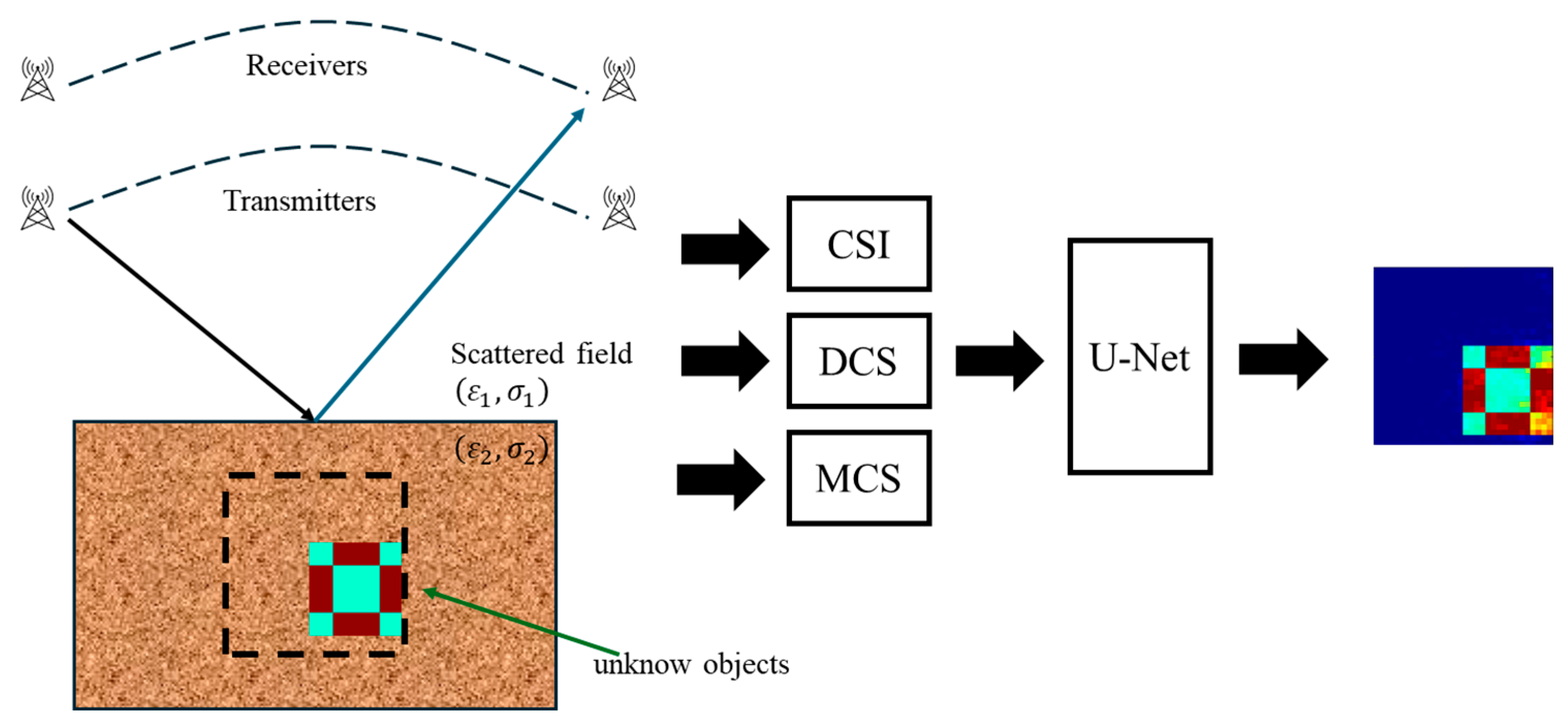
Figure 1.
Sensing and reconstruction architecture. The black arrows represent the incident wave, and the blue arrows represent the reflected wave.
Figure 1.
Sensing and reconstruction architecture. The black arrows represent the incident wave, and the blue arrows represent the reflected wave.
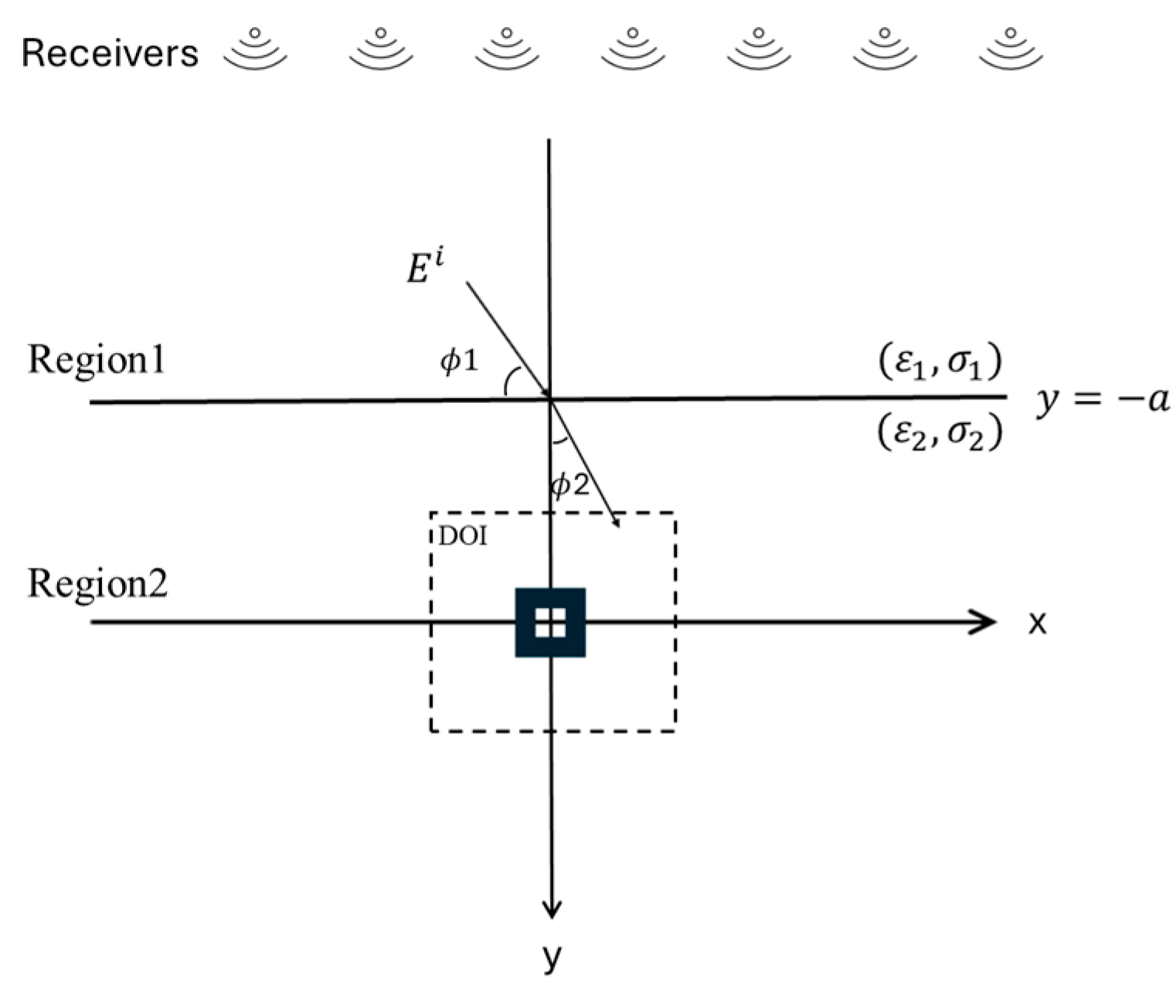
Figure 2.
Schematic diagram of a 2D dielectric object embedded in a half-space.
Figure 2.
Schematic diagram of a 2D dielectric object embedded in a half-space.
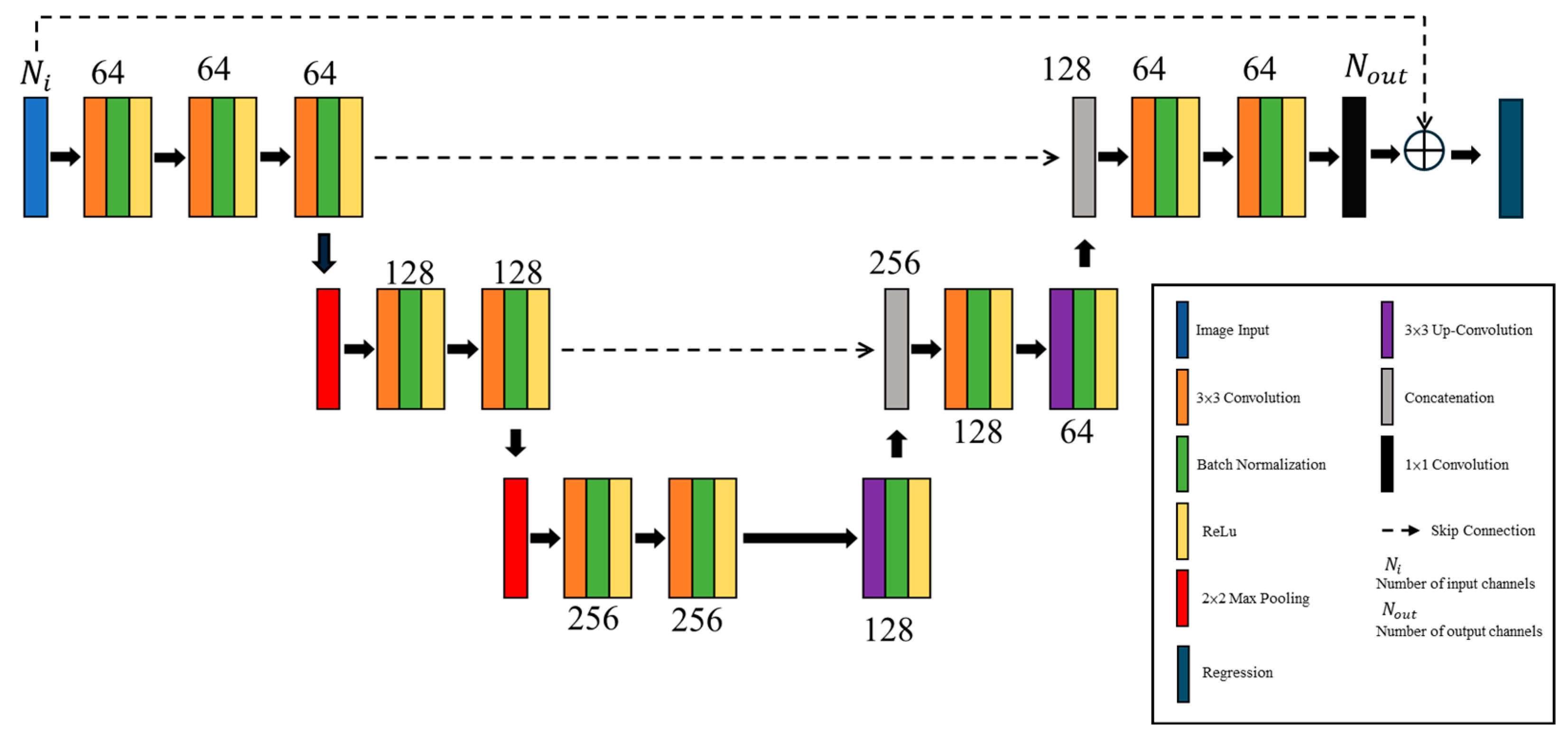
Figure 3.
U-Net architecture.
Figure 3.
U-Net architecture.
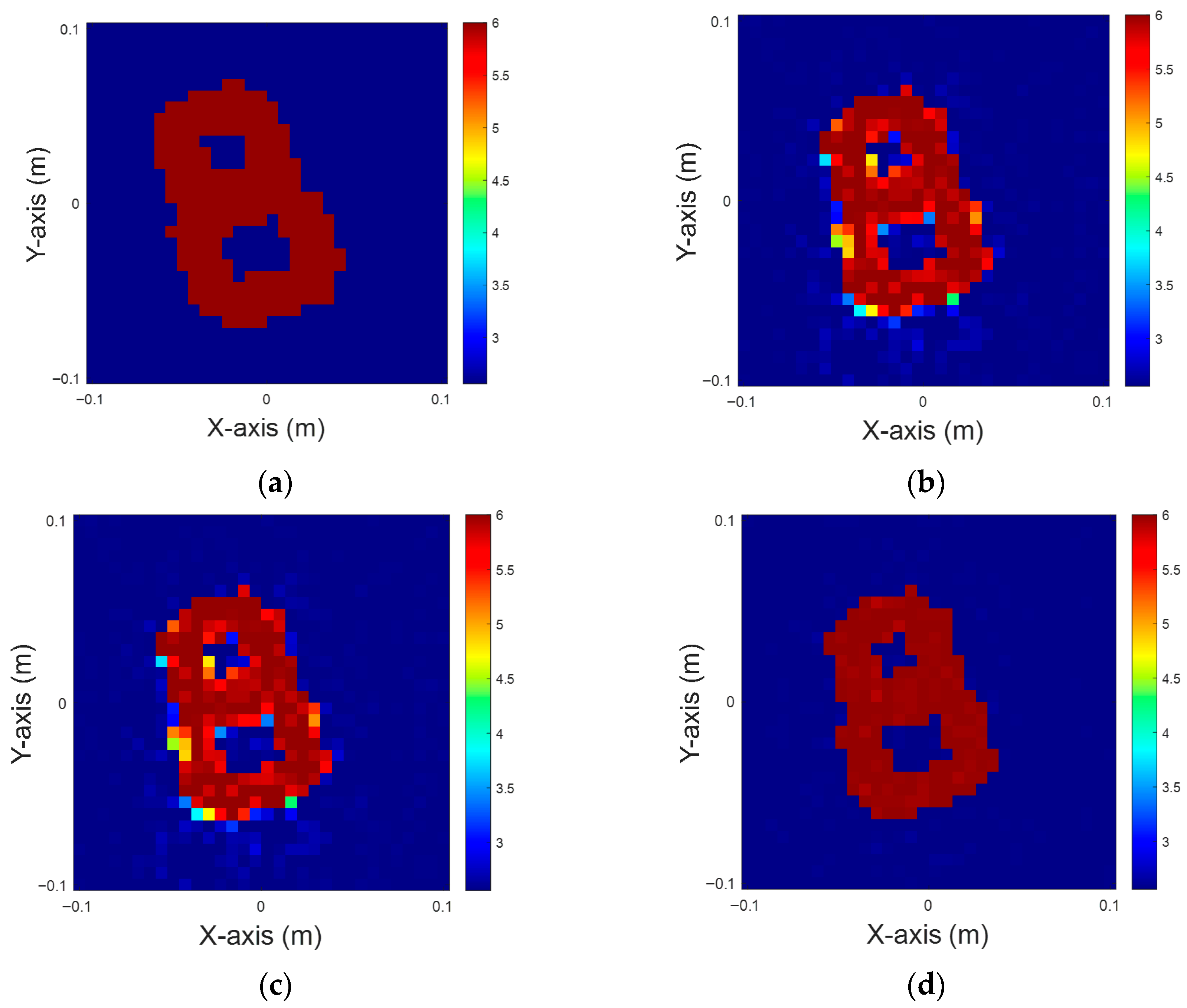
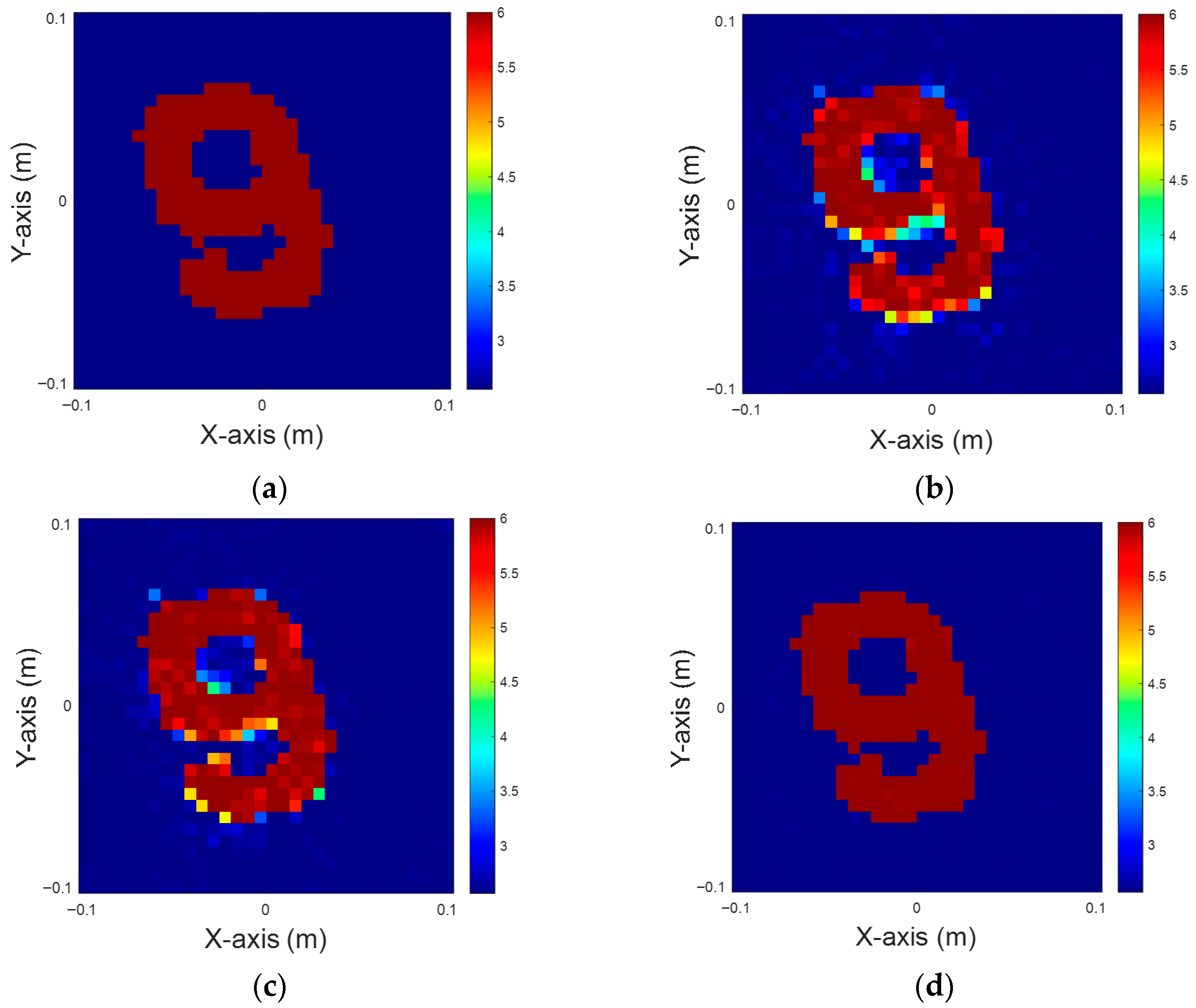
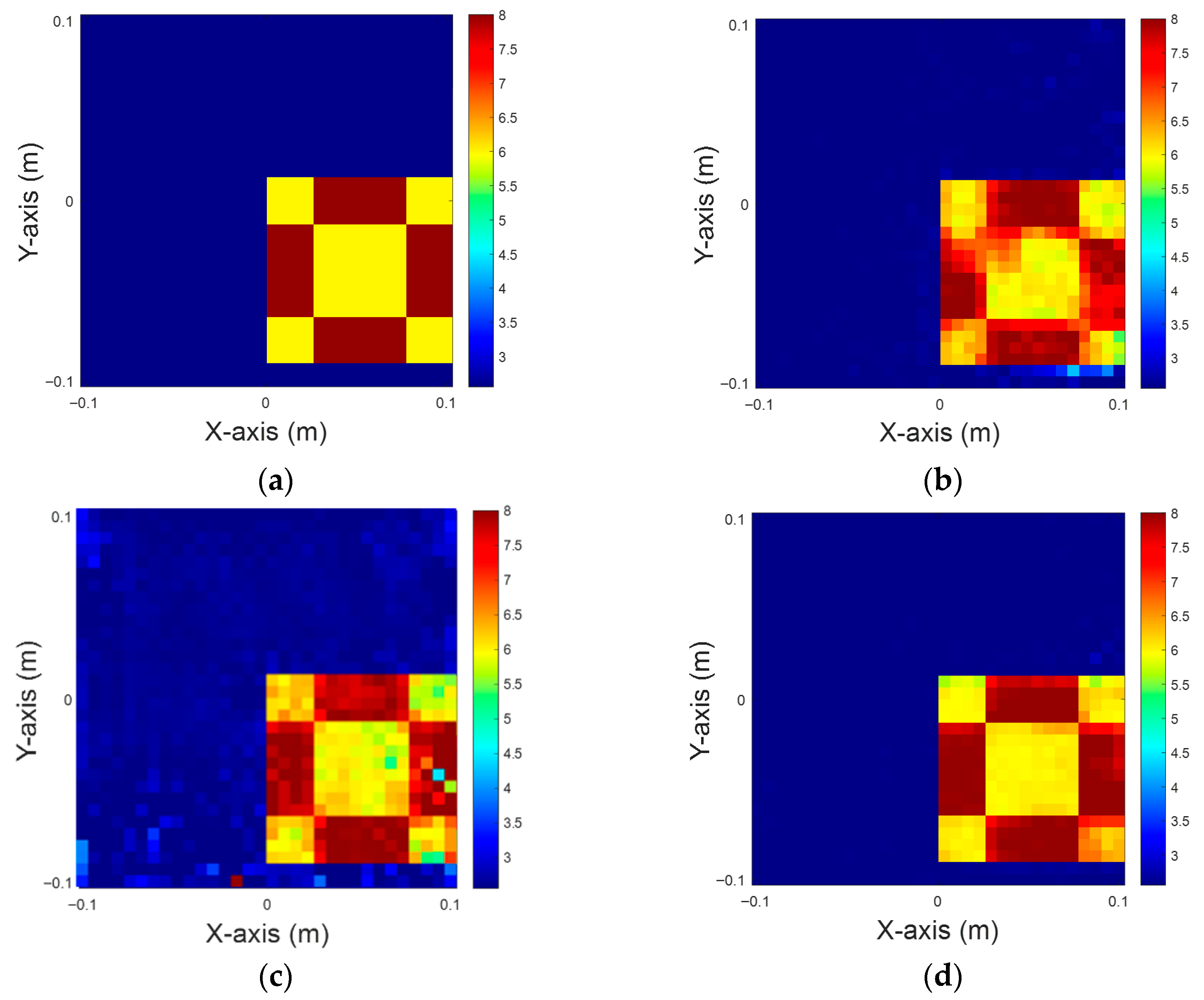
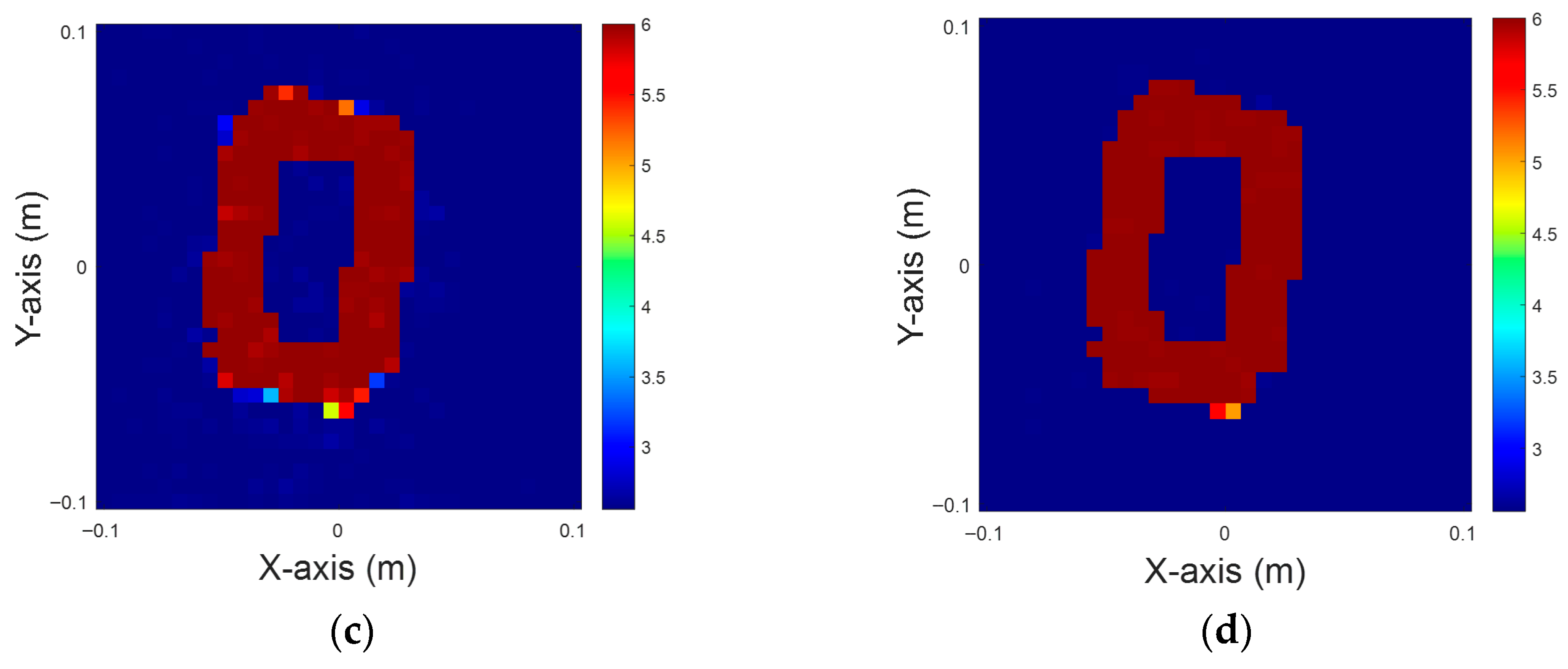
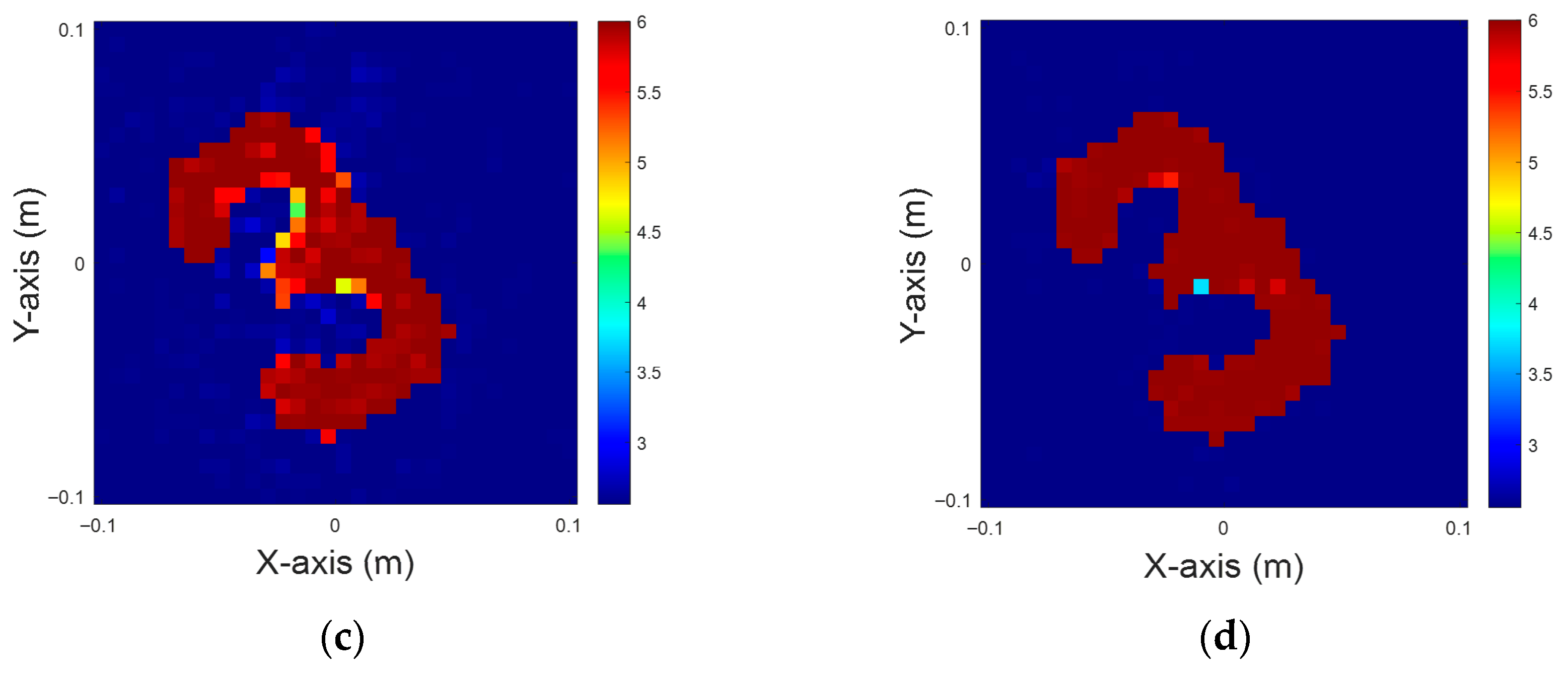
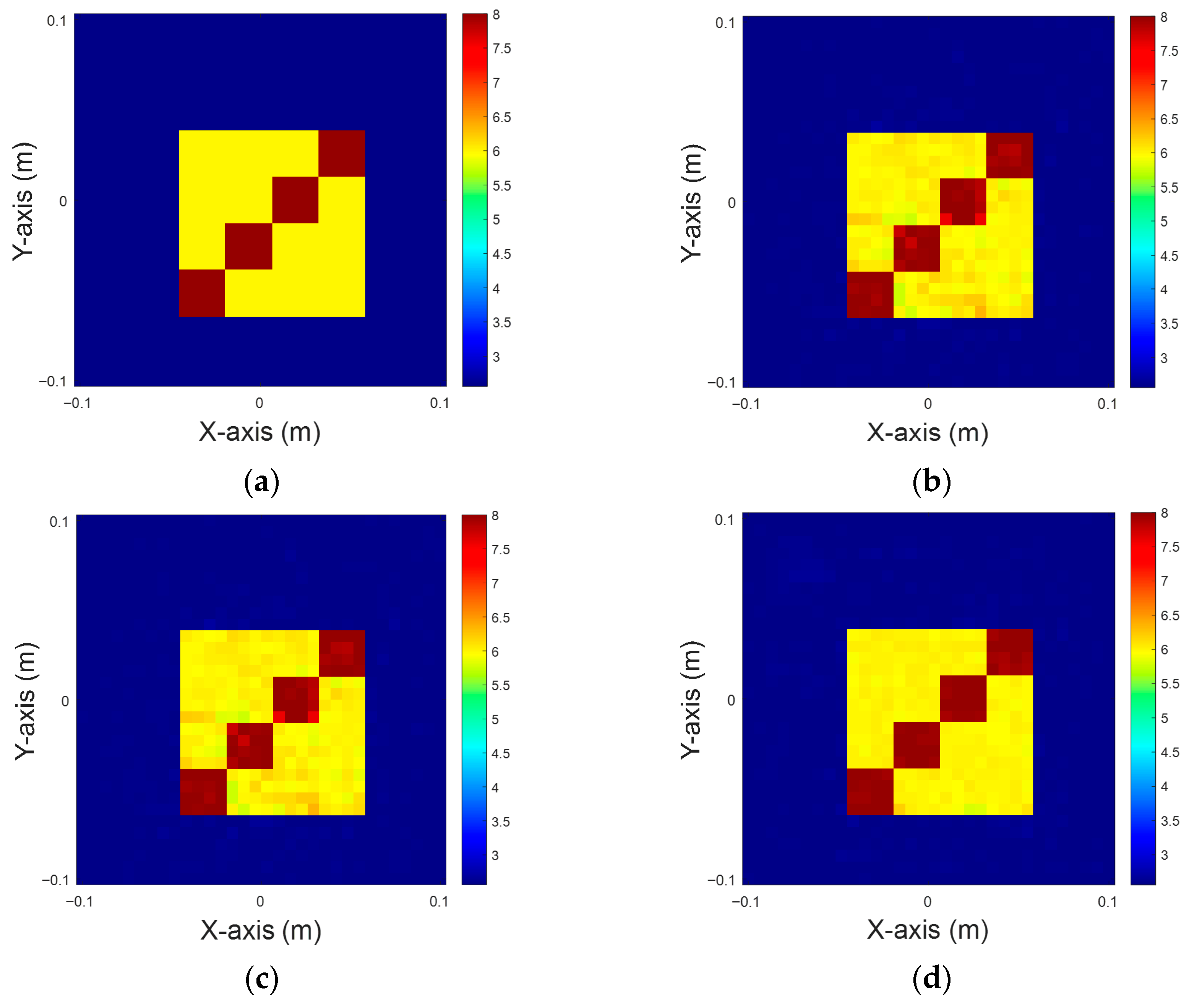
Figure 4.
Dielectric coefficient at six, with 5% noise. (a) Ground truth. (b) CSI, 10 iterations with U-Net. (c) DCS, three iterations with U-Net. (d) MCS, three iterations with U-Net.
Figure 4.
Dielectric coefficient at six, with 5% noise. (a) Ground truth. (b) CSI, 10 iterations with U-Net. (c) DCS, three iterations with U-Net. (d) MCS, three iterations with U-Net.
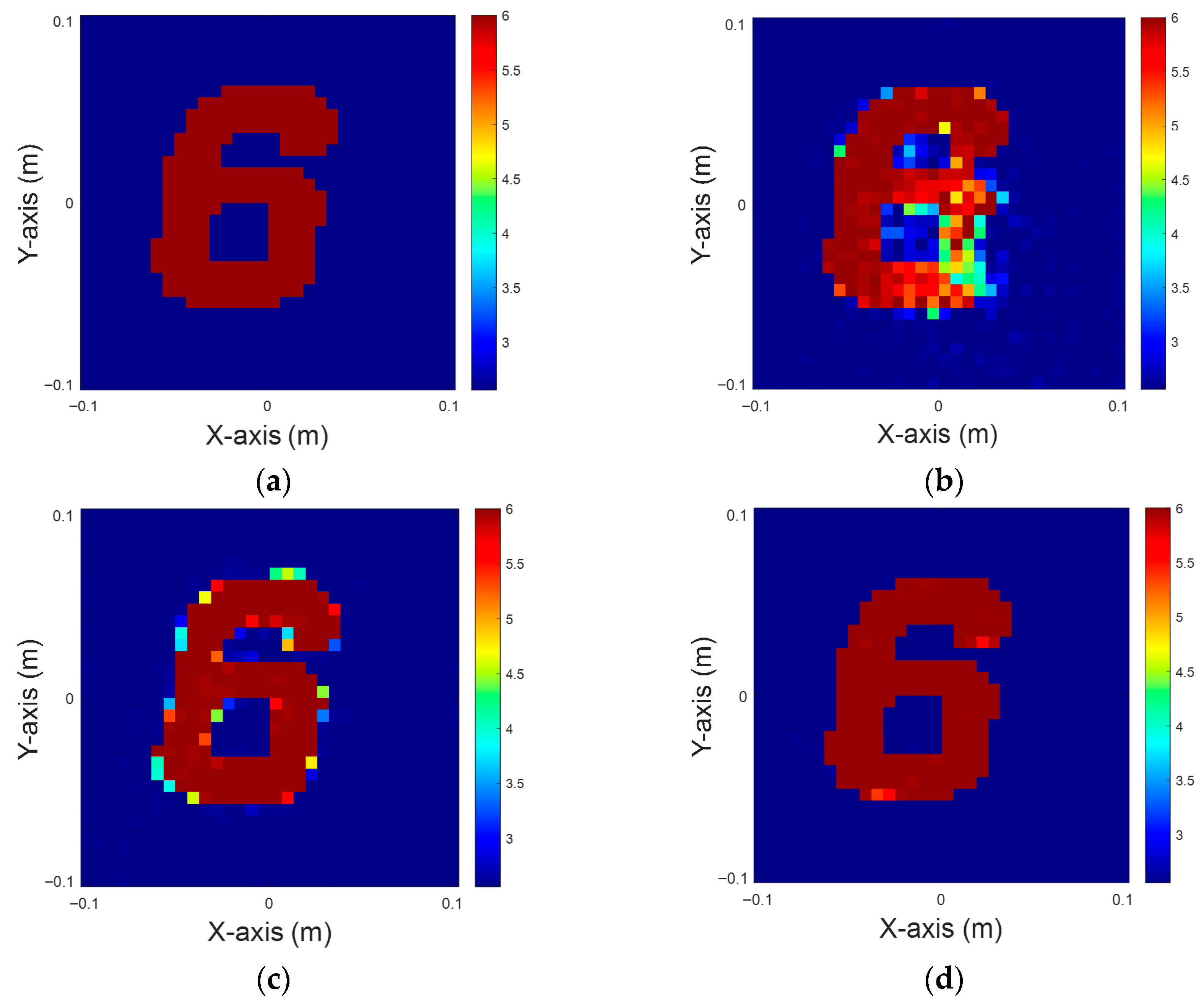
Figure 5.
Dielectric coefficient at six, with 10% noise. (a) Ground truth. (b) CSI, 10 iterations with U-Net. (c) DCS, three iterations with U-Net. (d) MCS, three iterations with U-Net.
Figure 5.
Dielectric coefficient at six, with 10% noise. (a) Ground truth. (b) CSI, 10 iterations with U-Net. (c) DCS, three iterations with U-Net. (d) MCS, three iterations with U-Net.
Figure 6.
Dielectric coefficient at six, with 15% noise. (a) Ground truth. (b) CSI, 10 iterations with U-Net. (c) DCS, three iterations with U-Net. (d) MCS, three iterations with U-Net.
Figure 6.
Dielectric coefficient at six, with 15% noise. (a) Ground truth. (b) CSI, 10 iterations with U-Net. (c) DCS, three iterations with U-Net. (d) MCS, three iterations with U-Net.
Figure 7.
Dielectric coefficient at six, with 20% noise. (a) Ground truth. (b) CSI, 10 iterations with U-Net. (c) DCS, three iterations with U-Net. (d) MCS, three iterations with U-Net.
Figure 7.
Dielectric coefficient at six, with 20% noise. (a) Ground truth. (b) CSI, 10 iterations with U-Net. (c) DCS, three iterations with U-Net. (d) MCS, three iterations with U-Net.
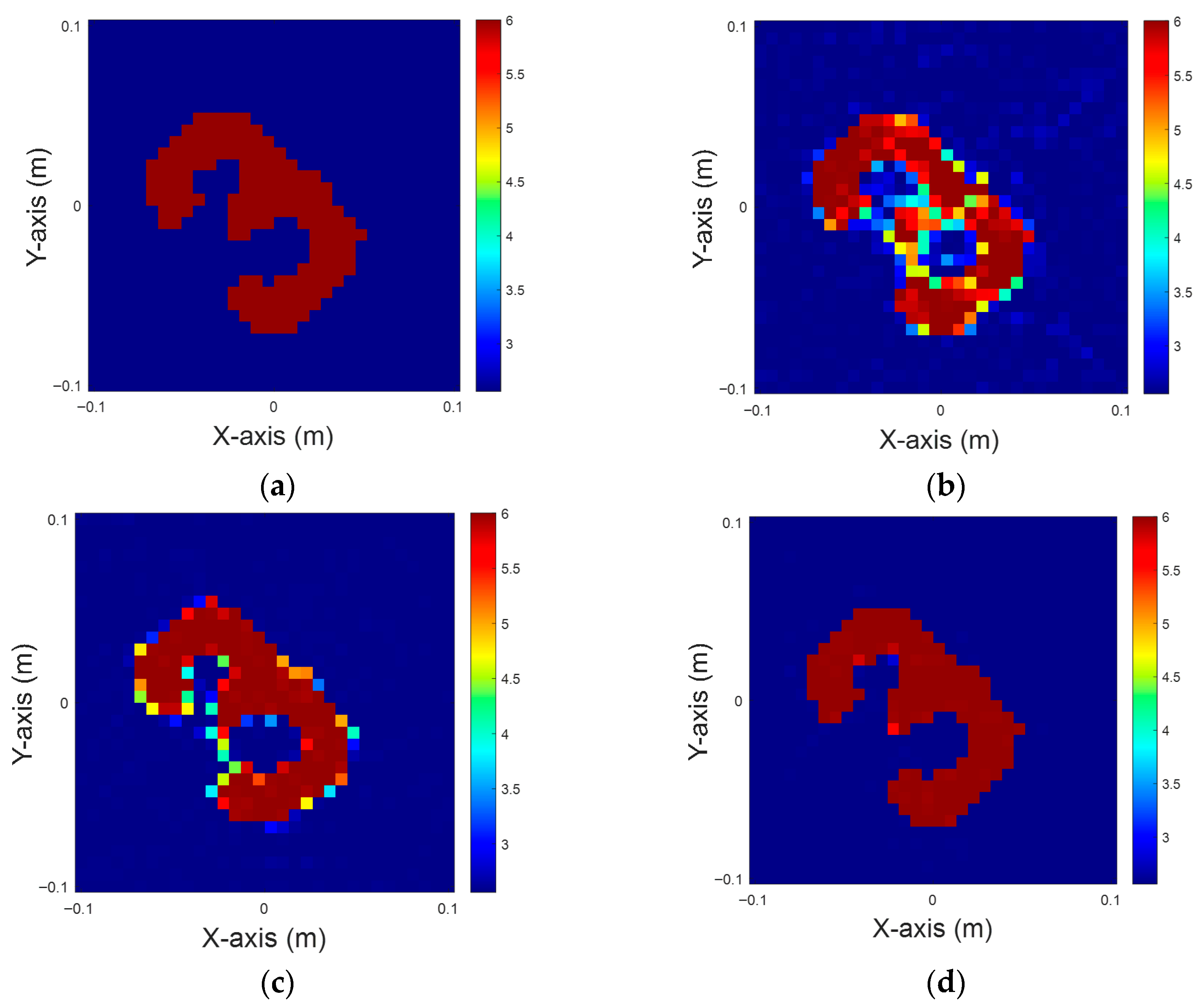
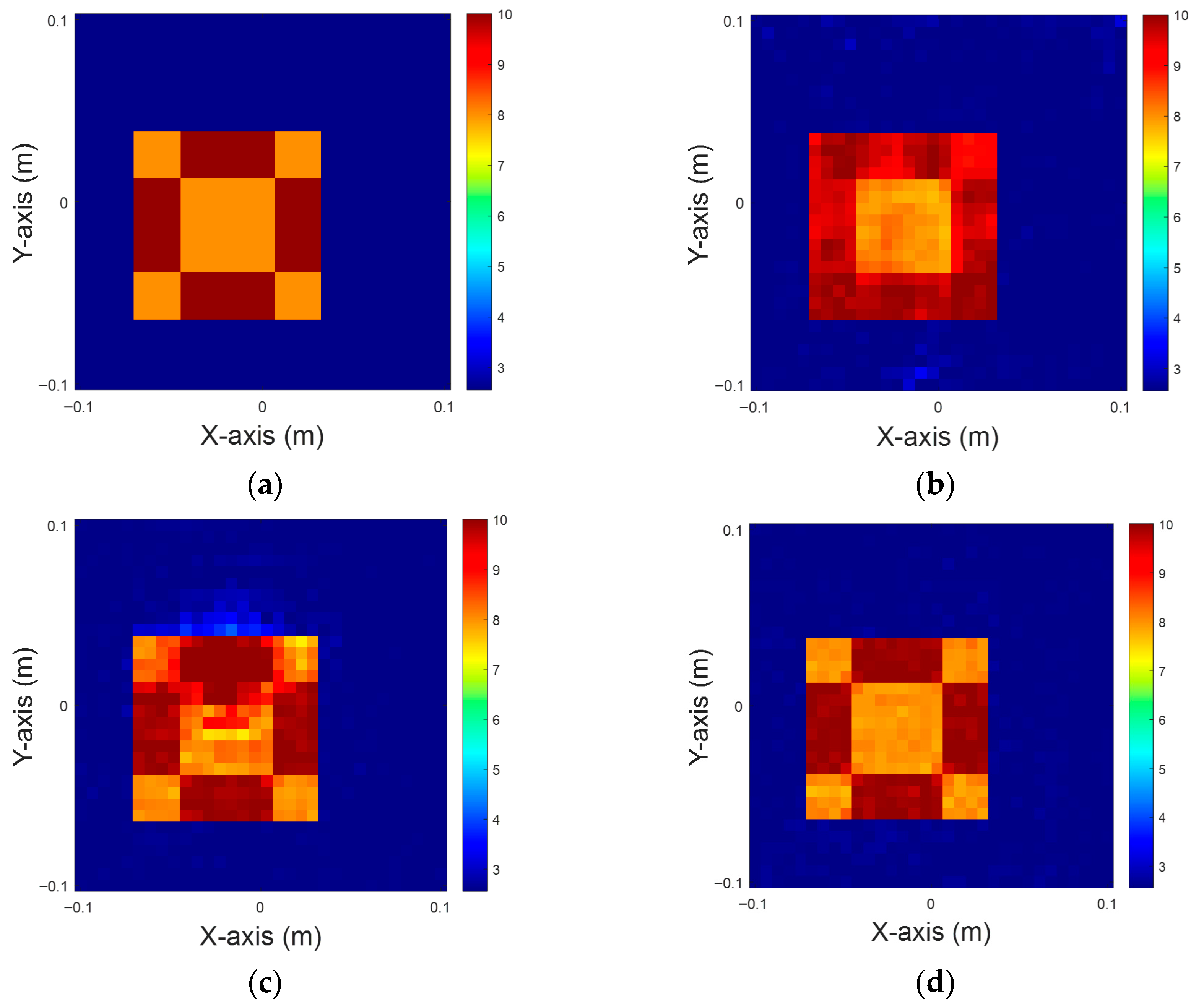
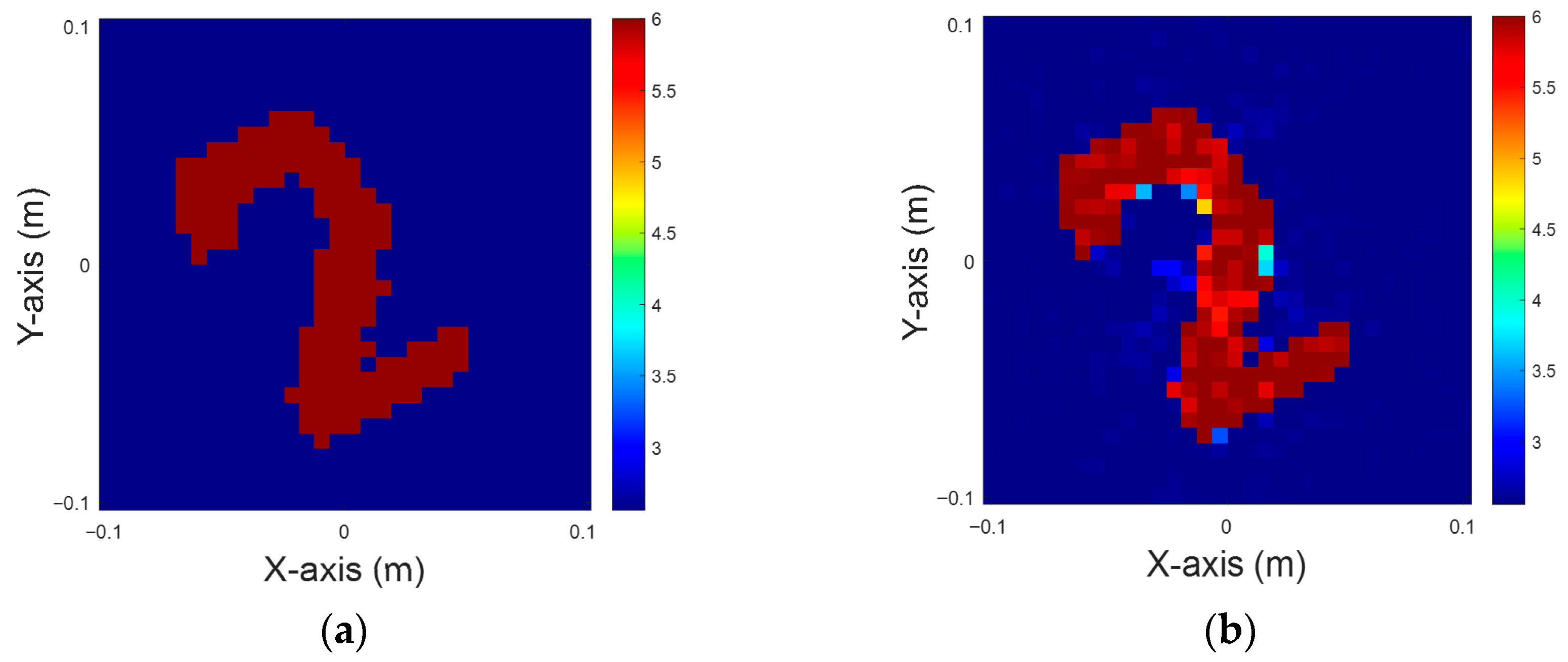
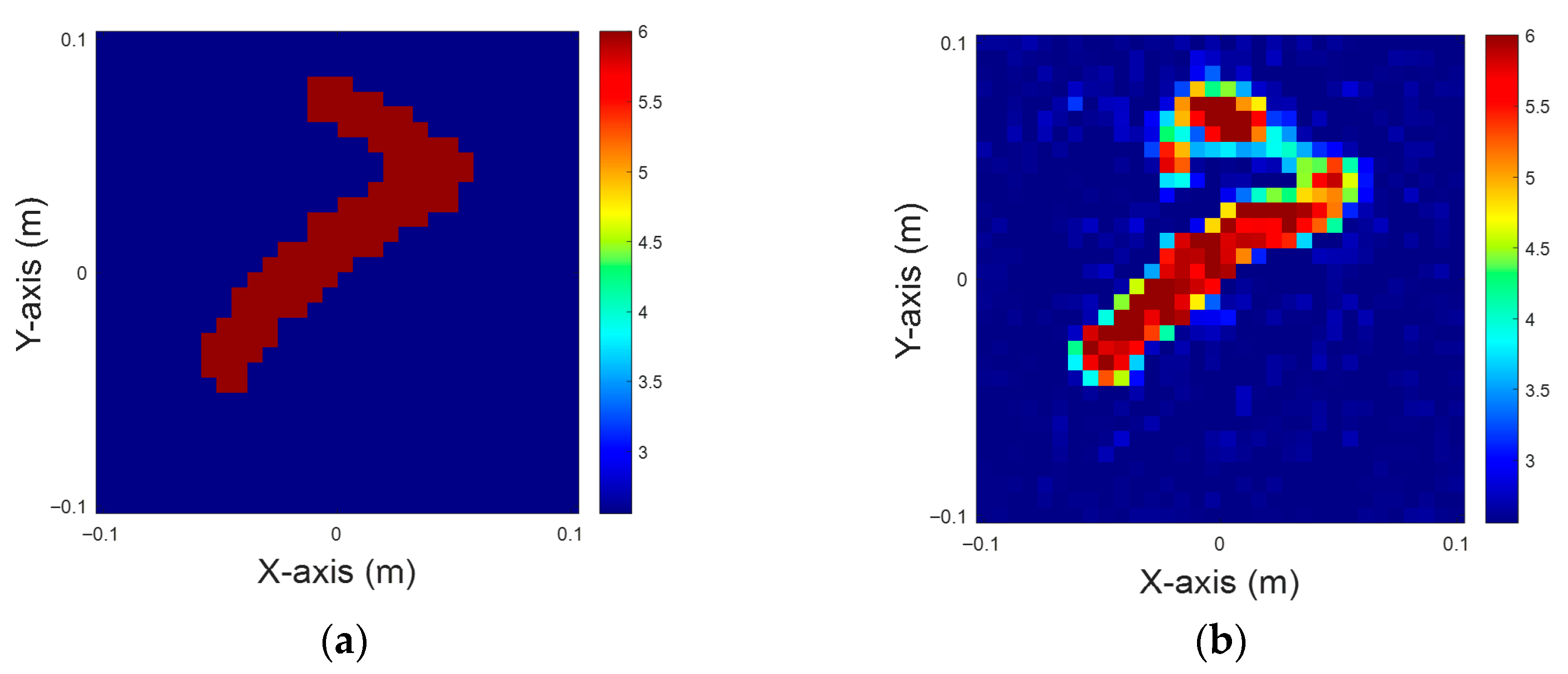
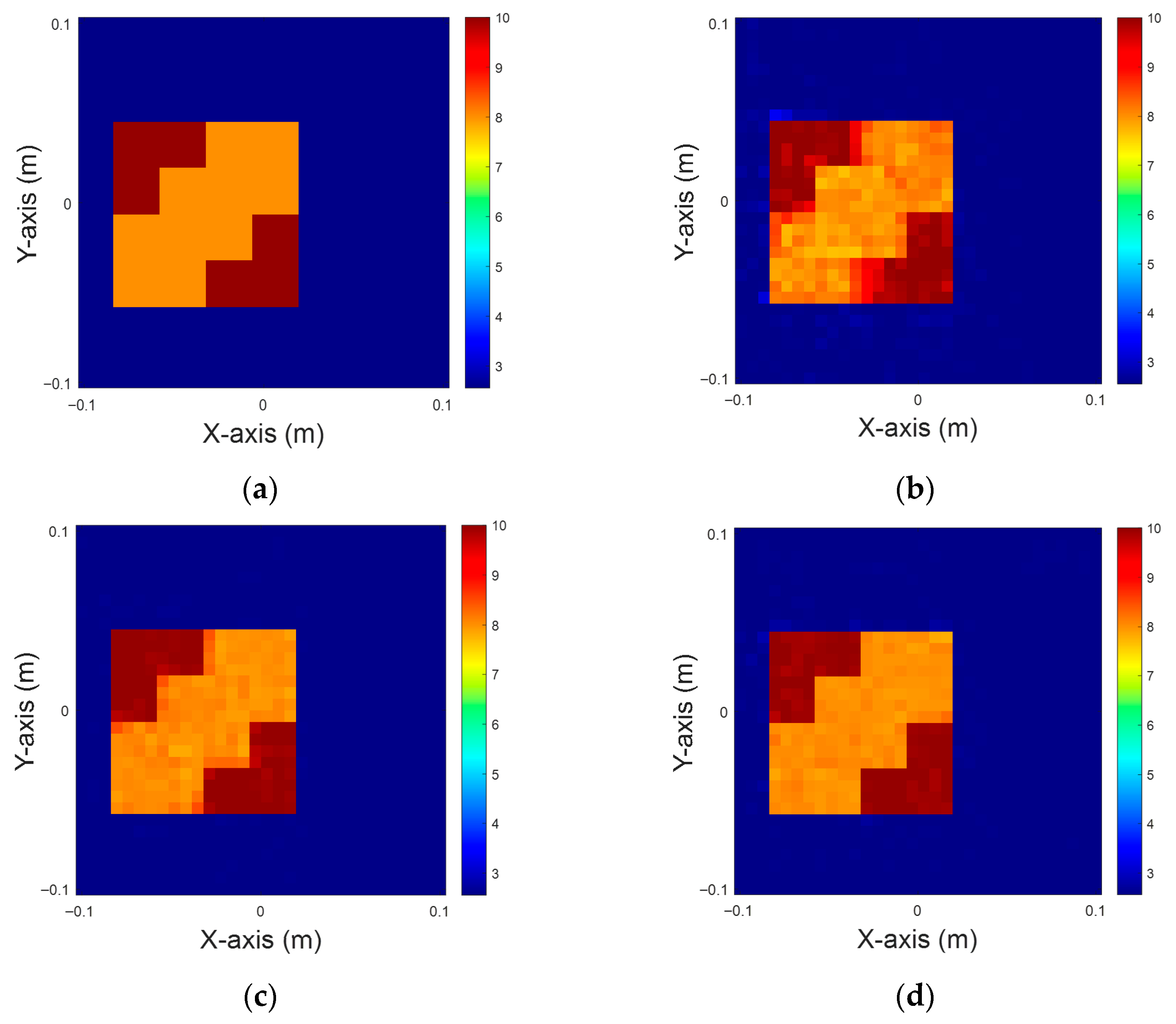
Figure 8.
Dielectric constant between four and six, with 5% noise for TM case. (a) Ground truth. (b) CSI, 10 iterations with U-Net. (c) DCS, three iterations with U-Net. (d) MCS, three iterations with U-Net.
Figure 8.
Dielectric constant between four and six, with 5% noise for TM case. (a) Ground truth. (b) CSI, 10 iterations with U-Net. (c) DCS, three iterations with U-Net. (d) MCS, three iterations with U-Net.
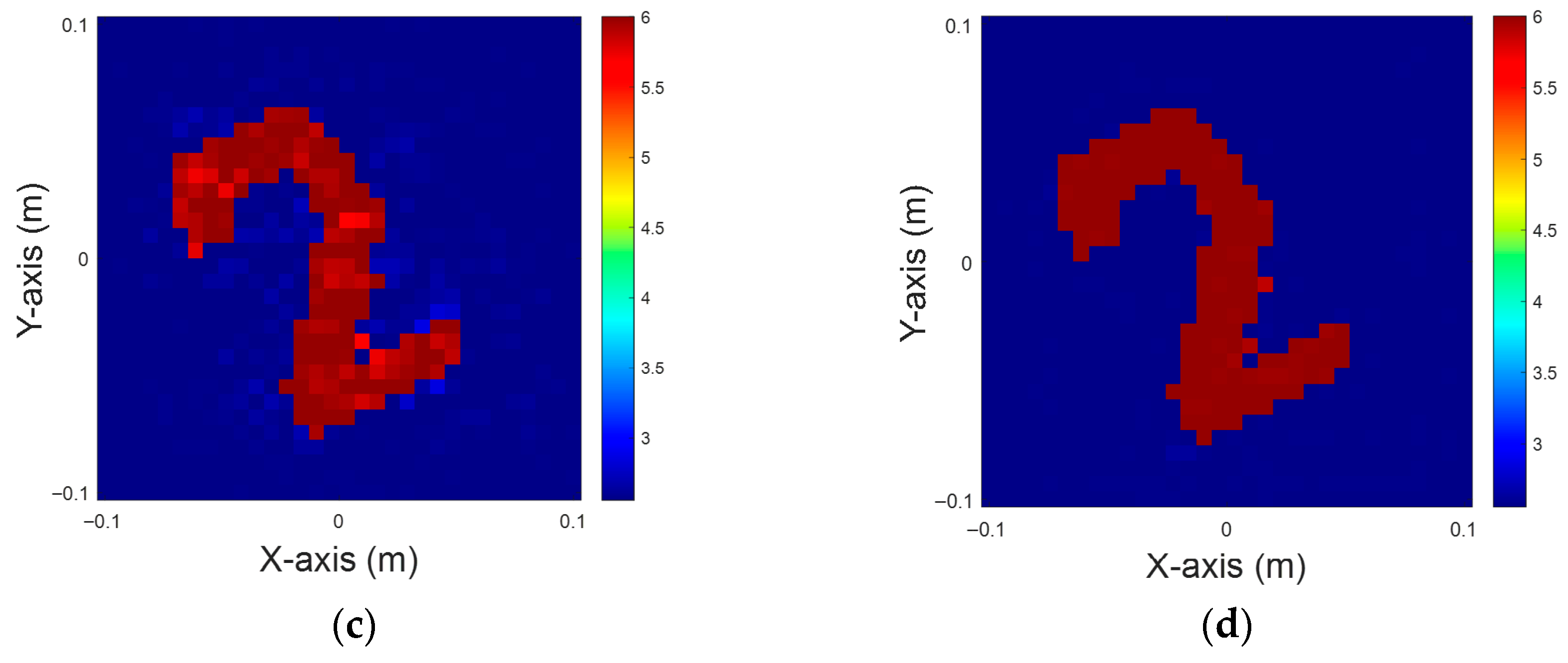
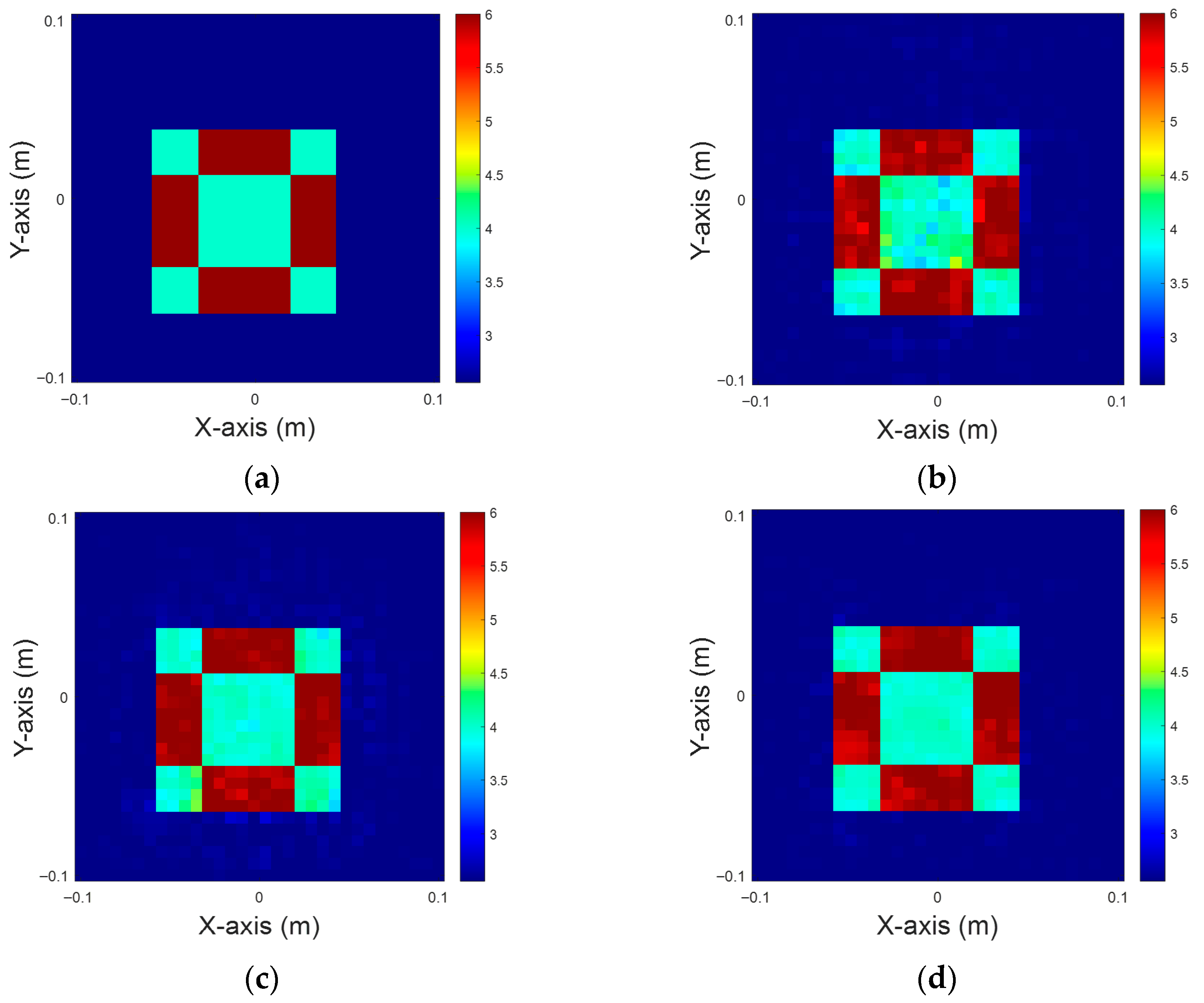
Figure 9.
Dielectric constant between six and eight, with 5% noise for TM case. (a) Ground truth. (b) CSI, 10 iterations with U-Net. (c) DCS, three iterations with U-Net. (d) MCS, three iterations with U-Net.
Figure 9.
Dielectric constant between six and eight, with 5% noise for TM case. (a) Ground truth. (b) CSI, 10 iterations with U-Net. (c) DCS, three iterations with U-Net. (d) MCS, three iterations with U-Net.
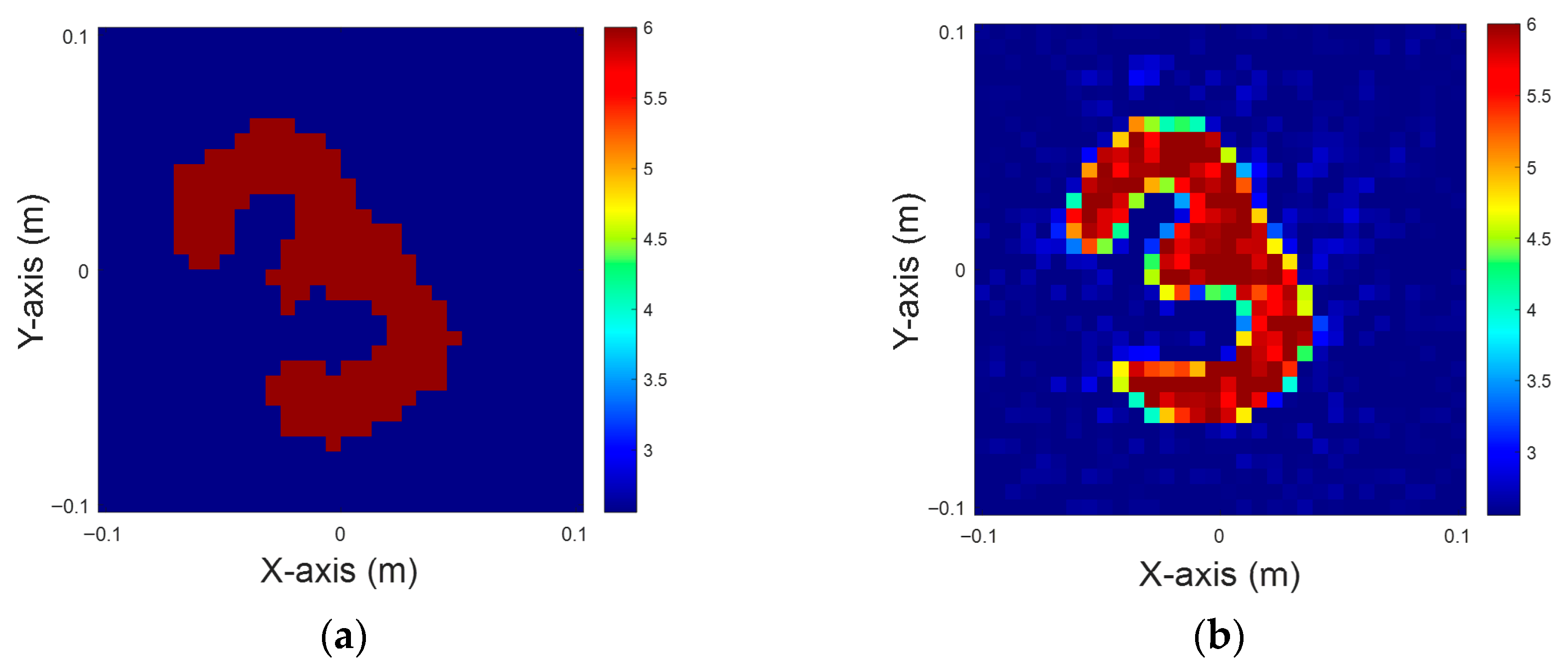
Figure 10.
Dielectric constant between 8 and 10, with 5% noise for TM case. (a) Ground truth. (b) CSI, 10 iterations with U-Net. (c) DCS, three iterations with U-Net. (d) MCS, three iterations with U-Net.
Figure 10.
Dielectric constant between 8 and 10, with 5% noise for TM case. (a) Ground truth. (b) CSI, 10 iterations with U-Net. (c) DCS, three iterations with U-Net. (d) MCS, three iterations with U-Net.
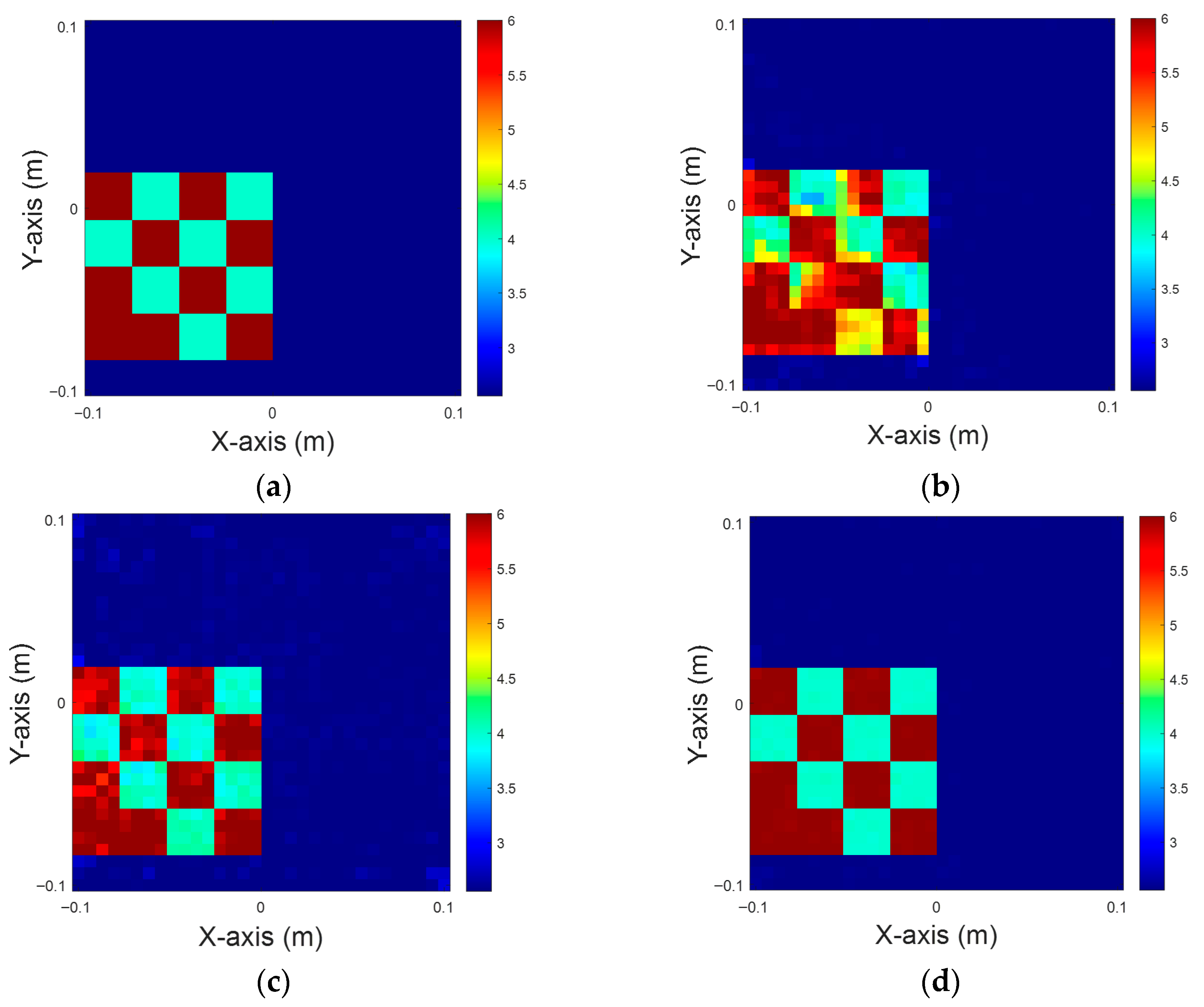
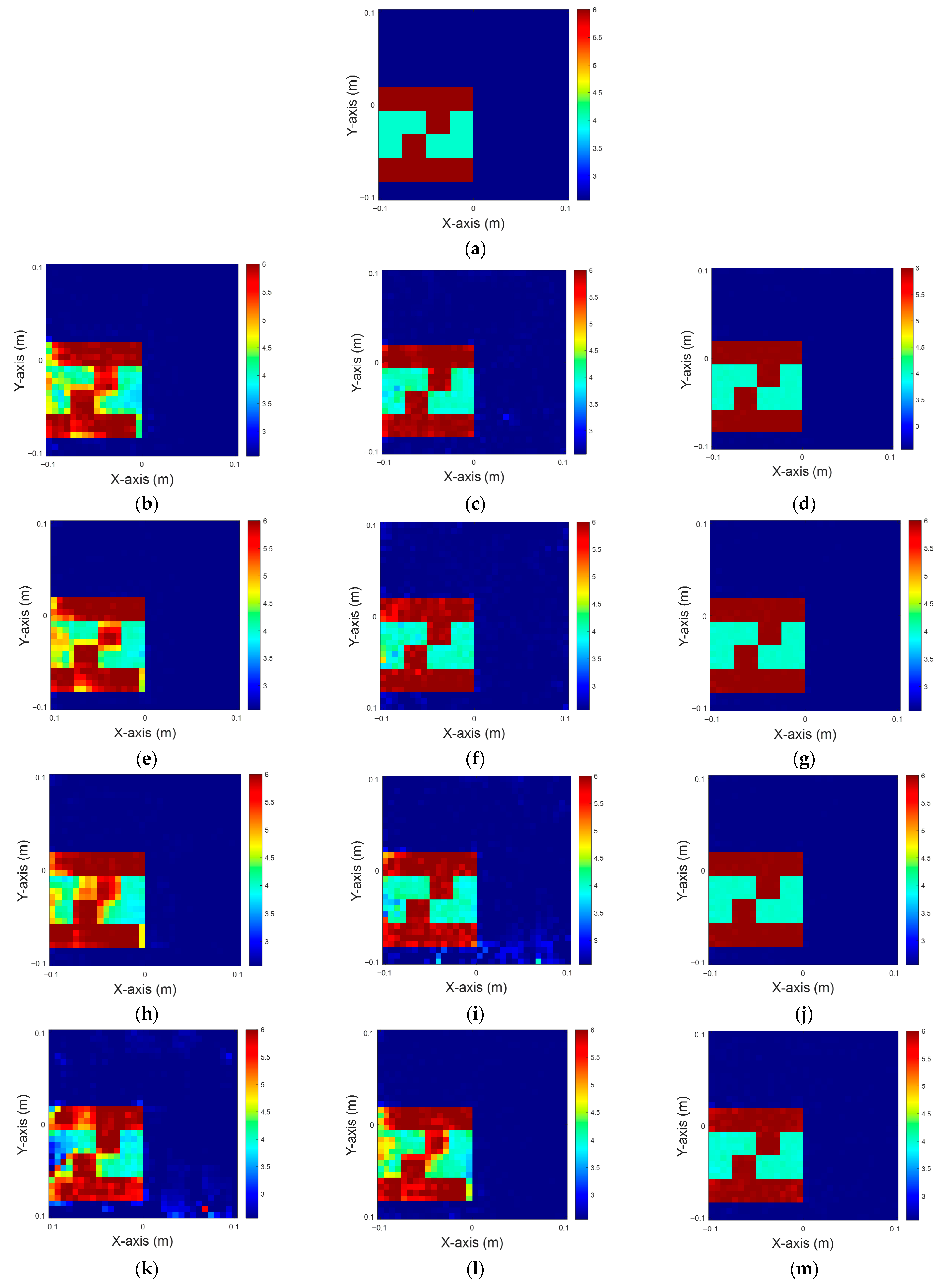
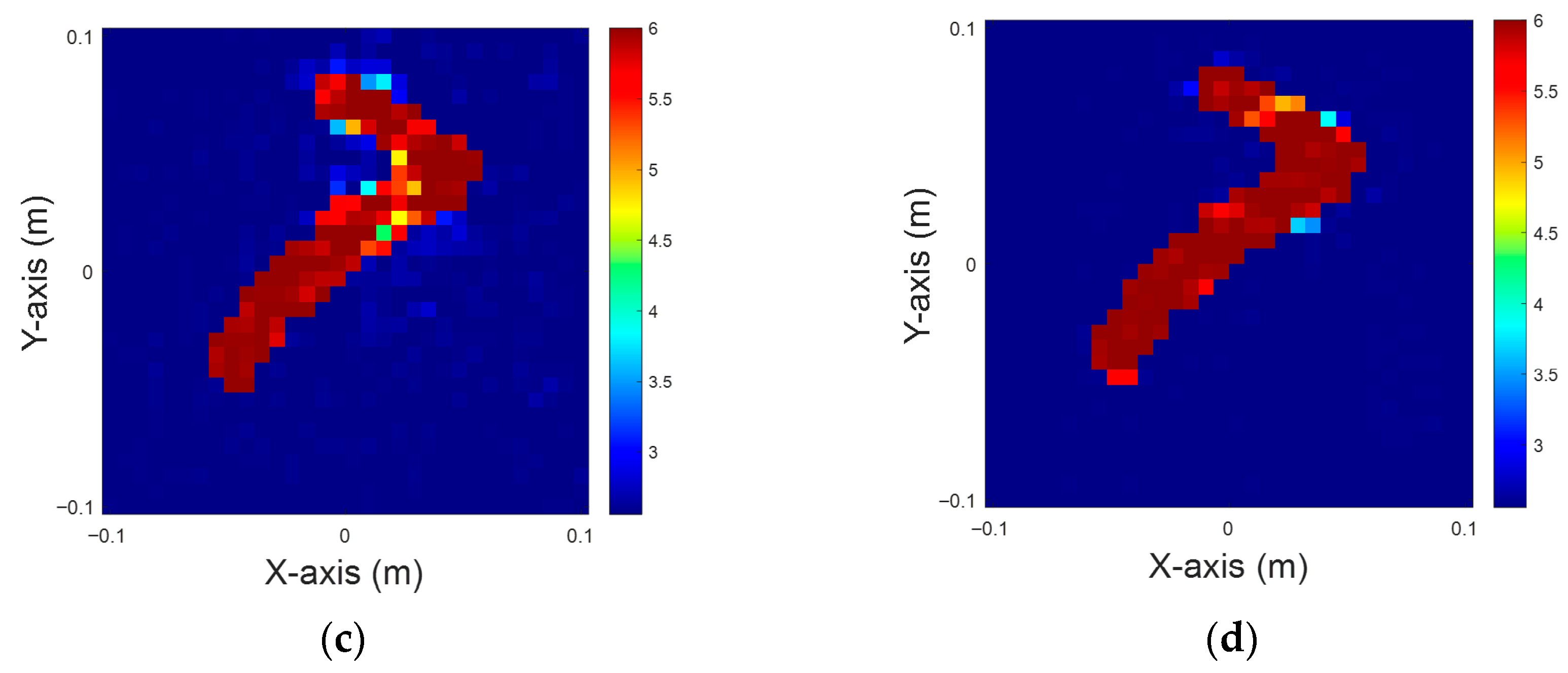
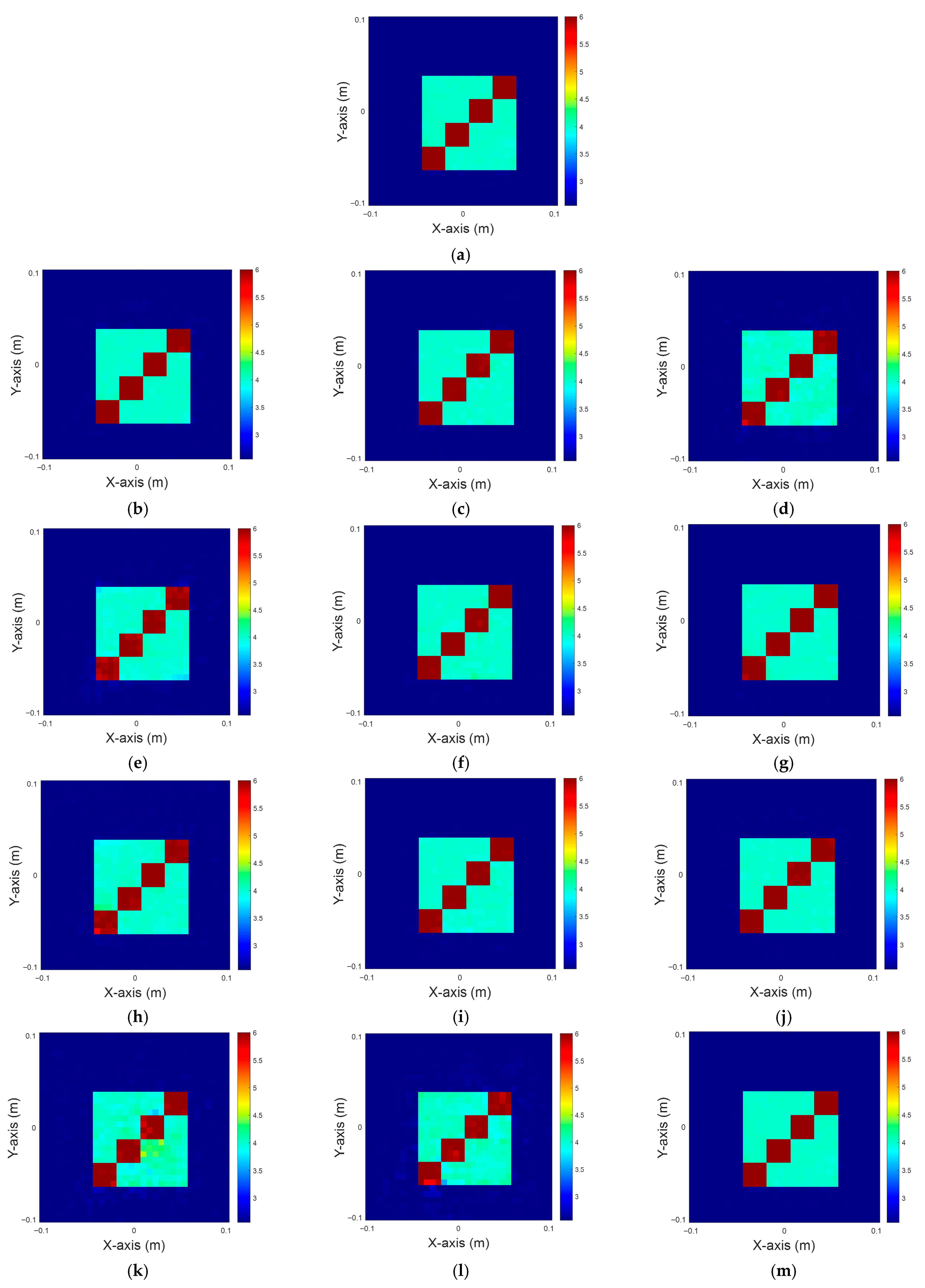
Figure 11.
Dielectric constant between four and six for TM case. (a) Ground truth; (b–d) 5% noise; (e–g) 10% noise; (h–j) 15% noise; (k–m) 20% noise.
Figure 11.
Dielectric constant between four and six for TM case. (a) Ground truth; (b–d) 5% noise; (e–g) 10% noise; (h–j) 15% noise; (k–m) 20% noise.
Figure 12.
Dielectric constant at six, with 5% noise for TE case. (a) Ground truth. (b) CSI, 10 iterations with U-Net. (c) DCS, three iterations with U-Net. (d) MCS, three iterations with U-Net.
Figure 12.
Dielectric constant at six, with 5% noise for TE case. (a) Ground truth. (b) CSI, 10 iterations with U-Net. (c) DCS, three iterations with U-Net. (d) MCS, three iterations with U-Net.
Figure 13.
Dielectric constant at six, with 10% noise for TE case. (a) Ground truth. (b) CSI, 10 iterations with U-Net. (c) DCS, three iterations with U-Net. (d) MCS, three iterations with U-Net.
Figure 13.
Dielectric constant at six, with 10% noise for TE case. (a) Ground truth. (b) CSI, 10 iterations with U-Net. (c) DCS, three iterations with U-Net. (d) MCS, three iterations with U-Net.
Figure 14.
Dielectric constant at six, with 15% noise for TE case. (a) Ground truth. (b) CSI, 10 iterations with U-Net. (c) DCS, three iterations with U-Net. (d) MCS, three iterations with U-Net.
Figure 14.
Dielectric constant at six, with 15% noise for TE case. (a) Ground truth. (b) CSI, 10 iterations with U-Net. (c) DCS, three iterations with U-Net. (d) MCS, three iterations with U-Net.
Figure 15.
Dielectric constant at six, with 20% noise for TE case. (a) Ground truth. (b) CSI, 10 iterations with U-Net. (c) DCS, three iterations with U-Net. (d) MCS, three iterations with U-Net.
Figure 15.
Dielectric constant at six, with 20% noise for TE case. (a) Ground truth. (b) CSI, 10 iterations with U-Net. (c) DCS, three iterations with U-Net. (d) MCS, three iterations with U-Net.
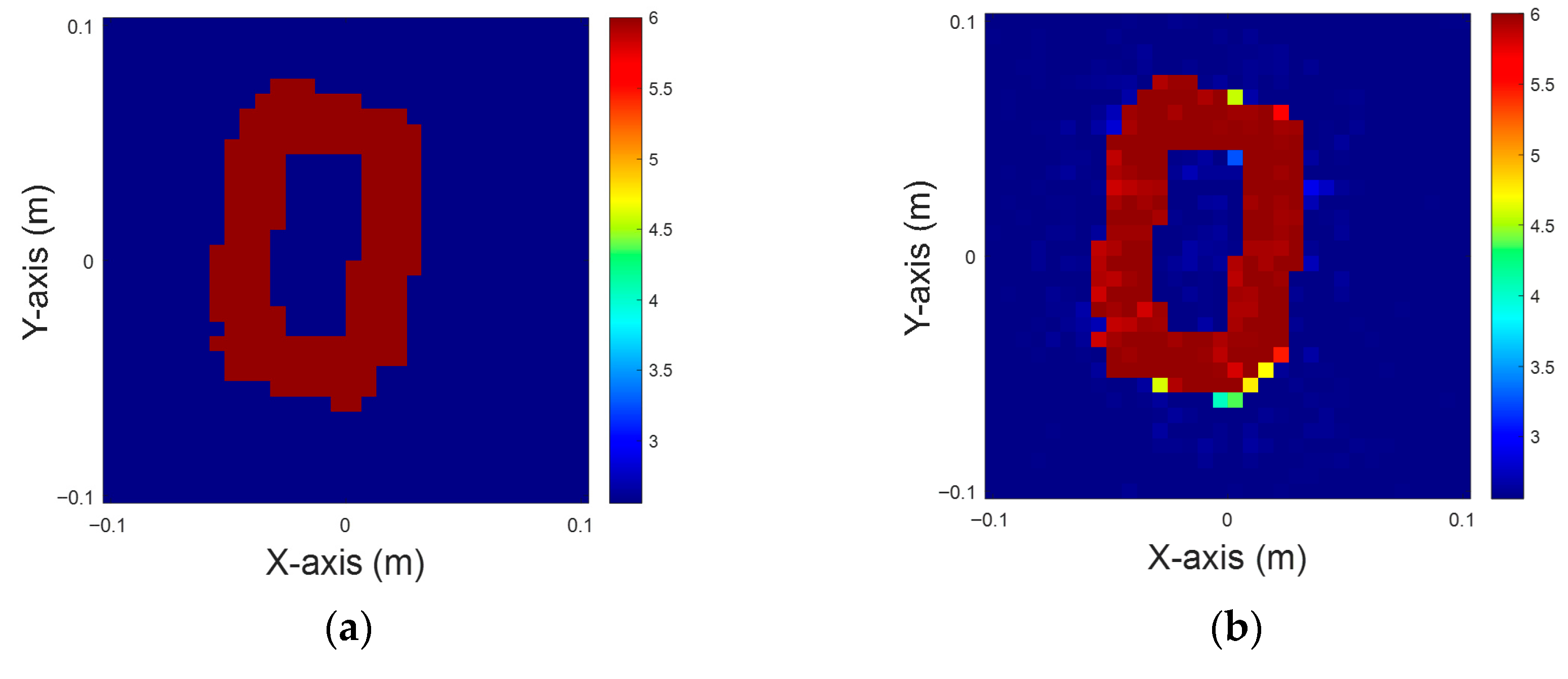
Figure 16.
Dielectric constant between four and six, with 5% noise for TE case. (a) Ground truth. (b) CSI, 10 iterations with U-Net. (c) DCS, three iterations with U-Net. (d) MCS, three iterations with U-Net.
Figure 16.
Dielectric constant between four and six, with 5% noise for TE case. (a) Ground truth. (b) CSI, 10 iterations with U-Net. (c) DCS, three iterations with U-Net. (d) MCS, three iterations with U-Net.
Figure 17.
Dielectric constant between six and eight, with 5% noise for TE case. (a) Ground truth. (b) CSI, 10 iterations with U-Net. (c) DCS, three iterations with U-Net. (d) MCS, three iterations with U-Net.
Figure 17.
Dielectric constant between six and eight, with 5% noise for TE case. (a) Ground truth. (b) CSI, 10 iterations with U-Net. (c) DCS, three iterations with U-Net. (d) MCS, three iterations with U-Net.
Figure 18.
Dielectric constant between 8 and 10, with 5% noise for TE case. (a) Ground truth. (b) CSI, 10 iterations with U-Net. (c) DCS, three iterations with U-Net. (d) MCS, three iterations with U-Net.
Figure 18.
Dielectric constant between 8 and 10, with 5% noise for TE case. (a) Ground truth. (b) CSI, 10 iterations with U-Net. (c) DCS, three iterations with U-Net. (d) MCS, three iterations with U-Net.
Figure 19.
Dielectric constant between four and six, with 5%, 10%, 15%, and 20% noise for TE case. (a) Ground truth; (b–d) 5% noise; (e–g) 10% noise; (h–j) 15% noise; (k–m) 20% noise.
Figure 19.
Dielectric constant between four and six, with 5%, 10%, 15%, and 20% noise for TE case. (a) Ground truth; (b–d) 5% noise; (e–g) 10% noise; (h–j) 15% noise; (k–m) 20% noise.
Table 1.
NRMSE and SSIM for dielectric constants at six, with 5% noise.
Table 1.
NRMSE and SSIM for dielectric constants at six, with 5% noise.
| | Method | CSI with U-Net | DCS with U-Net | MCS with U-Net |
|---|
| Performance | |
|---|
| NRMSE | 9.6% | 2.3% | 1.7% |
| SSIM | 88.5% | 90.1% | 98.6% |
Table 2.
NRMSE and SSIM for a dielectric constant at six, with 10% noise for TM case.
Table 2.
NRMSE and SSIM for a dielectric constant at six, with 10% noise for TM case.
| | Method | CSI with U-Net | DCS with U-Net | MCS with U-Net |
|---|
| Performance | |
|---|
| NRMSE | 12.6% | 4.5% | 2.1% |
| SSIM | 81.2% | 89.7% | 98.5% |
Table 3.
NRMSE and SSIM for a dielectric constant at six, with 15% noise for TM case.
Table 3.
NRMSE and SSIM for a dielectric constant at six, with 15% noise for TM case.
| | Method | CSI with U-Net | DCS with U-Net | MCS with U-Net |
|---|
| Performance | |
|---|
| NRMSE | 16.8% | 7.7% | 5.1% |
| SSIM | 78.8% | 86.5% | 94.7% |
Table 4.
NRMSE and SSIM for a dielectric constant at six, with 20% noise for TM case.
Table 4.
NRMSE and SSIM for a dielectric constant at six, with 20% noise for TM case.
| | Method | CSI with U-Net | DCS with U-Net | MCS with U-Net |
|---|
| Performance | |
|---|
| NRMSE | 24.7% | 13.7% | 3.1% |
| SSIM | 68.2% | 82.5% | 92.7% |
Table 5.
NRMSE and SSIM for a dielectric constant between four and six, with 5% noise for TM case.
Table 5.
NRMSE and SSIM for a dielectric constant between four and six, with 5% noise for TM case.
| | Method | CSI with U-Net | DCS with U-Net | MCS with U-Net |
|---|
| Performance | |
|---|
| NRMSE | 18.1% | 12.1% | 1.4% |
| SSIM | 77.7% | 92.5% | 95.7% |
Table 6.
NRMSE and SSIM for a dielectric constant between six and eight, with 5% noise for TM case.
Table 6.
NRMSE and SSIM for a dielectric constant between six and eight, with 5% noise for TM case.
| | Method | CSI with U-Net | DCS with U-Net | MCS with U-Net |
|---|
| Performance | |
|---|
| NRMSE | 20.1% | 16.1% | 2.3% |
| SSIM | 75.7% | 88.4% | 94.5% |
Table 7.
NRMSE and SSIM for a dielectric constant between 8 and 10, with 5% noise for TM case.
Table 7.
NRMSE and SSIM for a dielectric constant between 8 and 10, with 5% noise for TM case.
| | Method | CSI with U-Net | DCS with U-Net | MCS with U-Net |
|---|
| Performance | |
|---|
| NRMSE | 36.8% | 22.1% | 2.8% |
| SSIM | 65.1% | 71.3% | 92.8% |
Table 8.
NRMSE and SSIM for dielectric constants between four and six, with different noise levels for TM case.
Table 8.
NRMSE and SSIM for dielectric constants between four and six, with different noise levels for TM case.
| | Noise | 5% | 10% | 15% | 20% |
|---|
| Method/Performance | |
|---|
| CSI with U-Net | NRMSE | 14.5% | 22.8% | 31.2% | 38.3% |
| SSIM | 84.2% | 78.5% | 71.3% | 65.5% |
| DCS with U-Net | NRMSE | 8.8% | 10.4% | 19.6% | 23.3% |
| SSIM | 91.4% | 84.6% | 73.3% | 70.2% |
| MCS with U-Net | NRMSE | 2.6% | 3.1% | 3.8% | 5.6% |
| SSIM | 98.6% | 96.8% | 93.3% | 92.1% |
Table 9.
NRMSE and SSIM for a dielectric constant at six, with 5% noise for TE case.
Table 9.
NRMSE and SSIM for a dielectric constant at six, with 5% noise for TE case.
| | Method | CSI with U-Net | DCS with U-Net | MCS with U-Net |
|---|
| Performance | |
|---|
| NRMSE | 10.2% | 3.2% | 1.3% |
| SSIM | 93.1% | 95.2% | 98.9% |
Table 10.
NRMSE and SSIM for a dielectric constant at six, with 10% noise for TE case.
Table 10.
NRMSE and SSIM for a dielectric constant at six, with 10% noise for TE case.
| | Method | CSI with U-Net | DCS with U-Net | MCS with U-Net |
|---|
| Performance | |
|---|
| NRMSE | 10.2% | 3.2% | 1.3% |
| SSIM | 93.1% | 95.2% | 98.9% |
Table 11.
NRMSE and SSIM for a dielectric constant at six, with 15% noise for TE case.
Table 11.
NRMSE and SSIM for a dielectric constant at six, with 15% noise for TE case.
| | Method | CSI with U-Net | DCS with U-Net | MCS with U-Net |
|---|
| Performance | |
|---|
| NRMSE | 27.4% | 16.5% | 9.1% |
| SSIM | 74.5% | 80.3% | 93.2% |
Table 12.
NRMSE and SSIM for a dielectric constant at six, with 20% noise for TE case.
Table 12.
NRMSE and SSIM for a dielectric constant at six, with 20% noise for TE case.
| | Method | CSI with U-Net | DCS with U-Net | MCS with U-Net |
|---|
| Performance | |
|---|
| NRMSE | 29.5% | 13.7% | 6.1% |
| SSIM | 68.8% | 82.5% | 93.6% |
Table 13.
NRMSE and SSIM for a dielectric constant between four and six, with 5% noise for TE case.
Table 13.
NRMSE and SSIM for a dielectric constant between four and six, with 5% noise for TE case.
| | Method | CSI with U-Net | DCS with U-Net | MCS with U-Net |
|---|
| Performance | |
|---|
| NRMSE | 15.4% | 11.3% | 1.3% |
| SSIM | 88.6% | 90.5% | 95.6% |
Table 14.
NRMSE and SSIM for a dielectric constant between six and eight, with 5% noise for TE case.
Table 14.
NRMSE and SSIM for a dielectric constant between six and eight, with 5% noise for TE case.
| | Method | CSI with U-Net | DCS with U-Net | MCS with U-Net |
|---|
| Performance | |
|---|
| NRMSE | 15.4% | 11.3% | 1.3% |
| SSIM | 88.6% | 90.5% | 95.6% |
Table 15.
NRMSE and SSIM for a dielectric constant between 8 and 10, with 5% noise for TE case.
Table 15.
NRMSE and SSIM for a dielectric constant between 8 and 10, with 5% noise for TE case.
| | Method | CSI with U-Net | DCS with U-Net | MCS with U-Net |
|---|
| Performance | |
|---|
| NRMSE | 21.1% | 13.1% | 2.8% |
| SSIM | 85.2% | 89.3% | 93.8% |
Table 16.
NRMSE and SSIM for dielectric constants between four and six, with different noise levels for TE case.
Table 16.
NRMSE and SSIM for dielectric constants between four and six, with different noise levels for TE case.
| | Noise | 5% Noise | 10% Noise | 15% Noise | 20% Noise |
|---|
| Method/Performance | |
|---|
| CSI with U-Net | NRMSE | 4.6% | 5.2% | 63.7% | 14.3% |
| SSIM | 97.4% | 95.1% | 89.3% | 86.4% |
| DCS with U-Net | NRMSE | 3.4% | 4.4% | 5.6% | 12.3% |
| SSIM | 98.5% | 97.6% | 95.8% | 90.2% |
| MCS with U-Net | NRMSE | 1.3% | 2.1% | 2.8% | 3.6% |
| SSIM | 98.6% | 97.8% | 96.3% | 96.1% |
Table 17.
Computational resources of the three methods.
Table 17.
Computational resources of the three methods.
| | Method | CSI with U-Net | DCS with U-Net | MCS with U-Net |
|---|
| Resources | |
|---|
| Memory | 2.9 G | 2.8 G | 3 G |
| Computation Time | 179,288 s | 22,491 s | 21,077 s |