A New Bounding Procedure for Transportation Problems with Stepwise Costs

Abstract

Transportation planning often involves not only shipment costs but also setup costs associated with deploying vehicles or transport resources. In many practical logistics operations, this setup cost does not remain constant but increases stepwise with the number of vehicles used, reflecting economies of scale and scheduling thresholds. To capture this realistic feature, this study investigates the transportation problem with stepwise costs, where total costs combine shipment-dependent variable costs and vehicle activation costs. We develop a mixed-integer programming (MIP) model to represent the problem and propose an efficient algorithm based on variable-splitting reformulation and a row-and-column generation scheme. This approach dynamically introduces only the necessary variables and constraints, enabling the solution of large-scale instances that are otherwise computationally challenging. Numerical experiments show that the method produces high-quality solutions much faster than direct MIP solvers. The results highlight the model’s practical value in optimizing fleet utilization and transportation cost structures in real logistics and supply chain systems.

1. Introduction

In the era of globalization, enterprises are increasingly exposed to complex and volatile market environments. Under such conditions, competition among firms is not only reflected in product quality or pricing but also in the efficiency and sophistication of supply chain management. Within this framework, logistics supply chains are often regarded as the lifeline of enterprises, as they encompass the entire material flow from raw material procurement to final product delivery. Among the various functions of logistics, transportation plays a critical role, acting as the essential link that connects upstream and downstream processes. Effective transportation services enable the smooth coordination of supply and demand, improve responsiveness to market fluctuations, and ultimately enhance overall competitiveness.

Given its central role in determining both operational efficiency and overall profitability, the fixed-charge transportation problem (FCTP) has been one of the most widely studied models in operations research and logistics management [1]. Over several decades, it has attracted extensive scholarly attention and produced a rich body of theoretical results, as well as practical insights that continue to shape transportation planning and decision-making in industry. In its classical formulation, the FCTP assumes that transportation costs consist of two components: a variable cost that grows linearly with the amount shipped, and a setup cost that is triggered as soon as a shipping route is used, regardless of the load transported. This structure offers a convenient abstraction, enabling elegant linear programming models and efficient solution methods.

In practice, however, real-world logistics systems involve important additional complexities that the classical model does not capture. Most notably, shipments are executed by vehicles with finite capacity, and each vehicle that is deployed incurs a setup or activation cost that does not depend on how much of its capacity is actually utilized. Consequently, the cost for moving goods between a supply location and a demand location increases in a stepwise fashion, as the number of required vehicles rises with the total shipment volume. The cost function, combining a linear variable component with a discontinuous stepwise fixed component, captures an important feature abstracted from real-world logistics problems and motivates our theoretical investigation. Beyond this, actual logistics systems are more complex, involving dynamic demand, multimodal transportation, and other intricate factors that are also worth studying.

This stepwise cost structure makes the problem fundamentally different from the classical FCTP. While the FCTP already introduces combinatorial complexity through binary route-activation decisions, the vehicle-based cost structure adds another layer of difficulty, as the model must determine not only whether a route is used but also how many capacity-constrained vehicles are required. These characteristics significantly increase the modeling complexity and hinder the scalability of exact algorithms. However, this practically relevant setting has received limited attention, leaving a research gap between theoretical transportation models and real-world logistics systems where setup costs vary in discrete steps. As FCTP is a well-known NP-hard problem [2], and TPSC constitutes a strict generalization of FCTP, the NP-hardness of TPSC follows immediately. Consequently, solution times grow rapidly with problem size, motivating the development of new modeling and optimization techniques to bridge theory and practice in transportation planning.

To address these challenges, this paper makes the following contributions:

• We formulate a mixed-integer programming (MIP) model. Structural properties of optimal solutions are analyzed, revealing that they may be non-basic and providing insights for neighborhood design in local search.
• To overcome the weak relaxation of the base model, we propose a variable discretization reformulation and two classes of valid inequalities that significantly tighten bounds. A row-and-column generation (RCG) algorithm is then developed to dynamically introduce only essential variables and constraints for large-scale instances.
• A variable neighborhood descent (VND) is proposed to obtain the feasible solution from the fractional solution via rounding and refine it through problem-specific neighborhoods.
• Extensive experiments on benchmark instances demonstrate that the proposed method markedly improves lower bounds, yields near-optimal feasible solutions, and consistently outperforms direct MIP solvers in both quality and efficiency.

The remainder of this paper is organized as follows. Section 2 reviews related work on fixed-charge transportation problems. Section 3 introduces the problem definition and formulates the baseline mixed-integer programming model, together with the structural properties of optimal solutions. Section 4 presents the reformulation, valid inequalities, and the proposed bounding framework, which combines a row-and-column generation algorithm with a VND-based local search. Section 5 reports the computational results, and Section 6 concludes the paper with remarks and directions for future research.

2. Related Literature

The transportation problem has long been recognized as a fundamental research topic with broad applications in social and economic activities. Since the pioneering formulation by Hitchcock [3] in the context of production organization and rail transport, a substantial body of work has emerged. Subsequent contributions by Kantorovitch [4] and Chanas et al. [5] further enriched both the theoretical foundation and practical applications of TP. As research progressed and practical needs evolved, numerous variants of TP were introduced. In this study, we focus on the fixed-charge transportation problem (FCTP) and review the relevant literature in this domain.

Hirsch and Dantzig [6] first introduced the FCTP, establishing its mathematical formulation and proving that optimal solutions lie at extreme points of the feasible region. Building on this foundation, researchers have proposed numerous extensions and solution approaches. For example, Yang and Feng [7] considered a time-constrained FCTP that incorporates both cost and time dimensions, solved via tabu search. Buson et al. [8] developed a reduced-cost iterated local search heuristic for large-scale instances, while Fisk and McKeown [9] examined the pure FCTP and proposed a direct search method that exploits the embedded 0–1 knapsack structure. Mondal et al. [10] formulated multi-objective FCTP models with quantity-dependent costs and discount policies, solved via hybrid metaheuristics based on the artificial bee colony algorithm. Kartli [11] proposed integrated heuristic–metaheuristic algorithms that enhance solution quality for medium-sized instances. Zhu et al. [12] established new NP-hardness results and approximation schemes for the pure FCTP, whereas Allahdadi and Rivaz [13] extended FCTP formulations to rough interval uncertainty, broadening linear programming applications under imprecise data.

More complex logistics environments have also been explored. Adlakha et al. [14] designed a more-for-less heuristic for large-scale assignment-type FCTPs. Klose [15] studied the single-source variant of the problem. Xie and Jia [16] introduced a nonlinear FCTP, which was solved using a hybrid genetic algorithm. Safi and Razmjoo [17] considered interval-valued parameters and proposed solution schemes based on ordering relations of interval numbers. Pramanik et al. [18] modeled two-stage supply chain networks under Gaussian fuzzy settings, while Giri et al. [19] investigated fully fuzzy multi-item FCTPs. Paraskevopoulos et al. [20] studied multi-commodity transportation networks with fixed charges and proposed hybrid heuristics for effective solutions. Balaji et al. [21] introduced capacity constraints, solving them with genetic algorithms and simulated annealing. Cosma et al. [22,23] studied two-stage supply chain and transportation problems with fixed costs, introducing hybrid genetic algorithms and parallel methods that improve solution quality and scalability. From an exact optimization perspective, Legault et al. [24] developed a novel reformulation for the single-sink FCTP, significantly tightening relaxations and improving branch-and-cut efficiency. Most recently, Kartli et al. [25] proposed a new heuristic for the classical FCTP, demonstrating superior performance on benchmark tests.

Most of these studies assume that fixed costs are triggered solely by activating a route, independent of shipment size. In practice, however, transportation often involves more complex structures. For example, when inventory constraints or vehicle capacities require multi-stage shipments, fixed costs may increase once a shipment exceeds certain volume thresholds. This gives rise to the so-called step or two-step FCTP. Kowalski and Lev [26] analyzed structural properties of this variant, while El-Sherbiny [27] formulated it mathematically and proposed a mutation-based artificial immune algorithm for its solution. Collectively, these works illustrate complementary progress through metaheuristics, parallelization, and reformulation-based exact methods, offering valuable insights for tackling complex stepwise fixed-charge transportation problems. However, most existing approaches remain limited to simplified stepwise or two-step settings and do not explicitly capture the discrete activation of capacity-constrained vehicles. Moreover, few studies combine lower-bound strengthening with high-quality feasible solution generation in a unified framework, leaving room for methodological improvement.

This study differs from prior work by extending the two-step FCTP to a more realistic setting that explicitly incorporates vehicle capacity limits and activation-based stepwise costs. In the proposed formulation, each deployed vehicle incurs a fixed cost regardless of load, making the total fixed transportation cost a stepwise function of the number of vehicles used. This structure better reflects real logistics operations and introduces new modeling and computational challenges that existing approaches have not addressed.

3. Problem Formulation

To rigorously analyze the TPSC, we now present its formal problem formulation, including problem description, mixed-integer programming model, structural properties of optimal solutions, and its linear relaxation.

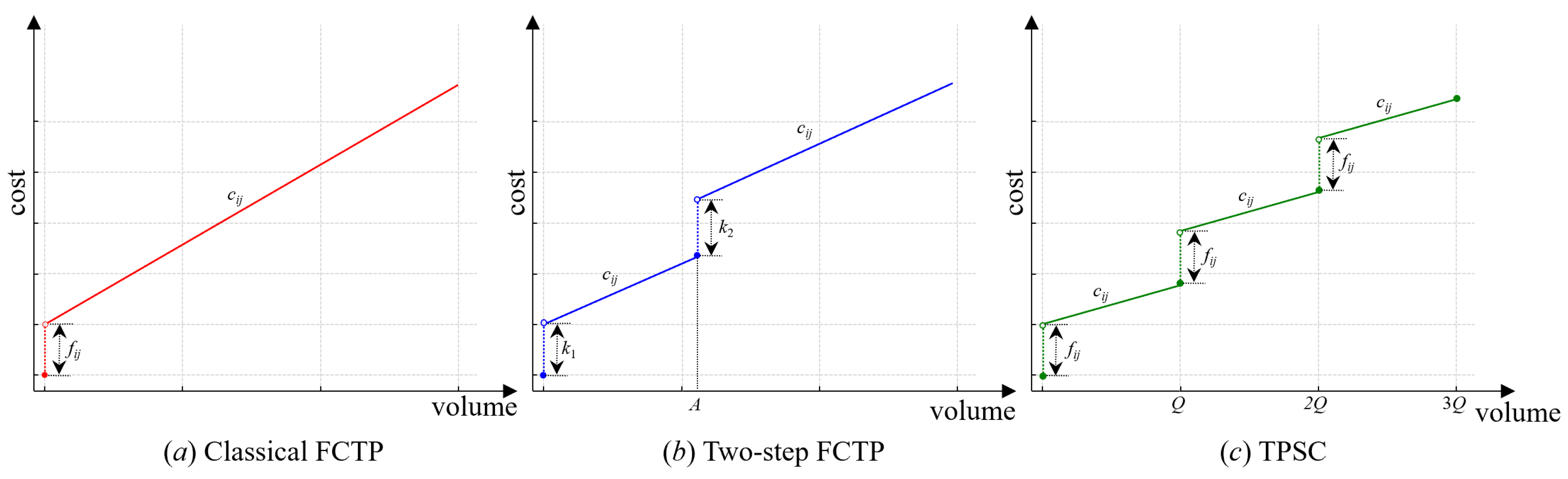
3.1. Problem Description

The TPSC can be formally described as follows. Consider a set of n supply nodes and a set of m demand nodes. The production capacity at each supply node and the demand requirement at each demand node are known in advance. Goods produced at any supply node can be delivered to any demand node. A single type of transport vehicle is used, each with limited capacity Q. During transportation, vehicles are loaded as fully as possible; however, when the volume transported is less than the vehicle capacity, one vehicle must still be deployed. The transportation cost consists of two parts: (i) a variable cost, which is proportional to the shipment volume, and (ii) a setup cost, which corresponds to the activation of a vehicle. Each time a vehicle is used, a setup cost is incurred regardless of whether the vehicle is fully loaded. The objective is to minimize the total transportation cost so that all supply, demand, and capacity constraints are satisfied.

Figure 1a shows the cost structure of the classical FCTP, where transport costs consist of variable costs proportional to shipment volume and fixed costs that are independent of volume but incurred whenever a route is used. The two-step FCTP is an extension of this model, which has been comprehensively studied by Kowalski et al. [26]. Its cost structure is illustrated in Figure 1b, where parameter A denotes a threshold of transported volume. If the shipment does not exceed A, the fixed cost is $k_1$; if it exceeds A, an additional fixed cost $k_2$ is incurred. Figure 1c depicts the cost function of the TPSC. As shown, the total setup cost depends on the number of vehicles activated: each deployed vehicle generates a fixed cost, and even if the vehicle is not fully loaded, the full setup cost of one vehicle is still applied.

3.2. Mixed-Integer Programming Model

The symbols and notation appearing in the model and in later sections are listed as follows:

• S: set of supply nodes, indexed by i.
• T: set of demand nodes, indexed by j.
• E: set of arcs from supply to demand, indexed by e.
• n: number of supply nodes.
• m: number of demand nodes.
• $c_{ij}$: unit transportation cost from supply node i to demand node j.
• $f_{ij}$: fixed setup cost of deploying one vehicle from supply node i to demand node j.
• $a_i$: available supply at node i.
• $b_j$: demand requirement at node j.
• $v_{ij}$: maximum transportable quantity from supply node i to demand node j, defined as $v_{ij}=min\{a_i,b_j\}$.
• Q: loading capacity of a single vehicle.
• $x_{ij}$: quantity shipped from supply node i to demand node j.
• $y_{ij}$: number of vehicles used to transport goods from i to j.

We assume that all supply quantities $a_i$, demand requirements $b_j$, and vehicle capacity Q are integer-valued. Moreover, the total supply is required to match the total demand, i.e., ${\sum }_{i\in S}{a}_i={\sum }_{j\in T}{b}_j$, which ensures the feasibility of the flow balance constraints. With these modeling assumptions and notation, a MIP formulation of the TPSC is given as follows:

$$\begin{array}{cc}\hfill \mathbf{\left(}{\mathbf{F}}_{\mathbf{0}}\mathbf{\right)} min & \sum _{i\in S}\sum _{j\in T}\left(c_{ij} x_{ij}+f_{ij} y_{ij}\right)\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill \mathrm{s}.\mathrm{t}. & \sum _{j\in T}{x}_{ij}=a_i,\forall i\in S\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill & \sum _{i\in S}{x}_{ij}=b_j,\forall j\in T\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill & x_{ij}\le Q y_{ij},\forall i\in S, \forall j\in T\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill & 0\le x_{ij}\le v_{ij},\forall i\in S, \forall j\in T\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill & y_{ij}\in {\mathbb{Z}}_{+},\forall i\in S, \forall j\in T\hfill \end{array}$$

(6)

The objective function (1) minimizes the total transportation cost, consisting of variable costs proportional to shipment volumes and fixed setup costs incurred by vehicle activation. Constraint (2) enforces supply conservation by requiring that the total outbound flow from each supply node equals its available production. Constraint (3) ensures demand satisfaction at each demand node. Constraint (4) imposes the vehicle capacity limit by linking the shipped volume on each route to the number of activated vehicles. Constraint (5) defines the feasible domain of shipment volumes. Finally, constraint (6) specifies that the number of vehicles is a nonnegative integer.

3.3. Properties of the Optimal Solution

Before presenting the reformulation and algorithmic framework, we first investigate the structural properties of the optimal solution, which provide important insights for model strengthening and algorithm design.

Proposition 1.

For the TPSC, an optimal solution is not necessarily a basic feasible solution (BFS) of the associated linear programming relaxation.

Proof. 

To verify this property, consider the following instance. $\left|S\right|=\left|T\right|=2, a_1=20, a_2=10, b_1=10, b_2=20, Q=3, c_{11}=10, c_{12}=10, c_{21}=20, c_{22}=10, f_{11}=f_{12}=f_{21}=f_{22}=30$. The balance constraints (2) and (3) yield $x_{12}=20-x_{11}, x_{21}=10-x_{11}, x_{22}=x_{11}, 0\le x_{11}\le 10.$ Hence, the feasible region of the transportation polytope is the line segment $\{(x_{11}, 20-x_{11}, 10-x_{11}, x_{11}):0\le x_{11}\le 10\},$ whose extreme points (and thus basic feasible solutions) occur at the endpoints: $x^{B_1}=(10,10,0,10)$ and $x^{B_2}=(0,20,10,0).$ Therefore, this instance admits exactly two BFS.

Let $x^{\prime }=\lambda x^{B_1}+(1-\lambda )x^{B_2}=(10\lambda , 20-10\lambda , 10(1-\lambda ), 10\lambda )$ with $0<\lambda <1$, so that $x^{\prime }$ is a strict convex combination of $x^{B_1}$ and $x^{B_2}$, and hence a feasible solution. Its objective value is

$$\begin{array}{c}\hfill z\left(x^{\prime }\right)=(400-100\lambda )+30· \left(⌈\frac{10\lambda }{3}⌉+⌈\frac{20-10\lambda }{3}⌉+⌈\frac{10(1-\lambda )}{3}⌉+⌈\frac{10\lambda }{3}⌉\right)\end{array}$$

(7)

Since the numerators of the terms inside the ceiling functions ($10\lambda$, $20-10\lambda$, and $10(1-\lambda )$) share a common multiple of 10, the ceiling values change only when these numerators cross multiples of 3. Consequently, the ceiling terms vary only at the breakpoints $\lambda \in \{0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9\}$. On each open interval between breakpoints, the second term of (7) is constant, and the first term strictly decreases in $\lambda$; therefore, the minimum over $(0,1)$ is reached at a breakpoint. Evaluating $z\left(\lambda \right)$ at these breakpoints gives $z\left(0.1\right)=750, z\left(0.2\right)=710, z\left(0.3\right)=700, z\left(0.4\right)=720, z\left(0.5\right)=680, z\left(0.6\right)=670, z\left(0.7\right)=690, z\left(0.8\right)=650, z\left(0.9\right)=640.$ Hence, the minimum over $0<\lambda <1$ is achieved at $\lambda =0.9$, with $x^{\prime }=(9,11,1,9)$ and $z\left(x^{\prime }\right)=640.$

The objective values of BFSs $x^{B_1}$ and $x^{B_2}$ are as follows:

$$\begin{array}{cc}\hfill z\left(x^{B_1}\right)& =10·(10+10+10)+30·\left(⌈{\displaystyle \frac{10}{3}}⌉+⌈{\displaystyle \frac{10}{3}}⌉+⌈{\displaystyle \frac{10}{3}}⌉\right)=660,\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill z\left(x^{B_2}\right)& =10·20+20·10+30·\left(⌈{\displaystyle \frac{20}{3}}⌉+⌈{\displaystyle \frac{10}{3}}⌉\right)=730.\hfill \end{array}$$

(9)

Thus, we have

$$\begin{array}{c}\hfill z\left(x^{\prime }\right)=640<min\{660,730\}=min\{z\left(x^{B_1}\right),z\left(x^{B_2}\right)\}.\end{array}$$

(10)

Since $x^{\prime }$ has four positive components while $m+n-1=3$, it is not a BFS. Therefore, there exists an optimal solution that is not a basic feasible solution.    □

The above example demonstrates that, unlike the classical transportation problem (TP), where every optimal LP solution can be chosen as a basic feasible solution (BFS), the transportation problem with stepwise costs (TPSC) may admit an optimal solution that is feasible but not basic. This structural difference carries two important implications. First, simplex-type algorithms, which traverse from one BFS to another, may fail to encounter certain optimal points that arise as convex combinations of BFSs, revealing a richer and more intricate relaxation geometry. Second, the existence of non-BFS optimal solutions provides theoretical motivation for designing advanced algorithms that move beyond simplex pivots. Since fractional vehicle variables $y_{ij}$ naturally appear in the relaxation, this structure can be exploited to construct tailored valid inequalities, rounding rules, or neighborhood moves within metaheuristic frameworks. In particular, the fact that optimality may occur at non-extreme points highlights the value of polyhedral strengthening and decomposition-based methods over pure simplex or direct branching approaches.

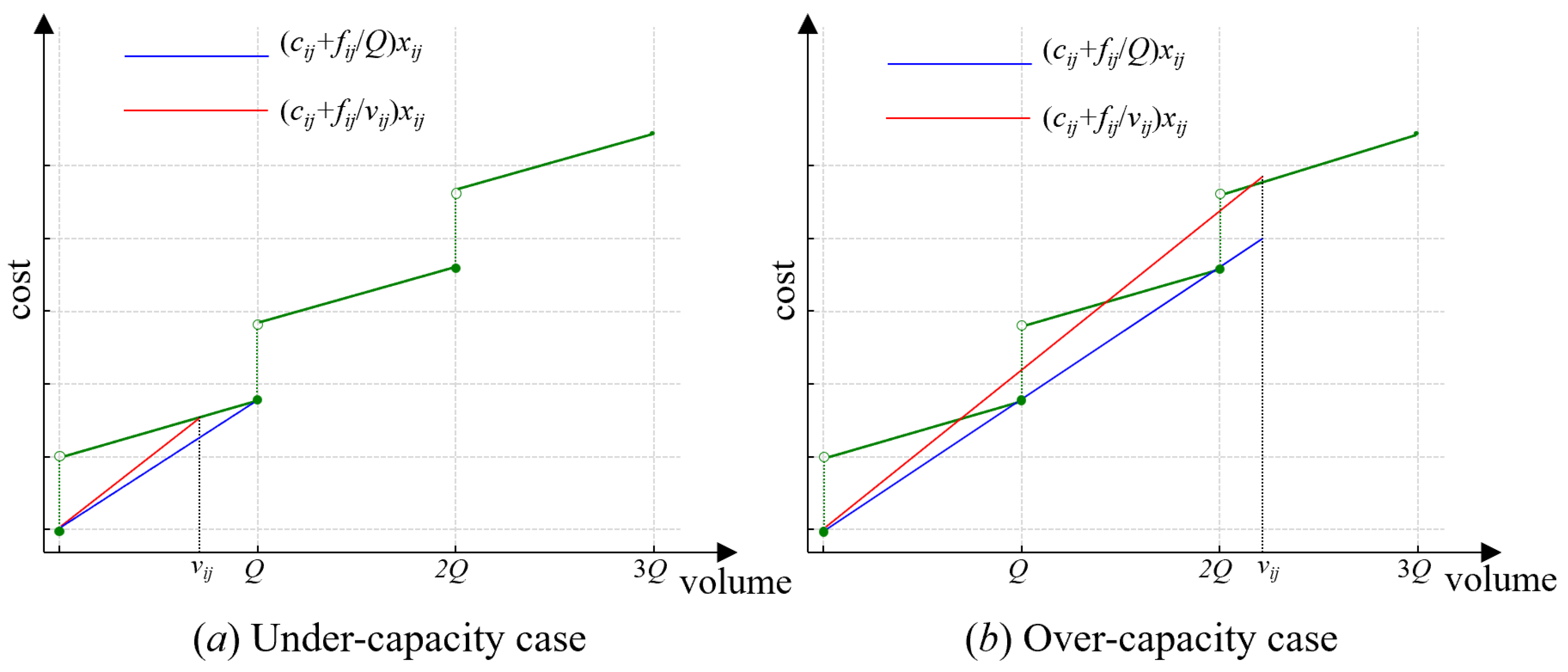
3.4. Linear Relaxation Model

In order to obtain a valid lower bound for $F_0$, we consider its LP relaxation, denoted by $L{F}_0$. The LP relaxation is obtained by relaxing the integrality requirements of the vehicle variables $y_{ij}$ while keeping all other constraints unchanged. This relaxation provides a tractable approximation of the original problem and serves as the basis for further reformulation and strengthening techniques developed in the subsequent sections.

From constraint (4), $x_{ij}\le Q y_{ij}$, and from constraint (5), $x_{ij}\le v_{ij}$. The shipment on arc $(i,j)$ must satisfy both: if $Q\le v_{ij}$, the capacity $Q y_{ij}$ dominates; otherwise the bound $v_{ij}$ is binding. The linear relaxation of $y_{ij}$ thus depends on the relation between $v_{ij}$ and Q.

Figure 2 illustrates how the relaxed transportation cost varies with shipment volume under the two cases. When $v_{ij}<Q$, the cost curve in Figure 2a corresponds to the red line, representing the objective of the linear relaxation. Conversely, when $v_{ij}\ge Q$, the curve in Figure 2b corresponds to the lower blue line, which depicts the relaxed objective function, ensuring that it never exceeds the original piecewise linear cost function for any shipment volume.

We define an auxiliary variable ${\overline{y}}_{ij}$ to represent the relaxed number of vehicles under the two cases:

$$\begin{array}{c}\hfill {\overline{y}}_{ij}=\left\{\begin{array}{cc}{\displaystyle \frac{x_{ij}}{Q}},\hfill & \mathrm{if} v_{ij}\ge Q,\hfill \\ {\displaystyle \frac{x_{ij}}{v_{ij}}},\hfill & \mathrm{if} v_{ij}<Q.\hfill \end{array}\right.\end{array}$$

(11)

In summary, the linear relaxation model ($L{F}_0$) can be written as

$$\begin{array}{cc}\hfill \mathbf{\left(}{\mathbf{LF}}_{\mathbf{0}}\mathbf{\right)} min& \sum _{i\in S}\sum _{j\in T}\left(c_{ij}+{\displaystyle \frac{f_{ij}}{min(Q,v_{ij})}}\right)x_{ij}\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill \mathrm{s}.\mathrm{t}. & \sum _{j\in T}{x}_{ij}=a_i,\forall i\in S\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill & \sum _{i\in S}{x}_{ij}=b_j,\forall j\in T\hfill \end{array}$$

(14)

In $L{F}_0$, the coefficients in constraints (13) and (14) are all equal to one, so the constraint matrix is totally unimodular. Since both the supply values $a_i$ and the demand values $b_j$ are integers, the relaxation $L{F}_0$ always admits an integer optimal solution.

4. Solution Method

To tackle the computational intractability of the mixed-integer model $F_0$ on large-scale instances—and the weak bounds provided by its linear relaxation $L{F}_0$—this section develops a reformulation-based bounding procedure. We first apply a variable splitting scheme to obtain an equivalent discretized model $F_1$, which preserves optimality while exposing additional structure. We then strengthen the linear relaxation $L{F}_1$ by introducing two families of valid inequalities—namely rounding inequalities and subset-cover inequalities—to tighten the lower bound and shrink the feasible region of the relaxation. Building on the reconstructed model, we design an RCG algorithm that starts from a restricted master problem and dynamically adds only the necessary rows and columns. This procedure iteratively produces improved lower bounds and dual solutions, enabling scalable exact optimization for large problem instances.

4.1. Discretized Reformulation

By discretizing the shipment volume on each route, the continuous decision variable $x_{ij}$ in the model $F_0$ is represented by a family of binary variables, which simplifies the model structure and exposes additional combinatorial properties. After incorporating valid inequalities, the discretized model can be efficiently solved using the RCG algorithm to obtain strong lower bounds as well as dual information to guide the search direction.

Based on model $F_0$, the transportation network is discretized into a set of arcs representing possible shipment quantities between supply and demand nodes. For any arc $(i,j)$, the feasible shipment volume q lies in $[1,v_{ij}]$, where $v_{ij}=min\{a_i,b_j\}$; when $q=0$, no goods are transported along that route. For each feasible shipment volume q, we define a binary variable:

$${\eta }_{ij}^q=\left\{\begin{array}{cc}1,\hfill & \mathrm{if} \mathrm{the} \mathrm{transported} \mathrm{quantity} \mathrm{from} i \mathrm{to} j \mathrm{equals} q,\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

Thus, the shipment variable $x_{ij}$ in $F_0$ can be expressed as

$$x_{ij}=\sum _{q=1}^{v_{ij}}q {\eta }_{ij}^q.$$

(15)

Let $g_{ij}^q$ denote the total cost (variable plus fixed) when q units are shipped from i to j, i.e.,

$$g_{ij}^q=\left\{\begin{array}{cc}{c}_{ij}q+f_{ij}⌈{\displaystyle \frac{q}{Q}}⌉,\hfill & \mathrm{if} v_{ij}\ge Q\hfill \\ c_{ij}q+f_{ij},\hfill & \mathrm{if} v_{ij}<Q.\hfill \end{array}\right.$$

(16)

The discretized model $F_1$ is then formulated as

$$\begin{array}{cc}\hfill \mathbf{\left(}{\mathbf{F}}_{\mathbf{1}}\mathrm{\right)} min & \sum _{i\in S}\sum _{j\in T}\sum _{q=1}^{v_{ij}}{g}_{ij}^q {\eta }_{ij}^q\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill \mathrm{s}.\mathrm{t}. & \sum _{j\in T}\sum _{q=1}^{v_{ij}}q {\eta }_{ij}^q=a_i,\forall i\in S,\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill & \sum _{i\in S}\sum _{q=1}^{v_{ij}}q {\eta }_{ij}^q=b_j,\forall j\in T,\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill & {\eta }_{ij}^q\in \{0,1\},\forall (i,j)\in E, q=1,\dots ,v_{ij}.\hfill \end{array}$$

(20)

The objective function (17) minimizes the total transportation cost across all supply–demand pairs. Constraints (18) ensure that the total quantity shipped from each supply node i equals its available supply $a_i$, while constraints (19) guarantee that each demand node j receives the required quantity $b_j$. Finally, constraints (20) define binary variables ${\eta }_{ij}^q$, indicating whether the q-th replicated arc of $(i,j)$ is used.

Relaxing the constraint (20) yields the linear relaxation, denoted as $L{F}_1$. We next present several propositions that describe its key properties.

Proposition 2.

The linear relaxations $L{F}_0$ and $L{F}_1$ have the same optimal value, i.e., $z\left(L{F}_0\right)=z\left(L{F}_1\right)$.

Proof. 

Let $\widehat{\eta }$ be an optimal solution to $L{F}_1$. In $L{F}_1$, the binary constraints on ${\eta }_{ij}^q$ are relaxed to $0\le {\eta }_{ij}^q\le 1$. Define the induced shipment variables ${\widehat{x}}_{ij}={\sum }_{q=1}^{v_{ij}}q {\widehat{\eta }}_{ij}^q,(i,j)\in E.$ Since $\widehat{\eta }$ satisfies (18) and (19), it follows that $\widehat{x}$ satisfies the supply and demand balance constraints of $L{F}_0$, (13) and (14). Hence, the induced vector $\widehat{x}$ is feasible to $L{F}_0$.

For each $(i,j)\in E$ and each $q\le v_{ij}$, using (16) we obtain

$$\begin{array}{c}\hfill g_{ij}^q=\left\{\begin{array}{cc}{c}_{ij}q+f_{ij}⌈q/Q⌉ \ge \left(c_{ij}+{\displaystyle \frac{f_{ij}}{Q}}\right)q,\hfill & v_{ij}\ge Q,\hfill \\ c_{ij}q+f_{ij} \ge \left(c_{ij}+{\displaystyle \frac{f_{ij}}{v_{ij}}}\right)q,\hfill & v_{ij}<Q,\hfill \end{array}\right.\end{array}$$

(21)

which yields

$$\begin{array}{c}\hfill \sum _{q=1}^{v_{ij}}{g}_{ij}^q {\widehat{\eta }}_{ij}^q \ge \left(c_{ij}+{\displaystyle \frac{f_{ij}}{min(Q,v_{ij})}}\right)\sum _{q=1}^{v_{ij}}q {\widehat{\eta }}_{ij}^q=\left(c_{ij}+{\displaystyle \frac{f_{ij}}{min(Q,v_{ij})}}\right){\widehat{x}}_{ij}.\end{array}$$

(22)

Summing over all arcs $(i,j)\in E$ gives

$$\begin{array}{c}\hfill \sum _{(i,j)\in E}\sum _{q=1}^{v_{ij}}{g}_{ij}^q {\widehat{\eta }}_{ij}^q \ge \sum _{(i,j)\in E}\left(c_{ij}+{\displaystyle \frac{f_{ij}}{min(Q,v_{ij})}}\right){\widehat{x}}_{ij}.\end{array}$$

(23)

Since $\widehat{\eta }$ is optimal for $L{F}_1$, the left-hand side is exactly $z\left(L{F}_1\right)$. The right-hand side equals the objective value of $L{F}_0$ evaluated at its feasible solution $\widehat{x}$. Therefore, the optimal value of $L{F}_1$ is no smaller than that of $L{F}_0$, i.e., $z\left(L{F}_1\right)\ge z\left(L{F}_0\right)$.

We now prove the converse. Let $\widehat{x}$ be any feasible solution to $L{F}_0$. We construct $\widehat{\eta }$ such that ${\sum }_{q=1}^{v_{ij}}q {\widehat{\eta }}_{ij}^q={\widehat{x}}_{ij}$ for all $(i,j)\in E$.

For arcs with $v_{ij}<Q$, set ${\widehat{\eta }}_{ij}^{v_{ij}}={\widehat{x}}_{ij}/v_{ij}$ and ${\widehat{\eta }}_{ij}^q=0$ for $q\ne v_{ij}$. Then $0\le {\widehat{\eta }}_{ij}^{v_{ij}}\le 1$, ${\sum }_{q}q {\widehat{\eta }}_{ij}^q={\widehat{x}}_{ij}$, and

$$\begin{array}{c}\hfill \sum _q{g}_{ij}^q {\widehat{\eta }}_{ij}^q=(c_{ij}{v}_{ij}+f_{ij}){\displaystyle \frac{{\widehat{x}}_{ij}}{v_{ij}}}=\left(c_{ij}+{\displaystyle \frac{f_{ij}}{v_{ij}}}\right){\widehat{x}}_{ij}.\end{array}$$

(24)

For arcs with $v_{ij}\ge Q$, let $m=\lfloor v_{ij}/Q\rfloor$ and $r={\widehat{x}}_{ij}/Q$. Define $t_k\in [0,1]$ for $k=m,m-1,\dots ,1$ by

$$\begin{array}{c}\hfill t_k=min \left\{1, {\displaystyle \frac{r-{\sum }_{\ell =k+1}^m\ell t_{\ell }}{k}}\right\},\end{array}$$

(25)

so that ${\sum }_{k=1}^{m}k t_k=r$. Set ${\widehat{\eta }}_{ij}^{kQ}=t_k$ for $k=1,\dots ,m$, and ${\widehat{\eta }}_{ij}^q=0$ for all other q. Then ${\sum }_{q}q {\widehat{\eta }}_{ij}^q={\widehat{x}}_{ij}$, and using $g_{ij}^{kQ}=c_{ij}\left(kQ\right)+f_{ij}k$,

$$\begin{array}{c}\hfill \sum _q{g}_{ij}^q {\widehat{\eta }}_{ij}^q=\sum _{k=1}^m\left(c_{ij}kQ+f_{ij}k\right)t_k=\left(c_{ij}+{\displaystyle \frac{f_{ij}}{Q}}\right){\widehat{x}}_{ij}.\end{array}$$

(26)

Thus, in both cases,

$$\begin{array}{c}\hfill \sum _q{g}_{ij}^q {\widehat{\eta }}_{ij}^q=\left(c_{ij}+{\displaystyle \frac{f_{ij}}{min(Q,v_{ij})}}\right){\widehat{x}}_{ij}, \forall (i,j)\in E.\end{array}$$

(27)

Summing over all arcs,

$$\begin{array}{c}\hfill \sum _{(i,j)\in E}\sum _q{g}_{ij}^q {\widehat{\eta }}_{ij}^q=\sum _{(i,j)\in E}\left(c_{ij}+{\displaystyle \frac{f_{ij}}{min(Q,v_{ij})}}\right){\widehat{x}}_{ij}.\end{array}$$

(28)

The left-hand side is the objective value of $L{F}_1$ at $\widehat{\eta }$, and the right-hand side is the objective value of $L{F}_0$ at $\widehat{x}$. Since $\widehat{x}$ was arbitrary among feasible solutions of $L{F}_0$, we conclude that $z\left(L{F}_1\right)\le z\left(L{F}_0\right).$

Combining the two inequalities proves $z\left(L{F}_1\right)=z\left(L{F}_0\right).$    □

The lower bound provided by $L{F}_1$ coincides with that of $L{F}_0$. Although $L{F}_1$ introduces additional binary-structured variables and is therefore less attractive to solve directly for bounding purposes, it enables the introduction of strong valid inequalities. This structural advantage makes $L{F}_1$ a more effective foundation for tightening relaxations and improving the quality of lower bounds.

4.2. Valid Inequalities

The Chvátal–Gomory (CG) cut [28] is a classical cutting-plane technique for integer programming. Given a valid linear inequality $u^{\top }x\le \beta$ for the LP relaxation and an integer vector x, the inequality ${\lfloor u\rfloor }^{\top }x\le \lfloor \beta \rfloor$ is also valid for all integer-feasible x.

Based on constraint (18), for any supply site $i\in S$, define a positive integer parameter $\sigma$ within the range $1<\sigma <a_i$. According to the CG-cut procedure, by applying floor rounding on a term-by-term basis, we obtain the following valid inequality:

$$\sum _{j\in T}\sum _{q=1}^{v_{ij}}⌊{\displaystyle \frac{q}{\sigma }}⌋{\eta }_{ij}^q\le ⌊{\displaystyle \frac{a_i}{\sigma }}⌋, \forall (i,\sigma )\in {\mathcal{R}}^1,$$

(29)

where ${\mathcal{R}}^1$ denotes the set of all pairs $(i,\sigma )$, i.e., ${\mathcal{R}}^1=\{(i,\sigma ):i\in S, \sigma \in {\mathbb{Z}}_{+}, 1<\sigma <a_i\}$.

By applying the same procedure to constraint (19), we obtain another valid inequality:

$$\sum _{i\in S}\sum _{q=1}^{v_{ij}}⌊{\displaystyle \frac{q}{\sigma }}⌋{\eta }_{ij}^q\le ⌊{\displaystyle \frac{b_j}{\sigma }}⌋, \forall (j,\sigma )\in {\mathcal{R}}^2,$$

(30)

where ${\mathcal{R}}^2$ denotes the set of all pairs $(j,\sigma )$, i.e., ${\mathcal{R}}^2=\{(j,\sigma ):j\in T, \sigma \in {\mathbb{Z}}_{+}, 1<\sigma <b_j\}$.

Moreover, for inequalities (29) and (30), replacing the floor operator with the ceiling operator reverses the inequality direction, thereby yielding two additional valid inequalities:

$$\sum _{j\in T}\sum _{q=1}^{v_{ij}}⌈{\displaystyle \frac{q}{\sigma }}⌉{\eta }_{ij}^q\ge ⌈{\displaystyle \frac{a_i}{\sigma }}⌉, \forall (i,\sigma )\in {\mathcal{R}}^1,$$

(31)

$$\sum _{i\in S}\sum _{q=1}^{v_{ij}}⌈{\displaystyle \frac{q}{\sigma }}⌉{\eta }_{ij}^q\ge ⌈{\displaystyle \frac{b_j}{\sigma }}⌉, \forall (j,\sigma )\in {\mathcal{R}}^2.$$

(32)

Subset-cover inequalities, originally studied in the context of set-covering [29] and vehicle-routing problems [30], constitute a well-known family of strong valid inequalities for capacitated problems. They exploit the relationship between limited supply (or capacity) and excessive demand to identify infeasible fractional solutions that satisfy the basic balance constraints but cannot correspond to any feasible integer solution. By enforcing that the excess demand of any subset of customers must be covered by vehicles or supplies outside a chosen subset, these inequalities significantly tighten the LP relaxation and are widely used in branch-and-cut algorithms for capacitated network design and vehicle routing.

The core idea of the subset-cover inequality in our context is as follows. Let $K\subseteq S$ denote a subset of supply nodes and $L\subseteq T$ denote a subset of demand nodes. If the total demand of L exceeds the total supply of K, i.e.,

$$\sum _{j\in L}{b}_j > \sum _{i\in K}{a}_i,$$

(33)

then part of the demand in L must necessarily be satisfied by supplies from $S\setminus K$. Consequently, the number of vehicles dispatched from $S\setminus K$ to L cannot be less than the shortage between the two quantities divided by the vehicle capacity Q.

Formally, let $\mathcal{C}$ denote the set of all pairs $(K,L)$ satisfying condition (33). For every $(K,L)\in \mathcal{C}$, the following subset-cover inequality holds:

$$\sum _{i\in S\setminus K}\sum _{j\in L}{y}_{ij} \ge ⌈{\displaystyle \frac{{\sum }_{j\in L}{b}_j-{\sum }_{i\in K}{a}_i}{Q}}⌉, \forall (K,L)\in \mathcal{C}.$$

(34)

By noting that $y_{ij}={\sum }_{q=1}^{v_{ij}}⌈\frac{q}{Q}⌉{\eta }_{ij}^q$, inequality (34) can be equivalently reformulated as

$$\sum _{i\in S\setminus K}\sum _{j\in L}\sum _{q=1}^{v_{ij}}⌈\frac{q}{Q}⌉{\eta }_{ij}^q \ge ⌈{\displaystyle \frac{{\sum }_{j\in L}{b}_j-{\sum }_{i\in K}{a}_i}{Q}}⌉, \forall (K,L)\in \mathcal{C}.$$

(35)

By incorporating inequalities (29)–(32) and  (35) into the constraints of ${\mathbf{LF}}_{\mathbf{1}}$, we obtain the relaxed model with valid inequalities, denoted as ${\mathbf{LF}}_{\mathbf{2}}$.

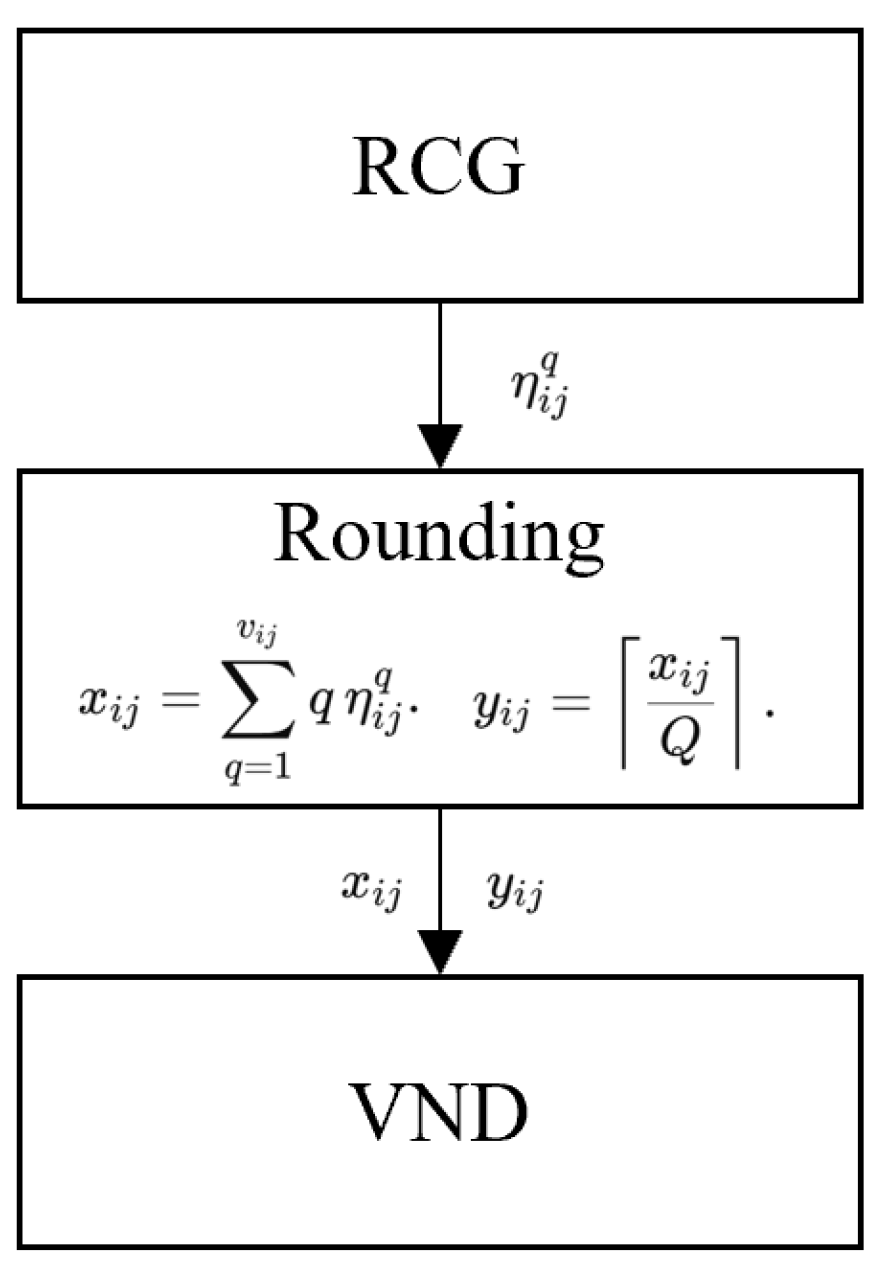
4.3. Lower Bounding Procedure

In the ${\mathbf{LF}}_{\mathbf{2}}$ model, there are ${\sum }_{i=1}^n{\sum }_{j=1}^m{v}_{ij}$ variables and at least $\left|m\right|+\left|n\right|+2{\sum }_{i=1}^n(a_i-2)+2{\sum }_{j=1}^m(b_j-2)+\left|\mathcal{C}\right|$ constraints. Even for small-scale instances, the number of constraints becomes extremely large. In particular, there exist exponentially many combinations $(K,L)$, implying that $\left|\mathcal{C}\right|$ grows exponentially. Therefore, although ${\mathbf{LF}}_{\mathbf{2}}$ is a linear program, solving it directly to optimality (or even near-optimality) in a reasonable time is highly challenging for standard optimization solvers such as CPLEX. To address this difficulty, we solve it within an RCG framework.

At each iteration, only a restricted subset of columns (variables) and rows (valid inequalities) of $L{F}_2$ are maintained in a restricted master problem (RMP). The RMP, which can be regarded as a tractable approximation of the full linear relaxation, is solved to optimality, yielding both primal and dual solutions. Based on the dual information, new variables with negative reduced costs are identified by evaluating the reduced costs.

Let ${\alpha }_i$ and ${\beta }_j$ denote the dual variables associated with the supply and demand balance constraints (18) and (19); ${\varphi }_{i\sigma }$ and ${\psi }_{j\sigma }$ the dual variables corresponding to the CG-cuts (29) and (30) with “≤” inequalities; ${\xi }_{i\sigma }$ and ${\zeta }_{j\sigma }$ the dual variables associated with the CG-cuts (31) and (32) with “≥” inequalities; and ${\gamma }_{KL}$ the dual variables corresponding to the subset-cover inequalities (35). The reduced cost of each variable ${\eta }_{ij}^q$ excluded from the current RMP is computed as follows.

$$\begin{array}{cc}\hfill R{C}_{ij}^q=& g_{ij}^q-q{\alpha }_i-q{\beta }_j-\sum _{\sigma :(i,\sigma )\in {\overline{\mathcal{R}}}^1}⌊\frac{q}{\sigma }⌋{\varphi }_{i\sigma }-\sum _{\sigma :(j,\sigma )\in {\overline{\mathcal{R}}}^2}⌊\frac{q}{\sigma }⌋{\psi }_{j\sigma }-\sum _{\sigma :(i,\sigma )\in {\overline{\mathcal{R}}}^1}⌈\frac{q}{\sigma }⌉{\xi }_{i\sigma }\hfill \\ \hfill & -\sum _{\sigma :(j,\sigma )\in {\overline{\mathcal{R}}}^2}⌈\frac{q}{\sigma }⌉{\zeta }_{j\sigma }-\sum _{\begin{array}{c}(K,L)\in \overline{\mathcal{C}}:i\notin K, j\in L\end{array}}⌈\frac{q}{Q}⌉{\gamma }_{KL},\forall (i,j,q)\in \mathcal{V}\setminus \overline{\mathcal{V}}.\hfill \end{array}$$

(36)

Here, ${\overline{\mathcal{R}}}^1$ denotes the index set of the cuts of types (29) and (31) that have already been generated, ${\overline{\mathcal{R}}}^2$ denotes the index set of the already generated cuts of types (30) and (32), and $\overline{\mathcal{C}}$ denotes the index set of the already generated subset-cover cuts (35). $\mathcal{V}$ and $\overline{\mathcal{V}}$ denote the index sets corresponding to all variables and to the variables that have already been generated, respectively. Columns with negative reduced cost, identified through (36), are added to the RMP. Once no further columns with negative reduced cost can be found, the procedure switches to row generation.

For each of the four families of CG cuts (29)–(32), the most violated inequality is identified by examining the sets ${\mathcal{R}}^1\setminus {\overline{\mathcal{R}}}^1$ and ${\mathcal{R}}^2\setminus {\overline{\mathcal{R}}}^2$. Since there exist exponentially many combinations $(K,L)$, identifying the most violated subset-cover inequality (35) is not straightforward. To achieve this, a dedicated separation problem must be solved.

Given an optimal solution $\overline{\eta }$ to the RMP, the combination $(K^{*},L^{*})\in \mathcal{C}\setminus \overline{\mathcal{C}}$ that most strongly violates inequality (34) can be identified by solving the following auxiliary MIP formulation. Here, ${\overline{\theta }}_{ij}={\sum }_q{\overline{\eta }}_{ij}^q$ represents the total assignment flow from supply i to demand j in the solution $\overline{\eta }$; $u_i$ is a binary variable for each supply node i, with $u_i=0$ if and only if $i\in K^{*}$ and $u_i=1$ otherwise; $v_j$ is a binary variable for each demand node j, with $v_j=1$ if and only if $j\in L^{*}$ and $v_j=0$ otherwise; and ${\delta }_{ij}$ is a binary variable equal to 1 if and only if $i\notin K^{*}$ and $j\in L^{*}$, and 0 otherwise. The model is formulated as follows.

$$\begin{array}{cc}\hfill \left(\mathbf{SP}\right) z^{*}=min & \sum _{i\in S}\sum _{j\in T}{\theta }_{ij}{\delta }_{ij},\hfill \end{array}$$

(37)

$$\begin{array}{cccc}\hfill \mathrm{s}.\mathrm{t}. & {\delta }_{ij}\ge u_i+v_j-1,\hfill & \hfill & \forall (i,j)\in E,\hfill \end{array}$$

(38)

$$\begin{array}{cc}\hfill & \sum _{i\in S}{a}_i{u}_i+\sum _{j\in T}{b}_j{v}_j \ge \sum _{i\in S}{a}_i+1,\hfill \end{array}$$

(39)

$$\begin{array}{cccc}\hfill & {\delta }_{ij}\in \{0,1\},\hfill & \hfill & \forall (i,j)\in E,\hfill \end{array}$$

(40)

$$\begin{array}{cccc}\hfill & u_i\in \{0,1\},\hfill & \hfill & \forall i\in S,\hfill \end{array}$$

(41)

$$\begin{array}{cccc}\hfill & v_j\in \{0,1\},\hfill & \hfill & \forall j\in T.\hfill \end{array}$$

(42)

By solving SP via a MIP solver, if the optimal objective value satisfies $z^{*}<1$, then for the optimal solution $\eta$ of ${\mathbf{LF}}_1$, there exists a subset pair $(K^{*},L^{*})\in \mathcal{C}$ for which inequality (34) is valid, where $K^{*}=\{ i\in S:u_i=0 \}$ and $L^{*}=\{ j\in T:v_j=1 \}$. Otherwise, inequality (34) is not applicable. For further details, the reader is kindly referred to [2], which provides a comprehensive treatment of related techniques for separating subset-cover inequalities in the context of the FCTP.

The iterative process of generating columns and rows continues until no column with a negative reduced cost and no violated inequality can be identified. At this stage, the algorithm converges and terminates, yielding a valid lower bound for the original problem. Notably, the integration of dynamic variable generation with adaptive cut management enables the restricted master problem to remain computationally tractable while progressively approaching the strength of the full relaxation. The overall RCG procedure, which formalizes this process and ensures convergence, is summarized in Algorithm 1.

Algorithm 1 Row-and-Column Generation for ${\mathrm{LF}}_{\mathbf{2}}$

1: Initialization: Solve ${\mathrm{LF}}_{\mathbf{0}}$ to obtain an integer solution X and construct initial columns. 2: repeat 3:    Solve the restricted master problem (RMP). 4:    Compute reduced costs of non-active variables. 5:    if negative reduced cost variables exist then 6:      Add corresponding columns to RMP. 7:    end if 8:    Check for violated valid inequalities from the cut families (29)–(32). 9:    if violated inequalities exist then 10:      Add them to RMP. 11:    end if 12:    Solve the subproblem (SP) to separate violated subset-cover inequalities. 13:    if violated inequalities exist then 14:      Add them to RMP. 15:    end if 16: until no negative reduced cost and no violated inequality are found 17: Output: Optimal solution of ${\mathrm{LF}}_{\mathbf{2}}$ and a valid lower bound.

Beyond its algorithmic role, the proposed RCG algorithm also provides managerial insights into the structural characteristics of the problem. By selectively generating variables and constraints, the procedure naturally highlights the dominant transportation patterns and the most critical capacity or cover relations. This not only improves computational efficiency but also offers a deeper understanding of which resources and routes primarily drive the overall solution. From a practical perspective, such information can guide decision makers in identifying bottlenecks, prioritizing capacity expansions, or redesigning allocation rules. Moreover, the sparsity of the final active set of columns and cuts suggests that only a small subset of decisions is truly essential for optimality, which can be exploited to design faster heuristics and more interpretable decision-support tools. In this sense, the RCG procedure goes beyond providing tight bounds—it also reveals actionable structural insights that enhance both planning efficiency and managerial decision-making.

4.4. Upper Bounding Procedure

The upper bound is obtained through a rounding procedure that transforms the fractional solution of the RMP into a feasible primal solution. This procedure guarantees feasibility with respect to supply and demand constraints and yields a valid, albeit not necessarily tight, upper bound for the problem. However, such solutions are seldom optimal due to the discrete stepwise cost structure and the fixed-charge characteristics of the model. To further improve solution quality, we introduce a local search (LS) procedure that iteratively explores neighborhoods specifically tailored to the structure of (F₀). By applying cycle adjustments, opening or closing vehicles, and rebalancing flows, the LS procedure systematically reduces total cost while maintaining feasibility. The connection between RCG and VND procedures is shown in Figure 3.

Let $X=(x,y)$ denote a feasible solution to (F₀). A neighborhood move transforms X into another feasible solution $X^{\prime }=(x^{\prime },y^{\prime })$. Four neighborhoods are considered:

• N1 (Cycle Adjustment in Open Arcs). Let $C=\{(i_1,j_1),(i_2,j_1),\dots ,(i_k,j_k),(i_1,j_k)\}$ be an even-length alternating cycle in the bipartite graph of open arcs, partitioned into “positive” $C^{+}$ and “negative” $C^{-}$. For $\theta >0$:

  $$\begin{array}{c}\hfill x_{ij}^{\prime }=\left\{\begin{array}{cc}{x}_{ij}+\theta ,\hfill & (i,j)\in C^{+},\hfill \\ x_{ij}-\theta ,\hfill & (i,j)\in C^{-},\hfill \\ x_{ij},\hfill & \mathrm{otherwise},\hfill \end{array}\right.\end{array}$$

  (43)

  subject to $0\le x_{ij}^{\prime }\le v_{ij}$ and $x_{ij}^{\prime }\le Q{y}_{ij}$. The cost variation is

  $$\begin{array}{c}\hfill \mathrm{\Delta }=\theta \left(\sum _{(i,j)\in C^{+}}{c}_{ij}-\sum _{(i,j)\in C^{-}}{c}_{ij}\right).\end{array}$$

  (44)
• N2 (Vehicle Opening with Cycle Adjustment). Consider a saturated or closed arc $(i,j)$. Opening a new vehicle increases $y_{ij}\leftarrow y_{ij}+1$, enlarging capacity by Q and incurring fixed cost $f_{ij}$. Inserting $(i,j)$ into an alternating cycle C, the cost change is

  $$\begin{array}{c}\hfill \mathrm{\Delta }=f_{ij}+\theta \left(\sum _{(p,q)\in C^{+}}{c}_{pq}-\sum _{(p,q)\in C^{-}}{c}_{pq}\right).\end{array}$$

  (45)
• N3 (Vehicle Closing). For an open arc $(i,j)$ with $y_{ij}>0$, if the load of one vehicle can be rerouted through feasible cycles, then $y_{ij}^{\prime }=y_{ij}-1$. The cost change is

  $$\begin{array}{c}\hfill \mathrm{\Delta }=-f_{ij}+{\mathrm{\Delta }}^{\mathrm{reroute}},\end{array}$$

  (46)

  where ${\mathrm{\Delta }}^{\mathrm{reroute}}$ denotes the net change in linear transportation costs.
• N4 (Intra-Arc Rebalancing). Within an arc $(i,j)$, flow can be redistributed across vehicles. If this eliminates one vehicle, then $y_{ij}^{\prime }=y_{ij}-1$, and the net cost variation is

  $$\begin{array}{c}\hfill \mathrm{\Delta }=-f_{ij}+{\mathrm{\Delta }}^{\mathrm{linear}},\end{array}$$

  (47)

  where ${\mathrm{\Delta }}^{\mathrm{linear}}$ is the change in linear costs due to reallocation.

We adopt a VND framework that explores the neighborhoods in increasing order of complexity. The overall upper bounding procedure is summarized in Algorithm 2

Algorithm 2 Upper Bounding Procedure for ${\mathrm{F}}_{\mathbf{0}}$

1: Step 1 (Initialization): Start from a feasible solution $(x,y)$ obtained by the rounding procedure. 2: Step 2 (Local Search): 3: repeat 4:    Construct the neighborhood of $(x,y)$ using: Cycle Adjustment (N1): Select an alternating cycle C in the bipartite network of open arcs. Adjust flows along C with step size $\theta$, preserving feasibility. Vehicle Opening (N2): For a saturated or closed arc $(i,j)$, increase $y_{ij}\leftarrow y_{ij}+1$ (open a new vehicle of capacity Q), insert $(i,j)$ into a cycle C, and adjust flows accordingly. Vehicle Closing (N3): For an open arc $(i,j)$ with $y_{ij}>0$, attempt to reroute the load of one vehicle through cycles. If successful, set $y_{ij}\leftarrow y_{ij}-1$. Intra-Arc Rebalancing (N4): Within a single arc $(i,j)$, redistribute flow among vehicles. If one vehicle becomes redundant, update $y_{ij}\leftarrow y_{ij}-1$. 5:    Evaluate all candidate moves and select the best improving neighbor $(x^{\prime },y^{\prime })$. 6:    if $(x^{\prime },y^{\prime })$ improves upon $(x,y)$ then 7:      Update $(x,y)\leftarrow (x^{\prime },y^{\prime })$. 8:    end if 9: until no improving neighbor is found or stopping criteria are met 10: Output: Improved feasible solution $(x,y)$ and its objective value.

To improve computational efficiency, several acceleration strategies are incorporated into the local search framework. These strategies include candidate-list restriction, first-improvement and incremental evaluation, adaptive neighborhood ordering, and occasional diversification with parallel evaluation to avoid premature convergence, detailed as follows:

• Candidate list reduction: restrict neighborhood exploration to the K most promising arcs, selected by indicators such as the marginal transportation cost $c_{ij}$ or the effective cost $c_{ij}+f_{ij}/Q$, thereby focusing computational effort on moves with the greatest potential benefit.
• First-improvement rule: accept the first improving move encountered, which reduces the number of evaluations per iteration and accelerates convergence compared with a best-improvement strategy.
• Incremental evaluation: maintain auxiliary data structures such as residual capacities $r_{ij}=Q{y}_{ij}-x_{ij}$ and arc-specific cost contributions, enabling incremental evaluation of candidate moves in $O\left(\right|C\left|\right)$ time.
• Adaptive neighborhood ordering: adopt a VND scheme that restarts from N1 whenever an improvement is found, ensuring that simple and computationally cheap adjustments are exploited before invoking more complex neighborhoods.
• Diversification: apply periodic perturbations or controlled restarts to enlarge the explored solution space, thereby avoiding premature convergence to poor-quality local optima.

5. Numerical Results

In this section, we present computational experiments to evaluate the proposed framework that integrates the RCG-based lower-bounding procedure with the VND-based upper-bounding procedure. The objectives are threefold: (i) to examine the impact of valid inequalities on strengthening the LP relaxation and to analyze the scalability and efficiency of the RCG algorithm, (ii) to evaluate the ability of VND to enhance solution quality by improving upper bounds, and (iii) to provide a comprehensive performance comparison between the proposed framework and a state-of-the-art commercial MIP solver in terms of solution quality, computational time, and scalability. The benchmark instances and computational environment are described below.

A suite of benchmark instances was generated following the procedure of Glover et al. [31], with modifications to incorporate the stepwise cost characteristics of the TPSC. The numbers of supply and demand nodes were fixed at $n=50$ and $m=100$. Supply quantities were uniformly distributed within $[400,800]$, while demands were sampled from $[200,400]$ under the condition of overall balance. Variable transportation costs were drawn from $[4,8]$. The vehicle capacity was set at two levels, $Q\in \{50,100\}$, and the setup cost for deploying a vehicle was sampled from four intervals: $[100,400]$, $[200,800]$, $[400,1600]$, and $[800,3200]$. Combining the two capacity levels with the four setup-cost intervals yields eight instance classes, denoted as A–H. Each class contains 15 independent instances, resulting in a total of 120 test instances that provide representative and diverse scenarios for performance evaluation.

All algorithms were implemented in C++ and compiled with Visual Studio 2023 (64-bit). LP and MIP models were solved using IBM ILOG CPLEX 20.1.0 with default parameter settings. All tests were executed on a Windows 10 workstation equipped with an Intel Xeon Platinum 2.4 GHz CPU, 16 GB RAM, and a 10 MB cache.

5.1. Effectiveness of Valid Inequalities and RCG Performance

This subsection examines the effect of valid inequalities on strengthening the LP relaxation. We compare two models: (i) the baseline formulation (${\mathrm{LF}}_{\mathbf{0}}$) and (ii) the discretized reformulation augmented with both classes of valid inequalities (${\mathrm{LF}}_{\mathbf{2}}$), solved by the RCG procedure. The evaluation focuses on three aspects: the tightness of the lower bounds, the relative improvement over the baseline, and the additional computational effort incurred.

Table 1. Comparison of lower bounds and computation times between ${\mathrm{LF}}_{\mathbf{0}}$ and ${\mathrm{LF}}_{\mathbf{2}}$.

Instances	${\mathbf{LF}}_0$				${\mathbf{LF}}_2$				${\mathbf{\Delta }}_{\mathbf{LB}}$ (%)
	Vars	Constr.	LB	CPU(s)	Cols	Cuts.	LB	CPU(s)
A	5000	150	372,112	$0.01$	852	2338	398,526	107	7.10
B	5000	150	414,680	$0.01$	931	2889	442,685	244	6.75
C	5000	150	788,565	$0.01$	1592	3064	854,425	173	8.35
D	5000	150	1,315,305	$0.01$	1767	3585	1,408,339	323	7.07
E	5000	150	242,430	$0.01$	1940	3271	266,388	179	9.88
F	5000	150	289,470	$0.01$	1054	3556	308,372	204	6.53
G	5000	150	480,300	$0.01$	1216	2632	515,102	141	7.25
H	5000	150	742,440	$0.01$	1016	3488	804,379	273	8.34

reports the average results over 15 instances for each class (A–H). For ${\mathrm{LF}}_{\mathbf{0}}$, it lists the number of variables (Vars), the number of constraints (Constr.), the optimal objective value providing a valid lower bound (LB) for the original problem, and the computation time (CPU(s)). For ${\mathrm{LF}}_{\mathbf{2}}$, it reports the number of columns (Cols) and cuts (Cuts) generated by the RCG procedure, together with the corresponding lower bound (LB) and computation time (CPU(s)); note that Cols and Cuts refer only to those generated in the restricted master problem, rather than the full set of variables and constraints in the complete formulation. The last column presents the relative improvement in the lower bound (${\mathrm{\Delta }}_{LB}$) obtained by ${\mathrm{LF}}_{\mathbf{2}}$ over ${\mathrm{LF}}_{\mathbf{0}}$.

As reported in Table 1, the baseline formulation ${\mathrm{F}}_{\mathbf{0}}$, when directly relaxed, provides relatively weak lower bounds that severely underestimate the problem’s true difficulty. By contrast, enhancing the discretized formulation with valid inequalities (${\mathrm{LF}}_{\mathbf{2}}$) substantially strengthens the relaxation, yielding relative improvements in the lower bound between 6.53% and 9.88% across all instance classes. This tightening effect highlights the crucial role of the inequalities in bridging the gap left by ${\mathrm{F}}_{\mathbf{0}}$’s weak relaxation. The improvement, however, comes at the expense of increased computation time, which grows from negligible levels in ${\mathrm{LF}}_{\mathbf{0}}$ to several hundred seconds in ${\mathrm{LF}}_{\mathbf{2}}$. Within the row-and-column generation (RCG) framework, the inequalities are introduced dynamically as additional cuts, while new allocation variables are generated as columns. This iterative enrichment yields a much tighter relaxation with far fewer variables and constraints than the full model, thereby maintaining scalability. By avoiding explicit enumeration of the entire discretized problem, RCG ensures that the enhanced formulation remains tractable for larger instances, confirming its role as a critical building block of the proposed framework.

Beyond these numerical gains, the results also offer methodological insights. First, the proposed inequalities effectively exploit problem structure: rounding inequalities eliminate fractional vehicle activations, while subset-cover inequalities rule out infeasible partial assignments. Second, the improvements remain stable across all instance classes, indicating that the inequalities generalize well across problem scales. Finally, by providing stronger lower bounds, the inequalities not only tighten the relaxation but also enhance the efficiency of the RCG process, as improved bounds accelerate pruning and focus the search more effectively.

5.2. Upper-Bound Improvement via VND

This subsection evaluates the quality of feasible solutions obtained by the proposed upper-bounding procedure. Two strategies are considered: (a) direct rounding of the fractional RMP solution, and (b) an enhanced approach that augments rounding with a VND-based local search exploiting problem-specific neighborhoods. The evaluation focuses on three performance indicators: the resulting upper bound (UB), the duality gap relative to the best lower bound obtained by solving ${\mathrm{LF}}_{\mathbf{2}}$ with RCG, and the computation time (CPU(s)).

Table 2. Comparison of upper bounds obtained by rounding with VND-based local search.

Instances	Rounding			VND			${\mathbf{\Delta }}_{\mathbf{UB}}$
	UB	Gap (%)	CPU(s)	UB	Gap (%)	CPU(s)
A	405,497	1.75	0.01	402,924	1.10	121	0.63
B	464,092	4.84	0.01	458,324	3.53	107	1.24
C	873,825	2.27	0.01	869,031	1.71	177	0.55
D	1,515,824	7.63	0.01	1,480,451	5.12	189	2.33
E	279,504	4.92	0.01	270,328	1.48	160	3.28
F	321,285	4.19	0.01	313,277	1.59	142	2.49
G	539,020	4.64	0.01	530,137	2.92	186	1.65
H	853,243	6.07	0.01	836,369	3.98	149	1.98

reports these measures for each instance class under both methods, with the last column ${\mathrm{\Delta }}_{UB}$ summarizing the relative improvement in solution quality achieved by VND.

As shown in Table 2, the rounding-only approach generates feasible solutions almost instantaneously, but the quality of these solutions is limited, with duality gaps between 6.85% and 9.67%. By incorporating VND-based local search, the upper bounds are consistently improved by several percentage points, leading to significantly smaller gaps, all below 4%. Importantly, this improvement is achieved with only modest additional runtime, which remains within three seconds even for the largest tested instances. These results demonstrate that the integration of local search into the upper-bounding procedure provides a clear and consistent benefit without sacrificing computational efficiency.

The findings also underscore the complementary nature of the two strategies. Rounding ensures rapid feasibility with negligible cost, serving as a reliable starting point, while local search leverages problem-specific neighborhoods—such as cycle adjustments and vehicle rebalancing—to systematically refine the solution. This combination not only delivers high-quality upper bounds but also narrows the duality gap to a practical level, reinforcing the scalability and robustness of the proposed framework.

5.3. Comparison with a State-of-the-Art MIP Solver

Finally, we present a comprehensive comparison between the proposed RCG&VND framework and a state-of-the-art commercial MIP solver applied directly to ${\mathrm{F}}_{\mathbf{0}}$. The evaluation considers three aspects: (i) the quality of lower and upper bounds, (ii) the duality gap of final solutions, and (iii) the computational runtime across all instance classes.

Table 3. Comprehensive Comparison between RCG&VND and CPLEX.

Instances	CPLEX				RCG&VND				${\mathbf{\Delta }}_{\mathbf{UB}}$ (%)	${\mathbf{\Delta }}_{\mathbf{LB}}$ (%)
	LB	UB	Gap (%)	CPU(s)	LB	UB	Gap (%)	CPU(s)
A	394,295	408,523	3.61	3600	398,526	402,924	1.10	228	1.37	1.07
B	439,313	462,855	5.36	3600	442,685	458,324	3.53	351	0.98	0.77
C	837,316	872,838	4.24	3600	854,425	869,031	1.71	350	0.44	2.04
D	1,396,903	1,499,496	7.34	3600	1,408,339	1,480,451	5.12	512	1.27	0.82
E	262,843	278,491	5.95	3600	266,388	270,328	1.48	339	2.93	1.35
F	304,757	319,050	4.69	3600	308,372	313,277	1.59	346	1.81	1.19
G	511,536	537,761	5.13	3600	515,102	530,137	2.92	327	1.42	0.70
H	796,474	851,746	6.94	3600	804,379	836,369	3.98	422	1.81	0.99

reports, for both CPLEX and RCG&VND, the lower bound (LB), the upper bound (UB), the optimality gap (Gap), and the computation time (CPU(s)). In addition, two performance indicators are included: ${\mathrm{\Delta }}_{UB}(\%)=100\times ({\mathrm{UB}}_{\mathrm{CPLEX}}-{\mathrm{UB}}_{\mathrm{VND}})/{\mathrm{UB}}_{\mathrm{CPLEX}}$, where a positive value indicates that VND achieves a better (lower) UB than CPLEX, and ${\mathrm{\Delta }}_{LB}(\%)=100\times ({\mathrm{LB}}_{\mathrm{RCG}}-{\mathrm{LB}}_{\mathrm{CPLEX}})/{\mathrm{LB}}_{\mathrm{CPLEX}}$, where a positive value indicates that RCG achieves a better (higher) LB than CPLEX. The optimality gap is calculated as $100\times (\mathrm{UB}-\mathrm{LB})/\mathrm{UB}$.

Table 3 provides a comprehensive comparison between the proposed RCG&VND framework and the commercial solver CPLEX. Under the 1-h time limit, CPLEX fails to close the duality gaps, which remain between 3.6% and 7.3% across the tested instances. In contrast, RCG&VND consistently yields tighter bounds: the lower bounds are improved by up to 2.0%, and the upper bounds are reduced by up to 2.9%, leading to significantly smaller gaps of 1.1–3.9%. These improvements stem from the fact that the proposed inequalities tighten the LP relaxation, raising the lower bound early, while the RCG procedure adds only the most influential variables and constraints, keeping the relaxation small and efficient. The VND-based local search then focuses on correcting the key structural sources of suboptimality, improving the upper bound. This coordinated tightening of both bounds enables convergence within about 600 s, compared with the full 3600-s budget required by CPLEX.

These findings demonstrate the effectiveness of combining lower-bound strengthening, row-and-column generation, and problem-specific local search. The framework not only narrows the duality gap but also produces high-quality feasible solutions within practical computation times. Overall, RCG&VND achieves a favorable balance between bound quality, solution accuracy, and scalability, clearly outperforming a state-of-the-art general-purpose solver on large-scale instances of the stepwise cost transportation problem.

6. Conclusions

This paper examined the transportation problem with stepwise costs, arising when vehicle setup costs increase with the number of vehicles deployed. We formulated a mixed-integer programming model, analyzed its structural properties, and addressed the weakness of its linear relaxation through a variable-splitting reformulation and valid inequalities. To handle the large scale of the discretized model, we designed an RCG algorithm that dynamically introduces only the most relevant variables and constraints. In addition, feasible solutions were generated via a rounding heuristic and subsequently improved through VND-based local search. Computational experiments on benchmark instances demonstrated that the proposed framework produces substantially tighter bounds, achieves high-quality feasible solutions, and consistently outperforms direct MIP solvers in both solution quality and efficiency. The study provides theoretical insights into stepwise cost modeling and a practical framework for large-scale transportation planning with vehicle activation costs.

Despite its theoretical value, the proposed model has certain limitations in practical applicability. Future research may build upon this work in several directions. Methodologically, richer neighborhoods and adaptive hybrid heuristics could be integrated into the local search procedure to improve convergence, while alternative polyhedral relaxations and decomposition schemes may yield tighter bounds. From an application perspective, extending the framework to address stochastic demand, multi-modal routing, or integrated production–distribution settings would further enhance its applicability and strengthen its relevance to complex supply chain planning problems with discrete and nonlinear cost structures.