Reducing Fuel Consumption in Aircraft: A Cruising Strategy-Based Approach

Abstract

The increasing environmental concerns related to aircraft carbon dioxide (CO₂) emissions call for efficient fuel-saving strategies. This study proposes an alternative cruising strategy to minimize fuel consumption during the cruise flight phase by introducing a two-phase maneuver consisting of a descent followed by a climb. Constraints related to both passenger comfort and aviator regulatory frameworks are considered to ensure the feasibility of the proposed strategy in real-world operational contexts. Using closed-form formulas of the aircraft’s fuel consumption, this strategy is compared against the conventional constant altitude cruise approach. Numerical simulations using data from a Boeing 767-300ER show that the proposed strategy can achieve reduction in fuel consumption at the cost of an increment in flight time. This can be achieved by repeating the proposed strategy as many times as needed according to the distance to be covered during the cruise flight phase.

1. Introduction

The introduction of jet engines in the 1950s revolutionized commercial aviation, particularly the cruise flight phase. Jet engine aircraft began operating at altitudes of 30,000 feet (9144 m) and speeds exceeding 430 knots (221 m/s), as occurred with the Boeing 707 [1] and the Douglas DC-8 [2]. This advancement not only reduced travel times but also allowed aircraft to fly above weather disturbances, minimizing turbulence and enhancing passenger comfort. Moreover, the improved efficiency of jet engines led to extended range capabilities, enabling the emergence of long-haul flights.

In contemporary aviation, aircraft normally operate following one of these cruising strategies: constant altitude cruise and step–climb cruise (see, e.g., [3] (pp. 341–344) and [4] (pp. 345–349)). Constant altitude cruise maintains a fixed altitude throughout, while step–climb cruise involves periodic step climbs during the cruise to maintain proximity to the optimum altitude for the airplane’s weight. In both strategies, the aircraft remains at a constant altitude for considerable periods.

These cruising strategies originated from the need to balance operational efficiency, air traffic management (ATM) requirements, aircraft performance capabilities, and compliance with environmental standards.

The cruise flight phase significantly impacts an aircraft’s overall fuel consumption and emissions, as it constitutes the majority of flight time. This flight phase remains an active area of study as researchers and industry professionals seek to enhance operational efficiency and fuel consumption.

The increasing impact of global warming is closely linked to the emission of greenhouse gases, particularly carbon dioxide (CO₂), which is significantly emitted by aircraft during flights. To address this environmental concern, based on closed-form formulas that describe jet engine fuel consumption, this research aims to optimize the fuel consumption of modern jet engine aircraft during the cruise phase by identifying specific piloting strategies that minimize fuel use.

Several frameworks have been proposed, which provide alternative strategies that aim to achieve optimal aircraft performance during cruise in terms of trajectory optimization, speed management, and fuel consumption [5,6,7,8,9]. Also, other works such as [10,11] address the problem of aerodynamic performance, which is also a fundamental factor in aircraft fuel consumption.

Some of the strategies provided consist of control algorithms. In [12,13], the trajectory optimization of aircraft during cruise is addressed as an optimal control problem. More specifically, in [12], a periodic (cyclic) optimal control problem is posed, where the aircraft’s speed, flight path angle, altitude, and mass are the state variables, and the lift coefficient and engine’s throttle (aircraft’s thrust capacity) are the control variables. The results yield a two-phase cyclic pattern in which the aircraft climbs at maximum thrust and consecutively descends at minimum thrust, obtaining a reduction in fuel consumption with such a trajectory. Moreover the authors of [13] pose a singular optimal control problem, with the aircraft’s speed and mass as state variables and the engine’s throttle as the control variable. Thatwork presents a numerical example in which a reduction in fuel consumption is also obtained at the expense of an increase in range and flight time. The problem presented in [12] is furthermore studied in [14], with the same state and control variables but allowing the engine’s throttle to provide intermediate values between the maximum and minimum thrust, once again providing a reduction in fuel consumption. Additional works that address this problem with similar methodologies can be found in [15,16,17,18,19]. Recently, other frameworks have also been proposed, providing alternative strategies with evolutionary [20,21] and machine learning algorithms [11,22,23] as prominent paradigms.

In this paper, a novel strategy for aircraft cruise is proposed to reduce fuel consumption, in which the cruise trajectory is flown in two consecutive maneuvers: one of descent and another of climb. Both maneuvers are subject to their respective flight path angle and altitude constraints. We aim to compare the proposed strategy with a constant altitude strategy in terms of fuel consumption. Specifically, our strategy uses a comprehensive mathematical model that considers the aircraft as an object with variable mass. Moreover, instead of considering only equations of the aircraft performance during the cruise flight phase, the optimisation problem combines those equations with specific equations of aircraft performance during climb and descent flight phases given in [24]. It should be mentioned that the closed-form equations of aircraft performance given in [24] are validated against Piano-X Aircraft Performance and Emissions software, which is known to yield results close to reality. To the best of our knowledge, embedding such closed-form equations into the optimization problem has not been done in previous works, and, although adding more complexity to the problem, it opens up a new pathway in the study of optimal aircraft fuel consumption during cruise. Assessing the safety and the operational concerns of the potential large-scale implementation of this novel strategy proposed is outside the scope of this paper. The aim of the paper is to motivate future research efforts to make it feasible.

The remainder of this paper is as follows. In Section 2, closed-form formulas of jet engine fuel consumption during aircraft’s cruise, climb, and descent flight phases are reviewed. Section 3 provides details of the proposed cruising strategy and the optimization problem to be solved. In Section 4, we present a method for numerically solving the optimization problem. In Section 5, we present a numerical example where the novel strategy proposed in this paper achieves fuel savings compared to the constant altitude strategy. A brief sensitivity analysis is also carried out to study how variations in the parameters impact the difference between the fuel consumption of the constant altitude strategy and the fuel consumption of the proposed strategy. The simulation is carried out for a Boeing 767-300ER. Finally, conclusions are given in Section 6.

2. Preliminaries

This section is dedicated to explaining how we calculate the aircraft’s fuel consumption during the cruise, climb, and descent flight phases. To that end, we first review the assumptions made in order to obtain such a mathematical model.

2.1. Assumptions

• The aircraft is considered a variable-mass system: fuel is being consumed as time goes on, and weight varies accordingly.
• Aircraft performance takes place in a two-dimensional plane that contains the interacting forces and the velocity vector.
• The air density and speed of sound are calculated using the International Civil Aviation Organization (ICAO) Standard Atmosphere model [25].
• Wind effects are not taken into account.
• Fuel consumption is only considered for the aircraft’s engines and under ideal conditions, that is, engines consume equal fuel quantities, and their degradation effects are not taken into account.
• For the cruise flight phase, the velocity vector remains constant in both magnitude and direction, and thrust specific fuel consumption (TSFC) is also constant under the conditions of constant velocity and altitude [26].
• For the climb and descent flight phases, the velocity vector remains constant in direction (due to constant angle of climb and descent, respectively) but not in magnitude. For such flight phases, the TSFC is modeled as a function of the aircraft’s rate of climb/descent, atmospheric (air density, speed of sound), and engine-specific (by-pass ratio, static thrust) parameters.
• The values of the lift and drag coefficients are based on the aircraft’s wing area, and the parabolic drag polar approach is used.

2.2. Fuel Consumption During the Cruise Flight Phase

According to the assumptions considered, the fuel consumption in the cruise flight phase is a function of time t and is deduced from [27] (Equations (2) and (20)):

$$C_{cr}\left(t\right)=m\left(0\right)\left(1-{\displaystyle \frac{1-\frac{1}{{\beta }_{cr}}tan\left(c_{j,cr}gt\sqrt{k{c}_{D,0}}\right)}{1+{\beta }_{cr}tan\left(c_{j,cr}gt\sqrt{k{c}_{D,0}}\right)}}\right),$$

(1)

where $g=9.80665$ m/${\mathrm{s}}^2$ is the gravitational acceleration on earth,

$${\beta }_{cr}={\displaystyle \frac{2gm\left(0\right)}{{\rho }_{cr}{v}_{cr}^{2}A}}\sqrt{{\displaystyle \frac{k}{c_{D,0}}}},$$

and the rest of the cruise flight phase parameters are defined in Table 1.

Table 1. Parameters of the cruise flight phase.

Symbol	Description
$c_{j,cr}$	Thrust specific fuel consumption
k	Induced drag factor
$c_{D,0}$	Zero-lift drag coefficient
$m\left(0\right)$	Initial cruise mass
${\rho }_{cr}$	Air density at cruise altitude
$v_{cr}$	Aircraft’s true airspeed during cruise
A	Total wing area

2.3. Fuel Consumption During the Climb and Descent Flight Phases

According to the assumptions considered, the fuel consumption C in the climb (descent) flight phase is a function of the altitude at which the aircraft is allowed to ascend (descend) and the climb (descent) angle $\gamma$. Considering an altitude segment in which the air density $\rho$ and the speed of sound a are constant, the fuel consumption is deduced from [24] (Equation (38)):

$$C(h_s,h_e,\gamma )={\int }_{{\eta }_s}^{{\eta }_e}{\rho }^{m+n}{\displaystyle \frac{\left({\xi }_1+\frac{{\xi }_2\eta }{a}\right)\left(F_1+\frac{F_2\eta }{a}\right){\eta }^2}{k_1+k_2\eta +k_3{\eta }^2}}d\eta ,$$

(2)

where the ending rate of climb (descent), ${\eta }_e$, depends on the altitude at the beginning and at the end of the climb (descent) flight phase, $h_s$ and $h_e$, respectively, and is implicitly given by

$$h_e-h_s={\int }_{{\eta }_s}^{{\eta }_e}{\displaystyle \frac{{\eta }^3}{k_1+k_2\eta +k_3{\eta }^2}}d\eta ,$$

(3)

with ${\eta }_s$ being the starting rate of climb (descent), and

$$\begin{array}{cc}\hfill {\xi }_1& =c\left(1-0.15{\lambda }^{0.65}\right){\rho }_0^{-m},\hfill \\ \hfill {\xi }_2& ={\displaystyle \frac{0.28{\xi }_1}{sin\left(\gamma \right)}}\left(1+0.063{\lambda }^2\right),\hfill \\ \hfill F_1& =N_e{F}_{N,0}\left(f_1+f_2\lambda \right){\rho }_0^{-n},\hfill \\ \hfill F_2& ={\displaystyle \frac{N_e{F}_{N,0}}{sin\left(\gamma \right)}}\left(f_3+f_4\lambda \right){\rho }_0^{-n},\hfill \end{array}$$

$$\begin{array}{cc}\hfill k_1& ={\displaystyle \frac{2g}{A{c}_L}}{(sin\left(\gamma \right))}^{3}cos\left(\gamma \right)F_1{\rho }^{n-1},\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill k_2& ={\displaystyle \frac{2g}{A{c}_L}}{(sin\left(\gamma \right))}^{3}cos\left(\gamma \right)F_2{\displaystyle \frac{{\rho }^{n-1}}{a}},\hfill \end{array}$$

$$\begin{array}{cc}\hfill k_3& =-gsin\left(\gamma \right)cos\left(\gamma \right)\left(btan\left(\gamma \right)+{\displaystyle \frac{\psi c_D}{c_L}}\right).\hfill \end{array}$$

(5)

The rest of the climb (descent) flight phase parameters are defined in Table 2.

Table 2. Parameters of the climb (descent) flight phase.

Symbol	Description
${\rho }_0$	Air density at sea level
$\lambda$	Jet engine by-pass ratio
$N_e$	Number of engines
$F_{N,0}$	Aircraft’s static thrust
$c_L$	Lift coefficient
$c_D$	Drag coefficient
$\psi$	Spillage drag effect
$b,c$ (climb)	$b=1$ and $c=1.55·{10}^{-5}$
$b,c$ (descend)	$b=-1$ and $c=0.45·{10}^{-5}$
$m,n,f_1,f_2,f_3,f_4$	Specific thrust parameters

The definition of $k_3$ in [24] (Equation (33)) contained a typo, which has been corrected in (5).

The closed-form expressions of (2) and (3), obtained by integrating rational functions with a second-degree polynomial in the denominator, are given in the Appendix A.

It should be mentioned that Equations (1) and (2) are validated in [24,27,28] with an example case provided by the Piano-X Aircraft Emissions and Performance software. Specifically, it is shown that the fuel consumption provided by the mathematical model here considered turns out to be very close to the fuel consumption given by the Piano-X software (v2008). Since the Piano-X software results are proven to be close to reality, it can be concluded that the mathematical model here considered also provides results close to reality. Other works that have also used Piano-X for validation can be found in [29,30,31,32,33], especially [34,35].

3. Problem Statement

The aim of our project is to compare two different cruising strategies to determine which one consumes less fuel. The first strategy, which is the proposed strategy, involves descending from the cruise altitude $h_{cr}$ to altitude $h_m$ at a constant descent angle (${\gamma }_d$), followed by ascending at constant climbing angle (${\gamma }_{cl}$) until the aircraft returns toits original cruise altitude. The aircraft remains within an altitude segment that goes from $h_{cr}$ to $h_m$, with $0<h_m<h_{cr}$. With this two-maneuver cruising strategy, the aircraft covers a horizontal distance d. From what remains of this paper, the proposed cruising strategy will be referred to as undulating cruise strategy. The second strategy, which is the constant altitude cruise strategy aforementioned, covers the same distance d by flying in a straight line while maintaining a constant cruise velocity ($v_{cr}$). We aim to compare these two strategies in terms of fuel consumption. Figure 1 shows a diagram of the two strategies.

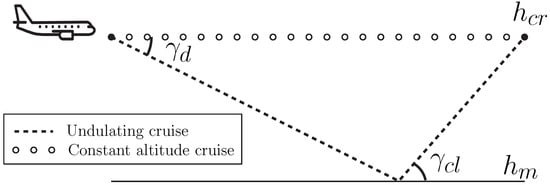
Figure 1. Diagram of the two strategies to be compared in terms of fuel consumption.

For the undulating cruise strategy, to compute from (2) and (3) the fuel consumption in the descent flight phase, $C(h_{cr},h_m,{\gamma }_d)$, we assume that ${\eta }_{sd}=v_{cr}tan\left({\gamma }_d\right)$, where ${\eta }_{sd}$ denotes the starting rate of descent. We denote by ${\eta }_{ed}$ the ending rate of descent, ${\eta }_e$, obtained from solving (3) by taking ${\eta }_s={\eta }_{sd}$. We assume that air density and speed of sound are constant in the altitude segment that goes from $h_{cr}$ to $h_m$.

To compute from (2) and (3) the fuel consumption in the climb flight phase, $C(h_m,h_{cr},{\gamma }_{cl})$, which ends when the aircraft returns to its original cruise altitude, we assume that ${\eta }_{scl}={\eta }_{ed}{\displaystyle \frac{tan\left({\gamma }_{cl}\right)}{tan\left({\gamma }_d\right)}}$, where ${\eta }_{scl}$ denotes the starting rate of climb. We denote by ${\eta }_{ecl}$ the ending rate of climb, ${\eta }_e$, obtained from solving (3) by taking ${\eta }_s={\eta }_{scl}$. The fuel consumption of the undulating cruise strategy is computed as

$$F{C}_1(h_m,{\gamma }_d,{\gamma }_{cl})=C(h_{cr},h_m,{\gamma }_d)+C(h_m,h_{cr},{\gamma }_{cl})+C_p,$$

where $C_p$ is the fuel consumed by the aircraft when transitioning from the descent to the ascent maneuver.

For the constant altitude cruise strategy, the time required to cover a horizontal distance d with constant cruise velocity $v_{cr}$ is $d/v_{cr}$. We approximate the horizontal distance covered, d, as

$$d(h_m,{\gamma }_d,{\gamma }_{cl})=(h_{cr}-h_m)\left({\displaystyle \frac{1}{tan(-{\gamma }_d)}}+{\displaystyle \frac{1}{tan\left({\gamma }_{cl}\right)}}\right).$$

(6)

Using (1), the fuel consumption of the constant altitude cruise strategy is computed as

$$F{C}_2(h_m,{\gamma }_d,{\gamma }_{cl})=C_{cr}\left({\displaystyle \frac{d(h_m,{\gamma }_d,{\gamma }_{cl})}{v_{cr}}}\right).$$

Now, we present the mathematical formulation of the optimization problem to be solved, which is expressed as the maximization of an objective function subject to a number of constraints. We aim to obtain the altitude $h_m$ and the descent and climb angles, ${\gamma }_d$ and ${\gamma }_{cl}$, respectively, that maximize the difference between the fuel consumption of each strategy. Specifically, we aim to solve the following maximization problem:

$$\begin{array}{cc}\hfill \underset{h_m,{\gamma }_d,{\gamma }_{cl}}{max}& F{C}_2(h_m,{\gamma }_d,{\gamma }_{cl})-F{C}_1(h_m,{\gamma }_d,{\gamma }_{cl})\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& h_{min}<h_m<h_{max}\hfill \\ \hfill & {\gamma }_{d_{min}}<{\gamma }_d<{\gamma }_{d_{max}}\hfill \\ \hfill & {\gamma }_{c{l}_{min}}<{\gamma }_{cl}<{\gamma }_{c{l}_{max}}\hfill \end{array}$$

(7)

The maximum and the minimum values of $h_m$ ($h_{max}$, $h_{min}$) depend on the air traffic control (ATC) rules that govern the flight levels allowed for flight operations. The maximum and minimum recommended values of ${\gamma }_d$ (${\gamma }_{d_{max}}$, ${\gamma }_{d_{min}}$) and ${\gamma }_{cl}$ (${\gamma }_{c{l}_{max}}$, ${\gamma }_{c{l}_{min}}$) depend on the specific aircraft and are determined by manufacturer limitations, aviation regulations, or passengers comfort considerations.

For the convenience of the reader Figure 2 shows the relationship between the variables $h_m$, ${\gamma }_d$, and ${\gamma }_{cl}$ and the objective function.

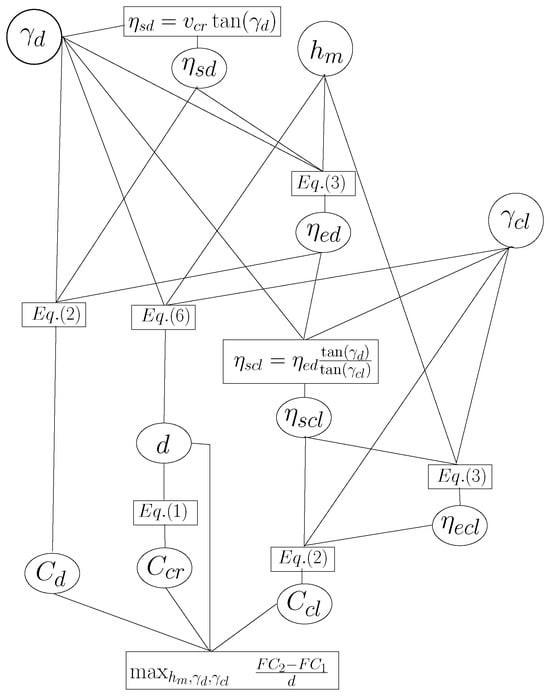
Figure 2. Relationship between the variables $h_m$, ${\gamma }_d$, and ${\gamma }_{cl}$ and the objective function.

4. Problem Resolution

As finding a maximum of the objective function analytically is not feasible, we present a method for numerically finding an approximate solution of the optimization problem (7), that is, to approximate the optimal values of the variables ($h_m$, ${\gamma }_d$ and ${\gamma }_{cl}$). To that end, we introduce the following change of variables:

$$\begin{array}{cc}\hfill h_m\prime & =tan\left({\displaystyle \frac{h_m-h_{min}}{h_{max}-h_{min}}}\pi -{\displaystyle \frac{\pi }{2}}\right),\hfill \\ \hfill {\gamma }_d\prime & =tan\left({\displaystyle \frac{{\gamma }_d-{\gamma }_{d_{min}}}{{\gamma }_{d_{max}}-{\gamma }_{d_{min}}}}\pi -{\displaystyle \frac{\pi }{2}}\right),\hfill \\ \hfill {\gamma }_{cl}\prime & =tan\left({\displaystyle \frac{{\gamma }_{cl}-{\gamma }_{c{l}_{min}}}{{\gamma }_{c{l}_{max}}-{\gamma }_{c{l}_{min}}}}\pi -{\displaystyle \frac{\pi }{2}}\right).\hfill \end{array}$$

It is easy to see that the optimization problem (7) can be rewritten as a maximization problem without constraints as follows:

$$\begin{array}{cc}\hfill \underset{h_m\prime ,{\gamma }_d\prime ,{\gamma }_{cl}\prime }{max}& F{C}_2(h_m,{\gamma }_d,{\gamma }_{cl})-F{C}_1(h_m,{\gamma }_d,{\gamma }_{cl})\hfill \end{array}$$

(8)

where

$$\begin{array}{cc}\hfill h_m& =h_{min}+{\displaystyle \frac{h_{max}-h_{min}}{\pi }}\left(arctan(h_m\prime )+{\displaystyle \frac{\pi }{2}}\right),\hfill \\ \hfill {\gamma }_d& ={\gamma }_{d_{min}}+{\displaystyle \frac{{\gamma }_{d_{max}}-{\gamma }_{d_{min}}}{\pi }}\left(arctan({\gamma }_d\prime )+{\displaystyle \frac{\pi }{2}}\right),\hfill \\ \hfill {\gamma }_{cl}& ={\gamma }_{c{l}_{min}}+{\displaystyle \frac{{\gamma }_{c{l}_{max}}-{\gamma }_{c{l}_{min}}}{\pi }}\left(arctan({\gamma }_{cl}\prime )+{\displaystyle \frac{\pi }{2}}\right).\hfill \end{array}$$

Now, in order to numerically solve (8), we can use one of the most known optimization methods for various variables, i.e., the so-called gradient descent or steepest descent method.

5. Numerical Example

In this section, we present a numerical example where the undulating cruise strategy achieves fuel savings compared to the constant altitude cruise strategy. First, the maximization problem is solved using the numerical method explained in Section 4. Then, a brief sensitivity analysis is carried out to study how variations in the parameters impact the difference between the fuel consumption of each strategy. Simulations are carried out using MATLAB version R2021a.

The selected aircraft is the Boeing 767-300ER flying a distance of 2170 nautical miles (nm), with $h_{cr}=10,668$ m or $35,000$ ft (see, e.g., [36,37]) $h_{max}=10,400$ m, $h_{min}=10,200$ m, ${\gamma }_{d_{min}}=-{10}^{°}$, ${\gamma }_{d_{max}}=-3^{°}$, ${\gamma }_{c{l}_{min}}=1.5^{°}$ and ${\gamma }_{c{l}_{max}}=3^{°}$.

Values of the parameters of the cruise flight phase are given in Table 3, and values of the parameters of the climb (descent) flight phase are given in Table 4.

Table 3. Values of parameters of the cruise flight phase.

Parameter	Value	Units
$c_{j,cr}$	1.72 $\times {10}^{-5}$	(kg/s)/N
k	0.04	-
$c_{D,0}$	0.0185	-
$m\left(0\right)$	128,965	kg
${\rho }_{cr}$	0.3796	kg/m3
$v_{cr}$	237.2	m/s
A	283.35	m2

Table 4. Values of parameters of the climb (descent) flight phase.

Parameter	Value	Units
${\rho }_0$	1.225	kg/m3
$\lambda$	5.31	-
$N_e$	2	-
$F_{N,0}$ (descend)	8263	kN
$F_{N,0}$ (climb)	162,523	kN
$c_L$	0.418	-
$c_D$	0.02221	-
$\psi$ (descend)	0.07	-
$\psi$ (climb)	1
m	0.08	-
n	0.7	-
$f_1$	0.88	-
$f_2$	−0.016	-
$f_3$	−0.3	-
$f_4$	0	-

For the cruise flight phase, the simulations performed in [27] provide values for thrust specific fuel consumption at cruise $c_{j,cr}$, lift-induced drag constant k, zero-lift drag coefficient $c_{D,0}$, aircraft’s initial cruise mass $m\left(0\right)$, air density at cruise altitude ${\rho }_{cr}$, and true airspeed during cruise $v_{cr}=237.2$ m/s or 460 knots (which is obtained from the Mach number equation at cruise, $M_{cr}=v_{cr}/a_{cr}$, considering a typical value of $M_{cr}=0.8$ [38]). Regarding the aircraft’s initial mass $m\left(0\right)$, the operating empty mass corresponds to $93,000$ kg, and the payload and fuel masses correspond to $11,465$ kg and $24,500$ kg, respectively. For the climb (descent) flight phase, the air density $\rho$ and the speed of sound a at the considered altitude segment are calculated with the standard atmospheric model [4]. Its values are $\rho =0.3796$ kg/m³ and $a=299$ m/s, respectively. Simulations performed in [27] provide values for $c_L$ and $c_D$ at the considered altitude segment. Values for $\psi$ were obtained from simulations performed using Piano-X Aircraft Emissions and Performance software (v2008) [39], and information referring to the spillage drag effect can be found in [40].

Data from the Boeing 767-300ER, such as the total wing area A and the number of engines $N_e$, can be found, for example, in [41,42]. The jet engine in our case corresponds to the CF6-80C2B2 [43], with $\lambda =5.31$, $F_{N,0}=162.5$ kN (climb) and $F_{N,0}=8.2$ kN (descent). Specific thrust parameters (m, n, $f_1$, $f_2$, $f_3$, $f_4$) can be found in [44] (pp. 67, 75).

In order to approximate the fuel consumed by the aircraft due to the transition from the descent to the ascent maneuver, $C_p$, we assume that stabilization in a climb, after the thrust increase and the pitch transition to nose-up, occurs in 8 s [45]. We approximate $C_p$ by the fuel consumed by the aircraft after 8 s in a climbing flight phase. From [24], we know that the average fuel consumption in the climb flight phase is $3.3$ kg/s. Therefore, we assume that $C_p=26.4$ kg.

Following the method presented in Section 4, we solve the maximization problem (7). The numerical solution obtained shows that following the undulating cruise strategy results in an optimal average fuel consumption per unit of distance of $3.9$ kg/km ($7.2$ kg/nm), when

$$\begin{array}{cc}\hfill h_m=& h_{min},\hfill \\ \hfill {\gamma }_d=& {\gamma }_{d_{max}},\hfill \\ \hfill {\gamma }_{cl}=& {\gamma }_{c{l}_{max}}.\hfill \end{array}$$

Since the average fuel consumption per unit distance of the constant altitude cruise strategy is $5.6$ kg/km ($10.4$ kg/nm), the optimal percentage of fuel saving is $31.4\%$. It is worth mentioning that to obtain this fuel saving, an increase in flying time is required, specifically an increase of $8.1\%$. Our results are aligned with those presented in [13], where the savings in fuel consumption per unit distance for a Boeing 747-400 are between 4% and 16% at the expense of an increase in flight time of 15.9%.

To study how variations on $h_m$, ${\gamma }_d$ and ${\gamma }_{cl}$ affect the difference between the fuel consumption of each strategy, a brief sensitivity analysis was carried out. Specifically, we varied the values of one of the variables within the allowable range in the optimization problem while keeping the values of the others at their optimal levels. Figure 3, Figure 4, and Figure 5 show the percentage of fuel saving achieved by varying $h_m$, ${\gamma }_d$, and ${\gamma }_{cl}$, respectively.

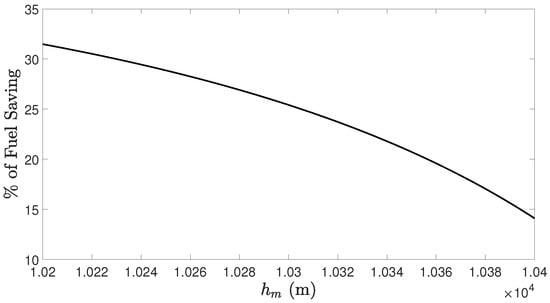
Figure 3. Percentage of fuel saving achieved for $10,200<h_m<10,400$, with ${\gamma }_d={\gamma }_{d_{max}}$ and ${\gamma }_{cl}={\gamma }_{c{l}_{max}}$.

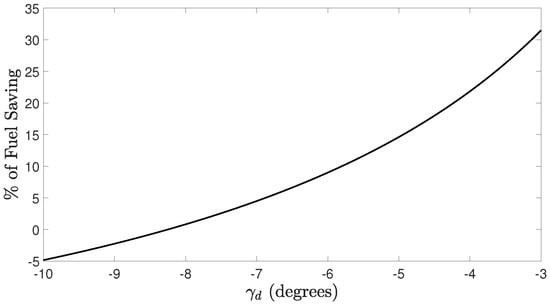
Figure 4. Percentage of fuel saving achieved for $-{10}^{°}<{\gamma }_d<-3^{°}$, with $h_m=h_{min}$ and ${\gamma }_{cl}={\gamma }_{c{l}_{max}}$.

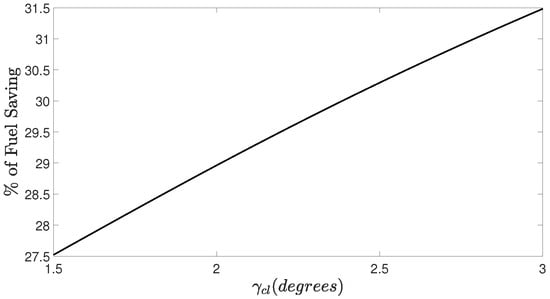
Figure 5. Percentage of fuel saving achieved for $1.5^{°}<{\gamma }_{cl}<3^{°}$, with $h_m=h_{min}$ and ${\gamma }_d={\gamma }_{d_{max}}$.

6. Conclusions

The results obtained in this study show that the optimal strategy for minimizing aircraft fuel consumption consists of allowing the aircraft to descend to the lowest possible altitude with the maximum allowable descent angle (as close as possible to zero). Subsequently, the aircraft should ascend with the maximum permitted climb angle to return to its original cruise altitude. The undulating cruise strategy should be repeated as many times as needed according to the distance to be covered during the cruise flight phase. The results obtained for the numerical example are consistent with those presented in [13].

Observe that our strategy resembles a cyclic two-phase pattern similar to the one proposed in [12], subject to a fixed flight path angle and altitude constraints, and with the descent maneuver first, followed subsequently by the climb maneuver. The main contribution of our undulating cruise strategy is that it uses a comprehensive mathematical model that considers the aircraft as an object with variable mass. Moreover, instead of considering only equations of the aircraft’s performance during the cruise flight phase, the optimisation problem combines those equations with specific equations of the aircraft performance during climb and descent flight phases given in [24], successfully obtaining a reduction in fuel consumption. These equations in [24] are validated against Piano-X Aircraft Performance and Emissions software, which is known to yield results close to reality. Hence, this work opens up a new pathway in the study of optimal aircraft fuel consumption during cruise.

Moreover, the optimization problem addressed in this study considers constraints related to both passenger comfort and aviator regulatory frameworks to ensure that the undulating cruise strategy meets real-world operational demands and adheres to established aviation standards. However, assessing the safety and the operational concerns of the potential large-scale implementation of this undulating cruise strategy proposed is outside the scope of this paper.

Among the factors analyzed, the descent angle appears to be the most critical in reducing fuel consumption. Small variations in this variable can have a significant impact on the efficiency of the strategy.

Finally, although the optimal strategy achieves considerable fuel savings, this benefit comes at the cost of increased flight time. The trade-off between fuel savings and flight duration must be considered in operational planning, especially for commercial flights where travel time is a key factor.