A Least-Squares Control Strategy for Asymptotic Tracking and Disturbance Rejection Using Tikhonov Regularization and Cascade Iteration
Abstract
1. Introduction
2. Statement of Problem
3. Approximate Cascade Controller
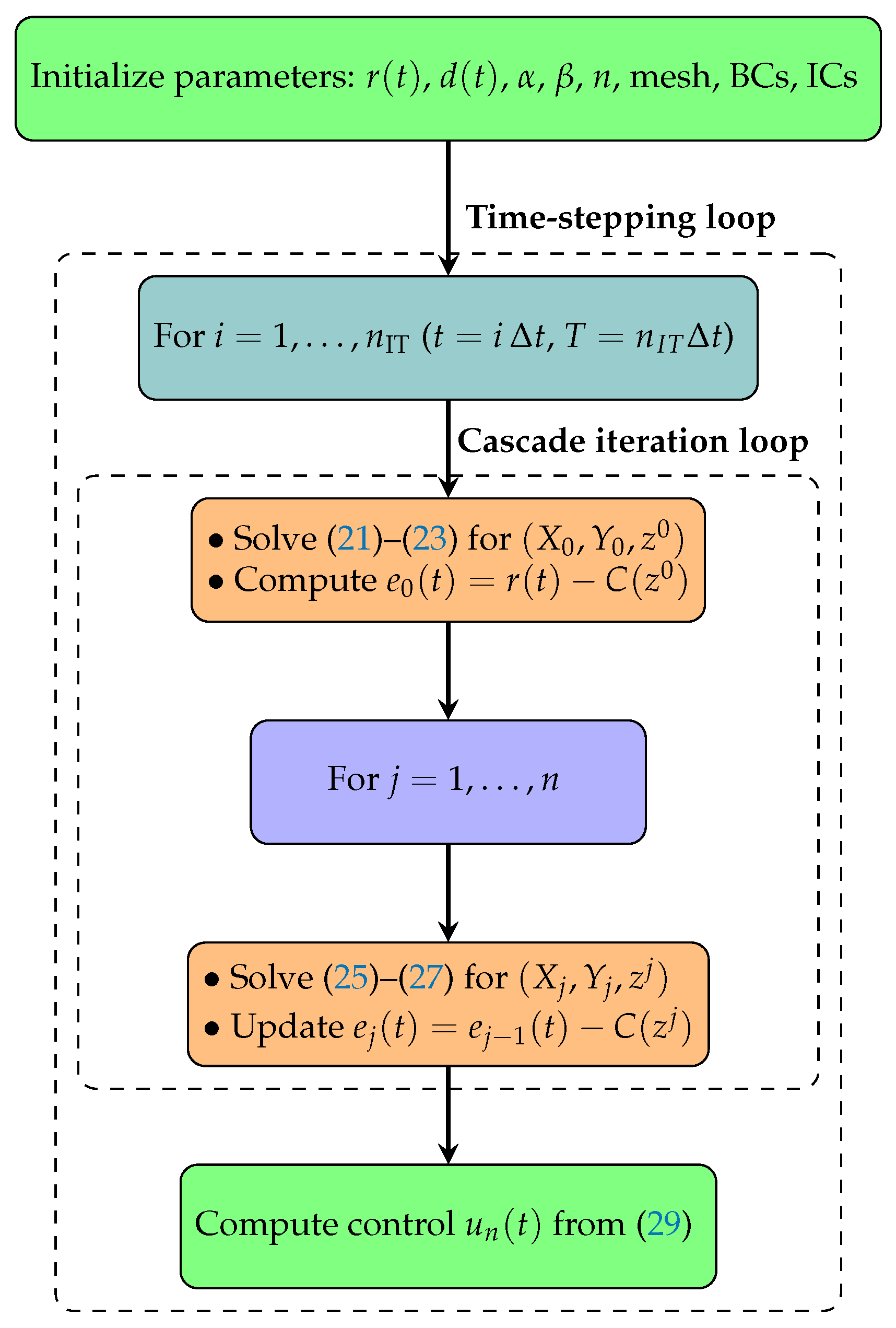
4. A Practical Solution Algorithm for the Controllers
5. Explicit Formulas for the Errors
6. Error Estimates for Finite-Dimensional Input and Output Spaces
7. Infinite-Dimensional Colocated Input and Output Spaces
- 1.
- Restriction Operator is defined for byOr, more simply .
- 2.
- Extension Operator is defined for by
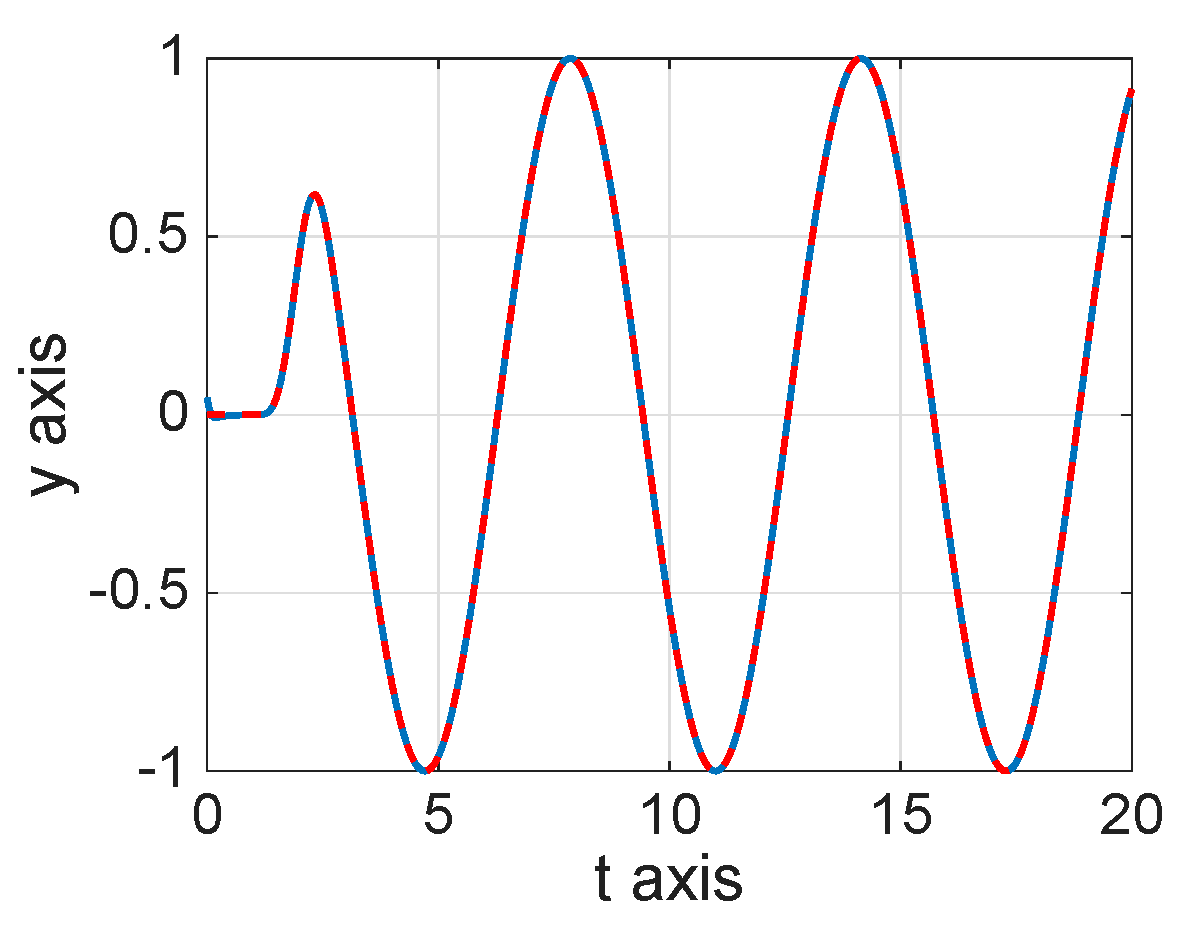
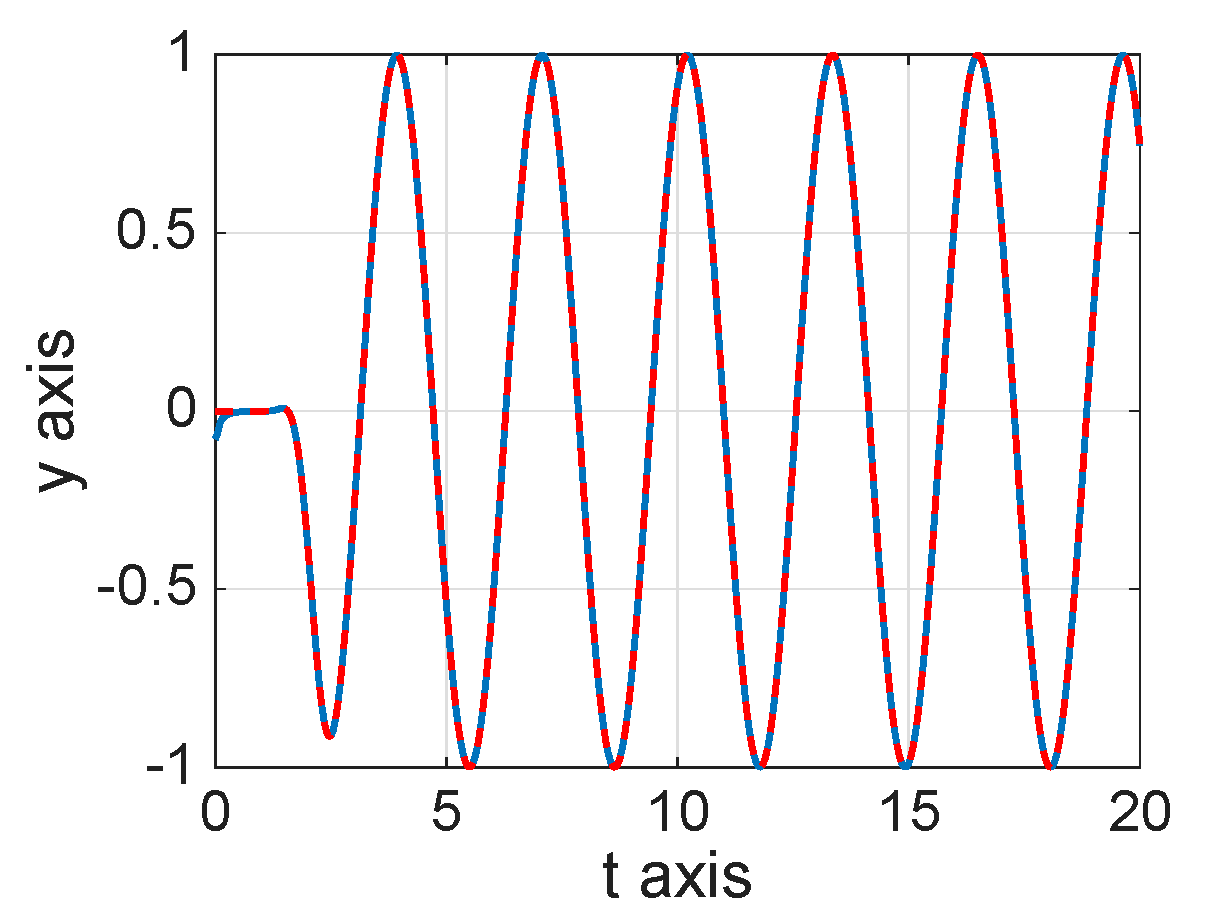
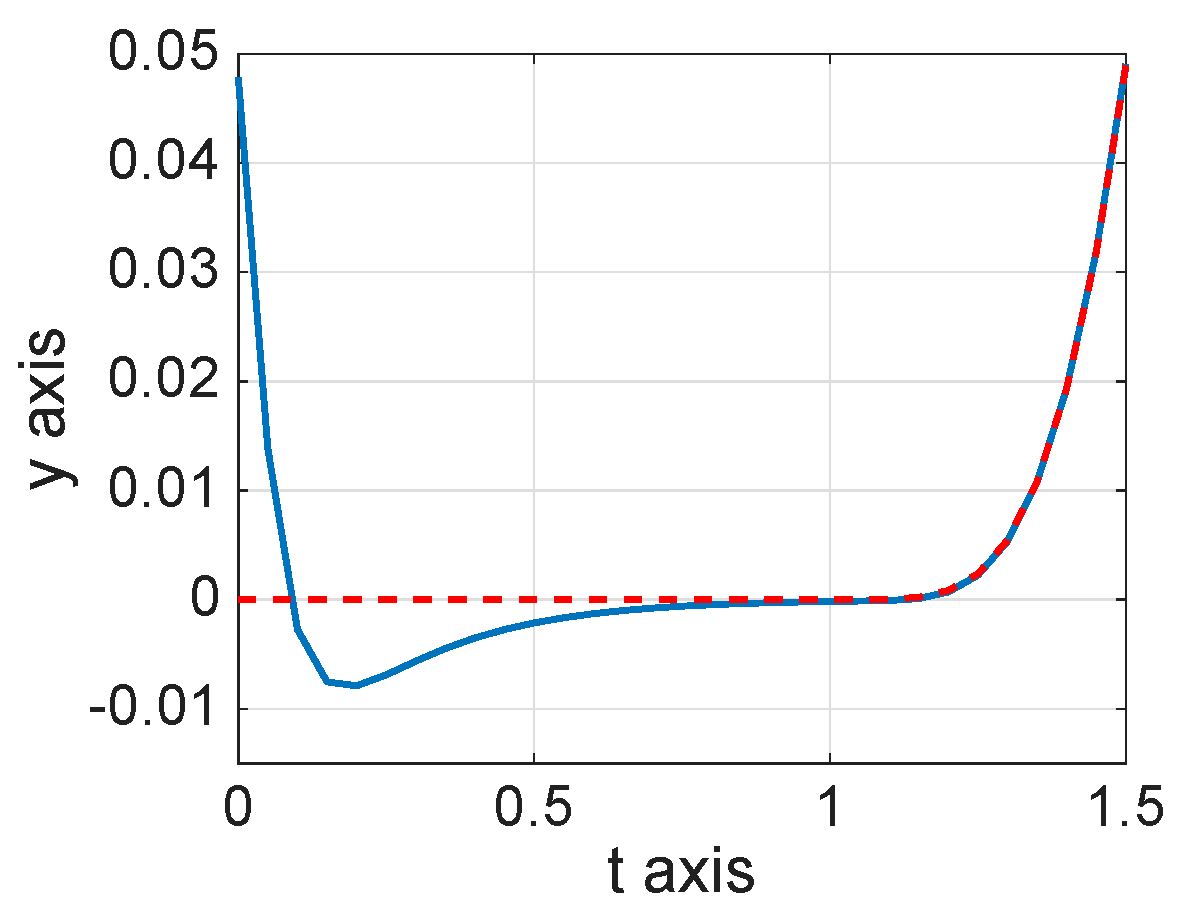
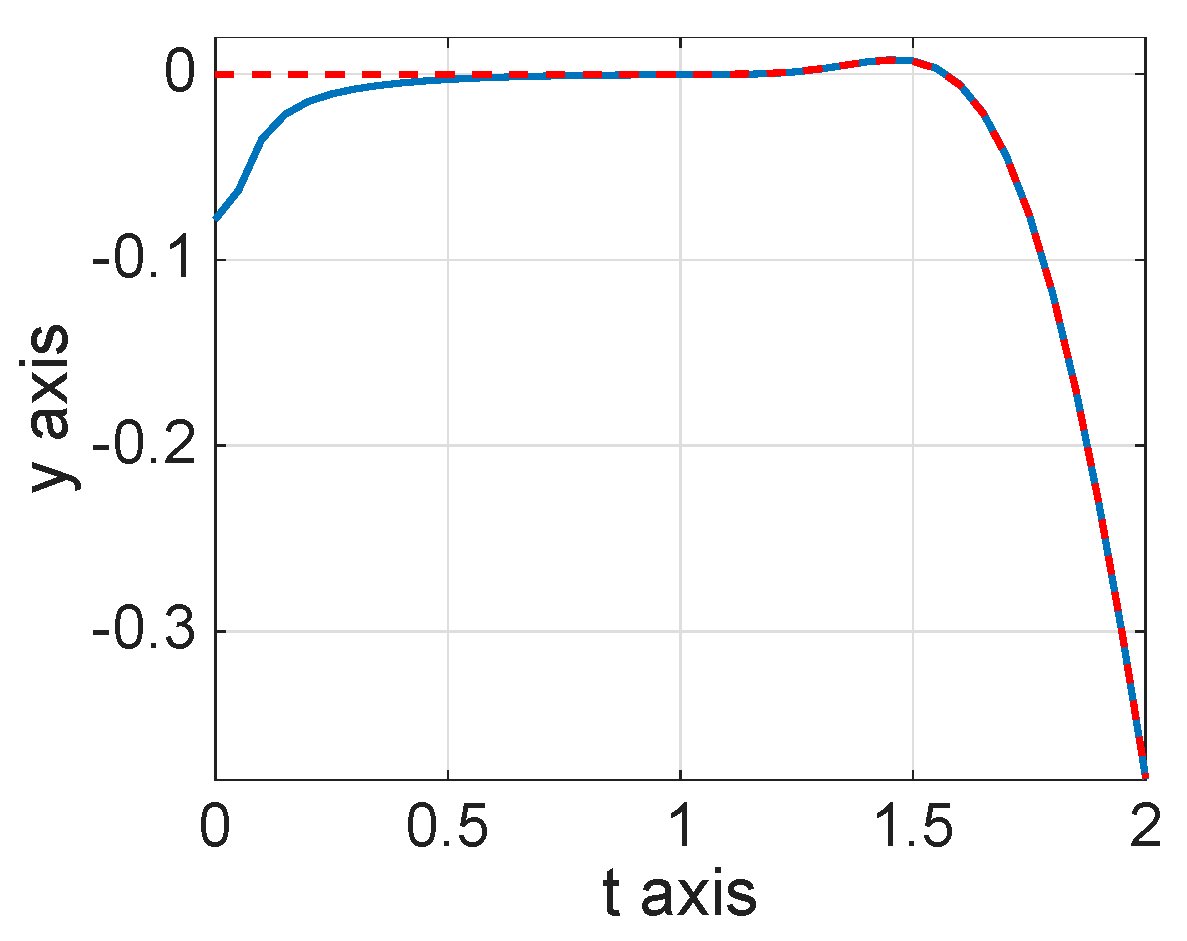
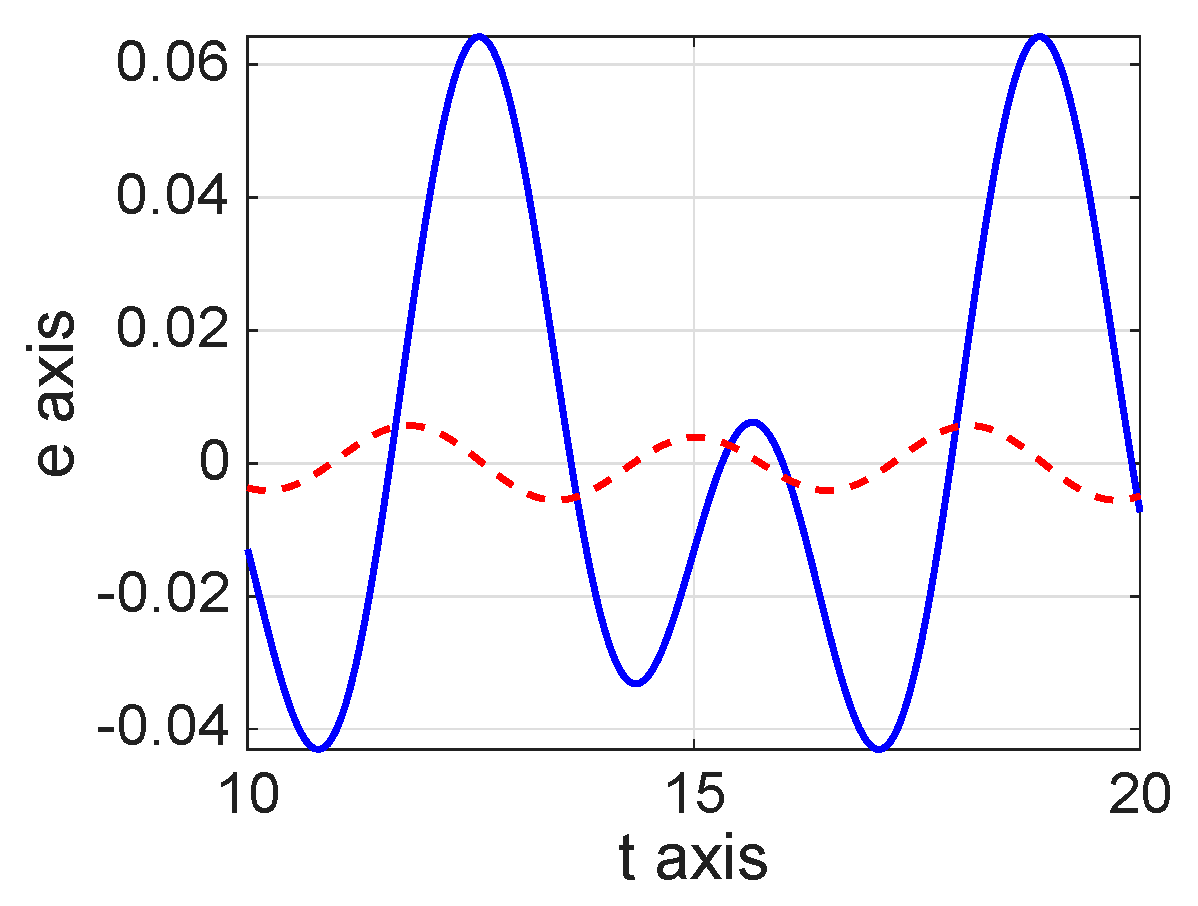
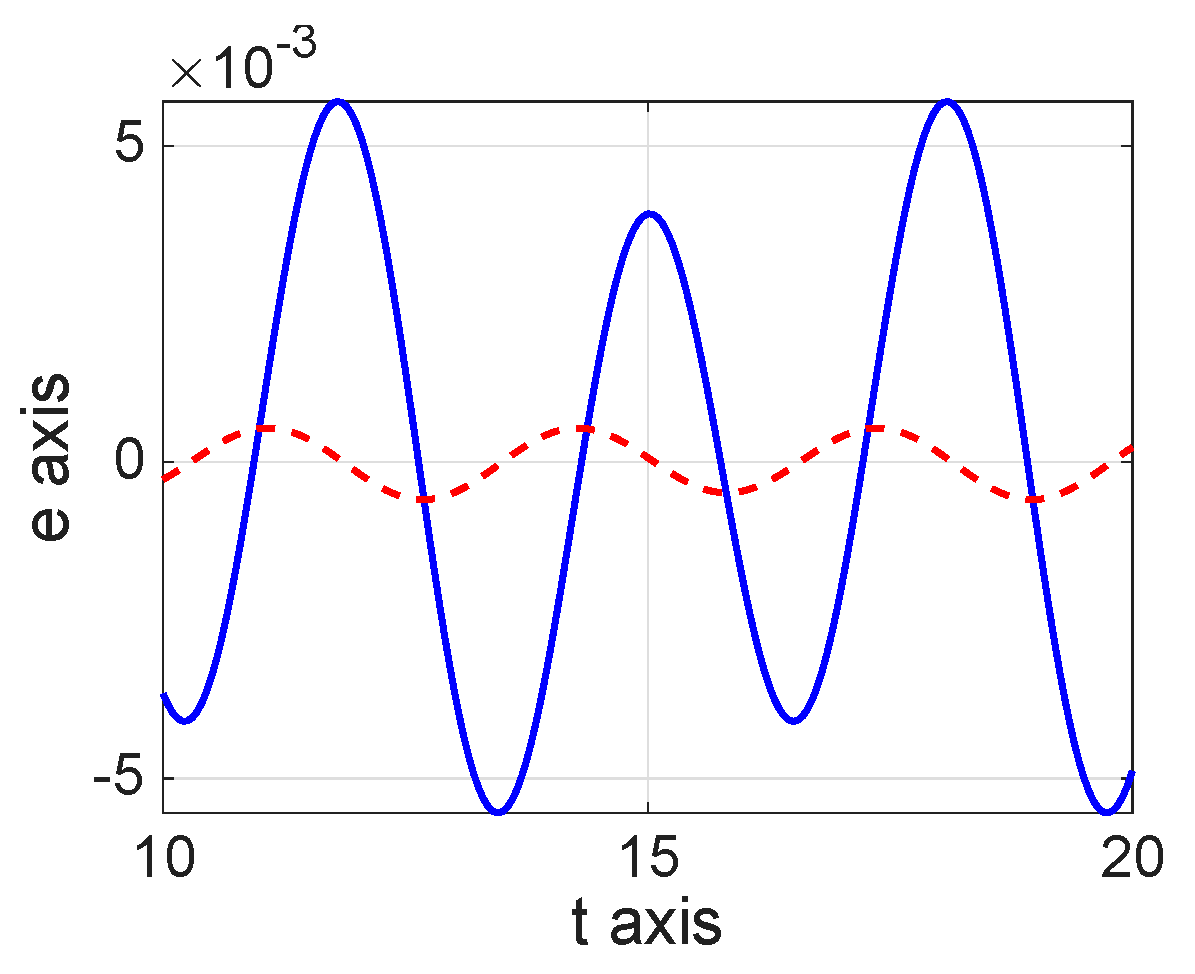
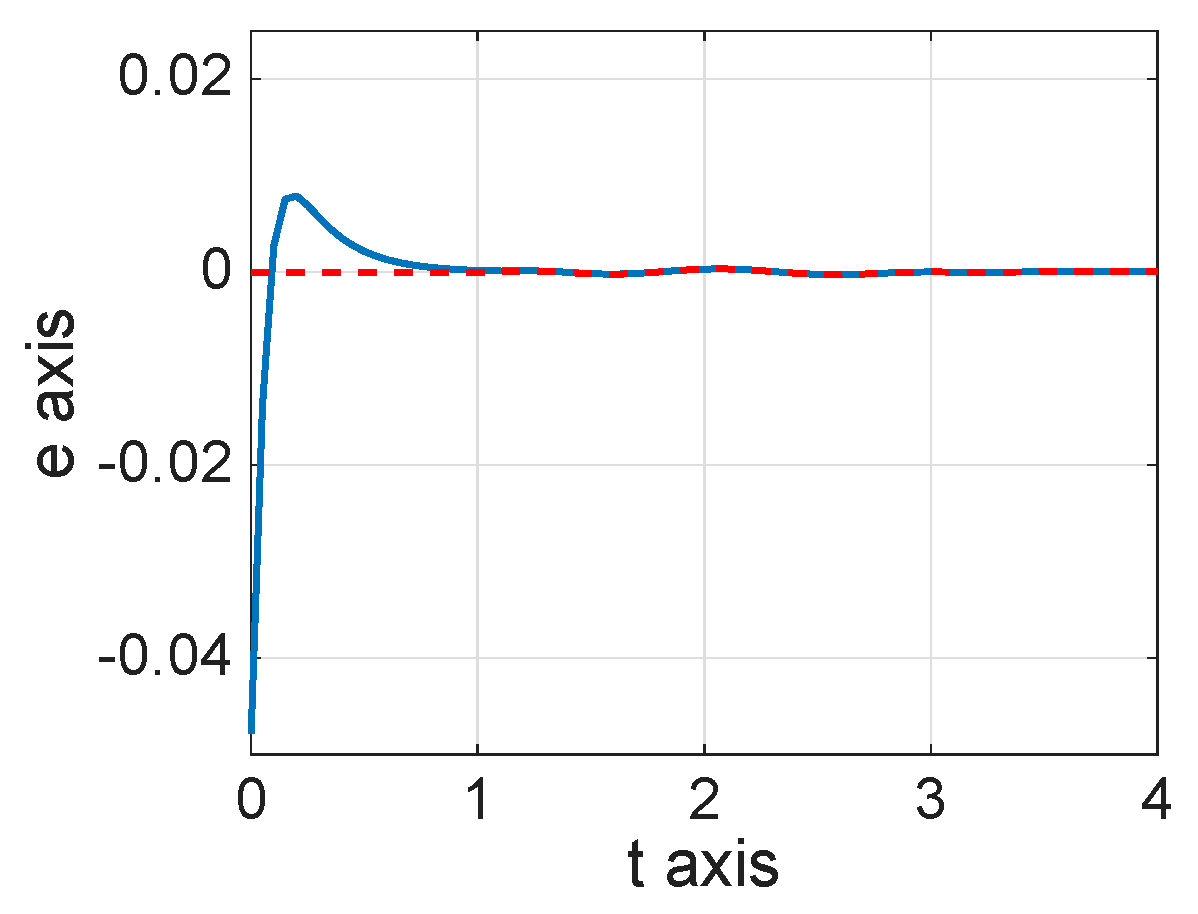
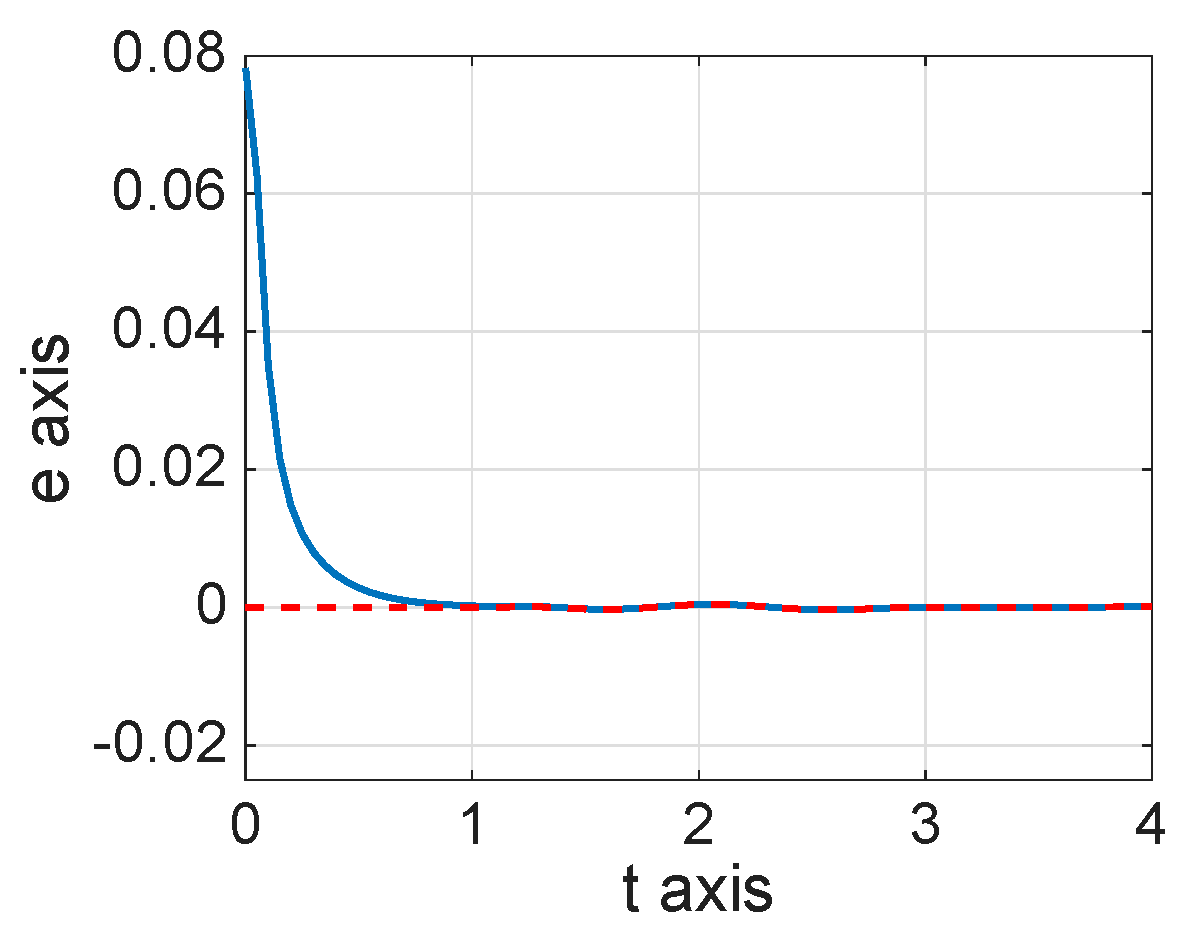
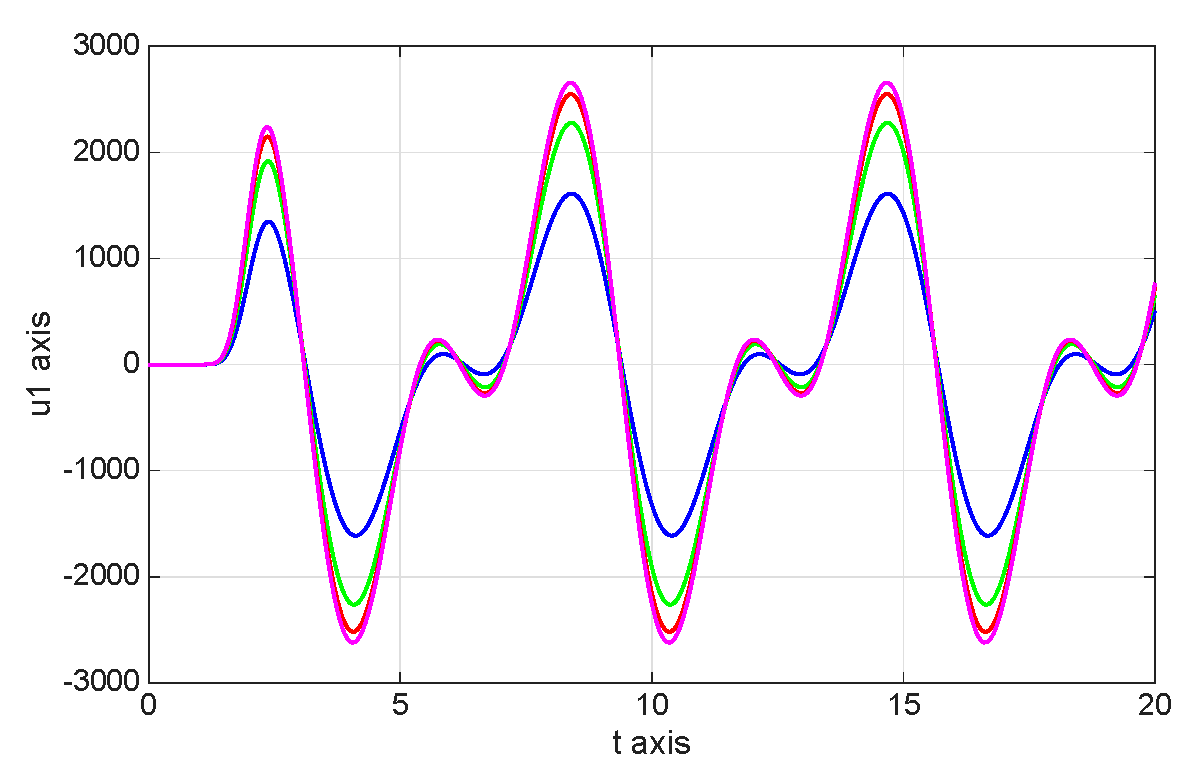
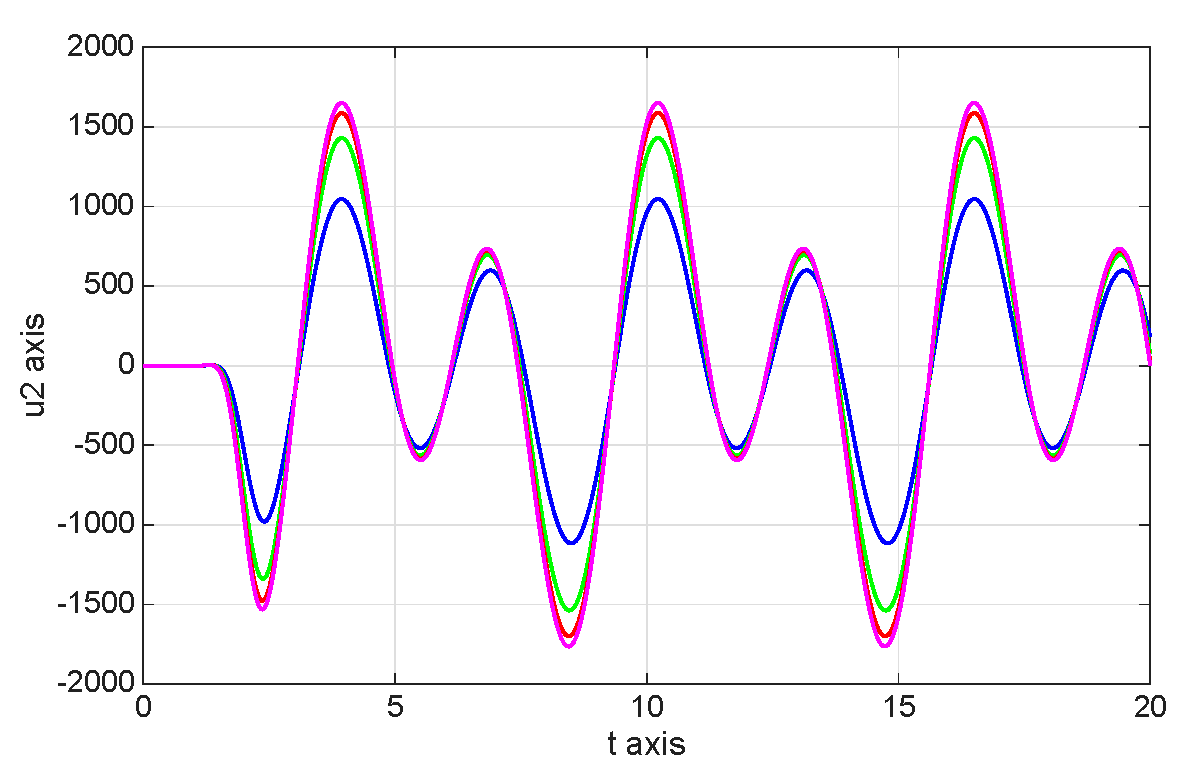
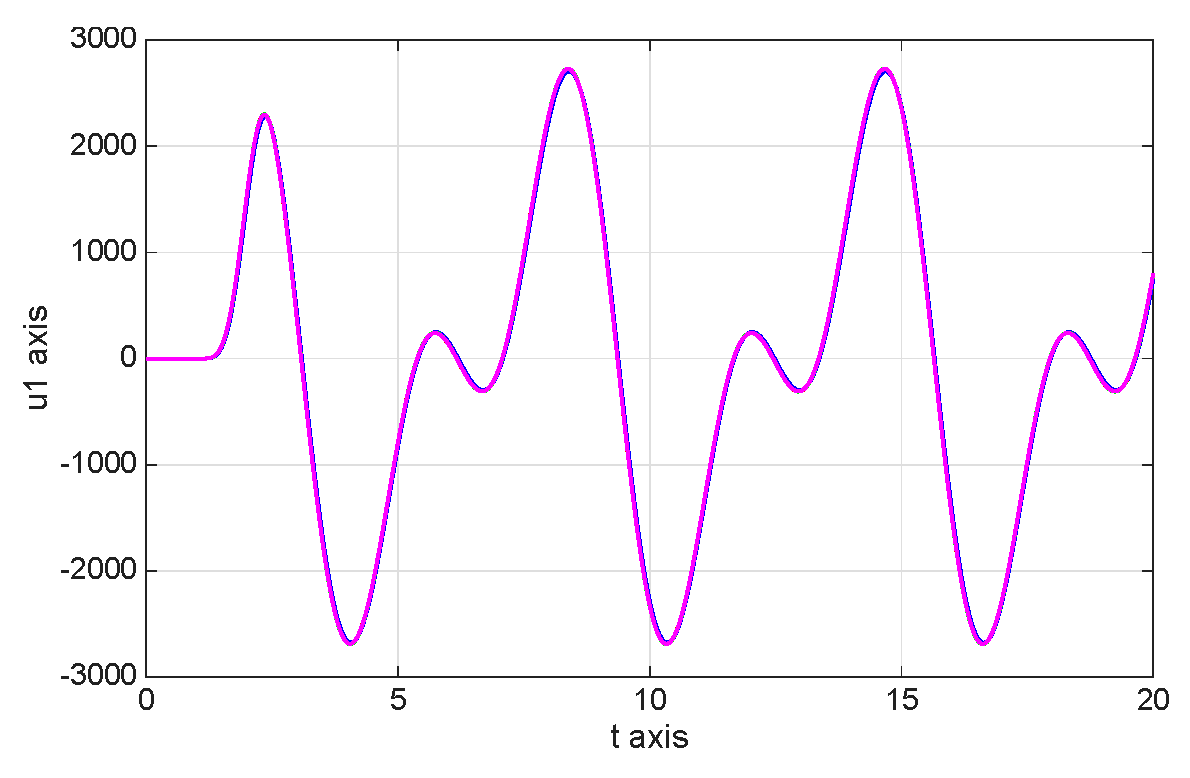
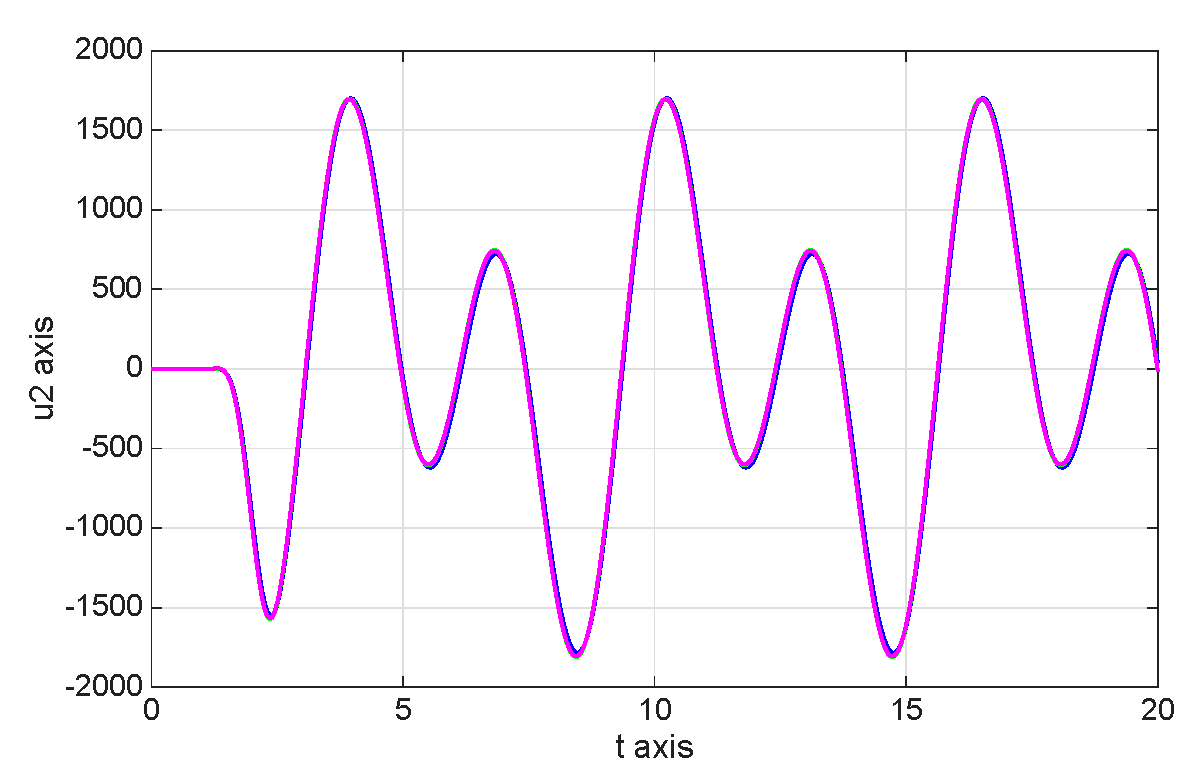
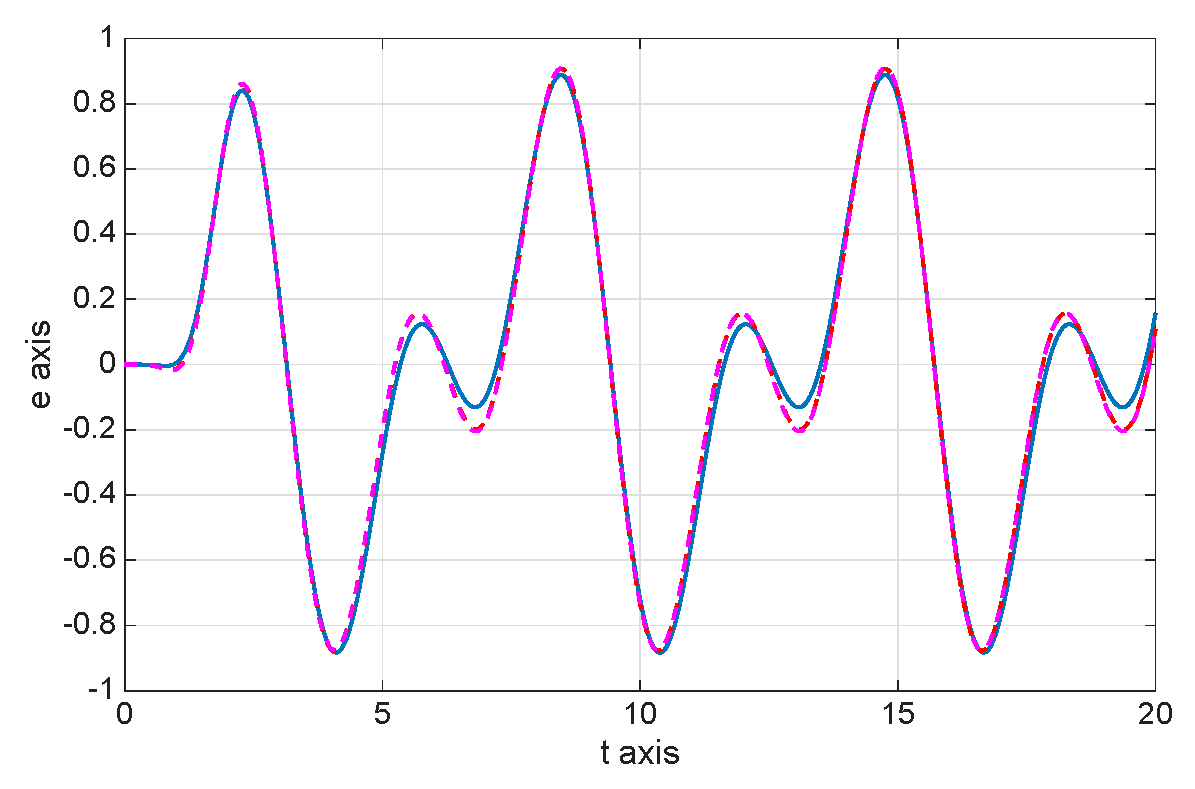
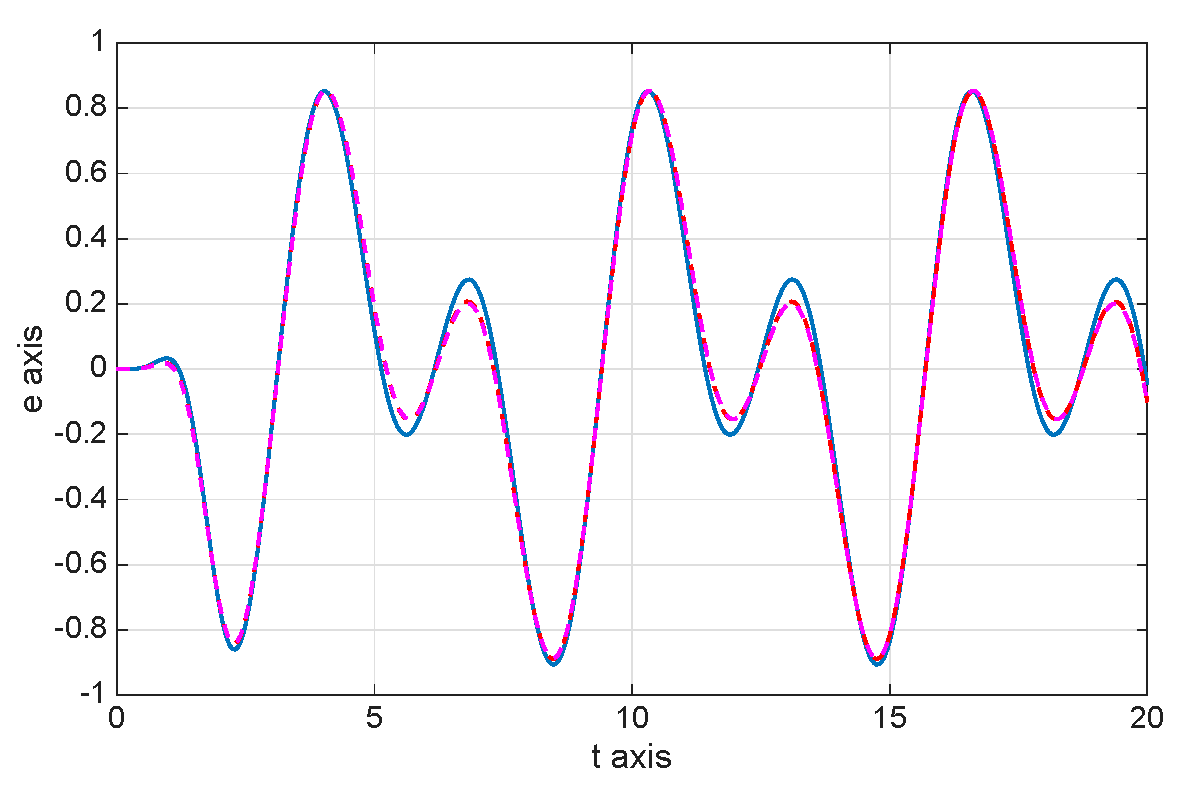
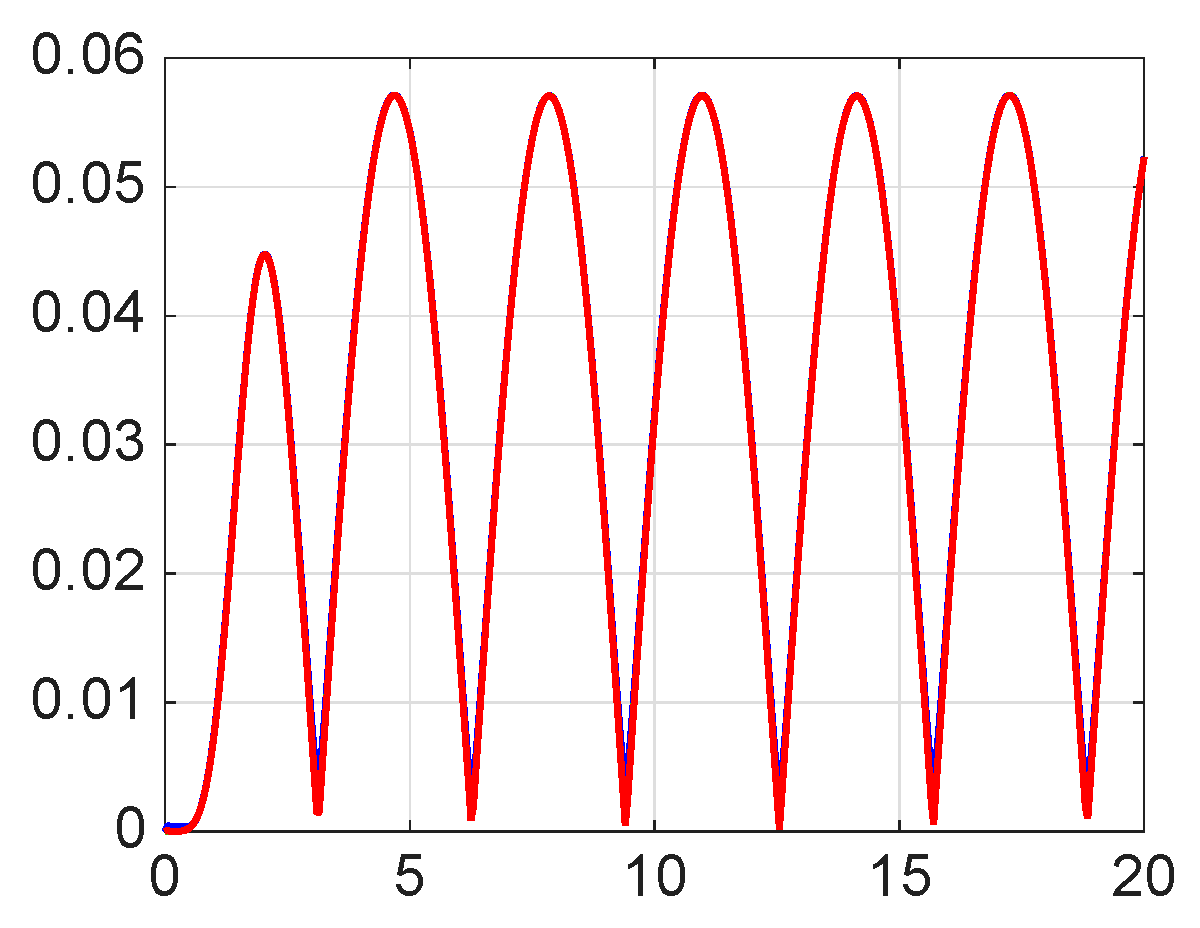
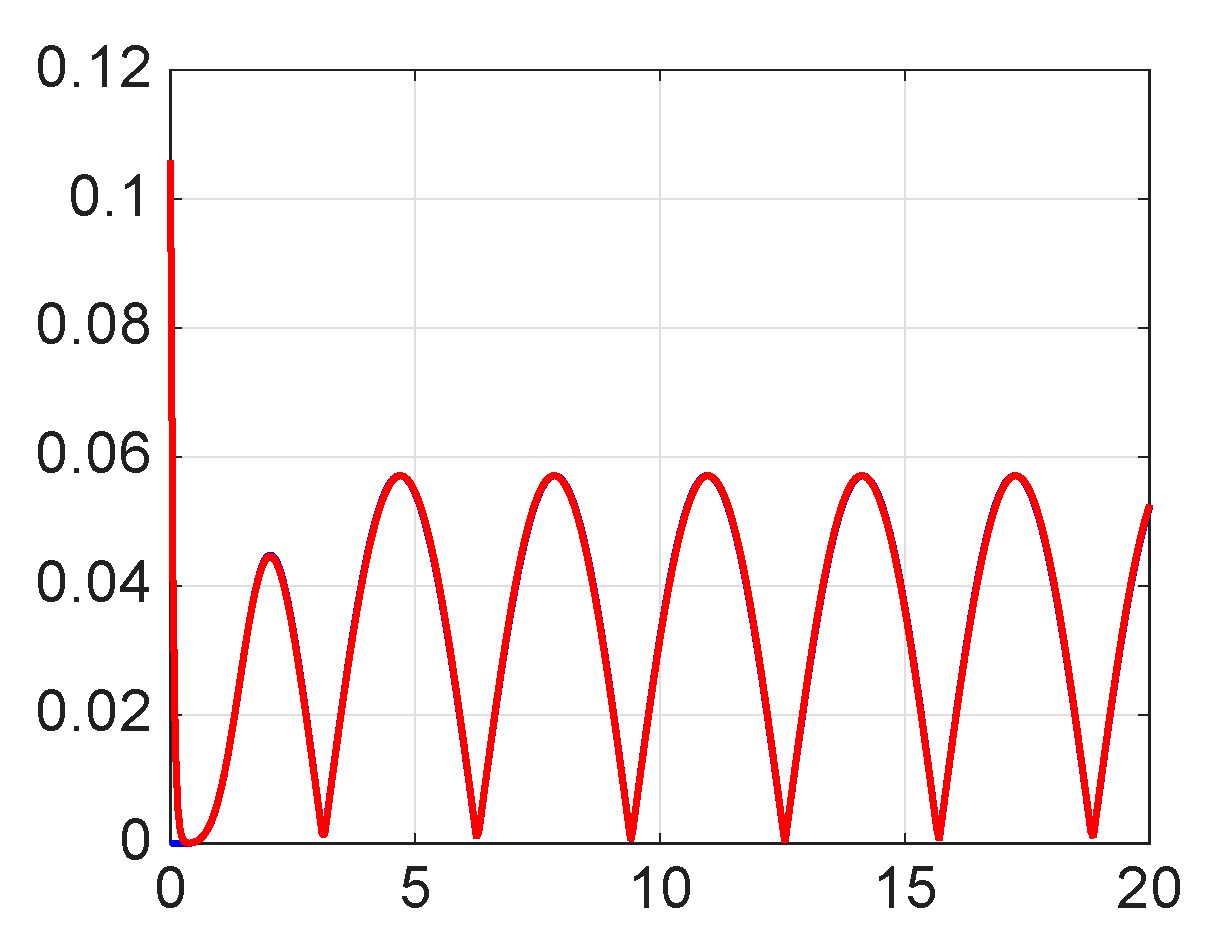
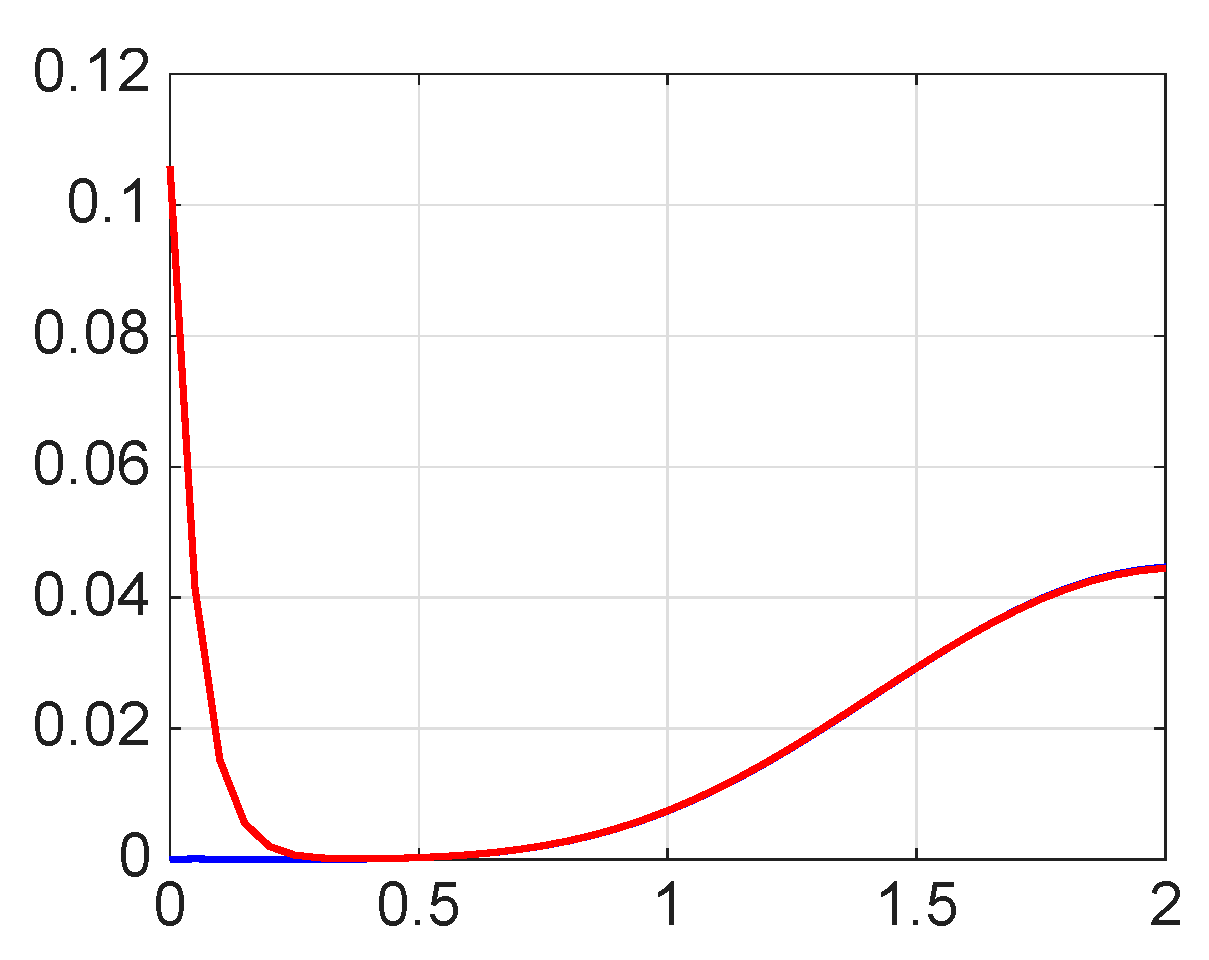
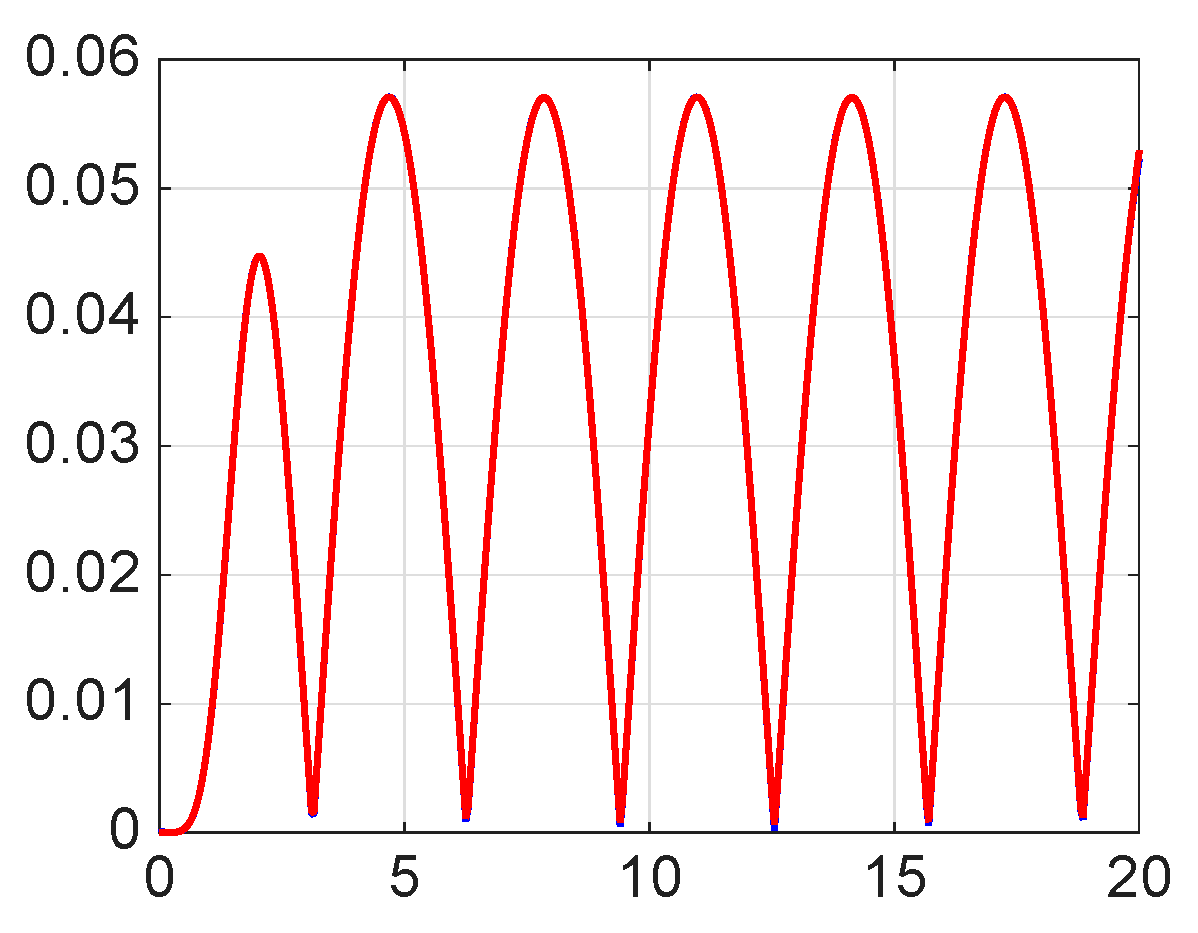
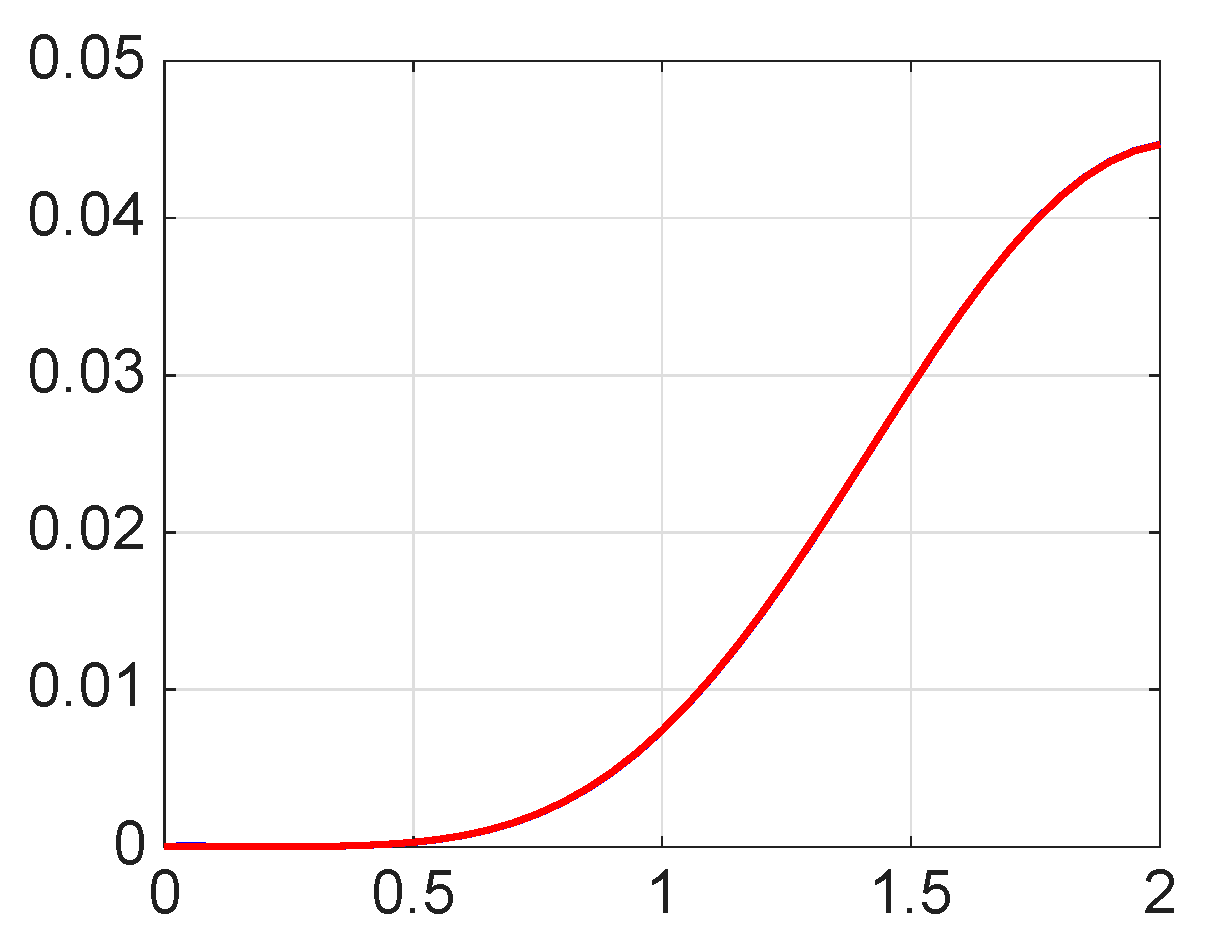
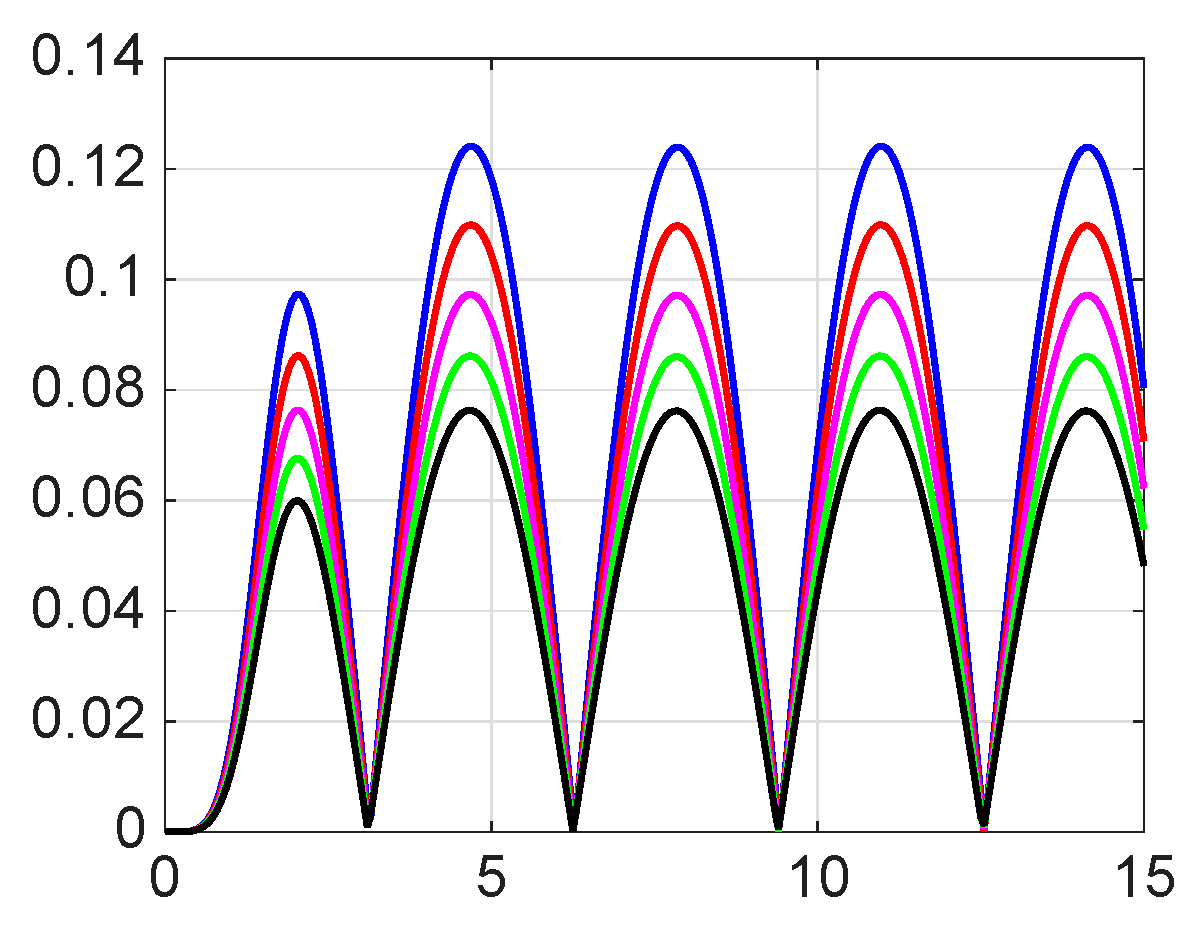
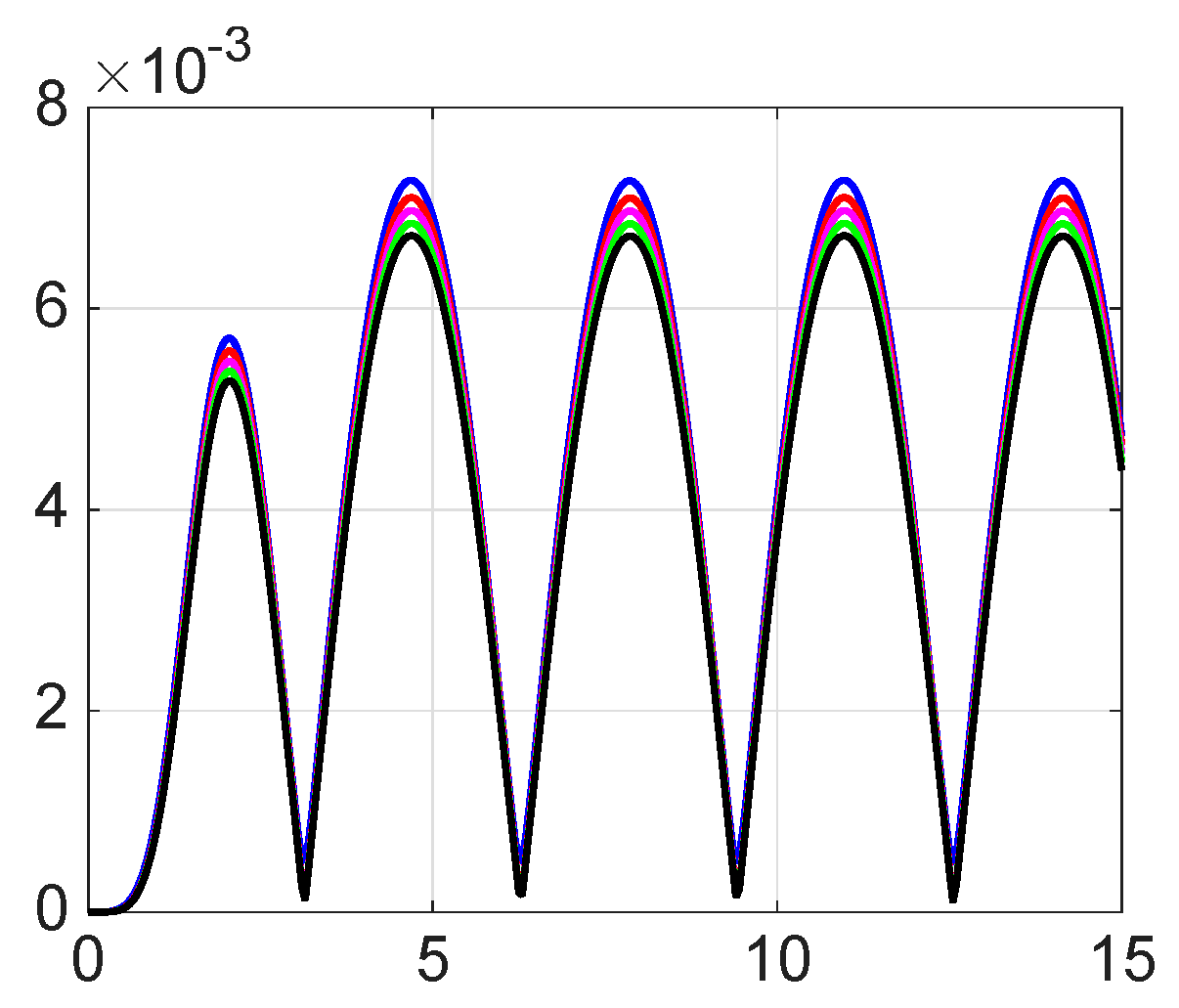
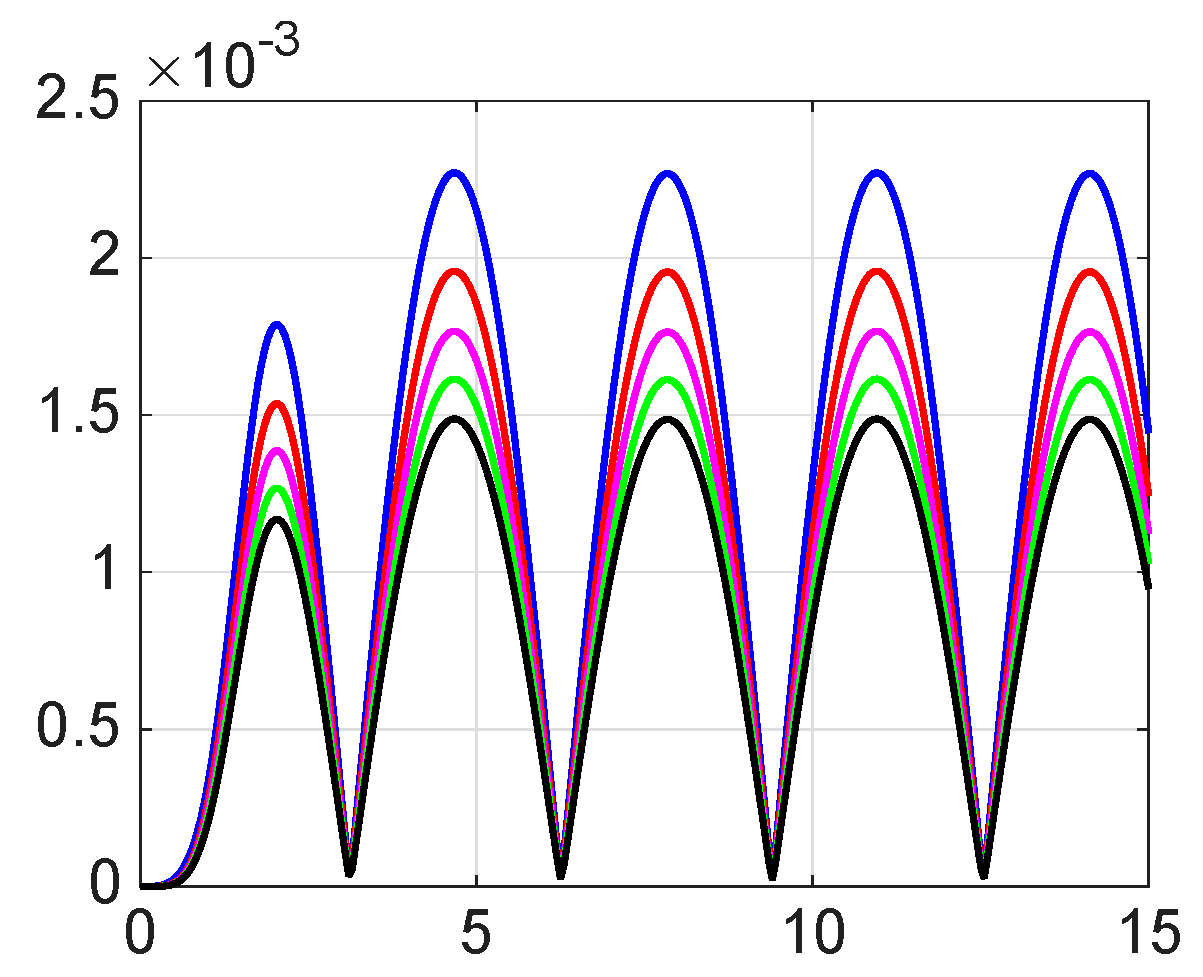
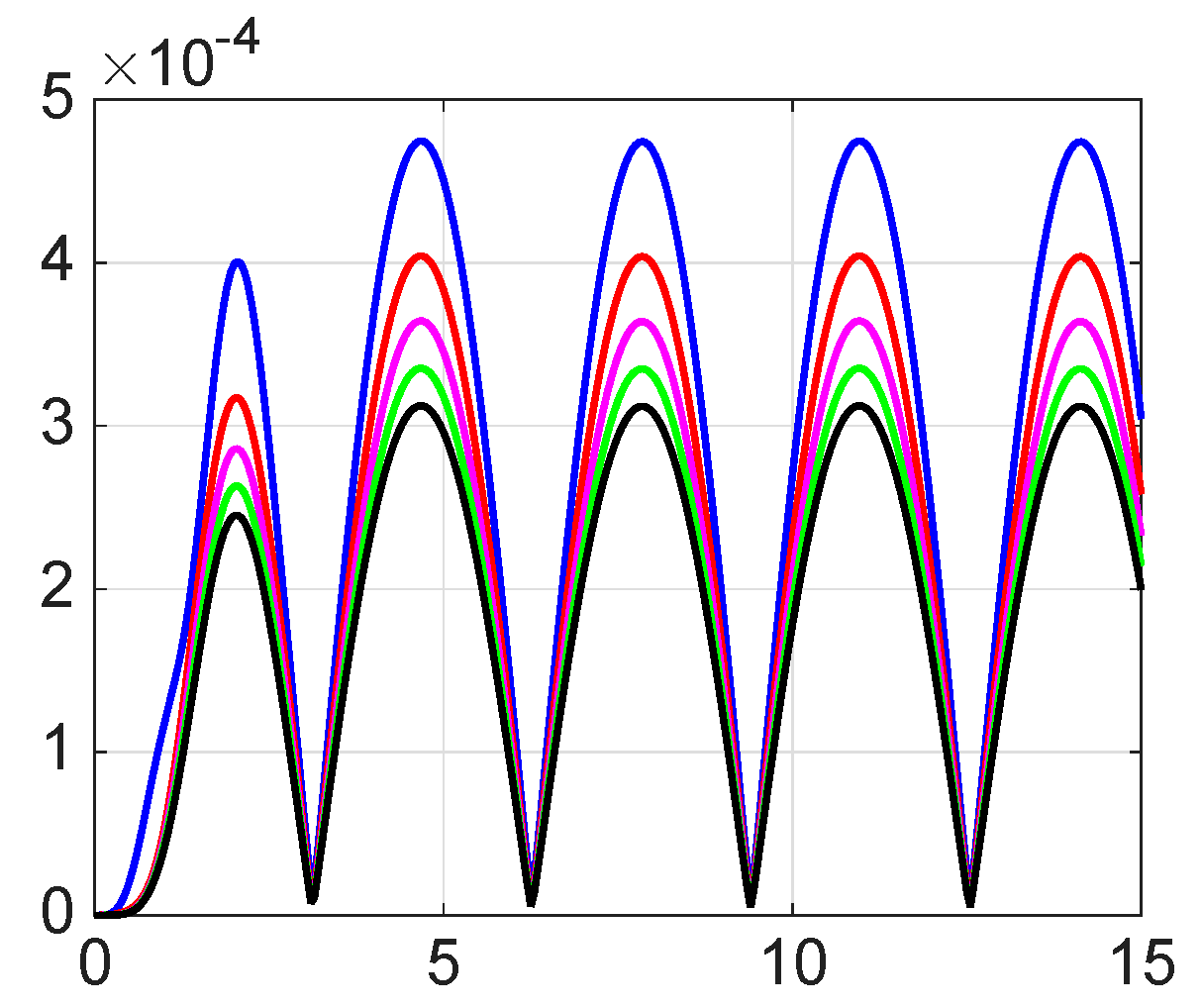
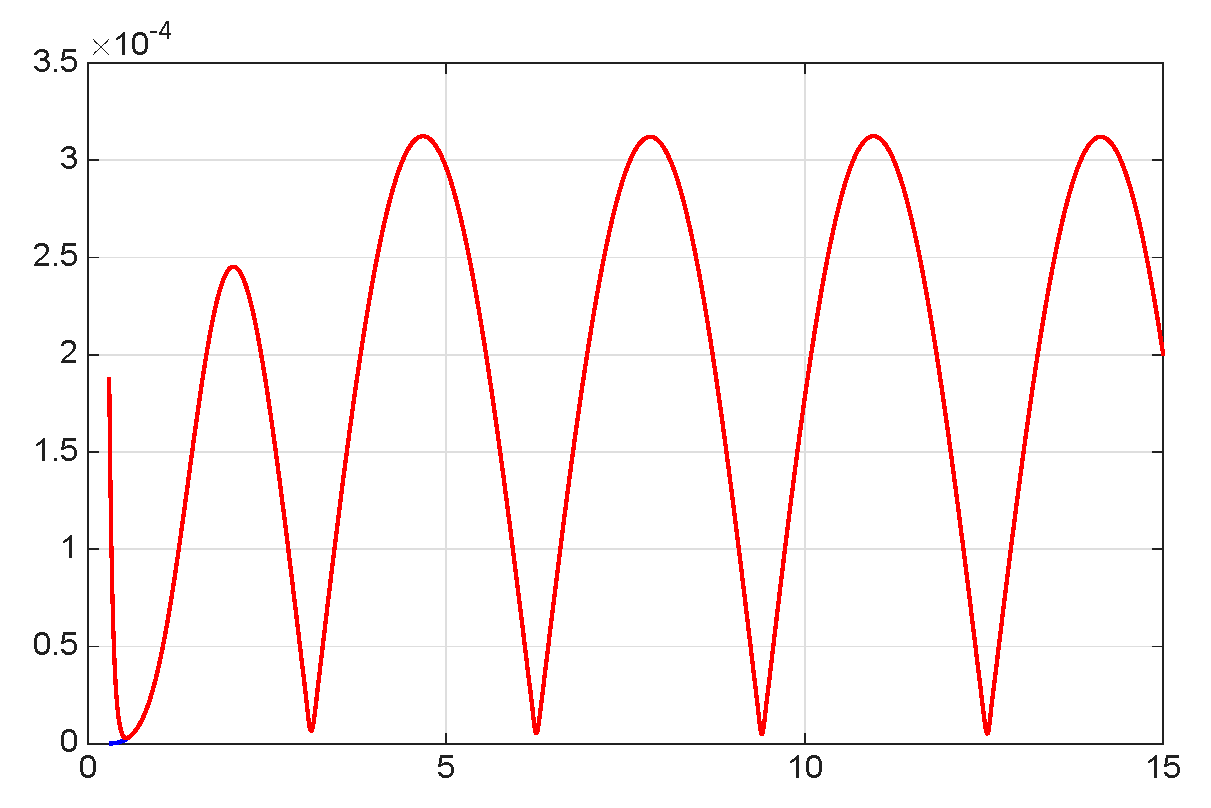
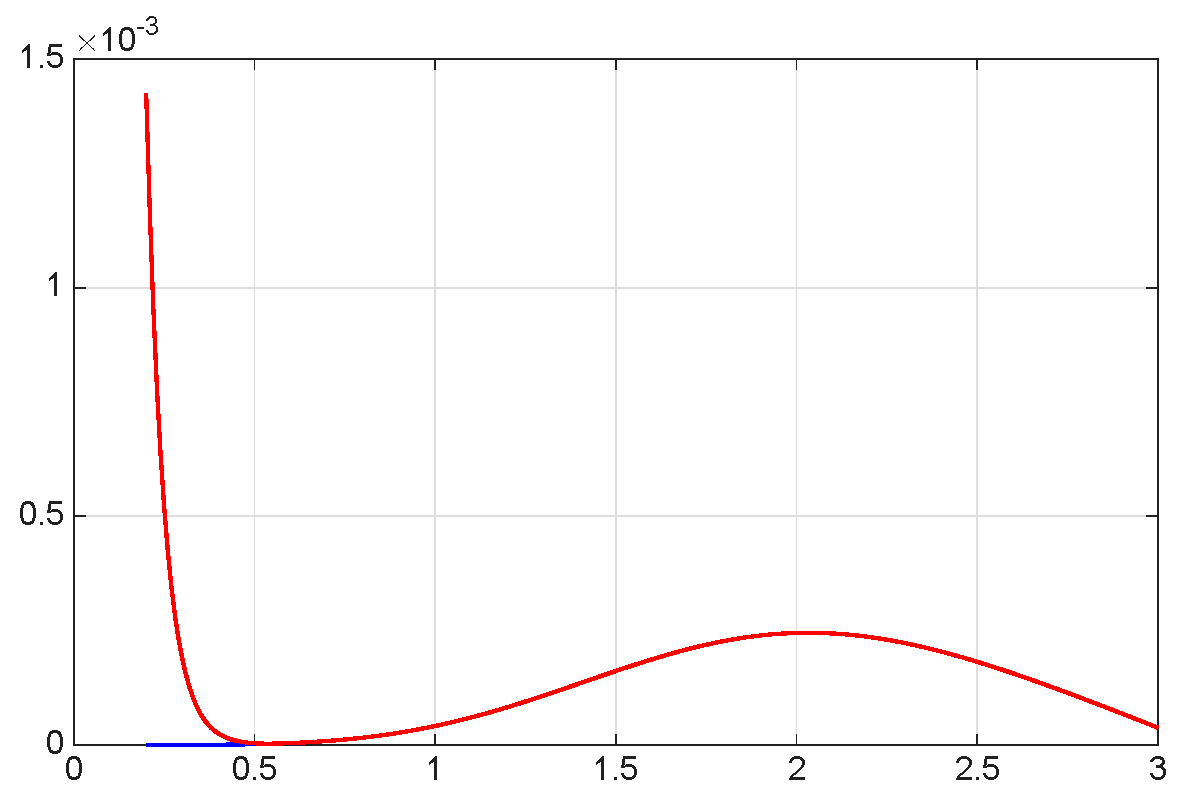
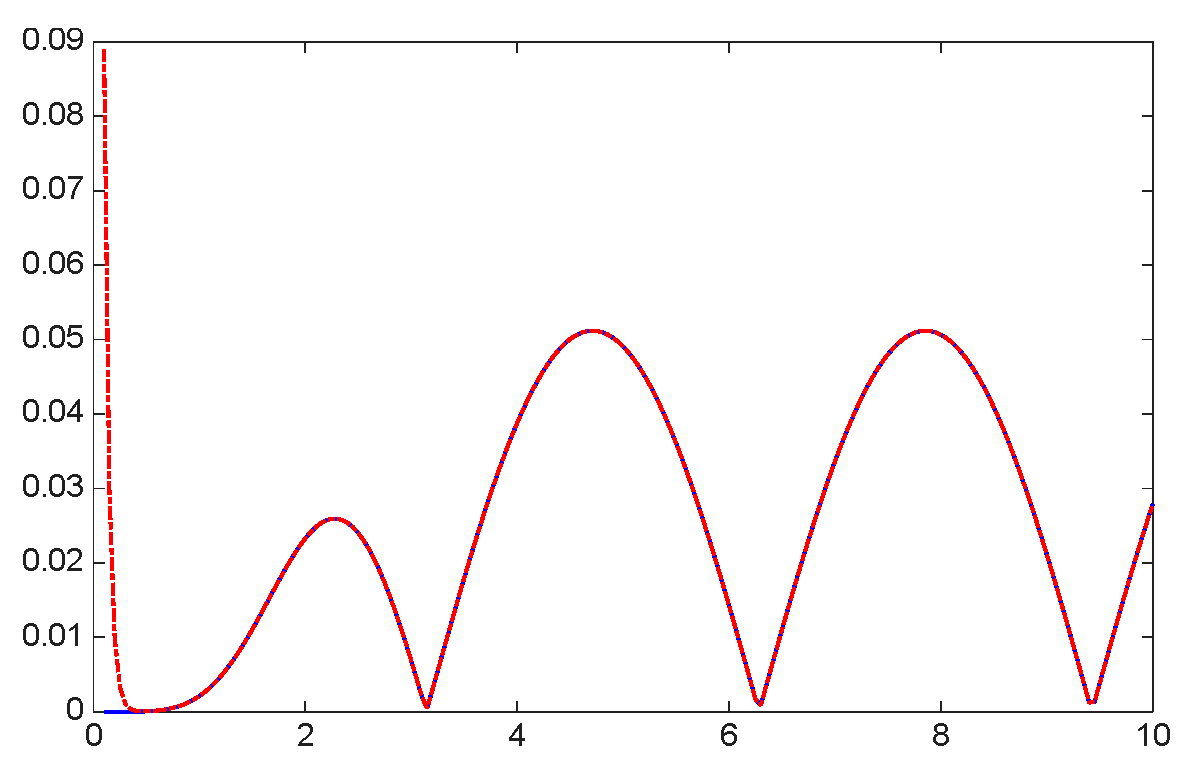
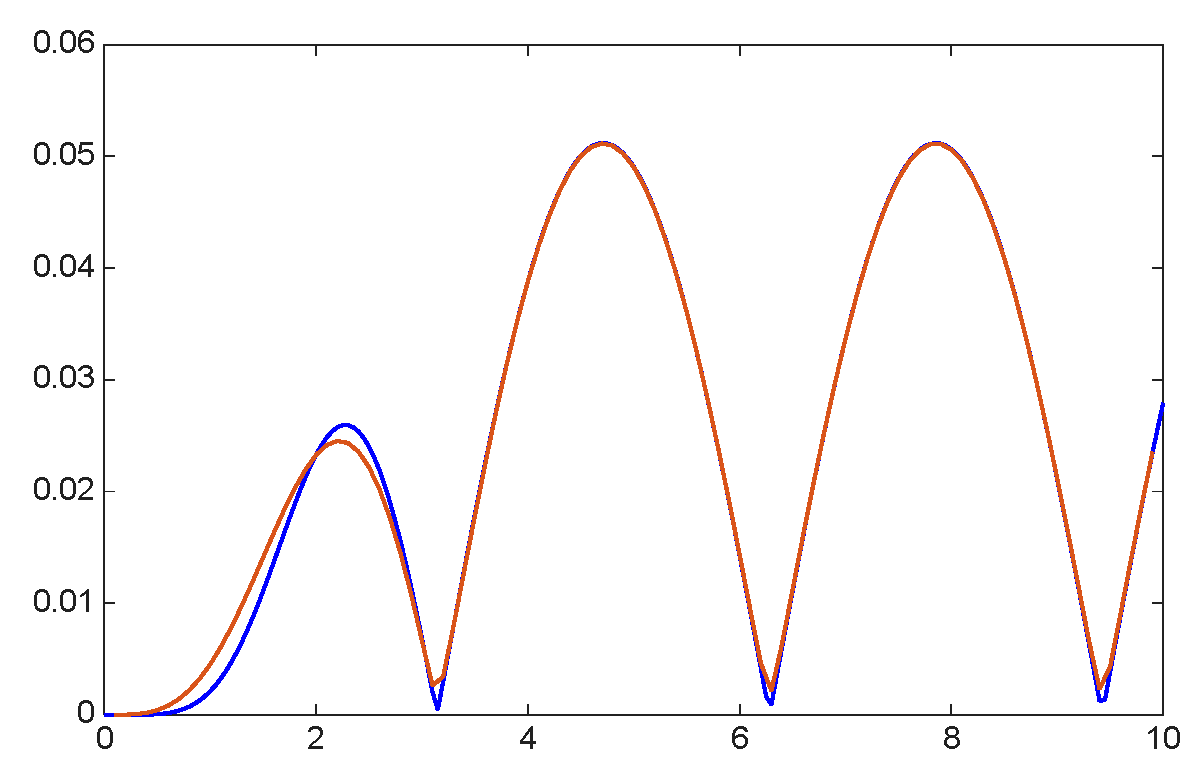
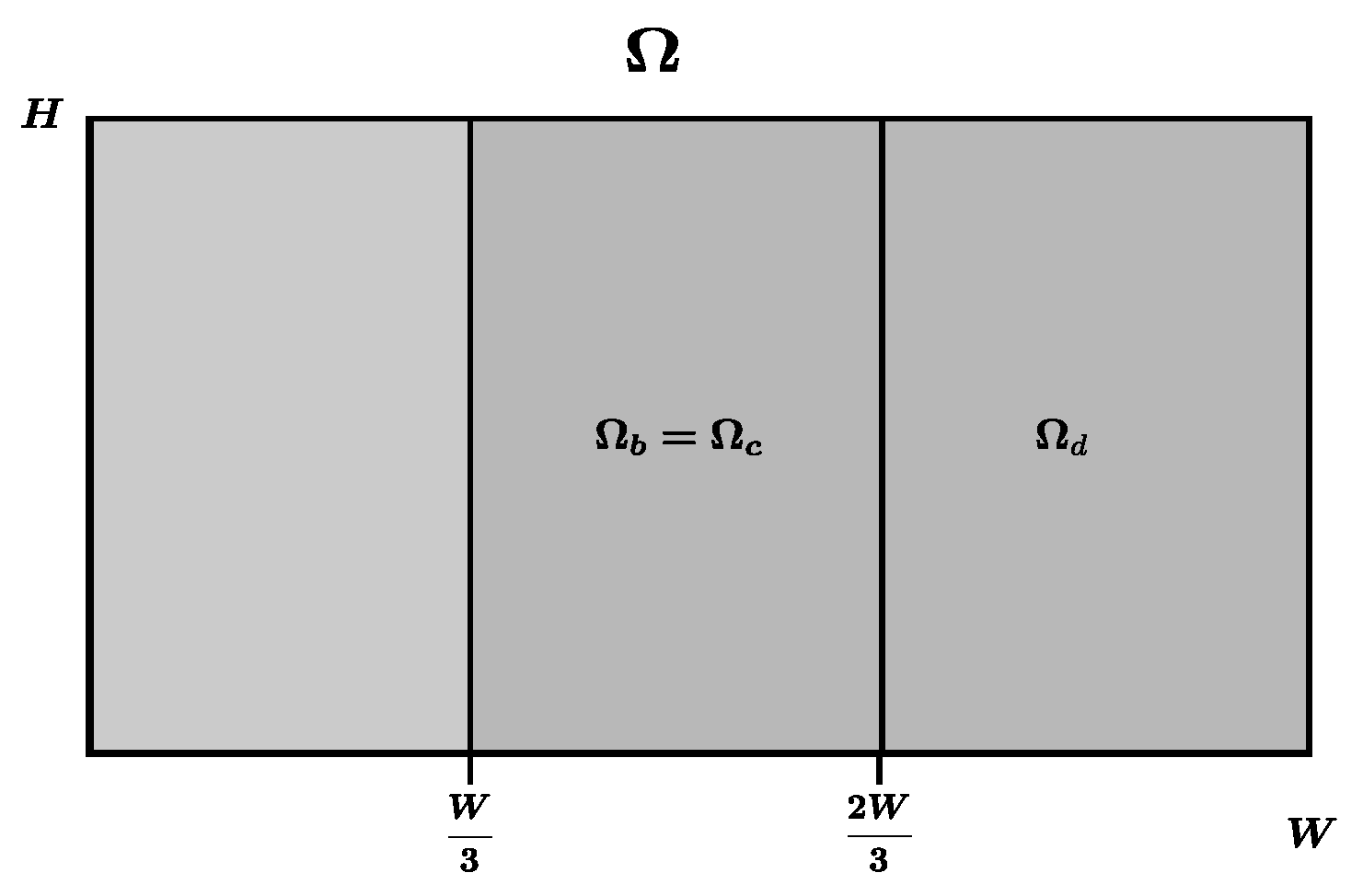
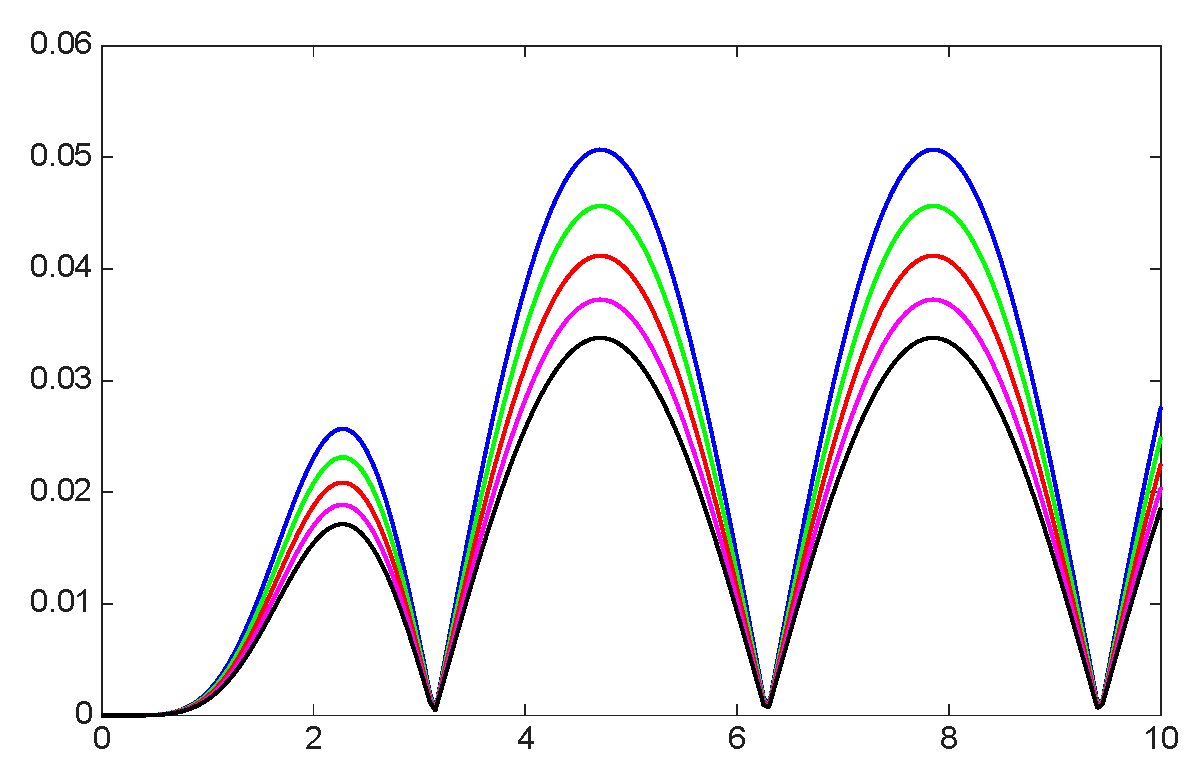
8. Numerical Simulations
9. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Motivation and Derivation of the Cascade Controller
The Cascade Controller
Appendix B. A Practical Solution Algorithm
Appendix C. Proof of Lemma 1
Appendix D. Analysis of the Errors
Appendix E. Error Estimates in the Case of Finite-Dimensional Input and Output Spaces
References
- Aulisa, E.; Gilliam, D. A Practical Guide to Geometric Regulation for Distributed Parameter Systems; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Burns, J.A.; He, X.; Hu, W. Feedback stabilization of a thermal fluid system with mixed boundary control. Comput. Math. Appl. 2016, 71, 2170–2191. [Google Scholar] [CrossRef]
- Deutscher, J.; Kerschbaum, S. Robust output regulation by state feedback control for coupled linear parabolic PIDEs. IEEE Trans. Autom. Control 2019, 65, 2207–2214. [Google Scholar] [CrossRef]
- Aulisa, E.; Gilliam, D.; Pathiranage, T. Analysis of an iterative scheme for approximate regulation for nonlinear systems. Int. J. Robust Nonlinear Control 2018, 28, 3140–3173. [Google Scholar] [CrossRef]
- Aulisa, E.; Gilliam, D.S.; Pathiranage, T.W. Analysis of the error in an iterative algorithm for asymptotic regulation of linear distributed parameter control systems. ESAIM Math. Model. Numer. Anal. 2019, 53, 1577–1606. [Google Scholar] [CrossRef]
- Aulisa, E.; Gilliam, D.S. Approximation methods for geometric regulation. arXiv 2021, arXiv:2102.06196. [Google Scholar]
- Francis, B.A.; Wonham, W.M. The internal model principle of control theory. Automatica 1976, 12, 457–465. [Google Scholar] [CrossRef]
- Francis, B.A. The linear multivariable regulator problem. SIAM J. Control Optim. 1977, 15, 486–505. [Google Scholar] [CrossRef]
- Hespanha, J.P. Linear Systems Theory, 2nd ed.; Princeton University Press: Princeton, NJ, USA, 2018. [Google Scholar]
- Azimi, A.; Koch, S.; Reichhartinger, M. Robust internal model-based control for linear-time-invariant systems. Int. J. Robust Nonlinear Control 2024, 34, 12476–12496. [Google Scholar] [CrossRef]
- Bymes, C.I.; Laukó, I.G.; Gilliam, D.S.; Shubov, V.I. Output regulation for linear distributed parameter systems. IEEE Trans. Autom. Control 2000, 45, 2236–2252. [Google Scholar] [CrossRef]
- Anderson, B.D.; Moore, J.B. Optimal Control: Linear Quadratic Methods, reprint edition ed.; Dover Publications: Mineola, NY, USA, 2007. [Google Scholar]
- Dorato, P.; Abdallah, C.; Cerone, V. Linear-Quadratic Control: An Introduction; Krieger Publishing Company: Malabar, FL, USA, 2000. [Google Scholar]
- Najafi Birgani, S.; Moaveni, B.; Khaki-Sedigh, A. Infinite horizon linear quadratic tracking problem: A discounted cost function approach. Optim. Control Appl. Methods 2018, 39, 1549–1572. [Google Scholar] [CrossRef]
- Bornemann, F.A. An adaptive multilevel approach to parabolic equations III. 2D error estimation and multilevel preconditioning. IMPACT Comput. Sci. Eng. 1992, 4, 1–45. [Google Scholar] [CrossRef]
- Tröltzsch, F. On the Lagrange–Newton–SQP method for the optimal control of semilinear parabolic equations. SIAM J. Control Optim. 1999, 38, 294–312. [Google Scholar] [CrossRef]
- McAsey, M.; Mou, L.; Han, W. Convergence of the forward-backward sweep method in optimal control. Comput. Optim. Appl. 2012, 53, 207–226. [Google Scholar] [CrossRef]
- Tröltzsch, F. Optimal Control of Partial Differential Equations: Theory, Methods and Applications; Graduate Studies in Mathematics; American Mathematical Society: Providence, RI, USA, 2010; Volume 112. [Google Scholar]
- Lee, Y.; Kouvaritakis, B. Constrained receding horizon predictive control for systems with disturbances. Int. J. Control 1999, 72, 1027–1032. [Google Scholar] [CrossRef]
- Camacho, E.F.; Bordons, C. Constrained model predictive control. In Model Predictive Control; Springer: Berlin/Heidelberg, Germany, 2007; pp. 177–216. [Google Scholar]
- Güttel, S.; Pearson, J.W. A rational deferred correction approach to parabolic optimal control problems. IMA J. Numer. Anal. 2018, 38, 1861–1892. [Google Scholar] [CrossRef]
- Leveque, S.; Pearson, J.W. Fast iterative solver for the optimal control of time-dependent PDEs with Crank–Nicolson discretization in time. Numer. Linear Algebra Appl. 2022, 29, e2419. [Google Scholar] [CrossRef]
- Aulisa, E.; Burns, J.A.; Gilliam, D.S. Approximate Error Feedback Controller for Tracking and Disturbance Rejection for Linear Distributed Parameter Systems. In Proceedings of the 2022 American Control Conference (ACC), Atlanta, GA, USA, 8–10 June 2022; pp. 976–981. [Google Scholar]
- Conway, J.B. A Course in Functional Analysis; Springer: Berlin/Heidelberg, Germany, 2019; Volume 96. [Google Scholar]
- Kato, T. Perturbation Theory for Linear Operators; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 132. [Google Scholar]
- Baumeister, J. Stable Solution of Inverse Problems; Springer: Berlin/Heidelberg, Germany, 1987. [Google Scholar]
- Kirsch, A. An Introduction to the Mathematical Theory of Inverse Problems, 3rd ed.; Applied Mathematical Sciences; Springer: Cham, Switzerland, 2021; Volume 120. [Google Scholar] [CrossRef]
- Morozov, V.A. Methods for Solving Incorrectly Posed Problems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Kress, R.; Maz’ya, V.; Kozlov, V. Linear Integral Equations; Springer: Berlin/Heidelberg, Germany, 1989; Volume 82. [Google Scholar]
- Hsiao, G.C.; Wendland, W.L. Boundary Integral Equations, 2nd ed.; Applied Mathematical Sciences; Springer: Cham, Switzerland, 2021; Volume 164. [Google Scholar] [CrossRef]
- Fallahnejad, M.; Kazemy, A.; Shafiee, M. Event-triggered H∞ stabilization of networked cascade control systems under periodic DoS attack: A switching approach. Int. J. Electr. Power Energy Syst. 2023, 153, 109278. [Google Scholar] [CrossRef]
- Du, Z.; Chen, C.; Li, C.; Yang, X.; Li, J. Fault-Tolerant H-Infinity Stabilization for Networked Cascade Control Systems with Novel Adaptive Event-Triggered Mechanism. IEEE Trans. Autom. Sci. Eng. 2025. early access. [Google Scholar] [CrossRef]
- Hecht, F.; Lance, G.; Trélat, E. PDE-Constrained Optimization Within FreeFEM; Open-Access Monograph; LJLL/Sorbonne Université: Paris, France, 2024. [Google Scholar]
- Schwartz, J.T. Linear Operators: Spectral Theory: Self Adjoint Operators in Hilbert Space; Interscience: Saint-Nom-la-Bretéche, France, 1963. [Google Scholar]
- Lewin, M. Spectral Theory and Quantum Mechanics; Universitext; Springer: Cham, Switzerland, 2024. [Google Scholar] [CrossRef]
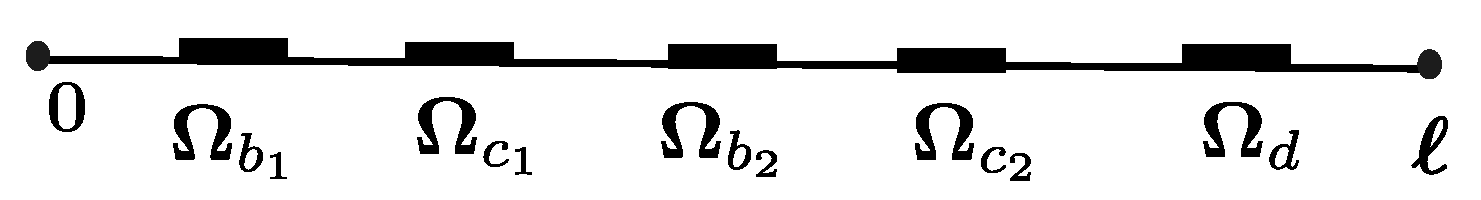
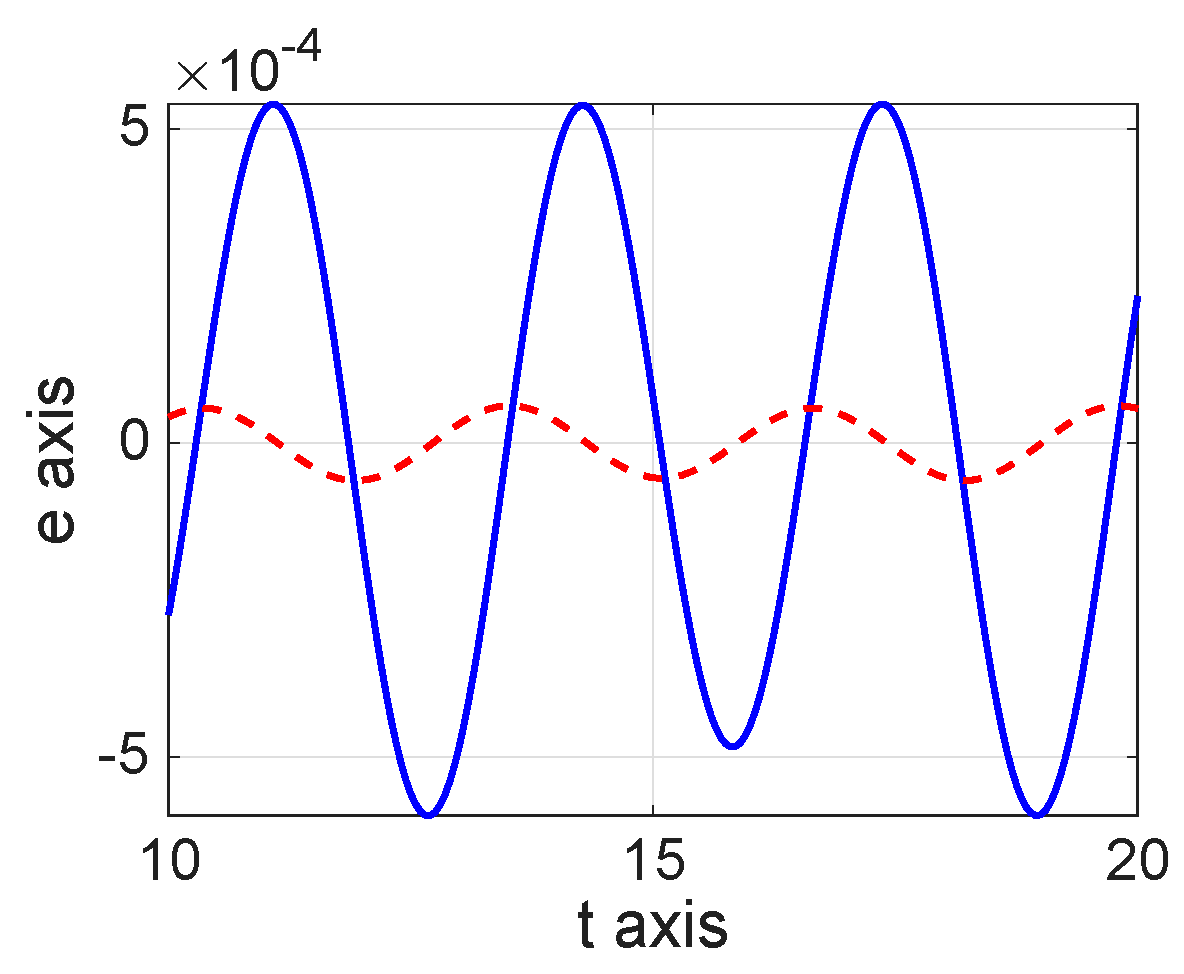
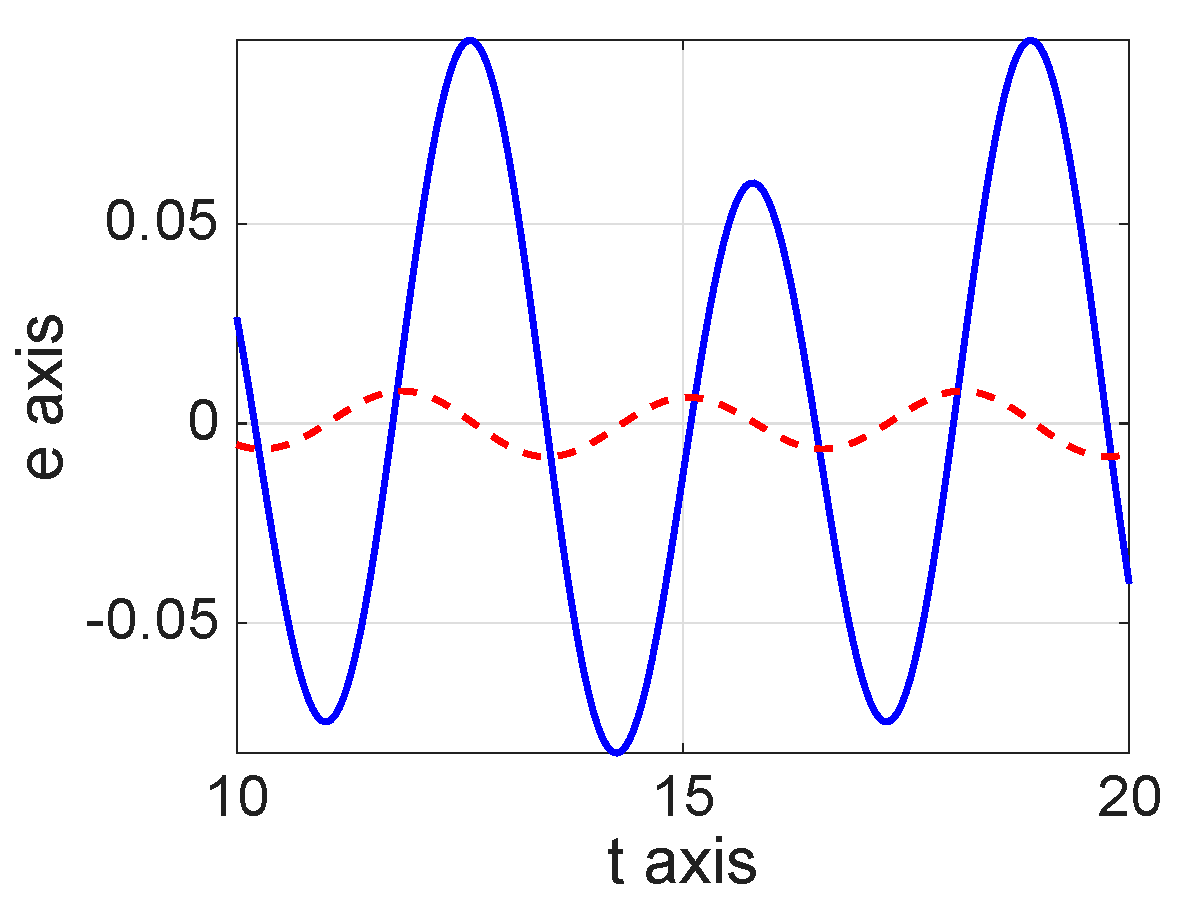
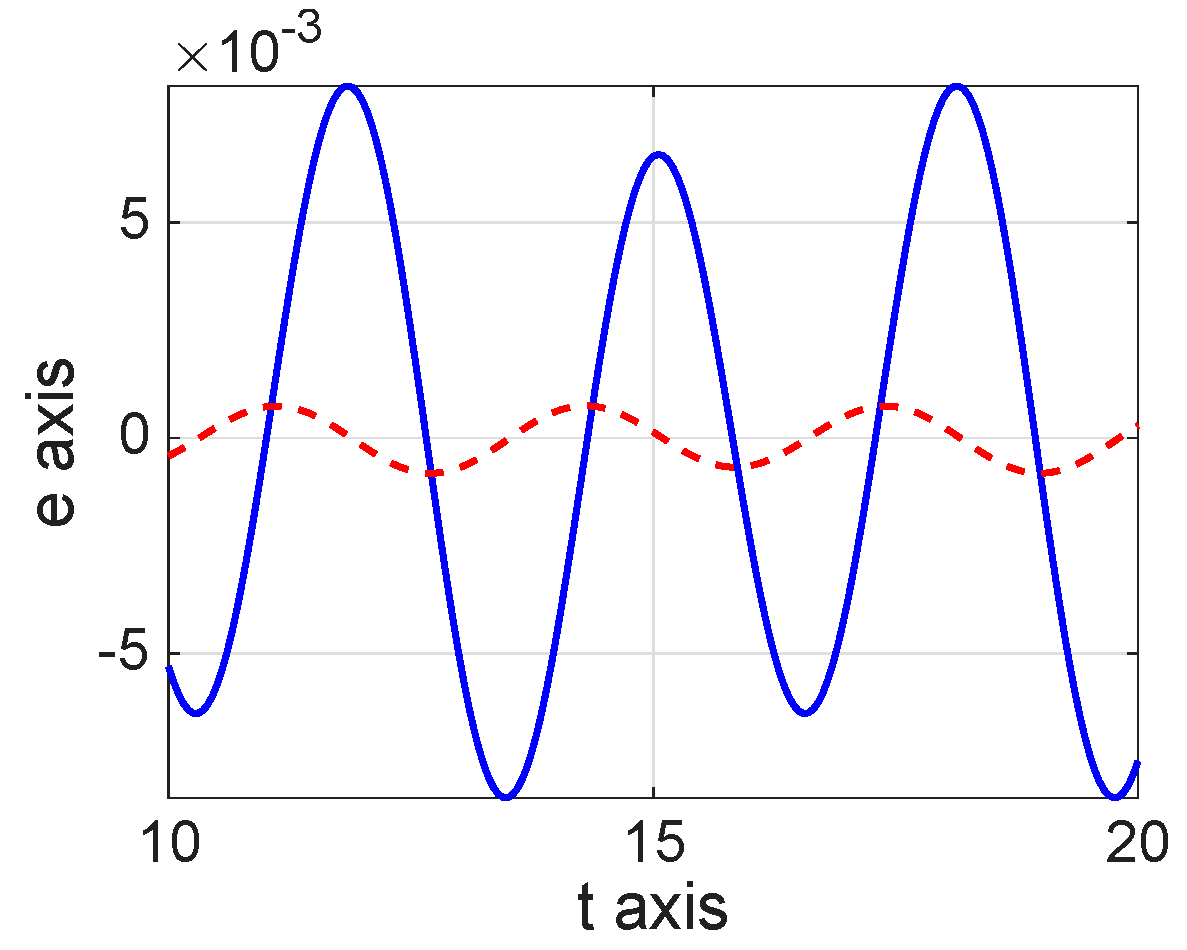
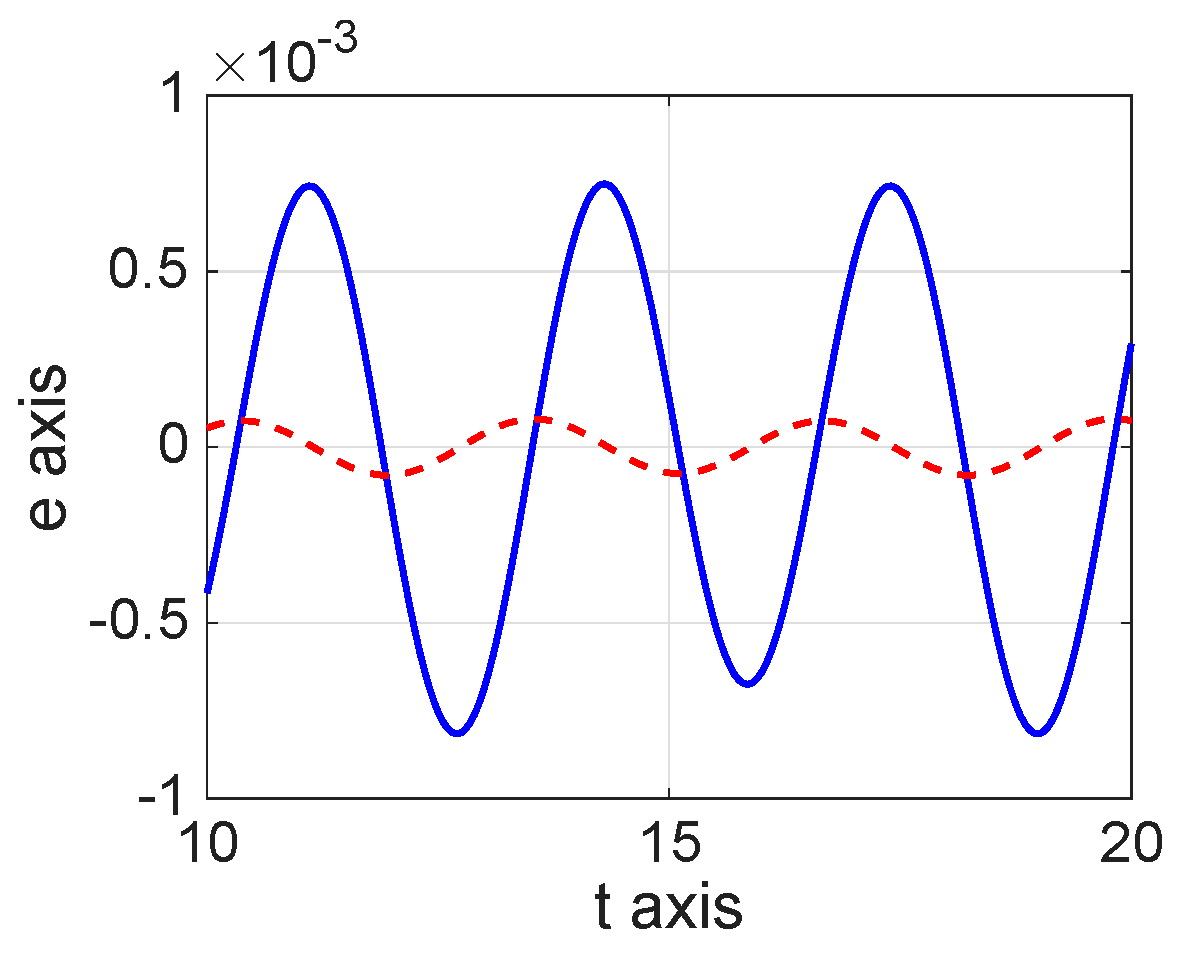
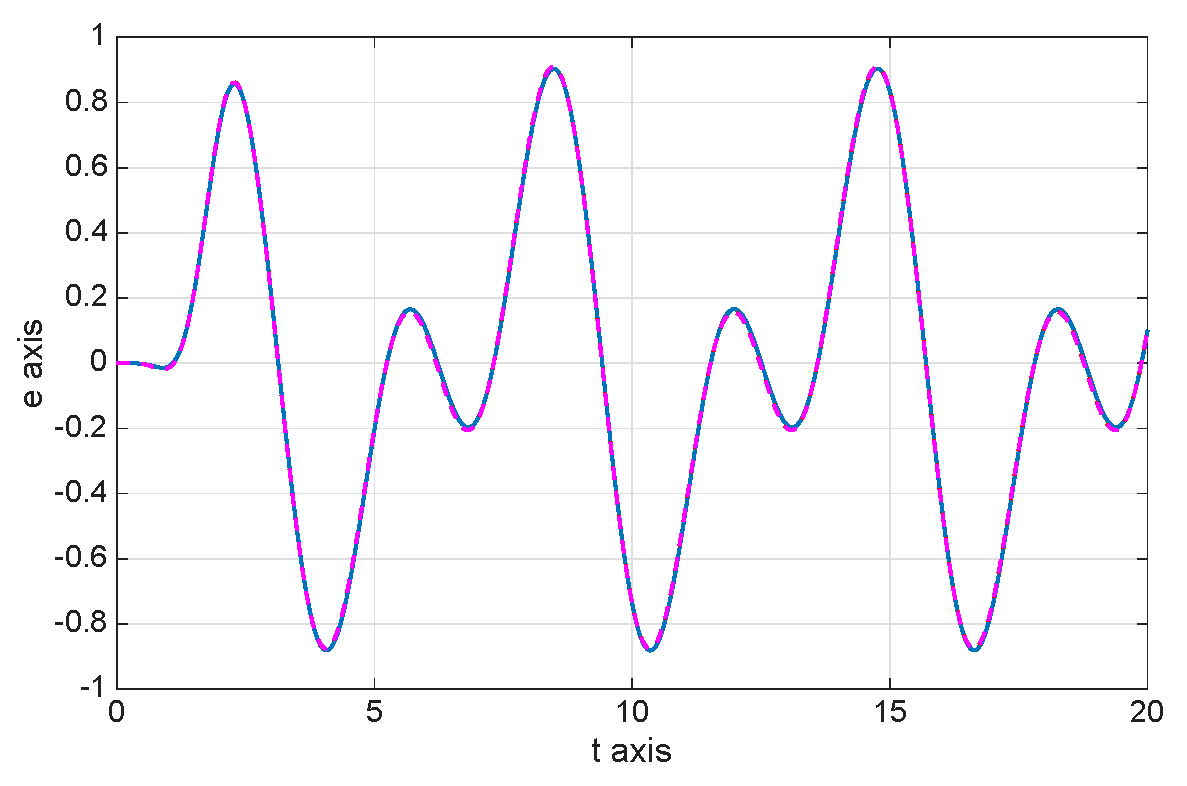
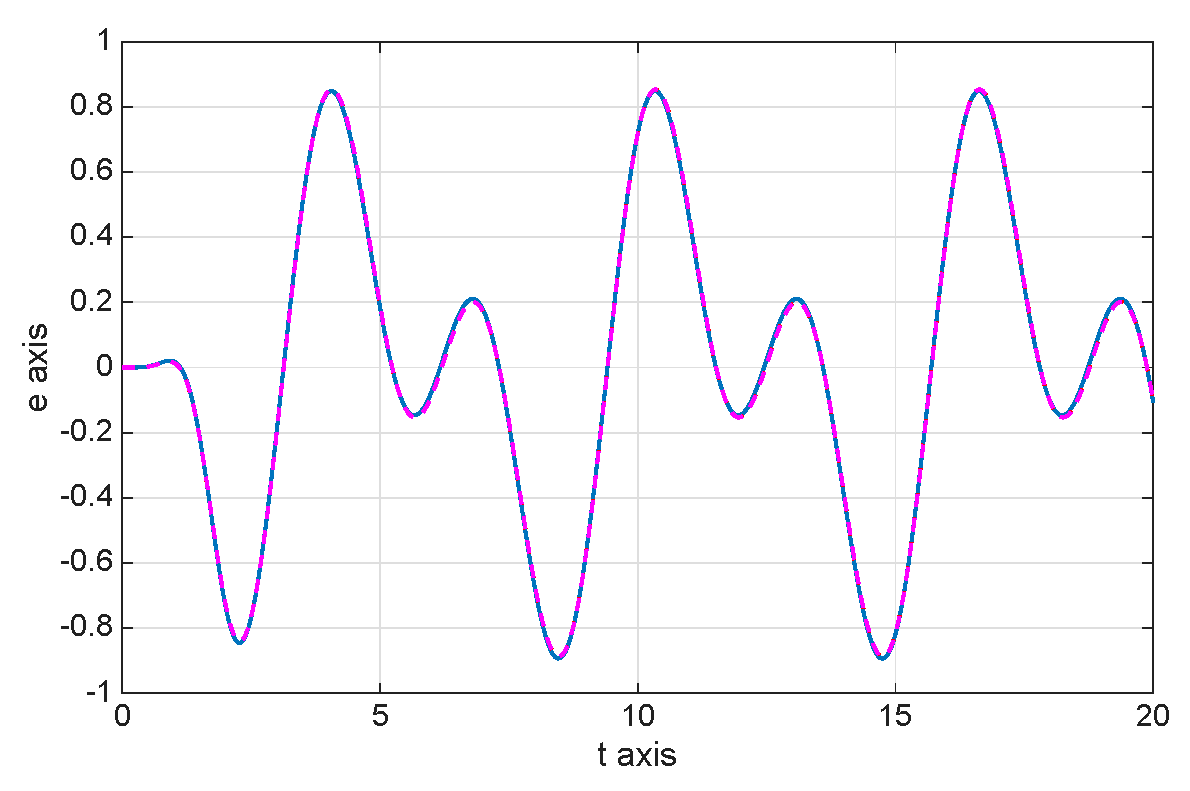
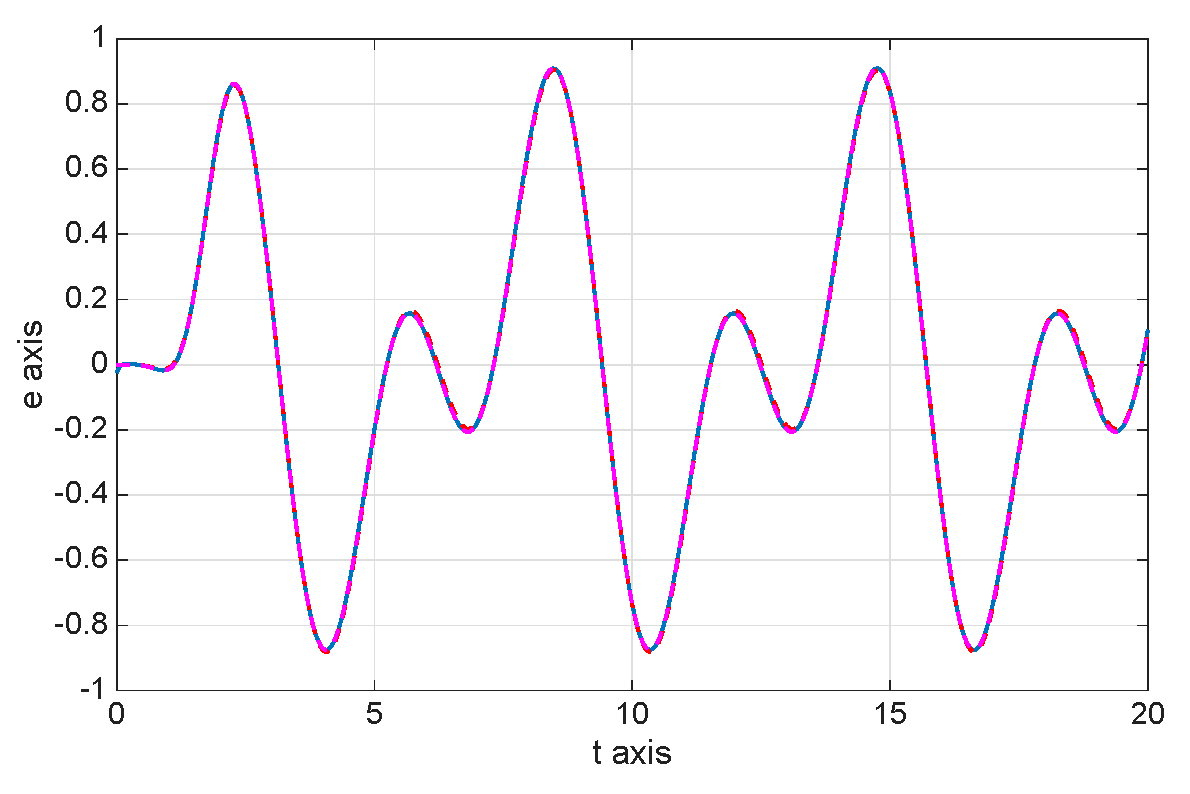
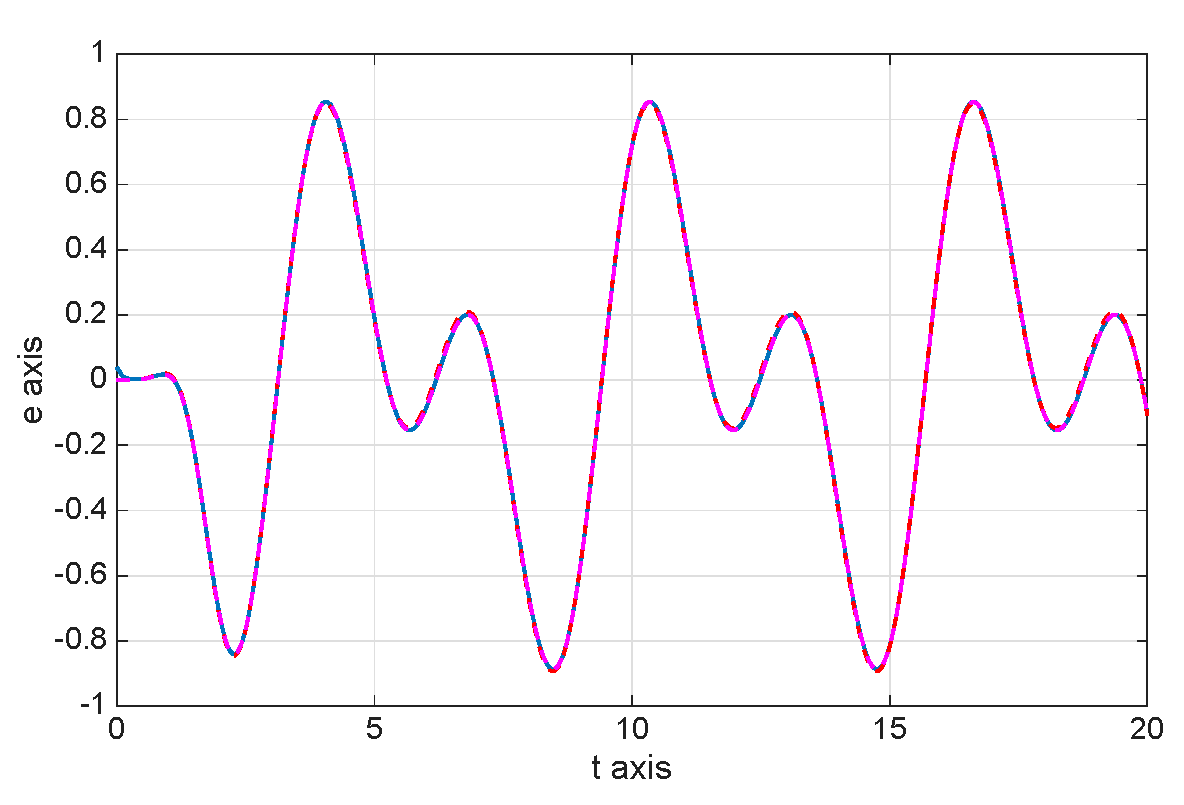
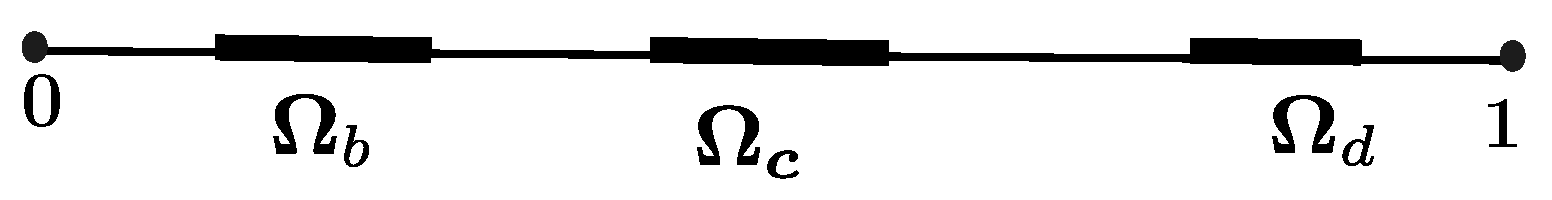
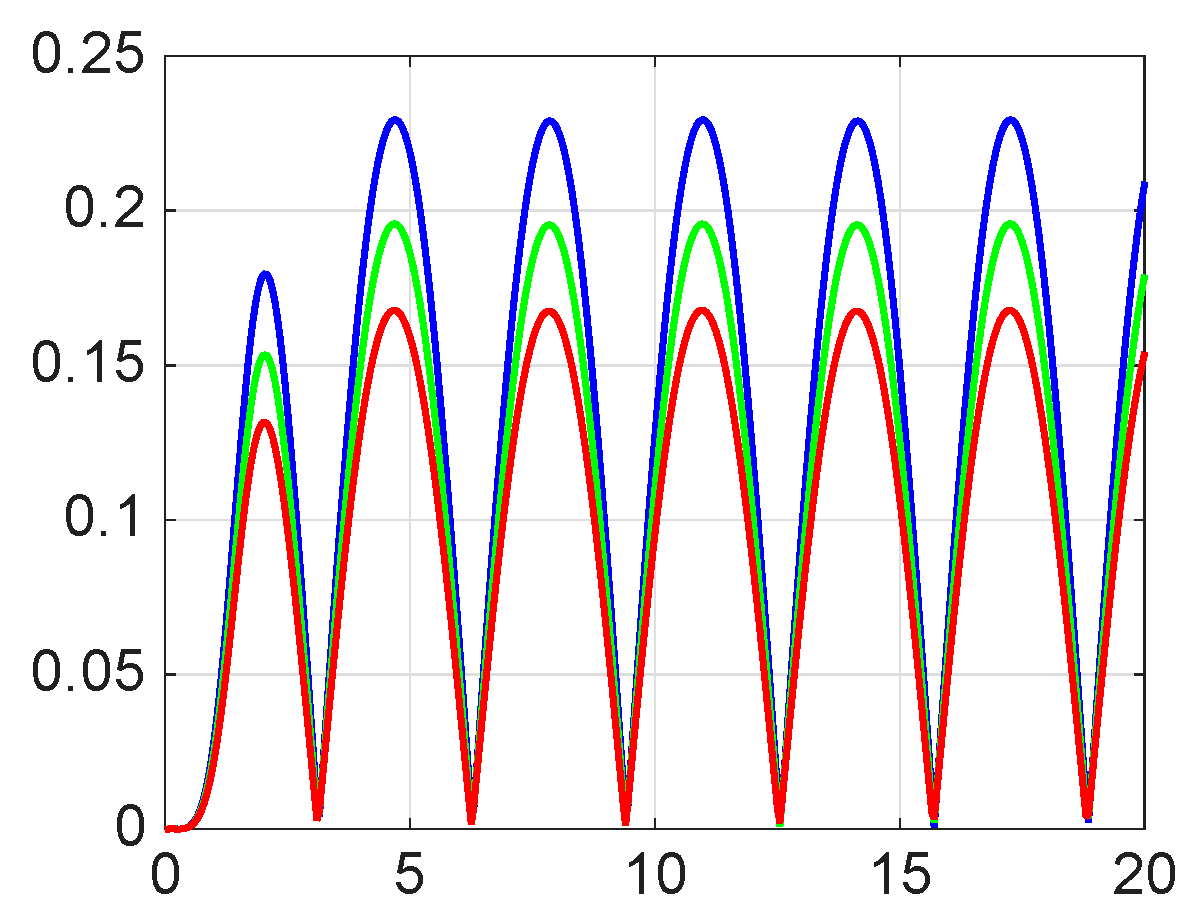
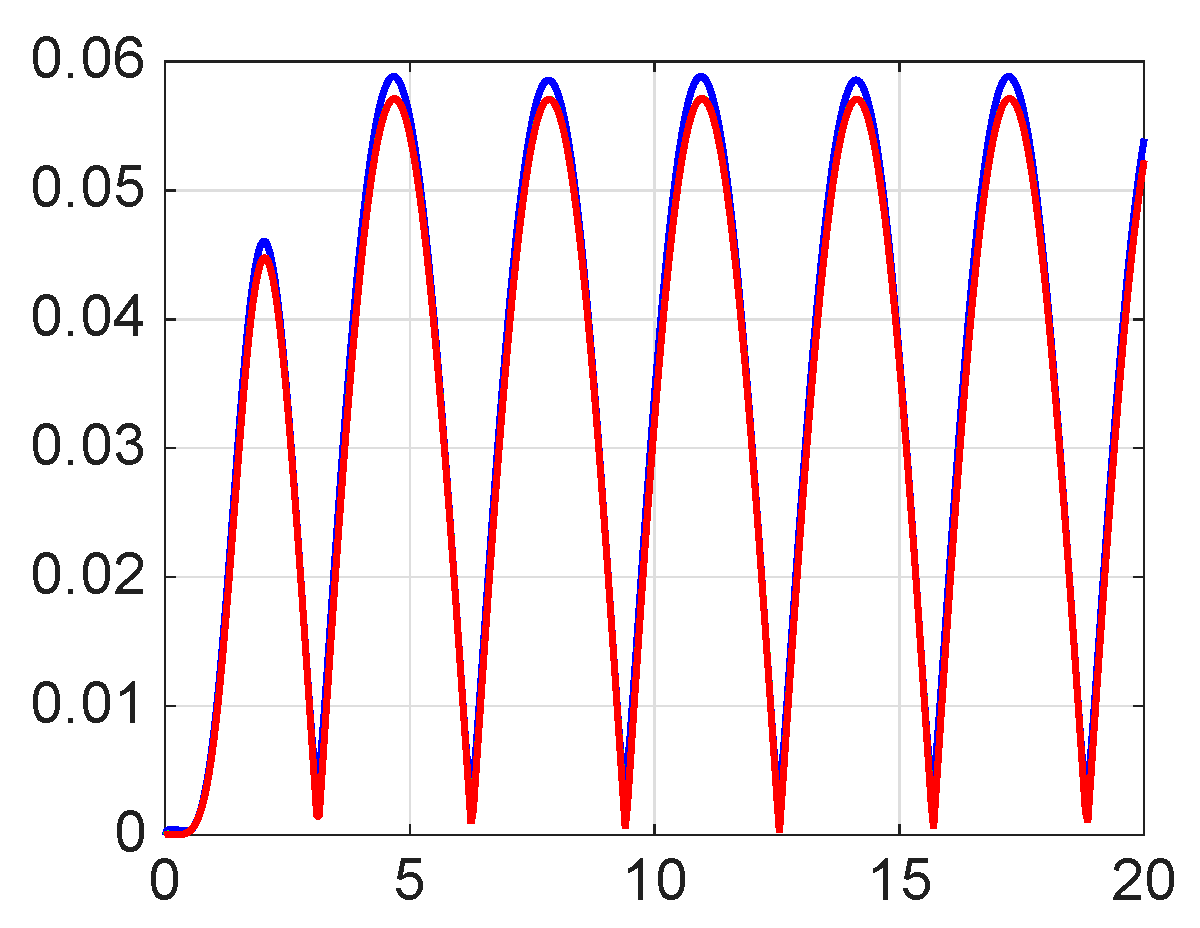
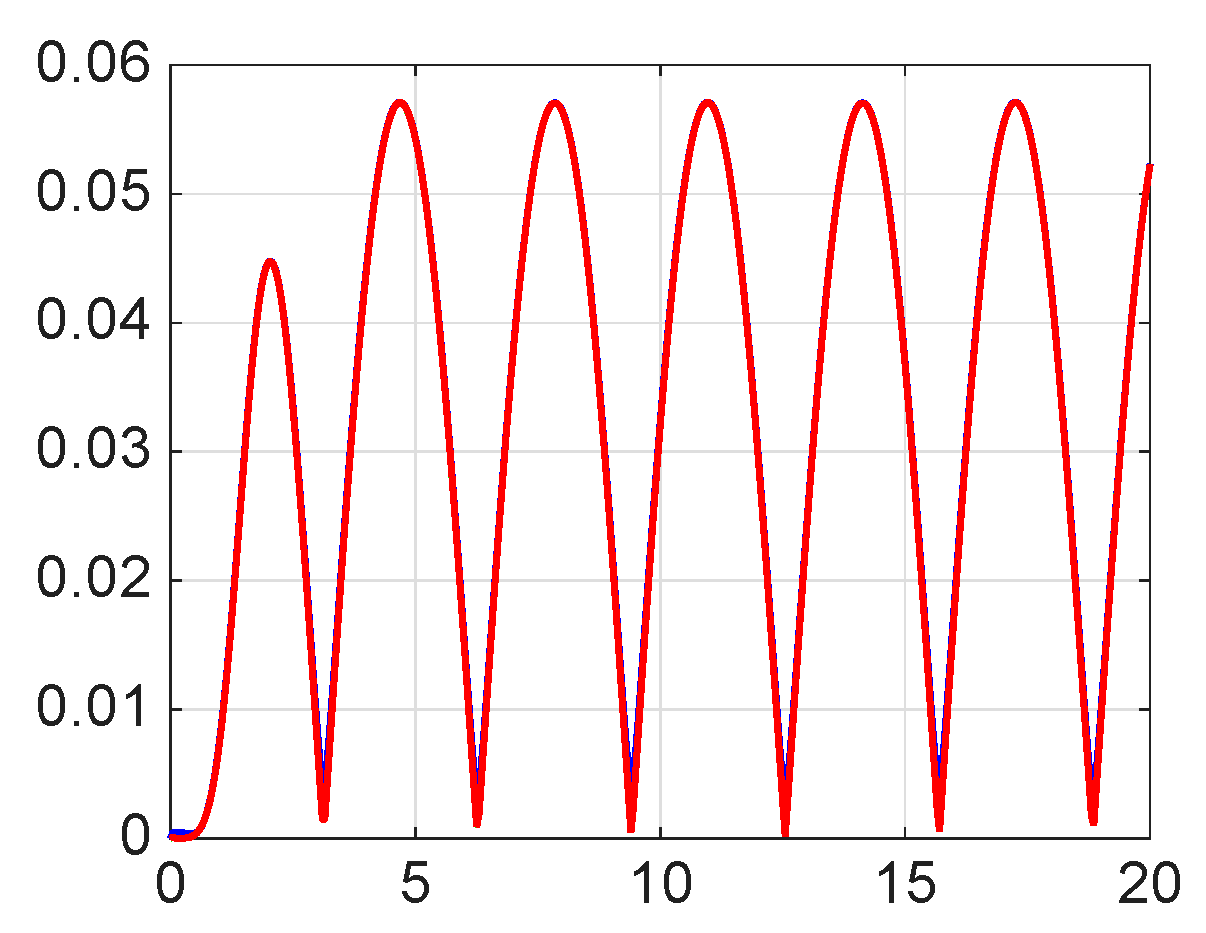
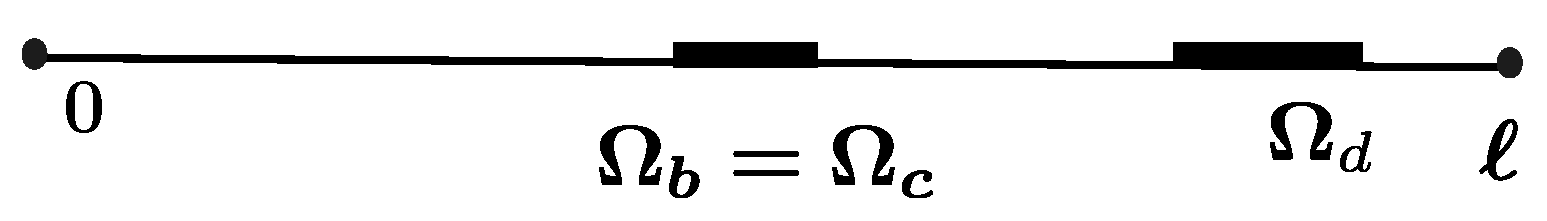
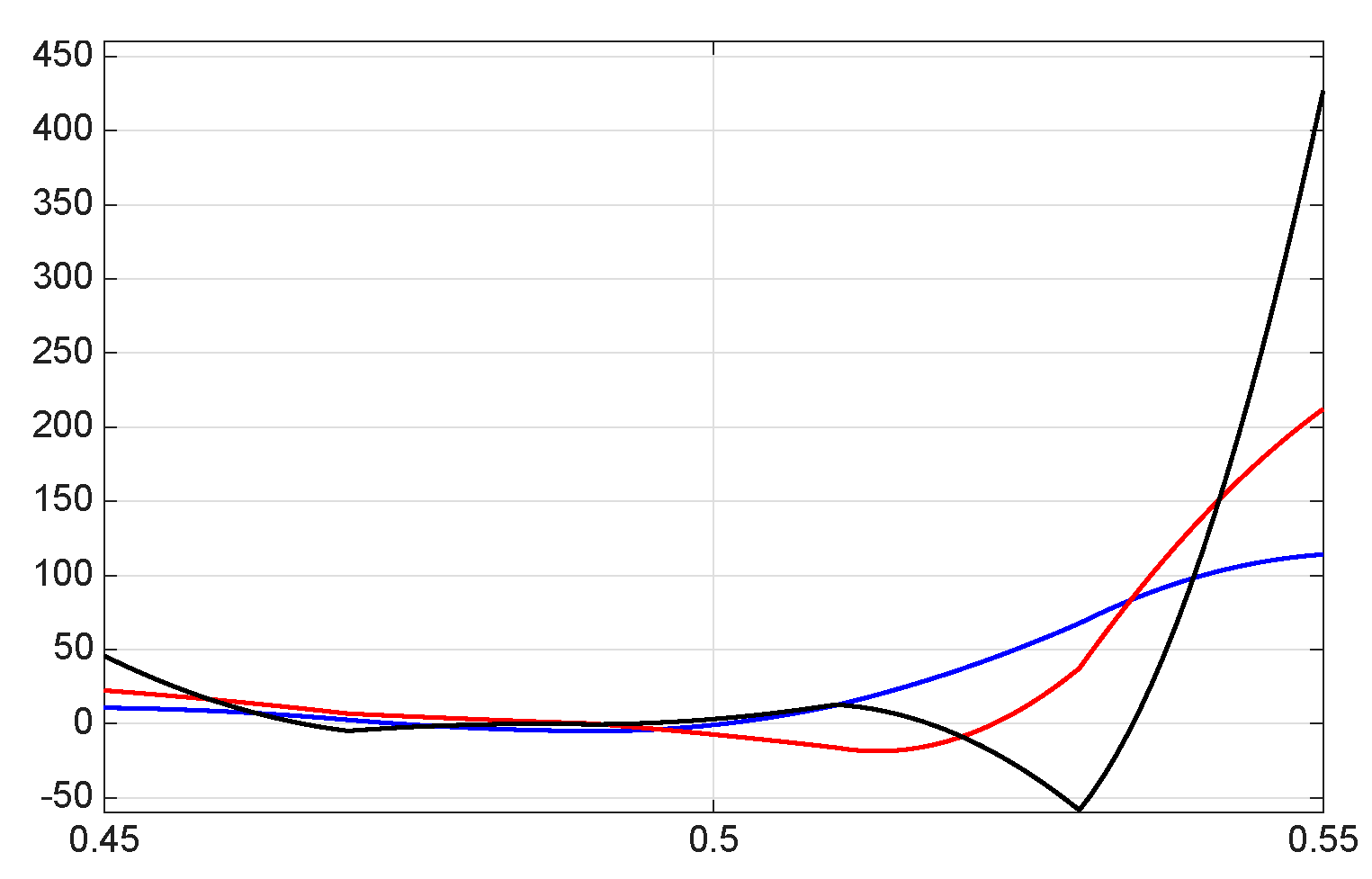
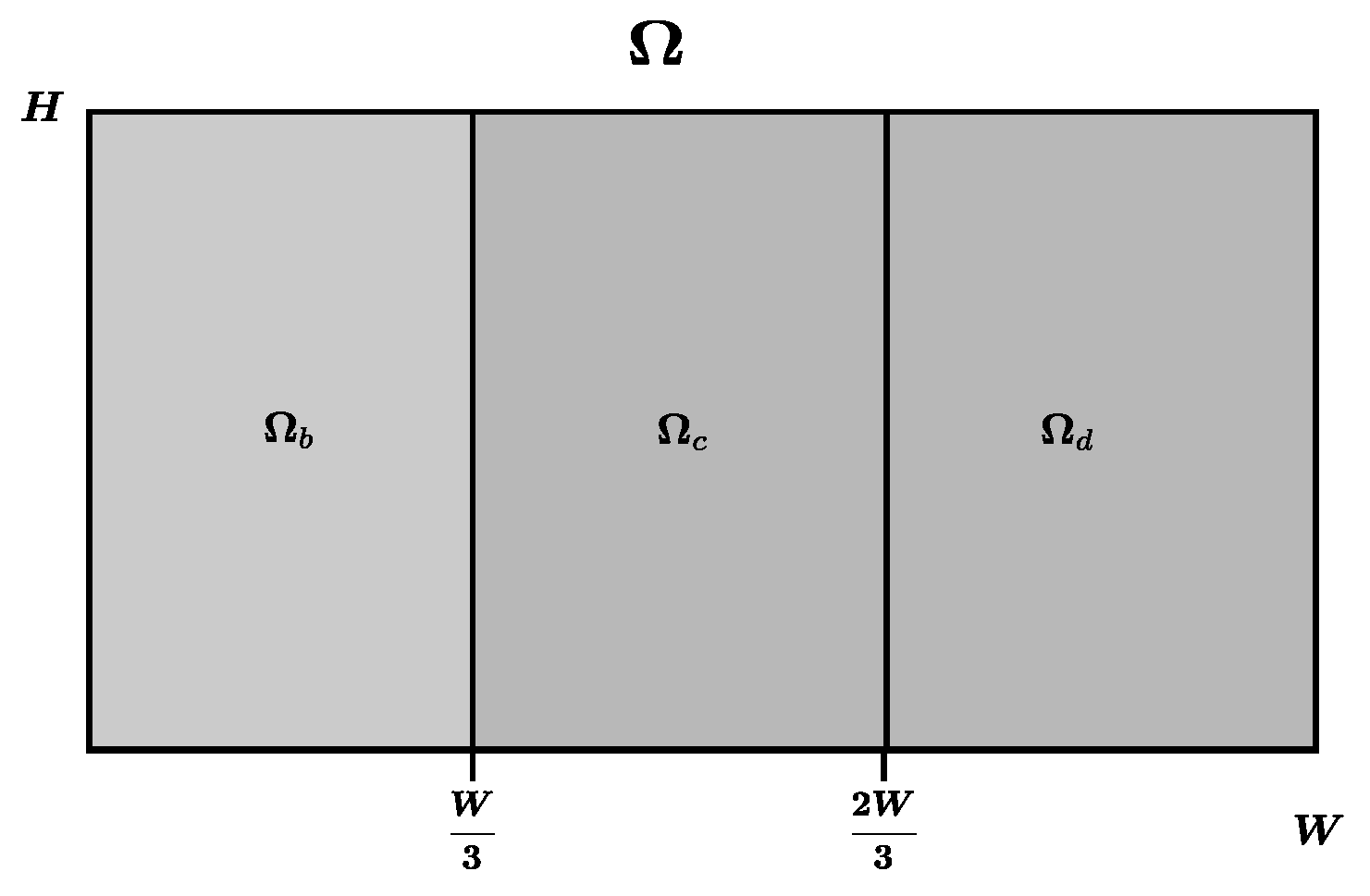
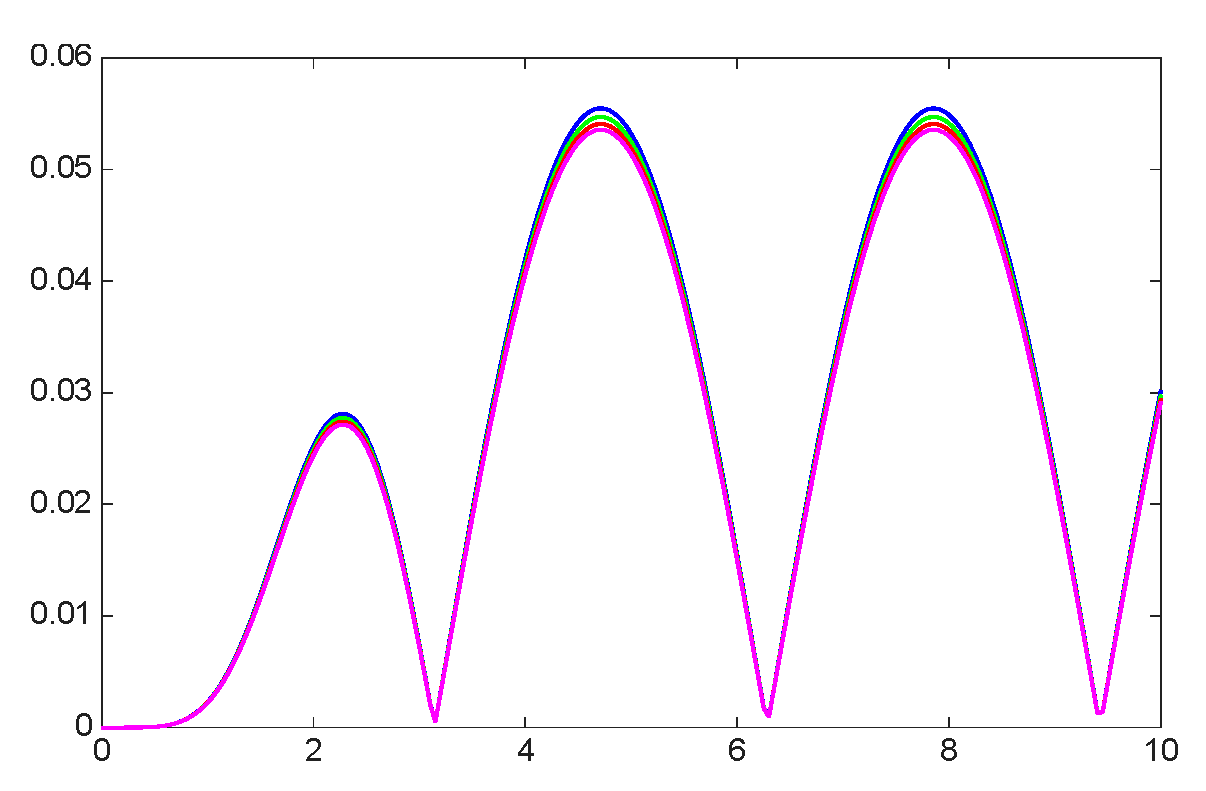
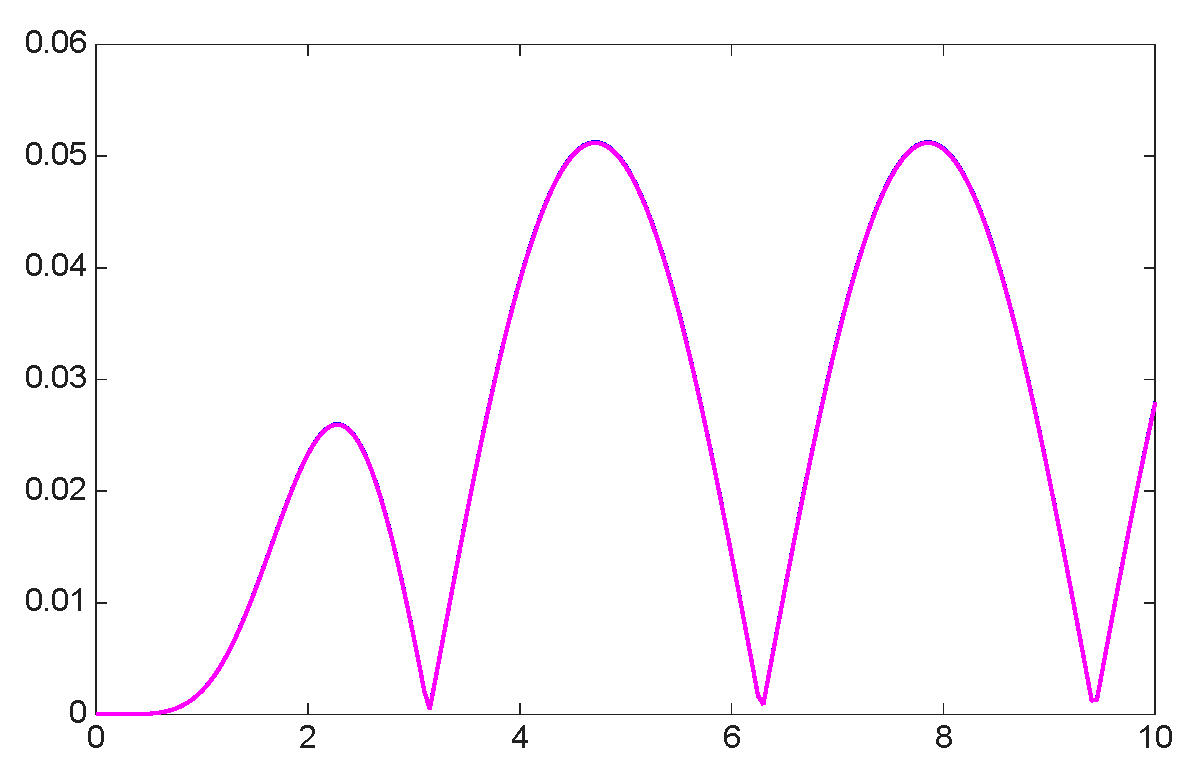
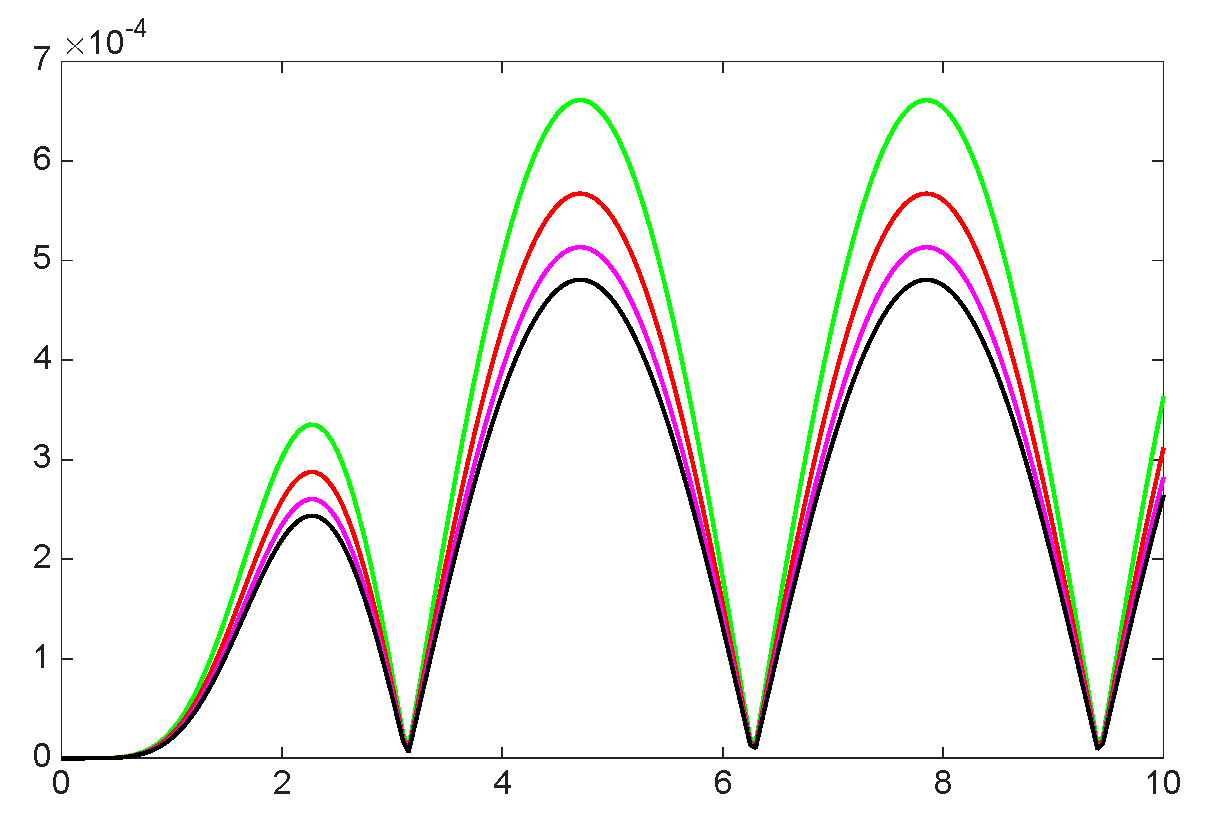
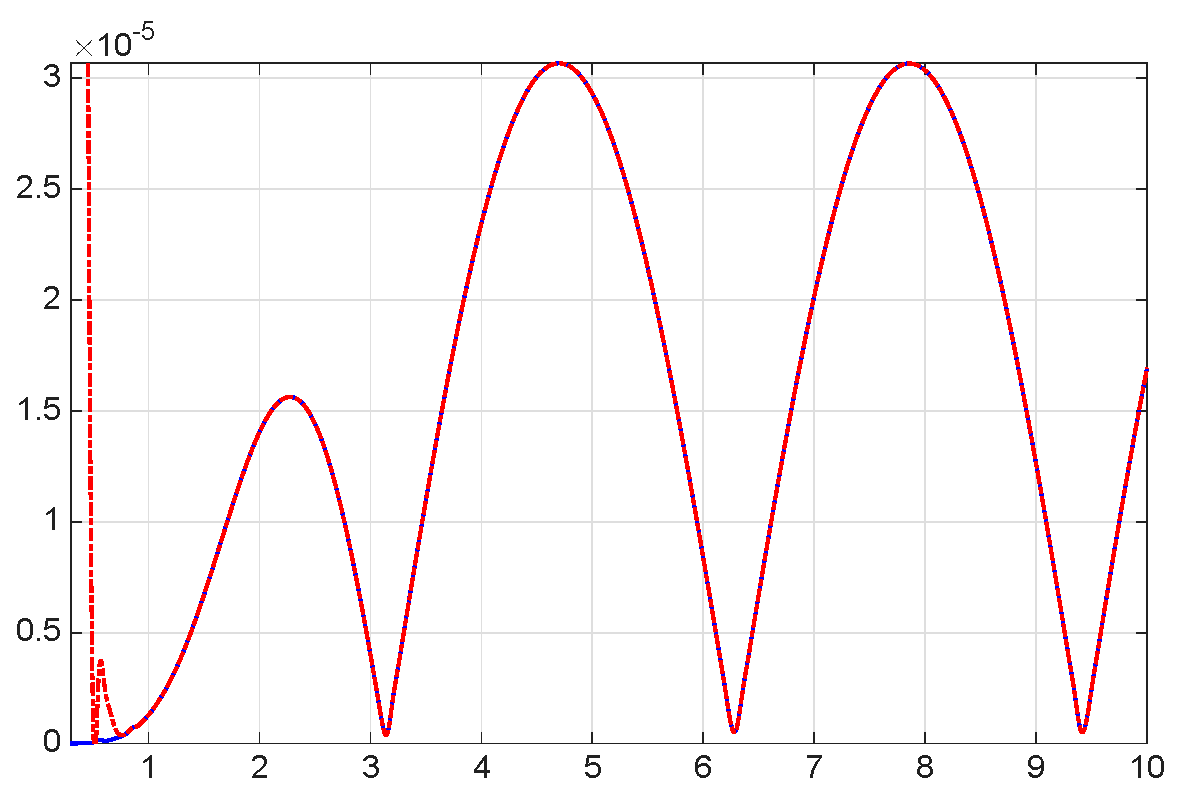
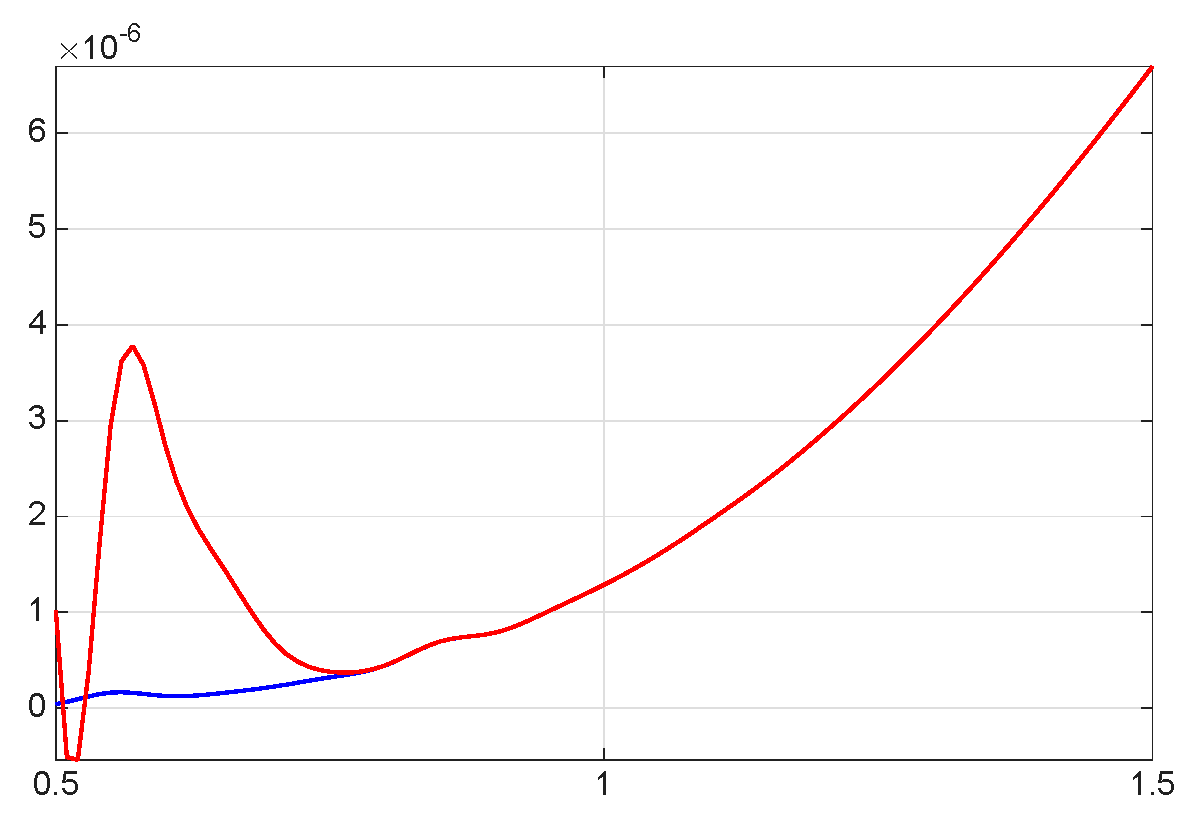
| 8.8800 × | 1.0400 × | 1.0060 × | |
| 8.6800 × | 9.7800 × | 9.8200 × |
| 0.8851 | 0.5238 | 0.6486 | 0.1369 | |
| 0.8852 | 0.9765 | 0.8622 | 0.8516 | |
| 0.8854 | 0.9817 | 0.9024 | 0.9014 | |
| 0.8856 | 0.9818 | 0.9137 | 0.9202 | |
| 0.8858 | 0.9820 | 0.9215 | 0.9315 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aulisa, E.; Chierici, A.; Gilliam, D.S. A Least-Squares Control Strategy for Asymptotic Tracking and Disturbance Rejection Using Tikhonov Regularization and Cascade Iteration. Mathematics 2025, 13, 3707. https://doi.org/10.3390/math13223707
Aulisa E, Chierici A, Gilliam DS. A Least-Squares Control Strategy for Asymptotic Tracking and Disturbance Rejection Using Tikhonov Regularization and Cascade Iteration. Mathematics. 2025; 13(22):3707. https://doi.org/10.3390/math13223707
Chicago/Turabian StyleAulisa, Eugenio, Andrea Chierici, and David S. Gilliam. 2025. "A Least-Squares Control Strategy for Asymptotic Tracking and Disturbance Rejection Using Tikhonov Regularization and Cascade Iteration" Mathematics 13, no. 22: 3707. https://doi.org/10.3390/math13223707
APA StyleAulisa, E., Chierici, A., & Gilliam, D. S. (2025). A Least-Squares Control Strategy for Asymptotic Tracking and Disturbance Rejection Using Tikhonov Regularization and Cascade Iteration. Mathematics, 13(22), 3707. https://doi.org/10.3390/math13223707







